向量的外积与混合积
高等数学高数课件 8.3数量积、向量积、混合积

的单位向量.
解
i j k i j c a b ax a y az 3 2
k
4 10 j 5k,
bx by bz 1 1 2
| c | 102 52 5 5,
c
|
c c
|
2
j
5
1 5
k
.
例7 在顶点为 A(1,1,2)、B(5,6,2) 和 C(1,3,1)
的三角形中, 求 AC 边上的高 BD.
解 AC 0,4,3, AB 4,5,0,
三角形 ABC 的面积为
S
Hale Waihona Puke 1 2|AC
AB
|
1 2
152
122
162
25 2
,
又
S
1 2
|
AC
|
|
BD
|,
|
AC |
42 (3)2 5,
所以
25 2
1 2
5
|
BD
|,
从而 | BD | 5.
例8
设向量
m
,
n,
p
两两垂直,
符合右手规则,
且
| m | 4,
2
3 .
(3) a b | b | Pr jba,
4 Pr
jba
a b |b |
3.
例2
证明向量
c
与向量
(a
c
)b
(b
c )a
垂直.
证 [(a c )b (b c )a] c
[(a c )b c (b c )a c]
(b c )[a c a c]
ax j ax
bx
bx
平面向量的向量积与混合积的应用

向量积在几何中的应用
02
面积计算
向量积在几何中可以用于计算平行四边形的面积 向量积可以用于计算三角形面积,公式为:面积 = (向量a × 向量b)的模 / 2 向量积还可以用于计算任意多边形的面积 向量积在计算面积方面具有广泛应用,是解决几何问题的重要工具之一
角度计算
向量积定义:两个向量a和b的向量积是一个向量,其模长等于以a和b为邻边的平行四边形的面 积,方向垂直于a和b所在的平面。
向量积与角度计算:向量积可以用于计算两向量的夹角,公式为cosθ=∣a·b∣∣a∣∣b∣。
向量积在几何中的应用:向量积可以用于解决与角度、方向和旋转相关的问题,例如确定点的位 置、判断直线的方向等。
YOUR LOGO
XX,a click to unlimited possibilities
平面向量的向量积与混合积的应用
汇报人:XX
汇报时间:20XX/01/01
目录
01.
向量积的定义 与性质
02.
向量积在几何 中的应用
03.
混合积的定义 与性质
04.
混合积在几何 中的应用
05.
向量积与混合 积在量积 和混合积的定义 和性质
运用向量的线性 组合和数量积等 技巧简化运算
注意运算中的符 号和顺序,避免 混淆和错误
结合具体例题进 行练习,提高运 算能力和准确性
避免计算错误的方法
仔细检查运算符号和括号
确保向量长度和夹角正确
使用数学软件进行验证
多次重复计算以避免误差
向量积与混合积的应用范围与限制
内积外积混和积

例: 证明一: 由定义
证明二:
35
例: 证明:
36
设 ( x1, y1, z1 ), ( x2 , y2 , z2 )
18
( x1, y1, z1 ), ( x2 , y2 , z2 )
( x1i y1 j z1k) ( x2i y2 j z2k) (自己算)
( y1z2 z1 y2 )i (z1 x2 x1z2 ) j ( x1 y2 y1 x2 )k
F
S
解: 根据物理知识,F 可以分解成水平方向分力Fx 和垂直方向分力 Fy 。其中只有与位移平行的分力
Fx 作功,而 Fy 不作功。
于是功W为: W=|F|cosθ|S|=|F||S|cosθ
为反映这一类物理现象,引入向量的内积。
3
内积及其运算规律
定义 两个向量α与β的内积是一个数,它等于
这两个向量的长度与它们夹角θ=(α,β)余弦的乘
x1 y2i j y1 y2 j2 z1 y2k j
x1z2i k y1z2 j k z1z2k 2
9
x1 x2 y1 y2 z1z2
(2) 2 x12 y12 z12 x12 y12 z12
(3) cos
解法一: (i 2 j) 2k
2i k 4 j k
2 j 4i
i jk
解法二: (i 2 j) 2k 1 2 0
00 2
20 10 12
i
j
k
02 02 00
4i 2 j
20
例: 求以 A(1, 2, 3) , B(2, 0, 5) , C(3, 0, 1) 为顶点的三 角形ABC的面积.
5-4内积、外积、混和积

a 2 135 例 设向量 a 的方向角分别为 60 120
求 a的坐标. 解
a1 cos a
a2 cos a a3 cos a
a1 a cos 2cos60 1
a2 a cos
2cos120 1
a3 a cos 2cos135 2
P1 P2
( x2 x1 )2 ( y2 y1 )2 ( z2 z1 )2
证 P P ( x2 x1 , y2 y1 , z2 z1 ) 1 2
P1 P2
( x2 x1 )2 ( y2 y1 )2 ( z2 z1 )2
(3) 两向量夹角的余弦公式
a (1, 1, 2)
例 已知向量 OA {1, 1, 2}和 OB {3, 1, 1} ,求向量 AB 的 方向余弦.
解 因为 AB 2, 2, 1 设其方向角是α,β,γ 又 AB ( 3 1)2 (1 ( 1))2 (1 2)2 3 所以
S 解 F 可以分解成水平方向分力Fx和垂直方向分力Fy , 其中只有与位移平行的分力Fx作功,而Fy不作功. 于是功 W=|F|cosθ |S|=|F| |S| cosθ 为反映这一类物理现象,引入向量的数量积.
1. 数量积的定义
定义 两个向量α与β的数量积是一个数,它等于这两个向量的模
与它们夹角余弦的乘积,记为
0 1 a 1 (a , a , a ) a1 a2 a3 a , , 1 2 3 a a a a a
(cos , cos , cos )
0 a 为与 a同方向的单位向量
空间的每一个向量都可以由它的模与方向余弦(或方向角)决定,特 别地,单位向量的方向余弦等于它的坐标.
向量的外积和混合积

x ( x, x )
三维空间:
x
k 1
n
2 k
设 x ( x1 , x2 , x3 )
y ( y1 , y2 , y3 )
12
则 x y x1 y1 x2 y2 x3 y3
2) 任意两向量之间的夹角定义:
( x, y) cos x y
1
平面解析几何是通过坐标法,把平面上的点与一 对有序的数对应起来,把平面上的图形和方程对应 起来,从而可以用代数方法来研究几何问题。空间 解析几何也是按照类似的方法建立起来的,它是在 三维坐标系中,用代数方法研究空间曲面和曲线性 质的一个数学分支。
2
§1 向量的外积与混合积
一、空间直角坐标系 三个坐标轴的正方向符合右手系。 即以右手握住 z 轴,右手的四个手指从正向 x 轴 以π/2 角度转向正向 y 轴时, 大拇指的指向就是 z 轴 z 竖轴 的正向。
z
R
M1
P
M2
Q
o
x
cos
x3 x x x
2 1 2 2 2 3
0 ,
0 ,
y
(cos , cos , cos )
0 .
表示线段OM 距离原点O 一个单位的点。
9
4、 向量的运算法则
设 x ( x1 , x2 , x3 ) y ( y1 , y2 , y3 ) 1)加法 (平行四边形法则) 即 x y ( x1 y1 , x2 y2 , x3 y3 ) 满足 a ) x y y x b) ( x y ) z x ( y z )
B(0, y , z )
8.4 向量的内积、外积、混合积

(a b a c b b b c ) (c a ) (a b a c b c ) (c a ) (a b ) c (a b ) a (a c ) c (a c ) a (b c ) c (b c ) a (a b ) c (b c ) a 2( a b ) c
4º 向量外积的坐标计算 设 a { a1 , a 2 , a 3 },b { b1 , b2 , b3 } , 则 a b ( a1i a 2 j a 3 k ) ( b1i b2 j b3 k )
C F OP s in(OP ,ˆ F )
C
方向: ( OP , F , C ) 形成右手系 于是力矩 C 可表示为:
C OP F
O
P
F
a b 的几何意义 :
b
a b a b sin( a ,ˆ b )
以 a , b 为邻边的平行四边形的面积
(4)
1 (3) a a a a1 a1 a 2 a 3
2 2 2
1 a12 a 2 2 a 3 2 i a2 a1 a 2 a 3
2 2 2
( a1i a 2 j a 3 k ) j a3 a1 a 2 a 3
j
(4) 如果 a , b 0 , 则 a
b ab 0
(5)
i j k , jk i , ki j
k
4-3R3中向量的外积和混合积

|| a × b || 2 =|| a || 2 ⋅ || b || 2 sin 2 (a ,∧ b) 2、解 、
=|| a || 2 ⋅ || b || 2 [1 − cos 2 (a ∧ b)]
=|| a || ⋅ || b || − || a || 2 ⋅ || b || 2 cos 2 (a ∧ b)
第四章 欧氏空间
第三节 R3中向量的外积和 混合积
几何向量的外积 几何向量的混合积 问题与思考
1
一、几何向量的外积
1、外积的定义
定义1 三维欧氏空间R 外积或 定义1 三维欧氏空间 3的两个向量α,β的外积或
向量积为 向量积为:γ =α×β 是一个几何向量: 是一个几何向量: γ 的模:‖γ‖=‖α‖‖β‖sin(α^β), 的模: ‖ , γ 的方向:既垂直于α,又垂直于β,其指向符合 的方向: 来确定。 右手规则从α 转向β 来确定。 中有一为零向量, 规定:若向量α,β 中有一为零向量, 则α×β =0.
∵ i×i=0,j×j =0,k×k =0, × ,× , × ,
(ax,)××=i,k×ii) = axbxi ×i i j×k (, x× =j, b , i×j =k, ×
j×i =-k,k×j =-i, i×k =-j. × , × , ×
=(ay bz- az by)i+(az bx- ax bz)j +(ax by- ay bx)k. ( ( (
解
i j k AC = {0,4,−3} AC × AB = 0 4 − 3 = 15i − 12 j − 16k 4 −5 0 AB = {4,−5,0}
B
三角形ABC的面积为 的面积为 三角形
S=
1.6 三矢量的混合积与双重外积

证 用向量的外积的坐标计算证明.
a (a1 , a2 , a3 ) b (b1 , b2 , b3 ) c (c1 , c2 , c3 )
设在直角坐标系下,
分别将上式左、右 用坐标表示, 即可得出两边相等.
性质1.6.7 (1) : Lagrang 恒等式
ac ad (a b) (c d ) (a c)(b d ) (b c)(a d ) bc bd 证: ( a b ) (c d ) (c d ) a b =((a c)d (a d )c) b (a c)(b d ) (b c)(a d ) ac a d bc bd
即
d b c d3 b3 x = a b c a1 b1 a2 b2 a3 b3
d1 d2
b1 b2
c1 c2 c3 c1 c2 c3
d c a a3 d3 c3 y = a b c a1 b1 c1 a2 b2 c2 a1 a2 b1 b2 d1 d2 a3 b3 c3
三个向量 a, b, c 共面的条件:
x1 a b c= x2 x3
y1 y2 y3
z1 z2 0. z3
例1:写出四点 P 1 ( x1 , y1 , z1 ), P 2 ( x2 , y2 , z2 ),
P3 ( x3 , y3 , z3 ), P4 ( x4 , y4 , z4 ) 共面的条件
§1.6 三矢量的混合积与双重外积
1.6.1三矢量的混合积
高等数学 第八章 第二节 数量积 向量积 混合积

5
第八章 第二节
16
例6 已知三点 A(1, 2 , 3 ) , B(3 , 4 , 5 ) , C( 2 , 4 , 7) ,求三
角形 ABC 的面积。
解: 如图
B
S ABC
=
1 2
AB
AC
sin
= 1 AB AC
A
C
2
i jk
= 1 2 2 2 = 1 (4 , − 6 , 2)
2
2
124
且 | m |= 4 , | n |= 2 , | p |= 3 ,计算 (m n) p 。
第八章 第二节
19
内容小结
1 向量的数量积 (结果是一个数量) ; 2 向量的向量积 (结果是一个向量) ; 3 数量积的坐标表示(对应坐标乘积之和) ; 4 向量积的坐标表示(行列式) ;
5 向量垂直的充要条件 (数量积为零) ;
= axbx + a yby + azbz
数量积的 坐标表达式 a b = (ax , a y , az ) (bx , by , bz )
= axbx + a yby + azbz
第八章 第二节
6
a
b
=
a x bx
+
a yby
+
azbz
a ⊥ b axbx + a yby + azbz
b
证: 如图, 设
CB = a , CA = b , AB = c
c B
C
aห้องสมุดไป่ตู้
则
c
2
=
cc
= (a − b)(a − b)
=
向量的外积与混合积

向量运算:外积与混合积在数学和物理学领域中,向量是一种重要的概念,它可以表示物理量的大小和方向。
向量的运算包括加法、数乘、内积、外积和混合积,其中外积和混合积是两种比较复杂的运算。
外积(叉乘)外积,又称叉乘或向量积,是两个向量之间的一种运算。
对于给定的两个三维向量$\\vec{a}$和$\\vec{b}$,它们的外积定义为一个新向量,记为$\\vec{a}\\times \\vec{b}$。
外积的计算公式如下:$$ \\vec{a} \\times \\vec{b} = \\begin{pmatrix} a_{1} \\\\ a_{2} \\\\ a_{3}\\end{pmatrix} \\times \\begin{pmatrix} b_{1} \\\\ b_{2} \\\\ b_{3}\\end{pmatrix} = \\begin{pmatrix} a_{2}b_{3} - a_{3}b_{2} \\\\ a_{3}b_{1} -a_{1}b_{3} \\\\ a_{1}b_{2} - a_{2}b_{1} \\end{pmatrix} $$在物理学中,外积经常用于描述两个向量之间的叉乘关系,并常用于计算力矩等物理量。
混合积(点乘)混合积,又称点乘或数量积,是三个向量之间的一种运算。
对于给定的三个向量$\\vec{a}$、$\\vec{b}$和$\\vec{c}$,它们的混合积定义为一个标量(纯数量),记为$\\vec{a} \\cdot (\\vec{b} \\times \\vec{c})$。
混合积的计算公式如下:$$ \\vec{a} \\cdot (\\vec{b} \\times \\vec{c}) = \\vec{a} \\cdot \\vec{d} =a_{1}d_{1} + a_{2}d_{2} + a_{3}d_{3} $$其中,$\\vec{d} = \\vec{b} \\times \\vec{c}$ 是$\\vec{b}$和$\\vec{c}$的叉积所得的向量。
向量的内积 外积 混合积课件

AMB . 解: MA (1, 1, 0 ), MB ( 1, 0, 1)
则 cos AMB MA MB MA MB
100 1
22 2
故
AMB
3
A
B M
例3. 设均匀流速为 v 的流体流过一个面积为 A 的平
面域 , 且 v 与该平面域的单位垂直向量 n 的夹角为 ,
求单位时间内流过该平面域的流体的质量P (流体密度
为 ) .
解: P A v cos
n 为单位向量
A vn
v n
A
单位时间内流过的体积
A v cos
例
4
已知a
(1,1,4) ,b
(1,2,2),求(1)
a ·b ;(2)a 与b 的夹角;(3)a 在b 上的投影.
v a r sin
v a
M
且 r v 符合右手法则 v r
lr
O
三、向量的混合积
1. 定义 已知三向量 a , b , c , 称数量
( a b ) c 记作 a, b,c
ab
为 a , b , c 的混合积 . 几何意义
以 a , b , c 为棱作平行六面体, 则其
例11. 证明四点 A(1,1,1), B( 4,5, 6 ),C( 2,3 ,3),
D(10,15,17 ) 共面 .
解: 因 [ AB , AC , AD ]
3 45
1 2 2 0 9 14 16
A
B C
D
故 A , B , C , D 四点共面 .
内容小结
设 a (ax , ay , az ) , b (bx ,by ,bz ) , c (cx , cy , cz )
向量内积、外积和混合积

向量内积、外积和混合积1 点乘1.1 定义点乘,也叫向量的内积、数量积。
两个向量的点乘结果是一个标量,不妨假定向量为a b 、,则点乘大小为: cos ,a b a b a b =<>令cos ,a b θ<>=,则[]0,θπ∈。
1.2 坐标表示设a =(x1,y1,z1),b =(x2,y2,z2),则:121212a b x x y y z z =++1.3 几何意义点乘的几何意义是:是一条边向另一条边的投影乘以另一条边的长度。
1.4 应用(1)计算两个矢量的夹角,取值范围为[]0,θπ∈。
这里有两个特殊值,当点乘为零时,则表示两个向量垂直;点乘取最大值(等于两个向量模的乘积)时,表示两个向量平行;(非零向量)(2)如果两个矢量均为单位矢量(即模为1),则点乘结果表示夹角余弦;(3)如果其中一个矢量是单位矢量,则点乘结果表示非单位矢量在单位矢量方向上的投影;(4)从视点到多边形任意一个顶点的矢量与多边形的法向量的点积的符号(>0)多边形在视点背面看不到应 删除。
(<0)多边形在视点的正面能看到。
(5)求平面外一点到平面的距离。
从该点向平面上的点画一条矢量再与平面的法向量点乘求的绝对值。
(6)方向角与方向余弦。
方向角定义为非零向量与坐标轴正向的夹角。
设于x, y, z 轴的夹角分别为,,αβγ,则:222cos ,cos ,cos cos cos cos y x za a a a a a αβγαβγ===++如果是单位向量,则()0cos ,cos ,cos a αβγ=。
2 叉乘2.1 定义叉乘,也叫向量的外积、向量积。
两个向量叉乘的结果仍为一向量,不妨设为c (x3,y3,z3)。
向量c 的方向与a,b 所在的平面垂直,且方向要用“右手法则”判断(用右手的四指先表示向量a 的方向,然后手指朝着手心的方向摆动到向量b 的方向,大拇指所指的方向就是向量c 的方向)。
向量内积、外积和混合积

向量内积、外积和混合积
向量的内积和外积在计算方式、几何意义以及各自的性质上都有区别。
具体如下:
1、计算方式不同
向量的内积(点乘/数量积),是对两个向量执行点乘运算,就是对这两个向量对应位一一相乘之后求和的操作;向量的外积,又叫叉乘、叉积向量积,其运算结果是一个向量而不是一个标量。
并且两个向量的外积与这两个向量组成的坐标平面垂直。
2、几何意义不同
内积(点乘)的几何意义包括:表征或计算两个向量之间的夹角;向量在a向量方向上的投影;在三维几何中,向量a和向量b 的外积结果是一个向量,有个更通俗易懂的叫法是法向量,该向量垂直于a和b向量构成的平面。
3、性质不同
内积性质:a^2≥0;当a^2=0时,必有a=0.(正定性);
(λa+μb)×c=λa×c+μb×c,对任意实数λ,μ成立(线性);cos∠(a,b)=a×b/(|a|×|b|);|a×b|≤|a||b|,等号只在a与b共线时成立。
向量外积的性质:a×b=-b×a(反称性);(λa+μb)×c=λ(a×c)+μ(b×c)(线性)。
4向量的内积、外积、混合积
2. 外积的的直接应用
(1).定理1: 两个向量 a , b 共线 a b 0.
特别地 , 如果 a 0,向量 b 沿向量 a 方向的正交分解为 b b1 b2 , 其中b1 // a , b2 a.则a b a b2 .
5i 6 j 3k 25 36 9
5 70
i
6 70
j
3 70
k.
例2. 已知向量 a (1,2,3), b ( 2,1, 2)求 a , b的夹角.
解 : cos a , b
a b ab
226 12 9
1 3
.
例3. 向量 a (1, 1,2), e (1,1,1)求 a在 e上的射影 .
3. 用直角坐标计算向量的内积
(1)定理 3 : 设向量 a , b 在直角坐标系 [O ; i , j , k ]下的坐标分别为 ( a1 , a 2 , a3 ) 与 (b1 , b2 , b3 ), 则它们的内积为 : a b a1b1 a 2 b2 a3b3 .
即 : ( a , b , c ) (b , c , a ) ( c , a , b ) (b , a , c ) ( c , b , a ) ( a , c , b ).
由定理 3, 显然有结论 : 推论 : ( a b ) c a (b c ).
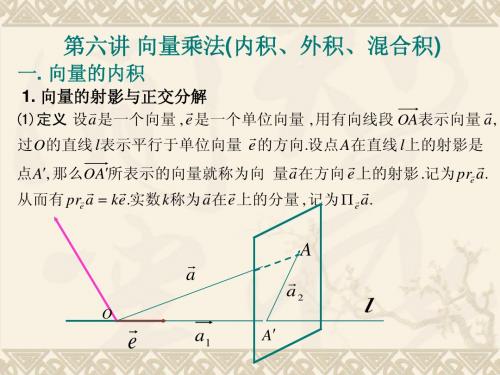
1. 向量的射影与正交分解
a
O
A
a2
A
e
l
a1
(2)正交分解
线性代数上10向量乘积

α×β =
x2 y2
x3 y3 x2
i−
x1 y1 z1 −
x3 y3 x1 y1
j+
x1 y1
x2 y2
k, x2 y2 z3
y2 z1 ∴ (α , β , γ ) = x1 y1
(α × β ) ⋅ γ =
x3 y3 z2 x2 y2
x3 y3
z2 +
x2 y2 z2
x1 y1 x3 y3 z3
(
)
5
3. 内积的应用 利用内积求长度. α ⋅β α ⋅β = (2) cos θ = 利用内积求夹角. 2 2 | α || β | α β
(3)α , β 垂直 ⇔< α , β >=
(1) | α |= α 2
π
2
, 记为 α ⊥ β .
α ⊥ β ⇔ α⋅β = 0.
在直角坐标系 {O; i, j, k} 下夹角的计算: 两向量 α = ( x1 , x 2 , x 3 ), β = ( y1 , y2 , y3 ) 夹角:
e11e22e33是一个空间仿射坐标系记332211321exexexxxx123112233yyyyeyeye利用内积的性质有112233112233xexexeyeyeye111112121313xyeexyeexyee212122222323xyeexyeexyee313132323333xyeexyeexyee111212313123121222323131232333yeeyeeyeexxxyeeyeeyeeyeeyeeyee??????????4111212313123121222323131232333yeeyeeyeexxxyeeyeeyeeyeeyeeyee??????????111213112321222323132333eeeeeeyxxxeeeeeeyeeeeeey????????????????????111213212223313233eeeeeeaeeeeeeeeeeee??????????112233xy称为仿射坐标系的度量矩阵
向量的积题型-概述说明以及解释

向量的积题型-概述说明以及解释1. 引言1.1 概述向量的积是高中数学中的一个重要概念,也是解决几何与代数问题的基础。
在数学中,我们常常遇到需要计算两个向量的积的情况,例如内积和外积。
内积也被称为点积,是两个向量乘积的数量积,结果是一个标量。
外积也被称为叉积,是两个向量乘积的向量积,结果是一个向量。
在几何中,向量的积有很多重要的应用。
内积可以用来求解向量的长度、夹角以及判定两条线段是否相交。
外积可以用来求解平面的面积、法向量等几何问题。
在物理中,向量的积还有更广泛的应用,例如力矩、磁场等。
本文将围绕向量的积这一主题展开讨论。
首先,我们将介绍内积和外积的定义和性质,包括计算公式和几何意义。
然后,我们将详细讨论内积和外积在几何和物理中的具体应用。
最后,我们将总结向量的积的重要性,并展望未来在数学和科学领域的应用前景。
通过深入学习向量的积的知识,我们可以更好地理解几何和代数问题,并能够灵活运用向量的积解决实际问题。
不仅如此,向量的积还是数学和物理领域中的基础概念,对于进一步学习和研究相关领域具有重要意义。
在接下来的正文部分,我们将逐一介绍向量的积的各个方面,包括内积和外积的定义、性质以及应用。
希望读者通过阅读本文,能够对向量的积有一个全面的了解,进一步提升数学水平和问题解决能力。
1.2 文章结构文章结构部分的内容如下:文章结构部分的主要目的是介绍整篇文章的组织和布局,让读者能够清楚地了解文章的主要部分和内容安排。
本文的结构如下:第一部分为引言,包括概述、文章结构和目的。
在这一部分,我们将简要介绍本篇文章的主题和目的,并概述各个章节的主要内容。
第二部分是正文,包括第一个要点和第二个要点。
在这一部分,我们将详细介绍向量的积题型的相关知识和技巧。
第一个要点将重点介绍某一种特定类型的向量积题目,并提供解题方法和实例。
第二个要点将介绍另一种类型的向量积题目,同样提供解题方法和实例。
通过这两个要点的介绍,读者将对向量的积题型有一个全面的了解。
向量的内积、外积、混合积

$(mathbf{a} + mathbf{b}) cdot (mathbf{c} times mathbf{d}) = mathbf{a} cdot (mathbf{c} times mathbf{d}) + mathbf{b} cdot (mathbf{c} times mathbf{d})$。
向量的内积、外积、混合积
目录
CONTENTS
• 向量内积 • 向量的外积 • 向量的混合积 • 向量内积、外积、混合积的应用
01
CHAPTER
向量内积
定义
向量内积定义为两个向量$mathbf{a}$ 和$mathbf{b}$的数量积,记作 $mathbf{a} cdot mathbf{b}$。其计 算公式为:$mathbf{a} cdot mathbf{b} = ||mathbf{a}|| times ||mathbf{b}|| times cos theta$,其中 $theta$是向量$mathbf{a}$和 $mathbf{b}$之间的夹角。
04
CHAPTER
向量内积、外积、混合积的 应用
在解析几何中的应用
计算向量的模
向量的模可以通过内积计算,即 $mathbf{u} cdot mathbf{u} = |mathbf{u}|^2$。
判断向量是否垂直
两个向量垂直当且仅当它们的内
积为0,即$mathbf{u}
cdot
mathbf{v} = 0$。
当两个向量正交时,它们的内积为0 。
向量的内积满足交换律和分配律,即 $mathbf{a} cdot mathbf{b} = mathbf{b} cdot mathbf{a}$和 $(mathbf{a} + mathbf{c}) cdot mathbf{b} = mathbf{a} cdot mathbf{b} + mathbf{c} cdot mathbf{b}$。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
( x y ) x y
11
5、 向量的内积(点积)
1) 定义: 对任意 x, y Rn , x 与 y 的内积为
x y ( x , y ) x k yk
n k 1
从定义可知,内积是只有大小没有方向的 说明: 的量(即数量),所以也称数量积。
M1 M 2 ( x2 x1 )2 ( y2 y1 ) 2 ( z2 z1 ) 2
7
当 x 1 时,称 x 为 单位向量。
3、向量的方向余弦 设非零向量 x 与三坐标轴的正向的夹角 , , , 称为方向角, cos , cos , cos 称为向量 x 的方向余弦。 说明: 1)方向余弦表示向量的方向;
z
R
M1
P
M2
Q
o
x
cos
x3 x x x
2 1 2 2 2 3
0 ,
0 ,
y
(cos , cos , cos )
0 .
表示线段OM 距离原点O 一个单位的点。
9
4、 向量的运算法则
设 x ( x1 , x2 , x3 ) y ( y1 , y2 , y3 ) 1)加法 (平行四边形法则) 即 x y ( x1 y1 , x2 y2 , x3 y3 ) 满足 a ) x y y x b) ( x y ) z x ( y z )
x ( x, x )
三维空间:
x
k 1
n
2 k
设 x ( x1 , x2 , x3 )
y ( y1 , y2 , y3 )
12
则 x y x1 y1 x2 y2 x3 y3
2) 任意两向量之间的夹角定义:
( x, y) cos x y
0 , 为 x 与 y的夹角。
x y x y cos 称为 y 在 x 方向上的投影。
y
x
结论:两向量的内积等于其中一个向量的模和 另一个向量在这向量的方向上的投影的乘积。 3)内积的重要性质:
x y x y 0
13
即 x1 y1 x2 y2 x3 y3 0
原点o 横轴 x
y 纵轴
空间直角坐标系
3
空间直角坐标系共有八个卦限 Ⅲ
z
Oyz 面
Ⅳ
Ozx面
Ⅱ
Oxy 面
Ⅶ Ⅷ
o
y
Ⅵ Ⅴ
Ⅰ
x
4
空间的点
1-1对应
有序数组(x , y , z)
特殊点的表示: O(0,0,0) 坐标轴上的点 D, E , F , 坐标面上的点 A, B, C ,
z
F (0,0, z )
1
平面解析几何是通过坐标法,把平面上的点与一 对有序的数对应起来,把平面上的图形和方程对应 起来,从而可以用代数方法来研究几何问题。空间 解析几何也是按照类似的方法建立起来的,它是在 三维坐标系中,用代数方法研究空间曲面和曲线性 质的一个数学分支。
2
§1 向量的外积与混合积
一、空间直角坐标系 三个坐标轴的正方向符合右手系。 即以右手握住 z 轴,右手的四个手指从正向 x 轴 以π/2 角度转向正向 y 轴时, 大拇指的指向就是 z 轴 z 竖轴 的正向。
x
2 x k 称为 x 的模或范数。 k 1
n
2 2 2 x x x x 说明:1)在空间三维坐标系中: 1 2 3
2)模为零的向量为零向量 0 , 零向量的方向是任意的。负向量为 x 3)向量 M1 M2 ( x2 x1 , y2 y1 , z2 z1 ) 的模为
2) i , j , k 分别表示沿 x, y, z 轴正向的单位向量; z M( x, y , z ) 3)R3中向量的坐标表示: a M1 M 2 k ( x2 x1 , y2 y1 , z2 z1
n x R 定义: 设 是 上的任意向量,定义 x 的长度为
2)向量 cos , cos , cos 是与 x方向相同的单位向量; z
R
P
M1
M2
Q
o
x
y
8
3)如 x x1 , x2 , x3 x1 则 cos 2 2 2 x1 x2 x3 x2 cos 2 2 2 x1 x2 x3
B(0, y , z )
C ( x , o, z )
P ( x, y, z )
E (0, y,0)
o
y
x
D( x,0,0)
A( x , y ,0)
5
二、向量的概念及性质 1、向量的定义 具有大小和方向的量。 空间上的向量: 有向线段(长度和方向) 3 向量表示:OM a R a xi yj zk a ( x , y , z ) 说明: 1)本书所研究的向量,只考虑其大小和方向, 不考虑其起点;
P1 (2, 2, 5), P2 ( 1, 6, 7) . 例1、设空间两点:
求:1)向量 P1 P2 在三个坐标轴上的投影; 2)向量 P1 P2 的模; 3)向量 P1 P2 的方向余弦; 4)与向量 P1 P2 方向一致的单位向量; 5)向量 P1 P2 在向量 M1 M 2 2, 2, 1上的投影;
6)向量 P1 P2 在向量 M1 M 2 2, 2, 1上的投影向量。
14
6、 向量的外积(叉积) 1) 定义: 设 x ( x1 , x2 , x3 ) y ( y1 , y2 , y3 ) x y i j k
x
x y
y
c) x y x y x y x y
10
2)减法
即 x y x ( y ) x ( x1 y1 , x2 y2 , x3 y3 )
y
x y
3)数乘 为任意实数, 则 x (x1 , x2 , x3 ) 满足 a ) ( x ) (x ) ( ) x b) ( ) x x x
