初中物理:柱体切割后压强的动态变化分析
压力压强变化分析解题思路小结——沪教版(上海)九年级上册
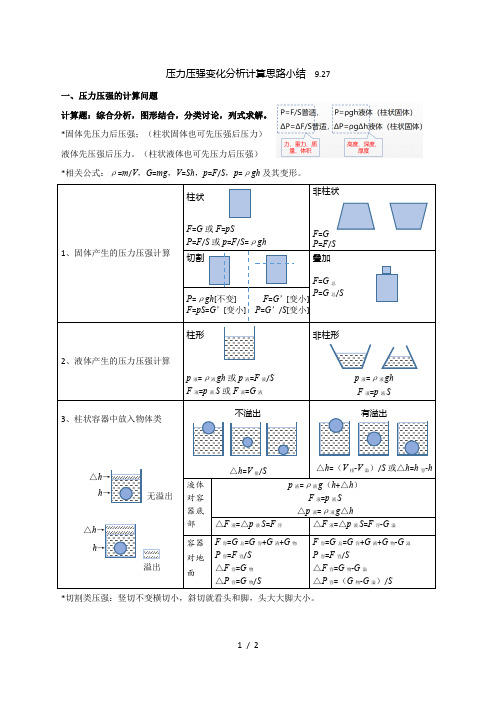
压力压强变化分析计算思路小结 9.27一、压力压强的计算问题计算题:综合分析,图形结合,分类讨论,列式求解。
*固体先压力后压强;(柱状固体也可先压强后压力) 液体先压强后压力。
(柱状液体也可先压力后压强)*相关公式:ρ=m /V ,G =mg ,V =Sh ,p =F /S ,p =ρgh 及其变形。
1、固体产生的压力压强计算柱状F =G 或F =pSP =F /S 或p =F /S =ρgh非柱状F =G P =F /S 切割叠加F =G 总 P =G 总/SP =ρgh [不变] F =G ’[变小] F =pS =G ’[变小] P =G ’/S [变小] 2、液体产生的压力压强计算柱形p 液=ρ液gh 或p 液=F 液/S F 液=p 液S 或F 液=G 液非柱形p 液=ρ液gh F 液=p 液S 3、柱状容器中放入物体类不溢出△h =V 排/S有溢出△h =(V 排-V 溢)/S 或△h =h 容-h液体对容器底部 p 液=ρ液g (h +△h )F 液=p 液S △p 液=ρ液g △h△F 液=△p 液S =F 浮 △F 液=△p 液S =F 浮-G 溢 容器对地面F 容=G 总=G 容+G 液+G 物 P 容=F 容/S △F 容=G 物 △P 容=G 物/SF 容=G 总=G 容+G 液+G 物-G 溢 P 容=F 容/S △F 容=G 物-G 溢△P 容=(G 物-G 溢)/S*切割类压强:竖切不变横切小,斜切就看头和脚,头大大脚大小。
△h → h →△h → h →溢出无溢出*液体对容器底部压力与重力的关系:柱形等,口大(G 液)大,底大(G 液)小。
二、压强压力的变化分析问题方法:公式推导(定性、定量)、数学比例、极限法、赋值法等 1、公式法:结合以上关系,用公式进行推导。
2、比例法ghShSg S Vg S mg S G S F p ρρρ======,F =G =mg =ρVg =ρhSg ; p 或F 与m 、V 、h 都可能成正比,此时p 或F 减少量或增加量与它们(m 、V 、h )都是成比例变化;hh F V V F m m F h h V V m m ∆=∆∆=∆∆=∆∆=∆∆=∆∆=∆F F F ,p p p p p p 或或或或 P 或F ,原来大,减小的比例(hhV V m m ∆∆∆或或)小或等(增大的比例大或等,或剩余的比例大),则后来的也大;【下同,其余情形大家自行分析】原来等,减小的比例大,则后来小;减小的比例等,则后来等;减小的比例小,则后来大; 原来小,减小的比例大或等,则后来小; 3、极限法当h (或V 或m )不同,截取相同h (或V 或m ),则h (或V 或m )小的先截完(p 和F 都为零),将此时压力或压强关系与原来的压力压强关系作比较,得出变化趋势。
初中物理压强变化题,解题思路

初中物理压强变化题,解题思路一、解题思路。
1. 固体压强变化。
对于柱状固体(如正方体、长方体、圆柱体等)放在水平面上时,根据p = (F)/(S)=(G)/(S)=(ρ Vg)/(S)=ρ gh(S为底面积,F = G为物体重力,ρ为物体密度,V为体积,h为物体的高度)。
如果是切割类问题,当沿水平方向切割时,压力F = G减小,S不变,根据p=(F)/(S)判断压强变化;当沿竖直方向切割时,F与S按比例减小,p=(F)/(S)不变(对于柱状固体p = ρ gh,h不变,p也不变)。
如果是叠加类问题,压力F增大,S不变(底面积不变的情况),压强p=(F)/(S)增大。
2. 液体压强变化。
根据p=ρ gh(ρ为液体密度,h为液体深度)。
如果是倒入或抽出液体问题,倒入液体时h增大,p增大;抽出液体时h减小,p减小。
如果是放入固体问题,当固体漂浮或悬浮时,F_浮 = G_物,根据F_浮=ρ_液gV_排,V_排的变化会引起h的变化从而影响液体压强p;当固体沉底时,也要分析V_排的变化情况来确定液体压强的变化。
二、出题、解析。
1. 固体压强变化题。
题目:一个正方体木块放在水平桌面上,正方体的边长为0.1m,木块的密度为0.6×10^3kg/m^3。
现将木块沿水平方向截去一半,求剩余部分对桌面的压强是多少?(g = 10N/kg)解析:正方体木块的体积V = L^3=(0.1m)^3=1×10^-3m^3。
木块的质量m=ρ V = 0.6×10^3kg/m^3×1×10^-3m^3=0.6kg。
木块的重力G = mg=0.6kg×10N/kg = 6N。
正方体的底面积S = L^2=(0.1m)^2=0.01m^2。
沿水平方向截去一半后,压力F=(G)/(2)=(6N)/(2)=3N,S不变。
根据p=(F)/(S),剩余部分对桌面的压强p=(3N)/(0.01m^2) = 300Pa。
上海市中考物理压强压轴题专题03柱体切割后浸入液体中,无液体溢出(含解析)

上海市中考物理压强压轴题:专题03 柱体切割后浸入液体中,无液体溢出一、常见题目类型1.将柱形物体沿水平方向切去某一厚度(体积或质量),并将切去部分浸没在容器的液体中(图1)。
2.将柱形物体沿竖直方向切去某一厚度(体积或质量),并将切去部分浸没在容器的液体中(图2)。
二、例题【例题1】如图1所示,均匀长方体甲和薄壁圆柱形容器乙置于水平地面上。
长方体甲的底面积为3S 。
容器乙足够高、底面积为2S ,盛有体积为5×10-3米3的水。
① 若甲的重力为20牛,底面积为5×10-4米2,求甲对地面的压强p 甲。
② 求乙容器中水的质量m 水。
③ 若将甲沿水平方向切去厚度为h 的部分,并将切去部分浸没在乙容器的水中时,甲对水平地面压强的变化量Δp 甲恰为水对乙容器底部压强增加量Δp 水的2倍。
求甲的密度ρ甲。
【答案】①40000帕;②5千克;③3×103千克/米3。
【解析】① F 甲=G 甲=20牛p 甲=F 甲/S 甲=20牛/5×104米2= 40000帕② m 水=ρ水V 水=1×103千克/米3×5×103米3=5千克图1乙甲图1 乙甲甲乙图2③甲对水平地面压强的变化量Δp甲即为切去厚度为h部分的压强Δp甲=ΔF甲/S甲=甲gh水对乙容器底部压强增加量Δp水为水升高的高度h水=3Sh/2SΔp水=水g h水=水g(3Sh/2S)因为Δp甲=2Δp水甲gh =2水g(3Sh/2S)所以ρ甲=3×103千克/米3【例题2】如图2所示,底面积为10-2米2、高为0.4米长方体甲(ρ甲=2×103千克/米3)和底面积为2×10-2米2的薄壁柱形容器乙放在水平地面上。
乙容器足够高,内盛有0.1米深的水。
甲乙(1)求甲的质量m甲。
(2)求水对乙容器底部的压强p水。
(3)现沿水平方向将长方体甲截取一定的厚度,并将截取部分竖直放入乙容器中,使得水对容器底部的压强最大,且长方体甲对地面的压强减少量最小,请求出甲对地面的压强减少量。
沪教版九年级压强切割与计算

第二讲固体压强变化知识梳理一、柱形固体压强计算1、用p=F/S=ρgh 计算固体压强,当物体自然放置在水平面上,且底面积与水平面充分接触,此时物体对水平面产生的压力大小(选填“大于”、“等于”或“小于”)物体的重力,即:F G;2、计算质地均匀的物体质量,m= ;3、计算柱形物体的体积,V= 。
二、固体切割压强判断知识点一:竖直切割柱形固体竖直切(包括切去质量、体积、厚度等),由公式可知,高度h 不变,压强保持,即压强变化量为。
知识点二:水平切割1、水平切相同高度,由公式:Δp= ,可求出压强的变化量。
若已知物体密度的大小关系,可以进一步判断压强变化量的大小关系。
由公式p′=,可判断切过之后的物体压强大小关系;2、切相同体积:①两个物体原来压强相等,水平切相同高度(或、)之后,剩余部分的压强一定是大物体的压强(选填“大于”、“等于”或“小于”)小物体的压强。
②两个物体原来质量(或压力)相等,沿水平切相同体积(或相同高度),剩余部分压强有种情况。
从开始切到小物体切完之前存在压强的情况。
③质量(或压力)相等,水平切去相同质量,压强的符号跟原来,即原来哪个物体的压强大,切过之后剩余部分压强还是哪个物体的大。
例题解析一、柱形固体压强计算【例1】如图所示,将一块砖平放、立放、侧放时,它对地面的压强()A.平放时最大B.立放时最大C.侧放时最大D.平放、立放、侧放时,一样大【例2】如图所示,两个完全相同的装满豆浆的密闭杯子,以下列四种不同的方式放在水平桌面上,若杯子上表面面积是下表面面积的 2 倍,它们对桌面的压强大小分别是p 甲、p 乙、p 丙、p 丁,则()A.p 甲<p 乙<p 丙<p 丁B.p 乙<p 甲<p 丁<p 丙C.p 乙<p 甲=p 丁<p 丙D.p 丙<p 乙<p 丁=p 甲【例3】甲、乙两个正方体放在水平地面上,它们对地面的压强相等,甲、乙密度之比是1:2, 则甲、乙的底面积之比是()A.1:2 B.2:1 C.1:4 D.4:1【例4】如图是小敏同学在探究甲、乙两种不同的固体物质的质量和体积的关系时得出的图象。
【初二物理】固体压强之切割问题-全国版

模块1:切割问题知识素材knowledge combing切割体压强计算学生素材常见固体切割方式(1)不同方向的切割问题(竖切、横切、斜切)a.对于柱体的水平切割,切去对应比例的、、,压力也变化相同的比例,同时压强也变化相同的比例;b.对于柱体的竖直切割,不改变固体的压强。
切去对应比例的、、,压力也变化相同的比例。
(2)不同条件的切割问题(比如切割相同高度、相同体积、相同质量等)常见压强变化类型(1)改变固体质量引起的压强变化。
(2)改变固体高度引起的压强变化(3)其他类型的问题,如改变体积引起的压强变化,可转化为上述类型,具体问题具体分析,择取合适的公式以简化计算过程。
h V m a V m Δp ==S ΔF =S ΔG S Δm ⋅g Δp =ρg Δh截图扫码领取课程资料1 实心均匀正方体静止在水平面上。
若在其右侧,按如图所示方式,沿竖直方向截去一部分后,则其质量、密度、对水平面的压力和压强四个物理量中,不变的是( )A.质量、密度B.压力、压强C.密度、压强D.密度、压力1 如图,一块长方体橡皮,重为,侧放于水平桌面上时,它与桌面的接触面积是,它对桌面的压强是Pa.若沿ab方向竖直向下切去一块,则剩余部分对桌面的压力 (选填“变大”或“变小”或“不变”)、压强 (填“变大”或“变小”或“不变”). 1 边长为、质量为的正方体放在水平桌面上,若沿如图所示的虚线去掉一半,其余部分不动,这时它对桌面的压强是。
如果沿如图所示的虚线去掉一半,其余部分不动,这时它对桌面的压强是 。
()1 如图所示,实心均匀正方体甲、乙对水平地面的压强均为,若沿竖直方向切去甲的一半,沿水平方向切去乙的一半,此时它们对地面的压强为和。
则下列判断正确的是( )例题20.6N 2×10m −32例题310cm 2kg a Pa b Pa g =10N/kg 例题4p 0p 甲p 乙截图扫码领取课程资料A. B. C. D. 1 如图所示,质量相同的甲、乙两个均匀实心正方体放在水平地面上。
专题15 均匀柱体、叠加柱体、切割体的压强(原卷版)-2022年中考物理二轮专项复习核心考点突破与必

专题15 均匀柱体、叠加柱体、切割体的压强【核心考点讲解】一、均匀柱体的压强1、密度均匀的柱状物体(圆柱、棱柱)对水平面的压强gh p ρ=。
2、推导过程:gh hg g p ρρρ=====SS S V S G S F 。
二、叠加柱体的压强1、运用SF =p 时,注意S 是受力面积,不一定等于底面积。
2、解题技巧:用未知量表示已知量的方程思想。
三、切割体的压强1、横向切割:压力变小,受力面积不变,压强减小。
2、纵向切割:柱形固体竖直切割后仍是柱体,可使用计算式gh p ρ=分析,压强不变。
3、不规则切割:压力和受力面积都改变,可使用割补法转化为柱体进行分析。
【必刷题型精练】1.(2021•凉山州中考)一块长方体合金块,重1.2N ,侧放于面积为1m 2的水平桌面上,它与桌面的接触面积是1×10﹣3m 2,下列说法正确的是( )。
①合金块对桌面的压强是1.2Pa②合金块对桌面的压强是1200Pa③若沿竖直方向切去一块,则剩余部分对桌面的压强不变④若沿水平方向切去一块,则剩余部分对桌面的压强不变A .①③B .②③C .①④D .②④2.(2020•襄阳中考)如图所示,甲、乙两个实心正方体物块放置在水平地面上,甲的边长大于乙的边长。
甲对地面的压强为p 1,乙对地面的压强为p 2.下列判断正确的是( )A .若甲、乙密度相等,将甲放到乙上,乙对地面的压强有可能变为p 1B .若甲、乙密度相等,将乙放到甲上,甲对地面的压强有可能变为p 2C.若甲、乙质量相等,将甲放到乙上,乙对地面的压强有可能变为p1D.若甲、乙质量相等,将乙放到甲上,甲对地面的压强有可能变为p23.(2021•崇左模拟)如图所示,体积相同的长方体甲、乙置于水平地面,其中甲、乙阴影部分为等大的正方形,甲、乙的密度分别为ρ甲、ρ乙,对地面的压强分别为p甲、p乙,将它们顺时针旋转90°,甲、乙对地面压强的变化量分别为△p甲、△p乙.△p甲<△p乙,则()A.ρ甲<ρ乙,p甲>p乙B.ρ甲<ρ乙,p甲<p乙C.ρ甲>ρ乙,p甲>p乙D.ρ甲>ρ乙,p甲<p乙4.(2021•长沙模拟)如图,水平面上放置了质地均匀的甲、乙两个实心圆柱体,它们的高度相同,质量相等,甲的底面积小于乙的底面积。
上海中考-专题2 压强变化 题型1 固体压强

题型一:固体压强竖直切割【考点】压强变化【解析】竖直方向切割后压强不变,剩余部分压强相等,则说明原来的压强相等,切去部分对地面的压强也相等;甲的密度大于乙的密度,那么甲的高度小于乙,所以甲的底面积小于乙。
由F pS =,知选择B 。
【答案】B【教学建议】注意给学生总结规律:柱体竖直切后压强不变,水平切后压强一定减小。
所以 本题在竖直切前两个正方体压强也是相同的。
【考点】压强变化【解析】由p gh ρ=可知,图(a )、(b )所示两种情况,剩余部分对水平地面的压强均不会发生变化。
故选D 。
例2.(★★)如图 (a)、(b)所示,若分别沿虚线方向切去放置在水平地面上实心正方体的左侧部分,则剩余部分对水平地面的压强 ( )A.只有图(a)所示情况会发生变化B.只有图(b)所示情况会发生变化C.图(a)、(b)所示两种情况均会发生变化D.图(a)、(b)所示两种情况均不会发生变化例1.(★★★)甲、乙两个实心均匀正方体(已知ρ甲>ρ乙)分别放在水平地面上。
若在两正方体右侧沿竖直方向各截去相同的体积,它们剩余部分对地面的压强相等。
则未截去前,两实心正方体对地面的压力F 甲、F 乙的关系是( )A.F 甲一定大于F 乙B.F 甲一定小于F 乙C.F 甲可能大于F 乙D.F 甲可能小于F 乙经典例题【答案】D【教学建议】此题是典型的柱状固体的压强切割问题,利用柱体竖直切后压强不变原理即可 得出正确答案。
题型二:固体压强水平切割【考点】压强变化【解析】水平切去相同质量,可以用旋转的方法,由于是正方体,旋转后对地面的压强仍然相等,水平切就可以转化为竖直切,压强相等,切去质量相等,则切去的底面积甲等于乙,甲的边长大于乙,所以甲切去的厚度就一定小于乙,故选A ;切去相同的体积,由公式V p g Sρ∆=,知甲的压强减少的小,所以甲剩下的压强一定大于乙的压强。
【答案】A【教学建议】把水平切割转化为竖直切割是一种非常有效的解题方法,尤其是对正方体物体, 有时会比常规的分析更快。
专题01压强计算(柱体切割叠放)-上海市2024年中考复习资料汇编(培优专用)
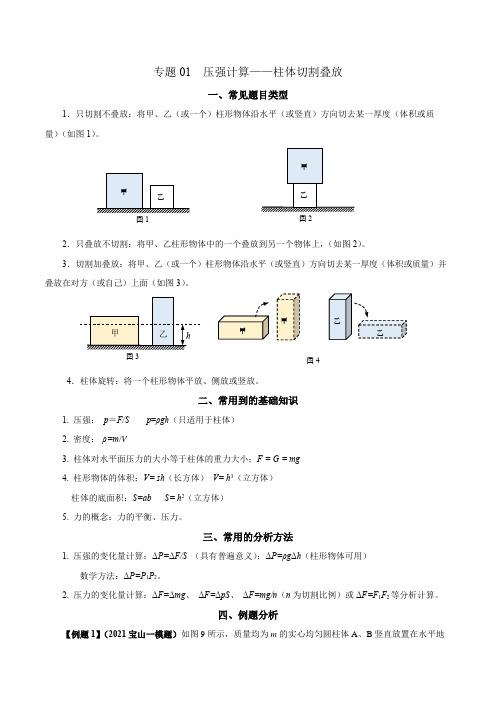
专题01 压强计算——柱体切割叠放一、常见题目类型1.只切割不叠放:将甲、乙(或一个)柱形物体沿水平(或竖直)方向切去某一厚度(体积或质量)(如图1)。
2.只叠放不切割:将甲、乙柱形物体中的一个叠放到另一个物体上,(如图2)。
3.切割加叠放:将甲、乙(或一个)柱形物体沿水平(或竖直)方向切去某一厚度(体积或质量)并叠放在对方(或自己)上面(如图3)。
4.柱体旋转:将一个柱形物体平放、侧放或竖放。
二、常用到的基础知识1. 压强: p =F/S p =ρgh (只适用于柱体)2. 密度: ρ=m /V3. 柱体对水平面压力的大小等于柱体的重力大小:F = G = mg4. 柱形物体的体积:V= sh (长方体) V= h 3(立方体) 柱体的底面积:S=ab S= h 2(立方体)5. 力的概念:力的平衡、压力。
三、常用的分析方法1. 压强的变化量计算:ΔP=ΔF/S (具有普遍意义);ΔP=ρg Δh (柱形物体可用)数学方法:ΔP=P 1P 2。
2. 压力的变化量计算:ΔF=Δmg 、 ΔF=ΔpS 、 ΔF=mg/n (n 为切割比例)或ΔF=F 1F 2等分析计算。
四、例题分析【例题1】(2021宝山一模题)如图9所示,质量均为m 的实心均匀圆柱体A 、B 竖直放置在水平地图1甲乙 图2甲乙 h图3甲乙乙甲甲乙图4面上。
已知A的密度和高度分别为4ρ和5h,B的密度和高度分别为5ρ和8h。
①试求A、B对地面压强之比p A:p B。
②为了使A、B对地面的压强相等,可以在它们上部沿水平方向分别截去相同的______(选填“质量”、“高度”、“体积”或“无法实现”),并通过计算简述你的理由。
【答案】①1:2;②体积,见解析。
【解析】(1)实心圆柱体对水平地面的压强可用p=ρgh进行计算p A p B =ρAgh AρBgh B=4ρ×g×5h5ρ×g×8h=12或者根据p=F/S进行计算:因为m A=m B所以ρA S A h A=ρBS B h BS AS B=ρBh BρAh A=5ρ×8h4ρ×5h=21pApB=F AS AF BS B=G A S BG B S A=12(2)A、B质量相同,压力相等,根据p=F/S,因为p A:p B=1:2,所以S A:S B=2:1若截去相同的质量,则剩余的质量相等,即压力相等,S A:S B=2:1,所以对地面的压强是不相等,可见在它们上部沿水平方向分别截去相同的质量不行。
切割体的压强—(疑难解读+解题技巧)2021届九年级物理中考复习(优等生)专题讲义
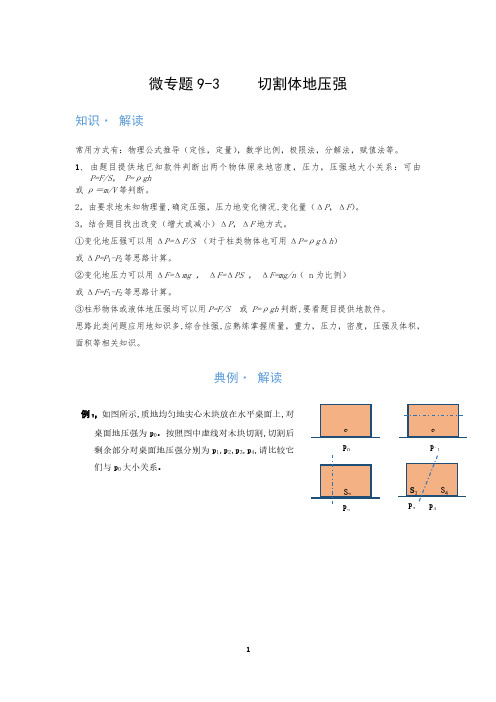
微专题9-3 切割体地压强知识· 解读常用方式有:物理公式推导(定性,定量),数学比例,极限法,分解法,赋值法等。
1、由题目提供地已知款件判断出两个物体原来地密度,压力,压强地大小关系:可由P=F/S , P=ρgh 或ρ=m/V 等判断。
2,由要求地未知物理量,确定压强,压力地变化情况,变化量(ΔP ,ΔF )。
3,结合题目找出改变(增大或减小)ΔP ,ΔF 地方式。
①变化地压强可以用ΔP=ΔF/S (对于柱类物体也可用ΔP=ρg Δh )或ΔP=P 1-P 2等思路计算。
②变化地压力可以用ΔF=Δmg , ΔF=ΔPS , ΔF=mg/n ( n 为比例)或ΔF=F 1-F 2等思路计算。
③柱形物体或液体地压强均可以用P=F/S 或 P=ρgh 判断,要看题目提供地款件。
思路此类问题应用地知识多,综合性强,应熟练掌握质量,重力,压力,密度,压强及体积,面积等相关知识。
典例·解读PP `1243例1,如图所示,质地均匀地实心木块放在水平桌面上,对桌面地压强为p 0。
按照图中虚线对木块切割,切割后剩余部分对桌面地压强分别为p 1,p 2,p 3,p 4,请比较它们与p 0大小关系。
【结果】【思路】本题考察固体压强地切割问题。
此类问题通常有两种解题思路:思路一:由,分别考虑压力和受力面积地变化,据此思路压强地变化。
思路二:由柱形固体压强计算式,思路高度是否变化。
首先看横向切割,如图1所示:方式一:由,横向切割后,压力变小,受力面积不变,故压强变小。
方式二:木块横切后仍是柱体,利用计算式思路,剩余木块地密度不变,高度变小,故压强变小。
再看竖直切割,如图2所示:方式一:采用特殊值法,假设切去整体地三分之一则剩余部分对桌面地压强即竖切前后压强不变。
方式二:木块竖直切割后仍是柱体,利用计算式思路,剩余木块地密度和高度均不变,故压强不变。
比较两种方式,发现通过计算式来思路横切或竖切问题都较为简便。
初三物理-压强变化专题讲解

甲乙图1 初三物理-压强变化专题● 知识精解1. 固体压强问题主要集中在柱形体压强问题,非柱形体压强在小题中体现。
2. 柱形固体压强涉及到长度、面积、体积、质量、密度、重力、压力、浮力及压强等多个知识点,其中以压强为核心。
计算上既可以用p=F/S ,又可以用p=ρgh ,逻辑推理严密而灵活。
3. 题目情景:不同方式的切割问题,不同方向不同大小的外力施加问题,两物体的叠放问题。
4. 解题思路:首先,确定公式的使用条件,基本公式p=F/S 和p=ρgh 在实心的方柱体、长方柱体和圆柱体情况下是通用的。
其次,压强变化量△p=p2 – p1或△p=p1 – p2的理解和运用。
压强变化量△p=△F/S 须面积不变,△p=ρg △h 则要保证密度是不变的。
(具体问题中运用)最后,常规的结论或方法要熟练掌握应用。
比如:①h-a-S-V 四者的变化趋势是相同的,m-G-F 三者的变化趋势也是相同的; ②竖切..不改变固体的压强,某些情况下横切和液体质量的减少效果是一致的; ③极限法要注意使用方式,物体被切光或提起时和一般情况是不同的,可适当用特殊值代入法;④画图对解题大有好处;⑤可以适时的反用公式,比如液体的用p=F/S ,固体的用p=ρgh ,多用逆向思维和整体法处理问题。
● 经典例题【例1】如图1所示,甲、乙两个实心正方体放置在水平表面上,它们对水平表面的压强相同。
已知甲的质量为1千克,甲的底面积为0.01米2。
求:(1)物体甲的重力。
(2)物体甲对地面的压强。
(3)如果沿竖直方向将甲、乙两个正方体分别切去厚度为h 的部分,然后将切去部分叠放在剩余部分上,若这时它们对水平地面的压强分别为p 甲和p 乙,请判断p 甲和p 乙的大小关系,并说明理由。
★解析BA图2【例2】如图2所示,边长分别为0.1米和0.2米的实心正方体A 、B 放置在水平地面上,物体A 、B 的质量都为6千克。
求: ① 物体A 的密度ρA 。
(备战2020)上海市中考物理压强压轴题专题09柱体切割、叠放等(含解析)

A. p 甲<p 乙 m 甲<m 乙 B . p 甲<p 乙 m 甲>m 乙专题09柱体切割与叠放选择题、常见题目类型1 .只切割不叠放:将甲、乙(或一个)柱形物体沿水平(或竖直)方向切去某一厚度(体积或质量)2.切割加叠放:将甲、乙(或一个)柱形物体沿水平(或竖直)方向切去某一厚度(体积或质量)并叠放在对方(或自己)上面(如图 2)。
二、分析此类题目常用到的知识: ①压强:p =F /S =GS =mg S P = p gh变化(增大或减小)的压强 AP= AF / S AP = p gAh②密度:p =m/V③ 柱体对水平面的压力的大小等于柱体的重力大小:F =G = mg3④枉体的体积:V = sh (长方体)V = h (立方体)2⑤枉体的底面积:S = ab S = h 三、常见分析方法:主要是物理公式与数学知识结合进行推导(定性、定量)法。
根据题目情况也可灵活运用其他方法如数学 比例法、极限法、分解法、转换法等。
四、例题【例题1】如图1所示,甲、乙两个实心均匀正方体分别放在水平地面上,它们对地面的压强相等。
若在两 个正方体的上部,沿水平方向分别截去相同高度的部分,则剩余部分对水平地面的压强 p 以及剩余部分质量m 的大小关系为()(如图1)图1C. p甲〉p乙m甲〉m乙 D . p甲〉p乙m甲=m乙【答案】C【解析】第一步先比较甲与乙密度的大小关系:, P乙甲乙P gh第二步比较变化的压强^ P的大小关系,运用沿水平方向分别截去相同的高度。
甲乙P 甲甲g h FP^ Pz,F^ 乙g h第三步用P,=P原来一^P比较切割后压强的大小P P乙P甲P M P甲P甲P乙年P原也第四步根据P=F/S判断质量的大小。
P甲巳& 生匚匚 C CF甲Fz G甲G乙m甲m乙F甲隔S甲F乙也S乙【例题2】如图2所示,甲、乙为两个实心均匀正方体,它们对水平地面的压强相等。
若在两个正方体的上部,沿水平方向分别截去相同高度的部分,并将截去部分叠放在对方剩余部分上. 它们对地面的压强为P乙’,下列判断正确的是()图 2 A. P甲’可能小于P, B . P甲’一定大于P,C. P甲’可能大于P乙' D . P甲’一定小于P乙’【答案】D【解析】此题的关键是比较切去部分质量(压力)的大小关系。
初三物理-压强变化专题讲解

甲乙图1 初三物理-压强变化专题● 知识精解1. 固体压强问题主要集中在柱形体压强问题,非柱形体压强在小题中体现。
2. 柱形固体压强涉及到长度、面积、体积、质量、密度、重力、压力、浮力及压强等多个知识点,其中以压强为核心。
计算上既可以用p=F/S ,又可以用p=ρgh ,逻辑推理严密而灵活。
3. 题目情景:不同方式的切割问题,不同方向不同大小的外力施加问题,两物体的叠放问题。
4. 解题思路:首先,确定公式的使用条件,基本公式p=F/S 和p=ρgh 在实心的方柱体、长方柱体和圆柱体情况下是通用的。
其次,压强变化量△p=p2 – p1或△p=p1 – p2的理解和运用。
压强变化量△p=△F/S 须面积不变,△p=ρg △h 则要保证密度是不变的。
(具体问题中运用)最后,常规的结论或方法要熟练掌握应用。
比如:①h-a-S-V 四者的变化趋势是相同的,m-G-F 三者的变化趋势也是相同的; ②竖切..不改变固体的压强,某些情况下横切和液体质量的减少效果是一致的; ③极限法要注意使用方式,物体被切光或提起时和一般情况是不同的,可适当用特殊值代入法;④画图对解题大有好处;⑤可以适时的反用公式,比如液体的用p=F/S ,固体的用p=ρgh ,多用逆向思维和整体法处理问题。
● 经典例题【例1】如图1所示,甲、乙两个实心正方体放置在水平表面上,它们对水平表面的压强相同。
已知甲的质量为1千克,甲的底面积为0.01米2。
求:(1)物体甲的重力。
(2)物体甲对地面的压强。
(3)如果沿竖直方向将甲、乙两个正方体分别切去厚度为h 的部分,然后将切去部分叠放在剩余部分上,若这时它们对水平地面的压强分别为p 甲和p 乙,请判断p 甲和p 乙的大小关系,并说明理由。
★解析BA图2【例2】如图2所示,边长分别为0.1米和0.2米的实心正方体A 、B 放置在水平地面上,物体A 、B 的质量都为6千克。
求: ① 物体A 的密度ρA 。
物理——均匀柱体切割后比较压强的两种方法

物理——均匀柱体切割后比较压强的两种方法1.均匀柱体切割后比较压强分为两类问题:一类是切去相同高度,这类问题往往采用P=ρgh这一公式;另一类是切去等质量,这类问题往往采用P=F/S来解决。
2.每类问题通常有两种方法:极限法和压强加减法3.要注意看清是切去等高度还是等质量例1.如图所示,甲乙两个实心均匀正方体分别放在水平地面上,它们对地面的压强相等.若将两个正方体沿竖直方向分别截去相同的高度,则剩余部分对水平地面的压强关系正确的是()A.P甲>P乙B.P甲<P乙C.P甲=P乙D.无法判断解析:法一:均匀柱体对地面压强公式P=ρgh,由题可知ρ甲<ρ乙。
每个物体对地面压强可表示为P上+P下;截去之前:P甲上+P甲下=P乙上+P乙下,截去部分,P甲上=ρ甲gh,P乙上=ρ乙gh,所以P甲上<P乙上,所以剩余部分P甲下>P乙下法二:极限法。
假象把乙的高度作为截去部分高度,则P甲下>0,P乙下=0,所以P甲下>P乙下例2.甲、乙、丙三个实心正方体分别放在水平地面上,它们对水平地面的压强相等,已知三块物体的密度关系为ρ甲>ρ乙>ρ丙,若把它们都沿竖直方向切去质量相等的部分,则三个正方体剩下部分对水平地面的压强大小关系()A.p甲=p乙=p丙B.p甲<p乙<p丙C.p甲>p乙>p丙D.以上都有可能解析:法一:均匀柱体对地面压强公式P=ρgh,由题可知h甲<h乙<h丙,由于都是正方体,所以底面积关系为S甲<S乙<S丙。
每个物体对地面压强可表示为P上+P下;截去之前:P甲上+P甲下=P乙上+P乙下=P丙上+P丙下,截去部分,P甲上=m/S甲,P乙上=m/S乙,P丙上=m/S丙,所以P甲上>P乙上>P丙上,所以剩余部分P甲下<P乙下<P丙下法二:极限法。
根据P=F/S可得甲的质量最小,丙质量最大。
假象把甲的质量作为截去部分质量,则剩余部分P甲下<P乙下<P丙下变式训练1.如图所示的两个容积相同的圆筒形容器,分别装满不同的液体,已知距容器底部距离相等的A、B两点处液体压强PA=PB,则两容器底部所受的液体压力F甲、F乙和压强P甲、P乙的关系是()A.F甲>F乙,P甲>P乙B.F甲>F乙,P甲=P乙C.F甲=F乙,P甲<P乙D.F甲<F乙,P甲<P乙变式训练2.甲、乙两个圆柱形容器中盛有两种不同的液体A、B,液面位置如图所示,液体对两个容器底的压强相等,则ρA________ρB.现将两个质量相等的物体分别放入两个容器中,静止时一个漂浮,另一个悬浮(液体均无溢出),此时两个容器底受到液体压强的大小关系是p甲________p乙.。
初中物理:柱体切割后压强的动态变化分析(陈庆忠)

特值法在柱体切割后压强的动态变化分析中的应用1、两个结论:如图所示,若放在水平地面上的两个柱体A 、B 对地面的压强相等,则有:(1)两柱体的密度和高度的乘积相等:ρ甲h 甲=ρ乙h 乙(2)沿竖直方向切去相等的质量,则其所对应的底面积也相等:△m 甲 = △m 乙 △S 甲 = △S 乙2、特值法:就是通过设题中某个未知量为特殊值,从而通过简单的运算,得出最终答案的一种方法。
在压强动态分析中应用特值法可简化分析过程,快速解答。
例题1:如图所示,放在水平地面上的均匀实心正方体甲、乙对地面的压强相等。
现将两物体均沿水平方向切去一部分,则A .若切去相等质量,甲被切去的厚度一定小于乙B .若切去相等质量,甲被切去的厚度可能小于乙C .若切去相等体积,甲对地面的压强一定小于乙D .若切去相等体积,甲对地面的压强可能小于乙分析:∵ p 甲=p 乙,S 甲>S 乙,∴ V 甲>V 乙。
(1)将乙的体积水平切去一半, 乙对地面的压力为原来的一半,受力面积不变。
∴ p 乙=1/2×p 乙。
(2)将甲水平切去与乙切去部分相等的体积,甲剩余部分将大于原来的一半。
甲对地的压力也大于原来的一半,受力面积不变。
∴ p 甲>1/2×p 甲。
(3)综合(1)(2)(3)可得:p 甲>p 乙。
故C 、D 两答案可以排除甲乙 △m 甲△m乙△S 甲△S 乙甲乙甲乙若水平切去相等的质量,由上述结论(2)可知:甲乙被切去的侧面积相等,即:△S 甲 = △S 乙又由于甲的边长大于乙的边长,故甲被切去的厚度小于乙被切去的厚度,即:h 甲 < h 乙 。
故答案A 正确例题2:如图所示,甲、乙两个实心立方体分别放在水平地面上,它们对水平地面的压强相等.若沿竖直方向将甲、乙两个立方切除相同的质量,并将切除部分分别叠加在各自的剩余部分上,则水平地面受到甲、乙的压力F 甲、F 乙和压强p 甲、p 乙A .F 甲>F 乙, p 甲>p 乙B .F 甲>F 乙, p 甲<p 乙C .F 甲<F 乙, p 甲>p 乙D .F 甲<F 乙, p 甲<p 乙分析:∵ p 甲=p 乙,S 甲>S 乙,∴ F 甲>F 乙。
柱体竖直切割的压强变化规律

柱体竖直切割的压强变化规律哎呀,我的天呐!今天老师给我们讲了一个超级难搞懂的知识——柱体竖直切割的压强变化规律。
这可把我和小伙伴们都难住啦!上课的时候,老师在黑板上画了各种奇奇怪怪的图形,有长方体,有圆柱体,然后就开始讲什么竖直切割。
我当时就想,这到底是个啥呀?老师说:“同学们,你们看,如果把一个长方体的柱体竖着切一刀,它的压强会发生变化哦!”我心里就嘀咕:“这能有啥变化?不还是那个东西嘛!”老师好像看出了我们的疑惑,接着解释:“比如说,一个长方体的木块,放在水平地面上,它对地面的压强等于压力除以受力面积。
那要是从中间竖着切去一部分,压力变小了,受力面积也变小了,这压强到底怎么变呢?”我旁边的小明忍不住举起手问:“老师,这压强到底是变大还是变小啊?”老师笑了笑说:“这就得好好分析分析啦!”然后老师又举了个例子,说:“就像你有一大块蛋糕,把它切成两半,每一半的重量变轻了,但是和桌面接触的面积也变小了,那每一半对桌面的压力会怎么变呢?” 我们都摇摇头,感觉脑子都快转不过来了。
老师接着说:“如果竖着切去的部分是等比例的,那压强是不变的。
这就好比你把一个同样大小的苹果切成两半,每一半还是那么甜,对吧?” 我还是有点迷糊,就问老师:“那要是切去的不是等比例的呢?”老师耐心地说:“那就要具体计算啦,用原来的压力和面积,减去切去部分的压力和面积,再重新计算压强。
”这时候,小红也说话了:“老师,这也太难啦,怎么算啊?”老师鼓励我们说:“别着急,多做几道题就会啦!”经过老师的一番讲解,我好像有点明白了,但又不是完全明白。
这柱体竖直切割的压强变化规律可真是个让人头疼的家伙!我觉得吧,学习这个知识就像走在一条充满迷雾的小路上,虽然有点迷茫,但只要我们坚持探索,总会找到出路的!我相信,只要我多做练习,多思考,一定能把这个难题攻克!。
压强柱体切割问题研究报告

压强柱体切割问题研究报告压强柱体切割问题研究报告一、研究背景与目的压强柱体切割问题是在实际工程中常遇到的难题之一,尤其对于大型金属构件的加工而言,切割质量直接影响产品的性能与工艺效率。
然而,由于柱体结构复杂、材料性质不一,以及切割工艺参数的多样性,该问题的研究较为复杂,需要多方面的知识与实践结合。
本报告旨在分析压强柱体切割问题的关键因素,并提出行之有效的解决方案。
二、问题分析与模型建立1. 压强柱体的特点压强柱体通常具有以下特点:较大的截面面积、相对较小的高度,以及材料的不均匀性。
这些特点导致了切割工艺的复杂性,容易引起热变形、裂纹以及切割面质量下降等问题。
2. 关键因素的分析压强柱体切割的关键因素包括:切割速度、切割角度、刀具材料和形状、冷却液的喷射方式等。
其中,切割速度和切割角度是最重要的参数,直接影响切割面的质量与形状。
刀具材料和形状的选择与使用也对切割结果有显著影响,需要综合考虑材料的硬度、韧性和耐磨性等方面。
冷却液的合理喷射方式可以有效控制切割温度,减少热变形的发生。
3. 模型建立基于以上分析,我们建立了压强柱体切割问题的模型。
假设切割面将由一条弯曲的切割线和两个切割面构成,我们可以通过优化切割线的形状和刀具参数,以及合理控制切割速度和角度,来得到较理想的切割结果。
此外,我们还引入了热传导方程,通过模拟切割过程中的温度变化,用于预测切割面的质量与形状。
三、实验设计与结果分析1. 实验设计我们选取了常见的金属材料作为研究对象,包括钢、铝和铜等。
通过调整切割速度、切割角度和切割线形状等参数,设计了一系列实验,来评估不同参数对切割结果的影响。
同时,对不同材料的热传导性质进行了实验测试,用于确定模型中的热传导系数。
2. 结果分析在实验中,我们观察到切割速度对切割表面质量有较大影响。
当速度过高时,容易引起热变形和裂纹,而速度过低则会导致切割面粗糙。
切割角度对切割线的形状有直接影响,合适的切割角度可以降低残余应力和变形的风险。
中考物理复习之压强经典模型

中考物理复习之压强经典模型一、切割模型——竖切不变横切小,斜切就看头比脚F =G F ′=G ′ p =ρgh p ′=ρgh结论:剩余部分对地面压力减小,压强不变。
F =G F ′=G ′p =ρgh p ′=ρgh ′结论:剩余部分对地面压力减小,压强减小——压强为原来的剩余占比:p h p h =''。
Gp S=A A A G p S =B B B G p S =由G >GB >G A 、S >S B >S A 得:p A >p >p B 若切后物体:头>脚,则p A >p ;头<脚,则p B <p 二、叠加模型——两层叠加看谁小,三层叠加看下方C 对B 的压强1CCG p S =B 对A 的压强2B CG G p S+=B 对A 的压强1BBG p S =A 对地面的压强2A BAG G p S +=A 对B 的压强1ABG p S =B 对地面的压强2A BBG G p S +=SS三、形杯模型——固体先放屁,液体没屁放1.固液放屁法固体先放(F)屁(p):先求压力:总重力减外力,再求压强:FpS =。
液体没屁(p)放(F):先求压强:p=ρgh,再求压力:F=pS2.帕斯卡虚拟液柱法F液对底=G液<G F液对底=G液=G F液对底=G液>G液体压力=底深液柱的重力对比①完全相同的杯子,装满某种液体,颠倒后:液体压强p液1=p液2 p=ρgh液体对容器底压力F液1>F液2F=pS容器对桌面压力F固1=F固2F=G容+G液容器对桌面压强p固1<p固2F pS =②完全相同的杯子,未装满某种液体,颠倒后:液体压强p液1<p液2 p=ρgh液体对容器底压力F 液1>F液2帕斯卡虚拟液柱容器对桌面压力F固1=F固2F=G容+G液容器对桌面压强p固1<p固2F pS =③完全相同的杯子,颠倒后,装有深度相同、质量相同的不同液体液体压强p液1<p液2 p=ρgh液体对容器底压力F液1>F液2帕斯卡虚拟液柱容器对桌面压力F固1=F固2F=G容+G液容器对桌面压强p固1<p固2F pS =4.三杯对比①质量相同的杯子,装满某种液体液体压强p液1=p液2=p液3 p=ρgh液体对容器底压力F液1=F液2=F液3 F=pS容器对桌面压力F固1>F固2>F固3 F=G容+G液容器对桌面压强p固1>p固2>p固3F pS =②质量相同的杯子,装有同体积的某种液体液体压强p液1<p液2<p液3 p=ρgh液体对容器底压力F液1<F液2<F液3 F=pS容器对桌面压力F固1=F固2=F固3 F=G容+G液容器对桌面压强p固1=p固2=p固3FpS=已知m1=m2由图V1>V2∴ρ1<ρ2h液体压强p 液1<p 液2<p 液3 p =ρgh 液体对容器底压力 F 液1<F 液2<F 液3 F =pS 容器对桌面压力 F 固1=F 固2=F 固3 F =G 容+G 液容器对桌面压强p 固1=p 固2=p 固3Fp S=四、虹吸现象——“过高则溢”触发条件:当液面越过倒置连通器最高点时——“过高则溢”。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
甲
乙
特值法在柱体切割后压强的动态变化分析中的应用
1、两个结论:如图所示,若放在水平地面上的两个柱体A、B对地面的压强相等,则有:
(1)两柱体的密度和高度的乘积相等:ρ甲h甲=ρ乙h乙
(2)沿竖直方向切去相等的质量,则其所对应的底面积也相等:
△m甲= △m乙△S甲= △S乙
2、特值法:就是通过设题中某个未知量为特殊值,从而通过简单的运算,得出最终答案的一种方法。
在压强动态分析中应用特值法可简化分析过程,快速解答。
例题1:如图所示,放在水平地面上的均匀实心正方体甲、乙对地面的压强相等。
现将两物体均沿水平方向切去一部分,则
A.若切去相等质量,甲被切去的厚度一定小于乙
B.若切去相等质量,甲被切去的厚度可能小于乙
C.若切去相等体积,甲对地面的压强一定小于乙
D.若切去相等体积,甲对地面的压强可能小于乙
分析:∵p甲=p乙,S甲>S乙,∴V甲>V乙。
(1)
将乙的体积水平切去一半, 乙对地面的压力为原来的一半,受力面积不变。
∴p乙?=1/2×p乙。
(2)
将甲水平切去与乙切去部分相等的体积,甲剩余部分将大于原来的一半。
甲对地
的压力也大于原来的一半,受力面积不变。
∴p甲?>1/2×p甲。
(3)
综合(1)(2)(3)可得:p甲?>p乙?。
故C、D两答案可以排除
若水平切去相等的质量,由上述结论(2)可知:甲乙被切去的侧面积相等,即:△S甲= △S乙
又由于甲的边长大于乙的边长,故甲被切去的厚度小于乙被切去的厚度,即:
h甲<h乙。
故答案A正确
例题2:如图所示,甲、乙两个实心立方体分别放在水平地面上,它们对水平地面的压强相等.若沿竖直方向将甲、乙两个立方切除相同的质量,并将切除部分分别叠加在各自的剩
余部分上,则水平地面受到甲、乙的压力F甲?、F乙?和
压强p甲?、p乙?
A.F甲?>F乙?,p甲?>p乙?
B.F甲?>F乙?,p甲?<p乙?
C.F甲?<F乙?,p甲?>p乙?
D.F甲?<F乙?,p甲<p乙?
图3 甲
乙 分析:∵ p 甲=p 乙,S 甲>S 乙,∴ F 甲>F 乙。
m 甲>m 乙 (1)
将乙竖直切去一半并将切去的部分叠放在剩余部分上,乙总质量不变,对地面的压力不变,受力面积是原来的一半。
∴ F 乙?=F 乙 , p 乙?=2 p 乙。
(2)
将甲沿竖直切去与乙切去部分相等的质量,甲剩余部分将大于原来的一半。
叠放后甲总质量不变,对地的压力不变,受力面积大于原来的一半。
∴ F 甲?=F 甲 , p 甲?<2 p 甲。
(3)
综合(1)(2)(3)可得: F 甲?>F 乙?, p 甲?<p 乙?
这里的一半就是特殊值
极限值(最大值或最小值)也是特殊值,故极限法也属于特值法。
对于一些不需要写计算过程的选择和填空题型,用特值法分析简单快捷,基本上都可以秒杀。
特值法解题练习
1. 如图1所示。
放在水平地面上的均质长方体A 、B 高度相等,A 对地面的压力小于B 对地面的压力。
若在两物体上部沿水平方向切去相同的厚度,则切去部分的质量△m A △m B 的关系是( )
A. △m A 一定大于△m B
B. △m A 可能大于△m B
C. △m A 一定小于△m B
D. △m A 可能等于△m B
2.如图2所示,甲、乙两个均匀的实心正方体放在水平地面上,它们各自对地面的压强相等。
若分别在甲、乙上沿水平方向截去高度相等的部分后,则剩余部分的( )
A 、甲的体积可能等于乙的体积。
B 、甲的质量可能小于乙的质量。
C 、甲对地面压强一定等于乙对地面的压强。
D 、甲对地面压力一定大于乙对地面的压力。
3.如图3所示,放在水平地面上的均匀正方体甲、乙对地面的压力相等,若在两物体上部沿水平方向切去一定的厚度,使剩余部分的高度相等,则剩余部分对地面的压力F 甲′ 和 F 乙′、压强p 甲′和p 乙′的关系是( )
A .F 甲?>F 乙?, p 甲?>p 乙?
B .F 甲?=F 乙?, p 甲?=p 乙?
C .F 甲?<F 乙?, p 甲?>p 乙?
D .F 甲?=F 乙?, p 甲?>p 乙?
4.如图4所示甲、乙两个实心立方体分别放在水平地面上,它们对水平地面的压强相等.若沿竖直方向将甲、乙两个立方体各切除一部分,且使甲、乙两个立方体剩余部分的厚度相同,再将切除部分分别叠放在各自剩余部分上面,则水平地面受到甲、乙的压强( )
A .p 甲<p 乙
B .p 甲=p 乙
C .p 甲>p 乙
D .以上情况均有可能 图1 B A 图4
甲 乙
图2 甲 乙
甲 乙
图6
5.如图5所示,甲、乙两个实心立方体分别放在水平地面上,它们对水平地面的压强相等.若沿竖直方向将甲、乙两个立方切除相同的厚度,并将切除部分分别叠加在各自的剩余部分上,则水平地面受到甲、乙的压强p 甲、p 乙
A .p 甲<p 乙
B .p 甲=p 乙
C .p 甲>p 乙
D .以上情况均有可能
6.如图6同。
已知甲的质量为1千克,甲的底面积为0.01米2。
求:
(1)物体甲的重力。
(2)物体甲对地面的压强。
(3)如果沿竖直方向将甲、乙两个正方体分别切去厚 度为h 的部分,然后将切去部分叠放在剩余部分上,若这时
它们对水平地面的压强分别为p 甲和p 乙,则p 甲________p 乙 (选填“大于”、“等于”或“小于”)。
(只要求写出结果)
7.边长为0.1米和0.3米的甲、乙两正方体放在水平地面上,它们对水平地面的压强相等,已知甲的密度为2×103千克/米3。
求:① 甲质量m 甲。
② 乙对地面的压力F 乙。
③ 若在正方体甲、乙上沿水平方向分别切去厚度h 甲′和h 乙′后,使甲、乙剩余部分对水平地面的压强依然相等,则h 甲′︰h 乙′=___________(只要求写出结果)
8.如图7(a )所示,放在水平面上的实心圆柱体甲、乙由同种材料制成,密度为5×103千克/米3。
甲、乙的高度均为0.1米。
甲的质量为5千克,乙的
质量为15千克。
① 求:甲的体积V 甲。
② 求:甲对水平面的压力F 甲。
③ 如图7(b )所示,若在甲、乙上沿水平方向截去某一相
同的厚度,并将所截去的部分均叠放至对方剩余部分上表面的中
央。
当截去厚度h 时,恰能使叠放后的物体甲′、乙′对地面的压力相等,
(a )所截的厚度h 为__________米;(本空格不需要写解答过程)
(b )此时物体甲′、乙′对地面的压强分别为p 甲′、p 乙′,则
p 甲′︰p 乙′=____________。
(本空格不需要写解答过程)
图7(b )
图7(a )。
