轴向拉伸和压缩练习题
项目三 轴向拉伸与压缩试题

【开始】单选题(分值=2分;答案=C;难度=基本题)在其他条件不变时,若受轴向拉伸的杆件横截面面积增加一倍,则杆件横截面上的正应力()。
A、4倍B、2倍C、1/2倍D、1/4倍【结束】【开始】单选题(分值=2分;答案=C;难度=水平题)在其他条件不变时,若受轴向拉伸的杆件杆长增加一倍,则杆件纵向线应变()。
A、增大B、减小C、不变D、不能确定【结束】【开始】单选题(分值=2分;答案=B;难度=基本题)弹性模量E与()有关。
A、应力和应变B、杆件的材料C、外力大小D、泊松比μ【结束】【开始】单选题(分值=2分;答案=B;难度=水平题)横截面面积不同的两根杆件,受到大小相同的轴向外力作用时,则()。
A、轴力相同,应力也相同B、轴力相同,应力不同C、轴力不同,应力也不同D、轴力不同,应力不同【结束】【开始】单选题(分值=2分;答案=A;难度=基本题)材料在轴向拉伸时,在比例极限内,线应变与()成正比。
A、正应力B、弹性模量EC、泊松比μD、都切应力【结束】【开始】单选题(分值=2分;答案=D;难度=基本题)危险截面的确定,对于杆件对象的工程设计是非常重要的,若杆件的材料相同,轴向拉伸杆件危险截面发生在()的截面上。
A、轴力最大、横截面面积最大B、轴力最小、横截面面积最小C、轴力最小、横截面面积最大D、轴力最大、横截面面积最小【结束】【开始】单选题(分值=2分;答案=D;难度=基本题)下列关于内力的说法中错误的是()。
A、由外力引起的杆件内各部分间的相互作用力B、内力随外力的改变而改变C、内力可由截面法求得D、内力不仅与外力有关,还与杆件的截面形状和尺寸有关【结束】【开始】单选题(分值=2分;答案=B;难度=基本题)对于塑性材料取()作为材料的极限应力。
A、弹性极限B、屈服极限C、比例极限D、强度极限【结束】【开始】单选题(分值=2分;答案=B;难度=基本题)轴向拉压杆的应力与杆件的()有关。
A、外力B、外力、截面面积和形状C、外力、截面面积和形状、材料D、外力、截面面积和形状、材料、杆长【结束】【开始】单选题(分值=2分;答案=D;难度=基本题)轴向拉压杆的纵向线应变与杆件的()有关。
轴向拉伸与压缩和剪切挤压练习题

轴向拉伸压缩练习题一、判断题:1.在弹性范围内,杆件的正应力和正应变成正比。
(对)2.轴向拉压杆横截面上,只有一种内力,有两种应力。
(对)3.胡克定律仅适用于杆件的弹性变形范围(对)4.低碳钢受拉破坏时有屈服阶段,中碳钢和合金钢都没有屈服阶段。
(错)5.铸铁扭转破坏沿45度螺旋面断裂是因剪应力先达到极限所致。
(错)6.低碳钢扭转破坏沿轴横截面断裂是因剪应力先达到极限所致。
(对)7.低碳钢压缩实验曲线一直是上扬的,因此极限强度为无穷。
(错)8. 弹性极限是材料保持弹性的最大极限值,可以不保持线性。
(错)9.比例极限是材料能保持线性的最大值,必在材料的弹性范围内。
(错)10.构件内力的大小不但与外力大小有关,还与材料的截面形状有关(错)11.杆件的某横截面上,若各点的正应力均为零,则该截面上的轴力为零。
(对)12.两根材料、长度都相同的等直柱子,一根的横截面积为A1,另一根为A2,且A2>A1 如图所示。
两杆都受自重作用。
则两杆最大压应力相等,最大压缩量也相等。
(对)13. 受集中力轴向拉伸的等直杆,在变形中任意两个横截面一定保持平行。
所以纵向纤维的伸长量都相等,从而在横截面上的内力是均匀分布的。
(错)14. 若受力物体内某电测得x和y方向都有线应变εx和εy,则x和y方向肯定有正应力σx 和σy。
(错)二、选择题1 塑性材料冷作硬化后,材料的力学性能发生了变化。
试判断以下结论哪一个是正确的:__ (A) 屈服应力提高,弹性模量降低;(B) 屈服应力提高,塑性降低;(C) 屈服应力不变,弹性模量不变;(D) 屈服应力不变,塑性不变。
2 低碳钢材料在拉伸实验过程中,不发生明显的塑性变形时,承受的最大应力应当小于的数值,有以下4种答案,请判断哪一个是正确的:_B_ (A) 比例极限;(B) 屈服极限;(C) 强度极限;(D) 许用应力。
3.关于低碳钢试样拉伸至屈服时,有以下结论,请判断哪一个是正确的:__ _ (A) 应力和塑性变形很快增加,因而认为材料失效;(B) 应力和塑性变形虽然很快增加,但不意味着材料失效;(C) 应力不增加,塑性变形很快增加,因而认为材料失效;(D) 应力不增加,塑性变形很快增加,但不意味着材料失效。
工程力学轴向拉伸与压缩答案
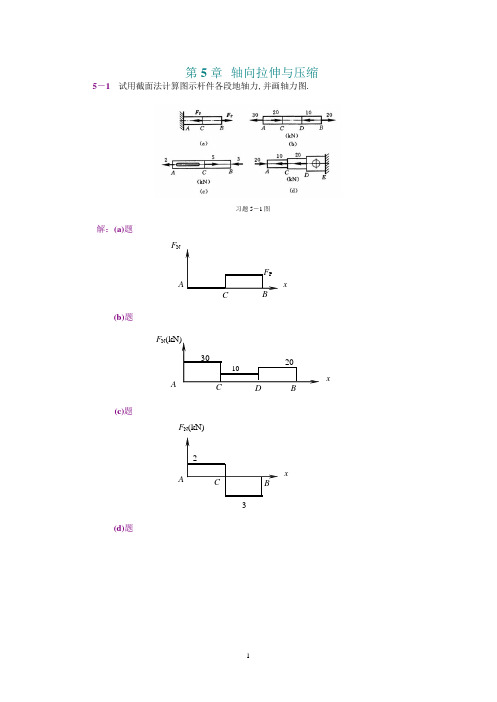
第5 章轴向拉伸与压缩5-1 试用截面法计算图示杆件各段地轴力,并画轴力图.习题5-1 图解:(a)题F Nx(b)题F NxA(c)题F N(kN)x-3(d)题F N-10x5-2 图示之等截面直杆由钢杆 ABC 与铜杆 CD 在 C 处粘接而成.直杆各部分地直径均为 d =36 mm ,受力如图所示.若不考虑杆地自重,试求 AC 段和 AD 段杆地轴向变形量 Δl AC和 Δl AD习题 5-2 图(F N ) l AB (F N ) l BC解: Δl AC =AB πd 2E s4+BC πd 2 E s 4 150 ×103 × 2000 +100 ×103 ×3000 4 = × = 2.947 mm(F N ) 200 ×103 l π ×362100 ×103 × 2500 × 4 Δl = Δl + CD CD = 2.947 + = 5.286 mm AD AC πd 2 E c4105 ×103 × π ×3625-3 长度 l =1.2 m 、横截面面积为 1.10×l0-3m 2 地铝制圆筒放置在固定地刚性块上;刚性板mC B −6 B 直径 d =15.0mm 地钢杆 BC 悬挂在铝筒顶端地刚性板上;铝制圆筒地轴线与钢杆地轴线重 合.若在钢杆地 C 端施加轴向拉力 F P ,且已知钢和铝地弹性模量分别为 E s =200GPa ,E a =70GPa ;轴向载荷 F P =60kN ,试求钢杆 C 端向下移动地距离.解:u A− u B −F l = P AB E a A a 3(其中 u A = 0)3∴ u =60 ×10 ×1.2 ×10= 0.935 mm B 70 ×10 3 ×1.10 ×10 −3 ×10 6钢杆 C 端地位移为F l60 ×103 × 2.1×103u = u + P BC = 0.935 + = 4.50 m m E s A s200 ×103 × π ×15245-4 螺旋压紧装置如图所示.现已知工件所受地压紧力为 F =4 kN .装置中旋紧螺栓 螺纹地内径 d 1=13.8 mm ;固定螺栓内径 d 2=17.3 mm .两根螺栓材料相同,其许用应力[σ ] =53.0 MPa .试校核各螺栓地强度是否安全.解:∑ M B = 0 ,F A = 2kN ∑ F y = 0 ,F B = 6kN习题 5-4 解图习题 5-4 图 σ = F A = 2000 = A π2000 × 42= 13.37 MPa < [σ ] ,安全. A A d 2 π ×13.8 ×104 σ = F B = 16000= 25.53 MPa <[σ ] ,安全. A B π ×17.32 ×10−645-5 现场施工所用起重机吊环由两根侧臂组成.每一侧臂 AB 和 BC 都由两根矩形截面 杆所组成,A 、B 、C 三处均为铰链连接,如图所示.已知起重载荷 F P =1200 kN ,每根矩形 杆截面尺寸比例 b/h =0.3,材料地许用应力[σ ]=78.5MPa .试设计矩形杆地截面尺寸 b 和 h .4⋅2FF N习题 5-5 图解:由对称性得受力图如习题 5-5 解图所示.∑ F y = 0 ,4F N cos α = F P 习题 5-5 解图F = F P = N 4 cos α 1200 ×103960 = 3.275 ×105 Nσ = F N A= F N 0.3h 2≤ [σ ]9602 + 42025h ≥ F N =0.3[σ ]3.275 ×100.3 × 78.5 ×106= 0.118m b = 0.3h ≥ 0.3 × 0.118 = 0.0354m = 35.4mmh = 118mm ,b = 35.4mm5-6 图示结构中 BC 和 AC 都是圆截面直杆,直径均为 d =20mm ,材料都是 Q235 钢, 其许用应力[σ ]=157MP .试求该结构地许用载荷.B习题 5-6 图习题 5-6 解图∑ F x = 0 , F B = 2F A (1)∑ F y= 0 ,2 F A + 23F B − F P = 0 2(2)1 + 3 F P = F B2(3)F ≤ [σ ] ⋅πd2B43 mdWs由式(1)、(2)得:F ≤ 1 + P2 = 1 + 23 ⋅π d 2 [σ ] 43 ⋅π × 202 ×10−4 ×157 ×106 = 67.4kN 4` (4)F P =2 (1 + 23 ) F A = 2 (1 + 2 3 ) ⋅[σ ]π 24= 90.28kN (5)比较(4)、(5)式,得 [F P ] = 67.4 kN5-7 图示地杆件结构中 1、2 杆为木制,3、4 杆为钢制.已知 1、2 杆地横截面面积A 1=A 2=4000 mm 2,3、4 杆地横截面面积 A 3=A 4=800 mm 2;1、2 杆地许用应力[σ]=20MPa , 3、4 杆地许用应力[σ ]=120 MPa .试求结构地许用载荷[F P ].习题 5-7 图P(a)3(b)解:1. 受力分析:由图(a )有5∑ F y = 0 , F 3 =F P 3 4 4由图(b )由∑ F x = 0 , F 1 = − 5 F 3 = − 3 F P∑ F x = 0 , F 4 = 4 F 3 = 5 43 F P2. 强度计算:5∑ F y = 0 , F 2= − 3F 3 = −F P| F 1 |>| F 2 || F 1 |≤ [σ w ] A 14 F ≤ A [σ ] 3P 1 w F ≤ 3 A [σ ] = 3 × 4000 ×10 −6 × 20 ×10 6 = 60 kN P 4 1 w4F 35F 3 > F 4 , ≤ [σ s ] , A 3F P ≤ [σ ]A 3 3F ≤3 [σ] A 3 ×120 ×10 6 × 800 ×10 −6= 57.6 kN[F P] = 57.6 kNa*5-8 由铝板和钢板组成地复合柱,通过刚性板承受纵向载 荷 F P =38 kN ,其作用线沿着复合柱地轴线方向.试确定:铝板和 钢板横截面上地正应力. 解:此为超静定问题.1. 平衡方程2. 变形协调方程:3. 物性关系方程:F Ns + F Na = F P Δl s = Δl a(1)(2)联立解得⎧F F Ns E s A sE s A s= FNaE a A a(3)习题 5-8 图⎪ Ns = E A E A F P ⎪ ⎨ ⎪F = s s + a E a A a a(压) F NaE A + E A P s s a aσ =F Ns =−E s F P = −E s F P s A E b h + E⋅ 2b h b hE + 2b hE s s 0 a 1 0 s 1 a9 3σ = − 200 ×10 ×385 ×10175MPa (压)= − s 0.03 × 0.05 × 200 ×109 + 2 × 0.02 × 0.05 × 70 ×109σa = F Na A = −b hE E a F P+ 2b hEa 0 s 1 aσ = −175E a E s = −17570 200= −61.25MPa (压)*5-9 铜芯与铝壳组成地复合棒材如图所示,轴向载荷通过两端刚性板加在棒材上. 现已知结构总长减少了 0.24 mm .试求:1.所加轴向载荷地大小; 2. 铜芯横截面上地正应力.习题 5-9 图F NcE A =F NaE A(1)E A E A σ aF = ΔlE c A c , F= ΔlE a A aF Nc + F Na = F P(2)Nc l NalF = F + F = ΔlE c A c + ΔlE a A aP Nc Nal l = Δl E A + E A( c c a a) l= 0.24 ×10−3 ⎧ π 2 =π ⎡ 2 2 ⎤⎫ = ⎨105 ×106 × ×(25 ×10−3 ) + 75 ×106 × × (60 ×10−3 ) − (25 ×10−3 ) ⎬ 30 ×10−3⎩ 4 4 ⎭ = 171 kNF =E c A cNc c c F P + E a A aF =E a A a Na c cF P + E a A a⎧ F Nc E c F P E c F P ⎪σ c = ⎪ A c ⎪ ∴ ⎨= E c A c + E a A a = E c ⋅ πd 2 4 + E a π 2 2 ⋅ (D− d ) 4 ⎪ = F Na ⎪ A a ⎪⎩ = πd 2E c 4E aF Pπ(D 2 − d 2 ) + E a 4 9 32. σ =4 ×105 ×10 ×171×1083.5MPa = c105 ×109 × π × 0.0252 + 70 ×109 × π × (0.062 − 0.025)2σa = σcE a = 83.5 × 70= 55.6MPa E c 105*5-10 图示组合柱由钢和铸铁制成,组合柱横截面为边长为 2b 地正方形,钢和铸铁 各占横截面地一半(b ×2b ).载荷 F P ,通过刚性板沿铅垂方向加在组合柱上.已知钢和铸铁 地弹性模量分别为 E s =196GPa ,E i =98.0GPa .今欲使刚性板保持水平位置,试求加力点地 位置 x =?解:∑ M 0 = 0 , (b ⋅ 2b σ 习题 5-10 图) ⋅( x − b ) = (b ⋅ 2b )σs i( 3 b − x )23∴σ σ s =iE sE i2 x − b = σ i3b − 2 x σ s(1)(2)代入(1)得σ i σ s4 x − 2b = 3b − 2 x5= 98 = 1196 2(2)∴ x = b 65-11 电线杆由钢缆通过旋紧张紧器螺杆稳固.已知钢缆地横截面面积为1×103 mm 2 ,E =200GPa ,[σ ] = 300MPa .欲使电杆有稳固力F R =100kN ,张紧器地螺杆需相对移动多少? 并校核此时钢缆地强度是否安全.F R习题 5-11 图解:(1)设钢缆所受拉力为 F N ,由平衡条件F N cos30°=F RF N =100/ cos30°=115.5kNΔl = F N l = 115.5 ×103 ×10 ×103= 6.67mm EA 200 ×103 ×103× 3 / 2张紧器地螺杆需相对移动 6.67mm .(2)钢缆地应力与强度σ = F N A = 115.5 ×10 103= 115.5MP a < [σ ]所以,强度安全.5-12 图示小车上作用着力 F P =15kN ,它可以在悬架地 AC 梁上移动,设小车对 AC梁地作用可简化为集中力.斜杆 AB 地横截面为圆形(直径 d =20mm),钢质,许用应力 [σ]=160MPa .试校核 AB 杆是否安全.3习题 5-12 图F N ABαF N ACF P习题 5-12 解图解:当小车开到 A 点时,AB 杆地受力最大,此时轴力为 F N A B .(1) 受力分析,确定 AB 杆地轴力 F N A B ,受力图如图 5-12 解图所示, 由平衡方程∑Fy= 0 ,F N AB sin α − F P = 0sin α =解得轴力大小为:0.8 0.82 +1.92F N AB = 38.7kN(2)计算应力σ = F N AB = F N AB = 4 × 38.7 ×10 =123 ×106Pa = 123MPa < [σ ] AB强度安全.A AB πd 2 4π × 202 ×10−65-13 桁架受力及尺寸如图所示.F P =30kN ,材料地抗拉许用应力[σ]+=120MPa , 抗压许用应力[σ]-=60MPa .试设计AC 及AD 杆所需之等边角钢钢号.(提示:利用附录B 型钢表.)F N AC45DAF N ADF PF RA习题 5-13 图习题 5-13 解图解:(1)受力分析,确定 AC 杆和 AD 杆地轴力 F N AC 、 F N AD ,对整体受力分析可得, F R A= F R B = F P 2= 15kN再取节点 A ,受力分析,受力图如图 5-13 解图所示,建立平衡方程D D 3 3 2 4 ∑F y = 0 , − F N AC sin 45 + F R A = 0解得 AC 杆轴力大小为:F N AC = 21.2kN(压)∑ F x = 0 , − F N AC cos 45 + F N AD = 0解得 AD 杆轴力大小为: F N AD = 15kN(拉)(2)强度条件拉杆:A AD = F N AD [σ ]+ = 15 ×10 120 = 125mm 2 压杆:(3)选择钢号A AC = F N AC [σ ]− = 21.2 ×10 60 = 353.3mm 2 拉杆: 20 × 20 × 4压杆: 40 × 40 × 55-14 蒸汽机地气缸如图所示.气缸内径D =560mm ,内压强p =2.5MPa ,活塞杆直径 d =100mm .所有材料地屈服极限σs =300MPa . (1)试求活塞杆地正应力及工作安全系数.(2)若连接气缸和气缸盖地螺栓直径为30mm ,其许用应力[σ]=60MPa ,求连接每个气缸盖 所需地螺栓数.习题 5-14 图解:(1)活塞杆受到地轴力为:⎡π (D 2 F = pA = p − d 2 ) ⎤ = 2.5⎡π (560 −1002 ) ⎤ = 596.12kN N ⎢ ⎥ ⎢ ⎥ ⎣ ⎦ ⎣ 4 ⎦活塞杆地正应力:σ =F N A 杆596.12 ×103 ) = = 75.9MPa π ×102 / 4 工作安全系数: (2)螺栓数mn = σ s σ= 300 = 3.95 75.93x 3 x y xm = F N = 596.12 ×10 = 14.1 个 A 栓 [σ ]栓 π × 302 / 4 × 60由于圆对称,取m =16个.5-15 图示为硬铝试件,h =200mm ,b =20mm .试验段长度l 0=70mm .在轴向拉力 F P =6kN 作用下,测得试验段伸长Δl 0=0.15mm ,板宽缩短Δb =0.014mm .试计算硬铝地弹 性模量E 和泊松比ν .习题 5-15 图解:(1)计算弹性模量Eε = Δl 0 l 0= 0.15 = 2.143 ×10−3 70σ = F P = 6 ×10 = 150MPa AE = σ = 20 × 2 150 ×106 = 70GPa ε 2.143 ×10−3 (2) 计算泊松比νε = Δb 0 b 0= − 0.014 = −7 ×10−4 20ε ν = y = − 7 ×10−4 = 0.327 ε 2.143 ×10−3上一章返回总目录下一章。
轴向拉伸与压缩练习题

轴向拉伸与压缩练习题在材料力学中,轴向拉伸与压缩是一种常见的载荷方式,它们用于研究材料的强度、刚度和变形特性。
这些练习题旨在帮助学生加深对轴向拉伸与压缩的理解,并提供实践应用的机会。
以下是一些典型的练习题,通过解答这些问题,我们可以更好地理解这一领域的概念和原理。
1. 假设一根钢杆的长度为L,直径为D,已知拉伸载荷为F,求该杆的应力和应变。
2. 一根弹性体的长度为L,横截面积为A,已知施加在该体上的拉伸载荷为F,它的徐变模量为E,求该体的应变。
3. 如果一根杆材受到的拉伸载荷逐渐增加,最终达到其屈服强度,该杆材会发生什么样的变形?4. 如果一根杆材受到的压缩载荷逐渐增加,最终达到其屈服强度,该杆材会发生什么样的变形?5. 如果一根杆材同时受到轴向拉伸和压缩两种载荷,该杆材会如何变形?6. 一根弹性体的长度为L,横截面积为A,已知施加在该体上的拉伸载荷为F,计算该体的应力。
7. 一块材料在受到拉伸载荷时,其应力与应变之间的关系可以通过应力-应变曲线来表示,请描述应力-应变曲线的特点。
8. 如果一根杆材在受到轴向拉伸时断裂,这可能是由于哪些原因导致的?9. 一根杆材经过轴向拉伸后恢复原状的能力被称为什么?10. 在材料力学中,有一种称为胶黏剪切的变形模式,你了解它吗?请简要描述一下。
以上是一些典型的轴向拉伸与压缩练习题,通过解答这些问题,我们可以更好地理解轴向拉伸与压缩的基本概念和应用。
在解答问题的过程中,我们也可以运用公式和原理来计算并分析材料的应力、应变和变形等性质。
同时,通过这些练习题,我们可以培养应用知识解决实际问题的能力。
要提醒的是,在进行轴向拉伸与压缩练习题时,我们应该注意准确的计算和合理的分析。
在解答问题时,可以尝试用不同的方法和途径来验证答案,以加深对知识的理解和掌握。
同时,在实践中,我们也可以通过学习和研究更多的相关材料,来进一步拓展和深化对轴向拉伸与压缩的理解。
通过轴向拉伸与压缩练习题的学习与实践,我们可以更好地掌握这一领域的知识和技能。
第一章轴向拉伸和压缩习题

第一章轴向拉伸和压缩习题一、单项选择题1、构件具有足够的抵抗破坏的能力,我们就说构件具有足够的A、刚度,B、稳定性,C、硬度,D、强度。
2、构件具有足够的抵抗变形的能力,我们就说构件具有足够的A、强度,B、稳定性,C、刚度,D、硬度。
3、单位面积上的内力称之为A、正应力,B、应力,C、拉应力,D、压应力。
4、与截面垂直的应力称之为A、正应力,B、拉应力,C、压应力,D、切应力。
5、轴向拉伸和压缩时,杆件横截面上产生的应力为A、正应力,B、拉应力,C、压应力,D、切应力。
6、胡克定律在下述哪个范围内成立?A、屈服极限,B、比例极限,C、强度极限,D、名义屈服极限。
时,试样将7、当低碳钢试样横截面上的实验应力σ =σsA、完全失去承载能力,B、断裂,C、产生较大变形,D、局部出现颈缩。
8、脆性材料具有以下哪种力学性质?A、试样拉伸过程中出现屈服现象,B、抗冲击性能比塑性材料好,C、若构件开孔造成应力集中现象,对强度没有影响。
D、抗压强度极限比抗拉强度极限大得多。
9、灰铸铁压缩实验时,出现的裂纹A、沿着试样的横截面,B、沿着与试样轴线平行的纵截面,C、裂纹无规律,D、沿着与试样轴线成45。
角的斜截面。
10、横截面都为圆的两个杆,直径分别为d和D ,并且d=0.5D。
两杆横截面上轴力相等两杆横截面上应力之比Ddσσ为 A 、2倍, B 、4倍, C 、8倍, D 、16倍。
二、填空题1、求内力常用的方法是 。
2、轴向拉伸和压缩时,虎克定律的两种表达形式为 ,3、通过低碳钢拉伸试验可知,反映材料抵抗弹性变形能力的指标是 ;反映材料强度的指标是 ;反映材料塑性的指标是 。
4、σ0.2表示材料的 。
5、与截面平行的应力称为 ;与截面垂直的应力称之为 。
6、 钢的弹性模量E=200Gpa ,铝的弹性模量E=71Gpa,试比较在同一应力作用下,哪种材料应变大? 。
7、轴向拉伸和压缩时,杆上所受外力或外力的合力与杆件的轴线 。
项目三 轴向拉压杆习题

项目三轴向拉伸与压缩一、填空题:1、内力是由引起的杆件内个部分间的。
2、求内力的基本方法是。
3、直杆的作用内力称。
其正负号规定为:当杆件受拉而伸长时为正,其方向截面。
4、截面法就轴力的步骤为:、、。
5、轴力图用来表达,画轴力图时用的坐标表示横截面位置,坐标表示横截面上的轴力。
6、轴力图中,正轴力表示拉力,画在轴的。
7、轴力的大小与外力有关。
与杆件截面尺寸、材料(有关、无关)。
8、应力是,反应了内力的分布集度。
单位,简称。
9、1pa= N/mm2 = N/m2。
1Mpa= pa。
10、直杆受轴力作用时的变形满足假设,根据这个假设,应力在横截面上分布,计算公式为。
11、正应力是指。
12、在荷载作用下生产的应力叫。
发生破坏是的应力叫。
许用应力是工作应力的;三者分别用符号、、表示。
13、当保证杆件轴向拉压时的安全,工作应力与许用应力应满足关系式:。
14、等截面直杆,受轴向拉压力作用时,危险截面发生在处。
而变截面杆,强度计算应分别进行检验。
15、轴向拉压杆的破坏往往从开始。
16、杆件在轴向力作用下长度的改变量叫,用表示。
17、胡克定律表明在范围内,杆件的纵向变形与及,与杆件的成正比。
18、材料的抗拉、压弹性模量用表示,反映材料的能力。
19、EA称作材料的,它反映了材料制成一定截面尺寸后的杆件的抗拉、压能力。
EA越大,变形越。
20、ε叫作,指单位长度的变形。
21、泊松比又叫,ν= ,应用范围为弹性受力范围。
二、计算题:1、试计算轴向拉压杆指定截面的轴力。
2、绘制图示杆件的轴力图。
3、求图示结构中各杆的轴力。
4、用绳索起吊管子如图所示。
若构件重W=10KN ,绳索的直径d=40mm ,许用30 20KNB 45C 455、图示支架中,荷载P=100KN。
杆1为圆形截面钢杆,其许用应力[σ]拉=150MPa,杆2位正方形截面木杆,其许用应力[σ]压=4MPa。
试确定钢杆的直径d和木杆截面的边长c。
C6、钢杆长l=2m,截面面积A=200 mm2,受到拉力P=32KN的作用,钢杆的弹性模量E=2.0×105MPa,试计算此钢杆的伸长量Δl。
工程力学:拉伸压缩 习题与答案

一、单选题1、拉压正应力计算公式s=F/A的适用条件是()。
A.应力小于弹性极限B.应力小于屈服极限C.应力小于比例极限D.外力的合力沿杆轴线正确答案:D2、材料经过冷作硬化后,其比例极限和塑性分别()。
A.提高,提高B.下降,不变C.下降,提高D.提高,下降正确答案:D3、假设一拉伸杆件的弹性模量E=300GPa,比例极限为 sp=300MPa,杆件受一沿轴线的拉力,测得轴向应变为e=0.0015,则该拉应力s的大小为()。
A.大于450MPaB.300MPa£s£450MPaC.450MPaD.小于300MPa正确答案:B4、受轴向拉伸的杆件,其最大切应力与轴线的角度为()。
A.30B.90C.45D.0正确答案:C5、一等直拉杆在两端承受拉力作用,若其一段为钢,另一段为铝,则两段的()。
A.应力不同,变形相同B.应力不同,变形不同C.应力相同,变形不同D.应力相同,变形相同正确答案:C6、脆性材料与塑性材料相比,其拉伸性能的最大特点是()。
A.没有明显的屈服阶段和塑性变形B.应力应变关系严格遵守虎克定律C.强度低、对应力集中不敏感D.强度极限比塑性材料高正确答案:A7、现有一两端固定、材料相同的阶梯杆,其大径与小径的横截面积之比为4:1, 杆的大径与小径长度相同,在大径与小径交界处施加一轴向力P,则杆的大径与小径所受轴力之比为()。
A.2:1B.1:1C.4:1D.1:2正确答案:C8、在低碳钢的拉伸实验中,材料的应力变化不大而变形显著增加的是()。
A.屈服阶段B.颈缩阶段C.强化阶段D.线弹性阶段正确答案:A9、现有两相互接触的平板,在垂直于板平面的方向上打一直径为d的销孔,使用直径d、许用切应力[τ]、许用挤压应力[sbs]的圆柱形销钉进行固定,两板的厚度均为h, 现分别在两板施加大小相同、方向相反的F,使两板有沿接触面相互错动的倾向,若要销钉不失效破坏,则要满足的条件是()。
材料力学 拉伸压缩 习题及参考答案

轴向拉伸和压缩 第二次 作业1. 低碳钢轴向拉伸的整个过程可分为 弹性阶段 、 屈服阶段 、 强化阶段 、 局部变形阶段 四个阶段。
2. 工作段长度100 mm l =,直径10 mm d =的Q235钢拉伸试样,在常温静载下的拉伸图如图所示。
当荷载F = 10kN 时,工作段的伸长∆l = 0.0607mm ,直径的缩小∆d = 0.0017mm 。
则材料弹性模量E = 210 GPa ,强度极限σb = 382 MPa ,泊松比μ = 0.28 ,断后伸长率δ = 25% ,该材料为 塑性 材料。
∆l / mmO0.0607253. 一木柱受力如图所示。
柱的横截面为边长20mm 的正方形,材料的弹性模量E =10GPa 。
不计自重,试求 (1)作轴力图;(2)各段柱横截面上的应力;(3)各段柱的纵向线应变;(4)柱端A 的位移。
100kN260kN解:(1)轴力图如图所示 (2)AC 段 310010250MPa 2020NAC AC AC F A σ-⨯===-⨯ CB 段 326010650MPa 2020NCB CB CB F A σ-⨯===-⨯ (3)AC 段 69250100.0251010NAC AC AC AC F EA E σε-⨯====-⨯ CB 段 69650100.0651010NCB CB CBCB F EA E σε-⨯====-⨯ (4)AC 段 0.025150037.5mm NAC ACAC AC AC ACF l l l EA ε∆===-⨯=- CB 段 0.065150097.5mm NCB CBCB CB CB CBF l l l EA ε∆===-⨯=- 柱端A 的位移 37.597.5135mm A AC CB l l ∆=∆+∆=--=-(向下)4. 简易起重设备的计算简图如图所示。
已知斜杆AB 用两根63×40×4不等边角钢组成,63×40×4不等边角钢的截面面积为A = 4.058cm 2,钢的许用应力[σ] = 170 MPa 。
拉伸与压缩试题

拉伸与压缩试题————————————————————————————————作者:————————————————————————————————日期:第二章 拉伸与压缩一、是非题2-1 、当作用于杆件两端的一对外力等值反向共线时则杆件产生轴向拉伸或压缩变形。
( ) 2-2 、关于轴力有下列几种说法: 1、轴力是作用于杆件轴线上的载荷( ) 2、轴力是轴向拉伸或压缩时杆件横截面上分布内力系的合力( )3、轴力的大小与杆件的横截面面积有关( )4、轴力的大小与杆件的材料无关( )2-3、 同一材料制成的阶梯杆及其受力如图2-1CD 段的横截面面积为ABC 和DE 段均为2A 分别用和表示截面上的轴力和正应力则有1、轴力321N N N F F F >> 。
( )2、正应力1σ>2σ>3σ。
( )2-4、 轴力越大,杆件越容易拉断,因此轴力的大小可以用来判断杆件的强度。
( )2-5 、一轴向拉伸的钢杆材料弹性模量E =200GP a,比例极限p σ=200MP a ,今测得其轴向线应变ε=0.0015,则由胡克定律得其应力εσE ==300MP a 。
( ) 2-6 、关于材料的弹性模量E,有下列几种说法:1、E 的量纲与应力的量纲相同。
( )2、E 表示弹性变形能力的大小。
( )3、各种牌号钢材的E 值相差不大。
( )4、橡皮的E 比钢材的E值要大。
( )5、从某材料制成的轴向拉伸试样,测的应力和相应的应变,即可求的其εσ=E 。
( ) 2-7 、关于横向变形系数(泊松比)μ,有下列几种说法:1、为杆件轴向拉、压时,横向应变ε'与纵向应变ε之比的绝对值。
( )2、 μ值越大,其横向变形能力越差。
( )3、各种材料的μ值都满足:0<μ≤0.5。
( )2-8、 受轴向拉、压的等直杆,若其总伸长为零,则有1、杆内各处的应变必为零。
( )2、杆内各点的位移必为零。
( )3、杆内各点的正应力必为零。
轴向拉伸和压缩习题集及讲解

第二章 轴向拉伸和压缩 第一节 轴向拉压杆的内力1.1 工程实际中的轴向受拉杆和轴向受压杆在工程实际中,经常有承受轴向拉伸荷载或轴向压缩荷载的等直杆。
例如图2-1a 所示桁架的竖杆、斜杆和上、下弦杆,图2-1b 所示起重机构架的各杆及起吊重物的钢索,图2-1c 所示的钢筋混凝土电杆上支承架空电缆的横担结构,BC 、AB 杆,此外,千斤顶的螺杆,连接气缸的螺栓及活塞连杆等都是轴间拉压杆。
钢木组合桁架d起重机图工程实际中的轴向受拉(压)杆1.2 轴向拉压杆的内力——轴力和轴力图bcx图用截面法求杆的内力为设计轴向拉压杆,需首先研究杆件的内力,为了显示杆中存在的内力和计算其大小,我们采用在上章中介绍过的截面法。
(如图2-2a )所示等直杆,假想地用一截面m -m 将杆分割为I 和II 两部分。
取其中的任一部分(例如I )为脱离体,并将另一部分(例如II )对脱离体部分的作用,用在截开面上的内力的合力N 来代替(图2-2b ),则可由静力学平衡条件:0 0X N P =-=∑求得内力N P =同样,若以部分II 为脱离体(图2-2c ),也可求得代表部分I 对部分II 作用的内力为N =P ,它与代表部分II 对部分I 的作用的内力等值而反向,因内力N 的作用线通过截面形心 即沿杆轴线作用,故称为轴力..。
轴力量纲为[力],在国际单位制中常用的单位是N (牛)或kN (千牛)。
为区别拉伸和压缩,并使同一截面内力符号一致,我们规定:轴力的指向离开截面时为正号轴力;指向朝向截面时为负号轴力。
即拉力符号为正,压力符号为负。
据此规定,图2-2所示m-m 截面的轴力无论取左脱离体还是右脱离体,其符号均为正。
1.3 轴力图当杆受多个轴向外力作用时,杆不同截面上的轴力各不相同。
为了形象表示轴力沿杆轴线的变化情况,以便于对杆进行强度计算,需要作出轴力图,通常用平行于杆轴线的坐标表示截面位置,用垂直杆轴线的坐标表示截面上轴力大小,从而给出表示轴力沿截面位置关系的图例,即为轴力图...。
工程力学习题册第五章 - 答案

第五章拉伸和压缩一、填空题1.轴向拉伸或压缩的受力特点是作用于杆件两端的外力__大小相等___和__方向相反___,作用线与__杆件轴线重合_。
其变形特点是杆件沿_轴线方向伸长或缩短__。
其构件特点是_等截面直杆_。
2.图5-1所示各杆件中受拉伸的杆件有_AB、BC、AD、DC_,受压缩的杆件有_BE、BD__。
图5-13.内力是外力作用引起的,不同的__外力__引起不同的内力,轴向拉、压变形时的内力称为_轴力__。
剪切变形时的内力称为__剪力__,扭转变形时的内力称为__扭矩__,弯曲变形时的内力称为__剪力与弯矩__。
4.构件在外力作用下,_单位面积上_的内力称为应力。
轴向拉、压时,由于应力与横截面__垂直_,故称为__正应力__;计算公式σ=F N/A_;单位是__N/㎡__或___Pa__。
1MPa=__106_N/m2=_1__N/mm2。
5.杆件受拉、压时的应力,在截面上是__均匀__分布的。
6.正应力的正负号规定与__轴力__相同,__拉伸_时的应力为__拉应力__,符号为正。
__压缩_时的应力为__压应力_,符号位负。
7.为了消除杆件长度的影响,通常以_绝对变形_除以原长得到单位长度上的变形量,称为__相对变形_,又称为线应变,用符号ε表示,其表达式是ε=ΔL/L。
8.实验证明:在杆件轴力不超过某一限度时,杆的绝对变形与_轴力__和__杆长__成正比,而与__横截面面积__成反比。
9.胡克定律的两种数学表达式为σ=Eε和ΔL=F N Lo/EA。
E称为材料的_弹性模量__。
它是衡量材料抵抗_弹性变形_能力的一个指标。
10.实验时通常用__低碳钢__代表塑性材料,用__灰铸铁__代表脆性材料。
11.应力变化不大,应变显著增大,从而产生明显的___塑性变形___的现象,称为__屈服___。
12.衡量材料强度的两个重要指标是__屈服极限___和__抗拉强度__。
13.采用___退火___的热处理方法可以消除冷作硬化现象。
材料力学第二章轴向拉伸与压缩作业习题

第二章 轴向拉伸与压缩1、试求图示各杆1-1和2-2横截面上的轴力,并做轴力图。
(1) (2)2、图示拉杆承受轴向拉力F =10kN ,杆的横截面面积A =100mm 2。
如以α表示斜截面与横截面的夹角,试求当α=10°,30°,45°,60°,90°时各斜截面上的正应力和切应力,并用图表示其方向。
3、一木桩受力如图所示。
柱的横截面为边长200mm 的正方形,材料可认为符合胡克定律,其弹性模量E =10GPa 。
如不计柱的自重,试求:(1)作轴力图;(2)各段柱横截面上的应力; (3)各段柱的纵向线应变;(4)柱的总变形。
4、(1)试证明受轴向拉伸(压缩)的圆截面杆横截面沿圆周方向的线应变d ε,等于直径方向的线应变d ε。
(2)一根直径为d =10mm 的圆截面杆,在轴向拉力F 作用下,直径减小0.0025mm 。
如材料的弹性摸量E =210GPa ,泊松比ν=0.3,试求轴向拉力F 。
(3)空心圆截面钢杆,外直径D =120mm,内直径d =60mm,材料的泊松比ν=0.3。
当其受轴向拉伸时, 已知纵向线应变ε=0.001,试求其变形后的壁厚δ。
5、图示A和B两点之间原有水平方向的一根直径d=1mm的钢丝,在钢丝的中点C加一竖直荷载F。
已知钢丝产生的线应变为ε=0.0035,其材料的弹性模量E=210GPa,钢丝的自重不计。
试求:(1) 钢丝横截面上的应力(假设钢丝经过冷拉,在断裂前可认为符合胡克定律);(2) 钢丝在C点下降的距离∆;(3) 荷载F的值。
6、简易起重设备的计算简图如图所示.一直斜杆AB应用两根63mm×40mm×4mm不等边角钢组[σ=170MPa。
试问在提起重量为P=15kN的重物时,斜杆AB是否满足强度成,钢的许用应力]条件?7、一结构受力如图所示,杆件AB,AD均由两根等边角钢组成。
已知材料的许用应力[σ=170MPa,试选择杆AB,AD的角钢型号。
材料力学答案- 轴向拉伸与压缩

习 题2-1 一木柱受力如图示,柱的横截面为边长20cm 的正方形,材料服从虎克定律,其弹性模量51010.0⨯=E MPa .如不计柱自重,试求:(1) 作轴力图;(2) 各段柱横截面上的应力;(3) 各段柱的纵向线应变;(4) 柱的总变形.解:(1) 轴力图(2) AC 段应力a a MP P σ5.2105.22.010100623-=⨯-=⨯-=CB 段应力a a MP P σ5.6105.62.010260623-=⨯-=⨯-=(3) AC 段线应变45105.2101.05.2-⨯-=⨯-==E σε CB 段线应变45105.6101.05.6-⨯-=⨯-==E σε(4) 总变形 m 3441035.15.1105.65.1105.2---⨯=⨯⨯-⨯⨯-=AB ∆2-2 图(a)所示铆接件,板件的受力情况如图(b)所示.已知:F =7 kN ,t =0.15cm ,b 1=0.4cm ,b 2=0.5cm ,b 3=0.6cml 。
试绘板件的轴力图,并计算板内的最大拉应力。
解:(2)a MP σ4.194101024.015.0767311=⨯⨯⨯⨯⨯=-a MP σ1.311101025.015.0767322=⨯⨯⨯⨯⨯=- a MP σ9.388101026.015.07673=⨯⨯⨯⨯=- 最大拉应力a MP σσ9.3883max ==2-3 直径为1cm 的圆杆,在拉力F =10 kN 的作用下,试求杆内最大剪应力,以及与横截面夹角为α=30o 的斜截面上的正应力与剪应力。
轴力图 (1)轴力图解:(1) 最大剪应力76max 22141210101063.66221F a d στππ-⨯===⨯⨯=MP ⨯ (2) ︒=30α界面上的应力()a MP ασσα49.952366.632cos 12=⨯=+= a MP αστα13.5530sin 66.632sin 2=⨯=⨯=︒2-4 图示结构中ABC 与CD 均为刚性梁,C 与D 均为铰接,铅垂力F =20kN 作用在C 铰,若(1)杆的直径d 1=1cm ,(2)杆的直径d 2=2cm ,两杆的材料相同,E =200Gpa ,其他尺寸如图示,试求(1)两杆的应力;(2)C 点的位移。
轴向拉伸和压缩习题附标准答案

第四章轴向拉伸和压缩、填空题1、杆件轴向拉伸或压缩时,其受力特点是:作用于杆件外力的合力的作用线与杆件轴线相_________ .2、轴向拉伸或压缩杆件的轴力垂直于杆件横截面,并通过截面_____________ .4、杆件轴向拉伸或压缩时,其横截面上的正应力是___________ 分布的.7、在轴向拉,压斜截面上,有正应力也有剪应力,在正应力为最大的截面上剪应力为________ .8杆件轴向拉伸或压缩时,其斜截面上剪应力随截面方位不同而不同,而剪应力的最大值发生在与轴线间的夹角为________ 的斜截面上.矚慫润厲钐瘗睞枥庑赖。
9、杆件轴向拉伸或压缩时,在平行于杆件轴线的纵向截面上,其应力值为_______ .10、胡克定律的应力适用范围若更精确地讲则就是应力不超过材料的________ 极限.11、杆件的弹必模量E表征了杆件材料抵抗弹性变形的能力,这说明杆件材料的弹性模量E值越大,其变形就越 ________ 聞創沟燴鐺險爱氇谴净。
12、在国际单位制中,弹性模量E的单位为________ .13、在应力不超过材料比例极限的范围内,若杆的抗拉(或抗压)刚度越_________ ,则变形就越小.15、低碳钢试样据拉伸时,在初始阶段应力和应变成___________ 关系,变形是弹性的,而这种弹性变形在卸载后能完全消失的特征一直要维持到应力为__________ 极限的时候.残骛楼諍锩瀨濟溆塹籟。
16、在低碳钢的应力一应变图上,开始的一段直线与横坐标夹角为a,由此可知其正切tg a在数值上相当于低碳钢的值.酽锕极額閉镇桧猪訣锥。
17、金属拉伸试样在屈服时会表现出明显的__________ 变形,如果金属零件有了这种变形就必然会影响机器正常工作.彈贸摄尔霁毙攬砖卤庑。
18、金属拉伸试样在进入屈服阶段后,其光滑表面将出现与轴线成_______ 角的系统条纹,此条纹称为__________ .謀养抟箧飆鐸怼类蒋薔。
建筑力学轴向拉伸与压缩概念题

第三章选择题1、 塑性材料的极限应力取 。
A .比例极限B .弹性极限C .屈服极限D .强度极限2、如图所示,轴向拉压杆1-1截面上的轴力等于 。
A .20NB .5NC .0ND .25N3、现有低碳刚和铸铁两种材料,在如图所示结构中,使用最合理的是A .①杆用低碳钢制造,②杆用铸铁制造B .②杆用低碳钢制造,①杆用铸铁制造C .①、②杆全部用铸铁制造4、下列结论中 是正确的。
( )A .材料力学主要研究各种材料的力学问题。
B .材料力学主要研究各种材料的力学性质。
C .材料力学主要研究杆件受力后变形与破坏的规律。
D .材料力学主要研究各类杆件中力与材料的关系。
5、轴向拉(压)时横截面上的正应力( )分布。
A .均匀 B.线性 C.假设均匀 D.抛物线6、杆件的抗拉刚度是( )。
A .EJ zB .GJ pC .GAD .EA7、直杆的两端受到一对等值、反向、作用线沿杆轴线的力。
杆件将产生( )变形。
A .拉压B .剪切C .弯曲D .扭转8、反映杆件横向应变与线应变之间关系的系数是 。
A .弹性模量B .泊松比C .延伸率D .截面收缩率9、杆件的应变与杆件的( )有关。
A .外力B .外力、截面C .外力、截面、材料D .外力、截面、杆长、材料10、杆件的变形与杆件的( )有关。
A .外力B .外力、截面C .外力、截面、材料D .外力、截面、杆长、材料11、两根相同截面,不同材料的杆件,受相同的外力作用,它们的纵向绝对变形( )。
A .相同B .不一定C .不相同12、两根相同截面、不同材料的杆件,受相同的外力作用,它们的应力( )。
A .相同B .不一定C .不相同13、构件抵抗变形的能力称( )。
A .刚度B .强度C .稳定性D .极限强度14、构件抵抗破坏的能力( )。
② ①PA.刚度B.强度C.稳定性D.极限强度15、构件保持原来平衡状态的能力称()。
A.刚度B.强度C.稳定性D.极限强度21、材料的强度指标是()。
轴向拉伸与压缩习题

轴向拉伸与压缩习题一、填空题1.在工程设计中,构件不仅要满足、和稳定性的要求,同时还必须符合经济方面的要求。
2、在式σ=eε中,比例系数e称作材料的拉压_______,相同材料的e值相同;它充分反映某种材料抵抗变形的能力,在其他条件相同时,ea越大,杆件的变形__________。
3、构件工作应力的最高极限叫做__________。
材料能承受的最大应力叫做材料__________。
4、材料抵抗弹性变形能力的指标就是____和_______。
5.在低碳钢的拉伸试验中,材料的应力变化不大而变形显著增加的现象称为。
二、选择题1.轴向弯曲或放大时,直杆横截面上的内力称作轴力,则表示为:()a.fnb.fsfqc.d.fjy2.材料的塑性指标有:()a.σu和δb.σs和ψc.σb和δd.δ和ψ3.截面上的内力大大,()a.与截面的尺寸和形状无关b.与截面的尺寸有关,但与截面的形状无关c.与截面的尺寸无关,但与截面的形状有关d.与截面的尺寸和形状都有关4.等横截面直杆在两个外力的促进作用下出现轴向放大变形时,这对外力所具有的特点一定就是等值、()。
a逆向、共线b反向,过截面形心c方向相对,促进作用线与杆轴线重合d方向相对,沿同一直线促进作用5.一阶梯形杆件受拉力p的作用,其截面1-1,2-2,3-3上的内力分别为n1,n2和n3,三者的关系为()。
an1≠n2n2≠n3bn1=n2n2=n3cn1=n2n2>n3dn1=n2n2<n36.图示阶梯形杆,cd段为铝,横截面面积为a;bc和de段为钢,横截面面积均为2a。
设1-1、2-2、3-3截面上的正应力分别为σ1、σ2、σ3,则其大小次序为()。
aσ1>σ2>σ3bσ2>σ3>σ1cσ3>σ1>σ2dσ2>σ1>σ37.轴向拉伸杆,正应力最大的截面和剪应力最大的截面()a分别是横截面、450斜截面b都是横截面c分别是450斜截面、横截面d都是450斜截面10.由变形公式δl=pl/ea即e=pl/aδl可知,弹性模量()a与载荷、杆长、横截面面积毫无关系b与载荷成正比c与杆长成正比d与横截面面积成正比11.在以下观点,()就是恰当的。
材料力学第二章轴向拉伸与压缩习题答案

解:
设每个螺栓承受的剪力为 ,则由
可得
螺栓的切应力
MPa MPa
∴螺栓满足剪切强度条件。
3-11图示矩形截面木拉杆的接头。已知轴向拉力 ,截面的宽度 ,木材顺纹的许用挤压应力 ,顺纹的许用切应力 。试求接头处所需的尺寸l和a。
解:
1.求支反力,作剪力图和弯矩图。
,
2.按正应力强度条件选择工字钢型号
由 ≤ ,得到
≥
查表选 14工字钢,其
, ,
3.切应力强度校核
满足切应力强度条件。
∴选择 14工字钢。
5-17图示木梁受移动载荷 作用。已知木材的许用正应力 ,许用切应力 , ,木梁的横截面为矩形截面,其高宽比 。试选择此梁的横截面尺寸。
≤
可得 ≤ ①
D点受力如图(b)所示,由平衡条件可得:
CD杆受压,压力为 ,由压杆的强度条件
≤
可得 ≤ ②
由①②可得结构的许用载荷为 。
3-8图示横担结构,小车可在梁AC上移动。已知小车上作用的载荷 ,斜杆AB为圆截面钢杆,钢的许用应力 。若载荷F通过小车对梁AC的作用可简化为一集中力,试确定斜杆AB的直径d。
截面上的剪力和弯矩为: ,
2.求1-1横截面上a、b两点的应力
5-10为了改善载荷分布,在主梁AB上安置辅助梁CD。若主梁和辅助梁的抗弯截面系数分别为 和 ,材料相同,试求a的合理长度。
解:
1.作主梁AB和辅助梁CD的弯矩图
2.求主梁和辅助梁中的最大正应力
主梁:
辅助梁:
3.求 的合理长度
轴向拉伸与压缩习题及解答

轴向拉伸与压缩习题及解答计算题1:利用截面法,求图2.1所示简支梁m — m 面的力分量。
解:〔1〕将外力F 分解为两个分量,垂直于梁轴线的分量F sin θ,沿梁轴线的分量F cos θ. (2)求支座A 的约束反力:xF∑=0,AxF∑=cos F θB M ∑=0, Ay F L=sin 3L F θAy F =sin 3Fθ (3)切开m — m ,抛去右半局部,右半局部对左半局部的作用力N F ,S F 合力偶M 代替 〔图1.12 〕。
图 2.1 图2.1(a) 以左半段为研究对象,由平衡条件可以得到xF∑=0, N F =—Ax F =—cos F θ〔负号表示与假设方向相反〕y F ∑=0, s F =Ay F =sin 3Fθ 左半段所有力对截面m-m 德形心C 的合力距为零sin θC M ∑=0, M=AyF 2L =6FL sin θ 讨论 对平面问题,杆件截面上的力分量只有三个:和截面外法线重合的力称为轴力,矢量与外法线垂直的力偶距称为弯矩。
这些力分量根据截面法很容易求得。
在材料力学课程中主要讨论平面问题。
计算题2:试求题2-2图所示的各杆1-1和2-2横截面上的轴力,并作轴力图。
解 〔a 〕如图〔a 〕所示,解除约束,代之以约束反力,作受力图,如题2-2图〔1a 〕所示。
利用静力学平衡条件,确定约束反力的大小和方向,并标示在题2-2图〔1a 〕中。
作杆左端面的外法线n ,将受力图中各力标以正负号,凡与外法线指向一致的力标以正号,反之标以负号,轴力图是平行于杆轴线的直线。
轴力图在有轴力作用处,要发生突变,突变量等与该处轴力的数值,对于正的外力,轴力图向上突变,对于负的外力,轴力图向下突变,如题2-2图〔2a 〕所示,截面1和截面2上的轴力分别为1N F =F 和2N F =—F 。
(b)解题步骤与题2-2〔a 〕一样,杆受力图和轴力图如题2-2〔1b 〕、〔2b 〕所示。
轴向拉伸与压缩习题答案

轴向拉伸与压缩习题答案轴向拉伸与压缩习题答案在学习力学的过程中,轴向拉伸与压缩是一个重要的概念。
它涉及到材料在受力作用下的变形与应力分布。
为了帮助大家更好地理解和掌握这个概念,下面将给出一些轴向拉伸与压缩的习题答案,希望对大家的学习有所帮助。
1. 一根长度为L的均匀杆,两端受到相等大小的拉力F,求杆的伸长量。
解析:根据胡克定律,杆的伸长量与拉力成正比,与杆的长度成反比。
因此,杆的伸长量可以表示为ΔL = (F/A) * L,其中A为杆的截面积。
2. 一根长度为L的均匀杆,两端受到相等大小的压力P,求杆的压缩量。
解析:与问题1类似,杆的压缩量也可以表示为ΔL = (P/A) * L。
3. 一根长度为L的均匀杆,在一端受到拉力F,在另一端受到压力P,求杆的伸长量。
解析:根据力的叠加原理,杆的伸长量可以表示为ΔL = [(F - P)/A] * L。
4. 一根长度为L的均匀杆,在一端受到拉力F,在另一端受到压力P,求杆的应力分布。
解析:根据胡克定律,杆的应力分布可以表示为σ = (F/A) - (P/A)。
5. 一根长度为L的均匀杆,在一端受到拉力F,在另一端受到压力P,如果杆的截面积不均匀,如何求杆的伸长量?解析:如果杆的截面积不均匀,可以将杆分成若干小段,每一小段的截面积近似看成常数。
然后分别计算每一小段的伸长量,再将其相加得到整个杆的伸长量。
6. 一根长度为L的均匀杆,在一端受到拉力F,在另一端受到压力P,如果杆的截面积不均匀,如何求杆的应力分布?解析:如果杆的截面积不均匀,可以将杆分成若干小段,每一小段的截面积近似看成常数。
然后分别计算每一小段的应力,再将其绘制成应力分布曲线。
通过以上习题的解析,我们可以看到轴向拉伸与压缩的问题都可以通过胡克定律来求解。
胡克定律是力学中的基本定律之一,它描述了弹性材料在小应变条件下的应力与应变之间的线性关系。
在轴向拉伸与压缩的情况下,胡克定律可以表示为σ = Eε,其中σ为应力,E为杨氏模量,ε为应变。
2020年10月自考《工程力学》2020第四章轴向拉伸与压缩习题答案及答案

第四章轴向拉伸与压缩习题答案1. 拉杆或压杆如图所示。
试用截面法求各杆指定截面的轴力,并画出各杆的轴力图。
解:(1)分段计算轴力杆件分为2段。
用截面法取图示研究对象画受力图如图,列平衡方程分别求得:F N1=F(拉);F N2=-F(压)(2)画轴力图。
根据所求轴力画出轴力图如图所示。
2. 拉杆或压杆如图所示。
试用截面法求各杆指定截面的轴力,并画出各杆的轴力图。
解:(1)分段计算轴力杆件分为3段。
用截面法取图示研究对象画受力图如图,列平衡方程分别求得:F N1=F(拉);F N2=0;F N3=2F(拉)(2)画轴力图。
根据所求轴力画出轴力图如图所示。
3. 拉杆或压杆如图所示。
试用截面法求各杆指定截面的轴力,并画出各杆的轴力图。
解:(1)计算A端支座反力。
由整体受力图建立平衡方程:∑F x=0,2kN-4kN+6kN-F A=0F A=4kN(←)(2)分段计算轴力杆件分为3段。
用截面法取图示研究对象画受力图如图,列平衡方程分别求得:F N1=-2kN(压);F N2=2kN(拉);F N3=-4kN(压)(3)画轴力图。
根据所求轴力画出轴力图如图所示。
4. 拉杆或压杆如图所示。
试用截面法求各杆指定截面的轴力,并画出各杆的轴力图。
解:(1)分段计算轴力杆件分为3段。
用截面法取图示研究对象画受力图如图,列平衡方程分别求得:F N1=-5kN(压); F N2=10kN(拉); F N3=-10kN (压)(2)画轴力图。
根据所求轴力画出轴力图如图所示。
5. 圆截面钢杆长l=3m,直径d=25mm,两端受到F=100kN的轴向拉力作用时伸长Δl=2.5mm。
试计算钢杆横截面上的正应力σ和纵向线应变ε。
解:6. 阶梯状直杆受力如图所示。
已知AD段横截面面积A AD=1000mm2,DB段横截面面积A DB=500mm2,材料的弹性模量E=200GPa。
求该杆的总变形量Δl AB。
解:由截面法可以计算出AC,CB段轴力F NAC=-50kN(压),F NCB=30kN(拉)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
q=4.2kN/m
FN26.5kN ③ 由强度条件求直径
0.4m
F Ay
4.25m
C FCx
FCy FN
由F A N4F dN 2得
d4F N 42 1 6 7 .0 5 1 1 0 0 6 3P N a 0.0141 m 14.1 m m
为了经济起见,选用钢拉杆的直径为14mm。其值略小于计算 结果,但是其工作正应力超过许用应力不到5%。
F N 2 F 1 F 2 1 0 k N 2 5 k N 3 5 k N 拉 力
F1=10kN
1F2=25kN 2 F3=55kN 3 F4=20kN
A1 B
2
C
Fx 0 FN3F4 0
FN3
F N 3 F 4 2 0 k N 压 力
FN1 10kN FN2 35kN
第二章 轴向拉伸和压缩
例 一等直杆受四个轴向外力作用,如图所示。试作轴力图
F1=10kN
1F2=25kN 2 F3=55kN
F4=20kN
A1 B
2
C
D
F1=10kN
FN1
Fx 0 FN1 F1 0 F N 1 F 1 1 0 k N 拉 力
F2=25kN
F1=10kN
FN2
Fx 0 FN2F1F20
得F N 1 5 0 k N 拉 F N 1
2-2截面
1 B 2C 3 D 40kN 30kN 20kN
Fx 0 FN230200
得 F N 21 0k N (拉 )
F N2
30kN 20kN
3-3截面
Fx 0 FN3200
得F N 3 2 0k N (压 )
FN / kN 50
F N3 10
2 1 0 1 0 9 P a 5 0 0 1 0 6 m 2 2 0 0 1 0 6 m 2
0.0286103m0.0286m m (缩短)
计算结果为负,说明整根杆发生了缩短
例 已知三铰屋架如图,承受竖向均布载荷,载荷的分布集度为 :q =4.2kN/m,屋架中的钢拉杆材料为Q235钢,[σ]=170MPa, 试选择钢拉杆的直径。(不计钢拉杆的自重)
l1=300
求:(1)AB、BC段的伸长量及杆
的总伸长量;(2)C截面相对B截面
的位移和C截面的绝对位移。
B B′
解:(1) 变形:物体受力以后
l2=200
发生尺寸和形状的改变。
C
l1
F N l1 E A1
40103N 300103m
210109Pa 400106m2
C′
0 .1 4 3 1 0 3 m = 0 .1 4 3 m m (伸长) 杆的总伸长量
B
C
F=40 kN
l2
FN l2 E A2
40103N 200103m
210109Pa 250106m2
l l1l2 0 .1 4 3 m m + 0 .1 5 2 m m
0.295mm (伸长)
0 .1 5 2 1 0 3 m = 0 .1 5 2 m m (伸长)
课堂练习 1. 已知: AAB =500mm2
q
F Ax
A
0.4m
F Ay
C
钢拉杆 8.5m
B
F B 0.4m
解:① 整体平衡求支反力
Fx0 FAx0
M B 0-F A y 8 .5 4 .2 9 .3 8 2 .5 0
FAy19.53kN
② 局部平衡求轴力
MC 0
F N 1 .4 24 2 .24 .6 5 2 1 9 .5 3 4 .2 50A
20kN
O
x
20
例 设例中的等直杆为实心圆截面,直径d=20mm。试求此 杆的最大工作应力。
F1=10kN
F2=25kN F3=55kN
F4=20kN
A
B
FN / kN
35
10
O
C
D
FN,max=35kN (BC段)
x
20
m a x F N A ,m a x F d N ,2 m a x 4 4 3 0 5 .0 2 1 m 0 3 2 N 1 1 1 .4 1 0 6 P a 1 1 1 .4 M P a
Fx0 FAx0
M B0-F A y164 2 2162
A
8m
F Ay
③求应力
C FCx
FCy
FN
② 局部平衡求轴力
MC 0
FN24228233680
FN672kN
FN A
672103 N 42104 m2
160106Pa
160MPa
例
A
已知: AB段:A1 =400mm2 BC段:A2 =250mm2 ,E=210GPa
课堂练习 1. 已知:q=40kN/m, []=160MPa C
试选择杆件的面积。
解: (1)计算拉杆的轴力
MA0 F N Bsin4 5 2 2 q 10
FNB56.6kN
A
45
B
(2)选择等边角钢型号
A FNB [ ]
56.6 103 N 160 106 Pa
3.54104m 2
q
2m FN B
危险截面:在研究拉(压)杆的强度问题时,通常把最大工作 正应力所在的横截面称为危险截面。
练习: 已知三铰屋架如图,承受竖向均布载荷,载荷的分 布集度为:q =42kN/m,屋架中的钢拉杆截面面积为42cm2 ,试求钢拉杆横截面的正应力。(不计钢拉杆的自重)
q
C
F Ax
A
钢拉杆
B
F Ay
16m
FB
解:① 整体平衡求支反力
=3.54cm2
A
B
F Ax
F Ay
q
2. 图示杆系中BC、AC杆的直径分别为d1=12m B
m,d2=18mm,两杆材料均为Q235钢,许用应 力[] = 170MPa,试按强度条件确定容许F值。
1
解: 取C节点为研究对象 F N 1 0 .8 9 7 F , F N 2 0 .7 3 2 F
A
B30kN
ABC =200mm2 ,E=210GPa 求:杆的总变形量。
解:(1)作轴力图 (2)计算变形
0.1m 0.3m
FN 20kN
lAClABlBC
FNABlAB EAAB
FNBClBC EABC
10kN
C 10kN x
1
2 0 1 0 3 N 0 .1 m1 0 1 0 3 N 0 .2 m
FN / kN
10
35
FN3 20kN O
3D F4=20kN
x
几点说明:
20
(1)荷载将杆件分成几段,就取几段截面来研究 (2)轴力大小与截面面积无关 (3)集中力作用处轴力图发生突变,突变值等于该集中力
例 试作轴力图 解:1-1截面
1
2
3
40kN 30kN 20kN
Fx 0 F N 14030200A
