构造全等三角形的常用方法
构造全等三角形的四种技巧

构造全等三角形的四种技巧在几何学中,全等三角形是一个非常重要的概念。
全等三角形是指两个或两个以上的三角形,它们的形状和大小完全相同。
理解并能够构造全等三角形,对于解决各种几何问题有着至关重要的作用。
以下是构造全等三角形的四种技巧:利用公理:全等三角形的公理是:如果两个三角形的三边对应相等,那么这两个三角形全等。
这个公理可以用来构造全等三角形。
确定你需要构造的全等三角形的所有边长,然后根据这些边长画出两个三角形。
这两个三角形的形状和大小将会完全相同。
利用角平分线:角平分线定理指出,一个角的平分线将对应的边分为两段,这两段与角的两边形成的两个小三角形是全等的。
通过这个定理,你可以通过一个角的平分线,构造出一个全等三角形。
利用中垂线:中垂线定理指出,一条中垂线将一个线段分为两段,这两段与线段的两端形成的两个小三角形是全等的。
这个定理可以用来构造全等三角形。
确定你需要构造的全等三角形的所有边长,然后通过中垂线将这些边分为两段。
这样,你就可以得到两个全等的三角形。
利用平行线:平行线定理指出,如果两条平行线被第三条直线所截,那么截得的对应线段成比例。
这个定理可以用来构造全等三角形。
确定你需要构造的全等三角形的所有边长,然后在两条平行线上画出对应的线段。
由于这些线段成比例,因此它们形成的两个小三角形是相似的。
如果这些相似三角形的对应边长度相等,那么它们就是全等的。
以上就是构造全等三角形的四种技巧。
理解和掌握这些技巧,对于解决各种几何问题有着重要的作用。
已知两个三角形全等,则它们对应边上的高也________;对应角平分线也________;对应边上的中线也________。
两个直角三角形全等,除了用定义外,还可以用以下________判定。
已知三角形ABC全等三角形DEF,且AB=18cm,BC=20cm,CA=15cm,则DE=________cm,DF=________cm,EF=________cm.做衣服需要依据身体部位的大小来选择布料,而教学则需要依据学生原有的知识基础来选择教学方法。
构造全等三角形的方法技巧

方法1 角形
利用“角平分线”构造全等三ห้องสมุดไป่ตู้
【方法归纳】 因角平分线本身已经具备 全等的三个条件中的两个(角相等和公共 边相等),故在处理角平分线问题时,常 作以下辅助线构造全等三角形: (1)在角的两边截取两条相等的线段; (2)过角平分线上一点作角两边的垂线.
思1.如图,AB∥CD,BE平分 ∠ABC,CE平分∠BCD,点E在AD 上,求证:BC=AB+CD. 考
2.如图,已知∠AOB=90°,OM是 ∠AOB的平分线,三角尺的直角顶点 P在射线OM上滑动,两直角边分别与 OA,OB交于点C,D,求证:PC= PD.
方法2 利用“截长补短法”构造全等 三角形
【方法归纳】 截长补短法的具体做法 :在某一条线段上截取一条线段与特定 线段相等,或将某条线段延长,使之与 特定线段相等,再利用三角形全等的有 关性质加以说明.这种方法适用于证明 线段的和、差、倍、分等类的题目.
3.如图,在△ABC中,AD平分 ∠BAC,∠C=2∠B,试判断AB, AC,CD三者之间的数量关系,并 说明理由.(想一想,你会几种方法)
方法3 利用“倍长中线法”构造全 等三角形
【方法归纳】 将中点处的线段延长 一倍,然后利用SAS证三角形全等.
6.已知:如图,AD,AE分别是 △ABC和△ABD的中线,且BA= BD.求证:AE=AC.
构造全等三角形的六种常用方法课件

构造方法简介
01
02
03
04
尺规作图法
利用尺规作图工具,通过已知 条件构造全等三角形。
翻折法
将已知三角形沿某条直线翻折, 得到与原三角形全等的三角形。
平移法
将已知三角形沿某方向平移一 定距离,得到与原三角形全等
的三角形。
旋转法
将已知三角形绕某点旋转一定 角度,得到与原三角形全等的
三角形。
02 方法一:SSS全 等法
感谢观看
拓展延伸:其他构造方法及应用场景
构造中位线
利用三角形中位线性质构 造全等三角形,常用于证 明线段相等或倍长中线等 问题。
构造角平分线
利用角平分线性质构造全 等三角形,常用于证明角 相等或线段成比例等问题。
构造垂直平分线
利用垂直平分线性质构造 全等三角形,常用于证明 线段相等或点共圆等问题。
THANKS
判定条件
两个三角形中,两个角及这两个角的夹边分别相等,则这两个三角形全等。
构造步骤这两个角的夹边相等,最后根据ASA判定条件证明两个三角形全等。
示例
在△ABC和△ADE中,∠BAC=∠DAE,∠B=∠D,AB=AD。根据ASA全等法,可以判定△ABC≌△ADE。
应用场景分析
1 2 3
解决角度和边长问题 当题目中给出两个角和它们的夹边相等时,可以 利用ASA全等法证明两个三角形全等,从而解决 与角度和边长相关的问题。
构造全等三角形 在几何证明题中,有时需要构造全等三角形以证 明某些线段或角度相等。ASA全等法是构造全等 三角形的常用方法之一。
辅助线策略 当遇到复杂的几何问题时,可以通过作辅助线构 造全等三角形,将问题转化为已知的全等三角形 问题,从而简化解题过程。
北师大版初二数学下册讲义《构造全等三角形的六种常用方法》

北师大版初二数学下册讲义《构造全等三角形的六种常用方法》【名师点睛】在进行几何题的证明或运算时,有时需要在图形中添加一些辅助线,辅助线能使题目中的条件比较集中,比较溶液找到一些量之间的关系,使数学问题较轻松的解决。
常见的辅助线作法有:翻折法、构造基础三角形法、旋转法、平行线法、倍长中线法和截长补短法,目的差不多上构造全等三角形。
[方法1]翻折法1.如图,在△ABC中,BE是∠ABC的角平分线,AD⊥BE,垂足为D,求证:∠2=∠1+∠C.解答:证明:∵BE是∠ABC的角平分线,AD⊥BE∴AB=FB∴∠2=∠AFB∵∠AFB=∠1+∠C∴∠2=∠1+∠C.[方法2]构造基础三角形法2.如图,在Rt△ABC中,∠ACB=90∘,AC=BC,∠ABC=45∘,点D为BC 的中点,CE⊥AD于点E,其延长线交AB于点F,连接DF.求证:∠ADC =∠BDF.解答:证明:作BG⊥CB,交CF的延长线于点G,如图所示:∵∠CBG=90∘,CF⊥AD∴∠CAD+∠ADC=∠BCG+∠ADC=90∘∴∠CAD=∠BCG在△ACD和△CBG中∠CAD=∠BCGAC=BC∠ACD=∠CBG=90∘∴△ACD ≌△CBG(ASA)∴CD=BG ,∠CDA=∠CGB∵CD=BD∴BG=BD∵∠ABC=45∘∴∠FBD=∠GBF=21∠CBG在△BFG 和△BFD 中BG=BD∠FBD=∠GBFBF=BF∴△BFG ≌△BFD(SAS)∴∠FGB=∠FDB∴∠ADC=∠BDF.[方法3]旋转法3.正方形ABCD 中,E 为BC 上的一点,F 为CD 上的一点,BE+DF=EF ,求∠EAF 的度数。
解答:延长EB 使得BG=DF ,连接AG ,在△ABG 和△ADF 中由AB=AD ,∠ABG=∠ADF=90∘,BG=DF可得△ABG ≌△ADF(SAS)∴∠DAF=∠BAG ,AF=AG又∵EF=DF+BE=EB+BG=EG ,AE=AE在△AEG 和△AEF 中,AE=AE ,GE=FE ,AG=AF∴△AEG ≌△AEF(SSS)∴∠EAG=∠EAF∵∠DAF+∠EAF+∠BAE=90∘∴∠EAG+∠EAF=90∘∴∠EAF=45∘.[方法4]平行线法4.如图,在△ABC中,∠BAC=60°,∠C=40°,AP平分∠BAC交B C于P,BQ平分∠ABC交AC于点Q,且AP与BQ相交于点O.求证:A B+BP=BQ+AQ.解答:证明:过点O作OD∥BC交AB于点D.∵OD∥BC∴∠ADO=∠ABC∵∠BAC=60°,∠C=40°∴∠ABC=80°∴∠ADO=80°∵BQ平分∠ABC∴∠ABQ=∠QBC=40°∴∠AQB=∠C+∠QBC=80°∴∠ADO=∠AQB∵AP平分∠BAC∴∠DAO=∠QAO=30°又∵OA=OA∴△ADO≌△AQO∴OD=OQ,AD=AQ又∵OD∥BP∴∠PBO=∠DOB又∵∠PBO=∠DBO∴∠DBO=∠DOB∴△DOB是等腰三角形∴BD=OD∴BD=OQ∵∠BAP=30°,∠ABQ=40°∴∠BOP=70°∵∠BAP=30°,∠ABC=80°∴∠APB=70°∴∠BOP=∠APB∴△BOP是等腰三角形∴BO=BP∴AB+BP=AD+DB+BP=AQ+OQ+BO=AQ+BQ,即AB+BP=BQ+AQ.[方法5]倍长中线法5.如图,△ABC中,D为BC的中点。
全等三角形的构造技巧(2020版)

全等三角形的构造技巧一、利用角平分线,构造全等三角形【方法剖析】因为角平分线本身已经具备全等的三个条件中的两个(角相等和公共边相等),故在处理角平分线问题时,常作以下辅助线构造全等三角形:(1)在角的两边截取两条相等的线段;(2)过角平分线上一点作角两边的垂线;(3)延长角平分线的垂线.(一)在角两边截取相等线段例1.如图,AB ∥CD ,BE 平分∠ABC ,CE 平分∠BCD ,点E 在AD 上,求证:BC =AB +CD.证明:在BC 上截取BF =AB ,连接EF.∵∠ABC 、∠BCD 的平分线交AD 于点E ,∴∠ABE =∠FBE ,∠BCE =∠DCE ,在△ABE 和△FBE 中,⎩⎪⎨⎪⎧AB =FB ,∠ABE =∠FBE ,BE =BE ,∴△ABE ≌△FBE.∴∠BAE =∠BFE.∵AB ∥CD ,∴∠BAE +∠CDE =180°.∴∠BFE +∠CDE =180°.∵∠BFE +∠CFE =180°,∴∠CFE =∠CDE.在△FCE 和△DCE 中,⎩⎪⎨⎪⎧∠CFE =∠CDE ,∠FCE =∠DCE ,CE =CE ,∴△FCE ≌△DCE.∴CF =CD.∴BC =BF +CF =AB +CD.练习:1.如图,BC >AB,BD 平分∠ABC 且AD=DC,求证: ∠A+∠C=1800. 分析:在边BC 上截取AB=BE,连接DE,则△BAD ≌△BED,这样,AD 转移到了DE 的位置,∠A 与∠C 就建立了联系。
也可看成 △BAD 翻折到了△BED 的位置。
(二)利用角平分线的性质,过角平分线上一点作角两边的垂线例1.如图,∠AOB =90°,将三角尺的直角顶点落在∠AOB 的平分线上的任意一点P ,使三角尺的两条直角边与∠AOB 的两边分别相交于点E 、F ,试证PE =PF.图1 图2分析:如图1,因为OC 是角平分线,所以本题可以过P 点作PM ⊥OA 于M ,PN ⊥OB 于N ,不难发现只要证明△PME ≌△PNF ,即可得到PE =PF ,根据∠PME =∠PNF =90°、PM =PN(角平 B A M N E F O P BA E F O P G AB C E DA B C E F D 分线性质)、∠MPE =∠NPF 这三个条件,利用ASA 可以证明△PME ≌△PNF 。
构造全等三角形的方法

构造全等三角形的方法
构造全等三角形的方法有以下几种:
1. SSS(side-side-side)法:给定两个三角形ABC和DEF,若它们的对应边长分别满足AB=DE,BC=EF,CA=FD,则可以得到两个全等三角形。
2. SAS(side-angle-side)法:给定两个三角形ABC和DEF,若它们的两对边长比值相等且夹角相等,即满足AB/DE = BC/EF,∠BAC = ∠EDF,则可以得到两个全等三角形。
3. ASA(angle-side-angle)法:给定两个三角形ABC和DEF,若它们的两对夹角相等且一对边长相等,即满足∠BAC = ∠EDF,∠ABC = ∠DEF,AC = DF,则可以得到两个全等三角形。
4. AAS(angle-angle-side)法:给定两个三角形ABC和DEF,若它们的两对夹角相等且一对角度之和为180,即满足∠BAC = ∠EDF,∠ABC + ∠BCA = ∠DEF + ∠EFD = 180,AB/DE ≠BC/EF,则可以得到两个全等三角形。
5. HL(hypotenuse leg)法:该方法适用于直角三角形。
给定两个直角三角形ABC和DEF,若它们的斜边和一对对边分别相等,即满足AC = DF,BC = EF,则可以得到两个全等三角形。
需要注意的是,在构造全等三角形时,要保证条件足够充分,即满足对应的几个条件才能得到全等三角形。
初中数学——构造全等三角形的五种常用方法

所以∠1=∠2. ∠1=∠2,
在△ACD 和△CBG 中,AC=CB, ∠ACD=∠CBG=90°,
所以△ACD≌△CBG(ASA). 所以∠ADC=∠G,CD=BG. 因为点 D 为 BC 的中点,所以 CD=BD.所以 BD=BG. 因为∠DBG=90°,∠DBF=45°,
所以∠GBF=∠DBG-∠DBF=90°-45°=45°.
解:如图,过点B作BG⊥BC交CF的延长线于点G. 因为∠ACB=90°,所以∠2+∠ACF=90°. 因为CE⊥AD, 所以∠AEC=90°. 所以∠1+∠ACF=180°-∠AEC=180°-90°=90°. 因为CE⊥AD,所以∠AEC=90°. 所以∠1+∠ACF=180°-∠AEC=180°-90°=90°.
在△AEH 和△AEF 中,AE=AE, EH=EF,
所以△AEH≌△AEF(SSS).
所以∠EAH=∠EAF.
所以∠EAF=12∠HAF=45°.
返回
方 法 4 倍长中线法
4.如图,在△ABC中,D为BC的中点.若AB=5, AC=3,求AD长度的取值范围. 解:如图,延长AD至点E,使DE= AD,连接BE. 因为D为BC的中点,所以CD=BD.
第四章 三角形
构造全等三角形的五种常用方法
方 法 1 翻折法
1.如图,在△ABC中,BE是∠ABC的平分线, AD⊥BE,垂足为D.试说明:∠2=∠1+∠C.
解:如图,延长AD交BC于点F(相当于将AB边向下翻 折,与BC边重合,A点落在F点处,折痕为BE). 因为BE平分∠ABC, 所以∠ABE=∠CBE. 因为BD⊥AD, 所以∠ADB=∠FDB=90°.
所以∠D=∠ABH=90°. AB=AD,
在△ABH 和△ADF 中,∠ABH=∠D=90°, BH=DF,
典中点全等三角形专训4 构造全等三角形的五种常用方法

典中点全等三角形专训4 构造全等三角形的五种常用方法
◐名师点金◑
在进行几何题的证明或计算时,需要在图形中添加一些辅助线辅助线能使题目中的条件比较集中,能比较多易找到一些量之间的关系,使教学问题较轻松地解决。
常见的辅助线作法:翻折法、构造法、旋转法、倍长中线法和截长(补短法,其目的都是构造全等三角形。
分法1:翻折法
1.如图,在△ABC中,BE是∠ABC的平分线,AD⊥BE,垂足为D求证:∠2=∠1+∠C
方法2:构造法
2.如图,在Rt△ABC中,∠ACB=90°,AC=BC,∠ABC=45°,点D为BC的中点,CE⊥AD于点E,其延长线交
AB于点F,连结DF。
求证:∠ADC=∠BDF
方法3:旋转法
3.如图,在正方形ABCD中,E为BC边上一点,F为CD边上一点,BE+DF=EF,求∠EAF的度数。
方法4:倍长中线法
4.如图,在△ABC中,D为BC的中点。
(1)求证:AB+AC>2AD
(2)若AB=5,AC=3,求AD的取值范围
方法5:截长(补短)法
5.如图,在四边形ABCD中,AB=AD,∠BAD=120°,∠B=∠ADC=90°.E,F分别是BC,CD上的点,且∠EAF=60°探究图中线段BE,EF,FD之间的数量关系并证明。
小专题(三) 构造全等三角形的常用方法

AB=FB, ∠ABE=∠FBE, BE=BE,
∴△ABE≌△FBE(SAS). ∴∠A=∠BFE.
∵AB∥CD, ∴∠A+∠D=180°. ∴∠BFE+∠D=180°. ∵∠BFE+∠CFE=180°, ∴∠CFE=∠D. 在△FCE和△DCE中,
方法2 利用“截长补短法”构造全等三角形
截长补短法的具体做法:在某一条线段上截取一条线 段与特定线段相等,或将某条线段延长,使之与特定线段 相等,再利用三角形全等的有关性质加以说明.这种方法 适用于证明线段的和、差、倍、分等题目.
2.如图,AB∥CD,BE平分∠ABC,CE平分∠BCD,点 E在AD上,求证:BC=AB+CD.
∠CFE=∠D, ∠FCE=∠DCE, CE=CE,
∴△FCE≌△DCE(AAS). ∴CF=CD. ∴BC=BF+CF=AB+CD.
3.(德州中考)问题背景: 如图1,在四边形ABCD中,AB=AD,∠BAD=120°, ∠B=∠ADC=90°.点E,F分别是BC,CD上的点,且 ∠EAF=60°.探究图中线段BE,EF,FD之间的数量关系. (1)小王同学探究此问题的方法是:延长FD到点G,使 DG=BE,连接AG.先证明△ABE≌△ADG,再证明 △AEF≌△AGF,可得出结论,他的结论应是 EF=BE+DF;
(2) 如图 2,若在四边形 ABCD 中,AB=AD, ∠B+∠D=180°.E,F 分别是 BC,CD 上的点,
且∠EAF=12∠BAD,上述结论是否仍然成立?并说明理由. 解:EF=BE+DF仍然成立. 理由:延长FD到G,使DG=BE,连接AG, ∵∠B+∠ADC=180°,∠ADC+∠ADG=180°, ∴∠B=∠ADG. 在△ABE和△ADG中,
全等三角形的构造方法
2.平行线法(或平移法)
若题设中含有中点可以试过中点作平行线或 中位线,对Rt△,有时可作出斜边的中线. 例 △ABC中,∠BAC=60°, ∠C=440°AP平分∠BAC交BC于P,BQ 平分∠ABC交AC于Q, 求证:AB+BP=BQ+AQ.
• 方法一 :本题也可以在AB截取AD=AQ,连OD, 构造全等三角形,即“截长补短法 ". • ⑵本题利用“平行法”解法也较多,举例如下: • ① 如图(2),过O作OD∥BC交AC于D,则 △ADO≌△ABO来解决. • ② 如图(3),过O作DE∥BC交AB于D,交 AC于E,则△ADO≌△AQO,△ABO≌△AEO来 解决. • ③ 如图(4),过P作PD∥BQ交AB的延长线 于D,则△APD≌△APC来解决. • ④ 如图(5),过P作PD∥BQ交AC于D,则 △ABP≌△ADP来解决
4.倍长中线法
• 题中条件若有中线,可延长一倍,以构造 全等三角形,从而将分散条件集中在一个 三角形内。 • 如图:AD是△ABC的中线,BE交AC于E, 交AD于F,且AE=BE. • 求证:AC=BF
• 证明:∵AD是△ABC的中线, ∴BD=CD. 方法一:延长AD至点M,使MD=FD,连接MC, 在△BDF和△CDM中, BD=CD ∠BDF=∠CDM DF=DM ∴△BDF≌△CDM(SAS). ∴MC=BF,∠M=∠BFM. ∵EA=EF, ∴∠EAF=∠EFA, ∵∠AFE=∠BFM, ∴∠M=∠MAC, ∴AC=MC, ∴BF=AC;
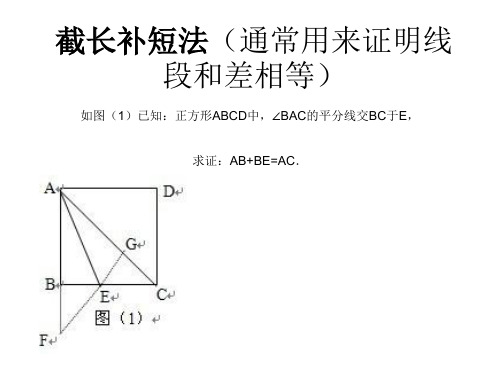
截长补短法(通常用来证明线 段和差相等)
如图(1)已知:正方形ABCD中,∠BAC的平分线交BC于E, 求证:AB+BE=AC.
• 方法一:补短法或补全法 延长AB至F使AF=AC, 证明:延长AB至F使AF=AC, ∵AE是∠BAC的平分线 ∴∠FAE=∠CAE ∵AF=AC ∵∠FAE=∠CAE AE=AE ∴△FAE≌△CAE ∴∠Eห้องสมุดไป่ตู้A=∠ECA=45° ∴△BFE是等腰直角三角形 ∴BE=BF ∴AF=AB+BF=AB+BE ∵AF=AC ∴AB+BE=AC解法 • 方法二:(截长法或分割法)在AC上截取 AG=AB
构造全等三角形的方法(优选.)

最新文件---------------- 仅供参考--------------------已改成-----------word文本 --------------------- 方便更改赠人玫瑰,手留余香。
全等三角形的构造方法全等三角形是初中数学中的重要内容之一,是今后学习其他内容的基础。
判断三角形全等公理有SAS、ASA、AAS、SSS和HL,如果能够直接证明三角形的全等的,直接根据相应的公理就可以证明,但是如果给出的条件不全,就需要根据已知的条件结合相应的公理来进行分析,先推导出所缺的条件然后再证明。
一些较难的一些证明问题要构造合适的全等三角形,把条件相对集中起来,再进行等量代换,就可以化难为易了。
构造方法有:1.截长补短法。
2.平行线法(或平移法):若题设中含有中点可以试过中点作平行线或中位线,对Rt△,有时可作出斜边的中线。
3.旋转法:对题目中出现有一个公共端点的相等线段时,可试用旋转方法构造全等三角形。
4.倍长中线法:题中条件若有中线,可延长一倍,以构造全等三角形,从而将分散条件集中在一个三角形内。
5.翻折法:若题设中含有垂线、角的平分线等条件的,可以试用轴对称性质,沿轴翻转图形来构造全等三角形。
下面举例说明几种常见的构造方法,供同学们参考.1.截长补短法(通常用来证明线段和差相等)“截长法”即把结论中最大的线段根据已知条件分成两段,使其中一段与较短线段相等,然后证明余下的线段与另一条线段相等的方法.“补短法”为把两条线段中的一条接长成为一条长线段,然后证明接成的线段与较长的线段相等,或是把一条较短的线段加长,使它等于较长的一段,然后证明加长的那部分与另一较短的线段相等.例1.如图所示,在Rt△ABC中,∠C=90°,BC=AC,AD平分∠BAC交BC于D,求证:AB=AC+CD.例2 已知:如图,AB=AC,E为AB上一点,F是AC延长线上一点,且BE=CF,EF交BC于点D.求证:DE=DF.(2)已知:如图,AB=AC,E为AB上一点,F是AC延长线上一点,且,EF交BC于点D,且D为EF的中点.求证:BE=CF.例3(北京市数学竞赛试题,天津市数学竞赛试题)如图所示,ABC是边长为1的NMAAMN正三角形,BDC ∆是顶角为120︒的等腰三角形,以D 为顶点作一个60︒的MDN ∠,点M 、N 分别在AB 、AC 上,求AMN ∆的周长.1.如图已知:正方形ABCD 中,∠BAC 的平分线交BC 于E ,求证:AB+BE=AC .2.(06年北京中考题)已知ABC ∆中,60A ∠=,BD 、CE 分别平分ABC ∠和.ACB ∠,BD 、CE 交于点O ,试判断BE 、CD 、BC 的数量关系,并加以证明.DOEC BA4321FDOE CB A3.已知:如图,ABCD是正方形,∠FAD=∠FAE. 求证:BE+DF=AE.如图,四边形ABPC中,,,,求证:.FEDCBA2.平行线法(或平移法)若题设中含有中点可以试过中点作平行线或中位线,对Rt△,有时可作出斜边的中线.例△ABC中,∠BAC=60°,∠C=440°AP平分∠BAC交BC于P,BQ平分∠ABC交AC于Q,求证:AB+BP=BQ+AQ.说明:⑴本题也可以在AB截取AD=AQ,连OD,构造全等三角形,即“截长补短法".⑵本题利用“平行法”解法也较多,举例如下:①如图(2),过O作OD∥BC交AC于D,则△ADO≌△ABO来解决.②如图(3),过O作DE∥BC交AB于D,交AC于E,则△ADO≌△AQO,△ABO≌△AEO来解决.③如图(4),过P作PD∥BQ交AB的延长线于D,则△APD≌△APC 来解决.④如图(5),过P作PD∥BQ交AC于D,则△ABP≌△ADP来解决.(本题作平行线的方法还很多,感兴趣的同学自己研究)3.旋转法对题目中出现有一个公共端点的相等线段时,可试用旋转方法构造全等三角形例.已知:如图(6),P为△ABC内一点,且PA=3,PB=4,PC=5,求∠APB的度数.分析:直接求∠APB的度数,不易求,由PA=3,PB=4,PC=5,联想到构造直角三角形.4.倍长中线法题中条件若有中线,可延长一倍,以构造全等三角形,从而将分散条件集中在一个三角形内。
证三角形全等的五种方法

证三角形全等的五种方法一、第一种方法是“边边边(SSS)”。
如果两个三角形的三边长度相应相等,那么我们就可以说这两个三角形全等。
比如,对于三角形ABC和三角形DEF,如果AB=DE,BC=EF以及AC=DF,那么三角形ABC与三角形DEF全等。
这种全等的方式十分明确,只要各边对应长度一致,不论角度如何都可以判定为全等。
二、第二种方法是“边角边(SAS)”。
若两个三角形有两边和它们之间的夹角对应相等,那么这两个三角形就可以被证明为全等。
比如,对于三角形ABC和三角形DEF,如果AB=DE,而且它们之间的夹角∠BAC=∠EDF,另外AC=DF,我们就可以断定三角形ABC和三角形DEF全等。
三、第三种方法是“角边角(ASA)”。
如果两个三角形的两个角和它们之间的边对应相等,那么他们就是全等的。
例如,对于三角形ABC和三角形DEF,如果∠BAC=∠EDF,且他们之间的边AC=DF,以及∠BCA=∠FDE,那么我们就可以认为三角形ABC全等于三角形DEF。
四、第四种方法是“角角边(AAS)”。
若两个三角形有两个角和任一边对应相等,那么它们就是全等的。
例如,对于三角形ABC和三角形DEF,如果∠BAC=∠EDF,∠BCA=∠FDE,并且边BC=EF,那么三角形ABC就全等于三角形DEF。
五、第五种方法是“右角三角形的斜边与一直角边(HL)”。
对于两个右角三角形,如果它们的斜边和一条直角边对应相等,那么我们就可以证明这两个三角形是全等的。
例如,对于三角形ABC和三角形DEF,如果∠BAC和∠EDF都是90°,且AC=DF(斜边),AB=DE(一条直角边),则三角形ABC和三角形DEF全等。
构造全等三角形种常用方法

构造全等三角形种常用方法在证明两个三角形全等时,选择三角形全等得五种方法(“SSS ”,“SA S”,“ASA ”,“AAS ”,“HL ”)中,至少有一组相等得边,因此在应用时要养成先找边得习惯。
如果选择找到了一组对应边,再找第二组条件,若找到一组对应边则再找这两边得夹角用“SAS ”或再找第三组对应边用“SSS ”;若找到一组角则需找另一组角(可能用“ASA ”或“AAS ”)或夹这个角得另一组对应边用“SAS”;若就就是判定两个直角三角形全等则优先考虑“HL ”。
上述可归纳为:搞清了全等三角形得证题思路后,还要注意一些较难得一些证明问题,只要构造合适得全等三角形,把条件相对集中起来,再进行等量代换,就可以化难为易了、下面举例说明几种常见得构造方法,供同学们参考、1、截长补短法例1、如图(1)已知:正方形ABCD 中,∠BAC 得平分线交B C于E ,求证:A B+BE=AC 、 解法(一)(补短法或补全法)延长AB 至F使AF=AC ,由已知△AEF ≌△AEC,∴∠F =∠ACE=45º, ∴BF =B E,∴AB+BE =A B+BF=AF=AC 、 解法(二)(截长法或分割法)在A C上截取AG=AB,由已知 △ AB E≌△AGE,∴EG=B E, ∠A GE=∠ABE,∵∠ACE =45º, ∴CG =EG, ∴AB +BE =AG+CG=AC、 2、平行线法(或平移法)若题设中含有中点可以试过中点作平行线或中位线,对Rt △,有时可作出斜边得中线、例2、△ABC 中,∠BAC=60°,∠C =40°A P平分∠BAC 交B C于P,B Q平分∠ABC 交A C于Q, 求证:A B+B P=BQ+A Q、证明:如图(1),过O 作O D∥BC 交AB 于D,∴∠ADO =∠ABC=180°-60°-40°=80°,又∵∠AQ O=∠C +∠QBC=80°,∴∠ADO=∠AQO ,又∵∠DA O=∠QAO ,OA=AO, ∴△ADO ≌△AQO,∴OD=O Q,AD=AQ ,又∵OD ∥BP,∴∠PBO=∠DOB ,又∵∠PBO=∠D BO,∴∠DBO=∠D OB,∴BD=O D,∴AB +BP=AD+DB+B P=A Q+OQ+B O=AQ+BQ 、说明:⑴本题也可以在AB 截取AD=AQ ,连OD,构造全等三角形,即“截长补短法”、⑵本题利用“平行法”解法也较多,举例如下: ① 如图(2),过O 作OD ∥BC 交AC 于D, 则△ADO ≌△ABO 来解决、 ② 如图(3),过O 作D E∥BC 交AB 于D,交AC 于E,则△ADO≌△AQ O,△A BO ≌△AE O来解决、 ③ 如图(4),过P作P D∥B Q交A B得延长线于D,则△A PD ≌△APC 来解决、 ④ 如图(5),过P 作PD ∥BQ 交A C于D, 则△AB P≌△ADP 来解决、 (本题作平行线得方法还很多,感兴趣A B C P Q D OO A B C P Q D图(2) A B C PQ D E 图(3) O A B C P Q图(4)DOA BCP Q 图(5)D OD得同学自己研究)、 3、旋转法对题目中出现有一个公共端点得相等线段时,可试用旋转方法构造全等三角形。
全等变换 构造全等三角形的常用方法 秦振

全等变换———构造全等三角形的常用方法秦 振(山东省枣庄市第九中学,277100) 全等三角形是平面几何的重要内容之一.证明三角形全等涉及的知识面广、难度大、技巧性强.下面介绍利用几何的全等变换构造全等三角形的常用方法,供大家参考.1 构造中心对称全等三角形一个三角形绕其某一点旋转180°,得到的三角形与原三角形是一对中心对称全等三角形.它的特点是对应边平行且相等或在同一直线上.其构造方法是将基本图形不完整部分补充完整,或过端点作平行线,或延长线段为原来的2倍.图1例1 如图1,■A BC 中,A D 为BC 的中线,∠1=∠2,∠3=∠4.求证:EF <BE +CF .分析:可构造中心对称全等三角形,将欲证三线段放在一个基本图形内.证明:如图1,延长ED 至点N ,使ND =DE .联结NF 、NC .因为∠1=∠5,BD =CD ,ND =DE ,所以,■BDE■C DN .则EB =CN .因为∠1+∠2+∠3+∠4=180°,∠1=∠2,∠3=∠4,所以,∠2+∠3=90°.则EF =NF .因为FN <CF +CN ,故EF <BE +CF .说明:当两线相交,交点为某线段中点时,可构造中心对称全等三角形.2 构造轴对称全等三角形把一个三角形沿着某条直线翻折180°与另一个三角形重合,这两个三角形就叫做轴对称全等三角形.满足下列条件可考虑构造轴对称全等三角形:相等线段或相等角关于某直线对称;有公共角;有对顶角;有角平分线或垂直平分线.图2例2 如图2,等腰Rt ■A BC 中,∠A =90°,D 为其内部一点,且∠A BD =30°,BD =BA .求证:A D =C D .分析:由于等腰直角三角形可看成是一条对角线将正方形分割而得的一半,因此可以以BC 为对称轴作轴对称全等三角形.证明:作点A 关于BC 的对称点A ′,联结A ′B 、A ′C 、A ′D .则四边形A BA ′C 为正方形.所以,BD =BA =BA ′=A ′C .又∠A ′B D =90°-30°=60°,所以,■BA ′D 为等边三角形.所以,BD =A ′D .由对称性知∠CA ′D =∠A B D .又A B =A ′C ,所以,■A ′C D■BA D .292006年第10期故A D =C D .说明:在三角形问题中,利用对称变换作辅助线构造对称全等三角形,将已知条件和要证明的结论集中在一起,建立某种联系,是解决此类问题的一条有效途径.3 构造平移型全等三角形把一个三角形沿某方向平移,得到的三角形与原三角形为平移型全等三角形.其特点是对应边平行且相等(或在同一直线上),对应角是同位角.图3例3 如图3,在■A BC 中,D 、E 为BC 边上的两点,且BD =EC .求证:A B +A C >A D +A E .分析:要证明的结论比较复杂,可利用三角形中的不等关系,构造全等三角形如下:将■A EC 平移到■A ′B D ,如图3,则线段A B 、AC 、A D 、A E 就集中在四边形A ′BDA 里.只要证明A B +A ′D >A D +A ′B 即可.证明:如图3,作BA ′∥EA ,则∠DBA ′=∠CEA ,BA ′=EA .联结A ′D ,交A B 于点F .因为B D =EC ,所以,■A ′BD■A EC .则A ′D =A C .因为FA ′+FB >A ′B ,FA +F D >A D ,所以,FA ′+FB +FA +F D >A ′B +A D ,A ′D +AB >A ′B +A D ,即 A B +AC >AD +AE .说明:一般地,有对应边平行或有同位角时可构造平移型全等三角形.4 构造旋转型全等三角形把一个三角形绕着某点旋转,得到的三角形与原三角形为旋转型全等三角形.用旋转法构造全等三角形,可以把分散的条件集中起来,易于找到条件与结论之间的关系.旋转时要注意确定旋转中心、旋转方向及旋转角度的大小.图4例4 如图4,D 、E 、F 分别为正■A BC 的边A B 、BC 、AC 的中点,P 为EC 上任意一点,■DPM 为正三角形.求证:EP =FM .分析:由题意,可以把■DM F 看成是■DPE 绕点D 逆时针旋转得到的.P 点转到M 点,E 点转到F 点,然后找到两个三角形全等的条件,进而得到结论.证明:如图4,联结DE 、DF .因为D 、E 、F 分别为正■A BC 的边A B 、BC 、A C 的中点,所以,DF ∥BC ,且DF =12BC ,DE ∥AC ,且DE =12AC .所以四边形DEC F 为平行四边形,且∠E DF =∠C =60°.又∠PD M =60°,所以,∠M DF =∠P DE .因为BC =AC ,所以,DF =DE .而DP =DM ,所以,■DFM■DEP .故EP =FM .说明:旋转法构造全等三角形常用于等腰三角形、等边三角形及正方形等图形中.30中学教与学。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
构造全等三角形的方法
方法一翻折法
1、如图,在△ABC中,BE是∠ABC的平分线,AD⊥BE,垂足为D.求证:∠2=∠1+∠C.
方法二补形法
2、如图,在Rt△ABC中,∠ACB=90°,AC=BC,点D为BC的中点,CE⊥AD于点E,其延长线交AB于点F,连接DF.求证:∠ADC=∠BDF.
方法三旋转法
3、如图,在正方形ABCD中,E为BC边上一点,F为CD边上一点,BE+DF=EF,求∠EAF.
方法四倍长中线法
4、如图,在△ABC中,D为BC的中点.(1)求证:AB+AC>2AD;(2)若AB=6,AC=2,求AD的取值范围.
方法五截长补短法
5、如图,在四边形ABCD中,AB=AD,∠BAD=120°,∠B=∠ADC=90°.E、F分别是BC、CD 上的点,且∠EAF=60°.探究图中线段BE、EF、FD之间的数量关系并证明.
方法六作垂线法
6、如图,∠AOB=90°,OM平分∠AOB,直角三角板的顶点P在射线OM上移动,两直角边分别与OA,OB相交于点C、D,问PC与PD相等吗?试说明理由.
方法七作平行线法
7、如图,△ABC中,∠BAC=60°,∠C=40°,AP平分∠BAC交BC于点P,BQ平分∠ABC 交AC于点Q.求证:AB+BP=BQ+AQ.。
