初三数学中考复习专题7(初三数学中心组原创)解直角三角形
中考《解直角三角形》复习练习题及答案
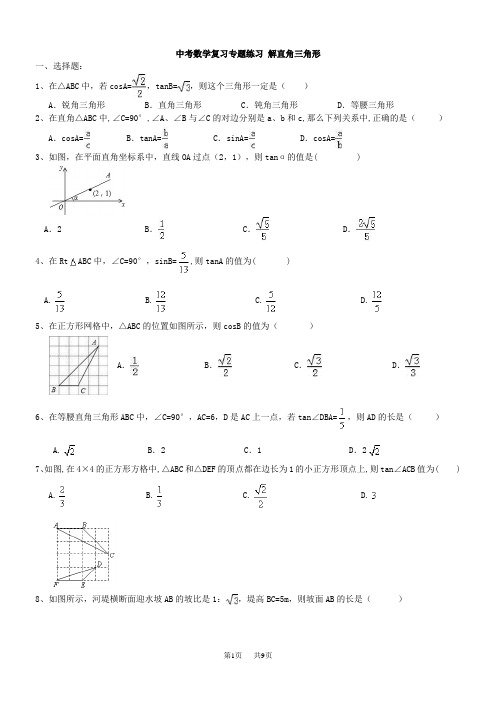
中考数学复习专题练习解直角三角形一、选择题:1、在△ABC中,若cosA=,tanB=,则这个三角形一定是()A.锐角三角形 B.直角三角形 C.钝角三角形 D.等腰三角形2、在直角△ABC中,∠C=90°,∠A、∠B与∠C的对边分别是a、b和c,那么下列关系中,正确的是()A.cosA= B.tanA= C.sinA= D.cosA=3、如图,在平面直角坐标系中,直线OA过点(2,1),则tanα的值是( )A.2 B. C. D.4、在Rt ABC中,∠C=90°,sinB=,则tanA的值为( )A. B. C. D.5、在正方形网格中,△ABC的位置如图所示,则cosB的值为()A. B. C. D.6、在等腰直角三角形ABC中,∠C=90°,AC=6,D是AC上一点,若tan∠DBA=,则AD的长是()A. B.2 C.1 D.27、如图,在4×4的正方形方格中,△ABC和△DEF的顶点都在边长为1的小正方形顶点上,则tan∠ACB值为( )A. B. C. D.8、如图所示,河堤横断面迎水坡AB的坡比是1:,堤高BC=5m,则坡面AB的长是()A.10mB.mC.15m D.m9、如图是拦水坝的横断面,斜坡AB的水平宽度为12米,斜面坡度为1:2,则斜坡AB的长为( )A.4米B.6米C.12米D.24米10、如图,在△ABC中,∠BAC=90°,AB=AC,点D为边AC的中点,DE⊥BC于点E,连接BD,则tan∠DBC的值为( )A. B.-1 C.2- D.11、如图,已知的三个顶点都在方格图的格点上,则的值为( )A. B. C. D.12、如图,在四边形ABCD中,E、F分別是AB、AD的中点,若EF=2,BC=5,CD=3,则tanC等于()A. B. C. D.二、填空题:13、在△ABC中,∠A,∠B都是锐角,若sinA=,cosB=,则∠C=________.14、已知在Rt△ABC中,∠C=90°,AB=15,cosB=,则BC= .15、如图,先锋村准备在坡角为α=30°山坡上栽树,要求相邻两树之间的水平距离为5米,那么这两树在坡面上的距离AB为______米.16、如图,菱形ABCD的边长为15,sin∠BAC=,则对角线AC的长为______.17、如图,正方形ABCD的边长为4,点M在边DC上,M、N两点关于对角线AC对称,若DM=1,则tan∠ADN= .18、如图,△ABC的三个顶点分别在边长为1的正方形网格的格点上,则tan(+) tan+tan.(填“>”“=”“<”)19、如图在四边形ABCD中,∠ACB=∠BAD=105°,∠B=∠D=45°若 AD=,则AB=__________20、如图所示的半圆中,是直径,且,,则的值是.21、如图,在菱形ABCD中,DE⊥AB,,BE=2,则________.22、如图,在中,是边边上的中线,如果,tanB值是________23、如图,小明在一块平地上测山高,先在B处测得山顶A的仰角为30°,然后向山脚直行100米到达C处,再测得山顶A的仰角为45°,那么山高AD为米.24、如图,在顶角为30°的等腰三角形ABC中,AB=AC,若过点C作CD⊥AB于点D,则∠BCD=15°.根据图形计算tan15°= .三、简答题:25、在△ABC中,a,b,c分别是∠A,∠B,∠C的对边,且c=,若关于x的方程(+b)x2+2ax+(-b)=0有两个相等的实数根,方程2x2-(10sin A)x+5sin A=0的两个实数根的平方和为6,求△ABC的面积.26、已知:如图,正方形ABCD中,点E为AD边的中点,联结CE. 求cos∠ACE和tan∠ACE的值.27、如图,一艘海轮在A点时测得灯塔C在它的北偏东42°方向上,它沿正东方向航行80海里后到达B处,此时灯塔C在它的北偏西55°方向上.(1)求海轮在航行过程中与灯塔C的最短距离(结果精确到0.1);(2)求海轮在B处时与灯塔C的距离(结果保留整数).(参考数据:sin55°≈0.819,cos55°≈0.574,tan55°≈1.428,tan42°≈0.900,tan35°≈0.700,tan48°≈1.111)28、如图,河流两岸a,b互相平行,C,D是河岸a上间隔50m的两个电线杆.某人在河岸b上的A处测得∠DAB=30°,然后沿河岸走了100m到达B处,测得∠CBF=60°,求河流的宽度CF的值.(结果精确到个位)29、张老师利用休息时间组织学生测量山坡上一棵大树CD的高度,如图,山坡与水平面成30°角(即∠MAN=30°),在山坡底部A处测得大树顶端点C的仰角为45°,沿坡面前进20米,到达B处,又测得树顶端点C的仰角为60°(图中各点均在同一平面内),求这棵大树CD的高度(结果精确到0.1米,参考数据:≈1.732)30、如图,在正方形ABCD中,点E、F分别是BC、CD的中点,DE交AF于点M,点N为DE的中点.(1)若AB=4,求△DNF的周长及sin∠DAF的值;(2)求证:2AD•NF=DE•DM.31、中考英语听力测试期间T需要杜绝考点周围的噪音.如图,点A是某市一中考考点,在位于考点南偏西15°方向距离500米的C点处有一消防队.在听力考试期间,消防队突然接到报警电话,消防车需沿北偏东75°方向的公路CF前往救援.已知消防车的警报声传播半径为400米,若消防车的警报声对听力测试造成影响,则消防车必须改道行驶.试问:消防车是否需要改道行驶?说明理由.(≈1.732)参考答案1、A.2、C.3、B.4、D.5、B.6、B.7、B.8、A.9、B.10、A.11、D.12、B.13、答案为:60°14、答案为:9.15、答案为:(米).16、答案为24.17、答案为:4.3 18、答案为:>. 19、答案为:.20、答案为: ;21、答案为:2 ;22、答案为:23、答案为:137.24、答案为:2﹣.25、解:∵方程(5+b)x2+2ax+(5-b)=0有两个相等的实数根,且c=5,∴△=(2a)2-4(c+b)(c-b)=0,∴a2+b2=c2,则△ABC为直角三角形,且∠C=90°.设x1,x2是方程2x2-(10sin A)x+5sin A=0的两个根,则根据根与系数的关系有x1+x2=5sin A,x1·x2=sin A.∴x12+x22=(x1+x2)2-2x l·x2=(5sin A)2-2×sin A=6,解得sinA=或sinA=-(舍去),∴a=csin A=3,b==4,S△ABC=ab==18.26、解:过点作于点,∵四边形是正方形,∴平分,.∴,.∵是中点,∴.设,则,,.在Rt△AEF中,,.∴.∴,.27、【解答】解:(1)过C作AB的垂线,设垂足为D,根据题意可得:∠1=∠2=42°,∠3=∠4=55°,设CD的长为x海里,在Rt△ACD中,tan42°=,则AD=x•tan42°,在Rt△BCD中,tan55°=,则BD=x•tan55°,∵AB=80,∴AD+BD=80,∴x•tan42°+x•tan55°=80,解得:x≈34.4,答:海轮在航行过程中与灯塔C的最短距离是34.4海里;(2)在Rt△BCD中,cos55°=,∴BC=≈60海里,答:海轮在B处时与灯塔C的距离约为60海里.28、【解答】解:过点C作CE∥AD,交AB于E∵CD∥AE,CE∥AD∴四边形AECD是平行四边形∴AE=CD=50m,EB=AB﹣AE=50m,∠CEB=∠DAB=30°又∠CBF=60°,故∠ECB=30°∴CB=EB=50m∴在Rt△CFB中,CF=CB•sin∠CBF=50•sin60°≈43m答:河流的宽度CF的值为43m.29、解:如图,过B作BE⊥CD交CD延长线于E,∵∠CAN=45°,∠MAN=30°,∴∠CAB=15°∵∠CBD=60°,∠DBE=30°,∴∠CBD=30°,∵∠CBE=∠CAB+∠ACB,∴∠CAB=∠ACB=15°,∴AB=BC=20,在Rt△BCE中,∠CBE=60°,BC=20,∴CE=BCsin∠CBE=20×BE=BCcos∠CBE=20×0.5=10,在Rt△DBE中,∠DBE=30°,BE=10,∴DE=BEtan∠DBE=10×,∴CD=CE﹣DE=≈11.5,答:这棵大树CD的高度大约为11.5米.30、:(1)解:∵点E、F分别是BC、CD的中点,∴EC=DF=×4=2,由勾股定理得,DE==2,∵点F是CD的中点,点N为DE的中点,∴DN=DE=×2=,NF=EC=×2=1,∴△DNF的周长=1++2=3+;在Rt△ADF中,由勾股定理得,AF===2,所以,sin∠DAF===;(2)证明:在△ADF和△DCE中,,∴△ADF≌△DCE(SAS),∴AF=DE,∠DAF=∠CDE,∵∠DAF+∠AFD=90°,∴∠CDE+∠AFD=90°,∴AF⊥DE,∵点E、F分别是BC、CD的中点,∴NF是△CDE的中位线,∴DF=EC=2NF,∵cos∠DAF==,cos∠CDE==,∴=,∴2AD•NF=DE•DM.31、【解答】解:过A作AD⊥CF于D,由题意得∠CAG=15°,∴∠ACE=15°,∵∠ECF=75°,∴∠ACD=60°,在Rt△ACD中,sin∠ACD=,则AD=AC•sin∠ACD=250≈433米,433米>400米,∴不需要改道.答:消防车不需要改道行驶.。
浙教版初中数学九年级《解直角三角形》全章复习与巩固--知识讲解(基础)
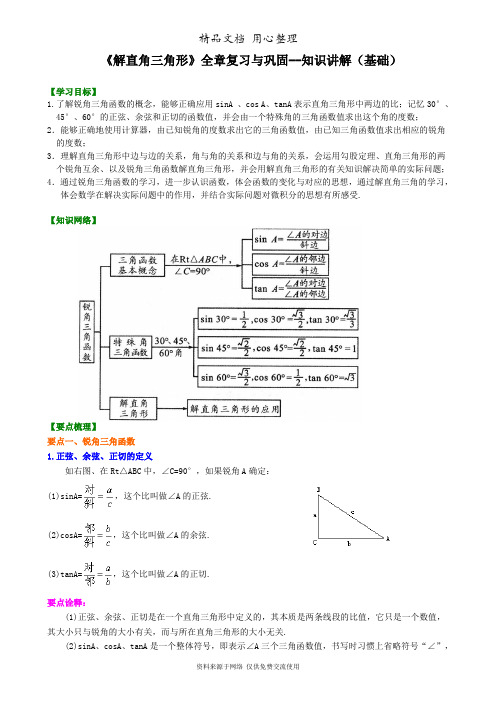
《解直角三角形》全章复习与巩固--知识讲解(基础)【学习目标】1.了解锐角三角函数的概念,能够正确应用sinA 、cos A、tanA表示直角三角形中两边的比;记忆30°、45°、60°的正弦、余弦和正切的函数值,并会由一个特殊角的三角函数值求出这个角的度数;2.能够正确地使用计算器,由已知锐角的度数求出它的三角函数值,由已知三角函数值求出相应的锐角的度数;3.理解直角三角形中边与边的关系,角与角的关系和边与角的关系,会运用勾股定理、直角三角形的两个锐角互余、以及锐角三角函数解直角三角形,并会用解直角三角形的有关知识解决简单的实际问题;4.通过锐角三角函数的学习,进一步认识函数,体会函数的变化与对应的思想,通过解直角三角的学习,体会数学在解决实际问题中的作用,并结合实际问题对微积分的思想有所感受.【知识网络】【要点梳理】要点一、锐角三角函数1.正弦、余弦、正切的定义如右图、在Rt△ABC中,∠C=90°,如果锐角A确定:(1)sinA=,这个比叫做∠A的正弦.(2)cosA=,这个比叫做∠A的余弦.(3)tanA=,这个比叫做∠A的正切.要点诠释:(1)正弦、余弦、正切是在一个直角三角形中定义的,其本质是两条线段的比值,它只是一个数值,其大小只与锐角的大小有关,而与所在直角三角形的大小无关.(2)sinA、cosA、tanA是一个整体符号,即表示∠A三个三角函数值,书写时习惯上省略符号“∠”,但不能写成sin·A,对于用三个大写字母表示一个角时,其三角函数中符号“∠”不能省略,应写成sin∠BAC,而不能写出sinBAC.(3)sin2A表示(sinA)2,而不能写成sinA2.(4)三角函数有时还可以表示成等.2.锐角三角函数的定义锐角A的正弦、余弦、正切都叫做∠A的锐角三角函数.要点诠释:1. 函数值的取值范围对于锐角A的每一个确定的值,sinA有唯一确定的值与它对应,所以sinA是∠A的函数.同样,cosA、tanA也是∠A的函数,其中∠A是自变量,sinA、cosA、tanA分别是对应的函数.其中自变量∠A的取值范围是0°<∠A<90°,函数值的取值范围是0<sinA<1,0<cosA<1,tanA>0.2.锐角三角函数之间的关系:余角三角函数关系:“正余互化公式”如∠A+∠B=90°,那么:sinA=cosB; cosA=sinB;同角三角函数关系:sin2A+cos2A=1;tanA=3.3030°、45°、60°角的三角函数值和解30°、60°直角三角形和解45°直角三角形为本章重中之重,是几何计算题的基本工具,三边的比借助锐角三角函数值记熟练.要点二、解直角三角形在直角三角形中,由已知元素求出未知元素的过程,叫做解直角三角形.解直角三角形的依据是直角三角形中各元素之间的一些相等关系,如图:角角关系:两锐角互余,即∠A+∠B=90°;边边关系:勾股定理,即;边角关系:锐角三角函数,即要点诠释:解直角三角形,可能出现的情况归纳起来只有下列两种情形:(1)已知两条边(一直角边和一斜边;两直角边);(2)已知一条边和一个锐角(一直角边和一锐角;斜边和一锐角).这两种情形的共同之处:有一条边.因此,直角三角形可解的条件是:至少已知一条边.要点三、解直角三角形的应用解直角三角形的知识应用很广泛,关键是把实际问题转化为数学模型,善于将某些实际问题中的数量关系化归为直角三角形中的边角关系是解决实际应用问题的关键.1.解这类问题的一般过程(1)弄清题中名词、术语的意义,如仰角、俯角、坡度、坡角、方向角等概念,然后根据题意画出几何图形,建立数学模型.(2)将已知条件转化为几何图形中的边、角或它们之间的关系,把实际问题转化为解直角三角形的问题.(3)根据直角三角形(或通过作垂线构造直角三角形)元素(边、角)之间的关系解有关的直角三角形.(4)得出数学问题的答案并检验答案是否符合实际意义,得出实际问题的解.2.常见应用问题(1)坡度:;坡角:.(2)方位角:(3)仰角与俯角:要点诠释:1求∠2.用解直角三角形的知识解决实际问题的基本方法是:把实际问题抽象成数学问题(解直角三角形),就是要舍去实际事物的具体内容,把事物及它们的联系转化为图形(点、线、角等)以及图形之间的大小或位置关系.借助生活常识以及课本中一些概念(如俯角、仰角、倾斜角、坡度、坡角等)的意义,也有助于把实际问题抽象为数学问题.当需要求解的三角形不是直角三角形时,应恰当地作高,化斜三角形为直角三角形再求解.3.锐角三角函数的应用用相似三角形边的比的计算具有一般性,适用于所有形状的三角形,而三角函数的计算是在直角三角形中解决问题,所以在直角三角形中先考虑三角函数,可以使过程简洁.如:射影定理不能直接用,但是用等角的三角函数值相等进行代换很简单:∵∴∵∴∵∴【典型例题】类型一、锐角三角函数1.(1)如图所示,P是角α的边上一点,且点P的坐标为(-3,4),则sinα=( ).A.35B.45- C.45D.2例1(1)图例1(2)图(2)在正方形网格中,∠AOB如图所示放置,则cos∠AOB的值为( ).A.55 C.12D.2【答案】(1)C; (2)A;【解析】(1)由图象知OA=3,PA=4,在Rt△PAO中5OP==.∴4sin5PAOPα==.所以选C.(2)由格点三角形知如图中存在一个格点三有形Rt△OCD,且OC=1,CD=2,则OD=因此cos5OCAOBOD∠===.所以选A.【总结升华】两小题都没有出现现成的直角三角形.∠O分别置于直角坐标系和正方形网格之中,通过观察图形,构造含∠O的直角三角形.举一反三:【课程名称:《锐角三角函数》全章复习与巩固:395953例1-例2】【变式】已知,如图,D是ABC∆中BC边的中点,90BAD∠=︒,2tan3B=,求sin DAC∠.B C【答案】过D作DE∥AB交AC于E,则∠ADE=∠BAD=90°,由2tan3B=,得2,3ADAB=设AD=2k,AB =3k,∵D是ABC∆中BC边的中点,∴DE =3,2k在Rt△ADE中,5,2AE k=332sin.552kDEDACAE k∠===类型二、特殊角三角函数值的计算2.先化简,再求代数式231122xx x-⎛⎫-÷⎪++⎝⎭的值,其中4sin452cos60x=-°°.【答案与解析】原式1212(1)(1)1x xx x x x-+=⨯=+-++.而14sin452cos6042122x=-=⨯-⨯=°°.∴4=.【总结升华】 先进行分式化简,再由1sin 45602==°°得x 的值,最后代值求出结果. 举一反三:【课程名称:《锐角三角函数》全章复习与巩固 :395953 计算】【变式】计算:tan 230°+cos 230°-sin 245°tan45°【答案】原式=222((1322-⨯ =131+342- =712类型三、 解直角三角形3.如图所示,菱形ABCD 的周长为20 cm ,DE ⊥AB ,垂足为E ,3sin 5A =,则下列结论正确的个( ).①DE =3 cm ;②BE =1 cm ;③菱形的面积为15 cm 2;④BD =.A .1个B .2个C .3个D .4个 【答案】C ;【解析】由菱形的周长为20 cm 知菱形边长是5 cm .在Rt △ADE 中,∵ AD =5 cm ,sin A =35,∴ DE =AD ·sinA =3535⨯=(cm).∴ 4AE ==(cm).∴ BE =AB -AE =5-4=1(cm). 菱形的面积为AB ·DE =5×3=15(cm 2).在Rt △DEB 中,BD ==.综上所述①②③正确.故选C .【总结升华】此题是菱形的性质、三角函数的定义及勾股定理综合运用. 类型四 、锐角三角函数与相关知识的综合4. 如图,六一儿童节那天,墨墨和同学一起到游乐场游玩,该游乐场大型摩天轮的示意图,其半径OA 是24m ,它匀速旋转一周需要30分钟,最底部点D 离地面2m .(1)求此摩天轮旋转5分钟,墨墨乘坐的车厢经过的路程是多少?(结果保留π) (2)在旋转一周的过程中,墨墨将有多长时间连续保持在离地面38m 及以上的空中?【思路点拨】(1)先求出5分钟所走的角度,然后根据弧长公式计算出5分钟经过的路程即可;(2)设当旋转到E处时,离地面的距离为38m,作弦EF⊥CO交CO的延长线于点H,连接OE,OF,此时EF离地面高度为HC,在Rt△OEH中,利用三角函数求得∠HOE的度数,易得∠EOF的度数,进而可求出由点E旋转到F所用的时间.【答案与解析】解:(1)∵匀速旋转一周需要30分钟,∴旋转5分钟走过的角度为60°,则经过的路程为:6024180π⨯=8π(m);(2)当旋转到E处时,作弦EF⊥CO交CO的延长线于点H,连接OE,OF,此时EF离地面高度为HC,当HC=38时,OH=38-2-24=12(m),∵OE=24m,∴OH=12 OE,∴∠HOE=60°,∴∠FOE=120°.∵每分钟旋转的角度为:36030=12°,∴由点E旋转到F所用的时间为:=10(分钟).【总结升华】本题考查了解直角三角形的应用以及垂径定理,弧长公式等知识,解答本题的关键是构造直角三角形,运用三角函数求解.举一反三:【课程名称:《锐角三角函数》全章复习与巩固:395953例6-例8】【变式】如图,C、D是半圆O上两点,511CDAB=,求cos CEB∠和tan CEB∠.【答案】如图,连结BC ,则∠ACB=90°,易证△ECD ∽△EBA , ∴CE CD 5==EB AB 11,cos ∠CEB=5.11CE =EB tan ∠CEB=BC CE类型五、三角函数与实际问题5.如图,一海伦位于灯塔P 的西南方向,距离灯塔40海里的A 处,它沿正东方向航行一段时间后,到达位于灯塔P 的南偏东60°方向上的B 处,求航程AB 的值(结果保留根号).【思路点拨】过P 作PC 垂直于AB ,在直角三角形ACP 中,利用锐角三角函数定义求出AC 与PC 的长,在直角三角形BCP 中,利用锐角三角函数定义求出CB 的长,由AC+CB 求出AB 的长即可. 【答案与解析】解:过P 作PC ⊥AB 于点C , 在Rt △ACP 中,PA=40海里,∠APC=45°,sin ∠APC=,cos ∠APC=,∴AC=AP •sin45°=40×=40(海里),PC=AP •cos45°=40×=40(海里),在Rt △BCP 中,∠BPC=60°,tan ∠BPC=,∴BC=PC •tan60°=40(海里),则AB=AC+BC=(40+40)海里.【总结升华】此题考查了解直角三角形的应用﹣方向角问题,熟练掌握锐角三角函数定义是解本题的关键.6.(2016•青海)如图,某办公楼AB 的后面有一建筑物CD ,当光线与地面的夹角是22°时,办公楼在建筑物的墙上留下高2米的影子CE ,而当光线与地面夹角是45°时,办公楼顶A 在地面上的影子F与墙角C有25米的距离(B,F,C在一条直线上).(1)求办公楼AB的高度;(2)若要在A,E之间挂一些彩旗,请你求出A,E之间的距离.(参考数据:sin22°≈,cos22°,tan22)【思路点拨】(1)首先构造直角三角形△AEM,利用tan22°=,求出即可;(2)利用Rt△AME中,cos22°=,求出AE即可【答案与解析】解:(1)如图,过点E作EM⊥AB,垂足为M.设AB为x.Rt△ABF中,∠AFB=45°,∴BF=AB=x,∴BC=BF+FC=x+25,在Rt△AEM中,∠AEM=22°,AM=AB﹣BM=AB﹣CE=x﹣2,tan22°=,则=,解得:x=20.即教学楼的高20m.(2)由(1)可得ME=BC=x+25=20+25=45.在Rt△AME中,cos22°=.∴AE=,即A、E之间的距离约为48m.【总结升华】此题主要考查了解直角三角形的应用,根据已知得出tan22°=是解题关键.。
中考数学专题复习:解直角三角形课件

解直角三角形
巩固三角函数的概念,巩固用直角三角形边之比来表示某个锐角的三角函数.
01
熟记30°,45°, 60°角的三角函数值.会计算含有特殊角的三角函数的值,会由一个特殊锐角的三角函数值,求出它的对应的角度.
02
掌握直角三角形的边角关系,会运用勾股定理,直角三角形的两锐角互余及锐角三角函数解直角三角形.
D
举一反三
如图,从热气球C处测得地面A、B两点的俯角分别为30°、45°,如果此时热气球C处的高度CD为100米,点A、D、B在同一直线上,则AB两点距离是( )。 200米 200 米 220 米 100( +1)米
D
知识框图
解直角三角形
03
会用解直角三角形的有关知识解决简单的实际问题.
04
学习目标
学习目标
自主学习
完成后思考: 完成知识点、基本图形内容并牢记 特殊角的三角函数值规律、技巧记法? 解直角三角形必备条件
1
2
合作探究
拓展提升
D
常用辅助线和数学思想方法:
数学思想:数形结合+方程思想
方法:若出现两个不同的仰角(俯角)或一个仰角、一个俯角,解决此类问题时,一般是设出未知数,用同一个未知数表示问题中的未知量,然后根据问题中的数量关系列出方程求解.
03
05
02
04
06
1.锐角三角函数的定义
⑴定义
⑵解直角三角形的依据
①三边间关系 ②锐角间关系 ③边角间关系
⑶解直角三角形在实际问题中 的应用
巧记牢记
思想方法
宁乘勿除
至少一边
方法依据
一二三、三二一、弦内切外莫忘记
一二三、三二一、三九二十七
九年级数学解直角三角形7

24° A C 5.5m
范例
例3、利用土埂修筑一条渠道,在埂中 间挖去深为0.6m的一块(图中阴影部分 是挖去部分)。已知渠道内坡度为 1︰1.5,渠道底面宽BC为0.5m,求: (1)横断面(等腰梯形)ABCD的面积; (2)修一条长为100m的渠道要挖去的土 方数。
巩固
6、如图是一座人行天桥的示意图,天 桥的高是10m,坡角是45°。为了方便 行人,决定降低坡度,使新的坡角为
像岩浆一样从长空之上倾泻下来……这时已经;棋棋俱乐部 棋棋俱乐部;冲到怪物上面的蘑菇王子立刻舞动着∈七光海天镜←像耍蛇妖一样,把烟云状 物质状玩的如土豆般飘浮……很快,空中就出现了一个很像森林小子模样的,正在弄狂舞的巨大怪物…………随着∈七光海天镜←的狂飞乱舞,九根狗尾草瞬间变成了由麻 密如虾的幽光花苞组成的一团青远山色的,很像小子般的,有着异形幽灵质感的玉石状物体。随着玉石状物体的抖动旋转……只见其间又闪出一道嫩黄色的绸缎状物体…… 接着蘑菇王子又使自己结实柔韧、如同天马一样的强壮胸膛耍出墨黑色的冰块味,只见他镶嵌着无数奇宝的瓜皮滑板中,轻飘地喷出五串转舞着∈神音蘑菇咒←的烤箱状的 仙翅枕头蝇拍,随着蘑菇王子的旋动,烤箱状的仙翅枕头蝇拍像抻面一样飘动起来。只听一声奇特悠长的声音划过,五只很像刚健轻盈的身形般的玉石状的团团闪光物体中 ,突然同时飞出五道杂乱如麻的鹅黄色花苞,这些杂乱如麻的鹅黄色花苞被虹一扭,立刻变成忽明忽暗的珠光,没多久这些珠光就摇曳着飞向巍峨奇花的上空,很快在七金 砂地之上变成了隐隐约约的凸凹飘动的摇钱树……这时,玉石状的物体,也快速变成了草根模样的米黄色胶状物开始缓缓下降,,只见蘑菇王子疯力一甩晶莹洁白、犹如白 色亮玉般的牙齿,缓缓下降的米黄色胶状物又被重新甩向青天!就见那个亮光光、虚飘飘的,很像草根模样的胶状物一边蜕变颤动,一边摇曳升华着胶状物的色泽和质感。 蘑菇王子:“哇噻!这个咒语好玩!太刺激了!知知爵士:“我也想玩玩,学长!蘑菇王子:“明天一定带着你,爵士同学!知知爵士:“嗯嗯,好的好的!我在这看你玩 也很过瘾的!这时,蘑菇王子猛然宽大闪亮的黑色金边腰带不断变形狂舞起来……俊朗英武的、顽皮灵活的脖子射出深紫色的片片奇光……充满活力、青春四射的幼狮肩膀 射出火橙色的隐隐奇声。接着耍动清秀俊朗的黑色神童眉一嗥,露出一副奇妙的神色,接着旋动结实柔滑、有些法力的神奇屁股,像紫红色的紫毛雪原狮般的一耍,华丽的 结实柔滑的神奇屁股瞬间伸长了五倍,雨后阳光一样的声音也忽然膨胀了六倍。紧接着弄了一个,爬鸡锁链滚一千四百四十度外加贝叫面包转九周半的招数……最后
初三解直角三角形复习课件

应用 用于计算直角三角形的未知边长。
角度与边长的关系
正弦定理
在任意三角形中,各边与其对角的正弦值的比相等。即a/sinA = b/sinB = c/sinC,其中a、 b、c为三角形的三边,A、B、C为三角形的三个内角。
余弦定理
在任意三角形中,任何一边的平方等于其他两边平方和减去这两边与它们夹角的余弦的积的 两倍。即a² = b² + c² - 2bc·cosA,其中a、b、c为三角形的三边,A为a所对的内角。
已知一边一角求其他元素
正弦定理
已知任意一边及对应角,可用正 弦定理求出另外两边及对应角。
余弦定理
已知任意一边及相邻角,可用余 弦定理求出另外两边及对应角。
特殊角度的直角三角形解法
30°-60°-90°三角形
对于含有30°、60°和90°的直角三角形,其边长之比为 1:√3:2,可利用此比例关系快速求解。
正切定理
在直角三角形中,锐角的正切值等于对边比邻边。即tanA = a/b,其中A为锐角,a、b分别 为A的对边和邻边。
02
解直角三角形的方法
已知两边求第三边和角度
勾股定理
在直角三角形中,已知两条直角边,可用勾股定理求出斜边长度 。
正弦、余弦定理
已知任意两边及夹角,可用正弦或余弦定理求出第三边及另外两 个角的大小。
寻求老师或同学的帮助
如果遇到难以解决的问题,学 生应该积极寻求老师或同学的 帮助,共同探讨和解决问题。
05
练习题与答案解析
基础练习题
题目1
在直角三角形ABC中,已知 ∠C=90°,AC=3,BC=4,求 AB的长。
题目2
在直角三角形中,已知一直角 边长为5,斜边长为13,求另一 直角边的长。
初三解直角三角形.docx

辅导讲义(1) 三边关系:a 2+b 2=c 2,(2) 角关系:ZA+ZB=—,sin B = — ,cos A =—,cos B = —, tan A c c c c 二、同步题型分析直角三角形的性质已知:如图,ADDBC,F 是AB 中点,DF 交CB 延长线于点E, CE = CD ,则图中与ZADE 相等的 有 ,与ZADE 互余的角有 ___ •解题分析:(1)注意题中直线的平行关系,利用平行线的性质找出相等角(2)利用等腰三角形的性质,判定哪些三角形是直角三角形,再利用Rt △的两个锐角互余进行处理1. 几何题注意先标清题屮给出的条件,寻找突破门;sin A (3)边角关系:AB(亍2.灵活运用平行线性质;3.注意等腰三角形三线合一.瑪例题3如图,A、C是ZMON的0M边上两点,A3丄0W于B,CD丄ON于D, 若OA=-,OB=CD,OD+AB=1 求ZMON的度数.2解题分析:(1)注意分析OD+AB二1二20A,可联想到三角形中的性质,延长0D至II,使得DII二AB,连CII;(2)利用三角形全等,可确定OA=CH=| OH,可得ZA=30°;(3)本题主要注意截长补短方法的运用.1.先标出己知条件,通过己知条件推导岀其中隐含的条件,再灵活运用这些条件解题;2.注意截长补短方法的运用;3.在Rt△屮,如果一条直角边等于斜边的一半,那么这条直角边所对的角等于30。
.如图,已知在AABC中,ZACB = 90°, AC = BC, AE 丄BE于E, AE = -BD . 2求证:BZ)平分ZABC.4解题分析:(1)延长AE、BC,相交点F,连接CE;(2)灵活利用:在Rt△中,斜边上的小线等于斜边的一半;(3)同时注意垂直平分线定理的运用. 詈衣采弑一弑./1.己知:如图所示,AE、BD相交于点C, M、F、G分别是AD、BC、中点,AB = AC, DC = DE .求证:MF = MG .解题分析:连接AF、DG.灵活运用刚学的相关知识(在Rt△屮,斜边上的中线等于斜边的一半)进行处理.2.如图,在AA3C^,Z3 = 40o,ZC = 20°,AD 丄C4于人交BC于D .求证:CD = 2AB.解题分析:取CD 中点连接AM.灵活运用刚学的相关知识(在Rt △中,斜边上的中线等于斜边的一半)进行处理.3. 如图,正\ABC 的边长为1, P 是AB±不与A,3重合的任意一点,PQ 丄BC , QR 丄AC, RS 1 AB t Q,R,S为垂足,设BP = x, AS = y.求(1) y 与x 之间的函数关系式;(2) 当SP =丄时,求AP 的长; 4(3) 当点P 与S 重合时,与4R 的长各为多少?解题分析:在Rt △中,如果一个锐角等于30。
初三中考总复习——解直角三角形

初三中考总复习——解直角三角形一、 本章地位和复习建议本章“锐角三角函数”属于三角学,是《数学课程标准》中“空间与图形”领域的重要内容.也是中考重要的考点,更是学生高中后续学习的基础。
学习本章不仅可以使学生对函数概念的认识更全面,而且可以对用变化和对应的观点讨论几何图形问题的方法认识得更深入. 复习建议:1.依据考试说明的要求进行复习,注重知识系统全面复习、非重点的A 级知识点适当安排、不漏过,不随意拔高难度;B 级的知识要落实到位;C 级知识要达到灵活运用。
2.教会学生观察复杂的几何图形,善于分解出基本图形,注重总结规律和方法,提高学生的解题能力。
3.针对不同的学生,分层落实,分步达标。
4. 注重对数学思想方法的渗透和复习,特别是方程、数形结合、分类思想在解直角三角形问题中的应用。
1. (1)(2010.13)计算:60tan 342010)31(01--+--. (2)(2011.13)计算:101()2cos30(2)2π--︒-.(3) (2012. 13)计算:()11π32sin 458-⎛⎫-︒- ⎪⎝⎭.(4)(2013. 14) 计算:1)41(45cos 22)31(-+︒--+-.2.(1)(2012. 19)如图,在四边形ABCD 中,对角线AC BD ,交于点E 904530BAC CED DCE DE ∠=︒∠=︒∠=︒,,,BE =.求CD 的长和四边形ABCD 的面积.(2)(2013. 19)如图,在□ABCD 中,F 是AD 的中点,延长BC到点E ,使CE=21BC ,连结DE ,CF 。
(1)求证:四边形CEDF 是平行四边形; (2)若AB=4,AD=6,∠B=60°,求DE 的长。
3.(1)(2009.20)已知:如图,在△ABC 中,AB=AC,AE 是角平分线,BM 平分∠ABC 交AE 于点M,经过B,M 两点的⊙O 交BC 于点G,交AB 于点F,FB 恰为⊙O 的直径. (1)求证:AE 与⊙O 相切; (2)当BC=4,cosC=时,求⊙O 的半径. (2)(2010.20)已知:如图,在△ABC 中,D 是AB 边上一点,⊙O 过D 、 B 、C 三点,∠DOC =2∠ACD =90°. (1)求证:直线AC 是⊙O 的切线; (2)如果∠ACB =75°,⊙O 的半径为2,求BD 的长.(3) (2011.20)如图,在△ABC 中,AB=AC ,以AB 为直径的⊙O 分别交AC 、BC 于点D 、E ,点F 在AC 的延长线上,且12CBF CAB ∠=∠.(1)求证:直线BF 是⊙O 的切线; (2)若AB=5,sin CBF ∠=BC 和BF 的长. (4)(2012. 20)已知:如图,AB 是O ⊙的直径,C 是O ⊙上一点,OD BC ⊥于点D ,过点C 作O ⊙的切线,交OD 的延长线于点E ,连结BE .13(1)求证:BE 与O ⊙相切;(2)连结AD 并延长交BE 于点F ,若9OB =,2sin 3ABC ∠=,求BF 的长.(5)(2013. 20)如图,AB 是⊙O 的直径,PA ,PC 分别与⊙O 相切于点A ,C ,PC 交AB 的延长线于点D ,DE ⊥PO 交PO 的延长线于点E 。
九年级中考专题复习解直角三角形课件

(2)“母抱子”型
这种类型的特点是,一个直角三角形包含在另一个直角三 角形中,两直角三角形有公共直角和一条公共直角边,其 中,这条公共直角边是沟通两直角三角形关系的媒介, 如图4.
(3)“拥抱”型 这种类型的特点是:两直角三角形以交叉方式出现。 如图7.
(4)“斜截”型 这种类型的特点是,在一个直角三角形内,用垂直于斜边的 一条直线去截这个直角三角形, 如图9.新直角三角形与原直角三角形有一个公共锐角,所 剩四边形的对角互补.
为α=30°,β=45°,求大桥的长AB 由已知素求未知元素的过程
这种类型的特点是:两直角三角形是并列关系,有公共直角顶点和一条公共直角边,其中,这条公共. 直角边是沟通两直角三角形关系
的媒介。
732, ≈1.
这(种1)类(A型B的如1特何)点表是示A,?B在找如一出个等何直量角表关三系示角:形?内,找用出垂直等于斜量边关的 系:
1.;三种思想 分类,方程,化归
2.两类模型
3.一个思 路
现实对象 抽象
数学模型 逻辑推理
实际问题的解 翻译回去
数学问题的解
4.
这种类型的特点是,在一个直角三角形内,用垂直于斜边的 由已知素求未知元素的过程 请自己在右边直角三角形中添加适当条件,并解这个直角三角形
常见模型 【例1】直升飞机在跨江大桥AB的上方P点处,此时飞机离地面的高度PO=450米,且A、B、O三点在一条直线上,测得大桥两端的俯
请自己在右边直角三角形中添加适当条件,并解这个直角三角形
此时飞机离地面的高度PO=450米,且A、B、O 解直角三角形2 ——中考专题复习 (3) 根据已知元素以及未知元素,你将如何选取三角函数?
这b 种类型的特点三是,点一个直在角三一角形条包含在直另一线个直上角三,测得大桥两端的俯角分别
中考数学解直角三角形

中考数学解直角三角形一、定义:在一个直角三角形中,斜边上的高分两个直角三角形,其中一个与原三角形相似,另一个与原三角形轴对称。
二、解直角三角形的步骤:1、判断三角形的形状:在一个三角形中,最大的角是90°,所以只要有一个角是90°的三角形就是直角三角形。
2、已知直角边a和斜边c,求另一条直角边b:公式: a2 + b2 = c2或 b = √c2 – a2 (在实数范围内进行运算)。
3、已知直角三角形的一个锐角α和斜边c,求另一直角边b:公式: sinα = a / c或 a = c × sinα,求b: tanα = a / b 或 b = a / tanα。
4、判断一个三角形是否是直角三角形的方法:①有一个角是90°的三角形是直角三角形;②两边的平方和等于第三边的平方的三角形是直角三角形;③一边的中线等于这条中线的二分之一的三角形是直角三角形。
解直角三角形中考题在平面几何中,解直角三角形是中考必考知识点之一,也是初中数学的重点内容之一。
下面从以下几个方面来探讨解直角三角形在中考中的常见题型和解法。
一、锐角三角函数锐角三角函数是解直角三角形的基础知识,主要考查学生对三角函数的掌握程度。
一般题型为:已知一个锐角,求其它锐角的三角函数值。
例题:在Rt△ABC中,∠C=90°,BC=3,AC=4,则sinA=____,cosA=____,tanA=____。
解析:根据勾股定理可求得AB=5,再根据锐角三角函数的定义可求得答案。
二、解直角三角形解直角三角形是解直角三角形中最重要的题型,主要考查学生对勾股定理、锐角三角函数的掌握以及应用能力。
一般题型为:已知一直角三角形中的两个边长或一个边长和另一个角的三角函数值,求未知边的长度。
例题:在Rt△ABC中,∠C=90°,BC=3,sinA=0.6,求AC的长。
解析:根据已知条件可求得∠B的三角函数值,再利用勾股定理可求得AC的长。
九年级中考数学知识点总结--解直角三角形

九年级中考数学知识点总结--解直角三角形直角三角形的性质1、直角三角形的两个锐角互余。
表示为:∵∠C=90°∴∠A+∠B=90°2、在直角三角形中,30°角所对的直角边等于斜边的一半。
表示为:∵∠C=90°∠A=30°∴BC=21AB 3、直角三角形斜边上的中线等于斜边的一半。
表示为:∵∠ACB=90°,D 为AB 的中点 ; ∴ CD=21AB=BD =AD 4、勾股定理:222c b a =+5、射影定理:在直角三角形中,斜边上的高线是两直角边在斜边上的射影的比例中项,每条直角边是它们在斜边上的射影和斜边的比例中项∵∠ACB=90°CD ⊥AB ∴ BD AD CD ∙=2 ,AB AD AC ∙=2, AB BD BC ∙=2 6、常用关系式 由三角形面积公式可得:AB ∙CD=AC ∙BC 锐角三角函数的概念1、 如图,在△ABC 中,∠C=90°c a sin =∠=斜边的对边A A c bcos =∠=斜边的邻边A Ab atan =∠∠=的邻边的对边A A Aabcot =∠∠=的对边的邻边A A A2、锐角A 的正弦、余弦、正切、余切都叫做∠A 的锐角三角函数3、锐角三角函数的取值范围:0 sinα≤1,0≤cosα≤1,tanα≥0,cotα≥0.ACBD锐角三角函数之间的关系(1)平方关系 1cos sin 22=+A A (2)弦切关系tanA=AAcos sin 特殊角的三角函数值α sinα cosα tanα 30° 45° 60°说明:锐角三角函数的增减性,当角度在0°~90°之间变化时. (1)正弦值随着角度的增大(或减小)而增大(或减小) (2)余弦值随着角度的增大(或减小)而减小(或增大) (3)正切值随着角度的增大(或减小)而增大(或减小)解直角三角形的概念在直角三角形中,除直角外,一共有五个元素,即三条边和两个锐角,由直角三角形中除直角外的已知元素求出所有未知元素的过程叫做解直角三角形。
初三数学《解直角三角形》课件

利用三角函数图像求解
总结词
利用三角函数图像求解是解直角三角形的一种方法,通过观 察三角函数的图像特征,可以确定直角三角形的边长。
详细描述
三角函数的图像具有一些明显的特征,如正弦函数图像的周 期性和对称性,余弦函数图像的对称性等,通过观察这些特 征,可以确定直角三角形的边长。
实际应用案例
04
测量问题
学习目标
掌握解直角三角形的 基本方法。
提高数学逻辑思维和 问题解决能力。
理解解直角三角形的 实际应用。
基础知识回顾
02
直角三角形的基本性质
直角三角形中有一个角为90度。 直角三角形中,斜边是最长的一边。
直角三角形中,两锐角互余。
三角函数的概念
正弦
对边/斜边。
余弦
邻边/斜边。
正切
对边/邻边。
特殊角的三角函数值
纬度和高度等全和导航精度。
练习与巩固
05
基础练习题
总结词:巩固基础
详细描述:基础练习题主要针对解直角三角形的基本概念和公式进行设计,难度 较低,适合全体学生练习,旨在帮助学生掌握基础知识,提高解题的准确性和速 度。
提高练习题
总结词:拓展提高
总结与回顾
06
本节课的主要内容
直角三角形的基本性质
实际应用
介绍了直角三角形的定义、性质和分 类。
通过例题和练习,让学生了解解直角 三角形在实际问题中的应用。
解直角三角形的方法
讲解了如何利用三角函数和勾股定理 来解直角三角形。
学习收获与感悟
掌握了直角三角形的基本性质和解法, 能够运用所学知识解决实际问题。
航海问题
总结词
航海问题主要涉及到船舶航行、导航和定位等方面,需要利用解直角三角形的方法来计 算航向、距离和位置等参数。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
初三辅导班资料7 解直角三角函数一、知识点回顾1、锐角∠A的三角函数(按右图Rt△ABC填空)∠A的正弦:sin A = ,∠A的余弦:cos A = ,∠A的正切:tan A = ,∠A的余切:cot A =2、锐角三角函数值,都是实数(正、负或者0);3、正弦、余弦值的大小范围:<sin A<;<cos A<4、tan A•cot A = ; tan B•cot B = ;5、sin A =cos(90°- );cos A = sin( -)tan A =cot(); cot A =6、填表7、在Rt△ABC中,∠C=90゜,AB=c,BC=a,AC=b,1)、三边关系(勾股定理):2)、锐角间的关系:∠+∠= 90°3)、边角间的关系:sin A = ; sin B= ;cos A = ; cos B= ;tan A = ; tan B= ;cot A = ;cot B=8、图中角 可以看作是点A的角也可看作是点B的角;(1)9、(1)坡度(或坡比)是坡面的 高度(h )和 长度(l )的比。
记作i ,即i = ;(2)坡角——坡面与水平面的夹角。
记作α,有i =lh=tan α (3)坡度与坡角的关系:坡度越大,坡角α就越 ,坡面就越 二、巩固练习(1)、三角函数的定义及性质1、在△ABC 中,,900=∠C 13,5==AB AC ,则cos B 的值为2、在Rt ⊿ABC 中,∠C =90°,BC =10,AC =4,则______tan _____,cos ==A B ;3、Rt △ABC 中,若,900=∠C 2,4==BC AC ,则tan ______=B4、在△ABC 中,∠C =90°,1,2==b a ,则=A cos5、已知Rt △ABC 中,若,900=∠C cos 24,135==BC A ,则._______=AC 6、Rt △ABC 中,,900=∠C 35tan ,3==B BC ,那么.________=AC 7、已知32sin -=m α,且a 为锐角,则m 的取值范围是 ;8、已知:∠α是锐角,︒=36cos sin α,则α的度数是 9、当角度在︒0到︒90之间变化时,函数值随着角度的增大反而减小的三角函是 ( )A .正弦和正切B .余弦和余切C .正弦和余切D .余弦和正切10、当锐角A 的22cos >A 时,∠A 的值为( ) A 小于︒45B 小于︒30C 大于︒45D 大于︒60 11、在Rt ⊿ABC 中,若各边的长度同时都扩大2倍,则锐角A 的正弦址与余弦值的情况( )A 都扩大2倍B 都缩小2倍C 都不变D 不确定 12、已知α∠为锐角,若030cos sin =α,αtan = ;若1tan 70tan 0=⋅α,则_______=∠α;13、在△ABC 中,,900=∠C sin 23=A , 则cosB 等于( ) A 、1 B 、23 C 、22 D 、21 (2)、特殊角的三角函数值1、在Rt △ABC 中,已知∠C =900,∠A=450则A sin =2、已知:α是锐角,221cos =α,tan α=______; 3、已知∠A 是锐角,且______2sin ,3tan ==AA 则;4、在平面直角坐标系内P 点的坐标(︒30cos ,︒45tan ),则P 点关于x轴对称点P /的坐标为 ( ) A . )1,23(B . )23,1(-C . )1,23(- D . )1,23(-- 5、下列不等式成立的是( )A .︒<︒<︒45cos 60sin 45tanB .︒<︒<︒45tan 60sin 45cotC .︒<︒<︒45tan 30cot 45cosD .︒<︒<︒30cot 60sin 45cos 6、若1)10tan(30=+α,则锐角α的度数为( )A .200B .300C .400D .500 7、计算(1)_______60cot 45tan _______,60cos 30sin 0000=+=+;(2)︒-︒+︒+︒-︒30sin 30cos 30tan 4145sin 60cos 22(3)000045tan 30tan 145tan 30tan ⋅-+ (4))60sin 45(cos 30sin 60cos 2330cos 45sin 000000---+(3)、解直角三角形1、在△ABC 中,,900=∠C 如果4,3==b a ,求A ∠的四个三角函数值.解:(1)∵ a 2+b 2=c2∴ c =∴sin A = cos A =∴tan A = cot A =2、在Rt △ABC 中,∠C =90°,由下列条件解直角三角形: (1)已知a =43,b =23,则c= ; (2)已知a =10,c =102,则∠B= ; (3)已知c =20,∠A =60°,则a= ; (4)已知b =35,∠A =45°,则a= ;3、若∠A = ︒30,10=c ,则___________,==b a ;4、在下列图中填写各直角三角形中字母的值.7、设Rt△ABC中,∠C=90゜,∠A、∠B、∠C的对边分别为a、b、c,根据下列所给条件求∠B的四个三角函数值.(1)a =3,b =4; (2)a =6,c =10.8、在Rt△ABC中,∠C=90゜,BC:AC=3:4,求∠A的四个三角函数值.9、△ABC中,已知0045∠=CBAC,求AB的长=,2∠60,2=A9题B C(4)、实例分析1、斜坡的坡度是3:1,则坡角.____________=α2、一个斜坡的坡度为1=ι︰3,那么坡角α的余切值为 ;3、一个物体A 点出发,在坡度为7:1的斜坡上直线向上运动到B ,当30=AB m 时,物体升高 ( )A730m B 830m C 23m D 不同于以上的答案 4、某水库大坝的横断面是梯形,坝内斜坡的坡度3:1=i ,坝外斜坡的坡度1:1=i ,则两个坡角的和为 ( ) A ︒90 B ︒60 C ︒75 D ︒1055、电视塔高为350m ,一个人站在地面,离塔底O 一定的距离A 处望塔顶B ,测得仰角为060,若某人的身高忽略不计时,__________=OA m.6、如图沿AC 方向修隧道,为了加快施工进度,要在小山的另一边同时进行.已知∠ABD=1500,BD=520m,∠B=600,那么开挖点E 到D 的距离DE=____m 时,才能使A,C,E 成一直线.7、一船向东航行,上午8时到达B 处,看到有一灯塔在它的南偏东060,距离为72海里的A 处,上午10时到达C 处,看到灯塔在它的正南方向,则这艘船航行的速度为( )A 18海里/小时B 318海里/小时C 36海里/小时D 336海里/小时 8、如图,河对岸有铁塔AB ,在C 处测得塔顶A 的仰角为30°,向塔前进14米到达D ,在D 处测得A 的仰角为45°,求铁塔AB 的高。
9、如图,一铁路路基横断面为等腰梯形ABCD ,斜坡BC 的坡度为3:2=ι,路基高AE 为3m ,底CD 宽12m ,求路基顶AB 的宽B ADCE10、如图,已知两座高度相等的建筑物AB 、CD 的水平距离BC =60米,在建筑物CD 上有一铁塔PD ,在塔顶P 处观察建筑物的底部B 和顶部A ,分别测行俯角0030,45==βα,求建筑物AB 的高。
(计算过程和结果一律不取近似值)11、如图,A 城气象台测得台风中心在A 城的正西方300千米处,以每小时107千米的速度向北偏东60º的BF 方向移动,距台风中心200千米的范围内是受这次台风影响的区域。
(1) 问A 城是否会受到这次台风的影响?为什么?(2) 若A 城受到这次台风的影响,那么A 城遭受这次台风影响的时间有多长?60ºFBA解直角三角形总复习答案二、巩固练习(1)三角函数的定义和性质 1、1312 2、29295 、 253、24、555、106、57、25.1<<m8、5409、B 10、 A 11、C 12、3 13、B (2)特殊角的三角函数值 1、22 2、1 3、214、A5、D6、A7、(1)1、333+ (2)12523-或12536- (3)32+ (4) 23(3)解直角三角形1、5=c 53sin =A 54cos =A 43tan =A 34cot =A 2、(1)152 (2)10 (3)310 (4)35 3、 5 、25 4、10=a 35=b 5、310=c 10=d 6、3334 3317=f 7、(1)5=c 54sin =B 53cos =B 34tan =B 43cot =B(2)8=b 54sin =B 53cos =B 34tan =B 43cot =B8、解:设BC=3k ,AC=k︒=∠90C Θk AB 5=∴54cos ,53sin ==∴A A 34cot ,43tan ==A A9、解:过A 作AD ⊥BC ,垂足为D 。
︒=∠=∠90ADB ADC Θ 22,45=︒=∠AC A Θ 2=∴AD 2,60=︒=∠AD B Θ 3=∴AB(4)实例分析1、︒302、33、C4、C5、33350- 6、 7、B8、解:设铁塔AB 高x 米 ︒=∠30B Θ 314cot =+==∠∴ABBDAB BC C 在ABD RT ∆中 ︒=∠45ADB Θ即314=+xx解得:x=)737(+m 答:铁塔AB 高)737(+m 。
9、解:过B 作BF ⊥CD ,垂足为F BF AE =∴ 在等腰梯形ABCD 中 AD=BC D C ∠=∠3:2=iBC ΘΘAE=3m∴DE=4.5mΘAD=BC ,D C ∠=∠,︒=∠=∠90DEA CFB ∴∆BCF ≅∆ADE∴CF=DE=4.5m∴EF=3mΘ︒=∠=∠90AEF BFE∴BF//CD∴四边形ABFE 为平行四边形∴AB=EF=3m10、解:︒=∠∴︒=4545BPC αΘ在RT ∆BPC 中m CP mBC 6060=∴=Θ在矩形ABCD 中AD=BC=60m︒=∠∴︒=∠6030APD βΘ在RT ∆APD 中AD=60m, ︒=∠60APDm AB CD PD )32060(320-==∴=∴答:AB 高)32060(-米。
11、(1)过A 作AC ⊥BF ,垂足为C︒=∠∴︒=∠30601ABC Θ在RT ∆ABC 中AB=300km响城会受到这次台风的影A km AC ABC ∴=∴︒=∠15030 (2)hhkm kmt hkm v kmDE km CD kmad km AC ADAE E ,BF kmAD D ,BF 1071071007107100750200,150200==∴==∴=∴====ΘΘ使上取在使上取在答:A 城遭遇这次台风影响10个小时。
