浙江省2018-2019学年高三下学期《立体几何》综合大题汇编(无答案)

合集下载

2018版高考数学浙江专用专题复习专题8 立体几何第50

一、选择题1.如图所示，已知三棱柱ABC －A1B 1C 1的侧棱与底面边长都相等，A 1在底面ABC 上的投影D 为BC 的中点，则异面直线AB 与CC 1所成的角的余弦值为( ) A.34B.54C.74D.342．已知正三棱柱ABC －A 1B 1C 1的体积为94，底面边长为3的正三角形．若P 为△A 1B 1C 1的中心，则P A 与平面ABC 所成角的大小为( ) A.π6B.π3C.π4D.23π 3．(2016·浙江五校高三第二次联考)如图，棱长为4的正方体ABCD －A 1B 1C 1D 1中，点A 在平面α内，平面ABCD 与平面α所成的二面角为30°，则顶点C 1到平面α的距离的最大值是( ) A ．2(2＋2) B ．2(3＋2) C ．2(3＋1)D ．2(2＋1)二、填空题4.如图，在等腰直角三角形ABD 中，∠BAD ＝90°，且等腰直角三角形ABD 与等边三角形BCD 所在平面垂直，E 为BC 的中点，则AE 与平面BCD 所成角的大小为________．5.如图所示，在三棱锥S －ABC 中，△SBC ，△ABC 都是等边三角形，且BC ＝1，SA ＝32，则二面角S －BC －A 的大小为________．6．在正方体ABCD －A 1B 1C 1D 1中，Q 是CC 1的中点，F 是侧面BCC 1B 1内的动点且A 1F ∥平面D 1AQ ，则A 1F 与平面BCC 1B 1所成角的正切值的取值范围为________．三、解答题7.如图所示，底面ABC 为正三角形，EA ⊥平面ABC ，DC ⊥平面ABC ，EA ＝AB＝2DC ＝2a ，设F 为EB 的中点． (1)求证：DF ∥平面ABC ；(2)求直线AD 与平面AEB 所成角的正弦值．8.(2016·辽宁沈阳二中月考)如图，在△ABC 中，∠ABC ＝45°，点O 在AB 上，且OB ＝OC ＝23AB ，PO ⊥平面ABC ，DA ∥PO ，DA ＝AO ＝12PO .(1)求证：PB ∥平面COD ； (2)求二面角O －CD －A 的余弦值．9．(2016·宁波二模)如图，正四棱锥S －ABCD 中，SA ＝AB ＝2，E ，F ，G 分别为BC ，SC ，CD 的中点．设P 为线段FG 上任意一点． (1)求证：EP ⊥AC ；(2)当P 为线段FG 的中点时，求直线BP 与平面EFG 所成角的余弦值．答案解析1．D2．B [因为AA 1⊥底面A 1B 1C 1，所以∠AP A 1为P A 与平面A 1B 1C 1所成的角．因为平面ABC ∥平面A 1B 1C 1，所以∠AP A 1为P A 与平面ABC 所成角，因为正三棱柱ABC －A 1B 1C 1的体积为94，底面三角形的边长为3，所以S △ABC ·AA 1＝94，可得AA 1＝ 3.又易知A 1P ＝1，所以tan ∠AP A 1＝AA 1A 1P ＝3，即∠AP A 1＝π3.] 3．B [过C 1，C 分别作平面α的垂线，垂足分别为点E ，F ，当平面AA 1C 1C 与平面ACF 重合时，顶点C 1到平面α的距离最大，即为C 1E ，此时∠CAF 为平面ABCD 与平面α所成的二面角，则∠CAF ＝30°，所以∠A 1AF ＝120°.设∠A 1AC 1＝θ，则sin θ＝63，cos θ＝33，所以sin ∠C 1AE ＝sin(120°－θ)＝32cos θ＋12sin θ＝32×33＋12×63＝12＋66.又AC 1＝43，所以C 1E ＝AC 1sin ∠C 1AF ＝43×(12＋66)＝2(3＋2)，故选B.]4．45°解析取BD 的中点F ，连接EF ，AF (图略)，易得AF ⊥BD ，AF ⊥平面BCD ，则∠AEF 就是AE 与平面BCD 所成的角，由题意知EF ＝12CD ＝12BD ＝AF ，所以∠AEF ＝45°，即AE 与平面BCD 所成的角为45°. 5．60° 6．[2,22]解析设平面AD 1Q 与直线BC 交于点G ，连接AG ，QG ，则G 为BC 的中点．分别取B 1B ，B 1C 1的中点M ，N ，连接A 1M ，MN ，A 1N ，如图所示． ∴A 1M ∥D 1Q ，∵A 1M ⊄平面D 1AQ ，D 1Q ⊂平面D 1AQ ，∴A 1M ∥平面D 1AQ ，同理可得MN ∥平面D 1AQ . ∵A 1M ，MN ⊆平面A 1MN ，A 1M ∩MN ＝M ， ∴平面A 1MN ∥平面D 1AQ .由此结合A 1F ∥平面D 1AQ ，可得直线A 1F ⊂平面A 1MN ，即点F 是线段MN 上的动点．设直线A 1F 与平面BCC 1B 1所成角为θ，移动点F 并加以观察，可得当点F 与M (或N )重合时，A 1F 与平面BCC 1B 1所成的角等于∠A 1MB 1，此时所成角θ达到最小值，满足tan θ＝A 1B 1B 1M ＝2；当点F 与MN 的中点重合时，A 1F 与平面BCC 1B 1所成角达到最大值，满足tan θ＝A 1B 122B 1M ＝22，∴A 1F 与平面BCC 1B 1所成角的正切值的取值范围为[2，22]． 7．(1)证明如图，过点F 作FH ∥EA 交AB 于点H ，连接HC . ∵EA ⊥平面ABC ，DC ⊥平面ABC ， ∴EA ∥DC . 又FH ∥EA ， ∴FH ∥DC . ∵F 是EB 的中点， ∴FH ＝12AE ＝DC .∴四边形CDFH 是平行四边形， ∴DF ∥HC .又HC ⊂平面ABC ，DF ⊄平面ABC ， ∴DF ∥平面ABC .(2)解 ∵△ABC 为正三角形，H 为AB 的中点， ∴CH ⊥AB .∵EA ⊥平面ABC ，CH ⊂平面ABC ，∴CH ⊥EA .又EA ∩AB ＝A ，EA ⊂平面AEB ，AB ⊂平面AEB ， ∴CH ⊥平面AEB . ∵DF ∥HC ， ∴DF ⊥平面AEB ，∴AF 为DA 在平面AEB 上的投影， ∴∠DAF 为直线AD 与平面AEB 所成的角．在Rt △AFD 中，AD ＝5a ，DF ＝3a ， sin ∠F AD ＝DF AD ＝155，∴直线AD 与平面AEB 所成角的正弦值为155. 8．(1)证明因为PO ⊥平面ABC ，AD ∥PO ，AB ⊂平面ABC ，所以PO ⊥AB ，DA ⊥AB .又DA ＝AO ＝12PO ，所以∠AOD ＝45°.因为OB ＝23AB ，所以OA ＝13AB ，所以OA ＝12OB ，又AO ＝12PO ，所以OB ＝OP ，所以∠OBP ＝45°，即OD ∥PB . 又PB ⊄平面COD ，OD ⊂平面COD ，所以PB ∥平面COD . (2)解如图，过A 作AM ⊥DO ，垂足为M ，过M 作MN ⊥CD 于N ，连接AN ，则∠ANM为二面角O－CD－A的平面角．设AD＝a，在等腰直角三角形AOD中，得AM＝22a，在直角三角形COD中，得MN＝33a，在直角三角形AMN中，得AN＝306a，所以cos∠ANM＝10 5.9．(1)证明设AC交BD于O点，∵S－ABCD为正四棱锥，∴SO⊥底面ABCD，BD⊥AC，又AC⊂平面ABCD，∴SO⊥AC，∵BD∩SO＝O，BD⊂平面SBD，SO⊂平面SBD，∴AC⊥平面SBD，∵E，F，G分别为BC，SC，CD的中点，∴FG∥SD，BD∥EG.又FG∩EG＝G，SD∩BD＝D，FG⊂平面EFG，EG⊂平面EFG，SD⊂BSD，BD⊂平面BSD，∴平面EFG∥平面BSD，∴AC⊥平面GEF.又∵PE⊂平面GEF，∴PE⊥AC.(2)解过B作BH⊥GE于H，连接PH，∵BD⊥AC，BD∥GH，∴BH∥AC，由(1)知AC ⊥平面GEF ，则BH ⊥平面GEF .∴∠BPH 就是直线BP 与平面EFG 所成的角．在Rt △BHP 中，BH ＝22，PH ＝132，PB ＝152，故cos ∠BPH ＝PH PB ＝19515.。

浙江高考试题分类汇编立体几何

浙江高考试题分类汇编立体几何The following text is amended on 12 November 2020.浙江高考试题分类汇编-立体几何一．选择题1．（2018 浙江 3）某几何体的三视图如图所示（单位：cm ），则该几何体的体积（单位：cm 2）是（）A. 2B. 4C. 6D. 82．（2018 浙江 6）.已知平面a ，直线m ，n 满足,m n αα⊄⊂，则“m ∥n ”是“m α”的（）A. 充分不必要条件B. 必要不充分条件C. 充分必要条件D. 既不充分也不必要条件3、（2018 浙江 8）已知道四棱锥S-ABCD 的底面是正方形，侧棱长均相等，E 是线段AB 上的点（不含端点），设SE 与BC 所成的角为1θ ，SE 与平面ABCD 所成的角为2θ，二面角S-AB-C 的平面角为3θ，则A. 123θθθ≤≤B. 321θθθ≤≤C. 132θθθ≤≤D. 231θθθ≤≤4．（2017 浙江 3）某几何体的三视图如图所示（单位：cm ），则该几何体的体积（单位：cm 3）是（）A ．+1B ．+3C ．+1D ．+35．（2017 浙江 9）如图，已知正四面体D﹣ABC（所有棱长均相等的三棱锥），P、Q、R分别为AB、BC、CA上的点，AP=PB，==2，分别记二面角D﹣PR﹣Q，D﹣PQ﹣R，D﹣QR﹣P的平面角为α、β、γ，则（）A．γ＜α＜βB．α＜γ＜βC．α＜β＜γD．β＜γ＜α6．（2015 浙江 2）某几何体的三视图如图所示（单位：cm），则该几何体的体积是（）A．8cm3B．12cm3C．D．7．（2015 浙江理 8）如图，已知△ABC，D是AB的中点，沿直线CD将△ACD折成△A′CD，所成二面角A′﹣CD﹣B的平面角为α，则（）A．∠A′DB≤αB．∠A′DB≥αC．∠A′CB≤αD．∠A′CB≥α8．（2014 浙江理3）某几何体的三视图（单位：cm）如图所示，则此几何体的表面积是（）A．90cm2B．129cm2C．132cm2D．138cm29．（2014浙江理3）某几何体的三视图（单位：cm）如图所示，则该几何体的体积是（）A．72cm3B．90cm3C．108cm3D．138cm3二．填空题1．（2016 浙江理11）某几何体的三视图如图所示（单位：cm），则该几何体的表面积是cm2，体积是cm3．2．（2016 浙江理14）如图，在△ABC中，AB=BC=2，∠ABC=120°．若平面ABC外的点P和线段AC上的点D，满足PD=DA，PB=BA，则四面体PBCD的体积的最大值是．3．（2016 浙江文 9）某几何体的三视图如图所示（单位：cm），则该几何体的表面积是cm2，体积是cm3．4．（2016 浙江文14）如图，已知平面四边形ABCD，AB=BC=3，CD=1，AD=，∠ADC=90°，沿直线AC将△ACD翻折成△ACD′，直线AC与BD′所成角的余弦的最大值是．5．（2015 浙江理 14）如图，三棱锥A﹣BCD中，AB=AC=BD=CD=3，AD=BC=2，点M，N分别是AD，BC的中点，则异面直线AN，CM所成的角的余弦值是．三．解答题1．（2018 浙江 19）如图，已知多面体ABC-A1B1C1，A1A、B1B，C1C均垂直于平面ABC，∠ABC=120°，A1A=4，C1C=1，AB=BC=B1B=2。

2019高考真题理分类汇编立体几何含答案解析选择题填空题.docx

专题05立体几何（选择题' 填空题）1.[2019年高考全国I卷理数】已知三棱锥P-ABC的四个顶点在球O的球面上，PA=PB=PC, &ABC是边长为2的正三角形，E, F分别是B4, 的中点，ZCEF=90。

,则球。

的体积为A. 8A/?兀B. 4\/6KC. 2A/6KD. y/6n【答案】D【解析】解法一：PA=PB = PC,AABC为边长为2的等边三角形，.•./>-ABC为正三棱锥，PBLAC,又E , F 分别为PA, AB 的中点，:.EF〃 PB , EF / AC ,又EF ICE, CE AC = C, :. EF± 平面PAC, :. PB L平面PAC ZAPB = 90。

,:. PA= PB = PC =也，P — ABC为正方体的一部分,2R = J2 + 2 + 2 = , 即R =寸!.，y= re—/?= 3-$/6 ,2 3 3 8故选D.解法二：设PA = PB = PC = 2x,分别为PA,AB 的中点，:.EF//PB,且EF=Lp3 = x,2 AABC为边长为2的等边三角形,.・.CF = B又ZCEF =90° , CE = 73-x2, AE^-PA^x,2△AEC中，由余弦定理可得cos ZEAC = x +4 ^-3 % ,2x2xx作PDLAC于。

，AD 1 X2+4-3+ X2 1PA = PC , \ D^jAC的中点，cosZEAC =——=—,J + x =—,PA 2x 4-x 2x12尤2 +1 = 2,尤？ = —, x ———，PA = PB — PC — y/^2，2 2又A8=8C=AC=2, .•.徵，您，PC两两垂直，:.2R = yj2 + 2 + 2=^6 > :.R = — , .-.V=-TI R3 =—71X 6^^ = J^7T ,故选D.2 3 3 8【名师点睛】本题主要考查学生的空间想象能力，补体法解决外接球问题.可通过线面垂直定理，得到三棱两两互相垂直关系，快速得到侧棱长，进而补体成正方体解决.2.[2019年高考全国II卷理数】设a, g为两个平面，则a//p的充要条件是A. a内有无数条直线与”平行B. a内有两条相交直线与”平行C. a,月平行于同一条直线D. a, 垂直于同一平面【答案】B【解析】由面面平行的判定定理知：。

2018学年高三下立体几何综合大题汇编

2018学年高三下立体几何综合大题汇编一、线面角1. （2018学年杭十四中4月月考19）如图，三棱柱111ABC A B C -所有的棱长均为2，1A B =1A B AC ⊥．（1）求证：111A C B C ⊥；（2）求直线AC 和平面11ABB A 所成角的余弦值．2. （2018学年浙江名校协作体高三上开学考19）如图，在三棱锥P ABC -中，PAC △和ABC △均为等腰三角形，且90APC BAC ∠=∠=︒，4PA AB ==．（1）判断AB PC ⊥是否成立，并给出证明；（2）求直线PB 与平面ABC 所成角的正弦值．C 1B 1A 1CBABCPA3. （2018学年浙江名校协作体高三下开学考19）四棱锥P ABCD -的底面为菱形，4AB =，60ABC ∠=︒， M 为PB 的中点，N 为BD 上一点，且13BN ND =．（1）求证：MN P 平面PAC ；（2）求证：PN ⊥平面ABCD ；（3）若5PA PC ==，PB =PN 与平面PCD 所成角的正弦值．4. （2018学年浙江重点中学高三上期末热身联考19）如图，等腰直角ABC △中，B ∠是直角，平面ABEF ⊥平面ABC ，2AF AB BE ==，60FAB ∠=︒，AF BE P ．（1）求证：BC BF ⊥；（2）求直线BF 与平面CEF 所成角的正弦值．PNMDCB A BCEFA5. （2019届超级全能生2月模拟19）如图，在三棱锥P ABC -中，2BAC π∠=，2AC =，BC BP ==，PC =，APC △的面积等于（1）求证：AC PB ⊥；（2）求直线AC 与平面PBC 所成角的正弦值．6. （2019届杭二仿真考19）如图，矩形ADFE 和梯形ABCD 所在平面互相垂直，AB CD ∥，90ABC ADB ∠=∠=︒，1CD =，2BC =．（1）求证：BE ∥平面DCF ；（2）当AE 的长为何值时，直线AD 与平面BCE 所成角的大小为45︒．7. （2019届湖丽衢9月质检19）如图，在四棱锥P ABCD -中，四边形ABCD 是直角梯形，且AD BC P ，BC CD ⊥，60ABC ∠=︒，22BC AD ==，3PC =，PAB △是正三角形，E 是PC 的中点．（1）求证：DE P 平面PAB ；（2）求直线BE 与平面PAB 所成角的正弦值．PBCAFEDC BAPBCD E A8. （2019届湖州三校4月模拟19）如图，在四棱锥E ABCD -中，底面ABCD 是边长为2的正方形，且DE =，平面ABCD ⊥平面ADE ，二面角A CD E --为30︒．（1）求证：AE ⊥平面CDE ；（2）求AB 与平面BCE 所成角的正弦值．9. （2019届湖州中学仿真考19）如图，已知四棱锥P ABCD -，底面ABCD 为边长为2的菱形，PA ⊥平面ABCD ，60ABC ∠=︒，E 是BC 的中点，PA AB =．（1）证明：AE PD ⊥；（2）若F 为PD 上的动点，求EF 与平面PAD 所成最大角的正切值．EDCBAFPDCBA10. （2019届稽阳联谊4月模拟19）在四棱锥P ABCD -中，PC ⊥平面ABCD ，BC AD ∥，BC AB ⊥，2PB AD ==，1AB BC ==，E 为棱PD 上的点．（1）若13PE PD =，求证：PB ∥平面ACE ；（2）若E 是PD 的中点，求直线PB 与平面ACE 所成角的正弦值．11. （2019届嘉丽4月模拟19）如图，在矩形ABCD 中，4AB =，3AD =，点E ，F 分别是线段DC ，BC 的中点，分别将DAE △沿AE 折起，CEF △沿EF 折起，使得D ，C 重合于点G ，连结AF ．（1）求证：平面GEF ⊥平面GAF ；（2）求直线GF 与平面GAE 所成角的正弦值．12. （2019届嘉兴9月基础测试20）如图，ABC △时候边长为2的正三角形，ABD △是以AB 为斜边的等腰直角三角形．已知2CD =．（1）求证：平面ABC ⊥平面ABD ；（2）求直线AC 与平面BCD 所成角的正弦值．EDBA PGFED CBABCDA13. （2019届金华十校4月模拟20）在四棱锥S ABCD -中，底面ABCD 为直角梯形，BC CD ⊥，1SC SD CD DA ====，2CB =，AD BC ∥，23SCB π∠=，E 为线段SB 上的中点．（1）证明：AE ∥平面SCD ；（2）求直线AE 与平面SBC 所成角的余弦值．14. （2019届金华一中5月模拟19）如图，在四棱锥P ABCD -中，底面ABCD 是菱形，60BAD ∠=︒，2AB =，1PA =，PA ABCD ⊥平面，E 是直线PC 的中点，F 是直线AB 的中点．（1）求证：BE ∥平面PDF ；（2）求直线BE 与平面PCD 所成角的正弦值．15. （2019届金丽衢十二校第二次联考19）三棱柱111ABC A B C -中，AB ⊥侧面11BCC B ，已知1BC =，1=3BCC π∠，12AB C C ==．（1）求证：1C B ⊥平面ABC ；（2）若E 在棱1C C (不包含端点1C C ，)上，且1EA EB ⊥，求1A E 与平面1AB E 所成角的正弦值．SEDC BFE DCBAP16. （2019届金丽衢十二校第一次联考19）如图，在四棱锥P ABCD -中，已知PA ⊥平面ABCD ，且四边形ABCD 为直角梯形，2ABC BAD π∠=∠=，2PA AD ==，1AB BC ==，点M 、E 分别是PA ，PD 的中点．（1）求证：CE P 平面BMD ；（2）点Q 为线段BP 中点，求直线PA 与平面CEQ 为所成角的余弦值．17. （2019届临海新昌乐清4月模拟19）已知多面体ABCDE 中，AE 、CD 均垂直于平面ABC ，120ABC ∠=︒，2AE CD =，AB BC CD ==，F 是BE 的中点．（1）求证：DF ∥平面ABC ；（2）求直线BD 与平面ABE 所成角的正弦值．BCEA 1B 1C 1A QEM PDCBA18. （2019届宁波4月模拟19）中国古代数学经典《数书九章》中，将底面为矩形且有一条侧棱与底面垂直的四棱锥称为“阳马”，将四个面都为直角三角形的四面体称之为“鳖臑”．在如图所示的阳马P ABCD -中，底面ABCD 是矩形，P A ⊥平面ABCD ，2PA AD ==，AB =AC 的中点O 为球心，AC 为直径的球面交PD 于M （异于点D ），交PC 于N （异于点C ）．（1）证明：平面AM PCD ⊥，并判断四面体MCDA 是否是鳖臑，若是，写出它每个面的直角（只需写出结论）；若不是，请说明理由；（2）求直线ON 与平面ACM 所成角的正弦值．19. （2019届宁波十校5月模拟19）如图，在四棱台1111ABCD A B C D -中，底面ABCD 是菱形，3ABC π∠=，11B BA B BC ∠=∠，16B BD π=，1122AB A B ==，12B B =，E 是CD 的中点．（1）求证：直线AC ⊥平面11BDD B ；（2）求直线1ED 与平面11ABB A 所成角的正弦值．BCDEFAD20.（2019届平湖5月模拟19）如图所示，在直角梯形ABCD中，90ADC∠=︒，CD AB∥，4AB=，2AD CD==，M为线段AB的中点，将ADC△沿AC折起，得到几何体P ABC-．（1）求证：AC PM⊥；（2）已知PM PB与平面APC所成角的正弦值．21.（2019届七彩阳光联盟第三次联考19）如图，在四棱锥P ABCD-中，BC⊥平面PCD，CD∥AB，22 AB CD==，BC PC==PD AB⊥．（1）求PD的长；（2）求直线AD与平面P AB所成角的正弦值．B1C1D1A1ODCBAMAPCBPDCBA22. （2019届七彩阳光联盟第一次联考19）如图，已知四棱锥P ABCD -，底面ABCD 为矩形，且侧面PAD ⊥平面PBC ，侧面PAD I 平面=PBC l ，PDC △为正三角形，2CD =．（1）求证：l BC P ；（2）求直线AB 与平面PAD 所成角的正弦值．23. （2019届衢州二中第二次模拟19）如图，正方形ABCD 所在平面外一点P 满足PE PF =，其中E 、F 分别是AB 、CD 的中点．（1）求证：EF PC ⊥；（2）若4AB =，PE PF ==且二面角P EF C --，求BC 与平面PEF 所成角的正弦值．24. （2019届衢州二中第一次模拟20）如图，已知矩形BCDE 所在平面与ABE △所在平面互相垂直，且AB AE ⊥，AB AE >．（1）若M 为AC 的中点，N 为BE 的中点，求证：MN ∥平面ADE ；（2）若2BE =，1DE =，且DE 与平面DAC，求ABE ∠的大小． BCDPAPF ED CBA25. （2019届绍兴3月模拟19）如图，四棱锥P ABCD -中，PA ⊥平面ABCD ，四边形ABCD 是矩形，且2PA AB ==，3AD =，E 是棱BC 上的动点，F 是线段PE 的中点．（1）求证：PB ⊥平面ADF ；（2）若直线DE 与平面ADF 所成角为30︒，求EC 的长．26. （2019届绍兴柯桥区5月模拟19）如图，在RT △ABC 中，90C ∠=︒，2CA =，CB =，现沿△ABC 的中位线DE 将△ADE 翻折至A DE '，使得二面角A DE A '--为60︒．（1）求证：A C ED '⊥；（2）求直线BA '与平面A DE '所成角的正弦值．EBCDPF EA27. （2019届嵊州5月模拟19）如图，已知四棱锥P ABCD -，AD BC ∥，90ABC ∠=︒，135ADP ∠=︒，AB =，22BC AD ==，2PB PD ==（1）求证：AB PD ⊥；（2）求直线PD 与平面PBC 所成的角的正弦值．28. （2019届台州4月模拟19）如图，棱锥P ABCD -的底面是菱形，2AB =，3DAB π∠=，侧面PAB垂直于底面ABCD ，且PAB △是正三角形．（1）求证：PD AB ⊥；（2）求直线PC 与平面PBD 所成角的正弦值．A'ED CBAP DCBABCDPA29. （2019届温州2月模拟19）在三棱锥D ABC -中，AD DC ⊥，AC CB ⊥，222AB AD DC ===，且平面ABD ⊥平面BCD ，E 为AC 的中点．（1）证明：AD BC ⊥；（2）求直线DE 与平面ABD 所成角的正弦值．30. （2019届温州5月模拟19）如图，四棱锥P ABCD -中，底面为直角梯形，AB ∥CD ，90BAD ∠=︒，24AB CD ==，PA CD ⊥，在锐角．．PAD △中，E 是边PD上一点，且3AD PD ED ===（1）求证：PB ∥平面ACE ；（2）当P A 的长为何值时，AC 与平面PCD 所成的角为30︒？31. （2019届温州8月模拟19）如图，在三棱柱111ABC A B C -中，12AA AC AB ==，90ABC ∠=︒，侧面11A ABB 为矩形，1=120A AC ∠︒．将111A B C △绕11A C 翻折至121A B C △，使2B 在平面11A ACC 内．（1）求证：1BC P 平面121A B B ；（2）求12C B 与平面11A ABB 所成角的正弦值．BCDEAACDEP32. （2019届温州九校第一次联考19）如图，将矩形ABCD 沿AE 折成二面角1D AE B --，其中E 为CD的中点，已知2AB =，=1BC ，11BD CD =，F 为1D B 的中点．（1）求证：CF P 平面1AD E ；（2）求AF 与平面1BD E 所成角的正弦值．33. （2019届永康5月模拟20）已知在等腰梯形ABGH 中，AB GH ∥，22AB GH HA ==，E ，F 分别为线段AH 和BG 的中点，现将四边形EFGH 沿直线EF 折成一个五面体AED BFC -．BCAB 1C 1B 2A 1BCDED 1FA（1）在线段BC 上是否存在点M ，使FM ∥平面ADE ，若存在，找出点M 的位置，若不存在，说明理由；（2）若二面角C EF B --的大小为60︒，求直线AC 与平面ABFE 所成角的正弦值．34. （2019届浙江百校联考19）如图，已知△P AD 为等边三角形，四边形ABCD 为直角梯形，AB ∥CD ，90DAB ∠=︒，平面P AD ⊥平面ABCD ，2AB AD CD ==，E 为PB 的中点．（1）求证：CE ∥平面P AD ；（2）求PB 与平面PCD 所成角的正弦值．35. （2019届浙江名校联盟第二次联考19）在四棱锥P ABCD -中，四边形ABCD 是边长为2的正方形，PB PD =，E F M 、、分别是棱AD PD PC 、、上的点，且=PF FD λu u u r u u u r ，AE ED λ=u u u r u u u r，若对任意()0,1λ∈，都有EF P 平面DBM ．（1）求PMMC的值；（2）若DM ，二面角M DB C --的大小为30︒，求直线PD 与平面BDM 所成角的正弦值．CDF EHGAPEDC BA36. （2019届浙江名校联盟第三次联考19）在所有棱长都相等的三棱柱111ABC A B C -中，1=60B BC ∠︒．（1）证明：1AB BC ⊥；（2）若二面角1A BC B --的大小为60︒，求1BC 与平面ABC 所成角的正弦值．37. （2019届浙江名校联盟第一次联考19）如图，在四棱锥P ABCD -中，PA ⊥平面ABCD ，AB CD ∥，4CD =，2PA AB BC AD ====，Q 为棱PC 上的点，且13PQ PC =．（1）证明：平面QBD ⊥平面ABCD ；（2）求直线QD 与平面PBC 所成角的正弦值．E FBC D PM AC 1B 1A 1CBA38. （2019届浙江三校第二次联考19）在斜三棱柱111ABC A B C -中，△ABC 是边长为2的正三角形，1A B =1160A AB A AC ∠=∠=︒．（1）证明：1平面平面A BC ABC ⊥；（2）求直线1BC 与平面11ABB A 所成角的正弦值．39. （2019届浙江三校第四次联考19）如图，在Rt ABC △中，90BAC ∠=︒，30B ∠=︒，D ，E 分别为BC ，AD 的中点，延长CE 交AB 于点F ，现将ACD △沿AD 折起，使二面角B AD C --的平面角大小为30︒．QPDC BAB 1C 1A 1CBA（1）求证：AD CF⊥；（2）求直线AB与平面ACD所成角的正弦值．40.（2019届浙江三校第一次联考19）如图，已知四棱锥A BCDE-中，2AB BC==，120ABC∠=︒，AE=CD BE∥，24BE CD==，60EBC∠=︒．（1）求证：EC ABC⊥平面；（2）求直线AD与平面ABE所成角的正弦值．41.（2019届镇海中学5月模拟19）如图，四棱锥P ABCD-的底面ABCD是边长为2的菱形，60ABC∠=︒，点M是棱PC的中点，PA⊥平面ABCD．（1）证明：PA∥平面BMD；（2）当PA长度为多少时，直线AM与平面PBC．FEDCB AE F DCB AC DEBA42. （2019届镇海中学考前练习19）如图，在四棱锥P ABCD -中，60APB BPD APD ∠=∠=∠=︒，2PB PD BC CD ====，3AP =．（1）证明：AP BD ⊥；（2）求PC 与平面PAB 所成角的正弦值．43. （2019届知行联盟5月模拟19）如图，在四棱锥E ABCD -中，底面ABCD 为正方形，AE CDE ⊥平面．已知1AE =，DE （1）证明：ADE ABCD ⊥平面平面；（2）求直线BE 与平面ACE 所成的角的正弦值．44. （2019届舟山中学5月模拟19）如图所示多面体EF ABCD -，其底面ABCD为矩形且AB =2BC =，四边形BDEF 为平行四边形，点F 在底面ABCD 内的投影恰好是BC 的中点．（1）已知G 为线段FC 的中点，证明：BG ∥平面AEF ；MPDBAPDCBAEDCBA（2）若二面角F BD C --的大小为3π，求直线AE 与平面BDEF 所成角的正弦值．45. （2019届诸暨5月模拟19）如图，在四棱锥P ABCD -中，底面是边长为2的菱形，60BAD ∠=︒，PB PD =（1）证明：平面PAC ⊥平面ABCD ；（2）设H 在AC 上，13AH AC =，若PH ．求PH 与平面PBC 所成角的正弦值．二、二面角46. （2018学年杭高高三下开学考19）如图（1），已知ABC △是边长为6的等边三角形，点D 、E 分别是边AB 、AC 上的点，且满足2AD CE ==．如图（2），将ADE △沿DE 折成四棱锥1A BCED -，且有平面1A DE ⊥平面BCED ．（1）求证：1A D ⊥平面BCED ；（2）记1A E 的中点为M ，求二面角1M DC A --的余弦值．FEDCBAHPDCBABCDEAMCBEDA 1图１图２47. （2019届杭二热身考20）在四棱锥P ABCD -中，底面ABCD 为菱形，60DAB ∠=︒，PC ⊥平面ABCD ，且2AB =，PC =F 是PA 的中点．（1）求证：CF ⊥平面PDB ；（2）求平面ADP 与平面BCP 所成锐二面角的余弦值．48. （2019届杭四仿真考19）在四棱锥P ABCD -中，PA ABCD ⊥底面，BAD ∠为直角，AB CD ∥，2AD CD AB ==，E 、F 分别为PC 、CD 的中点．（1）证明：APD BEF 平面∥平面；（2）设()0PA kAB k =>，且二面角E BD C --的平面角大于60°，求k 的取值范围．49. （2019届杭州4月模拟19）如图，四边形ABCD 为矩形，平面ABEF ⊥平面ABCD ，EF ∥AB ，90BAF ∠=o ，2AD =，1AB AF ==，点P 在线段DF 上．FPDCBAFEDCBAP（1）证明：AF ⊥平面ABCD ．（2）若二面角D AP C --PF 的长度．50. （2019届嘉兴一中5月模拟20）在四边形ABED 中，AB DE ∥，AB BE ⊥，点C 在AB 上，且AB CD ⊥，2AC BC CD ===，现将ACD △沿CD 折起，使点A 到达点P 的位置，且PE 与平面PBC 所成角为45︒．（1）求证：平面PBC ⊥平面DEBC ；（2）求二面角D PE B --的余弦值．51. （2019届绿色联盟5月模拟19）如图，圆的直径2AC =，B 为圆周上不与A ，C 重合的点，PA 垂直于圆所在的平面，45PCA ∠=︒．（1）求证：PB BC ⊥；（2）若BC B PC A --的余弦值．52. （2019届绿色联盟12月模拟19）在三棱锥P ABC -中，ABC △和ABP △均为等边三角形，PF EDC BAPE DCBACA2AB =，点P 在平面ABC 上的射影在ABC △内，已知直线PB 与平面ABC 所成角的正弦值为34．（1）求证：AB PC ⊥；（2）求二面角B AP C --的余弦值．53. （2019届七彩阳光联盟第二次联考19）如图，已知平行四边形ABCD ，满足45A ∠=︒，BC =，又H 为边DC 上一点，且满足BH DC ⊥，现将CBH △沿BH 翻折至PBH △处，使得PD PB ⊥．（1）求证：PD ⊥平面PBH ；（2）若1PD =，求钝二面角A PB H --的余弦值．54. （2019届上虞5月模拟19）已知等腰直角三角形ABC ，90C ∠=︒，D 、E 分别是AC 、AB 的中点，沿DE 将ADE △折起（如图），连接AC 、AB ．（1）设点P 为AC 的中点，求证：DP ⊥平面ABC ；（2）设Q 为BE 的中点，当ADE △折成二面角A DE B --为60︒时，求CQ 与面ABC 所成角的正弦值．BCPA BCHPDPQCDEBABCDEA55. （2019届余高、缙中、长中5月模拟19）如图，在三棱锥P ABC -中，G 是棱P A 的中点，PC AC ⊥，且2PB AB AC BC ====，1PC =．（1）求证：直线BG ⊥平面P AC ；（2）求二面角P AC B --的正弦值．56. （2019届浙江五校联考19）如图，已知ABC △中，AB BC ==AC =点A α∈平面，点B ，C 在平面α的同侧，且B ，C 在平面α上的射影分别为E ，D ，22BE CD ==．（1）求证：平面ABE ⊥平面BCDE ；（2）若M 是AD 中点，求平面BMC 与平面α所成锐二面角的余弦值；57. （2019届镇海中学最后一卷19）如图，在AOB △中，2AOB π∠=，6BAO π∠=，4AB =，D 为线段AB 的中点．若AOC △是AOB △绕直线AO 旋转而成的．记二面角B AO C --的大小为θ．（1）当平面COD ⊥平面AOB 时，求θ的值；（2）当2,23ππθ⎡⎤∈⎢⎥⎣⎦时，求二面角C OD B --的余弦值的取值范围．GPCBAαME DCBA三、距离、存在性等58. （2019届慈溪中学5月模拟19）在四面体D ABC -中，122AB AD CD ===，BD =，AC =BC AC ⊥．（1）求证：BC ⊥平面ACD ；DBCOA值．59. （2019届衢州五校联考19）如图，ABC △的外接圆O ，CD ⊥圆O 所在的平面，BE CD P ，4CD =，2BC =，且1BE =，tan AEB ∠=（1）证明：平面ADC ⊥平面BCDE ；（2）试问线段DE 上是否存在点M ，使得直线AM 与平面ACD 所成角的正弦值为27？若存在，确定点M 的位置；若不存在，请说明理由．60. （2019届绍兴一中4月模拟19）如图，四棱锥P ABCD -中，平面PAD ⊥平面ABCD ，底面ABCD 为梯形，AB CD ∥，2AB DC ==且PAD △与ABD △均为正三角形，E 为AD 的中点，G 为PAD △重心．C QDPBABEA（1）求证：GF ∥平面PDC ；（2）求三棱锥G PCD -的体积．61. （2019届浙北四校12月模拟19）如图，三棱柱111ABC A B C -的各棱长均为2，侧面11BCC B ⊥底面ABC ，侧棱1BB 与底面ABC 所成角为60︒．（1）求直线1A C 与底面ABC 所成的角；（2）在线段11A C 上是否存在点P ，使得平面1B CP ⊥平面11ACC A ？若存在，求出1C P 的长；若不存在，请说明理由．62. （2019届浙大附中5月模拟19）等边三角形ABC 的边长为3，点D 、E 分别是边AB 、AC 上的点，且满足12AD CE DB EA ==（如图1）．将ADE △沿DE 折起到1A DE △的位置，使二面角1A DE B --成直二 FG EPDCBAB 1C 1BA 1CA面角，连结1A B ，1A C （如图2）．（1）求证：1A D BCED ⊥平面；（2）在线段BC 上是否存在点P ，使直线1PA 与平面1A BD 所成的角为60o ？若存在，求出PB 的长，若不存在，请说明理由．63. （2019届浙江省模拟19）如图，在四棱锥P ABCD -中，底面ABCD 是边长为2的正方形，PAD△为等边三角形，E ，M 分别是AD ，PD的中点，PB = （1）求证：平面PBE ⊥平面ABCD ；（2）求点P 到平面ACM 的距离．64. （2019届浙江十校4月模拟19）如图，在四棱锥P ABCD -中，侧棱PA ⊥底面ABCD ，AD BC ∥，90ABC ∠=︒，1AD =,2PA AB BC ===，M 是棱PB 的中点．E DCBA 1EDCBA图2图1MPEDCBA（1）已知点E 在棱BC 上，且平面AM E ∥平面PCD ，试确定点E 的位置，并说明理由；（2）设点N 是线段CD 上的动点，当点N 在何处时，直线MN 与平面PAB 所成角最大？并求最大角的正弦值．NBCDPMA。

浙江省历年高考立体几何大题总汇

浙江省历年高考立体几何大题总汇(题目及答案)(总21页)--本页仅作为文档封面，使用时请直接删除即可----内页可以根据需求调整合适字体及大小--1.（本题满分15分）如图，平面PAC ⊥平面ABC ，ABC ∆是以AC 为斜边的等腰直角三角形。

,,E F O 分别为,,PA PB PC 的中点，16,10AC PA PC ===。

（I ）设C 是OC 的中点，证明：//PC 平面BOE ；（II ）证明：在ABO ∆内存在一点M ，使FM ⊥平面BOE ，并求点M 到OA ,OB 的距离。

2.如图，在棱长为1的正方体ABCD －A 1B 1C 1D 1中，P 是侧棱CC 1上的一点，CP=m ，（Ⅰ）试确定m ，使得直线AP 与平面BDB 1D 1所成角的正切值为32；（Ⅱ）在线段A 1C 1上是否存在一个定点Q ，使得对任意的m ，D 1Q 在平面APD 1上的射影垂直于AP ，并证明你的结论。

3. 如图甲，△ABC 是边长为6的等边三角形，E ，D 分别为AB 、AC 靠近B 、C的三等分点，点G 为BC 边的中点．线段AG 交线段ED 于F 点，将△AEDxyz沿ED 翻折，使平面AED ⊥平面BCDE ，连接AB 、AC 、AG 形成如图乙所示的几何体。

（I ）求证BC ⊥平面AFG ；（II ）求二面角B －AE －D 的余弦值．.4在如图所示的几何体中，EA ⊥平面ABC ，DB ⊥平面ABC ，AC BC ⊥，2AC BC BD AE ===，M 是AB 的中点．（1）求证：CM EM ⊥；（2）求CM 与平面CDE 所成的角5. 如图，矩形ABCD 和梯形BEFC 所在平面互相垂直，BE CF ∥，90BCF CEF ∠=∠=，3AD =2EF =．EMACBDD（Ⅰ）求证：AE ∥平面DCF ；（Ⅱ）当AB 的长为何值时，二面角A EF C --的大小为606. 如图，在矩形ABCD 中，点E ，F 分别在线段AB ，AD 上，AE=EB=AF=.432=FD 沿直线EF 将AEF ∆翻折成,'EF A ∆使平面⊥EF A '平面BEF.（I ）求二面角C FD A --'的余弦值；（II ）点M ，N 分别在线段FD ，BC 上，若沿直线MN 将四边形MNCD 向上翻折，使C与'A 重合，求线段FM 的长.7. 如图，在三棱锥P-ABC 中，AB ＝AC ，D 为BC 的中点，PO⊥平面ABC ，垂足O 落在线段AD 上，已知BC ＝8，PO ＝4，AO ＝3，OD ＝2（Ⅰ）证明：AP⊥BC；（Ⅱ）在线段AP 上是否存在点M ，使得二面角A-MC-B 为直二面角若存在，求出AM 的长；若不存在，请说明理由。

浙江省2018-2019学年高三下学期《立体几何》选择填空

2018学年高三下立体几何选填综合1.（2018学年杭髙高三下开学考14） a, b为空间中两条互相垂直的直线，等边三角形.毎C的边MC所在的直线与a, b都垂直，边-毎以2C为旋转轴旋转，直线与a所成角的最小值为___________________ ；当直线肋与a所成角在60。

时，肿与6所成角是______________ ・2.(2018学年杭十四中4月月考10)三棱锥A_BCD中，记二而角A — BC — D的大小为( )A.若AB 十AC>DB + DC,则ZBAC<ZBDCB・^AB + AC>DB + DC,则ZBAC>ABDCC・若BA + BD = CA + CD,且AD 丄BC,贝W>ZACDD・若AB + AC = DB + DC,且AD 丄BC,则6>ZACD3.（2018学年浙江名校协作体髙三下开学考14）四而体S-ABC中，SA丄而H是HSBC的垂心，且AH丄而SBC,则三对对棱与EC, SB与2C, SC与肋中互相垂直的有___________________ 对：若H也是5C的重心，贝IJ二而角S — BC —A的正弦值为_________ ・154.（2018学年浙江中重点中学髙三上期末热身联考10）如图，将边长为2的正方形ABCD沿PD、PC翻折至A. B两点重合，其中P是.15中点，在折成的三棱锥A（B）-PDC中，点0在平而PDC内运动，且直线“40与棱所成角为60。

，则点0运动的轨迹是（）A.圆B.椭圆C.双曲线D.抛物线5. （2018学年浙江重点中学髙三上期末热身联考17）平行六而体ABCD — ABCU 中，已知底而四边形 ABCD 为矩形，=英中 \AB\ = a , \AD\ = b , pL4,| = c,体对角线|A,C| = 1 ,则 c 的最大值为 ___________ ■6. （2019届慈溪中学5月模拟8）已知正方体ABCDfBCU 中，点E 在棱上运动，点F 在对角线BD 、上运动,设直线EF 与平面肋CD 所成的角为&，直线肪与平而別）耳所成的角为0,则（）7. （2019届杭二仿真考10）如图，三棱锥P-ABC 中，Q4丄平而ABC, ZB4C =壬，0为刃中点,下列说法中，正确说法的个数为（）（1） ZPBA + "CA + 乙BPC =兀；（2）记二而角P-BC-A, Q-BC-A 的平而角分别为q ,如,则q>2q ；（3）记△ABC,厶 QBC , aBC 的面积分别为 S 、, S 「则 S ；+S ；S4S ：：（4） cosZPBC <cosZPBQ cosZQBC ・ A ・0B ・1C ・2 D. 3A ・ 0>pC. 存在直线£只使得0 = 50°B ・ 0<pD. 存在直线EF,使得0 = 50。

浙江省历年高考立体几何大题总汇(题目与答案)

1.（本题满分15 分）如图，平面PAC ⊥平面ABC ，ABC 是以AC 为斜边的等腰直角三角形。

E,F ,O分别为PA, PB, PC 的中点，AC 16, PA PC 10 。

（I ）设 C 是OC 的中点，证明：PC // 平面BOE ；（II ）证明：在ABO 内存在一点M ，使FM ⊥平面BOE ，并求点M 到OA , OB 的距离。

zyx2.如图，在棱长为 1 的正方体ABCD －A1B1C1D1 中，P 是侧棱CC1 上的一点，CP=m ，（Ⅰ）试确定m，使得直线AP 与平面BDB 1D1 所成角的正切值为 3 2 ；（Ⅱ）在线段A1C1 上是否存在一个定点Q，使得对任意的m，D1Q 在平面APD 1 上的射影垂直于AP，并证明你的结论。

3. 如图甲，△ABC 是边长为 6 的等边三角形，E，D 分别为AB 、AC 靠近B、C 的三等分点，点G 为BC 边的中点．线段AG 交线段ED 于F 点，将△AED 沿ED 翻折，使平面AED ⊥平面BCDE ，连接AB 、AC 、AG 形成如图乙所示的几何体。

（I）求证BC⊥平面AFG ；（II）求二面角B－AE －D 的余弦值．.4 在如图所示的几何体中，EA 平面ABC，DB 平面ABC，AC BC ，AC BC BD 2AE ，M是AB的中点．（1）求证：CM EM ；D（2）求CM与平面CDE所成的角ECAMB4.如图，矩形ABCD 和梯形BEFC 所在平面互相垂直，BE ∥CF ，BCF CEF ，AD 3，E F 2．90D（Ⅰ）求证：AE ∥平面DCF ；AC （Ⅱ）当AB 的长为何值时，二面角 A EF C 的大小为60 ？BF E（第18 题）25.如图，在矩形ABCD 中，点E，F 分别在线段AB ，AD 上，AE=EB=AF= FD 4.沿直3线EF 将AEF 翻折成A' EF , 使平面A' EF 平面BEF.（I）求二面角A' FD C 的余弦值；（II ）点M ，N 分别在线段FD，BC 上，若沿直线MN 将四边形MNCD 向上翻折，使 C与A' 重合，求线段FM 的长.6.如图，在三棱锥P-ABC 中，AB ＝AC，D 为BC 的中点，PO⊥平面ABC ，垂足O 落在线段AD 上，已知BC＝8，PO＝4，AO＝3，OD＝2（Ⅰ）证明：AP⊥BC；（Ⅱ）在线段AP 上是否存在点M ，使得二面角A-MC-B 为直二面角？若存在，求出AM 的长；若不存在，请说明理由。

2018-2019年高考分类汇编：立体几何

2018-2019年高考立体几何真题1.(2018浙江)如图，已知多面体ABCA 1B 1C 1，A 1A ，B 1B ，C 1C 均垂直于平面ABC ，∠ABC =120°，A 1A =4，C 1C =1，AB =BC =B 1B =2.（1）证明：AB 1⊥平面A 1B 1C 1；（2）求直线AC 1与平面ABB 1所成的角的正弦值2.(2018浙江)已知四棱锥S −ABCD 的底面是正方形，侧棱长均相等，E 是线段AB 上的点(不含端点)，设SE 与BC 所成的角为θ1，SE 与平面ABCD 所成的角为θ2，二面角S −AB −C 的平面角为θ3，则( ) A . θ1≤θ2≤θ3 B . θ3≤θ2≤θ1 C . θ1≤θ3≤θ2 D . θ2≤θ3≤θ13.（2018江苏）在平行六面体1111ABCD A B C D -中，1AA AB =，111AB B C ⊥.求证：(1) AB //平面11A B C ；(2) 平面11ABB A ⊥平面1A BC .4.(2018全国1)如图，四边形ABCD 为正方形，E 、F 分别为AD ，BC 的中点，以DF 为折痕把△DFC 折起，使点C 到达点P 的位置，且PF ⊥BF. (1)证明:平面PEF ⊥平面ABFD ； (2)求DP 与平面ABFD 所成的角的正弦值.5.（2018全国2）如图，在三棱锥P-ABC中=4AB BC PA PB PC AC =====，O 为AC 中点。

（1）证明：PO ABC ⊥平面（2）若点M 在棱BC 上，且二面角M-AP-C 为030，C 1B 1A 1CBA(D 11B 1A 1DCBA求PC与平面PAM所成角的正弦值。

6.(2019全国1)如图，直四棱柱ABCD–A1B1C1D1的底面是菱形，AA1=4，AB=2，∠BAD=60°，E，M，N分别是BC，BB1，A1D的中点．（1）证明：MN∥平面C1DE；（2）求二面角A-MA1-N 的正弦值．7.(2019全国2)如图，长方体ABCD–A1B1C1D1的底面ABCD是正方形，点E在棱AA1上，BE ⊥EC1．（1）证明：BE⊥平面EB1C1；（2）若AE=A1E，求二面角B–EC–C1的正弦值．9.（2019浙江）如图，已知三棱柱ABC-A1B1C1，平面11A AC C⊥平面ABC，，，A1A=A1C=AC，E，F分别是AC，A1B1的中点.（1）证明：（2）求直线EF 与平面 A 1BC 所成角的余弦值10．（2019北京）如图，在四棱锥P –ABCD 中，PA ⊥平面ABCD ，AD ⊥CD ，AD ∥BC ，PA =AD =CD =2，BC =3．E 为PD 的中点，点F 在PC 上，且13PF PC =．（Ⅰ）求证：CD ⊥平面PAD ；（Ⅱ）求二面角F –AE –P 的余弦值；（Ⅲ）设点G 在PB 上，且23PG PB =．判断直线AG 是否在平面AEF 内，说明理由．11．（2019天津）如图，AE ⊥平面A B C D ，,CF AE AD BC ∥∥，,1,2AD AB AB AD AE BC ⊥====．（Ⅰ）求证：BF ∥平面ADE ；（Ⅱ）求直线CE 与平面BDE 所成角的正弦值；（Ⅲ）若二面角E BD F --的余弦值为13，求线段CF 的长．。

浙江省《立体几何》高考真题汇编

2014--2018浙江省《立体几何》高考真题汇编2014年浙江理（3）某几何体的三视图（单位：cm）如图所示，则此几何体的表面积是A. 902cm D. 1382cmcm C. 1322cm B. 12922014年浙江理 17、如图，某人在垂直于水平地面ABC的墙面前的点A 处进行射击训练.已知点A到墙面的距离为AB，某目标点P沿墙面上的射击线CM移动，此人为了准确瞄准目标点P，需计算由点A观察点P的仰角θ的大小.若15BCM∠=︒,则tanθ的最大值是=，30AB m=，25AC m(仰角θ为直线AP与平面ABC所成角)2014年浙江理 20.（本题满分15分）如图，在四棱锥A BCDE-中，平面ABC?平面BCDE ,AC=.==,190AB CD∠=∠=︒，2CDE BEDDE BE==,2(Ⅰ)证明：DE?平面ACD;(Ⅱ)求二面角B AD E--的大小.2014年浙江文 2. 设四边形ABCD的两条对角线为AC、BD，则“四边形ABCD为菱形”是“BDAC⊥”的（）A. 充分不必要条件B. 必要不成分条件C. 充要条件D. 既不充分也不必要条件2014年浙江文 3. 某几何体的三视图（单位：cm）若图所示，则该几何体的体积是（）A. 372cmB. 390cmC. 3108cmD. 3138cm2014年浙江文 10.如图，某人在垂直于水平地面ABC 的墙面前的点A 处进行射击训练，已知点A 刀枪面对而距离为AB ，某目标点P 沿墙面上的射线CM 移动，此人为了准确瞄准目标点P ，需计算由点A 观察点P 的仰角θ的大小（仰角θ为直线AP 与平面ABC 所成的角），若m AB 15=，m AC 25=，ο30=∠BCM ，则θtan 的最大值是（） A. 530 B. 1030 C.934 D. 9352014年浙江文6. 设m 、n 是两条不同的直线，α、β是两个不同的平面，则（）A.若n m ⊥，α//n ，则α⊥mB.若β//m ，αβ⊥，则α⊥mC.若β⊥m ，β⊥n ，α⊥n ，则α⊥mD.若n m ⊥，β⊥n ，αβ⊥，则α⊥m2014年浙江文 20、（本小题满分15分）如图，在四棱锥BCDE A -中，平面ABC ⊥平面BCDE ；90CDE BED ∠=∠=︒，2AB CD ==，1DE BE ==，2AC =. （1）证明：AC ⊥平面BCDE ；（2）求直线AE 与平面ABC 所成的角的正切值.2015年浙江理 2．（5分）（2015?浙江）某几何体的三视图如图所示（单位：cm ），则该几何体的体积是（）A ． 8cm 3B ． 12cm 3C ．D ．2015年浙江理 8．（5分）（2015?浙江）如图，已知△ABC，D 是AB 的中点，沿直线CD 将△ACD 折成△A′CD，所成二面角A′﹣CD ﹣B 的平面角为α，则（）A ． ∠A′DB≤αB ． ∠A′DB≥αC ． ∠A′CB≤αD ． ∠A′CB≥α2015年浙江理 13．（4分）（2015?浙江）如图，三棱锥A ﹣BCD 中，AB=AC=BD=CD=3，AD=BC=2，点M ，N 分别是AD ，BC 的中点，则异面直线AN ，CM 所成的角的余弦值是．2015年浙江理 17．（15分）（2015?浙江）如图，在三棱柱ABC ﹣A 1B 1C 1中，∠BAC=90°，AB=AC=2，A 1A=4，A 1在底面ABC 的射影为BC 的中点，D是B 1C 1的中点．（1）证明：A 1D⊥平面A 1BC ；（2）求二面角A 1﹣BD ﹣B 1的平面角的余弦值．2015年浙江文 2．（5分）与2015年浙江理的第2题相同2015年浙江文 7、如图，斜线段与平面所成的角为，为斜足，平面上的动点满足，则点的轨迹是（）A ．直线B ．抛物线B ．C ．椭圆D ．双曲线的一支AB α60o B αP 30∠PAB =o P2015年浙江文 4、设，是两个不同的平面，，是两条不同的直线，且，（）A ．若，则B ．若，则C ．若，则D ．若，则2015年浙江文 18. （本题满分15分）如图，在三棱柱ABC ﹣A 1B 1C 1中，∠BAC=90°，AB=AC=2，A 1A=4，A 1在底面ABC 的射影为BC 的中点，D 是B 1C 1的中点．(1)证明: ；(2)求直线和平面所成的角的正弦值.αβl m l α⊂m β⊂l β⊥αβ⊥αβ⊥l m ⊥//l β//αβ//αβ//l m 11D A BC A ⊥平面1A B 11B C B C2016浙江文 2. 已知互相垂直的平面交于直线l .若直线m ，n 满足m ∥α，n ⊥β，则（）∥l ∥n ⊥l ⊥n2016浙江文 9. 某几何体的三视图如图所示（单位：cm ），则该几何体的表面积是______cm 2,体积是______cm 3.2016浙江文 14．如图，已知平面四边形ABCD ，AB =BC =3，CD =1，AD=，∠ADC =90°．沿直线AC 将△ACD 翻折成△ACD'，直线AC 与BD'所成角的余弦的最大值是______．αβ，52016浙江文 18. （本题满分15分）如图，在三棱台ABC-DEF中，平面BCFE⊥平面ABC，∠ACB=90°，BE=EF=FC=1，BC=2，AC=3.（I）求证：BF ⊥平面ACFD；（II）求直线BD与平面ACFD所成角的余弦值.2016浙江理 2．（5分）已知互相垂直的平面α，β交于直线l，若直线m，n满足m∥α，n⊥β，则（）A．m∥l B．m∥n C．n⊥l D．m⊥n2016浙江理 11．（6分）某几何体的三视图如图所示（单位：cm），则该几何体的表面积是______cm2，体积是______cm3．2016浙江理 14．（4分）如图，在△ABC中，AB=BC=2，∠ABC=120°．若平面ABC外的点P和线段AC上的点D，满足PD=DA，PB=BA，则四面体PBCD 的体积的最大值是______．2016浙江理 17．（15分）如图，在三棱台ABC﹣DEF中，已知平面BCFE ⊥平面ABC，∠ACB=90°，BE=EF=FC=1，BC=2，AC=3，（Ⅰ）求证：BF⊥平面ACFD；（Ⅱ）求二面角B﹣AD﹣F的余弦值．2017年浙江3．某几何体的三视图如图所示（单位：cm），则该几何体的体积（单位：cm3）是（）A．+1B．+3 C．+1 D．+3π2π23π23π22017年浙江 9．如图，已知正四面体D–ABC（所有棱长均相等的三棱锥），P，Q，R分别为AB，BC，CA上的点，AP=PB，，分别记二面角D–PR–Q，D–PQ–R，D–QR–P的平面角为α，β，γ，则（）A．γ<α<βB．α<γ<βC．α<β<γD．β<γ<α2017年浙江 19．（本题满分15分）如图，已知四棱锥P–ABCD，△PAD 是以AD为斜边的等腰直角三角形，，CD⊥AD，PC=AD=2DC=2CB，E 为PD的中点．（Ⅰ）证明：平面PAB；（Ⅱ）求直线CE与平面PBC 所成角的正弦值．2BQ CRQC RA==//BC AD//CE2018年浙江省 3．某几何体的三视图如图所示（单位：cm ），则该几何体的体积（单位：cm 3）是（）A ．2B ．4C ．6D ．82018年浙江省 8．已知四棱锥S ?ABCD 的底面是正方形，侧棱长均相等，E 是线段AB 上的点（不含端点），设SE 与BC 所成的角为θ1，SE 与平面ABCD 所成的角为θ2，二面角S ?AB ?C 的平面角为θ3，则（）A ．θ1≤θ2≤θ3B ．θ3≤θ2≤θ1C ．θ1≤θ3≤θ2D ．θ2≤θ3≤θ12018年浙江省 19．（本题满分15分）如图，已知多面体ABCA 1B 1C 1，A 1A ，B 1B ，C 1C 均垂直于平面ABC ，∠ABC =120°，A 1A =4，C 1C =1，AB =BC =B 1B =2．（Ⅰ）证明：AB 1⊥平面A 1B 1C 1；（Ⅱ）求直线AC 1与平面ABB 1所成的角的正弦值．俯视图正视图。

浙江2019届高三数学汇编专题：4-6月份立体几何小题汇编(PDF版,含解析)

专题：4-6月立体几何小题汇编1.（1904杭州市T17）如图，已知矩形ABCD 中，AB =，1AD =，AF ⊥平面ABC ，且3AF =.E 为线段DC 上一点，沿直线AE 将DAE ∆翻折成'D AE ∆，M 为'BD 的中点.则三棱锥M BCF -体积的最小值是.【解析】我们设空间点P 到空间平面α的距离为d P -α.由于∆BCF 的面积113==1222BCP S BC FB ∆⋅⨯⨯.由于点'D 在空间的轨迹是以点A 为球心，半径为1AD =的部分球面，且3=2A BCF A FB d d --=，由此点'D 到平面BCF 的距离的最小值d D '-BCF ³d A -BCF -AD =12，从而11=24M BCF D BCF d d '--³，从而111=33412M BCF BCF M BCF V S d -∆-⋅³⨯=.2.（1904稽阳联考T9）已知正∆ABC 所在平面垂直平面α，且边BC 在平面α内，过AB 、AC 分别作两个平面β、γ（与正∆ABC 所在平面不重合），则以下结论错误．．的是A.存在平面β与平面γ，使得它们的交线l 和直线BC 所成角为90B.直线BC 与平面γ所成的角不大于60C.平面α与平面β所成锐二面角不小于60D.平面β与平面γ所成锐二面角不小于60【答案】D【解析】如图，设平面β与平面γ和平面α的交线分别为BD 、CD ，平面β与平面γ的交线l 即为直线BD .选项A ，显然当DB DC =时，BC AD ⊥，因此交线l 和直线BC 所成角为90︒，正确；选项B ，根据线面角的最小值可知，直线BC 与平面γ所成角不会超过直线BC 与平面γ内的直线AC 所成角（为60），正确；选项C ，设O 为BC 中点，则AO α⊥,过O 作BD 的垂线，垂足为H ，则平面α与平面β所成锐二面角的平面角为AHO ∠，从而tan AO AO AHO OH OB ∠=³=，从而60AHO ︒∠³，正确；选项D ，当点D 无限靠近线段BC 延长线时平面β与平面γ所成锐二面角就无限趋于零度，错误.3.（1904嘉丽衢联考T8）如图，在直三棱柱ABC -A 1B 1C 1中，AB =AC =1，BC =AA 1=点E ，O 分别是线段1C C ，BC 的中点，1113A F A A = ，分别记二面角F -OB 1-E ，F -OE -B 1，F -EB 1-O 的平面角为α，β，γ，则下列结论正确的是A.γβα>>B.αβγ>>C.αγβ>>D.γαβ>>【答案】D【解析】如图，设点F 在平面11BCC B 内的射影为点'F ，1OEB D 的内心为I ，如图，则点'F 到1OB ，OE ，1EB 的距离为1d ，2d ，3d ，由此可知，213d d d >>，故γαβ>>，选D.4.（1904金华十校T8）如图，AB 是平面α的斜线段，A 为斜足，点C 满足sin sin (0)CAB CBA ∠=∠>λλ，且在平面α内运动，则A.当1λ=时，点C 的轨迹是抛物B.当1λ=时，点C 的轨迹是一条直线C.当2λ=时，点C 的轨迹是椭圆D.当2λ=时，点C 的轨迹是双曲线抛物线【答案】B【解析】由于sin sin (0)CAB CBA BC AC ∠=∠>⇔=λλλ.当1λ=时，点C 的轨迹是线段AB 的中垂面与平面α的交线，因此其轨迹为一条直线；当2λ=时，点C 的轨迹是球面与平面α的相交部分，因此其轨迹为圆.因此选B.5.（1904台州高三T17）已知正方体1111ABCD A B C D -中，E 为BC 的中点，在平面1111A B C D 内，直线l //B 1D 1，设二面角A -l -E 的平面角为q ，当q 取最大值时，cos q =.【答案】2341【解析】如图1，连接11A C 交l 于G ，取CD 中点F ，连接EF 交AC 于M ，易知l EF //，则EF 与l 共面，易证11B D ⊥平面11A ACC ，因为l //B 1D 1，所以l ⊥平面11A ACC ,所以l AG ⊥，l MG ⊥，所以AGM ∠为二面角A l E --的平面角，如图2，问题转化为在直线11A C 上找一点G ，使AGM ∠最大，显然，当点G 在线11A C 段上时，AGM ∠最大，作GH AC ⊥，设正方体的棱长为1，则AM ，设AH x =，HM y =，则324x y +=，4tan tan()11x y AGM AGH AMH xy xy+∠=∠+∠==--，又29232x y xy +⎛⎫≤= ⎪⎝⎭，所以9032xy <≤，当932xy =时，max 242tan 23AGM ∠=，此时AGM ∠最大，23cos 41AGM ∠=.此时x y =，即H 为线段AM 的中点.6.（1904浙江十校T9）已知三棱柱ABC -A 1B 1C 1的所有棱长均相等，侧棱1A B .过1A B 作平面α与A 1B 平行，设平面α与平面11ACC A 的交线为l ，记直线l 与直线所成锐角分别为α，β，γ，则这三个角的大小关系为A.α>β>γB.α=β>γC.γ>β>αD.α>β=γ【答案】B【解析】连接A 1B 交AB 1于D ，取A 1C 1中点E ，则1//DE BC ，所以1//BC 平面AB 1E ，则平面α就是平面AB 1E ，交线l 就是直线AE ，AE 与CA 所成角γ就是AE 与平面ABC 所成角，由最小角定理知γ最小，AB ,BC 与AE 在平面ABC 内的射影CA 所成角相等，所以α=β.故α=β>γ，选B.7.(1905Z20T10)如图，棱长为2的正方体1111ABCD A B C D -的顶点A 在平面α上，棱AA 1与平面α所成的角为60︒，点A 1在平面α上的射影为O ，正方体ABCD -A 1B 1C 1D 1绕直线AA 1旋转，则当直线A 1O 与BC 1所成角最小时，侧面ABB 1A 1在平面α上的投影面积为A. D.2【答案】D【解析】直线1A O 与1BC 所成角最小即直线1A O 与1AD 所成角最小，由共面时夹角最小知此时平面11ABB A 与平面α的二面角大小为60︒，所以侧面11ABB A 在平面α上的投影面积为2.故选项D 正确.8.(1905慈溪中学T8)已知正方体ABCD -A 1B 1C 1D 1中，点E 在棱AB 上运动，点F 在对角线BD 1上运动，设直线EF 与平面ABCD 所成的角为q ，直线EF 与平面BDD 1所成的角为β，则A.q ³βB.q β≤C.存在直线EF ，使得D.存在直线EF ，使得【答案】D【解析】如图，过点F 作FM BD ⊥于点M ，连结EM ，则q =∠FEM ，过点E 作EN BD ⊥于点N ，连结FN ，则EFN β=∠，所以sin FM EF =q ，sin EN EF =β，因为FM 与EN 的大小不确定，故A,B 均不正确；由题知，二面角D 1-AB -D 的大小为45︒，二面角A -BD 1-D 的大小为60︒，由最大角原理知q ≤45︒，所以选项C 不正确；β≤60︒，所以选项D 正确.9.(1905杭州二中中旬T9)在《九章算术》中，将四个面都为直角三角形的四面体称之为鳖臑.如图，在鳖臑P -ABC 中，PA ⊥平面ABC ，AB ⊥BC ，且AP =AC =1，过点A 分别作AE ⊥PB 于点E ，AF ⊥PC 于点F ，连结EF ，当∆AEF 的面积最大值时，tan ∠BPC =A.14B.13C.12【答案】D【解析】由PA ⊥平面ABC ，AB ⊥BC ，AE ⊥PB ，得AE ⊥平面PBC ，AE PC ⊥，因为AF ⊥PC ，所以PC ⊥平面AEF ，且∆AEF 为直角三角形，∠AEF =90︒，AF =，要使∆AEF 的面积最大，即AE ⋅EF 最大，因为AE ⋅EF ≤AE 2+EF 22=14，当且仅当AE =EF =12时等号成立，此时tan ∠BPC =tan ∠EPF =EF PF =故选项D 正确.10.（1905杭州二中T10）如图，三棱锥P ABC -中，PA ⊥平面ABC ，2ABC π∠=,Q 为PA 中点，下列说法中①PBA PCA BPC π∠+∠+∠=；②记二面角P BC A --，Q BC A --的平面角分别为1q ，2q ，122>q q ；③记ABC ∆，QBC ∆，PBC ∆的面积分别为0S ，1S ，2S ，2220214S S S +≤；④cos cos cos PBC PBQ QBC ∠<∠⋅∠.正确说法的个数为A.0B.1C.2D.3【答案】C【解析】特殊化不妨令2AB AC AP ===，则有①5=6PBA PCA BPC ∠+∠+∠≠ππ，错误；②1tan =q ，22tan 2=q ，2tan 2∴q ，122∴<q q ，错误；③02S = ，1S =2S =2220214S S S ∴+≤成立；④1cos2PBC ∠= ，cos PBQ ∠=，cos QBC ∠=，cos cos cos PBC PBQ QBC ∴∠<∠⋅∠成立.11.（1905杭州高级T10）如图，在ABC ∆中，=120ABC ∠︒，2AB BC ==.在AC 边上取一点D （不含A ，C ），将ABD ∆沿线段BD 折起，得到PBD ∆.当平面PBD 垂直平面ABC 时，则P 到平面ABC 距离的最大值为B.2 D.142【答案】B【解析】过A 作AO BD ⊥，则点P 的轨迹是以O 为圆心，AO 为半径的圆.要使点P 到平面ABC 距离最大，只需要AO 最大即可.又=90AOB ∠ 知点O 的轨迹是以AB 为直径的圆，所以2AO AB ≤=.当且仅当BD AB ⊥时.12.（1905湖州中学T9）如图，已知三棱锥D ABC -中，平面DAB ⊥平面ABC ，记二面角D AC B --的平面角为α，直线DA 与平面ABC 所成角为β，直线AB 与平面ADC 所成角为γ，则A.αβγ³³B.βαγ³³C.αγβ³³D.γαβ³³【答案】A【解析】一方面，由二面角最大，可得αβ³；另一方面，直线DA 与平面ABC 所成角=DAB β∠，而DAB ∠可视作直线AB 与平面ADC 内直线AD 所成线线角.由线面角最小得βγ³.所以αβγ³³，选A.13.（1905嘉兴一中T9）如图，在三棱锥S ABC -中，SC ⊥平面ABC ，,E F 是棱SC 的两个三等分点，设二面角S AB F --、F AB E --、E AB C --的平面角分别为α，β，γ，则A.αβγ＞＞B.αγβ＞＞C.γβα＞＞D.γαβ＞＞【答案】C【解析】如图所示：作CD AB ⊥，连接,,ED FD SD ，因此SDF α=∠，EDF β=∠，EDC γ=∠.作出其平面图形，如下图：易得γβα>>，故选C.14.（1905金华一中T10）点P 到图形C 上每一个点的距离的最小值称为点P 到图形C 的距离，那么平面内到定圆C 的距离与到定点A 的距离相等的点的轨迹不可能是A.圆B.椭圆C.双曲线的一支D.直线【答案】D 【解析】设点P 到圆C C 上的距离为PM ,圆的半径为R ，依题得=PM PA ,若A 在圆外，得=PC PA PC PM CM R CA -=-=<，故点P 的轨迹是双曲线的一支；若A 在圆心，2R PA PM ==，故点P 的轨迹是圆；若A 在圆内，PA PC PM PC CM R AC +=+==>，故点P 的轨迹是椭圆；综上答案选D.15.（1905金色联盟T10）已知矩形ABCD ，4AB =，BC =BD 将BCD ∆折成'BC D .若点'C 在平面ABD 上的射影在ABD ∆内部（不包含边界），设二面角'C BD A --的平面角为α，二面角'C AD B --的平面角为β，'C D 与平面ABD 所成的角为γ，则α、β、γ三个角的大小关系是A.>>αγβB.>>βγαC.>>αβγD.>>γβα【答案】C【解析】如图，取AB 的中点G ，连接CG 交BD 于点O ，因为ABAD BC GB =,所以GBC ∆DAB ∆~，故BD CG ⊥，故点C '在底面上的射影E 在OG 上，过E 作AD EF ⊥，连接ED ，可得αOE C ='∠，βFE C ='∠，γDE C ='∠，因为ED EF EO <<，所以EDE C γEF E C βEO E C α'=>'=>'=tan tan tan ，所以>>αβγ.16．（1905宁波十校T10）如图，点P 是平面ABC 外一点，点D 是边AC 上的动点(不含端点)，且满足PD PA =，2PB BA BC ===，3ABC 2π∠=，则四面体P BCD -体积的最大值是 A.12 B.33 C.23 D.233【答案】C【解析】方法一：由2BP BA BC ===知，点P 在以B 为球心，半径为2的球上（除A ，C 外），又由PD PA =知，点P 在线段AD 的中垂面上，故对每一确定的点D ，点P 的轨迹是圆(除与平面ABC 的交点).设球B 的半径是2R =，圆的半径为r ，因为AD 的中垂面α⊥面ABC ，所以中垂面α在面ABC 上的投影是直线MN ，故球心B 到平面α的距离等价于点B 到直线MN 的距离.设(0AN x x =<<，则NH MB x ==-,所以2222222)(4r MP BP BM R x x ==-=-=--+，故点P 到平面ABC 距离为cos r q （q 为MP 与平面ABC 的法向量间的夹角），又因为1=sin 26BCD ABC ACD S S S AD AB x ∆∆∆π-=⋅⋅=，所以11cos 33P BCD BCD V S r x -∆=⋅⋅⋅=q q ，令(0t x =∈，故1=3V =q q ,故2(03V ∈，.故选C.方法二：由2BP BA BC ===知，点P 在以B 为球心，半径为2的球上（除A ，C 外），又由PD PA =知，点P 在线段AD 的中垂面上，即P 的轨迹为球与中垂面的交线圆（即如图以O 为圆心的圆）设CD x =，因AC ==，可得22x x AE ED ===，所以2x OB EF AF AE ==-=，可得OP =，因1=22BCD x S CD BF ∆⋅=，可得112333P BCD BCD V S OP -∆≤⋅⋅=⋅.当x =OP 与平面ABC 垂直时取等号，故选C.17.(1905宁波中学T10)在平面四边形ABCD 中，ABD ∆，BCD ∆均是以BD 为斜边的直角三角形，且2BD AB =，沿直线BD 将ABD ∆翻折成1A BD ∆，设1A D 与BC 所成的角为1q ，二面角1A BD C --的平面角为2q ，则A．对任意的1A ，总有12≤q q B.对任意的1A ，总有12≠q q C.对任意的1A ，总有160≠︒q D.对任意的1A ，总有126sin 4≤q 【答案】D【解析】过A 作AO BD ⊥于O ，在翻折过程中，点1A 的轨迹是以O 为圆心，半径为OA 的圆，这样形成两个圆锥，分别以B ，D 为顶点，底面均为圆O .取BC 中点E ，OE BD ⊥，则AOE ∠是二面角A BD C '--的平面角，于是AOE ∠=2q ，过D 作//DG CB ，则1GDA ∠是1A D 与BC 所成的角，即1GDA ∠=1[15,75]∈︒︒q ，所以选项C 不对，选项D 正确.下面说明选项A，B 不对①当2180=︒q 时，115=︒q ；20=︒q ，175=︒q ，所以选项A 不对.②注意到当2=q 90︒时，1cos =q 2q 从90 变化到0 时，设1A E t =，t 从1，1cos q 随着t 的减小由1cos =q 2cos q 随着t 的减小由0增大到1，根据连续性，存在某个t ，使得12cos cos =q q ，即12=q q ，所以选项B 不对.18.(1905七彩联盟T8)如图，在三棱锥S ABC -中，SC ⊥平面ABC ，E ，F 是棱SC 的两个三等分点，设二面角S AB F --、F AB E --、E AB C --的平面角分别为α、β、γ，则A.αβγ>>B.αγβ>>C.γβα>>D.γαβ>>【答案】C【解析】过C 作CG AB ⊥于G ，连接EG ，FG ，SG ，则SGF ∠=α，FGE ∠=β，EGC ∠=γ，不妨设3SC =，CG t =，则21tan 61tt =+α，21tan 21t t =+β，1tan t =γ，比较分母2262111t t+>+>，可得tan tan tan <<αβγ，于是<<αβγ，所以选C.19.(1905衢州二中二模T8)已知三棱锥BCD A -的所有顶点都在球O 的球面上，⊥AD 平面ABC ，︒=∠120BAC ，2=AD ，若球O 的表面积为π20，则三棱锥BCD A -的体积的最大值为A.33 B.332 C.3 D.32【答案】B【解析】设ABC ∆的外接圆为圆E ，由对称性，球心O 到平面ABC 的距离为112OE AD ==，因球O 的表面积为π20，所以球O ，所以小圆E 的半径为2r =，2sin120BC r =︒=，当AE BC ⊥时，BC 上高的最大值为1，所以ABC ∆，于是三棱锥BCD A -的体积的最大值为3，所以选B.20.（1905绍兴柯桥T8）如图，在棱长都相等的正三棱柱ABC -A 1B 1C 1中，D 是棱CC 1的中点，E 是AA 1上的动点.设AE =x ，随着x 的增大，平面BDE 与底面ABC 所成的锐二面角的平面角是A.增大B.先增大再减小C.减小D.先增大再减小【答案】D【解析】延长DE 、CA 交于点F ，过点C 作BF 的垂线，垂足为H ，易知当 90≤∠CBF 时，CH 逐渐变大，当 90=∠CBF 与CB 重合；当 90>∠CBF 时，CH 逐渐变小；另一方面，设二面角的平面角为θ，则CH DC θ=tan ，所以θ是减小后变大．21.（1905绍兴上虞T8）已知棱长都为2的正三棱柱111ABC A B C -的直观图如图，若正三棱柱111ABC A B C -绕着它的一条侧棱1AA 所在直线旋转，则它的侧视图可以为【答案】B【解析】显然A、D 是错误的，因为在矩形内部会有条AA 1所对应的实线或虚线，C 错误的原因在于矩形的底边应该是2．22.（1905绍兴嵊州T9）如图，已知三棱锥D ABC -，AB =AC =BC =2AD ，AB AD ⊥，记平面DAB ，平面DBC ，平面DAC 与底面ABC 所成的锐二面角分别为1q ，2q ，3q ，则A.123q q q ≤≤B.213q q q ≤≤C.132q q q ≤≤D.312q q q ≤≤【答案】B【解析】过A 作直线AB EF ⊥，且AB AF AE 21==，因为AD AB 2=，所以点D 在底面的投影必然在线段EF （不包活端点）之间，故1H D '2H D '<，记投影为D '，过D '作AC 、BC 的垂线，垂足分别为1H 、2H ，根据二面角的定义可得D A D D θ''=1tan ，22tan H D D D θ''=，13tan H D D D θ''=，由12H D D A H D '>'>'，所以答案是B．23.（1905绍兴一中数学试卷T9）如图，正方形网格纸中的实线图形是一个多面体的三视图，则该多面体各表面所在平面互相垂直的有A．2对B．3对C．4对D．5对【答案】C【解析】由三视图可以得到直观图如下图所示，显然由平面PAB ⊥平面PAD ，平面PCD ⊥平面PAD ，平面ABCD ⊥平面PAD ，因为平面PAB 与平面PCD 的交线与CD 平行，而CD AP ⊥，CD PD ⊥，故∠APD 是平面PAB 与平面PCD 的二面角的平面角，而∠APD =90°，故平面PAB ⊥平面PCD ，所以4对．24.（1905绍兴诸暨T10）如图，ABC ∆中，︒=∠=∠602B A ，点D 在BC 上，30BAD ∠=︒，将ABD ∆沿AD 旋转得到三棱锥B ADC '-，分别B A '，B D '记与平面ADC 所成角为α，β，则α，β的大小关系是A.2αβα<≤ B.23≤≤αβαC.2≤βα，23<≤αβα两种情况都存在D.存在某一位置使得3βα>【答案】A【解析】过点B 作AD 的垂线，垂足为点O ，由题意可得ABD ∆沿AD 旋转，B '的轨迹为圆，半径为BO ，设AC =，易得r =，BA ，2BD =，过点B '作BO 的垂线，垂足为H ，B H '∈，连接AH ，DH ，易得B H '⊥平面ADC ，则B AH α'∠=，βDH B =∠',所以sinB H B A α'=='sin 2B H B H B D β''=='，显然αβ<,因为B H '∈，所以1sin (0,2α∈，sin (0,]2β∈,sin 22sin cos 1sin sin αααββ=³=,所以sin 2sin αβ³，所以2αβ³，故选A．25.（1905温州三模T10）如图，矩形ABCD 中，，BC =，E 是AD 的中点，将ABE ∆沿BE 折起至A BE '∆，记二面角A BE D '--的平面角为α，直线A E '与平面BCDE 所成的角为β，A E '与BC 所成的角为γ，有如下两个命题：①对满足题意的任意的A '的位置，αβπ+≤；②对满足题意的任意的A '的位置，αγπ+≤．则A.命题①和命题②都成立B.命题①和命题②都不成立C.命题①成立，命题②不成立D.命题①不成立，命题②成立【答案】A【解析】①当α为锐角或直角或平角的时候，命题①和命题②都立；②当α为钝角时,连接AC ，交BE 于点F 易得AC EF ⊥，显然A FC α'∠=，A EA γ'∠=，A FA πα'∠=-，过点A '，作A H AF '⊥，垂足为H ，易得A H ABCD '⊥平面，A EH β'∠=，由最大角定理可得线面角A EH '∠≤面面角A FA πα'∠=-，所以βπα≤-，即+βαπ≤，故命题①成立；连接AA '，A F AF '=，A E AE '=，由余弦定理易得线线角A EA '∠≤面面角A FA πα'∠=-，+γαπ≤，故命题②成立．26.（1905学军中学T10）已知α，β为两个不重合的平面，m ，n 为两条不重合的直线，且m αβ= ，n β⊂.记直线m 与直线n 的夹角和二面角m αβ--均为1q ，直线n 与平面α的夹角为2q ，则下列说法正确的是A.若106πq <<,则122q q > B.若164ππq <<,则12tan 2tan q q >C.若143ππq <<,则12sin sin q q < D.若132ππq <<,则123cos cos 4q q >【答案】A【解析】如图，取直线n 上一点A ，过点A 作AH α⊥平面，垂足为H ，过点H 作HC m ⊥，连接AC ，HB ，易得AC m ⊥，所以1ABC ACH q ∠=∠=，2ABH q ∠=，由最小角定理可得线线角1q ³线面角2q ，故可以排除选项C；所以1sin AC AH AB AC q ==,2sin AH ABq =，则221sin sin q q =，2121sin 22sin cos 2sin sin q q q q q ==因为106πq <<，12sin (0,1)q ∈(0,1)，所以21sin 21sin q q <，而210223πq q <<<，所以必然有122q q >，故选项A 正确，同理可将B、D 选项2q 转换成1q ，发现无法比较大小．27.（1905浙江五校T10）如图，在三棱锥S ABC -中，SC AC =,SCB q ∠=,ACB πq ∠=-,二面角S BC A --的平面角为α，则A.αq ³B.SCA α∠³C.SBA α∠≤D.SBA α∠³（第8题图）SACB【答案】B【解析】由题意得三棱锥S ABC -可看成SBC ∆绕着ABS ∆的中线BC 翻折得到（与2015年浙江理科T8相似）取特殊值=0=ααπ，可快速排除A、C、D 选项过点S 作BC 的垂线交BC 于点D ，交AB 于点G ，连接SS '，则S DG α'∠=，S D SD '=，S C SC '=，SC SD ³，易得S DS S CS ''∠³∠所以S CA παπ'-³-∠即SCA α∠³，故选B.28.(1905镇海中学T17)已知棱长为4的正方体1111ABCD A B C D -中，点M 为1BC 的中点，点P 为11A CD ∆上一动点，且PD PM =，则点P 的轨迹长度为．【答案】【解析】由题知，点P 为DM 中垂面与11A CD ∆的交线，轨迹为线段．如图，分别作DM ，1DC ，11A D 中点E ，F ，G ．则1BDC ∆为等边三角形，1DM BC ⊥,则DM EF ⊥；在BGM ∆中，GD GM =，则DM GE ⊥.则点P 的轨迹为112GF AC ==．29．（1905知行联盟T9）如图，在ABC ∆中，36A ︒∠=，AD DB BC ==，点E 为线段AB 上一点，将ADE ∆绕DE 翻折，若在翻折过程中存在某个位置，使得AE CD ⊥，记q 为ADE ∠的最小值，则A.(15,20]q ︒︒∈ B.(20,25]q ︒︒∈C.(25,30]q ︒︒∈ D.(30,35]q ︒︒∈【答案】C【解析】如图，此题为翻折圆锥模型，AE ，CD 形成最大角为如图'A FA ∠，只需'90A FA ︒∠³即可.即''90(54)(90)AA F A AF ADE ADE ︒︒︒³∠+∠=-∠+-∠，即27ADE ︒∠³，即=27(25,30]q ︒︒︒∈．30．（1906镇海中学T15）已知二面角l αβ--为60︒，在其内部取点A ，在半平面α，β内分别取点B ，C ．若A 到l 的距离为1，则ABC ∆周长最小值为．【解析】如作图，点A 在以l 为轴，半径为1的圆柱面上，垂直l 作截面，得到右图，则此题转化为“将军饮马”模型之一，分别以两边m ，n 为对称轴作A 的对称点D ，E ，连接,D E 分别交m ，n 于B ，C ，则此时ABC ∆周长最小为DE ，因为60DOE∠=︒，BOC∠=︒，则120所以DE=。

2004—2019浙江高考真题《立体几何》汇编

2004−2019浙江高考真题《立体几何》汇编三视图1. （2009浙江文12理12）某几何体的三视图（单位：cm ）如图所示，则此几何体的体积是 3cm ．2. （2010浙江文8）某几何体的三视图（单位：cm ）如图所示，则此几何体的体积是（）A ．3352cm 3B ．3320cm 3C ．3224cm 3D ．3160cm 33. （2010浙江理12）若某几何体的三视图（单位：cm ）如图所示，则此几何体的体积是 3cm ．侧视图俯视图正视图侧视图俯视图侧视图俯视图4. （2011浙江文7）某几何体的三视图如图所示，则这个几何体的直观图可以是（）5. （2011浙江理3）某几何体的三视图如图所示，则这个几何体的直观图可以是（）6. （2012浙江文3）已知某三棱锥的三视图（单位：cm ）如图所示，则该三棱锥的体积是（）A ．13cmB ．23cmC ．33cmD ．63cmDC BA侧视图俯视图正视图DCB A 侧视图俯视图正视图侧视图俯视图正视图7. （2012浙江理11）已知某三棱锥的三视图（单位：cm ）如图所示，则该三棱锥的体积等于 3cm ．8. （2013浙江文5）已知某几何体的三视图（单位：cm ）如图所示，则该几何体的体积是（）A ．1083cmB ．1003cmC ．923cmD ．843cm9. （2013浙江理12）若某几何体的三视图（单位：cm ）如图所示，则此几何体的体积等于 3cm ．侧视图俯视图正视图俯视图侧视图正视图侧视图正视图3410. （2014浙江文3）某几何体的三视图（单位：cm ）如图所示，则该几何体的体积是（）A ．723cmB ．903cmC ．1083cmD ．1383cm11. （2014浙江理3）某几何体的三视图（单位：cm ）如图所示，则该几何体的表面积是（）A ．902cmB ．1292cmC ．1322cmD ．1382cm12. （2015浙江文2理2）某几何体的三视图如图所示（单位：cm ），则该几何体的体积是（）A ．83cmB ．123cmC ．3233cmD ．403cm俯视图侧视图正视图俯视图侧视图正视图侧视图正视图13. （2016浙江理11）某几何体的三视图如图所示（单位：cm ），则该几何体的表面积是 2cm ，体积是 3cm ．14. （2016浙江文9）某几何体的三视图如图所示（单位：cm ），则该几何体的表面积是 2cm ，体积是 3cm ．15. （2017浙江3）某几何体的三视图如图所示（单位：cm ），则该几何体的体积（单位：cm 3）是（）A ．12π+B ．32π+C ．312π+D ．332π+俯视图正视图316. （2018浙江3）某几何体的三视图如图所示（单位：cm ），则该几何体的体积（单位：3cm ）是（）A ．2B ．4C ．6D ．817. （2019浙江4）祖暅是我国南北朝时代的伟大科学家，他提出的“幂势既同，则积不容异”称为祖暅原理，利用该原理可以得到柱体的体积公式V Sh 柱体，其中S 是柱体的底面积，h 是柱体的高．若某柱体的三视图如图所示（单位：cm ），则该柱体的体积（单位：3cm ）是（） A ．158B ．162C ．182D ．324俯视图正视图俯视图侧视图正视图点、直线、平面位置关系18. （2005浙江文7理6）设α，β为两个不同的平面，l ，m 为两条不同的直线，且l α⊂，m β⊂．有如下两个命题：①若αβ∥，则l m ∥；②若l m ⊥，则αβ⊥．那么（） A ．①是真命题，②是假命题 B ．①是假命题，②是真命题C ．①②都是真命题D ．①②都是假命题19. （2007浙江文7理6）若P 是两条异面直线l ，m 外的任意一点，则（）A ．过点P 有且仅有一条直线与l ，m 都平行B ．过点P 有且仅有一条直线与l ，m 都垂直C ．过点P 有且仅有一条直线与l ，m 都相交D ．过点P 有且仅有一条直线与l ，m 都异面20. （2008浙江文9）对两条不相交的空间直线a 与b ，必存在平面α，使得（）A ．a α⊂，b α⊂B ．a α⊂，b α∥C ．a α⊥，b α⊥D ．a α⊂，b α⊥21. （2009浙江文4）设α，β是两个不同的平面，l 是一条直线，以下命题正确的是（）A ．若l α⊥，αβ⊥，则l β⊂B ．若l α∥，αβ∥，则l β⊂C ．若l α⊥，αβ∥，则l β⊥D ．若l α⊥，αβ⊥，则l β⊥22. （2010浙江理6）设l ，m 是两条不同的直线，α是一个平面，则下列命题正确的是（）A ．若l m ⊥，m α⊂，则l α⊥B ．若l α⊥，l m ∥，则m α⊥C ．若l α∥，m α⊂，则l m ∥D ．若l α∥，m α∥，则l m ∥23. （2011浙江文4）若直线l 不平行于平面α，且l α⊄，则（）A ．α内的所有直线与l 异面B ．α内不存在与l 平行的直线C ．α内存在唯一的直线与l 平行D ．α内的直线与l 都想交24. （2011浙江理4）下列命题中错误的是（）A ．如果αβ平面⊥平面，那么平面α内一定存在直线平行于平面βB ．如果αβ平面不垂直于平面，那么平面α内一定不存在直线垂直于平面βC ．如果αγ平面⊥平面，βγ平面⊥平面，l αβ=，那么l γ⊥平面D ．如果αβ平面⊥平面，那么平面α内所有直线都垂直于平面β25. （2012浙江文5）设直线l 是直线，α，β是两个不同的平面．（）A ．若l α∥，l β∥，则αβ∥B ．若l α∥，l β⊥，则αβ⊥C ．若αβ⊥，l α⊥，则l β⊥D ．若αβ⊥，l α∥，则l β⊥26. （2013浙江文4）设m ，n 是两条不同的直线，α，β是两个不同的平面．（）A ．若m α∥，n α∥，则m n ∥B ．若m α∥，m β∥，则αβ∥C ．若m n ∥，m α⊥，则n α⊥D ．若m α∥，αβ⊥，则m β⊥27. （2014浙江文6）设m ，n 是两条不同的直线，α，β是两个不同的平面．（）A ．若m n ⊥，n α∥，则m α⊥B ．若m β∥，βα⊥，则m α⊥C ．若m β⊥，n β⊥，n α⊥，则m α⊥D ．若m n ⊥，n β⊥，βα⊥，则m α⊥28. （2015浙江文4）设α，β是两个不同的平面，l ，m 是两条不同的直线，且l α⊂，m β⊂．（）A ．若l β⊥，则αβ⊥B ．若αβ⊥，则l m ⊥C ．若l β∥，则αβ∥D ．若αβ∥，则l m ∥29. （2016浙江文2理2）已知互相垂直的平面α，β交于直线l ，若直线m ，n 满足m α∥，n β⊥，则（） A ．m l ∥ B ．m n ∥C ．n l ⊥D ．m n ⊥30. （2018浙江6）已知平面α，直线m ，n 满足m α⊄，n α⊂，则“m n ∥”是“m α∥”的（）A ．充分不必要条件B ．必要不充分条件C ．充分必要条件D ．既不充分也不必要条件小题31. （2004浙江文15）已知α平面⊥β平面，l αβ=，P 是空间一点，且P 到平行α，β的距离分别是1，2，则点P 到l 的距离为．32. （2004浙江理16）已知平面α和平面β相交于直线l ，P 是空间一点，P A ⊥α，垂足为A ，PB ⊥β，垂足为B ，且1PA =，2PB =，若点A 在β内的射影与点B 在α内的射影重合，则点P 到l 的距离为．33. （2004浙江文10理10）如图，在正三棱柱111ABC A B C -中，已知1AB =，D 在棱1BB 上，且1BD =，若AD 与平面11AA C C 所成的角为α，则sin α=（） ABCDDB 1A 1C 1CBA34. （2005浙江文12理12）设M ，N 是直角梯形ABCD 两腰的中点，DE ⊥AB 于E （如图）．现将△ADE沿DE 折起，使二面角A DE B --为45°，此时点A 在平面BCDE 内的射影为点B ，则M ，N 的连线与AE 所成角的大小等于．35. （2006浙江文8）如图，正三棱柱111ABC A B C -的各棱长都为2，E ，F 分别是AB ，11A C 的中点，则EF 的长是（） A ．2BCD36. （2006浙江理9）如图，O 是半径为1的球的球心，点A ，B ，C 在球面上，OA ，OB ，OC 两两垂直，E ，F 分别是大圆弧AB 与AC 的中点，则点E ，F 在该球面上的球面距离是（） A ．4π B ．3π C ．2π D．4B 1C 1A 1FE CBA37. （2006浙江文14）如图，正四面体ABCD 的棱长为1，平面α过棱AB ，且CD α∥，则正四面体上的所有点在平面α内的射影构成的图形面积是．38. （2006浙江理14）正四面体ABCD 的棱长为1，棱AB ∥平面α，则正四面体上的所有点在平面α内的射影构成的图形面积的取值范围是．39. （2007浙江文17理16）已知点O 在二面角AB αβ--的棱上，点P 在α内，且45POB ∠=︒．若对于β内异于O 的任意一点Q ，都有45POQ ∠≥︒，则二面角AB αβ--的大小是．40. （2008浙江文15理14）如图，已知球O 的面上四点A ，B ，C ，D ，DA ⊥平面ABC ，AB ⊥BC ，DA AB BC ===O 的体积等于．BDACαBDACαDBCA41. （2008浙江理10）如图，AB 是平面α的斜线段．．．，A 为斜足．若点P 在平面α内运动，使得△ABP 的面积为定值，则动点P 的轨迹是（） A ．圆B ．椭圆C ．一条直线D ．两条平行直线42. （2009浙江理5）在三棱柱111ABC A B C -中，各棱长相等，侧棱垂直于底面，点D 是侧面11BB C C 的中心，则AD 与平面11BB C C 所成角的大小是（） A ．30° B ．45°C ．60°D ．90°43. （2009浙江理17）如图，在长方形ABCD 中，2AB =，1BC =，E 为DC 的中点，F 为线段EC （端点除外）上一动点，现将AFD △沿AF 折起，使平面ABD ⊥平面ABC ，在平面ABD 内过点D 作DK AB ⊥，K 为垂足，设AK t =，则t 的取值范围是．PABαKFDCBA44. （2012浙江理10）已知矩形ABCD ，1AB =，BC ．将△ABD 沿矩形的对角线BD 所在的直线进行翻折，在翻折过程中，（）A ．存在某个位置，使得直线AC 与直线BD 垂直B ．存在某个位置，使得直线AB 与直线CD 垂直C ．存在某个位置，使得直线AD 与直线BC 垂直D ．对于任意位置，三对直线“AC 与BD ”，“AB 与CD ”，“AD 与BC ”均不垂直45. （2013浙江理10）在空间中，过点A 作平面π的垂线，垂足为B ，记()B f A π=．设α，β是两个不同的平面，对空间任意一点P ，()1Q f f P βα=⎡⎤⎣⎦，()2Q f f P αβ⎡⎤=⎣⎦，恒有12PQ PQ =，则（） A ．α平面与β平面垂直 B ．α平面与β平面所成的（锐）二面角为45° C ．α平面与β平面平行 D ．α平面与β平面所成的（锐）二面角为60°46. （2014浙江文10理17）如图，某人在垂直于水平地面ABC 的墙面前的点A 处进行射击训练．已知点A 到墙面的距离为AB ，某目标点P 沿墙面上的射线CM 移动，此人为了准确瞄准目标点P ，需计算由点A 观察点P 的仰角θ的大小．若15m AB =，25m AC =，30BCM ∠=︒，则tan θ的最大值是．（仰角θ为直线AP 与平面ABC 所成角）PMCB A47. （2015浙江文7）如图，斜线段AB 与平面α所成的角为60︒，B 为斜足，平面α上的动点P 满足30PAB ∠=︒，则点P 的轨迹是（）A ．直线B ．抛物线C ．椭圆D ．双曲线的一支48. （2015浙江理8）如图，已知ABC △，D 是AB 的中点，沿直线CD 将ACD △翻折成A CD '△，所成（） A ．A DB α'∠≤B ．A DB α'∠≥C ．A CB α'∠≤D ．A CB α'∠≥49. （2015浙江理13）如图，在三棱锥A BCD -中，3AB AC BD CD ====，2AD BC ==，点M ，N 分别为AD ，BC 的中点，则异面直线AN ，CM 所成的角的余弦值是．αPBAA'DCBAMNDCBA50. （2016浙江文14）如图，已知平面四边形ABCD ，3AB BC ==，1CD =，AD =90ADC ∠=︒．沿直线AC 将△ACD 翻折成△ACD'，直线AC 与BD'所成角的余弦的最大值是．51. （2016浙江理14）如图，在△ABC 中，2AB BC ==，120ABC ∠=︒．若平面ABC 外的点P 和线段AC 上的点D ，满足PD DA =，PB BA =，则四面体PBCD 的体积的最大值是．52. （2017浙江9）如图，已知正四面体D ABC -（所有棱长均相等的三棱锥），P ，Q ，R 分别为AB ，BC ，CA 上的点，AP PB =，2BQ CRQC RA==，分别记二面角D PR Q --，D PQ R --，D QR P --的平面角为α，β，γ，则（） A ．γαβ<<B ．αγβ<<C ．αβγ<<D ．βγα<<D'DC APDCBARCQBP A D53. （2018浙江8）已知四棱锥S ABCD -的底面是正方形，侧棱长均相等，E 是线段AB 上的点（不含端点），设SE 与BC 所成的角为1θ，SE 与平面ABCD 所成的角为2θ，二面角S AB C --的平面角为3θ，则（） A ．123θθθ≤≤ B ．321θθθ≤≤ C ．132θθθ≤≤ D ．231θθθ≤≤54. （2019浙江8）设三棱锥V ABC -的底面是正三角形，侧棱长均相等，P 是棱VA 上的点（不含端点）．记直线PB 与直线AC 所成的角为α，直线PB 与平面ABC 所成的角为β，二面角P AC B --的平面角为γ，则（） A ．,βγαγ<< B ．,βαβγ<< C ．,βαγα<< D ．,αβγβ<<大题55. （2004浙江文19）如图，已知正方形ABCD 和矩形ACEF所在的平面互相垂直，AB =1AF =，M 是线段EF 的中点．（1）求证：AM ∥平面BDE ；（2）求证：AM ⊥平面BDF ；（3）求二面角A DF B --的大小．M FEDCBA56. （2004浙江理19）如图，已知正方形ABCD 和矩形ACEF所在的平面互相垂直，AB =1AF =，M 是线段EF 的中点．（1）求证：AM ∥平面BDE ；（2）求二面角A DF B --的大小；（3）试在线段AC 上确定一点P ，使得PF 与BC 所成的角是60︒．57. （2005浙江文18）如图，在三棱锥P ABC -中，AB BC ⊥，12AB BC PA ==，点O ，D 分别是AC ，PC 的中点，OP ⊥底面ABC ．（1）求证：OD ∥平面PAB ；（2）求直线OD 与平面PBC 所成角的大小．58. （2005浙江理18）如图，在三棱锥P ABC -中，AB BC ⊥，AB BC kPA ==，点O ，D 分别是AC ，PC 的中点，OP ⊥底面ABC ．（1）求证：OD ∥平面PAB ；（2）当12k =，求直线PA 与平面PBC 所成角的大小；（3）当k 取何值时，O 在平面PBC 内的射影恰好为PBC △的重心？MFEDCBA59. （2006浙江文17）如图，在四棱锥P ABCD -中，底面为直角梯形，AD BC ∥，90BAD ∠=︒，PA ⊥底面ABCD ，且2PA AD AB BC ===，M ，N 分别为PC ，PB 的中点．（1）求证：PB DM ⊥；（2）求BD 与平面ADMN 所成角．60. （2006浙江理17）如图，在四棱锥P ABCD -中，底面为直角梯形，AD BC ∥，90BAD ∠=︒，PA ⊥底面ABCD ，且2PA AD AB BC ===，M ，N 分别为PC ，PB 的中点．（1）求证：PB DM ⊥；（2）求CD 与平面ADMN 所成的角．61. （2007浙江理19）在如图所示的几何体中，EA ⊥平面ABC ，DB ⊥平面ABC ，AC ⊥BC ，且2AC BC BD AE ===，M 是AB 的中点．（1）求证：CM EM ⊥；（2）求CM 与平面CDE 所成的角．62. （2007浙江文20）在如图所示的几何体中，EA ⊥平面ABC ，DB ⊥平面ABC ，AC BC ⊥，且2AC BC BD AE ===，M 是AB 的中点．（1）求证：CM EM ⊥；（2）求DE 与平面EMC 所成角的正切值．63. （2008浙江文20理18）如图，矩形ABCD 和梯形BEFC 所在平面互相垂直，BE ∥CF ，90BCF CEF ∠=∠=︒，AD ，2EF =．（1）求证：AE DCF ∥平面；（2）当AB 的长为何值时，二面角A EF C --的大小为60°？64. （2009浙江文19）如图，DC ⊥平面ABC ，EB DC ∥，22AC BC EB DC ====，120ACB ∠=︒，P ，Q 分别为AE ，AB 的中点．（1）证明：PQ ACD ∥平面；（2）若AD 与平面ABE 所成角的正弦值．FEDCBA QPCDEBA65. （2009浙江理20）如图，平面PAC ⊥平面ABC ，ABC △是以AC 为斜边的等腰直角三角形，E ，F ，O 分别为P A ，PB ，AC 的中点，16AC =，10PA PC ==．（1）设G 是OC 的中点，证明：FG ∥平面BOE ；（2）证明：在ABO △内存在一点M ，使FM ⊥平面BOE ，并求点M 到OA ，OB 的距离．66. （2010浙江文20）如图，在平行四边形ABCD 中，2AB BC =，120ABC ∠=︒，E 为线段AB 的中点，将ADE △沿直线DE 翻折成A DE '△，使平面A DE '⊥平面BCD ，F 为线段A C '的中点．（1）求证：BF ∥平面A DE '；（2）设M 为线段DE 的中点，求直线FM 与平面A DE '所成角的余弦值．67. （2010浙江理20）如图，在矩形ABCD 中，点E ，F 分别在线段AB ，AD 上，243AE EB AF FD ====，沿直线EF 将AEF △翻折成A EF '△，使平面A EF '⊥平面BEF ．（1）求二面角A FD C '--的余弦值；（2）点M ，N 分别在线段FD ，BC 上，若沿直线MN 将四边形MNCD 向上翻折，使C 与A '中和，求线段FM 的长．GF EPOCBAA'MFED CBANM A'F EDCB A68. （2011浙江文20）如图，在三棱锥P ABC -中，AB AC =，D 为BC 的中点，PO ⊥平面ABC ，垂足O 落在线段AD 上．（1）证明：AP BC ⊥；（2）已知8BC =，4PO =，3AO =，2OD =，求二面角B AP C --的大小．69. （2011浙江理20）如图，在三棱锥P ABC -中，AB AC =，D 为BC 的中点，PO ⊥平面ABC ，垂足O 落在线段AD 上．已知8BC =，4PO =，3AO =，2OD =．（1）证明：AP BC ⊥；（2）在线段AP 上是否存在点M ，使得二面角A MC B --为直二面角？若存在，求出AM 的长；若不存在，请说明理由．70. （2012浙江文20）如图，在侧棱垂直底面的四棱柱1111ABCD A B C D -中，AD ⊥AB，AB =2AD =，4BC =，12AA =，E 是1DD 的中点，F 是平面11B C E 与直线1AA 的交点．（1）证明：（i ）11EF A D ∥；（ii ）111BA B C EF ⊥平面；（2）求1BC 与11B C EF 平面所成角的正弦值．OPDCBAOPDCBAD 1C 1B 1A 1EF B D CA71. （2012浙江理20）如图，在四棱锥P ABCD -中，底面是边长为的菱形，120BAD ∠=︒，且PA ABCD ⊥平面，PA =，M ，N 分别为PB ，PD 的中点．（1）证明：MN ∥平面ABCD ；（2）过点A 作AQ PC ⊥，垂足为点Q ，求二面角A MN Q --的平面角的余弦值．72. （2013浙江文20）如图，在四棱锥P ABCD -中，P A ⊥平面ABCD ，2AB BC ==，AD CD ==PA 120ABC ∠=︒．G 为线段PC 上的点．（1）证明：BD ⊥平面P AC ；（2）若G 为PC 的中点，求DG 与平面APC 所成的角的正切值；（3）若G 满足PC ⊥平面BGD ，求PGGC的值．73. （2013浙江理20）如图，在四面体A BCD -中，AD ⊥平面BCD ，BC CD ⊥，2AD =，BD =．M是AD 的中点，P 是BM 的中点，点Q 在线段AC 上，且3AQ QC =．（1）证明：PQ BCD ∥平面；（2）若二面角C BM D --的大小为60°，求BDC ∠的大小．QMNDABPGDB APQPMDBA74. （2014浙江文20）如图，在四棱锥A BCDE -中，平面ABC ⊥平面BCDE ，90CDE BED ∠=∠=︒，2AB CD ==，1DE BE ==，AC =（1）证明：AC BCDE ⊥平面；（2）求直线AE 与平面ABC 所成角的正切值．75. （2014浙江理20）如图，在四棱锥A BCDE -中，平面ABC ⊥平面BCDE ，90CDE BED ∠=∠=︒，2AB CD ==，1DE BE ==，AC（1）证明：DE ACD ⊥平面；（2）求二面角B AD E --的大小．76. （2015浙江文18）如图，在三棱柱111ABC A B C -中，90BAC ∠=︒，2AB AC ==，14AA =，1A 在底面ABC 的射影为BC 的中点，D 为11B C 的中点．（1）证明：11A D A BC ⊥平面；（2）求直线1A B 和平面11BB C C 所成的角的正弦值．BED CABED CAC 1B 1A 1DC BA77. （2015浙江理17）如图，在三棱柱111ABC A B C -中，90BAC ∠=︒，2AB AC ==，14AA =，1A 在底面ABC 的射影为BC 的中点，D 为11B C 的中点．（1）证明：11A D A BC ⊥平面；（2）求二面角11A BD B --的平面角的余弦值．78. （2016浙江文18）如图，三棱台ABC DEF -中，平面BCFE ⊥平面ABC ，90ACB ∠=︒，1BE EF FC ===，2BC =，3AC =．（1）求证：BF ⊥平面ACFD ；（2）求直线BD 与平面ACFD 所成角的余弦值．79. （2016浙江理17）如图，在三棱台ABC DEF -中，平面BCFE ⊥平面ABC ，90ACB ∠=︒，1BE EF FC ===，2BC =，3AC =．（1）求证：BF ⊥平面ACFD ；（2）求二面角B AD F --的平面角的余弦值．C 1B 1A 1DC BA80. （2017浙江19）如图，已知四棱锥P −ABCD ，△P AD 是以AD 为斜边的等腰直角三角形，BC ∥AD ，CD ⊥AD ，22PC AD DC CB ===，E 为PD 的中点．（1）证明：CE ∥平面P AB ；（2）求直线CE 与平面PBC 所成角的正弦值．81. （2018浙江19）如图，已知多面体111ABCA B C ，1A A ，1B B ，1C C 均垂直于平面ABC ，120ABC ∠=︒，14A A =，11C C =，12AB BC B B ===．（1）证明：1111AB A B C ⊥平面；（2）求直线1AC 与平面1ABB 所成的角的正弦值．82. （2019浙江19）如图，已知三棱柱111ABC A B C -，平面11A ACC ⊥平面ABC ，90ABC ∠=︒，30BAC ∠=︒，11A A AC AC ==，E ，F 分别是AC ，11A B 的中点．（1）证明：EF BC ⊥；（2）求直线EF 与平面1A BC 所成角的余弦值．ED CBAPC 1B 1A 1CBAC 1B 1A 1FECBA。

浙江高考2018、2019

(2018)3．某几何体的三视图如图所示(单位：cm)，则该几何体的体积(单位：cm3)是() CA．2 B．4C．6 D．8(2019)4．祖暅是我国南北朝时代的伟大科学家.他提出的“幂势既同，则积不容易”称为祖暅原理，利用该原理可以得到柱体体积公式V柱体=Sh，其中S是柱体的底面积，h是柱体的高.若某柱体的三视图如图所示，则该柱体的体积是（）BA．158 B．162C．182 D．32(2018)6．已知平面α，直线m，n满足m⊄α，n⊂α，则“m∥n”是“m∥α”的() A A．充分不必要条件B．必要不充分条件C．充要条件D．既不充分也不必要条件(2018)8．已知四棱锥S－ABCD的底面是正方形，侧棱长均相等，E是线段AB上的点(不含端点)，设SE与BC所成的角为θ1，SE与平面ABCD所成的角为θ2，二面角S－AB－C ，则() D的平面角为θA．θ1≤θ2≤θ3B．θ3≤θ2≤θ1C．θ1≤θ3≤θ2D．θ2≤θ3≤θ1(2019)8．设三棱锥V-ABC的底面是正三角形，侧棱长均相等，P是棱VA上的点（不含端点），记直线PB与直线AC所成角为α，直线PB与平面ABC所成角为β，二面角P-AC-B 的平面角为γ，则（）BA．β<γ，α<γB．β<α，β<γC．β<α，γ<αD．α<β，γ<β(2018)19.如图，已知多面体ABCA 1B 1C 1，A 1A ，B 1B ，C 1C 均垂直于平面ABC ，∠ABC ＝120°，A 1A ＝4，C 1C ＝1，AB ＝BC ＝B 1B ＝2.(1)证明：AB 1⊥平面A 1B 1C 1；(2)求直线AC 1与平面ABB 1所成的角的正弦值．.(2019)19.（本小题满分15分）如图，已知三棱柱111ABC A B C -，平面11A AC C ⊥平面ABC ,90ABC ∠=︒，1130,,,BAC A A AC AC E F ∠=︒==分别是AC ，A 1B 1的中点.（1）证明：EF BC ⊥；（2）求直线EF 与平面A 1BC 所成角的余弦值.35(2019)12．已知圆C 的圆心坐标是(0,)m ，半径长是r .若直线230x y -+=与圆相切于点(2,1)A --，则m =_____，r =______ .-(2018)2．双曲线－y 2＝1的焦点坐标是( )B A ．(－，0)，(，0) B ．(－2,0)，(2,0) C ．(0，－)，(0，)D ．(0，－2)，(0,2)(2019)2．渐近线方程为x ±y =0的双曲线的离心率是CA ．2B ．1CD ．2(2018)17．已知点P(0,1)，椭圆＋y2＝m(m＞1)上两点A，B满足＝2，则当m＝________时，点B横坐标的绝对值最大．5(2019)15．已知椭圆22195x y+=的左焦点为F，点P在椭圆上且在x轴的上方，若线段PF的中点在以原点O为圆心，OF为半径的圆上，则直线PF的斜率是(2018)21.如图，已知点P是y轴左侧(不含y轴)一点，抛物线C：y2＝4x上存在不同的两点A，B满足P A，PB的中点均在C上．(1)设AB中点为M，证明：PM垂直于y轴；(2)若P是半椭圆x2＋＝1(x＜0)上的动点，求△P AB面积的取值范围．(1)解设P(x0，y0)，A，B.因为P A，PB的中点在抛物线上，所以y1，y2为方程2＝4·，即y2－2y 0y＋8x0－＝0的两个不同的实根．所以y1＋y2＝2y0，所以PM垂直于y轴．(2)解由(1)可知所以|PM|＝(＋)－x＝－3x0，|y1－y2|＝2. 所以△P AB的面积S△P AB＝|PM|·|y1－y2|＝.因为＋＝1(－1≤x 0＜0)，所以－4x0＝－4－4x0＋4∈[4,5]，所以△P AB面积的取值范围是.(2019)21.（本小题满分15分）如图，已知点(10)F ，为抛物线22(0)y px p =>，点F 为焦点，过点F 的直线交抛物线于A 、B 两点，点C 在抛物线上，使得ABC △的重心G 在x 轴上，直线AC 交x 轴于点Q ，且Q 在点F 右侧.记,AFG CQG △△的面积为12,S S . （1）求p 的值及抛物线的标准方程；（2）求12S S 的最小值及此时点G 的坐标. （1）由题意得12p=，即p =2.所以，抛物线的准线方程为x =−1. （2）设()()(),,,,,A A B B c c A x y B x y C x y ，重心(),G G G x y .令2,0A y t t =≠，则2A x t =.由于直线AB 过F ，故直线AB 方程为2112t x y t-=+，代入24y x =，得 ()222140t y y t ---=，故24B ty =-，即2B y t =-，所以212,B tt ⎛⎫- ⎪⎝⎭.又由于()()11,33G A B c G A B c x x x x y y y y =++=++及重心G 在x 轴上，故220c t y t -+=，得242211222,2,,03t t C t t G t t t ⎛⎫⎛⎫-+⎛⎫⎛⎫-- ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭. 所以，直线AC 方程为()222y t t x t -=-，得()21,0Q t -. 由于Q 在焦点F 的右侧，故22t >.从而4224221244242222211|2|||322221222211|||1||2|23A ct t t FG y t S t t t t t S t t QG y t t t t -+-⋅⋅--====--+--⋅--⋅-. 令22m t =-，则m >0，1221222134324S m S m m m m =-=-=+++++….当m =12SS取得最小值1+，此时G （2，0）．(2019)12．已知圆C 的圆心坐标是(0,)m ，半径长是r .若直线230x y -+=与圆相切于点(2,1)A --，则m =_____，r =______.-(2018)3．某几何体的三视图如图所示(单位：cm)，则该几何体的体积(单位：cm 3)是( ) C A ．2 B ．4 C ．6D ．8(2019)4．祖暅是我国南北朝时代的伟大科学家.他提出的“幂势既同，则积不容易”称为祖暅原理，利用该原理可以得到柱体体积公式V 柱体=Sh ，其中S 是柱体的底面积，h 是柱体的高.若某柱体的三视图如图所示，则该柱体的体积是（）BA ．158B ．162C ．182D ．32(2018)6．已知平面α，直线m ，n 满足m ⊄α，n ⊂α，则“m ∥n ”是“m ∥α”的( ) A A ．充分不必要条件 B ．必要不充分条件 C ．充要条件 D ．既不充分也不必要条件(2018)8．已知四棱锥S －ABCD 的底面是正方形，侧棱长均相等，E 是线段AB 上的点(不含端点)，设SE 与BC 所成的角为θ1，SE 与平面ABCD 所成的角为θ2，二面角S －AB －C 的平面角为θ3，则( ) D A ．θ1≤θ2≤θ3 B ．θ3≤θ2≤θ1 C ．θ1≤θ3≤θ2D ．θ2≤θ3≤θ1(2019)8．设三棱锥V -ABC 的底面是正三角形，侧棱长均相等，P 是棱VA 上的点（不含端点），记直线PB 与直线AC 所成角为α，直线PB 与平面ABC 所成角为β，二面角P -AC -B 的平面角为γ，则（）B A ．β<γ，α<γ B ．β<α，β<γ C ．β<α，γ<α D ．α<β，γ<β(2018)19.如图，已知多面体ABCA 1B 1C 1，A 1A ，B 1B ，C 1C 均垂直于平面ABC ，∠ABC ＝120°，A 1A ＝4，C 1C ＝1，AB ＝BC ＝B 1B ＝2.(1)证明：AB 1⊥平面A 1B 1C 1；(2)求直线AC 1与平面ABB 1所成的角的正弦值．.(2019)19.（本小题满分15分）如图，已知三棱柱111ABC A B C -，平面11A AC C ⊥平面ABC ,90ABC ∠=︒，1130,,,BAC A A AC AC E F ∠=︒==分别是AC ，A 1B 1的中点.（1）证明：EF BC ⊥；（2）求直线EF 与平面A 1BC 所成角的余弦值.35(2018)2．双曲线－y 2＝1的焦点坐标是( )BA．(－，0)，(，0) B．(－2,0)，(2,0)C．(0，－)，(0，) D．(0，－2)，(0,2)(2019)2．渐近线方程为x±y=0的双曲线的离心率是CB．1 C D．2 A．2(2018)17．已知点P(0,1)，椭圆＋y2＝m(m＞1)上两点A，B满足＝2，则当m＝________时，点B横坐标的绝对值最大．5答案解析方法一如图，设A(x A，y A)，B(x B，y B)，由于椭圆具有对称性，不妨设点B 在第一象限，则x B＞0，y B＞0.∵P(0,1)，＝2，∴(－x A,1－y A)＝2(x B，y B－1)．∴－x A＝2x B，即x A＝－2x B.设直线AB：y＝kx＋1(k＞0)．将y＝kx＋1代入＋y2＝m，得(1＋4k2)x2＋8kx＋4－4m＝0.(*)∴x A＋x B＝－x B＝－，∴x B＝＝≤＝2，当且仅当＝4k，即k＝时，x B取到最大值2，此时方程(*)化为x2＋2x＋2－2m＝0，x A·x B＝－2＝－8，即2－2m＝－8，解得m＝5.当点B在其他象限时，同理可解．方法二设直线AB：y＝kx＋1(k≠0)，A(x A，y A)，B(x B，y B)．由P(0,1)，＝2，得x A＝－2x B.由得(1＋4k2)x2＋8kx＋4－4m＝0，∴x A＋x B＝－x B＝，x A x B＝－2＝.消去x B，得m＝1＋.|x B|＝＝≤2，当且仅当|k|＝时，|x B|max＝2，此时m＝5.(2019)15．已知椭圆22195x y+=的左焦点为F，点P在椭圆上且在x轴的上方，若线段PF的中点在以原点O为圆心，OF为半径的圆上，则直线PF的斜率是(2018)21.如图，已知点P是y轴左侧(不含y轴)一点，抛物线C：y2＝4x上存在不同的两点A，B满足P A，PB的中点均在C上．(1)设AB中点为M，证明：PM垂直于y轴；(2)若P是半椭圆x2＋＝1(x＜0)上的动点，求△P AB面积的取值范围．(1)解设P(x0，y0)，A，B.因为P A，PB的中点在抛物线上，所以y1，y2为方程2＝4·，即y 2－2y 0y ＋8x 0－＝0的两个不同的实根．所以y 1＋y 2＝2y 0，所以PM 垂直于y 轴． (2)解由(1)可知所以|PM |＝(＋)－x 0＝－3x 0，|y 1－y 2|＝2.所以△P AB 的面积 S △P AB ＝|PM |·|y 1－y 2|＝.因为＋＝1(－1≤x 0＜0)，所以－4x 0＝－4－4x 0＋4∈[4,5]，所以△P AB 面积的取值范围是.(2019)21.（本小题满分15分）如图，已知点(10)F ，为抛物线22(0)y px p =>，点F 为焦点，过点F 的直线交抛物线于A 、B 两点，点C 在抛物线上，使得ABC △的重心G 在x 轴上，直线AC 交x 轴于点Q ，且Q 在点F 右侧.记,AFG CQG △△的面积为12,S S.（1）求p 的值及抛物线的标准方程；（2）求12S S 的最小值及此时点G 的坐标.（1）由题意得12p=，即p =2. 所以，抛物线的准线方程为x =−1.（2）设()()(),,,,,A A B B c c A x y B x y C x y ，重心(),G G G x y .令2,0A y t t =≠，则2A x t =.由于直线AB 过F ，故直线AB 方程为2112t x y t-=+，代入24y x =，得 ()222140t y y t---=，故24B ty =-，即2B y t =-，所以212,B tt ⎛⎫- ⎪⎝⎭.又由于()()11,33G A B c G A B c x x x x y y y y =++=++及重心G 在x 轴上，故220c t y t -+=，得242211222,2,,03t t C t t G t t t ⎛⎫⎛⎫-+⎛⎫⎛⎫-- ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭. 所以，直线AC 方程为()222y t t x t -=-，得()21,0Q t -. 由于Q 在焦点F 的右侧，故22t >.从而4224221244242222211|2|||322221222211|||1||2|23A c t t t FG y t S t t t t t S t t QG y t t t t-+-⋅⋅--====--+--⋅--⋅-. 令22m t =-，则m >0，1221222134324S m S m m m m =-=-=+++++….当m =12S S取得最小值1+，此时G （2，0）．。

全国各地市历年高考立体几何题汇编(含参考答案).docx

全国各地市历年高考立体几何题汇编(含参考答案)(一)2018年高考立体几何题1.(北京理16)如图，在三棱柱ABC-me,中，CC~平面/此；D, E, F, G分别为必，AC,4G，B片的中点，AB=B(=yfs , A(=AA l=2.(I )求证：/以平面BEF-,(II )求二面角B-CAC、的余弦值；(III)证明：直线尸G与平面奶相交.2.(浙江-19)如图，已知多面体ABCAEG，AA, B、B,均垂直于平面,此；，"4，砂1，AB=B(=B Y B=2.(I )证明：刀3上平面(II)求直线WG与平面/蹈所成的角的正弦值.3.(课标III理T9)如图，边长为2的正方形ABCD所在的平面与半圆弧CD所在平面垂直, 肱是CQ上异于。

，。

的点.(1)证明：平面AMD1.平面BMC；(2)当三棱锥M -AB C体积最大时，求面MAB与面MCD所成二面角的正弦值.4.（课标II理-20）。

为AC的中如图，在三棱锥P-A8C 中，AB = BC = 2g, PA = PB = PC = AC = 4 ,(1)证明：POL平面ABC；(2)若点肱在棱BC上，且二面角为30。

，求PC与平面月皈所成角的正弦值.5.（课标I理-18）如图，四边形A3CZ)为正方形，分别为AD,B C的中点，以DF为折痕把△DPC折起, 使点C到达点F的位置，且PF LBF .(1)证明：平面PEF L平面ABFD；(2)求QP与平面A8FD所成角的正弦值.(二)2017年高考立体几何题1.(课标IIIS-19)如图，四面体，夙力中，△ABC是正三角形，△，⑦是直角三角形，/ABAZCBD, AB^BD.(1)证明：平面ACDL平面D(2)过的平面交彻于点&若平面北T把四面体⑦分成体积相等的两部分，求二面角D-AE-C的余弦值.2.（课标II理-19）如图，四棱锥巴ABCD中，侧面0〃为等边三角形且垂直于底面/次，AB = BC = -AD,ZBAD = ZABC = 90°, B是切的中 2点.(1)证明：直线CE〃平面0B；(2)点〃在棱PC上，且直线伽与底面/次所成角为45。

浙江省各地市高考数学联考试题分类大汇编(8)立体几何

一、选择题：6．(浙江省宁波市鄞州区2018年3月高考适应性考试文科)设m、n是不一样的直线，、是不一样的平面,以下四个命题中，正确的选项是（）A．若m//,n//,则m//nB．若m,n,则m//nC.．若,m ,则m D．若m,n,m//,n//,则//3．(浙江省部分要点中学2018年3月高三第二学期联考理科)一个空间几何体的主视图和左视图都是边长为1的正方形，俯视图是一个直径为1的圆，那么这个几何体的全面积为(▲)A．4πB ．2πC．3πD．3π2【答案】D4．(浙江省部分要点中学2018年3月高三第二学期联考理科)、为两个确立的订交平面，a、b为一对异面直线，以下条件中能使a、b所成的角为定值的有( ▲)10．(浙江省部分要点中学201 8年3月高三第二学期联考理科)在直三棱柱A1B1C1ABC中，BAC2，AB ACAA11，已知G和E分别为A1B1和CC1的中点，D与F分别为线段AC和AB上的动点(不包含端点)，若GD EF，则线段DF的长度的取值范围为(▲)A．【答案】A 5,1B．5,1C．25,1D．25,1 55556．(浙江省台州中学2018届高三放学期第二次统练文科)已知直线l平面，直线m//平面，以下命题中正确的选项是()（A）l m（B）l//m（C）l m//（D）l//m(4)(浙江省2018年2月三校联考高三文科)若直线l不平行于平面a，且l a，则(B)A.a内的全部直线与l异面B.a内不存在与l平行的直线C.a内存在独一的直线与l平行D.a内的直线与l都订交(5)(浙江省台州中学2018届高三放学期第一次统练理科)已知直线l∥平面α，P∈α，那么过点P且平行于直线l的直线(A)只有一条，不在平面α内(B)有无数条，不必定在平面α内(C)只有一条，且在平面α内(D)有无数条，必定在平面α内【答案】C555588 (单位：cm)，如右图所示，则该几何体的侧面积为正(主)视图侧(左)视图cm．【答案】80【分析】此题主要考察三视图表面积的问题。

2019年高考数学试题分类汇编立体几何

2019年高考理科数学试题立体几何
1．【2018年浙江卷】已知四棱锥S −ABCD 的底面是正方形，侧棱长均相等，E 是线段AB 上的点（不含端点），设SE 与BC 所成的角为θ1，SE 与平面ABCD 所成的角为θ2，二面角S −AB −C 的平面角为θ3，则
A.θ1≤θ2≤θ3
B.θ3≤θ2≤θ1
C.θ1≤θ3≤θ2
D.θ2≤θ3≤θ1【答案】D
从而因为，所以即
，选D.拓展：线线角找平行，线面角找垂直，面面角找垂面.
2．【2018年浙江卷】某几何体的三视图如图所示（单位：cm），则该几何体的体积（单位：cm 3）是
A.2
B.4
C.6
D.8
【答案】C
【解析】分析:先还原几何体为一直四棱柱，再根据柱体体积公式求结果.
详解：根据三视图可得几何体为一个直四棱柱，高为2，底面为直角梯形，上下底分别为1，2，梯形的高为2，因此几何体的体积为选C.
拓展：先由几何体的三视图还原几何体的形状,再在具体几何体中求体积或表面积等.
3．【2018年理新课标I 卷】已知正方体的棱长为1，每条棱所在直线与平面α所成的角相等，则α截此正方体所得截面面积的最大值为。

2018-2019学年高中新三维一轮复习数学浙江专版：板块

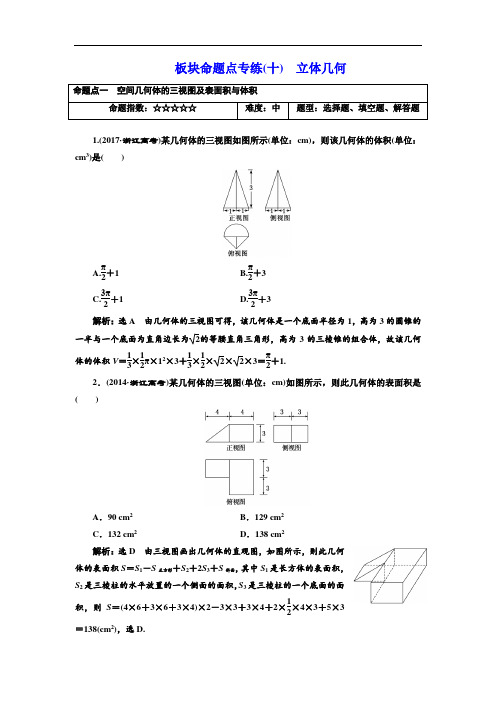
板块命题点专练(十) 立体几何1.(2017·浙江高考)某几何体的三视图如图所示(单位：cm)，则该几何体的体积(单位：cm 3)是( )A.π2＋1 B.π2＋3 C.3π2＋1 D.3π2＋3 解析：选A 由几何体的三视图可得，该几何体是一个底面半径为1，高为3的圆锥的一半与一个底面为直角边长为2的等腰直角三角形，高为3的三棱锥的组合体，故该几何体的体积V ＝13×12π×12×3＋13×12×2×2×3＝π2＋1.2．(2014·浙江高考)某几何体的三视图(单位：cm)如图所示，则此几何体的表面积是( )A ．90 cm 2B ．129 cm 2C ．132 cm 2D ．138 cm 2解析：选D 由三视图画出几何体的直观图，如图所示，则此几何体的表面积S ＝S 1－S 正方形＋S 2＋2S 3＋S 斜面，其中S 1是长方体的表面积，S 2是三棱柱的水平放置的一个侧面的面积，S 3是三棱柱的一个底面的面积，则S ＝(4×6＋3×6＋3×4)×2－3×3＋3×4＋2×12×4×3＋5×3＝138(cm 2)，选D.3．(2017·全国卷Ⅱ)如图，网格纸上小正方形的边长为1，粗实线画出的是某几何体的三视图，该几何体由一平面将一圆柱截去一部分后所得，则该几何体的体积为( )A ．90πB ．63πC ．42πD ．36π解析：选B 由题意知，该几何体由底面半径为3，高为10的圆柱截去底面半径为3，高为6的圆柱的一半所得，故其体积V ＝π×32×10－12×π×32×6＝63π.4．(2017·北京高考)某三棱锥的三视图如图所示，则该三棱锥的体积为( )A ．60B ．30C ．20D ．10解析：选D 如图，把三棱锥A -BCD 放到长方体中，长方体的长、宽、高分别为5,3,4，△BCD 为直角三角形，直角边分别为5和3，三棱锥A -BCD 的高为4，故该三棱锥的体积V ＝13×12×5×3×4＝10.5．(2016·浙江高考)某几何体的三视图如图所示(单位：cm)，则该几何体的表面积是________cm 2，体积是________cm 3.解析：由三视图还原几何体如图所示，下面长方体的长、宽都是4，高为2；上面正方体的棱长为 2.所以该几何体的表面积为(4×4＋2×4＋2×4)×2＋2×2×4＝80(cm 2)；体积为4×4×2＋23＝40(cm 3)．答案：80 406．(2017·山东高考)由一个长方体和两个14圆柱体构成的几何体的三视图如图，则该几何体的体积为________．解析：该几何体由一个长、宽、高分别为2,1,1的长方体和两个底面半径为1，高为1的四分之一圆柱体构成，所以V ＝2×1×1＋2×14×π×12×1＝2＋π2.答案：2＋π27．(2016·浙江高考)如图，在△ABC 中，AB ＝BC ＝2，∠ABC ＝120°.若平面ABC 外的点P 和线段AC 上的点D ，满足PD ＝DA ，PB ＝BA ，则四面体PBCD 的体积的最大值是________．解析：在△ABC 中，AB ＝BC ＝2，∠ABC ＝120°， ∴AC ＝22＋22－2×2×2×⎝⎛⎭⎫－12＝2 3. 设CD ＝x ，则AD ＝23－x ，∴PD ＝23－x ， ∴V P -BCD＝13S △BCD ·h ≤13·12BC ·CD ·sin 30°·PD ＝16x (23－x )≤16⎝ ⎛⎭⎪⎫x ＋23－x 22 ＝16×⎝⎛⎭⎫2322＝12，当且仅当x ＝23－x ，即x ＝3时取“＝”，此时PD ＝3，BD ＝1，PB ＝2，满足题意．故四面体PBCD 的体积的最大值为12.答案：121.(2016·全国卷Ⅲ)在封闭的直三棱柱ABC -A 1B 1C 1内有一个体积为V 的球．若AB ⊥BC ，AB ＝6，BC ＝8，AA 1＝3，则V 的最大值是( )A ．4πB ．9π2C ．6πD.32π3解析：选B 设球的半径为R ， ∵△ABC 的内切圆半径为6＋8－102＝2，∴R ≤2.又2R ≤3，∴R ≤32，∴V max ＝43×π×⎝⎛⎭⎫323＝9π2.故选B. 2．(2015·全国卷Ⅱ)已知A ，B 是球O 的球面上两点，∠AOB ＝90°，C 为该球面上的动点．若三棱锥O -ABC 体积的最大值为36，则球O 的表面积为( )A ．36πB ．64πC ．144πD ．256π 解析：选C 如图，设球的半径为R ，∵∠AOB ＝90°，∴S △AOB ＝12R 2.∵V O -ABC ＝V C -AOB ，而△AOB 面积为定值， ∴当点C 到平面AOB 的距离最大时，V O -ABC 最大，∴当C 为与球的大圆面AOB 垂直的直径的端点时，体积V O -ABC 最大，为13×12R 2×R ＝36，∴R ＝6，∴球O 的表面积为4πR 2＝4π×62＝144π.3．(2017·天津高考)已知一个正方体的所有顶点在一个球面上，若这个正方体的表面积为18，则这个球的体积为________．解析：由正方体的表面积为18，得正方体的棱长为 3. 设该正方体外接球的半径为R ，则2R ＝3，R ＝32，所以这个球的体积为43πR 3＝4π3×278＝9π2.答案：9π24．(2017·江苏高考)如图，在圆柱O 1O 2内有一个球O ，该球与圆柱的上、下底面及母线均相切．记圆柱O 1O 2的体积为V 1，球O 的体积为V 2，则V 1V 2的值是________．解析：设球O 的半径为R ，因为球O 与圆柱O 1O 2的上、下底面及母线均相切，所以圆柱的底面半径为R 、高为2R ，所以V 1V 2＝πR 2·2R 43πR 3＝32.答案：321.(2016·浙江高考)已知互相垂直的平面α，β交于直线l ，若直线m ，n 满足m ∥α，n ⊥β，则( )A ．m ∥lB ．m ∥nC ．n ⊥lD ．m ⊥n 解析：选C ∵α∩β＝l ，∴l ⊂β. ∵n ⊥β，∴n ⊥l .2．(2017·全国卷Ⅲ)在正方体ABCD -A 1B 1C 1D 1中，E 为棱CD 的中点，则( ) A ．A 1E ⊥DC 1 B ．A 1E ⊥BD C ．A 1E ⊥BC 1D ．A 1E ⊥AC 解析：选C 法一：由正方体的性质，得A 1B 1⊥BC 1，B 1C ⊥BC 1，A 1B 1∩B 1C ＝B 1，所以BC 1⊥平面A 1B 1CD . 又A 1E ⊂平面A 1B 1CD ，所以A 1E ⊥BC 1.法二：∵A 1E 在平面ABCD 上的投影为AE ，而AE 不与AC ，BD 垂直，∴B 、D 错； ∵A 1E 在平面BCC 1B 1上的投影为B 1C ，且B 1C ⊥BC 1， ∴A 1E ⊥BC 1，故C 正确；(证明：由条件易知，BC1⊥B1C，BC1⊥CE，又CE∩B1C＝C，∴BC1⊥平面CEA1B1.又A1E⊂平面CEA1B1，∴A1E⊥BC1.)∵A1E在平面DCC1D1上的投影为D1E，而D1E不与DC1垂直，故A错．3．(2017·全国卷Ⅰ)如图，在下列四个正方体中，A，B为正方体的两个顶点，M，N，Q为所在棱的中点，则在这四个正方体中，直线AB与平面MNQ不平行的是()解析：选A法一：对于选项B，如图所示，连接CD，因为AB∥CD，M，Q分别是所在棱的中点，所以MQ∥CD，所以AB∥MQ .又AB⊄平面MNQ，MQ⊂平面MNQ，所以AB∥平面MNQ.同理可证选项C、D中均有AB∥平面MNQ.故选A.法二：对于选项A，设正方体的底面对角线的交点为O(如图所示)，连接OQ，则OQ∥AB.因为OQ与平面MNQ有交点，所以AB与平面MNQ有交点，即AB与平面MNQ不平行，根据直线与平面平行的判定定理及三角形的中位线性质知，选项B、C、D中AB∥平面MNQ.故选A.4．(2017·山东高考)由四棱柱ABCD-A1B1C1D1截去三棱锥C1-B1CD1后得到的几何体如图所示．四边形ABCD为正方形，O为AC与BD的交点，E为AD的中点，A1E⊥平面ABCD.(1)证明：A1O∥平面B1CD1；(2)设M是OD的中点，证明：平面A1EM⊥平面B1CD1.证明：(1)取B1D1的中点O1，连接CO1，A1O1，因为ABCD-A1B1C1D1是四棱柱，所以A1O1∥OC，A1O1＝OC，因此四边形A1OCO1为平行四边形，所以A1O∥O1C，因为O1C⊂平面B1CD1，A1O⊄平面B1CD1，所以A1O∥平面B1CD1.(2)因为E，M分别为AD，OD的中点，所以EM∥AO.因为AO⊥BD，所以EM⊥BD，又A1E⊥平面ABCD，BD⊂平面ABCD，所以A1E⊥BD，因为B1D1∥BD，所以EM⊥B1D1，A1E⊥B1D1，又A1E⊂平面A1EM，EM⊂平面A1EM，A1E∩EM＝E，所以B1D1⊥平面A1EM，又B1D1⊂平面B1CD1，所以平面A1EM⊥平面B1CD1.5．(2017·北京高考)如图，在三棱锥P-ABC中，PA⊥AB，PA⊥BC，AB⊥BC，PA＝AB＝BC＝2，D为线段AC的中点，E为线段PC上一点．(1)求证：PA⊥BD；(2)求证：平面BDE⊥平面PAC；(3)当PA∥平面BDE时，求三棱锥E-BCD的体积．解：(1)证明：因为PA⊥AB，PA⊥BC，AB∩BC＝B，所以PA⊥平面ABC.又因为BD⊂平面ABC，所以PA⊥BD.(2)证明：因为AB＝BC，D为AC的中点，所以BD⊥AC.由(1)知，PA⊥BD，又AC∩PA＝A，所以BD⊥平面PAC.因为BD⊂平面BDE，所以平面BDE⊥平面PAC.(3)因为PA∥平面BDE，平面PAC∩平面BDE＝DE，所以PA∥DE.因为D为AC的中点，所以DE ＝12PA ＝1，BD ＝DC ＝ 2.由(1)知，PA ⊥平面ABC ，所以DE ⊥平面ABC .所以三棱锥E -BCD 的体积V ＝16 BD · DC · DE ＝13.三棱锥)，P ，Q ，R 分别为AB ，BC ，CA 上的点，AP ＝PB ，BQ QC ＝CRRA ＝2.分别记二面角D -PR -Q ，D -PQ -R ，D -QR -P 的平面角为α，β，γ，则( )A ．γ<α<βB ．α<γ<βC ．α<β<γD ．β<γ<α解析：选B 如图①，设O 是点D 在底面ABC 内的射影，过O 作OE ⊥PR ，OF ⊥PQ ，OG ⊥RQ ，垂足分别为E ，F ，G ，连接ED ，FD ，GD ，易得ED ⊥PR ，∴∠OED 就是二面角D -PR -Q 的平面角，∴α＝∠OED ，tan α＝ODOE ，同理tan β＝OD OF ，tan γ＝OD OG.底面的平面图如图②所示，以P 为原点建立平面直角坐标系，不妨设AB ＝2，则A (－1,0)，B (1,0)，C (0，3)，O ⎝⎛⎭⎫0，33， ∵AP ＝PB ，BQ QC ＝CRRA ＝2，∴Q ⎝⎛⎭⎫13，233，R ⎝⎛⎭⎫－23，33，则直线PR 的方程为y ＝－32x ，直线PQ 的方程为y ＝23x ，直线QR 的方程为y ＝ 33x ＋539，根据点到直线的距离公式，知OE ＝22121，OF ＝3939，OG ＝13， ∴OE >OG >OF ，∴tan α<tan γ<tan β，又α，β，γ为锐角， ∴α<γ<β.2．(2016·全国卷Ⅰ)平面α过正方体ABCD -A 1B 1C 1D 1的顶点A ，α∥平面CB 1D 1，α∩平面ABCD ＝m ，α∩平面ABB 1A 1＝n ，则m ，n 所成角的正弦值为( )A.32 B ．22C.33D.13解析：选A 如图，在正方体ABCD -A1B 1C 1D 1的上方接一个同等大小的正方体ABCD -A 2B 2C 2D 2，则过A 与平面CB 1D 1平行的是平面AB 2D 2，平面AB 2D 2∩平面AA 1B 1B ＝AB 2，即直线n 就是直线AB 2，由面面平行的性质定理知直线m 平行于直线B 2D 2，故m ，n 所成的角就等于AB 2与B 2D 2所成的角，在等边三角形AB 2D 2中，∠AB 2D 2＝60°，故其正弦值为32.3．(2016·浙江高考)如图，已知平面四边形ABCD ，AB ＝BC ＝3，CD ＝1，AD ＝5，∠ADC ＝90°，沿直线AC 将△ACD 翻折成△ACD ′，直线AC 与BD ′所成角的余弦的最大值是________．解析：如图，作D ′F ⊥AC 于点F ，作BE ⊥AC 于点E ，作FM 垂直于过点B 且平行于AC 的直线，垂足为M ，则∠D ′BM 是AC 与BD ′所成的角(或其补角)．在△AD ′C 中，D ′C ＝1， AD ′＝5，∠AD ′C ＝90°， ∴AC ＝6，D ′F ＝56，CF ＝66.在△BAC 中，BC ＝BA ＝3， BE ＝ 32－622＝ 152. 而AE ＝62，∴EF ＝62－66＝63. ∵MF ＝BE ＝ 152， ∴D ′M ＝ D ′F 2＋FM 2－2D ′F ·FM ·cos ∠D ′FM＝ 56＋152－2 56× 152cos ∠D ′FM ＝253－5cos ∠D ′FM .∵BM ＝EF ＝63， ∴BD ′＝D ′M 2＋BM 2＝9－5cos ∠D ′FM .∴cos ∠D ′BM ＝BM BD ′＝639－5cos ∠D ′FM ≤639－5＝66，当且仅当∠D ′FM 为0°时，等号成立． ∴直线AC 与BD ′所成角的余弦的最大值是66. 答案：664．(2017·浙江高考)如图，已知四棱锥P -ABCD ，△PAD 是以AD 为斜边的等腰直角三角形，BC ∥AD ，CD ⊥AD ，PC ＝AD ＝2DC ＝2CB ，E 为PD 的中点．(1)证明：CE ∥平面PAB ；(2)求直线CE 与平面PBC 所成角的正弦值．解：(1)证明：如图，设PA 的中点为F ，连接EF ，FB . 因为E ，F 分别为PD ，PA 的中点，所以EF ∥AD 且EF ＝12AD .又因为BC ∥AD ，BC ＝12AD ，所以EF ∥BC 且EF ＝BC ，即四边形BCEF 为平行四边形，所以CE ∥BF .因为BF ⊂平面PAB ，CE ⊄平面PAB ，所以CE ∥平面PAB .(2)分别取BC ，AD 的中点为M ，N . 连接PN 交EF 于点Q ，连接MQ ，BN . 因为E ，F ，N 分别是PD ，PA ，AD 的中点，所以Q 为EF 的中点，在平行四边形BCEF 中，MQ ∥CE . 由△PAD 为等腰直角三角形得PN ⊥AD . 由DC ⊥AD ，N 是AD 的中点得BN ⊥AD . 又PN ∩BN ＝N ，所以AD⊥平面PBN .由BC ∥AD 得BC ⊥平面PBN ，那么平面PBC ⊥平面PBN .过点Q 作PB 的垂线，垂足为H ，连接MH .则MH 是MQ 在平面PBC 上的射影，所以∠QMH 是直线CE 与平面PBC 所成的角．设CD ＝1.在△PCD 中，由PC ＝2，CD ＝1，PD ＝2得CE ＝2，在△PBN 中，由PN ＝BN ＝1，PB ＝3得QH ＝14，在Rt △MQH 中，QH ＝14，MQ ＝2，所以sin ∠QMH ＝28，所以直线CE 与平面PBC 所成角的正弦值是28.5.(2016·浙江高考)如图，在三棱台ABC -DEF 中，平面BCFE ⊥平面ABC ，∠ACB ＝90°，BE ＝EF ＝FC ＝1，BC ＝2，AC ＝3.(1)求证：BF ⊥平面ACFD ；(2)求二面角B -AD -F 的平面角的余弦值．解：(1)证明：延长AD ，BE ，CF 相交于一点K ，如图所示．因为平面BCFE ⊥平面ABC ，平面BCFE ∩平面ABC ＝BC ，且AC ⊥BC ，所以AC ⊥平面BCFE ，又因为BF ⊂平面BCFE ，因此BF ⊥AC .又因为EF ∥BC ，BE ＝EF ＝FC ＝1，BC ＝2，所以△BCK 为等边三角形，且F 为CK 的中点，则BF ⊥CK .又AC ∩CK ＝C ，所以BF ⊥平面ACFD .(2)过点F 作FQ ⊥AK 于Q ，连接BQ .因为BF ⊥平面ACFD ，所以BF ⊥AK ，则AK ⊥平面BQF ，所以BQ ⊥AK .所以∠BQF 是二面角B -AD -F 的平面角．在Rt △ACK 中，AC ＝3，CK ＝2，得AK ＝13，FQ ＝31313.在Rt △BQF 中，FQ ＝31313，BF ＝3，得cos ∠BQF ＝34.所以二面角B -AD -F 的平面角的余弦值为34.6．(2015·浙江高考)如图，在三棱柱ABC-A1B1C1中，∠BAC＝90°，AB＝AC＝2，A1A＝4，A1在底面ABC的射影为BC的中点，D是B1C1的中点．(1)证明：A1D⊥平面A1BC；(2)求二面角A1-BD-B1的平面角的余弦值．解：(1)证明：设E为BC的中点，连接AE，DE，A1E.由题意得A1E⊥平面ABC，所以A1E⊥AE.因为AB＝AC，所以AE⊥BC.故AE⊥平面A1BC.由D，E分别为B1C1，BC的中点，得DE∥B1B且DE＝B1B，从而DE∥A1A，DE＝A1A，所以四边形A1AED为平行四边形．故A1D∥AE.又因为AE⊥平面A1BC，所以A1D⊥平面A1BC.(2)作A1F⊥BD且A1F∩BD＝F，连接B1F.由AE＝EB＝2，∠A1EA＝∠A1EB＝90°，得A1B＝A1A＝4.由A1D＝B1D，A1B＝B1B，得△A1DB与△B1DB全等．由A1F⊥BD，得B1F⊥BD，因此∠A1FB1为二面角A1-BD-B1的平面角．由A1D＝2，A1B＝4，∠DA1B＝90°，得BD＝32，A1F＝B1F＝4 3，由余弦定理得cos∠A1FB1＝－1 8.。

专题19 立体几何综合-2019年高考数学母题题源系列(浙江专版)(原卷版)

专题19 立体几何综合【母题来源一】【2019年高考浙江卷】如图，已知三棱柱111ABC A B C -，平面11A ACC ⊥平面ABC ，90ABC ∠=︒，1130,,,BAC A A AC AC E F ∠=︒==分别是AC ，A 1B 1的中点．（1）证明：EF BC ⊥；（2）求直线EF 与平面A 1BC 所成角的余弦值．【答案】（1）证明见解析；（2）35．【解析】方法1：（1）如图，连接A 1E ，因为A 1A =A 1C ，E 是AC 的中点，所以A 1E ⊥AC ．又平面A 1ACC 1⊥平面ABC ，A 1E ⊂平面A 1ACC 1，平面A 1ACC 1∩平面ABC =AC ，所以，A 1E ⊥平面ABC ，则A 1E ⊥BC ．又A 1F ∥AB ，∠ABC =90°，故BC ⊥A 1F ．所以BC ⊥平面A 1EF ．因此EF ⊥BC ．（2）取BC 中点G ，连接EG ，GF ，则EGF A 1是平行四边形．由于A 1E ⊥平面ABC ，故A 1E ⊥EG ，所以平行四边形EGF A 1为矩形．由（1）得BC ⊥平面EGF A 1，则平面A 1BC ⊥平面EGF A 1，所以EF 在平面A 1BC 上的射影在直线A 1G 上．连接A 1G 交EF 于O ，则∠EOG 是直线EF 与平面A 1BC 所成的角（或其补角）．不妨设AC =4，则在Rt △A 1EG 中，A 1E EG由于O 为A 1G 的中点，故12A G EO OG ===所以2223cos 25EO OG EG EOG EO OG +-∠==⋅．因此，直线EF 与平面A 1BC 所成角的余弦值是35．方法2：（1）连接A 1E ，因为A 1A =A 1C ，E 是AC 的中点，所以A 1E ⊥AC ．又平面A 1ACC 1⊥平面ABC ，A 1E ⊂平面A 1ACC 1，平面A 1ACC 1∩平面ABC =AC ，所以，A 1E ⊥平面ABC ．如图，以点E 为原点，分别以射线EC ，EA 1为y ，z 轴的正半轴，建立空间直角坐标系E –xyz ．不妨设AC =4，则A 1（0，0，），B ，1，0），1B ，3,22F ，C (0，2，0)．因此33(,22EF =，(BC =．由0EF BC ⋅=得EF BC ⊥．（2）设直线EF 与平面A 1BC 所成角为θ．由（1）可得1=(310)=(02BC A C --，，，，，．设平面A 1BC 的法向量为n ()x y z =，，，由100BC A C ⎧⋅=⎪⎨⋅=⎪⎩n n ，得00y y ⎧+=⎪⎨=⎪⎩，取n (11)=，故||4sin |cos ,|=5|||EF EF EF θ⋅=〈〉=⋅n n n |，因此，直线EF 与平面A 1BC 所成的角的余弦值为35．【名师点睛】本题主要考查空间点、线、面位置关系，直线与平面所成的角等基础知识，同时考查空间想象能力和运算求解能力．【母题来源二】【2018年高考浙江卷】如图，已知多面体ABCA 1B 1C 1，A 1A ，B 1B ，C 1C 均垂直于平面ABC ，∠ABC =120°，A 1A =4，C 1C =1，AB =BC =B 1B =2．（1）证明：AB 1⊥平面A 1B 1C1；（2）求直线AC 1与平面ABB 1所成的角的正弦值．【答案】（1）证明见解析；（2）13．【解析】方法1：（1）由11112,4,2,,AB AA BB AAAB BB AB ===⊥⊥得111AB A B ==，所以2221111A B AB AA +=，故111AB A B ⊥．由2BC =，112,1,BB CC ==11,BB BC CC BC ⊥⊥得11B C 由2,120AB BC ABC ==∠=︒得AC = 由1CC AC ⊥，得1AC =所以2221111AB B C AC +=，故111AB B C ⊥．因此1AB ⊥平面111A B C ．（2）如图，过点1C 作111C D A B ⊥，交直线11A B 于点D ，连结AD ．由1AB ⊥平面111A B C 得平面111A B C ⊥平面1ABB ，由111C D A B ⊥得1C D ⊥平面1ABB ，所以1C AD ∠是1AC 与平面1ABB 所成的角．由111111BC A B AC ==111111cos C A B C A B ∠=∠=，所以1C D =，故111sin 13C D C AD AC ∠==．因此，直线1AC 与平面1ABB．方法2：（1）如图，以AC 的中点O 为原点，分别以射线OB ，OC 为x ，y 轴的正半轴，建立空间直角坐标系O -xyz ．由题意知各点坐标如下：111(0,(1,0,0),(0,(1,0,2),A B A B C因此11111(1(12),3),AB A B AC ==-=-uuu r uuu u r uuu u r由1110AB A B ⋅=uuu r uuu u r得111AB A B ⊥．由1110AB AC ⋅=uuu r uuu u r 得111AB AC ⊥．所以1AB ⊥平面111A B C ．（2）设直线1AC 与平面1ABB 所成的角为θ．由（1）可知11(1(0,0,2),AC AB BB ===u u u r u u u r u u u r设平面1ABB 的法向量(,,)x y z =n ．由10,0,AB BB ⎧⋅=⎪⎨⋅=⎪⎩uu u r uuu r n n即0,20,x z ⎧+=⎪⎨=⎪⎩可取(=n ．所以111|sin |cos ,||||AC AC AC θ⋅=〈〉==⋅n |n n |uuu ruuu r uuu r ．因此，直线1AC 与平面1ABB．【名师点睛】本题主要考查空间点、线、面位置关系，直线与平面所成的角等基础知识，同时考查空间想象能力和运算求解能力．【母题来源三】【2017年高考浙江卷】如图，已知四棱锥P –ABCD ，△P AD 是以AD 为斜边的等腰直角三角形，BC AD ∥，CD ⊥AD ，PC =AD =2DC =2CB ，E 为PD 的中点．（1）证明：CE ∥平面P AB ；（2）求直线CE 与平面PBC 所成角的正弦值．【答案】（1）证明见解析；（2．【解析】（1）如图，设P A 中点为F ，连接EF ，FB ．因为E ，F 分别为PD ，P A 中点，所以EF AD ∥且12EF AD =，又因为BC AD ∥，12BC AD =，所以EF BC ∥且EF BC =，即四边形BCEF 为平行四边形，所以CE BF ∥，因此CE ∥平面P AB ．（2）如图，分别取BC ，AD 的中点为M ，N ．连接PN 交EF 于点Q ，连接MQ ．因为E ，F ，N 分别是PD ，P A ，AD 的中点，所以Q 为EF 中点，在平行四边形BCEF 中，MQ//CE ．由△P AD 为等腰直角三角形得PN ⊥AD ．由DC ⊥AD ，N 是AD 的中点得BN ⊥AD ．所以AD ⊥平面PBN ，由BC //AD 得BC ⊥平面PBN ，那么平面PBC ⊥平面PBN ．过点Q 作PB 的垂线，垂足为H ，连接MH ． MH 是MQ 在平面PBC 上的射影，所以∠QMH 是直线CE 与平面PBC 所成的角．设CD =1．在△PCD 中，由PC =2，CD =1，CE ，在△PBN 中，由PN =BN =1，PB QH =14，在Rt △MQH 中，QH=14，MQ ，所以sin ∠QMH ，所以直线CE 与平面PBC ．【名师点睛】本题主要考查线面平行的判定定理、线面垂直的判定定理及面面垂直的判定定理，属于中档题．证明线面平行的常用方法：①利用线面平行的判定定理，使用这个定理的关键是设法在平面内找到一条与已知直线平行的直线，可利用几何体的特征，合理利用中位线定理、线面平行的性质或者构造平行四边形、寻找比例式证明两直线平行．②利用面面平行的性质，即两平面平行，在其中一平面内的直线平行于另一平面．本题（1）是就是利用方法①证明的．另外，本题也可利用空间向量求解线面角．【命题意图】高考对本部分内容的考查以能力为主，重点考查线面关系、面面关系及线面角的求解，考查数形结合的思想，空间想象能力及运算求解能力等．【命题规律】高考对该部分内容的考查主要有两种形式：一是利用立体几何的知识证明线面关系、面面关系；二是考查学生利用空间向量解决立体几何的能力，考查空间向量的坐标运算，以及平面的法向量等，难度属于中等偏上，解题时应熟练掌握空间向量的坐标表示和坐标运算，把空间立体几何问题转化为空间向量问题．【答题模板】运用空间向量坐标运算求空间角的一般步骤：（1）建立恰当的空间直角坐标系；（2）求出相关点的坐标；（3）写出向量坐标；（4）结合公式进行论证、计算；（5）转化为几何结论．【方法总结】1．直线与平面、平面与平面的平行与垂直的向量判定方法设直线l 的方向向量为a =(a 1，b 1，c 1)，平面α，β的法向量分别为μ=(a 2，b 2，c 2)，v =(a 3，b 3，c 3)，则（1）线面平行：l ∥α⇔a ⊥μ⇔a·μ=0⇔a 1a 2＋b 1b 2＋c 1c 2=0；（2）线面垂直：l ⊥α⇔a ∥μ⇔a =k μ⇔a 1=ka 2，b 1=kb 2，c 1=kc 2；（3）面面平行：α∥β⇔μ∥v ⇔μ=λv ⇔a 2=λa 3，b 2=λb 3，c 2=λc 3；（4）面面垂直：α⊥β⇔μ⊥v ⇔μ·v =0⇔a 2a 3＋b 2b 3＋c 2c 3=0．注意：用向量知识证明立体几何问题，仍然离不开立体几何中的定理．如要证明线面平行，只需要证明平面外的一条直线和平面内的一条直线平行，即化归为证明线线平行，用向量方法证明直线a ∥b ，只需证明向量a =λb （λ∈R ）即可．若用直线的方向向量与平面的法向量垂直来证明线面平行，仍需强调直线在平面外．2．利用向量求异面直线所成的角把角的求解转化为向量运算，“转化”是求异面直线所成角的关键，一般地，异面直线AC ，BD 的夹角β的余弦值为cos β=||||AC BD AC BD ⋅⋅uuu r uu u ruuur uu u r ．注意：两条异面直线所成的角α不一定是两直线的方向向量的夹角β，即cos α=|cos β|． 3．利用向量求直线与平面所成的角（1）分别求出斜线和它所在平面内的射影直线的方向向量，转化为求两个方向向量的夹角(或其补角)；（2）通过平面的法向量来求，即求出斜线的方向向量与平面的法向量所夹的锐角，取其余角就是斜线和平面所成的角．注意：直线和平面所成的角的正弦值等于平面法向量与直线方向向量夹角的余弦值的绝对值，即注意函数名称的变化．设直线l 的方向向量为a =(a 1，b 1，c 1)，平面α的法向量为μ=(a 3，b 3，c 3)，直线l 与平面α的夹角为π()20θθ≤≤，则||sin |cos ,|||||θ⋅==〈〉a a a μμμ． 4．用向量解决探索性问题的方法（1）确定点在线段上的位置时，通常利用向量共线来求．（2）确定点在平面内的位置时，充分利用平面向量基本定理表示出有关向量的坐标而不是直接设出点的坐标．（3）解题时，把要成立的结论当作条件，据此列方程或方程组，把“是否存在”问题转化为“点的坐标是否有解，是否有规定范围内的解”等，所以为使问题的解决更简单、有效，应善于运用这一方法解题．1．【浙江省浙南名校联盟2019届高三上学期期末联考】在三棱台111ABC A B C -中，ABC △是等边三角形，二面角1A BC B --的平面角为60︒，11BB CC =．（1）求证：1A A BC ⊥；（2）求直线AB 与平面11BCC B 所成角的正弦值．2．【重庆西南大学附属中学校2019届高三第十次月考】已知四棱锥P ABCD -中，底面ABCD 为菱形，60DAB ∠=︒，平面PAD ⊥平面ABCD ，2PA PD AD ===，点E ，F 分别为PD ，AB 上的一点，且2PE ED =，2BF FA =．（1）求证：AE //平面PFC ；（2）求PB 与平面PCD 所成角的正弦值．3．【浙江省2019年高考模拟训练卷三】在三棱锥P ABC -中，平面PAC ⊥平面ABC ，AQ QC =，2PA PC AB ===，1BC =，PB =（1）证明：BC BQ ⊥；（2）求直线AC 与平面PAB 所成角的正弦值．4．【河南省百校联盟2019届高三考前仿真试卷】如图，在几何体1111ACD A B C D -中，四边形11ADD A ，11CDD C 为矩形，平面11ADD A ⊥平面11CDD C ，11B A ⊥平面11ADD A ，1111,2AD CD AA A B ====，E 为棱1AA 的中点．（1）证明：11B C ⊥平面1CC E ；（2）求直线11B C 与平面1B CE 所成角的正弦值．5．【浙江省温州市2019届高三2月高考适应性测试】在三棱锥D ABC -中，AD DC ⊥，AC CB ⊥，222AB AD DC ===，且平面ABD ⊥平面BCD ，E 为AC 的中点．（1）证明：AD BC ⊥；（2）求直线DE 与平面ABD 所成的角的正弦值．6．【浙江省金华十校2019届第二学期高考模拟】在四棱锥S ABCD -中，底面ABCD 为直角梯形，BC CD ⊥，1SC SD CD DA ====，2CB =，AD BC ，23SCB π∠=，E 为线段SB 上的中点．（1）证明：AE 平面SCD ；（2）求直线AE 与平面SBC 所成角的余弦值．7．【安徽省1号卷A10联盟2019届高考最后一卷】如图，在四棱锥S ABCD -中，△BCD 为等边三角形，,120AD AB SD SB BAD ===∠=︒．（1）若点,M N 分别是线段,SC CD 的中点，求证：平面∥BMN 平面SAD ；（2）若二面角S BD C --为直二面角，求直线AC与平面SCD 所成角的正弦值．8．【浙江省台州市2019届高三上学期期末质量评估】如图，四棱锥P ABCD -中，PC 垂直平面ABCD ，AB AD ⊥，AB CD ∥，222PD AB AD CD ====，E 为PB 的中点．（1）证明：平面EAC ⊥平面PBC ；（2）求直线PD 与平面AEC 所成角的正弦值．。

浙江省2018-2019学年高三下学期《解三角形》选填汇编(无答案)

2018学年高三下解三角形选填题汇编1. （2018学年浙江名校协作体高三上开学考3）在ABC △中，角,,A B C 所对的边分别为,,a b c ，已知45,60,A B b =︒=︒=，则a =（）A B C D2. （2019届超级全能生2月模拟14）在ABC △中，,60AB AC BC A >==︒，ABC △的面积为则sin B = ，角平分线AM 的长度等于．3. （2019届嘉兴9月基础测试8）在ABC △中，角,,A B C 所对的边分别为,,a b c ，若53cos ,cos ,4135A B c ===，则a =（）A ．12B ．15C ．207D ．3074. （2019届金华十校4月模拟16）在ABC △中，A ，B ，C 内角所对的边分别为a ，b ，c ，已知2b =且cos cos 4sin sinc B b C a B C +=，则c 的最小值为．5. （2019届衢州五校联考15）在锐角ABC △中，角,,A B C 所对的边分别为,,a b c ，且2sin a B =，则A = ，若6,8a b c =+=，则ABC △的面积为．6. （2019届绍兴3月模拟14）在ABC △中，角,,A B C 所对的边分别为,,a b c ，若12cos ,33A b c ==，且ABC △b = ，sin C = ．7. （2019届温州2月模拟14）在ABC △中，45,6C AB =︒=，D 为BC 边上的点，且5,3AD BD ==，则cos B = ，AC = ．8. （2019届温州8月模拟14）在ABC △中，角,,A B C 所对的边分别为,,a b c ，AD 是BC 上的高，若3,60a AD A ==︒，则bc = ，b c += ．9. （2019届余高、缙中、长中5月模拟13）在锐角ABC △中，内角,,A B C 所对的边分别为,,a b c ，若2,3c A π==，则sin a C = ；a b +的取值范围是．10. （2019届浙江三校第一次联考14）已知ABC △的内角,,A B C 的对边分别为,,a b c ，若6A π=，(4cos b a B =+，且1b =，则B = ；ABC △的面积为．11. （2019届湖州中学仿真考12）如图，在山顶铁塔上B 处测得地面上有点A 的俯角60α=︒，在塔底C处测得A 处的俯角45β=︒．已知铁塔BC 部分的高为30米，则AB = ，山高CD = ．12. （2019届杭四仿真考6）在ABC △中，角A ，B ，C 的对边分别为a ，b ，c ，已知30B ∠=︒，ABC△的面积为32，且sin sin 2sin A C B +=，则b 的值为（）A．4+B．4-C1D113. （2019届杭二热身考14）ABC △中，2A B =，1BC =，则AC 的取值范围是，BA BC⋅的取值范围是_________．14. （2019届绿色联盟5月模拟16）如图，在宽8米的矩形教室MEFN 正前方有一块长6米的黑板AB ，学生座位区域CEFD 距黑板最近1米，在教室左侧边CE 上寻找黑板AB 的最大视角点P （即使APB ∠最大），则CP = 时，APB ∠最大．βαDC AB15. （2019届绿色联盟5月模拟14）在ABC △中，角,,A B C 所对的边分别为,,a b c ，若2222cos 20a c b bc A c +-+-=，()cos 1cos c A b C =-，且23C π=，则c = ；ABC △的面积S = ．16. （2019届知行联盟5月模拟14）在ABC △中，角A ，B ，C 所对的边分别为a ，b ，c，若a =1b =，60A ∠=︒，则c = ，ABC △的面积是．17. （2019届浙江三校第四次联考14）在ABC △中，角,,A B C 所对的边分别为,,a b c ，若()sin sin sin c C a A b a B =+-且1c =，则C = ；ABC △面积的最大值为．18. （2019届宁波十校5月模拟14）已知ABC △中，角,,A B C 所对的边分别为,,a b c ，ABC △的面积22sin S a C =，则（1）b aa b += ；（2）若10c =，角C 的平分线CM 交边AB 于点M ，且4CM =，则b = ．11NFD19. （2019届浙大附中5月模拟16）已知直角三角形ABC 中，直角边6AC =，点D 是边AC 上一定点，2CD =，点P 是斜边AB 上一动点，CP BD ⊥，则APC △面积的最大值是；线段DP 长度的最小值是．20. （2019届镇海中学最后一卷12）已知在ABC △中，()2sin 32,2cos32AB =︒︒，()cos 77,cos13BC =︒-︒，则AB BC ⋅= ，ABC △的面积为．21. （2019届七彩阳光联盟第三次联考13）在ABC △中，角,,A B C 所对的边分别为,,a b c ，222a c b ac +-=，2cos b a A =，2c =，则a = ，ABC △的面积为．22. （2019届衢州二中第二次模拟14）在ABC △中，2AB =，4B π=，6C π=，点P 是边BC 的中点，则AC = ；AP BC ⋅= ．23. （2019届舟山中学5月模拟13）在ABC △中，3,2BC AC A B ===，则cos B = ；若D 是BC 上一点且AD AC ⊥，则ABD △的面积为．24. （2019届绍兴一中4月模拟14）在锐角ABC △中，a =，3b =，sin A B +=A ∠= ；ABC △的面积是．25. （2019届浙江名校联盟第三次联考13）已知ABC △中，角A ，B ，C 所对的边分别为a ，b ,c ，若cos a A =，ABC △的面积S A = ；a 的最小值为．26. （2019届嘉丽4月模拟13）已知a ，b ，c 分别为ABC △的三边，若6a =，7b =，8c =，则cos C = ，ABC △的外接圆半径等于．27. （2019届嵊州5月模拟14）在ABC △中，2AB =，3AC =，边BC 上的中线2AD =，则BC = ，ABC △的面积为．28. （2019届杭州4月模拟13）在ABC △中，角A ,B ,C 所对的边分别为a ,b ,c ，已知1cos24C =-，则sin C = ；当2a =，2sin sin A C =时，则b = ．29. （2019届临海新昌乐清4月模拟15）在ABC △中，角,,A B C 所对的边分别为,,a b c ，若1,60c C ==︒，则b 的取值范围是．30. （2019届平湖5月模拟17）如图，矩形ABCD 中，2AB =，1AD =，M ，N 分别是边AB ，AD 上的点，设AM m =，AN n =，且m ，n 满足()()2111m n --=，则tan MCN ∠的最大值为．31. （2019届平湖5月模拟13）在ABC △中，已知45,cos A B =︒=若BC =D 为AB 的中点，则cos C ；CD 的长为．32. （2019届温州5月模拟14）如图，设ABC △是由3个全等的三角形与中间一个等边小三角形拼成的一个大等边三角形，设2DF AF =，AB EDF △的面积为．N D CB MABA33. （2019届稽阳联谊4月模拟14）在ABC △中，cos2C =，1BC =，5AC =，则cos C = ；sin A = ．34. （2019届上虞5月模拟7）如图，正方形ABCD 的边长为1，P 、Q 分别为边AB ，AD 上的点，当APQ △的周长为2时，则PCQ ∠的大小是（）A ．30︒B ．45︒C ．60︒D ．75︒35. （2019届上虞5月模拟4）在ABC △中，角,,A B C 所对的边长分别为,,a b c ，若2222a b c +=，则角C 的取值范围是（）A ．0,6π⎛⎤ ⎥⎝⎦B ．,64ππ⎛⎤ ⎥⎝⎦C ．0,3π⎛⎤⎥⎝⎦D ．,43ππ⎛⎤ ⎥⎝⎦36. （2019届浙江百校联考4）在ABC △中，角A ，B ，C 的对边分别是a ，b ，c，若c =，22a b -=，则角A 等于（） A ．4π B ．3π C ．2π D ．23πQAPBCD37. （2019届湖州三校4月模拟13）在ABC △中，内角A ，B ，C 所对的边分别为a ，b ，c ，已知tan +24A π⎛⎫= ⎪⎝⎭，则sin A 的值为，若4B π=，4a =，则ABC △的面积等于．38. （2019届浙江三校第二次联考14）在ABC △中角A ，B ，C 对应边分别为a ，b ，c ，120ABC ∠=︒，ABC ∠的平分线与AC 交点为D ，且1BD =，则11=a c+ ，ABC △面积的最小值是．39. （2019届台州4月模拟16）在ABC △中，AD 是BC 边上的中线，6ABD π∠=．若AB ，则CAD ∠= ；若22AC AD ==，则ABC △的面积为．40. （2019届余高、缙中、长中5月模拟13）在锐角ABC △中，内角,,A B C 所对的边分别为,,a b c ，若2,3c A π==，则sin a C = ；a b +的取值范围是．41. （2019届金华十校4月模拟16）在ABC △中，A ，B ，C 内角所对的边分别为a ，b ，c ，已知2b =且cos cos 4sin sinc B b C a B C +=，则c 的最小值为．42. （2019届绿色联盟12月模拟13）在ABC △中，角,,A B C 的对边分别为,,a b c ．已知4a =，3b =，且2A B =，B C ≠，则cos B = ，c = ．43. （2019届金丽衢十二校第二次联考14）在ABC △中，角,,A B C 的对边分别为,,a b c ，面积为()22213a c b +-，且C ∠为钝角，则tan B = ；ca 的取值范围是．44. （2019届湖丽衢9月质检14）已知ABC △，60A ∠=︒，D 是边AC 上一点，2AD DC =，2BD =，则AB = ；cos C = ．45. （2019届浙江名校联盟第一次联考14）在ABC △中，角,,A B C 的对边分别为,,a b c ，60A =︒，且ABC △a = ；若b c +=ABC △的面积为．。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

2018学年高三下立体几何综合大题汇编一、线面角1. （2018学年杭十四中4月月考19）如图，三棱柱111ABC A B C -所有的棱长均为2，1A B =1A B AC ⊥．（1）求证：111AC B C ⊥；（2）求直线AC 和平面11ABB A 所成角的余弦值．C 1B 1A 1CBA2. （2018学年浙江重点中学高三上期末热身联考19）如图，等腰直角ABC △中，B ∠是直角，平面ABEF ⊥平面ABC ，2AF AB BE ==，60FAB ∠=︒，AFBE ．（1）求证：BC BF ⊥；（2）求直线BF 与平面CEF 所成角的正弦值．BEFA3. （2019届超级全能生2月模拟19）如图，在三棱锥P ABC -中，2BAC π∠=，2AC =，BC BP ==，PC =APC △的面积等于（1）求证：AC PB ⊥；（2）求直线AC 与平面PBC 所成角的正弦值．PBCA4. （2019届杭二仿真考19）如图，矩形ADFE 和梯形ABCD 所在平面互相垂直，AB CD ∥，90ABC ADB ∠=∠=︒，1CD =，2BC =．（1）求证：BE ∥平面DCF ；（2）当AE 的长为何值时，直线AD 与平面BCE 所成角的大小为45︒．FEDC BA5. （2019届湖丽衢9月质检19）如图，在四棱锥P ABCD -中，四边形ABCD 是直角梯形，且AD BC ，BC CD ⊥，60ABC ∠=︒，22BC AD ==，3PC =，PAB △是正三角形，E 是PC 的中点．（1）求证：DE平面PAB ；（2）求直线BE 与平面PAB 所成角的正弦值．PBCD E A6. （2019届湖州三校4月模拟19）如图，在四棱锥E ABCD -中，底面ABCD 是边长为2的正方形，且DE =，平面ABCD ⊥平面ADE ，二面角A CD E --为30︒．（1）求证：AE ⊥平面CDE ；（2）求AB 与平面BCE 所成角的正弦值．EDCBA7. （2019届湖州中学仿真考19）如图，已知四棱锥P ABCD -，底面ABCD 为边长为2的菱形，PA ⊥平面ABCD ，60ABC ∠=︒，E 是BC 的中点，PA AB =．（1）证明：AE PD ⊥；（2）若F 为PD 上的动点，求EF 与平面PAD 所成最大角的正切值．FPDCBA8. （2019届稽阳联谊4月模拟19）在四棱锥P ABCD -中，PC ⊥平面ABCD ，BC AD ∥，BC AB ⊥，2PB AD ==，1AB BC ==，E 为棱PD 上的点．（1）若13PE PD =，求证：PB ∥平面ACE ；（2）若E 是PD 的中点，求直线PB 与平面ACE 所成角的正弦值．EDCBA P9. （2019届嘉丽4月模拟19）如图，在矩形ABCD 中，4AB =，3AD =，点E ，F 分别是线段DC ，BC 的中点，分别将DAE △沿AE 折起，CEF △沿EF 折起，使得D ，C 重合于点G ，连结AF ．（1）求证：平面GEF ⊥平面GAF ；（2）求直线GF 与平面GAE 所成角的正弦值．GFED CBA10. （2019届嘉兴9月基础测试20）如图，ABC △时候边长为2的正三角形，ABD △是以AB 为斜边的等腰直角三角形．已知2CD =．（1）求证：平面ABC ⊥平面ABD ；（2）求直线AC 与平面BCD 所成角的正弦值．BCDA11.（2019届金华十校4月模拟20）在四棱锥S ABCD-中，底面ABCD为直角梯形，BC CD⊥，1SC SD CD DA====，2CB=，AD BC∥，23SCBπ∠=，E为线段SB上的中点．（1）证明：AE∥平面SCD；（2）求直线AE与平面SBC所成角的余弦值．SED C BA12.（2019届金华一中5月模拟19）如图，在四棱锥P ABCD-中，底面ABCD是菱形，60BAD∠=︒，2AB=，1PA=，PA ABCD⊥平面，E是直线PC的中点，F是直线AB的中点．（1）求证：BE∥平面PDF；（2）求直线BE与平面PCD所成角的正弦值．FEDCBA P13. （2019届金丽衢十二校第二次联考19）三棱柱111ABC A B C -中，AB ⊥侧面11BCC B ，已知1BC =，1=3BCC π∠，12AB C C ==．（1）求证：1C B ⊥平面ABC ；（2）若E 在棱1C C (不包含端点1C C ，)上，且1EA EB ⊥，求1A E 与平面1AB E 所成角的正弦值．BCEA 1B 1C 1A14. （2019届金丽衢十二校第一次联考19）如图，在四棱锥P ABCD -中，已知PA ⊥平面ABCD ，且四边形ABCD 为直角梯形，2ABC BAD π∠=∠=，2PA AD ==，1AB BC ==，点M 、E 分别是PA ，PD 的中点．（1）求证：CE平面BMD ；（2）点Q 为线段BP 中点，求直线PA 与平面CEQ 为所成角的余弦值．QEM PDCBA15. （2019届临海新昌乐清4月模拟19）已知多面体ABCDE 中，AE 、CD 均垂直于平面ABC ，120ABC ∠=︒，2AE CD =，AB BC CD ==，F 是BE 的中点．（1）求证：DF ∥平面ABC ；（2）求直线BD 与平面ABE 所成角的正弦值．BCDEFA16.（2019届宁波4月模拟19）中国古代数学经典《数书九章》中，将底面为矩形且有一条侧棱与底面垂直的四棱锥称为“阳马”，将四个面都为直角三角形的四面体称之为“鳖臑”．在如图所示的阳马P ABCD-中，底面ABCD是矩形，P A⊥平面ABCD，2PA AD==，AB AC的中点O为球心，AC为直径的球面交PD于M（异于点D），交PC于N（异于点C）．（1）证明：平面AM PCD⊥，并判断四面体MCDA是否是鳖臑，若是，写出它每个面的直角（只需写出结论）；若不是，请说明理由；（2）求直线ON与平面ACM所成角的正弦值．D17. （2019届宁波十校5月模拟19）如图，在四棱台1111ABCD A B C D -中，底面ABCD 是菱形，3ABC π∠=，11B BA B BC ∠=∠，16B BD π=，1122AB A B ==，12B B =，E 是CD 的中点．（1）求证：直线AC ⊥平面11BDD B ；（2）求直线1ED 与平面11ABB A 所成角的正弦值．B 1C 1D 1A 1ODCBA18. （2019届平湖5月模拟19）如图所示，在直角梯形ABCD 中，90ADC ∠=︒，CD AB ∥，4AB =，2AD CD ==，M 为线段AB 的中点，将ADC △沿AC 折起，得到几何体P ABC -．（1）求证：AC PM ⊥；（2）已知PM =PB 与平面APC 所成角的正弦值．MAPC B19. （2019届七彩阳光联盟第三次联考19）如图，在四棱锥P ABCD -中，BC ⊥平面PCD ，CD ∥AB ，22AB CD ==，BC PC ==PD AB ⊥．（1）求PD 的长；（2）求直线AD 与平面P AB 所成角的正弦值．PDCBA20. （2019届七彩阳光联盟第一次联考19）如图，已知四棱锥P ABCD -，底面ABCD 为矩形，且侧面PAD ⊥平面PBC ，侧面PAD平面=PBC l ，PDC △为正三角形，2CD =．（1）求证：lBC ；（2）求直线AB 与平面PAD 所成角的正弦值．BCDPA21. （2019届衢州二中第二次模拟19）如图，正方形ABCD 所在平面外一点P 满足PE PF =，其中E 、F分别是AB 、CD 的中点．（1）求证：EF PC ⊥；（2）若4AB =，PE PF ==且二面角P EF C --，求BC 与平面PEF 所成角的正弦值．PF ED CBA22.（2019届衢州二中第一次模拟20）如图，已知矩形BCDE所在平面与ABE△所在平面互相垂直，且AB AE⊥，AB AE>．（1）若M为AC的中点，N为BE的中点，求证：MN∥平面ADE；（2）若2BE=，1DE=，且DE与平面DAC，求ABE∠的大小．E23.（2019届绍兴3月模拟19）如图，四棱锥P ABCD-中，PA⊥平面ABCD，四边形ABCD是矩形，且2PA AB==，3AD=，E是棱BC上的动点，F是线段PE的中点．（1）求证：PB⊥平面ADF；（2）若直线DE与平面ADF所成角为30︒，求EC的长．B C DP FEA△ABC 的中位线DE 将△ADE 翻折至A DE '，使得二面角A DE A '--为60︒．（1）求证：A C ED '⊥；（2）求直线BA '与平面A DE '所成角的正弦值．A'ED CBA25. （2019届嵊州5月模拟19）如图，已知四棱锥P ABCD -，AD BC ∥，90ABC ∠=︒，135ADP ∠=︒，AB ，22BC AD ==，2PB PD ==（1）求证：AB PD ⊥；（2）求直线PD 与平面PBC 所成的角的正弦值．P DCBA26. （2019届台州4月模拟19）如图，棱锥P ABCD -的底面是菱形，2AB =，3DAB π∠=，侧面PAB垂直于底面ABCD ，且PAB △是正三角形．（1）求证：PD AB ⊥；（2）求直线PC 与平面PBD 所成角的正弦值．BCDPA27. （2019届温州2月模拟19）在三棱锥D ABC -中，AD DC ⊥，AC CB ⊥，222AB AD DC ===，且平面ABD ⊥平面BCD ，E 为AC 的中点．（1）证明：AD BC ⊥；（2）求直线DE 与平面ABD 所成角的正弦值．BCDEA28.（2019届温州5月模拟19）如图，四棱锥P ABCD-中，底面为直角梯形，AB∥CD，90BAD∠=︒，24AB CD==，PA CD⊥，在锐角．．PAD△中，E是边PD上一点，且3AD PD ED===（1）求证：PB∥平面ACE；（2）当P A的长为何值时，AC与平面PCD所成的角为30︒？B ACDEP29. （2019届温州8月模拟19）如图，在三棱柱111ABC A B C -中，12AA AC AB ==，90ABC ∠=︒，侧面11A ABB 为矩形，1=120A AC ∠︒．将111A B C △绕11A C 翻折至121A B C △，使2B 在平面11A ACC 内．（1）求证：1BC 平面121A B B ；（2）求12C B 与平面11A ABB 所成角的正弦值．BCAB 1C 1B 2A 130. （2019届温州九校第一次联考19）如图，将矩形ABCD 沿AE 折成二面角1D AE B --，其中E 为CD的中点，已知2AB =，=1BC ，11BD CD =，F 为1D B 的中点．（1）求证：CF平面1AD E ；（2）求AF 与平面1BD E 所成角的正弦值．BCDED 1FA31.（2019届永康5月模拟20）已知在等腰梯形ABGH中，AB GHAB GH HA==，E，F分别为∥，22线段AH和BG的中点，现将四边形EFGH沿直线EF折成一个五面体AED BFC-．（1）在线段BC上是否存在点M，使FM∥平面ADE，若存在，找出点M的位置，若不存在，说明理由；（2）若二面角C EF B--的大小为60︒，求直线AC与平面ABFE所成角的正弦值．H GCDFEA32.（2019届浙江百校联考19）如图，已知△P AD为等边三角形，四边形ABCD为直角梯形，AB∥CD，90==，E为PB的中点．AB AD CDDAB∠=︒，平面P AD⊥平面ABCD，2（1）求证：CE∥平面P AD；（2）求PB与平面PCD所成角的正弦值．PED CAB33. （2019届浙江名校联盟第二次联考19）在四棱锥P ABCD -中，四边形ABCD 是边长为2的正方形，PB PD =，E F M 、、分别是棱AD PD PC 、、上的点，且=PF FD λ，AE ED λ=，若对任意()0,1λ∈，都有EF 平面DBM ．（1）求PMMC的值；（2）若DM M DB C --的大小为30︒，求直线PD 与平面BDM 所成角的正弦值．E FBC D PM A34. （2019届浙江名校联盟第三次联考19）在所有棱长都相等的三棱柱111ABC A B C -中，1=60B BC ∠︒．（1）证明：1AB BC ⊥；（2）若二面角1A BC B --的大小为60︒，求1BC 与平面ABC 所成角的正弦值．C 1B 1A 1CBA35. （2019届浙江名校联盟第一次联考19）如图，在四棱锥P ABCD -中，PA ⊥平面ABCD ，AB CD ∥，4CD =，2PA AB BC AD ====，Q 为棱PC 上的点，且13PQ PC =．（1）证明：平面QBD ⊥平面ABCD ；（2）求直线QD 与平面PBC 所成角的正弦值．QPDC BA36. （2019届浙江三校第二次联考19）在斜三棱柱111ABC A B C -中，△ABC 是边长为2的正三角形，1A B =1160A AB A AC ∠=∠=︒．（1）证明：1平面平面A BC ABC ⊥；（2）求直线1BC 与平面11ABB A 所成角的正弦值．B 1C 1A 1CBA37. （2019届浙江三校第四次联考19）如图，在Rt ABC △中，90BAC ∠=︒，30B ∠=︒，D ，E 分别为BC ，AD 的中点，延长CE 交AB 于点F ，现将ACD △沿AD 折起，使二面角B AD C --的平面角大小为30︒．（1）求证：AD CF ⊥；（2）求直线AB 与平面ACD 所成角的正弦值．FEDCBAEFDCA38. （2019届浙江三校第一次联考19）如图，已知四棱锥A BCDE -中，2AB BC ==，120ABC ∠=︒，AE =CD BE ∥，24BE CD ==，60EBC ∠=︒．（1）求证：EC ABC ⊥平面；（2）求直线AD 与平面ABE 所成角的正弦值．CDEA39.（2019届镇海中学5月模拟19）如图，四棱锥P ABCD-的底面ABCD是边长为2的菱形，60ABC∠=︒，点M是棱PC的中点，PA⊥平面ABCD．（1）证明：PA∥平面BMD；（2）当PA长度为多少时，直线AM与平面PBC所成角的正弦值为7．MPDBA40. （2019届镇海中学考前练习19）如图，在四棱锥P ABCD -中，60APB BPD APD ∠=∠=∠=︒，2PB PD BC CD ====，3AP =．（1）证明：AP BD ⊥；（2）求PC 与平面PAB 所成角的正弦值．PDCBA41. （2019届知行联盟5月模拟19）如图，在四棱锥E ABCD -中，底面ABCD 为正方形，AE CDE ⊥平面．已知1AE =，DE（1）证明：ADE ABCD ⊥平面平面；（2）求直线BE 与平面ACE 所成的角的正弦值．EDCBA42. （2019届舟山中学5月模拟19）如图所示多面体EF ABCD -，其底面ABCD为矩形且AB =2BC =，四边形BDEF 为平行四边形，点F 在底面ABCD 内的投影恰好是BC 的中点．（1）已知G 为线段FC 的中点，证明：BG ∥平面AEF ；（2）若二面角F BD C --的大小为3π，求直线AE 与平面BDEF 所成角的正弦值．FEDCBA43. （2019届诸暨5月模拟19）如图，在四棱锥P ABCD -中，底面是边长为2的菱形，60BAD ∠=︒，PB PD =（1）证明：平面PAC ⊥平面ABCD ；（2）设H 在AC 上，13AH AC =，若PH =．求PH 与平面PBC 所成角的正弦值．HPDCBA二、二面角44. （2018学年杭高高三下开学考19）如图（1），已知ABC △是边长为6的等边三角形，点D 、E 分别是边AB 、AC 上的点，且满足2AD CE ==．如图（2），将ADE △沿DE 折成四棱锥1A BCED -，且有平面1A DE ⊥平面BCED ．（1）求证：1A D ⊥平面BCED ；（2）记1A E 的中点为M ，求二面角1M DC A --的余弦值．BCDEAMCBEDA 1图１图２45. （2019届杭二热身考20）在四棱锥P ABCD -中，底面ABCD 为菱形，60DAB ∠=︒，PC ⊥平面ABCD ，且2AB =，PC =F 是PA 的中点．（1）求证：CF ⊥平面PDB ；（2）求平面ADP 与平面BCP 所成锐二面角的余弦值．FPDCBA46. （2019届杭四仿真考19）在四棱锥P ABCD -中，PA ABCD ⊥底面，BAD ∠为直角，AB CD ∥，2AD CD AB ==，E 、F 分别为PC 、CD 的中点．（1）证明：APD BEF 平面∥平面；（2）设()0PA kAB k =>，且二面角E BD C --的平面角大于60°，求k 的取值范围．FEDCBAP47. （2019届杭州4月模拟19）如图，四边形ABCD 为矩形，平面ABEF ⊥平面ABCD ，EF ∥AB ，90BAF ∠=，2AD =，1AB AF ==，点P 在线段DF 上．（1）证明：AF ⊥平面ABCD ．（2）若二面角D AP C --PF 的长度．PF EDC BA48.（2019届嘉兴一中5月模拟20）在四边形ABED中，AB DE∥，AB BE⊥，点C在AB上，且AB CD⊥，2AC BC CD===，现将ACD△沿CD折起，使点A到达点P的位置，且PE与平面PBC所成角为45︒．（1）求证：平面PBC⊥平面DEBC；（2）求二面角D PE B--的余弦值．PE D CBA49. （2019届绿色联盟5月模拟19）如图，圆的直径2AC =，B 为圆周上不与A ，C 重合的点，PA 垂直于圆所在的平面，45PCA ∠=︒．（1）求证：PB BC ⊥；（2）若BC =B PC A --的余弦值．CA50. （2019届绿色联盟12月模拟19）在三棱锥P ABC -中，ABC △和ABP △均为等边三角形，2AB =，点P 在平面ABC 上的射影在ABC △内，已知直线PB 与平面ABC 所成角的正弦值为34．（1）求证：AB PC ⊥；（2）求二面角B AP C --的余弦值．BCPA。