到达时间间隔与到达时刻的分布

合集下载

排队模型——精选推荐

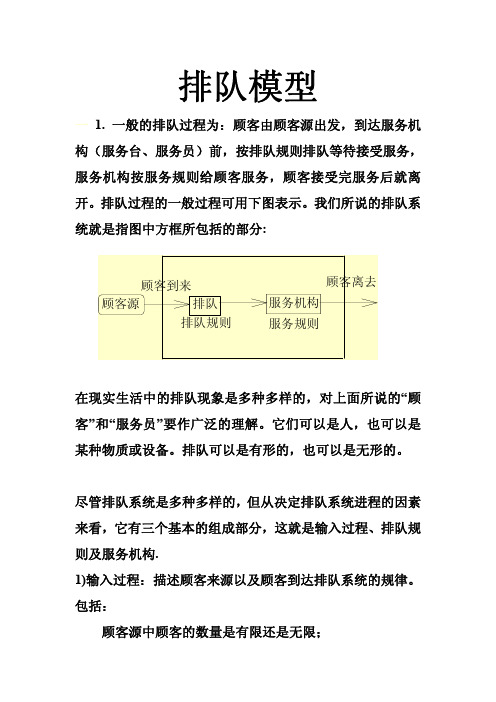
排队模型一 1. 一般的排队过程为：顾客由顾客源出发，到达服务机构（服务台、服务员）前，按排队规则排队等待接受服务，服务机构按服务规则给顾客服务，顾客接受完服务后就离开。

排队过程的一般过程可用下图表示。

我们所说的排队系统就是指图中方框所包括的部分:在现实生活中的排队现象是多种多样的，对上面所说的“顾客”和“服务员”要作广泛的理解。

它们可以是人，也可以是某种物质或设备。

排队可以是有形的，也可以是无形的。

尽管排队系统是多种多样的，但从决定排队系统进程的因素来看，它有三个基本的组成部分，这就是输入过程、排队规则及服务机构.1)输入过程：描述顾客来源以及顾客到达排队系统的规律。

包括：顾客源中顾客的数量是有限还是无限；顾客到达的方式是单个到达还是成批到达；顾客相继到达的间隔时间分布是确定型的还是随机型的，分布参数是什么，是否独立，是否平稳。

2)排队规则：描述顾客排队等待的队列和接受服务的次序。

包括：即时制还是等待制；等待制下队列的情况（是单列还是多列，顾客能不能中途退出，多列时各列间的顾客能不能相互转移）；等待制下顾客接受服务的次序（先到先服务，后到先服务，随机服务，有优先权的服务）。

3)服务机构：描述服务台(员)的机构形式和工作情况。

包括：服务台（员）的数目和排列情况；服务台（员）的服务方式；服务时间是确定型的还是随机型的，分布参数是什么，是否独立，是否平稳。

2.到达和服务过程的模型2.1 到达过程的模型用表示第i 个顾客到达的时间,.i t 称为第i 个到达时间间隔.1i i T t t +=−i 我们用的特征来刻画顾客到达过程. 最常见的情况是独立同分布. 用X 表示这样的随机变量.12,,T T 12,,T T 如果X 服从参数为λ的指数分布.这时1()()i E T E X λ==即平均每隔1λ来一个顾客.换句话说,单位时间理平均有λ个顾客到来.称λ为到达速率. 用表示到时刻t 为止到达的顾客总数,则在上面的假设下()N t ()()N t P t λ∼.除了指数分布外,常用的还有爱尔朗分布,其密度函数为1()(), 0.(1)!k RxR Rx e f x x k −−=≥− 这时2(), ()i i k k E T D T R R==. k 叫形状参数, R 叫速率参数.当取λ使得R k λ=, 则爱尔朗分布可以看成是k 个独立的服从参数为λ的指数分布随机变量的和的分布.2.2服务过程的模型一般总是认为不同顾客接受服务占用的时间长短是相互独立的. 用Y表示一个客户接受服务的时间长短, 它是一个随机变量.若Y的分布是参数为μ的指数分布, 意味着一个顾客的服务时间平均为1μ. 单位时间里可以完成的平均顾客数为μ.若Y服从形状参数为k, 速率参数为R kμ=的爱尔朗分布, 则平均服务时间为1μ, 根据爱尔朗分布的性质, 可以将Y看作是k个相继子服务的总时间, 每个子服务都服从参数为1kμ的指数分布且相互独立.在排队论中,我们常用如下字母表示特定的到达时间间隔或服务时间分布:M: i.i.d. 指数分布D: i.i.d. 的确定分布E k: i.i.d. 的形参为k的爱尔朗分布GI: 到达时间间隔是i.i.d. 的某种一般分布G: 服务时间是i.i.d. 的某种一般分布在处理实际排队系统时，需要把有关的原始资料进行统计，确定顾客到达间隔和服务时间的经验分布，然后按照统计学的方法确定符合哪种理论分布。

第三章泊松过程

定理设是{N (t), t≥0}一个强度为l的泊松过程，则对任意固定的t, N(t)服从泊松分布，即
P(N (t) = k ) = (lt)k e-l t
k!
k = 0,1, 2,L
二、泊松过程的数字特征与特征函数
1. 泊松过程的均值函数
mN (t) = E[N(t)]= lt
2. 泊松过程的方差函数
DN (t) = D[N(t)]= lt
3. 泊松过程的均方值函数
y
2 N
(t)
=
E[N
2
(t)]
=
DN
(t)
+
mN2
(t)
=
lt
+
(lt)2
4. 泊松过程的自相关函数
E(N (t1)N (t2 ))
令t2 ³ t1E{[N (t1)- N (0)][N (t2 )- N (t1)+ N (t1)]} 展开 E{[N(t1)- N (0)][N (t2 )- N(t1)]+ [N(t1)- N(0)]N(t1)} 展开 E{[N(t1)- N (0)][N (t2 )- N(t1)]}+ E{[N(t1)- N (0)]N (t1)} 增量独立E{[N(t1)- N(0)][N(t2 )- N(t1)]}+ E{[N(t1)- N(0)]N(t1)} 增量独立E[N (t1)- N (0)]E[N (t2 )- N (t1)]+ E{[N (t1)- N (0)]N (t1)}
mN (t) = 4t = DN (t)
RN (t1,t2 ) = 4 min(t1,t2 ) + 16t1t2 , t1,t2 Î T
CN (t1,t2 ) = 4 min(t1,t2 )

泊松过程的性质

到达时刻的分布
01
到达时刻的分布是均匀分布。在泊松过程中，到达时刻的概率密度函数为$f(t) = lambda e^{-lambda t}$，其中$t$是到达时刻。
02
到达时刻的期望和方差分别为 $E(T) = frac{1}{lambda}$和 $Var(T) = frac{1}{lambda^2}$ 。
泊松过程的性质
目录
CONTENTS
• 泊松过程的定义 • 泊松过程的性质 • 泊松过程的统计特性 • 泊松过程的扩展和推广 • 泊松过程的应用
01
CHAPTER
泊松过程的定义
泊松过程的基本概念
01
02
03
随机性
泊松过程是一种随机过程，其事件的发生具有随机性。
独立性
泊松过程中，任意两个不相交的时间区间内发生的事件相互独立。
马尔科夫到达过程是一种特殊的泊松过程，其中事件的发生概率只与当前状态有关，而与过去的状态无关。
在马尔科夫到达过程中，事件的发生是一个马尔科夫链的过程，即下一个事件的发生概率只取决于当前事件是否发生，而与之前的事件无关。这种过程具有无记忆性。
马尔科夫到达过程的数学表达通常使用马尔科夫链和概率论，通过状态转移概率和转移矩阵来描述。
平稳性
总结词
平稳性是指泊松过程的事件发生频率与时间无关，即单位时间内发生的事件数是一个常数。
详细描述
在泊松过程中，事件的发生频率是恒定的，不随时间的推移而改变。这意味着在任意一个固定的时间间隔内，事件发生的次数是一个随机变量，但其均值等于单位时间间隔内的事件发生率。
无后效性
总结词
无后效性是指泊松过程中，过去的事件不会影响未来的事件。

行车时刻表要素解读总结

行车时刻表要素解读总结行车时刻表是列车运行时的重要参考资料，它包含了车次、始发站、终到站、经停站和发车时间等关键信息。

准确地读懂行车时刻表有助于乘客了解列车的运行情况，合理安排行程。

以下是行车时刻表的要素解读总结。

1.车次：每个车次都有唯一的标识号码，用于区分不同的列车。

车次号通常由数字组成，例如G1、D2等。

2.始发站和终到站：始发站是列车出发的地点，终到站是列车的目的地。

这两项信息告诉乘客列车的运行方向和行程终点。

3.经停站：经停站是列车在途中停靠的站点。

行车时刻表通常会列出列车途经的主要车站，以方便乘客做出选择。

4.发车时间：发车时间是列车从始发站出发的具体时间。

行车时刻表按小时和分钟显示发车时间，例如13:30表示下午1点30分。

5.到达时间：到达时间是列车到达各站的具体时间。

行车时刻表通常会显示列车到达每个车站的预计时间，以便乘客合理安排行程。

6.时间间隔：时间间隔是指列车在各站之间的运行时间。

行车时刻表会列出列车在每个站点的停留时间和两个相邻站点之间的行车时间。

7.停靠站时间：停靠站时间是列车在每个车站停留的具体时间。

行车时刻表会标注列车在每个车站停靠的时间长度，以便乘客了解列车的停留时间。

8.班次间隔：班次间隔是指两个车次之间的时间间隔。

行车时刻表会显示不同车次之间的发车时间间隔，以便乘客选择合适的出行时机。

9.车票类型：行车时刻表通常会标注不同车次适用的车票类型，例如普通票、学生票、儿童票等。

10.备注：行车时刻表中可能会有一些特殊情况的备注，例如调整的发车时间、停运的车次等。

要正确读懂行车时刻表，乘客需要注意以下几点：1.确定乘车日期和始发站：行车时刻表根据日期和始发站不同而有所变化，乘客需要根据实际需要选择对应的时刻表。

2.关注车次和终到站：根据自己的出行需求，选择对应的车次和终到站，以确定列车的运行方向和终点。

3.计算到达时间：根据发车时间和时间间隔，计算出自己的到达时间。

(完整)排队论

5。

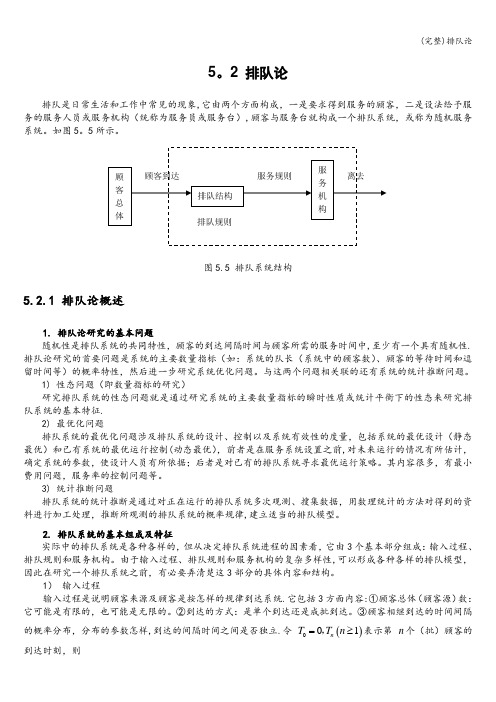
2 排队论排队是日常生活和工作中常见的现象,它由两个方面构成，一是要求得到服务的顾客，二是设法给予服务的服务人员或服务机构（统称为服务员或服务台）,顾客与服务台就构成一个排队系统，或称为随机服务系统。

如图5。

5所示。

图5.5 排队系统结构5.2.1 排队论概述1. 排队论研究的基本问题随机性是排队系统的共同特性，顾客的到达间隔时间与顾客所需的服务时间中,至少有一个具有随机性.排队论研究的首要问题是系统的主要数量指标（如：系统的队长（系统中的顾客数）、顾客的等待时间和逗留时间等）的概率特性，然后进一步研究系统优化问题。

与这两个问题相关联的还有系统的统计推断问题。

1) 性态问题（即数量指标的研究）研究排队系统的性态问题就是通过研究系统的主要数量指标的瞬时性质或统计平衡下的性态来研究排队系统的基本特征.2) 最优化问题排队系统的最优化问题涉及排队系统的设计、控制以及系统有效性的度量，包括系统的最优设计（静态最优）和已有系统的最优运行控制(动态最优），前者是在服务系统设置之前,对未来运行的情况有所估计，确定系统的参数，使设计人员有所依据；后者是对已有的排队系统寻求最优运行策略。

其内容很多，有最小费用问题，服务率的控制问题等。

3) 统计推断问题排队系统的统计推断是通过对正在运行的排队系统多次观测、搜集数据，用数理统计的方法对得到的资料进行加工处理，推断所观测的排队系统的概率规律,建立适当的排队模型。

2. 排队系统的基本组成及特征实际中的排队系统是各种各样的，但从决定排队系统进程的因素看，它由3个基本部分组成：输入过程、排队规则和服务机构。

由于输入过程、排队规则和服务机构的复杂多样性,可以形成各种各样的排队模型，因此在研究一个排队系统之前，有必要弄清楚这3部分的具体内容和结构。

1）输入过程输入过程是说明顾客来源及顾客是按怎样的规律到达系统.它包括3方面内容:①顾客总体（顾客源）数：它可能是有限的，也可能是无限的。

第4章离散事件仿真基础

(一)离散事件系统的仿真模型
1.仿真程序的主要成分采用步长法仿真的程序主要由以下部分组成:
– ①仿真时钟:提供仿真时间的当前值; – ②事件表:由策划和事件调度生成事件名称, 时间的二维表,即有关未来事件的表; – ③系统的状态变量:描述系统状态的变量; – ④初始化子程序:用于模型初始化; – ⑤事件子程序:每一类事件的服务子程序; – ⑥调度子程序:将未来事件插入事件表中的子程序;
顾客到达
忙
理发员忙否
排队等待
否服务服务完毕 (顾客离去) 置理发员闲
(1)实体(Entity) 实体是描述系统的三个基本要素之一.连续系统一样,离散事件也是由实体组成的. 在离散事件系统中的实体可以分为两大类: 临时实体和永久实体.
– 临时实体:在系统中只存在一段时间的实体称为临时实体.这类实体是由系统的外部到达并进人系统的,然后通过系统,并最终离开系统. 例4-1中的顾客显然是临时实体. – 永久性地驻留在系统中的实体称为永久实体. 例4-1中的服务员就是永久实体.
(3)活动(activity) 离散事件中的活动,通常用于表示两个可以区分的事件之间的过程,它标志着系统状态之间的转移.把实体所做的,或对实体施加的事件称为活动,它是实体在两个事件之间保持某一个状态的持续过程. 在例4-1中,顾客的到达事件与顾客的开始接受服务事件之间的过程可以称为一个活动,该活动使系统的状态(队长)发生变化, 从顾客开始接受服务到对该顾客服务完毕后离去的过程也可以被看成是一个活动, 它可能使队长减1或使服务员由忙转闲.
(二)离散事件系统仿真策略
因为离散事件模型的特点,实体活动,进程都是以事件为基础构成的,所以从事件, 活动,进程三个层次来组织事件构成了处理离散事件模型的三种典型的处理方法: 事件调度法,活动扫描法和进程交互法, 相应地要采用三种不同的仿真策略,在复杂系统仿真中,按进程来组织事件可以使众多的事件条理清晰,因而成为最通用的仿真方法.

排队论方法讲解

M－负指数分布 D－确定型分布 Ek k阶爱尔朗分布－阶爱尔朗分布
GI －一般相互独立的时间间隔分布 G －一般服务时间的分布
如 D/M/10/1000/∞ / F
排队论方法讲解
1.3 排队系统的运行指标
⑴ Ls：队长－系统中顾客数的期望： ⑵ Lq：：排队长－系统中等待服务的顾客数 Ln：：正在接受服务的顾客数 Ls=Lq+Ln ⑶ Ws：逗留时间：
排队论方法讲解
(3)普通性：普通性：普通性
内有2个或对于充分小的△t，在[t,t+△t]内有个或，内有多个顾客到达的概率极小,可以忽略不多个顾客到达的概率极小可以忽略不计,即 ∞ 即
∑ P (t , t + ∆t ) = o(∆t )
n=2 n
下面研究系统状态为n的概率分布：
= 1 − λ∆t − o(∆t )
P0 ( t , t + ∆ t ) = 1 − P1 ( t , t + ∆ t ) − ∑ Pn ( t , t + ∆ t )
n=2
∞
分为[0,t)和[t,t+△t), 将[0,t+△t)分为分为和则在时间段[0,t+△t)内到达个顾客的内到达n个顾客的则在时间段内到达概率为
n
由上结果可知,在长度为的时间段内到达由上结果可知在长度为t的时间段内到达在长度为 n个顾客的概率服从泊松分布个顾客的概率,服从泊松分布个顾客的概率服从泊松分布. 其中期望、其中期望、方差为 E[ N (t )] = D[ N (t )] = λt
排队论方法讲解
1.5.2 负指数分布

第5章排队系统和库存系统模型

第5章排队系统和库存系统模型
5.1 排队系统模型 5.2 库存系统模型
1
工业工程系
苏平
5.1 排队系统模型
排队系统的基本概念
排队系统的一般模型
2
工业工程系
苏平
5.1 排队系统模型
排队系统的构成及特性
顾客等待服务的对象。到达模式顾客进入系统的规律。服务台提供服务的机构、设备、人或程序排队规则顾客排队等待服务的次序。服务规则服务台为顾客提供服务的规则。服务时间顾客占用服务台的时间。
排队系统中的时间分布概述
确定性分布也称定长分布，顾客到达间隔时间和接受服务时间是一个确定的常数。指数分布顾客到达间隔时间或顾客接受服务的时间相互独立，具有相同的指数分布：
e t t 0 b (t ) t0 0
21
工业工程系
苏平
5.1 排队系统模型
顾客到达时间间隔和服务时间分布
排队系统中的时间分布概述
k阶爱尔郎分布顾客达到间隔时间或顾客接受服务的时间服从k阶爱尔郎分布：
k (k t ) k 1 k t b (t ) e (k 1)!
k=1时——指数分布 k≥30时——近似于正态分布 k→∞时——方差趋近于0
22
工业工程系
苏平
5.1 排队系统模型
S
( y R )h( y )
y R

其中h(y)是提前期需求量y的概率密度函数。
40
工业工程系
苏平
5.2 库存系统模型随机库存系统
每年所需费用为C，则
D D C C 0 C1 I C 2 S Q Q
将I ，S 表达式代入，可得

随机过程与排队论

随机过程与排队论任课教师:魏静萱副教授wjx@曾勇副教授第一节排队现象例一：电话系统：主叫用户和被叫用户之间提供语音服务，该服务承载于某条通信信道之上，即两个用户c个通道。

地需要一条通道，3个用户需要3个通道，4个用户需要6个通道。

一般的，n个用户需要2n球人口60亿，需要？通道。

海量通信接近天文数字。

解决：信道“公用”导致拥挤排队现象例二：排队现象举例排队系统的三大要素：1. 输入过程 2. 排队规则：队列允许的最大长度 3. 服务窗：顾客是怎样接受服务的1．输入过程：顾客按什么规则进入系统？一个个？成批？到达过程和到达时间间隔符合一定的分布，称到达分布。

假设：到达过程和到达时间是独立同分布的。

到达过程假定为平稳的，对时间是齐次的。

注：Markov 齐次过程如果一个过程只依赖于现在，而不是过去。

表1 输入过程的三种随机过程描述按顾客到达过程的不同概率特性分类： ① 定长输入（D ）：顾客等间隔到达，nc τ=n τ的分布函数为 1()()0n t c F t P t t cτ≥⎧=≤=⎨<⎩②Poisson 流输入(M): 系统的输入过程{M(t)>0}是Poission 流满足4个条件：a) M(t)取值为非负数b) P(M(0)=0)=1, 即时间间隔为0时到达系统的人数为0 c) 过程{M(t)} 具有平稳独立增量性 d) 每一个增量M(a+t)-M(a)非负，且服从参数为tλ的泊松分布(){()()}!k a t P M t a M a k e K λλ-+-==③ k 阶Erlang 输入(Ek)④ 一般独立输入(G)：顾客的到达过程{n τ}是独立同分布的随机变量序列，其分布函数可以是任意函数。

⑤ 成批到达系统：顾客一批批到达系统，每批相继到达的时间间隔为上述各种分布之一。

2．排队与服务规则① 损失制（无排队队列）：顾客到达时，系统被占用，顾客离去，不再回来。

高一物理必修一中的时间间隔与时刻常用的标志用语

高一物理必修一中的时间间隔与时刻常用的标志用语摘要：一、时间间隔与时刻的定义及区别二、时间间隔的常用标志用语三、时刻的常用标志用语四、实例解析正文：一、时间间隔与时刻的定义及区别在高一物理必修一中，我们学到了时间间隔和时刻这两个概念。

时间间隔是指两个时刻之间的时间长度，通常用秒、分钟、小时等单位表示。

时刻则是指某一瞬间的时间点，通常用具体的时间表示，如12:00、14:30 等。

时间间隔和时刻的区别在于，时间间隔是一个时间长度，而时刻是一个具体的时间点。

二、时间间隔的常用标志用语在描述时间间隔时，我们常用以下标志用语：1.“秒”：表示时间的基本单位，用于计量较短的时间间隔。

2.“分”：表示一分钟，用于计量较长的时间间隔。

3.“小时”：表示一小时，用于计量更长的时间间隔。

4.“天”：表示一天，用于计量较长的时间间隔。

5.“周”：表示一周，用于计量更长的时间间隔。

6.“月”：表示一个月，用于计量较长的时间间隔。

7.“年”：表示一年，用于计量较长的时间间隔。

三、时刻的常用标志用语在描述时刻时，我们常用以下标志用语：1.“点”：表示整点，如12:00、13:00 等。

2.“半”：表示半点，如12:30、13:30 等。

3.“刻”：表示一刻钟，如12:15、13:45 等。

4.“分”：表示分钟，如12:20、13:32 等。

四、实例解析假设有一个火车从甲站到乙站，甲、乙两站相距272 公里。

火车的行驶速度为每小时50 公里。

我们可以用时间间隔和时刻的标志用语来描述火车的行驶过程。

1.火车从甲站出发，行驶10 分钟后，火车到达了一个距离甲站25 公里的地方。

2.火车继续行驶20 分钟后，火车到达了乙站。

3.火车从甲站到乙站总共用了1 小时10 分钟。

北京交通大学硕士研究生课程《随机过程》4.1-2

在已知 N t n的条件下， S1， , Sn 的联合密度为
0, t 分为n 1个小部分，取ti为充分小量，
使得 t i -1 t i t i
4.1到达时间间隔与等待时间分布
P t i Δt i Si t i ,1 i n N t n
问题
10 该性质能否推广到 N t n，n 1的情形？
2 该性质是否是 Poisson 过程特有的？
0
4.1到达时间间隔与等待时间分布
补充知识—顺序统计量
10 定义：设 Y1 ,, Yn是n个随机变量，记 Yk 是 Y1 ,, Yn中第k个最小值， k 1,, n，则称 Y1 , Y2 ,, Yn 是对应于 Y1 ,, Yn的顺序统计量 .
k 1
s h k 1!
P N t n
k 1
e
h
h e
t s
t s e t n! n n k ! t
n k
1
s t
n k
1 t
4.1到达时间间隔与等待时间分布
说明：
s 1 P S k s N t n C t jk
又 P S 1 s , S1 s x S 2
s
P X 1 s, X 1 s x X 1 X 2 P X 1 du, X 2 s x u
0
P X 1 du, X 2 s x u P X 1 du, X 2 s x u
的分布，即 Erl an gn, , 密度函数为

排队系统

M—— 负指数分布(M是Markov的字头，因为负指数分布具有无记忆性，即Markov 性)。 D —— 确定性(Deterministic)。
X/Y/Z
其中， XEk—— k阶爱尔朗(Erlang)分布。 ——表示相继到达间隔时间的分布； YGI —— 一般相互独立(General Independent)的随机分布。 ——表示服务时间的分布； ZG —— 一般(General)随机分布。 ——表示并列的服务设备的数目。
工业工程与管理系
Industrial Engineering & Management
3.1 排队论的基本概念
排队模型的分类——例题
D/M/2
表示的是并行双服务机构的服务系统，客户到客户到达系统的间隔时间为确定的定长分布达的时间间隔符合定长分布，服务时间符合负系统服务机构的服务时间为负指数分布指数分布。系统并行的服务机构数量为2台（单队排队）
队列的度量
已知平均到达速率λ和平均服务速率μ,定义业务量强度u为
u
在某些场合下，到达的动态实体并不全都能够得到服务。因此有必要区分实际到达速率λ’以及得到服务的到达速率λ。
此时的业务量强度u为
' u
工业工程与管理系
Industrial Engineering & Management
合一般分布。系统的服务机构数量为1台
工业工程与管理系
Industrial Engineering & Management
3.2 到达时间间隔和服务时间分布引
收集顾客到达的时间间隔运用回归法等统计方法，计算得到到达模式分布的理论值
言
收集服务的时间统计值运用回归法等统计方法，计算得到服务时间分布的理论值

第六章-排队系统建模与仿真(New)

合计
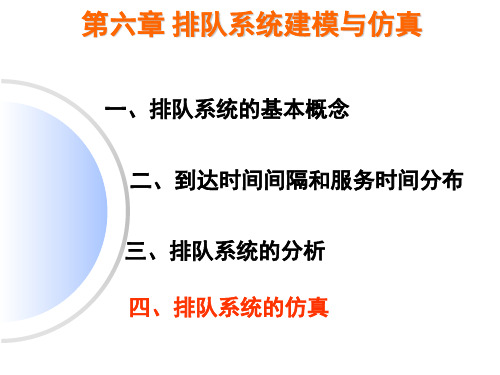
出现的次数ft 38 25 17 9 6 5 0 100
三、排队系统的分析
解：（1）计算平均到达速度：
nfn 2.1人 / 小时
100
平均手术时间：平均服务速度：
Ts
tft 100
0.37小时 / 人
1 1 2.5人 / 小时
Ts 0.4
（2）取λ=2.1，μ=2.5，通过统计检验方法的检验，可以认为病人到达数服从参数为2.1的泊松分布，手术时间服从参数为2.5的负指数分布。
服务员空闲否？
Y
开始服务
经过Si
服务完毕
N
排队等待
顾客离去
四、排队系统的仿真
仿真方法：手工仿真仿真初始条件：系统中没有顾客，即：排队的队列中没有顾客等待，服务台无服务对象。仿真开始：以第一个顾客到达时刻为仿真的起始点。
四、排队系统的仿真
? 事件何时出现？
在仿真中，通过随机数来产生！
四、排队系统的仿真
• M——负指数分布 • M/M/1表示相继到达时间为负指数分布，服务时间为负指数分布，单服务设备的模型。
三、排队系统的分析
1 单服务台M/M/1模型(M/M/1/∞/ ∞/FCFS)
（1）到达模式。动态实体源是无限的，动态实体单个到达，相互独立，一定时间的到达数服从泊松分布。
（2）排队规则。单对，且队列长度没有限制，先到先服务。
混合制
队列的度量
队列的度量
（1）服务强度
1
T0
n
1 Ts
ns
（2）实际业务强度u‘
u' ' 1
（3）服务设备利用率
n
三、排队系统的分析
随机排队系统的运行指标：在系统中动态实体数量的期望值Ls，在系统队列中等待的动态实体数量（队列长度）的期望值Lq。在系统中动态实体逗留时间的期望值Ws，在队列中动态实体等待时间（排队时间）的期望值Wq。

第三章poisson过程与更新过程解读

s,t 0, P(N (s t) N (s) k) (t)k et ,k N
k!
此即 N(s t) N(s) ~ P(t)
利用定理3.1.1 ,可得到Poission过程的等价定义:即
定义3.1.2 计数过程{N(t),t0}称为具有参数(或强度) λ 的Poission过程，如果 1）N(0)=0 ， 2）具有独立增量性，

{P M s t M s m | N s t N (s) n m
n0
P N s t N s n m}

n0
Cm nm
pm (1
p)n
(t)nm et
(n m)!
(n m)! pm (1 p)n (t)nm et
泊松过程的自相关函数
RN t1,t2 E N t1 N t2 min t1,t2 2t1t2
泊松过程的自协方差函数
CN t1,t2 min t1,t2
例 3.1.1 （Poisson过程在排队论中的应用）设某火车站售票从早上8:00开始，此售票处连续售票，乘客以 10人/小时的速率到达，求以下（1）9:00-10:00间最多有5名乘客来此购票的概率（2）10:00-11:00没有人来买票的概率（3）若已知8:00-11:00有10个人来买票，则9:00-10:00间有5名乘客买票的概率。例 3.1.2（事故发生次数及保险公司接到的索赔数）设保险公司接到的索赔请求为以Poisson过程{N(t)},又假设每次的赔付都是1，每月平均接到索赔要求为4次，则一年中保险公司要支付的金额平均是多少？
的分布函数是 F (x)

n 1
1 e x k 0

4-泊松过程

n n 1 2 1
n kn1
k1 !(k2 k1 )!(kn kn 1 )!
12
二、泊松过程的数字特征与一维特征函数
设 {N (t ), t 0} 是强度为的泊松过程，则
1. 均值函数 mN (t ) E( N (t )) t 2. 方差函数 DN (t ) D( N (t )) t
[例1] 设 N (t )为[0,t)时段内某电话交换台收到的
呼叫次数， t [0, )，N (t ) 的状态空间为 {0,1, 2,}，
且具有如下性质：（1） N (0) 0，即初始时刻未收到任何呼叫；（2）在[t,s)这段时间内收到的呼叫次数只与时间间隔s-t有关，而与时间起点t无关；（3）在任意多个不相重叠的时间间隔内收到
注:(4)中实际上假设了在足够小的时间间隔内出现一个质点的概率与时间间隔成正比，而出现质点数不少于2的概率是关于时间间隔的高阶无穷小——这一般是与实际情况相吻合的。
思考：试举个例子是计数过程而不是泊松过程。
9
[定理1]设 {N (t ), t T [0, )}是一强度为的泊松过程，则对任意固定的 t 0，N (t ) 服从泊松一维分布分布 (t ) ，即 k
P{N (t1 ) N (0) k1, N (t2 ) N (t1 ) k2 k1,, N (tn ) N (tn1 ) kn kn1}
P{N (t1 ) N (0) k1} P{N (t2 ) N (t1 ) k2 k1} P{N (tn ) N (tn 1 ) kn kn 1}
2 1
则称{N (t ), t T [0, )}是强度为的泊松过程。
k!

泊松过程、马尔科夫链

DX t X s t s ;
2 t DX t DX t X 0 t 0 t X
RX s, t st 1
s, t C X s, t RX t , s X t X s min
二、正态过程
1.定义
设{X(t),t∈T}是随机过程，若对任意正整数n和 t 1 , t 2 ,, t n T
X t1 , X t 2 ,, X t n 是n维正态随机变量，
则称{X(t),t∈T}是正态过程或高斯过程。
2.正态过程的一个重要性质
随机过程为正态过程的充分必要条件是其任意有限个状态的线性组合为一维正态随机变量。
2.平稳独立增量过程(齐次增量过程)
设{X(t),t≥0}是独立增量过程，若对任意0≤s<t,随机变量X(t)X(s)的分布仅依赖于t-s,而与起点s和终点t本身无关，则称 {X(t),t∈[0,+∞)}是平稳(也称齐次)独立增量过程.
二、泊松过程
1.计数过程
若N(t)表示到时刻t为止已发生的“事件A”的总数，且N(t)满足以下条件：
1N t 0; 2N t 取正整数； 3若s t，则N s N t ; 4当s t时，N t N s 等于区间 s, t 中发生的 “ 事件 A” 的次数 .
则随机过程{N(t),t≥0}为计数过程。
则称{W(t),t≥0}为维纳过程。
7.3 马尔科夫链
一、马尔科夫过程
马尔科夫过程是具有这样特性的过程：当已知随机过程现在时刻处于某状态时，此过程“将来”的情况便与“过去”的情况无关。这种特性通常称为无后效性。
设{X(t),t∈T}为随机过程，若对任意正整数n及 t 1 t 2 t n ,

泊松分布

它表示时间间隔(t0,t]内出现的质点数.“在 (t0,t]内出现k个质点”,即{N(t0,t)=k}是一随机事件,其概率记为 Pk(t0,t)=P{N(t0,t)=k},k=0,1,2, ….
2.泊松计数过程过程 : {N(t) ,t≥0} 称为强度为 λ 的泊松过程,如果满足条件: (1)在不相重叠的区间上的增量具有独立性;
在X(0)=0和方差函数为已知的条件下, 独立增量过程协方差函数可用方差函数表示为:
CX(s,t)X 2(min(s,t))
1、泊松过程举例（Poisson process ）
现实世界许多偶然现象可用泊松分布来描述, 大量自然界中的物理过程可以用泊松过程来刻画. 泊松过程是随机建模的重要基石,也是学习随机过程理论的重要直观背景.著名的例子包括盖格计数器上的粒子流,二次大战时伦敦空袭的弹着点,电话总机所接到的呼唤次数,交通流中的事故数,某地区地震发生的次数,细胞中染色体的交换等等.这类变化过程可粗略地假定为有相同的变化类型.我们所关心的是随机事件的数目,而每一变化可用时间或空间上的一个点来表示.这类过程有如下两个特性:一是时间和空间上的均匀性,二是未来的变化与过去的变化没有关系. 我们将基于这些性质来建立泊松过程的模型.
若t1<t2t3<t4,则在(t1,t2]内事件A发生的次数N(t2)-N(t1) 与在(t3,t4]内时间A发生的次数N(t4)-N(t3)相互独立,此时计数过程N(t)是独立增量过程.
若计数过程N(t)在(t,t+s]内(s>0),事件A发生的次数N(t+s)N(t)仅与时间差s有关,而与t无关,则计数过程N(t)是平稳独立增量过程.
注:由条件(3)知,泊松过程是平稳增量过程且E[X(t)]= t. 由于, =E[X(t)]/t表示单位时间内事件A发生的平均个数, 故称为此过程的速率或强度

齐次Poisson过程中到达时刻的分布

第44卷第3期数学的实践与认识、厂01．44．No．32014年2月MATHEMATICS IN PRA CTI CE AN D THE ORY F e b．、2014齐次Poisson过程中到达时刻的分布邵吉光，王军(北京交通大学理学院，北京100044)摘要：利用多项分布、区间分解等方法研究了齐次Poisson过程中粒子到达时刻的分布规律，对许多定理进行研究和推广，得到了更为一般的结果．关键词：Poisson过程；顺序统计量；多项分布；达到时刻1引言与准备齐次F'o isso n过程是一类重要的平稳过程，也是建立乎稳独立增量过程理论框架的基础之一【1】．其中的粒子来到时间间隔序列{x。

，n 2o)和粒子的到达时刻序列{&，n≥1)的诸多分布规律构成了Poisso n过程理论的重要组成部分．本文运用多项分布等方法导出了一系列到达时刻的概率密度函数．为方便起见，先给出基本的概念和引理．定义1若计数过程{Ⅳt，t≥o)满足：(1)No=o；(2)过程有独立增量性；(3)P(Ⅳs，t=n)=j=迎孚[e一^(2一“，则称{Ⅳt，t≥o)是强度为入的齐次Poisson过程【引．如～一而)=匙。

石A甄z,x+AzF=船。

鼍羞掣，定义2随机向量毒=(6，已，矗)的概率密度函数其中，△。

，。

斗A。

F是毒的分布函数F的他阶差分[3--4j，z=(Xl，z”～，z。

)，Ax=(△zl，△z2，，Ax。

)，0=(0，0，，o)．定义3推广的n重Bernoulli试验：n次重复独立的试验中，每次试验可能有若干个结果，把每次试验的可能结果记为A1，A2，，A，而P(Aj)=Pj，J=l，2，，r，且P1+P2++P，=1．称这类试验为推广的Bernoulli试验【引．引理1记K为Poisson过程{腿，￡之0}第n～1与扎个粒子到达的时间间隔，则有{义_，n≥o)i．i．d．，均服从exp(A)[61．引理2设{M，t≥0)为齐次Poisson过程，则有【2】P(肛=启f肌=n)=c盎(i)七(1一i)“一5，0<s<t，k=0，l，2，，扎此引理表明：条件随机变量(虬IⅣt=n)一6(n，；)，这就意味着，在不考虑次序情况下，已经到达的死个粒子中的任何一个，其到达时刻s皆服从(0，亡】上的均匀分布，且与其他到达时万方数据刻独立．232数学的实践与认识44卷出现后1次，A2出现也次，眯(㈦咄怠蚴幽，，A，出现k，次的概率为【5】双㈦地)=赢艄2p，kr，幻>0，；幻=礼引理4设随机变量∈1，已，，厶独立同(0，t】上均匀分布，则其顺序统计量(≤(1)，《(2)，，∈(”))的联合概率密度函数为【2】，4(￡1，￡2，，如)=豢，0<ti<t2< <t。

2-4到达时间的条件分布

0
0
sx
1 Fs x udFu，
0
所以，
s
xs
1 Fs x udFu 1 Fs x udFu．
0
x
19
化简上式，得 Fs Fx FsFx Fx s，所以 1 Fx s 1 Fs1 Fx．
令 Gx 1 Fx，则有 Gx s GsGx．
类似于定理 2.3.3 证明中的（2.3.4）式以后的证明部分，即得结论．
7
容易看到，对任意的 0 y1 y2 yn ，取充分小的 h 0 ，使得
0 y1 y1 h y2 y2 h y3 yn1 h yn yn h ，
则有
P y1 Y1 y1 h, y2 Y2 y2 h, , yn Yn yn h
P y1 Yi1 y1 h, y2 Yi2 y2 h, , yn Yin yn h ．
1
PN s
1, Nt Ns PNt 1
0
PN s
1 PNt PNt 1
Ns
0
s 1 es
s
0
et s
1!
0!
t 1 et
1!
s． t
4
这个定理说明，由于 Poisson 过程具有平
稳独立增量性，从而在已知时间间隔0, t
上有一事件发生的条件下，事件发生的时
间 X1 在 0, t上是“等可能性的”，即它的条件分布是 0, t上的均匀分布．
E
f
Sn
0
f
t
t n1 n 1!
e
t
dt
，
E
n 1
f
Sn
0
f
t
n 1
t n1 n 1!