医用物理学课件:第二章 流体力学
《医用物理学》教学课件:2-流体的运动

心脏
动脉系统 静脉系统
毛细管系统
血液流速与血管总截面积的关系
人体血液循 环示意图
3.连续性方程 S1v1 S2v2 其它例子
❖ 河道宽的地方 水流比较缓慢,而 河道窄处则水流 较急.
❖ 穿堂风 城市风
自学
例2-1:正常人心脏在一次搏动中泵出血液70cm3,每
分钟搏动75次.心脏主动脉的内径约2.5cm,腔静脉的
第二章 流体的运动
The Motion of Fluid
§2-1 理想流体的定常流动 §2-2 理想流体的伯努利方程 §2-3 黏性流体的运动
本章习题
P57
2-1, 2-5, 2-7, 2-8, 2-9, 2-10, 2-13
几个概念
流体:气体和液体的总称. 流体的特性——流动性:在外力的作用
下,流体的各部分之间很容易发生相 对位移. 流体特点:没有固定形状. 流体的研究对象:
毛细血管的平均血流速度
平静的长白山天池 活泼的长白山天池瀑布
?
§2-2 理想流体的伯努利方程
2.2.1 伯努利方程
2.2.2 伯努利方程的应用
2.2.3 应用伯努利方程 解题的步骤
丹·伯努利(Daniel Bernoull,1700—1782) 瑞士科学家. 1738年提 出了著名的伯努利方程
§2-2 理想流体的伯努利方程
内径约3.0cm,毛细血管横断面的总面积比主动脉的
横断面面积约大220-440倍.若将血液的循环看作是不
可压缩流体在刚性管道中的定常流动,试求:主动脉,
腔静脉和毛细血管的平均血流速度.
解:心脏输出血液的流量
Q V
S1v1
S 2
v2
Q 70106 75 m3/s 8.8105 m3/s 60
【医学PPT课件】流体力学

血液的功能
1. 運送各種物質:
如氧、養份、荷爾蒙的運送,與二氧化碳、 廢物的移除。
2. 保護作用:血液中含有許多抗體、白血球、
血小板,可消滅入侵的細菌、病毒,有外傷 時,血小板的凝固作用,可保護身體,以免 失血過多死亡。 3. 調節平衡作用: 血漿中有許多礦物質、水份、蛋白質,可調 節酸鹼度及體液體積
左心室將血液打入主動脈,經由大動脈及其分 枝而流到身體各部的細胞和組織,供應氧氣和 營養後,帶回代謝產物及二氧化碳,經上下腔 靜脈、大靜脈回流入右心房,稱為體循環。
• 肺循環(又稱小循環):
我們將剪應力及剪應率得這個關係式對各個流體做圖, 可得以下這個圖:
圖中有各式各樣的流體,讓我們來看看圖中這從原點出發, 並呈一直線的流體。這樣的流體我們定義為牛頓流體。牛 頓流體的剪應力對剪應率的比值恆為一定值。圖中的斜率 即代表所謂的黏滯係數,故牛頓流體的黏滯性是固定的, 反之亦然。但是大多數的流體皆不是牛頓流體,亦即它們 的黏滯性是會改變的,這些流體歸類為非牛頓流體,如上 圖所示的其他流體皆是。他們的剪應力對剪應率的比值稱 為apparent viscosity,它並不是一個常數,會隨情況而變。
循環系統
• 血液循環系統包括心臟和血管,心臟為推動 血液循環的原動力,各種血管為血液循環所 取路徑,而微血管則是血液與組織液間交換 物質的場所。
• 循環系統 功能:
1. 運送各種物質往來於體細胞之間使全身的細 胞發揮其本身的機能
2. 細胞代謝 3. 體液體積之恒定 4. 酸鹼度之恒定 5. 抵抗微生物之侵害
力學基本物理公式介紹
流體
血液中相關的力量
•垂直管壁的壓力pressure •管壁細胞抵抗撕裂的張力tensile stress •平行管壁的剪應力shear stress 這一次我們討論作用在血管內皮細胞上的力主要是剪應力 剪應力 SHEAR STRESS:
《医用物理学》教学课件:02第二章-流体的运动-3

(4)牛顿流体与非牛顿流体
遵从牛顿黏滞定律(剪切力、内摩擦力与形 变的关系)的流体称为牛顿流体(水、酒精、血 浆),不遵从牛顿黏滞定律的流体称为非牛顿流 体(血液、胶体溶液和燃料水溶液)。
一般来说,只含有相同物质的均匀流体多为 牛顿流体;而含有悬浮物或弥散物的流体为非牛 顿流体。
讨论 1.雷诺数无量纲,它是鉴别黏性流体 流动状态的唯一参数。
烟缕由层流转 变为湍流
不同雷诺数的圆柱绕流流场
讨论 3. 流体的黏度愈小,密度愈大,愈容易发生湍流。
• 流动相似性
雷诺数相等的流场具有相同的流动状态和性质。
流动的相似性原 理,在流体力学工程 的模拟实验中有着重 要的应用。如建立在 相似性原理基础上的 风洞、水洞试验(几何 相似的小尺度模型)。
非牛顿液体行为: /v_show/id_XMTU4MDc2MjI0.html?from=y1.2-1103.3.2-1.1-1-1-1
3. 湍流和雷诺数
(1)湍流(turbulent flow)
当流体流动的速度超过一定数 值时,流体将不再保持分层流动, 各流体层之间相互混淆,而且可以 出现涡旋。
Pd
1
g
P0
0
已知: Q 0.12m3 / s
P 2103 Pa SA 100cm2 SB 60cm2
hBA 2m
求: vA , vB , PB
解:SAvA SBvB
1 2
v2A
ghA
PA
1 2
vB2
ghB
PB
已知: SD 2SC h1 求:h2
解:h2 ?
PC ?
PA
括所需的实验器材,计算公式和实验步骤。
流体(医用物理)

gh v 2
1 Q 2 ( ) / g 0.46m 2 S
16
2-2 实际流体 一、牛顿粘性定律
17
2-2 实际流体 一、牛顿粘性定律
y x d dt
切应变
x
X
y
切应变率
v dv lim x 0 x dx
F1 L1 F2 L2 E P 1 S1 L 1P 2 S2 L2 E
流量守恒:
2 L2 P2 v S2 2
F2
L1 1 F1
v1 P 1 S1 h1 h2
(P 1P 2 )V E 1 1 2 ( mv2 mgh2 ) ( mv12 mgh1 ) 2 2 1 2 m( v2 v12 ) mg( h2 h1 ) 2 1 m 2 m P1 P2 ( v2 v12 ) g( h2 h1 ) 2 V V 1 2 P1 P2 ( v2 v12 ) g( h2 h1 ) 2 1 1 2 P1 v12 gh1 P2 v2 gh2 2 2
F P S
单位:Pa
N / m2
计示压强: 以当时当地大气压强为基准的压强
静压强:液体静止时的压强 在连通的同种静止液体中:
O
B A
P gh 常量
PA ghA PB ghB PA PB g( hB hA )
hA
h0
hB
PA PB gh
v1 S 2
Q S1v1 S2v2 S1 S2
2 g h 2 S12 S2
13
流体力学第二章ppt课件

P ghC A 225kN
yC
4 sin 60
11
6.6m
IC
b 12
h3
4 3
1.33m4
4m
C D
60° y
yD
yC
IC yC A
6.6
1.33 6.6 4
6.6
0.05
6.65m
yC
图解法(求解矩形平面)
1 水静压强分布图 用一定比例的线段表示压强的大小。 与作用面垂直的箭头表示压强的方向。
(H 13.6103 kg/m 3, 1103 kg/m 3 )
解题步骤
解:
已知断面1上作用着大气压, 因此可以从点1开始,通过等 , 压面,并应用流体静力学基 本方程式,逐点推算,最后 便可求得A点压强。
, 因2-2、3-3、4-4为等压面,根据静压强公式可得
p2 H g(1 2 )
p3 p2 g(3 2 )
根据力的作用方式不同
质量力:指某种力场作用在流体的每一个质点上,大小 与受作用的流体质量成正比的力。
lim X
FBX
V M m
单位质量力轴向分力
lim Y
FBY
V M m
lim Z
FBZ
V M m
单位:N/kg
表面力:是指作用于流体表面上,大小与作用表面积成 正比的力。
P
法向分力
p lim A A A
➢与两流层间的速度差du及流层的接触面积A成正比,和流层间距dy成反比。 ➢与流体种类有关。 ➢与流体的压力大小无关。
T A du dy
T A du 或 du
dy
dy
牛顿内摩擦定律
§1.3 流体的力学模型
医用物理学(第二章)PDF

二、湍流、雷诺数
3.层流和湍流的判别 Re<1000 Re>1500 Re:1000~1500
层流 湍流 湍流与层流均有可能
2011-9-22
25
三、粘性流体的伯努利方程
1. 连续性原理 S 1 v 1 = S 2 v 2
2. 伯努利方程
p1 +
1 2
ρ v12
+
ρ gh1
水银血压计:
z 开管水银压强计,充气带,打气球;
动脉收缩压: 动脉舒张压:
注意:
z 为间接测量方法;
z 所测得的血压为计示压强:p-p0
2011-9-22
35
2011-9-22
36
2011-9-22
37
第二章作业 P48-49: 2-4, 2-5, 2-6, 2-7,2-8,
2-9,2-15, 2-18
9 η(H)
f
z ESR与血浆密度与流动、 RBC密度、 RBC有效半径、 血液粘度、红细胞变形与聚集等因素有关。
2011-9-22
30
2-3 血液的流动
31
一、 血液循环的物理模型
血液循环系统: 体循环
z 左心室→主动脉→ 动脉→ 小 动脉 →毛细血管网→ 小静脉 → 静脉→腔静脉→ 右心房
2. 定常流动(steady flow) (1) 流线(stream line) a. 定义 b. 特点
(2) 定常流动:各点速度不 随时间而变,流线形状不随 时间而变。也称稳定流动。
3. 流管(flow tube)
2011-9-22
5
二、连续性原理
1. 流量(volume flux or flow rate) 单位时间流过截面的流体体积
《医学物理学》课件流体的运动

05
CATALOGUE
流体的流动规律
伯努利方程
伯努利方程表述了理想流体在重力场作稳定流动时,具有压力能、位能和动能三种形式,它们之间能 够互相转换,且总和保持不变。
伯努利方程是理想不可压缩、定常流动流体动量方程的变形,它反映了流体的压强、位置高度和速度 之间的关系。
连续方程
连续方程表述了单位时间流入、流出 控制体积的质量流量之差,等于体积 V中液体质量的变化率。
原因分析
重力是地球对物体的吸引力,因此物体受到的重力越大,其受到的 流体静压力也越大。
实例
在太空中,由于没有重力作用,液体无法保持一定的形状和位置, 会四处漂浮。
03
CATALOGUE
流体动力学
流体动压力
定义
流体动压力是指单位面积上垂直作用于流体微元上的动量力。
公式
流体动压力与流体的密度、速度和重力加速度有关,计算公式为: p = ρgh。
流体静压力与深度关系
深度对流体静压力的影响
流体静压力随深度的增加而增加。
原因分析
由于重力作用,越深处的流体受到的重力越大,因此流体静压力随 深度的增加而增加。
实例
在水中,水深每增加1米,水压就增加约9800帕斯卡。
流体静压力与重力关系
重力对流体静压力的影响
流体静压力与重力有关,重力越大,流体静压力越大。
案例二:肺换气过程模拟
肺换气的生理机制
肺换气是呼吸过程中氧气和二氧化碳交换的 过程,流体力学在肺换气过程中起着重要作 用。
肺功能评估
通过模拟肺换气过程,可以评估肺的功能状态,如 肺活量、通气量等,为诊断肺部疾病提供依据。
呼吸治疗
针对呼吸系统疾病,如哮喘、慢阻肺等,流 体力学方法可以帮助设计更有效的呼吸治疗 策略。
医用物理学课件:第二章 流体力学

压强为P2。
B
A
h
P1
1 2
流 v12
P2
1 2
流 v22
P1 P2 水银 gh
v22
v12
2gh
水银 流
S1v1
S2v2
v2
S1v1 S2
B A
h
v1 S2
2gh
S12
S
2 2
水银 流
Q v1 S1 S1S2
2gh
S12
S
2 2
习题二232629黏性流体的流动血液的流动例题本章总结一理解理想流体定常流动的概念二掌握连续性方程三掌握伯努利方程四掌握伯努利方程的应用常量水平管粗细均匀管常量黏性流体的流动一流体的黏性二黏性流体的伯努利方程三泊肃叶定律四斯托克斯黏滞公式五层流和湍流一流体的黏性1黏性流体的流动2层流黏性3牛顿黏滞定律4黏度5黏性液体的分类1黏性流体的流动黏性流体流动的速度不一致中轴线处最快2层流黏性层流示意图层流
压强能密度
2
流速、压强和高度的关系
势能密度
P 1 v2 gh 常量
2
1.量纲:压强(P)
2.静压强: P gh 动压强: 1 v2
2
3.理想流体定常流动的动力学方程
五、伯努利方程的应用
1、压强和流速的关系及举例(水平管) 2、压强和高度的关系及举例(均匀管) 3、伯努利方程的解题思路
压强和流速的关系
F PS 1.01105 4.23.5 1.5106 (N )
静止流体
潜水员和登山者所感知的压强通常叫做流体 静压强(Static pressure of fluids)。
F2 F1 mg
《医学物理学》课件流体的运动-(含多场合)

《医学物理学》课件流体的运动-(含多场合) 《医学物理学》课件——流体的运动一、引言流体力学是研究流体(液体和气体)运动规律及其与周围环境相互作用的学科。
在医学领域,流体力学有着广泛的应用,如血液流动、呼吸气流、药物输送等。
本课件将介绍流体的基本性质、流体运动的描述方法以及流体力学在医学中的应用。
二、流体的基本性质1.流体的定义与分类流体是一种无固定形状的物质,在外力作用下可以流动。
根据分子间作用力的不同,流体可分为液体和气体。
液体具有不可压缩性和粘滞性,而气体具有可压缩性和粘滞性。
2.流体的密度与压力密度是流体单位体积的质量,通常用ρ表示。
压力是流体分子对容器壁的撞击力,与流体深度和密度有关。
在静止的流体中,压力随深度增加而增大。
3.流体的粘滞性粘滞性是流体抵抗剪切变形的能力。
粘滞性越大,流体越难以流动。
牛顿流体和幂律流体是两种常见的流体类型,它们的粘滞性随剪切速率的变化而不同。
三、流体运动的描述方法1.拉格朗日法与欧拉法拉格朗日法通过追踪流体中某一质点的运动轨迹来描述流体运动。
欧拉法则从空间固定点观察流体运动,描述流体在某一时刻的速度场、压力场等。
2.流线、流管与流速分布流线是流体运动轨迹上各点的切线方向,流管是由一组流线组成的管状区域。
流速分布描述了流体在空间各点的速度大小和方向。
3.纳维-斯托克斯方程纳维-斯托克斯方程是描述流体运动的基本方程,包括质量守恒方程、动量守恒方程和能量守恒方程。
通过求解纳维-斯托克斯方程,可以得到流体运动的详细情况。
四、流体力学在医学中的应用1.血液流动血液是一种非牛顿流体,其流动特性对心血管系统的正常运行至关重要。
流体力学在研究心脏泵血、血管阻力、血流动力学等方面具有重要意义。
2.呼吸气流呼吸气流是气体在呼吸道中的运动。
流体力学在研究肺通气、气体交换、呼吸疾病等方面具有重要作用。
3.药物输送药物输送涉及药物在体内的输运和分布。
流体力学在研究药物在血管、组织间的传输过程以及药物释放等方面具有重要意义。
医学物理学-课件--流体的运动

Rf
8L R 4
泊肃叶定律另一表式: Q P Rf
返前后 回页页
例3-3(P38)
成年人主动脉的半径约为1.3×10-2m,问在
一段0.2m 距离内的流阻和压强降落ΔP为多少? 设血流量为1.00×10-4m3·s-1 ,η=
3.0×10-3pa·s.
解:
8L 83.01030.2 Rf R4 3.14(1.3102)4
即在水平管中流动的流体,
流速小的地方压强较大,
流速大的地方压强较小.
A B
喷雾器
水流抽气机
返前后 回页页
2.汾丘里流量计
∵ P11 212P21 222
S11S22
h
P1P2 gh
∴
2gh 1 S2 S12 S22
P2 S2
P1 υ1
S1
流体的流量:
QS11 S1S2
圆柱 机翼
返前后 回页页
三、稳定流动:
流场
vB B
C vC
A
vA
稳定流动(steady flow):流体中各 点的速度都不随时 间而变化.
(1)流线形状不变; (2)流线不相交.
返前后 回页页
返前后 回页页
流管(tube of flow):流体中通过一小截面 积周边各点的流线所围成的管状区域.
1
2
特例:P1P2 E
结论:粘性流体在均匀水平管中 流动需要一定的压强差来维持.
返前后 回页页
二、泊肃叶定律 (Poiseuille,s law)
稳定流动时: P1 F f
rR
f
压力差: F(P 1P 2)r2
内摩擦力:f 2rLd
《医用物理学》教学课件:2-流体的运动

毛细血管的平均血流速度
平静的长白山天池 活泼的长白山天池瀑布
?
§2-2 理想流体的伯努利方程
2.2.1 伯努利方程
2.2.2 伯努利方程的应用
2.2.3 应用伯努利方程 解题的步骤
丹·伯努利(Daniel Bernoull,1700—1782) 瑞士科学家. 1738年提 出了著名的伯努利方程
§2-2 理想流体的伯努利方程
流线(stream line): 在流体流过的空间作许多曲线,
曲线上每一点的切线方向和流经该处的流体质元的速度方向 一致——流线
流管(stream tube)
由流线围成的细管
2.1.3 定常流动(稳定流动)
一般流动: v(x、y、z、t) 定常流动: v(x、y、z)
任意空间点的流速都不随时间而改变
(2 P1 P2 )
(S12 S22)
Q v1S1 S1S2
2(P1 P2 )
(S12
S
2 2
)
已知: S1, S2 , h 求: Q v S
P1 P2 gh
Q S1S2
2gh S12 S22
伯努利方程
1 2
v12
gh1
P1
1 2
v22
gh2
P2
连续性方程 S1v1 S2v2
3.等压情况下流速与高度的关系
例:解释水龙头中的水流逐渐变细
2.2.2 伯努利方程的应用
1 2
v12
gh1
P1
1 2
v22
gh2
P2
1. 压强与高度的关系 当v1 v2时 P1 gh1 P2 gh2
h↑ 则 P↓
1. 压强与高度的关系
⑴ 体位对血压的影响
医用物理复习(医用物理).ppt

x暗
(2k
1)
L
2d
2、薄膜干涉
增透膜、增反膜条件
第10章 波动光学
二、衍射
1、单缝衍射 用半波带波分析明(暗)纹衍射角、位置 计算中央明纹和其他明纹(角)宽度
a sin
(2K
1)
2
明纹
K
暗纹
2、园孔衍射
s i n 1
1.2 2
d
艾里斑、瑞利判据、最小分辨角、分辨率
3、光栅衍射 分析主明纹衍射角、位置、缺级级次
欧姆定律的微分形式 J= E
1
R L
S
含源电路的欧姆定律 U AB IR
基尔霍夫电路定律
I 0
电容器的充电
t
uC (1 e )
IR 0
i
t
e
R
电容器的放电
t
uC e
i
t
e
R
第8章 振动和波
一、振动 1、简谐振动 x Acos(t 0 )
弹簧振子
k m
2、特征量 A, ,0
半衰期
平均寿命
T ln 2
1 T ln 2
放射性活度
A N ln 2 N
T
= 1 ( n 1)( 1 1 )
f
r1 r2
眼的光学系统:近点、远点、明视距离、正视眼、非正视眼的矫正
放大镜
25cm
f
光学显微镜
M m s 25cm
fo fe
Z 0.61
N .A
第13章 X射线
X射线的产生、强度、硬度
h max
1 2
mv2
eU
min
hc eU
1.242 ( nm ) U ( kV )
医用物理学,期末复习整理,.ppt
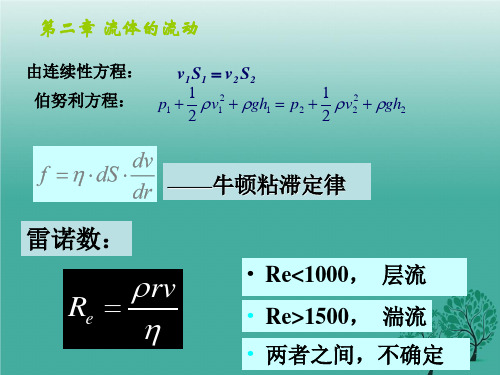
W Q2 ln RA 4πε0l RB
BA
与 W Q2 比较得:
2C
C 2πε0l ln RB
RA
例:面积均为 S 400cm2 的三块平行金属板,分别相距 d1 3mm, d2 6mm
,其中A板带电 q A 9 10 7 C ,B、C两板接地,不计边缘效应。
求(1) B板和C板上的感应电荷。 (2) A板的电势(以地为电势零点)。
例题:一个敞口圆筒容器,高度20cm,直径10cm,圆筒底部开一横截面
积为 10cm2 的小圆孔,水从圆筒顶部以140cm3 / s的流量由水管注入圆
筒内,问圆筒内的水面最终升高到多大高度?
解:圆筒截面
S1 0.785 10 2 m2 >>小孔截面 S2 104 m2 ,v2 2gh
达最高高度,流进液体等于流出的,
q C et / RC Qet / RC
UC
q C
(1 et / RC )
i dq et / RC
dt R
UC
q C
et / RC
i dq et / RC
dt R
例:电量Q(Q>0)均匀分布在长为L的细棒上,在细棒的延长 线上距细棒中心O距离为a的P点处放一带电量为q(q>0)的点电 荷,求带电细棒对该点电荷的静电力。
y(cm)
(2)写出该平面谐波的波动方程。
解、(1)A=0.1m
ω=
2
=πrad/s
T
10
0 20 40
x(m)
由x=0处,t=0.5s时 y=0 V<0 φ=0 故原点振动方程为y=0.1 cosπt
(2)λ=40m y=0.1 cos(πt-
2x )=0.1cos π(t- x )
医用物理学:02流体力学

根据功能原理,
p1∆V
−
p2∆V
=
(1 2
mv22
+
mgh2
)
−
(
1 2
mv12
+
mgh1 )
第8页
第2章 流体力学 血液流变学简介
h2
医用物理学
第2章 流体力学 血液流变学简介
p1∆V
−
p2∆V
=
(1 2
mv22
+
mgh2
)
−
(
1 2
mv12
+ mgh1)
p1∆V
+
1 2
mv12
+
mgh1
=
p2∆V
解:
p1
+
1 2
ρ v12
=
p2
p2
−
p1
=
1 2
ρ v12
=
ρ′gh
v1 =
2ρ′gh = ρ
2×103 ×9.8× 0.02 = 14 m⋅s−1 2
Q = v1S = 14×10×10−4 = 1.40 ×10−2 m3⋅ s−1 5分钟内采取的CO2气体为 1.40×10−2 × 5× 60 = 4.2 m3
2.3 伯努利方程
2.3.1 理想流体的伯努利方程
伯努利方程是关于理想流体作稳定流动时的运动规律. 伯 努利于1738年首先导出. 该方程可利用功能原理推导出来.
∆E
=
(1 2
mv
2 2
+
mgh2
)
−
(1 2
mv12
+
mgh1 )
压力的总功: A = A1 + A2 A = p1S1v1∆t + (− p2S2v2∆t) = p1∆V − p2∆V h1
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
• 流体:气体和液体
• 流体静力学:研究静止流体规律的学科 • 流体动力学:研究流体运动规律的学科
意义:研究血液循环和呼吸过程的基础。
本章内容
• 流体静力学 • 流体动力学:
– 运动的理想流体 – 运动的粘性流体
Density & Pressure
刚体——质量和力 流体——密度和压强
一、理想流体
• 定义:
–绝对不可压缩(即各处密度保持不变) –完全没有粘性(即没有内摩擦)
• 意义:理想模型 • 判断:实际流体分析
实际流体分析
• 压缩性:液体可近似为不可压缩;气体是可压缩 的,但在温度和压强不变的情况下,可认为密度 保持不变;
• 内摩擦:气体的内摩擦一般很小;水和酒精的内 摩擦也很小,但甘油和糖浆的内摩擦不能忽略。
密度 m m
V V
压强
p F F S S
标量,kg/m3
标量,N/m2, 帕[斯卡](Pa)
大气压
1atm 1.01105 pa (N/m2 ) 1.01106 bar (dyn/cm2 ) 760 torr 巴(达因/平方厘米)
1达因=10-5牛顿
760mmHg 1.03104 mmwater
p p0 gh
p1
y1
p2
mg
y2
F1
gauge pressure
在静力平衡流体中,一点的压强只与该点的深 度有关,与流体或容器的水平尺寸无关。
[例] 2-2 一个初学使用水下呼吸器的潜水者在游泳
池里练习潜水。在水面以下L处,在抛弃气罐前从 气罐吸足了气体使肺膨胀,然后游向水面。可是他 忽视了指导而没有在上升过程中呼气。当他到达水 面时,他受到外界的压强和他肺里的气压的差是 9.3kPa。问他出发时的深度是多少?他面对什么样 的致命危险?
Buoyancy
Fb m f g wV f g
漂浮 Fb G G mf g
[例] 2-4 漂浮在海面的冰山 的可见体积占整个冰山多 大比例?
已知冰和海水的密度分别为 0.917x103 kg/m3, 1.024x103 kg/m3
mg mf g
冰V 水V f
1 Vf 1 冰 1 0.917 0.10
F PS 1.01105 4.23.5 1.5106 (N )
静止流体
潜水员和登山者所感知的压强通常叫做流体 静压强(Static pressure of fluids)。
F2 F1 mg
F2
p2S p1S S (y 1 y 2)g
p2 p1 g (y 1 y 2)
absolute pressure
作原理
Archimedes’ Principle 阿基米德原理
When a body is completely or partially immersed in a fluid, the fluid exerts an upward force on the body equal to the weight of the displaced fluid.
例2-3如图所示,在一个水压机中,小活塞的直 径为1.0厘米,大活塞的直径为8.0厘米。将50牛 顿的力加到小活塞上,求作用于大活塞上的力 。 解 由帕斯卡定律,作用在两个活塞上的压强相 等,即
F2 F1 S2 S1
F2
S2 S1
F1
42 0.52
50
3200N
这就是汽车加油站中所用的液压千斤顶的基本工
1托/乇=133.322Pa
例 2-1一个起居室高2.4m,其地板的尺寸为长 4.2m宽3.5m。(空气在200C,1atm下密度为 1.21kg/m3)
(a)当压强为1.0 atm时,室内的空气有多重? (b)室内空气给地板的作用力有多大?
G mg Vg
2.44.23.51.219.8
418(N)
• 判断:当可压缩性和粘性只是影响运动的次要因 素,而其主要因素是流动性时,一般可采用理想 流体模型。
二、流线、流管、定常流动
B
C VB
VC
A VA
流线 特点:
图2.4 在进行风洞试验时, 烟在经过汽车的空气流中显 示流线
• 流线是随时间而变化的 ;
• 在任意时刻任意两条流线不可相交。
• 流管:在流体中作一微小的闭合曲线,通过 此曲线上的各点的流线所围成的细管。
In an incompressible liquid, the increase in the pressure at any point is transmitted undiminished to all other points in the liquid.
用液压杠杆可以将作用于一个给定距离的一个给 定的力转变为作用于一个较小距离的较大的力。
• 特点:流管内外的流体都不会穿越管壁
稳流/定常流动
B
C VB
VC
A
VA
流线
图2.3 一缕上升的烟雾从
• 定义:如果流体内各点的流稳速流的到非大稳小(湍和)流方的过渡。 向都不随时间而变化,称为定常流动 (steady flow,稳流)。
B
C VB
VC
A VA
流线 稳流时的特点 • 流线(流管)形状保持不变 • 密度分布保持不变 • 定常流动不一定是匀速流动 • 做定常流动的不一定是理想流体
p p0 gL p p p0 gL
L p
9300Pa
0.95m
g (1000kg / m 3)(9.8m / s 2)
测量压强
水银气压计
当气囊的压强降至心缩压以下时,血液湍 流通过血管射出,产生声振动,从听诊器可以 听到声音——称为 Korotkoff音或 K音。
Pascal’s Law 帕斯卡定律 & 液压杠杆
V
水
1.024
Iceberg
流体静力学小结
• Density & Pressure • Pascal’s Law帕斯卡定律 • Archimedes’ Principle 阿基米德原理 • 相关习题:习题二:2.1,2.2
运动的理想流体
一、理想流体 二、流线、流管、定常流动 三、连续性方程 四、伯努利方程 五、伯努利方程的应用 六、总结
三、定常流动的连续性方程
• 两个概念:体积流量、质量流量 • 连续性方程的推导 • 连续性方程的结论 • 连续性方程的应用举例
S
Sv11
v1Δt
图1-1.2 流管
