线段的中点坐标公式PPT幻灯片
线段的中点坐标公式

的分点C的坐标
2
2 1 (5)
解
x 2 1 1
4ቤተ መጻሕፍቲ ባይዱ (5) 1 21 3
2
y
3 1
1 4 2 1
64 2 1
2 3
2
因此分点C的坐标为(-
1 , 3
2) 3
2、线段的定比分点坐标公式
x x1 x2 , y y1 y2 ( 1)
1
1
练习 1、 设点C分线段AB成定比 ,求分点C的坐标:
设D,E,F分别是边BC,AC,AB的中点,求点D,E,F的坐标
解 点D的坐标为 (2, 3) 2
点E的坐标为 (1 , 1) 2
点F的坐标为 ( 1 , 1 ) 22
1、线段的中点坐标公式: x x1 x2 y y1 y2
2
2
例2 已知线段AB的中点M的坐标为(3, 1 ) ,端点A的坐标为(4,2)
使得 | AC |
1
y1) (x2
| CB |
,
y2 ) ,设C是线段AB上的一点,
试问:点C的坐标是多少?
2
y
.B
A.
C.
e2
o e1
x
思考:
如图,已知线段AB的两个端点A,B的坐标
分别为, (x1,
使得 | AC |
1
y1) (x2
| CB |
,
y2 ) ,设C是线段AB上的一点,
试问:点C的坐标是多少?
2
y
.B
C.
A.
e2
o e1
x
2、线段的定比分点坐标公式
(1)定比分点 在直线AB上任取一点C,使得AC λ CB ,我们称
求线段的中点坐标

求线段的中点坐标线段的中点坐标是指一条线段上的一点,该点与线段两个端点之间的长度相等。
计算线段的中点坐标的方法很简单,只需要将线段的两个端点的横坐标和纵坐标分别相加再除以2,即可得到中点的坐标。
设线段的两个端点分别为A(x1, y1)和B(x2, y2),中点的坐标为M(x, y)。
根据中点的定义,可以得到以下公式:x = (x1 + x2) / 2y = (y1 + y2) / 2下面我们通过一个具体的例子来演示如何计算线段的中点坐标。
例子:设线段的端点A为(2, 3),端点B为(8, 6),求线段AB的中点坐标。
根据上述公式,可以得到:x = (2 + 8) / 2 = 10 / 2 = 5y = (3 + 6) / 2 = 9 / 2 = 4.5所以线段AB的中点坐标为M(5, 4.5)。
在几何学中,线段的中点具有一些特殊的性质。
比如,线段的中点对称于线段两个端点,即如果在中点与线段两个端点之间画一条直线,这条直线将把线段平分为两段相等的部分。
此外,线段的中点也是线段的重心,即线段两个端点与中点连成的三条线段的长度相等。
计算线段的中点坐标在许多应用中是非常有用的。
例如,在计算机图形学中,中点坐标被广泛应用于计算图形的平移、旋转和缩放等操作中。
此外,在地理学中,也可以利用中点坐标来计算地图上两个点之间的中心点。
总之,计算线段的中点坐标是一项基本的几何计算,通过将线段的两个端点的横坐标和纵坐标分别相加再除以2,即可得到线段的中点坐标。
线段的中点具有一些特殊的性质,在许多应用中都能发挥重要作用。
希望本文能对读者有所帮助。
中点坐标公式及其应用

中点坐标公式中点坐标公式在平面直角坐标系中,如果线段AB 的端点A 、B 的坐标分别为A ),(11y x 、B ),(22y x ,则其中点P ),(n m 的坐标为 图形说明如图(1)所示. 以上便是线段的中点坐标公式.知道三个点中任意两个点的坐标,可以求出第三个点的坐标.如:抛物线)0(2≠++=a c bx ax y 与x 轴的两个交点分别为)0,()0,(21x x 、,则由中点中点坐标公式可知其对称轴为直线221x x x +=.再比如,如图(2)所示,在平面直角坐标系中,□ABCD 的顶点A 为(1,2),两条对角线交于点O,且点O (3,4),则端点C 的坐标可由中点坐标公式求得为(5,6).图(2)中点坐标公式的应用例1.(河南中考)已知抛物线)0(2≠++=a c bx ax y 与x 轴交于A 、B 两点,若点A 的坐标为)0,2(-,抛物线的对称轴为直线,2=x 则线段AB 的长为________. 例2(北京月考试题)已知:如图,抛物线c bx x y ++-=2经过直线3+-=x y 与坐标轴的两个交点A,B,此抛物线与x 轴的另一个交点为C,抛物线的顶点为D.(1)求该抛物线的解析式;(2)点M 为抛物线上的一个动点,求使△ABM 与△ABD 的面积相等的点M 的坐标.解:(1)由题意知:A(3,0),B(0,3)∵抛物线c bx x y ++-=2经过点A 、B ∴⎩⎨⎧==++-3039c c b 解之得:⎩⎨⎧==32c b∴该抛物线为322++-=x x y ; (2)∵D 为抛物线322++-=x x y 的顶点 ∴D(1,4)①过点D 作DM ∥AB,交抛物线于点M,此时△ABM 与△ABD 的面积相等.可设直线DM 为m x y +-= ∵D(1,4) ∴41=+-m ∴5=m∴直线DM 为5+-=x y 令5322+-=++-x x x 解之得:2,121==x x ∴3,421==y y ∴点M(2,3)(其中,点M(1,4)与点D(1,4)重合) ②∵A(3,0),B(0,3),D(1,4) ∴233322=+=AB ∴20222==+AD BD AB ∴BD ⊥AB延长DB 至点D′,使DB=B D′,并过点D′作直线AB 的平行线l ,l 与抛物线有两个交点,这两个交点即是符合题意的点M.设直线l 为n x y +-=,点D′为),(q p ∵B(0,3),D(1,4) ∴由中点坐标公式得:∴⎩⎨⎧=-=21q p ∴D′)2,1(- ∵直线l 经过点D′ ∴21=+n ∴1=n∴直线l 为1+-=x y 令1322+-=++-x x x 解之得:2173,217321-=+=x x ∴2171,217121+-=--=y y ∴点M 的坐标为⎪⎪⎭⎫⎝⎛--+2171,2173或⎪⎪⎭⎫⎝⎛+--2171,2173 综上所述,点M 的坐标为 (2,3)或⎪⎪⎭⎫⎝⎛--+2171,2173或⎪⎪⎭⎫⎝⎛+--2171,2173.。
平面直角坐标系线段中点坐标公式

平面直角坐标系线段中点坐标公式1. 中点的魅力大家好,今天咱们聊聊一个看似简单但又挺重要的概念——中点!你说,中点是什么?其实,它就是连接两点之间的一条线段的“中间人”。
想象一下,你在公园里和朋友散步,走着走着,突然发现那条长长的走道把你俩给分开了,别担心,中点就像是那道美丽的彩虹,把你俩连接起来。
它的坐标就是线段两端坐标的平均数,就像两个朋友一块分享冰淇淋,甜甜的,一点也不争!2. 中点坐标公式2.1 公式的来历要说到中点的坐标公式,我们得先弄明白两个点。
假设你有两个点,A(x₁, y₁)和B(x₂, y₂)。
那么,中点M的坐标就是用公式 M(x, y) 来表示的。
它的计算方法非常简单,x坐标是x₁和x₂的平均值,y坐标也是y₁和y₂的平均值。
换句话说,M的坐标就是:。
M(x, y) = (left(frac{x₁ + x₂{2, frac{y₁ + y₂{2right))。
简单吧?就像小孩子分享玩具一样,大家一起开心最重要。
2.2 公式的实际应用这个公式的用处可大了,生活中到处都能碰上它的身影!比如说,假设你在校园里和同学约好在操场见面,你们的位置分别在(2, 3)和(4, 5)。
用我们的中点公式一算,中点M的坐标就是:。
M(3, 4)这下,你俩就能在这个地方碰面,不用再东找西找,真是省时省力嘛!想象一下,你的生活就像一场大戏,中点就是那位调皮的小丑,负责让一切变得有趣和轻松。
3. 中点的趣味3.1 中点的几何意义中点不仅仅是数字的游戏,它还有深厚的几何背景。
想想看,一个线段的中点,实际上就是这个线段的“平衡点”。
在一个小朋友的天平上,如果一边放着苹果,另一边放着香蕉,只有在中间的那个点上,它们才能完美平衡。
这就是中点的魅力所在。
数学在我们身边,总是用最简单的方式告诉我们生活的真理。
3.2 生活中的应用而且,中点的概念在生活中还有很多实际应用!比如在建筑设计中,设计师常常需要找出某个结构的中心点,以确保一切都建得稳稳当当。
中点公式和距离公式

8. 1
两点间的距离与线段中点的坐标
巩 固 知 识 典 型 例 题
例1 解
求A(−3,1)、B(2,−5)两点间的距离. A、B两点间的距离为
| AB | (3 2)2 1 (5) 61.
2
第1题图
8. 1
两点间的距离与线段中点的坐标
运 用 知 识 强 化 练 习
,、 B(3, 在平面直角坐标系内,描出点 A(11) 4) .
故 | AD | (1 1)2 (2 0)2 2 2, 即BC边上的中线AD的长度为 2 2.
8. 1
两点间的距离与线段中点的坐标
1.已知点 A(2,3) 和点 B (8, 3),求线段AB中点的坐标.
运 用 知 识 强 化 练 习
5,0 .
2.已知ABC 的三个顶点为 A(2, 2)、B(4,6)、C (3, 2), 求AB边上的中线CD的长度.
作业
继 续 探 索 活 动 探 究
读书部分:阅读教材相关章节 书面作业:教材习题8.1 A(必做) 教材习题8.1 B(选做) 实践调查:编写一道关于求线段
中点坐标的问题并求解.
8. 1 两点间的距离与线段中点的坐标
学习效果
自 我 反 思 目 标 检 测
学习行为
学习方法
8. 1
两点间的距离与线段中点的坐标
已知点 M (0, 2),N (2, 2), 求线段MN的长度,并写出线段
自 我 反 思 目 标 检 测
MN的中点P的坐标.
MN 2; P 1, 2 .
8. 1
两点间的距离与线段中点的坐标
并计算两点之间的距离.
5.
8. 1
两点间的距离与线段中点的坐标
中职数学基础模块下册《两点间距离公式及中点坐标公式》PPT课件附课堂练习(投稿)

65.
求两点之间的距离:
(1)A(6,2),B(-2,5); (2)C(2,-4),D(7,2).
如图所示.设 M(x,y) 是 A(x1,y1) ,B(x2,y2) 的中点.
y
B2
B
M2 M
A A2
A1 O M1 B1 x
过 A,B,M 分别向 x 轴作垂线 AA1,BB1, MM1,垂足分别为 A1, B1 ,M1 ;
过 A,B,M 分别向 y 轴作垂线 AA2,BB2, MM2,垂足分别为A2, B2 ,M2 .
如图所示.设 M(x,y) 是 A(x1,y1),B(x2,y2) 的中点.
y
B2
B
M2 M
(1)你能说出垂足A1,A2,B1,B2, M1,M2的坐标吗? (2)点M是AB中点,M1是A1,B1的 中点吗?它们的坐标有怎样的关系?
3.直角三角形中勾股定理的内容是什么?
如图所示.设 A(x1,y1),B(x2,y2) .
y
B2
B
A A2 A1 O
C B1 x
过 A,B 分别向 x 轴作垂线 AA1,BB1,垂足分别为 A1,B1 ;
过 A,B 分别向 y 轴作垂线 AA2,BB2,垂足分别为 A2,B2 ;
其中直线 BB1 和 AA2 相交于 点C.
S3
计算 d=
d
2 x
d
2 y
;
S4 给出两点的距离d.
例1 已知ቤተ መጻሕፍቲ ባይዱA(2,-4),B(-2,3) ,求 |AB| .
解: 因为 x1=2,x2=-2,y1=-4,y2=3,
所以
dx=x2-x1=-2-2=-4, dy=y2-y1=3-(-4)=7.
3.3直线的交点坐标与距离公式ppt课件

一般式通过化简
y=
−
A B
x
+
C B
如何利用斜率、截距来判断两直线的位置关系?
4
直线方程:y = kx + b
y=
−
A B
x
+
C B
两直线平行
k1 k2 b1 b2
A1B2 A2B1
A1C2 A2C1
两直线重合
k1 k2 b1 b2
A1B2 A2B1
A1C2 A2C1
Ax0+C B
)
Q
P0Q是Rt⊿P0 RS斜边上的高 P0 由三角形面积公式可知 O
R (-
By0+C A
,
y0)
lx
|P0Q|·|RS|=|P0R|· |P0S|
即|P0Q|
=
|Ax0+By0+C| √A2+B2
点P0(x0,y0)到直线l:Ax+By+C=0的距离
d= |Ax0+By0+C| √A2+B2
l2: Ax+By+C2=0的距离,即为所求。
26
两ቤተ መጻሕፍቲ ባይዱ平行直线间的距离:
y 两条平行直线间的距离 是指夹在两条平行直线 间的公垂线段的长.
o
P l1
l2
Q x
两条平行线l1:Ax+By+C1=0 与
l2: Ax+By+C2=0的距离是 d
C1 - C2 A2 B2
27
练习
1.平行线2x-7y-8=0和6x-21y-1=0的距离是______; 2.两平行线3x-2y-1=0和6x-4y+2=0的距离是____.
线段的中点和分点公式

线段的中点和分点公式线段是指由两个端点所确定的一段直线。
在数学中,我们经常需要计算线段的中点和分点的坐标。
本文将介绍线段的中点和分点的计算公式,并且给出一些实际的应用例子。
1. 线段的中点公式线段的中点即为线段的中间点,离两个端点的距离相等。
如果我们已知线段的两个端点的坐标,可以使用下面的公式来计算线段的中点的坐标:中点的横坐标 = (端点1的横坐标 + 端点2的横坐标) / 2中点的纵坐标 = (端点1的纵坐标 + 端点2的纵坐标) / 2例如,假设线段的端点1为A(x1, y1)、端点2为B(x2, y2),我们可以使用上述公式来计算线段AB的中点的坐标。
这个中点的坐标可以表示为M((x1+x2)/2, (y1+y2)/2)。
2. 线段的分点公式线段的分点指的是线段上的任意一点,它将线段分成两个小线段。
如果我们已知线段的两个端点的坐标以及分点离端点1的距离比例(即所占线段总长度的比例),可以使用下面的公式来计算分点的坐标:分点的横坐标 = 端点1的横坐标 + (端点2的横坐标 - 端点1的横坐标) * 比例分点的纵坐标 = 端点1的纵坐标 + (端点2的纵坐标 - 端点1的纵坐标) * 比例例如,假设线段的端点1为A(x1, y1)、端点2为B(x2, y2),我们可以使用上述公式来计算线段AB上距离端点1长度比例为k的分点的坐标。
这个分点的坐标可以表示为P(x1 + (x2 - x1) * k, y1 + (y2 - y1) * k)。
3. 应用例子线段的中点和分点公式在几何学和物理学中有广泛的应用。
以下是一些例子:- 几何图形中的对称轴:对称轴是指一个几何图形的中心线,在轴上的任意一点到图形两侧的距离相等。
我们可以使用线段的中点公式来计算对称轴的坐标。
- 物体运动的中点和分点:在物理学中,我们经常需要计算物体在一段时间内的平均位置。
我们可以使用线段的中点公式来计算物体在两个时间点的中点位置,并使用线段的分点公式来计算物体在不同时间点的分点位置。
2.2.2直线的两点式方程 课件(共20张PPT)

所以所求直线方程为: + − 3 = 0或 = 2.
(,0)
Байду номын сангаас
例2 ⑴ 过点(1,2)并且在两个坐标轴上的截距相等的直线有几条?并求其方程.
(2) 过(1,2)并且在两个坐标轴上的截距的绝对值相等的直线有几条? 并求其方程.
解:三条
①当直线的两截距相等过原点时, = 2
②当直线的两截距相等不过原点时, + − 3 = 0
典例剖析
例3 三角形的顶点分别是(−5,0), (3, −3), (0,2),求边所在直线的方程,以及该边上
中线所在直线的方程.
变式1 求边上的垂直平分线所在直线的方程.
:5 + 3 − 6 = 0 = −
=
1
3
M ,
2
2
+
(1)在轴上的截距为2,在轴上的截距是3;
由截距式得:
x y
1
2 3
整理得:3x 2 y 6
0
(2)在轴上的截距为-5,在轴上的截距是6;
由截距式得:
x
y
1
5 6
整理得: 6 x 5 y 30 0
典例剖析
例2 ⑴ 过点(1,2)并且在两个坐标轴上的截距相等的直线有几条?并求其方程.
斜截式
斜率, 在轴上的纵截距
y kx b
斜
率
必
须
存
在
斜率不存在时,
直线方程为:x x0
思考:已知直线上两点1(1, 1), 2(2, 2)(其中1 ≠ 2, 1 ≠ 2 ),如何求出通过这两点的
两点间的距离及中点坐标公式
技师学院工业学校一体化翻转课堂教学设计方案PPT一、 课前预习1.提供课前教学资源:电子媒介及网络资源二、课堂教学流程设计1. 观察学生、教室,师生互致问候2. 核查上课人数3. 介绍布置教学任务,板书知识节点4. PPT 展示5. 学生独立完成任务6. 教师指导7. 上交任务8. 布置作业授课计划表(2课时)教学环节1、布教学容(知识点、技能点)*揭示课题学生活动学习、提问教师活动时间分配10分钟2-相关知识*创设情境兴趣导入3.相关知识【知识回顾】uuun平面直角坐标系中,设P1(x i,y i), P2(X2,y2),贝U RP2(x2x1,y2y1).*动脑思考探索新知【新知识】uuuu学习、提问写工作页展示小结及展示uiuur uuur uuuf, ----------------- ---------------------- ;IPP2I PP2 JRP2SPP2 VS x i)2 (y2 y i)2讲解、答疑30分钟指导40小结10(8. 1)教学过程8. 1两点间的距离与线段中点的坐标教学环节教学容(知识点、技能点)*动脑思考探索新知 【新知识】设线段的两个端点分别为 A (x i ,y 〔)和B (X 2,y 2),线段的中点为M (x o ,y 。
)(如图8—1),uuuu则 AM (X 0 X i ,y 0 y i ),学生活动教师活动时间分配教学过程uuuruuuu uuirMB g X 0,y 2 y o ),由于 M 为线段 AB 的中点,贝U AMMB,即X 0 X iX 2 X 0,(X 0 X i , y o y i ) (X 2X 0, y 2 y 。
), 即解 得y 。
y i V2y 0,X0c ,y° c . 2y /2] L. ---------1B(X 2, y 2)M(X0, y 0) A(X I , y i )O1 ----------------------- 1 1 才X。
线段的中点坐标公式

线段的中点坐标公式
设线段AB的坐标为A(x1,y1),B(x2,y2)。
线段的中点的坐标为
M(x,y)。
首先,我们知道线段的中点的横坐标是两个端点横坐标的平均值。
即
x=(x1+x2)/2
接下来,我们知道线段的中点的纵坐标也是两个端点纵坐标的平均值。
即y=(y1+y2)/2
所以,线段的中点坐标公式就是:
M(x,y)=((x1+x2)/2,(y1+y2)/2)。
这个公式可以用来求解任意线段的中点坐标。
例如,如果有一个线段的端点坐标为A(1,2),B(5,6)。
那么这个线
段的中点的坐标可以通过使用中点坐标公式进行计算。
将x1=1,y1=2,
x2=5,y2=6代入公式中,得到:
M(x,y)=((1+5)/2,(2+6)/2)=(3,4)。
所以,这个线段的中点的坐标是M(3,4)。
总结起来,线段的中点坐标公式是一个简单而有用的数学公式。
它将
线段的两个端点的坐标通过求平均值的方式得到了线段的中点的坐标。
这
个公式的求解方法简单明了,可以广泛应用于各个领域中。
坐标系中两点间公式和中点公式

在平面直角坐标系中,已知下列共线 各点:A(1,1)、B(3,4) 、C(5,7),
计算每两点间的距离.
B是AC的中点,那么 问 它们之间的坐标有什 题 么关系呢?
.y
7
.C
6.
.
5
4.
.B
3.
.2 .
1 . . A. . . . . . .
o 1 23 4 5 6 7 8x
设线段的两个端点分别为 A x1, y1 和 B x2, y2 ,线段的中
| P1P2 | (x2 x1)2 (y2 y1)2
已知平面上两点P1(x1,y1), P2(x2,y2), 如何求P1 P2的距离| P1 P2 |呢?
y
y
P1
P2
P2
P1
o
x
o
x
P1P2 x2 x1
P1P2 y2 y1
平面内两点之间公式:
| P1P2 | (x2 x1)2 ( y2 y1)2
• (1) A (8,-1) B (2,3) O4,1
• (2) A (-7,-3) B (5,-3) O-1,-3
• (3) A (-4,8) B (4,-4) O0,2
巩
固
例2 已知 ABC 的三个顶点为 A(1,0)、B(2,1)、C(0,3),试
知
识
求BC边上的中线AD的长度.
典
解 设BC的中点D坐标为D(xD , yD ),则由 B(2,1)、C(0,3) 得
例1 求A(2, −5 )、B(5,−1)两点间的距离. 解:由两点间的距离公式得,A、B两点间的距离为
AB x2 x12 y2 y12 (5 2)2 1 52
5
练习:求点B(1,5)与D(6,17)之间的距离
两点间的距离与线段中点的坐标

(如不规则形状、高维空间等)下的计算方法和应用仍需进一步探索。
02
精度与效率问题
在实际应用中,由于计算精度和效率的限制,可能导致距离和中点坐标
的计算结果存在一定误差,需要研究更为精确和高效的算法。
03
跨学科融合
未来研究可以进一步融合数学、计算机科学、物理学等多个学科的理论
和方法,推动两点间距离与线段中点坐标计算方法的创新和应用拓展。
05 常见问题及解决方法
计算错误问题
误用距离公式
01
确保使用正确的两点间距离公式,即根号下[(x2-x1)²+(y2-y1)²]
。
精度问题
02
在进行大量计算或处理复杂数据时,注意保持足够的精度,避
免误差累积。
运算顺序错误
03
遵循数学运算的优先级规则,先进行乘方和开方运算,再进行
加减乘除。
公式应用不当问题
在某些特定情况下,如两点极角相差不大或极径相近 时,可以近似地使用算术平均来估算中点坐标,但这 种方法存在一定的误差。
应用举例
在几何问题中,经常需要求解线段的 中点坐标,如求解三角形的重心、垂 心等问题。
在工程问题中,线段的中点坐标同样 具有广泛的应用,如求解建筑物的中 心点、道路的中线等问题。
在物理问题中,线段的中点坐标也具 有重要的应用,如求解质点的平均位 置、速度等问题。
线段中点坐标公式
给定线段的两个端点坐标,可以 通过取各维度坐标的平均值来计 算线段的中点坐标。
应用范围
两点间距离和线段中点坐标的计 算在几何、图形学、空间分析等 领域具有广泛应用,如计算物体 间的相对位置、路径规划、空间 插值等。
研究不足与展望
01
复杂场景下的应用
2.2.2直线的两点式方程课件-高二数学人教A版选择性必修第一册

方法三:设直线方程为xa+12y-a=1, ∵直线过点 A(-3,4),∴-a3+124-a=1. 整理,得 a2-5a-36=0,∴a=9 或 a=-4. ∴直线方程为x9+y3=1 或-x4+1y6=1, 即 x+3y-9=0 或 4x-y+16=0.
探究 4 本题采用 3 种方法有利于训练解题发散性思维,其 中方法三最简捷,一般已知截距条件时可优先考虑用截距式方程 求直线方程,没有特殊要求都要化成二元一次方程的形式.
例 3 求过点 A(4,1),且在坐标轴上截距相等的直线 l 的方 程.
【思路分析】 对于直线在两坐标轴上截距相等的问题,在使 用待定系数法求直线方程时,要注意方程形式的使用条件,避免丢 解.还可以设直线的点斜式方程,利用截距的定义,分别求出两截 距,这样就避免了丢解情况,此法对解决此类问题行之有效.
3.直线 3x-2y=4 的截距式方程是( D )
A.34x-y2=1
B.x1-y1=4 32
C.34x--y2=1
D.x4+-y2=1 3
4.已知△ABC 的顶点 A(0,5),B(1,-2),C(-6,4),则 BC 边上的中线所在直线方程为__8_x_-_5_y_+_2_5_=__0_____.
6.求经过点(-2,2)且与两坐标轴所围成的三角形面积为 1 的直线 l 的方程.
解析 由题意,知直线 l 在两坐标轴上的截距存在且不为零, 故可设所求直线 l 的方程为xa+yb=1,
由已知可得- 12|aa2||+b|=2b=1,1,解得ab==--12,或ab==21,. 所以-x1+-y2=1 或x2+y1=1, 故直线 l 的方程为 2x+y+2=0 或 x+2y-2=0.
(2)依题意知直线 l 与 AB 垂直,且过线段 AB 的中点.显然 直线 AB 的斜率存在,且 kAB=mm+-11--mm=-1,所以 kl=1,且 过点2m2-1,2m2+1,所以直线 l 的方程为 y-2m2+1=x- 2m2-1,即 x-y+1=0.故选 B.
线段的中点坐标公式PPT幻灯片
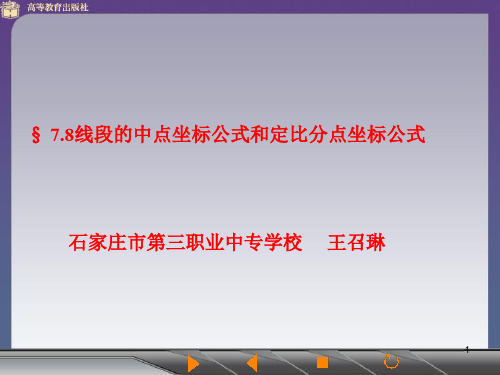
解
x 2 1 1
4 (5) 1 21 3
2
y
3 1
1 4 2 1
64 2 1
2 3
2
因此分点C的坐标为(-
1 , 3
2) 3
13
2、线段的定比分点坐标公式
x x1 x2 , y y1 y2 ( 1)
1
1
练习 1、 设点C分线段AB成定比 ,求分点C的坐标:
所以
x x1 x2 , y y1 y2 ( 1)
1
1
12
2、线段的定比分点坐标公式
x x1 x2 , y y1 y2 (知两点A(2,-3),B(-5,4),求分线段AB成定比
的分点C的坐标
2
2 1 (5)
,此时称分点C是外分点
17
课堂总结:
1、线段的中点坐标公式 2、线段的定比分点坐标公式
18
作业
P28 第3、4、6题
19
20
21
22
2
2
例2 已知线段AB的中点M的坐标为(3, 1 ) ,端点A的坐标为(4,2)
求端点B的坐标
2
解 设点B的坐标为 (x2 , y2 )
由公式得 3 4 x2 , 1 2 y2 2 22
解得 x2 2, y2 1
因此点B的坐标是(2,-1)
7
1、线段的中点坐标公式: x x1 x2 y y1 y2
2
2
练习 已知线段AB的中点M的坐标为 (8,-2) ,端点A的坐标为 (3,7)求端点B的坐标
解 点B的坐标为(13,-11)
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
x x1 x2 , y y1 y2 ( 1)
1
1
练习 1、 设点C分线段AB成定比 ,求分点C的坐标:
(1)A(3, 5), B(1, 4), 2
3
(2)A(4, 1), B(1, 7), 2
(3)A(1, 3), B(2, 5), 2
{即 (1 )x x1 x2 (1 ) y y1 y2
所以
x x1 x2 , y y1 y2 ( 1)
1
1
12
2、线段的定比分点坐标公式
x x1 x2 , y y1 y2 ( 1)
1
1
1
OM OA AM
OA
1
AB
1 2
OA (OB OA)
2
1
OA
1
OB
22
1
(OA
OB)
2
从而
OM
的坐标为
1 2
[(x1
,
y1 )
Hale Waihona Puke (x2 ,y2 )]
( x1
2
x2
,
A
y1 y2 ) 2
因此点M的坐标为 ( x1 x2 , y1 y2 )
试问:点C的坐标是多少?
2
y
.B
A.
C.
e2
o e1
x
10
思考:
如图,已知线段AB的两个端点A,B的坐标
分别为, (
使得 | AC
x1,
|
1
y1) (x2
| CB |
,
y2 ) ,设C是线段AB上的一点,
试问:点C的坐标是多少?
2
y
.B
C.
A.
e2
o e1
x
11
2、线段的定比分点坐标公式
(1)定比分点 在直线AB上任取一点C,使得AC λ CB ,我们称
点C分线段AB 成定比 ,此时称点C是线段AB的定比分点
(2)定比分点坐标公式
设定比分点C的坐标为(x, y),由 AC λ CB 得
(x x1, y y1) (x2 x, y2 y)
{ 由此得出
x x1 (x2 x)
y y1 ( y2 y)
2
2
例1 已知三角形ABC的顶点A,B,C的坐标分别为 (2,-1),(4,1),(6,-3),
设D,E分别是边BC,AC的中点,求点D,E的坐标
解
点D的坐标为( 4 6 , 1 (3)) (5,
y
1)
2
2
点E的坐标为
( 2 6 , 1 (3))
2
2
(4, 2)
o A
1
1
y
0 评注:1、点C在线段AB上,则定比
,
B
此时称分点C是内分点
A.
C.
e2
o e1
x
2、点C在线段BA(或AB)的延长线上,
0 则定比
,此时称分点C是外分点
17
课堂总结:
1、线段的中点坐标公式 2、线段的定比分点坐标公式
点F的坐标为 ( 1 , 1 ) 22
6
1、线段的中点坐标公式: x x1 x2 y y1 y2
2
2
例2 已知线段AB的中点M的坐标为(3, 1 ) ,端点A的坐标为(4,2)
求端点B的坐标
2
解 设点B的坐标为 (x2 , y2 )
由公式得 3 4 x2 , 1 2 y2 2 22
解得 x2 2, y2 1
因此点B的坐标是(2,-1)
7
1、线段的中点坐标公式: x x1 x2 y y1 y2
2
2
练习 已知线段AB的中点M的坐标为 (8,-2) ,端点A的坐标为 (3,7)求端点B的坐标
解 点B的坐标为(13,-11)
8
思考:
如图,已知线段AB的两个端点A,B的坐标
例3 已知两点A(2,-3),B(-5,4),求分线段AB成定比
的分点C的坐标
2
2 1 (5)
解
x 2 1 1
4 (5) 1 21 3
2
y
3 1
1 4 2 1
64 2 1
2 3
2
因此分点C的坐标为(-
1 , 3
2) 3
13
2、线段的定比分点坐标公式
2
2
15
2、线段的定比分点坐标公式
x x1 x2 , y y1 y2 ( 1)
1
1
y
0 评注:1、点C在线段AB上,则定比
,
此时称分点C是内分点
C.
B
A
e2
o e1
x
16
2、线段的定比分点坐标公式
x x1 x2 , y y1 y2 ( 1)
分别为, (
使得 | AC
x1,
|
1
y1) (x2
| CB |
,
y2 ) ,设C是线段AB上的一点,
试问:点C的坐标是多少?
2
y
.B
C.
A.
e2
o e1
x
9
思考:
如图,已知线段AB的两个端点A,B的坐标
分别为, (
使得 | AC
x1,
|
1
y1) (x2
| CB |
,
y2 ) ,设C是线段AB上的一点,
2、已知两点A(1,2),B(-1,3),设点C使得
AC 1 CB ,求点C的坐标 2
14
2、线段的定比分点坐标公式
x x1 x2 , y y1 y2 ( 1)
1
1
思考
什分当
么 样
点 坐
=1
子标
了公时
?式,
变定
为比
中点坐标公式
x x1 x2 y y1 y2
2
2
y M
e2
o e1
B x
3
1、线段的中点坐标公式:
如果线段AB的两个端点坐标分别为 (x1, y1 ) (x2 , y2 )
中点M的坐标记作(x, y),则
x x1 x2 y y1 y2
2
2
即线段的中点坐标等于它的两个端点坐标之和的一半
4
1、线段的中点坐标公式: x x1 x2 y y1 y2
B
.D x
.
E
C
5
1、线段的中点坐标公式: x x1 x2 y y1 y2
2
2
练习 已知三角形ABC的顶点A,B,C的坐标分别为 (2,3),(-3,4),(-1,-5),
设D,E,F分别是边BC,AC,AB的中点,求点D,E,F的坐标
解 点D的坐标为 (2, 3) 2
点E的坐标为 (1 , 1) 2
§ 7.8线段的中点坐标公式和定比分点坐标公式 石家庄市第三职业中专学校 王召琳
1
思考:
如图,已知线段AB的两个端点A,B的坐标
分别为, (x1, y1) (x2, y2 ) ,线段AB的中点M
的坐标是多少?
y
B
M
A
e2
o e1
x
2
1、线段的中点坐标公式:
分析:由于点M是线段AB的中点,因此
