第八讲容斥原理
2021国考笔试特训预测方法精讲-数量关系与资料分析 (全部讲义+笔记) (4)

方法精讲-数量 4(笔记)启智职教的店第八节容斥原理【知识点】1.两集合容斥原理。
(1)识别:多主体(两主体)、有交叉。
(2)公式:A+B-A∩B=总数-A、B都不满足个数。
(3)公式推导:如图所示,圈A和圈B,中学学的几何问题,就是求两个圈覆盖的面积,A+B,多加了中间相交的部分,所以减去A∩B,则等式可写为:A+B-A∩B=总-空白。
公务员考试中会把面积变成一些条件,例如满足条件1 的、满足条件2的、两个条件均满足的等。
(4)例如:我们班在线听课的有150人,有钱的有90人,任性的有70人,没钱不任性的有3人,求有钱任性的人数?答:该题为容斥原理问题,有钱的为90人,任性的有70人,“有钱的”为条件A,“任性的”为条件B,设有钱任性的为x人,根据公式B=总数-A、B都不满足个数,代入数据得90+70-x=150-3。
2.三集合容斥原理(一会讲)。
【例 1】(2019 江苏)市电视台向 150 位观众调查前一天晚上甲、乙两个频道的收视情况,其中 108 人看过甲频道,36 人看过乙频道,23 人既看过甲频道又看过乙频道,则受调查观众中在前一天晚上两个频道均未看过的人数是:A.17B.22C.29D.38【解析】例 1.“108 人看过甲频道,36 人看过乙频道”,出现两个主体,且两主体有交叉,属于两集合容斥原理问题,公式:A+B-A∩B=总数-都不满足的,代入数据,108+36-23=150-x,计算时结合选项,选项尾数不同,考虑尾数法, 8+6 尾数为 4,4-3 尾数为 1,则左边尾数为 1,右边 10-9 尾数才为 1,对应 C 项。
【选C】【注意】考试中一旦考查容斥原理问题,必须要拿分。
【例 2】(2018 广州)篮子里有苹果和梨两种水果若干个,将这些水果分发给 13 个人,每人最少拿一个,最多拿两个不同的水果。
已知有 9 个人拿到了苹果,有 8 个人拿到了梨,最后全部分完。
那么,有多少人只拿到了苹果?A.4B.5C.6D.7【解析】例 2.问“只拿到苹果”“已知有 9 个人拿到了苹果,有 8 个人拿到了梨”出现两个条件,总共有 13 人,肯定重复交叉,属于容斥原理问题。
升第八讲容斥原理之重叠问题

第八讲:容斥原理之重叠问题导入文氏图■■■■■■■■■■■■■■■文氏图,也叫维恩图”是由英国著名数学家Venn发明的.维恩(公元1834 年8月4日「公元1923 年4月4日)十九世纪英国著名的数学家和哲学家,生于英国赫尔.他1883 年获得理学博士学位,同年被选为英国皇家学会会员.维恩最主要的成就是系统解释并发展了几何表示的方法,也就是发明了文氏图.■他作出一系列・简单闭曲线(圆或更复杂的图形),将平面分为许多间隔.利用这种图表,维恩阐明了演绎推理的基本原理.为了进一步明确起见,他还引入了一些数学难题作为实例.虽然在维恩之前,莱布尼茨(Leibniz )已系统地运用过这类逻辑图,但今天这种逻辑图仍称作维恩图”另外, 维恩在概率论和逻辑学方面也有很大贡献,他的著作一一《机会逻辑》和《符号逻辑》,在19 世纪末20世纪初曾享有很高的声誉.除了数学以外,维恩还有一项较为特别的技能一一制作机器.他曾制作过一部板球发球机,当澳洲板球队在1909 年到访剑桥大学时,维恩的机器依然运作正常,并使他们其中一位成员打空四次.什么是容斥原理?这一讲我们主要学习和“包含”与“排除”有关的问题,这样的问题在生活中就有不少,比如吃瓜子.我们说吃掉了一斤瓜子,指的是带壳的瓜子,并非真的吃到肚子里一斤,因为这一斤中还“包含”着瓜子壳.如果要计算到底吃了多少,最简单的方法就是称一称瓜子壳,用原来的一斤“排除”掉瓜子壳的重量.瓜子的例子相对简单,一斤瓜子里一部分是瓜子仁,另一部分就是瓜子壳,两者各不相关.但本讲要学习的包含与排除问题要复杂一些,各部分之间会有重叠.比如一个办公室中每个人都至少爱喝茶或咖啡中的一种,已知有7个人爱喝茶,10个人爱喝咖啡,那能不能就说办公室里有17 个人呢?显然不能,因为可能有一些人既爱喝茶也爱喝咖啡,如果直接将喝茶的人数和喝咖啡的人数相加,会把既爱喝茶又爱喝咖啡的人计算2次,计算人数的时候要把这一部分减去才行.比如,如果有3个人既爱喝茶又爱喝咖啡,那总的人数就应该是7 + 10 - 3 = 14 人.这就是我们今天要来研究的问题一一有重叠的计数问题,即包含与排除问题•研究这种问题通常需要画出示意图,这样的示意图又叫做文氏图,下面我们就用文氏图推导两个对象的容斥原理公式.两个量之间的重叠例1、某班有34名同学参加了学校的运动会,其中有17名参加了跳绳,有20名参加了拔河,问:及参加了跳绳又参加了拔河的又多少人?如右图所示,如果要计算三个部分的总数,直接计算A+B 就会算多了,而多算的正好是共同部分,只要把多算的减掉就可以了•上述分析总结成公式就是:R总数=沖+丹一』、号重拄这个公式就是两个对象的容斥原理.练一练1、五年级有122 名学生参加语文、数学考试,每人至少有一门功课的成绩是优秀,其中语文成绩优秀的有65人,数学优秀的有87人•语文、数学都优秀的有多少人?2、在一次数学测试中有两道题全班同学都至少答对一题,答对第一题的有33人,答对第二题的又38人,两题都答对的又15人,问全班又多少人?3、学校文艺组每人至少会演奏一种乐器。
初中数学重点梳理:容斥原理

容斥原理知识定位在计数时,常常遇到这样的情况,作合并运算时会把重复的部分多算,需要减去;作排除运算时会把重复部分多减,需要加上,这就是容斥原理。
它的基本形式是: 记A 、B 是两个集合,属于集合A 的东西有A个,属于集合B 的东西有B个,既属于集合A 又属于集合B 的东西记为B A ,有BA 个;属于集合A 或属于集合B 的东西记为B A ,有BA 个,则有:B A =A +B -BA 。
知识梳理知识梳理1.容斥原理容斥原理可以用一个直观的图形来解释。
如图,左圆表示集合A ,右圆表示集合B ,两圆的公共部分表示B A ,两圆合起来的部分表示B A ,由图可知:B A =A +B -BA 。
容斥原理又被称作包含排除原理或逐步淘汰原则。
例题精讲【试题来源】【题目】在1到200的整数中,既不能被2整除,又不能被3整除的整数有多少个? 【答案】67【解析】根据容斥原理,应是200减去能被2整除的整数个数,减去能被3整除的整数个数,还要加上既能被2整除又能被3整除,即能被6整除的整数个数。
A BAB在1到200的整数中,能被2整除的整数个数为:2⨯1,2⨯2,…,2⨯100,共100个;在1到200的整数中,能被3整除的整数个数为:3⨯1,3⨯2,…,3⨯66,共66个;在1到200的整数中,既能被2整除又能被3整除,即能被6整除的整数个数为: 6⨯1,6⨯2,…,6⨯33,共33个;所以,在1到200的整数中,既不能被2整除,又不能被3整除的整数个数为:200-100-66+33=67(个)【知识点】容斥原理【适用场合】当堂例题【难度系数】3【试题来源】【题目】求1到100的自然数中,所有既不是2的倍数又不是3的倍数的整数之和S。
【答案】1633【解析】1到100的自然数中,所有自然数的和是:1+2+3+…+100=50501到100的自然数中,所有2的倍数的自然数和是:2⨯1+2⨯2+…+2⨯50=2⨯(1+2+3+…+50)= 2⨯1275=25501到100的自然数中,所有3的倍数的自然数和是:3⨯1+3⨯2+…+3⨯33=3⨯(1+2+3+…+33)= 3⨯561=16831到100的自然数中,所有既是2的倍数又是3的倍数,即是6的倍数的自然数和是:6⨯1+6⨯2+…+6⨯16=6⨯(1+2+3+…+16)= 6⨯136=816所以,1到100的自然数中,所有既不是2的倍数又不是3的倍数的整数之和S=5050-2550-1683+816=1633【知识点】容斥原理【适用场合】当堂例题【难度系数】3【试题来源】【题目】求不大于500而至少能被2、3、5中一个整除的自然数的个数。
第八讲容斥原理案例

|A|=17 |B|=30 |C|=13 |A∩B∩C|=5 |A∪B∪C|=|A|+|B|+|C| -|A∩B|-|A∩C|-|B∩C| +|A∩B∩C|=35 所以 |A∩B|+|A∩C|+|B∩C|=30 所求数目= |A|-|A∩B|-|A∩C| +|A∩B∩C| +|B|-|B∩C| |-|A∩B +|A∩B∩C| +|C|-|A∩C|-|B∩C| +|A∩B∩C| =60-2×30+3×5=15
70、36。问阴影部分(黄色)的面积是多少? A.15 B.16 C.14 D.18
11.三位专家为10幅作品投票,每位专家分别都投 出了5票,并且每幅作品都有专家投票。如果 三位专家都投票的作品列为A等,两位专家投 票的列为B等,仅有一位专家投票的作品列为 C等,则下列说法正确的是( D )。 A. A等和B等共6幅 B. B等和C等共7幅
120-(50+45+40-15-10-8+4)=14(人)
6.分母是1001的最简分数一共有多少个? 解:这一题实际上就是找分子中不能整除 1001 的数。由于 1001=7×11×13 ,所以就 是找不能被7,11,13整除的数。
如图
7的倍数143个 11的倍数91个
13
11 7
13的倍数77个
子一共被剪成了多少段?
59+39-19=79
9.在游艺会上,有100名同学抽到了标签分别为1至100的奖 券。按奖券标签号发放奖品的规则如下: (1)标签号为2的倍数,奖2支铅笔; (2)标签号为3的倍数,奖3支铅笔; (3)标签号既是2的倍数,又是3的倍数可重复领奖; (4)其他标签号均奖1支铅笔。那么游艺会为该项活动准备 的奖品铅笔共有多少支? 解:(50-16)×2+(33-16)×3+16×5+33×1=242
五年级第八讲容斥原理

容斥原理容斥原理:如果有s件东西,其中具有性质A的有a件,具有性质B 的有b件,既有性质A又有性质B的有c件,那么具有性质A或性质B的件数是:a+b-c既不具有性质A也不具有性质B的件数:s-(a+b-c)习题例1.两个长方形A和B的面积分别是21和9平方厘米,它们重叠部分C的面积为4平方厘米,这两个长方形盖住的面积是多少?例2.某校四年级共有132名学生,学生们自愿报名参加课外小组活动。
其中参加体育小组,科技小组的分别是39人、28人,即参加体育小组又参加科技小组的有12人。
问:(1)参加体育小组和科技小组共有多少人?(2)四年级有多少名学生既没参加体育小组又没参加科技小组?例3.在1-100的自然数中,能被3或5整除的数有几个?既不能被3整除又不能被5整除的数有几个?例4.一个班有学生42人,参加体育小组的有30人,参加文艺小组的25人,并且每个人都至少参加一个小组,这个班两小组都参加的有几人?例5.老师出了两道题,全班40人中,第一题有30人对,第二题有12人对,两道题都做对的有20人。
问:(1)第二题对第一题没做对的有多少人?(2)两题都没做对的有几个人?例6.400盏灯,各有一个开关控制(每拉一下开关,电灯的状态发生改变:亮的灭了,灭的亮了)。
现将其编号为1-400,初始状态全都关着。
然后将所有编号为5的倍数的电灯开关都拉一下,再将所有编号为7的倍数的电灯的开关都拉一下。
两次拉完后,灭了的电灯有多少盏?例7.在1-2010这2010个数中,既不能被8整除,又不能被12整除的数共有多少个?习题1.面积为1平方米的正方形桌面上放着两本书A和B,A和B的面积分别为294平方厘米、234平方厘米,两本书重叠部分的面积为100平方厘米。
求桌面没被两本书盖住的面积。
2.五年级一班有48人,其中会游泳的有21人,会滑冰的有12人,既会游泳又会滑冰的有6人,问两样都不会的有几人?3.50名学生面向老师排成一排,编号按顺序分别为1-50号。
容斥原理及其应用

容斥原理及其应用容斥原理是组合数学中一种重要的计数技巧,被广泛运用于排列组合、概率统计等领域。
它的核心思想是通过求出多个集合的交集和并集来计算所需的数量,从而避免重复计数,确保准确性和全面性。
本文将介绍容斥原理的基本概念、推导过程以及其在实际问题中的应用。
一、容斥原理的基本概念容斥原理是根据集合的性质和运算规则推导出的一种计数方法。
在给定一组集合时,容斥原理可以帮助我们计算这些集合的交集和并集的元素个数。
在具体运用中,我们将问题转化成求解几个集合的元素个数之和的问题。
容斥原理表达式如下:∣A1∪A2∪⋯∪An∣=∣A1∣+∣A2∣+⋯+∣An∣−∣A1∩A2∣−∣A1∩A3∣−⋯−∣An−1∩An∣+⋯+(−1)^n−1∣An−1∩An∣其中,∣A∣表示集合A的元素个数,∪表示集合的并集,∩表示集合的交集,n表示集合的数量。
二、容斥原理的推导过程容斥原理的推导过程可以通过数学归纳法来实现,下面简要介绍:首先,我们给定两个集合A和B,我们用∣A∣表示集合A的元素个数,用∣B∣表示集合B的元素个数。
如果我们要计算A和B的并集∣A∪B∣,那么可以采取如下步骤:1. 首先,我们直接将∣A∣和∣B∣相加,得到∣A∣+∣B∣。
2. 然后,我们需要减去重复计算的部分,即集合A和B的交集∣A∩B∣。
因为∣A∩B∣这部分元素已经在∣A∣和∣B∣中被计算了一次,所以需要减去∣A∩B∣。
通过以上步骤,我们得到了∣A∪B∣=∣A∣+∣B∣−∣A∩B∣。
这就是容斥原理的基本推导过程。
接下来,我们将容斥原理推广到更多集合的情况。
假设我们有三个集合A、B和C,我们想要计算它们的并集∣A∪B∪C∣,我们可以按照以下步骤进行:1. 首先,我们将∣A∣、∣B∣和∣C∣相加,得到∣A∣+∣B∣+∣C∣。
2. 然后,我们需要减去两两集合的交集部分,即∣A∩B∣、∣A∩C∣和∣B∩C∣。
这是因为这些部分元素在∣A∣、∣B∣和∣C∣中都被计算了一次,所以需要减去。
容斥原理

排列与布棋方案
一个棋盘由大小相同的正方形方格构 成,一个方格中允许放入一个棋子. 在向棋盘布棋时,要求任何两个棋子 既不能布在棋盘的同一行,也不能布 在同一列上.
排列 p1 p2 … pn 表示: 第一行的棋子放在第 p1 列 第二行的棋子放在第 p2 列 … 第 n 行的棋子放在第 pn 列
布棋方案
i 1
1i jm
| Ai Aj Ak | ... (1)m1 | A1 A2 ... Am |
1i jk m
定理: 设S为有穷集,P1,P2, …, Pm是m种性质,Ai是S中 具有性质Pi 的元素构成的子集, 是Ai 相对于S 的补集, i=1, 2, …, m. 则 S 中不具有性质P1, P2, …, Pm的元 素数为
i 1
1i jm
| Ai Aj Ak | ... (1)m | A1 A2 ... Am |
1i jk m
证明方法:数学归纳法、组合分析 证 组合分析. 若 x 不具有任何性质,则对等式右边贡献为:
1 0 + 0 0 + … +(1)m0 = 1 若 x 具有n 条性质,1nm, 则对等式右边的贡献为:
|A|=16, |B|=21, |E |=50, |~(A∪B)|=17 |A∩B| =|A|+|B|-|(A∪B)|
=|A|+|B|-(|E|-|~(A∪B)|)
=16+21-(50-17)=4 所以有4个人两项均得优。
例2
Pascal, Visual Basic, C
三门课程的上机。 三门课程的学生分别有110人,
| A1 A2 A3 A4 | 120 (60 40 24 17) (20 12 8 8 5 3) (4 2 1 1) 0
奥数五年级第八课 :容斥原理

您身边的个性化教育专家——问鼎教育
第八课容斥原理
概念在计数时,必须注意无一重复,无一遗漏。
为了使重叠部分不被重复计算,人们研究出一种新的计数方法,这种方法的基本思想是:先不考虑重叠的情况,把包含于某内容中的所有对象的数目先计算出来,然后再把计数时重复计算的数目排斥出去,使得计算的结果既无遗漏又无重复,这种计数的方法称为容斥原理。
例题例1 在一次校运动会上,甲班参加田赛的有15人,参加径赛的有12人,既参加田赛又参加了径赛的有7人,没有参加比赛的有21人,那么这个班有多少人?
例2两个边长分别为10厘米、4厘米的正方形重叠在一起,重叠部分的面积为4平方厘米,求这个图所能覆盖的面积。
例3 在1到100的全部自然数中,既不是6的倍数又不是5的倍数的数有多少个?
例4有50个学生,他们穿的裤子是白色的或者黑色的,上衣是蓝色的或红色的,若有14人穿的是蓝色上衣白裤子,31人穿黑裤子,18人穿红上衣,那么穿红上衣黑裤子的学生有多少人?
随堂练习:
1、一个旅行社有36人,其中会英语的有24人,会法语的有18人,两样都不会的4人,两样都会的有多少人?
2、4个边长是2厘米的正方形平放在桌子上,中间有一个边长是3厘米的正方形重叠在上面,求覆盖桌子的面积。
3、有一根长为240厘米的绳子,从一端开始每隔4厘米作一个记号,每隔6厘米也作一个记号,然后将标记有记号的地方剪断。
问:绳子共被剪成了多少段?
您身边的个性化教育专家——问鼎教育。
容斥原理(数学技巧点拨系列)

容斥原理【知识点讲解】1、原理容斥原理指把包含于某内容中的所有对象的数目先计算出来,然后再把计数时重复计算的数目排斥出去,使得计算的结果既无遗漏又无重复,这种计数的方法称为容斥原理。
2、解释由图可以直接看出各部分之间的关系由Venn图可知:(A∪B=A+B-A∩B)由Venn图可知:(A∪B∪C=A+B+C-A∩B-B∩C-C∩A+A∩B∩C)3、应用两类如果被计数的事物有A、B两类,那么,A类B类元素个数总和=属于A类元素个数+属于B类元素个数—既是A类又是B类的元素个数。
三类如果被计数的事物有A、B、C三类,那么,A类和B类和C类元素个数总和=A类元素个数+B类元素个数+C类元素个数—既是A类又是B类的元素个数—既是A类又是C类的元素个数—既是B类又是C类的元素个数+既是A类又是B类而且是C类的元素个数。
4、解题导语使用容斥原理一般用于集合相关问题中,但是此类思想在数学学习中仍有巨大作用。
例如在计数原理中使用间接法等等。
因此学习此类问题对数学能力的提升是有很大帮助的,它可以帮助你换一个角度看数学题,从而找到更简单的办法。
【例题详析】例1、(2020宁夏)《西游记》《三国演义》《水浒传》和《红楼梦》是中国古典文学瑰宝,并称为中国古典小说四大名著,六盘水市第七中学为了解我校学生阅读四大名著的情况,随机调查了100位学生,其中阅读过《西游记》或《红楼梦》的学生共有90位,阅读过《红楼梦》的学生共有80位,阅读过《西游记》且阅读过《红楼梦》的学生共有60位,则在调查的100位同学中阅读过《西游记》的学生人数为()A .80B .70C .60D .50【参考答案】B【详解】因为阅读过《西游记》或《红楼梦》的学生共有90位,阅读过《西游记》且阅读过《红楼梦》的学生共有60位,所以《西游记》与《红楼梦》两本书中只阅读了一本的学生共有90-60=30位,因为阅读过《红楼梦》的学生共有80位,所以只阅读过《红楼梦》的学生共有80-60=20位,所以只阅读过《西游记》的学生共有30-20=10位,故阅读过《西游记》的学生人数为10+60=70位,【方法解析】由两类的容斥原理得:总人数=阅读过《西游记》+阅读过《红楼梦》-阅读过《红楼梦》和《西游记》的,由此得阅读过《西游记》的学生人数=90+60-80=70(位)例2:某中学的学生积极参加体育锻炼,其中有96名学生喜欢足球或游泳,60名学生喜欢足球,82名学生喜欢游泳,则该中学既喜欢足球又喜欢游泳的学生有()名.A .62B .56C .46D .42【参考答案】C【详解】喜欢足球的学生、喜欢游泳的学生形成的集合分别记为A ,B ,依题意,集合A ,B ,A B 中元素个数分别为:()60,()82,()96n A n B n A B ==⋃=,则()()()()60829646n A B n A n B n A B ⋂=+-⋃=+-=,所以中学既喜欢足球又喜欢游泳的学生有46名.例3.某小学对小学生的课外活动进行了调查.调查结果显示:参加舞蹈课外活动的有63人,参加唱歌课外活动的有89人,参加体育课外活动的有47人,三种课外活动都参加的有24人,只选择两种课外活动参加的有46人,不参加其中任何一种课外活动的有15人.问接受调查的小学生共有多少人?()A .120B .144C .177D .192【参考答案】A 【详解】如图所示,用韦恩图表示题设中的集合关系,不妨将参加舞蹈、唱歌、体育课外活动的小学生分别用集合,,A B C 表示,则()63,()89,()47,()24card A card B card C card A B C ===⋂⋂=不妨设总人数为n ,韦恩图中三块区域的人数分别为,,x y z即()24,()24,()24card A B x card A C y card B C z ⋂=+⋂=+⋂=+46x y z ++=,由容斥原理:15()()()()()()()n card A card B card C card A B card A C card B C card A B C -=++-⋂-⋂-⋂+⋂⋂638947(24)(24)(24)24x y z =++-+-+-++解得:120n =【跟踪训练】一、单选题1.某校高三(1)班有50名学生,春季运动会上,有15名学生参加了田赛项目,有20名学生参加了径赛项目,已知田赛和径赛都参加的有8名同学,则该班学生中田赛和径赛都没有参加的人数为()A .27B .23C .15D .72.某网店统计了连续三天售出商品的种类情况:第一天售出19种商品,第二天售出13种商品,第三天售出18种商品;前两天都售出的商品有3种,后两天都售出的商品有4种.则该网店这三天售出的商品最少有().A.25种B.27种C.29种D.31种3.为了丰富同学们的课外生活,某班58名同学在选课外兴趣小组时,选择篮球小组的有28人,选择乒乓球小组的有36人,既没有选择篮球小组又没有选择乒乓球小组的有12人,那么选择篮球小组但没有选择乒乓球小组的人数为()A.8B.10C.18D.204.某班有50名同学,有20名同学既不选修足球课程也不选修篮球课程,有18名同学选修了足球课程,28名同学选修了篮球课程,则既选修了足球课程也选修了篮球课程的同学有()名A.10B.12C.14D.165.中共一大会址、江西井冈山、贵州遵义、陕西延安是中学生的几个重要的研学旅行地.某中学在校学生3000人,学校团委为了了解本校学生到上述红色基地研学旅行的情况,随机调查了500名学生,其中到过中共一大会址或井冈山研学旅行的共有40人,到过井冈山研学旅行的20人,到过中共一大会址并且到过井冈山研学旅行的恰有10人,根据这项调查,估计该学校到过中共一大会址研学旅行的学生大约有()人A.240B.180C.120D.606.某班45名学生参加“3·12”植树节活动,每位学生都参加除草、植树两项劳动.依据劳动表现,评定为“优秀”、“合格”2个等级,结果如下表:等级优秀合格合计项目除草301545植树202545若在两个项目中都“合格”的学生最多有10人,则在两个项目中都“优秀”的人数最多为()A.5B.10C.15D.207.高考“33 ”模式指考生总成绩由语文、数学、外语3个科目成绩和高中学业水平考试3个科目成绩组成.计入总成绩的高中学业水平考试科目,由考生根据报考高校要求和自身特长,在思想政治、历史、地理、物理、化学、生物6个科目中自主选择.某中学为了解本校学生的选择情况,随机调查了100位学生的选择意向,其中选择物理或化学的学生共有40位,选择化学的学生共有30位,选择物理也选择化学的学生共有10位,则该校选择物理的学生人数与该校学生总人数比值的估计值为()A.0.1B.0.2C.0.3D.0.48.移动支付、高铁、网购与共享单车被称为中国的新“四大发明”,某中学为了解本校学生中新“四大发明”的普及情况,随机调查了100位学生,共中使用过移动支付或共享单车的学生共90位,使用过移动支付的学生共有80位,使用过共享单车的学生且使用过移动支付的学生共有60位,则该校使用共享单车的学生人数与该校学生总数比值的估计值为()A.0.5B.0.6C.0.7D.0.89.某地对农户抽样调查,结果如下:电冰箱拥有率为45%,电视机拥有率为55%,洗衣机拥有率为65%,拥有上述三种电器的任意两种的占35%,三种电器齐全的为25%,那么一种电器也没有的农户所占比例是()A.20%B.10%C.15%D.12%10.某学校高三教师周一、周二、周三开车上班的人数分别是8,10,14,若这三天中至少有一天开车上班的职工人数是20,则这三天都开车上班的职工人数至多是()A.8B.7C.6D.5二、填空题11.学校运动会,某班所有同学都参加了羽毛球或乒乓球比赛,已知该班共有23人参加羽毛球赛,35人参加乒乓球赛,既参加羽毛球又参加乒乓球赛有6人,则该班学生数为______.12.某校高三(1)班有50名学生,春季运动会上,有15名学生参加了田赛项目,有20名学生参加了径赛项目,已知田赛和径赛都参加的有8名同学,则该班学生中田赛和径赛都没有参加的人数为__________.13.某单位共有员工85人,其中68人会骑车,62人会驾车,既会骑车也会驾车的人有57人,则既不会骑车也不会驾车的人有___________人.14.高一某班有学生45人,其中参加数学竞赛的有32人,参加物理竞赛的有28人,另外有5人两项竞赛均不参加,则该班既参加数学竞赛又参加物理竞赛的有___.人.15.某班有学生48人,经调查发现,喜欢打羽毛球的学生有35人,喜欢打篮球的学生有20人.设既喜欢打羽毛球,又喜欢打篮球的学生的人数为x,则x的最小值是_________.16.网络流行词“新四大发明’’是指移动支付、高铁、网购与共享单车.某中学为了解本校学生中“新四大发明”的普及情况,随机调查了100名学生,其中使用过移动支付或共享单车的学生共90名,使用过移动支付的学生共有80名,使用过共享单车的学生且使用过移动支付的学生共有60名,则该校使用共享单车的学生人数与该校学生总数比值的估计值为___________. 17.某班有39名同学参加数学、物理、化学课外研究小组,每名同学至多参加两个小组.已知参加数学、物理、化学小组的人数分别为26,15,13,同时参加数学和物理小组的有6人,同时参加物理和化学小组的有4人,则同时参见数学和化学小组有多少人__________. 18.某班共40人,其中24人喜欢篮球运动,16人喜欢乒乓球运动,6人这两项运动都不喜欢,则只喜欢其中一项运动的人数为________19.某班有45名同学参加语文、数学、英语兴趣小组.已知仅参加一个兴趣小组的同学有20人,同时参加语文和数学兴趣小组的同学有9人,同时参加数学和英语兴趣小组的同学有15人,同时参加语文和英语兴趣小组的同学有11人,则同时参加这三个兴趣小组的同学有人___________.20.某班进行集体活动,为活跃气氛,班主任要求班上60名同学从唱歌、跳舞、讲故事三个节目中至少选择一个节目、至多选两个节目为大家表演,已知报名参加唱歌、跳舞、讲故事的人数分别为40,20,30,同时参加唱歌和讲故事的有15人,同时参加唱歌和跳舞的有10人,则同时只参加跳舞和讲故事的人数为__________.21.对班级40名学生调查对A、B两事件的态度,有如下结果:赞成A的人数是全体的五分之三,其余的不赞成,赞成B的比赞成A的多3人,其余的不赞成,另外,对A、B都不赞成的学生数比对A、B都赞成的学生数的三分之一多1人,问对A、B都赞成的学生有________人. 22.2021年是中国共产党成立100周年,电影频道推出“经典频传:看电影,学党史”系列短视频,传扬中国共产党的伟大精神,为广大青年群体带来精神感召.现有《青春之歌》《建党伟业》《开国大典》三支短视频,某大学社团有50人,观看了《青春之歌》的有21人,观看了《建党伟业》的有23人,观看了《开国大典》的有26人.其中,只观看了《青春之歌》和《建党伟业》的有4人,只观看了《建党伟业》和《开国大典》的有7人,只观看了《青春之歌》和《开国大典》的有6人,三支短视频全观看了的有3人,则没有观看任何一支短视频的人数为________【参考答案】1.B【详解】设高三(1)班有50名学生组成的集合为U ,参加田赛项目的学生组成的集合为A ,参加径赛项目的学生组成的集合为B由题意集合A 有15个元素,B 有20个元素,A B 中有8个元素所以A B 有15+20827-=个元素.所以该班学生中田赛和径赛都没有参加的人数为5027=23-故选:B2.C【详解】解:因为前两天都售出的商品有3种,因此第一天售出且第二天没有售出的商品有19316-=(种);同理第三天售出的商品中有14种第二天未售出,有1种商品第一天未售出;所以三天商品种数最少时,是第三天中14种第二天未售出的商品都是第一天售出过的,此时商品总数是1416129+-=(种);分别用集合A 、B 、C 表示第一、第二和第三天售出的商品,则商品数最少时,如图所示.故选:C .3.B【详解】设既选择篮球小组又选择乒乓球小组的有x 人,则选择篮球小组但没有选择乒乓球小组的有()28x -人,选择乒乓球小组但没有选择篮球小组的有()36x -人.由题意可得()()12283658x x x +-+-+=,解得18x =,所以选择篮球小组但没有选择乒乓球小组的人数为2810x -=.【详解】设既选修了足球课程也选修了篮球课程的同学有x 名,由容斥原理得20182850x ++-=,解得16x =.故选:D.5.B【详解】如下图所示,设调查的学生中去过中共一大会址研学旅行的学生人数为x ,由题意可得()102040x -+=,解的30x =,因此,该学校到过中共一大会址研学旅行的学生的人数为303000180500⨯=.6.C【详解】用集合A 表示除草优秀的学生,B 表示植树优秀的学生,全班学生用全集U 表示,则U A ð表示除草合格的学生,则U B ð表示植树合格的学生,作出Venn 图,如图,设两个项目都优秀的人数为x ,两个项目都是合格的人数为y ,由图可得203045x x x y -++-+=,5x y =+,因为max 10y =,所以max 10515x =+=.故选:C .【详解】选择物理的学生人数为40301020-+=,即该校选择物理的学生人数与该校学生总人数比值的估计值为200.2100=.故选:B8.C【详解】根据题意使用过移动支付、共享单车的人数用韦恩图表示如下图,因此,该校使用共享单车的学生人数与该校学生总数比值的估计值700.7100=,故选C.9.A【详解】解:设农户总共为100家,则有55家农户有电视机,45家农户有电冰箱,65家农户有洗衣机,有25家农户同时拥有这三种电器,另外75家只有其中两种或一种或没有电器.设只有电冰箱和电视机的农户有a 家,只有电冰箱和洗衣机的农户有b 家,只有洗衣机和电视机的农户有c 家,只有电视机、电冰箱、洗衣机的分别有d 、e 、f 家,没有任何电器的农户有x 家.那么对于拥有电冰箱的农户可得出:2545a b e +++=①那么对于拥有电视机的农户可得出:2555a c d +++=②那么对于拥有洗衣机的农户可得出:2565b c f +++=③把上面三个式子相加可得:()290a b c d e f +++++=④对于拥有上述三种电器的任意两种的占35%,得到:35a b c ++=⑤把⑤代入④可得到20d e f ++=⑥因为农户共有100家,所以25100a b c d e f x +++++++=,把⑤和⑥代入上式得到20x =,即一种电器也没有的农户所占比例为20%,10.C【详解】解:设周三,周二,周一开车上班的职工组成的集合分别为A ,B ,C ,集合A ,B ,C 中元素个数分别为n A .,n B .,n C .,则n A .14=,n B .10=,n C .8=,()20n A B C ⋃⋃=,因为()n A B C n ⋃⋃=A .n +B .n +C .()()()()n A B n A C n B C n A B C -⋂-⋂-⋂+⋂⋂,且()()n A B n A B C ⋂⋂⋂ ,()()n A C n A B C ⋂⋂⋂ ,()()n B C n A B C ⋂⋂⋂ ,所以1410820()3()n A B C n A B C ++-+⋂⋂⋂⋂ ,即1410820()62n A B C ++-⋂⋂= .故选:C .11.52【详解】解:设参加羽毛球赛为集合A ,参加乒乓球赛为集合B ,依题意可得如下韦恩图:所以该班一共有1762952++=人;故答案为:5212.23【详解】由题意,15名参加田赛的同学中有7名没有参加径赛,20名参加径赛的同学中有12名没有参加田赛,所以参加田赛和径赛的同学共有781227++=人,综上,该班学生中田赛和径赛都没有参加的人数为502723-=人.13.12【详解】设会骑车的人组合的集合为A ,会驾车的人组成的集合为B ,既会骑车也会驾车的人组成的集合为集合C ,易知A B C = ,记card()A 表示集合A 中的元素个数,则有()()()()68625773card A B card A card B card A B =+-=+-= ,所以既不会骑车也不会驾车的人为857312-=.故答案为:1214.20【详解】设该班既参加数学竞赛又参加物理竞赛的学生人数为x ,以集合U 表示该班集体,集合A 表示参加数学竞赛的学生组成的集合,集合B 表示参加物理竞赛的学生组成的集合,如下图所示:由题意可得()()322856545x x x x -++-+=-=,解得20x =.故答案为:20.15.7【详解】设既不喜欢打羽毛球,又不喜欢打篮球的学生的人数为y ,则352048x y +-+=,即7x y -=,因为0y,所以7x .因为20x ,所以720x .故答案为:7.16.710##0.7【详解】根据题意,将使用过移动支付、共享单车的人数用如图所示的韦恩图表示,所以该校使用共享单车的学生人数与该校学生总数比值的估计值为6010710010+=.故答案为:710.17.5【详解】设参加数学、物理、化学小组的同学组成的集合分别为A ,B 、C ,同时参加数学和化学小组的人数为x ,因为每名同学至多参加两个小组,所以同时参加三个小组的同学的人数为0,如图所示:由图可知:20654939x x x -+++++-=,解得5x =,所以同时参加数学和化学小组有5人.故答案为:5.18.28【详解】6 人这两项运动都不喜欢,∴喜欢一项或两项运动的人数为40634-=人;∴喜欢两项运动的人数为:2416346+-=人,∴喜欢篮球的人数为24618-=人;喜欢乒乓球的人数为16610-=人;∴只喜欢其中一项运动的人数为181028+=人.故答案为:28.19.5【详解】以集合A 、B 、C 表示分别参加语文、数学、英语兴趣小组的学生,如下图所示:设同时参加这三个兴趣小组的同学有x 人,由图可得()()()209111555245x x x x x +-+-+-+=-=,解得5x =.故答案为:5.20.5【详解】参加唱歌、跳舞、讲故事的人分别用集合,,A B C 表示,作出Venn 图,如图,图中字母表示相应区域人数,则0n =,又40a b m ++=,20b c d ++=,30d e m ++=,15m =,10b =,60a b c d e m +++++=,则()()()a b m b c d d e m b m ++++++++--2a b c d e m =+++++,∴4020301510605d =++---=,∴同时只参加跳舞和讲故事的人数为5人.故答案为:5.21.18【详解】赞成A 的人数为340245⨯=,赞成B 的人数为24327+=,设对A 、B 都赞成的学生有x ,则112724403x x x x ++-++-=,解得18x =.故答案为:18.22.3【详解】把大学社团50人形成的集合记为全集U ,观看了《青春之歌》《建党伟业》《开国大典》三支短视频的人形成的集合分别记为A,B,C,依题意,作出韦恩图,如图,观察韦恩图:因观看了《青春之歌》的有21人,则只看了《青春之歌》的有214638---=(人),因观看了《建党伟业》的有23人,则只看了《建党伟业》的有234739---=(人),因观看了《开国大典》的有26人,则只看了《开国大典》的有2667310---=(人),因此,至少看了一支短视频的有3467891047++++++=(人),-=所以没有观看任何一支短视频的人数为50473。
第8讲容斥原理

第8讲容斥原理容斥原理是概率论和组合数学中的重要概念之一,它是一种用于计算多个事件的概率的推理方法。
容斥原理的核心思想是通过减去不重叠的事件的概率来计算多个事件的概率,从而得到它们的交集的概率。
容斥原理的一般形式可以表示为:P(A_1∪A_2∪A_3...)=S(A_1)+S(A_2)+S(A_3)-S(A_1∩A_2)-S(A_1∩A_3)-S(A_2∩A_3)+S(A_1∩A_2∩A_3)+...其中,P表示概率,A_i表示事件,S(A_i)表示事件A_i的概率,∪表示事件的并集,∩表示事件的交集。
容斥原理的核心思想是通过减去重叠部分的概率来计算多个事件的概率。
在上述公式中,第一项表示单独发生每个事件的概率,第二项表示两个事件同时发生的概率,第三项表示三个事件同时发生的概率,以此类推。
最后,通过交替相加和相减,得到多个事件的交集的概率。
容斥原理可以用来解决各种计数问题,如排列组合问题、集合的计数问题等。
它在概率论、组合数学、数论等领域里都有广泛的应用。
下面通过一个例子来理解容斥原理的具体应用。
例题:已知集合A中有n个元素,集合B中有m个元素,求集合A和集合B的并集中元素个数的期望值。
解答:首先,我们计算集合A中的元素在并集中出现的概率。
由于A中的每个元素在并集中的出现概率都相同,所以我们只需要计算一个元素出现的概率即可。
假设元素i出现在并集中的概率为p_i,那么由于每个元素的出现概率都相同,所以p_1+p_2+...+p_n=1而当一个元素出现在并集中时,它同时也是集合A和集合B中的元素,所以我们可以用容斥原理来计算元素i出现在并集中的概率。
通过容斥原理,我们可以得到集合A和集合B的并集中元素i出现的概率为:p_i=P(A_i)+P(B_i)-P(A_i∩B_i)其中P(A_i)表示元素i出现在集合A中的概率,P(B_i)表示元素i出现在集合B中的概率,P(A_i∩B_i)表示元素i同时出现在集合A和集合B中的概率。
升第八讲容斥原理之重叠问题

第八讲:容斥原理之重叠问题一、导入?文氏图文氏图,也叫“维恩图”,是由英国着名数学家 Venn 发明的.维恩(公元 1834 年 8 月 4 日─公元 1923 年 4 月 4 日)十九世纪英国着名的数学家和哲学家,生于英国赫尔.他 1883 年获得理学博士学位,同年被选为英国皇家学会会员.维恩最主要的成就是系统解释并发展了几何表示的方法,也就是发明了文氏图.他作出一系列简单闭曲线(圆或更复杂的图形),将平面分为许多间隔.利用这种图表,维恩阐明了演绎推理的基本原理.为了进一步明确起见,他还引入了一些数学难题作为实例.虽然在维恩之前,莱布尼茨(Leibniz)已系统地运用过这类逻辑图,但今天这种逻辑图仍称作“维恩图”另外,维恩在概率论和逻辑学方面也有很大贡献,他的着作——《机会逻辑》和《符号逻辑》,在 19 世纪末 20 世纪初曾享有很高的声誉.除了数学以外,维恩还有一项较为特别的技能——制作机器.他曾制作过一部板球发球机,当澳洲板球队在 1909 年到访剑桥大学时,维恩的机器依然运作正常,并使他们其中一位成员打空四次.什么是容斥原理?这一讲我们主要学习和“包含”与“排除”有关的问题,这样的问题在生活中就有不少,比如吃瓜子.我们说吃掉了一斤瓜子,指的是带壳的瓜子,并非真的吃到肚子里一斤,因为这一斤中还“包含”着瓜子壳.如果要计算到底吃了多少,最简单的方法就是称一称瓜子壳,用原来的一斤“排除”掉瓜子壳的重量.瓜子的例子相对简单,一斤瓜子里一部分是瓜子仁,另一部分就是瓜子壳,两者各不相关.但本讲要学习的包含与排除问题要复杂一些,各部分之间会有重叠.比如一个办公室中每个人都至少爱喝茶或咖啡中的一种,已知有 7 个人爱喝茶,10 个人爱喝咖啡,那能不能就说办公室里有 17 个人呢?显然不能,因为可能有一些人既爱喝茶也爱喝咖啡,如果直接将喝茶的人数和喝咖啡的人数相加,会把既爱喝茶又爱喝咖啡的人计算 2 次,计算人数的时候要把这一部分减去才行.比如,如果有 3 个人既爱喝茶又爱喝咖啡,那总的人数就应该是 7 + 10 ? 3 = 14 人.这就是我们今天要来研究的问题——有重叠的计数问题,即包含与排除问题.研究这种问题通常需要画出示意图,这样的示意图又叫做文氏图,下面我们就用文氏图推导两个对象的容斥原理公式. 两个量之间的重叠 例1、某班有34名同学参加了学校的运动会,其中有17名参加了跳绳,有20 名参加了拔河,问:及参加了跳绳又参加了拔河的又多少人? 如右图所示,如果要计算三个部分的总数,直接计算 A+B 就会算多了,而多算的正好是共同部分,只要把多算的减掉就可以了.上述分析总结成公式就是:这个公式就是两个对象的容斥原理.17+20-34=37-34=3(人)答:即参加跳绳又参加拔河的同学有3人。
容斥原理课

9、六年级一班有45名同学,每人都参加暑假体育培训班,其中足球班报25人,篮球班报20人,游泳班报30人,足球、篮球都报者有10人,足球、篮球都报者有12人。问三项都报的有多少人?
10、向50名同学调查春游去颐和园还是去动物园的态度,赞成去颐和园的人数是全体的 3/5,其余不赞成;赞成去动物园的比赞成去颐和园的学生多3人,其余不赞成,另外对去两处都不赞成的学生数比对去两处都赞成的学生数的1/3多1人,同时去颐和园和去动物园都赞成和都不赞成的学生各有多少人?
例9:甲、乙、丙同时给100盆花浇水。已知甲浇了78盆,乙浇了68盆,丙浇了58盆,那么3人都浇过的花最少有多少盆?
例10:某班同学参加期末测试,得优秀成绩的人数如下:数学20人,语文20人,英语20人,数学、英语两科都是优秀成绩的有8人,数学、语文两科成绩都是优秀的有7人,语文、英语两科成绩都是优秀的有9人,三科都没得优秀成绩的有3人。请问:这个班最多有多少人?最少有多少人?
例1:一个班有学生48人,每人至少参加跑步、跳高两项比赛中的一项。已知参加跑步的有37人,参加跳高的有40人,请问:这两项比赛都参加的学生有多少人?
例2:一次数学小测验只有两道题,结果全班有10人全对,第一题有25人做对,第二题有18人做错。问:两题都做错的有多少人?
例3:李老师出Biblioteka 两道题,全班40人中,第一道题有30人对,第2题有12人未做对,两题都做对的有20人。请问:
例6.六一班有学生46人,其中会骑自行车的有19人,会游泳的有25人,既会骑车又会游泳的有7人,既不会骑自行车又不会游泳的有多少人?
例7.有128位旅客,其中25人既不懂英语、又不懂法语,有98人懂英语,75人懂法语,请问:既懂英语、又懂法语的有多少人?
容斥原理及公式的证明
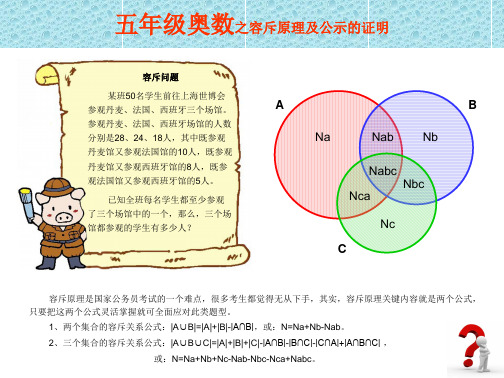
=50-(28+24+18)+(10+8+5) =3(人) 答:三个场馆都参观的有3人。
或:N=Na+Nb+Nc-Nab-Nbc-Nca+Nabc。
四年级奥数之容斥原理及公示的证明
பைடு நூலகம்
A
B
N1 Na
N4
N2
Nab Nb
Nabc
Nca N6
N7
Nbc N5
Nc
N3 C
定理: |A∪B∪C|=|A|+|B|+|C|-|A∩B|-|B∩C|-|C∩A|+|A∩B∩C| 或:N=(Na+Nb+Nc)-(Nab+Nbc+Nca)+Nabc
证明:设Na、Nb、Nc分别表示图A、B、C覆盖的 面积;Nab、Nbc、Nca分别表示图A和B、B和C、C和 A共同覆盖的面积;Nabc表示图A、B、C共同覆盖的面 积。再设N1、N2、N3、N4、N5、N6、N7分别表示7个 互不覆盖区域的面积;N表示7个互不覆盖区域的面积 总和。
则:N1=Na-Nab-Nca+Nabc, N2=Nb-Nab-Nbc+Nabc, N3=Nc-Nbc-Nca+Nabc N4=Nab-Nabc N5=Nbc-Nabc N6=Nca-Nabc N7=Nabc
五年级奥数之容斥原理及公示的证明
容斥问题
某班50名学生前往上海世博会 参观丹麦、法国、西班牙三个场馆。 参观丹麦、法国、西班牙场馆的人数 分别是28、24、18人,其中既参观 丹麦馆又参观法国馆的10人,既参观 丹麦馆又参观西班牙馆的8人,既参 观法国馆又参观西班牙馆的5人。
简单的容斥原理完整版课件

A
B
若对于三个有限集合A,B,C呢?
A∩B
A
A∩C
B
C
B∩C
A∩B∩C
三个集合的容斥原理
一般地,对任意三个有限集合A,B,C,有:
card(A∪B∪C)=card(A)+card(B)+card(C)-card(A∩B) -card(A∩C)-card(B∩C)+card(A∩B∩C).
例1.在100个学生中,音乐爱好者有56人,体育爱好 者有75人,既爱好音乐又爱好体育的有40人,那么 仅爱好音乐的有几人?仅爱好体育的有几人?两者 都不爱好的有几人?
A={圆珠笔、钢笔、橡皮、笔记本、方便面、汽水}
B={圆珠笔、铅笔、火腿肠、方便面}
card(A)=6, card(B)=4,
card(A∩B)=2,
card(A∪B)= 6+4-2
根据集合元素的互 异性
相同的元素只表示 一次!
两个集合的容斥原理
一般地,对任意两个有限集合A,B,有: card(A∪B)=card(A)+card(B)-card(A∩B).
A
音乐 爱好
者
B
体育 爱好者
变式:在100个学生中,音乐爱好者有56人,体育爱 好者有75人,那么既爱好音乐又爱好体育的人最多 有几人?最少有几人?
B
? A
音乐 爱好
体育 爱好
者
者
例2.已知集合 A {x N | 0 x 10000} ,求集合 A中不能被5或7整除的数的个数.
例2.已知集合 A {x N | 0 x 10000} ,求集合 A中不能被5或7整除的数的个数.
英语 六级
会计 师
最新容斥原理PPT课件

n !S (m ,m )A 1 A 2 ... A n n m C (n ,1 )(n 1 )m
( 1 )kC (n ,k)(nk)m ( 1 )nC (n ,n )0 m .
即:
S(m ,n)1 nC(n,k)(nk)m.
n!k0
例11 求方程x1+x2+x3=15的非负整数解的数目。 这个问题相当于15个相同的球放入3个不同的盒子的 不同方案数,为C(15+3-1,15)=C(17,2)。
A BC D 1 2 3 4
如左图,斜线区域表示禁区。
R(
)=1+6x+10x2+4x3,
方案数为:4!-6×3!+10×2!-4×1!=4。
例14 再解错排问题。 对应于棋盘上对角线格子为禁区的布子问题。
棋盘多项式为:
n
C = ··· R(C)(1x)n C(n,k)xk, k0 即:rk(C)=C(n,k)。
类似有:|A2∩A3|=0,|A2∩A4|=20!, |A2∩A5|=20!, |A3∩A4|=20!, |A3∩A5|=20!, |A4∩A5|=19!。
A1 A2 A3 0, A1 A2 A4 0,
A1 A2 A5 0, A1 A3 A4 0,
A1 A3 A5 0, A1 A4 A5 0,
ABCUA BCABBC
ACABC 4 n 3 3 n 3 2 n 1 .
例7 用26个英文字母作不允许重复的全排列,要求 排除dog,god,gum,depth,thing字样的出现,求 满足这些条件的排列数。
令Ai (i=1,2,3,4,5)分别表示出现以上五个单词之一的 排列的集合。
下面回到有禁区的排列问题,有如下的定理:
第八讲 容斥原理

第8讲 容斥原理一、知识点:容斥原理类型一:如果被统计的事物有甲、乙两类,那么,甲类或乙类个数=甲类个数+乙类个数-既甲类又乙类的物体个数 容斥原理类型类型二:如果被统计的事物有甲、乙两类,那么,既甲类又乙类的物体个数=甲类个数+乙类个数-甲类或乙类个数 容斥原理类型类型三:如果被统计的事物有甲、乙两类、既非甲类又非乙类,那么,既甲类又乙类的物体个数=甲类个数+乙类个数-(总体共有个数—既非甲类又非乙类个数)森林里住着很多动物,狮子大王派仙鹤去统计鸟的种数,蝙蝠跑去说:“我有翅膀,我算鸟类。
”仙鹤把蝙蝠统计进去了,结果得出森林中共有80种鸟类。
狮子大王又派大象去统计兽类的种类,蝙蝠又跑去说:“我没有羽毛,我算兽类。
”结果统计出森林中共有70种兽类。
最后狮子大王问:“森林中共有鸟类和兽类多少种?”狐狸军师听了仙鹤和大象的统计结果,向狮子大王报告:“森林中鸟类与兽类共计150种。
”这个统计对吗? 现在我们用维恩图表示:要求鸟类与兽类共多少种,可以:+得出结论:鸟类与兽类共多少种=鸟类+兽类— 蝙蝠这个故事反映的是一个数学原理,我们把这个数学原理称为包含排除原理,即容斥原理。
鸟类 80 种兽类 70种蝙蝠 1种鸟类与兽类共? 兽类70种鸟类—蝙蝠=79(种)二、例题讲解:包含与排除问题其实也叫容斥问题。
A AB B (韦恩图)(1)容斥原理的第一种类型:例题1:四年级(2)班每人都参加了一种兴趣小组,参加舞蹈组的有23人,参加合唱团的有40人,既参加舞蹈组又参加合唱团的有15人,全班共有多少人? 练习:1、四年甲班学生采集标本,采到昆虫标本的有26人,采到植物标本的有32人,两种豆采到的有10人,全班有学生多少人?2、学校文艺组每人至少会演奏一种乐器,已知会拉手风琴的有 24 人,会弹电子琴的有 17 人,其中两种乐器都会演奏的有 8 人。
这个文艺组一共有多少人?甲类乙类即甲 又乙 维恩图合唱团 40人舞蹈组 23人15人共?植物标本 32人昆虫标本 有26人10人共?如果被统计的事物有甲、乙两类,那么, 甲和乙的总个数=甲个数+乙个数-既是甲又是乙的个数。
什么是容斥原理

什么是容斥原理容斥原理是组合数学中的一种重要的计数方法,常常用于解决包含排列组合的问题。
容斥原理的核心思想是通过排除重复计数的方法,来求解包含多个集合的问题。
在实际问题中,容斥原理有着广泛的应用,特别是在概率统计、组合数学、计算机算法等领域。
首先,我们来了解一下容斥原理的基本概念。
假设有n个集合A1、A2、……、An,我们希望求解这些集合的并集的元素个数。
容斥原理告诉我们,这个并集的元素个数可以通过如下的公式来计算:|A1 ∪ A2 ∪……∪ An| = Σ|Ai| Σ|Ai ∩ Aj| + Σ|Ai ∩ Aj ∩ Ak| …… + (-1)^(n-1) |A1 ∩ A2 ∩……∩ An|。
其中,|A|表示集合A的元素个数,Σ表示求和运算。
公式右边的第一项是将所有集合的元素个数相加,第二项是将两两集合的交集的元素个数相减,第三项是将三个集合的交集的元素个数相加,以此类推。
最后一项是将所有集合的交集的元素个数相加,并且交替加减。
通过这个公式,我们可以清晰地看到容斥原理的核心思想,通过交替相加和相减集合的交集元素个数,来排除重复计数,最终得到并集的元素个数。
接下来,我们通过一个具体的例子来说明容斥原理的应用。
假设有一个集合包含了所有小于100的正整数中能被2、3或5整除的数,我们希望求解这个集合中元素的个数。
首先,我们分别求解能被2、3和5整除的数的个数,分别记为A2、A3和A5。
然后,我们求解能同时被2和3、2和5、3和5以及2、3和5整除的数的个数,分别记为A2∩3、A2∩5、A3∩5和A2∩3∩5。
最后,根据容斥原理的公式,我们可以得到集合中元素的个数:|A2 ∪ A3 ∪ A5| = |A2| + |A3| + |A5| |A2 ∩ A3| |A2 ∩ A5| |A3 ∩ A5| + |A2 ∩ A3 ∩ A5|。
通过具体的计算,我们可以得到最终的结果。
这个例子清晰地展现了容斥原理在实际问题中的应用,通过排除重复计数,我们可以准确地求解集合的并集元素个数。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第八讲容斥原理在一些计数问题中,经常遇到有关集合元素个数的计算。
我们用|A|表示有限集A的元素个数。
在并集的讨论中,已经知道,求两个集合并集的元素的个数,不能简单地把两个集合的元素个数相加,而要从两个集合个数之和中减去重复计算的元素个数,即减去交集的元素个数,用式子可表示成|A∪B|=|A|+|B|-|A∩B|我们称这一公式为包含与排除原理,简称容斥原理。
包含与排除原理告诉我们,要计算两个集合A、B的并集A∪B的元素的个数,可分以下两步进行:第一步分别计算集合A、B的元素个数,然后加起来,即先求|A|+|B|(意思是把A、B的一切元素都“包含”进来,加在一起);第二步从上面的和中减去交集的元素个数,即减去|A∩B|(意思是“排除”了重复计算的元素个数)。
例1 求不超过20的正整数中是2的数倍或3的倍数的数共有多少个。
分析与解:设I={1,2,3,…,19,20},A={I中2的倍数},B={I 中3的倍数}。
显然,题目要求计算并集|A∪B|的元素个数,即求|A∪B|。
易知,A={2,4,6,…,18,20},共有10个元素,即|A|=10,B={3,6,9,12,15,18},共有6个元素,即|B|=6。
A∩B={I中既是2的倍数又是3的倍数}={6,12,18}共有3个元素,即|A∩B|=3,所以|A∪B|=|A|+|B|-|A∩B|=10+6-3=13答:所求的数共有13个。
此题可直观地图示如下:图8-1中,A表示不超过20的正整数中2的倍数的集合。
B表示不超过20的正整数中3的倍数的集合。
在不超过20的正整数中既是2的倍数又是3的倍数的数有6,12,18,即A∩B中的数。
例2 某班统计考试成绩,数学得90分上的有25人;语文得90分以上的有21人;两科中至少有一科在90以上有38人。
问两科都在90分以上的有多少人?(1985年初一迎春杯数学竞赛试题)解:设A={数学成绩90分以上的学生),B={语文成绩90分以上的学生}。
那么,集合A∪B表示两科中至少有一科在90分以上的学生,由题意知|A|=25,|B|=21,A∪B=38。
现在要求两科都在90分以上的学生人数,即求|A∩B|。
由容斥原理得|A∩B|=|A|+|B|-|A∪B|=25+21-38=8答:两科都在90分以上的学生有8人。
在计算面积的问题中,有时也要用到容斥原理。
例3 边长为2的正方形与边长为3的正方形,如图8—2放在桌面上,它们所盖住的面积有多大?分析与解:如果把两个正方形的面积加起来,得22+32=13就会发现,多计算了一块阴影部分面积。
这块面积是1.52=2.25。
应该从上面的和中减去这一部分。
因此,两个正方形所盖住的面积应是22+32-1.52=13-2.25=10.75答:两个正方形所盖住的面积是10.75。
例4 有100位旅客,其中有10人既不懂英语又不懂俄语,有75人懂英语,83人懂俄语。
问既懂英语又懂俄语的有多少人?(1985年小学迎春杯数学竞赛试题)分析与解:设A={懂英语的旅客},B={懂俄语的旅客}。
那么,英语和俄语这两种语言中至少懂一种的旅客的集合为A∪B,而两种语言都懂的旅客的集合为A∩B。
题目要求|A∩B|。
由题意知,|A|=75,|B|=83,|A∪B|=100-10=90。
由容斥原理,得|A∩B|=|A|+|B|-|A∪B|=75+83-90=68答:既懂英语又懂俄语的旅客有68人。
对于任意三个有限集合A、B、C,我们可以将上面的容斥原理推广得到如下的公式:|A∪B∪C|=|A|+|B|+|C|-|A∩B|-|A∩C|-|B∩C|+|A∩B∩C|。
三个集合的容斥原理告诉我们,要计算并集A∪B∪C的元素个数,可以分三步进行:第一步求|A|+|B|+|C|;第二步减去|A∩B|,|A∩C|,|B∩C|;第三步加上|A∩B∩C|。
结合图8—3还可以作出如下说明。
由于A∪B∪C一般可分成如图的七个部分,或者说分成了七个不相交的子集。
其中Ⅰ、Ⅱ、Ⅲ部分的元素仅属于某个集合,而Ⅳ、V、Ⅵ部分的元素分别属于某两个集合,第Ⅶ部分则是三个集合的交集由于A∪B∪C的元素分别来自集合A、B、C,因此,先计算|A|+|B|+|C|。
在这个和里,Ⅰ、Ⅱ、Ⅲ部分的元素只计算了一次,而Ⅳ、V、Ⅵ部分的元素各计算了两次,第Ⅶ部分(A∩B∩C)的元素计算了三次。
在第二步减去|A∩B|,|A∩C|,|B∩C|后得|A|+|B|+|C|-|A∩B|-|A∩C|-|B∩C|。
这样显然消除了IV、V、VI部分的重复计算,但同时连续三次减去了第Ⅶ部分,于是第Ⅶ部分的元素个数都被减去了,因此必须补上第Ⅶ部分的元素个数,即再加上|A∩B∩C|,综上所述得|A∪B∪C|=|A|+|B|+|C|-|A∩B|-|A∩C|-|B∩C|+|A∩B∩C|。
例5 某校组织棋类比赛,分成围棋、中国象棋和国际象棋三个组进行。
参加围棋比赛的共有42人,参加中国象棋比赛的共有51人,参加国际象棋比赛的共有30人。
同时参加了围棋和中国象棋比赛的共有13人,同时参加了围棋和国际象棋比赛的7人,同时参加了中国象棋和国际象棋比赛的11人,其中三种棋赛都参加的3人。
问参加棋类比赛的共有多少人?解法1:设A={参加围棋比赛的人},B={参加中国象棋比赛的人},C={参加国际象棋比赛的人},那么参加棋类比赛的人的集合为A∪B∪C。
由题意知:|A|=42,|B|=,|C|=30,|A∩B|=13,|A∩C|=7,|B∩C|=11,|A∩B∩C|=3。
由容斥原理得|A∪B∪C|=|A|+|B|+|C|-|A∩B|-|A∪C|-|B∩C|+|A∩B∩C|=42+51+30-13-7-11+3=95(人)答:参加棋类比赛的共有95人。
解法2:利用文氏图逐个填写各区域所表示的集合元素的个数,然后求出最后结果。
设A、B、C分别表示参加围棋、中国象棋和国际象棋比赛的人的集合。
其文氏图分割成七个互不相交的区域。
区域Ⅶ(即A∩B∩C)表示三种棋赛都参加的数的集合。
由题意应填数字3。
区域IV表示仅参加围棋和中国象棋两项比赛的人的集合,其人数为13-3=10(人)。
区域Ⅵ表示仅参加围棋和国际象棋两项比赛的人的集合,其人数为7-3=4(人)。
区域Ⅰ表示只参加围棋一项比赛的人的集合,其人数为42-10-4-3=25(人)。
同理可把区域Ⅱ、Ⅲ、V所表示的集合的人数逐个算出,分别填入相应的区域内(图8—4)。
由此得出参加棋类比赛的总人数为25+30+15+15+10+8+4=3=95说明:解法2简单直观,不易出错。
由于各个区域所表示的集合的元素个数都计算出来了,因此提供了较多的信息,易于回答各种方式的提问。
例6边长分别为6,5,2的三个正方形,如图8—5所示放在桌面上。
问它们盖住的面积是多大?分析与解:这个问题可用容斥原理来解。
设R表示正方形区域ABCD,R1表示正方形区域A1B1C1D1,R2表示正方形区域A2B2C2D2。
那么R∩R1表示正方形区域BOD1M,R∩R2表示矩形区域A2FND2,R1∩R2表示矩形区域A2B2GE,R∩R1∩R2表示正方形区域A2FOE个正方形所盖住的部分为R∪R1∪R2。
如果用|R|表示区域R的面积,那么根据容斥原理可得|R∪R1∪R2|=|R|+|R1|+|R2|-|R∩R l|-|R∩R2|-|R1∩R2|+|R∩R1∩R2|=62+52+22-(32+2×1+1×2)+12=53答:三个正方形所盖住的面积为53。
例7 某班学生手中分别拿有红、黄、蓝三种颜色的球。
已知手中有红球的共有34人,手中有黄球的共有26人,手中有蓝球的共有18人。
其中手中有红、黄、蓝三种球的有6人。
而手中只有红、黄两种球的有9人,手中只有黄、蓝两种球的有4人,手中只有红、蓝两球的有3人,那么这个班共有多少人?(1986年初一迎春杯数学竞赛试题)分析与解:此题用填写文氏图各区域元素个数的方法来解较为简便,设A、B、C分别表示手中有红球、黄球、蓝球的人的集合。
由题意可逐一填出各区域元素的个数(如图)。
所以全班共有16+7+5+9+4+3+6=50(人)答:这个班共有50人。
这个题目也可以列式计算如下:(34+26+18)-(9+4+3)-2×6=50(人)例8求1到200的自然数中不能被2、3、5中任何一个数整除的数有多少?解:设A={1到200中间能被2整除的数},B={1到200中间能被3整除的数},C={1到200中间能被5整除的数}。
那么,A∩B={1到200中间能被2×3整除的数},A∩C={1到200中间能被2×5整除的数},B∩C={1到200中间能被3×5整除的数},A∩B∩C={1到200中间能被2×3×5整除的数}。
设[x]表示小于等于x的最大整数,那么|A|=[200/2]=100,|B|=[200/3]=66,|C|=[200/5]=40,|A∩B|=[200/6]=33,|A∩C|=[200/10]=20,|B∩C|=[200/15]=13,|A∩B∩C|=[200/30]=6。
根据容斥原理,1到200的自然数中至少能被2,3,5中一个数整除的数共有|A∪B∪C|=|A|+|B|+|C|-|A∩B|=|A∩C|-|B∩C|+|A∩B∩C|=100+66+40-33-20-13+6=146(个)所以1到200的自然数中不能被2,3,5中任何一个数整除的数共有200-146=54(个)习题八1.某班有团员23人。
这个班里男生共20人,问这个班女生团员比男生非团员多多少人?2.纸片面积为7,一张边长为2的正方形纸片,把这两张纸片放在桌面上覆盖的面积为8,问两张纸片重合部分的面积是多少?3.从1到100的自然数中,(1)不能被6和10整除的数有多少个?(2)至少能被2,3,5中一个数整除的数有多少个?4.盛夏的一天,有10个同学去冷饮店,向服务员交了一份需要冷饮的统计表:要可乐、雪碧、果汁的各有5人;可乐、雪碧都要的有3人;可乐、果汁都要的有2人;雪碧、果汁都要的有2人;三样都要的只有1人。
证明其中一定有1人这三种饮料都没有要。
5.对100个学生课外学科活动的调查结果如下:32人参加数学小组;20人参加英语小组,45人参加生物小组。
其中15人既参加了数学小组又参加了生物小组;7人既参加了英语小组又参加了数学小组;10人既参加了英语小组又参加了生物小组。
还有30人没有参加上述任何一个学科小组。
(1)求三个学科小组都参加的人数。
(2)在文氏图的八个区域内填入相应的学生人数。
其中A、B、C分别表示参加数学、英语和生物小组的学生的集合。
被调查的100个学生的集合为全集I。
