实验六 离散系统状态方程的求解
线性离散系统状态方程的解

Z变换法(2/7)
在Z反变换中对标量函数存在下述公式和性质:
Z 1 1 /(1 az 1 ) a k Z {W1 ( z )W2 ( z )} w1 (k i ) w2 (i )
1 i 0 k
Βιβλιοθήκη 其中W1(z)和W2(z)分别为w1(k)和w2(k)的Z变换。 将上述公式推广到向量函数和矩阵函数,则可得
离散卷积
Z变换法(3/7)—例3-14
因此,离散系统的状态方程的解为:
x(k ) G k x(0) G k j 1Hu( j )
j 0
k 1
该表达式与前面递推法求解结果一致。 例 已知某系统的状态方程和初始状态分别为 1 0 1 1 x(k 1) x( k ) u ( k ) x(0) 0.16 1 1 1
( k 1 , k0 ) G ( k ) ( k , k 0 ) ( k0 , k0 ) I
其解为
(k , k0 ) G(k 1)G(k 2)...G(k0 ) , k k0
线性时变离散系统状态方程的解(3/6)
与线性定常离散系统类似,线性时变离散系统的状态求解公 式可用迭代法证明。 对线性时变离散系统的状态方程,依次令k= k0, k0+1, k0+2, …,从而有
2. 引入状态转移矩阵概念和表示之后,线性连续系统和线 性离散系统的状态方程的求解公式在形式上一致,都由 零输入响应和零状态响应叠加组成, 只是相应的零状态响应在形式上略有不同,一为求 积分(卷积),一为求和(离散卷积),但本质是一致的。 3. 在由输入所引起的状态响应中,第k个时刻的状态只取决 于此采样时刻以前的输入采样值,而与该时刻的输入采 样值u(k)无关。
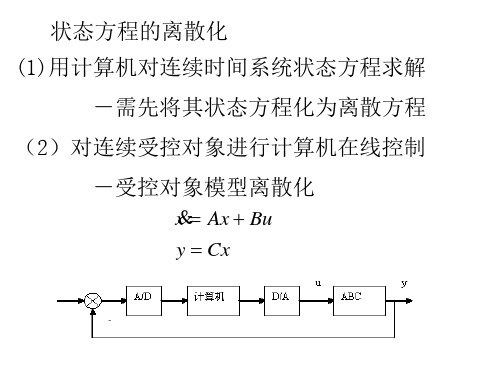
离散时间系统状态方程和输出方程的求解

2
5
0
D
0 0
q[0]
2 3
x[k] u[k]
离散系统的状态方程和输出方程的时域求解
离散系统的状态方程为:
q[k +1] Aq[k] Bx[k]
在给定系统的初始状态q[k0]后,可直接用迭代法进行求解。
q[k0 1] Aq[k0] Bx[k0] q[k0 2] Aq[k0 1] Bx[k0 1]
2
5 q1[k]
0
q2 [k ]
系统状态变量的初始状态及系统输入为:
q1[0] q2[0]
2
3
x[k] u[k]
在时域求解该系统的状态变量和输出。
离散系统的状态方程和输出方程的时域求解
解:状态方程和输出方程写成矩阵形式:
q[k +1] Aq[k] Bx[k]
在z域求解该系统的完全响应。
离散系统的状态方程和输出方程的z域求解
解:状态方程和输出方程写成矩阵形式:
离散系统的状态方程和输出方程的时域求解
[例] 已知描述某离散系统的状态方程和输出方程为
q1[k q2[k
1] 1]
0
1
6
1
5
q1[k ] q2 [k ]
0 1
x[k ]
6
y1[k ] y2 [k ]
1
zq[0]
[C (
zI
A)1
B
D]X
(
z)
Yzi (z)
Yzs ( z)
然后再对Q(z)和Y(z)进行z反变换即可得到q[k]和y[k]。
离散系统的状态空间表达式

(1)连续系统:用微分方程来表示,采用拉 普拉斯变换传递函数进行分析。
离散系统:用差分方程来描述,用Z变 换脉冲传递函数进行分析。
因此,离散系统的状态空间表达式可通过差 分方程或脉冲传递函数。
(2)离散系统的信号采用数字形式,输入和 输出都是脉冲序列或数字序列。计算机控制 系统属离散系统。
试写出其状态方程和输出方程 。
解:
x1 (k 1) 0
1
0 x1(k) 0
x2
(k
1)
0
0
1
x
2
(k
)
0
u(k)
x3 (k 1) 6 5 2x3 (k) 1
x1(k)
y(k) x(k) 1
0
0x2 (k)
x3 (k )
例1.10 已知 y(k+3)+2y(k+2)+5y(k+1) +6y(k)=3u(k+2)+2u(k+1)+6u(k)
脉冲传递函数:
G(z)
Y (z) u(z)
bmzm bm1zm1 b1z b0 zn an1zn1 a1z a0
二 、状态方程的建立
1、由差分方程
设T=1 输入仅有(kT)项,b0=1 整个方程可以写为: y(k+n)+an-1y(k+n-1)+……+a0y(k)=u(k) 设x1(k)=y(k) x2(k)=y(k+1)=x1(k+1) x3(k)=y(k+2)=x2(k+1) ……
xn(k)=y(k+n-1)=xn-1(k+1) xn(k+1)=y(k+n)=-a0 x1(k)-a1 x2(k)-
求解系统的状态方程

资料范本本资料为word版本,可以直接编辑和打印,感谢您的下载求解系统的状态方程地点:__________________时间:__________________说明:本资料适用于约定双方经过谈判,协商而共同承认,共同遵守的责任与义务,仅供参考,文档可直接下载或修改,不需要的部分可直接删除,使用时请详细阅读内容求解系统的状态方程一、实验设备PC计算机,MATLAB软件,控制理论实验台二、实验目的(1)掌握状态转移矩阵的概念。
学会用MATLAB求解状态转移矩阵(2)学习系统齐次、非齐次状态方程求解的方法,计算矩阵指数,求状态响应;(3)通过编程、上机调试,掌握求解系统状态方程的方法,学会绘制输出响应和状态响应曲线;(4)掌握利用MATLAB导出连续状态空间模型的离散化模型的方法。
三、实验原理及相关基础(1)参考教材P99~101“3.8利用MATLAB求解系统的状态方程”(2)MATLAB现代控制理论仿真实验基础(3)控制理论实验台使用指导实验内容(1)求下列系统矩阵A对应的状态转移矩阵(a)(b)代码:syms lambdaA=[lambda 0 0;0 lambda 0;0 0 lambda];syms t;f=expm(A*t)(c)代码:syms t;syms lambda;A=[lambda 0 0 0;0 lambda 1 0;0 0 lambda 1;0 0 0 lambda];f=expm(A*t)(2) 已知系统a) 用MATLAB求状态方程的解析解。
选择时间向量t,绘制系统的状态响应曲线。
观察并记录这些曲线。
(1)代码:A=[0 1; -2 -3];B=[3;0];C=[1 1];D=[0];u=1;syms t;f=expm(A*t);%状态转移矩阵x0=0;s1=f*B*u;s2=int(s1,t,0,t)%状态方程解析解状态曲线:(2)A=[0 1;-2 -3];syms t;f=expm(A*t);X0=[1;0];t=[0:0.5:10];for i=1:length(t);g(i)=double(subs(f(1),t(i)));endplot(t,g)状态转移矩阵syms lambdaA=[lambda 0 0;0 lambda 0;0 0 lambda];syms tf=expm(A*t)b) 计算系统在初始状态作用下状态响应和输出响应的数值解(用函数initial( )), 绘制系统的状态响应曲线和输出响应曲线。
离散化的状态方程
T ∫0
I ⋅ B ⋅ dt = BT
结论:上式为近似计算方法 例2.6 已知时变系统
0 5(1 − e −5t ) 5 5e −5t u ɺ x= x + −5t −5t 0 5(e − 1) 0 5(1 − e )
试将它离散化,并求出输入和初始条件分别为
0, x(0) = 0时,方程在采样时刻的近似解 u (t ) = 0 1
1 (3)H(T) = ∫ 0 0
T T 1/ 2(1−e )0 1 dt= ∫0 −2t e 1 0 −2t −2t
x 1 [( k + 1)T] x 1 (kT ) (4) = [G (T)] x (kT ) + [H (kT) U (kT)] x 2 [( k + 1)T] 2
归纳:将连续状态方程离散化步骤
1、求Φ(t )=e = L [ SI − A] 2、G(T ) = Φ(T ) = Φ(t ) t = T T At 3、求H (T ) = ∫0 e Bdt 4、求x[(k + 1)T ] = G(T ) x(kT ) + H (T )u (kT )
At
−1
−1
例2.5已知控制对象满足 1 x + 0u,求其离散化方程 ɺ = 0 x 0 1 −2
系统离散状态方程(T=0.1) 可见T较小时, x1[(k + 1)T ] 0.9 0.1 x1(kT ) 0 = + r (kT ) 两种方法得 x2[(k + 1)T ] − 0.1 0.9 x2 (kT ) 0.1 状态空间表 x1(kT ) 达式近似相 输出y(kT ) = [1 0] 等。 x2 (kT ) 离散方程求解可按2.3递推法或Z变换求解
K3.05-离散系统状态方程和输出方程

c12 c22
cq2
c1n
c2n
cqn
x1(k) x2(k) xn(k)
d11 d21 dq1
d12 d22
d1p
d2
p
f1 f2
dq2
dqp
fp
Y(k)
C
X(k)
D
f (k)
Y (k) CX (k) Df (k)
5பைடு நூலகம்
状态变量:x1(k), x2 (k)......, xn (k)
(3) 状态矢量、状态空间:
状态矢量:由状态变量构成的列矢量X(k) 。
x1(k)
X
(k
)
x2
(k
)
xn (k)
状态空间:状态矢量X(k) 所在的空间。
3
离散系统状态方程和输出方程 (4)状态方程:
描述状态与输入关系的一阶前向差分方程组。
离散系统状态方程和输出方程
知识点K3.05
离散系统状态方程和输出方程
主要内容:
1.状态变量 2.状态方程 3.输出方程
基本要求:
掌握离散系统状态方程和输出方程的基本概念
1
离散系统状态方程和输出方程
K3.05 离散系统状态方程和输出方程 (1)初始状态: 定义:离散系统在k0时刻的状态是最少数目的一组数, 知道了这组数和区间[k0,k]上的输入,就可以完全确定系 统在k时刻的输出,该组数即为初始状态,表示为:
一般形式:n阶系统,n个状态,p个输入。
x1(k 1) a11
x2
(k
1)
a21
a12
a22
a1n
a2n
x1(k)
x2
离散系统的状态空间描述状态方程

y( k ) x1 ( k ) h0u( k )
2019/1/5
13
写成矩阵形式,得到状态空间描述为:
1 x1 ( k 1) 0 x ( k 1) 0 0 2 x ( k 1 ) 0 n 1 0 xn ( k 1) a0 a1 0 1 0 0 x1 ( k ) h1 x2 ( k ) h2 0 u( k ) 1 xn1 ( k ) hn1 an1 xn ( k ) hn
y( k ) x1 ( k )
2019/1/5 10
写成矩阵形式,得到离散系统的状态空间表达式:
x1 ( k 1) 0 x ( k 1) 0 2 xn1 ( k 1) 0 xn ( k 1) a0 1 0 0 0 1 0 0 x1 ( k ) 0 x2 ( k ) 0 0 u( k ) 1 x n 1 ( k ) 0 an1 xn ( k ) b0
2019/1/5
8
4、将差分方程化为状态空间描述:或转换为Z传递函数,再求 离散系统差分方程描述形式:
y( k n) an1 y( k n 1) a1 y( k 1) a0 y( k ) bnu( k n) bn1u( k n 1) b0u( k ) ( k 0,1,2)
当初始状态 x(0) 0 时,对以下状态空间描述做Z变换:
x ( k 1) Gx( k ) Hu( k ) y( k ) Cx ( k ) Du( k )
§8.3 离散系统状态方程的建立

y(k)
输出方程 y (k)=–x1 (k) + x2(k)
第2页
二、由状态方程进行系统模拟
例:某离散系统的状态方程和输出方程为
⎡ x1 (k + 1) ⎤ ⎡1 2 4⎤ ⎡ x1 (k ) ⎤ ⎡1⎤ ⎢ x (k + 1)⎥ = ⎢1 2 0⎥ ⎢ x (k )⎥ + ⎢0⎥ f (k ) ⎥⎢ 2 ⎥ ⎢ ⎥ ⎢ 2 ⎥ ⎢ ⎢ ⎣ x3 (k + 1) ⎥ ⎦ ⎢ ⎣0 3 0 ⎥ ⎦⎢ ⎣ x3 (k ) ⎥ ⎦ ⎢ ⎣0 ⎥ ⎦
§8.3
离散系统状态方程的建立
与连续系统类似,具体方法为:
(1)由系统的输入-输出方程或系统函数,首先画出其信 号流图或框图; (2)选一阶子系统(迟延器)的输出作为状态变量; (3)根据每个一阶子系统的输入输出关系列状态方程; (4)在系统的输出端列输出方程。
第1页
例: 某离散系统的差分方程为 y(k) + 2y(k –1) –y(k –2) = f(k –1) –f(k –2) 列出其动态方程。
⎡ x1 (k ) ⎤ ⎥ ( ) y (k ) = [1 3 5]⎢ x k ⎢ 2 ⎥ ⎢ ⎣ x3 ( k ) ⎥ ⎦
画出该系统的信号流图
第3页
结果:
1
f( )
1 z -1 1 1 z -1 2 2 4 3
3 z-1
5
y( k ) x 3( k )
x 1( k )
x2(k )
第4页
−1
解:不难写出系统函数 画信号流图:
z −z H ( z) = −1 −2 1+ 2z − z
1
−2
设状态变量x1 (k) ,x2 (k) :
离散时间系统状态方程的求解.

或
An1u n 1 Z 1 zI A 1
项决定,即 本λ身n,0 只有当 时,n 式 n(02)才可给出完 整的 之结果λ。n
如果起始时刻选 n0 ,0并将上述对 值的n 限制以阶跃信号
的形式写入表达式,于是有
λ
n
Anλ 0un
零输入解
ni01 An1i Bxiun 1
零状态解
还可解得输出为
yn Cλ n Dxn
CAnλ0un
1 1
d2
d
2
n
1
n
n 1 1n2
2c2
3 2c31
n 1n 2 cn11n3
dm1
d
m1
1
n
n! m 1
!1nm1
m
1!cm1
m
! cm1
m 1!
2!
cm112
n 1! n m!
c nm k 1 1
三.离散系统状态方程的 z 变换解
和连续系统的拉氏变换方法类似,离散系统的 变z换方
零输入解
ni01 CAn1i Bxiun 1 Dxnun
零状态解
由两部分组成:
•一是起始状态经转移后在 n 时刻得到的响应分量;
•另一是对n 1 时刻以前的输入量的响应。它们分别
称为零输入解和零状态解。
其中 An称为离散系统的状态转移矩阵,它与连续系统中
的 e At 含义类似,也用符号 表示,写作n
法也使状态方程的求解显得容易一些。 由离散系统的状态方程和输出方程
λ n 1 Aλ n Bxn
yn
Cλ
n
Dxn
两边取 z 变换
zΛz zλ 0 AΛz BX z Y z CΛz DXz
离散时间系统状态方程的求解

§9.6 离散时间系统状态方程的求解概述:离散系统状态方程的求解和连续系统的求解方法类似,包括时域和变换域两种方法。
矢量差分方程的时域求解;An 的计算;离散系统状态方程的Z 变换解一.矢量差分方程的时域求解离散系统的状态方程表示为(1)此式为一阶差分方程,可以应用迭代法求解。
设给定系统的起始状态为:在 , 则按式(1)有 以下用迭代法,求 时刻的值:对于任意n 值,当 可归结为 (2)上式中,当 时第二项不存在,此时的结果只由第一项决定,即 本身,只有当 时,式(2)才可给出完整的 之结果。
如果起始时刻选 ,并将上述对 值的限制以阶跃信号的形式写入表达式,于是有还可解得输出为()()()n n n Bx A λλ+=+10n n =()0λn ()()()0001n n n Bx A λλ+=+()()nn n ,,3,200 ++()()()0001n n n Bx A λλ+=+()()()()()()1 112000000+++=+++=+n n n n n n Bx ABx λA Bx A λλ2()()()()()()()21 2230000000+++++=+++=+n n n n n n n Bx ABx Bx A λA Bx A λλ230n n >()()()()()()()()()∑-=--------+=-+++++=-+-=110002001000 1 1 11n ni in nn n n n n n n i n n n n n n n n Bx A λABx Bx A Bx A λA Bx A λλ 0n n =()0n λ0n n >()n λ00=n n ()()()()()⎪⎪⎭⎪⎪⎬⎫⎪⎪⎩⎪⎪⎨⎧-⎥⎦⎤⎢⎣⎡+=∑-=-- 零状态解零输入解10101n u i n u n n i i n Bx A λA λn ()()()n n n Dx C λy +=()()()()()()零状态解零输入解n u n n u i n u n i Dx Bx CA λCA i 1n n +-⎥⎦⎤⎢⎣⎡+=∑-=--1010由两部分组成:•一是起始状态经转移后在 时刻得到的响应分量 ;•另一是对时刻以前的输入量的响应。
第6章 离散系统状态空间分析

第6章 离散系统状态空间分析
以上针对线性定常差分方程介绍了状态方程的列写方法, 由于状态变量的选择不是惟一的,因此状态方程也不是 惟一的,上面只介绍了线性定常差分方程,而对于线性 时变差分方程也可以用上述类似的方法写出状态方程, 且可以得到形式上与时不变状态方程相同的时变状态方 程,只是由于时变差分方程的系数 ai,bj(i=1,2,…,n; j=0,1,…,m)都是 k的函数,即 ai(k),bj(k),因此,系数 矩阵A,B,C,D也都是k的函数,即A(k),B(k),C(k), D(k)。于是,对于线性时变差分方程所对应的状态方程 和输出方程的一般形式为:
第6章 离散系统状态空间分析
第6章 离散系统状态空间分析
第6章 离散系统状态空间分析
6.1 线性离散系统状态方程
离散时间系统可以用差分方程或脉冲传递函数来描述, 它们都是基于系统输入输出特性的描述。如何根据系统 的差分方程和 Z 传递函数描述得到它的基于输入 —— 状 态——输出的状态空间描述,是本节所要讨论的内容。
第6章 离散系统状态空间分析
x1 (k 1) 0 1 0 x1 (k ) 0 x (k 1) 0 0 1 x ( k ) 0 u (k ) 2 2 x3 (k 1) 6 3 5 x3 (k ) 2 x1 (k ) y ( k ) 1 0 0 x ( k ) 2 x3 (k )
第6章 离散系统状态空间分析
因而有关系式
zx1 ( z ) 2 x1 ( z ) U ( z ) zx2 ( z ) x2 ( z ) x3 ( z ) zx ( z ) x ( z ) U ( z ) 3 3
离散系统状态方程的解

t
零输入分量
零初值分量
一般需用计算机来求解。
线性离散系统状态方程的解
一. 线性连续系统的时间离散化 离散系统:自然离散系统 采样控制系统(由连续系统等间隔采样得到) 时间离散化问题的数学实质就是在一定的采样方式和保 持方式下,由系统的连续时间状态空间描述来导出其对 应的离散时间状态空间描述,并建立起两者的系数矩阵 间的关系式。
x[(k + 1)T ] = Φ (T ) x (kT ) +
( k +1)T
∫
Φ [(k + 1)T − τ ]Bu(τ )dτ
kT
= Φ (T ) x (kT ) +
( k +1)T
∫
Φ [(k + 1)T − τ ]Bdτ ⋅ u(kT )
kT
令 (k +1)T −τ = τ ′
有 : x [( k + 1) T ] = Φ ( T ) x ( kT ) + ∫ Φ (τ ′ ) B d ( − τ ′ ) ⋅ u ( kT )
又 Φ (t2 , t1 ) x (t1 )
分段转移
= Φ (t2 , t1 )Φ (t1 , t0 ) x (t0 )
3. Φ (t , t0 ) = Φ −1 (t0 , t )
转移可逆
QΦ (t0 , t ) ⋅Φ (t , t0 ) = Φ (t0 , t0 ) = I(互为逆)
三、时变非齐次状态方程的解:
(性质1)
3.化为A的有限多项式求解(Cayley-Hamilton法)
4.非奇异变换法
x = Px
A
性质10:e形(约当形)
性质11
∴ e At = Pe At P −1
《自动控制原理》线性定常离散系统状态方程的建立及求解

向量-矩阵形式为
x1 (k + 1) 0 1 0 0 x1 (k) 0
x2 (k
+ 1)
0
0
1
0
x2 (k)
0
= 0 0 0 0 + u(k)
xn−1
(k
+
1)
0
0
0
1
x
n−1
(k
)
0
xn (k + 1) − a0 − a1 − a2 − an−1 xn (k) 1
量和输入量:ai ,bi (i = 0,1,2,, n且an = 1) 为表征系统特性的常系
数。考虑初始条件为零时的z变换关系有
[ y(k)] = Y (z), [ y(k + i)] = ziY (z)
对式(9—87)两端取z变换并加以整理可得
G(z)
=
Y (z) U (z)
=
bn z n + bn−1 z n−1 + + b1 z + b0 z n + an−1 z n−1 + + a1 z + a0
(9-95)
三、线性定常离散动态方程的解
求解离散动态方程的方法友递推法和z变换法,这里只介绍常
用的递推法,对z变换法感兴趣的读者可参阅有关书籍。下面以解
离散化状态方程为例来说明如何使用递推法求解。令式(9-93)
中的k = 0,1,, k −1可得到 T,2T,, kT 时刻的状态,即
k = 0 : x(1) = (T )x(0) + G(T )u(0)
=
bn
+
z n−1 n−1
+
第八章(3) 离散系统状态方程的求解

在用状态分析系统时, 在用状态分析系统时,求状态转移矩阵(k) 是关键步骤. 是关键步骤. 例 8.4-1 已知矩阵 求其矩阵函数A 求其矩阵函数 k.
0 1 A= 2 1
矩阵A的特征方程为 解 矩阵 的特征方程为
λ 1 = λ2 λ 2 = 0 q( λ ) = det( λI A) = det 2 1 λ 方程有两个相异的特征根
其全解 x(k) = xx (k) + x f (k)
(3)求系统的输出
y(k) = Cx(k) + Df (k) = C(k)x(0) + C(k 1)B* f (k) + Df (k)
代入, 将 (k)代入,得零输入响应
1 k 1k ( 2) 1 0 ( 2) yx (k) = C(k)x(0) = = 1 , k ≥ 0 1 1 1 ( )k + ( 1)k ( )k 4 4 2
零输入解的象函数 零状态解的象函数
1
1
x(k) = (k)x(0) +(k 1)B* f (k)
于是, 于是,得状态转移矩阵 (k) = Ak = Z1{[zI A]1 z} 为了方便, 为了方便,定义
将它们代入, 将它们代入,得状态转移矩阵
1 1 k 1 0 1 k 1 k 2 1 k k (k) = A = ( ) + 2( ) + 4( 2) 4( 4) 1 4 0 1 2 4 1k 0 ( 2) = 1k 1k 1 k ( ) ( ) ( ) 4 4 2 0 1 4
i =0
k1
x(k) = (k)x(0) +(k 1)B* f (k)
x(k) = (k)x(0) + ∑(k 1 i )Bf (i)
离散时间系统状态方程的建立

ZT 1[C(zI A)1 B D]
x(n)
H(z)
Y (z)
C(zI
A)1 B D
X (z)
Hrm (z) Crk (zI A)k1k Bkm Drm
9
二、用状态变量法分析离散系统举例
例12 16 求图示离散系统的系统 函数H12 (z).
输出方程
:
yr1(n)
Crk
k 1 (n)
Drm
xm1(n)
2
状态方程
:
k 1 (n
1)
Akk k1 (n)
Bkm
xm1
(n)
输出方程
:
yr1(n)
Crk k1 (n)
Drm
xm1
(n)
延时单元
z 1
状态变量
3
例12 11 给定离散系统的方框图 ,列出系统的状态方程 .
选延时器的输出为状态变量
12.4 离散时间系统状态方程的建立
k个状态变
1(n 1) a111(n)量 a122 (n) a1kk (n) m个输入信
b11x1(n) b12 x2 (n) b1m xm (n)
号
2 (n 1) a211(n) a222 (n) a2kk (n)
b21x1(n) b22 x2 (n) b2m xm (n)
k (n 1) ak11(n) ak22 (n) akkk (n)
bk1x1(n) bk 2 x2 (n) bkmxm (n)
状态方程
:
k 1 (n
1)
Akk k1 (n)
Bkm
xm1
(n)
1
离散时间系统的输出方程
离散时间系统状态方程的解

(
)
λI G =
λ
1
0.16 λ + 1
= (λ + 0.2)(λ + 0.8) = 0
λ1 = 0.2; λ = 0.8
0 ~ 0 (0.2)k 0 0.2 0.2 ∴Λ = ; Φ(k ) = 0 = k 0 0.8 0.8 0 (0.8)
k
又求得
1 1 T = 0.2 0.8
该式右边第二项
5 4 k 1 k 1 ~ ~ 3 1 3 1[1] ∑ Φ( j )T Hu (k j 1) =∑ Φ( j ) 1 5 1 j =0 j =0 3 3
k 1
(0.2) j 0 3 k 1 3(0.2) j = ∑ = ∑ j j 0 (0.8) 2 j =0 2(0.8) j =0 3[1 + (0.2) + (0.2) 2 + L + (0.2) k 1 ] = 2 k 1 2[1 + (0.8) + (0.8) + L + (0.8) ] 5 1 17 k k 1 (0.2) k 0.4 [1 (0.2) ] 6 (0.2) + 2 ∴ ~ (k ) = x + = 22 k 3 4(0.8) 1 [1 (0.8) k ] (0.8) k 10 9 0.9 9
描述系统由t=0到t=kT状态的转移。
x ( k ) = φ ( k ) x ( 0 ) + ∑ φ ( k j 1) Hu ( j ) y ( k ) = Cx ( k ) + Du ( k )
j=0
k 1
二 、z变换法 对x(k+1)=Gx(k)+Hu(k) z变换:zx(z)-zx(0)=Gx(z)+Hu(z) (zI-G)x(z)=zx(0)+Hu(z) x(z)=[zI-G]-1zx(0)+ [zI-G]-1Hu(z) z反变换: [(zI[(zIx(k)=Z-1[(zI-G)-1z]x(0)+Z-1[(zI-G)-1Hu(z)]
第八章(3) 离散系统状态方程的求解

(2)求状态方程的解
x( k ) ( k ) x(0) ( k 1) B * f ( k )
将有关矩阵代入上式,得零输入解
1 k ( 2) x x ( k ) ( k ) x ( 0) 1 k 1 k ( ) ( ) 4 2 0 1 1 k 2 ( ) 4
1 2
2 1
矩阵函数Ak可表示成
Ak 0 I 1 A
k (1) 0 1 (1)
k
2 0 1 2
解得
1 k k 0 [2 2( 1) ] 3 1 k k 1 [2 ( 1) ] 3
将以上系数值β0、β1代入得
(3)求系统的输出
y( k ) Cx( k ) Df ( k ) C ( k ) x(0) C ( k 1) B * f ( k ) Df ( k )
将 ( k )代入,得零输入响应
1 k 1 k ( 2) 1 0 ( 2 ) y x ( k ) C ( k ) x(0) 1 1 , k 0 1 1 1 ( ) k ( ) k ( ) k 4 4 2
1 k 1 k 1 2 2 ( ) ( ) 2 2 * (k ) 2 , k 0 1 4 1 1 k 1 1 k 1 k k 2 ( ) ( ) ( ) ( ) 2 3 4 3 4 2
其全解 x( k ) x x ( k ) x f ( k )
C ( k ) x(0) h( k ) * f ( k )
式中
h( k ) C ( k 1) B D ( k )
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实验六 离散系统状态方程的求解
一、实验目的
(1)了解离散系统状态方程求解方法。
(2)了解离散系统信号流图化简的方法。
(3)了解函数ode45的调用方法。
二、实验原理
离散系统状态方程的一般形式为 x(k+1)=Ax(k)+Bf(k)
在些只对单输入的n 阶离散系统的状态议程求解。
一般采用递推迭代的方式求解,由裙的条件x(0)和激励f(0)求出k=1时的x(1),然后依次迭代求得所要求的x(0),……,x(n)的值。
编程时应注意,MATLAB 中变量下标不允许为零,则裙点的下标只能取1,第n 步的x 的下标为n+1。
三、涉及的MATLAB 函数
zeros(2,1)
y=lsim(sys,f,[],x0)
for i=1:n end
clear all
采用函数ode45可以求解微分方程。
其调用格式如下
[t,y]=ode45(odefun,tspan,y0)
其中,odefun 指状态方程的表达式,tspan 指状态方程对应的起止时间]t0,tf],y0指状态变量的初始状态。
四、实验内容与方法
1.验证性实验
采用MATLAB 语言编程,求解离散系统状态方程,并绘制状态变量的波形。
(1)已知离散系统的状态方程为 )(01)1()1(25.025.005.0)1()1(2121k f k x k x k x k x ⎥⎦
⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡++⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡++ 初始条件为x(0)=⎥⎦
⎤⎢⎣⎡-5.01,激励为f(k)=0.5ε(k),确定该状态方程x(k)前10步的解,并画出波形。
MATLAB 程序:
%离散系统状态求解
%A=input(‘系统矩阵 A=’)
%B=input(‘系数矩阵 B=’)
%x0=input(‘初始状态矩阵 x0=’)
%n=input(‘要求计算的步长n=’)
%f=input(‘输入信号f=’) %需求长度为n的数组
clear all
A=[0.5 0;0.25 0.25];
B=[1;0];
x0=[-1;0.5];
n=10;
f=[0 0.5*ones(1,n-1)];
x(:,1)=x0;
for i=1:n
x(:,i+1)=A*x(:,i)+B*f(i);
end
subplot(2,1,1);stem([0:n],x(1,:));
subplot(2,1,2);stem([0:n],x(2,:));
离散系统状态方程的求解结果如图6.1所示
图6-1 离散系统状态方程的求解(2)离散系统状态求解
MATLAB程序:
A=[0 1;-2 3];B=[0;1];
C=[1 1;2 -1];D=zeros(2,1);
x0=[1;-1];%初始条件
N=10;f=ones(1,N);
sys=ss(A,B,C,D,[]);
y=lsim(sys,f,[],x0);k=0:N-1;
subplot(2,1,1);
stem(k,y(:,1),'b');
subplot(2,1,2);stem(k,y(:,2),'b');
离散系统状态议程的求解结果如图6.2所示。
图6-2 离散系统状态方程的求解
2.程序设计实验
(1)离散系统状态方程为: x(k+1)=Ax(k)+Bf(k)
其中A=⎥⎦⎤⎢⎣⎡25.025.005.0,B=⎥⎦
⎤⎢⎣⎡01,初始状态⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡00)0()0(21x x ,激励f(k)=δ(k),确定该状态方程x(k)前10步的解,并画出波形。
MATLAB 程序:
%离散系统状态求解
%A=input(‘系统矩阵 A=’)
%B=input(‘系数矩阵 B=’)
%x0=input(‘初始状态矩阵 x0=’)
%n=input(‘要求计算的步长 n=’)
%f=input(‘输入信号 f=’) %需求长度为n 的数组
clear all
A=[0.5 0;0.25 0.25];
B=[1;0];
x0=[0;0];
n=10;
f=[1 zeros(1,n-1)];
x(:,1)=x0;
for i=1:n
x(:,i+1)=A*x(:,i)+B*f(i);
end
subplot(2,1,1);stem([0:n],x(1,:));
subplot(2,1,2);stem([0:n],x(2,:));
求解结果如图6.3所示:
图6-3 离散系统状态议程的求解
(2)描述离散时间系统的信号流图如图所示,确定该系统的系统函数(离散系统信号流图的形式与连续系统相同,只不过是变量s换为z,在此不再详述。
)。
MATLAB程序:
syms z;
Q=[0 0 0 0 0 0;2 0 -3 0 -2 0;0 1/z 0 0 0 0;3 0 1 0 0 0;0 0 0 1/z 0 0;1 0 0 0 2 0];
B=[1;0;0;0;0;0];
I=eye(size(Q));
H=(I-Q)\B;
H6=H(6);
pretty(H6);
执行后得到结果:
2
24 + 9 z + z
-------------
2
z + 3 z + 2。
