ADF检验
adf检验名词解释

ADF检验名词解释1. 什么是ADF检验?ADF(Augmented Dickey-Fuller)检验是一种用于时间序列数据的单位根检验方法。
单位根是指时间序列数据中存在非随机趋势,即数据具有持续性的特征。
ADF检验可以帮助我们判断一个时间序列数据是否具有单位根,从而确定其是否为稳定的平稳过程。
2. 单位根和平稳过程单位根是时间序列数据中的非随机趋势,它表示数据存在长期依赖关系,即过去的值对未来值有预测能力。
相反,平稳过程是指时间序列数据的统计特性在时间上保持不变,不受外部因素影响。
在经济学和金融学中,平稳过程是进行预测和建模的基础。
如果一个时间序列数据包含单位根,则其统计性质会发生变化,使得预测和建模变得困难。
3. ADF检验的原理ADF检验基于Dickey-Fuller回归模型,在该模型中,被解释变量是时间序列数据的差分值(将原始数据进行一阶差分),解释变量包括差分值、滞后差分值以及其他可能影响时间序列数据的因素。
ADF检验的原假设(H0)是存在单位根,即时间序列数据是非平稳的。
备择假设(H1)是不存在单位根,即时间序列数据是平稳的。
通过对回归模型进行估计和假设检验,我们可以判断原假设是否成立,并得出结论。
4. ADF检验的步骤步骤1:提取差分值首先,我们需要对原始时间序列数据进行差分操作,获得一阶差分值。
这样做可以消除数据中的线性趋势。
步骤2:构建ADF回归模型在ADF检验中,我们使用自回归模型(AR)来对差分后的数据进行建模。
这个模型包括一个滞后项和其他可能影响时间序列数据的因素。
步骤3:估计ADF模型参数通过最小二乘法估计ADF模型中的参数,并计算出参数的标准误差。
这些参数和标准误差将用于后续的统计推断。
步骤4:进行假设检验在ADF检验中,我们需要对回归系数进行假设检验。
常见的方法是计算t统计量,并与相应的临界值进行比较。
如果t统计量大于临界值,则可以拒绝原假设,认为时间序列数据是平稳的。
ADF检验
ADF检验
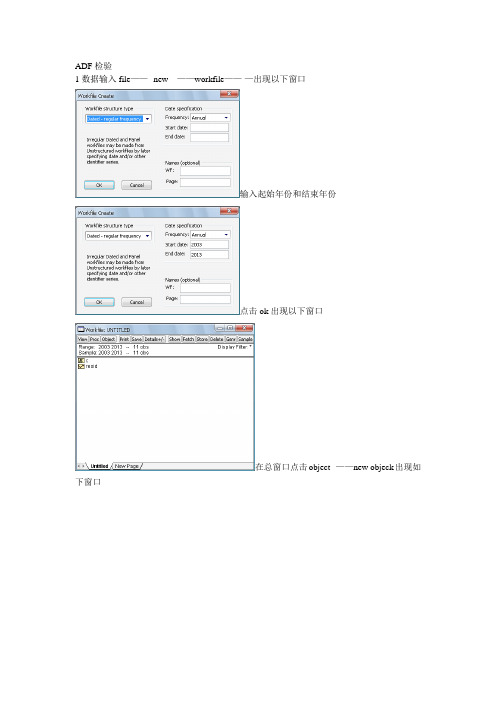
1数据输入file——--new---——workfile——-—出现以下窗口
输入起始年份和结束年份
点击ok出现以下窗口
在总窗口点击object--——new objeck出现如下窗口
选择poold点击ok
在此窗口中另起一行输入n,代表年份点击sheet
输入y?x?后点击ok(两者之间空一格)
点击edit+/-输入数据。
对两组数据取对数,得新的数据:p=log(y),q=log(x)。
可在eviews中点击Genr输入p=log(y)可自动产生对数数列。
对两个时间序列分别做ADF检验.
1。
eviews中选取时间序列P4,右键=》open.在新的窗口中点击view=》unit root test。
2.ADF检验需要对3个模型依次检验,所以在unit root test窗口中先①选:level、trend and intercept。
然后确认=》得到
第一行是所得t值,下面3行是临界值。
t=—2.0665〉临界值,因此非平稳.因此要继续检验②:level、intercept,假设还是非平稳。
继续检验③:level none.假设还是非平稳,则做一阶差分,即将level换成1st difference,将之前①②③从新来过,一旦t<临界值就可以停止了。
若level时,t值均大于临界值,则为非平稳序列.若1st difference的一阶差分时,变为平稳的,就是1阶单整,记为I(1),依次类推.。
python的adf检验代码

python的adf检验代码
ADF检验是用于检验时间序列数据是否具有平稳性的一种方法,常用于金融、经济等领域的数据分析。
Python中有多种库可以实现ADF检验,其中较为常用的是statsmodels库。
以下是一个简单的Python代码示例:
```python
import pandas as pd
import statsmodels.api as sm
# 读取数据
data = pd.read_csv('data.csv', index_col='date',
parse_dates=True)
# ADF检验
result = sm.tsa.stattools.adfuller(data['value'])
print('ADF统计量:', result[0])
print('p值:', result[1])
print('关键值:', result[4])
```
其中,data.csv是时间序列数据文件,包含日期和数值两列,示例数据如下:
```
date,value
2020-01-01,10.0
2020-01-02,11.5
2020-01-03,9.8
2020-01-04,12.3
2020-01-05,11.7
```
运行代码后,可以得到ADF统计量、p值以及关键值,通过p值和关键值的比较可以判断数据是否具有平稳性。
此外,还可以通过result[3]获取到检验所用的滞后阶数。
ADF检验

继续讨论:
对GDP的一阶差分进行检验
在10%的显著性水平下,单位根检验的临界值为 -3.2602,上述检验统计量值-3.62511小于相应DW临界值, 从而拒绝H0,表明我国1978——2003年D(GDP)序 列是平稳序列.
年度数据一般选择1或2年,月度数据一般选择6个月、12个月或者18个月, 季度数据一般4或者8。
ˆ ˆ ˆ
ˆ ˆ ˆ ... 0.786011
或
在1%、5%、10%三个显著性水平下,单位根检验的临界值分
别为- 4.4167、-3.6219、-3.2474,显然,上述
检验统计量值大于
相应DW临界值,从而接受 H 0 ,表明我国1978——2003年度GDP 序列存在单位根,是非平稳序列。
GDP序列,检验其是否为平稳序列。
方法1: 用时序图判断
由GDP的时序图初步判断序列是不平稳的(可以看出该序列可能 存在趋势项,若需用ADF检验则选择第三种模型进行检验)。
方法2: 用自相关系数图判断
中国GDP时间序列的自相关系数不是很快地(如滞后期K=2,3
趋于零,即缓慢下降,再次表明序列是非平稳的.
• 我们老师说样本较大时,选用bic ,较小 时用aic • 先找出最小的AIC和SIC(不是绝对值), 在此基础上看ADF检验是否通过,即判 断是否是平稳序列。 • 我一般是根据VAR模型的最优滞后阶 数-1作为协整的最优滞后阶数
• 根据赤池信息准则或舒瓦茨信息准则 • adf检验是在残差存在自相关时用的,滞 后阶数可以根据序列自相关和偏自相关 图确定
• 单位根是否应该包括常数项和趋势项可 以通过观察序列图确定,通过Quickgraph-line操作观察你的数据,若数据随 时间变化有明显的上升或下降趋势,则 有趋势项,若围绕0值上下波动,则没有 趋势项;其二,关于是否包括常数项有 两种观点,一种是其截距为非零值,则 取常数项,另一种是序列均值不为零则 取常数项。
r语言adf检验代码

r语言adf检验代码ADF检验是时间序列分析中常用的一种方法,用于检验时间序列数据是否具有单位根。
在R语言中,可以使用tseries包中的adf.test()函数进行ADF检验。
首先需要安装和加载tseries包:```rinstall.packages("tseries") # 安装tseries包library(tseries) # 加载tseries包```接下来,我们可以使用adf.test()函数进行ADF检验。
该函数有多个参数,其中最重要的是x和alternative参数。
x表示要进行ADF检验的时间序列数据,alternative表示备择假设。
在进行ADF检验时,我们通常会使用双侧假设(alternative="two.sided"),即假设时间序列数据既可能具有单位根,也可能不具有单位根。
以下是一个示例代码:```r# 生成一个随机游走序列set.seed(123)x <- cumsum(rnorm(100))# 进行ADF检验result <- adf.test(x, alternative = "two.sided")# 输出结果cat("ADF统计量:", result$statistic, "\n")cat("p值:", result$p.value, "\n")cat("1%临界值:", result$critical[[1]], "\n")cat("5%临界值:", result$critical[[2]], "\n")cat("10%临界值:", result$critical[[3]], "\n")```以上代码首先生成了一个长度为100的随机游走序列x,然后使用adf.test()函数对其进行ADF检验,并将结果赋值给result变量。
ADF检验

引自Ruey S. Tsay著,王辉、潘家柱译《金融时间序列分析》(第2版)DF检验为了检验资产的对数价格p t是否服从一个随机游动或一个带漂移的随机游动,对模型p t=ϕ1p t−1+e t (1)p t=ϕ0+ϕ1p t−1+e t (2)其中e t为误差项。
考虑原假设H0:ϕ1=1;H1:ϕ1<1,即是一个单位根检验问题。
一个方便的检验统计量就是在原假设下ϕ1的最小二乘估计的t−比。
对(1)式,由最小二乘法得ϕ1=p t−1p tTt=1t−1Tt=1,σe2=p t−ϕ1p t−12Tt=1其中p0=0,T为样本容量。
t−比为DF≡t−比=ϕ1−1ϕ1的标准差=p eTσe p t−12Tt=1这个t−比检验通常称为DF检验。
若e t为一个白噪声序列,其稍高于二阶的矩是有限的,则当T⟶∞时DF统计量趋于一个标准布朗运动的函数。
如果ϕ0=0但我们采用了(2)式,则所得的检验ϕ1=1的t−比将趋于另一种非标准的渐进分布。
上述两种情形都是用模拟方法来得到检验统计量的临界值。
然而如果ϕ0≠0且使用的是(2)式,则用来检验ϕ1=1的t−比是渐进正态的,但此时将需要很大的样本容量来保证渐进正态分布的使用。
ADF检验用x t表示一个AR(p)时间序列,为了验证序列是否存在单位根,通常人们采用ADF检验来验证,即可以用如下回归来进行假设检验(H0:β=1;H1:β<1):x t=c t+βx t−1+ϕiΔx t−i+e tp−1i=1其中c t是关于时间t的确定性函数,Δx j=x j−x j−1是x t的差分序列。
在实际中,c t可以是常数或者c t=ω0+ω1t。
β−1的t−比为ADF−检验=β−1β的标准差其中β为β的最小二乘估计,上述t−比就是著名的ADF检验。
注意到由于一阶差分,上面x t的式子等价于一个带确定性函数c t的AR(p)模型,可以改写为Δx t=c t+βc x t−1+ϕiΔx t−i+e tp−1i=1其中βc=β−1,相应的检验为H0:βc=0;H1:βc<0。
adf检验步骤详解stata

adf检验步骤详解stataADF检验主要用于时间序列数据,这是因为时间序列会存在不平稳的过程,不平稳的时间序列数据可能会带来t检验失败、自回归系数估计值有偏向的等问题,最后使用stata对数据跑回归可能是一个伪回归或者伪相关,因此得出来的回归结果就是不大可靠的。
在ADF检验当中比较重要的一个环节就是看滞后阶数是否显著(lags几期)之后回归。
接下来讲一下stata操作流程:首先,进行不带趋势项的DF检验,命令为dfullerlny(假如lny是经济产出变量),看DF统计量大不大于左边单侧检验,若小于,则可以拒绝“存在单位很”的原假设。
接着输入“dfullerlny,lags(xx)reg”,其中,xx可以是任何数字,用于检测最优滞后阶数,如果Z值一直不显著,可以使用PP检验,命令为:pperronlny。
如果PP检验还是不显著........那就用最有功效的DF-GLS检验,命令为:“dfglslny”,此时stata会给你一个表格,该表会显示数据在几阶的1%、5%、10%显不显著,这个时候再不显著,就证明该时间序列存在单位根。
发现数据存在单位根之后我们要将原假设变为平稳序列,这个时候要进行KPSS检验,命令为:“kpsslny,nottrend”。
接着stata会告诉你数据从几阶到几阶滞后,如果统计量均大于5%置信水平的统计值,则认为存在单位根,因此,进一步检验lny的差分是否平稳,命令为:dfglsdlny,如果表格显示滞后阶数介于几到几之间,那这个时候就可以拒绝原假设了,即认为差分dlny为平稳过程。
之后再进行kpss检验,命令为:“kpssdlny,nottrend”。
这个时候,我们就可以看到统计量均远小于5%的临界值,接受平稳过程的原假设,在最后填写ADF检验结果表格的时候就可以写上:“接受lny为a阶单整a(x)过程。
”然后上述过程对每个时间序列变量都进行一遍。
在最后的结果表格写上:“ADF 统计值、5%临界值、P值、平稳与否。
(完整版)ADF单位根检验_具体操作

ADF检验:
单位根检验,把数据输入Eviews之后,点击左上角的View--Unit Root Test,(但
好像更好用一些),之后可以选择一阶、二阶差分之后的序列是否存在单位根,同时可以选检验的方程中是否存在存在趋势项、常数项等。
一般进行ADF检验要分3步:
1 对原始时间序列进行检验,此时第二项选level,第三项选None.如果没通过检验,说明原始时间序列不平稳;
2 对原始时间序列进行一阶差分后再检验,即第二项选1st difference,第三
项选intercept,若仍然未通过检验,则需要进行二次差分变换;
3 二次差分序列的检验,即第二项选择2nd difference ,第四项选择Trend and intercept.一般到此时间序列就平稳了!
看结果:
1%,5%,10%指的是显著水平,如果ADF检验值(t值)大于某显著水平值(一般是5%),
则不通过检验,即存在单位根(不平稳),此时,可通过一阶差分再来查看单位根是否平稳,
p值指的是接受原假设的概率。
在报告上的写法:
:r=0
H
: r=1
H
1
,序列有单位根,非平缓。
反之……
如果ADF检验值>临界值,则接受H
(注:H
的写法,选中要设置为下标的字母,点击菜单栏格式——字体,选择效
果中的下标,确定。
或直接选中的那个红色项进行格式设置)
操作:图/line&symbol。
ADF单位的根检验具体操作

:ADF检验
单位根检验,把数据输入Eviews之后,点击左上角的View--Unit Root Test,
(但好像更好用一些),之后可以选择一阶、二阶差分之后的序列是否存在单
位根,同时可以选检验的方程中是否存在存在趋势项、常数项等。
一般进行ADF检验要分3步:
1 对原始时间序列进行检验,此时第二项选level,第三项选None.如果没通过检验,说明原始时间序列不平稳;
2 对原始时间序列进行一阶差分后再检验,即第二项选1st difference,第三
项选intercept,若仍然未通过检验,则需要进行二次差分变换;
3 二次差分序列的检验,即第二项选择2nd difference ,第四项选择Trend and intercept.一般到此时间序列就平稳了!
看结果:
1%,5%,10%指的是显著水平,如果ADF检验值(t值)大于某显著水平值(一般是5%),则不通
过检验,即存在单位根(不平稳),此时,可通过一阶差分再来查看单位根是否平稳,p值指的
是接受原假设的概率。
在报告上的写法:
H:r=0 0H: r=1
1如果ADF检验值>临界值,则接受H,序列有单位根,非平缓。
反之 0
(注:H的写法,选中要设置为下标的字母,点击菜单栏格式——字体,选择效
果中的下标,确定。
或直接选中的那个红色项进行格式设置)
/line&symbol 操作:图。
ADF检验
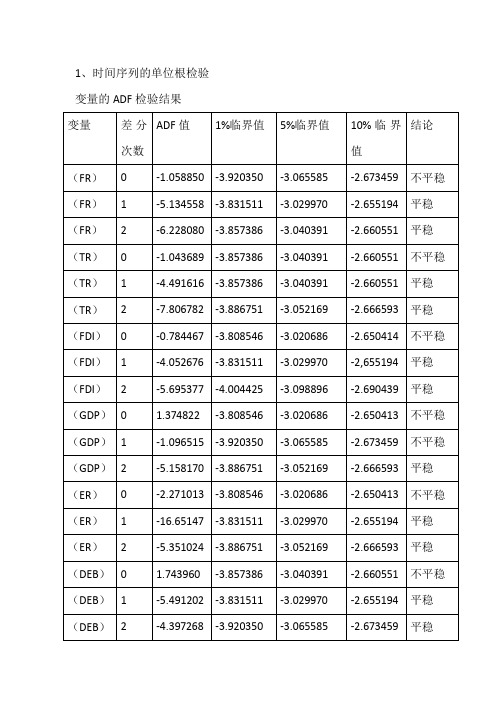
1、时间序列的单位根检验变量的ADF检验结果
说明:差分次数0代表未对数据进行差分;1代表数据的一阶差分;2代表数据的二阶差分
本文运用ADF(Augmented Dickey-Fuller test statistic)对时间序列进行单位根检验,检验Lg(FR)、Lg(TR)、Lg(FDI)、Lg(GDP)、Lg(ER)、Lg(DEB)、Lg(M2)的平稳性,并确定其单整阶数,单位根方程不包括常数项和时间序列项。
具体检验结果如上图所示。
从检验的结果来看,FR、TR、FDI、GDP、ER、DEB、M2均为原阶非平稳,FR、TR、FDI、ER、DEB、M2均为一阶平稳。
但是全体7组数据均为二阶单整。
2、时间序列的协整检验
通过ADF检验得知,FR、TR、FDI、GDP、ER、DEB、M2经过对数变换后都是二阶平稳序列,这是判定Lg(FR)、Lg(TR)、Lg(FDI)、Lg (GDP)、Lg(ER)、Lg(DEB)、Lg(M2)之间是否存在协整关系的前提条件。
平稳性检验公式学习平稳性检验的关键公式

平稳性检验公式学习平稳性检验的关键公式在统计学和经济学中,平稳性检验是一个重要的概念。
它用于确定时间序列数据是否表现出平稳性,即是否存在趋势、季节性或周期性。
本文将介绍平稳性检验的关键公式,帮助读者深入了解并应用这一方法。
1. 单位根检验公式单位根检验是最常用的平稳性检验方法之一。
它的核心思想是检验时间序列数据中是否存在单位根,若存在,则表明数据不具备平稳性。
单位根检验常用的公式是ADF(Augmented Dickey-Fuller)检验公式。
ADF检验基于以下模型:△Y_t = α + β t + γ Y_(t-1) + ∑_(i=1)^(p-1) θ_i △Y_(t-i) + ε_t其中,△表示差分操作,Y_t表示原始时间序列数据,α、β和γ分别是常数项、时间趋势项和滞后值系数,ε_t是误差项。
ADF检验的原假设是存在单位根,备择假设是不存在单位根。
通过对检验统计量的显著性检验,可以判断时间序列数据是否平稳。
2. 平稳性检验的拓展公式除了ADF检验,还有其他拓展的平稳性检验公式可以应用。
其中,KPSS(Kwiatkowski–Phillips–Schmidt–Shin)检验是另一个常用的方法。
KPSS检验模型可以表示为:Y_t = μ_t + ε_t其中,Y_t是时间序列数据,μ_t是趋势项,ε_t是误差项。
KPSS检验的原假设是数据是平稳的,备择假设是数据存在单位根。
通过对检验统计量的显著性检验,可以判断时间序列数据是否平稳。
3. 平稳性检验的实例为了更好地理解平稳性检验的应用,以下是一个实例:假设我们有一组月度销售额数据,我们想要判断这组数据是否表现出平稳性。
我们可以运用ADF检验和KPSS检验来进行判断。
首先,我们可以使用ADF检验公式来计算ADF统计量。
根据计算结果,如果ADF统计量的值显著小于某个临界值,我们可以拒绝原假设,即数据不具备单位根,从而表明数据是平稳的。
而对于KPSS检验,如果检验统计量的值显著小于某个临界值,我们可以拒绝备择假设,即数据存在单位根,从而表明数据是平稳的。
adf检验拒绝原假设的条件

adf检验拒绝原假设的条件
ADF检验是判断时间序列数据是否具有平稳性的一种常用方法。
当ADF 检验的统计值小于所设定的临界值时,我们拒绝原假设,即认为该时间序列不存在单位根,即该时间序列是平稳的。
那么ADF检验拒绝原假设的条件有哪些呢?
一、样本容量
首先,在进行ADF检验时,需要确保时间序列的样本容量足够大。
如果样本容量过小,可能会导致统计结果不可靠。
一般来说,样本容量应当大于50,最好是100以上。
二、数据的平稳性
在进行ADF检验之前,需要先对数据进行平稳性检验。
如果数据本身已经是平稳的,那么进行ADF检验的结果显然没有什么意义。
因此,需要对数据进行一定程度的平稳性处理,例如差分或对数变换等。
三、临界值的选择
ADF检验中,临界值的选择非常重要。
不同的置信水平和不同阶数的ADF检验所对应的临界值也不同。
因此,在进行ADF检验时,需要特别注意临界值的选择,以保证检验结果的准确性。
四、模型的选择
在进行ADF检验时,需要选择合适的模型。
如果模型选择不当,可能会影响到检验结果的准确性。
一般来说,需要根据数据的特点选择相应的模型,例如ARIMA模型、VAR模型等。
综上所述,ADF检验拒绝原假设的条件主要包括:样本容量足够大、数据具有一定的平稳性、选择合适的临界值和模型。
只有在以上条件都满足的情况下,我们才能够对时间序列的平稳性进行有效的判断。
使用R语言进行单位根检验介绍

使用R语言进行单位根检验介绍单位根检验是时间序列分析中的重要工具,用于检验一个时间序列是否具有单位根(即非平稳)。
单位根检验是判断时间序列是否稳定的关键步骤,因为只有稳定的时间序列才能应用很多经典时间序列建模技术。
在R语言中,有多种方法可以进行单位根检验。
本文将介绍常用的三种方法:ADF检验(Augmented Dickey-Fuller test)、PP检验(Phillips-Perron test)和KPSS检验(Kwiatkowski-Phillips-Schmidt-Shin test)。
1.ADF检验ADF检验是最常用的单位根检验方法之一,它的原假设是时间序列具有单位根,即非平稳。
在R中,可以使用`adf.test`函数进行ADF检验,其语法如下:```Radf.test(x, alternative = "stationary")```其中,参数`x`是待检验的时间序列,`alternative`指定备择假设,可以选择"stationary"表示平稳,或者"explosive"表示非平稳。
函数输出包括ADF统计量、p值和置信水平。
以下是一个例子:```R#假设我们有一个时间序列数据xresult <- adf.test(x, alternative = "stationary")#输出ADF统计量print(result$statistic)#输出p值print(result$p.value)```2.PP检验PP检验是另一种常用的单位根检验方法,它采用与ADF类似的方法,但在计算中采用了修正过的估计方法。
在R中,可以使用`pp.test`函数进行PP检验,其语法如下:```Rpp.test(x, alternative = "stationary")```与ADF检验相似,参数`x`是待检验的时间序列,`alternative`是备择假设。
ADF单位根检验 具体操作

ADF单位根检验具体操作
adf单位根检验-具体操作
ADF测试:
单位根检验,把数据输入eviews之后,点击左上角的view--unitroottest,(但
看起来好多了,
之后可以选择一阶、二阶差分之后的序列是否存在单位根,同时可以选检验的方程中是否存在存在趋势项、常数项等。
通常,ADF检查分为三个步骤:
1对原始时间序列进行检验,此时第二项选level,第三项选none.如果没通过检验,说明原始时间序列不平稳;
2在一阶差分后测试原始时间序列,即第二项选择第一个差分,第三项选择截距。
如果仍然无法通过测试,则需要进行二次差分转换;3.二次差序列检验,即第二项选择第二差,第四项选择趋势和接受,一般来说,该时间序列是稳定的!
看结果:
1%、5%和10%表示显著性水平。
如果ADF测试值(t值)大于某个显著性水平值(通常为5%),则无法通过测试,即存在单位根(不稳定)。
此时,可以通过一阶差来检查单位根是否稳定。
P值是指接受原始假设的概率。
在报告上的写法:h0:r=0h1:r=1
如果ADF测试值>临界值,则接受H0。
该序列有单位根且不平缓。
相反地
(注:h0的写法,选中要设置为下标的字母,点击菜单栏格式――字体,选择效
结果中的下标已确定。
(或直接选择设置)
的那个红色项进行格
操作:线条与符号。
r语言adf检验代码

r语言adf检验代码ADF检验是一种常用的时间序列分析方法,用于检验一个时间序列是否具有单位根。
单位根表示时间序列具有随机漂移,即序列中的值是随机游走的,没有明显的趋势。
如果时间序列存在单位根,则说明序列是非平稳的,难以进行进一步的分析和预测。
而ADF检验可以帮助我们判断一个时间序列是否平稳,从而为后续的分析提供基础。
在R语言中,我们可以使用“ur.df()”函数来进行ADF检验。
该函数位于“urca”包中,因此我们需要先安装并加载该包,然后才能使用该函数。
下面是一段示例代码,演示了如何使用R语言进行ADF检验:```R# 加载urca包library(urca)# 生成一个随机游走序列set.seed(123)random_walk <- cumsum(rnorm(100))# 进行ADF检验adf_test <- ur.df(random_walk, type = "trend", selectlags = "AIC")# 显示ADF检验结果summary(adf_test)```在上面的代码中,我们首先使用“cumsum()”函数生成了一个随机游走序列,该序列具有单位根。
然后,我们使用“ur.df()”函数对该序列进行ADF检验。
参数“type”指定了模型类型,这里我们选择了“trend”,表示模型中包含趋势项。
参数“selectlags”指定了滞后阶数的选择标准,这里我们选择了“AIC”准则。
最后,我们使用“summary()”函数显示了ADF检验的结果。
在结果中,我们关注的是测试统计量(Test Statistic)和p值(p-value)。
测试统计量用于判断时间序列是否具有单位根,如果测试统计量的绝对值大于对应的临界值,就可以拒绝单位根存在的假设,即序列是平稳的。
而p值则用于判断检验统计量是否显著,通常取0.05作为显著性水平。
如果p值小于0.05,则可以拒绝单位根存在的假设,即序列是平稳的。
stata中进行adf检验的命令

在Stata中进行ADF检验(Augmented Dickey-Fuller Test)是研究单位根(unit root)存在与否的一种常用方法。
单位根指的是时间序列数据中的根(根是指方程的解),如果单位根存在,意味着时间序列数据具有非平稳性。
而ADF检验则是用来检验单位根是否存在的统计方法。
在Stata中,进行ADF检验可以使用dfuller命令。
下面将详细介绍如何使用这个命令进行ADF检验。
1. 环境设置在使用dfuller命令之前,需要先加载Stata的时间序列数据扩展包(timeseries package)。
通过输入以下命令加载扩展包:ssc install tsset2. 数据准备在进行ADF检验之前,需要准备好相关的时间序列数据。
可以使用tsset命令将数据设置为Stata的时间序列数据格式。
tsset date这里的date是数据中表示日期的变量名,需要将其替换为实际使用的日期变量名。
3. 进行ADF检验使用dfuller命令可以进行ADF检验。
下面是该命令的基本语法:dfuller dependent_variable [if] [in], [options]其中,dependent_variable是要进行ADF检验的变量名。
可以使用if子句和in子句进行数据筛选。
在进行ADF检验时,需要考虑以下两个核心问题: - 是否包含截距项(constant):使用-c选项来指定。
如果添加了-c选项,表示模型中包含截距项。
如果没有添加该选项,则表示模型中不包含截距项。
- 是否包含时间趋势项(trend):使用-t选项来指定。
同样地,如果添加了-t选项,表示模型中包含时间趋势项。
如果没有添加该选项,则表示模型中不包含时间趋势项。
如果要进行包含截距项和时间趋势项的ADF检验,可以使用以下命令:dfuller dependent_variable, lags(#) trend其中,#需要用实际的滞后阶数替换,表示在ADF检验中使用的滞后阶数。
单位根检验法

单位根检验法单位根检验法是一种统计方法,用于检验时间序列数据是否具有单位根。
单位根表示时间序列中的变量存在随机游走的趋势,即序列呈现非平稳性。
单位根检验的目的是验证序列是否平稳,因为平稳性对于许多时间序列分析方法的有效性至关重要。
常用的单位根检验方法包括:ADF检验(Augmented Dickey-Fuller test):ADF检验是一种常用的单位根检验方法之一,它基于Dickey-Fuller检验,通过扩展模型以处理序列中的自相关性问题。
ADF检验的原假设是序列存在单位根,备择假设是序列是平稳的。
如果检验统计量小于一定的临界值,我们就可以拒绝原假设,认为序列是平稳的。
PP检验(Phillips-Perron test):PP检验也是一种基于Dickey-Fuller 检验的单位根检验方法,它通过对序列进行回归分析来检验序列的平稳性。
与ADF检验相比,PP检验的计算方式略有不同,但原理和假设检验的思想是相似的。
KPSS检验(Kwiatkowski-Phillips-Schmidt-Shin test):KPSS检验与ADF检验相反,它的原假设是序列是平稳的,备择假设是序列存在单位根。
如果检验统计量小于临界值,我们就可以接受原假设,认为序列是平稳的。
DF-GLS检验(Dickey-Fuller Generalized Least Squares test):DF-GLS 检验是ADF检验的一种泛化形式,它允许序列中的误差项存在序列相关性。
与ADF检验相比,DF-GLS检验在处理序列中的自相关性方面更加准确。
这些单位根检验方法在实践中经常用于验证时间序列数据的平稳性,从而为后续的时间序列分析提供可靠的基础。
在进行单位根检验时,需要注意选择合适的检验方法,并结合实际问题和数据特点进行分析和判断。
SPSSAU_计量经济研究_ADF检验

SPSS分析 SPSS教程 SPSSAU ADF检验单位根检验网页在线SPSSADF检验分析Contents1背景 (2)2理论 (2)3操作 (3)4 SPSSAU输出结果 (3)5文字分析 (3)6剖析 (3)单位根检验可用于检验时间序列是否存在单位根,如果存在单位根就说明为非平衡时间序列。
如果存在单位根即时间序列数据不平稳,通常不能进行后续的分析比如ARIMA模型。
此时可通过对数据进行差分,差分即相减的意思,比如2019年的数据减去2018年的数据,一阶差分其实就是增长的意思。
二阶差分是在一阶差分的基础上再次进行差分,物理意义相当于加速度。
如果二阶差分依旧不平稳,那说明数据比较糟糕,通常不会再进行进一步差分,因为其已经失去实际意义。
SPSSAU默认会自动进行单位根检验并且提供建议,如果原始数据序列不平稳,SPSSAU默认会进行一阶差分并且检验单位根,如果一阶差分依旧不平稳,SPSSAU会进行二阶差分并且检验。
如果二阶差分依旧不平稳,SPSSAU则最终以二阶差分为结点。
如果研究人员自行设置差分阶数,SPSSAU则按照研究人员设置进行检验。
特别提示:SPSSAU默认会智能分析单位根检验,如果原始数据存在单位根,SPSSAU则进行一阶差分并且检验单位根,如果一阶差分存在单位根,SPSSAU则会进行二阶差分并且检验单位根,并且以二阶差分结果作为终点。
如果研究人员自行设置差分阶数或者检验类型(通常不需要设置),SPSSAU默认以研究人员设置进行单位根检验。
ADF检验案例Contents1背景 (2)2理论 (2)3操作 (3)4 SPSSAU输出结果 (3)5文字分析 (3)6剖析 (3)1背景当前已经有阿里“双十一”历年(2009~2019年)的销售数据(时间序列数据),现希望对数据平稳性情况进行检验。
数据如下:年份阿里双十一销售额(亿元)20090.520109.3620115220121912013350201457120159122016120720171682.692018213520192684特别提示:时间序列的数据格式上,一定是时间从上至下递增,而且不能有间隔,比如2015,2017,2018这种数据少了2016,这类数据不能称为时间序列数据。
PP检验法和ADF检验法

第4节 PP 单位根检验法与ADF 单位根检验法DF 检验要求模型的随机扰动项t ε独立同分布。
但在实际应用中这一条件往往不能满足(如上一节中的有关例子)。
一般来说,如果估计模型的DW 值偏离2较大,表明随机扰动项是序列相关的,在这种情况下使用DF 检验可能会导致偏误,需要寻找新的检验方法。
本节我们将介绍在随机扰动项服从一般平稳过程的情况下,检验单位根的PP 检验法和ADF 检验法。
一、 PP (Phillips&Perron )检验首先考虑上一节情形二中扰动项为一平稳过程的单位根检验。
假设数据由(真实过程)φφ∑∞t t -1t t t j t -j j =0y =ρy +u ,u =(B)ε=ε (1) 产生,其中{}t ε独立同分布,∞<==2)(,0)(σεεt t D E 。
∑∞==0)(j j j B B ϕϕ,其中B 为滞后算子,其系数满足条件∞<∑∞=0j j j ϕ。
在回归模型t t t u y y ++=-1ρα中检验假设:0;1:0==αρH与DF 检验(情形二)一样,模型参数的OLS 估计为:⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛∑∑∑∑∑-----t t t t t t y y y y y y N 112111ˆˆρα 在1,0:0==ραH 成立时,上式可改写为:1121111t t t t t t ˆT y u ˆy y y u αρ-----⎛⎫⎛⎫⎛⎫= ⎪ ⎪ ⎪ ⎪ ⎪-⎝⎭⎝⎭⎝⎭∑∑∑∑∑ 以矩阵()12A diag T ,T =左乘上式两端,得()123122321111121111112211111t t t t t t t t t t t t ˆTyu T A A A ˆy yy u T T y T u T y u T y T y αρ------------------⎧⎫⎧⎫⎛⎫⎛⎫⎛⎫⎪⎪⎪⎪= ⎪ ⎪ ⎪⎨⎬⎨⎬⎪ ⎪ ⎪-⎪⎪⎪⎪⎝⎭⎝⎭⎝⎭⎩⎭⎩⎭⎛⎫⎛⎫⎪= ⎪ ⎪⎪⎝⎭⎝⎭∑∑∑∑∑∑∑∑∑∑利用有关单位根过程的极限分布(参见第2节),可得()12110221122000111112L W ()W (r )dr ˆT ˆT [W ()]W (r )dr W (r )dr λλαρλγλλ-⎛⎫⎛⎫⎛⎫⎪ ⎪−−→ ⎪ ⎪ ⎪ ⎪-- ⎪ ⎪⎝⎭⎝⎭⎝⎭⎰⎰⎰ 其中)1(σϕλ=,∑∞==0220s sϕσγ。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
仍以日本人口序列y t为例(数据见3.3)。
在工作文件窗口中双击y t序列,从而打开y t数据窗口。
点击View键,选择Unit Root Test功能,如下图,
则会弹出一个单位根检验对话框。
其中共有4种选项。
(1)检验方法(缺省选择是ADF检验),(2)所检验的序列(缺省选择是对原序列(Level)做单位根检验)。
(3)选择不同检验式(缺省选择是检验式中只包括截距项。
其他两种选择是检验式中包括趋势项和截距项,检验式中不包括趋势项和截距项。
(4)ADF检验式中选择差分项的最大滞后期数。
这里做的选择是(1)ADF 检验,(2)对原序列y t做单位根检验,(3)检验式中不包括趋势项和截距项。
点击OK 键。
得ADF检验结果如下。
相应的检验式是
∆= 0.0041 y t-1 + 0.2197∆ y t-1 + 0.1366∆ y t-1 + 0.2159∆ y t-1
(2.9) (2.4) (1.4) (2.3) DW = 2.05
输出的最上部分给出了检验结果。
因为ADF = 2.9283,分别大于不同检验水平的三个临界值,所以日本人口序列y t是一个非平稳序列。
在此情形下,应该继续对y t的差分序列进行单位根检验。
在序列y t窗口(即显示单位根检验结果的窗口)中,点击View键,选择Unit Root Test 功能,再次得到单位根检验对话框。
这时第二项选择应选1st difference,即检验∆y t。
第三项选择含截距项,第四项选择滞后2期。
点击OK键。
得ADF检验结果如下。
见输出结果的最上部分。
因为ADF = 3.5602,分别小于不同检验水平的三个临界值,所以日本人口差分序列∆ y t是一个平稳序列。
因此y t~ (1)。
3.对两个时间序列分别做ADF检验。
1.eviews中选取时间序列P4,右键=》open。
在新的窗口中点击view=》unit root test。
2.ADF检验需要对3个模型依次检验,所以在unit root test窗口中先①选:level、trend and intercept。
然后确认=》得到
第一行是所得t值,下面3行是临界值。
t=-2.0665>临界值,因此非平稳。
因此要继续检验②:level、intercept,假设还是非平稳。
继续检验③:level none。
假设还是非平稳,则做一阶差分,即将level换成1st difference,将之前①②③从新来过,一旦t<临界值就可以停止了。
若level时,t值均大于临界值,则为非平稳序列。
若1st difference的一阶差分时,变为平稳的,就是1阶单整,记为I(1),依次类推。
