第九章 直 平面 简单几何体
第九章直线、平面、简单几何体介绍

第九章(A)“直线、平面、简单几何体”简介《全日制普通高级中学教科书(试验修订本·必修)数学》第二册(下)的第九章(A)为《直线、平面、简单几何体》。
这一章是根据《全日制普通高级中学数学教学大纲(实验修订版)》中的“9(A)直线、平面、简单几何体”部分所规定的教学内容和教学目标而编写的。
它在原《立体几何》(必修本)的基础上作了较大的修改,精简了教学内容,减少了教学时间,在体系安排和内容的具体处理方法上也有所改革。
本章教学时间约需39课时,具体分配如下(仅供参考):一、空间直线和平面9.1平面约3课时9.2空间直线约5课时9.3直线与平面平行的判定和性质约3课时9.4直线与平面垂直的判定和性质约4课时9.5两个平面平行的判定和性质约3课时9.6两个平面垂直的判定和性质约3课时二、简单几何体9.7棱柱约4课时9.8棱锥约4课时9.9研究性课题:多面体欧拉公式的发现约3课时9.10球约4课时小结与复习约3课时一、内容与要求(一)本章主要内容是立体几何的基础知识和解决立体几何问题的基本思想方法本章的具体知识点主要包括:平面及其基本性质,平行直线,对应边分别平行的角,异面直线所成的角,异面直线的公垂线,异面直线的距离,直线和平面平行的判定与性质,直线和平面垂直的判定与性质,点到平面的距离,斜线在平面上的射影,直线和平面所成的角,三垂线定理及其逆定理,两个平面平行的判定与性质,平行平面间的距离,二面角及其平面角,两个平面垂直的判定与性质,棱柱,棱锥,平面图形与简单立体图形直观图的画法,多面体和正多面体,球。
(二)本章在体系编排上分为两大节:第一大节是“空间直线和平面”,第二大节是“简单几何体”1.直线和平面是最基本的几何元素,空间直线和平面的位置关系是立体几何的基础知识。
学好这一部分内容,对于学生在已有的平面图形知识基础上,建立空间观念,实现从平面图形到立体图形的认识飞跃,是非常重要的。
第一大节包括6小节,依次按照平面、空间直线、直线和平面平行、直线和平面垂直、两个平面平行、两个平面垂直的顺序编排。
直线平面简单几何体球

一个球与底面边长为a的正四棱锥的底面
和侧面都相切.若平行于棱锥
底面且与球相切的平面截棱锥,
所得的截面是一个边长为b的正
方形,求这个球的表面积.
解:过正四棱锥相对两个侧面的斜高作截
面,如图设O为球心,O1、O2
分别为截面和底面正方形的中
心,球与侧面的一个切点为C.
*
添加标题
添加标题
添加标题
添加标题
添加标题
添加标题
添加标题
添加标题
*
点评:求球的表面积的关键是求球的半径.求半径时,一般是根据截面圆的圆心与球的圆心的连线段、截面圆的弦长、球的半径三者之间的关系,通过解三角形来求得.
*
如图,A、B、C是表面积为 48π的球面上三点,AB=2, BC=4,∠ABC =60°,O为 球心.求直线OA与截面ABC 所成的角的大小. 解:连结AC,设O在 截面ABC上的射影是O′, 则O′为截面三角 形ABC外接圆的圆心,
*
已知过球面上A、B、C三点的截面和球心的距离等于球半径的一半,且AB=BC=CA=2,则球面面积是( ) A. B. C. D. 解:因为AB=BC=CA=2, 所以△ABC的外接圆半径为r= .设球的半 径为R,则 所以 , 所以
*
第九章 直线、平面、简单几何体
第 讲
球
考点 搜索
●球面、球体的概念,球的截面性质 ●地球的经纬度,球面距离 ●球的表面积和体积高考
高考 猜想
1. 考查有关球的表面积、体积和球面距离等的计算. 2. 考查球的截面问题的分析与计算.
与定点的距离_______________的点的集合,叫做球体,简称球,定点叫做球心,定长叫做球的半径,与定点距离__________的点的集合叫做球面. 用一个平面截一个球,所得的截面是________,且球心与截面圆心的连线________截面. 设球心到截面的距离为d,球半径为R,截面圆半径为r,则三者的关系是____________.
数学高考复习名师精品教案:第78课时:第九章 直线、平面、简单几何体-直线与平面、直线与直线所成的角

数学高考复习名师精品教案第78课时:第九章 直线、平面、简单几何体——直线与平面、直线与直线所成的角课题;直线与平面、直线与直线所成的角 一.复习目标:1.掌握直线与直线、直线与平面所成的角的概念,能正确求出线与线、线与面所成的角. 二.知识要点:1.异面直线,a b 所成角的定义: . 2.直线与平面所成角θ:(1)直线与平面平行或直线在平面内,则θ= . (2)直线与平面垂直,则θ= .(3)直线是平面的斜线,则θ定义为 . 3.最小角定理: .1.正方体1111ABCD A B C D -中,O 为,AC BD 的交点, 则1C O 与1A D 所成的角 ( )D()A 60 ()B 90 ()C arccos3 ()D arccos 62.,,PA PB PC 是从P 点引出的三条射线,每两条的夹角都是60 ,则直线PC 与平面APB 所成的角的余弦是( )()A 12 ()B ()C ()D 3.如图,在底面边长为2的正三棱锥ABC V-中,E 是BC的中点,若VAE ∆的面积是41,则侧棱VA 与底面所成角的大小为 . (结果用反三角函数值表示)四.例题分析:例1.在060的二面角βα--l 中,βα∈∈B A ,,已知A 、B 到l 的距离分别是2和4,且10=AB ,A 、B 在l 的射影分别为C 、D ,求:(1)CD 的长度;(2)AB和棱l 所成的角.例2.在棱长为4的正方体1111ABCD A B C D -中,O 是正方形1111A B C D 的中心,点P 在棱1CC 上,且14CC CP =.(Ⅰ)求直线AP 与平面11BCC B 所成的角的大小(结果用反三角函数值表示);(Ⅱ)设O 点在平面1D AP 上的射影是H ,求证:1D H AP ⊥.ABC VE· B 1PA CDA 1C 1D 1BO H·例3.在四棱锥P ABCD -中,底面ABCD 是正方形,侧棱PA ⊥底面ABCD ,AE PD ⊥,//,EF DC AM EF =.(1)证明MF 是异面直线AB 与PC 的公垂线;(2)若3PA AB =,求直线AC 与平面EAM 所成角的正弦值.五.课后作业:AMBCDF EP1.在正三棱柱111ABC A B C -中,已知1AB =,D 在1BB 上,且1BD =,若AD 与平面11AAC C 所成的角为α,则α=( )()A 13 ()B 4π ()C ()D 2.一直线和直二面角的两个面所成的角分别是,αβ,则αβ+的范围是( )()A [,)2ππ ()B [0,2π ()C (0,2π ()D [0,2π3.已知AB 是两条异面直线,AC BD 的公垂线段,1AB =,10AC BD ==,CD =则,AC BD 所成的角为 .4.如图,在三棱锥P ABC -中,ABC ∆是正三角形90PCA ∠= ,D 是PA 中点,二面角P AC B --为120,2,PC AB ==,(1)求证:AC BD ⊥; (2)求BD 与平面ABC 所成角.5.如图,已知直三棱柱111ABC A B C -中,90ACB ∠= ,侧面1AB 与侧面1AC 所成的ABCPD二面角为60 ,M 为1AA 上的点,1130A MC ∠= ,190CMC ∠= ,AB a =. (1)求BM 与侧面1AC 所成角的正切值;(2)求顶点A 到面1BMC 的距离.6.如图直四棱柱 1111ABCD A BC D -中,底面ABCD 是直角梯形,设090=∠=∠ABC BAD ,2,8BC AD ==,异面直线1AC 与D A 1互相垂直,(1)求证:D A 1⊥平面B AC 1;(2)求侧棱1AA 的长;(3)已知4AB =,求D A 1与平面11B ADC 所成的角.D 1C 1B 1A 1DCB A。
高中数学重点手册9——直线、平面、简单几何体

9.直线、平面、简单几何体「平面」平面是一个只描述而不定义的最基本的概念。
可以从下述几方面加深认识:①平面的最本质的一个属性就是具有无限延展性。
应注意把立体几何中的平面与日常接触到的平面严格加以区分,不能混为一谈。
作为立体几何概念的平面,已经不再具有平面形象物体的属性,它不计厚薄,不计质量,没有任何物理的或化学的属性。
②可以将平面几何中直线的无限延展性与立体几何中平面的无限延展性加以类比,从而加深对平面的认识:直线可以看成是一点沿一定方向运动以后形成的;平面可以看成是一条直线沿一定方向运动以后形成的。
一条直线把它所在平面分成两部分;一个平面把空间分成两部分。
「平面的画法及其表示法」用图形表示直线只有一种方法,而用图形表示平面的方法却不是惟一的。
它可以用常见的图形,如三角形、平行四边形、矩形、正方形、平面多边形和圆等表示。
总之,可以用任意封闭的平面图形表示平面。
值得注意的是,虽然是用有限的封闭图形表示具有无限延展性的平面,但不能动摇对平面无限延展性的认识。
立体几何中,通常用平行四边形表示平面,画表示水平平面的平行四边形时,通常把它的锐角画成45°,横边画成邻边的2倍,如图(1)所示,画非水平平面时,只要画成适当的平行四边形即可,如图(2)所示;画直立的平面时,应把一组对边用铅垂线表示,如图(3)所示。
一个平面通常用一个字母表示,如平面M,平在α,也可以用表示平面的平行四边形的顶点上的字母表示,如平面ABCD或平面AC。
「用集合符号表示点、直线和平面之间的基本关系」①点和平面的位置关系:点A在平面α内,记作A∈平面α;点B不在平面α内,记作B∉平面α。
②直线和平面的位置关系:直线l在平面M内,记作直线l⊂平面M,在不发生误会的前提下,可⊂;直线l不在平在M内,记作直线l⊂平面M。
以记作l M③平面和平面的位置关系:平面α和平面β相交于直线l,记作平面αI平面β=直线l。
「平面的基本性质」公理1:如果一条直线上的两点在一个平面内,那么这条直线上所有的点都在这个平面内。
第九章 直线、平面、简单几何体(B)2

第十章排列、组合和二项式定理课时作业53两个计数原理时间:45分钟分值:100分一、选择题(每小题5分,共30分)1.已知如图1的每个开关都有闭合、不闭合两种可能,因此5个开关共有25种可能,在这25种可能中,电路从P到Q接通的情况有()图1A.30种B.10种C.16种D.24种解析:5个开关闭合有1种接通方式;4个开关闭合有5种接通方式;3个开关闭合有8种接通方式;2个开关闭合有2种接通方式.故共有1+5+8+2=16(种).答案:C2.从正方体的8个顶点中任取3个为顶点作三角形,其中直角三角形的个数为() A.56 B.52C.48 D.40解析:正方体的每1个顶点引出3条棱,3条面对角线,每2条棱构成一个直角三角形两边,每1条面对角线与1条棱构成一直角三角形两边.所以以每1个顶点为直角顶点有6个直角三角形,所以共有6×8=48个直角三角形.答案:C3.(2009·湖南高考)从10名大学毕业生中选3人担任村长助理,则甲、乙至少有1人入选,而丙没有入选的不同选法的种数为() A.85 B.56C.49 D.28解析:分两类计算,C22C17+C12C27=49,故选C.答案:C4.将数字1,2,3,4,5,6排成一列,记第i个数为a i(i=1,2,…,6).若a1≠1,a3≠3,a5≠5,a1<a3<a5,则不同的排列方法种数为() A.18 B.30C.36 D.48解析:∵a1≠1且a1<a3<a5,∴(1)当a1=2时,a3为4或5,a5为6,此时有12种;(2)当a1=3时,a3仍为4或5,a5为6,此时有12种;(3)当a1=4时,a3为5,a5为6,此时有6种.∴共30种.答案:B5.(2009·广东高考)2010年广州亚运会组委会要从小张、小赵、小李、小罗、小王五名志愿者中选派四人分别从事翻译、导游、礼仪、司机四项不同工作,若其中小张和小赵只能从事前两项工作,其余三人均能从事这四项工作,则不同的选派方案共有() A.48种B.12种C.18种D.36种解析:若小张和小赵恰有1人入选,则共有C12C12A33=24种方案,若小张和小赵两人都入选,则共有A23A22=12种方案,故总共有24+12=36种方案.故选D.答案:D6.(2009·唐山质检)已知I={1,2,3},A、B是集合I的两个非空子集,且A中所有数的和大于B中所有数的和,则集合A、B共有() A.12对B.15对C.18对D.20对解析:依题意,当A、B均有一个元素时,有3对;当B有一个元素,A有两个元素时,有8对;当B有一个元素,A有三个元素时,有3对;当B有两个元素,A有三个元素时,有3对;当A、B均有两个元素时,有3对;共20对,选择D.答案:D二、填空题(每小题5分,共20分)7.用5种不同颜色给图中A、B、C、D4个区域涂色,规定每个区域只涂1种色,相邻区域涂不同颜色,则不同的涂色方法共有__________种.图2解析:A、B、C区域分别有5、4、3种涂法,因D可与A同色,则D区域有3种涂法,故共有5×4×3×3=180种.答案:1808.有一个机器猫(看作一点)在坐标平面内从原点出发,沿x轴跳动,每次向正方向或负方向跳1个单位,经过5次跳动机器猫落在点(3,0)(允许重复过此点)处,则机器猫不同的运动方法共有________种(用数字作答).解析:由已知条件可得,机器猫共向正方向跳动4次,向负方向跳动1次,所以该问题转化为机器猫向负方向跳动1次的所有情况.机器猫向负方向跳动1次的所有情况为:第k次跳动为向负方向跳动,k=1、2、3、4、5,共有5种情况.答案:59.(2009·浙江高考)甲、乙、丙3人站到共有7级的台阶上,若每级台阶最多站2人,同一级台阶上的人不区分站的位置,则不同的站法种数是________(用数字作答).解析:3个人各站一级台阶有A37=210种站法;3个人中有2个人站在一级,另一人站在另一级,有C23A27=126种站法,共有210+126=336种站法.故填336.答案:33610.(2009·陕西高考)某班有36名同学参加数学、物理、化学课外探究小组,每名同学至多参加两个小组.已知参加数学、物理、化学小组的人数分别为26、15、13,同时参加数学和物理小组的有6人,同时参加物理和化学小组的有4人,则同时参加数学和化学小组的有________人.图3解析:由题意知,同时参加三个小组的人数为0,令同时参加数学、化学人数为x人.20-x+6+5+4+9-x+x=36,x=8.答案:8三、解答题(共50分)11.(15分)某单位职工义务献血,在体检合格的人中,O 型血的共有28人,A 型血的共有7人,B 型血的共有9人,AB 型血的有3人.(1)从中任选1人去献血,有多少种不同的选法?(2)从四种血型的人中各选1人去献血,有多少种不同的选法?解:从O 型血的人中选1人有28种不同的选法,从A 型血的人中选1人有7种不同的选法,从B 型血的人中选1人有9种不同的选法,从AB 型血的人中选1人有3种不同的选法.(1)任选1人去献血,即无论选哪种血型的哪一个人,这件“任选1人去献血”的事情已完成,所以由分类计数原理,共有28+7+9+3=47种不同的选法.(2)要从四种血型的人中各选1人,即要在每种血型的人中依次选出1人后,这件“各选1人去献血”的事情才完成,所以用分步计数原理,共有28×7×9×3=5292种不同的选法.12.(15分)若a 、b ∈N ,且a +b ≤6,则以(a ,b )为坐标的不同的点共有多少个? 解:按a 的取值进行分类:当a =1时,b 的可取值有5个,对应着5个不同的点;当a =2时,b 的可取值有4个,对应着4个不同的点;当a =3时,b 的可取值有3个,对应着3个不同的点;当a =4时,b 的可取值有2个,对应着2个不同的点;当a =5时,b 的可取值有1个,对应着1个点.由分类计数原理,共有5+4+3+2+1=15个不同的点.13.(20分)设M ={1,2,3,…,100},从M 中选出3个不同的数,使它们成等差数列,最多可以组成多少个这样的等差数列?解:当公差d 取1时,可得1,2,3;2,3,4;…;98,99,100共98个等差数列.同理,当公差分别取2,3,…,49时,可依次有96,94,…,2个等差数列,并且每一个等差数列的倒序数列依然是等差数列,所以可得49(98+2)2×2=4900. 最多可组成4900个这样的等差数列.。
直线、平面、简单几何体第九章

第九章直线、平面、简单几何体空间图形是空间中一些点的集合.组成空间图形的点可都在同一平面内,也可都不在同一个平面内.各点不都在同一平面内的图形是立体图形.平面图形和立体图形是空间图形.将立体图形问题转化为平面图形解决.一空间直线和平面9.1平面1.平面几何中的平面、直线是无限延展的。
通常画直线的一部分来表示直线.也可以画出平面的一部分来表示平面. 通常画平行四边形来表示平面.当平面是水平放置的时候,常把平行四边形的锐角化成45°,横边画成邻边的2倍长.当一个平面的一部分被另一个平面遮住时,应把被遮部分的线段画成虚线或不画.先画两条交线或垂线.平面通常用希腊字母aβr等表示.如平面a平面β,也可用表示平行四边形的两个相对顶点字母表示,如平面AC.平面内有无数个点,平面可以认为是由它们内部的所有的点组成的点集,其中每个点都是它的元素.点A在平面a内,记作A∈a;点B 在平面a外,记作B不属于a.平面具有平整性和延展性.2.平面的基本性质公理1 如果一条直线上的两点在一个平面内,那么这条直线上所有的点都在这个平面内. 用符号表示为:A∈l,B∈l,A∈a,B∈a推出l在a公理2 如果两个平面有一个公共点,那么它们还有其他公共点,且所有这些公共点的集合是一条过这个公共点的直线.用符号表示为:P∈a ∩β推出∩β=l且P∈l公理3 经过不再同一条直线上的三点,有且只有一个平面.直线是由无数个点组成的集合.点P在直线l上,记作P∈l,点P 在直线l外,记作P¢l.如果直线l上所有的点都在平面a内,就说直线l在平面a内,或者说平面a经过直线l,记作l在a.否则,就说直线l在平面ɑ外,记作l¢ɑ.如果平面ɑ和β有一条公共直线l,平面ɑ和β就相交,交线是l,记作ɑ∩β=l在同一平面内作两直线平行和相交共有三种作法。
过ABC三点的平面可记作“平面ABC”推论1 经过一条直线和这条直线外的一点,有且只有一个平面.用符号表示为:A不属于ɑ可推出有且只有一个平面a,使A∈a,ɑ在a.推论2 经过两条相交直线,有且只有一个平面.用符号表示为:ɑ∩b=P 可推出有且只有一个平面a使ɑ在a,b在a。
高中数学第九章直线平面简单几何体B第30课多面体欧拉定理的发现2教案
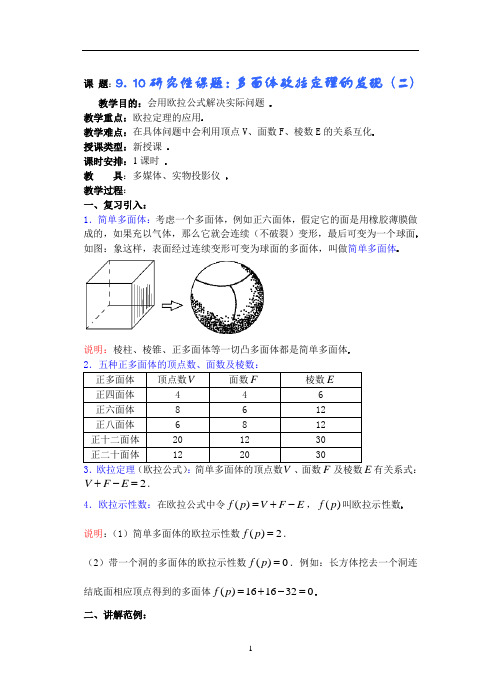
课 题:9.10研究性课题:多面体欧拉定理的发现 (二)教学目的:会用欧拉公式解决实际问题 教学重点:欧拉定理的应用教学难点:在具体问题中会利用顶点V 、面数F 、棱数E 的关系互化 授课类型:新授课 课时安排:1课时教 具:多媒体、实物投影仪 教学过程: 一、复习引入:1.简单多面体:考虑一个多面体,例如正六面体,假定它的面是用橡胶薄膜做成的,如果充以气体,那么它就会连续(不破裂)变形,最后可变为一个球面如图:象这样,表面经过连续变形可变为球面的多面体,叫做简单多面体说明:棱柱、棱锥、正多面体等一切凸多面体都是简单多面体 2.五种正多面体的顶点数、面数及棱数:3.欧拉定理(欧拉公式):简单多面体的顶点数、面数及棱数E 有关系式: 2V F E +-=.4.欧拉示性数:在欧拉公式中令()f p V F E =+-,()f p 叫欧拉示性数说明:(1)简单多面体的欧拉示性数()2f p =.(2)带一个洞的多面体的欧拉示性数()0f p =.例如:长方体挖去一个洞连结底面相应顶点得到的多面体()161632f p =+-=二、讲解范例:例1 由欧拉定理证明:正多面体只有正四面体、正六面体、正八面体、正十二面体、正二十面体这五种证明:设正多面体的每个面的边数为n ,每个顶点连有m 条棱,令这个多面体的面数为F ,每个面有n 条边,故共有nF 条边,由于每条边都是两个面的公共边,故多面体棱数2nFE =(1) 令这个多面体有V 个顶点,每一个顶点处有m 条棱,故共有mV 条棱由于每条棱有两个顶点,故多面体棱数2mVE = (2) 由(1)(2)得:2EF n =,2E V m =代入欧拉公式:222E EE m n+-=. ∴11112m n E+-= (3), ∵又3m ≥,3n ≥,但m ,n 不能同时大于3,(若3m >,3n >,则有11102m n +-≤,即10E≤这是不可能的)∴m ,n 中至少有一个等于3.令3n =,则1111032m E+-=>,∴116m >,∴5m ≤,∴35m ≤≤. 同样若3m =可得35n ≤≤.例2.欧拉定理在研究化学分子结构中的应用:1996年诺贝尔化学奖授予对发现60C 有重大贡献的三位科学家60是由60个C原子构成的分子,它是形如足球的多面体这个多面体有60个顶点,以每一个顶点为一端点都有三条棱,面的形状只有五边形和六边形,计算60C 分子中五边形和六边形的数目解:设60C 分子中有五边形x 个,六边形y 个60C 分子这个多面体的顶点数60V =,面数F x y =+,棱数1(360)2E =⨯⨯,由欧拉定理得:160()(360)22x y ++-⨯= (1),另一方面棱数可由多边形的边数和来表示,得11(56)(360)22x y +=⨯ (2),由(1)(2)得:12x =,20y =∴60C 分子中五边形有12个,六边形有20个例3.一个正多面体各个面的内角和为20π,求它的面数、顶点数和棱数解:由题意设每一个面的边数为m ,则(2)20F m ππ-=, ∴(2)20F m -=,∵2mFE =,∴10EF =+, 将其代入欧拉公式2V F E +-=,得12V =,设过每一个顶点的棱数为n ,则62n E V n ==,12n F m =得121262n n m +-=,即5213n m +=(1), ∵3m ≥,∴5n ≤,又3n ≥, ∴n 的可能取值为3,4,5,当3n =或4n =时(1)中m 无整数解; 当5n =,由(1)得3m =, ∴30E =, ∴20F =,综上可知:30E =,12V =,20F =.三、小结 :欧拉定理的应用;会用欧拉公式2V F E +-=解决简单多面体的顶点数、面数和棱数的计算问题 四、课后作业:⒈ 一个简单多面体的各面都是三角形,证明它的顶点数V 和面数F 有下面的关系:F =2V -4证明:∵23FE = ,V +F -E =2 ∴V +F -F 23=2 ∴F =2V -4 ⒉ 设一个凸多面体有V 个顶点,求证:它的各面多边形的内角和为(V-2)·360°解:设此多面体的上底面有V 上个顶点,下底面有V 下个顶点 将其下底面剪掉,抻成平面图形则 V 上·360°+(V 下-2)·180°+(V 下-2)·180° =(V 上+V 下-2)·360° =(V -2)360°⒊ 有没有棱数是7的简单多面体?说明理由 证明:∵V +F -E =2 , ∴V +F =7+2=9 ∵多面体的顶点数V ≥4,面数F ≥4∴只有两种情况V =4,F =5或V =5,F =4但是有4个顶点的多面体只有四个面,不可能是5个面有四个面的多面体是四面体,也只有四个面,不可能有5个面 ∴没有棱数是7的简单多面体⒋ 是否存在这样的多面体,它有奇数个面,且每一个在都有奇数条边 证明:设有一个多面体,有F (奇数)个面,并且每个面的边数F n n n 21,也都是奇数,则 E n n n F 221=+++但是上式左端是奇数个“奇数相加”,结果仍为奇数,可右端是偶数,这是不可能的∴不存在这样的多面体五、板书设计(略)六、课后记:。
直线平面和简单几何体ppt

平 面 的 基 本 性 质
性 质
A l
B
公理2:
A B C
l
P
公理3:
A B C
推论2:
ap b
推论3:
b a
平行直线
公理4 等角定理 判 定
直线和直线
相交直线 异面直线
线在面内
判
定
如果一条直线和一个平面内 斜线和平面所成的角,是这条斜 如果两个平行平面同时和第 垂线段和斜线段中: 如果和这个平面的一条斜线 平行于同一直线的两条直 两角两边分别平行 过平面外一点和平面内一点的直 的两条相交直线都垂直,那 线和这个平面的直线所成角的一 三个平面相交,那么它们的 如果平面外一条直线和这个平面 如果一个平面经过另一个平 的射影垂直,那么它也和这 如果一条直线和一个平面平行,经 线互相平行。 且方向相同,两角 如果两条直线同垂直于一个平 么这条直线垂直于这个平面。 射影相等的两条斜线段相等,射 线,和平面内不经过该点的直线 如果一个平面内有两条相交直 如果两平面垂直,那么在 交线平行。 切角中最小的角。 条斜线垂直。 内的一条直线平行,那么这条直 面的一条垂线,那么这两个 相等。 过这条直线的平面和这个平面相交, 影较长的斜线段也较长。 面,那么这两条直线平行。 是异面直线。 线都平行于另一个平面,那么 一个平面内垂直于交线的 如果两条平行直线中的一条 线和这个平面平行。 平面互相垂直。 如果两个平面平行,那么其 那么这条直线和交线平行。 在平面内的一条直线,如果 单直三面角余弦公式: 这两个平面平行。 直线垂直于另一个平面。 相等的斜线段的射影相等,较长 垂直于一个平面,那么另一 异面直线的距离公式。 中一个平面的直线平行于另 和这个平面的一条斜线垂直, cosA=cosBcosC 的斜线段的射影也较长。 条也垂直于这个平面。
第九章直线平面简单几何体(B)(第1课)基本性质(1)

课题:9.1平面的基本性质(一)教学目的:能够从日常生活实例中抽象出数学中所说的“平面”理解平面的无限延展性正确地用图形和符号表示点、直线、平面以及它们之间的关系初步掌握文字语言、图形语言与符号语言三种语言之间的转化教学重点:掌握点-直线-平面间的相互关系,并会用文字-图形-符号语言正确表示平面的无限延展性教学难点:(1)理解平面的无限延展性;(2)集合概念的符号语言的正确使用授课类型:新授课课时安排:1课时教具:多媒体、实物投影仪内容分析:立体几何课程是初等几何教育的内容之一,是在初中平面几何学习的基础上开设的,以空间图形的性质、画法、计算以及它们的应用为研究对象,以演绎法为研究方法立体几何的教学,使学生的认识水平从平面图形延拓至空间图形,完成由二维空间向三维空间的转化,发展学生的空间想象能力,逻辑推理能力和分析问题、解决问题的能力平面的概念和平面的性质是立体几何全部理论的基础事物形态的数学抽象,在立体几何中是只描述而不定义的原始概念,但平面是把三维空间图形转化为二维平面图形的主要媒介,在立体几何问题平面化的过程中具有重要的桥梁作用“立体几何”作为一门学生刚开始学习的学科,其内容对学生来说基本上是完全陌生的,应以“讲授法’的主,引导学生观察和想象,吸引学生的注意力,激发学生的学习兴趣,初步培养空间想象力本课是“立体几何”的起始课,应先把这一学科的内容作一大概介绍,包括课本的知而后引入“平面”概念,以类比的方式,联系直线的无限延伸性去理解平面的无限延展性,突破教学难点在进行“平面的画法”教学时,不仅要会画水平放置的平面,还应会画直立的平在用字母表示点、直线、平面三者间的关系时,应指明是借用了集合语句,并用列表法将这些关系归类,以便作为初学者的学生便于比较、记忆和运用9.1节,平面的基本性质共4个知识点:平面的表示法、平面的基本性质、公理的这一小节是整章的基础通过平面基本性质及其推论教师应该认识到培养学生的空间想象力主要是通过对图形性质的学习,使学生对图形的直观认识上升到理性认识,建立空间图形性质的正确概念,这样才能学好立体几何为了形成学生的空间观念,这一小节通过观察太阳(平行)光线照射物体形成影子的性先直观地了解平行射影的性质,这样就可正确地指导学生画空间图形这小节教学要求是,掌握平面的基本性质,直观了解空间图形在平面上的表示方法,会用斜二测画法画水平放置的平面图形的直观图和长方体、正方体的直观图教学过程:一、复习引入:平面图形就是由同一平面内的点、线所构成的图形平面图形以及我们学过的长方体、圆柱、圆锥等都是空间图形,空间图形就是由空间的点、线、面所构成的图形当我们把研究的范围由平面扩大到空间后,一些平面图形的基本性质,在空间仍然成立例如三角形全等、相似的充要条件,平行线的传递性等有些性质在研究范围扩大到空间后,是否仍然成立呢?例如,过直线外一点作直线的垂线是否仅有一条?到两定点距离相等的点的集合是否仅是连结两定点的线段的一条垂直平分线?二、讲解新课:1.平面的两个特征:①无限延展②平的(没有厚度)平面是没有厚薄的,可以无限延伸,这是平面最基本的属性部分,一条直线把平面分成两部分2.平面的画法:通常画平行四边形来表示平面(1)一个平面:水平放置和直立;当平面是水平放置的时候,通常把平行四边形的锐角画成45 ,横边画成邻边的2倍长,如图1(1).(2) 直线与平面相交,如图1(2)、(3),:(3)两个相交平面:画两个相交平面时,若一个平面的一部分被另一个平面遮住,应把被遮住部分的线段画成虚线或不画(如图2)平面的画法及其表示方法:①在立体几何中,常用平行四边形表示平面当平面水平放置时,通常把平行四边形的锐角画成45 ,横边画成邻边的两倍画两个平面相交时,当一个平面的一部分被另一个平面遮住时,应把被遮住的部分画成虚线或不画②一般用一个希腊字母α、β、γ……来表示,还可用平行四边形的对角顶点的字aβαBAβBAαβBAααβa图 2A(1)母来表示如平面α,平面AC 等 空间图形是由点、线、面组成的空间图形的基本元素是点、直线、平面而可以把直线、平面看成是点的集合,因此它们之间的关系除了用文字和图形表示外,还可借用集合中的符号语言来表示规定直线用两个大写的英文字母或一个小写的英文字母表示,点用一个大写的英文字母表示,而平面则用一个小写的希腊字母表示集合中“∈”的符号只能用于点与直线,点与平面的关系,“”和“”的符号只能用于直线与直线、直线与平面、平面与平面的关系,虽然借用于集合符号,但在读法上仍用几何语言α⊄(平面α外的直线a )表示α⊄a (平面α外的直线a )表示a α=∅ 或a α=三、讲解范例:例1将下列符号语言转化为图形语言: (1)A α∈,B β∈,A l ∈,B l ∈;(2)a α⊂,b β⊂,//a c ,b c p = ,αβ=解:说明:画图的顺序:先画大件(平面),再画小件(点、线)例2 将下列文字语言转化为符号语言:(1)点A 在平面α内,但不在平面β内;(2)直线a 经过平面α外一点M ; (3)直线l 在平面α内,又在平面β内(即平面α和β相交于直线解:(1)A ∈α,A ∉β; (2)M ∈a ,M ∉α; (3)l ∈α,l ∈β(即α β=l )例3 在平面α内有,,A O B 三点,在平面β内有,,B O C 三点,试画出它们的图形答案:右图四、课堂练习:1.判断下列命题的真假,真的打“√”,假的打“×”(1)可画一个平面,使它的长为4cm ,宽为2cm . ( ) (2)一条直线把它所在的平面分成两部分,一个平面把空间分成两部分.( ) (3)一个平面的面积为20 cm 2. ( ) (4)经过面内任意两点的直线,若直线上各点都在这个面内,那么这个面是平面.( ) 答案:(1)×(2)√(3)×(4)√ 2.观察(1)、(2)、(3)三个图形,模型说明它们的位置关系有什么不同,并用字母表示各个平面. 3.请将以下四图中,看得见的部分用实线描出.(3)(2)(1)(4)(3)(2)(1)4.如图所示,用符号表示以下各概念: ①点A 、B 在直线a 上 ;②直线a 在平面α内 ;点C 在平面α内 ; ③点O 不在平面α内 ;直线b 不在平面α内 . 答案:①,A a B a ∈∈ ②,a C αα⊂∈ ③,O b αα∉⊄5.①一条直线与一个平面会有几种位置关系 .②如图所示,两个平面α、β,若相交于一点,则会发生什么现象.③几位同学的一次野炊活动,带去一张折叠方桌,不小心弄坏了桌脚,有一生提议可将几根一样长的木棍,在等高处用绳捆扎一下作桌脚(如图所示),问至少要 几根木棍,才可能使桌面稳定?答案: ①3种 ②相交于经过这个点的一条直线 ③至少3根 五、小结 :平面的概念;平面的画法、表示方法及两个平面相交的画法;点、直线、平面间基本关系的文字语言,图形语言和符号语言之间关系的转换六、课后作业:试用集合符号表示下列各语句,并画出图形:(1)点A 在平面α内,但不在平面β内;(2)直线a 经过不属于平面α的点A ,且a 不在平面α内; (3)平面α与平面β相交于直线l ,且l 经过点P ; (4)直线l 经过平面α外一点P ,且与平面α相交于点M 七、板书设计(略)八、课后记:。
直线、平面、简单几何体优质课件

2.地球表面上从A地(北纬45°,东经120°)到B地(北纬
45°,东经30°)的最短距离为(地球半径为R)
(A)R (B)
πR
3.在北纬45o的圈上有甲、乙、丙三地,甲乙、乙丙之间
πR (C) 3
( C )
(D) πR
2
的经度差都是90o,则甲丙两地的球面距离是甲乙两地球
3 面距离的 ______倍 2
1 VA-BCD= (SABC+SBCD+SCDA+SDAB)· r 3 1 = · =16r 由16r=6√7 得内切球的半径为 r 3 7 48r 3 8
能力·思维·方法
【解题回顾】正如三角形的内切圆经常与面积发生关 系一样,多面体的内切球的半径也常与体积发生联系.
能力·思维·方法
9.在球内有相距14cm 的两个平行截面,它们的面积分别是 64πcm2 和 36πcm2,求球的表面积。 解:设球半径为R, (1)当截面在球心同侧,如图(1)
基础题例题
4.球的表面积膨胀为原来的 2 倍,膨胀后的体积为原来的 ( C) A. √2倍 B.2倍 C.2√2倍 D.4倍 2 2 5.棱长为2的正四面体的体积为_____________ 3
6.设P、A、B、C是球O面上的四点,且PA、PB、PC两两 互相垂直,若PA=PB=PC=a, 则球心O到截面ABC的距离 3 a 是______________ 6
直线、平面、简单几何体
要点·疑点·考点
一、多面体 1. 概念
(1)若干个平面多边形围成的几何体,叫多面体.
(2)把多面体的任何一面伸展为平面,如果所有其他各 面都在这个平面的同侧,这样的多面体叫凸多面体. (3)每个面都是有相同边数的正多边形,且以每个顶点 为其一端都有相同数目的棱的凸多面体,叫正多面体.
第九章直线平面简单几何体(B)(第6课)直线与平面平行平面与平面平行(1)

课 题:9.3直线与平面平行、平面与平面平行 (一)教学目的:1.掌握空间直线和平面的位置关系;2.掌握直线和平面平行的判定定理和性质定理,灵活运用线面平行的判定定理和性质定理实现“线线”“线面”平行的转化 教学重点:线面平行的判定定理和性质定理的证明及运用 教学难点:线面平行的判定定理和性质定理的证明及运用 授课类型:新授课 课时安排:1课时教 具:多媒体、实物投影仪 内容分析:本节有两个知识点,直线与平面和平面与平面平行,直线与平面、平面与平面平行特征性质这也可看作平行公理和平行线传递性质的推广直线与平面、平面与平面平行判定的依据是线、线平行这些平行关系有着本质上的联系通过教学要求学生掌握线、面和面、面平行的判定与性质这两个平行关系是下一大节学习共面向量的基础前面3节主要讨论空间的平行关系,其中平行线的传递性和平行平面的性质是这三小节的重点 教学过程:一、复习引入:1 空间两直线的位置关系 (1)相交;(2)平行;(3)异面2.公理4 :平行于同一条直线的两条直线互相平行推理模式://,////a b b c a c .3.等角定理:如果一个角的两边和另一个角的两边分别平行并且方向相同,那么这两个角相等4.等角定理的推论:如果两条相交直线和另两条相交直线分别平行,那么这两条直线所成的锐角(或直角)相等.5.空间两条异面直线的画法ab1AA6.异面直线定理:连结平面内一点与平面外一点的直线,和这个平面内不经过此点的直线是异面直线推理模式:,,,A B l B l ααα∉∈⊂∉⇒AB 与l 是异面直线7.异面直线所成的角:已知两条异面直线,a b ,经过空间任一点O 作直线//,//a a b b '',,a b ''所成的角的大小与点O 的选择无关,把,a b ''所成的锐角(或直角)叫异面直线,a b 所成的角(或夹角).为了简便,点O 通常取在异面直线的一条上2,0(π8.异面直线垂直:如果两条异面直线所成的角是直角,则叫两条异面直线垂直.两条异面直线,a b 垂直,记作a b ⊥.9.求异面直线所成的角的方法:(1)通过平移,在一条直线上找一点,过该点做另一直线的平行线;(2)找出与一条直线平行且与另一条相交的直线,那么这两条相交直线所成的角即为所求10.两条异面直线的公垂线、距离和两条异面直线都垂直相交....的直线,我们称之为异面直线的公垂线 在这两条异面直线间的线段(公垂线段)的长度,叫做两条异面直线间的距离.两条异面直线的公垂线有且只有一条二、讲解新课:1.直线和平面的位置关系(1)直线在平面内(无数个公共点);(2)直线和平面相交(有且只有一个公共点);(3)直线和平面平行(没有公共点)——用两分法进行两次分类.a α⊂,a A α= ,//a α.aαaα2.线面平行的判定定理:如果不在一个平面内的一条直线和平面内的一条直线平行,那么这条直线和这个平面平行. 推理模式:,,////lm l m l ααα⊄⊂⇒. 证明:假设直线l 不平行与平面α,∵l α⊄,∴l P α= ,若P m ∈,则和//l m 矛盾,若P m ∉,则l 和m 成异面直线,也和//l m 矛盾, ∴//l α.3. 线面平行的性质定理:如果一条直线和一个平面平行,经过这条直线的平面和这个平面相交,那么这条直线和交线平行. 推理模式://,,//l l m l m αβαβ⊂=⇒ . 证明:∵//l α,∴l 和α没有公共点, 又∵m α⊂,∴l 和m 没有公共点;即l 和m 都在β内,且没有公共点,∴//l m . 三、讲解范例:例1 已知:空间四边形ABCD 中,,E F 分别是,AB AD 的中点,求证://EF BCD 平面. 证明:连结BD ,在ABD ∆中, ∵,E F 分别是,AB AD 的中点,∴//EF BD ,EF BCD ⊄平面,BD BCD ⊂平面, ∴//EF BCD 平面.例2求证:如果过平面内一点的直线平行于与此平面平行的一条直线,那么这条直线在此平面内.已知://,,,//l P P m m l αα∈∈,求证:m α⊂. 证明:设l 与P 确定平面为β,且m αβ'= , ∵//l α,∴//l m ';又∵//l m ,,m m '都经过点P , ∴,m m '重合,∴m α⊂.例3 已知直线a ∥直线b ,直线a ∥平面α,b ⊄α, 求证:b ∥平面α 证明:过a 作平面β交平面α于直线∵a ∥α∴a ∥c 又∵a ∥b ∴b ∥c ,∴b ∥∵ b ⊄α, c ⊂α,∴b ∥α.FED CBAβαmlβαPmm 'a b.例4.已知直线a∥平面α,直线a∥平面β,平面α 平面β=b,求证//分析:利用公理4,寻求一条直线分别与a,b均平行,从而达到a∥b的目的.可借用已知条件中的a∥α及a∥β来实现.证明:经过a作两个平面γ和δ,与平面α和β分别相交于直线c和d,∵a∥平面α,a∥平面β,Array∴a∥c,a∥d,∴c∥d,又∵d⊂平面β,c∉平面β,∴c∥平面β,又c⊂平面α,平面α∩平面β=b,∴c∥b,又∵a∥c,所以,a∥b.四、课堂练习:1.选择题(1)以下命题(其中a,b表示直线,α表示平面)①若a∥b,b⊂α,则a∥α②若a∥α,b∥α,则a∥b③若a∥b,b∥α,则a∥α④若a∥α,b⊂α,则a∥b其中正确命题的个数是()(A)0个(B)1个(C)2个(D)3个(2)已知a∥α,b∥α,则直线a,b的位置关系①平行;②垂直不相交;③垂直相交;④相交;⑤不垂直且不相交.其中可能成立的有()(A)2个(B)3个(C)4个(D)5个(3)如果平面α外有两点A、B,它们到平面α的距离都是a,则直线AB和平面α的位置关系一定是()(A)平行(B)相交(C)平行或相交(D)AB⊂α(4)已知m,n为异面直线,m∥平面α,n∥平面β,α∩β=l,则l ()(A)与m,n都相交(B)与m,n中至少一条相交(C)与m,n都不相交(D)与m,n中一条相交答案:(1) A (2) D (3) C (4)C2.判断下列命题的真假(1)过直线外一点只能引一条直线与这条直线平行. ()(2)过平面外一点只能引一条直线与这个平面平行. ()(3)若两条直线都和第三条直线垂直,则这两条直线平行. ( ) (4)若两条直线都和第三条直线平行,则这两条直线平行. ( ) 答案:(1) 真 (2) 假 (3) 假 (4)真 3.选择题(1)直线与平面平行的充要条件是( ) (A )直线与平面内的一条直线平行 (B )直线与平面内的两条直线平行 (C )直线与平面内的任意一条直线平行 (D )直线与平面内的无数条直线平行(2)直线a ∥平面α,点A ∈α,则过点A 且平行于直线a 的直线 ( ) (A )只有一条,但不一定在平面α内 (B )只有一条,且在平面α内 (C )有无数条,但都不在平面α内 (D )有无数条,且都在平面α内(3)若a ⊄α,b ⊄α,a ∥α,条件甲是“a ∥b ”,条件乙是“b ∥α”,则条件甲是条件乙的 ( ) (A )充分不必要条件 (B )必要不充分条件 (C )充要条件 (D )既不充分又不必要条件 (4)A 、B 是直线l 外的两点,过A 、B 且和l 平行的平面的个数是 ( ) (A )0个 (B )1个 (C )无数个 (D )以上都有可能 答案:(1)D (2)B (3)A (4)D4.平面α与⊿ABC 的两边AB 、AC 分别交于D 、E ,且AD ∶DB =AE ∶EC , 求证:BC ∥平面α略证:AD ∶DB =AE ∶ECααα////BC DE BC DE BC ⇒⎪⎭⎪⎬⎫⊂⊄⇒ 5.空间四边形ABCD ,E 、F 分别是AB 、BC 的中点, 求证:EF ∥平面ACD .略证:E 、F 分别是AB 、BC 的中点α////EF ABC AC ACD EF AC EF ⇒⎪⎭⎪⎬⎫⊂⊄⇒ 6.经过正方体ABCD -A 1B 1C 1D 1的棱BB 1作一平面交平面AA 1D 1D 于E 1E ,求证:E 1E ∥B 1BC略证:11111111111////B BEE AA B BEE BB B BEE AA BB AA ⇒⎪⎭⎪⎬⎫⊂⊄1111111111111////EE AA EE B BEE A ADD A ADD AA B BEE AA ⇒⎪⎭⎪⎬⎫=⊂ 11111//////EE BB EE AA BB AA ⇒⎭⎬⎫7.选择题(1)直线a ,b 是异面直线,直线a 和平面α平行,则直线b 和平面α的位置关系是( ) (A )b ⊂α (B )b ∥α (C )b 与α相交 (D )以上都有可能(2)如果点M 是两条异面直线外的一点,则过点M 且与a ,b 都平行的平面 (A )只有一个 (B )恰有两个 (C )或没有,或只有一个 (D )有无数个 答案:(1)D (2)A 8.判断下列命题的真假.(1)若直线l ⊄α,则l 不可能与平面α内无数条直线都相交. ( ) (2)若直线l 与平面α不平行,则l 与α内任何一条直线都不平行 ( ) 答案:(1)假 (2)假9.如图,已知P 是平行四边形ABCD 所在平面外一点,M 、N 分别是AB 、PC 的中点(1)求证://MN 平面PAD ;(2)若4MN BC ==,PA = 求异面直线PA 与MN 所成的角的大小略证(1)取PD 的中点H ,连接AH ,DC NH DC NH 21,//=⇒AMNH AM NH AM NH ⇒=⇒,//为平行四边形 PAD AH PAD MN AH MN ⊂⊄⇒,,//PAD MN //⇒解(2): 连接AC 并取其中点为O ,连接OM 、ON ,则OM 平行且等于BC 的一半,ON 平行且等于PA 的一半,所以ONM ∠就是异面直线PA 与MN 所成1A的角,由4MN BC ==,PA =得,OM=2,ON=所以030=∠ONM ,即异面直线PA 与MN 成030的角10.如图,正方形ABCD 与ABEF 不在同一平面内,M 、N 分别在AC 、BF 上,且AM FN =求证://MN 平面CBE 略证:作AB NH AB MT //,//分别交BC 、BE 于T 、H 点AM FN =NH MT BNH CMT =⇒∆⇒≌从而有MNHT 为平行四边形CBE MN TH MN ////⇒⇒五、小结 :“线线”与“线面”平行关系:一条直线和已知平面平行,当且仅当这条直线平行于经过这条直线的平面和已知平面的交线. 六、课后作业:七、板书设计(略)八、课后记:E。
高中数学必修一第九章直线平面简单几何体(B)(第课)直线与平面垂直公开课教案课件课时训练练习教案课件

课 题:9.4直线和平面垂直 (一)教学目的: 1理解直线与平面垂直的定义; 2掌握直线与平面垂直的判定定理内容及论证过程; 3应用直线与平面垂直的判定定理解决问题教学重点:直线与平面垂直的判定定理内容及论证过程教学难点:直线与平面垂直的判定定理内容及论证过程授课类型:新授课课时安排:1课时教 具:多媒体、实物投影仪内容分析:本节包括两个知识点:直线和平面垂直及正射影和三垂线定理和平行射影的性质外,第二个重要性质就是空间的镜面对称直线与平面的垂直程就可以看到,证明的过程就是由平面的轴对称转换为空间的镜面对称的过程这一小节要特别重视判定定理的教学,要向学生指出定理证明过程的本质线定理是由直线和平面垂直判定定理得出的一个最重要的空间图形的性质,在传统几可学教育中这个定理占有极重要的地位,在这里,我们只重视概念的教学,减弱围绕三垂线定理的解题训练这是因为我们有更有效的向量工具处理空间的垂直问题这一小节的教学要求是,掌握直线和平面垂直的概念,掌握直线和平面垂直的判定定理,掌握三垂线定理及逆定理主要是理解定理的本质和直接应用不要进行大量的解题训练的教学这样就可减少课时,以加强空间向量的教学直线与平面垂直的定义是一个严格但不实用的定义,因而必须给出一个判定“直线与平面垂直”的判定定理而直线与平面是否垂直根据判定定理的要求,必须具备条件“a ⊥b ,a ⊥c ,b ∩c =B ,b ⊂α,c ⊂α”才能得到结论“a ⊥α”,至于为什么在上述条件下一定能得到“a ⊥α”这一结论便是本节课的一个主要内容教学过程:一、复习引入: 1观察空间直线和平面可知它们的位置关系有:(1)直线在平面内(无数个公共点);(2)直线和平面相交(有且只有一个公共点);(3)直线和平面平行(没有公共点)——用两分法进行两次分类它们的图形分别可表示为如下,符号分别可表示为a α⊂,a A α=,//a αaαaα线面平行的判定定理:如果不在一个平面内的一条直线和平面内的一条直线平行,那么这条直线和这个平面平行推理模式:,,////l m l m l ααα⊄⊂⇒ 3如果一条直线和一个平面平行,经过这条直线的平面和这个平面相交,那么这条直线和交线平行 推理模式://,,//l l m l αβαβ⊂=⇒二、讲解新课: 1 定义:如果一条直线和一个平面相交,并且和这个平面内的任意一条直线都垂直,我们就说这条直线和这个平面互相垂直其中直线叫做平面的垂线,平面叫做直线的垂面交点叫做垂足直线与平面垂直简称线面垂直,记作:a ⊥α画法:画直线和平面垂直时,通常要把直线画成和表示平面的平行四边形的一边垂直说明:①“任何”表示所有(提问:若直线与平面内的无数条直线垂直,则直线垂直与平面吗?如不是,直线与平面的位置关系如何?)②直线与平面垂直是直线与平面相交的一种特殊情况,在垂直时,直线与平面的交点叫做垂足③ a ⊥α等价于对任意的直线m ⊂α,都有a ⊥m利用定义,我们得到了判定线面垂直的最基本方法,同时也得到了线面垂直的最基本的性质2直线与平面垂直的判定定理:如果一条直线和一个平面内的两条相交直线都垂直,那么这条直线垂直于这个平面即 若l ⊥m ,l ⊥n ,m ∩n =B ,m ⊂α,n ⊂α,则l ⊥α已知:m 、n 是平面α内的两条相交直线,直线l 与α的交点为B ,且l ⊥m ,l ⊥n求证:l ⊥α分析:在α内平移m ,n ,使它们都通过点B ,这时m ,n 仍保持和l 垂直过点B 作任一条不与m ,n 重合的直线g ,如果我们能根据l ⊥m 且l ⊥n 推出l ⊥g ,那么就证明了直线l 和过点B 的所有直线都垂直,即l 垂直α为此,我们在l 上自点B 起于平面α的两侧分别截取BA=BA ′,于是m ,n βαm l都是线段AA ′的垂直平分线,它们上面的点到A 、A ′的距离相等 如果我们能证明g 上的点到A 、A ′的距离也相等,那么g 也是AA ′的垂直平分线,于是g 就垂直于l 在g 上任取一点E ,过点E 在α内作不通过点B 的直线,分别与m ,n 相交于点C 、D ,容易证明△ACD ≌A ′CD ,进而又可证明△ACE ≌△A ′CE于是EA=EA ′,g ⊥l一般地:证明:如果一条直线和平面内的两条相交直线都垂直,那么这条直线垂直于这个平面已知:,m n ''是平面α内的两条相交直线,直线l 与α的交点为B ,且,l m l n ''⊥⊥,求证:l α⊥证明:过点B 作//,//m m n n ''∵,l m l n ''⊥⊥ ∴,l m l n ⊥⊥,过B 任作直线a ,在l 上于α平面两侧分别截取BA BA '=,∴,m n 都是AA '的垂直平分线,∴,AD A D AC A C ''==,在a 上任取点E ,过E 在平面α内作不通过B 的直线分别与,m n 相交于点,C D ,∴ACD A CD '∆≅∆,∴ACD A CD '∠=∠,又AC A C '=,∴ACE A CE '∆≅∆,∴AE A E '=∴a l ⊥,∴l α⊥.三、讲解范例:例1 求证:如果两条平行直线中的一条垂直于一个平面,那么另一条也垂直于这个平面已知:a ∥b,a ⊥α 求证:b ⊥α证明:设m 是α内的任意一条直线 αααα⊥⇒⎭⎬⎫⊂⊥⇒⎭⎬⎫⊥⇒⎭⎬⎫⊂⊥b m m b b a m a m a // 本题的作用:要证b ⊥α,没有办法?而已知a ∥b ,只需证a ⊥α即可,在证题时起转移作用,但具体要证a ⊥α还需其他方法例2 过一点和已知平面垂直的直线只有一条已知:平面α和一点P求证:过点P 与α垂直的直线只有一条mb a α证明:不论P 在平面α内或外,设直线PA α⊥,垂足为A (或P )若另一直线PB α⊥,设,PA PBa αβ= ∴,PA a PB a ⊥⊥又∵,PA PB 在平面β所以过点P 与α垂直的直线只有一条例 3 有一根旗杆AB 高8m ,它的顶端A 挂一条长10m 的绳子,拉紧绳子并把它的下端放在地面上的两点(和旗杆脚不在同一直线上),C D ,如果这两点都和旗杆脚B 的距离是6m ,那么旗杆就和地面垂直,为什么?解:在ABC ∆和ABD ∆中,∵8,6,10AB m BC BD m AC AD m =====∴2222226810AB BC AC +=+== 2222226810AB BD AD +=+==∴90ABC ABD ∠=∠=即,AB BC AB BD ⊥⊥又∵,,B C D 不共线 ∴AB ⊥平面BCD ,即旗杆和地面垂直;例4 已知直线l ⊥平面α,垂足为A ,直线AP ⊥求证:AP 在α内证明:设AP 与l 确定的平面为β如果AP 不在α内,则可设α与β相交于直线AM∵l ⊥α,∴l ⊥AM又AP ⊥l ,于是在平面β内过点A 有两条直线垂直于l ,这是不可能的所以AP 一定在α内例5 求证:经过平面外一点有且只有一个平面和已知平面平行已知:P ∉α求证:过点P 有且只有一个平面β∥αEB A 证明:过平面α外一点P 作直线⊥l α,再过点P 作平面β,使⊥l β,则α∥β.因为过点P 且与α平行的平面必与α的垂线l 也垂直,而过点P 与l 垂直的平面是唯一的,所以过点P 且与α平行的平面只有一个.指出:由例2可得α∥β,α∥γ⇒β∥γ.例6 已知:空间四边形ABCD ,AB AC =,DB DC =,求证:BC AD ⊥证明:取BC 中点E ,连结,AE DE ,∵,AB AC DB DC ==,∴,AE BC DE BC ⊥⊥, ∴BC ⊥平面AED , 又∵AD ⊂平面AED , ∴BC AD ⊥.四、课堂练习:1.选择题(1)“直线l 垂直于平面α内的无数条直线”是“l ⊥α”的 ( )(A )充分条件(B )必要条件(C )充要条件(D )既不充分也不必要条件(2)如果一条直线l 与平面α的一条垂线垂直,那么直线l 与平面α的位置关系是( )(A )l ⊂α (B )l ⊥α (C )l ∥α (D )l ⊂α或l ∥α答案:(1)B (2)D2.填空题(1)过直线外一点作直线的垂线有 条;垂面有 个;平行线有 条;平行平面有 个.(2)过平面外一点作该平面的垂线有 条;垂面有 个;平行线有 条;平行平面有 个.答案:(1)无数,一,一,无数;(2)一,无数,无数,一3.能否作一条直线同时垂直于两条相交直线?能否作一条直线同时垂直于两个相交平面?为什么?答案:(能,而且有无数条) (不能) 拿一张矩形的纸对折后略为展开,竖立在桌面上,说明折痕为什么和桌面垂直答案:因为折痕垂直于桌面内的两条相交直线. 一条直线垂直于一个平面内的两条平行直线,这条直线垂直于这个平面吗?为什么?答案:不一定.因为这条直线可能与这个平面斜交或在其内. 6答案:是.假若有两个平面,αβ过点A 都于l 垂直,过这条公共垂线l 作一个不经过两平面,αβ的交线的平面γ,γ与,αβ分别相交于直线,,a b ab l A =且,l a l b ⊥⊥,,,l a b α⊂,从而有a b ,此与a b A =矛盾. 如果三条直线共点,且两两垂直,问其中一条直线是否垂直于另两条直线所确定的平面答案:是 8求证:一条线段的垂直平分面内任一点到这条线段两端点的距离相等 通过一条线段中点并且与这条线段垂直的平面,叫做这条线段的垂直平分面五、小结 :今天这节课,我们学习了直线和平面垂直的定义,这个定义最初用在判定定理的证明上,但用得较多的则是,如果直线l 垂直于平面α,那么l 就垂直于α内的任何一条直线;对于判定定理,判定线、面垂直,实质是转化成线、线垂直,从中不难发现立体几何问题解决的一般思路六、课后作业:七、板书设计(略)八、课后记:活动目的:教育学生懂得“水”这一宝贵资源对于我们来说是极为珍贵的,每个人都要保护它,做到节约每一滴水,造福子孙万代。
第九章 直线平面与简单几何体学生版

直线平面与简单几何体1、已知直线l ⊥平面α,直线m ⊂平面β,有下列四个命题:①α∥β⇒l ⊥m ;②α⊥β⇒ l ∥m ;③l ∥m ⇒α⊥β;④l ⊥m ⇒α∥β.其中正确的两个命题是 ( )A 、①与②B 、①与③C 、②与④D 、③与④1、B2、在正三棱锥中,相邻两侧面所成二面角的取值范围是( )A 、3ππ(,) B 、23ππ(,) C 、(0,2π) D 、23ππ(,)3 2、A3、如图,正方体ABCD -A 1B 1C 1D 1的棱长为1,点M 在A 上,且AM=31AB ,点P 在平面ABCD 上,且动点P 到直线A 1D 1的 距离的平方与P 到点M 的距离的平方差为 1,在平面直角坐标系xAy 中,动点P 的轨 迹方程是 .3、91322-=x y4.命题①空间直线a ,b ,c ,若a∥b,b∥c 则a∥c②非零向量、,若∥,∥则∥ ③平面α、β、γ若α⊥β,β⊥γ,则α∥γ ④空间直线a 、b 、c 若有a⊥b,b⊥c,则a∥c ⑤直线a 、b 与平面β,若a⊥β,c⊥β,则a∥c 其中所有真命题的序号是( )A .①②③ B.①③⑤ C.①②⑤ D.②③⑤ 5、(文)棱长为1的正方体ABCD -A 1B 1C 1D 1被以A 为球心,AB 为半径的球相截,则被截形体的表面积为( ) A .45π B .87π C .π D .47π选A6.某刺猬有2006根刺,当它蜷缩成球时滚到平面上,任意相邻的三根刺都可支撑住身体,且任意四根刺的刺尖不共面,问该刺猬蜷缩成球时,共有( )种不同的支撑身体的方式。
A .2006 B .4008 C .4012 D .2008 7.命题①空间直线a ,b ,c ,若a∥b,b∥c 则a∥c②非零向量c 、b 、a ,若a ∥b ,b ∥c 则a ∥c ③平面α、β、γ若α⊥β,β⊥γ,则α∥γ ④空间直线a 、b 、c 若有a⊥b,b⊥c,则a∥c ⑤直线a 、b 与平面β,若a⊥β,c⊥β,则a∥c 其中所有真命题的序号是( )A .①②③ B.①③⑤ C.①②⑤ D.②③⑤ 8、(文)棱长为1的正方体ABCD -A 1B 1C 1D 1被以A 为球心,AB 为半径的球相截,则被截形体的表面积为( )A .45π B .87π C .π D .47π 9、四边形ABCD 是︒=∠120A 的菱形,绕AC 将该菱形折成二面角D AC B --,记异面直线AC 、BD 所成角为α,AD 与平面ABC 所成角为β,当β+α最大时,二面角D AC B --等于( )A.3π B.2π C.2arctan D.22arctanBA xM10、将边长为3的正四面体以各顶点为顶点各截去(使截面平行于底面)边长为1的小正四面体,所得几何体的表面积为_____________ . .11.(理)在正三棱锥ABC S -中,M 、N 分别是棱SC 、BC 的中点,且AM MN ⊥,若侧棱32=SA ,则正三棱锥ABC S -外接球的表面积是( ) A .π12B .π32C .π36D .π4812、(文)已知ABCD 是同一球面上的四点,且每两点间距离相等,都等于2,则球心到平面BCD 的距离是( ) A .36B .66 C .126 D .186 13、正方体1111D C B A ABCD -,F E ,分别是1AA ,1CC 的中点,P 是1CC 上的动点(包括端点)过E 、D 、P 作正方体的截面,若截面为四边形,则P 的轨迹是 ( )A 、线段F C 1B 、线段CFC 、线段CF 和点1CD 、线段F C 1和一点C14、P 为ABC ∆所在平面外一点,PA 、PB 、PC 与平面ABC 所的角均相等,又PA 与BC 垂直,那么ABC ∆的形状可以是 。
第九章 直线、平面、简单的几何体

五. 例题
1. 两两相交且不过同一个点的三条 直线必在同一个平面内. 直线必在同一个平面内
2. 已知空间四边形 已知空间四边形ABCD, E、F、G、H 分别在边 、 、 、 AB、BC、CD、DA 上,并且 EH I FG = P 、 、 、 求证: 、 、 在同一直线上. 求证: B、D、P 在同一直线上
3. 推论 推论3
经过二条平行直线有且只有一个平面. 经过二条平行直线有且只有一个平面
α
A
b a
推论3 经过两条平行直线, 平行直线 推论 经过两条平行直线,有且只有一个平面
证明:设直线a 由平行线的定义, 证明:设直线a、b满足a平行于b ,由平行线的定义, 满足a平行于b 直线a 在同一平面内,这就是说,过直线a 直线a、b在同一平面内,这就是说,过直线a、b有平 面α。 设点A为直线a上任一点,则点A在直线b 设点A为直线a上任一点,则点A在直线b外,点A 和直线b在过直线a 的平面α 由公理3的推论1 和直线b在过直线a、b的平面α内,由公理3的推论1, 过点A和直线b的平面只有一个。过直线a 过点A和直线b的平面只有一个。过直线a、b的平面只 有一个。 有一个。
A ∈ l , B ∈ l , A ∈α , B ∈α ⇒ l ⊂ α
实例:当一直尺的边缘上任意两点放在平的桌 面上时,可以看到直尺的边缘就落在桌面上.
公理2 如果两个平面有一个公共点, 公理 如果两个平面有一个公共点,那么它们还 有其他公共点, 有其他公共点,且所有这些公共点的集合是一 条过这个公共点的直线。 条过这个公共点的直线。
1. 斜二测画法的规则: 斜二测画法的规则: (1)在已知图形中取水平平面,取互相垂直的轴 )在已知图形中取水平平面,取互相垂直的轴OX、 、 OY,画直观图时,把它画成对应的轴 O ′X ′、 O ′Y ′ , ,画直观图时,
数学高考复习名师精品教案:第82课时:第九章 直线、平面、简单几何体-球与多面体

数学高考复习名师精品教案第82课时:第九章直线、平面、简单几何体——球与多面体课题:球与多面体一.复习目标:1.了解多面体、正多面体的概念,了解多面体的欧拉公式,并利用欧拉公式解决有关问题;2.了解球、球面的概念, 掌握球的性质及球的表面积、体积公式, 理解球面上两点间距离的概念, 了解与球的有的内接、外切几何问题的解法.二.主要知识:1.欧拉公式;2.球的表面积;球的体积公式;3.球的截面的性质:.三.课前预习:1.一个凸多面体的顶点数为20,棱数为30,则它的各面多边形的内角和为( )D7200C6480 ()B5400 ()()A2160 ()2.一个四面体的所有棱长都为2,四个顶点在同一球面上,则此球的表面积是( )D6πC()()A3π()B4π()3.正四面体的中心到底面的距离与这四面体的高的比是 ( ) ()A 21 ()B 31 ()C 41 ()D 614.地球表面上从A 地(北纬45 ,东经120 )到B 地(北纬45 ,东经30 )的最短距离为(球的半径为R ) ( )()A 4Rπ ()B R π ()C 3Rπ ()D 2Rπ5.设,,,P A B C 是球O 面上的四点,且,,PA PB PC 两两互相垂直,若P A P B P C a===则球心O 到截面ABC 的距离是 . 四.例题分析:例1.已知三棱锥P A B C -内接于球, 三条侧棱两两垂直且长都为1, 求球的表面积与体积.例2.在北纬60 圈上有甲、乙两地,它们的纬度圆上的弧长等于2Rπ(R 为地球半径),求甲,乙两地间的球面距离。
例3.如图,球心到截面的距离为半径的一半,B C 是截面圆的直径,D 是圆周上一点,C A 是球O 的直径, (1) 求证:平面ABD ⊥平面A D C ; (2) 如果球半径是13,D 分 BC为两部分, 且 :1:2BD DC =,求A C 与BD 所成的角;(3) 如果:2BC D C =,求二面角B A C D --的大小。
第九章 直线、平面、简单几何体(B)
第九章直线、平面、简单几何体(B)课时作业45平面与空间直线时间:45分钟分值:100分一、选择题(每小题5分,共30分)1.若空间中有两条直线,则“这两条直线为异面直线”是“这两条直线没有公共点”的() A.充分非必要条件B.必要非充分条件C.充分必要条件D.既非充分又非必要条件答案:A2.设A,B,C,D是空间四个不同的点,在下列命题中,不正确...的是() A.若AC与BD共面,则AD与BC共面B.若AC与BD是异面直线,则AD与BC是异面直线C.若AB=AC,DB=DC,则AD=BCD.若AB=AC,DB=DC,则AD⊥BC答案:C3.在图1中,G、H、M、N分别是三棱柱的顶点或所在棱的中点,则表示直线GH、MN是异面直线的图形有()图1A.0个B.1个C.2个D.3个解析:题图(1)中,直线GH∥MN;图(2)中,G、H、N三点共面,但M∉面GHN,因此直线GH与MN异面;图(3)中GM∥HN,因此GH与MN共面;图(4)中,G、M、N三点共面,但H∉面GMN,∴GH与MN异面.所以图(2)、(4)中GH与MN异面.答案:C4.(2009·全国卷Ⅰ)已知三棱柱ABC-A1B1C1的侧棱与底面边长都相等,A1在底面ABC 上的射影为B图2C的中点,则异面直线AB与CC1所成的角的余弦值为( )A.34 B.54 C.74 D.34解析:设棱长为2,BC 的中点为D ,由题意,得AD = 3. 在Rt △A 1AD 中,A 1D =AA 21-AD 2=22-(3)2=1. 在Rt △A 1BD 中,A 1B =A 1D 2+BD 2= 2. ∵AA 1∥CC 1,∴AB 与AA 1所成的角∠A 1AB 即为AB 与CC 1所成的角. 在△A 1AB 中,由余弦定理,得cos ∠A 1AB =AA 21+AB 2-A 1B22AA 1·AB =4+4-22×2×2=34.答案:D5.直线l ⊂平面α,经过α外一点A 与l 、α都成30°角的直线有且只有( )A .1条B .2条C .3条D .4条解析:所求直线在平面α内的射影必与直线l 平行.这样的直线只有两条,故选B. 答案:B 6.(2008·辽宁高考)在正方体ABCD -A 1B 1C 1D 1中,E 、F 分别为棱AA 1、CC 1的中点,则在空间中与三条直线A 1D 1、EF 、CD 都相交的直线( )A .不存在B .有且只有两条C .有且只有三条D .有无数条解析:分别在异面直线A 1D 1、CD 上各任取一点M 、N ,则线段MN 的中点的轨迹构成一个平面α,显然直线EF 在平面α内.在EF 上任取一点P ,点P 和直线A 1D 1确定的平面与直线CD 交于点Q ,显然直线QP 与直线A 1D 1必有交点R ,即这样的直线有无穷多条.故选D.答案:D二、填空题(每小题4分,共20分)7.已知空间四边形的对角线相等,顺次连结它的各边中点所成的四边形是________. 解析:根据三角形中位线定理,连结各边中点的四边形的边分别等于对角线的一半,且对边分别平行,则构成平面图形,并且是平行四边形,再由四条边相等,即可判断为菱形.答案:菱形8.正方体ABCD -A 1B 1C 1D 1中,M 、N 、Q 分别为AB 、BB 1、C 1D 1的中点,过M 、N 、Q 的平面与正方体相交,截得的图形是________.解析:设正方体ABCD -A 1B 1C 1D 1中,P 、R 、S 分别为B 1C 1、D 1D 、AD 的中点,则六边形MNPQRS 即为平面MNQ 与正方体相交所得的截面图形,并且它是正六边形.∵面ABB 1A 1∥面CDD 1C 1,设平面MNQ 与平面DCC 1D 1的交线为R ′Q .则MN ∥QR ′. 而QR ∥DC 1∥AB 1∥MN ,据平行公理知过点Q 与MN 平行的直线有且只有一条. ∴QR 与QR ′重合,即R 与R ′重合(R ′为D 1D 的中点). ∵MN 不平行于A 1B 1,∴MN 与A 1B 1必相交,设交点为K ,可证得B 1K =BM .同理QP 与A 1B 1也一定相交,交点为K ′,且B 1K ′=QC 1=MB =B 1K .∴MN 与QP 相交于点K .于是过点M 、N 、Q 的平面MNQR 与平面MNPQ 重合, 即M 、N 、P 、Q 、R 共面于MNQ . 同理可证S 点也在此平面MNQ 内. 所以平面MNPQRS 是一平面图形. 易证得MN =PN =QP =QR =RS =SM .由等角定理可知∠MNP =∠QRS , ∠QPN =∠MSR ,∠SMN =∠RQP .连结MQ ,易证QM ∥PN ,在等腰梯形MNPQ 中, ∠QPN =∠MNP ,同理∠PQR =∠QPN .∴∠SMN =∠MNP =∠NPQ =∠PQR =∠QRS =∠RSM . ∴MNPQRS 为正六边形. 答案:正六边形9.(2009·四川高考)如图3,已知正三棱柱ABC -A 1B 1C 1的各条棱长都相等,M 是侧棱CC 1的中点,则异面直线AB 1和BM 所成的角的大小是______.图3解析:建立如图4所示的坐标系,O 为BC 中点,设三棱柱的棱长为2a ,则点A (3a,0,0),B (0,a,0),B 1(0,a,2a ),图4M (0,-a ,a ),则AB 1→·BM →=0,所以异面直线AB 1与BM 所成的角为90°. 答案:90°10.过正方体任意两个顶点的直线共有28条,其中异面直线有________对. 解析:由于以正方体的某四个顶点可以形成C 48-(6+6)=58个三棱锥(注:先从8个顶点中任选4个顶点有C 48种选法,其中四点共面的情形有两类:一类是所选的四个顶点恰好是某一个面的四个顶点时,此类有6种;另一类是所选的四个顶点刚好是该正方体的某一个对角面的四个顶点时,此类也有6种),而每个三棱锥的四条棱间能够形成3对异面直线,因此满足题意的异面直线对共有58×3=174对.答案:174三、解答题(共50分)11.(15分)如图5,在正方体ABCD -A 1B 1C 1D 1中,O 为正方形ABCD 的中点,H 为直线B 1D 与平面ACD 1的交点.求证:D 1、H 、O 三点共线.证明:连结BD ,B 1D 1则BD ∩AC =O ,如图6, ∵BB 1綊DD 1,∴四边形BB 1D 1D 为平面图形且为平行四边形,又H ∈B 1D ,B 1D ⊂平面BB 1D 1D ,则H ∈平面BB 1D 1D ,∵平面ACD 1∩平面BB 1D 1D =OD 1,∴H ∈OD 1. ∴D 1、H 、O 三点共线.图5图612.(15分)在正方体ABCD -A 1B 1C 1D 1中E 、F 分别为BB 1、CC 1的中点,求AE 、BF 所成角的余弦值.图7解:如图7,取DD 1中点M ,连结AM 、MF 、ME ,由AB 綊CD 綊MF 知四边形ABFM 为平行四边形∴AM ∥BF ,则AM 与AE 所夹锐角或直角为异面直线所成的角,设AB =1, 则在△AEM 中AE =AM =52,ME =2,∴cos ∠MAE =AM 2+AE 2-ME 22AM ·AE =15,即异面直线AE 、BF 所成角的余弦值为15.13.(20分)(2009·广东高考)如图8,已知正方体ABCD -A 1B 1C 1D 1的棱长为2,点E 是正方形BCC 1B 1的中心,点F ,G 分别是棱C 1D 1,AA 1的中点.设点E 1,G 1分别是点E ,G 在平面DCC 1D 1内的正投影.图8(1)求以E 为顶点,以四边形FGAE 在平面DCC 1D 1内的正投影为底面边界的棱锥的体积;(2)证明:直线FG 1⊥平面FEE 1;(3)求异面直线E 1G 1与EA 所成角的正弦值.解:(1)依题作点E 、G 在平面DCC 1D 1内的正投影E 1、G 1,则E 1、G 1分别为CC 1、DD 1的中点,连结EE 1、EG 1、ED 、DE 1,则所求为四棱锥E —DE 1FG 1的体积,其底面DE 1FG 1的面积为(2)证明:以D 为坐标原点,DA 、DC 、DD 1所在直线分别作x 轴,y 轴,z 轴,得E 1(0,2,1)、G 1(0,0,1),图9又G (2,0,1),F (0,1,2),E (1,2,1), 则FG 1→=(0,-1,-1),FE →=(1,1,-1),FE 1→=(0,1,-1), ∴FG 1→·FE →=0+(-1)+1=0, FG 1→·FE 1→=0+(-1)+1=0,即FG 1⊥FE ,FG 1⊥FE 1. 又FE 1∩FE =F ,∴FG 1⊥平面FEE 1.(3)E 1G 1→=(0,-2,0),EA →=(1,-2,-1),则cos 〈E 1G 1→,EA →〉=E 1G 1→·EA → |E 1G 1→||EA →|=26.设异面直线E 1G 1与EA 所成角为θ,则sin θ=1-23=33.∴异面直线E 1G 1与EA 所成角的正弦值为33.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第九章 直线 平面 简单几何体9.1三视图与空间坐标系1.(16北京 文11)某四棱柱的三视图如图所示,则该四棱柱的体积为__________.21侧(左)视图正(主)视图11【审题要津】由题设三视图,易知该几何体是以等腰梯形为底面的直四棱柱.以下只需根据图示数据,即可求解.解:依审题要津,所求为()1213122V +⨯=⨯=,故填32.【解法研究】依照三视图正确还原几何体是顺利求解的关键.(王墨森)2.(16浙江 文9理11)某几何体的三视图如图所示(单位:cm ),则该几何体的表面积是_______2cm ,体积是_______3cm【审题要津】由题设三视图可知,该几何体是如图所示的两个长方体的组合.据此即可根据题设数据求解.俯视图侧视图正视图222222244221121解:由每个长方体的表面积为()()22242440⨯⨯+⨯⨯=()2cm ,则知两个长方体的表面积为80()2cm ,注意到重合部分面积为()2228⨯⨯=()2cm ,故该几何体的表面积为80872-=()2cm ,而该几何体的体积则为()222432⨯⨯⨯=()3cm ,故填72,32.【解法研究】如由图示中阴影部分的面积为4()2cm ,而得所求面积为80476-=()2cm ,实属粗枝大叶.(王墨森)3.(16山东 文5理5)一个由半球和四棱锥组成的几何体,其三视图如图所示.则该几何体的体积为( ).A .1233+πB .1233+πC .1236+πD .216+π 【审题要津】结合主,左视图,进而关注俯视图中的实线和虚线,易知该几何体为半球与四棱锥的组合体,且作直径为边长为1的正方形对角线.据此即可根据题设给出的数据求解.解:依审题要津,3214212111232363V ⎛⎫=⨯π⨯+⨯⨯=π+ ⎪ ⎪⎝⎭.选C . 【解法研究】对于由不同几何体组合而成的几何体,关注其数量关系的同时,更要关心其位置关系.(李青峰)4.(16天津 文3)将一个长方形沿相邻三个面的对角线截去一个棱锥,得到的几何体的正视图与俯视图如图所示,则该几何体的侧(左)视图为( ).A .B .C .D .【审题要津】由题设长方体的正视图及俯视图,易知还原后的几何体为如解图所示的正四棱柱.注意到截割线的布局,问题易解. 解:继审题要津,选B .【解法研究】调准角度,缕清实线与虚线的不同意味,是顺利求解的关键.(王成维)5.(16新课标Ⅰ 文7理6)如图,某几何体的三视图是三个半径相等的圆俯视图111俯视图正视图及每个圆中两条相互垂直的半径.若该几何体的体积是283π,则它的表面积是( ). A .17πB .18πC .20πD .28π【审题要津】由题设三视图可知,该几何体是缺失了18的球体,其表面积是由78的球面及34个球大圆组成的.据此即可求解.解:继审题要津,设该几何体的体积和表面积分别是V S ,,则由374833V R 28π=⨯π=,可得2R =,进而可得2273484S R R =⨯π+⨯π=17π,故选A . 【解法研究】可借助右图的直观图理解审题要津的分析.(邵德彪)6.(16北京 理6)某三棱锥的三视图如图所示,则该三棱锥的体积为( ).A .16 B .13C .12D .1【审题要津】针对所求,首先应关注该三棱锥的高.由“主,左同高”,易知1h =,进而结合三视图, 可知三棱锥的底面为两直角边均为1的等腰直角三 角形,据此即可求解.解:依审题要津,该三棱锥的体积为11111326V =⨯⨯⨯=,故选A . 【解法研究】针对所求,在得知三棱锥的高1h =的基础上,对其底面的研究则是关键.本题标注字母,尤其是在题图中标注重叠字母的方法,既是“空间想象力”的“产品”,又是支持“空间想象力”的资源.借此沟通和整理三视图之间的“默契”,体现的也是数学思维的整体思想.据此还原出如解图所示的三棱锥的本来面目则不在话下.(王墨森)7.(16新课标Ⅲ 文10理9)如图,网格纸上小正方形的边长为1,粗实现画出的是某多面体的三视图,则 该多面体的表面积为( ).A .18365+B .54185+C .90D .81【审题要津】由三视图中标注的字母,可知该多1C A AC ) )侧(左)视图正(主)视图1111D DB AC面体是一个如图所示的斜四棱柱1111ABCD A B C D -, 其底面ABCD 是边长为3的正方形,且1A B ⊥平面ABCD ,16A B =.解:依审题要津,上下底面的面积均为339⨯=,前 后两个面的面积均为3618⨯=,由1A B ⊥平面ABCD 知1A B BC ⊥,又BC AB ⊥知BC ⊥平面11ABB A ,于是1BC BB ⊥,故四边形11BCC B 是矩形,又2213635AA =+=,所以左右两个面的面积均为95,由此可见,该四棱柱的表面积为54185+,故选B .【解法研究】解题的关键是由三视图分析出直观图,若以11ABB A ,11CDD C 为上,下底面,则此几何体为直四棱柱.(洪汪宝)8.(15安徽 文9理7)一个四面体的三视图如图所示,则该四面体的表面积是( ).A .13+B .122+C .23+D .22【审题要津】依题设,已知三视图还原成的四面体为如图所示的三棱锥S ABC -.在这里,平面SAC ⊥平面ABC ,点O 为AC 的中点.注意到其中相关线段上的数据标注,问题易解.解:继审题要津,显然有22112SB AB BC ===+=,所以SAB △与SBC△均为边长为2的等边三角形.与此同时,可知SAC BAC △≌△.综上可得,该四面体的表面积为()2312221232S ⎡⎤=⋅+⨯⨯=+⎢⎥⎣⎦,故选C . 【解法研究】注意到平面SAC ⊥平面ABC 是顺利求解的关键.(刘绍峰)9.(15新课标Ⅰ 文11理11)圆柱被一个平面截去一部分后与半球(半径为r )组成一个几何体,该几何体三视图中的正视图和俯视图如图所示,若该几何体的表面积为162+π,则r =( ).A .1B .2C .4D .8【审题要津】由题设几何体的正视图和俯视图,易知该几何体是由半个圆柱和半个球体组合而成的几何体.其直观图如图所示.据此即可根据相关数据确定r 值. 解:继审题要津,该几何体的表面积S 是由:①以r 为半径的半球面;r2rr2r1112121221正(主)视图侧(左)视图俯视图111122SO AC②以r 为半径的圆;③边长为2r 的正方形;④底面圆半径为r ,高为2r 的半圆柱的侧面展开图,四部分组成的,从而有()222221422542S r r r r r r r =⋅π+π++π⋅=π+ 于是由22542016r r π+=π+,解得4r =,故选C .【解法研究】依题设画出该几何体的直观图是难点,也是顺利求解的关键.(刘绍峰)10.(15北京 理5)某三棱锥的三视图如图所示,则该三棱锥的表面积是( ).A .25+B .45+C .225+D .5【审题要津】根据主、左同高;主、俯同宽的原则,又及题设三视图中标注的数据,易知还原后的几何体是如图所示的三棱锥S ABC -.其中ABC △及SAB △均为等腰三角形.设点D 为AB 的中点,联结SD CD ,,易知AB SD ⊥,AB CD ⊥.据此即可根据几何体中标注的相关数据求其表面积.解:继审题要津,在Rt SCD △中,2222125SD SC CD =+=+=. 在Rt SDB △中,()2222516SB SD BD =+=+=.在Rt SBC △中,()222615BC SB SC =-=-=.综上可知,三棱锥S ABC -的表面积 2SBC ABC SAB S S S S =++=△△△()()11525222522SC BC CD AB SD AB ⋅+⋅+⋅=++⨯=+,故选C . 【解法研究】关注三棱锥S ABC -的对称性,是从简求解的关键.(侯守一)11.(15福建 文9)某几何体的三视图如图所示,则该几何体的表面积等于( ).A .822+B .1122+C .1422+D .15【审题要津】由题设三视图及其中标注的数据,易知该几何体是一个如图所示的上、下底面为直角梯形的直四棱柱,其各棱之长如图标注.21正(主)视图侧(左)视图俯视图SD A 2111112解:继审题要津,该几何体的上、下两底面的面积之和为()11212132S ⎡⎤=+⨯=⎢⎥⎣⎦;侧面的4个矩形的面积之和为()211222822S =+++⨯=+,从而所求为121122S S S =+=+,故选B .【解法研究】审视三视图的要领,一是要关注实、虚线;二是要关注其中标注的数据.(刘绍峰)12.(15北京 文7)某四棱锥的三视图如图所示,该四棱锥最长棱的棱长为( ).A .1B .2C .3D .2【审题要津】由题设三视图,兼顾俯视图正方形中的对角线,易知还原后的几何体为如图所示的四棱锥S ABCD -,其中平面SBC 及平面SCD 均垂直于底面正方形ABCD ,且SBC △与SCD △均为腰长为1的等腰直角三角形.注意到1SC BC CD ===,则问题易解. 解:继审题要津,由SC ⊥平面ABCD ,又1SC BC CD AD AB =====,则知22112SB SD ==+=. 联结AC .由2AC =,则知()2222123SA SC AC =+=+=.故四棱锥S ABCD -中最长棱的棱长3SA =,选C .【解法研究】如果你能在如上的直观图中适当添加辅助线,你就会清楚:三视图还原成的四棱锥是由棱长为1的正方形截去两个与四棱锥S ABCD -完全相同的四棱锥后之所得.显然所求即为正方形的体对角线之长.(陈小鹏)13.(15新课标Ⅱ 文6理6)一个正方体被一个平面截去一部分后,剩余部分的三视图如图所示,则截去部分体积与剩余部分体积的比值为( ).A .18B .17 C .16D .15【审题要津】依题意,题设三视图所表示的几何体,是如图所示的正方体被截去一个三棱锥后的剩余部分.在这里,先关注三视图中的三个正方形,进而1221111 AS111正(主)视图侧(左)视图俯视图考察其中的对角线.这一审图意识至关重要.解:继审题要津,设原正方体的棱长为a ,则截去的三棱锥的体积为23111326a a a ⋅⋅=,于是剩余部分的体积为356a .从而所求为15,故选D . 【解法研究】如将截去的部分视为底面是腰长为a 的等腰直角三角形,高为a 的三棱锥,则知截去的体积为原正方体体积的16. (刘金泉)14.(15湖南 理10)某工件的三视图所示,现将该工件通过切削,加工成一个体积尽可能大的长方体,并使新工件的一个面落在原工件的一个面内,则原工件材料的利用率为( ). (材料利用率=新工件的体积/原工件的体积)A .89π B .169π C .)3421πD .)21221π【审题要津】由题设三视图及图中所标注的数据,易知原工件是一个底面圆半径为1,其高为2的圆锥.针对所求,如图所示,作该圆锥的轴截面PAB ,并使其过下底面在圆锥底面上的长方体的上底面的两个顶点E F ,.显然EF 即是长方体上底面矩形的对角线.为了求出长方体的体积,不妨设其长,宽,高分别为a b h ,,,并设其上,下底面的中心分别为1O ,2O .过E F ,两点作AB 的垂线,垂足分别为E F '',.显然12O F O F r '==,且01r <<.注意到12Rt Rt PO F PO B △∽△,则知1122PO O F PO O B =,即221h r-=,即22h r =-.于是长方体的体积为()22V abh ab r ==-.以下只需将ab 用r 来表示,即可利用函数的单调性完成所求.解:继审题要津,由()2222124a b O F r +==,可得()()()22222222222a b V ab r r r r +=-⋅-=-≤,()01r <<.当且仅当a b =,即长方体上,下底面均为正方形时,等号成立.令()2344 01y r r r =-<<,则2812y r r '=-,由0y '=,可得0r =或23r =.由此可见,当203r <<时,0y '>;当213r <<时,0y '<,故当23r =时,23max 226443327y ⎛⎫⎛⎫=⨯-⨯= ⎪ ⎪⎝⎭⎝⎭,即max 627V =.又圆锥的体积为2121233ππ⨯⨯=,因此所求为16382729⨯=ππ,故选A . 【解法研究】从作圆锥的轴截面入手是顺理成章的,使长方体上,下底面的长方形的对角线为轴截rO 2F E P O 1正视图侧视图俯视图112222面截圆锥的“切痕”更是必要的.对此应认真领会.本题在求导之前用到了且利用“均值不等式”推导了这样一个结论:圆内接矩形中,当长,宽相等时,即矩形为正方形时,其面积最大.对此也应有所感悟.(侯守一)15.(14安徽 文8理7)一个多面体的三视图如图所示,(文)则该几何体的体积是( ).A .233 B .476 C .6D .7(理)则该几何体的表面积为( ). A .213+ B .183+ C .21D .18【审题要津】针对所求,首先应画出该多面体的直观图.注意到题设三视图所标注的数据,应当想到该几何体的“母本”是一个正方体.为此可建立空间直角坐标系,并在其中构造如图所示的正方体1111ABCD A B C D -.解:继审题要津,结合三视图中标注的数据及其中实、虚斜线段的位置关系,易知该几何体是由正方体1111ABCD A B C D -在右后和左上分别截去小三棱锥1D MPN -及B EFG -所得.其体积为11232222111323V =⨯⨯-⨯⨯⨯⨯⨯=; 其表面积为()21364222132S ⎛⎫=⨯-+⨯⨯=+ ⎪⎝⎭,故文选A ,理选A .【解法研究】如解对照坐标系中的几何体的诸关键点所标注的字母,在三视图中也作出相应的标注,则对理解这种解法的思路,会更有帮助.(邵德彪)16.(14北京 理7)在空间直角坐标系O xyz -中,已知,()()()2 0 0 2 2 0 0 2 0A B C ,,,,,,,,,(1 12D ,,.若123S S S ,,分别是三棱锥D ABC -在xOy yOz zOx ,,坐标平面上的正投影图形的面积,则( ).A .123S S S ==B .21S S =且23S S ≠C .31S S =且32S S ≠D .32S S =且31S S ≠【审题要津】如图,在空间坐标系中描出A ,B ,C ,D 各点,并作出各点在三个坐标平面上的投影点,即可得到三棱锥D ABC -在各yzO D 2D 1S 3S 2S 1DC B A222111x yzGPN MD 1 A 1DFEC 1B 1CB A111111111111俯视图侧视图正视图坐标平面内的正投影,分别计算其面积即可作答.解:如图,点D 在xOy 面上的投影点()1 1 0,,恰好为AC 的中点;点D ,A ,B 在yOz 面上的投影分别为1D ()0 1 2,,,O ,C ;点D ,B ,C 在zOx 面上的投影分别为点2D ()1 0 2,,,A ,O ,于是121232 2ABC D OC D AO S S S S S S ======,△△△于是有123S S S >=,故选D .【解法研究】应熟悉以下规律:点()P x y z ,,在xOy ,yOz ,zOx 三个坐标平面上的正投影分别为()1 0P x y ,,,()20P y z ,,,()3 0P x z ,,.事实上,在O xyz -坐标系中描绘点()P x y z ,,,常常是先确定()1 0P x y ,,,而后将其沿Oz 方向平移z 个单位得到的.(邵德彪)17.(14湖北 文7理5)在如图所示的空间直角坐标系O xyz -中,一个四面体的顶点坐标分别是()0 0 2,,,()()()2 2 01 2 12 2 2,,,,,,,,.给出编号为①,②,③,④的四个图,则该四面体的正视图和俯视图分别为( ).A .①和②B .③和①C .④和③D .④和②【审题要津】为便于在空间直角坐标系中准确地描绘出题设四面体的四个顶点,不妨如图,先在空间直角坐标系中构造一个棱长为2的正方体1111ABCD A B C D -.解:继审题要津,显然有()10 0 2A ,,,()2 2 0C ,,,()12 2 2C ,,,而()1 2 1M ,,自然是正方形11CDD C 的中心.如图所示,该四面体11ACMC 的正视图为yOz 面内的11Rt A DD △(其中1M 为1DD 的中点);俯视图为xOy 面内的ACN △(其中N 为CD 的中点).对照四个选项,选D .【解法研究】借助构造正方体,并从三视图的原理入手,有助于弥补空间想象力的不足.(王成维)yz x N B 1AMD 1BC 1C M1A 1OD 222111③ ④②①yz xO2221 11。
