回归分析曲线拟合讲解
sup曲线拟合与回归分析 ppt课件

在一般情況下,只能找到一組 ,使得等號兩邊的
差異為最小,此差異可寫成
yA 2(yA )T(yA )
此即為前述的總平方誤差 E
MATLAB 提供一個簡單方便的「左除」(\)指
令,來解出最佳的
2020/12/27
10
線性迴歸:曲線擬合
利用「左除」來算出最佳的 值,並同時畫出 具有最小平方誤差的二次曲線
、
0
a
1、a
的一次式
2
令上述導式為零之後,我們可以得到一組三元一次
線性聯立方程式,就可以解出參數 佳值。
a
0、
a
1、a
的最
2
2020/12/27
8
線性迴歸:曲線擬合
假設 21 個觀察點均通過此拋物線,將這 21 個點帶入拋物線方程式,得到下列21個等式:
a0 a1 x1 a2 x12 y1 a0 a1 x2 a2 x2 2 y2
範例10-2: census01.m
load census.mat plot(cdate, pop, 'o');
% 載入人口資料 % cdate 代表年度,pop 代表人口總數
A = [ones(size(cdate)), cdate, cdate.^2];
y = pop; theta = A\y;
a0 a1 x21 a2 x212 y21
亦可寫成
1 1
x1
x2
x12 x22
1
2
y1
y2
1
x 21
x
212
3
y21
A
y
其中 2020/12/27
spss曲线拟合与回归分析
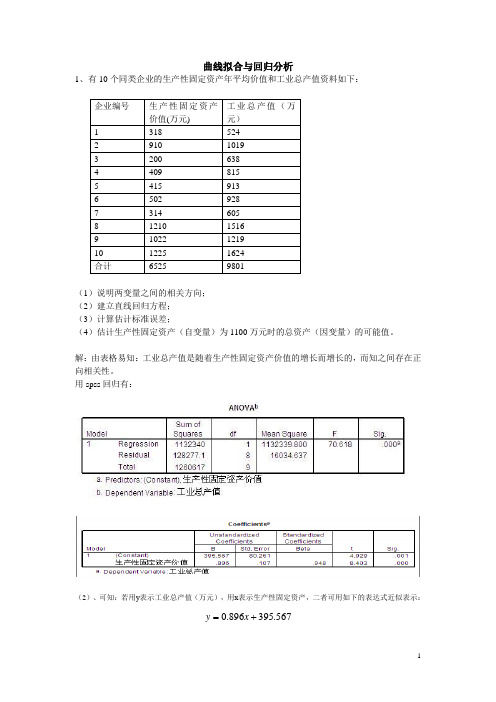
曲线拟合与回归分析1、有10个同类企业的生产性固定资产年平均价值和工业总产值资料如下:(1)说明两变量之间的相关方向;(2)建立直线回归方程;(3)计算估计标准误差;(4)估计生产性固定资产(自变量)为1100万元时的总资产(因变量)的可能值。
解:由表格易知:工业总产值是随着生产性固定资产价值的增长而增长的,而知之间存在正向相关性。
用spss回归有:(2)、可知:若用y表示工业总产值(万元),用x表示生产性固定资产,二者可用如下的表达式近似表示:=x.0+y.567395896(3)、用spss回归知标准误差为80.216(万元)。
(4)、当固定资产为1100时,总产值可能是(0.896*1100+395.567-80.216~0.896*1100+395.567+80.216)即(1301.0~146.4)这个范围内的某个值。
另外,用MATLAP也可以得到相同的结果:程序如下所示:function [b,bint,r,rint,stats] = regression1x = [318 910 200 409 415 502 314 1210 1022 1225];y = [524 1019 638 815 913 928 605 1516 1219 1624];X = [ones(size(x))', x'];[b,bint,r,rint,stats] = regress(y',X,0.05);display(b);display(stats);x1 = [300:10:1250];y1 = b(1) + b(2)*x1;figure;plot(x,y,'ro',x1,y1,'g-');industry = ones(6,1);construction = ones(6,1);industry(1) =1022;construction(1) = 1219;for i = 1:5industry(i+1) =industry(i) * 1.045;construction(i+1) = b(1) + b(2)* construction(i+1);enddisplay(industry);display( construction);end运行结果如下所示:b =395.56700.8958stats =1.0e+004 *0.0001 0.0071 0.0000 1.6035industry =1.0e+003 *1.02201.06801.11601.16631.21881.2736construction =1.0e+003 *1.2190 0.3965 0.3965 0.3965 0.3965 0.3965200400600800100012001400生产性固定资产价值(万元)工业总价值(万元)2、设某公司下属10个门市部有关资料如下:(1)、确定适宜的 回归模型; (2)、计算有关指标,判断这三种经济现象之间的紧密程度。
第八章 曲线拟合、回归和相关讲解

t
( y0 yp ) n 2
sy.x n 1 [n(x0 x)2 / sx2 ]
有n-2个自由度的t分布。由此能求得预报得总体值
得置信限
2 预报的平均值的假设检验
设y0是x=x0时y的预报值,它是从样本回归方程得到 的估计,即y0=a+bx0。设y p记对总体而言对应x=x0的y 的预报平均值,那么统计量
y=+x。下面是与正态分布有关的一些检验:
1 假设=c的检验
为了检验假设:回归系数等于某一特定值c,使
用统计量
t b n2
sy.x / sx
它具有n-2自由度的t分布。此结论也可用于从样本 值求总体回归系数的置信区间
2 预报值的假设检验
设y0是x=x0时y的预报值,它是从样本回归方程得到 的估计,即y0=a+bx0。设yp记对总体而言对应x=x0的y的 预报值,那么统计量
将所有点代入直线方程后相加,我们得到
y=an+bx(或 y a b x)
以及 xy=ax+bx2
这两个方程称为最小二乘的正规方程。由上 面的方程组我们可以达到a,b分别为:
a
yx2 nx2
xxy (x)2
,
b
nxy nx2
xy (x)2
, 其中b也可以写成
最小二乘法
若在近似n个数据点的集合
时,对一给定的曲线族的全
部曲线,其中有一条曲线的
性质:
d12
d
2 2
...
d
2 n
达最小值,则称该曲线为给 定曲线族中的最佳拟合曲 线。 有这样性质的一条曲线称为 在最小二乘意义上对数据的 拟合,该曲线称为最小二乘 回归曲线
回归分析(曲线拟合)算法探究

yi )
0
Q(a, b)
b
m
2 (a bxi
i 1
yi )xi
0
整理得到拟合曲线满足的方程:
ma
(
m i 1
xi )b
m i 1
yi
m
m
m
(
i 1
xi )a
(
i 1
xi2 )b
xi yi
i 1
最小二乘算法介绍
上式称为拟合曲线的法方程,可用消元法或者克莱姆方法解得:
m
yi
a i1 m xi yi i1
属性
text text text text Caption Caption Caption Caption Caption Caption Caption Caption Caption Scale Caption Caption Caption
值
自变量的观测值 因变量的观测值
X坐标名称 Y坐标名称 拟合类型 三次样条函数插值 最小二乘法 对数拟合 双曲线拟合 指数拟合
m
xi
i1
m
xi2
i1
m
m
xi
mm
mm
m
m
m
i1 m
( yi xi2 xi xi yi ) (m xi2 ( xi )2
xi
xi2
i1 i1
i1 i1
i1
i1
i1
i1
m
m
m
m
mHale Waihona Puke b (m xi yi xi yi ) (m xi2 ( xi )2 )
i 1
i1 i1
CH3COOC2H5 +Na+ +OH- = CH3 COO- +Na++C2H5OH 设NaOH和CH3COOC2H5 的初始浓度分别为a和b. 当a = b时, 有线性方程
回归分析曲线拟合通用课件

研究生物标志物与疾病之间的 关系,预测疾病的发生风险。
金融市场分析
分析股票价格、利率等金融变 量的相关性,进行市场预测和 风险管理。
社会科学研究
研究社会现象之间的相关关系 ,如教育程度与收入的关系、 人口增长与经济发展的线性回归模型
线性回归模型是一种预测模型,用于描 述因变量和自变量之间的线性关系。
SPSS实现
SPSS实现步骤 1. 打开SPSS软件; 2. 导入数据;
SPSS实现
01
3. 选择回归分析命令;
02
4. 设置回归分析的变量和选项;
03
5. 运行回归分析;
04
6. 查看并解释结果。
THANKS
感谢观看
回归分析曲线拟合通用课件
• 回归分析概述 • 线性回归分析 • 非线性回归分析 • 曲线拟合方法 • 回归分析的实践应用 • 回归分析的软件实现
01
回归分析概述
回归分析的定义
01
回归分析是一种统计学方法,用 于研究自变量和因变量之间的相 关关系,并建立数学模型来预测 因变量的值。
02
它通过分析数据中的变异关系, 找出影响因变量的主要因素,并 建立回归方程,用于预测和控制 因变量的取值。
线性回归模型的假设包括:误差项的独立性、误差项的同方差性、误差 项的无偏性和误差项的正态性。
对假设的检验可以通过一些统计量进行,如残差图、Q-Q图、Durbin Watson检验等。如果模型的假设不满足,可能需要重新考虑模型的建立 或对数据进行适当的变换。
03
非线性回归分析
非线性回归模型
线性回归模型的局限性
回归分析的分类
01
02
03
一元线性回归
生物统计学课件--17曲线拟合(回归)

一、对数函数曲线的拟合
1、对数方程的一般表达式: yˆ a b lg x
2、对数曲线 yˆ a b lg x 的图象
3、 yˆ a b lg x 直线化方法:
若令 lg x x` ,则有 yˆ a bx`
4、求 a 和 b 的值:
b SSx`y , SSx`
a y b x`
将up= y`= 0 代入 y`= a + bx`, 则有 :0 = a + bx`,
则有:x`= -a/b,
a
因为 x` = lgx,所以 x 10 b
此时的x即为半致死剂量,用LD50表示。
a
LD50 10 b
例题:用不同剂量的 射线照射小麦品种库斑克, 调查死苗率,得到以下结果:
剂量(Kr)x 14
a 10a` 101.6706 0.0214 b 10b` 100.1181 1.3125
yˆ 0.0214 1.3125 x
350
300
250
200
150
100
50
0
15
20
25
30
35
40
回归关系的检验:可以利用 b` 或者 r 进行检验,主要是对线 性关系的检验,线性回归或相关显著,则指数回归关系的拟 合就显著。
答:半致死剂量为18.6(Kr)
五、曲线的检验
有时将同一组数据,我们将其做指数函数或幂函数形式的变 换,都能得到X与Y的拟合曲线,并且可能在做线性回归关 系检验的时候,线性关系都显著,那么,究竟哪一条拟合曲 线是最好的呢?
一般情况下,以剩余平方和或称之为误差平方和的大小来判
断,即SSe最小时的拟合曲线为最好的曲线。
第五节 曲线拟合(非线性回归分析)
回归拟合曲线

回归拟合曲线回归拟合曲线是一种数据分析方法,用于确定数据之间的关系模式。
它可以帮助我们预测未来的趋势和变化。
本文将介绍回归拟合曲线的基本概念、常见的回归方法以及如何使用这些方法进行曲线拟合。
回归拟合曲线是通过找到最佳拟合线来描述两个或多个变量之间的关系。
拟合曲线可以是线性的,也可以是非线性的。
线性回归使用一条直线来拟合数据,而非线性回归使用其他类型的函数来拟合数据。
回归分析通常用于预测一个变量的值,基于已知的自变量值。
在回归拟合曲线中,有两个主要的变量:自变量和因变量。
自变量是我们用来预测因变量的变量,而因变量是我们想要预测的变量。
我们假设自变量能够解释因变量的变化。
回归分析的目标是找到自变量和因变量之间的关系,并使用这种关系来预测未来的因变量。
回归分析有很多不同的方法,包括线性回归、多项式回归、指数回归等。
线性回归是最简单的回归方法之一,它使用一条直线来拟合数据。
线性回归的基本原理是找到一条直线,使得这条直线与数据点的距离最小。
这种方法被广泛应用于各种领域,例如经济学、统计学和工程学等。
多项式回归是一种非线性回归方法,它使用多项式函数来拟合数据。
它可以适应各种曲线形态,并能更好地拟合非线性数据。
多项式回归的原理是在数据中添加多项式项,使得拟合曲线能够更好地适应数据点。
通过选择合适的多项式次数,我们可以调整曲线的形状和适应性。
指数回归是一种应用较广泛的非线性回归方法,它使用指数函数来拟合数据。
指数回归在研究生长速度、衰变速度等方面非常有用。
指数回归的原理是将因变量和自变量取对数,使拟合曲线变为线性形式。
然后使用线性回归分析来获得最佳拟合直线。
在进行回归拟合曲线之前,我们需要明确两个事项:回归分析的目标和回归模型的选择。
回归分析的目标是什么,决定了我们要解决什么问题。
回归模型的选择取决于我们的数据类型和问题需求。
回归分析在实际应用中非常有价值。
例如,在销售预测中,我们可以使用历史销售数据来预测未来销售额。
spss曲线拟合与回归分析

曲线拟合与回归分析1、有10个同类企业的生产性固定资产年平均价值和工业总产值资料如下:(1)说明两变量之间的相关方向;(2)建立直线回归方程;(3)计算估计标准误差;(4)估计生产性固定资产(自变量)为1100万元时的总资产(因变量)的可能值。
解:由表格易知:工业总产值是随着生产性固定资产价值的增长而增长的,而知之间存在正向相关性。
用spss回归有:(2)、可知:若用y表示工业总产值(万元),用x表示生产性固定资产,二者可用如下的表达式近似表示:=x.0+y.567395896(3)、用spss回归知标准误差为80.216(万元)。
(4)、当固定资产为1100时,总产值可能是(0.896*1100+395.567-80.216~0.896*1100+395.567+80.216)即(1301.0~146.4)这个范围内的某个值。
另外,用MATLAP也可以得到相同的结果:程序如下所示:function [b,bint,r,rint,stats] = regression1x = [318 910 200 409 415 502 314 1210 1022 1225];y = [524 1019 638 815 913 928 605 1516 1219 1624];X = [ones(size(x))', x'];[b,bint,r,rint,stats] = regress(y',X,0.05);display(b);display(stats);x1 = [300:10:1250];y1 = b(1) + b(2)*x1;figure;plot(x,y,'ro',x1,y1,'g-');industry = ones(6,1);construction = ones(6,1);industry(1) =1022;construction(1) = 1219;for i = 1:5industry(i+1) =industry(i) * 1.045;construction(i+1) = b(1) + b(2)* construction(i+1);enddisplay(industry);display( construction);end运行结果如下所示:b =395.56700.8958stats =1.0e+004 *0.0001 0.0071 0.0000 1.6035industry =1.0e+003 *1.02201.06801.11601.16631.21881.2736construction =1.0e+003 *1.2190 0.3965 0.3965 0.3965 0.3965 0.3965200400600800100012001400生产性固定资产价值(万元)工业总价值(万元)2、设某公司下属10个门市部有关资料如下:(1)、确定适宜的 回归模型; (2)、计算有关指标,判断这三种经济现象之间的紧密程度。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第三部分 线性回归
线性回归分为一元线性回归和多元线性回归。
一、一元线性回归:
1、涉及一个自变量的回归
2、因变量y与自变量x之间为线性关系
被预测或被解释的变量称为因变量(dependent variable),
用y表示
用来预测或用来解释因变量的一个或多个变量称为自变量
(independent variable),用x表示
计或预测因变量的取值
回归分析的模型
一、分类 按是否线性分:线性回归模型和非线性回归模型 按自变量个数分:简单的一元回归和多元回归
二、基本的步骤
利用SPSS得到模型关系式,是否是我们所要的? 要看回归方程的显著性检验(F检验)
回归系数b的显著性检验(T检验)
拟合程度R2
(注:相关系数的平方,一元回归用R Square,多元回归 用Adjusted R Square)
多元线性回归一般采用逐步回归方法-Stepwise。
(一) 一元线性回归模型
(linear n model)
1、描述因变量 y 如何依赖于自变量 x 和误差项 的方程称为回归模型
2、一元线性回归模型可表示为
y = b0 + b1 x +
Y是x 的线性函数
(部分)加上误差项
Remove:剔除变量。不进入方程模型的被选变量剔除。 Backward:向后消去 Forward:向前引入
Rule选项
选择一个用于指定分析个案的选择规则的变量。 选择规则包括: 等于、不等于、大于、小于、大于或等于、小于
或等于。 Value中输入相应变量的设定规则的临界值。
Statistics
独立性。独立性意味着对于一个特定的 x 值,
它所对应的ε与其他 x 值所对应的ε不相关;对于一 个特定的 x 值,它所对应的 y 值与其他 x 所对应的 y 值也不相关
估计的回归方程
(estimated regression equation)
1. 总体回归参数β0和β1是未知的,必须利用样本数 据去估计
回归分析的过程
在回归过程中包括:
Liner:线性回归 Curve Estimation:曲线估计
Binary Logistic: 二分变量逻辑回归 Multinomial Logistic:多分变量逻辑回归; Ordinal 序回归;Probit:概率单位回归; Nonlinear:非线性回归; Weight Estimation:加权估计; 2-Stage Least squares:二段最小平方法; Optimal Scaling 最优编码回归 我们只讲前面2个简单的(一般教科书的讲法)
第五步:如果点击OK,可以执行线性回归分析 操作。
Method选项
Enter:强迫引入法,默认选项。全部被选变量一次性进 入回归模型。
Stepwise:强迫剔除法。每一次引入变量时,概率F最小 值的变量将引入回归方程,如果已引入回归方程的变量 的F大于设定值,将被剔除回归方程。当无变量被引入 或剔除,时终止回归方程
b0 和 b1 称为模
型的参数
误差项 是随机
变量
注:线性部分反映了由于x的变化而引起的y的变
化;误差项反映了除x和y之间的线性关系之
外的随机因素对y的影响,它是不能由x和y之 间的线性关系所解释的变异性。
一元线性回归模型(基本假定)
1、因变量x与自变量y之间具有线性 关系
2、在重复抽样中,自变量x的取值 是固定的,即假定x是非随机的
3、因变量与自变量之间的关系用一个线性 方程来表示
线性回归的过程
一元线性回归模型确定过程 一、做散点图(Graphs ->Scatter->Simple)
目的是为了以便进行简单地观测(如: Salary与Salbegin的关系)。 二、建立方程 若散点图的趋势大概呈线性关系,可以建立线性方 程,若不呈线性分布,可建立其它方程模型,并比较R2 (-->1)来确定一种最佳方程式(曲线估计)。
2. 用样本统计量 bˆ0和 bˆ1代替回归方程中的未知参
数β0和β1 ,就得到了估计的回归方程
3. 一元线性回归中估计的回归方程为
yˆ = bˆ0 + bˆ1x
其中:bˆ0是估计的回归直线在 y 轴上的截距,bˆ1是直线的
斜率,它表示对于一个给定的 x 的值, yˆ 是 y 的估计值,
也表示 x 每变动一个单位时, y 的平均变动值
注:要对不同的自变量采用不同引入方法时, 选NEXT按钮把自变量归入不同自变量块中。
第三步:选择个案标签。在变量列表中选择变 量至个案标签中,而被选择的变量的标签用于 在图形中标注点的值。
第四步:选择加权二乘法(WLS)。在变量列 表框中选择变量至WLS中。但是该选项仅在被 选变量为权变量时选择。
模型拟合:复相关 系数、判定系数、
选项
调整R2、估计值的标 准误及方差分析
3 、误差项 满足条件
误差项 满足条件
正态性。 是一个服从正态分布的随机变量,
且期望值为0,即 ~N(0 , 2 ) 。对于一个给定的 x 值,y 的期望值为E(y)=b0+ b1x
方差齐性。对于所有的 x 值, 的方差一个特定
的值,的方差也都等于 2 都相同。同样,一个特定 的x 值, y 的方差也都等于2
第十讲 回归分析、线性回归和曲线估计
第一部分 上一讲回顾 第二部分 回归分析 第三部分 线性回归 第四部分 曲线估计
回归分析
什么是回归分析?
1、重点考察一个特定的变量(因变量),而 把其他变量(自变量)看作是影响这一变 量的因素,并通过适当的数学模型将变 量间的关系表达出来
2、利用样本数据建立模型的估计方程 3、对模型进行显著性检验 4、进而通过一个或几个自变量的取值来估
SPSS 线性回归分析
多元线性回归分析基本结构与一元线性回归相同。而 他们在SPSS下的功能菜单是集成在一起的。下面通过 SPSS操作步骤解释线性回归分析问题。
SPSS过程
步骤一:录入数据,选择分析菜单中的 Regression==>liner 打开线性回归分析对话框;
步骤二:选择被解释变量和解释变量。其中因 变量列表框中为被解释变量,自变量为回归分 析解释变量。
