2015-2019全国卷一理科数学真题汇编——统计概率、计数原理
2019年高考真题理科数学分类汇编专题10 概率与统计和计数原理(解析版)

专题10 概率与统计1.【2019年高考全国Ⅲ卷理数】《西游记》《三国演义》《水浒传》和《红楼梦》是中国古典文学瑰宝,并称为中国古典小说四大名著.某中学为了解本校学生阅读四大名著的情况,随机调查了100位学生,其中阅读过《西游记》或《红楼梦》的学生共有90位,阅读过《红楼梦》的学生共有80位,阅读过《西游记》且阅读过《红楼梦》的学生共有60位,则该校阅读过《西游记》的学生人数与该校学生总数比值的估计值为 A .0.5 B .0.6 C .0.7D .0.8【答案】C【解析】由题意得,阅读过《西游记》的学生人数为90-80+60=70,则其与该校学生人数之比为70÷100=0.7.故选C .【名师点睛】本题考查抽样数据的统计,渗透了数据处理和数学运算素养.采取去重法,利用转化与化归思想解题.2.【2019年高考全国Ⅱ卷理数】演讲比赛共有9位评委分别给出某选手的原始评分,评定该选手的成绩时,从9个原始评分中去掉1个最高分、1个最低分,得到7个有效评分.7个有效评分与9个原始评分相比,不变的数字特征是 A .中位数 B .平均数 C .方差D .极差 【答案】A【解析】设9位评委评分按从小到大排列为123489x x x x x x <<<<<.则①原始中位数为5x ,去掉最低分1x ,最高分9x 后剩余2348x x x x <<<<,中位数仍为5x ,A 正确; ②原始平均数1234891()9x x x x x x x =<<<<<,后来平均数23481()7x x x x x '=<<<,平均数受极端值影响较大,∴x 与x '不一定相同,B 不正确; ③2222111[()()()]9q S x x x x x x =-+-++-,22222381[()()()]7s x x x x x x '=-'+-'++-',由②易知,C 不正确;④原极差91x x =-,后来极差82x x =-,显然极差变小,D 不正确.故选A . 3.【2019年高考浙江卷】设0<a <1,则随机变量X 的分布列是则当a 在(0,1)内增大时, A .()D X 增大B .()D X 减小C .()D X 先增大后减小D .()D X 先减小后增大【答案】D【分析】研究方差随a 变化的增大或减小规律,常用方法就是将方差用参数a 表示,应用函数知识求解.本题根据方差与期望的关系,将方差表示为a 的二次函数,二次函数的图象和性质解题.题目有一定综合性,注重重要知识、基础知识、运算求解能力的考查. 【解析】方法1:由分布列得1()3aE X +=, 则2222111111211()(0)()(1)()333333926a a a D X a a +++=-⨯+-⨯+-⨯=-+, 则当a 在(0,1)内增大时,()D X 先减小后增大.故选D .方法2:则222221(1)222213()()()0[()]3399924a a a a D X E X E X a +-+=-=++-==-+,则当a 在(0,1)内增大时,()D X 先减小后增大.故选D .【名师点睛】易出现的错误有,一是数学期望、方差以及二者之间的关系掌握不熟,无从着手;二是计算能力差,不能正确得到二次函数表达式.4.【2019年高考江苏卷】已知一组数据6,7,8,8,9,10,则该组数据的方差是______________. 【答案】53【解析】由题意,该组数据的平均数为678891086+++++=,所以该组数据的方差是22222215[(68)(78)(88)(88)(98)(108)]63-+-+-+-+-+-=. 5.【2019年高考全国Ⅱ卷理数】我国高铁发展迅速,技术先进.经统计,在经停某站的高铁列车中,有10个车次的正点率为0.97,有20个车次的正点率为0.98,有10个车次的正点率为0.99,则经停该站高铁列车所有车次的平均正点率的估计值为______________. 【答案】0.98【分析】本题考查通过统计数据进行概率的估计,采取估算法,利用概率思想解题.【解析】由题意得,经停该高铁站的列车正点数约为100.97200.98100.9939.2⨯+⨯+⨯=,其中高铁个数为10201040++=,所以该站所有高铁平均正点率约为39.20.9840=. 【名师点睛】本题考查了概率统计,渗透了数据处理和数学运算素养,侧重统计数据的概率估算,难度不大.易忽视概率的估算值不是精确值而失误,根据分类抽样的统计数据,估算出正点列车数量与列车总数的比值.6.【2019年高考全国Ⅰ卷理数】甲、乙两队进行篮球决赛,采取七场四胜制(当一队赢得四场胜利时,该队获胜,决赛结束).根据前期比赛成绩,甲队的主客场安排依次为“主主客客主客主”.设甲队主场取胜的概率为0.6,客场取胜的概率为0.5,且各场比赛结果相互独立,则甲队以4∶1获胜的概率是______________. 【答案】0.18【分析】本题应注意分情况讨论,即前五场甲队获胜的两种情况,应用独立事件的概率的计算公式求解.题目有一定的难度,注重了基础知识、基本计算能力及分类讨论思想的考查.【解析】前四场中有一场客场输,第五场赢时,甲队以4:1获胜的概率是30.60.50.520.108,⨯⨯⨯=前四场中有一场主场输,第五场赢时,甲队以4:1获胜的概率是220.40.60.520.072,⨯⨯⨯=综上所述,甲队以4:1获胜的概率是0.1080.0720.18.q =+=【名师点睛】由于本题题干较长,所以,易错点之一就是能否静心读题,正确理解题意;易错点之二是思维的全面性是否具备,要考虑甲队以4:1获胜的两种情况;易错点之三是是否能够准确计算. 7.【2019年高考全国Ⅲ卷理数】为了解甲、乙两种离子在小鼠体内的残留程度,进行如下试验:将200只小鼠随机分成A ,B 两组,每组100只,其中A 组小鼠给服甲离子溶液,B 组小鼠给服乙离子溶液,每只小鼠给服的溶液体积相同、摩尔浓度相同.经过一段时间后用某种科学方法测算出残留在小鼠体内离子的百分比.根据试验数据分别得到如下直方图:记C 为事件:“乙离子残留在体内的百分比不低于5.5”,根据直方图得到P (C )的估计值为0.70. (1)求乙离子残留百分比直方图中a ,b 的值;(2)分别估计甲、乙离子残留百分比的平均值(同一组中的数据用该组区间的中点值为代表). 【答案】(1)a =0.35,b =0.10;(2)甲、乙离子残留百分比的平均值的估计值分别为4.05,6.00. 【解析】(1)由已知得0.70=a +0.20+0.15,故a =0.35. b =1–0.05–0.15–0.70=0.10.(2)甲离子残留百分比的平均值的估计值为 2×0.15+3×0.20+4×0.30+5×0.20+6×0.10+7×0.05=4.05. 乙离子残留百分比的平均值的估计值为3×0.05+4×0.10+5×0.15+6×0.35+7×0.20+8×0.15=6.00.8.【2019年高考全国Ⅱ卷理数】11分制乒乓球比赛,每赢一球得1分,当某局打成10:10平后,每球交换发球权,先多得2分的一方获胜,该局比赛结束.甲、乙两位同学进行单打比赛,假设甲发球时甲得分的概率为0.5,乙发球时甲得分的概率为0.4,各球的结果相互独立.在某局双方10:10平后,甲先发球,两人又打了X 个球该局比赛结束. (1)求P (X =2);(2)求事件“X =4且甲获胜”的概率. 【答案】(1)0.5;(2)0.1.【解析】(1)X =2就是10∶10平后,两人又打了2个球该局比赛结束, 则这2个球均由甲得分,或者均由乙得分. 因此P (X =2)=0.5×0.4+(1–0.5)×(1–0.4)=0.5.(2)X =4且甲获胜,就是10∶10平后,两人又打了4个球该局比赛结束, 且这4个球的得分情况为:前两球是甲、乙各得1分,后两球均为甲得分. 因此所求概率为[0.5×(1–0.4)+(1–0.5)×0.4]×0.5×0.4=0.1. 9.【2019年高考天津卷理数】设甲、乙两位同学上学期间,每天7:30之前到校的概率均为23.假定甲、乙两位同学到校情况互不影响,且任一同学每天到校情况相互独立.(1)用X 表示甲同学上学期间的三天中7:30之前到校的天数,求随机变量X 的分布列和数学期望; (2)设M 为事件“上学期间的三天中,甲同学在7:30之前到校的天数比乙同学在7:30之前到校的天数恰好多2”,求事件M 发生的概率. 【答案】(1)分布列见解析,()2E X ;(2)20243.【分析】本小题主要考查离散型随机变量的分布列与数学期望,互斥事件和相互独立事件的概率计算公式等基础知识.考查运用概率知识解决简单实际问题的能力.满分13分.【解析】(1)因为甲同学上学期间的三天中到校情况相互独立,且每天7:30之前到校的概率均为23,故2~(3,)3X B ,从而3321()C ()(),0,1,2,333kkkP X k k -===.所以,随机变量X 的分布列为随机变量X 的数学期望()323E X =⨯=.(2)设乙同学上学期间的三天中7:30之前到校的天数为Y , 则2~(3,)3Y B ,且{3,1}{2,0}M X Y X Y =====. 由题意知事件{3,1}X Y ==与{2,0}X Y ==互斥,且事件{3}X =与{1}Y =,事件{2}X =与{0}Y =均相互独立, 从而由(1)知()({3,1}{2,0})P M P X Y X Y =====(3,1)(2,0)P X Y P X Y ===+== (3)(1)(2)(0)P X P Y P X P Y ===+==824120279927243=⨯+⨯=. 10.【2019年高考北京卷理数】改革开放以来,人们的支付方式发生了巨大转变.近年来,移动支付已成为主要支付方式之一.为了解某校学生上个月A ,B 两种移动支付方式的使用情况,从全校学生中随机抽取了100人,发现样本中A ,B 两种支付方式都不使用的有5人,样本中仅使用A 和仅使用B 的学生的支付金额分布情况如下:(1)从全校学生中随机抽取1人,估计该学生上个月A ,B 两种支付方式都使用的概率;(2)从样本仅使用A 和仅使用B 的学生中各随机抽取1人,以X 表示这2人中上个月支付金额大于1000元的人数,求X 的分布列和数学期望;(3)已知上个月样本学生的支付方式在本月没有变化.现从样本仅使用A 的学生中,随机抽查3人,发现他们本月的支付金额都大于2000元.根据抽查结果,能否认为样本仅使用A 的学生中本月支付金额大于2000元的人数有变化?说明理由.【答案】(1)0.4;(2)分布列见解析,E (X )=1;(3)见解析.【解析】(1)由题意知,样本中仅使用A 的学生有18+9+3=30人,仅使用B 的学生有10+14+1=25人,A ,B 两种支付方式都不使用的学生有5人.故样本中A ,B 两种支付方式都使用的学生有100−30−25−5=40人.所以从全校学生中随机抽取1人,该学生上个月A ,B 两种支付方式都使用的概率估计为400.4100=. (2)X 的所有可能值为0,1,2.记事件C 为“从样本仅使用A 的学生中随机抽取1人,该学生上个月的支付金额大于1000元”,事件D 为“从样本仅使用B 的学生中随机抽取1人,该学生上个月的支付金额大于1000元”. 由题设知,事件C ,D 相互独立,且93141()0.4,()0.63025P C P D ++====. 所以(2)()()()0.24P X P CD P C P D ====,(1)()P X P CD CD == ()()()()P C P D P C P D =+ 0.4(10.6)(10.4)0.6=⨯-+-⨯0.52=,(0)()()()0.24P X P CD P C P D ====.所以X 的分布列为故X 的数学期望()00.2410.5220.241E X =⨯+⨯+⨯=.(3)记事件E 为“从样本仅使用A 的学生中随机抽查3人,他们本月的支付金额都大于2000元”. 假设样本仅使用A 的学生中,本月支付金额大于2000元的人数没有变化, 则由上个月的样本数据得33011()C 4060P E ==.答案示例1:可以认为有变化. 理由如下:P (E )比较小,概率比较小的事件一般不容易发生.一旦发生,就有理由认为本月的支付金额大于2000元的人数发生了变化,所以可以认为有变化. 答案示例2:无法确定有没有变化.理由如下: 事件E 是随机事件,P (E )比较小,一般不容易发生, 但还是有可能发生的,所以无法确定有没有变化.11.【2019年高考全国Ⅰ卷理数】为治疗某种疾病,研制了甲、乙两种新药,希望知道哪种新药更有效,为此进行动物试验.试验方案如下:每一轮选取两只白鼠对药效进行对比试验.对于两只白鼠,随机选一只施以甲药,另一只施以乙药.一轮的治疗结果得出后,再安排下一轮试验.当其中一种药治愈的白鼠比另一种药治愈的白鼠多4只时,就停止试验,并认为治愈只数多的药更有效.为了方便描述问题,约定:对于每轮试验,若施以甲药的白鼠治愈且施以乙药的白鼠未治愈则甲药得1分,乙药得1-分;若施以乙药的白鼠治愈且施以甲药的白鼠未治愈则乙药得1分,甲药得1-分;若都治愈或都未治愈则两种药均得0分.甲、乙两种药的治愈率分别记为α和β,一轮试验中甲药的得分记为X . (1)求X 的分布列;(2)若甲药、乙药在试验开始时都赋予4分,(0,1,,8)i p i =表示“甲药的累计得分为i 时,最终认为甲药比乙药更有效”的概率,则00p =,81p =,11i i i i p ap bp cp -+=++(1,2,,7)i =,其中(1)a P X ==-,(0)b P X ==,(1)c P X ==.假设0.5α=,0.8β=.(i)证明:1{}i i p p +-(0,1,2,,7)i =为等比数列;(ii)求4p ,并根据4p 的值解释这种试验方案的合理性. 【答案】(1)分布列见解析;(2)(i)证明见解析,(ii) 45 127p =,解释见解析. 【解析】X 的所有可能取值为1,0,1-.(1)(1)P X αβ=-=-,(0)(1)(1)P X αβαβ==+--, (1)(1)P X αβ==-,所以X 的分布列为(2)(i )由(1)得0.4,0.5,0.1a b c ===.因此110.40.5 0.1i i i i p p p p -+=++,故110.1()0.4()i i i i p p p p +--=-, 即114()i i i i p p p p +--=-. 又因为1010p p p -=≠, 所以1{}(0,1,2,,7)i i p p i +-=为公比为4,首项为1p 的等比数列.(ii )由(i )可得88776100p p p p p p p p =-+-++-+877610()()()p p p p p p =-+-++-81413p -=.由于8=1p ,故18341p =-, 所以44433221101( 411()327)(5())p p p p p p p p p p -=-+-+-+=-=. 4p 表示最终认为甲药更有效的概率,由计算结果可以看出,在甲药治愈率为0.5,乙药治愈率为0.8时, 认为甲药更有效的概率为410.0039257p =≈, 此时得出错误结论的概率非常小,说明这种试验方案合理.专题 计数原理1.【2019年高考全国Ⅲ卷理数】(1+2x 2 )(1+x )4的展开式中x 3的系数为 A .12 B .16 C .20 D .24【答案】A【解析】由题意得x 3的系数为3144C 2C 4812+=+=,故选A .【名师点睛】本题主要考查二项式定理,利用展开式通项公式求展开式指定项的系数.2.【2019年高考浙江卷理数】在二项式9)x 的展开式中,常数项是__________;系数为有理数的项的个数是__________.【答案】 5【解析】由题意,9)x 的通项为919C (0,1,29)rr r r T x r -+==,当0r =时,可得常数项为0919C T ==;若展开式的系数为有理数,则1,3,5,7,9r =,有246810T , T , T , T , T 共5个项.故答案为:5.【名师点睛】此类问题解法比较明确,首要的是要准确记忆通项公式,特别是“幂指数”不能记混,其次,计算要细心,确保结果正确.3.【2019年高考江苏卷理数】设2*012(1),4,n n n x a a x a x a x n n +=++++≥∈N .已知23242a a a =.(1)求n 的值;(2)设(1na +=+*,ab ∈N ,求223a b -的值.【答案】(1)5n =;(2)32-.【解析】(1)因为0122(1)C C C C 4n n n n n n n x x x x n +=++++≥,,所以2323(1)(1)(2)C ,C 26n nn n n n n a a ---====, 44(1)(2)(3)C 24nn n n n a ---==. 因为23242a a a =,所以2(1)(2)(1)(1)(2)(3)[]26224n n n n n n n n n ------=⨯⨯,解得5n =.(2)由(1)知,5n =.5(1(1n +=02233445555555C C C C C C =++++a =+解法一:因为*,a b ∈N ,所以024*********C 3C 9C 76,C 3C 9C 44a b =++==++=,从而222237634432a b -=-⨯=-.解法二:50122334455555555(1C C (C (C (C (C (=+++++02233445555555C C C C C C =--+-.因为*,a b ∈N ,所以5(1a -=-.因此225553((1(1(2)32a b a a -=+-=⨯-=-=-.【名师点睛】本题主要考查二项式定理、组合数等基础知识,考查分析问题能力与运算求解能力.。
全国高考试题(全国I卷)汇总(概率统计)

全国高考试题(全国I 卷)汇总《概率统计》1、【 2013 全国 I 卷 18】为了比较两种治疗失眠症的药(分别称为 A 药, B 药)的疗效,随机地选取 20 位患者服用 A 药, 20 位患者服用 B 药,这 40 位患者服用一段时间后,记录他们日平均增加的睡眠时间(单位: h ),试验的观测结果如下:服用 A 药的 20 位患者日平均增加的睡眠时间:0.6 1.2 2.7 1.5 2.8 1.8 2.2 2.3 3.2 3.52.5 2.6 1.2 2.7 1.5 2.93.0 3.1 2.3 2.4服用 B 药的 20 位患者日平均增加的睡眠时间:3.2 1.7 1.90.80.9 2.4 1.2 2.6 1.3 1.41.60.5 1.80.62.1 1.1 2.5 1.2 2.70.5(1)分别计算两组数据的平均数,从计算结果看,哪种药的疗效更好?(3)根据两组数据完成下面茎叶图,从茎叶图看,哪种药的疗效更好?A药B药0.1.2.3.2、【 2014 全国 I 卷 18】从某企业生产的某种产品中抽取100 件,测量这些产品的一项质量指标值,由测量表得如下频数分布表:质量指标值分组[75 , 85)[85 , 95)[95 , 105)[105 , 115)[115 , 125)频数62638228(I )在答题卡上作出这些数据的频率分布直方图:( II )估计这种产品质量指标值的平均数及方差(同一组中的数据用该组区间的中点值作代表);(III)根据以上抽样调查数据,能否认为该企业生产的这种产品符合“质量指标值不低于95 的产品至少要占全部产品的80%”的规定?频率 / 组距产品数据频率分布直方图0.0400.0380.0360.0340.0320.0300.0280.0260.0240.0220.0200.0180.0160.0140.0120.0100.0080.0060.0040.0020758595105115125质量指标值3、【 2015 全国 I 卷 19】某公司为确定下一年度投入某种产品的宣传费,需了解年宣传费x (单位:千元)对年销售量 y (单位: t )和年利润 z (单位:千元)的影响,对近8 年的宣传费 x i 和年销售量 y i i 1,2, L ,8 数据作了初步处理,得到下面的散点图及一些统计量的值.年 销 620 售600 量580 560 540 520 500480 11 1 1 1 1 1 1 1 1 1 13436 38 40 42 44 46 48 50 52 54 56年宣传费 /千元r urur 8888xy[来w( x ix) 2(w iw) 2(x ix)( y i y)(w i w)( y iy)源:]i 1i 1i 1i 146.6 56.3 6.8289.81.61469108.8表中 w i =xiur18, w =w i8 i 1(I )根据散点图判断,ya bx 与 y c dx ,哪一个适宜作为年销售量y 关于年宣传费x 的回归方程类型(给出判断即可,不必说明理由);(II )根据( I )的判断结果及表中数据,建立 y 关于 x 的回归方程;(III ) 已知这种产品的年利润z 与 x ,y 的关系为 z 0.2 y x ,根据( II )的结果回答下列问题:( i )当年宣传费 x 90 时,年销售量及年利润的预报值时多少?( i i )当年宣传费 x 为何值时,年利润的预报值最大?附:对于一组数据 (u 1 ,v 1) , (u 2 ,v 2 ) ,⋯⋯ ,(u n , v n ) ,其回归线 v u 的斜率和截距的最小二乘估计分别为:n^u i u viv^^β i 1n2vuu i u ,i 14、【 2016 全国 I 卷 19】某公司计划购买 1 台机器,该种机器使用三年后即被淘汰.机器有一易损零件,在购进机器时,可以额外购买这种零件作为备件,每个200 元 .在机器使用期间,如果备件不足再购买,则每个 500 元 .现需决策在购买机器时应同时购买几个易损零件,为此搜集并整理了 100 台这种机器在三年使用期内更换的易损零件数,得下面柱状图:频数2420161060161718192021更换的易损零件数记 x 表示 1 台机器在三年使用期内需更换的易损零件数,y 表示 1 台机器在购买易损零件上所需的费用(单位:元), n 表示购机的同时购买的易损零件数.(I )若n =19,求 y 与 x 的函数解析式;(II )若要求“需更换的易损零件数不大于n ”的频率不小于0.5,求n的最小值;(III )假设这 100 台机器在购机的同时每台都购买19个易损零件,或每台都购买20 个易损零件,分别计算这100 台机器在购买易损零件上所需费用的平均数,以此作为决策依据,购买 1 台机器的同时应购买19 个还是 20 个易损零件?。
2015年—2019年全国高考文理科数学试题各题考查主要知识点统计
11 三角函数图象与性质
12 立几外接球 13 曲线切线方程
三次奇函数切线 方程 三角形中线向量
三视图最短路径
抛物线直线数量 积 分段函数零点范 围 数学文化几何概 型 双曲线渐近线弦 长 正方体线面角面 积最值 线性规划
填 14 等比数列求和 空 题 15 独立事件概率
16 双曲线渐近线离心率
17 解三角形
概率均值茎叶图
翻折垂直体积
立几作图体积比
导数切线范围 椭圆面积不等式 极坐标参数方程
椭圆中点弦定值
导数单调性最大 值
极坐标参数方程
不等式选讲
不等式选讲
全国高考试题各题考查主要知识点统计 新课标 III 卷理科数学
全国新 课标 1
2019Ⅲ理 集合交集
2 复数运算
3 随机统计问题
4 二项式定理
5 等比数列通项
程序框图
8 抛物线与椭圆
数学文化古典概 型
9 三角函数性质
长方体异线角
三角函数化简求 10
值 11 双曲线离心率
函数与导数综合 12
问题
三角函数单调性
函数奇偶性对称 性求和 椭圆三角形离心 率
13 统计平均值
曲线的切线导数
填 14 函数奇偶性 空 题 15 解三角形
线性规划 三角恒等变换
数学文化与立体 圆锥线面角侧面
古典概型 抛物线垂直距 离 三角函数最值
函数奇偶性
长方体球体积
解三角形 等差数列等比 数列 平行体积 直方图独立性 检验 椭圆轨迹定点 导数单调性求 参 极坐标参数方 程 不等式选讲
4
2016Ⅱ文
2015Ⅱ文
集合交集 复数共轭 三角函数图像 正方体球表面积 抛物线求参
新课标全国卷1理科数学分类汇编——10.统计、概率分布列、计数原理

10.统计、概率分布列、计数原理(含解析)一、选择题【2017,2】如图,正方形ABCD 内的图形来自中国古代的太极图,正方形内切圆中的黑色部分和白色部分关于正方形的中心成中心对称.在正方形内随机取一点,则此点取自黑色部分的概率是( )A .14 B .π8 C .12 D .π4【2017,6】621(1)(1)x x++展开式中2x 的系数为( )A .15B .20C .30D .35【2016,4】某公司的班车在30:7,00:8,30:8发车,小明在50:7至30:8之间到达发车站乘坐班车,且到达发车丫的时候是随机的,则他等车时间不超过10分钟的概率是( ) A .31 B .21 C .32 D .43 【2015,10】25()x x y ++的展开式中,52x y 的系数为( )A .10B .20C .30D .60【2015,4】投篮测试中,每人投3次,至少投中2次才能通过测试.已知某同学每次投篮投中的概率为0.6,且各次投篮是否投中相互独立,则该同学通过测试的概率为( )A .0.648B .0.432C .0.36D .0.312【2014,5】4位同学各自在周六、周日两天中任选一天参加公益活动,则周六、周日都有同学参加公益活动的概率( )A .18B .38C .58D .78【2013,3】为了解某地区的中小学生的视力情况,拟从该地区的中小学生中抽取部分学生进行调查,事先已了解到该地区小学、初中、高中三个学段学生的视力情况有较大差异,而男女生视力情况差异不大.在下面的抽样方法中,最合理的抽样方法是( )A .简单随机抽样B .按性别分层抽样C .按学段分层抽样D .系统抽样【2013,9】设m 为正整数,2()mx y +展开式的二项式系数的最大值为a ,21()m x y ++展开式的二项式系数的最大值为b .若13a =7b ,则m =( )A .5B .6C .7D .8【2012,2】将2名教师,4名学生分成2个小组,分别安排到甲、乙两地参加社会实践活动,每个小组由1名教师和2名学生组成,不同的安排方案共有( ) A .12种B .10种C .9种D .8种【2011,8】512a x x x x ⎛⎫⎛⎫+- ⎪⎪⎝⎭⎝⎭的展开式中各项系数的和为2,则该展开式中常数项为( )A .40-B .20-C .20D .40【2011,4】有3个兴趣小组,甲、乙两位同学各自参加其中一个小组,每位同学参加各个小组的可能性相同,则这两位同学参加同一个兴趣小组的概率为( )A .13 B .12 C .23 D .34二、填空题 【2016,14】5)2(x x +的展开式中,3x 的系数是 .(用数字填写答案)【2014,13】8()()x y x y -+的展开式中22x y 的系数为 .(用数字填写答案) 【2012,15】某一部件由三个电子元件按下图方式连接 而成,元件1或元件2正常工作,且元 件3正常工作,则部件正常工作.设三个 电子元件的使用寿命(单位:小时)均服 从正态分布N (1000,502),且各个元件能否正常工作相互独立,那么该部件的使用寿命超过1000小时的概率为_________. 三、解答题【2017,19】为了监控某种零件的一条生产线的生产过程,检验员每天从该生产线上随机抽取16个零件,并测量其尺寸(单位:cm ).根据长期生产经验,可以认为这条生产线正常状态下生产的零件的尺寸服从正态分布N (μ,σ2).(1)假设生产状态正常,记X 表示一天内抽取的16个零件中其尺寸在(μ–3σ,μ+3σ)之外的零件数,求 P (X ≥1)及X 的数学期望;(2)一天内抽检零件中,如果出现了尺寸在(μ–3σ,μ+3σ)之外的零件,就认为这条生产线在这一天的生产过程可能出现了异常情况,需对当天的生产过程进行检查.(ⅰ)试说明上述监控生产过程方法的合理性; (ⅱ)下面是检验员在一天内抽取的16个零件的尺寸:经计算得16119.9716i i x x ===∑,0.212s ==≈,其中x i 为抽取的第i 个零件的尺寸,i =1,2, (16)用样本平均数x 作为μ的估计值ˆμ,用样本标准差s 作为σ的估计值ˆσ,利用估计值判断是否需对当天的生产过程进行检查?剔除ˆˆˆˆ(3,3)μσμσ-+之外的数据,用剩下的数据估计μ和σ(精确到0.01). 附:若随机变量Z 服从正态分布N (μ,σ2),则P (μ–3σ<Z <μ+3σ)=0.9974,0.997416≈0.95920.09≈.元件2元件3元件1【2016,19】某公司计划购买2台机器,该种机器使用三年后即被淘汰.机器有一易损零件,在购进机器时,可以额外购买这种零件作为备件,每个200元.在机器使用期间,如果备件不足再购买,则每个500元.现需决策在购买机器时应同时购买几个易损零件,为此搜集并整理了100台这种机器在三年使用期内更换的易损零件数,得下面柱状图: 以这100台机器更换的易损零件数的频率代替1台机器更换的易损零件数发生的概率,记X 表示2台机器三年内共需更换的易损零件数,n 表示购买2台机器的同时购买的易损零件数.(Ⅰ)求X 的分布列;(Ⅱ)若要求5.0)(≥≤n X P ,确定n 的最小值;(Ⅲ)以购买易损零件所需费用的期望值为决策依据,在19=n 与20=n 之中选其一,应选用哪个?【2015,19】某公司为确定下一年度投入某种产品的宣传费,需了解年宣传费x (单位:千元)对年销售量y (单位:t )和年利润z (单位:千元)的影响,对近8年的年宣传费i x 和年销售量i y (1,2,,8i =L )数据作了初步处理,得到下面的散点图及一些统计量的值.xyw821()ii x x =-∑821()ii w w =-∑81()()iii x x y y =--∑ 81()()iii w w yy =--∑46.6 563 6.8 289.8 1.6 1469 108.8表中i i w x =,8118i i w w ==∑(Ⅰ)根据散点图判断,y a bx =+与y c d x =+哪一个适宜作为年销售量y 关于年宣传费x 的回归方程类型?(给出判断即可,不必说明理由)(Ⅱ)根据(Ⅰ)的判断结果及数据,建立y 关于x 的回归方程;(III )已知这种产品的年利润z 与x ,y 的关系为0.2z y x =-,根据(Ⅱ)的结果回答下列问题: (i )年宣传费x =49时,年销售量及年利润的预报值是多少? (ii )年宣传费x 为何值时,年利润的预报值最大?附:对于一组数据1122(,),(,),,(,)n n u v u v u v L ,其回归直线v u αβ=+的斜率和截距的最小二乘估计分别为µ121()()()nii i nii uu v v uu β==-=--∑∑错误!未找到引用源。
2015-2019全国试卷(Ⅰ、Ⅱ、Ⅲ)高考汇编-统计概率

2015-2019全国高考数学试卷(Ⅰ、Ⅱ、Ⅲ)试题汇编-统计概率(2015年全国卷一19.)某公司为确定下一年度投入某种产品的宣传费,需了解年宣传费x(单位:千元)对年销售量y(单位:t)和年利润z(单位:千元)的影响.对近8年的年宣传费x i 和年销售量y i (i=1,2,…,8)数据作了初步处理,得到下面的散点图及一些统计量的值.xyw∑i=18(x i -x )2∑i=18(w i -w )2∑i=18(x i -x )(y i -y )∑i=18(w i -w )(y i -y )46.65636.8289.8 1.61469108.8表中w i =√x i ,w =18∑i=18w i .(Ⅰ)根据散点图判断,y=a+bx 与y=c+d √x 哪一个适宜作为年销售量y 关于年宣传费x 的回归方程类型?(给出判断即可,不必说明理由)(Ⅱ)根据(Ⅰ)的判断结果及表中数据,建立y 关于x 的回归方程;(Ⅲ)已知这种产品的年利润z 与x,y 的关系为z=0.2y-x.根据(Ⅱ)的结果回答下列问题: (i)年宣传费x=49时,年销售量及年利润的预报值是多少? (ii)年宣传费x 为何值时,年利润的预报值最大?附:对于一组数据(u 1,v 1),(u 2,v 2),…,(u n ,v n ),其回归直线v=α+βu 的斜率和截距的最小二乘估计分别为β^=∑i=1n(u i -u )(v i -v )∑i=1n(u i -u )2,α^=v -β^u .解:(Ⅰ)由散点图可以判断,y=c+d √x 适宜作为年销售量y 关于年宣传费x 的回归方程类型.(2分) (Ⅱ)令w=√x ,先建立y 关于w 的线性回归方程.由于d ^=∑i=18(w i -w )(y i -y )∑i=18(w i -w )2=108.81.6=68, c ^=y -d ^w =563-68×6.8=100.6,所以y 关于w 的线性回归方程为y ^=100.6+68w,因此y 关于x 的回归方程为y ^=100.6+68√x .(6分) (Ⅲ)(i)由(Ⅱ)知,当x=49时,年销售量y 的预报值 y ^=100.6+68√49=576.6,年利润z 的预报值z ^=576.6×0.2-49=66.32.(9分) (ii)根据(Ⅱ)的结果知,年利润z 的预报值 z ^=0.2(100.6+68√x )-x=-x+13.6√x +20.12. 所以当√x =13.62=6.8,即x=46.24时,z ^取得最大值.故年宣传费为46.24千元时,年利润的预报值最大.(12分)(2015全国二卷18.)某公司为了解用户对其产品的满意度,从A,B 两地区分别随机调查了20个用户,得到用户对产品的满意度评分如下:A 地区:62 73 81 92 95 85 74 64 53 7678 86 95 66 97 78 88 82 76 89B 地区: 73 83 62 51 91 46 53 73 64 8293 48 65 81 74 56 54 76 65 79(Ⅰ)根据两组数据完成两地区用户满意度评分的茎叶图,并通过茎叶图比较两地区满意度评分的平均值及分散程度(不要求计算出具体值,给出结论即可);A 地区B 地区456789(Ⅱ)根据用户满意度评分,将用户的满意度从低到高分为三个等级:满意度评分低于70分70分到89分不低于90分满意度等级不满意满意非常满意记事件C:“A地区用户的满意度等级高于B地区用户的满意度等级”.假设两地区用户的评价结果相互独立.根据所给数据,以事件发生的频率作为相应事件发生的概率,求C的概率.解:(Ⅰ)两地区用户满意度评分的茎叶图如下:A地区B地区4 6 83 5 1 3 6 46 4 2 6 2 4 5 56 8 8 6 4 37 3 3 4 6 99 2 8 6 5 1 8 3 2 17 5 5 2 9 1 3通过茎叶图可以看出,A地区用户满意度评分的平均值高于B地区用户满意度评分的平均值;A地区用户满意度评分比较集中,B地区用户满意度评分比较分散.(Ⅱ)记CA1表示事件:“A地区用户的满意度等级为满意或非常满意”;CA2表示事件:“A地区用户的满意度等级为非常满意”;CB1表示事件:“B地区用户的满意度等级为不满意”;CB2表示事件:“B 地区用户的满意度等级为满意”,则CA1与CB1独立,CA2与CB2独立,CB1与CB2互斥,C=CB1CA1∪CB2CA2. P(C)=P(CB1CA1∪CB2CA2) =P(CB1CA1)+P(CB2CA2) =P(CB1)P(CA1)+P(CB2)P(CA2).由所给数据得CA1,CA2,CB1,CB2发生的频率分别为1620,420,1020,820,故P(CA1)=1620,P(CA2)=420,P(CB1)=1020,P(CB2)=820,P(C)=1020×1620+820×420=0.48.(2016年全国一卷19.) 某公司计划购买2台机器,该种机器使用三年后即被淘汰.机器有一易损零件,在购进机器时,可以额外购买这种零件作为备件,每个200元.在机器使用期间,如果备件不足再购买,则每个500元.现需决策在购买机器时应同时购买几个易损零件,为此搜集并整理了100台这种机器在三年使用期内更换的易损零件数,得下面柱状图:以这100台机器更换的易损零件数的频率代替1台机器更换的易损零件数发生的概率,记X 表示2台机器三年内共需更换的易损零件数,n 表示购买2台机器的同时购买的易损零件数. (Ⅰ)求X 的分布列;(Ⅱ)若要求P(X≤n)≥0.5,确定n 的最小值;(Ⅲ)以购买易损零件所需费用的期望值为决策依据,在n=19与n=20之中选其一,应选用哪个? 解:(Ⅰ)由柱状图并以频率代替概率可得,一台机器在三年内需更换的易损零件数为8,9,10,11的概率分别为0.2,0.4,0.2,0.2.从而P(X=16)=0.2×0.2=0.04; P(X=17)=2×0.2×0.4=0.16;P(X=18)=2×0.2×0.2+0.4×0.4=0.24; P(X=19)=2×0.2×0.2+2×0.4×0.2=0.24;P(X=20)=2×0.2×0.4+0.2×0.2=0.2;P(X=21)=2×0.2×0.2=0.08;P(X=22)=0.2×0.2=0.04.(4分)所以X的分布列为X 16 17 18 19 20 21 22P 0.04 0.16 0.24 0.24 0.2 0.08 0.04(6分)(Ⅱ)由(Ⅰ)知P(X≤18)=0.44,P(X≤19)=0.68,故n的最小值为19.(8分)(Ⅲ)记Y表示2台机器在购买易损零件上所需的费用(单位:元).当n=19时,EY=19×200×0.68+(19×200+500)×0.2+(19×200+2×500)×0.08+(19×200+3×500)×0.04=4 040.(10分)当n=20时,EY=20×200×0.88+(20×200+500)×0.08+(20×200+2×500)×0.04=4 080.可知当n=19时所需费用的期望值小于n=20时所需费用的期望值,故应选n=19.(12分)(2016全国卷二18.)某险种的基本保费为a(单位:元),继续购买该险种的投保人称为续保人,续保人本年度的保费与其上年度出险次数的关联如下:上年度出险次数0 1 2 3 4 ≥5保费0.85a a 1.25a 1.5a 1.75a 2a设该险种一续保人一年内出险次数与相应概率如下:一年内出险次数0 1 2 3 4 ≥5概率0.30 0.15 0.20 0.20 0.10 0.05(Ⅰ)求一续保人本年度的保费高于基本保费的概率;(Ⅱ)若一续保人本年度的保费高于基本保费,求其保费比基本保费高出60%的概率;(Ⅲ)求续保人本年度的平均保费与基本保费的比值.解:(Ⅰ)设A表示事件:“一续保人本年度的保费高于基本保费”,则事件A发生当且仅当一年内出险次数大于1,故P(A)=0.2+0.2+0.1+0.05=0.55.(3分)(Ⅱ)设B表示事件:“一续保人本年度的保费比基本保费高出60%”,则事件B发生当且仅当一年内出险次数大于3,故P(B)=0.1+0.05=0.15.又P(AB)=P(B),故P(B|A)=P (AB )P (A )=P (B )P (A )=0.150.55=311.因此所求概率为311.(7分)(Ⅲ)记续保人本年度的保费为X 元,则X 的分布列为X 0.85a a 1.25a 1.5a 1.75a 2a P0.300.150.200.200.100.05EX=0.85a×0.30+a×0.15+1.25a×0.20+1.5a×0.20+1.75a×0.10+2a×0.05=1.23a. 因此续保人本年度的平均保费与基本保费的比值为1.23.(12分)(2016全国卷三18.)下图是我国2008年至2014年生活垃圾无害化处理量(单位:亿吨)的折线图.(Ⅰ)由折线图看出,可用线性回归模型拟合y 与t 的关系,请用相关系数加以说明;(Ⅱ)建立y 关于t 的回归方程(系数精确到0.01),预测2016年我国生活垃圾无害化处理量. 附注:参考数据:∑i=17y i =9.32,∑i=17t i y i =40.17,√∑i=17(y i -y )2=0.55,√7≈2.646.参考公式:相关系数r=∑i=1n(t i -t )(y -y )√∑i=1n(t i -t )∑i=1n (y i -y ),回归方程y ^=a ^+b ^t 中斜率和截距的最小二乘估计公式分别为:b ^=∑i=1n(t i -t )(y i -y )∑i=1n(t i -t )2,a ^=y -b ^t .解:(Ⅰ)由折线图中数据和附注中参考数据得t =4,∑i=17(t i -t )2=28,√∑i=17(y i -y )2=0.55,∑i=17(t i -t )(y i -y )=∑i=17t i y i -t ∑i=17y i =40.17-4×9.32=2.89,r≈2.890.55×2×2.646≈0.99.(4分)因为y 与t 的相关系数近似为0.99,说明y 与t 的线性相关程度相当高,从而可以用线性回归模型拟合y 与t 的关系.(6分) (Ⅱ)由y =9.327≈1.331及(Ⅰ)得b ^=∑i=17(t i -t )(y i -y )∑i=17(t i -t )2=2.8928≈0.10,a ^=y -b ^t =1.331-0.10×4≈0.93.所以,y 关于t 的回归方程为y ^=0.93+0.10t.(10分)将2016年对应的t=9代入回归方程得y ^=0.93+0.10×9=1.83. 所以预测2016年我国生活垃圾无害化处理量约为1.83亿吨.(12分)(2017全国卷一19.)为了监控某种零件的一条生产线的生产过程,检验员每天从该生产线上随机抽取16个零件,并测量其尺寸(单位:cm ).根据长期生产经验,可以认为这条生产线正常状态下生产的零件的尺寸服从正态分布2(,)N μσ.(1)假设生产状态正常,记X 表示一天内抽取的16个零件中其尺寸在(3,3)μσμσ-+之外的零件数,求(1)P X ≥及X 的数学期望;(2)一天内抽检零件中,如果出现了尺寸在(3,3)μσμσ-+之外的零件,就认为这条生产线在这一天的生产过程可能出现了异常情况,需对当天的生产过程进行检查.(ⅰ)试说明上述监控生产过程方法的合理性; (ⅱ)下面是检验员在一天内抽取的16个零件的尺寸:9.95 10.12 9.96 9.96 10.01 9.92 9.98 10.0410.26 9.91 10.13 10.02 9.22 10.04 10.05 9.95经计算得16119.9716i i x x ===∑,0.212s ==≈,其中i x 为抽取的第i 个零件的尺寸,1,2,,16i =⋅⋅⋅.用样本平均数x 作为μ的估计值ˆμ,用样本标准差s 作为σ的估计值ˆσ,利用估计值判断是否需对当天的生产过程进行检查?剔除ˆˆˆˆ(3,3)μσμσ-+之外的学科网数据,用剩下的数据估计μ和σ(精确到0.01).附:若随机变量Z 服从正态分布2(,)N μσ,则(33)0.997 4P Z μσμσ-<<+=,160.997 40.959 2=0.09≈.解:因此σ的估计值为0.0080.09≈.(2017全国卷一18.)淡水养殖场进行某水产品的新、旧网箱养殖方法的产量对比学|科网,收获时各随机抽取了100 个网箱,测量各箱水产品的产量(单位:kg )某频率直方图如下:(1) 设两种养殖方法的箱产量相互独立,记A 表示事件:旧养殖法的箱产量低于50kg, 新养殖法的箱产量不低于50kg,估计A 的概率;(2) 填写下面列联表,并根据列联表判断是否有99%的把握认为箱产量与养殖方法有关:(3) 根据箱产量的频率分布直方图,求新养殖法箱产量的中位数的估计值(精确到0.01)2()()()()()n ad bc K a b c d a c b d -=++++解:(2)220015.70510.82810010096104K ⨯==>⨯⨯⨯有99%的把握认为箱产量与养殖方法有关。
2019年高考数学全国统一考试概率统计分类详细解析及简易逻辑

数学分类解析一概率统计各地高考题.选择题:1.(安徽理)(10).设两个正态分布N (#i ,。
;)(0>0)和b ;)(%>0)的密度函数图像如图所示。
则有(A )A. 旧 v %b\ <a 2B. 丹 <穴2,0 >。
2C. "\>D. "\> 瞄%>2.(福建理)(5)某一批花生种子,2粒发芽的概率是 (B )16 96 192 256A.--- B. --- C. --- D.---625 625 625 62543.(福建文)(5)某一批花生种子,如果每1粒发芽的概率为石,那么播下3粒种子恰有2粒发芽的概率是(C)16 48k --- C.---125 1254.(广东理)(3).某校共有学生2000名,各年级男、女生人数如表1.已知在全校学生中随机抽取1名,抽到二年级女生的概率是0.19.现用分层抽样的方法在全校抽取64名学生,则应在三年级抽取的学生人数为(C )A. 24B. 18C. 16D. 12一年级二年级三年级女生373Xy男生377370Z5.(湖南理)4.设随机变量:服从正态分布N (2,9),若P (<>c+l )=P (〈<c —1),则c=(B )A.lB.2C.3D.46.(江西文)(11).电子钟一天显示的时间是从00:00到23:59,每一时刻都由四个数字组成,则一天中任一时刻显示的四个数字之和为23的概率为 (C)A.11801B .----2881C.---3601D ,4807. (辽宁理文)(7) . 4张卡片上分别写有数字1, 2, 3, 4,从这4张卡片中随机抽取2张,则取出的2张卡片上的数字之和为奇数的概率为(C )112 3A. — B. — C. — D.—3 2 3 48. (山东理)(7)在某地的奥运火炬传递活动中,有编号为1, 2, 3, 18的18名火炬手.若从中任选3人,则选出的火炬手的编号能组成3为公差的等差数列的概率为(B .)(A) — (B ) — (C)---51 68 3069. (山东理)(8)右图是根据《山东统计年整2007》中的资料作成的1997年至2006年我省城镇居民百户家庭人口数的茎叶 图.图中左边的数字从左到右分别表示城镇居民百户家庭人口数的百位数字和十位数字,右边的数字表示城镇居民百户家庭人口数的个位数字,从图中可以得到1997年至2006年我省城镇居民百户家庭人口数的平均数为(B)(A) 304.6(B) 303.6 (C)302.610.(山东文)9.从某项综合能力测试中抽取100人的成绩,统计如表,则这100人成绩的标准差为(B )(D)14082 9115 83 02 63 10 2 4 7(D)301.6分数54321人数2010303010A.n 2面D .----------5C. 38D.-510. (陕西文)(3).某林场有树苗30000棵,其中松树苗4000棵.为调查树苗的生长情况,采用分层抽样的方法抽取一个容量为150的样本,则样本中松树苗的数量为(C )A. 30B. 25C. 20D. 1511. (重庆理)(5)已知随机变量〈服从正态分布M3, a ),则P(〈<3)= (D)2(A)-(B) -(C) -(D)-5 4 3 212. (重庆文)(5)某交高三年级有男生500人,女生400人,为了解该年级学生的健康情况,从男生中任意抽取25人,从女生中任意抽取20人进行调查.这种抽样方法是(D)(A)简单随机抽样法(C)随机数表法(B)抽签法(D)分层抽样法13.(重庆文)(9)从编号为1,2,・“,10的10个大小相同的球中任取4个,则所取4个球的最大号码是6的概率为(B)2 3(C)y(D)y二.填空题:1.(广东文)(11).为了调查某厂工人生产某种产品的能力,随机抽查了20位工人某天生产该产品的数量.产品数量的分组区间为[45,55),[55,65),[65,75),[75,85),[85,95)由此得到频率分布直方图如图,则这20名工人中一天生产该产品数量在[55,75)的人数是13.2.(海南宁夏理文)(16).从甲、乙两品种的棉花中各抽测了25根棉花的纤维长度(单位:mm),结果如下:甲品种:271273280285285287292294295301303303307 308310314319323325325328331334337352乙品种:284292295304306307312313315315316318318 320322322324327329331333336337343356由以上数据设计了如下茎叶图甲乙31277550284542292587331304679403123556888553320224797413313673432356根据以上茎叶图,对甲、乙两品种棉花的纤维长度作比较,写出两个统计结论:①;②•以下任填两个:(1).乙品种棉花的纤维平均长度大于甲品种棉花的纤维平均长度(或:乙品种棉花的纤维长度普遍大于甲品种棉花的纤维长度).(2).甲品种棉花的纤维长度较乙品种棉花的纤维长度更分散•(或:乙品种棉花的纤维长度较甲品种棉花的纤维长度更集中(稳定).甲品种棉花的纤维长度的分散程度比乙品种棉花的纤维长度的分散程度更大).(3).甲品种棉花的纤维长度的中位数为307mm,乙品种棉花的纤维长度的中位数为318mm.(4).乙品种棉花的纤维长度基本上是对称的,而且大多集中在中间(均值附近).甲品种棉花的纤维长度除一个特殊值(352)夕卜,也大致对称,其分布较均匀.3.(湖北文)11.一个公司共有1000名员工,下设一些部门,要采用分层抽样方法从全体员工中抽取一个容量为50的样本,已知某部门有200名员工,那么从该部门抽取的工人数是10.4.(湖北文)14.明天上午李明要参加奥运志愿者活动,为了准时起床,他用甲、乙两个闹钟叫醒自己,假设甲闹钟准时响的概率是0.80,乙闹钟准时响的概率是0.90,则两个闹钟至少有一准时响的概率是0.98.5.(湖南理)15.对有n(nN4)个元素的总体{1,2,3,…刀}进行抽样,先将总体分成两个子总体{1,2,…,m}和(m+l>m+2,…,n}(m是给定的正整数,且2WmWn-2),再从每个子总体中各随机抽取2个元素组成样本,用坊表示元素i和f同时出现在样本中的4概率,则P|,,=--------;所有PiQWiVjW77)的和等于鱼.m(n—ni)6.(湖南文)(12)从某地区15000位老人中随机抽取500人,其生活能否自理的情况如下表所示:序号⑺分组睡眠时间组中值(G,)频数(人数)频率(Fj)1[4,5) 4.560.122[5,6) 5.5100.203[6,7) 6.5200.404[7,8)7.5100.205[8,9]8.540.08在上述统计数据的分析中,一部分计算见算法流程图,则输出的S的值为6.42.9.(上海理文)(7).在平面直角坐标系中,从六个点:A(0,0)、B(2,0)、C(l,l)、D(0,2)、3E(2,2)、F(3,3)中任取三个,这三点能构成三角形的概率是j(结果用分数表示)10.(上海理文)(9).已知总体的各个体的值由小到大依次为2,3,3,7,12,13.7,18.3,20,且总体的中位数为10.5,若要使该总体的方差最小,则a、》的取值分别是10.5和10.511.(上海文)8.在平面直角坐标系中,从五个点:A(O,O),3(2,0),C(L1),D(0,2),4£(2,2)中任取三个,这三点能构成三角形的概率是;(结果用分数表示).12.(天津文)(11).一个单位共有职工200人,其中不超过45岁的有120人,超过45岁的有80人.为了调查职工的健康状况,用分层抽样的方法从全体职工中抽取一个容量为25的样本,应抽取超过45岁的职工10人.13.三.解答题:1.(安徽理)(19).(本小题满分12分)为防止风沙危害,某地决定建设防护绿化带,种植杨树、沙柳等植物。
2015年全国各地高考数学试题及解答分类大全(概率、统计、统计案例、推理与证明)

8. (2015 湖北文)已知变量 x 和 y 满足关系 y 0.1x 1 ,变量 y 与 z 正相关. 下列结论中正确的
是( )
A. x 与 y 负相关, x 与 z 负相关
B. x 与 y 正相关, x 与 z 正相关
C. x 与 y 正相关, x 与 z 负相关
D. x 与 y 负相关, x 与 z 正相关
数为 x,由分层抽样的性质可得总体与样本中青年教师与老年教师的比例相等,即 320 16 ,解得 x9
x 180 .
考点:分层抽样.
3.(2015 福建理)为了解某社区居民的家庭年收入所年支出的关系,随机调查了该社区 5 户家庭,
得到如下统计数据表:
收入 x (万 8.2
8.6
10.0
11.3
11.9
则 card card F ( )
A. 50
【答案】D
B.100
C.150
D. 200
考点:推理与证明.
6.(2015
湖北理)在区间 [0,
1] 上随机取两个数
x, y
,记
p1 为事件“
x
y
1 2
”的概率,
p2
为事件
“|
x
y
|
1 2
”的概率,
p3
为事件“
xy
1 2
”的概率,则
(
)
A. p1 p2 p3
第 3页 (共 27页)
9.
(2015 湖北文)在区间[0,
1]
上随机取两个数
x,
y
,记
p1
为事件“
x
y
1 2
”
的概率,
p2
2015年全国卷1(理科数学)含答案

绝密★启用前2015年普通高等学校招生全国统一考试理科数学(全国Ⅰ卷)注意事项: 1.本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.第Ⅰ卷1至3页,第Ⅱ卷3至5页. 2.答题前,考生务必将自己的姓名、准考证号填写在本试题相应的位置. 3.全部答案在答题卡上完成,答在本试题上无效. 4. 考试结束后,将本试题和答题卡一并交回.第Ⅰ卷一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的.(1)设复数z 满足=i ,则|z |=【A 】 (A )1 (B(C(D )2(2)sin20°cos 10°-con 160°sin10°=【D 】 (A ) (B (C ) (D ) (3)设命题P :n N ,>,则P 为【C 】(A )n N , > (B ) n N , ≤ (C )n N , ≤ (D ) n N , =(4)投篮测试中,每人投3次,至少投中2次才能通过测试.已知某同学每次投篮投中的概率为0.6,且各次投篮是否投中相互独立,则该同学通过测试的概率为【A 】 (A )0.648 (B )0.432 (C )0.36 (D )0.312(5)已知M (x 0,y 0)是双曲线C :上的一点,F 1、F 2是C 上的两个焦点,若<0,则y 0的取值范围是【A 】1+z1z-12-12∃∈2n 2n⌝∀∈2n 2n ∃∈2n 2n∀∈2n 2n ∃∈2n 2n2212x y -=12MF MF ⋅(A )()(B )()(C )(,) (D )() (6)《九章算术》是我国古代内容极为丰富的数学名著,书中有如下问题:“今有委米依垣内角,下周八尺,高五尺.问:积及为米几何?”其意思为:“在屋内墙角处堆放米(如图,米堆为一个圆锥的四分之一),米堆底部的弧度为8尺,米堆的高为5尺,问米堆的体积和堆放的米各为多少?”已知1斛米的体积约为1.62立方尺,圆周率约为3,估算出堆放斛的米约有【B 】(A )14斛 (B )22斛 (C )36斛 (D )66斛(7)设D 为ABC 所在平面内一点,则【A 】(A ) (B )(C ) (D )(8)函数f (x )=的部分图像如图所示,则f (x )的单调递减区间为【D 】(A )(),k (b )(),k(C )(),k (D )(),k3-33BC CD =1433AD AB AC =-+1433AD AB AC=-4133AD AB AC =+4133AD AB AC =-(9)执行右面的程序框图,如果输入的t =0.01,则输出的n =【C 】 (A )5 (B )6 (C )7 (D )8(10)的展开式中,的系数为【C 】(A )10 (B )20 (C )30 (D )60(11)圆柱被一个平面截去一部分后与半球(半径为r )组成一个几何体, 该几何体三视图中的正视图和俯视图如图所示.若该几何体的 表面积为16 + 20,则r =【B 】 (A )1 (B )2 (C )4 (D )812.设函数f (x )=e x(2x -1)-ax +a ,其中a 1,若存在唯一的 整数x 0,使得f (x 0)0,则a 的取值范围是【D 】25()x x y ++52x y π2rr正视图俯视图r2rA .[,1)B . [)C . [)D . [,1)第II 卷本卷包括必考题和选考题两部分.第(13)题~第(21)题为必考题,每个试题考生都必须作答.第(22)题~第(24)题未选考题,考生根据要求作答. 二、填空题:本大题共3小题,每小题5分(13)若函数f (x )=xln (x)为偶函数,则a = 1 .(14)一个圆经过椭圆的三个顶点,且圆心在x 轴上,则该圆的标准方程为.(15)若x ,y 满足约束条件,则的最大值为 3 .(16)在平面四边形ABCD 中,∠A =∠B =∠C =75°,BC =2,则AB 的取值范围是.三.解答题:解答应写出文字说明,证明过程或演算步骤. (17)(本小题满分12分)S n 为数列{a n }的前n 项和.已知a n >0,(Ⅰ)求{a n }的通项公式: (Ⅱ)设,求数列}的前n 项和解:(I )由,可知可得即由于可得又,解得32e -33,24e -33,24e 32e 22325()24x y ±+=10040x x y x y -≥⎧⎪-≤⎨⎪+-≤⎩yx 2243n n n a a S +=+211124 3.n n n a a S ++++=+221112()4n n n n a a a a a +++-+-=2211112()()()n n n n n n a a a a a a a a +++++=-=+-0n a >1 2.n n a a +-=2111243a a a +=+111()3a a =-=舍去,所以是首相为3,公差为2的等差数列,通项公式为(II )由设数列的前n 项和为,则(18)如图,四边形ABCD 为菱形,∠ABC =120°, E ,F 是平面ABCD 同一侧的两点,BE ⊥平面ABCD , DF ⊥平面ABCD ,BE =2DF ,AE ⊥EC . (1)证明:平面AEC ⊥平面AFC(2)求直线AE 与直线CF 所成角的余弦值解:(I )连结BD ,设BDAC=G ,连结EG ,FG ,EF.在菱形ABCD 中不妨设GB=1.由ABC=120°,可得AG=GC=.由 BE 平面ABCD, AB=BC 可知AE=EC. 又AE EC ,所以EG=,且EG AC.在Rt EBG 中,可得BE=故DF=.在Rt FDG 中,可得FG=. 在直角梯形BDFE 中,由BD=2,BE=,DF=,{}n a 2 1.n a n =+21n a n =+111111().(21)(23)22123n n b a a n n n n +===-++++{}n b n T 12n nT b b b =+++1111111()()()()235572123.3(23)n n n n ⎡⎤=-+-++-⎢⎥++⎣⎦=+∠3⊥⊥3⊥∆222∆62222ABCFED可得FE=.从而又因为所以平面(I )如图,以G 为坐标原点,分别以GB ,GC 的方向为x 轴,y 轴正方向,为单位长,建立空间直角坐标系G-xyz.由(I )可得所以 故所以直线AE 与直线CF 所成直角的余弦值为.(19)某公司为确定下一年度投入某种产品的宣传费,需了解年宣传费x (单位:千元)对年销售量y (单位:t )和年利润z (单位:千元)的影响,对近8年的年宣传费x i 和年销售量y i (i =1,2,···,8)数据作了初步处理,得到下面的散点图及一些统计量的值.2222,EG FG EF EG FG +=⊥所以,.ACFG G EG AFC =⊥可得平面EG AEC ⊂平面AEC AFC ⊥平面GB(0(10(10),(02A E F C --,,,(132),(1AE CF ==-,,cos ,3AE CF AE CF AE CF ⋅==-⋅3-)2-)2-)(y i))(y i -)46.6 56.3 6.8289.81469108.8表中w i =, ,=(Ⅰ)根据散点图判断,y =a +bx 与y =c +哪一个适宜作为年销售量y 关于年宣传费x 的回归方程类型?(给出判断即可,不必说明理由)(Ⅱ)根据(Ⅰ)的判断结果及表中数据,建立y 关于x 的回归方程;(Ⅲ)以知这种产品的年利率z 与x 、y 的关系为z =0.2y -x .根据(Ⅱ)的结果回答下列问题:(i ) 年宣传费x =49时,年销售量及年利润的预报值是多少?(ii )年宣传费x 为何值时,年利率的预报值最大?附:对于一组数据(u 1 v 1),(u 2 v 2)…….. (u n v n ),其回归线v =u 的斜率和截距的最小二乘估计分别为:解: (I )由散点图可以判断,适宜作为年销售量y 关于年宣传费x 的回归方程类型。
2015-2019高考数学理科(全国卷和自主命题)分类汇编 专题13 计数原理

专题13 计数原理2019年1.【2019年高考全国Ⅲ卷理数】(1+2x 2 )(1+x )4的展开式中x 3的系数为 A .12 B .16 C .20 D .24【答案】A【解析】由题意得x 3的系数为3144C 2C 4812+=+=,故选A .2.【2019年高考浙江卷理数】在二项式9)x 的展开式中,常数项是__________;系数为有理数的项的个数是__________.【答案】 5【解析】由题意,9)x 的通项为919C (0,1,29)rr r r T x r -+==,当0r =时,可得常数项为0919C T ==;若展开式的系数为有理数,则1,3,5,7,9r =,有246810T , T , T , T , T共5个项.故答案为:5.3.【2019年高考江苏卷理数】设2*012(1),4,n n n x a a x a x a x n n +=++++≥∈N .已知23242a a a =.(1)求n 的值;(2)设(1n a +=+*,a b ∈N ,求223a b -的值. 【答案】(1)5n =;(2)32-.【解析】(1)因为0122(1)C C C C 4n n nn n n n x x x x n +=++++≥,,所以2323(1)(1)(2)C ,C 26n nn n n n n a a ---====, 44(1)(2)(3)C 24nn n n n a ---==. 因为23242a a a =,所以2(1)(2)(1)(1)(2)(3)[]26224n n n n n n n n n ------=⨯⨯,解得5n =.(2)由(1)知,5n =.5(1(1n +=+02233445555555C C C C C C =++++a =+解法一:因为*,a b ∈N ,所以024135555555C 3C 9C 76,C 3C 9C 44a b =++==++=,从而222237634432a b -=-⨯=-. 解法二:50122334455555555(1C C (C (C (C (C (=+++++02233445555555C C C C C C =--+-.因为*,a b ∈N ,所以5(1a =-.因此225553((1(1(2)32a b a a -=+-=+⨯-=-=-.2018年1.【2018年全国卷Ⅲ理】的展开式中 的系数为 A. 10 B. 20 C. 40 D. 80 【答案】C【解析】分析:写出 ,然后可得结果详解:由题可得,令 ,则 ,所以故选C.2.【2018年理数全国卷II 】我国数学家陈景润在哥德巴赫猜想的研究中取得了世界领先的成果.哥德巴赫猜想是“每个大于2的偶数可以表示为两个素数的和”,如 .在不超过30的素数中,随机选取两个不同的数,其和等于30的概率是 A.B.C.D.【答案】C【解析】分析:先确定不超过30的素数,再确定两个不同的数的和等于30的取法,最后根据古典概型概率公式求概率.详解:不超过30的素数有2,3,5,7,11,13,17,19,23,29,共10个,随机选取两个不同的数,共有 种方法,因为 ,所以随机选取两个不同的数,其和等于30的有3种方法,故概率为,选C.3.【2018年浙江卷】从1,3,5,7,9中任取2个数字,从0,2,4,6中任取2个数字,一共可以组成___________个没有重复数字的四位数.(用数字作答)【答案】12604.【2018年浙江卷】二项式的展开式的常数项是___________.【答案】7【解析】分析:先根据二项式展开式的通项公式写出第r+1项,再根据项的次数为零解得r,代入即得结果.详解:二项式的展开式的通项公式为,令得,故所求的常数项为5.【2018年理数天津卷】在的展开式中,的系数为____________.【答案】6.【2018年江苏卷】某兴趣小组有2名男生和3名女生,现从中任选2名学生去参加活动,则恰好选中2名女生的概率为________.【答案】【解析】分析:先确定总基本事件数,再从中确定满足条件的基本事件数,最后根据古典概型概率公式求概率.详解:从5名学生中抽取2名学生,共有10种方法,其中恰好选中2名女生的方法有3种,因此所求概率为7.【2018年江苏卷】已知5位裁判给某运动员打出的分数的茎叶图如图所示,那么这5位裁判打出的分数的平均数为________.【答案】90【解析】分析:先由茎叶图得数据,再根据平均数公式求平均数.详解:由茎叶图可知,5位裁判打出的分数分别为 , , , , ,故平均数为.8.【2018年理新课标I 卷】从2位女生,4位男生中选3人参加科技比赛,且至少有1位女生入选,则不同的选法共有_____________种.(用数字填写答案) 【答案】162017年1.【2017课标1,理6】621(1)(1)x x++展开式中2x 的系数为 A .15 B .20 C .30 D .35【答案】C【解析】试题分析:因为6662211(1)(1)1(1)(1)x x x x x ++=⋅++⋅+,则6(1)x +展开式中含2x 的项为2226115C x x ⋅=,621(1)x x ⋅+展开式中含2x 的项为44262115C x x x⋅=,故2x 前系数为151530+=,选C.2.【2017课标3,理4】()()52x y x y +-的展开式中x 3y 3的系数为 A .80- B .40- C .40 D .80【答案】C 【解析】3.【2017课标II ,理6】安排3名志愿者完成4项工作,每人至少完成1项,每项工作由1人完成,则不同的安排方式共有( )A .12种B .18种C .24种D .36种 【答案】D 【解析】试题分析:由题意可得,一人完成两项工作,其余两人每人完成一项工作,据此可得,只要把工作分成三份:有24C 种方法,然后进行全排列33A 即可,由乘法原理,不同的安排方式共有234336C A ⨯=种方法。
(完整)2015年高考理科数学试卷全国卷1含答案),推荐文档

2015年高考理科数学试卷全国卷11.设复数z 满足11zz+-=i ,则|z|=( ) (A )1 (B )2 (C )3 (D )2 2.o o o o sin 20cos10cos160sin10- =( ) (A )3-(B )3 (C )12- (D )123.设命题p :2,2nn N n ∃∈>,则p ⌝为( )(A )2,2nn N n ∀∈> (B )2,2nn N n ∃∈≤(C )2,2nn N n ∀∈≤ (D )2,=2nn N n ∃∈4.投篮测试中,每人投3次,至少投中2次才能通过测试。
已知某同学每次投篮投中的概率为0.6,且各次投篮是否投中相互独立,则该同学通过测试的概率为( ) (A )0.648 (B )0.432 (C )0.36 (D )0.3125.已知M (00,x y )是双曲线C :2212x y -=上的一点,12,F F 是C 上的两个焦点,若120MF MF •<u u u u r u u u u r,则0y 的取值范围是( )(A )(-33,33) (B )(-36,36) (C )(223-,223) (D )(23-,23)6.《九章算术》是我国古代内容极为丰富的数学名著,书中有如下问题:“今有委米依垣内角,下周八尺,高五尺。
问:积及为米几何?”其意思为:“在屋内墙角处堆放米(如图,米堆为一个圆锥的四分之一),米堆为一个圆锥的四分之一),米堆底部的弧长为8尺,米堆的高为5尺,问米堆的体积和堆放的米各为多少?”已知1斛米的体积约为1.62立方尺,圆周率约为3,估算出堆放斛的米约有( ) (A )14斛 (B )22斛 (C )36斛 (D )66斛7.设D 为ABC ∆所在平面内一点3BC CD =u u u r u u u r,则( )(A )1433AD AB AC =-+u u u r u u ur u u u r (B )1433AD AB AC =-u u u r u u u r u u u r(C )4133AD AB AC =+u u u u u r u u u r u u u r (D )4133AD AB AC =-u u u u u u u ru u u r u u u r8.函数()f x =cos()x ωϕ+的部分图像如图所示,则()f x 的单调递减区间为( )(A)13 (,),44 kk k Zππ-+∈(B)13(2,2),44k k k Zππ-+∈(C)13(,),44k k k Z-+∈(D)13(2,2),44k k k Z-+∈9.执行右面的程序框图,如果输入的t=0.01,则输出的n=()(A)5 (B)6 (C)7 (D)810.25()x x y++的展开式中,52x y的系数为()(A)10 (B)20 (C)30 (D)6011.圆柱被一个平面截去一部分后与半球(半径为r)组成一个几何体,该几何体三视图中的正视图和俯视图如图所示.若该几何体的表面积为16 + 20π,则r=()(A)1 (B)2 (C)4 (D)812.设函数()f x=(21)xe x ax a--+,其中a1,若存在唯一的整数x,使得()f x 0,则a的取值范围是()(A)[-32e,1)(B)[-32e,34)(C)[32e,34)(D)[32e,1)13.若函数f(x)=2ln()x x a x+为偶函数,则a=14.一个圆经过椭圆221164x y+=的三个顶点,且圆心在x轴的正半轴上,则该圆的标准方程为 .15.若,x y满足约束条件1040xx yx y-≥⎧⎪-≤⎨⎪+-≤⎩,则yx的最大值为 .16.在平面四边形ABCD中,∠A=∠B=∠C=75°,BC=2,则AB的取值范围是 .17.(本小题满分12分)n S 为数列{n a }的前n 项和.已知n a >0,2n n a a +=43n S +.(Ⅰ)求{n a }的通项公式; (Ⅱ)设11n n n b a a +=,求数列{n b }的前n 项和. 18.如图,四边形ABCD 为菱形,∠ABC=120°,E ,F 是平面ABCD 同一侧的两点,BE ⊥平面ABCD ,DF ⊥平面ABCD ,BE=2DF ,AE ⊥EC.(Ⅰ)证明:平面AEC ⊥平面AFC ;(Ⅱ)求直线AE 与直线CF 所成角的余弦值.19.某公司为确定下一年度投入某种产品的宣传费,需了解年宣传费x (单位:千元)对年销售量y (单位:t )和年利润z (单位:千元)的影响,对近8年的年宣传费i x 和年销售量i y (i =1,2,···,8)数据作了初步处理,得到下面的散点图及一些统计量的值.x ry u rw u r821()ii x x =-∑821()ii w w =-∑81()()iii x x y y =--∑ 81()()iii w w yy =--∑46.6 56.3 6.8 289.8 1.6 1469 108.8表中i i w x =,w u r =1881i i w =∑(Ⅰ)根据散点图判断,y=a+bx 与x y 关于年宣传费x 的回归方程类型?(给出判断即可,不必说明理由)(Ⅱ)根据(Ⅰ)的判断结果及表中数据,建立y 关于x 的回归方程;(Ⅲ)已知这种产品的年利率z 与x 、y 的关系为z=0.2y-x.根据(Ⅱ)的结果回答下列问题:(ⅰ)年宣传费x=49时,年销售量及年利润的预报值是多少? (ⅱ)年宣传费x 为何值时,年利率的预报值最大?附:对于一组数据11(,)u v ,22(,)u v ,……,(,)n n u v ,其回归线v u αβ=+的斜率和截距的最小二乘估计分别为:20.(本小题满分12分)在直角坐标系xoy 中,曲线C :y=24x 与直线y kx a =+(a >0)交与M,N 两点,(Ⅰ)当k=0时,分别求C 在点M 和N 处的切线方程;(Ⅱ)y 轴上是否存在点P ,使得当k 变动时,总有∠OPM=∠OPN ?说明理由.21.(本小题满分12分)已知函数f (x )=31,()ln 4x ax g x x ++=-. (Ⅰ)当a 为何值时,x 轴为曲线()y f x = 的切线;(Ⅱ)用min {},m n 表示m,n 中的最小值,设函数}{()min (),()(0)h x f x g x x => ,讨论h (x )零点的个数. 22.(本题满分10分)选修4-1:几何证明选讲 如图,AB 是的直径,AC 是的切线,BC 交于E.(Ⅰ)若D 为AC 的中点,证明:DE 是的切线;(Ⅱ)若3OA CE =,求∠ACB 的大小.23.(本小题满分10分)选修4-4:坐标系与参数方程 在直角坐标系xOy 中,直线1C :x =-2,圆2C :()()22121x y -+-=,以坐标原点为极点, x 轴的正半轴为极轴建立极坐标系. (Ⅰ)求1C ,2C 的极坐标方程; (Ⅱ)若直线3C 的极坐标方程为()4R πθρ=∈,设2C 与3C 的交点为M ,N ,求2C MN ∆的面积.24.(本小题满分10分)选修4—5:不等式选讲 已知函数=|x+1|-2|x-a|,a>0.(Ⅰ)当a=1时,求不等式f (x )>1的解集;(Ⅱ)若f (x )的图像与x 轴围成的三角形面积大于6,求a 的取值范围.【答案解析】 1.【答案】A 【解析】由11z i z +=-得,11i z i-+=+=(1)(1)(1)(1)i i i i -+-+-=i ,故|z|=1,故选A. 考点:本题主要考查复数的运算和复数的模等.2.【答案】D【解析】原式=o o o o sin 20cos10cos 20sin10+ =o sin30=12,故选D. 考点:本题主要考查诱导公式与两角和与差的正余弦公式. 3.【答案】C【解析】p ⌝:2,2nn N n ∀∈≤,故选C. 考点:本题主要考查特称命题的否定 4.【答案】A【解析】根据独立重复试验公式得,该同学通过测试的概率为22330.60.40.6C ⨯+=0.648,故选A.考点:本题主要考查独立重复试验的概率公式与互斥事件和概率公式 5.【答案】A【解析】由题知12(3,0),(3,0)F F -,220012x y -=,所以12MF MF •u u u u r u u u u r = 0000(3,)(3,)x y x y --•- =2220003310x y y +-=-<,解得033y <<,故选A.考点:双曲线的标准方程;向量数量积坐标表示;一元二次不等式解法. 6.【答案】B【解析】设圆锥底面半径为r ,则12384r ⨯⨯==163r =,所以米堆的体积为211163()5433⨯⨯⨯⨯=3209,故堆放的米约为3209÷1.62≈22,故选B.考点:圆锥的性质与圆锥的体积公式 7.【答案】A【解析】由题知11()33AD AC CD AC BC AC AC AB =+=+=+-=u u u r u u u r u u u r u u u r u u u r u u u r u u u r u u u r=1433AB AC -+u u ur u u u r ,故选A. 考点:平面向量的线性运算 8.【答案】D【解析】由五点作图知,1+4253+42πωϕπωϕ⎧=⎪⎪⎨⎪=⎪⎩,解得=ωπ,=4πϕ,所以()cos()4f x x ππ=+,令22,4k x k k Z πππππ<+<+∈,解得124k -<x <324k +,k Z ∈,故单调减区间为(124k -,324k +),k Z ∈,故选D. 考点:三角函数图像与性质9.【答案】C【解析】执行第1次,t=0.01,S=1,n=0,m=12=0.5,S=S-m=0.5,2mm ==0.25,n=1,S=0.5>t=0.01,是,循环,执行第2次,S=S-m=0.25,2mm ==0.125,n=2,S=0.25>t=0.01,是,循环, 执行第3次,S=S-m=0.125,2mm ==0.0625,n=3,S=0.125>t=0.01,是,循环,执行第4次,S=S-m=0.0625,2mm ==0.03125,n=4,S=0.0625>t=0.01,是,循环,执行第5次,S=S-m=0.03125,2mm ==0.015625,n=5,S=0.03125>t=0.01,是,循环,执行第6次,S=S-m=0.015625,2mm ==0.0078125,n=6,S=0.015625>t=0.01,是,循环,执行第7次,S=S-m=0.0078125,2mm ==0.00390625,n=7,S=0.0078125>t=0.01,否,输出n=7,故选C.考点:本题注意考查程序框图 10.【答案】C【解析】在25()x x y ++的5个因式中,2个取因式中2x 剩余的3个因式中1个取x ,其余因式取y,故52x y 的系数为212532C C C =30,故选 C.考点:本题主要考查利用排列组合知识计算二项式展开式某一项的系数.【名师点睛】本题利用排列组合求多项展开式式某一项的系数,试题形式新颖,是中档题,求多项展开式式某一项的系数问题,先分析该项的构成,结合所给多项式,分析如何得到该项,再利用排列组知识求解. 11.【答案】B【解析】由正视图和俯视图知,该几何体是半球与半个圆柱的组合体,圆柱的半径与球的半径都为r ,圆柱的高为2r ,其表面积为22142222r r r r r r πππ⨯+⨯++⨯=2254r r π+=16 + 20π,解得r=2,故选B.考点:简单几何体的三视图;球的表面积公式、圆柱的测面积公式 12.【答案】D【解析】设()g x =(21)xe x -,y ax a =-,由题知存在唯一的整数0x ,使得0()g x 在直线y ax a =-的下方.因为()(21)xg x e x '=+,所以当12x <-时,()g x '<0,当12x >-时,()g x '>0,所以当12x =-时,max [()]g x =12-2e -,当0x =时,(0)g =-1,(1)30g e =>,直线y ax a =-恒过(1,0)斜率且a ,故(0)1a g ->=-,且1(1)3g e a a --=-≥--,解得32e≤a <1,故选D.考点:本题主要通过利用导数研究函数的图像与性质解决不等式成立问题13.【答案】1【解析】由题知ln(y x =是奇函数,所以ln(ln(x x +- =22ln()ln 0a x x a +-==,解得a =1. 考点:函数的奇偶性 14.【答案】22325()24x y -+=【解析】设圆心为(a ,0),则半径为4a -,则222(4)2a a -=+,解得32a =,故圆的方程为22325()24x y -+=. 考点:椭圆的几何性质;圆的标准方程 15.【答案】3【解析】作出可行域如图中阴影部分所示,由斜率的意义知,yx是可行域内一点与原点连线的斜率,由图可知,点A (1,3)与原点连线的斜率最大,故yx的最大值为3.考点:线性规划解法16.【答案】【解析】如图所示,延长BA ,CD 交于E ,平移AD ,当A 与D 重合与E 点时,AB 最长,在△BCE 中,∠B=∠C=75°,∠E=30°,BC=2,由正弦定理可得sin sin BC BEE C=∠∠,即o o2sin 30sin 75BE=,解得BE AD ,当D 与C 重合时,AB 最短,此时与AB 交于F ,在△BCF 中,∠B=∠BFC=75°,∠FCB=30°,由正弦定理知,sin sin BF BC FCB BFC =∠∠,即o o2sin 30sin 75BF =,解得AB 的取值-).考点:正余弦定理;数形结合思想17.【答案】(Ⅰ)21n +(Ⅱ)11646n -+ 【解析】试题分析:(Ⅰ)先用数列第n 项与前n 项和的关系求出数列{n a }的递推公式,可以判断数列{n a }是等差数列,利用等差数列的通项公式即可写出数列{n a }的通项公式;(Ⅱ)根据(Ⅰ)数列{n b }的通项公式,再用拆项消去法求其前n 项和.试题解析:(Ⅰ)当1n =时,211112434+3a a S a +=+=,因为0n a >,所以1a =3,当2n ≥时,2211n n n n a a a a --+--=14343n n S S -+--=4n a ,即111()()2()n n n n n n a a a a a a ---+-=+,因为0n a >,所以1n n a a --=2,所以数列{n a }是首项为3,公差为2的等差数列, 所以n a =21n +; (Ⅱ)由(Ⅰ)知,n b =1111()(21)(23)22123n n n n =-++++,所以数列{nb }前n项和为12nb b b +++L =1111111[()()()]235572123n n -+-++-++L =11646n -+. 考点:数列前n 项和与第n 项的关系;等差数列定义与通项公式;拆项消去法18.【答案】(Ⅰ)见解析(Ⅱ)3【解析】 试题分析:(Ⅰ)连接BD ,设BD∩AC=G,连接EG ,FG ,EF ,在菱形ABCD 中,不妨设GB=1易证EG ⊥AC ,通过计算可证EG ⊥FG ,根据线面垂直判定定理可知EG ⊥平面AFC ,由面面垂直判定定理知平面AFC ⊥平面AEC ;(Ⅱ)以G 为坐标原点,分别以,GB GC u u u r u u u r的方向为x 轴,y 轴正方向,||GB u u u r为单位长度,建立空间直角坐标系G-xyz ,利用向量法可求出异面直线AE 与CF 所成角的余弦值. 试题解析:(Ⅰ)连接BD ,设BD∩AC=G,连接EG ,FG ,EF ,在菱形ABCD 中,不妨设GB=1,由∠ABC=120°,可得 由BE ⊥平面ABCD ,AB=BC 可知,AE=EC ,又∵AE ⊥EC ,∴EG ⊥AC ,在Rt △EBG 中,可得,故DF=2.在Rt △FDG 中,可得FG=2在直角梯形BDFE 中,由BD=2,,DF=2可得EF=2, ∴222EG FG EF +=,∴EG ⊥FG ,∵AC∩FG=G,∴EG ⊥平面AFC ,∵EG ⊂面AEC ,∴平面AFC ⊥平面AEC.(Ⅱ)如图,以G 为坐标原点,分别以,GB GC u u u r u u u r 的方向为x 轴,y 轴正方向,||GB u u u r为单位长度,建立空间直角坐标系G-xyz ,由(Ⅰ)可得A (0,,0),E (),F (-1,0,2),C (00),∴AE u u u r =(1),CF uuu r =(-1,,2) (10)分故cos ,||||AE CF AE CF AE CF ⋅<>==u u u r u u u r u u u r u u u r u u u r u u u r .所以直线AE 与CF. 考点:空间垂直判定与性质;异面直线所成角的计算;空间想象能力,推理论证能力19.【答案】(Ⅰ)y c =+适合作为年销售y 关于年宣传费用x 的回归方程类型;(Ⅱ)$100.6y =+46.24【解析】 试题分析:(Ⅰ)由散点图及所给函数图像即可选出适合作为拟合的函数;(Ⅱ)令w =先求出建立y 关于w 的线性回归方程,即可y 关于x 的回归方程;(Ⅲ)(ⅰ)利用y 关于x 的回归方程先求出年销售量y 的预报值,再根据年利率z 与x 、y 的关系为z=0.2y-x 即可年利润z 的预报值;(ⅱ)根据(Ⅱ)的结果知,年利润z 的预报值,列出关于x 的方程,利用二次函数求最值的方法即可求出年利润取最大值时的年宣传费用.试题解析:(Ⅰ)由散点图可以判断,y c =+适合作为年销售y 关于年宣传费用x 的回归方程类型.(Ⅱ)令w =y 关于w 的线性回归方程,由于$81821()()()iii ii w w yy dw w ==--=-∑∑=108.8=6816, ∴$cy dw =-$=563-68×6.8=100.6. ∴y 关于w 的线性回归方程为$100.668y w =+,∴y 关于x 的回归方程为$100.6y =+(Ⅲ)(ⅰ)由(Ⅱ)知,当x =49时,年销售量y 的预报值 $100.6y =+,576.60.24966.32z=⨯-=$. (ⅱ)根据(Ⅱ)的结果知,年利润z 的预报值0.2(100.620.12zx x =+-=-+$,=13.6=6.82,即46.24x =时,z $取得最大值. 故宣传费用为46.24千元时,年利润的预报值最大.……12分考点:非线性拟合;线性回归方程求法;利用回归方程进行预报预测;应用意识20.【答案】0y a --=0y a ++=(Ⅱ)存在【解析】试题分析:(Ⅰ)先求出M,N 的坐标,再利用导数求出M,N.(Ⅱ)先作出判定,再利用设而不求思想即将y kx a =+代入曲线C 的方程整理成关于x 的一元二次方程,设出M,N 的坐标和P 点坐标,利用设而不求思想,将直线PM ,PN 的斜率之和用a 表示出来,利用直线PM ,PN 的斜率为0,即可求出,a b 关系,从而找出适合条件的P 点坐标.试题解析:(Ⅰ)由题设可得)M a ,()N a -,或()M a -,)N a .∵12y x '=,故24x y =在x =,C 在,)a 处的切线方程为y a x -=-0y a --=.故24x y =在x =-处的到数值为,C 在(,)a -处的切线方程为y a x -=+0y a ++=.0y a --=0y a ++=.(Ⅱ)存在符合题意的点,证明如下:设P (0,b )为复合题意得点,11(,)M x y ,22(,)N x y ,直线PM ,PN 的斜率分别为12,k k .将y kx a =+代入C 得方程整理得2440x kx a --=.∴12124,4x x k x x a +==-. ∴121212y b y b k k x x --+=+=1212122()()kx x a b x x x x +-+=()k a b a+. 当b a =-时,有12k k +=0,则直线PM 的倾斜角与直线PN 的倾斜角互补,故∠OPM=∠OPN ,所以(0,)P a -符合题意.考点:抛物线的切线;直线与抛物线位置关系;探索新问题;运算求解能力21..【答案】(Ⅰ)34a =;(Ⅱ)当34a >-或54a <-时,()h x 由一个零点;当34a =-或54a =-时,()h x 有两个零点;当5344a -<<-时,()h x 有三个零点. 【解析】试题分析:(Ⅰ)先利用导数的几何意义列出关于切点的方程组,解出切点坐标与对应的a 值;(Ⅱ)根据对数函数的图像与性质将x 分为1,1,01x x x >=<<研究()h x 的零点个数,若零点不容易求解,则对a 再分类讨论.试题解析:(Ⅰ)设曲线()y f x =与x 轴相切于点0(,0)x ,则0()0f x =,0()0f x '=,即3002010430x ax x a ⎧++=⎪⎨⎪+=⎩,解得013,24x a ==. 因此,当34a =时,x 轴是曲线()y f x =的切线. (Ⅱ)当(1,)x ∈+∞时,()ln 0g x x =-<,从而()min{(),()}()0h x f x g x g x =≤<, ∴()h x 在(1,+∞)无零点.当x =1时,若54a ≥-,则5(1)04f a =+≥,(1)min{(1),(1)}(1)0h fg g ===,故x =1是()h x 的零点;若54a <-,则5(1)04f a =+<,(1)min{(1),(1)}(1)0h f g f ==<,故x =1不是()h x 的零点.当(0,1)x ∈时,()ln 0g x x =->,所以只需考虑()f x 在(0,1)的零点个数.(ⅰ)若3a ≤-或0a ≥,则2()3f x x a '=+在(0,1)无零点,故()f x 在(0,1)单调,而1(0)4f =,5(1)4f a =+,所以当3a ≤-时,()f x 在(0,1)有一个零点;当a ≥0时,()f x 在(0,1)无零点.(ⅱ)若30a -<<,则()f x 在(01)单调递增,故当x ()f x 取的最小值,最小值为f 14.①若f >0,即34-<a <0,()f x 在(0,1)无零点.②若f =0,即34a =-,则()f x 在(0,1)有唯一零点;③若f <0,即334a -<<-,由于1(0)4f =,5(1)4f a =+,所以当5344a -<<-时,()f x 在(0,1)有两个零点;当534a -<≤-时,()f x 在(0,1)有一个零点.…10分 综上,当34a >-或54a <-时,()h x 由一个零点;当34a =-或54a =-时,()h x 有两个零点;当5344a -<<-时,()h x 有三个零点. 考点:利用导数研究曲线的切线;对新概念的理解;分段函数的零点;分类整合思想22.【答案】(Ⅰ)见解析(Ⅱ)60°【解析】试题分析:(Ⅰ)由圆的切线性质及圆周角定理知,AE ⊥BC ,AC ⊥AB ,由直角三角形中线性质知DE=DC ,OE=OB ,利用等量代换可证∠DEC+∠OEB=90°,即∠OED=90°,所以DE 是圆O 的切线;(Ⅱ)设CE=1,由OA =得,AB=AE=x ,由勾股定理得BE ,由直角三角形射影定理可得2AE CE BE =⋅,列出关于x 的方程,解出x ,即可求出∠ACB 的大小.试题解析:(Ⅰ)连结AE ,由已知得,AE ⊥BC ,AC ⊥AB ,在Rt △AEC 中,由已知得DE=DC ,∴∠DEC=∠DCE ,连结OE ,∠OBE=∠OEB ,∵∠ACB+∠ABC=90°,∴∠DEC+∠OEB=90°,∴∠OED=90°,∴DE 是圆O 的切线.(Ⅱ)设CE=1,AE=x ,由已知得AB=BE ,由射影定理可得,2AE CE BE =⋅,∴2x =,解得x考点:圆的切线判定与性质;圆周角定理;直角三角形射影定理23.【答案】(Ⅰ)cos 2ρθ=-,22cos 4sin 40ρρθρθ--+=(Ⅱ)12【解析】 试题分析:(Ⅰ)用直角坐标方程与极坐标互化公式即可求得1C ,2C 的极坐标方程;(Ⅱ)将将=4πθ代入22cos 4sin 40ρρθρθ--+=即可求出|MN|,利用三角形面积公式即可求出2C MN V的面积. 试题解析:(Ⅰ)因为cos ,sin x y ρθρθ==,∴1C 的极坐标方程为cos 2ρθ=-,2C 的极坐标方程为22cos 4sin 40ρρθρθ--+=.……5分(Ⅱ)将=4πθ代入22cos 4sin 40ρρθρθ--+=,得240ρ-+=,解得1ρ=2ρ|MN|=1ρ-2ρ因为2C 的半径为1,则2C MN V 的面积o 11sin 452⨯=12. 考点:直角坐标方程与极坐标互化;直线与圆的位置关系24.【答案】(Ⅰ)2{|2}3x x <<(Ⅱ)(2,+∞) 【解析】试题分析:(Ⅰ)利用零点分析法将不等式f (x )>1化为一元一次不等式组来解;(Ⅱ)将()f x 化为分段函数,求出()f x 与x 轴围成三角形的顶点坐标,即可求出三角形的面积,根据题意列出关于a 的不等式,即可解出a 的取值范围.试题解析:(Ⅰ)当a=1时,不等式f (x )>1化为|x+1|-2|x-1|>1, 等价于11221x x x ≤-⎧⎨--+->⎩或111221x x x -<<⎧⎨++->⎩或11221x x x ≥⎧⎨+-+>⎩,解得223x <<, 所以不等式f (x )>1的解集为2{|2}3x x <<.(Ⅱ)由题设可得,12,1()312,112,x a x f x x a x a x a x a --<-⎧⎪=+--≤≤⎨⎪-++>⎩,所以函数()f x 的图像与x 轴围成的三角形的三个顶点分别为21(,0)3a A -,(21,0)B a +,(,+1)C a a ,所以△ABC 的面积为22(1)3a +. 由题设得22(1)3a +>6,解得2a >. 所以a 的取值范围为(2,+∞).考点:含绝对值不等式解法;分段函数;一元二次不等式解法。
2019高考试题汇编理科数学---概率统计

(Ⅲ)由题意结合概率的定义给出结论即可.
【详解】(Ⅰ)由题意可知,两种支付方式都是用的人数为: 人,则:
该学生上个月A,B两种支付方式都使用的概率 .
(Ⅱ)由题意可知,
仅使用A支付方法的学生中,金额不大于1000的人数占 ,金额大于1000的人数占 ,
【详解】方法1:由分布列得 ,则
,则当 在 内增大时, 先减小后增大.
方法2:则
故选D.
【点睛】易出现的错误有,一是数学期望、方差以及二者之间的关系掌握不熟,无从着手;二是计算能力差,不能正确得到二次函数表达式.
(Ⅲ)已知上个月样本学生的支付方式在本月没有变化.现从样本仅使用A的学生中,随机抽查3人,发现他们本月的支付金额都大于2000元.根据抽查结果,能否认为样本仅使用A的学生中本月支付金额大于2000元的人数有变化?说明理由.
【答案】(Ⅰ) ;
(Ⅱ)见解析;
(Ⅲ)见解析.
【解析】
【分析】
(Ⅰ)由题意利用古典概型计算公式可得满足题意的概率值;
.
(2019全国1理)21.为治疗某种疾病,研制了甲、乙两种新药,希望知道哪种新药更有效,为此进行动物实验.实验方案如下:每一轮选取两只白鼠对药效进行对比实验.对于两只白鼠,随机选一只施以甲药,另一只施以乙药.一轮的治疗结果得出后,再安排下一轮实验.当其中一种药治愈的白鼠比另一种药治愈的白鼠多4只时,就停止实验,并认为治愈只数多的药更有效.为了方便描述问题,约定:对于每轮实验,若施以甲药的白鼠治愈且施以乙药的白鼠未治愈则甲药得1分,乙药得 分;若施以乙药的白鼠治愈且施以甲药的白鼠未治愈则乙药得1分,甲药得 分;若都治愈或都未治愈则两种药均得0分.甲、乙两种药的治愈率分别记为 和 ,一轮实验中甲药的得分记为 .
2015高考理科数学一轮计数原理、概率复习题(带答案)

2015高考理科数学一轮计数原理、概率复习题(带答案)第1课时分类加法计数原理与分步乘法计数原理1.理解分类加法计数原理和分步乘法计数原理.2.会用分类加法计数原理和分步乘法计数原理分析和解决一些简单的实际问题.对应学生用书P167]【梳理自测】一、分类加法计数原理1.(教材改编)从3名女同学和2名男同学中选1人主持主题班会,则不同的选法种数为()A.6B.5C.3D.22.设x,y∈N且x+y≤3,则直角坐标系中满足条件的点M(x,y)共有()A.3个B.4个C.5个D.10个答案:1.B2.D◆以上题目主要考查了以下内容:完成一件事有n类不同的方案,在第一类方案中有m1种不同的方法,在第二类方案中有m2种不同的方法,……,在第n类方案中有mn种不同的方法,则完成这件事情共有N=m1+m2+…+mn种不同的方法.二、分步乘法计数原理1.(教材改编)由0,1,2,3这四个数字组成的四位数中,有重复数字的四位数共有()A.238个B.232个C.174个D.168个2.(教材改编)有不同颜色的四件衬衣与不同颜色的三条领带,如果一条领带与一件衬衣配成一套.则不同的配法种数是________.3.5位同学报名参加两个课外活动小组,每位同学限报其中的一个小组,则不同的报名方法共有________种.答案:1.C2.123.32◆以上题目主要考查了以下内容:完成一件事情需要分成n个不同的步骤,完成第一步有m1种不同的方法,完成第二步有m2种不同的方法,……,完成第n步有mn种不同的方法,那么完成这件事情共有N=m1•m2•…•mn种不同的方法.【指点迷津】1.两个特点分类加法计数原理的特点是独立、互斥;分步乘法计数原理的特点是关联、连续.解题时经常是两个原理交叉在一起使用,两个原理综合使用时,一般先分类,再分步,分类要标准明确,分步要步骤连续,有的题目也可能出现先分步,在“步”里面再分类.2.两个关键分类的关键在于要做到“不重不漏”,分步的关键在于要正确设计分步的步骤,既要合理分类,又要准确分步.对应学生用书P167]考向一分类加法计数原理(2014•浙江省名校联考)如果正整数a的各位数字之和等于6,那么称a 为“好数”(如:6,24,2013等均为“好数”),将所有“好数”从小到大排成一列a1,a2,a3,…,若an=2013,则n=()A.50B.51C.52D.53【审题视点】2013是四位数,故“好数”按四位数,按三大类分首位为0、1、2每一类再分,采用加法原理.【典例精讲】本题可以把数归为“四位数”(含0006等),因此比2013小的“好数”为0×××,1×××,2004,共三类数,其中第一类可分为:00××,01××,…,0600,共7类,共有7+6+…+2+1=28个数;第二类可分为:10××,11××,…,1500,共6类,共有6+5+4+3+2+1=21个数,故2013为第51个数,故n=51,选B.【答案】B【类题通法】(1)分类加法计数原理的特点①根据问题的特点能确定一个适合于它的分类标准;②完成这件事情的任何一种方法必须属于某一类.(2)使用分类加法计数原理应注意的问题分类时标准要明确,分类应做到不重不漏.1.从集合{1,2,3,…,10}中任意选出三个不同的数,使这三个数成等比数列,这样的等比数列的个数为()A.3B.4C.6D.8解析:选D.当公比为2时,等比数列可为1,2,4或2,4,8;当公比为3时,等比数列可为1,3,9;当公比为32时,等比数列可为4,6,9.同理,公比为12,13,23时,也有4个.考向二分步乘法原理(2012•高考辽宁卷)一排9个座位坐了3个三口之家,若每家人坐在一起,则不同的坐法种数为()A.3×3B.3×(3!)3C.(3!)4D.9!【审题视点】一家人视为一个整体,采用捆绑法,先排三个家庭,再排每个家庭的三口人.【典例精讲】第1步:3个家庭的全排列,方法数为3!,第2步:家庭内部3个人全排列,方法数为3!,共3个家庭,方法数为(3!)3;∴总数为(3!)×(3!)3=(3!)4,故选C.【答案】C【类题通法】(1)明确题目中所指的“完成一件事”是什么事,必须要经过几步才能完成这件事;(2)完成这件事需要分成若干个步骤,只有每个步骤都完成了才算完成这件事,缺少任何一步,这件事都不可能完成;(3)解决分步问题时要合理设计步骤、顺序,使各步互不干扰,还要注意元素是否可以重复选取.2.用数字2,3组成四位数,且数字2,3至少都出现一次,这样的四位数共有________个(用数字作答).解析:法一:用2,3组成四位数共有2×2×2×2=16(个),其中不出现2或不出现3的共2个,因此满足条件的四位数共有16-2=14(个).法二:满足条件的四位数可分为三类:第一类含有一个2,三个3,共有4个;第二类含有三个2,一个3共有4个;第三类含有二个2,二个3共有C24=6(个),因此满足条件的四位数共有2×4+C24=14(个).答案:14考向三两个原理的综合应用(2014•石家庄市模拟)为举办校园文化节,某班推荐2名男生、3名女生参加文艺技能培训,培训项目及人数分别为:乐器1人,舞蹈2人,演唱2人,每人只参加一个项目,并且舞蹈和演唱项目必须有女生参加,则不同的推荐方案的种数为________.(用数字作答)【审题视点】先分两类:参加乐器培训的是女生或男生,每一类中分步选舞蹈或演唱.【典例精讲】若参加乐器培训的是女生,则各有1名男生及1名女生分别参加舞蹈和演唱培训,共有3×2×2=12种方案;若参加乐器培训的是男生,则各有1名男生、1名女生及2名女生分别参加舞蹈和演唱培训,共有2×3×2=12种方案,所以共有24中推荐方案.【答案】24【类题通法】(1)解决此类综合题的关键在于区分该问题是“分类”还是“分步”.(2)解决既有“分类”又有“分步”的综合问题时,应“先分类,后分步”.3.已知集合M∈{1,-2,3),N∈{-4,5,6,-7},从两个集合中各取一个元素作为点的坐标,则这样的坐标在直角坐标系中可表示第一、二象限内不同的点的个数是()A.18B.10C.16D.14解析:选D.M中的元素作点的横坐标,N中的元素作点的纵坐标,在第一象限的点共有2×2个,在第二象限的点共有1×2个.N中的元素作点的横坐标,M中的元素作点的纵坐标,在第一象限的点共有2×2个,在第二象限的点共有2×2个.所求不同的点的个数是2×2+1×2+2×2+2×2=14(个).对应学生用书P168]两个原理不清,分步与排列混淆致误把3封信投到4个信箱,所有可能的投法共有()A.A34种B.C34种C.43种D.34种【正解】第1封信投到信箱中有4种投法;第2封信投到信箱也有4种投法;第3封信投到信箱也有4种投法.只要把这3封信投完,就做完了这件事情,由分步计数原理可得共有43种方法,故选C.【答案】C【易错点】(1)选择的标准出现错误,误认为每个信箱有三种选择,所以可能的投法有34种,没有注意到一封信只能投在一个信箱中.(2)与排列混淆,误认为3封信只能用三个信箱错选为A.(3)与组合混淆,错选为B,C34只表示适用了三个信箱,并没把信放入信箱,事情并没“完成”.【警示】(1)理清题目的条件、结论及完成的“事件”,合理选择分类原理和分步原理.(2)能否独立完成事情是区分分类还是分步的依据,如(1)中,把其中的一封信投到信箱里,并没有完成任务,所以只能看做其中的一步,而不是一类.(3)本题所完成的事是指:把3封信全部投到信箱,可以用一个信箱,也可用2、3个信箱,故采用分步完成.1.(2013•高考山东卷)用0,1,…,9十个数字,可以组成有重复数字的三位数的个数为()A.243B.252C.261D.279解析:选B.0,1,2…,9共能组成9×10×10=900(个)三位数,其中无重复数字的三位数有9×9×8=648(个),∴有重复数字的三位数有900-648=252(个).2.(2012•高考浙江卷)若从1,2,3,…,9这9个整数中同时取4个不同的数,其和为偶数,则不同的取法共有()A.60种B.63种C.65种D.66种解析:选D.共有4个不同的偶数和5个不同的奇数,要使和为偶数,则4个数全为奇数,或全为偶数,或2个奇数和2个偶数,故不同的取法有C45+C44+C25C24=66(种).3.(2013•高考福建卷)满足a,b∈{-1,0,1,2},且关于x的方程ax2+2x+b=0有实数解的有序数对(a,b)的个数为()A.14B.13C.12D.10解析:选B.当a=0时,关于x的方程为2x+b=0,此时有序数对(0,-1),(0,0),(0,1),(0,2)均满足要求;当a≠0时,Δ=4-4ab≥0,ab≤1,此时满足要求的有序数对为(-1,-1),(-1,0),(-1,1),(-1,2),(1,-1),(1,0),(1,1),(2,-1),(2,0).综上,满足要求的有序数对共有13个,选B.4.(2012•高考北京卷)从0,2中选一个数字,从1,3,5中选两个数字,组成无重复数字的三位数,其中奇数的个数为()A.24B.18C.12D.6解析:选B.从0,2中选一个数字,分两类:1)取0:此时0只能放在十位,再从1,3,5中任取两个数,在个位与百位进行全排列即可,列式为A23;2)取2:此时2可以放在十位或百位,再从1,3,5中任取两个放在剩余两位进行全排列,列式为2A23,∴满足条件的三位数的个数为A23+2A23=3A23=3×3×2=18.故选B.。
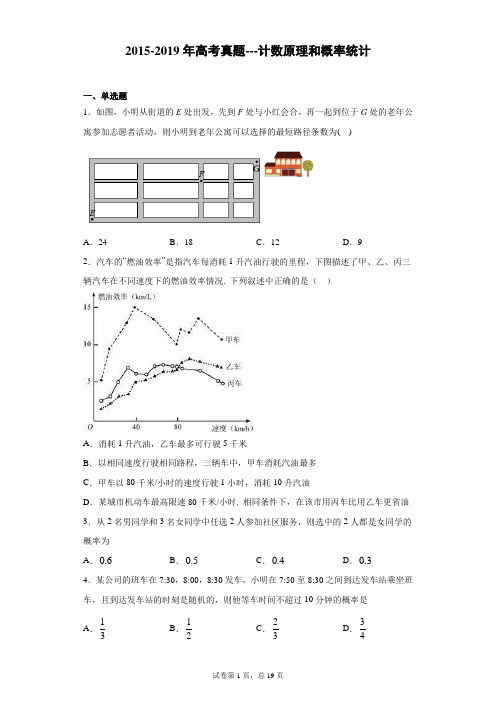
2015-2019年高考真题---计数原理和概率统计
2015-2019年高考真题---计数原理和概率统计一、单选题1.如图,小明从街道的E处出发,先到F处与小红会合,再一起到位于G处的老年公寓参加志愿者活动,则小明到老年公寓可以选择的最短路径条数为( )A.24 B.18 C.12 D.92.汽车的“燃油效率”是指汽车每消耗1升汽油行驶的里程,下图描述了甲、乙、丙三辆汽车在不同速度下的燃油效率情况. 下列叙述中正确的是()A.消耗1升汽油,乙车最多可行驶5千米B.以相同速度行驶相同路程,三辆车中,甲车消耗汽油最多C.甲车以80千米/小时的速度行驶1小时,消耗10升汽油D.某城市机动车最高限速80千米/小时. 相同条件下,在该市用丙车比用乙车更省油3.从2名男同学和3名女同学中任选2人参加社区服务,则选中的2人都是女同学的概率为A.0.6B.0.5C.0.4D.0.34.某公司的班车在7:30,8:00,8:30发车,小明在7:50至8:30之间到达发车站乘坐班车,且到达发车站的时刻是随机的,则他等车时间不超过10分钟的概率是A.13B.12C.23D.345.已知某批零件的长度误差(单位:毫米)服从正态分布()20,3N ,从中随机取一件,其长度误差落在区间(3,6)内的概率为( ) (附:若随机变量ξ服从正态分布()2,N μσ,则()68.26%P μσξμσ-<<+=,()2295.44%P μσξμσ-<<+=.)A .4.56%B .13.59%C .27.18%D .31.74%6.某城市为了解游客人数的变化规律,提高旅游服务质量,收集并整理了2014年1月至2016年12月期间月接待游客量(单位:万人)的数据,绘制了如图所示的折线图.根据该折线图,下列结论错误的是( )A .月接待游客量逐月增加B .年接待游客量逐年增加C .各年的月接待游客量高峰期大致在7,8月D .各年1月至6月的月接待游客量相对于7月至12月,波动性更小,变化比较平稳 7.有5支彩笔(除颜色外无差别),颜色分别为红、黄、蓝、绿、紫.从这5支彩笔中任取2支不同颜色的彩笔,则取出的2支彩笔中含有红色彩笔的概率为 A .45B .35C .25D .158.为了解某社区居民的家庭年收入所年支出的关系,随机调查了该社区5户家庭,得到如下统计数据表:根据上表可得回归直线方程ˆˆˆybx a =+,其中ˆˆˆ0.76,b a y bx ==-,据此估计,该社区一户收入为15万元家庭年支出为( ) A .11.4万元B .11.8万元C .12.0万元D .12.2万元9.为美化环境,从红、黄、白、紫4种颜色的花中任选2种花种在一个花坛中,余下的2种花种在另一个花坛中,则红色和紫色的花不在同一花坛的概率是 A .13B .12C .23D .5610.二项式()()1nx n N *+∈的展开式中2x项的系数为15,则n =( ) A .4B .5C .6D .711.我国古代数学名著《九章算术》有“米谷粒分”题:粮仓开仓收粮,有人送来米1534石,验得米内夹谷,抽样取米一把,数得254粒内夹谷28粒,则这批米内夹谷约为( ) A .134石B .169石C .338石D .1365石12.522x x ⎛⎫+ ⎪⎝⎭的展开式中4x 的系数为A .10B .20C .40D .8013.如图,正方形ABCD 内的图形来自中国古代的太极图,正方形内切圆中的黑色部分和白色部分关于正方形的中心成中心对称,在正方形内随机取一点,则此点取自黑色部分的概率是A .14B .8π C .12D .4π 14.某群体中的每位成员使用移动支付的概率都为p ,各成员的支付方式相互独立,设X 为该群体的10位成员中使用移动支付的人数, 2.4DX =,()()46P X P X =<=,则p = A .0.7B .0.6C .0.4D .0.315.(x 2+x +y )5的展开式中,x 5y 2的系数为 A .10B .20C .30D .6016.用数字0,1,2,3,4,5组成没有重复数字的五位数,其中比40000大的偶数共有 A .144个B .120个C .96个D .72个17.已知(1)n x 的展开式中第4项与第8项的二项式系数相等,则奇数项的二项式系数和为( ). A .122B .112C .102D .9218.从分别标有1,2,…,9的9张卡片中不放回地随机抽取2次,每次抽取1张.则抽到的2张卡片上的数奇偶性不同的概率是 A .518B .49C .59D .7919.若某群体中的成员只用现金支付的概率为0.45,既用现金支付也用非现金支付的概率为0.15,则不用现金支付的概率为 A .0.3B .0.4C .0.6D .0.720.下图所示的茎叶图记录了甲、乙两组各5名工人某日的产量数据(单位:件)若这两组数据的中位数相等,且平均值也相等,则x 和y 的值分别为A .5,5B .3,5C .3,7D .5,721.(1+2x 2 )(1+x )4的展开式中x 3的系数为 A .12B .16C .20D .2422.演讲比赛共有9位评委分别给出某选手的原始评分,评定该选手的成绩时,从9个原始评分中去掉1个最高分、1个最低分,得到7个有效评分.7个有效评分与9个原始评分相比,不变的数字特征是 A .中位数 B .平均数 C .方差D .极差23.从分别写有1,2,3,4,5的5张卡片中随机抽取1张,放回后再随机抽取1张,则抽得的第一张卡片上的数大于第二张卡片上的数的概率为( ) A .110B .35C .310D .2524.两位男同学和两位女同学随机排成一列,则两位女同学相邻的概率是( )A .16B .14C .13D .1225.设复数()()1,z x yi x y R =-+∈,若1z ≤,则y x ≥的概率为( ) A .3142π+B .112π+ C .1142π-D .112π- 26.若样本数据1210,,,x x x ⋅⋅⋅的标准差为8,则数据121x -,221x -,⋅⋅⋅,1021x -的标准差为( ) A .8B .15C .16D .3227. 重庆市2013年各月的平均气温(℃)数据的茎叶图如下:则这组数据的中位数是 ( ) A .19 B .20 C .21.5D .2328.已知变量x 和y 满足关系0.11y x =-+,变量y 与z 正相关. 下列结论中正确的是( )A .x 与y 负相关,x 与z 负相关B .x 与y 正相关,x 与z 正相关C .x 与y 正相关,x 与z 负相关D .x 与y 负相关,x 与z 正相关29.在区间[0,1]上随机取两个数,x y ,记1p 为事件“12x y +≤”的概率,2p 为事件“12xy ≤” 的概率,则( ) A .1212p p << B .1212p p << C .2112p p << D .2112p p << 30.用数字1,2,3,4,5组成没有重复数字的五位数,其中奇数的个数为 A .24 B .48 C .60D .7231.某地区经过一年的新农村建设,农村的经济收入增加了一倍.实现翻番.为更好地了解该地区农村的经济收入变化情况,统计了该地区新农村建设前后农村的经济收入构成比例.得到如下饼图:则下面结论中不正确的是 A .新农村建设后,种植收入减少B .新农村建设后,其他收入增加了一倍以上C .新农村建设后,养殖收入增加了一倍D .新农村建设后,养殖收入与第三产业收入的总和超过了经济收入的一半 32.在区间上随机取两个数,x y ,记1p 为事件“12x y +≥”的概率,2p 为事件“12x y -≤”的概率,3p 为事件“12xy ≤”的概率,则 ( ) A .123p p p << B .231p p p << C .312p p p <<D .321p p p <<33.我国数学家陈景润在哥德巴赫猜想的研究中取得了世界领先的成果.哥德巴赫猜想是“每个大于2的偶数可以表示为两个素数的和”,如30723=+.在不超过30的素数中,随机选取两个不同的数,其和等于30的概率是 A .112B .114C .115D .11834.已知随机变量i ξ满足P (i ξ=1)=p i ,P (i ξ=0)=1—p i ,i =1,2.若0<p 1<p 2<12,则 A .1E()ξ<2E()ξ,1D()ξ<2D()ξ B .1E()ξ<2E()ξ,1D()ξ>2D()ξ C .1E()ξ>2E()ξ,1D()ξ<2D()ξD .1E()ξ>2E()ξ,1D()ξ>2D()ξ35.如果3个正整数可作为一个直角三角形三条边的边长,则称这3个数为一组勾股数,从1,2,3,4,5中任取3个不同的数,则这3个数构成一组勾股数的概率为( ) A .310B .15C .110D .12036.在区间[]0,2上随机地取一个数x ,则事件“121-1log 2x ≤+≤()1”发生的概率为( )A.34B.23C.13D.1437.生物实验室有5只兔子,其中只有3只测量过某项指标,若从这5只兔子中随机取出3只,则恰有2只测量过该指标的概率为A.23B.35C.25D.15二、解答题38.某超市计划按月订购一种酸奶,每天进货量相同,进货成本每瓶4元,售价每瓶6元,未售出的酸奶降价处理,以每瓶2元的价格当天全部处理完.根据往年销售经验,每天需求量与当天最高气温(单位:℃)有关.如果最高气温不低于25,需求量为500瓶;如果最高气温位于区间[20,25),需求量为300瓶;如果最高气温低于20,需求量为200瓶.为了确定六月份的订购计划,统计了前三年六月份各天的最高气温数据,得下面的频数分布表:以最高气温位于各区间的频率估计最高气温位于该区间的概率.(1)求六月份这种酸奶一天的需求量不超过300瓶的概率;(2)设六月份一天销售这种酸奶的利润为Y(单位:元),当六月份这种酸奶一天的进货量为450瓶时,写出Y的所有可能值,并估计Y大于零的概率.39.已知某单位甲、乙、丙三个部门的员工人数分别为24,16,16.现采用分层抽样的方法从中抽取7人,进行睡眠时间的调查.(I)应从甲、乙、丙三个部门的员工中分别抽取多少人?(II)若抽出的7人中有4人睡眠不足,3人睡眠充足,现从这7人中随机抽取3人做进一步的身体检查.(i)用X表示抽取的3人中睡眠不足..的员工人数,求随机变量X的分布列与数学期望;(ii)设A为事件“抽取的3人中,既有睡眠充足的员工,也有睡眠不足的员工”,求事件A发生的概率.40.改革开放以来,人们的支付方式发生了巨大转变.近年来,移动支付已成为主要支付方式之一.为了解某校学生上个月A ,B 两种移动支付方式的使用情况,从全校所有的1000名学生中随机抽取了100人,发现样本中A ,B 两种支付方式都不使用的有5人,样本中仅使用A 和仅使用B 的学生的支付金额分布情况如下:支付金额支付方式(Ⅰ)估计该校学生中上个月A ,B 两种支付方式都使用的人数;(Ⅱ)从样本仅使用B 的学生中随机抽取1人,求该学生上个月支付金额大于2000元的概率;(Ⅲ)已知上个月样本学生的支付方式在本月没有变化.现从样本仅使用B 的学生中随机抽查1人,发现他本月的支付金额大于2000元.结合(Ⅱ)的结果,能否认为样本仅使用B 的学生中本月支付金额大于2000元的人数有变化?说明理由.41.海水养殖场进行某水产品的新、旧网箱养殖方法的产量对比,收获时各随机抽取了100个网箱,测量各箱水产品的产量(单位:kg ), 其频率分布直方图如下:(1)记A 表示事件“旧养殖法的箱产量低于50kg”,估计A 的概率;(2)填写下面列联表,并根据列联表判断是否有99%的把握认为箱产量与养殖方法有关:(3)根据箱产量的频率分布直方图,对两种养殖方法的优劣进行较。
-2019年全国一卷理科试题汇编---概率统计试题

全国一卷分类汇编(2013年-2019年)——概率统计一、概率与排列组合1、(2013全国1卷.理3)为了解某地区的中小考生视力情况,拟从该地区的中小考生中抽取部分考生进行调查,事先已了解到该地区小学、初中、高中三个学段考生的视力情况有较大差异,而男女生视力情况差异不大,在下面的抽样方法中,最合理的抽样方法是( )A 、简单随机抽样B 、按性别分层抽样C 、按学段分层抽样D 、系统抽样2.(2014全国1卷.理5)4位同学各自在周六、周日两天中任选一天参加公益活动,则周六、周日都有同学参加公益活动的概率为( ) A 、81 B 、83 C 、85 D 、873、(2015全国1卷.理4)投篮测试中,每人投3次,至少投中2次才能通过测试。
已知某同学每次投篮投中的概率为 ,且各次投篮是否投中相互独立,则该同学通过测试的概率为( ) A 、B 、C 、D 、4. (2016全国1卷.理4)某公司的班车在7:00,8:00,8:30发车,小明在7:50至8:30之间到达发车站乘坐班车, 且到达发车站的时刻是随机的,则他等车时间不超过10分钟的概率是( ) A 、31 B 、21 C 、32 D 、43 5.(2017全国1卷.理2)如图,正方形ABCD 内的图形来自中国古代的太极图.正方形内切圆中的黑色部分和白色部分关于正方形的中心成中心对称.在正方形内随机取一点,则此点取自黑色部分的概率是( ) A .14B .π8C .12D .π4二、二项式定理1、(2013全国1卷.理9)设m 为正整数,2()mx y +展开式的二项式系数的最大值为a ,21()m x y ++展开式的二项式系数的最大值为b ,若13a =7b ,则m = ( ) A 、5B 、6C 、7D 、82、(2014全国1卷.理13)()()8x y x y -+的展开式中27x y 的系数为________.(用数字填写答案)3、(2015全国1卷.理10)25()x x y ++的展开式中,52x y 的系数为( )A 、10B 、20C 、30D 、604、(2016全国1卷.理14)5)2(x x +的展开式中,3x 的系数是 .(用数字填写答案)5.(2017全国1卷.理6)621(1)(1)x x++展开式中2x 的系数为( ) A 、15B 、20C 、30D 、356、(2018全国1卷.理3)某地区经过一年的新农村建设,农村的经济收入增加了一倍,实现翻番,为更好地了解该地区农村的经济收入变化情况,统计了该地区新农村建设前后农村的经济收入构成比例,得到如下饼图:则下面结论中不正确的是 A .新农村建设后,种植收入减少B .新农村建设后,其他收入增加了一倍以上C .新农村建设后,养殖收入增加了一倍D .新农村建设后,养殖收入与第三产业收入的总和超过了经济收入的一半 7、(2018全国1卷.理10)下图来自古希腊数学家希波克拉底所研究的几何图形.此图由三个半圆构成,三个半圆的直径分别为直角三角形ABC 的斜边BC ,直角边AB ,AC .△ABC 的三边所围成的区域记为I ,黑色部分记为II ,其余部分记为III .在整个图形中随机取一点,此点取自I ,II ,III 的概率分别记为p 1,p 2,p 3,则 A .p 1=p 2B .p 1=p 3C .p 2=p 3D .p 1=p 2+p 38、(2018全国1卷.理15)从2位女生,4位男生中选3人参加科技比赛,且至少有1位女生入选,则不同的选法共有_____________种.(用数字填写答案)9、(2019全国1卷.理6)我国古代典籍《周易》用卦描述万物的变化。
2019年高考数学理试题分类汇编:统计与概率(含答案)
2019 年高考数学理试题分类汇编统计与概率一、选择题1、( 2019 年北京高考)袋中装有偶数个球,其中红球、黑球各占一半.甲、乙、丙是三个空盒.每次从袋中任意取出两个球,将其中一个球放入甲盒,如果这个球是红球,就将另一个球放入乙盒,否则就放入丙盒.重复上述过程,直到袋中所有球都被放入盒中,则()A. 乙盒中黑球不多于丙盒中黑球B.乙盒中红球与丙盒中黑球一样多C.乙盒中红球不多于丙盒中红球D.乙盒中黑球与丙盒中红球一样多【答案】 C2、( 2019 年山东高考)某高校调查了200 名学生每周的自习时间(单位:小时),制成了如图所示的频率分布直方图,其中自习时间的范围是[17.5,30] ,样本数据分组为[17.5,20),[20,22.5),[22.5,25),[25,27.5),[27.5,30] .根据直方图,这200 名学生中每周的自习时间不少于 22.5 小时的人数是( A )56(B)60(C)120(D)140【答案】 D3、( 2019 年全国 I 高考)某公司的班车在7:30, 8:00, 8:30 发车,小明在 7:50 至 8:30 之间到达发车站乘坐班车,且到达发车站的时刻是随机的,则他等车时间不超过10 分钟的概率是1123(A )3( B)2(C)3(D)4【答案】 B4、( 2019年全国 II 高考)从区间0,1 随机抽取 2n 个数x1,x2,⋯,x n,y1,y2,⋯,y n,构成n 个数对x1, y1, x2 , y2,⋯,x n , y n,其中两数的平方和小于 1 的数对共有m个,则用随机模拟的方法得到的圆周率的近似值为( A)【答案】 C 4n2n4m2m m(B)( C)(D)m n n5、( 2019 年全国 III 高考)某旅游城市为向游客介绍本地的气温情况,绘制了一年中月平均最高气温和平均最低气温的雷达图。
图中 A 点表示十月的平均最高气温约为150C, B 点表示四月的平均最低气温约为50C。
2015年全国统一高考真题数学试卷(理科)(新课标ⅰ)(含答案及解析)

2015年全国统一高考数学试卷(理科)(新课标Ⅰ)一、选择题(共12小题,每小题5分,满分60分)1.(5分)设复数z满足=i,则|z|=()A.1B.C.D.22.(5分)sin20°cos10°﹣cos160°sin10°=()A.B.C.D.3.(5分)设命题p:∃n∈N,n2>2n,则¬p为()A.∀n∈N,n2>2n B.∃n∈N,n2≤2nC.∀n∈N,n2≤2n D.∃n∈N,n2=2n4.(5分)投篮测试中,每人投3次,至少投中2次才能通过测试.已知某同学每次投篮投中的概率为0.6,且各次投篮是否投中相互独立,则该同学通过测试的概率为()A.0.648B.0.432C.0.36D.0.3125.(5分)已知M(x0,y0)是双曲线C:=1上的一点,F1,F2是C的左、右两个焦点,若<0,则y0的取值范围是()A.B.C.D.6.(5分)《九章算术》是我国古代内容极为丰富的数学名著,书中有如下问题:”今有委米依垣内角,下周八尺,高五尺.问:积及为米几何?“其意思为:”在屋内墙角处堆放米(如图,米堆为一个圆锥的四分之一),米堆底部的弧长为8尺,米堆的高为5尺,问米堆的体积和堆放的米各为多少?“已知1斛米的体积约为1.62立方尺,圆周率约为3,估算出堆放的米约有()A.14斛B.22斛C.36斛D.66斛7.(5分)设D为△ABC所在平面内一点,,则()A.B.C.D.8.(5分)函数f(x)=cos(ωx+φ)的部分图象如图所示,则f(x)的单调递减区间为()A.(kπ﹣,kπ+),k∈z B.(2kπ﹣,2kπ+),k∈zC.(k﹣,k+),k∈z D.(,2k+),k∈z9.(5分)执行如图所示的程序框图,如果输入的t=0.01,则输出的n=()A.5B.6C.7D.810.(5分)(x2+x+y)5的展开式中,x5y2的系数为()A.10B.20C.30D.6011.(5分)圆柱被一个平面截去一部分后与半球(半径为r)组成一个几何体,该几何体三视图中的正视图和俯视图如图所示.若该几何体的表面积为16+20π,则r=()A.1B.2C.4D.812.(5分)设函数f(x)=e x(2x﹣1)﹣ax+a,其中a<1,若存在唯一的整数x0使得f(x0)<0,则a的取值范围是()A.[)B.[)C.[)D.[)二、填空题(本大题共有4小题,每小题5分)13.(5分)若函数f(x)=xln(x+)为偶函数,则a=.14.(5分)一个圆经过椭圆=1的三个顶点.且圆心在x轴的正半轴上.则该圆标准方程为.15.(5分)若x,y满足约束条件.则的最大值为.16.(5分)在平面四边形ABCD中,∠A=∠B=∠C=75°.BC=2,则AB的取值范围是.三、解答题:17.(12分)S n为数列{a n}的前n项和,已知a n>0,a n2+2a n=4S n+3(I)求{a n}的通项公式:(Ⅱ)设b n=,求数列{b n}的前n项和.18.(12分)如图,四边形ABCD为菱形,∠ABC=120°,E,F是平面ABCD同一侧的两点,BE丄平面ABCD,DF丄平面ABCD,BE=2DF,AE丄EC.(Ⅰ)证明:平面AEC丄平面AFC(Ⅱ)求直线AE与直线CF所成角的余弦值.19.(12分)某公司为确定下一年度投入某种产品的宣传费,需了解年宣传费x (单位:千元)对年销售量y(单位:t)和年利润z(单位:千元)的影响,对近8年的年宣传费x i和年销售量y i(i=1,2,…,8)数据作了初步处理,得到下面的散点图及一些统计量的值.(x i﹣)2(w i﹣)2(x i﹣)(y i﹣)(w i﹣)(y i﹣)46.6563 6.8289.8 1.61469108.8表中w i=i,=(Ⅰ)根据散点图判断,y=a+bx与y=c+d哪一个适宜作为年销售量y关于年宣传费x的回归方程类型?(给出判断即可,不必说明理由)(Ⅱ)根据(Ⅰ)的判断结果及表中数据,建立y关于x的回归方程;(Ⅲ)已知这种产品的年利润z与x、y的关系为z=0.2y﹣x.根据(Ⅱ)的结果回答下列问题:(i)年宣传费x=49时,年销售量及年利润的预报值是多少?(ii)年宣传费x为何值时,年利润的预报值最大?附:对于一组数据(u1 v1),(u2 v2)…..(u n v n),其回归线v=α+βu的斜率和截距的最小二乘估计分别为:=,=﹣.20.(12分)在直角坐标系xOy中,曲线C:y=与直线l:y=kx+a(a>0)交于M,N两点.(Ⅰ)当k=0时,分別求C在点M和N处的切线方程.(Ⅱ)y轴上是否存在点P,使得当k变动时,总有∠OPM=∠OPN?(说明理由)21.(12分)已知函数f(x)=x3+ax+,g(x)=﹣lnx(i)当a为何值时,x轴为曲线y=f(x)的切线;(ii)用min{m,n}表示m,n中的最小值,设函数h(x)=min{f(x),g(x)}(x>0),讨论h(x)零点的个数.选修4一1:几何证明选讲22.(10分)如图,AB是⊙O的直径,AC是⊙O的切线,BC交⊙O于点E.(Ⅰ)若D为AC的中点,证明:DE是⊙O的切线;(Ⅱ)若OA=CE,求∠ACB的大小.选修4一4:坐标系与参数方程23.(10分)在直角坐标系xOy中,直线C1:x=﹣2,圆C2:(x﹣1)2+(y﹣2)2=1,以坐标原点为极点,x轴的正半轴为极轴建立极坐标系.(Ⅰ)求C1,C2的极坐标方程;(Ⅱ)若直线C3的极坐标方程为θ=(ρ∈R),设C2与C3的交点为M,N,求△C2MN的面积.选修4一5:不等式选讲24.(10分)已知函数f(x)=|x+1|﹣2|x﹣a|,a>0.(Ⅰ)当a=1时,求不等式f(x)>1的解集;(Ⅱ)若f(x)的图象与x轴围成的三角形面积大于6,求a的取值范围.2015年全国统一高考数学试卷(理科)(新课标Ⅰ)参考答案与试题解析一、选择题(共12小题,每小题5分,满分60分)1.(5分)设复数z满足=i,则|z|=()A.1B.C.D.2【考点】A8:复数的模.【专题】11:计算题;5N:数系的扩充和复数.【分析】先化简复数,再求模即可.【解答】解:∵复数z满足=i,∴1+z=i﹣zi,∴z(1+i)=i﹣1,∴z==i,∴|z|=1,故选:A.【点评】本题考查复数的运算,考查学生的计算能力,比较基础.2.(5分)sin20°cos10°﹣cos160°sin10°=()A.B.C.D.【考点】GP:两角和与差的三角函数.【专题】56:三角函数的求值.【分析】直接利用诱导公式以及两角和的正弦函数,化简求解即可.【解答】解:sin20°cos10°﹣cos160°sin10°=sin20°cos10°+cos20°sin10°=sin30°=.故选:D.【点评】本题考查诱导公式以及两角和的正弦函数的应用,基本知识的考查.3.(5分)设命题p:∃n∈N,n2>2n,则¬p为()A.∀n∈N,n2>2n B.∃n∈N,n2≤2n C.∀n∈N,n2≤2n D.∃n∈N,n2=2n【考点】2J:命题的否定.【专题】5L:简易逻辑.【分析】根据特称命题的否定是全称命题即可得到结论.【解答】解:命题的否定是:∀n∈N,n2≤2n,故选:C.【点评】本题主要考查含有量词的命题的否定,比较基础.4.(5分)投篮测试中,每人投3次,至少投中2次才能通过测试.已知某同学每次投篮投中的概率为0.6,且各次投篮是否投中相互独立,则该同学通过测试的概率为()A.0.648B.0.432C.0.36D.0.312【考点】C8:相互独立事件和相互独立事件的概率乘法公式.【专题】5I:概率与统计.【分析】判断该同学投篮投中是独立重复试验,然后求解概率即可.【解答】解:由题意可知:同学3次测试满足X∽B(3,0.6),该同学通过测试的概率为=0.648.故选:A.【点评】本题考查独立重复试验概率的求法,基本知识的考查.5.(5分)已知M(x0,y0)是双曲线C:=1上的一点,F1,F2是C的左、右两个焦点,若<0,则y0的取值范围是()A.B.C.D.【考点】KC:双曲线的性质.【专题】11:计算题;5D:圆锥曲线的定义、性质与方程.【分析】利用向量的数量积公式,结合双曲线方程,即可确定y0的取值范围.【解答】解:由题意,=(﹣﹣x0,﹣y0)•(﹣x0,﹣y0)=x02﹣3+y02=3y02﹣1<0,所以﹣<y0<.故选:A.【点评】本题考查向量的数量积公式,考查双曲线方程,考查学生的计算能力,比较基础.6.(5分)《九章算术》是我国古代内容极为丰富的数学名著,书中有如下问题:”今有委米依垣内角,下周八尺,高五尺.问:积及为米几何?“其意思为:”在屋内墙角处堆放米(如图,米堆为一个圆锥的四分之一),米堆底部的弧长为8尺,米堆的高为5尺,问米堆的体积和堆放的米各为多少?“已知1斛米的体积约为1.62立方尺,圆周率约为3,估算出堆放的米约有()A.14斛B.22斛C.36斛D.66斛【考点】LF:棱柱、棱锥、棱台的体积.【专题】5F:空间位置关系与距离.【分析】根据圆锥的体积公式计算出对应的体积即可.【解答】解:设圆锥的底面半径为r,则r=8,解得r=,故米堆的体积为××π×()2×5≈,∵1斛米的体积约为1.62立方,∴÷1.62≈22,故选:B.【点评】本题主要考查椎体的体积的计算,比较基础.7.(5分)设D为△ABC所在平面内一点,,则()A.B.C.D.【考点】96:平行向量(共线).【专题】5A:平面向量及应用.【分析】将向量利用向量的三角形法则首先表示为,然后结合已知表示为的形式.【解答】解:由已知得到如图由===;故选:A.【点评】本题考查了向量的三角形法则的运用;关键是想法将向量表示为.8.(5分)函数f(x)=cos(ωx+φ)的部分图象如图所示,则f(x)的单调递减区间为()A.(kπ﹣,kπ+),k∈z B.(2kπ﹣,2kπ+),k∈zC.(k﹣,k+),k∈z D.(,2k+),k∈z【考点】HA:余弦函数的单调性.【专题】57:三角函数的图像与性质.【分析】由周期求出ω,由五点法作图求出φ,可得f(x)的解析式,再根据余弦函数的单调性,求得f(x)的减区间.【解答】解:由函数f(x)=cos(ωx+ϕ)的部分图象,可得函数的周期为=2(﹣)=2,∴ω=π,f(x)=cos(πx+ϕ).再根据函数的图象以及五点法作图,可得+ϕ=,k∈z,即ϕ=,f(x)=cos (πx+).由2kπ≤πx+≤2kπ+π,求得2k﹣≤x≤2k+,故f(x)的单调递减区间为(,2k+),k∈z,故选:D.【点评】本题主要考查由函数y=Asin(ωx+φ)的部分图象求解析式,由周期求出ω,由五点法作图求出φ的值;还考查了余弦函数的单调性,属于基础题.9.(5分)执行如图所示的程序框图,如果输入的t=0.01,则输出的n=()A.5B.6C.7D.8【考点】EF:程序框图.【专题】5K:算法和程序框图.【分析】由已知中的程序框图可知:该程序的功能是利用循环结构计算并输出变量n的值,模拟程序的运行过程,分析循环中各变量值的变化情况,可得答案.【解答】解:第一次执行循环体后,S=,m=,n=1,不满足退出循环的条件;再次执行循环体后,S=,m=,n=2,不满足退出循环的条件;再次执行循环体后,S=,m=,n=3,不满足退出循环的条件;再次执行循环体后,S=,m=,n=4,不满足退出循环的条件;再次执行循环体后,S=,m=,n=5,不满足退出循环的条件;再次执行循环体后,S=,m=,n=6,不满足退出循环的条件;再次执行循环体后,S=,m=,n=7,满足退出循环的条件;故输出的n值为7,故选:C.【点评】本题考查的知识点是程序框图,当循环的次数不多,或有规律时,常采用模拟循环的方法解答.10.(5分)(x2+x+y)5的展开式中,x5y2的系数为()A.10B.20C.30D.60【考点】DA:二项式定理.【专题】11:计算题;5P:二项式定理.【分析】利用展开式的通项,即可得出结论.=,【解答】解:(x2+x+y)5的展开式的通项为T r+1令r=2,则(x2+x)3的通项为=,令6﹣k=5,则k=1,∴(x2+x+y)5的展开式中,x5y2的系数为=30.故选:C.【点评】本题考查二项式定理的运用,考查学生的计算能力,确定通项是关键.11.(5分)圆柱被一个平面截去一部分后与半球(半径为r)组成一个几何体,该几何体三视图中的正视图和俯视图如图所示.若该几何体的表面积为16+20π,则r=()A.1B.2C.4D.8【考点】L!:由三视图求面积、体积.【专题】5Q:立体几何.【分析】通过三视图可知该几何体是一个半球拼接半个圆柱,计算即可.【解答】解:由几何体三视图中的正视图和俯视图可知,截圆柱的平面过圆柱的轴线,该几何体是一个半球拼接半个圆柱,∴其表面积为:×4πr2+×πr22r×2πr+2r×2r+×πr2=5πr2+4r2,又∵该几何体的表面积为16+20π,∴5πr2+4r2=16+20π,解得r=2,故选:B.【点评】本题考查由三视图求表面积问题,考查空间想象能力,注意解题方法的积累,属于中档题.12.(5分)设函数f(x)=e x(2x﹣1)﹣ax+a,其中a<1,若存在唯一的整数x0使得f(x0)<0,则a的取值范围是()A.[)B.[)C.[)D.[)【考点】51:函数的零点;6D:利用导数研究函数的极值.【专题】2:创新题型;53:导数的综合应用.【分析】设g(x)=e x(2x﹣1),y=ax﹣a,问题转化为存在唯一的整数x0使得g (x0)在直线y=ax﹣a的下方,求导数可得函数的极值,数形结合可得﹣a>g (0)=﹣1且g(﹣1)=﹣3e﹣1≥﹣a﹣a,解关于a的不等式组可得.【解答】解:设g(x)=e x(2x﹣1),y=ax﹣a,由题意知存在唯一的整数x0使得g(x0)在直线y=ax﹣a的下方,∵g′(x)=e x(2x﹣1)+2e x=e x(2x+1),∴当x<﹣时,g′(x)<0,当x>﹣时,g′(x)>0,∴当x=﹣时,g(x)取最小值﹣2,当x=0时,g(0)=﹣1,当x=1时,g(1)=e>0,直线y=ax﹣a恒过定点(1,0)且斜率为a,故﹣a>g(0)=﹣1且g(﹣1)=﹣3e﹣1≥﹣a﹣a,解得≤a<1故选:D.【点评】本题考查导数和极值,涉及数形结合和转化的思想,属中档题.二、填空题(本大题共有4小题,每小题5分)13.(5分)若函数f(x)=xln(x+)为偶函数,则a=1.【考点】3K:函数奇偶性的性质与判断.【专题】51:函数的性质及应用.【分析】由题意可得,f(﹣x)=f(x),代入根据对数的运算性质即可求解.【解答】解:∵f(x)=xln(x+)为偶函数,∴f(﹣x)=f(x),∴(﹣x)ln(﹣x+)=xln(x+),∴﹣ln(﹣x+)=ln(x+),∴ln(﹣x+)+ln(x+)=0,∴ln(+x)(﹣x)=0,∴lna=0,∴a=1.故答案为:1.【点评】本题主要考查了偶函数的定义及对数的运算性质的简单应用,属于基础试题.14.(5分)一个圆经过椭圆=1的三个顶点.且圆心在x轴的正半轴上.则该圆标准方程为(x﹣)2+y2=.【考点】K3:椭圆的标准方程.【专题】5D:圆锥曲线的定义、性质与方程.【分析】利用椭圆的方程求出顶点坐标,然后求出圆心坐标,求出半径即可得到圆的方程.【解答】解:一个圆经过椭圆=1的三个顶点.且圆心在x轴的正半轴上.可知椭圆的右顶点坐标(4,0),上下顶点坐标(0,±2),设圆的圆心(a,0),则,解得a=,圆的半径为:,所求圆的方程为:(x﹣)2+y2=.故答案为:(x﹣)2+y2=.【点评】本题考查椭圆的简单性质的应用,圆的方程的求法,考查计算能力.15.(5分)若x,y满足约束条件.则的最大值为3.【考点】7C:简单线性规划.【专题】59:不等式的解法及应用.【分析】作出不等式组对应的平面区域,利用目标函数的几何意义,利用数形结合确定的最大值.【解答】解:作出不等式组对应的平面区域如图:(阴影部分ABC).设k=,则k的几何意义为区域内的点到原点的斜率,由图象知OA的斜率最大,由,解得,即A(1,3),k OA==3,即的最大值为3.故答案为:3.【点评】本题主要考查线性规划的应用,结合目标函数的几何意义以及直线的斜率,利用数形结合的数学思想是解决此类问题的基本方法.16.(5分)在平面四边形ABCD中,∠A=∠B=∠C=75°.BC=2,则AB的取值范围是(﹣,+).【考点】HT:三角形中的几何计算.【专题】15:综合题;2:创新题型;58:解三角形.【分析】如图所示,延长BA,CD交于点E,设AD=x,AE=x,DE=x,CD=m,求出x+m=+,即可求出AB的取值范围.【解答】解:方法一:如图所示,延长BA,CD交于点E,则在△ADE中,∠DAE=105°,∠ADE=45°,∠E=30°,∴设AD=x,AE=x,DE=x,CD=m,∵BC=2,∴(x+m)sin15°=1,∴x+m=+,∴0<x<4,而AB=x+m﹣x=+﹣x,∴AB的取值范围是(﹣,+).故答案为:(﹣,+).方法二:如下图,作出底边BC=2的等腰三角形EBC,B=C=75°,倾斜角为150°的直线在平面内移动,分别交EB、EC于A、D,则四边形ABCD即为满足题意的四边形;当直线移动时,运用极限思想,①直线接近点C时,AB趋近最小,为﹣;②直线接近点E时,AB趋近最大值,为+;故答案为:(﹣,+).【点评】本题考查求AB的取值范围,考查三角形中的几何计算,考查学生的计算能力,属于中档题.三、解答题:17.(12分)S n为数列{a n}的前n项和,已知a n>0,a n2+2a n=4S n+3(I)求{a n}的通项公式:(Ⅱ)设b n=,求数列{b n}的前n项和.【考点】8E:数列的求和;8H:数列递推式.【专题】54:等差数列与等比数列.【分析】(I)根据数列的递推关系,利用作差法即可求{a n}的通项公式:(Ⅱ)求出b n=,利用裂项法即可求数列{b n}的前n项和.【解答】解:(I)由a n2+2a n=4S n+3,可知a n+12+2a n+1=4S n+1+3两式相减得a n+12﹣a n2+2(a n+1﹣a n)=4a n+1,即2(a n+1+a n)=a n+12﹣a n2=(a n+1+a n)(a n+1﹣a n),∵a n>0,∴a n+1﹣a n=2,∵a12+2a1=4a1+3,∴a1=﹣1(舍)或a1=3,则{a n}是首项为3,公差d=2的等差数列,∴{a n}的通项公式a n=3+2(n﹣1)=2n+1:(Ⅱ)∵a n=2n+1,∴b n===(﹣),∴数列{b n}的前n项和T n=(﹣+…+﹣)=(﹣)=.【点评】本题主要考查数列的通项公式以及数列求和的计算,利用裂项法是解决本题的关键.18.(12分)如图,四边形ABCD为菱形,∠ABC=120°,E,F是平面ABCD同一侧的两点,BE丄平面ABCD,DF丄平面ABCD,BE=2DF,AE丄EC.(Ⅰ)证明:平面AEC丄平面AFC(Ⅱ)求直线AE与直线CF所成角的余弦值.【考点】LM:异面直线及其所成的角;LY:平面与平面垂直.【专题】5F:空间位置关系与距离;5G:空间角;5H:空间向量及应用.【分析】(Ⅰ)连接BD,设BD∩AC=G,连接EG、EF、FG,运用线面垂直的判定定理得到EG⊥平面AFC,再由面面垂直的判定定理,即可得到;(Ⅱ)以G为坐标原点,分别以GB,GC为x轴,y轴,|GB|为单位长度,建立空间直角坐标系G﹣xyz,求得A,E,F,C的坐标,运用向量的数量积的定义,计算即可得到所求角的余弦值.【解答】解:(Ⅰ)连接BD,设BD∩AC=G,连接EG、EF、FG,在菱形ABCD中,不妨设BG=1,由∠ABC=120°,可得AG=GC=,BE⊥平面ABCD,AB=BC=2,可知AE=EC,又AE⊥EC,所以EG=,且EG⊥AC,在直角△EBG中,可得BE=,故DF=,在直角三角形FDG中,可得FG=,在直角梯形BDFE中,由BD=2,BE=,FD=,可得EF==,从而EG2+FG2=EF2,则EG⊥FG,(或由tan∠EGB•tan∠FGD=•=•=1,可得∠EGB+∠FGD=90°,则EG⊥FG)AC∩FG=G,可得EG⊥平面AFC,由EG⊂平面AEC,所以平面AEC⊥平面AFC;(Ⅱ)如图,以G为坐标原点,分别以GB,GC为x轴,y轴,|GB|为单位长度,建立空间直角坐标系G﹣xyz,由(Ⅰ)可得A(0,﹣,0),E(1,0,),F(﹣1,0,),C(0,,0),即有=(1,,),=(﹣1,﹣,),故cos<,>===﹣.则有直线AE与直线CF所成角的余弦值为.【点评】本题考查空间直线和平面的位置关系和空间角的求法,主要考查面面垂直的判定定理和异面直线所成的角的求法:向量法,考查运算能力,属于中档题.19.(12分)某公司为确定下一年度投入某种产品的宣传费,需了解年宣传费x (单位:千元)对年销售量y(单位:t)和年利润z(单位:千元)的影响,对近8年的年宣传费x i和年销售量y i(i=1,2,…,8)数据作了初步处理,得到下面的散点图及一些统计量的值.(x i ﹣)2(w i ﹣)2(x i ﹣)(y i ﹣)(w i ﹣)(y i ﹣)46.6563 6.8289.8 1.61469108.8表中w i =i ,=(Ⅰ)根据散点图判断,y=a+bx与y=c+d哪一个适宜作为年销售量y关于年宣传费x的回归方程类型?(给出判断即可,不必说明理由)(Ⅱ)根据(Ⅰ)的判断结果及表中数据,建立y关于x的回归方程;(Ⅲ)已知这种产品的年利润z与x、y的关系为z=0.2y﹣x.根据(Ⅱ)的结果回答下列问题:(i)年宣传费x=49时,年销售量及年利润的预报值是多少?(ii)年宣传费x为何值时,年利润的预报值最大?附:对于一组数据(u1 v1),(u2 v2)…..(u n v n),其回归线v=α+βu的斜率和截距的最小二乘估计分别为:=,=﹣.【考点】BK:线性回归方程.【专题】5I:概率与统计.【分析】(Ⅰ)根据散点图,即可判断出,(Ⅱ)先建立中间量w=,建立y关于w的线性回归方程,根据公式求出w,问题得以解决;(Ⅲ)(i)年宣传费x=49时,代入到回归方程,计算即可,(ii)求出预报值得方程,根据函数的性质,即可求出.【解答】解:(Ⅰ)由散点图可以判断,y=c+d适宜作为年销售量y关于年宣传费x的回归方程类型;(Ⅱ)令w=,先建立y关于w的线性回归方程,由于==68,=﹣=563﹣68×6.8=100.6,所以y关于w的线性回归方程为=100.6+68w,因此y关于x的回归方程为=100.6+68,(Ⅲ)(i)由(Ⅱ)知,当x=49时,年销售量y的预报值=100.6+68=576.6,年利润z的预报值=576.6×0.2﹣49=66.32,(ii)根据(Ⅱ)的结果可知,年利润z的预报值=0.2(100.6+68)﹣x=﹣x+13.6+20.12,当==6.8时,即当x=46.24时,年利润的预报值最大.【点评】本题主要考查了线性回归方程和散点图的问题,准确的计算是本题的关键,属于中档题.20.(12分)在直角坐标系xOy中,曲线C:y=与直线l:y=kx+a(a>0)交于M,N两点.(Ⅰ)当k=0时,分別求C在点M和N处的切线方程.(Ⅱ)y轴上是否存在点P,使得当k变动时,总有∠OPM=∠OPN?(说明理由)【考点】KH:直线与圆锥曲线的综合.【分析】(I)联立,可得交点M,N的坐标,由曲线C:y=,利用导数的运算法则可得:y′=,利用导数的几何意义、点斜式即可得出切线方程.(II)存在符合条件的点(0,﹣a),设P(0,b)满足∠OPM=∠OPN.M(x1,y1),N(x2,y2),直线PM,PN的斜率分别为:k1,k2.直线方程与抛物线方程联立化为x2﹣4kx﹣4a=0,利用根与系数的关系、斜率计算公式可得k1+k2=.k1+k2=0⇔直线PM,PN的倾斜角互补⇔∠OPM=∠OPN.即可证明.【解答】解:(I)联立,不妨取M,N,由曲线C:y=可得:y′=,∴曲线C在M点处的切线斜率为=,其切线方程为:y﹣a=,化为.同理可得曲线C在点N处的切线方程为:.(II)存在符合条件的点(0,﹣a),下面给出证明:设P(0,b)满足∠OPM=∠OPN.M(x1,y1),N(x2,y2),直线PM,PN的斜率分别为:k1,k2.联立,化为x2﹣4kx﹣4a=0,∴x1+x2=4k,x1x2=﹣4a.∴k1+k2=+==.当b=﹣a时,k1+k2=0,直线PM,PN的倾斜角互补,∴∠OPM=∠OPN.∴点P(0,﹣a)符合条件.【点评】本题考查了导数的运算法则、利用导数的几何意义研究切线方程、直线与抛物线相交问题转化为方程联立可得根与系数的关系、斜率计算公式,考查了推理能力与计算能力,属于中档题.21.(12分)已知函数f(x)=x3+ax+,g(x)=﹣lnx(i)当a为何值时,x轴为曲线y=f(x)的切线;(ii)用min{m,n}表示m,n中的最小值,设函数h(x)=min{f(x),g(x)}(x>0),讨论h(x)零点的个数.【考点】6E:利用导数研究函数的最值;6H:利用导数研究曲线上某点切线方程.【专题】2:创新题型;53:导数的综合应用.【分析】(i)f′(x)=3x2+a.设曲线y=f(x)与x轴相切于点P(x0,0),则f(x0)=0,f′(x0)=0解出即可.(ii)对x分类讨论:当x∈(1,+∞)时,g(x)=﹣lnx<0,可得函数h(x)=min { f(x),g(x)}≤g(x)<0,即可得出零点的个数.当x=1时,对a分类讨论:a≥﹣,a<﹣,即可得出零点的个数;当x∈(0,1)时,g(x)=﹣lnx>0,因此只考虑f(x)在(0,1)内的零点个数即可.对a分类讨论:①当a≤﹣3或a≥0时,②当﹣3<a<0时,利用导数研究其单调性极值即可得出.【解答】解:(i)f′(x)=3x2+a.设曲线y=f(x)与x轴相切于点P(x0,0),则f(x0)=0,f′(x0)=0,∴,解得,a=.因此当a=﹣时,x轴为曲线y=f(x)的切线;(ii)当x∈(1,+∞)时,g(x)=﹣lnx<0,∴函数h(x)=min { f(x),g(x)}<0,故h(x)在x∈(1,+∞)时无零点.当x=1时,若a≥﹣,则f(1)=a+≥0,∴h(x)=min { f(1),g(1)}=g(1)=0,故x=1是函数h(x)的一个零点;若a<﹣,则f(1)=a+<0,∴h(x)=min { f(1),g(1)}=f(1)<0,故x=1不是函数h(x)的零点;当x∈(0,1)时,g(x)=﹣lnx>0,因此只考虑f(x)在(0,1)内的零点个数即可.①当a≤﹣3或a≥0时,f′(x)=3x2+a在(0,1)内无零点,因此f(x)在区间(0,1)内单调,而f(0)=,f(1)=a+,∴当a≤﹣3时,函数f(x)在区间(0,1)内有一个零点,当a≥0时,函数f(x)在区间(0,1)内没有零点.②当﹣3<a<0时,函数f(x)在内单调递减,在内单调递增,故当x=时,f(x)取得最小值=.若>0,即,则f(x)在(0,1)内无零点.若=0,即a=﹣,则f(x)在(0,1)内有唯一零点.若<0,即,由f(0)=,f(1)=a+,∴当时,f(x)在(0,1)内有两个零点.当﹣3<a时,f(x)在(0,1)内有一个零点.综上可得:a<时,函数h(x)有一个零点.当时,h(x)有一个零点;当a=或时,h(x)有两个零点;当时,函数h(x)有三个零点.【点评】本题考查了导数的运算法则、利用导数的几何意义研究切线方程、利用导数研究函数的单调性极值,考查了分类讨论思想方法、推理能力与计算能力,属于难题.选修4一1:几何证明选讲22.(10分)如图,AB是⊙O的直径,AC是⊙O的切线,BC交⊙O于点E.(Ⅰ)若D为AC的中点,证明:DE是⊙O的切线;(Ⅱ)若OA=CE,求∠ACB的大小.【考点】N9:圆的切线的判定定理的证明.【专题】5B:直线与圆.【分析】(Ⅰ)连接AE和OE,由三角形和圆的知识易得∠OED=90°,可得DE是⊙O的切线;(Ⅱ)设CE=1,AE=x,由射影定理可得关于x的方程x2=,解方程可得x 值,可得所求角度.【解答】解:(Ⅰ)连接AE,由已知得AE⊥BC,AC⊥AB,在RT△ABC中,由已知可得DE=DC,∴∠DEC=∠DCE,连接OE,则∠OBE=∠OEB,又∠ACB+∠ABC=90°,∴∠DEC+∠OEB=90°,∴∠OED=90°,∴DE是⊙O的切线;(Ⅱ)设CE=1,AE=x,由已知得AB=2,BE=,由射影定理可得AE2=CE•BE,∴x2=,即x4+x2﹣12=0,解方程可得x=∴∠ACB=60°【点评】本题考查圆的切线的判定,涉及射影定理和三角形的知识,属基础题.选修4一4:坐标系与参数方程23.(10分)在直角坐标系xOy中,直线C1:x=﹣2,圆C2:(x﹣1)2+(y﹣2)2=1,以坐标原点为极点,x轴的正半轴为极轴建立极坐标系.(Ⅰ)求C1,C2的极坐标方程;(Ⅱ)若直线C3的极坐标方程为θ=(ρ∈R),设C2与C3的交点为M,N,求△C2MN的面积.【考点】Q4:简单曲线的极坐标方程.【专题】5S:坐标系和参数方程.【分析】(Ⅰ)由条件根据x=ρcosθ,y=ρsinθ求得C1,C2的极坐标方程.(Ⅱ)把直线C3的极坐标方程代入ρ2﹣3ρ+4=0,求得ρ1和ρ2的值,结合圆的半径可得C2M⊥C2N,从而求得△C2MN的面积•C2M•C2N的值.【解答】解:(Ⅰ)由于x=ρcosθ,y=ρsinθ,∴C1:x=﹣2 的极坐标方程为ρcosθ=﹣2,故C2:(x﹣1)2+(y﹣2)2=1的极坐标方程为:(ρcosθ﹣1)2+(ρsinθ﹣2)2=1,化简可得ρ2﹣(2ρcosθ+4ρsinθ)+4=0.(Ⅱ)把直线C3的极坐标方程θ=(ρ∈R)代入圆C2:(x﹣1)2+(y﹣2)2=1,可得ρ2﹣(2ρcosθ+4ρsinθ)+4=0,求得ρ1=2,ρ2=,∴|MN|=|ρ1﹣ρ2|=,由于圆C2的半径为1,∴C2M⊥C2N,△C2MN的面积为•C2M•C2N=•1•1=.【点评】本题主要考查简单曲线的极坐标方程,点的极坐标的定义,属于基础题.选修4一5:不等式选讲24.(10分)已知函数f(x)=|x+1|﹣2|x﹣a|,a>0.(Ⅰ)当a=1时,求不等式f(x)>1的解集;(Ⅱ)若f(x)的图象与x轴围成的三角形面积大于6,求a的取值范围.【考点】R5:绝对值不等式的解法.【专题】59:不等式的解法及应用.【分析】(Ⅰ)当a=1时,把原不等式去掉绝对值,转化为与之等价的三个不等式组,分别求得每个不等式组的解集,再取并集,即得所求.(Ⅱ)化简函数f(x)的解析式,求得它的图象与x轴围成的三角形的三个顶点的坐标,从而求得f(x)的图象与x轴围成的三角形面积;再根据f(x)的图象与x轴围成的三角形面积大于6,从而求得a的取值范围.【解答】解:(Ⅰ)当a=1时,不等式f(x)>1,即|x+1|﹣2|x﹣1|>1,即①,或②,或③.解①求得x∈∅,解②求得<x<1,解③求得1≤x<2.综上可得,原不等式的解集为(,2).(Ⅱ)函数f(x)=|x+1|﹣2|x﹣a|=,由此求得f(x)的图象与x轴的交点A (,0),B(2a+1,0),故f(x)的图象与x轴围成的三角形的第三个顶点C(a,a+1),由△ABC的面积大于6,可得[2a+1﹣]•(a+1)>6,求得a>2.故要求的a的范围为(2,+∞).【点评】本题主要考查绝对值不等式的解法,体现了转化、分类讨论的数学思想,属于中档题.。
2015年高考数学真题概率和统计 答案

2015年高考数学真题分类汇编 专题11 概率和统计 文20.【2015高考安徽,文17】某企业为了解下属某部门对本企业职工的服务情况,随机访问50名职工,根据这50名职工对该部门的评分,绘制频率分布直方图(如图所示),其中样本数据分组区间为[40,50],[50,60],,[80,90],[90,100](Ⅰ)求频率分布图中a 的值;(Ⅱ)估计该企业的职工对该部门评分不低于80的概率;(Ⅲ)从评分在[40,60]的受访职工中,随机抽取2人,求此2人评分都在[40,50]的概率.【答案】(Ⅰ)0.006;(Ⅱ)0.4;(Ⅲ)110【解析】(Ⅰ)因为110)028.02022.00018.0004.0(=⨯+⨯+++a ,所以006.0=a(Ⅱ)由所给频率分布直方图知,50名受访职工评分不低于80的频率为4.010)018.0022.0(=⨯+, 所以该企业职工对该部门评分不低于80的概率的估计值为0.4.(Ⅲ)受访职工评分在[50,60)的有:50×0.006×10=3(人),即为321,,A A A ; 受访职工评分在[40,50)的有: 50×0.004×40=2(人),即为21,B B .从这5名受访职工中随机抽取2人,所有可能的结果共有10种,它们是{}{}{}{},,,,,,,,21113121B A B A A A A A{}{}{}{}{}{},,,,,,,,,,,,2123132212312B B B A B A B A B A A A 又因为所抽取2人的评分都在[40,50)的结果有1种,即{}21,B B ,故所求的概率为101=p . 【考点定位】本题主要考查了频率分布直方图、概率和频率的关系、古典概型等基础知识.【名师点睛】利用频率分布直方图解题的时,注意其表达的意义,同时要理解频率是概率的估计值这一基础知识;在利用古典概型解题时,要注意列出所有的基本事件,千万不可出现重、漏的情况.21.【2015高考北京,文17】(本小题满分13分)某超市随机选取1000位顾客,记录了他们购买甲、乙、丙、丁四种商品的情况,整理成如下统计表,其中“√”表示购买,“×”表示未购买.(I )估计顾客同时购买乙和丙的概率;(II )估计顾客在甲、乙、丙、丁中同时购买3中商品的概率;(III )如果顾客购买了甲,则该顾客同时购买乙、丙、丁中那种商品的可能性最大? 【答案】(I )0.2;(II )0.3;(III )同时购买丙的可能性最大. 【解析】试题分析:本题主要考查统计表、概率等基础知识,考查学生的分析问题解决问题的能力、转化能力、计算能力.(I )由统计表读出顾客同时购买乙和丙的人数200,计算出概率;(II )先由统计表读出顾客在甲、乙、丙、丁中同时购买3中商品的人数100200+,再计算概率;(III )由统计表读出顾客同时购买甲和乙的人数为200,顾客同时购买甲和丙的人数为100200300++,顾客同时购买甲和丁的人数为100,分别计算出概率,再通过比较大小得出结论.试题解析:(Ⅰ)从统计表可以看出,在这1000位顾客中,有200位顾客同时购买了乙和丙,所以顾客同时购买乙和丙的概率可以估计为2000.21000=. (Ⅱ)从统计表可以看出,在在这1000位顾客中,有100位顾客同时购买了甲、丙、丁,另有200位顾客同时购买了甲、乙、丙,其他顾客最多购买了2种商品.所以顾客在甲、乙、丙、丁中同时购买3种商品的概率可以估计为1002000.31000+=.(Ⅲ)与(Ⅰ)同理,可得:顾客同时购买甲和乙的概率可以估计为2000.21000=, 顾客同时购买甲和丙的概率可以估计为1002003000.61000++=,顾客同时购买甲和丁的概率可以估计为1000.11000=,所以,如果顾客购买了甲,则该顾客同时购买丙的可能性最大. 考点:统计表、概率.【名师点晴】本题主要考查的是统计表和古典概型,属于中档题.解题时一定要抓住重要字眼“估计”和“最大”,否则很容易失分.解此类统计表的试题一定要理解透彻题意,提取必要的信息.解本题需要掌握的知识点是古典概型概率公式,即()A P A =包含的基本事件的个数基本事件的总数.22.【2015高考福建,文18】全网传播的融合指数是衡量电视媒体在中国网民中影响了的综合指标.根据相关报道提供的全网传播2015年某全国性大型活动的“省级卫视新闻台”融合指数的数据,对名列前20名的“省级卫视新闻台”的融合指数进行分组统计,结果如表所示.(Ⅰ)现从融合指数在[4,5)和[]7,8内的“省级卫视新闻台”中随机抽取2家进行调研,求至少有1家的融合指数在[]7,8的概率;(Ⅱ)根据分组统计表求这20家“省级卫视新闻台”的融合指数的平均数. 【答案】(Ⅰ)910;(Ⅱ)6.05. 【解析】解法一:(I )融合指数在[]7,8内的“省级卫视新闻台”记为1A ,2A ,3A ;融合指数在[)4,5内的“省级卫视新闻台”记为1B ,2B .从融合指数在[)4,5和[]7,8内的“省级卫视新闻台”中随机抽取2家的所有基本事件是:{}12,A A ,{}13,A A ,{}23,A A ,{}11,A B ,{}12,A B ,{}21,A B ,{}22,A B ,{}31,A B ,{}32,A B ,{}12,B B ,共10个.其中,至少有1家融合指数在[]7,8内的基本事件是:{}12,A A ,{}13,A A ,{}23,A A ,{}11,A B ,{}12,A B ,{}21,A B ,{}22,A B ,{}31,A B ,{}32,A B ,共9个.所以所求的概率910P =. (II )这20家“省级卫视新闻台”的融合指数平均数等于28734.5 5.5 6.57.5 6.0520202020⨯+⨯+⨯+⨯=. 解法二:(I )融合指数在[]7,8内的“省级卫视新闻台”记为1A ,2A ,3A ;融合指数在[)4,5内的“省级卫视新闻台”记为1B ,2B .从融合指数在[)4,5和[]7,8内的“省级卫视新闻台”中随机抽取2家的所有基本事件是:{}12,A A ,{}13,A A ,{}23,A A ,{}11,A B ,{}12,A B ,{}21,A B ,{}22,A B ,{}31,A B ,{}32,A B ,{}12,B B ,共10个.其中,没有1家融合指数在[]7,8内的基本事件是:{}12,B B ,共1个. 所以所求的概率1911010P =-=. (II )同解法一.【考点定位】1、古典概型;2、平均值.【名师点睛】本题考差古典概型和平均数,利用古典概型的“等可能”“有限”性的特点,能方便的求出概率.由实际意义构造古典概型,首先确定试验的样本空间结构并计算它所含样本点总数,然后再求出事件A 所含基本事件个数,代入古典概型的概率计算公式;根据频率分布表求平均数,对于每组的若干个数可以采取区间中点值作为该组数据的数值,再求平均数.23.【2015高考广东,文17】(本小题满分12分)某城市100户居民的月平均用电量(单位:度),以[)160,180,[)180,200,[)200,220,[)220,240,[)240,260,[)260,280,[]280,300分组的频率分布直方图如图2.(1)求直方图中x 的值;(2)求月平均用电量的众数和中位数;(3)在月平均用电量为[)220,240,[)240,260,[)260,280,[]280,300的四组用户中,用分层抽样的方法抽取11户居民,则月平均用电量在[)220,240的用户中应抽取多少户? 【答案】(1)0.0075;(2)230,224;(3)5. 【解析】试题分析:(1)由频率之和等于1可得x 的值;(2)由最高矩形的横坐标中点可得众数,由频率之和等于0.5可得中位数;(3)先计算出月平均用电量为[)220,240,[)240,260,[)260,280,[]280,300的用户的户数,再计算抽取比例,进而可得月平均用电量在[)220,240的用户中应抽取的户数.试题解析:(1)由()0.0020.00950.0110.01250.0050.0025201x ++++++⨯=得:0.0075x =,所以直方图中x 的值是0.0075 (2)月平均用电量的众数是2202402302+= 因为()0.0020.00950.011200.450.5++⨯=<,所以月平均用电量的中位数在[)220,240内,设中位数为a ,由()()0.0020.00950.011200.01252200.5a ++⨯+⨯-=得:224a =,所以月平均用电量的中位数是224(3)月平均用电量为[)220,240的用户有0.01252010025⨯⨯=户,月平均用电量为[)240,260的用户有0.00752010015⨯⨯=户,月平均用电量为[)260,280的用户有0.0052010010⨯⨯=户,月平均用电量为[]280,300的用户有0.0025201005⨯⨯=户,抽取比例11125151055==+++,所以月平均用电量在[)220,240的用户中应抽取12555⨯=户 考点:1、频率分布直方图;2、样本的数字特征(众数、中位数);3、分层抽样.【名师点晴】本题主要考查的是频率分布直方图、样本的数字特征(众数、中位数)和分层抽样,属于中档题.解题时一定要注意频率分布直方图的纵轴是频率组距,否则很容易出现错误.解本题需要掌握的知识点是频率分布直方图、样本的数字特征(众数、中位数)和分层抽样,即在频率分布直方图中,各小长方形的面积的总和等于1,众数是最高矩形的横坐标中点,中位数左边和右边的直方图的面积相等,=⨯频率频率组距组距,=样本容量抽取比例总体容量.24.【2015高考湖南,文16】(本小题满分12分)某商场举行有奖促销活动,顾客购买一定金额的商品后即可抽奖,抽奖方法是:从装有2个红球12,A A 和1个白球B 的甲箱与装有2个红球12,a a 和2个白球12,b b 的乙箱中,各随机摸出1个球,若摸出的2个球都是红球则中奖,否则不中奖。
2015年高考数学真题分类汇编:专题(12)概率和统计(理科)及答案

专题十二 概率和统计1.【2015高考重庆,理3】重庆市2013年各月的平均气温(o C )数据的茎叶图如下:0891258200338312则这组数据的中位数是( )A 、19B 、20C 、21.5D 、23 【答案】B .【解析】从茎叶图知所有数据为8,9,12,15,18,20,20,23,23,28,31,32,中间两个数为20,20,故中位数为20,选B ..【考点定位】本题考查茎叶图的认识,考查中位数的概念.【名师点晴】本题通过考查茎叶图的知识,考查样本数据的数字特征,考查学生的数据处理能力.2.【2015高考广东,理4】袋中共有15个除了颜色外完全相同的球,其中有10个白球,5个红球。
从袋中任取2个球,所取的2个球中恰有1个白球,1个红球的概率为( ) A .1 B. 2111 C. 2110 D. 215【答案】B .【解析】从袋中任取2个球共有215105C =种,其中恰好1个白球1个红球共有1110550C C =种,所以从袋中任取的2个球恰好1个白球1个红球的概率为5010=10521,故选B . 【考点定位】排列组合,古典概率.【名师点睛】本题主要考查排列组合,古典概率的计算和转化与化归思想应用、运算求解能力,解答此题关键在于理解所取2球恰好1个白球1个红球即是分步在白球和红球各取1个球的组合,属于容易题.3.【2015高考新课标1,理4】投篮测试中,每人投3次,至少投中2次才能通过测试。
已知某同学每次投篮投中的概率为0.6,且各次投篮是否投中相互独立,则该同学通过测试的概率为( )(A )0.648 (B )0.432 (C )0.36 (D )0.312【答案】A【解析】根据独立重复试验公式得,该同学通过测试的概率为22330.60.40.6C ⨯+=0.648,故选A.【考点定位】本题主要考查独立重复试验的概率公式与互斥事件和概率公式【名师点睛】解答本题时,先想到所求事件是恰好中3次与恰好中2次两个互斥事件的和,而这两个事件又是实验3次恰好分别发生3次和2次的独立重复试验,本题很好考查了学生对独立重复试验和互斥事件的理解和公式的记忆与灵活运用,是基础题,正确分析概率类型、灵活运用概率公式是解本题的关键.4.【2015高考陕西,理11】设复数(1)z x yi =-+(,)x y R ∈,若||1z ≤,则y x ≥的概率为( )A .3142π+B .1142π-C .112π- D .112π+【答案】B【考点定位】1、复数的模;2、几何概型.【名师点晴】本题主要考查的是复数的模和几何概型,属于中档题.解几何概型的试题,一般先求出实验的基本事件构成的区域长度(面积或体积),再求出事件A 构成的区域长度(面积或体积),最后代入几何概型的概率公式即可.解本题需要掌握的知识点是复数的模和几何概型的概率公式,即若z a bi =+(a 、R b ∈),几何概型的概率公式()P A =()()A 构成事件的区域长度面积或体积试验的全部结果所构成的区域长度面积或体积.5.【2015高考陕西,理2】某中学初中部共有110名教师,高中部共有150名教师,其性别比例如图所示,则该校女教师的人数为( )A .167B .137C .123D .93【答案】B【解析】该校女老师的人数是()11070%150160%137⨯+⨯-=,故选B . 【考点定位】扇形图.【名师点晴】本题主要考查的是扇形图,属于容易题.解题时一定要抓住重要字眼“女教师”,否则很容易出现错误.扇形统计图是用整个圆表示总数,用圆内各个扇形的大小表示各部分数量占总数的百分数.通过扇形图可以很清晰地表示各部分数量同总数之间的关系. 6.【2015高考湖北,理2】我国古代数学名著《九章算术》有“米谷粒分”题:粮仓开仓收粮,有人送来米1534石,验得米内夹谷,抽样取米一把,数得254粒内夹谷28粒,则这批米内夹谷约为( )A .134石B .169石C .338石D .1365石 【答案】B【解析】依题意,这批米内夹谷约为169153425428=⨯石,选B. 【考点定位】用样本估计总体.【名师点睛】《九章算术》是中国古代第一部数学专著,是算经十书中最重要的一种.该书内容十分丰富,系统总结了战国、秦、汉时期的数学成就.本题“米谷粒分”是我们统计中的用样本估计总体问题.7.【2015高考安徽,理6】若样本数据1x ,2x ,⋅⋅⋅,10x 的标准差为8,则数据121x -,221x -,⋅⋅⋅,1021x -的标准 差为( )(A )8 (B )15 (C )16 (D )32【答案】C【解析】设样本数据1x ,2x ,⋅⋅⋅,10x 8=,即方差64DX =,而数据121x -,221x -,⋅⋅⋅,1021x -的方差22(21)2264D X DX -==⨯,所以其标16=.故选C.【考点定位】1.样本的方差与标准差的应用.【名师点睛】已知随机变量X 的均值、方差,求X 的线性函数Y aX b =+的均值、方差和标准差,可直接用X 的均值、方差的性质求解.若随机变量X 的均值EX 、方差DX 、标Y aX b =+的均值aEX b +、方差2a DX 、标准差.8.【2015高考湖北,理4】设211(,)X N μσ ,222(,)Y N μσ ,这两个正态分布密度曲线如图所示.下列结论中正确的是( )A .21()()P Y P Y μμ≥≥≥B .21()()P X P X σσ≤≤≤C .对任意正数t ,()()P X t P Y t ≤≥≤D .对任意正数t ,()()P X t P Y t ≥≥≥【答案】C【考点定位】正态分布密度曲线. 【名师点睛】正态曲线的性质①曲线在x 轴的上方,与x 轴不相交. ②曲线是单峰的,它关于直线μ=x 对称. ③曲线在μ=x 处达到峰值πσ21.④曲线与x 轴之间的面积为1.⑤当σ一定时,曲线随着μ的变化而沿x 轴平移,如图甲所示⑥μ一定时,曲线的形状由σ确定.σ越大,曲线越“矮胖”,总体分布越分散;σ越小.曲线越“瘦高”.总体分布越集中.如图乙所示.9.【2015高考福建,理4】为了解某社区居民的家庭年收入所年支出的关系,随机调查了该社区5户家庭,得到如下统计数据表:收入为15万元家庭年支出为( )A .11.4万元B .11.8万元C .12.0万元D .12.2万元 【答案】B【解析】由已知得8.28.610.011.311.9105x ++++==(万元),6.27.58.08.59.885y ++++==(万元),故 80.76100.4a =-⨯=,所以回归直线方程为ˆ0.760.4yx =+,当社区一户收入为15万元家庭年支出为ˆ0.76150.411.8y =⨯+=(万元),故选B .【考点定位】线性回归方程.【名师点睛】本题考查线性回归方程,要正确利用平均数公式计算和理解线性回归方程的意义,属于基础题,要注意计算的准确性.10.【2015高考湖北,理7】在区间[0,1]上随机取两个数,x y ,记1p 为事件“12x y +≥”的概率,2p 为事件“1||2x y -≤”的概率,3p 为事件“12xy ≤”的概率,则 ( ) A .123p p p << B .231p p p << C .312p p p << D .321p p p <<【答案】B【解析】因为,[0,1]x y ∈,对事件“12x y +≥”,如图(1)阴影部分1S , 对事件“1||2x y -≤”,如图(2)阴影部分2S , 对为事件“12xy ≤”,如图(3)阴影部分3S ,由图知,阴影部分的面积从下到大依次是132S S S <<,正方形的面积为111=⨯, 根据几何概型公式可得231p p p <<.(1) (2) (3) 【考点定位】几何概型.【名师点睛】对于几何概型的概率公式中的“测度”要有正确的认识,它只与大小有关,而与形状和位置无关,在解题时,要掌握“测度”为长度、面积、体积、角度等常见的几何概型的求解方法.11.【2015高考山东,理8】已知某批零件的长度误差(单位:毫米)服从正态分布()20,3N ,从中随机取一件,其长度误差落在区间(3,6)内的概率为( )(附:若随机变量ξ服从正态分布()2,N μσ ,则()68.26%P μσξμσ-<<+= ,()2295.44%P μσξμσ-<<+=。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2015-2019全国卷一理科数学真题汇编——统计概率、计数原理
【2019.理.6】我国古代典籍《周易》用“卦”描述万物的变化.每一“重卦”由从下到上排列的6个爻组成,爻分为阳爻“”和阴爻“”,下图就是一重卦.在所有重卦中随机取一重卦,则该重卦恰有3个阳爻的概率是( ) A.
516 B.1132 C.2132
D.1116
【2019.理.15】甲乙两队进行篮球决赛,采取七场四胜制(当一队赢得四场胜利时,该对获胜,决赛结束)根据前期的比赛成绩,甲队的主客场安排依次为“主主客客主客主”设甲队主场取胜的概率为0.6,客场取胜的概率为0.5,且各场比赛相互独立,则甲队以4:1获胜的概率是 .
【2019.理.21】为治疗某种疾病,研制了甲、乙两种新药,希望知道哪种新药更有效,为此进行动物实验.实验方案如下:每一轮选取两只白鼠对药效进行对比实验.对于两只白鼠,随机选一只施以甲药,另一只施以乙药.一轮的治疗结果得出后,再安排下一轮实验.当其中一种药治愈的白鼠比另一种药治愈的白鼠多4只时,就停止实验,并认为治愈只数多的药更有效.为了方便描述问题,约定:对于每轮实验,若施以甲药的白鼠治愈且施以乙药的白鼠未治愈则甲药得1分,乙药得1-分;若施以乙药的白鼠治愈且施以甲药的白鼠未治愈则乙药得1分,甲药得1-分;若都治愈或都未治愈则两种药均得0分.甲、乙两种药的治愈率分别记为α和β,一轮实验中甲药的得分记为
X .
(1)求X 的分布列;
(2)若甲药、乙药在实验开始时都赋予4分,(0,1,,8)i p i =L 表示“甲药的累计得分为i 时,最终认为甲药比乙药更有效”的概率,则00p =,81p =,11i i i i p ap bp cp -+=++(1,2,,7)i =L ,其中(1)a P X ==-,
(0)b P X ==,(1)c P X ==.假设0.5α=,0.8β=.
(i )证明:1{}(0,1,2,,7)i i p p i +-=L 为等比数列; (ii )求4p ,并根据4p 的值解释这种实验方案的合理性.
【2018.理.3】某地区经过一年的新农村建设,农村的经济收入增加了一倍.实现翻番.为更好地了解该地区农村的经济收入变化情况,统计了该地区新农村建设前后农村的经济收入构成比例.得到如下饼图:
则下面结论中不正确的是( ) A .新农村建设后,种植收入减少
B .新农村建设后,其他收入增加了一倍以上
C .新农村建设后,养殖收入增加了一倍
D .新农村建设后,养殖收入与第三产业收入的总和超过了经济收入的一半
【2018.理.10】下图来自古希腊数学家希波克拉底所研究的几何图形,此图由三个半圆构成,三个半圆的直径分别为直角三角形ABC 的斜边BC ,直角边AB ,AC ,ABC △的三边所围成的区域记为Ⅰ,黑色部分记为Ⅱ,其余部分记为Ⅲ,在整个图形中随机取一点,此点取自Ⅰ,Ⅱ,Ⅲ的概率分别记为1p ,2p ,3p ,则( ) A .12p p =
B .13p p =
C .23p p =
D .123p p p =+
【2018.理.15】从2位女生,4位男生中选3人参加科技比赛,且至少有1位女生入选,则不同的选法共有________种.(用数字填写答案)
【2018.理.21】某工厂的某种产品成箱包装,每箱200件,每一箱产品在交付用户之前要对产品作检验,如检验出不合格品,则更换为合格品,检验时,先从这箱产品中任取20件作检验,再根据检验结果决定是否对余下的所有产品作检验,设每件产品为不合格品的概率都为()01p p <<,且各件产品是否为不合格品相互独立. ⑴记20件产品中恰有2件不合格品的概率为()f p ,求()f p 的最大值点0p ;
⑵现对一箱产品检验了20件,结果恰有2件不合格品,以⑴中确定的0p 作为p 的值.已知每件产品的检验费用为2元,若有不合格品进入用户手中,则工厂要对每件不合格品支付25元的赔偿费用. (i )若不对该箱余下的产品作检验,这一箱产品的检验费用与赔偿费用的和记为X ,求EX ; (ii )以检验费用与赔偿费用和的期望值为决策依据,是否该对这箱余下的所有产品作检验?
【2017.理.2】如图,正方形ABCD 内的图形来自中国古代的太极图.正方形内切圆中的黑色部分和白色部分关于正方形的中心成中心对称.在正方形内随机取一点,则此点取自黑色部分的概率是
A .
14
B .
π8 C .1
2
D .
π
4
【2017.理.9】
为了监控某种零件的一条生产线的生产过程,检验员每天从该生产线上随机抽取16个零
件,并测量其尺寸(单位:cm ).根据长期生产经验,可以认为这条生产线正常状态下生产的零件的尺寸服从正态分布2
(,)N μσ.
(1)假设生产状态正常,记X 表示一天内抽取的16个零件中其尺寸在(3,3)μσμσ-+之外的零件数,求
(1)P X ≥及X 的数学期望;
(2)一天内抽检零件中,如果出现了尺寸在(3,3)μσμσ-+之外的零件,就认为这条生产线在这一天的生产过程可能出现了异常情况,需对当天的生产过程进行检查.
(ⅰ)试说明上述监控生产过程方法的合理性; (ⅱ)下面是检验员在一天内抽取的16个零件的尺寸:
9.95 10.12 9.96
9.96
10.01 9.92
9.98
10.04 10.26
9.91
10.13 10.02 9.22
10.04 10.05
9.95
经计算得16119.9716i i x x ===∑,16162
22211
11()(16)0.2121616i i i i s x x x x ===-=-≈∑∑,其中i x 为抽取的第i 个零件的尺寸,1,2,,16i =⋅⋅⋅.
用样本平均数x 作为μ的估计值ˆμ
,用样本标准差s 作为σ的估计值ˆσ,利用估计值判断是否需对当天的生产过程进行检查?剔除ˆˆˆˆ(3,3)μ
σμσ-+之外的数据,用剩下的数据估计μ和σ(精确到0.01). 附:若随机变量Z 服从正态分布2
(,)N μσ,则(33)0.997 4P Z μσμσ-<<+=,
160.997 40.959 2=,0.0080.09≈.
【2016.理.4】某公司的班车在7:30,8:00,8:30发车,小明在7:50至8:30之间到达发车站乘坐班车,且到达发车站的时刻是随机的,则他等车时间不超过10分钟的概率是( ) (A )
13(B )12(C )23(D )34
【2016.理.19】
某公司计划购买2台机器,该种机器使用三年后即被淘汰.机器有一易损零件,在购进机器时,可以额外购买这种零件作为备件,每个200元,.在机器使用期间,如果备件不足再购买,则每个500元.现需决策在购买机器时应同时购买几个易损零件,为此搜集并整理了100台这种机器在三年使用期内更换的易损零件数,得下面柱状图: 以这100台机器更换的易损零件数的频率代替1台机器更换的易损零件数发生的概率,记X 表示2台机器三年内共需更换的易损零件数,n 表示购买2台机器的同时购买的易损零件数. (I )求X 的分布列;
(II )若要求()0.5P X n ≤≥,确定n 的最小值;
(III )以购买易损零件所需费用的期望值为决策依据,在19n =与20n =之中选其一,应选用哪个?
【2015.理.4】投篮测试中,每人投3次,至少投中2次才能通过测试.已知某同学每次投篮投中的概
率为0.6,且各次投篮是否投中相互独立,则该同学通过测试的概率为 (A )0.648 (B )0.432 (C )0.36 (D )0.312
(19)某公司为确定下一年度投入某种产品的宣传费,需了解年宣传费x (单位:千元)对年销售量y (单位:t )和年利润z (单位:千元)的影响,对近8年的年宣传费x i 和年销售量y i (i =1,2,···,8)数据作了初步处理,得到下面的散点图及一些统计量的值.
x r
y u r
w u r
8
i=1
∑
(x i -x r )2
8
i=1
∑
(w i -w u r )2
8
i=1
∑
(x i -x r
)(y i -
y u r )
8
i=1
∑
(w i -
w u r )(y i -y u r )
46.6 56.3 6.8 289.8 1.6 1469
108.8
表中w i =i x , ,w u r =
1
8
8
i=1
∑
i w
(Ⅰ)根据散点图判断,y =a +bx 与y =c +d x 哪一个适宜作为年销售量y 关于年宣传费x 的回归方程类型?(给
出判断即可,不必说明理由)
(Ⅱ)根据(Ⅰ)的判断结果及表中数据,建立y 关于x 的回归方程;
年宣传费(千元)
年销售量
(Ⅲ)以知这种产品的年利率z与x、y的关系为z=0.2y-x.根据(Ⅱ)的结果回答下列问题:(i)年宣传费x=49时,年销售量及年利润的预报值是多少?
(ii)年宣传费x为何值时,年利率的预报值最大?
附:对于一组数据(u1v1),(u2v2)…….. (u n v n),其回归线v=αβ
+u的斜率和截距的最小
二乘估计分别为: (1)
2
1
()()
,
()
n
i i
i
n
i
i
u u v v
v u
u u
βαβ=
=
--
==-
-
∑
∑。
