计算切线方位角
缓和曲线圆曲线计算公式

缓和曲线、竖曲线、圆曲线、匝道(计算公式)一、缓和曲线上的点坐标计算已知:①缓和曲线上任一点离ZH点的长度:l②圆曲线的半径:R③缓和曲线的长度:l0④转向角系数:K(1或-1)⑤过ZH点的切线方位角:α⑥点ZH的坐标:xZ,yZ计算过程:说明:当曲线为左转向时,K=1,为右转向时,K=-1,公式中n的取值如下:当计算第二缓和曲线上的点坐标时,则:l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与计算第一缓和曲线时相反xZ,yZ为点HZ的坐标切线角计算公式:二、圆曲线上的点坐标计算已知:①圆曲线上任一点离ZH点的长度:l②圆曲线的半径:R③缓和曲线的长度:l0④转向角系数:K(1或-1)⑤过ZH点的切线方位角:α⑥点ZH的坐标:xZ,yZ计算过程:说明:当曲线为左转向时,K=1,为右转向时,K=-1,公式中n的取值如下:当只知道HZ点的坐标时,则:l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与知道ZH点坐标时相反xZ,yZ为点HZ的坐标三、曲线要素计算公式公式中各符号说明:l——任意点到起点的曲线长度(或缓曲上任意点到缓曲起点的长度)l1——第一缓和曲线长度l2——第二缓和曲线长度l0——对应的缓和曲线长度R——圆曲线半径R1——曲线起点处的半径R2——曲线终点处的半径P1——曲线起点处的曲率P2——曲线终点处的曲率α——曲线转角值四、竖曲线上高程计算已知:①第一坡度:i1(上坡为“+”,下坡为“-”)②第二坡度:i2(上坡为“+”,下坡为“-”)③变坡点桩号:SZ④变坡点高程:HZ⑤竖曲线的切线长度:T⑥待求点桩号:S计算过程:五、超高缓和过渡段的横坡计算已知:如图,第一横坡:i1第二横坡:i2过渡段长度:L待求处离第二横坡点(过渡段终点)的距离:x 求:待求处的横坡:i解:d=x/Li=(i2-i1)(1-3d2+2d3)+i1六、匝道坐标计算已知:①待求点桩号:K②曲线起点桩号:K0③曲线终点桩号:K1④曲线起点坐标:x0,y0⑤曲线起点切线方位角:α0⑥曲线起点处曲率:P0(左转为“-”,右转为“+”)⑦曲线终点处曲率:P1(左转为“-”,右转为“+”) 求:①线路匝道上点的坐标:xy②待求点的切线方位角:αT计算过程:注:sgn(x)函数是取符号函数,当x0时sgn(x)=1,当x=0时sgn(x)=0。
道路曲线高程计算公式

高速公路的一些线路坐标、高程计算公式(缓和曲线、竖曲线、圆曲线、匝道) 一、缓和曲线上的点坐标计算已知:①缓和曲线上任一点离ZH点的长度:l②圆曲线的半径:R③缓和曲线的长度:l0④转向角系数:K(1或-1)⑤过ZH点的切线方位角:α⑥点ZH的坐标:xZ,yZ计算过程:说明:当曲线为左转向时,K=1,为右转向时,K=-1,公式中n的取值如下:当计算第二缓和曲线上的点坐标时,则:l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与计算第一缓和曲线时相反xZ,yZ为点HZ的坐标切线角计算公式:二、圆曲线上的点坐标计算已知:①圆曲线上任一点离ZH点的长度:l②圆曲线的半径:R③缓和曲线的长度:l0④转向角系数:K(1或-1)⑤过ZH点的切线方位角:α⑥点ZH的坐标:xZ,yZ计算过程:说明:当曲线为左转向时,K=1,为右转向时,K=-1,公式中n的取值如下:当只知道HZ点的坐标时,则:l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与知道ZH点坐标时相反xZ,yZ为点HZ的坐标三、曲线要素计算公式公式中各符号说明:l——任意点到起点的曲线长度(或缓曲上任意点到缓曲起点的长度)l1——第一缓和曲线长度l2——第二缓和曲线长度l0——对应的缓和曲线长度R——圆曲线半径R1——曲线起点处的半径R2——曲线终点处的半径P1——曲线起点处的曲率P2——曲线终点处的曲率α——曲线转角值四、竖曲线上高程计算已知:①第一坡度:i1(上坡为“+”,下坡为“-”)②第二坡度:i2(上坡为“+”,下坡为“-”)③变坡点桩号:SZ④变坡点高程:HZ⑤竖曲线的切线长度:T⑥待求点桩号:S计算过程:五、超高缓和过渡段的横坡计算已知:如图,第一横坡:i1第二横坡:i2过渡段长度:L待求处离第二横坡点(过渡段终点)的距离:x 求:待求处的横坡:i解:d=x/Li=(i2-i1)(1-3d2+2d3)+i1六、匝道坐标计算已知:①待求点桩号:K②曲线起点桩号:K0③曲线终点桩号:K1④曲线起点坐标:x0,y0⑤曲线起点切线方位角:α0⑥曲线起点处曲率:P0(左转为“-”,右转为“+”)⑦曲线终点处曲率:P1(左转为“-”,右转为“+”)求:①线路匝道上点的坐标:x,y②待求点的切线方位角:αT计算过程:。
方位角的计算公式

计算公式一、 方位角的计算公式1. 字母所代表的意义:x 1:QD 的X 坐标 y 1:QD 的Y 坐标 x 2:ZD 的X 坐标 y 2:ZD 的Y 坐标 S :QD ~ZD 的距离 α:QD ~ZD 的方位角2. 计算公式:()()212212y y x x S -+-=1)当y 2- y 1>0,x 2- x 1>0时:1212x x y y arctg--=α2)当y 2- y 1<0,x 2- x 1>0时:1212360x x y y arctg --+︒=α 3)当x 2- x 1<0时:1212180x x y y arctg--+︒=α 二、 平曲线转角点偏角计算公式1. 字母所代表的意义:α1:QD ~JD 的方位角 α2:JD ~ZD 的方位角 β:JD 处的偏角2. 计算公式:β=α2-α1(负值为左偏、正值为右偏)三、 平曲线直缓、缓直点的坐标计算公式1. 字母所代表的意义:U :JD 的X 坐标 V :JD 的Y 坐标 A :方位角(ZH ~JD )T :曲线的切线长,2322402224R L L D tg R L R T ss s -+⎪⎪⎭⎫ ⎝⎛+=D :JD 偏角,左偏为-、右偏为+2. 计算公式:直缓(直圆)点的国家坐标:X ′=U+Tcos(A+180°)Y ′=V+Tsin(A+180°)缓直(圆直)点的国家坐标:X ″=U+Tcos(A+D)Y ″=V+Tsin(A+D)四、 平曲线上任意点的坐标计算公式1. 字母所代表的意义:P :所求点的桩号B :所求边桩~中桩距离,左-、右+ M :左偏-1,右偏+1C :JD 桩号 D :JD 偏角 L s :缓和曲线长 A :方位角(ZH ~JD ) U :JD 的X 坐标 V :JD 的Y 坐标T :曲线的切线长,2322402224R L L D tg R L R T ss s -+⎪⎪⎭⎫ ⎝⎛+=I=C -T :直缓桩号 J=I+L :缓圆桩号s L DRJ H -+=180π:圆缓桩号K=H+L :缓直桩号2. 计算公式: 1)当P<I 时中桩坐标:X m =U+(C -P)cos(A+180°) Y m =V+(C -P)sin(A+180°) 边桩坐标:X b =X m +Bcos(A+90°) Y b =Y m +Bsin(A+90°)2)当I<P<J 时()s230RL I P MA O π-︒+= ()()2390R I P I P G ---=中桩坐标:X m =U+Tcos(A+180°)+GcosO Y m =V+Tsin(A+180°)+GsinO()s290RL I P W π-︒=边桩坐标:X b =X m +Bcos(A+MW+90°) Y b =Y m +Bsin(A+MW+90°)3)当J<P<H 时()()R J P L M A R J P R L M A O s s πππ-+︒+=⎪⎭⎫⎝⎛-︒+︒+=909090 ()RJ P R G π-︒=90sin2中桩坐标:()O G R L M A R L L A T U X s ss m cos 30cos 90180cos 23+⎪⎭⎫⎝⎛︒+⎪⎪⎭⎫ ⎝⎛-+︒++=π ()O G R L M A R L L A T V Y s ss m sin 30sin 90180sin 23+⎪⎭⎫ ⎝⎛︒+⎪⎪⎭⎫ ⎝⎛-+︒++=π ()RJ P W π-︒=90边桩坐标:X b =X m +Bcos(O+MW+90°) Y b =Y m +Bsin(O+MW+90°)4)当H<P<K 时()sRL K P MMD A O π230180-︒-︒++= ()2390R P K P K G ---= 中桩坐标:X m =U+Tcos(A+MD)+GcosO Y m =V+Tsin(A+MD)+GsinO()s290RL K P W π-︒=边桩坐标:X b =X m +Bcos(A+MD -MW+90°) Y b =Y m +Bsin(A+MD -MW+90°)5)当P>K 时中桩坐标:X m =U+(T+P -K)cos(A+MD) Y m =V+(T+P-K)sin(A+MD) 边桩坐标:X b =X m +Bcos(A+MD+90°) Y b =Y m +Bsin(A+MD+90°)注:计算公式中距离、长度、桩号单位:“米”;角度测量单位:“度”;假设要以“弧度”为角度测量单位,请将公式中带°的数字换算为弧度。
切线方位角计算

曲线上点的切线方位角计算公式:
圆曲线:±1*起点到计算点的圆心角+起点的切线方位角(ZY)
完全对称缓和曲线:
第一缓和曲线:±1*ZH到计算点的缓和曲线长^2/(2*R*Ls)*(180/PI())+ZH点的切线方位角。
圆曲线:±1*(Ls/(2*R)+HY到计算点的圆弧曲线长度/R)*(180/PI())+ZH点的切线方位角。
第二缓和曲线:1*HZ到计算点的缓和曲线长^2/(2*R*Ls)*(180/PI())+HZ点的切线方位角+180。
不对称缓和曲线:
第一缓和曲线:±1*ZH到计算点的缓和曲线长^2/(2*R*Ls1)*(180/PI())+ZH点的切线方位角。
圆曲线:±1*(Ls1/(2*R)+HY到计算点的圆弧曲线长度/R)*(180/PI())+ZH点的切线方位角。
第二缓和曲线:1*HZ到计算点的缓和曲线长^2/(2*R*Ls2)*(180/PI())+HZ点的切线方位角+180。
高速公路的一些线路坐标、高程计算公式

高速公路的一些线路坐标、高程计算公式(缓和曲线、竖曲线、圆曲线、匝道)一、缓和曲线上的点坐标计算已知:①缓和曲线上任一点离ZH点的长度:l②圆曲线的半径:R③缓和曲线的长度:l0④转向角系数:K(1或-1)⑤过ZH点的切线方位角:α⑥点ZH的坐标:xZ,yZ计算过程:说明:当曲线为左转向时,K=1,为右转向时,K=-1,公式中n的取值如下:当计算第二缓和曲线上的点坐标时,则:l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与计算第一缓和曲线时相反xZ,yZ为点HZ的坐标切线角计算公式:二、圆曲线上的点坐标计算已知:①圆曲线上任一点离ZH点的长度:l②圆曲线的半径:R③缓和曲线的长度:l0④转向角系数:K(1或-1)⑤过ZH点的切线方位角:α⑥点ZH的坐标:xZ,yZ计算过程:说明:当曲线为左转向时,K=1,为右转向时,K=-1,公式中n的取值如下:当只知道HZ点的坐标时,则:l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与知道ZH点坐标时相反xZ,yZ为点HZ的坐标三、曲线要素计算公式公式中各符号说明:l——任意点到起点的曲线长度(或缓曲上任意点到缓曲起点的长度)l1——第一缓和曲线长度l2——第二缓和曲线长度l0——对应的缓和曲线长度R——圆曲线半径R1——曲线起点处的半径R2——曲线终点处的半径P1——曲线起点处的曲率P2——曲线终点处的曲率α——曲线转角值四、竖曲线上高程计算已知:①第一坡度:i1(上坡为“+”,下坡为“-”)②第二坡度:i2(上坡为“+”,下坡为“-”)③变坡点桩号:SZ④变坡点高程:HZ⑤竖曲线的切线长度:T⑥待求点桩号:S计算过程:五、超高缓和过渡段的横坡计算已知:如图,第一横坡:i1第二横坡:i2过渡段长度:L待求处离第二横坡点(过渡段终点)的距离:x 求:待求处的横坡:i解:d=x/Li=(i2-i1)(1-3d2+2d3)+i1六、匝道坐标计算已知:①待求点桩号:K②曲线起点桩号:K0③曲线终点桩号:K1④曲线起点坐标:x0,y0⑤曲线起点切线方位角:α0⑥曲线起点处曲率:P0(左转为“-”,右转为“+”)⑦曲线终点处曲率:P1(左转为“-”,右转为“+”)求:①线路匝道上点的坐标:x,y②待求点的切线方位角:αT计算过程:注:sgn(x)函数是取符号函数,当x<0时sgn(x)=-1,当x>0时sgn(x)=1,当x=0时sgn(x)=0。
圆 缓和曲线中线上点位切线方位角计算

P
曲线左偏时:k -1 HZ
HZ切 曲线左偏
P
曲线右偏
P切 HZ
HZ切
圆曲线线路中线点位切线方位角计算
3、HY~HY段切线方切线方位角分析:
• k4+900点在JD3的曲线YH-HZ段上,由所给已知条件知:
• 本曲线为右偏,其HZ点切线方位角为 HZ切 9703526
(3)求k2+300点切线方位角
• k2+300点在JD3的圆+缓和曲线上,由所给已知条件知:
• 本曲线为右偏,其ZH点切线方位角为 ZH切 7102635
解: l k p kZH K 2 300 K 2 206.253 93.747
l 2 180 001127 2Rl0
曲线右偏:k 1
• 本曲线为右偏,其ZH点切线方位角为 ZH切 7102635
解:
0
l0 2R
180
30 16 57
曲线右偏: k 1
K P K HY 180 104257
R
0 405954
p切 ZH切 k
7102635 405954 7602629
加入缓和曲线后的切线坐标系
4、YH~HZ段切线方位角计算
(1)求p点切线的切偏角
l2 180 2Rl0
l kHZ kP
P切
P
HZ
HZ切 曲线左偏
P
曲线右偏
P切 HZ
HZ切
加入缓和曲线后的切线坐标系
4、YH~HZ段切线方位角计算
(2)求p点切线方位角 p切
p切 HZ切 k
曲线右偏时:k 1
P切
解:
l kHZ kP K4 946.780 K4 900 46.780
方位角及坐标计算

方位角及坐标计算公路工程各点方位角及坐标计算公式(一)各点方位角计算:1、第一直线段(K0~ZH):F=arctgΔY/ΔX注:直线方位角要考虑象限角才能定出正确线路走向 2、第一缓和曲线段(KZH~KHY):δ1=(K0-KZH)2/(2RLh)×180/π 3、圆曲线段(KHY~KYH):δ2=[2(K0-KZH)-Lh]/2R×180/π δ2=(KHY-KZH)/2R×180/π+(K0-KHY)/R×180/π无缓和曲线时:δ2=(K0-KHY)/R×180/π(即圆曲线圆心角) 4、第二缓和曲线段(KYH~KHZ):δ3=(KHZ-K0)2/(2RLh)×180/π 5、第二直线段(KHZ~KZH):F±α (左偏时F-α,右偏时F+α)注:K0――计算点的程α――曲线交点偏角Lh――缓和曲线长(注意有时第一和第二缓和曲线长不一样)(二)各点坐标计算XZH=XJD-T?CosF XHZ=XJD+T?Cos(F±α) YZH=YJD-T?SinF YHZ=YJD+T?Sin(F±α) 1、第一直线段:X=XZH+(K0-KZH)?CosF 中桩Y=YZH+(K0-KZH)?SinF X边=X中±B?Cos(F-Δ)边桩Y边=Y中±B?Sin(F-Δ)注:B――中桩至所求点的距离(左幅时为+B,右幅时为-B,当设计轴线与线路不垂直时B取斜长,即B/SinΔ)设计轴线线路方向。
BΔ 图S-12、第一缓和曲线段: XX=XZH-Y′?Sinθ+X′?Cosθ X X′ X′ 中桩′Y=YZH+Y′?Cosθ+X′?Sinθ Y ZH Y θ HZX边=X中±B?Cos(F+μδ1-Δ) HY YH 边桩Y边=Y中±B?Sin(F+μδ1-Δ)JD Y′ 注:(本公式只适用与图S-2线形)图S-2 μ――曲线左转为-1,右转为+1θ――线路方位角与Y轴所夹的锐角,见图S-2 Y′=L-L5/(40R2Lh2);X′=L3/(6RLh)-L7/(336R3Lh3);(R―圆曲线半径,L―缓和曲线上任一点至曲线起点长度)3、圆曲线段:X=XHY+2R?Sinφ?Cos(F+μ(ξ+φ))中桩Y=YHY+2R?Sinφ?Sin(F+μ(ξ+φ)) X边=X中±B?Cos(F+μδ2-Δ)边桩Y边=Y中±B?Sin(F+μδ2-Δ)注:φ=(K0-KHY)/2R×180/π;ξ=(KHY-KZH)/2R×180/π 4、第二缓和曲线段:X=XHZ-Y′?Sinθ+X′?Cosθ 中桩Y=YHZ-Y′?Cosθ-X′?Sinθ X边=X中±B?Cos(F+μδ1-Δ)边桩Y边=Y中±B?Sin(F+μδ1-Δ)注:1、本公式只适用与图S-2线形,其他线形可根据本线形公式变换2、式中符号与第一缓和曲线意义相同3、注意有时第一缓和曲线长和第二缓和曲线长不一样4、第二直线段:X=XHZ+(K0-KHZ)?Cos(F±α)中桩Y=YHZ+(K0-KHZ)?Sin(F±α) X边=X中±B?Cos(F±α-Δ)边桩Y边=Y中±B?Sin(F±α-Δ)注:F――第一直线段的方位角(三)用CASIO fx-4500P计算已知坐标点在线路上的里程和距中线距离 1、直线段(已知坐标X、Y)Pol(X-XHZ,Y-YHZ):K=V?Cos(F-W)+KHZ B=V?Sin(F-W)注: 1、在fx-4500P中计算结果存入变量储存区V和W,要显示储存区内容时按RCL V 、 W 键。
缓和曲线)计算公式
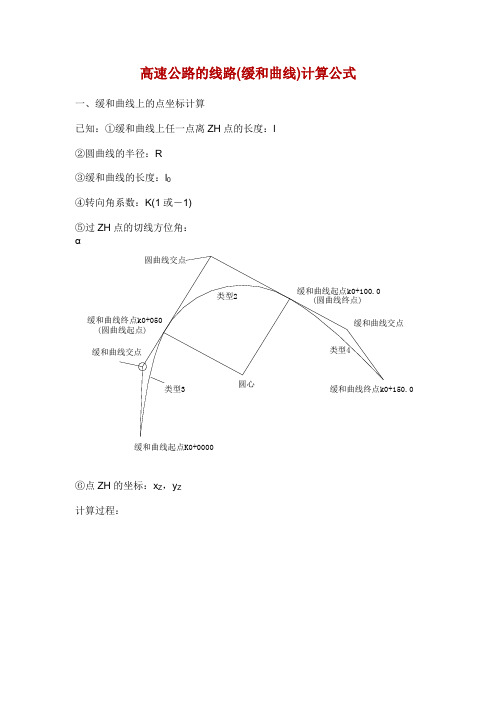
高速公路的线路(缓和曲线)计算公式一、缓和曲线上的点坐标计算已知:①缓和曲线上任一点离ZH点的长度:l②圆曲线的半径:R③缓和曲线的长度:l0④转向角系数:K(1或-1)⑤过ZH点的切线方位角:α⑥点ZH的坐标:x Z,y Z计算过程:说明:当曲线为左转向时,K=1,为右转向时,K=-1,公式中n的取值如下:当计算第二缓和曲线上的点坐标时,则:l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与计算第一缓和曲线时相反x Z,y Z为点HZ的坐标切线角计算公式:二、圆曲线上的点坐标计算已知:①圆曲线上任一点离ZH点的长度:l②圆曲线的半径:R③缓和曲线的长度:l0④转向角系数:K(1或-1)⑤过ZH点的切线方位角:α⑥点ZH的坐标:x Z,y Z计算过程:说明:当曲线为左转向时,K=1,为右转向时,K=-1,公式中n的取值如下:当只知道HZ点的坐标时,则:l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与知道ZH点坐标时相反x Z,y Z为点HZ的坐标三、曲线要素计算公式公式中各符号说明:l——任意点到起点的曲线长度(或缓曲上任意点到缓曲起点的长度)l1——第一缓和曲线长度l2——第二缓和曲线长度l0——对应的缓和曲线长度R——圆曲线半径R1——曲线起点处的半径R2——曲线终点处的半径P1——曲线起点处的曲率P2——曲线终点处的曲率α——曲线转角值四、竖曲线上高程计算已知:①第一坡度:i1(上坡为“+”,下坡为“-”)②第二坡度:i2(上坡为“+”,下坡为“-”)③变坡点桩号:S Z④变坡点高程:H Z⑤竖曲线的切线长度:T⑥待求点桩号:S计算过程五、超高缓和过渡段的横坡计算已知:如图,第一横坡:i1第二横坡:i2过渡段长度:L待求处离第二横坡点(过渡段终点)的距离:x 求:待求处的横坡:i解:d=x/Li=(i2-i1)(1-3d2+2d3)+i1六、匝道坐标计算已知:①待求点桩号:K②曲线起点桩号:K0③曲线终点桩号:K1④曲线起点坐标:x0,y0⑤曲线起点切线方位角:α0⑥曲线起点处曲率:P0(左转为“-”,右转为“+”)⑦曲线终点处曲率:P1(左转为“-”,右转为“+”)求:①线路匝道上点的坐标:x,y ②待求点的切线方位角:αT计算过程:。
竖曲线计算公式加强版

缓和曲线、竖曲线、圆曲线、匝道(计算公式)一、缓和曲线上的点坐标计算已知:①缓和曲线上任一点离ZH点的长度:l②圆曲线的半径:R③缓和曲线的长度:l0④转向角系数:K(1或-1)⑤过ZH点的切线方位角:α⑥点ZH的坐标:xZ,yZ计算过程:说明:当曲线为左转向时,K=1,为右转向时,K=-1,公式中n的取值如下:当计算第二缓和曲线上的点坐标时,则:l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与计算第一缓和曲线时相反xZ,yZ为点HZ的坐标切线角计算公式:二、圆曲线上的点坐标计算已知:①圆曲线上任一点离ZH点的长度:l②圆曲线的半径:R③缓和曲线的长度:l0④转向角系数:K(1或-1)⑤过ZH点的切线方位角:α⑥点ZH的坐标:xZ,yZ计算过程:说明:当曲线为左转向时,K=1,为右转向时,K=-1,公式中n的取值如下:当只知道HZ点的坐标时,则:l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与知道ZH点坐标时相反xZ,yZ为点HZ的坐标三、曲线要素计算公式公式中各符号说明:l——任意点到起点的曲线长度(或缓曲上任意点到缓曲起点的长度)l1——第一缓和曲线长度l2——第二缓和曲线长度l0——对应的缓和曲线长度R——圆曲线半径R1——曲线起点处的半径R2——曲线终点处的半径P1——曲线起点处的曲率P2——曲线终点处的曲率α——曲线转角值四、竖曲线上高程计算已知:①第一坡度:i1(上坡为“+”,下坡为“-”)②第二坡度:i2(上坡为“+”,下坡为“-”)③变坡点桩号:SZ④变坡点高程:HZ⑤竖曲线的切线长度:T⑥待求点桩号:S计算过程:S、SZ为里程数据,往往有些人计算时误入,用等实际计算的距离计算!!五、超高缓和过渡段的横坡计算已知:如图,第一横坡:i1第二横坡:i2过渡段长度:L待求处离第二横坡点(过渡段终点)的距离:x求:待求处的横坡:i解:d=x/Li=(i2-i1)(1-3d2+2d3)+i1三、匝道坐标计算已知:①待求点桩号:K②曲线起点桩号:K0③曲线终点桩号:K1④曲线起点坐标:x0,y0⑤曲线起点切线方位角:α0⑥曲线起点处曲率:P0(左转为“-”,右转为“+”)⑦曲线终点处曲率:P1(左转为“-”,右转为“+”) 求:①线路匝道上点的坐标:xy②待求点的切线方位角:αT计算过程:注:sgn(x)函数是取符号函数,当x0时sgn(x)=1,当x=0时sgn(x)=0。
曲线及缓和曲线计算公式

《坐标计算》一、缓和曲线上的点坐标计算已知:①缓和曲线上任一点离ZH点的长度:l②圆曲线的半径:R③缓和曲线的长度:l0④转向角系数:K(1或-1)⑤过ZH点的切线方位角:α⑥点ZH的坐标:xZ,yZ计算过程:说明:当曲线为左转向时,K=1,为右转向时,K=-1,公式中n的取值如下:当计算第二缓和曲线上的点坐标时,则:l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与计算第一缓和曲线时相反xZ,yZ为点HZ的坐标切线角计算公式:二、圆曲线上的点坐标计算已知:①圆曲线上任一点离ZH点的长度:l②圆曲线的半径:R③缓和曲线的长度:l0④转向角系数:K(1或-1)⑤过ZH点的切线方位角:α⑥点ZH的坐标:xZ,yZ计算过程:说明:当曲线为左转向时,K=1,为右转向时,K=-1,公式中n的取值如下:当只知道HZ点的坐标时,则:l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与知道ZH点坐标时相反xZ,yZ为点HZ的坐标三、曲线要素计算公式公式中各符号说明:l——任意点到起点的曲线长度(或缓曲上任意点到缓曲起点的长度)l1——第一缓和曲线长度l2——第二缓和曲线长度l0——对应的缓和曲线长度R——圆曲线半径R1——曲线起点处的半径R2——曲线终点处的半径P1——曲线起点处的曲率P2——曲线终点处的曲率α——曲线转角值四、竖曲线上高程计算已知:①第一坡度:i1(上坡为“+”,下坡为“-”)②第二坡度:i2(上坡为“+”,下坡为“-”)③变坡点桩号:SZ④变坡点高程:HZ⑤竖曲线的切线长度:T⑥待求点桩号:S计算过程:五、超高缓和过渡段的横坡计算已知:如图,第一横坡:i1第二横坡:i2过渡段长度:L待求处离第二横坡点(过渡段终点)的距离:x求:待求处的横坡:i解:d=x/Li=(i2-i1)(1-3d2+2d3)+i1六、匝道坐标计算已知:①待求点桩号:K②曲线起点桩号:K0③曲线终点桩号:K1④曲线起点坐标:x0,y0⑤曲线起点切线方位角:α0⑥曲线起点处曲率:P0(左转为“-”,右转为“+”)⑦曲线终点处曲率:P1(左转为“-”,右转为“+”)求:①线路匝道上点的坐标:x,y②待求点的切线方位角:αT计算过程:。
线路中线上点位切线方位角计算

已知条件
2、地面上(如图)
控制点坐标及高程
控制点的实际位置
第二部分
如何求一条直线的方位角?
如何求一条直线的方位角?
1、首先找一条方位角已知的直线
• 对于铁路、公路线路来说,应选择曲线起点或终点的切线
2、求待求直线与已知直线间的夹角
• 求线路中线点切线与曲线起点或终点的切线的切偏角
3、直线的方位角等于
AP AB
B
A
P
第三部分
直线段线路中线点切线方位角计算
直线段线路中线点切线方位角计算 某高速公路直线、曲线、交角见下表
直线段线路中线点切线方位角计算
导线点 JD1
ZY
导线点 圆曲线
导线点 JD2
导线点 ZH P
YZ
导线点
HY 缓 导线点
JD3 YH
圆 导线点
导线点 HZ
3
180
101259
p切 ZY切 k
5004033 101259 4902734
第五部分
圆+缓和曲线线路中线点位 切线方位角计算
圆+缓和曲线线路中线点位切线方位角计算
1、已知条件
ZH点切线方位角 圆曲线半径 缓和曲线长
主点里程
ZH切
P
P切
P切
ZH切
P
ZH
曲线右偏
ZH
4、YH~HZ段切线方位角计算
(1)求p点切线的切偏角
l2 180 2Rl0
l kHZ kP
P切 HZ
P
HZ切 曲线左偏
P
曲线右偏
P切 HZ
HZ切
加入缓和曲线后的切线坐标系
4、YH~HZ段切线方位角计算
非完整缓和曲线坐标计算

非完整缓和曲线坐标计算公路、铁路主干线一般线形采用曲线基本型,而在公路匝道部分常采用线形单元组合形式,组合线形的坐标计算只能按线形单元分段计算。
通常设计文件中提供各特征点的桩号、坐标、切线方位角。
圆曲线计算较为简单,这里主要讨论非完整缓和曲线的桩点的坐标计算。
一、计算ZH(HZ)点的坐标已知数据:如图4.9.1所示,起点p的半径Rp ,桩号Lp坐标Xp、Yp,切线方位角αp,缓和曲线参数A。
式中各项计算如下:图4.9.1 非完整缓和曲线αpZ的计算:其中Δp——右偏用“-”,左偏用“+”。
ZH切线坐标方位角:其中βp——左偏用“+”,右偏用“-”(ZH换成HZ时,左偏用“-”,右偏用“+”)。
二、计算缓和曲线切线坐标系各点坐标计算出缓和曲线起点坐标后即可按式4.8.2计算各中线点坐标。
三、计算施工坐标系坐标切线坐标系转换为施工坐标系需要进行坐标平移和转轴计算,当转向角为右时按式(4.9.7)、(4.9.8)计算;当转向角为左时按式(4.9.9)、(4.9.10)计算。
(1)当转向角为右时:(2)当转向角为左时:式中 Xi ,Yi——路线统一坐标系坐标;x i ,yi——切线坐标;α——转向点之间的切线方位角。
【例4.9.1】如图4.9.2所示,起点P处半径RP =9 579.228 m,桩号lP=0+889.975,XP =19 698.065,YP=28 469.399,起点的切线方位角αP=82°34′06″,缓和曲线参数A=60。
与缓和曲线相接的圆曲线半径R=55 m,公切点的桩号lGQ=K0+824.896试计算K0+860的坐标。
图4.9.2 非完整缓和曲线【解】(1)计算ZH的桩号和XZH ,YZH:(左偏)用“+”:(2)计算αZH切线方位角:(3)计算K0+860坐标:+860点切线坐标系坐标:x=30.30 m,y=1.293 m(计算过程略)+860点施工坐标系坐标:。
竖曲线要素计算

[转]缓和曲线、竖曲线、圆曲线、匝道(计算公式)来源:王维超的日志一、缓和曲线上的点坐标计算已知:①缓和曲线上任一点离ZH点的长度:l②圆曲线的半径:R③缓和曲线的长度:l0④转向角系数:K(1或-1)⑤过ZH点的切线方位角:α⑥点ZH的坐标:xZ,yZ计算过程:说明:当曲线为左转向时,K=1,为右转向时,K=-1,公式中n的取值如下:当计算第二缓和曲线上的点坐标时,则:l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与计算第一缓和曲线时相反xZ,yZ为点HZ的坐标切线角计算公式:二、圆曲线上的点坐标计算已知:①圆曲线上任一点离ZH点的长度:l②圆曲线的半径:R③缓和曲线的长度:l0④转向角系数:K(1或-1)⑤过ZH点的切线方位角:α⑥点ZH的坐标:xZ,yZ计算过程:说明:当曲线为左转向时,K=1,为右转向时,K=-1,公式中n的取值如下:当只知道HZ点的坐标时,则:l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与知道ZH点坐标时相反xZ,yZ为点HZ的坐标三、曲线要素计算公式公式中各符号说明:l——任意点到起点的曲线长度(或缓曲上任意点到缓曲起点的长度)l1——第一缓和曲线长度l2——第二缓和曲线长度l0——对应的缓和曲线长度R——圆曲线半径R1——曲线起点处的半径R2——曲线终点处的半径P1——曲线起点处的曲率P2——曲线终点处的曲率α——曲线转角值四、竖曲线上高程计算已知:①第一坡度:i1(上坡为“+”,下坡为“-”)②第二坡度:i2(上坡为“+”,下坡为“-”)③变坡点桩号:SZ④变坡点高程:HZ⑤竖曲线的切线长度:T⑥待求点桩号:S计算过程:五、超高缓和过渡段的横坡计算已知:如图,第一横坡:i1第二横坡:i2过渡段长度:L待求处离第二横坡点(过渡段终点)的距离:x 求:待求处的横坡:i解:d=x/Li=(i2-i1)(1-3d2+2d3)+i1六、匝道坐标计算已知:①待求点桩号:K②曲线起点桩号:K0③曲线终点桩号:K1④曲线起点坐标:x0,y0⑤曲线起点切线方位角:α0⑥曲线起点处曲率:P0(左转为“-”,右转为“+”)⑦曲线终点处曲率:P1(左转为“-”,右转为“+”)求:①线路匝道上点的坐标:xy②待求点的切线方位角:αT计算过程:注:sgn(x)函数是取符号函数,当x0时sgn(x)=1,当x=0时sgn(。
缓和曲线,圆曲线上任意一点切线方位角如何计算

[引用回复][搜索][献花][顶贴]
第6楼
2008-6-9 18:42:00
以下是引用片段:
以下是引用660在2008-6-8 21:26:00的发言:
例:JD=52+285.156 N=154678.69 E=404862.108 前FWJ=124°22°11° 后FWJ=140°18°49° 半径R=800 第一缓和曲线LS1=80 第二缓和曲线LS2=80 问:52+150和52+327各点切线方位角如何计算?
本贴得筑龙币:0等级得币:0 版主奖励:0 贴主答谢:0 献花赠币:0] 得信誉分:0
本贴评定等级:0执行评定版主:夏夜
[定制广告]路桥软件免费下载!
-
夏夜
ΨЖ
位置:
湖南
信誉:
84
专业:
路桥
发贴:
1799
[留言][电邮][主页][BLOG]
[引用回复][搜索][献花][顶贴]
第5楼
2008-6-9 7:27:00
[引用回复][搜索][献花][顶贴]
第9楼
2008-6-9 23:37:00
夏夜版主:我想请你计算一下52+327点的切线方位角?
本贴得筑龙币:0等级得币:0 版主奖励:0 贴主答谢:0 献花赠币:0] 得信誉分:0
本贴评定等级:0执行评定版主:夏夜
[定制广告]工程总结别发愁 这里来找你需要
夏夜
ΨЖ
第8楼
2008-6-9 22:53:00
不知道什么时候才用得着计算任意点方位角呀?
本贴得筑龙币:0等级得币:0 版主奖励:0 贴主答谢:0 献花赠币:0] 得信誉分:0
计算切线方位角

某匝道的由五段线元(直线+完整缓和曲线+圆曲线+非完整缓和曲线+直线)组
成,各段线元的要素(起点里程S0、起点坐标X0 Y0、起点切线方位角F0、线元长度
LS、起点曲率半径R0、止点曲率半径RN、线 元左右偏标志Q)如下:
S0 X0 Y0 F0 LS R0 RN Q
500.000 19942.837 28343.561 125 16 31.00 269.256 1E45 1E45 0
769.256 19787.340 28563.378 125 16 31.00 37.492 1E45 221.75 -1
806.748 19766.566 285945 -1
请问线元 起点到500 在到直缓769.256 在到缓圆806.748 在到圆缓919.527 在到缓直999.812 起点切线方位角分别是 125 16 31.00 125 16 31.00 120 25 54.07
91 17 30.63 80 40 50.00
919.527 19736.072 28701.893 91 17 30.63 80.285 221.75 9579.228 -1
999.812 19744.038 28781.659 80 40 50.00 100.000 1E45 1E45 0
推荐答案 按路线前进方向有JD1(为曲线之前的交点), ZH, HY, JD2 QZ, YH, HZ, 一般JD1与JD2的坐标已知,可根据方位角计算公式求的过两交点直线的方位角。也就是ZH到JD2线段的方位角(记作A),那么在曲线段上任意一点的方位角=A + 曲线段对应的圆心角B。 当计算点在第一缓和段上时: B=(计算点的桩号-ZH点桩号) /(2*R) 这里R为圆曲线的半径,算出的结果单位是弧度。当在圆曲线段上时 B = Ls/2R + (计算点的桩号-HY点桩号)/R 上述公式中的R均为圆曲线半径。 当在第二缓和段上时以此累加。上述的情况为路线右转,若为左转 就改为 任意一点的方位角=A - 曲线段对应的圆心角B。 还需要注意的是 缓和曲线一定弧长所对应的圆心角计算式为 a = 弧长 / 2倍的R, 而 圆曲线上 为 a = 弧长 / R,这些其实都是基础知识,希望能帮到你~~
圆曲线中边桩坐标计算公式

圆曲线中边桩坐标计算公式: L=F-H;注:L---所求点曲线长;F---所求点里程;H---圆曲线起点(ZY点桩号里程)X=XZY+2×R×SIN(L÷2R)×COS{α±(L÷2R)}+S×COS{α±(L÷R)+M}; Y =YZY+2×R×SIN(L÷2R)×SIN{α±(L÷2R)}+S×SIN{α±(L÷R)+M}. 注:α---线路方位角;M---所求边桩与路线的夹角;S---所求边桩至中桩的距离;"±"---曲线左偏取“-”右偏取“+”;当S=0时为中桩坐标。
经高速公路施工一线使用效果很好。
记住在公式中加入Excel的Radians()函数将度转为弧度即可轻松方便地使用,从ZY点坐标准确快速推算地计算出整条圆曲线。
注意要分清左偏右偏两种情况。
高速公路线路坐标计算公式:高速公路的一些线路坐标、高程计算公式(缓和曲线、竖曲线、圆曲线、匝道)一、缓和曲线上的点坐标计算已知:①缓和曲线上任一点离ZH点的长度:l②圆曲线的半径:R③缓和曲线的长度:l④转向角系数:K(1或-1)⑤过ZH点的切线方位角:α⑥点ZH的坐标:xZ ,yZ计算过程:说明:当曲线为左转向时,K=1,为右转向时,K=-1,公式中n的取值如下:当计算第二缓和曲线上的点坐标时,则:l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与计算第一缓和曲线时相反xZ ,yZ为点HZ的坐标切线角计算公式:二、圆曲线上的点坐标计算已知:①圆曲线上任一点离ZH点的长度:l②圆曲线的半径:R③缓和曲线的长度:l④转向角系数:K(1或-1)⑤过ZH点的切线方位角:α⑥点ZH的坐标:xZ ,yZ计算过程:说明:当曲线为左转向时,K=1,为右转向时,K=-1,公式中n的取值如下:当只知道HZ点的坐标时,则:l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与知道ZH点坐标时相反xZ ,yZ为点HZ的坐标三、曲线要素计算公式公式中各符号说明:l——任意点到起点的曲线长度(或缓曲上任意点到缓曲起点的长度)l1——第一缓和曲线长度l2——第二缓和曲线长度l——对应的缓和曲线长度R——圆曲线半径R1——曲线起点处的半径R2——曲线终点处的半径P1——曲线起点处的曲率P2——曲线终点处的曲率α——曲线转角值四、竖曲线上高程计算已知:①第一坡度:i1(上坡为“+”,下坡为“-”)②第二坡度:i2(上坡为“+”,下坡为“-”)③变坡点桩号:SZ④变坡点高程:HZ⑤竖曲线的切线长度:T⑥待求点桩号:S计算过程:五、超高缓和过渡段的横坡计算已知:如图,第一横坡:i1第二横坡:i2过渡段长度:L待求处离第二横坡点(过渡段终点)的距离:x求:待求处的横坡:i解:d=x/Li=(i2-i1)(1-3d2+2d3)+i1六、匝道坐标计算已知:①待求点桩号:K②曲线起点桩号:K③曲线终点桩号:K1④曲线起点坐标:x0,y⑤曲线起点切线方位角:α⑥曲线起点处曲率:P(左转为“-”,右转为“+”)⑦曲线终点处曲率:P1(左转为“-”,右转为“+”)求:①线路匝道上点的坐标:x,y②待求点的切线方位角:αT计算过程:注:sgn(x)函数是取符号函数,当x<0时sgn(x)=-1,当x>0时sgn(x)=1,当x=0时sgn(x)=0。
公路卵形曲线任意点坐标和切线方位角的计算方法

公路卵形曲线任意点坐标和切线方位角的计算方法
张玲玲;张志伟
【期刊名称】《兰州交通大学学报》
【年(卷),期】2007(026)001
【摘要】针对公路卵形曲线段上任意点坐标和过该点的切线方位角的计算、测设问题,结合工程实例,将卵形曲线转化为完整缓和曲线的一部分,进而推导了简洁、实用、易懂的计算公式.此种计算公式在应用计算机编程计算方面也比较实用.
【总页数】3页(P86-88)
【作者】张玲玲;张志伟
【作者单位】兰州交通大学,土木工程学院,甘肃,兰州,730070;中铁十三局集团,第五工程有限公司,吉林,长春,130033
【正文语种】中文
【中图分类】TB22
【相关文献】
1.道路缓和曲线任意点坐标及方位角的计算方法 [J], 樊志军
2.卵形曲线要素及其上任意点坐标的严密算法 [J], 任克林
3.应用弦长与弦方位角、切线方位角推算公路曲线坐标 [J], 翁黎辉
4.非对称缓和平曲线任意点坐标及方位角计算 [J], 马志平
5.道路卵形回旋线任意点坐标及方位角计算方法 [J], 叶松林
因版权原因,仅展示原文概要,查看原文内容请购买。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
如何将直曲表元素转换为线元法所需要的元素(起点坐标,方位角)?在此现感
谢各位前辈了!…………………………………………………………
谢谢发贴:+4 分【测量空间】[0
本文可共享补充点击修改共享补充New!查看楼主其它文章<<返回→回复内容只查看楼主与本人回复
沙发:duzhitao11-1-10 16:5
计算呀
2楼:清晰楼主11-1-10 20:24
能具体说说吗?谢谢!
3楼:gmh45345311-1-13 9:32
可以用卡西欧计算器计算,也可以用软件计算,你的程序是线元法的吧,其实主要是计算出分段曲线的切线方位角就可以了,之后自己编个EXCEL表就哦了
4楼:清晰楼主11-1-13 14:59
前辈你有没有具体的手算方法或公式给我发一份,谢谢!
5楼:zhangliwei020211-1-14 16:16评:+8
分
计算看看
6楼:yuan198991011-1-15 7:53我也来学习学习,如果有也发一份给我252149547@ 7楼:123hezheng11-1-17 20:48我也来学习一下有的话发289699412@谢谢啦
8楼:半边书生11-1-19 20:57直线上的切线方位角不变
缓和曲线的转角=Ls/2/R(弧度)
圆曲线的转角=Lc/R(弧度)
所以,已知起点切线方位角为A(弧度)的情况下
ZH点的切线方位角=A
HY点的切线方位角=A+Ls/2/R
YH点的切线方位角=A+Ls/2/R+Lc/R
HZ点的切线方位角=A+Ls/R+Lc/R,同时应与本交点到下一交点的坐标方位角相等。
上式中,Ls为缓和曲线长,Lc为圆曲线长,R为圆曲线半径,曲线左偏时加负号。
各主点的坐标相信你如果懂积木法算桩坐标的话应该都可以计算得出,同时记得将HZ 点的坐标计算值和交点法算得的坐标相较以检验。
9楼:公道翁11-1-29 16:42
分两步计算:1、计算曲线要素
P=S²÷(24R);Q=S÷2-S³÷(240R²);T=(P+R)tan|0.5B|+Q;L=πRB÷180+S
ZH(C)=A-T;HY(D)=C+S;YH(H)=C+L-S;HZ(G)=C+L
式中:F----方位角;A----交点桩号;B-----路线偏角(左偏为负,右偏为正),R----半径;S---缓和曲线长
T----切线长;L-----曲线长
2、计算方位角:ZH=F;HY=F+S÷2R;HZ=F+B;YH=HZ-S÷2R;(当F<0时S÷2R为负,大于0时为正)
10楼:明学军11-2-8 20:20
8楼楼主:我用你的计算方法检查我已做过的隧道工,,YH点和HZ点不对啊,HY 点是对的,请你再核实一下,给我回复!谢啦,QQ:764207279
11楼:半边书生11-2-22 16:42
自己去下载吧
/down_view.asp?id=1279&author=%u534A%u8FB9%u4E66%u75 1F。
