矩阵分析 4
矩阵分析引论第四版课后练习题含答案

矩阵分析引论第四版课后练习题含答案简介《矩阵分析引论》是矩阵分析领域的经典教材之一,已经发行了四个版本。
该书主要以线性代数、矩阵理论和应用为主要内容,重点介绍了矩阵分析的基本概念、原理和应用。
本文主要介绍该书第四版中的课后练习题及其答案。
提供的资料本文为矩阵分析引论第四版课后练习题及其答案,包含了第一章到第五章的所有习题和答案。
其中,习题从简单到复杂,大部分习题都有详细的解答过程和答案。
内容概述第一章引言第一章主要介绍了矩阵分析的历史和基本概念、性质、符号等。
本章习题主要涉及了矩阵、向量、矩阵运算等基本概念和性质。
第二章基本概念和变换第二章主要介绍了线性变换的基本概念和性质,以及线性代数中的一些重要定理和定理的证明。
本章习题主要涉及了线性变换、矩阵的秩和标准型、特征值和特征向量等内容。
第三章矩阵运算第三章主要介绍了矩阵运算的基本概念和性质,包括矩阵乘法、逆矩阵、行列式等。
本章习题主要涉及矩阵运算的基本操作和应用。
第四章矩阵分解第四章主要介绍了矩阵分解的基本概念和应用,包括特征值分解、奇异值分解、QR分解等。
本章习题主要涉及了矩阵特征值和特征向量、矩阵的奇异值分解等内容。
第五章线性方程组和特征值问题第五章主要介绍了解线性方程组和求特征值的方法,包括高斯消元法、LU分解、带状矩阵、雅可比迭代等。
本章习题主要涉及了线性方程组的解法、矩阵的特征值问题等内容。
结语本文介绍了矩阵分析引论第四版课后练习题及其答案。
对于学习矩阵分析的同学,课后习题是一个非常重要的练习和提升自己能力的途径。
本文所提供的习题和答案可以帮助读者巩固和提高自己的矩阵分析能力。
同时,本文也希望能够帮助更多的人学习矩阵分析,并成为矩阵分析领域的专家。
矩阵分析课件(1-1,4)

显然, 例1.1.1 1.1.3都是实数域R上的线性空间.下面再举 几个例子 :
例1.1.4 设A为实m n矩阵, 易证 : 齐次线性方程组Ax 0的所有 解(包括零解)的集合构成实数域R上的线性空间.这个空间为方 程组 Ax 0的解空间, 也称为矩阵A的核或零空间, 常记为N ( A).
称n阶方阵
a11 a21 P= a n1
a12 a22 an 2
a1n a2 n ann
是由基1 , 2 ,
, n到基1 , 2 ,
, n的过渡矩阵。于是上 ,n ) P
式可写成(1 , 2 ,
, n)=(1 , 2 ,
n n
1=(0,0,
T ,1)是 Rn的一组基,称 1 , 2 , , n为Rn的
标准正交基。
例1.2.1 试证:线性空间 R[ x ]n a0 a1 x
是n维的,并求a0 a1 x ,( x a )n1 下的坐标。
an1 x n1 ai R
定义1.3.1 设W 为域F 上的n维线性空间V的子集合,若 W 中元素满足
(1) 若, W , 则+ W ; (2) W , F , 则 W .
则称W 是线性空间V的一个子空间。
a1i a 2i , n ) ani
( i 1, 2,
, n)
把这n个关系式用矩阵可表示为
( 1 , 2 , , n ) (1 , 2 , a11 a21 , n ) a n1 a12 a22 an 2 a1n a2 n ann
矩阵分析第4章课件

矩阵满秩分解不唯一;但同一矩阵的两个满
秩分解的因式矩阵之间存在密切的关系( 见P153,定理4.1.2).
ACrmn r=rank A min{m,n} A的秩等于它的行秩、列秩或行列式秩。A的行( 列)秩是它的最大线性无关组的行(列)数;A 的行列式秩是它的非0子式的最大阶数。 A=BC rank A rank B & rank A rank C
1
初等变换与初等矩阵性质
①3类初等矩阵都是可逆的(行列式不为0). ②将A依次作初等矩阵P1,…,Pr对应的行(列)初等变
换等价于左(右)乘A以可逆矩阵Pr,…,P1(P1,…,Pr).
③可适当选第一类初等矩阵的乘积P使PA(AP)的 行(列)是A的行(列)的任意排列.可适当选第三类 初等矩阵P(i,j(k))中的k使P(i,j(k))A的(i,j) 元变为0.可适当选第二类初等矩阵P(i(k))中的k 使P(i(k))A的非零(i,i)元变为1.综合起来推出: Er 0 存在初等矩阵的乘积P和Q,使 PAQ= 0 0 m n 其中r=rank A.一般地,ACr 都 Er 0 存在m,n阶可逆阵P和Q使 PAQ=
a11 a1n AB ann
b11 b1n a11b11 * bnn annbnn
a11 a1n 1/ a11 * 1 1 A , aii 0 det A 0 A det A a 1/ a nn nn
1 C11 1 2 C21 1 C22 2 n Cn1 1 Cn 2 2 ... Cnn n
Teadiva的SWOT矩阵分析
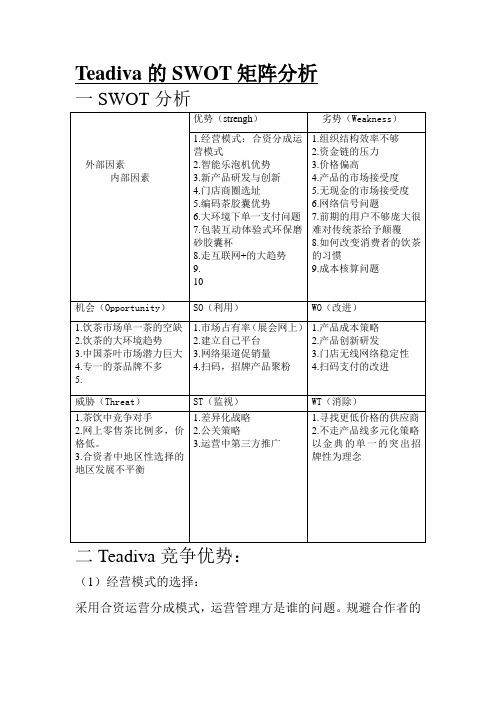
Teadiva的SWOT矩阵分析一SWOT分析外部因素内部因素优势(strengh)劣势(Weakness)1.经营模式:合资分成运营模式2.智能乐泡机优势3.新产品研发与创新4.门店商圈选址5.编码茶胶囊优势6.大环境下单一支付问题7.包装互动体验式环保磨砂胶囊杯8.走互联网+的大趋势9.101.组织结构效率不够2.资金链的压力3.价格偏高4.产品的市场接受度5.无现金的市场接受度6.网络信号问题7.前期的用户不够庞大很难对传统茶给予颠覆8.如何改变消费者的饮茶的习惯9.成本核算问题机会(Opportunity)SO(利用)WO(改进)1.饮茶市场单一茶的空缺2.饮茶的大环境趋势3.中国茶叶市场潜力巨大4.专一的茶品牌不多5. 1.市场占有率(展会网上)2.建立自己平台3.网络渠道促销量4.扫码,招牌产品聚粉1.产品成本策略2.产品创新研发3.门店无线网络稳定性4.扫码支付的改进威胁(Threat)ST(监视)WT(消除)1.茶饮中竞争对手2.网上零售茶比例多,价格低。
3.合资者中地区性选择的地区发展不平衡1.差异化战略2.公关策略3.运营中第三方推广1.寻找更低价格的供应商2.不走产品线多元化策略以金典的单一的突出招牌性为理念二Teadiva竞争优势:(1)经营模式的选择:采用合资运营分成模式,运营管理方是谁的问题。
规避合作者的投资风险和前期投资费用。
(2)品牌优势:1.充分利用“半DIY的互动体验式的环保磨砂胶囊杯”的运用,在消费者需求的中心由产品转向包装服务,在由服务转向客户体验的时代,Teadiva创立了一种以“Teadiva 互动体验”为特点饮茶新模式,与一般茶饮店的区别在于Teadiva赋予了一杯茶更丰富的体验和更深层次茶文化的内涵。
2.智能乐泡泡茶优势,Teadiva智能饮茶设备全球首家独创式智能饮茶设备,拥有多项国家专利技术,智能识别每款胶囊茶,一键式的操作,降低操作难度,标准化操作使门店口感达到统一。
矩阵分析引论--第四章--矩阵的奇异值分解-向量范数、向量范数

n
定义 E
xi2 .
证明
a,
都与
b
E 等价.
i 1
利用 a
x11 xn n
( x1 ,, xn )连续,
在单位球面
S
y
(
y1 ,,
yn
n
)
i 1
yi2
1
上
取得最大值M与最小值m.
目录 上页 下页 返回 结束
第四章第一二节 向量范数、矩阵范数
第二节 矩阵范数
定义4-2 设A P nn ,定义非负实数 A, 满足下列条件: (1) 正定性:当A 0时,A 0; (2) 齐次性:kA k A (k P); (3) 三角不等式: A B A B . (4) AB A B . 则称非负实数||A||为n×n方阵的范数.
则称非负实数||||为向量 的范数.
此时称线性空间V 为线性赋范空间.
目录 上页 下页 返回 结束
第四章第一二节 向量范数、矩阵范数
设V是内积空间, V ,定义: ( , ),
则 • 是V上的一个范数,称为由内积引出的范数.
向量范数的性质:
P124, 1
(1) 0 0 ;
(2) 0时, 1 1 ;
A F
n
2
aij
tr( AH A)
i , j1
是与 2相容的方阵范数. 称为 F 范数.
注:当U为酉矩阵时,有
F范数的优点
A的酉相似矩阵的F 范数相同.
目录 上页 下页 返回 结束
第四章第一二节 向量范数、矩阵范数
常用的矩阵范数
n
(1)
A
1
max
1 jn i 1
aij
矩阵分析知识点总结

矩阵分析知识点总结一、矩阵的基本概念1.1 矩阵的定义矩阵是由数个数排成的矩形阵列。
矩阵可以用大写字母表示。
1.2 矩阵的基本要素- 元素:矩阵中的每一个数称为矩阵的元素。
- 维数:矩阵的行数和列数称为矩阵的维数。
行和列的个数分别称为行数和列数。
1.3 矩阵的类型- 方阵:行数等于列数的矩阵称为方阵。
- 零矩阵:所有元素都是 0 的矩阵称为零矩阵。
- 对角矩阵:除了主对角线上的元素外,其它元素都是 0 的矩阵称为对角矩阵。
1.4 矩阵的表示- 横标法:按行标的顺序把元素排列成一串数,两个 4× 3 的矩阵可以表示为 12 个数。
- 纵标法:按纵标的顺序把元素排列成一串数。
1.5 矩阵的运算- 矩阵的加法- 矩阵的数乘- 矩阵的乘法1.6 矩阵的转置- 行变列,列变行,得到的新矩阵称为原矩阵的转置。
- 性质: (AT)T = A1.7 矩阵的逆- 若矩阵 A 有逆矩阵 A-1, 则 A × A-1 = A-1 × A = E- 矩阵 A 有逆矩阵的充分必要条件是 A 是可逆的。
- 克拉默法则:若一个 n 阶矩阵可逆,且 Ax = b,则 x = A-1b1.8 矩阵的秩- 行最简形矩阵都是行等价的。
其秩等于不为零的行数。
- 同样列最简形矩阵都是列等价的。
其秩等于不为零的列数。
- 行秩等于列秩。
1.9 矩阵的特征值和特征向量- 特征值:如果数λ和非零向量 x ,使得Ax = λx 成立,则称λ 是矩阵 A 的特征值。
非零向量x 称为特征值λ 对应的特征向量。
- 矩阵 A 所有特征值的集合称为 A 的谱。
- 若λ1,λ2,···,λn 互不相同,相应的特征向量组 x1,x2,···,xn 线性无关,则它们构成一组 A 的特征向量基。
1.10 矩阵的奇异值- 奇异值:对于矩阵A(λ1, λ2, ···, λn),λ1,λ2,···,λn称为矩阵 A 的奇异值。
矩阵分析 史荣昌 魏丰 第三版 第一章-第四章 期末复习总结

定义:若v1 ∩ v =0,则称v1与v 2 的和空间v1 + v 2 是直和,用记号v1 ⊕ v 2 表示
交
定理:设v1与v 2 是线性空间 v 的两个子空间,则下列命题是等价的
与
和
1) v1 + v 2 是直和
直和
2) dim(v1 + v 2 )= dim v1 + dim v 2
3)
设
α1, αn1
α α α 定理:(1) R(T)=span{T( 1 ),T( 2 ),……T( n )} (2)rank(T)=rank(A)(A 为线性映射在基下的矩阵表示)
值
域
性质:
设 A 是 n 维线性空间V1 到 m 维线性空间V2 的线性映射,α1,α2, αn
是V1
的一组基,β1,
β
2
,
,βm
是V2 的一组基。线性映射 A 在这组基下的矩阵表示是 m*n 矩阵 A=( A1,A2, An
特征子
空间
V 性质:特征子空间 λi 是线性变换 T 的不变子空间。
定义:设v1和v 2 是数域 F 上的两个线性空间,映射 A:v1 → v 2 ,如果对任何两个向量 α1,α2 ∈ v1和任何数λ ∈ F
有 A( α1 + α2 )=A( α1 )+A( α2 ),A( λα1 )= λ A( α1 ),便称 映射 A 是由v 1到v 2 的线性映射
α1,α
2
,
αr
生成的子空间为
T
的不变子空间。
0 0 an,r +1 ann
λ α λ λ λ 定义:设 T 是数域 F 上 n 维线性空间 V 的线性变换,如果 V 中存在非零向量α,使得 T(α)= 0 , 0 ∈F.那么称 0 是 T 的一个特征值,称α是 T 的属于 0 的一个特征向量。
分析04-矩阵的特征值

矩阵的特征值与特征向量的计算
产生迭代向量序列
(由x 的某一分量的相邻二次结果之比 可得出1),而相应的特征向量为 x ( k 1) 。
实际上, 由式(4-1)可得 :
x ( k 1) Ax( k ) Ak 1 x ( 0) Ak 1 ( i ui )
i 1 k i k 1ui 11 1u1 2k 1u2 n k 1un i 2 n i 1 n n
当n不大时,如n4 解特征方程,可求出全部特征值 (n 3较难)当 n较大(n>5),计算量会增大得惊人, 且不可能求得准确结果,还可能出现不稳定,所以当n稍 大一般不直接求解特征方程,而根据实际问题的需要,介 绍相应的一些行之有效的数值解法
第四章 矩阵的特征值与特征向量的计算
4-4
W
矩阵的特征值与特征向量的计算概述(续1)
x(k+1)为1对应的特征向量收敛到1u1+…+mum
W Y
两 点 注 释(续2)
( k 1) xi ( xi k )
x
( k 1)
( k 1) 1
x
( 0)
可构造向量序列
所以乘幂法实际上是,对于给定的初始向量 x ( 0) ( 零向量)由迭代法:
x
( k 1)
第四章
W Y
u
i 1
n
i i
1u1 2u 2 nU n
x
( k 1)
Ax
(k )
Ax
(k )
(k 0,1,, )
(4 -1)
5. 若 , 输出 , x, 停机; 否则, 转6
6. 若k<N,置k+1k, ,转3;否则, 输出失败信息,停机。
矩阵分析与计算--04-矩阵分解-01-Jordan标准型

则 A( ) 的 k 级行列式因子为
Dk ( ) d1 ( )d 2 ( ) d k ( ), k 1,2, r.
26
2)(定理4) 矩阵的Smith标准形是唯一的. 证:设 矩阵 A( ) 的标准形为
A( ) 与C ( ) 等价.
16
2) A( )与 B( ) 等价 存在一系列初等矩阵
P1 PS , Q1 Qt 使 A( ) P1 PS B( )Q1 Qt .
17
七、λ-矩阵的对角化
都等价于下列形式的矩阵
d1 ( ) d 2 ( )
19
1 2 1 1 2 0 [1,3] 1 3 1 1 2 1 2 1 1 3 1 0 2 0 3 2 0 0 1 2 0 [21(2 1),[31( 1)]] 0 3 2
2.(定理2)任意一个非零的 s n 的 一矩阵 A( ) 称之为 A( )的 Smith标准 形.
d r ( )
0
0
其中 r 1, d i ( ) ( i 1,2, 多项式,且
, r ) 是首项系数为1的
d i ( ) d i 1 ( ) ( i 1,2,
1
( )
1
i行 j行 1
14
② 初等矩阵皆可逆.
p( i , j )1 p( i , j )
p( i (c ))1 p( i ( 1 c ))
p( i , j( ( ))) p( i , j( ( )))
矩阵分析课件-2024鲜版

特征多项式求解技巧
特征多项式定义
设A为n阶矩阵,则行列式|λE-A|称为A的 特征多项式。
VS
求解技巧
通过求解特征多项式|λE-A|=0的根,可以 得到矩阵A的特征值。对于具体的求解过程, 可以采用行列式性质、降阶法、因式分解 等方法进行化简和计算。
2024/3/28
20
对角化条件及判别方法
03
$(AB)' = A'B + AB'$,其中$A(t)$和$B(t)$是可乘 的矩阵函数。
26
常见矩阵函数求导公式
若$A(t) = [a_{ij}(t)]$是对角矩阵函数,则$A'(t) = [a_{ij}'(t)]$。
若$A(t) = sin(Bt)$或$cos(Bt)$,其中$B$是常数矩 阵,则可以通过将$sin(x)$和$cos(x)$的幂级数展开
欧拉法具有一阶精度且计算简单但误差较大。
02
龙格-库塔法
一种高精度求解一阶常微分方程的数值方法,通过多步迭代提高精度。
四阶龙格-库塔法具有较高的精度和稳定性,在实际应用中广泛使用。
2024/3/28
03
有限差分法
一种求解偏微分方程的数值方法,通过将连续问题离散化并构造差分格
式进行求解。有限差分法适用于规则区域且易于编程实现但精度受限于
对角化条件
一个n阶矩阵A可以对角化的充分必要条件是A有n个线性无关的特征向量。
判别方法
判断一个矩阵是否可以对角化,可以通过求解其特征值和特征向量,然后判断是否有n个线性无关的特征向量。 如果存在n个线性无关的特征向量,则矩阵可以对角化;否则,矩阵不能对角化。
2024/3/28
21
矩阵分析 总结

矩阵分析总结矩阵分析是一门数学领域中的重要课程,它研究的是关于矩阵的性质、操作和应用的内容。
通过矩阵分析,我们能够更好地理解和解决许多实际问题,如线性方程组、最小二乘法、特征值问题等。
本文将对矩阵分析的基本概念、相关定理以及应用进行总结。
矩阵是一个按照矩形排列的数表,它可以用来表示线性映射或线性变换。
矩阵的基本运算包括加法、数乘、矩阵乘法和转置。
其中,矩阵乘法是矩阵分析的核心内容之一,它能够将一个矩阵与另一个矩阵相乘,得到一个新的矩阵。
矩阵乘法满足结合律,但不满足交换律。
在矩阵分析中,我们还常常关注矩阵的行列式和逆矩阵。
行列式是一个标量值,它可以用来判断一个矩阵是否可逆。
当行列式不等于零时,我们可以通过一系列运算求得矩阵的逆矩阵。
逆矩阵可以将原矩阵与其逆矩阵相乘得到单位矩阵。
矩阵分析还研究了特征值和特征向量的问题。
特征值是一个数,它可以描述矩阵线性变换的特征。
特征向量是一个非零向量,与特征值相关联。
特征值与特征向量满足一个基本关系式,即矩阵乘以特征向量等于特征值乘以特征向量。
通过求解特征值和特征向量,我们可以对矩阵进行相似变换或对称双对角化处理。
除了上述基本概念和定理,矩阵分析还有许多重要的应用。
其中包括线性方程组的求解、最小二乘法、矩阵的奇异值分解、矩阵的多项式表达等。
线性方程组的求解是矩阵分析中的基本问题之一,通过高斯消元法或矩阵的LU分解,我们可以较快地求解出线性方程组的解。
最小二乘法是矩阵分析的另一个重要应用,它主要用于解决数据拟合和参数估计的问题。
通过最小二乘法,我们可以找到一个近似解,使得观测值和模型的预测值之间的残差平方和最小。
矩阵的奇异值分解是对矩阵的一种分解形式,它可以将矩阵分解为三个矩阵的乘积,其中一个是奇异值矩阵,表示矩阵的奇异值。
奇异值分解在图像处理、数字信号处理等领域有广泛的应用。
总的来说,矩阵分析是一门重要的数学课程,它研究了矩阵的基本性质、运算和应用。
通过学习矩阵分析,我们能够更好地理解线性代数和线性方程组的相关概念,掌握常见的运算方法,并能够应用于实际问题的求解。
四矩阵特征值与特征向量的计算

四矩阵特征值与特征向量的计算矩阵特征值和特征向量是矩阵分析中非常重要的概念,它们在各个领域的应用非常广泛。
特征值和特征向量可以帮助我们理解矩阵的性质,解决方程组,降维和主成分分析等问题。
在本文中,我们将讨论如何计算矩阵的特征值和特征向量的方法和应用。
首先,我们来介绍一下矩阵的特征值和特征向量的定义。
对于一个n阶矩阵A,如果存在一个非零向量x和一个实数λ,使得Ax=λx,则λ称为A的特征值,x称为对应于特征值λ的特征向量。
特征方程为,A-λI,=0,其中I是n阶单位矩阵。
求解特征方程,可以得到矩阵的特征值。
接下来,我们来讨论几种求解矩阵特征值和特征向量的方法。
1.特征值分解法特征值分解法是最常用的求解特征值和特征向量的方法之一、对于一个n阶矩阵A,特征值分解可以将其分解为A=PDP^(-1),其中P是由特征向量组成的矩阵,D是一个对角矩阵,对角线上的元素是矩阵A的特征值。
这种方法在计算上较为复杂,但可以得到全部的特征值和特征向量。
2.幂法幂法是一种迭代法,用来计算矩阵的最大特征值和对应的特征向量。
幂法的基本思想是不断迭代一个向量,直到其收敛到矩阵的特征向量。
算法的步骤如下:(1)任意选择一个非零向量x0作为初始向量;(2) 迭代计算xk=Ax(k-1),其中k表示迭代次数;(3) 标准化向量,即xk=xk/,xk,保证向量的模为1;(4) 判断向量是否收敛,如果满足收敛条件,则停止迭代,向量收敛到的值为矩阵的特征向量,特征值为Axk/ xk。
3.QR算法QR算法是一种迭代法,用于计算矩阵的全部特征值和特征向量。
QR 算法的基本思想是不断进行QR分解,直到得到上三角矩阵,对角线上的元素即为矩阵的特征值。
算法的步骤如下:(1)将矩阵A分解为QR,其中Q是正交矩阵,R是上三角矩阵;(2)令A=RQ,继续进行QR分解;(3)重复第二步,直到矩阵变为上三角矩阵;(4)上三角矩阵的对角线元素即为矩阵的特征值。
矩阵分析lecture4内积空间

令 x ∈V2 ,则 x ∈V ,由第二式有:
x = x1 + x3
这里, x1 ∈V1, x3 ∈V3 。又因为 x ⊥ x1 ,所以,
0 = ( x, x1 ) = ( x1 + x3, x1 ) = ( x1, x1 ) + ( x3, x1 )
但 x3 ⊥ x1 ,故 (x3, x1) = 0 ,从而 (x1, x1) = 0 ,于是 x1 = 0 , x = x3 ∈V3 ; 即V2 ⊆ V3 。
定理 1:设 V 是内积空间, x, y 是 V 中任意两个向量,则有:
(x, y)2 ≤ (x, x)( y, y)
且等号成立当且仅当 x, y 线性相关时成立。
证明:设 t 为任意实数,则根据内积定义 (x − ty, x − ty) ≥ 0 。
即对任意实数 t,
( y, y)t2 − 2(x, y)t + (x, x) ≥ 0
| x |= (x, x)
由此,C—S 不等式即:
| (x, y) |≤| x | ⋅ | y |
从而: ±(x, y) ≤| x | ⋅ | y | 进一步,当 x ≠ 0, y ≠ 0 时,我们有
(x, y) ≤ 1 xy −1 ≤ (x, y) ≤ 1
xy
可用等式
cosϕ = (x, y) xy
则 e3 ≠ 0 ,再由 (e3, e1) = 0, (e3, e2 ) = 0 得
β1
=
−
( f3, e1 ) (e1, e1 )
,
β2
=
−
( f3, e2 (e2 , e2
) )
按此方法做下去,若已作出正交组 e1, e2,", en−1 则令
矩阵分析 第三章内积空间、正规矩阵1-4节

四、长度及其性质
记为 . 1、定义: 非负实数 ( , )称为向量的长度, 2、 单位向量: 1 , 则称 为单位向量. 设 1 0 注 :当 0时, 为单位向量
上页
下页
返回
3、 性质: (1) 非负性: 0, 当且仅当 0 时 0;
( 2) 齐次性: ; ( 3) 三角不等式: .
满足以下条件:
i 1
i 1
(1) (, ) ( , ) ; (2) (k, ) k (, ); (3) ( , ) (, ) ( , ); (4) (, ) 0, 当且仅当 0时等号成立. 则称V为C上的酉空间, (, )称为内积. 而
ii
4、 内积表示式: 设内积空间V中基 1, 2, , n的度量矩阵为G 且, 在基下的坐标为 , , (, ) X T GY . X Y 则
证: (1, 2, , n ) X, (1, 2, , n )Y,
G (1, 2, , n )T (1, 2, , n ). (, ) T [(1, 2, , n ) X ]T [(1, 2, , n )Y ] X T [( 1, 2, , n )T ( 1, 2, , n )]Y X T GY . 注: V为酉空间, (, ) Y H GX 若 则
上页
下页
返回
5、 不同基下度量矩阵的关 设 1, 2, , n; 1, 2, , n为内 系: 积空间V中的基且度量矩阵为 , , A B 过渡矩阵为C, B C T AC 则
证: A ( 1, 2, , n )T ( 1, 2, , n ). B ( 1, 2, , n )T ( 1, 2, , n ),
矩阵分析课后习题答案

矩阵分析课后习题答案矩阵分析是一门重要的数学学科,广泛应用于各个领域,如物理学、工程学和经济学等。
通过矩阵分析,我们可以更好地理解和解决实际问题。
然而,学习矩阵分析过程中,经常会遇到各种复杂的习题,给学生带来困扰。
在这篇文章中,我将为大家提供一些常见矩阵分析课后习题的答案,希望能够帮助大家更好地掌握这门学科。
1. 矩阵乘法的性质矩阵乘法是矩阵分析中的基础概念,了解其性质对于解决复杂的习题非常重要。
下面是几个常见的矩阵乘法性质的答案:- 乘法结合律:对于三个矩阵A、B和C,满足(A*B)*C = A*(B*C)。
- 乘法分配律:对于三个矩阵A、B和C,满足A*(B+C) = A*B + A*C。
- 乘法单位元:对于任意矩阵A,满足A*I = I*A = A,其中I为单位矩阵。
2. 矩阵的转置和逆矩阵矩阵的转置和逆矩阵是矩阵分析中常见的概念,它们在解决线性方程组和求解特征值等问题中起到重要作用。
以下是一些常见的矩阵转置和逆矩阵的答案:- 矩阵的转置:矩阵A的转置记作A^T,即将A的行变为列,列变为行。
- 逆矩阵的存在性:如果一个n阶矩阵A存在逆矩阵A^-1,那么AA^-1 =A^-1A = I,其中I为单位矩阵。
- 逆矩阵的计算:对于2阶矩阵A = [a b; c d],如果ad-bc≠0,则A的逆矩阵为A^-1 = 1/(ad-bc) * [d -b; -c a]。
3. 矩阵的特征值和特征向量特征值和特征向量是矩阵分析中的重要概念,它们在解决线性方程组和矩阵对角化等问题中起到关键作用。
以下是一些常见的特征值和特征向量的答案:- 特征值和特征向量的定义:对于一个n阶矩阵A,如果存在一个非零向量x和一个标量λ,使得Ax = λx,那么λ称为A的特征值,x称为对应于λ的特征向量。
- 特征值的计算:特征值可以通过解方程|A-λI|=0来计算,其中I为单位矩阵。
- 特征向量的计算:对于给定的特征值λ,可以通过求解(A-λI)x=0来计算对应的特征向量。
矩阵分析

⎡J1 0
P −1
AP
=
⎢ ⎢ ⎢
0
J2
⎢ ⎣
0
0
0⎤
0
⎥ ⎥
,
⎥
⎥ Js⎦
s
∑ 其中 Ji ( i = 1,2,…, s )为 ni 阶 Jordan 块, ni = n 。 i=1
显然 Jordan 矩阵之对角线上元素就是其全部特征值,而相似变换不改变矩阵特征值, 所以这些也是原矩阵全部特征值。 Jordan 矩阵(标准型)的计算:
* c2 0
*⎤
*
⎥ ⎥
。
A3 ⎥⎦
⎡c1 *
依此类推即可得 H n−1
H2
H1
A
=
⎢ ⎢ ⎢
0
c2
⎢ ⎣
0
0
*⎤
*
⎥ ⎥ ⎥
=
R
,即
A
=
H1H 2
⎥ cn ⎦
H n−1R 。
定义 8:矩阵的 Hermite 标准型满足如下三个条件:
(1) 非 0 行数等于矩阵秩,
(2) 每个非 0 行之第一个非 0 元素为 1,
k =0
k =0
若 λ1,λ2,…,λn 为 A 的全部特征值,则必有
n −1
∑ g(λi ) = bk λik ( i = 1,2,…,n ); k =0
当 λi 为 m 重根时还有
n−1
∑ g ( j) (λi ) = k(k −1) (k − j +1)bk λik ( j = 1,2,…, m −1)。 k= j
征值,则 f A(λ0 ) = 0 。
定义2:设 A 为 n 阶方阵,称
f A (λ) =| λI − A |= λn + a1λn−1 + + an−1λ + an
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
0 0
0 0
1 0
2 0
3 0
所以 Rank(A) 1,且此矩阵的第三,第四,第五
列任意一列都是线性无关的,所以选取哪一列构成 列满秩矩阵均可以。
选取
B
1 2
C 21 1
,
C 0 0 1 2
3
C 15 1
也可以选取
B
2 4
C 21 1
,
C 0
0
1 2
1
3
2
C 15 1
0 1 0 1 1 (3) 0 2 0 1 1
,
R 是正线上三角矩阵,R1 是
正线下三角矩阵。
A
证明:先证明分解的存在性。将矩阵 按列分块得到
A 1 2 L n
ACn
Байду номын сангаас
由于
nn ,所以
1, 2 , L , n
是线性无关的。利用 Schmidt 正交化与单位化方法, 先得到一组正交向量组
1, 2, L , n
再单位化,这样得到一组标准正交向量组
4 8 6 2 8 10
解 :(1)对此矩阵只实施行变换可以得到
1 2 1 0 1 2 1 2 0 1 1 1
1
221
3
3
0
0
1
1
2 4 3 1 4 5 0 0 0 0
2 0
1 0
M
4 8 6 2 8 10 0 0 0 0 0 0
由此可知 Rank( A) 2,且该矩阵第一列,第三列 是线性无关的。选取
值为 5.
(2)由于
AAH
2 0
0 4
显然 AAH 的特征值为 2,4,所以 A 的奇异值
为 2,2。
例 2 证明:正规矩阵的奇异值为其非零特征值 的模长。
定理:设 A Crmn ,
1 2 L r
是 A 的 r 个奇异值,那么存在 m 阶酉矩阵 U
和 n 阶酉矩阵 V 使得
UH
AV
0
0 0
U°
1
U
是酉矩阵,而 R°R1 是一个正线上三
角矩阵,由前面的结论可知
因此有
U°
1
U
I
,
R°R1 I
U° U , R° R
因为有 ACnnn ,所以 AT Cnnn ,按照分解
的存在性可知 AT U° R°
其中 U° U nn , R° 是正线上三角矩阵。于是 A R°T U°T R1U1
U U1 U2 ,其中
U1 Urmr ,
U2
U m(mr ) mr
于是有
UU12HH
AAH
U1
2
U2
0
0 0
从而有
U1H AAHU1 2 , U2H AAHU 2 0
令 V1 AHU11 ,那么容易验证
U
H 2
A
0.
V1 U r nr , V1HV1 Ir
选取 V2 使得 V V1 V2 是酉矩阵, 则
使得
A H1U UH2
且这样的分解式是唯一的。同时有
AH
A
H
2 2
,
AAH H12
则
AH A R1H R1 R2H R2
因为 AH A 是正定的 Hermite 矩阵(为什么?),
由正定二次型的等价定理可知,其三角分解是唯一
的,故 R1 R2 ,进一步有 U1 U2 。
例 1 :求下列矩阵的正交三角分解
1 1 1
A 1 0
0
0 1 0
0 0
1
解: 容易判断出 AC343,即
1 B 1
2 4
1
2 3
C2
42
6
,
C
1 0
2 0
0 1
1 1
1 2
1 1
C2
26
同样,我们也可以选取
1 B 1
2 4
0
1 1
C2
42
2
M (r2 r1)
,
C
1 0
2 0
1 1
0 1
1 2
2 1
C 26 2
0 0 1 2 3 (2) 0 0 2 4 6
解:对此矩阵只实施行变换可以得到
如何求此分解表达式?特别要注意下面的关系式
AH
A
V
2
0
0 0
nn
V
H
AAH
U
2
0
0 0
mm
U
H
即
AH AV
V
2
0
0
0
nn
AAHU
U
2
0
0 0 mm
由此可知 V H 的列向量就是 AH A 的标准正交特 征向量;而 U H的列向量就是 AAH 的标准正交特
征向量。
例 :求下列矩阵的奇异值分解表达式
证明:假设矩阵 A 的前 r 个列向量是线性无关的,对 矩阵 A只实施行初等变换可以将其化成
Ir D
0
0
即存在 P Cmmm 使得
于是有
PA
Ir 0
D
0
A
P1
Ir 0
Ir
D BC
其中
B
P 1
Ir
0
Cr mr
,C
Ir
D Crrn
如果 A的前 r 列线性相关,那么只需对 A 作列变换
U
0 1
1 0
再计算 AAH 的标准正交特征向量,解得分别与 5,
2,0,0 对应的两个标准正交特征向量
1 5
0
1
2
0 0
, 5
2
1 0 1
2
,
2
3
2
0
1
0
5
, 5
4
1 1
0 0
2 2
由这四个标准正交特征向量组成矩阵 V ,所以有
1
5
0
V
1, 2, L , n
并且向量组之间有如下关系
1 c111 2 c211 c222 3 c311 c322 c333
LLLL
n cn11 cn22 L L cnnn
其中 cii i 0, i 1, 2,L , n ,于是有
A 1 2 L n
1 2 L
c11 c21 L
n
由这三个标准正交特征向量组成矩阵 V ,所以有
1 0 0 V 0 1 0
0 0 1
再计算 AH A 的标准正交特征向量,解得分别与5,
0 对应的两个标准正交特征向量
1
1
2
5
,
5
2
2
1
5
5
由这两个标准正交特征向量组成矩阵 U , 那么有
1
U
2
5 5
2
5
1
5
于是可得奇异值分解式为
1 2 (1) A 0 0
0 0
0 1
(2) A 1 0 0 2
1
0
解 : (1)容易计算 AAH 的特征值为 5,0,0, 所以 A 的奇异值为 5 。下面计算 AAH 的标准
正交特征向量,解得分别与 5,0,0对应的三个标 准正交特征向量
1 0 0
1 0 ,2 1 ,3 0
0 0 1
5
AV 0
0
0
0
U
H
0
1 0 0 5 0 1
0
1
0
0
0
0
1
0
0 0
2
5 5
2
5
1
5
解 :(2)容易计算
AH
A
2 0
0 5
那么 A 的非零奇异值为 5 , 2 ,AH A 对应于
特征值 5,2 的标准特征向量为
1
0 1 ,
2
1 0
由这两个标准正交特征向量组成矩阵 U
那么有
A 1 2 3 1 2 3
2
2 2
2
2
0
6 2
6 6
UR
0
0
2 3
3
2 2 1 (2) A 0 2 2
2 1 2
解:首先判断出
A
C 33 3
,由定理可知必存
在 U U 33 ,以及三阶正线上三角矩阵 R 使得
A UR
推论:设 A Crmn ,则 A 可分解为 A U1R1L2U2
0 3 0 2 2
解:对此矩阵只实施行变换可以得到
0 1 0 0 0 0 0 0 1 1
0 0 0 0 0
r2 r1,
1 r1 ( 3 )
r1(2) r2
(3r1 2r2 ) r3
所以 Rank(A) 2 ,且容易看出此矩阵的第二列 和第四列是线性无关的,选取
1 B 2
3
C
0 0
其中 R1 是正线下三角矩阵,而 U1 U nn 。
此结论也可以被推广为
定理:设 A Crmr ,则 A 可以唯一地分解为
A UR
其中 R 是 r 阶正线上三角矩阵,U Urmr ,即
U 是一个次酉矩阵。
证明:分解的存在性证明,同上面的例题完全一样。
分解的唯一性证明。设
A U1R1 U2 R2
0
V1HV2
U 1 H 1
AV2
由上式可得
U1H AV2 0
U H AV
UU12HH
A
V1
V2
UU12HH
AV1 AV1
U1H U2H
AV2 AV2
0
0 0
这里,要注意 U2H A 0. 我们称此定理为奇异值分解定理。称表达式
