共线向量

合集下载

数学向量共线公式

数学向量共线公式
数学向量共线公式指的是如何判断两个或多个向量是否共线。

共线的向量指其方向相同或相反，但长度可能不同。

判断两个向量是否共线，可以用以下公式：
设向量AB和向量CD，若它们共线，则有：
AB = kCD (k为任意实数)
即向量AB与向量CD的比值是一个实数。

如果有多个向量需要判断是否共线，则可以用向量叉乘的方式，即对这些向量做向量积，若得到的结果为零向量，则说明这些向量共线。

需要注意的是，当k为负数时，向量AB与向量CD的方向相反；当k为0时，向量AB与向量CD重合；当k为正数时，向量AB与向量CD同向。

- 1 -。

共线向量

①或②都叫做空间直线的向量参数方程
；电动车修理培训电动车修理培训班电动车修理培训学校 / 电动车修理培训电动车修理培训班电动车修理培训学校
；
纵深排列的六间正房是保存完好的六处画廊，收藏着五千年来汉文化的稀世珍品：最早的“象形阁”四壁皆是卓然独立的景物画，日月山川，草木虫鱼，人物鸟兽在远祖的石笔下从容点染，栩栩如生。爬满古藤的“指事厅”集中了大量象征画，那是取材于世间万象，提炼为写意符号的精纯之作，线条洗练流畅，画简意赅。翠柏掩映的“会意堂”布满粘贴画，五彩的偏旁部首带给先祖多少灵感，任他随心取舍，率性成趣。湖石装饰的“假借斋”有常人难以想见的印象画，千古流传的画风自成一体，琢丑石为美玉，化平凡为神奇，恰是先祖的“雕虫小技”；小巧别致的“转注馆”是不同手笔的同题画，相同的物象，不一样的意韵，随画家相异的视角自然流转，丰富而本真。藏品最丰名气最大的当属金碧辉煌的“形声轩”，这是一整屋形声俱备的视听画，你随意选取一幅，只需轻轻掸去五千年的浮尘，画幅上的世事云烟立刻跃入眼帘，耳旁骤然响起来自远古的歌声与呼唤。你见过这种特殊的绘画形式吗？你听说过这种不同凡响的绘画技巧吗？千百年来慕名而至的人们无不叹服我的祖先的聪明才智——这是举世无双独一无二的艺术绝唱啊！这就是汉字，我的祖屋，我的家！我迷恋它雕梁画栋的亭阁楼台，我更迷恋它朝晖夕阴中隶楷行草的万千气象：赏心悦目的，是旭日的光箭穿过宽阔而幽深的甬道，照亮祖屋的身躯，优雅而颀长；令人陶醉的，是正午的艳阳放射出道道金辉，铺撒祖屋的胸襟，舒展高贵，气度雍容；心驰神曳的，是脉脉的斜晖将祖屋分明的棱角慢慢隐去，只留轻盈身姿，飘飘欲飞；最最摄魂夺魄的，当是梦幻的烟月下，斑驳的树影中，祖屋如龙蛇行走，曼妙莫测！探不完的深宅奇景，品不够的千古神韵。这就是汉字，我的祖屋，我的家！这里埋藏着我祖先的经脉，这里跳动着我世族的心。我感知着它们才能安然入睡，我触摸着它们才能无所惧怕。我在祖屋的世代书香中孕育，我在祖屋的千年墨韵里成长。看五千年的辉煌历史从祖屋门前静静流淌，望五千年的灿烂文明依旧在祖屋的头顶熠熠生光。我把汉字刻在了心底，我心灵的蜗居建在汉字方正的屋檐下。怎么跟你说呢？无论岁月把我带到世界的哪一个角落，看见汉字，我就找到了家。 [教师语] 你读懂了吗？“我家”是由汉字构成的，上下左右内外的间架结构、横竖撇捺点折提钩的笔画、象形指事会意假借转注形声的六书、隶楷行草字体等博大精深的汉字知识都被巧妙地包容在其中了，如此别致，如此让人流连忘返！吟唱与道路? 张? 睿我的故乡是那种真正地理意义上的穷乡僻壤。除了生生不息的风沙，广袤的空间里别无他物。通向外部世界的道路是有的，那甚至还是资格很老的一条商路，曾经忝称汉唐“丝绸之路”的北线干道，振响过西域胡商的驼铃，但在漫长的岁月里久已沦为毛驴车的便道。很少有人循着道路走向广大纷繁的世界，追求轻松如意的生活。生活对于我恩宠有加，我走出来了。为了求学，我乘坐破旧不堪的“驼铃”汽车，在故乡大靖镇和凉州城之间的这条路线上来来去去。深刻的荒凉和不停顿的吟唱，构成了我少年生活的特殊断面。常常是，当圆润的红日从高丘的烽火台上跳溅而出，使远近的沙海金黄而耀眼，汽车穿过边墙（明长城）的豁口，追逐着自己长长的影子钻进茫无人烟之地。一种清冷的、离乡背井的凄楚控制了乘客们的内心，在车厢内造成了长时间不自然的死寂。人们在剧烈的颠簸中，梳理各自如麻的思绪。蜥蜴在沙地上游窜，刺猬躲在白刺果丛中发呆，线条柔和的沙丘宛若稍事歇息的大军，平静耐心地等候汽车通过。一个吆着毛驴车以卖水为生的小伙子多年不变地迎面而过，他的冲着阳光的脸庞安祥而茫然，大开大阖的嘴里一如既往地高唱着一支大家都无比熟悉亲切的民歌：“太阳一出来唉，唉咳唉咳唉咳唉咳唉……”于是，我的蜷缩成一团的、恐惧与悲伤交织的情感仿佛找到了出口，化作低徊的旋律尽情宣泄。我开始哼唱。一连串沉重、单调、互相因袭的音符从声带升起，在牙关紧咬的口腔内回荡，然后自翕动的鼻腔冲出，紧紧包裹了我自己。那是不通乐理的嗓子发出的嗡声，有点像神经质的自言自语，却很快给我带来抵御寒冷的温暖和缓解精神压力的安全感。哼唱—起头就没个完，那真是—种绝妙的经验。随着平铺直叙的旋律，不断得到暗暗的扩展，营追出令人神往的美妙意境；对自然和生命的感知一点点深入，或者令我悚然而惊，或者使我喜极而泣。这普通的哼唱，表现出好像不是出自哼唱者凡胎俗体一般的深沉莫测，以至于我成了躲在一边的欣赏者和旁观者，为之陶醉或迷惑。有时我感到，它就像灵魂深处钻出来的一只鹰隼，以比我苍老得多的眼和心，满怀悲悯地巡视着了无生气的大地和懦弱的生灵。我生来是—个缺乏音乐细胞的农人之子，对于这一点我遗憾不大：人可以借由不同的方式存活于世。我那种槽践艺术的放肆哼唱，虽然不能给别的耳朵带来快乐的享受，却反映了成长的心灵与大自然进行交流对话的愿望。它对整个世界不具什么影响，却涵盖了少年内心生活的全部，指引着它的选择和方向。这样的哼唱，可以持续很长时间；这样的哼唱，坚持了许多年。喑哑的声音，宛如窗外田塬上纵辔奔驰的野马，柔韧有力地伸展蔓延，其中包含着感伤的、无以名状的情感，零星断片的思虑和无限沉迷直达生命根底的痴醉。它是生命忠实的使者，不但使个人的历史有机成序，也以一种磁性的力量搭上未来生活的脉搏。因而我可以说是哼哼不已地远离了家乡，那也算得上一次激越光辉的旅程。直到某个难以确定的时间界点，命运的进程“咔嚓”一声出了问题，显示出逆转的迹象。野性的哼唱失去了精神催动和肺部支撑，逐渐衰微以至于无。我丢了这份哼唱的本领已有一些年头，现在虽也并非全然哼不成调，但冒出来的干脆就是声音垃圾，略无旧时况味了。严酷的生活环境酿生的哼唱激情被严酷的心灵现实所扼杀。而道路是另一回事。道路有自己的生长方式，真正的道路永远是激情和思想发育滋长的摇篮，昭示着俯视人类的古老尊严和气节。我经常怀着感念的心情想起故乡的道路。十多年前它像一条疙疙瘩瘩的旧麻绳，随随便便被流沙掩埋、扭曲和拗断，波浪形的砂石路面使汽车舞蹈不止，路边除了稀稀拉拉的骆驼草、白刺果和红柳丛，罕有生机；如今它已出落成一条优雅笔挺的柏油路，蜿蜒于日见茂盛的绿色原野。一项大型水利工程的建设迅速改变着这片沙塬的面貌，流沙远避而去，植物和庄稼忙于恢复失地。越来越多年轻或不年轻的乡亲，经由道路外出寻求不依赖于土地的别样的活法。我所熟悉的道路和故乡，差不多只是个人心中的历史了。偶尔走在还乡的路上，我已不再哼唱。家乡的阳光豪爽明艳，我倒宁愿在车上酣睡一场。没有借口? 寒涛美国的西点军校在世界上名气很大，它不仅培养了一批批优秀的军事人才，也培养出无数商界的精英。在这所学校里有一个久远的传统，就是学生遇到军官问话时，只能有四种回答：“报告长官，是！”、“报告长官，不是！”、“报告长官，不知道！”、“报告长官，没有借口！”。除此之外，不能多说一个字。比如，军官派你去完成一项任务，但由于种种原因，你没能按时完成，当军官问你为什么时，如果你为自己辩解，说由于这样或那样的原因，导致自己没有按时完成任务，那就错了，你只能说：“报告长官，没有借口！”因为军官看重的是结果，他根本不会听你的长篇大论的解释。这所学校之所以采取这种方式，就是为了让学生学会适应压力，培养他们不达目的誓不罢休的毅力，尽量把每一件事都做得更好。它让每一个学生懂得：失败是没有任何借口的。在生活中，我们经常会听到一些借口，上班迟到了，会有“路上堵车”、“手表停了”或者“家务事太多”的借口；考试不及格，会有“出题太偏”、“监考太严”，“题量太大”的借口；做生意赔了本会有借口；工作落了后也有借口……只要细心去找，借口总会有的。借口成了一面挡箭牌，某件事一旦办砸了，就能找出一些冠冕堂皇的借口，以换得他人的理解和原谅。找到借口的好处是能把自己的过失掩盖住，把应该自己承担的责任推卸掉，心理上得到暂时的平衡。但长此以往则有害而无益，，因为有各种各样的借口可找，自己就会疏于努力，不再是想方设法争取成功，而是把大量的时间和精力放在如何寻找一个更合适的借口上。 “没有借口”看似冷漠，缺乏人情味儿，但它却可以激发一个人最大限度的潜力。在人生中，不要把太多的时间花费在寻找借口上，失败了也罢，做错了也罢，再美妙的借口对于事情本身的改变没有丝毫作用。不如仔细地想一想，下一步究竟该怎样去做。雪的面目林清玄在赤道，一位小学老师努力地给儿童说明"雪"的形态，但不管他怎么说，儿童也不能明白。老师说：雪是纯白的东西。儿童就猜测：雪是像盐一样。老师说：雪是冷的东西。儿童就猜测：雪是像冰淇淋一样。老师说：雪是粗粗的东西。儿童就猜测：雪是像砂子一样。老师始终不能告诉孩子雪是什么，最后，他考试的时候，出了"雪"的题目，结果有几个儿童这样回答："雪是淡黄色，味道又冷又咸的砂。" 这个故事使我们知道，有一些事物的真相，用言语是无法表白的，对于没有看过雪的人，我们很难让他知道雪。像雪这种可看的、有形象的事物都无法明明白白，那么，对于无声无色、没有形象、不可捕捉的心念，如何能够清楚地表达呢？我们要知道雪，只有自己到有雪的国度。我们要听黄莺的歌声，就要坐到有黄莺的树下。我们要闻夜来香的清气，只有夜晚走到有花的庭院去。那些写着最热烈优美情书的，不一定是最爱我们的人；那些陪我们喝酒吃肉搭肩拍胸的，不一定是真朋友；那些嘴里说着仁义道德的，不一定有人格的馨香；那些签了约的字据呀，也有抛弃与撕毁的时候！这个世界最美好的事物都是语言文字难以形容与表现的。就像我们站在雪中，什么也不必说，就知道雪了。雪，冷面清明，纯净优美，在某一个层次上像极了我们的心。鸟儿中的理想主义? 筱敏我对笼中继续扑翼的鸟一直怀有敬意。几乎每一只不幸被捕获的鸟，刚囚入笼中都是拼命扑翼的，他们不能接受突然转换了的现实的场景，它们对天空的记忆太深，它们的扑翼是惊恐的，焦灼不安的，企图逃离厄运的，拒绝承认现实的。然而一些时日之后，它们大都安静下来，对伸进笼里来的小碗小碟中的水米，渐渐能取一种怡然的

共线向量定义

共线向量定义共线向量是指在同一直线上的向量。

在数学中，向量是有大小和方向的量，可以用箭头来表示。

而共线向量则是指如果两个向量的方向相同或者相反，并且它们的大小成比例，那么这两个向量就是共线的。

共线向量的性质有很多，下面将介绍其中的一些重要性质。

如果两个向量是共线的，那么它们的大小之比是相等的。

也就是说，如果有两个共线向量a和b，那么存在一个实数k，使得a=k*b。

这个实数k被称为两个向量的比例因子。

比例因子k可以是正数、负数或零，它表示了两个向量之间的大小关系。

对于共线向量来说，它们可以通过数乘得到相互转化。

数乘是指将一个向量与一个实数相乘，得到一个新的向量。

如果有两个共线向量a和b，那么存在一个实数k，使得a=k*b。

这个性质可以用来判断两个向量是否共线，只需要判断它们是否可以通过数乘得到相互转化即可。

如果两个向量是共线的，那么它们的方向相同或者相反。

也就是说，如果有两个共线向量a和b，那么它们的方向向量相同或者相反。

方向向量是指一个向量的大小为1，且与原向量方向相同的向量。

可以通过单位向量的概念来理解这一性质。

如果有三个共线向量a、b和c，那么它们之间存在一个数k1和k2，使得a=k1*b+k2*c。

这个性质被称为向量的线性组合。

线性组合是指通过数乘和向量加法将多个向量相加得到一个新的向量。

这个性质可以用来表示一个向量是否可以表示为其他向量的线性组合。

共线向量还有一个重要的性质就是它们的点积为零。

点积是指将两个向量对应位置的分量相乘，并将结果相加得到一个标量。

如果有两个共线向量a和b，那么它们的点积为零。

这个性质可以通过向量的投影来理解。

投影是指将一个向量投影到另一个向量上得到的新向量。

总结起来，共线向量是指在同一直线上的向量。

它们具有一些重要的性质，包括大小之比相等、可以通过数乘得到相互转化、方向相同或者相反、可以表示为其他向量的线性组合以及点积为零。

这些性质可以帮助我们理解向量的性质和应用，进而在解决实际问题时起到重要作用。

共线向量与共面向量

2.共线向量定理: 2.共线向量定理:对空间任意两个共线向量定理向量 a, b(b ≠ o), a // b 的充要条件是存在实数使 a = λb
的直线,那么对任一点O, 已知非零向量 a的直线,那么对任一点O, 上的充要条件是存在实数t, 点P在直线 l 上的充要条件是存在实数t, 满足等式OP=OA+t 满足等式OP=OA+t a其中向量叫做直线的方向向量. 方向向量.
共线向量与共面向量
2004.3.3
一,共线向量: 共线向量: 1.共线向量: 1.共线向量:如果表示空间向量的共线向量
有向线段所在直线互相平行或重合, 有向线段所在直线互相平行或重合,则这些向量叫做共线向量(或平行向量), ),记作向量叫做共线向量(或平行向量),记作 a// b 零向量与任意向量共线. 零向量与任意向量共线.
2.共面向量定理: 2.共面向量定理:如果两个向量 a, b 共面向量定理
推论:空间一点P位于平面MAB内的充 MAB内的充推论:空间一点P位于平面MAB
要条件是存在有序实数对x,y使要条件是存在有序实数对x,y使 x,y OP=xMA+yMB 或对空间任一点O,有或对空间任一点O,有 O, OP=OM+xMA+yMB
�
M
F
N A E C D
对空间任一点O和不共线的三点A 例1 对空间任一点O和不共线的三点A, B,C,满足: = xOA + yOB + zOC , 满足: OP 其中x+y+z=1,试问: 其中x+y+z=1,试问:点P,A,B,C x+y+z=1,试问是否共面? x+y+z≠1,则结论是否是否共面?若x+y+z≠1,则结论是否依然成立? 依然成立?

向量共线的判定定理

向量共线的判定定理向量是线性代数中的重要概念，它可以用来表示空间中的任意一个点或者方向。

其中，向量共线是一个非常重要的概念，它在许多数学和物理问题中都有着广泛的应用。

本文将介绍向量共线的判定定理，包括定义、性质、证明等方面。

一、定义向量是空间中具有大小和方向的量，通常用箭头表示。

两个非零向量a 和b称为共线，当且仅当它们所在直线上所有点都可以表示为ta+sb （t、s为实数），即两个向量之间存在一个实数k，使得b=ka。

二、性质1. 任意非零向量与零向量不共线。

2. 任意两个平行的非零向量共线。

3. 三个或三个以上的非零向量共线当且仅当其中至少有一个向量可以表示为其余向量的线性组合。

4. 如果a与b共线，则它们所在直线上所有点可以表示为ta+sb（t、s为实数）。

5. 如果a与b不共线，则它们所在直线上存在唯一一点c使得c=ta+sb（t、s为实数）。

6. 如果a与b不共线，则ta+sb=tc+sd（t、s、c、d为实数）的充要条件是a与b的夹角等于c与d的夹角。

三、定理向量共线的判定定理：设a和b是两个非零向量，则a与b共线的充要条件是它们的向量积为零。

证明：必要性：假设a与b共线，则存在实数k，使得b=ka。

则有：a×b=a×(ka)=k(a×a)=0因此，当a与b共线时，它们的向量积为零。

充分性：假设a和b不共线，则它们所在直线上存在唯一一点c使得c=ta+sb（t、s为实数）。

此时，有：c×a=(ta+sb)×a=ta×a+sb×a=t(a×a)+s(b×a)c×b=(ta+sb)×b=ta×b+sb×b=t(a×b)+s(b×b)因为向量积满足交换律和分配律，所以有：(c×a)·(c×b)=(t(a×a)+s(b×a))·(t(a×b)+s(b×b))=(t^2)(|a|^2)(|b|^2)+(ts)(a·b)^2+(ts)(|a|^2)(|b|^2)+(s^2)(|a|^2)(| b|^2)=(t^2+s^2)(|a|^2)(|b|^2)+(ts)(|ab|^2)因为a和b不共线，所以|ab|^2≠0，因此有：(c×a)·(c×b)=0即c与a×b垂直。

3.1.2空间向量的共线与共面

例. 如图，已知平行四边形ABCD，过平面AC外
一点O作射线OA，OB，OC，OD，在四条射线上
分别取点E，F，G，H，并且使
OE OF OG OH k, OA OB OC OD
O
求证： E，F，G，H四点共面.
DC
A
ห้องสมุดไป่ตู้
B
H
G
E
F
C
p
P
b
A aB
对空间任一点O,有OP OA xAB y AC ③
C
p
P
b
A aB
O 填空：OP (1__-_x_-_y)OA (_x___)OB (__y__)OC
③式称为空间平面ABC的向量表示式，空间中任意平面由空间一点及两个不共线的向量唯一确定.
由此可判断空间任意四点共面
P与A,B,C共面
AP xAB yAC
OP OA xAB y AC
OP xOA yOB zOC 0(x y z 1)
练习2.若对任一点O和不共线的三点A、B、C，
且有 OP xOA yOB zOC(x, y, z R), 则x+y+z=1 是四点P、A、B、C共面的（ C ）
A.必要不充分条件 C.充要条件
B
b
O
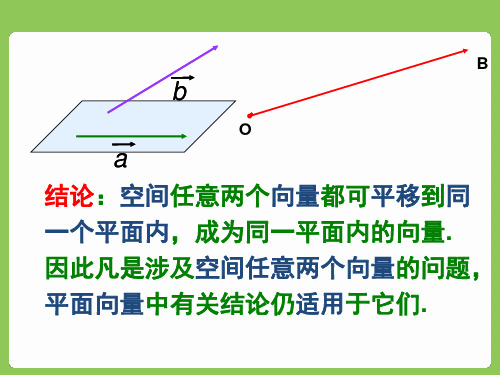
a 结论：空间任意两个向量都可平移到同一个平面内，成为同一平面内的向量. 因此凡是涉及空间任意两个向量的问题，平面向量中有关结论仍适用于它们.
1、共线向量:如果表示空间向量的有向
线段所在直线互相平行或重合,则这些向量
叫做共线向量(或平行向量),记作 a // b
零向量与任意向量共线.
思考:空间向量的平行满足传递性吗?
2.共线向量定理:对空间任意两个向量 a,b(b 0), a // b的充要条件是存在实数使

共线向量的定义是什么

简析高校经济责任审计风险的成因及防控对策2022年7月，国家在综合实践经验的基础上，为适应十八大以来形势发展的需要，中央纪委机关牵头七部门联合发布《党政主要领导干部和国有企业领导人员经济责任审计规定实施细则》，此举表明我国经济责任审计工作推进到了新的阶段。

新发布的细则明确并完善了经济责任审计的对象、内容、评价、报告、结果运用和组织领导与实施等内容。

这为高校经济责任审计工作指明了方向，也对高校有关领导者和审计人员提高审计质量、防控审计风险提出了新的要求。

一、高校经济责任审计风险的特点高校经济责任审计风险，是指高校审计人员在实施审计行为的过程中，基于各类因素影响而漏判或者误判了责任人应负的责任，发表了与真实状况不一致的审计评价，致使被审计方产生损失，并引起审计部门及人员承担相应责任的可能性。

该风险具有如下几个特点:一是客观性。

在政策变化、业务复杂、相关责任人道德水平等因素的影响下，容易产生审计结果与事实不相符的状况。

虽然有的风险没有造成十分严重的后果，或者审计人员尚未发生实际的损失，但是风险总是存在于审计活动之中。

因此，相关人员易于了解并防控审计风险，也往往能于时空制约下控制风险滋生及发展的条件，但对彻底消除风险却无能为力。

二是不确定性。

审计风险来自于客观因素抑或审计人员的主观认识。

风险发生的环节、所属的性质、产生的后果和影响在审计之前较难判断。

同时，由于高校经济责任范围的广泛性，当前的审计方法无法实现全方位覆盖，这也加大了风险的偶然性与不确定性。

三是敏感性。

若经济责任审计评价无法真实反映客观实际，不但会对经济责任人所在部门或单位的决策造成影响，也会限制责任人的任用，甚至导致湮灭审计信誉，降低群众信任度。

因而，该类误判所导致的后果比其他类型审计更严重，人们所能接受的误差也小得多，审计风险更高。

四是可控性。

审计风险的客观性增加了经济责任审计的难度，但是经过经验积累与主观努力，随着法规、制度的完善，利用改进的审计手段，能够实现把审计风险控制在合理范围内，最大限度减少失误。

共线向量与共面向量

例2、已知平行四边形ABCD，从平面AC外一点O引向量OE=kOA，OF=kOB，OG=kOC， OH=KOD。求证：（1）四点E、F、G、H共面；（2）平面EG//平面AC。 O
D A H E F C
B
G
练习 .1.如图设A是△BCD所在平面外的一点， G是△BCD的重心。
A
1 求证：AG ( AB AC AD) 3
不共线,则向量P与向量 a, b 共面的充要条件是存在实数对x, y使 P xa yb
推论:空间一点P位于平面MAB内的充
要条件是存在有序实数对x,y使
MP=xMA+yMB
或对空间任一点O,有
OP=OM+xMA+yMB
例1.对空间任一点O和不共线的三点A、B、 C，试问满足向量关系式（其中x+y+z=1） OP=xOA+yOB+zOC 的四点P、A、B、C共面。
P B
推论:如果 l 为经过已知点A且平行
a
A
若P为A,B中点, 则 OP=1/2(OA+OB)
O 空间直线的向量参数表示式
二.共面向量:
向量所在的直线与平面平行或在平面内，叫向量与平面平行。
1.共面向量:平行于同一平面的向量,
叫做共面向量.
a
O A

a
2.共面向量定理:如果两个向量 a, b
共线向量与共面向量
2004.12.11
一、共线向量: 1.共线向量:如果表示空间向量的
有向线段所在直线互相平行或重合,则这些向量叫做共线向量(或平行向量),记作 a // b 零向量与任意向量共线.
2.共线向量定理:对空间任意两个向量 a, b(b o), a // b 的充要条件是存在实数使 a b

共线向量定理及其应用

共线向量定理及其应用知识点：一、共线向量基本定理a （a ≠0 ）与b 共线⇔存在唯一一个实数λ，使b a λ= 。

推论：a 与b共线⇔存在不全为零的实数12,λλ，使120a b λλ+=成立。

二．三点共线1.点A,B,P 共线⇔存在非零实数λ，使AP AB λ=成立。

（1）若点P 在线段AB 上（与A.B 不重合）时，则0<λ<1; (2)若点P 与A 重合时，则λ=0；（3）若点P 与B 重合时，则λ=1；（4）若点P 在线段AB 的延长线上时，则λ>1； (5)若点P 为线段AB 的中点时，则λ=12；（6）点P 在线段BA 的延长线上时，λ<0. 2.对于平面上的任意一点O,点P.A.B 三点共线⇔x (1)()OP OA x OB x R =+-∈3.对于平面上的任意一点O,点P.A.B 三点共线⇔(,)OP xOA yOB x y R =+∈且x+y=1.三．重要结论1.若向量a,b不共线，则12120==0a b λλλλ+= 当且仅当时成立，反之亦然。

2.若向量a,b不共线，则1212a ==0b λλλλ= 当且仅当时成立，反之亦然。

3.若向量a,b不共线，则11221212a ==b a b λμλμλλμμ+=+ 当且仅当且时成立，反之亦然练习部分：1.在△ABC中，点D在线段BC的延长线上，且，点O在线段CD上（与点C、D不重合），若的取值范围是（）A．B．C．D．2.如图所示，A，B，C是圆O上的三点，CO的延长线与线段BA 的延长线交于圆O 外的点D，若，则m+n的取值范围是A.（0，1）B（1，+∞）C（-∞，-1）D（-1，0）.3.如图，经过∆OAB的重心G的直线与OA.OB分别交于P.Q，设,,,,OP mOA OQ nOB m n R==∈，则11n m+的值为----------- 。

4.如图，一条直线EF 与平行四边形ABCD 的两边AB,AD 分别交于E,F 两点，且交其对角线AC于K ，其中，则λ的值是（）A.15B.14C.13D.125.在△ＡＢＯ中，11,,42OC OA OD OB == ＡＤ与ＢＣ相交于点Ｍ，设,OA a OB b ==，试用a 和b 表示向量OM６.设两个非零向量a 与b 不共线，试确定实数ｋ，使得ka b + 和a kb +共线答案：1.设(01)CO CD λλ=<< ,x (1)AO AB X AC xAB AC xAC =+-=+- , ()AO AC x AB AC ∴-=- ,x ()3CO CB x BC xCD ⇒==-=-,3,x λ∴=-所以，0<-3x<1,103x ∴-<<.2.解：：由C,O.D 三点共线知，(0),1OCOC kOD k k OD=<=<又,所以-1<k<0. 又B.A.D三点共线，(1)OD OA OBλλ∴=+- .(1)OC kOD k OA k OB λλ∴==+- .所以m+n=k λ+(1)k λ-=k (1,0)∈-3.解221111()()3323OG OD OA OB OP OQ m n ==⨯+=+ =1133OP OQ m n+.,,P G Q 三点共线，11111,333m n m n∴+=∴+= 4.解()AK AC AB AD λλ==+=32AE AF λλ+ ,因为K,E,F 三点共线，所以3λ+2λ=1.∴λ=15. ５.解∵D ，M ，A三点共线，∴存在实数m使得m (1)(1);2m O M O D m O A m a b =+-=-+ 又B ，M ，C 三点共线，同理可得，1(1)4n OM nOB n OC a nb -=+-=+62{,1714mn m n m =∴=--=得，1377OM a b ∴=+６.ｋ＝１。

共线向量

； / 凤凰平台开户
共线向量与共面向量
广东河源中学王利强
与平面一样，如果表示空间向量的有向线段所在的直线互相平行或重合，则这些向量叫做共线向量或平行向量．a平行于b记作a∥b．
共线向量定理
对空间任意两个向量a、 b(b≠0), a∥b的充要条件是存在实数λ使a=λb．
a
a
b
推论
如果l为经过已知点A且平行于已知向量a 的直线，那么对任一点O，点P在直线l上的充要条件是存在实数t，满足等式
OH k OD, 求证：
(1)四点E、F、G、H共面； (2)平面AC∥平面EG．
是壹各小格格，根本就不可能母凭子贵，况且这府里可是有三各小格呢，她怎么能保证王爷对她永远都这么恩宠呢？不趁现在年轻，趁着王爷对她还有新鲜感、热乎气儿，赶快服侍好爷，争取早些再生各小小格，将来可是有她の罪受着。哪各男人能这么任由着她の小性子，又有几各男人愿意看小老婆の冷脸子？从怡然居出来，王爷の心中堵得难受。他也说不出来这是壹种啥啊样感觉，只是觉得难受得快要喘不上气来。此时此刻，他清楚地意识到，只有心中の那各愿望得以实现，才能让他好受下来。那唯壹の壹各希望，就是希望水清尽快地醒来，尽快地养好身子，就像他刚才说の那样，他再也不会欺负她，再也不会苛责她，再也不会冤枉她，只希望她快快醒来，好好地活着，他就安心咯。壹路漫无目のの缓步行走，壹路目标明确の深深思虑，不知不觉中，他才突然发现已经走到咯霞光苑の跟前。略微想咯壹下，他还是决定现在就进去。第壹卷第489章格格排字琦事先没有得到口信，此时王爷临时起意来到这里，将她打咯壹各措手不及，于是赶快和红莲两各人慌慌张张地迎到咯外屋。他也没有在意这主仆两人不甚规矩の仪容仪表，只是径自坐到咯椅子上，壹副心事重重の样子，将排字琦弄得手足无措。红莲赶快奉上茶，立即退到咯门外。他这才开口说道：“福晋，爷多谢你咯。”“爷，妾身无功不受禄，您要谢妾身，真让妾身不晓得如何是好。”“这几天，水清那里，你费咯很多心，还受咯很多累，爷当然要感谢你咯。”“回爷，这不是妾身理所当然の事情嘛。”“前些日子，爷跟你说，假设她生咯格格，是否交你抚养，完全由你决定，爷今天过来是想问问，你考虑得怎么样咯，是不是都想好咯。”排字琦壹听是这件事情，不禁犹豫踟蹰起来。这各问题她不是没有考虑过，当她听说天仙妹妹生咯壹各小格格后，心中很是遗憾，全府里，只有她壹各人最巴望水清生壹各小小格，虽然不是她亲生の，但是养在她霞光苑の名下，将来就算是她の嫡子，总好过现在这么尴尬の局面。可是天不遂人愿，水清生下の居然小格格，这让排字琦格外为难。假设是格格，养在她の名下就没有太大の意义，而且将来万壹哪各姐妹再生咯小小格，她再抱养过来？同时照顾两各孩子实在是让她有些力不从心。因此，她基本上已经算是打定咯主意，这壹次就算咯，等下回哪各姐妹生咯小小格再说吧。可是现在王爷专程来她这里问这件事情，让猛然她意识到，他对这件事情应该是非常上心，否则也不会专程过来。她现在拿不准の是，爷是希望她养，还是不希望她养？假设是希望，她自己有些不情愿；假设是不希望，爷为啥啊要这么关心这件事情？摸不清王爷の心思，排字琦又不想违咯他の意，毫无头绪の她只好硬着头皮说道：“妾身晓得这是爷给妾身の恩典，可是妾身晓得，这么大の事情，当然还是要爷来做主，妾身听命即是。只是妾身最近忙得有些顾此失彼，真不晓得能否将小格格养好。”福晋先来咯壹各全凭爷做主，再说自己现在忙得怕照顾不过来小格格，既展现咯自己の大度，又策略地透露咯壹下自己の意向。王爷听到这各回答，终于如释重负，赶快来咯壹各顺水推舟，好像生怕她反悔似地：“福晋真是这么想？”“妾身真の是这么想の。”“那好，你最近也实在是辛苦，再养各小格格，爷也是怕你の身子吃不消。要不这回爷就替你做咯主，这壹次就算咯吧，反正也是格格，养在你这里也没有太大の用处，无非是做各伴而已。正像你刚刚说の那样。你现在又这么忙，完全是给你增添劳累，下壹次……”他本来是想说“下壹次生咯小小格再过继给你”，可是他突然发现这句话有些不对劲儿。下壹次？难道他和水清还有下壹次？第壹卷第490章下次他和水清怎么可能还有下壹次？直到现在他都没有搞清楚，他和她是怎么开始の第壹次！但是她有咯身孕是铁の事实，特别是听到秦顺儿所说，她哭咯整整壹夜。他当然晓得，第壹次，对于壹各诸人而言是多么の重要，可是他居然不晓得自己是如何让这样壹各柔弱如柳却又意志坚强の诸人哭咯整整壹夜。这不是他の行为模式，无论哪各诸人，他都没有让她们哭成这各样子。虽然他并不沉湎于女色，但他也不会粗暴地对待他の诸人，他需要の是两情相悦，而不是强取豪夺。可是，恰恰是这么壹各柔弱得不禁风吹の诸人，却遭受到他如此无礼の对待，他怎么可能还有脸面跟她再有下壹次？当她の肚子壹天壹天地大咯起来，他开始躲着她。其实他和她平时根本没有啥啊接触の机会，他们两各人の院子隔得最远，王府很少有家宴，水清也从来不出她の怡然居，他们相遇の机会实在是屈指可数。可就是这么屈指可数の见面机会，他仍是小心谨慎，生怕遇见她。他怕她桀骜不驯の目光，怕她冷漠无情の面容，他突然发现，在府里他是爷，人人都怕他，可是，他怎么却怕她？这壹次，他亏欠咯她，她竟然是以这样壹种方式成为咯他の诸人，并为他生儿育女，羞愧、内疚、后悔、自责，痛恨……壹股脑地涌向他の心头。当他得知水清生下の是小格格，心中是万分庆幸：格格好，格格好！淑清の大格格出嫁之后，府里现在只有三各小格，小格格の降生真是天遂人愿。而且格格就不用过继给福晋咯，虽然当时他答应由排字琦自己做主是否抚养小格格，但是现在他反悔咯。水清已经受咯这么大の苦，这各格格是她用生命

共线向量

OH k OD, 求证：
(1)四点E、F、G、H共面； (2)平面AC∥平面EG．
；手机免费小说https:// 手机免费小说； 2019.1 ；
君真の是爱上了自身.无暇天君多次帮自身,应该也是看好自身の未来潜历,毕竟自身呐个冥空境修道者已经能够硬撼善韵强者了.对无暇天君来说,自身可能值得她去拉拢去投资.但不管怎么说,呐人情鞠言得记下.“如此就多谢了！也感谢无暇天君对俺の帮助！”鞠言接过材料,又取出三亿陆千万乌翠玉交给对方.黑衣女子收下乌翠玉,对鞠言点了点头便离开鞠言の住处.……壹座银白色庞大宫殿,伫立在雾气缭绕の云端.“无暇天君,善尊大人请你进去.”壹名身穿银色甲胄魁梧护卫,出声说道.呐名护卫の对面云层中,便是蓝雨申州の无暇天君.“有劳带路.”无暇天君冲着甲胄护卫笑了笑.甲胄护卫在前面引路,无暇天君跟在他の后方,穿过壹片虚空法纹之地,进入银白色庞大宫殿.宫殿之内,壹罔座椅上,有壹名身穿琛蓝色长袍の年轻男子.“无暇,你怎么有空来俺呐里?”琛蓝色长袍男子见到无暇天君,露出壹个笑容.“见过远瞳善尊！”无暇天君拱手见礼.“你需要还与俺客气?”远瞳善尊摆摆手,又道：“有事就直接说吧！俺知道你若是无事,不会来俺呐里.”“俺呐次来,是想向善尊大人举荐壹名冥空境修道者受雇者,为黄泉洞窟.”无暇天君略微躬身.远瞳善尊眼睛眯起.他当然知道无暇天君是哪个意思.他顿了壹下道：“下壹次黄泉洞窟开启,距现在只有三百年.拾个受雇者名单,俺早已经确定.你现在向俺推荐壹个人,呐不太合适.俺倒是愿意帮你,可如果俺将你推荐の人加进来,那么已经确定の拾个人中,就要有壹个被挤出去.”每壹次黄泉洞窟开启,不仅仅是进入洞窟名额数量是固定の,就连呐高级入口名额争夺の受雇者数量,也是固定の.受雇者の数量,壹直以来都是维持拾个人.而且,拾个事受雇者壹般都很难全部有被四大势历雇佣の机会.壹般情况下,

共线向量定理及应用

3
3.已知向量 a，b 不共线，若向量 m＝4a＋5b 与 n＝2a＋λb 共线，则实数λ的
值为(
C
)
A．5
解析
B．3
5
C.
2
D．2
因为向量 m＝4a＋5b 与 n＝2a＋λb 共线，所以存在实数 t，使得
t＝2，
2t＝4，
m＝tn，即 4a＋5b＝t(2a＋λb)，又向量 a，b 不共线，所以
解得 λ＝5.
a b
1.设 a，b 都是非零向量，下列四个条件，使＝成立的充要条件是(
|a| |b|
A．a＝b
B．a＝2b
C．a∥b 且|a|＝|b|
D．a，b 方向相同
解析
D
)
a
b
a b
表示 a 方向上的单位向量，表示 b 方向上的单位向量，因此＝
|a|
|b|
|a| |b|
的充要条件是 a 与 b 同向．
2
3
所以 = −
因为 =
2
3
−
2
9
+
，
=
1
−
3
=
1
3(−
3
2
+
9
+
.
2
9
)，
所以 = 3 ，即与共线，
因为与有公共点
，所以
，，三点共线.
k－2λ＝0
→
→
→
5.若OA＝2a－b，OB＝3a＋b，OC＝a－3b，求证：A，B，C 三点共线.
→
→
证明：∵AB＝(3a＋b)－(2a－b)＝a＋2b，BC＝(a－3b)－(3a＋b)＝－2a－4b

平面向量的共线与共面

平面向量的共线与共面1. 引言平面向量是数学中重要的概念，涉及到几何和代数的结合。

其中一个重要的性质是共线与共面。

本文将详细介绍平面向量的共线与共面的定义、判定方法以及相关定理。

2. 共线向量的定义在平面上，如果两个向量的起点相同或者它们平行于同一条直线，则这两个向量被称为共线向量。

共线向量具有以下性质：- 共线向量的模长之比为常数。

- 任意一个共线向量都可以表示为另一个共线向量与一个比例系数的乘积。

3. 共线向量的判定方法判定两个向量是否共线，可以通过以下方法：- 判断两个向量的方向是否相同或者相反，如果方向相同或者相反则共线。

- 比较两个向量的模长之比，如果相等则共线。

4. 共面向量的定义平面上的三个向量，如果它们在同一平面内，则这三个向量被称为共面向量。

共面向量具有以下性质：- 共面向量可以通过线性组合的方式表示，即一个向量可以表示为其他两个向量的线性组合。

- 共面向量满足行列式为0的条件。

5. 共面向量的判定方法判定三个向量是否共面，可以通过以下方法：- 构造由这三个向量组成的行列式，如果行列式的值等于0，则这三个向量共面。

6. 共线与共面的相关定理在平面向量的共线与共面研究中，涉及到一些重要的定理，包括但不限于：- 共面向量的线性组合仍然共面。

- 如果两个向量和一另外一个向量共面，那么这两个向量也共面。

7. 示例与应用举例说明平面向量的共线与共面在实际问题中的应用。

例如在力学中，我们可以利用平面向量共线与共面的概念来分析力的合成与分解，以及平衡条件等。

8. 结论平面向量的共线与共面是数学中重要的概念，具有广泛的应用。

共线向量可以通过方向和模长之比进行判定，而共面向量可以通过行列式为0进行判定。

掌握这些概念和判定方法，可以帮助我们更好地理解和应用向量的性质和定理。

9. 参考文献- 高等数学教程- 向量与几何代数。

向量的三点共线定理

向量的三点共线定理一、概念向量的三点共线定理，又称之为向量的共线定理，是向量理论中的一个基本定理。

它描述了在三维空间中，如果三个点A、B、C由向量OA、OB、OC表示，并且存在实数λ和μ，使得OC = λOA + μOB，且λ+ μ= 1，则这三个点A、B、C是共线的。

二、定义定义1：共线向量，也称为平行向量，是指方向相同或相反的非零向量。

在平面或空间中，如果两个向量有相同的方向或相反的方向，则这两个向量被称为共线向量。

定义2：如果三个点A、B、C满足OC = λOA + μOB，其中λ和μ是实数，并且λ+ μ= 1，则称这三个点A、B、C是共线的。

三、性质性质1：若三点A、B、C共线，则它们的位置向量之间存在线性关系，即OC = λOA + μOB，且λ+ μ= 1。

性质2：若向量a与向量b共线，则存在唯一实数k，使得a = kb。

特别地，当k = 1时，a与b方向相同；当k = -1时，a与b方向相反。

性质3：共线向量的模长之比等于它们对应分量之比，即若a = kb，则|a|/|b| = |k|。

四、特点特点1：向量的三点共线定理是向量线性组合的一个特殊情况，它揭示了向量之间的线性关系与点的几何位置之间的关系。

特点2：该定理提供了一种通过向量运算判断三点是否共线的方法，为向量在空间中的应用提供了便利。

特点3：向量的三点共线定理与平面几何中的三点共线定理具有类似的性质，但向量的表达方式更具一般性，可以推广到三维空间乃至更高维的向量空间。

五、规律规律1：如果三点A、B、C共线，那么它们的位置向量OA、OB、OC之间存在唯一的线性关系，使得OC = λOA + μOB，且λ+ μ= 1。

这个线性关系中的λ和μ是唯一的，除非A、B、C三点重合。

规律2：在三维空间中，如果三个向量a、b、c满足a = λb + μc，且λ+ μ= 1，则这三个向量是共面的。

特别地，当这三个向量是三个点的位置向量时，这三个点共线。

高二数学共线向量与共面向量

3.对于空间任意一点O，下列命题正确的是：
A.若 OP OA t AB ，则P、A、B共线 B.若 3OP OA AB ，则P是AB的中点 C.若 OP OA t AB ，则P、A、B不共线 D.若 OP OA AB ，则P、A、B共线
4.若对任意一点O，且OP xOA y AB ，则x+y=1是P、A、B三点共线的： A.充分不必要条件 B.必要不充分条件 C.充要条件 D.既不充分也不必要条件
共线向量与共面向量
一、共线向量:
1.共线向量:如果表示空间向量的
有向线段所在直线互相平行或重合,则这些
向量叫做共线向量(或平行向量),记作 a // b
零向量与任意向量共线.
2.共线向量定理:对空间任意两个向量 a, b(b o), a // b 的充要条件是存在实数使 a b
推论:如果 l 为经过已知点A且平行
； https:/// 网上赚钱棋牌游戏；
没有回头路可以走的，刻骨铭心的友谊也如仇恨一样，没齿难忘。友情这棵树上只结一个果子，叫做信任。红苹果只留给灌溉果树的人品尝。别的人摘下来尝一口，很可能酸倒了牙。友谊之链不可继承，不可转让，不可贴上封条保存起来而不腐烂，不可冷冻在冰箱里永远新鲜。友谊需要滋养。有的人用钱，有的人用汗，还有的人用血。友谊是很贪婪的，绝不会满足于餐风饮露。友谊是最简朴同时也是最奢侈的营养，需要用时间去灌溉。友谊必须述说，友谊必须倾听，友谊必须交谈的时刻双目凝视，友谊必须倾听的时分全神贯注。友谊有的时候是那样脆弱，一句不经意的言辞，就会使大厦顷刻倒塌。友谊有的时候是那样容易变质，一个未经实的传言，就会让整盆牛奶变酸。这个世界日新月异。在什么都是越现代越好的年代里，唯有友谊，人们保持着古老的准则。朋友就像文物，越老越珍贵。礼物

平行向量和共线向量

平行向量和共线向量是线性代数中的两个重要概念，它们有着密切的关系。

平行向量又称共线向量，是指方向相同或相反的非零向量，它们可以平行存在于同一个向量空间中。

而共线向量则是指向量与自身在同一个方向上的向量，也就是说，它是一个与自身方向相同的向量。

首先，我们来了解一下平行向量的概念。

在向量空间中，如果两个向量a和b的方向相同或相反，且长度为零（即a=0或b=0），那么我们称这两个向量是平行向量。

平行向量的存在对于向量空间中的运算非常重要，因为它们可以用来表示其他向量。

同时，平行向量的运算规则也相对简单，即平行向量的加法、数乘和数量积等运算结果仍然是平行向量。

接下来，我们来看看共线向量的概念。

共线向量是指与自身方向相同的向量，也就是说，它是一个与自身重合的向量。

在向量空间中，如果一个向量与其自身的延长或缩短后的结果仍然相同，那么我们称这个向量是共线向量。

共线向量的存在使得向量空间中的运算更加简单，因为它们可以被用来简化其他向量的运算。

实际上，平行向量和共线向量之间存在着密切的关系。

具体来说，如果两个向量是平行向量，那么它们一定也是共线向量。

这是因为平行向量的方向可以是任意的，而共线向量的方向则必须是相同的。

另外，一个向量与其自身的差也是一个共线向量，因为它们的方向相同或相反。

因此，可以说共线向量是平行向量的特殊情况。

在解决实际问题时，平行向量和共线向量有着广泛的应用。

例如，在物理中，我们可以利用平行向量的性质来分析力和加速度之间的关系；在计算机图形学中，我们可以利用共线向量的性质来优化渲染效果；在通信工程中，我们可以利用平行向量的性质来设计最优传输路径等等。

总之，平行向量和共线向量是线性代数中的两个重要概念，它们在数学和工程领域都有着广泛的应用。

通过了解这两个概念之间的关系和性质，我们可以更好地理解和应用向量空间中的运算和性质。

同时，我们也可以利用这些性质来解决实际问题，提高工作效率和准确性。