4.4.1积分区间无限的广义积分
无穷限的广义积分.

cos
x 0
.
极限不存在
sin xdx
是发散的
若认为积分区间关于原点对称,被积函数为
奇函数,按定积分公式③计算就错了.
例3 计算广义积分 ex sin xdx . 0
解 先计算定积分 Aex sin xdx 0
A
0
e
x
sin
xdx
A 0
sin
xd
ex
ex
sin
x
A 0
A ex cos xdx
a
f xdx
lim Ft Fa F Fa; t
b
f xdx
Fb lim Ft Fb F ; t
f
xdx
lim
t
F
t
lim
t
F
t
F F .
(2)当
f x为奇函数时,
f
x
dx
不能按积
分区间关于原点对称的定积分处理为零。因为
f
xdx
lim
A
B
A
f
xdx,
B
这里A与B是相互独立的.
3.例题
例1
计算广义积分
0 e
x
dx
.
解
0exdx
ex
0
1.
y
这个广义积分值的几
何意义是,当t
时,图5-7中阴影部
1
y ex
分向左无限延伸,但 其面积却有极限值1 .
t
ox
图5-7
例2 计算广义积分 sin xdx .
解
sin
xdx
0 sin
xdx
0
sin
xdx
广义积分

(a 0).
x a 为被积函数的无穷间断点。
0
a
dx dx a lim 0 2 2 0 a x a2 x2
a
arcsin x lim 0 a 0
y
y
1 a2 x2
a lim arcsin 0 。 0 a 2
第五章
第四节
广 义 积 分
本节主要内容
一、无限区间上的广义积分 二、无界函数的广义积分
一、无限区间上的广义积分;
(一)无限区间上的广义积分的概念 定义1
设f ( x )在[a,)上连续,取b a, 记
a
f ( x )dx xlim f ( x )dx
a a
例5
1 证明 p dx当p 1时收敛,当p 1时发散。 1 x
证: 当p 1时,
1 1 1 1 p dx 1 p [ p1 ]1 p 1; x 1 x
当p 1时, 1 dx [ln x ]1 , 故原积分发散; p 1 x 当p 1时, 1 1 ] p dx [ p1 1 , (1 p) x 1 x
1 a
o
a x
1 例12 证明广义积分 0 q dx 当 q 1时收敛,当 x q 1时,广义积分发散。
1
证:(1) q 1,
0
1
11 1 dx 0 dx ln x 1 , q 0 x x
*
, q 1, 1 1 x ( 2) q 1, q dx 1 , q 1, 0 x 1 q 0* 1 q
b a a
b
广义积分

b
a
f ( x )dx
此时也称瑕积分收敛,否则称瑕积分 发散.
a
b b
3.定义 设 f ( x ) 在 [a, c) (c, b] 上连续,并且
lim f ( x ) ,如果 f ( x )dx和 f ( x )dx
c b
xc
a
c
同时收敛,则称它们的和为函数 f ( x ) 在 [a , b] 上的瑕积分. 记作:
例10 求
3
1
x 1 x3
0
dx.
1 3
1 解 令 x t 则 x t dx t dt 3 1 2 6 1 1 x t 1 3 t dt 1 0 1 x 3 dx 0 3 2 (1 t ) 1 1 t (1 t ) dt 0 t (1 t ) 3 3 1 1 ( )( ) 1 2 1 1 1 2 . ( , ) 3 (1) 3 3 2 2
2
即瑕积分发散.
总结
定义及以下两个特殊广义积分: 无穷积分 1
1 dx p x
p 1 时收敛, p 1 时发散.
瑕积分
1
0
1 dx ( p 0) p x p 1 时收敛, p 1 时发散.
三. 函数 定义 广义积分 (r ) 0 x e dx (r 0)
1 1 1 2 0 1 2 1 1 2 1 1 2
2 3
dt
2 2 ln 2
即广义积分收敛,值为 2 2 ln 2.
例5.讨论广义积分 0
解
1 i 因 xlm p 0 x
1
1 dx ( p 0) 的敛散性. p x
无穷限广义积分的计算

指导教师:陈一虎作者简介:陈雪静(1986-),女,陕西咸阳人,数学与应用数学专业2008级专升本1班.无穷限广义积分的计算陈雪静(宝鸡文理学院 数学系,陕西 宝鸡 721013)摘 要: 文章归纳总结了利用数学分析、复变函数、积分变换、概率论统计理论等知识计算无穷限广义积分的几种方法.在学习中运用这几种方法可开拓视野,激发学习数学的兴趣.关键词: 广义积分;收敛;计算方法广义积分是《高等数学》学习中的一个难点知识,广义积分的概念不仅抽象,而且计算方法灵活,不易掌握.广义积分包括两大类,一类是积分区间无穷型的广义积分,另一类是积分区间虽为有穷,但被积函数在该区间内含有有限个无穷型间断点(瑕点)的广义积分.一般的判别法是对积分区间无穷型的广义积分,先将积分限视为有限的积分区间按常义积分处理,待积分求出原函数后再考查其极限是否存在,在用此极限去判定原积分是否收敛.对于第二类广义积分,我们可将积分区间改动,使被积函数在改动后的积分区间内成为有界函数再按常义积分处理,求出原函数之后考查它在原积分区间上的极限是否收敛.但是有些被积函数的原函数不易求出或无法用初等函数表示,使得广义积分无法用常规方法计算,因此需寻求其它的计算方法.本文主要研究无穷限广义积分的计算方法,主要方法包括利用广义积分定义、参量积分、变量代换、二重积分、留数定理、级数展开、概率论知识以及拉普拉斯变换等方法.1 无穷限广义积分的定义定义1 设函数()f x 在区间[,)a +∞上连续,取t a >.如果极限lim ()d tat f x x →+∞⎰存在,则称此极限为函数()f x 在无穷区间[,)a +∞上的反常积分(也称作广义积分),记作()d af x x +∞⎰,即()d af x x +∞⎰=lim ()d tat f x x →+∞⎰;这时也称反常积分()d a f x x +∞⎰收敛;如果上述极限不存在,函数()f x 在无穷区间[,)a +∞上的反常积分()d af x x +∞⎰就没有意义,习惯上称为反常积分()d af x x +∞⎰发散,这时记号()d af x x +∞⎰不再表示数值了.类似地,设函数()f x 在区间(,]b -∞上连续,取t b <. 如果极限lim ()d btt f x x →-∞⎰存在,则称此极限为函数()f x 在无穷区间(,]b -∞上的反常积分,记作()d b f x x -∞⎰,即()d bf x x -∞⎰=lim ()d btt f x x →-∞⎰;这时也称反常积分()d b f x x -∞⎰收敛;如果上述极限不存在,就称反常积分()d bf x x-∞⎰发散.设函数()f x 在无穷区间(,)-∞+∞内连续,如果广义积分()d cf x x -∞⎰和()d cf x x +∞⎰(c 为常数)都收敛,则称上述两个反常积分之和为函数()f x 在无穷区间(,)-∞+∞内的广义积分,记作()f x dx +∞-∞⎰,即()d f x x +∞-∞⎰=()d cf x x -∞⎰+()d cf x x +∞⎰=lim ()d ctt f x x →-∞⎰+lim ()d tct f x x →+∞⎰这时也称广义积分()d f x x +∞-∞⎰收敛;否则就称反常积分()d f x x +∞-∞⎰发散.上述反常积分统称为积分区间为无穷区间的广义积分或无穷限广义积分.2 无穷限广义积分的计算方法2.1利用广义积分的定义求无穷限广义积分由定义计算可以分两步:1求定积分()d Aaf x x ⎰=()F A .需要说明的是原函数()F A 均指有限形式.2取极限lim ()d AaA f x x →+∞⎰=lim A →+∞()F A .例1[1]计算23121()d 1x x x+∞++⎰解 =23121lim()d 1bb x x x →+∞++⎰231121lim[d d ]1b b b x x x x→+∞=++⎰⎰ 2111lim[2arctan ]2bbb x x →+∞=-211lim[2arctan arctan1]22b b b →+∞=--+ 2π11lim 2arctan lim 222b b b b →+∞→+∞=--+ π122=+ 2.2利用含参量积分的理论求无穷限广义积分含参量积分:10()e d s x s x x +∞--Γ=⎰(0s >)1110(,)(1)d p q p q x x x --B =-⎰ (0,0p q >>)统称为欧拉积分.其中()s Γ称为格马函数.(,)p q B 称为贝塔函数.且有递推公式(1)()s s s Γ+=Γ 及 1(,)(,1)1q p q p q p q -B =B -+-.因此在计算广义积分时看所给广义积分当,,s p q 为何值时对应的欧拉积分,然后用欧拉积分公式直接算出广义积分的值.例2[5] 求220e d n x x x +∞-⎰(n 为正整数)解 此广义积分与表达式相似,因此可用Γ函数法求解.220ed n x x x +∞-⎰=limA →+∞220ed An x x x -⎰2t x =21201lim e d 2A n t A t t --→+∞⎰=12112e d n t t t +∞+--⎰==121()2n Γ+=121[()1]2n Γ-+ =121()2n -1()2n Γ-=121()2n -3()2n -3()2n Γ-17(21)2n n +-注:1()2Γ=2.3利用变量代换法求无穷限广义积分有些函数的原函数不易求出或直接积分不出来,但如果对被积函数施以变量代换,在辅以一定的技巧就可以求出这类积分.作变量带换时,首先要对被积函数的结构进行分析,然后再看积分限与被积函数的关系.变换的方向是求出原函数或求出一个含原积分的方程,从而求得所含广义积分的值.例3[2] 求I=401d 1x x +∞+⎰解 令x=1t ,则I=204d d 11t t x t +∞-+⎰上式加上I=04d 11t t +∞+⎰ 得2I=2401d 1t t t +∞++⎰=202211d 1t t t t +∞++⎰=021d()1()2t t t t +∞--+⎰故2.4利用二重积分理论计算无穷限广义积分.利用二重积分理论计算广义积分时,应分两步: 1把广义积分巧妙的化为一个二重积分.2计算二重积分,从而间接的计算出广义积分的值. 例4[5]计算广义积分2ed x x +∞-⎰解 由于20ed x x +∞-⎰=2e d y y +∞-⎰所以22[ed ]x x +∞-⎰=22ed ed x y x y +∞+∞--⋅⎰⎰而22e d e d x y x y +∞+∞--⋅⎰⎰=22()e d d xy Dx y -+⎰⎰ 其中D=[0,)[0,)∞⨯∞故()22ed x x +∞-⎰=22()e d d x y Dx y -+⎰⎰而22()e d d xy Dx y -+⎰⎰=π42ed x x +∞-⎰=2. 例5[3]计算广义积分I=0sin sin e d pxbx axx x+∞--⎰ 解 因为sin sin bx ax x-=cos()d ba xy y ⎰ 所以I=0sin sin e d px bx ax x x+∞--⎰=0e (cos()d )d bpx axy y x +∞-⎰⎰=0d e cos()d b px ax xy y +∞-⎰⎰=0d e cos()d b px ay xy x +∞-⎰⎰=22d bap y p y +⎰=arctan b p -arctan ap. 2.5积分号下求导法计算无穷限广义积分.收敛因子法:此方法是对被积函数引入一个收敛因子,因子中有一个参数, 对参数(不一定是收敛因子中的参数)求导,有时可求得原积分的值.在此情况下引入的收敛因子加强了原积分的收敛性(如条件收敛的成为绝对收敛,或求导后发散的,变成一致收敛).这样使积分号下求导条件得以满足.一般采用e kx -(k>0)作为收敛因子.例65]求积分0sin d axx x+∞⎰(0a ≥) 解 引入积分因子e px -(p >0)作积分()F p =0sin e d px axx x+∞-⎰ ()F p '=0e cos d px ax x +∞-⎰=22pp a+ 故 ()F p = arctana p +C =arctan ap(显然C =I(0)=0)由此有 0lim arctanp a p +→=π2所以 I=π2 故同样可得 0sin d ax x x +∞⎰=-π2(0)a <2.6积分号下求积分法算无穷限广义积分这种方法是将被积函数中某一因子表为一个适当的积分.于是将原积分化成二次积分.交换这两个积分的顺序,就可求出所给的积分.例7[2]求积分I=2cos d 1xx x β+∞+⎰(0)β> 解 由201e sin d 1xy y y x+∞-=+⎰,于是 I=0cos d e sin d xy x x y y β+∞+∞-⋅⎰⎰=0sin d e cos d xy y y x x β+∞+∞-⋅⎰⎰=22sin d y yy yβ+∞+⎰y t β==2sin d 1t tt t β+∞+⎰由20d sin d d 1I x x x x ββ+∞=-+⎰,有d d I β=I -所以 I =C e β-为了确定C ,令0β=. 得 020d π12x I C x +∞===+⎰故πe 2I β-=.2.7利用复变函数理论中的留数定理计算无穷限广义积分.定理1[5] 设函数()f z 在实轴上处处解析,在上半平面Im 0z >除有限个孤立奇点1,2z z ⋅⋅⋅n z 外处处解析,且存在常数00R >,0M >,0δ>,使得当0z R >,且Im 0z >时, 1()M f z zδ+≤,则1()d 2πi [(),]nk k f x x Res f z z +∞-∞==∑⎰推论 1[5]设()()()P z f z Q z =是有理函数,()P z 与()Q z 为z 的n ,m 次多项,多项式()Q z 的次数比()P z 至少高2次,()Q z 在实轴上没有零点,1,2z z ⋅⋅⋅n z 是()f z 在上半平面Im 0z >的孤立奇点,则1()d 2πi [(),]nk k f x x Res f z z +∞-∞==∑⎰例84]计算广义积分22222d ()()x x x a x b +∞-∞++⎰解 因为22222()()()z f z z a z b =++,显然()f z 满足推论的条件,且1z =i a ,2z =i b 是()f z 在上半平面的孤立奇点,这两个点都是()f z 的一级极点,因此有22222ai Re [(),i]lim[(i)]()()z z s f z a z a z a z b →=-++ 2222i()a ab a -=- 222i()aa b =- 同理Re [(),i]s f z b =222i()bb a - 故22222d ()()x x x a x b +∞-∞++⎰=2πi [222()a i a b -+222()bi b a -] =πa b+ 2.8级数展开法求广义积分利用无穷级数计算广义积分也是常用的一种技巧.常有两种方法. 其一是将被积函数展成级数以求积分;其二是将无穷区间上的广义积分表示成级数的形式以求积分.例92]求积分I=2e cos 2d x bx x +∞-⎰解 利用余弦函数的幂级数展开以及指数函数的展开式0e !nxn x n ∞==∑ (2)!2!(21)!n n n n =⋅-我们有2ecos 2d x bx x +∞-⎰=22200(1)(2)ed (2)!n n x n n b x x n ∞+∞-=-∑⎰=22200(1)(2)e d (2)!n n x nn b x x n ∞+∞-=-∑⎰=0n ∞=20()2!nn b n ∞=-∑2b - 例10[5]计算广义积分1ln d (1)xx x x +∞-⎰. 解 由于1ln d (1)xx x x +∞-⎰=211n n∞=-∑ 而211n n∞=∑=2π6 故原式=-2π6.利用级数展开求积分,展开的仅是被积函数的某个因子,“展开因子”选择应是其展开的级数形式比较简单;展开的级数连同被积函数剩下的因子可逐项积分;这些积分容易求出.因此记住一些常用函数的展开式及一些数项级数的和对积分计算是有益的.2.9利用概率统计知识求无穷限广义积分.例11[5] 计算广义积分I=0sin sin e d pxbx axx x+∞--⎰. 解因为22()x f x -=为标准的正态分布密度函数所以()d f x x +∞-∞⎰= 1.即22d x x +∞--∞⎰=1.所以2201d 2xx +∞-=⎰即22ed x x +∞--∞⎰令222x u -=⇒u =⇒20e d uu +∞-⎰220e d x x +∞-2 2.10用拉普拉斯变换求无穷限广义积分定义2[6] 设()f t 在0t ≥上有定义,且积分0()()e d st F s f t t +∞-=⎰(s 是复变参量)关于某一范围内的s 收敛,则由这个积分确定的函数0()()e d st F s f t t +∞-=⎰称为函数()f t 的拉普拉斯变换.并记做[()]L f t ,即[()]L f t =0()()e d st F s f t t +∞-=⎰,其中的()F s 称为()f t 的像函数,()f t 称为()F s 的像原函数.定理 2[5] (Laplace 变换存在定理) 设函数()f t 在0t ≥的任何有限区间内分段连续,并且当t →+∞时, ()f t 的增长速度不超过某一指数函数,即存在常数0M >,和00s >,使得在[0,]+∞上,0()e s t f t M ≤,则在半平面0Re s s >上,[()]L f t 存在,且()F s =[()]L f t 是s 的解析函数.其中0s 称为()f t 的增长指数.性质1[1](积分性质)若[()]()L f t F p =,则0()[()d ]tF p L f t t p=⎰(p 为复数) (1)性质2[1](终值性质) 若[()]()L f t F p =,且()p F p 的所有奇点全在p 平面的部0lim ()lim ()t p f t p F p →+∞→=⋅ (2)性质3[1] 若[()]()L f t F p =,()F p 在Re 0p >上解析,且0()d n t f t t +∞⎰收敛,则0(1)lim ()n n p F p →-存在,且(1)lim ()()d n nn p F p t f t t +∞→-=⎰(3)证明 [()]()L f t F p = 由微分性知 ()n F p =[()()]n L t f t -[()]n L t f t =(1)()n n F p -由性质1 0(1)()[()d ]n n t nF p L t f t t p-=⎰所以由性质2 00(1)()lim[()d ]lim n n t nt p F p t f t t p→+∞→-=⎰即 0()d n t f t t +∞⎰=0(1)lim ()n n p F p →-特别的,0n =时,有()d lim ()p f t t F p +∞→=⎰. (4)性质4[1](象函数的积分性质)若[()]()L f t F p =,且积分()d F p p ∞⎰收敛()[]()d p f t L F p p t∞=⎰. (5)性质 5[1]设[()]()L f t F p =,且()d F p p ∞⎰与0()d f t t t∞⎰皆收敛,则 0()()d d f t F p p t t∞∞=⎰⎰(6) 证明 由(5)式,()[]()d p f t L F p p t∞=⎰ 由(4)式,()d f t t t∞⎰=0lim ()d p p F p p ∞→⎰()d F p p ∞=⎰例12[4] 求sin ()tf t t =的拉普拉斯变换,并求积分0sin d t t t+∞⎰.解 由定理2,因为0()1e f t ≤⋅,故在s 的实部大于零上, 拉普拉斯变换存在,且esin d stt t ω+∞-⎰=22e [sin cos ]st s t t s ωωωω---+=22s ωω+于是 22[sin ]L t s ωωω=+ (在s 的实部大于零) 那么 2sin 1[]1t L t s =+ 由命题4知 sin []t L t =21d 1s s s +∞+⎰=πarctan 2s -在利用命题5知0sin d t t t +∞⎰=201d 1s s +∞+⎰=π2. 例13[6] 计算下列积分30e sin d t t t t +∞-⎰ 解 21[sin ]1L t s =+, 由微分性质知, 22212[sin ]()1(1)s L t t s s '=-=++ 但是另一方面 0[sin ]sin e st L t t t t dt +∞-=⋅⎰当3s =时,即30e sin d t t t t +∞-⎰=2232(1)s s +=350致谢:本文在写作过程中得到陈一虎老师的指导.在此表示感谢!参考文献:[1] 白水周.无穷限广义积分的几种有效解法[J].开封大学学报,2000,14(1):49-50.[2] 李绍成.论广义积分的计算[J].绵阳农专学报:自然科学版,1996,13(2):65-70.[3] 数学分析.华东师范大学数学系[M].高等教育出版社,2001.[4] 宋叔尼,孙涛.复变函数与积分变换[M].北京:科学出版社,2006.[5] 刘开生,杨钟玄.无穷限广义积分的几种计算方法[J].天水师范学院学报:自然科学版,2002,22(2):9-10.[6] 盖云英,包革军.复变函数与积分变换学习指导[M].科学出版社,2004.Ways of calculating limitless generalized integralCHEN Xue-Jing(Department of Mathematic,Baoji University of Arts and Science Baoji 721013,Shaanxi ,China) Abstract:ways of calculating generlazed integral are given by using maths analysis, complex variable and integral transform, complex function and proabability statistical theroy. In the study the use of these methods can broaden their horizons, stimulate interest in learning mathematics.Key words:generalized integration; convergence; calculation method.。
无穷限的广义积分

b
c
b
f ( x )dx
16
思考题
积分 ∫0
1
ln x dx 的瑕点是哪几点? x −1
2010-1-4
广义积分(22)
17
思考题解答 积分 ∫0
1
ln x dx 可能的瑕点是 x = 0, x −1
x =1
ln x 1 = lim = 1, ∵ lim x →1 x x →1 x − 1
ln x ∵ lim =∞ x →0 x − 1
∴ x = 1 不是瑕点,
是瑕点,
∴ x=0
∴ ∫0
2010-1-4
1
ln x dx x −1
的瑕点是 x = 0.
广义积分(22) 18
2010-1-4 广义积分(22) 12
a −ε
1 例 6 证明广义积分 ∫0 q dx 当q < 1时收敛,当 x q ≥ 1时发散.
1
11 1 dx = ∫0 dx = [ln x ]1 = +∞ , 证 (1) q = 1, ∫0 q 0 x x ⎧+ ∞, q > 1 1− q 1 1 1 ⎡x ⎤ ⎪ ( 2) q ≠ 1, ∫ q dx = ⎢ ⎥ = ⎨ 1 ,q<1 0 x ⎣1 − q ⎦ 0 ⎪ ⎩1 − q 1 因此当q < 1时广义积分收敛,其值为 ; 1− q 当q ≥ 1时广义积分发散.
广义积分(22)
10
设函数 f ( x ) 在区间[a , b]上除点 c (a < c < b ) 外连 续,而在点 c 的邻域内无界.如果两个广义积分
∫a f ( x )dx 和 ∫c
b
c
b
f ( x )dx 都收敛,则定义
广义积分

∫−∞ f ( x )dx = ∫−∞ f ( x )dx + ∫0
= lim
+∞
0
+∞
f ( x )dx
∫a f ( x )dx + blim ∫0 a → −∞ → +∞
0
b
f ( x )dx
极限存在称广义积分收敛;否则称广义积分发散. 极限存在称广义积分收敛;否则称广义积分发散.
例1 计算广义积分 ∫− ∞ 解
1
例7 计算广义积分 解
∫
2
1
dx . x ln x
∫1
2
dx 2 dx = lim ∫1+ε x ln x ε →0+ x ln x
2
= lim ∫1+ε
ε → 0+
ε → 0+
d (ln x ) 2 = lim [ln(ln x )]1+ε ε → 0+ ln x
= lim [ln(ln 2) − ln(ln(1 + ε ))]
b
b
上连续, 设函数 f ( x ) 在区间 ( −∞ ,+∞ ) 上连续 , 如果 广义积分 ∫− ∞ f ( x )dx 和 ∫0
0 +∞
f ( x )dx 都收敛 , 则 都收敛,
+∞
称上述两广义积分之和为函数 f ( x ) 在无穷区间
( −∞ ,+∞ ) 上的广义积分,记作 ∫− ∞ f ( x )dx . 上的广义积分,
= lim ∫a
ε → +0
c −ε
f ( x )dx
b
f ( x )dx + lim
b
《无穷限广义积分》课件

参考文献
• 张三. 《无穷限广义积分教程》. 2019. • 李四. 《无穷限广义积分导论》. 2020. • 王五. 《无穷限广义积分及其应用》. 2021.
2
分部积分法
探索分部积分法在计算无穷限广义积分中的应用技巧和有效性。
3
日常计算中的技巧
分享在日常应用中计算无穷限广义积分时的小技巧和实用方法。
4. 特殊函数与应用
伽马函数
介绍伽马函数及其性质,探索 其在数学和物理学中的重要应 用。
贝塞尔函数
了解贝塞尔函数及其在科学与 工程领域中的实际应用和重要 性。
《无穷限广义积分》PPT课件
本课件介绍无穷限广义积分的基本概念与定义,探讨其与普通积分的比较, 以及无穷限广义积分的重要性及应用领域。
1. 介绍
基本概念与定义
了解无穷限广义积分的基本概念及其精确定义。
与普通积分的比较
比较无穷限广义积分与普通积分的异同,探讨其适用范围及优势。
重要性及应用领域
探索无穷限广义积分在数学、物理、统计学等领域的重要性及应用。
应用:统计学、物理 学等
探索无穷限广义积分在统计学、 物理学等领域的广泛应用和实 际价值。
5. 总结与展望
重要性再强调
总结无穷限广义积分的重要性,强调其在数学以及多个领域的实际应用。
发展历程与未来研究
回顾无穷限广义积分的发展历程,并展望未来在该领域中的研究方向。
推广与应用前景
探讨无穷限广义积分的推广和未来应用前景,展示其潜力和发展空间。
2. 收敛性与发散性
外延收敛与内延发散
深入了解无穷限广义积分的外延 收敛和内延敛 和绝对收敛的定义及判别法。
收敛性判别法
了解用于判断无穷限广义积分收 敛性的常用判别法和证明方法。
Maple

BJUT
3.集合的运算 (1)集合的基数 集合中元素的个数称为集合的基数,在Maple中求集合的基数通 过调用函数nops来实现。 >A:={x1,x2,0,{3}}; >B:={x3,x5,{a,b},{a}}; >nops(A);
BJUT
(2)集合相等 当A、B两个集合的元素完全相同时,称集合A与B相等,记为A=B.通 过调用函数evalb来判断两个集合是否相等,也可以使用函数 member来判断一个元素是否属于某个集合。 >A:={1,2,3,4}; >B:={1,2,4,5}; >C:={4,2,3,1}; >evalb(A=B); >evalb(A=C); >member(3,B);
BJUT
分段函数求偏导 >f(x,y):=piecewise(x^2+y^2<>0,x*y/(x^2+y^2),x^2+y^2=0,0); >diff(f(x,y),x); >diff(f(x,y),y); >diff(f(x,y),x,y); >simplify(%);
BJUT
4.4.2 导数的应用 导数的应用很多,如求运动物体的速度和加速度、曲线的切线 方程、函数的最值、函数的单调性的判定等。下面以函数单调性的 判定为例。(回忆利用导数判定单调性的条件及方法) >f:=x->exp(x)-x-1; >f1:=diff(f(x),x); >assume(x>0); >is(f1>0); >assume(x<0); >is(f1<0); 函数assume可指定假设,而函数is可查询对象属性是否成立,返回 true,表示成立;返回false,表示不成立;返回faile,表示不确定
无限区间广义积分

∫ f (x)dx和
∫
+∞ a
+∞ f (x)dx都收敛,则称广义积分−∞
∫
f (x)dx收敛,
+∞ 否则称广义积分−∞
∫
f (x)dx发散 .
上述三种方法统称为无穷区间上的广义积分.
例2 求 ∫
+∞
+∞ −3x e dx. 0
解 ∫0 e−3xdx = lim ∫0e−3xdx
b b→+∞
1 b −3x = − lim ∫0e d(−3x) 3b→+∞
∫
定义为所求开口图形的 面积,并称定积分的极 A为函 限 为函 A 1 + 1 ∞ [, 数 = 2 在区间1 + ∞)的广义积分,记作∫ y dx,即 2 1 x x + 1 ∞ b 1 ∫1 2dx = blim ∫1 2dx. →+∞ x x
定义1 设函数 (x)在区间a,+∞)上连续,取 > a f [ b
无限区间广义积分
一、无限区间上的广义积分
一、无穷区间的广义积分
1 例1 求曲线 = 2 直线 =1及 轴为边界的开口图 y x x x 形 或称区域 的面积 ( ) .
1 由曲线 = 2 , 直线 =1, x = b(b >1)及 轴所围成 y x Ox x A 计算: 的曲边梯形的面积 ,可以用下面的定积分 1 1 1 b 1 A = ∫1 2 dx = − = −( −1) =1− , x1 b b x 10 1 1 10 1 当b =10时, = ∫1 2 dx = − A =1− = 0.9 , x1 10 x
∫
0 −∞
1
2
1+ x
dx
0 1 = lim a dx 2 a→−∞ 1 + x
4.4.1积分区间无限广义积分

二、1、n!; 2、0; 3、(1)n n!.
三、当k 1时收敛于 1 (b a)1k ; 当k 1时发散. 1 k
0 , x 0
四、
x
f
(t )dt
1
4
x2
,
0
x
2.
x 1 , 2 x
4.4 广义积分(41)
24
4.4.2 被积函数无界的广义积分
设函数 f ( x)在区间(a, b]上连续,而在点a 的右
0 a
0 c
否则,就称广义积分
b
a
f ( x)dx 发散.
定义中 c 称
为函数的瑕点,所以,此积分亦称瑕积分.
4.4 广义积分(41)
27
a dx
例10 计算广义积分 0 a2 x2
解
lim 1 , xa0 a2 x2
(a 0).
x a为被积函数的无穷间断点.
a dx
a dx lim
4.4.1 积分区间无限的广义积分
设函数 f ( x)在区间[a,)上连续,取b a . 若
极限
lim
b
b
a
f
( x)dx
存在,则称此极限为函数
f
(
x)
在无穷区间[a,)上的广义积分(无穷积分),
记作
b
f ( x)dx lim f ( x)dx.
a
b a
当极限存在时,称广义积分收敛;当极限不存在 时,称广义积分发散.
11
即
F (b)
b
a
f
( x)dx
在[a, )
也上有上界.
由
定理
1
可知,积分
a
f
无穷限广义积分

(3) a [ f (x) g(x)]d x a f (x) d x a g(x) d x .
(4)
u(x)v(x) d x
a
u(x)v(x)
a
u(x)v(x) d x .
a
(5) 无穷积分也可按照定积分的换元法进行计算.
(6) 若在[a, ) 上 f (x) g(x) , 则
d x x1 p
a xp 1 p
,
a
a 1 p , p 1
p 1, p 1.
发散 收敛
例3
计算
cos x d x .
0
解
cos x d x sin x
0
0
lim sin x sin 0 , x
由于 lim sin x 不存在,故原积分
的敛散性.
因为
lim
x
x
1
x3 x2
lim x2 x 1
x x2
,
故无穷积分
1
x3 d x 1 x2
是发散的.
例7
判别无穷积分 d x 的敛散性 . 1 x 1 x2
解 因为
lim x2 1 lim x 1, ( p 2 1) x x 1 x2 x 1 x2
cos x d x
发散 .
x
0
无穷积分的基本运算性质
设以下所有出现的积分均存在,则
a
(1) f (x) d x f (x) d x .
a
其它类型的无穷 积分的情形类似 于此.
《无穷限的广义积分》课件

瑕积分的定义
这是对于含瑕点函数的积分,它可以被分成瑕点和良好积分两个部分。
瑕积分的判定
同样有相应的分析判定方法。
技巧
1
分部积分法
将一个积分式子分成两个部分,做出新的代表性表达式,这种方法叫做分部积分 法。
2
换元积分法
更换成代表性更强的太极变量,可以大幅度简化积分式子。
无穷限积分的收敛与发散
2
穷限积分则将该积分的上限或下限设置 为无穷大或负无穷大,从而使积分具有
无穷限积分只有在区间内的函数满足一
物理意义。
定的条件时,才会有收敛的情况。若不
满足条件,则是发散的。
判定
比较判定法
与积分值相对比的方法
极限判定法
与极限值相对比的方法
积分判定法
对函数的其他方法
瑕积分
什么是瑕积分
Publications.
《无穷限的广义积分》 PPT课件
欢迎来到本课程,今天我们将学习无穷限广义积分的概念、定义、收敛性测 试、技巧和应用。
引言
广义积分是对于微积分基础学习的进一步拓展,而无穷限积分指的是积分区 间上界或下界为无穷大的积分。在本节中,我们将学习广义积分和无穷限积 分的相关概念。
定义
1
无穷限积分的定义
定义一个物理意义不明确的积分,而无
3
三角函数积分法
高等数学以及微积分课程中讲解了三角函数的复杂性,这种方法可以使用求导知 识对三角函数进行积分。
应用
计算无穷限积分
我们有许多种计算无穷限积分的方法
计算瑕积分
在计算瑕积分中,就需要运用这些积分技巧。
4.4广义积分
0
6 、广义积分 ∫
x
−∞
1− x 的几何意义是______ ______________ f ( t )dt 的几何意义是______________
________ __; = ________;
________________________. ________________________.
b
+∞
∫−a f (x) dx a→+∞
a
v.p.∫ f (x) dx (c为瑕点, a < c < b)
a
c−ε f (x) dx + b f (x) dx = lim ∫ ∫c+ε + a ε →0
注意: 注意 主值意义下广义积分存在不等于一般意义下 广义积分收敛 .
例题 试证
注意到: Γ(1) = ∫
+∞ −x e dx 0
=1
= L= n!Γ(1)
(2) 当s → 0+时, Γ(s) → +∞. 证:
Γ(s +1) Q Γ(s) = , Γ(1) = 1 s 且可证明Γ(s) 在s > 0连续,
∴s → 0 时, Γ(s) → +∞
(3) 余元公式:
+
当s = 1 时, 有 2
4.4 广义积分 广义积分
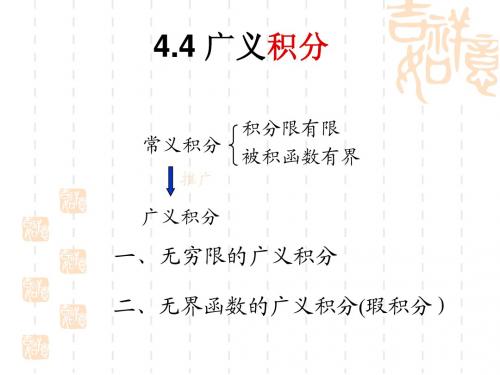
积分限有限 被积函数有界
常义积分
推广
广义积分
一、无穷限的广义积分 二、无界函数的广义积分(瑕积分)
一、无穷限的广义积分 无穷限的广义积分 广义
引例. 引例 曲线 和直线 及 x 轴所围成的开口曲
边梯形的面积 可记作
x2 其含义可理解为 b b dx −1 A = lim ∫ 2 = lim 1 x b→+∞ x 1 b→+∞
广 义 积 分

广义积分
前面介绍的定积分有两个限制条件:积分 区间有限和被积函数有界.实际问题中还需要某 些函数在无穷区间上的积分以及某些无界函数在 有限区间上的积分.因此要求将定积分概念加以 推广,这就是广义积分.广义积分包括无穷区间 的广义积分和无界函数的广义积分两类.
一、 无穷区间的广义积分
定义2
二、 无界函数的广义积分
【例35】
二、 无界函数的广义积分
【例36】
二、 无界函数的广义积分
【例37】
二、 无界函数的广义积分
【例38】
பைடு நூலகம்
二、 无界函数的广义积分
二、 无界函数的广义积分
由这个递推公式不难看出该积分收敛.特别地,对任何正整 数n
Γ(n+1)=n!
Γ(n+1)=nΓ(n)=n(n-1)Γ(n-1)=…=n!Γ(1)
以及∫baf(x)dx收敛和发散的概念.
(6-13)
二、 无界函数的广义积分
定义5
设f(x)在区间[a,b]上除点c(a<c<b) limx→cf(x)=∞,如果两个广义积分∫caf(x)dx和∫bcf(x)dx 都收敛,则称广义积分∫baf(x)dx收敛
∫baf(x)dx=∫caf(x)dx+∫bcf(x)dx; (6-14) 否则,称其没有意义或发散.
∫baf(x)dx=limε→0+∫ba+εf(x)dx, (6-12) 此时称广义积分∫baf(x)dx存在或收敛;否则称广义积分 ∫baf(x)dx没有意义或发散.这种广义积分又称为瑕积分,a为瑕点.
类似地,可定义f(x)在区间[a,b) ∫baf(x)dx=limε→0+∫b-εaf(x)dx
高数广义积分

0
f ( x )dx与
0
f ( x )dx中有一个发散 ,
f x dx发散.
3
例1 计算广 义积分
dx 1 x 2 .
y
a o
y
1 1 x2
解
由 (3) 式得
b
x
0 dx dx dx 1 x 2 1 x 2 0 1 x 2 0 b dx dx lim lim 0 1 x2 a a 1 x 2 b
f ( x )dx 不再表示数值了.
a
类似地
设 f ( x ) C , b, a b. 如果
I 1 lim
a a
b
f ( x )dx 存在。
即
b
f ( x )dx ,
b
f x dx lim
a a
f x dx.
b
(2)
这时也称广义积分
t
1 . 2 p
6
例3
证明
dx 当 p>1 时 收敛; ( a 0 ) a x p 当 p≤1 时 发散。 解:当 p=1 时
a
dx ln x a lim ln x ln a ; x x
当 p ≠1 时
a
dx xp
a 1 p x , p 1 1 p a ,
(1,1)
a
dx ( a 0) p x
当 p>1 时 收敛; 当 p≤1 时 发散。 O
4.4 积分法(二)

x a 时,
t
2
,
a
a
a x dx 2 02 a 2 1 sin 2 t a cos tdt
2 2 2
2a 02 cos tdt a 02 1 cos 2t dt 2 a2 a 2 a sin 2t 02 . 2 2 2
x3 cos xdx 0.
第4章 积分及其应用
例5 求
解 设
a
a
a 2 x 2 dx(a 0).
由定积分的对称性知, a
a
a x dx 2
2 2
a
0
a 2 x 2 dx.
x a sin t ,则 dx a cos tdt .
当 x 0 时, t 0; 当 于是
a f xdx 0 f xdx 0 f xdx 20 f x dx.
a a a a
第4章 积分及其应用
例4 设 f x x cos x ,则 1 f x dx ___.
3
1
解 因为 f x 在 1,1 上是奇函数,所以
1
1
第4章 积分及其应用
例 7 求 arcsin xdx .
1 2 0
解 在公式(4-7)中,取u arcsin x, dv dx ,即 v x ,于是 0 arcsin xdx [ x arcsin x] |0 0 xd (arcsin x)
1 2 1 2 1 2
1 1 xdx 1 2 2 arcsin 0 ( 1 x ) d ( 1 x ) 2 0 2 2 1 x 12 2 1 3 2 2(1 x ) |0 1 12 2 12 2
无穷区间上的广义积分

定积分的概念中,积分区间[a,b] 是一个有限区间,但在
科学技术中有时会遇到区间是无限区间,为此需要将定积 分的概念加以扩展,得到下列无穷区间上的广义积分的概 念.
2021/4/21
1
定义 4.2 设函数 f (x) 在 [a, + )上连续, 取实 数 b > a,如果极限
补例 计算 0 xexdx.
解 用分部积分法,得
0 xe xdx 0 xde x xe x 0 0 e xdx
ex 0 1.
其中 lim xex x
lim
x
x ex
lim
x
1 ex
0,
即 xex 0 0.
2021/4/21
8
例 2
求
1
1 x2
dx.
解
1 1 x2 dx
arctan x ( ) .
2
2
补例 判断 cos xdx 的 收 敛 性. 0
解
cos
xdx
sin
x
.
0
0
由于当 x + 时,sin x 没有极限,所以原广义积
分发散 .
2021/4/21
9
补例
判断
dx
的 收 敛 性.
e x ln x
解
dx d ln x ln ln x
解 用分部积分法,得
xexdx xdex xex exdx
0
0
0
0
0 ex (0 e0 ) 1. 0
注:以上实际
lim xex
x
lim
x
x ex
lim
x
1 ex
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
f ( x )dx lim
a a
f ( x )dx .
当极限存在时,称广义积分收敛;当极限不存在 时,称广义积分发散.
4.4 广义积分(41) 4
一般地,设函数 f ( x ) 在区间 ( , ) 上连续 , 若广义积分 f ( x )dx 和 0 f ( x )dx 都收敛, 则称 上述两广义积分之和为函数 f ( x ) 在无穷区间
证
设 a b , 由 0 f ( x) g( x) 及 a g( x )dx
b b
的收敛性,得 a f ( x )dx a g( x )dx a g( x )dx ,
4.4 广义积分(41) 11
即
F (b) f ( x )dx 在 [a, ) 也上有上界. 由 a
4.4.1 积分区间无限的广义积分
设函数 f ( x ) 在区间[a , ) 上连续,取 b a . 若
f ( x )dx 存在,则称此极限为函数 f ( x ) 极限 blim a
b
在无穷区间[a , ) 上的广义积分(无穷积分) , 记作
a
f ( x )dx lim f ( x )dx .
pa pb
b
px
e dx blim p a
px
b
e ap e e , p0 lim p b p p p0 ,
即当 p 0 时收敛,当 p 0 时发散.
4.4 广义积分(41) 9
4.4 广义积分(41) 10
定理 2(比较审敛原理)设函数 f ( x ), g( x ) 在区 间 [a, ) 上连续, 且 0 f ( x) g( x) ,(a x ) , 则当无穷积分 a g( x )dx 收敛时,a f ( x )dx 也收 敛;当无穷积分 a f ( x )dx 发散时, a g( x )dx 也 发散.
无穷积分的审敛法
定理1 设函数 f ( x ) 在区间 [a ,) 上连续, 且 f ( x ) 0.若函数 F ( x ) f ( t )dt
a x
在 [a ,) 上有界,则广义积分 f ( x )dx 收敛.
a
证略.
定理1,对于非负函数的无穷积分有下
面的比较收敛原理.
b
定理 1 可知,积分 a f ( x )dx 收敛.
当积分 a f ( x )dx 发散时, 显然 a g( x )dx
发散. 否则,由上面的结果得 a f ( x )dx 收敛 的矛盾.
4.4 广义积分(41)
12
定理 3(比较审敛法 1)
设函数 f ( x ) 在区间
例1 计算广义积分 解
dx . 2 1 x
0 dx dx dx 2 2 1 x 0 1 x 1 x2
lim
a
0
a
b dx dx 2 lim b 0 1 x 2 1 x
0 b
lim arctan x a lim arctan x 0
a b
π π lim arctan a lim arctan b π. a b 2 2
4.4 广义积分(41) 6
例2 计算广义积分 解
2 π
1 1 sin dx . 2 x x
2 π
1 1 1 1 sin dx 2 sin d 2 x x π x x
[a, ),(a 0) 上连续,且 f ( x ) 0 .若存在常数
M M 0 及 p 1 ,使得 f ( x ) p (a x ) ,则 x
a
f ( x )dx 收敛;若存在常数 N 0 ,使得
N x
f ( x)
1 dx 当 p 1时收敛, p x
证 (1) p 1,1
, p 1 1 x ( 2) p 1, dx 1 p 1 x , p1 1 p 1 p1 1 因此当 p 1 时广义积分收敛,其值为 ; p1 当 p 1 时广义积分发散.
1 p
4.4 广义积分(41) 8
1 1 d x , d x ln x p 1 1 x x
例4
证明广义积分
a
e px dx 当 p 0 时收敛,
当 p 0 时发散.
证 当p=0时,积分显然发散. 否则
a
e
px
e dx blim a
பைடு நூலகம்
1 1 1 cos lim 2 sin d blim b π x x x
b
b
2 π
1 π lim cos cos 1. b b 2
4.4 广义积分(41) 7
例 3 证明广义积分 1 当 p 1时发散.
b a
b
当极限存在时,称广义积分收敛;当极限不存在 时,称广义积分发散.
4.4 广义积分(41) 3
类似地,设函数 f ( x ) 在区间 ( , b]上连续,取
f ( x )dx 存在,则称此极限为 a b . 若极限 alim a
b
函数 f ( x ) 在无穷区间 ( , b]上的广义积分(无 穷积分) ,记作
0
( , )上的广义积分(无穷积分) ,记作
f ( x )dx
0
f ( x )dx
0
f ( x )dx
b
lim f ( x )dx lim f ( x )dx
a a
b 0
0
极限存在称广义积分收敛;否则称广义积分发散.
4.4 广义积分(41) 5
