圆锥曲线习题精选精讲

合集下载

圆锥曲线-高中数学好题精练精讲解析版

一、单选题（本大题共8小题，共40分。

在每小题列出的选项中，选出符合题目的一项）1.已知椭圆mx2+y22=1的焦距为2，则实数m=( )A. 13B. 16C. 16或12D. 13或12.已知等差数列{a n}满足4a3=3a2，则{a n}中一定为零的项是( )A. a6B. a7C. a8D. a93.已知数列{a n}中，a3=2,a7=1.若{1a n}为等差数列，则a5=( )A. 23B. 32C. 43D. 344.设等差数列{a n}的前n项和为S n，且S5=15,S10=80，则S20=( )A. 145B. 250C. 360D. 4005.已知等差数列{a n}的首项为1，前n项和为S n，且对任意n≠7，S n<S7，则( )A. S13<0B. S14>0C. S15<0D. S16>06.已知数列{a n}，{b n}是等差数列，其前n项和分别为S n，T n，且S nT n =2n−34n−3，则a1+a9b2+b10=( )A. 1541B. 511C. 715D. 19417.已知双曲线E的中心为原点，F(3,0)是E的焦点，过F的直线l与E相交于A，B两点，且AB的中点为N(−12,−15)，则E的方程为( )A. x23−y26=1 B. x24−y25=1 C. x26−y23=1 D. x25−y24=18.抛物线y2=2px(p>0)的焦点为F，准线为l，A，B是抛物线上的两个动点，且满足∠AFB=π3，设线段AB的中点M在l上的投影为N，则|MN||AB|的最大值是A. 1B. √32C. √33D. 2二、多选题（本大题共4小题，共20分。

在每小题有多项符合题目要求）9.已知等差数列{a n}的前n项和为S n，a1<0，S7=S12，则( )A. 数列{a n }是递减数列B. a 10=0C. S n <0时，n 的最大值是18D. S 2<S 1610.已知抛物线y 2=4x 的焦点为F ，顶点为O ，过点F 的直线l 与抛物线交于A ，B 两点，A 在第一象限，若|AF|=3|FB|，则下列结论正确的是( ) A. 直线l 的斜率为√ 3 B. 线段AB 的长度为163C. OA ⊥OBD. 以AF 为直径的圆与y 轴相切11.已知F 1，F 2是椭圆x 2a 12+y 2b 12=1(a 1>b 1>0)和双曲线x 2a 22−y 2b 22=1(a 2>0,b 2>0)的公共焦点，P 是它们的一个公共点，且∠F 1PF 2=π3，则以下结论正确的是 ( )A. a 12−b 12=a 22−b 22 B. b 12=3b 22 C. 14e 12+14e 22=1D. e 12+e 22的最小值为1+√ 3212.数学家华罗庚曾说：“数缺形时少直观，形少数时难入微.”事实上，很多代数问题可以转化为几何问题加以解决.例如，与√ (x −a)2+(y −b)2相关的代数问题，可以转化为点A(x,y)与点B(a,b)之间的距离的几何问题.结合上述观点，下列结论正确的是( )A. 函数f(x)=√ x 2+4x +8−√ x 2−4x +8有1个零点B. 函数g(x)=√ x 2+4x +8−√ x 2−4x +8−2有2个零点C. 函数ℎ(x)=√ x 2+4x +8+√ x 2−4x +8有最小值4√ 2D. 关于x 的方程√ x 2+4x +8+√ x 2−4x +8=6的解为x =±3√ 55三、填空题（本大题共4小题，共20分） 13.经过A (2,√ 22)，B (√ 2,√ 32)两点的椭圆的标准方程为______．14.设双曲线C ：x 2a 2−y 2b2=1(a >0,b >0)的左、右焦点分别为F 1，F 2，若过点F 2且斜率为√ 3的直线l 与双曲线的右支交于A ，B 两点，则该双曲线的离心率的取值范围为________________．15.如图所示，高脚杯的轴截面为抛物线，往杯中缓慢倒水，当杯中的水深为2cm时，水面宽度为6cm，当水面再上升1cm时，水面宽度为________cm．16.已知数列{a n}满足a2n−a2n−1=3n−2，a2n+1+a2n=3n−1(n∈N∗)，则数列{a n}的前40项和2S40=．四、解答题（本大题共6小题，共72分。

圆锥曲线高考题精讲 2

y
A
60
o
B
F
x
2 y2 x 15、椭圆 1 的左焦点为 F，直线 x=m 与椭圆相交 4 3
于点 A,B，当 FAB 的周长最大时， FAB 的面积是________。
3
[解] | AF 1 | | BF 1 | | AB | 4a, 而| A 1F 1 | | B 1F 1 | | A 1B 1 | | A 1F 1 | | B 1F 1 | | A 1F 2 | | B 1F 2 | 4a,
k2 3 . 2
2 y2 x 20、如图，椭圆 C0 : 2 2 1(a b 0, a，b 为常数)， a b 2 动圆 C1 : x2 y 2 t1 ， b t1 a .点 A 1, A 2 分别为 C0 的左，右顶点， C1 与 C0 相交于 A，B，C，D 四点. (1)求直线 AA 1 与直线 A 2 B 交点 M 的轨迹方程;
x
16. (key)5 / 6
y
n
B
n
o
m
A
m
F
x
y
M
o
N
A x
17 .
y
M
oБайду номын сангаас
N
A x
2 x 18、已知椭圆 C1 : y2 1, 椭圆 C2 以 C1 的长轴为短轴，且与 4 （1）求椭圆 C2 的方程；（2）设 O 为坐标原点， C1 有相同的离心率。
点 A，B 分别在椭圆 C1 和 C2 上， OB 2OA ，求直线 AB 的方程。
2 2
且 a, b, c 互不相同，在所有这些方程所表示的曲线中，不同的抛物线共有（ B ）条 A、28 B、32 C、36 D、48

(完整版)圆锥曲线的综合经典例题(含答案解析)

经典例题精析类型一：求曲线的标准方程1. 求中心在原点,一个焦点为且被直线截得的弦AB的中点横坐标为的椭圆标准方程.思路点拨：先确定椭圆标准方程的焦点的位置（定位），选择相应的标准方程，再利用待定系数法确定、（定量）.解析：方法一：因为有焦点为，所以设椭圆方程为，,由，消去得，所以解得故椭圆标准方程为方法二：设椭圆方程,,,因为弦AB中点,所以，由得,（点差法）所以又故椭圆标准方程为.举一反三：【变式】已知椭圆在x轴上的一个焦点与短轴两端点连线互相垂直，且该焦点与长轴上较近的端点的距离为.求该椭圆的标准方程.【答案】依题意设椭圆标准方程为()，并有，解之得，,∴椭圆标准方程为2．根据下列条件，求双曲线的标准方程.（1）与双曲线有共同的渐近线，且过点；（2）与双曲线有公共焦点，且过点解析：（1）解法一：设双曲线的方程为由题意，得，解得，所以双曲线的方程为解法二：设所求双曲线方程为（），将点代入得，所以双曲线方程为即（2）解法一：设双曲线方程为－=1由题意易求又双曲线过点，∴又∵，∴，故所求双曲线的方程为.解法二：设双曲线方程为，将点代入得，所以双曲线方程为.总结升华：先根据已知条件确定双曲线标准方程的焦点的位置（定位），选择相应的标准方程，再利用待定系数法确定、.在第（1）小题中首先设出共渐近线的双曲线系方程.然后代点坐标求得方法简便.第（2）小题实轴、虚轴没有唯一给出.故应答两个标准方程.(1)求双曲线的方程，关键是求、，在解题过程中应熟悉各元素（、、、及准线）之间的关系，并注意方程思想的应用.(2)若已知双曲线的渐近线方程，可设双曲线方程为（）.举一反三：【变式】求中心在原点，对称轴在坐标轴上且分别满足下列条件的双曲线的标准方程.（1）一渐近线方程为，且双曲线过点.（2）虚轴长与实轴长的比为，焦距为10.【答案】（1）依题意知双曲线两渐近线的方程是,故设双曲线方程为，∵点在双曲线上，∴，解得，∴所求双曲线方程为.（2）由已知设, ,则()依题意，解得.∴双曲线方程为或.3．求满足下列条件的抛物线的标准方程，并求对应抛物线的准线方程：（1）过点；（2）焦点在直线：上思路点拨：从方程形式看，求抛物线的标准方程仅需确定一次项系数；从实际分析，一般需结合图形确定开口方向和一次项系数两个条件，否则，应展开相应的讨论解析：（1）∵点在第二象限，∴抛物线开口方向上或者向左当抛物线开口方向左时，设所求的抛物线方程为（），∵过点，∴，∴，∴，当抛物线开口方向上时，设所求的抛物线方程为（），∵过点，∴，∴，∴，∴所求的抛物线的方程为或，对应的准线方程分别是，.（2）令得，令得，∴抛物线的焦点为或当焦点为时，，∴，此时抛物线方程；焦点为时，，∴，此时抛物线方程为∴所求的抛物线的方程为或，对应的准线方程分别是，.总结升华：这里易犯的错误就是缺少对开口方向的讨论，先入为主，设定一种形式的标准方程后求解，以致失去一解.求抛物线的标准方程关键是根据图象确定抛物线开口方向，选择适当的方程形式，准确求出焦参数P.举一反三：【变式1】分别求满足下列条件的抛物线的标准方程.（1）焦点为F(4,0)；（2）准线为；（3）焦点到原点的距离为1；（4）过点（1，－2）；（5）焦点在直线x-3y+6=0上.【答案】（1）所求抛物线的方程为y2=16x；（2）所求抛物线的标准方程为x2=2y；（3）所求抛物线的方程y2=±4x或x2=±4y；（4）所求抛物线的方程为或；（5）所求抛物线的标准方程为y2=－24x或x2=8y.【变式2】已知抛物线的顶点在原点，焦点在轴负半轴上，过顶点且倾角为的弦长为，求抛物线的方程.【答案】设抛物线方程为()，又弦所在直线方程为由，解得两交点坐标,∴，解得.∴抛物线方程为.类型二：圆锥曲线的焦点三角形4．已知、是椭圆（）的两焦点，P是椭圆上一点，且，求的面积.思路点拨：如图求的面积应利用，即.关键是求.由椭圆第一定义有,由余弦定理有，易求之.解析：设,,依题意有(1)2-(2)得，即.∴.举一反三：【变式1】设为双曲线上的一点，是该双曲线的两个焦点，若，则的面积为（）A．B．C．D．【答案】依据双曲线的定义有，由得、，又，则，即，所以，故选A.【变式2】已知双曲线实轴长6，过左焦点的弦交左半支于、两点，且，设右焦点，求的周长.【答案】：由双曲线的定义有: ，，两式左、右分别相加得(.即∴.故的周长.【变式3】已知椭圆的焦点是,直线是椭圆的一条准线.①求椭圆的方程；②设点P在椭圆上,且,求.【答案】① .②设则，又.【变式4】已知双曲线的方程是.（1）求这双曲线的焦点坐标、离心率和渐近线方程；（2）设和是双曲线的左、右焦点，点在双曲线上，且，求的大小【答案】（1）由得，∴，，.焦点、，离心率，渐近线方程为.（2），∴∴【变式5】中心在原点，焦点在x轴上的一个椭圆与双曲线有共同焦点和，且，又椭圆长半轴与双曲线实半轴之差为4，离心率之比.（1）求椭圆与双曲线的方程；（2）若为这两曲线的一个交点，求的余弦值.【答案】（1）设椭圆方程为()，双曲线方程，则，解得∵,∴, .故所求椭圆方程为，双曲线方程为.（2）由对称性不妨设交点在第一象限.设、.由椭圆、双曲线的定义有:解得由余弦定理有.类型三：离心率5．已知椭圆上的点和左焦点，椭圆的右顶点和上顶点，当，（O为椭圆中心）时，求椭圆的离心率.思路点拨：因为，所以本题应建立、的齐次方程，使问题得以解决.解析：设椭圆方程为（），，，则，即.∵，∴，即，∴.又∵，∴.总结升华：求椭圆的离心率，即求的比值，则可由如下方法求.（1）可直接求出、；（2）在不好直接求出、的情况下，找到一个关于、的齐次等式或、用同一个量表示；（3）若求的取值范围，则想办法找不等关系.举一反三：【变式1】如图，和分别是双曲线的两个焦点，和是以为圆心，以为半径的圆与该双曲线左支的两个交点，且是等边三角形，则双曲线的离心率为（）A．B．C．D．【答案】连接，则是直角三角形，且，令，则，，即，，所以，故选D.【变式2】已知椭圆（）与x轴正半轴交于A点，与y轴正半轴交于B点，F点是左焦点，且，求椭圆的离心率.法一：,,∵, ∴,又,，代入上式，得，利用代入，消得,即由，解得,∵,∴.法二：在ΔABF中，∵，，∴，即下略）【变式3】如图，椭圆的中心在原点, 焦点在x轴上, 过其右焦点F作斜率为1的直线, 交椭圆于A、B两点, 若椭圆上存在一点C, 使. 求椭圆的离心率.【答案】设椭圆的方程为（），焦距为,则直线l的方程为:,由，消去得,设点、,则∵＋, ∴C点坐标为.∵C点在椭圆上,∴.∴∴又∴∴【变式4】设、为椭圆的两个焦点，点是以为直径的圆与椭圆的交点，若，则椭圆离心率为_____.【答案】如图，点满足，且.在中，有：∵，∴,令此椭圆方程为则由椭圆的定义有,,∴又∵，∴，，∴∴，∴，即.6．已知、为椭圆的两个焦点，为此椭圆上一点，且.求此椭圆离心率的取值范围；解析：如图，令, ,,则在中，由正弦定理，∴，令此椭圆方程为(),则,,∴即（），∴, ∴,∵,且为三角形内角，∴，∴,∴, ∴.即此椭圆离心率的取值范围为.举一反三：【变式1】已知椭圆，F1，F2是两个焦点，若椭圆上存在一点P，使，求其离心率的取值范围.【答案】△F1PF2中，已知，|F1F2|=2c，|PF1|+|PF2|=2a，由余弦定理：4c2=|PF1|2+|PF2|2-2|PF1||PF2|cos120°①又|PF1|+|PF2|=2a ②联立①②得4c2=4a2-|PF1||PF2|，∴【变式2】椭圆的焦点为，，两条准线与轴的交点分别为，若，则该椭圆离心率的取值范围是（）Ａ．Ｂ．Ｃ．Ｄ．【答案】由得，即，解得，故离心率.所以选D.【变式3】椭圆中心在坐标系原点，焦点在x轴上，过椭圆左焦点F的直线交椭圆P、Q两点，且OP⊥OQ，求其离心率e的取值范围．【答案】e∈[,1)【变式4】双曲线(a＞1,b＞0)的焦距为2c,直线过点(a,0)和(0,b),且点(1,0)到直线的距离与点(-1,0)到直线的距离之和s≥c．求双曲线的离心率e的取值范围．【答案】直线的方程为bx+ay-ab=0．由点到直线的距离公式,且a＞1,得到点(1,0)到直线的距离．同理得到点(-1,0)到直线的距离．=．由s≥c,得≥c,即5a≥2c2．于是得5≥2e2．即4e4-25e2+25≤0．解不等式,得≤e2≤5．由于e＞1,所以e的取值范围是．类型五：轨迹方程7．已知中，,,为动点，若、边上两中线长的和为定值15.求动点的轨迹方程.思路点拨：充分利用定义直接写出方程是求轨迹的直接法之一.应给以重视解法一：设动点,且,则、边上两中点、的坐标分别为,.∵,∴,即.从上式知，动点到两定点,的距离之和为常数30，故动点的轨迹是以,为焦点且,,的椭圆，挖去点.∴动点的轨迹方程是().解法二：设的重心，,动点,且，则.∴点的轨迹是以,为焦点的椭圆（挖去点），且,,.其方程为().又, 代入上式，得()为所求.总结升华：求动点的轨迹，首先要分析形成轨迹的点和已知条件的内在联系，选择最便于反映这种联系的坐标形式，建立等式，利用直接法或间接法得到轨迹方程.举一反三：【变式1】求过定点且和圆:相切的动圆圆心的轨迹方程.【答案】设动圆圆心, 动圆半径为,.（1）动圆与圆外切时，，（2）动圆与圆内切时，，由（1）、（2）有.∴动圆圆心M的轨迹是以、为焦点的双曲线，且,,.故动圆圆心的轨迹方程为.【变式3】已知圆的圆心为M1，圆的圆心为M2，一动圆与这两个圆外切，求动圆圆心P的轨迹方程.【答案】设动圆圆心P（x，y），动圆的半径为R，由两圆外切的条件可得：，.∴.∴动圆圆心P的轨迹是以M1、M2为焦点的双曲线的右支，其中c=4，a=2，∴b2=12，故所求轨迹方程为.【变式4】若动圆与圆:相外切，且与直线:相切，求动圆圆心的轨迹方程.法一：设,动圆半径，动圆与直线切于点，点.依题意点在直线的左侧，故∵,∴.化简得, 即为所求.法二：设,作直线：.过作于，交于，依题意有, ∴,由抛物线定义可知，点的轨迹是以为顶点，为焦点，：为准线的抛物线.故为所求.。

高中生圆锥曲线练习题及讲解

高中生圆锥曲线练习题及讲解圆锥曲线是高中数学中的一个重要概念，通常包括椭圆、双曲线和抛物线。

下面是一些圆锥曲线的练习题以及相应的讲解。

### 练习题1：椭圆的标准方程给定一个椭圆的两个焦点距离为2c，且长轴长度为2a，求椭圆的标准方程。

解答步骤：1. 根据椭圆的性质，我们知道长轴和短轴的关系为 \( a^2 = b^2 +c^2 \)。

2. 题目给出 \( 2c \) 和 \( 2a \)，可以求出 \( c \) 和 \( a \) 的值。

3. 将 \( c \) 和 \( a \) 的值代入上述公式，求出 \( b \) 的值。

4. 最终，椭圆的标准方程为 \( \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 \)。

### 练习题2：双曲线的渐近线已知双曲线的方程为 \( \frac{x^2}{a^2} - \frac{y^2}{b^2} = 1 \)，求其渐近线方程。

解答步骤：1. 双曲线的渐近线方程可以通过 \( \frac{x^2}{a^2} -\frac{y^2}{b^2} = 0 \) 得到。

2. 将上述方程简化，得到 \( y = \pm \frac{b}{a}x \)。

3. 这就是双曲线的渐近线方程。

### 练习题3：抛物线的焦点和准线给定抛物线的方程 \( y^2 = 4ax \)，求其焦点和准线。

解答步骤：1. 抛物线的焦点位于 \( (a, 0) \)。

2. 准线方程为 \( x = -a \)。

3. 焦点和准线是抛物线的重要特征，可以通过方程直接得出。

### 练习题4：圆锥曲线的参数方程已知椭圆的参数方程为 \( x = a \cos(\theta) \) 和 \( y = b\sin(\theta) \)，求其标准方程。

解答步骤：1. 将参数方程中的 \( \cos(\theta) \) 和 \( \sin(\theta) \) 替换为 \( x/a \) 和 \( y/b \)。

圆锥曲线综合精讲精炼

圆锥曲线综合精讲精炼知识点睛一、圆锥曲线的几何特征综合注：只讨论了其中一种情况二、圆锥曲线与直线的位置关系 1. 圆锥曲线与直线的交点的个数问题把圆锥曲线方程与直线方程联立消去y (或x )，整理得到关于x (或y )的方程20ax bx c ++=(或20ay by c ++=)，判断方程的解的个数．2. 圆锥曲线与直线的相交弦长问题设斜率为(0)k k ≠的直线l 与圆锥曲线C 相交于A ，B 两点，11()A x y ，，22()B x y ，，则1212||||AB x x y y==-=-．3.弦的中点问题点差法在求解圆锥曲线并且题目中交代直线与圆锥曲线相交和被截的线段的中点坐标时，设出直线与圆锥曲线的两个交点坐标，代入圆锥曲线的方程并作差，从而求出直线的斜率，然后利用中点坐标求出直线方程．精讲精练1.实数变量m，n满足221m n+=，则坐标()m n mn+，表示的点的轨迹是（）A．椭圆B．双曲线的一支C．抛物线D．抛物线的一部分2.已知抛物线24y x=的准线与双曲线2221(0)xy aa-=>相交于A，B两点，且F是抛物线的焦点，若△F AB是直角三角形，则双曲线的离心率为（）ABC．2 D．33.已知M是214y x=上一点，F为抛物线的焦点．若点A在圆22(1)(4)1C x y-+-=：上，则||||MA MF+的最小值为（）A．2B．4C．8D．104.已知抛物线22(0)y px p=>上一点(1)(0)M m m>，到其焦点的距离为5，双曲线2221(0)xy aa-=>的左顶点为A，若双曲线的一条渐近线与直线AM平行，则实数a的值是（）A．19B．125C．15D．135. 已知(07)A ，，(07)B -，，(122)C ，，以C 为一个焦点的椭圆经过A ，B 两点，则椭圆的另一个焦点F 的轨迹方程是（）A ．221(1)48x y y -=-≤ B ．221(1)48x y y -=≥ C ．221(1)48y x x -=-≤D ．221(1)48y x x -=≥6. 设点A 为圆22(1)1x y -+=上的动点，P A 是圆的切线，且||1PA =，则P 点的轨迹方程为（）A ．22y x =B ．22(1)4x y -+=C ．22y x =-D ．22(1)2x y -+=7. 已知抛物线28y x =的焦点为F ，直线(2)y k x =-与此抛物线相交于P ，Q 两点，则11||||FP FQ +=（） A ．12B ．1C ．2D ．48. 已知椭圆C ：22221(0)x y a b a b+=>>的左焦点为F ，椭圆C 与过原点的直线相交于A ，B 两点，连接AF ，BF ．若||10AB =，||6AF =，4cos 5ABF ∠=，则C 的离心率e =__________．9. 点P 是双曲线221221(00)x y C a b a b-=>>：，与圆2222x y a b +=+的一个交点，且21122PF F PF F ∠=∠，其中1F ，2F 分别是双曲线1C 的左、右焦点，则双曲线1C 的离心率为__________．10. 椭圆22143x y +=的左焦点为F ，直线x =m 与椭圆相交于点A ，B ．当△F AB 的周长最大时，△F AB 的面积是__________．11. 椭圆2212x y +=的一条弦被点11( )22，平分，则这条弦所在的直线方程是__________________．12. 如图，设P 是圆2225x y +=上的动点，点D 是P 在x 轴上的投影，M 为PD上一点，且4||||5MD PD =．（1）当P 在圆上运动时，求点M 的轨迹C 的方程；（2）求过点(3 0)，且斜率为45的直线被C 所截线段的长度．13. 已知椭圆22114xC y +=：，椭圆2C 以1C 的长轴为短轴，且与离心率．（1）求椭圆2C 的方程；（2）设O 为坐标原点，点A ，B 分别在椭圆1C ，2C 上，若 =2OB OA −→−→，求直线AB 的方程．14. 如图，双曲线22221(00)x y a b a b-=>>，的一条渐近线方程是y =，坐标原点到直线AB 的距离为32，其中(0)A a ，，(0)B b -，．（1）求双曲线的方程；（2）若1B 是双曲线虚轴在y 轴正半轴上的端点，过点B 作直线交双曲线于点M ，N ，求11B M B N ⊥时，直线MN 的方程．回顾与思考________________________________________________________ ________________________________________________________ _______________________________________________________ 【参考答案】知识点睛一、222c a b=-222c a b=+精讲精练1．D 2．B 3．B 4．D5．A6．D 7．A8．5 7910．3 11．1324 y x=-+12．（1）2212516x y+=；（2）41513．（1）221416x y+=；（2）y x=±14．（1）22139x y-=；（2）3y=-。

专题50 圆锥曲线(多选题部分)(解析版)

专题50 圆锥曲线（多选题部分）一、题型选讲题型一、圆锥曲线定义与性质的考查例1、（202年山东卷）已知曲线22:1C mx ny +=（） A ．若0m =，0n >，则C 是两条直线 B ．若0m n =>，则CC ．若0m n >>，则C 是椭圆，其焦点在x 轴上D ．若0mn <，则C是双曲线，其渐近线方程为y = 【答案】AD【详解】对于A ，若0m =，0n >，则2:1C ny =即y =，为两条直线，故A 正确；对于B ，若0m n =>，则221:C x y n +=，所以CB 错误；对于C ，若0m n >>，则110m n<<，所以22:1C mx ny +=即22:111x y C m n +=为椭圆，且焦点在y 轴上，故C 错误；对于D ，若0mn <，则22:111x y C m n +=为双曲线，且其渐近线为y ==，故D 正确.例2、已知双曲线C过点(且渐近线方程为3y x =±，则下列结论正确的是（） A ．C 的方程为2213x y -=B ．CC ．曲线21x y e -=-经过C 的一个焦点 D．直线10x -=与C 有两个公共点【答案】AC【详解】对于A：由双曲线的渐近线方程为3y x =±，可设双曲线方程为223x y λ-=，把点代入，得923λ-=，即1λ=．∴双曲线C 的方程为2213x y -=，故A 正确；对于B ：由23a =，21b =，得2c =，∴双曲线C=，故B 错误；对于C ：取20x +=，得2x =-，0y =，曲线21x y e +=-过定点(2,0)-，故C 正确；对于D ：双曲线的渐近线0x ±=，直线10x --=与双曲线的渐近线平行，直线10x -=与C 有1个公共点，故D 不正确．故选：AC ．例3、（2020·山东济南外国语学校高三月考）已知双曲线的左、右焦点分别为为双曲线上一点，且，若，则对双曲线中的有关结论正确的是（） A ．B ．C ．D ．【答案】ABCD【解析】由双曲线的定义知：，由，在中，由余弦定理可得：，22221(0,0)x y a b a b-=>>12,,F F P122PF PF =12sin 4F PF ∠=,,,a b c e e =2e =b =b =12212,4PF PF PF a PF a -==∴=12sin F PF ∠=121cos 4F PF ∠=±12PF F △222416412244a a c a a +-=±⨯⨯解得或，，或，又，可得或故选：ABCD例4、已知双曲线，若的离心率最小，则此时（）A．BC ．双曲线的一个焦点坐标为D【答案】AB【解析】因为，所以双曲线的焦点在轴上，所以，，所以．又双曲线的离心率，则．因为，所以，当且仅当，即时，等号成立，则双曲线的离心率最小时，，，，则双曲，故A ，B 正确；双曲线的焦点坐标为（，0），故C 错误；焦点，故D 错误.故选：AB ．题型二圆锥曲线的综合性问题例5、的椭圆为“黄金椭圆”．如图，已知椭圆C ：22221(0)x y a b a b +=>>，12,A A 分别为左、右顶点，1B ，2B 分别为上、下顶点，1F ，2F 分别为左、右焦点，P 为椭圆上一点，则满足下列条件能使椭圆C 为“黄金椭圆”的有（）224c a =226c a=2ce a∴==2c a ∴=c =222c a b =+b =b =()222:104x y C m m m m -=>-+C 2m =0y ±=)0m >C x 2a m =224b m m =-+224c m =+c e a =222244c m e m a m m+===+0m >244e m m =+≥=4m m=2m =C 22a =26b =28c =0y ±=±()0y +=2==A ．2112212A F F A F F ⋅= B ．11290F B A ∠=︒C ．1PF x ⊥轴，且21//PO A BD ．四边形221AB A B 的内切圆过焦点1F ，2F【答案】BD【详解】∵椭圆2222:1(0)x y C a b a b+=>>∴121212(,0),,0),(0,),(0,),(,0),(,)(0A a A a B b B b F c F c ---对于A ，若2112212A F F A F F ⋅=，则22()(2)a c c -=，∴2a c c -=，∴13e =，不满足条件，故A 不符合条件；对于B ，11290F B A ︒∠=，∴222211112A F B F B A =+ ∴2222()a c a a b +=++，∴220c ac a +-= ∴210e e +-=，解得e =e =，故B 符合条件；对于C ，1PF x ⊥轴，且21//PO A B ，∴2,b P c a ⎛⎫- ⎪⎝⎭∵21PO A B k k =∴2b c ab a =--，解得 ∵，∴b c =222a b c =+a =∴，不满足题意，故C不符合条件；对于D，四边形的内切圆过焦点即四边形的内切圆的半径为c，∴∴，∴，解得（舍去）或，∴，故D符合条件．例6、已知椭圆()22:10x yC a ba b+=>>的左、右焦点分别为1F，2F且122F F=，点()1,1P在椭圆内部，点Q在椭圆上，则以下说法正确的是（）A．1QF QP+的最小值为1B．椭圆C的短轴长可能为2C．椭圆C的离心率的取值范围为⎛⎝⎭D．若11PF FQ=，则椭圆C【答案】ACD【详解】A.因为12||2F F，所以22(1,0),||1F PF=，所以122||||||||||1QF QP QF QP PF+=+≥=，当2,,Q F P，三点共线时，取等号，故正确；B．若椭圆C的短轴长为2，则1,2b a==，所以椭圆方程为22121x y+=，11121+>，则点P在椭圆外，故错误；C．因为点(1,1)P在椭圆内部，所以111a b+<，又1a b-=，所以1b a=-，所以1111+<-a a，即2310a a-+>，解得236(1244a+++>==，12+>，所以12=<e，所以椭圆C的离心率的取值范围为，故正确；2cea===1221A B A B12,F F1221A B A B ab=422430c a c a-+=42310e e-+=235e+=235e-=51e-=D ．若11PF FQ =，则1F 为线段PQ 的中点，所以(3,1)Q --，所以911+=a b，又1a b -=，即21190-+=a a ，解得a ====，所以椭圆C，故正确．例7、（2020·山东高三开学考试）已知双曲线，过其右焦点的直线与双曲线交于两点、，则（）A ．若、同在双曲线的右支，则的斜率大于B ．若在双曲线的右支，则最短长度为C ．的最短长度为D ．满足的直线有4条【答案】BD【解析】易知双曲线的右焦点为，设点、，设直线的方程为，当时，直线的斜率为，联立，消去并整理得. 则，解得. 对于A 选项，当时，直线轴，则、两点都在双曲线的右支上，此时直线的斜率不存在，A 选项错误；对于B 选项，，B 选项正确；对于C 选项，当直线与轴重合时，，C 选项错误；对于D 选项，当直线与轴重合时，；当直线与轴不重合时，由韦达定理得，， 22:1916x y C -=F l A B A B l 43A FA 2AB 32311AB =C ()5,0F ()11,A x y ()22,B x y l 5x my =+0m ≠l 1k m=225169144x my x y =+⎧⎨-=⎩x ()221691602560m y my -++=()()222222169016042561699610m m m m ⎧-≠⎪⎨∆=-⨯-=+>⎪⎩34m ≠0m =l x ⊥A B l min 532F c a A =-=-=l x 32263AB a ==<l x 2611AB a ==≠l x 122160169m y y m +=--122256169y y m =-由弦长公式可得，解得或.故满足的直线有条，D 选项正确. 故选：BD.例8、（2020·江苏扬州中学高二月考）已知椭圆的左、右焦点分别为，且，点在椭圆内部，点在椭圆上，则以下说法正确的是（）A ．的最小值为B ．椭圆的短轴长可能为2C ．椭圆的离心率的取值范围为D ．若，则椭圆【答案】ACD【解析】A. 因为，所以，所以，当，三点共线时，取等号，故正确；B.若椭圆的短轴长为2，则，所以椭圆方程为，，则点在椭圆外，故错误；C. 因为点在椭圆内部，所以，又，所以，所以，即，解得，所以，所以椭圆的离心率的取值范围为，故正确；()2122961169m AB y y m +=-==-()226161611169m m +==-4m =±m =11AB =4()22:10x y C a b a b+=>>1F 2F 122F F =()1,1P Q 1QF QP +21a -C C ⎛ ⎝⎭11PF FQ =C 122F F =()221,0,1=F PF 1222221+=-+≥-=-QF QP a QF QP a PF a 2,,Q F P C 1,2b a ==22121x y +=11121+>P ()1,1P 111a b+<1a b -=1b a =-1111+<-a a 2310a a -+>(2136244++>==a >12=<e C 10,2⎛⎫⎪ ⎪⎝⎭D. 若，则为线段的中点，所以，所以，又，即，解得，所以椭圆的，故正确.故选：ACD例9、（2020届山东省枣庄、滕州市高三上期末）在平面直角坐标系xOy 中，抛物线2:2C y px =(0)p >的焦点为F ，准线为l.设l 与x 轴的交点为K ，P 为C 上异于O 的任意一点，P 在l 上的射影为E ，EPF ∠的外角平分线交x 轴于点Q ，过Q 作QN PE ⊥交EP 的延长线于N ，作QM PF ⊥交线段PF 于点M ，则（）A ．||||PE PF =B ．||||PF QF =C ．||||PN MF =D ．||||PN KF =【答案】ABD 【解析】由抛物线的定义，PE PF =，A 正确；∵//PN QF ，PQ 是FPN ∠的平分线，∴FQP NPQ FPQ ∠=∠=，∴||||PF QF =，B 正确；若||||PN MF =，由PQ 是外角平分线，QN PE ⊥，QM PF ⊥得QM QN =，从而有PM PN =，于是有PM FM =，这样就有QP QF =，PFQ ∆为等边三角形，60FPQ ∠=︒，也即有60FPE ∠=︒，11PF FQ =1F PQ ()3,1Q --911+=a b1a b -=21190-+=a a 21122244++===a =C这只是在特殊位置才有可能，因此C 错误；连接EF ，由A 、B 知PE QF =，又//PE QF ，EPQF 是平行四边形，∴EF PQ =，显然EK QN =，∴KF PN =，D 正确．二、达标训练1、（2020·山东高三其他模拟）关于双曲线与双曲线，下列说法正确的是（）.A ．它们有相同的渐近线B ．它们有相同的顶点C ．它们的离心率不相等D ．它们的焦距相等【答案】CD【解析】双曲线的顶点坐标，渐近线方程：，离心率为：，焦距为10．双曲线，即：，它的顶点坐标，渐近线方程：，离心率为：，焦距为10．所以它们的离心率不相等，它们的焦距相等．故选：．2、（2020届山东省滨州市高三上期末）已知双曲线C ：22221(0,0)x y a b a b -=>>的左、右焦点分别为1(5,0)F -，2(5,0)F ，则能使双曲线C 的方程为221169x y -=的是( )A ．离心率为54B ．双曲线过点95,4⎛⎫ ⎪⎝⎭C ．渐近线方程为340±=x yD ．实轴长为4【答案】ABC【解析】由题意，可得：焦点在x 轴上，且5c =；A 选项，若离心率为54，则4a =，所以2229b c a =-=，此时双曲线的方程为：221169x y -=，故A 正确；221:1916x y C -=222:1916y x C -=-221:1916x y C -=(3,0)430x y ±=53222:1916y x C -=-221169x y -=(4,0)±340±=x y 54CDB 选项，若双曲线过点95,4⎛⎫ ⎪⎝⎭，则22222812516125a b a b c ⎧⎪⎪-=⎨⎪+==⎪⎩，解得：22169a b ⎧=⎨=⎩；此时双曲线的方程为：221169x y -=，故B 正确；C 选项，若双曲线的渐近线方程为340±=x y ，可设双曲线的方程为：22(0)169x y m m -=>，所以216925c m m =+=，解得：1m =，所以此时双曲线的方程为：221169x y -=，故C 正确； D 选项，若实轴长为4，则2a =，所以22221b c a =-=，此时双曲线的方程为：224121x y -=，故D 错误；故选：ABC.3、（2020届山东省德州市高三上期末）已知抛物线2:2C y px =()0p >的焦点为F经过点F ，直线l 与抛物线C 交于点A 、B 两点（点A 在第一象限），与抛物线的准线交于点D ，若8AF =，则以下结论正确的是（） A ．4p = B ．DF FA =C ．2BD BF =D ．4BF =【答案】ABC 【解析】如下图所示：分别过点A 、B 作抛物线C 的准线m 的垂线，垂足分别为点E 、M .抛物线C 的准线m 交x 轴于点P ，则PF p =，由于直线l 60，//AE x 轴，60EAF ∴∠=，由抛物线的定义可知，AE AF =，则AEF ∆为等边三角形，60EFP AEF ∴∠=∠=，则30PEF ∠=，228AF EF PF p ∴====，得4p =，A 选项正确；2AE EF PF ==，又//PF AE ，F ∴为AD 的中点，则DF FA =，B 选项正确；60DAE ∴∠=，30ADE ∴∠=，22BD BM BF ∴==（抛物线定义），C 选项正确； 2BD BF =，118333BF DF AF ∴===，D 选项错误. 故选：ABC.4、（2020届山东省日照市高三上期末联考）过抛物线24y x =的焦点F 作直线交抛物线于A ，B 两点，M为线段AB 的中点，则（） A ．以线段AB 为直径的圆与直线32x =-相离 B ．以线段BM 为直径的圆与y 轴相切 C ．当2AF FB =时，92AB = D ．AB 的最小值为4【答案】ACD【解析】对于选项A ，点M 到准线1x =-的距离为()1122AF BF AB +=，于是以线段AB 为直径的圆与直线1x =-一定相切，进而与直线32x =-一定相离：对于选项B ，显然AB 中点的横坐标与12BM 不一定相等，因此命题错误. 对于选项C ，D ，设()11,A x y ，()22,B x y ，直线AB 方程为1x my =+，联立直线与抛物线方程可得2440y my --=，124y y =-，121=x x ，若设()24,4A a a ，则211,4B aa ⎛⎫- ⎪⎝⎭，于是21221424AB x x p a a=++=++，AB 最小值为4；当2AF FB =可得122y y =-， 142a a ⎛⎫=-- ⎪⎝⎭，所212a =，92AB =.故选:ACD.5、（2020届山东省临沂市高三上期末）已知P 是椭圆C ：2216x y +=上的动点，Q 是圆D ：()22115x y ++=上的动点，则（）A ．CB ．C 的离心率为6C ．圆D 在C 的内部D ．PQ 【答案】BC【解析】2216x y += a ∴=，1b =c ∴===C 的焦距为c e a ===.设(), P x y （x ≤≤，则()()22222256441111665555x x y x x PD ⎛⎫++=++-=++≥> ⎪⎝⎭=，所以圆D 在C 的内部，且PQ =. 故选：BC .6、（2020届山东省烟台市高三上期末）已知抛物线2:4C y x =的焦点为F 、准线为l ，过点F 的直线与抛物线交于两点()11,P x y ，()22,Q x y ，点P 在l 上的射影为1P ，则（） A ．若126x x +=，则8PQ =B ．以PQ 为直径的圆与准线l 相切C ．设()0,1M ，则1PM PP +≥D ．过点()0,1M 与抛物线C 有且仅有一个公共点的直线至多有2条【答案】ABC【解析】对于选项A,因为2p =,所以122x x PQ ++=,则8PQ =,故A 正确；对于选项B,设N 为PQ 中点,设点N 在l 上的射影为1N ,点Q 在l 上的射影为1Q ,则由梯形性质可得111222PP QQ PF QF PQ NN ++===,故B 正确；对于选项C,因为()1,0F ,所以1PM PP PM PF MF +=+≥=故C 正确；对于选项D,显然直线0x =,1y =与抛物线只有一个公共点,设过M 的直线为1y kx =+, 联立214y kx y x=+⎧⎨=⎩,可得()222410k x k x +-+=,令0∆=,则1k =,所以直线1y x =+与抛物线也只有一个公共点,此时有三条直线符合题意,故D 错误；故选：ABC7、（2020·福清西山学校高二期中）在平面直角坐标系中，动点与两个定点和连线的斜率之积等于，记点的轨迹为曲线，直线：与交于，两点，则（） A ．的方程为B ．C ．的渐近线与圆相切D ．满足的直线仅有1条【答案】AC【解析】设点，整理得，所以点的轨迹为曲线的方程为，故A 正确；又离心率，故B 不正确；圆的圆心到曲线的渐近线为的距离为，又圆的半径为1，故C 正确；直线与曲线的方程联立整理得，设，，且，xOy P ()1F)2F 13P E l ()2y k x =-E A B E 221(3x y x -=≠E E ()2221x y -+=AB =l (),P xy 13=2213x y -=P E 221(3x y x -=≠e ==()2221x y -+=()20，E y x =1d ==()2221x y -+=l E ()2221(3y k x x y x ⎧=-⎪⎨-=≠⎪⎩()222213+121230k x x k k ---=()()1122,,A B x y x y ，()()()224214441312312+1>0kk kk ∆=----=2130k -≠有，所以，要满足，则需或或，当,此时，而曲线E 上，所以满足条件的直线有两条，故D 不正确，故选：AC .2122221212123+,1313x xx k x kk k ---==--)221+13k AB k===-AB =)221+13k k=-0k =1k =1k =-0k =)()AB ，x ≠。

高考数学圆锥曲线习题精选精讲可编辑

学前教育理论与实务袁玉长春光华学院．第三章学前教育观第一节学前教育的价值第二节学前教育的发展第三节学前教育的目标第四节科学学前教育观的树立学前儿童的因材施教第五节第一节学前教育的价值一、学前教育在儿童发展中的作用学前教育对于儿童的成长至关重要。

无论是对胎儿，还是对婴儿，或是对幼儿，只要有适宜的教育和训练，就能得到很好的成长与发展。

（一）保证胎儿健康的出生胎儿在5个月，听觉系统的发育已基本完善，6－7个月时能分辨出母亲的情感。

孕妇的情绪会通过神经——体液的变化，去影响胎儿的血液供应、呼吸、胎动等。

（二）保证婴儿及时的成长婴儿期是学前儿童发展的第二个重要时期。

有研究者认为：儿童八个月-2岁这段时期是特别重要的，因为语言、好奇心、智能和社会化的发展等基础都是在此期间奠定的、脑科学研究的人员发现：每个人的学习能力的50%是在生命的头4年发展起来的，早期学习不但不会剥夺童年的换了，而且能够为儿童提供各种发展的良机。

1.母乳喂养有利于婴儿免疫能力的增强。

母乳喂养对婴儿的呼吸道有保护作用，能降低呼吸道的发病率，母乳中含有较多的疾病免疫的因子，有助于刺激婴儿免疫系统的成熟。

母乳最佳喂养方式：产后半小时开始喂奶；出生后4个月内坚持母乳喂养，4-6个月开始添加辅食，具体月龄依婴儿生长情况而定，6个月月龄的婴儿均应添加辅食。

2.母亲注意卫生保健有利于婴儿的生长发育。

在婴儿哺乳期间，母亲吸烟，分泌的乳汁会减少，并增加婴儿的支气管和肺炎发生率。

3.成人重视体育锻炼，有助于婴儿健康成长。

成人注意语言刺激有利于婴儿4.的智力发展。

成人注意激发阅读兴趣有益于5.婴儿良好品行的塑造。

．成人注意音乐刺激有助于婴儿6.的情感陶冶。

（三）保证幼儿迅速的发展1.重视体育锻炼，能促进幼儿身心健康成长。

重视音乐训练，能提高幼儿的智力水平。

2.3.幼儿期教育能为儿童做好入学准备。

研究表明：上过幼儿园的儿童与未上过幼儿园的儿童相比，适应小学生活的能力更强，语文、数学平均成绩更高，当班干部、三好学生的比例更大。

圆锥曲线习题精选精讲

圆锥曲线1.圆锥曲线的两个定义：（1）第一定义中要重视“括号”内的限制条件：椭圆中，与两个定点F 1，F 2的距离的和等于常数2a ，且此常数2a 一定要大于21F F ，当常数等于21F F 时，轨迹是线段F 1F 2，当常数小于21F F 时，无轨迹；双曲线中，与两定点F 1，F 2的距离的差的绝对值等于常数2a ，且此常数2a 一定要小于|F 1F 2|，定义中的“绝对值”与2a ＜|F 1F 2|不可忽视。

若2a ＝|F 1F 2|，则轨迹是以F 1，F 2为端点的两条射线，若2a ﹥|F 1F 2|，则轨迹不存在。

若去掉定义中的绝对值则轨迹仅表示双曲线的一支。

如（1）已知定点)0,3(),0,3(21F F -，在满足下列条件的平面上动点P 的轨迹中是椭圆的是 A ．421=+PF PF B ．621=+PF PF C ．1021=+PF PFD ．122221=+PF PF （答：C ）；（2）方程8表示的曲线是_____（答：双曲线的左支）（2）第二定义中要注意定点和定直线是相应的焦点和准线，且“点点距为分子、点线距为分母”，其商即是离心率e 。

圆锥曲线的第二定义，给出了圆锥曲线上的点到焦点距离与此点到相应准线距离间的关系，要善于运用第二定义对它们进行相互转化。

如已知点)0,22(Q 及抛物线42x y =上一动点P （x ,y ）,则y+|PQ|的最小值是_____（答：2）2.圆锥曲线的标准方程（标准方程是指中心（顶点）在原点，坐标轴为对称轴时的标准位置的方程）：（1）椭圆：焦点在x 轴上时12222=+by a x （0a b >>）⇔{cos sin x a y b ϕϕ==（参数方程，其中ϕ为参数），焦点在y 轴上时2222bx a y +＝1（0ab >>）。

方程22Ax By C +=表示椭圆的充要条件是什么？（ABC ≠0，且A ，B ，C 同号，A ≠B ）。

圆锥曲线(解析版)--2024年高考真题和模拟题数学好题汇编

圆锥曲线1(新课标全国Ⅱ卷)已知曲线C ：x 2+y 2=16(y >0)，从C 上任意一点P 向x 轴作垂线段PP ，P 为垂足，则线段PP 的中点M 的轨迹方程为()A.x 216+y 24=1(y >0)B.x 216+y 28=1(y >0)C.y 216+x 24=1(y >0)D.y 216+x 28=1(y >0)【答案】A【分析】设点M (x ,y )，由题意，根据中点的坐标表示可得P (x ,2y )，代入圆的方程即可求解.【详解】设点M (x ,y )，则P (x ,y 0),P (x ,0)，因为M 为PP 的中点，所以y 0=2y ，即P (x ,2y )，又P 在圆x 2+y 2=16(y >0)上，所以x 2+4y 2=16(y >0)，即x 216+y 24=1(y >0)，即点M 的轨迹方程为x 216+y 24=1(y >0).故选：A2(全国甲卷数学(理))已知双曲线C :y 2a 2-x 2b 2=1(a >0,b >0)的上、下焦点分别为F 10,4 ,F 20,-4 ，点P -6,4 在该双曲线上，则该双曲线的离心率为()A.4B.3C.2D.2【答案】C【分析】由焦点坐标可得焦距2c ，结合双曲线定义计算可得2a ，即可得离心率.【详解】由题意，F 10,-4 、F 20,4 、P -6,4 ，则F 1F 2 =2c =8，PF 1 =62+4+4 2=10，PF 2 =62+4-4 2=6，则2a =PF 1 -PF 2 =10-6=4，则e =2c 2a =84=2.故选：C .3(新高考天津卷)双曲线x 2a 2-y 2b 2=1(a >0，b >0)的左、右焦点分别为F 1、F 2.P 是双曲线右支上一点，且直线PF 2的斜率为2．△PF 1F 2是面积为8的直角三角形，则双曲线的方程为()A.x 28-y 22=1B.x 28-y 24=1C.x 22-y 28=1D.x 24-y 28=1【答案】C【分析】可利用△PF 1F 2三边斜率问题与正弦定理，转化出三边比例，设PF 2 =m ，由面积公式求出m ，由勾股定理得出c ，结合第一定义再求出a .【详解】如下图：由题可知，点P 必落在第四象限，∠F 1PF 2=90°，设PF 2 =m ，∠PF 2F 1=θ1,∠PF 1F 2=θ2，由k PF 2=tan θ1=2，求得sin θ1=25，因为∠F 1PF 2=90°，所以k PF 1⋅k PF 2=-1，求得k PF 1=-12，即tan θ2=12，sin θ2=15，由正弦定理可得：PF 1 :PF 2 :F 1F 2 =sin θ1:sin θ2:sin90°=2:1:5，则由PF 2 =m 得PF 1 =2m ,F 1F 2 =2c =5m ，由S △PF 1F 2=12PF 1 ⋅PF 2 =12m ⋅2m =8得m =22，则PF 2 =22,PF 1 =42,F 1F 2 =2c =210,c =10，由双曲线第一定义可得：PF 1 -PF 2 =2a =22，a =2,b =c 2-a 2=8，所以双曲线的方程为x 22-y 28=1.故选：C4(新课标全国Ⅰ卷)(多选)造型可以做成美丽的丝带，将其看作图中曲线C 的一部分.已知C 过坐标原点O .且C 上的点满足横坐标大于-2，到点F (2,0)的距离与到定直线x =a (a <0)的距离之积为4，则()A.a =-2B.点(22,0)在C 上C.C 在第一象限的点的纵坐标的最大值为1D.当点x 0,y 0 在C 上时，y 0≤4x 0+2【答案】ABD【分析】根据题设将原点代入曲线方程后可求a，故可判断A的正误，结合曲线方程可判断B的正误，利用特例法可判断C的正误，将曲线方程化简后结合不等式的性质可判断D的正误.【详解】对于A：设曲线上的动点P x,y，则x>-2且x-22+y2×x-a=4，因为曲线过坐标原点，故0-22+02×0-a=4，解得a=-2，故A正确.对于B：又曲线方程为x-22+y2×x+2=4，而x>-2，故x-22+y2×x+2=4.当x=22,y=0时，22-22×22+2=8-4=4，故22,0在曲线上，故B正确.对于C：由曲线的方程可得y2=16x+22-x-22，取x=32，则y2=6449-14，而6449-14-1=6449-54=256-24549×4>0，故此时y2>1，故C在第一象限内点的纵坐标的最大值大于1，故C错误.对于D：当点x0,y0在曲线上时，由C的分析可得y20=16x0+22-x0-22≤16x0+22，故-4x0+2≤y0≤4x0+2，故D正确.故选：ABD.【点睛】思路点睛：根据曲线方程讨论曲线的性质，一般需要将曲线方程变形化简后结合不等式的性质等来处理.5(新课标全国Ⅱ卷)(多选)抛物线C：y2=4x的准线为l，P为C上的动点，过P作⊙A:x2+(y-4)2=1的一条切线，Q为切点，过P作l的垂线，垂足为B，则()A.l与⊙A相切B.当P，A，B三点共线时，|PQ|=15C.当|PB|=2时，PA⊥ABD.满足|PA|=|PB|的点P有且仅有2个【答案】ABD【分析】A选项，抛物线准线为x=-1，根据圆心到准线的距离来判断；B选项，P,A,B三点共线时，先求出P 的坐标，进而得出切线长；C选项，根据PB=2先算出P的坐标，然后验证k PA k AB=-1是否成立；D选项，根据抛物线的定义，PB=PF，于是问题转化成PA=PF的P点的存在性问题，此时考察AF的中垂线和抛物线的交点个数即可，亦可直接设P点坐标进行求解.【详解】A选项，抛物线y2=4x的准线为x=-1，⊙A的圆心(0,4)到直线x=-1的距离显然是1，等于圆的半径，故准线l和⊙A相切，A选项正确；B选项，P,A,B三点共线时，即PA⊥l，则P的纵坐标y P=4，由y2P=4x P，得到x P=4，故P(4,4)，此时切线长PQ=PA2-r2=42-12=15，B选项正确；C选项，当PB=2时，xP=1，此时y2P=4x P=4，故P(1,2)或P(1,-2)，当P(1,2)时，A(0,4),B(-1,2)，k PA=4-20-1=-2，k AB=4-20-(-1)=2，不满足k PA k AB=-1；当P(1,-2)时，A(0,4),B(-1,2)，k PA=4-(-2)0-1=-6，k AB=4-(-2)0-(-1)=6，不满足k PA k AB=-1；于是PA⊥AB不成立，C选项错误；D选项，方法一：利用抛物线定义转化根据抛物线的定义，PB=PF，这里F(1,0)，于是PA=PB时P点的存在性问题转化成PA=PF时P点的存在性问题，A(0,4),F(1,0)，AF中点12,2，AF中垂线的斜率为-1kAF =14，于是AF的中垂线方程为：y=2x+158，与抛物线y2=4x联立可得y2-16y+30=0，Δ=162-4×30=136>0，即AF的中垂线和抛物线有两个交点，即存在两个P点，使得PA=PF，D选项正确.方法二：(设点直接求解)设Pt24,t，由PB⊥l可得B-1,t，又A(0,4)，又PA=PB，根据两点间的距离公式，t416+(t-4)2=t24+1，整理得t2-16t+30=0，Δ=162-4×30=136>0，则关于t的方程有两个解，即存在两个这样的P点，D选项正确.故选：ABD6(新课标全国Ⅰ卷)设双曲线C:x2a2-y2b2=1(a>0,b>0)的左右焦点分别为F1、F2，过F2作平行于y轴的直线交C于A，B两点，若|F1A|=13,|AB|=10，则C的离心率为．【答案】3 2【分析】由题意画出双曲线大致图象，求出AF2，结合双曲线第一定义求出AF1，即可得到a,b,c的值，从而求出离心率.【详解】由题可知A ,B ,F 2三点横坐标相等，设A 在第一象限，将x =c 代入x 2a 2-y 2b 2=1得y =±b 2a ，即A c ,b 2a ,B c ,-b 2a ，故AB =2b 2a =10，AF 2 =b 2a=5，又AF 1 -AF 2 =2a ，得AF 1 =AF 2 +2a =2a +5=13，解得a =4，代入b 2a=5得b 2=20，故c 2=a 2+b 2=36,，即c =6，所以e =c a =64=32.故答案为：327(新高考北京卷)已知抛物线y 2=16x ，则焦点坐标为．【答案】4,0【分析】形如y 2=2px ,p ≠0 的抛物线的焦点坐标为p2,0，由此即可得解.【详解】由题意抛物线的标准方程为y 2=16x ，所以其焦点坐标为4,0 .故答案为：4,0 .8(新高考北京卷)已知双曲线x 24-y 2=1，则过3,0 且和双曲线只有一个交点的直线的斜率为．【答案】±12【分析】首先说明直线斜率存在，然后设出方程，联立双曲线方程，根据交点个数与方程根的情况列式即可求解.【详解】联立x =3与x 24-y 2=1，解得y =±52，这表明满足题意的直线斜率一定存在，设所求直线斜率为k ，则过点3,0 且斜率为k 的直线方程为y =k x -3 ，联立x 24-y 2=1y =k x -3 ，化简并整理得：1-4k 2x 2+24k 2x -36k 2-4=0，由题意得1-4k 2=0或Δ=24k 2 2+436k 2+4 1-4k 2 =0，解得k =±12或无解，即k =±12，经检验，符合题意.故答案为：±12.9(新高考天津卷)(x -1)2+y 2=25的圆心与抛物线y 2=2px (p >0)的焦点F 重合，A 为两曲线的交点，则原点到直线AF 的距离为．【答案】45/0.8【分析】先求出圆心坐标，从而可求焦准距，再联立圆和抛物线方程，求A 及AF 的方程，从而可求原点到直线AF 的距离.【详解】圆(x -1)2+y 2=25的圆心为F 1,0 ，故p2=1即p =2，由x -12+y 2=25y 2=4x可得x 2+2x -24=0，故x =4或x =-6(舍)，故A 4,±4 ，故直线AF :y =±43x -1 即4x -3y -4=0或4x +3y -4=0，故原点到直线AF 的距离为d =45=45，故答案为：4510(新高考上海卷)已知抛物线y 2=4x 上有一点P 到准线的距离为9，那么点P 到x 轴的距离为．【答案】42【分析】根据抛物线的定义知x P =8，将其再代入抛物线方程即可.【详解】由y 2=4x 知抛物线的准线方程为x =-1，设点P x 0,y 0 ，由题意得x 0+1=9，解得x 0=8，代入抛物线方程y 2=4x ，得y 20=32，解得y 0=±42，则点P 到x 轴的距离为42．故答案为：42．11(新课标全国Ⅰ卷)已知A (0,3)和P 3,32 为椭圆C :x 2a 2+y 2b 2=1(a >b >0)上两点.(1)求C 的离心率;(2)若过P 的直线l 交C 于另一点B ，且△ABP 的面积为9，求l 的方程．【答案】(1)12(2)直线l 的方程为3x -2y -6=0或x -2y =0.【分析】(1)代入两点得到关于a ,b 的方程，解出即可；(2)方法一：以AP 为底，求出三角形的高，即点B 到直线AP 的距离，再利用平行线距离公式得到平移后的直线方程，联立椭圆方程得到B 点坐标，则得到直线l 的方程；方法二：同法一得到点B 到直线AP 的距离，再设B x 0,y 0 ，根据点到直线距离和点在椭圆上得到方程组，解出即可；法三：同法一得到点B 到直线AP 的距离，利用椭圆的参数方程即可求解；法四：首先验证直线AB 斜率不存在的情况，再设直线y =kx +3，联立椭圆方程，得到点B 坐标，再利用点到直线距离公式即可；法五：首先考虑直线PB 斜率不存在的情况，再设PB :y -32=k (x -3)，利用弦长公式和点到直线的距离公式即可得到答案；法六：设线法与法五一致，利用水平宽乘铅锤高乘12表达面积即可.【详解】(1)由题意得b=39a2+94b2=1，解得b2=9a2=12，所以e=1-b2a2=1-912=12.(2)法一：k AP=3-320-3=-12，则直线AP的方程为y=-12x+3，即x+2y-6=0，AP=0-32+3-3 22=352，由(1)知C:x212+y29=1，设点B到直线AP的距离为d，则d=2×9352=1255，则将直线AP沿着与AP垂直的方向平移1255单位即可，此时该平行线与椭圆的交点即为点B，设该平行线的方程为：x+2y+C=0，则C+65=1255，解得C=6或C=-18，当C=6时，联立x212+y29=1x+2y+6=0，解得x=0y=-3或x=-3y=-32，即B0,-3或-3,-3 2，当B0,-3时，此时k l=32，直线l的方程为y=32x-3，即3x-2y-6=0，当B-3,-3 2时，此时k l=12，直线l的方程为y=12x，即x-2y=0，当C=-18时，联立x212+y29=1x+2y-18=0得2y2-27y+117=0，Δ=272-4×2×117=-207<0，此时该直线与椭圆无交点.综上直线l的方程为3x-2y-6=0或x-2y=0.法二：同法一得到直线AP的方程为x+2y-6=0，点B到直线AP的距离d=125 5，设B x0,y0，则x0+2y0-65=1255x2012+y209=1，解得x0=-3y0=-32或x0=0y0=-3，即B0,-3或-3,-3 2，以下同法一.法三：同法一得到直线AP的方程为x+2y-6=0，点B到直线AP的距离d=125 5，设B 23cos θ,3sin θ ，其中θ∈0,2π ，则有23cos θ+6sin θ-6 5=1255，联立cos 2θ+sin 2θ=1，解得cos θ=-32sin θ=-12或cos θ=0sin θ=-1，即B 0,-3 或-3,-32，以下同法一；法四：当直线AB 的斜率不存在时，此时B 0,-3 ，S △PAB =12×6×3=9，符合题意，此时k l =32，直线l 的方程为y =32x -3，即3x -2y -6=0，当线AB 的斜率存在时，设直线AB 的方程为y =kx +3，联立椭圆方程有y =kx +3x 212+y 29=1，则4k 2+3 x 2+24kx =0，其中k ≠k AP ，即k ≠-12，解得x =0或x =-24k 4k 2+3，k ≠0，k ≠-12，令x =-24k 4k 2+3，则y =-12k 2+94k 2+3，则B -24k 4k 2+3,-12k 2+94k 2+3同法一得到直线AP 的方程为x +2y -6=0，点B 到直线AP 的距离d =1255，则-24k4k 2+3+2×-12k 2+94k 2+3-65=1255，解得k =32，此时B -3,-32 ，则得到此时k l =12，直线l 的方程为y =12x ，即x -2y =0，综上直线l 的方程为3x -2y -6=0或x -2y =0.法五：当l 的斜率不存在时，l :x =3,B 3,-32,PB =3,A 到PB 距离d =3，此时S △ABP =12×3×3=92≠9不满足条件.当l 的斜率存在时，设PB :y -32=k (x -3)，令P x 1,y 1 ,B x 2,y 2 ，y =k (x -3)+32x 212+y 29=1 ，消y 可得4k 2+3 x 2-24k 2-12k x +36k 2-36k -27=0，Δ=24k 2-12k 2-44k 2+3 36k 2-36k -27 >0，且k ≠k AP ，即k ≠-12，x 1+x 2=24k 2-12k 4k 2+3x 1x 2=36k 2-36k -274k 2+3,PB =k 2+1x 1+x 2 2-4x 1x 2=43k 2+13k 2+9k +2744k 2+3 ，A 到直线PB 距离d =3k +32k 2+1,S △PAB =12⋅43k 2+13k 2+9k +2744k 2+3⋅3k +32 k 2+1=9，∴k =12或32，均满足题意，∴l :y =12x 或y =32x -3，即3x -2y -6=0或x -2y =0.法六：当l 的斜率不存在时，l :x =3,B 3,-32,PB =3,A 到PB 距离d =3，此时S △ABP =12×3×3=92≠9不满足条件.当直线l 斜率存在时，设l :y =k (x -3)+32，设l 与y 轴的交点为Q ，令x =0，则Q 0,-3k +32，联立y =kx -3k +323x 2+4y 2=36，则有3+4k 2 x 2-8k 3k -32x +36k 2-36k -27=0，3+4k 2x 2-8k 3k -32x +36k 2-36k -27=0，其中Δ=8k 23k -322-43+4k 2 36k 2-36k -27 >0，且k ≠-12，则3x B =36k 2-36k -273+4k 2,x B =12k 2-12k -93+4k 2，则S =12AQ x P -x B =123k +32 12k +183+4k 2=9，解的k =12或k =32，经代入判别式验证均满足题意.则直线l 为y =12x 或y =32x -3，即3x -2y -6=0或x -2y =0.12(新课标全国Ⅱ卷)已知双曲线C :x 2-y 2=m m >0 ，点P 15,4 在C 上，k 为常数，0<k <1．按照如下方式依次构造点P n n =2,3,... ，过P n -1作斜率为k 的直线与C 的左支交于点Q n -1，令P n 为Q n -1关于y 轴的对称点，记P n 的坐标为x n ,y n .(1)若k =12，求x 2,y 2；(2)证明：数列x n -y n 是公比为1+k1-k的等比数列；(3)设S n 为△P n P n +1P n +2的面积，证明：对任意的正整数n ，S n =S n +1.【答案】(1)x 2=3，y 2=0(2)证明见解析(3)证明见解析【分析】(1)直接根据题目中的构造方式计算出P 2的坐标即可；(2)根据等比数列的定义即可验证结论；(3)思路一：使用平面向量数量积和等比数列工具，证明S n 的取值为与n 无关的定值即可.思路二：使用等差数列工具，证明S n 的取值为与n 无关的定值即可.【详解】(1)由已知有m =52-42=9，故C 的方程为x 2-y 2=9.当k =12时，过P 15,4 且斜率为12的直线为y =x +32，与x 2-y 2=9联立得到x 2-x +322=9.解得x =-3或x =5，所以该直线与C 的不同于P 1的交点为Q 1-3,0 ，该点显然在C 的左支上.故P 23,0 ，从而x 2=3，y 2=0.(2)由于过P n x n ,y n 且斜率为k 的直线为y =k x -x n +y n ，与x 2-y 2=9联立，得到方程x 2-k x -x n +y n 2=9.展开即得1-k 2 x 2-2k y n -kx n x -y n -kx n 2-9=0，由于P n x n ,y n 已经是直线y =k x -x n +y n 和x 2-y 2=9的公共点，故方程必有一根x =x n .从而根据韦达定理，另一根x =2k y n -kx n 1-k 2-x n =2ky n -x n -k 2x n1-k 2，相应的y =k x -x n +y n =y n +k 2y n -2kx n1-k 2.所以该直线与C 的不同于P n 的交点为Q n2ky n -x n -k 2x n 1-k 2,y n +k 2y n -2kx n1-k 2，而注意到Q n 的横坐标亦可通过韦达定理表示为-y n -kx n 2-91-k 2x n ，故Q n 一定在C 的左支上.所以P n +1x n +k 2x n -2ky n 1-k 2,y n +k 2y n -2kx n1-k 2.这就得到x n +1=x n +k 2x n -2ky n 1-k 2，y n +1=y n +k 2y n -2kx n1-k 2.所以x n +1-y n +1=x n +k 2x n -2ky n 1-k 2-y n +k 2y n -2kx n1-k 2=x n +k 2x n +2kx n 1-k 2-y n +k 2y n +2ky n 1-k 2=1+k 2+2k 1-k2x n -y n =1+k 1-k x n -y n .再由x 21-y 21=9，就知道x 1-y 1≠0，所以数列x n -y n 是公比为1+k 1-k 的等比数列.(3)方法一：先证明一个结论：对平面上三个点U ,V ,W ，若UV =a ,b ，UW =c ,d ，则S △UVW =12ad -bc .(若U ,V ,W 在同一条直线上，约定S △UVW =0)证明：S △UVW =12UV ⋅UW sin UV ,UW =12UV ⋅UW 1-cos 2UV ,UW =12UV⋅UW 1-UV ⋅UWUV ⋅UW 2=12UV 2⋅UW 2-UV ⋅UW 2=12a 2+b 2c 2+d 2-ac +bd2=12a 2c 2+a 2d 2+b 2c 2+b 2d 2-a 2c 2-b 2d 2-2abcd =12a 2d 2+b 2c 2-2abcd =12ad -bc2=12ad -bc .证毕，回到原题.由于上一小问已经得到x n +1=x n +k 2x n -2ky n 1-k 2，y n +1=y n +k 2y n -2kx n 1-k 2，故x n +1+y n +1=x n +k 2x n -2ky n 1-k 2+y n +k 2y n -2kx n 1-k 2=1+k 2-2k 1-k 2x n +y n=1-k1+k x n +y n .再由x 21-y 21=9，就知道x 1+y 1≠0，所以数列x n +y n 是公比为1-k 1+k 的等比数列.所以对任意的正整数m ，都有x n y n +m -y n x n +m=12x n x n +m -y n y n +m +x n y n +m -y n x n +m -12x n x n +m -y n y n +m -x n y n +m -y n x n +m =12x n -y n x n +m +y n +m -12x n +y n x n +m -y n +m =121-k 1+k m x n -y n x n +y n-121+k 1-k mx n +y n x n -y n =121-k 1+k m -1+k 1-k m x 2n -y 2n=921-k 1+k m -1+k 1-k m .而又有P n +1P n =-x n +1-x n ,-y n +1-y n ，P n +1P n +2=x n +2-x n +1,y n +2-y n +1 ，故利用前面已经证明的结论即得S n =S △P n P n +1P n +2=12-x n +1-x n y n +2-y n +1 +y n +1-y n x n +2-x n +1 =12x n +1-x n y n +2-y n +1 -y n +1-y n x n +2-x n +1 =12x n +1y n +2-y n +1x n +2 +x n y n +1-y n x n +1 -x n y n +2-y n x n +2=12921-k 1+k -1+k 1-k +921-k 1+k -1+k 1-k -921-k 1+k 2-1+k 1-k 2.这就表明S n 的取值是与n 无关的定值，所以S n =S n +1.方法二：由于上一小问已经得到x n +1=x n +k 2x n -2ky n 1-k 2，y n +1=y n +k 2y n -2kx n 1-k 2，故x n +1+y n +1=x n +k 2x n -2ky n 1-k 2+y n +k 2y n -2kx n 1-k 2=1+k 2-2k 1-k2x n +y n =1-k1+k x n +y n .再由x 21-y 21=9，就知道x 1+y 1≠0，所以数列x n +y n 是公比为1-k1+k的等比数列.所以对任意的正整数m ，都有x n y n +m -y n x n +m=12x n x n +m -y n y n +m +x n y n +m -y n x n +m -12x n x n +m -y n y n +m -x n y n +m -y n x n +m =12x n -y n x n +m +y n +m -12x n +y n x n +m -y n +m =121-k 1+k m x n -y n x n +y n-121+k 1-k mx n +y n x n -y n =121-k 1+k m -1+k 1-k m x 2n -y 2n =921-k 1+k m -1+k 1-k m.这就得到x n +2y n +3-y n +2x n +3=921-k 1+k -1+k1-k=x n y n +1-y n x n +1，以及x n +1y n +3-y n +1x n +3=921-k 1+k 2-1+k 1-k 2=x n y n +2-y n x n +2.两式相减，即得x n +2y n +3-y n +2x n +3 -x n +1y n +3-y n +1x n +3 =x n y n +1-y n x n +1 -x n y n +2-y n x n +2 .移项得到x n +2y n +3-y n x n +2-x n +1y n +3+y n x n +1=y n +2x n +3-x n y n +2-y n +1x n +3+x n y n +1.故y n +3-y n x n +2-x n +1 =y n +2-y n +1 x n +3-x n .而P n P n +3 =x n +3-x n ,y n +3-y n ，P n +1P n +2 =x n +2-x n +1,y n +2-y n +1 .所以P n P n +3 和P n +1P n +2平行，这就得到S △P n P n +1P n +2=S △P n +1P n +2P n +3，即S n =S n +1.【点睛】关键点点睛：本题的关键在于将解析几何和数列知识的结合，需要综合运用多方面知识方可得解.13(全国甲卷数学(理)(文))设椭圆C :x 2a 2+y 2b 2=1(a >b >0)的右焦点为F ，点M 1,32 在C 上，且MF ⊥x 轴．(1)求C 的方程；(2)过点P 4,0 的直线与C 交于A ,B 两点，N 为线段FP 的中点，直线NB 交直线MF 于点Q ，证明：AQ ⊥y 轴．【答案】(1)x 24+y 23=1(2)证明见解析【分析】(1)设F c ,0 ，根据M 的坐标及MF ⊥x 轴可求基本量，故可求椭圆方程.(2)设AB :y =k (x -4)，A x 1,y 1 ，B x 2,y 2 ，联立直线方程和椭圆方程，用A ,B 的坐标表示y 1-y Q ，结合韦达定理化简前者可得y 1-y Q =0，故可证AQ ⊥y 轴.【详解】(1)设F c ,0 ，由题设有c =1且b 2a =32，故a 2-1a =32，故a =2，故b =3，故椭圆方程为x 24+y 23=1.(2)直线AB 的斜率必定存在，设AB :y =k (x -4)，A x 1,y 1 ，B x 2,y 2 ，由3x 2+4y 2=12y =k (x -4) 可得3+4k 2 x 2-32k 2x +64k 2-12=0，故Δ=1024k 4-43+4k 2 64k 2-12 >0，故-12<k <12，又x 1+x 2=32k 23+4k 2,x 1x 2=64k 2-123+4k 2，而N 52,0 ，故直线BN :y =y 2x 2-52x -52 ，故y Q =-32y 2x 2-52=-3y 22x 2-5，所以y 1-y Q =y 1+3y 22x 2-5=y 1×2x 2-5 +3y 22x 2-5=k x 1-4 ×2x 2-5 +3k x 2-42x 2-5=k 2x 1x 2-5x 1+x 2 +82x 2-5=k2×64k 2-123+4k 2-5×32k 23+4k 2+82x 2-5=k128k 2-24-160k 2+24+32k 23+4k 22x 2-5=0，故y 1=y Q ，即AQ ⊥y 轴.【点睛】方法点睛：利用韦达定理法解决直线与圆锥曲线相交问题的基本步骤如下：(1)设直线方程，设交点坐标为x 1,y 1 ,x 2,y 2 ；(2)联立直线与圆锥曲线的方程，得到关于x (或y )的一元二次方程，注意Δ的判断；(3)列出韦达定理；(4)将所求问题或题中的关系转化为x 1+x 2、x 1x 2(或y 1+y 2、y 1y 2)的形式；(5)代入韦达定理求解.14(新高考北京卷)已知椭圆方程C ：x 2a 2+y 2b 2=1a >b >0 ，焦点和短轴端点构成边长为2的正方形，过0,t t >2 的直线l 与椭圆交于A ，B ，C 0,1 ，连接AC 交椭圆于D ．(1)求椭圆方程和离心率；(2)若直线BD 的斜率为0，求t ．【答案】(1)x 24+y 22=1,e =22(2)t =2【分析】(1)由题意得b =c =2，进一步得a ，由此即可得解；(2)说明直线AB 斜率存在，设AB :y =kx +t ,t >2 ，A x 1,y 1 ,B x 2,y 2 ，联立椭圆方程，由韦达定理有x 1+x 2=-4kt 1+2k 2,x 1x 2=2t 2-42k 2+1，而AD :y =y 1-y 2x 1+x 2x -x 1 +y 1，令x =0，即可得解.【详解】(1)由题意b =c =22=2，从而a =b 2+c 2=2，所以椭圆方程为x 24+y 22=1，离心率为e =22；(2)显然直线AB 斜率存在，否则B ,D 重合，直线BD 斜率不存在与题意不符，同样直线AB 斜率不为0，否则直线AB 与椭圆无交点，矛盾，从而设AB :y =kx +t ,t >2 ，A x 1,y 1 ,B x 2,y 2 ，联立x 24+y 22=1y =kx +t ，化简并整理得1+2k 2x 2+4ktx +2t 2-4=0，由题意Δ=16k 2t 2-82k 2+1 t 2-2 =84k 2+2-t 2 >0，即k ,t 应满足4k 2+2-t 2>0，所以x 1+x 2=-4kt 1+2k 2,x 1x 2=2t 2-42k 2+1，若直线BD 斜率为0，由椭圆的对称性可设D -x 2,y 2 ，所以AD :y =y 1-y 2x 1+x 2x -x 1 +y 1，在直线AD 方程中令x =0，得y C =x 1y 2+x 2y 1x 1+x 2=x 1kx 2+t +x 2kx 1+t x 1+x 2=2kx 1x 2+t x 1+x 2 x 1+x 2=4k t 2-2 -4kt +t =2t =1，所以t =2，此时k 应满足4k 2+2-t 2=4k 2-2>0k ≠0 ，即k 应满足k <-22或k >22，综上所述，t =2满足题意，此时k <-22或k >22.15(新高考天津卷)已知椭圆x 2a 2+y 2b 2=1(a >b >0)椭圆的离心率e =12．左顶点为A ，下顶点为B ，C 是线段OB 的中点，其中S △ABC =332．(1)求椭圆方程．(2)过点0,-32的动直线与椭圆有两个交点P ，Q ．在y 轴上是否存在点T 使得TP ⋅TQ ≤0恒成立．若存在求出这个T 点纵坐标的取值范围，若不存在请说明理由．【答案】(1)x 212+y 29=1(2)存在T 0,t -3≤t ≤32，使得TP ⋅TQ ≤0恒成立.【详解】(1)因为椭圆的离心率为e =12，故a =2c ，b =3c ，其中c 为半焦距，所以A -2c ,0 ,B 0,-3c ,C 0,-3c 2 ，故S △ABC=12×2c ×32c =332，故c =3，所以a =23，b =3，故椭圆方程为：x 212+y 29=1.(2)若过点0,-32 的动直线的斜率存在，则可设该直线方程为：y =kx -32，设P x 1,y 1 ,Q x 2,y 2 ,T 0,t ，由3x 2+4y 2=36y =kx -32可得3+4k 2 x 2-12kx -27=0，故Δ=144k 2+1083+4k 2 =324+576k 2>0且x 1+x 2=12k 3+4k 2,x 1x 2=-273+4k 2,而TP =x 1,y 1-t ,TQ=x 2,y 2-t ，故TP ⋅TQ =x 1x 2+y 1-t y 2-t =x 1x 2+kx 1-32-t kx 2-32-t =1+k 2 x 1x 2-k 32+t x 1+x 2 +32+t 2=1+k 2 ×-273+4k 2-k 32+t ×12k 3+4k 2+32+t 2=-27k 2-27-18k 2-12k 2t +332+t 2+3+2t 2k 23+4k 2=3+2t2-12t -45 k 2+332+t 2-273+4k 2，因为TP ⋅TQ ≤0恒成立，故3+2t 2-12t -45≤0332+t 2-27≤0，解得-3≤t ≤32.若过点0,-32的动直线的斜率不存在，则P 0,3 ,Q 0,-3 或P 0,-3 ,Q 0,3 ，此时需-3≤t ≤3，两者结合可得-3≤t ≤32.综上，存在T 0,t-3≤t ≤32 ，使得TP ⋅TQ ≤0恒成立.【点睛】思路点睛：圆锥曲线中的范围问题，往往需要用合适的参数表示目标代数式，表示过程中需要借助韦达定理，此时注意直线方程的合理假设.16(新高考上海卷)已知双曲线Γ:x 2-y 2b2=1,(b >0),左右顶点分别为A 1,A 2，过点M -2,0 的直线l 交双曲线Γ于P ,Q 两点.(1)若离心率e =2时，求b 的值．(2)若b =263,△MA 2P 为等腰三角形时，且点P 在第一象限，求点P 的坐标．(3)连接OQ 并延长，交双曲线Γ于点R ，若A 1R ⋅A 2P=1，求b 的取值范围．【答案】(1)b =3(2)P 2,22 (3)0,3 ∪3,303【详解】(1)由题意得e =c a =c1=2，则c =2，b =22-1=3．(2)当b =263时，双曲线Γ:x 2-y 283=1，其中M -2,0 ，A 21,0 ，因为△MA 2P 为等腰三角形，则①当以MA 2为底时，显然点P 在直线x =-12上，这与点P 在第一象限矛盾，故舍去；②当以A 2P 为底时，MP =MA 2 =3，设P x ,y ，则 x 2-3y 28=1(x +2)2+y 2=9, 联立解得x =-2311y =-81711 或x =-2311y =81711或x =1y =0 ，因为点P 在第一象限，显然以上均不合题意，舍去；(或者由双曲线性质知MP >MA 2 ，矛盾，舍去)；③当以MP 为底时，A 2P =MA 2 =3，设P x 0,y 0 ，其中x 0>0,y 0>0，则有x 0-1 2+y 20=9x 20-y 2083=1，解得x 0=2y 0=22，即P 2,22 ．综上所述：P 2,22 .(3)由题知A 1-1,0 ,A 21,0 ，当直线l 的斜率为0时，此时A 1R ⋅A 2P=0，不合题意，则k l ≠0，则设直线l :x =my -2，设点P x 1,y 1 ,Q x 2,y 2 ，根据OQ 延长线交双曲线Γ于点R ，根据双曲线对称性知R -x 2,-y 2 ，联立有x =my -2x 2-y 2b2=1⇒b 2m 2-1 y 2-4b 2my +3b 2=0，显然二次项系数b 2m 2-1≠0，其中Δ=-4mb 2 2-4b 2m 2-1 3b 2=4b 4m 2+12b 2>0，y 1+y 2=4b 2m b 2m 2-1①，y 1y 2=3b 2b 2m 2-1②，A 1R =-x 2+1,-y 2 ,A 2P=x 1-1,y 1 ，则A 1R ⋅A 2P=-x 2+1 x 1-1 -y 1y 2=1，因为P x 1,y 1 ,Q x 2,y 2 在直线l 上，则x 1=my 1-2，x 2=my 2-2，即-my 2-3 my 1-3 -y 1y 2=1，即y 1y 2m 2+1 -y 1+y 2 3m +10=0，将①②代入有m 2+1 ⋅3b 2b 2m 2-1-3m ⋅4b 2m b 2m 2-1+10=0，即3b 2m 2+1 -3m ⋅4b 2m +10b 2m 2-1 =0化简得b 2m 2+3b 2-10=0，所以 m 2=10b 2-3, 代入到 b 2m 2-1≠0, 得 b 2=10-3b 2≠1, 所以 b 2≠3,且m 2=10b 2-3≥0，解得b 2≤103，又因为b >0，则0<b 2≤103，综上知，b 2∈0,3 ∪3,103 ，∴b ∈0,3 ∪3,303．【点睛】关键点点睛：本题第三问的关键是采用设线法，为了方便运算可设l :x =my -2，将其与双曲线方程联立得到韦达定理式，再写出相关向量，代入计算，要注意排除联立后的方程得二次项系数不为0.一、单选题1(2024·福建泉州·二模)若椭圆x 2a 2+y 23=1(a >0)的离心率为22，则该椭圆的焦距为()A.3B.6C.26或3D.23或6【答案】D【分析】分焦点在x 轴或y 轴两种情况，求椭圆的离心率，求解参数a ，再求椭圆的焦距.【详解】若椭圆的焦点在x 轴，则离心率e =a 2-3a =22，得a 2=6，此时焦距2c =26-3=23，若椭圆的焦点在y 轴，则离心率e =3-a 23=22，得a 2=32，此时焦距2c =23-32=6，所以该椭圆的焦距为23或6.故选：D2(2024·河北衡水·三模)已知双曲线C ：x 2a 2-y 2b 2=1(a >0，b >0)，圆O 1:(x -2)2+y 2=4与圆O 2:x 2+(y -1)2=1的公共弦所在的直线是C 的一条渐近线，则C 的离心率为()A.3B.2C.5D.6【答案】C【详解】因为O 1:(x -2)2+y 2=4，O 2:x 2+(y -1)2=1，所以两圆方程相减可得y =2x ，由题意知C 的一条渐近线为y =2x ，即ba =2，双曲线C 的离心率e =c a =c 2a 2=a 2+b 2a 2=1+b 2a2=5．故选：C ．3(2024·北京·三模)已知双曲线E :3mx 2-my 2=3的一个焦点坐标是0,2 ，则m 的值及E 的离心率分别为()A.-1,233B.-1,2C.1，2D.102,10【答案】A【详解】依题意，双曲线E :3mx 2-my 2=3化为：y 2-3m -x 2-1m=1，则-3m +-1m =22，解得m =-1，双曲线y 23-x 2=1的离心率e =23=233.故选：A4(2024·贵州贵阳·三模)过点A (-3,-4)的直线l 与圆C :(x -3)2+(y -4)2=9相交于不同的两点M ，N ，则线段MN 的中点P 的轨迹是()A.一个半径为10的圆的一部分B.一个焦距为10的椭圆的一部分C.一条过原点的线段D.一个半径为5的圆的一部分【答案】D【详解】设P (x ,y )，根据线段MN 的中点为P ，则CP ⊥MN ，即CP ⊥AP ，所以CP ⋅AP =0，又A (-3,-4),C (3,4),AP =(x +3,y +4),CP =(x -3,y -4)，所以(x +3)(x -3)+(y +4)(y -4)=0，即x 2+y 2=25，所以点P 的轨迹是以(0,0)为圆心，半径为5的圆在圆C 内的一部分，故选：D .5(2024·湖南·模拟预测)已知点A 1,0 ，点B -1,0 ，动点M 满足直线AM ，BM 的斜率之积为4，则动点M 的轨迹方程为()A.x 24-y 2=1B.x 24-y 2=1(x ≠±1)C.x 2-y 24=1D.x 2-y 24=1(x ≠±1)【答案】D【详解】设动点M (x ,y )由于A 1,0 ，B -1,0 ，根据直线AM 与BM 的斜率之积为4．整理得y x +1⋅y x -1=4，化简得：x 2-y 24=1(x ≠±1)．故选：D6(2024·陕西榆林·三模)在平面直角坐标系xOy 中，把到定点F 1-a ,0 ,F 2a ,0 距离之积等于a 2(a >0)的点的轨迹称为双纽线.若a =2，点P x 0,y 0 为双纽线C 上任意一点，则下列结论正确的个数是()①C 关于x 轴不对称②C 关于y 轴对称③直线y =x 与C 只有一个交点④C 上存在点P ，使得PF 1 =PF 2 A.1个 B.2个C.3个D.4个【答案】C【详解】①设M x ,y 到定点F 1-2,0 ,F 22,0 的距离之积为4，可得(x +2)2+y 2.(x -2)2+y 2=4，整理得x 2+y 2 2=8x 2-y 2 ，即曲线C 的方程为x 2+y 2 2=8x 2-y 2 ，由x 用-x 代换，方程没变，可知曲线C 关于y 轴对称，由y 用-y 代换，方程没变，可知曲线C 关于x 轴对称，由x 用-x 代换，y 用-y 同时代换，方程没变，可知曲线C 关于原点对称，图象如图所示：所以①不正确，②正确；③联立方程组x 2+y 2 2=8x 2-y 2y =x，可得x 4=0，即x =0，所以y =0，所以直线y =x 与曲线C 只有一个交点O (0,0)，所以③正确.④原点O 0,0 满足曲线C 的方程，即原点O 在曲线C 上，则OF 1 =OF 2 ，即曲线C 上存在点P 与原点O 重合时，满足PF 1 =PF 2 ，所以④正确.故选:C .7(2024·福建泉州·二模)双曲线C :x 2a 2-y 2b 2=1(a >0,b >0)，左、右顶点分别为A ，B ，O 为坐标原点，如图，已知动直线l 与双曲线C 左、右两支分别交于P ，Q 两点，与其两条渐近线分别交于R ，S 两点，则下列命题正确的是()A.存在直线l ，使得BQ ⎳OSB.当且仅当直线l 平行于x 轴时，|PR |=|SQ |C.存在过(0,b )的直线l ，使得S △ORB 取到最大值D.若直线l 的方程为y =-22(x -a ),BR =3BS ，则双曲线C 的离心率为3【答案】D【详解】解：对于A 项：与渐近线平行的直线不可能与双曲线有两个交点，故A 项错误；对于B 项：设直线l :y =kx +t ，与双曲线联立y =kx +tx 2a2-y 2b2=1，得：b 2-a 2k 2 x 2-2a 2ktx -a 2t 2+a 2b 2 =0，其中b 2-a 2k 2≠0，设P x 1,y 1 ,Q x 2,y 2 ，由根与系数关系得：x 1+x 2=2a 2kt b 2-a 2k 2,x 1x 2=-a 2b 2+a 2t 2b 2-a 2k 2，所以线段PQ 中点N x 1+x 22,y 1+y 22 =a 2kt b 2-a 2k 2,a 2k 2tb 2-a 2k2+t，将直线l :y =kx +t ，与渐近线y =b a x 联立得点S 坐标为S at b -ak ,btb -ak，将直线l :y =kx +t 与渐近线y =-b a x 联立得点R 坐标为R -at b +ak ,btb +ak ，所以线段RS 中点M a 2kt b 2-a 2k 2,a 2k 2tb 2-a 2k2+t，所以线段PQ 与线段RS 的中点重合．所以，对任意的直线l ，都有|PR |=|PQ |-|RS |2=|SQ |，故B 项不正确；对于C 项：因为|OB |为定值，当k 越来越接近渐近线y =-b a x 的斜率-ba 时，S △ORB 趋向于无穷，所以S △ORB 会趋向于无穷，不可能有最大值，故C 项错误；对于D 项：联立直线l 与渐近线y =bax ，解得Sa 22b +a ,ab2b +a，联立直线l 与渐近线y =-b a x ，解得R a 2-2b +a ,ab2b -a由题可知，BR =3BS ，3y S =y R +2y B ,3ab2b +a =ab2b -a ，解得b =2a ，所以e =1+b 2a2=1+(2a )2a 2=3，故D 项正确．故选：D ．【点睛】方法点睛：求解椭圆或双曲线的离心率的三种方法：①定义法：通过已知条件列出方程组，求得a ,c 得值，根据离心率的定义求解离心率e ；②齐次式法：由已知条件得出关于a ,c 的二元齐次方程，然后转化为关于e 的一元二次方程求解；③特殊值法：通过取特殊值或特殊位置，求出离心率.8(2024·河南·二模)已知双曲线C :x 2a 2-y 2b 2=1(a >0,b >0)的左，右焦点分别为F 1,F 2,O 为坐标原点，焦距为82，点P 在双曲线C 上，OP =OF 2 ，且△POF 2的面积为8，则双曲线的离心率为()A.2B.22C.2D.4【答案】C【详解】因为△POF 2的面积为8，所以△PF 1F 2的面积为16.又OP =OF 2 ，所以OP =OF 2 =OF 1 =12F 1F 2，所以△PF 1F 2为直角三角形，且PF 1⊥PF 2.设PF 1 =m ，PF 2 =n ，所以m -n =2a ,m 2+n 2=4c 2，所以mn =m 2+n 2 -(m -n )22=4c 2-4a 22=2b 2，所以S △PF 1F 2=12mn =b 2=16，又b >0，所以b =4.焦距为2c =82，所以c =42，则a 2=c 2-b 2=(42)2-16=16，所以a =4，则离心率e =424=2.故选：C .9(2024·重庆·三模)已知抛物线y 2=4x 的焦点为F ，过点F 的直线l 交抛物线于A ，B 两点，点A 在第一象限，点O 为坐标原点，且S △AOF =2S △BOF ，则直线l 的斜率为()A.22B.3C.1D.-1【答案】A 【详解】如图：设直线倾斜角为α，抛物线的准线l ：x =-1作AM ⊥l 于M ，根据抛物线的定义，AM =AF =DF +AF ⋅cos α=2+AF ⋅cos α，所以|AF |=21-cos α，类似的|BF |=21+cos α.由S △AOF =2S △BOF 知|AF |=2|BF |，得cos α=13，故k =tan α=22.故选：A10(2024·黑龙江齐齐哈尔·三模)设F 为抛物线C :y =ax 2的焦点，若点P (1,2)在C 上，则|PF |=()A.3B.52C.94D.178【答案】D【详解】依题意，2=a ×12，解得a =2，所以C :x 2=y 2的准线为y =-18，所以|PF |=2+18=178，故选:D ．11(2024·山东泰安·二模)设抛物线x 2=4y 的焦点为F ，过抛物线上点P 作准线的垂线，设垂足为Q ，若∠PQF =30°，则PQ =()A.43B.433C.3D.233【答案】A【详解】如图所示：设 M 为准线与x 轴的交点，因为∠PQF =30°，且PF =PQ ，所以∠PFQ =30°,∠QPF =120°，因为FM ⎳PQ ，所以∠QFM =30°，而在Rt△QMF中，QF=FMcos30°=232=433，所以PF=PQ=QF2÷cos30°=233÷32=43.故选：A.二、多选题12(2024·江西·模拟预测)已知A-2,0，B2,0，C1,0，动点M满足MA与MB的斜率之积为-3 4，动点M的轨迹记为Γ，过点C的直线交Γ于P，Q两点，且P，Q的中点为R，则()A.M的轨迹方程为x24+y23=1B.MC的最小值为1C.若O为坐标原点，则△OPQ面积的最大值为32D.若线段PQ的垂直平分线交x轴于点D，则R点的横坐标是D点的横坐标的4倍【答案】BCD【详解】对于选项A，设M x,y，因为A-2,0，B2,0，所以k MA⋅k MB=yx+2⋅yx-2=-34，化简得x24+y23=1x≠±2，故A错误；对于选项B，因为x24+y23=1x≠±2，则a=2，b=3，则c=a2-b2=1，所以C1,0为椭圆的右焦点，则MCmin=a-c=2-1=1，故B正确；对于选项C，设PQ的方程 x=my+1，代入椭圆方程，得3m2+4y2+6my-9=0，设P x1,y1,Q x2,y2，则y1+y2=-6m3m2+4,y1y2=-93m2+4，Δ=36m2+363m2+4>0，所以S△OPQ=12OCy1-y2=12y1+y22-4y1y2=12-6m3m2+42+363m2+4=6m2+13m2+4，令m2+1=t≥1，则S△OPQ=6t3t2+1=63t+1t，令g t =3t+1tt≥1，则S△OPQ=6g t，t≥1,g t =3-1t2=3t2-1t2>0，g t 在1,+∞为增函数，g t ≥g1 =4，g t min=4，所以S△OPQmax=64=32，当且仅当t=1时即m=0等号成立，故C正确；对于选项D，因为Rx1+x22,y1+y22，x1+x22=m y1+y22+1=-3m23m2+4+1=43m2+4，y1+y22=-3m3m2+4，所以R43m2+4,-3m3m2+4，则x R=43m2+4，设D x D ,0 ，则k PQ ⋅k RD =1m ⋅3m3m 2+4x D -43m 2+4=-1，则x D =13m 2+4，所以x R x D=43m 2+413m 2+4=4，则R 点的横坐标是D 点的横坐标的4倍，故D 正确.故选：BCD .【点睛】关键点点睛：本题求解的关键有两个：一是利用面积公式得出面积表达式，结合导数得出最值；二是根据垂直平分得出点之间的关系.13(2024·江苏常州·二模)双曲线具有光学性质：从双曲线一个焦点发出的光线经过双曲线镜面反射，其反射光线的反向延长线经过双曲线的另一个焦点．如图，双曲线E :x 24-y 26=1的左、右焦点分别为F 1,F 2，从F 2发出的两条光线经过E 的右支上的A ,B 两点反射后，分别经过点C 和D ，其中AF 2 ,BF 2共线，则()A.若直线AB 的斜率k 存在，则k 的取值范围为-∞,-62 ∪62,+∞ B.当点C 的坐标为210,10 时，光线由F 2经过点A 到达点C 所经过的路程为6C.当AB ⋅AD =AB 2时，△BF 1F 2的面积为12D.当AB ⋅AD =AB 2时，cos ∠F 1F 2A =-1010【答案】ABD【详解】如图所示，过点F 2分别作E 的两条渐近线的平行线l 1,l 2，则l 1,l 2的斜率分别为62和-62，对于A 中，由图可知，当点A ,B 均在E 的右支时，k <-62或k >62，所以A 正确；对于B 中，光线由F 2经过点A 到达点C 所经过的路程为F 2A +AC =F 1A -2a +AC =F 1C -2a =(210+10)2+(10-0)2-4=6，所以B 正确；对于C 中，由AB ⋅AD =AB 2，得AB ⋅AD -AB =0，即AB ⋅BD=0，所以AB ⊥BD ，设BF 1 =n ，则BF 2 =n -2a =n -4，因为∠ABD =π2，所以n 2+(n -4)2=(2c )2=40，整理得n 2-4n -12=0，解得n =6或n =-2(舍去)，所以BF 1 =6，BF 2 =2，所以△BF 1F 2的面积S =12BF 1 ⋅BF 2 =6，所以C 错误；对于D 项，在直角△F 1BF 2中，cos ∠F 1F 2B =BF 2 F 1F 2=2210=1010，所以cos ∠F 1F 2A =-cos ∠F 1F 2B =-1010，所以D 正确．故选：ABD ．14(2024·重庆·三模)已知双曲线C :x 2a 2-y 216=1(a >0)的左，右焦点分别为F 1,F 2,P 为双曲线C 上点，且△PF 1F 2的内切圆圆心为I (3,1)，则下列说法正确的是()A.a =3B.直线PF 1的斜率为14C.△PF 1F z 的周长为643D.△PF 1F 2的外接圆半径为6512【答案】ACD【详解】如图1，由条件，点P 应在双曲线C 的右支上，设圆I 分别与△PF 1F 2的三边切于点M ､N ､A ，则由题A 3,0 ，且PM =PN ,F 1M =F 1A ，F 2N =F 2A ，又∵PF 1 -PF 2 =F 1M -F 2N =AF 1 -F 2A =x A +c -c -x A =2x A =2a ∴a =x A =3，A 选项正确；由选项A 得F 1-5,0 ,F 25,0 ，连接IF 1、IF 2、IA ，则tan ∠IF 1A =IA AF 1=18，所以k PF 1=tan ∠PF 1A =tan2∠IF 1A =2tan ∠IF 1A 1-tan 2∠IF 1A=1663，B 选项错误；同理，tan ∠PF 2A =tan2∠IF 2A =43，∴tan ∠F 1PF 2=-tan ∠PF 1A +∠PF 2A =-125，∴⇒tan∠F 1PF 22=32，所以由焦三角面积公式得S △F 1PF 2=b 2tan∠F 1PF 22=323，又S △F 1PF 2=PF 1+PF 2+F 1F 2 r2，故得PF 1 +PF 2 +F 1F 2 =643，∴△PF 1F 2的周长为643，C 选项正确；由tan ∠F 1PF 2=-125⇒sin ∠F 1PF 2=1213，由正弦定理F 1F 2sin ∠F 1PF 2=2R 得R =6512，D 选项正确.故选：ACD .【点睛】关键点睛：求直线PF 1的斜率、△PF 1F z 的周长、△PF 1F 2的外接圆半径的关键是根据已知条件F 1A 、F 2A 、IA 以及与各个所需量的关系即可求出∠PF 1A =2∠IF 1A 、∠PF 2A =2∠IF 2A 和∠F 2PF 1.15(2024·湖北襄阳·二模)抛物线C :x 2=2py 的焦点为F ，P 为其上一动点，当P 运动到(t ,1)时，|PF |=2，直线l 与抛物线相交于A 、B 两点，下列结论正确的是()A.抛物线的方程为：x 2=8yB.抛物线的准线方程为：y =-1。

高中数学圆锥曲线经典考点及例题专题讲解

圆锥曲线的综合问题考纲解读 1.求圆锥曲线过定点问题；2.利用圆锥曲线求定值、常数值；3.利用圆锥曲线求变量的取值范围，最值问题；4.利用圆锥曲线求解探索性、存在性问题．考点一圆锥曲线过定点问题|方法突破[例1] (2018·淄博模拟)椭圆C ：x 2a 2＋y 2b 2＝1(a >b >0)的离心率为12，其左焦点到点P (2,1)的距离为10.(1)求椭圆C 的标准方程．(2)若直线l ：y ＝kx ＋m 与椭圆C 相交于A ，B 两点(A ，B 不是左、右顶点)，且以AB 为直径的圆过椭圆C 的右顶点．求证：直线l 过定点，并求出该定点的坐标．[解析] (1)因为左焦点(－c,0)到点P (2,1)的距离为10，所以(2＋c )2＋1＝10，解得c ＝1.又e ＝c a ＝12，解得a ＝2，所以b 2＝a 2－c 2＝3.所以所求椭圆C 的方程为x 24＋y 23＝1.(2)证明：设A (x 1，y 1)，B (x 2，y 2)，由⎩⎪⎨⎪⎧y ＝kx ＋m ，x 24＋y 23＝1，消去y 得(3＋4k 2)x 2＋8mkx ＋4(m 2－3)＝0， Δ＝64m 2k 2－16(3＋4k 2)(m 2－3)>0，化为3＋4k 2>m 2.所以x 1＋x 2＝－8mk 3＋4k 2，x 1x 2＝4(m 2－3)3＋4k 2.y 1y 2＝(kx 1＋m )(kx 2＋m )＝k 2x 1x 2＋mk (x 1＋x 2)＋m 2＝3(m 2－4k 2)3＋4k 2.因为以AB 为直径的圆过椭圆右顶点D (2,0)，k AD ·k BD ＝－1，所以y 1x 1－2·y 2x 2－2＝－1，所以y 1y 2＋x 1x 2－2(x 1＋x 2)＋4＝0，所以3(m 2－4k 2)3＋4k 2＋4(m 2－3)3＋4k 2＋16mk 3＋4k 2＋4＝0.化为7m 2＋16mk ＋4k 2＝0，解得m 1＝－2k ，m 2＝－2k7.且满足3＋4k 2－m 2>0.当m ＝－2k 时，l ：y ＝k (x －2)，直线过定点(2,0)与已知矛盾；当m ＝－2k7时，l ：y ＝k ⎝⎛⎭⎫x －27，直线过定点⎝⎛⎭⎫27，0. 综上可知，直线l 过定点⎝⎛⎭⎫27，0 .[方法提升][母题变式]若本例的条件“以AB 为直径的圆过椭圆C 的右顶点”，改为“以AB 为直径的圆过椭圆C 的左顶点”．则直线l 是否还过定点？若过定点，求出该定点的坐标；若不过定点，说明理由．解析：设A (x 1，y 1)，B (x 2，y 2)，由⎩⎪⎨⎪⎧y ＝kx ＋m ，x 24＋y 23＝1，消去y 得(3＋4k 2)x 2＋8mkx ＋4(m 2－3)＝0， Δ＝64m 2k 2－16(3＋4k 2)(m 2－3)>0，化为3＋4k 2>m 2. 所以x 1＋x 2＝－8mk 3＋4k 2，x 1x 2＝4(m 2－3)3＋4k 2.y 1y 2＝(kx 1＋m )(kx 2＋m )＝k 2x 1x 2＋mk (x 1＋x 2)＋m 2＝3(m 2－4k 2)3＋4k 2.因为以AB 为直径的圆过椭圆左顶点D (－2,0)，k AD ·k BD ＝－1，所以y 1x 1＋2·y 2x 2＋2＝－1，所以y 1y 2＋x 1x 2＋2(x 1＋x 2)＋4＝0，所以3(m 2－4k 2)3＋4k 2＋4(m 2－3)3＋4k 2－16mk 3＋4k 2＋4＝0.化为7m 2－16mk ＋4k 2＝0，解得m 1＝2k ，m 2＝2k 7.且满足3＋4k 2－m 2>0.当m ＝2k 时，l ：y ＝k (x ＋2)，直线过定点(－2,0)与已知矛盾；当m ＝2k7时，l ：y ＝k ⎝⎛⎭⎫x ＋27，直线过定点⎝⎛⎭⎫－27，0. 综上可知，直线l 过定点⎝⎛⎭⎫－27，0.考点二圆锥曲线的定值问题|方法突破[例2] 已知椭圆C ：x 24＋y 23＝1.若直线l ：y ＝kx ＋m 与椭圆C 相交于A ，B 两点，且k OA ·k OB＝－34(O 为坐标原点)，判断△AOB 的面积是否为定值，若为定值，求出定值；若不为定值，说明理由．[解析] 设A (x 1，y 1)，B (x 2，y 2)，由⎩⎪⎨⎪⎧y ＝kx ＋m ，x 24＋y 23＝1得(3＋4k 2)x 2＋8mkx ＋4(m 2－3)＝0，则由Δ＝64m 2k 2－16(3＋4k 2)(m 2－3)>0，得3＋4k 2－m 2>0.又x 1＋x 2＝－8mk3＋4k 2，x 1x 2＝4(m 2－3)3＋4k 2，∴y 1y 2＝(kx 1＋m )(kx 2＋m )＝k 2x 1x 2＋mk (x 1＋x 2)＋m 2＝3(m 2－4k 2)3＋4k 2.又由k OA ·k OB ＝－34，得y 1y 2x 1x 2＝－34，即y 1y 2＝－34x 1x 2，∴3(m 2－4k 2)3＋4k 2＝－34·4(m 2－3)3＋4k 2，即2m 2－4k 2＝3. 又|AB |＝1＋k 2(x 1＋x 2)2－4x 1x 2＝24(1＋k 2)3＋4k 2.点O 到直线AB 的距离为d ＝|m |1＋k2＝ 2－12(1＋k 2)≥2－12＝62. S △AOB ＝12|AB |d ＝1224(1＋k 2)3＋4k 2·|m |1＋k 2＝12 24(1＋k 2)m 2(3＋4k 2)(1＋k 2)＝12243＋4k 2·3＋4k 22＝ 3. [方法提升]已知椭圆x 2a 2＋y 2b 2＝1(a >b >0)的左焦点F 1(－1,0)，长轴长与短轴长的比是2∶ 3.(1)求椭圆的方程；(2)过F 1作两直线m ，n 交椭圆于A ，B ，C ，D 四点，若m ⊥n ，求证：1|AB |＋1|CD |为定值．解析：(1)由已知得⎩⎪⎨⎪⎧2a ∶2b ＝2∶3，c ＝1，a 2＝b 2＋c 2.解得a ＝2，b ＝ 3.故所求椭圆方程为x 24＋y 23＝1.(2)证明：由已知F 1(－1,0)，当直线m 不垂直于坐标轴时，可设直线m 的方程为y ＝k (x ＋1)(k ≠0)．由⎩⎪⎨⎪⎧y ＝k (x ＋1)，x 24＋y 23＝1，得(3＋4k 2)x 2＋8k 2x ＋4k 2－12＝0. 由于Δ>0，设A (x 1，y 1)，B (x 2，y 2)，则有x 1＋x 2＝－8k 23＋4k 2，x 1x 2＝4k 2－123＋4k 2，|AB |＝(1＋k 2)[(x 1＋x 2)2－4x 1x 2] ＝(1＋k 2)⎣⎢⎡⎦⎥⎤⎝⎛⎭⎫－8k 23＋4k 22－4×4k 2－123＋4k 2 ＝12(1＋k 2)3＋4k 2.同理|CD |＝12(1＋k 2)3k 2＋4.所以1|AB |＋1|CD |＝3＋4k 212(1＋k 2)＋3k 2＋412(1＋k 2)＝7(1＋k 2)12(1＋k 2)＝712.当直线m 垂直于坐标轴时，此时|AB |＝3，|CD |＝4；或|AB |＝4，|CD |＝3，1|AB |＋1|CD |＝13＋14＝712. 综上，1|AB |＋1|CD |为定值712.考点三圆锥曲线中的范围(最值)问题|模型突破[例3] (2018·聊城模拟)椭圆x 2a 2＋y 2b 2＝1(a >b >0)的左、右焦点分别为F 1，F 2，P 是椭圆上的一点，l ：x ＝－a 2c ，且PQ ⊥l ，垂足为Q ，若四边形PQF 1F 2为平行四边形，则椭圆的离心率的取值范围是( )A.⎝⎛⎭⎫12，1B.⎝⎛⎭⎫0，12 C.⎝⎛⎭⎫0，22 D.⎝⎛⎭⎫22，1[解析] 设点P (x 1，y 1)，由于PQ ⊥l ，故|PQ |＝x 1＋a 2c ，因为四边形PQF 1F 2为平行四边形，所以|PQ |＝|F 1F 2|＝2c ，即x 1＋a 2c ＝2c ，则有x 1＝2c －a 2c >－a ，所以2c 2＋ac －a 2>0，即2e 2＋e －1>0，解得e <－1或e >12，由于0<e <1，所以12<e <1，即椭圆离心率的取值范围是⎝⎛⎭⎫12，1. [答案] A [模型解法][高考类题]1．(2015·高考重庆卷)设双曲线x 2a 2－y 2b 2＝1(a >0，b >0)的右焦点为F ，右顶点为A ，过F作AF 的垂线与双曲线交于B ，C 两点，过B ，C 分别作AC ，AB 的垂线，两垂线交于点D .若D 到直线BC 的距离小于a ＋a 2＋b 2，则该双曲线的渐近线斜率的取值范围是( )A ．(－1,0)∪(0,1)B ．(－∞，－1)∪(1，＋∞)C ．(－2，0)∪(0，2)D ．(－∞，－2)∪(2，＋∞)解析：如图所示，由题意知BC 为双曲线的通径，所以|BC |＝2b 2a ，则|BF |＝b 2a .又|AF |＝c －a ，因为BD ⊥AC ，DC ⊥AB ，所以点D 在x 轴上，由Rt △BF A ∽Rt △DFB ，得|BF |2＝|AF |·|FD |，即(b 2a )2＝(c －a )|FD |，所以|FD |＝b 4a 2(c －a )，则由题意知b 4a 2(c －a )<a ＋a 2＋b 2，即b 4a 2(c －a )<a ＋c ，所以b 4<a 2(c －a )(a ＋c )，即b 4<a 2(c 2－a 2)，即b 4<a 2b 2，所以0<b 2a 2<1，解得0<b a <1，而双曲线的渐近线斜率为±ba ，所以双曲线的渐近线斜率的取值范围是(－1,0)∪(0,1)，故选A.答案：A2．(2017·高考浙江卷)如图，已知抛物线x 2＝y ，点A ⎝⎛⎭⎫－12，14，B ⎝⎛⎭⎫32，94，抛物线上的点P (x ，y )⎝⎛⎭⎫－12<x <32.过点B 作直线AP 的垂线，垂足为Q .(1)求直线AP 斜率的取值范围； (2)求|P A |·|PQ |的最大值．解析：(1)设直线AP 的斜率为k ，k ＝x 2－14x ＋12＝x －12.因为－12<x <32，所以直线AP 斜率的取值范围是(－1,1)．(2)联立直线AP 与BQ 的方程⎩⎨⎧kx －y ＋12k ＋14＝0，x ＋ky －94k －32＝0，解得点Q 的横坐标是x Q ＝－k 2＋4k ＋32(k 2＋1).因为|P A |＝1＋k 2⎝⎛⎭⎫x ＋12＝1＋k 2(k ＋1)，|PQ |＝1＋k 2(x Q －x )＝－(k －1)(k ＋1)2k 2＋1，所以|P A |·|PQ |＝－(k －1)(k ＋1)3，令f (k )＝－(k －1)(k ＋1)3. 因为f ′(k )＝－(4k －2)(k ＋1)2，所以f (k )在区间⎝⎛⎭⎫－1，12上单调递增，⎝⎛⎭⎫12，1上单调递减，因此当k ＝12时，|P A |·|PQ |取得最大值2716.考点四圆锥曲线的存在性问题|方法突破[例4] 已知椭圆C ：x 2a 2＋y 2b 2＝1(a >b >0)的离心率为22，点P (0,1)和点A (m ，n )(m ≠0)都在椭圆C 上，直线P A 交x 轴于点M .(1)求椭圆C 的方程，并求点M 的坐标(用m ，n 表示)；(2)设O 为原点，点B 与点A 关于x 轴对称，直线PB 交x 轴于点N .问：y 轴上是否存在点Q ，使得∠OQM ＝∠ONQ ？若存在，求点Q 的坐标；若不存在，说明理由．[解析] (1)由题意得⎩⎪⎨⎪⎧b ＝1，c a ＝22，a 2＝b 2＋c 2.解得a 2＝2.故椭圆C 的方程为x 22＋y 2＝1.设M (x M,0)．因为m ≠0，所以－1<n <1. 直线P A 的方程为y －1＝n －1m x ，所以x M ＝m 1－n ，即M (m1－n，0)．(2)因为点B 与点A 关于x 轴对称，所以B (m ，－n )．设N (x N,0)，则x N ＝m1＋n.“存在点Q (0，y Q )使得∠OQM ＝∠ONQ ”等价于“存在点Q (0，y Q )使得|OM ||OQ |＝|OQ ||ON |”，即y Q 满足y 2Q ＝|x M ||x N |.因为x M ＝m 1－n ，x N ＝m 1＋n ，m 22＋n 2＝1，所以y 2Q ＝|x M ||x N |＝m 21－n 2＝2. 所以 y Q ＝2或y Q ＝－ 2.故在y 轴上存在点Q ，使得∠OQM ＝∠ONQ ，点Q 的坐标为(0，2)或(0，－2)． [方法提升][跟踪训练](2018·徐州模拟)在平面直角坐标系xOy 中，经过点(0，2)且斜率为k 的直线l 与椭圆x 22＋y 2＝1有两个不同的交点P 和Q .(1)求k 的取值范围．(2)设椭圆与x 轴正半轴、y 轴正半轴的交点分别为A ，B ，是否存在常数k ，使得向量OP →＋OQ →与AB →垂直？如果存在，求k 值；如果不存在，请说明理由．解析：(1)由已知条件，直线l 的方程为y ＝kx ＋2，代入椭圆方程得x 22＋(kx ＋2)2＝1，整理得⎝⎛⎭⎫12＋k 2x 2＋22kx ＋1＝0.①直线l 与椭圆有两个不同的交点P 和Q 等价于①中 Δ＝8k 2－4⎝⎛⎭⎫12＋k 2 ＝4k 2－2>0，解得k <－22或k >22. 即k 的取值范围为⎝⎛⎭⎫－∞，－22∪⎝⎛⎭⎫22，＋∞.(2)不存在，理由如下：设P (x 1，y 1)，Q (x 2，y 2)，则OP →＋OQ →＝(x 1＋x 2，y 1＋y 2)，由方程①得，x 1＋x 2＝－42k1＋2k 2，y 1＋y 2＝k (x 1＋x 2)＋22＝－42k 21＋2k 2＋2 2.因为(OP →＋OQ →)⊥AB →，AB →＝(－2，1)，所以(x 1＋x 2)·(－2)＋y 1＋y 2＝0，即：－42k 1＋2k 2·(－2)－42k 21＋2k 2＋22＝0.解得：k ＝－24，由(1)知k 2>12，与此相矛盾，所以不存在常数k 使OP →＋OQ →与AB →垂直．[考点二](2015·高考全国卷Ⅱ)已知椭圆C ：x 2a 2＋y 2b 2＝1(a >b >0)的离心率为22，点(2，2)在C 上．(1)求C 的方程；(2)直线l 不过原点O 且不平行于坐标轴，l 与C 有两个交点A ，B ，线段AB 的中点为M .证明：直线OM 的斜率与直线l 的斜率的乘积为定值．解析：(1)由题意有a 2－b 2a ＝22，4a 2＋2b 2＝1，解得a 2＝8，b 2＝4. 所以C 的方程为x 28＋y 24＝1.(2)证明：设直线l ：y ＝kx ＋b (k ≠0，b ≠0)，A (x 1，y 1)，B (x 2，y 2)，M (x M ，y M )．将y ＝kx ＋b 代入x 28＋y 24＝1得(2k 2＋1)x 2＋4kbx ＋2b 2－8＝0. 故x M ＝x 1＋x 22＝－2kb2k 2＋1，y M ＝k ·x M ＋b ＝b2k 2＋1.于是直线OM 的斜率k OM ＝y M x M ＝－12k ，即k OM ·k ＝－12.所以直线OM 的斜率与直线l 的斜率的乘积为定值．。

（完整版）圆锥曲线知识点+例题+练习含答案（整理）.docx

（完整版）圆锥曲线知识点+例题+练习含答案（整理）.docx圆锥曲线⼀、椭圆：（ 1）椭圆的定义：平⾯内与两个定点F1 , F2的距离的和等于常数（⼤于| F1 F2 |）的点的轨迹。

其中：两个定点叫做椭圆的焦点，焦点间的距离叫做焦距。

注意： 2a | F1F2 | 表⽰椭圆；2a | F1F2|表⽰线段F1F2； 2a| F1F 2 |没有轨迹；（2）椭圆的标准⽅程、图象及⼏何性质：中⼼在原点，焦点在x 轴上中⼼在原点，焦点在y 轴上标准⽅程图形x2y2y2x2a2b 21( a b 0)a 2b21(ab 0)yB 2yB 2P F2 PA 1 A 2x A 1xA 2OF1O F21B 1FB 1顶点对称轴焦点焦距离⼼率通径2b2aA1 (a,0), A2 (a,0)A1( b,0), A2 (b,0)B1 (0, b), B2(0, b)B1( 0,a), B2 (0, a) x 轴，y轴；短轴为2b，长轴为2aF1 (c,0), F2(c,0)F1 ( 0,c), F2 (0,c)| F1 F2 | 2c(c 0)c2 a 2 b 2(0 e 1) （离⼼率越⼤，椭圆越扁）a（过焦点且垂直于对称轴的直线夹在椭圆内的线段）3．常⽤结论：（1）椭圆x2y21(a b 0) 的两个焦点为F1, F2，过F1的直线交椭圆于A, B两a2 b 2点，则ABF 2的周长=（2）设椭圆x2y2221( a b 0)左、右两个焦点为 F1, F2，过 F1且垂直于对称轴的直线a b交椭圆于 P, Q 两点，则 P, Q 的坐标分别是| PQ |⼆、双曲线：（ 1）双曲线的定义：平⾯内与两个定点F1 , F2的距离的差的绝对值等于常数（⼩于| F1F2 | ）的点的轨迹。

其中：两个定点叫做双曲线的焦点，焦点间的距离叫做焦距。

注意： | PF1 || PF2 | 2a 与 | PF2 | | PF1 |2a （ 2a| F1F2 | ）表⽰双曲线的⼀⽀。

圆锥曲线(课堂讲义和例题)

专题1 焦长与焦比体系】过椭圆的一个焦点的弦与另一个焦点围成的三角形的周长是．【例2】过椭圆的一个焦点F 作弦AB ，若，，则的数值为（） A ． B ．C ．D ．与、斜率有关【例3】设直线与椭圆相交于A 、B 两个不同的点，与x 轴相交于点F .（1）证明：；（2）若F 是椭圆的一个焦点，且，求椭圆的方程．【例4】设椭圆中心在坐标原点，焦点在轴上，一个顶点，离心率为. （1）求椭圆的方程；（2）若椭圆左焦点为，右焦点，过且斜率为1的直线交椭圆于，求的面积.秒杀秘籍：椭圆焦长以及焦比问题体:过椭圆的左焦点F 1的弦与右焦点F 2围成的三角形的周长是4a ；焦长公式：A 是椭圆上一点，、是左、右焦点，为，过，c 是椭圆半焦距，则（1）；（2）；（3）．体面积：，．证明：（1）如图所示，，故；（2）设由余弦定理得；整理得；整理得则过焦点的弦长.（焦长公式）焦比定理：过椭圆的左焦点F 1的弦，，令，即，代入弦长公式可得．yO F 2AB xF 1【例5】已知椭圆C：的左右顶点为A，B，点P为椭圆C上不同于A，B，的一点，且直线P A，PB的斜率之积为；（1）求椭圆的离心率；（2）设为椭圆C的左焦点，直线l过点F与椭圆C交与不同的两点M，N，且求直线l的斜率．【例6】（2014•安徽）设F1，F2分别是椭圆E：的左、右焦点，过点F1的直线交椭圆E于A、B两点，若，轴，则椭圆E的方程为．【例7】（2011•浙江）设F1，F2分别为椭圆的焦点，点A，B在椭圆上，若,则点A的坐标是．【例8】（2014•安徽）设F1，F2分别是椭圆E：的左、右焦点，过点F1的直线交椭圆E于A，B两点，．（1）若，的周长为16，求；（2）若，求椭圆E的离心率．_________.【例10】过双曲线的左焦点F 1作倾斜角为的直线交双曲线于A 、B 两点，则=________.【例11】已知双曲线的左、右焦点分别为，．过的直线与双曲线的右支相交于，两点，若，若是以为顶角的等腰三角形，则双曲线的离心率为（） A ． B ．C ．D ．注意：关于这类型焦比双曲线求离心率的题目很多，通常需要利用双曲线的几何性质把拥有焦比的较长的那段用关于的式子表示出来，再利用（交一支）或者（交两支）得出离心率.证明：1．；同理. 2．．3．设O 到AB 的距离为,则，故． 4．，． 5．；；；．关于抛物线的焦长公式及定理（A 为直线与抛物线右交点，B 为左交点，为AB 倾斜角） 1．；2． 3．；4．设，则； 5．设AB 交准线于点P ，．【例12】已知抛物线C ：的焦点为F ，直线与C 交于A ，B （A 在x 轴上方）两点，若，则m 的值为（） A ．B ．C ．D ．【例13】已知抛物线的方程为，过其焦点F 的直线与抛物线交于A 、B 两点，且，O 为坐标原点，则的面积和的面积之比为（） A ． B ． C ． D ．【例14】过抛物线的焦点F 的直线l 交抛物线于点A 、B ，交其准线于点C ，若，且则此抛物线的方程为（）若交于两支时，，代入弦长公式可得．秒杀秘籍：抛物线焦长公式及性质 1．．2．．3．．4．设,则．5．设AB 交准线于点P ，则；．秒杀秘籍：过焦点的弦与其中垂线的性质 1.设椭圆焦点弦的中垂线与长轴的交点为，则与之比是离心率的一半（如图）。

高考数学圆锥曲线典型例题(必考)

高考数学圆锥曲线典型例题(必考)9.1 椭圆典例精析题型一求椭圆的标准方程【例1】已知点P 在以坐标轴为对称轴的椭圆上，点P 到两焦点的距离分别为453和253，过P 作长轴的垂线恰好过椭圆的一个焦点，求椭圆的方程. 【解析】故所求方程为x 25＋3y 210＝1或3x 210＋y 25＝1.【点拨】(1)在求椭圆的标准方程时，常用待定系数法，但是当焦点所在坐标轴不确定时，需要考虑两种情形，有时也可设椭圆的统一方程形式：mx 2＋ny 2＝1(m ＞0，n ＞0且m ≠n )；(2)在求椭圆中的a 、b 、c 时，经常用到椭圆的定义及解三角形的知识.【变式训练1】已知椭圆C 1的中心在原点、焦点在x 轴上，抛物线C 2的顶点在原点、焦点在x 轴上.小明从曲线C 1，C 2上各取若干个点(每条曲线上至少取两个点)，并记录其坐标(x ，y ).由于记录失误，使得其中恰有一个点既不在椭圆C 1上，也不在抛物线C 2上.小明的记录如下：据此，可推断椭圆C 1的方程为 . x 212＋y 26＝1.题型二椭圆的几何性质的运用【例2】已知F 1、F 2是椭圆的两个焦点，P 为椭圆上一点，∠F 1PF 2＝60°. (1)求椭圆离心率的范围；(2)求证：△F 1PF 2的面积只与椭圆的短轴长有关.【解析】(1)e 的取值范围是[12，1).(2)21F PF S ＝12mn sin 60°＝33b 2，【点拨】椭圆中△F 1PF 2往往称为焦点三角形，求解有关问题时，要注意正、余弦定理，面积公式的使用；求范围时，要特别注意椭圆定义(或性质)与不等式的联合使用，如|PF 1|·|PF 2|≤(|PF 1|＋|PF 2|2)2，|PF 1|≥a －c . 【变式训练2】已知P 是椭圆x 225＋y 29＝1上的一点，Q ，R 分别是圆(x ＋4)2＋y 2＝14和圆(x －4)2＋y 2＝14上的点，则|PQ |＋|PR |的最小值是 .【解析】最小值为9.题型三有关椭圆的综合问题【例3】(2010全国新课标)设F 1，F 2分别是椭圆E ：x 2a 2＋y 2b 2＝1(a ＞b ＞0)的左、右焦点，过F 1斜率为1的直线l 与E 相交于A ，B 两点，且|AF 2|，|AB |，|BF 2|成等差数列.(1)求E 的离心率；(2)设点P (0，－1)满足|PA |＝|PB |，求E 的方程.(1) 22.(2)为x 218＋y 29＝1.【变式训练3】已知椭圆x 2a 2＋y2b 2＝1(a ＞b ＞0)的离心率为e ，两焦点为F 1，F 2，抛物线以F 1为顶点，F 2为焦点，P 为两曲线的一个交点，若|PF 1||PF 2|＝e ，则e 的值是( )A.32B.33C.22D.63【解析】选B 题型思有关椭圆与直线综合问题【例4】【2012高考浙江理21】如图，椭圆C ：2222+1x y a b =(a ＞b ＞0)的离心率为12，其左焦点到点P (2，1)的距离为10．不过原点O 的直线l 与C 相交于A ，B 两点，且线段AB被直线OP 平分．(Ⅰ)求椭圆C 的方程；(Ⅱ) 求∆ABP 的面积取最大时直线l 的方程． .【变式训练4】【2012高考广东理20】在平面直角坐标系xOy 中，已知椭圆C 1：22221(0)x y a b a b+=>>的离心率e=23，且椭圆C 上的点到Q （0，2）的距离的最大值为3. （1）求椭圆C 的方程；（2）在椭圆C 上，是否存在点M （m,n ）使得直线l ：mx+ny=1与圆O ：x 2+y 2=1相交于不同的两点A 、B ，且△OAB 的面积最大？若存在，求出点M 的坐标及相对应的△OAB 的面积；若不存在，请说明理由．总结提高1.椭圆的标准方程有两种形式，其结构简单，形式对称且系数的几何意义明确，在解题时要防止遗漏.确定椭圆需要三个条件，要确定焦点在哪条坐标轴上(即定位)，还要确定a 、 b 的值(即定量)，若定位条件不足应分类讨论，或设方程为mx 2＋ny 2＝1(m ＞0，n ＞0，m ≠n )求解.2.充分利用定义解题，一方面，会根据定义判定动点的轨迹是椭圆，另一方面，会利用椭圆上的点到两焦点的距离和为常数进行计算推理.3.焦点三角形包含着很多关系，解题时要多从椭圆定义和三角形的几何条件入手，且不可顾此失彼，另外一定要注意椭圆离心率的范围.练习1（2009全国卷Ⅰ理）已知椭圆22:12x C y +=的右焦点为F ,右准线为l ，点A l ∈，线段AF 交C 于点B ，若3FA FB =u u u r u u u r ,则||AF u u u u r=( )A. 2B. 2C.3D. 3 选A.2（2009浙江文）已知椭圆22221(0)x y a b a b+=>>的左焦点为F ，右顶点为A ，点B 在椭圆上，且BF x ⊥轴，直线AB 交y 轴于点P ．若2AP PB =u u u r u u u r，则椭圆的离心率是（） A 32 C ．13 D ．12【答案】D3.（2009江西卷理）过椭圆22221x y a b+=(0a b >>)的左焦点1F 作x 轴的垂线交椭圆于点P ，2F 为右焦点，若1260F PF ∠=o ，则椭圆的离心率为 A ．22 B ．33 C ．12D ．13 【答案】B 4.【2012高考新课标理4】设12F F 是椭圆2222:1(0)x y E a b a b +=>>的左、右焦点，P 为直线32ax =上一点，12PF F ∆是底角为30o 的等腰三角形，则E 的离心率为（） ()A 12 ()B 23 ()C 34 ()D 45【答案】C5【2012高考四川理15】椭圆22143x y +=的左焦点为F ，直线x m =与椭圆相交于点A 、B ，当FAB ∆的周长最大时，FAB ∆的面积是____________。

【精编】圆锥曲线知识整理及练习(含解析)

圆锥曲线与方程一、轨迹方程求法:1.求曲线方程的一般步骤:①建系，②设动点，③限制条件，④代入，⑤化简．简记为：建、设、限、代、化．2.求曲线方程的关键是找关系列等式，常见方法为直译法和代入法(相关点法)．二、圆锥曲线的定义与性质：1.椭圆定义的理解:当||||||2121F F PF PF =+时，点P 的轨迹是；当||||||2121F F PF PF <+时，点P 的轨迹是． 2.双曲线定义的理解：(1)若没有“绝对值”，则动点的轨迹是．当|MF 1|－|MF 2|＝2a 时，曲线仅表示焦点所对应的一支；当|MF 1|－|MF 2|＝－2a 时，曲线仅表示焦点所对应的一支． (2)当2a ＝|F 1F 2|时，则动点的轨迹是；当2a ＞|F 1F 2|时，动点轨迹；当2a ＝0时，动点的轨迹是． 3.双曲线定义的理解：(1)平面内与一个定点F 和一条定直线l (不经过点F)的距离相等的点的轨迹叫做抛物线． (2)注意：定点F 不在定直线l 上，否则动点M 的轨迹不是抛物线，而是过点F 垂直于直线l 的一条直线．三、圆锥曲线知识要点：1.(1)椭圆上点到焦点最大值为，最小值为 . (2)椭圆焦点三角形周长问题：2.直线与椭圆的位置关系通过解直线方程与椭圆方程组成的方程组，对解的个数进行讨论．通常消去方程组中的一个变量，得到关于另一变量的一元二次方程．(1)Δ＞0⇔直线与椭圆相交⇔有两个公共点； (2)Δ＝0⇔直线与椭圆相切⇔有且只有一个公共点； (3)Δ＜0⇔直线与椭圆相离⇔无公共点． 3.直线与双曲线的位置关系一般地，设直线l ：y ＝kx ＋m(m ≠0)，双曲线C ：x 2a 2－y 2b 2＝1，联立、化简，得(b 2－a 2k 2)x 2－2a 2mkx－a 2m 2－a 2b 2＝0.(1)当b 2－a 2k 2＝0，即k ＝±b a 时，直线l 与双曲线的渐近线平行，直线l 与双曲线交于一点.(2)当b 2－a 2k 2≠0，即k ≠±b a 时，Δ＝(－2a 2mk)2－4(b 2－a 2k 2)(－a 2m 2－a 2b 2).若Δ>0⇒l 与C 有两个公共点，此时相交. 若Δ＝0⇒l 与C 有一个公共点，相切. 若Δ<0⇒l 与C 无公共点，相离. 4.直线与抛物线的的位置关系要解决直线与抛物线的位置关系问题，可把直线方程与抛物线方程联立，消去y(或消去x)得出关于x(或关于y)的一个方程Ax 2＋Bx ＋C ＝0，其中二次项系数A 有可能为0，此时直线与抛物线有一个交点．当二次项系数A ≠0时，Δ＝B 2－4AC. 若Δ＜0，则直线与抛物线没有公共点；若Δ＝0，则直线与抛物线有且只有一个公共点；若Δ＞0，则直线与抛物线有两个不同的公共点．5.弦长问题通常将直线方程与圆锥曲线方程联立，得到关于x(或y)的一元二次方程，然后求出根与系数的关系，再求弦长，从而绕过求直线与圆锥曲线的交点坐标．若直线y ＝kx ＋b 与圆锥曲线交于A(x 1，y 1)，B(x 2，y 2)两点，则|AB|＝1＋k 2|x 1－x 2|＝1＋k 2·（x 1＋x 2）2－4x 1x 2，或|AB|＝1＋1k2·|y 1－y 2|＝1＋1k2（y 1＋y 2）2－4y 1y 2. 6.中点弦问题(点差法)(1)利用端点在曲线上，坐标满足方程，将端点坐标分别代入椭圆方程，然后作差，构造出中点坐标和斜率的关系，具体如下：已知A(x 1，y 1)，B(x 2，y 2)是椭圆x 2a 2＋y2b 2＝1(a>b>0)上的两个不同的点，M(x 0，y 0)是线段AB 的中点，则⎩⎪⎨⎪⎧x 21a 2＋y 21b2＝1， ①x 22a 2＋y 22b2＝1. ②由①－②，得1a 2(x 21－x 22)＋1b 2(y 21－y 22)＝0，变形得y 1－y 2x 1－x 2＝－b 2a 2·x 1＋x 2y 1＋y 2＝－b 2a 2·x 0y 0，即k AB ＝－b 2x 0a 2y 0.(2)问：直线与双曲线相交于两点时，其中点弦所在直线斜率如何表示？(3)问：直线与抛物线相交于两点时，其中点弦所在直线斜率如何表示？7.抛物线的焦半径和焦点弦问题(1)以AB 为直径的圆必与准线相切． (2)|AB|＝2(x 0＋p2)(焦点弦长与中点关系)．(3)|AB|＝x 1＋x 2＋p(焦点弦长与端点关系). (4)若直线AB 的倾斜角为α，则|AB|＝2psin 2α. (5)A ，B 两点的横坐标之积、纵坐标之积为定值，即x 1x 2＝p 24， y 1y 2＝－p 2.(6)1|AF|＋1|FB|＝2p. (7)抛物线焦点弦所在直线方程可设为2p my x +=.圆锥曲线练习一、选择题1．抛物线y＝2x2的焦点坐标是( )A.10,2⎛⎫⎪⎝⎭B.12⎛⎫⎪⎝⎭， C.10,8⎛⎫⎪⎝⎭D.18⎛⎫⎪⎝⎭，2．已知双曲线22221x ya b-=(a>0，b>0)的两条渐近线互相垂直，则该双曲线的离心率是( )A．2 32 D. 3 23．设椭圆22221x ya b+= (a>b>0)的左、右焦点分别为F1，F2，上顶点为B.若|BF2|＝|F1F2|＝2，则该椭圆的方程为( )A.22143x y+= B.2213xy+= C.2212xy+= D.2214xy+=4．设P是双曲线22219x ya-= (a>0)上一点，双曲线的一条渐近线方程为3x－2y＝0，F1，F2分别是双曲线的左、右焦点，若|PF1|＝3，则|PF2|＝( )A．1或5 B．6 C．7 D．85．已知抛物线y2＝2px(p＞0)，过点C(－4,0)作抛物线的两条切线CA，CB，A，B为切点，若直线AB经过抛物线y2＝2px的焦点，△CAB的面积为24，则以直线AB为准线的抛物线的标准方程是( ) A．y2＝4x B．y2＝－4x C．y2＝8x D．y2＝－8x6．探照灯反射镜的轴截面是抛物线的一部分，光源位于抛物线的焦点处，已知灯口的直径为60 cm，灯深40 cm，则抛物线的标准方程可能是( )A．y2＝254x B．y2＝454x C．x2＝－452y D．x2＝－454y7.我们把由半椭圆22221x ya b+= (x≥0)与半椭圆22221y xb c+=(x<0)合成的曲线称作“果圆”(其中a2＝b2＋c2，a>b>c>0)，如图所示，其中点F0，F1，F2是相应椭圆的焦点．若△F0F1F2是边长为1的等边三角形，则a，b的值分别为( ) 7，3 1 C．5,3 D．5,48．设双曲线C：22xa－y2＝1(a>0)与直线l：x＋y＝1相交于两个不同的点，则双曲线C的离心率e的取值范围为( )A.2⎛⎝ B ．，＋∞) C. 2⎛⎫+∞ ⎪ ⎪⎝⎭ D. 2⎛ ⎝∪，＋∞)9．(多项选择)θ是任意实数，则方程x 2＋y 2sin θ＝4的曲线可能是( ) A ．椭圆 B ．双曲线 C ．抛物线 D ．圆10.(多项选择)已知椭圆的长轴长为10，其焦点到中心的距离为4，则这个椭圆的标准方程为( )A.22110084x y += B. 221259x y += C.22184100x y += D. 221259y x += 11．(多项选择)设F 为抛物线C ：y 2＝3x 的焦点，过F 且倾斜角为30°的直线交C 于A ，B 两点，则( )A ．|AB |＝12 B ．OA OB ⋅＝－2716C ．y A y B ＝－3D ．x A x B ＝3 12．(多项选择)设圆锥曲线Γ的两个焦点分别为F 1，F 2.若曲线Γ上存在点P 满足|PF 1|∶|F 1F 2|∶|PF 2|＝4∶3∶2，则曲线Γ的离心率等于( ) A.12 B ．2 C. 32 D. 23二、填空题13．以双曲线221412x y -=的焦点为顶点，顶点为焦点的椭圆方程为________． 14．已知二次曲线2214x y m +=，当m ∈[－2，－1]时，该曲线的离心率的取值范围是______． 15．抛物线y 2＝8x 的焦点到双曲线221169x y -=渐近线的距离为________，双曲线右焦点到抛物线准线的距离为________．16．设F 1，F 2分别是椭圆2212516x y +=的左、右焦点，P 为椭圆上任一点，点M 的坐标为(6,4)，则|PM |＋|PF 1|的最大值为________．三、解答题17．命题p ：方程22126x y m m -=-表示焦点在y 轴上的椭圆；命题q ：方程22111x y m m +=+-表示双曲线．(1)若命题p 为真命题，求m 的取值范围； (2)若命题q 为假命题，求m 的取值范围．18．已知抛物线的顶点在原点，它的准线过双曲线22221x ya b-= (a>0，b>0)的一个焦点，并且这条准线与双曲线的两焦点的连线垂直，抛物线与双曲线交于点P362⎛⎝，，求抛物线的方程和双曲线的方程．19．已知抛物线y2＝2px(p＞0)上点T(3，t)到焦点F的距离为4.(1)求t，p的值；(2)如图所示，设A，B是抛物线上分别位于x轴两侧的两个动点，且OA OB⋅＝5(其中O为坐标原点)．求证直线AB必过定点，并求出该定点的坐标．20．已知抛物线C：y2＝2px(p＞0)的焦点为F(1,0)，抛物线E：x2＝2py的焦点为M.(1)若过点M的直线l与抛物线C有且只有一个交点，求直线l的方程；(2)若直线MF与抛物线C交于A，B两点，求△OAB的面积．21．给定椭圆C：22221x ya b+= (a＞b＞0)，称圆心在原点O22a b+的圆是椭圆C的“准圆”．已知椭圆的离心率e 6x2＋y2＝4.(1)求椭圆C的方程；(2)点P是椭圆C的“准圆”上的动点，过点P作椭圆的切线l1，l2，交“准圆”于点M，N.当点P 为“准圆”与y轴正半轴的交点时，求直线l1，l2的方程，并证明l1⊥l2.22．在平面直角坐标系xOy 中，已知椭圆E ：x 2a 2＋y 2b 2＝1(a ＞b ＞0)的离心率为32，上顶点为B ，直线l ：y ＝12x 与椭圆E 交于C ，D 两点，且△BCD 的面积为2．(1)求椭圆E 的标准方程；(2)设点P 是椭圆E 上一点，过点P 引直线m ，其倾斜角与直线l 的倾斜角互补．若直线m 与椭圆E 相交，另一交点为Q ，且直线m 与x ，y 轴分别交于M ，N ，求证：QM 2＋QN 2为定值．23．已知椭圆C ：x 2a 2＋y 24＝1，F 1、F 2为椭圆的左、右焦点，A 、B 为椭圆的左、右顶点，点P 为椭圆上异于A 、B 的动点，且直线P A 、PB 的斜率之积为－12．(1)求椭圆C 的方程；(2)若动直线l 与椭圆C 有且仅有一个公共点，试问：在x 轴上是否存在两个定点，使得这两个定点到直线l 的距离之积为4？若存在，求出两个定点的坐标；若不存在，请说明理由．24．已知椭圆22221x y a b+= (a >b >0)的离心率e ＝63A (0，－b )和B (a,0)的直线与原点的距离为32. (1)求椭圆的方程；(2)已知定点E (－1,0)，若直线y ＝kx ＋2(k ≠0)与椭圆交于C ，D 两点，问：是否存在k 的值，使以CD 为直径的圆过E 点，请说明理由．圆锥曲线练习参考答案1．【答案】C【解析】抛物线的标准方程为x 2＝12y ，焦点在y 轴上，∴焦点坐标为10,8⎛⎫⎪⎝⎭. 2．【答案】C 【解析】由题可知y ＝b a x 与y ＝－b a x 互相垂直，可得－b a ·ba＝－1，则a ＝b .由离心率的计算公式，可得e 2＝22c a ＝222a b a +＝2，e ＝2.3．【答案】A【解析】∵|BF 2|＝|F 1F 2|＝2，∴a ＝2c ＝2，∴a ＝2，c ＝1，∴b ＝3.∴椭圆的方程为22143x y +=. 4．【答案】C【解析】双曲线22219x y a -=的一条渐近线方程为3x －2y ＝0，故a ＝2.又P 是双曲线上一点，故||PF 1|－|PF 2||＝4，而|PF 1|＝3，则|PF 2|＝7. 5．【答案】D【解析】由抛物线的对称性知A ,2p p ⎛⎫⎪⎝⎭，B ,2p p ⎛⎫- ⎪⎝⎭，则S △CAB ＝1422p ⎛⎫+ ⎪⎝⎭×2p ＝24，解得p ＝4，直线AB 的方程为x ＝2，所以所求抛物线的标准方程为y 2＝－8x . 6．【答案】C【解析】如果设抛物线的方程为y 2＝2px (p >0)，则抛物线过点(40,30)，从而有302＝2p ×40，即2p ＝452，所以所求抛物线方程为y 2＝452x .虽然选项中没有y 2＝452x ，但C 中的2p ＝452符合题意． 7.【答案】A【解析】∵|OF 2|＝22b c -＝12，|OF 0|＝c ＝3|OF 2|＝32，∴b ＝1，∴a2＝b 2＋c 2＝1＋34＝74，得a ＝72.8．【答案】D【解析】由2221,1x y a x y ⎧-=⎪⎨⎪+=⎩消去y 并整理得(1－a 2)x 2＋2a 2x －2a 2＝0.由于直线与双曲线相交于两个不同的点，则1－a 2≠0⇒a 2≠1，且此时Δ＝4a 2(2－a 2)>0⇒a 2<2，所以a 2∈(0,1)∪(1,2)．另一方面e，则a 2＝211e -，从而e∈⎝∪，＋∞)． 9．【答案】ABD【解析】由于θ∈R ，对sin θ的值举例代入判断．sin θ可以等于1，这时曲线表示圆，sin θ可以小于0，这时曲线表示双曲线，sin θ可以大于0且小于1，这时曲线表示椭圆． 10.【答案】BD【解析】因为椭圆的长轴长为10，其焦点到中心的距离为4，所以210,4,a c =⎧⎨=⎩解得a ＝5，b 2＝25－16＝9.所以当椭圆焦点在x 轴时，椭圆方程为221259x y +=；当椭圆焦点在y 轴时，椭圆方程为221259y x +=. 11．【答案】AB【解析】抛物线C ：y 2＝3x 的焦点为F 304⎛⎫ ⎪⎝⎭，，所以AB 所在的直线方程为y34x ⎛⎫- ⎪⎝⎭.将y34x ⎛⎫- ⎪⎝⎭代入y 2＝3x ，整理得x 2－212x ＋916＝0. 设A (x A ，y A )，B (x B ，y B )，由根与系数的关系得x A ＋x B ＝212，x A x B ＝916，故D 错误，22A B y y ＝3x A ·3x B ＝9x A x B ＝8116，∴y 1y 2＝－94，故C 错误． OA OB ⋅＝x A x B ＋y A y B ＝916－94＝－2716，故B 正确．由抛物线的定义可得|AB |＝x A ＋x B ＋p ＝212＋32＝12，故选A 、B. 12．【答案】AC【解析】设圆锥曲线的离心率为e ，由|PF 1|∶|F 1F 2|∶|PF 2|＝4∶3∶2，知①若圆锥曲线为椭圆，则由椭圆的定义，得e ＝1212||||||F F PF PF +＝342+＝12；②若圆锥曲线为双曲线，则由双曲线的定义，得e ＝1212||||||F F PF PF -＝342-＝32.综上，所求的离心率为12或32.故选A 、C. 13．【答案】2211612x y += 【解析】双曲线焦点(±4,0)，顶点(±2,0)，故椭圆的焦点为(±2,0)，顶点(±4,0)．14．【答案】56⎡⎤⎢⎥⎣⎦，【解析】∵m ∈[－2，－1]，∴曲线方程化为2214x y m-=-，曲线为双曲线， ∴e ＝4.∵m ∈[－2，－1]，∴2≤e ≤215．【答案】657 【解析】抛物线y 2＝8x 的焦点F (2,0)，双曲线221169x y -=的一条渐近线方程为y ＝34x ，即3x －4y ＝0，则点F (2,0)到渐近线3x －4y ＝0＝65.双曲线右焦点的坐标为(5,0)，抛物线的准线方程为x ＝－2，所以双曲线右焦点到抛物线准线的距离为7.16．【答案】15【解析】由椭圆的定义知|PF 1|＋|PF 2|＝10，|PF 1|＝10－|PF 2|，|PM |＋|PF 1|＝10＋|PM |－|PF 2|，易知M 点在椭圆外，连接MF 2并延长交椭圆于点P (图略)，此时|PM |－|PF 2|取最大值|MF 2|，故|PM |＋|PF 1|的最大值为10＋|MF 2|＝1015. 17．【解析】(1)根据题意，得60,20,(6)2,m m m m -<⎧⎪>⎨⎪-->⎩解得0＜m ＜2，故命题p 为真命题时，m 的取值范围为(0,2)．(2)若命题q 为真命题，则(m ＋1)(m －1)＜0，解得－1＜m ＜1，故命题q 为假命题时，m 的取值范围为(－∞，－1]∪[1，＋∞)．18．【解析】依题意，设抛物线的方程为y 2＝2px (p >0)，∵点P 32⎛ ⎝在抛物线上，∴6＝2p ×32.∴p ＝2， ∴所求抛物线的方程为y 2＝4x .∵双曲线的左焦点在抛物线的准线x ＝－1上，∴c ＝1，即a 2＋b 2＝1，又点P 32⎛ ⎝在双曲线上，∴229614a b-=，解方程组222219614a b a b⎧+=⎪⎨-=⎪⎩ 得221434a b ⎧=⎪⎪⎨⎪=⎪⎩或2298a b ⎧=⎪⎨=-⎪⎩ (舍去)． ∴所求双曲线的方程为4x 2－43y 2＝1. 19．【解析】(1)由已知得3＋2p ＝4，∴p ＝2，∴抛物线的方程为y 2＝4x ，代入可解得t ＝±(2)设直线AB 的方程为x ＝my ＋n ，A 211,4y y ⎛⎫ ⎪⎝⎭，B 222,4y y ⎛⎫ ⎪⎝⎭.由2,4x my n y x=+⎧⎨=⎩得y 2－4my －4n ＝0，则y 1＋y 2＝4m ，y 1y 2＝－4n .由OA OB ⋅＝5，得212()16y y ＋y 1y 2＝5，∴y 1y 2＝－20或y 1y 2＝4(舍去)．即－4n ＝－20，∴n ＝5，∴直线AB 过定点(5,0)．20．【解析】(1)因为抛物线C ：y 2＝2px (p ＞0)的焦点为F (1,0)，抛物线E ：x 2＝2py 的焦点为M ，所以p ＝2，M (0，1)．①当直线l 的斜率不存在时，其方程为x ＝0，满足题意．②当直线l 的斜率存在时，设方程为y ＝kx ＋1，代入y 2＝4x ，得k 2x 2＋(2k －4)x ＋1＝0.当k ＝0时，x ＝14，满足题意，直线l 的方程为y ＝1；当k ≠0时，令Δ＝(2k －4)2－4k 2＝0，解得k ＝1，所以直线l 的方程为y ＝x ＋1.综上，直线l 的方程为x ＝0或y ＝1或y ＝x ＋1. (2)结合(1)知抛物线C 的方程为y 2＝4x ，直线MF 的方程为y ＝－x ＋1.联立24,1y x y x ⎧=⎨=-+⎩得y 2＋4y －4＝0，设A (x 1，y 1)，B (x 2，y 2)，则y 1＋y 2＝－4，y 1y 2＝－4，所以|y 1－y 2|＝，所以S △OAB ＝12|OF |·|y 1－y 2|＝. 21．【解析】(1)由准圆方程为x 2＋y 2＝4，得a 2＋b 2＝4，椭圆的离心率e ＝c aab ＝1， ∴椭圆的标准方程：23x ＋y 2＝1. (2)∵准圆x 2＋y 2＝4与y 轴正半轴的交点为P (0，2)，设过点P (0,2)且与椭圆相切的直线为y ＝kx ＋2，联立，得222,1,3y kx x y =+⎧⎪⎨+=⎪⎩整理，得 (1＋3k 2)x 2＋12kx ＋9＝0.∵直线y ＝kx ＋2与椭圆相切，∴Δ＝144k 2－4×9(1＋3k 2)＝0，解得k ＝±1，∴l 1，l 2的方程为y ＝x ＋2，y ＝－x ＋2.∵k 1l ＝1，k 2l ＝－1，∴k 1l ·k 2l ＝－1，则1l ⊥2l .22．【解析】 (1)由e ＝c a ＝32，得c 2＝34a 2，b 2＝14a 2，联立⎩⎪⎨⎪⎧y ＝12x ，x 2＋4y 2＝a 2得D ⎝⎛⎭⎫22a ，24a ，所以CD ＝2⎝⎛⎭⎫22a 2＋⎝⎛⎭⎫24a 2＝102a ，又上顶点B ⎝⎛⎭⎫0，a 2到直线l 的距离为d ＝a 5，所以△BCD 的面积为S ＝12CD ·d ＝12×102a ×a 5＝24a 2＝2，解得a 2＝4，即椭圆的方程为x 24＋y 2＝1． (2)法一设Q (x 1，y 1)，则x 214＋y 21＝1，因为直线m 与直线l 的倾斜角互补，所以k m ＝－k 1＝－12，所以直线m 的方程为y －y 1＝－12(x －x 1)，令y ＝0，得M (x 1＋2y 1，0)；令x ＝0，得N ⎝⎛⎭⎫0，12x 1＋y 1．所以QM 2＋QN 2＝(2y 1)2＋y 21＋x 21＋⎝⎛⎭⎫12x 12＝54x 21＋5y 21＝5⎝⎛⎭⎫x 214＋y 21＝5．法二设P (x 0，y 0)，则x 204＋y 20＝1，因为直线m 与直线l 的倾斜角互补，所以k m ＝－k l ＝－12，所以直线m 的方程为y －y 0＝－12(x －x 0)，令y ＝0，得M (x 0＋2y 0，0)；令x ＝0，得N ⎝⎛⎭⎫0，12x 0＋y 0．联立⎩⎨⎧x 24＋y 2＝1，y －y 0＝－12（x －x 0）消去x ，得8y 2－4y (x 0＋2y 0)＋(x 0＋2y 0)2－4＝0，解得Q ⎝⎛⎭⎫2y 0，12x 0，所以QM 2＋QN 2＝x 20＋14x 20＋4y 20＋y 20＝5⎝⎛⎭⎫x 204＋y 20＝5． 23．【解析】(1)A (－a ，0)，B (a ，0)，设P (x 0，y 0)，则x 20a 2＋y 204＝1，依题意y 0x 0＋a ·y 0x 0－a＝－12，得a 2＝8， ∴椭圆标准方程为x 28＋y 24＝1． (2)①当直线l 的斜率存在时，设直线l 的方程为y ＝kx ＋p ，代入椭圆方程得 (1＋2k 2)x 2＋4kpx ＋2p 2－8＝0，因为直线l 与椭圆C 有且只有一个公共点，所以Δ＝16k 2p 2－4(1＋ 2k 2)(2p 2－8)＝8(4＋8k 2－p 2)＝0，即4＋8k 2＝p 2．设x 轴上存在两个定点(s ，0)，(t ，0)，使得这两个定点到直线l 的距离之积为4，则|ks ＋p |k 2＋1·|kt ＋p |k 2＋1＝|k 2st ＋kp （s ＋t ）＋p 2|k 2＋1＝4．即 (st ＋ 4)k ＋p (s ＋t )＝0(*)，或(st ＋ 12)k 2＋(s ＋t )kp ＋8＝0 (**)由(*)恒成立，得⎩⎪⎨⎪⎧st ＋4＝0，s ＋t ＝0，解得⎩⎪⎨⎪⎧s ＝2，t ＝－2或⎩⎪⎨⎪⎧s ＝－2，t ＝2(**)不恒成立． ②当直线l 的斜率不存在，即直线l 的方程为x ＝±22时，定点(－2，0)、F 2(2，0)到直线l 的距离之积(22－2)(22＋2)＝4．综上，存在两个定点(2，0)、(－2，0)，使得这两个定点到直线l 的距离之积为定值4．24．【解析】(1)直线AB 的方程为：bx －ay －ab ＝0.依题意2ca⎧=⎪⎪⎨=1ab⎧=⎪⎨=⎪⎩∴椭圆方程为23x＋y2＝1.(2)假设存在这样的k值，由222,330,y kxx y=+⎧⎨+-=⎩得(1＋3k2)x2＋12kx＋9＝0.∴Δ＝(12k)2－36(1＋3k2)>0.解得k＞1或k＜－1.①设C(x1，y1)，D(x2，y2)，则12212212,13913kx xkx xk⎧+=-⎪⎪+⎨⎪=⎪+⎩②而y1y2＝(kx1＋2)(kx2＋2)＝k2x1x2＋2k(x1＋x2)＋4.要使以CD为直径的圆过点E(－1,0)，当且仅当CE⊥DE时成立，则121211y yx x⋅++＝－1.即y1y2＋(x1＋1)(x2＋1)＝0.∴(k2＋1)x1x2＋(2k＋1)(x1＋x2)＋5＝0.③将②式代入③整理解得k＝76.经验证k＝76使①成立．综上可知，存在k＝76，使得以CD为直径的圆过点E.。

专题12 圆锥曲线压轴小题常见题型全归纳(精讲精练)(原卷版)

专题12 圆锥曲线压轴小题常见题型全归纳【命题规律】1、圆锥曲线的定义、方程与几何性质是每年高考必考的内容．一是求圆锥曲线的标准方程；二是求椭圆或双曲线的离心率、与双曲线的渐近线有关的问题；三是抛物线的性质及应用问题．多以选择、填空题的形式考查，难度中等．2、通过对椭圆、双曲线、抛物线的定义、方程及几何性质的考查，着重考查了数学抽象、数学建模、逻辑推理与数学运算四大核心素养．【核心考点目录】核心考点一：阿波罗尼斯圆与圆锥曲线核心考点二：蒙日圆核心考点三：阿基米德三角形核心考点四：仿射变换问题核心考点五：圆锥曲线第二定义核心考点六：焦半径问题核心考点七：圆锥曲线第三定义核心考点八：定比点差法与点差法核心考点九：切线问题核心考点十：焦点三角形问题核心考点十一：焦点弦问题核心考点十二：圆锥曲线与张角问题核心考点十三：圆锥曲线与角平分线问题核心考点十四：圆锥曲线与通径问题核心考点十五：圆锥曲线的光学性质问题核心考点十六：圆锥曲线与四心问题【真题回归】1．（2022·天津·统考高考真题）已知抛物线212,,y F F =分别是双曲线22221(0,0)x y a b a b-=>>的左、右焦点，抛物线的准线过双曲线的左焦点1F ，与双曲线的渐近线交于点A ，若124F F A π∠=，则双曲线的标准方程为（） A ．22110x y -=B ．22116y x -=C ．2214y x -=D ．2214x y -=2．（2022·全国·统考高考真题）设F 为抛物线2:4C y x =的焦点，点A 在C 上，点(3,0)B ，若AF BF =，则AB =（）A ．2B ．C ．3D ．3．（2022·全国·统考高考真题）已知椭圆2222:1(0)x y C a b a b+=>>的离心率为13，12,A A 分别为C 的左、右顶点，B 为C 的上顶点．若121BA BA ⋅=-，则C 的方程为（） A ．2211816x y +=B ．22198x yC ．22132x y +=D ．2212x y +=4．（多选题）（2022·全国·统考高考真题）已知O 为坐标原点，点(1,1)A 在抛物线2:2(0)C x py p =>上，过点(0,1)B -的直线交C 于P ，Q 两点，则（） A ．C 的准线为1y =- B ．直线AB 与C 相切 C ．2|OP OQ OA ⋅>D ．2||||||BP BQ BA ⋅>5．（多选题）（2022·全国·统考高考真题）已知O 为坐标原点，过抛物线2:2(0)C y px p =>焦点F 的直线与C 交于A ，B 两点，其中A 在第一象限，点(,0)M p ，若||||AF AM =，则（）A ．直线AB 的斜率为B ．||||OB OF =C ．||4||AB OF >D ．180OAM OBM ∠+∠<︒6．（2022·全国·统考高考真题）已知椭圆2222:1(0)x y C a b a b+=>>，C 的上顶点为A ，两个焦点为1F ，2F ，离心率为12．过1F 且垂直于2AF 的直线与C 交于D ，E 两点，||6DE =，则ADE 的周长是________________．7．（2022·全国·统考高考真题）设点(2,3),(0,)A B a -，若直线AB 关于y a =对称的直线与圆22(3)(2)1x y +++=有公共点，则a 的取值范围是________．8．（2022·全国·统考高考真题）已知直线l 与椭圆22163x y +=在第一象限交于A ，B 两点，l 与x 轴，y 轴分别交于M ，N 两点，且||||,||MA NB MN ==l 的方程为___________．【方法技巧与总结】1、在利用圆锥曲线的定义求轨迹方程时，若所求的轨迹符合某种圆锥曲线的定义，则根据定义判定轨迹曲线并写出方程．有时还要注意轨迹是不是完整的曲线，如果不是完整的曲线，则应对其中的变量x 或y 进行限制．2、应用圆锥曲线的定义时，要注意定义中的限制条件．在椭圆的定义中，要求122a F F >；在双曲线的定义中，要求2a <12F F ；在抛物线的定义中，定直线不经过定点．此外，通过到定点和到定直线的距离之比为定值可将三种曲线统一在一起，称为圆锥曲线．3、圆锥曲线定义的应用主要有：求标准方程，将定义和余弦定理等结合使用，研究焦点三角形的周长、面积，求弦长、最值和离心率等．4、用解析法研究圆锥曲线的几何性质是通过方程进行讨论的，再通过方程来研究圆锥曲线的几何性质．不仅要能由方程研究曲线的几何性质，还要能运用儿何性质解决有关问题，如利用坐标范围构造函数或不等关系等．【核心考点】核心考点一：阿波罗尼斯圆与圆锥曲线【典型例题】例1．（2023·全国·高三专题练习）设双曲线222116x y b-=的左右两个焦点分别为1F 、2F ，P 是双曲线上任意一点，过1F 的直线与12F PF ∠的平分线垂直，垂足为Q ，则点Q 的轨迹曲线E 的方程________；M 在曲线E 上，点(8,0)A ，(5,6)B ，则12AM BM +的最小值________．例2．（2023·全国·高三专题练习）希腊著名数学家阿波罗尼斯与欧几里得、阿基米德齐名．他发现：“平面内到两个定点,A B 的距离之比为定值()1λλ≠的点的轨迹是圆”．后来，人们将这个圆以他的名字命名，称为阿波罗尼斯圆，简称阿氏圆．已知在平面直角坐标系xOy 中，()2,1A -，()2,4B -，点P 是满足12λ=的阿氏圆上的任一点，则该阿氏圆的方程为____；若点Q 为抛物线:E 24y x =上的动点，Q 在y 轴上的射影为H ，则PA PQ QH ++的最小值为______．例3．（2022春·江苏镇江·高二校考期中）在平面上给定相异两点A ，B ，设点P 在同一平面上且满足||||PA PB λ=，当 0λ>且1λ≠时，P 点的轨迹是一个圆，这个轨迹最先由古希腊数学家阿波罗尼斯发现，故我们称这个圆为阿波罗尼斯圆．现有双曲线22221(0,0)x y a b a b-=>>， 12,F F 分别为双曲线的左､右焦点，A ，B 为双曲线虚轴的上､下端点，动点P 满足||2||PB PA =， PAB 面积的最大值为4．点M ，N 在双曲线上，且关于原点O 对称，Q 是双曲线上一点，直线QM 和QN 的斜率满足 3QM QN k k ⋅=，则双曲线方程是 ______________ ；过2F 的直线与双曲线右支交于C ，D 两点（其中C 点在第一象限），设点M ､N 分别为 12CF F △､12DF F △的内心，则MN 的范围是 ____________ ．核心考点二：蒙日圆【典型例题】例4．（2023·全国·高三专题练习）蒙日圆涉及的是几何学中的一个著名定理，该定理的内容为：椭圆上两条互相垂直的切线的交点必在一个与椭圆同心的圆上，该圆称为原椭圆的蒙日圆，若椭圆()22:102x y C a a a+=>+的蒙日圆为226x y +=，则=a （） A ．1 B ．2 C ．3 D ．4例5．（2023·全国·高三专题练习）“蒙日圆”涉及几何学中的一个著名定理，该定理的内容为：椭圆上两条互相垂直的切线的交点必在一个与椭圆同心的圆上，该圆称为原椭圆的蒙日圆．若椭圆C ：2211x y a a+=+(0)a >的离心率为12，则椭圆C 的蒙日圆方程为（） A ．229x y += B ．227x y += C ．225x y += D ．224x y +=例6．（2023春·四川乐山·高二四川省乐山沫若中学校考期中）加斯帕尔·蒙日（图1）是18～19世纪法国著名的几何学家，他在研究圆锥曲线时发现：椭圆的任意两条互相垂直的切线的交点都在同一个圆上，其圆心是椭圆的中心，这个圆被称为“蒙日圆”（图2）．则椭圆 22:154x y C +=的蒙日圆的半径为（）A ．3B ．4C ．5D ．6核心考点三：阿基米德三角形【典型例题】例7．（2023·高二课时练习）抛物线上任意两点A ，B 处的切线交于点P ，称PAB 为“阿基米德三角形”，当线段AB 经过抛物线的焦点F 时，PAB 具有以下特征： ①P 点必在抛物线的准线上；②PF AB ⊥．若经过抛物线24y x =的焦点的一条弦为AB ，“阿基米德三角形”为PAB ，且点P 的纵坐标为4，则直线AB 的方程为（）A ．210x y --=B ．220x y +-=C ．210x y +-=D ．220x y --=例8．（2023·全国·高三专题练习）阿基米德（Archimedes ，公元前287年-公元前212年），出生于古希腊西西里岛叙拉古（今意大利西西里岛上），伟大的古希腊数学家、物理学家，与高斯、牛顿并称为世界三大数学家．有一类三角形叫做阿基米德三角形．．．．．．．（过抛物线的弦与过弦端点的两切线所围成的三角形），他利用“通近法”得到抛物线的弦与抛物线所围成的封闭图形的面积等于阿基米德三角形面积的23（即右图中阴影部分面积等于PAB 面积的23）．若抛物线方程为22(0)y px p =>，且直线2p x =与抛物线围成封闭图形的面积为6，则p =（）A ．1B ．2C ．32D ．3例9．（2023·全国·高三专题练习）阿基米德（公元前287年～公元前212年）是古希腊伟大的物理学家、数学家和天文学家．他研究抛物线的求积法得出著名的阿基米德定理，并享有“数学之神”的称号．抛物线的弦与过弦的端点的两条切线所围成的三角形被称为阿基米德三角形．如图，PAB 为阿基米德三角形．抛物线22(0)x py p =>上有两个不同的点()()1122,,,A x y B x y ，以A ，B 为切点的抛物线的切线,PA PB 相交于P ．给出如下结论，其中正确的为（）（1）若弦AB 过焦点，则ABP 为直角三角形且90APB ︒∠=；（2）点P 的坐标是1212,22x x x x +⎛⎫ ⎪⎝⎭；（3）PAB 的边AB 所在的直线方程为()121202x x py x x x --=+；（4）PAB 的边AB 上的中线与y 轴平行（或重合）．A ．（2）（3）（4）B ．（1）（2）C ．（1）（2）（3）D ．（1）（3）（4）核心考点四：仿射变换问题【典型例题】例10．（2023·全国·高三专题练习）已知直线l 与椭圆22142x y +=交于M ，N 两点，当OM ON k k ⋅=______，MON △面积最大，并且最大值为______．记1122(,),(,)M x y N x y ，当MON △面积最大时，2212x x +=_____﹐2212y y +=_______．Р是椭圆上一点，OP OM ON λμ=+，当MON △面积最大时，22λμ+=______．例11．（2023·全国·高三专题练习）过椭圆22143x y +=的右焦点F 的直线与椭圆交于A ，B 两点，则AOB面积最大值为_______．例12．（2023·全国·高三专题练习）已知椭圆22:12x C y +=左顶点为A ，,P Q 为椭圆C 上两动点，直线PO 交AQ 于E ，直线QO 交AP 于D ，直线,OP OQ 的斜率分别为12,k k 且1212k k =-，,AD DF AE EQ λμ==（,λμ是非零实数），求22λμ+=______________．核心考点五：圆锥曲线第二定义【典型例题】例13．（2023·全国·高三专题练习）设F 为抛物线2:6C y x =的焦点，过F 且倾斜角为60°的直线交C 于A ，B 两点，则AB =（）A B ．8 C ．12 D ．例14．（2023·全国·高三专题练习）过抛物线24y x =焦点F 的直线与该抛物线及其准线都相交，交点从左到右依次为A ，B ，C ．若2AB BF =，则线段BC 的中点到准线的距离为（） A ．3B ．4C ．5D ．6例15．（2023·全国·高三专题练习）如图，过抛物线22(0)y px p =>的焦点F 的直线交抛物线于点A ，B ，交其准线l 于点C ，若F 是AC 的中点，且4AF =，则线段AB 的长为（）A ．5B ．6C ．163D ．203核心考点六：焦半径问题【典型例题】例16．（2023·全国·高三专题练习）已知点P 是双曲线22184x y -=上的动点，1F ，2F 为该双曲线的左右焦点，O 为坐标原点，则12||||||PF PF OP +的最大值为（）A ．B ．2C D例17．（2023·全国·高三专题练习）已知双曲线222:1(0)4x y C a α-=>的右支上的点0(P x ，0)y 满足121||3||(PF PF F =，2F 分别是双曲线的左右焦点），则00(cy c x +为双曲线C 的半焦距）的取值范围是（） A．)∞+ B ．[2，25)2C ．25)2D ．[2，例18．（2023·全国·高三专题练习）已知点P 是双曲线22221(0,0)x y a b a b-=>>上的动点，1F ，2F 是左、右焦点，O 是坐标原点，若12||PF PF OP +，则双曲线的离心率为（）AB C ．32D ．2核心考点八：圆锥曲线第三定义【典型例题】例19．（江苏省南京市中华中学2022-2023学年高二下学期初数学试题）椭圆C ：22143x y +=的左、右顶点分别为1A ，2A ，点P 在C 上且直线1PA 的斜率的取值范围是[]2,1--，那么直线2PA 斜率的取值范围是（） A ．33,84⎡⎤⎢⎥⎣⎦B ．13,24⎡⎤⎢⎥⎣⎦C ．1,12⎡⎤⎢⎥⎣⎦D ．3,14⎡⎤⎢⎥⎣⎦例20．（2023·全国·高三专题练习）椭圆22:143x y C +=的左、右顶点分别为1A ，2A ，点P 在C 上且直线2PA 的斜率的取值范围是[3-，1]-，那么直线1PA 斜率的取值范围是（）A ．1[4，3]4B ．1[2，3]4C ．1[2，1]D ．3[4，1]例21．（2023·全国·高三专题练习）已知O 为坐标原点，椭圆22221(0)x y a b a b+=>>的左、右焦点分别是12F F 、，过点1F 且斜率为k 的直线与圆222x y a +=交于A ，B 两点（点B 在x 轴上方），线段1F B 与椭圆交于点M ，2MF 延长线与椭圆交于点N ，且122||,2AF MB MF F N ==，则椭圆的离心率为___________，直线1AF 的斜率为___________．例22．（2023·全国·高三专题练习）设椭圆22221(0)x y a b a b+=>>长轴的两个顶点分别为A 、B ，点C 为椭圆上不同于A 、B 的任一点，若将ABC ∆的三个内角记作A 、B 、C ，且满足3tan 3tan tan 0A B C ++=，则椭圆的离心率为（）A B ．13C D ．23核心考点八：定比点差法与点差法【典型例题】例23．（2023·全国·高三专题练习）已知斜率为k 的直线l 与椭圆22:143x y C +=交于A ，B 两点，线段AB的中点为(1,)M m （0m >），那么k 的取值范围是（）A ．12k <-B ．1122k -<<C ．12k >D ．12k <-，或12k >例24．（2023·全国·高三专题练习）已知椭圆22:143x y C +=，过点()11P ，的直线l 与椭圆C 交于,A B 两点，若点P 恰为弦AB 中点，则直线l 斜率是（） A ．3-B ．13-C ．34-D ．43-例25．（2023·全国·高三专题练习）已知椭圆2222:1(0)x y a b a b Γ+=>>内有一定点(1,1)P ，过点P 的两条直线1l ，2l 分别与椭圆Γ交于A 、C 和B 、D 两点，且满足AP PC λ=，BP PD λ=，若λ变化时，直线CD 的斜率总为14-，则椭圆Γ的离心率为A B ．12C D 核心考点九：切线问题【典型例题】例26．（2023·全国·高三专题练习）已知过圆锥曲线221x y m n+=上一点(),o o P x y 的切线方程为001x x y y m n +=．过椭圆221124x y +=上的点()3,1A -作椭圆的切线l ，则过A 点且与直线l 垂直的直线方程为（） A ．30x y --= B ．-20x y += C ．2330x y +-=D ．3100x y --=例27．（2023·全国·高三专题练习）已知点()1,0A -､()10B ,，若过A ､B 两点的动抛物线的准线始终与圆228x y +=相切，该抛物线焦点的轨迹是某圆锥曲线的一部分，则该圆锥曲线是（）A ．椭圆B ．圆C ．双曲线D ．抛物线例28．（2023·全国·高三专题练习）设P 是双曲线C ：22221(0,0)x y a b a b -=>>在第一象限内的动点，O 为坐标原点，双曲线C 在P 点处的切线的斜率为m ，直线OP 的斜率为n ，则当1ln ln b a m n a b mn++++取得最小值时，双曲线C 的离心率为（）AB ．2CD核心考点十：焦点三角形问题【典型例题】例29．（2023春·河南洛阳·高二宜阳县第一高级中学校考阶段练习）已知椭圆2212516x y +=的左、右焦点分别为1F 、2F ，点P 在椭圆上，若16PF =，则12PF F △的面积为（）A ．8B ．C ．16D ．例30．（2023·全国·高三专题练习）椭圆两焦点分别为()13,0F ，()23,0F -，动点P 在椭圆上，若12PF F △的面积的最大值为12，则此椭圆上使得12F PF ∠为直角的点P 有（） A ．0个B ．1个C ．2个D ．4个例31．（2023·全国·高三专题练习）双曲线221169x y -=的左、右焦点分别1F 、2F ，P 为双曲线右支上的点，12PF F △的内切圆与x 轴相切于点C ，则圆心I 到y 轴的距离为（）A ．1B ．2C ．3D ．4例32．（2023·全国·高三专题练习）已知(P 在双曲线22214x y b-=上，其左、右焦点分别为1F 、2F ，三角形12PF F 的内切圆切x 轴于点M ，则2MP MF ⋅的值为（）A ．1B ．1C ．2D ．核心考点十一：焦点弦问题【典型例题】例33．（2023·全国·高三专题练习）已知抛物线()2:20C y px p =>的焦点F 与椭圆2212516x y +=的右焦点重合．斜率为()0k k >直线l 经过点F ，且与C 的交点为A ，B ．若3AF BF =，则直线l 的方程是（）A 0y --=B ．40y --C ．390x y --=D ．330x y --=例34．（2023·全国·高三专题练习）抛物线24y x =的焦点弦被焦点分成长是m 和n 的两部分，则m 与n 的关系是（） A ．m ＋n ＝mnB ．m ＋n ＝4C ．mn ＝4D ．无法确定例35．（2023春·河南南阳·高二统考期中）如图所示，1F ，2F 是双曲线C ：22221()00a x y a b b >-=>，的左、右焦点，过1F 的直线与C 的左、右两支分别交于A ，B 两点．若22345AB BF AF =∶∶∶∶，则双曲线的离心率为（）A ．2BC D核心考点十二：圆锥曲线与张角问题【典型例题】例36．（2023·全国·高三专题练习）定义：点P 为曲线L 外的一点，,A B 为L 上的两个动点，则APB ∠取最大值时，APB ∠叫点P 对曲线L 的张角．已知点P 为抛物线2:4C y x =上的动点，设P 对圆22:(3)1M x y -+=的张角为θ，则cos θ的最小值为___________．例37．（2023春·山东·高二山东省实验中学校考阶段练习）已知椭圆22221(0)x y C a b a b +=>>：的左、右焦点分别为1F ，2F ，点P 在C 上，直线PF 2与y 轴交于点Q ，点P 在线段2F Q 上，1QPF 的内切圆的圆心为I ，若12IF F △为正三角形，则12F PF ∠=___________，C 的离心率的取值范围是___________．核心考点十三：圆锥曲线与角平分线问题【典型例题】例38．（2022春·广东广州·高二校联考期中）已知椭圆2222:1(0)x y C a b a b+=>>的左､右焦点分别为12,,F F P为C 上不与左､右顶点重合的一点，I 为12PF F △的内心，且12322IF IF PI +=，则C 的离心率为（）A ．13B ．25C D 例39．（2023春·辽宁铁岭·高二昌图县第一高级中学校考期中）双曲线22221x y a b -=的左右焦点分别为1F 、2F ，P 是双曲线右支上一点，I 为12PF F △的内心，PI 交x 轴于Q 点，若12FQ PF =，且:2:1PI IQ =，则双曲线的离心率e 的值为（） A ．2B ．32C D ．53例40．（2023·全国·高三专题练习）已知椭圆()2222:10x y C a b a b+=>>的两个焦点1F ，2F 与短轴的两个端点1B ，2B 都在圆221x y +=上，P 是C 上除长轴端点外的任意一点，12F PF ∠的平分线交C 的长轴于点M ，则12MB MB +的取值范围是（）A ．⎡⎣B ．⎡⎣C ．⎡⎣D ．2,⎡⎣核心考点十四：圆锥曲线与通径问题【典型例题】例41．（2023·全国·高三专题练习）在平面直角坐标系xOy 中，以点()14,0F ，()28,9F 为焦点的动椭圆与双曲线221412x y -=的右支有公共点，则椭圆通径的最小值为______．例42．（2023·全国·高三专题练习）过抛物线2:2(0)T y px p =>的焦点F 的直线与T 交于,A B 两点，且2AF FB =，T 的准线l 与x 轴交于C ，CBF 的面积为T 的通径长为___________．例43．（2023·全国·高三专题练习）过双曲线的焦点与双曲线实轴垂直的直线被双曲线截得的线段的长称为双曲线的通径，其长等于22b a（a 、b 分别为双曲线的实半轴长与虚半轴长）．已知双曲线222:1x C y a -=（0a >）的左、右焦点分别为1F 、2F ，若点M 是双曲线C 上位于第四象限的任意一点，直线l 是双曲线的经过第二、四象限的渐近线，MQ l ⊥于点Q ，且1MQ MF +的最小值为3，则双曲线C 的通径为__________．核心考点十五：圆锥曲线的光学性质问题【典型例题】例44．（2023·全国·高三专题练习）椭圆有这样的光学性质：从椭圆的一个焦点出发的光线，经椭圆反射后，反射光线经过椭圆的另一个焦点，今有一个水平放置的椭圆形台球盘，点A 、B 是它的焦点，长轴长为2a ，焦距为2c ，静放在点A 的小球（小球的半径不计），从点A 沿直线出发，经椭圆壁反弹后第一次回到点A 时，小球经过的路程是（） A ．4aB ．2()a c -C ．2()a c +D ．以上答案均有可能例45．（2023·全国·高三专题练习）双曲线的光学性质为：从双曲线一个焦点发出的光，经过反射后，反射光线的反向延长线都汇聚到双曲线的另一个焦点上，若双曲线E 的焦点分别为1F ，2F ，经过2F 且与1F 2F 垂直的光线经双曲线E 反射后，与1F 2F 成45°角，则双曲线E 的离心率为（）AB1 C．D．1例46．（2023·全国·高三专题练习）抛物线有如下光学性质：由其焦点射出的光线经抛物线反射后，沿平行于抛物线对称轴的方向射出；反之，平行于抛物线对称轴的入射光线经抛物线反射后必过抛物线的焦点．已知抛物线2:4C y x =，一条平行于x 轴的光线1l 从点()8,4P 射入，经过C 上的点A 反射后，再经C 上另一点B 反射后，沿直线2l 射出，则AB =（） A ．7B ．174C ．214D ．254核心考点十六：圆锥曲线与四心问题【典型例题】例47．（2023·全国·高三专题练习）已知椭圆Γ：22143x y +=，过其左焦点1F 作直线l 交椭圆Γ于P ，A 两点，取P 点关于x 轴的对称点B ．若G 点为PAB 的外心，则1PAGF =（） A ．2B ．3C ．4D ．以上都不对例48．（2023·全国·高三专题练习）双曲线22122:1(0,0)x y C a b a b-=>>的渐近线与抛物线22:2(0)C x py p =>交于点,,A O B ，若抛物线2C 的焦点恰为AOB ∆的内心，则双曲线1C 的离心率为（）A ．32BC4D ．122例49．（2023·全国·高三专题练习）已知双曲线C ：22221(0,0)x y a b a b-=>>的左、右焦点分别是1F ，2F ，P是双曲线右支上一点，且212PF F F ⊥，I 和G 分别是12PF F △的内心和重心，若IG 与x 轴平行，则双曲线的离心率为（） AB ．2C ．3D ．4例50．（2023·全国·高三专题练习）记椭圆C ：2221x y +=的左右焦点为1F ，2F ，过2F 的直线l 交椭圆于A ，B ，A ，B 处的切线交于点P ，设12F F P 的垂心为H ，则PH 的最小值是（）ABCD【新题速递】一、单选题1．（2023春·福建泉州·高三阶段练习）已知椭圆E ：221164x y +=的左右顶点分别为1A ，2A ，圆1O 的方程为()22114x y ⎛++= ⎝⎭，动点P 在曲线E 上运动，动点Q 在圆1O 上运动，若12A A P △的面积为PQ 的最大值和最小值分别为m 和n ，则m n +的值为（）AB ．C ．D ．2．（2023·河南郑州·高三阶段练习）公元656年，唐代李淳风注《九章算术》时提到祖暅的开立圆术．祖暅在求球体积时，使用一个原理：“幂势既同，则积不容异”．“幂”是截面积，“势”是立体的高．意思是两个同高的几何体，如在等高处的截面面积相等﹐则体积相等．更详细点说就是，界于两个平行平面之间的两个立体，被任一平行于这两个平面的平面所截，如果两个截面的面积相等，则这两个几何体的体积相等．上述原理在中国被称为祖暅原理，国外则一般称之为卡瓦列利原理．已知将双曲线22:182x y C -=与直线2y =±围成的图形绕y 轴旋转一周得到一个旋转体E ，则旋转体E 的体积是（）A ．32π3B ．64π3C ．80π3D ．160π33．（2023·广西南宁·南宁二中校考一模）设12F F 、是双曲线22:1810y C x -=的左、右两个焦点，O 为坐标原点，点P 在C 上且1212OP PF PF =-，则1PF O 的面积为（） A ．5B ．8C ．10D ．124．（2023·全国·高三校联考阶段练习）在平面直角坐标系中，已知点()20M ，，()10N -，，动点()Q x y ，满足2QM QN =，过点()31-，的直线与动点Q 的轨迹交于A ，B 两点，记点Q 的轨迹的对称中心为C ，则当ABC 面积取最大值时，直线AB 的方程是（）A ．4y x =+B ．4y x =-+C ．24y x =+D ．24y x =-+5．（2023春·北京大兴·高三校考阶段练习）数学美的表现形式不同于自然美或艺术美那样直观，它蕴藏于特有的抽象概念，公式符号，推理论证，思维方法等之中，揭示了规律性，是一种科学的真实美．平面直角坐标系中，曲线22:C x y x y +=+就是一条形状优美的曲线，对于此曲线，给出如下结论：①曲线C 围成的图形的面积是2π+； ②曲线C 上的任意两点间的距离不超过2；③若(),P m n 是曲线C 上任意一点，则3m n +-的最小值是1．其中正确结论的个数为（） A ．0B ．1C ．2D ．36．（2023春·重庆·高三统考阶段练习）已知点P 为抛物线()220y px p =>上一动点，点Q 为圆22:(1)(4)1C x y ++-=上一动点，点F 为抛物线的焦点，点P 到y 轴的距离为d ，若PQ d +的最小值为2，则p =（） A ．12p =B ．1p =C ．2p =D ．4p =7．（2023·全国·高三专题练习）如图所示，1F ，2F 是双曲线C ：22221x y a b -=（0a >，0b >）的左、右焦点，C 的右支上存在一点B 满足12BF BF ⊥，1BF 与C 的左支的交点A 满足221212sin sin BF AF F AF B F F ∠=∠，则双曲线C的离心率为（）A ．3B．CD8．（2023·北京·高三专题练习）在平面直角坐标系中，,A B 是直线x y m +=上的两点，且10AB =．若对于任意点()()cos ,sin 02πP θθθ≤<，存在,A B 使90APB ∠=成立，则m 的最大值为（） A．B．C．D．9．（2023·全国·高三专题练习）用平面截圆柱面，当圆柱的轴与α所成角为锐角时，圆柱面的截线是一个椭圆．著名数学家Dandelin 创立的双球实验证明了上述结论．如图所示，将两个大小相同的球嵌入圆柱内，使它们分别位于α的上方和下方，并且与圆柱面和α均相切．给出下列三个结论：①两个球与α的切点是所得椭圆的两个焦点；②椭圆的短轴长与嵌入圆柱的球的直径相等；③当圆柱的轴与α所成的角由小变大时，所得椭圆的离心率也由小变大．其中，所有正确结论的序号是（） A ．①B ．②③C ．①②D ．①③10．（2023春·内蒙古赤峰·高三统考阶段练习）已知圆22:4O x y +=和圆22:4210M x y x y ++-+=相交于A ，B 两点，下列说法中错误的是（）． A ．圆O 与圆M 有两条公切线 B ．圆O 与圆M 关于直线AB 对称 C ．线段ABD ．E ，F 分别是圆O 和圆M 上的点，则EF的最大值为4二、多选题11．（2023·全国·高三校联考阶段练习）已知F 是抛物线2:2C x y =的焦点，,A B 是抛物线C 上的两点，O 为坐标原点，则（）A ．若AF y ⊥轴，则1AF =B ．若2AF =，则AOFC ．AB 长度的最小值为2D ．若AOB 90∠=，则8OA OB ⋅≥12．（2023·江苏苏州·苏州中学校考模拟预测）已知椭圆()2222:10x y C a b a b+=>>的左，右焦点分别为12,F F ，长轴长为4，点)P在椭圆C 外，点Q 在椭圆C 上，则（）A ．椭圆C的离心率的取值范围是⎫⎪⎪⎝⎭B ．当椭圆C1QF的取值范围是2⎡⎣ C ．存在点Q 使得210QF QF ⋅=D ．1211QF QF +的最小值为2 13．（2023·全国·高三专题练习）已知O 为坐标原点，抛物线C ：22y px =（0p >）的焦点F 为()1,0，过点()3,2M 的直线l 交抛物线C 于A ，B 两点，点P 为抛物线C 上的动点，则（） A ．PM PF +的最小值为B ．C 的准线方程为=1x -C ．4OA OB ⋅≥-D ．当PF l ∥时，点P 到直线l 的距离的最大值为14．（2023·全国·高三专题练习）已知抛物线22y x =的焦点为F ，()11,M x y ，()22,N x y 是抛物线上两点，则下列结论正确的是（） A ．点F 的坐标为1,08⎛⎫ ⎪⎝⎭B ．若直线MN 过点F ，则12116x x =-C ．若MF NF λ=，则MN 的最小值为12 D ．若32MF NF +=，则线段MN 的中点P 到x 轴的距离为58三、填空题15．（2023春·甘肃兰州·高三兰化一中校考阶段练习）已知抛物线C ：y 2=2px （p >0）的焦点F 与椭圆22143x y +=的右焦点重合，点M 是抛物线C 的准线上任意一点，直线MA ，MB 分别与抛物线C 相切于点A ，B ．设直线MA ，MB 的斜率分别为1212,,k k k k ⋅=则______16．（2023·全国·高三校联考阶段练习）已知双曲线22221()00a x y a bb >-=>，的离心率2≥e ，直线1y x =-+交双曲线于点M ，N ，O 为坐标原点且OM ON ⊥，则双曲线实轴长的最小值是__________．17．（2023春·重庆·高三统考阶段练习）已知圆221:4C x y +=与圆222:(1)(1)10C x y +++=相交于A ，B 两点，则||AB =________．18．（2023·全国·高三专题练习）已知抛物线C ：22y px =（0p >）的准线方程为2x =-，焦点为F ，准线与x 轴的交点为A ､B 为抛物线C |2||BF AB =，则点F 到AB 的距离为______．19．（2023·全国·高三专题练习）已知实数x ，y 满足：22(2)(1)1x y ++-=，则 1 2 x y -+的取值范围是______．20．（2023·江苏苏州·苏州中学校考模拟预测）已知抛物线M ：24x y =，圆C ：22(3)4x y +-=，在抛物线M 上任取一点P ，向圆C 作两条切线PA 和PB ，切点分别为A ，B ，则CA CB ⋅的取值范围是______ ．。

上海高二数学圆锥曲线专题精讲

上海高二数学圆锥曲线专题精讲一、知识回顾1. 椭圆、双曲线、抛物线的标准方程与几何性质椭圆双曲线抛物线定义 1．到两定点F 1,F 2的距离之和为定值2a(2a>|F 1F 2|)的点的轨迹 1．到两定点F 1,F 2的距离之差的绝对值为定值2a(0<2a<|F 1F 2|)的点的轨迹2．与定点和直线的距离之比为定值e 的点的轨迹.（0<e<1） 2．与定点和直线的距离之比为定值e 的点的轨迹.（e>1）与定点和直线的距离相等的点的轨迹. 图形方程标准方程 12222=+b y a x (b a >>0) 12222=-b y a x (a>0,b>0) y 2=2px 参数方程为离心角）参数θθθ(sin cos ⎩⎨⎧==b y a x 为离心角）参数θθθ(tan sec ⎩⎨⎧==b y a x ⎩⎨⎧==pt y pt x 222(t 为参数) 范围 ─a ≤x ≤a ，─b ≤y ≤b |x| ≥ a ，y ∈R x ≥0 中心原点O （0，0）原点O （0，0）顶点 (a,0), (─a,0), (0,b) , (0,─b)(a,0), (─a,0) (0,0)对称轴 x 轴，y 轴；长轴长2a,短轴长2b x 轴，y 轴; 实轴长2a, 虚轴长2b.x 轴焦点 F 1(c,0), F 2(─c,0) F 1(c,0), F 2(─c,0))0,2(p F 焦距 2c （c=22b a -） 2c （c=22b a +）离心率 )10(<<=e ace )1(>=e ace e=1准线x=c a 2±x=ca 2±2p x -= 渐近线y=±ab x焦半径 ex a r ±=)(a ex r ±±=2p x r += 通径ab 22 ab 22 2p焦参数c a 2ca 2P2. 椭圆、双曲线、抛物线的标准方程的其他形式及相应性质.3. 等轴双曲线4. 共轭双曲线5. 方程y 2=ax 与x 2=ay 的焦点坐标及准线方程.6.共渐近线的双曲线系方程.二、几种常见求轨迹方程的方法 1．直接法由题设所给(或通过分析图形的几何性质而得出)的动点所满足的几何条件列出等式，再用坐标代替这等式，化简得曲线的方程，这种方法叫直接法．例1(1)求和定圆x 2+y 2=k 2的圆周的最小距离等于k 的动点P 的轨迹方程； (2)过点A(a ，o)作圆O ∶x 2+y 2=R 2(a ＞R ＞o)的割线，求割线被圆O 截得弦的中点的轨迹． 2．定义法利用所学过的圆的定义、椭圆的定义、双曲线的定义、抛物线的定义直接写出所求的动点的轨迹方程，这种方法叫做定义法．例2 设Q 是圆x 2+y 2=4上的动点，另有点(3,0),A 线段AQ 的垂直平分线l 交半径OQ 于点P ，当Q 点在圆周上运动时，求点P 的轨迹方程． 3．相关点法若动点P(x ，y)随已知曲线上的点Q(x 0，y 0)的变动而变动，且x 0、y 0可用x 、y 表示，则将Q 点坐标表达式代入已知曲线方程，即得点P 的轨迹方程．这种方法称为相关点法(或代换法)．例3 已知抛物线y2=x+1，定点A(3，1)、B为抛物线上任意一点，点P在线段AB上，且有BP∶PA=1∶2，当B点在抛物线上变动时，求点P的轨迹方程．例4.垂直于y轴的直线与y轴及抛物线y2=2(x–1)分别交于点A和点P，点B在y轴上且点A分OB的比为1:2，求线段PB中点的轨迹方程.4．待定系数法求圆、椭圆、双曲线以及抛物线的方程常用待定系数法求．例4 已知抛物线y2=4x和以坐标轴为对称轴、实轴在y轴上的双曲线仅有两个公共点，又直线y=2x被双曲线截得线段长等于25，求此双曲线方程．三、点、直线与圆锥曲线的位置关系1．点P(x0，y0)和圆锥曲线C：f(x，y)=0的位置关系有：点P在曲线C上、点P在曲线C内部(含焦点区域)、点P在曲线的外部(不含焦点的区域)．2．直线l：Ax+By+C=0和圆锥曲线C：f(x，y)=0的位置关系可分为：相交、相切、相离．这三种位置关系的条件是：设直线l:Ax+By+C=0,圆锥曲线C：f(x,y)=0 ; 由(,)0Ax By CF x y++=⎧⎨=⎩消去y（或x）得：ax2+bx+c=0 (a≠0) ;令Δ=b2-4ac, 则（1）Δ>0⇔相交；（2）Δ=0⇔相切（3）Δ<0⇔相离.注意：直线与抛物线、双曲线有一个公共点是直线与抛物线、双曲线相切的必要条件，但不是充分条件．二、例题例1若直线y=kx+1与焦点在x轴上的椭圆2215x ym+=总有公共点，求m的取值范围．提示：分别从曲线和方程与数形结合思想两个角度分析、解题.例2椭圆C:22143x y+=上有相异两点关系直线l: y=4x+m 对称，求m的取值范围．点拨1：对称点在直线 l’ ： 14y x n =-+上，且l ’与椭圆C 有两个不同的交点，可用“判别式法”.点拨2：两对称点P 1(x 1，y 1)，P 2(x 2，y 2)连线的中点M (x 0，y 0)在椭圆C 内，可用“内点法”．说明：判别式法和内点法，是解决圆锥曲线上存在两点关于直线的对称的一般方法例3.已知抛物线C ：y=─x 2+mx─1,点A(3,0),B(0,3)，若抛物线C 与线段AB 有两个交点，求m 的取值范围.提示：转化为一元二次方程根的分布. 例4.过椭圆C ：12222=+b y a x (a>b>0)上一动点P 向圆O ：x 2+y 2=b 2引两条切线PA 、PB ，切点分别是A 、B ，直线AB 与x 轴，y 轴分别交于M ，N 两点，求△MON 面积的最小值点拨：充分利用平几知识解题.四、与圆锥曲线有关的几种典型题 1．圆锥曲线的弦长求法设圆锥曲线C ∶f(x ，y)=0与直线l ∶y=kx+b 相交于A(x1，y1)、B(x 2，y2)两点，则弦长|AB|为：(2)若弦AB 过圆锥曲线的焦点F ，则可用焦半径求弦长，|AB|=|AF|+|BF|．例1 过抛物线214y x =-的焦点作倾斜角为α的直线l 交抛物线于A 、B 两点，且|AB |=8，求倾斜角α．2．与圆锥曲线有关的最值(极值)的问题在解析几何中求最值，关键是建立所求量关于自变量的函数关系，再利用代数方法求出相应的最值．注意点是要考虑曲线上点坐标(x ，y )的取值范围．例2 已知x 2+4(y -1)2=4，求：(1)x 2+y 2的最大值与最小值；(2)x +y 的最大值与最小值． 3．与圆锥曲线有关的证明问题它涉及到线段相等、角相等、直线平行、垂直的证明方法，以及定点、定值问题的判断方法．。

高考圆锥曲线知识点及相关习题精解(含答案)

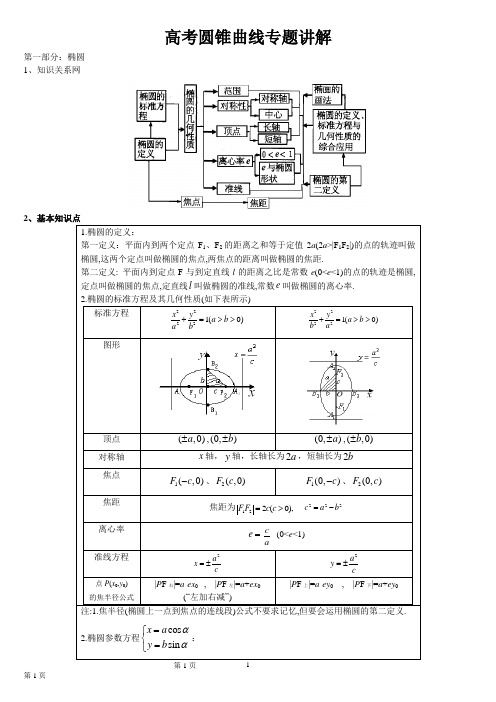
高考圆锥曲线专题讲解第一部分：椭圆 1、知识关系网2、基本知识点1.椭圆的定义：第一定义：平面内到两个定点F 1、F 2的距离之和等于定值2a (2a >|F 1F 2|)的点的轨迹叫做椭圆,这两个定点叫做椭圆的焦点,两焦点的距离叫做椭圆的焦距.第二定义: 平面内到定点F 与到定直线l 的距离之比是常数e (0<e <1)的点的轨迹是椭圆,定点叫做椭圆的焦点,定直线l 叫做椭圆的准线,常数e 叫做椭圆的离心率. 2.椭圆的标准方程及其几何性质(如下表所示)标准方程22221(0)x y a b a b+=>> 22221(0)x y a b b a +=>> 图形顶点 (,0)a ±,(0,)b ± (0,)a ±,(,0)b ±对称轴 x 轴，y 轴，长轴长为2a ，短轴长为2b焦点 1(,0)F c -、2(,0)F c1(0,)F c -、2(0,)F c焦距焦距为122(0),F F c c => 222c a b =-离心率 e =c a(0<e <1)准线方程2a x c=±2a y c=±点P (x 0,y 0) 的焦半径公式|P F 右|=a -ex 0 , |P F 左|=a +ex 0(“左加右减”)|P F 上|=a -ey 0 , |P F 下|=a +ey 0注:1.焦半径(椭圆上一点到焦点的连线段)公式不要求记忆,但要会运用椭圆的第二定义. 2.椭圆参数方程cos sin x a y b αα=⎧⎨=⎩：如图点(cos ,sin )N a b αα的轨迹为椭圆.3、典型例题例1.F 1，F 2是定点，且|F 1F 2|=6，动点M 满足|MF 1|+|MF 2|=6，则M 点的轨迹方程是( ) (A)椭圆 (B)直线 (C)圆 (D)线段例2. 已知ABC ∆的周长是16，)0,3(-A ，B )0,3(, 则动点的轨迹方程是( )(A)1162522=+y x (B))0(1162522≠=+y y x (C)1251622=+y x (D))0(1251622≠=+y y x 例3. 若F (c ，0)是椭圆22221x y a b+=的右焦点，F 与椭圆上点的距离的最大值为M ，最小值为m ，则椭圆上与F 点的距离等于2M m+的点的坐标是( ) (A)(c ，2b a ±) 2()(,)b B c a-± (C)(0，±b ) (D)不存在例4. 如果椭圆221259x y +=上有一点P ，它到左准线的距离为2.5，那么P 点到右焦点的距离与到左焦点的距离之比是( )。

圆锥曲线(文科)解答题20题-备战高考数学冲刺横向强化精练精讲(解析版)

圆锥曲线（文科）解答题20题1．（2020年全国统一高考数学试卷（文科）（新课标Ⅱ））已知椭圆C 1：22221x y a b+=(a >b >0)的右焦点F 与抛物线C 2的焦点重合，C 1的中心与C 2的顶点重合．过F 且与x 轴垂直的直线交C 1于A ，B 两点，交C 2于C ，D 两点，且|CD |=43|AB |．（1）求C 1的离心率；（2）若C 1的四个顶点到C 2的准线距离之和为12，求C 1与C 2的标准方程．【答案】（1）12；（2）1C ：2211612x y+=，2C ： 28y x =.【分析】（1）根据题意求出2C 的方程，结合椭圆和抛物线的对称性不妨设,A C 在第一象限，运用代入法求出,,,A B C D 点的纵坐标，根据4||||3CD AB =，结合椭圆离心率的公式进行求解即可；（2）由（1）可以得到椭圆的标准方程，确定椭圆的四个顶点坐标，再确定抛物线的准线方程，最后结合已知进行求解即可；【详解】解：（1）因为椭圆1C 的右焦点坐标为：(c,0)F ,所以抛物线2C 的方程为24y cx =，其中22c a b -不妨设,A C 在第一象限，因为椭圆1C 的方程为：22221x ya b+=，所以当x c =时，有222221c y b y a b a +=⇒=±，因此,A B 的纵坐标分别为2b a ，2b a-；又因为抛物线2C 的方程为24y cx =，所以当x c =时，有242y c c y c =⋅⇒=±，所以,C D 的纵坐标分别为2c ，2c -，故22||b AB a=，||4CD c =.由4||||3CD AB =得2843b c a=，即2322()c c a a ⋅=-，解得2c a =-（舍去），12c a =.所以1C 的离心率为12.（2）由（1）知2a c =，3b c =，故22122:143x y C c c+=，所以1C 的四个顶点坐标分别为(2,0)c ，(2,0)c -，3)c ，(0,3)c ，2C 的准线为x c =-. 由已知得312c c c c +++=，即2c =. 所以1C 的标准方程为2211612x y +=，2C 的标准方程为28y x =.【点睛】本题考查了求椭圆的离心率，考查了求椭圆和抛物线的标准方程，考查了椭圆的四个顶点的坐标以及抛物线的准线方程，考查了数学运算能力.2．（2021年全国高考乙卷数学（文）试题）已知抛物线2:2(0)C y px p =>的焦点F 到准线的距离为2．（1）求C 的方程;（2）已知O 为坐标原点，点P 在C 上，点Q 满足9PQ QF =，求直线OQ 斜率的最大值.【答案】（1）24y x =；（2）最大值为13.【分析】（1）由抛物线焦点与准线的距离即可得解；（2）设()00,Q x y ，由平面向量的知识可得()00109,10P x y -，进而可得20025910y x +=，再由斜率公式及基本不等式即可得解. 【详解】（1）抛物线2:2(0)C y px p =>的焦点,02p F ⎛⎫⎪⎝⎭，准线方程为2p x =-，由题意，该抛物线焦点到准线的距离为222p p p ⎛⎫--== ⎪⎝⎭，所以该抛物线的方程为24y x =；（2）设()00,Q x y ，则()00999,9PQ QF x y ==--，所以()00109,10P x y -，由P 在抛物线上可得()()200104109y x =-，即20025910y x +=，所以直线OQ 的斜率000220001025925910OQ y y y k y x y ===++，当00y =时，0OQ k =；当00y ≠时，0010925OQ k y y =+，当00y >时，因为0092530y y +≥，此时103OQk <≤，当且仅当00925y y =，即035y =时，等号成立；当00y <时，0OQ k <；综上，直线OQ 的斜率的最大值为13.【点睛】关键点点睛：解决本题的关键是利用平面向量的知识求得点Q 坐标的关系，在求斜率的最值时要注意对0y 取值范围的讨论.3．（2021年全国高考甲卷数学（理）试题）抛物线C 的顶点为坐标原点O ．焦点在x 轴上，直线l ：1x =交C 于P ，Q 两点，且OP OQ ⊥．已知点()2,0M ，且M 与l 相切．（1）求C ，M 的方程；（2）设123,,A A A 是C 上的三个点，直线12A A ，13A A 均与M 相切．判断直线23A A 与M 的位置关系，并说明理由．【答案】（1）抛物线2:C y x =，M 方程为22(2)1x y -+=；（2）相切，理由见解析【分析】（1）根据已知抛物线与1x =相交，可得出抛物线开口向右，设出标准方程，再利用对称性设出,P Q 坐标，由OP OQ ⊥，即可求出p ；由圆M 与直线1x =相切，求出半径，即可得出结论；（2）先考虑12A A 斜率不存在，根据对称性，即可得出结论；若121323,,A A A A A A 斜率存在，由123,,A A A 三点在抛物线上，将直线121223,,A A A A A A 斜率分别用纵坐标表示，再由1212,A A A A 与圆M 相切，得出2323,y y y y +⋅与1y 的关系，最后求出M 点到直线23A A 的距离，即可得出结论. 【详解】（1）依题意设抛物线200:2(0),(1,),(1,)C y px p P y Q y =>-，20,1120,21OP OQ OP OQ y p p ⊥∴⋅=-=-=∴=，所以抛物线C 的方程为2y x =，(0,2),M M 与1x =相切，所以半径为1，所以M 的方程为22(2)1x y -+=；（2）设111222333(),(,),(,)A x y A x y A x y若12A A 斜率不存在，则12A A 方程为1x =或3x =，若12A A 方程为1x =，根据对称性不妨设1(1,1)A ，则过1A 与圆M 相切的另一条直线方程为1y =，此时该直线与抛物线只有一个交点，即不存在3A ，不合题意；若12A A 方程为3x =，根据对称性不妨设12(3,A A 则过1A 与圆M 相切的直线13A A为3)y x -，又131********A A y y k y x x y y -====∴=-+， 330,(0,0)x A =，此时直线1323,A A A A 关于x 轴对称，所以直线23A A 与圆M 相切；若直线121323,,A A A A A A 斜率均存在，则121323121323111,,A A A A A A k k k y y y y y y ===+++，所以直线12A A 方程为()11121y y x x y y -=-+，整理得1212()0x y y y y y -++=，同理直线13A A 的方程为1313()0x y y y y y -++=，直线23A A 的方程为2323()0x y y y y y -++=， 12A A 与圆M相切，1=整理得22212121(1)230y y y y y -++-=，13A A 与圆M 相切，同理22213131(1)230y y y y y -++-=所以23,y y 为方程222111(1)230y y y y y -++-=的两根，2112323221123,11y y y y y y y y -+=-⋅=--，M 到直线23A A 的距离为：21223122123213|2|21()1()1y y y y y -+=+++--22112222111111(1)4y y y y +===+-+，所以直线23A A 与圆M 相切；综上若直线1213,A A A A 与圆M 相切，则直线23A A 与圆M 相切. 【点睛】关键点点睛：（1）过抛物线上的两点直线斜率只需用其纵坐标（或横坐标）表示，将问题转化为只与纵坐标（或横坐标）有关；（2）要充分利用1213,A A A A 的对称性，抽象出2323,y y y y +⋅与1y 关系，把23,y y 的关系转化为用1y 表示.4．（2019年全国统一高考数学试卷（理科）（新课标Ⅲ））已知曲线C ：y =22x ，D 为直线y =12-上的动点，过D 作C 的两条切线，切点分别为A ，B .（1）证明：直线AB 过定点：（2）若以E (0，52)为圆心的圆与直线AB 相切，且切点为线段AB 的中点，求四边形ADBE 的面积.【答案】(1)见详解；(2) 3或2【分析】（1）可设11(,)A x y ，22(,)B x y ，1(,)2D t -然后求出A ，B 两点处的切线方程，比如AD ：1111()2y x x t +=-，又因为BD 也有类似的形式，从而求出带参数直线AB 方程，最后求出它所过的定点.（2）由(1)得带参数的直线AB 方程和抛物线方程联立，再通过M 为线段AB 的中点，EM AB ⊥得出t 的值，从而求出M 坐标和EM 的值，12,d d 分别为点,D E 到直线AB 的距离，则21221,1d t d t =+=+.【详解】(1)证明：设1(,)2D t -,11(,)A x y ,则21112y x =．又因为212y x =，所以y'x =.则切线DA 的斜率为1x ，故1111()2y x x t +=-，整理得112210tx y -+=. 设22(,)B x y ，同理得222210tx y -+=.11(,)A x y ,22(,)B x y 都满足直线方程2210tx y -+=.于是直线2210tx y -+=过点,A B ，而两个不同的点确定一条直线，所以直线AB 方程为2210tx y -+=.即2(21)0tx y +-+=，当20,210x y =-+=时等式恒成立．所以直线AB 恒过定点1(0,)2.（2）由（1）得直线AB 的方程为12y tx =+. 由2122y tx x y ⎧=+⎪⎪⎨⎪=⎪⎩，可得2210x tx --=，于是2121212122,1,()121x x t x x y y t x x t +==-+=++=+212|||2(1)AB x x t =-=+.设12,d d 分别为点,D E 到直线AB的距离，则12d d ==因此，四边形ADBE 的面积()(2121||32S AB d d t =+=+设M 为线段AB 的中点，则21,2M t t ⎛⎫+ ⎪⎝⎭，由于EM AB ⊥，而()2,2EM t t =-，AB 与向量(1,)t 平行，所以()220t t t +-=，解得0=t 或1t =±.当0=t 时，3S =；当1t =±时S =因此，四边形ADBE 的面积为3或【点睛】此题第一问是圆锥曲线中的定点问题和第二问是求面积类型，属于常规题型，按部就班的求解就可以．思路较为清晰，但计算量不小．5．（2019年全国统一高考数学试卷（文科）（新课标Ⅱ））已知12,F F 是椭圆2222:1(0)x y C a b a b+=>>的两个焦点，P 为C 上一点，O 为坐标原点．（1）若2POF 为等边三角形，求C 的离心率；（2)如果存在点P ，使得12PF PF ⊥，且12F PF △的面积等于16，求b 的值和a 的取值范围.【答案】(1) 31e =；（2）4b =，a 的取值范围为[42,)+∞. 【分析】（1）先连结1PF ，由2POF 为等边三角形，得到1290F PF ∠=，2PF c =，13PF c =；再由椭圆定义，即可求出结果；（2）先由题意得到，满足条件的点(,)P x y 存在，当且仅当12162y c ⋅=，1y yx c x c⋅=-+-，22221x y a b +=，根据三个式子联立，结合题中条件，即可求出结果. 【详解】（1）连结1PF ，由2POF 为等边三角形可知：在12F PF △中，1290F PF ∠=，2PF c =，13PF c ，于是1223a PF PF c c =+=，故椭圆C 的离心率为3113c e a ===+；（2）由题意可知，满足条件的点(,)P x y 存在，当且仅当12162y c ⋅=，1y y x c x c⋅=-+-，22221x y a b +=，即16c y = ① 222x y c += ②22221x y a b += ③ 由②③以及222a b c =+得422b y c =，又由①知22216y c=，故4b =；由②③得22222()a x c b c=-，所以22c b ≥，从而2222232a b c b =+≥=，故42a ≥当4b =，42a ≥P . 故4b =，a 的取值范围为[42,)+∞. 【点睛】本题主要考查求椭圆的离心率，以及椭圆中存在定点满足题中条件的问题，熟记椭圆的简单性质即可求解，考查计算能力，属于中档试题.6．（2019年全国统一高考数学试卷（文科）（新课标Ⅰ））已知点A ，B 关于坐标原点O 对称，│AB │ =4，⊙M 过点A ，B 且与直线x +2=0相切．（1）若A 在直线x +y =0上，求⊙M 的半径．（2）是否存在定点P ，使得当A 运动时，│MA │－│MP │为定值？并说明理由．【答案】（1）2或6；（2）见解析. 【分析】（1）设(),A t t -，(),B t t -，根据AB 4=，可知t =M 必在直线y x =上，可设圆心(),M a a ；利用圆心到20x +=的距离为半径和MA MB r ==构造方程，从而解出r ；（2）当直线AB 斜率存在时，设AB 方程为：y kx =，由圆的性质可知圆心M 必在直线1=-y x k 上；假设圆心坐标，利用圆心到20x +=的距离为半径和r MA =构造方程，解出M 坐标，可知M 轨迹为抛物线；利用抛物线定义可知()1,0P 为抛物线焦点，且定值为1；当直线AB 斜率不存在时，求解出M 坐标，验证此时()1,0P 依然满足定值，从而可得到结论. 【详解】（1）A 在直线0x y +=上 ∴设(),A t t -，则(),B t t -又AB 4= 2816t ∴=，解得：t =M 过点A ，B ∴圆心M 必在直线y x =上设(),M a a ，圆的半径为rM 与20x +=相切 2r a ∴=+又MA MB r ==，即((222a a r +=((()2222a a a ∴+=+，解得：0a =或4a =当0a =时，2r ；当4a =时，6r =M ∴的半径为：2或6（2）存在定点()1,0P ，使得1MA MP -= 说明如下：A ，B 关于原点对称且AB 4=∴直线AB 必为过原点O 的直线，且2OA =①当直线AB 斜率存在时，设AB 方程为：y kx = 则M 的圆心M 必在直线1=-y x k上设(),M km m -，M 的半径为rM 与20x +=相切 2r km ∴=-+又222224r MA OA OMk m m ==+++22224km k m m ∴-+++，整理可得：24m km =-即M 点轨迹方程为：24y x =，准线方程为：1x =-，焦点()1,0FMA r =，即抛物线上点到2x =-的距离 ∴1MA MF =+ 1MA MF ∴-=∴当P 与F 重合，即P 点坐标为()1,0时，1MA MP -=②当直线AB 斜率不存在时，则直线AB 方程为：0x =M ∴在x 轴上，设(),0M n224n n ∴++0n =，即()0,0M 若()1,0P ，则211MA MP -=-=综上所述，存在定点()1,0P ，使得MA MP -为定值. 【点睛】本题考查圆的方程的求解问题、圆锥曲线中的定点定值类问题.解决本定点定值问题的关键是能够根据圆的性质得到动点所满足的轨迹方程，进而根据抛物线的定义得到定值，进而验证定值符合所有情况，使得问题得解.7．（2019年北京市高考数学试卷（文科））已知椭圆2222:1x y C a b+=的右焦点为(1,0)，且经过点(0,1)A .（Ⅰ）求椭圆C 的方程；（Ⅱ）设O 为原点，直线:(1)l y kx t t =+≠±与椭圆C 交于两个不同点P ，Q ，直线AP 与x 轴交于点M ，直线AQ 与x 轴交于点N ，若|OM |·|ON |=2，求证：直线l 经过定点. 【答案】（Ⅰ）2212x y +=；（Ⅱ）见解析. 【分析】(Ⅰ)由题意确定a ,b 的值即可确定椭圆方程；(Ⅱ)设出直线方程，联立直线方程与椭圆方程确定OM ,ON 的表达式，结合韦达定理确定t 的值即可证明直线恒过定点. 【详解】（Ⅰ）因为椭圆的右焦点为(1,0)，所以1225；因为椭圆经过点(0,1)A ,所以1b =，所以2222a b c =+=，故椭圆的方程为2212x y +=. （Ⅱ）设1122(,),(,)P x y Q x y联立2212(1)x y y kx t t ⎧+=⎪⎨⎪=+≠⎩得222(12)4220k x ktx t +++-=，21212224220,,1212kt t x x x x k k -∆>+=-=++，121222()212t y y k x x t k +=++=+，222212121222()12t k y y k x x kt x x t k-=+++=+. 直线111:1y AP y x x --=，令0y =得111x x y -=-，即111x OM y -=-；同理可得221x ON y -=-. 因为2OM ON =,所以1212121212211()1x x x x y y y y y y --==---++；221121t t t -=-+，解之得0=t ，所以直线方程为y kx =，所以直线l 恒过定点(0,0). 【点睛】解决直线与椭圆的综合问题时，要注意：(1)注意观察应用题设中的每一个条件，明确确定直线、椭圆的条件；(2)强化有关直线与椭圆联立得出一元二次方程后的运算能力，重视根与系数之间的关系、弦长、斜率、三角形的面积等问题．8．（2020年全国统一高考数学试卷（文科）（新课标Ⅰ））已知A 、B 分别为椭圆E ：2221x y a+=（a >1）的左、右顶点，G 为E 的上顶点，8AG GB ⋅=，P 为直线x =6上的动点，PA 与E 的另一交点为C ，PB 与E 的另一交点为D ．（1）求E 的方程；（2）证明：直线CD 过定点.【答案】（1）2219x y +=；（2）证明详见解析.【分析】（1）由已知可得：(),0A a -， (),0B a ，()0,1G ，即可求得21AG GB a ⋅=-，结合已知即可求得：29a =，问题得解.（2）设()06,P y ，可得直线AP 的方程为：()039y y x =+，联立直线AP 的方程与椭圆方程即可求得点C 的坐标为20022003276,99y y y y ⎛⎫-+ ⎪++⎝⎭，同理可得点D 的坐标为2002200332,11y y y y ⎛⎫-- ⎪++⎝⎭，当203y ≠时，可表示出直线CD 的方程，整理直线CD 的方程可得：()02043233y y x y ⎛⎫=- ⎪-⎝⎭即可知直线过定点3,02⎛⎫ ⎪⎝⎭，当203y =时，直线CD ：32x =，直线过点3,02⎛⎫⎪⎝⎭，命题得证. 【详解】（1）依据题意作出如下图象：由椭圆方程222:1(1)x E y a a+=>可得：(),0A a -， (),0B a ，()0,1G∴(),1AG a =，(),1GB a =- ∴218AG GB a ⋅=-=，∴29a =∴椭圆方程为：2219x y +=（2）证明：设()06,P y ，则直线AP 的方程为：()()00363y y x -=+--，即：()039y y x =+联立直线AP 的方程与椭圆方程可得：()2201939x y y y x ⎧+=⎪⎪⎨⎪=+⎪⎩，整理得：()2222000969810y x y x y +++-=，解得：3x =-或20203279y x y -+=+将20203279y x y -+=+代入直线()039y y x =+可得：02069y y y =+所以点C 的坐标为20022003276,99y y y y ⎛⎫-+ ⎪++⎝⎭. 同理可得：点D 的坐标为2002200332,11y y y y ⎛⎫-- ⎪++⎝⎭ 当203y ≠时，∴直线CD 的方程为：0022*******22000022006291233327331191y y y y y y y x y y y y y y ⎛⎫-- ⎪++⎛⎫⎛⎫--⎝⎭-=- ⎪ ⎪-+-++⎝⎭⎝⎭-++，整理可得：()()()2220000002224200000832338331116963y y y y y y y x x y y y y y +⎛⎫⎛⎫--+=-=- ⎪ ⎪+++--⎝⎭⎝⎭ 整理得：()()0002220004243323333y y y y x x y y y ⎛⎫=+=- ⎪---⎝⎭所以直线CD 过定点3,02⎛⎫⎪⎝⎭．当203y =时，直线CD ：32x =，直线过点3,02⎛⎫ ⎪⎝⎭．故直线CD 过定点3,02⎛⎫⎪⎝⎭．【点睛】本题主要考查了椭圆的简单性质及方程思想，还考查了计算能力及转化思想、推理论证能力，属于难题.9．（2020年北京市高考数学试卷）已知椭圆2222:1x y C a b+=过点(2,1)A --，且2a b =．（Ⅰ）求椭圆C 的方程：（Ⅱ）过点(4,0)B -的直线l 交椭圆C 于点,M N ,直线,MA NA 分别交直线4x =-于点,P Q ．求||||PB BQ 的值．【答案】（Ⅰ）22182x y +=；（Ⅱ）1.【分析】(Ⅰ)由题意得到关于a ,b 的方程组，求解方程组即可确定椭圆方程；(Ⅱ)首先联立直线与椭圆的方程，然后由直线MA ,NA 的方程确定点P ,Q 的纵坐标，将线段长度的比值转化为纵坐标比值的问题，进一步结合韦达定理可证得0P Q y y +=，从而可得两线段长度的比值. 【详解】(1)设椭圆方程为：()222210x y a b a b+=>>，由题意可得：224112a ba b⎧+=⎪⎨⎪=⎩，解得：2282a b ⎧=⎨=⎩，故椭圆方程为：22182x y +=.(2)设()11,M x y ，()22,N x y ，直线MN 的方程为：()4y k x =+，与椭圆方程22182x y +=联立可得：()222448x k x ++=，即：()()222241326480k x k x k +++-=，则：2212122232648,4141k k x x x x k k --+==++. 直线MA 的方程为：()111122y y x x ++=++，令4x =-可得：()()()1111111141214122122222P k x k x y x y x x x x ++-++++=-⨯-=-⨯-=++++，同理可得：()()222142Q k x y x -++=+.很明显0P Q y y <，且：PQPB y PQy =，注意到： ()()()()()()()()122112121242424421212222P Q x x x x x x y y k k x x x x +++++⎛⎫+++=-++=-+⨯ ⎪++++⎝⎭，而：()()()()()122112124242238x x x x x x x x +++++=+++⎡⎤⎣⎦ 2222648322384141k k k k ⎡⎤⎛⎫--=+⨯+⎢⎥ ⎪++⎝⎭⎣⎦()()()22226483328412041k k k k -+⨯-++=⨯=+，故0,P Q P Q y y y y +==-.从而1PQPB y BQy ==. 【点睛】解决直线与椭圆的综合问题时，要注意：(1)注意观察应用题设中的每一个条件，明确确定直线、椭圆的条件；(2)强化有关直线与椭圆联立得出一元二次方程后的运算能力，重视根与系数之间的关系、弦长、斜率、三角形的面积等问题．10．（2020年天津市高考数学试卷）已知椭圆22221(0)x y a b a b +=>>的一个顶点为(0,3)A -，右焦点为F ，且||||OA OF =，其中O 为原点．（Ⅰ）求椭圆的方程；（Ⅱ）已知点C 满足3OC OF =，点B 在椭圆上（B 异于椭圆的顶点），直线AB 与以C 为圆心的圆相切于点P ，且P 为线段AB 的中点．求直线AB 的方程．【答案】（Ⅰ）221189x y +=；（Ⅱ）132y x =-，或3y x =-．【分析】（Ⅰ）根据题意，并借助222a b c =+，即可求出椭圆的方程；（Ⅱ）利用直线与圆相切，得到CP AB ⊥，设出直线AB 的方程，并与椭圆方程联立，求出B 点坐标，进而求出P 点坐标，再根据CP AB ⊥，求出直线AB 的斜率，从而得解. 【详解】（Ⅰ）椭圆()222210x y a b a b+=>>的一个顶点为()0,3A -，∴3b =，由OA OF =，得3c b ==，又由222a b c =+，得2228313a =+=，所以，椭圆的方程为221189x y +=；（Ⅱ）直线AB 与以C 为圆心的圆相切于点P ，所以CP AB ⊥，根据题意可知，直线AB 和直线CP 的斜率均存在，设直线AB 的斜率为k ，则直线AB 的方程为3y kx ，即3y kx =-，2231189y kx x y =-⎧⎪⎨+=⎪⎩，消去y ，可得()2221120k x kx +-=，解得0x =或21221k x k =+. 将21221k x k =+代入3y kx =-，得222126321213k y k k k k =⋅--=++，所以，点B 的坐标为2221263,2121k k k k ⎛⎫- ⎪++⎝⎭，因为P 为线段AB 的中点，点A 的坐标为()0,3-，所以点P 的坐标为2263,2121kk k -⎛⎫ ⎪++⎝⎭，由3OC OF =，得点C 的坐标为()1,0，所以，直线CP 的斜率为222303216261121CPk k k k k k --+=-+-+=，又因为CP AB ⊥，所以231261k k k ⋅=--+，整理得22310k k -+=，解得12k =或1k =. 所以，直线AB 的方程为132y x =-或3y x =-. 【点睛】本题考查了椭圆标准方程的求解、直线与椭圆的位置关系、直线与圆的位置关系、中点坐标公式以及直线垂直关系的应用，考查学生的运算求解能力，属于中档题.当看到题目中出现直线与圆锥曲线位置关系的问题时，要想到联立直线与圆锥曲线的方程. 11．（2020年新高考全国卷Ⅰ数学高考试题（山东））已知椭圆C ：22221(0)x y a b a b+=>>2()2,1A ．（1）求C 的方程：（2）点M ，N 在C 上，且AM AN ⊥，AD MN ⊥，D 为垂足．证明：存在定点Q ，使得DQ 为定值．【答案】（1）22163x y +=；（2）详见解析.【分析】（1）由题意得到关于,,a b c 的方程组，求解方程组即可确定椭圆方程.（2）设出点M ，N 的坐标，在斜率存在时设方程为y kx m =+, 联立直线方程与椭圆方程，根据已知条件，已得到,m k 的关系，进而得直线MN 恒过定点，在直线斜率不存在时要单独验证，然后结合直角三角形的性质即可确定满足题意的点Q 的位置. 【详解】（1）由题意可得：2222222411c aa b a b c ⎧=⎪⎪⎪+=⎨⎪=+⎪⎪⎩，解得：2226,3a b c ===，故椭圆方程为：22163x y +=.(2) 设点()()1122,,,M x y N x y ，若直线MN 斜率存在时，设直线MN 的方程为：y kx m =+，代入椭圆方程消去y 并整理得：()22212k 4260x kmx m +++-=，可得122412km x x k +=-+，21222612m x x k -=+，因为AM AN ⊥，所以·0AM AN =，即()()()()121222110x x y y --+--=，根据1122,kx m y kx m y =+=+,代入整理可得：()()()()22121212140x x km k x x km ++--++-+=，所以()()()22222264k 121401212m km km k m k k -⎛⎫++---+-+= ⎪++⎝⎭，整理化简得()()231210k m k m +++-=，因为2,1A （）不在直线MN 上，所以210k m +-≠，故23101k m k ++=≠，，于是MN 的方程为2133y k x ⎛⎫=-- ⎪⎝⎭()1k ≠，所以直线过定点直线过定点21,33P ⎛⎫- ⎪⎝⎭.当直线MN 的斜率不存在时，可得()11,N x y -，由·0AM AN =得：()()()()111122110x x y y --+---=，得()1221210x y -+-=，结合2211163x y +=可得：2113840x x -+=，解得：123x =或22x =（舍）.此时直线MN 过点21,33P ⎛⎫- ⎪⎝⎭.令Q 为AP 的中点，即41,33Q ⎛⎫⎪⎝⎭，若D 与P 不重合，则由题设知AP 是Rt ADP △的斜边，故12DQ AP ==，若D 与P 重合，则12DQ AP =，故存在点41,33Q ⎛⎫⎪⎝⎭，使得DQ 为定值.【点睛】关键点点睛：本题的关键点是利用AM AN ⊥得 ·0AM AN =，转化为坐标运算，需要设直线MN 的方程，点()()1122,,,M x y N x y ，因此需要讨论斜率存在与不存在两种情况，当直线MN 斜率存在时，设直线MN 的方程为：y kx m =+，与椭圆方程联立消去y 可12x x +，12x x 代入·0AM AN =即可，当直线MN 的斜率不存在时，可得()11,N x y -，利用坐标运算以及三角形的性质即可证明，本题易忽略斜率不存在的情况，属于难题. 12．（2018年全国普通高等学校招生统一考试理数（全国卷II ））设抛物线24C y x =：的焦点为F ，过F 且斜率为(0)k k >的直线l 与C 交于A ，B 两点，||8AB =．（1）求l 的方程；（2）求过点A ，B 且与C 的准线相切的圆的方程．【答案】(1) y =x –1,(2)()()223216x y -+-=或()()22116144x y -++=．【详解】分析：(1)根据抛物线定义得12AB x x p =++，再联立直线方程与抛物线方程，利用韦达定理代入求出斜率，即得直线l 的方程；（2）先求AB 中垂线方程，即得圆心坐标关系，再根据圆心到准线距离等于半径得等量关系，解方程组可得圆心坐标以及半径，最后写出圆的标准方程.详解：（1）由题意得F （1，0），l 的方程为y =k （x –1）（k >0）．设A （x 1，y 1），B （x 2，y 2）．由()214y k x y x ⎧=-⎨=⎩得()2222240k x k x k -++=． 216160k ∆=+=，故212224k x x k ++=．所以()()21224411k AB AF BF x x k +=+=+++=．由题设知22448k k +=，解得k =–1（舍去），k =1．因此l 的方程为y =x –1．（2）由（1）得AB 的中点坐标为（3，2），所以AB 的垂直平分线方程为()23y x -=--，即5y x =-+．设所求圆的圆心坐标为（x 0，y 0），则()()002200051116.2y x y x x =-+⎧⎪⎨-++=+⎪⎩，解得0032x y =⎧⎨=⎩，或00116.x y =⎧⎨=-⎩，因此所求圆的方程为()()223216x y -+-=或()()22116144x y -++=．点睛：确定圆的方程方法(1)直接法：根据圆的几何性质，直接求出圆心坐标和半径，进而写出方程． (2)待定系数法①若已知条件与圆心(),a b 和半径r 有关，则设圆的标准方程依据已知条件列出关于,,a b r 的方程组，从而求出,,a b r 的值；②若已知条件没有明确给出圆心或半径，则选择圆的一般方程，依据已知条件列出关于D 、E 、F 的方程组，进而求出D 、E 、F 的值．13．（2018年全国普通高等学校招生统一考试文科数学（新课标I 卷））设抛物线22C y x =：，点()20A ，，()20B -，，过点A 的直线l 与C 交于M ，N 两点．（1）当l 与x 轴垂直时，求直线BM 的方程；（2）证明：ABM ABN ∠=∠．【答案】（1）112y x =+或112y x =--；（2）见解析. 【分析】（1）首先根据l 与x 轴垂直，且过点()20A ，，求得直线l 的方程为2x =，代入抛物线方程求得点M 的坐标为()2,2或()2,2-，利用两点式求得直线BM 的方程；（2）设直线l 的方程为2x ty =+，点()11,M x y 、()22,N x y ，将直线l 的方程与抛物线的方程联立，列出韦达定理，由斜率公式并结合韦达定理计算出直线BM 、BN 的斜率之和为零，从而得出所证结论成立. 【详解】（1）当l 与x 轴垂直时，l 的方程为2x =，可得M 的坐标为()2,2或()2,2-．所以直线BM 的方程为112y x =+或112y x =--；（2）设l 的方程为2x ty =+，()11,M x y 、()22,N x y ，由222x ty y x =+⎧⎨=⎩，得2240y ty --=，可知122y y t +=，124y y =-．直线BM 、BN 的斜率之和为()()()()()()()()21122112121212122244222222BM BN x y x y ty y ty y y yk k x x x x x x +++++++=+==++++++()()()()()()1212121224244202222ty y y y t tx x x x ++⨯-+⨯===++++，所以0BM BN k k +=，可知BM 、BN 的倾斜角互补，所以ABM ABN ∠=∠.综上，ABM ABN ∠=∠. 【点睛】该题考查的是有关直线与抛物线的问题，涉及到的知识点有直线方程的两点式、直线与抛物线相交的综合问题、关于角的大小用斜率来衡量，在解题的过程中，第一问求直线方程的时候，需要注意方法比较简单，需要注意的就是应该是两个，关于第二问，涉及到直线与曲线相交都需要联立方程组，之后韦达定理写出两根和与两根积，借助于斜率的关系来得到角是相等的结论.14．（2018年全国卷Ⅲ文数高考试题文档版）已知斜率为k 的直线l 与椭圆22143x y C +=：交于A ，B 两点．线段AB 的中点为(1,)(0)M m m >．（1）证明：12k <-；（2）设F 为C 的右焦点，P 为C 上一点，且0FP FA FB ++=．证明：2FP FA FB =+．【答案】（1）证明见解析（2）证明见解析【详解】分析：（1）设而不求，利用点差法，或假设直线方程，联立方程组，由判别式和韦达定理进行证明．（2）先求出点P 的坐标，解出m ，得到直线l 的方程，联立直线与椭圆方程由韦达定理进行求解．详解：（1）设()11A x y ，，()22B x y ，，则2211143x y +=，2222143x y +=．两式相减，并由1212=y y k x x --得1212043x x y y k +++⋅=．由题设知1212x x +=，122y y m +=，于是34k m =-．由题设得211,043m m +<>∴302m <<，故12k <-．（2）由题意得F （1，0）．设()33P x y ，，则()()()()33112211100x y x y x y -+-+-=，，，，．由（1）及题设得()31231x x x =-+=，()31220y y y m =-+=-<．又点P 在C 上，所以34m =，从而312P ⎛⎫- ⎪⎝⎭，，3||=2FP ．于是()()222211111||1131242x xFA x y x ⎛⎫=-+-+-- ⎪⎝⎭．同理2||=22x FB -．所以()121|43|||2FA FB x x +=-+=．故2||=||+||FP FA FB ．点睛：本题主要考查直线与椭圆的位置关系，第一问利用点差法，设而不求可减小计算量，第二问由已知得求出m ，得到FP ,再有两点间距离公式表示出,FA FB ，考查了学生的计算能力，难度较大．15．（2017年全国普通高等学校招生统一考试文科数学（新课标2卷精编版））设O 为坐标原点，动点M 在椭圆C 22:12x y +=上，过M 作x 轴的垂线，垂足为N ，点P 满足2NP NM =.（1）求点P 的轨迹方程；（2）设点Q 在直线3x =-上，且1OP PQ ⋅=.证明：过点P 且垂直于OQ 的直线l 过C 的左焦点F .【答案】（1）222x y +=；（2）见解析. 【详解】（1）设P （x ，y ），M （00,x y ）,则N （0,0x ），00NP (x ,),NM 0,x y y =-=（）由NP 2NM =得00x x y y ==，. 因为M （00,x y ）在C 上，所以22x 122y +=. 因此点P 的轨迹为222x y +=.由题意知F （-1,0），设Q （-3，t ），P （m ，n ），则()()OQ 3t PF 1m n OQ PF 33m tn =-=---⋅=+-，，，，， ()OP m n PQ 3m t n ==---，，（，）.由OP PQ 1⋅=得-3m-2m +tn-2n =1，又由（1）知222m n +=，故3+3m-tn=0.所以OQ PF 0⋅=，即OQ PF ⊥.又过点P 存在唯一直线垂直于OQ ，所以过点P 且垂直于OQ 的直线l 过C 的左焦点F.点睛:定点、定值问题通常是通过设参数或取特殊值来确定“定点”是什么、“定值”是多少，或者将该问题涉及的几何式转化为代数式或三角问题，证明该式是恒成立的. 定点、定值问题同证明问题类似，在求定点、定值之前已知该值的结果，因此求解时应设参数，21运用推理，到最后必定参数统消，定点、定值显现.16．（2017年全国1卷（文数））设A ，B 为曲线C ：y ＝24x 上两点，A 与B 的横坐标之和为4．（1）求直线AB 的斜率；（2）设M 为曲线C 上一点，C 在M 处的切线与直线AB 平行，且AM ⊥BM ，求直线AB 的方程．【答案】（1）1；（2）y ＝x ＋7．【分析】（1）设A (x 1，y 1)，B (x 2，y 2)，直线AB 的斜率k ＝1212y y x x --＝124x x+，代入即可求得斜率；（2）由（1）中直线AB 的斜率，根据导数的几何意义求得M 点坐标，设直线AB 的方程为y ＝x ＋m ，与抛物线联立，求得根，结合弦长公式求得AB ，由AM BM ⊥知，|AB |＝2|MN |，从而求得参数m . 【详解】解：（1）设A (x 1，y 1)，B (x 2，y 2)，则x 1≠x 2，y 1＝214x ，y 2＝224x ，x 1＋x 2＝4，于是直线AB 的斜率k ＝1212y y x x --＝124x x+＝1．（2）由y ＝24x ，得y ′＝2x ．设M (x 3，y 3)，由题设知32x ＝1，解得x 3＝2，于是M (2，1)．设直线AB 的方程为y ＝x ＋m ，故线段AB 的中点为N (2，2＋m )，|MN |＝|m ＋1|．将y ＝x ＋m 代入y ＝24x 得x 2－4x －4m ＝0．当Δ＝16(m ＋1)>0，即m >－1时，x 1，2＝2±1m + 从而|AB |2x 1－x 2|＝()421m +由题设知|AB |＝2|MN |，即()421m +2(m ＋1)，解得m ＝7．所以直线AB 的方程为y ＝x ＋7．17．（2016年全国2卷（文数））已知A 是椭圆E ：22143x y +=的左顶点，斜率为()0k k >的直线交E 于A ，M 两点，点N 在E 上，MA NA ⊥.试卷第22页，共26页（Ⅰ）当AM AN =时，求AMN 的面积（Ⅱ）当2AM AN =时，证明：32k <<. 【答案】（Ⅰ）14449；（Ⅱ）详见解析. 【解析】试题分析：（Ⅰ）先求直线AM 的方程，再求点M 的纵坐标，最后求AMN ∆的面积；（Ⅱ）设()11,M x y ，将直线AM 的方程与椭圆方程组成方程组，消去y ，用k 表示1x ，从而表示AM ，同理用k 表示AN ，再由2AM AN =求k 的取值范围. 试题解析：（Ⅰ）设11(,)M x y ，则由题意知10y >. 由已知及椭圆的对称性知，直线AM 的倾斜角为π4.又(2,0)A -，因此直线AM 的方程为2y x =+. 将2x y =-代入22143x y +=得27120y y -=. 解得0y =或127y =，所以1127y =.因此AMN ∆的面积11212144227749AMN S ∆=⨯⨯⨯=. （Ⅱ）将直线AM 的方程(2)(0)y k x k =+>代入22143x y +=得 2222(34)1616120k x k x k +++-=.由2121612(2)34k x k -⋅-=+得2122(34)34k x k -=+，故22121212134k AM x k k+=++=+. 由题设，直线AN 的方程为，故同理可得2121k k AN +=. 由2AM AN =得222343+4kk k =+，即3246380k k k -+-=. 设32()4638f t t t t =-+-，则k 是()f t 的零点，22()121233(21)0f t t t t +=-'=-≥，所以()f t 在(0,)+∞单调递增.又(3)153260,(2)60f f ==，因此()f t 在(0,)+∞有唯一的零点，且零点k 在(3,2)32k <. 【考点】椭圆的性质，直线与椭圆的位置关系【名师点睛】对于直线与椭圆的位置关系问题，通常将直线方程与椭圆方程联立进行求解，注意计算的准确性.请考生在第22~24题中任选一题作答，如果多做，则按所做的第一题计分.2318．（2016新课标全国卷Ⅰ文科）在直角坐标系xOy 中，直线l :y =t (t ≠0)交y 轴于点M ，交抛物线C ：22(0)y px p =>于点P ，M 关于点P 的对称点为N ，连结ON 并延长交C 于点H .（Ⅰ）求OH ON；（Ⅱ）除H 以外，直线MH 与C 是否有其它公共点？说明理由. 【答案】（1）2；（2）没有. 【分析】（Ⅰ）先确定2,,t N t ON p ⎛⎫ ⎪⎝⎭的方程为py x t =，代入22y px =整理得2220px t x -=，解得21220,t x x p ==，因此22(,2)t H t p ，所以N 为OH 的中点，即||2||OH ON =. （Ⅱ）直线MH 的方程为2py t x t-=，与22y px =联立得22440y ty t -+=，解得122y y t ==，即直线MH 与C 只有一个公共点，即可得出结论.【详解】（Ⅰ）由已知得()20,,,2t M t P t p ⎛⎫⎪⎝⎭. 又N 为M 关于点P 的对称点，故2,,t N t ON p ⎛⎫ ⎪⎝⎭的方程为py x t =，代入22y px =整理得2220px t x -=，解得21220,t x x p ==，因此22(,2)t H t p，所以N 为OH 的中点，即||2||OH ON =. （Ⅱ）直线MH 与C 除H 以外没有其它公共点. 理由如下：直线MH 的方程为2py t x t-=，即2()t x y t p =-，代入22y px =，得22440y ty t -+=，解得122y y t ==，即直线MH 与C 只有一个公共点，所以除H 以外直线MH 与C 没有其它公共点. 【点睛】高考解析几何解答题大多考查直线与圆锥曲线的位置关系,直线与圆锥曲线的位置关系试卷第24页，共26页是一个很宽泛的考试内容,主要由求值、求方程、求定值、求最值、求参数取值范围等几部分组成；解析几何中的证明问题通常有以下几类：证明点共线或直线过定点；证明垂直；证明定值问题.其中考查较多的圆锥曲线是椭圆与抛物线,解决这类问题要重视方程思想、函数思想及化归思想的应用.19．（2021·新疆昌吉·高三阶段练习（文））已知椭圆2222:1(0)x y C a b a b+=>>的左､右顶点分別为12,A A ，右焦点为F （1，0），且椭圆C 的离心率为12，M ，N 为椭圆C 上任意两点，点P 的坐标为（4，t ）（t ≠0），且满足1122,AM MP A N NP λλ==. （1）求椭圆C 的方程；（2）证明：M ，F ，N 三点共线. 【答案】（1）22143x y +=；（2）证明见解析. 【分析】（1）根据椭圆的焦点坐标及离心率求椭圆参数，写出椭圆方程即可.（2）设()()1122,,,M x y N x y ，由题设易知1,,A M P 共线，2,,A N P 共线，利用向量共线的坐标表示有()()22112222292x y y x +=-，再由M ，N 在椭圆上可得()12122580x x x x -++=，最后由11(1,)FM x y =-，22(1,)FN x y =-结合分析法证明结论. （1）椭圆C 的右焦点为(1,0)F ，且离心率为12，∴a =2，c =1，则b 2=a 2-c 2=3， ∴椭圆C 的方程为22143x y +=.（2）由（1）知，12,A A 的坐标分别为(2,0),(2,0)-，设()()1122,,,M x y N x y ， ∴111(2,)AM x y =+，1(6,)A P t =，222(2,)A N x y =-，2(2,)A P t =， ∵11AM MP λ=，22A N NP λ=，25∴1,,A M P 三点共线，2,,A N P 三点共线，即()()11226222y t x y t x ⎧=+⎪⎨=-⎪⎩，整理得1122322y x y x +=-，两边平方得()()22112222292x y y x +=-，① 又M ，N 在椭圆上，则22112222334334y x y x ⎧=-⎪⎪⎨⎪=-⎪⎩，代入①并化简得()12122580x x x x -++=，又11(1,)FM x y =-，22(1,)FN x y =-，∴要证M ，F ，N 三点共线，只需证()()211211y x y x -=-，即112211y x y x -=-，只需证()112221321x x x x +-=--，整理得()12122580x x x x -++=，∴M ，F ，N 三点共线. 【点睛】关键点点睛：第二问，设()()1122,,,M x y N x y ，由向量共线得1122322y x y x +=-，利用分析法结合向量共线的坐标表示只需证112211y x y x -=-，最后由M ，N 在椭圆上求证即可.20．（2021·宁夏·石嘴山市第三中学高三阶段练习（文））已知椭圆C ：()222210x y a b a b +=>>的左焦点为F ，离心率为12，过点F 且垂直于x 轴的直线交C 于,A B 两点，3AB =（1）求椭圆的标准方程；（2）若直线l 过点()4,0M -且与椭圆相交于A ，B 两点，求ABF 面积最大值及此时直线l 的斜率. 【答案】（1）22143x y += （2332114± 【分析】（1）根据题意得22221223c a ba abc ⎧=⎪⎪⎪=⎨⎪=+⎪⎪⎩，再解方程即可得答案；（2）设直线l 的方程为4x my =-，设()11,A x y ，()22,B x y ，进而将直线l 的方程与椭圆试卷第26页，共26页方程联立，并结合韦达定理得ABFS =，再令)0t t =>，结合基本不等式求解即可. （1）解：由题知：2222122231c a a bb ac a b c ⎧=⎪=⎧⎪⎪⎪=⇒=⎨⎨⎪⎪=⎩=+⎪⎪⎩ 所以椭圆22:143x y C +=.（2）设直线l 的方程为4x my =-，设()11,A x y ､()22,B x y ，与椭圆方程联立得224143x my x y =-⎧⎪⎨+=⎪⎩，消去x 得()223424360m y my +-+=.则()()2225764363414440m m m ∆=-⨯+=->，所以24m >.由根与系数的关系知1222434m y y m +=+，1223634y y m =+，所以1232ABFSy y =-=①令)0t t =>，则①式可化为21818163163ABFt St t t ==++当且仅当163t t =，即t =.此时3m =±l的斜率为14±.27。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

若2a ＝|F 1F 2|，则轨迹是以F 1，F 2为端点的两条射线，若2a ﹥|F 1F 2|，则轨迹不存在。

若去掉定义中的绝对值则轨迹仅表示双曲线的一支。

圆锥曲线的第二定义，给出了圆锥曲线上的点到焦点距离与此点到相应准线距离间的关系，要善于运用第二定义对它们进行相互转化。

方程22Ax By C +=表示椭圆的充要条件是什么？（ABC ≠0，且A ，B ，C 同号，A ≠B ）。

如（1）已知方程12322=-++ky k x 表示椭圆，则k 的取值范围为____（答：11(3,)(,2)22--- ）；（2）若R y x ∈,，且62322=+y x ，则y x +的最大值是____，22y x+的最小值是___2）（2）双曲线：焦点在x 轴上：2222by a x - =1，焦点在y 轴上：2222bx a y -＝1（0,0a b >>）。

方程22Ax By C +=表示双曲线的充要条件是什么？（ABC ≠0，且A ，B 异号）。

如（1）双曲线的离心率等于25，且与椭圆14922=+y x 有公共焦点，则该双曲线的方程_______（答：2214x y -=）；（2）设中心在坐标原点O ，焦点1F 、2F 在坐标轴上，离心率2=e 的双曲线C 过点)10,4(-P ，则C 的方程为_______（答：226xy -=）（3）抛物线：开口向右时22(0)y px p =>，开口向左时22(0)y px p =->，开口向上时22(0)x py p =>，开口向下时22(0)x py p =->。

3.圆锥曲线焦点位置的判断（首先化成标准方程，然后再判断）：（1）椭圆：由x2,y2分母的大小决定，焦点在分母大的坐标轴上。

如已知方程12122=-+-my m x 表示焦点在y 轴上的椭圆，则m 的取值范围是__（答：)23,1()1,( --∞）（2）双曲线：由x2,y2项系数的正负决定，焦点在系数为正的坐标轴上；（3）抛物线：焦点在一次项的坐标轴上，一次项的符号决定开口方向。

特别提醒：（1）在求解椭圆、双曲线问题时，首先要判断焦点位置，焦点F 1，F 2的位置，是椭圆、双曲线的定位条件，它决定椭圆、双曲线标准方程的类型，而方程中的两个参数,a b ，确定椭圆、双曲线的形状和大小，是椭圆、双曲线的定形条件；在求解抛物线问题时，首先要判断开口方向；（2）在椭圆中，a 最大，222ab c =+，在双曲线中，c 最大，222c a b =+。

4.圆锥曲线的几何性质：（1）椭圆（以12222=+by a x （0a b >>）为例）：①范围：,a x a b y b -≤≤-≤≤；②焦点：两个焦点(,0)c ±；③对称性：两条对称轴0,0x y==，一个对称中心（0,0），四个顶点(,0),(0,)a b ±±，其中长轴长为2a ，短轴长为2b ；④准线：两条准线2a x c=±； ⑤离心率：c e a =，椭圆⇔01e <<，e 越小，椭圆越圆；e 越大，椭圆越扁。

如（1）若椭圆1522=+my x 的离心率510=e ，则m 的值是__（答：3或325）；（2）以椭圆上一点和椭圆两焦点为顶点的三角形的面积最大值为1时，则椭圆长轴的最小值为__（答：22）（2）双曲线（以22221x y a b-=（0,0a b >>）为例）：①范围：x a ≤-或,x a y R ≥∈；②焦点：两个焦点(,0)c ±；③对称性：两条对称轴0,0x y==，一个对称中心（0,0），两个顶点(,0)a ±，其中实轴长为2a ，虚轴长为2b ，特别地，当实轴和虚轴的长相等时，称为等轴双曲线，其方程可设为22,0x y k k -=≠；④准线：两条准线2ax c=±； ⑤离心率：cea=，双曲线⇔1e >，等轴双曲线⇔e =e 越小，开口越小，e 越大，开口越大；⑥两条渐近线：by x a=±。

如（1）双曲线的渐近线方程是023=±y x ，则该双曲线的离心率等于______）；（2）双曲线221ax by -=:a b = （答：4或14）；（3）设双曲线12222=-by a x （a>0,b>0）中，离心率e ∈[2,2],则两条渐近线夹角θ的取值范围是________（答：[,]32ππ）；（3）抛物线（以22(0)y px p =>为例）：①范围：0,x y R ≥∈；②焦点：一个焦点(,0)2p，其中p 的几何意义是：焦点到准线的距离；③对称性：一条对称轴0y =，没有对称中心，只有一个顶点（0,0）；④准线：一条准线2px =-； ⑤离心率：c e a=，抛物线⇔1e =。

如设R a a ∈≠,0，则抛物线24ax y =的焦点坐标为________（答：)161,0(a）； 5、点00(,)P x y 和椭圆12222=+by a x （0a b >>）的关系：（1）点00(,)P x y 在椭圆外⇔2200221x y a b +>；（2）点00(,)P x y 在椭圆上⇔22220b y a x +＝1；（3）点00(,)P x y 在椭圆内⇔2200221x y a b+<6．直线与圆锥曲线的位置关系：（1）相交：0∆>⇔直线与椭圆相交； 0∆>⇒直线与双曲线相交，但直线与双曲线相交不一定有0∆>，当直线与双曲线的渐近线平行时，直线与双曲线相交且只有一个交点，故0∆>是直线与双曲线相交的充分条件，但不是必要条件；0∆>⇒直线与抛物线相交，但直线与抛物线相交不一定有0∆>，当直线与抛物线的对称轴平行时，直线与抛物线相交且只有一个交点，故0∆>也仅是直线与抛物线相交的充分条件，但不是必要条件。

如（1）若直线y=kx+2与双曲线x 2-y 2=6的右支有两个不同的交点，则k 的取值范围是_______（答：(-315,-1)）；（2）直线y ―kx ―1=0与椭圆2215x y m +=恒有公共点，则m 的取值范围是_______（答：[1，5）∪（5，+∞））；（3）过双曲线12122=-y x 的右焦点直线交双曲线于A 、B 两点，若│AB ︱＝4，则这样的直线有_____条（答：3）；（2）相切：0∆=⇔直线与椭圆相切；0∆=⇔直线与双曲线相切；0∆=⇔直线与抛物线相切；（3）相离：0∆<⇔直线与椭圆相离；0∆<⇔直线与双曲线相离；0∆<⇔直线与抛物线相离。

特别提醒：（1）直线与双曲线、抛物线只有一个公共点时的位置关系有两种情形：相切和相交。

如果直线与双曲线的渐近线平行时,直线与双曲线相交,但只有一个交点；如果直线与抛物线的轴平行时,直线与抛物线相交,也只有一个交点；（2）过双曲线2222by a x -＝1外一点00(,)P x y 的直线与双曲线只有一个公共点的情况如下：①P 点在两条渐近线之间且不含双曲线的区域内时，有两条与渐近线平行的直线和分别与双曲线两支相切的两条切线，共四条；②P 点在两条渐近线之间且包含双曲线的区域内时，有两条与渐近线平行的直线和只与双曲线一支相切的两条切线，共四条；③P 在两条渐近线上但非原点，只有两条：一条是与另一渐近线平行的直线，一条是切线；④P 为原点时不存在这样的直线；（3）过抛物线外一点总有三条直线和抛物线有且只有一个公共点：两条切线和一条平行于对称轴的直线。

如（1）过点)4,2(作直线与抛物线x y 82=只有一个公共点，这样的直线有______（答：2）；（2）过点(0,2)与双曲线116922=-y x 有且仅有一个公共点的直线的斜率的取值范围为______（答：4,3⎧⎪±⎨⎪⎪⎩⎭）；（3）过双曲线1222=-y x 的右焦点作直线l 交双曲线于A 、B两点，若=AB 4，则满足条件的直线l 有____条（答：3）；（4）对于抛物线C ：x y 42=，我们称满足0204x y <的点),(00y x M 在抛物线的内部，若点),(00y x M 在抛物线的内部，则直线l ：)(200x x yy +=与抛物线C 的位置关系是_______（答：相离）；（5）过抛物线x y 42=的焦点F 作一直线交抛物线于P 、Q 两点，若线段PF 与FQ 的长分别是p 、q ，则=+qp 11_______（答：1）；（6）设双曲线191622=-y x 的右焦点为F ，右准线为l ，设某直线m 交其左支、右支和右准线分别于R Q P ,,，则PFR ∠和QFR ∠的大小关系为___________(填大于、小于或等于) （答：等于）；（7）求椭圆284722=+y x 上的点到直线01623=--y x的最短距离（答：）；（8）直线1+=ax y 与双曲线1322=-y x 交于A 、B 两点。

①当a 为何值时，A 、B 分别在双曲线的两支上？②当a 为何值时，以AB为直径的圆过坐标原点？（答：①(；②1a =±）； 7、焦半径（圆锥曲线上的点P 到焦点F 的距离）的计算方法：利用圆锥曲线的第二定义，转化到相应准线的距离，即焦半径r ed=，其中d 表示P 到与F 所对应的准线的距离。

圆锥曲线习题精选精讲

圆锥曲线-高中数学好题精练精讲解析版

圆锥曲线高考题精讲 2

(完整版)圆锥曲线的综合经典例题(含答案解析)

高中生圆锥曲线练习题及讲解

圆锥曲线综合精讲精炼

专题50 圆锥曲线(多选题部分)(解析版)

高考数学圆锥曲线习题精选精讲可编辑

圆锥曲线习题精选精讲

圆锥曲线(解析版)--2024年高考真题和模拟题数学好题汇编

高中数学圆锥曲线经典考点及例题专题讲解

（完整版）圆锥曲线知识点+例题+练习含答案（整理）.docx

圆锥曲线(课堂讲义和例题)

高考数学圆锥曲线典型例题(必考)

【精编】圆锥曲线知识整理及练习(含解析)

专题12 圆锥曲线压轴小题常见题型全归纳(精讲精练)(原卷版)

上海 高二 数学 圆锥曲线专题精讲

高考圆锥曲线知识点及相关习题精解(含答案)

圆锥曲线(文科)解答题20题-备战高考数学冲刺横向强化精练精讲(解析版)

圆锥曲线高考题精讲 2

上海高二数学圆锥曲线专题精讲