理论力学第一章习题
1-8章的习题答案理论力学.doc

第一章静力学公理和物体的受力分析一、选择题与填空题1.C2.ACD3.A, B两处约束力的方向如图所示60°第二章平面力系一、选择题与填空题■1. B; D。
2. B。
3. F;向上。
4. B。
5. 4^M;方向与水平线成60角,指向 23L右下。
6. 10kN; 10kN ; 5kN; 5kN。
7. 100kN;水平向右。
二•计算题1. F B - -70 KN F AX =70 KN ,F Ay =120 KN , M A二-30KN m2. F AX - -qa F BX二 F qa F Ay =qa F F By 二 qa - F3. F= -5kN F Dy = 4.33kN F E-4.33kN F C =24.41kND xF B^ -17.08kN F AX=F BX = -5kN l^y = -14.08kN M A=T4.66kN mF AX =10N FAy =20N M A =15N mF CD =14.1N6F Ax=2.5kN F Ay=—2.16kN M A=」kN ,m F c =20.33kN7 F B=40kNF AX = —10kNFA ^-20kN M -50kN m F cx = 40kNF ey = 0F HX =300N F Hy =100N第三章空间力系少2(-8. F A ^ = -100N F Ay 二-300N F Ex 二-300N F Ey =100N F °y 二 200N整=一一A > X Y m 一:J E £c X一、选择题与填空题f—- - Fa 6 Fa 1.B。
2.B。
3. M x(F)=O ; M y(F) —H2 44.F x=-40.2N; F y=30-2N; M z=240.2 N m。
5.F z= F sin :;F y= F cos :cos :;M x(F)二 F(ccos'cos : bsin )。
理论力学习题答案

第三章 空间力系
一、是非题判断题
3.1.1对一空间任意力系,若其力多边形自行封闭,则该力系的主矢为零。 (∨)
平面力系中,若其力多边形自行闭合,则力系平衡。(×)
3.1.2只要是空间力系就可以列出6 个独立的平衡方程。 (×)
2.3.4悬臂式吊车的结构简图如图所示,由DE、AC二杆组成,A、B、C为铰链连接。已知P1=5kN,P2=1kN,不计杆重,试求杆AC杆所受的力和B点的支反力。
(答案:FBx=3.33kN,FBy=0.25kN,FAC=6.65kN)
2.3.5由AC和CD构成的组合粱通过铰链C连接,它的支承和受力如图所示,已知均布载荷强度q=10kN/m,力偶矩M=40kN.m,不计梁重,求支座A、B、D的约束反力和铰链C处所受的力。
3.1.3若由三个力偶组成的空间力偶系平衡,则三个力偶矩矢首尾相连必构成自行封闭的三角形。(∨)
3.1.4空间汇交力系平衡的充分和必要条件是力系的合力为零;空间力偶系平衡的充分和必要条件是力偶系的合力偶矩为零。(∨)
二、填空题
3.2.1若一空间力系中各力的作用线平行于某一固定平面,则此力系有5个独立的平衡方程。
3.3.3如图所示,三圆盘A、B、C的半径分别为15cm、10cm、5cm,三根轴OA、OB、OC在同一平面内,∠AOB为直角,三个圆盘上分别受三个力偶作用,求使物体平衡所需的力F和α角。
3.3.4某传动轴由A、B两轴承支承。圆柱直齿轮的节圆直径d=17.3cm,压力角 =20º,在法兰盘上作用一力偶矩为M=1030N.m的力偶,如轮轴的自重和摩擦不计,求传动轴匀速转动时A、B两轴承的约束反力。(答案:FAx=4.2kN,FAz=1.54kN,FBz=7.7kN,FBz.=2.79kN)
(最新整理)1-8章习题答案 理论力学.doc

第一章 静力学公理和物体的受力分析一、选择题与填空题 1.C 2.ACD3.A ,B 两处约束力的方向如图所示。
4.5F ,方向与5F 方向相反。
5.60°。
6. 铅直向上。
第二章 平面力系一、选择题与填空题 1.B ;D 。
2.B 。
3.2F ;向上。
4.B 。
5.LM 334;方向与水平线成︒60角,指向右下。
6.10kN ;10kN ;5kN ;5kN 。
7. 100kN ;水平向右。
二.计算题1. 70-=BF KN 70=AxF KN ,120=Ay F KN ,30A M KN m =-⋅ 2. qa F Ax -= qa F F Bx += F qa F Ay += F qa F By -=3. kN5-=Dx FkN33.4=Dy FkN33.4=E FkN41.24=C FkN08.17-=By FkN 5-='=BxAx F FkN08.14-=Ay F m kN 66.14⋅-=A M4.5.N10=Ax FN20=Ay F m N 15⋅=A M N 1.14=CD F6.kN5.2=AxF kN 16.2-=Ay F m kN 8⋅-=A M kN33.20=C F7. kN 40=B FkN10-=Ax FkN20-=Ay F m kN 50⋅-=A MkN40=Cx F 0=Cy F8. N100-=Ax F N300-=Ay FN300-=Ex F N100=Ey F N200=Dy FN 300=Hx F N100=Hy F第三章 空间力系一、选择题与填空题1.B 。
2.B 。
3. 0)(=F M x ;2)(FaF M y -= ;46)(Fa F M z = 。
4. F x =240-N ;F y =302N ;M z =2402m N ⋅。
5.sin z F F ϕ=;cos cos y F F ϕβ=;()(cos cos sin )x M F F c b ϕβϕ=+。
理论力学习题答案

理论力学习题答案(总26页)--本页仅作为文档封面,使用时请直接删除即可----内页可以根据需求调整合适字体及大小--2第一章 静力学公理和物体的受力分析一、是非判断题在任何情况下,体内任意两点距离保持不变的物体称为刚体。
( ∨ ) 物体在两个力作用下平衡的必要与充分条件是这两个力大小相等、方向相反,沿同一直线。
( × ) 加减平衡力系公理不但适用于刚体,而且也适用于变形体。
( × ) 力的可传性只适用于刚体,不适用于变形体。
( ∨ ) 两点受力的构件都是二力杆。
( × ) 只要作用于刚体上的三个力汇交于一点,该刚体一定平衡。
( × ) 力的平行四边形法则只适用于刚体。
( × ) 凡矢量都可以应用平行四边形法则合成。
( ∨ ) 只要物体平衡,都能应用加减平衡力系公理。
( × ) 凡是平衡力系,它的作用效果都等于零。
( × ) 合力总是比分力大。
( × ) 只要两个力大小相等,方向相同,则它们对物体的作用效果相同。
( × )若物体相对于地面保持静止或匀速直线运动状态,则物体处于平衡。
( ∨ )当软绳受两个等值反向的压力时,可以平衡。
( × )静力学公理中,二力平衡公理和加减平衡力系公理适用于刚体。
( ∨ )静力学公理中,作用力与反作用力公理和力的平行四边形公理适用于任何物体。
( ∨ )凡是两端用铰链连接的直杆都是二力杆。
( × )如图所示三铰拱,受力F ,F 1作用,其中F 作用于铰C 的销子上,则AC 、BC 构件都不是二力构件。
( × )图3二、填空题力对物体的作用效应一般分为 外 效应和 内 效应。
对非自由体的运动所预加的限制条件称为 约束 ;约束力的方向总是与约束所能阻止的物体的运动趋势的方向 相反 ;约束力由 主动 力引起,且随 主动 力的改变而改变。
理论力学第一章习题

理论力学第一章习题
1-1重力为P的圆球放在板AC与墙壁AB之间,如图所示。
设板AC自重不计,试画出板和球的受力图。
1-2梁AB的A端为滚动铰链支座,B端为固定铰链支座。
杆CD的C端靠在光滑墙壁上,两杆在D处用铰链连接,如图所示。
如果在E处作用铅直力F,不计重力,分别画出杆CD和AB的受力图。
1-3平面承重支架如图所示,在C点上作用荷载F,若不计各杆件的重力,试分别画出杆AC 和BD的受力图。
1-4球体的重力为G,放在如图所示的光滑接触面上,今在球心O作用水平向左的力P后使球处于静止状态。
画出球体的受力图。
1-5匀质杆AB的重力为G,放在光滑的半圆槽内,并在如图所示的位置处于静止状态。
画出杆AB在平衡时的受力图。
1-6图为汽车制动机构的示意图。
已知司机脚踏制动蹬的力为P,平衡时拉杆CD为水平。
A 和D均为固定铰链支座,C处为铰链连接。
如果不计机构的重量和摩擦,画出制动蹬AB 的受力图。
理论力学习题解答第一章

第一章 静力学基本概念
1-1 考虑力对物体作用的运动效应,力是( A )。
A.滑动矢量
B.自由矢量
C.定位矢量
1-2 如图1-18所示,作用在物体A 上的两个大小不等的力1F 和2F ,沿同一直线但方向相反,则其合力可表为( C )。
A.1F –2F
B.2F - 1F
C.1F +2F
图1-18 图1-19 1-3 F =100N ,方向如图1-19所示。
若将F 沿图示x ,y 方向分解,则x 方向分力的大小 x F = C N ,y 方向分力的大小y F = ___B __ N 。
A. 86.6
B. 70.0
C. 136.6
D.25.9
1-4 力的可传性只适用于 A 。
A. 刚体
B. 变形体
1-5 加减平衡力系公理适用于 C 。
A. 刚体;
B. 变形体;
C. 刚体和变形体。
1-6 如图1-20所示,已知一正方体,各边长a ,沿对角线BH 作用一个力F ,则该力在x 1轴上的投影为 A 。
A. 0
B. F/2
C. F/6
D.-F/3
1-7如图1-20所示,已知F=100N ,则其在三个坐标轴上的投影分别为:
Fx Fy Fz
图1-20 图1-21。
理论力学习题
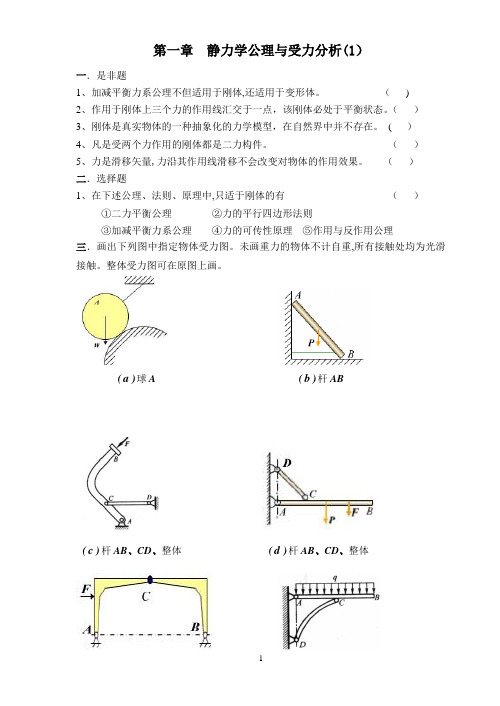
第一章静力学公理与受力分析(1)一.是非题1、加减平衡力系公理不但适用于刚体,还适用于变形体。
()2、作用于刚体上三个力的作用线汇交于一点,该刚体必处于平衡状态。
()3、刚体是真实物体的一种抽象化的力学模型,在自然界中并不存在。
( )4、凡是受两个力作用的刚体都是二力构件。
()5、力是滑移矢量,力沿其作用线滑移不会改变对物体的作用效果。
()二.选择题1、在下述公理、法则、原理中,只适于刚体的有()①二力平衡公理②力的平行四边形法则③加减平衡力系公理④力的可传性原理⑤作用与反作用公理三.画出下列图中指定物体受力图。
未画重力的物体不计自重,所有接触处均为光滑接触。
整体受力图可在原图上画。
)a(球A )b(杆ABd(杆AB、CD、整体)c(杆AB、CD、整体)- 1 -)e(杆AC、CB、整体)f(杆AC、CD、整体四.画出下列图中指定物体受力图。
未画重力的物体不计自重,所有接触处均为光滑接触.多杆件的整体受力图可在原图上画。
)a(球A、球B、整体)b(杆BC、杆AC、整体- 2 -- 3 -第一章 静力学公理与受力分析(2)一.画出下列图中指定物体受力图。
未画重力的物体不计自重,所有接触处均为光滑接触。
整体受力图可在原图上画。
WADB CE Original FigureAD B CEWWFAxF AyF BFBD of the entire frame)a (杆AB 、BC 、整体)b (杆AB 、BC 、轮E 、整体)c (杆AB 、CD 、整体)d (杆BC 带铰、杆AC 、整体)e(杆CE、AH、整体)f(杆AD、杆DB、整体)g(杆AB带轮及较A、整体)h(杆AB、AC、AD、整体- 4 -- 5 -第二章 平面汇交和力偶系一.是非题1、因为构成力偶的两个力满足F = — F ',所以力偶的合力等于零。
( )2、用解析法求平面汇交力系的合力时,若选用不同的直角坐标系,则所求得的合力不同。
理论力学习题及答案(全)

第一章静力学基础一、是非题1.力有两种作用效果,即力可以使物体的运动状态发生变化,也可以使物体发生变形。
()2.在理论力学中只研究力的外效应。
()3.两端用光滑铰链连接的构件是二力构件。
()4.作用在一个刚体上的任意两个力成平衡的必要与充分条件是:两个力的作用线相同,大小相等,方向相反。
()5.作用于刚体的力可沿其作用线移动而不改变其对刚体的运动效应。
()6.三力平衡定理指出:三力汇交于一点,则这三个力必然互相平衡。
()7.平面汇交力系平衡时,力多边形各力应首尾相接,但在作图时力的顺序可以不同。
()8.约束力的方向总是与约束所能阻止的被约束物体的运动方向一致的。
()二、选择题1.若作用在A点的两个大小不等的力F1和F2,沿同一直线但方向相反。
则其合力可以表示为。
①F1-F2;②F2-F1;③F1+F2;2.作用在一个刚体上的两个力F A、F B,满足F A=-F B的条件,则该二力可能是。
①作用力和反作用力或一对平衡的力;②一对平衡的力或一个力偶。
③一对平衡的力或一个力和一个力偶;④作用力和反作用力或一个力偶。
3.三力平衡定理是。
①共面不平行的三个力互相平衡必汇交于一点;②共面三力若平衡,必汇交于一点;③三力汇交于一点,则这三个力必互相平衡。
4.已知F1、F2、F3、F4为作用于刚体上的平面共点力系,其力矢关系如图所示为平行四边形,由此。
①力系可合成为一个力偶;②力系可合成为一个力;③力系简化为一个力和一个力偶;④力系的合力为零,力系平衡。
5.在下述原理、法则、定理中,只适用于刚体的有。
①二力平衡原理;②力的平行四边形法则;③加减平衡力系原理;④力的可传性原理;⑤作用与反作用定理。
三、填空题1.二力平衡和作用反作用定律中的两个力,都是等值、反向、共线的,所不同的是。
2.已知力F沿直线AB作用,其中一个分力的作用与AB成30°角,若欲使另一个分力的大小在所有分力中为最小,则此二分力间的夹角为度。
理论力学习题及解答1
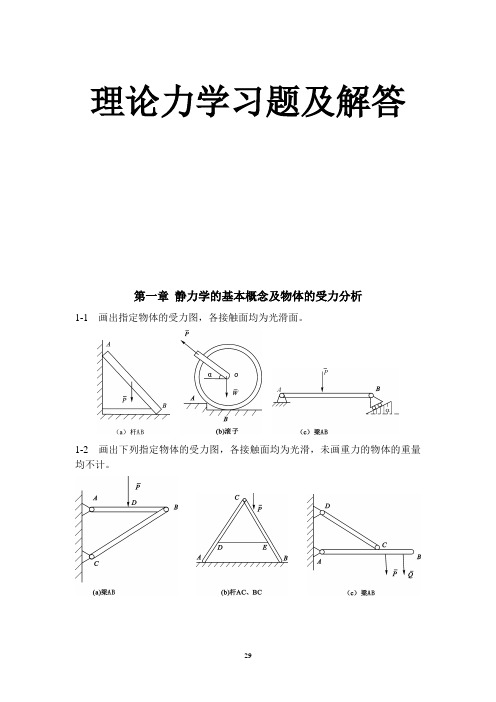
理论力学习题及解答第一章静力学的基本概念及物体的受力分析1-1 画出指定物体的受力图,各接触面均为光滑面。
1-2 画出下列指定物体的受力图,各接触面均为光滑,未画重力的物体的重量均不计。
1-3 画出下列各物体以及整体受力图,除注明者外,各物体自重不计,所有接触处均为光滑。
(a) (b)(c) (d)(e) (f)第二章平面一般力系2-1 物体重P=20kN,用绳子挂在支架的滑轮B上,绳子的另一端接在铰车D 上,如图所示。
转动铰车,物体便能升起,设滑轮的大小及滑轮转轴处的摩擦忽略不计,A、B、C三处均为铰链连接。
当物体处于平衡状态时,试求拉杆AB和支杆CB所受的力。
2-2 用一组绳悬挂重P=1kN的物体,求各绳的拉力。
2-3 某桥墩顶部受到两边桥梁传来的铅直力P1=1940kN,P2=800kN及制动力T=193kN,桥墩自重W=5280kN,风力Q=140kN。
各力作用线位置如图所示,求将这些力向基底截面中心O简化的结果,如能简化为一合力,试求出合力作用线的位置。
2-4 水平梁的支承和载荷如图所示,试求出图中A、B处的约束反力。
2-5 在图示结构计算简图中,已知q=15kN/m,求A、B、C处的约束力。
2-6 图示平面结构,自重不计,由AB、BD、DFE三杆铰接组成,已知:P=50kN,M=40kN·m,q=20kN/m,L=2m,试求固定端A的反力。
图2-6 图2-72-7 求图示多跨静定梁的支座反力。
2-8 图示结构中各杆自重不计,D、E处为铰链,B、C为链杆约束,A为固定端,已知:q G=1kN/m,q=1kN/m,M=2kN·m,L1=3m,L2=2m,试求A、B、C 处约束反力。
图2-8 图2-92-9 支架由两杆AO、CE和滑轮等组成,O、B处为铰链,A、E是固定铰支座,尺寸如图,已知:r=20cm,在滑轮上吊有重Q=1000N的物体,杆及轮重均不计,试求支座A和E以及AO杆上的O处约束反力。
理论力学第一章题及解答(文末)

理论⼒学第⼀章题及解答(⽂末)第⼀章思考题1.1平均速度与瞬时速度有何不同?1.2 在极坐标系中,r v r =,θθ r v =.为什么2θ r r a r-=⽽⾮r ?为什么θθ r r a 20+=⽽⾮θθ r r +?你能说出r a 中的2θ r -和θa 中另⼀个θ r 出现的原因和它们的物理意义吗?1.3 在内禀⽅程中,n a 是怎样产⽣的?为什么在空间曲线中它总沿着主法线⽅向?当质点沿空间运动时,副法线⽅向的加速度b a 等于零,⽽作⽤⼒在副法线⽅向的分量b F ⼀般不等于零,这是不是违背了⽜顿运动定律呢?1.4 在怎样的运动中只有τa ⽽⽆n a ?在怎样的运动中⼜只有n a ⽽⽆τa ?在怎样的运动中既有n a ⽽⽆τa ?1.5dt r d 与dt dr 有⽆不同?dt v d与dtdv 有⽆不同?试就直线运动与曲线运动分别加以讨论. 1.6⼈以速度v 向篮球⽹前进,则当其投篮时应⽤什么⾓度投出?跟静⽌时投篮有何不同?1.7⾬点以匀速度v 落下,在⼀有加速度a 的⽕车中看,它⾛什么路经?1.8某⼈以⼀定的功率划船,逆流⽽上.当船经过⼀桥时,船上的渔竿不慎落⼊河中.两分钟后,此⼈才发现,⽴即返棹追赶.追到渔竿之处是在桥的下游600⽶的地⽅,问河⽔的流速是多⼤?1.9物体运动的速度是否总是和所受的外⼒的⽅向⼀致?为什么?1.10在那些条件下,物体可以作直线运动?如果初速度的⽅向和⼒的⽅向⼀致,则物体是沿⼒的⽅向还是沿初速度的⽅向运动?试⽤⼀具体实例加以说明.1.11质点仅因重⼒作⽤⽽沿光滑静⽌曲线下滑,达到任⼀点时的速度只和什么有关?为什么是这样?假如不是光滑的将如何?1.12为什么被约束在⼀光滑静⽌的曲线上运动时,约束⼒不作功?我们利⽤动能定理或能量积分,能否求出约束⼒?如不能,应当怎样去求?1.13质点的质量是1千克,它运动时的速度是k j i v 323++=,式中i 、j 、k 是沿x 、y 、z 轴上的单位⽮量。
理论力学第一章质点力学习题(带答案解析)

《理论力学》第一章质点力学一、单选题(共22题)1、如图,下面三个坐标系分别为()①②③A 、直角坐标系、极坐标系、自然坐标系;B 、直角坐标系、自然坐标系、极坐标系;C 、自然坐标系、极坐标系、直角坐标系;D 、极坐标系、直角坐标系、自然坐标系;正确答案:A2、速度表达式:①z y x e z e y e x v ++=;②θθe r e r v r +=;③t e dtds v =分别在自然坐标系、极坐标系、直角坐标系下的排序为:A 、①②③;B 、②①③;C 、③②①;D 、①③②。
正确答案:C3、加速度表达式:①z y x e z e y e x a ++=;②n t e v e v a 2ρ+=;③θθθθe r r e r r a r )2()(2++-=分别在自然坐标系、极坐标系、直角坐标系下的排序为:A 、①②③;B 、②③①;C 、③②①;D 、①③②。
正确答案:B4、以初速v 0与水平面成θ角抛出物体,不计空气阻力,则在最高点轨道的曲率半径为()A 、∞;B 、0C 、g v /0;D 、g v /)cos 20θ(正确答案:D解析:物体在最高点只有水平速度θcos 0v v x =,进行受力分析,由牛二有g v v m mg x /)cos 202θρρ(=⇒=。
5、质点的功能原理可写为E W ∆=∆,其中W ∆应为()。
A 、所有力的总功;B 、保守力的总功;C 、外力及内部非保守力的总功;D 、外力的总功正确答案:C解析:C 。
功能原理:外力及内部非保守力的总功等于系统机械能的改变量。
6、下列()状态属于平衡状态。
.A 、匀加速直线运动B 、静止状态C 、减速运动D 、定轴加速转动正确答案:B7、物体的平衡是指物体相对于地球处于()状态A 、静止B 、静止或匀速直线运动C 、加速运动D 、减速运动正确答案:B8、作用于刚体上的两个力平衡的充分必要条件是这两个力()。
A 、大小相等B 、大小相等,方向相反C 、大小相等,方向相反,作用在一条直线D 、无关系正确答案:C9、对物体系的各个物体进行受力分析时,要用到作用和反作用定律,但应当注意,作用力和反作用力总是同时存在的,并()。
《理论力学》第一章基本概念及基本原理

第一章 基本概念及基本原理[习题1-1] 支座受力F ,已知kN F 10=,方向如图所示, 求力沿y x ,轴及沿'',y x 轴分解的结果,并求力F 在各轴上的投影.解:(1)F 沿y x ,轴分解的结果把F 沿y x ,轴分解成两个分力,如图所示. →→→→=⨯==i i i F F x 66.8866.01030cos 0)(kN →→→→=⨯==j j j F F y 55.01030sin 0)(kN (2)F 沿'',y x 轴分解的结果把F 沿'',y x 轴分解成两个分力,如图所示. 由图可知,力三角形是等腰三角形.故:→→→==''10'i i F F x )(kN→→→-=⨯-=''018.575cos 102'j j F y )(kN (3) F 在y x ,轴上的投影)(66.8866.01030cos 0kN F F x =⨯==)(55.01030sin 0kN F F y =⨯== (4) F 在'',y x 轴上的投影)(66.8866.01030cos 0'kN F F x =⨯==)(59.275cos 1075cos 00'kN F F y -=-=-=[习题1-2] 已知N F 1001=,N F 502=,N F 603=N F 804=,各力方向如图所示,试分别求各力在x 轴y 轴上的投影. 解:)(6.86866.010030cos 011N F F x =⨯==)(505.010030sin 011N F F y =⨯==)(305350cos 222N F F x =⨯==α力沿x,y 轴的分解图力沿x ’,y ’轴的分解图力沿x ’,y ’轴的投影图xF yFy 'x F ')(405450sin 222N F F y -=⨯-=-=α 0060cos 333=⨯==αF F x)(60160sin 333N F F y =⨯==α)(57.56135cos 80cos 0444N F F x -===α)(57.56135sin 80sin 0444N F F y ===α[习题1-3] 计算图中321,,F F F 三个力分别在z y x ,,轴上的投影.已知kN F 21=,kN F 12= , kN F 33=. 解:)(2.16.025311kN F F x -=⨯-=⨯-= )(6.18.025411kN F F y =⨯=⨯=01=z F)(424.05345sin 1cos sin 02222kN F F x =⨯⨯==θγ )(566.05445sin 1sin sin 02222kN F F y=⨯⨯==θγ)(707.045cos 1cos 0222kN F F z =⨯==γ03=x F03=y F)(333kN F F z ==[习题1-4] 已知kN F T 10=,求T F 分别在z y x ,,轴上的投影. 解:(591.75353510sin 22222F F T Txy =+++⨯==γ)(51.6355591.7cos 22kN F F Txy Tx =+⨯==θ题1-2图)3,)0,)(91.3353591.7sin 22kN F F Txy Ty =+⨯==θ)(51.6535510cos 222kN F F T Tz -=++⨯-=-=γ[习题1-5] 力F 沿正六面体的对角线AB 作用,kN F 100=,求F 在ON 上的投影. 解:如图所示,F 在AC 线上的投影为:)(345.88400300400400400100cos 22222kN CAB F F F OB AC =+++⨯===5.0400200tan ==NOD 057.265.0arctan ==NOD 00043.1857.2645=-=BONF 在ON 线上的投影为:)(811.8343.18cos 345.88cos 0kN BON F F O B O N ===[习题1-6] 已知N F 10=,其作用线通过A(4,2,0),B(1,4,3)两点,如图所示.试求力F 在沿CB 的T 轴上的投影. 解: 61.313)42()14(22==-+-=AD69.413361.322==+=AB 2361.322=-=DGF 在AD 上的投影为:M)(697.769.461.310cos N BAD F F AD =⨯== )(40.669.4310sin N BAD F F z =⨯==)(264.461.32697.7cos N ADG F F AD y =⨯==)(396.661.33697.7sin N ADG F F AD x =⨯==F 在T 轴上的投影为:)(251.75340.654264.4cos cos kN ECB F BCD F F z y T =⨯+⨯=+= [习题1-7] 图中圆轮在力F 和矩为M 的力偶作用下保持平衡,这是否说明一个力可与一个力偶平衡? 解:图中圆轮在力F 和矩为M 的力偶作用下保持平衡,这不能说明一个力可与一个力偶平衡.因为轮子的圆心处 有支座,该支座反力R 与F 构成一力偶,力偶矩),(F R M 与M 等值,共面,反向,故圆轮保持平衡.[习题1-8] 试求图示的力F 对A 点之矩,已知m r 2.01=m r 5.02=,N F 300=.010012030cos 60sin )30sin (60cos )(r F r r F F M A ⋅+--=)(15232.023300)5.02.05.0(5.0300)(m N F M A ⋅-=⨯⨯⨯+⨯-⨯-= [习题1-9] 试求图示绳子张力T F 对A 点及对B 点的矩.已知kN F T 10=,m l 2=,m R 5.0=,030=α.解:)(530sin 10sin 0kN F F T Tx ===α)(66.830cos 10cos 0kN F F T Ty ===α )(732.1866.0260sin 0m l OC =⨯==)(15.0260cos 0m l AC =⨯==)()()(Ty A Tx A T A F M F M F M +=)30cos 5.01(66.8)30sin 5.0732.1(500+⨯+-⨯-=)(5m kN ⋅=)()()(Ty B Tx B T B F M F M F M +=)30cos 5.01(66.8)30sin 5.0732.1(500-⨯--⨯-=)(320.12m kN ⋅-=[习题1-10] 已矩正六面体的边长为c b a ,,,沿AC 作用一力F ,试求力F 对O 点的矩矢量表达式. 解:zy xF F F c bak j iF M →→→=)(0式中,2222222222cos cos c b a Fa b a a c b a b a F F F x ++-=+⋅+++⋅-=⋅-=θγ2222222222sin cos cb a Fb ba b cb a b a F F F y ++-=+⋅+++⋅-=⋅-=θγ222222sin cb a Fc cb ac F F F z ++=++⋅==γ故cb ac b ak j i c b a FF M --++=→→→2220)(cc bak j i c b a F200222→→→++=baj ic c b a F→→⋅++=2222)(2222→→-++=j a i b c b a cF[习题1-11] 钢绳AB 中的张力kN F T 10=.写出该张力T F 对O 点的矩的矢量表达式.解:2)21()01(22=-+-=BC2318)04()12()10(222==-+-+-=ABzy xF F F k j iF M 42)(0→→→=式中,)(357.22123210cos cos kN F F T Tx =⋅⋅=⋅=θγ )(357.22123210sin cos kN F F T Ty -=⋅⋅-=⋅-=θγ)(428.923410sin kN F F T Tz -=⋅-=-=γ故428.9357.2357.2420)(0--=→→→k j i F M 357.2357.24428.9357.22---=→→→→jiki)(357.24)357.2428.9(2→→→→--⨯---=j i k i →→→-+-=k j i 714.4428.9428.9[习题1-12] 已知力→→→→+-=k j i F 32,其作用点的位置矢→→→→++=k j i r A 423,求力F 对位置矢为→→→→++=k j i r B 的一点B 的矩(力以N 计,长度m 以计).A解:→→→→→⨯-=⨯=F r r F r F M B A AB B )()(式中,→→→→++=k j i r A 423,→→→→++=k j i r B ,=-→→)(B A r r →→→++k j i 312 →→→→+-=k j i F 32故, =)(F M B ⨯++→→→)312(k j i )32(→→→+-k j i=-=→→→132312k j i=--→→→240312k j i 23522---→→→→k k j i 5222---=→→→k j i)425(2→→→+---=k j i→→→-+=k j i 8410 )(m N ⋅[习题1-13] 工人启闭闸门时,为了省力,常常用一根杆子插入手轮中,并在杆的一端C 施加力,以转动手轮.设手轮直径m AB 6.0=,AC 轩长m l 2.1=,在C 端用N F C 100=的力能将闸门开启,若不借用杆子而直接在手轮A,B 施加力偶),('F F ,问F 至少应多大才能开启闸门? 解:支座O 反力O R 与C F 构成一力偶),(0C F R 若要闸门能打开,则),('F F 与),(0C F R 必须 等效,即它们的力偶矩相等:)3.02.1(1006.0-⨯=⨯F )(150N F =[习题1-14] 作下列指定物体的示力图.物体重量,除图上已注明者外,均略去不计.假设接触处都是光滑的.。
理论力学题库第一章

应用物理专业理论力学题库-第一章一、填空题1. 在质点运动学中)(t r 给出质点在空间任一时刻所占据的位置,故其表示了质点的运动规律,被称为质点的运动学方程。
2. 运动质点在空间一连串所占据的点形成的一条轨迹,被称为轨道。
3. 一个具有一定几何形状的宏观物体在机械运动中的物质性体现在:不能有两个或两个以上的物体同时占据同一空间;不能从空间某一位置突然改变到另一位置。
4. 质点的运动学方程是时间t 的单值的、连续的函数。
5. 质点的运动轨道的性质,依赖于参考系的选择。
6. 平面极坐标系中速度的表达式是 ,其中 称为径向速度, 称为横向速度。
7. 平面极坐标系中,径向速度是由位矢的量值变化引起的,横向速度是由位矢的方向改变引起的。
8. 平面极坐标系中加速度的表达式是 ,其中 称为径向加速度, 称为横向加速度。
9. 自然坐标系中加速度的表达式是 ,其中两项分别称为 和 。
10.自然坐标系中,切向加速度是由于速度的量值改变引起的,法向加速度是由于速度的方向改变引起的。
11.对于切向加速度τa 与法向加速度n a ,质点运动时,只存在切向加速度,做变速率直线运动;只存在法向加速度,做匀速率曲线运动;切向加速度与法向加速度同时存在,则做变速曲线运动;切向加速度与法向加速度都不存在,则做匀速直线运动。
12.我们通常把物体相对于“静止”参考系的运动叫做绝对运动,物体相对于运动参考系的运动叫做相对运动,物体随运动参考系一起运动而具有相对于静止参考系的运动,叫做牵连运动。
13.绝对速度等于牵连速度与相对速度的矢量和。
14.绝对加速度等于牵连加速度与相对加速度的矢量和。
15.已知0是S '系相对于S 系的加速度,在相对于S 系作加速直线运动的参考系S '中观察质点的运动时,质点的速度υ'和加速度a '和在S 系中所观察到的υ和a 不同,分别写出它们的关系式:υυυ'+=0,a '+=0。
理论力学第一章的习题.doc

第一章习题1.4 细杆绕点以角速转动,并推动小环C 在固定的钢丝上滑动。
图中的为已知常数,试求小球的速度及加速度的量值。
解 如题1.4.1图所示,绕点以匀角速度转动,在上滑动,因此点有一个垂直杆的速度分量点速度又因为所以点加速度OL O ωAB d A BOCLxθd 第1.4题图OL O C AB C 22x d OC v +=⨯=⊥ωωC dx d d v v v 222sec sec cos +====⊥⊥ωθωθθωθ= C θθθω ⋅⋅⋅⋅==tan sec sec 2d dt dv a ()2222222tan sec 2d x d x d +==ωθθω1.5 矿山升降机作加速度运动时,其变加速度可用下式表示:式中及为常数,试求运动开始秒后升降机的速度及其所走过的路程。
已知升降机的初速度为零。
解 由题可知,变加速度表示为由加速度的微分形式我们可知代入得对等式两边同时积分 可得 :(为常数)代入初始条件:时,,故即 又因为 所以对等式两边同时积分,可得:⎪⎭⎫ ⎝⎛-=T t c a 2sin 1πc T t ⎪⎭⎫ ⎝⎛-=T t c a 2sin 1πdtdv a =dt T t c dv ⎪⎭⎫ ⎝⎛-=2sin 1πdt T t c dv t v⎰⎰⎪⎭⎫⎝⎛-=002sin 1πD Ttc Tct v ++=2cos2ππD 0=t 0=v c TD π2-=⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛-+=12cos 2T t T t c v ππdtds v =dt T t T t c ⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛-+12cos 2ππ=ds ⎥⎦⎤⎢⎣⎡⎪⎭⎫⎝⎛-+=t T t T T t c s 2sin 22212πππ1.6 一质点沿位失及垂直于位失的速度分别为及,式中及是常数。
试证其沿位矢及垂直于位失的加速度为解 由题可知质点的位矢速度(1)沿垂直于位矢速度 (2)又因为, 即 (3) (4) 对③求导(5) 对④求导(6)根据课本的推导可知 沿位矢方向加速度(7) 垂直位矢方向加速度(8)把(3)(4)(5)(6)代入(7)(8)式中可得r λμθλμ⎪⎭⎫ ⎝⎛+-r rr μλμθθμλ,222r λ=//v μθ=⊥v r rλ= μθθ==⊥r v rμθθ= θμμθθrrr +-=2()2θr r a -=()θθr r a 2+=⊥rr a 222//θμλ-=⎪⎭⎫ ⎝⎛+=⊥r a μλμθr rr 2 λ λ = = rr λ = = // v1.7 试自出发,计算及。
胡汉才编著《理论力学》课后习题答案 第1章静力学基本概念

第一章 静力学基本概念
1-1 考虑力对物体作用的运动效应,力是( A )。
A.滑动矢量
B.自由矢量
C.定位矢量
1-2 如图1-18所示,作用在物体A 上的两个大小不等的力1F 和2F ,沿同一直线但方向相
反,则其合力可表为( C )。
A.1F –2F
B.2F - 1F
C.1F +2F
图1-18 图1-19 1-3 F =100N ,方向如图1-19所示。
若将F 沿图示x ,y 方向分解,则x 方向分力的大小 x F = C N ,y 方向分力的大小y F = ___B __ N 。
A. 86.6
B. 70.0
C. 136.6
D.25.9
1-4 力的可传性只适用于 A 。
A. 刚体
B. 变形体
1-5 加减平衡力系公理适用于 C 。
A. 刚体;
B. 变形体;
C. 刚体和变形体。
1-6 如图1-20所示,已知一正方体,各边长a ,沿对角线BH 作用一个力F ,则该力在x 1轴上的投影为 A 。
A. 0
B. F/2
C. F/6
D.-F/3
1-7如图1-20所示,已知F=100N ,则其在三个坐标轴上的投影分别为: Fx = -402N ,Fy = 302N ,Fz = 502 N 。
图1-20 图1-21。
理论力学练习册及答案
由速度合成定理 作速度平行四边形。
由加速度合成定理 作加速度图。
取 方向投影,得:
再取动点杆O1C上C点,动系固连套筒B上,定系固连机架。
由速度合成定理 作速度平行四边形。
由加速度合成定理:
作加速度图。
取 方向投影,得:
取 方向投影,得:
第八章 刚体平面运动
8-1.已知图示机构滑块B,沿水平方向按规律SB=0.01t2+0.18t m移动,通过连杆AB带动半径R=0.1 m的轮子沿水平方向只滚不滑。求当t=1 s时,点A和点C在图示位置的速度和加速度。
解:当 时,
由于杆AB作瞬时平动,且P为轮C
的速度瞬心,故有:
8-2.曲柄OA=17 cm,绕定轴O转动的角速度ωOA=12 rad/s,AB=12 cm,BD=44 cm,滑块C、D分别沿着铅垂与水平滑道运动,在图示瞬时OA铅垂,求滑块C与D的速度。
2、研究滑块A运动副,求 ,
3、分别作套筒o运动副、滑块A运动副
加速度图,
4、研究杆BE,作O、A加速度图,
5、分别列O、A点加速度投影式求解
7-7.圆盘半径OA=r,可绕其边缘上一点A转动,从而带动直杆BC绕B点转动,AB=3r,且直杆与圆盘始终相切,当圆盘中心运动到AB连线上时,圆盘转动的角速度为ω,角加速度为ε,求此瞬时直杆BC的角速度和角加速度。
8-5.滑块B、D在铅直导槽中滑动,通过连杆BA及CD与轮子A相连,各连接处都是光滑铰链。轮A放在水平面上,AB=10 cm,CD=13 cm。在图示瞬时,即轮心A至两铅垂导槽的距离均为8 cm时,可在水平面上自由滚动的轮子,其轮心速度νA=30 cm/s,方向水平向右。求此时滑块D的速度。
理论力学习题答案 第三版

e2ω 2r 4
( ) ( ) ( ) =
a2
1− e2
2
a2 1− e2 [1 −
2
+r2
− 2ar 1 − e 2
+ r2ω 2 ]
r2e2
( ) r 2ω 2 ( ) = a2 1 − e 2
⎡ e2 r 2 − r 2 + 2ar 1 − e2
⋅⎢ ⎣
1− e2
- 12 -
又因为 所以 把⑥代入⑤
既可化为 对等式两边积分 所以
x& = yy& p
v 2 = x& 2 + y& 2
y& 2
=
v2
1+
y2 p2
⑥
p2
⎜⎜⎝⎛1+
v
y2 p2
1
⎞2 ⎟⎟ ⎠
⋅
dv dy
=
−2kv2
⋅
y3
⎜⎜⎝⎛1 +
p2 y2
3
⎞2 ⎟⎟ ⎠
dv = −2kp dy
v
y2 + p2
d 2 + x2 d
又因为θ& = ω 所以 C 点加速度
( ) a
=
dv dt
= ωd ⋅ 2 secθ
⋅ secθ
⋅ tan⋅ θ&
=
2dω 2 sec 2 θ
ta n θ
=
2ω 2 x d 2 d2
+
x2
1.5 矿山升降机作加速度运动时,其变加速度可用下式表示:
a
= c⎜⎛1 − sin
πt
⎞ ⎟
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第一章习题细杆OL 绕O 点以角速ω转动,并推动小环C 在固定的钢丝AB 上滑动。
图中的d 为已知常数,试求小球的速度及加速度的量值。
解 如题1.4.1图所示,A BOCLxθd 第1.4题图OL 绕O 点以匀角速度转动,C 在AB 上滑动,因此C 点有一个垂直杆的速度分量22x d OC v +=⨯=⊥ωωC 点速度dx d d v v v 222sec sec cos +====⊥⊥ωθωθθ 又因为ωθ=&所以C 点加速度θθθω&⋅⋅⋅⋅==tan sec sec 2d dt dv a ()2222222tan sec 2d x d x d +==ωθθω矿山升降机作加速度运动时,其变加速度可用下式表示:⎪⎭⎫ ⎝⎛-=T t c a 2sin1π 式中c 及T 为常数,试求运动开始t 秒后升降机的速度及其所走过的路程。
已知升降机的初速度为零。
解 由题可知,变加速度表示为⎪⎭⎫ ⎝⎛-=T t c a 2sin1π 由加速度的微分形式我们可知dtdv a =代入得dtT t c dv ⎪⎭⎫ ⎝⎛-=2sin 1π 对等式两边同时积分dt T t c dv t v⎰⎰⎪⎭⎫ ⎝⎛-=002sin 1π可得 :D Ttc T ct v ++=2cos2ππ(D 为常数)代入初始条件:0=t 时,0=v ,故cT D π2-=即⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛-+=12cos 2T t T t c v ππ 又因为dtds v =所以dt T t T t c ⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛-+12cos 2ππ =ds对等式两边同时积分,可得:⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛-+=t T t T T t c s 2sin 22212πππ一质点沿位失及垂直于位失的速度分别为r λ及μθ,式中λ及μ是常数。
试证其沿位矢及垂直于位失的加速度为⎪⎭⎫ ⎝⎛+-r rr μλμθθμλ,222解 由题可知质点的位矢速度r λ=//v (1)沿垂直于位矢速度μθ=⊥v (2)又因为 , 即 r r λ=& (3)μθθ==⊥r v &rμθθ=& (4) 对③求导(5) 对④求导θμμθθ&&&&rr r +-=2(6)根据课本的推导可知 沿位矢方向加速度()2θ&&&r r a -= (7) 垂直位矢方向加速度()θθ&&&&r r a 2+=⊥ (8)把(3)(4)(5)(6)代入(7)(8)式中可得rr a 222//θμλ-=⎪⎭⎫ ⎝⎛+=⊥r a μλμθr r// v rr r 2试自θθsin ,cos r y r x ==出发,计算x &&及y &&。
并由此推出径向加速度r a 及横向加速度θa 。
解 由题可知⎩⎨⎧==θθsin cos r y r x ①②对①求导θθθ&&&sin cos r r x -= ③ 对③求导 θθθθθθθcos sin sin 2cos 2&&&&&&&&&r r r r x ---=④对②求导 θθθcos sin &&&r r y +=⑤对⑤求导 θθθθθθθsin cos cos 2sin 2&&&&&&&&&r r r r y -++=⑥对于加速度a ,我们有如下关系见题1.7.1图题1.7.1图θθsin cos y x a r &&&&+= ⑾把④⑥代入 ⑾得2θ&&&r r a r -= 同理可得θθθ&&&&r r a 2+=一飞机在静止空气中每小时的速率为100千米。
如果飞机沿每边为6千米的正方形飞行,2()cos (2)sin x r r r r θθθθθ=--+&&&&&&&&&即2()sin (2)cos y r r r r θθθθθ=--+&&&&&&&&&即sin cos a x y θθθ=-+&&&&且风速为每小时28千米,方向与正方形的某两边平行,则飞机绕此正方形飞行一周,需时多少?解 正方形如题1.14.1图。
CD3v由题可知h km v v /28==风牵设风速B A →,h km v /100=相,当飞机B A →,h km h km v /128/)28100(1=+= h km h km v D B /96/28100,222=-=→h km h km v D C /72/)28100(,3=-=→=→4,v A D h km h km /96/2810022=-故飞机沿此边长6h km /正方形飞行一周所需总时间min 16515192499667269661286==⎪⎭⎫ ⎝⎛+++=h h t2风v 相题1.14.2图风v v 题1.14.3图小船M 被水冲走后,由一荡桨人以不变的相对速度朝岸上A 点划回。
假定河流速度1 2沿河宽不变,且小船可以看成一个质点,求船的轨迹。
解 以A 为极点,岸为极轴建立极坐标如题.图.题1.17.1图船沿垂直于r 的方向的速度为,船沿径向r 方向的速度为和沿径向的分量的合成,即①--② ②/①得 ,对两积分: 设为常数,即C r k k +=+-αα11cos 2sin ln ln 代入初始条件0r r =时,0ϕϕ=.设,200αϕ=有,cos 2sin ln ln 01010αα+--=k k r C 得101110sin cos cos sin αααα-++-⋅=k kk k r r将质量为m 的质点竖直抛上于有阻力的媒质中。
设阻力与速度平方成正比,即22gv mk R =。
如上抛时的速度为0v ,试证此质点又落至投掷点时的速度为Ck, 2,12Crsin ln 2 tan ln ln 12 d rdrcot sin 1 22 1 1 cos sin dtdr dtd r12sin 122011vk v v +=解 质点从抛出到落回抛出点分为上升和下降阶段.取向上为正各力示意图如题1.19.1图,上升时 下降时 题1.19.1图则两个过程的运动方程为: 上升22yg mk mg y m &&&--= ① 下降:②对上升阶段:()221v k g dtdv+-= ()221v k g dyvdvdt dy dy dv +-== 即gdy vk vdv-=+221 对两边积分gdy vk vdv h v ⎰⎰-=+022010所以()2221ln 21v k gk h +=③ 即质点到达的高度. 对下降阶段:2 2 y g mk mgy m即()21221ln 21v k gk h --= ④ 由③=④可得202011vk v v +=重为W 的不受摩擦而沿半长轴为a 、半短轴为b 的椭圆弧滑下,此椭圆的短轴是竖直的。
如小球自长2轴的端点开始运动时,其初速度为零,试求小球在到达椭圆的最低点时它对椭圆的压力。
gdy v kvdv h v2 2 0 12 2 gv k -g dyvdvdt dy dy dv解 建立如题1.28.1图所示直角坐标.题1.28.1图椭圆方程 12222=+by a x ① 从A 滑到最低点B ,只有重力做功.机械能守恒.即221mv mgb =②设小球在最低点受到椭圆轨道对它的支持力为N 则有:③ρ为B 点的曲率半径. B A →的轨迹:221axb y --=得2221ax abx y -=';2322211⎪⎪⎭⎫ ⎝⎛-⋅=''a x ab y 又因为()223211ab y y k ='+''==ρ所以⎪⎪⎭⎫ ⎝⎛+=⨯+=+=2222212a b W mgh a b mg mv mg N ρ 故根据作用力与反作用力的关系小球到达椭圆最低点对椭圆压力为⎪⎪⎭⎫ ⎝⎛+2221a b W 方向垂直轨道向下.检验下列的力是否是保守力。
如是,则求出其势能。
()a 233206y bx y abz F x -=,y bx abxz F y 43106-=,218abxyz F z =()b ()()()z F y F x F z y x k j i F ++=2v mmgN解 (a )保守力F 满足条件0F =⨯∇对题中所给的力的表达式 ,代入上式 即()()()22=+--+-+-=⎪⎪⎭⎫ ⎝⎛∂∂-∂∂+⎪⎭⎫ ⎝⎛∂∂-∂∂+⎪⎪⎭⎫ ⎝⎛∂∂-∂∂=∂∂∂∂∂∂=⨯∇kj i kj i F F F k j i F zyxy 40abx 6abz y 40bx 6abzy 18abz y 18abz 18abxz 18abxz y F x F x F z F z F y F z y x 333322x y z x y z所以此力是保守力,其势为()()()()()()()()()()()324,,0,,20,,0,0,4300000233z y,x,0,0,0x6518106d 206F abxyz y bx dz abxyz dy y bx abxzx y bx y abz dz F dy F dx V z y x y x y x x ,x,,,zy-=-----++-=⋅-=⎰⎰⎰⎰⎰drF(b)同(a ),由=⎪⎪⎭⎫ ⎝⎛∂∂-∂∂+⎪⎭⎫ ⎝⎛∂∂-∂∂+⎪⎪⎭⎫ ⎝⎛∂∂-∂∂=∂∂∂∂∂∂=⨯∇k j i k j i F y F x F x F z F z F y F F F F z y x x y zx y z zyx所以此力F 是保守力,则其势能为dzF dy F dx F d V BABABx Az z z y y y x x ⎰⎰⎰⎰---=⋅-=rF已知作用在质点上的力为za y a x a F z a y a x a F z a y a x a F z y x 333231232221131211++=++=++= 式中系数()3,2,1,=j i a ij 都是常数。
问这些ij a 应满足什么条件,才有势能存在?如这些条件满足,试计算其势能。
解 要满足势能的存在,即力场必须是无旋场,亦即力为保守力,所以0=⨯∇F 即⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧∂∂=∂∂∂∂=∂∂∂∂=∂∂x F zF x F yF z F yF zx yx yz 得⎪⎩⎪⎨⎧===311321122332aa a a a a ()3,2,1,=j i a ij 为常数满足上式关系,才有势能存在。
