全等三角形证明过程训练(习题与答案及解析)
11.2 三角形全等的判定(SSS)(含答案)

11.2 三角形全等的判定(SSS)题号一1 二2 三3 四4 五5 六6 七7 八8 得分度的反复训练才能取得跟多的收获,我们设计的试卷主要就是从这点出发,所以从你下载这张试卷开始,就与知识接近了一步。
◆课堂测控测试点边边边1.如图,点B,E,C,F在同一直线上,AB=DE,AC=DF,BE=CF,∠A=•43°,求∠D的度数,下面是小红同学的求解过程,请你说明每一步的理由.解:因为BE=CF,所以BE+EC=CF+EC,即BC=EF.在△ABC与△DEF中,,,AB DEAC DFBC EF=⎧⎪=⎨⎪=⎩所以△ABC≌△DEF().所以∠D=∠A=43°().2.已知:如图,C是AB的中点,AD=CE,CD=BE,求证:△ACD≌△CBE.◆课后测控3.如图,AC=BD,AB=DC,求证:∠B=∠C.4.已知:如图,点A,C,B,D都在一条直线上,AC=BD,AM=CN,BM=DN.求证:AM∥CN.5.三月三放风筝,下图是小明制作的风筝,他根据DE=DF,EH=FH,不用度量,就知道∠DEH=∠DFH.请你用所学知识给予证明.◆拓展测控6.有一块三角形的厚铁板(如图),根据实际生产需要,工人师傅要把∠MAN平分开,现在他手边只有一把尺子(没有刻度)和一根细绳,•你能帮助工人师傅想个办法吗?并说明你这样做的理由.答案:1.SSS 全等三角形对应角相等2.∵C是AB的中点,∴AC=BC.在△ACD与△CBE中,,,,AC CBAD CECD BE=⎧⎪=⎨⎪=⎩∴△ACD≌△CBE(SSS).[总结反思]三条边对应相等的两个三角形全等,•运用此结论可证明两个三角形全等.3.证明:在△ABD与△DCA中,,,,AB DCDB ACAD DA=⎧⎪=⎨⎪=⎩∴△ABD≌△DCA(SSS),∴∠B=∠C.[解题规律]证明线段相等或角相等时,常证明它们所在的两个三角形全等,本题中证明两个三角形全等已具备两个条件,运用公共边这个隐含条件是解题关键.4.∵AC=BD,∴AC+CB=BD+CB,即AB=CD.在△AMB和△CND中,,,,AM CNBM DNAB CD=⎧⎪=⎨⎪=⎩∴△AMB≌△CND(SSS).∴∠A=∠NCD,∴AM∥CN.[解题技巧]题目中条件AC=BD不能直接用来证明,可运用等式的性质变为AB=CD.5.证明:连结DH.在△DEH和△DFH中,,,.DE DFEH FHDH DH=⎧⎪=⎨⎪=⎩∴△DEH≌△DFH(SSS),∴∠DEH=∠DFH.[解题规律]连结EH即将原图形分成一对三角形,利用公共边运用SSS可得两个三角形全等.6.用绳子的一定长度在AM,AN边上截取AB=AC,再选取适当长度的绳子,将其对折,得绳子的中点D,把绳子的两端点固定在B,C两点,拽住绳子中点D,向外拉直BD和CD,•再在铁板上点出D的位置,作射线AD,则AD平分∠MAN.理由如下:如图,∵在△ABD和△ACD中,,,,AB ACBD CDAD AD=⎧⎪=⎨⎪=⎩∴△ABD≌△ACD(SSS),∴∠BAD=∠CAD,即AD平分∠MAN.[解题技巧]这是一道实际应用问题,通过构造两个三角形全等将∠MAN平分,•解题关键是得到绳子的中点并拉直绳子,从而可知DB=DC.可以编辑的试卷(可以删除)This document is collected from the Internet, which is convenient for readers to use. If there is any infringement, please contact the author and delete it immediately.。
八年级全等三角形专题练习(解析版)

一、八年级数学全等三角形解做题压轴题〔难〕1. 〔1〕如图〔1〕,:在△ ABC中,N BAC=90.,AB二AC,直线m经过点A, 8口,直线m, CE J_直线m,垂足分别为点D、E.证实:DE=BD+CE.〔2〕如图〔2〕,将〔1〕中的条件改为:在△ ABC中,AB=AC, D、A、E三点都在直线m 上,并且有N BDA=Z AEC=Z BAC=.,其中.为任意锐角或钝角.请问结论DE=BD+CE是否成立? 如成立,请你给出证实;假设不成立,请说明理由.〔3〕拓展与应用:如图〔3〕 , D、E是D、A、E三点所在直线m上的两动点〔D、A、E 三点互不重合〕,点F为N BAC平分线上的一点,且△ ABF和^ ACF均为等边三角形,连接BD、CE,假设N BDA=Z AEC=Z BAC,试判断△ DEF 的形状.【答案】(1)见解析(2)成立(3) 4DEF为等边三角形【解析】解:(1)证实:BDL直线m, CEJ_直线m,,N BDA=N CEA=900.: Z BAC=90°, /. Z BAD+Z CAE=90°.•/ Z BAD+Z ABD=90°, /. Z CAE=Z ABD.又AB二“AC〞,「・△ ADB合△ CEA (AAS) . /. AE=BD, AD=CE./. DE=,,AE+AD=H BD+CE.(2)成立.证实如下:: Z BDA =Z BAC=a , /. Z DBA+Z BAD=Z BAD+Z CAE=180°-O r . /. Z DBA=Z CAE.Z BDA=Z AEC=., AB=AC,「・△ AD於△ CEA (AAS). /. AE=BD, AD=CE.DE二AE+AD=BD+CE.(3)△ DEF为等边三角形.理由如下:由(2)知,△ ADB合△ CEA, BD=AE, Z DBA =Z CAE,: △ ABF 和^ ACF 均为等边三角形,J Z ABF=Z CAF=60°.・•, Z DBA+Z ABF=Z CAE+Z CAF. /. Z DBF=Z FAE.; BF=AF,,•・丛DBF合△ EAF (AAS) . /. DF=EF, Z BFD=Z AFE.・•, Z DFE=Z DFA+z AFE=Z DFA+Z BFD=60°.・•.A DEF为等边三角形.(1)由于DE=DA+AE,故由AAS证△ ADB合4 CEA,得出DA=EC, AE=BD,从而证得DE=BD+CE.(2)成立,仍然通过证实△ ADB2 J CEA,得出BD=AE, AD=CE,所以DE=DA+AE=EC+BD.(3)由△ ADB2△ CEA得BD=AE, NDBA=N CAE,由△ ABF和△ ACF均等边三角形,得Z ABF=Z CAF=60°, FB=FA,所以N DBA+N ABF=N CAE+N CAF,即N DBF二N FAE,所以△ DBF^ △ EAF,所以FD=FE, Z BFD=Z AFE,再根据N DFE=Z DFA+Z AFE=Z DFA+Z BFD=60°得到△ DEF是等边三角形.2.如图1,在正方形ABCD中,P是对角线BD上的一点,点E在AD的延长线上,且PA=PE, PE 交CD 于 F〔1〕证实:PC=PE;〔2〕求N CPE的度数:〔3〕如图2,把正方形ABCD改为菱形ABCD,其他条件不变,当N ABC=12〔T时,连接【答案】(1)证实见解析(2) 90° (3) AP=CE【解析】【分析】(1)、根据正方形得出AB=BC, ZABP=ZCBP=45%结合PB=PB得出aABP g^CBP,从而得出结论:⑵、根据全等得出NBAP=NBCP, ZDAP=ZDCP,根据PA=PE得出NDAP=NE,即ZDCP=ZE,易得答案;(3)、首先证实4ABP和^CBP全等,然后得出PA=PC, NBAP=NBCP,然后得出NDCP二NE,从而得出NCPF=NEDF=60°,然后得出AEPC是等边三角形,从而得出AP=CE.【详解】⑴、在正方形ABCD 中,AB=BC, ZABP=ZCBP=45%在ZkABP 和4CBP 中,XV PB=PB AAABP^ACBP (SAS) , ,PA=PC, VPA=PE>:.PC=PE;⑵、由(1)知,A ABP^ACBP,.\ZBAP=ZBCP, JNDAP=NDCP,VPA=PE, .\ZDAP=ZE> /. ZDCP=ZE. VZCFP=ZEFD (对顶角相等), A180° - ZPFC - ZPCF=1800 - ZDFE - NE, BPZCPF=ZEDF=90<>:⑶、AP = CE理由是:在菱形ABCD 中,AB=BC, NABP二NCBP,在2\ABP ^lACBP 中,XV PB=PB /.△ABP^ACBP (SAS),,PA二PC, NBAP=NDCP,VPA=PE,,PC=PE,,NDAP=NDCP, V PA=PC,/DAP=NE, A ZDCP=ZE V ZCFP=ZEFD (对顶角相等),A180°- ZPFC - ZPCF=180° - ZDFE - NE, RPZCPF=ZEDF=180° - ZADC=180° - 120°=60°, AAEPC 是等边三角形,,PC=CE, AAP=CE考点:三角形全等的证实3.如图,在AA8C中,NAC8为锐角,点£>为射线8C上一动点,连接AO.以AO为直角边且在AD的上方作等腰直角三角形ADF.图①图②图③〔1〕假设A3 = AC, ABAC = 90°①当点.在线段BC上时〔与点3不重合〕,试探讨CF与8.的数量关系和位置关系:②当点O在线段C的延长线上时,①中的结论是否仍然成立,请在图2中而出相应的图形并说明理由;〔2〕如图3,假设ABwAC, ABAC90° , ZBC4 = 45°,点.在线段8C上运动,试探究CF与8.的位置关系.【答案】〔1〕①CF_LBD,证实见解析:②成立,理由见解析:〔2〕 CF1BD,证实见解析.【解析】【分析】〔1〕①根据同角的余角相等求出NCAF=NBAD,然后利用"边角边"证实4ACF和4ABD全等,②先求出NCAF=NBAD,然后与①的思路相同求解即可:〔2〕过点A作AE_LAC交BC于E,可得4ACE是等腰直角三角形,根据等腰直角三角形的性质可得AC=AE, NAED=45.,再根据同角的余角相等求出NCAF=NEAD,然后利用“边角边〞证实4ACF 和4AED全等,根据全等三角形对应角相等可得NACF=NAED,然后求出ZBCF=90°,从而得到CFJ_BD.【详解】解:〔1〕①•••NBAC=90°, 4ADF是等腰直角三角形,.\ZCAF+ZCAD=90% ZBAD+ZACD=90°,.\ZCAF=ZBAD,在4ACF和4ABD中,VAB=AC, ZCAF=ZBAD, AD=AF,.,.△ACF^AABD〔SAS〕,.・.CF=BD, ZACF=ZABD=45",ZACB=45",AZFCB=90°,.-.CF±BD:②成立,理由如下:如图2:VZCAB=ZDAF=90%,ZCAB+ ZCAD= ZDAF+ ZCAD, 即NCAF=NBAD,在aACF和AABD中,VAB=AC, ZCAF=ZBAD, AD=AF, AAACF^AABD(SAS), ACF=BD, NACF=NB,VAB=AC, ZBAC=90%AZB=ZACB=45%/. Z BCF= ZACF+ ZACB=45o+45o=90°,ACF1BD:(2)如图3,过点A作AE_LAC交BC于E,•/ ZBCA=45",••.△ACE是等腰直角三角形,,AC=AE, NAED=45°, VZCAF+ZCAD=90°, ZEAD+ZCAD=90%,NCAF=NEAD,在4ACF和4AED中,VAC=AE, NCAF=NEAD, AD=AF,.•.△ACF^AAED(SAS), /. ZACF=ZAED=45\,ZBCF= ZACF+ ZBCA=45o+45°=90°, ACF1BD.【点睛】此题考查全等三角形的动点问题,综合性较强,有一定难度,需要熟练掌握全等三角形的判定和性质进行综合运用.4.如图〔1〕,在△A3C中,ZA = 90°, A3 = AC,点.是斜边8C的中点,点E, 产分别在线段A3, 4c上,且NEDF = 90..〔1〕求证:△.所为等腰直角三角形:〔2〕假设△ABC的面积为7,求四边形AEDF•的面积:〔3〕如图〔2〕,如果点E运动到A8的延长线上时,点尸在射线C4上且保持ZEDF = 90°,△.石尸还是等腰直角三角形吗.请说明理由.【答案】〔1〕证实见解析;〔2〕 3.5:〔3〕是,理由见解析.【解析】【分析】〔1〕由题意连接AD,并利用全等三角形的判定判定△ BD年△ ADF〔ASA〕,进而分析证得△.瓦'为等腰直角三角形;〔2〕由题意分析可得S网边形AEDF=S MDF+S AADE=S ABDE+S ACDF,以此进行分析计算求出四边形AEDF的面积即可;〔3〕根据题意连接AD,运用全等三角形的判定判定△ BDE^ △ ADF〔ASA〕,进而分析证得△.所为等腰直角三角形.【详解】解:〔1〕证实:如图①,连接AD.「N BAC=90°,AB=AC,点D是斜边BC的中点,/. AD±BC , AD=BD,・•, Z 1=Z B=45°,Z EDF=90% Z 2+Z 3=90%又,Z 3+Z 4=90°,/. Z 2=Z 4,在^ BDE 和^ ADF 中,Z 1=Z B, AD=BD,Z 2=Z 4,/. △ BDE合 , ADF(ASA),・•, DE二DF,又;Z EDF=90\・•・ ADEF为等腰直角三角形.(2)由(1)可知DE=DF, NON 6=45., 又「N 2+N 3=90°, Z 2+Z 5=90%J Z 3=Z 5,A ADE级△ CDF,・' S N边H,AEDF=S AADF+S CADE二S ABDE+S^CDF,S MBC=2 S 网边毛AEDF,S wijn;AEDF=3.5.(3)是,如图②,连接AD.•/ Z BAC=90\ AB=AC, D 是斜边BC 的中点,/. AD±BC Z AD=BD ,「・Z 1=45°,Z DAF=180°-Z l=180°-45°=135% Z DBE=180°-Z ABC=180°-45°=135%/. Z DAF=Z DBE,「Z EDF=90\/. Z 3+Z 4=90%又;Z 2+Z 3=90°,「・Z 2=Z 4,在仆BDE 和a ADF 中,Z DAF=Z DBE, AD=BD,N 2=Z 4,△ BDE合△ ADF(ASA),・•.DE=DB又:Z EDF=90\.•.A DEF为等腰直角三角形.【点睛】此题考查等腰直角三角形的性质以及全等三角形的判定与性质,根据题意作辅助线构造出全等三角形是解题的关键.5.如图,在MBC中,ZC = 90°, AC = 3, BC = 7,点.是8c边上的动点,连接AD,以AO为斜边在A.的下方作等腰直角三角形AO石.(1)填空:AABC的面积等于—;(2)连接CE,求证:CE是NAC3的平分线;(3)点.在6C边上,且CO = 1,当.从点.出发运动至点3停止时,求点E相应的运动路程.王O 1 _【答案】〔I〕—:〔2〕证实见解析:〔3〕 3点【解析】【分析】〔1〕根据直角三角形的面积计算公式直接计算可得:〔2〕如下图作出辅助线,证实△AEM名ADEN 〔AAS〕,得至I] ME=NE,即可利用角平分线的判定证实:〔3〕由〔2〕可知点E在NACB的平分线上,当点D向点B运动时,点E的路径为一条直线,再根据全等三角形的性质得出CN=!〔AC + C.〕,根据CD的长度计算出CE的长度即可.【详解】解:〔1〕 ZC = 90°, AC = \ BC = 7= -ACxBC = -x3x7 = — ,故答案为:—2〔2〕连接CE,过点E作EMLAC于点M,作EN_LBC于点N,AZEMA=Z END=90°,XVZACB=90SAZMEN=90%AZMED+Z DEN=90°,•••△ADE是等腰直角三角形AZAED=90\ AE=DEA ZAEM+Z MED=90%, ZAEM=Z DEN,在△AEM 与ZkDEN 中,ZEMA=Z END=90% ZAEM=Z DEN, AE=DEAAAEM^ADEN 〔AAS〕/. ME=NE,点E 在NACB 的平分线上, 即CE 是NAC3的平分线工(3)由(2)可知,点E 在NACB 的平分线上,・•・当点D 向点B 运动时,点E 的路径为一条直线,VAAEM^ADEN,AM=DN,即 AC-CM=CN-CD在 RtZiCME 与 RtZkCNE 中,CE=CE, ME=NE,ARtACME^RtACNE (HL)ACM=CN.,.CN=;(AC + CO),又YNMCE 二NNCE=45°, ZCME=90\・,. CE= y/2CN = —(AC + CD).2当 AC=3, CD=CO=1 时,CE=](3 + 1) = 2&当 AC=3, CD=CB=7 时,5CE=r (3 + 7) = 5 虚,点E 的运动路程为:50-20 = 30,£【点睛】此题考查了全等三角形的综合证实题,涉及角平分线的判定,几何中动点问题,全等三角 形的性质与判定,解题的关键是综合运用上述知识点.6.如图1,在长方形ABCD 中,AB=CD=5 cm, BC=12 cm,点P 从点B 出发,以2cm/s 的 速度沿BC 向点C 运动,设点P 的运动时间为ts.(1) PC=—cm :(用含t 的式子表示)■I) I)(2)当t 为何值时,△ABPg^DCP?.(3)如图2,当点P从点B开始运动,此时点Q从点C出发,以vcm/s的速度沿CD向点D运动,是否存在这样的v值,使得某时刻4ABP与以P, Q, C为顶点的直角三角形全等?假设存在,请求出v的值:假设不存在,请说明理由.【答案】(1) (12-2/); (2)1 = 3;(3)存在,P = 2或忏1【解析】【分析】(1)根据P点的运动速度可得BP的长,再利用BC的长减去BP的长即可得到PC的长:(2)先根据三角形全等的条件得出当BP=CP,列方程求解即得;(3)先分两种情况:当BP=CQ, AB=PC 时,△ABPgZ\PCQ:或当BA=CQ, PB=PC 时,△ABPgaQCP,然后分别列方程计算出t的值,进而计算出v的值.【详解】解:(1)当点P以2cm/s的速度沿BC向点C运动时间为ts时3P = 2/57•・• BC = \2cin:.PC = BC-BP = (n-2i)cm故答案为:(12—27)(2) MBP = ^DCP・•. BP = CP・•・ 2/= 12-2/解得1 = 3.(3)存在,理由如下:①当BP=CQ, AB=PC 时,ZiABP名△PCQ,1. PC=AB=5.•.BP=BC-PC=12-5=7•・• BP = Item:.2t=7解得t=3.5.\CQ=BP=7,那么 3.5v=7解得y = 2.②当B4 = C.,PB = PC 时,MBP = \QCP,: BC = ncm,BP = CP = -BC = 6c7〃 2V BP = Item:.2t = 6解得/ = 3CQ = 3vcm,: AB = CQ = 5cm, 3v = 5解得U3综上所述,当u = 2或i,=,时,A48尸与以P, Q,C为顶点的直角三角形全等.【点睛】此题考查全等三角形的判定及性质和矩形的性质,解题关键是将动态情况化为某一状态情况,并以这一状态为等量关系建立方程求解.7.:在MBC中,AB = AC,ZBAC = 90° ,尸Q为过点4的一条直线,分别过B、C两点作8M_LP0,CN_L尸.,垂足分别为M、N.(1)如图①所示,当P.与BC边有交点时,求证:MN = CN — BM ;(2)如图②所示,当与6C边不相交时,请写出线段8M、CN和MN之间的数量关系,并说明理由. 【答案】(1)见解析:(2) MN = BM + CN (或BM = MN — CN或CN = MN-BM ),理由见解析【解析】【分析】(1)根据条件先证AAA/i运ACN4,得到AM = CN,BM = AN,即可证得MN = CN — BM: (2)由(1)知AAMBYACNA,得到4M =CN,8M = AN,即可确定MN = BM + CN.【详解】证实:・・・BM_LPQ,CN_LP0,・•. ZAMB=ZCAN=90°,V ZBAC=90 ° ,AZCAN+ZACN=90°,ZCAN+ZBAM=90°(或NCW + NAC/V = NC4N+NMM)・•. ZBAM = ZACN,在AAMB和ACN4中,'ZAMB = 4CNA・.• ZBAM = AACN , AB = CA:.AAM“ACN4(A4S),.・.AM =CN,BM =AN,,: MN = AM-AN,:.MN = CN — BM.(2) MN = BM + CN (或BM=MN-CN或CN = MN-BM) .理由:•.・BM_LPQ,CN_LP.,・•・ ZAMB=ZCAN=90°,V ZBAC=90 ° ,.\ZCAN+ZACN=90°,ZCAN+ZBAM=90°(或NCW + NAC/V = NC4N+NBAM ),:.ZBAM = ZACN,在AAMB和ACNA中,'AAMB = ZCNAZ.B\M = ZACN , AB = CA:.AAM*ACNA( AAS),.・.AM =CN,BM =AN,:.MN = AN + AM = BM+CN.【点睛】此题考察三角形全等的应用,正确确定全等三角形是解题关键,由此得到对应相等的线段,确定它们之间的和差关系得到80、CN和MN之间的关系式.8.操作发现:如图,己知"配和"DE均为等腰三角形,AB=AC, AD=AE,将这两个三角形放置在一起,使点8, D, E在同一直线上,连接CE.(1)如图1, ZABC= ZACB= ZADE= ZAED=55Q,求证:△BADgZkCAE;(2)在(1)的条件下,求N8EC的度数:拓广探索:(3)如图2,假设NC48=NEAD=120.,8D=4, CF为aBCE中8E边上的高,请直接写出讦的长度.【答案】(1)见解析:(2) 70°; (3) 2【解析】【分析】(1)根据SAS证实△BADg/kCAE即可.(2)利用全等三角形的性质解决问题即可.(3)同法可证4BAD丝ZkCAE,推出EC=BD=4,由NBEC=NBAC=12O0,推出NFCE=30°即可解决问题.(1)证实:如图1中,图1Z ABC=^ ACB = Z ADE=N AED, /. Z EAD=Z CAB,:.Z EAC=A DAB,AE=AD. AC=AB9:.△ BAD^ & CAE (SAS).(2)解:如图1中,设AC交8E于O. •「N A8C=N4C8 = 55°,/. Z 84c=180° - 110° = 70°,BAD^△ CAE,Z ABO=Z ECO,Z EOC=ZAOB,・•, Z CEO = Z 840=70°,即 N BEC= 70°.(3)解:如图2中,A图2Z C48 = N EAD=120\•. Z BAD=A CAE,:AB=AC, AD=AE.△ BAD^ 4 CAE 〔SAS〕,•. Z BAD=A ACE. 8D=EC=4,同理可证N BEC- 8AC=120°,Z F£C=60%CFLEF,Z F=90",•. Z FCE=30\1•. EF=-EC=2. 2此题属于三角形综合题,考查了全等三角形的判定和性质等知识,解题的关键是正确寻找全等三角形解决问题,属于中考常考题型.9.在等边aABC中,点.是边8C上一点.作射线AO,点3关于射线AO的对称点为点E.连接CE并延长,交射线AO于点〔1〕如图,连接AE,①AE与AC的数量关系是;②设NBA尸=a,用.表示NBCF的大小;〔2〕如图,用等式表示线段A尸,CF.所之间的数量关系,并证实.【答案】⑴①AB二AE;②NBCF=.:(2)AF-EF=CF,理由见详解.【解析】【分析】(1)①根据轴对称性,即可得到答案;②由釉对称性,得:AE二AB, NBAF=NEAF=.,由△A3C是等边三角形,得AB=AC, ZBAC=ZACB=60° ,再根据等腰三角形的性质和三角形内角和等于180°,即可求解:(2)作NFCG=60°交AD于点G,连接BF,易证AFCG是等边三角形,得GF=FC,再证△ACG会ABCF(SAS),从而得AG=BF,进而可得至lj结论.【详解】(1)①•・•点4关于射线的对称点为点E , AAB和AE关于射线AD的对称,AAB=AE.故答案是:AB=AE;②•.•点3关于射线的对称点为点E , ,AE二AB, NBAF=NEAF=.,•二△A3c是等边三角形,AAB=AC, ZBAC=ZACB=60" ,:.ZEAC=60° -2a, AE=AC,ZACE=1[180 - (60 - 2a)] = 60 +6?,A ZBCF=ZACE-ZACB=60 +a-60°=a .(2) AF-EF=CF,理由如下:作NFCG=60.交AD于点G,连接BF,•••NBAF=NBCF=a , NADB=NCDF,A ZABC=ZAFC=60c ,••.△FCG是等边三角形,AGF=FC,•二△A3c是等边三角形,ABC=AC, ZACB=60° , AZACG=ZBCF=« .在AACG和ABCF中,CA = CBZACG = ABCF , CG = CF,AACG 仝ABCF(SAS),.,.AG=BF,•・•点4关于射线AO的对称点为点E , .\AG=BF=EF,VAF-AG=GF,.\AF-EF=CE【点睛】此题主要考查等边三角形的性质和三角形全等的判定和性质定理,添加辅助线,构造全等三角形,是解题的关键.10.如图,AA8C是等边三角形,点.在边4c上〔“点D不与A,C重合〕,点石是射线5c上的一个动点〔点E不与点8,C重合〕,连接OE,以OE为边作作等边三角形hDEF,连接CF.〔1〕如图1,当.石的延长线与A3的延长线相交,且CF在直线OE的同侧时,过点D 作DG//AB, DG 交BC 于点、G ,求证:CF = EG ;〔2〕如图2,当.石反向延长线与A8的反向延长线相交,且.,尸在直线OE的同侧时,求证:CD = CE+CF;〔3〕如图3,当OE反向延长线与线段A8相交,且.,厂在直线O石的异侧时,猜测CD、CE、CP之间的等量关系,并说明理由.【答案】〔1〕证实见详解;〔2〕证实见详解:〔3〕 CF = CO-CE,理由见详解.【解析】【分析】(1)由AABC 是等边三角形,DG//AB,得NCDG=NA=60° , NACB=60.,ACDG 是等边三角形,易证AGDE仝ACDF(SAS),即可得到结论:(2)过点D作DG〃AB交BC于点G,易证A GDE仝△ CDF(SAS),即可得到结论;(3)过点D作DG〃AB交BC于点G,易证A GDE仝A CDF(SAS),即可得到结论.【详解】(1)•・• AA3C是等边三角形,DG//AB, :.ZCDG=ZA=60° , ZACB=60° , ・•. ACQG是等边三角形,.\DG=DC.是等边三角形, .,.DE=DF, ZEDF=60° , A ZCDG-ZGDF=ZEDF-ZGDF,即:ZGDE=ZCDF, 在4 GDE和八CDF中,DE = DFNGDE = NCDF ,DG = DC.,.△GDE^A CDF(SAS),:.CF = EG ;(2)过点D作DG〃AB交BC于点G,如图2,•・• AABC是等边三角形,DG//AB、:.ZCDG=ZA=60° , ZACB=60" ,••・ACDG是等边三角形,:.DG=DC.•••ADE/是等边三角形,,DE=DF, ZEDF=60c ,A ZCDG-ZCDE=ZEDF-ZCDE> 即:ZGDE=ZCDF, 在4 GDE和^ CDF中,DE = DFNGDE = ZCDF ,DG = DC.,.△GDE^ACDF(SAS),:・CF = GE,••. CD = CG = CE+GE = CE+CF(3)CF = CD + CE,理由如下:过点D作DG〃AB交BC于点G,如图3,•・・AA8C是等边三角形,DGUAB, .,.ZCDG=ZA=60° , ZACB=60" ,,ACDG是等边三角形, ADG=DC=GC.•・• ADEF是等边三角形, ,DE=DF, ZEDF=60° ,A ZCDG+ZCDE=ZEDF+ZCDE,即:NGDE=NCDF, 在A GDE和4 CDF中,DE = DFNGDE = ZCDF , DG = DCAAGDE^ACDF(SAS),,CF = G£=GC+CE=CD+CE.【点睛】此题主要考查等边三角形的性质和三角形全等的判定和性质定理,添加辅助线,构造全等三角形,是解题的关键.。
全等三角形证明中考题精选[有答案解析]
![全等三角形证明中考题精选[有答案解析]](https://img.taocdn.com/s3/m/abb0f9f733687e21ae45a9aa.png)
全等三角形证明中考题精选[有答案解析]七年级数学下---全等三角形证明题1如图,已知人。
是厶ABC勺中线,分别过点B、C作BEL AD于点E,CF丄AD交AD的延长线于点F,求证:BE=CF2•如图1,将两个完全相同的三角形纸片ABC和DEC重合放置,其中/(1)操作发现:如图2,固定△ ABC使厶DEC绕点C旋转,当点D恰好落在AB边上时,填空:①线段DE与AC的位置关系是_____________②设△ BDC的面积为$,△ AEC的面积为S,则(2)猜想论证S与S2的数量关系是 _____________当厶DEC绕点C旋转到如图3所示的位置时,小明猜想(1)中S与S2的数量关系仍然成立,并尝试分别作出了△BDC ffiA AEC中BC CE边上的高,请你证明小明的猜想.(3)拓展探究已知/ABC=60,点D是角平分线上一点,BD=CD=, DE// AB交BC于点E (如图4).若在射线BA 上存在点F,使S A DC=S BDE,请直接写出相应的BF的长.3.如图,把一个直角三角形ACB(/ACB=90 )绕着顶点B顺时针旋转60°,使得点C旋转到AB 边上的一点D,点A旋转到点E的位置.F, G分别是BD BE上的点,BF=BG延长CF与DG交于点H. (1)求证:CF=DG (2)求出/ FHG勺度数.全等三角形证明中考题精选[有答案解析]4•如图所示,在△ ABC 中,D E 分别是AB AC 上的点,DE// BQ 如图①,然后将厶ADE 绕A 点顺 时针旋转一定角度,得到图②,然后将 BD CE 分别延长至M N,使DM=BD EN=CE 得到图③, 请解答下列问题:(1)若AB=AC 请探究下列数量关系:① 在图②中,BD 与CE的数量关系是_ _ ;② 在图③中,猜想AM 与 AN 的数量关系、/ MAN 与/BAC 的数量关系,并证明你的猜想;(2)若AB=I?AC( k > 1),按上述操作方法,得到图④,请继续探究: AM 与 AN 的数量关系、/ MAN 与/BAC 的数量关系,直接写出你的猜想,不必证明.4. (1)如图,在△ ABC ffiA ADE 中, AB 二AC AD=AE Z BAC K DAE=90 .① 当点D 在AC 上时,如图1,线段BD CE 有怎样的数量关系和位置关系? 直接写出你猜想的结论;② 将图1中的△ ADE 绕点A 顺时针旋转口角(O °VaV 90°),如图2,线段BD CE 有怎样的数量 关系和位置关系?请说明理由.(2)当厶ABC^P ^ADE 满足下面甲、乙、丙中的哪个条件时,使线段 BD CE 在(1)中的位置关系 仍然成立?不必说明理由.甲: AB AC=AD AE=1, / BAC K DA 字90°;乙:AB AC=AD AE M 1,K BAC K DAE=90 ;丙: 6. CD 经过/ BCA 顶点C 的一条直线,CA=CB E, F 分别是直线CD 上两点,且/ BEC K CFA Ka.(1)若直线CD 经过/ BCA 的内部,且E, F 在射线CD 上,请解决下面两个问题:①如图 1,若/ BCA=90 , Ka =90°,则 BE ______________ CF; EF ___________ |BE - AF| (填“〉”, “v”或“=”);②如图2,若0°<Z BCA : 180°,请添加一个关于Ka 与/ BCA 关系的条件—AB: AC=AD AE M 1,/ BAC K DAE^ 90E__________ ,使①中的两个结论仍然成立,并证明两个结论成立.7. 如图,已知 AB=AC (1)若 CE=BD 求证:GE=G ;⑵若CE=mBD (m 为正数),试猜想GE 与 GD 有何关系.(只写结论,不证明)8. (1)已知:如图①,在△ AOBf^A COD 中, OA=OJ 3OC=OD / AOB M COD=60,求证:① AC=BD ②/ APB=6(度;(2)如图②,在△ AOBf^A COD 中,若 OA=OBOC=O , / AOB M COD a ,贝U AC 与 BD 间的等量关系式为 _____________ ; Z APB 的大小为 _____________ ;(3)如图③,在△ AOBf^ACOD 中,若 OA=?OBOC=?OD(k > 1),Z AOB ZCOD a ,贝U AC 与 BD间的等量关系式为 10.已知:EG// AF, AB=AC DE=DF 求证:BE=CF参考答案与试题解析(2)如图3,若直线CD 经过/ BCA 的外部,/ a =Z BCA 请提出EF, BE AF 三条线段数量关系的 合理猜想(不要求证明)•Z APB 的大小为 _____2. 解:(1)①DEC绕点C旋转点D恰好落在AB边上,••• AC=CD:/ BAC=90 -Z B=90°- 30° =60°,二厶ACD是等边三角形,•••/ ACD=60,又TZ CDE Z BAC=60 ,:Z ACD Z CDE 二DE// AC;②T Z B=30°,Z C=90,二CD=AC=AB /• BD=AD=AC2根据等边三角形的性质,△ ACD的边AC AD上的高相等,•••△ BDC的面积和△ AEC的面积相等(等底等高的三角形的面积相等),即S=S2;故答案为:DE// AC S=S;(2)如图,•「△ DEC是由厶ABC绕点C旋转得到,••• BC=CE AC=CD T Z ACN Z BCN=90,Z DCM Z BCN=180 - 90° =90°,•••Z ACN Z DCM T在厶ACNm DCM中,fZACM=ZDCHI ZCND=ZH=90°,[AC=CD•△ACN^A DCM( AAS, • AN=DM•△ BDC的面积和△ AEC的面积相等(等底等高的三角形的面积相等),即S i=S2;3、解(1)证明:•••在厶CBF ft^ DBG K答.fBC=BD答《二,:BF=BG•△CBF^A DBG( SAS , • CF=DQ(2)解:•••△ CBF^A DBG •Z BCF Z BDG又T Z CFB Z DFH •Z DHF Z CBF=60 ,•Z FHG=180 -Z DHF=180 - 60°=120°.4、解答:解:(1)①结论:BD=CE BDL CE②结论:BD=CE BDL CE;理由如下:T Z BAC Z DAE=90• Z BAC-Z DAC Z DAE-Z DAC 即Z BAD Z CAE ft^ ABD与△ ACE中, AB=ACT*4皿ZCAE •△ABD^A ACE(SAS • BD=CEb AD=AE延长BD交AC于F,交CE于H.在厶ABF 与厶HCF 中,T Z ABF=/ HCF Z AFB=/ HFC •Z CHF Z BAF=90••• BDL CE(2)结论:乙.AB AC=AD AE / BAC K DAE=905.6.解答:解:(1)①IK BCA=90,/a =90°,.・.K BCE K CBE=90,/ BCE K ACF=90 , • K CBE K ACF v CA=CB K BEC K CFA •△ BCE^A CAF •- BE=CF EF=|BE- AF|. ②所填的条件是:Ka +K BCA=180 . I AE=AD 卩. 7 •••△ CAE^A BAD( SAS , AC 二 AB • / ACE K ABD v DM=BD EN=CE • BM=CN 在厶 ABM ffiA ACN 中, r 瓏二 CN ••• ZAC14=ZAbr 〔AB 二AC • △ ABMm ACN( SAS , • AM=AN •/ BAM K CAN 即K MAN K BAC (2)AM=?AN 在厶BADfy CAE 中 解答: / CAE=/ BAD K MAN K BAC全等三角形证明中考题精选[有答案解析]证明:在厶 BCE 中,/ CBE# BCE=180 -Z BEC=180 — /a. v/ BCA=180 —/a,•••/ CBE Z BCE Z BCA 又v/ ACF Z BCE Z BCA CBE Z ACF又v BC=CA / BEC Z CFA •△BCE^A CAF( AAS •- BE=CF CE=AF又v EF=C- CE, • EF=|BE- AF|.(2) EF=BE+AF7.解证明:(1)过D作DF// CE交BC于F,答: 贝UZ E=Z GDF v AB=AC •/ ACB Z ABC/ DF/ CE •/ DFB Z ACB•Z DFB Z ACB Z ABC • DF=DB v CE=BD •- DF=CE 在厶GDF^ GEC中, (ZE 二ZGDFI ZDGF=ZEGC ,[DF=EC•△GDF^A GEC(AAS. • GE=GD• / AOB Z BOC Z COD Z BOC 即:/ AOC Z BOD 答:又v OA=OB OC=OD •△ AOC^A BOD • AC=BD②由①得:/ OAC Z OBDv/ AEO Z PEB / APB=180 — (/ BEP+Z OBD, / AOB=180 —(/ OAC Z AEO , • Z APB Z AOB=60 .(2) AC=BD a(3) AC=?BD 180°—a.。
2020年秋人教版八年级数学上册第12章《全等三角形证明过程训练》(讲义及答案)

人教版八年级数学上册第12章全等三角形证明过程训练(讲义、随堂测试、习题)➢ 课前预习1. 判定三角形全等的方法有______,______,______,______.要证三角形全等需要找_____组条件,其中必须有_____.2. 在做几何题时,我们往往借助对图形的标注来梳理信息,进而把条件直观化,请学习下图中的标注.①如图1,在四边形ABCD 中,AB ∥CD ,AD ∥BC .②如图2,在四边形ABCD 中,连接BD ,∠ABD =∠CDB ,∠ADB =∠CBD ,∠A =∠C .③如图3,在四边形ABCD 中,连接AC ,BD 相交于点O ,AO =OC ,BO =DO .D C BA ××AB CDOABCD图1图2图33. 数学推理中,有理有据地思考和表达是一项基本的数学素养,请走通思路后,完整书写过程.如图是一个易拉罐的纵截面示意图,易拉罐的上下底面互相平行(AB ∥CD ),用吸管吸饮料时,若∠1=110°,求∠2的度数.➢ 知识点睛1. 直角三角形全等的判定定理:_________________________.2. 已知:如图,在△ABC 与△A′B′C′中,∠C =∠C′=90°,AB =A′B′,AC =A′C′.321DC BA求证:△ABC ≌△A′B′C′.C'B'A'CB A证明:如图,在Rt △ABC 和Rt △A′B′C′中AB A'B'AC A'C'=⎧⎨=⎩(已知)(已知) ∴Rt △ABC ≌Rt △A′B′C′(HL )➢ 精讲精练1. 如图,AC =AD ,∠C ,∠D 是直角,将上述条件标注在图中,则___________≌___________,从而BC ________BD .D CBA 2. 如图,DE ⊥AB 于E ,DF ⊥AC 于F ,AE =AF ,则_____≌______,从而DE =______.ABCD EF3. 已知:如图,AB =CD ,AF =CE ,DE ⊥AC 于E ,BF ⊥AC 于F .求证:△ABF ≌△CDE .ABCDEF4.已知:如图,∠B=∠D=90°,如果要使△ABC≌△ADC,那么还需要一个条件,这个条件可以是_________________,理由是____________;这个条件也可以是_______________,理由是____________;这个条件也可以是_______________,理由是____________;这个条件还可以是_______________,理由是____________.ABC D ABCDE Fl第4题图第5题图5.如图,直线l过正方形ABCD的顶点B,点A,C到直线l的距离分别是1和2,则EF的长为_________.6.已知:如图,在Rt△ABC中,∠C=90°,AD平分∠BAC交BC于D,DE⊥AB于E.求证:△ACD≌△AED.E DC7. 已知:如图,点B ,E ,C ,F 在同一直线上,AC ∥DF 且AC =DF ,BE =CF .求证:△ABC ≌△DEF .FE DC B A8. 如图,在正方形ABCD 中,∠A =∠ABC =90°,AB =BC ,E ,F 分别是AB ,AD 上的点,已知CE ⊥BF ,垂足为M . 求证:BE =AF .ABCDEFM9. 已知:如图,在△ABC 中,∠ACB =90°,AC =BC ,D 为AB 上一点,连接CD ,AE ⊥CD 于E ,BF ⊥CD 交CD 的延长线于F .求证:CF =AE .10. 已知:如图,在△ABC 中,∠B =∠C =60°,D ,E ,F 分别为边BC ,AB ,AC 上的点,且BE =CD ,∠EDF =60°.求证:ED =DF .FED CBAAB DE F【参考答案】➢课前预习1.SAS,SSS,ASA,AAS3,边2.略3.解:如图∵AB∥CD∴∠1=∠3∵∠1=110°∴∠3=110°∵∠2+∠3=180°∴∠2=180°-∠3=180°-110°➢ 知识点睛 1. SAS ,SSS ,ASA ,AAS ,HL ➢精讲精练1. Rt △CAB ,Rt △DAB ,=2. Rt △AED ,Rt △AFD ,DF3. 证明:如图,∵DE ⊥AC ,BF ⊥AC ∴∠DEC =∠BFA =90° 在Rt △ABF 和Rt △CDE 中,AB CD AF CE =⎧⎨=⎩(已知)(已知) ∴Rt △ABF ≌Rt △CDE (HL ) 4. AB =AD ,HLBC =DC ,HL ∠BAC =∠DAC ,AAS ∠BCA =∠DCA ,AAS 5. 36. 证明:如图,∵DE ⊥AB ∴∠DEA =90° ∵∠C =90° ∴∠C =∠DEA ∵AD 平分∠BAC ∴∠CAD =∠EAD 在△ACD 和△AED 中C DEA CAD AED AD AD ∠=∠⎧⎪∠=∠⎨⎪=⎩(已证)(已证)(公共边) ∴△ACD ≌△AED (AAS ) 7. 证明:如图,21A BC DE F第8题图∵AC ∥DF∵BE =CF ∴BE +EC =CF +EC 即BC =EF在△ABC 和△DEF 中1 2 AC DF BC EF =⎧⎪∠=∠⎨⎪=⎩(已知)(已证)(已证) ∴△ABC ≌△DEF (SAS ) 8. 证明:如图,∵∠ABC =90° ∴∠ABF+∠MBC =90° ∵AE ⊥BF ∴∠CMB =90° ∴∠MBC +∠BCE =90° ∴∠ABF =∠BCE 在△ABF 和△BCE 中A EBC AB BC ABF BCE ∠=∠⎧⎪=⎨⎪∠=∠⎩(已知)(已知)(已证) ∴△ABF ≌△BCE (ASA )∴AF =BE (全等三角形对应边相等) 9. 证明:如图,第9题图321A BDE F∵∠ACB =90° ∴∠1+∠2=90° ∵AE ⊥CD ,BF ⊥CD ∴∠F =∠AEC =90° ∴∠3+∠2=90° ∴∠1=∠3在△BCF 和△CAE 中1 3 F AEC BC CA ∠=∠⎧⎪∠=∠⎨⎪=⎩(已证)(已证)(已知) ∴△BCF ≌△CAE (AAS )∴CF =AE (全等三角形对应边相等) 10. 证明:如图,∵∠B =60° ∴∠1+∠2=120° ∵∠EDF =60° ∴∠2+∠3=120° ∴∠1=∠3在△BDE 和△CFD 中1 3 BE CD B C ∠=∠⎧⎪=⎨⎪∠=∠⎩(已证)(已知)(已知) ∴△BDE ≌△CFD (ASA )∴ED =DF (全等三角形对应边相等)全等三角形证明过程训练(随堂测试)1. 已知:如图,在△ABC 中,AD ⊥BC 于点D ,E 为AD 上一点,且BE =AC ,如果要使△BDE ≌△ADC ,那么还需要一个条件,这个条件可以是____________________,理由是_________;这个条件也可以是__________________,理由是_________; 这个条件也可以是__________________,理由是_________; 这个条件还可以是__________________,理由是_________.2. 已知:如图,在△ABC 中,D 为BC 边的中点,过点C 作 CF ⊥AD 于点F ,过点B 作BE ⊥AD ,交AD 的延长线于点E . 求证:CF =BE . 证明:如图,ED CB A 第10题图321A BCD E FF DCA【参考答案】1. DE =DC ,HLBD =AD ,HL ∠EBD =∠CAD ,AAS ∠BED =∠C ,AAS 2. 证明:如图,∵CF ⊥AD ,BE ⊥AD ∴∠CFD=∠BED =90° ∵D 为BC 边的中点 ∴CD =BD在△CFD 和△BED 中∴△CFD ≌△BED (AAS )∴CF =BE (全等三角形对应边相等)全等三角形证明过程训练(习题)1 2 CFD BED CD BD ∠=∠⎧⎪=⎨⎪=⎩(已证)∠∠(对顶角相等)(已证)第2题图➢ 例题示范例1:已知:如图,在正方形ABCD 中,AB =CB ,∠ABC =90°.E 为正方形内一点,BE ⊥BF ,BE =BF ,EF 交BC 于点G . 求证:AE =CF . 【思路分析】 ① 读题标注:② 梳理思路:要证AE =CF ,可以把它们放在两个三角形中证全等.观察发现,放在△ABE 和△CBF 中进行证明.要证全等,需要三组条件,其中必须有一组边相等. 由已知得,AB =CB ;BE =BF ;根据条件∠ABC =90°,BE ⊥BF ,推理可得∠1=∠2. 因此由SAS 可证两三角形全等.【过程书写】(在演草部分先进行规划,然后书写过程) 证明:如图 ∵BE ⊥BF ∴∠EBF =90° ∴∠2+∠EBC =90° ∵∠ABC =90° ∴∠1+∠EBC =90° ∴∠1=∠2在△ABE 和△CBF 中12AB CB BE BF =⎧⎪∠=∠⎨⎪=⎩(已知)(已证)(已知)∴△ABE ≌△CBF (SAS )∴AE =CF (全等三角形对应边相等)➢ 巩固练习11. 如图,PD ⊥AB ,PE ⊥AC ,垂足分别为点D ,E ,且PD =PE ,将上述条件标注在图中,易得___________≌___________,从而AD =__________.21G FE DCB A GABC DEF第1题图第2题图12. 已知:如图,AB ⊥BD 于点B ,CD ⊥BD 于点D ,如果要使△ABD ≌△CDB ,那么还需要添加一组条件,这个条件可以是_______________,理由是_____________;这个条件也可以是_____________,理由是_____________;这个条件也可以是_____________,理由是_____________;这个条件还可以是_____________,理由是_____________.13. 已知:如图,C 为BD 上一点,AC ⊥CE ,AC =CE ,∠ABC =∠CDE =90°.若AB =4,DE =2,则BD 的长为______.14. 已知:如图,点A ,E ,F ,B 在同一条直线上,CE ⊥AB 于点E ,DF ⊥AB 于点F ,BC =AD ,AE =BF . 求证:△CEB ≌△DFA .15. 如图,点C ,F 在BE 上,∠1=∠2,BF =EC ,∠A =∠D .求证:△ABC ≌△DEF .PEDCBADC B A ED CBAF E DC BA16. 已知:如图,点A ,B ,C ,D 在同一条直线上,且AC =BD ,BE ∥CF 证:△ABE ≌△DCF .17. 已知:如图,在△ABC 中,AD ⊥BC ,CE ⊥AB ,垂足分别为点D ,E ,AD 与CE 相交于点H ,AE =CE . 求证:AH =CB .FDCBA HEA➢思考小结1.要证明边或者角相等,可以考虑边或者角所在的两个三角形_______;要证明三角形全等,需要准备_____组条件,其中有一组必须是_______相等.2.阅读材料我们是怎么做几何题的?例1:已知:如图,AB=AD,AC=AE,∠BAE=∠DAC.求证:∠B=∠D.EBC A第一步:读题标注,把题目信息转移到图形上(请把条件标注在图上)第二步:分析特征走通思路①要求∠B=∠D,考虑放在两个三角形里面证全等,把∠B放在△ABC中,把∠D放在△ADE中,只需要证明这两个三角形全等即可.②要证明△ABC≌△ADE,需要找三组条件,由已知得AB=AD,AC=AE,还差一组条件,根据∠BAE=∠DAC,同时加上公共角∠CAE,可得∠BAC=∠DAE,利用SAS可得两个三角形全等.第三步:规划过程过程分成三块:①由∠BAE=∠DAC,可得∠BAC=∠DAE;②由SAS得△ABC≌△ADE;③由全等得∠B=∠D.第四步:过程书写【参考答案】➢巩固练习1.Rt△ADP,Rt△AEP,AE2.AD=CB,HLAB=CD,SAS∠A=∠C,AAS∠ADB=∠CBD,ASA3. 64.证明:如图,∵CE ⊥AB ,DF ⊥AB ∴∠CEB =∠DFA =90° ∵AE =BF ∴AE +EF =BF +EF 即AF =BE在Rt △CEB 和Rt △DFA 中BC AD BE AF =⎧⎨=⎩(已知)(已证) ∴Rt △CEB ≌Rt △DFA (HL ) 5. 证明:如图,∵BF =EC ∴BF +FC =EC+FC 即BC =EF在△ABC 和△DEF 中1 2 A D BC EF =⎧⎪=⎨⎪=⎩∠∠(已知)∠∠(已知)(已证) ∴△ABC ≌△DEF (AAS ) 6. 证明:如图,∵AC =BD ∴AC -BC =BD -BC 即AB =DC ∵BE ∥CF ∴∠1=∠2 ∵∠1+∠3=180° ∠2+∠4=180° ∴∠3=∠4 ∵AE ∥DF ∴∠A =∠D在△ABE 和△DCF 中3 4 AB DC A D =⎧⎪=⎨⎪=⎩∠∠(已证)(已证)∠∠(已证) ∴△ABE ≌△DCF (ASA ) 7. 证明:如图,第5题图4321A B CDF∵AD ⊥BC ∴∠ADC =90° ∴∠1+∠2=90° ∵CE ⊥AB∴∠AEH =∠CEB =90° ∴∠3+∠4=90° ∵∠2=∠4 ∴∠1=∠3在△AEH 和△CEB 中3 1 AEH CEB AE CE =⎧⎪=⎨⎪=⎩∠∠(已证)(已知)∠∠(已证) ∴△AEH ≌△CEB (ASA )∴AH =CB (全等三角形对应边相等)➢ 思考小结1. 全等;3,边第6题图3124AB DEH。
全等三角形证明之二次全等,附练习题含答案

全等三角形证明之二次全等学案➢ 知识梳理1.遇到与角有关的计算和证明时,常见的思考角度: 由平行想到同位角;内错角;同旁内角;由垂直想到直角三角形两锐角互余;同角或等角的余角相等; 由外角想到三角形的一个外角等于和它不相邻的两个内角的和.例1:已知:如图,CD ⊥AB 于点D ,BE ⊥AC 于点E ,且BD =CE ,BE 交CD 于点O .求证:AO 平分∠BAC . 【思路分析】 ① 读题标注:② 梳理思路:要证AO 平分∠BAC ,则需证明∠DAO =∠EAO . 要证∠DAO =∠EAO ,则需证明△AOD ≌△AOE .要证△AOD ≌△AOE ,需找三组条件,其中必须有一组边.分析发现,AO =AO ,∠ADO =∠AEO =90°,已经有了两组条件,还需要一组条件. 从已知条件出发,发现BD =CE ,∠BDO =∠CEO =90°,又因为∠1=∠2,可证明△BOD ≌△COE .由△BOD ≌△COE ,可为上面的全等准备一组条件OD =OE .至此,在△AOD 和△AOE 中三组条件找全,利用HL 可以证明全等,从而得出结论. 【过程书写】 证明:如图 ∵CD ⊥AB ,BE ⊥AC∴∠ADO =∠AEO =∠BDO =∠CEO =90° 在△BOD 和△COE 中12BDO CEO BD CE ∠=∠⎧⎪∠=∠⎨⎪=⎩(对顶角相等)(已证)(已知) ∴△BOD ≌△COE (AAS )∴OD =OE (全等三角形对应边相等) 在Rt △AOD 和Rt △AOE 中AO AO OD OE=⎧⎨=⎩(公共边)(已证)∴Rt △AOD ≌Rt △AOE (HL )∴∠DAO =∠EAO (全等三角形对应角相等) ∴AO 平分∠BAC21O EDC BAABCDEO➢ 练习题1. 已知:如图,点C 为线段AB 上一点,在△ACM ,△CBN 中,AC =CM ,BC =CN ,∠ACM =∠BCN =60°,连接AN 交CM 于点E ,连接BM 交CN 于点F . 求证:①△CAN ≌△CMB ;②△CEN ≌△CFB .2. 已知:如图,在正方形ABCD 中,AD =AB ,∠D =∠ABC =∠BAD =90°,E ,F 分别为CD ,BC 边上的点,且∠EAF =45°,延长CB 到点G ,使BG =DE ,连接EF ,AG .求证:①△ADE ≌△ABG ;②EF =DE +BF .3. 已知:如图,∠A =∠D =90°,AC ,BD 相交于点E ,BE =CE .求证:△ABC ≌△DCB .4. 已知:如图,点A ,E ,F ,C 在同一直线上,AE =CF ,过点E ,F 分别作ED ⊥AC 于点E ,FB ⊥AC 于点F ,连接AB ,CD ,BD ,BD 交AC 于点G ,AB =CD .求证:△DEG ≌△BFG .NMCFE AG AB CEDF EDAFCBGEDA5. 已知:如图,AB =AC ,BD =CD ,AD 与BC 相交于点O .求证:AD ⊥BC .6. 已知:如图,在Rt △ABE 和Rt △ACF 中,∠E =∠F =90°,BE =CF .BE 与AC 相交于点M ,与CF 相交于点D ,AB 与CF 相交于点N ,∠EAC =∠FAB .求证:AM =AN .7. 已知:如图,在△ABC 中,AD 是∠BAC 的平分线,点D 是BC 的中点,DF ⊥AB 于F ,DE ⊥AC 于E .试猜想AB 和AC 的数量关系,并证明你的猜想.8. 已知:如图,△ABC 是等边三角形,AB =BC =AC ,∠ABC =∠ACB =60°,点E ,F 分别在AB ,AC 边上,∠EDF =60°,BD =CD ,∠DBC =∠DCB =30°,∠BDC =120°,延长AC 到点G ,使CG =BE . 求证:①△EBD ≌△GCD ;②△EFD ≌△GFD .B O DANFCBM EDF C BE DAGFE C BA9. 已知:如图,AB =AC ,BD =CD ,E 是线段AD 延长线上一点.求证:△ABE ≌△ACE .10. 已知:如图,∠ACB =∠ADB =90°,AD =BC ,CE ⊥AB 于点E ,DF ⊥AB 于点F .求证:CE =DF .11. 已知:如图,点C ,D 在线段BE 上,BD =EC ,CA ⊥AB 于点A ,DF ⊥EF 于点F ,且AB =EF .求证:CF =DA .12. 已知:如图,在△PBC 中,D 为PB 上一点,PD =PC ,延长PC 到点A ,使得PA =PB ,连接AD ,交BC 于点O ,连接PO . 求证:OD =OC .DCBAFE DCBFEDCBAOBDPCA【参考答案】1. 证明:如图,①∵∠ACM =∠BCN =60° ∴∠MCN =60° ∴∠ACN =∠MCB =120° 在△CAN 和△CMB 中,AC MC ACN MCB CN CB =⎧⎪∠=∠⎨⎪=⎩(已知)(已证)(已知) ∴△CAN ≌△CMB (SAS ) ②∵△CAN ≌△CMB∴∠ANC =∠MBC (全等三角形对应角相等) ∵∠ECN =60°;∠FCB =60° ∴∠ECN =∠FCB 在△CEN 和△CFB 中,ECN FCB CN CB ENC FBC ∠=∠⎧⎪=⎨⎪∠=∠⎩(已证)(已知)(已证) ∴△CEN ≌△CFB (ASA ) 2. 证明:如图,①∵∠D =∠ABC =90° ∴∠ABG =90° ∴∠D =∠ABG在△ADE 和△ABG 中,AD AB D ABG DE BG =⎧⎪∠=∠⎨⎪=⎩(已知)(已证)(已知) ∴△ADE ≌△ABG (SAS ) ②∵△ADE ≌△ABG (已证) ∴AE =AG (全等三角形对应边相等) ∠EAD =∠GAB (全等三角形对应角相等) ∵∠EAF =45°;∠BAD =90° ∴∠BAF +∠EAD =45° ∴∠BAF +∠GAB =45° 即∠GAF =∠45° ∴∠GAF =∠EAF 在△AFE 和△AFG 中,AE AGEAF GAFAF AF =⎧⎪∠=∠⎨⎪=⎩(已证)(已证)(公共边)∴△AFE ≌△AFG (SAS )∴EF =GF (全等三角形对应边相等) ∵GF =BG +BF ∴EF =DE +BF 3. 证明:如图,在△AEB 和△DEC 中,A DAEB DECBE CE ∠=∠⎧⎪∠=∠⎨⎪=⎩(已知)(对顶角相等)(已知) ∴△AEB ≌△DEC (AAS )∴AB =DC (全等三角形对应边相等) 在Rt △ABC 和Rt △DCB 中,BC CBAB DC=⎧⎨=⎩(公共边)(已证) ∴△ABC ≌△DCB (HL ) 4. 证明:如图,∵AE =CF ∴AE+EF =CF+EF 即AF =CE∵DE ⊥AC ;BF ⊥AC ∴∠AFB =∠CED =90° 在Rt △ABF 和Rt △CDE 中,AB CDAF CE =⎧⎨=⎩(已知)(已证) ∴Rt △ABF ≌Rt △CDE (HL ) ∴BF =DE (全等三角形对应边相等) 在△DEG 和△BFG 中,DEG BFG EGD FGBDE BF ∠=∠⎧⎪∠=∠⎨⎪=⎩(已证)(对顶角相等)(已证) ∴△DEG ≌△BFG (AAS ) 5. 证明:如图,在△ABD 和△ACD 中,AB AC BD CDAD AD =⎧⎪=⎨⎪=⎩(已知)(已知)(公共边) ∴△ABD ≌△ACD (SSS )∴∠BAD =∠CAD (全等三角形对应角相等) 在△BAO 和△CAO 中,AB ACBAO CAOAO AO =⎧⎪∠=∠⎨⎪=⎩(已知)(已证)(公共边) ∴△BAO ≌△CAO (SAS )∴∠AOB =∠AOC (全等三角形对应角相等) ∵∠AOB +∠AOC =180° ∴∠AOB =90° ∴AD ⊥BC 6. 证明:如图,∵∠EAC =∠FAB∴∠EAC +∠BAC =∠FAB +∠BAC 即∠BAE =∠CAF 在△ABE 和△ACF 中,BAE CAF E FBE CF ∠=∠⎧⎪∠=∠⎨⎪=⎩(已证)(已知)(已知) ∴△ABE ≌△ACF (AAS )∴AE =AF (全等三角形对应边相等) 在△AEM 和△AFN 中;E F AE AFEAM FAN ∠=∠⎧⎪=⎨⎪∠=∠⎩(已知)(已证)(已知) ∴△AEM ≌△AFN (ASA )∴AM = AN (全等三角形对应边相等) 7. AB =AC ,理由如下:证明:如图, ∵DF ⊥AB ;DE ⊥AC∴∠AFD =∠AED =∠BFD =∠CED =90° ∵AD 平分∠BAC ∴∠FAD =∠EAD 在△AFD 和△AED 中;AFD AED FAD EADAD AD ∠=∠⎧⎪∠=∠⎨⎪=⎩(已证)(已证)(公共边) ∴△AFD ≌△AED (AAS )∴DF =DE ,AF =AE (全等三角形对应边相等) ∵点D 是BC 的中点 ∴BD =CD在Rt △BFD 和Rt △CED 中BD CDDF DE=⎧⎨=⎩(已证)(已证) F E DCB∴Rt △BFD ≌Rt △CED (HL ) ∴BF =CE (全等三角形对应边相等) ∴AF +BF =AE +CE即AB =AC8. 证明:如图,①∵∠ABC =∠ACB =60°,∠DBC =∠DCB =30° ∴∠DBE =∠ABC+∠DBC =90° ∠DCG =180°-∠ACB -∠DCB =90° ∴∠DBE =∠DCG在△EBD 和△GCD 中,B DBE DCD CDGBE CG ∠=∠=⎧⎪⎨⎪=⎩(已知)(已证)(已知) ∴△EBD ≌△GCD (SAS ) ②∵△EBD ≌△GCD (已证)∴DE =DG (全等三角形对应边相等)∠EDB =∠GDC (全等三角形对应角相等) ∵∠BDC =120°,∠EDF =60° ∴∠EDB +∠CDF =60° ∴∠GDC +∠CDF =60° 即∠GDF =60° ∴∠EDF =∠GDF在△EFD 和△GFD 中,D DE DGEDF GDFF DF =∠=∠⎧⎪⎨⎪=⎩(已证)(已证)(公共边) ∴△EFD ≌△GFD (SAS ) 9. 证明:如图,在△ABD 和△ACD 中,AB ACBD CDAD AD ⎧⎪⎨⎪=⎩==(已知)(已知)(公共边) ∴△ABD ≌△ACD (SSS )∴∠BAD =∠CAD (全等三角形对应角相等) 在△ABE 和△ACE 中,A AB ACBAE CAEE AE =∠=∠⎧⎪⎨⎪=⎩(已知)(已证)(公共边) ∴△ABE ≌△ACE (SAS ) 10. 证明:如图,在Rt △ACB 和Rt △BDA 中,BC B BAADA ==⎧⎨⎩(公共边)(已知) ∴Rt △ACB ≌Rt △BDA (HL ) ∴AC =BD (全等三角形对应边相等) ∠CAB =∠DBA (全等三角形对应角相等) ∵CE ⊥AB ,DF ⊥AB ∴∠CEA =∠DFB =90° 在△ACE 和△BDF 中,CEA DFBCAE DBFAC BD ⎧⎪⎨∠=∠∠=⎪∠⎩=(已证)(已证)(已证) ∴△ACE ≌△BDF (AAS )∴CE =DF (全等三角形对应边相等) 11. 证明:如图,∵CA ⊥AB ,DF ⊥EF ∴∠CAB =∠DFE =90° ∵BD =EC ∴BD +DC =EC +DC 即BC =ED在Rt △ABC 和Rt △FED 中,BC EDAB FE =⎧⎨=⎩(已证)(已知) ∴Rt △ABC ≌Rt △FED (HL )∴∠B =∠E (全等三角形对应角相等) 在△ABD 和△FEC 中,AB FE B EBD EC =⎧⎪∠=∠⎨⎪=⎩(已知)(已证)(已知) ∴△ABD ≌△FEC (SAS )∴CF =DA (全等三角形对应边相等) 12. 证明:如图,在△ADP 和△BCP 中,PD PCAPD BPCPA PB =⎧⎪∠=∠⎨⎪=⎩(已知)(公共角)(已知) ∴△ADP ≌△BCP (SAS )∴∠A =∠B (全等三角形对应角相等) ∵PD =PC ,PB =PA ∴PD -PB =PA -PC 即BD =AC在△BOD 和△AOC 中,BOD AOCB ABD AC ⎧⎪∠=∠⎪=∠⎩=⎨∠(对顶角相等)(已证)(已证) ∴△BOD ≌△AOC (AAS )∴OD =OC (全等三角形对应边相等)。
全等三角形练习题及答案

全等三角形练习题及答案.求证如图已知C B =BC :AC.=C A AB,=B A AC,A C AB,A B ,:.1''''⊥'⊥'2.已知:如图,△ABC 中,点E 、F 分别在AB 、AC 边上,点D 是BC 边中点,且EF ∥BC,DE=DF . 求证:∠B=∠C3. 已知:如图,AC=AB,AE=AD,∠1=∠2.求证:∠3=∠44. 已知:如图 , AB=DC ,AD=BC , O 是BD 中点 ,过O 的直线分别与DA 、BC 的延长线交于E 、F . 求证:OE=OF5. 已知:如图,AB=AC,AE 平分∠BAC.求证:∠DBE=∠DCE .6. 已知:如图:AB=CD , BE=CF , AF=DE.求证:△ABE≌△DCF7. 已知:如图,∠1=∠2,BD=CD,求证:AD是∠BAC的平分线.8. 已知:如图,AD是BC上的中线,且DF=DE.求证:BE∥CF.9. 如图,已知:AC=DF,AC∥FD,AE=DB,求证:△ABC≌△DEF10. 已知:如图,点B,E,C,F在同一直线上,AB∥DE,且AB=DE,BE=CF.求证:AC∥DF.答案1. C B =BC C A B BAC C A B =BAC AC B +C CA =AC B +B BA 90=C CA =B BA AC A C AB,A B :''''''''''''⊥'⊥'∴≌△∴△∠∠即∠∠∠∠∴°∠∠∴∵证明 2. 证:∵BD=CD,EF ∥BC∴∠1=∠2,∠3=∠4∵DE=DF,∴∠2=∠4∴∠1=∠3∵D 是BC 的中点,∴BD=DC,又∠1=∠3,DE=DF ∴△BED ≌△CFD(SAS)∴∠B=∠C3. 证明:∵∠1=∠2∴∠1+∠5=∠2+∠5,即∠EAC=∠DAB 在△EAC 和△DAB 中∵∠∠AC ABEAC DABAE AD ===⎡⎣⎢⎢⎢⎢∴△EAC ≌△DAB(SAS)∴∠3=∠44. 提示:先证△ABD ≌△CDB , 再证△DOE ≌△BOF .5. 证明:在△ABE 和△ACE 中 ∵∠∠平分∠AB ACABE BAC AE AE ===⎡⎣⎢⎢⎢⎢12()∴△ABE ≌△ACE(SAS)∴BE=CE ∠3=∠ 4在△EBD 和△ECD 中∵∠∠BE CEDE ED ===⎡⎣⎢⎢⎢⎢34∴△EBD ≌△ECD(SAS) ∴∠DBE=∠DCE6. 证 明:∵AF=DE , ∴AF+FE=DE+EF .即AE=DF 在△ABE 和△DCF 中AB=CD , BE=CF , AE=DF , ∴△ABE ≌△DCF(SSS).7. 证明:∵BD=CD,∠1=∠2, ∴∠ADB=∠ADCAD=AD∴△ADB ≌△ADC(SAS) ∴∠BAD=∠CAD .即AD 平分∠BAC .8. 证:∵D 是BC 的中点,∴BD=CD ∵∠1=∠2,DF=DE,∴△BED ≌△CFD(SAS) ∴∠E=∠CFD∴BE ∥CF9. 证明:∵AE=BD∴AB=DE∵AC=DF AC ∥DF∴∠1=∠2∴△ABC ≌△DEF(SAS)10. 证明:∵BE=CF∴BE+EC=CF+EC 即BC=EF 又 AB ∥DE∴∠B=∠DEF∵AB=DE∴△ABC ≌△DEF∴∠ACB=∠F∴AC ∥DF。
(完整版)全等三角形练习题及答案

全等三角形练习题及答案1、下列判定直角三角形全等的方法,不正确的是()A、两条直角边对应相等。
B、斜边和一锐角对应相等。
C、斜边和一条直角边对应相等。
D、两锐角相等。
2、在△ABC中,∠B=∠C,与△ABC全等的三角形有一个角是100°,那么在△ABC中与这100°角对应相等的角是()A.∠AB.∠BC.∠CD.∠B或∠C3、下列各条件中,不能作出唯一三角形的是()A.已知两边和夹角B.已知两角和夹边C.已知两边和其中一边的对角 D.已知三边4、在△ABC与△DEF中,已知AB=DE;∠A=∠D;再加一个条件,却不能判断△ABC与△DEF全等的是().A. BC=EF B.AC=DFC.∠B=∠E D.∠C=∠F5、使两个直角三角形全等的条件是()A.一锐角对应相等B.两锐角对应相等C.一条边对应相等D.两条直角边对应相等6、在△ABC和△A'B'C'中有①AB=A'B',②BC=B'C',③AC=A'C',④∠A=∠A',⑤∠B=∠B',⑥∠C=∠C',则下列各组条件中不能保证△ABC≌△A'B'C'的是()A、①②③B、①②⑤C、①②④D、②⑤⑥7、如图,已知∠1=∠2,欲得到△ABD≌△ACD,还须从下列条件中补选一个,错误的选法是()A、∠ADB=∠ADCB、∠B=∠CC、DB=DCD、AB=AC8、如图,△ABC≌△ADE,若∠BAE=120°,∠BAD=40°,则∠BAC的度数为A. 40°B. 80°C.120°D. 不能确定9、如图,AE=AF,AB=AC,EC与BF交于点O,∠A=600,∠B=250,则∠EOB的度数为()A.600 B.700C.750D.85010、如图,已知AB=DC,AD=BC,E.F在DB上两点且BF=DE,若∠AEB=120°,∠ADB=30°,则∠BCF= ( )A. 150°B.40°C.80°D. 90°11、①两角及一边对应相等②两边及其夹角对应相等③两边及一边所对的角对应相等④两角及其夹边对应相等,以上条件能判断两个三角形全等的是( )A.①③ B.②④ C.②③④ D.①②④12、下列条件中,不能判定两个三角形全等的是()A.三条边对应相等 B.两边和一角对应相等C.两角及其一角的对边对应相等 D.两角和它们的夹边对应相等13、如图,已知,,下列条件中不能判定⊿≌⊿的是()(A)(B)(C)(D)∥14、如图,AB与CD交于点O,OA=OC,OD=OB,∠A=50°,∠B=30°,则∠D的度数为().A.50° B.30° C.80° D.100°15、如图,△ABC中,AD⊥BC于D,BE⊥AC于E,AD与BE相交于点F,若BF=AC,则∠ABC的度数是.16、在△ABC和△中,∠A=44°,∠B=67°,∠=69°,∠=44°,且AC=则这两个三角形全等(填“一定”或“不一定”)17、如图,,,,在同一直线上,,,若要使,则还需要补充一个条件:或.18、(只需填写一个你认为适合的条件)如图,已知∠CAB=∠DBA,要使△ABC≌△BAD,需增加的一个条件是。
最新北师大版七年级下册三角形全等的证明练习题以及答案
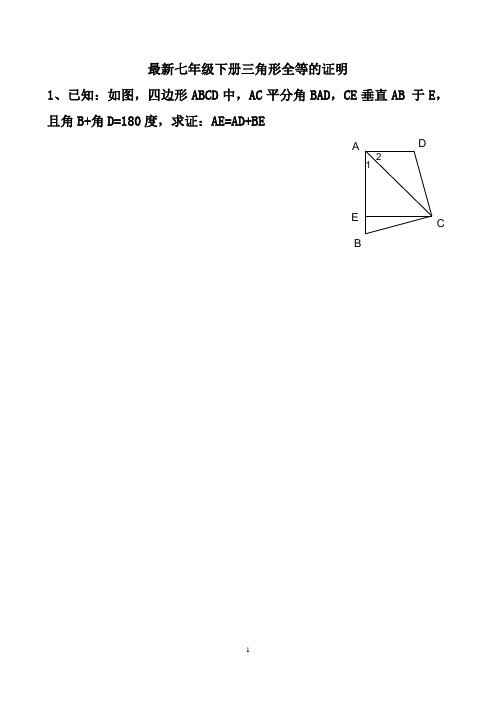
最新七年级下册三角形全等的证明1、已知:如图,四边形ABCD中,AC平分角BAD,CE垂直AB 于E,且角B+角D=180度,求证:AE=AD+BEA B DCE 122、已知,如图,AB=CD,DF⊥AC于F,BE⊥AC于E,DF=BE。
求证:AF=CE。
FE A CDB3、已知,如图,AB ⊥AC ,AB =AC ,AD ⊥AE ,AD =AE 。
求证:BE =CD 。
AEDC B4、如图,DE⊥AB,DF⊥AC,垂足分别为E、F,请你从下面三个条件中任选出两个作为已知条件,另一个为结论,推出一个正确的命题。
①AB=AC ②BD=CD ③BE=CFBD C5、如图,△ABC中,AB=AC,过A作GE∥BC,角平分线BD、CF 交于点H,它们的延长线分别交GE于E、G,试在图中找出三对全等三角形,并对其中一对给出证明。
E G6、如图,在△ABC中,点D在AB上,点E在BC上,BD=BE。
(1)请你再添加一个条件,使得△BEA≌△BDC,并给出证明。
你添加的条件是:________ ___(2)根据你添加的条件,再写出图中的一对全等三角形:______________(不再添加其他线段,不再标注或使用其他字母,不必写出证明过程)7、已知:如图,AB⊥BC,AD⊥DC,AB=AD,若E是AC上一点。
求证:EB=ED。
DA E CB8、已知:如图,AB、CD交于O点,CE//DF,CE=DF,AE=BF。
求证:∠ACE=∠BDF。
AB CDEFO9、已知:如图,△ABC中,AD⊥BC于D,E是AD上一点,BE的延长线交AC于F,若BD=AD,DE=DC。
求证:BF⊥AC。
AE FDB C10、. 已知:如图,△ABC 和△A 'B 'C '中,∠BAC=∠B 'A 'C ',∠B=∠B ',AD 、A 'D '分别是∠BAC 、∠B 'A 'C '的平分线,且AD=A 'D '。
求证:△ABC ≌△A’B’C’。
8年级数学人教版上册同步练习全等三角形三角形全等的判定(含答案解析)

8年级数学人教版上册同步练习全等三角形三角形全等的判定(含答案解析)12.1全等三角形12.2三角形全等的判定专题一三角形全等的判定1.如图,BD是平行四边形ABCD的对角线,∠ABD的平分线BE交AD于点E,∠CDB 的平分线DF交BC于点F.求证:△ABE≌△CDF.2.如图,在△ABC中,D是BC边上的点(不与B,C重合),F,E分别是AD及其延长线上的点,CF∥BE. 请你添加一个条件,使△BDE≌△CDF (不再添加其他线段,不再标注或使用其他字母),并给出证明.(1)你添加的条件是:__________;(2)证明:3.如图,△ABC中,点D在BC上,点E在AB上,BD=BE,要使△ADB≌△CEB,还需添加一个条件.(1)给出下列四个条件:①AD=CE;②AE=CD;③∠BAC=∠BCA;④∠ADB=∠CEB;请你从中选出一个能使△ADB≌△CEB的条件,并给出证明;(2)在(1)中所给出的条件中,能使△ADB≌△CEB的还有哪些?直接在题后横线上写出满足题意的条件序号.__________________.专题二全等三角形的判定与性质4.如图,已知△ABC中,∠ABC=45°,AC=4,H是高AD和BE的交点,则线段BH的长度为()A6B.4 C.23D.55.【2013·襄阳】如图,在△ABC中,AB=AC,AD⊥BC于点D,将△ADC绕点A顺时针旋转,使AC与AB重合,点D落在点E处,AE的延长线交CB的延长线于点M,EB的延长线交AD的延长线于点N.求证:AM=AN.NMEDB CA6.【2012·泸州】如图,△ABC是等边三角形,D是AB边上一点,以CD为边作等边三角形CDE,使点E﹨A在直线DC的同侧,连接AE.求证:AE∥BC.专题三全等三角形在实际生活中的应用7.如图,有两个长度相同的滑梯靠在一面墙上.已知左边滑梯的高度AC与右边滑梯水平方向的长度DF相等,则这两个滑梯与地面夹角∠ABC与∠DFE的度数和是()A.60°B.90°C.120°D.150°8.有一座小山,现要在小山A﹨B的两端开一条隧道,施工队要知道A﹨B两端的距离,于是先在平地上取一个可以直接到达A和B的点C,连接AC并延长到D,使CD=CA,连接BC并延长到E,使CE=CB,连接DE,那么量出DE的长,就是A﹨B两端的距离,你能说说其中的道理吗?9.已知如图,要测量水池的宽AB,可过点A作直线AC⊥AB,再由点C观测,在BA延长线上找一点B′,使∠ACB′=∠ACB,这时只要量出AB′的长,就知道AB的长,对吗?为什么?状元笔记【知识要点】1.全等三角形能够完全重合的两个三角形叫做全等三角形.2.全等三角形的性质全等三角形的对应边相等,全等三角形的对应角相等.3.三角形全等的判定方法(1)三边分别相等的两个三角形全等(简写成“边边边”或“SSS”).(2)两边和它们的夹角分别相等的两个三角形全等(简写成“边角边”或“SAS”).(3)两角和它们的夹边分别相等的两个三角形全等(简写成“角边角”或“ASA”).(4)两个角和其中一个角的对边分别相等的两个三角形全等(简写成“角角边”或“AAS”).4.直角三角形全等的判定方法斜边和一条直角边分别相等的两个直角三角形全等(简写成“斜边﹨直角边”或“HL”).【温馨提示】1.两个三角形全等的条件中必须有一条边分别相等,只有角分别相等不能证明两个三角形全等.2.有两边和其中一边的对角分别相等的两个三角形不一定全等.3.“HL”定理指的是斜边和一条直角边分别相等,而不是斜边和直角分别相等.【方法技巧】1.应用全等三角形性质解决问题的前提是准确地确定全等三角形的对应边和对应角,其规律主要有以下几点:(1)以对应顶点为顶点的角是对应角;(2)对应顶点所对应的边是对应边;(3)公共边(角)是对应边(角);(4)对顶角是对应角;(5)最大边(角)是对应边(角),最小边(角)是对应边(角).全等三角形的对应边和对应角可以依据字母的对应位置来确定,如若△ABC≌△DEF,说明A与D,B与E,C与F是对应点,则∠ABC与∠DEF是对应角,边AC与边DF 是对应边.2.判定两个三角形全等的解题思路:SAS SSS AAS SAS ASA AAS ASA AAS ⎧⎧⎨⎪⎩⎪⎪⎧⎪⎪⎪⎧⎪⎪⎨⎨⎪⎨⎪⎪⎪⎪⎪⎩⎩⎪⎪⎧⎪⎨⎪⎩⎩找夹角——已知两边找另一边——边为角的对边——找任一角——找夹角的另一边——已知一边一角边为角的邻边找夹边的另一角——找边的对角——找夹边——已知两角找任一边——参考答案:1.证明:平行四边形ABCD 中,AB=CD ,∠A=∠C ,AB ∥CD , ∴∠ABD=∠CDB .∵∠ABE=21∠ABD ,∠CDF=21∠CDB ,∴∠ABE=∠CDF .在△ABE 与△CDF 中,⎪⎩⎪⎨⎧∠=∠=∠=∠CDF ABE CDAB C A ∴△ABE ≌△CDF . 2.解:(1)DC BD =(或点D 是线段BC 的中点),ED FD =,BE CF =中任选一个即可﹒ (2)以DC BD =为例进行证明: ∵CF ∥BE ,∴∠FCD ﹦∠EBD .又∵DC BD =,∠FDC =∠EDB , ∴△BDE ≌△CDF . 3.解:(1)添加条件②,③,④中任一个即可,以添加②为例说明. 证明:∵AE=CD ,BE=BD , ∴AB=CB .又∠ABD=∠CBE ,BE=BD , ∴△ADB ≌△CEB . (2)③④.4.B 解析:∵∠ABC =45°,AD ⊥BC ,∴AD =BD ,∠ADC =∠BDH , ∠AHE =∠BHD =∠C .∴△ADC ≌△BDH .∴BH =AC =4.故选B . 5.证明:如图所示,M∵△AEB由△ADC旋转而得,∴△AEB≌△ADC.∴∠3=∠1,∠6=∠C.∵AB=AC,AD⊥BC,∴∠2=∠1,∠7=∠C.∴∠3=∠2,∠6=∠7.∵∠4=∠5,∴∠ABM=∠ABN.又∵AB=AB,∴△AMB≌△ANB.∴AM=AN.6.证明:∵△ABC和△EDC是等边三角形,∴∠BCA=∠DCE=60°.∴∠BCA-∠ACD=∠DCE-∠ACD,即∠BCD=∠ACE.在△DBC和△EAC中,BC=AC,∠BCD=∠ACE,DC=EC,∴△DBC≌△EAC(SAS).∴∠DBC=∠EAC.又∵∠DBC=∠ACB=60°,∴∠ACB=∠EAC.∴AE∥BC.7.B 解析:∵滑梯﹨墙﹨地面正好构成直角三角形,又∵BC=EF,AC=DF,∴Rt△ABC≌Rt△DEF.∴∠ABC=∠DEF,∵∠DEF+∠DFE=90°,∴∠ABC+∠DFE=90°.故选B.8.解:在△ABC和△CED中,AC=CD,∠ACB=∠ECD,EC=BC,∴△ABC≌△CED.∴AB=ED.即量出DE的长,就是A﹨B两端的距离.9.解:对.理由:∵AC ⊥AB,∴∠CAB=∠CAB′=90°. 在△ABC 和△AB′C 中,ACB ACB AC AC CAB CAB =⎧⎪=⎨⎪=⎩∠∠′,,∠∠′, ∴△ABC ≌△AB′C (ASA ). ∴AB′=AB .。
全等三角形的性质及判定(习题及答案)

全等三角形的性质及判定(习题)例题示范例1:已知:如图,C 为AB 中点,CD=BE,CD∥BE.求证:△ACD≌△CBE.【思路分析】①读题标注:DDBB②梳理思路:要证全等,需要三组条件,其中必须有一组边相等.由已知得,CD=BE;根据条件C 为AB 中点,得AC=CB;这样已经有两组条件都是边,接下来看第三边或已知两边的夹角.由条件CD∥BE,得∠ACD=∠B.发现两边及其夹角相等,因此由 SAS 可证两三角形全等.【过程书写】先准备不能直接用的两组条件,再书写全等模块.过程书写中需要注意字母对应.证明:如图∵C 为AB 中点ACEACE∴AC =CB ∵CD ∥BE ∴∠ACD =∠B 在△ACD 和△CBE 中 AC = CB(已证)ACD = B (已证) CD = BE (已知) ∴△ACD ≌△CBE (SAS )EC巩固练习1. 如图,△ABC ≌△AED ,有以下结论:①AC =AE ;②∠DAB =∠EAB ;③ED =BC ;④∠EAB =∠DAC . 其中正确的有( ) A .1 个B .2 个C .3 个D .4 个EAA1F EBC 2BDCD第 1 题图第 2 题图2. 如图,B ,C ,F ,E 在同一直线上,∠1=∠2,BF =EC ,要使△ABC ≌△DEF ,还需要添加一组条件, 这个条件可以是 ,理由是 ; 这个条件也可以是 ,理由是 ; 这个条件还可以是,理由是.3. 如图,D 是线段 AB 的中点,∠C =∠E ,∠B =∠A ,找出图中的一对全等三角形是,理由是.AC AG DFHB E B D第3 题图第4 题图4.如图,AB=AD,∠BAE=∠DAC,要使△ABC≌△ADE,还需要添加一组条件,这个条件可以是,理由是;这个条件也可以是,理由是;这个条件还可以是,理由是.BCDF5. 如图,将两根钢条 AA' , BB' 的中点连在一起,使 AA' , BB'可以绕着中点 O 自由旋转,这样就做成了一个测量工具,A'B' 的长等于内槽宽 AB .其中判定△OAB ≌△ OA'B' 的理由是 ()A .SASB .ASAC .SSSD .AASA B'A'E第 5 题图第 6 题图6. 要测量河两岸相对的两点 A ,B 的距离,先在 AB 的垂线 BF上取两点 C ,D ,使 CD =BC ,再定出 BF 的垂线 DE ,使 A ,C ,E 在一条直线上(如图所示),可以说明△E DC ≌△ABC ,得 ED =AB ,因此测得 ED 的长就是 AB 的长.判定△EDC ≌ △ABC 最恰当的理由是( ) A .SASB .ASAC .SSSD .AAA7. 已知:如图,M 是 AB 的中点,∠1=∠2,∠C =∠D .求证:△AMC ≌△BMD . 【思路分析】 ① 读题标注: ② 梳理思路: C DA要证全等,需要 组条件,其中必须有一组 相等.由已知得:=,= .A OB根据条件,得= .因此,由可证两三角形全等.【过程书写】证明:如图8.已知:如图,点B,F,C,E 在同一条直线上,且BC=EF,AB∥DE,AB=DE.A求证:△ABC≌△DEF.CB F E【思路分析】①读题标注:②梳理思路:D要证全等,需要组条件,其中必须有一组相等.由已知得:= ,= .根据条件,得= .因此,由可证两三角形全等.【过程书写】证明:如图思考小结1.两个三角形全等的判定有,, _,,其中AAA,SSA 不能证明三角形全等,请举反例进行说明.2.如图,A,B 两点分别位于一个池塘的两端,小明想用绳子测量A,B 间的距离,但绳子不够长,一个叔叔帮他出了这样一个主意:先在地上取一个可以直接到达A 点和B 点的点C,连接AC 并延长到D,使CD=CA;连接BC 并延长到E,使CE=CB ,连接DE 并测量出它的长度,DE 的长度就是A,B 间的距离.你能说明其中的道理吗A ECB D【参考答案】 巩固练习1. B2. AC =DF ,SAS ;∠B =∠E ,ASA ;∠A =∠D ,AAS3. △BCD ≌△AED ,AAS4. AC =AE ,SAS ;∠B =∠D ,ASA ;∠C =∠E ,AAS5. A6. B7. ①略②3,边∠1,∠2;∠C ,∠DM 是 AB 的中点,AM ,BM AAS【过程书写】证明:如图, ∵M 是 AB 的中点 ∴AM =BM在△AMC 和△BMD 中C =D (已知) 1 = 2 (已知) AM = BM (已证) ∴△AMC ≌△BMD (AAS ) 8. ①略②3,边BC ,EF , AB ,DE AB ∥DE ,∠B ,∠E SAS【过程书写】证明:如图, ∵AB ∥DE∴∠B =∠E在△ABC 和△DEF 中 AB = DE (已知)B = E (已证) BC = EF (已知)∴△ABC ≌△DEF (SAS )思考小结1. SAS ,SSS ,ASA ,AASAAA 反例:大小三角板SSA 反例:作图略2. 证明:如图,在△ABC 和△DEC 中AC = DC (已知)ACB = DCE (对顶角相等) BC = EC (已知) ∴△ABC ≌△DEC (SAS )∴AB =DE (全等三角形对应边相等) 即 DE 的长度就是 A ,B 间的距离。
(完整)全等三角形难题及答案
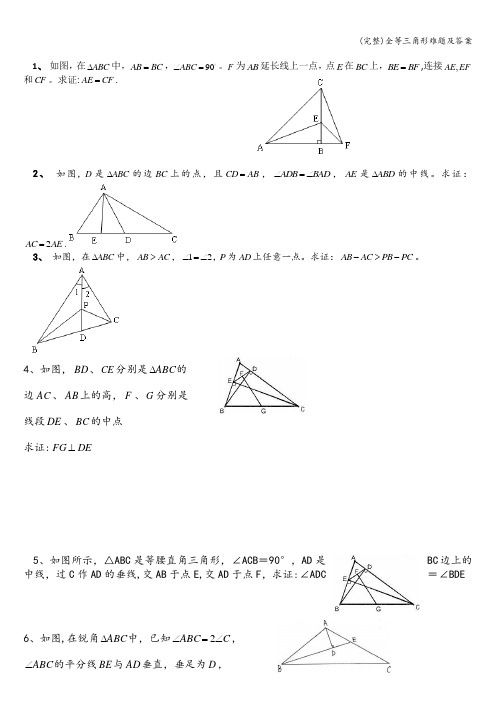
1、 如图,在ABC ∆中,AB BC =,90ABC ∠=。
F 为AB 延长线上一点,点E 在BC 上,BE BF =,连接,AE EF 和CF 。
求证:AE CF =.2、 如图,D 是ABC ∆的边BC 上的点,且CD AB =,ADB BAD ∠=∠,AE 是ABD ∆的中线。
求证:2AC AE =.3、 如图,在ABC ∆中,AB AC >,12∠=∠,P 为AD 上任意一点。
求证:AB AC PB PC ->-。
4、如图,BD 、CE 分别是ABC ∆的边AC 、AB 上的高,F 、G 分别是线段DE 、BC 的中点求证:DE FG ⊥5、如图所示,△ABC 是等腰直角三角形,∠ACB =90°,AD 是BC 边上的中线,过C 作AD 的垂线,交AB 于点E,交AD 于点F ,求证:∠ADC=∠BDE6、如图,在锐角ABC ∆中,已知C ABC ∠=∠2,ABC ∠的平分线BE 与AD 垂直,垂足为D ,若cm BD 4=,求AC 的长参考答案1、 思路分析:可以利用全等三角形来证明这两条线段相等,关键是要找到这两个三角形.以线段AE 为边的ABE ∆绕点B 顺时针旋转90到CBF ∆的位置,而线段CF 正好是CBF ∆的边,故只要证明它们全等即可。
解答过程:90ABC ∠=,F 为AB 延长线上一点∴90ABC CBF ∠=∠=在ABE ∆与CBF ∆中AB BC ABC CBF BE BF =⎧⎪∠=∠⎨⎪=⎩∴ABE CBF ∆≅∆(SAS)∴AE CF =。
解题后的思考:利用旋转的观点,不但有利于寻找全等三角形,而且有利于找对应边和对应角。
小结:利用三角形全等证明线段或角相等是重要的方法,但有时不容易找到需证明的三角形。
这时我们就可以根据需要利用平移、翻折和旋转等图形变换的观点来寻找或利用辅助线构造全等三角形。
2、 思路分析:要证明“2AC AE =”,不妨构造出一条等于2AE 的线段,然后证其等于AC 。
八年级全等三角形简单证明题及答案(15道)

∴BC=ED.
全等三角形的判定与性 质.
01
如图,在△ABC中, ∠C=90°,点D是AB边上的 一点,DM⊥AB,且 DM=AC,过点M作 ME∥BC交AB于点E.求证: △ABC≌△MED。
02
证明:∵MD⊥AB,
∴∠MDE=∠C=90°,
∵ME∥BC,
∴∠B=∠MED,
在△ABC与△MED中, ∠B=∠MED ∠C=∠EDM DM=AC ,
∠D=∠B , ∴△ADF≌△CBE(ASA), ∴AF=CE, ∴AF+EF=CE+EF,即
AE=CF.
全等三角形的判定与性 质.
11.在△ABC中,AB=CB,∠ABC=90°,F为AB延 长线上一点,点E在BC上,且AE=CF.求证: Rt△ABE≌Rt△CBF;
证明:∵∠ABC=90°,
角平分线的性质;全等三角形的判定与性质.
全等三角形的判定.
如图,在△ABC中, AB=AC,AD平分 ∠BAC.求证: ∠DBC=∠DCB.
解:∵AD平分∠BAC, ∴∠BAD=∠CAD. ∴在△ACD和△ABD中 AB=AC ∠BAD=∠CAD
AD=AD , ∴△ACD≌△ABD, ∴BD=CD, ∴∠DBC=∠DCB.
:∵AC平分∠BAD,
∴∠BAC=∠DAC,
在△ABC和△ADC中, AB=AD ∠BAC=∠DAC AC=AC ,
∴△ABC≌△ADC.
全等三角形的判定.
9.如图,已知 点E,C在线段
BF上, BE=CF, AB∥DE, ∠ACB=∠F.
求证: △ABC≌△DEF
.
证明:∵AB∥DE,
∴∠B=∠DEF.
全等三角形的判定与性质.
全等三角形经典题型50题(含答案解析)
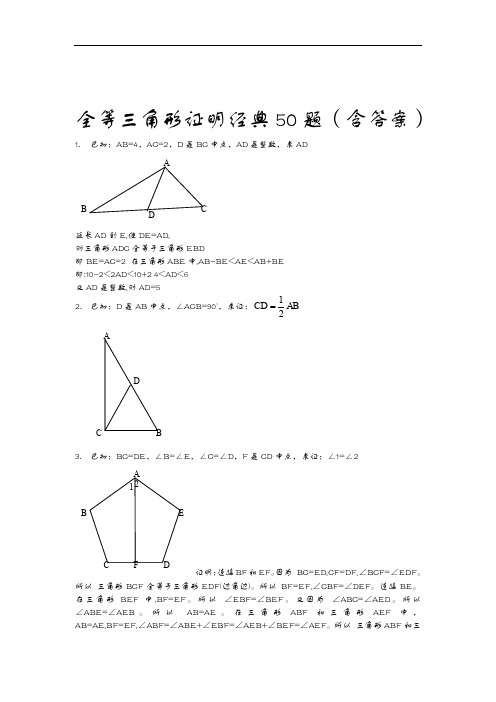
全等三角形证明经典50题(含答案)1. 已知:AB=4,AC=2,D 是BC 中点,AD 是整数,求AD延长AD 到E,使DE=AD,则三角形ADC 全等于三角形EBD即BE=AC=2 在三角形ABE 中,AB-BE<AE<AB+BE 即:10-2<2AD<10+2 4<AD<6 又AD 是整数,则AD=52. 已知:D 是AB 中点,∠ACB=90°,求证:12CD AB3. 已知:BC=DE ,∠B=∠E ,∠C=∠D ,F 是CD 中点,求证:∠1=∠2证明:连接BF 和EF 。
因为 BC=ED,CF=DF,∠BCF=∠EDF 。
所以 三角形BCF 全等于三角形EDF(边角边)。
所以 BF=EF,∠CBF=∠DEF 。
连接BE 。
在三角形BEF 中,BF=EF 。
所以 ∠EBF=∠BEF 。
又因为 ∠ABC=∠AED 。
所以 ∠ABE=∠AEB 。
所以 AB=AE 。
在三角形ABF 和三角形AEF 中,AB=AE,BF=EF,∠ABF=∠ABE+∠EBF=∠AEB+∠BEF=∠AEF 。
所以 三角形ABF和三ADBC角形AEF 全等。
所以 ∠BAF=∠EAF (∠1=∠2)。
4. 已知:∠1=∠2,CD=DE ,EF//AB ,求证:EF=AC证明:过E 点,作EG//AC ,交AD 延长线于G 则∠DEG=∠DCA ,∠DGE=∠2又∵CD=DE ∴⊿ADC ≌⊿GDE (AAS )∴EG=AC ∵EF//AB ∴∠DFE=∠1∵∠1=∠2∴∠DFE=∠DG E ∴EF=EG ∴EF=AC5. 已知:AD 平分∠BAC ,AC=AB+BD ,求证:∠B=2∠C证明:在AC 上截取AE=AB ,连接ED ∵AD 平分∠BAC ∴∠EAD=∠BAD 又∵AE=AB ,AD=AD ∴⊿AED ≌⊿ABD (SAS )∴∠AED=∠B ,DE=DB ∵AC=AB+BDAC=AE+CE ∴CE=DE ∴∠C=∠E DC ∵∠AED=∠C+∠EDC=2∠C ∴∠B=2∠C6. 已知:AC 平分∠BAD ,CE ⊥AB ,∠B+∠D=180°,求证:AE=AD+BE证明: 在AE 上取F ,使EF =EB ,连接CF 因为CE ⊥AB 所以∠CEB =∠CEF =90° 因为EB =EF ,CE =CE , 所以△CEB ≌△CEF 所以∠B =∠CFE 因为∠B +∠D =180°,∠CFE +∠CFA =180° 所以∠D =∠CFA 因为AC 平分∠BAD 所以∠DAC =∠FAC 又因为AC =AC 所以△ADC ≌△AFC (SAS ) 所以AD =AF 所以AE =AF +FE =AD +BE12. 如图,四边形ABCD 中,AB ∥DC ,BE 、CE 分别平分∠ABC 、∠BCD ,且点E 在AD 上。
三角形全等的判定“角边角与角角边”(6种题型)-2023年新八年级数学题型(人教版)(解析版)

三角形全等的判定“角边角与角角边”(6种题型)【知识梳理】一、全等三角形判定——“角边角”两角和它们的夹边对应相等的两个三角形全等(可以简写成“角边角”或“ASA ”).要点诠释:如图,如果∠A =∠'A ,AB =''A B ,∠B =∠'B ,则△ABC ≌△'''A B C .二、全等三角形判定——“角角边” 1.全等三角形判定——“角角边”两个角和其中一个角的对边对应相等的两个三角形全等(可以简写成“角角边”或“AAS ”)要点诠释:由三角形的内角和等于180°可得两个三角形的第三对角对应相等.这样就可由“角边角”判定两个三角形全等,也就是说,用角边角条件可以证明角角边条件,后者是前者的推论.2.三个角对应相等的两个三角形不一定全等.如图,在△ABC 和△ADE 中,如果DE BC ,那么∠ADE =∠B ,∠AED =∠C ,又∠A =∠A ,但△ABC 和△ADE 不全等.这说明,三个角对应相等的两个三角形不一定全等.【考点剖析】题型一:用“角边角”直接证明三角形全等例1.如图,∠A =∠B ,AE =BE ,点D 在 AC 边上,∠1=∠2,AE 和BD 相交于点O .求证:△AEC ≌△BED ;【详解】∵AE 和BD 相交于点O ,∴∠AOD=∠BOE .在△AOD 和△BOE 中,∠A=∠B ,∴∠BEO=∠2.又∵∠1=∠2,∴∠1=∠BEO ,∴∠AEC=∠BED .在△AEC 和△BED 中,A B AE BEAEC BED ∠∠⎧⎪⎨⎪∠∠⎩===∴△AEC ≌△BED (ASA ).【变式1】如图,AB =AD ,∠1,DA 平分∠BDE .求证:△ABC ≌△ADE .【解答】证明:∵∠1=∠2,∴∠1+∠DAC =∠2+∠DAC ,∴∠BAC =∠DAE ,∵AB =AD ,∴∠ADB =∠B ,∵DA 平分∠BDE .∴∠ADE =∠ADB ,∴∠ADE =∠B ,在△ABC和△ADE中,{∠ADE=∠B AB=AD∠BAC=∠DAE,∴△ABC≌△ADE(ASA).【变式2】如图,已知∠1=∠2,∠3=∠4,要证BC=CD,证明中判定两个三角形全等的依据是()A.角角角B.角边角C.边角边D.角角边【分析】已知两角对应相等,且有一公共边,利用全等三角形的判定定理进行推理即可.【解答】解:在△ABC与△ADC中,{∠1=∠2 AC=AC∠3=∠4,则△ABC≌△ADC(ASA).∴BC=CD.故选:B.【变式3】(2022•长安区一模)已知:点B、E、C、F在一条直线上,AB∥DE,AC∥DF,BE=CF.求证:△ABC≌△DEF.【解答】证明:∵AB∥DE,∴∠B=∠DEF,∵AC∥DF,∴∠ACB=∠F,∵BE=CF,∴BE+EC=CF+EC,即BC =EF ,在△ABC 和△DEF 中,{∠B =∠DEFBC =EF ∠ACB =∠F,∴△ABC ≌△DEF (ASA ). 题型二:用“角边角”间接证明三角形全等例2.如图,已知AB ∥CD ,AB =CD ,∠A =∠D .求证:AF =DE .【详解】证明:∵AB //CD ,∴∠B =∠C ,在△ABF 和△DCE 中,A D AB CD BC ∠=∠⎧⎪=⎨⎪∠=∠⎩,∴△ABF ≌△DCE (ASA ),∴AF =DE .【变式1】已知:如图,E ,F 在AC 上,AD ∥CB 且AD =CB ,∠D =∠B .求证:AE =CF .【答案与解析】证明:∵AD ∥CB∴∠A =∠C在△ADF 与△CBE 中A C AD CB D B ∠=∠⎧⎪=⎨⎪∠=∠⎩∴△ADF ≌△CBE (ASA )∴AF =CE ,AF +EF =CE +EF故得:AE =CF【变式2】如图,AB =AC ,AB ⊥AC ,AD ⊥AE ,且∠ABD =∠ACE .求证:BD =CE .【详解】∵AB ⊥AC ,AD ⊥AE ,∴∠BAE +∠CAE =90°,∠BAE +∠BAD =90°,∴∠CAE =∠BAD .又AB =AC ,∠ABD =∠ACE ,∴△ABD ≌△ACE (ASA ).∴BD =CE .【变式3】如图,要测量河两岸相对两点A 、B 间的距离,在河岸BM 上截取BC =CD ,作ED ⊥BD 交AC 的延长线于点E ,垂足为点D .(DE ≠CD )(1)线段 的长度就是A 、B 两点间的距离(2)请说明(1)成立的理由.【解答】解:(1)线段DE 的长度就是A 、B 两点间的距离;故答案为:DE ;(2)∵AB ⊥BC ,DE ⊥BD∴∠ABC =∠EDC =90°又∵∠ACB =∠DCE ,BC =CD∴△ABC ≌△CDE (ASA )∴AB =DE .【变式4】如图,G 是线段AB 上一点,AC 和DG 相交于点E.请先作出∠ABC 的平分线BF ,交AC 于点F ;然后证明:当AD∥BC,AD =BC ,∠ABC=2∠ADG 时,DE =BF.【答案与解析】证明: ∵AD∥BC,∴∠DAC=∠C∵BF 平分∠ABC∴∠ABC=2∠CBF∵∠ABC=2∠ADG∴∠CBF=∠ADG在△DAE 与△BCF 中 ⎪⎩⎪⎨⎧∠=∠=∠=∠C DAC BCAD CBF ADG ∴△DAE≌△BCF(ASA )∴DE=BF【变式5】已知:如图,在△MPN 中,H 是高MQ 和NR 的交点,且MQ =NQ .求证:HN =PM.【答案】证明:∵MQ 和NR 是△MPN 的高,∴∠MQN =∠MRN =90°,又∵∠1+∠3=∠2+∠4=90°,∠3=∠4∴∠1=∠2在△MPQ 和△NHQ 中,12MQ NQ MQP NQH ∠=∠⎧⎪=⎨⎪∠=∠⎩∴△MPQ ≌△NHQ (ASA )∴PM =HN【变式6】如图,已知224m ABC S =△,AD 平分BAC ∠,且AD BD ⊥于点D ,则ADC S =△________2m .【答案】12【详解】解:如图,延长BD 交AC 于点E ,∵AD 平分BAC ∠,AD BD ⊥,∴BAD EAD ∠=∠,90ADB ADE ∠=∠=︒.∵AD AD =,∴()ADB ADE ASA ≌.∴BD DE =.∴ABD AED S S =△△,BCD ECD S S =. ∴12ABD BCD AED ECD ABC S S S S S =++=△△△△△.即12ADC ABC S S =.∵224m ABC S =△,∴212m ADC S =△.故答案为:12.【变式7】(2022秋•苏州期中)如图,△ABC 中,AD 是BC 边上的中线,E ,F 为直线AD 上的点,连接BE ,CF ,且BE ∥CF .(1)求证:△BDE ≌△CDF ;(2)若AE =13,AF =7,试求DE 的长.【解答】(1)证明:∵AD 是BC 边上的中线,∴BD =CD ,∵BE ∥CF ,∴∠DBE =∠DCF ,在△BDE 和△CDF 中,,∴△BDE ≌△CDF (ASA );(2)解:∵AE =13,AF =7,∴EF =AE ﹣AF =13﹣7=6,∵△BDE ≌△CDF ,∴DE =DF ,∵DE +DF =EF =6,∴DE =3.题型三:用“角角边”直接证明三角形全等例3.如图,在四边形ABCD中,E是对角线AC上一点,AD∥BC,∠ADC=∠ACD,∠CED+∠B=180°.求证:△ADE≌△CAB.【解答】证明:∵∠ADC=∠ACD,∴AD=AC,∵AD∥BC,∴∠DAE=∠ACB,∵∠CED+∠B=180°,∠CED+∠AED=180°,∴∠AED=∠B,在△ADE与△CAB中,{∠DAE=∠ACB ∠AED=∠BAD=AC,∴△ADE≌△CAB(AAS).【变式】(202210块高度都是2cm的相同长方体小木块,垒了两堵与地面垂直的木墙,木墙之间刚好可以放进一个等腰直角三角板(AC=BC,∠ACB=90°),点C在DE上,点A和B 分别与木墙的顶端重合.(1)求证:△ADC≌△CEB;(2)求两堵木墙之间的距离.【解答】(1)证明:由题意得:AC=BC,∠ACB=90°,AD⊥DE,BE⊥DE,∴∠ADC=∠CEB=90°,∴∠ACD+∠BCE=90°,∠ACD+∠DAC=90°,∴∠BCE=∠DAC在△ADC 和△CEB 中,∴△ADC ≌△CEB (AAS ); (2)解:由题意得:AD =2×3=6(cm ),BE =7×2=14(cm ),∵△ADC ≌△CEB ,∴EC =AD =6cm ,DC =BE =14cm ,∴DE =DC +CE =20(cm ),答:两堵木墙之间的距离为20cm .题型四:用“角角边”间接证明三角形全等例4、已知:如图,AB ⊥AE ,AD ⊥AC ,∠E =∠B ,DE =CB .求证:AD =AC .【答案与解析】证明:∵AB ⊥AE ,AD ⊥AC ,∴∠CAD =∠BAE =90°∴∠CAD +∠DAB =∠BAE +∠DAB ,即∠BAC =∠EAD在△BAC 和△EAD 中BAC EAD B E CB=DE ∠=∠⎧⎪∠=∠⎨⎪⎩∴△BAC ≌△EAD (AAS )∴AC =AD【变式】已知:如图,90ACB ∠=︒,AC BC =,CD 是经过点C 的一条直线,过点A 、B 分别作AE CD ⊥、 BF CD ⊥,垂足为E 、F ,求证:CE BF =.【答案与解析】证明:∵ CD AE ⊥,CD BF ⊥∴︒=∠=∠90BFC AEC∴︒=∠+∠90B BCF∵,90︒=∠ACB∴︒=∠+∠90ACF BCF∴B ACF ∠=∠在BCF ∆和CAE ∆中⎪⎩⎪⎨⎧=∠=∠∠=∠BC AC B ACE BFC AEC∴BCF ∆≌CAE ∆(AAS )∴BF CE =【总结升华】要证BF CE =,只需证含有这两个线段的BCF ∆≌CAE ∆.同角的余角相等是找角等的好方法.题型五:“边角边”与“角角边”综合应用例5.如图,120CAB ABD ∠+∠=AD 、BC 分别平分CAB ∠、ABD ∠,AD 与BC 交于点O .(1)求AOB ∠的度数;(2)说明AB AC BD =+的理由.【答案】(1)120°;(2)见解析【详解】解:(1)∵AD ,BC 分别平分∠CAB 和∠ABD ,∠CAB +∠ABD =120°,∴∠OAB +∠OBA =60°,∴∠AOB =180°-60°=120°;(2)在AB 上截取AE =AC ,∵∠CAO=∠EAO,AO=AO,∴△AOC≌△AOE(SAS),∴∠C=∠AEO,∵∠C+∠D=(180°-∠CAB-∠ABC)+(180°-∠ABD-∠BAD)=180°,∴∠AEO+∠D=180°,∵∠AEO+∠BEO=180°,∴∠BEO=∠D,又∠EBO=∠DBO,BO=BO,∴△OBE≌△OBD(AAS),∴BD=BE,又AC=AE,∴AC+BD=AE+BE=A B.【变式】如图(1)在△ABC中,∠ACB=90°,AC=BC,直线MN经过点C,且AD⊥MN于点D,BE⊥MN于点E.(1)求证:①△ADC≌△CEB;②DE=AD+BE.(2)当直线MN绕点C旋转到图(2)的位置时,DE、AD、BE又怎样的关系?并加以证明.【答案】(1)①证明见解析;②证明见解析;(2)DE=AD-BE,证明见解析.【详解】解:(1)①证明:∵AD⊥DE,BE⊥DE,∴∠ADC=∠BEC=90°,∵∠ACB=90°,∴∠ACD+∠BCE=90°,∠DAC+∠ACD=90°,∴∠DAC=∠BCE,在△ADC 和△CEB 中,CDA BEC DAC ECB AC BC ∠=∠⎧⎪∠=∠⎨⎪=⎩∴△ADC ≌△CEB (AAS ).②证明:由(1)知:△ADC ≌△CEB ,∴AD =CE ,CD =BE ,∵DC +CE =DE ,∴AD +BE =DE .(2)成立.证明:∵BE ⊥EC ,AD ⊥CE ,∴∠ADC =∠BEC =90°,∴∠EBC +∠ECB =90°,∵∠ACB =90°,∴∠ECB +∠ACE =90°,∴∠ACD =∠EBC ,在△ADC 和△CEB 中,ACD CBE ADC BEC AC BC ∠=∠⎧⎪∠=∠⎨⎪=⎩,∴△ADC ≌△CEB (AAS ),∴AD =CE ,CD =BE ,∴DE =EC -CD =AD -BE .题型六:尺规作图——利用角边角或角角边做三角形例6、已知三角形的两角及其夹边,求作这个三角形已知:∠α,∠β和线段c ,如图4-4-21所示.图4-4-21求作:△ABC ,使∠A =∠α,∠B =∠β,AB =c .作法:(1)作∠DAF =∠α;图4-4-224-4-23(2)在射线AF 上截取线段AB =c ;图4-4-24(3)以B 为顶点,以BA 为一边,在AB 的同侧作∠ABE =∠β,BE 交AD 于点C .△ABC 就是所求作的三角形.[点析] 我们这样作出的三角形是唯一的,依据是两角及其夹边分别相等的两个三角形全等. 例7.已知:角α,β和线段a ,如图4-4-29所示,求作:△ABC ,使∠A =∠α,∠B =∠β,BC =a .图4-4-29[解析] 本题所给条件是两角及其中一角的对边,可利用三角形内角和定理求出∠C ,再利用两角夹边作图. 解: 如图4-4-30所示:(1)作∠γ=180°-∠α-∠β;(2)作线段BC =a ;(3)分别以B ,C 为顶点,以BC 为一边作∠CBM =∠β,∠BCN =∠γ;(4)射线BM ,CN 交于点A .△ABC 就是所求作的三角形.图4-4-30【变式】(2022春·陕西·七年级陕西师大附中校考期中)尺规作图已知:α∠,∠β和线段a ,求作ABC ,使A α∠=∠,2B β∠=∠,AB a =.要求:不写作法,保留作图痕迹,标明字母.【详解】解:如图,△ABC即为所求..【过关检测】一、单选题A.带①去B.带②去C.带③去D.①②③都带去【答案】A【分析】根据全等三角形的判定可进行求解【详解】解:第①块不仅保留了原来三角形的两个角还保留了一边,则可以根据ASA来配一块一样的玻璃.故选:A.【点睛】此题主要考查了全等三角形的判定方法的开放性的题,要求学生将所学的知识运用于实际生活中,要认真观察图形,根据已知选择方法.≌过程中,先作2.(2023春·广东佛山·七年级校考期中)如图,在用尺规作图得到DBC ABCDBC ABC ∠=∠,再作DCB ACB ∠=∠,从而得到DBC ABC ≌,其中运用的三角形全等的判定方法是( )A .SASB .ASAC .AASD .SSS【答案】B 【分析】根据题意分析可得DBC ABC ∠=∠,DCB ACB ∠=∠,再加上公共边BC BC =,根据AAS ,即可判断DBC ABC ≌.【详解】解:∵得DBC ABC ∠=∠, BC BC =,DCB ACB ∠=∠,∴DBC ABC≌()ASA , 故选:B .【点睛】本题考查了作一个角等于已知角,全等三角形的判定,熟练掌握全等三角形的判定定理是解题的关键.3.(2023春·重庆沙坪坝·七年级重庆一中校考期末)如图,OC 平分AOB ∠,点P 是射线OC 上一点,PM OB ⊥于点M ,点N 是射线OA 上的一个动点,连接PN ,若6PM =,则PN 的长度不可能是( )【答案】D 【分析】如图所示,过点P 作PH OA ⊥于H ,证明POH POM △≌△得到6PH PM ==,由垂线段最短可知PN PH ≥,由此即可得到答案.【详解】解:如图所示,过点P 作PH OA ⊥于H ,∵PM OB ⊥,∴90PHO PMO ==︒∠∠,∵OC 平分AOB ∠,∴POH POM ∠=∠,又∵OP OP =,∴()AAS POH POM △≌△,∴6PH PM ==,由垂线段最短可知PN PH ≥,∵(264036=>,∴6,∴四个选项中,只有D 选项符合题意,故选:D .【点睛】本题主要考查了全等三角形的性质与判定,垂线段最短,实数比较大小,正确作出辅助线构造全等三角形是解题的关键. 4.(2023春·陕西咸阳·七年级统考期末)如图,AD BC ∥,ABC ∠的平分线BP 与BAD ∠的平分线AP 相交于点P ,作PE AB ⊥于点E ,若4PE =,则点P 到AD 与BC 的距离之和为( )A .4B .6C .8D .10【答案】C【分析】如图所示,过点P 作FG AD ⊥与F ,延长FP 交BC 于G ,先证明AD FG ⊥,由角平分线的定义得到EBP GBP =∠∠,进而证明EBP GBP △≌△得到4PG PE ==,同理可得4PF PE ==,则8FG PF PG =+=,由此即可得到答案.【详解】解:如图所示,过点P 作FG AD ⊥与F ,延长FP 交BC 于G ,∵AD BC ∥,∴AD FG ⊥,∵PE AB ⊥,∴90PFA PEA PEB PGB ====︒∠∠∠∠,∵BP 平分ABC ∠,∴EBP GBP =∠∠,又∵BP BP =,∴()AAS EBP GBP △≌△,∴4PG PE ==,同理可得4PF PE ==,∴8FG PF PG =+=,∴点P 到AD 与BC 的距离之和为8,故选C .【点睛】本题主要考查了平行线的性质,全等三角形的性质与判定,角平分线的定义,平行线间的距离等等,正确作出辅助线构造全等三角形是解题的关键. 5.(2023春·福建福州·七年级福建省福州第十六中学校考期末)如图,90C ∠=︒,点M 是BC 的中点,DM 平分ADC ∠,且8CB =,则点M 到线段AD 的最小距离为( )A .2B .3C .4D .5【答案】C 【分析】如图所示,过点M 作ME AD ⊥于E ,证明MDE MDC △≌△,得到ME MC =,再根据线段中点的定义得到142ME MC BC ===,根据垂线段最短可知点M 到线段AD 的最小距离为4.【详解】解:如图所示,过点M 作ME AD ⊥于E ,∴90MED C ==︒∠∠,∵DM 平分ADC ∠,∴MDE MDC =∠∠,又∵MD MD =,∴()AAS MDE MDC △≌△,∴ME MC =,∵点M 是BC 的中点,8CB =,∴142ME MC BC ===,∴点M 到线段AD 的最小距离为4,故选:C .【点睛】本题主要考查了全等三角形的性质与判定,角平分线的定义,垂线段最短等等,正确作出辅助线构造全等三角形是解题的关键.6.(2023·全国·八年级假期作业)如图,点E 在ABC 外部,点D 在ABC 的BC 边上,DE 交AC 于F ,若123∠=∠=∠,AE AC =,则( ).A .ABD AFE △≌△B .AFE ADC ≌△△ C .AFE DFC ≌△△D .ABC ADE △≌△ 【答案】D 【分析】首先根据题意得到BAC DAE ∠=∠,E C ∠=∠,然后根据ASA 证明ABC ADE △≌△.【详解】解:∵12∠=∠,∴12DAC DAC ∠+∠=∠+∠,∴BAC DAE ∠=∠,∵23∠∠=,AFE DFC ∠=∠,∴E C ∠=∠,∴在ABC 和ADE V 中,BAC DAE AC AEC E ∠=∠⎧⎪=⎨⎪∠=∠⎩, ∴()ASA ABC ADE ≌△△, 故选:D .【点睛】此题主要考查全等三角形的判定,解题的关键是熟知全等三角形的判定定理.7.(2023·浙江·八年级假期作业)小明不慎将一块三角形的玻璃摔碎成如图所示的四块(即图中标有1、2、3、4的四块)你认为将其中的哪一块带去,就能配一块与原来一样大小的三角形?应该带( )A .带①去B .带②去C .带③去D .①②③都带去【答案】B 【分析】本题应先假定选择哪块,再对应三角形全等判定的条件进行验证.【详解】解:①、③、④块玻璃不同时具备包括一完整边在内的三个证明全等的要素,所以不能带它们去, 只有第②块有完整的两角及夹边,符合ASA ,满足题目要求的条件,是符合题意的.故选:B .【点睛】本题主要考查三角形全等的判定,看这4块玻璃中哪个包含的条件符合某个判定.判定两个三角形全等的一般方法有:SSS 、SAS 、ASA 、AAS . 8.(2023春·浙江宁波·七年级校考期末)如图,ABC 的两条高AD 和BF 相交于点E ,8AD BD ==,10AC =,2AE =,则BF 的长为( )A .11.2B .11.5C .12.5D .13【答案】A 【分析】先证明BDE ADC △≌△,可得 6DE DC ==,14BC =,而10AC =,再由等面积法可得答案.【详解】解:∵ABC 的两条高AD 和BF 相交于点E ,∴90ADB ADC BFA ∠=∠=︒=∠,∵AEF BED ∠=∠,∴DBE DAC ∠=∠,∵8AD BD ==,2AE =,∴BDE ADC △≌△,6DE =,∴6DE DC ==,∴14BC =,而10AC =,由等面积法可得:111481022BF ⨯⨯=⨯⨯,解得:11.2BF =;故选A【点睛】本题考查的是三角形的内角和定理的应用,全等三角形的判定与性质,等面积法的应用,证明BDE ADC △≌△是解本题的关键. 9.(2023春·辽宁沈阳·七年级沈阳市第一二六中学校考阶段练习)如图,抗日战争期间,为了炸毁敌人的碉堡,需要测出我军阵地与敌人碉堡的距离.我军战士想到一个办法,他先面向碉堡的方向站好,然后调整帽子,使视线通过帽檐正好落在碉堡的底部点B ;然后转过身保持刚才的姿势,这时视线落在了我军阵地的点E 上;最后,他用步测的办法量出自己与E 点的距离,从而推算出我军阵地与敌人碉堡的距离,这里判定ABC DEF ≌△△的理由可以是( )A . SSSB . SASC . ASAD . AAA【答案】C 【分析】根据垂直的定义和全等三角形的判定定理即可得到结论.【详解】解:∵士兵的视线通过帽檐正好落在碉堡的底部点B ,然后转过身保持刚才的姿势,这时视线落在了我军阵地的点E 上,∴A D ∠=∠,∵AC BC ⊥,DF EF ^,∴90ACB DFE ∠=∠=︒,∵AC DF =,∴判定ABC DEF ≌△△的理由是ASA . 故选C .【点睛】本题主要考查了全等三角形的应用,分析题意找到相等的角和边判定三角形的全等是解题的关键.10.(2023春·四川达州·八年级统考期末)如图,已知BP 是ABC ∠的平分线,AP BP ⊥,若212cm BPC S =△,则ABC 的面积( )A .224cmB .230cmC .236cmD .不能确定【答案】A【分析】延长AP 交BC 于点C ,根据题意,易证()ASA ABP DBP ≌,因为APC △和DPC △同高等底,所以面积相等,根据等量代换便可得出2224cm ABC BPC S S ==.【详解】如图所示,延长AP ,交BC 于点D ,,∵AP BP ⊥,∴90APB DPB ∠=∠=︒,∵BP 是ABC ∠的角平分线,∴ABP DBP ∠=∠,在ABP 和DBP 中,ABP DBP BP BP APB DPB ∠=∠⎧⎪=⎨⎪∠=∠⎩, ∴()ASA ABP DBP ≌,∴AP DP =,∴ABP DBP S S =△△,∵APC △和DPC △同底等高,∴APC DPC S S =△,∴PBC DPB DPC ABP APC S S S S S =+=+△△△△,∴2224ABC BPC S S cm ==,故选:C .【点睛】本题考查了三角形的角平分线和全等三角形的判定,解题的关键是熟练运用三角形的角平分线和全等三角形的判定.二、填空题 11.(2023·浙江·八年级假期作业)如图,D 在AB 上,E 在AC 上,且B C ∠=∠,补充一个条件______后,可用“AAS ”判断ABE ACD ≌.【答案】BE CD =或AE AD =【分析】由于两个三角形已经具备B C ∠=∠,A A ∠=∠,故要找边的条件,只要不是这两对角的夹边即可.【详解】解:∵B C ∠=∠,A A ∠=∠,∴若用“AAS ”判断ABE ACD ≌,可补充的条件是BE CD =或AE AD =;故答案为:BE CD =或AE AD =.【点睛】本题考查了全等三角形的判定,熟知掌握判定三角形全等的条件是解题的关键.七年级期末)如图,在ABC 中, 【答案】ASA【分析】由AD BC ⊥、AD 平分BAC ∠、AD AD =可得出两个三角形对应的两个角及其夹边相等,于是可以利用ASA 判定这两个三角形全等.【详解】∵AD BC ⊥,∴90BDA CDA ︒=∠=∠.∵AD 平分BAC ∠,∴BAD ∠CAD =∠.在ABD △与ACD 中,BDA CDA AD AD BAD CAD ∠=∠⎧⎪=⎨⎪∠=∠⎩ ∴()ASA ABD ACD ≌.故答案为:ASA【点睛】本题考查了三角形全等的判定条件,解题的关键是找到两个三角形对应的边角相等. 13.(2023春·陕西榆林·七年级统考期末)如图,AB CD ⊥,且AB CD =,连接AD ,CE AD ⊥于点E ,BF AD ⊥于点F .若8CE =,5BF =,4EF =,则AD 的长为________.【答案】9【分析】只要证明(AAS)ABF CDE ≌,可得8AF CE ==,5BF DE ==,推出AD AF DF =+即可得出答案.【详解】解:∵AB CD ⊥,CE AD ⊥,BF AD ⊥,∴90AFB CED ∠=∠=︒,90A D ∠+∠=︒,90C D ∠=∠=︒,∴A C ∠=∠,∵AB CD =,∴(AAS)ABF CDE ≌,∴8AF CE ==,5BF DE ==,∵4EF =,∴()8549AD AF DF =+=+−=,故答案为:9.【点睛】本题考查全等三角形的判定与性质,解题的关键是正确寻找全等三角形解决问题,属于中考常考题型. 14.(2023春·山东枣庄·七年级统考期末)如图,A ,B 两个建筑物分别位于河的两岸,为了测量它们之间的距离,可以沿河岸作射线BF ,且使BF AB ⊥,在BF 上截取BC CD =,过D 点作DE BF ⊥,使E C A ,,在一条直线上,测得16DE =米,则A ,B 之间的距离为______米.【答案】16【分析】根据已知条件可得ABC EDC △≌△,从而得到DE AB =,从而得解.【详解】∵BF AB DE BF ⊥⊥,,∴90B EDC ∠=∠=°,∵90B EDC ∠=∠=,BC CD BCA DCE =∠=∠,,∴()ASA ABC EDC ≌△△,∴DE AB =.又∵16DE =米,∴16AB =米,即A B ,之间的距离为16米.【点睛】此题主要考查全等三角形的应用,解题的关键是熟知全等三角形的判定方法.15.(2023·广东茂名·统考一模)如图,点A 、D 、C 、F 在同一直线上,AB DE ∥,AD CF =,添加一个条件,使ABC DEF ≌△△,这个条件可以是______.(只需写一种情况)【答案】BC EF ∥或B E ∠=∠或BCA EFD ∠=∠或AB DE =(答案不唯一)【分析】先证明A EDF ∠=∠及AC DF =,然后利用全等三角形的判定定理分析即可得解.【详解】解∶BC EF ∥或B E ∠=∠或BCA EFD ∠=∠或AB DE =,理由是∶∵AB DE ∥,∴A EDF ∠=∠,∵AD CF =,∴AD CD CF CD +=+即AC DF =,当BC EF ∥时,有BCA EFD ∠=∠,则() ASA ABC DEF ≌, 当BCA EFD ∠=∠时,则() ASA ABC DEF ≌, 当B E ∠=∠时,则() AAS ABC DEF ≌, 当AB DE =时,则() SAS ABC DEF ≌,故答案为∶BC EF ∥或B E ∠=∠或BCA EFD ∠=∠或AB DE =.【点睛】本题考查了对全等三角形的判定定理的应用,掌握全等三角形的判定定理有SAS , ASA , AAS , SSS 是解题的关键. 16.(2023春·上海虹口·七年级上外附中校考期末)如图,有一种简易的测距工具,为了测量地面上的点M 与点O 的距离(两点之间有障碍无法直接测量),在点O 处立竖杆PO ,并将顶端的活动杆PQ 对准点M ,固定活动杆与竖杆的角度后,转动工具至空旷处,标记活动杆的延长线与地面的交点N ,测量点N 与点O 的距离,该距离即为点M 与点O 的距离.此种工具用到了全等三角形的判定,其判定理由是______.【答案】两个角及其夹边对应相等的两个三角形全等【分析】根据全等三角形的判定方法进行分析,即可得到答案.【详解】解:在POM 和PON △中,90OP OPPOM PON ⎪=⎨⎪∠=∠=︒⎩, ()ASA POM PON ∴≌,∴判定理由是两个角及其夹边对应相等的两个三角形全等,故答案为:两个角及其夹边对应相等的两个三角形全等.【点睛】本题考查了全等三角形的判定,熟练掌握全等三角形的判定方法是解题关键.【答案】 = 180BCA α∠+∠=︒【分析】①求出90BEC AFC ∠=∠=︒,CBE ACF ∠=∠,根据AAS 证BCE CAF ≌△△,推出BE CF =,CE AF =即可得出结果;②求出CBE ACF ∠=∠,由AAS 证BCE CAF ≌△△,推出BE CF =,CE AF =即可得出结果.【详解】解:①90BCA ∠=︒,90α∠=︒,90BCE CBE ∴∠+∠=︒,90BCE ACF ∠+∠=︒,CBE ACF ∴∠=∠,在BCE 和CAF V 中,BEC CFACB CA ⎪∠=∠⎨⎪=⎩,(AAS)BCE CAF ∴△≌△,BE CF ∴=,CE AF =,||||EF CF CE BE AF ∴=−=−,②α∠与BCA ∠应满足180BCA α∠+∠=︒,在BCE 中,180180CBE BCE BEC α∠+∠=︒−∠=︒−∠,180BCA α∠=︒−∠,BCA CBE BCE ∴∠=∠+∠,ACF BCE BCA ∠+∠=∠,CBE ACF ∴∠=∠,在BCE 和CAF V 中,CBE ACF BEC CFACB CA ∠=∠⎧⎪∠=∠⎨⎪=⎩,(AAS)BCE CAF ∴△≌△, BE CF ∴=,CE AF =,||||EF CF CE BE AF ∴=−=−,故答案为:=,180BCA α∠+∠=︒.【点睛】本题是三角形综合题,主要考查了全等三角形的判定与性质、三角形的面积计算、三角形的外角性质等知识;解题的关键是判断出BCE CAF ≌△△. ABC 的角平分线,过点【答案】4【分析】延长CE 与BA 的延长线相交于点F ,利用ASA 证明ABD △和ACF △全等,进而利用全等三角形的性质解答即可.【详解】解:如图,延长CE 与BA 的延长线相交于点F ,90EBF F ∠+∠=︒,90ACF F ∠+∠=︒,EBF ACF ∴∠=∠,在ABD △和ACF △中,EBF ACF AB ACBAC CAF ∠=∠⎧⎪=⎨⎪∠=∠⎩,()ASA ABD ACF ∴≌, BD CF ∴=,BD Q 是ABC ∠的平分线,EBC EBF ∴∠=∠.在BCE 和BFE △中,BE BECEB FEB ⎪=⎨⎪∠=∠⎩,()ASA BCE BFE ∴≌, CE EF ∴=,2CF CE ∴=,24BD CF CE ∴===.故答案为:4.【点睛】本题主要考查了全等三角形的性质和判定,理解题意、灵活运用全等三角形的判定与性质是解题的关键.三、解答题【答案】(1)见解析(2)5【分析】(1)首先根据垂直判定AB EF ∥,得到ABC F ∠=∠,再利用AAS 证明即可;(2)根据全等三角形的性质可得9AB CF ==,4BC EF ==,再利用线段的和差计算即可.【详解】(1)解:∵CD AB ⊥,EF CE ⊥,∴AB EF ∥,∴ABC F ∠=∠,在ABC 和CFE 中,ACB EAC CE ⎪∠=∠⎨⎪=⎩, ∴()AAS ABC CFE △△≌; (2)∵ABC CFE △△≌, ∴9AB CF ==,4BC EF ==,∴5BF CF BC =−=.【点睛】本题考查了全等三角形的判定和性质,平行线的判定和性质,解题的关键是找准条件,证明三角形全等. 20.(2023春·陕西西安·七年级西安市铁一中学校考期末)如图,A ,C ,D 三点共线,ABC 和CDE 落在AD 的同侧,AB CE ∥,BC DE =,B D ∠=∠.求证:AB CE AD +=.【答案】见解析【分析】证明()AAS ABC CDE ≌,得出AB CD =,BC CE =,即可证明结论.【详解】解:∵AB CE ∥,∴A DCE ∠=∠,∵B D ∠=∠,BC DE =,∴()AAS ABC CDE ≌,∴AB CD =,BC CE =,∴AB CE CD AC AD +=+=.【点睛】本题主要考查了平行线的性质,三角形全等的判定和性质,解题的关键是熟练掌握三角形全等的判定方法证明ABC CDE △≌△.21.(2022秋·八年级课时练习)已知αβ∠∠,和线段a (下图),用直尺和圆规作ABC ,使A B AB a αβ∠=∠∠=∠=,,.【答案】见解析 【分析】先作出线段AB a =,再根据作与已知角相等的角的尺规作图方法作DAB EBA αβ∠=∠∠=∠,即可得到答案.【详解】解:作法如下图.1.作一条线段AB a =.2.分别以A ,B 为顶点,在AB 的同侧作DAB EBA αβ∠=∠∠=∠,,DA 与EB 相交于点C .ABC 就是所求作的三角形.【点睛】本题主要考查了三角形的尺规作图,熟知相关作图方法是解题的关键.22.(2023春·全国·七年级专题练习)如图,已知ABC ,请根据“ASA”作出DEF ,使DEF ABC ≌.【答案】见解析【分析】先作MEN B ∠=∠,再在EM 上截取ED BA =,在EN 上截取EF BC =,从而得到DEF ABC ≌.【详解】解:如图,DEF 为所作.【点睛】本题考查了作图-复杂作图:解决此类题目的关键是熟悉基本几何图形的性质,结合几何图形的基本性质把复杂作图拆解成基本作图,逐步操作.也考查了全等三角形的判定. 23.(2023春·山西太原·七年级校考阶段练习)如图,点B 、F 、C 、E 在同一条直线上,已知FB CE =,AB DE ∥,ACB DFE ∠=∠,试说明:AC DF =.【答案】见解析【分析】利用ASA 定理证明三角形全等,然后利用全等三角形的性质分析求解.【详解】解:∵FB CE =,∴FB FC CE FC +=+,即BC EF =,∵AB DE ∥,∴B E ∠=∠,在ABC 和DEF 中B E BC EF ACB DFE ∠=∠⎧⎪=⎨⎪∠=∠⎩∴ABC DEF ≌△△, ∴AC DF =.【点睛】此题主要考查了全等三角形的判定,关键是掌握判定两个三角形全等的一般方法:SSS 、SAS 、ASA 、AAS 、HL .三角形全等的判定是中考的热点,一般以考查三角形全等的方法为主,判定两个三角形全等,先根据已知条件或求证的结论确定三角形,然后再根据三角形全等的判定方法,看缺什么条件,再去证什么条件.24.(2020秋·广东广州·八年级海珠外国语实验中学校考阶段练习)如图,已知:EC AC =,BCE DCA ∠=∠,A E ∠=∠.求证:AB ED =.【答案】见解析【分析】先求出ACB ECD ∠=∠,再利用“角边角”证明ABC 和EDC △全等,然后根据全等三角形对应边相等证明即可.【详解】证明:∵BCE DCA ∠=∠,∴BCE ACE DCA ACE ∠+∠=∠+∠,即ACB ECD ∠=∠.在ABC 和EDC △中,∵ACB ECD AC ECA E ∠=∠⎧⎪=⎨⎪∠=∠⎩,∴()ASA ABC EDC ≌△△.∴AB ED =.【点睛】本题考查了全等三角形的判定和性质,熟练掌握全等三角形的判定定理是解题的关键.25.(2023春·福建宁德·七年级校考阶段练习)如图,点B ,F ,C ,E 在直线l 上(F ,C 之间不能直接测量),点A ,D 在l 异侧,测得AB DE =,AB DE ∥,A D ∠=∠.(1)求证:ABC DEF ≌△△; (2)若10BE =,3BF =,求FC 的长度.【答案】(1)见解析(2)4【分析】(1)由AB DE ∥,得ABC DEF ∠=∠,而AB DE =,A D ∠=∠,即可根据全等三角形的判定定理“ASA ”证明ABC DEF ≌△△; (2)根据全等三角形的性质得BC EF =,则3BF CE ==,即可求得FC 的长度.【详解】(1)解:证明:∵AB DE ∥,∴ABC DEF ∠=∠,在ABC 和DEF 中,A D AB DE ABC DEF ∠=∠⎧⎪=⎨⎪∠=∠⎩ ∴()ASA ABC DEF ≌△△; (2)解:由(1)知()ASA ABC DEF ≌△△,∴BC EF =, ∴BF FC CE FC +=+,∴3BF CE ==,∵10BE =,∴10334FC BE BF CE =−−=−−=,∴FC 的长度是4.【点睛】此题重点考查全等三角形的判定与性质、平行线的性质等知识,根据平行线的性质证明ABC DEF ∠=∠是解题的关键. 26.(2023·浙江·八年级假期作业)如图,ABC 中,BD CD =,连接BE ,CF ,且BE CF ∥.(1)求证:BDE CDF ≌;(2)若15AE =,8AF =,试求DE 的长.【答案】(1)证明见解析(2)72【分析】(1)根据平行线的性质可得BED CFD Ð=Ð,根据全等三角形的判定即可证明;(2)根据全等三角形的性质可得DE DF =,即可求得.【详解】(1)证明:∵BE CF ∥,∴BED CFD Ð=Ð,∵BDE CDF ∠=∠,BD CD =,∴()AAS BDE CDF ≌;(2)由(1)结论可得DE DF =,∵1587EF AE AF =−=−=,∴72DE =.【点睛】全等三角形的判定和性质,熟练掌握平行线的性质,全等三角形的判定和性质是解题的关键. 27.(2023春·江西鹰潭·七年级校考阶段练习)将两个三角形纸板ABC 和DBE 按如图所示的方式摆放,连接DC .已知DBA CBE ∠=∠,BDE BAC ∠=∠,AC DE DC ==.(1)试说明ABC DBE ≌△△.(2)若72ACD ∠=︒,求BED ∠的度数.【答案】(1)见解析(2)36BED ∠=︒【分析】(1)利用AAS 证明三角形全等即可;(2)全等三角形的性质,得到BED BCA ∠=∠,证明()SSS DBC ABC ≌,得到1362BCD BCA ACD ∠=∠=∠=︒,即可得解.【详解】(1)解:因为DBA CBE ∠=∠,所以DBA ABE CBE ABE ∠+∠=∠+∠,即DBE ABC ∠=∠.在ABC 和DBE 中,ABC DBE BAC BDEAC DE ∠=∠⎧⎪∠=∠⎨⎪=⎩, 所以()AAS ABC DBE ≌. (2)因为ABC DBE ≌△△, 所以BD BA =,BCA BED ∠=∠.在DBC △和ABC 中,DC AC CB CBBD BA =⎧⎪=⎨⎪=⎩, 所以()SSS DBC ABC ≌, 所以1362BCD BCA ACD ∠=∠=∠=︒,所以36BED BCA ∠=∠=︒.【点睛】本题考查全等三角形的判定和性质.解题的关键是证明三角形全等. 28.(2023春·河南驻马店·七年级统考期末)如图,线段AD 是ABC 的中线,分别过点B 、C 作AD 所在直线的垂线,垂足分别为E 、F .(1)请问BDE 与CDF 全等吗?说明理由;(2)若ACF △的面积为10,CDF 的面积为6,求ABE 的面积.【答案】(1)BDE CDF ≌△△,见解析 (2)22【分析】(1)利用AAS 证明三角形全等即可.(2)根据中线性质,得到,ABD ACD ACF CDF CDF ==+=△△△△△BDE △S S S S S S ,结合ABEABD BDE S S S =+△△△计算即可. 【详解】(1)BDE CDF ≌△△,理由如下: ∵AD 是ABC 的中线,∴BD CD =,∵BE AE ⊥,CF AE ⊥,∴90BED CFD ∠=∠=︒,在BDE 和CDF 中,BED CFD BDE CDFBD CD ∠=∠⎧⎪∠=∠⎨⎪=⎩∴()AAS BDE CDF ≌.(2)∵10ACF S =△,6CDF S =△,BDE CDF ≌,∴10616ACD ACF CDF S S S =+=+=△△△,6BDE CDF S S ==,∵BD CD =∴ABD △和ACD 是等底同高的三角形∴16ABD ACD S S ==△△∴16622ABE ABD BDE S S S =+=+=△△△.【点睛】本题考查了三角形全等的判定和性质,中线的性质,三角形面积的计算,熟练掌握三角形全等的判定和性质,中线的性质是解题的关键. 29.(2019·七年级单元测试)(1)求证:等边三角形内的任意一点到两腰的距离之和等于定长.(提示:添加辅助线证明)(2)如图所示,在三角形ABC 中,点D 是三角形内一点,连接DA 、DB 、DC ,若,=∠=∠AB AC ADB ADC ,求证:AD 平分BAC ∠.【答案】(1)详见解析;(2)详见解析.【分析】(1)已知点P 是等边三角形ABC 内的任意一点,过点P 分别作三边的垂线,分别交三边于点D 、点E 、点F .求证PD PE PF ++为定长,即可完成证明;(2)(面积法)过点A 作AE BD ⊥交BD 延长线于点E ,再过点A 作AF CD ⊥交CD 延长线于点F.因为ADB ADC ∠=∠,所以ADE ADF ∠=∠,因此(AAS)ADF ADE ≅,得到AF AE =.进而AFC AEB ≅,得到ABD ACD ∠=∠,因此BAD CAD ∠=∠,即AD 平分BAC ∠.【详解】(1) 已知:等边如图三角形ABC ,P 为三角形ABC 内任意一点,PD ⊥AB, PF ⊥AC, PE ⊥BC, 求证:PD+PE+PF 为定值.证明:如图:过点A 作AG BC ⊥,垂足为点G ,分别连接AP 、BP 、CP .∵ABC ABP BCP CAP S S S S =++, ∴11112222BC AG BC PE AC PF AB PD =++又∵BC=AB=AC∴AG=PE+PF+PD,即PD PE PF AG ++=定长.∴等边三角形内的任意一点到两腰的距离之和等于定长.(2)过点A 作AE BD ⊥交BD 延长线于点E ,再过点A 作AF CD ⊥交CD 延长线于点F.∵ADB ADC ∠=∠,∴ADE ADF ∠=∠,又∵AD=AD∴(AAS)ADF ADE ≅,∴AF AE =∴AFC AEB ≅,∴ABD ACD ∠=∠,∴BAD CAD ∠=∠,即AD 平分BAC ∠.【点睛】本题考查了等边三角形的性质和全等三角形的性质和判定,其中做出辅助线是解答本题的关键.。
11.2三角形全等的判定(HL)练习题及答案

11.2三角形全等的判定(HL)◆随堂检测1. 如图,AC=AD,∠C,∠D是直角,你能说明BC与BD相等吗?2.如图,两根长相等的绳子,一端系在旗杆上,另一端分别固定在地面的两个木桩上,两根木桩到旗杆底部的距离相等吗?请说明理由。
3. 如图,已知AD⊥BE,垂足C是BE的中点,AB=DE.求证:AB//DE.◆典例分析CDA B例:已知△ABC和△A′B′C′中,AB=A′B′,AC=A′C′,如 AD、A′D′分别是BC、B′C′边上的高,且 AD=A′D′.问△ABC与△A′B′C′是否全等?如果全等,给出证明.如果不全等,请举出反例.错解:这两个三角形全等.证明如下:如图1,在Rt△ABD和 Rt△A′B′D′中,∵AB=A′B′,AD=A′D′∴Rt△ABD≌Rt△A′B′D′.∴BD=B′D′同理可证 DC=D′C′,∴BC=B′C′在△ABC和△A′B′C′中,∵AB=A′B′,AC=A′C′,BC=B′C′,∴△ABC≌△A′B′C′.评析:这两个三角形不一定全等.当这两个三角形均为钝角(或锐角)三角形时全等;若一个是锐角三角形,一个是钝角三角形时就不可能全等.如图2,虽有AB=A′B′,AC=A′C′,但BC≠B′C′,因此这两个三角形不全等.◆课下作业●拓展提高4.把下列说明Rt△ABC≌Rt△DEF的条件或根据补充完整.(1) _______,∠A=∠D ( ASA )(2) AC=DF,________ (SAS)(3) AB=DE,BC=EF ( )(4) AC=DF, ______ ( HL )(5) ∠A=∠D, BC=EF ( )(6) ________,AC=DF ( AAS )5.小明既无圆规,又无量角器,只有一个三角板,他是怎样画角平分线的呢?他的具体做法如下:在已知∠AOB的两边上,分别取OM=ON,再分别过点M、N作OA、OB的垂线交点为P,画射线OP.则OP平分∠AOB。
三角形全等的判定方法压轴题五种模型全攻略(解析版)

三角形全等的判定方法压轴题五种模型全攻略【考点导航】目录【典型例题】【考点一用SAS证明两三角形全等】【考点二用ASA证明两三角形全等】【考点三用AAS证明两三角形全等】【考点四用SSS证明两三角形全等】【考点五添一个条件使两三角形全等】【过关检测】【典型例题】【考点一用SAS证明两三角形全等】1(2023春·江苏苏州·七年级校联考阶段练习)如图,在△ABC中,AC>AB,射线AD平分∠BAC,交BC 于点E,点F在边AB的延长线上,AF=AC,连接EF.(1)求证:△AEC≌△AEF.(2)若∠AEB=50°,求∠BEF的度数.【答案】(1)证明见解析(2)80°【分析】(1)由射线AD平分∠BAC,可得∠CAE=∠FAE,进而可证△AEC≌△AEF SAS;(2)由△AEC≌△AEF SAS,可得∠C=∠F,由三角形外角的性质可得∠AEB=∠CAE+∠C=50°,则∠FAE+∠F=50°,根据∠FAE+∠F+∠AEB+∠BEF=180°,计算求解即可.【详解】(1)证明:射线AD平分∠BAC,∴∠CAE=∠FAE,在△AEC和△AEF中,∵AC=AF∠CAE=∠FAEAE=AE,∴△AEC≌△AEF SAS;(2)解:∵△AEC≌△AEF SAS,∴∠C =∠F ,∵∠AEB =∠CAE +∠C =50°,∴∠FAE +∠F =50°,∵∠FAE +∠F +∠AEB +∠BEF =180°,∴∠BEF =80°,∴∠BEF 为80°.【点睛】本题考查了角平分线,全等三角形的判定与性质,三角形外角的性质,三角形内角和定理.解题的关键在于对知识的熟练掌握与灵活运用.【变式训练】1(2023春·云南昭通·九年级校考阶段练习)如图,点A 、C 、F 、D 在同一直线上,AF =DC ,∠A =∠D ,AB =DE .求证:△ABC ≌△DEF.【答案】见解析【分析】由AF =CD ,可求得AC =DF ,利用SAS 可得出结论.【详解】解:∵ AF =CD ,∴AF -FC =CD -FC ,即AC =DF ,在△ABC 和△DEF 中,AB =DE∠A =∠D AC =DF,∴△ABC ≌△DEF (SAS ).【点睛】本题主要考查全等三角形的判定,掌握全等三角形的判定方法是解题的关键.2(2023春·四川成都·七年级统考期末)如图在△ABC 中,D 是BC 边上的一点,AB =DB ,BE 平分∠ABC ,交AC 边于点E ,连接DE.(1)求证:△ABE ≌△DBE ;(2)若∠A =100°,∠C =40°,求∠DEC 的度数.【答案】(1)证明见解析(2)60°【分析】(1)根据BE 平分∠ABC ,可得∠ABE =∠DBE ,进而利用SAS 证明△ABE ≌△DBE 即可;(2)根据全等三角形的性质可得∠BDE =∠A =100°,再由三角形外角的性质即可求解.【详解】(1)解:∵BE 平分∠ABC ,∴∠ABE =∠DBE .∵AB=DB,BE=BE,∴△ABE≌△DBE SAS;(2)解:∵△ABE≌△DBE,∴∠BDE=∠A=100°,∴∠DEC=∠BDE-∠C=60°.【点睛】本题主要考查了全等三角形的判定和性质,三角形外角的性质,熟练掌握全等三角形的判定和性质定理是解题的关键.3(2023春·江苏泰州·七年级统考期末)如图,在△ABC和△ADE中,AB=AC,AD=AE,∠BAC=∠DAE=90°,连接BD、CE.(1)求证:△ABD≌△ACE.(2)图中BD和CE有怎样的关系?试证明你的结论.【答案】(1)见详解(2)见详解【分析】(1)先证明∠BAD=∠EAC,又因为AB=AC,AD=AE,即可求出三角形全等;(2)根据△ABD≌△ACE,得到∠ACE=∠ABD,进而证得∠ABD+∠DBC+∠ACB=90°,等量代换得∠ACE+∠DBC+∠ACB=90°即∠ECB+∠DBC=90°,再利用内角和,即可证明垂直.【详解】(1)解:∵∠BAC=∠DAE=90°∴∠BAC+∠CAD=∠DAE+∠CAD∴∠BAD=∠EAC∵AB=AC,AD=AE∴△ABD≌△ACE.(2)解:如图,设BD和CE交点为F∵△ABD≌△ACE∴∠ACE=∠ABD∵∠BAC=90°∴∠ABD+∠DBC+∠ACB=90°∴∠ACE+∠DBC+∠ACB=90°即∠ECB+∠DBC=90°∴∠BFC=180°-∠ECB+∠DBC=90°∴BD⊥CE.【点睛】此题考查全等三角形的判定和性质,和角与角之间关系,解题的关键是根据SAS三角形全等.4(2023·江苏南通·统考一模)如图,点A,B,C,D在同一条直线上,AB=CD=13BC,AE=DF,AE∥DF.(1)求证:△AEC ≌△DFB ;(2)若S △AEC =6,求四边形BECF 的面积.【答案】(1)见解析(2)9【分析】(1)由AE ∥DF ,得∠A =∠D ,进一步证得AC =DB ,根据边角边求证△AEC ≌△DFB SAS ;(2)以AC 为底作EH 为高,则S △AEC =12EH ∙AC ,S △BCE =12EH ·BC ,由AB =CD =13BC ,求得S △BEC =34S △AEC=4.5;求证△BEC ≌△CFB SAS ,得S △BEC =S △CFB ,所以S 四边形BECF =2S △BEC =9.【详解】(1)证明:∵AE ∥DF ,∴∠A =∠D ,∵AB =CD ,∴AC =DB ,在△AEC 和△DFB 中,AE =DF∠A =∠DAC =DB∴△AEC ≌△DFB SAS ;(2)解:在△AEC 中,以AC 为底作EH 为高,∴S △AEC =12EH ∙AC ,S △BCE =12EH ∙BC ,∵AB =CD =13BC ,∴AC =43BC ,∵S △AEC =6,∴S △BEC =34S △AEC =4.5,∵△AEC ≌△DFB ,∴∠ACE =∠DBF ,EC =FB ,在△BEC 和△CFB 中,EC =FB∠BCE =∠CBF BC =CB,∴△BEC ≌△CFB SAS ,∴S △BEC =S △CFB ,∴S 四边形BECF =2S △BEC =9.【点睛】本题考查平行的性质,全等三角形的判定和性质,三角形面积计算;能够灵活运用全等三角形性质是解题的关键.【考点二用ASA 证明两三角形全等】1(2023春·广东惠州·八年级校考期中)如图,BC ∥EF ,点C ,点F 在AD 上,AF =DC ,∠A =∠D .求证:△ABC ≌△DEF.【答案】见解析【分析】首先根据平行线的性质可得∠ACB =∠DFE ,利用等式的性质可得AC =DF ,然后再利用ASA 判定△ABC ≌△DEF 即可.【详解】证明:∵BC ∥EF ,∴∠ACB =∠DFE ,∵AF =DC ,∴AF +CF =DC +CF ,即AC =DF ,在△ABC 和△DEF 中,∠A =∠DAC =DF ∠ACB =∠DFE,∴△ABC ≌△DEF ASA .【点睛】本题考查三角形全等的判定方法,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.【变式训练】1(2023·校联考一模)如图,点A 、D 、B 、E 在同一条直线上,若AD =BE ,∠A =∠EDF ,∠E =∠ABC .求证:AC =DF.【答案】见解析【分析】由AD =BE 知AB =ED ,结合∠A =∠EDF ,∠E =∠ABC ,依据“ASA ”可判定△ABC ≌△DEF ,依据两三角形全等对应边相等可得AC =DF .【详解】证明:∵AD =BE ,∴AD +BD =BE +BD ,即AB =ED ,在△ABC 和△DEF 中,∠ABC =∠EAB =ED ∠A =∠EDF,∴△ABC≌△DEF ASA,∴AC=DF.【点睛】本题主要考查全等三角形的判定与性质,掌握全等三角形的判定与性质是解题的关键.2(2023·浙江温州·温州市第八中学校考三模)如图,在△ABC和△ECD中,∠ABC=∠EDC=90°,点B为CE中点,BC=CD.(1)求证:△ABC≌△ECD.(2)若CD=2,求AC的长.【答案】(1)见解析(2)4,见解析【分析】(1)根据ASA判定即可;(2)根据△ABC≌△ECD ASA和点B为CE中点即可求出.【详解】(1)证明:∵∠ABC=∠EDC=90°,BC=CD,∠C=∠C,∴△ABC≌△ECD ASA(2)解:∵CD=2,△ABC≌△ECD ASA,∴BC=CD=2,AC=CE,∵点B为CE中点,∴BE=BC=CD=2,∴CE=4,∴AC=4;【点睛】本题考查全等三角形的判定和性质,掌握全等三角形的判定条件是解答本题的关键.【考点三用AAS证明两三角形全等】1(2023·广东汕头·广东省汕头市聿怀初级中学校考三模)如图,点E在△ABC边AC上,AE=BC,BC∥AD,∠CED=∠BAD.求证:△ABC≌△DEA【答案】证明见解析【分析】根据平行线的性质,得到∠DAC=∠C,再根据三角形外角的性质,得出∠D=∠BAC,即可利用“AAS”证明△ΑBC≌△DEA.【详解】证明:∵BC∥AD,∴∠DAC=∠C,∵∠CED=∠BAD,∠CED=∠D+∠DAC,∠BAD=∠DAC+∠BAC,∴∠D=∠BAC,在△ABC和△DEA中,∠BAC=∠D ∠C=∠DAC BC=AE,∴△ΑBC≌△DEA AAS.【点睛】本题考查了全等三角形的判定,平行线的性质,三角形外角的性质,熟练掌握全等三角形的判定定理是解题关键.【变式训练】1(2023·浙江温州·统考二模)如图,AB=BD,DE∥AB,∠C=∠E.(1)求证:△ABC≅△BDE.(2)当∠A=80°,∠ABE=120°时,求∠EDB的度数.【答案】(1)见解析(2)40°【分析】(1)根据平行线的性质,利用三角形全等的判定定理即可证明;(2)根据三角形全等的性质和平行线的性质即可求解【详解】(1)解:∵DE∥AB,∴∠BDE=∠ABC,又∵∠E=∠C,BD=AB,∴△ABC≅△BDE.(2)解:∵∠A=80°,△ABC≅△BDE,∴∠A=∠BDE=80°,∵∠ABE=120°,∴∠ABD=40°,∵DE∥AB,∴∠EDB=40°.【点睛】本题考查了平行线的性质,三角形全等的判定和性质,熟练掌握各知识点,利用好数形结合的思想是解本题的关键.2(2023秋·八年级课时练习)如图,已知点C是线段AB上一点,∠DCE=∠A=∠B,CD=CE.(1)求证:△ACD ≌△BEC ;(2)求证:AB =AD +BE .【答案】(1)见解析(2)见解析【分析】(1)由∠DCE =∠A 得∠D +∠ACD =∠ACD +∠BCE ,即∠D =∠BCE ,从而即可证得△ACD ≌△BEC ;(2)由△ACD ≌△BEC 可得AD =BC ,AC =BE ,即可得到AC +BC =AD +BE ,从而即可得证.【详解】(1)证明:∵∠DCE =∠A ,∴∠D +∠ACD =∠ACD +∠BCE ,∴∠D =∠BCE ,在△ACD 和△BEC 中,∠A =∠B∠D =∠BCE CD =EC,∴△ACD ≌△BEC AAS ;(2)解:∵△ACD ≌△BEC ,∴AD =BC ,AC =BE ,∴AC +BC =AD +BE ,∴AB =AD +BE .【点睛】本题主要考查了全等三角形的判定与性质,熟练掌握全等三角形的判定与性质是解题的关键.【考点四用SSS 证明两三角形全等】1(2023·云南玉溪·统考三模)如图,点B ,E ,C ,F 在一条直线上,AB =DF ,AC =DE ,BE =CF ,求证:△ABC ≌△DFC.【答案】见解析【分析】根据题意,运用“边边边”的方法证明三角形全等.【详解】证明:∵BE =CF ,∴BE +CE =CF +CE ,即BC =EF ,在△ABC 和△DFE 中,AB =DFAC =DEBC =FE∴△ABC ≌△DFE (SSS ).【点睛】本题主要考查三角形全等的判定,掌握全等三角形的判定方法解题的关键.【变式训练】1(2023·云南·统考中考真题)如图,C 是BD 的中点,AB =ED ,AC =EC .求证:△ABC ≌△EDC.【答案】见解析【分析】根据C 是BD 的中点,得到BC =CD ,再利用SSS 证明两个三角形全等.【详解】证明:∵C 是BD 的中点,∴BC =CD ,在△ABC 和△EDC 中,BC =CDAB =ED AC =EC,∴△ABC ≌△EDC SSS 【点睛】本题考查了线段中点,三角形全等的判定,其中对三角形判定条件的确定是解决本题的关键.2(2023春·全国·七年级专题练习)如图,已知∠E =∠F =90°,点B ,C 分别在AE ,AF 上,AB =AC ,BD =CD.(1)求证:△ABD ≌△ACD ;(2)求证:DE =DF .【答案】(1)见解析(2)见解析【分析】(1)直接根据SSS 证明即可.(2)根据(1)得∠EAD =∠FAD ,然后证明△AED ≌△AFD 即可.【详解】(1)解:证明:在△ABD 和△ACD 中,AB =ACAD =AD BD =CD∴△ABD ≌△ACD (SSS ).(2)解:由(1)知△ABD ≌△ACD (SSS ),∴∠EAD =∠FAD ,在△AED和△AFD中,∠E=∠F∠EAD=∠FAD AD=AD∴△AED≌△AFD(AAS),∴DE=DF.【点睛】本题考查了全等三角形的性质与判定,熟记全等三角形的性质与判定是解题关键.【考点五添一个条件使两三角形全等】1(2023春·宁夏银川·七年级校考期末)如图,在△ABC和△FED中,AD=FC,∠A=∠F,要使△ABC≌△FED,需添加的一个条件是.【答案】AB=EF(∠B=∠E或∠ACB=∠FDE答案不唯一)【分析】要使△ABC≌△FED,现有一边一角分别对应相等,还少一个条件,可结合图形选择利用求解即可.【详解】解:∵AD=FC,∴AC=FD又∵∠A=∠F,∴添加AB=EF,利用SAS可以证明△ABC≌△FED;添加∠B=∠E,利用AAS可以证明△ABC≌△FED;添加∠ACB=∠FDE,利用ASA可以证明△ABC≌△FED故答案为:AB=EF(∠B=∠E或∠ACB=∠FDE(.【点睛】本题考查三角形全等的判定方法;判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.添加时注意:AAA、SSA不能判定两个三角形全等,不能添加,根据已知结合图形及判定方法选择条件是正确解答本题的关键.【变式训练】1(2023·北京大兴·统考二模)如图,点B,E,C,F在一条直线上,AC∥DF,BE=CF,只需添加一个条件即可证明△ABC≌△DEF,这个条件可以是(写出一个即可).【答案】AC=DF或∠A=∠D或∠ABC=∠DEF或AB∥DE(答案不唯一).【分析】根据SAS,AAS或ASA添加条件即可求解.【详解】解:∵AC∥DF,∴∠ACB=∠DFE,∵BE=CF,∴BE+EC=CF+EC,即BC=EF,则有边角AS两个条件,要添加一个条件分三种情况,(1)根据“SAS”,则可添加:AC=DF,(2)根据“ASA”,则可添加:∠ABC=∠DEF或AB∥DE,(3)根据“AAS”,则可添加:∠A=∠D,故答案为:AC=DF或∠ABC=∠DEF或AB∥DE或∠A=∠D(答案不唯一).【点睛】本题考查了全等三角形的判定,解此题的关键是熟练掌握全等三角形的几种判断方法.2(2023春·山东青岛·七年级统考期末)如图,点E,F在BC上,BE=CF,∠AFB=∠DEC,请你添加一个条件(不添加字母和辅助线),使得△ABF≌△DCE,你添加的条件是.【答案】AF=DE或∠ABF=∠DCE或∠A=∠D【分析】本题要判定△ABF≌△DCE,已知∠AFB=∠DEC,由BE=CF可得BF=CE,那么只需添加一个条件即可.添边可以是AF=DE或添角可以是∠ABF=∠DCE或∠A=∠D.【详解】解:所添加条件为:AF=DE或∠ABF=∠DCE或∠A=∠D,∵BE=CF,∴BE+EF=CF+EF,即BF=CE,添加:AF=DE,在△ABF和△DCE中,AF=DE∠AFB=∠DECBF=CE,∴△ABF≌△DCE SAS;添加:∠ABF=∠DCE,在△ABF和△DCE中,∠ABF=∠DCEBF=CE∠AFB=∠DEC,∴△ABF≌△DCE ASA添加:∠A=∠D,在△ABF和△DCE中,∠A=∠D∠AFB=∠DECBF=CE,∴△ABF≌△DCE AAS.故答案为:AF=DE或∠ABF=∠DCE或∠A=∠D.【点睛】本题考查三角形全等的判定方法,解题的关键是掌握判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.3(2023秋·八年级课前预习)如图,AB=AC,D,E分别是AB,AC上的点,要使△ABE≌△ACD,则还需添加的条件是.(只需填写一个合适的条件即可,图中不能再添加其他点或线)【答案】AE=AD或∠B=∠C或∠AEB=∠ADC(答案不唯一)【分析】根据全等三角形的判定方法即可求解.【详解】解:①∵AB=AC,∠A=∠A,AE=AD,∴△ABE≌△ACD(SAS),∴添加的条件为AE=AD;②∵∠B=∠C,AB=AC,∠A=∠A,∴△ABE≌△ACD(ASA),∴添加的条件为∠B=∠C;③∵∠A=∠A,∠AEB=∠ADC,AB=AC,∴△ABE≌△ACD(ASA),∴添加的条件为∠AEB=∠ADC;综上所述,添加的条件为AE=AD或∠B=∠C或∠AEB=∠ADC,故答案为:AE=AD或∠B=∠C或∠AEB=∠ADC(答案不唯一).【点睛】本题主要考查全等三角形的判定,掌握以上知识是解题的关键.【过关检测】一、单选题1(2023春·四川达州·七年级四川省大竹中学校考期末)如图,已知BE=DF,AF∥CE,不能使△ABF≌△CDE的是()A.BF=DEB.AF=CEC.AB∥CDD.∠A=∠C【答案】A【分析】根据BE =DF ,可得BF =DE ,根据AF ∥CE ,可得∠AFE =∠CEF ,由等角的补角相等可得∠AFB =∠CED ,然后根据全等三角形的判定定理逐一判断即可.【详解】解:∵BE =DF ,∴BF =DE ,∵AF ∥CE ,∴∠AFE =∠CEF ,∴∠AFB =∠CED .A 、添加BF =DE 时,不能判定△ABF ≌△CDE ,故选项符合题意;B 、添加AF =CE ,根据SAS ,能判定△ABF ≌△CDE ,故选项不符合题意;C 、由AB ∥CD 可得∠B =∠D ,所以添加AB ∥CD ,根据ASA ,能判定△ABF ≌△CDE ,故选项不符合题意;D 、添加∠A =∠C ,根据AAS ,能判定△ABF ≌△CDE ,故选项不符合题意;故选:A .【点睛】本题重点考查了三角形全等的判定定理,普通两个三角形全等共有四个定理,即AAS 、ASA 、SAS 、SSS ,直角三角形可用HL 定理,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.2(2023秋·河南漯河·八年级校考期末)如图,∠A =∠B ,AE =BE ,点D 在AC 边上,∠1=∠2,AE 和BD 相交于点O ,若∠1=42°,则∠BDE 的度数为()A.71°B.69°C.67°D.65°【答案】B【分析】证明△BED ≌△AEC ,得到DE =CE ,∠C =∠BDE 等边对等角,求出∠C 的度数,即可.【详解】解:∵∠A =∠B ,∠BOE =∠AOD ,∴∠2=∠3,∵∠1=∠2,∴∠1=∠3,∴∠BED =∠AEC ,又AE =BE ,∴△BED ≌△AEC ,∴DE =CE ,∠C =∠BDE ,∴∠CDE =∠C =12180°-∠1 =69°,∴∠BDE =69°.【点睛】本题考查全等三角形的判定和性质,等腰三角形的判定和性质.解题的关键是证明三角形全等.3(2023春·辽宁丹东·八年级校考期中)如图,在△PAB中,PA=PB,M,N,K分别是PA,PB,AB上的点,且AM=BK,BN=AK,若∠MKN=42°,则∠P的度数为()A.42°B.74°C.84°D.96°【答案】D【分析】根据等腰三角形的性质得出两个底角相等,根据三角形全等的判定定理得出∠AMK=∠BKN,根据三角形的外角性质得出∠A的度数,即可得答案.【详解】解:∵PA=PB,∴∠A=∠B,∵AM=BK,BN=AK,∴△AMK≌△BKN,∴∠AMK=∠BKN,∵∠MKB=∠A+∠AMK=∠MKN+∠BKN,∴∠A=∠MKN=42°,∴∠P=180°-2×42°=96°.故选:D.【点睛】本题考查等腰三角形的性质、全等三角形的判定与性质、三角形内角和定理及三角形外角性质,熟练掌握相关判定定理及性质是解题关键.二、填空题4(2023春·山东青岛·七年级统考期末)如图,∠l=∠2,现要添加一个条件使△ABD≌△ACD,可以添加.(只添一个即可).【答案】CD=BD(答案不唯一)【分析】根据三角形全等的判定方法进行解答即可.【详解】解:∵∠l=∠2,∴180°-∠1=180°-∠2,即∠ADC =∠ADB ,∵AD =AD ,∴添加条件CD =BD ,根据SAS 证明△ABD ≌△ACD ;添加条件∠C =∠B ,根据AAS 证明△ABD ≌△ACD ;添加条件∠CAD =∠BAD ,根据ASA 证明△ABD ≌△ACD .故答案为:CD =BD (答案不唯一).【点睛】本题主要考查了三角形全等的判定,解题的关键是熟练掌握三角形全等的判定方法,SAS ,AAS ,ASA ,HL ,SSS .5(2023秋·湖南娄底·八年级统考期末)如图,∠ACB =90°,AC =BC ,BE ⊥CE 于E ,AD ⊥CE 于D .下面四个结论:①∠ABE =∠BAD ;②△CBE ≌△ACD ;③AB =CE ;④AD -BE =DE ,其中正确的有.【答案】①②④【分析】由BE ⊥CE 于E ,AD ⊥CE 于D ,得BE ∥AD ,则∠ABE =∠BAD ,可判断①正确;根据“同角的余角相等”推导出∠BCE =∠CAD ,即可证明△CBE ≌△ACD ,可判断②正确;由垂线段最短可证明AB >BC ,BC >CE ,则AB >CE ,可判断③错误;由CE =AD ,BE =CD ,且CE -CD =DE ,得AD -BE =DE ,可判断④正确,于是得到问题的答案.【详解】∵BE ⊥CE ,AD ⊥CE ,∴AD ∥BE ,∴∠ABE =∠BAD ,故①正确;∵∠E =∠ADC =∠ACB =90°,∴∠BCE =∠CAD =90°-∠ACD ,在△CBE 和△ACD 中,∠E =∠ADC∠BCE =∠CAD BC =CA,∴△CBE ≌△ACD AAS ,故②正确;∵BC ⊥AC ,CE ⊥BE ,∴AB >BC ,BC >CE ,∴AB >CE ,故③错误;∵△CBE ≌△ACD ,∴CE =AD ,BE =CD ,∵CE -CD =DE ,∴AD -BE =DE ,故④正确;故答案为:①②④.【点睛】此题考查了同角的余角相等、垂线段最短、平行线的判定与性质、全等三角形的判定与性质等知识,证明∠BCE =∠CAD 及△CBE ≌△ACD 是解题的关键.6(2023秋·江苏淮安·八年级淮安市浦东实验中学校考开学考试)如图,已知正方形ABCD中,边长为10cm,点E在AB边上,BE=6cm.如果点P在线段BC上以4cm/s的速度由B点向C点运动.同时,点Q在线段CD上以acm/s的速度由C点向D点运动.当a=时,△EBP和△PCQ全等.【答案】4或24 5【分析】分两种情况:当△EBP≌△PCQ时和当△EBP≌QCP时,根据边对应相等,分别求出a的值即可.【详解】解:当△EBP≌△PCQ时,此时BE=CP,BP=CQ,则有BP=4t=at,CP=BC-BP=10-4t=6,此时t=1,a=4,当△EBP≌QCP时,此时BE=CQ,BP=CP,则有CQ=at=6,CP=BC-BP=10-4t=4t,此时t=54,a=245,综上所述,a的值为4或24 5,故答案为:4或24 5.【点睛】本题主要考查了全等三角形的性质,熟练掌握全等三角形的性质,采用分类讨论的思想是解题的关键.三、解答题7(2023春·上海嘉定·七年级校考期末)如图,在四边形ABCD中,AD∥BC,点E为对角线BD上一点,∠A=∠BEC,且AD=BE.(1)求证:△ABD≌△ECB;(2)如果∠BDC=75°,求∠ADB的度数.【答案】(1)见解析(2)∠ADB=30°【分析】(1)由平行线性质可得∠ADB=∠CBE,再由ASA可证△ABD≌△ECB;(2)由全等三角形的性质可得BD=BC,由等腰三角形的性质可求出∠DBC=30°,再由两直线平行内错角相等即可求解.【详解】(1)证明∵AD∥BC,∴∠ADB=∠CBE,在△ABD和△ECB中,∠A=∠BECAD=BE∠ADB=∠CBE,∴△ABD≌△ECB ASA;(2)∵△ABD≌△ECB,∴BD=BC,∴∠BDC=∠BCD=75°,∴∠DBC=180°-∠BDC-∠BCD=30°,∵AD∥BC,∴∠ADB=∠DBC=30°.【点睛】本题考查了全等三角形的判定和性质,平行线的性质,三角形内角和,熟练掌握两直线平行内错角相等是解答本题的关键.8(2023秋·江苏·八年级校考周测)如图,在△ABC中,∠ACB=90°,AC=BC,AE是BC边上的中线,过C作CF⊥AE,垂足为F,过B作BD⊥BC交CF的延长线于D.(1)试说明AE=CD;(2)若AC=12cm,求BD的长.【答案】(1)见解析(2)BD=6cm【分析】(1)由题意可得∠D+∠DCB=90°,∠DCB+∠AEC=90°,即∠D=∠AEC,根据“AAS”可证△DBC≌△ECA,可得;(2)先求出,然后根据全等三角形的性质即可求解.【详解】(1)∵,,∴,,∴,∵,,∴,∴;(2)∵,,∴.∵是边上的中线,∴.∵,∴.【点睛】本题考查了全等三角形的判定与性质,熟练运用全等三角形的判定是本题的关键.9(2023秋·湖南长沙·八年级长沙市开福区青竹湖湘一外国语学校校考开学考试)如图所示,在中,于D,于E,与交于点F,且.(1)求证:;(2)已知,求的长.【答案】(1)见解析(2)【分析】(1)根据垂直的定义得出,再根据同角的余角相等得出,然后由证明即可;(2)由全等三角形的性质得出,再根据线段的和差即可解决问题.【详解】(1)证明:∵,,∴,∴,∴,在和中∴,(2)解:∵,∴,∵,∴,∴;【点睛】此题考查了全等三角形的判定与性质的应用,证明三角形全等是解决问题的关键,属于中考常考题型.10(2023春·四川成都·七年级成都实外校考期末)已知:如图,点是等边三角形内一点,且,外一点满足,平分.(1)求证:;(2)求的度数.(3)若,试判断与的位置关系,并说明理由.【答案】(1)见解析(2)(3),理由见解析【分析】(1)由三角形是等边三角形和可得,由角平分线的性质可得,由“”即可证明;(2)由三角形是等边三角形和可得,,由“”证明,从而得到,再由,;(3)由全等三角形的性质可得,由等腰三角形的性质可得,令交于点,通过计算得出,最后由三角形内角和定理可得出,从而得到答案.【详解】(1)证明:三角形是等边三角形,,,,平分,,在和中,,;(2)解:三角形是等边三角形,,,在和中,,,,,,由(1)得,,;(3)解:,理由如下:由(1)得,,,由(2)得,,,,,,如图,令交于点,,则,,,.【点睛】本题主要考查了等边三角形的性质、三角形全等的判定与性质、等腰三角形的性质、三角形内角和定理、角平分线的性质,熟练掌握等边三角形的性质、三角形全等的判定与性质、等腰三角形的性质、三角形内角和定理、角平分线的性质,是解题的关键.11(2023春·四川达州·七年级校考期末)如图,在中,,,点在线段上运动(不与、重合),连接,作,交线段于.(1)当时,,;点从向的运动过程中,逐渐变(填“大”或“小”);(2)当等于多少时,,请说明理由.(3)在点的运动过程中,与的长度可能相等吗?若可以,请直接写出的度数,请说明理由.【答案】(1);;小;(2),理由见解析;(3)可能相等,,理由见解析【分析】(1)现根据邻补角的定义,得到,进而得到,然后利用三角形内角和定理,得到,,又因为点从向的运动过程中,逐渐增大,所以逐渐变小;(2)利用三角形内角和定理,得到,根据平角的性质,得到,进而得到,再根据“”证明,即可得到答案;(3)根据等边对等角的性质,得到,再利用三角形内角和定理,得出,由三角形外角的性质,得到,进而得到,最后利用邻补角,即可求出的度数.【详解】(1)解:,,,,,,,,点从向的运动过程中,逐渐增大,逐渐变小,故答案为:;;小;(2)解:当时,,理由如下:,,又,,,,当时,,,在和中,,,即当时,,;(3)解:在点的运动过程中,与的长度可能相等,理由如下:,,,,,,,,.【点睛】本题考查了邻补角,三角形内角和定理,全等三角形的判定和性质,等腰三角形的判定和性质,三角形外角的性质,灵活运用相关知识解决问题是解题关键.12(2023春·广东梅州·八年级校考开学考试)在四边形中.(1)如图1,,,,分别是,上的点,且,探究图中,,之间的数量关系.小林同学探究此问题的方法是:延长到点,使.连接,先对比与结论是;(2)如图2,在四边形中,,,、分别是,上的点,且,则上述结论是否仍然成立,请说明理由.(3)如图3,在四边形中,,,若点在的延长线上,点在的延长线上,若,请写出与的数量关系,并给出证明过程.【答案】(1),理由见解析(2)成立,理由见解析(3),证明见解析【分析】(1)延长到点,使,连接,可判定,进而得出,,再判定,可得结论;(2)延长到点,使,连接,先判定,进而得出,,再判定,可得结论;(3)在延长线上取一点,使得,连接,先判定,再判定,得出,最后根据,推导得到【详解】(1)解:结论:.理由:如图1,延长到点,使,连接,在和中,,,,,,,,在和中,,,.故答案为:;(2)解:仍成立,理由:如图2,延长到点,使,连接,,,,在和中,,,,,,,,在和中,,,;(3)解:结论:.理由:如图3,在延长线上取一点,使得,连接,,,,在和中,,,,,在和中,,,,,,,即,.【点睛】本题属于三角形综合题,主要考查了全等三角形的判定以及全等三角形的性质的综合应用,解题的关键是作辅助线构造全等三角形,根据全等三角形的对应角相等进行推导变形.解题时注意:同角的补角相等.。
八年级数学上册《三角形全等的判定》练习题及答案

八年级数学上册《三角形全等的判定》练习题及答案学校:___________姓名:___________班级:___________一、单选题1.如图,//BC EF ,BC EF =,要使得ABC DEF △≌△,需要补充的条件不能是( )A .B E ∠=∠ B .AB DE =C .AD CF = D .//AB DE2.如图,已知ABC ,用直尺和圆规按以下步骤作出DEF .(1)画射线DM ,以点D 为圆心,AB 长为半径画弧,与DM 交于点E ;(2)分别以D ,E 为圆心,线段AC ,BC 长为半径画弧,两弧相交于点F ;(3)连接DF ,EF .则能用于证明ABC DEF ≌△△的依据是( )A .SSSB .SASC .ASAD .AAS3.如图,由AB =AC ,∠B =∠C ,便可证得BAD ∠CAE ,其全等的理由是( )A .SSSB .SASC .ASAD .AAS4.如图,在矩形ABCD 中,DE 平分ADC ∠交BC 于点E ,点F 是CD 边上一点(不与点D 重合).点P 为DE 上一动点,PE PD <,将DPF ∠绕点P 逆时针旋转90°后,角的两边交射线DA 于H ,G 两点,有下列结论:∠DH DE =;∠DP DG =;∠DG DF +;∠DP DE DH DC ⋅=⋅,其中一定正确的是( )A .∠∠B .∠∠C .∠∠D .∠∠5.已知:如图AB //EF ,BC ∠CD ,则∠α,∠β,∠γ之间的关系是( )A .βαγ∠=∠+∠B .180αβγ∠+∠+∠=C .90αβγ∠+∠-∠=D .90βγα∠+∠-∠=6.如图所示,E 是正方形ABCD 的对角线BD 上一点,EF ∠BC ,EG ∠CD ,垂足分别是F 、G .若CG =3,CF =4,则AE 的长是( )A .3B .4C .5D .7二、填空题7.如图,在Rt ABC 中,90C ∠=︒,10AC =,5BC =,线段PQ AB =,P ,Q 两点分别在AC 和过点A 且垂直于AC 的射线AO 上运动,当AP =__________时,ABC 和PQA △全等.8.如图,AB 是∠O 的直径,AC 是∠O 的切线,A 为切点,连接BC ,与∠O 交于点D ,连接OD .若82AOD ∠=︒,则C ∠=_________︒.9.正方形ABCD 在平面直角坐标系中的位置如图所示,点A 的坐标为(2,0),点B 的坐标为(0,4).若反比例函数y =k x(k ≠0)的图象经过点C ,则k 的值为 _____.10.如图,已知l 1∠l 2,MN 分别和直线1l 、2l 交于点A 、B ,ME 分别和直线1l 、2l 交于点C 、D ,点P 在MN 上(P 点与A 、B 、M 三点不重合)如果点P 在直线AB 运动时,α∠、β∠、γ∠之间有何数量关系______.11.如图,EFG 和HIJ 都是等边三角形,连接HG ,EI 交于点P ,则EPH ∠=_________度.12.如图,ABC 中,AB AC =,AD BD ⊥于点D ,20BAD ∠=︒,若2BC BD =,则BAC ∠的度数为 _____.三、解答题13.如图,已知ABC(1)用直尺和圆规按下列要求作图:(保留作图痕迹)在BC 上作点D ,使点D 到AB 和AC 的距离相等;过点B 作//BE AD 交CA 的延长线于E ;(2)若AF BE ⊥,垂足为F ,证明BF EF =.14.在∠ABC 中,D 是BC 的中点,DE ∠AB ,DF ∠AC ,垂足分别是E ,F .(1)若BE =CF ,求证:AD 是∠ABC 的角平分线.(2)若AD 是∠ABC 的角平分线,求证:BE =CF .15.如图,AB CD ,AD 与BC 交于点O ,40C ∠=︒,80AOB ∠=︒,求A ∠的度数.16.在ABC 中,AB AC =,D 是BC 边的中点,E 、F 分别是AD 、AC 边上的点.(1)如图∠,连接BE 、EF ,若ABE EFC ∠=∠,求证:BE EF =;(2)如图∠,若B 、E 、F 在一条直线上,且45ABE BAC ∠=∠=︒,探究BD 与AE 的数量之间有何等量关系,并说明理由;17.如图,在Rt DEF △和Rt ABC 中,90D A ∠=∠=︒,30E ∠=︒,45C ∠=︒,AC 与DF 相交于点G ,若105FGC ∠=︒,请判断EF 与BC 是否平行?并说明理由.18.如图,点D ,E 分别在OA ,OB 上,点P 在OC 上,且PD PE =.若180ODP OEP ∠+∠=︒,求证:OC 平分AOB ∠.参考答案:1.B【分析】根据全等三角形的判定定理判断解答即可.【详解】解:A 、∠BC ∠EF ,∠∠ACB =∠DFE ,又∠B =∠E ,BC =EF ,∠∠ABC ∠∠DEF (ASA ),正确,不符合题意;B 、根据全等三角形的判定定理,不能证明∠ABC ∠∠DEF ,错误,符合题意;C 、∠BC ∠EF ,∠∠ACB =∠DFE ,∠AD=CF ,∠AD+DC=CF+DC ,∠AC=DF ,∠BC=EF ,∠ACB =∠DFE ,AC=DF ,∠∠ABC ∠∠DEF (SAS ),正确,不符合题意;D 、∠BC ∠EF ,AB ∠DE ,∠∠ACB =∠DFE ,∠BAC =∠EDF ,又BC=EF ,∠∠ABC ∠∠DEF (AAS ),正确,不符合题意,故选:B .【点睛】本题考查全等三角形的判定、平行线的性质,熟练掌握全等三角形的判定是解答的关键.2.A【分析】根据作图方法可知,DE AB =,DF AC =,EF BC =,由此可解.【详解】解:根据作图的步骤(1)知DE AB =,由步骤(2)知DF AC =,EF BC =,根据三组边对应相等(SSS ),可证ABC DEF ≌△△. 故答案为:A .【点睛】本题考查尺规作图和全等三角形的判定,根据作图的方法判断出两个三角形的三条边对应相等是解题的关键.3.C【分析】根据全等三角形的判定定理解答即可.【详解】解:在BAD 和CAE 中,A A AB AC B C ∠=∠⎧⎪=⎨⎪∠=∠⎩, ∠BAD ∠CAE ()ASA ,故选:C .【点睛】本题考查了全等三角形的判定,熟练掌握全等三角形的判定定理是解本题的关键.4.D【分析】根据旋转的性质判断得()GPH DPF ASA ∆≅∆,可判断∠正确,证PDHCDE ∆∆可判断∠正确,从而得出结果.【详解】解:根据旋转的性质可知,90DPH GPF ∠=∠=︒,∠DE 平分ADC ∠,∠45HDP ∠=︒,∠45DHP PDH PDF ∠=∠=∠=︒,∠PH =PD ,∠90DPH GPF ∠=∠=︒∠GPH DPF ∠=∠在GPH ∆和DPF ∆中, ∠GHP FDP PH PD GPH DPF ∠=∠⎧⎪=⎨⎪∠=∠⎩∠()GPH DPF ASA ∆≅∆∠HG DF =∠45PDH ∠=︒∠DH =∠DF DG GH DG DH +=+==故∠正确;∠45PDH PDF ∠=∠=︒,90DPH DCE ∠=∠=︒∠PDHCDE ∆∆ ∠DH DP DE CD= 即DP DE DH DC ⋅=⋅,故∠正确;根据已知条件无法证明∠DH =DE ,∠DP =DG .故选:D .【点睛】本题主要考查矩形的性质、三角形的全等、三角形的相似,掌握相关知识并灵活应用是解题的关键.5.C【分析】分别过C 、D 作AB 的平行线CM 和DN ,由平行线的性质可得到最终结果.【详解】如图,分别过C 、D 作AB 的平行线CM 和DN ,,,,,,,90,90,AB EF AB CM DN EF BCM MCD NDC NDE BC CD BCD BCM MCD NDCNDE αγααβαβγ∴∴∠=∠∠=∠∠=∠⊥∴∠=∠+∠=∠+∠=∠+∠-∠=︒∴∠+∠-∠=︒故选:C .【点睛】本题主要考查平行线的性质,掌握平行线的性质是解题的关键,即∠两直线平行,同位角相等;∠两直线平行,内错角相等;∠两直线平行,同旁内角互补.6.C【分析】由“SAS”可证△ABE ∠∠CBE ,可得AE =CE ,可证四边形CFEG 是矩形,可得GC =EF =3,∠EFC =90°,由勾股定理可求解.【详解】解:如图,连接CE ,∠四边形ABCD 是正方形,∠AB =BC ,∠ABD =∠CBD =45°,在△ABE 和△CBE 中,AB BC ABE CBE BE BE =⎧⎪∠=∠⎨⎪=⎩,∠∠ABE ∠∠CBE (SAS ),∠AE =CE ,∠EF ∠BC ,EG ∠CD ,∠BCD =90°,∠四边形CFEG 是矩形,∠GC =EF =3,∠EFC =90°,∠CE5,∠AE =5,故选:C .【点睛】本题考查了正方形的性质,全等三角形的判定和性质,勾股定理,灵活运用这些性质解决问题是解题的关键.7.5或10【分析】当AP =5或10时,∠ABC 和∠PQA 全等,根据HL 定理推出即可.【详解】解:∠∠C =90°,AO ∠AC ,∠∠C =∠QAP =90°,∠当AP =5=BC 时,在Rt ∠ACB 和Rt ∠QAP 中∠AB PQ BC AP =⎧⎨=⎩, ∠Rt ∠ACB ∠Rt ∠QAP (HL ),∠当AP =10=AC 时,在Rt ∠ACB 和Rt ∠P AQ 中AB PQ AC AP =⎧⎨=⎩, ∠Rt ∠ACB ∠Rt ∠P AQ (HL ),故答案为:5或10.【点睛】本题考查了全等三角形的判定定理的应用,注意:判定两直角三角形全等的方法有ASA ,AAS ,SAS ,SSS ,HL .8.49【分析】利用同弧所对的圆周角等于圆心角的一半求得∠B =12∠AOD =41°,根据AC 是∠O 的切线得到∠BAC =90°,即可求出答案.【详解】解:∠∠AOD =82°,∠∠B =12∠AOD =41°,∠AC 为圆的切线,A 为切点,∠∠BAC =90°,∠∠C =90°-41°=49°故答案为49.【点睛】此题考查圆周角定理,圆的切线的性质定理,直角三角形两锐角互余,正确理解圆周角定理及切线的性质定理是解题的关键.9.24【分析】过点C 作CE ∠y 轴,由正方形的性质得出∠CBA =90°,AB =BC ,再利用各角之间的关系得出∠CBE =∠BAO ,根据全等三角形的判定和性质得出OA =BE =2,OB =CE =4,确定点C 的坐标,然后代入函数解析式求解即可.【详解】解:如图所示,过点C 作CE ∠y 轴,∠点B(0,4),A(2,0),∠OB=4,OA=2,∠四边形ABCD为正方形,∠∠CBA=90°,AB=BC,∠∠CBE+∠ABO=90°,∠∠BAO+∠ABO=90°,∠∠CBE=∠BAO,∠∠CEB=∠BOA=90°,,∠ABO BCE∠OA=BE=2,OB=CE=4,∠OE=OB+BE=6,∠C(4,6),将点C代入反比例函数解析式可得:k=24,故答案为:24.【点睛】题目主要考查正方形的性质,全等三角形的判定和性质,反比例函数解析式的确定等,理解题意,综合运用这些知识点是解题关键.10.∠α+∠β=∠γ【分析】根据平行线的性质可求出它们的关系,从点P作平行线,平行于AC,根据两直线平行内错角相等可得出.【详解】解:如图,过点P作AC的平行线PO,∠AC∠PO,∠∠β=∠CPO,又∠AC∠BD,∠PO∠BD,∠∠α=∠DPO ,∠∠α+∠β=∠γ,故答案为:∠α+∠β=∠γ.【点睛】本题主要考查了两直线平行,内错角相等,正确作出辅助线是解题的关键.11.60【分析】根据等边三角形的性质可证∠FIH ∠∠GJI ,再证明∠FGH ∠∠GEI ,根据全等三角形的性质可得∠FGH =∠GEI ,从而可得∠GEI +∠HGE =60°,根据外角的性质可得∠EPH 的度数.【详解】解:在等边∠EFG 中,∠F =∠FGE =60°,FG =GE ,∠∠FHI +∠FIH =120°,在等边∠HIJ 中,∠HIJ =60°,HI =JI ,∠∠FIH +∠JIG =120°,∠∠FHI =∠JIG ,在∠FIH 和∠GJI 中,F G FHI GIJ HI JI ∠=∠⎧⎪∠=∠⎨⎪=⎩,∠∠FIH ∠∠GJI (AAS ),∠FH =GI ,在∠FGH 和∠GEI 中,FH GI F G FG GE =⎧⎪∠=∠⎨⎪=⎩,∠∠FGH ∠∠GEI (SAS ),∠∠FGH =∠GEI ,∠∠FGH +∠HGE =60°,∠∠GEI +∠HGE =60°,∠∠EPH =60°,故答案为:60【点睛】本题考查了全等三角形的判定和性质,等边三角形的性质等,熟练掌握全等三角形的判定和性质是解题的关键.12.40︒【分析】如图(见详解),根据等腰三角形的三线合一性质,过点A 作AE BC ⊥于点E ,可证RT ABE RT ABD △≌△,即可求出BAC ∠的度数.【详解】解:如图,过点A 作AE BC ⊥于点E ,∠AB =AC ,∠E 是BC 的中点,且AE 平分BAC ∠.∠2BC BD =,∠BD =BE .在RT ABE 和RT ABD 中,()AB AB RT ABE RT ABD HL BD BE =⎧⇒⎨=⎩△≌△, ∠20BAD BAE CAE ∠=∠=∠=︒.∠40BAC ∠=︒.故答案为:40︒.【点睛】本题考查等腰三角形的三线合一性质以及直角三角形全等的判定定理,正确运用定理进行判定是解题的关键.13.(1)见解析;(2)见解析【分析】(1)作∠BAC 的平分线,交BC 于D ,作∠ABE =∠BAD ,交CA 延长线于E 即可;(2)根据已知条件,利用ASA 证明∠AFE ∠∠AFB ,可得结果.【详解】解:(1)如图所示,AD 和BE 即为所作;(2)∠BE ∠AD ,AF ∠BE ,∠∠DAF =180°-90°=90°,∠EAF +∠CAD =90°,即∠BAF +∠BAD =90°,由(1)可知:∠BAD =∠CAD ,∠∠CAD +∠BAF =90°,∠∠BAF =∠EAF ,∠∠AFE =∠AFB =90°,AF =AF ,∠∠AFE ∠∠AFB (ASA ),∠EF =BF .【点睛】本题考查了尺规作图,平行线的性质,角平分线的判定,全等三角形的判定和性质,正确的作出图形是解题的关键.14.(1)证明见解析;(2)证明见解析【分析】(1)根据D 是BC 的中点可得BD DC =,根据 DE ∠AB 可得90DEB DFC ∠=∠=︒,利用直角三角形全等的判定和性质可得Rt Rt BDE CDF ≌,DE =DF ,再用角平分线得判定定理即可证明;(2)根据角平分线的性质得到DE =DF ,根据D 是BC 的中点可得BD DC =,再用HL 证明Rt Rt BDE CDF ≌,最后用全等三角形对应边相等证明.(1)证明:∠DE ∠AB ,DF ∠AC ,∠∠BDE 与∠DCF 是直角三角形.在Rt∠BDE 与Rt∠CDF 中,BD CD BE CF=⎧⎨=⎩, ∠Rt∠BDE ∠Rt∠CDF (HL ),∠DE =DF .又∠DE ∠AB ,DF ∠AC ,∠AD 是∠ABC 的角平分线;(2)∠AD 是∠ABC 的角平分线,DE ∠AB 于E ,DF ∠AC 于F ,∠DE =DF ,∠AD 是BC 边的中线,∠BD =CD .在Rt∠BDE 和Rt∠CDF 中,BD CD DE DF =⎧⎨⎩=, ∠Rt∠BDE ∠Rt∠CDF (HL ),∠BE =CF .【点睛】本题考查直角三角形全等的判定(HL ),角平分线的性质定理和判定定理,用HL 证明Rt∠BDE ∠Rt∠CDF 是解题的关键.15.60︒【分析】由AB 与CD 平行,利用两直线平行内错角相等求出B 的度数,在AOB 中,利用三角形内角和定理即可求出A ∠的度数.【详解】解:∠AB CD ,40C ∠=︒,∠40B C ∠=∠=︒,∠180A B AOB ∠+∠+∠=︒,∠18060∠=︒-∠-∠=︒A AOB B .【点睛】此题考查了平行线的性质以及三角形内角和定理,熟练掌握平行线的性质及三角形内角和定理是解本题的关键.16.(1)证明见解析;(2)2AE BD =,理由见解析【分析】(1)AD 为线段BC 的垂直平分线,垂直平分线的性质可得∠ABC =∠ACB ,BE =CE ,通过角的等量替换可得∠ACE =∠EFC ,再证边长相等即可.(2)由(1)可得∠ABE =∠ACE ,直角三角形证明全等即可得出.(1)连接CE ,AB AC =,D 是BC 边的中点,AD ∴为线段BC 的垂直平分线,A ABC CB =∠∠,BE CE ∴=,EBC ECB ∴∠=∠,ABC EBC ACB ECB ∴∠-∠=∠-∠,即ABE ACE =∠∠,ABE EFC ∠=∠,ACE EFC ∴∠=∠,EF CE ∴=,BE EF ∴=;(2)连接CE ,由(1)可得ABE ACE =∠∠,45ABE BAC ∠=∠=︒,ABF ∴和CEF △都是等腰直角三角形,AF BF CF EF ∴==,,CBF EAF ∴≌△△,BC AE ∴=,2AE BD ∴=;(注:辅助线连接CE 不要求)17.EF BC ∥,理由见解析【分析】过G 点作GH BC ∥,根据平行线的性质,角的和差关系,三角形内角和定理可得∠F =∠FGH ,再根据平行线的判定即可求解.【详解】解:EF BC ∥.理由如下:过G 点作GH BC ∥,∠∠C =45°,90A ∠=︒,∠∠CGH =45°,∠∠FGC =105°,∠∠FGH =105°−45°=60°,在Rt ∠DEF 中,∠D =90°,∠E =30°,∠∠F =60°,∠∠F =∠FGH ,∠EF GH ∥,∠EF BC ∥.【点睛】本题考查了平行线的判定与性质,三角形内角和定理,关键是熟悉两条直线都和第三条直线平行,那么这两条直线平行.18.见解析【分析】过点P 作PF OA ⊥,PH OB ⊥,证明∠PDF ∠∠PEH ,得出PF PH =,根据角平分线的判定定理得出OC 平分AOB ∠.【详解】证明:过点P 作PF OA ⊥,PH OB ⊥,∠90PFD PHE ∠=∠=︒∠180ODP OEP ∠+∠=︒,180PEB OEP ∠+∠=︒∠ODP PEB ∠=∠在∠PDF 和∠PEH 中PFD PHE PDF PEH PF PH ∠=∠⎧⎪∠=∠⎨⎪=⎩∠∠PDF ∠∠PEHPF PH ∴=,∠OC 平分AOB ∠.【点睛】本题考查了角平分线的判定定理,全等三角形的性质与判定,掌握角平分线的判定定理是解题的关键.。
全等三角形的证明及计算大题专项训练(30道)(含答案)

全等三角形的证明及计算大题专项训练(30道)考卷信息:本套训练卷共30题,培优篇15题,拔尖篇15题,题型针对性较高,覆盖面广,选题有深度,可深化学生对全等三角形工具的应用及构造全等三角形!1.(2021春•道里区期末)如图,点A ,C 在EF 上,AD ∥BC ,DE ∥BF ,AE =CF .(1)求证:△ADE ≌△CBF ;(2)直接写出图中所有相等的线段(AE =CF 除外).【解题思路】(1)利用ASA 证明△ADE ≌△CBF 即可;(2)根据△ADE ≌△CBF 即可得图中所有相等的线段.【解答过程】(1)证明:∵AD ∥BC∴∠DAC =∠BCA ,又∵∠DAC +∠EAD =180°,∠BCA +∠FCB =180°,∴∠EAD =∠FCB ,∵DE ∥BF ,∴∠E =∠F ,在△ADE 和△CBF 中,{∠EAD =∠FCB AE =CF ∠E =∠F,∴△ADE ≌△CBF (ASA ),(2)∵△ADE ≌△CBF ,∴ED =FB ,DA =BC ,EC =F A .∵AD ∥BC ,∴∠DAC =∠BCA ,在△ADC 和△CBA 中,{AD =CB ∠DAC =∠CBA AC =CA,∴△ADC ≌△CBA (SAS ),∴AB =CD ;∴图中所有相等的线段有:ED =FB ,DA =BC ,AB =CD ,EC =F A .2.(2021春•宁德期末)如图,AB ,CD 交于点O ,AC =DB ,∠ACD =∠DBA .(1)说明△AOC ≌△DOB 的理由;(2)若∠ACD =94°,∠CAO =28°,求∠OCB 的度数.【解题思路】(1)直接利用AAS 即可证明△AOC ≌△DOB ;(2)利用三角形外角的性质得到∠COB ,再根据△AOC ≌△DOB 得到OC =OB ,即可求得∠OCB .【解答过程】解:(1)在△AOC 和△DOB 中,{∠AOC =∠DOB ∠ACO =∠DBO AC =DB,∴△AOC ≌△DOB (AAS );(2)∵∠ACD =94°,∠CAO =28°,∴∠COB =∠ACD +∠CAO =122°,∵△AOC ≌△DOB ,∴OC =OB ,∴∠OCB =(180°﹣122°)÷2=29°.3.(2021春•沙坪坝区校级期末)如图,在△ABC 中,AC =BC ,点D 在AB 边上,点E 在BC 边上,连接CD ,DE .已知∠ACD =∠BDE ,CD =DE .(1)猜想AC 与BD 的数量关系,并证明你的猜想;(2)若AD =3,BD =5,求CE 的长.【解题思路】(1)利用AAS 证明△ADC ≌△BED ,即可得结论;(2)结合△ADC ≌△BED ,可得AC =BD =5,BE =AD =3,进而可得CE 的长.【解答过程】解:(1)AC =BD ,理由如下:∵AC =BC ,∴∠A =∠B ,在△ADC 和△BED 中,{∠A =∠B ∠ACD =∠BED CD =DE,∴△ADC ≌△BED (AAS ),∴AC =BD ;(2)由(1)知:△ADC ≌△BED ,∴AC =BD =5,BE =AD =3,∴BC =AC =5,∴CE =BC ﹣BE =2.4.(2021春•渝中区校级期末)如图,点E 在△ABC 的边AC 上,且∠ABE =∠C ,AF 平分∠BAE 交BE 于F ,FD ∥BC 交AC 于点D .(1)求证:△ABF ≌△ADF ;(2)若BE =7,AB =8,AE =5,求△EFD 的周长.【解题思路】(1)根据平行线的性质得到∠ADF =∠C ,等量代换得到∠ABF =∠ADF ,由角平分线的定义得到∠BAF =∠CAF ,根据全等三角形的判定定理即可得到结论;(2)根据全等三角形的性质得到AD =AB =8,BF =DF ,由线段的和差得到DE =AD =AE =8﹣5=3,根据三角形的周长公式即可得到结论.【解答过程】解:(1)∵FD ∥BC ,∴∠ADF =∠C ,∵∠ABF =∠C ,∴∠ABF =∠ADF ,∵AF 平分∠BAE ,∴∠BAF =∠CAF ,在△ABF 和△ADF 中,{∠BAF =∠DAF ∠ABF =∠ADF AF =AF,∴△ABF ≌△ADF (AAS );(2)∵△ABF ≌△ADF ,∴AD =AB =8,BF =DF ,∵AE =5,∴DE =AD ﹣AE =8﹣5=3,∴△EFD 的周长=EF +DF +DE =EF +BF +DE =BE +DE =7+3=10.5.(2021春•北碚区校级期末)如图,已知D 是AC 上一点,AB =DA ,AB +DC =ED ,AE =BC .(1)求证:△ABC ≌△DAE ,(2)若∠BAE =125°,求∠DCB 的度数.【解题思路】(1)根据SSS 证明三角形全等即可.(2)利用全等三角形的性质以及三角形内角和定理求解即可.【解答过程】(1)证明:∵DE =AB +DC ,AB =AD ,∴DE =AD +DC =AC ,在△ABC 和△DAE 中,{AB =AD AC =DE BA =AE,∴△ABC ≌△DAE (SSS ).(2)解:∵△ABC ≌△DAE ,∴∠EAD =∠B ,∴∠B +∠BAC =∠EAD +∠BAC =∠EAB =125°,∴∠DCB =180°﹣(∠B +∠BAC )=180°﹣125°=55°.6.(2021春•莱芜区期末)如图,已知AD 、BC 相交于点O ,AB =CD ,AM ⊥BC 于点M ,DN ⊥BC 于点N ,BN =CM .(1)求证:△ABM ≌△DCN ;(2)试猜想OA 与OD 的大小关系,并说明理由.【解题思路】(1)根据HL 可证明:△ABM ≌△DCN ;(2)根据AAS 证明△AMO ≌△DNO 可得结论.【解答过程】(1)证明:∵BN =CM ,∴BN +MN =MN +CM ,即CN =BM ,∵AM ⊥BC 于点M ,DN ⊥BC 于点N ,∴∠AMB =∠DNC =90°,在Rt △ABM 和Rt △DCN 中,{AB =CD BM =CN, ∴Rt △ABM ≌Rt △DCN (HL );(2)解:OA =OD ,理由如下:∵Rt △ABM ≌Rt △DCN ,∴AM =DN ,在△AMO 和△DNO 中,{∠AOM =∠DNO ∠AMO =∠DNO AM =DN,∴△AMO ≌△DNO (AAS ),∴OA =OD .7.(2021春•静安区期末)如图,已知四边形ABCD 中,AB ∥CD ,AD ∥BC .E 为BD 上一点,且BE =AD ,∠DEF =∠ADC ,EF 交BC 的延长线于点F .(1)AD 和BC 相等吗?为什么?(2)BF 和BD 相等吗?为什么?【解题思路】(1)根据平行线的性质和全等三角形的判定和性质得出△ABD 与△CDB 全等,进而利用全等三角形的性质解答即可;(2)根据平行线的性质和全等三角形的判定和性质得出△EFB 与△CDB 全等,进而解答即可.【解答过程】解:(1)AD =CB ,理由如下:∵AD ∥BC ,∴∠ABD =∠CDB ,同理可得,∠ADB =∠CBD ,在△ABD 与△CDB 中,{∠ABD =∠CDB BD =DB ∠ADB =∠CBD,∴△ABD ≌△CDB (ASA ),∴AD =CB ;(2)BF =BD ,理由如下:∵AD =CB ,BE =AD ,∴BC =BE ,∵∠DEF =∠ADC ,∴∠DEF ﹣∠DBF =∠ADC ﹣∠ADB ,即∠EFB =∠CDB ,在△EFB 与△CDB 中,{∠EFB =∠CDB BC =BE ∠FBE =∠DBC,∴△EFB ≌△CDB (ASA ),∴FB =DB .8.(2021春•沙坪坝区校级月考)如图,△ABC 中,CD ⊥AB ,垂足为D .BE ⊥AC ,垂足为G ,AB =CF ,BE =AC .(1)求证:AE =AF ;(2)求∠EAF 的度数.【解题思路】(1)利用SAS 证明△AEB ≌△F AC 可证明结论;(2)由全等三角形的性质可得∠E =∠CAF ,由余角的定义可求得∠EAF 的度数.【解答过程】(1)证明:∵CD ⊥AB ,BE ⊥AC ,∴∠CAD +∠ACD =∠CAD +∠EBA =90°,∴∠ACD =∠EBA ,在△AEB 和△F AC 中,{AB =FC ∠EBA =∠ACF BE =CA,∴△AEB ≌△F AC (SAS ),∴AE =F A ;(2)解:∵△AEB ≌△F AC ,∴∠E =∠CAF ,∵∠E +∠EAG =90°,∴∠CAF +∠EAG =90°,即∠EAF =90°.9.(2021春•铁岭月考)已知:如图,AB =AC ,∠1=∠2.(1)找出图中的所有全等三角形(直接写出);(2)求证:AD =AE .【解题思路】(1)直接根据全等三角形的判定可得答案;(2)先根据SAS 证得△ABF ≌△ACF ,再根据ASA 证得△BDF ≌△CEF ,然后根据全等三角形的性质可得结论.【解答过程】解:(1)△ABF ≌△ACF ,△BDF ≌△CEF ,△ADF ≌△AEF ,△ADC ≌△AEB ;(2)证明:在△ABF 和△ACF 中,{AB =AC ∠1=∠2AF =AF,∴△ABF ≌△ACF (SAS ),∴∠B =∠C ,BF =CF .在△BDF 和△CEF 中,{∠B =∠C BF =CF ∠BFD =∠CFE,∴△BDF ≌△CEF (ASA ),∴BD =CE ,∴AB ﹣BD =AC ﹣CE ,∴AD =AE .10.(2021•南岗区模拟)已知:在△ABC 和△DBE 中,AB =DB ,BC =BE ,其中∠ABD =∠CBE .(1)如图1,求证:AC =DE ;(2)如图2,AB =BC ,AC 分别交DE ,BD 于点F ,G ,BC 交DE 于点H ,在不添加任何辅助线的情况下,请直接写出图2中的四对全等三角形.【解题思路】(1)根据SAS 证明△ABC 与△DBE 全等,利用全等三角形的性质解答即可.(2)根据全等三角形的判定解答即可.【解答过程】证明:(1)∵∠ABD =∠CBE ,∴∠ABD +∠DBC =∠CBE +∠DBC ,即∠ABC =∠DBE ,在△ABC 与△DBE 中,{AB =DB ∠ABC =∠DBE BC =BE,∴△ABC ≌△DBE (SAS ),∴AC =DE ;(2)由(1)得△ABC ≌△DBE ,∴∠A =∠D ,∠C =∠E ,AB =DB ,BC =BE ,∴AB =BE ,∵AB =BC ,∴∠A =∠C ,∴∠A =∠E ,在△ABG 与△EBH 中,{∠A =∠E AB =BE ∠ABD =∠EBC,∴△ABG ≌△EBH (ASA ),∴BG =BH ,在△DBH 与△CBG 中,{BG =BH ∠DBH =∠CBG DB =CB,∴△DBH ≌△CBG (SAS ),∴∠D =∠C ,∵DB =CB ,BG =BH ,∴DG =CH ,在△DFG 与△CFH 中,{∠DFG =∠CFH ∠D =∠C DG =CH,∴△DFG ≌△CFH (AAS ).11.(2021•三水区一模)如图,AB =AC ,直线l 过点A ,BM ⊥直线l ,CN ⊥直线l ,垂足分别为M 、N ,且BM =AN .(1)求证△AMB ≌△CNA ;(2)求证∠BAC =90°.【解题思路】(1)由HL证明△AMB≌△CNA即可;(2)先由全等三角形的性质得∠BAM=∠ACN,再由∠CAN+∠ACN=90°,得∠CAN+∠BAM=90°,即可得出结论.【解答过程】证明:(1)∵BM⊥直线l,CN⊥直线l,∴∠AMB=∠CNA=90°,在Rt△AMB和Rt△CNA中,{AB=CABM=AN,∴Rt△AMB≌Rt△CNA(HL);(2)由(1)得:Rt△AMB≌Rt△CNA,∴∠BAM=∠ACN,∵∠CAN+∠ACN=90°,∴∠CAN+∠BAM=90°,∴∠BAC=180°﹣90°=90°.12.(2021•广州模拟)如图,在△ABC中,∠ACB=90°,AC=BC,点E是∠ACB内部一点,连接CE,作AD⊥CE,BE⊥CE,垂足分别为点D,E.(1)求证:△BCE≌△CAD;(2)若BE=5,DE=7,则△ACD的周长是30.【解题思路】(1)根据条件可以得出∠E=∠ADC=90°,进而得出△CEB≌△ADC;(2)利用(1)中结论,根据全等三角形的性质即可解决问题;【解答过程】(1)证明:∵BE ⊥CE ,AD ⊥CE ,∴∠E =∠ADC =90°,∴∠EBC +∠BCE =90°.∵∠BCE +∠ACD =90°,∴∠EBC =∠DCA .在△BCE 和△CAD 中,{∠E =∠ADC ∠EBC =∠DCA BC =AC,∴△BCE ≌△CAD (AAS );(2)解:∵:△BCE ≌△CAD ,BE =5,DE =7,∴BE =DC =5,CE =AD =CD +DE =5+7=12.∴由勾股定理得:AC =13,∴△ACD 的周长为:5+12+13=30,故答案为:30.13.(2020春•越秀区校级期中)已知:△ABN 和△ACM 的位置如图所示,∠1=∠2,AB =AC ,AM =AN . 求证:(1)∠BAN =∠CAM ;(2)∠ODA =∠OEA .【解题思路】(1)由∠1=∠2,则∠1+∠MAN =∠2+∠MAN ,即∠BAN =∠CAM ;(2)先证△ACM ≌△ABN (SAS ),得∠M =∠N ,再证△ADN ≌△AEM (ASA ),即可得出结论.【解答过程】证明:(1)∵∠1=∠2,∴∠1+∠MAN =∠2+∠MAN ,即∠BAN =∠CAM ;(2)在△ACM 和△ABN 中,{AM =AN ∠CAM =∠BAN AC =AB,∴△ACM ≌△ABN (SAS ),∴∠M =∠N ,在△ADN 和△AEM 中,{∠DAN =∠EAM AN =AM ∠N =∠M,∴△ADN ≌△AEM (ASA ),∴∠NDA =∠MEA ,即∠ODA =∠OEA .14.(2020•江北区模拟)如图,在△ABC 中,AD 是BC 边上的中线,E 是AB 边上一点,过点C 作CF ∥AB ,交ED 的延长线于点F .(1)求证:△BDE ≌△CDF ;(2)当AD ⊥BC ,AE =2,CF =1时,求AC 的长.【解题思路】(1)根据平行线的性质得到∠B =∠FCD ,∠BED =∠F ,由AD 是BC 边上的中线,得到BD =CD ,于是得到结论;(2)根据全等三角形的性质得到BE =CF =1,求得AB =AE +BE =3,于是得到结论.【解答过程】证明:∵CF ∥AB ,∴∠B =∠FCD ,∠BED =∠F ,∵AD 是BC 边上的中线,∴BD =CD ,在△BDE 和△CDF 中,{∠B =∠FCD ∠BED =∠F BD =CD,∴△BDE ≌△CDF (AAS );(2)∵△BDE ≌△CDF ,∴BE =CF =1,∴AB =AE +BE =2+1=3,∵AD ⊥BC ,BD =CD ,∴AC =AB =3.15.(2020秋•萧山区月考)如图,已知在△ABC 中,BD ⊥AC 于D ,CE ⊥AB 于E ,F 是BD 上一点,BF =AC ,G 是CE 延长线上一点,CG =AB ,连接AG ,AF .(1)试说明∠ABD =∠ACE ;(2)探求线段AF ,AG 有什么关系?并请说明理由.【解题思路】(1)根据的等角的余角相等,即可证明∠ACG =∠ABF ;(2)根据SAS 推出△ABF ≌△GCA 即可解决问题;【解答过程】(1)证明:∵BD 、CE 是△ABC 的高,∴∠ADB =∠AEC =90°,∴∠ABF +∠BAD =90°,∠GCA +∠BAD =90°,∴∠ABF =∠GCA ,(2)结论:AF =AG ,AF ⊥AG .理由如下:在△ABF 和△GCA 中,{AB =CG ∠ABF =∠GCA BF =AC,∴△ABF ≌△GCA (SAS ),∴AF =AG ,∠GAC =∠AFB ,∵∠AFB=∠ADB+∠F AD,∠GAC=∠GAF+∠F AD,∴∠GAF=∠ADF,∵∠ADF=90°,∴∠GAF=90°,∴AG⊥AF,AG=AF.16.(2021•张家界模拟)如图,四边形ABCD中,AB=BC=2CD,AB∥CD,∠C=90°,E是BC的中点,AE与BD相交于点F,连接DE(1)求证:△ABE≌△BCD;(2)判断线段AE与BD的数量关系及位置关系,并说明理由;(3)若CD=1,试求△AED的面积.【解题思路】(1)由平行线的性质得出∠ABE+∠C=180°,得出∠ABE=90°=∠C,再证出BE=CD,由SAS证明△ABE≌△BCD即可;(2)由全等三角形的性质得出AE=BD,证出∠ABF+∠BAE=90°,得出∠AFB=90°,即可得出结论;(3)由全等三角形的性质得出BE=CD=1,求出CE=BC﹣BE=1,得出CE=CD,△AED的面积=梯形ABCD的面积﹣△ABE的面积﹣△CDE的面积,即可得出答案.【解答过程】(1)证明:∵AB∥CD,∴∠ABE+∠C=180°,∵∠C=90°,∴∠ABE=90°=∠C,∵E是BC的中点,∴BC=2BE,∵BC=2CD,∴BE=CD,在△ABE和△BCD中,{AB=BC∠ABE=∠CBE=CD,∴△ABE≌△BCD(SAS);(2)解:AE=BD,AE⊥BD,理由如下:由(1)得:△ABE≌△BCD,∴AE=BD,∵∠BAE=∠CBD,∠ABF+∠CBD=90°,∴∠ABF+∠BAE=90°,∴∠AFB=90°,∴AE⊥BD;(3)解:∵△ABE≌△BCD,∴BE=CD=1,∵AB=BC=2CD=2,∴CE=BC﹣BE=1,∴CE=CD,∴△AED的面积=梯形ABCD的面积﹣△ABE的面积﹣△CDE的面积=12(1+2)×2−12×2×1−12×1×1=3 2.17.(2020秋•台江区校级期中)如图,A,B,C三点共线,D,C,E三点共线,∠A=∠DBC,EF⊥AC 于点F,AE=BD.(1)求证:C是DE的中点;(2)求证:AB=2CF.【解题思路】(1)过D 作DH ⊥AC 的延长线与H ,根据全等三角形的判定证得△AEF ≌△BDH ,得到EF =DH ,再证得△EFC ≌△DHC 得到CE =CD ,即可证得即可证得结论;(2)由(1)得,△AEF ≌△BDH ,△EFC ≌△DHC ,根据全等三角形的性质得到AF =BH ,CF =CH ,再根据线段的和差即可证得结论.【解答过程】证明:(1)过D 作DH ⊥AC 的延长线与H ,∴∠EFC =∠DHC =90°,在△AEF 和△BDH 中,{∠A =∠DBC ∠AFE =∠BHD =90°AE =BD,∴△AEF ≌△BDH (AAS ),∴EF =DH ,在△EFC 和△DHC 中,{∠FCE =∠HCD ∠EFC =∠DHC =90°EF =DH,∴△EFC ≌△DHC (AAS ),∴CE =CD ,∴C 是DE 的中点;(2)由(1)得,△AEF ≌△BDH ,△EFC ≌△DHC ,∴AF =BH ,CF =CH ,∴AB +BF =BF +FH ,FH =2FC ,∴AB =FH ,∴AB =2CF .18.(2021春•铁岭月考)如图,△AOC 和△BOD 中,OA =OC ,OB =OD ,∠AOC =∠BOD =α(0<α<90°),AD 与BC 交于点P .(1)求证:△AOD ≌△COB ;(2)求∠APC (用含α的式子表示);(3)过点O 分别作OM ⊥AD ,ON ⊥BC ,垂足分别为点M 、N ,请直接写出OM 和ON 的数量关系.【解题思路】(1)由∠AOC =∠BOD ,可得∠AOD =∠COB ,然后根据SAS 可得结论;(2)根据全等三角形的性质得∠OAD =∠OCB ,再根据三角形外角性质可得答案;(3)根据全等三角形的性质得∠MAO =∠NCO ,由垂直定义得∠AMO =∠CNO ,再根据全等三角形的判定与性质可得结论.【解答过程】解:(1)∵∠AOC =∠BOD ,∴∠AOC +∠COD =∠BOD +∠COD ,∴∠AOD =∠COB ,在△AOD 和△COB 中,{OA =OC ∠AOD =∠COB OD =OB,∴△AOD ≌△COB (SAS );(2)由(1)可知△AOD ≌△COB ,∴∠OAD =∠OCB ,令AD 与OC 交于点E ,则∠AEC =∠OAD +∠AOC =∠OCB +∠APC ,∴∠AOC =∠APC ,∵∠AOC =α,∴∠APC =α;(3)∵△AOD ≌△COB ,∴∠P AP =∠BCO ,即∠MAO =∠NCO ,∵OM ⊥AD ,ON ⊥BC ,∴∠AMO =∠CNO =90°,在△AOM 和△CON 中,{∠MAO =∠NCO ∠AMO =∠CNO OA =OC,∴△AOM ≌△CON (AAS ),∴OM =ON .19.(2020秋•花都区月考)如图所示,BD 、CE 是△ABC 的高,点P 在BD 的延长线上,CA =BP ,点Q 在CE 上,QC =AB .(1)探究P A 与AQ 之间的关系;(2)若把(1)中的△ABC 改为钝角三角形,AC >AB ,∠A 是钝角,其他条件不变,上述结论是否成立?画出图形并证明你的结论.【解题思路】(1)由条件可得出∠1=∠2,可证得△APB ≌△QAC ,可得结论;(2)根据题意画出图形,结合(1)可证得△APB ≌△QAC ,可得结论.【解答过程】(1)结论:AP =AQ ,AP ⊥AQ 证明:∵BD 、CE 是△ABC 的高, ∴BD ⊥AC ,CE ⊥AB ,∴∠1+∠CAB =90°,∠2+∠CAB =90°, ∴∠1=∠2,在△QAC 和△APB 中,{QC =AB ∠1=∠2CA =BP,∴△QAC ≌△APB (SAS ),∴AQ =AP ,∠QAC =∠P ,而∠DAP +∠P =90°,∴∠DAP +∠QAC =90°,即∠QAP =90°,∴AQ ⊥AP ;即AP =AQ ,AP ⊥AQ ;(2)上述结论成立,理由如下:如图所示:∵BD 、CE 是△ABC 的高,∴BD ⊥AC ,CE ⊥AB ,∴∠1+∠CAE =90°,∠2+∠DAB =90°, ∵∠CAE =∠DAB ,∴∠1=∠2,在△QAC 和△APB 中,{QC =AB ∠1=∠2CA =BP,∴△QAC ≌△APB (SAS ),∴AQ =AP ,∠QAC =∠P ,∵∠PDA =90°,∴∠P +∠P AD =90°,∴∠QAC +∠P AD =90°,∴∠QAP =90°,∴AQ ⊥AP ,即AP =AQ ,AP ⊥AQ .20.(2020春•萍乡期末)在△ABC 中,AB =AC ,D 是直线BC 上一点,以AD 为一边在AD 的右侧作△ADE ,使AE =AD ,∠DAE =∠BAC ,连接CE ,设∠BAC =∠1,∠DCE =∠2.(1)如图①,当点D 在线段BC 上移动时,试说明:∠1+∠2=180°;(2)如图②,当点D 在线段BC 的延长线上移动时,请猜测∠1与∠2有怎样的数量关系?并说明理由.【解题思路】(1)由“SAS ”可证△BAD ≌△CAE ,可得∠ACE =∠ABD ,由三角形的内角和定理可得结论;(2)由“SAS ”可证△BAD ≌△CAE ,可得∠ACE =∠ABD ,由三角形的内角和定理和平角的定义可得结论.【解答过程】证明:(1)∵∠DAE =∠BAC ,∴∠BAD =∠CAE ,在△ABD 和△ACE 中,{AB =AC ∠BAD =∠CAE AD =AE,∴△BAD ≌△CAE (SAS ),∴∠ACE =∠ABD ,∵∠BAC +∠ABD +∠ACB =180°,∴∠BAC +∠ACB +∠ACE =∠BAC +∠BCE =180°,∴∠1+∠2=180°;(2)∠1=∠2,理由如下:∵∠DAE =∠BAC ,∴∠BAD =∠CAE ,在△ABD 和△ACE 中,{AB =AC ∠BAD =∠CAE AD =AE,∴△BAD ≌△CAE (SAS ),∴∠ACE =∠ABD ,∵∠BAC +∠ABD +∠ACB =180°,∠ACE +∠ACB +∠DCE =180°,∴∠1=∠2.21.(2020春•揭阳期末)已知△ABC ,点D 、F 分别为线段AC 、AB 上两点,连接BD 、CF 交于点E .(1)若BD ⊥AC ,CF ⊥AB ,如图1所示,试说明∠BAC +∠BEC =180°;(2)若BD 平分∠ABC ,CF 平分∠ACB ,如图2所示,试说明此时∠BAC 与∠BEC 的数量关系;(3)在(2)的条件下,若∠BAC =60°,试说明:EF =ED .【解题思路】(1)根据余角的性质得到∠DEC =∠BAC ,由于∠DEC +∠BEC =180°,即可得到结论;(2)根据角平分线的性质得到∠EBC =12∠ABC ,∠ECB =12∠ACB ,于是得到结论;(3)作∠BEC 的平分线EM 交BC 于M ,由∠BAC =60°,得到∠BEC =90°+12∠BAC =120°,求得∠FEB =∠DEC =60°,根据角平分线的性质得到∠BEM =60°,推出△FBE ≌△EBM ,根据全等三角形的性质得到EF =EM ,同理DE =EM ,即可得到结论.【解答过程】解:(1)∵BD ⊥AC ,CF ⊥AB ,∴∠DCE +∠DEC =∠DCE +∠F AC =90°,∴∠DEC =∠BAC ,∠DEC +∠BEC =180°,∴∠BAC +∠BEC =180°;(2)∵BD 平分∠ABC ,CF 平分∠ACB ,∴∠EBC =12∠ABC ,∠ECB =12∠ACB ,∠BEC =180°﹣(∠EBC +∠ECB )=180°−12(∠ABC +∠ACB )=180°−12(180°﹣∠BAC )=90°+12∠BAC ;(3)作∠BEC 的平分线EM 交BC 于M ,∵∠BAC =60°,∴∠BEC =90°+12∠BAC =120°,∴∠FEB =∠DEC =60°,∵EM 平分∠BEC ,∴∠BEM =60°,在△FBE 与△EBM 中,{∠FBE =∠EBM BE =BE ∠FEB =∠MEB,∴△FBE ≌△EBM (ASA ),∴EF =EM ,同理DE =EM ,∴EF =DE .22.(2020秋•淇滨区校级期中)(1)如图1所示,△ACB 和△ECD 都是等腰三角形,A 、C 、D 三点在同一直线上,连接BD 、AE ,并延长AE 交BD 于点F ,试判断AE 与BD 的数量关系及位置关系,并证明你的结论.(2)若△ECD 绕顶点C 顺时针转任意角度后得到图2,图1中的结论是否仍然成立?请说明理由.【解题思路】(1)根据SAS 推出△ACE ≌△BCD ,根据全等三角形的性质得出∠CAE =∠DBC ,根据∠ACB =90°求出∠CAE +∠AEC =90°,求出∠DBC +∠BEF =90°,根据三角形内角和定理求出∠BFE =90°即可;(2)根据SAS 推出△ACE ≌△BCD ,根据全等三角形的性质得出∠CAE =∠DBC ,根据∠ACB =90°求出∠CAE +∠AOC =90°,求出∠DBC +∠BOE =90°,根据三角形内角和定理求出∠BFO =90°即可.【解答过程】(1)AE ⊥BD .证明:在△ACE 和△BCD 中{AC =BC ∠ACE =∠BCD CE =CD∴△ACE ≌△BCD (SAS ),∴∠CAE =∠DBC ,∵∠ACB =90°,∴∠CAE +∠AEC =90°,∵∠CAE =∠DBC ,∠AEC =∠BEF ,∴∠DBC +∠BEF =90°,∴∠BFE =180°﹣90°=90°,∴AE ⊥BD ;(2)解:结论还成立,理由是:∵∠ACB =∠ECD ,∴∠ACB +∠BCE =∠ECD +∠BCE ,即∠ACE =∠BCD ,在△ACE 和△BCD 中{AC =BC ∠ACE =∠BCD CE =CD∴△ACE≌△BCD(SAS),∴∠CAE=∠DBC,∵∠ACB=90°,∴∠CAE+∠AOC=90°,∵∠CAE=∠DBC,∠AOC=∠BOE,∴∠DBC+∠BOE=90°,∴∠BFO=180°﹣90°=90°,∴AE⊥BD.23.(2020秋•蒙阴县期中)在△ABC中,∠ACB=90°,AC=BC,直线MN经过点C,且AD⊥MN于点D,BE⊥MN于点E.(1)当直线MN绕着点C旋转到如图1所示的位置时,求证:①△ADC≌△CEB;②DE=AD+BE;(2)当直线MN绕着点C旋转到如图2所示的位置时,①找出图中一对全等三角形;②DE、AD、BE之间有怎样的数量关系,并加以证明.【解题思路】(1)根据余角和补角的性质易证得∠DAC=∠ECB,已知∠ADC=∠CEB=90°,AC=CB,根据全等三角形的判定AAS即可证明△ADC≌△CEB,根据各边的相等关系即可得DE=AD+BE.(2)同理可证得△ADC≌△CEB,再根据各边的相等关系可得DE=AD﹣BE.【解答过程】(1)证明:∵AD⊥MN,BE⊥MN,∴∠ADC=∠CEB=90°,∴∠DAC+∠ACD=90°,∵∠ACB=90°,∴∠ACD+∠BCE=180°﹣90°=90°,∴∠DAC=∠ECB;在△ADC和△CEB中,∠ADC=∠CEB,∠DAC=∠ECB,AC=CB,∴△ADC≌△CEB(AAS)①,(7分)∴DC=EB,AD=CE,∴DE=AD+BE.(9分)(2)解:同理可得△ADC≌△CEB①;(11分)∴AD=CE,CD=BE,∴DE=AD﹣BE②.(14分)24.(2018秋•环翠区期末)(1)如图1,在四边形ABCD中,AB=AD,∠B=∠D=90°,E、F分别是边BC、CD上的点,若∠EAF=12∠BAD,可求得EF、BE、FD之间的数量关系为BE+DF=EF.(只思考解题思路,完成填空即可,不必书写证明过程)(2)如图2,在四边形ABCD中,AB=AD,∠B+∠ADC=180°,E、F分别是边BC、CD延长线上的点,若∠EAF=12∠BAD,判断EF、BE、FD之间的数量关系还成立吗,若成立,请完成证明,若不成立,请说明理由.【可借鉴第(1)问的解题经验】【解题思路】(1)线段EF、BE、FD之间的数量关系是BE+DF=EF.如图1中,延长CB至M,使BM =DF,连接AM,利用全等三角形的性质解决问题即可.(2)结论:EF+DF=BE.如图2中,在BE上截取BM=DF,连接AM,证明△ABM≌△ADF(SAS),推出AM=AF,∠BAM=∠DAF,再证明△AEM≌△AEF(SAS),可得结论.【解答过程】解:(1)线段EF、BE、FD之间的数量关系是BE+DF=EF.如图1,延长CB至M,使BM=DF,连接AM,∵∠ABC +∠D =180°,∠ABC +∠1=180°,∴∠1=∠D ,在△ABM 和△ADF 中,{AB =AD ∠1=∠D BM =DF,∴△ABM ≌△ADF (SAS ),∴AM =AF ,∠3=∠2,∵∠EAF =12∠BAD ,∴∠4+∠4=∠EAF ,∴∠GAM =∠3+∠4=∠2+∠4=∠EAF ,在△MAE 和△F AE 中,{AM =AF ∠MAE =∠FAE AE =AE,∴△MAE ≌△F AE (SAS ),∴EF =EM ,∵EM =BM +BE =BE +DF ,∴EF =BE +FD ;故答案为:BE +DF =EF .(2)结论:EF +DF =BE .理由:在BE 上截取BM =DF ,连接AM ,∵∠B +∠ADC =180°,∠ADC +∠ADE =180°,∴∠B =∠ADF ,在△ABM 与△ADF 中,{BM =DF ∠ABM =∠ADF AB =AD,∴△ABM ≌△ADF (SAS ),∴AM =AF ,∠BAM =∠DAF ,∵∠EAF =12∠BAD ,∴∠EAF =∠EAM ,在△AEM 与△AEF 中,{AM =AF ∠EAF =∠EAM AE =AE,∴△AEM ≌△AEF (SAS ),∴EM =EF ,即BE ﹣BM =EF ,即BE ﹣DF =EF ,∴EF +DF =BE .25.(2021春•和平区期末)如图,在△ABC 中,AC =BC ,点D 在边AB 上,AB =4BD ,连接CD ,点E ,F 在线段CD 上,连接BF ,AE ,∠BFC =∠AEC =180°﹣∠ACB .(1)①∠FBC 与∠ECA 相等吗?说明你的理由;②△FBC 与△ECA 全等吗?说明你的理由;(2)若AE =11,EF =8,则请直接写出BF 的长为 3 ;(3)若△ACE 与△BDF 的面积之和为12,则△ABC 的面积为 48 .【解题思路】(1)①连接BC ,由已知及∠AEC =180°﹣∠AED ,可得到∠ACB =∠AED .再证明∠CAE =∠BCF ,由三角形内角和定理可得∠FBC =∠ECA ;②利用“ASA ”证明△FBC ≌△ECA ;(2)由(1)中全等三角形的结论及已知可得到BF 的长;(3)由(1)中结论可得S △FBC =S △ECA ,所以S △ECA +S △BDF =12=S △FBC +S △BDF =S △DBC ,根据AB =4BD ,可得到S △DBC =14S △ABC =12,从而可得△ABC 的面积.【解答过程】解:(1)①∠FBC =∠ECA ,理由如下:连接BC ,如右图.∵∠BFC =∠AEC =180°﹣∠ACB ,且∠AEC =180°﹣∠AED ,∴∠ACB =∠AED .由外角定理可得∠AED =∠ACD +∠CAE ,又∠ACB =∠ACD +∠BCF ,∴∠CAE =∠BCF ,由三角形内角和定理可得∠FBC =∠ECA .②△FBC 与△ECA 全等,理由如下:在△FBC 和△ECA 中,{∠FBC =∠ECA BC =CA ∠BCF =∠CAE,∴△FBC ≌△ECA (ASA ).(2)由(1)中②可知,FC =AE =11,BF =CE ,又EF =8,∴CE =FC ﹣EF =11﹣8=3,∴BF =3,故答案为:3.(3)由(1)中结论可知S△FBC=S△ECA,∴S△ECA+S△BDF=12=S△FBC+S△BDF=S△DBC,又AB=4BD,∴S△DBC=14S△ABC=12,∴S△ABC=48.故答案为:48.26.(2020•岱岳区一模)已知∠ABC=90°,点D是直线AB边上的点,AD=BC.(1)如图1,点D在线段AB上,过点A作AF⊥AB,且AF=BD,连接DC、DF、CF,试判断△CDF 的形状并说明理由;(2)如图2,点D在线段AB的延长线上,点F在点A的左侧,其他条件不变,以上结论是否仍然成立?请说明理由.【解题思路】(1)利用SAS证明△F AD≌△DBC,再利用全等三角形的性质得出FD=DC,即可判断三角形的形状;(2)利用SAS证明△F AD和△DBC全等,再利用全等三角形的性质得出FD=DC,∠FDC=90°,即可得出结论.【解答过程】(1)△CDF是等腰直角三角形,理由如下:∵AF⊥AB,∴∠A=90°,在△F AD和△DBC中,∵{AF=BD∠A=∠B=90°AD=BC,∴△F AD≌△DBC(SAS),∴∠ADF=∠BCD,DF=DC,∵∠BDC+∠BCD=90°,∴∠ADF+∠CDB=90°,∴∠FDC=180°﹣90°=90°,又∵DF=DC,∴△CDF是等腰直角三角形;(2)仍然成立,理由如下:∵AF⊥AB,∴∠A=90°,在△F AD和△DBC中,∵{AF=BD∠A=∠DBC=90°AD=BC,∴△F AD≌△DBC(SAS),∴∠ADF=∠BCD,DF=DC,∵∠BDC+∠BCD=90°,∴∠ADF+∠BDC=90°,即∠FDC=90°,又∵DF=DC,∴△CDF是等腰直角三角形.27.如图(1),线段AD∥BC,连接AB、CD,取CD中点E,连接AE,AE平分∠BAD.(1)线段AB与AD、BC之间存在怎样的等量关系?请说明理由.(2)如果点C在AB的左侧,其他条件不变,如图(2)所示,那么(1)中的结论还成立吗?如果成立,请说明理由;如果不成立,请写出新的结论,并说明理由.【解题思路】(1)延长AE ,BF 交于点F ,即可求证△ADE ≌△FCE ,即可求得CF =AD ,AB =BF ,即可求得AB =AD +BC ;(2)不成立,新的结论为:AB +BC =AD .延长AE ,BF 交于点F ,可证△ADE ≌△FCE 和AB =BF ,即可解题.【解答过程】解:(1)延长AE ,BF 交于点F ,∵AE 平分∠BAD ,∴∠BAF =∠DAF ,∵AD ∥BC ,∴∠AFB =∠DAF ,∴AB =BF ,在△ADE 和△FCE 中,{∠DAE =∠EFC ∠AED =∠FEC DE =CE,∴△ADE ≌△FCE (AAS ),∴CF =AD ,∵BF =BC +CF ,∴AB =BC +AD ;(2)不成立,新结论为:AB =AD ﹣BC .延长AE ,BF 交于点F ,证明:∵AE 平分∠BAD ,∴∠BAF =∠DAF ,∵AD ∥BC ,∴∠AFB =∠DAF ,∴AB =BF ,在△ADE 和△FCE 中,{∠DAE =∠EFC ∠AED =∠FEC DE =CE,∴△ADE ≌△FCE (AAS ),∴CF =AD ,∵BF +BC =CF ,∴AB +BC =AD .28.(2021春•章丘区期末)如图,CD 是经过∠BCA 顶点C 的一条直线,CA =CB ,E 、F 分别是直线CD 上两点,且∠BEC =∠CF A =α.(1)若直线CD 经过∠BCA 的内部,且E 、F 在射线CD 上.①如图1,若∠BCA =90°,α=90°,则BE = CF ;②如图2,若0°<∠BCA <180°,请添加一个关于α与∠BCA 关系的条件 α+∠BCA =180° ,使①中的结论们然成立,并说明明理由;(2)如图3,若线CD 经过∠BCA 的外部,a =∠BCA ,请提出关于EF ,BE ,AF 三条线段数量关系的合理猜想,并简述理由.【解题思路】(1)由∠BCA =90°,∠BEC =∠CF A =α=90°,可得∠CBE =∠ACF ,从而可证△BCE ≌△CAF ,故BE =CF .(2)若BE =CF ,则可使得△BCE ≌△CAF .根据题目已知条件添加条件,再使得一对角相等,△BCE ≌△CAF 便可得证.(3)题干已知条件可证△BCE ≌△CAF ,故BE =CF ,EC =F A ,从而可证明EF =BE +AF .【解答过程】解:(1)∵∠BEC =∠CF A =α=90°,∴∠BCE +∠CBE =180°﹣∠BEC =90°.又∵∠BCA =∠BCE +∠ACF =90°,∴∠CBE =∠ACF .在△BCE 和△CAF 中,{∠BEC =∠CFA ,∠CBE =∠ACF ,BC =AC .∴△BCE ≌△CAF (AAS ).∴BE =CF .(2)α+∠BCA =180°,理由如下:∵∠BEC =∠CF A =α,∴∠BEF =180°﹣∠BEC =180°﹣α.又∵∠BEF =∠EBC +∠BCE ,∴∠EBC +∠BCE =180°﹣α.又∵α+∠BCA =180°,∴∠BCA =180°﹣α.∴∠BCA =∠BCE +∠ACF =180°﹣α.∴∠EBC =∠FCA .在△BCE 和△CAF 中,{∠CBE =∠ACF ,∠BEC =∠CFA ,BC =CA .∴△BCE ≌△CAF (AAS ).∴BE =CF .(3)EF =BE +AF ,理由如下:∵∠BCA =α,∴∠BCE +∠ACF =180°﹣∠BCA =180°﹣α.又∵∠BEC =α,∴∠EBC +∠BCE =180°﹣∠BEC =180°﹣α.∴∠EBC =∠FCA .在△BEC 和△CF A 中,{∠EBC =∠FCA ,∠BEC =∠FCA ,BC =CA .∴△BEC ≌△CF A (AAS ).∴BE =CF ,EC =F A .∴EF =EC +CF =F A +BE ,即EF =BE +AF .29.(2020春•南岸区期末)在∠MAN 内有一点D ,过点D 分别作DB ⊥AM ,DC ⊥AN ,垂足分别为B ,C .且BD =CD ,点E ,F 分别在边AM 和AN 上.(1)如图1,若∠BED =∠CFD ,请说明DE =DF ;(2)如图2,若∠BDC =120°,∠EDF =60°,猜想EF ,BE ,CF 具有的数量关系,并说明你的结论成立的理由.【解题思路】(1)根据题目中的条件和∠BED =∠CFD ,可以证明△BDE ≌△CDF ,从而可以得到DE =DF ;(2)作辅助线,过点D 作∠CDG =∠BDE ,交AN 于点G ,从而可以得到△BDE ≌△CDG ,然后即可得到DE =DG ,BE =CG ,再根据题目中的条件可以得到△EDF ≌△GDF ,即可得到EF =GF ,然后即可得到EF ,BE ,CF 具有的数量关系.【解答过程】解:(1)∵DB ⊥AM ,DC ⊥AN ,∴∠DBE =∠DCF =90°,在△BDE 和△CDF 中,∵{∠BED =∠CFD ,∠DBE =∠DCF ,BD =CD ,∴△BDE ≌△CDF (AAS ).∴DE =DF ;(2)EF =FC +BE ,理由:过点D 作∠CDG =∠BDE ,交AN 于点G ,在△BDE 和△CDG 中,{∠EBD =∠GCD BD =CD ∠BDE =∠CDG,∴△BDE ≌△CDG (ASA ),∴DE =DG ,BE =CG .∵∠BDC =120°,∠EDF =60°,∴∠BDE +∠CDF =60°.∴∠FDG =∠CDG +∠CDF =60°,∴∠EDF =∠GDF .在△EDF 和△GDF 中,{DE =DG ∠EDF =∠GDF DF =DF,∴△EDF ≌△GDF (SAS ).∴EF =GF ,∴EF=FC+CG=FC+BE.30.(2021春•揭东区期末)已知点C为线段AB上一点,分别以AC、BC为边在线段AB同侧作△ACD和△BCE,且CA=CD,CB=CE,∠ACD=∠BCE,直线AE与BD交于点F.(1)如图1,求证:△ACE≌△DCB.(2)如图1,若∠ACD=60°,则∠AFB=120°;如图2,若∠ACD=90°,则∠AFB=90°;(3)如图3,若∠ACD=β,则∠AFB=180°﹣β(用含β的式子表示)并说明理由.【解题思路】(1)求出∠ACE=∠DCB,根据SAS证出两三角形全等即可;(2)根据全等三角形性质得出∠AEC=∠DBC,∠CDB=∠CAE,求出∠EAB+∠DBA=∠ACD,∠AFB =180°﹣(∠EAB+∠DBC),代入求出即可;(3)根据全等三角形性质得出∠AEC=∠DBC,∠CDB=∠CAE,求出∠EAB+∠DBA=∠ACD,∠AFB =180°﹣(∠EAB+∠DBC),代入求出即可.【解答过程】(1)证明:∵∠ACD=∠BCE,∴∠ACD+∠DCE=∠BCE+∠DCE,∴∠ACE=∠DCB,在△ACE和△DCB中∵{AC=CD∠ACE=∠DCB CE=CB,∴△ACE≌△DCB;(2)解:∵∠ACD=60°,∴∠CDB+∠DBC=∠ACD=60°,∵△ACE≌△DCB,∴∠AEC=∠DBC,∠CDB=∠CAE,∴∠CAE+∠DBC=60°,∴∠AFB=180°﹣60°=120°;当∠ACD=90°时,∵∠ACD=90°,∴∠CDB+∠DBC=∠ACD=90°,∵△ACE≌△DCB,∴∠AEC=∠DBC,∠CDB=∠CAE,∴∠CAE+∠DBC=90°,∴∠AFB=180°﹣90°=90°;故答案为:120°,90°;(3)解:当∠ACD=β时,∠AFB=180°﹣β,理由是:∵∠ACD=β,∴∠CDB+∠DBC=∠ACD=β,∵△ACE≌△DCB,∴∠AEC=∠DBC,∠CDB=∠CAE,∴∠CAE+∠DBC=β,∴∠AFB=180°﹣(∠CAE+∠DBC)=180°﹣β;故答案为:180°﹣β.。
1.3探索三角形全等的条件(6)(分层练习)解析版

1.3 探索三角形全等的条件(6)分层练习1.图中是全等的三角形是()A.甲和乙B.乙和丁C.甲和丙D.甲和丁【答案】B【分析】比较三条边的长度一致的就是全等三角形.【详解】解:比较三角形的三边长度,发现乙和丁的长度完全一样,即为全等三角形,故选:B.2.将三根木条钉成一个三角形木架,这个三角形木架具有稳定性.解释这个现象的数学原理是()A.SSS B.SAS C.ASA D.AAS【答案】A【分析】根据三根木条即为三角形的三边长,利用全等三角形判定定理确定唯一三角形即可得.【详解】解:三根木条即为三角形的三边长,即为利用SSS确定三角形,故选:A.3.如图,AC=FD,BC=ED,要利用“SSS”来判定△ABC和△FED全等时,下面的4个条件中:①AE=FB;②AB=FE;③AE=BE;④BF=BE,可利用的是()A.①或②B.②或③C.①或③D.①或④【答案】A【分析】根据全等三角形的SSS判定条件解答即可.【详解】解:∵AE=FB,∴AE+BE=FB+BE,∴AB=FE,在△ABC和△FED中,AC=FDBC=ED,AB=FE∴△ABC≌△FED(SSS),∵AE=BE和BF=BE推不出AB=FE,∴可利用的是①或②,故选:A.4.如图,在△ABC中,AB=AC,D为BC的中点,则下列结论中:①△ABD≌△ACD;②∠B=∠C;③AD平分∠BAC;④AD⊥BC,其中正确的个数为( )A.1个B.2个C.3个D.4个【答案】D【分析】由D为BC中点可得BD=CD,利用SSS即可证明△ABD≌△ACD,根据全等三角形的性质逐一判断即可.【详解】∵D为BC的中点,∴BD=CD,又∵AB=AC,AD为公共边∴△ABD≌△ACD(SSS),故①正确,∴∠B=∠C,∠BAD=∠CAD,∠ADB=∠ADC,∵∠ADB+∠ADC=180°,∴∠ADB=∠ADC=90°,即AD⊥BC,故②③④正确.综上所述:正确的结论有①②③④共4个,故选D.【答案】3【分析】根据已知利用全等三角形的判定方法SSS得出全等三角形即可.【详解】解:全等三角形共有3对,△ACE≅△ADE,△ACB≅△ADB,△ECB≅△EDB,理由:在△ECB和△EDB中EB=EBEC=ED,BC=BD∴△ECB≅△EDB(SSS),在△ACE和△ADE中AC=ADAE=AE,EC=ED∴△ACE≅△ADE(SSS),在△ACB和△ADB中AB=ABAC=AD,BC=BD∴△ACB≅△ADB(SSS).故答案为:3.8.如图,点E、F在BD上,且AB=CD,BF=DE,AE=CF,试说明:点O是AC的中点.请你在横线上补充其推理过程或理由.解:因为BF=DE,所以BF―EF=DE―EF,因为AB=CD,AE=CF,所以_______________(理由:SSS)所以∠B=∠D(理由:_________________)因为∠AOB=∠COD(理由:_________________)所以△ABO≌△CDO所以__________________(理由:全等三角形对应边相等)所以点O是AC中点.【答案】△ABE≌△CDF,全等三角形对应角相等,对顶角相等,AO=CO【分析】由“SSS”可证△ABE≌△CDF,可得∠B=∠D,由“AAS”可证△ABO≌△CDO,可得AO=CO,即可求解.【详解】解:因为BF=DE,所以BF―EF=DE―EF,因为AB=CD,AE=CF,所以△ABE≌△CDF(理由:SSS),所以∠B=∠D(理由:全等三角形对应角相等),因为∠AOB=∠COD(理由:对顶角相等),所以△ABO≌△CDO,所以AO=CO(理由:全等三角形对应边相等),所以点O是AC中点,故答案为:△ABE≌△CDF,全等三角形对应角相等,对顶角相等,AO=CO.9.如图,AB=AD,BC=CD,AC、BD相交于E,由这些条件可以得到若干结论,请你写出其中3个正确结论(不要添加字母和辅助线,并对其中一个给出证明)结论1:结论2:结论3:证明:【答案】结论1:△ABC≌△ADC结论2:∠BCA=∠DCA结论3:AC平分∠BAD证明结论3,见详解【分析】结合题意,得出三个结论;利用“SSS”证明△ABC≌△ADC,由全等三角形的性质即可证明AC平分∠BAD.【详解】结论1:△ABC≌△ADC结论2:∠BCA=∠DCA结论3:AC平分∠BAD证明结论3:在△ABC和△ADC中,AB=ADAC=ACCB=CD,∴△ABC≌△ADC(SSS),∴∠BAC=∠DAC,即AC平分∠BAD.10.如图,AD=CB,E,F是AC上两动点,且有DE=BF(1)若E,F运动如图①所示的位置,且有AF=CE,求证:△ADE≌△CBF;(2)若E,F运动如图②所示的位置,仍有AF=CE,那么△ADE≌△CBF还成立吗?为什么?(3)若E,F不重合,AD和CB平行吗?说明理由.【答案】(1)详见解析;(2)成立,证明详见解析;(3)AD与CB不一定平行,理由详见解析.【分析】(1)根据AF=CE可得AF+EF=CE+EF,即AE=CF,利用SSS即可证明△ADE≌△CBF;(2)根据AF=CE可得AF-EF=CE-EF,即AE=CF,利用SSS即可证明△ADE≌△CBF;(3)根据已知两个条件,不能判定△ADE≌△CBF,不能确定∠A=∠C,即可得AD和CB不一定平行.【详解】(1)∵AF=CE,∴AF+EF=CE+EF,即AE=CF,在△ADE和△CBF中AD=CB DE=BF AE=CF,∴△ADE≌△CBF.(2)成立.理由如下:∵AF=CE,∴AF-EF=CE-EF,即AE=CF,在△ADE和△CBF中AD=CB DE=BF AE=CF,∴△ADE≌△CBF.(3)AD与CB不一定平行,理由如下:∵只给了两组对应相等的边,∴不能判定△ADE≌△CBF,∴不能判定∠A与∠C的大小关系,∴AD与CB不一定平行.11.中国现役的第五代隐形战斗机歼—20的机翼如图,为适应空气动力的要求,两个翼角∠A,∠B必须相等. 制造中,工作人员只需用刻度尺测量PA=PB,CA=CB就能满足要求,说明理由.【分析】连接PC,证明△APC≌△BPC(SSS)即可证明∠A=∠B;【详解】解:如图所示,连接PC,∵PA=PB,PC=PC,AC=BC,∴△APC≌△BPC(SSS),∴∠A=∠B;12.如图,在四边形ABCD中,CB⊥AB于点B,CD⊥AD于点D,点E,F分别在AB,AD上,AE AF=,CE=CF.若AE=8,CD=6,求四边形AECF的面积.【答案】)8【分析】连接AC ,证明△ACE ≌△ACF ,则S △ACE =S △ACF ,根据三角形面积公式求得S △ACF 与S △ACE ,根据S 四边形AECF =S △ACF +S △ACE 求解即可;【详解】解:连接AC ,如图,在△ACE 和△ACF 中AE =AF CE =CF AC =AC∴△ACE ≌△ACF (SSS ).∴S △ACE =S △ACF ,∠FAC =∠EAC .∵CB ⊥AB ,CD ⊥AD ,∴CD =CB =6.∴S △ACF =S △ACE =12AE ·CB =12×8×6=24.∴S 四边形AECF =S △ACF +S △ACE =24+24=48.(1)【旧题重现】《学习与评价》19P 有这样一道习题:如图①,AD 、A ′D ′分别是△ABC 和△A ′B ′C ′的BC 、B C ¢¢边上的中线,AD A D ¢¢=,AB =A ′B ′,BC =B ′C ′.求证:△ABC≌△A ′B ′C ′.证明的途径可以用下面的框图表示,请填写其中的空格..(2)【深入研究】如图②,AD 、A ′D ′分别是△ABC 和△A ′B ′C ′的BC 、B C ¢¢边上的中线,AD A D ¢¢=,AB =A ′B ′,AC =A ′C ′.判断△ABC 与△A ′B ′C ′是否仍然全等.(3)【类比思考】下列命题中是真命题的是 .(填写相应的序号)①两角和第三个角的角平分线分别相等的两个三角形全等;②一边和这条边上的中线以及高分别相等的两个三角形全等;③斜边和斜边上的高分别相等的两个直角三角形全等;④两边和第三边上的高分别相等的两个三角形全等;⑤底边和一腰上的中线分别相等的两个等腰三角形全等.【答案】(1)①BD =12BC ;②B ′D ′=12B ′C ′;③AD =A ′D ′;④∠B =∠B ′(2)全等,见解析(3)①②③⑤【分析】(1)根据三角形中线的定义及全等三角形的判定与性质可得出答案;(2)延长AD 至E ,使DE =AD ,连接BE ,延长A ′D ′至E ′,使D ′E ′=A ′D ′,连接B ′E ′.证明△ADC≌△EDB(SAS ).由全等三角形的性质得出AC =EB ,∠DAC =∠E ,同理A ′C ′=E ′B ′,∠D ′A ′C ′=∠E ′.证明△ABE≌△A ′B ′E ′(SSS ).得出∠BAE =∠B ′A ′E ′,∠E =∠E ′.则可证明△ABC≌△A ′B ′C ′(SAS );(3)根据全等三角形的判定方法可得出结论.【详解】(1)证明:∵AD 是△ABC 的中线,∴BD =12BC ,∵A ′D ′分别是△A ′B ′C ′的中线,∴B ′D ′=12B ′C ′,∵BC =B ′C ′,∴BD =B ′D ′,在△ABD 和△A ′B ′D ′中,BD =B ′D ′AD =A ′D ′AB =A ′B ′,∴△ABD≌△A ′B ′D ′(SSS ),∴∠B =∠B ′,在△ABC 和△A ′B ′C ′中,AB =A ′B ′∠B =∠B ′BC =B ′C ′,∴△ABC≌△A ′B ′C ′(SAS ).故答案为:①BD =12BC ;②B ′D ′=12B ′C ′;③AD =A ′D ′;④∠B =∠B ′;(2)解:△ABC 与△A ′B ′C ′仍然全等,理由如下:延长AD 至E ,使DE =AD ,连接BE ,延长A ′D ′至E ′,使D ′E ′=A ′D ′,连接B ′E ′.∵AD 和A ′D ′分别是△ABC 和△A ′B ′C ′的BC 和B ′C ′边上的中线,∴BD =CD ,B ′D ′=C ′D ′.在△ADC 和△EDB 中,AD =DE ∠ADC =∠BDE BD =CD,∴△ADC≌△EDB(SAS ).∴AC=EB,∠DAC=∠E,同理A′C′=E′B′,∠D′A′C′=∠E′.∵AC=A′C′,∴EB=E′B′.∵AD=A′D′,AD=DE,A′D′=D′E′,∴AE=A′E′.∵AB=A′B′,∴△ABE≌△A′B′E′(SSS).∴∠BAE=∠B′A′E′,∠E=∠E′.∴∠DAC=∠D′A′C′.∴∠BAC=∠B′A′C′,又AB=A′B′,AC=A′C′,∴△ABC≌△A′B′C′(SAS),(3)①两角和第三个角的角平分线分别相等的两个三角形全等,正确,符合题意;②一边和这条边上的中线以及高分别相等的两个三角形全等,正确,符合题意;③斜边和斜边上的高分别相等的两个直角三角形全等,正确,符合题意;④两边和第三边上的高分别相等的两个三角形全等,说法错误,如图,在△ABC与△AB C′中,AB=AB,AC=A C′,高AD相同,但是△ABC与△AB C′不全等.故④不符合题意;⑤底边和一腰上的中线分别相等的两个等腰三角形全等,正确,符合题意.故答案为:①②③⑤.(初步探索)(1)如图1:在四边形ABCD中,AB=AD,∠B=∠ADC=90°,E、F分别是BC、CD上的点,且EF=BE+FD,探究图中∠BAE、∠FAD、∠EAF之间的数量关系.小明同学探究此问题的方法是:延长FD 到点G,使DG=BE.连接AG,先证明△ABE≌△ADG,再证明△AEF≌△AGF,可得出结论,他的结论应是___________;(灵活运用)(2)如图2,若在四边形ABCD中,AB=AD,∠B+∠D=180°,E、F分别是BC、CD上的点,且EF=BE+FD,上述结论是否仍然成立,并说明理由.【答案】(1)∠BAE+∠FAD=∠EAF,证明见解析(2)成立,理由见解析【分析】(1)如图1,延长FD到点G,使DG=BE,连接AG,先证明△ABE≌△ADG,得到∠BAE=∠DAG,AE=AG,再证明△AEF≌△AGF,得到∠EAF=∠GAF =∠DAG+∠DAF =∠BAE+∠DAF 即可;(2)同(1)证明即可.【详解】(1)解:∠BAE+∠FAD=∠EAF.理由如下:如图1,延长FD到点G,使DG=BE,连接AG,∵∠B=∠ADC=90°,∴∠ADG=∠B=90°,∵DG=BE,AB=AD,∴△ABE≌△ADG(SAS),∴∠BAE=∠DAG,AE=AG,∵EF=BE+FD,DG=BE,∴EF=DG+FD=GF,又∵AE=AG,AF=AF,∴△AEF≌△AGF(SSS),∴∠EAF=∠GAF =∠DAG+∠DAF =∠BAE+∠DAF.故答案为:∠BAE+∠FAD=∠EAF;(2)解:如图2,延长FD到点G,使DG=BE,连接AG,∵∠B+∠ADF=180°,∠ADG+∠ADF=180°,∴∠B=∠ADG,又∵AB=AD,∴△ABE≌△ADG(SAS),∴∠BAE=∠DAG,AE=AG,∵EF=BE+FD=DG+FD=GF,AF=AF,∴△AEF≌△AGF(SSS),∴∠EAF=∠GAF =∠DAG+∠DAF =∠BAE+∠DAF.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
E B 1 2
G
C
E
G
⎨
⎩
全等三角形证明过程训练(习题)
例题示范
例 1:已知:如图,在正方形 ABCD 中,AB =CB ,∠ABC =90°.E A
D
为正方形内一点,BE ⊥BF ,BE =BF ,EF 交 BC 于点 G . 求证:AE =CF .
【思路分析】 A D ① 读题标注:
B
C
F
② 梳理思路: F
要证 AE =CF ,可以把它们放在两个三角形中证全等.观察发现,放在△ABE 和△CBF 中进行证明. 要证全等,需要三组条件,其中必须有一组边相等. 由
已知得,AB =CB ;BE =BF ;
根据条件∠ABC =90°,BE ⊥BF ,推理可得∠1=∠2. 因此由 SAS 可证两三角形全等.
【过程书写】(在演草部分先进行规划,然后书写过程) 证明:如图
∵BE ⊥BF ∴∠EBF =90°
∴∠2+∠EBC =90° ∵∠ABC =90°
∴∠1+∠EBC =90° ∴∠1=∠2
在△ABE 和△CBF 中
⎧ A B = CB ⎪
∠1 = ∠2 ⎪BE = BF (已知) (已证) (已知) ∴△ABE ≌△CBF (SAS )
∴AE =CF (全等三角形对应边相等)
过程规划:
1.准备不能直接用的条件: ∠1=∠2
2.证明△ABE ≌△CBF
3.根据全等性质得,AE =CF
E
巩固练习
1.
如图,PD ⊥AB ,PE ⊥AC ,垂足分别为点 D ,E ,且 P D =PE , 将
上述条件标注在图中,易得 ≌ , 从而 A D = .
A
D
B C
第 1 题图 第 2 题图
2.
已知:如图,AB ⊥BD 于点 B ,CD ⊥BD 于点 D ,如果要使 △ABD ≌△CDB ,那么还需要添加一组条件, 这个条件可以是 ,理由是 ; 这个条件也可以是 ,理由是 ; 这个条件也可以是 ,理由是 ; 这个条件还可以是
,理由是
.
3.
已知:如图,C 为 BD 上一点,AC ⊥CE ,AC =CE ,∠ABC = ∠CDE =90°.若 A B =4,DE =2,则 B D 的长为 .
A
C
4.
已知:如图,点 A ,E ,F ,B 在同一条直线上,CE ⊥AB 于点 E ,DF ⊥AB 于点 F ,BC =AD ,AE =BF . 求证:△CEB ≌△DFA .
A
C D
F
2 1
5.
如图,点 C ,F 在 BE 上,∠1=∠2,BF =EC ,∠A =∠D . 求
证:△ABC ≌△DEF .
A
D
F
6.
已知:如图,点 A ,B ,C ,D 在同一条直线上,且 A C =BD , BE ∥CF ,AE ∥DF .求证:△ABE ≌△DCF .
过程规划:
过程规划:
E
H
7.
已知:如图,在△ABC 中,AD ⊥BC ,CE ⊥AB ,垂足分别为 点 D ,E ,AD 与 C E 相交于点 H ,AE =CE .
A
求证:AH =CB .
B
D
C
思考小结
1. 要证明边或者角相等,可以考虑边或者角所在的两个三角形
;要证明三角形全等,需要准备 _组条件,其中 有一组必须是 相等.
过程规划:
2.阅读材料
我们是怎么做几何题的?
例 1:已知:如图,AB=AD,AC=AE,∠BAE=∠DAC.
求证:∠B=∠D. E
B 第一步:读题标注,把题目信息转移到图形上(请把条件标注
在图上)
第二步:分析特征走通思路 C A
① 要求∠B=∠D,考虑放在两个三角形里面证全等,把∠B
放在△ABC 中,把∠D 放在△ADE 中,只需要证明这两 D
个三角形全等即可.
② 要证明△ABC ≌△ADE ,需要找三组条件,由已知得
AB=AD,AC=AE,还差一组条件,根据∠BAE=∠DAC,同
时加上公共角∠CAE,可得∠BAC=∠DAE,利用 SAS 可
得两个三角形全等.
第三步:规划过程
过程分成三块:
① 由∠BAE=∠DAC,可得∠BAC=∠DAE;
② 由SAS 得△ABC≌△ADE;
③ 由全等得∠B=∠D.第
四步:过程书写
A
B
3 2 1
4 C
D
⎩
⎨
⎩ 【参考答案】 巩固练习
1. Rt △ADP ,Rt △AEP ,AE
2. AD =CB ,HL
AB =CD ,SAS ∠A =∠C ,AAS
∠ADB =∠CBD ,ASA 3. 6
4. 证明:如图,
∵CE ⊥AB ,DF ⊥AB ∴∠CEB =∠DFA =90° ∵AE =BF
∴AE +EF =BF +EF 即 AF =BE
在 Rt △CEB 和 Rt △DFA 中 ⎧BC = AD (已知) ⎨
BE = AF (已证) ∴Rt △CEB ≌Rt △DFA (HL ) 5. 证明:如图,
∵BF =EC
∴BF +FC =EC+FC 即 BC =EF
在△ABC 和△DEF 中 ⎧ A = ∆ (已知) ⎪
1 =
2 (已知) ⎪BC = EF (已证) ∴△ABC ≌△DEF (AAS ) F
6. 证明:如图,
∵AC =BD
∴AC -BC =BD -BC 即 AB =DC ∵BE ∥CF ∴∠1=∠2
∵∠1+∠3=180°
E
3
E
4 H 2
1
⎨ ⎩
⎨ ⎩
∠2+∠4=180° ∴∠3=∠4 ∵AE ∥DF ∴∠A =∠D
在△ABE 和△DCF 中 ⎧ 3 = 4 (已证) ⎪
AB = DC (已证) ⎪ A = ∆ (已证) ∴△ABE ≌△DCF (ASA ) 7. 证明:如图,
A
∵AD ⊥BC ∴∠ADC =90° ∴∠1+∠2=90° ∵CE ⊥AB
∴∠AEH =∠CEB =90° ∴∠3+∠4=90° ∵∠2=∠4 ∴∠1=∠3
在△AEH 和△CEB 中 ⎧ AEH = XEB (已证) ⎪
AE = CE (已知) ⎪ 3 = ∠1 (已证) ∴△AEH ≌△CEB (ASA )
∴AH =CB (全等三角形对应边相等)
思考小结
1. 全等;3,边。
