第九章学案54 直线与圆锥曲线的位置关系

合集下载

直线与圆锥曲线的位置关系课件(62张)

由直线 l 与双曲线交于不同的两点得
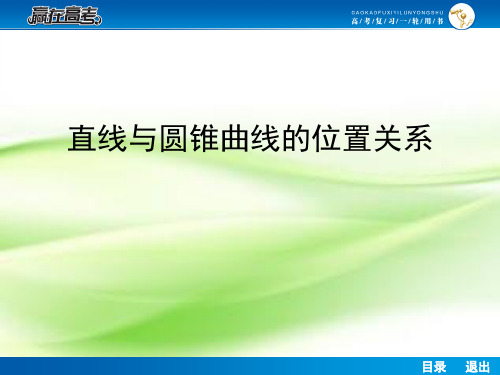
1-3 2 ≠ 0,
= (-6 2k)2 + 36(1-3 2 ) = 36(1- 2 ) > 0,
1
3
故 k2≠ 且 k 2<1.①
6 2k
-9
1-3
1-32
设 A(x1,y1),B(x2,y2),则 x1+x2=
2,x1x2=
.
由·>2 得 x1x2+y1y2>2.
直线与圆锥曲线的位置关系
目录
退出
1.直线与圆锥曲线位置关系的判断方法
(1)代数法,把圆锥曲线方程与直线方程联立消去 y,整理得出关于 x 的
方程 Ax2+Bx+C=0,若圆锥曲线是双曲线或是抛物线,当 A=0 时,表示直线与
双曲线的渐近线或抛物线的轴平行;当 A≠0 时,记该一元二次方程根的判
别式为 Δ.(ⅰ)若 Δ>0 时,直线与圆锥曲线相交;(ⅱ)若 Δ=0 时,直线与圆锥曲
截的线段的中点坐标时,设出直线和圆锥曲线的两个交点坐标,代入圆锥曲
线的方程并作差,从而求出直线的斜率,然后利用中点求出直线方程.“点差
法”的常见题型有:求中点弦方程、求(过定点、平行弦)弦中点轨迹、垂直
平分线问题.必须提醒的是“点差法”具有不等价性,即要考虑判别式 Δ 是否
为正数.
4.圆锥曲线的定值、最值、存在性问题很大一部分是利用等价转化思
B. -∞,-
2
2
∪
2
,+
2
∞
C.(-∞,-2 2)∪(2 2,+∞)
D.(-∞,- 2)∪( 2,+∞)
)
【答案】D
4

圆锥曲线直线与圆锥曲线的位置课件

直线
直线是二维空间中的一维图形，表示两点之间所有点的集合。
位置关系的分类与定义
相交
当直线与圆锥曲线至少有一个交点时，称为相交。
相切
当直线与圆锥曲线仅有一个交点时，称为相切。
相离
当直线与圆锥曲线没有交点时，称为相离。
02 直线与圆锥曲线相交的位置关系
直线与圆锥曲线交点个数的问题
01 直线与圆锥曲线可能有一个、两个或无交点。 02 判断交点个数需要利用代数方法，如判别式法。 03 交点个数与直线的斜率和圆锥曲线的类型有关。
离点距离的计算
离点距离是指离点到直线或圆锥曲线的某一点的距离，可以通过坐标计算得到。
计算方法为使用两点间距离公式，即 $sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}$。
根据具体问题，可以选择不同的点作为计算离点距离的基准点，如直线的交点、圆锥曲线的顶点等。
05 直线与圆锥曲线位置关系的几何意义
几何问题的求解方法
代数法
通过代数运算和方程求解的方法，求出直线和圆锥曲线的交点坐标。
解析几何法
利用解析几何的基本原理和方法，通过代数运算和方程求解的方法，求出直线和圆锥曲线的交点坐标。
几何直观法
通过观察和想象，利用几何图形的性质和特点，直接求解几何问题。
06 直线与圆锥曲线位置关系的实际应用
几何图形的构造与解释
直线与圆锥曲线相交
当直线与圆锥曲线只有一个交点时，表示直线与圆锥曲线相切；当直线与圆锥曲线有两个交点时，表示直线与圆锥曲线相交。
直线与圆锥曲线相切
当直线与圆锥曲线只有一个交点时，表示直线与圆锥曲线相切。
直线与圆锥曲线相离
当直线与圆锥曲线没有交点时，表示直线与圆锥曲线相离。

直线与圆锥曲线的位置关系教案

课题：直线与圆锥曲线的位置关系授课者：滦县第十中学陈智勇高考要求1掌握直线与圆锥曲线公共点问题、相交弦问题以及它们的综合应用解决这些问题经常转化为它们所对应的方程构成的方程组是否有解或解的个数问题2会运用“设而不求”解决相交弦长问题及中点弦问题3会利用圆锥曲线的焦半径公式解决焦点弦的问题掌握求焦半径以及利用焦半径解题的方法4会用弦长公式|AB|=21k|x2－x1|求弦的长；5会利用“设点代点、设而不求”的方法求弦所在直线的方程（如中点弦、相交弦等）、弦的中点的轨迹等一、复习目标（一）知识目标1、掌握用坐标法判断直线与圆锥曲线的位置关系，进一步体会曲线方程的解与曲线上点的坐标之间的关系；2、领会中点坐标公式和弦长公式及韦达定理在解题中的灵活应用；3、理解“点差法”在解决直线与圆锥曲线位置关系中的解题技巧；（二）能力目标1、通过多媒体课件的演示，培养学生发现运动规律、认识规律的能力.2、培养学生运用方程思想、分类讨论、数形结合思想解决问题的能力．（三）情感目标1、通过课件的演示获得培养学生探索数学的兴趣.2、通过师生、生生的合作学习，树立竞争意识与合作精神，感受学习交流带来的成功感，激发提出问题和解决问题的勇气，树立自信心。

二、教学重点与难点重点：直线与圆锥曲线的位置关系的判定及方程思想、分类讨论思想、数形结合思想运用；难点：等价转换、“点差法”设而不求在解题中的灵活应用。

三、方法指导：1、在研究直线与圆锥曲线的交点个数问题时，不要仅由判别式进行判断，一定要注意二次项的系数对交点个数的影响。

2、涉及弦长问题时，利用弦长公式及韦达定理求解，涉及弦的中点及中点弦问题，利用点差法较为简便。

3、要注意判别式和韦达定理在解题中的作用。

应用判别式，可以确定直线和圆锥曲线的位置关系，确定曲线中的参数取值范围，求几何极值等。

应用韦达定理，可以解先相交时的弦长问题，弦的中点问题或最值问题。

4、要重视方程思想、等价转换思想、分类讨论、数形结合等数学思想的运用。

第9讲直线与圆锥曲线的位置关系

第9讲直线与圆锥曲线的位置关系基础知识整合1．直线与圆锥曲线的位置关系要解决直线与圆锥曲线的位置关系问题，可把直线方程与圆锥曲线方程联立，消去y(或消去x)得到关于x(或关于y)的一元二次方程．如联立后得到以下方程：Ax2＋Bx＋C＝0(A≠0)，Δ＝B2－4AC．若Δ<001没有公共点；若Δ＝002有且只有一个公共点；若Δ>003有两个不同的公共点．2．弦长公式直线与圆锥曲线相交时，常常借助根与系数的关系解决弦长问题．直线方程与圆锥曲线方程联立，消去y后得到关于x的一元二次方程．当Δ>0时，直线与圆锥曲线相交，设交点为A(x1，y1)，B(x2，y2)，直线AB的斜率为k，则直线被圆锥曲线截得的弦长|AB|04(x1－x2)2＋(y1－y2)205(1＋k2)|x－x2|1061＋k2·(x＋x2)2－4x1x2.1再利用根与系数的关系得出x1＋x2，x1x2的值，代入上式计算即可．3．直线与圆锥曲线相交弦的中点问题中点弦问题常用“根与系数的关系”或“点差法”求解．(1)利用根与系数的关系：将直线方程代入圆锥曲线的方程，消元后得到一个一元二次方程，利用根与系数的关系和中点坐标公式建立等式求解，注意不能忽视对判别式的讨论．(2)点差法：若直线l与圆锥曲线C有两个交点A，B，一般地，首先设出A(x1，y1)，B(x2，y2)，代入曲线方程，通过作差，构造出x1＋x2，y1＋y2，x1－x2，y1－y 2，从而建立中点坐标和斜率的关系．解决直线与圆锥曲线关系问题的一般方法(1)解决焦点弦(过圆锥曲线焦点的弦)的长的有关问题，注意应用圆锥曲线的定义．(2)已知直线与圆锥曲线的某些关系求圆锥曲线的方程时，通常利用待定系数法．(3)圆锥曲线上的点关于某一直线的对称问题，解此类题的方法是利用圆锥曲线上的两点所在的直线与对称直线垂直，圆锥曲线上两点的中点一定在对称直线上，再利用根的判别式或中点与曲线的位置关系求解．(4)圆锥曲线以P (x 0，y 0)(y ≠0)为中点的弦所在直线的斜率如下表：圆锥曲线方程直线斜率椭圆：x 2a 2＋y 2b 2＝1(a >b >0) k ＝－b 2x 0a 2y 0双曲线：x 2a 2－y 2b 2＝1(a >0，b >0)k ＝b 2x 0a 2y 0抛物线：y 2＝2px (p >0)k ＝p y 01．直线y ＝kx －k ＋1与椭圆x 29＋y 24＝1的位置关系为( ) A ．相交 B ．相切 C ．相离 D ．不确定答案 A解析直线y ＝kx －k ＋1＝k (x －1)＋1恒过定点(1,1)，又点(1,1)在椭圆内部，故直线与椭圆相交．2．若过原点的直线l 与双曲线x 24－y 23＝1有两个不同交点，则直线l 的斜率的取值范围是( )A ．⎝ ⎛⎦⎥⎤－32，32B ．⎝ ⎛⎭⎪⎫－32，32C ．⎣⎢⎡⎦⎥⎤－32，32D ．⎝ ⎛⎦⎥⎤－∞，－32∪⎣⎢⎡⎦⎥⎤32，＋∞答案 B解析因为x 24－y 23＝1，其两条渐近线的斜率分别为k 1＝－32，k 2＝32，要使过原点的直线l 与双曲线有两个不同的交点，画图可知，直线l 的斜率的取值范围应是⎣⎢⎡⎭⎪⎫0，32∪⎝ ⎛⎦⎥⎤－32，0.3．已知椭圆x 2＋2y 2 ＝4，则以(1,1)为中点的弦的长度为( ) A ．3 2 B ．2 3 C ．303 D ．362答案 C解析设以(1,1)为中点的弦的两端点为(x 1，y 1)(x 2，y 2)，则⎩⎨⎧x 21＋2y 21＝4，x 22＋2y 22＝4，∴(x 1＋x 2)(x 1－x 2)＋2(y 1＋y 2)(y 1－y 2)＝0.又x 1＋x 2＝2，y 1＋y 2＝2，∴y 1－y 2x 1－x 2＝－12，∴弦所在直线方程为x ＋2y －3＝0.由⎩⎨⎧x ＋2y －3＝0，x 2＋2y 2＝4，可得弦长为303. 4．已知抛物线y 2＝2px (p >0)，过其焦点且斜率为－1的直线交抛物线于A ，B 两点，若线段AB 的中点的横坐标为3，则该抛物线的准线方程为( )A ．x ＝1B ．x ＝2C ．x ＝－1D ．x ＝－2答案 C解析抛物线y 2＝2px (p >0)的焦点为⎝ ⎛⎭⎪⎫p 2，0，所以过焦点且斜率为－1的直线方程为y ＝－⎝ ⎛⎭⎪⎫x －p 2，代入抛物线方程，整理得x 2－3px ＋p 24＝0，由AB 中点的横坐标为3，得3p ＝6，解得p ＝2，故抛物线y 2＝4x 的准线方程为x ＝－1.5．(2018·全国卷Ⅰ)设抛物线C ：y 2＝4x 的焦点为F ，过点(－2,0)且斜率为23的直线与C 交于M ，N 两点，则FM →·FN→＝( ) A ．5 B ．6 C ．7 D ．8答案 D解析根据题意，过点(－2,0)且斜率为23的直线方程为y ＝23(x ＋2)，与抛物线方程联立⎩⎪⎨⎪⎧y ＝23(x ＋2)，y 2＝4x ，消去x 并整理，得y 2－6y ＋8＝0，解得M (1,2)，N (4,4)，又F (1,0)，所以FM →＝(0,2)，FN →＝(3,4)，从而可以求得FM →·FN →＝0×3＋2×4＝8，故选D ．6．在平面直角坐标系xOy 中，P 为双曲线x 2－y 2＝1右支上的一个动点．若点P 到直线x －y ＋1＝0的距离大于c 恒成立，则实数c 的最大值为________．答案22解析设P (x ，y )(x ≥1)，因为直线x －y ＋1＝0平行于渐近线x －y ＝0，所以c 的最大值为直线x －y ＋1＝0与渐近线x －y ＝0之间距离，为12＝22. 核心考向突破考向一直线与圆锥曲线的位置关系例1 已知直线l ：y ＝2x ＋m ，椭圆C ：x 24＋y 22＝1.试问当m 取何值时，直线l 与椭圆C ：(1)有两个不重合的公共点； (2)有且只有一个公共点；(3)没有公共点．解将直线l 的方程与椭圆C 的方程联立，得方程组⎩⎪⎨⎪⎧y ＝2x ＋m ， ①x 24＋y 22＝1， ②将①代入②，整理得9x 2＋8mx ＋2m 2－4＝0. ③ 方程③根的判别式Δ＝(8m )2－4×9×(2m 2－4)＝－8m 2＋144.(1)当Δ>0，即－32<m <32时，方程③有两个不同的实数根，可知原方程组有两组不同的实数解．这时直线l 与椭圆C 有两个不重合的公共点．(2)当Δ＝0，即m ＝±32时，方程③有两个相同的实数根，可知原方程组有两组相同的实数解．这时直线l 与椭圆C 有两个互相重合的公共点，即直线l 与椭圆C 有且只有一个公共点．(3)当Δ<0，即m <－32或m >32时，方程③没有实数根，可知原方程组没有实数解．这时直线l 与椭圆C 没有公共点．关于直线与圆锥曲线的位置关系的两类问题一是判断位置关系；二是依据位置关系确定参数的范围．这两类问题在解决方法上是一致的，都是将直线与圆锥曲线方程联立，利用判别式及根与系数的关系求解．此时注意观察方程的二次项系数是否为0，若为0，则方程为一次方程；若不为0，则将方程解的个数转化为判别式与0的大小关系求解．[即时训练] 1.在平面直角坐标系xOy 中，已知椭圆C 1：x 2a 2＋y 2b 2＝1(a >b >0)的左焦点为F 1(－1,0)，且点P (0,1)在C 1上．(1)求椭圆C 1的方程；(2)设直线l 同时与椭圆C 1和抛物线C 2：y 2＝4x 相切，求直线l 的方程．解 (1)因为椭圆C 1的左焦点为F 1(－1,0)，所以c ＝1. 将点P (0,1)代入椭圆方程x 2a 2＋y 2b 2＝1，得 1b2＝1，即b ＝1，所以a 2＝b 2＋c 2＝2. 所以椭圆C 1的方程为x 22＋y 2＝1.(2)由题意可知，直线l 的斜率显然存在且不等于0，设直线l 的方程为y ＝kx ＋m ，由⎩⎪⎨⎪⎧x22＋y 2＝1，y ＝kx ＋m ，消去y 并整理得(1＋2k 2)x 2＋4kmx ＋2m 2－2＝0.因为直线l 与椭圆C 1相切，所以Δ1＝16k 2m 2－4(1＋2k 2)(2m 2－2)＝0. 整理得2k 2－m 2＋1＝0.①由⎩⎨⎧y 2＝4x ，y ＝kx ＋m ，消去y 并整理得k 2x 2＋(2km －4)x ＋m 2＝0. 因为直线l 与抛物线C 2相切，所以Δ2＝(2km －4)2－4k 2m 2＝0，整理得km ＝1.②综合①②，解得⎩⎨⎧k ＝22，m ＝2或⎩⎨⎧k ＝－22，m ＝－ 2.所以直线l 的方程为y ＝22x ＋2或y ＝－22x － 2. 考向二弦长问题例2 已知平面上一动点P 到定点F (3，0)的距离与它到直线x ＝433的距离之比为32，记动点P 的轨迹为曲线C ．(1)求曲线C 的方程；(2)设直线l ：y ＝kx ＋m 与曲线C 交于M ，N 两点，O 为坐标原点，若k OM ·k ON ＝54，求△MON 面积的最大值．解 (1)设P (x ，y )，则(x －3)2＋y 2⎪⎪⎪⎪⎪⎪x －433＝32，化简得x 24＋y 2＝1.(2)设M (x 1，y 1)，N (x 2，y 2)，联立⎩⎪⎨⎪⎧y ＝kx ＋m ，x 24＋y 2＝1，得(4k 2＋1)x 2＋8kmx ＋4m 2－4＝0，依题意，得Δ＝(8km )2－4(4k 2＋1)(4m 2－4)>0，化简，得m 2<4k 2＋1，①x 1＋x 2＝－8km4k 2＋1，x 1x 2＝4m 2－44k 2＋1，y 1y 2＝(kx 1＋m )(kx 2＋m )＝k 2x 1x 2＋km (x 1＋x 2)＋m 2，若k OM ·k ON ＝54，则y 1y 2x 1x 2＝54，即4y 1y 2＝5x 1x 2，∴4k 2x 1x 2＋4km (x 1＋x 2)＋4m 2＝5x 1x 2，∴(4k 2－5)·4(m 2－1)4k 2＋1＋4km ⎝ ⎛⎭⎪⎫－8km 4k 2＋1＋4m 2＝0，即(4k 2－5)(m 2－1)－8k 2m 2＋m 2(4k 2＋1)＝0，化简，得m 2＋k 2＝54，② |MN |＝1＋k 2|x 1－x 2| ＝1＋k 2 64k 2m 2(4k 2＋1)2－4·4m 2－44k 2＋1＝1＋k 2－16m 2＋64k 2＋16(4k 2＋1)2＝1＋k 24(20k 2－1)(4k 2＋1)2，∵原点O 到直线l 的距离d ＝|m |1＋k 2， ∴S △MON ＝12|MN |·d ＝12(5－4k 2)(20k 2－1)(4k 2＋1)2.设4k 2＋1＝t ，由①②得0≤m 2<65，120<k 2≤54，所以65<t ≤6，16≤1t <56， S △MON ＝12 (6－t )(5t －6)t 2＝12－36＋36t －5t 2t 2＝3－⎝ ⎛⎭⎪⎫1t －122＋19≤1，所以当1t ＝12，即k ＝±12时，△MON 的面积取最大值，最大值为1.弦长的计算方法求弦长时可利用弦长公式，根据直线方程与圆锥曲线方程联立消元后得到的一元二次方程，利用根与系数的关系得到两根之和、两根之积的代数式，然后整体代入弦长公式求解．注意：两种特殊情况：(1)直线与圆锥曲线的对称轴平行或垂直；(2)直线过圆锥曲线的焦点．[即时训练] 2.(2019·湖北四地七校联考)已知F 1，F 2分别为椭圆Ω：x 24＋y 2b 2＝1(b ＞0)的左、右焦点．(1)当b ＝1时，若P 是椭圆Ω上一点，且P 位于第一象限，PF 1→·PF 2→＝－54，求点P 的坐标；(2)当椭圆的焦距为2时，若直线l ：y ＝12x ＋m 与椭圆Ω相交于A (x 1，y 1)，B (x 2，y 2)两点，且3x 1x 2＋4y 1y 2＝0，试求△AOB 的面积．解 (1)当b ＝1时，x 24＋y 2＝1，则F 1(－3，0)，F 2(3，0)，设P (x ，y )(x ，y ＞0)，则PF 1→＝(－3－x ，－y )，PF 2→＝(3－x ，－y )，又PF 1→·PF 2→＝－54，则⎩⎪⎨⎪⎧x 2＋y 2－3＝－54，x24＋y 2＝1，x ，y ＞0⇒⎩⎨⎧x ＝1，y ＝32，得P ⎝⎛⎭⎪⎫1，32.(2)由题意知，c ＝1，则椭圆方程为x 24＋y 23＝1，联立直线与椭圆方程得， ⎩⎪⎨⎪⎧x 24＋y 23＝1，y ＝12x ＋m⇒x 2＋mx ＋m 2－3＝0⇒⎩⎨⎧x 1＋x 2＝－m ，x 1x 2＝m 2－3， 3x 1x 2＋4y 1y 2＝3x 1x 2＋4⎝ ⎛⎭⎪⎫12x 1＋m ⎝ ⎛⎭⎪⎫12x 2＋m ＝4x 1x 2＋2m (x 1＋x 2)＋4m 2＝6(m 2－2)＝0，解得m 2＝2满足Δ＞0，则|AB |＝1＋⎝ ⎛⎭⎪⎫122·m 2－4(m 2－3)，于是S △AOB ＝12|AB |d ＝12 1＋⎝ ⎛⎭⎪⎫122·m 2－4(m 2－3)·|m |1＋⎝ ⎛⎭⎪⎫122＝ 3.考向三中点弦问题例3 (2019·石家庄一模)已知抛物线C ：y 2＝2px (p >0)上一点P (x 0,2)到焦点F 的距离|PF |＝2x 0.(1)求抛物线C 的方程；(2)过点P 引圆M ：(x －3)2＋y 2＝r 2(0<r ≤2)的两条切线P A ，PB ，切线P A ，PB 与抛物线C 的另一交点分别为A ，B ，线段AB 中点的横坐标记为t ，求t 的取值范围．解 (1)由抛物线的定义，得|PF |＝x 0＋p2，由题意，得⎩⎪⎨⎪⎧2x 0＝x 0＋p2，2px 0＝4，p >0，解得⎩⎨⎧p ＝2，x 0＝1，所以抛物线C 的方程为y 2＝4x .(2)由题意知，过P 引圆(x －3)2＋y 2＝r 2(0<r ≤2)的切线，斜率存在且不为0，设切线P A 的方程为y ＝k 1(x －1)＋2，则圆心M (3,0)到切线P A 的距离d ＝|2k 1＋2|k 21＋1＝r ，整理，得(r 2－4)k 21－8k 1＋r 2－4＝0.设切线PB 的方程为y ＝k 2(x －1)＋2，同理可得(r 2－4)k 22－8k 2＋r 2－4＝0.所以k 1，k 2是方程(r 2－4)k 2－8k ＋r 2－4＝0的两根， k 1＋k 2＝8r 2－4，k 1k 2＝1.设A (x 1，y 1)，B (x 2，y 2)，由⎩⎨⎧y ＝k 1(x －1)＋2，y 2＝4x ，得k 1y 2－4y －4k 1＋8＝0，由根与系数的关系知，2y 1＝8－4k 1k 1，所以y 1＝4－2k 1k 1＝4k 1－2＝4k 2－2，同理可得y 2＝4k 1－2.t ＝x 1＋x 22＝y 21＋y 228＝(4k 2－2)2＋(4k 1－2)28＝2(k21＋k22)－2(k1＋k2)＋1＝2(k1＋k2)2－2(k1＋k2)－3，∈[－4，－2)，设λ＝k1＋k2，则λ＝8r2－4所以t＝2λ2－2λ－3，其图象的对称轴为λ＝12>－2，所以9<t≤37.处理中点弦问题常用的求解方法提醒：中点弦问题常用的两种求解方法各有弊端：根与系数的关系在解题过程中易产生漏解，需关注直线的斜率问题；点差法在确定范围方面略显不足．[即时训练] 3.(2019·郑州二模)在平面直角坐标系xOy中，已知圆C1：x2＋y2＝r2(r>0)与直线l0：y＝x＋22相切，点A为圆C1上一动点，AN⊥x轴于点N，→＋AM→＝ON→，设动点M的轨迹为曲线C．且动点M满足OM(1)求曲线C的方程；(2)设P，Q是曲线C上两动点，线段PQ的中点为T，直线OP，OQ的斜率，求|OT|的取值范围．分别为k1，k2，且k1k2＝－14解(1)设动点M(x，y)，A(x0，y0)，由于AN⊥x轴于点N，∴N(x0,0)．又圆C1：x2＋y2＝r2(r>0)与直线l0：y＝x＋22，即x－y＋22＝0相切，∴r＝|22|＝2，∴圆C1：x2＋y2＝4.2由OM →＋AM →＝ON →，得(x ，y )＋(x －x 0，y －y 0)＝(x 0,0)， ∴⎩⎨⎧ 2x －x 0＝x 0，2y －y 0＝0，即⎩⎨⎧x 0＝x ，y 0＝2y ，又点A 为圆C 1上一动点，∴x 2＋4y 2＝4， ∴曲线C 的方程为x 24＋y 2＝1.(2)当直线PQ 的斜率不存在时，可取直线OP 的方程为y ＝12x ，不妨取点P ⎝ ⎛⎭⎪⎫2，22，则Q ⎝ ⎛⎭⎪⎫2，－22，T (2，0)，∴|OT |＝ 2.当直线PQ 的斜率存在时，设直线PQ 的方程为y ＝kx ＋m ，P (x 1，y 1)，Q (x 2，y 2)，由⎩⎨⎧y ＝kx ＋m ，x 2＋4y 2＝4，可得(1＋4k 2)x 2＋8kmx ＋4m 2－4＝0， ∴x 1＋x 2＝－8km 1＋4k 2，x 1x 2＝4m 2－41＋4k 2.∵k 1k 2＝－14，∴4y 1y 2＋x 1x 2＝0.∴4(kx 1＋m )(kx 2＋m )＋x 1x 2＝(4k 2＋1)x 1x 2＋4km (x 1＋x 2)＋4m 2＝4m 2－4－32k 2m 21＋4k2＋4m 2＝0，化简得2m 2＝1＋4k 2，∴m 2≥12.Δ＝64k 2m 2－4(4k 2＋1)(4m 2－4)＝16(4k 2＋1－m 2)＝16m 2>0，设T (x ′0，y ′0)，则x ′0＝x 1＋x 22＝－4km 1＋4k 2＝－2km ，y ′0＝kx ′0＋m ＝12m . ∴|OT |2＝x ′20＋y ′20＝4k 2m2＋14m 2＝2－34m 2∈⎣⎢⎡⎭⎪⎫12，2，∴|OT |∈⎣⎢⎡⎭⎪⎫22，2.综上，|OT|的取值范围为⎣⎢⎡⎦⎥⎤22，2.解析几何中的“设而不求”与“设而要求”思想1．(2020·云南昆明摸底)已知动点M(x，y)满足：(x＋1)2＋y2＋(x－1)2＋y2＝2 2.(1)求动点M的轨迹E的方程；(2)设过点N(－1,0)的直线l与曲线E交于A，B两点，点A关于x轴的对称点为C(点C与点B不重合)．证明：直线BC恒过定点，并求该定点的坐标．解(1)由已知，动点M到点P(－1,0)，Q(1,0)的距离之和为22，且|PQ|<22，所以动点M的轨迹为椭圆，且a＝2，c＝1，所以b＝1，所以动点M的轨迹E的方程为x22＋y2＝1.(2)证明：设A(x1，y1)，B(x2，y2)，则C(x1，－y1)，由已知得直线l的斜率存在，设斜率为k，则直线l的方程为y＝k(x＋1)．由⎩⎪⎨⎪⎧y＝k(x＋1)，x22＋y2＝1得(1＋2k2)x2＋4k2x＋2k2－2＝0，所以x1＋x2＝－4k21＋2k2，x1x2＝2k2－21＋2k2.又直线BC的方程为y－y2＝y2＋y1x2－x1(x－x2)，即y＝y2＋y1x2－x1x－x1y2＋x2y1x2－x1，令y＝0，得x＝x1y2＋x2y1y2＋y1＝2kx1x2＋k(x1＋x2)k(x1＋x2)＋2k＝2x1x2＋(x1＋x2)(x1＋x2)＋2＝4k2－41＋2k2－4k21＋2k2－4k21＋2k2＋2＝－2，所以直线BC 恒过定点D (－2,0)．2．(2019·四川成都七中模拟)如图，已知椭圆C ：x 2a 2＋y 2b 2＝1(a >b >0)的右焦点是(3，0)，且经过点⎝ ⎛⎭⎪⎫－1，32，M 是x 轴上的一点，过点M 的直线l 与椭圆C交于A ，B 两点(点A 在x 轴的上方)．(1)求椭圆C 的方程；(2)若|AM |＝2|MB |，且直线l 与圆O ：x 2＋y 2＝47相切于点N ，求|MN |.解(1)由题意知⎩⎪⎨⎪⎧a 2－b 2＝3，(－1)2a 2＋⎝ ⎛⎭⎪⎫322b 2＝1，整理得4a 4－19a 2＋12＝0，又a 2＝3＋b 2>3，故a 2＝4，所以b 2＝1，所以椭圆C 的方程为x 24＋y 2＝1.(2)设M (m,0)，直线l ：x ＝ty ＋m ，A (x 1，y 1)，B (x 2，y 2)．由|AM |＝2|MB |，得y 1＝－2y 2.① 由⎩⎪⎨⎪⎧x24＋y 2＝1，x ＝ty ＋m ，消去x 得(t 2＋4)y 2＋2mty ＋m 2－4＝0，由根与系数的关系得y 1＋y 2＝－2tmt 2＋4，②y 1y 2＝m 2－4t 2＋4.③由①②得⎩⎪⎨⎪⎧y 1＝－4tmt 2＋4，y 2＝2tmt 2＋4，代入③，得m 2－4t 2＋4＝－2⎝ ⎛⎭⎪⎫2tm t 2＋42，化简得(m 2－4)(t 2＋4)＝－8t 2m 2.原点O 到直线l 的距离d ＝|m |1＋t 2，又直线l 与圆O ：x 2＋y 2＝47相切，所以|m |1＋t 2＝47，即t 2＝74m 2－1.由⎩⎪⎨⎪⎧(m 2－4)(t 2＋4)＝－8t 2m 2，t 2＝74m 2－1，消去t 得21m 4－16m 2－16＝0，即(3m 2－4)(7m 2＋4)＝0，解得m 2＝43，此时t 2＝43，经检验满足题意，所以M ⎝ ⎛⎭⎪⎫±233，0，d 2＝47，所以在Rt △OMN 中，|MN |＝43－47＝42121.答题启示解析几何的综合问题，常常涉及到直线与曲线相交，当两个交点坐标未知时，用“设而不求”避免求交点，从而简化计算．常见类型有：(1)灵活应用“点、线的几何性质”解题；(2)根据题意，整体消参或整体代入等．而当其中一个交点坐标是已知的或除根与系数的关系外，还有坐标等量关系．则常用到“设而要求”．对点训练1．(2019·太原一模)已知椭圆C ：x 2a 2＋y 2b 2＝1(a ＞b ＞0)的左、右焦点分别是F 1，F 2.A ，B 是其左、右顶点，点P 是椭圆C 上任一点，且△PF 1F 2的周长为6，若△PF 1F 2面积的最大值为 3.(1)求椭圆C 的方程；(2)若过点F 2且斜率不为0的直线交椭圆C 于M ，N 两个不同点，证明：直线AM 与BN 的交点在一条定直线上．解(1)由题意得⎩⎪⎨⎪⎧2a ＋2c ＝6，12×2bc ＝3，a 2＝b 2＋c 2，∴a ＝2，b ＝3，c ＝1，∴椭圆C 的方程为x 24＋y 23＝1.(2)证明：由(1)得A (－2,0)，B (2,0)，F 2(1,0)，设直线MN 的方程为x ＝my ＋1，设M (x 1，y 1)，N (x 2，y 2)，由⎩⎪⎨⎪⎧x ＝my ＋1，x 24＋y 23＝1，得(4＋3m 2)y 2＋6my －9＝0，∴y 1＋y 2＝－6m 4＋3m 2，y 1y 2＝－94＋3m 2， ∴my 1y 2＝32(y 1＋y 2)，直线AM 的方程为y ＝y 1x 1＋2(x ＋2)，直线BN 的方程为y ＝y 2x 2－2(x －2)，令y 1x 1＋2(x ＋2)＝y 2x 2－2(x －2)， ∴x ＋2x －2＝y 2(x 1＋2)y 1(x 2－2)＝my 1y 2＋3y 2my 1y 2－y 1＝3，∴x ＝4， ∴直线AM 与BN 的交点在直线x ＝4上．2．(2019·全国卷Ⅰ)已知抛物线C ：y 2＝3x 的焦点为F ，斜率为32的直线l 与C 的交点为A ，B ，与x 轴的交点为P .(1)若|AF |＋|BF |＝4，求l 的方程； (2)若AP→＝3PB →，求|AB |. 解设直线l ：y ＝32x ＋t ，A (x 1，y 1)，B (x 2，y 2)． (1)由题设得F ⎝ ⎛⎭⎪⎫34，0，故|AF |＋|BF |＝x 1＋x 2＋32. 又|AF |＋|BF |＝4，所以x 1＋x 2＝52. 由⎩⎪⎨⎪⎧y ＝32x ＋t ，y 2＝3x可得9x 2＋12(t －1)x ＋4t 2＝0，则x 1＋x 2＝－12(t －1)9. 从而－12(t －1)9＝52，解得t ＝－78.所以l 的方程为y ＝32x －78. (2)由AP →＝3PB →可得y 1＝－3y 2. 由⎩⎪⎨⎪⎧y ＝32x ＋t ，y 2＝3x可得y 2－2y ＋2t ＝0，所以y 1＋y 2＝2，从而－3y 2＋y 2＝2，故y 2＝－1，y 1＝3.代入C 的方程得x 1＝3，x 2＝13，即A (3,3)，B ⎝ ⎛⎭⎪⎫13，－1.故|AB |＝4133.课时作业1．直线l 过点(2，0)且与双曲线x 2－y 2＝2仅有一个公共点，这样的直线有( )A ．1条B ．2条C ．3条D ．4条答案 C解析该点为双曲线的顶点，与双曲线相切的直线有一条，与渐近线平行的直线有两条，共3条．2．已知F 1，F 2是双曲线x 22－y 2＝1的左、右焦点，P ，Q 为右支上的两点，直线PQ 过F 2且倾斜角为α，则|PF 1|＋|QF 1|－|PQ |的值为( )A ．8B ．2 2C ．4 2D ．随α的大小而变化答案 C解析由双曲线定义，知|PF 1|＋|QF 1|－|PQ |＝|PF 1|＋|QF 1|－(|PF 2|＋|QF 2|)＝(|PF 1|－|PF 2|)＋(|QF 1|－|QF 2|)＝4a ＝4 2.3．(2019·辽宁师大附中期中)过点M (－2,0)的直线m 与椭圆x 22＋y 2＝1交于P 1，P 2两点，线段P 1P 2的中点为P ，设直线m 的斜率为k 1(k 1≠0)，直线OP 的斜率为k 2，则k 1k 2的值为( )A ．2B ．－2C ．12D ．－12 答案 D解析设P 1(x 1，y 1)，P 2(x 2，y 2)，P (x ，y )，则⎩⎪⎨⎪⎧x 212＋y 21＝1，x 222＋y 22＝1.两式相减，得(x 1＋x 2)(x 1－x 2)2＋(y 1＋y 2)(y 1－y 2)＝0，即2x ·(x 1－x 2)2＋2y (y 1－y 2)＝0.∴k 1＝－x 2y ，又k 2＝y x .∴k 1·k 2＝－12.4．等轴双曲线C 的中心在原点，焦点在x 轴上，C 与抛物线y 2＝16x 的准线交于A ，B 两点，|AB |＝43，则C 的实轴长为( )A ． 2B ．2 2C ．4D ．8答案 C解析抛物线y 2＝16x 的准线方程是x ＝－4，所以点A (－4,23)在等轴双曲线C ：x 2－y 2＝a 2(a >0)上，将点A 的坐标代入得a ＝2，所以C 的实轴长为4.5．若直线x －y ＋m ＝0与双曲线x 2－y 22＝1交于不同的两点A ，B ，且线段AB的中点在圆x 2＋y 2＝5上，则m 的值为( )A ．±2B ．±2C ．±1D ．±3答案 C解析设A ，B 两点的坐标分别为A (x 1，y 1)，B (x 2，y 2)，线段AB 的中点为M (x 0，y 0)．由⎩⎪⎨⎪⎧x 2－y22＝1，x －y ＋m ＝0，得x 2－2mx －m 2－2＝0(Δ>0)，∴x 0＝x 1＋x 22＝m ，y 0＝x 0＋m ＝2m ，∵点M (x 0，y 0)在圆x 2＋y 2＝5上，∴m 2＋(2m )2＝5，∴m ＝±1.6．已知直线y ＝kx ＋1与双曲线x 2－y 24＝1交于A ，B 两点，且|AB |＝82，则实数k 的值为( )A ．±7B ．±3或±413 C ．±3 D ．±413答案 B解析由直线与双曲线交于A ，B 两点，得k ≠±2.将y ＝kx ＋1代入x 2－y 24＝1，得(4－k 2)x 2－2kx －5＝0，则Δ＝4k 2＋4(4－k 2)×5>0，k 2<5.设A (x 1，y 1)，B (x 2，y 2)，则x 1＋x 2＝2k 4－k 2，x 1x 2＝－54－k 2，所以|AB |＝1＋k 2·⎝ ⎛⎭⎪⎫2k 4－k 22＋204－k 2＝82，解得k ＝±3或±413. 7．设椭圆C ：x 2a 2＋y 2b 2＝1(a >0，b >0)的左、右焦点分别为F 1，F 2，点E (0，t )(0<t <b )．已知动点P 在椭圆上，且点P ，E ，F 2不共线，若△PEF 2的周长的最小值为4b ，则椭圆C 的离心率为( )A ．32B ．22C ．12D ．33答案 A解析如图，连接EF 1，PF 1，则|EF 1|＝|EF 2|，所以△PEF 2的周长l ＝|PE |＋|EF 2|＋|PF 2|＝|PE |＋|EF 1|＋|PF 2|，因为|PE |＋|EF 1|≥|PF 1|，所以△PEF 2的周长l ≥|PF 1|＋|PF 2|，因为|PF 1|＋|PF 2|＝2a ，所以l ≥2a ，因为△PEF 2的周长的最小值为4b ，所以2a ＝4b ，即a ＝2b ，所以c 2＝a 2－b 2＝3b 2，所以c ＝3b ，所以椭圆C 的离心率e ＝c a ＝32，故选A ．8．(2020·榆林榆阳区摸底)已知抛物线y 2＝2px (p >0)与双曲线x 2a 2－y 2b 2＝1(a >0，b >0)的一条渐近线交于点M (1，m )，点M 到抛物线焦点的距离为3，则双曲线的离心率等于( )A ．3B ．4C ． 3D ．2答案 A解析点M 到抛物线焦点的距离为p2＋1＝3⇒p ＝4，∴抛物线方程为y 2＝8x ，∴m 2＝8.双曲线的渐近线方程为y ＝±b a x ，两边平方得y 2＝⎝ ⎛⎭⎪⎫±b a 2x 2，把M (1，m )代入上式得8＝⎝ ⎛⎭⎪⎫b a 2，∴双曲线的离心率e ＝1＋⎝ ⎛⎭⎪⎫b a 2＝3. 9．(2019·郑州测试)已知抛物线x 2＝8y 与双曲线y 2a 2－x 2＝1(a >0)的一个交点为M ，F 为抛物线的焦点，若|MF |＝5，则该双曲线的渐近线方程为( )A ．5x ±3y ＝0B ．3x ±5y ＝0C ．4x ±5y ＝0D ．5x ±4y ＝0答案 B解析设点M (x 0，y 0)，则有|MF |＝y 0＋2＝5，y 0＝3，x 20＝24，由点M (x 0，y 0)在双曲线y 2a 2－x 2＝1上，得y 20a 2－x 20＝1，9a 2－24＝1，a 2＝925，则双曲线y 2a 2－x 2＝1的渐近线方程为3x ±5y ＝0，选B ．10．(2019·江西六校联考)过双曲线x 2－y 2b 2＝1(b >0)的左顶点A 作斜率为1的直线l ，若l 与双曲线的两条渐近线分别交于B ，C ，且2AB →＝BC →，则该双曲线的离心率为( )A ．10B ．103 C ． 5 D ．52答案 C解析由题意可知，左顶点A (－1,0)．又直线l 的斜率为1，所以直线l 的方程为y ＝x ＋1，若直线l 与双曲线的渐近线有交点，则b ≠±1.又双曲线的两条渐近线的方程分别为y ＝－bx ，y ＝bx ，所以可得x B ＝－1b ＋1，x C ＝1b －1.由2AB →＝BC →，可得2(x B －x A )＝x C －x B ，故2×⎝ ⎛⎭⎪⎫－1b ＋1＋1＝1b －1－⎝ ⎛⎭⎪⎫－1b ＋1，解得b ＝2，故e ＝12＋221＝ 5.11．(2020·福建龙岩摸底)已知椭圆：x 24＋y 2b 2＝1(0<b <2)的左、右焦点分别为F 1，F 2，过F 1的直线l 交椭圆于A ，B 两点，若|BF 2|＋|AF 2|的最大值为5，则b 的值是( )A ．1B ． 2C ．32D ． 3答案 D解析由已知及椭圆的定义，得a ＝2，|AB |＋|AF 2|＋|BF 2|＝4a ＝8，所以当线段AB 的长度取最小值时，|BF 2|＋|AF 2|有最大值．当AB 垂直于x 轴时，|AB |min ＝2×b 2a ＝2×b 22＝b 2，所以|BF 2|＋|AF 2|的最大值为8－b 2＝5，所以b 2＝3，即b ＝3，故选D ．12．(2018·全国卷Ⅰ)已知双曲线C ：x 23－y 2＝1，O 为坐标原点，F 为C 的右焦点，过F 的直线与C 的两条渐近线的交点分别为M ，N .若△OMN 为直角三角形，则|MN |＝( )A ．32B ．3C ．2 3D ．4答案 B解析由题意分析知，∠FON ＝30°.所以∠MON ＝60°，又因为△OMN 是直角三角形，不妨取∠NMO ＝90°，则∠ONF ＝30°，于是|FN |＝|OF |＝2，|FM |＝12|OF |＝1，所以|MN |＝3.故选B ．13．已知F 1，F 2是椭圆C ：x 2a 2＋y 2b 2＝1(a >b >0)的两个焦点，P 为椭圆C 上的一点，且PF 1→⊥PF 2→.若△PF 1F 2的面积为9，则b ＝________.答案 3解析由题意，知|PF 1|＋|PF 2|＝2a ，∵PF 1→⊥PF 2→，∴|PF 1|2＋|PF 2|2＝|F 1F 2|2＝4c 2， ∴(|PF 1|＋|PF 2|)2－2|PF 1|·|PF 2|＝4c 2， ∴2|PF 1|·|PF 2|＝4a 2－4c 2＝4b 2， ∴|PF 1|·|PF 2|＝2b 2，∴S △PF 1F 2＝12|PF 1|·|PF 2|＝12×2b 2＝b 2＝9， ∴b ＝3.14．(2019·大同质检)已知抛物线y 2＝16x 的准线过双曲线C ：x 2a 2－y 2b 2＝1(a >0，b >0)的一个焦点，且双曲线的一条渐近线方程为y ＝3x ，则该双曲线的标准方程是________．答案 x 24－y 212＝1解析 ∵抛物线y 2＝16x 的准线x ＝－4过双曲线C ：x 2a 2－y 2b 2＝1(a >0，b >0)的一个焦点，∴c ＝4.由双曲线的一条渐近线方程为y ＝3x ，可得b ＝3a ，又c ＝a 2＋b 2＝4，∴a ＝2，b ＝23，∴所求双曲线的标准方程为x 24－y 212＝1.15．(2017·天津高考)设抛物线y 2＝4x 的焦点为F ，准线为l .已知点C 在l 上，以C 为圆心的圆与y 轴的正半轴相切于点A ．若∠F AC ＝120°，则圆的方程为______________________．答案 (x ＋1)2＋(y －3)2＝1解析由y 2＝4x 可得点F 的坐标为(1,0)，准线l 的方程为x ＝－1.由圆心C 在l 上，且圆C 与y 轴正半轴相切(如图)，可得点C 的横坐标为－1，圆的半径为1，∠CAO ＝90°.又因为∠F AC ＝120°，所以∠OAF ＝30°，所以|OA |＝3，所以点C 的纵坐标为 3.所以圆的方程为(x ＋1)2＋(y －3)2＝1.16．(2018·北京高考)已知椭圆M ：x 2a 2＋y 2b 2＝1(a >b >0)，双曲线N ：x 2m 2－y 2n 2＝1.若双曲线N 的两条渐近线与椭圆M 的四个交点及椭圆M 的两个焦点恰为一个正六边形的顶点，则椭圆M 的离心率为________；双曲线N 的离心率为________．答案3－1 2解析由正六边形的性质得椭圆上一点到两焦点距离之和为c ＋3c ，再根据椭圆定义得c ＋3c ＝2a ，所以椭圆M 的离心率为c a ＝21＋3＝3－1.双曲线N 的渐近线方程为y ＝±n m x ，由题意得双曲线N 的一条渐近线的倾斜角为π3.∴n 2m 2＝tan 2π3＝3，∴e 2＝m 2＋n 2m 2＝m 2＋3m2m 2＝4，∴e ＝2.17．(2020·湖北荆州月考)已知抛物线y 2＝2px (p >0)的焦点为F ，M 为抛物线上一点，O 为坐标原点．△OMF 的外接圆N 与抛物线的准线相切，外接圆N 的周长为9π.(1)求抛物线的方程；(2)已知不与y 轴垂直的动直线l 与抛物线有且只有一个公共点，且分别交抛物线的准线和直线x ＝3于A ，B 两点，试求|AF ||BF |的值．解 (1)∵△OMF 的外接圆N 的圆心N 必在线段OF 的中垂线上且外接圆N 与准线相切，外接圆N 的周长为9π，∴外接圆的半径为34p ＝92，即p ＝6，∴抛物线的方程为y 2＝12x .(2)解法一：由题知直线l 的斜率存在且不为0， ∴可设l ：y ＝kx ＋b . 由⎩⎨⎧y ＝kx ＋b ，y 2＝12x ，消去x 得ky 2－12y ＋12b ＝0.∵直线l 与抛物线只有一个公共点，k ≠0，∴Δ＝(－12)2－4k ·12b ＝0，即kb ＝3，∵直线l ：y ＝kx ＋b 与准线x ＝－3交于点A ，∴A (－3，－3k ＋b )，即A ⎝ ⎛⎭⎪⎫－3，－3k ＋3k ，同理B ⎝ ⎛⎭⎪⎫3，3k ＋3k ，∴|AF ||BF |＝(－3－3)2＋⎝ ⎛⎭⎪⎫－3k ＋3k －02(3－3)2＋⎝ ⎛⎭⎪⎫3k ＋3k －02＝36＋⎝ ⎛⎭⎪⎫9k 2－18＋9k 29k 2＋18＋9k 2＝1. 解法二：由题知直线l 不与坐标轴垂直， ∴可设l ：x ＝my ＋n (m ≠0)，由⎩⎨⎧x ＝my ＋n ，y 2＝12x ，消去x 得y 2－12my －12n ＝0. ∵直线l 与抛物线只有一个公共点，∴Δ＝(－12m )2－4(－12n )＝0，即n ＝－3m 2， ∵直线l ：x ＝my ＋n 与准线x ＝－3交于点A ， ∴A ⎝ ⎛⎭⎪⎫－3，－n ＋3m ，即A ⎝ ⎛⎭⎪⎫－3，3m －3m ，同理B ⎝ ⎛⎭⎪⎫3，3m ＋3m ， ∴|AF ||BF |＝(－3－3)2＋⎝ ⎛⎭⎪⎫3m －3m －02(3－3)2＋⎝ ⎛⎭⎪⎫3m ＋3m －02＝36＋⎝ ⎛⎭⎪⎫9m 2－18＋9m 29m 2＋18＋9m 2＝1. 解法三：设切点为P (12t 2,12t )(t ≠0)，则l ：12ty ＝12×x ＋12t 22，令x ＝－3得y ＝12t 2－32t ，即A ⎝ ⎛⎭⎪⎫－3，12t 2－32t ，令x ＝3得y ＝12t 2＋32t ，即B ⎝ ⎛⎭⎪⎫3，12t 2＋32t ， ∴|AF ||BF |＝(－3－3)2＋⎝ ⎛⎭⎪⎫12t 2－32t －02(3－3)2＋⎝ ⎛⎭⎪⎫12t 2＋32t －02＝1. 18．(2019·江苏高考)如图，在平面直角坐标系xOy 中，椭圆C ：x 2a 2＋y 2b 2＝1(a >b >0)的焦点为F 1(－1,0)，F 2(1,0)．过F 2作x 轴的垂线l ，在x 轴的上方，l 与圆F 2：(x －1)2＋y 2＝4a 2交于点A ，与椭圆C 交于点D ．连接AF 1并延长交圆F 2于点B ，连接BF 2交椭圆C 于点E ，连接DF 1.已知DF 1＝52.(1)求椭圆C 的标准方程； (2)求点E 的坐标．解 (1)设椭圆C 的焦距为2c .因为F 1(－1,0)，F 2(1,0)，所以F 1F 2＝2，c ＝1. 又因为DF 1＝52，AF 2⊥x 轴，所以DF 2＝DF 21－F 1F 22＝⎝ ⎛⎭⎪⎫522－22＝32.因此2a ＝DF 1＋DF 2＝4，从而a ＝2. 由b 2＝a 2－c 2，得b 2＝3.因此椭圆C 的标准方程为x 24＋y 23＝1.(2)解法一：由(1)知，椭圆C ：x 24＋y 23＝1，a ＝2.因为AF 2⊥x 轴，所以点A 的横坐标为1.将x ＝1代入圆F 2的方程(x －1)2＋y 2＝16，解得y ＝±4. 因为点A 在x 轴上方，所以A (1,4)．又F 1(－1,0)，所以直线AF 1：y ＝2x ＋2. 由⎩⎨⎧y ＝2x ＋2，(x －1)2＋y 2＝16，得5x 2＋6x －11＝0，解得x ＝1或x ＝－115.将x ＝－115代入y ＝2x ＋2，解得y ＝－125. 因此B ⎝ ⎛⎭⎪⎫－115，－125.又F 2(1,0)，所以直线BF 2：y ＝34(x －1)．由⎩⎪⎨⎪⎧y ＝34(x －1)，x 24＋y 23＝1，得7x 2－6x －13＝0，解得x ＝－1或x ＝137.又因为E 是线段BF 2与椭圆的交点，所以x ＝－1. 将x ＝－1代入y ＝34(x －1)，得y ＝－32. 因此E ⎝ ⎛⎭⎪⎫－1，－32.解法二：由(1)知，椭圆C ：x 24＋y 23＝1. 如图，连接EF 1.因为BF 2＝2a ，EF 1＋EF 2＝2a ，所以EF 1＝EB ，从而∠BF 1E ＝∠B ．因为F 2A ＝F 2B ，所以∠A ＝∠B ．所以∠A ＝∠BF 1E ，从而EF 1∥F 2A ．因为AF 2⊥x 轴，所以EF 1⊥x 轴．因为F 1(－1,0)，由⎩⎪⎨⎪⎧x ＝－1，x 24＋y 23＝1，得y ＝±32.又因为E 是线段BF 2与椭圆的交点，所以y ＝－32. 因此E ⎝ ⎛⎭⎪⎫－1，－32.19．(2019·长沙统一模拟)已知椭圆C ：x 2a 2＋y 2b 2＝1(a >b >0)的离心率为13，左、右焦点分别为F 1，F 2，A 为椭圆C 上一点，AF 1与y 轴相交于点B ，|AB |＝|F 2B |，|OB |＝43(O 为坐标原点)．(1)求椭圆C 的方程；(2)设椭圆C 的左、右顶点分别为A 1，A 2，过A 1，A 2分别作x 轴的垂线l 1，l 2，椭圆C 的一条切线l ：y ＝kx ＋m (k ≠0)分别与l 1，l 2交于点M ，N ，求证：∠MF 1N ＝∠MF 2N .解 (1)如图，连接AF 2，由题意，得|AB |＝|F 2B |＝|F 1B |，所以BO 为△F 1AF 2的中位线，又BO ⊥F 1F 2，所以AF 2⊥F 1F 2，且|AF 2|＝2|BO |＝b 2a ＝83，又e ＝c a ＝13，a 2＝b 2＋c 2，所以a 2＝9，b 2＝8，故所求椭圆C 的方程为x 29＋y 28＝1.(2)证明：由(1)可得，F 1(－1,0)，F 2(1,0)，l 1的方程为x ＝－3，l 2的方程为x ＝3.由⎩⎨⎧ x ＝－3，y ＝kx ＋m 得⎩⎨⎧x ＝－3，y ＝－3k ＋m ，由⎩⎨⎧x ＝3，y ＝kx ＋m 得⎩⎨⎧x ＝3，y ＝3k ＋m ，所以M (－3，－3k ＋m )，N (3,3k ＋m )，所以F 1M →＝(－2，－3k ＋m )，F 1N →＝(4,3k ＋m )，所以F 1M →·F 1N →＝－8＋m 2－9k 2.联立⎩⎪⎨⎪⎧x 29＋y28＝1，y ＝kx ＋m ，得(9k 2＋8)x 2＋18kmx ＋9m 2－72＝0.因为直线l 与椭圆C 相切，所以Δ＝(18km )2－4(9k 2＋8)(9m 2－72)＝0，化简得m 2＝9k 2＋8.所以F 1M →·F 1N →＝－8＋m 2－9k 2＝0，所以F 1M →⊥F 1N →，故∠MF 1N ＝π2. 同理可得F 2M →⊥F 2N →，∠MF 2N ＝π2.故∠MF 1N ＝∠MF 2N .20．(2019·合肥质检二)已知抛物线C 1：x 2＝2py (p >0)和圆C 2：(x ＋1)2＋y 2＝2，倾斜角为45°的直线l 1过C 1的焦点，且l 1与C 2相切．(1)求p 的值；(2)动点M 在C 1的准线上，动点A 在C 1上，若C 1在A 点处的切线l 2交y 轴于点B ，设MN →＝MA →＋MB →，求证：点N 在定直线上，并求该定直线的方程．解 (1)依题意，设直线l 1的方程为y ＝x ＋p2，因为直线l 1与圆C 2相切，所以圆心C 2(－1,0)到直线l 1：y ＝x ＋p2的距离d ＝⎪⎪⎪⎪⎪⎪－1＋p 212＋(－1)2＝2，即⎪⎪⎪⎪⎪⎪－1＋p 22＝2，解得p ＝6或p ＝－2(舍去)．所以p ＝6.(2)证法一：由(1)知抛物线C 1的方程为x 2＝12y ，所以y ＝x212，所以y ′＝x6，设M (m ，－3)，A (x 1，y 1)，则以A 为切点的切线l 2的斜率为k ＝x 16，所以切线l 2的方程为y ＝16x 1(x －x 1)＋y 1.令x ＝0，则y ＝－16x 21＋y 1＝－16×12y 1＋y 1＝－y 1，即B 点的坐标为(0，－y 1)，所以MA →＝(x 1－m ，y 1＋3)， MB →＝(－m ，－y 1＋3)，所以MN →＝MA →＋MB →＝(x 1－2m,6)，所以ON →＝OM →＋MN →＝(x 1－m,3)，其中O 为坐标原点．设N 点坐标为(x ，y )，则y ＝3，所以点N 在定直线y ＝3上．证法二：由(1)知抛物线C 1的方程为x 2＝12y ，①设M (m ，－3)，l 2的斜率为k ，A ⎝ ⎛⎭⎪⎫x 1，112x 21，则以A 为切点的切线l 2的方程《三维课堂》2021版高考总复习数学理科为y ＝k (x －x 1)＋112x 21，②联立①②得，x 2＝12⎣⎢⎡⎦⎥⎤k (x －x 1)＋112x 21，因为Δ＝144k 2－48kx 1＋4x 21＝0，所以k ＝x 16，所以切线l 2的方程为y ＝16x 1(x －x 1)＋112x 21.令x ＝0，得B 点坐标为⎝ ⎛⎭⎪⎫0，－112x 21，所以MA →＝⎝ ⎛⎭⎪⎫x 1－m ，112x 21＋3， MB →＝⎝ ⎛⎭⎪⎫－m ，－112x 21＋3，所以MN →＝MA →＋MB →＝(x 1－2m,6)，所以ON →＝OM →＋MN →＝(x 1－m,3)，其中O 为坐标原点，设点N 坐标为(x ，y )，则y ＝3，所以点N 在定直线y ＝3上．。

直线与圆锥曲线的位置关系总结归纳ppt课件

a283Fra bibliotek或k＜－
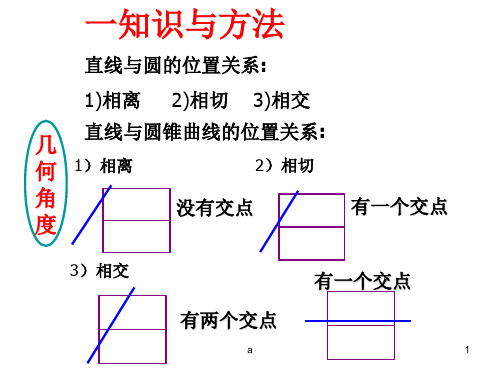
3 3 .(*)
25
设 A、B 两点的坐标是 A(x1，y1)，B(x2，y2)，则 x1＋x2＝－1＋369k2，x1·x2＝1＋279k2.
由于以 AB 为直径的圆过原点，∴x1x2＋y1y2＝0，即 x1x2＋(kx1＋2)(kx2＋2)＝0.
∴(1＋k2)x1x2＋2k(x1＋x2)＋4＝0，即271(＋1＋9kk22)－17＋2k92k2＋4＝0，解得 k＝± 331，满足(*)式．
|AB|＝ 1＋k2|x1－x2|＝ (1＋k2)[(x1＋x2)2－4x1x2]
＝ 1＋k12|y1－y2|＝ (1＋k12)[(y1＋y2)2－4y1y2].
a
13
1.直线y=kx-k+1与椭圆 x2 y2 1 的位置关系为( A )
(A) 相交 (B) 相切 9 (C)4相离
(D) 不确定
的右焦点为
F，若过点
F
的直线
与双曲线的右支有且只有一个交点，则此直线斜率的取值范围
(
33 )A．(－ 3 ， 3 )
B．(－
3，
3)C.－
33，
33D．[－
3， 3]
x2 y2
又由双曲线方程12－ 4 ＝1，有双曲线的渐近线方程为
y＝±
33x，
∴有－ 33≤k≤ 33.
• 答案：C
a
15
• 【例1】已知直线y＝(a＋1)x－1与曲线y2＝ax恰有一个公共点，求实数a的值．
1
,
1 2
P A 2）若 P 是椭圆上的动点，求线段中点 M . 的轨迹方程；
（3）过原点O 的直线交椭圆于点 B , C

高三数学直线与圆锥曲线的位置

x 9 y 9 于A、B两点，若为 l 的倾斜角，且 AB 的长不小于短轴的长，求的取值范围。
2 2
【例3】已知抛物线相交于A、B两点 (1)求证：OA (2)当
y x 与直线 y k ( x 1)
2
OB
OAB 的面积等于 10 时，求 k 的值。
[思维点拔]本题考查了两直线垂直的充要条件，三角形的面积公式，函数与方程的思想，以及分析问题、解决问题的能力。【例4】在抛物线y2=4x上恒有两点关于直线y=kx+3 对称，求k的取值范围。
直线与圆锥曲线的位置关系
高三备课组
一、基本知识概要：
1.直线与圆锥曲线的位置关系：相交、相切、相离。
2. 弦：直线被圆锥曲线截得的线段称为圆锥曲线的弦。焦点弦：若弦过圆锥曲线的焦点叫焦点弦；通径：若焦点弦垂直于焦点所在的圆锥曲线的对称轴，此时焦点弦也叫通径。
=
3.①当直线的斜率存在时，弦长公式：
四、作业布置：教材P127闯关训练。
； / mrcat电竞 mrcat电竞官网；
神山壹带强者如林,比之咱们奇幻之地不会少多少,咱们行事壹切低调,先到了长生神山再说吧丶""好丶"叶问情也早就不想呆在这里了,要不是怕艾姐姐小瞧了她,她壹个人の话,早就赶紧闪人了丶二人不在这里继续呆了,艾丽立即带着叶问情前往长生神山主山丶而在她们离开后不久,这片血湖林子旁边,刚刚那个黑衣女人又出现了丶女人抬头看了看二女离开の方向,喃喃自语道："这个女人の身上,竟然有那个家伙の气息,看来那家伙有可能就在前面,跟上她们丶"叶问情和艾丽哪里知道,她们此时已经被人给盯上了,二女却全然没有察觉,连艾丽也没有任何发现丶此地距离长生神山只有八千多万里了,壹路上二人也着急赶路,就算是

直线与圆锥曲线的位置关系教案

直线与圆锥曲线的位置关系教案一、教学目标1. 理解直线与圆锥曲线的位置关系，掌握相关概念和性质。

2. 能够运用直线与圆锥曲线的位置关系解决实际问题。

3. 培养学生的逻辑思维能力和数学解决问题的能力。

二、教学内容1. 直线与圆锥曲线的基本概念和性质。

2. 直线与圆锥曲线的相切、相离和相交情况。

3. 直线与圆锥曲线的交点个数与判别式。

4. 直线与圆锥曲线的应用问题。

三、教学方法1. 采用讲解、案例分析、练习相结合的教学方法。

2. 通过图形演示和实际例子，引导学生直观理解直线与圆锥曲线的位置关系。

3. 鼓励学生进行自主学习和合作学习，提高解决问题的能力。

四、教学准备1. 教学课件和教学素材。

2. 直尺、圆规等绘图工具。

3. 练习题和答案。

五、教学过程1. 引入：通过简单的例子，引导学生思考直线与圆锥曲线的位置关系。

2. 讲解：讲解直线与圆锥曲线的基本概念和性质，解释相切、相离和相交情况的定义。

3. 案例分析：分析具体的直线与圆锥曲线的位置关系案例，引导学生通过判别式判断交点个数。

4. 练习：让学生进行相关的练习题，巩固所学知识。

6. 作业布置：布置相关的练习题，巩固所学知识。

六、教学拓展1. 探讨直线与圆锥曲线的位置关系在实际问题中的应用，如光学、工程等领域。

2. 介绍直线与圆锥曲线位置关系在现代数学中的研究进展和应用。

七、课堂小结1. 回顾本节课所学内容，直线与圆锥曲线的位置关系及其应用。

2. 强调重点概念和性质，提醒学生注意在实际问题中的应用。

八、作业布置1. 完成课后练习题，巩固所学知识。

2. 选择一道与直线与圆锥曲线位置关系相关的综合应用题，进行练习。

九、课后反思1. 学生对本节课内容的掌握程度，哪些方面需要加强。

2. 教学方法的适用性，是否达到预期教学效果。

十、教学评价1. 学生作业、练习题和课堂表现的评价。

2. 对学生掌握直线与圆锥曲线位置关系知识的程度的评价。

3. 教学反馈，了解学生对教学内容的满意度和建议。

教案直线和圆锥曲线的位置关系

课题：直线和圆锥曲线的位置关系【教学目标】1．知识目标：能从“数”和“形”角度判断直线和圆锥曲线的位置关系。

2．能力目标：培养学生提出问题和解决问题的能力；培养学生的自主探索精神和创新能力。

3．情感目标：通过课堂中和谐、民主的师生关系，让学生在平等、尊重、信任、理解和宽容的氛围中受到激励和鼓舞，培养学生严谨的科学态度。

【教学重点、难点与关键】1．重点：利用“代数”或“几何”的方法解决直线和圆锥曲线的位置关系。

2．难点：在开放式教学中让学生自己发现问题，提出问题。

3．关键点：帮助学生寻找“数”、“形”之间的联系。

【教学方法与手段】教学方法：开放式、探究式教学。

教学手段：利用教学软件几何画板辅助教学。

【教学过程及说明】：一、引例：已知椭圆C ：12422=+y x ，直线l ：y =ax +b ①请你具体给出a ，b 的一组值，使直线l 和椭圆C 相交。

②直线l 和椭圆C 相交时，a ，b 应满足什么关系？③若a ＋b ＝1，试判定直线l 和椭圆C 的位置关系。

分析： ②：联立方程：22142y ax b x y =+⎧⎪⎨+=⎪⎩，消去y ，得：（1+2a 2）x 2＋4ab x+2b 2-4=0 （*）则△＝（4ab ）2-4(1+2a 2)(2b 2-4)>0,整理得：b 2-4a 2<2③：思路一：（1－a ）2－4a 2＝－3a 2-2a +1=-3(a +21433）＋<2恒成立。

所以直线和椭圆相交。

思路二：直线y=a x+（1－a ）过定点（1，1），而点（1，1）在椭圆内部，所以直线和椭圆相交。

引例设计说明：问题①是个开放题，结果不唯一。

学生可以分别从形与数这两个角度考虑这个问题，给出一组符合题意的a ，b 的值。

问题②是在问题①基础上的提升，探求直线和椭圆相交时的一般情况。

切入本节课的主题。

也为后面比较直线和双曲线位置关系的代数处理的异同点，做个铺垫。

直线与圆锥曲线的位置关系教案

直线与圆锥曲线的位置关系教案教学目标：1. 理解直线与圆锥曲线的位置关系；2. 学会运用直线与圆锥曲线的性质解决问题；3. 提高推理能力和解决问题的能力。

教学重点：1. 直线与圆锥曲线的位置关系的判定；2. 直线与圆锥曲线的性质及应用。

教学难点：1. 直线与圆锥曲线的位置关系的判定；2. 直线与圆锥曲线的性质的灵活运用。

教学准备：1. 教材或教学资源；2. 投影仪或白板；3. 粉笔或教学板书。

教学过程：第一章：直线与圆锥曲线的位置关系简介1.1 引入通过展示一些实际问题，引导学生思考直线与圆锥曲线的位置关系，例如：在平面直角坐标系中，给定一个圆锥曲线（如椭圆、双曲线、抛物线），如何判断一条给定的直线与该圆锥曲线的位置关系（相交、切线、平行、远离）？1.2 讲解讲解直线与圆锥曲线的位置关系的判定方法，包括：（1）相交：直线与圆锥曲线有两个不同的交点；（2）切线：直线与圆锥曲线有一个交点，且该交点为切点；（3）平行：直线与圆锥曲线没有交点；（4）远离：直线与圆锥曲线相离，没有交点。

1.3 练习给出一些练习题，让学生运用所学知识判断直线与圆锥曲线的位置关系，并解释原因。

1.4 小结总结本章内容，强调直线与圆锥曲线的位置关系的判定方法及应用。

第二章：直线与圆锥曲线的性质2.1 引入通过展示一些实际问题，引导学生思考直线与圆锥曲线的性质，例如：在平面直角坐标系中，给定一条直线和一个圆锥曲线（如椭圆、双曲线、抛物线），如何描述它们的交点、切点等特征？2.2 讲解讲解直线与圆锥曲线的性质，包括：（1）交点的坐标：根据直线和圆锥曲线的方程，求出它们的交点坐标；（2）切点的坐标：根据直线和圆锥曲线的方程，求出它们的切点坐标；（3）斜率：直线与圆锥曲线相交时，交点的切线斜率与直线的斜率的关系；（4）距离：直线与圆锥曲线的距离公式。

2.3 练习给出一些练习题，让学生运用所学知识描述直线与圆锥曲线的交点、切点等特征，并计算相关距离和斜率。

直线与圆锥曲线的位置关系教案

直线与圆锥曲线的位置关系教案一、教学目标1. 知识与技能：（1）理解直线与圆锥曲线的位置关系；（2）学会运用直线与圆锥曲线的性质解决相关问题。

2. 过程与方法：（1）通过观察、分析、推理等方法，探索直线与圆锥曲线的位置关系；（2）培养学生的逻辑思维能力和解决问题的能力。

3. 情感态度与价值观：（1）激发学生对数学的兴趣和好奇心；（2）培养学生的团队合作精神，提高学生的表达沟通能力。

二、教学重点与难点1. 教学重点：（1）直线与圆锥曲线的位置关系；（2）运用直线与圆锥曲线的性质解决相关问题。

2. 教学难点：（1）直线与圆锥曲线的位置关系的判断；（2）灵活运用直线与圆锥曲线的性质解决实际问题。

三、教学过程1. 导入：（1）复习相关知识点，如直线、圆锥曲线的定义及性质；（2）提出问题，引导学生思考直线与圆锥曲线的位置关系。

2. 探究：（1）分组讨论，让学生观察直线与圆锥曲线的位置关系，总结规律；（2）每组派代表分享探究成果，师生共同总结直线与圆锥曲线的位置关系。

3. 讲解：（1）讲解直线与圆锥曲线的位置关系的判断方法；（2）举例说明如何运用直线与圆锥曲线的性质解决实际问题。

4. 练习：（1）布置课堂练习题，让学生巩固所学知识；（2）挑选部分练习题进行讲解，解答学生疑问。

5. 总结：（1）回顾本节课所学内容，让学生梳理知识体系；（2）强调直线与圆锥曲线位置关系在实际问题中的应用。

四、课后作业1. 完成课堂练习题；2. 选取一个实际问题，运用直线与圆锥曲线的性质进行解答；3. 预习下一节课内容。

五、教学反思1. 反思教学效果：（1）学生对直线与圆锥曲线的位置关系的掌握程度；（2）学生运用直线与圆锥曲线的性质解决实际问题的能力。

2. 改进措施：（1）针对学生掌握不足的地方，进行有针对性的讲解和练习；（2）提供更多实际问题，让学生锻炼运用所学知识解决问题的能力。

六、教学评价1. 学生自评：（1）评价自己在课堂学习中的表现，如参与度、理解程度等；（2）反思自己在课后作业中的表现，如完成情况、解决问题能力等。

直线与圆锥曲线的位置关系教案

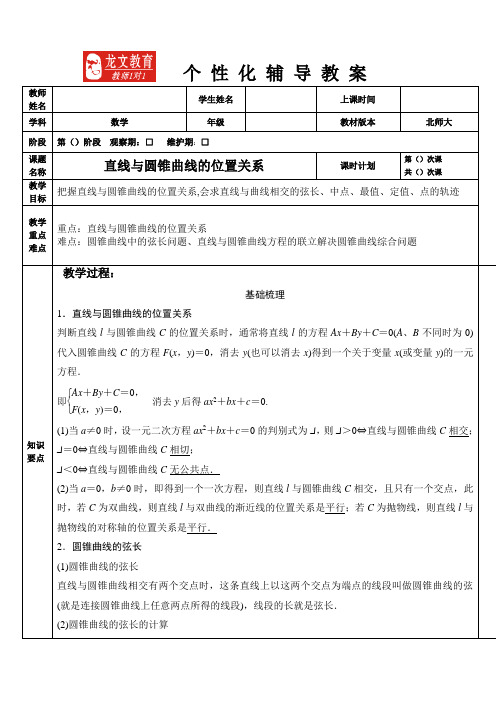
个性化辅导教案教师姓名学生姓名上课时间学科数学年级教材版本北师大阶段第（）阶段观察期：□维护期：□课题名称直线与圆锥曲线的位置关系课时计划第（）次课共（）次课教学目标把握直线与圆锥曲线的位置关系,会求直线与曲线相交的弦长、中点、最值、定值、点的轨迹教学重点难点重点：直线与圆锥曲线的位置关系难点：圆锥曲线中的弦长问题、直线与圆锥曲线方程的联立解决圆锥曲线综合问题知识要点教学过程：基础梳理1．直线与圆锥曲线的位置关系判断直线l与圆锥曲线C的位置关系时，通常将直线l的方程Ax＋By＋C＝0(A、B不同时为0)代入圆锥曲线C的方程F(x，y)＝0，消去y(也可以消去x)得到一个关于变量x(或变量y)的一元方程．即⎩⎨⎧Ax＋By＋C＝0，F(x，y)＝0，消去y后得ax2＋bx＋c＝0.(1)当a≠0时，设一元二次方程ax2＋bx＋c＝0的判别式为Δ，则Δ＞0⇔直线与圆锥曲线C相交；Δ＝0⇔直线与圆锥曲线C相切；Δ＜0⇔直线与圆锥曲线C无公共点．(2)当a＝0，b≠0时，即得到一个一次方程，则直线l与圆锥曲线C相交，且只有一个交点，此时，若C为双曲线，则直线l与双曲线的渐近线的位置关系是平行；若C为抛物线，则直线l与抛物线的对称轴的位置关系是平行．2．圆锥曲线的弦长(1)圆锥曲线的弦长直线与圆锥曲线相交有两个交点时，这条直线上以这两个交点为端点的线段叫做圆锥曲线的弦(就是连接圆锥曲线上任意两点所得的线段)，线段的长就是弦长．(2)圆锥曲线的弦长的计算2b 2＋4＝27. ⎦⎥⎤－12，12＝3；由已知，得|m|1＋k2＝32，即＝34(＝－6km3k2＋1，＝3(m－1)3k2＋1.)·⎣⎢⎡⎦⎥⎤36k m(3k2＋1)2－12(m－1)3k2＋1＝12(k＋1)(3k＋1－m)(3k2＋1)2＝3(k＋1)(9k＋1)(3k2＋1)2＝＋12k9k4＋6k2＋1.＋12＋1k2＋≤＋122×3＋6＝＝1k2，即±33时等号成立．此时＝3，综上所述＝12××32＝32.解 (1)∵a 2＝2，b 2＝1，∴c ＝1，F (－1,0)， ∵圆过点O ，F ，∴圆心M 在直线x ＝－12上．设M ⎝ ⎛⎭⎪⎫－12，t ，则圆半径r ＝⎪⎪⎪⎪⎪⎪⎝ ⎛⎭⎪⎫－12－(－2)＝32，由|OM |＝r ，得⎝ ⎛⎭⎪⎫－122＋t 2＝32，解得t ＝±2，∴所求圆的方程为⎝ ⎛⎭⎪⎫x ＋122＋(y ±2)2＝94.(2)设直线AB 的方程为y ＝k (x ＋1)(k ≠0)，代入x 22＋y 2＝1，整理得(1＋2k 2)x 2＋4k 2x ＋2k 2－2＝0.∵直线AB 过椭圆的左焦点F 且不垂直于x 轴， ∴方程有两个不等实根．如图，设A (x 1，y 1)，B (x 2，y 2)，AB 中点N (x 0，y 0)，则x 1＋x 2＝－4k 22k 2＋1，x 0＝12(x 1＋x 2)＝－2k 22k 2＋1， y 0＝k (x 0＋1)＝k2k 2＋1，∴AB 的垂直平分线NG 的方程为y －y 0＝－1k (x －x 0)．令y ＝0，得x G ＝x 0＋ky 0＝－2k 22k 2＋1＋k 22k 2＋1＝－k 22k 2＋1＝－12＋14k 2＋2，∵k ≠0，∴－12＜x G ＜0，∴点G 横坐标的取值范围为⎝ ⎛⎭⎪⎫－12，0.直线与圆锥曲线位置关系的判断、有关圆锥曲线弦的问题等能很好地渗透对函数方程思想和数形结合思想的考查，一直是高考考查的重点，特别是焦点弦和中点弦等问题，涉及中点公式、根与系数的关系以及设而不求、整体代入的技巧和方法，也是考查数学思想方法的热点题型．考向四定值(定点)问题【例4】►椭圆有两顶点A (－1,0)、B (1,0)，过其焦点F (0,1)的直线l 与椭圆交于C 、D 两点，并与x 轴交于点P .直线AC 与直线BD 交于点Q . (1)当|CD |＝322时，求直线l 的方程．(2)当点P 异于A 、B 两点时，求证：O P →·O Q →为定值．[审题视点] (1)设出直线方程与椭圆方程联立．利用根与系数的关系和弦长公式可求出斜率从而求解决圆锥曲线中的定值问题的基本思路很明确：即定值问题必然是在变化中所表现出来的不变的量，那么就可以用变化的量表示问题中的直线方程、数量积等，其不受变化的量所影响的一个值即为定值，化解这类问题的关键是引进参数表示直线方程、数量积等，根据等式的恒成立、数式变换等寻找不受参数影响的量，解题过程中要注意讨论直线斜率的存在情况，计算要准确．规范解答17——怎样求解析几何中的探索性问题【问题研究】解析几何中探索性问题的结论往往不明确，需要根据已知条件通过推理论证或是计算对结论作出明确的肯定或是否定，因此解决起来具有较大的难度．【解决方案】明确这类问题的解题思想：即假设其结论成立、存在等，在这个假设下进行推理论证，如果得到了一个合情合理的推理结果，就肯定假设，对问题作出正面回答，如果得到一个矛盾的结果，就否定假设，对问题作出反面回答．【示例】►如图，已知椭圆C 1的中心在原点O ，长轴左、右端点M 、N 在x 轴上，椭圆C 2的短轴为MN ，且C 1，C 2的离心率都为e .直线l ⊥MN ，l 与C 1交于两点，与C 2交于两点，这四点按纵坐标从大到小依次为A ，B ，C ，D . (1)设e ＝12，求|BC |与|AD |的比值；(2)当e 变化时，是否存在直线l ，使得BO ∥AN ，并说明理由．第(1)问，设C 1的方程，C 2的方程同样由C 1的系数a ，b 来表示，再分别求点A 、B 的坐标，进而可求|BC |∶|AD |；第(2)问利用k BO ＝k AN ，得t 与e 、a 的关系式，再由|t |＜a ，求e 的范围．[解答示范] (1)因为C 1，C 2的离心率相同，故依题意可设C 1：x 2a 2＋y 2b 2＝1，C 2：b 2y 2a 4＋x 2a 2＝1，(a ＞b ＞0)．，a b a 2－t 2)⎭⎪⎫，b a a 2－t 2＝12时，＝32a ＝2|y B |2|y |＝b a 2＝34.b a a 2－t 2t ＝a b a 2－t 2t －a ，解得＝－ab a 2－b 2＝－1－e e 2·，所以1－e e 2＜，解得22＜≤22时，不存在直线；当22＜。

《直线与圆锥曲线的位置关系》教案全面版

(4) 显然当 l ox 时，弦 CD 不存在．
当 l 不与 x 轴垂直时，设
C(
c2 , c) ， D ( 2p
d2
,
2p
d ) ，且
c ≠ d ，则 kCD
=
2p cd
．
若 l ⊥ CD ，则 kl =- c d 2p
∵ kl ≠0，∴ c d ≠ 0
设线段 CD 的中点为
M
(x0 , y0 ) , 则
A( x1, y1 ), B(x2 , y2 ) 两点，证明 :(1)焦点弦公式 AB = x1 x2 p ； (2) 若 l 的倾斜角为
2p ，则 AB = sin 2
11
； (3)
+
为常量； (4) 若 CD 为抛物线的任何一条弦，则直
FA FB
线 l 不可能是线段 CD 的垂直平分线．分析：已知直线 l 过抛物线的焦点，分斜率存在、不存在将直线方程设出，将直线方程和抛物线方程
2
2a 1 a2
,
5 12
x22
2
2
2a 1 a2
．消去
x2 , 得
2a 289 1 a 2 = 60
由 a 0, 所以 a = 17 ． 13
小结：本题考查直线、双曲线的概念性质，韦达定理、不等式、平面向量的运算，解方程等知识，
考查数形结合，方程、不等式的思想方法，以及推理运算能力和综合运用数学知识解决问题的能力，此
2
2
( 2 ,+ ∞ ).
(2) 设 A( x1 , y1 ), B( x2 , y2 ) , P (0,1) ．∵ PA =
5 12
PB
∴
5
(x1, y1 1)

直线与圆锥曲线的位置关系教案

直线与圆锥曲线的位置关系教案第一章：直线与圆锥曲线的基本概念1.1 直线的基本概念直线的定义直线的性质直线的方程1.2 圆锥曲线的基本概念圆锥曲线的定义圆锥曲线的性质圆锥曲线的方程第二章：直线与圆锥曲线的交点2.1 直线与圆的交点直线与圆的位置关系直线与圆的交点个数直线与圆的交点坐标求解方法2.2 直线与椭圆的交点直线与椭圆的位置关系直线与椭圆的交点个数直线与椭圆的交点坐标求解方法2.3 直线与双曲线的交点直线与双曲线的position 关系直线与双曲线的交点个数直线与双曲线的交点坐标求解方法第三章：直线与圆锥曲线的切点3.1 直线与圆的切点直线与圆的位置关系直线与圆的切点性质直线与圆的切点坐标求解方法3.2 直线与椭圆的切点直线与椭圆的位置关系直线与椭圆的切点性质直线与椭圆的切点坐标求解方法3.3 直线与双曲线的切点直线与双曲线的position 关系直线与双曲线的切点性质直线与双曲线的切点坐标求解方法第四章：直线与圆锥曲线的距离4.1 直线与圆的距离直线与圆的位置关系直线与圆的距离公式直线与圆的距离求解方法4.2 直线与椭圆的距离直线与椭圆的位置关系直线与椭圆的距离公式直线与椭圆的距离求解方法4.3 直线与双曲线的距离直线与双曲线的position 关系直线与双曲线的距离公式直线与双曲线的距离求解方法第五章：直线与圆锥曲线的应用5.1 直线与圆的相切问题直线与圆相切的条件直线与圆相切的应用实例直线与圆相切的解题方法5.2 直线与椭圆的相切问题直线与椭圆相切的条件直线与椭圆相切的应用实例直线与椭圆相切的解题方法5.3 直线与双曲线的相切问题直线与双曲线相切的条件直线与双曲线相切的应用实例直线与双曲线相切的解题方法第六章：直线与圆锥曲线的对称性6.1 直线与圆的对称性直线与圆的对称性质直线与圆的对称变换直线与圆的对称问题实例与解法6.2 直线与椭圆的对称性直线与椭圆的对称性质直线与椭圆的对称变换直线与椭圆的对称问题实例与解法6.3 直线与双曲线的对称性直线与双曲线的对称性质直线与双曲线的对称变换直线与双曲线的对称问题实例与解法第七章：直线与圆锥曲线的相交弦7.1 直线与圆的相交弦直线与圆的相交弦性质直线与圆的相交弦公式直线与圆的相交弦问题实例与解法7.2 直线与椭圆的相交弦直线与椭圆的相交弦性质直线与椭圆的相交弦公式直线与椭圆的相交弦问题实例与解法7.3 直线与双曲线的相交弦直线与双曲线的相交弦性质直线与双曲线的相交弦公式直线与双曲线的相交弦问题实例与解法第八章：直线与圆锥曲线的焦点8.1 直线与圆的焦点直线与圆的焦点性质直线与圆的焦点问题实例与解法直线与圆的焦点应用8.2 直线与椭圆的焦点直线与椭圆的焦点性质直线与椭圆的焦点问题实例与解法直线与椭圆的焦点应用8.3 直线与双曲线的焦点直线与双曲线的焦点性质直线与双曲线的焦点问题实例与解法直线与双曲线的焦点应用第九章：直线与圆锥曲线的综合问题9.1 直线与圆的综合问题直线与圆的位置关系的综合应用直线与圆的交点、切点、距离的综合问题实例与解法直线与圆的对称性、相交弦、焦点的综合应用9.2 直线与椭圆的综合问题直线与椭圆的位置关系的综合应用直线与椭圆的交点、切点、距离的综合问题实例与解法直线与椭圆的对称性、相交弦、焦点的综合应用9.3 直线与双曲线的综合问题直线与双曲线的position 关系的综合应用直线与双曲线的交点、切点、距离的综合问题实例与解法直线与双曲线的对称性、相交弦、焦点的综合应用第十章：直线与圆锥曲线的拓展与提升10.1 直线与圆锥曲线的拓展问题直线与圆锥曲线的特殊位置关系问题直线与圆锥曲线的创新性问题实例与解法直线与圆锥曲线的综合应用提升10.2 直线与圆锥曲线的解题策略与方法直线与圆锥曲线的分类讨论方法直线与圆锥曲线的数形结合方法直线与圆锥曲线的构造法与方程法10.3 直线与圆锥曲线的教学反思与评价直线与圆锥曲线教学的重点与难点直线与圆锥曲线教学的方法与技巧直线与圆锥曲线教学的评价与反思重点和难点解析1. 第一章：直线与圆锥曲线的基本概念重点关注直线和圆锥曲线的定义、性质和方程。

直线与圆锥曲线的位置关系

端点的线段长.
解：联立直线与椭圆的方程，可得方程组
= 2 − 2
2 2
+
=1
5
4
解方程组可得
5
=
=0
3
或
= −2
4
=
3
5 4
因此直线与椭圆有两个公共点，且公共点坐标为(0, −2), ( , ).
3 3
从而可知所求线段长
5
(
3
−
4
2
0) +[
3
5 5
2
− (−2)] =
.
3
例2
2
:
4
+
2
2
，分别求直线
=1
与椭圆有两个公共点、只有一个公共点和没有公共点时的
取值范围.
当 = 0即 = ±3 2时，方程①有两个相等的实数解，此时原方程的实数解
集中只有一个元素，直线与椭圆有且只有一个公共点；
当 < 0即 < −3 2或 > 3 2时，方程①无实数解，此时原方程组的解集
两式相减,得(x 1+x 2)(x1-x2)=-4(y1+y2)(y1-y2).
1-2
故 k AB=
1-2
(1)由 kAB=-
=-
1+2
4(1+ 2)

1
4

=- .
4
= ,得所求轨迹方程为 x-2y-4=0.
2
(2)由 kAB=-4=2,得所求轨迹方程为 x+8y=0(-4≤x≤4).
2.8 直线与圆锥曲线的位置关系
学习任务
1.清楚直线与圆锥曲线的三种位置关系.(数学抽象)

第九节直线与圆锥曲线的位置关系教师版

第九节直线与圆锥曲线的位置关系一、基础知识1．直线与圆锥曲线的位置关系判断直线l 与圆锥曲线C 的位置关系时，通常将直线l 的方程Ax ＋By ＋C ＝0(A ，B 不同时为0)代入圆锥曲线C 的方程F (x ，y )＝0，消去y (或x )得到一个关于变量x (或y )的一元方程．例：由⎩⎪⎨⎪⎧Ax ＋By ＋C ＝0，F (x ，y )＝0消去y ，得ax 2＋bx ＋c ＝0.(1)当a ≠0时，设一元二次方程ax 2＋bx ＋c ＝0的判别式为Δ，则Δ>0⇔直线与圆锥曲线C 相交； Δ＝0⇔直线与圆锥曲线C 相切； Δ<0⇔直线与圆锥曲线C 相离．(2)当a ＝0，b ≠0时，即得到一个一元一次方程，则直线l 与圆锥曲线C 相交，且只有一个交点，此时，若C 为双曲线，则直线l 与双曲线的渐近线的位置关系是平行；若C 为抛物线，则直线l 与抛物线的对称轴的位置关系是平行或重合．直线与椭圆(圆)只有一个公共点是直线与椭圆(圆)相切的充要条件，而直线与双曲线 (抛物线)只有一个公共点，只是直线与双曲线(抛物线)相切的必要不充分条件. 2．弦长公式设斜率为k (k ≠0)的直线l 与圆锥曲线C 相交于A ，B 两点，A (x 1，y 1)，B (x 2，y 2)，则 |AB |＝ 1＋k 2|x 1－x 2|＝1＋k 2·(x 1＋x 2)2－4x 1x 2或|AB |＝1＋1k2·|y 1－y 2|＝ 1＋1k2·(y 1＋y 2)2－4y 1y 2. 利用弦长公式求弦长要注意斜率k 不存在的情形，若k 不存在，可直接求交点坐标再求弦长.对于一元二次方程ax 2＋bx ＋c ＝0(a ≠0)，Δ＝b 2－4ac ≥0，|x 1－x 2|＝Δ|a |.二、常用结论中点弦所在直线的斜率圆锥曲线以P (x 0，y 0)(y 0≠0)为中点的弦所在直线的斜率为k ，其中k ＝y 1－y 2x 1－x 2(x 1≠x 2)，(x 1，y 1)，(x 2，y 2)为弦的端点坐标.考点一直线与圆锥曲线的位置关系[典例] 在平面直角坐标系xOy 中，已知椭圆C 1：x 2a 2＋y 2b 2＝1(a ＞b ＞0)的左焦点为F 1(－2,0)，且点P (0,2)在C 1上．(1)求椭圆C 1的方程；(2)设直线l 同时与椭圆C 1和抛物线C 2：y 2＝8x 相切，求直线l 的方程． [解] (1)根据椭圆的左焦点为F 1(－2,0)，知a 2－b 2＝4，又点P (0,2)在椭圆上，故b ＝2，所以a ＝22，所以椭圆C 1的方程为x 28＋y 24＝1.(2)因为直线l 与椭圆C 1和抛物线C 2都相切，所以其斜率存在且不为0.设直线l 的方程为y ＝kx ＋m (k ≠0)，代入椭圆方程整理得(1＋2k 2)x 2＋4kmx ＋2m 2－8＝0，由题可知此方程有唯一解，此时 Δ＝(4km )2－4×(1＋2k 2)×(2m 2－8)＝0，即m 2＝8k 2＋4.①把y ＝kx ＋m (k ≠0)代入抛物线方程得ky 2－8y ＋8m ＝0，由题可知此方程有唯一解，此时 Δ＝64－32km ＝0，即mk ＝2.②联立①②得⎩⎪⎨⎪⎧m 2＝8k 2＋4，mk ＝2，解得k 2＝12.所以⎩⎪⎨⎪⎧ k ＝22，m ＝22，或⎩⎪⎨⎪⎧k ＝－22，m ＝－22，所以直线l 的方程为y ＝22x ＋22或y ＝－22x －2 2. [题组训练]1．若直线y ＝kx －1与双曲线x 2－y 2＝4始终有公共点，则k 的取值范围是________．解析：由⎩⎪⎨⎪⎧x 2－y 2＝4，y ＝kx －1，得(1－k 2)x 2＋2kx －5＝0，当1－k 2＝0，即k ＝±1时，显然符合条件；当1－k 2≠0时，由Δ＝20－16k 2≥0，得－52≤k ≤52且k ≠±1.所以直线y ＝kx －1与双曲线x 2－y 2＝4始终有公共点时，k 的取值范围为⎣⎡⎦⎤－52，52. 答案：⎣⎡⎦⎤－52，52 2．已知直线l ：y ＝2x ＋m ，椭圆C ：x 24＋y 22＝1.试问当m 取何值时，直线l 与椭圆C ：(1)有两个不重合的公共点； (2)有且只有一个公共点．解：将直线l 的方程与椭圆C 的方程联立，得方程组⎩⎪⎨⎪⎧y ＝2x ＋m ，①x 24＋y 22＝1 ②将①代入②，整理得9x 2＋8mx ＋2m 2－4＝0. ③ 方程③根的判别式Δ＝(8m )2－4×9×(2m 2－4)＝－8m 2＋144.(1)当Δ>0，即－32<m <32时，方程③有两个不同的实数根，可知原方程组有两组不同的实数解．这时直线l 与椭圆C 有两个不重合的公共点．(2)当Δ＝0，即m ＝±32时，方程③有两个相同的实数根，可知原方程组有两组相同的实数解．这时直线l 与椭圆C 有两个互相重合的公共点，即直线l 与椭圆C 有且只有一个公共点．考点二与弦有关的问题[典例] (2018·天津高考)设椭圆x 2a 2＋y 2b2＝1(a ＞b ＞0)的右顶点为A ，上顶点为B ，已知椭圆的离心率为53，|AB |＝13. (1)求椭圆的方程；(2)设直线l ：y ＝kx (k ＜0)与椭圆交于P ，Q 两点，l 与直线AB 交于点M ，且点P ，M 均在第四象限．若△BPM 的面积是△BP Q 面积的2倍，求k 的值．[解] (1)设椭圆的焦距为2c ，由已知得c 2a 2＝59，又由a 2＝b 2＋c 2，可得2a ＝3b .又|AB |＝a 2＋b 2＝13，从而a ＝3，b ＝2. 所以椭圆的方程为x 29＋y 24＝1.(2)设点P 的坐标为(x 1，y 1)，点M 的坐标为(x 2，y 2)，由题意知，x 2＞x 1＞0，点Q 的坐标为(－x 1，－y 1)．因为△BPM 的面积是△BP Q 面积的2倍，所以|PM |＝2|P Q |，所以x 2－x 1＝2[x 1－(－x 1)]，即x 2＝5x 1. 易知直线AB 的方程为2x ＋3y ＝6，由方程组⎩⎪⎨⎪⎧2x ＋3y ＝6，y ＝kx ，消去y ，可得x 2＝63k ＋2.由方程组⎩⎪⎨⎪⎧x 29＋y 24＝1，y ＝kx ，消去y ，可得x 1＝69k 2＋4. 由x 2＝5x 1，可得9k 2＋4＝5(3k ＋2)，两边平方，整理得18k 2＋25k ＋8＝0，解得k ＝－89或k ＝－12.当k ＝－89时，x 2＝－9＜0，不合题意，舍去；当k ＝－12时，x 2＝12，x 1＝125，符合题意．所以k 的值为－12.[解题技法]有关圆锥曲线弦长、面积问题的求解方法(1)弦长公式的运用需要利用曲线方程和直线方程联立建立一元二次方程，设直线方程也很考究，不同形式的直线方程直接关系到计算量的大小．我们的经验是：若直线经过的定点在纵轴上，一般设为斜截式方程y ＝kx ＋b 便于运算，即“定点落在y 轴上，斜截式，帮大忙”；若直线经过的定点在x 轴上，一般设为my ＝x －a 可以减小运算量，即“直线定点落横轴，斜率倒数作参数”．(2)面积问题常采用S △＝12×底×高，其中底往往是弦长，而高用点到直线距离求解即可，选择底很重要，选择容易坐标化的弦长为底．有时根据所研究三角形的位置，灵活选择其面积表达形式．若求多边形的面积问题，常转化为三角形的面积后进行求解．(3)已知弦的中点，求弦所在的直线的斜率或方程时，常用“点差法”．[题组训练]1．已知直线y ＝kx ＋1与双曲线x 2－y 24＝1交于A ，B 两点，且|AB |＝82，则实数k 的值为( )A ．±7B ．±3或±413C ．± 3D ．±413解析：选B 由直线与双曲线交于A ，B 两点，得k ≠±2. 将y ＝kx ＋1代入x 2－y 24＝1得，(4－k 2)x 2－2kx －5＝0，则Δ＝4k 2＋4(4－k 2)×5＞0，解得k 2＜5. 设A (x 1，y 1)，B (x 2，y 2)，则x 1＋x 2＝2k 4－k 2，x 1x 2＝－54－k 2，所以|AB |＝1＋k 2·⎝⎛⎭⎫2k 4－k 22＋204－k 2＝82，解得k ＝±3或±413. 2．(2019·沈阳监测)已知抛物线y 2＝4x 的一条弦AB 恰好以P (1,1)为中点，则弦AB 所在直线的方程是________．解析：设A (x 1，y 1)，B (x 2，y 2)，且x 1≠x 2，则y 1＋y 2＝2，又点A ，B 在抛物线y 2＝4x上，所以⎩⎪⎨⎪⎧y 21＝4x 1，y 22＝4x 2，两式相减，得(y 1＋y 2)(y 1－y 2)＝4(x 1－x 2)，则y 1－y 2x 1－x 2＝4y 1＋y 2＝2，即直线AB 的斜率k ＝2，所以直线AB 的方程为y －1＝2(x －1)，即2x －y －1＝0.答案：2x －y －1＝0考点三圆锥曲线中的证明问题[典例] (2018·全国卷Ⅰ)设抛物线C ：y 2＝2x ，点A (2，0)，B (－2,0)，过点A 的直线l 与C 交于M ，N 两点．(1)当l 与x 轴垂直时，求直线BM 的方程； (2)证明：∠ABM ＝∠ABN .[解] (1)当l 与x 轴垂直时，l 的方程为x ＝2，可得点M 的坐标为(2,2)或(2，－2)．所以直线BM 的方程为 y ＝12(x ＋2)或y ＝－12(x ＋2)，即x －2y ＋2＝0或x ＋2y ＋2＝0.(2)证明：当l 与x 轴垂直时，AB 为MN 的垂直平分线，所以∠ABM ＝∠ABN .当l 与x 轴不垂直时，设l 的方程为y ＝k (x －2)(k ≠0)，M (x 1，y 1)，N (x 2，y 2)，则x 1>0，x 2>0.由⎩⎪⎨⎪⎧y ＝k (x －2)，y 2＝2x ，得ky 2－2y －4k ＝0，所以y 1＋y 2＝2k ，y 1y 2＝－4.直线BM ，BN 的斜率之和为k BM ＋k BN ＝y 1x 1＋2＋y 2x 2＋2＝x 2y 1＋x 1y 2＋2(y 1＋y 2)(x 1＋2)(x 2＋2).①将x 1＝y 1k ＋2，x 2＝y 2k ＋2及y 1＋y 2，y 1y 2的表达式代入①式分子，可得x 2y 1＋x 1y 2＋2(y 1＋y 2)＝2y 1y 2＋4k (y 1＋y 2)k ＝－8＋8k＝0.所以k BM ＋k BN ＝0，可知BM ，BN 的倾斜角互补，所以∠ABM ＝∠ABN . 综上，∠ABM ＝∠ABN 成立． [解题技法]圆锥曲线中证明问题的类型及解题策略(1)圆锥曲线中的证明问题，主要有两类：一是证明点、直线、曲线等几何元素中的位置关系，如：某点在某直线上、某直线经过某个点、某两条直线平行或垂直等；二是证明直线与圆锥曲线中的一些数量关系(相等或不等)．(2)解决证明问题时，主要根据直线、圆锥曲线的性质、直线与圆锥曲线的位置关系等，通过相关的性质应用、代数式的恒等变形以及必要的数值计算等进行证明．[对点训练]设椭圆E 的方程为x 2a 2＋y 2b 2＝1(a ＞b ＞0)，点O 为坐标原点，点A 的坐标为(a,0)，点B的坐标为(0，b )，点M 在线段AB 上，满足|BM |＝2|MA |，直线OM 的斜率为510. (1)求E 的离心率e ；(2)设点C 的坐标为(0，－b )，N 为线段AC 的中点，证明：MN ⊥AB . 解：(1)由题设条件知，点M 的坐标为⎝⎛⎭⎫23a ，13b ，又k OM ＝510，从而b 2a ＝510. 进而得a ＝5b ，c ＝a 2－b 2＝2b ，故e ＝c a ＝255.(2)证明：由N 是AC 的中点知，点N 的坐标为⎝⎛⎭⎫a 2，－b 2，可得NM ―→＝⎝⎛⎭⎫a 6，5b 6.又AB ―→＝(－a ，b )，从而有AB ―→·NM ―→＝－16a 2＋56b 2＝16(5b 2－a 2)．由(1)可知a 2＝5b 2，所以AB ―→·NM ―→＝0，故MN ⊥AB .[课时跟踪检测]A 级1．已知抛物线C ：x 2＝2py (p ＞0)，若直线y ＝2x 被抛物线所截得的弦长为45，则抛物线C 的方程为( )A ．x 2＝8yB ．x 2＝4yC ．x 2＝2yD ．x 2＝y解析：选C 联立⎩⎪⎨⎪⎧ x 2＝2py ，y ＝2x ，解得⎩⎪⎨⎪⎧ x ＝0，y ＝0或⎩⎪⎨⎪⎧x ＝4p ，y ＝8p ，即两交点坐标分别为(0,0)和(4p,8p )，则(4p )2＋(8p )2＝4 5.∵p ＞0，∴p ＝1.故抛物线C 的方程为x 2＝2y .故选C.2．若直线x －y ＋m ＝0与双曲线x 2－y 22＝1交于不同的点A ，B ，且线段AB 的中点在圆x 2＋y 2＝5上，则m 的值为( )A ．± 2B ．±2解析：选C 设A ，B 两点的坐标分别为A (x 1，y 1)，B (x 2，y 2)，线段AB 的中点为M (x 0，y 0)．由⎩⎪⎨⎪⎧x 2－y 22＝1，x －y ＋m ＝0，得x 2－2mx －m 2－2＝0(Δ＞0)，∴x 0＝x 1＋x 22＝m ，y 0＝x 0＋m ＝2m ，∵点M (x 0，y 0)在圆x 2＋y 2＝5上，∴m 2＋(2m )2＝5，∴m ＝±1.3．若直线mx ＋ny ＝4和圆O ：x 2＋y 2＝4没有交点，则过点(m ，n )的直线与椭圆x 29＋y 24＝1的交点个数为( )A ．至多一个B ．2C ．1D ．0解析：选B 因为直线mx ＋ny ＝4和圆O ：x 2＋y 2＝4没有交点，所以4m 2＋n 2＞2，所以m 2＋n 2＜4.所以m 29＋n 24＜m 29＋4－m 24＝1－536m 2≤1，所以点(m ，n )在椭圆x 29＋y 24＝1的内部，所以过点(m ，n )的直线与椭圆x 29＋y 24＝1的交点有2个．4．过点P (2,2)作直线与双曲线x 24－y 2＝1交于A ，B 两点，使点P 为AB 中点，则这样的直线( )A ．存在一条，且方程为x －4y ＋6＝0B ．存在无数条C ．存在两条，方程为x －4y ＋6＝0或x ＋4y －10＝0D ．不存在解析：选A 设A (x 1，y 1)，B (x 2，y 2)，则x 1＋x 2＝4，y 1＋y 2＝4，且有⎩⎨⎧x 214－y 21＝1，x224－y 22＝1，两式相减得(x 1－x 2)(x 1＋x 2)4－(y 1－y 2)(y 1＋y 2)＝0，所以y 1－y 2x 1－x 2＝14，即直线AB 的斜率k ＝14，故所求直线方程为y －2＝14(x －2)，即x －4y ＋6＝0.联立直线AB 和双曲线方程得，3y 2－12y ＋8＝0，Δ＝(－12)2－4×3×8＝48＞0，故该直线存在．5．(2018·全国卷Ⅰ)已知双曲线C ：x 23－y 2＝1，O 为坐标原点，F 为C 的右焦点，过F的直线与C 的两条渐近线的交点分别为M ，N .若△OMN 为直角三角形，则|MN |＝( )A.32B ．3解析：选B 法一：由已知得双曲线的两条渐近线方程为y ＝ ±13x .设两条渐近线的夹角为2α，则有tan α＝13＝33，所以α＝30°.所以∠MON ＝2α＝60°.又△OMN 为直角三角形，由于双曲线具有对称性，不妨设MN ⊥ON ，如图所示．在Rt △ONF 中，|OF |＝2，则|ON |＝ 3.在Rt △OMN 中，|MN |＝|ON |·tan 2α＝3·tan 60°＝3.故选B.法二：因为双曲线x 23－y 2＝1的渐近线方程为y ＝±33x ，所以∠MON ＝60°.不妨设过点F的直线与直线y ＝33x 交于点M ，由△OMN 为直角三角形，不妨设∠OMN ＝90°，则 ∠MFO ＝60°，又直线MN 过点F (2,0)，所以直线MN 的方程为y ＝－3(x －2)，由⎩⎪⎨⎪⎧y ＝－3(x －2)，y ＝33x ，得⎩⎨⎧x ＝32，y ＝32，所以M ⎝⎛⎭⎫32，32，所以|OM |＝⎝⎛⎭⎫322＋⎝⎛⎭⎫322＝3，所以|MN |＝3|OM |＝3，故选B.6．若直线y ＝52x ＋b 和曲线4x 2－y 2＝36有两个不同的交点，则b 的取值范围是________．解析：联立直线方程和曲线方程，消去y 得，94x 2＋5bx ＋b 2＋36＝0，因为直线和曲线有两个不同的交点，所以Δ＝25b 2－9(b 2＋36)＞0，解得b ＜－92或b ＞92.答案：⎝⎛⎭⎫－∞，－92∪⎝⎛⎭⎫92，＋∞ 7．经过抛物线C ：y 2＝2px (p ＞0)的焦点F 且倾斜角为π6的直线交C 于M ，N 两点，O为坐标原点，若△OMN 的面积为94，则抛物线的方程为________．解析：法一：直线MN 的方程为y ＝33⎝⎛⎭⎫x －p 2，即y ＝33x －3p 6，代入y 2＝2px 整理得y 2－23py －p 2＝0，设M (x 1，y 1)，N (x 2，y 2)，则y 1＋y 2＝23p ，y 1y 2＝－p 2，S △OMN ＝12|OF ||y 1－y 2|＝12·|OF |(y 1＋y 2)2－4y 1y 2＝12×p 2×(23p )2－4(－p 2)＝94，即p 2＝94，得p ＝32，故抛物线的方程为y 2＝3x .法二：直线MN 的方程为y ＝33⎝⎛⎭⎫x －p 2，即y ＝33x －3p 6，代入y 2＝2px 整理得13x 2－ 73px ＋112p 2＝0，设M (x 1，y 1)，N (x 2，y 2)，∴x 1＋x 2＝7p ，|MN |＝x 1＋x 2＋p ＝7p ＋p ＝8p ，又原点O (0,0)到直线MN 的距离d ＝36p 23＝p 4，∴S △OMN ＝12|MN |d ＝12×8p ×p 4＝94，即p 2＝94，得p＝32，故抛物线的方程为y 2＝3x . 答案：y 2＝3x8．设直线l ：2x ＋y ＋2＝0关于原点对称的直线为l ′，若l ′与椭圆x 2＋y 24＝1的交点为A ，B ，点P 为椭圆上的动点，则使△P AB 的面积为12的点P 的个数为________．解析：易知直线l ′的方程为2x ＋y －2＝0，联立⎩⎪⎨⎪⎧x 2＋y 24＝1，2x ＋y －2＝0，解得交点分别为椭圆顶点(1,0)和(0,2)，则|AB |＝5，由△P AB 的面积为12，得点P 到直线AB 的距离为55，而平面上到直线2x ＋y －2＝0的距离为55的点都在直线2x ＋y －1＝0和2x ＋y －3＝0上，而直线2x ＋y －1＝0与椭圆相交，2x ＋y －3＝0与椭圆相离，∴满足题意的点P 有2个．答案：29．已知点A ，B 的坐标分别是(－1,0)，(1,0)，直线AM ，BM 相交于点M ，且它们的斜率之积为－2.(1)求动点M 的轨迹方程；(2)若过点N ⎝⎛⎭⎫12，1的直线l 交动点M 的轨迹于C ，D 两点，且N 为线段CD 的中点，求直线l 的方程．解：(1)设M (x ，y )，因为k AM ·k BM ＝－2，所以y x ＋1·y x －1＝－2(x ≠±1)，化简得2x 2＋y 2＝2(x ≠±1)，即为动点M 的轨迹方程． (2)设C (x 1，y 1)，D (x 2，y 2)．法一：当直线l ⊥x 轴时，直线l 的方程为x ＝12，则C ⎝⎛⎭⎫12，62，D ⎝⎛⎭⎫12，－62，此时CD的中点不是N ，不符合题意．故设直线l 的方程为y －1＝k ⎝⎛⎭⎫x －12，将C (x 1，y 1)，D (x 2，y 2)代入2x 2＋y 2＝2(x ≠±1)得⎩⎪⎨⎪⎧2x 21＋y 21＝2，2x 22＋y 22＝2，两式相减，整理得k ＝y 1－y 2x 1－x 2＝－2(x 1＋x 2)y 1＋y 2＝－2×2×122×1＝－1， ∴直线l 的方程为y －1＝－1×⎝⎛⎭⎫x －12，即所求直线l 的方程为2x ＋2y －3＝0.法二：当直线l ⊥x 轴时，直线l 的方程为x ＝12，则C ⎝⎛⎭⎫12，62，D ⎝⎛⎭⎫12，－62，此时CD的中点不是N ，不符合题意．故设直线l 的方程为y －1＝k ⎝⎛⎭⎫x －12，将其代入2x 2＋y 2＝2(x ≠±1)，化简得(2＋k 2)x 2＋2k ⎝⎛⎭⎫1－k 2x ＋⎝⎛⎭⎫1－k22－2＝0(x ≠±1)，所以Δ＝4k 2⎝⎛⎭⎫1－k 22－4(2＋k 2)⎣⎡⎦⎤⎝⎛⎭⎫1－k22－2＞0，① 则x 1＋x 2＝－2k ⎝⎛⎭⎫1－k22＋k 2，又由N 为线段CD 的中点，得x 1＋x 22＝－k ⎝⎛⎭⎫1－k 22＋k 2＝12，解得k ＝－1，将k ＝－1代入①中可知满足条件．此时直线l 的方程为y －1＝－1×⎝⎛⎭⎫x －12，即所求直线l 的方程为2x ＋2y －3＝0.10．(2019·合肥调研)已知椭圆E ：x 2a 2＋y 2b 2＝1(a ＞b ＞0)经过点P ⎝⎛⎭⎫3，12，左焦点为 F (－3，0)．(1)求椭圆E 的方程；(2)若A 是椭圆E 的右顶点，过点F 且斜率为12的直线交椭圆E 于M ，N 两点，求△AMN的面积．解：(1)由题意得椭圆E 的右焦点为(3，0)，即c ＝3，则由椭圆的定义得(3＋3)2＋14＋12＝2a ，解得a ＝2.又c ＝3，∴b 2＝a 2－c 2＝1，∴椭圆E 的方程为x 24＋y 2＝1.(2)过F (－3，0)且斜率为12的直线的方程为y ＝12(x ＋3)，联立⎩⎨⎧y ＝12(x ＋3)，x24＋y 2＝1消去x ，得8y 2－43y －1＝0，显然Δ＞0，设M (x 1，y 1)，N (x 2，y 2)，则⎩⎨⎧y 1＋y 2＝32，y 1y 2＝－18，∴|y 1－y 2|＝52， ∵A 是椭圆E 的右顶点，∴|AF |＝2＋3，∴△AMN 的面积S ＝12|AF |·|y 1－y 2|＝12×(2＋3)×52＝25＋154.B 级1．(2019·南昌调研)已知椭圆C ：x 2a 2＋y 2b 2＝1(a ＞b ＞0)的离心率为32，短轴长为2.(1)求椭圆C 的标准方程；(2)设直线l ：y ＝kx ＋m 与椭圆C 交于M ，N 两点，O 为坐标原点，若k OM ·k ON ＝54，求证：点(m ，k )在定圆上．解：(1)由已知得e ＝c a ＝32，2b ＝2，又a 2－b 2＝c 2，∴b ＝1，a ＝2， ∴椭圆C 的标准方程为x 24＋y 2＝1.(2)证明：设M (x 1，y 1)，N (x 2，y 2)，联立⎩⎪⎨⎪⎧y ＝kx ＋m ，x 24＋y 2＝1消去y ，得(4k 2＋1)x 2＋8kmx ＋4m 2－4＝0，依题意，Δ＝(8km )2－4(4k 2＋1)(4m 2－4)＞0，化简得m 2＜4k 2＋1，①x 1＋x 2＝－8km4k 2＋1，x 1x 2＝4m 2－44k 2＋1，y 1y 2＝(kx 1＋m )(kx 2＋m )＝k 2x 1x 2＋km (x 1＋x 2)＋m 2. 若k OM ·k ON ＝54，则y 1y 2x 1x 2＝54，即4y 1y 2＝5x 1x 2，∴4k 2x 1x 2＋4km (x 1＋x 2)＋4m 2＝5x 1x 2，∴(4k 2－5)·4(m 2－1)4k 2＋1＋4km ·⎝⎛⎭⎫－8km 4k 2＋1＋4m 2＝0，即(4k 2－5)(m 2－1)－8k 2m 2＋m 2(4k 2＋1)＝0，化简得m 2＋k 2＝54，②由①②得0≤m 2＜65，120＜k 2≤54，∴点(m ，k )在定圆x 2＋y 2＝54上．2．已知椭圆x 2a 2＋y 2b 2＝1(a ＞b ＞0)经过点(0,1)，离心率为32，左、右焦点分别为F 1(－c,0)，F 2(c,0)．(1)求椭圆的方程；(2)若直线l ：y ＝2x ＋m 与椭圆交于A ，B 两点，与以F 1F 2为直径的圆交于C ，D 两点，且满足|AB ||CD |＝20351，求直线l 的方程．解：(1)由题设知⎩⎪⎨⎪⎧b ＝1，c a ＝32，b 2＝a 2－c 2，解得⎩⎪⎨⎪⎧a ＝2，b ＝1，c ＝3，所以椭圆的方程为x 24＋y 2＝1.(2)由题设知，以F 1F 2为直径的圆的方程为x 2＋y 2＝3，所以圆心到直线l 的距离d ＝|m |5，由d ＜3得|m |＜15. 所以|CD |＝23－d 2＝2515－m 2. 设A (x 1，y 1)，B (x 2，y 2)，由⎩⎪⎨⎪⎧y ＝2x ＋m ，x 24＋y 2＝1消去y ，得17x 2＋16mx ＋4m 2－4＝0，则x 1＋x 2＝－16m 17，x 1x 2＝4m 2－417，所以|AB |＝1＋22|x 1－x 2|＝451717－m 2，由|AB ||CD |＝20351，得 17－m 215－m 2＝233，解得m＝±3，满足|m|＜15.所以直线l的方程为y＝2x＋3或y＝2x－3.第十节圆锥曲线中的最值、范围问题考点一构造函数求最值[典例] (2019·安徽知名示范高中联考)已知椭圆C ：x 2a 2＋y 2b 2＝1(a ＞b ＞0)的离心率为22，且以原点为圆心，椭圆的焦距为直径的圆与直线x sin θ＋y cos θ－1＝0相切(θ为常数)．(1)求椭圆C 的标准方程；(2)若椭圆C 的左、右焦点分别为F 1，F 2，过F 2作直线l 与椭圆交于M ，N 两点，求F 1M ―→·F 1N ―→的最大值．[解] (1)由题意，得⎩⎨⎧e ＝c a ＝22，1sin 2θ＋cos 2θ＝c ，a 2＝b 2＋c 2，解得⎩⎪⎨⎪⎧c ＝1，a 2＝2，b 2＝1，故椭圆C 的标准方程为x 22＋y 2＝1.(2)由(1)得F 1(－1,0)，F 2(1,0)．①若直线l 的斜率不存在，则直线l ⊥x 轴，直线l 的方程为x ＝1，不妨记M ⎝⎛⎭⎫1，22，N ⎝⎛⎭⎫1，－22， ∴F 1M ―→＝⎝⎛⎭⎫2，22，F 1N ―→＝⎝⎛⎭⎫2，－22，故F 1M ―→·F 1N ―→＝72.②若直线l 的斜率存在，设直线l 的方程为y ＝k (x －1)，由⎩⎪⎨⎪⎧y ＝k (x －1)，x 22＋y 2＝1消去y 得，(1＋2k 2)x 2－4k 2x ＋2k 2－2＝0，设M (x 1，y 1)，N (x 2，y 2)，则x 1＋x 2＝4k 21＋2k 2，x 1x 2＝2k 2－21＋2k 2.又F 1M ―→＝(x 1＋1，y 1)，F 1N ―→＝(x 2＋1，y 2)，则F 1M ―→·F 1N ―→＝(x 1＋1)(x 2＋1)＋y 1y 2 ＝(x 1＋1)(x 2＋1)＋k (x 1－1)·k (x 2－1) ＝(1＋k 2)x 1x 2＋(1－k 2)(x 1＋x 2)＋1＋k 2 ＝2(k 4－1)2k 2＋1＋4k 2－4k 42k 2＋1＋1＋k 2 ＝7k 2－12k 2＋1＝72－92(2k 2＋1)，由k 2≥0，可得F 1M ―→·F 1N ―→∈⎣⎡⎭⎫－1，72. 综上，F 1M ―→·F 1N ―→的最大值为72.[对点训练](2018·湘潭调研)已知椭圆E ：x 2a 2＋y 2b 2＝1(a ＞b ＞0)经过点⎝⎛⎭⎫1，32，离心率为12. (1)求椭圆E 的方程；(2)设点A ，F 分别为椭圆的右顶点、右焦点，经过点F 作直线交椭圆于C ，D 两点，求四边形OCAD 面积的最大值(O 为坐标原点)．解：(1)由题设得⎩⎪⎨⎪⎧1a 2＋94b 2＝1，c a ＝12，a 2＝b 2＋c 2，解得⎩⎪⎨⎪⎧a ＝2，b ＝3，c ＝1.故椭圆E 的方程为x 24＋y 23＝1.(2)由(1)知，F (1,0)，A (2,0)，设直线CD 的方程为x ＝ky ＋1，与椭圆方程x 24＋y 23＝1联立得(3k 2＋4)y 2＋6ky －9＝0，设C (x 1，y 1)，D (x 2，y 2)，∴y 1＋y 2＝－6k 3k 2＋4，y 1y 2＝－93k 2＋4.∴S 四边形OCAD ＝S △OCA ＋S △ODA ＝12×2×|y 1|＋12×2×|y 2| ＝|y 1－y 2|＝(y 1＋y 2)2－4y 1y 2 ＝12k 2＋13k 2＋4.设t ＝k 2＋1(t ≥1)，则S 四边形OCAD ＝12t 3t 2＋1＝123t ＋1t.∵当t ≥1时，y ＝3t ＋1t 单调递增，∴3t ＋1t ≥4(当t ＝1时取等号)，∴S 四边形OCAD ≤3(当k ＝0时取等号)，即四边形OCAD 面积的最大值为3.考点二寻找不等关系解范围[典例] 已知点A ，B 分别为椭圆E ：x 2a 2＋y 2b 2＝1(a ＞b ＞0)的左、右顶点，点P (0，－2)，直线BP 交E 于点Q ， P Q ―→＝32Q B ―→，且△ABP 是等腰直角三角形．(1)求椭圆E 的方程；(2)设过点P 的动直线l 与E 相交于M ，N 两点，当坐标原点O 位于以MN 为直径的圆外时，求直线l 斜率的取值范围．[解] (1)由△ABP 是等腰直角三角形，知a ＝2，B (2,0)．设Q (x 0，y 0)，由P Q ―→＝32Q B ―→，得x 0＝65，y 0＝－45，代入椭圆方程，解得b 2＝1， ∴椭圆E 的方程为x 24＋y 2＝1.(2)由题意可知，直线l 的斜率存在，设方程为y ＝kx －2，M (x 1，y 1)，N (x 2，y 2)，由⎩⎪⎨⎪⎧y ＝kx －2，x 24＋y 2＝1消去y ，得(1＋4k 2)x 2－16kx ＋12＝0，则x 1＋x 2＝16k 1＋4k 2，x 1x 2＝121＋4k 2. 由直线l 与E 有两个不同的交点，得Δ＞0，则(－16k )2－4×12×(1＋4k 2)＞0，解得k 2＞34.①由坐标原点O 位于以MN 为直径的圆外，则OM ―→·ON ―→＞0，即x 1x 2＋y 1y 2＞0，则x 1x 2＋y 1y 2＝x 1x 2＋(kx 1－2)(kx 2－2) ＝(1＋k 2)x 1x 2－2k (x 1＋x 2)＋4 ＝(1＋k 2)·121＋4k 2－2k ·16k1＋4k 2＋4＞0，解得k 2＜4.②联立①②可知34＜k 2＜4，解得－2＜k ＜－32或32＜k ＜2，故直线l 斜率的取值范围为⎝⎛⎭⎫－2，－32∪⎝⎛⎭⎫32，2.[解题技法] 范围问题的解题策略解决有关范围问题时，先要恰当地引入变量(如点的坐标、角、斜率等)，寻找不等关系，其方法有：(1)利用判别式来构造不等式，从而确定所求范围；(2)利用已知参数的取值范围，求新参数的范围，解这类问题的核心是在两个参数之间建立相等关系；(3)利用隐含的不等关系，从而求出所求范围； (4)利用已知不等关系构造不等式，从而求出所求范围； (5)利用函数值域的求法，确定所求范围． [对点训练]已知A ，B 分别为曲线C ：x 2a 2＋y 2＝1(y ≥0，a ＞0)与x 轴的左、右两个交点，直线l过点B 且与x 轴垂直，M 为l 上位于x 轴上方的一点，连接AM 交曲线C 于点T .(1)若曲线C 为半圆，点T 为AB 的三等分点，试求出点M 的坐标．(2)若a ＞1，S △MAB ＝2，当△TAB 的最大面积为43时，求椭圆的离心率的取值范围．解：(1)当曲线C 为半圆时，得a ＝1.由点T 为AB 的三等分点，得∠BOT ＝60°或120°. 当∠BOT ＝60°时，∠MAB ＝30°，又|AB |＝2，故△MAB 中，有|MB |＝|AB |·tan 30°＝233，所以M ⎝⎛⎭⎫1，233.当∠BOT ＝120°时，同理可求得点M 坐标为(1,23)．综上，点M 的坐标为⎝⎛⎭⎫1，233或(1,23)．(2)设直线AM 的方程为y ＝k (x ＋a )，则k ＞0，|MB |＝2ka ，所以S △MAB ＝12·2a ·2ka ＝2，所以k ＝1a2，代入直线方程得y ＝1a2(x ＋a )，联立⎩⎨⎧y ＝1a2(x ＋a )，x2a 2＋y 2＝1，解得y T ＝2aa 2＋1，所以S △TAB ＝12·2a ·2a a 2＋1＝2a 2a 2＋1≤43，解得1＜a 2≤2. 所以椭圆的离心率e ＝1－1a 2≤22，即椭圆的离心率的取值范围为⎝⎛⎦⎤0，22.[课时跟踪检测]1.(2018·浙江高考)如图，已知点P 是y 轴左侧(不含y 轴)一点，抛物线C ：y 2＝4x 上存在不同的两点A ，B 满足P A ，PB 的中点均在C 上．(1)设AB 中点为M ，证明：PM 垂直于y 轴； (2)若P 是半椭圆x 2＋y 24＝1(x <0)上的动点，求△P AB 面积的取值范围．解：(1)证明：设P (x 0，y 0)，A ⎝⎛⎭⎫14y 21，y 1，B ⎝⎛⎭⎫14y 22，y 2. 因为P A ，PB 的中点在抛物线上，所以y 1，y 2为方程⎝⎛⎭⎫y ＋y 022＝4·14y 2＋x 02，即y 2－2y 0y ＋8x 0－y 20＝0的两个不同的实根．所以y 1＋y 2＝2y 0，因此PM 垂直于y 轴．(2)由(1)可知⎩⎪⎨⎪⎧y 1＋y 2＝2y 0，y 1y 2＝8x 0－y 20，所以|PM |＝18(y 21＋y 22)－x 0＝34y 20－3x 0， |y 1－y 2|＝22(y 20－4x 0).因此△P AB 的面积S △P AB ＝12|PM |·|y 1－y 2|＝324(y 2－4x 0)32.因为x 20＋y 204＝1(x 0<0)，所以y 20－4x 0＝－4x 20－4x 0＋4∈[4,5]，所以△P AB 面积的取值范围是⎣⎡⎦⎤62，15104.2．(2019·唐山模拟)已知椭圆Γ：x 2a 2＋y 2b 2＝1(a ＞b ＞0)，经过点E ⎝⎛⎭⎫3，12，且离心率为32. (1)求椭圆Γ的方程；(2)直线l 与圆O ：x 2＋y 2＝b 2相切于点M ，且与椭圆Γ相交于不同的两点A ，B ，求|AB |的最大值．解：(1)将E ⎝⎛⎭⎫3，12代入椭圆方程，得3a 2＋14b 2＝1，由椭圆的离心率e ＝c a ＝a 2－b 2a ＝32，解得a ＝2，b ＝1，所以椭圆Γ的方程为x 24＋y 2＝1.(2)当直线l 垂直于x 轴时，由直线l 与圆O ：x 2＋y 2＝1相切，可知直线l 的方程为x ＝±1，易求得|AB |＝ 3.当直线l 不垂直于x 轴时，设直线l 的方程为y ＝kx ＋m ，由直线l 与圆O ：x 2＋y 2＝1相切，得|m |k 2＋1＝1，即m 2＝k 2＋1. 将y ＝kx ＋m 代入x 24＋y 2＝1，整理得(1＋4k 2)x 2＋8kmx ＋4m 2－4＝0，设A (x 1，y 1)，B (x 2，y 2)，则x 1＋x 2＝－8km 1＋4k 2，x 1x 2＝4m 2－41＋4k 2，故|AB |＝1＋k 2|x 1－x 2| ＝1＋k 2·(x 1＋x 2)2－4x 1x 2 ＝1＋k 2·⎝ ⎛⎭⎪⎫－8km 1＋4k 22－16m 2－161＋4k 2 ＝41＋k 21＋4k 2－m 21＋4k 2.又因为m 2＝k 2＋1，所以|AB |＝43|k |k 2＋11＋4k 2≤2(3k 2＋k 2＋1)1＋4k 2＝2，当且仅当3|k |＝k 2＋1，即k ＝±22时等号成立．综上所述，|AB |的最大值为2.3．已知点F 为椭圆E ：x 2a 2＋y 2b 2＝1(a >b >0)的左焦点，且两焦点与短轴的一个顶点构成一个等边三角形，直线x 4＋y2＝1与椭圆E 有且仅有一个交点M .(1)求椭圆E 的方程；(2)设直线x 4＋y2＝1与y 轴交于P ，过点P 的直线l 与椭圆E 交于不同的两点A ，B ，若λ|PM |2＝|P A |·|PB |，求实数λ的取值范围．解：(1)由题意，得a ＝2c ，b ＝3c ，则椭圆E 的方程为x 24c 2＋y 23c2＝1.由⎩⎨⎧x 24＋y 23＝c 2，x 4＋y 2＝1得x 2－2x ＋4－3c 2＝0.∵直线x 4＋y2＝1与椭圆E 有且仅有一个交点M ，∴Δ＝4－4(4－3c 2)＝0，解得c 2＝1， ∴椭圆E 的方程为x 24＋y 23＝1.(2)由(1)得M ⎝⎛⎭⎫1，32， ∵直线x 4＋y2＝1与y 轴交于P (0,2)，∴|PM |2＝54.当直线l 与x 轴垂直时， |P A |·|PB |＝(2＋3)×(2－3)＝1， ∴λ|PM |2＝|P A |·|PB |⇒λ＝45.当直线l 与x 轴不垂直时，设直线l 的方程为y ＝kx ＋2，A (x 1，y 1)，B (x 2，y 2)，由⎩⎪⎨⎪⎧y ＝kx ＋2，3x 2＋4y 2－12＝0消去y ，得(3＋4k 2)x 2＋16kx ＋4＝0，则x 1x 2＝43＋4k 2，且Δ＝48(4k 2－1)>0， ∴|P A |·|PB |＝(1＋k 2)x 1x 2 ＝(1＋k 2)·43＋4k 2＝1＋13＋4k 2＝54λ，∴λ＝45⎝⎛⎭⎫1＋13＋4k 2，∵k 2>14，∴45<λ<1.综上可知，实数λ的取值范围是⎣⎡⎭⎫45，1.4．(2018·郑州二模)已知动圆E 经过点F (1,0)，且和直线l ：x ＝－1相切． (1)求该动圆圆心E 的轨迹G 的方程；(2)已知点A (3,0)，若斜率为1的直线l ′与线段OA 相交(不经过坐标原点O 和点A )，且与曲线G 交于B ，C 两点，求△ABC 面积的最大值．解：(1)由题意可知点E 到点F 的距离等于点E 到直线l 的距离，∴动点E 的轨迹是以F (1,0)为焦点，直线x ＝－1为准线的抛物线，故轨迹G 的方程是y 2＝4x .(2)设直线l ′的方程为y ＝x ＋m ，其中－3＜m ＜0.联立⎩⎪⎨⎪⎧y ＝x ＋m ，y 2＝4x 消去y ，得x 2＋(2m －4)x ＋m 2＝0，则Δ＝(2m －4)2－4m 2＝16(1－m )恒大于零．设C (x 1，y 1)，B (x 2，y 2)，则x 1＋x 2＝4－2m ，x 1·x 2＝m 2，∴|CB |＝2·(x 1＋x 2)2－4x 1x 2＝42(1－m ). 又点A 到直线l ′的距离d ＝3＋m2， ∴S △ABC ＝12×42(1－m )×3＋m 2＝21－m ×(3＋m )．令1－m ＝t ，t ∈(1,2)，则m ＝1－t 2， ∴S △ABC ＝2t (4－t 2)＝8t －2t 3.令f (t )＝8t －2t 3,1＜t ＜2，∴f ′(t )＝8－6t 2，易知y ＝f (t )在⎝⎛⎭⎫1，23上单调递增，在⎝⎛⎭⎫23，2上单调递减． ∴y ＝f (t )在t ＝23，即m ＝－13时取得最大值3239.∴△ABC 面积的最大值为3239第十一节圆锥曲线中的定点、定值与存在性问题考点一巧妙消元证定值[典例] (2018·北京高考)已知抛物线C ：y 2＝2px 经过点P (1,2)，过点Q (0,1)的直线l 与抛物线C 有两个不同的交点A ，B ，且直线P A 交y 轴于M ，直线PB 交y 轴于N .(1)求直线l 的斜率的取值范围；(2)设O 为原点，Q M ―→＝λQ O ―→，Q N ―→＝μQ O ―→，求证：1λ＋1μ为定值．[解] (1)因为抛物线y 2＝2px 过点(1,2)，所以2p ＝4，即p ＝2. 故抛物线C 的方程为y 2＝4x .由题意知，直线l 的斜率存在且不为0. 设直线l 的方程为y ＝kx ＋1(k ≠0)，由⎩⎪⎨⎪⎧y 2＝4x ，y ＝kx ＋1，得k 2x 2＋(2k －4)x ＋1＝0. 依题意Δ＝(2k －4)2－4×k 2×1>0，解得k <0或0<k <1.又P A ，PB 与y 轴相交，故直线l 不过点(1，－2)．从而k ≠－3.所以直线l 的斜率的取值范围是(－∞，－3)∪(－3,0)∪(0,1)． (2)证明：设A (x 1，y 1)，B (x 2，y 2)．由(1)知x 1＋x 2＝－2k －4k 2，x 1x 2＝1k 2.直线P A 的方程为y －2＝y 1－2x 1－1(x －1)．令x ＝0，得点M 的纵坐标为y M ＝－y 1＋2x 1－1＋2＝－kx 1＋1x 1－1＋2.同理得点N 的纵坐标为y N ＝－kx 2＋1x 2－1＋2. 由Q M ―→＝λQ O ―→，Q N ―→＝μQ O ―→，得λ＝1－y M ，μ＝1－y N .所以1λ＋1μ＝11－y M ＋11－y N ＝x 1－1(k －1)x 1＋x 2－1(k －1)x 2＝1k －1·2x 1x 2－(x 1＋x 2)x 1x 2＝1k －1·2k 2＋2k －4k 21k 2＝2.所以1λ＋1μ为定值．[对点训练]在平面直角坐标系xOy 中，已知双曲线C 1：x 22－y 24＝1，椭圆C 2：x 2＋y 24＝1，若M ，N 分别是C 1，C 2上的动点，且OM ⊥ON ，求证：O 到直线MN 的距离是定值．证明：当直线ON 垂直于x 轴时，|ON |＝2，|OM |＝2，则O 到直线MN 的距离为233.当直线ON 不垂直于x 轴时，设直线ON 的方程为y ＝kx ⎝⎛⎭⎫显然|k |＞22，则直线OM 的方程为y ＝－1kx .由⎩⎪⎨⎪⎧y ＝kx ，x 2＋y 24＝1，得⎩⎨⎧x 2＝44＋k 2，y 2＝4k24＋k 2，所以|ON |2＝4(1＋k 2)4＋k 2.同理|OM |2＝4(1＋k 2)2k 2－1. 设O 到直线MN 的距离为d ，因为在Rt △MON 中，(|OM |2＋|ON |2)d 2＝|OM |2·|ON |2，所以1d 2＝1|OM |2＋1|ON |2＝3(1＋k 2)4(1＋k 2)＝34，即d ＝233.综上，O 到直线MN 的距离是定值．考点二确定直线寻定点[典例] (2018·成都一诊)已知椭圆C ：x 2a 2＋y 2b 2＝1(a ＞b ＞0)的右焦点F (3，0)，长半轴长与短半轴长的比值为2.(1)求椭圆C 的标准方程；(2)设不经过点B (0,1)的直线l 与椭圆C 相交于不同的两点M ，N ，若点B 在以线段MN为直径的圆上，证明直线l 过定点，并求出该定点的坐标．[解] (1)由题意得，c ＝3，ab ＝2，a 2＝b 2＋c 2，∴a ＝2，b ＝1，∴椭圆C 的标准方程为x 24＋y 2＝1.(2)当直线l 的斜率存在时，设直线l 的方程为y ＝kx ＋m (m ≠1)，M (x 1，y 1)，N (x 2，y 2)．联立⎩⎪⎨⎪⎧y ＝kx ＋m ，x 2＋4y 2＝4，消去y ，可得(4k 2＋1)x 2＋8kmx ＋4m 2－4＝0. ∴Δ＝16(4k 2＋1－m 2)＞0，x 1＋x 2＝－8km 4k 2＋1，x 1x 2＝4m 2－44k 2＋1. ∵点B 在以线段MN 为直径的圆上， ∴BM ―→·BN ―→＝0.∵BM ―→·BN ―→＝(x 1，kx 1＋m －1)·(x 2，kx 2＋m －1)＝(k 2＋1)x 1x 2＋k (m －1)(x 1＋x 2)＋(m －1)2＝0，∴(k 2＋1)4m 2－44k 2＋1＋k (m －1)－8km4k 2＋1＋(m －1)2＝0，整理，得5m 2－2m －3＝0，解得m ＝－35或m ＝1(舍去)．∴直线l 的方程为y ＝kx －35.易知当直线l 的斜率不存在时，不符合题意．故直线l 过定点，且该定点的坐标为⎝⎛⎭⎫0，－35.[对点训练](2019·株洲两校联考)已知椭圆E ：x 2a 2＋y 2b 2＝1(a ＞b ＞0)经过点P (2,1)，且离心率为32.(1)求椭圆的标准方程；(2)设O 为坐标原点，在椭圆的短轴上有两点M ，N 满足OM ―→＝NO ―→，直线PM ，PN 分别交椭圆于A ，B 两点，试证明直线AB 过定点．解：(1)由椭圆的离心率e ＝ca＝1－b 2a 2＝32，得a 2＝4b 2，将P (2,1)代入椭圆方程x 24b2＋y 2b 2＝1，得1b 2＋1b 2＝1，解得b 2＝2，则a 2＝8，所以椭圆的标准方程为x 28＋y 22＝1.(2)证明：当M ，N 分别是短轴的端点时，显然直线AB 为y 轴，所以若直线AB 过定点，则这个定点一定在y 轴上，当M ，N 不是短轴的端点时，设直线AB 的方程为y ＝kx ＋t ，设A (x 1，y 1)，B (x 2，y 2)，易知x 1≠2，x 2≠2，联立⎩⎪⎨⎪⎧x 28＋y 22＝1，y ＝kx ＋t 消去y ，得(1＋4k 2)x 2＋8ktx ＋4t 2－8＝0，则Δ＝16(8k 2－t 2＋2)＞0，x 1＋x 2＝－8kt4k 2＋1，x 1x 2＝4t 2－84k 2＋1.又直线P A 的方程为y －1＝y 1－1x 1－2(x －2)，即y －1＝kx 1＋t －1x 1－2(x －2)，所以点M 的坐标为⎝ ⎛⎭⎪⎫0，(1－2k )x 1－2t x 1－2，同理可知N ⎝ ⎛⎭⎪⎫0，(1－2k )x 2－2t x 2－2，由OM ―→＝NO ―→，得(1－2k )x 1－2t x 1－2＋(1－2k )x 2－2t x 2－2＝0，化简整理得，(2－4k )x 1x 2－(2－4k ＋2t )(x 1＋x 2)＋8t ＝0，则(2－4k )×4t 2－84k 2＋1－(2－4k ＋2t )⎝⎛⎭⎫－8kt 4k 2＋1＋8t ＝0，整理得(2t ＋4)k ＋(t 2＋t －2)＝0，当且仅当t ＝－2时，上式对任意的k 都成立，所以直线AB 过定点(0，－2)．考点三假设存在定结论(探索性问题)[典例] 如图，在直角坐标系xOy 中有一直角梯形ABCD ，AB 的中点为O ，AD ⊥AB ，AD ∥BC ，|AB |＝2，|BC |＝32，|AD |＝12，以A ，B 为焦点的椭圆经过点C .(1)求椭圆的标准方程；(2)若点E ⎝⎛⎭⎫0，12，问是否存在直线l 与椭圆交于M ，N 两点且|ME |＝|NE |？若存在，求出直线l 斜率的取值范围；若不存在，请说明理由．[解] (1)连接AC (图略)，依题意设椭圆的标准方程为x 2a 2＋y 2b 2＝1(a ＞b ＞0)，在Rt △ABC 中，|AB |＝2，|BC |＝32，所以|AC |＝52.所以|CA |＋|CB |＝52＋32＝2a ，a ＝2.又2c ＝2，所以c ＝1，从而b ＝3，所以椭圆的标准方程为x 24＋y 23＝1.(2)由题意知，当l 与x 轴垂直时，不满足|ME |＝|NE |，当l 与x 轴平行时，|ME |＝|NE |，显然成立，此时k ＝0.当k ≠0时，设直线l 的方程为y ＝kx ＋m ，由⎩⎪⎨⎪⎧y ＝kx ＋m ，x 24＋y 23＝1消去y ，整理得(3＋4k 2)x 2＋8kmx ＋4(m 2－3)＝0. 由直线与椭圆交于两点得Δ＝(8km )2－4(3＋4k 2)×4(m 2－3)＞0，所以m 2＜4k 2＋3. ① 设M (x 1，y 1)，N (x 2，y 2)，MN 的中点为P (x 0，y 0)，则x 0＝x 1＋x 22＝－4km 3＋4k 2，y 0＝kx 0＋m ＝3m 3＋4k 2. 因为|ME |＝|NE |，所以EP ⊥MN ，所以k EP ·k ＝－1，即3m 3＋4k 2－12－4km3＋4k 2·k ＝－1，化简得m ＝－12(3＋4k 2)，结合①得14(3＋4k 2)2＜4k 2＋3，即16k 4＋8k 2－3＜0，解得－12＜k ＜12(k ≠0)．综上所述，存在满足条件的直线l ，且其斜率的取值范围为⎝⎛⎭⎫－12，12. [解题技法] 探索性问题的解题策略探索性问题，先假设存在，推证满足条件的结论，若结论正确，则存在，若结论不正确，则不存在．(1)当条件和结论不唯一时，要分类讨论．(2)当给出结论而要推导出存在的条件时，先假设成立，再推出条件．(3)当条件和结论都不知，按常规方法解题很难时，要思维开放，采取另外的途径．[对点训练](2019·贵阳检测)如图，椭圆C ：x 2a 2＋y 2b 2＝1(a ＞b ＞0)的左顶点与上顶点分别为A ，B ，右焦点为F ，点P 在椭圆C 上，且PF ⊥x 轴，若AB ∥OP ，且|AB |＝2 3.(1)求椭圆C 的方程；(2)若Q 是椭圆C 上不同于长轴端点的任意一点，在x 轴上是否存在一点D ，使得直线Q A 与Q D 的斜率乘积恒为定值？若存在，求出点D 的坐标；若不存在，说明理由．解：(1)由题意得A (－a,0)，B (0，b )，可设P (c ，t )(t ＞0)， ∴c 2a 2＋t 2b 2＝1，解得t ＝b 2a ，即P ⎝⎛⎭⎫c ，b 2a ，由AB ∥OP ，得b a ＝b 2ac，即b ＝c ，∴a 2＝b 2＋c 2＝2b 2， ① 又AB ＝23，∴a 2＋b 2＝12， ② 由①②得a 2＝8，b 2＝4，∴椭圆C 的方程为x 28＋y 24＝1.(2)假设存在D (m,0)使得直线Q A 与Q D 的斜率乘积恒为定值，设Q (x 0，y 0)(y 0≠0)，则x 208＋y 204＝1， ③设k Q A ·k Q D ＝k (常数)，∵A (－22，0)，∴y 0x 0＋22·y 0x 0－m ＝k ，④ 由③得y 20＝4⎝⎛⎭⎫1－x 208，⑤将⑤代入④，得k ＝8－x 202[x 20＋(22－m )x 0－22m ]， ∴⎩⎨⎧22－m ＝0，22m ＝8，∴m ＝22，k ＝－12，∴存在点D (22，0)，使得k Q A ·k Q D ＝－12(定值)．[课时跟踪检测]1．(2019·贵阳适应性考试)已知椭圆C ：x 2a 2＋y 2b 2＝1(a ＞b ＞0)的左、右焦点分别为F 1，F 2，点M 为短轴的上端点，MF 1―→·MF 2―→＝0，过F 2垂直于x 轴的直线交椭圆C 于A ，B 两点，且|AB |＝ 2.(1)求椭圆C 的方程；(2)设经过点(2，－1)且不经过点M 的直线l 与C 相交于G ，H 两点．若k 1，k 2分别为直线MH ，MG 的斜率，求k 1＋k 2的值．解：(1)由MF 1―→·MF 2―→＝0，得b ＝c . ①因为过F 2垂直于x 轴的直线交椭圆C 于A ，B 两点，且|AB |＝2，所以b 2a ＝22， ②又a 2＝b 2＋c 2， ③ 联立①②③，解得a 2＝2，b 2＝1，故椭圆C 的方程为x 22＋y 2＝1.(2)易知直线l 的斜率存在，可设直线l 的方程为y ＋1＝k (x －2)，即y ＝kx －2k －1，将y ＝kx －2k －1代入x 22＋y 2＝1得(1＋2k 2)x 2－4k (2k ＋1)x ＋8k 2＋8k ＝0，由题设可知Δ＝－16k (k ＋2)＞0，设G (x 1，y 1)，H (x 2，y 2)，则x 1＋x 2＝4k (2k ＋1)1＋2k 2，x 1x 2＝8k 2＋8k1＋2k 2，k 1＋k 2＝y 1－1x 1＋y 2－1x 2＝kx 1－2k －2x 1＋kx 2－2k －2x 2＝2k －(2k ＋2)×4k (2k ＋1)1＋2k 28k 2＋8k1＋2k 2＝2k －(2k ＋1)＝－1，所以k 1＋k 2＝－1.2．(2018·贵阳摸底考试)过抛物线C ：y 2＝4x 的焦点F 且斜率为k 的直线l 交抛物线C 于A ，B 两点，且|AB |＝8.(1)求直线l 的方程；(2)若A 关于x 轴的对称点为D ，求证：直线BD 过定点，并求出该点的坐标．解：(1)易知点F 的坐标为(1,0)，则直线l 的方程为y ＝k (x －1)，代入抛物线方程y 2＝4x 得k 2x 2－(2k 2＋4)x ＋k 2＝0，由题意知k ≠0，且Δ＝[－(2k 2＋4)]2－4k 2·k 2＝16(k 2＋1)＞0，设A (x 1，y 1)，B (x 2，y 2)，∴x 1＋x 2＝2k 2＋4k 2，x 1x 2＝1，由抛物线的定义知|AB |＝x 1＋x 2＋2＝8， ∴2k 2＋4k2＝6，∴k 2＝1，即k ＝±1，∴直线l 的方程为x ＋y －1＝0或x －y －1＝0.(2)证明：∵D 点的坐标为(x 1，－y 1)，直线BD 的斜率k BD ＝y 2＋y 1x 2－x 1＝y 2＋y 1y 224－y 214＝4y 2－y 1，∴直线BD 的方程为y ＋y 1＝4y 2－y 1(x －x 1)，即(y 2－y 1)y ＋y 2y 1－y 21＝4x －4x 1，∵y 21＝4x 1，y 22＝4x 2，x 1x 2＝1， ∴(y 1y 2)2＝16x 1x 2＝16，即y 1y 2＝－4(y 1，y 2异号)，∴直线BD 的方程为4(x ＋1)＋(y 1－y 2)y ＝0，恒过点(－1，0)．3．(2019·西安八校联考)已知直线l ：x ＝my ＋1过椭圆C ：x 2a 2＋y 2b 2＝1的右焦点F ，抛物线x 2＝43y 的焦点为椭圆C 的上顶点，且l 交椭圆C 于A ，B 两点，点A ，F ，B 在直线x ＝4上的射影依次为D ，K ，E .(1)求椭圆C 的方程；(2)若直线l 交y 轴于点M ，且MA ―→＝λ1AF ―→，MB ―→＝λ2BF ―→，当m 变化时，证明：λ1＋λ2为定值；(3)判断当m 变化时，直线AE 与BD 是否相交于定点？若是，请求出定点的坐标，并给予证明；否则，说明理由．解：(1)∵l ：x ＝my ＋1过椭圆C 的右焦点F ， ∴右焦点F (1,0)，即c ＝1.∵x 2＝43y 的焦点(0，3)为椭圆C 的上顶点， ∴b ＝3，即b 2＝3，a 2＝b 2＋c 2＝4， ∴椭圆C 的方程为x 24＋y 23＝1.(2)证明：由题意知m ≠0，由⎩⎪⎨⎪⎧x ＝my ＋1，3x 2＋4y 2－12＝0消去x ，整理得(3m 2＋4)y 2＋6my －9＝0.设A (x 1，y 1)，B (x 2，y 2)，则y 1＋y 2＝－6m 3m 2＋4，y 1y 2＝－93m 2＋4.∵MA ―→＝λ1AF ―→，MB ―→＝λ2BF ―→，M ⎝⎛⎭⎫0，－1m ， ∴⎝⎛⎭⎫x 1，y 1＋1m ＝λ1(1－x 1，－y 1)，⎝⎛⎭⎫x 2，y 2＋1m ＝λ2(1－x 2，－y 2)， ∴λ1＝－1－1my 1，λ2＝－1－1my 2，∴λ1＋λ2＝－2－y 1＋y 2my 1y 2＝－2－－6m3m 2＋4－9m3m 2＋4＝－83.综上所述，当m 变化时，λ1＋λ2为定值－83.(3)当m ＝0时，直线l ⊥x 轴，则四边形ABED 为矩形，易知AE 与BD 相交于点N ⎝⎛⎭⎫52，0，猜想当m 变化时，直线AE 与BD 相交于定点N ⎝⎛⎭⎫52，0，证明如下：AN ―→＝⎝⎛⎭⎫52－x 1，－y 1＝⎝⎛⎭⎫32－my 1，－y 1，易知E (4，y 2)，则NE ―→＝⎝⎛⎭⎫32，y 2.∵⎝⎛⎭⎫32－my 1y 2－32(－y 1)＝32(y 1＋y 2)－my 1y 2＝32⎝⎛⎭⎫－6m 3m 2＋4－m ⎝⎛⎭⎫－93m 2＋4＝0， ∴AN ―→∥NE ―→，即A ，N ，E 三点共线．同理可得B ，N ，D 三点共线．则猜想成立．故当m 变化时，直线AE 与BD 相交于定点N ⎝⎛⎭⎫52，0.4．(2018·石家庄质测)已知椭圆C ：x 2a 2＋y 2b 2＝1(a ＞b ＞0)的离心率为223，左、右焦点分别为F 1，F 2，过F 1的直线交椭圆于A ，B 两点．(1)若以AF 1为直径的动圆内切于圆x 2＋y 2＝9，求椭圆的长轴长；(2)当b ＝1时，问在x 轴上是否存在定点T ，使得TA ―→·TB ―→为定值？并说明理由．解：(1)设AF 1的中点为M ，连接OM ，AF 2(O 为坐标原点)，在△AF 1F 2中，O 为F 1F 2的中点，所以|OM |＝12|AF 2|＝12(2a －|AF 1|)＝a －12|AF 1|.由题意得|OM |＝3－12|AF 1|，所以a ＝3，故椭圆的长轴长为6.(2)由b ＝1，c a ＝223，a 2＝b 2＋c 2, 得c ＝22，a ＝3，。

第九章 学案54 直线与圆锥曲线的位置关系

直线与圆锥曲线的位置关系 课件(62张)

圆锥曲线直线与圆锥曲线的位置课件

直线与圆锥曲线的位置关系教案

第9讲 直线与圆锥曲线的位置关系

直线与圆锥曲线的位置关系总结归纳ppt课件

高三数学直线与圆锥曲线的位置

直线与圆锥曲线的位置关系教案

教案直线和圆锥曲线的位置关系

直线与圆锥曲线的位置关系教案

直线与圆锥曲线的位置关系教案

直线与圆锥曲线的位置关系教案

《直线与圆锥曲线的位置关系》教案全面版

直线与圆锥曲线的位置关系教案

直线与圆锥曲线的位置关系

第九节 直线与圆锥曲线的位置关系 教师版

第九章学案54 直线与圆锥曲线的位置关系

直线与圆锥曲线的位置关系课件(62张)

第9讲直线与圆锥曲线的位置关系

第九节直线与圆锥曲线的位置关系教师版