不定积分,定积分复习题及答案

合集下载

积分微分知识点及习题和答案（仅供参考）

积分微分知识点及习题和答案（仅供参考）仅供参考积分和微分积分一般分为不定积分、定积分和微积分三种1、不定积分设F(x) 是函数f(x) 的一个原函数,我们把函数f(x) 的所有原函数F(x)+C （C 为任意常数）叫做函数f(x) 的不定积分. 记作∫f(x)dx其. 中∫叫做积分号, f(x) 叫做被积函数, x 叫做积量,f(x)dx 叫做被积式,C 叫做积分常数,求已知函数的不定积分的过程叫做对这个函数进行积分.由定义可知：求函数f(x) 的不定积分,就是要求出f(x) 的所有的原函数,由原函数的性质可知,只要求出函数f(x) 的一个原函数,再加上任意的常数C,就得到函数f(x) 的不定积分.也可以表述成,积分是微分的逆运算,即知道了导函数,求原函数.2、定积分众所周知,微积分的两大部分是微分与积分.微分实际上是求一函数的导数,而积分是已知一函数的导数,求这一函数.所以,微分与积分互为逆运算.实际上,积分还可以分为两部分.第一种,是单纯的积分,也就是已知导数求原函数,而若F(x) 的导数是f(x), 那么F(x)+C （C 是常数）的导数也是f(x), 也就是说,把f(x) 积分,不一定能得到F(x), 因为F(x)+C 的导数也是f(x),C 是无穷无尽的常数,所以f(x) 积分的结果有无数个, 是不确定的,我们一律用F(x)+C 代替,这就称为不定积分.而相对于不定积分,就是定积分.所谓定积分,其形式为∫f(x) dx 上(限 a 写在∫上面,下限 b 写在∫下面).之所以称其为定积分, 是因为它积分后得出的值是确定的,是一个数,而不是一个函数.定积分的正式名称是黎曼积分,详见黎曼积分.用自己的话来说,就是把直角坐标系上的函数的图象用平行于y 轴的直线把其分割成无数个矩形,然后把某个区间[a,b] 上的矩形累加起来,所得到的就是这个函数的图象在区间[a,b] 的面积.实际上,定积分的上下限就是区间的两个端点a、b.我们可以看到,定积分的本质是把图象无限细分,再累加起来,而积分的本质是求一个函数的原函数.它们看起来没有任何的联系,那么为什么定积分写成积分的形式呢?定积分与积分看起来风马牛不相及,但是由于一个数学上重要的理论的支撑,使得它们有了本质的密切关系.把一个图形无限细分再累加,这似乎是不可能的事情,但是由于这个理论, 可以转化为计算积分.这个重要理论就是大名鼎鼎的牛顿-莱布尼兹公式,它的内容是：若F'(x)=f(x) 那么∫f(x) dx(上限 a 下限b)=F(a)-F(b)牛顿-莱布尼兹公式用文字表述,就是说一个定积分式的值,就是上限在原函数的值与下限在原函数的值的差.正因为这个理论,揭示了积分与黎曼积分本质的联系,可见其在微积分学以至更高等的数学上的重要地位,因此,牛顿-莱布尼兹公式也被称作微积分基本定理.3、微积分积分是微分的逆运算,即知道了函数的导函数,反求原函数.在应用上,积分作用不仅如此, 它被大量应用于求和,通俗的说是求曲边三角形的面积,这巧妙的求解方法是积分特殊的性质决定的。

不定积分+定积分及其应用习题附带答案

1．设是在上的一个原函数,且为奇函数,则是 ( )()F x ()f x (),-∞+∞()F x ()f x A ．偶函数 B ．奇函数C ．非奇非偶函数 D ．不能确定2．已知的一个原函数为,的一个原函数为,则的一个原函数()f x cos x ()g x 2x ()f g x ⎡⎤⎣⎦为 ( )A ．B ． 2x 2cos x C ． D ．2cos x cos x3．设为连续导函数,则下列命题正确的是 ( )()f x A ． ()()1222f x dx f x c '=+⎰B ．()()22f x dx f x c'=+⎰C ． ()()()222f x dx f x ''=⎰D ．()()2f x dx f x c'=+⎰4．设且()22cos sin f x x '= ,则=( )()00f =()f x A ． B ． 212x x -212x -C ． D ．1x -313x x-5．设是的一个原函数,则2xe-()f x ( )()02()limx f x x f x x∆→-∆-=∆A ． B ．22xe -28xe-C ． D ．22xe--24xe-6．设,则=( )()xf x e -=()ln f x dx x'⎰A ．B ． 1x-c +ln x c -+C ．D ． 1c x+ln x c +7．若是的一个原函数,则ln x x ()f x =()f x '8．设的一个原函数为()()tan 2f x k x =,则 2ln cos 23x k =9．若,则()2f x dx x c =+⎰=()231x f x dx -⎰10．()()2cos 2sin 2d θθθ=⎰11．若,则()()f x dx F x c =+⎰()xx ef e dx --=⎰12．若,则()ln cos f x x '=⎡⎤⎣⎦()f x =13．计算()23x xe dx +⎰14．计算()()sin ln cos ln x x dx x⎡⎤⎡⎤⎣⎦⎣⎦⎰15．计算ln(tan )sin cos x dxx x ⎰16．计算21arctan1x dx x +⎰17．计算11sin dx x+⎰18．计算19．计算20．计算21．计算22．计算23. 计算()221tan xex dx+⎰24．已知的一个原函数为,求()f x sin x x()3x f x dx '⎰1、解:可导奇函数的导函数必为偶函数.必为偶函数.选A()()f x F x '∴=2、解:(1),()()cos sin f x x x '==- ()()()22sin 2g x x x f g x x'==∴=-⎡⎤⎣⎦(2)()2cos 2cos (sin )xx x '=- 选B sin 2x =-∴3、解:()()12222f x dx f x d x''=⎰⎰()122f x c =+选A4、解：(1)()22cos 1cos f x x '=- ()1f x x'∴=- (2)()22x f x x c=-+且得()00f =0c =,选A ()22x f x x =-5、解：(1)原式=()()()022limx f x x f x x∆→-∆--⎡⎤⎣⎦-2∆()2f x '=-(2)()2xF x e-= ()()222x xf x e e --'∴==-(3) 原式= 选D222(2)4xx ee ----=6、解：(1)()()ln ln ln f x dx f x d xx''=⎰⎰()ln f x c=+(2)(),xf x e -= ()1lnln 1ln x xf x e ex-∴===(3)原式=选C 1c x+7、解：(1)()ln F x x x= ()()1ln f x F x x'∴==+(2) ()()11ln f x x x''=+=8、解：()2ln cos 23F x x =()()2sin 223cos 2xf x x -∴=-故 ()()4tan 21ln 3x F x x '=-=+43k =-9、解：原式=()()331113f x d x ---⎰()3113x c =--+10、解：原式=2222cos sin 4sin cos d θθθθθ-⎰221144sin cos d d θθθθ=-⎰⎰11cot tan 44t cθθ=--+或1csc 2c θ⎛⎫=-+ ⎪⎝⎭11、解：原式=()()xxx f edeF e c----=-+⎰12、解：()ln cos f x dx xdx'=⎡⎤⎣⎦⎰⎰()1ln sin f x x c =+()1sin sin c x xf x e c e -==⋅13、解:原式=()22323x xx x e e dx ⎡⎤++⋅⎢⎥⎣⎦⎰()2923xxxe dx dx e dx=++⎰⎰⎰219232ln 91ln 3x x xx e e c ⋅⋅=++++14、解:原式=()()sin ln cos ln ln x x d x⋅⎰()()sin ln sin ln x d x =⎰=()21sin ln 2x c +⎡⎤⎣⎦15、解:原式=()2ln tan tan cosx dxx x⎰()ln tan tan tan x d xx=⎰()()ln tan ln tan x d x =⎰ ()21ln tan 2x c =+⎡⎤⎣⎦16、解:原式=221arctan11x dx x x ⎛⎫+ ⎪⎝⎭⎰21arctan111x d x x ⎛⎫=- ⎪⎝⎭⎛⎫+ ⎪⎝⎭⎰11arctan arctand x x=-⎰211arctan 2cx ⎛⎫=-+ ⎪⎝⎭17、解:原式=21sin 1sin xdx x --⎰21sin cos cos x dx dx x x=-⎰⎰2cos tan cos d xx x =+⎰1tan cos x cx=-+18、解:2,1,2t x t dx tdt==-=原式=()2221211tdt dt tt t=++⎰⎰=2arctan t c+c+回代19、解:令2tan ,sec x t dx tdt==原式=32tan sec sec ttdtt⎰=2tan sec td t⎰()2sec 1sec t d t=-⎰31sec sec 3t t c =-+()()3122221113x x c +-++回代20、解:令2sin ,2cos x t dx tdt ==原式=2cos 2sin cos t dtt t ⎰1csc 2tdt =⎰()1ln csc cot 2t t c -+公式12c 回代21、解:(倒代换)令211,x dx dt t t-==原式==-11arcsin 333t c =-=-+13arcsin 3c x-+回代13arccos 3c x=+(注:(三角代换)令3sec ,x t =,3sec tan dx t tdt =原式=3sec tan 19sec tan 3t t dt t c t t =+⎰)13arccos 3c x+回代22、解:2,1,xt e t ==+ ()222ln 1,1tx tdx dtt=+=+原式=222211211t t t dt dtt t ⋅+-=++⎰⎰=()2arctan t t c-+2c-+回代23、解：原式=()221tan2tan xex x dx++⎰2tan 2tan x d x e xdx=+⎰⎰2x e 222tan tan 22tan x x x e x x e dx e xdx =-⋅⋅+⎰⎰22tan 2tan x x e x x e dx =-⋅⎰22tan x xe dx +⎰2tan x e x c=+24、解： ()sin x F x x= ()()2cos sin x x xf x F x x -'∴==原式()3x df x =⎰()()323x f x f x x dx=-⋅⎰2222cos sin cos sin 3x x x x x x x x dx x x --=⋅-⎰2cos sin 3sin 3sin x x x x xd x xdx=--+⎰⎰2cos sin 3sin 3sin 3sin x x x x x x xdx xdx =--++⎰⎰2cos 4sin 6cos x x x x x c=--+1．设初等函数在区间有定义，则在上一定（）()f x [],a b ()f x [],a b A ．可导 B ．可微C ．可积D ．不连续2．若连续，下列各式正确的是（）f A ．()()ba d f x dx f x dx =⎰B ．()()df x dx f x dx dx =⎰C ． ()()bx d f t dt f x dx =⎰D ．()()xad f t dt f x dx =⎰3. 下列关系式中正确的是（）A ．B ．21100x x e dx e dx =⎰⎰211x x e dx e dx≥⎰⎰C ．D ．以上都不对211x x e dx e dx ≤⎰⎰4．下列各式中，正确的是（）A ．B ．2101x e dx ≤≤⎰211x e dx e≤≤⎰C ． D ．以上都不对2120x e e dx e ≤≤⎰5．下列函数在区间上可用牛顿——莱布尼兹公式的是（）[]1,1-AB ．C1x 6．设在上，[],a b ()()()0,'0,''0f x f x f x ><>记，，，则有（）()110S f x dx =⎰()()2S f b b a =⋅-()()32b aS f b f a -=+⎡⎤⎣⎦A ． B ．123S S S <<213S S S <<C ． D ．312S S S<<231S S S <<7．xx →=8．设连续，且，则 ()f x ()()xe xF x f t dt -=⎰()'F x =9．设连续，则 ()'f x 1'2x f dx ⎛⎫= ⎪⎝⎭⎰10．设则()()120121f x f x dx x=-+⎰ ()1f x dx =⎰11．设连续，且则 ()f x ()21301,(1)x f t dt x x -=+>⎰()8f =12．设，则y 的极小值为()01xy t dt =-⎰13．方程，确定，求cos 0yx t e dt tdt +=⎰⎰()y y x =0x dydx=14．设在连续，且满足，求 ()f x []0,1()()13243f x x x f x dx =-⎰()f x 15．讨论方程在区间内实根的个数4013101xx dt t --=+⎰()0,116．设在连续，且在单调减少，讨论在区间()f x [],a b (),a b ()()1xa F x f t dt x a=-⎰的单调性(),a b 17．求()22220limx t xx t e dt te dt→⎰⎰18．设其中为连续函数，求()()2xa x F x f t dt x a=-⎰f ()lim x a F x →19．设，且可导，，求()()01122xf t dt f x =-⎰()f x ()0f x ≠()f x20．若为连续的奇函数，判别的奇偶性()f x ()0xf t dt ⎰21．1321sin x x x dx-⎡⎤⎣⎦⎰22．已知，求221x t e dt -⎰()1xf x dx⎰23．1⎰24．设连续，证明()f x 并由此计算()()20sin 2sin f x dx f x dx ππ=⎰⎰0π⎰1、解：初等函数在定义区间内必连续，连续必可积。

(完整版)不定积分习题与答案

不定积分(A)求下列不定积分dx~~2X(x 2)2dxdx2) xV x2x .2dx 4) 1 x1、1) 3)5)7) 2、1) 3) 5) 7) 9) 11) 13) 15) 17)2 3X 53^△dx cos2x2 ；~2~dx6)cos xsin xX 3(2e )dxx求下列不定积分(第一换元法)(1 —y^'xYxdX8) x3(3 2x) dxsin t ..dtxtdxcosxsin xdx2) 32 3xdx,) xl n x In (I n x)xcos(x2)dxsinx , 厂dxcos xdx2x2 1sin 2xcos3xdxdxx x6) e e“、cos3xdx12)tan3x secxdx14)3x9 x2dx16)______ 13cos2 x—dx4sin x10 2arccosxdxarctan x ,dx 18) x(1 x)3、求下列不定积分（第二换元法）1) 2)sinxdx3) 4)2x----------- d x, (a 0)2 2.a x5)7) 4、1) 3) 5)7) 5、1)2)3)dx6)dx1 \2xdxx -J x28)dx1 T x2求下列不定积分（分部积分法）xSnxdxx2In xdxx2arcta nxdxIn2xdx求下列不定积分（有理函数积分）3xdxx 32x 32x 3xdxx(x21)1、一曲线通过点方程。

2、已知一个函数2)4)6)8)arcs inxdxe 2x sin -dx2x2cosxdx2 2 xx cos dx2(B)（M,3），且在任一点处的切线斜率等于该点的横坐标的倒数,F（x）的导函数为1 x2，且当x 1时函数值为2求该曲线的，试求此函数。

3、证明：若f(x)dx F(x)c，则f (ax b)dx 丄F(axa b) c,(a 0)o sin x4、设f(x)的一个原函数为求xf(x)dx。

(完整版)不定积分习题与答案

不定积分（Ａ）１、求下列不定积分１）⎰2xdx ２）⎰xxdx2３）dxx⎰-2)2(４）dxxx⎰+221 ５）⎰⋅-⋅dxxxx32532 ６）dxxxx⎰22sincos2cos７）dxxe x32(⎰+　８）dxxxx)11(2⎰-２、求下列不定积分（第一换元法）１）dxx⎰-3)23( ２）⎰-332xdx３）dttt⎰sin４）⎰)ln(lnln xxxdx５）⎰xxdxsincos ６）⎰-+xx eedx７）dxxx)cos(2⎰ ８）dxxx⎰-4313９）dxxx⎰3cossin10）dxxx⎰--249111）⎰-122xdx 12）dxx⎰3cos13)⎰xdxx3cos2sin 14)⎰xdxx sectan315)dxxx⎰+23916)dxxx⎰+22sin4cos3117)dxxx⎰-2arccos211018)dxxxx⎰+)1(arctan3、求下列不定积分（第二换元法）１）dxxx⎰+211 ２）dxx⎰sin３）dxxx⎰-42４）⎰>-)0(,222adxxax５）⎰+32)1(xdx ６）⎰+xdx21７）⎰-+21xxdx ８）⎰-+211xdx４、求下列不定积分（分部积分法）　１）inxdxxs⎰ ２）⎰xdxarcsin３）⎰xdxx ln2４）dxxe x⎰-2sin2５）⎰xdxx arctan2 ６）⎰xdxx cos2７）⎰xdx2ln ８）dxxx2cos22⎰５、求下列不定积分（有理函数积分）１）dxxx⎰+33２）⎰-++dxxxx1033223）⎰+)1(2xxdx （Ｂ）1、一曲线通过点)3,(2e，且在任一点处的切线斜率等于该点的横坐标的倒数，求该曲线的方程。

2、已知一个函数)(xF的导函数为211x-，且当1=x时函数值为π23，试求此函数。

3、证明：若⎰+=c x F dx x f )()(，则)0(,)(1)(≠++=+⎰a cb ax F a dx b ax f 。

不定积分,定积分复习题及答案

姓名: 上海第二工业大学不定积分、定积分测验试卷学号: 班级: 成绩: 、选择题：(每小格3分，共30分) 竺仝为f(x)的一个原函数，且 a = 0，贝U x sinax sin ax 3 C ； (B ) 2 C ； ( C ) a x a x e x在(」：，：：)上不定积分是F(x) C , 1、设(A ) 2、若 (A ) F(xH x_0 ；-e^+oxcO (B ) F(x)二(C ) < xe, xAO . F(x) x [-e +2,x v0 (D ) 3、设 (A ) (B ) (C ) (D ) 匸^dx 应等于( ) a 竺坐C ； ax sin ax (D) — x 则 F(x)二( ■ xe c,_xI e c 2,x ： 0 F (V 0 j —e , x < 01, x 0 f(x)二 0, x =0,F(x) f(t)dt ，则( -1,x ：：0 F(x)在x = 0点不连续; F(x)在内连续，在x = 0点不可导; F(x)在(_：：「：)内可导，且满足 F (x) = f (x)； F(x)在(-：：, =)内可导，但不一定满足 F (x)二f(x)。

4、极限啊 x tsin tdt 」 =( x 2 t 2dt(A)- 1； (D ) 2 b 5、设在区间[a,b]上 f (x) 0, f (x) :: 0, f (x) 0。

令 s 二 f (x)dx , s 2 二 ' a(B ) 0； (C ) 1 ； f(b)(b-a)& =2【f (a ) f (b)](b-a)，则((A ) 3 ：：： s 2::: S 3 ； (B ) s :::3 ：：： S 3；(C )sj::: S 1：：： S 2 ；(D) S 2：：：、填空题：(每小格3分，共30分)1、计算Md X2、计算 xta n 2 xdxX3、设 x _1，求,1 -t)dt1 + x ， x 04、设 f (x )、「x 01设f(x)的一个原函数是e-x ，则它的一个导函数是 ______________________2 1 2、设］f (x)dx =1, f (2) =2，贝V ［xf (2x)dx = _______________ 。

(完整版)不定积分习题与答案

不定积分（Ａ）１、求下列不定积分１）⎰2xdx２）⎰xxdx2３）dxx⎰-2)2(４）dxxx⎰+221５）⎰⋅-⋅dxxxx32532６）dxxxx⎰22sincos2cos７）dxxe x)32(⎰+８）dxxxx)11(2⎰-２、求下列不定积分（第一换元法）１）dxx⎰-3)23(２）⎰-332xdx３）dttt⎰sin４）⎰)ln(lnln xxxdx５）⎰xxdxsincos６）⎰-+xx eedx７）dxxx)cos(2⎰８）dxxx⎰-4313９）dxxx⎰3cossin10）dxxx⎰--249111）⎰-122xdx12）dxx⎰3cos13)⎰xdxx3cos2sin14)⎰xdxx sectan315)dxxx⎰+23916)dxxx⎰+22sin4cos3117)dxxx⎰-2arccos211018)dxxxx⎰+)1(arctan3、求下列不定积分（第二换元法）１）dxxx⎰+211２）dxx⎰sin３）dxxx⎰-42４）⎰>-)0(,222adxxax５）⎰+32)1(xdx６）⎰+xdx21７）⎰-+21xxdx８）⎰-+211xdx４、求下列不定积分（分部积分法）１）inxdxxs⎰２）⎰xdxarcsin３）⎰xdxx ln2４）dxxe x⎰-2sin2５）⎰xdxx arctan2６）⎰xdxx cos2７）⎰xdx2ln８）dxxx2cos22⎰５、求下列不定积分（有理函数积分）１）dx xx⎰+33２）⎰-++dxxxx1033223）⎰+)1(2xxdx（Ｂ）1、一曲线通过点)3,(2e，且在任一点处的切线斜率等于该点的横坐标的倒数，求该曲线的方程。

2、已知一个函数)(xF的导函数为211x-，且当1=x时函数值为π23，试求此函数。

3、证明：若⎰+=c x F dx x f )()(，则)0(,)(1)(≠++=+⎰a cb ax F a dx b ax f 。

不定积分、定积分及其几何应用(部分含答案)

不定积分、定积分及其几何应用1、⎰+.d )ln (ln 123x x x x求Cx x +--21)ln (22、.sin 1d ⎰+xx求⎰-dx x x2cos sin 1=-+tan cos .x xc 13、求⎰-dxe x114、.d csc 4⎰x x 求.cot cot 313c x x +--5、⎰.d cos 3x x 求.sin 31sin 3c x x +-6、.d )(ln 112x x x⎰-求.)arcsin(ln c x +7、求⎰+.d )1(35x x xc x x ++++323)1(123138、.d 1323x xx ⎰+⋅求9、⎰-.4d 2xx x求10、⎰-dxxx24求　11、.4d 22⎰-x xx求12、⎰xx x d 2sin cos 2求x x x d cos sin 23⎰⋅.cos 214c x +-=13、.1d 23⎰-x xx求.211arccos 2122c x x x+-+14、.d cos 23x x x ⎰⋅求().cos sin 21222c x x x ++15、 .d 2432x xx x ⎰-求　c x x +-12174517245416、⎰'=t t f t f t t t f d )()(,cos )(ln 求设ct t t +-⋅sin cos17、．求⎰+202sin 8sin πdx xx2ln 6118、．求⎰+1012dx ex )13(3-e 19、．求⎰-+121x x dx4π20、．⎰+401dx xx3ln 221、 ⎰-1224．求dx x x 233-π22、．求⎰-eex x x dx)ln 1(ln 23、求⎰π02sin xdxx 24、．求⎰π02cos xdx x 25、求⎰-+21 2121sin 1－dxxx26、⎰+2232)sin (cos ππ－dxx x 27、如果.,612ln 2x e dtxt求π=-⎰28、求．⎰403cos sin πdx xxx 214-π29、．求⎰-3232)4(x dx)12(33-29、．，计算：dx e x⎰∞+-0)21min(⎰⎰+∞-+2ln 2ln 021dx e dx x =+1221(ln )30、．　求，，设⎰--⎪⎩⎪⎨⎧≤<-≤=1 32)(1010)(dx x f x x x xe x f x 1243--e π31、．求⎰∞++122)1(x x dx41π-32、．求dx x x x ⎰∞+++1222)1(21⎰∞+++122)111(dxx x =+14π33、设，求⎪⎩⎪⎨⎧<+≥+=-01011)(x e e x xx f xx⎰∞--2)1( dx x f 34、设，求⎪⎩⎪⎨⎧<≥+=011)(22x e x x x f x ⎰∞-1)(dx x f 35、()⎰∞+-+311x x dx求42π36、设为连续函数，满足，求)(x f C 98)()(1816120+++=⎰⎰x x dt t f t dt t f x x)(x f 37、设有连续的二阶导数，且，求)(x f a b f b a f ='=')()(，⎰'''ba dxx f x f )()(38、．　计算设⎰⎰==-11 )()(22dt t tf I dx e t f t x 39、⎰⎰++++1021021)]1ln(1[大小与不计算积分，试比较dx x dx x x x 40、⎰⎰+-10102)1ln()2(大小与不计算积分，试比较dx x dx x x 41、若间有什么关系？与问的原函数为xe xf x e x f xx )(,)(⎰'dxx f x )(并求42、若间有什么关系？与问的原函数为xxx f x x x f sin )(,sin )(⎰'dx x f x )(并求、．为自然数，、求)()1(4310n dx xx n⎰-,sin 2t x =令　原式=+⎰22102cos n tdtπ=+2221()!!()!!n n 44、nn nx n a n n dx e x f a x x x x x f 220lim )2()21()()1(21210)(∞→-==⎩⎨⎧≤≤-≤≤=⎰ ，，求：，，设函数()()()1202112　a f x edx xedx x e dx n nxnxnx ==+----⎰⎰⎰=-+--11222ne e n n ()=1()lim lim()21222　n n n n n n a e e →∞→∞--=-+45、设，为偶函数，且[]上连续　，在，)0()()(>-a a a x x f ϕ)(x ϕ（常数），证明：k x f x f =-+)()(⎰⎰=-aaadxx k dx x x f 0)()()(ϕϕ⎰⎰+=-aa dx x x f dx x x f 00)()()()(ϕϕ左边⎰⎰+-=aadxx x f dx x x f 0)()()()(ϕϕ=⎰c x dxaϕ()046、)()0()()()()(1x F x dt t f xx F x f x ''≠=∞+-∞⎰，求　可导，且，在设113xf x '()47、设，求dt ttx f x ⎰=21sin )(⎰10)(dx x xf 原式=)11(cos 21)(21102-=⎰dx x f 48、为偶函数．证明：函数⎰++=xdt t t x F 02)1ln()()()1ln()()(02u t dt t t x F x x-=++=-∞+-∞∈∀⎰- ， =-+-⎰ln()12u u du x=++⎰ln()u u dux120 =F x ()∴　为偶函数F x ()49、为偶函数．证明：设)( , )cos 21ln()(02x F dt x t x x F ⎰+-=πF x x t x dt()ln(cos )-=++⎰1220πt u x u x du =--+-⎰ππln(cos )()1220=-+⎰ln(cos )1220x u x du π=F x ()221d d 0d )(502=+-⎰=-=t tx u txu et t x x 所确定的，求是由方程、若22e具有连续导数．，求及，、已知)(,)2(1)(0)2(21)2(5110220x f dx x f x dx x f f f ⎰⎰''=='=（0）52、试求抛物线和抛物线相切于纵坐标y=3处的切线及x 轴所围成的平面1)2(2-=-x y 图形面积。

不定积分-定积分复习题及答案

（A ） F ( x ) = ⎨ ；（B ） F ( x ) = ⎨ ⎩ -e - x + c , x < 0 ⎩ -e - x + c + 2, x < 03、设 f ( x ) = ⎨0, x = 0 , F ( x ) = ⎰ f (t )dt ，则（）⎪ -1, x < 0 ⎰ t sin tdt⎰ t2dt2上海第二工业大学不定积分、定积分测验试卷姓名：学号：班级：成绩：一、选择题：（每小格 3 分，共 30 分）1、设 sin x f (ax ) 为 f ( x ) 的一个原函数，且 a ≠ 0 ，则 ⎰x adx 应等于（）（A ） sin ax sin ax sin ax sin ax+ C ；（B ） + C ；（C ） + C ；（D ） + Ca 3 x a 2 x ax x2、若 e x 在 (-∞, +∞) 上不定积分是 F ( x ) + C ，则 F ( x ) = （）⎧e x + c , x ≥ 0 ⎧e x + c , x ≥ 01 2⎧e x , x ≥ 0 ⎧e x , x ≥ 0（C ） F ( x ) = ⎨ ；（D ） F ( x ) = ⎨⎩ -e - x + 2, x < 0 ⎩ -e - x , x < 0⎧1, x > 0 ⎪ x；⎩（A ） F ( x ) 在 x = 0 点不连续；（B ） F ( x ) 在 (-∞, +∞) 内连续，在 x = 0 点不可导；（C ） F ( x ) 在 (-∞, +∞) 内可导，且满足 F '( x ) = f ( x ) ；（D ） F ( x ) 在 (-∞, +∞) 内可导，但不一定满足 F '( x ) = f ( x ) 。

4、极限 lim x →0x 0x＝（）（A ）－1；（B ）0；（C ）1；（D ）25、设在区间[a , b ] 上 f ( x ) > 0, f '( x ) < 0, f ''( x ) > 0 。

2023-2024经济数学(2)复习题答案详解

增．
填空题
1．
1
1 4x
2
dx
（
） d arctan2x ．
解：d arctan2x 2 dx ，所以， 1 dx 1 d arctan2x ．
1 4x2
1 4x2
2
2．
x
f
ln x f ln x
dx
解：
x
f
ln x f ln x
dx
f
ln x f ln x
d
ln
x
．
f
1
ln
x
df
(ln
x)
2
解：f xy，x y x2 y 2 xy (x y)2 xy ．令 xy s ，x y t ，则 f s，t t 2 s ，
故， f x，y y 2 x ．
填空题
15．若 z 2x2 3xy y2 ，则 2 z
．
xy
解： z 4x 3y ， 2 z 3．
x
xf
xdx
5
0
xdf
x
xf
5 (x)
0
5
0
f
xdx
5
f
(5)
3
7
．
填空题
5．
1
x
1 x2
2dx
1
．
偶倍奇零
1
解： x
1 x2 2dx
1 x2 2x 1 x2 1 x2 dx
1
2x
1 x2
1 dx
1
1
1
1
1dx 2 ． 1
6．
x2
1 dx 2x 2
xd
ln
x
ln

定积分复习

0(xsinx)2 dx；
e
（10）ò -
1022)(1xmdx ；（11）ò
p
lnx dx ；（12）ò 20x cos xdx .
1
e
1
11.已知.. f(0) = 1, f (2) = 3, f ￠(2) = 5 ，试计算ò0
xf ￠
￠￠(2x)dx .
35 6
b
1
15
1
(5) -ln |1+ 3 cos x | +C; (6) -(3 -2x) + C; (7) -3 -2x + C; (8) -ln |1 -10 x | +C;
3 cosxx +
(9) -ln |1 -3e | +C; (10) ln | x -5x + 7| +C; (11) -e + C; (12) 2eC;
211
(arcsin x2)
dx ；（2）ò-
332423sinxx dx .
21-xx + 2x +1
7.计算下列定积分:
（1）ò
p
xdx；（2）ò xdx；（3）òp
2 12 sin
1
dx ；（4）ò
p
-322cos1pxdx；
203cossinx1022(x +1)1 xx
12.设.. f(x) 在区间[a, b] 上具有二阶连续导数，且.. f(a) = f (b) = 0 ，证明：..
1
f ￠￠(x)(x -a)(x -b)dx
ò 2 ò=
babaxdxf()

微积分(I)复习(不定积分与定积分)

7） b f ( x)dx
b
f ( x)dx
a
a
8）估值定理
若m f ( x) M ,则
b
m(b a) a f ( x)dx M (b a)
9）中值定理
若f ( x) C[a, b], 则存在 [a, b],
使得
b
f ( x)dx
f ( )( b a).
a
10）广义中值定理
若f ( x) C[a, b], g( x) R[a, b]且在[a, b]
上不变号, 则存在 [a, b], 使得
b
b
a f ( x)g( x)dx f ( )a g( x)dx .
(四)变上限定积分
x2 a2 dx.
x
解令 x asec t, 则
原式

a tant asec t

asin t cos2 t
dt

a
sin 2 t cos2 t
dt

a
tan 2
tdt
a (sec 2 t 1)dt a sec2 tdt dt
a d tant dt a tant at C
限值为f ( x)在[a, b]上的定积分，记作
b
n
a
f ( x)dx

lim
0 k1
f (k )xk
此时称f ( x)在[a, b]上可积.
2.定积分的几何意义
b f ( x)dx表示f ( x)与x轴及直线x a, a
x b之间所围面积的代数和.

(整理)§4不定积分习题与答案.

3、 (1) ln csct cot t c
（ 2） 2( x cos x sin x ) c
x2 4
2
（ 3） 2(tan
arccos ) c
2
x
a2
x
(4) (arcsin
2
a
x a2
a2
x2)
c
x
(5)
c
1 x2
(6) 2x ln(1 2x) c
精品文档
精品文档
1 (7) (arcsin x ln x
(3) ln x 1 ln( x 2 1) c 2
(4) ln x
1 ln x 1
1 ln( x2
1)
1 arctanx
c
2
4
2
1 x2 1
3
2x 1
(5) 2 ln x2 x 1
arctan 3
3
c
1、设曲线 y
(B)
f ( x) ，由导数的几何意义： y
11 ， dx
ln x
c ，点 (e2 ,3) 代入即可。
１） (3 2x) 3dx
dx
２）
3 2 3x
３） sin t dt t
精品文档
dx
４）
x ln xln(ln x)
精品文档
５）
dx
cos x sin x
７） x cos(x2 ) dx
dx
６）
ex e x ８） 3 x3 dx
1 x4
９）
sin x
3
dx
cos x
10）
1 x dx
9 4x2
dx
x2 )
c
3

不定积分与定积分典型例题

不定积分与定积分典型例题(二)典型例题1.填空题(1)若/(X)的一个原函数为lnx2,则/(x)= ____________ .答案：-X(2)__________________________________ 若j* f(x)dx = sin 2x + c ,则f (x) ______________________ .答案：2cos2x(3)若Jcosxdx= _______________答案：sinx + c(4)J de .答案：e』+c(5)J(sinx)dx = ________________ ・答案：sinx + c(6)若j* f(x)dx = F(x) 4- c ,则J /(2A - 3)ck = 答案：丄F(2x — 3) + c2(7)若j* f\x)dx = F(x) + c» 则j*xf(\ -x~)ck = 答案：一丄F(l_/)+ c2(8)j^sin xcos2x-x2+ x)dx = __________ ・答案：-？3(9)£||ln(A2 + l)dx = ____________________ .答案：o(10)J°e2v d¥= _______ .答案：-22.单项选择题(1)下列等式成立的是()・A. dj/(x)cLv = f(x)答案：D （3）（）答案：A （4）下列定积分中积分值为0的是（）・ -XC ・ f (x 3 +cosx)d¥D ・ f (x 2 +sinx)(iv J-ffJ-JT答案:A (5)设/(x)是连续的奇函数，则泄积分£/(x)ch =() A. 0 B./(x)cLv C. £ /(A )dv D. 2j° f(x)dx答案：A （6）下列无穷积分收敛的是（）・C.厂丄drD. JJ X e _2v d.v答案：D 3.计算题(1)J(2x-l),o dx-解：j(2x-l),u ck = |j(2x-l)10d(2¥-1) = J-(2x-l)u +cA .| ^inxdv B ・ C. —J f(x)dx = f(x)答案：c (2) 以下等式成立的是( A. In xdx = d(—) x C.dx 77D. Jd/W = /W)B ・ sin xdx = d(cosx)D. 3v dx = — In 3 A. /(x)-/(x) + cC. —x 2f'(x) + cB ・ xf\x) + c D ・(x + l)/3 + cLsin 丄(2) J —1 sm-] j ] 解：\— ¥ = - fsin —d — =cos_ + c J x" J xx x⑶ j'n_e v (4 + e r )2dA-解：「y hzdv =丄「(1 + 5In 小/(1 + 5Inx)=丄(1 + 5Inx)2 =-1(36-1) = - Ji r s Ji in in ?解：f xe'di =xe A 一 f e v dx-=4 •证明题⑴证明等式 = £[/(-X )+ /(X )]dA- •证明 J a /3dY = J 丿⑴山 + £ /(x)dv令 x = -t i 则 dY = -df,且当 x = -a 时，t =a > x = 0 时，t = 0 于是 f° /(T)d(“) = -f°/(-r)dr=f fl /(-r)dz= f7(-x)d.r J-n JO JO所以= J ： /(-x)dY + £ fMdx = £[/(-A -) + /(x)]dx(2)设厂(x)在S0]上连续，证明:\h xf'\X }dx = [bf\b) - f(b)]-[af\a) - /⑷]证明利用分部积分法，[灯0皿=[炖• 3 =时©) ][ — f f f (x)dx=bf(b) - af(a) - /(x)|：-W f (b) - f(b)] - - f(a)] e v (4 + e v )~dx = £ (4 + e l )2d(4 + e v )= (4 + e v )= 1(216-64) = 1^。

不定积分和定积分习题

f ( x) f ( x)dx f x df x 1 2 f x C 2
1 cos x sin 2 x C 2 2 1 x sin x
2
不定积分 dx 2 x x 1
u x 1
1 3 ln x 1dx 3
2 x ln x 1 dx

不定积分

e cos 2 x 2 e sin 2 xdx
x x
e
x
cos 2 xdx cos 2 xde
x
e x cos 2 x 2 sin 2 xde x
2 d x x 1 1 3 dx 2 2 2 x x 1 2 x x 1 3 1 dx 2 ln x x 1 2 2 2 2 3 1 x 2 2
......

不定积分

e
3 x
x 3 ue
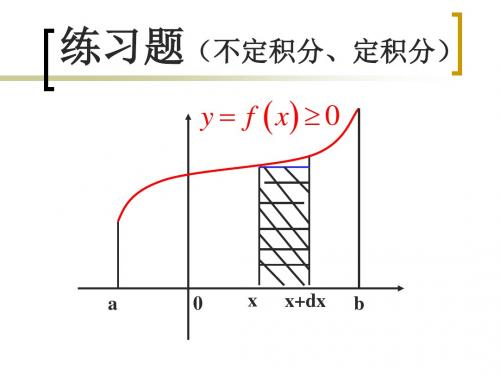
练习题（不定积分、定积分）
y f x 0
a
0
x
x+dx
b
不定积分

sin x 已知 f ( x) 的一个原函数为，求 f ( x) f ( x)dx 1 x sin x 2 sin x cos x sin x 解： f x 2 1 x sin x 1 x sin x
x
sin x cos x 1 d sin x 1 sin 4 x dx 2 1 sin 2 x 2 1 2 arctan sin x C 2 x 2 dx dx 2 x 2 x 2 x 2 1

积分测试题及答案

积分测试题及答案一、单选题（每题2分，共10分）1. 以下哪个函数的不定积分是 \(\ln|x|\)？A. \(1/x\)B. \(x^2\)C. \(e^x\)D. \(\sin(x)\)答案：A2. 计算定积分 \(\int_{0}^{1} x^2 dx\) 的结果是多少？A. \(1/3\)B. \(1/2\)C. \(2/3\)D. \(1\)答案：A3. 函数 \(e^{-x}\) 的不定积分是什么？A. \(-e^{-x} + C\)B. \(e^{-x} + C\)C. \(-e^x + C\)D. \(e^x + C\)答案：A4. 以下哪个函数是奇函数？A. \(f(x) = x^2\)B. \(f(x) = x^3\)C. \(f(x) = \sin(x)\)D. \(f(x) = \cos(x)\)答案：B5. 计算定积分 \(\int_{-1}^{1} \sin(x) dx\) 的结果是多少？A. \(0\)B. \(2\)C. \(-2\)D. \(\pi\)答案：A二、填空题（每题3分，共15分）1. 函数 \(\cos(x)\) 的不定积分是 ________。

答案：\(\sin(x) + C\)2. 定积分 \(\int_{0}^{\pi/2} \cos(x) dx\) 的结果是 ________。

答案：\(1\)3. 函数 \(f(x) = 2x\) 的原函数是 ________。

答案：\(x^2 + C\)4. 函数 \(\ln(x)\) 的不定积分是 ________。

答案：\(x\ln(x) - x + C\)5. 定积分 \(\int_{1}^{e} \frac{1}{x} dx\) 的结果是 ________。

答案：\(1\)三、计算题（每题10分，共20分）1. 计算不定积分 \(\int (3x^2 - 2x + 1) dx\)。

答案：\(x^3 - x^2 + x + C\)2. 计算定积分 \(\int_{0}^{2} (x^2 - 4x + 5) dx\)。

(整理)不定积分习题与答案.

不定积分（Ａ）１、求下列不定积分１）⎰2xdx２）⎰xxdx2３）dxx⎰-2)2(４）dxxx⎰+221５）⎰⋅-⋅dxxxx32532６）dxxxx⎰22sincos2cos７）dxxe x)32(⎰+８）dxxxx)11(2⎰-２、求下列不定积分（第一换元法）１）dxx⎰-3)23(２）⎰-332xdx３）dttt⎰sin４）⎰)ln(lnln xxxdx５）⎰xxdxsincos６）⎰-+xx eedx７）dxxx)cos(2⎰８）dxxx⎰-4313９）dxxx⎰3cossin10）dxxx⎰--249111）⎰-122xdx12）dxx⎰3cos13)⎰xdxx3cos2sin14)⎰xdxx sectan315)dxxx⎰+23916)dxxx⎰+22sin4cos3117)dxxx⎰-2arccos211018)dxxxx⎰+)1(arctan3、求下列不定积分（第二换元法）１）dxxx⎰+211２）dxx⎰sin３）dxxx⎰-42４）⎰>-)0(,222adxxax６）⎰+xdx2 1７）⎰-+21xxdx８）⎰-+211xdx４、求下列不定积分（分部积分法）１）inxdxxs⎰２）⎰xdxarcsin３）⎰xdxx ln2４）dxxe x⎰-2sin2５）⎰xdxx arctan2６）⎰xdxx cos2７）⎰xdx2ln８）dxxx2cos22⎰５、求下列不定积分（有理函数积分）１）dx xx⎰+33２）⎰-++dxxxx1033223）⎰+)1(2xxdx（Ｂ）1、一曲线通过点)3,(2e，且在任一点处的切线斜率等于该点的横坐标的倒数，求该曲线的方程。

2、已知一个函数)(xF的导函数为211x-，且当1=x时函数值为π23，试求此函数。

3、证明：若⎰+=c x F dx x f )()(，则)0(,)(1)(≠++=+⎰a cb ax F a dx b ax f 。

不定积分练习题及答案(可打印修改)

2
2
2
2
22) ln 1 e2x ex c 23) x cot x ln sin x x ln csc x cot x c sin x
24) 1 (x 1)96 3 (x 1)97 3 (x 1)98 1 (x 1)99 c 25)e2x tan x c
96
97
98
9
26) arctan x 1 (arctan x)2 1 ln x2 c
1 arcsin
x c
2
(B) arcsin x c
(D) arcsin(2x 1) c
(C) 2arcsin(2x 1) c
16、若f在(x上) 的[某a,b原] 函数为零，则在上必有__[a_,_b]
( A) f (x)的原函数恒等于零；的(B不) f定(x积) 分恒等于零；
(C) f (x)恒等于零；不(D恒) f等(x于) 零, 但导函数恒为零。f '(x)
f
1 (x)
dx
__________;
9、、 f '(ln x) 1 x, f (x) ________;
10、、、、、、、f、、(、x) (a,b)
(a,b) f (x) ______;
( A)、、、、、、、、、、、、、、、、、 (B)
(C)
(D)
11、、、 xf (x)dx x sin x sin xdx, f (x) ______;
arctan x
(26)
dx
x2 (1 x2 )
arctan ex
(27)
dx
e2x
(28)设f求(s：in2 x) x , sin x
x f (x)dx 1 x
(29)已知f的(x一) 个原函数为求：ln2 x, xf '(x)dx

不定积分与定积分复习与典型复习题解答

不定积分与定积分复习与典型复习题解答(一)内容1.原函数与不定积分：原函数的概念；不定积分的定义、性质，积分基本公式；求不定积分的直接积分法、第一换元积分法和分部积分法。

2.定积分：定积分的定义(用牛顿−莱布尼兹公式作定义)、性质和计算。

3.广义积分（简单的无穷限积分） (二)要求1.理解原函数与不定积分的概念、性质，掌握积分基本公式，掌握用直接积分法、第一换元积分法和分部积分法求不定积分的方法。

2.了解定积分的概念、性质，会计算一些简单的定积分。

（三）典型例题1．填空题（1）若)(x f 的一个原函数为2ln x ，则=)(x f 。

解：因为c x dx x f +=⎰2ln )( 所以=)(x f x xx 222= （2）若⎰+=c x x x f 2sin d )(，则=)(x f ．解：=)(x f x 2cos 2（3）若c x x x x f +=⎰ln d )(，则=')(x f ．解：=)(x f 1ln +x ，=')(x f x1（4）=⎰-x x d e d 2．解：=⎰-x x d e d 2dx e x 2-（5）='⎰x x d )(sin ．解：='⎰x x d )(sin c x +sin（6）若⎰+=c x F x x f )(d )(，则⎰=-x x f d )32( ．解：⎰=-x x f d )32(c x F x d x f +-=--⎰)32(21)32()32(21 （7）若⎰+=c x F x x f )(d )(，则⎰=-x x xf d )1(2 ．解：⎰=-x x xf d )1(2c x F x d x f +--=---⎰)1(21)1()1(21222 （8） .______d )2cos (sin 112=-⎰-x x x x 解：322d )2cos (sin 12112112-=-=-=-⎰⎰⎰--dx x dx x x x x x （9）=+⎰e 12d )1ln(d d x x x . 解：=+⎰e12d )1ln(d d x x x（10）x x d e 02⎰∞-= ．解：x x d e 02⎰∞-21)1(lim 21lim 21lim 20202=-===-∞→-∞→-∞→⎰a a ax a ax a e e dx e 2．单项选择题（1）下列等式成立的是（）． A ．)(d )(d dx f x x f x=⎰ B ．)(d )(x f x x f ='⎰ C ．)(d )(d x f x x f =⎰ D ．)()(d x f x f =⎰ 解：应选A（2）若c x x x f x +=⎰22e d )(，则=)(x f （）. A. )1(e 22x x x + B. x x 22e 2 C. x x 2e 2 D. x x 2e解：因为c x x x f x +=⎰22e d )(，两边同时对x 求导得： =+=x x e x xe x f 22222)()1(e 22x x x + 应选A（3）以下计算正确的是（）A ．3ln 3d d 3xxx = B ．)1(d 1d 22x x x +=+ C ．x xxd d = D ．)1d(d ln x x x =解：应选A（4）=''⎰x x f x d )(（）A. c x f x f x +-')()(B. c x f x +')(C. c x f x +')(212 D. c x f x +'+)()1(解：=''⎰x x f x d )(⎰⎰+-'='-'='c x f x f x dx x f x f x x f xd )()()()()( 应选A（5）⎰-x a x d d 2=（）．A ．x a 2-B ．x a a x d ln 22--C ．x a x d 2-D ．c x a x +-d 2 答：应选C（6）如果等式⎰+-=--C x x f xx11e d e )(，则=)(x f （） A.x 1- B. 21x -C. x 1D. 21x解：由⎰+-=--C x x f x x11e d e )(两边对x 求导，得：)]1([)(211xe ex f xx---=--，=)(x f 21x - 应选B（7）若⎰+10d )2(x k x = 2，则k =（）．A ．1B ．-1C ．0D ．21解：因为⎰+10d )2(x k x 21)(102=+=+=k kx x 所以1=k 应选A（8）下列定积分中积分值为0的是（）．A ．x xx d 2e e 11⎰--- B ．x xx d 2e e 11⎰--+ C ．x x x d )cos (3⎰-+ππ D ．x x x d )sin (2⎰-+ππ解：令2)(xx e e x f --=则)(2)(x f e e x f xx -=-=-- 所以函数2)(xx e e x f --=是奇函数因此x xx d 2e e 11⎰---=0 应选A （9）设)(x f 是连续的奇函数，则定积分=⎰aa x x f -d )(（）A ．⎰0-d )(2a x x fB ．⎰0-d )(a x x fC ．⎰ax x f 0d )( D ． 0 答：应选D（10）下列无穷积分收敛的是（）．A ．⎰∞+0d in x x sB ．⎰∞+-02d e x xC ．⎰∞+1d 1x x D ．⎰∞+1d 1x x答：应选B 3．计算题（1）⎰+-x xxx x d sin 33解：⎰+-x xxx x d sin 33⎰⎰⎰+-=xdx dx x dx x sin 13c x x x +--=c o s32ln 323（2）x x d )12(10⎰- 解：x x d )12(10⎰-c x x d x +-+⋅=--=+⎰11010)12(110121)12()12(21 c x +-=11)12(221（3）x x x d 1sin2⎰解：x xx d 1sin2⎰c x x d x +=-=⎰1cos )1(1sin(4)x x x d )e 1(e 22ln 0+⎰ 解：x x x d )e 1(e 22ln 0+⎰319389)1(31)1()1(2ln 0322ln 0=-=+=++=⎰x x x e e d e (5)x x xd ln 51e1⎰+ 解：x x x d ln 51e 1⎰+⎰⎰++=+=ee x d x x d x 11)ln 51()ln 51(51ln )ln 51( 21)16(101)ln 51(215112=-=+⋅=ex(6)x x x d e 10⎰ 解：x xe xd 10⎰1)1(1011010=--=-=-==⎰⎰e e ee dx e xexde x xx x(7)⎰π20d sin x x x解：⎰20d sin πx x x )cos cos (cos 202020⎰⎰--=-=πππxdx x x x xd101sin 20=-==πx4.证明题(1)证明等式⎰⎰+-=-aaa x x f x f x x f 0)]()([)(d d 证明：⎰⎰⎰+=--aa aa dx x f dx x f dx x f 00)()()(考虑积分⎰-0)(a dx x f ，令t x -=，则dt dx -=，从而⎰⎰⎰⎰⎰-=-=--=--=-aaaaadx x f dt t f dt t f dt t f dx x f 0)()()(])[()(所以⎰⎰⎰+=--aaaadx x f dx x f dx x f 00)()()(⎰⎰⎰+-=+-=aa adx x f x f dx x f dx x f 0)]()([)()((2)设)(x f ''在],[b a 上连续，证明：)]()([)]()([)(a f a f a b f b f b dx x f x ba -'--'=''⎰ 证明：⎰⎰⎰'-'='=''ba ba ba b a dx x f x f x x f xd dx x f x )()()()()]()([)()()()()(a f b f a f a b f b x f a f a b f b ba '-'-'-'=-'-'=)]()([)]()([a f a f a b f b f b -'--'=。