最全拉氏变换计算公式

合集下载

最全拉氏变换计算公式

1最全拉氏变换计算公式1. 拉氏变换的基本性质 1线性定理齐次性)()]([s aF t af L =叠加性)()()]()([2121s F s F t f t f L ±=±2微分定理一般形式=-=][ '- -=-=----=-∑11)1()1(1222)()()0()()(0)0()(])([)0()(])([k k k k nk k n n nn dt t f d t f f s s F s dt t f d L f sf s F s dt t f d L f s sF dt t df L ）（初始条件为0时)(])([s F s dtt f d L n nn = 3积分定理一般形式∑⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰==+-===+=++=+=nk t n n k n n nn t t t dt t f s s s F dt t f L sdt t f s dt t f s s F dt t f L sdt t f s s F dt t f L 101022022]))(([1)(])()([]))(([])([)(]))(([])([)(])([个共个共初始条件为0时n n n ss F dt t f L )(]))(([=⎰⎰个共4 延迟定理（或称t 域平移定理）)()](1)([s F e T t T t f L Ts -=--5 衰减定理（或称s 域平移定理） )(])([a s F e t f L at +=-6 终值定理 )(lim )(lim 0s sF t f s t →∞→=7 初值定理 )(lim )(lim 0s sF t f s t ∞→→=8 卷积定理)()(])()([])()([21021021s F s F d t f t f L d f t f L tt =-=-⎰⎰τττττ22．常用函数的拉氏变换和z 变换表序号拉氏变换E(s)时间函数e(t) Z 变换E(z)1 1δ(t) 12 Tse --11∑∞=-=0)()(n T nT t t δδ1-z z 3 s1 )(1t1-z z 4 21s t2)1(-z Tz5 31s 22t32)1(2)1(-+z z z T6 11+n s!n t n)(!)1(lim 0aT n n n a ez z a n -→-∂∂- 7 as +1 at e - aTe z z-- 8 2)(1a s +atte- 2)(aT aT e z Tze ---9 )(a s s a+ ate--1))(1()1(aT aT e z z z e ----- 10 ))((b s a s ab ++-bt at e e --- bTaT e z ze z z ----- 11 22ωω+s t ωsin1cos 2sin 2+-T z z Tz ωω 12 22ω+s st ωcos1cos 2)cos (2+--T z z T z z ωω13 22)(ωω++a s t e atωsin - aTaT aT eT ze z Tze 22cos 2sin ---+-ωω 14 22)(ω+++a s a st eatωcos -aTaT aT e T ze z T ze z 222cos 2cos ---+--ωω15aT s ln )/1(1- T t a /az z -33．用查表法进行拉氏反变换用查表法进行拉氏反变换的关键在于将变换式进行部分分式展开，然后逐项查表进行反变换。

拉氏变换公式

拉普拉斯变换的数学方法微分定理
机械工程控制基础
第二章拉普拉斯变换的数学方法多重微分
（2－21）
原函数的高阶导数像函数中s的高次代数式
机械工程控制基础第二章拉普拉斯变换的数学方法
例2-5：利用导数性质求以下函数的象函数：
（1）f(t)=cos(ωt) （2）f(t)=δ(t)
eas f ( )es d 0
eas F (s)
（2－24）
原函数平移像函数乘以 e-s
机械工程控制基础第二章拉普拉斯变换的数学方法
例2-8：求f(t)的象函数
f(t)
A
T O
f ’(t)
解：
t
f(t)= f ’(t)+ f ’’(t) =Aε(t) -Aε(t-T)
例2-6：利用积分性质求函数f(t)=t的象函数
解：f(t)=t
t
( )d
0
L[f(t)]= 1 1 ss

1 s2
机械工程控制基础第二章拉普拉斯变换的数学方法衰减定理（复位移定理）
（2－23）
原函数乘以指数函数e-at像函数F(S)在复数域中作位移a
机械工程控制基础第二章拉普拉斯变换的数学方法例2-7：求 et sint 的拉氏变换解：直接用复位移定理得：
由于 δ(t)=dε(t)/dt
L[ (t)] L[d (t) / dt]
=s 1 - 0 s
=1
机械工程控制基础
第二章拉普拉斯变换的数学方法积分定理
机械工程控制基础
第二章拉普拉斯变换的数学方法多重积分
（2－22）
原函数的n重积分像函数中除以sn
机械工程控制基础第二章拉普拉斯变换的数学方法

拉氏变换

A01 r 1 A02 r 2 p0 t f (t ) [ t t A0 r ]e (r 1)! (r 2)! Ar 1e pr1t An e pnt t0
13
例：解：
s3 求反变换。 ( s 2) 2 ( s 1) A01 A02 A3 F ( s) 2 s 2 s 1 ( s 2) s3 A01 [ ( s 2) 2 ] s 2 1 ( s 2) 2 ( s 1) F (s)
定义：
1 c j f (t ) F ( s)e st ds 2j c j
根据上式求反变换显然很复杂，一般采用下面的方法求反变换。设F(s)为：
b0 s m b1s m1 bm1s bm F ( s) a0 s n a1s n1 an1s an
F (s)
f (t ) te2t 2e2t 2et (t 2)e2t 2et
t 0
14
习题一、求拉氏变换
(1) f (t ) 0.5(1 cos3t ) (3) f (t ) e at sin t (2) f (t ) 1 e t e 4t (4) f (t ) te 2t
1
1
例：已知解：
F ( s)
F (s)
s 1 s ( s 2 s 1)
求 f(t)
A A s A2 s 1 0 21 s( s 2 s 1) s s s 1
s0 0 s1, 2 1 j 3 0.5 j 0.866 2 2
三个极点：
( n1) (0) 0 特别，当初值 f (0) f (0) f (0) f

拉氏变换常用公式

拉氏变换常用公式拉普拉斯变换是一种重要的数学工具，用于求解线性常系数常微分方程和线性差分方程。

在控制工程、信号与系统、电路分析等领域中，拉普拉斯变换被广泛应用。

下面是拉普拉斯变换中一些常用的公式：1.输入信号：f(t)的拉普拉斯变换：F(s) = L[f(t)] = ∫[0,∞] (e^(-st))(f(t)) dt2.单位阶跃函数u(t)的拉普拉斯变换：U(s)=L[u(t)]=1/s3.延时函数f(t-T)的拉普拉斯变换：L[f(t-T)]=e^(-Ts)F(s)4.积分操作的拉普拉斯变换：L[∫[0,t]f(τ)dτ]=1/sF(s)5.导数操作的拉普拉斯变换：L[dⁿf(t) / dtⁿ] = sⁿF(s) - sⁿ⁻¹f(0) - sⁿ⁻²f'(0) - ... - f⁽ⁿ⁻¹⁾(0)6.二阶导数操作的拉普拉斯变换：L[d²f(t) / dt²] = s²F(s) - sf(0) - f'(0)7.卷积操作的拉普拉斯变换：L[f(t)*g(t)]=F(s)G(s)8.乘法操作的拉普拉斯变换：L[f(t)g(t)]=F(s)*G(s)9.常用单位阶跃函数和冲激函数的拉普拉斯变换：(1)f(t)=u(t)的拉普拉斯变换：F(s)=L[u(t)]=1/s(2)f(t)=t^nu(t)的拉普拉斯变换：F(s)=L[t^nu(t)]=n!/s^(n+1)(3) f(t) = e^(at) u(t)的拉普拉斯变换：F(s) = L[e^(at) u(t)] = 1 / (s - a)(4) f(t) = sin(ωt) u(t)的拉普拉斯变换：F(s) = L[sin(ωt) u(t)] = ω / (s² + ω²) (5) f(t) = cos(ωt) u(t)的拉普拉斯变换：F(s) = L[cos(ωt) u(t)] = s / (s² + ω²) (6)f(t)=δ(t)的拉普拉斯变换：F(s)=L[δ(t)]=1(7) f(t) = e^(at) δ(t)的拉普拉斯变换：F(s) = L[e^(at) δ(t)] = 1 / (s - a)(8) f(t) = sin(ωt) δ(t)的拉普拉斯变换：F(s) = L[sin(ωt) δ(t)] = ω / (s² + ω²)(9) f(t) = cos(ωt) δ(t)的拉普拉斯变换：F(s) = L[cos(ωt) δ(t)] = s / (s² + ω²)拉普拉斯变换的公式非常有用，可以将时域问题转化为复频域问题，从而更容易进行分析和求解。

拉氏变换常用公式

拉氏变换常用公式拉氏变换是一种重要的数学工具，常被用于信号处理、系统分析、电路设计等领域。

在进行拉氏变换时，我们常用到一些常用的公式，这些公式是解决问题的关键。

本文将介绍一些常用的拉氏变换公式，以及其在实际应用中的意义和用法。

1. 基本定义拉氏变换是一种将时域函数转换为复频域函数的方法。

它定义如下：F(s) = L{f(t)} = ∫[0,∞)e^(-st) f(t) dt其中，F(s)表示拉氏变换结果，L表示拉氏变换算子，f(t)表示时域函数，s表示复频域变量。

2. 常见公式以下是一些常用的拉氏变换公式：2.1 常数函数L{1} = 1/s2.2 单位阶跃函数L{u(t)} = 1/s2.3 指数函数L{e^(at)} = 1/(s-a)，其中a为常数2.4 正弦函数L{sin(at)} = a/(s^2 + a^2)2.5 余弦函数L{cos(at)} = s/(s^2 + a^2)2.6 钟形函数L{rect(t)} = 1/sinc(s/2)，其中sinc(x) = sin(x)/x2.7 基本运算拉氏变换具有一些基本运算规则，如时移、倍乘和微分等。

这些运算可以用于求解更复杂的函数对应的拉氏变换。

详细的运算规则可以参考相应的数学教材。

3. 实际应用拉氏变换在信号处理、系统分析和电路设计等领域有着广泛的实际应用。

3.1 信号处理在信号处理中，常常需要对信号进行滤波、频域分析等操作。

通过将信号进行拉氏变换，可以将复杂的时域信号转换为频域函数，便于对信号特性的分析和处理。

3.2 系统分析拉氏变换在系统分析中有着重要的作用。

通过将系统的输入和输出进行拉氏变换，可以得到系统的传递函数，进而分析系统的频率响应、稳定性等性质。

3.3 电路设计在电路设计中，拉氏变换可以用于求解电路的导纳、阻抗等参数。

通过将电路的输入和输出进行拉氏变换，可以得到电路的传输函数，进而进行电路的设计和优化。

综上所述，拉氏变换是一种重要的数学工具，广泛应用于信号处理、系统分析、电路设计等领域。

Laplace拉氏变换公式表

419附录A 拉普拉斯变换及反变换1.表A-1拉氏变换的基本性质1线性定理齐次性)()]([s aF t af L =叠加性)()()]()([2121s F s F t f t f L ±=±2微分定理一般形式=−=][ ′− −=−=−−−−=−∑11)1()1(1222)()()0()()(0)0()(])([)0()(])([k k k k nk k n n nn dt t f d t f f s s F s dt t f d L f sf s F s dt t f d L f s sF dt t df L ⋮）（初始条件为0时)(])([s F s dtt f d L n nn =3积分定理一般形式��∑∫∫∫∫∫∫∫∫∫∫∫==+−===+=++=+=nk t n n k n n nn t t t dt t f s s s F dt t f L sdt t f s dt t f s s F dt t f L sdt t f s s F dt t f L 101022022]))(([1)(])()([]))(([])([)(]))(([])([)(])([个共个共⋯⋯⋮初始条件为0时�nn n ss F dt t f L )(]))(([=∫∫个共⋯4延迟定理（或称t 域平移定理）)()](1)([s F e T t T t f L Ts −=−−5衰减定理（或称s 域平移定理）)(])([a s F e t f L at +=−6终值定理)(lim )(lim 0s sF t f s t →∞→=7初值定理)(lim )(lim 0s sF t f s t ∞→→=8卷积定理)()(])()([])()([21021021s F s F d t f t f L d f t f L tt =−=−∫∫τττττ4202．表A-2常用函数的拉氏变换和z 变换表序号拉氏变换E(s)时间函数e(t)Z 变换E(z)11δ(t)12Tse −−11∑∞=−=0)()(n T nT t t δδ1−z z 3s1)(1t 1−z z 421s t2)1(−z Tz 531s 22t 32)1(2)1(−+z z z T 611+n s !n t n )(!)1(lim 0aTn n n a e z z a n −→−∂∂−7as +1at e −aTe z z−−82)(1a s +atte−2)(aT aT e z Tze −−−9)(a s s a +ate−−1))(1()1(aT aT e z z z e −−−−−10))((b s a s a b ++−bt at e e −−−bT aT e z ze z z −−−−−1122ωω+s t ωsin 1cos 2sin 2+−T z z Tz ωω1222ω+s s tωcos 1cos 2)cos (2+−−T z z T z z ωω1322)(ωω++a s t e atωsin −aTaT aT e T ze z Tze 22cos 2sin −−−+−ωω1422)(ω+++a s a s teatωcos −aTaT aT e T ze z T ze z 222cos 2cos −−−+−−ωω15aT s ln )/1(1−Tt a /az z −4213．用查表法进行拉氏反变换用查表法进行拉氏反变换的关键在于将变换式进行部分分式展开，然后逐项查表进行反变换。

拉氏变换详解

称为拉氏反变换。记为 L1[ F (s)] 。
由F(s)可按下式求出
f
(t)

L1[F (s)]

1
2
j
C j

C j
F (s)est ds(t

0)
式中C是实常数，而且大于F(s)所有极点的实部。
直接按上式求原函数太复杂，一般都用查拉氏变换表的方法求拉氏反变换，但F(s)必须是一种能直接查到的原函数的形式。 12
2.常用函数的拉氏变换
数学知识回顾
(1)例1.求阶跃函数f(t)=A·1(t)的拉氏变换。

F (s) Ae st dt

A e st

A
0
s
0
s
1
单位阶跃函数f(t)=1(t)的拉氏变换为 s 。
(2)例2.求单位脉冲函数f(t)=δ(t)的拉氏变换。
lim lim
F (s) (t)est dt
3
证：根据拉氏变换的定义有
L[
f
(t)]

0
f
(t)est dt

s
0
f
(t)est dt

f
(t )e st
0
sF(s) f (0)
原函数二阶导数的拉氏变换
L[ f (t)] sL[ f (t)] f (0) s[sF (s) f (0)] f (0)
则象函数及其自变量都增加（或减小）同
样倍数。即：L[ f ( t )] aF (as)
证：
a L[ f ( t )] f ( t )est dt
a 0a

拉氏变换

确定。可对应于平面上的点 (x, y)，这样表示复数的
平面称为复平面或 z 平面。其中 x 轴称为实轴，y
轴称为虚轴。
y
Z（a，b）
z=a+bi uuur OZ (a,b)
O
x
复数的表示
• 代数形式： z x iy
• 三角形式： z r(cos i sin ) r | z | Arg z
例1
求 : f (t) sin( t)的象函数
解
F(s)
sin(t )

1

2
j
(e j t

e j t
)

1 2j

S
1
j

S
1
j

S2 2
注：欧拉公式 re jt r[cos(t) sin(t)]
2）. 微分性质
➢ 斜坡信号（Ramp Function）
r(t)

R

t

u(t)

Rt 0
r（t）
t0 t0
u(t)-----单位阶跃函数
Rt t g（）=R

时间 t
斜坡信号为匀速信号，适于测试匀速系统。
➢抛物线信号（Parabolic Function）
r
(t
)

0.5R

t
2

u(t
)

0.5R 0
t
s0
f (0 ) lim f (t) lim SF (S)
t0
s
证：
df (t) dt

sF (s)

拉氏逆变换的公式

拉氏逆变换的公式L^-1{F(s)} = 1/2πj ∫[γ-j∞, γ+j∞] F(s)e^(st) ds其中，L^-1代表拉氏逆变换操作，F(s)代表拉氏变换后的函数，j代表虚数单位，t代表时间，γ为一条垂直于虚轴的直线，γ应该位于F(s)函数的所有极点的右侧。

换句话说，拉氏逆变换可以通过对拉氏变换后的函数F(s)在复平面上所有的极点进行逆时针积分来恢复原始函数。

逆变换的结果是一个时间域函数，它描述了信号或系统在时域上的响应。

拉氏逆变换的计算通常是通过查找拉氏变换表或使用部分分式分解的方法进行。

当拉氏变换的函数F(s)包含多个不同的极点时，我们可以将其分解为简单的分式形式，然后使用逆变换表格来找到每个分式对应的原始函数。

部分分式分解的方法允许我们将复杂的函数分解为简单的形式，从而方便进行逆变换的计算。

此外，还有一些常见的拉氏逆变换公式，例如：1.L^-1{1/s}=1这是一个简单的逆变换，它表示拉氏变换中的常数1/s在逆变换后变为了常数1。

2. L^-1{1/(s-a)} = e^(at)这个逆变换公式表示了一个带有指数增长项的逆变换，其中a是实数。

3. L^-1{s/(s^2+a^2)} = sin(at)这个逆变换公式表示了一个正弦函数，其中a是实数。

这些公式只是拉氏逆变换的一些基本示例，还有很多其他的逆变换公式可用于恢复各种不同类型的函数。

在实际应用中，可以根据具体的拉氏变换函数来选择合适的逆变换公式进行计算。

总结起来，拉氏逆变换是一种通过对拉氏变换函数进行逆时针积分来恢复原始函数的数学变换。

逆变换的公式包括基本的逆变换公式以及部分分式分解方法。

拉氏逆变换在信号处理和控制理论中发挥着重要的作用，它允许我们在时域上分析和处理各种信号和系统。

Laplace拉氏变换公式表

Laplace拉氏变换公式表1. 常数变换：对于常数C，其拉普拉斯变换为C/s，其中s是复数频率。

2. 幂函数变换：对于幂函数t^n，其中n为实数，其拉普拉斯变换为n!/s^(n+1)。

3. 指数函数变换：对于指数函数e^(at)，其中a为实数，其拉普拉斯变换为1/(sa)。

4. 正弦函数变换：对于正弦函数sin(at)，其中a为实数，其拉普拉斯变换为a/(s^2+a^2)。

5. 余弦函数变换：对于余弦函数cos(at)，其中a为实数，其拉普拉斯变换为s/(s^2+a^2)。

6. 双曲正弦函数变换：对于双曲正弦函数sinh(at)，其中a为实数，其拉普拉斯变换为a/(s^2a^2)。

7. 双曲余弦函数变换：对于双曲余弦函数cosh(at)，其中a为实数，其拉普拉斯变换为s/(s^2a^2)。

8. 指数衰减正弦函数变换：对于指数衰减正弦函数e^(at)sin(bt)，其中a和b为实数，其拉普拉斯变换为b/(s+a)^2+b^2。

9. 指数衰减余弦函数变换：对于指数衰减余弦函数e^(at)cos(bt)，其中a和b为实数，其拉普拉斯变换为s+a)/(s+a)^2+b^2。

10. 指数增长正弦函数变换：对于指数增长正弦函数e^(at)sin(bt)，其中a和b为实数，其拉普拉斯变换为b/(sa)^2+b^2。

Laplace拉氏变换公式表11. 幂函数与指数函数的乘积变换：对于函数t^n e^(at)，其中n为实数，a为实数，其拉普拉斯变换为n!/(sa)^(n+1)。

12. 幂函数与正弦函数的乘积变换：对于函数t^n sin(at)，其中n为实数，a为实数，其拉普拉斯变换可以通过分部积分法得到。

13. 幂函数与余弦函数的乘积变换：对于函数t^n cos(at)，其中n为实数，a为实数，其拉普拉斯变换可以通过分部积分法得到。

14. 指数函数与正弦函数的乘积变换：对于函数e^(at) sin(bt)，其中a和b为实数，其拉普拉斯变换为b/(sa)^2+b^2。

拉氏变换常用公式

附录A 拉普拉斯变换及反变换表A-1 拉氏变换的基本性质表A-2 常用函数的拉氏变换和z变换表用查表法进行拉氏反变换用查表法进行拉氏反变换的关键在于将变换式进行部分分式展开，然后逐项查表进行反变换。

设)(s F 是s 的有理真分式1110111)()()(a s a s a s a b s b s b s b s A s B s F n n n n m m m m ++++++++==---- （m n >）式中系数n n a a a a ,,...,,110-，m m b b b b ,,,110- 都是实常数；n m ,是正整数。

按代数定理可将)(s F 展开为部分分式。

分以下两种情况讨论。

① 0)(=s A 无重根这时，F(s)可展开为n 个简单的部分分式之和的形式。

∑=-=-++-++-+-=ni ii n n i i s s c s s c s s c s s c s s c s F 12211)( （F-1）式中，n s s s ,,,21 是特征方程A(s)＝0的根。

i c 为待定常数，称为F(s)在i s 处的留数，可按下式计算： )()(lim s F s s c i s s i i-=→ （F-2）或iss i s A s B c ='=)()( （F-3）式中，)(s A '为)(s A 对s 的一阶导数。

根据拉氏变换的性质，从式（F-1）可求得原函数[]⎥⎦⎤⎢⎣⎡-==∑=--n i i i s s c L s F L t f 111)()(＝ts n i iie c -=∑1 (F-4) ②0)(=s A 有重根设0)(=s A 有r 重根1s ，F(s)可写为())()()()(11n r rs s s s s s s B s F ---=+ =nn i i r r r r r r s s c s s c s s c s s c s s c s s c -++-++-+-++-+-++-- 11111111)()()( 式中，1s 为F(s)的r 重根，1+r s ，…, n s 为F(s)的n-r 个单根；其中，1+r c ，…, n c 仍按式(F-2)或(F-3)计算，r c ，1-r c ，…, 1c 则按下式计算：)()(lim 11s F s s c r s s r -=→)]()([lim111s F s s dsdc r s s r -=→-)()(lim !11)()(1s F s s dsd j c r j j s s jr -=→- (F-5))()(lim )!1(11)1()1(11s F s s dsd r c r r r s s --=--→原函数)(t f 为 [])()(1s F Lt f -=⎥⎦⎤⎢⎣⎡-++-++-+-++-+-=++---n n i i r r r r r r s s c s s c s s c s s c s s c s s c L 111111111)()()( t s nr i i t s r r r r ie c e c t c t r c t r c ∑+=---+⎥⎦⎤⎢⎣⎡+++-+-=1122111)!2()!1( （F-6）。

拉氏变换表(包含计算公式)[1]1

1拉氏变换及反变换公式1. 拉氏变换的基本性质 1线性定理齐次性)()]([s aF t af L =叠加性)()()]()([2121s F s F t f t f L ±=±2微分定理一般形式=-=][ '- -=-=----=-∑11)1()1(1222)()()0()()(0)0()(])([)0()(])([k k k k nk k n n nn dt t f d t f f s s F s dt t f d L f sf s F s dt t f d L f s sF dt t df L ）（初始条件为0时)(])([s F s dtt f d L n nn = 3积分定理一般形式∑⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰==+-===+=++=+=nk t n n k n n nn t t t dt t f s s s F dt t f L sdt t f s dt t f s s F dt t f L sdt t f s s F dt t f L 101022022]))(([1)(])()([]))(([])([)(]))(([])([)(])([个共个共初始条件为0时n n n ss F dt t f L )(]))(([=⎰⎰个共4 延迟定理（或称t 域平移定理） )()](1)([s F e T t T t f L Ts -=--5 衰减定理（或称s 域平移定理） )(])([a s F e t f L at +=-6 终值定理 )(lim )(lim 0s sF t f s t →∞→=7 初值定理 )(lim )(lim 0s sF t f s t ∞→→=8 卷积定理)()(])()([])()([21021021s F s F d t f t f L d f t f L tt =-=-⎰⎰τττττ22．常用函数的拉氏变换和z 变换表序号拉氏变换E(s)时间函数e(t) Z 变换E(z)1 1δ(t) 12 Tse --11∑∞=-=0)()(n T nT t t δδ1-z z 3 s1 )(1t1-z z 4 21s t2)1(-z Tz5 31s 22t32)1(2)1(-+z z z T6 11+n s!n t n)(!)1(lim 0aT n n n a ez z a n -→-∂∂- 7 as +1 at e - aTe z z-- 8 2)(1a s +atte- 2)(aT aT e z Tze ---9 )(a s s a+ ate--1))(1()1(aT aT e z z z e ----- 10 ))((b s a s ab ++-bt at e e --- bTaT e z ze z z ----- 11 22ωω+s t ωsin1cos 2sin 2+-T z z Tz ωω 12 22ω+s st ωcos1cos 2)cos (2+--T z z T z z ωω13 22)(ωω++a s t e atωsin - aTaT aT eT ze z Tze 22cos 2sin ---+-ωω 14 22)(ω+++a s a st eatωcos -aTaT aT e T ze z T ze z 222cos 2cos ---+--ωω15aT s ln )/1(1- T t a /az z -33．用查表法进行拉氏反变换用查表法进行拉氏反变换的关键在于将变换式进行部分分式展开，然后逐项查表进行反变换。

Laplace拉氏变换公式表

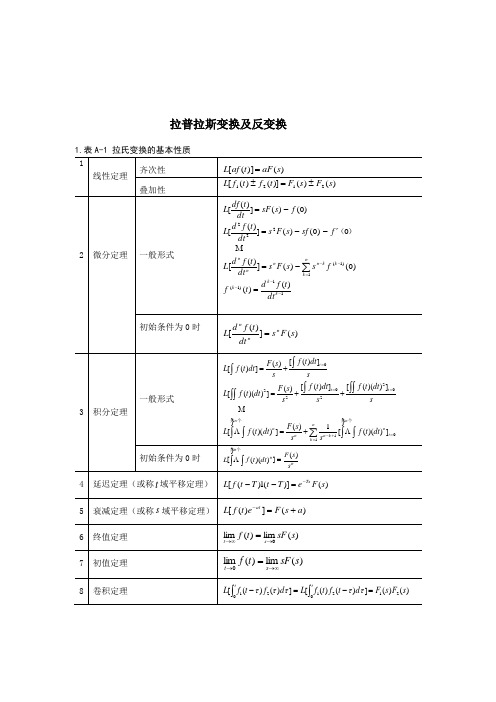
拉普拉斯变换及反变换3．用查表法进行拉氏反变换用查表法进行拉氏反变换的关键在于将变换式进行部分分式展开，然后逐项查表进行反变换。

设)(s F 是s 的有理真分式1110111)()()(a s a sa s ab s b sb sb s A s B s F n n nn m m m m ++++++++==---- （m n >）式中系数n n a a a a ,,...,,110-，m m b b b b ,,,110- 都是实常数；n m ,是正整数。

按代数定理可将)(s F 展开为部分分式。

分以下两种情况讨论。

① 0)(=s A 无重根这时，F(s)可展开为n 个简单的部分分式之和的形式。

∑=-=-++-++-+-=ni ii nn ii s s c s s c s s c s s c s s c s F 12211)( （F-1）式中，n s s s ,,,21 是特征方程A(s)＝0的根。

i c 为待定常数，称为F(s)在i s 处的留数，可按下式计算：)()(lim s F s s c i s s i i-=→ （F-2）或is s i s A s B c ='=)()( （F-3）式中，)(s A '为)(s A 对s 的一阶导数。

根据拉氏变换的性质，从式（F-1）可求得原函数[]⎥⎦⎤⎢⎣⎡-==∑=--n i i i s s c L s F L t f 111)()(＝ts ni i ie c -=∑1 (F-4)② 0)(=s A 有重根设0)(=s A 有r 重根1s ，F(s)可写为())()()()(11n r rs s s s s s s B s F ---=+=nn ii r r r r rr s s c s s c s s c s s c s s c s s c -++-++-+-++-+-++-- 11111111)()()(式中，1s 为F(s)的r 重根，1+r s ，…, n s 为F(s)的n-r 个单根；其中，1+r c ，…, n c 仍按式(F-2)或(F-3)计算，r c ，1-r c ，…, 1c 则按下式计算：)()(lim 11s F s s c rs s r -=→)]()([lim111s F s s dsd c rs s r -=→-)()(lim!11)()(1s F s s dsdj c rj j s s j r -=→- (F-5))()(lim)!1(11)1()1(11s F s s dsdr c rr r s s --=--→原函数)(t f 为 [])()(1s F L t f -=⎥⎦⎤⎢⎣⎡-++-++-+-++-+-=++---n n i i r r r r r r s s c s s c s s c s s c s s c s s c L 111111111)()()( ts nr i it s r r r r i ec e c t c t r c t r c ∑+=---+⎥⎦⎤⎢⎣⎡+++-+-=1122111)!2()!1(（F-6）。

拉氏变换常用公式

拉氏变换常用公式拉氏变换是一种重要的数学工具，广泛应用于信号处理、控制系统分析和电路设计等领域。

本文将介绍拉氏变换常用的公式，包括重要的拉氏变换和反变换公式，以及一些常见的拉氏变换性质。

1. 拉氏变换公式拉氏变换公式是将一个时间域函数变换成复频域的函数。

以下是一些常用的拉氏变换公式：（1）常数信号的拉氏变换：如果输入信号为常数，即f(t)=A，其拉氏变换为F(s) = A/s，其中A 为常数。

（2）指数信号的拉氏变换：指数信号的拉氏变换公式为：f(t) = e^(at) -> F(s) = 1/(s-a)，其中a为常数。

（3）单位冲激信号的拉氏变换：单位冲激信号的拉氏变换公式为：f(t) = δ(t) -> F(s) = 1，其中δ(t)表示单位冲激函数。

（4）正弦信号的拉氏变换：正弦信号的拉氏变换公式为：f(t) = sin(ωt) -> F(s) = ω/(s^2 + ω^2)。

其中ω为正弦信号的频率。

2. 拉氏反变换公式拉氏反变换是将复频域函数转换回时间域函数的过程，以下是一些常用的拉氏反变换公式：（1）常数信号的拉氏反变换：对于F(s) = A/s，其拉氏反变换为f(t) = A。

（2）指数信号的拉氏反变换：对于F(s) = 1/(s - a)，其拉氏反变换为f(t) = e^(at)，其中a为常数。

（3）单位冲激信号的拉氏反变换：对于F(s) = 1，其拉氏反变换为f(t) = δ(t)。

（4）正弦信号的拉氏反变换：对于F(s) = ω/(s^2 + ω^2)，其拉氏反变换为f(t) = sin(ωt)。

3. 拉氏变换的性质拉氏变换具有一些重要的性质，其中包括线性性质、时间平移性质、频率平移性质、频率缩放性质、卷积定理等，这些性质对于信号处理和系统分析非常有用。

（1）线性性质：拉氏变换具有线性性质，即对于输入信号f1(t)和f2(t)，以及相应的拉氏变换F1(s)和F2(s)，有以下性质成立：a1*f1(t) + a2*f2(t) -> a1*F1(s) + a2*F2(s)。

(完整word版)拉氏变换常用公式

附录 A 拉普拉斯变换及反变换表 A-1 拉氏变换的基天性质齐次性1线性定理叠加性一般形式微分定理2初始条件为0 时一般形式积分定理3初始条件为0 时4延缓定理（或称 t 域平移定理）5衰减定理（或称 s域平移定理）6终值定理7初值定理8卷积定理L[ af (t )] aF ( s)L[ f1 ( t) f 2 (t )] F1 (s) F2 ( s)L[ df (t ) ] sF ( s) f (0)dtd 2 f (t )s2F (s) sf ( 0) f（）L[ dt2] 0Ld nf (t ) s n F (s) n s n k f (k 1) (0)dt n k 1f ( k 1) ( t) d k 1 f (t)dt k 1L[ d n f (t ) ] s n F ( s)dt nL[ f (t)dt]F (s) [ f (t)dt]t 0s sL[ f (t )(dt)2 ] F (s)[ f (t )dt]t 0 [ f (t)( dt)2]t 0s2 ss2共 n个n共n个nF (s) 1 nL[ f (t )(dt) ] 1 [ f (t)( dt) ]t 0n n ks k 1 s共n个L[ f (t )(dt) n ] F ( s)s nL[ f (t T )1(t T )]Tse F (s)L[ f (t)e at ] F (s a)lim f (t) lim sF (s)t s0lim f (t) lim sF(s)t 0st tL[ 0 f1 (t) f2 ( )d ] L[ 0 f1(t ) f2 (t)d ]F1( s)F2 (s)序表 A-2 常用函数的拉氏变换和z 变换表号1 2 3 456 拉氏变换E(s)111 e Ts1s12s13s1s n 1时间函数e(t)δ(t)T (t )(t nT )n01(t )tt 22t nn!Z 变换 E(z)1zz 1zz 1Tz2T 2 z(z 1)2( z 1) 3lim ( 1) nnn( zaT)a 0 n! a z e7 1s a e atzaTz e81( s a) 2 teataTTze9101112131415as(s a)b a(s a)(s b)s2 2ss2 2(s a) 2 2s a2 2(s a)1s (1/ T ) ln a1 e ate at e btsin tcos te at sin te at cos ta t / T(1 e aT )z(z 1)( z e aT )z zz e aT z e bTzsin Tz2 2z cos T 1z2z(z cos T )2z cos T 1ze aT sin Tz2 2ze aT cos T e 2 aTz 2 ze aT cos Tz2 2ze aT cos T e 2 aTzz a用查表法进行拉氏反变换用表法行拉氏反的关在于将式行部分分式睁开，而后逐表行反。

拉氏变换

p f(+∞) = lim pF(p)= lim p→ 0 p →0 p + a
=0
3 2t + 3 = 解： f(0) = lim f(t) = lim t →0 (t + 1)(t + 2) t→0 2 2t + 3 f(+∞) = lim f(t)= lim =0 t →∞ (t + 1)(t + 2) t→∞
1 p = - 2 p p + 16
16 = p(p2 +16)
二、平移性质
若 L[f(t)] = F(p)，则 L at f(t)] = F(p - a) [e
(a是数常）
ω 解： L[sinωt] = Q 2 2 p +ω
∴L[e sinωt] =
-at -at
例3、求L[e sinωt]
上式两端取拉氏变换，并根据拉氏变换的线性性质及滞后性质，得
3c 2c c
o
a
2a 3a
t
L[f(t)] = c{L[u(t)] + L[u(t - a)] + L[u(t - 2a)] + L}
1 1 -ap 1 - 2ap 当p>0时，上端右 = c( + e + e + L) 式的等比级数收敛 p p p c c 1 - ap - 2ap = (1 + e + e + L) = ⋅ (p > 0) -ap p p 1- e
[a 则，L 1f1(t) + a2f2 (t)] a1L[f1(t)] + a2L[f 2 (t)] =
= F (p) + F (p) 1 2

拉氏变换常用公式

常用拉普拉斯变换总结1、指数函数,其中,A 与a 为常数。

2、阶跃函数,其中,A 为常数。

3、单位阶跃函数0010)(><⎩⎨⎧=t t t u s t e t u L st 1d )]([0==⎰∞-4、斜坡函数000)(≥<⎩⎨⎧=t t Att f ,其中,A 为常数。

20d s A t e s A st ==⎰∞-A ＝1时得斜坡函数称为单位斜坡函数,发生在t=t 0时刻得单位斜坡函数写成r(t-t 0)5、单位斜坡函数6、正弦函数,其中A 为常数。

)(t f t 图2.3正弦函数和余弦函数)(t f t(a)(b)00根据欧拉公式: 拉式变换为:同理余弦函数得拉式变换为:7、脉动函数,其中,A 与t 0为常数。

脉动函数可以瞧做就是一个从t ＝0开始得高度为A /t 0得阶跃函数,与另一个从t ＝t 0开)(21sin t j t j e e j t ωωω--=始得高度为A /t 0得负阶跃函数叠加而成。

8、脉冲函数脉冲函数就是脉动函数得一种特殊极限情况。

9、单位脉冲函数当面积A =1得脉冲函数称为单位脉冲函数,或称为狄拉克(Disac)函数,量值为无穷大且持续时间为零得脉冲函数纯属数学上得一种假设,而不可能在物理系统中发生。

但就是,如果系统得脉动输入量值很大,而持续时间与系统得时间常数相比较非常小时,可以用脉冲函数去近似地表示脉动输入。

当描述脉冲输入时,脉冲得面积大小就是非常重要得,而脉冲得精确形状通常并不重要。

脉冲输入量在一个无限小得时间内向系统提供能量。

单位脉冲函数可以瞧作就是单位阶跃函数u(t-t 0)在间断点t=t 0上得导数,即相反,如若对单位脉冲函数积分:积分得结果就就是单位阶跃函数 u(t-t 0)利用脉冲函数得概念,我们可以对包含不连续点得函数进行微分,从而得到一些脉冲,这些脉冲得量值等于每一个相应得不连续点上得量值。

10、加速度函数,其中,A 为常数。