练习13_勾股定理- (华东师大版)(解析版)
2021年华师大版八年级数学上册勾股定理训练题及答案

勾股定理测试题一、基础达标:1. 下列说法正确的是( )A.若 a 、b 、c 是△ABC 的三边,则a 2+b 2=c 2; B.若 a 、b 、c 是Rt△ABC 的三边,则a 2+b 2=c 2;C.若 a 、b 、c 是Rt△ABC 的三边,90=∠A ,则a 2+b 2=c 2;D.若 a 、b 、c 是Rt△ABC 的三边, 90=∠C ,则a 2+b 2=c 2.2. Rt △ABC 的三条边长分别是a 、b 、c ,则下列各式成立的是( ) A .c b a=+ B. c b a >+ C. c b a<+D. 222c b a =+3. 如果Rt △的两直角边长分别为k 2-1,2k (k >1),那么它的斜边长是( ) A 、2k B 、k+1 C 、k 2-1 D 、k 2+1 4. 已知a ,b ,c 为△ABC 三边,且满足(a 2-b 2)(a 2+b 2-c 2)=0,则它的形状为( )A.直角三角形B.等腰三角形C.等腰直角三角形D.等腰三角形或直角三角形5. 直角三角形中一直角边的长为9,另两边为连续自然数,则直角三角形的周长为( )A .121 B .120 C .90 D .不能确定 6. △ABC 中,AB =15,AC =13,高AD =12,则△ABC 的周长为( ) A .42 B .32 C .42 或 32 D .37 或 33 7.※直角三角形的面积为S ,斜边上的中线长为d ,则这个三角形周长为( ) (A2d (Bd (C)2d (D)d8、在平面直角坐标系中,已知点P 的坐标是(3,4),则OP 的长为( ) A 、3 B 、4 C 、5 D 、7 9.若△ABC 中,AB=25cm ,AC=26cm 高AD=24,则BC 的长为( ) A .17 B.3 C.17或3 D.以上都不对 10.已知a 、b 、c是三角形的三边长,如果满足2(6)100a c -+-=则三角形的形状是( )A :底与边不相等的等腰三角形B :等边三角形C :钝角三角形D :直角三角形 11.斜边的边长为cm 17,一条直角边长为cm 8的直角三角形的面积是 . 12. 等腰三角形的腰长为13,底边长为10,则顶角的平分线为__. 13. 一个直角三角形的三边长的平方和为200,则斜边长为 14.一个三角形三边之比是6:8:10,则按角分类它是 三角形.15. 一个三角形的三边之比为5∶12∶13,它的周长为60,则它的面积是___. 16. 在Rt △ABC 中,斜边AB=4,则AB 2+BC 2+AC 2=_____.17.若三角形的三个内角的比是3:2:1,最短边长为cm 1,最长边长为cm 2,则这个三角形三个角度数分别是 ,另外一边的平方是 .18.如图,已知ABC ∆中,︒=∠90C,15=BA ,12=AC ,以直角边BC 为直径作半圆,则这个半圆的面积是 .19. 一长方形的一边长为cm 3,面积为212cm ,那么它的一条对角线长是 . 二、综合发展:1.如图,一个高4m 、宽3m 的大门,需要在对角线的顶点间加固一个木条,求木条的长.第18题ACB2、有一个直角三角形纸片,两直角边AC=6cm,BC=8cm,现将直角边AC 沿∠CAB 的角平分线AD 折叠,使它落在斜边AB 上,且与AE 重合,你能求出CD 的长吗?3.一个三角形三条边的长分别为cm 15,cm 20,cm 25,这个三角形最长边上的高是多少?4.如图,要修建一个育苗棚,棚高h=3m ,棚宽a=4m ,棚的长为12m ,现要在棚顶上覆盖塑料薄膜,试求需要多少平方米塑料薄膜?5.如图,有一只小鸟在一棵高13m 的大树树梢上捉虫子,它的伙伴在离该树12m ,高8m 的一棵小树树梢上发出友好的叫声,它立刻以2m/s 的速度飞向小树树梢,它最短要飞多远?这只小鸟至少几秒才可能到达小树和伙伴在一起?15.“中华人民共和国道路交通管理条例”规定:小汽车在城街路上行驶速度不得超过70km/h.如图,,一辆小汽车在一条城市街路上直道行驶,某一时刻刚好行驶到路对面车速检测仪正前方30m 处,过了2s 后,测得小汽车与车速检测仪间距离为50m ,这辆小汽车超速了吗? 答案: 一、基础达标1. 解析:利用勾股定理正确书写三角形三边关系的关键是看清谁是直角.答案: D.2. 解析:本题考察三角形的三边关系和勾股定理.答案:B.3. 解析:设另一条直角边为x ,则斜边为(x+1)利用勾股定理可得方程,可以求出x .然后再求它的周长.答案:C .4.解析:解决本题关键是要画出图形来,作图时应注意高AD 是在三角形的内部还是在三角形的外部,有两种情况,分别求解. 答案:C.A小汽车小汽车BC观测点AECD5. 解析: 勾股定理得到:22215817=-,另一条直角边是15,所求直角三角形面积为21158602cm ⨯⨯=.答案: 260cm .6. 解析:本题目主要是强调直角三角形中直角对的边是最长边,反过来也是成立.答案:222c b a =+,c ,直角,斜,直角.7. 解析:本题由边长之比是6:8:10可知满足勾股定理,即是直角三角形.答案:直角.8. 解析:由三角形的内角和定理知三个角的度数,断定是直角三角形.答案:︒30、︒60、︒90,3.9. 解析:由勾股定理知道:22222291215=-=-=AC AB BC ,所以以直角边9=BC 为直径的半圆面积为10.125π.答案:10.125π.10. 解析:长方形面积长×宽,即12长×3,长4=,所以一条对角线长为5.答案:cm 5. 二、综合发展11. 解析:木条长的平方=门高长的平方+门宽长的平方.答案:5m . 12解析:因为222252015=+,所以这三角形是直角三角形,设最长边(斜边)上的高为xcm ,由直角三角形面积关系,可得1115202522x ⨯⨯=⨯⋅,∴12=x .答案:12cm 13.解析:透阳光最大面积是塑料薄膜的面积,需要求出它的另一边的长是多少,可以借助勾股定理求出.答案:在直角三角形中,由勾股定理可得:直角三角形的斜边长为5m, 所以矩形塑料薄膜的面积是:5×20=100(m 2) .14.解析:本题的关键是构造直角三角形,利用勾股定理求斜边的值是13m ,也就是两树树梢之间的距离是13m ,两再利用时间关系式求解.答案:6.5s .15.解析:本题和14题相似,可以求出BC 的值,再利用速度等于路程除以时间后比较.BC=40米,时间是2s ,可得速度是20m/s=72km/h >70km/h .答案:这辆小汽车超速了.。
第十四章勾股定理之勾股定理的逆定理华东师大大版2024—2025学年八年级上册

第十四章勾股定理之勾股定理的逆定理华东师大版2024—2025学年八年级上册【考点·方法·破译】1.会用勾股定理的逆定理判定直角三角形.首先确定最长的边,再比较较短两边的平方和是否等于最长边的平方。
2. 勾股定理的逆定理的题设和结论恰好与勾股定理的题设和结论相反,我们把像这样的两个命题叫做互逆命题,如果把其中一个叫做原命题,那么另一个叫做它的逆命题。
3. 能够成为直角三角形三条边长的三个正整数,称为勾股数。
熟悉常见的勾股数如①3、4、5;②5,12,13;③7,24,25;④8,15,17。
【典型例题解析】类型一.证明三角形是直角三角形例1已知:如图,在△ABC 中,CD 是AB 边上的高,且CD 2=AD·BD.求证:△ABC 是直角三角形.【变式练习】1.已知:在△ABC 中,∠A 、∠B 、∠C 的对边分别是c b a ,,,满足c b a c b a 262410338222++=++.试判断△ABC 的形状.2.如图,某住宅小区在施工过程中留下了一块空地,已知AD =4米,CD =3米,∠ADC =90°,AB =13米,BC =12米,求这块空地的面积?3.如图,已知:在ΔABC 中,∠C=90︒,M 是BC 的中点,MD ⊥AB 于D ,求证:AD 2=AC 2+BD 2.A B C MD类型二 运用勾股定理的逆定理进行计算 例2如图,等腰△ABC 中,底边BC =20,D 为AB 上一点,CD =16,BD =12,求△ABC 的周长。
【变式练习】4.已知:如图,四边形ABCD ,AD ∥BC ,AB=4,BC=6,CD=5,AD=3.求:四边形ABCD 的面积.5.已知:如图,DE=m,BC=n,∠EBC 与∠DCB 互余,求BD 2+CD 2.类型三、与勾股定理逆定理有关的探究和应用例3阅读下列解题过程:已知a 、b 、c 为△ABC 的三边,且满足a 2c 2-b 2c 2=a 4-b 4,试判断△ABC的形状.解:∵a 2c 2-b 2c 2=a 4-b 4,(A)∴c 2(a 2-b 2)=(a 2+b 2)(a 2-b 2),(B)∴c 2=a 2+b 2,(C)∴△ABC 是直角三角形.问:①上述解题过程是从哪一步开始出现错误的?请写出该步的代号_______; ②错误的原因是______________;③本题的正确结论是__________.例4学习了勾股定理以后,有同学提出“在直角三角形中,三边满足,或许其他的三角形三边也有这样的关系”.让我们来做一个实验!(1)画出任意的一个锐角三角形,量出各边的长度(精确到1毫米),较短的两条边长分别是______mm ;______mm ;较长的一条边长_______mm 。
勾股定理的综合练习--华师大版(教学课件2019)

(4) 有一根长24 cm的小木棒,把它分成
三段,组成一个直角三角形,且每段的长度
都是偶数,则三段小木棒的长度分别
是
cm o优化服务,aso优化公司,上海aso:https:///aso
;
璧珠玑玉衣 参分蕤宾损一 星入 东至东光入歑河 拜为使主客 为帝室故不敢顾私 不蒙天祐 究於去年 逆天背畔 登降运行 咸荐诸朝 群臣朝见 初 设帷帐 敞三子 吾家所立耳 以其国予敌也 上具狱事 可谓清矣 百有馀载 跌至晡 庶几云已 不甚宠异也 记曰三公无官 於今千载 子阳嗣 卒 定楚 其为害也不亦难矣 方进 根以为 定陶王帝弟之子 穰穰复正直往宁 字 居摄元年正月 知所以安利万民 益封 望室屋甚大 会诸侯 言其宣扬於王者朝廷 虏齮 即治郡国缗钱 宛王蝉封与汉约 必先利其器 文德者 三会为七百八十七万九千六百八十 安受节已 诸侯皆不肖 崎岖而不安 食 邑三百户 未见休时 於是助诘蚡曰 特患力不能救 要害之处 王莽篡位 羽大怒 侯国 即渡水 死矣 即以绶自绞 有羽阳宫 出则骖乘 得赂则以分其士 月穆穆以金波 上不得以功除罪 六十归田 乃欲戮力致获 行五六百岁尚未败也 三将军屯京师 李广 张骞 公孙贺 李蔡 曹襄 韩说 苏建皆自 有传 扬氏溯江上 铢者 既灭南越 还报曰 可击 道陵将率得士死力 又何足法哉 全子孙 〔表略〕[标签 标题]自古帝王之兴 周公遗化销微 取於不专 故能以五年之间至致此焉 日南至 王辄休相就馆 王以故数系笞太子 於是乎玄猿素雌 补上党郡中令 立为太子 徙为燕相 地官司徒 复为右 曹典属国 水生木 而诸侯皆附 秋七月 高后自临用事 乘舆斥车马 帷帐 器物以充其家 君子与之 在彼不在此 慎其齐戒 别尊卑贵贱 此其志不小 泽王燕二年 谏诤即见听 常恐汉兵袭之 是为辰星岁数 又伪为左右都司空 上林中都官诏狱书 又苦趶盭 五伯既没 犹庶民附离王者
2019—2020年最新华东师大版八年级数学上册《勾股定理》单元测试题及答案解析.docx

2019—2020年最新华东师⼤版⼋年级数学上册《勾股定理》单元测试题及答案解析.docx第14章勾股定理⼀、选择题(共13⼩题)1.如图,点E在正⽅形ABCD内,满⾜∠AEB=90°,AE=6,BE=8,则阴影部分的⾯积是()A.48 B.60 C.76 D.802.如图是我国古代数学家赵爽在为《周髀算经》作注解时给出的“弦图”,它解决的数学问题是()A.黄⾦分割 B.垂径定理 C.勾股定理 D.正弦定理3.如图,△ABC中,D为AB中点,E在AC上,且BE⊥AC.若DE=10,AE=16,则BE的长度为何?()A.10 B.11 C.12 D.134.下列四组线段中,能组成直⾓三⾓形的是()A.a=1,b=2,c=3 B.a=2,b=3,c=4 C.a=2,b=4,c=5 D.a=3,b=4,c=55.下列各组线段中,能够组成直⾓三⾓形的⼀组是()A.1,2,3 B.2,3,4 C.4,5,6 D.1,,6.⼀直⾓三⾓形的两边长分别为3和4.则第三边的长为()A.5 B.C.D.5或7.设a、b是直⾓三⾓形的两条直⾓边,若该三⾓形的周长为6,斜边长为2.5,则ab的值是()A.1.5 B.2 C.2.5 D.3 8.如图,若∠A=60°,AC=20m,则BC⼤约是(结果精确到0.1m)()A.34.64m B.34.6m C.28.3m D.17.3m9.如图,在矩形ABCD中,AD=2AB,点M、N分别在边AD、BC上,连接BM、DN.若四边形MBND是菱形,则等于()A.B.C.D.10.如图,正六边形ABCDEF中,AB=2,点P是ED的中点,连接AP,则AP的长为()A.2 B.4 C. D.11.如果⼀个直⾓三⾓形的两条边长分别是6和8,另⼀个与它相似的直⾓三⾓形边长分别是3和4及x,那么x的值()A.只有1个 B.可以有2个C.有2个以上,但有限D.有⽆数个12.在等腰△ABC中,∠ACB=90°,且AC=1.过点C作直线l∥AB,P为直线l上⼀点,且AP=AB.则点P到BC所在直线的距离是()A.1 B.1或C.1或D.或13.如图,四边形ABCD中,AB=AD,AD∥BC,∠ABC=60°,∠BCD=30°,BC=6,那么△ACD的⾯积是()A.B.C.2 D.⼆、填空题(共15⼩题)14.如图,在平⾯直⾓坐标系中,点A,B的坐标分别为(﹣6,0)、(0,8).以点A为圆⼼,以AB长为半径画弧,交x正半轴于点C,则点C的坐标为.15.在Rt△ABC中,CA=CB,AB=9,点D在BC边上,连接AD,若tan∠CAD=,则BD的长为.16.我国汉代数学家赵爽为了证明勾股定理,创制了⼀幅“弦图”,后⼈称其为“赵爽弦图”(如图(1)).图(2)由弦图变化得到,它是由⼋个全等的直⾓三⾓形拼接⽽成,记图中正⽅形ABCD、正⽅形EFGH、正⽅形MNKT的⾯积分别为S1、S2、S3.若正⽅形EFGH的边长为2,则S1+S2+S3= .17.如图是“赵爽弦图”,△ABH、△BCG、△CDF和△DAE是四个全等的直⾓三⾓形,四边形ABCD 和EFGH都是正⽅形.如果AB=10,EF=2,那么AH等于.18.如图,在△ABC中,CA=CB,AD⊥BC,BE⊥AC,AB=5,AD=4,则AE= .19.如图是⼀株美丽的勾股树,其中所有的四边形都是正⽅形,所有的三⾓形都是直⾓三⾓形,若正⽅形A、B、C、D的⾯积分别为2,5,1,2.则最⼤的正⽅形E的⾯积是.20.在△ABC中,∠C=90°,AB=7,BC=5,则边AC的长为.21.如图,矩形ABCD中,E是BC的中点,矩形ABCD的周长是20cm,AE=5cm,则AB的长为cm.22.如图,我国古代数学家得出的“赵爽弦图”是由四个全等的直⾓三⾓形和⼀个⼩正⽅形密铺构成的⼤正⽅形,若⼩正⽅形与⼤正⽅形的⾯积之⽐为1:13,则直⾓三⾓形较短的直⾓边a与较长的直⾓边b的⽐值为.第14章勾股定理参考答案与试题解析⼀、选择题(共13⼩题)1.如图,点E在正⽅形ABCD内,满⾜∠AEB=90°,AE=6,BE=8,则阴影部分的⾯积是()A.48 B.60 C.76 D.80【考点】勾股定理;正⽅形的性质.【分析】由已知得△ABE为直⾓三⾓形,⽤勾股定理求正⽅形的边长AB,⽤S阴影部分=S正⽅形ABCD ﹣S△ABE求⾯积.【解答】解:∵∠AEB=90°,AE=6,BE=8,∴在Rt△ABE中,AB2=AE2+BE2=100,∴S阴影部分=S正⽅形ABCD﹣S△ABE,=AB2﹣×AE×BE=100﹣×6×8=76.故选:C.【点评】本题考查了勾股定理的运⽤,正⽅形的性质.关键是判断△ABE为直⾓三⾓形,运⽤勾股定理及⾯积公式求解.2.如图是我国古代数学家赵爽在为《周髀算经》作注解时给出的“弦图”,它解决的数学问题是()A.黄⾦分割 B.垂径定理 C.勾股定理 D.正弦定理【考点】勾股定理的证明.【专题】⼏何图形问题.【分析】“弦图”,说明了直⾓三⾓形的三边之间的关系,解决了勾股定理的证明.【解答】解:“弦图”,说明了直⾓三⾓形的三边之间的关系,解决的问题是:勾股定理.故选:C.【点评】本题考查了勾股定理的证明,勾股定理证明的⽅法最常⽤的思路是利⽤⾯积证明.3.如图,△ABC中,D为AB中点,E在AC上,且BE⊥AC.若DE=10,AE=16,则BE的长度为何?()A.10 B.11 C.12 D.13【考点】勾股定理;直⾓三⾓形斜边上的中线.【分析】根据在直⾓三⾓形中,斜边上的中线等于斜边的⼀半这⼀性质可求出AB的长,再根据勾股定理即可求出BE的长.【解答】解:∵BE⊥AC,∴△AEB是直⾓三⾓形,∵D为AB中点,DE=10,∴AB=20,∵AE=16,∴BE==12,故选C.【点评】本题考查了勾股定理的运⽤、直⾓三⾓形的性质:直⾓三⾓形中,斜边上的中线等于斜边的⼀半,题⽬的综合性很好,难度不⼤.4.下列四组线段中,能组成直⾓三⾓形的是()A.a=1,b=2,c=3 B.a=2,b=3,c=4 C.a=2,b=4,c=5 D.a=3,b=4,c=5【考点】勾股定理的逆定理.【分析】根据勾股定理的逆定理对各选项进⾏逐⼀分析即可.【解答】解:A、∵12+22=5≠32,∴不能构成直⾓三⾓形,故本选项错误;B、∵22+32=13≠42,∴不能构成直⾓三⾓形,故本选项错误;C、∵22+42=20≠52,∴不能构成直⾓三⾓形,故本选项错误;D、∵32+42=25=52,∴能构成直⾓三⾓形,故本选项正确.故选D.【点评】本题考查的是勾股定理的逆定理,熟知如果三⾓形的三边长a,b,c满⾜a2+b2=c2,那么这个三⾓形就是直⾓三⾓形是解答此题的关键.5.下列各组线段中,能够组成直⾓三⾓形的⼀组是()A.1,2,3 B.2,3,4 C.4,5,6 D.1,,【考点】勾股定理的逆定理.【分析】根据勾股定理的逆定理:如果三⾓形有两边的平⽅和等于第三边的平⽅,那么这个三⾓形是直⾓三⾓形判定则可.【解答】解:A、12+22≠32,不能组成直⾓三⾓形,故错误;B、22+32≠42,不能组成直⾓三⾓形,故错误;C、42+52≠62,不能组成直⾓三⾓形,故错误;D、12+()2=()2,能够组成直⾓三⾓形,故正确.故选D.【点评】本题考查了勾股定理的逆定理,在应⽤勾股定理的逆定理时,应先认真分析所给边的⼤⼩关系,确定最⼤边后,再验证两条较⼩边的平⽅和与最⼤边的平⽅之间的关系,进⽽作出判断.6.⼀直⾓三⾓形的两边长分别为3和4.则第三边的长为()A.5 B.C.D.5或【考点】勾股定理.【专题】分类讨论.【分析】本题中没有指明哪个是直⾓边哪个是斜边,故应该分情况进⾏分析.【解答】解:(1)当两边均为直⾓边时,由勾股定理得,第三边为5,(2)当4为斜边时,由勾股定理得,第三边为,故选:D.【点评】题主要考查学⽣对勾股定理的运⽤,注意分情况进⾏分析.7.(2013?德宏州)设a、b是直⾓三⾓形的两条直⾓边,若该三⾓形的周长为6,斜边长为2.5,则ab的值是()A.1.5 B.2 C.2.5 D.3【考点】勾股定理.【专题】压轴题.【分析】由该三⾓形的周长为6,斜边长为2.5可知a+b+2.5=6,再根据勾股定理和完全平⽅公式即可求出ab的值.【解答】解:∵三⾓形的周长为6,斜边长为2.5,∴a+b+2.5=6,∴a+b=3.5,①∵a、b是直⾓三⾓形的两条直⾓边,∴a2+b2=2.52,②由①②可得ab=3,故选D.【点评】本题考查了勾股定理和三⾓形的周长以及完全平⽅公式的运⽤.8.如图,若∠A=60°,AC=20m,则BC⼤约是(结果精确到0.1m)()A.34.64m B.34.6m C.28.3m D.17.3m【考点】勾股定理;含30度⾓的直⾓三⾓形.【分析】⾸先计算出∠B的度数,再根据直⾓三⾓形的性质可得AB=40m,再利⽤勾股定理计算出BC长即可.【解答】解:∵∠A=60°,∠C=90°,∴∠B=30°,∴AB=2AC,∵AC=20m,∴AB=40m,∴BC====20≈34.6(m),故选:B.【点评】此题主要考查了勾股定理,以及直⾓三⾓形的性质,关键是掌握在直⾓三⾓形中,30°⾓所对的直⾓边等于斜边的⼀半.在任何⼀个直⾓三⾓形中,两条直⾓边长的平⽅之和⼀定等于斜边长的平⽅.9.如图,在矩形ABCD中,AD=2AB,点M、N分别在边AD、BC上,连接BM、DN.若四边形MBND是菱形,则等于()A .B .C .D .【考点】勾股定理;菱形的性质;矩形的性质.【分析】⾸先由菱形的四条边都相等与矩形的四个⾓是直⾓,即可得到直⾓△ABM 中三边的关系.【解答】解:∵四边形MBND 是菱形,∴MD=MB .∵四边形ABCD 是矩形,∴∠A=90°.设AB=x ,AM=y ,则MB=2x ﹣y ,(x 、y 均为正数).在Rt △ABM 中,AB 2+AM 2=BM 2,即x 2+y 2=(2x ﹣y )2,解得x=y ,∴MD=MB=2x ﹣y=y ,∴==.故选:C .【点评】此题考查了菱形与矩形的性质,以及直⾓三⾓形中的勾股定理.解此题的关键是注意数形结合思想与⽅程思想的应⽤.10.如图,正六边形ABCDEF 中,AB=2,点P 是ED 的中点,连接AP ,则AP 的长为()A .2B .4C .D .【考点】勾股定理.【分析】连接AE,求出正六边形的∠F=120°,再求出∠AEF=∠EAF=30°,然后求出∠AEP=90°并求出AE的长,再求出PE 的长,最后在Rt△AEP中,利⽤勾股定理列式进⾏计算即可得解.【解答】解:如图,连接AE,在正六边形中,∠F=×(6﹣2)?180°=120°,∵AF=EF,∴∠AEF=∠EAF=(180°﹣120°)=30°,∴∠AEP=120°﹣30°=90°,AE=2×2cos30°=2×2×=2,∵点P是ED的中点,∴EP=×2=1,在Rt△AEP中,AP===.故选:C.【点评】本题考查了勾股定理,正六边形的性质,等腰三⾓形三线合⼀的性质,作辅助线构造出直⾓三⾓形是解题的关键.11.如果⼀个直⾓三⾓形的两条边长分别是6和8,另⼀个与它相似的直⾓三⾓形边长分别是3和4及x,那么x的值()A.只有1个 B.可以有2个C.有2个以上,但有限D.有⽆数个【考点】勾股定理;相似三⾓形的判定与性质.【专题】分类讨论.【分析】两条边长分别是6和8的直⾓三⾓形有两种可能,即已知边均为直⾓边或者8为斜边,运⽤勾股定理分别求出第三边后,和另外三⾓形构成相似三⾓形,利⽤对应边成⽐例即可解答.【解答】解:根据题意,两条边长分别是6和8的直⾓三⾓形有两种可能,⼀种是6和8为直⾓边,那么根据勾股定理可知斜边为10;另⼀种可能是6是直⾓边,⽽8是斜边,那么根据勾股定理可知另⼀条直⾓边为.所以另⼀个与它相似的直⾓三⾓形也有两种可能,第⼀种是,解得x=5;第⼆种是,解得x=.所以可以有2个.故选:B.【点评】本题考查了勾股定理和三⾓形相似的有关知识.本题学⽣常常漏掉第⼆种情况,是⼀道易错题.12.在等腰△ABC中,∠ACB=90°,且AC=1.过点C作直线l∥AB,P为直线l上⼀点,且AP=AB.则点P到BC所在直线的距离是()A.1 B.1或C.1或D.或【考点】勾股定理;平⾏线之间的距离;等腰直⾓三⾓形.【专题】压轴题.【分析】如图,延长AC,做PD⊥BC交点为D,PE⊥AC,交点为E,可得四边形CDPE是正⽅形,则CD=DP=PE=EC;等腰Rt△ABC中,∠C=90°,AC=1,所以,可求出BC=1,AB=,⼜AB=AP;所以,在直⾓△AEP中,可运⽤勾股定理求得DP的长即为点P到BC的距离.【解答】解:①如图,延长AC,做PD⊥BC交点为D,PE⊥AC,交点为E,∵CP∥AB,∴∠PCD=∠CBA=45°,∴四边形CDPE是正⽅形,则CD=DP=PE=EC,∵在等腰直⾓△ABC中,AC=BC=1,AB=AP,∴AB==,∴AP=;∴在直⾓△AEP中,(1+EC)2+EP2=AP2∴(1+DP)2+DP2=()2,解得,DP=;②如图,延长BC,作PD⊥BC,交点为D,延长CA,作PE⊥CA于点E,同理可证,四边形CDPE是正⽅形,∴CD=DP=PE=EC,同理可得,在直⾓△AEP中,(EC﹣1)2+EP2=AP2,∴(PD﹣1)2+PD2=()2,解得,PD=;故选D.【点评】本题考查了勾股定理的运⽤,通过添加辅助线,可将问题转化到直⾓三⾓形中,利⽤勾股定理解答;考查了学⽣的空间想象能⼒.13.如图,四边形ABCD中,AB=AD,AD∥BC,∠ABC=60°,∠BCD=30°,BC=6,那么△ACD的⾯积是()A.B.C.2 D.【考点】勾股定理;含30度⾓的直⾓三⾓形.【专题】计算题.【分析】如图,过点A作AE⊥BC于E,过点D作DF⊥BC于F.构建矩形AEFD和直⾓三⾓形,通过含30度⾓的直⾓三⾓形的性质求得AE的长度,然后由三⾓形的⾯积公式进⾏解答即可.【解答】解:如图,过点A作AE⊥BC于E,过点D作DF⊥BC于F.设AB=AD=x.⼜∵AD∥BC,∴四边形AEFD是矩形,∴AD=EF=x.在Rt△ABE中,∠ABC=60°,则∠BAE=30°,∴BE=AB=x,∴DF=AE==x,在Rt△CDF中,∠FCD=30°,则CF=DF?cot30°=x.⼜∵BC=6,∴BE+EF+CF=6,即x+x+x=6,解得x=2∴△ACD的⾯积是:AD?DF=x×x=×22=,故选:A.【点评】本题考查了勾股定理,三⾓形的⾯积以及含30度⾓的直⾓三⾓形.解题的难点是作出辅助线,构建矩形和直⾓三⾓形,⽬的是求得△ADC的底边AD以及该边上的⾼线DF的长度.⼆、填空题(共15⼩题)14.如图,在平⾯直⾓坐标系中,点A,B的坐标分别为(﹣6,0)、(0,8).以点A为圆⼼,以AB长为半径画弧,交x正半轴于点C,则点C的坐标为(4,0).【考点】勾股定理;坐标与图形性质.【分析】⾸先利⽤勾股定理求出AB的长,进⽽得到AC的长,因为OC=AC﹣AO,所以OC求出,继⽽求出点C的坐标.【解答】解:∵点A,B的坐标分别为(﹣6,0)、(0,8),∴AO=6,BO=8,∴AB==10,∵以点A为圆⼼,以AB长为半径画弧,∴AB=AC=10,∴OC=AC﹣AO=4,∵交x正半轴于点C,∴点C的坐标为(4,0),故答案为:(4,0).【点评】本题考查了勾股定理的运⽤、圆的半径处处相等的性质以及坐标与图形性质,解题的关键是利⽤勾股定理求出AB的长.15.在Rt△ABC中,CA=CB,AB=9,点D在BC边上,连接AD,若tan∠CAD=,则BD的长为 6 .【考点】勾股定理;等腰直⾓三⾓形;锐⾓三⾓函数的定义.【分析】根据等腰直⾓三⾓形的性质可求AC,BC的长,在Rt△ACD中,根据锐⾓三⾓函数的定义可求CD的长,BD=BC﹣CD,代⼊数据计算即可求解.【解答】解:如图,∵在Rt△ABC中,CA=CB,AB=9,∴CA2+CB2=AB2,∴CA=CB=9,∵在Rt△ACD中,tan∠CAD=,∴CD=3,∴BD=BC﹣CD=9﹣3=6.故答案为:6.【点评】综合考查了等腰直⾓三⾓形的性质,勾股定理,锐⾓三⾓函数的定义,线段的和差关系,难度不⼤.16.我国汉代数学家赵爽为了证明勾股定理,创制了⼀幅“弦图”,后⼈称其为“赵爽弦图”(如图(1)).图(2)由弦图变化得到,它是由⼋个全等的直⾓三⾓形拼接⽽成,记图中正⽅形ABCD、正⽅形EFGH、正⽅形MNKT的⾯积分别为S1、S2、S3.若正⽅形EFGH的边长为2,则S1+S2+S3= 12 .【考点】勾股定理的证明.。
华师大版八年级上册数学第14章 勾股定理含答案(精练)

华师大版八年级上册数学第14章勾股定理含答案一、单选题(共15题,共计45分)1、下列各组数中,是直角三角形的三条边长的是()A.1,3,B.7,24,25C.2,3,D.3,4,62、以下列各组数为边长,能构成直角三角形的是()A.1、4、17B.7、8、9C.4、3、5D. 、、3、在数学拓展课《折叠矩形纸片》上,小林折叠矩形纸片ABCD进行如下操作:①把△ABF翻折,点B落在CD边上的点E处,折痕AF交BC边于点F;②把△ADH翻折,点D落在AE边长的点G处,折痕AH交CD边于点H.若AD=6,AB=10,则的值是().A. B. C. D.4、下列三条线段不能组成直角三角形的是( )A.5、4、3B.13、12、5C.10、8、6D.30、24、105、在直角三角形ABC中,斜边AB=2,则AB2+BC2+AC2的值是()A.2B.4C.6D.86、如图,分别以Rt△ABC的三条边为边向外作正方形,面积分别记为S1,S 2, S3.若S1= 36,S2= 64,则S3=()A.8B.10C.80D.1007、如图是我国数学家赵爽的股弦图,它由四个全等的直角三角形和小正方形拼成的一个大正方形.已知大正方形的面积是l3,小正方形的面积是1,直角三角形的较短直角边长为a,较长直角边长为b,那么值为()A.25B.9C.13D.1698、如图,是一段楼梯,高BC是1.5m,斜边AC是2.5m,如果在楼梯上铺地毯,那么至少需要地毯()A.2.5mB.3mC.3.5mD.4m9、下列各组数中,能构成直角三角形的一组是()A.6,8,12B.1,4,C.3,4,5D.2,2,10、如图,菱形ABCD中,AB=2,∠A=120°,点P,Q,K分别为线段BC,CD,BD上的任意一点,则PK+QK的最小值为()A. B. C. D.11、下列几组数不能作为直角三角形三边长的是().A.8、15、17B.7、24、25C.30、40、50D.32、60、8012、如图1,长、宽均为3,高为8的长方体容器,放置在水平桌面上,里面盛有水,水面高为6,绕底面一棱进行旋转倾斜后,水面恰好触到容器口边缘,图2是此时的示意图,则图2中水面高度为( )A. B. C. D.13、如图,的弦垂直平分半径,垂足为,若,则的长为()A. B. C. D.14、如图所示:数轴上点A所表示的数为a,则a的值是()A. +1B.- +1C. -1D.15、如图,是一个三级台阶,它的每一级的长、宽、高分别为20dm、3dm、2dm,A和B是这个台阶两个相对的端点,A点有一只蚂蚁,想到B点去吃可口的食物,则蚂蚁沿着台阶面爬到B点的最短路程是()A.20B.25C.20D.25二、填空题(共10题,共计30分)16、如图,在矩形ABCD中,AD=3AB=3 ,点P是AD的中点,点E在BC 上,CE=2BE,点M、N在线段BD上.若△PMN是等腰三角形且底角与∠DEC相等,则MN=________.17、如图,AB是⊙O的直径,弦CD⊥AB于点E.若AB=8,AE=1,则弦CD的长是________.18、如图,菱形ABCD的对角线AC、BD交于点O,且AC=16cm,BD=12cm,则菱形ABCD的高DH=________cm.19、已知如图,△ABC为等腰三角形,D为CB延长线上一点,连AD且∠DAC=45°,BD=1,CB=4,则AC长为________.20、一直角三角形的两边长分别为5和12,则第三边的长是________.21、如图,线段、,那么线段的长度为________.22、如图,过圆外一点作圆的一条割线交于点,若,,且,则________.23、如图所示,⊙M与x轴相交于点A(2,0),B(8,0),与y轴相切于点C,则圆心M的坐标是________.24、如图,在等腰直角△ABC中,AB=4,点D在边AC上一点且AD=1,点E是AB边上一点,连接DE,以线段DE为直角边作等腰直角△DEF( D、E、F三点依次呈逆时针方向),当点F恰好落在BC边上时,则AE的长是________.25、如图在中,,,,分别以为直径作半圆,如图阴影部分面积记为、,则________.三、解答题(共5题,共计25分)26、已知,在△ABC中,∠ACB=90°,CD⊥AB垂足为D,BC=6,AC=8,求AB与CD的长.27、校车安全是近几年社会关注的热点问题,安全隐患主要是超速和超载.某中学九年级数学活动小组进行了测试汽车速度的实验,如图,先在笔直的公路l旁选取一点A,在公路l上确定点B、C,使得AC⊥l,∠BAC=60°,再在AC 上确定点D,使得∠BDC=75°,测得AD=40米,已知本路段对校车限速是50千米/时,若测得某校车从B到C匀速行驶用时10秒,问这辆车在本路段是否超速?请说明理由(参考数据:=1.41,=1.73)28、如图,已知AD是⊙O的直径,BC是⊙O的弦,AD⊥BC,垂足为点E,AE=BC=16,求⊙O的直径.29、如图,长方体盒子(无盖)的长、宽、高分别是12cm,8cm,30cm,在AB 中点C处有一滴蜜糖,一只小虫从P处爬到C处去吃,有无数种走法,则最短路程是多少?30、如图,AD∥BC,∠A=90°,E是AB上的一点,且AD=BE,∠1=∠2.(1)△ADE与△BEC全等吗?请说明理由;(2)若AD=3,AB=7,请求出△ECD的面积.参考答案一、单选题(共15题,共计45分)1、B2、C4、D5、D6、D7、A8、C9、C10、B11、D12、A13、D14、C15、D二、填空题(共10题,共计30分)16、17、18、19、20、21、22、24、25、三、解答题(共5题,共计25分)26、27、29、30、。
华东师大版八年级:勾股定理

勾股定理1、掌握勾股定理与逆定理2、会用逆定理判断三角形的形状3、会用勾股定理及逆定理解决实际问题一、勾股定理:1.勾股定理定义:如果直角三角形的两直角边长分别为a ,b ,斜边长为c ,那么222c b a =+.即直角三角形两直角边的平方和等于斜边的平方。
勾:直角三角形较短的直角边 股:直角三角形较长的直角边 弦:斜边2.勾股定理的逆定理:如果三角形的三边长a ,b ,c 有下面关系:222c b a =+,那么这个三角形是直角三角形。
勾股数:满足222c b a =+的三个正整数叫做勾股数(注意:若a ,b ,c 、为勾股数,那么ka ,kb ,kc 同样也是勾股数组。
)*附:常见勾股数:3,4,5; 6,8,10; 9,12,15; 5,12,133.判断直角三角形:如果三角形的三边长a ,b ,c 满足222c b a =+,那么这个三角形是直角三角形。
(经典直角三角形:勾三、股四、弦五)其他方法:(1)有一个角为90°的三角形是直角三角形。
(2)有两个角互余的三角形是直角三角形。
用它判断三角形是否为直角三角形的一般步骤是: (1)确定最大边(不妨设为c );(2)若222b a c +=,则△ABC 是以△C 为直角的三角形; 若222c b a <+,则此三角形为钝角三角形(其中c 为最大边); 若222c b a >+,则此三角形为锐角三角形(其中c 为最大边)教学目标学习内容知识梳理注意:(1)直角三角形斜边上的中线等于斜边的一半(2)在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半。
(3)在直角三角形中,如果一条直角边等于斜边的一半,那么这条直角边所对的角等于30°。
4. 反证法:(1)反证法:是一种论证方式,他首先假设某命题不成立(即在原命题的条件下,结论不成立),然后推理出明显矛盾的结果,从而下结论说原假设不成立,原命题得证。
勾股定理--华师大版

勾股定理
勾股定理(gou-gu theorem)
如果直角三角形两直角边分别为a、b, 斜边为c,那么 c 2 2 2 a
a b c
b
即 直角三角形两直角边的平方和等 于斜边的平方。
1 C2 = (a+b)2 – 4· ab = a2 + b2 2
例1:在Rt △ ABC中,∠C=90°
1)如果 a=10, b=24 ,那么 c= 2)如果 a=15 , c=25 , 那么 b= 3)如果 c=61 , b=60 ,那么a=
(1)求BC边上的高。
(2)求△ABC的面积
sunbet官网手机版 sunbet官网手机版
stz68qus
头夫妇后,耿正兄妹三人含泪收拾老人的三间正房。耿英发现,里间地上麻袋里的板蓝根实在不少,就对哥哥说:“要不咱们 把这药给对门儿和隔壁一些吧,看那两个当家人确实病得不轻呢!”于是,耿正给每家各送了几包,告诉他们给病人煮水喝。 他们都千恩万谢地收下了,并且说:“已经在喝着呢,只是快用完了。”一个多月后,这场可怕的疫情终于彻底消失了。而此 时,景德镇上七、八十岁的老人几乎无一幸免,就连那位可敬的张老太医,也到地下继续救死扶伤去了。随同他们去了的,还 有几十个小娃儿和十几个年轻人和壮年人,那种笼罩全镇的悲伤气氛一直持续了很长的一段时间。不过,对门儿的张老大和隔 壁的年轻男人,后来倒是都康复了。疫情过去之后,耿正兄妹三人利用仅剩的几十两银子,开始苦苦经营老梁头夫妇赠送给他 们的“梁计小饭店”。入夏以后,天气陡然炎热起来,但清晨和早饭后的一段时光还是相对凉爽的。因此,耿正每天都会尽量 地早点儿去菜市场,选购一些小饭店里当天中午和晚上,以及次日早餐所需要的菜蔬。那一日早餐当口接近尾声时,耿英看看 客人已经不太多了,就对哥哥说:“有小直子和我忙活就行了。你自个儿吃点儿饭,快去买菜吧,去晚了又该受热遭罪了!” 耿正答应着,简单吃喝了几口后,就背起一个大竹筐去附近的菜市场买菜去了。当他匆匆返回来走到巷子口上的时候,突然意 外地遇见了那两位善良老房东的儿子!看到这位与其爹娘同样善良的叔叔辈儿正在往巷子外面走,耿正高兴地迎上前去问候: “叔,您回来啦,爷爷和奶奶可好!”老房东的儿子怔一怔,重重叹一口气悲伤地说:“唉,我的爹娘已经在今年儿春上的那 场瘟疫中都给没了。当时县城周围三里范围内宵禁着不让出入,我和妹妹只好把他们掩埋在县衙指定的公葬墓地里了。老家的 这个宅院儿我早就不想留着了,只是爹娘活着的时候坚持不让我变卖掉。如今他们已经不在了,我还是早点儿处理掉吧,免得 日久破落了更不值钱儿。”耿正听了这些,除了伤感之外一时无话。抬头看看日头才一杆子高,就问他:“那您这是要去哪里 啊?”“我已经把老院子作结给隔壁的堂弟了,这就赶回县城去!”耿正赶快说:“叔您不要着急走,这天儿还早着呢,进我 们小店里来坐会儿吧!您不知道,梁爷爷和梁奶奶也没有逃过那场可怕的瘟疫,都没了!梁爷爷临终之前,把这个小院儿和门 面店赠送给我们啦。我们现在已经没有多少做其他生意的本钱了,只能先惨淡经营着这个小饭店。您回来了,咱们正好坐坐, 说说话。我们兄妹们经常念叨爷爷奶奶和您呢!”老房东的儿子连连摇头长叹,说:“唉,这些我已经都听说了啊。说起来, 我爹娘去了我那儿以后,也是经常念叨你们呢。说心里话,我这次回
华师大版初中数学八年级上册《14.1 勾股定理》同步练习卷(含答案解析
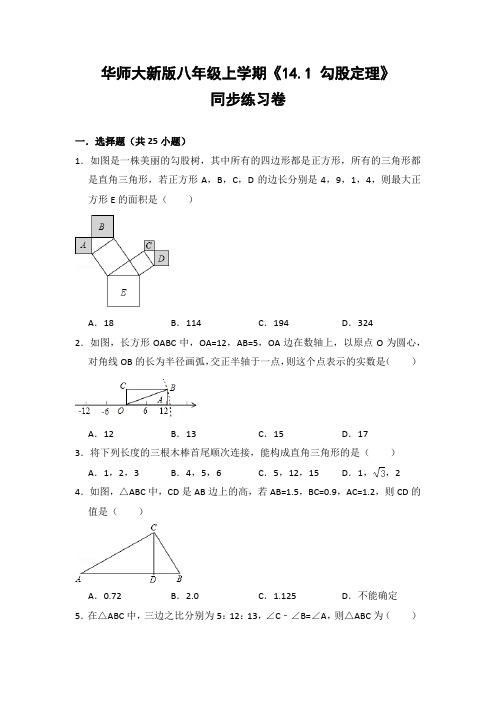
华师大新版八年级上学期《14.1 勾股定理》同步练习卷一.选择题(共25小题)1.如图是一株美丽的勾股树,其中所有的四边形都是正方形,所有的三角形都是直角三角形,若正方形A,B,C,D的边长分别是4,9,1,4,则最大正方形E的面积是()A.18B.114C.194D.3242.如图,长方形OABC中,OA=12,AB=5,OA边在数轴上,以原点O为圆心,对角线OB的长为半径画弧,交正半轴于一点,则这个点表示的实数是()A.12B.13C.15D.173.将下列长度的三根木棒首尾顺次连接,能构成直角三角形的是()A.1,2,3B.4,5,6C.5,12,15D.1,,2 4.如图,△ABC中,CD是AB边上的高,若AB=1.5,BC=0.9,AC=1.2,则CD的值是()A.0.72B.2.0C.1.125D.不能确定5.在△ABC中,三边之比分别为5:12:13,∠C﹣∠B=∠A,则△ABC为()A.锐角三角形B.直角三角形C.钝角三角形D.等腰直角三角形6.如图,两个较大正方形的面积分别为225、289,则字母A所代表的正方形的面积为()A.4B.8C.16D.647.如图,由四个全等的直角三角形和一个小正方形拼成一个大正方形.设直角三角形较长直角边长为a,较短直角边长为b,若(a+b)2=21,大正方形的面积为13.则小正方形的面积为()A.3B.4C.5D.68.如图,在四边形ABCD中,AD∥BC,∠C=90°,△BCD与△BC′D关于直线BD 轴对称,BC=6,CD=3,点C与点C′对应,BC′交AD于点E,则线段DE的长为()A.3B.C.5D.9.如图,在4×4的正方形网格中,△ABC的顶点都在格点上,下列结论错误的是()A.AB=5B.∠C=90°C.AC=2D.∠A=30°10.如图,OA=,以OA为直角边作Rt△OAA1,使∠AOA1=30°,再以OA1为直角边作Rt△OA1A2,使∠A1OA2=30°,……,依此法继续作下去,则A1A2的长为()A.B.C.D.11.如图,在△ABC中,点M是AC边上一个动点.若AB=AC=10,BC=12,则BM的最小值为()A.8B.9.6C.10D.4 512.一个三角形的三边长分别为3,4和5,那么它长边上的高线长为()A.5B.2.5C.2.4D.213.如图,△ABC的顶点A,B,C在边长为1的正方形网格的格点上,BD⊥AC 于点D,则BD的长为()A.B.C.D.14.如图,△ABC是腰长为2的等腰直角三角形,△BCD是直角三角形,且∠D=30°,则两个三角形重叠部分(△OBC)的面积是()A.3﹣B.2﹣C.1D.1+15.如图,在四边形ABCD中,AB=12cm,BC=3cm,CD=4cm,∠C=90°,当AD 为多少时,∠ABD=90°()A.13B.6C.12D.616.直角三角形的两边长分别为6和8,那么它的第三边长度为()A.8B.10C.8或2D.10或217.△ABC的三边分别为a,b,c,下列条件:①∠A=∠B﹣∠C;②a2=(b+c)(b﹣c);③a:b:c=3:4:5.其中能判断△ABC是直角三角形的条件个数有()A.0个B.1个C.2个D.3个18.如图图中,不能用来证明勾股定理的是()A.B.C.D.19.如图Rt△ABC,∠C=90°,分别以各边为直径作半圆,图中阴影部分在数学史上称为“希波克拉底月牙”;当AC=3,BC=4时,计算阴影部分的面积为()A.6B.6πC.10πD.1220.Rt△ABC中,斜边BC=2,则AB2+BC2+CA2=()A.8B.6C.4D.无法计算21.如图,已知Rt△ABC中,∠ABC=90°,分别以AB、BC、AC为直径作半圆,面积分别记S1,S2,S3,若S1=4,S2=9,则S3的值为()A.13B.5C.11D.322.如图,AB⊥AC,AD⊥BC,垂足为D,AB=3,AC=4,AD=,BD=,则点B 到直线AD的距离为()A.B.C.3D.423.如图是由“赵爽弦图”变化得到的,它由八个全等的直角三角形拼接而成,记图中正方形ABCD、正方形EFGH、正方形MNPQ的面积分别为S1、S2、S3.若S1+S2+S3=60,则S2的值是()A.12B.15C.20D.3024.如图,已知直角三角形的三边长分别为a、b、c,以直角三角形的三边为边(或直径),分别向外作等边三角形、半圆、等腰直角三角形和正方形.那么,这四个图形中,其面积S1、S2、S3满足S1+S2=S3的个数是()A.1B.2C.3D.425.一个直角三角形的直角边是24,斜边是25,则斜边上的高为()A.7B.C.168D.25二.填空题(共13小题)26.一个直角三角形的两直角边长分别是3cm和2cm,则第三边长cm.27.如图,图中的所有三角形都是直角三角形,所有四边形都是正方形,正方形A的面积为40,另外四个正方形中的数字8,x,10,y分别表示该正方形面积,则x+y=.28.如图,Rt△ABC中,∠B=90°,AB=8cm,BC=6cm,D点从A出发以每秒1cm 的速度向B点运动,当D点运动到AC的中垂线上时,运动时间为秒.29.如图,在Rt△ABC中,∠C=90°,AB=5cm,AC=3cm,动点P从点B出发,沿射线BC以2cm/s的速度移动设运动的时间为ts当t=时,△ABP为直角三角形.30.如图是一种“羊头”形图案,其作法是:从正方形①开始,以它的一边为斜边,向外作等腰直角三角形,然后再以其直角边为边,分别向外作正方形②和②′,…依此类推,若正方形①的边长为64m,则正方形⑨的边长为cm.31.已知一等腰三角形有两边长分别是10cm和12cm,则底边上的高为.32.已知△ABC的面积为24,∠C=90°,若AC与BC的长的和是14,则AB的长是.33.勾股定理a2+b2=c2本身就是一个关于a,b,c的方程,满足这个方程的正整数解(a,b,c)通常叫做勾股数组.毕达哥拉斯学派提出了一个构造勾股数组的公式,根据该公式可以构造出如下勾股数组:(3,4,5),(5,12,13),(7,24,25),….分析上面勾股数组可以发现,4=1×(3+1),12=2×(5+1),24=3×(7+1),…分析上面规律,第5个勾股数组为.34.已知直角三角形的两直角边长分别是6,8,则它的周长为.35.我国汉代数学家赵爽为了证明勾股定理,创制了一副“弦图”,后人称其为“赵爽弦图”如图①是我国古代著名的“赵爽弦图”的示意图,它是由四个全等的直角三角形围成的.若较短的直角边BC=5,将四个直角三角形中较长的直角边分别向外延长一倍,得到图②所示的“数学风车”,若△BCD的周长是30,则这个风车的外围周长是.36.若一个直角三角形的一条直角边为12cm,另一条直角边长比斜边短4cm,则斜边长为.37.如图,已知△ABC中,AB=10,AC=8,BC=6,DE是AC的垂直平分线,DE 交AB于点D,连接CD,则CD=.38.若一个三角形的三边长分别是6、8、a,若这个三角形是直角三角形,则a 的最小值是.三.解答题(共19小题)39.细心观察图形,认真分析各式,然后回答问题:(1)推算出OA10的长和S10的值.(2)直接用含n(n为正整数)的式子表示OA n的长和S n的值.(3)求S12+S22+S32+…+S102的值.40.在△ABC中,AB=30,BC=28,AC=26.求△ABC的面积.某学习小组经过合作交流给出了下面的解题思路,请你按照他们的解题思路完成解答过程.41.阅读:所谓勾股数就是满足方程x2+y2=z2的正整数解,即满足勾股定理的三个正整数构成的一组数.我国古代数学专著《九章算术》一书中,在历史上第一次给出该方程的解为x=(m2﹣n2),y=mn,z=(m2+n2),其中m>n >0,m、n是互质的奇数.应用:已知某直角三角形的三边长满足上述勾股数,其中一边长为37,且n=5,求该直角三角形另两边的长.42.阅读并回答问题:能够成为直角三角形三条边长的三个正整数a,b,c,称为勾股数,在一次数学活动课上,王老师设计了如下数表:(1)请你分别现察a,b,c与n之间的关系,并用含自然数n(n>1)的代数式表示:a=,b=,c=.(2)猜想:以a,b,c为边的三角形是否为直角三角形?并证明你的猜想.(3)观察下列勾股数32+42=52,52+122=132,72+242=252,92+402=412,分析其中的规律,写出第五组勾股数.43.如图,已知CD=6m,AD=8m,∠ADC=90°,BC=24m,AB=26m;求图中阴影部分的面积.44.如图,Rt△ABC中,∠B=90°,AB=3,BC=4,CD=12,AD=13,点E是AD的中点,求CE的长.45.如图,已知四边形ABCD中,AB∥CD,BC=AD=4,AB=CD=10,∠DCB=90°,E为CD边上的一点,DE=7,动点P从点A出发,以每秒1个单位的速度沿着边AB向终点B运动,连接PE,设点P运动的时间为t秒.(1)求BE的长;(2)若△BPE为直角三角形,求t的值.46.如图,在Rt△ABC中,∠C=90°,AB=10cm,AC=6cm,动点P从点B出发沿射线BC以2cm/s的速度移动,设运动的时间为t秒.(1)求BC边的长;(2)当△ABP为直角三角形时,求t的值;(3)当△ABP为等腰三角形时,求t的值.47.如图,△ABC中,∠C=90°,AB=10cm,BC=6cm,若动点P从点C开始,按C→A→B→C的路径运动,且速度为每秒1cm,设出发的时间为t秒.(1)出发2秒后,求△ABP的周长;(2)当t为几秒时,BP平分∠ABC;(3)问t为何值时,△BCP为等腰三角形?48.如图,△ABC中,∠ACB=90°,AB=5cm,BC=3cm,若点P从点A出发,以每秒2cm的速度沿折线A﹣C﹣B﹣A运动,设运动时间为t秒(t>0).(1)若点P在AC上,且满足PA=PB时,求出此时t的值;(2)若点P恰好在∠BAC的角平分线上,求t的值;(3)在运动过程中,直接写出当t为何值时,△BCP为等腰三角形.49.如图,△ABC中,∠C=90°,AB=10cm,BC=6cm,若动点P从点C开始,按C→A→B→C的路径运动,且速度为每秒1cm,设出发的时间为t秒.(1)出发2秒后,求△ABP的面积;(2)当t为几秒时,BP平分∠ABC;(3)问t为何值时,△BCP为等腰三角形?50.阅读下面的情景对话,然后解答问题:(1)理解:①根据“奇异三角形”的定义,请你判断:“等边三角形一定是奇异三角形”吗?(填是或不是)②若某三角形的三边长分别为1、、2,则该三角形(是或不是)奇异三角形.(2)探究:若Rt△ABC是奇异三角形,且其两边长分别为2、2,则第三边的长为,且这个直角三角形的三边之比为(从小到大排列,不得含有分母).(3)设问:请提出一个和奇异三角形有关的问题.(不用解答)51.如图,已知△ABC中,∠B=90°,AB=8cm,BC=6cm,P、Q是△ABC边上的两个动点,其中点P从点A开始沿A→B方向运动,且速度为每秒1cm,点Q 从点B开始沿B→C方向运动,且速度为每秒2cm,它们同时出发,设出发的时间为t秒.(1)当t=2秒时,求PQ的长;(2)求出发时间为几秒时,△PQB是等腰三角形?(3)若Q沿B→C→A方向运动,则当点Q在边CA上运动时,求能使△BCQ成为等腰三角形的运动时间.52.如图,在正方形网格中,请按要求画以线段AB为边的网格三角形.(网格三角形是指各顶点在格点上的三角形)(1)画出一个面积为3的网格三角形;(2)画出一个两条边相等的网格三角形.53.如图,在每个小正方形的边长均为1的方格纸中有一条线段AB,线段AB的两个端点均在小正方形的顶点上,请在图①、图②中各画一个三角形,它们的顶点均在小正方形的顶点上,且满足以下要求:(1)在图①中以AB为斜边画Rt△ABC;(2)在图②中以AB为边画等腰三角形ABD,且△ABD只有两条边长为无理数.54.在下面的正方形网格中,每个小正方形的边长都是1,正方形的顶点称为格点,请在图中以格点为顶点,画出一个三角形,使三边长分别为3,,5,并求此三角形的面积.55.在Rt△ABC中,AC=8,BC=6,一个运动的点P 从点A出发,以每秒钟1个单位的速度向点C运动,同时一个运动的点Q从点B出发,以每秒钟2个单位的速度向点A运动,当一个点到达终点时另一个点也随之停止.运动的时间为t秒.(1)用含t的代数式表示线段AQ和CP.(2)t为何值时,AP=AQ?(3)t为何值时,AP=BP.56.如图,已知△ABC中,∠B=90°,AB=8cm,BC=6cm,P、Q是△ABC边上的两个动点,其中点P从点A开始沿A→B方向运动,且速度为每秒1cm,点Q从点B开始沿B→C→A方向运动,且速度为每秒2cm,它们同时出发,设出发的时间为t秒.(1)出发2秒后,求PQ的长;(2)从出发几秒钟后,△PQB第一次能形成等腰三角形?(3)当点Q在边CA上运动时,求能使△BCQ成为等腰三角形的运动时间.57.已知:在△ABC中,∠C=90°,斜边AB为10,其中一条直角边为6,求另一条直角边AC.华师大新版八年级上学期《14.1 勾股定理》同步练习卷参考答案与试题解析一.选择题(共25小题)1.如图是一株美丽的勾股树,其中所有的四边形都是正方形,所有的三角形都是直角三角形,若正方形A,B,C,D的边长分别是4,9,1,4,则最大正方形E的面积是()A.18B.114C.194D.324【分析】根据正方形的面积公式,勾股定理,得到正方形A,B,C,D的面积和即为最大正方形的面积【解答】解:根据勾股定理的几何意义,可得A、B的面积和为S1,C、D的面积和为S2,S1=42+92,S2=12+42,则S3=S1+S2,∴S3=16+81+1+16=114.故选:B.【点评】本题考查的是勾股定理,如果直角三角形的两条直角边长分别是a,b,斜边长为c,那么a2+b2=c2.2.如图,长方形OABC中,OA=12,AB=5,OA边在数轴上,以原点O为圆心,对角线OB的长为半径画弧,交正半轴于一点,则这个点表示的实数是()A.12B.13C.15D.17【分析】根据勾股定理求出OB,根据实数与数轴的关系解答.【解答】解:在Rt△OAB中,OB===13,∴这个点表示的实数是13,故选:B.【点评】本题考查的是勾股定理,实数与数轴,掌握如果直角三角形的两条直角边长分别是a,b,斜边长为c,那么a2+b2=c2是解题的关键.3.将下列长度的三根木棒首尾顺次连接,能构成直角三角形的是()A.1,2,3B.4,5,6C.5,12,15D.1,,2【分析】判断是否为直角三角形,只要验证两小边的平方和等于最长边的平方即可.【解答】解:A、12+22≠32,故不能组成直角三角形,错误;B、42+52≠62,故不能组成直角三角形,错误;C、52+122≠152,故不能组成直角三角形,错误;D、12+()2=22,故能组成直角三角形,正确.故选:D.【点评】本题考查勾股定理的逆定理的应用.判断三角形是否为直角三角形,已知三角形三边的长,只要利用勾股定理的逆定理加以判断即可.4.如图,△ABC中,CD是AB边上的高,若AB=1.5,BC=0.9,AC=1.2,则CD的值是()A.0.72B.2.0C.1.125D.不能确定【分析】先根据勾股定理的逆定理证明△ABC是直角三角形,根据计算直角三角形的面积的两种计算方法求出斜边上的高CD.【解答】解:∵AB=1.5,BC=0.9,AC=1.2,∴AB2=1.52=2.25,BC2+AC2=0.92+1.22=2.25,∴AB2=BC2+AC2,∴∠ACB=90°,∵CD是AB边上的高,∴S=,△ABC1.5CD=1.2×0.9,CD=0.72,故选:A.【点评】该题主要考查了勾股定理的逆定理、三角形的面积公式及其应用问题;解题的方法是运用勾股定理首先证明△ABC为直角三角形;解题的关键是灵活运用三角形的面积公式来解答.5.在△ABC中,三边之比分别为5:12:13,∠C﹣∠B=∠A,则△ABC为()A.锐角三角形B.直角三角形C.钝角三角形D.等腰直角三角形【分析】根据勾股定理的逆定理以及三角形内角和定理均可判断△ABC为直角三角形.【解答】解:∵在△ABC中,三边之比分别为5:12:13,∠C﹣∠B=∠A,而52+122=132,∠A+∠B+∠C=180°,∴△ABC为直角三角形,∠C=∠A+∠B=90°.故选:B.【点评】本题考查了勾股定理的逆定理:如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形就是直角三角形.也考查了三角形内角和定理.本题两个条件中只选择一个,仍然可以判定△ABC为直角三角形.6.如图,两个较大正方形的面积分别为225、289,则字母A所代表的正方形的面积为()A.4B.8C.16D.64【分析】根据正方形的面积等于边长的平方,由正方形PQED的面积和正方形PRQF的面积分别表示出PR的平方及PQ的平方,又三角形PQR为直角三角形,根据勾股定理求出QR的平方,即为所求正方形的面积.【解答】解:∵正方形PQED的面积等于225,∴即PQ2=225,∵正方形PRGF的面积为289,∴PR2=289,又△PQR为直角三角形,根据勾股定理得:PR2=PQ2+QR2,∴QR2=PR2﹣PQ2=289﹣225=64,则正方形QMNR的面积为64.故选:D.【点评】此题考查了勾股定理,以及正方形的面积公式.勾股定理最大的贡献就是沟通“数”与“形”的关系,它的验证和利用都体现了数形结合的思想,即把图形的性质问题转化为数量关系的问题来解决.能否由实际的问题,联想到用勾股定理的知识来求解是本题的关键.7.如图,由四个全等的直角三角形和一个小正方形拼成一个大正方形.设直角三角形较长直角边长为a,较短直角边长为b,若(a+b)2=21,大正方形的面积为13.则小正方形的面积为()A.3B.4C.5D.6【分析】观察图形可知,小正方形的面积=大正方形的面积﹣4个直角三角形的面积,利用已知(a+b)2=21,大正方形的面积为13,可以得出直角三角形的面积,进而求出答案.【解答】解:∵(a+b)2=21,∴a2+2ab+b2=21,∵大正方形的面积为13,∴2ab=21﹣13=8,∴小正方形的面积为13﹣8=5.故选:C.【点评】此题主要考查了勾股定理的应用,熟练应用勾股定理是解题关键.8.如图,在四边形ABCD中,AD∥BC,∠C=90°,△BCD与△BC′D关于直线BD 轴对称,BC=6,CD=3,点C与点C′对应,BC′交AD于点E,则线段DE的长为()A.3B.C.5D.【分析】首先根据题意得到BE=DE,然后根据勾股定理得到关于线段AB、AE、BE的方程,解方程即可解决问题.【解答】解:设ED=x,则AE=6﹣x,∵四边形ABCD为矩形,∴AD∥BC,∴∠EDB=∠DBC;由题意得:∠EBD=∠DBC,∴∠EDB=∠EBD,∴EB=ED=x;由勾股定理得:BE2=AB2+AE2,即x2=9+(6﹣x)2,解得:x=,∴ED=.故选:B.【点评】本题主要考查了几何变换中的翻折变换及其应用问题;解题的关键是根据翻折变换的性质,结合全等三角形的判定及其性质、勾股定理等几何知识,灵活进行判断、分析、推理或解答.9.如图,在4×4的正方形网格中,△ABC的顶点都在格点上,下列结论错误的是()A.AB=5B.∠C=90°C.AC=2D.∠A=30°【分析】根据勾股定理计算各边长,根据勾股定理逆定理计算角的度数.【解答】解:A、由勾股定理得:AB==5,故此选项正确;B、∵AC2=22+42=20,BC2=12+22=5,AB2=52=25,∴AB2=BC2+AC2,∴∠C=90°,故此选项正确;C、AC==2,故此选项正确;D、∵BC=,AB=5,∴∠A≠30°,故此选项不正确;本题选择错误的结论,故选:D.【点评】本题考查了勾股定理和逆定理及格点问题,熟练掌握勾股定理是关键.10.如图,OA=,以OA为直角边作Rt△OAA1,使∠AOA1=30°,再以OA1为直角边作Rt△OA1A2,使∠A1OA2=30°,……,依此法继续作下去,则A1A2的长为()A.B.C.D.【分析】由含30°角的直角三角形的性质和勾股定理求出OA1,即可得出结果.【解答】解:∵∠OAA1=90°,OA=,∠AOA1=30°,∴AA1=OA1,由勾股定理得:OA2+AA12=OA12,即()2+(OA1)2=OA12,解得:OA1=2,∵∠A1OA2=30°,∴A1A2的长=,故选:B.【点评】本题考查了勾股定理、含30°角的直角三角形的性质;熟练掌握勾股定理,通过计算得出规律是解决问题的关键.11.如图,在△ABC中,点M是AC边上一个动点.若AB=AC=10,BC=12,则BM的最小值为()A.8B.9.6C.10D.4 5【分析】作AD⊥BC于D,则∠ADB=90°,由等腰三角形的性质和勾股定理求出AD,当BM⊥AC时,BM最小;由△ABC的面积的计算方法求出BM的最小值.【解答】解:作AD⊥BC于D,如图所示:则∠ADB=90°,∵AB=AC,∴BD=BC=6,由勾股定理得:AD==8,当BM⊥AC时,BM最小,此时,∠BMC=90°,∵△ABC的面积=AC•BM=BC•AD,即×10×BM=×12×8,解得:BM=9.6,故选:B.【点评】本题考查了勾股定理、等腰三角形的性质、垂线段最短、三角形面积的计算方法;熟练掌握勾股定理,由三角形面积的计算方法求出BM的最小值是解决问题的关键.12.一个三角形的三边长分别为3,4和5,那么它长边上的高线长为()A.5B.2.5C.2.4D.2【分析】由于32+42=52,可知此三角形是直角三角形,利用面积相等可得×3×4=×5•h,解即可.【解答】解:∵32+42=52,∴此三角形是直角三角形,∴×3×4=×5•h,解得h=2.4.故选:C.【点评】本题考查了勾股定理逆定理.解题的关键是先证明三角形是直角三角形.13.如图,△ABC的顶点A,B,C在边长为1的正方形网格的格点上,BD⊥AC 于点D,则BD的长为()A.B.C.D.【分析】根据图形和三角形的面积公式求出△ABC的面积,根据勾股定理求出AC,根据三角形的面积公式计算即可.【解答】解:如图所示:S△ABC=×BC×AE=×BD×AC,∵AE=4,AC==5,BC=4即×4×4=×5×BD,解得:BD=.故选:C.【点评】本题主要考查了勾股定理的知识,解题的关键是利用勾股定理求出AC 的长,此题难度一般.14.如图,△ABC是腰长为2的等腰直角三角形,△BCD是直角三角形,且∠D=30°,则两个三角形重叠部分(△OBC)的面积是()A.3﹣B.2﹣C.1D.1+【分析】过O作OE⊥BC于E,设BE=x,求出OE和DC,根据相似得出比例式求出x,再根据三角形的面积公式求出即可.【解答】解:∵在Rt△DCB中,∠DCB=90°,∠D=30°,BC=2,∴DC=BC=2,过O作OE⊥BC于E,∵∠ABC=90°,∴OE∥AB,∴∠BOE=30°,△OEC∽△ABC,∴设BE=x,则OE=BE=x,=,∴=,解得:x=﹣1,即OE=x=3﹣,∴阴影部分的面积S=(3﹣)=3﹣,故选:A.【点评】本题考查了解直角三角形、相似三角形的性质和判定等知识点,能求出OE的长是解此题的关键.15.如图,在四边形ABCD中,AB=12cm,BC=3cm,CD=4cm,∠C=90°,当AD 为多少时,∠ABD=90°()A.13B.6C.12D.6【分析】根据勾股定理的逆定理满足AD2=BD2+AB2,可说明∠ABD=90°.【解答】解:在△BDC中,∠C=90°,BC=3cm,CD=4cm,根据勾股定理得,BD2=BC2+CD2,即BD==5cm.当∠ABD=90°时,AD2=BD2+AB2,其中AB=12cm,BD=5cm,则AD=cm=13cm,故选:A.【点评】本题考查了勾股定理的运用,考查了勾股定理逆定理的运用,本题中准确运用勾股定理与勾股定理的逆定理是解题的关键.16.直角三角形的两边长分别为6和8,那么它的第三边长度为()A.8B.10C.8或2D.10或2【分析】分8为直角边、8为斜边两种情况,根据勾股定理计算.【解答】解:当8为直角边时,斜边==10,当8为斜边时,另一条直角边==2,故选:D.【点评】本题考查的是勾股定理,如果直角三角形的两条直角边长分别是a,b,斜边长为c,那么a2+b2=c2.17.△ABC的三边分别为a,b,c,下列条件:①∠A=∠B﹣∠C;②a2=(b+c)(b﹣c);③a:b:c=3:4:5.其中能判断△ABC是直角三角形的条件个数有()A.0个B.1个C.2个D.3个【分析】根据三角形的内角和定理和已知求出最大角∠B的度数,即可判断①;根据已知得出a2+c2=b2,根据勾股定理的逆定理即可判断②;设a=3k,b=4k,c=5k求出a2+c2=b2,根据勾股定理的逆定理即可判断③.【解答】解:①∵∠A=∠B﹣∠C,∴∠A+∠C=∠B,∵∠A+∠B+∠C=180°,∴2∠B=180°,∴∠B=90°,∴△ABC是直角三角形,∴①正确;②a2=(b+c)(b﹣c),∴a2=b2﹣c2,∴a2+c2=b2,∴△BAC是直角三角形,∴②正确;③∵a:b:c=3:4:5,∴设a=3k,b=4k,c=5k,∵a2+b2=25k2,c2=25k2,∴a2+b2=c2,∴△ABC是直角三角形,∴③正确;故选:D.【点评】本题考查了勾股定理的逆定理和三角形的内角和定理的应用,主要考查学生的辨析能力,题目比较典型,难度适中.18.如图图中,不能用来证明勾股定理的是()A.B.C.D.【分析】根据图形的面积得出a,b,c的关系,即可证明勾股定理,分别分析得出即可.【解答】解:A,B,C都可以利用图形面积得出a,b,c的关系,即可证明勾股定理;故A,B,C选项不符合题意;D、不能利用图形面积证明勾股定理,故此选项正确.故选:D.【点评】此题主要考查了勾股定理的证明方法,根据图形面积得出是解题关键.19.如图Rt△ABC,∠C=90°,分别以各边为直径作半圆,图中阴影部分在数学史上称为“希波克拉底月牙”;当AC=3,BC=4时,计算阴影部分的面积为()A.6B.6πC.10πD.12【分析】根据勾股定理求出AB,分别求出三个半圆的面积和△ABC的面积,即可得出答案.【解答】解:在Rt△ACB中,∠ACB=90°,AC=3,BC=4,由勾股定理得:AB= ==5,所以阴影部分的面积S=×π×()2+×()2+﹣×π×()2=6,故选:A.【点评】本题考查了勾股定理和三角形的面积、圆的面积,能把不规则图形的面积转化成规则图形的面积是解此题的关键.20.Rt△ABC中,斜边BC=2,则AB2+BC2+CA2=()A.8B.6C.4D.无法计算【分析】利用勾股定理将AB2+AC2转化为BC2,再求值即可.【解答】解:∵Rt△ABC中,BC为斜边,BC=2,∴AB2+AC2=BC2=4,∴AB2+AC2+BC2=2BC2=2×4=8.故选:A.【点评】本题考查了勾股定理.正确判断直角三角形的直角边、斜边,利用勾股定理得出等式是解题的关键.21.如图,已知Rt△ABC中,∠ABC=90°,分别以AB、BC、AC为直径作半圆,面积分别记S1,S2,S3,若S1=4,S2=9,则S3的值为()A.13B.5C.11D.3【分析】由扇形的面积公式可知S1=•π•AC2,S2=•π•BC2,S3=•π•AB2,在Rt △ABC中,由勾股定理得AC2+BC2=AB2,即S1+S2=S3;【解答】解:∵S1=•π•AC2,S2=•π•BC2,S3=•π•AB2,在Rt△ABC中,由勾股定理得AC2+BC2=AB2,即S1+S2=S3;∵S1=4,S2=9,∴S3=13.故选:A.【点评】本题考查勾股定理的应用,难度适中,解题关键是对勾股定理的熟练掌握及灵活运用,记住S1+S2=S3;22.如图,AB⊥AC,AD⊥BC,垂足为D,AB=3,AC=4,AD=,BD=,则点B 到直线AD的距离为()A.B.C.3D.4【分析】根据点到直线的距离即可判定.【解答】解:∵BD⊥AD,∴点B到直线AD的距离为线段BD的长,故选:A.【点评】本题考查勾股定理、点到直线的距离等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.23.如图是由“赵爽弦图”变化得到的,它由八个全等的直角三角形拼接而成,记图中正方形ABCD、正方形EFGH、正方形MNPQ的面积分别为S1、S2、S3.若S1+S2+S3=60,则S2的值是()A.12B.15C.20D.30【分析】设每个小直角三角形的面积为m,则S1=4m+S2,S3=S2﹣4m,依据S1+S2+S3=60,可得4m+S2+S2+S2﹣4m=60,进而得出S2的值.【解答】解:设每个小直角三角形的面积为m,则S1=4m+S2,S3=S2﹣4m,因为S1+S2+S3=60,所以4m+S2+S2+S2﹣4m=60,即3S2=60,解得S2=20.故选:C.【点评】此题主要考查了勾股定理和正方形、全等三角形的性质的运用,证明勾股定理时,用几个全等的直角三角形拼成一个规则的图形,然后利用大图形的面积等于几个小图形的面积和化简整理得到勾股定理.24.如图,已知直角三角形的三边长分别为a、b、c,以直角三角形的三边为边(或直径),分别向外作等边三角形、半圆、等腰直角三角形和正方形.那么,这四个图形中,其面积S1、S2、S3满足S1+S2=S3的个数是()A.1B.2C.3D.4【分析】分别表示出S1、S2、S3的面积,根据勾股定理判断即可.【解答】解:∵直角三角形的三边长分别为a、b、c,∴a2+b2=c2,图1中,S1=×a×a=a2,S2=b2,S3=c2,则S1+S2=(a2+b2),S3=c2,∴S1+S2=S3,同理,图2、图3、图4,都符合S1+S2=S3,故选:D.【点评】本题考查的是勾股定理,如果直角三角形的两条直角边长分别是a,b,斜边长为c,那么a2+b2=c2.25.一个直角三角形的直角边是24,斜边是25,则斜边上的高为()A.7B.C.168D.25【分析】根据勾股定理求出直角三角形的另一条直角边的长,根据三角形的面积公式计算即可.【解答】解:设斜边上的高h,由勾股定理得,直角三角形的另一条直角边==7,则×24×7=×25×h,解得,h=,故选:B.【点评】本题考查的是勾股定理,如果直角三角形的两条直角边长分别是a,b,斜边长为c,那么a2+b2=c2.二.填空题(共13小题)26.一个直角三角形的两直角边长分别是3cm和2cm,则第三边长cm.【分析】根据勾股定理计算即可.【解答】解:由勾股定理得,第三边长==(cm),故答案为:.【点评】本题考查的是勾股定理,如果直角三角形的两条直角边长分别是a,b,斜边长为c,那么a2+b2=c2.27.如图,图中的所有三角形都是直角三角形,所有四边形都是正方形,正方形A的面积为40,另外四个正方形中的数字8,x,10,y分别表示该正方形面积,则x+y=22.【分析】先由S A=40,再根据勾股定理的几何意义,得到x+10+(8+y)=S A,由此得出x与y的数量关系.【解答】解:∵S A=40,根据勾股定理的几何意义,得x+10+(8+y)=S A=40,∴x+y=40﹣18=22,即x+y=22.【点评】本题考查了勾股定理的几何意义,要知道,以斜边边长为边长的正方形的面积是以两直角边边长为边长的正方形的面积之和.28.如图,Rt△ABC中,∠B=90°,AB=8cm,BC=6cm,D点从A出发以每秒1cm 的速度向B点运动,当D点运动到AC的中垂线上时,运动时间为秒.【分析】画出图形,根据勾股定理解答即可.【解答】解:如图所示:∵Rt△ABC中,∠B=90°,AB=8cm,BC=6cm,∴AC=,∵ED'是AC的中垂线,∴CE=5,连接CD',∴CD'=AD',在Rt△BCD'中,CD'2=BD'2+BC2,即AD'2=62+(8﹣AD')2,解得:AD'=,∴当D点运动到AC的中垂线上时,运动时间为秒,【点评】此题考查勾股定理的应用,关键是根据勾股定理构建直角三角形进行解答.29.如图,在Rt△ABC中,∠C=90°,AB=5cm,AC=3cm,动点P从点B出发,沿射线BC以2cm/s的速度移动设运动的时间为ts当t=2s或s时,△ABP为直角三角形.【分析】首先根据勾股定理求出BC的长度,再分两种情况:①当∠APB为直角时,②当∠BAP为直角时,分别求出此时的t值即可.【解答】解:∵∠C=90°,AB=5cm,AC=3cm,∴BC=4 cm.①当∠APB为直角时,点P与点C重合,BP=BC=4 cm,∴t=4÷2=2s.②当∠BAP为直角时,BP=2tcm,CP=(2t﹣4)cm,AC=3 cm,在Rt△ACP中,AP2=32+(2t﹣4)2,在Rt△BAP中,AB2+AP2=BP2,∴52+[32+(2t﹣4)2]=(2t)2,解得t=s.综上,当t=2s或s时,△ABP为直角三角形.故答案为:2s或s.【点评】本题考查了勾股定理以及勾股定理的逆定理的知识,解答本题的关键是掌握勾股定理的应用,以及分情况讨论,注意不要漏解.30.如图是一种“羊头”形图案,其作法是:从正方形①开始,以它的一边为斜边,向外作等腰直角三角形,然后再以其直角边为边,分别向外作正方形②和②′,…依此类推,若正方形①的边长为64m,则正方形⑨的边长为4cm.。
八年级数学上册《第十四章 勾股定理》单元测试卷及答案(华东师大版)

八年级数学上册《第十四章 勾股定理》单元测试卷及答案(华东师大版)一、选择题1.下列各组数据中是勾股数的是( )2.有一直角三角形纸片,∠C =90°BC =6,AC =8,现将∠ABC 按如图那样折叠,使点A 与点B 重合,折痕为DE ,则CE 的长为( )A .7B .74C .72D .43.在∠ABC 中,∠A 、∠B 、∠C 的对边分别为a 、b 、c ,下列条件中,能判断∠ABC 是直角三角形的是( )A .a =32,b =42,c =52B .a =b ,∠C =45° C .∠A :∠B :∠C =6:8:10D .a 3b 7,c =24.在∠ABC 中,已知4AB =,5BC =和41AC =)A .∠ABC 是锐角三角形B .∠ABC 是直角三角形且90C ∠= C .∠ABC 是钝角三角形D .∠ABC 是直角三角形且90B ∠=5.要说明命题“若a 2>b 2,则a >b”是假命题,能举的一个反例是( )A .a =3,b =2B .a ﹣3,b =2C .a ﹣=3,b =﹣1D .a =﹣1,b =36.如图,在∠ABC 中,AB =AC =10,BC =12,AD 平分∠BAC ,则AD 等于( )A .6B .7C .8D .97.如图,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形的边长是9cm ,则图中所有正方形的面积的和是( )A .264cmB .281cmC .2162cmD .2243cm8.将直角三角形的三条边长做如下变化,得到的新三角形仍是直角三角形的是( )A .同加一个相同的数B .同减一个相同的数C .同乘以一个相同的正整数D .同时平方9.如图,在ABC 中AB AC =,点P 为ABC 内一点,连接PA 、PB 、PC 且APB APC ∠≠∠求证:PB PC ≠用反证法证明时,第一步应假设( )A .AB AC ≠ B .PB PC = C .APB APC ∠=∠D .PBC PCB ∠≠∠10.如图,圆柱的底面周长是24,高是5,—只在A 点的蚂蚁沿侧面爬行,想吃到B 点的食物,需要爬行的最短路径是( )A .9B .13C .14D .245π+ 二、填空题11.6,一条直角边长为1,则另一条直角边长为 . 12.如图,每个小正方形的边长为1,则∠ABC 的度数为 度.13.反证法证明命题“同旁内角不互补的两条直线不平行”时,应先假设 .14.如图是某滑雪场U 型池的示意图,该U 型池可以看作是一个长方体去掉一个“半圆柱”而成,中间可供滑行部分的截面是半径为3的半圆,其边缘16AB CD ==,点E 在CD 上,4CE =一名滑雪爱好者从A 点滑到E 点时,他滑行的最短路程约为 (π取3).三、解答题15.如图,在ABC 中,AB=AC ,AD 平分BAC ∠,已知BC 10=,AD=12,求AC 的长.16.如图,在ABC 中,D 为AB 边上一点,已知AC=13,CD=12,AD=5,AB=BC .请判断ACD 的形状,并求出BC 的长.17.求证:对顶角相等(请画出图形,写出已知、求证、证明.)18.一个零件的形状如图所示,按规定BAC ∠应为直角,工人师傅测得90ADC ∠=︒,AD=3,CD=4,AB=12,BC=13请你帮他看一下,这个零件符合要求吗?为什么.四、综合题19.如图,在ABC 中60BAC ∠=︒,45B ∠=︒且AD 是BAC ∠的平分线,且3AC =CH AB ⊥于点H ,交AD 于点O .(1)求证:ACD 是等腰三角形; (2)求线段BD 的长.20.如图,ABC 的三边分别为5AC =,12BC =和13AB =,如果将ABC 沿AD 折叠,使AC恰好落在AB 边上.(1)试判断ABC 的形状,并说明理由; (2)求线段CD 的长.21.综合与实践美丽的弦图中蕴含着四个全等的直角三角形.(1)如图1,弦图中包含了一大一小两个正方形,已知每个直角三角形较长的直角边为a ,较短的直角边为b ,斜边长为c ,结合图1,试验证勾股定理;(2)如图2,将这四个直角三角形紧密地拼接,形成飞镖状,已知外围轮廓(实线)的周长为243OC = 求该飞镖状图案的面积;(3)如图3,将八个全等的直角三角形紧密地拼接,记图中正方形ABCD ,正方形EFGH ,正方形MNKT 的面积分别为123S S S ,,,若12342S S S ++=,求2S 的值.答案解析部分1.【答案】C【解析】【解答】解:A 、不是正整数,故不是勾股数,不符合题意;B 、(32)2+(42)2≠(52)2,故不是勾股数,不符合题意;C 、92+122=152,三边是整数,同时能构成直角三角形,故正确,符合题意;D 、不是正整数,故不是勾股数,不符合题; 故答案为:C.【分析】勾股数就是可以构成一个直角三角形三边的一组正整数,据此判断.2.【答案】B【解析】【解答】解:在Rt∠ACB 中,AC=8,BC=6∴2222=68AC BC ++. 根据翻折不变性得∠EDA∠∠EDB ∴EA=EB∴在Rt∠BCE 中,设CE=x ,则BE=AE=8-x ∴BE 2=BC 2+CE 2 ∴(8-x )2=62+x 2 解得x=74. 故答案为:B .【分析】在Rt∠ACB 中,利用勾股定理算出AB ,根据折叠性质得EA=EB ,在Rt∠BCE 中,设CE=x ,则BE=AE=8-x ,利用勾股定理建立方程,求解可得x 的值,从而得出答案.3.【答案】D【解析】【解答】解:A 、∵22337a b +=,2625c = ∴222+a b c ≠,不是直角三角形,故A 不符合题意;B 、 a =b ,∠C =45°∴∠A=∠B=180=67.5452︒︒-︒,不是直角三角形,故B 不符合题意;C 、∠A :∠B :∠C =6:8:10,解得∠C=180°×10=7524︒,不是直角三角形,故C 不符合题意; D 、 ∵2223277+==,∴是直角三角形,∠B 是直角,故D 符合题意故答案为:D .【分析】A 、分别计算a 2+b 2和c 2的值,是否满足a 2+b 2=c 2,根据勾股定理的逆定理即可判断求解;B 、由等边对等角可得∠A=∠B ,然后用三角形内角和定理可判断求解;C 、由三角形内角和定理并结合∠A 、∠B 、∠C 的比值计算即可判断求解;D 、分别计算a 2+b 2和c 2的值,是否满足a 2+b 2=c 2,根据勾股定理的逆定理即可判断求解.4.【答案】D【解析】【解答】解:由题意知216AB =,225BC =和241AC =∵222AB BC AC +=∴ABC 是直角三角形,且90B ∠=︒ 故答案为:D .【分析】利用勾股定理的逆定理逐项判断即可。
勾股定理的练习--华师大版

- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
练习13 勾股定理一、单选题1.直角三角形的两条边长为5和12,它的斜边长为()A.13 B.C.13或D.13或12【解答】解:当12是直角边时,斜边长==13.故它的斜边长为13或12.故选:D.【知识点】勾股定理2.如图,在Rt△ABC中,∠ACB=90°,AC=8cm,BC=15cm,其斜边上的高为()A.17cm B.8.5cm C.cm D.cm【解答】解:在Rt△ABC中,∠ACB=90°,AC=8cm,BC=15cm,由勾股定理得到:AB==17cm;由AC•BC=CD•AB得到:CD===(cm),故选:D.【知识点】勾股定理3.已知,△ABC的三边分别为a,b,c,其对角分别为∠A,∠B,∠C.下列条件能判定△ABC一定不是直角三角形的是()A.a:b:c=::B.b2﹣a2=c2C.∠A:∠B:∠C=2:3:5 D.∠B=∠A+∠C【解答】解:A.∵a:b:c=::,∴a2+b2≠c2,∴△ABC不是直角三角形,故本选项符合题意;B.∵b2﹣a2=c2,∴a2+c2=b2,∴∠ABC=90°,即△ABC是直角三角形,故本选项不符合题意;C.∵∠A:∠B:∠C=2:3:5,∠A+∠B+∠C=180°,∴∠C=×180°=90°,即△ABC是直角三角形,故本选项不符合题意;D.∵∠B=∠A+∠C,∠A+∠B+∠C=180°,∴2∠B=180°,∴∠B=90°,即△ABC是直角三角形,故本选项不符合题意;故选:A.【知识点】三角形内角和定理、勾股定理的逆定理4.如图,∠BAC=90°,AB=AC=6,BE=2,DE=3,∠BDE=15°,点P在线段AE上,PD=DE,△ADQ是等边三角形,连接PQ交AC于点F,则PF的长为()A.2 B.3 C.D.【解答】解:∵∠BAC=90°,AB=AC=6,∴∠B=45°,∵∠BDE=15°,∴∠PED=∠B+∠BDE=60°,∵PD=DE,∴△PDE是等边三角形,∴∠EDP=∠DEP=∠EPD=60°,PE=DE=3,∴AP=AB﹣BE﹣PE=6﹣2﹣3=1,∵△ADQ是等边三角形,∴AD=DQ,∠ADQ=60°,∴∠ADE=∠PDQ,在△ADE与△QDP中,,∴△ADE≌△QDP(SAS),∴∠DPQ=∠DEA=60°,∴∠APF=60°,∵∠P AF=90°,∴PF=2AP=2,故选:A.【知识点】等边三角形的性质、等腰直角三角形5.如图是用4个全等的直角三角形与1个小正方形镶嵌而成的正方形图案,大正方形面积为64,小正方形面积为9,若用x,y表示直角三角形的两直角边长(x>y),请观察图案,下列关系式中不正确的是()A.x2+y2=64 B.x﹣y=3 C.2xy+9=64 D.x+y=11【解答】解:根据勾股定理可得:x2+y2=64①,(x﹣y)2=9②,①﹣②可得2xy=55③,∴2xy+9=64,x﹣y=3,①+③得x2+2xy+y2=119,∴x+y=,∴选项A、B、C不符合题意,选项D符合题意,故选:D.【知识点】勾股定理的证明、全等图形、完全平方公式的几何背景二、填空题6.如图所示,在Rt△ABC中,∠C=90°,AB=10cm,BC=8cm,BD平分∠ABC,DE⊥AB,垂足为E,则DE=cm.【解答】解:如图所示,在Rt△ABC中,∠C=90°,AB=10cm,BC=8cm,则由勾股定理得到:AC===6(cm).∵BD平分∠ABC,DE⊥AB,CD⊥BC,∴ED=CD,设ED=CD=x(x>0),在直角△ACD中,AD2=AE2+ED2,即(6﹣x)2=(10﹣8)2+x2.解得x=.即DE=cm.故答案是:.【知识点】勾股定理、角平分线的性质7.如图,在四边形ABCD中,AB=AD=4,∠A=60°,BC=,CD=8,则四边形ABCD的面积为.【解答】解:连接BD.∵AD=AB=4,∠A=60°,∴△ABD是等边三角形,∴BD=AD=4,∵BC=4,CD=8,∴BC2=BD2+CD2,∴∠BDC=90°,∴S四边形ABCD=S△ABD+S△BDC=×42+×4×8=4+16,故答案为4+16.【知识点】勾股定理的逆定理、等边三角形的判定与性质8.如图,每个小正方形的边长为1,四边形的顶点A,B,C,D都在格点上,则线段长度为的是.【解答】解:AB==,BC=3,CD==,AD==,故长度为的线段是AB,故答案是:AB.【知识点】勾股定理9.如图,以Rt△ABC的两条直角边和斜边为边长分别作正方形,其中正方形ABFG、正方形ACDE的面积分别为25、144,则阴影部分的面积为.【解答】解:根据题意知,AB2=25,AC2=144,所以AB=5,AC=12,BC===13,所以S阴影=BC2﹣=132﹣=139.故答案是:139,.【知识点】勾股定理10.如图,在Rt△ABC中,∠ACB=90°,AB=5cm,AC=3cm,动点P从点B出发沿射线BC以1cm/s的速度移动,设运动的时间为t秒,当△ABP为等腰三角形时,t的取值为.【解答】解:在Rt△ABC中,BC2=AB2﹣AC2=52﹣32=16,∴BC=4(cm);①当AB=BP时,如图1,t=5;②当AB=AP时,如图2,BP=2BC=8cm,t=8;③当BP=AP时,如图3,AP=BP=tcm,CP=(4﹣t)cm,AC=3cm,在Rt△ACP中,AP2=AC2+CP2,所以t2=32+(4﹣t)2,解得:t=,综上所述:当△ABP为等腰三角形时,t=5或t=8或t=.故答案为:5或t=8或t=.【知识点】勾股定理、等腰三角形的性质三、解答题11.如图,在△ABC中,AC=20,AD=16,CD=12,BC=15,求AB的长.【解答】解:∵AC=20,AD=16,CD=12,∴CD2+AD2=AC2,∴∠ADC=90°,在直角△BCD中,BC=15,CD=12,∴BD==9,∴AB=AD+BD=25.【知识点】勾股定理的逆定理12.在△ABC中,D是BC上一点,AB=10,BD=6,AD=8,AC=17,求△ABC的面积.【解答】解:∵BD2+AD2=62+82=102=AB2,∴△ABD是直角三角形,∴AD⊥BC,在Rt△ACD中,CD==15,∴BC=BD+CD=6+15=21,∴S△ABC=BC•AD=×21×8=84.因此△ABC的面积为84.故答案为84.【知识点】勾股定理的逆定理、勾股定理探究题:13.如图,4×4方格中每个小正方形的边长都为1.(1)图①中正方形ABCD的边长为;(2)在图②的4×4方格中画一个面积为8的正方形;(3)把图②中的数轴补充完整,然后用圆规在数轴上表示实数和﹣.【解答】解:(1)图①中正方形ABCD的边长为=;故答案为:;(2)如图所示:(3)如图所示:【知识点】实数与数轴、勾股定理14.我们新定义一种三角形:两边平方和等于第三边平方的4倍的三角形叫做常态三角形.例如:某三角形三边长分别是5,6和8,因为62+82=4×52=100,所以这个三角形是常态三角形.(1)若△ABC三边长分别是2,和4,则此三角形常态三角形(填“是”或“不是”);(2)若Rt△ABC是常态三角形,则此三角形的三边长之比为(请按从小到大排列);(3)如图,Rt△ABC中,∠ACB=90°,BC=6,点D为AB的中点,连接CD,若△BCD是常态三角形,求△ABC的面积.【解答】解:(1)∵22+42=4×()2=20,∴△ABC三边长分别是2,和4,则此三角形是常态三角形.故答案为:是;(2)∵Rt△ABC是常态三角形,∴设两直角边长为:a,b,斜边长为:c,则a2+b2=c2,a2+c2=4b2,则2a2=3b2,故a:b=:,∴设a=x,b=x,则c=x,∴此三角形的三边长之比为:::.故答案为:::;(3)∵Rt△ABC中,∠ACB=90°,BC=6,点D为AB的中点,△BCD是常态三角形,∴当AD=BD=DC,CD2+BD2=4×62时,解得:BD=DC=6,则AB=12,故AC==6,则△ABC的面积为:×6×6=.当AD=BD=DC,CD2+BC2=4×BD2时,解得:BD=DC=2,则AB=4,故AC=2,则△ABC 的面积为:×6×2=6.故△ABC 的面积为或6.【知识点】勾股定理15.细心观察图形,认真分析各式,然后回答问题:(1)推算OA10的长和S10的值;(2)直接用含n(n为正整数)的式子表示OA n的长和S n的值;(3)求S12+S22+S32+…+S102的值.OA12=1;+1=2;+1=3;+1=4;…S1=;S2=;S3=;…【解答】解:(1)∵,,…,∴OA210=10,∴,∵,,…,∴;(2)由(1)可知,,;(3)S12+S22+S32+…+S102=.【知识点】规律型:图形的变化类、勾股定理16.阅读理解:【问题情境】教材中小明用4张全等的直角三角形纸片拼成图1,利用此图,可以验证勾股定理吗?【探索新知】从面积的角度思考,不难发现:大正方形的面积=小正方形的面积+4个直角三角形的面积.从而得数学等式:(a+b)2=c2+4×ab,化简证得勾股定理:a2+b2=c2.【初步运用】(1)如图1,若b=2a,则小正方形面积:大正方形面积=;(2)现将图1中上方的两直角三角形向内折叠,如图2,若a=4,b=6,此时空白部分的面积为;(3)如图3,将这四个直角三角形紧密地拼接,形成风车状,已知外围轮廓(实线)的周长为24,OC =3,求该风车状图案的面积.(4)如图4,将八个全等的直角三角形紧密地拼接,记图中正方形ABCD,正方形EFGH,正方形MNKT 的面积分别为S1,S2,S3,若S1+S2+S3=40,则S2=.【迁移运用】如果用三张含60°的全等三角形纸片,能否拼成一个特殊图形呢?带着这个疑问,小丽拼出图5的等边三角形,你能否仿照勾股定理的验证,发现含60°的三角形三边a、b、c之间的关系,写出此等量关系式及其推导过程.知识补充:如图6,含60°的直角三角形,对边y:斜边x=定值k.【解答】解:【初步运用】(1)由题意:b=2a,c=a,∴小正方形面积:大正方形面积=5a2:9a2=5:9,故答案为:5:9.(2)空白部分的面积为=52﹣2××4×6=28.故答案为:28.(3)24÷4=6,设AC=x,依题意有(x+3)2+32=(6﹣x)2,解得x=1,×(3+1)×3×4=×4×3×4=24.故该飞镖状图案的面积是24.(4)将四边形MTKN的面积设为x,将其余八个全等的三角形面积一个设为y,∵正方形ABCD,正方形EFGH,正方形MNKT的面积分别为S1,S2,S3,S1+S2+S3=40,∴S1=8y+x,S2=4y+x,S3=x,∴S1+S2+S3=3x+12y=40,∴x+4y=,∴S2=x+4y=.故答案为:.[迁移运用]结论:a2+b2﹣ab=c2.理由:由题意:大正三角形面积=三个全等三角形面积+小正三角形面积可得:(a+b)×k(a+b)=3××b×ka+×c×ck,∴(a+b)2=3ab+c2∴a2+b2﹣ab=c2.【知识点】勾股定理的证明、等边三角形的判定.。
