飞行力学第三章机动性
飞行力学复习

6、飞机的续航性能
基本性能
多高、多快
续航性能
多远、多久
定常直线飞行 准定常直线飞行
➢主要指标
航程L、航时T、活动半径R
➢按任务的两类续航性能计算问题
❖给定飞行状态,确定续航性能 ❖选择飞行状态和发动机工作状态,使得续航性能最佳
➢技术航程/航时,实用航程/航时
典型巡航飞行剖面
Lss
Lxh
Lxih
Tss
性。由M
z
(mz
)或M
C z
y
(
mzC
y
)的符号决定
(2)、纵向静稳定性与飞机重心和焦点之间的关系
mcy z
xG
xF
mcy z
0
xG
xF
纵向静稳定
mcy z
0
xG
xF
纵向静不稳定
mzcy=0 xG=xF 纵向中立静稳定
Cy
(3)静稳定裕度
Cy1
K n xF xG
(4)纵向平衡
Cy0 O
沉浮模态 长周期模态
特征 周期长,频率低,衰减慢的振荡运动; Δ α、ωz基本不变:该模态幅值小; 质心运动参数Δ V主要表现出沉浮模态特点;
原因
质量m,恢复力 YV V ,G 与阻尼 (PV QV )V 等
大
小
小
恢复慢,衰减慢(甚至发散)的振荡运动
典型参数
(7)纵向动态飞行品质要求
概述
飞行品质要求或规范是确保飞行安全和顺利完成预定 任务必须满足的要求,也是各类飞机的设计和使用过 程中必须满足的要求。
正常操纵响应(以定直平飞为基准)
• 油门—— 推油门加速,收油门减速; • 纵杆—— 推杆低头,拉杆抬头; • 横杆—— 左压杆左滚,右压杆右滚; • 脚蹬—— 左蹬舵左偏航,右蹬舵右偏航。
大气飞行力学第2-1章补充机动性能

大气飞行力学--机动性能
11
积分得
ΔH = ∫
θ
0
V 2 ( n y cos γ s − cos θ ) dH dθ = ln g ( n y cos γ s − 1) dθ
直线俯冲段
⎧ G dV = Pky − Q + G sin θ xh ⎪ ⎨ g dt ⎪Y = G cos θ xh ⎩
慢车推力近似 为零
改出段
⎧ dV ⎪m dt = ( Pky − Q ) − G sin θ ⎪ ⎨ ⎪ dθ = g (n − cos θ ) ⎪ dt V y ⎩
剩余推力近似 为零
dV V sin θ =− dθ n y − cos θ dV sin θ dθ =− V n y − cos θ
大气飞行力学--机动性能
⎧G dV ⎪ g dt = Pky − Q − G sin θ ⎪ ⎨ ⎪G V dθ = Y − G cos θ ⎪ g dt ⎩
大气飞行力学--机动性能
铅垂面质心运动 的一般方程。 可数值求解。
8
3、跃升性能计算方法 能量法
假设:ΔP的平均作用为零,飞机总能量不变。
G 2 进入跃升 E0 = H 0G + V0 2g G 退出跃升 E1 = H 1G + V12 2g
1 t= g dV G V1 dV = V0 n g V0 ΔP x t1 G V1 VdV L = Vdt = t0 g V0 ΔP
∫
V1
∫
∫
∫
大气飞行力学--机动性能
7
二、跃升
衡量飞机由动能换取势能、迅速获取高度优势 的能力,即高度机动性。
1、指标
ΔH max ,
Δ t ΔH
某型飞行器的飞行力学性能分析

某型飞行器的飞行力学性能分析随着航空工业的不断发展,各种新型飞行器层出不穷。
其设计和研发过程中需要进行严密的飞行力学性能分析,以保证其空气动力学性能、机动性能及飞行稳定性。
本文将根据某型飞行器,进行飞行力学性能分析。
一、飞行器的主要构成部分某型飞行器主要由机翼、螺旋桨、机身、尾舵及控制系统等部分组成。
其中,机翼作为飞行器的主要升力构件,螺旋桨提供飞行器的推力,机身作为承载构件,尾舵及控制系统用于操纵飞行器。
二、飞行器气动力分析1.升力机翼是飞行器的主要升力构件,其升力主要来自于机翼下表面空气流动速度的加速。
升力与机翼的几何形状、攻角、气动面积以及来流速度等因素有关。
当飞行器飞行时,机翼下表面气流速度增加,从而实现机翼产生升力的目的。
2.阻力阻力是指飞行器所受空气阻力,主要包括风阻、涡阻、摩擦阻力等。
阻力与机翼的几何形状、来流速度、攻角以及表面光滑程度等因素有关。
为了减小飞行器的阻力,可以采用减小机身横截面积、优化机翼的形状等方法。
3.侧滑力侧滑力是指由于来流不稳定而引起的飞行器侧向运动的力,主要通过侧滑角进行计算。
当飞行器出现侧滑时,侧面产生了横向加速度,从而产生侧向气动力,进一步影响了飞行器的飞行方向。
三、机动性能分析飞行器的机动性能指其完成不同飞行任务过程中所需的能力,主要包括爬升、俯冲、滚转、俯仰等。
1.爬升能力爬升能力指飞行器在飞行时,垂直方向的速度变化能力。
其主要包括垂直爬升速度、爬升率以及最大可爬升高度等。
2.俯冲能力俯冲能力是指飞行器在垂直方向上的下降速度、下降率及最大可俯冲深度等。
3.滚转能力滚转能力是指飞行器进行侧滚动作时,所需的时间及相关的性能指标。
其主要与飞行器侧翼结构的参数、侧翼的攻角、机头高度等因素有关。
4.俯仰能力俯仰能力是指飞行器进行俯仰动作时,所需的时间及相关的性能指标。
飞行器的攻角变化率、机头高度、侧翼结构等对其俯仰能力均有影响。
四、飞行稳定性分析飞行稳定性是指飞行器在飞行过程中保持稳定的能力,主要包括方向稳定性、纵向稳定性和横向稳定性。
第三章 飞行空气动力学

第三章- 飞行空气动力学飞行空气动力学介绍作用于飞机上的力的相互关系和由相关力产生的效应。
作用于飞机的力至少在某些方面,飞行中飞行员做的多好取决于计划和对动力使用的协调以及为改变推力,阻力,升力和重力的飞行控制能力。
飞行员必须控制的是这些力之间的平衡。
对这些力和控制他们的方法的理解越好,飞行员执行时的技能就更好。
下面定义和平直飞行(未加速的飞行)相关的力。
推力是由发动机或者螺旋桨产生的向前力量。
它和阻力相反。
作为一个通用规则,纵轴上的力是成对作用的。
然而在后面的解释中也不总是这样的情况。
阻力是向后的阻力,由机翼和机身以及其他突出的部分对气流的破坏而产生。
阻力和推力相反,和气流相对机身的方向并行。
重力由机身自己的负荷,乘客,燃油,以及货物或者行礼组成。
由于地球引力导致重量向下压飞机。
和升力相反,它垂直向下地作用于飞机的重心位置。
升力和向下的重力相反,它由作用于机翼的气流动力学效果产生。
它垂直向上的作用于机翼的升力中心。
在稳定的飞行中,这些相反作用的力的总和等于零。
在稳定直飞中没有不平衡的力(牛顿第三定律)。
无论水平飞行还是爬升或者下降这都是对的。
也不等于说四个力总是相等的。
这仅仅是说成对的反作用力大小相等,因此各自抵消对方的效果。
这点经常被忽视,而导致四个力之间的关系经常被错误的解释或阐明。
例如,考虑下一页的图3-1。
在上一幅图中的推力,阻力,升力和重力四个力矢量大小相等。
象下一幅图显示的通常解释说明(不保证推力和阻力就不等于重力和升力)推力等于阻力,升力等于重力。
必须理解这个基本正确的表述,否则可能误解。
一定要明白在直线的,水平的,非加速飞行状态中,相反作用的升力和重力是相等的,但是它们也大于相反作用的推力和阻力。
简而言之,非加速的飞行状态下是推力和阻力大小相等,而不是说推力和阻力的大小和升力重力相等,基本上重力比推力更大。
必须强调的是,这是在稳定飞行中的力平衡关系。
总结如下:向上力的总和等于向下力的总和向前力的总和等于向后力的总和对旧的“推力等于阻力,升力等于重力”公式的提炼考虑了这样的事实,在爬升中,推力的一部分方向向上,表现为升力,重力的一部分方向向后,表现为阻力。
8、飞行力学第三章-机动性

Va本身与H1有关, 需迭代求解。
飞行器飞行力学
28
计算步骤:
估计: Va
由 H1
H1
H0
1 2g
(V02
Va2 )
c
Maa Va / c
CL.a
求得
Va
2W
CL.a S
迭代达到计算精度。
➢给定H0,若V0↑, 则ΔH↑。
Hmax
1 2g
(V02max
Va2 )
➢E0↑, 则H1↑。
H1
(H0
V02 2g
W 2g
V02
E1
H1W
W 2g
V12
H
H1
H0
1 2g
(V02
V12 )
问题: 若V0↑, V1↓,则△H↑,与飞机特性无关?
共73页
飞行器飞行力学
27
➢给定V0、H0,求ΔHmax
分析 若V1↓,则ΔH↑。
V1下限: V1 Va
2W
C L.a S
Hmax
H1
H0
1 2g
(V02
Va2 )
共73页
共73页
飞行器飞行力学
35
3.2飞机在铅垂平面内的机动飞行性能 五、筋斗
在铅垂平面内作360度的曲线运动的一种机动飞行。
最小允许机动速度
共73页
(Va )机动
2nzW
CL.a S
nz (Va )lf
飞行器飞行力学
Level flight
36
3.3 飞机在水平平面内的机动飞行性能
水平面机动:
衡量飞机改变速度方向的能力,即方向机动性。 盘旋 : 水平面内连续转弯不小于360度的机动。 转弯: 飞行方向连续变化小于360度的机动。
飞行力学部分作业答案(1)

+ (sinθa sinφa sinψ a + cosφa cosψ a )C − (sinθa cosφa sinψ a − sinφa cosψ a )
m
dvzg dt
= −sinθT
cosϕ + cosφ cosθT sin ϕ + sinθaC + sinφa
cosθaC − cosφa
sin θ
cosφ
sinψ
− sinφ
cosψ
cosφ cosθ
Lga
=
ccoossθθaa
cosψ a sinψ a
− sinθa
sinθa sinφa cosψ a − cosφa sinψ a sinθa sinφa sinψ a + cosφa cosψ a
sin φa cosθa
+ (sinθa sinφa cosψ a − cosφa sinψ a ) C − (sinθa cosφa cosψ a + sinφa sinψ a ) L
m dvyg dt
= cosθ sinψ T cosϕ
− (sinθ cosφ sinψ
− sinφ cosψ
)T sin ϕ − cosθa sinψ a D
= 0.1019
2
2
CD = 0.014 + 0.08CL2
CD = 0.0152
D = 8771N
代入方程求得T = 38771N
3.5
χɺ = V R
得:
R
=
V ω
=
300 / 3.6 3.14 /15
=
机动性

在飞机需要快速灭速时,为改机的减速性能,应尽量收小油门,减小发动机推力,同时可打开减速板或扰流 板。
高度机动性反映的是飞机改变一定飞行高度的能力。通常把高度机动性与速度机动性结合在一起,统称为飞 机在铅垂面内的机动飞行性能。
需要说明的是,飞机在正常的航路爬升和下降的飞行过程中,飞行高度虽然也随着飞行时间的变化而变化, 但此时,飞行速度变化率和飞行航迹角变化率相对较小,因而被归入“准定常”飞行范畴。
(1)盘旋
飞机在水平面内作等速圆周飞行,叫做盘旋飞行,如图1所示。通常坡度(坡度即指飞机倾斜的程度)小于 45°时,叫做小坡度盘旋;大于45°时,叫做大坡度盘旋。盘旋和转弯的操纵动作完全相同,只是转弯的角度不 到360°而已。
图1飞机盘旋
盘旋一周所需的时间越短,盘旋半径越小,方向机动性就越好。在作战时,希望盘旋半径越小越好,这时就 要尽量使飞机倾斜坡度加大,以增大使飞机作曲线运动的改变坡度时,需要相应地改变升力的大小,坡度越大,则所需的升力也就越大,因此 飞机的过载也就越大。如表5.1所列,不同坡度盘旋时飞机对应了不同的过载系数。
为了实现更大的机动性,人们通过不懈的努力,通过使用推力矢量技术等途径,已经能够克服失速迎角的限 制,进行过失速机动。例如眼镜蛇机动、钟摆机动、钩子机动、榔头机动、赫布斯特机动。
飞行力学知识点
《飞行动力学》掌握知识点第一章掌握知识点如下:1)现代飞机提高最大升力系数采取的措施包括边条翼气动布局或近耦鸭式布局。
2)飞行器阻力可分为摩擦阻力、压差阻力、诱导阻力、干扰阻力和激波阻力等。
3)试描述涡喷发动机的三种特性:转速(油门)特性,速度特性,高度特性并绘出变化曲线。
(P7)答:涡轮喷气发动机的性能指标推力T和耗油率f C等均随飞行状态、发动机工作状态而改变。
下面要简单介绍这些变化规律,即发动机的特性曲线,以供研究飞行性能时使用。
1)转速(油门特性)在给定调节规律下,高度和转速一定时,发动机推力和耗油率随转速的变化关系,称为转速特性。
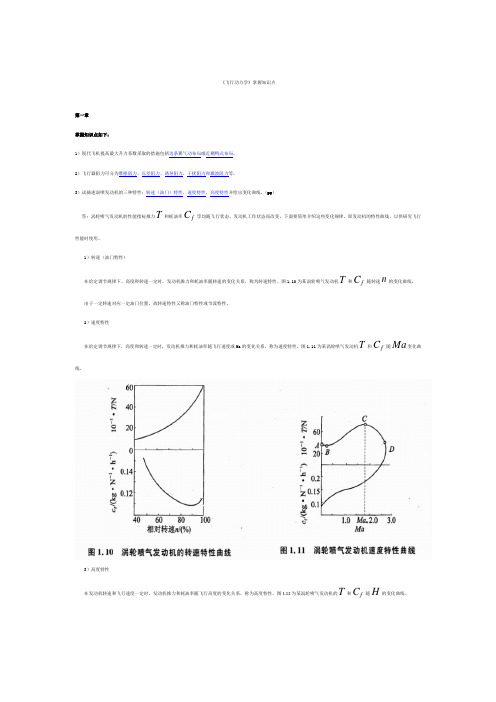
图1.10为某涡轮喷气发动机T和f C随转速n的变化曲线。
由于一定转速对应一定油门位置,故转速特性又称油门特性或节流特性。
2)速度特性在给定调节规律下,高度和转速一定时,发动机推力和耗油率随飞行速度或Ma的变化关系,称为速度特性。
图1.11为某涡轮喷气发动机T和f C随Ma变化曲线。
3)高度特性在发动机转速和飞行速度一定时,发动机推力和耗油率随飞行高度的变化关系,称为高度特性。
图1.12为某涡轮喷气发动机的T和f C随H的变化曲线。
第二章掌握知识点如下:1)飞机飞行性能包括平飞性能、上升性能、续航性能和起落性能。
2)飞机定直平飞的最小速度受到哪些因素的限制?(P40)答:最小平飞速度m in V 是指飞机在某一高度上能作定直平飞的最小速度。
1)受最大升力系数m ax L C 限制的理想最小平飞速度S C W V L ρmax min 2=;2)受允许升力系数a L C .限制的最小允许使用平飞速度S C W V a L a ρ.2=;3)受抖动升力系数sh L C .限制的抖动最小平飞速度SC W V sh L sh ρ.2=; 4)受最大平尾偏角m ax .δL C 限制的最小平飞速度SC W V L ρδδmax max .min 2)(=;5)发动机可用推力a T 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
= V sinγ
入 段
⎨⎪W V dγ
⎪⎩ g dt
= Lcos μ − W cosγ
dH =
V 2 sin γ
dγ g(nn cos μ − cosγ )
速度矢量滚转角μ
升力方向与含速矢的铅垂面 的夹角 。
在对称面内 与速矢垂直
Oxkzk平面
“+”:右翼下沉
飞行器飞行力学2010
∫ 积分得 ΔH = γ dH dγ = V 2 ln (nn cos μ − cosγ )
机动性能
第三章: 引言
定常直线飞行 非定常机动飞行
运动参数和轨迹均随时间变化
常规机动:水平加减速、跃升、俯冲、筋斗、 盘旋、转弯、上升转弯、半滚倒转等
特殊战术机动:桶滚、剪刀叉、split-s等
过失速机动:眼镜蛇、Herbst、尾冲等
飞行器飞行力学2010
第三章: 引言(续) 掌握 机动飞行的受力特性、运动特性; 机动性能的评估指标; 机动性能的计算模型和方法; 机动性能的影响因素; 机动飞行的稳定性和操纵性,控制律设计等
ΔH max
=
H1
−
H0
=
1 2g
(V02
− Va2 )
Va本身与H1有关, 需迭代求解。
飞行器飞行力学2010
计算步骤:
估计: Va′
由 H1′
H1′
=
H0
+
1 2g
(V02
− Va′2 )
c′
Maa′ = Va′ / c′
C
′
L.a
求得
Va′′=
2W
C
′
L.a
ρ
′S
迭代达到计算精度。
¾给定H0,若V0↑, 则ΔH↑。
1、性能指标
ΔHmax , Δt ΔH
2、跃升动力学方程
⎧W ⎪⎪ g
dV dt
=T
− D−W
sin γ
⎪⎨W ⎪⎩ g
V
dγ
dt
=
L−W
cos γ
铅垂面质心运动的 一般方程。 可数值求解。
飞行器飞行力学2010
3、跃升性能计算方法 ¾能量法
假设:ΔT的平均做功为零,飞机总机械能不变。
进入跃升 退出跃升
飞行器飞行力学2010
3.2飞机在铅垂平面内的机动飞行性能 五、筋斗
高度损失: ΔH = V 2 − V12 = V12 [( nz − cosγ 1 )2 − 1]
2g 2g nz − 1
算例计算
垂直俯冲,V1 = 338m / s,
nz = 6,V = 406m / s;ΔH = 2565m; nz = 8,V = 386m / s;ΔH = 1784m。
改出俯冲时高度损失大,为安全起见,要有一定高度储 备,同时,增加改出时的过载。
H max .d
=
(H0
+
V02 2g
)max
− Va2 2g
=
(H0
+
V2 0max 2g
)max
−
Va2 2g
¾示例
Hmax.d Hmax.a
Ma
Hmax.d~Hmax.a的动力 高度飞行范围,可持
续一段减速平飞
H=13500m,Ma=2.05→Hmax.d=23000m>> Hmax.a=19500m
− D) −W
sin γ
⎨ ⎪
dγ
⎪⎩ dt
=
g V
(nz
−
cos γ
)
dV = − V sin γ dγ nz − cosγ
dV = − sinγ dγ
V
nz − cosγ
飞行器飞行力学2010
积分得改出速度
过载不变
V
= V1
nz − cosγ 1
nz − 1
近似认为推力与阻力相等,根据能量守恒得
nr = nx ir + ny rj + nz kr
切向(纵向)
过载 nτ
沿飞行速 度矢方向
水平面内 垂直于速矢
铅垂面内 垂直于速矢
飞行器飞行力学2010
一、运动与过载的关系
♦ 无侧滑、推力沿速度方向时航迹坐标系中的 质心运动方程
⎪⎧m ⎪
dV dt
=T − D−W
sin γ
⎪2010
第三章: 引言(续)
¾机动性定义
飞机在一定时间内改变飞行状态(飞行高度、 飞行速度大小和飞行方向)的能力。
机动性能指标是针对典型机动动作来定义。
¾机动动作分类
铅垂平面内机动 水平加减速、跃升、俯冲、筋斗等
水平平面内机动
盘旋、转弯等 空间机动
斜筋斗、上升转弯、半滚倒转等
飞行器飞行力学2010
⎪⎪⎩⎪⎪⎨⎧VddVtddγt=
g(nx − sinγ ) = g(nz − cosγ
)
飞行器飞行力学2010
一、运动与过载的关系(续)
转弯速率
dγ
dt
=
g V
(nz
−
cos γ
)
=
g V
(nn
−
cos γ
)
转弯半径
Rv
= V / dγ
dt
=
V2
g(nn − cosγ )
飞行器飞行力学2010
一、运动与过载的关系(续)
ΔH max
=
1 2g
(V02max
− Va2 )
¾E0↑, 则H1↑。
H1
=
(H0
+
V02 2g
)
−
V12 2g
H1
→
max
⇔
⎪⎩⎪⎨⎧V(H1 →0 +mV2i0g2n),V→1
= Va max
飞行器飞行力学2010
3.2飞机在铅垂平面内的机动飞行性能
三、动升限
H
通过跃升可以达到的最 大高度, Hmax.d
0 dγ
g (nn cos μ − 1)
直线俯冲段
慢车推力近似 为零
因为 得
⎧W
⎪ ⎨
g
dV dt
=T − D−W
sin γ
⎪⎩L = W cosγ
dV dt
=
dV dH
dH dt
= Vv
dV dH
= V sin γ
dV dH
dV
=−
g [1 − Ta − CD
1 ρV 2 S
2
]
dH V
W sin γ
= >
<
1 1
1
,感觉同静止 ,超重 ,失重
机动飞行时驾驶员将感受到等于自身重量n倍的力
飞行器飞行力学2010
3.2 飞机在铅垂平面内的机动飞行性能
一、平飞加减速
衡量飞机改变速度大小的能力,即速度机动性。
1、指标
加减速时间:
t , t 0.7Vmax →0.97Vmax Vmax →0.7Vmax (亚音速飞机 )
受H、W、构形、油门影响:一般加速时满油 门;减速时小油门,并打开减速装置。
¾示例(发动机加力)
H(m) 5000 15000
△V(m/s) 222→250 222→250
平均△T(N) 12260 2940
飞行器飞行力学2010
加速时间(s) 11.3 47
加减速性能与构造参数关系
⎪⎧ dV = g (T − D) ⎨ dt W ⎪⎩L = W
飞行器飞行力学2010
二、过载限制(续)
1、极限过载
飞机的迎角达到失速迎角时的法向过载,与CLmax对应.
2、可用过载
nn.l
=
qSC Lmax W
最大舵偏角时飞机飞机所能产生的法向过载nn.a.这里的最 大舵偏角应考虑飞机的操纵效能、失速及结构强度限制.
3、需用过载 飞机实现某机动时所需的法向过载nn.R.
E0 = E1
E0
=
H 0W
+
W 2g
V02
E1
=
H1W
+
W 2g
V12
ΔH
=
H1
−
H0
=
1 2g
(V02
− V12 )
问题: 若V0↑, V1↓,则△H↑,与飞机特性无关?
飞行器飞行力学2010
¾给定V0、H0,求ΔHmax
分析 若V1↓,则ΔH↑。
V1下限: V1 ≥ Va =
2W
C L.a ρS
dχ
dt
=
Lsin μ
定义
⎪⎪⎩− mV
dγ
dt
= − Lcos μ + W cosγ
⎧ dV
⎪ ⎪
dt
=
g(nx
− sin γ )
⎪⎨V ⎪
cos γ
dχ
dt
=
gn y
⎪ ⎪⎩V
dγ
dt
= g(nz − cosγ )
飞行器飞行力学2010
⎪⎧nx ⎪
=
T−D W
⎪⎨ n y ⎪
=
Lsin μ
W
⎪ ⎪⎩nz
飞行器飞行力学2010
速度变化
⎧⎪⎪⎪⎨加极速限段速:度:D <H−↓W⇒siDnγ↑⇒=WddVtsi>n
0
γ
⇒ ⇒
V Vd
↑
.l
=
2(T − W sin γ ) / ρCD S
⎪ ⎪减速段:H
↓, D
>
−W
sin γ
⇒
dV
<
0⇒V
