广义斐波那契数列的性质及推广
广义fibonacci数列与广义黄金分割数

广义fibonacci数列与广义黄金分割数
广义Fibonacci数列与广义黄金分割数是一组非常有趣的数学理论,在互联网上得到了广泛的普及,从而得到了深入探究。
首先,让我们来看看这两个理论。
广义Fibonacci数列是一组性质相似的数字,用于描述自然界中的某种周期性的现象,如多倍生物的出现次数,种子的分散,落叶的重现,动物的繁殖等等。
这组数字的组成为:1,1,2,3,5,8,13,21,34,55,89,144等等。
可以看到,每一个数字都是前两个数字的总和,即斐波那契数列的定义。
而广义黄金分割数则是由古希腊数学家阿基米德提出的一个重要概念,即一条长度分割为两部分,且其中最小部分等于最大部分的1.618倍时,称之为黄金分割数。
这个概念被广泛用于各种建筑图形的设计,也被用于文学、美术、艺术以及自然界中的许多景观的构成,此外,它还是群论的基础之一。
在互联网上,广义Fibonacci数列与广义黄金分割数都得到了广泛的使用,尤其是广义Fibonacci数列,它不仅被用于自然界中的现象,也常常被用于技术分析和投资计划等方面,被认为是投资市场趋势的重要参考标准,用于增加投资收益。
在音乐制作方面,它也被认为是一种适合曲调剧情发展的有效方式。
此外,在互联网上还有一些其他用途,如服务器设备的故障模拟、用户侧重的收集与汇总、搜索引擎的搜索结果排名等等,都是运用这两种理论的典型案例。
总之,广义Fibonacci数列与广义黄金分割数以及它们在互联网开发过程中的应用,是数学界有趣且值得被深入探究的课题之一。
随着人们对互联网新技术的持续研究和运用,它们在未来也将会被越来越多地利用,实现更多惊喜。
斐波那契数列介绍、编程实现及推广

斐波那契数列介绍、编程实现及推⼴斐波那契数列是⼀列规律很简单、明显的数列,它的第0项是0,第1项是1,第2项是1,依此类推,之后每⼀项是之前两数的和。
⾸⼏个数是:0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946 ……(OEIS )编程实现最容易想到的实现⽅法,可以设⼀个数组,⾸两项是0和1,从n=2项起,每⼀项是之前两项之和,循环依次赋值,这⾥代码略去。
下⾯介绍另⼏种实现⽅法。
⽤递归⽅法实现:static long getItemRecursive(int index){if (index < 1) return 0;if (index == 1) return 1;return getItemRecursive(index - 1) + getItemRecursive(index - 2);}这种实现⽅式最直观,但会很耗时,若⽅法名为fib,当index为5时,fib(5)的计算过程如下:1. fib(5)2. fib(4) + fib(3)3. (fib(3) + fib(2)) + (fib(2) + fib(1))4. ((fib(2) + fib(1)) + (fib(1) + fib(0))) + ((fib(1) + fib(0)) + fib(1))5. (((fib(1) + fib(0)) + fib(1)) + (fib(1) + fib(0))) + ((fib(1) + fib(0)) + fib(1))由上⾯可以看出,这种算法对于相似的⼦问题进⾏了重复的计算,因此不是⼀种⾼效的算法。
实际上,该算法的运算时间是指数级增长的。
另外两种递归实现(C#):static long getItem2(int index){return getItemRecursive2(0, 1, 0, index);}static long getItemRecursive2(int curr, int next, int currIndex, int index){if (currIndex == index){return curr;}else{return getItemRecursive2(next, curr + next, currIndex + 1, index);}}static void getItemRecursive1(out long a2, out long a1, int index){if (index <= 1){a2 = 1;a1 = 0;}else{long m2, m1;getItemRecursive1(out m2, out m1, index - 1);a1 = m2;a2 = m2 + m1;}}利⽤动态规划:static long getItem(int index){long n0 = 0, n1 = 1;if (index < 1) return n0;if (index == 1) return n1;long sn;for (int i = 2; i <= index; i++){sn = n0 + n1;n0 = n1;n1 = sn;//或者以下⽅法//n1 = n0 + n1;//n0 = n1 - n0;//或者以下⽅法//n0 = n1 ^ (n0 + n1);//n1 = n1 ^ n0;//n0 = n1 ^ n0;}return n1;}利⽤矩阵乘法、快速幂的实现:这种⽅式当计算较⼤项(index⼤于65535)时,所花费的时间要⽐前⾯的⽅法花费的时间少⾄少⼀个数量级。
斐波那契数列及其性质

裴波纳契数列及其性质在现实生活中,我们经常会遇到类似“数列”变化的一系列经济问题,裴波纳契数列出现在我们生活中的方方面面,一些问题不仅可以用裴波纳契数列表示,而且本质上就是裴波纳契数列,可见裴波纳契数列在很多数学分支都有很广泛的应用,因此研究裴波纳契数列非常必要。
本文通过探讨裴波纳契数列的性质,进一步掌握数列的数字排列、增减变化、波动趋势等数项之间的变化规律,继而给出一系列与裴波纳契数列相关问题的解决方案,特别是对中学数学教育中,如何让学生巧妙解题具有启发作用。
1. 裴波纳契数列的由来斐波那契,公元13世纪意大利数学家,在他的著作《算盘书》中记载着这样一个“兔子繁殖问题”:假定有一对大兔子,每一个月可生下一对小兔子,并且生下的这一对小兔子两个月后就具有繁殖能力。
假如一年内没有发生死亡,那么,从一对小兔子开始,一年后共有多少对兔子?问题的解答思路:将每个月的兔子总对数列出来即可(需考虑到每个月具有生殖能力的兔子的对数),如下:月份 1 2 3 4 5 6 7 8 9 10 111213小兔子数(对) 1 0 1 1 2 3 5 8 13 21345589大兔子数(对)0 1 1 2 3 5 8 13 21345589144兔子总数(对) 1 1 2 3 5 8 13 21345589144233所以一年后(即第13个月初),繁殖的兔子共有233对。
仔细观察,可以看出上面列出的兔子对数呈现出一个有趣的变化规律:即从第3个月起,每个月的兔子对数都是前两个月的兔子对数之和,把这些数字按照相同的规律推算到无穷多项,就构成了一列数列:1、1、2、3、5、8、13、21、34、55……,人们就把它称为裴波纳契数列,而将这个数列中的每一项称为“裴波纳契数”。
2. 生活中常见的裴波纳契数列数学模型:假如我们把设为裴波纳契数列,不难发现数列是由递推关系式:,,……,所给出的一个数列。
从而,我们就可以轻而易举地算出两年,三年……以后的兔子数。
关于斐波那契数列的性质的简单证法及其推广和应用

关于斐波那契数列的性质的简单证法及其推广和应用
斐波那契数列是一种十分有名的数列,它可以通过以下公式定义:
F(n)=F(n-1)+F(n-2),其中F(1)=1,F(2)=1。
斐波那契数列有三个主要的性质:(1)它是一个等比数列,称为斐波那契数列的比率;(2)它是一个自相似的数列,每一项都是它的前两项之和;(3)它的后n项的和等于
Fn+2减去1。
证明斐波那契数列的性质,首先要证明它是一个等比数列,即F(n)/F(n-1)是一个常数,
也就是斐波那契数列的比率,因为F(n)/F(n-1)=F(n-1)/F(n-2)=φ,所以得证。
其次要证明斐波那契数列是一个自相似的数列,因为F(n)=F(n-1)+F(n-2),所以得证。
最后要证明斐
波那契数列的后n项的和等于Fn+2减去1,这可以从公式F(n)=F(n-1)+F(n-2)推出,F(n-1)是F(n)和F(n-2)的和,F(n-2)也是F(n)和F(n-3)的和,因此F(n-1)+F(n-2)=FN+FN-3,
把它继续推导出F(n)+F(n-1)+F(n-2)=FN+2-1,因此得证。
斐波那契数列的这些性质不仅仅对斐波那契数列有效,它也可以推广到其他数列。
例如,
求解斐波数列时,我们也可以把它看作是一种等差数列,用它的性质可以简化求解问题的过程。
斐波那契数列的性质还可以应用于许多实际的工程项目中。
在科学计算中,它常常被用来进行存储内容和检索操作,这大大降低了检索数据所需要的内存空间大小;在数学形式中,它可以用来表示某一定性关系。
综上所述,斐波那契数列的性质可以简单证明,并且可以推广应用到各种数列,在工程科学计算中也有广泛的应用。
斐波那契数列的性质整理
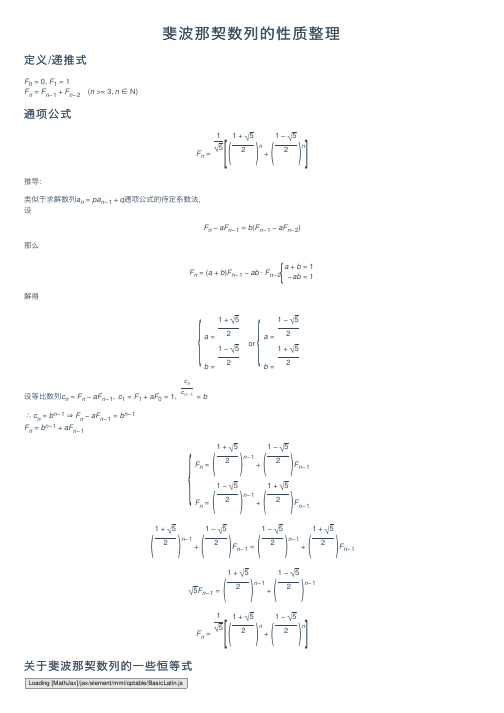
斐波那契数列的性质整理定义/递推式F0=0,F1=1F n=F n−1+F n−2(n>=3,n∈N)通项公式F n=1√51+√52n+1−√52n推导:类似于求解数列a n=pa n−1+q通项公式的待定系数法,设F n−aF n−1=b(F n−1−aF n−2)那么F n=(a+b)F n−1−ab⋅F n−2a+b=1−ab=1解得a=1+√5 2b=1−√52ora=1−√52b=1+√52设等⽐数列c n=F n−aF n−1,c1=F1+aF0=1,c nc n−1=b∴c n=b n−1⇒F n−aF n−1=b n−1 F n=b n−1+aF n−1F n=1+√52n−1+1−√52Fn−1F n=1−√52n−1+1+√52Fn−11+√52n−1+1−√52Fn−1=1−√52n−1+1+√52Fn−1√5F n−1=1+√52n−1+1−√52n−1F n=1√51+√52n+1−√52n关于斐波那契数列的⼀些恒等式[()()]{ {{{()()()()()()()()()()[()()] Loading [MathJax]/jax/element/mml/optable/BasicLatin.js1: F 1+F 2+⋯+F n =F n +2−12: F 21+F 22+⋯+F 2n =F n F n +13: F 1+F 3+F 5+⋯+F 2n −1=F 2n 4: F 2+F 3+F 6+⋯+F 2n =F 2n +1−15: F n =F m F n −m +1+F m −1F n −m6: F n −1F n +1=F 2n +(−1)n 证明:1~4.都是⽤类似的⽅法。
⽐如1: F 1=F 3−F 1,F 2=F 4−F 3,⋯,F n =F n +2−F n +1类似的分解。
然后求和就能获得结果了。
对于5:F n =F n −1+F n −2=2F n −2+F n −3=3F n −3+2F n −4=5F n −4+3F n −5=⋯=F m F n −m +1+F m −1F n −m看出系数的规律了,2=1+1,3=2+1,5=3+2,……⽤数学归纳法严谨证明⼀下:1)当m =2时,F n =F 2F n −2+1+F 2−1F n −2=F n −1+F n −2成⽴。
斐波那契数列的拓展

目录页
Contents Page
1. 斐波那契数列定义 2. 斐波那契数列性质 3. 拓展斐波那契数列 4. 拓展数列的性质 5. 生成函数与公式 6. 拓展数列的应用 7. 与其他数列的关系 8. 结论与未来研究
斐波那契数列的拓展
斐波那契数列定义
斐波那契数列定义
斐波那契数列的定义
▪ 拓展斐波那契数列的性质
1.拓展斐波那契数列的一些新性质:如相邻两项的比值仍然趋近于黄金分割比例,数列中的数 字仍然频繁出现在自然界中等。 2.性质的应用:这些性质可以用于解决一些实际问题,如在优化问题、图形学等领域中的应用 。 ---
拓展斐波那契数列
▪ 拓展斐波那契数列与其他数学问题的联系
1.与其他数学问题的联系:拓展斐波那契数列与许多数学问题有着密切的联系,如与黄金分割 、杨辉三角、Catalan数等问题的联系。 2.联系的应用:这些联系可以帮助我们更好地理解拓展斐波那契数列的性质和应用,同时也可 以用于解决其他数学问题。 ---
1.斐波那契数列有很多拓展和变体,如卢卡斯数列、佩尔数列 等,它们都具有类似的性质和应用。 2.在数学研究上,斐波那契数列的拓展和变体也引发了许多深 入的研究和探索。 3.通过对斐波那契数列的拓展和变体进行研究,可以进一步揭 示数列的本质和应用价值。
斐波那契数列的拓展
斐波那契数列性质
斐波那契数列性质
生成函数与公式
生成函数与组合结构的对应关系
1.生成函数与组合结构之间存在一一对应关系。 2.通过对应关系可以深入理解生成函数的组合意义和解释。 3.探讨对应关系在组合结构分析和计数中的应用价值。 ---
生成函数的未来发展趋势和前沿方向
1.生成函数在组合数学和计算机科学等领域仍具有广泛的研究 前景和应用潜力。 2.探讨生成函数的未来发展趋势,包括新算法、新模型和新应 用等方向。 3.分析前沿方向的研究热点和挑战,提出未来的发展方向和展 望。
高三数学 教案 斐波那契数列通项公式推导过程

斐波那契数列斐波那契数列,又称黄金分割数列、因数学家列昂纳多·斐波那契以兔子繁殖为例子而引入,故又称为“兔子数列”,指的是这样一个数列:1、1、2、3、5、8、13、21、34、……在数学上,斐波纳契数列以如下被以递推的方法定义:F(1)=1,F(2)=1, F(n)=F(n-1)+F(n-2)(n>=3,n∈N*)在现代物理、准晶体结构、化学等领域,斐波纳契数列都有直接的应用,为此,美国数学会从1963年起出版了以《斐波纳契数列季刊》为名的一份数学杂志,用于专门刊载这方面的研究成果。
定义斐波那契数列指的是这样一个数列1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233,377,610,987,1597,2584,4181,6765,10946,17711,28657,46368........自然中的斐波那契数列这个数列从第3项开始,每一项都等于前两项之和。
斐波那契数列的定义者,是意大利数学家列昂纳多·斐波那契,生于公元1170年,卒于1250年,籍贯是比萨。
他被人称作“比萨的列昂纳多”。
1202年,他撰写了《算盘全书》(Liber Abacci)一书。
他是第一个研究了印度和阿拉伯数学理论的欧洲人。
他的父亲被比萨的一家商业团体聘任为外交领事,派驻地点于阿尔及利亚地区,列昂纳多因此得以在一个阿拉伯老师的指导下研究数学。
他还曾在埃及、叙利亚、希腊、西西里和普罗旺斯等地研究数学。
通项公式递推公式斐波那契数列:1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, ...如果设F(n)为该数列的第n项(n∈N*),那么这句话可以写成如下形式::F(n)=F(n-1)+F(n-2)显然这是一个线性递推数列。
通项公式(如上,又称为“比内公式”,是用无理数表示有理数的一个范例。
) 注:此时通项公式推导方法一:利用特征方程(线性代数解法)线性递推数列的特征方程为:x²=x+1解得,.则∵∴解得方法二:待定系数法构造等比数列1(初等代数解法)设常数r,s .使得则r+s=1,-rs=1n≥3时,有……联立以上n-2个式子,得:∵,上式可化简得:那么……(这是一个以为首项、以为末项、为公比的等比数列的各项的和)。
斐波那契数列的性质

斐波那契数列的性质斐波那契递推式:斐波那契通项公式:求证过程如下:斐波那契和矩阵的关系:描述这个。
那还是描述矩阵和线性递推式的关系吧线性递推式。
即F(n)和F(n-1),F(n-2),F(n-3),F(n-4)...其阶均是⼀次的关系。
如F(n)=2F(n-1)+F(n-2).F(n)=F(n-1)+2F(n-3)+4F(n-4)...矩阵可以求解这样的递推式。
也就是说可以快速计算F(n).时间复杂度可以到达log(n)级别。
先介绍⼀下我们需要⽤到的关于矩阵的知识。
描述矩阵规模时:n⾏m列。
即⼤⼩为n*m.矩阵乘法:形状上:2*2 和 2*3 的矩阵乘积后,结果是2*3的矩阵。
即 a*b 矩阵和 c*d的矩阵乘积结果是a*d的矩阵。
其中b和c必须相等。
原因看下⾯。
运算法则:对于结果矩阵的第i⾏第j列的位置的结果是由前⼀个矩阵的对应的⾏。
和后⼀个矩阵对应的列。
对应位置 乘积和获得的。
⽐如第1⾏第1列的11.是由前矩阵的第⼀⾏(1,3)和后矩阵的第⼀列(2,3)对应位置乘 积和。
1*2+3*3 = 11 获得的。
如果上述b和c如果不相等。
那么会有地⽅"失配"没有数值可以进⾏ 计算。
不符合矩阵乘法定义。
矩阵乘法性质: 矩阵乘法不符合交换律。
符合结合律。
(具体不分析了。
稍加思考即得。
)矩阵的幂运算:即计算以下式⼦。
其中朴素想法可以通过⼀步⼀步矩阵乘法来获得结果矩阵。
但是从宏观⾓度上去想。
我们把矩阵的乘法理解成⼀种普通的数的乘法。
我们现在要计算数的幂。
可以类⽐快速幂。
那么矩阵也有矩阵的快速幂。
分治思想。
具体实现其实就是快速幂把乘法那部分改成矩阵乘法即可。
代码百度上有很多。
等下我会放⼀份。
(acdreamer矩阵的模板)矩阵计算递推式。
⽐如:对于F(n)=aF(n-1)+bF(n-2)我们可以构造矩阵和矩阵⼆者乘积为:会发现经过⼀次乘积。
我们可以获得矩阵。
那么我们再将这个矩阵乘⼀次就会得到F(3),F(2)的矩阵。
斐波那契数列2

一个完整的升跌循环: 一级波(红色粗):1+1=2 二级波(蓝色中):5+3=8 三级波(黑色细):21+13=34 四级波(未画出):89+55=144
斐波那契数列与大自然的很多现象有密切 的关系,该数列还有很多不为人知的奥秘 等着人们去发现、去研究。
波浪理论认为证券市场应该遵循一定的周期周而 复始地向前发展。股价的上下波动也是按照某种 规律进行的。这种理论最基本的形式认为每个完 整的周期包含8浪,其中5浪上升, 3浪下降。在周 期的上升阶段, 每1浪均以数字编号。1浪、3浪和 5浪是上升浪, 称为主浪,点1, 3, 5为顶点, 而2浪 和4浪的方向与上升趋势的方向相反, 因为2浪和4 浪分别是对1浪和3浪的调整, 故称为调整浪, 点2, 4为底点,上述5浪完成后, 出现了一个浪形式的 调整, 这3个波浪分别用字母a, b, c 来表示。其中 b 为顶点, a, c 为底点
斐波那契协会和《斐波那契季刊》
斐波那契1202年在《算盘书》中从兔子问题得到斐波那契数列之后, 并没有进一步探讨此序列,且在19世纪初以前,也没有人认真研究过它。 没想到过了几百年之后,十九世纪末和二十世纪,这一问题派生出广泛 的应用,从而突然活跃起来,成为热门的研究课题。有人比喻说,“有 关斐波那契数列的论文,甚至比斐波那契的兔子增长得还快”,以致 1 9 6 3 年 成 立 了 斐 波 那 契 协 会 ,
1 月 11 对 月 对 2 3 月 2 对 4 月 3 对 5 月 5 对 6 月 8 对 7 月 13 对
可以将结果以列表形式给出:
1月 1 7月 13
2月 1 8月 21
3月 2 9月 34
4月 3
5月 5
斐波那契数列在三对角行列式计算中的应用

λ1
1 -
( λ2
qλ1n
-
qλ2n
+ pλ1 λ2n + 1
- pλ2 λ1n )
.
三、斐波那契数列在行列式计算中的应用
在三对角行列 式 的 计 算 中,利 用 降 阶 展 开 定 理 得 到 行
列式的递推关系式,这个递推关系式经常满足( 广义) 斐波
那契数列的条件,所 以 利 用 斐 波 那 契 数 列 的 通 项 公 式 来 计
一、引 言
斐波那契在《算盘书》中提出了一个有趣的兔子问题:
一般而言,兔子在 出 生 两 个 月 后,就 有 繁 殖 能 力,一 对 兔 子 每个月能生出一对小兔子来. 如果所有兔都不死,那么一年 以后可以繁殖多少对兔子?
分析 第一个月小兔子没有繁殖能力,所以还是一对;
两个月后,生下一对小兔,总数是两对; 三个月以后老兔子 又生下一对,因 为 小 兔 子 还 没 有 繁 殖 能 力,所 以 一 共 是 三
0
0
0 … 1 α+β
其中 α,β 是复数且 α≠β.
解 降阶展开可得 Dn = ( α + β) Dn - 1 - αβDn - 2 ,其 中
D1 = α + β,D2 = α2 + αβ + β2 ,则 Dn 是广义斐波那契数列,由
引理
2
整理可得
Dn
=
αn +1 α
- -
βn +1 . β
( 二) 斐波那契数列在变形的三条形行列式中的应用
可得
λ1
=1
+ 槡5 2
,λ2
=1
- 槡5 2
,从而有
( ( )( ) ( )( ) ) |Fn |
斐波那契数列的几条性质及其证明

斐波那契数列的几条性质及其证明斐波那契数列也叫兔子数列,它的前几项是1、1、2、3、5、8、13、21、34、55……,递推公式是:n a =1-n a +2-n a ,其中1a =2a =1。
1、斐波那契数列前n 项的和等于第n +2项的值减去1。
即:1a +2a +…+1-n a +n a =2+n a -1证明:左边=2a +1a +2a +…+1-n a +n a -2a=(2a +1a )+2a +…+1-n a +n a -2a根据递推公式n a =1-n a +2-n a 得:上式 =(3a +2a )+…+1-n a +n a -2a 以此类推最后得:左边=1+n a +n a -2a =2+n a -2a =2+n a -1。
等式得证。
2、斐波那契数列前n 项的平方和等于第n 项和第n +1项的值乘积。
即:21a +22a +……+2n a =n a 1+n a证明:根据递推公式n a =1-n a +2-n a 得,左边=21a +2a (3a -1a )+3a (4a -2a )+……+n a (1+n a -1-n a )=21a +2a 3a - 1a 2a +3a 4a -2a 3a +……+n a 1+n a -1-n a n a因为21a =1a 2a ,所以合并同类项后得,左边=n a 1+n a 。
等式得证。
3、斐波那契数列前n 项相邻两项乘积之和,当n 是奇数时等于第n +1项的值的平方,当n 是偶数时等于第n 项和第n +2项的值之积。
即:1a 2a +2a 3a +……+n a 1+n a 当n 是奇数时等于21+n a ,当n 是偶数时等于n a 2+n a 。
证明:(1)、当n 是奇数时,1a 2a +2a 3a +……+n a 1+n a =21+n a左边=1a 2a +2a (4a -2a )+3a 4a +4a (6a -4a )+……+1-n a (1+n a -1-n a )+n a 1+n a =1a 2a +2a 4a -2a 2a +3a 4a +4a 6a -4a 4a +……+1-n a 1+n a -1-n a 1-n a +n a 1+n a 因为1a 2a =2a 2a ,所以上式=2a 4a +3a 4a +4a 6a -4a 4a +……+1-n a 1+n a -1-n a 1-n a +n a 1+n a =(2a +3a )4a -4a 4a +(4a +5a )6a -6a 6a +……-1-n a 1-n a +(1-n a +n a )1+n a根据递推公式n a =1-n a +2-n a 得:上式 =4a 4a -4a 4a +6a 6a -6a 6a +……+1-n a 1-n a -1-n a 1-n a +1+n a 1+n a=21+n a等式得证。
广义斐波那契数列的性质及推广

( 1 0 )
、
— } ∞J n + l
令X = 0 , Y =1 , r = 1 , S =1 , 有r : + 4 ≠ 0 , 满足 l < I I , 代入( 1 0 )
列 的黄 金数 。
=0 . 6 1 8
这个 数 就 叫黄 金 数 , 记作 ∞。 下 面 分 情 况 讨 论广 义 斐 波 那 契 数
①当, +4 s=0时 ,
设矩阵A的特征多项式为厂 ( ) , 即, ( ) = 一 A I = 乙, 一 ,
用, ( ) 除 , 设商 为 ‘ p ( 九 ), 余式 为 p l L+ P 。 根据 哈 密 顿一凯 莱定 理
1 通 项公 式 的求 解
上 述 递 推 关 系 用 矩 阵 运 算 表 示 , 即 :
令A = 1 0 1 } , = 一 一 1 , 则 上 式 简 记 为 = r - - , 即 :
=
二 2 ] 3 广义斐波那契数列的黄金数
( 1 )
, 厂 =
{ / 2 } 、{ / } , 限 干篇 幅 , 笔 者不 一 -7 1 1 举。
总结: 广 义斐 波 那 契 数 列 求 和 的 关 键 , 在 于分 析 { } 的 通 项 公 式 由哪 几部 分 组 成 。 一 般 可 化 为 等 差 数 列 与等 比数 列 积 的组 合 形 式。 故 将 广义 斐 波 那 契 数 列 求 和 变 形 , 例如求解 数列 { ( 一 1 ) } 、
,
∑
fibonacci型数列及其性质

fibonacci型数列及其性质
Fibonacci序列是由意大利数学家莱昂纳多·斐波那契(Leonard Fibonacci)在《计算书》中提出来的一个数字序列。
该数列从第三项开始,每一项都等于前两项之和,形如:0、1、1、2、3、5、8、13、21、34、55、89……
斐波那契数列具有以下性质:
1. 数列中任意一项均等于其前两项之和;
2. 数列中的第一项和第二项均为1;
3. 斐波那契数列的每一项都可以表达成这样的形式:Fn=Fn-1+Fn-2;
4. 斐波那契数列包含有0、1和负数;
5. 斐波那契数列中任意一项都可以表示成如下形式:Fn=A*φ^n+(1-A)*(-φ)^n,φ=(1+√5)/2;
6. 斐波那契数列在自然数中循环出现;
7. 斐波那契数列中任一项与它的前两项比值之比例接近黄金分割数φ。
fibonacci数列为什么那么重要,所有关于数学的书几乎都会提到?

fibonacci数列为什么那么重要,所有关于数学的书几乎都会提到?因为斐波那契数列在数学和生活以及自然界中都非常有用。
一句话先回答问题:因下面我就尽我所能,讲述一下斐波那契数列。
一、起源和定义斐波那契数列最早被提出是印度数学家Gopala,他在研究箱子包装物件长度恰好为1和2时的方法数时首先描述了这个数列。
也就是这个问题:有n个台阶,你每次只能跨一阶或两阶,上楼有几种方法?而最早研究这个数列的当然就是斐波那契(Leonardo Fibonacci)了,他当时是为了描述如下情况的兔子生长数目:第一个月初有一对刚诞生的兔子第二个月之后(第三个月初)它们可以生育每月每对可生育的兔子会诞生下一对新兔子兔子永不死去这个数列出自他赫赫有名的大作《计算之书》(没有维基词条,坑),后来就被广泛的应用于各种场合了。
这个数列是这么定义的:The On-Line Encyclopedia of Integer Sequences? (OEIS?)序号为A000045 - OEIS(注意,并非满足第三条的都是斐波那契数列,卢卡斯数列(A000032 - OEIS)也满足这一特点,但初始项定义不同)二、求解方法讲完了定义,再来说一说如何求对应的项。
斐波那契数列是编程书中讲递归必提的,因为它是按照递归定义的。
所以我们就从递归开始讲起。
1.递归求解int Fib(int n){return n < 2 ? 1 : (Fib(n-1) + Fib(n-2));}这是编程最方便的解法,当然,也是效率最低的解法,原因是会出现大量的重复计算。
为了避免这种情况,可以采用递推的方式。
2.递推求解int Fib[1000];Fib[0] = 0;Fib[1] = 1;for(int i = 2;i < 1000;i++) Fib[i] = Fib[i-1] + Fib[i-2];递推的方法可以在O(n)的时间内求出Fib(n)的值。
一类广义斐波那契数列及其应用_张纪平

13 ( 9)
假设 x 是有理数 , 并记 x =
q , 其中, p , q 互质 , 代入式( 9) 得 p p 2 = pq + k q2 . 2 4m kq 2 是整数. 于是 4m 2 w ( 10)
下面的讨论将得出矛盾, 从而说明 x 是无理数 . 假设 q 有一质数因子 w , 使得 2m 不以 w 做为其因子 . 那么 p 2 = ( p q + kq2 ) w . w 4m w 因此 , p 含有质数因子 w , 从而含有因子 w , 即说明 p 含有因子 w . 这与 p 、 q 互质相矛盾. q 2 k q 由此可见 , q 整除 2m, 1. 现将式( 10) 改写为 p = p q + q. 2m 2m 2m 因为 k 2m 1 , 由式 ( 10) 得 p 2 = pq + k q q 2m 2m pq + q. 注意到 x 1, 而 x = 1 不满足
[ 1] [ 2] [ 3] 吴振奎 . 斐波那契数列 [ M ] . 沈阳 : 辽宁教育出版社 , 1987. 周苹濒 . F - 型数列的某些性质 [ J ] . 厦门数学通讯 . 1987, ( 4) : 3- 6. 陈传璋 . 数学分析 [ M ] . 北京 : 教育出版社 , 1989.
0, 故由式 ( 7) 得
又由式( 3) 可递推得, 对任意自然数 n、 j, A 2 | x n+ j - x n | A 2 | x n+ j - x n | < | x n+ j + 1 - x n+ 1 | = 2. ( A 1 + A 2 x n ) ( A 1 + A 2 x n+ j ) [ A 1 + A 2 / ( 4A 1 ) ] A2 记B = 2 , 容易验证 0 < B < 1. 根据引理 1 知数列{ x n } 是基本列 . 证毕. [ A 1 + A 2 / ( 4A 1 ) ]
斐波那契数列资料

斐波那契数列资料斐波那契数列斐波那契数列⼀、简介斐波那契数列(Fibonacci),⼜称黄⾦分割数列,由数学家斐波那契最早以“兔⼦繁殖问题”引⼊,推动了数学的发展。
故斐波那契数列⼜称“兔⼦数列”。
斐波那契数列指这样的数列:1,1,2,3,5,8,13,……,前两个数的和等于后⾯⼀个数字。
这样我们可以得到⼀个递推式,记斐波那契数列的第i项为F i,则F i=F i-1+F i-2.兔⼦繁殖问题指设有⼀对新⽣的兔⼦,从第三个⽉开始他们每个⽉都⽣⼀对兔⼦,新⽣的兔⼦从第三个⽉开始⼜每个⽉⽣⼀对兔⼦。
按此规律,并假定兔⼦没有死亡,10个⽉后共有多少个兔⼦?这道题⽬通过找规律发现答案就是斐波那契数列,第n个⽉兔⼦的数量是斐波那契数列的第n项。
⼆、性质如果要了解斐波那契数列的性质,必然要先知道它的通项公式才能更简单的推导出⼀些定理。
那么下⾯我们就通过初等代数的待定系数法计算出通项公式。
令常数p,q满⾜F n-pF n-1=q(F n-1-pF n-2)。
则可得:F n-pF n-1=q(F n-1-pF n-2)=q2(F n-2-pF n-3)=…=q n-2(F2-pF1)⼜∵F n-pF n-1=q(F n-1-pF n-2)∴F n-pF n-1=qF n-1-pqF n-2F n-1+F n-2-pF n-1-qF n-1+pqF n-2=0(1-p-q)F n-1+(1+pq)F n-2=0∴p+q=1,pq=-1是其中的⼀种⽅程组∴F n-pF n-1= q n-2(F2-pF1)=q n-2(1-p)=q n-1F n=q n-1+pF n-1=q n-1+p(q n-2+p(q n-3+…))=q n-1+pq n-2+p2q n-3+…+p n-1不难看出,上式是⼀个以p/q为公⽐的等⽐数列。
将它⽤求和公式求和可以得到:⽽上⾯出现了⽅程组p+q=1,pq=-1,可以得到p(1-p)=-1,p2-p-1=0,这样就得到了⼀个标准的⼀元⼆次⽅程,配⽅得p2-p+0.25=1.25,(p-0.5)2=1.25,p=±√1.25+0.5。
斐波那切数列

斐波那切数列一、斐波那切数列的基本内容斐波那契数列又称“那波列”,是斐波那契对数和欧拉乘积的一个特例,指由任意大于0的奇数(非零自然数)按照它们的指数的比例关系排成的数列。
在数学中,斐波那契数列被定义为一个从小到大依次为formula_1, formula_2,formula_3,…formula_n,包含有formula_i个项的数列。
该数列第i项的系数formula_4,叫做这个数列的通项公式。
其中formula_5表示上述各项的指数的乘积,且formula_6。
二、斐波那切数列在古典数论中的地位斐波那切数列是斐波那契数列和帕斯卡三角形数的推广,它是古典数论中两个最重要的数学结果之一。
所谓帕斯卡三角形数,就是以3、 5、 7为顶点的等边三角形数,共有11种,其中的一种就是斐波那契数列。
欧拉曾经把他的乘法公式中的下标P改成g,并且将公式改写成为:即欧拉乘积中出现的g指的就是g。
并且将欧拉的证明公布于众,后人将它记录成为欧拉恒等式:但他们之间也存在着密切联系。
首先,帕斯卡三角形数与斐波那契数列的通项公式相同;其次,斐波那契数列与三角形数之间有着深刻的对应关系,如斐波那契数列中的第一项正好是三角形数的第一项。
因此,三角形数的每一项都可以用斐波那契数列的前两项相乘来得到。
三、斐波那契数列的意义在数学中,斐波那契数列是很有价值的概念,它的出现标志着近代数学的开始。
作为计算的工具,它已被应用于高等数学的某些分支,其中最重要的是微分学。
斐波那契数列被普遍认为是用来解析微分方程的工具,它的许多性质在高等数学的发展中起了十分重要的作用,是现代数学基础的一部分。
斐波那契数列的发现不仅提供了确定无疑的例证,而且提供了大量重要的函数和图形。
二者不仅保持着某种数学上的同构关系,而且由于这两个概念的紧密联系,使人感到似乎是同一个定理的两个方面。
比如说,我们知道某一个函数f( x)=ax2+bx+c,并且利用费马大定理可以得出,只要知道函数f( x)=ax2+bx+c,我们就能找到函数f的定义域和值域;再如,从自变量的递增区间的极限函数导出某函数的极限;从数列的极限导出某函数的极限,等等。
斐波那契的初步推广与探讨

斐波那契数列的初步推广晏文能 08数① 200803011034摘要:斐波那契数列是递推数列中的一类,他是先给定数列的开始两项,然后由这两项相加的第三项,再用第二、三项相加得第四项,如此依次递推的数列,即数列中任意相连三项的第三项等于前两项之和。
现本文将对斐波那契数列中的由先给定开始两项初步推广至先给定开始三项,再由已给定三项相加得第四项,依次递推,即所得数列中任意相连四项的第四项等于前三项之和,并对其通项公式进行初步的探讨。
关键词:数列;递推;求和。
一、斐波那契数列的通项公式简介。
斐波那契数列指的是这样一个数列:1、1、2、3、5、8、13、21、……这个数列从第三项开始,每一项都等于前两项之和。
它的通项公式的推导如下:设常数r,s使得F(n)-r*F(n-1)=s*[F(n-1)-r*F(n-2)]则r+s=1,-rs=1n≥3时,有F(n)-r*F(n-1)=s*[F(n-1)-r*F(n-2)]F(n-1)-r*F(n-2)=s*[F(n-2)-r*F(n-3)]F(n-2)-r*F(n-3)=s*[F(n-3)-r*F(n-4)]……F(3)-r*F(2)=s*[F(2)-r*F(1)]将以上n-2个式子相乘,得:F(n)-r*F(n-1)=[s^(n-2)]*[F(2)-r*F(1)]∵s=1-r,F(1)=F(2)=1上式可化简得:F(n)=s^(n-1)+r*F(n-1)那么:F(n)=s^(n-1)+r*F(n-1)= s^(n-1) +a*s^(n-2) +a^2*F(n-2)= s^(n-1) +a*s^(n-2) +a^2*s^(n-3) +a^3*F(n-3)……= s^(n-1) +a*s^(n-2) +a^2*s^(n-3) +……+a^(n-2)*s +a^(n-1)*F(1) = s^(n-1) +a*s^(n-2) +a^2*s^(n-3) +……+a^(n-2)*s +a^(n-1) (这是一个以s^(n-1)为首项、以r^(n-1)为末项、r/s为公比的等比数列的各项的和)=[s^(n-1)-r^(n-1)*r/s]/(1-r/s)=(s^n -a^n)/(s-r)r+s=1, -rs=1的一解为s=(1+√5)/2,r=(1-√5)/2则F(n)=(1/√5)*{[(1+√5)/2]^n - [(1-√5)/2]^n}若令F﹙n﹚=a﹙n﹚则:有趣的是:这样一个完全是自然数的数列,通项公式居然是用无理数来表达的。
