数学竞赛之窗2010年模拟题解答(11-20)
2010年全国高中数学联赛一试试题及答案

6. 两人轮流投掷骰子否则轮由另 一人投掷.先投掷人的获胜概率是
84 . 119 21 7 = ,从而先投掷人的获胜概率为 36 12
解:同时投掷两颗骰子点数和大于 6 的概率为
7 5 7 5 7 + ( )2 × + ( )4 × + " 12 12 12 12 12 7 1 84 . = × = 25 119 12 1− 144
2
数学竞赛之窗博客/
g ( y ) max = a 2 + 3a − 2 = 8 ⇒ a = 2 ,
所以 g ( y ) min = 2
1 + 3 × 2 −1 − 2 = − . 4 1 综上 f ( x) 在 x ∈ [ −1,1] 上的最小值为 − . 4
解二:如图, PC = PC1 , PA1 = PB . 设 A1 B 与 AB1 交于点 O, 则
OA1 = OB, OA = OB1 , A1 B ⊥ AB1 .
因为 PA = PB1 , 所以 PO ⊥ AB1 ,
从而 AB1 ⊥ 平面 PA1 B . 过 O 在平面 PA1 B 上作 OE ⊥ A1 P ,垂足为 E . 连结 B1 E ,则 ∠B1 EO 为二面角 B − A1 P − B1 的平面角. 设 AA1 = 2 ,则易求得
2
3 ≤ a ≤ 12 . 2
解:令 sin x = t ,则原函数化为 g (t ) = ( −at + a − 3)t ,即
2
g (t ) = −at 3 + (a − 3)t .
由
− at 3 + (a − 3)t ≥ −3 , − at (t 2 − 1) − 3(t − 1) ≥ 0 ,
2010年模拟考试数学试题答案

tan ABO
1 ……………………………………………
OB 4
2
.2 分
∴ OA= 2,即 A 的坐标为 (0, 2),点 B 的坐标为 (4, 0)……………… 3 分
OA OB
∵ CE⊥ x 轴,∴ CE∥ OA,∴
………………………………
CE BE
∵ OE=2,∴ CE=3.∴点 C 的坐标是 (- 2, 3)…………………………
∴ OE ON , AE CN .
ห้องสมุดไป่ตู้
又∵ MOE MON 450 , OM OM , ∴ OME OMN . ∴ MN ME AM AE . ∴ MN AM CN , ∴ p MN BN BM AM CN BN BM AB BC 4.
∴在旋转正方形
OABC 的过程中, p 值无变化 . …………… 10 分
∴一共调查了 3x+4x+ 5x+ 8x+ 2x= 66(人 ) ……………………………………………
∴捐款数不少于
20 元的概率是 30 66
5 11
.…………………………………………………
3分 5分
数学 第 1 页 ( 共 6 页)
(2) 由(1) 可知,这组数据的众数是 20(元 ),中位数是 15(元 ).…………………………… 7 分 (3) 全校学生共捐款 (9× 5+ 12×10+ 15×15+ 24×20+ 6× 30)÷ 66× 2310= 36750(元 ) ………………… 10 分
2y ……………………… 4 分 xy
x 3y =
2 y ………………………………………… 6 分
xy xy
= x y =1. xy
…………………………………………… 7 分
2010全国初中数学竞赛题及答案

三、解答题(共4题,每题20分,共80分)11.如图,△ABC 为等腰三角形,AP 是底边BC 上的高,点D 是线段PC 上的一点,BE 和CF 分别是△ABD 和△ACD 的外接圆直径,连接EF . 求证: tan EF PAD BC∠=.证明:如图,连接ED ,FD . 因为BE 和CF 都是直径,所以ED ⊥BC , FD ⊥BC ,可得…………(20分)12.如图,抛物线2y ax bx =+(a >0)与双曲线y x=相交于点A ,B . 已知点A 的坐标为(1,4),点B 在第三象限内,且△AOB 的面积为3(O 为坐标原点).(1)求实数a ,b ,k 的值;(2)过抛物线上点A 作直线AC ∥x 轴,交抛物线于另一点C ,求所有满足△EOC ∽△AOB 的点E 的坐标.(第11题)解:(1)因为点A (1,4)在双曲线k y x=上, 所以k=4. 故双曲线的函数表达式为xy 4=. 设点B (t ,4t ),0t <,AB 所在直线的函数表达式为y mx n =+,则有 44m n mt n t =+⎧⎪⎨=+⎪⎩,, 解得4m t =-,4(1)t n t +=. 于是,直线AB 与y 轴的交点坐标为4(1)0,t t +⎛⎫ ⎪⎝⎭,故 ()141132AOB t S t t∆+=⨯-=(),整理得22320t t +-=, 解得2t =-,或t =1(舍去).所以点B 的坐标为(2-,2-). ⎧⎨⎩=B '(2-,2)是CO 的延长1OA 到点1E ,使得1OE =12OA ,这时点1E (8,2-)是符合条件的点.(ii )作△BOA 关于x 轴的对称图形△2B OA ',得到点2A (1,4-);延长2OA 到点2E ,使得2OE =22OA ,这时点E 2(2,8-)是符合条件的点.所以,点E 的坐标是(8,2-),或(2,8-). …………(20分)13.求满足22282p p m m ++=-的所有素数p 和正整数m ..解:由题设得(21)(4)(2)p p m m +=-+, 所以(4)(2)p m m -+,由于p 是素数,故(4)p m -,或(2)p m +. ……(5分)(1)若(4)p m -,令4m kp -=,k 是正整数,于是2m kp +>,2223(21)(4)(2)p p p m m k p >+=-+>,故23k <,从而1k =. 所以4221m p m p -=⎧⎨+=+⎩,,解得59.p m =⎧⎨=⎩, …………(10分) (2)若(2)p m +,令2m kp +=,k 是正整数.当5p >时,有46(1)m kp kp p p k -=->-=-,223(21)(4)(2)(1)p p p m m k k p >+=-+>-,故(1)3k k -<,从而1k =,或2.由于(21)(4)(2)p p m m +=-+是奇数,所以2k ≠,从而1k =.于是4212m p m p -=+⎧⎨+=⎩,, 这不可能.当5p =时,2263m m -=,9m =;当3p =,2229m m -=,无正整数解;当2p =时,2218m m -=,无正整数解.综上所述,所求素数p =5,正整数m =9. …………(20分)14.从1,2,…,2010这2010个正整数中,最多可以取出多少个数,使得所取出的数中任意三个数之和都能被33整除?解:首先,如下61个数:11,1133+,11233+⨯,…,116033+⨯(即1991)满足题设条件. …………(5分)另一方面,设12n a a a <<< 是从1,2,…,2010中取出的满足题设条件的数,对于这n 个数中的任意4个数i j k m a a a a ,,,,因为33()i k m a a a ++, 33()j k m a a a ++,所以 33()j i a a -.因此,所取的数中任意两数之差都是33的倍数. …………(10分)设133i i a a d =+,i =1,2,3,…,n . 由12333()a a a ++,得12333(33333)a d d ++, …………(15分)故20分)。
高州市2010年学科竞赛数学试卷答案
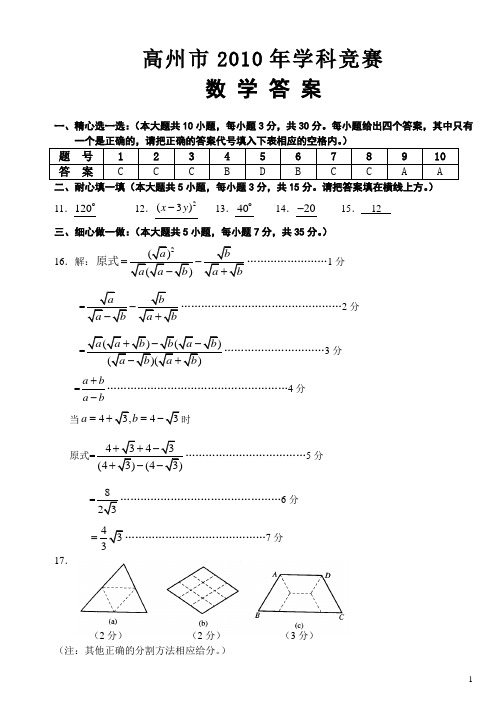
高州市2010年学科竞赛数 学 答 案一、精心选一选:(本大题共10小题,每小题3分,共30分。
每小题给出四个答案,其中只有11.120 12.2(3)x y - 13.40 14.20- 15. 12三、细心做一做:(本大题共5小题,每小题7分,共35分。
)16.解:=原式……………………1分…………………………………………2分3分=a ba b +-………………………………………………4分当44a b ==时原式5分…………………………………………6分=7分17.(2分) (2分) (3分)(注:其他正确的分割方法相应给分。
)18.解:作DE ⊥BC 于E ,DF ⊥AB 于F ,……………………1分则30,60DCE ADF ∠=∠=四边形DEBF 为矩形,……………………………………2分在,1000500Rt CDE CD DE =∴= 中米米500FB ∴=米…………………………3分45,30ACB DCB ∠=∠= 15ACD ∴∠=90B ∠= 又 45CAB ∴∠=又453015CAD CAB DAF ∠=∠-∠=-=ACD CAD ∴∠=∠1000AD CD ∴==米………………………………4分 在3,sin 6010005003()2Rt ADF AF AD =⋅=⨯= 中米…………5分 …………………………6分答:山高AB 为50031)米……………………………………7分19、解:设甲工种招x 人,两工种每月要付工资总额为y 元,则乙工种招(150-x )人, (1)分依题意得1502,x x -≥………………2分得050x ≤≤…………………………3分10015015x ≤-≤………………4分即:甲工种招工不多于50人,乙工种不少于100人时,每月所付工资总额最少。
……5分 又8001000(150)150000200(050)y x x x x =+-=-≤≤50,140000(x y ∴==当时最小元)………………………………6分答:甲工种招人不多于50人,乙工种招人不少于100人时,工资总额最少。
2010年全国 初中数学联赛(含答案)

12010年全国初中数学联合竞赛试题参考答案第一试一、选择题:(本题满分42分,每小题7分)1.若a ,b ,c 均为整数且满足1010()()1a b a c -+-=,则||||||a b b c c a -+-+-=( )A .1B .2C .3D .4【答案】 B【解析】 因为()()10101a b a c ---=,而左边的两个加数都是非负整数,所以一个等于0,另一个等于1,也就是说,a ,b ,c 三个数中有两个相等,另一个和它们相差1.因此,所求的和式中,两项等于1,另一项等于2,结果为2.2.若实数a ,b ,c 满足等式3||6a b =,49||6a b c =,则c 可能取的最大值为( )A .0B .1C .2D .3【答案】 C【解析】 为了使c 尽量大,a 应该尽量大,b 应该尽量小.因为它们都是非负数,3a ,0b =,不难观察到所求答案为2.3.若a ,b 是两个正数,且1110,a b b a--++= 则( )2A .103a b <+≤B .113a b <+≤C .413a b <+≤D .423a b <+≤. 【答案】 C【解析】 去分母之后得到()()110a a b b ab -+-+=,即220a ab b a b ++--=.给定a 和b 是两个正数,那么如果让它们中的一个等于0,则另一个等于0或14.若方程2310x x --=的两根也是方程420x ax bx c +++=的根,则2a b c +-的值为 ( )A .13-B .9-C .6D .0【答案】 A【解析】 这需要使得前者是后者的因式,用综合除法可得,余式为()()33310a b x a c +++++,它应该等于0.所以两个系数都为0,特别地,()()333210a b a c ++-++,所以所求答案为13-.5.在ABC △中,已知60CAB ∠=︒,D ,E 分别是边AB ,AC 上的点,且60AED ∠=︒,ED DB CE +=,2CDB CDE ∠=∠,则DCB ∠= ( )A .15oB .20oC .25oD .30o【答案】 B【解析】 观察可得ADE △为正三角形,6.对于自然数n ,将其各位数字之和记为n a ,如2009200911a =+++=,201020103a =+++=,则312320092010a a a a a +++++=L ( )A .28062B .28065C .28067D .28068.【答案】 D【解析】 根据弃九法,它和1到2010的和被9除的余数相等.每连续9个自然数之和被9整除,2010被9除余3,1236++=,所以只有D 符合.二、填空题:(本题满分28分,每小题7分)1.已知实数x ,y 满足方程组33191x y x y ⎧+=⎨+=⎩,,则22x y += .【答案】 13【解析】 第一式除以第二式可得2219x xy y -+=,第二式平方可得2221x xy y ++=,那么所求答案就是()1921313⨯+÷=.2.二次函数2y x bx c =++的图象与x 轴正方向交于A ,B 两点,与y 轴正方向交于点C .已知3AB ,30CAO ∠=︒,则c = .【答案】 19【解析】 观察可知A 必须在B 左边,否则B 会跑到x 轴负半轴上.设A 的横坐标为a ,则C 的纵坐标3,23AC =,2AB a =.因此,考虑两根之积,33a a ⨯,3a =319=. 3.在等腰直角ABC △中,5AB BC ==,P 是ABC △内一点,且5PA ,5PC =,则PB = .4【答案】 10【解析】 设()00B ,,()50A ,,()05C ,,根据熟知的勾三股四弦五,可观察到()31P ,,(另一个点在三角形外,不符合),所以10PB =.4.将若干个红、黑两种颜色的球摆成一行,要求两种颜色的球都要出现,且任意中间夹有5个或10个球的两个球必为同一种颜色的球.按这种要求摆放,最多可以摆放 个球.【答案】 15【解析】 也就是说,编号之差为6或11的两个球颜色相同.下面从1号球开始,依次写出颜色相同的球的编号:11261711516104159314821371→→→→→→→→→→→→→→→→→也就是说,如果有17个球,则全部同色;如果超过17个,则任何连续17个同色,也不行.如果有16个,则上面的圈去掉17号球仍然是一条链,仍然不行;如果有15个,则上面的圈去掉17号球和16号球后断成两部分,所以可以.第二试 (A )一.(本题满分20分)设整数()a b c a b c ≥≥,,为三角形的三边长,满足22213a b c ab ac bc ++---=,求符合条件且周长5不超过30的三角形的个数.【解析】 由已知等式可得222()()()26a b b c a c -+-+-= ①令a b m -=,b c n -=,则a c m n -=+,其中m ,n 均为自然数.于是,等式①变为222()26m n m n +++=,即2213m n mn ++= ②由于m ,n 均为自然数,判断易知,使得等式②成立的m ,n 只有两组:31m n =⎧⎨=⎩,,和13.m n =⎧⎨=⎩,⑴ 当3m =,1n =时,1b c =+,34a b c =+=+.又a ,b ,c 为三角形的三边长,所以b c a +>,即(1)4c c c ++>+,解得3c >.又因为三角形的周长不超过30,即(4)(1)30a b c c c c ++=++++≤,解得253c ≤. 因此2533c <≤, 所以c 可以取值4,5,6,7,8,对应可得到5个符合条件的三角形.6⑵ 当1m =,3n =时,3b c =+,14a b c =+=+.又a ,b ,c 为三角形的三边长,所以b c a +>,即(3)4c c c ++>+,解得1c >.又因为三角形的周长不超过30,即(4)(3)30a b c c c c ++=++++≤,解得233c ≤. 因此2313c <≤, 所以c 可以取值2,3,4,5,6,7,对应可得到6个符合条件的三角形.综合可知:符合条件且周长不超过30的三角形的个数为5611+=.二.(本题满分25分)已知等腰三角形ABC △中,AB AC =,C ∠的平分线与AB 边交于点P ,M 为ABC △的内切圆I e 与BC 边的切点,作MD AC ∥,交I e 于点D .证明:PD 是I e 的切线.【解析】 过点P 作I e 的切线PQ (切点为Q )并延长,交BC 于点N .因为CP 为ACB ∠的平分线,所以ACP BCP ∠=∠.又因为PA 、PQ 均为I e 的切线,所以APC NPC ∠=∠.IP QNB7又CP 公共,所以ACP NCP △≌△,所以PAC PNC ∠=∠.由NM QN =,BA BC =,所以QNM BAC △≌△,故NMQ ACB ∠=∠,所以MQ AC ∥.又因为MD AC ∥,所以MD 和MQ 为同一条直线.又点Q 、D 均在I e 上,所以点Q 和点D 重合,故PD 是I e 的切线.三.(本题满分25分)已知二次函数2y x bx c =+-的图象经过两点()1P a ,,()210Q a ,. ⑴ 如果a ,b ,c 都是整数,且8c b a <<,求a ,b ,c 的值.⑵ 设二次函数2y x bx c =+-的图象与x 轴的交点为A 、B ,与y 轴的交点为C .如果关于x 的方程20x bx c +-=的两个根都是整数,求ABC △的面积.【解析】 点()1P a ,、()210Q a ,在二次函数2y x bx c =+-的图象上,故1b c a +-=,4210a c a +-=,解得93b a =-,82c a =-.⑴ 由8c b a <<知8293938a a a a -<-⎧⎨-<⎩,,解得13a <<.又a 为整数,所以2a =,9315b a =-=,8214c a =-=.⑵ 设m ,n 是方程的两个整数根,且m n ≤,旗开得胜8由根与系数的关系可得39m n b a +=-=-,28mn c a =-=-,消去a ,得98()6mn m n -+=-,两边同时乘以9,得8172()54mn m n -+=-,分解因式,得(98)(98)10m n --=.所以9819810m n -=⎧⎨-=⎩,,或982985m n -=⎧⎨-=⎩,,或9810981m n -=-⎧⎨-=-⎩,,或985982m n -=-⎧⎨-=-⎩,,解得12m n =⎧⎨=⎩,,或109139m n ⎧=⎪⎪⎨⎪=⎪⎩,,或2979m n ⎧=-⎪⎪⎨⎪=⎪⎩,,或19323m n ⎧=⎪⎪⎨⎪=⎪⎩,,又m ,n 是整数,所以后面三组解舍去,故1m =,2n =.因此,()3b m n =-+=-,2c mn =-=-,二次函数的解析式为232y x x =-+.易求得点A 、B 的坐标为()10,和()20,,点C 的坐标为()02,, 所以ABC △的面积为1(21)212⨯-⨯=.第二试 (B )旗开得胜9一.(本题满分20分)设整数a ,b ,c 为三角形的三边长,满足22213a b c ab ac bc ++---=,求符合条件且周长不超过30的三角形的个数(全等的三角形只计算1次).【解析】 不妨设a b c ≥≥,由已知等式可得222()()()26a b b c a c -+-+-= ①令a b m -=,b c n -=,则a c m n -=+,其中m ,n 均为自然数.于是,等式①变为222()26m n m n +++=,即2213m n mn ++= ②由于m ,n 均为自然数,判断易知,使得等式②成立的m ,n 只有两组:31m n =⎧⎨=⎩,,和13.m n =⎧⎨=⎩,⑴ 当3m =,1n =时,1b c =+,34a b c =+=+.又a ,b ,c 为三角形的三边长,所以b c a +>,即(1)4c c c ++>+,解得3c >.又因为三角形的周长不超过30,即(4)(1)30a b c c c c ++=++++≤,解得253c ≤. 因此2533c <≤,旗开得胜10所以c 可以取值4,5,6,7,8,对应可得到5个符合条件的三角形.⑵ 当1m =,3n =时,3b c =+,14a b c =+=+.又a ,b ,c 为三角形的三边长,所以b c a +>,即(3)4c c c ++>+,解得1c >.又因为三角形的周长不超过30,即(4)(3)30a b c c c c ++=++++≤,解得233c ≤. 因此2313c <≤, 所以c 可以取值2,3,4,5,6,7,对应可得到6个符合条件的三角形.综合可知:符合条件且周长不超过30的三角形的个数为5611+=.二.(本题满分25分)题目和解答与(A )卷第二题相同.三.(本题满分25分)题目和解答与(A )卷第三题相同.第二试 (C )11一.(本题满分20分)题目和解答与(B )卷第一题相同.二.(本题满分25分)题目和解答与(A )卷第二题相同.三.(本题满分25分)设p 是大于2的质数,k 为正整数.若函数2(1)4y x px k p =+++-的图象与x 轴的两个交点的横坐标至少有一个为整数,求k 的值.【解析】 由题意知,方程2(1)40x px k p +++-=的两根1x ,2x 中至少有一个为整数.由根与系数的关系可得12x x p +=-,12(1)4x x k p =+-,从而有()()()()12121222241x x x x x x k p ++=+++=- ①⑴ 若1k =,则方程为22(2)0x px p ++-=,它有两个整数根2-和2p -.⑵ 若1k >,则10k ->.因为12x x p +=-为整数,如果1x ,2x 中至少有一个为整数,则1x ,2x 都是整数.又因为p 为质数,由①式知1|2p x +或2|2p x +.不妨设1|2p x +,则可设12x mp +=(其中m 为非零整数),则由①式可得212k x m-+=,12故()()12122k x x mp m -+++=+,即1214k x x mp m-++=+. 又12x x p +=-,所以14k p mp m--+=+, 即1(1)4k m p m-++= ② 如果m 为正整数,则(1)(11)36m p ++⨯=≥,10k m->, 从而1(1)6k m p m-++>,与②式矛盾. 如果m 为负整数,则(1)0m p +<,10k m-<, 从而1(1)0k m p m-++<,与②式矛盾. 因此,1k >时,方程2(1)40x px k p +++-=不可能有整数根.综上所述,1k =.旗开得胜13。
2010年全国初中数学联赛模拟卷

图3
1. A C内接于Q0, 2A B D是边 B C上的中点 , / B 若 _ C+L A 9 。则 AA C _ A D C= 0 , B 是
三角形.
第 7期
2 1 全 国初 中数 学联 赛模 拟 卷 0 0年
・
4 4・
中学教研 ( 数学)
21 0 0生
2010年 全 国 初 中 数 学 联 赛 模 拟 卷
一
、
选择题
1已知 : AA C中, C 9 。 /A C=1。A . 在 B LA B= 0 , B _ 5 ,C=1则 B , C的长为
(
)
A2 .+
A 二者 均 为有 理数 .
A. 0o 8
4 ≤ 5
B. O。 5
c≤ 2 . 6 7 <
C. 40。
D-≤ 莩 . ) , ≤
(
D. O。 2
5 如 图 1 已知在 AA C中 ,B= C / A . , B A A , _B C和 /A B 的平 分线 相 交 于 点 D, A _ C / DC= _
l. 4 已知线 段 A B是 o0 的弦 , P是 优 弧A 上 一个 动点 ( 点 B P不与 , 重合 ) 直线 z /A B的平分 线. , 是_P
/ 、
() 1 画图并 证 明 : 当点 P在 优弧 船 上运 动时 , A B 的平 分 线 z 定点 Q / P _ 过 .
・ 5・ 4
三、 解答 题
l. 同学买某种铅笔 , 3某 当他买了 . , 2 付了 Y , 7 支 元( Y都是整数 ) , 时 营业员说 :你要再多买 l , “ 0支 我就总
2010年北京市中学生数学竞赛高一年级初赛试题及参考解答

A B C 内 一点 , 且满 足 2 PA +
∋
&& ∋
3 P B + 6 PC = 0, 试 确 定 P CA 的面积之比. 6. 如图 5, 凸四边形 A B CD 中, ( B A D + ( A D C = 240 ), E 和 F 分 别是边 A D 、 B C 的中点 , EF =
) ] , 而已知这个函数是奇函数 , 其必要 2 = k ,所
条件是在 0 点的函数值为 0, 即 3 以 的最小值是 6 .
2 . 答: ( B) . b 理由 为直线 O P 的斜率, 其最小值为 a b O C 的斜率 , 其最大值为 OA 的斜率, 所以 的 a p q 最大值为 , 最小值为 . m n 3 . 答 : ( C) . 理由 在 A BC 所在平面上取一点 O , ∗ + + 即 P A + P B + PC = 2 A B ,
2010 年 7 月上
第 397 期 ( 高中 )
数 学 竞 赛 之 窗
S PC 1 A 1 , 6# 2 + S PA B . S PB C . S PCA = 6 . 2 . 3 . 6. 答: 28 . 解 延长 B A 、 CD 相交于点 P , 由 ( BA D + ( A D C = 240 ) , 得 ( BP C = 60 ). 连接 BD , 取 BD 的中点 G, 连接 EG, FG, 则 由三角形中位线定理, 知 GE / BP, GF / PC, 所 1 1 以 ( EGF = 120 ), EG = A B, FG = CD. 2 2 在 E GF 中, 由余弦定理得 E F 2 = EG 2 + F G 2 - 2EG FG cos 120 ) AB 2 CD 2 AB CD = + + , 2 2 2 2 2 2 AB CD AB CD 即 + + 2 2 2 2 S
2010年大学生数学竞赛试题及解答

(1)计算积分222,0,0.xxee dx xαβαβ--+∞->>⎰解 方法一 直接利用分部积分法得222xxee dx xαβ--+∞-⎰221()()xxeedx xαβ+∞--'=--⎰221(22)()xxxexe dx xαβαβ+∞--=--+-⎰22(22)xxeedx αβαβ+∞--=--⎰)22(2πβπα⋅-⋅-=)(αβπ-=;方法二 不妨设0αβ<<,由于dyexe e yxxx⎰---=-βαβα2222,而积分2yxe dx +∞-⎰关于y 在[,]αβ上一致收敛,故可交换积分次序222xxee dx xαβ--+∞-⎰2yxdx edy βα+∞-=⎰⎰2yxdy edxβα+∞-=⎰⎰dy y⎰=βαπ21)(αβπ-=;方法三 将0β>固定,记222(),0xxee I dx xαβαα--+∞-=>⎰ , 可证()I α在(0,)+∞上收敛.设[,),0αδδ∈+∞> , 因为22xxe eαδ--≤,而2xedx δ∞-⎰+0收敛,所以由Weierstrass 判别法知道2xedx α∞-⎰+0对[,)αδ∈+∞一致收敛.所以可以交换微分运算和积分运算的次序, 即222()()xxee I dx xαβαα--+∞∂-'=∂⎰2()xedx α+∞-=-⎰12πα=-.由δ的任意性,上式在(0,)+∞上成立. 所以 ()I C απα=-+,由于()0,,I C βπβ==所以)()(αβπα-=I ,即dx xe exx⎰∞+---0222βα)(αβπ-=.(2)若关于x 的方程211kx x +=,()0k >在区间()0,+∞内有唯一的实数解,求常数k.解:设()211f x kx x=+-,则有()32f x k x'=-,当1320,x k ⎛⎫⎛⎫ ⎪∈ ⎪ ⎪⎝⎭⎝⎭时,()0f x '<;当132,x k ⎛⎫⎛⎫ ⎪∈+∞ ⎪ ⎪⎝⎭⎝⎭时,()0f x '>. 由此()f x 在132x k ⎛⎫= ⎪⎝⎭处达到最小值,又()211f x kx x=+-在()0,+∞内有唯一的零点,必有1320f k ⎛⎫⎛⎫ ⎪= ⎪ ⎪⎝⎭⎝⎭,13322102k k k ⎛⎫⎛⎫+-= ⎪ ⎪⎝⎭⎝⎭, 3212331214k ⎛⎫⎛⎫ ⎪+= ⎪ ⎪⎝⎭⎝⎭,22714k ⋅=, 所以233k =.(3)设函数()f x 在区间[],a b 上连续,由积分中值公式,有()()()xaf t dt x a f ξ=-⎰,()a x b ξ≤≤≤,若导数()f a +'存在且非零,求lim x aax aξ+→--.解:()()()()()()()xaf t f a dt x a f f a ξ-=--⎰,()()()()()()21xaaa f t f a dt x af f a x a ξξξ--=⋅----⎰, 由条件,可知()()()1l i m x aaf f a f a ξξ+→+-='-,()()()()()()()()21lim lim 22xax ax af t f a dtf x f a f a x a x a +++→→--'==--⎰,故有1lim 2x aax aξ+→-=-.二、设函数()f x 在0x =附近可微,()00f =,()0f a '=,定义数列22212n n x f f f n n n ⎛⎫⎛⎫⎛⎫=+++ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭.证明:{}n x 有极限并求其值.证明:由导数的定义, 对于任意0ε>,存在0δ>,当0||x δ<<时,有()f x a xε-<.于是()()()a x f x a x εε-<<+,()0x δ<<从而,当1nδ->时,有21k nnδ<<,()()222kk k a f a n n n εε⎛⎫-<<+ ⎪⎝⎭,其中1,2,,k n = .对于上式求和,得到()()2211nnn k k k k a x a nnεε==-<<+∑∑,即()()1122n n n a x a nnεε++-<<+,令n →∞,有()()11lim lim 22nn n n a x x a εε→∞→∞-≤≤≤+,由0ε>的任意性,得到 lim 2n n a x →∞=.设()f x 在()1,1-上有定义,在0x =处可导,且()00f =.证明:()210lim2nn k f k f n →∞='⎛⎫= ⎪⎝⎭∑.三、设函数f在[0,)+∞上一致连续,且对任何[0,1]x ∈,有()0limn f x n →∞+=,证明:()0lim x f x →+∞=。
2010年全国初中数学联合竞赛-试题参考答案及评分标准

2010年全国初中数学联合竞赛试题参考答案及评分标准说明:评阅试卷时,请依据本评分标准.第一试,选择题和填空题只设7分和0分两档;第二试各题,请严格按照本评分标准规定的评分档次给分,不要再增加其他中间档次.如果考生的解答方法和本解答不同,只要思路合理,步骤正确,在评卷时请参照本评分标准划分的档次,给予相应的分数.第一试一、选择题(本题满分42分,每小题7分)本题共有6小题,每题均给出了代号为D C B A ,,,的四个答案,其中有且仅有一个是正确的.将你所选择的答案的代号填在题后的括号内.每小题选对得7分;不选、选错或选出的代号字母超过一个(不论是否写在括号内),一律得0分.1. 已知z y x ,,满足x z z y x +=-=532,则zy y x 25+-的值为 ( ) (A )1. (B )31. (C )31-. (D )21. 【答】B.解 由x z z y x +=-=532得x z x y 23,3==,所以31333525=+-=+-x x x x z y y x ,故选(B ). 注:本题也可用特殊值法来判断.2.当x 分别取值20071,20061,20051,…,21,1,2,…,2005,2006,2007时,计算代数式2211xx +-的值,将所得的结果相加,其和等于 ( ) (A )-1. (B )1. (C )0. (D )2007.【答】C.解 因为=+-++-222211)1(1)1(1n n n n 011112222=+-++-n n n n ,即当x 分别取值n 1,n n (为正整数)时,计算所得的代数式的值之和为0;而当1=x 时,0111122=+-.因此,当x 分别取值20071,20061,20051,…,21,1,2,…,2005,2006,2007时,计算所得各代数式的值之和为0.故选(C ).3. 设c b a ,,是△ABC 的三边长,二次函数2)2(2b a cx x ba y ----=在1=x 时取最小值b 58-,则△ABC 是 ( ) (A )等腰三角形. (B )锐角三角形. (C )钝角三角形. (D )直角三角形.【答】D.解 由题意可得⎪⎪⎩⎪⎪⎨⎧-=----=---,5822,1)2(2b b a c b a b a c 即⎪⎩⎪⎨⎧==+,53,2b c a c b 所以b c 53=,b a 54=,因此222b c a =+,所以△ABC 是直角三角形. 故选(D ).4. 已知锐角△ABC 的顶点A 到垂心H 的距离等于它的外接圆的半径,则∠A 的度数是( )(A )30°. (B )45°. (C )60°. (D )75°. 【答】C.解 锐角△ABC 的垂心在三角形内部,如图,设△ABC 的外心为O ,D 为BC 的中点,BO 的延长线交⊙O 于点E ,连CE 、AE ,则CE //AH ,AE //CH ,则OD CE AH OB 2===,所以∠OBD =30°,∠BOD =60°,所以∠A =∠BOD =60°.故选(C ).5.设K 是△ABC 内任意一点,△KAB 、△KBC 、△KCA 的重心分别为D 、E 、F ,则ABC DEF S S △△:的值为 ( )(A )91. (B )92. (C )94. (D )32. 【答】A.解 分别延长KD 、KE 、KF ,与△ABC 的三边AB 、BC 、CA 交于点M 、N 、P ,由于D 、E 、F 分别为△KAB 、△KBC 、△KCA 的重心,易知M 、N 、P 分别为AB 、BC 、CA 的中点,所以ABC MNP S S △△41=. 易证△D E F ∽△M N P ,且相似比为3:2,所以M N P D E F S S △△2)32(=A B C S △4194⋅=A B C S △91=. 所以:DEF S △19ABC S =△.故选(A ). 6.袋中装有5个红球、6个黑球、7个白球,从袋中摸出15个球,摸出的球中恰好有3个红球的概率是 ( )(A )101. (B )51. (C )103. (D )52. 【答】B.解 设摸出的15个球中有x 个红球、y 个黑球、z 个白球,则z y x ,,都是正整数,且7,6,5≤≤≤z y x ,15=++z y x .因为13≤+z y ,所以x 可取值2,3,4,5.当2=x 时,只有一种可能,即7,6==z y ;当3=x 时,12=+z y ,有2种可能,7,5==z y 或6,6==z y ;当4=x 时,11=+z y ,有3种可能,7,4==z y 或6,5==z y 或5,6==z y ; 当5=x 时,10=+z y ,有4种可能,7,3==z y 或6,4==z y 或5,5==z y 或4,6==z y .因此,共有1+2+3+4=10种可能的摸球结果,其中摸出的球中恰好有3个红球的结果有2种,所以所求的概率为51102=.故选(B ). 二、填空题(本题满分28分,每小题7分)1. 设121-=x ,a 是x 的小数部分,b 是x -的小数部分,则=++ab b a 333____1___.解 ∵12121+=-=x ,而3122<+<,∴122-=-=x a . 又∵12--=-x ,而2123-<--<-,∴22)3(-=---=x b .∴1=+b a ,∴=++ab b a 333=++-+ab b ab a b a 3))((221)(3222=+=++-b a ab b ab a . 2. 对于一切不小于2的自然数n ,关于x 的一元二次方程22(2)20x n x n -+-=的两个根记作n n b a ,(2≥n ),则)2)(2(122--b a )2)(2(133--+b a +)2)(2(120072007--+b a =.10034016- 解 由根与系数的关系得2+=+n b a n n ,22n n a b n ⋅=-,所以=--)2)(2(n n b a (2-n n b a 4)++n n b a 222(2)42(1)n n n n =--++=-+, 则11111()(2)(2)2(1)21n n a b n n n n =-=----++, )2)(2(122--b a )2)(2(133--+b a +)2)(2(120072007--+b a =11111111111003()()()()22334200720082220084016⎡⎤--+-++-=--=-⎢⎥⎣⎦. 3. 已知直角梯形ABCD 的四条边长分别为6,10,2====AD CD BC AB ,过B 、D 两点作圆,与BA 的延长线交于点E ,与CB 的延长线交于点F ,则BF BE -的值为____4_____.解 延长CD 交⊙O 于点G ,设DG BE ,的中点分别为点N M ,,则易知DN AM =.因为10==CD BC ,由割线定理,易证DG BF =,所以42)(2)(2==-=-=-=-AB AM BM DN BM DG BE BF BE .4. 若64100+a 和64201+a 均为四位数,且均为完全平方数,则整数a 的值是___17____.解 设264100m a =+,264201n a =+,则100,32<≤n m ,两式相减得 ))((10122m n m n m n a -+=-=,因为101是质数,且101101<-<-m n ,所以101=+m n ,故1012-=-=n m n a .代入264201n a =+,整理得020*******=+-n n ,解得59=n ,或343=n (舍去).所以171012=-=n a .第二试 (A )AB CD E F G M N一、 (本题满分20分)设n m ,为正整数,且2≠m ,如果对一切实数t ,二次函数mt x mt x y 3)3(2--+=的图象与x 轴的两个交点间的距离不小于2t n +,求n m ,的值.解 因为一元二次方程03)3(2=--+mt x mt x 的两根分别为mt 和3-,所以二次函数mt x mt x y 3)3(2--+=的图象与x 轴的两个交点间的距离为3mt +.由题意,32mt t n+≥+,即22(3)(2)mt t n +≥+,即222(4)(64)90m t m n t n -+-+-≥. 由题意知,042≠-m ,且上式对一切实数t 恒成立,所以⎪⎩⎪⎨⎧≤----=∆>-,0)9)(4(4)46(,042222n m n m m 22,4(6)0,m mn >⎧⇒⇒⎨-≤⎩⎩⎨⎧=>,6,2mn m 所以⎩⎨⎧==,2,3n m 或⎩⎨⎧==.1,6n m 二、(本题满分25分)如图,四边形ABCD 是梯形,点E 是上底边AD 上一点,CE 的延长线与BA 的延长线交于点F ,过点E 作BA 的平行线交CD 的延长线于点M ,BM 与AD 交于点N .证明:∠AFN =∠DME . 证明 设MN 与EF 交于点P ,∵NE //BC , ∴△PNE ∽△PBC ,∴PCPE PB PN =, ∴PC PN PE PB ⋅=⋅. 又∵ME //BF ,∴△PME ∽△PBF ,∴PF PE PB PM =, ∴PF PM PE PB ⋅=⋅.∴PF PM PC PN ⋅=⋅,故PFPC PN PM = 又∠FPN =∠MPE ,∴△PNF ∽△PMC ,∴∠PNF =∠PMC ,∴NF//MC∴∠ANF =∠EDM.又∵ME//BF ,∴∠FAN =∠MED.∴∠ANF +∠FAN =∠EDM +∠MED ,∴∠AFN=∠DME.三、 (本题满分25分)已知a 是正整数,如果关于x 的方程056)38()17(23=--+++x a x a x 的根都是整数,求a 的值及方程的整数根. A B CD E F M N P解 观察易知,方程有一个整数根11=x ,将方程的左边分解因式,得[]056)18()1(2=+++-x a x x因为a 是正整数,所以关于x 的方程 056)18(2=+++x a x (1)的判别式0224)18(2>-+=∆a ,它一定有两个不同的实数根.而原方程的根都是整数,所以方程(1)的根都是整数,因此它的判别式224)18(2-+=∆a 应该是一个完全平方数.设22224)18(k a =-+(其中k 为非负整数),则224)18(22=-+k a ,即 224)18)(18(=-+++k a k a .显然k a ++18与k a -+18的奇偶性相同,且1818≥++k a ,而8284562112224⨯=⨯=⨯=,所以⎩⎨⎧=-+=++,218,11218k a k a 或⎩⎨⎧=-+=++,418,5618k a k a 或⎩⎨⎧=-+=++,818,2818k a k a 解得⎩⎨⎧==,55,39k a 或⎩⎨⎧==,26,12k a 或⎩⎨⎧==,10,0k a 而a 是正整数,所以只可能⎩⎨⎧==,55,39k a 或⎩⎨⎧==.26,12k a 当39=a 时,方程(1)即056572=++x x ,它的两根分别为1-和56-.此时原方程的三个根为1,1-和56-.当12=a 时,方程(1)即056302=++x x ,它的两根分别为2-和28-.此时原方程的三个根为1,2-和28-. 第二试 (B )一、(本题满分20分)设n m ,为正整数,且2≠m ,二次函数mt x mt x y 3)3(2--+=的图象与x 轴的两个交点间的距离为1d ,二次函数nt x n t x y 2)2(2+-+-=的图象与x 轴的两个交点间的距离为2d .如果21d d ≥对一切实数t 恒成立,求n m ,的值.解 因为一元二次方程03)3(2=--+mt x mt x 的两根分别为mt 和3-,所以31+=mt d ;一元二次方程02)2(2=+-+-nt x n t x 的两根分别为t 2和n -,所以n t d +=22. 所以,21d d ≥22)2()3(23n t mt n t mt +≥+⇔+≥+⇔ 09)46()4(222≥-+-+-⇔n t n m t m (1)由题意知,042≠-m ,且(1)式对一切实数t 恒成立,所以⎪⎩⎪⎨⎧≤----=∆>-,0)9)(4(4)46(,042222n m n m m 22,4(6)0,m mn >⎧⇒⇒⎨-≤⎩⎩⎨⎧=>,6,2mn m 所以⎩⎨⎧==,2,3n m 或⎩⎨⎧==.1,6n m 二、(本题满分25分)题目和解答与(A )卷第二题相同. 三、(本题满分25分)设a 是正整数,二次函数a x a x y -+++=38)17(2,反比例函数xy=,如果两个函数的图象的交点都是整点(横坐标和纵坐标都是整数的点),求a 的值. 解 联立方程组⎪⎩⎪⎨⎧=-+++=,56,38)17(2x y a x a x y 消去y 得a x a x -+++38)17(2x56=,即 056)38()17(23=--+++x a x a x ,分解因式得[]056)18()1(2=+++-x a x x (1)显然11=x 是方程(1)的一个根,(1,56)是两个函数的图象的一个交点.因为a 是正整数,所以关于x 的方程 056)18(2=+++x a x (2)的判别式0224)18(2>-+=∆a ,它一定有两个不同的实数根.而两个函数的图象的交点都是整点,所以方程(2)的根都是整数,因此它的判别式224)18(2-+=∆a 应该是一个完全平方数.设22224)18(k a =-+(其中k 为非负整数),则224)18(22=-+k a ,即 224)18)(18(=-+++k a k a .显然k a ++18与k a -+18的奇偶性相同,且1818≥++k a ,而8284562112224⨯=⨯=⨯=,所以⎩⎨⎧=-+=++,218,11218k a k a 或⎩⎨⎧=-+=++,418,5618k a k a 或⎩⎨⎧=-+=++,818,2818k a k a 解得⎩⎨⎧==,55,39k a 或⎩⎨⎧==,26,12k a 或⎩⎨⎧==,10,0k a而a 是正整数,所以只可能⎩⎨⎧==,55,39k a 或⎩⎨⎧==.26,12k a当39=a 时,方程(2)即056572=++x x ,它的两根分别为1-和56-,此时两个函数的图象还有两个交点)56,1(--和)1,56(--.当12=a 时,方程(2)即056302=++x x ,它的两根分别为2-和28-,此时两个函数的图象还有两个交点)28,2(--和)2,28(--.第二试 (C )一、(本题满分25分)题目和解答与(B )卷第一题相同.二、(本题满分25分)题目和解答与(A )卷第二题相同.三、(本题满分25分)设a 是正整数,如果二次函数a x a x y 710)232(22-+++=和反比例函数xa y 311-=的图象有公共整点(横坐标和纵坐标都是整数的点),求a 的值和对应的公共整点. 解 联立方程组⎪⎩⎪⎨⎧-=-+++=,311,710)232(22x a y a x a x y 消去y 得a x a x 710)232(22-+++=113a x -,即0113)710()232(223=-+-+++a x a x a x ,分解因式得[]0311)12()12(2=-+++-a x a x x (1)如果两个函数的图象有公共整点,则方程(1)必有整数根,从而关于x 的一元二次方程 0311)12(2=-+++a x a x (2) 必有整数根,所以一元二次方程(2)的判别式∆应该是一个完全平方数,而224)18(10036)311(4)12(222-+=++=--+=∆a a a a a .所以224)18(2-+a 应该是一个完全平方数,设22224)18(k a =-+(其中k 为非负整数),则224)18(22=-+k a ,即224)18)(18(=-+++k a k a .显然k a ++18与k a -+18的奇偶性相同,且1818≥++k a ,而8284562112224⨯=⨯=⨯=,所以 ⎩⎨⎧=-+=++,218,11218k a k a 或⎩⎨⎧=-+=++,418,5618k a k a 或⎩⎨⎧=-+=++,818,2818k a k a 解得⎩⎨⎧==,55,39k a 或⎩⎨⎧==,26,12k a 或⎩⎨⎧==,10,0k a而a 是正整数,所以只可能⎩⎨⎧==,55,39k a 或⎩⎨⎧==.26,12k a 当39=a 时,方程(2)即0106512=-+x x ,它的两根分别为2和53-,易求得两个函数的图象有公共整点)53,2(-和)2,53(-.当12=a 时,方程(2)即025242=-+x x ,它的两根分别为1和25-,易求得两个函数的图象有公共整点)25,1(-和)1,25(-.。
2010年全国高中数学联赛试题及解答

10. (20 分)已知抛物线 y 2 6 x 上的两个动点 A x1 , y1 和B x2 , y2 ,其中 x1 x2 且 x1 x2 4 .线段 AB 的垂直平分线与 x 轴交于点 C ,求 ABC 面积的最大值. x x y y2 解法一:设线段 AB 的中点为 M ( x0 , y0 ) ,则 x0 1 2 2, y0 1 , 2 2
答案:
A1 C1 B1
设正三棱柱的棱长为 2, 则 B 1,0,0 , B1 1,0, 2 , A1 1,0, 2 , P 0, 3,1 . 从而,
BA1 2,0, 2 , BP 1, 3,1 , B1 A1 2,0,0 , B1 P 1, 3, 1 .
当 t 0, 1 时(1)总成立;
1 3 对 0 t 1,0 t 2 t 2 ;对 1 t 0, t 2 t 0 .从而可知 a 12 . 4 2
3. 双曲线 x2 y 2 1 的右半支与直线 x 100 围成的区域内部(不含边界)整点(纵横坐标均为整数的 点)的个数是 答案:9800. 解:由对称性知,只要先考虑 x 轴上方的情况,设 y k k 1, 2,
从而
3a 3a 8 b c 1 0 , z 2 2 ,由 0 z 2 1 知 a . 4 4 3 解法二: f x 3ax2 2bx c . 设 g x f x 1 ,则当 0 x 1 时, 0 g x 2 .
k AB y2 y1 y y1 6 3 . 22 y12 y2 y1 y0 x2 x1 y2 6 6
线段 AB 的垂直平分线的方程是
2010年全国高中数学联赛试题与参考答案

2010年全国高中数学联合竞赛一试试题一、填空题(本题满分64分,每小题8分)1.函数()5243f x x x =--的值域是______________.2.已知函数2(cos 3)sin y a x x =-的最小值为3-,则实数a 的取值范围是_____________.3.双曲线221x y -=的右半支与直线100x =围成的区域内部(不含边界)整点(纵横坐标均为整数的点)的个数是___________.4.已知{}n a 是公差不为0的等差数列,{}n b 是等比数列,其中1122533,1,,3a b a b a b ====,且存在常数,αβ使得对每一个正整数n 都有log n n a b αβ=+,则αβ+=____________.5. 函数2()32(0,1)x x f x a a a a =+->≠在区间[1,1]x ∈-上的最大值为8,则它在这个区间上的最小值是___________________.6. 两人轮流投掷骰子,每人每次投掷两颗,第一个使两颗骰子点数和大于6者为胜,否则轮由另一人投掷.先投掷人的获胜概率为_________________.7.正三棱柱111ABC A B C -的9条棱长都相等,P 是1CC 的中点,二面角11B A P B α--=,则sin α=_____________.8.方程2010x y z ++= 满足x y z ≤≤的正整数解(,,)x y z 的个数是_____________.二、解答题(本题满分56分)9.(本小题满分16分)已知函数32()(0)f x ax bx cx d a =+++≠,当01x ≤≤时,|()|1f x '≤,试求a 的最大值.10. (本小题满分20分)已知抛物线26y x =上的两个动点11(,)A x y 和22(,)B x y ,其中12x x ≠且124x x +=.线段AB 的垂直平分线与x 轴交于点C ,求△ABC 面积的最大值.11. (本小题满分20分)证明:方程32520x x +-=恰有一个实根r ,且存在唯一的严格递增正整数列{}n a ,使得31225a a a r r r =+++ .2010年全国高中数学联合竞赛加试试题一、(本题满分40分)如图,锐角三角形ABC的外心为O,K是边BC上一点(不是边BC的中点),D是线段AK延长线上一点,直线BD与AC交于点N,直线CD与AB交于点M.求证:若OK MN⊥,则,,,A B D C四点共圆.二、(本题满分40分)设k是给定的正整数,12r k=+.记()()f r f r r r==⎡⎤⎢⎥(1),(1)()(()),2l lf r f f r l-=≥().证明:存在正整数m ,使得()()m f r 为一个整数.这里,x ⎡⎤⎢⎥表示不小于实数x 的最小整数,例如11,112⎡⎤==⎡⎤⎢⎥⎢⎥⎢⎥.三、(本题满分50分)给定整数2n >,设正实数12,,,n a a a 满足1k a ≤,1,2,,k n = ,记12,1,2,,.kk a a a A k n k+++==求证:1112nnk k k k n a A ==--<∑∑.四、(本题满分50分)一种密码锁的密码设置是在正n 边形12n A A A 的每个顶点处赋值0和1两个数中的一个,同时在每个顶点处涂染红、蓝两种颜色之一,使得任意相邻的两个顶点的数字或颜色中至少有一个相同.问:这种密码锁共有多少种不同的密码设置.2010年全国高中数学联合竞赛一试试题参考答案与评分标准一、填空题1.[3]-.2.3122a -≤≤ 3.9800. 4. 3335.14-. 6.1217. 7.104. 8.336675. 1.2..3.由对称性知,只需先考虑x 轴上方的情况,设(1,2,,99)y k k == 与双曲线右半支交于点k A ,与直线100x =交于点k B ,则线段k k A B 内部的整点个数为99k -,从而在x 轴上方区域内部整点的个数为991(99)9949k k =-=⨯∑,又x 轴上有98个整点,则所求整点个数为24999+98=9800⨯⨯. 4.5.6.=1217. 7.8.二、解答题9.10.11.2010年全国高中数学联合竞赛加试试题参考答案与评分标准一、二、三、四、。
2010年数学周报杯全国初中数学竞赛试题及详细解答

中国教育学会中学数学教学专业委员会“《数学周报》杯”2010年全国初中数学竞赛试题详细解答一、选择题(共5小题,每小题7分,共35分.其中有且只有一个选项是正确的. 请将正确选项的代号填入题后的括号里,不填、多填或错填都得0分) 1.若20 10a b b c ==,,则a b b c++的值为( ) (A )1121 (B )2111 (C )11021 (D )21011【答案】D【解析1】由题设知0c ≠,10,20200b c a b c ===,于是200102101011a b c c b c c c ++==++. 【解析2】 由题设知0b ≠,于是12012101111110a ab bc b c b +++===+++,故选D. 2.若实数,a b 满足21202a ab b -++=,则a 的取值范围是( ) (A )2a ≤- (B )4a ≥ (C )2a ≤-或4a ≥ (D )24a -≤≤【答案】C 【解析】21202b ab a -++=可以看作是关于b 的一元二次方程,因为b 是实数,所以21202b ab a -++=的判别式21()41(2)02a a ∆--⨯⨯+≥=,即2280a a --≥,(2)(4)0a a +-≥,解得2a ≤-或4a ≥.故a 的取值范围是2a ≤-或4a ≥,故选C . 3.如图,在四边形ABCD 中,135,120B C ∠=∠= ,23AB =,422BC =-, 42CD =,则AD 边的长为( )(A )26 (B )64(C )64+ (D )622+【答案】(D )【解析1】如图1,过点A 作AE BC ⊥交CB 的延长线于点E ,过点D 作DF BC ⊥交BC的延长线于点F ,过点A 作AG DF ⊥于点G ,135ABC ∠= ,∴45ABE BAE ∠=∠=在Rt AEB ∆中,2sin 2362BE AE AB BAE ==⋅∠=⨯=,又∵120BCD ∠= ,∴60DCF ∠=,cos6022,sin6026CF CD DF CD ==== , 于是46EF BE BC CF =++=+.在Rt ADG ∆中,46,AG EF ==+2666DG DF GF DF AE =-=-=-=,根据勾股定理得2222(46)(6)28864(726)226AD AG DG =+=++=+=+=+.【解析2】如图2,过点A 作AE BC ∥交CD 于E ,AF DC ⊥交DC 的延长线于F ;过点B作BM AE ⊥于M ; 过点C 作CN AE ⊥于N ,135ABC ∠= ,∴45ABM BAM ∠=∠= , 2sin 452362BM AM AB ==⋅=⨯= ∵四边形BMNC 为矩形,∴6CN BM ==,422MN BC ==-在Rt CNE ∆中,30NCE ∠= ,60CEN ∠= , tan302,NE CN =⋅= 22CE = 462AE AM MN NE =++=+-,22DE CD CE =-=462cos cos602EF AE FEA AE +-=⋅∠=⋅= 43326sin sin 602AF AE FEA AE +-=⋅∠=⋅=43262DF DE EF ++=+=,在Rt ADF ∆中, 22224332643264(72622622AD AF DF ⎛⎫⎛⎫+-++=+=+=+=+ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭)【解析3】如图3,过点A 作AE BC ∥交CD 于E ,过点B作BM AE ⊥于M ; 过点C 作CN AE ⊥于N ,则四边形BMNC 为矩形,ABM ∆为等腰直角三角形62ABBM AM ===,在Rt CEN ∆中,030NCE ∠=, 由6CN =得0tan 6tan302NE CN NCE =⋅∠=⨯=,22CE =,422MN BC ==-,462AE AM MN NE =++=+-,22ED CD CE =-=,又0120AED BCD ∠=∠=,在AED ∆中,根据余弦定理得, 2222cos AD AE ED AE ED AED =+-⋅∠220(462)(22)2(462)(22)cos120=+-+-⨯+-⨯⨯2(226)=+ 于是226AD =+,故选(D ).(说明:本题与1991年全国初中数学联合竞赛第一试填空第4题类型完全相同,只是数值不同)4.在一列数123x x x ,,,……中,已知11=x ,1121444k k k k x x -⎛--⎫⎡⎤⎡⎤=+-- ⎪⎢⎥⎢⎥⎣⎦⎣⎦⎝⎭(2k ≥),(取整符号[]a 表示不超过实数a 的最大整数,例如[]2.62=,[]0.20=),则2010x 等于( )(A) 1 (B) 2 (C) 3 (D) 4【答案】B【解析】由11=x 和1121444k k k k x x -⎛--⎫⎡⎤⎡⎤=+-- ⎪⎢⎥⎢⎥⎣⎦⎣⎦⎝⎭可得11x =,22x =,33x =, 44x =,51x =,62x =,73x =,84x =,……,归纳可得 41421,2,k k x x ++==434(1)3,4k k x x ++==,(k 为自然数),因2010=4×502+2,故2010x =2. 5.如图,在平面直角坐标系xOy 中,等腰梯形ABCD 的顶点坐标分别为A (1,1),B (2,-1),C (-2,-1),D (-1,1).y 轴上一点P (0,2)绕点A 旋转180°得点P 1,点P 1绕点B 旋转180°得点P 2,点P 2绕点C 旋转180°得点P 3,点P 3绕点D 旋转180°得点P 4,……,重复操作依次得到点P 1,P 2,…, 则点P 2010的坐标是( ).(A )(2010,2) (B )(2010,2-)(C )(2012,2-) (D )(0,2)【答案】B【解析1】由已知得,点1P ,2P 的坐标分别为12(2,0),(2,2)P P -,记222 )P a b (,,其中222,2a b ==-,根据对称关系,依次可以求得:322(42)P a b --,--,422(2)P a b ++,4,(第5题)522(2)P a b ---,,622(4)P a b +,,令662(,)P a b ,同样可以求得,点10P 的坐标为(624,a b +),即1022(42,)P a b ⨯+,因2010=4⨯502+2,故点2010P 的坐标为(2010,2-). 【解析2】由已知得,12(2,0),(2,2)P P -,34(6,0),(4,2),P P -56(2,0),(6,2),P P --789101112(10,0),(8,2),(6,0),(10,2),(14,0),(12,2),P P P P P P ---- 归纳可得4142434(1)(24,0),(42,2),(64,0),(44,2)k k k k P k P k P k P k ++++-+---+(k 为自然数) 因2010=4⨯502+2,故点2010P 的坐标为(2010,2-). 二、填空题(共5小题,每小题7分,共35分)6.已知51a =-,则3227212a a a +--的值等于 .【答案】0【解析】由已知得2(1)5a +=,224a a +=,于是原式=22222(2)321236123(2)1234120a a a a a a a a a ++--=+-=+-=⨯-=.7.一辆客车、一辆货车和一辆小轿车在一条笔直的公路上朝同一方向匀速行驶.在某一时刻,客车在前,小轿车在后,货车在客车与小轿车的正中间.过了10分钟,小轿车追上了货车;又过了5分钟,小轿车追上了客车;再过t 分钟,货车追上了客车,则t = .【答案】15 【解析1】画出某一时刻三辆车的位置示意图,如图所示,设在某一时刻,货车与客车、小轿车的距离均为S 千米,小轿车、货车、客车的速度分别为a b c ,,(千米/分),并设货车经x 分钟追上客车,依题意得()10a b S -= ① , ()152a c S -= ② , ()x b c S -= ③由①②,得30b c S -=(),与③比较得,x =30,故 3010515t =--=(分).【解析2】设在某一时刻,客车在前,小轿车在后,货车在客车与小轿车的正中间,客车与小轿车间隔为2,则小轿车与货车的速度差为110,小轿车与客车的速度差为2210515=+,则货车与客车的速度差为211151030-=,货车追上了客车需113030÷=分钟,所以货车追上了客车,需再过3010515t =--=分钟. 8.如图,在平面直角坐标系xOy 中,多边形OABCDE 的顶点坐标分别是O (0,0),A (0,6),B (4,6),C (4,4),D (6,4),E (6,0).若直线l 经过点M (2,3),且将多边形OABCDE 分割成面积相等的两部分,则直线l 的函数表达式是 .【答案】11133y x =-+ 【解析】如图,延长BC 交x 轴于点F ;连接,OB AF ;连接,CE DF ,且相交于点N .则(4,0)F ,由已知得点(2,3)M 是OB AF 与的中点,即点M 为矩形ABFO 的中心,所以直线l 把矩形ABFO 分成面积相等的两部分.又因为点(5,2)N 是矩形CDEF 的中心,所以, 过点(5,2)N 的直线把矩形CDEF 分成面积相等的两部分.于是,直线MN 即为所求的直线l .设直线l 的函数表达式为(0)y kx b k =+≠,则2352k b k b =⎧⎨+=⎩+,,解得 1311.3k b ⎧=-⎪⎪⎨⎪=⎪⎩,, 故所求直线l 的函数表达式为11133y x =-+. 9.如图,射线AM ,BN 都垂直于线段AB ,点E 为AM 上一点,过点A 作BE 的垂线AC 分别交,BE BN 于点,F C ,过点C 作AM 的垂线CD ,垂足为D .若CD CF =,则 AE AD= . 【答案】 215- 【解析】如图,因Rt AFB ∆∽Rt ABC ∆,所以AB AF AC AB=, 即2AB AF AC =⋅.∵AB CD CF ==,∴2()CF AF AF CF =⋅+ , 即210AF AF CF CF ⎛⎫+-= ⎪⎝⎭,解得512AF CF -=, 或512AF CF --=(舍去). (第8题)答案图(第8题)(第9题)又∵Rt AFE Rt CFB ∆∆∽,∴512AE AF BC CF -==,而AD BC =,故AE AD =512-. 10.对于i =2,3,…,k ,正整数n 除以i 所得的余数为1i -.若n 的最小值0n 满足020003000n <<,则正整数k 的最小值为 . 【答案】9【解析】因为1n +为2 3 k ,,,的倍数,所以n 的最小值0n 满足[]012 3 n k += ,,,,(其中[]2 3 k ,,,表示2 3 k ,,,的最小公倍数) 由于[]2 3 8840,= ,,,[]2 3 92520 = ,,,,[]2 3 102520= ,,,,[]2 3 1127720= ,,,,因此满足020003000n <<的正整数k 的最小值为9. 三、解答题(共4题,每题20分,共80分)11(A).如图,抛物线2y ax bx =+(a >0)与双曲线k y x=相交于点A ,B . 已知点A 的坐标为(1,4),点B 在第三象限内,且△AOB 的面积为3(O 为坐标原点).(1)求实数a ,b ,k 的值;(2)过抛物线上点A 作直线AC ∥x 轴,交抛物线于另一点C ,求所有满足△EOC ∽△AOB 的点E 的坐标.解:(1)因为点A (1,4)在双曲线k y x=上,所以k=4. 故双曲线的函数表达式为x y 4=.设点4(,),0B t t t <, AB 所在直线的函数表达式为y mx n =+,则有44m n mt n t=+⎧⎪⎨=+⎪⎩,, 解得4m t =-,4(1)t n t +=. 故44(1)t y x t t +=-+,于是,直线AB 与y 轴的交点坐标为4(1)0,t t +⎛⎫ ⎪⎝⎭, 故()141132AOB t S t t∆+=⨯-=(),整理得22320t t +-=,解得2t =-,或12t =(舍去). 故点B 的坐标为(2,2)--.(第11(A)题)因为点(1,4),(2,2)A B --都在抛物线2(0)y ax bx a =+>上,所以4422a b a b +=⎧⎨-=-⎩,,解得13.a b =⎧⎨=⎩, …………(10分) (2)由(1)知23y x x =+,因为AC x 轴且(1,4)A ,所以令4y =,得234x x +=,解得4x =-,或1x =,故(4,4)C -,于是42OC =. 又22OB =,所以2OC OB=. 设抛物线2(0)y ax bx a =+>与x 轴负半轴相交于点D , 则点D 的坐标为(3-,0). 因为45COD BOD ∠=∠= ,所以90COB =. (i )将AOB ∆绕点O 顺时针旋转90︒,得到△1B OA '.此时,点(2,2)B '-是OC 的中点,点1(4,1)A -,延长1OA 到点1E ,使得112OE OA =,这时点1(8,2)E -是符合条件的点. (ii )作AOB ∆关于x 轴的对称图形2A OB '∆,得到点2(1,4)A -;延长2OA 到点2E ,使得222OE OA =,这时点2(2,8)E -是符合条件的点.故点E 的坐标是(8,2)-,或(2,8)-. …………(20分)11(B). 设实数a ,b 满足:2231085100a ab b a b -++-=,求u =29722a b ++的最小值.解:由已知得,(2)(34)5(2)0a b a b a b --+-=,即(2)(345)0a b a b --+=,所以20a b -=,或3450a b -+=.…………(5分)(i )当20a b -=,即2a b =时,22297223672236(1)34u a b b b b =++=++=+-, 于是当1b =-时,u 的最小值为34-,此时2a =-,1b =-.…………(15分)(ii )当3450a b -+=,即345a b =-时, 2222(3)722(45)72216322716(1)11u a b b b b b b =++=-++=++=++, 于是1b =-时,u 的最小值为11,此时3a =-,1b =-.综上可知,u 的最小值为34-.…………(20分)12(A). 如图,ABC ∆为锐角三角形,点,P Q 为边BC 上的两点,ABP ∆和ACQ ∆的外接(第11(A)题)答案图圆圆心分别为1O 和2O ,试判断1BO 的延长线与2CO 的延长线的交点D 是否可能在ABC ∆的外接圆上,并说明理由.解:答案是否定的,即1BO 的延长线与2CO 的延长线的交点D 不可能在△ABC 的外接圆上. ……(5分)理由如下:如图,连接1O P ,设直线1BO 与直线2CO 的交点为D ,则11180902BO P O BP BAP ︒-∠∠==︒-∠,22180902QO C O CQ CAQ -∠∠==︒-∠ , 所以 12180O BP O CQ BAP CAQ ∠+∠=︒-∠-∠,即180180()BDC BAP CAQ -∠=-∠+∠ , 故BDC BAP CAQ ∠=∠+∠.……(15分) 由于点P Q ,为边BC 上的两点,所以BAP CAQ BAC ∠+∠≠∠,即BDC BAC ∠≠∠ 因此,点D 不在△ABC 的外接圆上.…………(20分)12(B).如图,△ABC 为等腰三角形,AP 是底边BC 上的高,点D 是线段PC 上的一点,BE 和CF 分别是△ABD 和△ACD 的外接圆直径,连接EF . 求证:tan EF PAD BC∠=.证明:如图,连接,ED FD .(第12A 题) (第12A 题)答案图(第12(B )题)(第12(B)题)答案图因为BE 和CF 都是直径,所以,ED BC FD BC ⊥⊥,因此,,D E F 三点共线. …(5分) 连接,AE AF ,则AEF ABC ACB AFD ∠=∠=∠=∠,所以,AEF ∆∽ABC ∆…(10分) 过点A 作AH EF ⊥于H ,则AH PD =. 由AEF ∆∽ABC ∆,可得EF AH BC AP =, 从而EF PD BC AP =,所以 tan PD EF PAD AP BC∠==. …………(20分) 13(A). 实数,a b 使得关于,x y 的方程组2221.....................0...xy x xy ax bx a ⎧-=⎨+++=⎩①②有实数解(,)x y . (1)求证2y ≥;(2)求22a b +的最小值. 解: (1)(证法1)由方程①知0x ≠,且211x y x x x+==+ ∴112y x x x x=+=+≥(当且仅当1x =时取等号). 即2y ≥……(5分) (或书写如下:)由方程①知0x ≠,且211x y x x x+==+. 所以,当0x >时,2y ≥;当0x <时,2y ≤-,故2y ≥. …………(5分)(证法2)由方程①得210x xy -+=,此方程可视为关于x 的一元二次方程,由于x 为实数,故2()40,y ∆=--≥即2y ≥.…………(5分)(2)(解法1) 由方程①得21x xy =-③,将③代入方程②,得2(1)0x y ax y b x a +-++=,即2()0x y ay b ++=,∵0x ≠, ∴20y ay b ++=④.由于方程组有实数解,故方程20y ay b ++=④在2y ≤-,或2y ≥的范围内至少有一个实数根.(i )当4a ≤时,有2422a a b ---≤-,或2422a ab -+-≥, 故2440a b a -≥-≥,或2440a b a -≥+≥,即24a b ≥+或2(4)a b ≤-+.若40b +≥,即4b ≥-时,202b a ≥+≥或202b a ⎛⎫≤-+≤ ⎪⎝⎭,由此得22244b a b ≥++,于是 222222255844541616244()445554555a b b b b b b ⎡⎤⎛⎫⎛⎫+≥++=++-+=++≥⎢⎥ ⎪ ⎪⎝⎭⎝⎭⎢⎥⎣⎦ (当且仅当45b =-时,上式取等号,此时85a =±.) 若40b +<,即4b <-时,对于满足24a b ≥+,或2(4)a b ≤-+的任意实数a , 均有2216165a b +>>.…………(15分) (ii )当4a >时,2216165a b +>> . 综上(i )、(ii )可知,22a b +的最小值为516.………(20分) (解法2:)由方程①得21x xy =-③,将③代入方程②,得2(1)0xy a xy bx a +-++=,即2()0x y ay b ++=,∵0x ≠, ∴20y ay b ++=,2()b y ay =-+2222222234()2a b a y ay a a y ay y ⎡⎤+=+-+=+++⎣⎦∴22333224222(1)2111y y y y a a y y y y ⎡⎤⎛⎫⎛⎫=++⋅+-+⎢⎥ ⎪ ⎪+++⎢⎥⎝⎭⎝⎭⎣⎦2362422(1)11y y y a y y y ⎛⎫=++-+ ⎪++⎝⎭234222(1)11y y y a y y ⎛⎫=+++ ⎪++⎝⎭ 于是,当3201y a y +=+时,22a b +有最小值421y y +, 又∵2y ≥,244,16,y y ≥≥∴241111,416y y ≤≤,241111541616y y +≤+=∴ 从而24116115y y ≥+,即421651y y ≥+(当且仅当2y =±时取等号) 故当2y =±时,85a = ,22a b +有最小值165. (解法3:) 由方程①得21xy x =+③,将③代入②得22(1)0x y ax bx a ++++=,即2()()0a y x bx a y ++++=④(i) 当0a y +=,即y a =-时,方程④变为0bx =,由方程①知0x ≠,∴0b =, 此时②变为22()0a x ax a -++=,即2(1)0a x ax ++=,若0a =,则由方程②得20xy =,因0x ≠,故0y =,由(1)知0y ≠,从而0a ≠, ∴210x ax ++=,∵x 为不等于0的实数,∴240a ∆=-≥,24a ≥,∴2224a b a +=≥(当且仅当2y =±,即2a = 时取等号)………(10分) (ii)当0a y +≠,即y a ≠-时,方程④可视为关于x 的一元二次方程.∵x 为不等于0的实数,∴224()0b a y ∆=-+≥,∴224()b a y ≥+, ∴222222222444164()5845()5555a b a a y a ay y a y y y +≥++=++=++≥≥ (当且仅当22244(),0,45b a y a y y =++==同时成立,即2y =±,85a = 时取等号) 综上(i)、(ii)可知,22a b +的最小值为165.………(20分) 13(B). 求满足22282p p m m ++=-的所有素数p 和正整数m .解:由题设得(21)(4)(2)p p m m +=-+,所以(4)(2)p m m -+,由于p 是素数,故(4)p m -,或(2)p m +. ……(5分)(1)若(4)p m -,令4m kp -=,k 是正整数,则2=6,m kp kp ++>又∵p 是素数∴1,p > 从而321p p >+,于是2223(21)(4)(2),p p p m m k p >+=-+>故23k <,从而1k =.所以4221m p m p -=⎧⎨+=+⎩,,解得59.p m =⎧⎨=⎩, …………(10分) (2)若(2)p m +,令2m np +=,n 是正整数.当5p >时,有4(2)66(1)m m np np p p n -=+-=->-=-,223(21)(4)(2)(1)p p p m m n n p >+=-+>-,故(1)3n n -<,从而1n =或2n =. 由于(21)(4)(2)p p m m +=-+是奇数,故2n ≠,从而1n =.于是4212m p m p -=+⎧⎨+=⎩,,,解得79p m =-⎧⎨=-⎩,这不符合题意. 当5p =时,2263m m -=,解得9m =;当3p =,2229m m -=,无正整数解;当2p =时,2218m m -=,无正整数解.综上所述,所求素数5p =,正整数9m =.…(20分)14(A).从1,2,…,2010这2010个正整数中,最多可以取出多少个数,使得所取出的数中任意三个数之和都能被33整除?解:首先,如下的61个数:11,1133+,11233+⨯,…,116033+⨯(即1991)满足题设条件. …………(5分)另一方面,设12,,,n a a a (12n a a a <<< )是从1,2,…,2010中取出的满足题设条件的数,对于这n 个数中的任意4个数i j k m a a a a ,,,,因为33()i k m a a a ++,33()j k m a a a ++,故33()j i a a -.即所取的数中任意两数之差都是33的倍数.(10分) 设133i i a a d =+,i =1,2,3,…,n .由12333()a a a ++,得12333(33333)a d d ++, 所以1333a ,111a ,即111a ≥. ……(15分)1201011613333n n a a d --=≤<,60n d ≤. 所以,61n ≤.综上所述,n 的最大值为61. …………(20分)14(B). 将凸五边形ABCDE 的5条边和5条对角线染色,且满足任意有公共顶点的两条线段不同色,求颜色数目的最小值.解:由于顶点A 是4条线段AB AC AD AE ,,,的公共点,因此至少需要4种颜色. 若只有4种颜色,不妨设为红、黄、蓝、绿,则每个顶点引出的4条线段的颜色包含红、黄、蓝、绿各1种,因此,红色的线段共有52条,矛盾.故至少需要5种颜色. …(10分) 下面的例子说明5种颜色可以将这10条线段染为满足条件的颜色. 将AB CE ,染为1号颜色;将BC DA ,染为2号颜色;将CD EB ,染为3号颜色;将DE AC ,染为4号颜色;将EA BD ,染为5号颜色,则任意有公共顶点的两条线段不同色.综上所述,颜色数目的最小值为5. ……(20分)。
#2010全国初中数学竞赛试题及参考答案

中国教育学会中学数学教课专业委员会“《数学周报》杯” 2010 年全国初中数学比赛试题参照答案一、选择题 <共 5 小题,每题 7 分,共 35 分 .此中有且只有一个选项是正确的 .请将正确选项的代号填入题后的括号里,不填、多填或错填都得0 分)EdIGbSrxq7.若a,b10 ,则ab的值为 < ).120b cbc<A )11<B )21<C )110<D )210211121 11a ba 120 1 210解: D 由题设得b .bcc1 1111b102.若实数 a , b 知足1a ab b 2 2 0 ,则 a 的取值范围是 <).2<A )a 2 <B )a 4<C ) a ≤ 2或 a ≥4 <D ) 2 ≤ a ≤ 4解 .C因为 b 是实数,所以对于 b 的一元二次方程 b 2ab1 a2 012的鉴别式= ( a)24 1 ( a 2) ≥0, 解得 a ≤ 2 或 a ≥4.23.如图,在四边形 ABCD 中,∠ B = 135°,∠ C =120°,AB= 2 3 , BC=4 2 2 ,CD = 4 2 ,则 AD 边的长为< ). EdIGbSrxq7<A ) 2 6<B )4 6<C ) 46<D )2 2 6题)<第 3 解: D如图,过点 A ,D 分别作 AE , DF 垂直于直线BC ,垂足分别为 E ,F .由已知可得BE=AE= 6 ,CF = 2 2 ,DF =2 6 ,<第 3题)于是 EF=4+ 6 .点 A 作 AG⊥ DF,垂足 G.在 Rt△ADG 中,依据勾股定理得AD(4 6)2( 6)2(224)2=226 .4.在一列数x1,x2,x3,⋯⋯中,已知x11,且当k≥2,x k x k 1 1k 1k 2 444<取整符号 a 表示不超数 a 的最大整数,比如 2.62, 0.20), x2010等于<).(A> 1(B> 2(C> 3(D> 4EdIGbSrxq7解: B由 x 1和k1k 2可得x k x k 1 1 4144x11,x2 2 , x3 3 , x4 4 ,x5 1 , x6 2 , x7 3 , x8 4 ,⋯⋯因为 2010=4×502+2,所以x2010 =2.5.如,在平面直角坐系xOy 中,等腰梯形ABCD 的点坐分A<1 , 1),B<2,- 1), C<- 2,- 1), D <- 1, 1). y 上一点 P<0, 2)点 A 旋 180 °得点P1,点 P1点 B 旋 180°得点 P2,点 P2点 C 旋 180°得点 P3,点 P3点 D 旋 180°得点 P4,⋯⋯,重复操作挨次得到点P1,P2,⋯ ,点P2010的坐是<).EdIGbSrxq7<A)<2010,2) <B)<2010, 2 )<C)<2018, 2 )<D)<0,2)<第 5题)解: B 由已知能够获得,点P1, P2的坐分<2,0),<2, 2 ).P(a ,b ) ,此中 a2, b2.22222依据称关系,挨次能够求得:P3 ( 4 a2,- 2- b2 ) , P4 (2a2,4b2 ) , P5 ( a2, 2b2 ) , P6 (4a2,b2 ) .令 P (a , b )662,相同能够求得,点P的坐标为<4 a ,b62),即10P < 42 a ,b ),2210因为 2010=4502+2,所以点P2010的坐标为<2010, 2 ).二、填空题6.已知a= 5 -1,则2a3+ 7a2- 2a- 12的值等于.解: 0由已知得 (a+1>2=5,所以 a2+2a=4,于是2a3+ 7a2- 2a-12=2a3+4a2+3a2-2a- 12=3a2+6a-12= 0.7.一辆客车、一辆货车和一辆小轿车在一条笔挺的公路上朝同一方向匀速行驶.在某一时辰,客车在前,小轿车在后,货车在客车与小轿车的正中间.过了10 分钟,小轿车追上了货车;又过了 5 分钟,小轿车追上了客车;再过t 分钟,货车追上了客车,则t =. EdIGbSrxq7解: 15设在某一时辰,货车与客车、小轿车的距离均为S 千 M ,小轿车、货车、客车的速度分别为 a,b, c <千 M/ 分),并设货车经x 分钟追上客车,由题意得EdIGbSrxq710 a b S ,①15 a c 2S ,②x b c S .③由①②,得 30( b c) S ,所以,x=30.故 t30 10 5 15 <分).8.如图,在平面直角坐标系xOy 中,多边形 OABCDE 的极点坐标分别是 O<0, 0),A<0, 6), B<4, 6), C<4, 4), D <6 , 4), E<6, 0).若直线 l 经过点 M <2,3),且将多边形 OABCDE 切割成面积相等的两部分,则直线 l 的函数表达式是. EdIGbSrxq7解: y 1 x+11<第 8题)33如图,延伸 BC 交 x 轴于点 F;连结 OB,AF;连结 CE,DF ,且订交于点 N.<第 8题由已知得点 M<2, 3)是 OB,AF 的中点,即点 M 为矩形 ABFO 的中心,所以直线 l 把矩形 ABFO 分红面积相等的两部分.又因为点N<5, 2)是矩形CDEF 的中心,所以, EdIGbSrxq7过点 N<5, 2)的直线把矩形 CDEF 分红面积相等的两部分.于是,直线 MN 即为所求的直线 l .设直线 l 的函数表达式为 y kxb ,则 2k+,b3,5k b2k1,111 .解得3 ,故所求直线 l 的函数表达式为 y x+113 3b.39.如 ,射 AM , BN 都垂直于 段 AB ,点 E AM 上一点, 点 A 作 BE 的垂 AC分 交 BE , BN 于点 F , C , 点 C 作 AM 的垂 CD ,垂足D .若 CD =CF ,AE . EdIGbSrxq7AD解:5 12见题图,设 FC m, AF n .因为 Rt △AFB ∽Rt △ ABC ,所以 AB 2<第 9题)AF AC .又因为 FC =DC =AB ,所以m 2n(n,即 ( n )2 n 1 0,m)m m解得n5 1 ,或 n 5 1 <舍去).m2 m2又 Rt △ AFE ∽ Rt △ CFB,所以AEAEAF n 5 1 , 即AD BC FC m2AE = 5 1. AD 210. 于 i=2 , 3 ,⋯, k ,正整数 n 除以 i 所得的余数i - 1 .若 n 的最小 n 0 足2000 n 0 3000 , 正整数 k 的最小 .EdIGbSrxq7解:9因为 n 1 2,3, ,k的倍数,所以 n 的最小n 0 足n 0 1 2,3, , k ,此中 2,3,, k表示 2,3,, k 的最小公倍数.因为 2,3,,8840,2,3,,92520,2,3,,102520,2,3,,1127720,所以知足 2000 n03000 的正整数k的最小值为9.三、解答 <共 4 ,每 20 分,共 80 分)11.如图,△ ABC 为等腰三角形, AP 是底边 BC 上的高,点 D 是线段 PC 上的一点,BE和 CF 分别是△ABD 和△ACD的外接圆直径,连结 EF.求证:tanEF.EdIGbSrxq7PADBC明:如,接 ED, FD. 因为 BE 和 CF 都<第 11 题)是直径,所以ED⊥ BC,FD⊥ BC,所以 D,E,F 三点共 .⋯⋯⋯⋯<5分)接 AE, AF,AEFABC ACBAFD ,所以,△ ABC∽△ AEF.⋯⋯⋯⋯ <10 分)<第 11 题)作 AH⊥ EF,垂足 H , AH=PD. 由△ ABC∽△ AEF 可得EF AH ,EF PD ,BC AP进而BC APPD EF. ⋯⋯⋯⋯ <20 分)所以tan PADAP BC k订交于点12.如图,抛物线y ax2bx <a0)与双曲线y A, B. 已知点 A 的坐标x为 <1, 4),点 B 在第三象限内,且△AOB 的面积为 3<O 为坐标原点) .EdIGbSrxq7<1)务实数a, b, k 的值;<2)过抛物线上点 A 作直线AC∥ x 轴,交抛物线于另一点 C ,求全部 足△EOC ∽△ AOB 的点 E 的坐 .解: <1)因为点A<1, 4)在双曲所以 k= 4. 故双曲 的函数表达式yk <第 12 题)上,x 4 y.x点 B<t , 4), t0 , AB 所在直 的函数表达式y mx n , 有t4 m ,n 44(t1) 4 mt , 解得 m, n.t ntt于是,直 AB 与 y 的交点坐0, 4( t1) ,故tSAOB( )3 ,整理得 2t23t2 0 ,1 4 t 1 1 t2 t解得 t2 ,或 t = 1<舍去).所以点B 的坐 <2 , 2 ).2因为点 A , B 都在抛物 yax 2 bx <a0)上,所以a b,a,解得⋯⋯⋯⋯ <10 分)4a 2b,b 3.2<2)如 ,因为 AC ∥ x ,所以C<4 ,4),于是CO = 42 .又 BO=2 2 ,所以CO2 .BO抛物y ax 2 bx <a 0 )与 x 半 订交于点D , 点 D 的坐 <3 ,0).<第 12 题)因为∠ COD =∠ BOD = 45 ,所以∠ COB= 90 .<i )将△ BOA 点O 旋90 ,获得△ B OA 1 . ,点 B ( 2 , 2>是 CO 的中点,点 A 1 的坐 <4, 1) .延 OA 1 到点 E 1 ,使得 OE 1 = 2OA 1 , 点 E 1 <8, 2 )是切合条件的点.<ii )作△ BOA 对于 x 的 称 形△B OA 2 ,获得点 A 2 <1, 4 );延 OA 2 到点E 2 ,使得 OE 2 = 2OA 2 , 点 E 2<2, 8 )是切合条件的点. EdIGbSrxq7所以,点 E 的坐 是 <8, 2 ),或<2 ,8 ) .⋯⋯⋯⋯ <20 分)13.求知足 2 p 2 p 8 m 2 2m 的全部素数 p 和正整数 m..解: 由 得 p(2 p 1)(m 4)( m 2) ,所以 p (m 4)(m2) ,因为 p 是素数,故 p (m 4) ,或 p (m 2) . ⋯⋯ <5 分)<1)若 p (m4) ,令 m4kp , k 是正整数,于是 m 2 kp ,3 p 2p(2 p 1)(m 4)( m 2) k 2 p 2 ,故 k 23 ,进而 k1 .m4 ,p,⋯⋯⋯⋯ <10 分)所以解得m2 2 p ,m 9.1<2)若 p ( m 2) ,令 m2 kp , k 是正整数 .当 p 5 ,有 m4kp 6 kpp p(k 1) ,3p 2p(2 p 1) (m 4)( m 2) k (k 1) p 2 ,故 k(k 1) 3 ,进而 k 1 ,或 2.因为 p(2 p 1) ( m 4)(m 2) 是奇数,所以k 2 ,进而 k1 .m 42 p,1于是, m 2p不行能 .当 p5 , m 22m 63 , m 9 ;当 p 3 , m 22m 29 ,无正整数解;当 p2 , m 22m18 ,无正整数解 .上所述,所求素数p=5,正整数 m=9.⋯⋯⋯⋯ <20 分)14.从1,2,⋯, 20102010 个正整数中,最多能够拿出多少个数,使得所拿出的数中随意三个数之和都能被33 整除? EdIGbSrxq7解: 第一,以下 61 个数: 11, 11 33, 11 2 33 ,⋯, 11 6033 <即 1991) 足条件 .⋯⋯⋯⋯ <5 分) EdIGbSrxq7另一方面,a 1 a 2a n 是从 1, 2,⋯, 2010 中拿出的 足 条件的数,于 n 个数中的随意4 个数 a i , a j , a k , a m ,因为33 (a i a k a m ) ,33 (a j a k a m ) ,所以33 (a j a i ) .所以,所取的数中随意两数之差都是33 的倍数 .⋯⋯⋯⋯ <10 分)a i a133d i,i=1,2,3,⋯,n.由 33 (a a a ) ,得 33 (3a33d233d3) ,1231所以 333a1, 11 a1,即a1≥11.⋯⋯⋯⋯ <15 分)d n a n a1≤2010 1161 ,3333故 d n≤60.所以,n≤61.上所述, n 的最大61.⋯⋯⋯⋯<20分)声明:全部资料为自己采集整理,仅限个人学习使用,勿做商业用途。
全国大学生数学竞赛初赛2010年第二届《非数学专业》竞赛题目及答案解析高清无水印版

的 对 称 式 方 程 为 l1 :
1
1
0
,记两直线的方向向量分别为
l1 1, 1, 0 ,l2 4, 2, 1 ,两直线上两定点分别为P1(0, 0, 0), P2(2, 1, 3),并记
a
P1P2
2, 1, 3 ,l1
l2
1, 1,6;
a
l1
l2
| 2 1 18 |
19
其中 x, y, z | x2 y2 z2 1 而
a2 b2 c2
x2dV a x2 dx
a
y2 z2
dy dz
x2
a x2
a
ab 1
x2 a2
dx
4a 3bc 15
.
1
b2 c2
a2
4
或者使用换元法,有
x2dV
2
d
d
1
a
2r
2
0
0
0
sin2
cos2
abcr2
x2
dy
D
4xd x
dy
0.
6
C
x4 y2
的值为常数.
(1) 设 L 为正向闭曲线(x 2)2 y2 1 . 证明:
2xy d x (x)d y 0;
L
x4 y2
2xy d x (x)d y
(2) 求函数(x) ; (3) 设C 是围绕原点的光滑简单正向闭曲线,求
C
x4 y2
.
2xy d x (x)d y
【参考答案】设
L
x4 y2
I ,将曲线L 分割成两段L L1 L2 。设L0 不经过原点的
光滑曲线,使得 L0 L1 和 L0 L2 分别组成围绕原点的分段光滑闭曲线. 由已知条件可知 L0 L1 和
2010年全国高中数学联赛广东赛区预赛试卷及详细答案

2010年全国高中数学联赛广东省赛区预赛试题及详细答案一、填空题:本大题共8小题,每小题8分,共64分.把答案填在横线上. 1.方程2log sin 2x x π+=在区间(0,]2π上的实根个数为_________________.解:设2()log sin 2f x x x π=+-,则1()cos ln2f x x x π'=+,∵02x π<≤,∴0cos 1x ≤<,又0ln12π<<,∴()0f x '>,即在区间(0,]2π上单调递增,故方程2log sin 2x x π+=在区间(0,]2π上有且只有一个实根. 2.设数列118()3n -⎧⎫⨯-⎨⎬⎩⎭的前n 项和为n S ,则满足不等式1|6|125n S -<的最小整数n 是______. 解:易知数列118()3n -⎧⎫⨯-⎨⎬⎩⎭是首项是8,公比是13-的等比数列,∴18[1()]1366()131()3n n n S --==----,于是1|6|125n S -<⇔112132503125n n --<⇔>,∵53243250=<,63729250=>,故最小整数n 是7.3.已知n (n N ∈,2n ≥)是常数,且1x ,2x , ,n x 是区间0,2π⎡⎤⎢⎥⎣⎦内任意实数,则函数1212231(,,,)sin cos sin cos sin cos n n f x x x x x x x x x =+++ 的最大值等于_________.解:∵222a b ab +≤,∴1212231(,,,)sin cos sin cos sin cos n n f x x x x x x x x x =+++22222223112sin cos sin cos sin cos 222n x x x x x x +++≤+++2222221122(sin cos )(sin cos )(sin cos )2n n x x x x x x ++++++= 2n =,故所求函数的最大值等于2n.4.圆周上给定10个点,每两点连一条弦,如果没有三条弦交于圆内一点,那么,这些弦在圆内一共有_________________个交点.解:圆周上任意四点构成一个四边形,四边形的两条对角线的交点必在圆内,所以四边形的个数与每两条弦的交点数相等,故有410109872101234C ⨯⨯⨯==⨯⨯⨯个交点.5.一只虫子沿三角形铁圈爬行,在每个顶点,它都等机会地爬向另外两个顶点之一,则它在n 次爬行后恰好回到起始点的概率为_________________.解:由已知条件第n 次到达起始点的概率记为n a ,则到其他两点的概率为1n a -,则第1n +次到达起始点的概率为11(1)2n n a a +=-;所以接下来构造一个等比数列来进行计算.即1111()323n n a a +-=--,其中10a =,所以111()22(1)2332n n n n na ---+-==⋅.答案:22(1)32n n n +-⋅ 6.设O 是平面上一个定点,A ,B ,C 是平面上不共线的三个点,动点P 满足||||AC ABOP OA AC AB λλ-=+,其中[0,)λ∈+∞,则点P 的轨迹为_________________. 解:∵||||AC AB OP OA AC AB λλ-=+ ,∴()||||AB ACOP OA AB AC λ-=++ , 即()||||AB AC AP AB AC λ=+,又||AB AB ,||ACAC为单位向量,由向量加法的平行四边形法则,知点P 的轨迹为BAC ∠的平分线.7.对给定的整数m ,符号()m ϕ表示{}1,2,3中使()m m ϕ+能被3整除的唯一值,那么201020102010(21)(22)(23)ϕϕϕ-+-+-=_________________.解:由二项式定理知,20101005100524(31)31p ==+=+,即20102被3除余1,∴2010(21)3ϕ-=,2010(22)1ϕ-=2010(23)2ϕ-=, 故201020102010(21)(22)(23)6ϕϕϕ-+-+-=.8.分别以直角三角形的两条直角边a ,b 和斜边c 为轴将直角三角形旋转一周,所得旋转体的体积依次为a V ,b V ,c V ,则22a b V V +与2(2)c V 的大小关系是_________________.解: ∵222222222222222()()()3399a b V V b a a b a b a b a b c ππππ+=+=+=,224422242244(2)(2())()399c ab a b V h a b c c cπππ''=⋅+==⋅,∴作商,有22422222222222()(2)1(2)444a b c V V c a b ab V a b a b a b++==≥=,故222(2)a b c V V V +≥. 二、解答题:本大题共3小题,共56分. 解答应写出文字说明、证明过程或演算步骤.1.(本小题满分16分)是否存在实数a ,使直线1y ax =+和双曲线2231x y -=相交于两点A 、B ,且以AB 为直径的圆恰好过坐标系的原点?解:设交点A 、B 的坐标为11(,)A x y 、22(,)B x y ,由22131y ax x y =+⎧⎨-=⎩消去y ,得 22(3)220a x ax ---=,由韦达定理,得12223a x x a +=-, ① 12223x x a -=-, ② ∵以AB 为直径的圆恰好过坐标系的原点,∴OA OB ⊥,∴12120x x y y +=,即1212(1)(1)0x x ax ax +++=,整理,得21212(1)()10a x x a x x ++++=③将①②代入③,并化简得22103a a -=-,∴1a =±,经检验,1a =±确实满足题目条件,故存在实数a满足题目条件.2.(本小题满分20分)求证:不存在这样的函数{}:1,2,3f Z →,满足对任意的整数x ,y ,若{}||2,3,5x y -∈,则()()f x f y ≠.证明:假设存在这样的函数f ,则对任意的整数n ,设()f n a =,(5)f n b +=,其中{},1,2,3a b ∈,由条件知a b ≠.由于|(5)(2)|3n n +-+=,|(2)|2n n -+=,∴(2)f n a +≠且(2)f n b +≠,即(2)f n +是{}1,2,3除去a ,b 后剩下的那个数,不妨设(2)f n c +=又由于|(5)(3)|2n n +-+=,|(3)|3n n -+=,∴(3)(2)f n f n +=+.以1n +代替n ,得(4)(3)(2)f n f n f n +=+=+,但这与|(4)(2)|2n n +-+=矛盾! 因此假设不成立,即不存在这样的函数f . 3.(本小题满分20分)设非负实数a ,b ,c 满足1a b c ++=,求证:19(19)4abc ab bc ca abc ≤++≤+ 证明:先证左边的不等式.∵1a b c ++=,∴222222()()3ab bc ca ab bc ca a b c a b ab b c bc a c ac abc ++=++++=++++++639abc abc abc ≥+=再证右边的不等式. 不妨设a b c ≥≥,注意到条件1a b c ++=,得314()9()4()()9ab bc ca abc a b c a b c ab bc ca abc -+++=++-+++++()()()()()()a a b a c b b a b c c c a c b =--+--+--()[()()]()()0a b a a c b b c c c a c b =----+--≥,所以1(19)4ab bc ca abc ++≤+,综上,19(19)4abc ab bc ca abc ≤++≤+.。
