7.3高斯型求积公式
高斯求积公式

x m ( x)dx,
0
x f ( x)dx 0.389111 f (0.821162)
0.277556 f (0.289949).
由于非线性方程组较复杂, 故一般不通过解方程
通常 n 2就很难求解.
求xk 及Ak (k 0,1,, n) ,
而从分析高斯点的特性来构造高斯求积公式.
7
1
0
x f ( x)dx A0 f ( x0 ) A 1 f ( x1 ).
x0 0.821162, A0 0.389111,
x1 0.289949; A1 0.277556.
m 0,1, ,2n 1.
这样,高斯公式是 A xm
k 0 1
n
k
b
a
4
根据定义要使求积公式具有 2n 1次代数精度,只要对
f ( x) x (m 0,1, ,2n 1),
m
令 a f ( x) ( x)dx Ak f ( xk ),
b k 0
n
精确成立,
m A x x k ( x)dx, k 0 m k b a n
a
a
10
由于求积公式是插值型的, 即
b a n 1
它对于q( x) H n 是精确的,
n
P( x) ( x) ( x)dx 0. q( x) ( x)dx A q( x
b a k 0 k
k
).
再注意到
n1 ( xk ) 0 (k 0,1,,n),
知
q( xk ) f ( xk ) (k 0,1,,n),
第07章 03-高斯型求积公式

第七章
§7.7 数值微分
数值积分与微分
泰勒公式是建立数值微分的工具之一,设 h x1 x0 ,
根据泰勒公式可得:
f x0 h f x0 f x0 O h h h h f x0 f x0 2 2 f x0 O h2 h
1 t
0
1
t
2
dt 。
解:(1)首项系数为1的三次勒让德多项式为:
3 2 d x 1 3! 3 3 3 x x x 3 6! dx 5 3 3 , x1 0, x2 取其零点 x0 作为高斯点 5 5 3
第七章
§7.6 高斯求积公式
N
(充分性得证)
第七章
§7.6 高斯求积公式
数值积分与微分
定理7.6 表明,若能够找到满足
N+1次多项式 N 1 x ,则积分公式的高斯点就确定了, 从而确定了一个高斯型求积公式。为此,引入勒让德 (Legendre)多项式。 定义:一个仅以区间[-1, 1]上的高斯点 xi i 0 为零点的
j 0
N
关于高斯求积公式的误差有如下结论:高斯积分公式 的误差是可控的,稳定性比其他积分方法好。特别当
f x 在[-1, 1] 上连续时,高斯型求积公式必收敛。
第七章
数值积分与微分
总结
1 梯形求积公式和辛普生求积公式是低精度的方法,但对 于光滑性较差的函数有时比用高精度方法能得到更好的 效果。复化梯形公式和辛普生求积公式,精度较高,计 算较简,使用非常广泛。 2 龙贝格求积方法,算法简单,当节点加密提高积分近似 程度时,前面的计算结果可以为后面的计算使用,因此, 对减少计算量很有好处。并有比较简单的误差估计方法。 3 Gauss型求积,它的节点是不规则的,所以当节点增加时, 前面计算的函数值不能被后面利用。计算过程比较麻烦, 但精度高,特别是对计算无穷区间上的积分和旁义积分, 则是其他方法所不能比的。
高斯求积公式
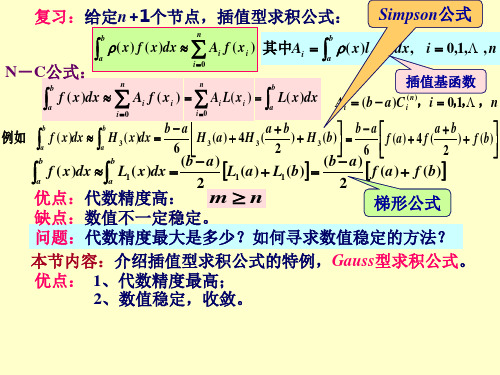
定理4 求积公式(2.2)是Gauss型的 Gauss点a<x0<…<xn <b
是[a,b]上关于权 ( x)的n+1次正交多项式的根。
分析:“充分性”即是引理1的结论。以下只证必要性
“必要性”,即Gauss点作为节点正是n+1次正交多项式的根。
只需证 n1(x) 关于( x) 正交。 证明:取2n 1次多项式f ( x) n1( x)q( x) ( x x0 ) ( x xn )q( x),
q( x)为次数 n的多项式。
则有
b
Gauss点 的 定 义
a ( x)n1( x)q( x)dx
n
Akn1 ( xk )q( xk ) 0,
k 0
由于左端等于0,即( n1 ( x),q( x)) 0,
n1 ( x)在a, b上关于权 ( x)是n 1次正交多项式,
则 x(k k 0,1, ,n)是n 1次正交多项式 n1( x)的根。
max
a
a
2、收敛性 引理2 对于有限闭区间[a, b] 上的任何连续函数 f ( x)有
lim R[ f ] 0
(2.4)
n
证明 : [a, b] 上的连续函数 f ( x) 可以用代数多项式一致逼近,
对任意给定的
max |
a xb
f
0,
(x
存在某个多项式
) qm ( x) | b
2 (
qm (x x)dx
由
b
a ( x)H2n1( x)dx
n
Ak H 2n1( xk )
k0
b
n
Ak f ( xk ) (
k0
b
( x) f ( x)dx I( f ))
高斯求积公式-数值分析课程设计2

一、 引言介绍高斯型求积公式,并使用其求积分⎰=1sin I xdx 。
要求:数值实验结果要体现出随高斯点的增加误差的变化。
我们知道,求积公式⎰∑=≈bani i ix f Adx x f 0)()( (1.1)含有22+n 个待定常数i x 及),,2,1,0(n i A i =,如果它具有n 次代数精确度,则它应使1+m 个方程mk dx x x A bakni ki i ,,2,1,0,==⎰∑= (1.2)精确成立。
作为插值型求积公式(1.1)它至少具有n 次代数精确度;另一方面,令)())(()(101n n x x x x x x x ---=+ ω,则对22+n 次多项式)()(21x x f n +=ω而言,(7.5.1)右端为零,而左端严格大于零,即(7.5.1)式对22+n 次多项式)(21x n +ω不准确成立。
但要确定方程组(7.5.2)中的22+n 个待定常数i x 与i A ,最多需要给出22+n 个独立条件,所以m最大取12+n 。
因此,插值型求积公式(1.1)的代数精确度最小是n ,最大是12+n .由此可见,高斯公式的代数精度比牛顿-科特斯公式高,求解高斯求积公式的关键就是解出上述2n+2个待定常数。
为解决上述问题,首先要先给出三个定理:定理一:以n x x x ,,,10 为节点的插值型求积公式(7.5.1)具有12+n 次代数精确度的充要条件是以这些节点为零点的多项式)())(()(101n n x x x x x x x ---=+ ω与任意次数不超过n 的多项式)(x P 均在区间],[b a 上正交,即⎰=+ban dx x x P 0)()(1ω (1.3)定理二:高斯公式(1.1)的求积系数k A 全为正,且nk dx x l dx x l A bak bak k ,1,0,)()(2===⎰⎰(1.4)定理三:对于高斯公式(1.1),其余项为dxx fn f R ban n ⎰+++=)()()!22(1)(21)22(ωη (1.5)其中).())(()(],,[101n n x x x x x x x b a ---=∈+ ωη证明 以n x x x ,,,10 为节点构造)(x f 的埃尔米特插值多项式)(x H),()(i i x f x H = ni x f x H i i ,1,0),()(='='因为)(x H 是12+n 次多项式,而它的余项是)()()!22(1)()(21)22(x fn x H x f n n +++=-ωξ所以高斯公式(7.5.1)对)(x H 能准确成立,即∑∑⎰====ni i in i iibax f Ax H A dx x H 0)()()(从而dxx fn dxx H dx x f x f A dx x f f R n ban babani i i ba)()()!22(1)()()()()(21)22(0++=⎰⎰⎰∑⎰+=-=-=ωξ若)()22(x fn +在区间],[b a 上连续,由于)(21x n +ω在],[b a 上不变号,故应用积分中值定理可得],[,)()()!22(1)(21)22(b a dx x fn f R ban n ∈+=⎰++ηωη上述定理说明,与牛顿—科兹公式进行比较,高斯公式不但具有高精度,而且它还是数值稳定的,但是节点和求积系数的计算比较麻烦。
高斯求积公式

3 3 )+ f( ), 求积公式为 ∫ f ( x )dx ≈ f ( − -1 3 3 1 2 3 4 3 4 2 4 4 对于f ( x) = x , I ( f ) = ∫ x dx = ≠ Q( x) = (− ) + ( ) = -1 5 3 3 9
1
只要证明 ∀ 2 n + 2次多项式 f ( x ), I ( f ) = ∫ f ( x )dx ≠ ∑ Ak f ( x k ) a k =0 即可。 = Q( f )即可。 2 2 则 事实上, 事实上,令f ( x ) = [( x − x 0 )( x − x1 )L( x − x n )] = ω n +1 ( x ), f ( x ) ≥ 0,
⇒ m = 3 = 2 × 1 + 1。 一般地, 一般地,对于任意求积节点 a ≤ x0 < x1 < L< xn ≤ b ,任意求积 b 系数, 系数,求积公式 I ( f ) = ∫ f ( x )dx ≈ ∑ Ak f ( x k ) = Q ( f )的代数精度 a m < 2n + 2。 分析: 分析: n b
§2 Gauss型求积公式 型求积公式
本节 问题 关键
例4 求节点 x0,x1 ,使插值型求积公式
∫
1
−1
f ( x)dx ≈ A0 f ( x0 ) + A1 f ( x1 )
( 2 .1 )
具有尽可能高的代数精度。 具有尽可能高的代数精度。 分析:四个未知量A 分析:四个未知量 0,A1,x0,x1,并知道插值型求积公式的 代数精度最高。因此按插值型求积公式来 求积公式来求 代数精度最高。因此按插值型求积公式来求A0,A1。 x − x0 x − x1 待定, l , l1 ( x) = , 解:x0 , x1待定,0 ( x) =
7.3高斯型求积公式

ωn+1 ( x ) = ∏ ( x − xk ) 与任何次数不超过 n 的多项式
k =0
n
Pn ( x ) 在积分区间上关于权函数 ρ ( x ) 均正交, 即
∫
b a
ρ ( x )ωn+1 ( x ) Pn ( x )dx = 0。 (2)
( 即高斯点xk 是[a,b]上关于权函数
ρ ( x )的n+1次多项式Pn+1 ( x )的根 )
6
3
7 4 ±0.8611363116 ±0.3399810436 0.3478548451 0.6521451549
±0.9491079123 ±0.7415311856 ±0.4058451514 0
0.1294849662 0.2797053915 0.3818300505 0.4179591837
2 A 0 + A1 = ; 3 2 x0 A0 + x0 A0 = ; 5 2 x 02 A 0 + x 12 A 1 = ; 7
3 x 0 A 0 + x 13 A 1 =
2 . 9 ≥ 2
由于非线性方程组,通常 n
就很难求解.
而从分析高斯点的特性来构造高斯求积公式.
高斯点的基本特性
尽管高斯点的确定原则上可以化为代数问题, 但是由于所归结的方程组是非线性的,而它的 求解存在实质性的困难,所以我们要从研究高 斯点的基本特性着手解决高斯公式的构造问题。
∫
b a
ωn+1 ( x ) P ( x )dx = 0
(即高斯点xk 是[a,b]上的n+1次多项式Pn +1 ( x )的根)
定理7- 2: 带权插值求积公式 ∫a ρ ( x ) f ( x )dx = ∑ Ak f ( xk ) 其结点 xk
高斯求积公式

定义4 定义4
如果求积公式(5.1)具有 2n +1次代数精度,
则称其节点 xk (k = 0,1 ⋯, n) 为高斯点 高斯点,相应公式(5.1)称 高斯点 , 为高斯求积公式 高斯求积公式. 高斯求积公式
3
根据定义要使(5.1)具有 2n +1次代数精度,只要对
充分性. 对于 ∀f (x) ∈H2n+1, 用 ωn+1(x) 除 f (x) , , 记商为 P(x),余式为 q(x) 即 f (x) = P(x)ωn+1(x) + q(x) , 其中 P(x),q(x)∈Hn. 由(5.5)可得
∫
b
a
f (x)ρ(x)dx = ∫ q(x)ρ(x)dx.
b a
18
令它对 f (x) =1, x 都准确成立,有
A + A = 2; 0 1 A − 1 + A 1 = 0. 1 0 3 3
由此解出 A = A =1, 从而得到两点高斯-勒让德求积公式 0 1
∫
1
1 −
f (x)dx ≈ f (−
1 1 ) + f (− ). 3 3
b n→ ∞ k =0 a n
16
4.5.2
高斯高斯-勒让德求积公式
在高斯求积公式(5.1)中,若取权函数 ρ(x) =1, 区间为
[−11 则得公式 , ],
n
∫
1
−1
f (x)dx ≈ ∑A f (xk ). k
k =0
(5.9)
由于勒让德多项式是区间 [−11]上的正交多项式,因此, , 勒让德多项式 P 1(x) 的零点就是求积公式(5.9)的高斯点. n+ 形如(5.9)的高斯公式称为高斯-勒让德求积公式. 高斯-勒让ρ(x) ≥ 0, 由积分中值定理得(5.1)的余项为
gauss型求积公式

gauss型求积公式一、Gauss型求积公式的基本概念。
1. 定义。
- 在数值积分中,Gauss型求积公式是一种高精度的求积公式。
对于积分∫_a^bf(x)ρ(x)dx(其中ρ(x)为权函数),Gauss型求积公式的形式为∫_a^bf(x)ρ(x)dx≈∑_i = 1^nA_if(x_i)。
这里x_i称为求积节点,A_i称为求积系数,n为求积公式的节点个数。
2. 特点。
- 高精度:Gauss型求积公式具有很高的代数精度。
对于n个节点的Gauss型求积公式,其代数精度为2n - 1。
这意味着对于次数不超过2n-1的多项式f(x),该求积公式能精确成立,即∫_a^bP_m(x)ρ(x)dx=∑_i = 1^nA_iP_m(x_i),其中m≤slant2n - 1,P_m(x)是m次多项式。
- 节点分布:Gauss型求积公式的节点x_i不是等距分布的。
这些节点是关于权函数ρ(x)正交的多项式的零点。
例如,当ρ(x) = 1,[a,b]=[- 1,1]时,对应的正交多项式是勒让德多项式P_n(x),Gauss型求积公式的节点就是勒让德多项式的零点。
二、求积节点与求积系数。
1. 求积节点的确定。
- 以勒让德 - Gauss求积公式为例(ρ(x)=1,[a,b]=[-1,1]),求积节点x_i是勒让德多项式P_n(x)的零点。
勒让德多项式P_n(x)可以通过递推公式(n + 1)P_n +1(x)=(2n + 1)xP_n(x)-nP_n - 1(x),P_0(x)=1,P_1(x)=x来计算。
通过求解P_n(x)=0得到求积节点x_i。
2. 求积系数的计算。
- 求积系数A_i可以通过多种方法计算。
一种常见的方法是利用正交性条件。
对于勒让德 - Gauss求积公式,求积系数A_i可以通过公式A_i=(2)/((1 -x_i)^2)[P_{n'(x_i)]^2}计算,其中P_n'(x)是勒让德多项式P_n(x)的导数。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
∫
b
(2) x n ρ ( x)dx
a
∫
b
存在 n = 1,2,L
则称ρ(x)是[a,b]上的一个权函数。
正交多项式
在高等数学中介绍付立叶级数时,曾提到函数系 1, cosx, sinx, cos2x, sin2x,…, cosnx, sinnx,… 中,由于任意两个函数乘积在区间[-π,+π]上的积分 都等于零,则说这个函数系在[-π,+π]上是正交的, 并称这个函数系为正交函数系。 定义1(a) 定义1(a):设函数f(x),g(x)∈[a,b],且 1(a)
第七章 微积分的数值计算方法
7.3 高斯型求积公式
7.3 高斯型求积公式
代数精度的概念:一个求积公式的准确程度
问题: 是否有比等距节点的Newton-Cotes型求积公式 问题 是否有比等距节点的 型求积公式 更高代数精度的求积公式? 最高能达到多大? 更高代数精度的求积公式 最高能达到多大
注:对于一般的插值求积公式
(2) 递推公式 P ( x) = x P0 ( x ) = 1, 1 (n + 1) Pn +1 ( x ) = (2n + 1) xPn ( x ) − nPn −1 ( x ) n = 1, 2,L
(3)
Pn ( − x ) = ( −1) n Pn ( x )
(4) 所有根都是单根, 并在( −1,1)上关于原点对称分布.
∫
b
a
ρ ( x)ωn +1 ( x) Pn ( x)dx = 0。
(即高斯点xk 是[a,b]上关于权函数ρ ( x )的n+1次 正交多项式Pn +1 ( x )的根)
常见的正交多项式及高斯求积公式
•勒让德多项式(Legendre) •切比雪夫多项式(Chebyshev) •拉盖尔多项式(Laguerre) •埃尔米特多项式 (Hermite )
高斯高斯-勒让德求积公式
1. 勒让德(Legendre)多项式: 定义在区间 [ −1,1] 上 n 阶勒让德(Legendre)多项式 P0 ( x ) = 1 1 dn Pn ( x ) = n [( x 2 − 1) n ] 2 n ! dx n n = 1, 2,L 是正交的函数系,其 n + 1 阶勒让德多项式 Pn +1 ( x ) 与任 何次数不超过 n 的多项式 P ( x ) 在区间[-1,1]上均正交, 即
Ak 0.1713244924 0.3607615730 0.4679139346 0.1294849662 0.2797053915 0.3818300505 0.4179591837
6
3
7 4 0.3478548451 0.6521451549
5
±0.9061798459 ±0.5384693101 0
∫
1 −1 1− x 2
1
Tn +1 ( x ) P ( x )dx = 0
2. Chebyshev多项式的性质 多项式的性质: 多项式的性质
(1) Chebyshev多项式{Tn }∞=0 是[ −1,1]上带权ρ ( x ) = n 的正交多项式组,即 0, m ≠ n π 1 T ( x )T ( x ) n (Tm , Tn ) = ∫ m dx = , m = n ≠ 0 −1 1 − x2 2 π , m = n = 0 (2)递推公式
b k =0
n
所有次数不超过m 的多项式均能准确成立, 但对于 m + 1 次多项式不一定准确成立, 则称该数值求积公式具有 m 次代数精度。
高斯求积公式
定义7-2: 若插值求积公式 ∫ f ( x )dx ≈ ∑ Ak f ( xk )
a k =0
b
n
具有 2n + 1 次代数精度,则称该插值求积公式 为高斯求积公式,其中结点 xk 称为高斯点; 求积系数 Ak 称为高斯求积系数。
ωn +1 ( x) = ∏ ( x − xk ) 与任何次数不超过 n 的多项式
k =0
n
P( x) 在积分区间上均正交, 即 ∫ ωn +1 ( x) P( x)dx = 0
a
b
Gauss求积公式的特点: 1. 代数精度达到最高2n+1(针对n+1个节点而言) 2. 高斯点xk 是[a,b]上的n+1次正交多项式Pn +1 ( x )的根)
n 1 2
xk 0 ±0.5773502692 ±0.7745966692 0 ±0.8611363116 ±0.3399810436
Ak 2 1 0.5555555556 0.8888888889
n
xk ±0.9324695142 ±0.6612093865 ±0.2386191861 ±0.9491079123 ±0.7415311856 ±0.4058451514 0
定理7-2: 带权插值求积公式 ∫a ρ ( x ) f ( x )dx ≈ ∑ Ak f ( xk ) 其结点 xk
b k =0 n
为带权高斯点的充要条件是以这些点为零点的多项式
ωn +1 ( x) = ∏ ( x − xk ) 与任何次数不超过 n 的多项式
k =0
n
Pn ( x) 在积分区间上关于权函数 ρ ( x) 均正交, 即
b k =0 n
具有 2n + 1 次代数精度, 则称该带权插值求积公式为带权高斯求积公式, 其中结点 xk 称为带权高斯点; 求积系数 Ak 称为带权高斯求积系数。
权函数
定义:设[a,b]是有限或无限区间, ρ(x)是定义在[a,b]上 定义 的非零可积函数,若其满足
(1) ρ ( x)dx > 0
称为在[a,b]上带权 ρ ( x ) 正交序列,
ϕ j ( x ) 称为[a,b]上带权 ρ (x ) 的 n 次正交多项式。
高斯点与正交多项式的零点
定理7-1: 插值求积公式 ∫ f ( x)dx ≈ ∑ Ak f ( xk ) 其节点 xk 为
b a k =0 n
高斯点的充要条件是以这些点为零点的多项式
T1 ( x ) = x, T0 ( x ) = 1, Tn +1 ( x ) + Tn −1 ( x ) = 2 xTn ( x )
(3) 所有根都是单根, 在( − 1,1)上与原点对称分布,且Tn ( x )的n个根为 x k = cos (2k − 1)π ,( k = 1, 2,L , n ) 2n
1 1− x 2
3. Gauss - Chebyshev求积公式 以 Tn +1 ( x ) 的 n + 1 个零点作为区间 [ −1,1] 上的带权高斯点, 其带权插值求积公式
n 1 1 ∫−1 1− x f ( x )dx ≈ ∑ Ak f ( xk ) k =0 (2k + 1)π 为Tn +1的零点, xk = cos 2n + 2 1 π 1 Ak = ∫−1 1− x lk ( x )dx = n + 1
高斯积分公式的数值稳定型
设lk ( x ), k = 0,1,L , n为Lagrange基函数. lk2 ( x ) ≥ 0为2n次代数多项式, 其Gauss数值积分 等于精确积分,即有 0<∫ ρ ( x )lk2 ( x )dx = ∑ Alk2 ( xi ) = Ak , i
定义2 定义
最高幂项的系数为 a n ≠ 0 的 n 次多项式
ϕ j ( x ), j = 0,1,L ,若满足(两两正交) :
0, j ≠ k (ϕ j ,ϕ k ) = ∫ ρ ( x )ϕ j ( x )ϕ k ( x )d ( x ) = a Ak > 0, j = k
b
则 {ϕ j ( x )}
( f , g ) =
∫
b a
f ( x ) g ( x )d x = 0
则称f(x)与g(x)在[a,b]上正交.
正交多项式
定义1(b):设函数f(x),g(x)∈[a,b],且 定义
( f , g ) =
∫
b a
ρ ( x ) f ( x ) g ( x ) dx
= 0
称为权函数 称为权函数 则称f(x)与g(x)在[a,b]上带权ρ(x)正交.
定义7-3: 若带权插值求积公式 ∫a ρ ( x ) f ( x )dx ≈ ∑ Ak f ( xk ) 对
b k =0 n
所有次数不超过 m 的多项式 f ( x ) 均能准确成立, 但对 m + 1 次多项式不一定准确成立, 则称该带权插值求积公式具有 m 次代数精度。
定义7-4: 若带权插值求积公式 ∫a ρ ( x ) f ( x )dx ≈ ∑ Ak f ( xk )
2 2 n +1
( x)
有
I= ∫ f ( x )dx > 0,
a n n k =0
b
而数值积分
2 I n 43;1 ( xk ) = 0 k =0
故最高可能代数精度为2n+1.
高斯求积公式
定义7-1:如果求积公式 ∫a f ( x )dx ≈ ∑ Ak f ( xk ) 对于
∫
b
a
f ( x )dx ≈ ∑ Ak f ( xk )
k =0
n
来说,不管在积分区间上的 n + 1 个插值结点 xk 如 何选取,其代数精度至少为 n ;而只要选取合适的 xk 与 Ak,此插值求积公式的代数精度达到最大。
对于给定的求积节点,代数精度最高的求积公式 是插值型求积公式. 事实上,插值型求积公式的 代数精度完全由求积节点的分布所决定. 节点数目 固定后, 节点分布不同,所达到的代数精度也不同.
