电磁场的边界关系
电磁场的边界条件

将⑧代入⑨,得: sin 2 cos 1 sin 1 cos 2 sin(1 2 ) rs sin 2 cos 1 sin 1 cos 2 sin(1 2 )
2n1 cos 1 ts n1 cos 1 n2 cos 2
对绝大多数物质, 1 2
所以得到方程:
E1 y z E1' y z E2 y z
z 0
⑥
代入边界条件,可得:
k1 cos 1 A1s k1' cos 1' A1' s k2 cos 2 A2 s
k1 k1' 整理得: cos 1 A1s cos 1' A1' s cos 2 A2 s k2 k2' k1 sin 2 将 代入上式,得: k2 sin 1
AB BC CD DA
针对麦克斯韦 方程组积分形 式的第三个与 第四个方程, 建立如左图模 型,积分可得
E2t CD ( E2 n DF E1n FA) 0
E1t E2t 同理可得 H1t =H 2t
电磁场边界条件
(1)电场强度E 在分界面上的平行分量连续。
从右图可以看出, 对于s光:
Ex 0 E y ES Ez 0
根据几何关系,可知:
k x k sin 1 , k y 0, k z k cos 1
对于单色平面光波: E0 e E
i[t ( k x x k y y k z z )]
将上面的结论带 i[1t ( k sin 1 x k cos1 z )] E E0 e 入方程可得: 对于s光,可以分解为:
i ( k2 sin 2 x )
【精品】第八讲:麦克斯韦方程组、电磁场的边界条件
第八讲:麦克斯韦方程组、电磁场的边界条件2.6麦克斯韦方程组2.7电磁场的边值关系1、了解麦克斯韦方程组的建立过程,掌握它的基本性质;2、了解边界上场不连续的原因,能导出电磁场的边值关系;3、掌握电磁场方程微分形式和边界形式的联系与区别。
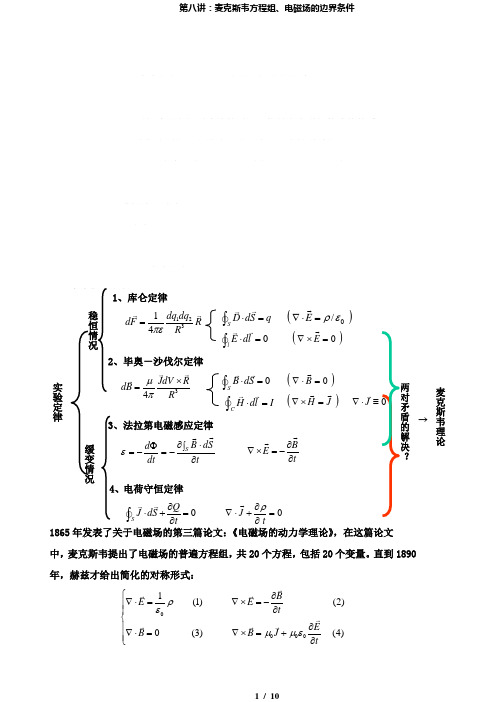
重点:1)麦克斯韦方程组的基本性质;2)电磁场的边值关系 难点:电磁场切向边值关系的推导 讲授法、讨论 2学时2.6麦克斯韦方程组(Maxwell ’sEquations )一、麦克斯韦方程1865年发表了关于电磁场的第三篇论文:《电磁场的动力学理论》,在这篇论文中,麦克斯韦提出了电磁场的普遍方程组,共20个方程,包括20个变量。
直到1890 年,赫兹才给出简化的对称形式:00001(1)(2)0(3)(4)BE E tE B B J tρεμμε⎧∂∇⋅=∇⨯=-⎪∂⎪⎨∂⎪∇⋅=∇⨯=+⎪∂⎩实验定律3、法拉第电磁感应定律4、电荷守恒定律12314dq dq dF RR πε=S D dS q ⋅=⎰0l E dl ⋅=⎰34JdV R dB R μπ⨯=0SB dS ⋅=⎰()0=⋅∇B CH dl I ⋅=⎰()JH =⨯∇tB E ∂∂-=⨯∇ 0=∂∂+⋅∇tJ ρ 0J ∇⋅≡对矛盾的解决麦克斯韦理论稳恒况缓变情况2、毕奥-沙伐尔定律1、库仑定律()/ερ=⋅∇E()=⨯∇E t S d B dt d S ∂⎰⋅∂-=Φ-= ε0S QJ dS t ∂⋅+=∂⎰→上式即为真空中的麦克斯韦方程组,其中(2)(4)含有对时间的偏导数,对应 运动方程,(1)(3)为约束方程。
二、麦克斯韦方程组的基本性质 1、线性性麦克斯韦方程组是一组线性方程,表明场服从迭加原理。
2、自洽性方程组各个方程彼此协调,且与电荷守恒定律协调。
如(2)式和(3)式一致:由(2)式有:()0=∂⋅∂∇-=⨯∇⋅∇tBE⇒C B =⋅∇ ,考虑到静磁时0=⋅∇B,所以取0=C 。
第五节边值关系

第四节电磁场边值关系
一、介质边界面上的电磁现象
1 导体在静电平衡时的边界行为:
导体静电平衡时,场量的突变发生在界面上。因 为: 内部场强 外部场强
E内 0 E外 0
1)求 Dt 关系:
E2t E1t D2t
2
ห้องสมุดไป่ตู้
D1t
1
2 1
D2t D1t
2)求 En 关系:
D2n D1n E2n 2 E1n1 2 1
E2n E1n
3)求 Bt 关系:
H 2t H1t B2t
2
B1t
1
2 1 B2t B1t
B 向量的法向关系: 将 B dS 0
s
用到小柱体上,可得
n ( B2 B1 ) 0
或 讨论:
B2n B1n 0
1)界面上 f 0 ,Dn 在两侧有突变。 界面上 f 0 ,Dn 在两侧连续。 2)界面两侧 Bn 线总连续。B2n B1n 3)已知 P n (P2 P ) 1
dl1 dl2
n
2 1
1
dl dl
将
L
H dl j f dS D
s s
t
dS
dl1
用到边界的长方形回路上去
L H dl l1 H1 dl1 l2 H 2 dl2 H dl h H1 l1 H2 l2 ( H1 H2 ) l s j f dS 回路面积 j f dS I 当 h 0 I f (l et ) f l (n e ) l (n f ) D dS 0 s t ( H1 H 2 ) l (n f ) l
电磁场的边界条件与电磁波的辐射和传播

电磁场的边界条件与电磁波的辐射和传播[摘要]:本文结合相关示意图简要总结了电磁场的边界条件,在参考大量相关文献的基础上,由边界条件出发分析了交变电磁场传播的原理,联系实际解释了电磁场的辐射和传播。
关键字:电磁场;电磁波;边界条件;辐射;传播。
一、电磁场的边界条件电磁场在两种不同媒质分界面上,从一侧过渡到另一侧时,场矢量E、D、B、H一般都有一个跃变。
电磁场的边界条件就是指场矢量的这种跃变所遵从的条件,也就是两侧切向分量之间以及法向分量之间的关系。
电磁场的边界条件可以由麦克斯韦方程组的积分形式推出,它实际上是积分形式的极限结果。
这些边界条件是:n·(D1-D2)=ρs; (1)n×(E1-E2)=0; (2)n·(B1-B2)=0; (3)n×(H1-H2)=J)s。
(4)式中n为两媒质分界面法线方向的单位矢量,场矢量E、D、B、H的下标1或2分别表示在媒质1或2内紧靠分界面的场矢量,ρ为分界面上的自由电荷面密度,J为分界面上的传导电流面密度。
式(1)表示在分界面两侧电位移矢量D的法向分量的差等于分界面上的自由电荷面密度。
当分界面上无自由电荷时,两侧电位移矢量的法向分量相等,即其法向分量是连续的。
式(2)表示在分界面两侧电场强度E的切向分量是连续的。
式(3)表示在分界面两侧磁通密度B的法向分量是连续的。
式(4)表示在分界面两侧磁场强度H的切向分量的差等于分界面上的表面传导电流面密度。
当分界面上无表面传导电流时,两侧磁场强度的切向分量相等,即其切向分量是连续的。
当媒质2为理想导体时,E2、D2、B2、H2等于零,式(1)表示D1的法向分量等于自由电荷面密度;式(2)表示E1无切向分量.式(3)表示B1的法向分量为零;式(4)表示H1的切向分量等于表面传导电流面密度,并且与电流方向正交。
二、电磁波的辐射和传播电磁波的产生与发射是通过天线来实现的。
由振荡电路产生的强大交变讯号通过互感耦合到天线上,天线就有交变电流产生,如下图所示。
电磁场的源与边界条件

q 所趋近的极限值就定义为点 P 的电 V
(r ) lim
式中 r 是源点的位失。
V 0
q dq V dV
2、 电荷面密度 在实际问题中,常会遇到电荷分布在薄层内的情况,如果薄层的厚度趋近于零,可近似 认为电荷分布在曲面上, 可以用电荷面密度 S (r ) 来描述其分布。 设曲面 S 上任一面元 S 内所包围的电荷量为 q ,则 S (r ) 定义为
3、磁感应强度 B 的散度、旋度和边界条件 (1)磁感应强度 B 的散度 根据磁通连续性原理的微分形式可知恒定磁场为无散场,故
B0
磁通连续性原理表明自然界无孤立的磁荷存在。上式即为麦克斯韦第二方程的微分形式。 (2)磁感应强度 B 的旋度 根据安培环路定理可得恒定磁场的磁感应强度 B 的旋度为
二、
电流及电流分布
电荷做定向运动形成电流,通常以电流强度来描述其大小。在电磁理论研究中,常用到 体电流模型,面电流模型和线电流模型。 1、 体电流 电荷在某一体积内定向流动形成的电流成为体电流。体电 流在导体内某一截面的分布用电流密度矢量 J 来描述,其定义 为:空间任一点 J 的方向是该点正电荷运动的方向, J 的大小 等于通过该点与 J 垂直的单位面积的电流,即
Nqd dS P dS P endS
因此,穿出闭合面 S 的正电荷为 P dS 。与之对应,留在闭合面 S 内的极化电荷量为
S
q p P dS PdV
S V
又由于
qP P dV
V
故有
P P
(2)极化强度 P 的旋度 对于各向同性和线性介质,有 P e 0 E ,其中合成电场强度 E 为自由电荷产生的外 电场 E 0 和极化电荷产生的附加电场 E 的叠加,由于两种电场强度的旋度都为零,故
电动力学-第一章-1.5 电磁场边值关系

j
0
t
2、库仑定律
F
1
4 0
V1 V2
12
r3
rd1d 2
1 Q1Q2 r.
40 r3
3、毕奥——萨伐尔定律
r B
xr
0 4
V
Jr
xr ' rr
r3
dV
'
4、法拉第定律
L
E
dl
S
B ds t
5、洛仑兹力
F Fe Fm q(E v B)
整体
f
(
E
v
B)
4
3
r23 r13
f
D
r23 r13 3
f
1 r2
,
r
r2
ÑS E dS V f dV
P e0E
D 1 e 0E E
4 r2D 4 3
r3 r13
f
D
r3 r13 3
f
1 r2
, r2
r
r1
E D
P
1
0
D
注意球内球外的ε不同
D 0,r r1
r
f
0
P
理想导体表面边界条件σ=∞
• 设介质1为理想导体,理想导体内电场为 0(否则J为∞),对应的磁场也为0
• 介质2边界上的场强满足
en H ar en E 0
en D f
en B 0
理想介质σ=0
• 如果媒质1和2为理想介质,在求时变场时 认为表面不存在自由面电荷和面电流
D 0E P P e0E
H B M
0
M
D
mH
0
1
e
电磁场的源与边界条件

根据安培环路定理可得恒定磁场的磁感应强度 B 的旋度为
当有磁介质存在时,上式变为
B 0J B 0 (J JM )
式中 J 为传导电流密度, J M 为磁化电流密度。
(3)磁感应强度 B 的边界条件 将积分形式的麦克斯韦第三方程应用于如图 4 所示的圆
柱,易得
en (B1 B2 ) 0 上式表明磁感强度的法向分量是连续的。
球的极限当带电体的尺寸相对于观察点至带电体的距离可以忽略时,就可以认为电荷分布于
带电体中心上,即将带电体抽象为一个几何点。点电荷的电荷密度分布可以用数学上的 (r )
来描述。
二、 电流及电流分布
电荷做定向运动形成电流,通常以电流强度来描述其大小。在电磁理论研究中,常用到 体电流模型,面电流模型和线电流模型。 1、 体电流
移矢量的切向分量是不连续的(两种介质的 通常不等)。
3、磁感应强度 B 的散度、旋度和边界条件
(1)磁感应强度 B 的散度 根据磁通连续性原理的微分形式可知恒定磁场为无散场,故 B0
磁通连续性原理表明自然界无孤立的磁荷存在。上式即为麦克斯韦第二方程的微分形式。 (2)磁感应强度 B 的旋度
即
故有
(P1 P2 ) enS SPS
en (P1 P2 ) SP 上式表明极化强度的法向分量是不连续的。一般情况下,其切向分量也不连续。
7、磁化强度 M 的散度、旋度和边界条件
7/9
电磁场与电磁波
第二章 电磁场的基本规律
学习报告
(1)磁化强度 M 的散度
对于各向同性和线性磁介质, M m H ,由于 H 的散度为零,故
自然界中存在两种电荷:正电荷和负电荷。带电体上所带的电荷是以离散的方式分布的, 任何带电体的电荷量都是基元电荷的整数倍,但在研究宏观电磁现象时,人们关注的是大量 微观带电粒子的整体效应,因此可以认为电荷是以一定形式连续分布的,并用电荷密度来描 述电荷的分布。 1、 电荷体密度
电磁场的边界条件

电磁场与电磁波
第 2 章
电磁场的基本规律
§8
边界条件的推证 (1) 电磁场量的法向边界条件
ΔS
媒质1
en
S
媒质2
D1
Δh
在两种媒质的交界面上任取一
点P,作一个包围点P 的扁平圆柱 曲面S,如图表示。 令Δh →0,则由
P
D2
即 同理 ,由
S
D dS
d
x
π ez sin( z ) cos(t k x x) (A/m) 0 d k x E0
(2) z = 0 处导体表面的电流密度为
J S ez H
z 0
πE0 ey sin(t k x x ) 0 d
(A/m)
z = d 处导体表面的电流密度为
J S ( ez ) H
E1 ( z , t ) ex [60 cos(15 108 t 5 z ) 20 cos(15 108 t 5 z )] V/m
媒质2中的电场强度为
(1)试确定常数A的值;(2)求磁场强度 H 1 ( z , t ) 和 H 2 ( z , t ) ; (3)验证 H 1 ( z , t ) 和 H 2 ( z , t ) 满足边界条件。
H1 1 1 E1x E1 ey t 1 1 z 1 e y [300sin(15 108 t 5 z ) 100sin(15 108 t 5 z)] 0
将上式对时间 t 积分,得
1 2 7 8 H1 ( z , t ) ey [2 10 cos(15 10 t 5 z ) 10 7 cos(15 108 t 5 z )] A/m 0 3
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
§1-6电磁场的边值关系
应用小圆柱体:则上式左边面积应遍及整个 圆柱体表面:则
B d 顶 B d 壁 B d 底 B d
设圆柱体的面积很小,可以认为B在此范围 内是常数:
则上式变为 :
B 1 n 1 A B 2 n 2 A 壁 B d 0
§1-6电磁场的边值关系
两E •种dl形式的 B 麦t•克d斯韦方程组:EBt
D •d Q
•D
B • d 0
•B0
H •dlI D t•d
H jD t
§1-6电磁场的边值关系
电磁场的波动 性:
E
B t
D
E
0
B 0
E
B
(1) (2)
(3)
B 0
H
j
D t
B
t
E
t
(4)
j E
电导率
D E
介电常数
H
1
B
磁导率
§1-6电磁场的边值关系
无限大、均匀、透明介质中电磁场的波动
方程:
2E 2B22tBE 2
t2
2
2 x2
2 y2
2 z2
§1-6电磁场的边值关系
(2)波动方程解的基本形式:
平面电磁波:
E f 1 ( z v ) f t 2 ( z v )t
球面波简谐表达:E A ( r,tA )1 eA rx 1ic (k p o k r s r t)t 0
r
0
A 柱(r面,t)波简A rc 谐o 表k达 sr :t0
E A exi(k p rt)
r
0
§1-6电磁场的边值关系
(3)从表达式中可以获得的信息: 介质折射率: 传播速度与方向: 偏振方向: 周期、频率、角频率: 空间周期、空间频率、空间角频率: 平面电磁波的性质:
在光学中,常常要处理光波从一种介质到另一 种介质的传播问题,由于两种介质的物理性质 不同(分别以1、1 和2、2 表征),在两 种介质的分界面上,电磁场将不连续,但他们 之间仍存在一定关系,通常把这种关系称为电 磁场的边值关系。
§1-6电磁场的边值关系
由于界面两侧的电磁场在介面上并不连续, 因此不能从麦克斯韦方程的微分形式出发来
,此外长方形的高h0,
则沿BC, DA的积分趋于0,
并且,由于面积趋向于零,而 B t
为有限量,则
Edl (
AB
BC
CD D)AE•dl
于是:
B t •d0
A E • d l B C E • d l D 0 或 E 1 t 1 l E 2 t 2 l 0
§1-6电磁场的边值关系
式中 n1,n分2 别为柱顶和柱底的外法线单位矢 量。当高 h0时
上式第三式也趋于零,并且柱顶和柱底趋近 分界面。
以 n 表示分界面法线方向的单位矢量(方向 从介质2指向介质1)则有 :
nn 1 n 2
§1-6电磁场的边值关系
于是:
n•(B1B2)0或
B1n B2n
电磁场的边界关系
§1-6电磁场的边值关系
1.前面内容回顾: 2.分界面上电磁场法向分量的关系: 3.分界面上电磁场切向分量的关系:
§1-6电磁场的边值关系
一、内容回顾: 1.对已讲内容的要求: (1).了解光的电磁理论、电磁场的波动性; (2).彻底掌握光波在介质中的传播速率、介
质折射率的物理意义及其表达式; (3).深入理解平面、球面、柱面简谐光波场
s 1 SdtA2 1 cos2(krt)dt
0
0
1A2 1 A2
2
2
通常可以写为:
I A2
计算光强时可以用:
~ ~ I A 2E E *
§1-6电磁场的边值关系
二、本节内容的说明:
为了解释一平面波(单色简谐)射向界面时, 其反射波、折射波传播方向的改变规律和振幅 改变规律(前者为反射定律,后者为折射定 律)。
推导,而应从积分形式出发来讨论:
积分形式的麦克斯韦方程 :
D
d
Q
B E Hd
d
dl l I
0
B t
D t
d d
§1-6电磁场的边值关系
三、分界面上法向分量 n1
:
δS
δh
n
ε1μ1
ε2μ2
n2
设:在分界面上作出一个扁平的小圆柱体的 Nhomakorabea 高为 h
圆面B 积为d s 0 ,由上第2式 :
的时间、空间特性,以及描述平面、球面、 柱面简谐光波的数学表达式中各项参数的物 理意义;
§1-6电磁场的边值关系
(4).牢固地掌握光强的概念和计算相对光 强的方法;
2.已讲授的基本结论: (1).光的电磁理论、电磁场的波动性:
光的电磁理论的提出是人们在电磁学方面已有了 深入研究的结果。1864年麦克斯韦把电磁规律总 结为麦克斯韦方程组,建立起完整的经典电磁理 论,同时指出光也是一种电磁波,从而产生了光 的电磁理论。
上式表明,在通过分界面时,
磁感应强度B虽然整个的发生跃变,但它 的法向分量却是连续的。
§1-6电磁场的边值关系
在各向同性、均匀、透明介质中,
由于其Q=0则,同样由 D •d Q
可以得到: n•(D 1D 2)0或
D1n D2n
即:在分界面上没有自由电荷的情况下,电感 强度的法向分量 也是连续的。
§1-6电磁场的边值关系
(4)关于光强的概念:
若单位时间内穿过与K相垂直的单位面积的 为能量S (功率密度) ,通常把S在接收器
能分辨的时间间隔内的平均值叫做电磁波 的强度I。
表达式:
1
I
s
sdt
0
考虑到传播方向,可以定义波印廷矢量
S
1
EB
§1-6电磁场的边值关系
平面电磁波的强度:
球面电磁波:
柱面电磁波:A (r,t)1 rB 1(rv)tB 2(rv)t
E A rC 1 (r v) tC 2(r v)t
§1-6电磁场的边值关系
三种基本形式的简谐表达:
平面波简谐表达: E A co 2 s (z v)t E A ei ( x k r p t )
§1-6电磁场的边值关系
四、电磁场切向分量的关系:
把小圆柱换成一个矩形面积ABCD如图1-
19所示:由于
A
ε1μ1 t
δl
t1
B
δh
EdlBtdε2μ2
D
t
2
C
dlE取 dAlB (C 切 ADB线 BC方 C向 D, D)AE则 •dlBtd
§1-6电磁场的边值关系
若AB和CD长度很短,则在两线段内E 可认 为是常数;在介质1和介质2内分别为E1和E2
