运筹学第一章线性规划与单纯形法
合集下载
运筹学
11
目录
（三）LP问题的标准型
1.为了讨论LP问题解的概念和解的性质以及对LP问题求 解方便，必须把LP问题的一般形式化为统一的标准型：
minz=c1x1+c2x2+…+cnxn
j =1 a11 x2 + a12 x2 + + a1n xn = b1 a x + a x + + a x = b n 2n n 2 21 2 22 2 简 aij x j = bi (i = 1,2, L , m) s.t 化 j =1 x j ≥ 0( j = 1,2,L , n) am1 x2 + am 2 x2 + + amn xn = bm x1 , x2 , , xn ≥ 0
A ( 0 ,3 ) 10 15 , ) B( 7 7 5 C ( ,0 ) 2
max
Z = 5 x1 + 4 x 2
3 x 1 + 5 x 2 ≤ 15 2 x1 + x 2 ≤ 5 2 x 1 + 2 x 2 ≤ 11 x1 , x 2 ≥ 0
Z=
110 7
2x1+2x2=11
C 2.5
5x1+4x2=0 红线为目标函数的等值线 等值线. 红线为目标函数的等值线
j i= 1
j
(1.4) (1.5) (1.6)
ì n a ij x j = s .t . j = 1 í 1.从代数的角度看： x j 0 1.
b
i
可行解（Feasible Solution)： 满足约束条件(1.5)和(1.6)的 解X=(x1,x2,…,xn)T称为可行解。所有可行解构成可行解集， 即可行域。 最优解(Optimal Solution): 而使目标函数达到最大值的可 行解称为最优解，对应的目标函数值称为最优值。 求解LP问题就是求其最优解和最优值，但从代数的角 17 度去求是困难的。 目录
第1章-线性规划及单纯形法-课件(1)
✓ x1、 x2 0
IБайду номын сангаас
设备
1
原材料 A 4
原材料 B 0
利润
2
II 资源限量
2 8 台时
0
16kg
4
12kg
3
第一章 线性规划及单纯形法 运筹学
该计划的数学模型
✓ 目标函数 ✓ 约束条件
Max Z = 2x1 + 3x2
x1 + 2x2 8 4x1 16 4x2 12 x1、 x2 0
x1
✓ 美国航空公司关于哪架飞机用于哪一航班和哪些 机组人员被安排于哪架飞机的决策。
✓ 美国国防部关于如何从现有的一些基地向海湾运 送海湾战争所需要的人员和物资的决策。
✓ ……
第一章 线性规划及单纯形法 运筹学
二、线性规划问题的数学模型
✓ 1、一般形式 ✓ 2、简写形式 ✓ 3、表格形式 ✓ 4、向量形式 ✓ 5、矩阵形式
1、唯一最优解
max Z 2 x 1 3 x 2
2 x 1 2 x 2 12 ⑴
x1 4 x1
2 x2
8 16
⑵ ⑶
4 x 2 12 ⑷
x 1 0 , x 2 0
1 234 56
x2
⑶ ⑷
(4，2)
0 1 234 5678
x1
⑵
⑴
✓最优解：x1 = 4,x2 = 2，有唯一最优解Z=14。
第一章 线性规划及单纯形法 运筹学
三、线性规划模型的标准形式
✓ 1、标准形式 ✓ 2、转换方式
第一章 线性规划及单纯形法 运筹学
1、标准形式
maZx cjxj
xj
aijxj 0
bi
运筹学线性规划与单纯形法
整理课件
16
Max Z= x1-2x2+3x3' -3x3" + 0x4 +0x5 s.t. x1+x2+ x3' - x3" +x4 =7
x1-x2+ x3' - x3" -x5=2
-3x1+x2+2x3' -2x3" =5 x1, x2,x3',x3", x4,x5 0
第一节小结：建立模型；三个组成要素；四种形式； 化为标准形（4个条件5点）
.
9x1+4x2 ≤ 360
90 80 60 40 20
4x1+5x2 ≤200
B C
HI G
Z=70x1+120x2 3x1+10x2 ≤300
0
20 D40 E 60
80 1F00 x1
整理课件
30
二、解的几种可能情况
1．唯一最优解。目标函数直线与凸多边形只有 一个切点； 2．无穷多最优解，目标函数图形与某个约束条 件平行。 3．无界解（无最优解）----可行域无界。一般是 漏了一些约束条件。 4．无可行解----可行域为空。
Ⅰ
Ⅱ 计划期可用能力
2
2
12
1
2
8
4
0
16
0
4
12
2
3
问：应如何安排生产计划，才能使总利润最大？
整理课件
3
解：用数学的语言进行描述:
1.决策变量：设产品I、II的产量分别为 x1、x2 2.目标函数：问题要求获取利润最大，该公司获取
利润为2 x1 + 3 x2，令z = 2 x1 + 3 x2，则max z = 2 x1 + 3 x2， max z 是该公司获取利润的目标 值，它是变量x1、 x2的函数，称为目标函数。
运筹学第1章：线性规划问题及单纯型解法
原料甲 原料乙 最低含量 VA 0.5 0.5 2 VB1 1.0 0.3 3 VB2 0.2 0.6 1.2 VD 0.5 0.2 2 0.3 0.5 单价
分别代表每粒胶丸中甲, 设 x1, x2分别代表每粒胶丸中甲, 乙两种原料的用量
5
例3,合理下料问题 , 分别代表采用切割方案1~8的套数, 的套数, 设 xj 分别代表采用切割方案 的套数
19
( f(x
)= 3
6
1.2.2 单纯型法的基本思路
确定初试基础可行解
检查是否为 最优解? 最优解?
是
求最优解的目标函数值
否 确定改善方向
求新的基础可行解
20
1.2.3 单纯型表及其格式
IV CB III XB II x1 b c1 a11 a21 c1′′= cn+1 xn+1 b1 c2′′= cn+2 xn+2 b2 x2 … xn c2 … cn a12 … a1n a22 … a2n I xn+1 cn+1 1 0 0 zn+1 xn+2 cn+2 0 1 0 zn+2 … … … … … … xn+m cn+m 0 0 1 zn+m
OBJ : max f ( x) = 6x1 + 4x2 2x1 + x2 ≤ 10 铜资源约束 x1 + x2 ≤ 8 铅资源约束 s.t. x2 ≤ 7 产量约束 x1, x2 ≥ 0 产量不允许为负值 最优解: x1 = 2, x2 = 6, max f ( x) = 36.
4
例2,配料问题(min, ≥) ,配料问题(
2 max 1 O 1 2 3 4 D 5 6 7 H 8
清华大学运筹学课件(完整课件)
2x1 + 3x2 ≤ 4 x1,x2 ≥ 0
化标准型
max z = x1 + 3x2 + 0x3 + 0x4
x1 + 2x2 + x3 = 3
2x1 + 3x2
+ x4 = 4
x1,x2,x3,x4 ≥ 0
系数矩阵
1 A 2
2 3
1 0
0 1
p1
p2
p3 p4 , 则 B p3 p4
取x3、x4为基变量,令非基变量x1= x2=0 ∴ 初始基可行解：X(0) = (0 0 3 4)T
③
3
z = 2x1 + 4x2，此时表示 目标函数的直线与表示
Q2(4,2)
① *
条件①的直线平行，
o
最优点在线段Q3Q2上。
即存在无穷多最优解。
4 Q1
x1
7
(3)无界解
[eg.5]
max z = 2x1 + 3x2 4x1 ≤ 16 x1，x2 ≥ 0
则x2 → ∞，z → ∞。 即存在无界解。
对于
n
m
max z c j x j cni xni
j 1
i 1
n
aij x j xni bi
i 1, , m
j1
x
j
0
j 1, , n m
设 xni 为基变量可行,i 1,, m
x j为非基变量, j 1,, n
n
xni bi aij x j j 1
代入目标函数
产品Ⅱ生产x2件。
4x1
≤ 16
这里z为利润函数，
4x2 ≤ 12
max z:表示求z的最大值。
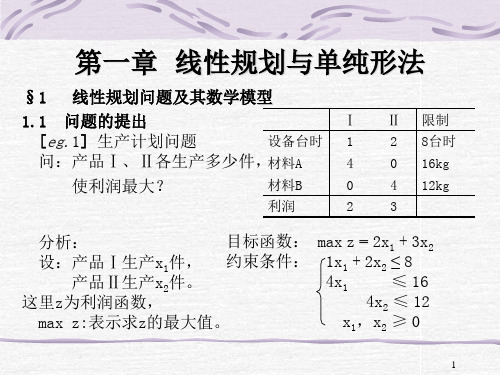
化标准型
max z = x1 + 3x2 + 0x3 + 0x4
x1 + 2x2 + x3 = 3
2x1 + 3x2
+ x4 = 4
x1,x2,x3,x4 ≥ 0
系数矩阵
1 A 2
2 3
1 0
0 1
p1
p2
p3 p4 , 则 B p3 p4
取x3、x4为基变量,令非基变量x1= x2=0 ∴ 初始基可行解：X(0) = (0 0 3 4)T
③
3
z = 2x1 + 4x2，此时表示 目标函数的直线与表示
Q2(4,2)
① *
条件①的直线平行，
o
最优点在线段Q3Q2上。
即存在无穷多最优解。
4 Q1
x1
7
(3)无界解
[eg.5]
max z = 2x1 + 3x2 4x1 ≤ 16 x1，x2 ≥ 0
则x2 → ∞，z → ∞。 即存在无界解。
对于
n
m
max z c j x j cni xni
j 1
i 1
n
aij x j xni bi
i 1, , m
j1
x
j
0
j 1, , n m
设 xni 为基变量可行,i 1,, m
x j为非基变量, j 1,, n
n
xni bi aij x j j 1
代入目标函数
产品Ⅱ生产x2件。
4x1
≤ 16
这里z为利润函数，
4x2 ≤ 12
max z:表示求z的最大值。
运筹学第一章
OR1
30
1.1.3解的概念
概念： 1、可行解：满足所有约束条件的解。 2、可行域：即可行解的集合。所有约束条件的交 集，也就是各半平面的公共部分。满足所有约 束条件的解的集合，称为可行域。 3、凸集：集合内任意两点的连线上的点均属于这 个集合。如：实心球、三角形。线性规划的可 行域是凸集。
OR1
OR1
27
线性规划图解法例题
（无界解）
max z x 2 y x y 1 2 x 4 y 3 x 0, y 0
OR1
28
线性规划图解法例题
（无解）
min z x 2 y x y 2 2 x 4 y 3 x 0, y 0
请问该 医院至 少需要 多少名 护士？
5
例题2建模
目标函数：min Z=x1+x2+x3+x4+x5+x6 约束条件： x1+x2 ≥70
x2+x3 ≥60 x3+x4 ≥ 50 x4+x5 ≥20 x5+x6 ≥30 非负性约束：xj ≥0,j=1,2,…6
OR1
6
例题3：运输问题
三个加工棉花的加工厂，并且有三个仓库供应棉花，各 供应点到各工厂的单位运费以及各点的供应量与需求量 分别如下表所示：问如何运输才能使总的运费最小？
OR1
14
总
结
从以上 5 个例子可以看出，它们都属于优化问题，它们 的共同特征： 1 、每个问题都用一组决策变量表示某一方案；这组决 策变量的值就代表一个具体方案，一般这些变量取值是 非负的。 2 、存在一定的约束条件，这些约束条件可以用一组线 性等式或线性不等式来表示。 3 、都有一个要求达到的目标，它可用决策变量的线性 函数（称为目标函数）来表示。按问题的不同，要求目 标函数实现最大化或最小化。 满足以上三个条件的数学模型称为线性规划的数学模型。
30
1.1.3解的概念
概念： 1、可行解：满足所有约束条件的解。 2、可行域：即可行解的集合。所有约束条件的交 集，也就是各半平面的公共部分。满足所有约 束条件的解的集合，称为可行域。 3、凸集：集合内任意两点的连线上的点均属于这 个集合。如：实心球、三角形。线性规划的可 行域是凸集。
OR1
OR1
27
线性规划图解法例题
（无界解）
max z x 2 y x y 1 2 x 4 y 3 x 0, y 0
OR1
28
线性规划图解法例题
（无解）
min z x 2 y x y 2 2 x 4 y 3 x 0, y 0
请问该 医院至 少需要 多少名 护士？
5
例题2建模
目标函数：min Z=x1+x2+x3+x4+x5+x6 约束条件： x1+x2 ≥70
x2+x3 ≥60 x3+x4 ≥ 50 x4+x5 ≥20 x5+x6 ≥30 非负性约束：xj ≥0,j=1,2,…6
OR1
6
例题3：运输问题
三个加工棉花的加工厂，并且有三个仓库供应棉花，各 供应点到各工厂的单位运费以及各点的供应量与需求量 分别如下表所示：问如何运输才能使总的运费最小？
OR1
14
总
结
从以上 5 个例子可以看出，它们都属于优化问题，它们 的共同特征： 1 、每个问题都用一组决策变量表示某一方案；这组决 策变量的值就代表一个具体方案，一般这些变量取值是 非负的。 2 、存在一定的约束条件，这些约束条件可以用一组线 性等式或线性不等式来表示。 3 、都有一个要求达到的目标，它可用决策变量的线性 函数（称为目标函数）来表示。按问题的不同，要求目 标函数实现最大化或最小化。 满足以上三个条件的数学模型称为线性规划的数学模型。
线性规划
一、线性规划问题的提出
(1) 根据影响所要达到目的的因素确定决策变 量； (2) 由决策变量所受的限制条件确定决策变量 所要满足的约束条件； (3) 由决策变量和所要达到目的之间的函数关 系确定目标函数
线性规划问题是什么样的一类问题呢？ 线性规划问题是什么样的一类问题呢？ 请看案例-----请看案例-----例1(资源的合理利用问题) 资源的合理利用问题) 某工厂在下一个生产周期内生 产 甲、乙两种产品，要消耗 A、B和C三种资源，已知每件产 品对这三种资源的消耗、这三 种资源的现有数量和每件产品 可获得的利润如表所示. 可获得的利润如表所示.问：如 何安排生产计划，使得既能充 分利用现有资源又使总利润最 大？
线性规划问题的一般形式
max（min） max（min）Z = c1 x1+c2 x2 + … + cn xn
一般形式 (1.1a)
s.t.a11 x1 + a12 x2 + … + a1n xn ≤（或=，≥）b1
a21 x1 + a22 x2 + … + a2n xn ≤（或=，≥）b2
… …
例4 、七桥问题
200多年前东普鲁士（德国）-----哥尼斯堡 200多年前东普鲁士（德国）-----哥尼斯堡
A D B
C A
D C
B
例5、婚姻问题
三个女儿待嫁、三个追求者、一夫一妻制
大 A B C 3 5 26 中 27 10 28 小 1 5 11
例6、中国邮递员问题
中国科学家管梅谷------一个邮递员送完信后 中国科学家管梅谷------一个邮递员送完信后 所走过的路最短
销地 产地
B1
B2
(1) 根据影响所要达到目的的因素确定决策变 量； (2) 由决策变量所受的限制条件确定决策变量 所要满足的约束条件； (3) 由决策变量和所要达到目的之间的函数关 系确定目标函数
线性规划问题是什么样的一类问题呢？ 线性规划问题是什么样的一类问题呢？ 请看案例-----请看案例-----例1(资源的合理利用问题) 资源的合理利用问题) 某工厂在下一个生产周期内生 产 甲、乙两种产品，要消耗 A、B和C三种资源，已知每件产 品对这三种资源的消耗、这三 种资源的现有数量和每件产品 可获得的利润如表所示. 可获得的利润如表所示.问：如 何安排生产计划，使得既能充 分利用现有资源又使总利润最 大？
线性规划问题的一般形式
max（min） max（min）Z = c1 x1+c2 x2 + … + cn xn
一般形式 (1.1a)
s.t.a11 x1 + a12 x2 + … + a1n xn ≤（或=，≥）b1
a21 x1 + a22 x2 + … + a2n xn ≤（或=，≥）b2
… …
例4 、七桥问题
200多年前东普鲁士（德国）-----哥尼斯堡 200多年前东普鲁士（德国）-----哥尼斯堡
A D B
C A
D C
B
例5、婚姻问题
三个女儿待嫁、三个追求者、一夫一妻制
大 A B C 3 5 26 中 27 10 28 小 1 5 11
例6、中国邮递员问题
中国科学家管梅谷------一个邮递员送完信后 中国科学家管梅谷------一个邮递员送完信后 所走过的路最短
销地 产地
B1
B2
管理运筹学 易错判断题整理
主要内容： 1 存储费 2 订货费 3 生产成本 4.缺货成本 5 订货提前期 6 订货点 7 （s,S）型存储 2 确定性存储的4种形式，要会画图。 判断题： 1 在其他费用不变的情况下，随着单位缺货费的增加， 最优订货批量将相应减少。× 2 其他费用不变，订货费用的增加将导致订货批量的减少。 × 3 在需求量为常数，订货提前期为0的经济订货批量存储模型中， 4 最优订货批量随一次订货费的增大而增大，随存储费用的增加而减小。 √
× 5 如果运输问题或者转运问题模型中，Cij 都是产地i到销地j的最小 运输费用，则运输问题同转运问题将得到相同的最优解。
√
第三章：目标规划
主要内容： 1 描述目标规划建模的思路以及他的数学模型同一般线性 数学模型的相同和不同点。 2 解释下列变量：1正负偏差变量 2绝对约束和目标约束 3 优先因子与权系数。 3 目标规划图解法的步骤。 4 目标规划 目标函数特点。 判断题： 1 目标规划模型中，可以不含有绝对约束但是必须含有目 标约束。
第一章：线性规划及单纯形法
2.1单纯形法和两阶段法大M法 主要内容
1 线性规划数学模型的结构及各要素的特征。 2 求解线性规划时可能出现哪几种结果。 3 叙述线性规划问题的可行解、基解、基可行解、最优解 的概念及上述解之间的关系。
4 单纯性法的计算步骤，如何在单纯性表中判别问题是具 有唯一最优解、无穷多最优解、无界解。
√ 4 动态规划的基本方程保证各阶段内决策的独立进行，可以不考虑这之前和之后 决策的如何进行。
√
第六章：网络规划
主要内容：
6.1 1 通常用G=（v,e）表示一个图，试描述符号V,E及表达式的含义。 2 解释下列名词，说明区别。1 端点，相邻，关联边， 2 环，多重边，简单图 3链，初等链 4. 圈，初等圈，简单圈。 5.回路，初等路6.节点的次，悬挂点，悬挂边，孤立点 7. 连通图，连通分图 ，支撑子图8. 有向图，基础图，赋权图 3 描述树，图的支撑树，最小支撑树的概念。 4 描述Dijkstra算法的基本思想和步骤。 5 最大流问题是线性规划问题，说明其线性形式。 6 什么是增光链，为什么不存在关于可行流f的增广链，就是最大流。 7截集，截量以及最大流最小截量定理。 8 最小费用最大流的概念。
× 5 如果运输问题或者转运问题模型中，Cij 都是产地i到销地j的最小 运输费用，则运输问题同转运问题将得到相同的最优解。
√
第三章：目标规划
主要内容： 1 描述目标规划建模的思路以及他的数学模型同一般线性 数学模型的相同和不同点。 2 解释下列变量：1正负偏差变量 2绝对约束和目标约束 3 优先因子与权系数。 3 目标规划图解法的步骤。 4 目标规划 目标函数特点。 判断题： 1 目标规划模型中，可以不含有绝对约束但是必须含有目 标约束。
第一章：线性规划及单纯形法
2.1单纯形法和两阶段法大M法 主要内容
1 线性规划数学模型的结构及各要素的特征。 2 求解线性规划时可能出现哪几种结果。 3 叙述线性规划问题的可行解、基解、基可行解、最优解 的概念及上述解之间的关系。
4 单纯性法的计算步骤，如何在单纯性表中判别问题是具 有唯一最优解、无穷多最优解、无界解。
√ 4 动态规划的基本方程保证各阶段内决策的独立进行，可以不考虑这之前和之后 决策的如何进行。
√
第六章：网络规划
主要内容：
6.1 1 通常用G=（v,e）表示一个图，试描述符号V,E及表达式的含义。 2 解释下列名词，说明区别。1 端点，相邻，关联边， 2 环，多重边，简单图 3链，初等链 4. 圈，初等圈，简单圈。 5.回路，初等路6.节点的次，悬挂点，悬挂边，孤立点 7. 连通图，连通分图 ，支撑子图8. 有向图，基础图，赋权图 3 描述树，图的支撑树，最小支撑树的概念。 4 描述Dijkstra算法的基本思想和步骤。 5 最大流问题是线性规划问题，说明其线性形式。 6 什么是增光链，为什么不存在关于可行流f的增广链，就是最大流。 7截集，截量以及最大流最小截量定理。 8 最小费用最大流的概念。
运筹学第一章
max z = - x1’ +2x2 +3（ x3’ - x3” ） - x1’ +x2 – ( x3’ - x3” )-x4 = 9 st. 3x1’ +2x2 -4 ( x3’ - x3” )-x5= 7 x1’ +2x2 - 3 ( x3’ - x3” ) = 6 x1’ ≥ 0, x2 ≥ 0, x3’ ≥0 x3” ≥0
3.线性规划问题的标准形式 线性规划问题的标准形式 max z =- x1-2x2 -3x3 2 x1’+x2 +(x3’ - x3” )+ x4 = 9 3 x1’ +x2 +2 (x3’ - x3” ) –x5 = 4 st. -4 x1’ +2x2 +3 (x3’ - x3” ) =6 x1’ ≥ 0, x2 ≥0, x3’ ≥0 x3” ≥0
例1-1-2 ---1 min z = x1+2x2 +3x3 ﹣2 x1+x2 +x3 ≤9 st. ﹣3 x1+x2 +2x3 ≥ 4
4 x1－2x2 － 3x3 =﹣6
x1 ≤0, x2 ≥0, x3 无约束。 （1）min z = x1+2x2 +3x3 令Z=-Z’ min Z=min（-z ’）=max z ’
第一章 讲解内容
第一节： 第一节：线性规划问题及其数学模型 第二节： 第二节：线性规划问题的几何意义 第三节：单纯形法 第三节： 第四节： 第四节：单纯形法的计算过程 第五节： 第五节：单纯形法的进一步讨论 第六节： 第六节：应用案例
第一章 线性规划问题及其数学模型 1. 问题的提出 2.图解法（重点） 3. 线性规划问题的标准形式 4.线性规划问题的解的概念（重点、难点）
3.线性规划问题的标准形式 线性规划问题的标准形式 max z =- x1-2x2 -3x3 2 x1’+x2 +(x3’ - x3” )+ x4 = 9 3 x1’ +x2 +2 (x3’ - x3” ) –x5 = 4 st. -4 x1’ +2x2 +3 (x3’ - x3” ) =6 x1’ ≥ 0, x2 ≥0, x3’ ≥0 x3” ≥0
例1-1-2 ---1 min z = x1+2x2 +3x3 ﹣2 x1+x2 +x3 ≤9 st. ﹣3 x1+x2 +2x3 ≥ 4
4 x1－2x2 － 3x3 =﹣6
x1 ≤0, x2 ≥0, x3 无约束。 （1）min z = x1+2x2 +3x3 令Z=-Z’ min Z=min（-z ’）=max z ’
第一章 讲解内容
第一节： 第一节：线性规划问题及其数学模型 第二节： 第二节：线性规划问题的几何意义 第三节：单纯形法 第三节： 第四节： 第四节：单纯形法的计算过程 第五节： 第五节：单纯形法的进一步讨论 第六节： 第六节：应用案例
第一章 线性规划问题及其数学模型 1. 问题的提出 2.图解法（重点） 3. 线性规划问题的标准形式 4.线性规划问题的解的概念（重点、难点）
运筹学[第一章线性规划与单纯形法]山东大学期末考试知识点复习
![运筹学[第一章线性规划与单纯形法]山东大学期末考试知识点复习](https://img.taocdn.com/s3/m/83512a81ba0d4a7303763a31.png)
第一章线性规划与单纯形法1．线性规划问题的数学模型(1)一般形式(2)标准型式]2．数学模型化为标准型(1)若目标函数实现最小化，则min z=-max z'(令z'=-z)(2)若约束方程为不等式，则若约束方程为“≤”不等式左端+松驰变量(≥0)=右端若约束方程为“≥”不等式左端-剩余变量(≥0)=右端(3)若存在取值无约束的变量x k(1≤k≤咒)，则在标准型中x k=x'k-x"k(其中x k=x'，x"k≥0)3．线性规划的解线性规划问题：(1)可行解：满足约束条件②和③的解X=(x1，x2，…，x n)T。
(2)最优解：使目标函数①达到最大值的可行解。
(3)基：设A为约束方程组②的m×n阶系数矩阵，设n＞m，其秩为m，B 为矩阵A中的一个m×m阶的满秩子矩阵，则称B为线性规划问题的一个基。
不失一般性，设B中每一个列向量P j(j=1，2，…，m)称为基向量，与基向量PJ对应的变量x j称为基变量。
除基变量以外的变量为非基变量。
(4)基本解：在约束方程组②中，令所有非基变量x m+1=x m+2=…=x n=0，此时方程组②有唯一解X B=(x1，x2，…，x m)T，将此解加上非基变量取0的值有X=(x1，x2，…，x m，0，0…，0)T，称X为线性规划问题的基本解。
(5)基本可行解：满足非负条件③的基本解。
(6)可行基：对应于基本可行解的基。
4．初始基可行解的确定(1)直接从A中观察到存在一个初始可行基。
(2)对所有约束条件是“≤”形式的不等式，可利用化为标准型的方法，在每个约束条件左端加上一个松弛变量，这m个松弛变量就构成一个基变量，则对应的m个向量组成的单位矩阵B就是线性规划问题的一个可行基。
(3)对所有约束条件是“≥”形式的不等式以及等式约束情况，采用人造基的方法。
即对不等式约束的左端减去一个非负的剩余变量后，再加上一个非负的人工变量；对于等式约束的左端再加上一个非负的人工变量。
运筹学基础及应用第五版胡运权第一章
问题的提出 某企业计划生产Ⅰ、Ⅱ两种产品。这两种产品都要分别在A、B、C、D四种不同设备上加工。生产每件产品Ⅰ需占用各设备分别为2、1、4、0h，生产每件产品Ⅱ，需占用各设备分别为2、2、0、4h。已知各设备计划期内用于生产这两种产品的能力分别为12、8、16、12h，又知每生产一件产品Ⅰ企业能获得2元利润，每生产一件产品Ⅱ企业能获得3元利润，问企业应安排生产两种产品各多少件，使总的利润收入为最大。
xi 0
aij
aLj
xL 0
i
∴ P1 , P2,······,PL-1, PL+1,······ Pm, Pj 线性无关。
∴ X1 也为基本可行解。
四、最优性检验和解的判别
令
，其中 随基的改变而改变
X1 = (x1 0- a1j ,x2 0- a2j ,···,xm 0- amj ,0,···,,···,0)T
必要性：X非基本可行解 X非凸集顶点 不失一般性，设X=(x1,x2,······,xm,0,0,······,0)T，为非基本可行解， ∵ X为可行解，
证：等价于 X非基本可行解X非凸集顶点
又 X是非基本可行解， ∴ P1,P2,······,Pm线性相关，即有 1P1+2P2+······+mPm=0， 其中1，2，······，m不全为0，两端同乘≠0，得 1P1+2P2+······+mPm=0，······（2）
∵ >0, 1->0 ，当xj=0， 必有yj=zj=0
∴
pjyj =
j=1
n
pjyj=b ······(1)
j=1
r
pjzj =
j=1
n
pjzj=b ······(2)
xi 0
aij
aLj
xL 0
i
∴ P1 , P2,······,PL-1, PL+1,······ Pm, Pj 线性无关。
∴ X1 也为基本可行解。
四、最优性检验和解的判别
令
，其中 随基的改变而改变
X1 = (x1 0- a1j ,x2 0- a2j ,···,xm 0- amj ,0,···,,···,0)T
必要性：X非基本可行解 X非凸集顶点 不失一般性，设X=(x1,x2,······,xm,0,0,······,0)T，为非基本可行解， ∵ X为可行解，
证：等价于 X非基本可行解X非凸集顶点
又 X是非基本可行解， ∴ P1,P2,······,Pm线性相关，即有 1P1+2P2+······+mPm=0， 其中1，2，······，m不全为0，两端同乘≠0，得 1P1+2P2+······+mPm=0，······（2）
∵ >0, 1->0 ，当xj=0， 必有yj=zj=0
∴
pjyj =
j=1
n
pjyj=b ······(1)
j=1
r
pjzj =
j=1
n
pjzj=b ······(2)
运筹学第1章线性规划及单纯形法复习题
max (min)
Z = CX
AX ≤ ( = , ≥ ) b X ≥ 0
3、线性规划的标准形式 、
ma0
4、线性规划问题的解 、 （一）求解方法
一 般 有 两种方法 图 解 法 单纯形法 两个变量、 两个变量、直角坐标 三个变量、 三个变量、立体坐标
适用于任意多个变量、 适用于任意多个变量、但需将 一般形式变成标准形式
（二）线性规划问题的解
1、解的概念 可行解：满足约束条件② 的解为可行解。 ⑴ 可行解：满足约束条件②、③的解为可行解。 所有解的集合为可行解的集或可行域。 所有解的集合为可行解的集或可行域。 最优解： 达到最大值的可行解。 ⑵ 最优解：使目标函数①达到最大值的可行解。 ⑶ 基：B是矩阵A中m×m阶非奇异子矩阵 是矩阵A ≠0）， ），则 是一个基。 （∣B∣≠0），则B是一个基。
§2 图 解 法
例一、 例一、 max
Z = 2 x 2 x 2 x 4 x
2 2 1
+ 3 x
2
2 x1 + x + 1 4 x1 x1 ≥
≤ 12 ≤ 8 ≤ 16 ≤ 12
2
⑴ ⑵ ⑶ ⑷
2
0, x
≥ 0
max
Z = 2 x1 + 3 x 2 x 2 x
2 2
当xj=0时, 必有 j=zj=0, 因此 时 必有y
∑P x = ∑P y = ∑P z
j =1
r
r
r
r
j
j
j =1
j
j
j =1
j
j
=b
∑(y
j =1
j
− z j ) Pj = 0
运筹学第一章
第一章、 线性规划和单纯形法1.1 线性规划的概念一、线性规划问题的导出1．(引例) 配比问题——用浓度为45%和92%的硫酸配置100t 浓度为80%的硫酸。
取45%和92%的硫酸分别为x1和x2t,则有： 求解二元一次方程组得解。
目的相同，但有5种不同浓度的硫酸可选（30%，45%，73%，85%，92%）会出现什么情况？设取这5种硫酸分别为 x1、x2、x3、x4、x5 t, 则有： ⎩⎨⎧⨯=++++=++++1008.092.085.073.045.03.01005432154321x x x x x x x x x x 请问有多少种配比方案？为什么？哪一种方案最好？假设5种硫酸价格分别为：400，700，1400，1900，2500元/t ，则有：2.生产计划问题如何制定生产计划，使三种产品总利润最大？考虑问题：⎩⎨⎧⨯=+=+1008.092.045.01002121x x x x ⎪⎩⎪⎨⎧=≥⨯=++++=++++++++=5,,2,1,01008.092.085.073.045.03.0100..250019001400700400543215432154321 j x x x x x x x x x x x t s x x x x x MinZ j（1）何为生产计划？（2）总利润如何描述？（3）还要考虑什么因素？（4）有什么需要注意的地方（技巧）？（5）最终得到的数学模型是什么？二、线性规划的定义和数学描述（模型）1．定义：对于求取一组变量xj (j =1,2,......,n)，使之既满足线性约束条件，又使具有线性表达式的目标函数取得极大值或极小值的一类最优化问题称为线性规划问题，简称线性规划。
2.配比问题和生产计划问题的线性规划模型的特点：用一组未知变量表示要求的方案，这组未知变量称为决策变量；存在一定的限制条件，且为线性表达式；有一个目标要求（最大化，当然也可以是最小化），目标表示为未知变量的线性表达式，称之为目标函数； 对决策变量有非负要求。
第1章线性规划与单纯形法
26
线性规划问题的数学模型
7. 线性规划问题的解
线性规划问题
n
max Z cj xj (1) j 1
s.t
n j 1
aij
xj
bi
(i 1, 2,
, m) (2)
x
j
0,
j
1, 2,
, n (3)
求解线性规划问题，就是从满足约束条件(2)、(3)的方程组 中找出一个解，使目标函数(1)达到最大值。
解： Max z = 3x1–5x2’+5x2”–8x3 +7x4 s.t. 2x1–3x2’+3x2”+5x3+6x4+x5= 28 4x1+2x2’-2x2”+3x3-9x4-x6= 39 -6x2’+6x2”-2x3-3x4-x7 = 58 x1 ,x2’,x2”,x3 ,x4 ,x5 ,x6 ,x7 ≥ 0
x1 , x2 0, x3无约束
解:（１）因为x3无符号要求 ，即x3取正值也可取负值，标准 型中要求变量非负，所以
用 x3 x3 替换 x3 ，且 x3 , x3 0
20
线性规划问题的数学模型
(2) 第一个约束条件是“≤”号，在“≤”左端加入松驰变量x4， x4≥0,化为等式；
(3) 第二个约束条件是“≥”号，在“≥”左端减去剩余变量x5， x5≥0；
11
线性规划问题的数学模型
3. 建模条件 (1) 优化条件：问题所要达到的目标能用线型函数描述，且 能够用极值 （max 或 min）来表示；
(2) 限定条件：达到目标受到一定的限制，且这些限制能够 用决策变量的线性等式或线性不等式表示；
(3) 选择条件：有多种可选择的方案供决策者选择，以便找 出最优方案。
线性规划问题的数学模型
7. 线性规划问题的解
线性规划问题
n
max Z cj xj (1) j 1
s.t
n j 1
aij
xj
bi
(i 1, 2,
, m) (2)
x
j
0,
j
1, 2,
, n (3)
求解线性规划问题，就是从满足约束条件(2)、(3)的方程组 中找出一个解，使目标函数(1)达到最大值。
解： Max z = 3x1–5x2’+5x2”–8x3 +7x4 s.t. 2x1–3x2’+3x2”+5x3+6x4+x5= 28 4x1+2x2’-2x2”+3x3-9x4-x6= 39 -6x2’+6x2”-2x3-3x4-x7 = 58 x1 ,x2’,x2”,x3 ,x4 ,x5 ,x6 ,x7 ≥ 0
x1 , x2 0, x3无约束
解:（１）因为x3无符号要求 ，即x3取正值也可取负值，标准 型中要求变量非负，所以
用 x3 x3 替换 x3 ，且 x3 , x3 0
20
线性规划问题的数学模型
(2) 第一个约束条件是“≤”号，在“≤”左端加入松驰变量x4， x4≥0,化为等式；
(3) 第二个约束条件是“≥”号，在“≥”左端减去剩余变量x5， x5≥0；
11
线性规划问题的数学模型
3. 建模条件 (1) 优化条件：问题所要达到的目标能用线型函数描述，且 能够用极值 （max 或 min）来表示；
(2) 限定条件：达到目标受到一定的限制，且这些限制能够 用决策变量的线性等式或线性不等式表示；
(3) 选择条件：有多种可选择的方案供决策者选择，以便找 出最优方案。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
发展
二战结束后, 运筹学很快深入到工业、商业、政府部门等, 并得到了 迅速发展；运筹学在中国研究及应用从20世纪50年代中期开始。
1957年, 我国在建筑业和纺织业中首先应用运筹学. 1958年, 开始在交通运输、工业、农业、水利建设、邮电等方面陆 续得到推广应用 20世纪60年代起, 在钢铁和石油部门得到了比较全面、深入的应用 1965年起统筹法在建筑业、大型设备维修计划等方面的应用取得可 喜的进展. 1970年在全国大部分省、市和部门推广优选法 70年代中期, 最优化方法在工程设计界受到了广泛的重视, 并在许多 方面取得成果; 排队论开始应用于矿山、港口、电信及计算机设计 等方面; 图论用于线路布置、计算机设计、化学物品的存放等 70年代后期, 存储论在应用汽车工业等方面获得成功 近年来, 运筹学已趋向研究和解决规模更大、更复杂的问题, 并与系 统工程紧密结合.
军事起源
{资料} 当时德国的潜水艇严重威胁盟军的运输船, 1942年, 美国大
西洋舰队主持反潜战的官员贝克(W.D.Baker)请求成立反潜战运筹 组, 麻省理工学院的物理学家莫尔斯(P. W.Morse)被请来担任计划与 监督.
莫尔斯领导的小组经过多方实地调查, 提出两条重要建议： 1. 将反潜攻击由反潜舰艇投掷水雷改为由飞机投掷深水炸弹; 仅当 潜艇浮出水面或刚下潜时, 方投掷深水炸弹; 深水炸弹的定深(指 起爆深度)由100-200英尺, 修正为20-50英尺. 2. 改进运送物资的船队及护航舰艇编队的方式, 由小规模多批次, 改进为加大规模、减少批次, 可使损失减少，军方采用了上述建 议, 重创德国潜艇舰队, 最终成功地打破了德国的海上封锁.
管理起源
•爱尔朗（Erlong）的排队论公式
1909－1920年间，丹麦哥本哈根电话公司工程师 爱尔朗陆续发表了关于电话通路数量等方面的分析 与计算公式。尤其是1909年的论文“概率与电话通 话理论”，开创了运筹学的重要分支－－排队论。
带有拥挤效应的服务行业如通讯业、交通运输业等都隐含排 队论的问题。
经济起源
经济学理论对运筹学的影响是和数理经济学学派紧密联系 的 数理经济学对运筹学, 特别是对线性规划的影响可以从 魁奈(Qusnay)1758年发表的《经济表》算起. 最著名的经济学家沃尔拉斯(Walras)研究了经济平衡问 题, 后来的经济学家对其数学形式继续研究并得到深入 发展. 1928年 冯.诺伊曼以研究二人零和对策的一系列论文为 “对策论”奠基. 1932年, 又提出了广义经济平衡模型. 1939年, 苏联的康托洛维奇发表《生产组织和计划中的 数学方法》. 这些工作都可以看作是运筹学的先驱工作
管理起源
第一次世界大战前就已经发展成熟的古典管理学派, 对运 筹学的产生和发展影响很大。 1911年, 泰勒出版了著名的《科学管理原理》一书. 书 中, 泰勒的管理思想和理论, 概括起来主要有以下三个 观点： 科学管理的根本目的是谋求最高工作效率。 达到最高工作效率的重要手段是科学的管理方法。 实施科学管理要求精神上的彻底变革。
军事起源
{二战期间} 1939年, 由英国曼彻斯特大学物理学家、英国战斗 机司令部科学顾问、战后获得诺贝尔奖的布莱凯特 (P.M.S.Blackett)为首, 组建了一个代号为“Blackett 马戏团”的研究小组, 专门就改进防空系统进行研究 二战中, 除英国外, 美国、加拿大等国也相继成立 了军事运筹研究小组,解决战争中提出的运筹学课题. 其中最著名的工作之一是改进深水炸弹的起爆深度.
军事起源
1951年, 莫尔斯和金博尔出版了(1946年内部出版 , 1951年公开出版)第一本运筹学专著:《运筹学的 方法》(The Methods of Operations Research). 书中总结了第二次世界大战中运筹学的军事应用, 并给出了运筹学的一个著名定义
运筹学 是为执行部门对它们控制下的“业务”活 动采取决策提供定量依据的科学方法.
来历及定义
二战期间, 英国为了研究“如何最好地运用空军及新发明 的雷达保护国家”, 成立了一个由各方面专家组成的交 叉学科小组.这就是最早的运筹学小组, 它的任务是进行“ 作战研究”(Operational Research). 后来, 美国从事这方面研究的科学家又称之为“ Operations Research”, 简称为 O.R. O.R.的中文译名“运筹学”取自成语“运筹帷幄之中，决胜 千里之外”，具有运用筹划，出谋献策，以策略取胜等内 涵。目前国外的《管理科学》（Management Science ）与《运筹学》的内容基本相同
管理起源
弗兰克·杰尔布雷斯夫妇. 有影响的著作有:《动作研究》(1911年)、《科学管 理入门》(1912年)以及《疲劳研究》(1916年)等. 他们的研究比泰勒的研究更为细致和广泛, 其重要 贡献在以下几方面： 提出动作研究和动作经济原理 疲劳研究. 注意到了工作、工人和环境之间的相互影响.
《 运筹学》
陈克东
上海工程技术大学——管理学院
“ 一门科学只有成功的应用数学时， 才算达到了完善的地步 ”
------------- 马克
思
运筹学的发展：三个来源
军 事 管 理 经 济
军事起源
运筹学思想方法的起源可追溯到古代 我国先秦时期诸子著作中就存在许多朴素的运筹思 想. 《孙子兵法》中有丰富的运筹思想. 在国外, 运筹学思想也可追溯到很早以前. 如阿基 米德、达芬奇、伽利略等都研究过作战问题
军事起源
战争结束时, 英美及加拿大军队中工作的运筹学工 作者已超过了700人. 正是由于战争需要的促进, 以及大批著名科学家的参与, 运筹学得到迅速发展 . 之后, 运筹学从单纯军事和战争中的应用研究, 扩 展到经济和管理领域, 并形成了自己的理论与方法 . 1948年, 美国麻省理工学院（MIT）率先开设了 运筹学课程, 许多大学群起效法, 内容也日益丰富 。
根据以上观点泰勒提出管理制度: 最佳动作原理; 合理的 日工作量或恰当的工作定额原理; 刺激性付酬制度等.
管理起源
与泰勒同时代的, 对管理改革作出贡献的还有一些 学者 亨利· 甘特 甘特的贡献主要有以下几点： 提出了一种“工资任务加奖金”的工资制度 1903年, 发明了“甘特图”. 至今还在实践中使用, 并发展为统筹方法 强调管理民主和重视人的领导方式