立体几何中的最值问题答案
高中数学立体几何中的最值问题专题辅导

高中数学立体几何中的最值问题 海红楼 立体几何主要研究空间中点、线、面之间的位置关系,与空间图形有关的线段、角、体积等最值问题常常在试题中出现。
下面举例说明解决这类问题的常用方法。
一、运用变量的相对性求最值例1. 在正四棱锥S-ABCD 中,SO ⊥平面ABCD 于O ,SO=2,底面边长为2,点P 、Q 分别在线段BD 、SC 上移动,则P 、Q 两点的最短距离为( )A. 55B. 552C. 2D. 1解析:如图1,由于点P 、Q 分别在线段BD 、SC 上移动,先让点P 在BD 上固定,Q 在SC 上移动,当OQ 最小时,PQ 最小。
过O 作OQ ⊥SC ,在Rt △SOC 中,552=OQ 中。
又P 在BD 上运动,且当P 运动到点O 时,PQ 最小,等于OQ 的长为552,也就是异面直线BD 和SC 的公垂线段的长。
故选B 。
图1二、定性分析法求最值例2. 已知平面α//平面β,AB 和CD 是夹在平面α、β之间的两条线段。
AB ⊥CD ,AB=3,直线AB 与平面α成30°角,则线段CD 的长的最小值为______。
解析:如图2,过点B 作平面α的垂线,垂足为O ,连结AO ,则∠BAO=30°。
过B 作BE//CD 交平面α于E ,则BE=CD 。
连结AE ,因为AB ⊥CD ,故AB ⊥BE 。
则在Rt △ABE 中,BE=AB ·tan ∠BAE ≥AB ·tan ∠BAO=3·tan30°=3。
故3≥CD 。
图2三、展成平面求最值例3. 如图3-1,四面体A-BCD 的各面都是锐角三角形,且AB=CD=a ,AC=BD=b ,AD=BC=c 。
平面α分别截棱AB 、BC 、CD 、DA 于点P 、Q 、R 、S ,则四边形PQRS 的周长的最小值是( )A. 2aB. 2bC. 2cD. a+b+c图3-1解析:如图3-2,将四面体的侧面展开成平面图形。
2 第2课时 空间距离与立体几何中的最值(范围)问题(选用)

第2课时 空间距离与立体几何中的最值(范围)问题(选用)空间中的距离问题如图,平面P AD ⊥平面ABCD ,四边形ABCD 为正方形,△P AD 是直角三角形,且P A =AD =2,点E ,F ,G 分别是线段P A ,PD ,CD 的中点.(1)求证:平面EFG ⊥平面P AB ; (2)求点A 到平面EFG 的距离.【解】 如图,建立空间直角坐标系A -xyz ,则A (0,0,0),B (2,0,0),C (2,2,0),D (0,2,0),P (0,0,2),E (0,0,1),F (0,1,1),G (1,2,0).(1)证明:因为EF →=(0,1,0),AP →=(0,0,2),AB →=(2,0,0),所以EF →·AP →=0×0+1×0+0×2=0,EF →·AB →=0×2+1×0+0×0=0,所以EF ⊥AP ,EF ⊥AB .又因为AP ,AB ⊂平面P AB ,且P A ∩AB =A , 所以EF ⊥平面P AB .又EF ⊂平面EFG ,所以平面EFG ⊥平面P AB . (2)设平面EFG 的一个法向量为n =(x ,y ,z ),则⎩⎪⎨⎪⎧n ·EF →=(x ,y ,z )·(0,1,0)=0,n ·EG →=(x ,y ,z )·(1,2,-1)=0,所以{y =0,,x +2y -z =0.取n =(1,0,1),又AE →=(0,0,1),所以点A 到平面EFG 的距离d =|AE →·n ||n |=12=22.(1)空间中的各种距离一般都可以转化为求点与点、点与线、点与面的距离.①点点距:点与点的距离,以这两点为起点和终点的向量的模;②点线距:点M 到直线a 的距离,若直线的方向向量为a ,直线上任一点为N ,则点M 到直线a 的距离为d =|MN →|·sin 〈MN →,a 〉;③线线距:两平行线间的距离转化为点线距离,两异面直线间的距离转化为点面距离或者直接求公垂线段的长度;④点面距:点M 到平面α的距离,若平面α的法向量为n ,平面α内任一点为N ,则点M 到平面α的距离d =|MN →||cos 〈MN →,n 〉|=|MN →·n ||n |.(2)利用空间向量求空间距离问题,首先应明确所求距离的特征,恰当选用距离公式求解.1.如图,P ABCD 是正四棱锥,ABCD -A 1B 1C 1D 1是正方体,其中AB =2,P A =6,则B 1到平面P AD 的距离为________.解析:以A 1为原点,以A 1B 1所在直线为x 轴,A 1D 1所在直线为y 轴,A 1A 所在直线为z 轴建立空间直角坐标系A 1xyz ,则AD →=(0,2,0),AP →=(1,1,2),设平面P AD 的法向量是m =(x ,y ,z ),所以由⎩⎪⎨⎪⎧m ·AD →=0,m ·AP →=0,可得⎩⎪⎨⎪⎧2y =0,x +y +2z =0.取z =1,得m =(-2,0,1),因为B 1A →=(-2,0,2),所以B 1到平面P AD 的距离d =|B 1A →·m ||m |=65 5.答案:6552.如图,在长方体ABCD -A 1B 1C 1D 1中,AB =4,BC =3,CC 1=2.(1)求证:平面A 1BC 1∥平面ACD 1; (2)求平面A 1BC 1与平面ACD 1的距离.解:(1)证明:因为AA 1綊CC 1,所以四边形ACC 1A 1为平行四边形,所以AC ∥A 1C 1. 又AC ⊄平面A 1BC 1,A 1C 1⊂平面A 1BC 1,所以AC ∥平面A 1BC 1.同理可证CD 1∥平面A 1BC 1. 又AC ∩CD 1=C ,AC ⊂平面ACD 1,CD 1⊂平面ACD 1, 所以平面A 1BC 1∥平面ACD 1.(2)以B 1为原点,分别以B 1A 1→,B 1C 1→,B 1B →的方向为x 轴,y 轴,z 轴的正方向建立如图所示的空间直角坐标系B 1xyz ,则A 1(4,0,0),A (4,0,2),D 1(4,3,0),C (0,3,2),A 1A →=(0,0,2),AC →=(-4,3,0),AD 1→=(0,3,-2),设n =(x ,y ,z )为平面ACD 1的一个法向量, 则⎩⎪⎨⎪⎧n ·AC →=0,n ·AD 1→=0,即⎩⎪⎨⎪⎧-4x +3y =0,3y -2z =0,取n =(3,4,6),所以所求距离d =|A 1A →|×|cos 〈n ,A 1A →〉|=|n ·A 1A →||n |=1232+42+62=126161, 故平面A 1BC 1与平面ACD 1的距离为126161.立体几何中的最值(范围)问题(1)(2020·宁波十校联考)如图,平面P AB ⊥平面α,AB ⊂α,且△P AB 为正三角形,点D 是平面α内的动点,ABCD 是菱形,点O 为AB 中点,AC 与OD 交于点Q ,l ⊂α,且l ⊥AB ,则PQ 与l 所成角的正切值的最小值为( )A.-3+372B.3+372C.7 D .3(2)(2020·温州高考模拟)如图,在三棱锥A -BCD 中,平面ABC ⊥平面BCD ,△BAC 与△BCD 均为等腰直角三角形,且∠BAC =∠BCD =90°,BC =2,点P 是线段AB 上的动点,若线段CD 上存在点Q ,使得直线PQ 与AC 成30°的角,则线段P A 长的取值范围是( )A.⎝⎛⎭⎫0,22 B.⎣⎡⎦⎤0,63 C.⎝⎛⎭⎫22,2 D.⎝⎛⎭⎫63,2【解析】 (1)如图,不妨以CD 在AB 前侧为例.以点O 为原点,分别以OB 、OP 所在直线为y 、z 轴建立空间直角坐标系O -xyz ,设AB =2,∠OAD =θ(0<θ<π),则P (0,0,3),D (2sin θ,-1+2cos θ,0),所以Q ⎝⎛⎭⎫23sin θ,23cos θ-13,0, 所以QP →=⎝⎛⎭⎫-23sin θ,13-23cos θ,3, 设α内与AB 垂直的向量n =(1,0,0),PQ 与直线l 所成角为φ, 则cos φ=⎪⎪⎪⎪⎪⎪⎪⎪QP →·n |QP →||n |=⎪⎪⎪⎪⎪⎪-23sin θ329-49cos θ=sin θ8-cos θ=1-cos 2θ8-cos θ.令t =cos θ(-1<t <1),则s =1-t 28-t ,s ′=t 2-16t +1(8-t )2,令s ′=0,得t =8-37,所以当t =8-37时,s 有最大值为16-67. 则cos φ有最大值为16-67,此时sin φ取最小值为67-15.所以正切值的最小值为67-1516-67=3+372.故选B. (2)以C 为原点,CD 所在直线为x 轴,CB 所在直线为y 轴,过C 作平面BCD 的垂线为z 轴,建立空间直角坐标系C xyz ,则A (0,1,1),B (0,2,0),C (0,0,0),设Q (q ,0,0),AP →=λAB →=(0,λ,-λ)(0≤λ≤1),则PQ →=CQ →-CP →=CQ →-(CA →+AP →)=(q ,0,0)-(0,1,1)-(0,λ,-λ)=(q ,-1-λ,λ-1),因为直线PQ 与AC 成30°的角, 所以cos 30°=|CA →·PQ →||CA →|·|PQ →|=22·q 2+(1+λ)2+(λ-1)2=2q 2+2λ2+2=32, 所以q 2+2λ2+2=83,所以q 2=23-2λ2∈[0,4],所以⎩⎨⎧23-2λ2≥023-2λ2≤4,解得0≤λ≤33,所以|AP →|=2λ∈⎣⎡⎦⎤0,63,所以线段P A 长的取值范围是⎣⎡⎦⎤0,63. 故选B.【答案】 (1)B (2)B(1)求解立体几何中的最值问题,需要先确定最值的主体,确定题目中描述的相关变量,然后根据所求,确定是利用几何方法求解,还是转化为代数(特别是函数)问题求解.利用几何方法求解时,往往利用几何体的结构特征将问题转化为平面几何中的问题进行求解,如求几何体表面距离的问题.利用代数法求解时,要合理选择参数,利用几何体中的相关运算构造目标函数,再根据条件确定参数的取值范围,从而确定目标函数的值域,即可利用函数最值的求解方法求得结果.(2)用向量法解决立体几何中的最值问题,不仅简捷,更减少了思维量.用变量表示动点的坐标,然后依题意用向量法求其有关几何量,构建有关函数,从而用代数方法即可求其最值.1.(2020·浙江省五校联考模拟)如图,棱长为4的正方体ABCD -A 1B 1C 1D 1,点A 在平面α内,平面ABCD 与平面α所成的二面角为30°,则顶点C 1到平面α的距离的最大值是( )A .2(2+2)B .2(3+2)C .2(3+1)D .2(2+1)解析:选B.如图所示,作C 1O ⊥α,交ABCD 于点O ,交α于点E ,由题得O 在AC 上,则C 1E 为所求,∠OAE =30°, 由题意,设CO =x ,则AO =42-x , C 1O =16+x 2,OE =12OA =22-12x ,所以C 1E =16+x 2+22-12x ,令y = 16+x 2+22-12x ,则y ′=x16+x 2-12=0,可得x =43, 所以x =43时,顶点C 1到平面α的距离的最大值是2(3+2). 2.(2020·浙江省名校协作体高三联考)如图,在梯形ABCD 中,AB ∥CD ,AD =DC =CB =1,∠ABC =60°,四边形ACFE 为矩形,平面ACFE ⊥平面ABCD ,CF =1.(1)求证:BC ⊥平面ACFE ;(2)点M 在线段EF 上运动,设平面MAB 与平面FCB 所成二面角的平面角为θ(θ≤90°),试求cos θ的取值范围.解:(1)证明:在梯形ABCD 中,因为AB ∥CD ,AD =DC =CB =1,∠ABC =60°,所以AB =2,所以AC 2=AB 2+BC 2-2AB ·BC ·cos 60°=3, 所以AB 2=AC 2+BC 2,所以BC ⊥AC ,因为平面ACFE ⊥平面ABCD ,平面ACFE ∩平面ABCD =AC ,BC ⊂平面ABCD ,所以BC ⊥平面ACFE .(2)如图所示,由(1)可建立分别以直线CA ,CB ,CF 为x 轴,y 轴,z 轴的空间直角坐标系C -xyz ,令FM =λ(0≤λ≤3),则C (0,0,0),A (3,0,0),B (0,1,0),M (λ,0,1),所以AB →=(-3,1,0),BM →=(λ,-1,1),设n 1=(x ,y ,z )为平面MAB 的一个法向量,由⎩⎪⎨⎪⎧n 1·AB →=0n 1·BM →=0,得⎩⎪⎨⎪⎧-3x +y =0λx -y +z =0,取x =1,则n 1=(1,3,3-λ),因为n 2=(1,0,0)是平面FCB 的一个法向量, 所以cos θ=|n 1·n 2||n 1|·|n 2|=11+3+(3-λ)2×1=1(λ-3)2+4,因为0≤λ≤3,所以当λ=0时,cos θ有最小值77, 当λ=3时,cos θ有最大值12,所以cos θ∈⎣⎡⎦⎤77,12.[基础题组练]1.(2020·宁波市镇海中学高考模拟)在直三棱柱A 1B 1C 1ABC 中,∠BAC =π2,AB =AC=AA 1=1,已知点G 和E 分别为A 1B 1和CC 1的中点,点D 与F 分别为线段AC 和AB 上的动点(不包括端点),若GD ⊥EF ,则线段DF 的长度的取值范围为( )A.⎣⎡⎭⎫55,1B.⎣⎡⎦⎤55,1C.⎝⎛⎭⎫255,1D.⎣⎡⎭⎫255,1解析:选A.建立如图所示的空间直角坐标系A -xyz ,则A (0,0,0),E ⎝⎛⎭⎫0,1,12,G ⎝⎛⎭⎫12,0,1, F (x ,0,0),D (0,y ,0), 由于GD ⊥EF ,所以x +2y -1=0, DF =x 2+y 2=5⎝⎛⎭⎫y -252+15, 由x =1-2y >0,得y <12,所以当y =25时,线段DF 长度的最小值是15,当y =0时,线段DF 长度的最大值是1,又不包括端点,故y =0不能取,故选A. 2.(2020·杭州市学军中学高考数学模拟)如图,三棱锥P -ABC 中,已知P A ⊥平面ABC ,AD ⊥BC 于点D ,BC =CD =AD =1,设PD =x ,∠BPC =θ,记函数f (x )=tan θ,则下列表述正确的是( )A .f (x )是关于x 的增函数B .f (x )是关于x 的减函数C .f (x )关于x 先递增后递减D .f (x )关于x 先递减后递增解析:选C.因为P A ⊥平面ABC ,AD ⊥BC 于点D ,BC =CD =AD =1,PD =x ,∠BPC =θ,所以可求得AC =2,AB =5,P A =x 2-1,PC =x 2+1,BP =x 2+4,所以在△PBC 中,由余弦定理知 cos θ=PB 2+PC 2-BC 22BP ·PC=2x 2+42x 2+1x 2+4.所以tan 2θ=1cos 2θ-1=(x 2+1)(x 2+4)(x 2+2)2-1=x 2(x 2+2)2.所以tan θ=x x 2+2=1x +2x ≤12 x ·2x =24(当且仅当x =2时取等号),所以f (x )关于x 先递增后递减.3.(2020·义乌市高三月考)如图,边长为2的正△ABC 的顶点A 在平面γ上,B ,C 在平面γ的同侧,点M 为BC 的中点,若△ABC 在平面γ上的射影是以A 为直角顶点的△AB 1C 1,则M 到平面γ的距离的取值范围是________.解析:设∠BAB 1=α,∠CAC 1=β,则AB 1=2cos α,AC 1=2cos β,BB 1=2sin α,CC 1=2sin β,则点M 到平面γ的距离d =sin α+sin β,又|AM |=3,则|B 1C 1|=23-d 2,即cos 2α+cos 2β=3-(sin 2α+2sin αsin β+sin 2β).也即sin αsin β=12,所以d =sin α+sin β=sin α+12sin α≥2,因为sin α<1,sin β<1,所以12sin α<1,所以12<sin α<1,所以当sinα=12或1时,d =32,则2≤d <32.答案:⎣⎡⎭⎫2,32 4.(2020·杭州市学军中学高考数学模拟)如图,在二面角A -CD -B 中,BC ⊥CD ,BC =CD =2,点A 在直线AD 上运动,满足AD ⊥CD ,AB =3.现将平面ADC 沿着CD 进行翻折,在翻折的过程中,线段AD 长的取值范围是________.解析:由题意得AD →⊥DC →,DC →⊥CB →,设平面ADC 沿着CD 进行翻折的过程中,二面角A CD B 的夹角为θ,则〈DA →,CB →〉=θ,因为AB →=AD →+DC →+CB →,所以平方得AB →2=AD →2+DC →2+CB →2+2AD →·DC →+2CB →·AD →+2DC →·CB →, 设AD =x ,因为BC =CD =2,AB =3, 所以9=x 2+4+4-4x cos θ, 即x 2-4x cosθ-1=0,即cos θ=x 2-14x .因为-1≤cos θ≤1,所以-1≤x 2-14x≤1,即⎩⎪⎨⎪⎧x 2-1≤4x x 2-1≥-4x ,即⎩⎪⎨⎪⎧x 2-4x -1≤0x 2+4x -1≥0,则⎩⎪⎨⎪⎧2-5≤x ≤2+5,x ≥-2+5或x ≤-2- 5.因为x >0,所以5-2≤x ≤5+2, 即AD 的取值范围是[5-2,5+2]. 答案:[5-2,5+2]5.(2020·金丽衢十二校联考)如图,在三棱锥D -ABC 中,已知AB =2,AC →·BD →=-3,设AD =a ,BC =b ,CD =c ,则c 2ab +1的最小值为________.解析:设AD →=a ,CB →=b ,DC →=c ,因为AB =2,所以|a +b +c |2=4⇒a 2+b 2+c 2+2(a ·b +b ·c +c ·a )=4,又因为AC →·BD →=-3,所以(a +c )·(-b -c )=-3⇒a ·b +b ·c +c ·a +c 2=3,所以a 2+b 2+c 2+2(3-c 2)=4⇒c 2=a 2+b 2+2,所以a 2+b 2+2ab +1≥2ab +2ab +1=2,当且仅当a=b 时,等号成立,即c 2ab +1的最小值是2.答案:26.(2020·温州十五校联合体期末考试)在正四面体P -ABC 中,点M 是棱PC 的中点,点N 是线段AB 上一动点,且AN →=λAB →,设异面直线NM 与AC 所成角为α,当13≤λ≤23时,则cos α的取值范围是________.解析:设点P 到平面ABC 的射影为点O ,以AO 所在直线为y 轴,OP 所在直线为z 轴,过点O 作BC 的平行线为x 轴,建立空间直角坐标系O -xyz ,如图.设正四面体的棱长为43,则有A (0,-4,0),B (23,2,0),C (-23,2,0),P (0,0,42),M (-3,1,22).由AN →=λAB →,得N (23λ,6λ-4,0).从而有NM →=(-3-23λ,5-6λ,22),AC →=(-23,6,0).所以cos α=|NM →·AC →||NM →||AC →|=3-2λ24λ2-4λ+3,设3-2λ=t ,则53≤t ≤73. 则cos α=12 t 2t 2-4t +6=12 6⎝⎛⎭⎫1t 2-4·1t +1,因为13<37≤1t ≤35,所以51938≤cos α≤71938. 答案:⎣⎡⎦⎤51938,71938 7.如图,在△ABC 中,∠B =π2,AB =BC =2,点P 为AB 边上一动点,PD ∥BC 交AC 于点D .现将△PDA 沿PD 翻折至△PDA ′,使平面PDA ′⊥平面PBCD .(1)当棱锥A ′PBCD 的体积最大时,求P A 的长;(2)若点P 为AB 的中点,点E 为A ′C 的中点,求证:A ′B ⊥DE .解:(1)设P A =x ,则P A ′=x ,所以V A ′PBCD =13P A ′·S 底面PBCD =13x ⎝⎛⎭⎫2-x 22. 令f (x )=13x ⎝⎛⎭⎫2-x 22=2x 3-x 36(0<x <2), 则f ′(x )=23-x 22.当x 变化时,f ′(x ),f (x )的变化情况如下表: x⎝⎛⎭⎫0,233 233 ⎝⎛⎭⎫233,2 f ′(x )+ 0 - f (x ) 单调递增 极大值 单调递减由上表易知,当P A =x =23时,V A ′PBCD 取最大值. (2)证明:取A ′B 的中点F ,连接EF ,FP .由已知,得EF 綊12BC 綊PD . 所以四边形EFPD 是平行四边形,所以ED ∥FP .因为△A ′PB 为等腰直角三角形,所以A ′B ⊥PF .所以A ′B ⊥DE .8.(2020·杭州市第一次高考科目数学质量检测)如图,在三棱柱ABC -A 1B 1C 1中,AA 1⊥平面ABC ,平面A 1BC ⊥平面A 1ABB 1.(1)求证:AB ⊥BC ;(2)设直线AC 与平面A 1BC 所成的角为θ,二面角A 1BC A 的大小为φ,试比较θ和φ的大小关系,并证明你的结论.解:(1)证明:过点A 在平面A 1ABB 1内作AD ⊥A 1B 于D ,因为平面A 1BC ⊥平面A 1ABB 1,平面A 1BC ∩平面A 1ABB 1=A 1B ,所以AD ⊥平面A 1BC ,又因为BC ⊂平面A 1BC ,所以AD ⊥BC .因为AA 1⊥平面ABC ,所以AA 1⊥BC .又因为AA 1∩AD =A ,所以BC ⊥侧面A 1ABB 1,又因为AB ⊂平面A 1ABB 1,故AB ⊥BC .(2)连接CD ,由(1)知∠ACD 是直线AC 与平面A 1BC 所成的角.又∠ABA 1是二面角A 1BC A 的平面角.则∠ACD =θ,∠ABA 1=φ.在Rt △ADC 中,sin θ=AD AC ,在Rt △ADB 中, sin φ=AD AB.由AB <AC , 得sin θ<sin φ,又0<θ,φ<π2, 所以θ<φ.[综合题组练]1.(2020·温州市高考数学模拟)如图,在矩形ABCD 中,AB AD=λ(λ>1),将其沿AC 翻折,使点D 到达点E 的位置,且二面角C -AB -E 为直二面角.(1)求证:平面ACE ⊥平面BCE ;(2)设点F 是BE 的中点,二面角E -AC -F 的平面角的大小为θ,当λ∈[2,3]时,求cos θ的取值范围.解:(1)证明:因为二面角C -AB -E 为直二面角,AB ⊥BC,所以BC ⊥平面ABE ,所以BC ⊥AE .因为AE ⊥CE ,BC ∩CE =C ,所以AE ⊥平面BCE .因为AE ⊂平面ACE ,所以平面ACE ⊥平面BCE .(2)如图,以E 为坐标原点,以AD 长为一个单位长度,建立如图所示的空间直角坐标系E -xyz ,则AB =λ,A (0,1,0),B (λ2-1,0,0),C (λ2-1,0,1),E (0,0,0),F ⎝ ⎛⎭⎪⎫λ2-12,0,0, 则EA →=(0,1,0),EC →=(λ2-1,0,1),设平面EAC 的法向量为m =(x ,y ,z ),则⎩⎪⎨⎪⎧y =0λ2-1·x +z =0,取x =1,则m =(1,0,-λ2-1). 同理得平面F AC 的一个法向量为n =(2,λ2-1,-λ2-1). 所以cos θ=m ·n |m |·|n |=λ2+1λ·2(λ2+1)=22·1+1λ2 . 因为λ∈[2,3],所以cos θ∈⎣⎡⎦⎤53,104. 2.如图,在四棱锥P -ABCD 中,已知P A ⊥平面ABCD ,且四边形ABCD 为直角梯形,∠ABC =∠BAD =π2, P A =AD =2,AB =BC =1.(1)求平面P AB 与平面PCD 所成二面角的余弦值;(2)点Q 是线段BP 上的动点,当直线CQ 与DP 所成的角最小时,求线段BQ 的长.解:以{AB →,AD →,AP →}为正交基底建立如图所示的空间直角坐标系A -xyz ,则各点的坐标为B (1,0,0),C (1,1,0),D (0,2,0),P (0,0,2).(1)由题意知,AD ⊥平面P AB ,所以AD →是平面P AB 的一个法向量,AD →=(0,2,0).因为PC →=(1,1,-2),PD →=(0,2,-2).设平面PCD 的法向量为m =(x ,y ,z ),则⎩⎪⎨⎪⎧m ·PC →=0,m ·PD →=0, 即⎩⎪⎨⎪⎧x +y -2z =0,2y -2z =0.令y =1,解得z =1,x =1. 所以m =(1,1,1)是平面PCD 的一个法向量.从而cos 〈AD →,m 〉=AD →·m |AD →||m |=33, 所以平面P AB 与平面PCD 所成二面角的余弦值为33. (2)因为BP →=(-1,0,2),设BQ →=λBP →=(-λ,0,2λ)(0≤λ≤1),又CB →=(0,-1,0),则CQ →=CB →+BQ →=(-λ,-1,2λ),又DP →=(0,-2,2),从而cos 〈CQ →,DP →〉=CQ →·DP →|CQ →||DP →|=1+2λ10λ2+2. 设1+2λ=t ,t ∈[1,3],则cos 2〈CQ →,DP →〉=2t 25t 2-10t +9=29⎝⎛⎭⎫1t -592+209≤910.当且仅当t =95,即λ=25时,|cos 〈CQ →,DP →〉|的最大值为31010. 因为y =cos x 在⎝ ⎛⎭⎪⎫0,π2上是减函数, 所以此时直线CQ 与DP 所成角取得最小值. 又因为BP =12+22=5,所以BQ =25BP =255.。
立体几何中的最值问题-高三数学备考练习

问题29立体几何中的最值问题一、考情分析立体几何中的最值问题一般涉及到距离、面积、体积、角度等四个方面,此类问题多以规则几何体为载体,涉及到几何体的结构特征以及空间线面关系的逻辑推理、空间角与距离的求解等,题目较为综合,解决此类问题一般可从两个方面思考:一是函数法,即利用传统方法或空间向量的坐标运算,建立所求的目标函数,转化为函数的最值问题求解;二是直接法,即根据几何体的结构特征或平面几何中的相关结论,直接判断最值. 纵观近几年高考对于组合体的考查,重点放在与球相关的外接与内切问题上.要求学生有较强的空间想象能力和准确的计算能力,才能顺利解答.从实际教学来看,这部分知识是学生掌握最为模糊,看到就头疼的题目.分析原因,除了这类题目的入手确实不易之外,主要是学生没有形成解题的模式和套路,以至于遇到类似的题目便产生畏惧心理.二、经验分享1.解决立体几何中的最值问题常见方法有:(1)建立函数法是一种常用的最值方法,很多情况下,我们都是把这类动态问题转化成目标函数,最终利用代数方法求目标函数的最值.解题途径很多,在函数建成后,可用一次函数的端点法;二次数的配方法、公试法;有界函数界值法(如三角函数等)及高阶函数的拐点导数法等.(2)公理与定义法通常以公理与定义作依据,直接推理问题的最大值与最小值,一般的公理与定理有:两点之间以线段为最短,分居在两异面直线上的两点的连线段中,以它们的公垂线段为短.球面上任意两点间的连线中以过这两点与球心的平面所得圆的劣弧长为最短等.如果直接建立函数关系求之比较困难,而运用两异面直线公垂线段最短则是解决问题的捷径.(3)解不等式法是解最值问题的常用方法、在立体几何中同样可利用不等式的性质和一些变量的特殊不等关系求解:如最小角定理所建立的不等关系等等.(4)展开体图法是求立体几何最值的一种特殊方法,也是一种常用的方法,它可将几何题表面展开,也可将几何体内部的某些满足条件的部分面展开成平面,这样能使求解问题,变得十分直观,由难化易.(5)变量分析法是我们要透过现象看本质,在几何体中的点、线、面,哪些在动,哪些不动,要分析透彻,明白它们之间的相互关系,从而转化成求某些线段或角等一些量的求解最值总题的方法.除了上述5种常用方法外,还有一些使用并不普遍的特殊方法,可以让我们达到求解最值问题的目的,这就是:列方程法、极限思想法、向量计算法等等其各法的特点与普遍性,大家可以通过实例感受其精彩内涵与思想方法所在.2.决定棱锥体积的量有两个,即底面积和高,当研究其体积的最值问题时,若其中有一个量确定,则只需另一个量的最值;若两个量都不确定,可通过设变量法,将体积表示为变量的函数解析式,利用函数思想确定其最值;将空间问题转化为平面问题是转化思想的重要体现,通过旋转到一个平面内,利用两点之间距离最短求解3.解决几何体体积最值问题的方法(1) 根据条件建立两个变量的和或积为定值,利用基本不等式求体积的最值;通过建立相关函数式,将所求的最值问题转化为函数的最值问题求解,此法应用最为广泛;由图形的特殊位置确定最值,如垂直求解球与棱柱、棱锥的接、切问题时,一般过球心及接、切点作截面,把空间问题转化为平面图形与圆的接、切问题,再利用平面几何知识寻找几何中元素间的关系求解.4.解题时,通常应注意分析题目中所有的条件,首先应该在充分理解题意的基础上,分析是否能用公理与定义直接解决题中问题;如果不能,再看是否可将问题条件转化为函数,若能写出确定的表意函数,则可用建立函数法求解;再不能,则要考虑其中是否存在不等关系,看是否能运用解等不式法求解;还不行则应考虑是否可将其体图展开成平面,这样依次从本文所标定的方法顺序思考,必能找到解题的途径三、题型分析(一) 距离最值问题1.空间中两点间距离的最值问题A C与BD上,求MN的最小值. 【例1】正方体的棱长为1,M、N分别在线段11【分析】方法一,该题可以结合正方体的结构特征,将其转化为两异面直线的距离来求;方法二,可设出变量,构建相应的函数,利用函数的最值求解;方法三,建立空间直角坐标系,利用点的坐标以及距离公式表示出目标函数,然后利用函数方法求解最值.A C与BD是异面直线,所以当MN是两直线的共垂线段时,MN 【解析】方法一(定义转化法)因为直线11取得最小值.取11A C 的中点P ,BD 的中点Q .则线段PQ 就是两异面直线11A C 与BD 的共垂线段.下证明之.在矩形11BDD B 中,PQ 为中位线,所以1//PQ BB , 又因为1BB ⊥平面ABCD ,所以PQ ⊥平面ABCD 又因为BD ⊆平面ABCD , 所以PQ BD ⊥. 同理可证11PQ A C ⊥, 而,,所以线段PQ 就是两异面直线11A C 与BD 的共垂线段,且1PQ =. 由异面直线公垂线段的定义可得,故MN 的最小值为1.方法二:(参数法)如图,取11A C 的中点P ,BD 的中点Q .则线段PQ 就是两异面直线11A C 与BD 的共垂线段.由正方体的棱长为1可得1PQ =.连结AC ,则11//AC A C ,所以BQC ∠为两异面直线11A C 与BD 所成角. 在正方形ABCD 中,AC BD ⊥,所以.过点M 作MH AC ⊥,垂足为H ,连结NH ,则//MH PQ ,且.设PM m =,QN t =,则QH m =. 在Rt QNH ∆中, ,在Rt MHN ∆中,.显然,当0m n ==时,2MN 取得最小值1,即MN 的最小值为1.方法三:(向量法)如图,以D 为坐标原点,分别以射线DA 、DC 、1DD 为x 、y 、z 轴建立空间直角坐标系.设DN m =,1A M n =.则,即;,即.所以,故当2m n ==时,2MN 取得最小值1,即MN 的最小值为1.【点评】空间中两点距离的最值,最基本的方法就是利用距离公式建立目标函数,根据目标函数解析式的结构特征求解最值.对于分别在两个不同对象上的点之间距离的最值,可以根据这两个元素之间的关系,借助立体几何中相关的性质、定理等判断并求解相应的最值.如【典例1】中的两点分别在两条异面直线上,显然这两点之间距离的最小值即为两异面直线的公垂线段的长度.另外注意直线和平面的距离,两平面的距离等的灵活运用.【小试牛刀】【湖南省长沙市2019届上学期高三统一检测】设正方体的棱长为,为的中点,为直线上一点,为平面内一点,则,两点间距离的最小值为()A. B. C. D.【答案】B【解析】结合题意,绘制图形结合题意可知OE是三角形中位线,题目计算距离最短,即求OE与两平行线的距离,,所以距离d,结合三角形面积计算公式可得,解得,故选B。
立体几何中线段长度的最值问题
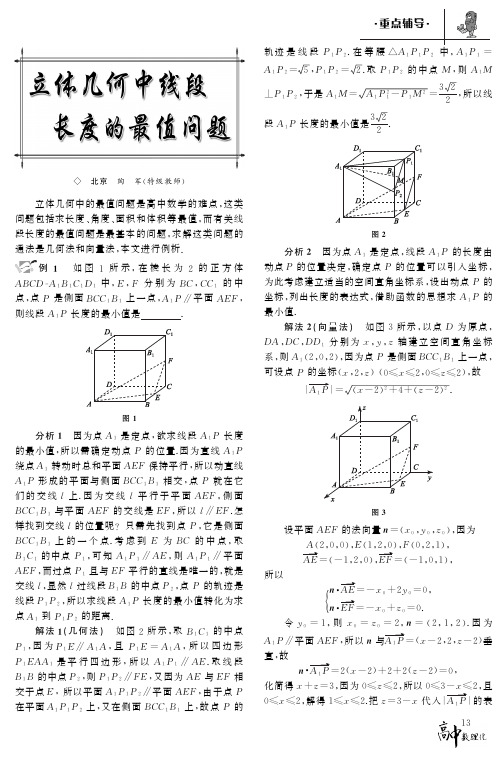
重点辅导Җ㊀北京㊀陶㊀军(特级教师)㊀㊀立体几何中的最值问题是高中数学的难点,这类问题包括求长度㊁角度㊁面积和体积等最值,而有关线段长度的最值问题是最基本的问题,求解这类问题的通法是几何法和向量法,本文进行例析.例1㊀如图1所示,在棱长为2的正方体A B C D GA 1B 1C 1D 1中,E ,F 分别为B C ,C C 1的中点,点P 是侧面B C C 1B 1上一点,A 1P ʊ平面A E F ,则线段A 1P 长度的最小值是.图1分析1㊀因为点A 1是定点,欲求线段A 1P 长度的最小值,所以需确定动点P 的位置.因为直线A 1P 绕点A 1转动时总和平面A E F 保持平行,所以动直线A 1P 形成的平面与侧面B C C 1B 1相交,点P 就在它们的交线l 上.因为交线l 平行于平面A E F ,侧面B C C 1B 1与平面A E F 的交线是E F ,所以l ʊE F .怎样找到交线l 的位置呢?只需先找到点P ,它是侧面B C C 1B 1上的一个点.考虑到E 为B C 的中点,取B 1C 1的中点P 1,可知A 1P 1ʊA E ,则A 1P 1ʊ平面A E F ,而过点P 1且与E F 平行的直线是唯一的,就是交线l ,显然l 过线段B 1B 的中点P 2,点P 的轨迹是线段P 1P 2,所以求线段A 1P 长度的最小值转化为求点A 1到P 1P 2的距离.解法1(几何法)㊀如图2所示,取B 1C 1的中点P 1,因为P 1E ʊA 1A ,且P 1E =A 1A ,所以四边形P 1E A A 1是平行四边形,所以A 1P 1ʊA E .取线段B 1B 的中点P 2,则P 1P 2ʊF E ,又因为A E 与E F 相交于点E ,所以平面A 1P 1P 2ʊ平面A E F ,由于点P 在平面A 1P 1P 2上,又在侧面B C C 1B 1上,故点P 的轨迹是线段P 1P 2.在等腰әA 1P 1P 2中,A 1P 1=A 1P 2=5,P 1P 2=2.取P 1P 2的中点M ,则A 1M ʅP 1P 2,于是A 1M =A 1P 21-P 1M 2=322,所以线段A 1P 长度的最小值是322.图2分析2㊀因为点A 1是定点,线段A 1P 的长度由动点P 的位置决定,确定点P 的位置可以引入坐标,为此考虑建立适当的空间直角坐标系,设出动点P 的坐标,列出长度的表达式,借助函数的思想求A 1P 的最小值.解法2(向量法)㊀如图3所示,以点D 为原点,D A ,D C ,D D 1分别为x ,y ,z 轴建立空间直角坐标系,则A 1(2,0,2),因为点P 是侧面B C C 1B 1上一点,可设点P 的坐标(x ,2,z )(0ɤx ɤ2,0ɤz ɤ2),故|A 1P ң|(x -2)2+4+(z -2)2.图3设平面A E F 的法向量n =(x 0,y 0,z 0),因为A (2,0,0),E (1,2,0),F (0,2,1),A E ң=(-1,2,0),E F ң=(-1,0,1),所以n A E ң=-x 0+2y 0=0,n E F ң=-x 0+z 0=0.{令y 0=1,则x 0=z 0=2,n =(2,1,2).因为A 1P ʊ平面A E F ,所以n 与A 1P ң=(x -2,2,z -2)垂直,故n A 1P ң=2(x -2)+2+2(z -2)=0,化简得x +z =3,因为0ɤz ɤ2,所以0ɤ3-x ɤ2,且0ɤx ɤ2,解得1ɤx ɤ2.把z =3-x 代入|A 1P ң|的表31重点辅导达式,整理得|A 1P ң|=2(x -32)2+92,x ɪ[1,2],故当x =32时,|A 1P ң|取得最小值322.例2㊀如图4所示,在棱长为2的正方体A B C D GA 1B 1C 1D 1中,E 为B C 的中点,点P 在线段D 1E 上,点P 到直线C C 1的距离的最小值为.图4分析1㊀求点P 到直线C C 1的距离的最小值,就是找点P 到直线C C 1的垂线段P Q 长度的最小值.求线段P Q 的长度涉及空间上两个动点长度的距离问题,不易处理.注意到C C 1ʅ平面A B C D ,P Q ʅC C 1,则P Q ʊ平面A B C D .因此,我们可以把P Q 正投影在平面A B C D 上,点P 在平面A B C D 上的正投影H 落在线段D E 上,点Q 在平面A B C D 上的正投影是点C ,于是P Q =H C ,求P Q 的最小值转化为在平面A B C D 上求定点C 与线段D E 上的动点H 之间距离的最小值,就是求定点C 到D E 的距离.解法1(几何法)㊀如图5所示,过点P 作P Q ʅC C 1,Q 为垂足,因为C C 1ʅ平面A B CD ,所以P Q ʊ平面A B C D ,过点P 作PH ʅDE ,H 为垂足,则PH ʅ平面A B C D ,所以PH ʊQ C ,且P Q ʊH C ,Q C ʅH C ,故四边形P Q C H 是矩形,P Q =H C ,在R t әC D E 中,当C H ʅD E 时,C H 长度最小,因为C E =1,C D =2,D E =5,所以C H =1ˑ25=255,故点P 到直线C C 1的距离的最小值为255.图5分析2㊀设点P 到直线C C 1的距离为P Q ,因为P ,Q 分别在线段D 1E 和C C 1上,故可以引入两个变量控制点P ,Q 的位置.设E P ң=λE D 1ң(0ɤλɤ1),C Q ң=μC C 1ң(0ɤμɤ1),根据正方体的特殊性建立适当的空间直角坐标系,利用向量的坐标运算推出点P ,Q 的坐标,进而用λ,μ表示P Q ң,利用P Q ң C C 1ң=0找出λ,μ的关系式,代入P Q 长度的表达式,转化为一元函数求最值.解法2(向量法)㊀如图6所示,以D 为原点,D A ,D C ,D D 1分别为x ,y ,z 轴建立空间直角坐标系,则D 1(0,0,2),E (1,2,0),C 1(0,2,2),C (0,2,0),E D 1ң=(-1,-2,2),由于点P 在线段D 1E 上,可设E P ң=λE D 1ң(0ɤλɤ1),即E P ң=(-λ,-2λ,2λ),由此得点P 的坐标为(,,).图6过点P 作P Q 垂直于C C 1,Q 为垂足,设点Q 的坐标(0,2,m ),P Q ң=(λ-1,2λ,m -2λ),C C 1ң=(0,0,2),因为P Q ңʅC C 1ң,所以P Q ң C C 1ң=0,即2(m -2λ)=0,m =2λ,P Q ң=(λ-1,2λ,0),|P Q ң|=(λ-1)2+(2λ)2+02=5(λ-15)2+45,λɪ[0,1].当λ=15,P Q 取得最小值255.综上所述,利用几何法求线段长度的最值,要点是先用立体几何知识确定动点的轨迹,再用平面几何知识求最值;利用向量法求线段长度的最值,要点是建立适当的坐标系,设出动点坐标,建立线段长度的表达式,借助向量知识把题目中的几何条件合理转化为代数条件,找到动点坐标的关系,把线段长度的表达式转化为一元函数,用函数的思想求最值.(作者单位:北京市怀柔区第一中学)41。
高数140招之71-立体几何中的最值问题的解题策略

一、与线段长有关的最值问题【典例1】在直三棱柱ABC A 1B 1C 1中,底面为直角三角形, ∠ACB =90°,AC =6,BC =CC 1=2,P 是BC 1上一动点,如图所示,则CP +PA 1的最小值为________.[解析]PA 1在平面A 1BC 1内,PC 在平面BCC 1内,将其铺平后转化为平面上的问题.铺平平面A 1BC 1,平面BCC 1,如图所示,计算得A 1B =AB 1=210,BC 1=2.又A 1C 1=6,故△A 1BC 1是∠A 1C 1B =90°的直角三角形. 设P 是BC 1上任一点,CP +PA 1≥A 1C ,即当A 1,P ,C 三点共线时,CP +PA 1有最小值. 在△A 1C 1C 中,由余弦定理得A 1C =62+ 2 2-2×6×2×cos 135°=52, 故(CP +PA 1)min =52.【变式练习】1.如图所示,在棱长为1的正方体ABCD A 1B 1C 1D 1的面对角线A 1B 上存在一点P ,使得AP +D 1P 取得最小值,则此最小值为()A .2B.6+22C .2+2 D.2+2解析:选D将△A 1AB 与△A 1BD 1放在同一平面内,如图所示.连接AD 1,则AD 1为AP +D 1P 的最小值.因为AA 1=A 1D 1=1,∠AA 1D 1=90°+45°=135°,所以由余弦定理得AD 1=AA 21+A 1D 21-2×AA 1×A 1D 1×cos 135°=2+2. 2.某三棱锥的三视图如图所示,且三个三角形均为直角三角形,则xy 的最大值为________.解析:由三视图知三棱锥如图所示,底面ABC 是直角三角形,AB ⊥BC , PA ⊥平面ABC ,BC =27, PA 2+y 2=102,(27)2+PA 2=x 2, 因此xy =x 102-[x 2- 27 2] =x128-x 2≤x 2+ 128-x 22=64,当且仅当x 2=128-x 2,即x =8时取等号,因此xy 的最大值是64.3.已知直三棱柱ABC A 1B 1C 1的侧棱长为6,且底面是边长为2的正三角形,用一平面截此棱柱,与侧棱AA 1,BB 1,CC 1分别交于三点M ,N ,Q ,若△MNQ 为直角三角形,则该直角三角形斜边长的最小值为()A .22B .3C .23D .4解析:选C 如图,不妨设N 在B 处,设AM =h ,CQ =m ,则MB 2=h 2+4,BQ 2=m 2+4,MQ 2=(h -m )2+4,由MB 2=BQ 2+MQ 2,得m 2-hm +2=0.Δ=h 2-8≥0⇒h 2≥8,该直角三角形斜边MB =4+h 2≥23,故该直角三角形斜边长的最小值为23.故选C.二、与面积有关的最值问题【典例2】已知正四面体S ABC 的棱长为1,如果一个高为36的长方体能在该正四面体内任意转动,则该长方体的长和宽形成的长方形的面积的最大值为________.解析:如图,易知正四面体S ABC 的内切球的球心O 必在高线SH 上,延长AH 交BC 于点D ,则D 为BC 的中点,连接SD ,设内切球切SD 于点E ,连接AO .因为H 是正三角形ABC 的中心,所以AH ∶DH =2∶1.易得Rt △OAH ∽Rt △DSH ,所以OA OH =DSDH=3,可得OA =3OH =SO ,因此SH =4OH ,可得内切球的半径R =OH =14SH .因为正四面体S ABC 的棱长为1,所以在Rt △DSH中,DS =SH 2+DH 2= 4R 2+(13×32)2=32,解得R 2=124.要满足一个高为36的长方体能在该正四面体内任意转动,则长方体的体对角线长不超过正四面体内切球的直径,设该长方体的长和宽分别为x ,y ,其长和宽形成的长方形的面积为S ,则4R 2≥(36)2+x 2+y 2,所以x 2+y 2≤112,所以S =xy ≤x 2+y 22≤124,当且仅当x =y =612时等号成立,即该长方体的长和宽形成的长方形的面积的最大值为124. 【变式练习】1.(2018·全国卷Ⅰ)已知正方体的棱长为1,每条棱所在直线与平面α所成的角都相等,则α截此正方体所得截面面积的最大值为() A .334B .233C .324D .32【答案】A【解析】如图所示,在正方体ABCD A 1B 1C 1D 1中,平面AB 1D 1与棱A 1A ,A 1B 1,A 1D 1所成的角都相等,又正方体的其余棱都分别与A 1A ,A 1B 1,A 1D 1平行,故正方体ABCD A 1B 1C 1D 1的每条棱所在直线与平面AB 1D 1所成的角都相等.如图所示,取棱AB ,BB 1,B 1C 1,C 1D 1,D 1D ,DA 的中点E ,F ,G ,H ,M ,N ,则正六边形EFGHMN 所在平面与平面AB 1D 1平行且面积最大,此截面面积为S 正六边形EFGHMN =6×12×22×22×sin 60°=334.故选A.2.已知球O 是正三棱锥A BCD 的外接球,BC =3,AB =23,点E 在线段BD 上,且BD =3BE ,过点E 作球O 的截面,则所得截面中面积最小的截面圆的面积是________.【答案】2π【解析】如图,设△BCD 的中心为点O 1,球O 的半径为R ,则A ,O ,O 1三点共线.连接O 1D ,O 1E ,OD ,OE ,则O 1D =3,AO 1=AD 2-O 1D 2=3.在Rt △OO 1D 中,R 2=3+(3-R )2,即R =2,所以OO 1=1.在△O 1DE 中,DE =23BD =2,∠O 1DE =30°,所以由余弦定理得O 1E =3+4-2×3×2× cos 30°=1.所以OE =2.过点E 作圆O 的截面,当截面与OE 垂直时,截面的面积最小,此时截面圆的半径为22-(2)2=2,所以截面圆的面积为2π.3.在长方体ABCD A 1B 1C 1D 1中,AB =AD =4,AA 1=2.过点A 1作平面α与AB ,AD 分别交于M ,N 两点,若AA 1与平面α所成的角为45°,则截面A 1MN 面积的最小值是________.【答案】2π【解析】如图,过点A 作AE ⊥MN ,连接A 1E ,因为A 1A ⊥平面ABCD ,所以A 1A ⊥MN ,所以MN ⊥平面A 1AE ,所以A 1E ⊥MN ,平面A 1AE ⊥平面A 1MN ,所以∠AA 1E 为AA 1与平面A 1MN 所成的角,所以∠AA 1E =45°,在Rt △A 1AE 中,因为AA 1=2,所以AE =2,A 1E =22,在Rt △MAN 中,由射影定理得ME ·EN =AE 2=4,由基本不等式得MN =ME +EN ≥2ME ·EN =4,当且仅当ME =EN ,即E 为MN 的中点时等号成立,所以截面A 1MN 面积的最小值为12×4×22=42.三、与体积有关的最值问题【典例3】(2017·全国卷Ⅰ)如图,圆形纸片的圆心为O ,半径为5 cm ,该纸片上的等边三角形ABC 的中心为O .D ,E ,F 为圆O 上的点,△DBC ,△ECA ,△FAB 分别是以BC ,CA ,AB 为底边的等腰三角形.沿虚线剪开后,分别以BC ,CA ,AB 为折痕折起△DBC ,△ECA ,△FAB ,使得D ,E ,F 重合,得到三棱锥.当△ABC 的边长变化时,所得三棱锥体积(单位:cm 3)的最大值为________.【答案】415【解析】如图,连接OD 交BC 于点G ,由题意知,OD ⊥BC .易得OG =36BC ,设OG =x ,则BC =23x ,DG =5-x , S △ABC =12×23x ×3x =33x 2,故所得三棱锥的体积V =13×33x 2× 5-x 2-x 2=3x 2×25-10x =3×25x 4-10x 5.令f (x )=25x 4-10x 5,x ∈(0,52),则f ′(x )=100x 3-50x 4,令f ′(x )>0,即x 4-2x 3<0,得0<x <2; 令f ′(x )<0,得2<x <52,则当x ∈(0,52)时,f (x )≤f (2)=80, ∴V ≤3×80=415.∴所求三棱锥的体积的最大值为415.【变式练习】1.(2018·全国卷Ⅲ)设A ,B ,C ,D 是同一个半径为4的球的球面上四点,△ABC 为等边三角形且其面积为93,则三棱锥D ABC 体积的最大值为()A .123B .183C .243D .543【答案】B【解析】由等边△ABC 的面积为93,可得34AB 2=93,所以AB =6,所以等边△ABC的外接圆的半径为r =33AB =23.设球的半径为R ,球心到等边△ABC 的外接圆圆心的距离为d ,则d =R 2-r 2=16-12=2.所以三棱锥D ABC 高的最大值为2+4=6,所以三棱锥D ABC 体积的最大值为13×93×6=183.2.已知圆锥的侧面展开图是半径为3的扇形,则该圆锥体积的最大值为________. 【答案】23π【解析】由题意得圆锥的母线长为3,设圆锥的底面半径为r ,高为h ,则h =9-r 2,所以圆锥的体积V =13πr 2h =13πr 29-r 2=13π9r 4-r 6.设f (r )=9r 4-r 6(r >0),则f ′(r )=36r 3-6r 5,令f ′(r )=36r 3-6r 5=6r 3(6-r 2)=0,得r =6,所以当0<r <6时,f ′(r )>0,f (r )单调递增;当r >6时,f ′(r )<0,f (r )单调递减,所以f (r )max =f (6)=108,所以V max =13π×108=23π.3.已知A ,B ,C 是球O 的球面上三点,且AB =AC =3,BC =33,D 为该球面上的动点,球心O 到平面ABC 的距离为球半径的一半,则三棱锥D ABC 体积的最大值为________.【答案】274【解析】如图,在△ABC 中, ∵AB =AC =3,BC =33, ∴由余弦定理可得cos A =32+32- 33 22×3×3=-12,∴sin A =32.设△ABC 外接圆O ′的半径为r ,则3332=2r ,得r =3.设球的半径为R ,连接OO ′,BO ′,OB , 则R 2=(R 2)2+32,解得R =23.由图可知,当点D 到平面ABC 的距离为32R 时,三棱锥D ABC 的体积最大,∵S △ABC =12×3×3×32=934,∴三棱锥D ABC 体积的最大值为13×934×33=274.4.如图,等腰梯形ABCD 中,AB ∥CD ,AD =AB =BC =1,CD =2,E 为CD 的中点,将△ADE 沿AE 折到△APE 的位置.(1)证明:AE ⊥PB ;(2)当四棱锥P ABCE 的体积最大时,求二面角A PE C 的余弦值.解:(1)证明:在等腰梯形ABCD 中,连接BD ,交AE 于点O , ∵AB ∥CE ,AB =CE ,∴四边形ABCE 为平行四边形, ∴AE =BC =AD =DE ,∴△ADE 为等边三角形, ∴在等腰梯形ABCD 中,∠C =∠ADE =π3,BD ⊥BC ,∴BD ⊥AE .如图,翻折后可得OP ⊥AE ,OB ⊥AE ,又OP ⊂平面POB ,OB ⊂平面POB ,OP ∩OB =O ,∴AE ⊥平面POB ,∵PB ⊂平面POB ,∴AE ⊥PB .(2)当四棱锥P ABCE 的体积最大时,平面PAE ⊥平面ABCE .又平面PAE ∩平面ABCE =AE ,PO ⊂平面PAE ,PO ⊥AE ,∴OP ⊥平面ABCE .以O 为坐标原点,OE所在的直线为x 轴,OB 所在的直线为y 轴,OP 所在的直线为z轴,建立空间直角坐标系,由题意得,P(0,0,32),E(12,0,0),C(1,32,0),∴PE―→=(12,0,-32),EC―→=(12,32,0),设平面PCE的法向量为n1=(x,y,z),则{·n1=0,·n1=0,)即{12x-32z=0,12x+32y=0,)设x=3,则y=-1,z=1,∴n1=(3,-1,1)为平面PCE的一个法向量,易知平面PAE的一个法向量为n2=(0,1,0),cos n1,n2 =n1·n2|n1||n2|=-11×5=-55.由图知所求二面角APEC为钝角,∴二面角APEC的余弦值为-5 5 .[解题技法]立体几何中的最值问题的解题策略空间几何体中的某些对象,如点、线、面,在约束条件下运动,带动相关的线段长度、体积等发生变化,进而就有了面积与体积的最值问题.定性分析:在空间几何体的变化过程中,通过观察运动点的位置变化,确定其相关量的变化规律,进而发现相关面积或体积的变化规律,求得其最大值或最小值.定量分析:将所求问题转化为某一个相关量的问题,即转化为关于其中一个量的函数,求其最大值或最小值的问题.根据具体情况,有函数法、不等式法、三角函数法等多种方法可供选择.。
2020年高考数学专题复习第2课时空间距离与立体几何中的最值(范围)问题(选用)

空间距离与立体几何中的最值(范围)问题(选用)空间中的距离问题如图,平面PAD ⊥平面ABCD ,四边形ABCD 为正方形,△PAD 是直角三角形,且PA =AD =2,E ,F ,G 分别是线段PA ,PD ,CD 的中点.(1)求证:平面EFG ⊥平面PAB ; (2)求点A 到平面EFG 的距离.【解】 如图,建立空间直角坐标系Axyz ,则A (0,0,0),B (2,0,0),C (2,2,0),D (0,2,0),P (0,0,2),E (0,0,1),F (0,1,1),G (1,2,0).(1)证明:因为EF →=(0,1,0),AP →=(0,0,2),AB →=(2,0,0),所以EF →·AP →=0×0+1×0+0×2=0,EF →·AB →=0×2+1×0+0×0=0,所以EF ⊥AP ,EF ⊥AB .又因为AP ,AB ⊂平面PAB ,且PA ∩AB =A ,所以EF ⊥平面PAB . 又EF ⊂平面EFG ,所以平面EFG ⊥平面PAB . (2)设平面EFG 的一个法向量为n =(x ,y ,z ),则⎩⎪⎨⎪⎧n ·EF →=(x ,y ,z )·(0,1,0)=0,n ·EG →=(x ,y ,z )·(1,2,-1)=0,所以⎩⎪⎨⎪⎧y =0,x +2y -z =0.取n =(1,0,1),又AE →=(0,0,1),所以点A 到平面EFG 的距离d =|AE →·n ||n |=12=22.(1)空间中的各种距离一般都可以转化为求点与点、点与线、点与面的距离. ①点点距:点与点的距离,以这两点为起点和终点的向量的模;②点线距:点M 到直线a 的距离,若直线的方向向量为a ,直线上任一点为N ,则点M 到直线a 的距离为d =|MN →|·sin〈MN →,a 〉;③线线距:两平行线间的距离转化为点线距离,两异面直线间的距离转化为点面距离或者直接求公垂线段的长度;④点面距:点M 到平面α的距离,若平面α的法向量为n ,平面α内任一点为N ,则点M 到平面α的距离d =|MN →||cos 〈MN →,n 〉|=|MN →·n ||n |.(2)利用空间向量求空间距离问题,首先应明确所求距离的特征,恰当选用距离公式求解.1.如图,P ABCD 是正四棱锥,ABCD A 1B 1C 1D 1是正方体,其中AB =2,PA =6,则B 1到平面PAD 的距离为________.解析:以A 1B 1所在直线为x 轴,A 1D 1所在直线为y 轴,A 1A 所在直线为z 轴建立空间直角坐标系,则AD →=(0,2,0),AP →=(1,1,2),设平面PAD 的法向量是m =(x ,y ,z ), 所以由⎩⎪⎨⎪⎧m ·AD →=0,m ·AP →=0,可得⎩⎪⎨⎪⎧2y =0,x +y +2z =0.取z =1,得m =(-2,0,1),因为B 1A →=(-2,0,2),所以B 1到平面PAD 的距离d =|B 1A →·m ||m |=65 5.答案:6552.如图,在长方体ABCD A 1B 1C 1D 1中,AB =4,BC =3,CC 1=2.(1)求证:平面A 1BC 1∥平面ACD 1; (2)求平面A 1BC 1与平面ACD 1的距离.解:(1)证明:因为AA 1綊CC 1,所以四边形ACC 1A 1为平行四边形,所以AC ∥A 1C 1. 又AC ⊄平面A 1BC 1,A 1C 1⊂平面A 1BC 1, 所以AC ∥平面A 1BC 1.同理可证CD 1∥平面A 1BC 1. 又AC ∩CD 1=C ,AC ⊂平面ACD 1,CD 1⊂平面ACD 1, 所以平面A 1BC 1∥平面ACD 1.(2)以B 1为原点,分别以B 1A 1→,B 1C 1→,B 1B →的方向为x 轴,y 轴,z 轴的正方向建立如图所示的空间直角坐标系,则A 1(4,0,0),A (4,0,2),D 1(4,3,0),C (0,3,2),A 1A →=(0,0,2),AC →=(-4,3,0),AD 1→=(0,3,-2),设n =(x ,y ,z )为平面ACD 1的一个法向量, 则⎩⎪⎨⎪⎧n ·AC →=0,n ·AD 1→=0,即⎩⎪⎨⎪⎧-4x +3y =0,3y -2z =0,取n =(3,4,6),所以所求距离d =|A 1A →|×|cos 〈n ,A 1A →〉|=|n ·A 1A →||n |=1232+42+62=126161,故平面A 1BC 1与平面ACD 1的距离为126161.立体几何中的最值(范围)问题(1)(2019·宁波十校联考)如图,平面PAB ⊥平面α,AB ⊂α,且△PAB 为正三角形,点D 是平面α内的动点,ABCD 是菱形,点O 为AB 中点,AC 与OD 交于点Q ,l ⊂α,且l ⊥AB ,则PQ 与l 所成角的正切值的最小值为( )A . -3+372B . 3+372C .7D .3(2)(2019·温州高考模拟)如图,在三棱锥A BCD 中,平面ABC ⊥平面BCD ,△BAC 与BCD 均为等腰直角三角形,且∠BAC =∠BCD =90°,BC =2,点P 是线段AB 上的动点,若线段CD 上存在点Q ,使得直线PQ 与AC 成30°的角,则线段PA 长的取值范围是( )A .⎝ ⎛⎭⎪⎫0,22 B .⎣⎢⎡⎦⎥⎤0,63 C .⎝⎛⎭⎪⎫22,2 D .⎝⎛⎭⎪⎫63,2 【解析】 (1)如图,不妨以CD 在AB 前侧为例.以O 为原点,分别以OB 、OP 所在直线为y 、z 轴建立空间直角坐标系,设AB =2,∠OAD =θ(0<θ<π),则P (0,0,3),D (2sin θ,-1+2cos θ,0),所以Q ⎝ ⎛⎭⎪⎫23sin θ,23cos θ-13,0,所以QP →=⎝ ⎛⎭⎪⎫-23sin θ,13-23cos θ,3,设α内与AB 垂直的向量n =(1,0,0),PQ 与l 所成角为φ,则cos φ=⎪⎪⎪⎪⎪⎪⎪⎪QP →·n |QP →||n |=⎪⎪⎪⎪⎪⎪⎪⎪-23sin θ329-49cos θ=sin θ8-cos θ=1-cos 2θ8-cos θ.令t =cos θ(-1<t <1),则s =1-t 28-t ,s ′=t 2-16t +1(8-t )2,令s ′=0,得t =8-37,所以当t =8-37时,s 有最大值为16-67.则cos φ有最大值为16-67,此时sin φ取最小值为67-15. 所以正切值的最小值为67-1516-67=3+372.故选B.(2) 以C 为原点,CD 所在直线为x 轴,CB 所在直线为y 轴,过C 作平面BCD 的垂线为z 轴,建立空间直角坐标系,则A (0,1,1),B (0,2,0),C (0,0,0),设Q (q ,0,0),AP →=λAB →=(0,λ,-λ)(0≤λ≤1),则PQ →=CQ →-CP →=CQ →-(CA →+AP →)=(q ,0,0)-(0,1,1)-(0,λ,-λ)=(q ,-1-λ,λ-1),因为直线PQ 与AC 成30°的角, 所以cos 30°=|CA →·PQ →||CA →|·|PQ →|=22·q 2+(1+λ)2+(λ-1)2=2q 2+2λ2+2=32, 所以q 2+2λ2+2=83,所以q 2=23-2λ2∈[0,4],所以⎩⎪⎨⎪⎧23-2λ2≥023-2λ2≤4,解得0≤λ≤33,所以|AP →|=2λ∈⎣⎢⎡⎦⎥⎤0,63,所以线段PA 长的取值范围是⎣⎢⎡⎦⎥⎤0,63. 故选B.【答案】 (1)B (2)B(1)求解立体几何中的最值问题,需要先确定最值的主体,确定题目中描述的相关变量,然后根据所求,确定是利用几何方法求解,还是转化为代数(特别是函数)问题求解.利用几何方法求解时,往往利用几何体的结构特征将问题转化为平面几何中的问题进行求解,如求几何体表面距离的问题.利用代数法求解时,要合理选择参数,利用几何体中的相关运算构造目标函数,再根据条件确定参数的取值范围,从而确定目标函数的值域,即可利用函数最值的求解方法求得结果.(2)用向量法解决立体几何中的最值问题,不仅简捷,更减少了思维量.用变量表示动点的坐标,然后依题意用向量法求其有关几何量,构建有关函数,从而用代数方法即可求其最值.1.(2019·浙江省五校联考模拟)如图,棱长为4的正方体ABCD A 1B 1C 1D 1,点A 在平面α内,平面ABCD 与平面α所成的二面角为30°,则顶点C 1到平面α的距离的最大值是( )A .2(2+2)B .2(3+2)C .2(3+1)D .2(2+1)解析:选B.如图所示,作C 1O ⊥α,交ABCD 于O ,交α于E ,由题得O 在AC 上,则C 1E 为所求,∠OAE =30°, 由题意,设CO =x ,则AO =42-x ,C 1O =16+x 2,OE =12OA =22-12x ,所以C 1E =16+x 2+22-12x ,令y =16+x 2+22-12x ,则y ′=x16+x 2-12=0,可得x =43,所以x =43时,顶点C 1到平面α的距离的最大值是2(3+2).2.(2019·浙江省名校协作体高三联考)如图,在梯形ABCD 中,AB ∥CD ,AD =DC =CB =1,∠ABC =60°,四边形ACFE 为矩形,平面ACFE ⊥平面ABCD ,CF =1.(1)求证:BC ⊥平面ACFE ;(2)点M 在线段EF 上运动,设平面MAB 与平面FCB 所成二面角的平面角为θ(θ≤90°),试求cos θ的取值范围.解:(1)证明:在梯形ABCD 中,因为AB ∥CD ,AD =DC =CB =1,∠ABC =60°,所以AB =2,所以AC 2=AB 2+BC 2-2AB ·BC ·cos 60°=3, 所以AB 2=AC 2+BC 2,所以BC ⊥AC ,因为平面ACFE ⊥平面ABCD ,平面ACFE ∩平面ABCD =AC ,BC ⊂平面ABCD ,所以BC ⊥平面ACFE .(2)如图所示,由(1)可建立分别以直线CA ,CB ,CF 为x 轴,y 轴,z 轴的空间直角坐标系,令FM =λ(0≤λ≤3),则C (0,0,0),A (3,0,0),B (0,1,0),M (λ,0,1),所以AB →=(-3,1,0),BM →=(λ,-1,1),设n 1=(x ,y ,z )为平面MAB 的一个法向量,由⎩⎪⎨⎪⎧n 1·AB →=0n 1·BM →=0,得⎩⎨⎧-3x +y =0λx -y +z =0,取x =1,则n 1=(1,3,3-λ),因为n 2=(1,0,0)是平面FCB 的一个法向量, 所以cos θ=|n 1·n 2||n 1|·|n 2|=11+3+(3-λ)2×1 =1(λ-3)2+4,因为0≤λ≤3,所以当λ=0时,cos θ有最小值77, 当λ=3时,cos θ有最大值12,所以cos θ∈⎣⎢⎡⎦⎥⎤77,12.空间中的距离(1)点与点之间的距离⎩⎪⎨⎪⎧利用空间两点间的距离公式利用空间向量的模长利用辅助线转化为平面距离(2)点线距离⎩⎪⎨⎪⎧转化为两点间距离求解利用向量法求解(3)点面之间距离⎩⎪⎨⎪⎧等积法求解向量法求解立体几何中的最值(范围)问题 (1)几何体的面积、体积的最值(范围) (2)空间角(或空间角三角函数值)的最值(范围) (3)空间距离的最值(范围) 求解方法⎩⎪⎨⎪⎧①构造函数法②转化为平面问题③引入参数利用向量法[基础达标]1.(2019·宁波市镇海中学高考模拟)在直三棱柱A 1B 1C 1ABC 中,∠BAC =π2,AB =AC=AA 1=1,已知G 和E 分别为A 1B 1和CC 1的中点,D 与F 分别为线段AC 和AB 上的动点(不包括端点),若GD ⊥EF ,则线段DF 的长度的取值范围为( )A .⎣⎢⎡⎭⎪⎫55,1 B .⎣⎢⎡⎦⎥⎤55,1 C .⎝⎛⎭⎪⎫255,1 D .⎣⎢⎡⎭⎪⎫255,1 解析:选A.建立如图所示的空间直角坐标系,则A (0,0,0),E ⎝ ⎛⎭⎪⎫0,1,12,G ⎝ ⎛⎭⎪⎫12,0,1, F (x ,0,0),D (0,y ,0),由于GD ⊥EF ,所以x +2y -1=0,DF =x 2+y 2=5⎝ ⎛⎭⎪⎫y -252+15, 由x =1-2y >0,得y <12,所以当y =25时,线段DF 长度的最小值是15,当y =0时,线段DF 长度的最大值是1,又不包括端点,故y =0不能取,故选A. 2. (2019·杭州市学军中学高考数学模拟)如图,三棱锥P ABC 中,已知PA ⊥平面ABC ,AD ⊥BC 于D ,BC =CD =AD =1,设PD =x ,∠BPC =θ,记函数f (x )=tan θ,则下列表述正确的是( )A .f (x )是关于x 的增函数B .f (x )是关于x 的减函数C .f (x )关于x 先递增后递减D .f (x )关于x 先递减后递增解析:选C.因为PA ⊥平面ABC ,AD ⊥BC 于D ,BC =CD =AD =1,PD =x ,∠BPC =θ, 所以可求得AC =2,AB =5,PA =x 2-1,PC =x 2+1,BP =x 2+4, 所以在△PBC 中,由余弦定理知cos θ=PB 2+PC 2-BC 22BP ·PC =2x 2+42x 2+1x 2+4. 所以tan 2θ=1cos 2θ-1=(x 2+1)(x 2+4)(x 2+2)2-1=x2(x 2+2)2.所以tan θ=x x 2+2=1x +2x ≤12x ·2x=24(当且仅当x =2时取等号),所以f (x )关于x 先递增后递减.3.(2019·义乌市高三月考)如图,边长为2的正△ABC 的顶点A 在平面γ上,B ,C 在平面γ的同侧,M 为BC 的中点,若△ABC 在平面γ上的射影是以A 为直角顶点的△AB 1C 1,则M 到平面γ的距离的取值范围是________.解析:设∠BAB 1=α,∠CAC 1=β,则AB 1=2cos α,AC 1=2cos β,BB 1=2sin α,CC 1=2sin β,则点M 到平面γ的距离d =sin α+sin β,又|AM |=3,则|B 1C 1|=23-d 2,即cos 2α+cos 2β=3-(sin 2α+2sin αsin β+sin 2β).也即sin αsin β=12,所以d=sin α+sin β=sin α+12sin α≥2,因为sin α<1,sin β<1,所以12sin α<1,所以12<sin α<1,所以当sin α=12或1时,d =32,则2≤d <32.答案:⎣⎢⎡⎭⎪⎫2,324. (2019·杭州市学军中学高考数学模拟)如图,在二面角A CD B 中,BC ⊥CD ,BC =CD =2,点A 在直线AD 上运动,满足AD ⊥CD ,AB =3.现将平面ADC 沿着CD 进行翻折,在翻折的过程中,线段AD 长的取值范围是________.解析:由题意得AD →⊥DC →,DC →⊥CB →,设平面ADC 沿着CD 进行翻折的过程中,二面角A CD B 的夹角为θ,则〈DA →,CB →〉=θ,因为AB →=AD →+DC →+CB →,所以平方得AB →2=AD →2+DC →2+CB →2+2AD →·DC →+2CB →·AD →+2DC →·CB →, 设AD =x ,因为BC =CD =2,AB =3, 所以9=x 2+4+4-4x cos θ,即x 2-4x cos θ-1=0,即cos θ=x 2-14x.因为-1≤cos θ≤1,所以-1≤x 2-14x≤1,即⎩⎪⎨⎪⎧x 2-1≤4x x 2-1≥-4x ,即⎩⎪⎨⎪⎧x 2-4x -1≤0x 2+4x -1≥0,则⎩⎨⎧2-5≤x ≤2+5,x ≥-2+5或x ≤-2- 5.因为x >0,所以5-2≤x ≤5+2, 即AD 的取值范围是[5-2,5+2]. 答案:[5-2,5+2]5.(2019·金丽衢十二校联考)如图,在三棱锥D ABC 中,已知AB =2,AC →·BD →=-3,设AD =a ,BC =b ,CD =c ,则c 2ab +1的最小值为________.解析:设AD →=a ,CB →=b ,DC →=c ,因为AB =2,所以|a +b +c |2=4⇒a 2+b 2+c 2+2(a ·b +b ·c +c ·a )=4,又因为AC →·BD →=-3,所以(a +c )·(-b -c )=-3⇒a ·b +b ·c +c ·a +c 2=3,所以a 2+b 2+c 2+2(3-c 2)=4⇒c 2=a 2+b 2+2,所以a 2+b 2+2ab +1≥2ab +2ab +1=2,当且仅当a=b 时,等号成立,即c 2ab +1的最小值是2.答案:26.(2019·温州十五校联合体期末考试)在正四面体P ABC 中,点M 是棱PC 的中点,点N 是线段AB 上一动点,且AN →=λAB →,设异面直线NM 与AC 所成角为α,当13≤λ≤23时,则cos α的取值范围是________.解析:设点P 到平面ABC 的射影为点O ,以AO 所在直线为y 轴,OP 所在直线为z 轴,过点O 作BC 的平行线为x 轴,建立空间直角坐标系,如图.设正四面体的棱长为43,则有A (0,-4,0),B (23,2,0),C (-23,2,0),P (0,0,42),M (-3,1,22).由AN →=λAB →,得N (23λ,6λ-4,0).从而有NM →=(-3-23λ,5-6λ,22),AC →=(-23,6,0). 所以cos α=|NM →·AC →||NM →||AC →|=3-2λ24λ2-4λ+3,设3-2λ=t ,则53≤t ≤73.则cos α=12t 2t 2-4t +6=126⎝ ⎛⎭⎪⎫1t 2-4·1t+1,因为13<37≤1t ≤35,所以51938≤cos α≤71938.答案:⎣⎢⎡⎦⎥⎤51938,719387.如图,在△ABC 中,∠B =π2,AB =BC =2,P 为AB 边上一动点,PD ∥BC 交AC 于点D .现将△PDA 沿PD 翻折至△PDA ′,使平面PDA ′⊥平面PBCD .(1)当棱锥A ′PBCD 的体积最大时,求PA 的长; (2)若P 为AB 的中点,E 为A ′C 的中点,求证:A ′B ⊥DE . 解:(1)设PA =x ,则PA ′=x ,所以V A ′PBCD =13PA ′·S 底面PBCD =13x ⎝ ⎛⎭⎪⎫2-x 22.令f (x )=13x ⎝⎛⎭⎪⎫2-x 22=2x 3-x36(0<x <2),则f ′(x )=23-x22.当x 变化时,f ′(x ),f (x )的变化情况如下表:(2) 证明:取A ′B 的中点F ,连接EF ,FP .由已知,得EF 綊12BC 綊PD .所以四边形EFPD 是平行四边形,所以ED ∥FP . 因为△A ′PB 为等腰直角三角形,所以A ′B ⊥PF . 所以A ′B ⊥DE .8. (2019·杭州市第一次高考科目数学质量检测)如图,在三棱柱ABC A 1B 1C 1中,AA 1⊥平面ABC ,平面A 1BC ⊥平面A 1ABB 1.(1)求证:AB ⊥BC ;(2)设直线AC 与平面A 1BC 所成的角为θ,二面角A 1BC A 的大小为φ,试比较θ和φ的大小关系,并证明你的结论.解:(1)证明:过点A 在平面A 1ABB 1内作AD ⊥A 1B 于D , 因为平面A 1BC ⊥平面A 1ABB 1, 平面A 1BC ∩平面A 1ABB 1=A 1B , 所以AD ⊥平面A 1BC , 又因为BC ⊂平面A 1BC , 所以AD ⊥BC .因为AA 1⊥平面ABC ,所以AA 1⊥BC . 又因为AA 1∩AD =A , 所以BC ⊥侧面A 1ABB 1, 又因为AB ⊂平面A 1ABB 1, 故AB ⊥BC .(2)连接CD ,由(1)知∠ACD 是直线AC 与平面A 1BC 所成的角. 又∠ABA 1是二面角A 1BC A 的平面角. 则∠ACD =θ,∠ABA 1=φ.在Rt △ADC 中,sin θ=AD AC,在Rt △ADB 中, sin φ=AD AB.由AB <AC ,得sin θ<sin φ,又0<θ,φ<π2,所以θ<φ. [能力提升]1.(2019·温州市高考数学模拟)如图,在矩形ABCD 中,AB AD=λ(λ>1),将其沿AC 翻折,使点D 到达点E 的位置,且二面角C AB E 为直二面角.(1)求证:平面ACE ⊥平面BCE ;(2)设F 是BE 的中点,二面角E AC F 的平面角的大小为θ,当λ∈[2,3]时,求cosθ的取值范围.解:(1)证明:因为二面角C AB E 为直二面角,AB ⊥BC, 所以BC ⊥平面ABE ,所以BC ⊥AE .因为AE ⊥CE ,BC ∩CE =C ,所以AE ⊥平面BCE . 因为AE ⊂平面ACE ,所以平面ACE ⊥平面BCE .(2)如图,以E 为坐标原点,以AD 长为一个单位长度,建立如图所示的空间直角坐标系,则AB =λ,A (0,1,0),B (λ2-1,0,0),C (λ2-1,0,1),E (0,0,0),F ⎝ ⎛⎭⎪⎫λ2-12,0,0,则EA →=(0,1,0),EC →=(λ2-1,0,1), 设平面EAC 的法向量为m =(x ,y ,z ),则⎩⎨⎧y =0λ2-1·x +z =0,取x =1,则m =(1,0,-λ2-1). 同理得平面FAC 的一个法向量为n =(2,λ2-1,-λ2-1).所以cos θ=m ·n |m |·|n |=λ2+1λ·2(λ2+1)=22·1+1λ2.因为λ∈[2,3], 所以cos θ∈⎣⎢⎡⎦⎥⎤53,104.2.如图,在四棱锥P ABCD 中,已知PA ⊥平面ABCD ,且四边形ABCD 为直角梯形,∠ABC =∠BAD =π2, PA =AD =2,AB =BC =1.(1)求平面PAB 与平面PCD 所成二面角的余弦值;(2)点Q 是线段BP 上的动点,当直线CQ 与DP 所成的角最小时,求线段BQ 的长. 解:以{AB →,AD →,AP →}为正交基底建立如图所示的空间直角坐标系A xyz ,则各点的坐标为B (1,0,0),C (1,1,0),D (0,2,0),P (0,0,2).(1)由题意知,AD ⊥平面PAB ,所以AD →是平面PAB 的一个法向量,AD →=(0,2,0). 因为PC →=(1,1,-2),PD →=(0,2,-2). 设平面PCD 的法向量为m =(x ,y ,z ), 则m ·PC →=0,m ·PD →=0,即⎩⎪⎨⎪⎧x +y -2z =0,2y -2z =0.令y =1,解得z =1,x =1. 所以m =(1,1,1)是平面PCD 的一个法向量.从而cos 〈AD →,m 〉=AD →·m |AD →||m |=33,所以平面PAB 与平面PCD 所成二面角的余弦值为33. (2)因为BP →=(-1,0,2),设BQ →=λBP →=(-λ,0,2λ)(0≤λ≤1), 又CB →=(0,-1,0),则CQ →=CB →+BQ →=(-λ,-1,2λ), 又DP →=(0,-2,2),从而cos 〈CQ →,DP →〉=CQ →·DP →|CQ →||DP →|=1+2λ10λ2+2. 设1+2λ=t ,t ∈[1,3],则cos 2〈CQ →,DP →〉=2t 25t 2-10t +9=29⎝ ⎛⎭⎪⎫1t -592+209≤910.当且仅当t =95,即λ=25时,|cos 〈CQ →,DP →〉|的最大值为31010.因为y =cos x 在⎝⎛⎭⎪⎫0,π2上是减函数,所以此时直线CQ 与DP 所成角取得最小值. 又因为BP =12+22=5, 所以BQ =25BP =255.。
立体几何中体积与面积最值问题的解法

1 声明本文首先以体积最大和面积最小的物体为例,讨论它们的最大/小值的解决方案。
接下来,给定指定的条件,通过拉格朗日型最优化技术对最大化体积最小化面积问题进行剖析。
最后,在说明了结果及其分析之后,讨论此类问题的求解思路及扩展性。
2 体积最大和面积最小的物体体积最大和面积最小的物体是立体几何的典型问题,它可以被看作是一种拉格朗日型优化问题,即在完成最大化体积和最小化面积的条件下寻求平衡点。
典型的体积最大和面积最小物体有球形、柱形、长方体等,也可以拓展到多边形,例如三角形等。
2.1 球形球形是一种立体几何体,其体积最大,面积最小,可以通过满足一定条件解决最大体积最小面积问题。
大体积最小面积问题的解法主要有两种:1) 根据体积最大的物体的方程,可以求出球的半径r,其中`V=4/3πr^3`;2) 因为球的周长是最长,周长和平面面积是相关的,因此可以求出球的周长C,从而计算球的面积`S=4πr^2`;这两个方程使用上面的公式,可以求出球的体积和面积。
根据拉格朗日型优化例子求出:当半径r=1时,体积最大,体积V=4/3πr^3=4.19,面积最小,面积S=4πr^2=12.57;当半径r=2时,体积最小,体积V=33.51,面积最大,面积S=50.27。
2.2 柱形柱形也是一种常用的立体几何物体,它的体积最大,面积最小的条件也可以满足。
柱的体积的最大/小值可以利用柱体的内切球的半径r求出,其中`V=πr²h`; 柱的面积最大/小值可以求出其元表面积`S=(2πrh+2πr²)`。
根据拉格朗日型优化例子求出:当半径r=1时,体积最大,体积V=πr²h=2.14,面积最小,面积S=2πr²+2πrh=10.30;当半径r=2时,体积最小,体积V=12.56,面积最大,面积S=18.85。
2.3 长方体长方体也是常用的立体几何物体,其体积最大,面积最小的条件也可以满足。
长方体的体积的最大/小值可以利用它的公式`V=a*b*c`进行求解,其中a,b,c分别为直角坐标三边的长度;长方体的表面积最大/小值可以求出其元表面积`S=2(a*b+b*c+a*c)`。
立体几何第三讲 空间几何体得最值问题

分清定量与变量,然后根据变量的取值情况,利用函数法或平面几何的相关结论判断相应的
最值.如该题中确定三棱锥底面的面积最值是关键.
【玩转跟踪】在棱长为 1 的正方体 ABCD A1B1C1D1 中,点 P1, P2 分别是线段 AB 、BD1(不
包括端点)上的动点,且线段 P1P2 平行于 平面 A1 ADD1 ,则四面体 P1P2 AB 的体积的最大值
锥 P-AEF 的底面积和高,高为定值时,底面积最大,则体积最大.
【解析】因为 PA 平面 ABC, BC 平面 ABC,所以 PABC 又因为 BCAC, PA AC A ,所以 BC 平面 PAC,又 AF 平面 PAC,所以 BCAF , 又 AFPC, PC BC C ,所以 AF 平面 PBC,即 AFEF 。EF 是 AE 在平面 PBC 上的 射影,因为 AEPB ,所以 EFPB ,即 PE 平面 AEF。在三棱锥 P AEF 中, AP AB 2, AEPB ,
5
.
5
又 P 在 BD 上运动,且当 P 运动到点 O 时,PQ 最小,等于 OQ 的长为 2 5 ,也就是异面直 5
线 BD 和 SC 的公垂线段的长.故选 B. 2.几何体表面上的最短距离问题
【例 2】正三棱柱 ABC—A1B1C1 中,各棱长均为 2,M 为 AA1 中点,N 为 BC 的中点,则 在棱柱的表面上从点 M 到点 N 的最短距离是多少?并求之.
又∵ 0<α+β<π,∴(α+β)max=π-arctan 2 ,(α+β)min=π-arctan2 2 .
【迁移运用】
1.【西藏日喀则一中高三 10 月检测】已知正三C 的距离为1,点 是线段 的中点,过点 作球 的截面,则截面面
立体几何中的翻折、轨迹及最值(范围)问题--备战2022年高考数学配套word试题(创新设计版)

立体几何中的翻折、轨迹及最值(范围)问题)1.翻折问题是立体几何的一类典型问题,是考查实践能力与创新能力的好素材.解答翻折问题的关键在于画好折叠前后的平面图形与立体图形,并弄清折叠前后哪些发生了变化,哪些没有发生变化.解题时我们要依据这些变化的与未变化的量来分析和解决问题.而表面展开问题是折叠问题的逆向思维、过程,一般地,涉及多面体表面的距离问题不妨将它展开成平面图形试一试.2.在立体几何中,某些点、线、面按照一定的规则运动,构成各式各样的轨迹,探求空间轨迹与探求平面轨迹类似,应注意几何条件,善于基本轨迹转化.对于较为复杂的轨迹,常常要分段考虑,注意特定情况下的动点的位置,然后对任意情形加以分析判定,也可转化为平面问题.对每一道轨迹命题必须特别注意轨迹的纯粹性与完备性.3.立体几何中的体积最值问题一般是指有关距离的最值、角的最值或面积、体积的最值.其一般方法有:(1)几何法:通过证明或几何作图,确定图形中取得最值的特殊位置,再计算它的值;(2)代数方法:分析给定图形中的数量关系,选取适当的自变量及目标函数,确定函数解析式,利用函数的单调性、有界性,以及不等式的均值定理等求出最值.题型一立体几何中的翻折问题【例1】(2019·全国Ⅲ卷)图①是由矩形ADEB,Rt△ABC和菱形BFGC组成的一个平面图形,其中AB=1,BE=BF=2,∠FBC=60°.将其沿AB,BC折起使得BE与BF重合,连接DG,如图②.(1)证明:图②中的A,C,G,D四点共面,且平面ABC⊥平面BCGE;(2)求图②中的二面角B-CG-A的大小.(1)证明由已知得AD∥BE,CG∥BE,所以AD∥CG,所以AD ,CG 确定一个平面,从而A ,C ,G ,D 四点共面.由已知得AB ⊥BE ,AB ⊥BC ,且BE ∩BC =B ,BE ,BC ⊂平面BCGE , 所以AB ⊥平面BCGE .又因为AB ⊂平面ABC ,所以平面ABC ⊥平面BCGE .(2)解 作EH ⊥BC ,垂足为H .因为EH ⊂平面BCGE ,平面BCGE ⊥平面ABC ,平面BCGE ∩平面ABC =BC , 所以EH ⊥平面ABC .由已知,菱形BCGE 的边长为2,∠EBC =60°,可求得BH =1,EH = 3. 以H 为坐标原点,HC →的方向为x 轴的正方向,建立如图所示的空间直角坐标系H-xyz ,则A (-1,1,0),C (1,0,0),G (2,0,3),CG→=(1,0,3),AC →=(2,-1,0).设平面ACGD 的法向量为n =(x ,y ,z ),则⎩⎪⎨⎪⎧CG →·n =0,AC →·n =0,即⎩⎨⎧x +3z =0,2x -y =0. 所以可取n =(3,6,-3).又平面BCGE 的法向量可取m =(0,1,0),所以cos 〈n ,m 〉=n ·m |n ||m |=32.因此二面角B -CG -A 的大小为30°.【训练1】 (2021·浙江名师预测卷四)在梯形ABCD 中,对角线AC 与BD 交于点O ,AD =2AB =2BC =2CD .将△BCD 沿BD 翻折至△BPD ,且满足平面ABP ⊥平面BPD .(1)求证:二面角P -BD -A 是直二面角;(2)(一题多解)求直线PD 与平面P AO 所成角的正弦值的大小.(1)证明由已知条件易得∠BAD=60°,∠BDA=30°,AB⊥BD.在△BPD中,过点D作DH⊥BP,交BP的延长线于点H.∵平面ABP⊥平面BPD,平面ABP∩平面BPD=BP,∴DH⊥平面ABP,∵AB⊂平面ABP,∴DH⊥AB.又∵BD∩DH=D,∴AB⊥平面BPD,∵AB⊂平面ABD,∴平面ABD⊥平面BPD.即二面角P-BD-A是直二面角.(2)解法一过点P作PG⊥BD,交BD于点G,则G是BD的中点.由(1)可知平面PBD⊥平面ABD,又∵平面PBD∩平面ABD=BD,∴PG⊥平面ABD.设OB=1,则OP=1,OA=2,AB=BP=3,∵AB⊥平面BPD,∴AB⊥BP,∴AP=AB2+BP2=6,由余弦定理得cos∠AOP=OA2+OP2-AP22OA·OP=-14,则sin∠AOP=15 4.设点D到△AOP的距离为h,∵V P-AOD=V D-AOP,∴13·PG·S△AOD=13·h·S△AOP,∵PG=32,S△AOD=12×2×2·sin2π3=3,S△AOP=12×1×2×154=154,∴h=215 5,∵PD =3,∴直线PD 与平面P AO 所成角θ的正弦值sin θ=h PD =255.法二 分别取BD ,AD 的中点E ,F ,连接EP ,EF ,则EF ∥AB .由(1)可知AB ⊥平面BPD ,∴EF ⊥平面BPD ,∴EF ⊥BD ,EF ⊥EP .∵PB =PD ,∴PE ⊥BD ,以点E 为坐标原点,EF→,ED →,EP →的方向为x 轴、y 轴、z 轴的正方向建立空间直角坐标系.设OB =1,可得P ⎝⎛⎭⎪⎫0,0,32,D ⎝ ⎛⎭⎪⎫0,32,0, A ⎝ ⎛⎭⎪⎫3,-32,0,O ⎝ ⎛⎭⎪⎫0,-12,0. ∴PD →=⎝ ⎛⎭⎪⎫0,32,-32,P A →=⎝⎛⎭⎪⎫3,-32,-32, AO→=(-3,1,0). 设平面P AO 的法向量为n =(x ,y ,z ),则⎩⎪⎨⎪⎧P A →·n =0,AO →·n =0,即⎩⎨⎧3x -32y -32z =0,-3x +y =0, 令x =1,则n =(1,3,-1),∴直线PD 与平面P AO 所成角θ的正弦值为sin θ=|cos 〈n ,PD →〉|=|n ·PD →||n |·|PD →|=255. 题型二 立体几何中的轨迹问题【例2】 (1)已知在平行六面体ABCD -A 1B 1C 1D 1中,AA 1与平面A 1B 1C 1D 1垂直,且AD =AB ,E 为CC 1的中点,P 在对角面BB 1D 1D 所在平面内运动,若EP 与AC 成30°角,则点P 的轨迹为( )A .圆B .抛物线C .双曲线D .椭圆(2)已知正方体ABCD -A 1B 1C 1D 1的棱长为1,点P 是平面AC 内的动点, 若点P 到直线A 1D 1的距离等于点P 到直线CD 的距离,则动点P 的轨迹所在的曲线是()A.抛物线B.双曲线C.椭圆D.直线答案(1)A(2)B解析(1)因为在平行六面体ABCD-A1B1C1D1中,AA1与平面A1B1C1D1垂直,且AD=AB,所以该平面六面体ABCD-A1B1C1D1是一个底面为菱形的直四棱柱,所以对角面BB1D1D⊥底面ABCD,AC⊥对角面BB1D1D.取AA1的中点F,则EF∥AC,因为EP与AC成30°角,所以EP与EF成30°角.设EF与对角面BB1D1D 的交点为O,则EO⊥对角面BB1D1D,所以点P的轨迹是以EO为轴的一个圆锥的底面,故选A.(2)如图,以A为原点,AB为x轴、AD为y轴,建立平面直角坐标系.设P(x,y),作PE⊥AD于E、PF⊥A1D1于F,连接EF,易知|PF|2=|PE|2+|EF|2=x2+1,又作PN⊥CD于N,则|PN|=|y-1|.依题意|PF|=|PN|,即x2+1=|y-1|,化简得x2-y2+2y=0,故动点P的轨迹为双曲线,选B.【训练2】(1)在正方体ABCD-A1B1C1D1中,点M,N分别是线段CD,AB上的动点,点P是△A1C1D内的动点(不包括边界),记直线D1P与MN所成角为θ,若θ的最小值为π3,则点P的轨迹是()A.圆的一部分B.椭圆的一部分C.抛物线的一部分D.双曲线的一部分(2)如图,AB是平面α的斜线段,A为斜足,若点P在平面α内运动,使得△ABP 的面积为定值,则动点P的轨迹是()A.圆B.椭圆C.一条直线D.两条平行直线答案(1)B(2)B解析(1)延长D1P交底面ABCD的内部于点Q,连接QD,则∠D1QD为直线D1Q 与底面ABCD所成的角,也就是直线D1P与MN所成角θ的最小值,故∠D1QD=π3,从而∠DD1Q=π6,所以D1Q的轨迹是以D1D为轴,顶点为D1,母线D1Q与轴D1D的夹角为π6的圆锥面的一部分,则点P的轨迹就是该部分圆锥面与△A1C1D面(不包括边界)的交线,而△A1C1D面所在平面与轴D1D斜交,故点P 的轨迹是椭圆的一部分.(2)由于线段AB 是定长线段,而△ABP 的面积为定值,所以动点P 到线段AB 的距离也是定值.由此可知空间点P 在以AB 为轴的圆柱侧面上.又P 在平面内运动,所以这个问题相当于一个平面去斜切一个圆柱(AB 是平面的斜线段)得到的切痕是椭圆.P 的轨迹就是圆柱侧面与平面α的交线是椭圆.题型三 立体几何中的长度、面积、体积的最值(范围)问题【例3】 (1)如图,正三棱锥S -ABC 的底面边长为2a ,E 、F 、G 、H 分别为SA ,SB ,CB ,CA 的中点,则四边形EFGH 的面积的取值范围是( )A .(0,+∞) B.⎝ ⎛⎭⎪⎫33a 2,+∞ C.⎝ ⎛⎭⎪⎫36a 2,+∞ D.⎝ ⎛⎭⎪⎫12a 2,+∞ (2)(2021·“超级全能生”联考)在长方体ABCD -A 1B 1C 1D 1中,底面ABCD 是边长为4的正方形,侧棱AA 1=t (t >4),点E 是BC 的中点,点P 是侧面ABB 1A 1内的动点(包括四条边上的点),且满足tan ∠APD =4tan ∠EPB ,则四棱锥P -ABED 的体积的最大值是( )A.433 B .16 3 C.1633 D.6439答案 (1)B (2)C解析 (1)因为E 、F 、G 、H 分别为SA ,SB ,CB ,CA 的中点,∴EF 綉12AB ,HG綉12AB ,∴EF 綉HG ,同理,EH 綉FG ,所以EFGH 为平行四边形,又∵S -ABC 为正三棱锥,∴SC ⊥AB ,∴EF ∥AB ,FG ∥SC ,所以EF ⊥FG ,从而四边形EFGH 为矩形,其面积S =GH ·GF =12a ·SC ,当正三棱锥的高→0时,SC →正三角形ABC的外接圆的半径233a ,所以四边形EFGH 的面积→33a 2,选B.(2)作PF ⊥AB ,垂足为点F ,在长方体ABCD -A 1B 1C 1D 1中,DA ⊥平面ABB 1A 1,CB ⊥平面ABB 1A 1,在Rt △P AD 和Rt △PBC 中,所以tan ∠APD =AD AP ,tan ∠EPB=BE PB .因为tan ∠APD =4tan ∠EPB ,BE =12BC =12AD ,所以PB =2AP .因为平面ABB 1A 1⊥平面ABCD ,平面ABB 1A 1∩平面ABCD =AB ,PF ⊥AB ,所以PF ⊥平面ABCD .设PF =h ,AF =x ,则BF =4-x ,x ∈[0,4],由PB =2AP ,得h 2+(4-x )2=4(x 2+h 2),即h 2=-x 2-83x +163.因为函数y =-x 2-83x +163在[0,4]上单调递减,所以当x =0时,(h 2)max =163,即h max =433,所以四棱锥P -ABED 的体积的最大值(V P -ABED )max =13×12×(2+4)×4×433=1633,故选C.【训练3】 (1)在棱长为6的正方体ABCD -A 1B 1C 1D 1中,M 是BC 中点,点P 是平面DCC 1D 1所在的平面内的动点,且满足∠APD =∠MPC ,则三棱锥P -BCD 体积的最大值是( )A .36B .12 3C .24D .18 3(2)(2021·镇海中学模拟)已知棱长为1的正方体ABCD -A 1B 1C 1D 1,球O 与正方体的各条棱相切,P 为球O 上一点,Q 是△AB 1C 的外接圆上的一点,则线段PQ 长的取值范围是________.答案 (1)B (2)⎣⎢⎡⎦⎥⎤3-22,3+22 解析 (1)因为AD ⊥平面D 1DCC 1,则AD ⊥DP ,同理BC ⊥平面D 1DCC 1,则BC ⊥CP ,∠APD =∠MPC ,则△P AD ∽△PMC ,∵AD =2MC ,则PD =2PC ,下面研究点P 在面ABCD 的轨迹(立体几何平面化),在平面直角坐标系内设D (0,0),C (6,0),D 1(0,6),C 1(6,6),设P (x ,y ),因为PD =2PC ,所以x 2+y 2=2(x -6)2+y 2,化简得(x -8)2+y 2=16,该圆与CC 1的交点纵坐标最大,交点为(6,23),三棱锥P -BCD 的底面BCD 的面积为18,要使三棱锥P -BCD 体积最大,只需高最大,当P 在CC 1上且CP =23时棱锥的高最大,V =13·18·23=12 3.(2)因为球O 与正方体的各条棱相切,所以球心O 为正方体的中心,切点为各条棱的中点,则易得|OP |=22.△AB 1C 为边长为2的等边三角形,设其外接圆的圆心为M ,则易得|MB 1|=63.在正方体ABCD -A 1B 1C 1D 1中,易得BD 1⊥平面AB 1C ,则OM ⊥MB 1.又因为|OB |=32,|MB |=33,所以|OM |=36,则|OQ |=|OB 1|=|OM |2+|MB 1|2=32,所以|PQ |max =|OQ |+|OP |=3+22,|PQ |min =|OQ |-|OP |=3-22,即线段PQ 的取值范围为⎣⎢⎡⎦⎥⎤3-22,3+22一、选择题1.已知线段AB 垂直于定圆所在的平面,B ,C 是圆上的两点,H 是点B 在AC 上的射影,当C 运动时,点H 运动的轨迹( )A .是圆B .是椭圆C .是抛物线D .不是平面图形答案 A解析 设在定圆内过点B 的直径与圆的另一个交点为点D ,过点B 作AD 的垂线,垂足为点E ,连接EH ,CD .因为BD 为定圆的直径,所以CD ⊥BC ,又因为AB 垂直于定圆所在的平面,所以CD ⊥AB ,又因为AB ∩BC =B ,所以CD ⊥平面ABC ,所以CD ⊥BH ,又因为BH ⊥AC ,AC ∩CD =C ,所以BH ⊥平面ACD ,所以BH ⊥EH ,所以动点H 在以BE 为直径的圆上,即点H 的运动轨迹为圆,故选A.2.设P 是正方体ABCD -A 1B 1C 1D 1的对角面BDD 1B 1(含边界)内的点,若点P 到平面ABC 、平面ABA 1、平面ADA 1的距离相等,则符合条件的点P ( )A .仅有一个B .有有限多个C .有无限多个D .不存在答案 A解析 与平面ABC ,ABA 1距离相等的点位于平面ABC 1D 1上;与平面ABC ,ADA 1距离相等的点位于平面AB 1C 1D 上;与平面ABA 1,ADA 1距离相等的点位于平面ACC 1A 1上;据此可知,满足题意的点位于上述平面ABC 1D 1,平面AB 1C 1D ,平面ACC 1A 1的公共点处,结合题意可知,满足题意的点仅有一个.3.(2021·温州中学模拟)如图所示,用一边长为2的正方形硬纸,按各边中点垂直折起四个小三角形,做成一个蛋巢,将体积为4π3的鸡蛋(视为球体)放入其中,蛋巢形状保持不变,则鸡蛋(球体)离蛋巢底面的最短距离为( )A.5+12B.5-12C.3+12D.3-12答案 D解析 因为蛋巢的底面是边长为1的正方形,所以过四个顶点截鸡蛋所得的截面圆的直径为1.又因为鸡蛋(球体)的体积为4π3,所以球的半径为1,所以球心到截面圆的距离d =1-14=32,则截面圆到球体最低点的距离为1-32,而蛋巢的高度为12,故鸡蛋(球体)到蛋巢底面的最短距离为12-⎝⎛⎭⎪⎫1-32=3-12,故选D. 4.(2021·温州适考)如图,在△ABC 中,点M 是边BC 的中点,将△ABM 沿着AM 翻折成△AB ′M ,且点B ′不在平面AMC 内,点P 是线段B ′C 上一点.若二面角P -AM -B ′与二面角P -AM -C 的平面角相等,则直线AP 经过△AB ′C 的( )A .重心B .垂心C .内心D .外心答案 A解析因为二面角P-AM-B′与二面角P-AM-C的平面角相等,所以点P到两个平面的距离相等,所以V P-AB′M=V P-ACM,即V A-PB′M=V A-PCM.因为两三棱锥的高相等,故S△PB′M =S△PCM,故B′P=CP,故点P为CB′的中点,所以直线AP经过△AB′C的重心,故选A.5.(2021·浙江名师预测卷一)如图,在四棱锥P-ABCD中,底面ABCD为正方形,侧面P AD为正三角形,且侧面P AD⊥底面ABCD,已知在侧面P AD内存在点Q,满足PQ⊥QD,则当AQ最小时,二面角A-CD-Q的余弦值是()A.2-34 B.2+34C.2-62 D.2+64答案 D解析取PD的中点M,因为四边形ABCD为正方形,所以CD⊥AD,又平面P AD⊥平面ABCD,且平面P AD∩平面ABCD=AD,CD⊂平面ABCD,所以CD⊥平面P AD,所以CD⊥QD,则二面角A-CD-Q的平面角是∠ADQ,又因为点Q的轨迹是以M为圆心的圆,如图,当|AQ|最小时,∠ADQ=∠ADP-∠QDP=60°-45°=15°,即二面角A-CD-Q的余弦值为cos 15°=cos(60°-45°)=2+6 4,故选D.6.(2021·浙江新高考仿真卷二)如图所示,在棱长为1的正方体ABCD-A1B1C1D1中,P,Q分别为BD1,BB1上的动点,则△C1PQ周长的最小值为()A.215 3B.4+2 2C.4+83 2D.213 3答案 B解析连接B1D1,BC1,由图易得△C1PQ的三边分别在三棱锥B-B1C1D1的三个侧面上,将三棱锥B-B1C1D1的侧面展开成平面图形,如图,可得四边形BC1D1C1′为直角梯形,当C1′,P,Q,C1四点共线时,△C1PQ的周长最小,最小值为C1′D21+D1C21=4+22,即△C1PQ的周长的最小值为4+22,故选B.7.(2021·上虞区期末调测)在棱长均为23的正四面体ABCD中,M为AC的中点,E为AB的中点,P是DM上的动点,Q是平面ECD上的动点,则AP+PQ的最小值是()A.3+112 B.3+ 2C.534D.2 3答案 A解析 如图,作MG ⊥CE 于点G ,连接DG .由已知得平面CDE ⊥平面ABC ,又平面CDE ∩平面ABC =CE ,则MG ⊥平面CDE ,故DG 为DM 在平面CDE 上的射影.将半平面ADM 沿DM 翻折至与半平面DMG 所成二面角为180°,记翻折后的点A 即A ′到DG 的距离为h A ,则h A 为△A ′DG 的边DG 上的高,且AP +PQ =A ′P +PQ ≥h A .因为MG =12AE =32,DM =DC 2-⎝ ⎛⎭⎪⎫AC 22=3,则sin ∠MDG=MG DM =36,故cos ∠MDG =336.又∠ADM =∠A ′DM =π6,所以sin ∠A ′DG =sin ⎝ ⎛⎭⎪⎫∠MDG +π6=336×12+36×32=3+3312,所以AP +PQ的最小值h A =A ′D sin ∠A ′DG =11+32.故选A. 二、填空题8.在正方体ABCD -A 1B 1C 1D 1中,点P 在侧面BCC 1B 1及其边界上运动,总有AP ⊥BD 1,则动点P 的轨迹为________. 答案 线段B 1C解析 易证BD 1⊥平面ACB 1,所以满足BD 1⊥AP 的所有点P 都在一个平面ACB 1上.而已知条件中的点P 是在侧面BCC 1B 1及其边界上运动,因此,符合条件的点P 在平面ACB 1与平面BCC 1B 1的交线上,故所求的轨迹为线段B 1C .9.已知正方体ABCD -A 1B 1C 1D 1的棱长为3,长为2的线段MN 的一个端点M 在DD 1上运动,另一个端点N 在底面ABCD 上运动,则MN 的中点P 的轨迹与正方体的面所围成的几何体的体积为________. 答案 π6解析 连接DP ,因为MN =2,所以PD =1,因此点P 的轨迹是一个以D 为球心,1为半径的球面在正方体内的部分,所以点P的轨迹与正方体的表面所围成的几何体的体积为球的体积的18,即V=18×43π×13=π6.10.已知在矩形ABCD中,AB=3,BC=a,若P A⊥平面AC,在BC边上取点E,使PE⊥DE,若满足条件的E点有两个时,则a的取值范围是________.答案(6,+∞)解析连接AE,由三垂线逆定理可知DE⊥AE,要使满足条件的E点有两个则须使以AD为直径的圆与BC有两个交点,所以半径长a2>3,∴a>6.11.如图,已知∠ACB=90°,DA⊥平面ABC,AE⊥DB交DB于E,AF⊥DC交DC于F,且AD=AB=2,则三棱锥D-AEF体积的最大值为________.答案2 6解析因为DA⊥平面ABC,所以DA⊥AB,AD⊥BC,∵AE⊥DB,又AD=AB=2,∴DE=2,又因为BC⊥AC,AC∩AD=A,所以BC⊥平面ACD,所以平面BCD⊥平面ACD,∵AF⊥DC,平面BCD∩平面ACD=CD,所以AF⊥平面BCD,所以AF⊥EF,BD⊥EF,所以BD⊥平面AEF,由AF2+EF2=AE2=2≥2AF·EF可得AF·EF≤1,所以S△AEF ≤12,所以三棱锥D-AEF体积的最大值为13×2×12=26.12.如图,在长方形ABCD中,AB=2,BC=1,E为DC的中点,F为线段EC(端点除外)上一动点.现将△AFD 沿AF 折起,使平面ABD ⊥平面ABC .在平面ABD 内过点D 作DK ⊥AB ,K 为垂足.设AK =t ,则t 的取值范围是________.答案 ⎝ ⎛⎭⎪⎫12,1解析 如图,在平面ADF 内过D 作DH ⊥AF ,垂足为H ,连接HK .过F 点作FP ∥BC 交AB 于点P.设∠F AB =θ,则cos θ∈⎝ ⎛⎭⎪⎫22,255.设DF =x ,则1<x <2, ∵平面ABD ⊥平面ABC ,平面ABD ∩平面ABC =AB ,DK ⊥AB ,DK ⊂平面ABD ,∴DK ⊥平面ABC ,又AF ⊂平面ABC ,∴DK ⊥AF . 又∵DH ⊥AF ,DK ∩DH =D ,DK ,DH ⊂平面DKH , ∴AF ⊥平面DKH ,∴AF ⊥HK ,即AH ⊥HK . 在Rt △ADF 中,AF =1+x 2,∴DH =x 21+x 2, ∵△ADF 和△APF 都是直角三角形,PF =AD , ∴Rt △ADF ≌Rt △FP A ,∴AP =DF =x . ∵△AHD ∽△ADF ,∴cos θ=11+x 2t =x1+x 2. ∴x =1t .∵1<x <2,∴1<1t <2,∴12<t <1. 三、解答题13.(2018·全国Ⅰ卷)如图,四边形ABCD 为正方形, E ,F 分别为AD ,BC 的中点,以DF 为折痕把△DFC 折起,使点C 到达点P 的位置,且PF ⊥BF .(1)证明:平面PEF ⊥平面ABFD ; (2)求DP 与平面ABFD 所成角的正弦值.(1)证明 由已知可得,BF ⊥PF ,BF ⊥EF ,又PF ∩EF =F ,PF ,EF ⊂平面PEF ,所以BF ⊥平面PEF .又BF ⊂平面ABFD ,所以平面PEF ⊥平面ABFD . (2)解 作PH ⊥EF ,垂足为H .由(1)得,PH ⊥平面ABFD .以H 为坐标原点,分别以FB→,HF →,HP →的方向为x 轴、y 轴、z 轴的正方向,|BF →|为单位长,建立如图所示的空间直角坐标系H -xyz .由(1)可得,DE ⊥PE .又DP =2,DE =1,所以PE = 3.又PF =1,EF =2,故EF 2=PE 2+PF 2,所以PE ⊥PF . 可得PH =32,EH =32.则H (0,0,0),P ⎝ ⎛⎭⎪⎫0,0,32,D ⎝ ⎛⎭⎪⎫-1,-32,0,DP →=⎝ ⎛⎭⎪⎫1,32,32,HP →=⎝ ⎛⎭⎪⎫0,0,32为平面ABFD 的一个法向量.设DP 与平面ABFD 所成角为θ, 则sin θ=⎪⎪⎪⎪⎪⎪⎪⎪HP →·DP →|HP →||DP →|=343=34. 所以DP 与平面ABFD 所成角的正弦值为34.14.(2021·杭州二中仿真模拟)如图,平面四边形ABCD 关于直线AC 对称,∠A =60°,∠C =90°,CD =2.把△ABD 沿BD 折起.(1)若二面角A -BD -C 的余弦值为33,求证:AC ⊥平面BCD ; (2)若AB 与平面ACD 所成的线面角为30°时,求AC 的长. 解 (1)取BD 的中点E ,连接AE ,CE . 因为AB =AD ,CB =CD , 所以AE ⊥BD ,CE ⊥BD , 又AE ∩CE =E ,所以BD ⊥平面ACE ,所以BD ⊥AC , 所以∠AEC 是二面角A -BD -C 的平面角.在△AEC 中,AC 2=AE 2+CE 2-2AE ·CE cos ∠AEC =4,则AC 2+CE 2=AE 2, 所以AC ⊥CE .因为CE ∩BD =E ,CE ,BD ⊂平面BCD , 所以AC ⊥平面BCD .(2)由(1)得以点C 为坐标原点建立如图所示的空间直角坐标系,则C (0,0,0),B (2,0,0),D (0,2,0). 设A (m ,m ,n ),则BA→=(m -2,m ,n ),CA →=(m ,m ,n ),CD →=(0,2,0). 设平面ACD 的法向量n =(x ,y ,z ), 则⎩⎪⎨⎪⎧n ·CA →=0,n ·CD →=0,即⎩⎨⎧xm +ym +zn =0,2y =0,取⎩⎨⎧x =n ,y =0,z =-m ,所以n =(n ,0,-m ), 因为BA =22,所以(m -2)2+m 2+n 2=8, 则|cos 〈BA→,n 〉|=|n (m -2)-mn |22m 2+n 2=12,解得m 2=n 2,解得m =2或m =-23, 所以AC =23或AC =23 3.。
立体几何最值问题-高考数学一题多解

立体几何最值问题-高考数学一题多解一、攻关方略事物的空间形成,总是表现为不同维数且遵循由低维到高维的发展规律,所谓升维策略,就是把维数、抽象水平较低的或局部的问题转化为维数、抽象水平较高或整体性较强的整体间的关系问题,通过对整体性质或关系的考虑,使原问题获得解决的策略,如平面图形通过翻折或旋转成为空间图形就是二维向三维的转化与变换.在解题时,考虑把高维空间的问题转化为低维空间的问题,这种处理问题的方法叫降维法,也可称之为降维策略,如将立体几何问题转化为平面几何问题.实际上,许多立体几何问题如求空间角、空间距离等,通常总是转化为平面内的问题,通过计算来解决的,当然将空间角、空间距离转变为平面角、平面上点线距离这一步是需要证明的.在立体几何学习中经常碰到几何体中有变角或变动的线段,此时必须根据题意列出沟通已知量与变量之间的关系,运用函数与方程的思想来处理,立体几何中由于动点的变化引起的最值,通常建立关于与动点相关的角度的目标函数,转化为函数最值问题求解.若在空间图形中建立空间直角坐标系,利用向量坐标法,结合条件得到方程(组),则可用解方程(组)求出结果,利用函数与方程的思想方法还可以解空间图形中涉及线面关系、面面关系的探究性问题.真可谓:翻折旋转二维升三,空间问题降维处理.点动角变牵动图形,立几最值函数搞定.1.如图所示,圆形纸片的圆心为O ,半径为5cm ,该纸片上的等边三角形ABC 的中心为O .D 、E 、F 为圆O 上的点,DBC △、ECA △、FAB 分别是以BC 、CA 、AB 为底边的等腰三角形,沿虚线剪开后,分别以BC 、CA 、AB 为折痕折起DBC △、ECA △、FAB ,使得D 、E 、F 重合,得到三棱锥.当ABC 的边长变化时,所得三棱锥体积(单位:cm 3)的最大值为______.【针对训练】2.点P 在ABC 所在平面α外,PA α⊥,PB PC ==,3tan 2PBC ∠=,则点A 到平面PBC 的距离的最大值是______.3.如图所示,在ABC 中,2AB BC ==,120ABC ∠=︒.若平面ABC 外的点P 和线段AC 上的点D ,满足PD DA =,PB BA =,则四面体P BCD -的体积的最大值是______.4.已知底面边长为2的正三棱锥-P ABC ,其表面展开图是123PP P ,如图所示,求123PP P 的各边长及此三棱锥的体积V .5.已知球的直径4SC =,A 、B 是该球面上的两点,30ASC BSC ∠=∠=︒,则三棱锥S ABC -的体积的最大值为______.(2021全国新高考Ⅰ卷19)6.已知直三棱柱111ABC A B C -中,侧面11AA B B 为正方形,2AB BC ==,E ,F 分别为AC 和1CC 的中点,D 为棱11A B 上的点.11BF A B ⊥(1)证明:BF DE ⊥;(2)当1B D 为何值时,面11BB C C 与面DFE 所成的二面角的正弦值最小?(2022新高考1卷)7.已知正四棱锥的侧棱长为l ,其各顶点都在同一球面上.若该球的体积为36π,且333l ≤≤)A .8118,4⎡⎤⎢⎥⎣⎦B .2781,44⎡⎤⎢⎥⎣⎦C .2764,43⎡⎤⎢⎥⎣⎦D .[18,27](2022年全国乙卷(文数)第12题)8.已知球O 的半径为1,四棱锥的顶点为O ,底面的四个顶点均在球O 的球面上,则当该四棱锥的体积最大时,其高为()A .13B .12C D .2(2022年全国乙卷(文数)第18题)9.如图,四面体ABCD 中,AD CD ⊥,AD CD =,ADB BDC ∠=∠,E 为AC 的中点.(1)证明:平面BED ⊥平面ACD ;(2)设2AB BD ==,60ACB ∠=︒,点F 在BD 上,当AFC △的面积最小时,求三棱锥F ABC -的体积.10.如图,已知平面四边形ABCD ,AB=BC=3,CD=1,ADC=90°.沿直线AC 将ACD 翻折成ACD '△,直线AC 与BD '所成角的余弦的最大值是________.11.已知四边形ABCD ,2AB BD DA ===,BC CD ==ABD △沿BD 折起,使二面角A BD C --的大小在5,66ππ⎡⎤⎢⎥⎣⎦内,则直线AB 与CD 所成角的余弦值取值范围是()A .08⎡⎢⎣⎦,B .08⎡⎢⎣⎦,C .01⎡⎫⎪⎢⎪⎣⎦⎣⎭ D .88⎢⎣⎦,参考答案:1.3【分析】先求得所求三棱锥体积的表达式,然后利用导数或基本不等式求得体积的最大值.【详解】解法一:由题意可知,折起后所得三棱锥为正三棱锥,当ABC 的边长变化时,设ABC 的边长为()0a a >cm ,则ABC 的面积为24a .DBC △的高为56a -,则正三棱锥的高为=∴2503->,∴0a <<.∴所得三棱锥的体积213412V a =⨯=.令45253t a a =-,则34100t a =',由0t '=,得a =此时所得三棱锥的体积最大,为3.解法二:如图所示,连接OD 交BC 于点G ,由题意知,OD BC ⊥,OG 是等边三角形ABC 内切圆半径,21π1sin 3232BC BC OG ⨯⨯=⨯⨯,解得OG =,∴OG 的长度与BC 的长度成正比.设OG x =,则BC =,5DG x =-,2132ABC S x =⨯=△,则所得三棱锥的体积2213V =⨯=令()452510f x x x =-,50,2x ⎛⎫∈ ⎪⎝⎭.则()3410050f x x x '=-,令()0f x '≥,即4320x x -≤,得02x <≤.则当50,2x ⎛⎫∈ ⎪⎝⎭时,()()280f x f =≤,∴V ≤.∴所求三棱锥的体积的最大值为3.解法三:如图所示,连接OE 交AC 于点H ,连接AO 、OC ,设OH x =.则AC =,5EH x =-,三棱锥D ABC -2ABC S = ,D ABC V -=2≤=,当且仅当104x x =-,即2x =时取等号.∴所求三棱锥的体积的最大值为3.【点睛】本题为平面图形折叠成空间图形,当折叠终止时,几何体是一个正三棱锥,这个正三棱锥底面边长是一个变元,从而导致三棱锥体积的变化,特别要提醒的是,在折叠问题中,必须注意到折叠过程中哪些要素在变化,哪些要素始终保持不变,其中不变要素见核心要素.根据平面图形的性质,寻找不变的数量关系以及直线与直线平行和垂直的位置关系,是解决折叠问题的突破口,因此折叠问题要通过变图、想图、构图、用图的过程,积极思考,体会解题程序方向性,直击问题的本质,折叠问题既要看清平面转化为空间的过程,又要了解三维空间图形问题的平面化处理,两者是互通的.在建立体积表达式的函数模型之后,结合函数思想求最值,通常用导数法,也可考虑运用基本不等式的方法.策略一:以动正三角形AEC 的边长为变元建立函数关系式,运用导数法求其最大值.策略二:以动正三角形ABC 的中心到边的距离为变元建立函数关系式,运用导数法求其最大值.策略三:以动正三角形ABC 的中心到边的距离为变元建立函数关系式,运用基本不等式求最大值,注意等号成立的条件.2【分析】法一,取BC 的中点D ,连接AD 、PD ,设ADP θ∠=,用θ的正余弦表示AD ,PD ,再利用等体积法求解作答.法二,作PD BC ⊥于点D ,连接AD ,作AF PD ⊥于点F ,证明AF ⊥平面PBC ,再利用均值不等式求解作答.【详解】解法一,取BC 的中点D ,连接AD 、PD ,如图,因PB PC =,则PD BC ⊥,而3tan2PBC ∠=,有sin PBC ∠=则有sin PD PB PBC =⋅∠=PA ⊥平面ABC ,,AD BC ⊂平面ABC ,则PA AD ⊥,PA BC ⊥,又,,PA PD P PA PD ⋂=⊂平面PAD ,因此BC ⊥平面PAD ,AD ⊂平面PAD ,则AD BC ⊥,在Rt PAD △中,令(0,)2ADP πθ∠=∈,sin ,cos PA PD AD PD θθ==,设点A 到平面PBC 的距离为h ,11,22PBC ABC S BC PD S BC AD =⋅=⋅ ,由A PBC P ABC V V --=得:1133PBC ABC S h S PA ⋅=⋅ ,即1122BC PD h BC AD PA ⋅⋅=⋅⋅,于是得cos sin 2AD PA PD PD h PD PD θθθ⋅⋅==,当且仅当22=πθ,即4πθ=时取等号,所以点A 到平面PBC解法二,在PBC 中,作PD BC ⊥于点D ,连接AD ,作AF PD ⊥于点F,如图,PA ⊥平面ABC ,BC ⊂平面ABC ,则PA BC ⊥,又,,PA PD P PA PD ⋂=⊂平面PAD ,因此BC ⊥平面PAD ,而BC ⊂平面PBC ,则有平面PAD ⊥平面PBC ,又平面PAD ⋂平面PBC PD =,AF ⊂平面PAD ,因此AF ⊥平面PBC ,即AF 就是点A 到平面PBC 的距离,而3tan 2PBC ∠=,有sin PBD ∠=sin PD PB PBD =⋅∠=,在Rt PAD △中,22211()1222PA AD PD PA AD AF PD PD PD PD +⋅=≤==当且仅当3PA AD ==时取等号,所以点A 到平面PBC3.12##0.5【分析】先求得四面体P BCD -体积的表达式,利用基本不等式或函数的单调性求得体积的最大值.【详解】解法一:由2AB BC ==,120ABC ∠=︒,可得AC =要求四面体P BCD -的体积,关键是寻找底面三角形BCD 的面积BCD S △和点P 到平面BCD 的距离h ,易知2h ≤.设AD x =,则DP x =,DC x =,()12sin 3022DBC xS x =⨯⨯⨯︒=△,其中(0,x ∈,且h x ≤.∴2111366622P BCDBCD x x x x V S h h x -⎛⎫-+=⨯=≤≤= ⎪ ⎪⎝⎭△.当且仅当x x =,即x =P BCD -的体积的最大值是12.解法二:设PD AD x ==,∵PB PA =,PBD ABD ≌△△,1133P BCD BCD V S h -=⨯=△(h 为三棱锥P BCD -的高).当平面PBD ⊥平面BDC 时,使四面体PBCD 的体积较大.作PH BD ⊥,垂足为H ,则PH ⊥平面BCD ,sin sin h PH PD PDB x ADB ==⋅∠=⋅∠.此时,()211sin sin sin 662P BCDx x V ADB ADB ADB -=⋅∠≤∠=∠⎝⎭,当且仅当x =1sin 2P BCD V ADB -=∠,当90ADB ∠=︒,即AD BD ⊥时,P BCD V -最大值为12.解法三:∵13P BCD BCD V S h -=⨯△(h 为三棱锥P BCD -的高),在ABC 中,2AB BC ==,120ABC ∠=︒,则AC =30BAC BCA ∠=∠=︒,设(0PD DA x x ==<<,则DC x =-,1sin 22BCD xS BC CD BCA =⨯⋅∠=△.在ABD △中,由余弦定理,有2222cos BD AD AB AD AB BAC =+-⋅∠.代入整理得BD =PBD △中,由余弦定理,有222cos 2PB BD PD PBD PB BD+-∠=⋅,代值整理得cos PBD ∠∴sin PBD ∠=.过P 作PM BD ⊥,垂足为M ,则PM 为四面体P BCD -的高.∴sin h PM PB PBM ==∠故111336P BCDBCD V S h -===△,t =,∵0x <<12t ≤<,∴224x t -=-.2141466P BCDt V t t t--⎛⎫=⨯=- ⎪⎝⎭在[)1,2t ∈上单调递减.∴当1t =,即x =P BCD -的体积最大为1411612P BCD V --=⨯=.4.1213234PP PP P P ===,3【分析】由12APB CBP ≌△△,分析可得123PP P 是边长为4的正三角形,再由13P ABC ABC S PO V -=⋅ 结合题干数据求解即可.【详解】由题图可知1P 、B 、2P 三点共线,∴12APBCBP ≌△△.∵60ABC ∠=︒,∴1260ABP CBP ∠=∠=︒,1APB △和2CBP △都是正三角形.∴124PP =.同理可知其他两边长也是4,∴123PP P 是边长为4的正三角形.折叠后是棱长为2的正四面体-P ABC ,如图所示.设顶点P 在底面内的投影为O ,连结BO 并延长,交AC 于点D ,则D 为AC 的中点,O 为ABC 的重心,PO ⊥底面ABC .AO AB ==,PO ==.故133P ABC ABC V S PO -=⋅=△.5.2【分析】过AB 作与SC 垂直的截面ABM .通过13S ABC ABM V SC S -=⋅△,分析即得解.【详解】过AB 作平面ABM SC ⊥且SC 平面ABM M =,如图所示,由题意知SAC 、SBC △均为直角三角形.∵4SC =,30ASC BSC ∠=∠=︒,故SAC SBC ≅ ,∴SA =,2CA =,∴SA ACAM BM SC⋅==.∴2141sin 2sin 2332S ABCABM V SC S AMB AMB -=⋅=⨯⨯∠=∠≤△.∴三棱锥S ABC -体积的最大值为2.故答案为:26.(1)证明见解析;(2)112B D =【分析】(1)方法二:通过已知条件,确定三条互相垂直的直线,建立合适的空间直角坐标系,借助空间向量证明线线垂直;(2)方法一:建立空间直角坐标系,利用空间向量求出二面角的平面角的余弦值最大,进而可以确定出答案;【详解】(1)[方法一]:几何法因为1111,//BF AB AB AB ⊥,所以BF AB ⊥.又因为1AB BB ⊥,1BF BB B ⋂=,所以AB ⊥平面11BCC B .又因为2AB BC ==,构造正方体1111ABCG A B C G -,如图所示,过E 作AB 的平行线分别与AG BC ,交于其中点,M N ,连接11,AM BN ,因为E ,F 分别为AC 和1CC 的中点,所以N 是BC 的中点,易证1Rt Rt BCF B BN ≅ ,则1CBF BBN ∠=∠.又因为1190BBN BNB ∠+∠=︒,所以1190CBF BNB BF BN ∠+∠=︒⊥,.又因为111111,BF AB BN AB B ⊥= ,所以BF ⊥平面11A MNB .又因为ED ⊂平面11A MNB ,所以BF DE ⊥.[方法二]【最优解】:向量法因为三棱柱111ABC A B C -是直三棱柱,1BB ∴⊥底面ABC ,1B B AB ∴⊥11//A B AB ,11BF A B ⊥,BF AB ∴⊥,又1BB BF B ⋂=,AB ∴⊥平面11BCC B .所以1,,BA BC BB 两两垂直.以B 为坐标原点,分别以1,,BA BC BB 所在直线为,,x y z 轴建立空间直角坐标系,如图.()()()0,0,0,2,0,0,0,2,0,B A C ∴()()()1110,0,2,2,0,2,0,2,2B A C ,()()1,1,0,0,2,1E F .由题设(),0,2D a (02a ≤≤).因为()()0,2,1,1,1,2BF DE a ==--,所以()()0121120BF DE a ⋅=⨯-+⨯+⨯-=,所以BF DE ⊥.[方法三]:因为11BF A B ⊥,11//A B AB ,所以BF AB ⊥,故110BF A B ⋅= ,0BF AB ⋅=,所以()11BF ED BF EB BB B D ⋅=⋅++ ()11=BF B D BF EB BB ⋅+⋅+ 1BF EB BF BB =⋅+⋅ 11122BF BA BC BF BB ⎛⎫=--+⋅ ⎪⎝⎭11122BF BA BF BC BF BB =-⋅-⋅+⋅ 112BF BC BF BB =-⋅+⋅111cos cos 2BF BC FBC BF BB FBB =-⋅∠+⋅∠1=2202-⨯⨯,所以BF ED ⊥.(2)[方法一]【最优解】:向量法设平面DFE 的法向量为(),,m x y z =,因为()()1,1,1,1,1,2EF DE a =-=--,所以00m EF m DE ⎧⋅=⎨⋅=⎩ ,即()0120x y z a x y z -++=⎧⎨-+-=⎩.令2z a =-,则()3,1,2m a a =+-因为平面11BCC B 的法向量为()2,0,0BA =,设平面11BCC B 与平面DEF 的二面角的平面角为θ,则cos m BA m BA θ⋅=⋅==当12a =时,2224a a -+取最小值为272,此时cos θ=所以()minsin θ=112B D =.[方法二]:几何法如图所示,延长EF 交11A C 的延长线于点S ,联结DS 交11B C 于点T ,则平面DFE 平面11B BCC FT =.作1BH FT ⊥,垂足为H ,因为1DB ⊥平面11BB C C ,联结DH ,则1D H B ∠为平面11BB C C 与平面DFE 所成二面角的平面角.设1,B D t =[0,2],t ∈1B T s =,过1C 作111//CG AB 交DS 于点G .由111113C S C G SA A D ==得11(2)3C G t =-.又1111B D BT C G C T=,即12(2)3t s s t =--,所以31t s t =+.又111B H BT C F FT =,即11B H =,所以1B H =所以DH ==则11sin B D DHB DH∠===所以,当12t =时,()1min 3sin 3DHB ∠=.[方法三]:投影法如图,联结1,FB FN,DEF 在平面11BB C C 的投影为1BN F ,记面11BB C C 与面DFE 所成的二面角的平面角为θ,则1cos B NF DEFS S θ=.设1(02)BD t t =≤≤,在1Rt DB F中,DF ==在Rt ECF中,EF =D 作1B N 的平行线交EN 于点Q .在Rt DEQ △中,DE ==在DEF 中,由余弦定理得222cos 2DF EF DE DFE DF EF+-∠=⋅=,sin DFE ∠1sin 2DFE S DF EF DFE =⋅∠ =13,2B NF S = 1cos B NF DFES S θ==,sin θ,当12t =,即112B D =,面11BB C C与面DFE 所成的二面角的正弦值最小,最小值为3.【整体点评】第一问,方法一为常规方法,不过这道题常规方法较为复杂,方法二建立合适的空间直角坐标系,借助空间向量求解是最简单,也是最优解;方法三利用空间向量加减法则及数量积的定义运算进行证明不常用,不过这道题用这种方法过程也很简单,可以开拓学生的思维.第二问:方法一建立空间直角坐标系,利用空间向量求出二面角的平面角是最常规的方法,也是最优方法;方法二:利用空间线面关系找到,面11BB C C 与面DFE 所成的二面角,并求出其正弦值的最小值,不是很容易找到;方法三:利用面DFE 在面11BB C C 上的投影三角形的面积与DFE △面积之比即为面11BB C C 与面DFE 所成的二面角的余弦值,求出余弦值的最小值,进而求出二面角的正弦值最小,非常好的方法,开阔学生的思维.7.C【分析】设正四棱锥的高为h ,根据题意求出正四棱锥的底面边长与高的关系,再利用导数求解即可.【详解】设球体的半径为R ,由题知:34363R ππ=,所以球的半径3R =.设正四棱锥的底面边长为2a ,高为h ,则222222l h a h =+=+,22232(3)a h =+-,所以26h l =,2222a l h =-所以正四棱锥的体积42622411214()=333366936l l l V Sh a h l l ⎛⎫==⨯⨯=⨯-⨯- ⎪⎝⎭,设()641=936x f x x ⎛⎫- ⎪⎝⎭,3x ≤≤,所以()5233112449696x x f x x x ⎛⎫⎛⎫-'=-= ⎪⎝⎭⎝⎭,当3x ≤≤()0f x ¢>,()f x 为增函数,当x <≤()0f x '<,()f x 为减函数,所以当l =时,正四棱锥的体积V 取最大值,最大值为643,又3l =时,274V =,l =814V =,所以正四棱锥的体积V 的最小值为274,所以该正四棱锥体积的取值范围是276443⎡⎤⎢⎥⎣⎦,.故选:C 8.C【分析】令四棱锥底面四边形外接圆半径为r ,用r 表示四棱锥的高及底面四边形面积最大值,再借助导数求解作答.【详解】设该四棱锥底面四边形为ABCD ,平面ABCD 截球O 所得小圆半径为r ,则球心O到平面ABCD 的距离h =设四边形ABCD 对角线,AC BD 的夹角为α,则1sin 2ABCD S AC BD α=⋅,于是得该四棱锥的体积:12sin 22sin 36623ABCD V S h BD r r rπα=⋅=⋅≤⋅⋅=当且仅当对角线,AC BD 是截面小圆互相垂直的两条直径,即四边形ABCD 为正方形时取等号,令2(0,1)r x =∈,有23r =23(),(0,1)f x x x x =-∈,求导得:22()233()3f x x x x x '=-=-,当203x <<时,()0f x '>,当213x <<时,()0f x '<,因此函数()f x 在2(0,)3上单调递增,在2(,1)3上单调递减,当23x =时,23max 224()(()3327f x =-=,从而当223r =时,max 222(333r =⨯⨯max V =,此时3h ==,故选:C9.(1)证明见解析;【分析】(1)利用线面垂直的判定定理可得AC ⊥平面BED ,然后根据面面垂直的判定定理可得平面BED ⊥平面ACD ;(2)首先判断出三角形AFC 的面积最小时F 点的位置,然后求得F 到平面ABC 的距离,从而求得三棱锥F ABC -的体积或利用等积法及锥体的体积公式即得.【详解】(1)AD CD = ,ADB BDC ∠=∠,BD BD =,ADB CDB ∴≅ ,AB BC ∴=,又E 为AC 的中点.AC BE ∴⊥,AD CD = ,E 为AC 的中点.AC DE ∴⊥,又BE DE E = ,BE ⊂平面BED ,DE ⊂平面BED ,AC ∴⊥平面BED ,又AC ⊂ 平面ACD ,∴平面BED ⊥平面ACD ;(2)方法一:依题意2AB BD BC ===,60ACB ∠=︒,三角形ABC 是等边三角形,所以2,1,AC AE CE BE ====由于,AD CD AD CD =⊥,所以三角形ACD 是等腰直角三角形,所以1DE =,所以222DE BE BD +=,即DE BE ⊥,由于AC BE E ⋂=,,AC BE ⊂平面ABC ,所以DE ⊥平面ABC ,由于ADB CDB ≅△△,所以FBA FBC ∠=∠,由于BF BFFBA FBC AB CB =⎧⎪∠=∠⎨⎪=⎩,所以FBA FBC ≅ ,所以AF CF =,所以EF AC ⊥,由于12AFC S AC EF =⋅⋅ ,所以当EF 最短时,三角形AFC 的面积最小,过E 作EF BD ⊥,垂足为F ,在Rt BED △中,1122BE DE BD EF ⋅⋅=⋅⋅,解得2EF =,所以13,222DF BF DF ===-=,所以34BF BD =,过F 作FH BE ⊥,垂足为H ,则//FH DE ,又DE ⊥平面ABC ,所以FH ⊥平面ABC ,且34FH BF DE BD ==,所以34FH =,所以111323324F ABC ABC V S FH -=⋅⋅=⨯⨯=方法二:AB BC = ,60ACB ∠=︒,2AB =ABC ∴ 是边长为2的等边三角形,BE ∴=连接EF ,由于ADB CDB ≅△△,所以FBA FBC ∠=∠,由于BF BFFBA FBC AB CB =⎧⎪∠=∠⎨⎪=⎩,所以FBA FBC ≅ ,所以AF CF =,所以EF AC ⊥,由于12AFC S AC EF =⋅⋅ ,所以当EF 最短时,三角形AFC 的面积最小,即EF BD ⊥时,AFC △的面积最小,,,2AD CD AD CD AC ⊥== ,E 为AC 的中点,∴1DE =,222DE BE BD +=,BE ED ∴⊥,在Rt BED △中,1122BE DE BD EF ⋅⋅=⋅⋅,解得2EF =,∴32BF ,113222BEF S BF EF ∴=⋅=⋅11233F ABC A BEF C BEF BEF V V V S AC ---∴=+=⋅=⋅= .10.6【分析】取AC 中点O ,连接OB ,过点O 作Oz ⊥平面ABC ,以点O 为原点建立空间直角坐标系,设二面角D AC B '--的大小为α,把直线A C 与BD '所成角的余弦表示为α的函数,求出函数最大值作答.【详解】在ACD 中,90ADC ∠= ,1,CD AD ==则AC =,过D 作DH AC ⊥于H ,连接D H ',如图,显然D H AC '⊥,ACD 绕直线AC 旋转过程中,线段DH 绕点H 在垂直于直线AC 的平面γ内旋转到D H ',取AC 中点O ,连接OB ,因3AB BC ==,有OB AC ⊥,OB =,,663CD ADD H DH CH OH AC⋅'=====,过点O 作Oz ⊥平面ABC ,以点O 为原点,射线,,OB OA Oz 分别为,,x y z 轴非负半轴,建立空间直角坐标系,则A ,B ,(0,2C -,显然有//Oz 平面γ,设二面角D AC B '--的大小为[0,]απ∈,有(,,sin )636D αα'-,则有(,sin )6236BD αα=--' ,CA的方向向量为(0,1,0)n = ,设直线AC 与BD '所成的角为θ,于是得||cos |cos ,|||||n BD n BD n BD θ'⋅'=〈〉=='因[0,]απ∈,则1cos 1α-≤≤,于是得cos 6θ=,当且仅当cos 1α=取等号,所以直线AC 与BD '11.A【分析】取BD 中点O ,连接AO ,CO ,以O 为原点建立空间直角坐标系,利用二面角A BD C --的大小θ的正余弦表示,AB CD的坐标,利用空间向量建立函数关系求解作答.【详解】取BD 中点O ,连接AO ,CO ,而AB =BD =DA =2,BC =CD,则CO ⊥BD ,AO ⊥BD ,且CO =1,AOAOC ∠是二面角A BD C --的平面角,令5[,]66AOC ππθ∠=∈,显然有BD ⊥平面AOC ,BD ⊂平面BCD ,则平面AOC ⊥平面BCD ,在平面AOC 内过O 作Oz OC ⊥,而平面AOC I 平面BCD OC =,因此Oz ⊥平面BCD ,即射线,,OC OD Oz 两两垂直,以O 为原点,射线,,OC OD Oz 分别为,,x y z轴非负半轴,建立空间直角坐标系,如图,则(0,1,0),(1,0,0),(0,1,0)B C D -,)A θθ,,1,),(1,1,0)BA CD θθ==-,设直线AB 与CD 所成的角为α,则||cos |cos ,|||||AB CD AB CD AB CD α⋅=〈〉==,由5[,66ππθ∈得:cos [,]22θ∈,15122θ-≤≤,则5|1|[0,2θ∈,于是得cos[0,]α∈,8.所以直线AB与CD 所成角的余弦值取值范围是[0,]8故选:A答案第18页,共18页。
立体几何压轴小题:06空间线段以及线段之和最值问题(含解析)

第6讲空间线段以及线段之和最值问题一、单选题1.(2024·湖北·校联考模拟预测)已知四棱锥P ABCD -的底面为矩形,AB =4BC =,侧面PAB 为正三角形且垂直于底面ABCD ,M 为四棱锥P ABCD -内切球表面上一点,则点M 到直线CD 距离的最小值为()A 2B1C .2D .12.(2024上·江西萍乡·高二统考期末)以等腰直角三角形斜边BC 上的高AD 为折痕,把ABD △和ACD 折成60的二面角.若AB ,()1DM xDA yDB x y DC =++--,其中,x y ∈R ,则DM 的最小值为()A B .7C .14D .73.(2024上·四川成都·高三树德中学校考期末)如图,已知正方体1111ABCD A B C D -的棱长为2,P 为底面正方形ABCD 内(含边界)的一动点,则下列结论中:①若点Q 为1CC 的中点,则1PA PQ +②过点P 作与1AD 和1BA 都成π6的直线,可以作四条;③若点P 为BC 的中点时,过点C 作与直线1D P 垂直的平面α,则平面α截正方体1111ABCD A B C D -的截面周长为④若点P 到直线1BB 与到直线AD 的距离相等,CD 的中点为E ,则点P 到直线AE 的最短距离是3510.其中正确的命题有()A .4个B .3个C .2个D .1个4.(2024·全国·高三专题练习)在空间直角坐标系O xyz -中,已知点()1,0,2A ,()0,2,1B ,点C ,D 分别在x 轴,y 轴上,且AD BC ⊥,那么CD的最小值是()AB C D5.(2024上·黑龙江大庆·高三校考阶段练习)已知直四棱柱1111ABCD A B C D -的底面ABCD 为矩形,1AA =且该棱柱外接球O 的表面积为20π,E 为线段AB 上一点.则当该四棱柱的体积取最大值时,1D E CE +的最小值为()A .6BC .2D .二、多选题6.(2024下·山东·高三校联考开学考试)在长方体1111ABCD A B C D -中,12,1,AB AA AD E ===为11A B 的中点,点P 满足1(01)DP DB λλ=<<,则()A .若M 为1A D 的中点,则三棱锥P BEM -体积为定值B .存在点P 使得AP BE ⊥C .当23λ=时,平面PBC 截长方体1111ABCD A B C D -D .若Q为长方体1111ABCD A B C D -外接球上一点,23λ=,则3QE QP +7.(2024·广西南宁·南宁三中校联考一模)在边长为2的正方体1111ABCD A B C D -中,动点M 满足1AM xAB y AD z AA =++,(,,R x y z ∈且0,0,0)x y z ≥≥≥,下列说法正确的是()A .当[]1,0,0,14x z y ==∈时,1B M MD +B .当11,2x y z ===时,异面直线BM 与1CD 所成角的余弦值为5C .当1x y z ++=,且AM =MD .当1,0x y z +==时,AM 与平面11AB D 8.(2024下·江西·高三校联考开学考试)化学中经常碰到正八面体结构(正八面体是每个面都是正三角形的八面体),如六氟化硫(化学式6SF )、金刚石等的分子结构.将正方体六个面的中心连线可得到一个正八面体(如图1),已知正八面体E ABCD F --的(如图2)棱长为2,则()A .正八面体E ABCD F --的内切球表面积为8π3B .正八面体E ABCD F --的外接球体积为8π3C .若点P 为棱EB 上的动点,则AP CP +的最小值为D .若点Q 为棱AF 上的动点,则三棱锥E QBC -的体积为定值2239.(2024下·安徽·高三池州市第一中学校联考开学考试)已知棱长为2的正方体1111ABCD A B C D -中,动点M 在棱1DD 上,记平面1BC M 截正方体所得的截面图形为Ω,则()A .平面1A BC ⊥平面11BC DB .不存在点M ,使得直线CM //平面11BA CC .1B M CM +的最小值为D .Ω的周长随着线段DM 长度的增大而增大10.(2024下·江西上饶·高二上饶市第一中学校考开学考试)在正方体1111ABCD A B C D -中,4AB E F =,,分别为1,BB CD 的中点,点P 满足1,[0,1]BP BC =∈λλ,则()A .1A F ⊥平面1AD EB .三棱锥1P AD E -的体积与P 点的位置有关C .1DP B P +的最小值为4+D .当10,3λ⎛⎤∈ ⎥⎝⎦时,平面PEF 截正方体的截面形状为五边形11.(2024下·湖北·高二应城市第一高级中学校联考开学考试)棱长为1的正方体1111ABCD A B C D -中,点P满足1DP DD DA λμ=+,[]0,1λ∈,[]0,1u ∈,则下面结论正确的是:()A .当λμ=时,1BP AC ⊥B .当12μ=时,三棱锥11C PB C -的体积为定值C .当1λμ+=时,直线CP 与平面11BCC B 所成的角不可能为π3D .当1λμ+=时,PC PB +12.(2024下·重庆·高三重庆八中校考开学考试)已知正四棱柱1111ABCD A B C D -的底面边长为1,12AA =,点P 在底面ABCD 内运动(含边界),点Q 满足[]1,0,1CQ mCC m =∈ ,则()A .当12m =时,1A P PQ +B .当14m =时,存在点P ,使1A PQ ∠为直角C .当78m =时,满足11D P A Q ⊥的点P 的轨迹平行平面1C BD D .当116m =时,满足1A P PQ ⊥的点P 的轨迹围成的区域的面积为π413.(2023上·河北保定·高三校联考阶段练习)在三棱锥1A ABC -中,1A A ⊥平面ABC ,AB AC ⊥,13AA AB AC ===,P 为1A BC 内的一个动点(包括边界),AP 与平面1A BC 所成的角为45 ,则()A .1A P -B .1A P C .有且仅有一个点P ,使得1A P BC ⊥D .所有满足条件的线段AP 形成的曲面面积为414.(2024上·江苏常州·高三统考期末)在棱长为2的正方体1111ABCD A B C D -中,P 在线段1BD 上运动(包括端点),下列说法正确的有()A .存在点P ,使得⊥CP 平面1A DBB .不存在点P ,使得直线1C P 与平面1A DB 所成的角为30 C .PC PD +的最小值为D .以P 为球心,PA 为半径的球体积最小时,被正方形11ADD A 截得的弧长是π315.(2024上·安徽蚌埠·高二统考期末)如图,正方体1111ABCD A B C D -的棱长为2,点M ,N 分别是棱11A D ,CD 的中点,点P 在四边形ABCD 内,若PM =,则下列结论正确的有()A .MN BD⊥B .MN //1A BC .点P 的轨迹长度为πD .PN 116.(2024上·江苏南京·高二南京市第九中学校考期末)已知正方体1111ABCD A B C D -的棱长为1,点E 满足()101,01BE BC BB λμλμ=+≤≤≤≤,则()A .若λμ=,则1BC AE⊥B .若1λμ+=,则1B C 平面1A DEC .若1λμ+=,则1AE D E +D .若221λμ+=,则AE 与平面11BB C C 的所成角为定值π417.(2024上·湖南·高二湖南师大附中校考期末)下列有关正方体的说法,正确的有()A .正方体的内切球、棱切球、外接球的半径之比为B .若正方体1111ABCD A BCD -的棱长为1,Q 为正方体侧面11BCC B 上的一个动点,,EF 为线段1AC 的两个三等分点,则QE QF +C .若正方体8个顶点到某个平面的距离为公差为1的等差数列,则正方体的棱长为D .若正方体ABCD A B C D -''''的棱长为3,点P 在棱CC '上,且2PC PC =',则三棱锥B D AP '-'的外接球表面积为99π418.(2024上·山西太原·高三统考期末)在棱长为1的正方体1111ABCD A B C D -中,E 为线段1B C 的中点,点P 和Q 分别满足111D P D C λ=,11D Q D B μ=,其中λ,[0,1]μ∈,则下列结论正确的是()A .当12λ=时,三棱锥Q PDE -的体积为定值B .当12μ=时,四棱锥Q ABCD -的外接球的表面积是9π4C .当1λ=时,不存在μ使得11PQ BD ⊥D .PQ EQ +的最小值为619.(2024上·湖南衡阳·高二统考期末)已知四棱台1111ABCD A B C D -的底面为正方形,棱1AA ⊥底面ABCD ,且11122AD AA A D ===,则下列说法正确的是()A .直线1CD 与平面1A BD 相交B .若直线1AC 与平面11BDD B 交于点M ,则M 为线段1AC 的中点C .平面1ACD 将该四棱台分成的大、小两部分体积之比为5:2D .若点,P Q 分别在直线11,AA CD 上运动,则线段PQ 20.(2024上·宁夏固原·高二统考期末)如图,在长方体1111ABCD A B C D -中,14,2,3,AB BC CC M ===为11B C 的中点,,P Q 分别是直线1,CC AM 上的动点,则下列结论正确的是()A .三棱锥A BDM -的体积为4B .1AC =C .直线1,AC BDD .PQ 21.(2023上·福建泉州·高三福建省泉州第一中学校考阶段练习)在正方体1111ABCD A B C D -中,4AB E F =,,分别为1,BB CD 的中点,,点P 满足1B B C P λ=,[]01λ∈,,则()A .1A F ⊥平面1AD EB .三棱锥1P AD E -的体积与P 点的位置有关C .1DP B P +的最小值为4+D .当10,3λ⎛⎫∈ ⎪⎝⎭时,平面PEF 截正方体的截面形状为五边形22.(2023上·河北石家庄·高三石家庄市第二十七中学校考阶段练习)已知正方体1111ABCD A B C D -的棱长为1,点P 满足1CP CD CC λμ=+,其中[][],0,10,1λμ∈∈,以下结论正确的是()A .当1λ=时,1B P AC⊥B .当λμ=时,DP AP +C .当1B P PC ⊥时,BP 的最大值2D .若1B P 与平面11CC D D 所成角为π4,则点P 的轨迹长度为π23.(2023上·山东·高三校联考阶段练习)如图,已知菱形ABCD 的边长为2,60ADC ∠=︒,将ACD 沿AC 翻折为三棱锥-P ABC ,点P 为翻折过程中点D 的位置,则下列结论正确的是()A .无论点P 在何位置,总有AC PD ⊥B .点P 存在两个位置,使得1P ABC V -=成立C .当PB =AD 旋转所形成的曲面的面积为2D .当2PB =时,M 为PB 上一点,则AM CM +的最小值为24.(2023·山西临汾·校考模拟预测)如图,在正四棱柱1111ABCD A B C D -中,122AA AB ==,E ,F ,N 分别是棱1CC ,11C D ,1AA 的中点,P 是NC 上一点,Q 在平面ABCD 内,则()A .CN ⊥平面BDEB .直线BE 与1A F 是异面直线C .当BP 取得最小值时,BP PQ +61+D .直线NC 与平面BDE 的交点是BDE △的外心25.(2023上·山东济南·高二山东省济南市莱芜第一中学校考阶段练习)已知正方体1111ABCD A B C D -的棱长为1,P 为线段11A C 上任意一点,下列说法正确的是()A .1PD BD ⊥B .动点P 到线段BD 2C .P 是11A C 中点时,直线PD 与平面1A BD 所成的角的正弦值是23D .三棱锥1P A BD -体积最大时,若点M 满足1OM xOA yOB zOD =++,其中1x y z ++=,则PM 的2326.(2023上·黑龙江大庆·高三大庆实验中学校考期末)如图,已知正方体1111ABCD A B C D -的棱长为2,P 为底面正方形ABCD 内(含边界)的一动点,则下列结论正确的是()A .存在点P ,使得1C P ⊥平面11B CD B .三棱锥111B A D P -的体积为定值C .当点P 在棱CD 上时,1PA PB +的最小值为2+D .若点P 到直线1BB 与到直线AD 的距离相等,CD 的中点为E ,则点P 到直线AE 27.(2024上·湖南长沙·高三长沙一中校考阶段练习)四棱锥P ABCD -的底面为正方形,PA 与底面垂直,2PA =,1=AB ,动点M 在线段PC 上,则()A .不存在点M ,使得AC BM ⊥B .MB MD +C .四棱锥P ABCD -的外接球表面积为6πD .点M 到直线AB 28.(2024上·黑龙江哈尔滨·高三哈尔滨三中校考期末)在棱长为1的正方体1111ABCD A B C D -中,下列结论正确的有()A .11//AC 平面1B CDB .点1C 到平面1B CD 的距离为22C .当P 在线段11CD 上运动时,三棱锥11A B PC -的体积不变D .若Q 为正方体侧面11BCC B 上的一个动点,,EF 为线段1AC 的两个三等分点,则QE QF +的最小值为3三、填空题29.(2024上·广东·高二统考期末)如图,正方形ABCD 和正方形ABEF 的边长都是1,且它们所在的平面所成的二面角D AB F --的大小是60︒,则直线AC 和BF 夹角的余弦值为.若,M N 分别是,AC BF 上的动点,且AM BN =,则MN 的最小值是.30.(2024上·江西九江·高二统考期末)如图,正三棱锥-P ABC 中,三条侧棱,,PA PB PC 两两垂直且相等,2,PA M =为PC 的中点,N 为平面ABC 内一动点,则NM NP +的最小值为.31.(2024上·浙江宁波·高三余姚中学校联考期末)在棱长为1的正方体1111ABCD A B C D -中,,,E F M 分别是棱1111,,B C C D AB 的中点,,G H 分别是线段1,AC EF 上的动点,则GH GM +的最小值为.32.(2024上·河北邯郸·高二统考期末)如图,正三棱柱111ABC A B C -的底面边长为2,侧棱长为3,D 为BC的中点,设()1111,01A P A B DQ DC λλλ==≤≤,则PQ 的最小值为.33.(2024上·四川成都·高三石室中学校考期末)如图,在三棱锥111A A B C -中,1AA ⊥平面111A B C ,11190A B C ∠=︒,11111222A B A A B C ===,P 为线段1AB 的中点,,M N 分别为线段1AC 和线段11B C 上任意一点,MN+的最小值为.34.(2024上·重庆·高二统考期末)一种糖果的包装纸由一个边长为3的正方形和两个等腰直角三角形组成(如图1),沿AD ,BC 将这两个三角形折起到与平面ABCD 垂直(如图2),连接EF ,AE ,CF ,AC ,若点G 满足DG xDA yDC zDF =++且1x y z ++=,则||EG 的最小值为.35.(2024上·上海·高二上海市复旦中学校考期末)已知在直三棱柱111ABC A B C -中,底面为直角三角形,90ACB ∠=︒,6AC =,1BC CC ==P 是1BC 上一动点,则1CP PA +的最小值为.36.(2023上·河北石家庄·高二石家庄一中校考阶段练习)正方体1111ABCD A B C D -的棱长为2,点M 在线段DC 上,且DM ,动点P 在正方形ABCD 内运动(含边界),若1D P =,则当1B P 取得最小值时,三棱锥1B MPB -外接球的表面积为37.(2024·河南·方城第一高级中学校联考模拟预测)在棱长为1的正方体1111ABCD A B C D -中,M ,N 分别为线段1A D 和11B D 上的动点,且12D N DM =,则MN 的最小值为.38.(2024·全国·模拟预测)如图,在长方体1111ABCD A B C D -中,3AB =,12BC CC ==,M ,N 分别为BC ,1CC 的中点,点P 在矩形11BCC B 内运动(包括边界),若1//A P 平面AMN ,则1A P 取最小值时,三棱锥1P MA B-的体积为.39.(2023上·上海·高二格致中学校考阶段练习)已知直三棱柱111ABC A B C -,底面三角形ABC 是等腰直角三角形,其中B 为直角顶点,且13,AB AA ==D 为棱1AA 的中点,点M 为平面BCD 的一动点,则11B M C M +的最小值是.第6讲空间线段以及线段之和最值问题一、单选题1.(2024·湖北·校联考模拟预测)已知四棱锥P ABCD -的底面为矩形,AB =4BC =,侧面PAB 为正三角形且垂直于底面ABCD ,M 为四棱锥P ABCD -内切球表面上一点,则点M 到直线CD 距离的最小值为()A 2B1C .2D .1【答案】B【解析】如图,设四棱锥的内切球的半径为r ,取AB 的中点为H ,CD 的中点为N ,连接PH ,PN ,HN ,球O 为四棱锥P ABCD -的内切球,底面ABCD 为矩形,侧面PAB 为正三角形且垂直于底面ABCD ,则平面PHN 截四棱锥P ABCD -的内切球O 所得的截面为大圆,此圆为PHN 的内切圆,半径为r ,与HN ,PH 分别相切于点E ,F ,平面PAB ⊥平面ABCD ,交线为AB ,PH ⊂平面PAB ,PAB 为正三角形,有PH AB ⊥,PH ∴⊥平面ABCD ,HN ⊂平面ABCD ,PH HN ∴⊥,AB =4BC =,则有3PH =,4HN =,5PN =,则PHN 中,()113434522PHN S r =⨯⨯=++ ,解得1r =.所以,四棱锥P ABCD -内切球半径为1,连接ON .PH ⊥Q 平面ABCD ,CD ⊂平面ABCD ,CD PH ∴⊥,又CD HN ⊥,,PH HN Ì平面PHN ,PH HN H = ,CD \^平面PHN ,ON ⊂ 平面PHN ,可得ON CD ⊥,所以内切球表面上一点M 到直线CD 的距离的最小值即为线段ON 的长减去球的半径,又ON ==所以四棱锥P ABCD -内切球表面上的一点M 到直线CD 1.故选:B.2.(2024上·江西萍乡·高二统考期末)以等腰直角三角形斜边BC 上的高AD 为折痕,把ABD △和ACD 折成60的二面角.若AB ,()1DM xDA yDB x y DC =++--,其中,x y ∈R ,则DM 的最小值为()A .21B C .14D .7【答案】D【解析】由已知得,AD BD AD CD ⊥⊥,所以BDC ∠是ABD △和ACD 折成60 的二面角的平面角,所以60BDC ∠= ,又AB =,所以1AB AC AD BD CD =====,222+2cos 601BC AD CD AD CD =-⋅⋅= ,所以1BC =,因为()1DM xDA yDB x y DC =++-- ,其中,x y ∈R ,所以点M 在平面ABC 内,则DM的最小值为点D 到平面ABC 的距离,设点D 到平面ABC 的距离为h ,因为,AD BD AD CD ⊥⊥,BD CD D ⋂=,BD ⊂平面BDC ,CD ⊂平面BDC ,所以AD ⊥平面BDC ,所以AD 是点A 到平面BDC 的距离,所以111111sin 332A BDC BDC V AD S BDC -=⨯⨯=⨯⨯⨯⨯⨯∠=又ABC 中,1AB AC BC ===,所以2223cos 24AB AC BC BAC AB AC +-∠==⋅⋅,所以7sin 4BAC ∠=,则11sin 2244ABC S AB AC BAC =⋅⋅∠==,所以1133412D ABC ABC V h S h -=⨯⨯=⨯⨯ ,解得h DM 的最小值为7,故选:D.3.(2024上·四川成都·高三树德中学校考期末)如图,已知正方体1111ABCD A B C D -的棱长为2,P 为底面正方形ABCD 内(含边界)的一动点,则下列结论中:①若点Q 为1CC 的中点,则1PA PQ +②过点P 作与1AD 和1BA 都成π6的直线,可以作四条;③若点P 为BC 的中点时,过点C 作与直线1D P 垂直的平面α,则平面α截正方体1111ABCD A B C D -的截面周长为④若点P 到直线1BB 与到直线AD 的距离相等,CD 的中点为E ,则点P 到直线AE 的最短距离是10.其中正确的命题有()A .4个B .3个C .2个D .1个【答案】C【解析】在棱长为2的正方体1111ABCD A B C D -中,延长QC 到Q ',使1CQ '=,由点Q 为1CC 的中点,得平面ABCD 是线段QQ '的中垂面,连接111,A Q A C ',则PQ PQ '=,111PA PQ PA PQ AQ ''+=+≥===,当且仅当点P 为直线1A Q '与平面ABCD 的交点时取等号,①正确;连接1BC ,四边形11ABC D 是正方体1AC 的对角面,则四边形11ABC D 是矩形,即11//BC AD ,显然1111A B BC AC ==,则11π3A BC ∠=,11A BC ∠的平分线与直线11,BA BC 都成π6的角,显然在空间过点B 作与直线11,BA AD 都成π6角的直线只有1条,则过空间任意点作与直线11,BA AD 都成π6角的直线只有1条,②错误;当点P 为BC 的中点时,取1,BB BA 的中点,F G ,连接1,,,CG CF GF C P ,显然Rt BCF ≌1Rt CC P ,则1BCF CC P ∠=∠,111π2CPC BCF CPC CC P ∠+∠=∠+∠=,即有1CF C P ⊥,而11D C ⊥平面11BCC B ,CF ⊂平面11BCC B ,则11CF D C ⊥,又1111111,,D C C P C D C C P =⊂ 平面11D C P ,于是CF ⊥平面11D C P ,而1D P ⊂平面11D C P ,因此1CF D P ⊥,同理1CG D P ⊥,显然,,CG CF C CG CF =⊂ 平面CGF ,所以CGF △是平面α截正方体1111ABCD A B C D -所得截面,其周长为25GF CG CF ++=,③错误;由于1BB ⊥平面ABCD ,则点P 到直线1BB 距离等于PB ,即点P 到点B 的距离等于它到直线AD 的距离,因此点P 轨迹是以点B 为焦点,直线AD 为准线的抛物线在正方形ABCD 及内部,以线段AB 中点O 为原点,建立如图所示的平面直角坐标系,点P 轨迹方程为24(02)y x y =≤≤,直线AE 的方程为22y x =+,令000(,21)P x x x ≤,因此点P 到直线AE :220x y -+=的距离0020|222|213()25525x x d x -+=-+,于是当014x =,即点1(,1)4P 时,min 3510d =所以正确命题的个数为2.故选:C4.(2024·全国·高三专题练习)在空间直角坐标系O xyz -中,已知点()1,0,2A ,()0,2,1B ,点C ,D 分别在x 轴,y 轴上,且AD BC ⊥,那么CD的最小值是()AB C .2D 【答案】B【解析】设(),0,0C x ,()0,,0D y ,且()1,0,2A ,()0,2,1B ,∴()1,,2AD y =-- ,(),2,1BC x =-- ,又AD BC ⊥,∴220AD BC x y ⋅=--+=,即22x y +=.∵(),,0CD x y =-,∴CD =当且仅当45y =时等号成立.故选:B5.(2024上·黑龙江大庆·高三校考阶段练习)已知直四棱柱1111ABCD A B C D -的底面ABCD 为矩形,1AA =且该棱柱外接球O 的表面积为20π,E 为线段AB 上一点.则当该四棱柱的体积取最大值时,1D E CE +的最小值为()A .6BC .2D .【答案】D【解析】设外接球O 的半径为R ,则球O 的表面积24π20πS R ==,所以R设矩形ABCD 的长和宽分别为x 和y ,则((2222x y ++=,所以228x y+=,)111122ABCD A B C D V x y -=≤+=,当且仅当2x y ==时取等号,即底面为边长为2的正方形时,四棱柱的体积最大.则有14BC ===,将平面ABCD 沿AB 展开,与11ABC D 处于同一平面,则11D E EC D C +≥=即平面图形中1,,D E C 三点共线时,1D E CE +有最小值故选:D 二、多选题6.(2024下·山东·高三校联考开学考试)在长方体1111ABCD A B C D -中,12,1,AB AA AD E ===为11A B 的中点,点P 满足1(01)DP DB λλ=<<,则()A .若M 为1A D 的中点,则三棱锥P BEM -体积为定值B .存在点P 使得AP BE ⊥C .当23λ=时,平面PBC 截长方体1111ABCD A B C D -D .若Q为长方体1111ABCD A B C D -外接球上一点,23λ=,则3QE QP +【答案】ACD【解析】对于A :因为M 为1A D 的中点,E 为11A B 的中点,所以1//DB EM ,1DB ⊄面BEM ,EM ⊂面BEM ,所以1//DB 面BEM ,故A 正确;则P 到面BEM 的距离为定值,所以体积为定值.对于B :AP 在平面11ABB A 的投影为1AB ,设P 在平面11ABB A 的投影为G ,则G 在直线1AB 上.则PG ⊥平面11ABB A ,BE ⊂平面11ABB A ,所以PG BE ⊥,若AP BE ⊥,PG AP P ⋂=,所以BE ⊥平面APG ,1AB ⊂平面APG ,则1AB BE ⊥,因为四边形11ABB A 为正方形,所以1AB 与BE 不垂直,所以B 错.对于C :平面PCD 与平面1B CD 重合,平面1B CD 与平面11DCB A 重合,所以延长CP 会与11A B 有交点,因为123DP DB =,所以延长CP 与11A B 交于点E ,取11C D 中点F ,则平面PBC 截长方体1111ABCD A B C D -所得截面为矩形BCFE C 正确;对于D :长方体1111ABCD A B C D -外接球球心为1B D 中点,半径为132,23DP DB =,由阿氏球得,在直线1B D 上必存在一点N ,使得3QP QN =,此时点N 在1DB 延长线上,且满足13B N =,以D 为原点,建系如图,13,6DB DN ==所以12DN DB =,则()4,2,4N ,因为()1,1,2E ,所以min min (3)()QE QP QE QN NE +=+==D 正确.故选:ACD.7.(2024·广西南宁·南宁三中校联考一模)在边长为2的正方体1111ABCD A B C D -中,动点M 满足1AM xAB y AD z AA =++,(,,R x y z ∈且0,0,0)x y z ≥≥≥,下列说法正确的是()A .当[]1,0,0,14x z y ==∈时,1B M MD +B .当11,2x y z ===时,异面直线BM 与1CD 所成角的余弦值为105C .当1x y z ++=,且3AM =时,则M 的轨迹长度为3D .当1,0x y z +==时,AM 与平面11AB D 所成角的正弦值的最大值为3【答案】AD【解析】对于A ,在AB 上取点H ,使14AH AB = ,在DC 上取点K ,使14DK DC =,因为[]1,0,0,14x z y ==∈,即14AM AB y AD =+ ,故M 点在HK 上,将平面11B HKC 与平面AHKD 沿着HK 展开到同一平面内,如图:连接1B D 交HK 于P ,此时,,B P D 三点共线,1B M MD +取到最小值即1B D 的长,由于113,422AH AB BH ==∴= ,则152B H ==,故11513,22A B B D =+=∴即此时1B M MD +A 正确;对于B ,由于11,2x y z ===时,则111122AM AB AD AA AC CC =++=+ ,此时M 为1CC 的中点,取11C D 的中点为N ,连接,,BM MN BN,则1MN CD ∥,故BMN ∠即为异面直线BM 与1CD 所成角或其补角,又112MN CD BM ===3BN ===,故2222223cos 2BM MN BN BMN BM MN +-+-∠===⋅而异面直线所成角的范围为π(0,]2,故异面直线BM 与1CD B 错误;对于C ,当1x y z ++=时,可得点M 的轨迹在1A BD 内(包括边界),由于1CC ⊥平面ABCD ,BD ⊂平面ABCD ,故1CC BD ⊥,又BD AC ⊥,11,,AC CC C AC CC =⊂ 平面1ACC ,故BD ⊥平面1ACC ,1AC ⊂平面1ACC ,故1BD AC ⊥,同理可证11A B AC ⊥,11,,A B BD B A B BD =⊂ 平面1A BD ,故1AC ⊥平面1A BD ,设1AC 与平面1A BD 交于点P ,由于11113222324A A BD A ABD VV --=⨯⨯==⨯⨯,1A BD 为边长为A 到平面1A BD的距离为43AP =若AM =,则MP =,即M 点落在以P 为圆心,3为半径的圆上,P 点到1A BD 三遍的距离为31223<,即M 点轨迹是以P 为圆心,3为半径的圆的一部分,其轨迹长度小于圆的周长42π3,C 错误;对于D ,因为11,B D BD BD ⊄∥平面11AB D ,11B D ⊂平面11AB D ,故BD ∥平面11AB D ,因为当1,0x y z +==时,AM AB AD =+,即M 在BD 上,点M 到平面11AB D 的距离等于点B 到平面11AB D 的距离,设点B 到平面11AB D 的距离为d ,则111111111142223323B AB D ABB ABB D V V S A D --==⋅=⨯⨯⨯⨯= ,11AB D 为边长为(12114333A BD S d d ⋅=⨯= ,解得3d =,又M 在BD 上,当M 为BD 的中点时,AM ,设直线AM 与平面11AB D 所成角为π,[0,2θθ∈,则3sind AM AM θ==AM 与平面11AB D D 正确,故选:AD8.(2024下·江西·高三校联考开学考试)化学中经常碰到正八面体结构(正八面体是每个面都是正三角形的八面体),如六氟化硫(化学式6SF )、金刚石等的分子结构.将正方体六个面的中心连线可得到一个正八面体(如图1),已知正八面体E ABCD F --的(如图2)棱长为2,则()A .正八面体E ABCD F --的内切球表面积为8π3B .正八面体E ABCD F --的外接球体积为8π3C .若点P 为棱EB 上的动点,则AP CP +的最小值为D .若点Q 为棱AF 上的动点,则三棱锥E QBC -的体积为定值223【答案】ACD【解析】对于A 项,设该正八面体内切球的半径为r ,由内切球的性质可知正八面体的体积111822sin60222323V r =⨯⨯⨯⨯⨯⋅=⨯⨯⨯ ,解得3r =,故它的内切球表面积为28π4π3⨯=⎝⎭,故A 项正确;对于B 项,设该正八面体外接球的半径为R ,由图知,ABCD 是正方形,222OA OB OC OD ====,在Rt EOB △中,OE ==,利用对称性知OF =故点O 为正八面体外接球的球心,则R =,所以正八面体外接球的体积为3,故B 项错误;对于C 项,如图,因ABE 与BCE 是边长为2的全等的正三角形,可将BCE 翻折到BCE ' ,使其与ABE 共面,从而得到一个菱形ABC E '.连接AC 与BE 相交于点P ,此时,AP EB C P EB '⊥⊥,322AP C P '==⨯则AP CP +取得最小值为故C 项正确;对于D 项,易知AF //EC ,因为AF ⊄平面,EBC EC ⊂平面EBC ,所以AF //平面EBC ,所以1122323E QBC Q EBC A EBC E ABC V V V V ----====⨯⨯⨯=三棱锥三棱锥三棱锥三棱锥,故D 项正确.故选:ACD.9.(2024下·安徽·高三池州市第一中学校联考开学考试)已知棱长为2的正方体1111ABCD A B C D -中,动点M 在棱1DD 上,记平面1BC M 截正方体所得的截面图形为Ω,则()A .平面1A BC ⊥平面11BC DB .不存在点M ,使得直线CM //平面11BA CC .1B M CM +的最小值为D .Ω的周长随着线段DM 长度的增大而增大【答案】ACD【解析】由于正方体的对角面相互垂直,故A 正确;当点M 与1D 重合时,直线CM //平面11BA C ,故B 错误;将四边形11DCC D 翻折至与四边形11BB D D 共面,则11B M CM B C +≥=C 正确;当0DM =时,Ω为1BC D ,且1BC D 的周长为当2DM =时,Ω为四边形11ABC D ,且四边形11ABC D 的周长为4+当02DM <<时,如图,过点M 作MN //1AD ,易得MN //1BC ,所以Ω为四边形1MNBC ,设DM x =,四边形1MNBC 的周长为l ,则()l x =,所以()l x '=()0l x '>,解得04x <<,所以()l x 在()0,2上单调递增,所以Ω的周长随着线段DM 长度的增大而增大,故D 正确.故选:ACD .10.(2024下·江西上饶·高二上饶市第一中学校考开学考试)在正方体1111ABCD A B C D -中,4AB E F =,,分别为1,BB CD 的中点,点P 满足1,[0,1]BP BC =∈λλ,则()A .1A F ⊥平面1AD EB .三棱锥1P AD E -的体积与P 点的位置有关C .1DP B P +的最小值为4+D .当10,3λ⎛⎤∈ ⎥⎝⎦时,平面PEF 截正方体的截面形状为五边形【答案】AD【解析】A 选项,以D 为坐标原点,以1,,DA DC DD 所在直线为,,x y z 轴建立空间直角坐标系,则11(4,0,0),(4,4,2),(0,0,4),(0,2,0),(4,0,4)A E D F A =则11(4,0,4),(4,2,4),(0,4,2)AD A F AE =-=--= ,11(4)(4)024(4)0,A F AD ⋅=-⨯-+⨯+⨯-=1(4)024(4)20,A F AE ⋅=-⨯+⨯+-⨯=所以111,A F AD A F AE ⊥⊥,又1,AE AD A AE ⋂=⊂平面11,AD E AD ⊂平面1AD E ,所以1A F ⊥平面1AD E ,故A 正确;B 选项,因为在正方体1111ABCD A BCD -中,11//AB C D 且11AB C D =,所以四边形11ABC D 为平行四边形,因此11//BC AD ,又1BC ⊂/平面11,AED AD ⊂平面1AED ,所以1//BC 平面1AED ,因此棱1BC 上的所有点到平面1AED 的距离都相等,又P 是棱1BC 上的动点,所以三棱锥1P AED -的体积始终为定值,故B 错;C 选项,11(4,4,0),(0,4,4),(4,4,4)B C B ,因为1,[0,1]BP BC =∈λλ,所以(44,4,4)P -λλ,所以1(44,4,4),(4,0,44)DP B P =-=-- λλλλ,2211323232323216DP B P DP B P λλλλ+=+=-+-+ 2211322432822λλ⎛⎫⎛⎫=-+-+ ⎪ ⎪⎝⎭⎝⎭[0,1]λ∈又,当12λ=时,1DP B P +有最小值,最小值为2622C 错误;D 选项,连接EC ,取1AA 中点为G ,当EC 与1BC 交点为点P 时,平面PEF 截正方体截面图形ECDG 为四边形,如下图1,此时11~,~,,PM MC PM BM PMC EBC PMB C CB EB BC CC BC == ,此时13λ=,当103λ<<时,如下图2,截面为五边形EBFKL ,故D 正确;故选∶AD11.(2024下·湖北·高二应城市第一高级中学校联考开学考试)棱长为1的正方体1111ABCD A B C D -中,点P满足1DP DD DA λμ=+,[]0,1λ∈,[]0,1u ∈,则下面结论正确的是:()A .当λμ=时,1BP AC ⊥B .当12μ=时,三棱锥11C PB C -的体积为定值C .当1λμ+=时,直线CP 与平面11BCC B 所成的角不可能为π3D .当1λμ+=时,PC PB +【答案】ABC 【解析】根据正方体可建立如图所示的空间直角坐标系,则()()()()0,0,0,1,0,0,1,1,0,0,1,0,A B C D ()()()()11110,0,1,1,0,1,1,1,1,0,1,1A B C D .故()()10,0,1,0,1,0DD DA ==- ,因为1DP DD DA λμ=+,故()0,,DP μλ=- ,故()0,1,P μλ-对于A ,当λμ=时,()0,1,P λλ-,故()1,1,BP λλ=--,而()11,1,1AC = ,故1110BP AC λλ⋅=-+-+= ,故1BP AC ⊥,故A 成立.对于B ,因为()0,1,P μλ-,故P 在平面11ADD A ,故P 到平面11B C C 的距离为1,而11B C C △的面积为定值,故11P C B C V -为定值,故11C PB C V -为定值,故B 正确.对于C ,()0,,P λλ,故()1,1,CP λλ=-- ,而平面11BCC B 的法向量为()1,0,0AB =,设直线CP 与平面11BCC B 所成的角为θ,则sin AB CP AB CP θ⋅= 因为[]0,1λ∈,故23131424λ⎛⎫≤-+≤ ⎪⎝⎭,故sin 232θ≤,故θ不可能为π3,故C 错误.对于D ,由C 的分析可得()0,,P λλ且()1,1,CP λλ=-- ,()1,,BP λλ=-,故PC PB +==,设(),0M λ,1,2N S ⎛⎛⎝⎭⎝⎭,1,2N ⎛ ⎝⎭',如下图,故))PC PB MN MS MNMS '+=+=+S'D 错误.12.(2024下·重庆·高三重庆八中校考开学考试)已知正四棱柱1111ABCD A B C D -的底面边长为1,12AA =,点P 在底面ABCD 内运动(含边界),点Q 满足[]1,0,1CQ mCC m =∈ ,则()A .当12m=时,1A P PQ +B .当14m =时,存在点P ,使1A PQ ∠为直角C .当78m =时,满足11D P A Q ⊥的点P 的轨迹平行平面1C BD D .当116m =时,满足1A P PQ ⊥的点P 的轨迹围成的区域的面积为π4【答案】ACD【解析】以D 为坐标原点,1,,DA DC DD 所在直线分别为,,x y z 轴,建立空间直角坐标系,则()()11,0,2,0,1,1A Q ,则点Q 关于平面ABCD 的对称点为()0,1,1Q '-,连接1A Q ',与平面ABCD 的交点即为使得1A P PQ +取最小值的点P ,此时11A P PQ AQ +=='A 正确;B 选项,当14m =时,()111,0,2,0,1,2A Q ⎛⎫ ⎪⎝⎭,设(),,0P s t ,则()222114A P s t =-++,()222114PQ s t =+-+,22111711224A Q ⎛⎫=++-=⎪⎝⎭,令22211A P PQ A Q +=,即()()222211714144s t s t -++++-+=,故()()2222110s t s t -+++-=,则需满足10,0,0,10s s t t -===-=,不合要求,故不存在点P ,使1A PQ ∠为直角,B 错误;C 选项,当78m =时,()()1171,0,2,0,1,,0,0,24A Q D ⎛⎫ ⎪⎝⎭,设(),,0P s t ,则()()11710,1,1,0,21,1,,,,244A Q D P s t ⎛⎫⎛⎫=-=--=- ⎪ ⎪⎝⎭⎝⎭ ,()11111,1,,,2042A Q D P s t s t ⎛⎫⋅=--⋅-=-++= ⎪⎝⎭ ,在平面ABCD 中画出(),,0P s t 点的轨迹,如图所示,其轨迹为线段MN ,其中,M N 分别为,AD AB 的中点,其中//MN BD ,又BD ⊂平面1C BD ,MN ⊄平面1C BD ,故//MN 平面1C BD ,当78m =时,满足11D P A Q ⊥的点P 的轨迹平行平面1C BD ,C 正确;D 选项,当116m =时,()111,0,2,0,1,8A Q ⎛⎫ ⎪⎝⎭,设(),,0P s t ,则()111,,2,,1,8A P s t PQ s t ⎛⎫=--=-- ⎪⎝⎭ ,则()221111,,2,1,084A P PQ s t s t s s t t ⎛⎫⋅=--⋅--=-+-+-= ⎪⎝⎭ ,即22111224s t ⎛⎫⎛⎫-+-= ⎪ ⎪⎝⎭⎝⎭,故点P 的轨迹为以11,22⎛⎫ ⎪⎝⎭为圆心,12为半径的圆,刚好与正方形ABCD 相切,故面积为211ππ24⎛⎫= ⎪⎝⎭,当116m =时,满足1A P PQ ⊥的点P 的轨迹围成的区域的面积为1π4,D 正确.故选:ACD13.(2023上·河北保定·高三校联考阶段练习)在三棱锥1A ABC -中,1A A ⊥平面ABC ,AB AC ⊥,13AA AB AC ===,P 为1A BC 内的一个动点(包括边界),AP 与平面1A BC 所成的角为45 ,则()A .1A P -B .1A P C .有且仅有一个点P ,使得1A P BC ⊥D .所有满足条件的线段AP 【答案】ACD【解析】因为1A A ⊥平面ABC ,,AB AC ⊂平面ABC ,所以11,A A AB A A AC ⊥⊥,又1,3AB AC AA AB AC ⊥===,所以11A B AC BC ===取BC 的中点M ,则1,AM BC A M BC ⊥⊥,又11,,AM A M M AM A M =⊂ 平面1A AM ,所以BC ⊥平面1A AM ,过A 作1AH A M ⊥于H ,因为AH ⊂平面1A AM ,所以AH BC ⊥,又11,,A M BC M A M BC =⊂ 平面1A BC ,所以AH ⊥平面1A BC ,所以APH ∠为AP 与平面1A BC 所成的角的平面角,因为1A A ⊥平面ABC ,AM ⊂平面ABC ,则1A A AM ⊥,又在1Rt A AM V中,113,2A A AM BC ==1A M =所以11AA AM AH A M ⋅=因为45APH ∠=︒,所以AH HP =,AP =所以点P 轨迹是以H1A BC内部的一部分,如图,所以1A P的最小值为1A H HP -,故A 正确;由于轨迹圆部分在平面1A BC 外部,所以1A P的最大值不等于1A H HP +,故B 错误;因为BC ⊥平面1A AM ,1A M ⊂平面1A AM ,所以1BC A M ⊥,若1A P BC ⊥,则点P 在线段1A M 上,有且仅有一个点P 满足题意,故C 正确;动线段AP 形成的曲面为圆锥AH 侧面积的一部分,易知三棱锥1A A BC -是正三棱锥,AH ⊥平面1A BC ,故H 为等边1A BC 的中心,所以11133HM A M ==,因为11cos 2HM B HM HB ∠==,所以1π4B HM ∠=,因为π2π23142π4-⨯⨯=,所以曲面面积为圆锥侧面面积的14,圆锥AH侧面积为π=,所以所有满足条件的动线段AH形成的曲面面积为4,故D 正确.故选:ACD.14.(2024上·江苏常州·高三统考期末)在棱长为2的正方体1111ABCD A B C D -中,P 在线段1BD 上运动(包括端点),下列说法正确的有()A .存在点P ,使得⊥CP 平面1A DBB .不存在点P ,使得直线1C P 与平面1A DB 所成的角为30 C .PC PD +的最小值为D .以P 为球心,PA 为半径的球体积最小时,被正方形11ADD A 截得的弧长是π3【答案】BCD 【解析】方法一:如图,以D 为原点,分别以1,,DA DC DD 为,,x y z 轴建立空间直角坐标系,()2,2,0B ,()10,0,2D ,()2,0,0A ,()10,2,2C ,()12,2,2BD =-- ,()12,2,2AC =-,1BP BD λ=,则()22,22,2P λλλ--,对于A ,因为1111ABCD A B C D -为正方体,所以11AB A B ⊥,11AD A D⊥由三垂线定理得11AC A B ⊥,11AC A D ⊥,因为111A B A D A = ,11,A B A D ⊂平面1A DB ,所以1AC ⊥平面1A DB ,()12,2,2AC =-是平面1A BD 一个法向量,假设⊥CP 面1A DB ,则()22,2,2CP λλλ=--与()2,2,2-共线矛盾,假设不成立,A 错.对于B ,若存在P ,1C P 与1A DB 所成角为30 ,则160AC P ∠= 或120︒,11,60C A C P 〈〉= 或120︒,111112C A C P C A C P ⋅∴=λ=假设不成立,B 对.对于C,PC PD +==.表示(),0P λ与2,33E ⎛⎝⎭,1,33F⎛- ⎝⎭距离之和,1PEPF EF +≥=,PC PD +≥C 对.对于D,PA =13λ=时PA 最小,442,,333P ⎛⎫⎪⎝⎭,PA =,设截面小圆的圆心为N ,半径为r ,则NP ⊥平面11ADD A ,所以42,0,33N ⎛⎫ ⎪⎝⎭,3r ==,因为3NA ==,所以球与面11ADD A N 因为190A AD ∠=︒,所以Q 在正方形11ADD A内轨迹为半圆,弧长12233=⋅⋅=ππ,选项D 正确;。
专题17 立体几何中的最值问题【解析版】

第四章立体几何专题17 立体几何中的最值问题【压轴综述】在立体几何中,判定和证明空间的线线、线面以及面面之间的位置关系(主要是平行与垂直的位置关系),计算空间图形中的几何量(主要是角与距离)是两类基本问题.在涉及最值的问题中主要有三类,一是距离(长度)的最值问题;二是面(体)积的最值问题;三是在最值已知的条件下,确定参数(其它几何量)的值.从解答思路看,有几何法(利用几何特征)和代数法(应用函数思想、应用基本不等式等)两种,都需要我们正确揭示空间图形与平面图形的联系,并有效地实施空间图形与平面图形的转换.要善于将空间问题转化为平面问题:这一步要求我们具备较强的空间想象能力,对几何体的结构特征要牢牢抓住,有关计算公式熟练掌握.一、涉及几何体切接问题最值计算求解与球有关的组合体问题,一种是内切,一种是外接.解题时要认真分析图形,明确切点和接点的位置,确定有关元素间的数量关系,并作出合适的截面图,如球内切于正方体,切点为正方体各个面的中心,正方体的棱长等于球的直径;球外接于正方体,正方体的顶点均在球面上,正方体的体对角线长等于球的直径等.通过作截面,把空间问题转化为平面图形与圆的接、切问题,再利用平面几何知识寻找几何中元素间的关系求解.这样才能进一步将空间问题转化为平面内的问题;二.涉及角的计算最值问题1. 二面角的平面角及其求法有:定义法、三垂线定理及其逆定理、找公垂面法、射影公式、向量法等,依据题目选择方法求出结果.2.求异面直线所成角的步骤:一平移,将两条异面直线平移成相交直线.二定角,根据异面直线所成角的定义找出所成角.三求角,在三角形中用余弦定理或正弦定理或三角函数求角.四结论.3.线面角的计算:(1)利用几何法:原则上先利用图形“找线面角”或者遵循“一做----二证----三计算”. (2)利用向量法求线面角的方法(i分别求出斜线和它在平面内的射影直线的方向向量,转化为求两个方向向量的夹角(或其补角);(ii)通过平面的法向量来求,即求出斜线的方向向量与平面的法向量所夹的锐角(钝角时取其补角),取其余角就是斜线和平面所成的角.下面通过例题说明应对这类问题的方法与技巧.【压轴典例】例1.(2018·全国高考真题(理))已知正方体的棱长为1,每条棱所在直线与平面 所成的角都相等,则α截此正方体所得截面面积的最大值为( )A .4B C .4D 【答案】A 【解析】根据相互平行的直线与平面所成的角是相等的, 所以在正方体1111ABCD A B C D -中,平面11AB D 与线11111,,AA A B A D 所成的角是相等的,所以平面11AB D 与正方体的每条棱所在的直线所成角都是相等的, 同理平面1C BD 也满足与正方体的每条棱所在的直线所成角都是相等, 要求截面面积最大,则截面的位置为夹在两个面11AB D 与1C BD 中间的,,所以其面积为26(424S =⨯⋅=,故选A. 例2.(2018·全国高考真题(文))设A B C D ,,,是同一个半径为4的球的球面上四点,ABC △为等边三角形且其面积为D ABC -体积的最大值为( )A .B .C .D .【答案】B 【解析】 如图所示,点M 为三角形ABC 的中心,E 为AC 中点,当DM ⊥平面ABC 时,三棱锥D ABC -体积最大 此时,OD OB R 4===2ABCSAB == AB 6∴=,点M 为三角形ABC 的中心2BM 3BE ∴==Rt OMB ∴中,有OM 2==DM OD OM 426∴=+=+=()max 163D ABC V -∴=⨯=故选B.例3.(2017·全国高考真题(理))a ,b 为空间中两条互相垂直的直线,等腰直角三角形ABC 的直角边AC 所在直线与a ,b 都垂直,斜边AB 以直线AC 为旋转轴旋转,有下列结论: ①当直线AB 与a 成60°角时,AB 与b 成30°角; ②当直线AB 与a 成60°角时,AB 与b 成60°角; ③直线AB 与a 所成角的最小值为45°; ④直线AB 与a 所成角的最大值为60°.其中正确的是________.(填写所有正确结论的编号) 【答案】②③ 【解析】由题意知,a 、b 、AC 三条直线两两相互垂直,画出图形如图, 不妨设图中所示正方体边长为1, 故|AC |=1,|AB|=斜边AB 以直线AC 为旋转轴,则A 点保持不变,B 点的运动轨迹是以C 为圆心,1为半径的圆,以C 坐标原点,以CD 为x 轴,CB 为y 轴,CA 为z 轴,建立空间直角坐标系, 则D (1,0,0),A (0,0,1),直线a 的方向单位向量a =(0,1,0),|a |=1, 直线b 的方向单位向量b =(1,0,0),|b |=1,设B 点在运动过程中的坐标中的坐标B ′(cos θ,sin θ,0), 其中θ为B ′C 与CD 的夹角,θ∈[0,2π),∴AB ′在运动过程中的向量,'AB =(cos θ,sin θ,﹣1),|'AB|=设'AB 与a 所成夹角为α∈[0,2π], 则cos α()()10102'cos sin a AB θθ--⋅==⋅,,,,|sin θ, ∴α∈[4π,2π],∴③正确,④错误. 设'AB 与b 所成夹角为β∈[0,2π],cos β()()'1100''AB b cos sin AB bbAB θθ⋅-⋅===⋅⋅,,,,θ|, 当'AB 与a 夹角为60°时,即α3π=,|sin θ|3πα===, ∵cos 2θ+sin 2θ=1,∴cos β2=|cos θ|12=,∵β∈[0,2π],∴β3π=,此时'AB 与b 的夹角为60°, ∴②正确,①错误. 故答案为:②③.例4.(2017·全国高考真题(理))如图,圆形纸片的圆心为O ,半径为5 cm ,该纸片上的等边三角形ABC 的中心为O .D ,E ,F 为圆O 上的点,△DBC ,△ECA ,△FAB 分别是以BC ,CA ,AB 为底边的等腰三角形.沿虚线剪开后,分别以BC ,CA ,AB 为折痕折起△DBC ,△ECA ,△FAB ,使得D ,E ,F 重合,得到三棱锥.当△ABC 的边长变化时,所得三棱锥体积(单位:cm 3)的最大值为______.【答案】【解析】如下图,连接DO 交BC 于点G ,设D ,E ,F 重合于S 点,正三角形的边长为x (x >0),则13OG x =x =.∴5FG SG x ==-,SO h ====,∴三棱锥的体积21133ABC V S h x =⋅==.设()455n x x x =-,x >0,则()3420n x x x '=,令()0n x '=,即4340x =,得x =()n x 在x =处取得最大值.∴max 48V ==例5.(2016·浙江高考真题(理))如图,在ABC中,AB=BC=2,∠ABC=120°.若平面ABC外的点P和线段AC上的点D,满足PD=DA,PB=BA,则四面体PBCD的体积的最大值是 .【答案】【解析】中,因为,所以.由余弦定理可得,所以.设,则,.在中,由余弦定理可得.故.在中,,.由余弦定理可得,所以.由此可得,将ABD沿BD翻折后可与PBD重合,无论点D在任何位置,只要点D的位置确定,当平面PBD⊥平面BDC时,四面体PBCD的体积最大(欲求最大值可不考虑不垂直的情况).过作直线的垂线,垂足为.设,则,即,解得.而 的面积.当平面PBD⊥平面BDC 时:四面体的体积.观察上式,易得,当且仅当,即时取等号,同时我们可以发现当时,取得最小值,故当时,四面体的体积最大,为例6.(2019·安徽芜湖一中高三开学考试)在Rt AOB ∆中,6OAB π∠=,斜边4AB =.Rt AOC ∆可以通过Rt AOB ∆以直线AO 为轴旋转得到,且二面角B AO C --是直二面角.动点D 的斜边AB 上.(1)求证:平面COD ⊥平面AOB ;(2)求直线CD 与平面AOB 所成角的正弦的最大值.【答案】(1)详见解析;(2【解析】(1)AOB ∆为直角三角形,且斜边为AB ,2AOB π∴∠=.将Rt AOB ∆以直线AO 为轴旋转得到Rt AOC ∆,则2AOC π∠=,即OC AO ⊥.二面角B AO C --是直二面角,即平面AOC ⊥平面AOB .又平面AOC I 平面AOB AO =,OC ⊂平面AOC ,OC ∴⊥平面AOB .OC ⊂Q 平面COD ,因此,平面COD ⊥平面AOB ;(2)在Rt AOB ∆中,6OAB π∠=,斜边4AB =,122OB AB ∴==且3OBA π∠=. 由(1)知,OC ⊥平面AOB ,所以,直线CD 与平面AOB 所成的角为ODC ∠.在Rt OCD ∆中,2COD π∠=,2OC OB ==,CDsin OC ODC CD ∴∠==当⊥OD AB 时,OD 取最小值,此时sin ODC ∠取最大值,且sin3OD OB π==因此,sin 7OC ODC CD ∠==≤=,即直线CD 与平面AOB 所成角的正弦的最大值为7. 例7.(2019·深圳市高级中学高三月考(文))如图,AB 是圆O 的直径,点C 是圆O 上异于A ,B 的点,PO 垂直于圆O 所在的平面,且PO =OB =1.(1)若D 为线段AC 的中点,求证:AC⊥平面PDO ; (2)求三棱锥P -ABC 体积的最大值; (3)若,点E 在线段PB 上,求CE +OE 的最小值.【答案】(1)见解析;(2);(3)【解析】(1)证明:在△AOC中,因为OA=OC,D为AC的中点,所以AC⊥DO.又PO垂直于圆O所在的平面,所以PO⊥AC.因为DO∩PO=O,所以AC⊥平面PDO.(2)解:因为点C在圆O上,所以当CO⊥AB时,C到AB的距离最大,且最大值为1.又AB=2,所以△ABC面积的最大值为.又因为三棱锥P-ABC的高PO=1,故三棱锥P-ABC体积的最大值为.(3)解:在△POB中,PO=OB=1,∠POB=90°,所以.同理,所以PB=PC=BC.在三棱锥P-ABC中,将侧面BCP绕PB旋转至平面BC′P,使之与平面ABP共面,如图所示.当O,E,C′共线时,CE+OE取得最小值.又因为OP=OB,,所以垂直平分PB,即E为PB的中点.从而,即CE+OE的最小值为.例8.(2016·江苏高考真题)现需要设计一个仓库,它由上下两部分组成,上部分的形状是正四棱锥,下部分的形状是正四棱柱(如图所示),并要求正四棱柱的高是正四棱锥的高的4倍.(1)若则仓库的容积是多少? (2)若正四棱锥的侧棱长为,则当为多少时,仓库的容积最大?【答案】(1)312(2)【解析】(1)由PO 1=2知OO 1=4PO 1=8. 因为A 1B 1=AB=6,所以正四棱锥P-A 1B 1C 1D 1的体积正四棱柱ABCD-A 1B 1C 1D 1的体积所以仓库的容积V=V 锥+V 柱=24+288=312(m 3).(2)设A 1B 1=a (m ),PO 1=h (m ),则0<h<6,OO 1=4h.连结O 1B 1.因为在中,所以,即于是仓库的容积,从而.令,得或(舍).当时,,V 是单调增函数;当时,,V 是单调减函数.故时,V 取得极大值,也是最大值.因此,当m 时,仓库的容积最大.【压轴训练】1.(2019·四川石室中学高三开学考试(文))在ABC △中,已知AB =BC =045ABC ∠=,D 是边AC 上一点,将ABD △沿BD 折起,得到三棱锥A BCD -.若该三棱锥的顶点A 在底面BCD 的射影M 在线段BC 上,设BM x =,则x 的取值范围为( )A.(B.C.D.(【答案】B 【解析】由将ABD △沿BD 折起,得到三棱锥A BCD -,且A 在底面BCD 的射影M 在线段BC 上, 如图2所示,AM ⊥平面BCD ,则AM BD ⊥, 在折叠前图1中,作AM BD ⊥,垂足为N ,在图1中过A 作1AM BC ⊥于点1M ,当运动点D 与点C 无限接近时,折痕BD 接近BC ,此时M 与点1M 无限接近,在图2中,由于AB 是直角ABM ∆的斜边,BM 为直角边,所以BM AB <, 由此可得1BM BM AB <<,因为ABC ∆中,045ABC AB BC ∠===,由余弦定理可得AC =所以1BM ==BM <<由于BM x =,所以实数x 的取值范围是,故选B .2.(2019·四川高三月考(文))已知球O 表面上的四点A ,B ,C ,P 满足AC BC ==2AB =.若四面体PABC 体积的最大值为23,则球O 的表面积为( ) A .254πB .254π C .2516π D .8π【答案】A 【解析】当平面ABP 与平面ABC 垂直时,四面体ABCP 的体积最大.由AC BC ==2AB =,得90ACB ︒∠=.设点Р到平面ABC 的距离为h,则112323h ⨯=,解得2h =. 设四面体ABCP 外接球的半径为R ,则()22221R R =-+,解得5R=4.所以球O 的表面积为2525444ππ⎛⎫⨯= ⎪⎝⎭. 故选:A .3.(2019·湖南雅礼中学高三月考(理))圆锥的母线长为2,其侧面展开图的中心角为θ弧度,过圆锥顶点的截面中,面积的最大值为2,则θ的取值范围是( ) A.),2π B.π⎡⎤⎣⎦C.}D.,2π⎫⎪⎪⎣⎭【答案】A 【解析】设轴截面的中心角为α,过圆锥顶点的截面的顶角为β,且βα≤ 过圆锥顶点的截面的面积为:122sin β2sin β2⨯⨯⨯=, 又过圆锥顶点的截面中,面积的最大值为2, 故此时β2π=,故απ2π≤<圆锥底面半径r )2sin22α=∈ ∴侧面展开图的中心角为θ弧度2sin222πsin22απα⨯⨯==∈),2π 故选:A.4.(2019·安徽高考模拟(理))如图,已知四面体ABCD 为正四面体,1AB =,E ,F 分别是AD ,BC 中点.若用一个与直线EF 垂直,且与四面体的每一个面都相交的平面α去截该四面体,由此得到一个多边形截面,则该多边形截面面积最大值为( )A .14B C D .1【答案】A 【解析】将正四面体补成正方体,如下图所示:EF α⊥ ∴截面为平行四边形MNKL ,可得1NK KL +=又//KL BC ,//KN AD ,且AD BC ⊥ KN KL ∴⊥ 可得2124MNKLNK KL S NK KL +⎛⎫=⋅≤=⎪⎝⎭四边形(当且仅当NK KL =时取等号) 本题正确选项:A5.(2019·湖北高三月考(理))若一个四棱锥底面为正方形,顶点在底面的射影为正方形的中心,且该四棱锥的体积为9,当其外接球表面积最小时,它的高为( )A .3B .C .D .【答案】A 【解析】设正方形的边长为a ,则四棱锥的高为227h a =,则其外接圆的半径r =.设球的半径为R ,则()222h R r R -+=,解得44222272727210844108a a R a a a =+=++94≥=,当且仅当42274108a a =,即3a =时等号成立,此时,四棱锥的高为2272739h a ===.故选A. 6.(2019·四川雅安中学高三开学考试(文))已知三棱锥D ABC -四个顶点均在半径为R 的球面上,且AB BC ==2AC =,若该三棱锥体积的最大值为1,则这个球的表面积为( )A.50081πB.1009πC.259πD.4π【答案】B 【解析】AB BC ==2AC = 222AB BC AC ∴+= AB BC ∴⊥112ABC S AB BC ∆∴=⋅= 如下图所示:若三棱锥D ABC -体积最大值为1,则点D 到平面ABC 的最大距离:3d = 即:3DO '=设球的半径为R ,则在Rt OAO '∆中:()22213R R =+-,解得:53R =∴球的表面积:210049S R ππ==本题正确选项:B7.(2017·山西高三(理))两球1O 和2O 在棱长为1的正方体1111ABCD A B C D -的内部,且互相外切,若球1O 与过点A 的正方体的三个面相切,球2O 与过点1C 的正方体的三个面相切,则球1O 和2O 的表面积之和的最小值为( )A .(32pB .(42pC .(32p +D .(42p【答案】A 【解析】设球1O 与球2O 的半径分别为r 1,r 2,∴r 1+r 2r 1+r 2)= r 1+r 2=32-,r 1+r 2⩾球1O 与球2O 的面积之和为: S =4π(21r+21r)=4π(r 1+r 2)2−8π12r r ⩾()212π1+−2π()231+=(6−)π,当且仅当r 1=r 2时取等号其面积最小值为(6−π. 故选A.8.(2019·广东高考模拟(理))平面四边形ABCD 中,AD AB ==CD CB ==且AD A B ⊥,现将ABD ∆沿对角线BD 翻折成A BD '∆,则在A BD '∆折起至转到平面BCD 的过程中,直线A C '与平面BCD 所成最大角的正切值为( )A .2B .12C D 【答案】D 【解析】 取BD 的中点O,则,,,A B A D BC CD A O BD CO BD '''==∴⊥⊥即BD ⊥平面A OC ',从而平面BCD ⊥平面A OC ',因此A '在平面BCD 的射影在直线OC 上,即A CO '∠为直线A C '与平面BCD 所成角,因为AD AB ==CD CB ==AD AB ⊥,所以111,2sin sin sin 22A O A O OC A CO OA C OA C OC '''''==∴∠=∠=∠≤,即A CO '∠最大值为π6,因此直线A C '与平面BCD 所成最大角的正切值为πtan63=,选D.9.(2019·云南省玉溪第一中学高二月考(理))已知底面边长为,侧棱长为S ABCD -内接于球1O .若球2O 在球1O 内且与平面ABCD 相切,则球2O 的直径的最大值为__________. 【答案】8 【解析】如图所示,正四棱锥S ABCD -内接于球1O ,1SO 与平面ABCD 交于点O ,正方形ABCD 中,4AB AO ==,在直角三角形SAO 中,2SO ===,设球1O 的半径为R ,则在直角三角形1OAO 中,222(2)4R R -+=, 解得5R =, 所以球1O 的直径为10,当求2O 与平面ABCD 相切且与球1O 相切时,球2O 的直径最大, 又因为球2SO =,所以球2O 的直径的最大值为1028-=.10.(2019·山西高三月考)已知三棱锥P ABC -的四个顶点都在半径为3的球面上,AB AC ⊥,则该三棱锥体积的最大值是__. 【答案】323【解析】如图所示,设,AB m AC n ==,则12ABCS mn ∆=,ABC ∆3,三棱锥P ABC -的体积公式为221113)3)3234m n mn +⨯≤⨯,设224m n t +=,则1()3f t t =,1()33f t '⎫=+⎪⎭,令()0f t '=,解得8t =,()f t 在()0,8单增,[]8,9单减,max 32()(8)3f t f ∴==, 所以三棱锥P ABC -体积最大值为32311.(2019·云南师大附中高三月考)在直三棱柱111ABC A B C -中,90BAC ∠=︒且14BB =,设其外接球的球心为O ,已知三棱锥O -ABC 的体积为2,则球O 的表面积的最小值是_____________. 【答案】28π 【解析】 如图,在Rt ABC △中,设AB c =,=AC b ,则BC =, 取BC ,11B C 的中点分别为2O ,1O ,则2O ,1O 分别为Rt ABC △和111Rt A B C △的外接圆的圆心,连接2O 1O ,又直三棱柱111ABC A B C -的外接球的球心为O ,则O 为2O 1O 的中点,连接OB ,则OB 为三棱柱外接球的半径.设半径为R ,因为直三棱柱111ABC A B C -,所以1214BB O O ==,所以三棱锥O ABC -的高为2,即22OO =,又三棱锥O ABC -体积为2,所以1122632O ABC V bc bc -=⨯⨯=⇒=.在2Rt OO B △中,22222221()4424b c R BC OO +⎛⎫=+=+=+ ⎪⎝⎭⎝⎭, 所以2=4πS R =球表22224π4π()16π2π16π12π16π28π4b c b c bc ⎛⎫++=+++=+=⎪⎝⎭≥,当且仅当b c =时取“=”,所以球O 的表面积的最小值是28π,故答案为28π.12.(2019·湖南高三月考(文))已知三棱锥A BCD -满足3AB BD DC CA ====,则该三棱锥体积的最大值为________.【答案】【解析】取AD 中点E ,连接BE ,CE ,因为3AB BD DC CA ====, 所以BE AD ⊥,CE AD ⊥,且BE CE =,由题意可得,当平面⊥BAD 平面CAD 时,棱锥的高最大,等于BE ,此时体积也最大; 所以此时该三棱锥体积为113sin sin 362-∆=⋅⋅=⋅⋅⋅∠⋅=⋅∠A BCD ACD V S BE CA CD ACD BE CE ACD ,设ACD θ∠=,则sin 3cos 22πθθ-⎛⎫=⋅=⎪⎝⎭CE CD , 所以239cos sin 9sin cos 9sin sin 222222θθθθθθ-⎛⎫=⋅=⋅=- ⎪⎝⎭A BCD V , 令sin2θ=x ,因为0θπ<<,所以0sin12θ<<,设3()=-f x x x ,01x <<,则2()13'=-f x x ,由2()130'=->f x x 得03x <<;由2()130'=-<f x x 得13x <<;所以函数3()=-f x x x 在⎛ ⎝⎭上单调递增,在⎫⎪⎪⎝⎭上单调递减;所以max ()33279⎛==-= ⎝⎭f x f ,因此三棱锥体积的最大值为99-=⋅=A BCD V故答案为13.(2019·河南高三月考(文))已知三棱锥P ABC -的四个顶点均在同一个球面上,底面ABC ∆满足BA BC ==2ABC π∠=,若该三棱锥体积的最大值为3.则其外接球的体积为________.【答案】323π 【解析】 如图所示:设球心为O ,ABC △所在圆面的圆心为1O ,则1OO ⊥平面ABC ;因为BA BC ==2ABC π∠=,所以ABC △是等腰直角三角形,所以1O 是AC 中点;所以当三棱锥体积最大时,P 为射线1O O 与球的交点,所以113p ABC ABC V PO S -=⋅⋅;因为132ABCS==,设球的半径为R ,所以11PO PO OO R R =+==+(1333R ⋅⋅=,解得:2R =,所以球的体积为:343233R ππ=.14.(2019·四川双流中学高三月考(文))已知球的直径4DC =,A ,B 是该球面上的两点,6ADC BDC π∠=∠=,则三棱锥A BCD -的体积最大值是______.【答案】2 【解析】因为球的直径4DC =,且6ADC BDC π∠=∠=,所以2AC BC ==,AD BD ==13A BCD BCD V S h -∆=⨯⨯(其中h 为点A 到底面BCD 的距离),故当h 最大时,A BCD V -的体积最大,即当面ADC ⊥面BDC 时,h 最大且满足42h =⨯h =112232A BCD V -=⨯⨯⨯=.15.(2019·河北高三月考)在四棱锥P ABCD -中,PD AC ⊥,AB ⊥平面PAD ,底面ABCD 为正方形,且3CD PD +=,若四棱锥P ABCD -的每个顶点都在球O 的球面上,则球O 的表面积的最小值为_____. 【答案】6π 【解析】∵AB ⊥平面PAD ,∴AB PD ⊥,又PD AC ⊥,∴PD ⊥平面ABCD ,则四棱锥P ABCD -可补形成一个长方体,球O 的球心为PB 的中点,设()03CD x x =<<,则3PD x =-.从而球O 的表面积为()2243126x πππ⎡⎤=-+≥⎣⎦⎝⎭. 故答案为6π 16.(2016·浙江高考真题(文))如图,已知平面四边形ABCD ,AB=BC=3,CD=1,直线AC 将ACD 翻折成ACD',直线AC 与BD' 所成角的余弦的最大值是______.【解析】试题分析:如图,连接BD′,设直线AC 与'BD 所成的角为θ.O 是AC 的中点.由已知得AC =,以OB 为x 轴, OA 为y 轴,过O 与平面ABC 垂直的直线为z 轴,建立空间直角坐标系,则0,2A ⎛⎫ ⎪ ⎪⎝⎭, 2B ⎛⎫ ⎪ ⎪⎝⎭, 0,2C ⎛⎫- ⎪ ⎪⎝⎭.作DH AC ⊥于H ,连接D′H翻折过程中, 'D H 始终与AC 垂直, 则2CD CH CA ===则3OH = DH ==因此'cos ,sin 636D αα⎛⎫-- ⎪ ⎪⎝⎭(设∠DHD′=α),则'BD αα⎛⎫= ⎪ ⎪⎝⎭,与CA 平行的单位向量为()0,1,0n =,所以cos cos ',BD n θ= ''BD n BD n⋅==,所以cos 1α=-时, cos θ.17.(2019·重庆一中高三开学考试(理))已知正方形ABCD 的边长为ABC ∆沿对角线AC 折起,使平面ABC ⊥平面ACD ,得到如图所示的三棱锥B-ACD .若O 为AC 的中点,点M ,N 分别为DC ,BO 上的动点(不包括端点),且BN CM =,则当三棱锥N-AMC 的体积取得最大值时,点N 到平面ACD 的距离为______.【答案】1【解析】由题意知,BO AC ⊥,而平面ABC ⊥平面ACD ,所以BO ⊥平面ACD ,易知BO =2,设BN x =,三棱锥N AMC -的高为NO ,则2NO x =-,由三棱锥体积公式得211=(2)(1)3233N AMC V y x x -=⨯⨯⨯-=--+,∴x =1时,y max =3.此时,211NO =-=. 故本题正确答案为1.18.(2019·浙江高三开学考试)如图,在棱长为2的正方体1111ABCD A B C D -中,点M 是AD 中点,动点P 在底面ABCD 内(不包括边界),使四面体1A BMP 体积为23,则1C P 的最小值是___________.【解析】由已知得四面体1A BMP 体积1122,33A MBP MBP V S -∆=⨯⨯=所以1,MBP S ∆=设P 到BM 的距离为h ,则11,2MBP S h ∆==解得h =所以P 在底面ABCD 内(不包括边界)与BM 的线段l 上, 要使1C P 的最小,则此时P 是过C 作BM 的垂线的垂足.点C 到BM 的距离为,5所以5CP =此时()1min 5C P ==19.(2019·安徽合肥一中高考模拟(文))如图,在棱长为 1 的正方体1111ABCD A B C D -中,点M 是AD 的中点,动点P 在底面ABCD 内(不包括边界),若1//B P 平面1A BM ,则1C P 的最小值是____.【解析】 取BC 中点N ,连结11,,B D B N DN ,作CO DN ⊥,连1C O ,因为面1//B DN 面面1A BM ,所以动点P 在底面ABCD 内的轨迹为线段DN , 当点P 与点O 重合时,1C P 取得最小值,因为1112252DN CO DC NC CO ⋅=⋅⇒==,所以1min 1()5C P C O ====. 20.(2019·湖南高三期末(文))点P 在正方体1111ABCD A B C D -的侧面11BCC B 及其边界上运动,并保持1AP BD ⊥,若正方体边长为2,则PB 的取值范围是__________.【答案】2⎤⎦【解析】连结1AB ,AC ,1CB ,易知平面11ACB BD ⊥,故P 点的轨道为线段1CB ,当P 在1CB 当P 与C 或1B 重合时:最大值为2则PB 的取值范围是2⎤⎦.故答案为:2⎤⎦。
立体几何中的最值问题

如 图 5所 示 , 了 制 作 一 个 圆 为
例 2 三 棱 锥 SABC - 中 , 条棱 长为 , 余 棱 长 一 其 均 为 1 求 a为 何 值 时 ,
最 大 , 求最 大值 . 并 如图 3设 s , c—n ,
ቤተ መጻሕፍቲ ባይዱ形 灯笼 , 要 制 作 4个 全 等 的 先
形 骨架 , 总计 耗用 9 6m 铁 丝 , . 用 S I 塑 料 片制 成 圆柱 的侧 I T
1 )利 用 一 次 、 次 、 比 例 函 数 性 质 求 最 值 二 反
■r’,-
何性 质 . 比较 常用 的性 质如 :1 )两 点之 间以直 线段 最
短 ; )垂 线段 最短 等. 2
■■ _
例 3 ( 0 9 全 国卷 )已知二 面角 z 的大小 20 年
为 6 。动 点 P、 分别在 平 面 a J内 , 0, Q 、 9 P到 p的距离 为
) .
B 2; C 2 ; D 4
的侧 面绕 行 2周到 达 A 点 的最 短路线 的长 为
.
如 图 4 分别 作 Q , A一
析 a于 A , AC ̄ Z于 C PBj 口于 B , _ PD - Z于 D , l -
C B 则 AC Q、 D, Q= PDB
C
。 c
和下 底面 ( 安装 上 底 面 ) 不 .当
析
其余 棱长 均为 1 取 ,
柱 底 面 半 径 r取 何 值 时 , S取 得 最大 值?并 求 出该 最 大值 ( 果 结 图5
罐
AB 中点 H , 接 HS HC, 连 、
图 3
精 确 到 0 0 ) . 1m。 .
立体几何动点最值问题

立体几何动点最值问题
立体几何动点最值问题是指在立体几何空间中,给定一些特定条件下,求一个动点的某个值的最大或最小值。
这类问题广泛应用于建筑设计、机械工程、地理测量等领域。
在解决立体几何动点最值问题时,通常需要利用几何性质和数学方法进行分析和求解。
下面以两个典型的问题为例进行拓展说明。
问题一:在一个正方体中,找到离一个定点最远的顶点。
解答:首先,我们找到这个正方体的中心点,然后根据对称性可以知道,离中心点最远的顶点就是通过连接中心点和一个面的对角线的顶点。
因此,我们可以通过计算这个对角线的长度,并找出最长的对角线来确定离定点最远的顶点。
问题二:在一个球体上,找到离球心最远的点。
解答:根据球体的几何性质,离球心最远的点是球体表面上的点。
因此,我们可以通过计算球心到球面上各点的距离,并找出最大距离的点来确定离球心最远的点。
在实际应用中,立体几何动点最值问题的解决往往需要结合具体的条件和约束条件进行分析和求解。
这些问题可能涉及到线段、面积、体积等几何量的计算,以及最优化等数学方法的运用。
因此,解决这类
问题需要理解立体几何的基本概念和性质,并熟练掌握相关的计算和求解技巧。
专题4.4 立体几何中最值问题(解析版)

一.方法综述高考试题将趋于关注那些考查学生运用运动变化观点处理问题的题目,而几何问题中的最值与范围类问题,既可以考查学生的空间想象能力,又考查运用运动变化观点处理问题的能力,因此,将是有中等难度的考题.此类问题,可以充分考查图形推理与代数推理,同时往往也需要将问题进行等价转化,比如求一些最值时,向平面几何问题转化,这些常规的降维操作需要备考时加强关注与训练.立体几何中的最值问题一般涉及到距离、面积、体积、角度等四个方面,此类问题多以规则几何体为载体,涉及到几何体的结构特征以及空间线面关系的逻辑推理、空间角与距离的求解等,题目较为综合,解决此类问题一般可从三个方面思考:一是函数法,即利用传统方法或空间向量的坐标运算,建立所求的目标函数,转化为函数的最值问题求解;二是根据几何体的结构特征,变动态为静态,直观判断在什么情况下取得最值;三是将几何体平面化,如利用展开图,在平面几何图中直观求解.二.解题策略类型一距离最值问题【例1】【河南省焦作市2019届高三三模】在棱长为4的正方体ABCD﹣A1B1C1D1中,点E、F分别在棱AA1和AB上,且C1E⊥EF,则|AF|的最大值为()A.B.1 C.D.2【答案】B【解析】以AB,AD,AA1所在直线为x,y,z轴,建立空间直角坐标系如图所示,则C1(4,4,4),设E(0,0,z),z∈[0,4],F(x,0,0),x∈[0,4],则|AF|=x.=(4,4,4﹣z),=(x,0,﹣z).因为C1E⊥EF,所以,即:z2+4x﹣4z=0,x=z﹣.当z=2时,x取得最大值为1.|AF|的最大值为1.故选:B.【指点迷津】建立空间直角坐标系,求出坐标,利用C 1E⊥EF,求出|AF|满足的关系式,然后求出最大值即可.利用向量法得到|AF|的关系式是解题的关键,故选D.【举一反三】1、【江西省吉安市2019届高三上学期期末】若某几何体的三视图如图所示,则该几何体的最长棱的棱长为A.B.C.D.【答案】A【解析】解:根据三视图知,该几何体是一个正四棱锥,画出图形如图所示;则,,底面CDEB,结合图形中的数据,求得,在中,由勾股定理得,同理求得,.故选:A .2、【河南省顶级名校2019届高三第四次联合测评】在侧棱长为的正三棱锥中,侧棱OA ,OB ,OC 两两垂直,现有一小球P 在该几何体内,则小球P 最大的半径为 A . B . C .D .【答案】B 【解析】当小球与三个侧面,,及底面都相切时,小球的体积最大此时小球的半径最大,即该小球为正三棱锥的内切球设其半径为由题可知因此本题正确选项:3、如右图所示,在棱长为2的正方体1111ABCD A B C D 中, E 为棱1CC 的中点,点,P Q 分别为面1111A B C D和线段1B C 上的动点,则PEQ ∆周长的最小值为_______.【解析】将面1111A B C D 与面11BB C C 折成一个平面,设E 关于11B C 的对称点为M ,E 关于1B C 对称点为N,则PEQ ∆周长的最小值为MN ==类型二 面积的最值问题【例2】【河南省郑州市2019年高三第二次质量检测】在长方体中,,,分别是棱的中点,是底面内一动点,若直线与平面没有公共点,则三角形面积的最小值为( )A .B .C .D .【答案】C 【解析】补全截面EFG 为截面EFGHQR 如图,其中H 、Q 、R 分别为、的中点,易证平面ACD 1∥平面EFGHQR ,∵直线D 1P 与平面EFG 不存在公共点, ∴D 1P∥面ACD 1,∴D 1P 面ACD 1,∴P ∈AC ,∴过P 作AC 的垂线,垂足为K ,则BK=,此时BP 最短,△PBB 1的面积最小,∴三角形面积的最小值为,故选:C.【指点迷津】截面问题,往往涉及线面平行,面面平行定义的应用等,考查空间想象能力、逻辑思维能力及计算求解能力.解题的关键是注意明确截面形状,确定几何量.本题由直线与平面没有公共点可知线面平行,补全所给截面后,易得两个平行截面,从而确定点P所在线段,得解.【举一反三】1、【湖南省衡阳市2019届高三二模】如图,直角三角形,,,将绕边旋转至位置,若二面角的大小为,则四面体的外接球的表面积的最小值为()A.B.C.D.【答案】B【解析】如图,,,分别为,,的中点,作面,作面,连,,易知点即为四面体的外接球心,,,.设,,则,,,.【处理一】消元化为二次函数..【处理二】柯西不等式..所以.2、如图,在正四棱柱1111D C B A ABCD -中,2,11==AA AB ,点P 是平面1111D C B A 内的一个动点,则三棱锥ABC P -的正视图与俯视图的面积之比的最大值为( )A .1B .2C .21D .41 【答案】BABC P -的正视图与俯视图的面积之比的最大值为2;故选B .3、【福建省2019届高三模拟】若某几何体的三视图如图所示,则该几何体的所有侧面和底面中,面积的最大值为( )A .2B .C .3D .【答案】C【解析】由三视图可得,该几何体的直观图如图所示,其中,为的中点,平面,,.所以,,.又因为,,所以,故,所以.故选C.类型三体积的最值问题【例3】如图,已知平面平面,,、是直线上的两点,、是平面内的两点,且,,,,,是平面上的一动点,且有,则四棱锥体积的最大值是()A. B. C. D.【答案】A【指点迷津】本题主要考查面面垂直的性质,棱锥的体积公式以及求最值问题. 求最值的常见方法有①配方法:若函数为一元二次函数,常采用配方法求函数求值域,其关键在于正确化成完全平方式,并且一定要先确定其定义域;②换元法;③不等式法;④单调性法;⑤图像法,本题首先根据线面关系将体积最值转化为函数求最值问题,然后应用方法①解答的. 【举一反三】1、已知AD 与BC 是四面体ABCD 中相互垂直的棱,若6AD BC ==,且60ABD ACD ∠=∠=,则四面体ABCD 的体积的最大值是A. B. C. 18 D. 36 【答案】A2、如图,已知平面l αβ=,A 、B 是l 上的两个点,C 、D 在平面β内,且,,DA CB αα⊥⊥4AD =,6,8AB BC ==,在平面α上有一个动点P ,使得APD BPC ∠=∠,则P ABCD -体积的最大值是( )A. B.16 C.48 D.144 【答案】C 【解析】,,DA DA βααβ⊂⊥∴⊥面.,,DA CB αα⊥⊥PAD ∴∆和PBC ∆均为直角三角形.,APD BPC PAD ∠=∠∴∆∽PBC ∆.4,8,2AD BC PB PA ==∴=.学科&网过P 作PM AB ⊥,垂足为M .则PM β⊥.令AM t =,()t R ∈.则2222PA AM PB BM -=-,即()222246PA t PA t -=--,2124,PA t PM ∴=-∴=底面四边形ABCD 为直角梯形面积为()1486362S =+⨯=.学科&网136483P ABCD V -∴=⨯=.故C 正确.3.【河南省八市重点高中联盟“领军考试”2019届高三第三次测评】已知一个高为l 的三棱锥,各侧棱长都相等,底面是边长为2的等边三角形,内有 一个体积为的球,则的最大值为( ) A . B .C .D .【答案】A 【解析】依题意,当球与三棱锥的四个面都相切时,球的体积最大, 该三棱锥侧面的斜高为,,,所以三棱锥的表面积为,设三棱锥的内切球半径为, 则三棱锥的体积,所以,所以,所以,故选A.类型四 角的最值问题【例4】如图,四边形ABCD 和ADPQ 均为正方形,它们所在的平面互相垂直,动点M 在线段PQ 上,E 、F 分别为AB 、BC 的中点.设异面直线EM 与AF 所成的角为θ,则θcos 的最大值为.【答案】25【解析】建立坐标系如图所示.设1AB =,则11(1,,0),(,0,0)22AF E =.设(0,,1)(01)M y y ≤≤,则1(,,1)2EM y =-,由于异面直线所成角的范围为(0,]2π,所以cos θ==.2281145y y +=-+,令81,19y t t +=≤≤,则281161814552y y t t+=≥++-,当1t =时取等号.所以2cos 5θ==≤=,当0y =时,取得最大值.C【指点迷津】空间的角的问题,只要便于建立坐标系均可建立坐标系,然后利用公式求解.解本题要注意,空间两直线所成的角是不超过90度的.几何问题还可结合图形分析何时取得最大值.当点M 在点P 处时,EM 与AF 所成角为直角,此时余弦值为0(最小),当点M 向左移动时,.EM 与AF 所成角逐渐变小,点M 到达点Q 时,角最小,余弦值最大. 【举一反三】1、矩形ABCD 中,,,将△ABC 与△ADC 沿AC 所在的直线进行随意翻折,在翻折过程中直线AD 与直线BC 成的角范围(包含初始状态)为( )A.B.C.D.【答案】C2、在正方体1111D C B A ABCD -中,O 是BD 中点,点P 在线段11D B 上,直线OP 与平面BD A 1所成的角为α,则αsin 的取值范围是( ) A .]33,32[B .]21,31[C .]33,43[D .]31,41[ 【答案】A3.【云南省昆明市云南师范大学附属中学2019届高三上学期第四次月考】如图,在正方体中,点P为AD的中点,点Q为上的动点,给出下列说法:可能与平面平行;与BC所成的最大角为;与PQ一定垂直;与所成的最大角的正切值为;.其中正确的有______写出所有正确命题的序号【答案】【解析】解:由在棱长为1的正方体中点P为AD的中点,点Q为上的动点,知:在中,当Q为的中点时,,由线面平行的判定定理可得PQ与平面平行,故正确;在中,当Q为的中点时,,,,可得,故错误;在中,由,可得平面,即有,故正确;在中,如图,点M为中点,PQ与所成的角即为PQ与所成的角,当Q与,或重合时,PQ与所成的角最大,其正切值为,故正确;在中,当Q 为的中点时,PQ 的长取得最小值,且长为,故正确.故答案为:.4、在正四面体P ABC -中,点M 是棱PC 的中点,点N 是线段AB 上一动点,且AN AB λ=,设异面直线NM 与AC 所成角为α,当1233λ≤≤时,则cos α的取值范围是__________.【答案】,3838⎡⎢⎣⎦ 【解析】设P 到平面ABC 的射影为点O ,取BC 中点D ,以O 为原点,在平面ABC 中,以过O 作DB 的平行线为x 轴,以OD 为y 轴,以OP 为z 轴,建立空间直角坐标系,如图,设正四面体P −ABC的棱长为则()()(((0,4,0,,,,A B C P M --,由AN AB λ=,得(),64,0N λ-,∴((),56,NM AC λ=--→-=-,∵异面直线NM 与AC 所成角为α, 1233λ≤≤,∴2NM AC cos NM AC α⋅==⋅,设32t λ-=,则5733t 剟∴222111124626()41t cos t t t tα==-+-⋅+,∵1313375t <剟cos α.∴cos α的取值范围是⎣⎦.三.强化训练一、选择题1、【甘肃省2019届高三第一次高考诊断】四棱锥的顶点均在一个半径为3的球面上,若正方形的边长为4,则四棱锥的体积最大值为()A.B.C.D.【答案】D【解析】设正方形的中心为,当在于球心的连线上时,四棱锥高最高,由于底面面积固定,则高最高时,四棱锥体积取得最大值.设高为,,球的半径为,故,解得.故四棱锥的体积的最大值为.故选D.2.【广东省东莞市2019届高三第二次调研】已知一个四棱锥的正主视图和俯视图如图所示,其中,则该四棱锥的高的最大值为A.B.C.4 D.2【答案】A【解析】解:如图所示,由题意知,平面平面ABCD,设点P到AD的距离为x,当x最大时,四棱锥的高最大,因为,所以点P的轨迹为一个椭圆,由椭圆的性质得,当时,x取得最大值,即该四棱锥的高的最大值为.故选:A.3.【四川省教考联盟2019届高三第三次诊断】已知四棱锥的底面四边形的外接圆半径为3,且此外接圆圆心到点距离为2,则此四棱锥体积的最大值为()A.12 B.6 C.32 D.24【答案】A【解析】由锥体的体积公式v=,可知,当s和h都最大时,体积最大.由题得顶点P到底面ABCD的距离h≤2.当点P在底面上的射影恰好为圆心O时,即PO⊥底面ABCD时,PO最大=2,即,此时,即四边形ABCD为圆内接正方形时,四边形ABCD的面积最大,所以此时四边形ABCD的面积的最大值=,所以.故选:A4.【安徽省蚌埠市2019届高三第一次检查】某三棱锥的三视图如图所示,网格纸上小正方形的边长为1,三棱锥表面上的点M在俯视图上的对应点为A,三棱锥表面上的点N在左视图上的对应点为B,则线段MN的长度的最大值为A .B .C .D .【答案】D 【解析】由三视图可知,该三棱锥的底面是直角三角形, 一条侧棱与底面垂直(平面),为几何体的直观图如图,在上,重合,当与重合时, 线段的长度的最大值为.故选D .5.如图,在矩形ABCD 中, 2,1AB AD ==,点E 为CD 的中点, F 为线段CE (端点除外)上一动点现将DAF ∆沿AF 折起,使得平面ABD ⊥平面ABC 设直线FD 与平面ABCF 所成角为θ,则sin θ的最大值为( )A.13 B. 4 C. 12 D. 23【答案】C 【解析】如图:在矩形中,过点作的垂线交于点,交于点设,6.【2019年4月2019届高三第二次全国大联考】已知正四面体的表面积为,点在内(不含边界). 若,且,则实数的取值范围为( ) A . B . C .D .【答案】A 【解析】 设正四面体的棱长为则,解得则正四面体的高为记点到平面、、的距离分别为则因为,所以,则故又,故即实数的取值范围为本题正确选项:二、填空题7.【山东省青岛市2019届高三3月一模】在四棱锥中,底面是边长为2的正方形,面,且,若在这个四棱锥内有一个球,则此球的最大表面积为__________.【答案】【解析】在这个四棱锥内有一个球,则此球的最大表面积时,对应的球应该是内切球,此时球的半径最大,设内切球的球心为O半径为R,连接球心和ABCD四个点,构成五个小棱锥,根据体积分割得到,五个小棱锥的体积之和即为大棱锥的体积,,根据AB垂直于AD,PD垂直于AB 可得到AB垂直于面PDA,故得到AB垂直于PA,同理得到BC垂直于PC,表面积为:,此时球的表面积为:.故答案为:.8.【陕西省西安地区陕师大附中、西安高级中学、高新一中、铁一中学、西工大附中等八校2019届高三3月联考】如图,已知正四棱柱和半径为的半球O,底面ABCD在半球O底面所在平面上,,,,四点均在球面上,则该正四棱柱的体积的最大值为______.【答案】4【解析】设正四棱柱的高为h,底面棱长为a,则正四棱柱的底面外接圆直径为,所以,.由勾股定理得,即,得,其中,所以,正四棱柱的体积为,其中,构造函数,其中,则,令,得.当时,;当时,.所以,函数在处取得极大值,亦即最大值,则.因此,该正四棱柱的体积的最大值为4.9.【陕西省西安地区陕师大附中、西安高级中学、高新一中、铁一中学、西工大附中等八校2019届高三3月联考】如图,已知圆柱和半径为的半球O,圆柱的下底面在半球O底面所在平面上,圆柱的上底面内接于球O,则该圆柱的体积的最大值为_____.【答案】2π【解析】解:设圆柱的底面圆半径为r,高为h;则h2+r2=R2=3;所以圆柱的体积为V=πr2h=π(3﹣h2)h=π(3h﹣h3);则V′(h)=π(3﹣3h2),令V′(h)=0,解得h=1;所以h∈(0,1)时,V′(h)>0,V(h)单调递增;h∈(1,)时,V′(h)<0,V(h)单调递减;所以h=1时,V(h)取得最大值为V(1)=2π.故答案为:2π.10.【江西省上饶市2019届高三二模】一个棱长为的正方体形状的铁盒内放置一个正四面体,且能使该正四面体在铁盒内任意转动,则该正四面体的体积的最大值是_____.【答案】【解析】由题该正四面体在铁盒内任意转动,故其能在正方体的内切球内任意转动,内切球半径为6,设正四面体棱长为a, 将此正四面体镶嵌在棱长为x的正方体内,如图所示:则x=,外接球的球心和正方体体心O重合,∴外接球的球半径为:=6,a=4又正四面体的高为∴该正四面体的体积为故答案为11.【河北省衡水市第二中学2019届高三上期中】已知体积为的正四棱锥外接球的球心为,其中在四棱锥内部.设球的半径为,球心到底面的距离为.过的中点作球的截面,则所得截面圆面积的最小值是___________.【答案】【解析】如图取底面的中心为,连接平面,且球心在上,由条件知,,连接,,则,于是底面的边长为.又,故四棱锥的高是,所以,即,从而,,于是,过的中点的最小截面圆是以点为圆心的截面圆,该截面圆的半径是,故所求面积为.12.【江西省临川第一中学等九校2019届高三3月联考】如图所示,三棱锥的顶点,,,都在同一球面上,过球心且,是边长为2等边三角形,点、分别为线段,上的动点(不含端点),且,则三棱锥体积的最大值为__________.【答案】【解析】过球心,又是边长为的等边三角形,,,三角形是等腰直角三角形,,,又因为,在平面内,由线面垂直的判定定理可得平面,即平面,设,,则三棱锥体积,当且仅当,即时取等号,故答案为.13.【安徽省蚌埠市2019届高三下学期第二次检查】正三棱锥中,,点在棱上,且.正三棱锥的外接球为球,过点作球的截面,截球所得截面面积的最小值为__________.【答案】【解析】因为,所以,所以,同理,故可把正三棱锥补成正方体(如图所示),其外接球即为球,直径为正方体的体对角线,故,设的中点为,连接,则且,所以,当平面时,平面截球的截面面积最小,此时截面为圆面,其半径为,故截面的面积为.填.14.【江西师范大学附属中学2019高三上学期期末】若一个四棱锥的底面为正方形,顶点在底面的射影为正方形的中心,且该四棱锥的体积为9,当其外接球的体积最小时,它的高为_________.【答案】【解析】设四棱锥底面边长为a,高为h,底面对角线交于O,由条件四棱锥P-ABCD为正四棱锥,其外接球的球心M在高PO上,设外接球半径为R,在直角三角形MAO中,,又该四棱锥的体积为9,所以所以,,,时,时,所以时R极小即R最小,此时体积最小.故答案为3.15.【江西省上饶市2019届高三二模】已知正方体的棱长为,平面与对角线垂直且与每个面均有交点,若截此正方体所得的截面面积为,周长为,则的最大值为______.【答案】【解析】因为平面与对角线垂直,所以平面与对角面平行,作出图象,为六边形,设则,所以,由对称性得平面过对角线中点时截面面积取最大值为,则的最大值为.16.【河南省洛阳市2019届高三第二次统考】正四面体中,是的中点,是棱上一动点,的最小值为,则该四面体内切球的体积为_____.【答案】【解析】如下图,正方体中作出一个正四面体将正三角形和正三角形沿边展开后使它们在同一平面内,如下图:要使得最小,则三点共线,即:,设正四面体的边长为,在三角形中,由余弦定理可得:,解得:,所以正方体的边长为2,正四面体的体积为:,设四正面体内切球的半径为,由等体积法可得:,整理得:,解得:,所以该四面体内切球的体积为.17.【2019届湘赣十四校高三联考第二次考试】如图,正三棱锥的高,底面边长为4,,分别在和上,且,当三棱锥体积最大时,三棱锥的内切球的半径为________.【答案】【解析】设,,当时,取得最大值,此时为中点,经过点,且,,所以可求,,因此易求,,,,又∵,∴.。
立体几何最值问题如何应对

j 例 3 已知 四棱锥 PA C 底 面 AB D 为菱形 , - B D, C
频 率较高 , 决 此类 问题 的关 键 是 构 造 函 数关 系 , 解 进
而求 函数 的最值 , 常用 的方 法主要 有 以下几种 .
1 导 数 法
,- 一
P _ 面 A C AB = 6。E, Aj平 B D, C 0 , F分 别 是 B , C 的 CP
EFG H .
』・D √  ̄ 0 J ll5 / 孚 . , × 2 lB I
1 一
因为 二面 角 EAF C 为锐 角 , 所求 二 面角 的余 弦 值 - - 故
为 .
( ) B =b 则 A D 11 D= 2 。, 1Hl一 2设 C , B _B1 c A c 1 ab V皿 FCG -
√ 一 ,以积一a 11 , 1譬所体 号h32 z 设 2 Z a1 = /4 6
Y 2 1a一寺n , 一4a~3 当 Y取最值时, 。则 8。 a,
Y 一4 a 一3 , 8 。 a =0 解得 a 一0或 a .当 a 一4 一4时 , 体
积最 大 , 时 ^ 此 一 2 基 本 不 等 式 法 1 一 一2答 案为 2 2 . .
( )设 AB=2 2 AA1 a 在 AB D— B C D 内 —2 , C A 1 1
IF I vz0 眦像 1一 A0 + + . 一 , z一 1
m . F一 A'
,
随机 选 取 一 点 , 该 点 取 自 于 几 何 体 A AB E 记 F-
量. D=( 3 3 0 , 以 又B 一√ , ,)所
cos m 一
厂 析 ( 证明 在 方 BDABC , Q 1 解 ) : 长 体A C — 中 D
专题06 立体几何中的动点及最值范围问题(解析版)

专题06 立体几何中动点及最值范围问题题型一、角度、长度最值范围问题(多选)1、设动点P 在正方体1111ABCD A B C D -的对角线1BD 上,记11D P D B λ=当APC ∠为钝角时,则实数可能的取值是( ) A .12B .23C .13D .1【答案】AB【分析】首先以D 为原点,DA ,DC ,1DD 分别为x ,y ,z 轴建立空间直角坐标系,根据题意得到0PA PC ⋅<,再解不等式即可得到答案.【解析】以D 为原点,DA ,DC ,1DD 分别为x ,y ,z 轴建立空间直角坐标系,如图所示:设正方体的边长为1,则()1,0,0A ,()1,1,0B ,()0,1,0C ,()10,0,1D ,()11,0,1D A =-,()10,1,1D C =-,()11,1,1D B =-,所以()11,,D P D B λλλλ==-. 又因为()()()11,,1,0,11,,1PA PD D A λλλλλλ=+=--+-=---,()()()11,,0,1,1,1,1PC PD DC λλλλλλ=+=--+-=---, 因为APC ∠为钝角,所以0PA PC ⋅<,即()()()()()()()2111=1310λλλλλλλ--+--+---<,解得113λ<<.故选AB【名师点睛】本题主要考查空间向量的数量积运算,属于简单题.2、如图,正方体1111ABCD A B C D -,点P 在1AB 上运动(不含端点),点E 是AC 上一点(不含端点),设EP 与平面1ACD 所成角为θ,则cosθ的最小值为( )A .13B .33C .53D .63答案: A 解析:由已知求出AC 的中点1E 与1B 的连线与平面1ACD 所成角的余弦值,在1AB 上(不含端点)任取一点P ,在平面1AB E 内过P 作11//PE B E ,则EP 与平面1ACD 所成角11OE B θ=∠,可得1cos 3θ=,结合选项即可得答案.详解:解:如图,由正方体的性质,可得1B D ⊥平面1AD C ,且1B 在平面1AD C 上的射影O 为△1AD C 的外心.设正方体的棱长为1,则△1AD C 的边长为2, 当1E 为AC 的中点时,11162326OE =-=, 1116122B E =+=,此时11616cos 362OE B ==. 在1AB 上(不含端点)任取一点P ,在平面1AB E 内过P 作11//PE B E ,则EP 与平面1ACD 所成角11OE B θ=∠,可得1cos 3θ=.结合选项可知,cos θ的最小值为13.故选:A .3、三棱柱111ABC A B C -的侧棱与底面垂直,11AA AB AC ===,AB AC ⊥,N 是BC 的中点,点P 在11A B 上,且满足111A P A B λ=,当直线PN 与平面ABC 所成的角取最大值时,λ的值为( )A .12B .22C .32D .255【答案】A【分析】建立空间直角坐标系,利用向量的夹角公式,求出直线PN 与平面ABC 所成的角,即可求得结论.【解析】如图,以AB ,AC ,1AA 分别为x ,y ,z 轴,建立空间直角坐标系A xyz -,则(,P λ0,1),11,,122PN λ⎛⎫=-- ⎪⎝⎭,平面ABC 的一个法向量为(0,n =0,1)设直线PN 与平面ABC 所成的角为θ,21sin 15()24PN nPN nθλ⋅∴==⋅-+, ∴当12λ=时,25(sin )5max θ=,此时角θ最大.故选A . 【名师点睛】本题考查了向量法求线面角的求法,考查了函数最值的求法,是基础题,解题时要认真审题,注意向量法的合理运用.4、如图所示,在正方体1111ABCD A B C D -中,点E 为线段AB 的中点,点F 在线段AD 上移动,异面直线1B C 与EF 所成角最小时,其余弦值为( )A .0B .12C .105D .1116【答案】C【分析】以D 为原点,DA 为x 轴,DC 为y 轴,1DD 为z 轴,建立空间直角坐标系,利用向量法能求出异面直线1B C 与EF 的夹角的余弦值,根据夹角最小即可求得结果.【解析】以D 为原点,DA 为x 轴,DC 为y 轴,1DD 为z 轴,建立空间直角坐标系,在正方体1111ABCD A B C D -中, 点E 为线段AB 的中点,设正方体棱长为2, 则1(0,0,0),(2,1,0),(2,2,2),(0,2,0)D E B C ,1(2,0,2)B C =--,设(),0,0F m ()02m ≤≤,(2,1,0)EF m =--,设异面直线1B C 与EF 的夹角为θ,则1212|||2(2)|cos ||||122(2)1211(2)EF B C m EF B C m m θ⋅-⨯-===⋅⋅-+⋅+-, 异面直线1B C 与EF 所成角最小时,则cos θ最大,即0m =时,210cos 51102141θ===⋅+.故选C .【名师点睛】本题考查异面直线及其所成的角的余弦值,解题方法是建立空间直角坐标系,用空间向量法表示距离、求角,属于中档题.5、如图,已知正方体1111ABCD A B C D -的棱长为1,,E F 分别是棱11,AD B C 上的中点.若点P 为侧面正方形11ADD A 内(含边)动点,且存在,x y R ∈使1B P xBE yBF =+成立,则点P 的轨迹长度为A .12B .1C 5D .2π 【答案】C【分析】根据向量共面判断出1//B P 平面BEF ,由面面平行得到P 点的轨迹,在直角三角形中求出边长即可.【解析】因为1B P xBE yBF =+成立,所以1B P BE BF 、、共面,即1//B P 平面BEF , 如图,取11A D 中点Q ,连接1B Q 、1B A 、AQ , 根据正方体的性质得,1//B Q BE ,1//B A FE , 且111=B QB A B ,=FEBE E ,所以平面1//B AQ 平面BEF ,所以点P 在AQ 上运动,点P 的轨迹为线段AQ ,因为11A A =,112AQ =, 由勾股定理得151+=42QA =,故选C .题型二、动点问题(多选)1、如图,棱长为1的正方体1111ABCD A B C D -中,P 为线段1A B 上的动点(不含端点),则下列结论正确的是A .平面11D A P ⊥平面1A APB .//BC 平面11AD PC .三棱锥1D CDP -的体积为定值 D .直线1D P 与AC 所成的角可能是6π【答案】AC【解析】对于A 中,在正方体1111ABCD A B C D -中,可得1111,A D AA A D AB ⊥⊥,又由1AA AB A =,所以11A D ⊥平面1A AP ,因为11A D ⊂平面11D A P ,所以平面11D A P ⊥平面1A AP ,所以A 正确; 对于B 中,在正方体1111ABCD A B C D -中,可得11//BC A D , 所以11,,,B C A D 四点共面,所以B 不正确; 对于C 中,因为1111122CDD S=⨯⨯=,点P 到平面1CDD 的距离为1BC =, 所以三棱锥1D CDP -的体积为定值,所以C 正确;对于D 中,以D 为原点,DA 为x 轴,DC 为y 轴,1DD 为z 轴,建立空间直角坐标系,可得1(0,0,1),(1,0,0),(0,1,0)D A C ,设(1,,)(01,01)P a b a b <<<<, 则1(1,,1),(1,1,0)D P a b AC =-=-, 则11221cos ,01(1)2D P AC D P AC D P ACa b ⋅==<⋅++-⋅,当1a =时,1,2D P AC π=;当0,1a b ==时,13,4D P AC π=, 所以直线1D P 与AC 所成的角的范围是(,)42ππ,所以D 不正确.故选AC【名师点睛】此类问题解答中熟记正方体的几何结构特征,熟练应用转化顶点,利用等体积法求解三棱锥的体积,以及合理利用空间向量的夹角公式求解异面直线所成的角是解答的关键.(多选)2、如图,在三棱柱111ABC A B C -中,侧棱1AA ⊥底面111A B C ,90BAC ︒∠=,11AB AC AA ===,D 是棱1CC 的中点,P 是AD 的延长线与11A C 的延长线的交点.若点Q 在直线1B P 上,则下列结论错误的是( ).A .当Q 为线段1B P 的中点时,DQ ⊥平面1A BD B .当Q 为线段1B P 的三等分点时,DQ ⊥平面1A BDC .在线段1B P 的延长线上,存在一点Q ,使得DQ ⊥平面1A BD D .不存在点Q ,使DQ 与平面1A BD 垂直 【答案】ABC【分析】以1A 为坐标原点,11A B ,11A C ,1A A 所在直线分别为x 轴、y 轴、z 轴建立空间直角坐标系,求得平面1A BD 的一个法向量(,,)n x y z =,假设DQ ⊥平面1A BD ,且11B Q B P λ=,得到11DQ DB BQ =+=11,12,2λλ⎛⎫--+- ⎪⎝⎭,则(2,1,2)n =-与11,12,2DQ λλ⎛⎫=--+- ⎪⎝⎭共线,研究1112122124λλ---+===-是否有解即可. 【解析】以1A 为坐标原点,11A B ,11A C ,1A A 所在直线分别为x 轴、y 轴、z 轴建立空间直角坐标系,则由1(0,0,0)A ,1(1,0,0)B ,1(0,1,0)C ,(1,0,1)B ,10,1,2D ⎛⎫ ⎪⎝⎭,(0,2,0)P ,所以1(1,0,1)A B =,110,1,2A D ⎛⎫= ⎪⎝⎭,1(1,2,0)B P =-,111,1,2DB ⎛⎫=-- ⎪⎝⎭.设平面1A BD 的一个法向量为(,,)n x y z =,则11012n A B x z n A D y z ⎧⋅=+=⎪⎨⋅=+=⎪⎩, 取2z =-,则2x =,1y =,所以平面1A BD 的一个法向量为(2,1,2)n =-.假设DQ ⊥平面1A BD ,且11(1,2,0)(,2,0)BQ B P λλλλ==-=-, 则11DQ DB BQ =+=11,12,2λλ⎛⎫--+- ⎪⎝⎭. 因为DQ 也是平面1A BD 的法向量,所以(2,1,2)n =-与11,12,2DQ λλ⎛⎫=--+- ⎪⎝⎭共线,所以1112122124λλ---+===-成立,但此方程关于λ无解. 因此不存在点Q ,使DQ 与平面1A BD 垂直,故选ABC .(多选)3、在长方体1111ABCD A B C D -中,23AB =12AD AA ==,,,P Q R 分别是11,,AB BB AC 上的动点,下列结论正确的是 A .对于任意给定的点P ,存在点Q 使得1D P CQ ⊥ B .对于任意给定的点Q ,存在点R 使得1D R CQ ⊥ C .当1AR A C ⊥时,1AR D R ⊥D .当113AC A R =时,1//D R 平面1BDC 【答案】ABD【分析】如图所示建立空间直角坐标系,计算142D P CQ b ⋅=-,()12222D R CQ b λλ⋅=--,134AR D R ⋅=-,10D R n ⋅=,得到答案.【解析】如图所示,建立空间直角坐标系,设()2,,0P a ,0,23a ⎡⎤∈⎣⎦,()2,23,Q b ,[]0,2b ∈,设11A R AC λ=,得到()22,23,22R λλλ--,[]0,1λ∈. ()12,,2P a D -=,()2,0,CQ b =,142D P CQ b ⋅=-,当2b =时,1D P CQ ⊥,A 正确;()122,23,2D R λλλ=--,()12222D R CQ b λλ⋅=--,取22bλ=+时,1D R CQ ⊥,B 正确;1AR A C⊥,则()()12,23,222,23,2212440AR AC λλλλλλ⋅=--⋅--=-+-+=, 14λ=,此时11333313,,,,02222224AR D R ⎛⎫⎛⎫⋅=-⋅-=-≠ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭,C 错误; 113AC A R =,则4234,,333R ⎛⎫ ⎪ ⎪⎝⎭,14232,,333D R ⎛⎫=- ⎪ ⎪⎝⎭,设平面1BDC 的法向量为(),,n x y z =,则10n BD n DC ⎧⋅=⎪⎨⋅=⎪⎩,解得()3,1,3n =-,故10D R n ⋅=,故1//D R 平面1BDC ,D 正确. 故选ABD .【点睛】本题考查了空间中的线线垂直,线面平行,意在考查学生的计算能力和空间想象能力,推断能力. 题型三、确定点的位置1、如图,在三棱柱111ABC A B C -中,四边形11AAC C 是边长为3的正方形,1CC BC ⊥,1BC =,2AB =.(1)证明:平面1A BC ⊥平面1ABC ;(2)在线段1A B 上是否存在点M ,使得1CM BC ⊥,若存在,求1BMBA 的值;若不存在,请说明理由.【答案】(1)证明见解析;(2)14. 【解析】(1)在ABC 中,3AC =1BC =,2AB =,满足222AC BC AB +=,所以AC BC ⊥,又1CC BC ⊥,1CC AC C =,所以BC ⊥面11ACC A ,又1AC ⊂面11ACC A ,所以1BC A C ⊥,又四边形11AAC C 是边长为3的正方形,所以11AC AC ⊥,又1BCAC C =,所以1AC ⊥面1A CB ,又1AC ⊂平面1ABC ,所以平面1A BC ⊥平面1ABC ;(2)在线段1A B 上存在点M ,使得1CM BC ⊥,且114BM BA =, 理由如下:由(1)得,以点C 为原点,1,,CA CB CC 所在直线分别为,,x y z 轴建立空间直角坐标系,如图所示,则()3,0,0A,()0,0,0C ,()0,1,0B ,13,0,3A ,(13C ,设(),,M x y z ,1BM BA λ=,所以(),1,3,3x y z λ-=-,解得3x λ=,1y λ=-,3z λ=,所以()3,13CM λλλ=-,(10,1,3C B =-,要使1CM BC ⊥,则需10CM BC ⋅=,即130λλ--=,解得14λ=,故114BM BA =.2、如图,在多面体ABCDP 中,ABC 是边长为4的等边三角形,PA AC =,22BD CD ==,42PC PB ==,点E 为BC 的中点,平面BDC ⊥平面ABC .(1)求证://DE 平面PAC(2)线段BC 上是否存在一点T ,使得二面角T DA B --为直二面角?若存在,试指出点T 的位置;若不存在,请说明理由.【答案】(1)证明见解析;(2)存在,T 为线段BC 上靠近点C 的八等分点. 【分析】(1)根据题目条件证明DE ⊥平面ACE ,从而得到DE //PA ,得出DE //平面PAC ;(2)建立空间直角坐标系,假设存在点(),0,0T λ,计算平面TDA 和平面BDA 的法向量,使法向量数量积为零,然后求解λ,根据λ的值确定点T 的位置. 【解析】(1)因为22BD CD ==ABC 是边长为4的等边三角形, 所以((2222222216BD CD BC +=+==,所以BDC 是等腰直角三角形,90BDC ∠=︒.又点E 为BC 的中点,所以DE BC ⊥.因为平面BDC ⊥平面ABC ,平面BDC ⋂平面ABC BC =,所以DE ⊥平面ABC . 因为42PC PB ==,4PA AC AB ===,所以222224432PA AC PC +=+==,222224432PA AB PB +=+==,所以PAB △与PAC 都是直角三角形,故PA AC ⊥,PA AB ⊥. 又AC AB A ⋂=,所以PA ⊥平面ABC ,所以DE PA ∥. 因为PA ⊂平面PAC ,DE ⊄平面PAC ,所以DE 平面PAC .(2)连接AE ,以E 为原点,EC ,EA ,ED 所在直线分别为x ,y ,z 轴,建立如图所示的空间直角坐标系,则()0,23,0A ,()2,0,0B -,()2,0,0C ,()0,0,2D ,设存在(),0,0T λ,使得二面角T DA B --为直二面角,易知22λ-≤≤,且0λ≠. 设平面BAD 的法向量为()1111,,n x y z =,则由()2,0,2BD =,()0,23,2AD =-,得1111030x z y z +=⎧⎪⎨-+=⎪⎩,令11z =,得111x x =-,133y =,故131,,13n ⎛⎫=- ⎪ ⎪⎝⎭.设平面TAD 的法向量为()2222,,n x y z =,则由(),0,2DT λ=-,(),23,0AT λ=-,得222220,230x z x y λλ-=⎧⎪⎨-=⎪⎩,令21z =,得22x λ=,233y =,故223,,13n λ⎛⎫= ⎪ ⎪⎝⎭. 由122233133cos ,074433n n λλ-+⨯+==⨯+,得12103λ-+=,故32λ=. 所以当T 为线段BC 上靠近点C 的八等分点时,二面角T DA B --为直二面角.3、如图,三棱柱111ABC A B C -中,AB ⊥侧面11BB C C ,已知13BCC π∠=,1BC =,12AB C C ==,点E 是棱1C C 的中点.(1)求证:1C B ⊥平面ABC ; (2)求二面角11A EB A --的余弦值;(3)在棱CA 上是否存在一点M ,使得EM 与平面11A B E 所成角的正弦值为21111,若存在,求出CM CA 的值;若不存在,请说明理由.【答案】(1)证明见解析(225(3)存在,13CM CA =或523CM CA =.【解析】(1)由题意,因为1BC =,12CC =,13BCC π∠=,所以13BC又所以22211BC BC CC +=,所以1BC BC ⊥,因为AB ⊥侧面11BB C C ,所以1AB BC ⊥.又因为AB BC B ⋂=,AB ,BC ⊂平面ABC ,所以直线1C B ⊥平面ABC . (2)以B 为原点,分别以BC ,1BC 和BA 的方向为x ,y 和z 轴的正方向建立如图所示的空间直角坐标系,则()0,0,2A ,()13,0B -,132E ⎛⎫⎪ ⎪⎝⎭,()13,2A -,设平面1AB E 的一个法向量为()111,,n x y z =,()13,2AB =--,13,,222AE ⎛⎫=- ⎪ ⎪⎝⎭因为100n AB n AE ⎧⋅=⎨⋅=⎩,所以11111132013202x z x y z ⎧--=⎪⎨-=⎪⎩,令13y =,则11x =,所以()1,3,1n =设平面11A B E 的一个法向量为(),,m x y z =,()110,0,2A B =-,133,,222A E ⎛⎫=-- ⎪ ⎪⎝⎭, 因为11100m A B m A E ⎧⋅=⎪⎨⋅=⎪⎩,所以20332022z x y z -=⎧⎪⎨--=⎪⎩,令3y =,则1x =,所以()1,3,0m =,2m =,5n =,4m n ⋅=,所以425cos ,525m n m n m n⋅===.设二面角11A EB A --为α,则25cos cos ,5m n α==. 所以设二面角11A EB A --的余弦值为255. (3)假设存在点M ,设(),,M x y z ,因为CM CA λ=,[]0,1λ∈,所以()()1,,1,0,2x y z λ-=-,所以()1,0,2M λλ-所以13,,222EM λλ⎛⎫=-- ⎪ ⎪⎝⎭设平面11A B E 的一个法向量为()1,3,0m =,所以22132112211132424λλλ--=⎛⎫-++ ⎪⎝⎭,得2693850λλ-+=.即()()312350λλ--=,所以13λ=或523λ=,所以13CM CA =或523CM CA =.【名师点睛】本题考查了线面平行的判定与证明,以及空间角的求解问题,意在考查学生的空间想象能力和逻辑推理能力,解答中熟记线面位置关系的判定定理和性质定理,通过严密推理是线面位置关系判定的关键,同时对于立体几何中角的计算问题,往往可以利用空间向量法,通过求解平面的法向量,利用向量的夹角公式求解. 强化训练(多选)1、如图所示,正方体1111ABCD A B C D -中,1AB =,点P 在侧面11BCC B 及其边界上运动,并且总是保持1AP BD ⊥,则以下四个结论正确的是A .113P AA D V -=B .点P 必在线段1BC 上 C .1AP BC ⊥D .//AP 平面11AC D【答案】BD【分析】根据三棱锥体积公式求得116P AA D V -=,知A 错误;以D 为坐标原点建立空间直角坐标系,利用空间向量法可得到1CP x B C →→=-,11AP BC →→⋅=,AP →垂直于平面11AC D 的法向量n →,由此可确定,,B C D 的正误.【解析】对于A ,P 在平面11BCC B 上,平面11//BCC B 平面1AA D ,P ∴到平面1AA D 即为C 到平面1AA D 的距离,即为正方体棱长,1111111113326P AA D AA D V S CD -∴=⋅=⨯⨯⨯⨯=△,A 错误;对于B ,以D 为坐标原点可建立如下图所示的空间直角坐标系:则()1,0,0A ,(),1,P x z ,()1,1,0B ,()10,0,1D ,()11,1,1B ,()0,1,0C()1,1,AP x z →∴=-,()11,1,1BD →=--,()11,0,1B C →=--,1AP BD ⊥,1110AP BD x z →→∴⋅=--+=,x z ∴=,即(),1,P x x ,(),0,CP x x →∴=,1CP x B C →→∴=-,即1,,B P C 三点共线,P ∴必在线段1B C 上,B 正确;对于C ,()1,1,AP x x →=-,()11,0,1BC →=-,111AP BC x x →→∴⋅=-+=,AP ∴与1BC 不垂直,C 错误;对于D ,()11,0,1A ,()10,1,1C ,()0,0,0D ,()11,0,1DA →∴=,()10,1,1DC →=, 设平面11AC D 的法向量(),,n x y z →=,1100n DA x z n DC y z ⎧⋅=+=⎪∴⎨⋅=+=⎪⎩,令1x =,则1z =-,1y =,()1,1,1n →∴=-, 110AP n x x →→∴⋅=-+-=,即AP n →→⊥,//AP ∴平面11ACD ,D 正确. 故选BD .【点睛】本题考查立体几何中动点问题相关命题的辨析,涉及到三棱锥体积公式、动点轨迹、线线垂直关系和线面平行关系等知识;解题关键是熟练应用空间向量法来验证相关结论.2、如图,在边长为2的正方体1111ABCD A B C D -中,E 为BC 的中点,点P 在底面ABCD 上移动,且满足11B P D E ⊥,则线段1B P 的长度的最大值为( )A .45B .2C .2D .3【答案】D【分析】以点D 为坐标原点,DA 、DC 、1DD 所在直线分别为x 、y 、z 轴建立空间直角坐标系,设点(),,0P x y ,根据110B P D E ⋅=得出x 、y 满足的关系式,并求出y 的取值范围,利用二次函数的基本性质求得1B P 的最大值.【解析】如下图所示,以点D 为坐标原点,DA 、DC 、1DD 所在直线分别为x 、y 、z 轴建立空间直角坐标系D xyz -,则点()12,2,2B 、()10,0,2D 、()1,2,0E ,设点()(),,002,02P x y x y ≤≤≤≤,()11,2,2D E =-,()12,2,2B P x y =---,11D E B P ⊥,()112224220B P D E x y x y ∴⋅=-+-+=+-=,得22x y =-,由0202x y ≤≤⎧⎨≤≤⎩,得022202y y ≤-≤⎧⎨≤≤⎩,得01y ≤≤, ()()2221224548B P x y y y ∴=-+-+=-+01y ≤≤,当1y =时,1B P 取得最大值3.故选D .3、在长方体1111ABCD A B C D -中,已知底面ABCD 为正方形,P 为11A D 的中点,2AD =,13AA =,点Q 为正方形ABCD 所在平面内的一个动点,且满足2QC QP =.则线段BQ 的长度的最大值是( )A .2B .4C .6D .前三个答案都不对【答案】C【分析】先以D 点为坐标原点,分别以DA ,DC ,1DD 所在方向为x 轴,y 轴,z 轴正方向,建立空间直角坐标系,由题意得到(0,2,0)C ,()1,0,3P ,(2,2,0)B ,设(,,0)Q x y ,由2QC QP =,得到22(2)(2)4-++=x y ,再由圆上的点与定点距离的问题,即可求出结果.【解析】以D 点为坐标原点,分别以DA ,DC ,1DD 所在方向为x 轴,y 轴,z 轴正方向,建立如图所示的空间直角坐标系,因为在长方体1111ABCD A B C D -中,已知底面ABCD 为正方形,P 为11A D 的中点,2AD =,13AA =(0,2,0)C ,(1,3P ,(2,2,0)B ,因为点Q 为正方形ABCD 所在平面内的一个动点,设(,,0)Q x y , 因为2QC QP =,所以()2222(2)213+-=⋅-++x y x y ,整理得:22(2)(2)4-++=x y ,即点Q 可看作圆22(2)(2)4-++=x y 上的点, 又22(2)(2)=-+-BQ x y ,所以BQ 表示圆22(2)(2)4-++=x y 上的点与定点(2,2)之间的距离, 因此22max (22)(22)426=-+--+=+=BQ r (其中r表示圆22(2)(2)4-++=x y 的半径.)故选C . 【名师点睛】本题主要考查立体几何中的轨迹问题,涉及圆上的点到定点距离的最值,灵活运用转化与化归的思想即可,属于常考题型.4、如图,已知正方体ABCD -A 1B 1C 1D 1棱长为8,点H 在棱AA 1上,且HA 1=2,在侧面BCC 1B 1内作边长为2的正方形EFGC 1,P 是侧面BCC 1B 1内一动点,且点P 到平面CDD 1C 1距离等于线段PF 的长,则当点P 在侧面BCC 1B 1运动时,2HP 的最小值是( )A .87B .88C .89D .90【答案】B【分析】建立空间直角坐标系,过点H 作1HM BB ⊥,垂足为M ,连接MP ,得出222HP HM MP =+,当MP 最小时,2HP 最小,利用空间直角坐标系求2HP 的最小值.【解析】如图,建立空间直角坐标系,过点H 作1HM BB ⊥,垂足为M ,连接MP ,则HM PM ⊥,所以222HP HM MP =+,当MP 最小时,2HP 最小, 过P 作1PN CC ⊥,垂足为N ,设(,8,)P x z ,则(2,8,6),(8,8,6),(0,8,)F M N z ,且08,08x z ≤≤≤≤,因为PN PF =,所以22(2)(6)x z x -+-=,化简得244(6)x z -=-,所以222222(8)(6)(8)441260(6)2424MP x z x x x x x =-+-=-+-=-+=-+≥, 当6x =时,2MP 取得最小值24,此时222282488HP HM MP =+=+=, 所以2HP 的最小值为88,故选B .5、如图,在棱长为2的正方体1111ABCD A B C D -中,E 为BC 的中点,点P 在底面ABCD 上(包括边界....)移动,且满足11B P D E ⊥,则线段1B P 的长度的最大值为A .55B .25C .2D .3【答案】D【分析】以D 为原点,DA 为x 轴,DC 为y 轴,1DD 为z 轴,建立空间直角坐标系,利用向量法能求出线段1B P 的长度的最大值.【解析】以D 为原点,DA 为x 轴,DC 为y 轴,1DD 为z 轴,建立空间直角坐标系,设P (a ,b ,0),则1D (0,0,2),E (1,2,0),1B (2,2,2),1B P =(a −2,b −2,−2),1D E =(1,2,−2), 因为1B P ⊥1D E ,()1122240B P D E a b ∴⋅=-+-+=, 所以a +2b −2=0,01b ≤≤,所以点P 的轨迹是一条线段,()()()()2222221224224548a b b B P b b b -+-+==+-+=-+, 由二次函数的性质可得当1b =时,2548b b -+可取到最大值9, 所以线段1B P 的长度的最大值为3.故选D .6、如图所示,在正方体1111ABCD A B C D -中,点P 是底面1111D C B A 内(含边界)的一点,且//AP 平面1DBC ,则异面直线1A P 与BD 所成角的取值范围为A .3,44ππ⎡⎤⎢⎥⎣⎦B .,42ππ⎡⎤⎢⎥⎣⎦C .,32ππ⎡⎤⎢⎥⎣⎦D .2,33ππ⎡⎤⎢⎥⎣⎦【答案】C【分析】连接111,,AB AD B D ,则点P 在线段11B D 上,以D 为坐标原点建立坐标系,利用向量方法可求出范围. 【解析】过A 作平面α平面1DBC ,点P 是底面1111D C B A 内(含边界)的一点,且//AP 平面1DBC ,则P ∈平面α,即P 在α与平面1111D C B A 的交线上,连接111,,AB AD B D ,11DD BB =,则四边形11BDD B 是平行四边形,11B D BD ∴,11B D ∴平面1DBC ,同理可证1AB ∥平面1DBC ,∴平面11AB D ∥平面1DBC ,则平面11AB D 即为α,点P 在线段11B D 上,以D 为坐标原点,1,,DA DC DD 建立如图坐标系,设正方体棱长为1,则()0,0,0D ,()1,1,0B ,()1,0,0A ,设(),,1P λλ,[]0,1λ∈,()1,1,0DB ∴=,()1,,1AP λλ=-,21DB AP λ∴⋅=-,2DB =,2222AP λλ=-+,设1A P 与BD 所成角为θ,则()22221211cos 2121DB APDB AP λλθλλλλ⋅--===-+⋅-+ 221313442121324λλλ=-=--+⎛⎫-+ ⎪⎝⎭,当12λ=时,cos θ取得最小值为0, 当0λ=或1时,cos θ取得最大值为12,10cos 2θ∴≤≤,则32ππθ≤≤.故选C .7、如图,三棱锥V ABC -的侧棱长都相等,底面ABC 与侧面VAC 都是以AC 为斜边的等腰直角三角形,E 为线段AC 的中点,F 为直线AB 上的动点,若平面VEF 与平面VBC 所成锐二面角的平面角为θ,则cos θ的最大值是A .33 B .23C 5D 6【答案】D【分析】连接BE ,以E 为原点,EB 为x 轴,EC 为y 轴,EV 为z 轴,建立空间直角坐标系,求出平面VBC 的一个法向量m ,平面VEF 的一个法向量n ,利用cos m n m nθ⋅=即可求解.【解析】底面ABC 与侧面VAC 都是以AC 为斜边的等腰直角三角形, 则Rt ABC Rt VAC ≅,所以VA VC BA BC === 设2VA VC BA BC VB =====,由E 为线段AC 的中点,则2VE BV ==, 由222VE BE VB +=,所以VE EB ⊥,以E 为原点,EB 为x 轴,EC 为y 轴,EV 为z 轴, 建立空间直角坐标系,如图所示:则()2,0C ,)2,0,0B,(2V ,设(),2,0F x x -,(0,2,2VC =-,(2,0,2VB =-,(2EV =,(,2,2VF x x =,设平面VBC 的一个法向量()111,,m x y z =,则00m VC m VB ⎧⋅=⎨⋅=⎩,即1111220220z x ⎧+=⎪⎨-=⎪⎩,令11x =,则11y =,11z =,所以()1,1,1m =. 设平面VEF 的一个法向量()222,,n x y z =,则00n EV n VF ⎧⋅=⎨⋅=⎩,即(222220220z x x x y z ⎧=⎪⋅+-⋅+=⎪⎩,解得20z =,令21y =,则221x x =-, 所以21,1,0n x ⎛⎫=- ⎪ ⎪⎝⎭, 平面VEF 与平面VBC 所成锐二面角的平面角为θ,则22cos 22232m n x m n x xθ⋅==-+,将分子、分母同除以1x,可得=令()2266632f x x x ⎛=-+=-+ ⎝⎭,当2x =时,()min 3f x =,则cos θ3=. 故选D【点睛】本题考查了空间向量法求二面角、考查了基本运算求解能力,解题的关键是建立恰当的空间直角坐标系,属于中档题.8、已知MN 是正方体内切球的一条直径,点P 在正方体表面上运动,正方体的棱长是2,则PM PN →→⋅的取值范围为 A .[]0,4 B .[]0,2C .[]1,4D .[]1,2【答案】B【分析】利用向量的线性运算和数量积运算律可将所求数量积化为21PO →-,根据正方体的特点可确定PO →的最大值和最小值,代入即可得到所求范围. 【解析】设正方体内切球的球心为O ,则1OM ON ==,2PM PN PO OM PO ON PO PO OM ON OM ON →→→→→→→→→→→→⎛⎫⎛⎫⎛⎫⋅=+⋅+=+⋅++⋅ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭,MN 为球O 的直径,0OM ON →→∴+=,1OM ON →→⋅=-,21PM PN PO →→→∴⋅=-,又P 在正方体表面上移动,∴当P 为正方体顶点时,PO →最大,最大值为;当P 为内切球与正方体的切点时,PO →最小,最小值为1,[]210,2PO →∴-∈,即PM PN →→⋅的取值范围为[]0,2.故选B .【点睛】本题考查向量数量积的取值范围的求解问题,关键是能够通过向量的线性运算将问题转化为向量模长的取值范围的求解问题.7、在正四面体D ABC -(所有棱长均相等的三棱锥)中,点E 在棱AB 上,满足2AE EB =,点F 为线段AC 上的动点.设直线DE 与平面DBF 所成的角为α,则A .存在某个位置,使得DE BF ⊥B .存在某个位置,使得4FDB π∠=C .存在某个位置,使得平面DEF ⊥平面DACD .存在某个位置,使得6πα=【答案】C【分析】设正四面体D ABC -的底面中心为点O ,连接DO ,则DO ⊥平面ABC ,以点O 为坐标原点,OB 、OD 所在直线分别为x 、z 轴建立空间直角坐标系,设正四面体D ABC -的棱长为2,然后利用空间向量法逐一分析求解可得结果. 【解析】如下图所示,设正四面体D ABC -的底面中心为点O ,连接DO ,则DO ⊥平面ABC ,以点O 为坐标原点,OB 、OD 所在直线分别为x 、z 轴建立空间直角坐标系, 设正四面体D ABC -的棱长为2,则31,0A ⎛⎫- ⎪ ⎪⎝⎭、23B ⎫⎪⎪⎝⎭、3C ⎛⎫ ⎪ ⎪⎝⎭、26D ⎛ ⎝⎭、31,03E ⎫-⎪⎪⎝⎭,设,03F λ⎛⎫- ⎪ ⎪⎝⎭,其中11λ-≤≤, 对于A 选项,若存在某个位置使得DE BF ⊥,31,333DE ⎛⎫=-- ⎪ ⎪⎝⎭,(),0BF λ=-,1103DE BF λ∴⋅=--=,解得3λ=-,不合乎题意,A 选项错误;对于B 选项,若存在某个位置使得4FDB π∠=,,33DF λ⎛=-- ⎝⎭,23DB ⎛=⎝⎭,cos ,DF DB DF DB DF DBλ⋅<>====⋅B选项错误;对于C 选项,设平面DAC 的一个法向量为()111,,m x y z =,1,DA ⎛=-- ⎝⎭,DC ⎛=-⎝⎭,由1111113033303m DA x y z m DC x y z ⎧⋅=---=⎪⎪⎨⎪⋅=-+-=⎪⎩,取11z =-,得()22,0,1m =-,设平面DEF 的一个法向量为()222,,n x y z =,31,3DE ⎛=- ⎝⎭,,DF λ⎛=- ⎝⎭, 由22222231033333n DE x y z n DF x y z λ⎧⋅=--=⎪⎪⎨⎪⋅=-+=⎪⎩,取y =,则()221n λ=+-,若存在某个位置,使得平面DEF ⊥平面DAC ,则2190m n λ⋅=+=,解得[]31,17λ=-∈-,合乎题意,C 选项正确;对于D 选项,设平面DBF 的一个法向量为()333,,u x y z =,2326,0,33DB ⎛⎫=- ⎪ ⎪⎝⎭,326,,33DF λ⎛⎫=-- ⎪ ⎪⎝⎭, 由333332326033326033u DB x z u DF x y z λ⎧⋅=-=⎪⎪⎨⎪⋅=-+-=⎪⎩,令z λ=,则()2,6,u λλ=,若存在某个位置,使得6πα=,即()()22612131sin cos ,6227272363u DE u DE u DEλλπλλ++⋅==<>===⋅⨯++⨯,整理得254120λλ-+=,162400∆=-<,该方程无解,D 选项错误. 故选C.【点评】本题考查利用空间向量法求解空间角以及利用空间向量法处理动点问题,计算量大,属于难题.10、如图,直三棱柱111ABC A B C -的底面是边长为6的等边三角形,侧棱长为2,E 是棱BC 上的动点,F 是棱11B C 上靠近1C 点的三分点,M 是棱1CC 上的动点,则二面角A FM E --的正切值不可能...是A .3155B .2155C .6D .5【答案】B【分析】建立空间直角坐标系,求得二面角A FM E --的余弦值,进而求得二面角A FM E --的正切值,求得正切值的最小值,由此判断出正确选项.【解析】取BC 的中点O ,连接OA ,根据等边三角形的性质可知OA BC ⊥,根据直三棱柱的性质,以O 为原点建立如图所示的空间直角坐标系.则()()0,33,0,1,0,2A F ,设()()3,0,02M t t ≤≤. 则()()1,33,2,2,0,2AF FM t =-=-. 设平面AMF 的一个法向量为(),,m x y z =,则()3320220m AF x z m FM x t z ⎧⋅=-+=⎪⎨⋅=+-=⎪⎩,令1y =,得633363,1,66t m t t ⎛= --⎝⎭. 平面FME 的一个法向量是()0,1,0n =,所以222cos ,28120252633363166m n m n m nt t t t t ⋅===⋅-+⎛⎫⎛⎫-++ ⎪ ⎪--⎝⎭⎝⎭,所以2sin ,1cos ,m n m n =-222710821628120252t t t t -+=-+所以二面角A FM E--的正切值为()sin ,27 cos,m nf tm n===因为02t≤≤,所以111466t-≤≤--,216125405-=-⨯结合二次函数的性质可知当1165t=--时,()f t5=;当1166t=--时,()f t=,所以()f t∈⎣,所以二面角A FM E--.故选B.【点睛】本小题主要考查二面角的求法,考查数形结合的数学思想方法,属于难题.11、直四棱柱ABCD﹣A1B1C1D1中,侧棱长为6,底面是边长为8的菱形,且∠ABC =120°,点E在边BC上,且满足BE=3EC,动点M在该四棱柱的表面上运动,并且总保持ME⊥BD1,则动点M的轨迹围成的图形的面积为_____;当MC与平面ABCD所成角最大时,异面直线MC1与AC所成角的余弦值为_____.【答案】,17【分析】由题意可知M的轨迹为过E且与直线1BD垂直的平面与直四棱柱的截面的边界,根据直棱柱的结构特征和底面棱形的性质,由线面垂直的定义可得截面与下底面的截线是与AC平行的,进而确定截面与与AB的交点F,建立空间直角坐标系,利用坐标方法求得截面与1BB的交点G,进而得到所求面积,根据线面角的定义可得M与G重合时MC与平面ABCD所成角最大,利用空间向量可求异面直线所成角的余弦值.【解析】如图,在直四棱柱1111ABCD A B C D-中,因为底面是菱形,侧棱垂直底面,所以AC ⊥平面11BDD B ,所以1BD AC ⊥.在AB 上取F ,使得3BF FA =,连接EF ,则//EF AC ,1⊥BD EF .记AC 与BD 的交点为O ,以O 为坐标原点,建立如图所示的空间直角坐标系O xyz -,则()4,0,0B ,()14,0,6D -,()1,33,0E .在1BB 上取一点G ,记为()4,0,G t ,于是()18,0,6BD =-,()3,33,EG t =-. 由12460BD EG t ⋅=-+=,得4t =,即12BG GB =, 所以EFG 的边为点M 的运动轨迹. 由题意得22213FG BF BG =+=33836344EF AC ==⨯= 动点M 的轨迹围成的图形的面积为()()22163213331532⨯-=显然当M 与G 重合时,MC 与平面ABCD 所成角最大. 因为()4,0,4M ,()10,43,6C ,所以()14,43,2MC =-. 因为AC 的一个方向向量为()0,1,0n =,所以1251cos ,17MC n =即异面直线1MC 与AC 251. 【点睛】本题考查点、线、面的位置关系,考查空间动点的轨迹,涉及线面垂直的判定与性质,异面直线所成的角,线面角,利用空间直角坐标系和空间向量确定点的位置和求异面直线所成的角,考查直观想象与数学运算的核心素养.属中档题,难度较大.12、如图,在直三棱柱111ABC A B C -中,已知90ABC ∠=︒,P 为侧棱1CC 上任意一点,Q 为棱AB 上任意一点,PQ 与AB 所成角为α,PQ 与平面ABC 所成的角为β,则α与β的大小关系为( )A .αβ=B .αβ<C .αβ>D .不能确定【答案】C【分析】建立空间直角坐标系设()()(),0,,0,,00,0,0P x z Q y x y z >≥≥,利用空间向量法分别求得cos ,cos αβ,然后根据(0,],0,22ππαβ⎡⎤∈∈⎢⎥⎣⎦,利用余弦函数的单调性求解.【解析】建立如图所示空间直角坐标系:设()()(),0,,0,,00,0,0P x z Q y x y z >≥≥,则()(),,,0,,0QP x y z QB y =-=-,所以2222,,QP QB y QP x y z QB y ⋅==++=,所以222cos QP QB y QP QBx y zα⋅==⋅++,又(0,],0,22ππαβ⎡⎤∈∈⎢⎥⎣⎦,222sin QP CP z QPx y zβ⋅==++,所以22222cos x y x y zβ+=++,所以cos cos βα>,因为cos y x = 在0,2π⎛⎫⎪⎝⎭上递减,所以αβ>,故选C 13、如图,在四棱柱1111ABCD A B C D -中,底面ABCD 为正方形,侧棱1AA ⊥底面ABCD ,3AB =,14AA =,P 是侧面11BCC B 内的动点,且1AP BD ⊥,记AP 与平面11BCC B 所成的角为θ,则tan θ的最大值为( )A .43B .53C .2D .259【答案】B【分析】建立空间直角坐标系,利用向量法能求出线面角的正切值的最大值. 【解析】以1,,DA DC DD 所在直线分别为,,x y z 轴,建立空间直角坐标系, 设(,3,)P x z ,则1(3,3,),(3,3,4)AP x z BD =-=--,11,0AP BD AP BD ⊥∴⋅=,33(3)3340,4x z z x ∴---⨯+=∴=, 22225||(3)6916BP x z x x ∴=-+=-+225488191625255x ⎛⎫=-+ ⎪⎝⎭, ||5tan ||3AB BP θ∴=,tan θ∴的最大值为53.故选B .14、如图,在棱长都相等的正三棱柱111ABC A B C -中,D 是棱1CC 的中点,E 是棱1AA 上的动点.设AE x =,随着x 增大,平面BDE 与底面ABC 所成锐二面角的平面角是( )A .增大B .先增大再减小C .减小D .先减小再增大【答案】D【解析】设正三棱柱111ABC A B C -棱长为2,,02AE x x =≤≤, 设平面BDE 与底面ABC 所成锐二面角为α,以A 为坐标原点,过点A 在底面ABC 内与AC 垂直的直线为x 轴,1,AC AA 所在的直线分别为,y z 轴建立空间直角坐标系,则3,1,0),(0,2,1),(0,0,),(3,1,1),(0,2,1)B D E x BD ED x =-=-,设平面BDE 的法向量(,,)m s t k =,则m BDm ED⎧⊥⎨⊥⎩,即302(1)0s t k t x k ⎧-++=⎪⎨+-=⎪⎩,令3k =33,1t x s x =-=+,所以平面BDE 的一个法向量(1,33,23)m x x =+-, 底面ABC 的一个法向量为(0,0,1)n =,222233cos |cos ,|115(1)3(1)12()24m n x x x α=<>==++-+-+当1(0,)2x ∈,cos α随着x 增大而增大,则α随着x 的增大而减小,当1(,2)2x ∈,cos α随着x 增大而减小,则α随着x 的增大而增大.故选D .【点睛】本题考查空间向量法求二面角,应用函数思想讨论二面角的大小,考查直观想象、数学计算能力,素养中档题.15、如图所示,在正方体1111ABCD A B C D -中,点P 是底面1111D C B A 内(含边界)的一点,且//AP 平面1DBC ,则异面直线1A P 与BD 所成角的取值范围为( )A .3,44ππ⎡⎤⎢⎥⎣⎦B .,42ππ⎡⎤⎢⎥⎣⎦C .,32ππ⎡⎤⎢⎥⎣⎦D .2,33ππ⎡⎤⎢⎥⎣⎦【答案】C【解析】过A 作平面α平面1DBC ,点P 是底面1111D C B A 内(含边界)的一点,且//AP 平面1DBC ,则P ∈平面α,即P 在α与平面1111D C B A 的交线上,连接111,,AB AD B D ,11DD BB =,则四边形11BDD B 是平行四边形,11B D BD ∴,11B D ∴平面1DBC ,同理可证1AB ∥平面1DBC ,∴平面11AB D ∥平面1DBC ,则平面11AB D 即为α,点P 在线段11B D 上,以D 为坐标原点,1,,DA DC DD 建立如图坐标系,设正方体棱长为1,则()0,0,0D ,()1,1,0B ,()1,0,0A ,设(),,1P λλ,[]0,1λ∈,()1,1,0DB ∴=,()1,,1AP λλ=-,21DB AP λ∴⋅=-,2DB =,2222AP λλ=-+,设1A P 与BD 所成角为θ,则()22221211cos 2121DB APDB AP λλθλλλλ⋅--===-+⋅-+221313442121324λλλ=-=--+⎛⎫-+⎪⎝⎭12λ=时,cos θ取得最小值为0, 当0λ=或1时,cos θ取得最大值为12,10cos 2θ∴≤≤,则32ππθ≤≤.故选C .16、如图,矩形ABCD 中,222AB AD ==E 为边AB 的中点,将ADE 沿直线DE 翻折成1A DE △.在翻折过程中,直线1A C 与平面ABCD 所成角的正弦值最大为( )A .1024- B .66C .514-D .55【答案】A【解析】分别取DE ,DC 的中点O ,F ,则点A 的轨迹是以AF 为直径的圆, 以,OA OE 为,x y 轴,过O 与平面AOE 垂直的直线为z 轴建立坐标系,则()2,1,0C -,平面ABCD 的其中一个法向量为n = (0,0.1), 由11A O =,设()1cos ,0,sin A αα,则()1cos 2,1,sin CA αα=+-, 记直线1A C与平面ABCD 所成角为θ,则211|sin 1cos sin 4cos 64cos 6||CA nCA n αθαα⋅-===++⋅,设3153535102cos ,,sin 222416444t t t αθ-⎡⎤⎛⎫=+∈=-+≤-=⎪⎢⎥⎣⎦⎝⎭ 所以直线1A C 与平面ABCD 所成角的正弦值最大为1024-,故选A . (多选)17、在正方体1111ABCD A B C D -中,若棱长为1,点,E F 分别为线段11B D 、1BC 上的动点,则下列结论正确结论的是( )A .1DB ⊥面1ACD B .面11//AC B 面1ACDC .点F 到面1ACD 的距离为定值33D .直线AE 与面11BB D D 所成角的正弦值为定值13【答案】ABC【分析】以A 为坐标原点建立空间直角坐标系,利用共线向量可表示出动点,E F 的坐标,利用空间向量判断线面垂直、面面平行、求解点到面的距离和直线与平面所成角的方法依次验证各个选项即可得到结果.【解析】以A 为坐标原点可建立如下图所示的空间直角坐标系:由题意知:()0,0,0A ,()1,0,0B ,()1,1,0C ,()0,1,0D ,()10,0,1A ,()11,0,1B ,()11,1,1C ,()10,1,1D ,设(),,1E x y ,111B E B D λ→→=,即()()1,,0,,0x y λλ-=-,()1,,1E λλ∴-, 设()1,,F y z '',1BF BC μ→→=,即()()0,,0,,y z μμ''=,()1,,F μμ∴. 对于A ,()11,1,1DB →=-,()1,1,0AC →=,()10,1,1AD →=,11100DB AC DB AD ⎧⋅=⎪∴⎨⋅=⎪⎩,1DB AC ∴⊥,11DB AD ⊥, 又1,AC AD ⊂平面1ACD ,1AC AD A =,1DB ∴⊥平面1ACD ,A 正确;对于B ,1DB ⊥平面1ACD ,()11,1,1DB →∴=-为平面1ACD 的一个法向量,()111,1,0A C →=,()11,0,1A B →=-,111110DB A C DB A B ⎧⋅=⎪∴⎨⋅=⎪⎩,111DB AC ∴⊥,11DB A B ⊥, 又111,A C A B ⊂平面11A C B ,1111AC A B A =,1DB ∴⊥平面11A C B ,∴平面11//AC B平面1ACD ,B 正确;对于C ,()1,,AF μμ→=,∴点F 到面1ACD 的距离111333AF DB d DB →→→⋅===,为定值,C 正确;对于D ,几何体为正方体,AC ∴⊥平面11BB D D ,()1,1,0AC →∴=是平面11BB D D 的一个法向量,又()1,,1AE λλ→=-,设直线AE 与平面11BB D D 所成角为θ,则21sin 2222AC AEAC AEθλλ→→→→⋅==⋅-+⋅,不是定值,D 错误.故选ABC .(多选)18、如图所示,正方体1111ABCD A B C D -中,1AB =,点P 在侧面11BCC B 及其边界上运动,并且总是保持1AP BD ⊥,则以下四个结论正确的是( )A .113P AA D V -=B .点P 必在线段1BC 上 C .1AP BC ⊥D .//AP 平面11AC D【答案】BD【分析】根据三棱锥体积公式求得116P AA D V -=,知A 错误;以D 为坐标原点建立空间直角坐标系,利用空间向量法可得到1CP x B C →→=-,11AP BC →→⋅=,AP →垂直于平面11AC D 的法向量n →,由此可确定,,B C D 的正误.【解析】对于A ,P 在平面11BCC B 上,平面11//BCC B 平面1AA D ,P ∴到平面1AA D 即为C 到平面1AA D 的距离,即为正方体棱长,1111111113326P AA D AA D V S CD -∴=⋅=⨯⨯⨯⨯=△,A 错误;对于B ,以D 为坐标原点可建立如下图所示的空间直角坐标系:则()1,0,0A ,(),1,P x z ,()1,1,0B ,()10,0,1D ,()11,1,1B ,()0,1,0C()1,1,AP x z →∴=-,()11,1,1BD →=--,()11,0,1B C →=--,1AP BD ⊥,1110AP BD x z →→∴⋅=--+=,x z ∴=,即(),1,P x x ,(),0,CP x x →∴=,1CP x B C →→∴=-,即1,,B P C 三点共线,P ∴必在线段1B C 上,B 正确; 对于C ,()1,1,AP x x →=-,()11,0,1BC →=-,111AP BC x x →→∴⋅=-+=,AP ∴与1BC 不垂直,C 错误;对于D ,()11,0,1A ,()10,1,1C ,()0,0,0D ,()11,0,1DA →∴=,()10,1,1DC →=,设平面11AC D 的法向量(),,n x y z →=,1100n DA x z n DC y z ⎧⋅=+=⎪∴⎨⋅=+=⎪⎩,令1x =,则1z =-,1y =,()1,1,1n →∴=-, 110AP n x x →→∴⋅=-+-=,即AP n →→⊥,//AP ∴平面11ACD ,D 正确.故选BD . (多选)19、如图所示,棱长为1的正方体1111ABCD A B C D -中,P 为线段1A B 上的动点(不含端点),则下列结论正确的是( )。
例谈立体几何最值问题的几种解法

思路探寻立体几何最值问题侧重于考查同学们的空间想象、逻辑推理和数学运算等能力.常见的立体几何最值问题是求立体几何图形中某条线段、某个角、体积、表面积的最值,那么如何求解呢?一、利用函数思想在大多数情况下,我们可以把与动点有关的立体几何问题看作函数问题来求解.以其中某一个量,如动点的坐标、线段的长、角的大小为变量,建立关于该变量的关系式,并将其视为函数式,即可利用一次函数、二次函数、三角函数的性质和图象求得最值.例1.如图1,正方体ABCD-A1B1C1D1的棱长为1,P为AA1的中点,M在侧面AA1B1B上,若D1M⊥CP,则ΔBCM).C.5D.2图1图2解:过M作MG⊥平面ABCD,垂足为G,作GH⊥BC于点H,连接MH,以D为坐标原点,建立如图2所示的空间直角坐标系,可得D()0,0,0,C()0,1,0,A()1,0,0,P()1,0,12,D1(0,0,1),B()1,1,0.设M()1,a,b,则D1M=()1,a,b-1,CP=()1,-1,12,∵D1M⊥CP,∴ D1M⋅ CP=12b-a+12=0,∴b=2a-1,∴CH=1-a,MG=2a-1,∴MH=()1-a2+()2a-12=5a2-6a+2,∴SΔBCM=12BC⋅MH=1=可知当a=35时,ΔBCM面积取最小值,为SΔBCM=12×=故选B.在建立空间直角坐标系后,设出点M的坐标,以a、b为变量,构建关于a的函数式SΔBCM=然后将5a2-6a+2看作二次函数式,对其配方,根据二次函数的性质即可知函数在a=35时取最小值.二、运用基本不等式在解答立体几何最值问题时,我们往往可以先根据立体几何中的性质、定义、定理求得目标式;然后将其进行合理的变形,采用拆项、凑系数、补一次项,去掉常数项等方式,配凑出两式的和或积,就可以直接运用基本不等式来求得最值.在运用基本不等式求最值时,要把握三个条件:一正、二定、三相等.例2.已知三棱锥P-ABC的4个顶点均在球心为O、直径为23的球面上,PA=2,且PA,PB,PC两两垂直.当PC+AB取最大值时,三棱锥O-PAB的体积为().A. C.6解:∵PA,PB,PC两两互相垂直,∴三棱锥P-ABC可补全为如图3所示的长方体.则长方体的外接球即为三棱锥P-ABC的外接球,∴PA2+PB2+PC2=()232=12,又PA=2,∴PB2+PC2=10,∵AB2=PA2+PB2=2+PB2,∴PC2+AB2=2+PB2+PC2=12,∴()PC+AB2-2PC⋅AB=12,又PC⋅AB≤()PC+AB22,∴12=()PC+AB2-2PC⋅AB≥()PC+AB2-2()PC+AB22=12()PC+AB2,当且仅当PC=AB时取等号,∴()PC+AB max=26,此时PC=AB=6,PB=图347思路探寻AB 2-PA 2=2,∴V O -PAB =12V C -PAB =16S △PAB ⋅PC =112PA ⋅PB⋅PC =112×2×2×6故选B.根据长方体的性质得到()PC +AB 2-2PC ⋅AB =10后,可发现该式中含有PC 、AB 的和与积,根据基本不等式a +b ≥2ab 求解,即可得到三棱锥O -PAB 的体积.三、转化法运用转化法求解立体几何最值问题有两种思路.一是将问题转化为平面几何问题.先将几何体的表面展开,或将几何体内部满足条件的某些面展开成平面;再在平面内利用平面几何知识,如正余弦定理、两点间的距离最短、三角形的两边之和大于第三边等求解,这样问题就变得十分直观,容易求解了.另一种思路是根据题意和几何图形中的点、线、面的位置关系,明确其中改变的量和不变的量及其关系,根据简单几何体的性质、表面积公式、体积公式,将问题转化为求某些线段或角的最值.再结合简单几何体的性质,几何图形中点、线、面的位置关系求得最值例3.如图4,在正三棱柱ABC -A 1B 1C 1中,AA 1=AB =2,D 在A 1C 上,E 是A 1B 的中点,则()AD +DE 2的最小值是().A.6-7 B.27 C.3+7 D.5+7图4图5解:将平面A 1BC 与平面A 1AC 翻折到同一平面上,连接AE ,如图5所示,设AE ⋂A 1C =F .由题意可知A 1A =AC =BC =2,A 1C =A 1B =22,所以AA 21+AC 2=A 1C 2,所以AA 1⊥AC ,则∠AA 1C =45°,由余弦定理可得cos∠BA 1C =A 1B 2+A 1C 2-BC 22A 1B ⋅A 1C=8+8-42×22×22=34,则sin∠BA 1C =1-cos 2∠BA 1C =故cos∠AA 1B =cos ()∠AA 1C +∠BA 1C =cos ∠AA 1C cos ∠BA 1C -sin ∠AA 1C sin ∠BA 1C =32-148.因为E 是A 1B 的中点,所以A 1E =2,由余弦定理可得AE 2=AA 21+A 1E 2-2AA 1⋅A 1E cos∠BA 1A=4+2-2×2×2×32-148=3+7.因为D 在A 1C 上,所以AD +DE ≥AE ,当A 、E 、D 三点共线时,等号成立,则()AD +DE 2≥3+7.故选C .将平面A 1BC 与平面A 1AC 翻折到同一平面上,就可以把立体几何问题转化为平面几何问题,即可根据勾股定理和余弦定理求得A 1E 以及AE 的值.分析图形可知当A 、E 、D 三点共线时,AD +DE 取得最大值,再结合余弦定理求解即可.例4.已知球O 的表面积为60π,四面体P -ABC 内接于球O ,ΔABC 是边长为6的正三角形,平面PBC ⊥平面ABC ,则四面体P -ABC 体积的最大值为().A.18B.27C.32D.81解:因为球O 的表面积为60π,所以球的半径R ==15,由题意知四面体P -ABC 底面三角形的面积为定值,要使四面体的体积最大,只须使顶点P 到底面的距离最大,又因为平面PBC ⊥平面ABC ,所以当PB =PC 时,点P 到底面的距离最大,而ΔABC 外接圆的半径r =62sin60°=23,则O 到面ABC 的距离为d =R 2-r 2=3,且O 到面PBC 的距离为h =12r =3,设点P 到平面ABC 的距离为H ,则R 2=()H -d 2+h 2,解得H =33,此时体积最大值为V max =13×12×6×6×sin60°×33=27.故选B.解答本题,首先根据球的表面积求得球的半径;再根据题意和几何体的特征明确当PB =PC 时,点P 到底面的距离最大;最后根据外接圆的性质、勾股定理求出点P 到底面的距离,即可求出最大值.除了上述三种方法外,有时还可采用定义法、构造法来求立体几何最值问题的答案.总之,同学们在解题时,要先根据题意和几何体的结构特征寻找取得最值的情形,求得目标式;然后根据目标式的特征,选用合适的方法求最值.(作者单位:贵州省江口中学)48。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
立体几何中的最值问题一、线段长度最短或截面周长最小问题例1. 正三棱柱ABC —A 1B 1C 1中,各棱长均为2,M 为AA 1中点,N 为BC 的中点,则在棱柱的表面上从点M 到点N 的最短距离是多少?并求之.解析: (1)从侧面到N ,如图1,沿棱柱的侧棱AA 1剪开,并展开,则MN =22AN AM +=22)12(1++=10(2)从底面到N 点,沿棱柱的AC 、BC 剪开、展开,如图2.则MN =︒⋅-+120cos 222AN AM AN AM =21312)3(122⨯⨯⨯++=34+∵34+<10 ∴m in MN =34+.例2.如图,正方形ABCD 、ABEF 的边长都是1,而且平面ABCD 、ABEF 互相垂直。
点M 在AC 上移动,点N 在BF 上移动,若CM=BN=a ).20(<<a (1)求MN 的长;(2)当a 为何值时,MN 的长最小; (3)当MN 长最小时,求面MNA 与面MNB 所成的二面角α的大小。
解析:(1)作MP ∥AB 交BC 于点P ,NQ ∥AB 交BE 于点Q ,连接PQ ,依题意可得MP ∥NQ ,且MP=NQ ,即MNQP 是平行四边形。
∴MN=PQ,由已知,CM=BN=a,CB=AB=BE=1, ∴2==BF AC ,21,21a BQ a CP ==, 即2a BQ CP ==, ∴=+-==22)1(BQ CP PQ MN )20(21)22()2()21(222<<+-=+-a a aa(2)由(1)知: 2222==MN a 时,当,的中点时,分别移动到即BF AC N M ,, 22的长最小,最小值为MN(3)取MN 的中点G ,连接AG 、BG ,∵AM=AN,BM=BN ,∴AG ⊥MN,BG ⊥MN ,∴∠AGB 即为二面角α的平面角。
又46==BG AG ,所以由余弦定理有31464621)46()46(cos 22-=••-+=α。
故所求二面角)31arccos(-=α。
例3. 如图,边长均为a 的正方形ABCD 、ABEF 所在的平面所成的角为)20(πθθ<<。
点M 在AC 上,点N 在BF 上,若AM=FN ,(1)求 A证:MN//面BCE ; (2)求证:MN ⊥AB;(3)求MN 的最小值.解析:(1)如图,作MG//AB 交BC 于G, NH//AB 交BE 于H, MP//BC 交AB 于P, 连PN, GH , 易证MG//NH,且MG=NH, 故MGNH 为平行四边形,所以MN//GH , 故MN//面BCE ;(2)易证AB ⊥面MNP, 故MN ⊥AB ;(3)MPN ∠即为面ABCD 与ABEF 所成二面角的平面角,即θ=∠MPN ,设AP=x , 则BP=a -x , NP=a -x , 所以:θcos )(2)(22x a x x a x MN ---+= 22)cos 1(21)2)(cos 1(2a ax θθ-+-+=, 故当2ax =时,MN有最小值a )cos 1(21θ-. 例4.如图,正方形ABCD 、ABEF 的边长都是1,而且平面ABCD 、ABEF 互相垂直。
点M 在AC 上移动,点N 在BF 上移动,若CM=x ,BN=y, ).2,0(<<y x (1)求MN 的长(用x,y 表示);(2)求MN 长的最小值,该最小值是否是异面直线AC ,BF 之间的距离。
解析:在面ABCD 中作MP ⊥AB 于P ,连PN ,则MP ⊥面ABEF ,所A B F E CD PNM以MP ⊥PN ,PB=1-AP=x 22在∆PBN 中,由余弦定理得:PN 2=02245cos 2)22(xy y x -++ xy y x -+=2221,在PMN Rt ∆中,MN=xy y x x PN MP -++-=+2222221)221(1222+--+=x xy y x ).2,0(<<y x ;(2)MN 1222+--+=x xy y x 31)322(43)2(22+-+-x x y ,故当322=x ,32=y 时,MN 有最小值33。
且该最小值是异面直线AC ,BF 之间的距离。
例5. 如图,在ΔABC 中,∠ACB =90°,BC =a,AC =b,D 是斜边AB 上的点,以CD 为棱把它折成直二面角A —CD —B 后,D 在怎样的位置时,AB 为最小,最小值是多少?解析: 设∠ACD =θ,则∠BCD =90°-θ,作AM ⊥CD 于M ,BN ⊥CD 于N ,于是AM =bsin θ,CN =asin θ.∴MN =|asin θ-bcos θ|,因为A —CD —B 是直二面角,AM ⊥CD ,BN ⊥CD ,∴AM 与BN 成90°的角,于是AB =22222)cos sin (cos sin θθθθb a a b -++=θ222sin ab b a -+≥ab b a -+22. ∴当θ=45°即CD 是∠ACB 的平分线时,AB 有最小值,最小值为ab b a -+22.例6. 正三棱锥A-BCD ,底面边长为a ,侧棱为2a ,过点B 作与侧棱AC 、AD 相交的截面,在这样的截面三角形中,求(1)周长的最小值;(2)周长为最小时截面积的值,(3)用这周长最小时的截面截得的小三棱锥的体积与三棱锥体积之比.解析:(1)沿侧棱AB 把正三棱锥的侧面剪开展成平面图.如图1,当周长最小时,EF 在直线BB ′上,∵ΔABE ≌ΔB ′AF ,∴AE =AF ,AC =AD ,∴B ′B ∥CD ,∴∠1=∠2=∠3,∴BE =BC =a ,同理B ′F =B ′D =a.∵ΔFDB ′∽ΔADB ′,∴BD DF '=B A B D '',a DF =a a 2=21,∴DF =21a,AF =23a.又∵ΔAEF ∽ΔACD ,∴BB ′=a+43a+a =411a,∴截面三角形的周长的最小值为411a.(2)如图2,∵ΔBEF 等腰,取EF 中点G ,连BG ,则BG ⊥EF.∴BG =22EG BE -=22)83(a a -=855a ∴S ΔBEF =21·EF ·BG =21·43a ·855a =64553a 2. (3)∵V A-BCD =V B-ACD ,而三棱锥B —AEF ,三棱锥B —ACD 的两个高相同,所以它们体积之比于它们的两底面积之比,即CAD B AEF B V V --=ACD AEF S S △△=22CD EF =169 评析 把曲面上的最短路线问题利用展开图转化为平面上两点间距离的问题,从而使问题得到解决,这是求曲面上最短路线的一种常用方法.本题中的四面体,其中任何一个面都可以做为底面,因而它可有四个底面和与之对应的四条高,在解决有关三棱锥体积题时,需要灵活运用这个性质.二、面积最值问题例7. 如图1所示,边长AC =3,BC =4,AB =5的三角形简易遮阳棚,其A 、B 是地面上南北方向两个定点,正西方向射出的太线与地面成30°角,试问:遮阳棚ABC 与地面成多大角度时,才能保证所遮影面ABD 面积最大?解析: 易知,ΔABC 为直角三角形,由C 点引AB 的垂线,垂足为Q ,则应有DQ 为CQ 在地面上的斜射影,且AB 垂直于平面CQD ,如图2所示.因太与地面成30°角,所以∠CDQ =30°,又知在ΔCQD 中,CQ =512,由正弦定理,有 ︒30sin CQ =QCD QD ∠sin 即 QD =56sin ∠QCD. 为使面ABD 的面积最大,需QD 最大,这只有当∠QCD =90°时才可达到,从而∠CQD = 60°.故当遮阳棚ABC 与地面成60°角时,才能保证所遮影面ABD 面积最大.例8. 在三棱锥A —BCD 中,ΔABC 和ΔBCD 都是边长为a 的正三角形,二面角A —BC —D =φ,问φ为何值时,三棱锥的全面积最大。
解析:S ΔBAC =S ΔBCD =43a 2为常量,所以三棱锥全面积的大小取决于S ΔABD 与S ΔACD 的大小,由于ΔABD ≌ΔACD ,所以只求S ΔACD 何时面积取最大值即可。
∵S ΔACD =21asin ∠ACD ,所以当∠ACD =90°时面积最大,问题得解。
解 如图,取BC 中点M ,连AM 、DM ,∴ΔABC 和ΔBCD 都是正三角形,∴∠AMD 是二面角A-BC-D 的平面角,∠AMD =φ,又∵ΔABD ≌ΔACD ,且当∠ACD =90°时,ΔACD 和ΔABD 面积最大,此时AD =2a ,在ΔAMD 中,由余弦定理cos ∠AMD =-31, ∴当φ=π-arccos 31时,三棱锥A-BCD 的全面积最大。
点评 本题将求棱锥全面积的最大值,转化为求ΔACD 面积的最大值,间接求得φ角。
例9、一个圆锥轴截面的顶角为1200,母线为1,过顶点作圆锥的截面中,最大截面面积为 。
分析:本题是截面问题中的常见题,设圆锥的轴截面顶角是α,母线长为l ,则截面面积S max =⎪⎪⎩⎪⎪⎨⎧∈∈],2[21)2,0(sin 2122ππαπααl l ,本题轴截面顶角为1200,∴最大面积为21。
例10、圆柱轴截面的周长L 为定值,求圆柱侧面积的最大值。
分析:设圆柱的底面直径和高分别为d,h,则有:2(d+h )=L,d+h=L/2,S 侧=πdh ≤π22⎪⎭⎫ ⎝⎛+h d =162l π(当且仅当d=h 时取“=”)。
