1空间几何体的结构练习题.
专题14 空间几何体的结构、面积与体积(练)【解析版】

第一篇热点、难点突破篇专题14空间几何体的结构、面积与体积(练)【对点演练】一、单选题1.(2022秋·北京·高三统考阶段练习)已知圆柱的上、下底面的中心分别为1O,2O,过直O O的平面截该圆柱所得的截面是面积为12的正方形,则该圆柱的体积为()线12A.B.12πC.D.则该圆台的体积为()A.36πB.40πC.42πD.45πOO的长度===,1O为ABC的外接圆的圆心,球O的表面积为64π,则1AB BC AC为()B.2C.D.3A【答案】C【分析】由已知求得球O的半径4r=,即可求R=,根据正弦定理求出ABC外接圆半径2出结果.O的半径为r,球O的半径为R.【详解】设圆1依题意得ABC 为等边三角形,则由正弦定理得O 的表面积为如图,根据球的截面性质得2d OA ==的扇形,则该圆锥的侧面积为( ) A .π B .3π2C D .点作球O 的截面,则最小截面的面积为( ) A .3π B .4πC .5πD .6π子,其形状可以看成一个正四面体.广东流行粽子里放蛋黄,现需要在四角状粽子内部放入一个蛋黄,蛋黄的形状近似地看成球,当这个蛋黄的表面积是9π时,则该正四面体的高的最小值为()A.4B.6C.8D.10实物图,石碾子主要由碾盘、碾滚(圆柱形)和碾架组成.碾盘中心设竖轴(碾柱),连碾架,架中装碾滚,以人推或畜拉的方式,通过碾滚在碾盘上的滚动达到碾轧加工粮食作物的目的.若推动拉杆绕碾盘转动2周,碾滚的外边缘恰好滚动了5圈,碾滚与碾柱间的距离忽略不计,则该圆柱形碾滚的高与其底面圆的直径之比约为()A.3:2B.5:4C.5:3D.4:3一卷中称轴截面为等腰直角三角形的圆锥为直角圆锥.若一个直角圆锥的侧面积为,则该圆锥的体积为( )A .B .C .D .9π中,地球静止同步卫星的轨道位于地球赤道所在平面,轨道高度为h (轨道高度是指卫星到地球表面的距离).将地球看作是一个球心为O ,半径r 为的球,其上点A 的纬度是指OA 与赤道平面所成角的度数.地球表面上能直接观测到一颗地球静止同步轨道卫星点的纬度最大值为α,记卫星信号覆盖地球表面的表面积为22(1cos )S r πα=-(单位:2km ),若458h r =,则S 占地球表面积的百分比约为( ) A .26% B .34% C .42% D .50%【答案】C【分析】设C 表示卫星,过CO 作截面,截地球得大圆O ,过C 作圆O 的切线,CA CB ,线段CO 交圆O 于E ,得AOC α∠=,在直角三角形中求出cos α后,可计算两者面积比.【详解】设C 表示卫星,过CO 作截面,截地球得大圆O ,过C 作圆O 的切线,CA CB ,线段CO 交圆O 于E ,如图,则AOC α∠=,r OE =,CE h =,OA CA ⊥,二、填空题10.(2022秋·江苏徐州·高三期末)已知圆柱的高为8,该圆柱内能容纳半径最大的球的表面积为36π,则圆柱的体积为______.【答案】72π【分析】先分析半径最大的球不可能为圆柱的内切球,所以此球是与圆柱侧面与下底面相切的球,就能求出圆柱底面半径,然后根据圆柱的体积公式可得.【详解】圆柱内能容纳半径最大的球的表面积为36π,设此球半径为r,则24π36π3r r=⇒=如果圆柱有内切球,又因为圆柱的高为8,所以内切球半径为43>,说明这个圆柱内能容纳半径最大的球,与圆柱侧面和下底面相切,与上底面相离,易得圆柱底面半径为3,圆柱的体积为2π3872π⋅⨯=故答案为:72π【冲刺提升】一、单选题1.(2022秋·广东东莞·高三统考期末)已知一个装满水的圆台形容器的上底半径为6,下底半径为1,高为,若将一个铁球放入该容器中,使得铁球完全没入水中,则可放入的铁球的体积的最大值为()A.B.C D.108π【答案】B【分析】作出体积最大时的剖面图,分析出此时圆与上底,两腰相切,建立合适直角坐标系,()53,05<<t=-533)32332=模拟预测)某工厂要生产容积为为侧面成本的2倍,为使成本最小,则圆柱的高与底面半径之比应为()A.1B.1C.2D.4 2圆柱上下底的总面积为3.(2022·浙江·模拟预测)如图,正方体1111的棱长为1,,E F 分别为棱BC ,11的中点,则三棱锥1B AEF -的体积为( )A .524B .316C .29D .181AB ES =因为正方体ABCD A B C D -的棱长为1, 所以111(,1,0),(0,1,1),(1,22AE AB AF =-==-的法向量为(,,)n x y z =112n AE x n AB y z ⎧⋅=-⎪⎨⎪⋅=+⎩所以(2,1,1)n =-,F 平面1AB E 的距离为2AF n n-+⋅=又因为1AB =,121122AB EAB S⎫==⋅⎪⎭所以三棱锥故选:AF ,G ,H 分别是SA ,SB ,BC ,AC 的中点,则四边形EFGH 面积的取值范围是( ) A .()0,∞+ B .⎫∞⎪⎪⎝⎭ C .⎫+∞⎪⎪⎝⎭D .1,2⎛⎫+∞ ⎪⎝⎭【答案】B【分析】画出图形,求出,EF HG ,说明EFHG 是矩形,结合图形,说明S 点在ABC 平面时,面积最小,求出即可得到范围 【详解】如图所示:由正三棱锥S ABC -的底面边长是2,因为E 、F 、G 、H 分别是SA 、SB 、BC 、AC 的中点,设ABC 的中心为SC OA >=所以EFGH 所以四边形且4BC =,6BD =,面ABC 与面BCD 夹角正弦值为1,则空间四边形ABCD 外接球与内切球的表面积之比为( )A B C D 【答案】C【分析】根据空间四边形ABCD 的线面关系可得DB ⊥平面ABC ,则空间四边形ABCD 可以内接于圆柱中,根据圆柱的外接球半径求得空间四边形ABCD 的外接球半径R ,又根据内切球的几何性质用等体积法可求得空间四边形ABCD 的内切球半径r ,即可得空间四边形ABCD 外接球与内切球的表面积之比.【详解】解:面ABC 与面BCD 夹角正弦值为1,∴面ABC ⊥面BCD ,又面ABC ⋂面BCD BC =,DB BC DB ⊥⊂面BCD ,DB ∴⊥平面ABC ,则空间四边形ABCD 可以内接于圆柱12O O 中,如下图所示:点在上底面圆周上,ABC三个顶点在下底面圆周上,则圆柱O O的外接球即空间四边连接OA,则球心为为正ABC4sin6032BC=︒1111333ABC ABD ADC BCDS r S r S r S r⋅+⋅+⋅+⋅,,所以()22142132832ADCS=⨯⨯-=,44612ABC ABD ADC BCDS S S S⨯⨯⨯=+++⨯外接球与内切球的表面积之比为6.(2022秋·湖南长沙·高三长郡中学校考阶段练习)三棱锥A BCD -中,AB BC AD CD BD AC ======,则三棱锥A BCD -的外接球的表面积为( )A .20πB .28πC .32πD .36π23AB AD ==且E 为BD 中点,AE BD ∴⊥,AE AB ∴=又AE CE =120, 过BCD △的外心作平面同理过ABD △l l O ''=,易知连接O E ',O 为BCD △又在OO E '中,603=,∴得27O C O O ''=,即外接球半径7=,故外接球表面积28π=.故选:B7.(2022秋·天津河东·高三统考期末)一个球与一个正三棱柱(底面为等边三角形,侧棱与底面垂直)的两个底面和三个侧面都相切,若棱柱的体积为)A.16πB.4πC.8πD.32π8.(2022秋·黑龙江牡丹江·高三牡丹江一中校考期末)如图截角四面体是一种半正八面体,可由四面体经过适当的截角,即截去四面体的四个顶点所产生的多面体.如图,将棱长为3的正四面体沿棱的三等分点作平行于底面的截面得到所有棱长均为1的截角四面体.则该截角四面体的表面积是______.正六边形每个内角均为2π111A B C 中,点P 在棱1BB 上,且1PA PC ⊥,当1APC 的面积取最小值时,三棱锥-P ABC 的外接球的表面积为______.【答案】28π时,1APC 面积取得最小值,补形后三棱锥的外接球,求出外接球半径和表面积【详解】由勾股定理得:AB =,则16PA =(7x y ++1APC S =2169y +,即2x =其中长方体的外接球的直径为,平面PAB ⊥平面PCD ,则P ABCD -体积的最大值为__________.PO ⊥平面ABCD ,PE CD⊥CD平面POE∴⊥,CD OE底面ABCD是边长为∴⊥,CD BCOE⊂平面ABCD OE BC∴,同理可得:OF∥O E F三点共线故,,∥,且有EF BC设平面PAB⋂平面∥AB CD AB,∴∥∥l AB⊥PE CD平面PAB∴⊥平面PEPF⊂平面∴⊥PE PF不妨设PE22∴+x y且2OP=-即2y m11.(2023·广西梧州·统考一模)边长为1的正方形ABCD 中,点M ,N 分别是DC ,BC 的中点,现将ABN ,ADM △分别沿AN ,AM 折起,使得B ,D 两点重合于点P ,连接PC ,得到四棱锥P AMCN -.(1)证明:平面APN ⊥平面PMN ;(2)求四棱锥P AMCN -的体积. ,所以PMN 为直角三角形,即PMN S=111111222AMN ABN ADM CMN ABCD S S S S S =---=-⨯⨯⨯-⨯正方形设点P 到平面AMN 的距离为h ,由A PMN P V V --=1133PMN AMN S PA S h ⋅=⋅△△,即13188h ⨯=,得h =)AMN MCN S S h +=AMCN 的体积为全国·高三对口高考)如题图,是圆锥底面的圆心,ABC 是底面的内接正三角形.P 为DO 上一点,90APC ∠=︒.(1)求证:PC ⊥平面PAB ;(2)若DO =.求三棱锥-P ABC 的体积. 因为ABC 是底面的内接正三角形,CO AB ⊥,PO OC ⋂AB ⊥平面PC ⊂平面AB PC ⊥,PA AB A =,⊥平面PAB(2)解:设圆锥的母线为l,底面半径为r,则圆锥的侧面积为ππ,即,=603所以,在等腰直角三角形APC。
高考数学大一轮复习配套课时训练:第七篇 立体几何 第1节 空间几何体的结构及三视图和直观图(含答案)

第七篇立体几何(必修2)第1节空间几何体的结构及三视图和直观图课时训练练题感提知能【选题明细表】A组一、选择题1.(2013山东烟台模拟)如图是底面半径为1,母线长均为2的圆锥和圆柱的组合体,则该组合体的侧(左)视图的面积为( C )(A)8π(B)6π(C)4+(D)2+解析:该组合体的侧(左)视图为其中正方形的边长为2,三角形为边长为2的三角形,所以侧(左)视图的面积为22+×22×=4+,故选C.2.(2013山东莱州模拟)一个简单几何体的正(主)视图,侧(左)视图如图所示,则其俯视图不可能为①长方形;②直角三角形;③圆;④椭圆.其中正确的是( C )(A)①(B)② (C)③ (D)④解析:当该几何体的俯视图为圆时,由三视图知,该几何体为圆柱,此时,正(主)视图和侧(左)视图应相同,所以该几何体的俯视图不可能是圆,其余都有可能.故选C.3.(2013韶关市高三调研)某几何体的三视图如图所示,根据图中标出的数据,可得这个几何体的表面积为( B )(A)4+4 (B)4+4(C) (D)12解析:由三视图知该几何体为正四棱锥P ABCD,底面边长为2,高PO=2,如图所示,取CD的中点E,连接OE、PE,则PE==,因此几何体的表面积为2×2+×2×4×=4+4,故选B.4.如果一个水平放置的图形的斜二测直观图是一个底角为45°,腰和上底均为1的等腰梯形,那么原平面图形的面积是( A )(A)2+(B)(C)(D)1+解析:由题意画出斜二测直观图及还原后原图,由直观图中底角均为45°,腰和上底长度均为1,得下底长为1+,所以原图上、下底分别为1,1+,高为2的直角梯形.所以面积S=(1++1)×2=2+.故选A.5.(2013北京东城区模拟)已知一个三棱锥的三视图如图所示,其中三个视图都是直角三角形,则在该三棱锥的四个面中,直角三角形的个数为( D )(A)1 (B)2 (C)3 (D)4解析:由题意可知,几何体是三棱锥,其放置在长方体中形状如图所示,利用长方体模型可知,此三棱锥A BCD的四个面中,全部是直角三角形.故选D.6.(2013广州市毕业班测试(二))一个圆锥的正(主)视图及其尺寸如图所示,若一个平行于圆锥底面的平面将此圆锥截成体积之比为1∶7的上、下两部分,则截面的面积为( C )(A)π(B)π (C)π(D)4π解析:由题意知,该几何体是底面半径为3,高为4的圆锥.由截面性质知截面圆半径为×3=,故截面的面积为π·()2=,故选C.7.下面是关于四棱柱的四个命题:①若有两个侧面垂直于底面,则该四棱柱为直四棱柱;②若过两个相对侧棱的截面都垂直于底面,则该四棱柱为直四棱柱;③若四个侧面两两全等,则该四棱柱为直四棱柱;④若四棱柱的四条对角线两两相等,则该四棱柱为直四棱柱.其中真命题为( D )(A)①②(B)①③(C)②③(D)②④解析:对于①,平行六面体的两个相对侧面与底面垂直且互相平行,而另两个相对侧面可能与底面不垂直,则不是直棱柱,故①假;对于②,两截面的交线平行于侧棱,且垂直于底面,故②真;对于③,作正四棱柱的两个平行菱形截面,可得满足条件的斜四棱柱(如图(1)所示),故③假;对于④,四棱柱一个对角面的两条对角线,恰为四棱柱的对角线,故对角面为矩形,于是侧棱垂直于底面的一条对角线,同样侧棱也垂直于底面的另一条对角线,故侧棱垂直于底面,故④真.故选D.二、填空题8.如图所示的Rt△ABC绕着它的斜边AB旋转一周得到的图形是.解析:过Rt△ABC的顶点C作线段CD⊥AB,垂足为D,所以Rt△ABC绕着它的斜边AB旋转一周后应得到的是以CD作为底面圆的半径的两个圆锥的组合体.答案:两个圆锥的组合体9.一个几何体的正(主)视图为一个三角形,则这个几何体可能是下列几何体中的(填入所有可能的几何体前的编号).①三棱锥;②四棱锥;③三棱柱;④四棱柱;⑤圆锥;⑥圆柱.解析:显然①②⑤均有可能;当三棱柱放倒时,其正(主)视图可能是三角形,所以③有可能,④不可能.答案:①②③⑤10.如图,点O为正方体ABCD A′B′C′D′的中心,点E为平面B′BCC′的中心,点F为B′C′的中点,则空间四边形D′OEF在该正方体的各个面上的投影可能是(填出所有可能的序号).解析:空间四边形D′OEF在正方体的平面DCC′D′上的投影是①;在平面BCC′B′上的投影是②;在平面ABCD上的投影是③,而不可能出现投影为④的情况.答案:①②③11.(2013山东烟台模拟)如图,三棱柱的侧棱长为2,底面是边长为2的正三角形,AA1⊥面A1B1C1,正(主)视图是边长为2的正方形,俯视图为正三角形,则侧(左)视图的面积为.解析:因为俯视图为正三角形,所以俯视图的高为,侧视图为两直角边分别为2、的矩形,所以侧(左)视图的面积为2.答案:2三、解答题12.(2013西工大附中模拟)已知四棱锥P ABCD的三视图如图所示,求此四棱锥的四个侧面的面积中最大值.解:由三视图可知该几何体是如图所示的四棱锥,顶点P在底面的射影是底面矩形的顶点D.底面矩形边长分别为3,2,△PDC是直角三角形,直角边为3与2,所以S△PDC=×2×3=3.△PBC是直角三角形,直角边长为2,,三角形的面积为×2×=.△PAB是直角三角形,直角边长为3,2;其面积为×3×2=3.△PAD也是直角三角形,直角边长为2,2,三角形的面积为×2×2=2. 所以四棱锥P ABCD的四个侧面中面积最大的是前面三角形的面积为3.13.圆台的一个底面周长是另一个底面周长的3倍,轴截面的面积等于392 cm2,母线与轴的夹角为45°,求这个圆台的高、母线长和底面半径.解:圆台的轴截面如图.设圆台的上、下底面半径分别为x cm和3x cm,延长AA1交OO1的延长线于点S.在Rt△SOA中,∠ASO=45°,则∠SAO=45°.所以SO=AO=3x,OO1=2x.又×(6x+2x)×2x=392,解得x=7.所以圆台高OO母线长l=OO1=14 cm,底面半径分别为7 cm和21 cm.B组14.(2013广州高三调研)已知四棱锥P ABCD的三视图如图所示,则四棱锥P ABCD的四个侧面中面积最大的是( C )(A)3 (B)2(C)6 (D)8解析:四棱锥如图所示,PM=3,×4×=2,S△PDC=S△PAB=×4×3=6,S△PBC=S△PAD=×2×3=3,故四个侧面中面积最大的是6.15.(2013北京西城检测)三棱锥D ABC及其三视图中的正视图和侧视图如图所示,则棱BD的长为.解析:取AC的中点E,连结BE,DE,由正(主)视图可知BE⊥AC,BE⊥DE.DC⊥平面ABC且DC=4,BE=2,AE=EC=2.所以BC====4,即BD====4.答案:416.三棱锥V ABC的底面是正三角形,顶点在底面ABC上的射影为正△ABC的中心,其三视图如图所示:(1)画出该三棱锥的直观图;(2)求出侧(左)视图的面积.解:(1)直观图如图所示.(2)根据三视图间的关系可得BC=2,作AM⊥BC于M,连结VM,过V作VO⊥AM于O,过O作EF∥BC交AB,AC于F、E,则△VEF即侧(左)视图.由=,得EF=.又VA=4,AM==3.则AO=2,VO===2.××2=4.所以S即侧(左)视图的面积为4.。
2023年高考数学一轮复习精讲精练(新高考专用)专题33:空间几何体(练习版)

专题33:空间几何体精讲温故知新一.空间几何体的结构1.多面体一般地,由若干个平面多边形围成的几何体叫做多面体。
围成多面体的各个多边形叫做多面体的面;两个面的公共边叫做多面体的棱;棱与棱的公共点叫做多面体的顶点。
2.旋转体一条平面曲线,包括直线,绕它所在平面内的一条定直线旋转所成的曲面叫做旋转面。
封闭的旋转面围成的几何体叫做旋转体。
这条定直线叫做旋转体的轴。
3.棱柱一般地,有两个面互相平行,其余各面都是四边形,并且相邻两个四边形的公共边都互相平行,由这些面所围成的多面体叫做棱柱。
在棱柱中,两个互相平行的面叫做棱柱的底面,它们是全等的多边形,其余各面叫做棱柱的侧面,它们都是平行四边形,相邻两边的公共边叫做棱柱的侧棱,侧面和底面的公共顶点叫做棱柱的顶点。
棱柱的底面可以是三角形、四边形、五边形,我们把这样的棱柱分别叫做三棱柱、四棱柱、五棱柱。
一般地,我们把侧面垂直于底面的棱柱叫做直棱柱,侧面不垂直于底面的棱柱叫做斜棱柱,底面是正多边形的,直棱柱叫做正棱柱,底面是平行四边形的四棱柱,也叫做平行六面体。
4.棱锥一般地,有一个面是多边形,其余各面都是有一个公共顶点的三角形,由这些面所围成的多面体叫做棱锥。
这个多边形面叫做棱锥的底面,有公共顶点的各个三角形面叫做棱锥的侧面,相邻两边的公共边叫做棱锥的侧棱,这侧面的公共顶点叫做棱锥的顶点。
棱锥,用表示顶点和各面各顶点的字母来表示,其中三棱锥又叫四面体,底面是正多边形并且顶点与底面中心的连线垂直于底面的棱锥叫做正棱锥。
5.棱台用一个平行于圆锥底面的平面去截棱锥,我们把底面和截面之间那部分多面体叫做棱台。
在棱台中,原棱锥的底面和截面分别叫做棱台的下底面和上底面面,类似于棱柱、棱锥,棱台也有侧面、侧棱和顶点。
6.圆柱与矩形的一边所在直线为旋转轴,其余三边旋转一周形成的面所围成的旋转体叫做圆柱。
旋转轴叫做圆柱的轴,垂直于轴的边旋转而成的圆面,叫做圆柱的底面,平行的边旋转而成的曲面叫做圆柱的侧面,无论旋转到什么位置,平行于轴的边叫做圆柱侧面的母线。
空间几何体的结构特征习题(绝对物超所值)

空间几何体的结构特征1.在下列四个几何体中,它们的三视图(主视图、左视图、俯视图)中有且仅有两个相同,而一 个不同的几何体是( )A .(1)(2)(3)B .(2)(3)(4)C .(1)(3)(4)D .(1)(2)(4)2.如图,已知圆锥的底面半径为10r =,点Q 为半圆弧AB 的中点,点P 为母线SA 的中点.若PQ 与SO 所成角为4π,则此圆锥的全面积与体积分别为( )A .100051006,3ππB .10005100(16),3ππ+ C .100031003,3ππ D .10003100(13),3ππ+3.已知曲线24y x =-与x 轴的交点为,A B ,分别由,A B 两点向直线作垂线,垂足为,沿直线将平面折起,使ACD BCD ⊥平面平面,则四面体ABCD 的外接球的表面积为 ( )A .16πB .12πC .8πD .6π 4.多面体的三视图如图所示,则该多面体的体积为( )(单位cm ) A .3216 B .332C .216D . 32 5.如图,圆锥的底面直径2AB =,母线长3VA =,点C 在母线VB 上,且1VC =,有一只蚂蚁沿圆锥的侧面从点A 到达点C ,则这只蚂蚁爬行的最短距离是( ) A .13 B .7 C .433 D .3326.在四棱锥ABCD V -中,1B ,1D 分别为侧棱VB ,VD 的中点,则四面体11CD AB 的体积与四棱锥ABCD V -的体积之比为( )A .6:1B .5:1C .4:1D .3:1ACD y x =,C D y x=PSAQOBAV CB7.一个组合体的主视图和左视图相同,如图,其体积为,则图中的为A.4B.4.5C.5D.8.已知棱长为2的正方体的俯视图是一个面积为2的正方形,则该正方体的正视图的面积不可能等于 A.21- B.2 C.21+ D.22 9.已知直线l ,平面,,αβγ,则下列能推出//αβ的条件是 A.l α⊥,//l β B.//l α,//l β C.α⊥γ,γβ⊥ D.//αγ,//γβ10.如图,已知某品牌墨水瓶的外形三视图和尺寸,则该墨水瓶的容积为(瓶壁厚度忽见解析不计)A .π8+B .π48+C .π16+D .π416+11.已知某几何体的三视图如图所示,则该几何体的体积为 ( ) A . B . C . D . 12.多面体MN ABCD -的底面ABCD 矩形,其正(主)视图和侧(左)视图如图,其中正(主)视图为等腰梯形,侧(左)视图为等腰三角形,则该多面体的体积为 ( )A .163B .6C .203 D .613.几何体的三视图如下,则它的体积是( )A.B .C .D .14.若三角形内切圆半径为r ,三边长分别为c b a ,,,则三角形的面积为)(21c b a r s ++=,根据类比思想,若四面体内切球半径为R ,四个面的面积分别为4321,,,S S S S ,则这个四面体的体积为( )A .)(614321S S S S R V +++=B .)(414321S S S S R V +++= C .)(314321S S S S R V +++= D .)(214321S S S S R V +++=373a π331612a π+3712a π333a π+332112 5.5x 22πx3415.若l 、m 、n 是互不相同的空间直线,α、β是不重合的平面,则下列命题中为真命题的是( ) A .若//,,l n αβαβ⊂⊂,则//l n B .若,l n m n ⊥⊥,则//l m C .若,l αβα⊥⊂,则l β⊥ D .若,//l l αβ⊥,则αβ⊥16.三棱锥ABC -S 中,底面ABC 为等腰直角三角形,2,BC BA == 侧棱32SC SA ==,二面角B -AC -S 的余弦值为55,则此三棱锥外接球的表面积为( ) A.π16 B.π12 C.π8 D.π417.已知c b ,,a 是三条不同的直线,命题:“a ∥b 且c b c a ⊥⇒⊥”是真命题,如果把c b ,,a 中的两条直线换成两个平面,在所得3个命题中,真命题的个数为( ) A.0 B.1 C.2 D.319.三棱柱111ABC A B C -的侧棱与底面垂直,11AA AB AC ===,AB AC ⊥,N 是BC 的中点,点P 在11A B 上,且满足111A P A B λ=,直线PN 与平面ABC 所成角θ的正切值取最大值时λ的值为( ) A.12 B.22C.32D.255 20.在四面体ABCD 中,AB AD ⊥,1AB AD BC CD ====,且平面ABD ⊥平面BCD ,M 为AB 中点,则CM 与平面ABD 所成角的正弦值为( ) A.22B.33C.32D.6321.在长方体1111ABCD A B C D -中,13,4,5AB AD AA ===,O 为1D C 与1DC 的交点,则三棱锥O ABC -的体积为( )A.5 B.10 C.15 D.3022.若某几何体的三视图(单位:cm )如图所示,则此几何体的体积是( ) A . B . C . D .(2428)π-3cm 24.若是互不相同的空间直线,是不重合的平面,则下列命题正确的是( ) A. B.C. D. 26.一个几何体的三视图如图,则该几何体的体积为 A .π B .π2 C .π3 D .π6,//l l αβαβ⊥⇒⊥,//l n m n l m ⊥⊥⇒,l l αβαβ⊥⊂⇒⊥//,,//l n l n αβαβ⊂⊂⇒,αβ,,l m n 3cm (1828)π-3cm (2420)π-3cm (1820)π-侧视图正视图俯视图11221=R28.某几何体的三视图如图所示,则该几何体的体积为A.π2 B.2π2 C.3πD.23π29.已知三角形所在平面与矩形所在平面互相垂直,,,若点都在同一球面上,则此球的表面积等于A. B.. C.π12 D.π2030.某几何体三视图如图所示,其中三角形的三边长与圆的直径均为2,则该几何体体积为()A.32833π+B.3233π+C.4333π+D.433π+31.一个几何体的三视图如图所示,其中俯视图是一个正方形,则这个几何体的体积是()A.64 B.32 C.16 D.833.如图,网格纸上小正方形的边长为,粗线画出的是某多面体的三视图,则该多面体的体积为()A. B. C. D.34.如图,矩形ABCD中,AB=2AD,E为边AB的中点,将△ADE沿直线DE翻折成△A1DE.若M为线段A1C的中点,则在△ADE翻折过程中,下面四个命题中不正确的是A.|BM|是定值 B.点M在某个球面上运动C.存在某个位置,使DE⊥A1 C D.存在某个位置,使MB//平面A1DE35.如图所示是一个几何体的三视图,则这个几何体外接球的表面积为()A.8π B.16π C.32π D.64π36.一个几何体的三视图如图所示,那么这个几何体的体积为()A.16πB.6πC.4πD.864332336432313π43πP A B C D、、、、90APD︒∠=2PA PD AB===ABCDPAD俯视12411侧视12411主视37.某三棱锥的正视图如图所示,则在下列图①②③④中,所有可能成为这个三棱锥的俯视图的是( )① ② ③ ④(A )①②③ (B )①②④ (C )②③④ (D )①②③④ 39.设m 、n 是两条不同的直线,α、β是两个不同的平面,则( ) A .若n m ⊥,α//n ,则α⊥m B .若β//m ,αβ⊥,则α⊥mC .若β⊥m ,β⊥n ,α⊥n ,则α⊥mD .若n m ⊥,β⊥n ,αβ⊥,则α⊥m 40.如图,是一个几何体的三视图,其中主视图、左视图是直角边长为2的等腰直角三角形,俯视图为边长为2的正方形,则此几何体的表面积为( ). (A )8+42 (B )8+43 (C )662+ (D )8+22+2341.如图,网格纸上小正方形边长为1,粗线是一个棱锥的三视图,则此棱锥的体积为( ).(A )38 (B )34(C )34 (D )3242.已知直线m 和平面α,β,则下列四个命题中正确的是(A )若αβ⊥,m β⊂,则m α⊥ (B )若//αβ,//m α,则//m β (C )若//αβ,m α⊥,则m β⊥ (D )若//m α,//m β,则//αβ 43.某四棱锥的三视图如图所示,其中正(主)视图是等腰直角三角形,侧(左)视图是等腰三角形,俯视图是正方形,则该四棱锥的体积是 (A )23 (B )43 (C )53 (D )8344.设三棱柱的侧棱垂直于底面,所有棱长都a ,顶点都在一个球面上,则该球的表面积大小为( ) (A )2a π(B )273a π(C )2113a π(D )25a π 45.已知一个几何体的三视图是三个全等的边长为1的正方形,如图所示,则它的体积为( )(A )16 (B )13 (C )23 (D )56正视图主视图 左视图俯视图俯视图正视图 侧视图46.如图,四棱柱1111D C B A ABCD -中,E 、F 分别是1AB 、1BC 的中点.下列结论中,正确的是( ) A .1BB EF ⊥ B .//EF 平面11A ACC C .BD EF ⊥D .⊥EF 平面11B BCC47.一个四面体如图,若该四面体的正视图(主视图)、侧视图(左视图)和俯视图都是直角边长为1的等腰直角三角形,则它的体积=V ( ) A .21 B .31 C .61 D .12148.如图,网格纸上小正方形的边长为1,粗实线画出的是某多面体的三视图,则该多面体的各条棱中,最长的棱的长度为( ) A .22 B .6 C .3 D .2350.一个几何体的三视图如右图所示,则该几何体的表面积为( ) A .32 B .6262++ C .12 D .3262++ 51.如图所示是一个几何体的三视图,则该几何体的表面积为( )A .4+2B .2+C .2+2D .4+ 52.点A 、B 、C 、D 在同一球面上,D A ⊥平面C AB ,D C 5A =A =,3AB =,C 4B =,则该球的表面积为( ) A .252π B .12523πC .50πD .503π 53.已知某锥体的正视图和侧视图如图2,其体积为233,则该锥体的俯视图可以是( )54.已知球O 的直径4=PQ ,C B A ,,是球球面上的三点,是正三角形,且,则三棱锥ABC P -的体积为 ( ) A .B .C .D . 55.一个四面体的顶点在空间直角坐标系o xyz -中的坐标分别是(1,0,1),(1,1,0),(0,1,1),(0,0,0),画该四面体三视图中的主视图时,以zox 平面为投影面,则得到主视图可以为( )56.若某几何体的三视图如图所示,则此几何体的体积等于( ) A .752B .30C .75D .15 57.某几何体的三视图如图所示,其中正视图是两底边长分别为1,2的直角梯形,俯视图是斜边为3的等腰直角三角形,该几何体的体积是( ) A .1 B .2 C .47 D .49 58.一个几何体的三视图如图所示,则该几何体的外接球的体积为( )A .32πB .92πC .43πD .83π221俯视图左视图 主视图AB CDEFGH4327233439433 30=∠=∠=∠CPQ BPQ APQ ABC ∆O59.一只蚂蚁从正方体 1111ABCD A B C D -,的顶点A 处出发,经正方体的表面,按最短路线爬行到达顶点1C 位置,则下列图形中可以表示正方体及蚂蚁最短爬行路线的正视图是A .①②B .①③C .②④D .③④ 60.如图是一个几何体的三视图,则该几何体的体积是( )(A )54 (B )27 (C )18 (D ) 961.设,是两条不同的直线,,是两个不同的平面,下列命题中正确的是( ) A .若//,//,m n αα则//m n B .若,,,m m αββα⊥⊥⊄则//m α C .若,,m αβα⊥⊂则m β⊥ D .若,,//,//,m n m n ααββ⊂⊂则//αβ62.已知三条直线若和b 是异面直线,b 和c是异面直线,那么直线a 和的位置关系是( )A .平行B .相交C .异面D .平行、相交或异面63.四棱锥的三视图如图所示,则最长的一条侧棱的长度是( )A. B . C . D . 64.一个空间几何体的三视图如图所示,则该几何体的体积为A.403 B .803C .40D .80 65.如图,四棱锥ABCD P -中,,, 和都是等边三角形,则异面直线与所成角的大小为( )A .B .C . 60D . 4575 90BDCPAPB CD PAD ∆PAB ∆AD BC 2= 90=∠=∠BAD ABC 2213529c a ,,,a b c βαn m66. 给出下列关于互不相同的直线m 、l 、n 和平面α、β的四个命题: ①若α⊂m ,A l =α ,点m A ∉,则l 与m 不共面;② 若m 、l 是异面直线,α//l ,α//m ,且l n ⊥,m n ⊥,则α⊥n ; ③ 若α//l ,β//m ,βα//,则m l //;④ 若,,,,,则, 其中为真命题的是( )A .①③④B .②③④C .①②④D .①②③ 67.某几何体三视图如图所示,则该几何体的体积为( ) A .23 B .1 C .43 D .3269.某几何体的三视图如图所示,则该几何体的体积为 ( ) A.61 B.21 C.32 D.65 70.如图,在正方形ABCD 中,F E ,分别是CD BC ,的中点,沿EF AF AE ,,把正方形折成一个四面体,使D C B ,,三点重合,重合后的点记为P ,点P 在AEF ∆内的射影为.则下列说法正确的是( )A.O 是AEF ∆的垂心B.O 是AEF ∆的内心C.O 是AEF ∆的外心D.O 是AEF ∆的重心71.某几何体的三视图如图所示,则该几何体的体积为( ) A.61 B.21 C.32 D.65 72.设,l m 是两条不同的直线,,αβ是两个不同的平面,则下列命题为真命题的是( ) A .若//,//,//m l m l αα则 B .若,,//m l m l αα⊥⊥则C .若//,,//,l m l m αβαβ⊥⊥则D .若,//,,//,//m m l l αββααβ⊂⊂则O βα//β//m β//l A m l = α⊂m α⊂l 112正视图侧视图俯视图正视侧视俯视111正视图侧视图俯视图11174.一个几何体的三视图如图所示,则该几何体的体积的是( )(A ) (B ) (C )(D )75.一个四棱锥的三视图如图所示,其中侧视图为正三角形,则该四棱锥的体积是 ,四棱锥侧面中最大侧面的面积是 . 76.若3,),,3,1(),0,2,2(π>=<==b a z b a ,则z 等于( )A.B.C.D.77.已知向量)3,2,1(=a ,点)(0,1,0A ,若a AB 2-=,则点B 的坐标是( )A.(-2,-4,-6)B.(2,4,6)C.(2,3,6)D.(-2,-3,-6) 78.对于空间的一条直线m 和两个平面,αβ,下列命题中的真命题是( ) A .若//,//,m m αβ则//αβ B .若//,//,m m αβ则αβ⊥ C .若,,m m αβ⊥⊥则//αβ D .若,,m m αβ⊥⊥则αβ⊥79.一个几何体的三视图如图所示,其中俯视图与左视图均为半径是2的圆,则这个几何体的表面积是( )A .24πB .16πC .12πD .8π 80.已知,m n 表示两条不同直线,α表示平面,下列说法正确的是( ) A .若,m m n α⊥⊥,则//n α B .若,m n αα⊥⊂,则m n ⊥ C .若//,m m n α⊥,则n α⊥ D .若//,//m n αα,则//m n81.设,l m 是两条不同的直线,,αβ是两个不同的平面,则下列命题为真命题的是( )A .若//,//,//m l m l αα则B .若,,//m l m l αα⊥⊥则C .若//,,//,l m l m αβαβ⊥⊥则D .若,//,,//,//m m l l αββααβ⊂⊂则7152233476侧(左)视图正(主)视图俯视图211122 11111 1 正视图侧视图俯视图正视俯视左视82.下图为一个几何体的三视图,尺寸如图所示,则该几何体的体积为A. B. C. D. 83.如图是一个几何体的三视图(侧视图中的弧线是半圆),则该几何体的表面积是( ).A .20+3πB .24+3πC .20+4πD .24+4π84.已知三棱锥的三视图如图所示,则它的外接球的表面积为( ).A .4πB .8πC .12πD .16π86. 一个空间几何体的三视图及部分数据如图所示,则这个几何体的体积是( )A .3B .25C .21D .23 87.一个四棱锥的侧棱长都相等,底面是正方形,其正(主)视图如右图所示该四棱锥侧面积和体积分别是( )A .B .C .D .8,8 88.平面四边形中,,,BD CD ⊥,将其沿对角线BD 折成四面体A BCD '-,使平面A BD '⊥平面BCD ,若四面体A BCD '-的顶点在同一个球面上,则该球的体积为 ( )A .32πB .3πC .23π D .2π 89.设,是两条不同的直线,,,是三个不同的平面,给出下列四个命题:①⊥,∥,则⊥; ②若⊥,⊥,则∥;③若∥,∥, ⊥,则⊥; ④若m αγ⋂=,=,∥ ,则∥.其中正确命题的序号是A .①和③B .②和③C .③和④D .①和④βαn m n γ⋂βγm αm γββαβαγβγαn m αn αm γβαn m 2BD =1AB AD CD ===ABCD 84(51),3+845,345,8435327π+35327π+433327π+32327π+90.如图,已知正方体的棱长为4,点,分别是线段,上的动点,点P 是上底面内一动点,且满足点P 到点F 的距离等于点P 到平面的距离,则当点P 运动时,的最小值是( )A .5B .4C .42D .2592.如下图所示是一个几何体的三视图,则该几何体的表面积为( )A .B .C .D .93.一个几何体的三视图如图所示,则该几何体的体积等于( )A 、263π+B 、463π+C 、283π+D 、483π+94.已知某几何体的三视图如图,则该几何体的表面积是( ) A.24 B.3662+ C.36 D.95.一个简单几何体的正视图、侧视图如右图所示,则其俯视图不可能为....①长方形;②正方形;③圆;④椭圆.中的( )A.①②B.②③C.③④D.①④96.如图,正三棱柱111C B A ABC -的正视图是边长为4的正方形,则此正三棱柱的侧视图的面积为( )A .16B .32C .34D .3836122+2222主视图 左视图2俯视图 64+622+62+624+PE 11ABB A 1111A B C D 11C D AB F E 1111ABCD A B C D -AB C 1A 1B 1C 2 2 4 主视图97.一个锥体的主视图和左视图如下图所示,下面选项中,不可能是该锥体的俯视图的是( )98.设α,β,γ为平面,m ,n 为直线,则m β⊥的一个充分条件是( )A .αβ⊥,n αβ= ,m n ⊥B .m αγ= ,αγ⊥,βγ⊥C .αβ⊥,βγ⊥,m α⊥D .n α⊥,n β⊥,m α⊥99.在直三棱柱中,,,则点到平面的距离为A. B . C . D .3 102.若一个底面为正三角形、侧棱与底面垂直的棱柱的三视图如下图所示,则这个棱柱的体积为( )A .B . C. D.104.关于直线,及平面,,下列命题中正确的是A .若,,则B .若,,则C .若,,则D .若,,则105.某几何体的三视图如图所示,其中俯视图是半圆,则该几何体的表面积为A .3π32+B .π3+C .3π2D .5π32+ 106.三棱锥P ABC -中,PA PB PC ==,456AB BC CA ===,,,若ABC ∆的外接圆恰好是三棱锥P ABC -外接球O 的一个大圆,则三棱锥P ABC -的体积为( )A .10B .20C .30D .40107.已知某几何体的三视图如图所示,其中,正视图和侧视图都是由三角形和半圆组成,俯视图是由圆和内接三角形组成,则该几何体体积为( )m α⊥l m ⊥//l ααβ⊥//l βl α⊥//l m //m α//l α//l m m αβ= //l αβαm l 6327336312俯视图侧视图正视图33433432341A BC A 11AA =2AB AC BC ===111ABC A B C -A .21+32πB .21+66π C .41+36π D .21+32π 108.已知某几何体的三视图如图所示,其中网格纸的小正方形的边长是1,则该几何体 的表面积为( )A .4B .4+42C .8+42D .8+22109.一个几何体的三视图如图所示,则该几何体的体积为( )A .412π+B .124π+C .1212π+D .44π+110.设m 、n 是两条不同的直线,α、β是两个不同的平面,给出下列四个命题:①若//m n ,//m α,则//n α; ②若αβ⊥,//m α,则m β⊥;③若αβ⊥,m β⊥,则//m α; ④若m n ⊥,m α⊥,n β⊥,则αβ⊥.其中假命题的个数是( )A .1B .2C .3D .4111.一块橡胶泥表示的几何体的三视图如图所示,将该橡胶泥揉成一个底面边长为8的正三角形的三棱锥,则这个三棱锥的高为( )A .33B .63C .93D .183112.如图所示的三个直角三角形是一个体积为20cm 3的几何体的三视图,则h=( )cmA .4B .2C .1D .12113.已知正四棱柱ABCD —A 1B 1C 1D 1中,AA 1=2AB ,则CD 与平面BDC 1所成角的正弦值等于( )A .23 B .33 C .23D .13114.已知四面体OABC 各棱长为1,D 是棱OA 的中点,则异面直线BD 与AC 所成角的余弦值( ) A.33 B.14 C.36 D.283224116.设,是两条不同的直线,,是两个不同的平面,下列命题中正确的是( )A.若则B.若则C .若则 D.若则117.已知三条直线若和是异面直线,和是异面直线,那么直线和的位置关系是( )A.平行B.相交C.异面D.平行、相交或异面119.半径为的半圆卷成一个圆锥,圆锥的体积为( ) A. B . C . D . 120.如图,正方体的棱长为,线段上有两个动点,且,则下列结论中错误..的是( )A .B .平面C .三棱锥的体积为定值D .的面积与的面积相等BEF ∆AEF ∆BEF A -ABCD //EF BE AC ⊥EBD1B 1C1D FC A 1A21=EF E F 、11D B 11111D C B A ABCD -316R π3324R π336R π333R πR c a c b b a ,,,a b c //αβ,,//,//,m n m n ααββ⊂⊂m β⊥,,m αβα⊥⊂//m α,,,m m αββα⊥⊥⊄//m n //,//,m n ααβαn m本卷由系统自动生成,请仔细校对后使用,答案仅供参考。
高一数学必修2__1.1空间几何体的结构(练习题)
必修2 1.1空间几何体的结构(练习题)一、选择题1.在棱柱中()A.只有两个面平行 B.所有的棱都平行C.所有的面都是平行四边形 D.两底面平行,且各侧棱也互相平行2.将图1所示的三角形线直线l旋转一周,可以得到如图2所示的几何体的是哪一个三角形()3.若一个平行六面体的四个侧面都是正方形,则这个平行六面体是()A.正方体 B.正四棱锥C.长方体D.直平行六面体4.下面命题中,正确的是()①底面是正方形,侧面都是等腰三角形的棱锥是正四棱锥;②对角线相等的四棱柱必是直棱柱;③底面边长相等的直四棱柱为正四棱柱;④四个面都是全等的三角形的几何体是正四面体5.如图一个封闭的立方体,它6个表面各标出1、2、3、4、5、6这6个数字,现放成下面3个不同的位置,则数字l、2、3对面的数字是()A.4、5、6 B.6、4、5 C.5、4、6 D.5、6、46.如图,能推断这个几何体可能是三棱台的是()A.A1B1=2,AB=3,B1C1=3,BC=4B.A1B l=1,AB=2,B l C l=1.5,BC=3,A1C1=2,AC=3C.A l B l=1,AB=2,B1C l=1.5,BC=3,A l C l=2,AC=4D.AB=A1B1,BC=B1C1,CA=C1A17.有下列命题(1)在圆柱的上、下底面的圆周上各取一点,则这两点的连线是圆柱的母线;(2)圆锥顶点与底面圆周上任意一点的连线是圆锥的母线;(3)在圆台上、下底面圆周上各取一点,则这两点的连线是圆台的母线;(4)圆柱的任意两条母线所在的直线是互相平行的.其中正确的是()A.(1)(2) B.(2)(3) C.(1)(3) D.(2)(4)8.下列命题中错误的是()A.圆柱的轴截面是过母线的截面中面积最大的一个B.圆锥的轴截面是所有过顶点的截面中面积最大的一个C.圆台的所有平行于底面的截面都是圆D.圆锥所有的轴截面是全等的等腰三角形9.一个三棱锥四个面中,是直角三角形的最多有()A.1个 B.2个 C.3个 D.4个10.图,这是一个正方体的表面展开图,若把它再折回成正方体后,有下列命题:①点H与点C重合;②点D与点M与点R重合;③点B与点Q重合;④点A与点S重合.其中正确命题的序号是_______________.(注:把你认为正确的命题的序号都填上)11.高为H的水瓶中注水,注满为止,如果注水量V与水深h的函数关系的图象如图所示,那么水瓶的形状是_______________.三、解答题12.察以下几何体的变化,通过比较,说出他们的特征.13.一个圆锥截成圆台,已知圆台的上下底面半径的比是1∶4,母线长为10cm,求圆锥的母线长__________.。
空间几何体的结构1.1第1课时 棱柱、棱锥、棱台的结构特征

1.空间几何体的定义
空间中的物体都占据着空间的一部分, 若只考虑这些物体的_形__状___和_大__小___,
而不考虑其他因素,那么由这些物体抽 象出来的空间图形就叫做空间几何体.
[问题1] 图片(1)(2)(3)中的物体的形状有何特点? [提示] 由若干个平面多边形围成. [问题2] 图片(4)(5)(6)(7)的物体的形状与(1)(2)(3) 中有何不同?图片(4)(5)(6)(7)中的几何体可否看作 平面图形绕某定直线旋转而成? [提示] 表面是由平面与曲面围成.可以。
DCFD′. 其中四边形ABEA′和四边形DCFD′是底面, A′D′,EF,BC,AD为侧棱.
8.如 图 , 已 知 长 方 体 ABCD- A1B1C1D1,过 BC 和 AD 分别作 一 个 平 面 交 底 面 A1B1C1D1 于 EF、PQ,则长方体被分成的三 个几何体中,棱柱的个数是________.
答案: D
下列的几何体是多面体吗?
答:这些不但是多面体,他们还是多面体 当中的一种,叫做棱锥。
你们思考一下这些棱锥有什么共同特点?
2.棱锥的结构特征
什么是棱锥? 一般地,有一 个面是多边形,其余 各面都是有一个公共 点的三角形,由这些 面围成的多面体叫做 棱锥. 记为:棱锥S-ABCD
多边形 三角形
D'
E'
C'
D A'
B'
S A'B'C'D'E' S ABCDE
S' H '2 SH 2
E
O
C
AB
3. 棱台的结构特征
什么是棱台? 一般地,用一个平行于棱锥底面的平面去截 棱锥,底面和截面中间的部分的多面体叫做棱台.
高中数学必修2(人教A版)第一章几何空间体1.1知识点总结含同步练习及答案

描述:例题:描述:高中数学必修2(人教A版)知识点总结含同步练习题及答案第一章 空间几何体 1.1 空间几何体的结构一、学习任务认识柱、锥、台、球及其简单组合体的结构特征,能运用这些结构特征描述现实生活中简单物体的结构.二、知识清单典型空间几何体空间几何体的结构特征 组合体展开图 截面分析三、知识讲解1.典型空间几何体空间几何体的概念只考虑物体的形状和大小,而不考虑其他因素,那么由这些物体抽象出来的空间图形就叫做空间几何体.2.空间几何体的结构特征多面体由若干个平面多边形围成的几何体叫做多面体.围成多面体的各个多边形叫做多面体的面;相邻两个面的公共边叫做多面体的棱;棱与棱的公共点叫做多面体的顶点;连接不在同一个面上的两个顶点的线段叫做多面体的对角线.按多面体的面数可把多面体分为四面体、五面体、六面体.其中,四个面均为全等的正三角形的四面体叫做正四面体.旋转体由一个平面图形绕它所在的平面内的一条定直线旋转所形成的封闭几何体叫做旋转体.这条定直线叫做旋转体的轴.棱柱的结构特征一般地,有两个面互相平行,其余各面都是四边形,且每相邻两个四边形的公共边都互相平行,由这些面所围成的多面体叫做棱柱(prism).棱柱中,两个互相平行的面叫做底面,简称底;其余各面叫做棱柱的侧面;相邻侧面的公共边叫做棱柱的侧棱;侧棱与底面的公共顶点叫做棱柱的用一个平行于棱锥底面的平面去截棱锥,得到两个几何体,一个是______,另一个是______.解:棱锥;棱台.⋯⋯余各面叫做棱柱的侧面;相邻侧面的公共边叫做棱柱的侧棱;侧棱与底面的公共顶点叫做棱柱的顶点.底面是三角形、四边形、五边形的棱柱分别叫做三棱柱、四棱柱、五棱柱,可以用表示底面各顶点的字母或一条对角线端点的字母表示棱柱,如下图的六棱柱可以表示为棱柱或棱柱 .侧棱与底面不垂直的棱柱叫做斜棱柱;侧棱与底面垂直的棱柱叫做直棱柱;底面是正多边形的直棱柱叫做正棱柱;底面是平行四边形的棱柱叫做平行六面体;侧棱与底面垂直的平行六面体叫做直平行六面体.棱锥的结构特征一般地,有一个面是多边形,其余各面都是有一个公共顶点的三角形,由这些面所围成的多面体叫做棱锥(pyramid).这个多边形面叫做棱锥的底面或底;有公共顶点的各个三角形面叫做棱锥的侧面;各侧面的公共顶点叫做棱锥的顶点;相邻侧面的公共边叫做棱锥的侧棱.底面是三角形、四边形、五边形的棱锥分别叫做三棱锥、四棱锥、五棱锥其中三棱锥又叫四面体.棱锥也用表示顶点和底面各顶点的字母或者用表示顶点和底面一条对角线端点的字母来表示,如下图的四棱锥表示为棱锥 或者棱锥 .棱锥的底面是正多边形,且它的顶点在过底面中心且与底面垂直的直线上,这个棱锥叫做正棱锥.正棱锥各侧面都是全等的等腰三角形,这些等腰三角形底边上的高都相等,叫做棱锥的斜高.⋯⋯⋯⋯ABCDEF−A′B′C′D′E′F′DA′⋯⋯⋯⋯S−ABCD S−AC棱台的结构特征用一个平行于棱锥底面的平面去截棱锥,底面与截面之间的部分,这样的多面体叫做棱台(frustum of a pyramid).原棱锥的底面和截面分别叫做棱台的下底面和上底面;其他各面叫做棱台的侧面;相邻两侧面的公共边叫做棱台的侧棱;两底面的距离叫做棱台的高.由正棱锥截得的棱台叫做正棱台,正棱台的各个侧面都是全等的等腰梯形,这些等腰梯形的高叫做棱台的斜高.圆柱的结构特征以矩形的一边所在直线为旋转轴,其余三边旋转形成的面所围成的旋转体叫做圆柱(circular cylinder).旋转轴叫做圆柱的轴;垂直于轴的边旋转而成的圆面叫做圆柱的底面;平行于轴的边旋转而成的曲面叫做圆柱的侧面;无论旋转到什么位置,不垂直于轴的边都叫做圆柱侧面的母线.圆锥的结构特征以直角三角形的一条直角边所在直线为旋转轴,其余两边旋转形成的面所围成的旋转体叫做圆锥(circular cone).圆台的结构特征例题:用平行于圆锥底面的平面去截圆锥,底面与截面之间的部分叫做圆台(frustum of a cone).棱台与圆台统称为台体.球的结构特征以半圆的直径所在直线为旋转轴,半圆面旋转一周形成的旋转体叫做球体,简称球(solid sphere).半圆的圆心叫做球的球心,半圆的半径叫做球的半径,半圆的直径叫做球的直径.球常用表示球心的字母 表示.O下列命题中,正确的是( )A.有两个面互相平行,其余各面都是四边形的几何体叫棱柱B.棱柱中互相平行的两个面叫做棱柱的底面C.棱柱的侧面是平行四边形,而底面不是平行四边形D.棱柱的侧棱长相等,侧面是平行四边形解:D如图(1),满足 A 选项条件,但不是棱柱;对于 B 选项,如图(2),构造四棱柱,令四边形 是梯形,可知 ,但这两个面不能作为棱柱的底面;C选项中,若棱柱是平行六面体,则它的底面是平行四边形.ABCD−A1B1C1D1ABCD面AB∥面DCB1A1C1D1若正棱锥的底面边长与侧棱长相等,则该棱锥一定不是( )A.三棱锥 B.四棱锥 C.五棱锥 D.六棱锥解:D如下图,正六边形 中,,那么正六棱锥中,,即侧棱长大于底面边长.ABCDEF OA=OB=⋯=AB S−ABCDEF SA>OA=AB描述:3.组合体简单组合体的构成有两种基本形式:一种是由简单几何体拼接而成,一种是由简单几何体截去或挖去一部分而成.如图所示的几何体中,是台体的是( )A.①② B.①③ C.③ D.②③解:C利用棱台的定义求解.①中各侧棱的延长线不能交于一点;②中的截面不平行于底面;③中各侧棱的延长线能交于一点且截面与底面平行.有下列四种说法:①圆柱是将矩形旋转一周所得的几何体;②以直角三角形的一直角边为旋转轴,旋转所得几何体是圆锥;③圆台的任意两条母线的延长线,可能相交也可能不相交;④半圆绕其直径所在直线旋转一周形成球.其中错误的有( )A.个 B. 个 C. 个 D. 个解:D圆柱是矩形绕其一条边所在直线旋转形成的几何体,故①错;以直角三角形的一条直角边所在直线为轴,旋转一周,才能构成圆锥,②错;圆台是由圆锥截得,故其任意两条母线延长后一定交于一点,③错;半圆绕其直径所在直线旋转一周形成的是球面,故④错误.1234例题:描述:4.展开图空间形体的表面在平面上摊平后得到的图形,是画法几何研究的一项内容.描述图中几何体的结构特征.解:图(1)所示的几何体是由两个圆台拼接而成的组合体;图(2)所示的几何体是由一个圆台挖去一个圆锥得到的组合体;图(3)所示的几何体是在一个圆柱中间挖去一个三棱柱后得到的组合体.下图中的几何体是由哪个平面图形旋转得到的( )解:D)不在同一平面内的有______对.3内.解:C描述:例题:5.截面分析截面用平面截立体图形所得的封闭平面几何图形称为截面.平行截面、中截面与立体图形底面平行的截面称为平行截面,等分立体图形的高的平行截面称为中截面.轴截面包含立体图形的轴线的截面称为轴截面.球截面球的截面称为球截面.球的任意截面都是圆,其中通过球心的截面称为球的大圆,不过球心的截面称为球的小圆.球心与球的截面的圆心连线垂直于截面,并且有 ,其中 为球的半径, 为截面圆的半径, 为球心到截面的距离.+=r 2d 2R 2R r d 下面几何体的截面一定是圆面的是( )A.圆台 B.球 C.圆柱 D.棱柱解:B如图所示,是一个三棱台 ,试用两个平面把这个三棱台分成三部分,使每一部分都是一个三棱锥.解:如图,过 ,, 三点作一个平面,再过 ,, 作一个平面,就把三棱台分成三部分,形成的三个三棱锥分别是 ,,.ABC −A ′B ′C ′A ′B C A ′B C ′ABC −A ′B ′C ′−ABC A ′−B B ′A ′C ′−BC A ′C ′如图,正方体 中,,, 分别是 ,, 的中点,那么正方体中过点 ,, 的截面形状是( )A.三角形 B.四边形 C.五边形 D.六边形ABCD −A 1B 1C 1D 1P Q R AB AD B 1C 1P QR作截面图如图所示,可知是六边形.ii)若两平行截面在球心的两侧,如图(2)所示,则 解:四、课后作业 (查看更多本章节同步练习题,请到快乐学)答案:1.如图,能推断这个几何体可能是三棱台的是 .A .B .C .D .C ()=2,AB =3,=3,BC =4A 1B 1B 1C 1=1,AB =2,=1.5,BC =3,=2,AC =3A 1B 1B 1C 1A 1C 1=1,AB =2,=1.5,BC =3,=2,AC =4A 1B 1B 1C 1A 1C 1AB =,BC =,CA =A 1B 1B 1C 1C 1A 1答案:2. 纸制的正方体的六个面根据其方位分别标记为上、下、东、南、西、北.现在沿该正方体的一些棱将正方体剪开、外面朝上展平,得到如图所示的平面图形,则标" "的面的方位是 .A .南B .北C .西D .下B △()3. 向高为 的水瓶中注水,注满为止,如果注水量 与水深 的函数关系的图象如图所示,那么水瓶的形状是.A .H V h ()高考不提分,赔付1万元,关注快乐学了解详情。
第一章1.1-1.1.2圆柱、圆锥、圆台、球、简单组合体的结构特征

第一章空间几何体1.1 空间几何体的结构1.1.2 圆柱、圆锥、圆台、球、简单组合体的结构特征A级基础巩固一、选择题1.下列几何体中是旋转体的是()①圆柱②六棱锥③正方体④球体⑤四面体A.①和⑤B.①C.③和④D.①和④解析:圆柱、球体是旋转体,其余均为多面体.答案:D2.如图所示的简单组合体的结构特征是()A.由两个四棱锥组合成的B.由一个三棱锥和一个四棱锥组合成的C.由一个四棱锥和一个四棱柱组合成的D.由一个四棱锥和一个四棱台组合成的解析:这个8面体是由两个四棱锥组合而成.答案:A3.下图是由哪个平面图形旋转得到的()解析:图中几何体由圆锥、圆台组合而成,可由A 中图形绕图中虚线旋转360°得到.答案:A4.如图所示的几何体是从一个圆柱中挖去一个以圆柱的上底面为底面,下底面圆心为顶点的圆锥而得到的.现用一个平面去截这个几何体,若这个平面平行于底面,那么截面图形为( )解析:截面图形应为图C 所示的圆环面.答案:C5.用长为4,宽为2的矩形做侧面围成一个圆柱,此圆柱轴截面面积为( )A .8 B.8π C.4π D.2π解析:若矩形的长为圆柱底面周长,则2πR =4.所以2R =4 π. 因此圆柱轴截面面积S 1=2R ·2=8 π. 若矩形的宽为圆柱底面周长,则2πr =2.所以2r=2π,则圆柱轴截面面积S2=2r·4=8π.综上可知,圆柱的轴截面面积为8π.答案:B二、填空题6.等腰三角形绕底边上的高所在的直线旋转180°,所得几何体是________.解析:结合旋转体及圆锥的特征知,所得几何体为圆锥.答案:圆锥7.给出下列说法:①圆柱的母线与它的轴可以不平行;②圆锥的顶点、圆锥底面圆周上任意一点及底面圆的圆心三点的连线,都可以构成直角三角形;③在圆台的上、下两底面圆周上各取一点,则这两点的连线是圆台的母线;④圆柱的任意两条母线所在的直线是互相平行的.其中正确的是____________(填序号).解析:由旋转体的形成与几何特征可知①③错误,②④正确.答案:②④8.如图是一个几何体的表面展成的平面图形,则这个几何体是__________.答案:圆柱三、解答题9.指出如图①②所示的图形是由哪些简单几何体构成的.解:分割原图,使它的每一部分都是简单几何体.图①是由一个三棱柱和一个四棱柱拼接而成的简单组合体. 图②是由一个圆锥和一个四棱柱拼接而成的简单组合体.10.如图所示,用一个平行于圆锥SO 底面的平面截这个圆锥,截得圆台上、下底面的半径分别2 cm 和5 cm ,圆台的母线长是12 cm ,求圆锥SO 的母线长.解:如图,过圆台的轴作截面,截面为等腰梯形ABCD ,由已知可得上底半径O 1A =2 cm ,下底半径OB =5 cm ,且腰长AB =12 cm.设截得此圆台的圆锥的母线长为l ,则由△SAO 1∽△SBO ,可得l -12l =25,所以l =20 cm. 故截得此圆台的圆锥的母线长为20 cm.B 级 能力提升1.如图所示的平面中阴影部分绕中间轴旋转一周,形成的几何体形状为( )A.一个球体B.一个球体中间挖出一个圆柱C.一个圆柱D.一个球体中间挖去一个长方体解析:外面的圆旋转形成一个球,里面的长方形旋转形成一个圆柱.所有形成的几何为一个球体挖出一个圆柱.答案:B2.一个半径为5 cm的球,被一平面所截,球心到截面圆心的距离为4 cm,则截面圆面积为__________cm2.解析:如图所示,过球心O作轴截面,设截面圆的圆心为O1,其半径为r.由球的性质,OO1⊥CD.在Rt△OO1C中,R=OC=5,OO1=4,则O1C=3,所以截面圆的面积S=π·r2=π·O1C2=9π.答案:9π3.如图,底面半径为1,高为2的圆柱,在A点有一只蚂蚁,现在这只蚂蚁要围绕圆柱由A点爬到B点,问蚂蚁爬行的最短距离是多少?解:把圆柱的侧面沿AB剪开,然后展开成为平面图形——矩形,如图所示,连接AB′,即为蚂蚁爬行的最短距离.因为AB=A′B′=2,AA′为底面圆的周长,且AA′=2π×1=2π.所以AB′=A′B′2+AA′2=4+(2π)2=21+π2,所以蚂蚁爬行的最短距离为21+π2.。
空间几何体结构

空间几何体的结构(P5)例题7.下列结论正确的是()A.各个面都是三角形的几何体是三棱锥B.以正方形的一条对角线为轴旋转一周围成的几何体叫圆锥C.棱锥的侧棱长与底面多边形的边长都相等,则此棱锥可能是正六棱锥D.圆锥的顶点与底面圆周上的任意一点的连线都是母线解析:选D.三棱锥的侧面是有公共顶点的三角形,A错;以正方形的一条对角线为轴旋转一周围成的几何体为两个圆锥组成的一个组合体,B错;六棱锥的侧棱长大于底面多边形的边长,C错;D正确.答案:D反思:正确把握几何体的定义,理解其结构特征,明确旋转体的形成。
P7 例15.(2012·山东省济宁第三次质检)在一个倒置的正三棱锥容器内放入一个钢球,钢球恰与棱锥的四个面都接触,过棱锥的一条侧棱和高作截面,正确的截面图形是( B )答案:B.分析:由于球与侧棱不相交,因此截面图不可能存在截面圆与三角形都相切,排除A,D,又圆锥的高一定过球心,因此在截面图中三角形的高一定过截面圆的圆心,排除C,故选B.反思:首先要明确简单组合体的的结构特征,其次要有一定的空间想象能力.(P8)1.以下四个命题:①正棱锥的所有侧棱相等;②直棱柱的侧面都是全等的矩形;③圆柱的母线垂直于底面;④用经过旋转轴的平面截圆锥,所得的截面一定是全等的等腰三角形.其中,正确的命题个数为( )(A)4 (B)3 (C)2 (D)11.【解析】选B.由正棱锥的定义可知所有侧棱相等,故①正确;由于直棱柱的底面不一定是正多边形,故侧面矩形不一定全等,因此②不正确;由圆柱母线的定义可知③正确;结合圆锥轴截面的作法可知④正确.综上,正确的命题有3个.(P8)9.如图,在透明塑料制成的长方体ABCD-A1B1C1D1容器内灌进一些水,将容器底面一边BC固定于地面上,再将容器倾斜,随着倾斜度的不同,有下列四个命题:①水的部分始终呈棱柱状;②水面四边形EFGH的面积不改变;③棱A1D1始终与水面EFGH平行;④当E∈AA1时,AE+BF是定值.其中正确命题的序号是________(填上所有可能的序号).答案:①③④[解析]由于容器一边BC固定于水平地面上,所以随着容器倾斜度的变化,水面四边形EFGH的一组对边EH和FG始终与BC平行且相等,而另一对边EF与GH是变化的,因此A1D1与水面平行,且水的部分是一个棱柱(BC为垂直于两底的侧棱),由于水的体积不变,故棱柱的底面面积不变,因此AE+BF为定值.(P8)12.[2013·北京卷] 如图1-2,在正方体ABCD-A1B1C1D1中,P为对角线BD1的三等分点,P到各顶点的距离的不同取值有()1-2A.3个B.4个C.5个D.6个12.答案:B[解析] 设棱长为1,∵BD1=3,∴BP=33,D1P=2 33.联结AD1,B1D1,CD1,得△ABD1≌△CBD1≌△B1BD1,∴∠ABD1=∠CBD1=∠B1BD1,且cos∠ABD1=3 3,联结AP,PC,PB1,则有△ABP≌△CBP≌△B1BP,∴AP=CP=B1P=63,同理DP=A1P=C1P=1,∴P到各顶点的距离的不同取值有4个.--------------------------------------------------------------------------------------------------------------- 1.给出以下命题:①底面是矩形的平行六面体是长方体;②直角三角形绕着它的一边旋转一周形成的几何体叫做圆锥;③四棱锥的四个侧面可以都是直角三角形.其中说法正确的序号是________.1.③[解析] 命题①不是真命题,因为底面是矩形,若侧棱不垂直于底面,这时四棱柱是斜平行六面体;命题②不是真命题,直角三角形绕着它的一条直角边旋转一周形成的几何体叫做圆锥,如果绕着它的斜边旋转一周,形成的几何体则是两个具有共同底面的圆锥;命题③是真命题,如图所示,在四棱锥P-ABCD中,底面ABCD是矩形,P A⊥平面ABCD,则可以得到四个侧面都是直角三角形,故填③.7.(易错题)一正方体内接于一个球,经过球心作一个截面,则截面的可能图形为_________(只填写序号).7.【解析】当截面与正方体的某一面平行时,可得①,将截面旋转可得②,继续旋转,过正方体两顶点时可得③,即正方体的对角面,不可能得④.答案:①②③2.充满气的车轮内胎可由下面某个图形绕对称轴旋转而成,这个图形是( )解析:选项A得到的是空心球;D得到的是球;选项C得到的是车轮内胎;B得到的是空心的环状几何体,故选C.答案:C8.(金榜预测)一个几何体的正视图为一个三角形,则这个几何体可能是下列几何体中的________(填入所有可能的几何体前的编号).①三棱锥 ②四棱锥 ③三棱柱 ④四棱柱 ⑤圆锥⑥圆柱11.已知正方体ABCD —A 1B 1C 1D 1的棱长为1,P 是AA 1的中点,E 是BB 1上一点,如图所示,求PE +EC 的最小值.解:把面A 1ABB 1和面B 1BCC 1展成平面图形,如图所示,PE +EC 的最小值即为线段PC 的长.由于AP =PA 1=12,AC =2,所以PC =22+⎝ ⎛⎭⎪⎫122=172, 所以PE +EC 的最小值为172. 评析:“化折为直”是求空间几何体表面上折线段最小值问题的基本方法,其途径是将各侧面展开.12.如图所示,在长方体ABCD -A 1B 1C 1D 1中,AB =3,BC =2,BB 1=1,求由A 到C1在长方体表面上的最短距离为多少?解析:展开1如图(1)所示:AC1=52+12=26;展开2如图(2)所示:AC1=32+32=32;展开3如图(3)所示:AC1=42+22=2 5.由A到C1在长方体表面上的最短距离为3 2.。
2025年高考数学一轮复习-空间几何体的结构、表面积和体积-专项训练【含答案】

2025年高考数学一轮复习-空间几何体的结构、表面积和体积-专项训练一、基本技能练1.下列说法中,正确的是()A.棱柱的侧面可以是三角形B.若棱柱有两个侧面是矩形,则该棱柱的其他侧面也是矩形C.正方体的所有棱长都相等D.棱柱的所有棱长都相等2.如图所示的等腰梯形是一个几何图形的斜二测直观图,其底角为45°,上底和腰均为1,下底为2+1,则此直观图对应的平面图形的面积为()A.1+2B.2+2C.2+22D.4+223.如图所示,正方体的棱长为2,以其所有面的中心为顶点的多面体的体积为()A.4B.43D.3C.234.已知在梯形ABCD中,∠ABC=π2,AD∥BC,BC=2AD=2AB=2,则将梯形ABCD绕AD所在的直线旋转一周而形成的曲面所围成的几何体的表面积为() A.(5+2)π B.(4+2)πC.(5+22)πD.(3+2)π5.如图,位于西安大慈恩寺的大雁塔,是唐代玄奘法师为保存经卷、佛像而主持修建的,是我国现存最早的四方楼阁式砖塔.塔顶可以看成一个正四棱锥,其侧棱与底面所成的角为45°,则该正四棱锥的一个侧面与底面的面积之比为()A.3∶2B.2∶2C.3∶3D.3∶46.过圆锥的轴作截面,如果截面为正三角形,则称该圆锥为等边圆锥.已知在一等边圆锥中,过顶点P 的截面与底面交于CD ,若∠COD =90°(O 为底面圆心),且S △PCD =72,则这个等边圆锥的表面积为()A.2π+2πB.3πC.2π+3πD.π+3π7.如图,四边形ABCD 是边长为2的正方形,ED ⊥平面ABCD ,FC ⊥平面ABCD ,ED =2FC =2,则四面体ABEF 的体积为()A.13B.23C.1D.438.黄金分割是指将整体一分为二,较大部分与整体部分的比值等于较小部分与较大部分的比值,其比值为5-12,约为0.618.这个比例被公认为是最能引起美感的比例,因此被称为黄金比.在几何世界中有很多黄金图形,在三角形中,如果相邻两边之比等于黄金比,且它们夹角的余弦值为黄金比值,那么这个三角形一定是直角三角形,且这个三角形称为黄金分割直角三角形.在正四棱锥中,以黄金分割直角三角形的长直角边作为正四棱锥的高,黄金分割直角三角形的短直角边的边长作为底面正方形的边心距(正多边形的边心距是正多边形的外接圆圆心到正多边形某一边的距离),斜边作为正四棱锥的斜高,这样得到的正四棱锥称为黄金分割正四棱锥.在黄金分割正四棱锥中,以该正四棱锥的高为边长的正方形的面积与该正四棱锥的侧面积之比为()A.5-12B.5+12C.1D.149.如图,在棱长为2的正方体ABCD-A′B′C′D′中,点E,F,G分别是棱A′B′,B′C′,CD的中点,则由点E,F,G确定的平面截正方体所得的截面多边形的面积等于________.10.已知圆锥的顶点为S,底面圆周上的两点A,B满足△SAB为等边三角形,且面积为43,又知圆锥轴截面的面积为8,则圆锥的侧面积为________.11.如图,已知正三棱柱ABC-A1B1C1的各棱长均为2,点D在棱AA1上,则三棱锥D-BB1C1的体积为________.12.已知三棱锥S-ABC中,∠SAB=∠ABC=π2,SB=4,SC=213,AB=2,BC =6,则三棱锥S-ABC的体积为________.二、创新拓展练13.(多选)攒尖是我国古代建筑中屋顶的一种结构形式,宋代称为撮尖,清代称攒尖,通常有圆形攒尖、三角攒尖、四角攒尖、八角攒尖,也有单檐和重檐之分,多见于亭阁式建筑、园林建筑.下面以四角攒尖为例,如图,它的屋顶部分的轮廓可近似看作一个正四棱锥.已知此正四棱锥的侧面与底面所成的锐二面角为θ,这个角接近30°.若取θ=30°,侧棱长为21米,则()A.正四棱锥的底面边长为6米B.正四棱锥的底面边长为3米C.正四棱锥的侧面积为243平方米D.正四棱锥的侧面积为123平方米14.(多选)如图,正方体ABCD-A1B1C1D1的棱长为1,线段B1D1上有两个动点E,F,且EF=12,则下列结论中错误的是()A.AC⊥AFB.EF∥平面ABCDC.三棱锥A-BEF的体积为定值D.△AEF的面积与△BEF的面积相等15.(多选)《九章算术》是《算经十书》中最重要的一部,其中将有三条棱互相平行且有一个面为梯形的五面体称为“羡除”,则()A.“羡除”有且仅有两个面为三角形B.“羡除”一定不是台体C.不存在有两个面为平行四边形的“羡除”D.“羡除”至多有两个面为梯形16.(多选)如图,四边形ABCD为正方形,ED⊥平面ABCD,FB∥ED,AB=ED=2FB.记三棱锥E-ACD,F-ABC,F-ACE的体积分别为V1,V2,V3,则()A.V3=2V2B.V3=V1C.V3=V1+V2D.2V3=3V1参考答案与解析一、基本技能练1.答案C解析棱柱的侧面都是平行四边形,选项A错误;其他侧面可能是平行四边形,选项B错误;棱柱的侧棱与底面边长并不一定相等,选项D错误;易知选项C正确.2.答案B解析∵平面图形的直观图是一个底角为45°,腰和上底长均为1的等腰梯形,∴平面图形为直角梯形,且直角腰长为2,上底边长为1,下底边长为2+1,∴平面图形的面积S=1+1+22×2=2+ 2.故选B.3.答案B解析易知该几何体是由上、下两个全等的正四棱锥组成的,其中正四棱锥底面边长为2,棱锥的高为1,所以该多面体的体积V =2×13×(2)2×1=43.4.答案A解析因为在梯形ABCD 中,∠ABC =π2,AD ∥BC ,BC =2AD =2AB =2,所以将梯形ABCD 绕AD 所在的直线旋转一周得到的几何体是一个底面半径为1,高为2的圆柱挖去一个底面半径为1,高为1的圆锥后剩余的部分,如图所示.所以该几何体的表面积S =π×12+2π×1×2+π×1×12+12=(5+2)π.5.答案D解析设塔顶是正四棱锥P -ABCD (如图),PO 是正四棱锥的高.设正四棱锥底面边长为a ,则底面面积S 1=a 2,因为AO =22a ,∠PAO =45°,所以PA =2×22a =a ,所以△PAB 是正三角形,其面积为S 2=34a 2,所以S 2∶S 1=34a 2∶a 2=3∶4.6.答案B解析如图,连接PO ,设圆锥的母线长为2a ,则圆锥的底面圆的半径为a ,高为PO =3a .由已知得CD =2a ,PC =PD =2a ,则S △PCD =12×2a ×(3a )2+22a 2=72,从而可得a =1,圆锥的表面积为πa ×2a +πa 2=3πa 2=3π.7.答案B解析∵ED ⊥平面ABCD 且AD ⊂平面ABCD ,∴ED ⊥AD .∵在正方形ABCD 中,AD ⊥DC ,又DC ∩ED =D ,DC ,ED ⊂平面CDEF ,∴AD ⊥平面CDEF .易知FC =ED2=1,V A -BEF =V ABCDEF -V F -ABCD -V A -DEF .∵V E -ABCD =13·ED ·S 正方形ABCD =13×2×2×2=83,V B -EFC =13·BC ·S △EFC =13×2×2×1×12=23,∴V ABCDEF =V E -ABCD +V B -EFC =83+23=103.又V F -ABCD =13·FC ·S 正方形ABCD =13×1×2×2=43,V A -DEF =13·AD ·S △DEF =13×2×2×2×12=43,∴V A -BEF =V ABCDEF -V F -ABCD -V A -DEF =103-43-43=23.故选B.8.答案D解析如图,在黄金分割正四棱锥P -ABCD 中,O 是正方形ABCD 的中心,PE 是正四棱锥的斜高,设OE =a ,则CD =2a ,∴Rt△POE为黄金分割直角三角形,则OEPE=5-12,∴PE=5+12,则PO=PE2-OE2=1+52a,∴以该正四棱锥的高为边长的正方形的面积S=PO2=1+52a2,又正四棱锥的四个侧面是全等的,∴S侧=4S△PCD=4×12×CD×PE=2(1+5)a2,∴该正四棱锥的高为边长的正方形的面积与该正四棱锥的侧面积之比为1 4 .9.答案332解析分别取AD,CC′和AA′的中点为P,M,N,可得出过E,F,G三点的平面截正方体所得截面为正六边形EFMGPN,则正六边形的边长MG=CG2+CM2=222+2221,故截面多边形的面积S=6×34×12=332.10.答案82π解析设圆锥的母线长为l,由△SAB为等边三角形,且面积为43,所以12l 2sin π3=43,解得l =4;又设圆锥底面半径为r ,高为h ,则由轴截面的面积为8,得rh =8;又r 2+h 2=l 2=16,解得r =h =22,所以圆锥的侧面积S =πrl =π·22·4=82π.11.答案233解析如图,取BC 的中点O ,连接AO .∵正三棱柱ABC -A 1B 1C 1的各棱长均为2,∴AC =2,OC =1,则AO = 3.∵AA 1∥平面BCC 1B 1,∴点D 到平面BCC 1B 1的距离为3.又S △BB 1C 1=12×2×2=2,∴V D -BB 1C 1=13×2×3=233.12.答案43解析∵∠ABC =π2,AB =2,BC =6,∴AC =AB 2+BC 2=22+62=210.∵∠SAB =π2,AB =2,SB =4,∴AS =SB 2-AB 2=42-22=2 3.由SC =213,得AC 2+AS 2=SC 2,∴AC ⊥AS .又∵SA ⊥AB ,AC ∩AB =A ,AC ,AB ⊂平面ABC ,∴AS ⊥平面ABC .∴AS 为三棱锥S -ABC 的高,∴V 三棱锥S -ABC =13×12×2×6×23=4 3.二、创新拓展练13.答案AC解析如图,在正四棱锥S -ABCD 中,O 为正方形ABCD 的中心,H 为AB 的中点,则∠SHO 为侧面SAB 与底面ABCD 所成的锐二面角,且SH ⊥AB ,∠SHO =30°,设底面边长为2a ,所以OH =AH =a ,OS =33a ,SH =233.在Rt △SAH 中,a 2=21,解得a =3,所以正四棱锥的底面边长为6米,侧面积为S =12×6×23×4=243(平方米).14.答案AD解析由题意及图形知,当点F 与点B 1重合时,∠CAF =60°,故A 错误;由正方体ABCD -A 1B 1C 1D 1的两个底面平行,EF ⊂平面A 1B 1C 1D 1,知EF ∥平面ABCD ,故B 正确;由几何体的性质及图形知,三角形BEF 的面积是定值,点A 到平面DD 1B 1B 的距离是定值,故可得三棱锥A -BEF 的体积为定值,故C 正确;由图形可以看出,B 到直线EF 的距离与A 到直线EF 的距离不相等,故△AEF 的面积与△BEF 的面积不相等,故D 错误.故选AD.15.答案ABC解析由题意知AE ∥BF ∥CD ,四边形ACDE 为梯形,如图所示.选项A ,由题意知“羡除”有且仅有两个面为三角形,故A 正确;选项B ,因为AE ∥BF ∥CD ,所以“羡除”一定不是台体,故B 正确;选项C ,假设四边形ABFE 和四边形BCDF 为平行四边形,则AE ∥BF ∥CD ,且AE =BF =CD ,即四边形ACDE 为平行四边形,与已知四边形ACDE 为梯形矛盾,故不存在,故C 正确;选项D ,若AE ≠BF ≠CD ,则“羡除”有三个面为梯形,故D 错误.故选ABC.16.答案CD 解析如图,连接BD 交AC 于O ,连接OE ,OF .设AB =ED =2FB =2,则AB =BC =CD =AD =2,FB =1.因为ED ⊥平面ABCD ,FB ∥ED ,所以FB ⊥平面ABCD ,所以V 1=V E -ACD =13S △ACD ·ED =13×12AD ·CD ·ED =13×12×2×2×2=43,V 2=V F -ABC =13S △ABC ·FB =13×12AB ·BC ·FB =13×12×2×2×1=23.因为ED ⊥平面ABCD ,AC ⊂平面ABCD ,所以ED ⊥AC ,又AC ⊥BD ,且ED ∩BD =D ,ED ,BD ⊂平面BDEF ,所以AC ⊥平面BDEF .因为OE ,OF ⊂平面BDEF ,所以AC ⊥OE ,AC ⊥OF .易知AC=BD=2AB=22,OB=OD=12BD=2,OF=OB2+FB2=3,OE=OD2+ED2=6,EF=BD2+(ED-FB)2=(22)2+(2-1)2=3,所以EF2=OE2+OF2,所以OF⊥OE.又OE∩AC=O,OE,AC⊂平面ACE,所以OF⊥平面ACE,所以V3=V F-ACE=13S△ACE·OF=13×12AC·OE·OF=13×12×22×6×3=2,所以V3≠2V2,V1≠V3,V3=V1+V2,2V3=3V1,所以选项A,B不正确,选项C,D正确.故选CD.。
高一数学空间几何体试题答案及解析
高一数学空间几何体试题答案及解析1.某三棱锥的三视图如图所示,该三棱锥的体积为()A.B.C.D.【答案】A【解析】由三视图知,几何体是一个三棱锥,底面是直角边长为的直角三角形,面积是,三棱锥的一条侧棱与底面垂直,且长度是,这是三棱锥的高,三棱锥的体积是.故选A.【考点】本题考查由三视图求面积、体积.2.已知一空间几何体的三视图如图所示,它的表面积是()A.B.C.D.3【答案】C【解析】该几何体是三棱柱,如下图,,其表面积为。
故选C。
【考点】柱体的表面积公式点评:由几何体的三视图来求出该几何体的表面积或者体积是一个考点,这类题目侧重考察学生的想象能力。
3.已知某一几何体的正(主)视图与侧(左)视图如图,则在下列图形中,可以是该几何体的俯视图的图形有()A.①②③⑤B.②③④⑤C.①③④⑤D.①②③④【答案】D【解析】俯视图为⑤的几何体的侧视图如下,这与题目不相符,而①②③④符合题意。
故选D。
【考点】三视图点评:本题考查简单空间图形的三视图,考查空间想象能力,是基础题.4.如图是某直三棱柱(侧棱与底面垂直)被削去上底后的直观图与三视图中的侧(左)视图、俯视图,在直观图中,是的中点,侧(左)视图是直角梯形,俯视图是等腰直角三角形,有关数据如图所示.(1)求出该几何体的体积;(2)若是的中点,求证:∥平面;(3)求证:平面⊥平面.【答案】(1)4 (2)主要证明∥ (3)主要证明平面【解析】解:(1)由题意可知,四棱锥中,平面平面,,所以,平面,又,,则四棱锥的体积为.(2)连接,则∥,∥,又,所以四边形为平行四边形,∴∥,∵平面,平面,所以,∥平面.(3)∵,是的中点,∴⊥,又在直三棱柱中可知,平面平面,∴平面,由(2)知,∥,∴平面,又平面,所以,平面平面.【考点】平面与平面垂直的判定;棱柱、棱锥、棱台的体积;直线与平面平行的判定.点评:本题考查的知识点是直线与平面平行的判定,棱锥的体积,平面与平面垂直的判定,其中(1)的关键是由面面垂直的性质定理可得AB⊥平面ACDE,(2)的关键是分析出四边形ANME为平行四边形,即AN∥EM,(3)的关键是熟练掌握空间线线垂直,线面垂直与面面垂直之间的相互转化.5.如图是长方体被一平面所截得到的几何体,四边形为截面,长方形为底面,则四边形的形状为( )A.梯形B.平行四边形C.可能是梯形也可能是平行四边形D.不确定【答案】B【解析】因为,长方体中相对的平面互相平行,所以,被平面截后,EF,GH平行且相等,GF,EH 平行且相等,故四边形的形状为平行四边形,选B。
高二数学同步单元练习(必修2) 专题01 空间几何体的结构(AB卷) Word版含解析

(测试时间:120分钟满分:150分)第Ⅰ卷(共60分)一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.下列图形中,不是三棱柱的展开图的是()答案:C2.有两个面平行的多面体不可能是()A.棱柱B.棱锥C.棱台D.以上都错解析:选B棱柱、棱台的上、下底面是平行的,而棱锥的任意两面均不平行.3.关于棱柱,下列说法正确的是()A.只有两个面平行B.所有的棱都相等C.所有的面都是平行四边形D.两底面平行,侧棱也互相平行4.正五棱柱中,不同在任何侧面且不同在任何底面的两顶点的连线称为它的对角线,那么一个正五棱柱对角线的条数共有()A.20 B.15C.12 D.10解析:选D从正五棱柱的上底面1个顶点与下底面不与此点在同一侧面上的两个顶点相连可得2条对角线,故共有5×2=10条对角线.5.下列命题中正确的是()A.用一个平面去截棱锥,棱锥底面和截面之间的部分是棱台B.两个底面平行且相似,其余各面都是梯形的多面体是棱台C.棱台的底面是两个相似的正方形D.棱台的侧棱延长后必交于一点解析:选D A中的平面不一定平行于底面,故A错;B中侧棱不一定交于一点;C中底面不一定是正方形.6.观察如图的四个几何体,其中判断不正确的是()A.①是棱柱B.②不是棱锥C.③不是棱锥D.④是棱台解析:结合棱柱、棱锥、棱台的定义可知①是棱柱,②是棱锥,④是棱台,③不是棱锥,故B错误.答案:B7.纸质的正方体的六个面根据其方位分别标记为上、下、东、南、西、北.现在沿该正方体的一条棱将正方体剪开,外面朝上展平得到右侧的平面图形,则标“△”的面的方位是()A.南B.北C.西D.下答案:B8.如图,在三棱台A'B'C'-ABC中,截去三棱锥A'-ABC,则剩余部分是()A.三棱锥B.四棱锥C.三棱柱D.三棱台解析:剩余部分是四棱锥A'-BCC'B'.答案:B9.棱锥的侧面和底面可以都是()A.三角形B.四边形C.五边形D.六边形解析:三棱锥的侧面和底面均是三角形.答案:A10.在下列四个平面图形中,每个小四边形皆为正方形,其中可以沿相邻正方形的公共边折叠围成一个正方体的图形是()解析:动手将四个选项中的平面图形折叠,看哪一个可以折叠围成正方体即可.答案:C11.如图,将装有水的长方体水槽固定底面一边后倾斜一个小角度,则倾斜后水槽中的水形成的几何体是()A.棱柱B.棱台C.棱柱与棱锥的组合体D.不能确定形状.答案:A12.用一个平面去截四棱锥,不可能得到()A.棱锥B.棱柱C.棱台D.四面体解析:根据棱椎的特点,侧棱不平行,所以肯定得不到棱柱答案:B第Ⅱ卷(共90分)二、填空题(本大题共4小题,每题5分,满分20分,将答案填在答题纸上)13.面数最少的棱柱为________棱柱,共有________个面围成.解析:棱柱有相互平行的两个底面,其侧面至少有3个,故面数最少的棱柱为三棱柱,共有五个面围成.答案:三 514.如图,M是棱长为2 cm的正方体ABCD-A1B1C1D1的棱CC1的中点,沿正方体表面从点A 到点M的最短路程是________ cm.答案:1315.侧棱垂直于底面的棱柱叫做直棱柱.侧棱不垂直于底面的棱柱叫做斜棱柱.底面是正多边形的直棱柱叫做正棱柱.底面是平行四边形的四棱柱叫做平行六面体.侧棱与底面垂直的平行六面体叫做直平行六面体.底面是矩形的直平行六面体叫做长方体.棱长都相等的长方体叫做正方体.请根据上述定义,回答下面的问题:(1)直四棱柱________是长方体;(2)正四棱柱________是正方体.(填“一定”、“不一定”、“一定不”)解析:根据上述定义知:长方体一定是直四棱柱,但是直四棱柱不一定是长方体;正方体一定是正四棱柱,但是正四棱柱不一定是正方体.答案:(1)不一定(2)不一定16.一个棱柱有10个顶点,所有的侧棱长的和为60 cm,则每条侧棱长为cm.解析:n棱柱有2n个顶点,因为此棱柱有10个顶点,所以此棱柱为五棱柱.又棱柱的侧棱都相等,五条侧棱长的和为60 cm,可知每条侧棱长为12 cm.答案:12三、解答题(本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.)17.观察下列四张图片,结合所学知识说出这四个建筑物主要的结构特征.18.给出两块正三角形纸片(如图所示),要求将其中一块剪拼成一个底面为正三角形的三棱锥模型,另一块剪拼成一个底面是正三角形的三棱柱模型,请设计一种剪拼方案,分别用虚线标示在图中,并作简要说明.解:如图(1)所示,沿正三角形三边中点连线折起,可拼得一个底面为正三角形的三棱锥.如图(2)所示,正三角形三个角上剪出三个相同的四边形,其较长的一组邻边边长为三角形边长的14,有一组对角为直角,余下部分按虚线折成,可成为一个缺上底的底面为正三角形的三棱柱,而剪出的三个相同的四边形恰好拼成这个底面为正三角形的棱柱的上底. 19.按下列条件分割三棱台ABC-A 1B 1C 1(不需要画图,各写出一种分割方法即可). (1)一个三棱柱和一个多面体; (2)三个三棱锥.20.正三棱台的上、下底面边长及高分别为1,2,2,则它的斜高是多少? 解析:如图,MF=OF-O'E=. 在Rt △EMF 中,∵EM=2, ∴EF=.所以斜高是21.如图,在棱锥A-BCD中,截面EFG平行于底面,且AE∶AB=1∶3,已知△DBC的周长是18,求△EFG的周长.解:由已知得EF∥BD,FG∥CD,EG∥BC,∴△EFG∽△BDC.∴.又,∴.∴△EFG的周长=18×=6.22.如图,在长方体ABCD-A1B1C1D1中,AB=3,BC=4,A1A=5,现有一只甲壳虫从A出发沿长方体表面爬行到C1来获取食物,试画出它的最短爬行路线,并求其路程的最小值.(测试时间:120分钟满分:150分)第Ⅰ卷(共60分)一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.观察如图所示的4个几何体,其中判断正确的是( )A.①是棱台 B.②是圆台C.③是棱锥 D.④不是棱柱2.下列关于母线的叙述正确的是( )①在圆柱上、下底面的圆周上各取一点,则这两点的连线是圆柱的母线;②圆锥顶点与底面圆周上任意一点的连线是圆锥的母线;③在圆台上、下底面的圆周上各取一点,则这两点的连线是圆台的母线;④圆柱的任意两条母线所在的直线是互相平行的.A.①② B.②③C.①③ D.②④D ①③中两点的连线可能不在侧面上,因此不一定是母线;②中两点的连线符合母线的条件;④中圆柱任意一条母线与圆柱的轴所在的直线平行,因此圆柱的任意两条母线所在的直线是互相平行的.3.下列判断正确的是( )A.棱柱中只能有两个面互相平行B.底面是正方形的直四棱柱是正四棱柱C.底面是正六边形的棱台是正六棱台D.底面是正方形的四棱锥是正四棱锥B A错误,比如四棱柱;B正确;C错误,还应满足正棱台上下底面中心的连线垂直于底面;D错误,还应满足顶点在底面的投影为底面的中心.4.若一正方体沿着表面几条棱裁开放平得到如图L112所示的展开图,则在原正方体中( )A.AB∥CD B.AB∥EFC.CD∥GH D. AB∥GHC 折回原正方体如图所示,则C与E重合,D与B重合,显然CD∥GH.5.如图所示的四个长方体中,由如图所示的纸板折成的是( )D 根据纸板的折叠情况及特殊面的阴影部分可以判断正确选项是D.6.给出下列三个命题:①底面为正多边形,且有相邻两个侧面与底面垂直的棱柱是正棱柱;②直角三角形绕其任一边所在直线旋转一周所形成的几何体都是圆锥;③棱台的上、下底面可以不相似,但侧棱长一定相等.其中正确命题的个数是( )A.0 B.1 C.2 D.37.如图所示,若Ω是长方体ABCDA1B1C1D1被平面EFGH截去几何体EFGHB1C1后得到的几何体,其中E为线段A1B1上异于B1的点,F为线段BB1上异于B1的点,且EH∥A1D1,则下列结论中不正确的是( )A.EH∥FG B.四边形EFGH是矩形C.Ω是棱柱 D.Ω是棱台D 根据棱台的定义(侧棱的延长线必交于一点,即棱台可以还原成棱锥)可知,几何体Ω不是棱台.8.下列命题正确的是( )A.矩形的平行投影一定是矩形B.梯形的平行投影一定是梯形C.两条相交直线的投影可能平行D.一条线段中点的平行投影仍是这条线段投影的中点9.如图所示的一个几何体,哪一个是该几何体的俯视图( )答案:C10.如图所示,下列几何体各自的三视图中,有且仅有两个视图相同的是( )A.①② B.①③ C.①④ D.②④D11.一个长方体去掉一个小长方体,所得几何体的正视图与侧视图分别如图所示,则该几何体的俯视图为( )答案:C12.如图所示的正方体中,M、N分别是AA1、CC1的中点,作四边形D1MBN,则四边形D1MBN在正方体各个面上的正投影图形中,不可能出现的是( )答案:D第Ⅱ卷(共90分)二、填空题(本大题共4小题,每题5分,满分20分,将答案填在答题纸上)13.关于如图所示的几何体的正确说法为________.(填序号)图L116①这是一个六面体;②这是一个四棱台;③这是一个四棱柱;④这是一个被截去一个三棱柱的四棱柱①③④由图易知①③④正确.14.一个无盖的正方体盒子展开后的平面图如图L117所示,A,B,C是展开图上的三点,则在正方体盒子中∠ABC=________.15.下列说法中错误的是__________.(填序号)①圆柱的轴截面是过母线的截面中面积最大的;②球的所有截面中过球心的截面的面积最大;③圆台的所有平行于底面的截面都是圆面;④圆锥的所有轴截面都是全等的等腰直角三角形.④根据旋转体的定义可知,圆锥的所有轴截面是全等的等腰三角形.16.若一个三棱柱的三视图如图所示,则这个三棱柱的高(两底面之间的距离)和底面边长分别是________和________.答案:2 4解析三棱柱的高同侧视图的高,侧视图的宽度恰为底面正三角形的高,故底边长为4.三、解答题(本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.)17.在下面图形中,图(b)是图(a)中实物画出的正视图和俯视图,你认为正确吗?如果不正确,请找出错误并改正,然后画出侧视图(尺寸不作严格要求).18.如图是截去一角的长方体,画出它的三视图.解该图形的三视图如图所示.19.如图,螺栓是棱柱和圆柱的组合体,画出它的三视图.解该物体是由一个正六棱柱和一个圆柱组合而成的,正视图反映正六棱柱的三个侧面和圆柱侧面,侧视图反映正六棱柱的两个侧面和圆柱侧面,俯视图反映该物体投影后是一个正六边形和一个圆(中心重合).它的三视图如图所示.20.用小立方体搭成一个几何体,使它的正视图和俯视图如图所示,搭建这样的几何体,最多要几个小立方体?最少要几个小立方体?解由于正视图中每列的层数即是俯视图中该列的最大数字,因此,用的立方块数最多的情况是每个方框都用该列的最大数字,即如图①所示,此种情况共用小立方块17块.而搭建这样的几何体用方块数最少的情况是每列只要有一个最大的数字,其他方框内的数字可减少到最少的1,即如图②所示,这样的摆法只需小立方块11块.21.有两个面互相平行,其余各面都是平行四边形的几何体是棱柱吗?备特征③.22.如图所示,四边形ABCD绕边AD所在的直线EF旋转,其中AD∥BC,AD⊥CD.当点A选在射线DE上的不同位置时,形成的几何体大小、形状不同,比较其不同点.(测试时间:120分钟满分:150分)第Ⅰ卷(共60分)一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.下列说法正确的是()A.矩形的平行投影一定是矩形B.梯形的平行投影一定是梯形C.两条相交直线的平行投影可能平行D.若一条线段的平行投影是一条线段,则中点的平行投影仍为这条线段投影的中点答案:D2.在一个几何体的三视图中,正视图和俯视图如图,则相应的侧视图可以为()解析:此空间几何体是由一个半圆锥和一个三棱锥拼接而成的一个简单组合体,由其正视图和俯视图可知其相应的侧视图可为D.答案:D3.(2016山西大同一中高二月考)如果用表示1个立方体,用表示2个立方体叠加,用表示3个立方体叠加,那么如图中由7个立方体摆成的几何体,从正前方观察,可画出平面图形是()解析:由题意和图可知,左边和右边各为1个正方体,用表示;当中为3个正方体,用表示;上面为2个正方体,用表示.故选B.答案:B4.(2016山西太原五中高二月考)一个简单几何体的正视图、侧视图如图所示,则其俯视图不可能为①长方形;②直角三角形;③圆;④椭圆.其中正确的是()A.①B.②C.③D.④解析:其俯视图若为圆,则正视图中的长度与侧视图中的宽度应一样,由图中可知其正视图与侧视图的宽度不一样,因此其俯视图不可能是圆.故选C.答案:C5.(2016安徽蚌埠一中高二期中)已知正六棱柱的底面边长和侧棱长均为2 cm,其三视图中的俯视图如图所示,则其侧视图的面积是()A.4 cm2B.2 cm2C.8 cm2D.4 cm2答案:A6.关于几何体的三视图,下列说法正确的是( )A.正视图反映物体的长和宽B.俯视图反映物体的长和高C.侧视图反映物体的高和宽D.正视图反映物体的高和宽答案:C 由三视图的特点可知选项C正确.7.在原来的图形中,两条线段平行且相等,则在直观图中对应的两条线段( )A.平行且相等 B.平行不相等C.相等不平行 D.既不平行也不相等答案:A 由斜二测画法规则知平行性是不变的,长度的变化在平行时相同,故仍平行且相等.8.一个几何体的三视图如图L121所示,这个几何体可能是一个( )A.三棱锥B.底面不规则的四棱锥C.三棱柱D.底面为正方形的四棱锥答案:C 根据三视图,几何体为一个倒放的三棱柱.9.如图是水平放置的三角形的直观图,D′是△A′B′C′中B′C′边的中点,A′B′,A′D′,A′C′三条线段对应原图形中的线段AB,AD,AC,那么( )A.最短的是ACB.最短的是ABC.最短的是ADD.无法确定谁最短10.如图L123所示,已知四边形ABCD的直观图是一个边长为1的正方形,则原图形的周长为( )A.2 2 B.6 C.8 D.4 2+2图L123图L12411.图L124为水平放置的正方形ABCO,在直角坐标系中点B的坐标为(2,2),则用斜二测画法画出的正方形的直观图中,点B′到O′x′轴的距离为( )A.12B.22C. 1D.2答案:B 因为BC垂直于x轴,所以在直观图中B′C′的长度是1,且与O′x′轴的夹角是45°,所以B′到O′x′轴的距离是22.12.用斜二测画法画出的某平面图形的直观图如图L125所示,AB平行于y′轴,BC,AD平行于x′轴.已知四边形ABCD的面积为2 2 cm2,则原平面图形的面积为( )图L125A.4 cm2B.4 2 cm2C.8 cm2D.8 2 cm2答案:C 依题意可知∠BAD=45°,则原平面图形为直角梯形,且上下底边的长分别与BC,AD相等,高为梯形ABCD的高的2 2倍,所以原平面图形的面积为8 cm2.第Ⅱ卷(共90分)二、填空题(本大题共4小题,每题5分,满分20分,将答案填在答题纸上)13.太阳光线与地面成60°的角,照射在地面上的一个皮球上,皮球在地面上的投影长是10,则皮球的直径是.解析:直径d=10sin 60°=15.答案:1514.在棱长为1的正方体ABCD-A1B1C1D1中,对角线AC1在六个面上的正投影长度总和是.解析:正方体的对角线AC1在各个面上的正投影是正方体各个面上的对角线,因而其长度都为,所以所求总和为6.答案:615.一个几何体的正视图为一个三角形,则这个几何体可能是下列几何体中的.(填入所有可能的几何体前的编号)①三棱锥;②四棱锥;③三棱柱;④四棱柱;⑤圆锥;⑥圆柱.答案:①②③⑤16.(2012·杭州检测)如图Rt△O′A′B′是一平面图形的直观图,直角边O′B′=1,则这个平面图形的面积是________.解析:∵O′B′=1,∴O′A′=2,∴在Rt△OAB中,∠AOB=90°,OB=1,OA=22,∴S △AOB =12×1×22= 2.答案: 2三、解答题 (本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.) 17. 一个水平放置的平面图形的斜二测直观图是直角梯形ABCD ,如图所示,∠ABC =45°,AB =AD =1,DC ⊥BC ,原平面图形的面积为________.答案:2+2218.画出下列几何体的三视图.解:几何体的三视图如图所示:19.如图,该几何体是由一个长方体木块锯成的. (1)判断该几何体是否为棱柱;(2)画出它的三视图.解:(1)是棱柱.因为该几何体的前、后两个面互相平行,其余各面都是矩形,而且相邻矩形的公共边都互相平行.(2)该几何体的三视图如图.20.如图是某圆锥的三视图,求其底面积和母线长.21.已知正三棱锥VABC的正视图、侧视图和俯视图如图L1215所示.(1)画出该三棱锥的直观图;(2)求出侧视图的面积.图L1215解:(1)三棱锥的直观图如图所示. (2)根据三视图间的关系可得BC =2 3. 由俯视图可知三棱锥底面三角形的高为2 3×32=3. ∵三棱锥的高在底面上的投影是底面的中心,且其到点A 的距离为底面△ABC 高的23,∴底面中心到点A 的距离为23×3=2,∴侧视图中VA =42-22=2 3,∴S △VBC =12×2 3×2 3=6.22.如图所示,画出水平放置的四边形OBCD 的直观图.。
人教A版高中数学必修2《1.1 空间几何体的结构 习题1.1》_7
D A B CE F 1 A 1 E D 1 B 1C 1 F 空间几何体:如果我们只考虑物体占用空间部分的形状和大小,而不考虑其它因素,那么由这些物体抽象出来的空间图形,就叫做空间几何体。
探究点1 多面体和旋转体观察下面的图片,这些图片中的物体具有怎样的形状?日常生活中我多面体:一般地,我们把由若干个平面多边形围成的几何体叫做多面体。
注:1围成多面体的各个多边形叫做多面体的面2、相邻两面的公共边叫做多面体的棱。
3、棱与棱的公共点叫做多面体的顶点。
旋转体:我们把由一个平面图形绕它所在平面内的一条定直线旋转所形成的封闭几何体叫做旋转体。
注、这条定直线叫做旋转体的轴。
探究点2、棱柱的结构特征 96 7 8棱柱:有两个面相互平行,其余各面都是四边形,并且每相邻的两个四边形的公共边都互相平行,由这些面所围成的空间几何体叫做棱柱。
如图。
棱柱的表示:如何判断一个多面体是不是棱柱?练习:下面的几何体中,哪些是棱柱?棱柱的分类:探究点3、棱锥的结构特征定义:有一个面是多边形,其余各面都是有一个公共顶点的三角形,由这些面所围成的多面体叫做棱锥.棱锥的分类:探究点4 棱台的结构特征定义:用一个平行与棱锥底面的平面去截棱锥,底面与截面之间的部分,这样的多面体叫做棱台。
(如图)。
探究点5 圆柱的结构特征圆柱:以矩形的一边所在的直线为旋转轴,其余三边旋转形成的面所围成的旋转体叫做圆柱。
(如图)探究点6、 圆锥的结构特征定义:以矩形的一边所在直线为旋转轴,其余三边旋转形成的曲面所围成的旋转体叫做圆柱。
探究点7、球的结构特征球的定义:以半圆的直径所在直线为旋转轴,半圆面旋转一周形成的旋转体叫做球体,简称球。
小结:O。
高中数学必修2课后习题答案(精心整理)

1.剩下的几何体是棱柱,截去的几何体也是棱柱;它们分别是五棱柱和三棱柱。
2.左侧几何体的主要结构特征:圆柱和棱柱组成的简单组何体;中间几何体的主要结构特征:下部和上部都是一个圆柱截去一个圆柱组成的简单组何体;右侧几何体的主要结构特征:下部是一个圆柱体,上部是一个圆柱截去一个圆柱组成的简单组何体。
2. 提示:三角形任意两边之和大于第三边。
3. 设直角三角形的两条直角边长分别为a,b,斜边长为c,以直角边BC所在直线为轴,其余各边旋转一周形成的曲面围成的几何体是圆锥,其体积为 ,同理,以直角边AC所在直线为轴,其余各边旋转一周形成的曲面围成的几何体是圆锥,其体积为 ,以斜边AB所在直线为轴,其余各边旋转一周形成的曲面围成的几何体是两个圆锥组合而成的简单组合体。
10.它们的表面积分别为 cm2, cm2, cm2;体积分别为 cm3, cm3, cm3;三视图略。
B组
1. (1)略
(2)表面积为 (3117)cm2,体积为 (12728) cm3;
(3)略。
2.水不会从水槽流出。
3.如右图所示的正方体,其中 分别为下底面和上底面中心,以 所在直线为轴,在转动过程中 的轨迹即是纸篓面。
1.略。
2.(1)√ (2)× (3)× (4)√
3.A
4.略
5.略
习题 1.2
A组
1.略
2.(1)三棱柱 (2)圆台 (3)四棱柱 (4)四棱柱与圆柱组合而成的简单组合体
3~5.略
B组
1~2.略
3.此题答案不唯一,一种答案是由15个小正方体组合而成的简单组合体,如图
1.3 空间几何体的表面积与体积
1.2 空间几何体的三视图和直观图
练习(第 15 页)
高考复习 第8篇 第1讲 空间几何体及其表面积与体积知识点+例题+练习 含答案
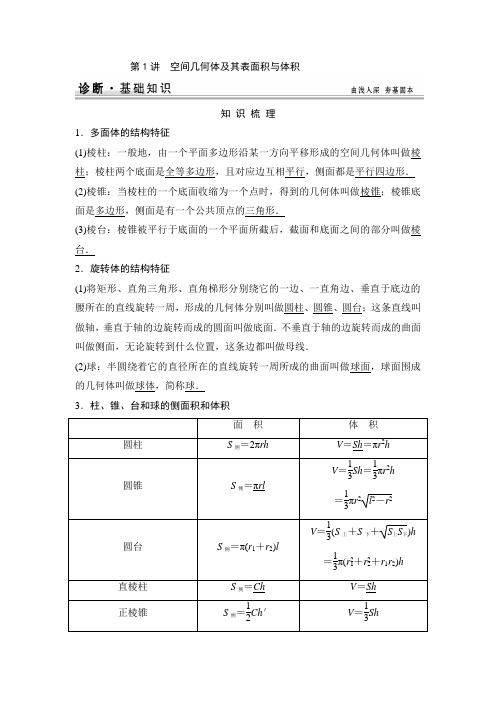
第1讲空间几何体及其表面积与体积知识梳理1.多面体的结构特征(1)棱柱:一般地,由一个平面多边形沿某一方向平移形成的空间几何体叫做棱柱;棱柱两个底面是全等多边形,且对应边互相平行,侧面都是平行四边形.(2)棱锥:当棱柱的一个底面收缩为一个点时,得到的几何体叫做棱锥;棱锥底面是多边形,侧面是有一个公共顶点的三角形.(3)棱台:棱锥被平行于底面的一个平面所截后,截面和底面之间的部分叫做棱台.2.旋转体的结构特征(1)将矩形、直角三角形、直角梯形分别绕它的一边、一直角边、垂直于底边的腰所在的直线旋转一周,形成的几何体分别叫做圆柱、圆锥、圆台;这条直线叫做轴,垂直于轴的边旋转而成的圆面叫做底面.不垂直于轴的边旋转而成的曲面叫做侧面,无论旋转到什么位置,这条边都叫做母线.(2)球:半圆绕着它的直径所在的直线旋转一周所成的曲面叫做球面,球面围成的几何体叫做球体,简称球.3.柱、锥、台和球的侧面积和体积面积体积圆柱S侧=2πrh V=Sh=πr2h圆锥S侧=πrlV=13Sh=13πr2h=13πr2l2-r2圆台S侧=π(r1+r2)lV=13(S上+S下+S上S下)h=13π(r21+r22+r1r2)h直棱柱S侧=Ch V=Sh正棱锥S侧=12Ch′V=13Sh续表4.(1)棱柱、棱锥、棱台的表面积就是各面面积之和.(2)圆柱、圆锥、圆台的侧面展开图分别是矩形、扇形、扇环形;它们的表面积等于侧面积与底面面积之和.辨析感悟1.柱体、锥体、台体与球的面积(1)圆柱的一个底面积为S,侧面展开图是一个正方形,那么这个圆柱的侧面积是2πS.(×)(2)设长方体的长、宽、高分别为2a,a,a,其顶点都在一个球面上,则该球的表面积为3πa2.(×)2.柱体、锥体、台体的体积(3)(教材练习改编)若一个球的体积为43π,则它的表面积为12π.(√)(4)在△ABC中,AB=2,BC=3,∠ABC=120°,使△ABC绕直线BC旋转一周所形成的几何体的体积为9π.(×)3.柱体、锥体、台体的展开与折叠(5)将圆心角为2π3,面积为3π的扇形作为圆锥的侧面,则圆锥的表面积等于4π.(√)(6)(2014·青州模拟改编)将边长为a的正方形ABCD沿对角线AC折起,使BD=a,则三棱锥D-ABC的体积为312a3.(×)[感悟·提升]两点注意一是求几何体的体积,要注意分割与补形.将不规则的几何体通过分割或补形将其转化为规则的几何体求解.二是几何体展开、折叠问题,要抓住前后两个图形间的联系,找出其中的量的关系.考点一空间几何体的结构特征【例1】给出下列四个命题:①有两个侧面是矩形的棱柱是直棱柱②侧面都是等腰三角形的棱锥是正棱锥③侧面都是矩形的直四棱柱是长方体④底面为正多边形,且有相邻两个侧面与底面垂直的棱柱是正棱柱其中不正确的命题为________.解析对于①,平行六面体的两个相对侧面也可能是矩形,故①错;对于②,对等腰三角形的腰是否为侧棱未作说明(如图),故②错;对于③,若底面不是矩形,则③错;④正确.答案①②③规律方法解决该类题目需准确理解几何体的定义,要真正把握几何体的结构特征,并且学会通过举反例对概念进行辨析,即要说明一个命题是错误的,设法举出一个反例即可.【训练1】设有以下四个命题:①底面是平行四边形的四棱柱是平行六面体;②底面是矩形的平行六面体是长方体;③直四棱柱是直平行六面体;④棱台的相对侧棱延长后必交于一点.其中真命题的序号是________.解析命题①符合平行六面体的定义,故命题①是正确的.底面是矩形的平行六面体的侧棱可能与底面不垂直,故命题②是错误的.因为直四棱柱的底面不一定是平行四边形,故命题③是错误的.命题④由棱台的定义知是正确的. 答案 ①④考点二 几何体的表面积与体积【例2】 如图所示,四棱锥P -ABCD 的底面ABCD 是半径为R 的圆的内接四边形,其中BD 是圆的直径,∠ABD =60°,∠BDC =45°, △ADP ∽△BAD . (1)求线段PD 的长;(2)若PC =11R ,求三棱锥P -ABC 的体积. 解 (1)∵BD 是圆的直径,∴∠BAD =90°, 又∵△ADP ∽△BAD ,∴AD BA =DP AD , ∠PDA =∠BAD =90°, DP =AD 2BA =(BD sin 60°)2BD sin 30°=4R 2×342R ×12=3R . ∴DP 的长为3R .(2)在Rt △BCD 中,BC =CD =BD cos 45°=2R , ∵PD 2+CD 2=9R 2+2R 2=11R 2=PC 2,∴PD ⊥CD , 又∠PDA =90°,AD ∩CD =D ,∴PD ⊥底面ABCD , 则S △ABC =12AB ·BC sin(60°+45°) =12R ·2R ⎝ ⎛⎭⎪⎫32×22+12×22=3+14R 2.所以三棱锥P -ABC 的体积为V P -ABC =13·S △ABC ·PD =13·3+14R 2·3R =3+14R 3.规律方法 求几何体的体积问题,可以多角度、全方位地考虑问题,常采用的方法有“换底法”、“分割法”、“补体法”等,尤其是“等积转化”的数学思想方法应高度重视.【训练2】 (2014·苏州模拟)一个正三棱台的上、下底面边长分别是3 cm 和6 cm ,高是32 cm.(1)求三棱台的斜高;(2)求三棱台的侧面积和表面积. 解(1)设O 1、O 分别为正三棱台ABC -A 1B 1C 1的上、下底面正三角形的中心,如图所示,则O 1O =32,过O 1作O 1D 1⊥B 1C 1,OD ⊥BC ,则D 1D 为三棱台的斜高;过D 1作D 1E ⊥AD 于E ,则D 1E =O 1O =32, 因O 1D 1=36×3=32,OD =36×6=3,则DE =OD -O 1D 1=3-32=32.在Rt △D 1DE 中, D 1D =D 1E 2+ED 2=⎝ ⎛⎭⎪⎫322+⎝ ⎛⎭⎪⎫322=3(cm). (2)设c 、c ′分别为上、下底的周长,h ′为斜高, S 侧=12(c +c ′)h ′=12(3×3+3×6)×3=2732(cm 2),S 表=S 侧+S 上+S 下=2732+34×32+34×62=9934(cm 2).故三棱台斜高为 3 cm ,侧面积为2732 cm 2,表面积为9934 cm 2.考点三 球与空间几何体的接、切问题【例3】 (1)(2013·新课标全国Ⅱ卷)已知正四棱锥O -ABCD 的体积为322,底面边长为3,则以O 为球心,OA 为半径的球的表面积为________.(2)(2013·辽宁卷改编)已知直三棱柱ABC -A 1B 1C 1的6个顶点都在球O 的球面上,若AB =3,AC =4,AB ⊥AC ,AA 1=12,则球O 的半径为________.审题路线 (1)根据正四棱锥的体积求高⇒求底面正方形的对角线长⇒由勾股定理求OA ⇒由球的表面积公式求解.(2)BC 为过底面ABC 的截面圆的直径⇒取BC 中点D ,则球心在BC 的垂直平分线上,再由对称性求解. 解析 (1)设正四棱锥的高为h , 则13×(3)2×h =322,解得h =322. 又底面正方形的对角线长为2×3= 6. 所以OA =⎝ ⎛⎭⎪⎫3222+⎝ ⎛⎭⎪⎫622= 6. 故球的表面积为S 球=4π×(6)2=24π.(2)因为在直三棱柱中AB =3,AC =4,AA 1=12,AB ⊥AC ,所以BC =5,且BC 为过底面ABC 的截面圆的直径,取BC 中点D ,则OD ⊥底面ABC ,则O 在侧面BCC 1B 1内,矩形BCC 1B 1的对角线长即为球的直径,所以2r =122+52=13,即r =132.答案 (1)24π (2)132规律方法 解决球与其他几何体的切、接问题,关键在于仔细观察、分析,弄清相关元素的关系和数量关系,选准最佳角度作出截面(要使这个截面尽可能多地包含球、几何体的各种元素以及体现这些元素之间的关系),达到空间问题平面化的目的.【训练3】(2012·辽宁卷)已知点P,A,B,C,D是球O表面上的点,P A⊥平面ABCD,四边形ABCD是边长为23的正方形.若P A=26,则△OAB的面积为________.解析根据球的内接四棱锥的性质求解.如图所示,线段PC就是球的直径,设球的半径为R,因为AB=BC=23,所以AC=2 6.又P A=26,所以PC2=P A2+AC2=24+24=48,所以PC=43,所以OA=OB=23,所以△AOB是正三角形,所以S=12×23×23×32=3 3.答案3 3考点四几何体的展开与折叠问题【例4】(1)如图所示,在边长为4的正方形纸片ABCD中,AC与BD相交于O,剪去△AOB,将剩余部分沿OC,OD折叠,使OA,OB重合,则以A,B,C,D,O为顶点的四面体的体积为________.(2)如图所示,在直三棱柱ABC-A1B1C1中,△ABC为直角三角形,∠ACB=90°,AC=4,BC=CC1=3.P是BC1上一动点,沿棱柱表面使CP+P A1最小,则最小值为________.解析 (1)折叠后的四面体如图所示.OA ,OC ,OD 两两相互垂直,且OA =OC =OD =22,体积V =13 S △OCD ·OA =13×12×(22)3=823.(2)由题意知,A 1P 在几何体内部,把面BB 1C 1C 沿BB 1展开与面AA 1B 1B 在一个平面上,如图所示,连接A 1C 即可. 则A 1、P 、C 三点共线时,CP +P A 1最小, ∵∠ACB =90°,AC =4,BC =C 1C =3,∴A 1B 1=AB =42+32=5,∴A 1C 1=5+3=8,∴A 1C =82+32=73.故CP +P A 1的最小值为73.答案 (1)823 (2)73规律方法 (1)有关折叠问题,一定要分清折叠前后两图形(折前的平面图形和折叠后的空间图形)各元素间的位置和数量关系,哪些变,哪些不变.(2)研究几何体表面上两点的最短距离问题,常选择恰当的母线或棱展开,转化为平面上两点间的最短距离问题.【训练4】如图为一几何体的展开图,其中ABCD是边长为6的正方形,SD=PD=6,CR=SC,AQ=AP,点S,D,A,Q共线,点P,D,C,R共线,沿图中虚线将它们折叠起来,使P,Q,R,S四点重合,则需要________个这样的几何体,可以拼成一个棱长为6的正方体.解析由题意知,将该展开图沿虚线折叠起来以后,得到一个四棱锥P-ABCD(如图所示),其中PD⊥平面ABCD,因此该四棱锥的体积V=13×6×6×6=72,而棱长为6=3个这样的几何体,才能拼成的正方体的体积V=6×6×6=216,故需要21672一个棱长为6的正方体.答案 31.对于基本概念和能用公式直接求出棱柱、棱锥、棱台与球的表面积的问题,要结合它们的结构特点与平面几何知识来解决.2.求三棱锥的体积时要注意三棱锥的每个面都可以作为底面,例如三棱锥的三条侧棱两两垂直,我们就选择其中的一个侧面作为底面,另一条侧棱作为高来求体积.3.与球有关的组合体问题,一种是内切,一种是外接.解题时要认真分析图形,明确切点和接点的位置,确定有关元素间的数量关系,并作出合适的截面图,如球内切于正方体,切点为正方体各个面的中心,正方体的棱长等于球的直径;球外接于正方体,正方体的顶点均在球面上,正方体的体对角线长等于球的直径.方法优化5——特殊点在求解几何体的体积中的应用【典例】 (2012·山东卷)如图,正方体ABCD -A 1B 1C 1D 1的棱长为1,E ,F 分别为线段AA 1,B 1C 上的点,则三棱锥D 1-EDF 的体积为________.[一般解法] 三棱锥D 1-EDF 的体积即为三棱锥F -DD 1E 的体积.因为E ,F 分别为AA 1,B 1C 上的点,所以在正方体ABCD -A 1B 1C 1D 1中△EDD 1的面积为定值12,F 到平面AA 1D 1D 的距离为定值1,所以VF -DD 1E =13×12×1=16. [优美解法] E 点移到A 点,F 点移到C 点,则VD 1-EDF =VD 1-ADC =13×12×1×1×1=16. [答案] 16[反思感悟] (1)一般解法利用了转化思想,把三棱锥D 1-EDF 的体积转化为三棱锥F -DD 1E 的体积,但这种解法还是难度稍大,不如采用特殊点的解法易理解、也简单易求.(2)在求几何体体积时还经常用到等积法、割补法. 【自主体验】 如图,在三棱柱ABC-A1B1C1中,侧棱AA1与侧面BCC1B1的距离为2,侧面BCC1B1的面积为4,此三棱柱ABC-A1B1C1的体积为________.解析补形法将三棱柱补成四棱柱,如图所示.记A1到平面BCC1B1的距离为d,则d=2.则V三棱柱=12V四棱柱=12S四边形BCC1B1·d=12×4×2=4.答案 4基础巩固题组(建议用时:40分钟)一、填空题1.以下命题:①以直角三角形的一边为轴旋转一周所得的旋转体是圆锥;②以直角梯形的一腰为轴旋转一周所得的旋转体是圆台;③圆柱、圆锥、圆台的底面都是圆;④一个平面截圆锥,得到一个圆锥和一个圆台.其中正确命题的个数是________.解析命题①错,因为这条边若是直角三角形的斜边,则得不到圆锥.命题②题,因这条腰必须是垂直于两底的腰.命题③对.命题④错,必须用平行于圆锥底面的平面截圆锥才行.答案 12.在正方体上任意选择4个顶点,它们可能是如下各种几何形体的四个顶点,这些几何形体是________(写出所有正确结论的编号).①矩形;②不是矩形的平行四边形;③有三个面为等腰直角三角形,有一个面为等边三角形的四面体;④每个面都是等边三角形的四面体;⑤每个面都是直角三角形的四面体.解析①显然可能;②不可能;③取一个顶点处的三条棱,连接各棱端点构成的四面体;④取正方体中对面上的两条异面对角线的四个端点构成的几何体;⑤正方体ABCD-A1B1C1D1中,三棱锥D1-DBC满足条件.答案①③④⑤3.在三棱锥S-ABC中,面SAB,SBC,SAC都是以S为直角顶点的等腰直角三角形,且AB=BC=CA=2,则三棱锥S-ABC的表面积是________.解析设侧棱长为a,则2a=2,a=2,侧面积为3×12×a2=3,底面积为34×22=3,表面积为3+ 3.答案3+ 34.若圆锥的侧面积为2π,底面面积为π,则该圆锥的体积为________.解析 设圆锥的底面圆半径为r ,高为h ,母线长为l ,则⎩⎪⎨⎪⎧ πrl =2π,πr 2=π,∴⎩⎪⎨⎪⎧r =1,l =2.∴h =l 2-r 2=22-12= 3.∴圆锥的体积V =13π·12·3=33π. 答案 33π5.(2012·新课标全国卷改编)平面α截球O 的球面所得圆的半径为1,球心O 到平面α的距离为2,则此球的体积为________. 解析如图,设截面圆的圆心为O ′,M 为截面圆上任一点,则OO ′=2,O ′M =1,∴OM =(2)2+1=3,即球的半径为3,∴V =43π(3)3=43π.答案 43π 6.如图所示,已知一个多面体的平面展开图由一个边长为1的正方形和4个边长为1的正三角形组成,则该多面体的体积是________.解析 由题知该多面体为正四棱锥,底面边长为1,侧棱长为1,斜高为32,连接顶点和底面中心即为高,可求得高为22,所以体积V =13×1×1×22=26. 答案 267.(2013·天津卷)已知一个正方体的所有顶点在一个球面上,若球的体积为9π2,则正方体的棱长为________.解析 设正方体的棱长为a ,外接球的半径为R ,由题意知43πR 3=9π2,∴R 3=278,而R =32.由于3a 2=4R 2,∴a 2=43R 2=43×⎝ ⎛⎭⎪⎫322=3,∴a = 3.答案 38.如图,在多面体ABCDEF 中,已知ABCD 是边长为1的正方形,且△ADE ,△BCF 均为正三角形,EF ∥AB ,EF =2,则该多面体的体积为________.解析 如图,分别过点A ,B 作EF 的垂线,垂足分别为G ,H ,连接DG ,CH ,容易求得EG =HF =12,AG =GD =BH =HC =32,∴S △AGD =S △BHC =12×22×1=24,∴V =V E -ADG +V F -BHC +V AGD -BHC =2V E -ADG +V AGD -BHC =13×24×12×2+24×1=23. 答案 23 二、解答题 9.如图,在三棱锥P -ABC 中,AC =BC =2,∠ACB =90°,AP =BP =AB ,PC ⊥AC .(1)求证:PC ⊥AB ;(2)求点C 到平面APB 的距离. (1)证明 取AB 中点D ,连接PD ,CD .因为AP =BP ,所以PD ⊥AB , 因为AC =BC ,所以CD ⊥AB .因为PD ∩CD =D ,所以AB ⊥平面PCD .因为PC ⊂平面PCD ,所以PC ⊥AB . (2)解 设C 到平面APB 的距离为h ,则由题意,得AP =PB =AB =AC 2+BC 2=22, 所以PC =AP 2-AC 2=2.因为CD =12AB =2,PD =32PB =6, 所以PC 2+CD 2=PD 2,所以PC ⊥CD .由(1)得AB ⊥平面PCD ,于是由V C -APB =V A -PDC +V B -PDC , 得13·h ·S △APB =13AB ·S △PDC ,所以h =AB ·S △PDCS △APB=22×12×2×234×(22)2=233.故点C 到平面APB 的距离为233.10.有一个倒圆锥形容器,它的轴截面是一个正三角形,在容器内放一个半径为r 的铁球,并注入水,使水面与球正好相切,然后将球取出,求这时容器中水的深度.解 如图所示,作出轴截面,因轴截面是正三角形,根据切线性质知当球在容器内时,水的深度为3r ,水面半径BC 的长为3r ,则容器内水的体积为 V =V 圆锥-V 球=13π(3r )2·3r - 43πr 3=53πr 3,将球取出后,设容器中水的深度为h , 则水面圆的半径为33h ,从而容器内水的体积为 V ′=13π⎝ ⎛⎭⎪⎫33h 2h =19πh 3,由V =V ′,得h =315r .能力提升题组 (建议用时:25分钟)一、填空题1.已知球的直径SC =4,A ,B 是该球球面上的两点,AB =3,∠ASC =∠BSC =30°,则棱锥S -ABC 的体积为________.解析 由题意知,如图所示,在棱锥S -ABC 中,△SAC ,△SBC 都是有一个角为30°的直角三角形,其中AB =3,SC =4,所以SA =SB =23,AC =BC =2,作BD ⊥SC 于D 点,连接AD ,易证SC ⊥平面ABD ,因此V S -ABC =13×34×(3)2×4= 3. 答案 32.(2014·南京模拟)如图,在直三棱柱ABC -A 1B 1C 1中,AB =1,BC =2,AC =5,AA 1=3,M 为线段B 1B 上的一动点,则当AM +MC 1最小时,△AMC 1的面积为________.解析 如图,当AM +MC 1最小时,BM =1,所以AM 2=2,C 1M 2=8,AC 21=14,于是由余弦定理,得cos ∠AMC 1=AM 2+MC 21-AC 212AM ·MC 1=-12,所以sin ∠AMC 1=32,S △AMC 1=12×2×22×32= 3. 答案 33.如图,已知正三棱柱ABC -A 1B 1C 1的底面边长为2 cm 、高为5 cm ,则一质点自点A 出发,沿着三棱柱的侧面绕行两周到达点A 1的最短路线的长为________cm. 解析 根据题意,利用分割法将原三棱柱分割为两个相同的三棱柱,然后将其展开为如图所示的实线部分,则可知所求最短路线的长为52+122=13 cm.答案 13 二、解答题4.如图1,在直角梯形ABCD 中,∠ADC =90°,CD ∥AB ,AB =4,AD =CD =2,将△ADC 沿AC 折起,使平面ADC ⊥平面ABC ,得到几何体D -ABC ,如图2所示.(1)求证:BC ⊥平面ACD ; (2)求几何体D -ABC 的体积.(1)证明 在图中,可得AC =BC =22, 从而AC 2+BC 2=AB 2, 故AC ⊥BC ,又平面ADC ⊥平面ABC , 平面ADC ∩平面ABC =AC , BC ⊂平面ABC , ∴BC ⊥平面ACD .(2)解 由(1)可知,BC 为三棱锥B -ACD 的高,BC =22,S △ACD =2,∴V B -ACD =13S △ACD ·BC =13×2×22=423,由等体积性可知,几何体D -ABC 的体积为423.。
空间几何体的结构

3. 底面是正多边形的直棱柱叫做正棱柱.
观察下面的几何体,哪些是棱柱?
练习:1.观察长方体,共有多少对平行平面? 能做为棱柱底面的有多少对?
D
C
A
D
B
C
B
A
探究4:
观察右边的棱柱,共有多少 对平行平面?能作为棱柱的 底面的有几对? 答:四对平行平面;只有一 对可以作为棱柱的底面.
棱柱的任何两个平行平面都可以作为棱柱 的底面吗? 答:不是.
B、由简单几何体截去或挖 去一部分而成
练一练:将一个直角梯形绕其较短的底所在
的直线旋转一周得到一个几何体,关于该几何 体的以下描绘中,正确的是( D )
A、是一个圆台
B、是一个圆柱
C、是一个圆柱和一个圆锥的简单组合体 D、是一个圆柱被挖去一个圆锥后所剩的几何体
练习:见P8页A组第3题,第4题,第5题.
练习:下列几何体是不是棱台,为什么?
(1)
(2)
想一想,怎样给多面体分类呢? 答:可以按面数分类,多面体有几个面就 称为几面体。如:三棱锥是四面体,四棱柱 是六面体. 练习:见P8页A组第1题的(1),(2),(3)小题. 思考:棱柱、棱锥和棱台都是多面体,当 底面发生变化时,它们能否互相转化?
E’
答:都是棱柱.
棱锥
棱锥的有关概念
顶点
棱锥中,这个多边形面 叫做棱锥的底面或底,有 公共顶点的各个三角形 面叫做棱锥的侧面,各侧 面的公共顶点叫做棱锥 的顶点,相邻侧面的公共 边叫做棱锥的侧棱。 棱锥的表示
S 侧面 侧棱
D
C 底面
B
A
用表示顶点和底面各顶点的字母表示,如图所 示的棱锥表示为:“棱锥S—ABCD”
D A B
1.1.2空间几何体的结构限时
空间几何体的结构1.在棱柱中()A.只有两个面平行B.所有的棱都平行C.所有的面都是平行四边形D.两底面平行,且各侧棱也互相平行2.将图1所示的三角形线直线l旋转一周,可以得到如图2所示的几何体的是哪一个三角形()3.如图一个封闭的立方体,它6个表面各标出1、2、3、4、5、6这6个数字,现放成下面3个不同的位置,则数字l、2、3对面的数字是()A.4、5、6 B.6、4、5 C.5、4、6 D.5、6、44.如图,能推断这个几何体可能是三棱台的是()A.A1B1=2,AB=3,B1C1=3,BC=4B.A1B l=1,AB=2,B l C l=1.5,BC=3,A1C1=2,AC=3C.A l B l=1,AB=2,B1C l=1.5,BC=3,A l C l=2,AC=4D.AB=A1B1,BC=B1C1,CA=C1A15.有下列命题(1)在圆柱的上、下底面的圆周上各取一点,则这两点的连线是圆柱的母线;(2)圆锥顶点与底面圆周上任意一点的连线是圆锥的母线;(3)在圆台上、下底面圆周上各取一点,则这两点的连线是圆台的母线;(4)圆柱的任意两条母线所在的直线是互相平行的.其中正确的是()A.(1)(2)B.(2)(3)C.(1)(3)D.(2)(4)6.图1是由图2中的哪个平面图旋转而得到的()二、填空题7如图,长方体ABCD—A1B l C l D1中,AD=3,AA l=4,AB=5,则从A点沿表面到C l的最短距离为______.8在三棱锥S—ABC中,SA=SB=SC=1,∠ASB=∠ASC=∠BSC=30°,如图,一只蚂蚁从点A出发沿三棱锥的表面爬行一周后又回到A点,则蚂蚁爬过的最短路程为_____.9高为H的水瓶中注水,注满为止,如果注水量V与水深h的函数关系的图象如图所示,那么水瓶的形状是______.10图,这是一个正方体的表面展开图,若把它再折回成正方体后,有下列命题:①点H与点C重合;②点D与点M与点R重合;③点B与点Q重合;④点A与点S重合.其中正确命题的序号是____.(注:把你认为正确的命题的序号都填上)。
专题8.1 空间几何体的结构特征及表面积体积(练习)【必考点专练】2023届高考数学二轮复习专题

专专8.1空间几何体的结构特征及表面积体积一、单选题1. 给出下列命题中正确的是( )A. 棱柱被平面分成的两部分可以都是棱柱B. 底面是矩形的平行六面体是长方体C. 棱柱的底面一定是平行四边形D. 棱锥的底面一定是三角形2. 已知A ,B ,C 为球O 的球面上的三个点,1O 为ABC 的外接圆.若1O 的面积为4π,1AB BC AC OO ===,则球O 的表面积为( )A. 64πB. 48πC. 36πD. 32π3. 设A ,B ,C ,D 是同一个半径为4的球的球面上四点,ABC 为等边三角形且其面积为D ABC -体积的最大值为( )A. B. C. D.4. 已知圆锥的顶点为S ,母线SA ,SB 所成角的余弦值为78,SA 与圆锥底面所成角为45︒,若SAB 的面积为,则该圆锥的侧面积为(( )A. B. C. D.5. 埃及胡夫金字塔是古代世界建筑奇迹之一,它的形状可视为一个正四棱锥,以该四棱锥的高为边长的正方形面积等于该四棱锥一个侧面三角形的面积,则其侧面三角形底边上的高与底面正方形的边长的比值为( )A.14B.12C.14+ D.12+ 6. 已知边长为2的等边三角形ABC ,D 为BC 的中点,以AD 为折痕,将ABC 折成直二面角B AD C --,则过A ,B ,C ,D 四点的球的表面积为( )A. 3πB. 4πC. 5πD. 6π7. 已知三棱锥P ABC -中,PA ,PB ,PC 两两垂直,且长度相等.若点P ,A ,B ,C都在半径为1的球面上,则球心到平面ABC 的距离为( )A.36B.12C.13D.328. 沙漏是古代的一种计时装置,它由两个形状完全相同的容器和一个狭窄的连接管道组成,开始时细沙全部在上部容器中,细沙通过连接管道全部流到下部容器所需要的时间称为该沙漏的一个沙时.如图,某沙漏由上下两个圆锥组成,圆锥的底面直径和高均为8cm ,细沙全部在上部,其高度为圆锥高度的2(3细管长度忽略不计).假设该沙漏每秒钟漏下30.02cm 的沙,且细沙全部漏入下部后,恰好堆成一个盖住沙漏底部的圆锥沙堆.以下结论正确的是( )A. 沙漏的侧面积是2165cm πB. 沙漏中的细沙体积为31024cm πC. 细沙全部漏入下部后此锥形沙堆的高度约为1.2cmD. 该沙漏的一个沙时大约是1985秒( 3.14)π≈9. 如图所示,在直三棱柱111ABC A B C -中,11AA =,3AB BC ==,1cos 3ABC ∠=, P 是1A B 上的一动点,则1AP PC +的最小值为( )A. 5B. 7C. 13+D. 310. 在棱长为1的正方体1111ABCD A B C D -中,E ,F ,G ,H 分别为11A B ,11C D ,AB ,CD 的中点,点P 从G 出发,沿折线GBCH 匀速运动,点Q 从H 出发,沿折线HDAG 匀速运动,且点P 与点Q 运动的速度相等,记以E ,F ,P , Q 四点为顶点的三棱锥的体积为V ,点P 运动的路程为x ,在02x 时,V 与x 满足的函数解析式的图象应为( )A.B.C.D.二、多选题11. 将边长为2的正方形沿对角线BD 折成直二面角BD A C --,如图所示,点E ,F 分别为线段BC,AD 的中点,则( )A. EF BC ⊥B. 四面体BCD A -的表面积为4+23C. 四面体BCD A -的外接球的体积为823π D. 过EF 且与BD 平行的平面截四面体BCD A -所得截面的面积为212. 如图,在棱长为1的正方体1111ABCD A B C D -中,P 为线段11B D 上一动点(包括端点),则以下结论正确的有( )A. 三棱锥1P A BD -的体积为定值13B. 过点P 平行于平面1A BD 的平面被正方体1111ABCD A B C D -截得的多边形的面积为32C. 直线1PA 与平面1A BD 所成角的正弦值的范围为D. 当点P 与1B 重合时,三棱锥1P A BD -的外接球的体积为32π13. 如图,在三棱锥P ABC -中,D 、E 、F 分别为棱PC 、AC 、AB 的中点,PA ⊥平面ABC ,90ABC ∠=︒,6,8,AB PA BC ===则( )A. 三棱锥D BEF -的体积为6B. 直线PB 与直线DF 垂直C. 平面DEF 截三棱锥P ABC -所得的截面面积为12D. 点P 与点A 到平面BDE 的距离相等三、填空题14. 正方体1111ABCD A B C D -的棱长为2,则平面11AC D 与平面ABCD 所成角为__________;设P 为1CC 的中点,过点A ,P ,1D 的平面截该正方体所得截面的面积为__________.15. 中国有悠久的金石文化,印信是金石文化的代表之一.印信的形状多为长方体、正方体或圆柱体,但南北朝时期的官员独孤信的印信形状是“半正多面体”(图1).半正多面体是由两种或两种以上的正多边形围成的多面体.半正多面体体现了数学的对称美.图2是一个棱数为48的半正多面体,它的所有顶点都在同一个正方体的表面上,且此正方体的棱长为1.则该半正多面体共有__________个面,其棱长为__________.16. 学生到工厂劳动实践,利用3D 打印技术制作模型,如图,该模型为长方体1111ABCD A B C D -挖去四棱锥O EFGH -后所得的几何体,其中O 为长方体的中心,,,,E F G H 分别为所在棱的中点,==6AB BC cm ,1=4AA cm ,3D 打印所用的材料密度为30.9/g cm ,不考虑打印损耗,制作该模型所需原料的质量为__________.g17. 如图,在平面四边形PQRS 中,2QPS π∠=,2QSR π∠=, 2.PQ PS SR ===将该平面图形沿线QS 折成一个直二面角P QS R --,三棱锥P QRS -的体积为__________ ,三棱锥P QRS -的外接球的体积为__________ .18. 如图,在一个底面边长为2,侧棱长为10的正四棱锥-P ABCD 中,大球1O 内切于该四棱锥,小球2O 与大球1O 及四棱锥的四个侧面相切,则小球2O 的体积为__________.四、解答题19. 如图,四边形ABCD 为菱形,G 为AC 与BD 的交点,BE ⊥平面.ABCD(1)证明:平面AEC ⊥平面BED ;(2)若120ABC ︒∠=,AE EC ⊥,三棱锥E ACD -,求该三棱锥的侧面积.答案和解析1.【答案】A解:平行于棱柱底面的平面可以把棱柱分成两个棱柱,故A 正确; 三棱柱的底面是三角形,故C 错误;底面是矩形的平行六面体的侧面不一定是矩形,故它也不一定是长方体,故B 错误; 四棱锥的底面是四边形,故D 错误. 故选:.A2.【答案】A解:由题意可知图形如图:1O 的面积为4π,可得12O A =,由题知ABC 是等边三角形,根据等边三角形性质, 得13sin 602AO AB ︒=,13322AO AB =, 123AB BC AC OO ∴====,外接球的半径为:22114R AO OO =+=,球O 的表面积:24464.ππ⨯⨯=故选:.A3.【答案】B解:ABC 为等边三角形且面积为2AB =6AB =, 设球心为O ,三角形ABC 的外心为O ',显然D 为O O '的延长线与球的交点时,三棱锥的体积最大.如图:2362332O C '=⨯⨯=,224(23)2OO '=-=,则三棱锥D ABC -高的最大值为:6, 则三棱锥D ABC -体积的最大值为:2136618 3.34⨯⨯⨯= 故选:.B4.【答案】A解:因为2211sin 22SAB Sl ASB l =∠==,所以l =l =,所以r =,则12.2S rl rl πππ=⨯==⋅=侧 故选:.A5.【答案】C解:设正四棱锥的高为h ,底面边长为a ,侧面三角形底边上的高为h ',则依题意有:因此有222151()4()2()10(224a h h h h ah a a a '''+'-='⇒--=⇒=负值舍去); 故选:.C6.【答案】C解:如图所示:边长为2的等边三角形ABC ,D 为BC 的中点,以AD 为折痕, 将ABC 折成直二面角B AD C --,则AD ,BD ,DC 两两垂直, 将四面体ABCD 扩展为以D 为顶点的长方体,其中 3AD =,1BD CD ==,设过A ,B ,C ,D 四点的球的半径为r , 故:2(2)1135r =++=, 所以:254r =, 所以254454S r πππ==⋅=, 故过A ,B ,C ,D 四点的球的表面积为5.π 故选:.C7.【答案】C解:三棱锥P ABC -中,PA ,PB ,PC 两两垂直,且长度相等,∴此三棱锥的外接球即以PA ,PB ,PC 为三边的正方体的外接球O ,且体对角线为球O 的直径,球O 的半径为1,设正方体的边长为a 2=,解得a =,∴PA PB PC ===, 球心到截面ABC 的距离即正方体中心到截面ABC 的距离, 设P 到截面ABC 的距离为h ,则正三棱锥P ABC -的体积13ABCV Sh =⨯13PABS PC =⨯31132=⨯⨯,由勾股定理易知ABC 的正三角形,2ABCS==,则3111332h =⨯⨯,23h ∴=, 由正方体的几何形状可知,直线PO 经过三菱锥P ABC -以P 为顶点的高线, 所以球心到平面ABC 的距离为113h -=, ∴球心(即正方体中心)O 到截面ABC 的距离为1.3故选:.C8.【答案】D解:对于A ,沙漏的侧面积为,故A 错误;对于B ,设细沙在上部时,细沙的底面半径为r ,则28433r cm =⨯=, 所以细沙的体积为23118161024()33381V cm ππ=⨯⨯=,故B 错误; 对于C ,设细沙流入下部后的高度为1h ,根据细沙体积不变可知:,解得1642.427h cm =≈,故C 错误; 对于D ,该沙漏的一个沙时为:10241024 3.140.025*********π⨯÷=⨯≈秒,故D 正确. 故选:.D9.【答案】B解:连接1BC ,得11A BC ,以1A B 所在直线为轴,将11A BC 所在平面旋转到平面11ABB A ,设点1C 的新位置为C ',连接AC ',则AC '即为1AP PC +的最小值, 由题意知11AA =,3AB BC ==,1cos 3ABC ∠=,得112A B BC AC ='='=,1160AA B BAC ∠=∠'=︒, 所以在1AAC '中,114212()7.2AC '=+-⨯⨯⨯-= 故选.B10.【答案】C解:(1)当102x时,点P 与点Q 运动的速度相等根据下图得出:面OEF 把几何体PEFQ 分割为相等的几何体,111122OEFS=⨯⨯=,P 到面OEF 的距离为x , 112223263PEFQ P OEF x xV V x -==⨯⨯=⋅=四面体三棱锥,(2)当1322x <<时,P 在BC 上,Q 在AD 上, P 到平面OEF 的距离为12,111122OEFS =⨯⨯=, 1111223226PEFQ P OEF V V -==⨯⨯⨯==四面体三棱锥定值.(3)当322x 时,111122OEFS =⨯⨯=,P 到面OEF 的距离为2x -, 112122(2)3233PEFQ P OEF V V x x -==⨯⨯⨯-=-四面体三棱锥,,故选:.C11.【答案】BCD解:选项A ,如图,取BD 中点为原点,建立空间直角坐标系,坐标如下:(0,-2,0)B ,(2,0,0)C ,22(,-,0)22E ,22(0,,)22F ,(0,0,2)A ,22EF=(,2,)22∴-,BC=(2,2,0),22EF BC=-2+22+0=1022∴⋅⨯⨯⨯≠,EF ∴与BC 不垂直,故A 错误;选项B ,22|AC |+=2+2=2AO CO =,∴四面体的表面积131131=+++=22+22+22+22=23+4222222ABC ABD ACD BCD S S S S S ∆∆∆∆⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯,故B 正确;选项C ,BCD ∆外接圆半径=2r ,锥高=2h ,外接球半径R 满足222()+=R h r R -,解得=2R ,∴四面体外接球体积为3482=33R ππ⋅⋅,故C 正确;选项D ,如图,分别取AB ,CD 中点M ,N ,MF//BD ,EN//BD ,1MF=EN=BD=22,∴四边形ENFM 为平行四边形,EN//BD ,EN ⊂平面ENFM ,BD/⊂平面ENFM ,BD//∴平面ENFM ,由选项A 可知22(,,0)22N ,22(0,-,)22M ,EN=(0,2,0),22EM=(,0,)22-,EN EM=0∴⋅,EN EM ∴⊥,ENFM ∴是矩形,面积=EN ME=21=2S ⨯⨯,故D 正确.12.【答案】BCD解:A 选项:111211213226P A BD A PBD V V --==⨯⨯⨯⨯=,A 不正确; B 选项:此平面为平面11B D C ,故三角形11B D C 的面积为233(2)42⨯=,B 选项正确; C 选项:设点P 到平面1A BD 的距离为h , 由1116P A BD A PBD V V --==知,点P 到平面1A BD 的距离为33h =,当点P 在线段11B D 上运动时,1max ||1(PA P =为端点时),1min 2||2PA =, 设直线1PA 与平面1A BD 所成角为θ,,则,C 正确;D 选项:11190B BD B A D ︒∠=∠=,所以三棱锥1P A BD -的外接球的球心为1B D 的中点, 故外接球半径为32,三棱锥1P A BD -的外接球的体积为32π,D 正确. 故选.BCD13.【答案】ACD解:D ,E 分别为棱PC ,AC 的中点,则//DE PA , 又PA ⊥平面ABC ,则DE ⊥平面ABC ,即DE ⊥平面FBE , 90ABC ︒∠=,6AB PA ==,8BC =,所以13462EFB S ∆=⨯⨯=,132DE PA ==,所以三棱锥D BEF -的体积为16363⨯⨯=,故A 正确;假设PB DF ⊥,PA ⊥平面ABC ,BC ⊂平面ABC ,BC PA ∴⊥,又BC AB ⊥,PA AB A ⋂=,PA ,AB ⊂平面PAB ,BC ∴⊥平面PAB ,E ,F 分别为AC ,AB 的中点,//EF BC ∴,EF ∴⊥平面PAB , AB ⊂平面PAB ,EF AB ∴⊥,DE ⊥平面ABC ,AB ⊂平面ABC ,AB DE ∴⊥,EF DE E ⋂=,EF ,DE ⊂平面DEF ,AB ∴⊥平面DEF ,DF ⊂平面DEF ,AB DF ∴⊥,又假设PB DF ⊥,AB PB B ⋂=,AB ,PB ⊂平面PAB ,DF ∴⊥平面PAB , 显然不成立,不符合题意,故假设不成立,故B 错误;取PB 的中点Q ,连DQ ,FQ ,则//DQ EF ,DQ EF =,四边形DQFE 为平行四边形,DE ⊥平面EFB ,EF ⊂平面EFB ,DE EF ⊥, 所以平行四边形DEFQ 为矩形,3DE =,4EF =,所以截面面积为12,故C 正确;因为//DE PA ,PA ⊂/平面BDE ,DE ⊂平面BDE ,所以//PA 平面.BDE 所以点P 与点A 到平面BDE 的距离相等,故D 正确; 故选.ACD14.【答案】4π 92解:连接1BC ,在正方体1111ABCD A B C D -中,易知11//AB C D 且11AB C D =,则四边形11ABC D 为平行四边形,即B ∈平面11AC D ,因为正方体中,AB BC ⊥,1AB BB ⊥,且1,BC BB ⊂平面11BB C C , 则AB ⊥侧面11BB C C ,所以1AB BC ⊥, 又平面11AC D ⋂平面ABCD AB =,则1C BC ∠即等于平面11AC D 与平面ABCD 所成的角,所以11tan 1CC C BC BC∠==, 即14C BC π∠=;取BC 中点为Q ,连接PQ ,AQ ,因为P 为1CC 的中点,则1//PQ BC , 又11//AD BC ,则1//PQ AD ,即A ,1D ,P ,Q 四点共面, 即梯形1AD PQ 即为过点A ,P ,1D 的平面截该正方体所得截面,因为正方体棱长为2,则11AD BC ===,11PC BQ ==,所以112PQ BC ==,AQ ==1PD == 即梯形1AD PQ 为等腰梯形,分别作1PM AD ⊥于点M ,1PN AD ⊥于点N ,则11122AD NM AD PQ D M AN --====,所以2PM ===, 因此梯形1AD PQ 的面积为故答案为:4π;9.215.【答案】261-解:该半正多面体中间层是一个正八棱柱,有8个侧面, 故该半正多面体共有888226+++=个面;设其棱长为x ,因为每个顶点都在棱长为1的正方体上,则122x x x ++=,解得 1.x =故答案为26 1.-16.【答案】118.8解:该模型为长方体1111ABCD A B C D -,挖去四棱锥O EFGH -后所得的几何体,其中O 为长方体的中心,E ,F ,G ,H ,分别为所在棱的中点,6AB BC cm ==,14AA cm =,∴该模型体积为:1111ABCD A B C D O EFGH V V ---11664(46432)332=⨯⨯-⨯⨯-⨯⨯⨯⨯314412132()cm =-=,3D 打印所用原料密度为30.9/g cm ,不考虑打印损耗,∴制作该模型所需原料的质量为:1320.9118.8().g ⨯=故答案为118.8.17.【答案】43解:如图,平面PQS ⊥平面QRS ,且平面PQS ⋂平面QRS QS =,QS SR ⊥, SR ∴⊥平面PQS ,PQ ⊂平面PQS ,从而SR PQ ⊥,PQ PS ⊥,且PS SR S ⋂=,PQ ∴⊥平面PRS ,PR ⊂平面PRS ,得PQ PR ⊥,QR ∴是三棱锥P QRS -的外接球的直径,在Rt QSR 中,2223QR QS SR =+=,则球的半径3R =,则外接球的体积为34433R ππ=; 三棱锥P QRS -的体积为1114222.3323PQSSSR ⨯=⨯⨯⨯⨯=故答案为:43;43.π18.【答案】24解:设O 为正方形ABCD 的中心,AB 的中点为M ,连接PM ,OM ,PO , 则=1OM ,22=-=10-1=3PM PA AM ,=9-1=22PO ,如图,在截面PMO 中,设N 为球1O 与平面PAB 的切点,则N 在PM 上,且1O N PM ⊥,设球1O 的半径为R ,则1=O N R , 因为1sin ==3OM MPO PM ∠,所以111=3NO PO ,则1=3PO R , 11=+=4=22PO PO OO R ,所以2=2R , 设球1O 与球2O 相切于点Q ,则=-2=2PQ PO R R ,设球2O 的半径为r , 同理可得=4PQ r ,所以2==24R r , 故小球2O 的体积342V=r =324ππ, 故答案为2.24π19.【答案】证明:(1)四边形ABCD 为菱形,AC BD ∴⊥,BE ⊥平面ABCD ,AC ⊂平面ABCD ,AC BE ∴⊥,BD ,BE ⊂平面BED ,BD BE B ⋂=, 则AC ⊥平面BED ,AC ⊂平面AEC ,∴平面AEC ⊥平面BED ;解:(2)设AB x =,在菱形ABCD 中,由120ABC ︒∠=, 得2AG GC x ==,2x GB GD ==,BE ⊥平面ABCD ,BG ⊂平面ABCD ,BE BG ∴⊥,则EBG 为直角三角形,1322EG AC AG x ∴===, 则2222BE EG BG x =-=, 三棱锥E ACD -的体积3116632243V AC GD BE x =⨯⋅⋅==, 解得2x =,即2AB =,120ABC ︒∠=,22212cos 44222()122AC AB BC AB BC ABC ∴=+-⋅∠=+-⨯⨯⨯-=,即1223AC ==,在三个直角三角形EBA ,EBD ,EBC 中,斜边AE EC ED ==,AE EC ⊥,EAC ∴为等腰三角形,则22212AE EC AC +==, 即2212AE =,26AE ∴=,则6AE =,∴从而得6AE EC ED ===,EAC ∴的面积1166322S EA EC =⨯⋅=⨯⨯=,在等腰三角形EAD 中,过E 作EF AD ⊥于F , 则6AE =,112122AF AD ==⨯=, 则22(6)15EF =-=,EAD ∴的面积和ECD 的面积均为12552S =⨯⨯=,故该三棱锥的侧面积为32 5.+。
解空间几何体的结构——选择(基础题)

空间几何体的结构选择(基础题)1.下列各组几何体中全是多面体的一组是()A.三棱柱四棱台球圆锥B.三棱柱四棱台正方体圆台C.三棱柱四棱台正方体六棱锥D.圆锥圆台球半球解:选项A中的球和圆锥是旋转体,A不正确;B中的圆台是旋转体,所以B不正确;D中的四个几何体全是旋转体,所以D不正确;只有C中的四个几何体符合多面体概念.故选C.2.若正四棱台的上底边长为2,下底边长为8,高为4则它的表面积为()A.50 B.100C.248 D.以上答案都不对解:∵上底的边心距为1,下底的边心距为4,高是4,∴斜高为=5,故侧面积等于4××5=100.它的表面积为S=100+22+82=168.故选:D.3.某四面体的三视图如图所示.该四面体的六条棱的长度中,最大的是()A.2 B.2 C.2 D.4解:由三视图可知原几何体为三棱锥,其中底面△ABC为俯视图中的钝角三角形,∠BCA为钝角,其中BC=2,BC边上的高为2,PC⊥底面ABC,且PC=2,由以上条件可知,∠PCA为直角,最长的棱为PA或AB,在直角三角形PAC中,由勾股定理得,PA===2,又在钝角三角形ABC中,AB==.故选C.4.下列四种说法中:①有两个面平行,其余各面都是平行四边形的几何体叫棱柱②相等的线段在直观图中仍然相等③一个直角三角形绕其一边旋转一周所形成的封闭图形叫圆锥④用一个平面去截棱锥,底面与截面之间的部分组成的几何体叫棱台正确的个数是()A.0 B.1 C.2 D.3解:有两个面平行,其余各面都是平行四边形,并且相邻的两个平行四边形的公共边都相互平行,这些面围成的几何体叫棱柱,故①错误.②相等的线段在直观图中仍然相等,不一定相等,不正确;③根据一个直角三角形绕其一个直角边边旋转一周所形成的封闭图形叫圆锥,可得不正确;④用平行于底面的平面去截棱锥,底面与截面之间的部分组成的几何体叫棱台,不正确.故选A.5.下列命题中,正确的是()A.底面是正方形的四棱柱是正方体B.棱锥的高线可能在几何体之外C.有两个面互相平行,其余各面是平行四边形的几何体是棱柱D.有一个面是多边形,其余各面都是三角形的几何体是棱锥解:底面是正方形的四棱柱不一定是正方体,故A错误;斜棱锥的高线有可能在几何体之外,故B正确;根据棱柱的定义可得,有两个面互相平行,其余各面是平行四边形的几何体不一定是棱柱,故C错误;有一个面是多边形,其余各面是有公共顶点的三角形的几何体是棱锥,故D错误.故选:B.6.下列说法正确的是()A.圆锥的侧面展开图是一个等腰三角形B.棱柱的两个底面全等且其余各面都是矩形C.任何一个棱台的侧棱必交于同一点D.过圆台侧面上一点有无数条母线解:在A中,圆锥的侧面展开后是一个扇形,不是等腰三角形,故A错误;在B中,棱柱的两个底面全等且其余各面都是平行四边形,故B错误;在C中,由棱台的定义得任何一个棱台的侧棱必交于同一点,故C正确;在D中,过圆台侧面上一点有且只有1数条母线,故D错误.故选:C.7.下列结论,其中正确的个数是()①梯形的直观图可能是平行四边形②三棱锥中,四个面都可以是直角三角形③如果一个棱锥的各个侧面都是等边三角形,这个棱锥不可能是六棱锥④底面是矩形的平行六面体是长方体.A.1 B.2 C.3 D.4解:①梯形的直观图可能是平行四边形;不正确,因为平行x轴的线段长度不变;②三棱锥中,四个面都可以是直角三角形;正确,一条棱长垂直底面直角三角形的一个锐角,即可满足题意.③如果一个棱锥的各个侧面都是等边三角形,这个棱锥不可能是六棱锥;错误,满足条件,结果是正六边形.④底面是矩形的平行六面体是长方体.棱长不垂直底面,不正确.故选A.8.下列几何体是组合体的是()A.B.C.D.解:选项A是圆锥体,B是圆柱体,C是球体,D是圆台与圆锥体的组合体.故选:D.9.在空间中有下列四个命题:①有两组对边相等的四边形是平行四边形;②四边相等的四边形是菱形;③两组对边分别平行的四边形是平行四边形;④连接空间四边形各边中点的四边形一定是梯形.其中正确命题的个数为()A.1 B.2 C.3 D.4解:四边相等和两组对边相等的四边形可以是空间四边形,故①②错误,连接空间四边形各边中点的四边形一定是平行四边形,故④错误,两组对边分别平行的四边形是平行四边形,正确,故正确命题的个数为1个,故选:A10.以下说法正确的是()A.球的截面中过球心的截面面积未必最大B.圆锥截去一个小圆锥后剩下来的部分是圆台C.棱锥截去一个小棱锥后剩下来的部分是棱台D.用两个平行平面去截圆柱,截得的中间部分还是圆柱解:在A中,球的截面中过球心的截面面积最大,故A错误;在B中,圆锥截去一个小圆锥后剩下来的部分是圆台,由圆台的定义知B正确;在C中,棱锥截去一个小棱锥后剩下来的部分有可是棱台,有可能不是棱台,故C错误;在D中,用两个平行平面去截圆柱,如果沿纵切面方向截得的中间部分不是圆柱,故D错误.故选:B.12.如图几何体中不是柱体的有()A.1个B.2个C.3个D.4个解:①是三棱柱,②的上下两个平面不平行,不是三棱柱,③是四棱柱,④是圆柱,⑤是四棱柱,⑥是四棱台,⑦三棱锥;∴不是柱体的为②⑥⑦,共3个.故选C.14.下列说法正确的是()A.以直角三角形一边为轴旋转所得的旋转体是圆锥B.用一个平面去截圆锥,得到一个圆锥和一个圆台C.正棱锥的棱长都相等D.棱柱的侧棱都相等,侧面是平行四边形解:对于A,以直角三角形的一直角边为轴旋转所得的旋转体是圆锥,斜边为轴旋转所得的旋转体是组合体,故A错误.对于B,用平行与底面的平面去截圆锥,得到一个圆锥和一个圆台,否则不是,故B错误;对于C,正棱锥的侧棱长都相等,底边棱长不一定相等,故C错误;对于D,棱柱的侧棱都相等,侧面是平行四边形,D正确.故选:D.15.下列命题中正确的是()A.用一个平面去截棱锥,棱锥底面和截面之间的部分是棱台B.有两个面平行,其他面都是平行四边形的几何体叫棱柱C.棱台的底面是两个相似的正方形D.棱台的侧棱延长后必交于一点解:在A中,用一个平行于底面的平面去截棱锥,棱锥底面和截面之间的部分是棱台,故A 不正确;在B中,两个底面平行且相似,其余各面都是梯形的多面体是棱台,侧棱不一定相交于一点,故B不正确.在C中,棱台的底面是两个相似的多边形,故C错误;在D中,由棱台的性质得棱台的侧棱延长后必交于一点,故D正确.故选:D.16.下列结论正确的是()A.圆锥的顶点与底面圆周上的任意一点的连线都是母线B.以三角形的一条边所在直线为旋转轴,其余两边绕旋转轴旋转形成的曲面所围成的几何体叫圆锥C.棱锥的侧棱长与底面多边形的边长都相等,则该棱锥可能是六棱锥D.各个面都是三角形的几何体是三棱锥解:在A中,由圆锥的定义知:圆锥的顶点与底面圆周上的任意一点的连线都是母线,故A 正确;在B中,如图,若△ABC不是直角三角形,或△ABC是直角三角形但旋转轴不是直角边,所得的几何体都不是圆锥,故B错误;在C中,若该棱锥是六棱锥,由题设知,它是正六棱锥,正六棱锥的侧棱长必大于底面边长,这与题设矛盾,故C错误;在D中,三棱锥每个面都是三角形,但是每个面都是三角形的几何体不一定是三棱锥,2个一样的三棱锥上下拼接成一个六面体,它每个面都是三角形,故D错误.故选:A.17.若一个长方体共顶点的三个面的对角线长分别是a,b,c,则长方体的对角线长是()A.B.C.D.解:设同一顶点的三条棱分别为x,y,z,则x2+y2=a2,y2+z2=b2,x2+z2=c2得x2+y2+z2=(a2+b2+c2),则对角线长为.故选:B.18.如图是正方体的表面展开图,则图中的直线AB,CD在原正方体中是()A.平行 B.相交成60°角C.异面成60°角D.异面垂直解:把正方体的表面展开图变形为正方体,B与D重合,此时AB=AC=BC,∴△ABC为等边三角形,即∠ABC=60°,则图中的直线AB,CD在原正方体中是相交成60°角,故选:B.19.在长方体ABCD﹣A1B1C1D1中,底面ABCD是边长为的正方形,AA1=3,E是AA1的中点,过C1作C1F⊥平面BDE与平面ABB1A1交于点F,则等于()A.B.C.D.解:连结AC、BD,交于点O,∵四边形ABCD是正方形,AA1⊥底面ABCD,∴BD⊥平面ACC1A1,则当C1F与EO垂直时,C1F⊥平面BDE,∵F∈平面ABB1A1,∴F∈AA1,在矩形ACC1A1中,△C1A1F∽△EAO,则=,∵A1C1=2AO=,AE=,∴A1F=,∴AF=,∴=.故选:C.20.下面没有体对角线的一种几何体是()A.三棱柱B.四棱柱C.五棱柱D.六棱柱解:三棱柱,四棱锥,五棱柱,六棱柱,底面分别为三角形,四边形,五边形,六边形,三角形没有对角线,所以三棱柱没有对角线.故选:A.22.如图所示是正方体的平面展开图,在这个正方体中()①BM与ED平行②CN与BE是异面直线;③CN与BM成60°角;④DM与BN垂直.A.①②③B.②④ C.③④ D.②③④解:由题意画出正方体的图形如图:显然①②不正确;③CN与BM成60°角,即∠ANC=60°正确;④DM⊥平面BCN,所以④正确;故选C.23.有下列三种说法①侧棱垂直于底面的棱柱是直棱柱②底面是正多边形的棱柱是正棱柱③棱柱的侧面都是平行四边形.其中正确说法的个数是()A.0 B.1 C.2 D.3解:①侧棱垂直于底面的棱柱是直棱柱,正确;②底面是正多边形的直棱柱是正棱柱,不正确;③棱柱的侧面都是平行四边形,正确,故选:C.24.如图所示,是一个正方体的表面展开图,则图中“2”所对的面是()A.1 B.7 C.快D.乐解:由已知中的正方体表面展开图可得:2和7对面,0和快对面,1和乐对面,故选:B25.如图,将无盖正方体纸盒展开,直线AB,CD在原正方体中的位置关系是()A.平行 B.相交成60°C.相交且垂直D.异面直线解:将正方体还原得到A,B,C,D的位置如图因为几何体是正方体,所以连接AC,得到三角形ABC是等边三角形,所以∠ABC=60°;故选:B.26.半径为R的半圆卷成底面最大的圆锥,所得圆锥的高为()A.B.C.D.解:半径为R的半圆弧长为πR,圆锥的底面圆的周长为πR,圆锥的底面半径为:,所以圆锥的高:=.故选:B.27.若圆锥的侧面展开图是圆心角为120°、半径为l的扇形,则这个圆锥的表面积与侧面积的比是()A.4:3 B.2:1 C.5:3 D.3:2解:圆锥的侧面积=π×12×=圆锥的底面半径=2π×1×÷2π=,圆锥的底面积==,圆锥的表面积=侧面积+底面积=,∴这个圆锥的表面积与侧面积的比=4:3.故选A28.在正四棱锥V﹣ABCD中(底面是正方形,侧棱均相等),AB=2,VA=,且该四棱锥可绕着AB任意旋转,旋转过程中CD∥平面α,则正四棱锥V﹣ABCD在平面α内的正投影的面积的取值范围是()A.[2,4] B.(2,4] C.[,4] D.[2,2]解:由题意,侧面上的高为=,∴侧面的面积为=2,又由于底面的面积为2×2=4,当正四棱锥的高平行于面时面积最小是2,∴正四棱锥V﹣ABCD在面α内的投影面积的取值范围是[2,4],故选:A.29.观察如图所示几何体,其中判断正确的是()A.①是棱台 B.②是圆台 C.③是棱锥 D.④不是棱柱解:图形①,不满足棱台的定义,所以①不正确;图形②,不满足圆台的定义,所以②不正确;图形③满足棱锥的定义,所以③正确;图形④是棱柱,所以④的判断不正确.故选:C.30.正四棱锥的侧棱长是底面长的k倍,则k的取值范围是()A.(0,+∞)B.(,+∞})C.(,+∞)D.(,+∞)解:如图所示,设正四棱锥V﹣ABCD底面中心为O,BC=a,则VB=ka,易知OB=a;在Rt△VOB中,cos∠VBO==,∵∠VBO∈(0,),∴0<<1,∴,解得k>;∴k的取值范围是(,+∞).32.用一个平面去截四棱锥,不可能得到()A.棱锥 B.棱柱 C.棱台 D.四面体解:∵棱柱的上下底面是相同的,∴用一个平面去截四棱锥,不可能得到棱柱.故选:B.33.正四面体的内切球球心到一个面的距离等于这个正四面体高的()A.B.C.D.解:球心到正四面体一个面的距离即球的半径r,连接球心与正四面体的四个顶点.把正四面体分成四个高为r的三棱锥,所以4×S•r=•S•h,r=h.(其中S为正四面体一个面的面积,h为正四面体的高)答案:C.35.如图所示,观察四个几何体,其中判断正确的是()A.①是棱台 B.②是圆台 C.③是棱锥 D.④不是棱柱解:图①不是由棱锥截来的,所以①不是棱台;图②上、下两个面不平行,所以②不是圆台;图③是棱锥.图④前、后两个面平行,其他面是平行四边形,且每相邻两个四边形的公共边平行,所以④是棱柱.故选C.37.下列说法中不正确的是()A.棱柱的各个侧面都是平行四边形B.棱锥的侧面都是三角形C.棱台的所有侧棱都相等D.圆柱的任意两条母线互相平行解:棱柱的侧面是平行四边形,正确;棱锥的侧面是有公共顶点的三角形,正确棱台的各条棱不一定都相等,不正确,圆柱的任意两条母线互相平行,正确,故选:C.38.下列关于棱锥、棱台的说法,其中不正确的是()A.棱台的侧面一定不会是平行四边形B.棱锥的侧面只能是三角形C.由四个面围成的封闭图形只能是三棱锥D.棱锥被平面截成的两部分不可能都是棱锥解:在A中,棱台的侧面是梯形,故A正确;在B中,由棱锥的定义得棱锥的侧面只能是三角形,故B正确;在C中,由棱锥的定义得四个面围成的封闭图形只能是三棱锥,故C正确;在D中,棱锥被平面截成的两部分有可能都是棱锥,故D错误.故选:D.42.如图是由哪个平面图形旋转得到的()A.B.C.D.解:图中所给的几何体是由上部的圆锥和下部的圆台组合而成的,故轴截面的上部是直角三角形,下部为直角梯形构成,故选 D.43.将半径为1的圆分割成面积之比为1:2:3的三个扇形作为三个圆锥的侧面,设这三个圆锥底面半径依次为r1,r2,r3,那么r1+r2+r3的值为()A.B.2 C.D.1解:∵2πr1=,∴r1=,同理,∴r1+r2+r3=1,故选:D.45.一个底面半径为2cm的圆柱形容器内盛有高度为6cm的水,现将一个母线长为cm 的圆锥形物体完全浸入水中,容器里水的高度上升到7cm,则该圆锥的高为()A.1cm B.2cm C.3cm D.cm解:圆锥的体积V=π×22×1=4π,设圆锥的高为h,则圆锥的底面半径r=,∴V==4π,解得h=1或h=3.当h=1时,r==2>2,不符合题意.故选:C.47.如图,已知半径为2的半圆中,BC为直径,O为圆心,点A在半圆弧上,且AB=AC,则图中阴影部分绕直线BC旋转一周所形成的几何体的体积为()A.B.C.16π D.32π解:半圆绕BC旋转一周所得球体的体积V球==.三角形ABC绕BC旋转一周所得几何体体积V′==.∴阴影部分绕BC旋转一周所得几何体体积V=V球﹣V′=.故选:A.48.若一个圆锥的轴截面是等边三角形,则该圆锥的侧面积与底面积的比等于()A.3 B.2 C.D.解:设圆锥的底面半径为r,则母线l=2r,∴S侧=πrl=2πr2,S底=πr2,∴=2.故选:B.49.将直角三角形绕它的一个直角边所在的直线旋转一周,形成的几何体一定是()A.圆锥 B.圆柱 C.圆台 D.以上均不正确解:由旋转体的定义,将直角三角形绕它的一个直角边所在的直线旋转一周,形成的几何体为圆锥故选A50.一竖立在地面上的圆锥形物体的母线长为4m,侧面展开图的圆心角为,则这个圆锥的体积等于()A.πm3 B.πm3C.πm3D.πm3解:设圆锥的底面半径为r,圆锥形物体的母线长l=4m,侧面展开图的圆心角为,故2πr=l,解得:r=m,故圆锥的高h==m,故圆锥的体积V==πm3,故选:D。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1.1空间几何体的结构练习题
1、在棱柱中(
A .只有两个面平行
B .所有的棱都平行
C .所有的面都是平行四边形
D .两底面平行,且各侧棱也互相平行
2、下列说法错误的是 (
A :由两个棱锥可以拼成一个新的棱锥
B :由两个棱台可以拼成一个新的棱台
C :由两个圆锥可以拼成一个新的圆锥
D :由两个圆台可以拼成一个新的圆台
3、下列说法正确的是 (
A :以直角三角形的一边为轴旋转而成几何体是圆锥
B :圆柱、圆锥、圆台的底面都是圆面
C :以直角梯形的一腰为轴旋转成的是圆台
D :圆锥的侧面展开图为扇形,这个扇形所在的圆的半径等于圆锥底面圆的半径
4、下列关于长方体的叙述不正确的是 (
A :长方体的表面共有 24个直角
B :长方体中相对的面都互相平行
C :长方体中某一底面上的高的长度就是两平行底面间的距离:
D ;两底面间的棱互相平行且相等的六面体是长方体
5、将图 1所示的三角形线
直线 l 旋转一周,可以得到
如图 2所示的几何体的是哪
一个三角形(
6、如图一个封闭的立方体,它 6个表面各标出 1、2、 3、 4、 5、 6这 6个数字,现放成下面 3个不同
的位置,则数字 l 、 2、 3对面的数字是(
A . 4、 5、 6 B. 6、 4、 5 C . 5、 4、 6 D . 5、 6、 4
7、如图,能推断这个几何体可能是三棱台的是 (
A . A 1
B 1=2, AB =3, B 1
C 1=3, BC =4
B . A 1B l =1, AB =2, B l
C l =1.5, BC =3, A 1C 1=2, AC =3
C . A l B l =1, AB =2, B 1C l =1.5, BC =3, A l C l =2, AC =4
D . AB =A 1B 1, BC =B 1C 1, CA =C 1A 1
8、有下列命题(1在圆柱的上、下底面的圆周上各取一点,则这两点
的连线是圆柱的母线; (2圆锥顶点与底面圆周上任意一点的连线是圆
锥的母线; (3在圆台上、下底面圆周上各取一点,则这两点的连线是圆台的母线; (4圆柱的任意两条母线所在的直线是互相平行的;其中正确的是(
A . (1 (2 B. (2 (3 C. (1 (3 D. (2 (4
9、下列命题中错误的是(
A .圆柱的轴截面是过母线的截面中面积最大的一个 B.圆锥的轴截面是所有过顶点的截面中面积最大的一个
C .圆台的所有平行于底面的截面都是圆面 D.圆锥所有的轴截面是全等的等腰三角形
10、图 1是由图 2中的哪个平面图旋转而得到的(
1.2空间几何体的三视图和直观图练习题
1.若一个几何体的三视图都是等腰三角形,则这个几何体可能是 (
A .圆锥
B .正四棱锥
C .正三棱锥
D .正三棱台
2.说出下列三视图表示的几何体是(
A .正六棱柱
B .正六棱锥
C .正六棱台
D .正六边形
3.下列说法正确的是(
A .互相垂直的两条直线的直观图一定是互相垂直的两条直线
B .梯形的直观图可能是平行四边形
C .矩形的直观图可能是梯形
D .正方形的直观图可能是平行四边形
4.如右图所示,该直观图表示的平面图形为(
A .钝角三角形
B .锐角三角形
C .直角三角形
D .正三角形
5.下列几种说法正确的个数是(
①相等的角在直观图中对应的角仍然相等
②相等的线段在直观图中对应的线段仍然相等
③平行的线段在直观图中对应的线段仍然平行
④线段的中点在直观图中仍然是线段的中点
A . 1
B . 2
C . 3
D . 4
6.哪个实例不是中心投影(
A .工程图纸
B .小孔成像
C .相片
D .人的视觉
7.关于斜二测画法画直观图说法不正确的是 (
A .在实物图中取坐标系不同,所得的直观图有可能不同
B .平行于坐标轴的线段在直观图中仍然平行于坐标轴
C .平行于坐标轴的线段长度在直观图中仍然保持不变
D .斜二测坐标系取的角可能是 135°
8.下列几种关于投影的说法不正确的是(
A .平行投影的投影线是互相平行的
B .中心投影的投影线是互相垂直的影
C .线段上的点在中心投影下仍然在线段上
D .平行的直线在中心投影中不平行
9. 在一个倒置的正三棱锥容器内放入一个钢球, 钢球恰与棱锥的四个面都接触, 过棱锥的一条侧棱和高作截面, 正确的截面图形是(
A B C D
10.一个三角形在其直观图中对应一个边长为 1正三角形,原三角形的面积为(
A . 46
B . 4
C . 23
D . 26。
