必修4第三章---三角恒等变换单元教学设计
人教版高一数学必修四3.2简单的三角恒等变换教案

三角恒等变换一、教学目标1:能够熟练运用两角之差及两角之和的正余弦、正切公式解决问题; 2:辅助角公式的应用;3:能够解决三角函数的图像与性质有关的综合应用问题。
二、教学重点与难点 与辅助角公式相关的三角函数综合问题三、教学过程1、复习•引入 两角和与差的正弦公式()sin αβ+=_________________________________()sin αβ-=_________________________________ 口答:利用公式展开sin 4πα⎛⎫+ ⎪⎝⎭=_____________________ 反之,αα化简为只含正弦的三角比的形式,则可以是αα=_____________________________ 尝试:将以下各式化为只含有正弦的形式,即化为)sin(βα+A ()0A >的形式(11cos 2αα+ (2)sin αα2、辅助角公式•推导对于一般形式ααcos sin b a +(a 、b 不全为零),如何将表达式化简为只含有正弦的三角比形式?sin cos ))a b αααααβ++其中辅助角β由cos sin ββ⎧=⎪⎪⎨⎪=⎪⎩β(通常πβ20<≤)的终边经过点(,)a b------------------我们称上述公式为辅助角公式,其中角β为辅助角。
3、例题•反馈例1、试将以下各式化为)sin(βα+A ()0A >的形式.(11cos 2αα- (2)ααcos sin +(3αα (4)ααcos 4sin 3-例2、试将以下各式化为)sin(βα+A (),[,0ππβ-∈>A )的形式.(1)sin cos αα-(2)ααsin cos - (3)cos αα-例3、若sin(50)cos(20)3x x +++=,且0360x ≤<,求角x 的值。
例42)cos()12123x x ππ+++=,且 02x π-<<,求sin cos x x -的值。
人教版高中必修4(B版)第三章三角恒等变换课程设计

人教版高中必修4(B版)第三章三角恒等变换课程设计一、课程背景本课程设计是针对高中必修课程《数学四》(B版)第三章三角恒等变换的教学实践。
在本章节中,学生将学习三角函数的基本概念,包括正弦、余弦、正切等;以及三角函数的基本性质、图像特征等知识。
在此基础上,进一步学习三角恒等变换的定义、性质、应用等内容,帮助学生感受数学美妙,拓展学生的数学思维和实际应用能力。
二、课程目标•知识目标1.掌握三角函数的概念、性质、基本图像和相关公式;2.掌握三角恒等变换的概念、性质和基本应用;3.理解三角恒等变换与三角函数图像的关系,培养学生对数学美的感悟。
•能力目标1.能灵活应用三角函数及其相关公式;2.能理解并应用三角恒等变换在实际问题中得到解决;3.能有效运用数学知识解决实际问题,并能形成自己的思考方式。
•情感目标1.通过学习,培养学生感受数学美妙的情感和兴趣;2.让学生理解数学是实践中最常用的一门学科;3.激发学生爱思考、勇于探究、善于合作的精神。
三、课程内容1.三角函数基础知识复习;2.三角恒等变换;3.三角函数图像变化。
四、教学方法1.讲授法:通过课堂讲解,准确阐述三角恒等变换的基本概念、性质、公式等,并通过简单的计算题、实例演练等方式帮助学生掌握相关知识;2.实践结合法:通过实际问题的解答,引导学生思考、动手解决,培养学生的数学实践能力;3.合作学习法:通过小组讨论、合作解题等方式,让学生在团队中相互交流、借鉴、提高彼此能力。
五、教学设计第一节课时间:1学时主要内容:三角函数基础知识复习1.引入三角函数知识,介绍正弦、余弦、正切的定义、符号、图像及基本性质;2.以例子为主,提高学生对于三角函数的计算能力;3.通过课堂测验,及时调整教学内容,帮助弱势学生摆脱困境。
第二节课时间:1学时主要内容:三角恒等变换1.引入三角恒等变换的定义、本质及重要性;2.提出三角恒等变换相关的公式,并进行简单的计算;3.通过实例演示,帮助学生理解三角恒等变换在证明中的应用。
高中数学必修四教案-简单的三角恒等变换三

3.2简单的三角恒等变换(三) 教学目标(一) 知识与技能目标熟练掌握三角公式及其变形公式.(二) 过程与能力目标抓住角、函数式得特点,灵活运用三角公式解决一些实际问题.(三) 情感与态度目标培养学生观察、分析、解决问题的能力.教学重点和、差、倍角公式的灵活应用.教学难点如何灵活应用和、差、倍角公式的进行三角式化简、求值、证明. 教学过程例1:教材P141面例4例1. 如图,已知OPQ 是半径为1,圆心角为3π的扇形,C 是扇形弧上的动点,ABCD 是扇形的内接矩形.记∠COP =α,求当角α取何值时,矩形ABCD 的面积最大?并求出这个最大面积.例2:把一段半径为R(分别设边与角为自变量)解:(1)如图,设矩形长为l ,则面积224l R l S +=, 所以,4)()4(22222222l R l l R l S +-=-=当且仅当,224222R R l == 即R l 2=时,2S 取得最大值44R ,此时S 取得最大值22R ,矩形的宽为R RR 2222=即长、宽相等,矩形为圆内接正方形. (2)设角为自变量,设对角线与一条边的夹角为θ,矩形长与宽分别为 θsin 2R 、θcos 2R ,所以面积θθθ2sin 2sin 2cos 22R R R S =⨯=.而12sin ≤θ,所以22R S ≤,当且仅当12sin =θ时,S 取最大值22R ,所以当且仅当︒=902θ即︒=45θ时, S 取最大值,此时矩形为内接正方形.变式:已知半径为1的半圆,PQRS 是半圆的内接矩形如图,问P 点在什么位置时,矩形的面积最大,并求最大面积时的值.解:设,α=∠SOP 则,cos ,sin αα==OS SP故S 四边形PQRS ααα2sin cos 2sin =⨯=故α为︒45时,1max =S课堂小结建立函数模型利用三角恒等变换解决实际问题.课后作业1. 阅读教材P.139到P.142;2. 《习案》作业三十五.O。
高中数学人教A版必修4教案-3.2_简单的三角恒等变换_教学设计_教案_3

教学准备1. 教学目标三角恒等变形的关键是熟练掌握公式及应用, 掌握公式的逆用和变形三角恒等变形包括三角函数的求值、化简与证明题;2. 教学重点/难点三角恒等变形的关键是熟练掌握公式及应用, 掌握公式的逆用和变形三角恒等变形包括三角函数的求值、化简与证明题;3. 教学用具4. 标签教学过程【知识点精讲】三角恒等变形的关键是熟练掌握公式及应用, 掌握公式的逆用和变形三角恒等变形包括三角函数的求值、化简与证明题;三角函数式的求值的类型一般可分为:(1)“给角求值”:给出非特殊角求式子的值。
仔细观察非特殊角的特点,找出和特殊角之间的关系,利用公式转化或消除非特殊角(2)“给值求值”:给出一些角得三角函数式的值,求另外一些角得三角函数式的值。
找出已知角与所求角之间的某种关系求解(3)“给值求角”:转化为给值求值,由所得函数值结合角的范围求出角。
(4)“给式求值”:给出一些较复杂的三角式的值,求其他式子的值。
将已知式或所求式进行化简,再求之三角函数式常用化简方法:切割化弦、高次化低次三角恒等式的常用证明方法:(1)化繁到简法;(2)左右归一法;(3)变更命题法注意点:灵活角的变形和公式的变形重视角的范围对三角函数值的影响,对角的范围要讨论【例题选讲】解答:见《走向高考》p51例4【课堂小结】三角函数式的求值的关键是熟练掌握公式及应用, 掌握公式的逆用和变形1.三角函数式的求值的类型一般可分为:(1)“给角求值”:给出非特殊角求式子的值。
仔细观察非特殊角的特点,找出和特殊角之间的关系,利用公式转化或消除非特殊角(2)“给值求值”:给出一些角得三角函数式的值,求另外一些角得三角函数式的值。
找出已知角与所求角之间的某种关系求解(3)“给值求角”:转化为给值求值,由所得函数值结合角的范围求出角。
(4)“给式求值”:给出一些较复杂的三角式的值,求其他式子的值。
将已知式或所求式进行化简,再求之2.三角函数式常用化简方法:切割化弦、高次化低次3.三角恒等式的常用证明方法:(1)化繁到简法;(2)左右归一法;(3)变更命题法4.利用三角恒等变换研究三角函数的性质;注意点:灵活角的变形和公式的变形重视角的范围对三角函数值的影响,对角的范围要讨论【作业布置】《走向高考》p52 5. 6 . 7。
人教版高中数学必修四第三章 三角恒等变换全章教案

3.1.1 两角差的余弦公式一、教学目标掌握用向量方法建立两角差的余弦公式.通过简单运用,使学生初步理解公式的结构及其功能,为建立其它和(差)公式打好基础.二、教学重、难点1. 教学重点:通过探索得到两角差的余弦公式;2. 教学难点:探索过程的组织和适当引导,这里不仅有学习积极性的问题,还有探索过程必用的基础知识是否已经具备的问题,运用已学知识和方法的能力问题,等等.三、学法与教学用具1. 学法:启发式教学2. 教学用具:多媒体四、教学设想:(一)导入:我们在初中时就知道 2cos 452=,3cos302=,由此我们能否得到()cos15cos 4530?=-=大家可以猜想,是不是等于cos 45cos30-呢?根据我们在第一章所学的知识可知我们的猜想是错误的!下面我们就一起探讨两角差的余弦公式()cos ?αβ-=(二)探讨过程:在第一章三角函数的学习当中我们知道,在设角α的终边与单位圆的交点为1P ,cos α等于角α与单位圆交点的横坐标,也可以用角α的余弦线来表示,大家思考:怎样构造角β和角αβ-?(注意:要与它们的正弦线、余弦线联系起来.)展示多媒体动画课件,通过正、余弦线及它们之间的几何关系探索()cos αβ-与cos α、cos β、sin α、sin β之间的关系,由此得到cos()cos cos sin sin αβαβαβ-=+,认识两角差余弦公式的结构.思考:我们在第二章学习用向量的知识解决相关的几何问题,两角差余弦公式我们能否用向量的知识来证明?提示:1、结合图形,明确应该选择哪几个向量,它们是怎样表示的?2、怎样利用向量的数量积的概念的计算公式得到探索结果?展示多媒体课件比较用几何知识和向量知识解决问题的不同之处,体会向量方法的作用与便利之处.思考:()cos ?αβ+=,()()cos cos αβαβ+=--⎡⎤⎣⎦,再利用两角差的余弦公式得出()()()()cos cos cos cos sin sin cos cos sin sin αβαβαβαβαβαβ+=--=-+-=-⎡⎤⎣⎦(三)例题讲解例1、利用和、差角余弦公式求cos 75、cos15的值.解:分析:把75、15构造成两个特殊角的和、差.()231cos 75cos 4530cos 45cos30sin 45sin 302222=+=-=⨯=()231cos15cos 4530cos 45cos30sin 45sin 30222=-=+=⨯=点评:把一个具体角构造成两个角的和、差形式,有很多种构造方法,例如:()cos15cos 6045=-,要学会灵活运用.例2、已知4sin 5α=,5,,cos ,213παπββ⎛⎫∈=- ⎪⎝⎭是第三象限角,求()cos αβ-的值.解:因为,2παπ⎛⎫∈ ⎪⎝⎭,4sin 5α=由此得3cos 5α===-又因为5cos ,13ββ=-是第三象限角,所以12sin 13β===- 所以3541233cos()cos cos sin sin 51351365αβαβαβ⎛⎫⎛⎫⎛⎫-=+=-⨯-+⨯-=- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭点评:注意角α、β的象限,也就是符号问题.(四)小结:本节我们学习了两角差的余弦公式,首先要认识公式结构的特征,了解公式的推导过程,熟知由此衍变的两角和的余弦公式.在解题过程中注意角α、β的象限,也就是符号问题,学会灵活运用.(五)作业:15012.P T T -3.1.2两角和与差的正弦、余弦、正切公式(1)教案一、教学分析1.两角和与差的正弦、余弦、正切公式是在研究了两角差的余弦公式的基础上,进一步研究具有“两角和差”关系的正弦、余弦、正切公式的.在这些公式的推导中,教科书都把对照、比较有关的三角函数式,认清其区别,寻找其联系和联系的途径作为思维的起点,如比较cos(α-β)与cos(α+β),它们都是角的余弦只是角形式不同,但不同角的形式从运算或换元的角度看都有内在联系,即α+β=α-(-β)的关系,从而由公式C(α-β)推得公式C(α+β),又如比较sin(α-β)与cos(α-β),它们包含的角相同但函数名称不同,这就要求进行函数名的互化,利用诱导公式(5)(6)即可推得公式S(α-β)、S(α+β)等.2.通过对“两角和与差的正弦、余弦、正切公式”的推导,揭示了两角和、差的三角函数与这两角的三角函数的运算规律,还使学生加深了数学公式的推导、证明方法的理解.因此本节内容也是培养学生运算能力和逻辑思维能力的重要内容,对培养学生的探索精神和创新能力,发现问题和解决问题的能力都有着十分重要的意义.3.本节的几个公式是相互联系的,其推导过程也充分说明了它们之间的内在联系,让学生深刻领会它们的这种联系,从而加深对公式的理解和记忆.本节几个例子主要目的是为了训练学生思维的有序性,逐步培养他们良好的思维习惯,教学中应当有意识地对学生的思维习惯进行引导,例如在面对问题时,要注意先认真分析条件,明确要求,再思考应该联系什么公式,使用公式时要具备什么条件等.另外,还要重视思维过程的表述,不能只看最后结果而不顾过程表述的正确性、简捷性等,这些都是培养学生三角恒等变换能力所不能忽视的. 二、三维目标1.知识与技能:在学习两角差的余弦公式的基础上,通过让学生探索、发现并推导两角和与差的正弦、余弦、正切公式,了解它们之间的内在联系,并通过强化题目的训练,加深对公式的理解,培养学生的运算能力及逻辑推理能力,从而提高解决问题的能力.2.过程与方法:通过两角和与差的正弦、余弦、正切公式的运用,会进行简单的求值、化简、恒等证明,使学生深刻体会联系变化的观点,自觉地利用联系变化的观点来分析问题,提高学生分析问题解决问题的能力.3.情感态度与价值观:通过本节学习,使学生掌握寻找数学规律的方法,提高学生的观察分析能力,培养学生的应用意识,提高学生的数学素质.三、重点难点教学重点:两角和与差的正弦、余弦、正切公式及其推导.教学难点:灵活运用所学公式进行求值、化简、证明.四、课时安排2课时五、教学设想第1课时(一)导入新课思路 1.(旧知导入)教师先让学生回顾上节课所推导的两角差的余弦公式,并把公式默写在黑板上或打出幻灯片,注意有意识地让学生写整齐.然后教师引导学生观察cos(α-β)与cos(α+β)、sin(α-β)的内在联系,进行由旧知推出新知的转化过程,从而推导出C (α+β)、S (α-β)、S (α+β).本节课我们共同研究公式的推导及其应用.思路2.(问题导入)教师出示问题,先让学生计算以下几个题目,既可以复习回顾上节所学公式,又为本节新课作准备.若sin α=55,α∈(0,2π),cos β=1010,β∈(0,2π),求cos(α-β),cos(α+β)的值.学生利用公式C (α-β)很容易求得cos (α-β),但是如果求cos (α+β)的值就得想法转化为公式C (α-β)的形式来求,此时思路受阻,从而引出新课题,并由此展开联想探究其他公式.(二)推进新课、新知探究、提出问题①还记得两角差的余弦公式吗?请一位同学到黑板上默写出来.②在公式C (α-β)中,角β是任意角,请学生思考角α-β中β换成角-β是否可以?此时观察角α+β与α-(-β)之间的联系,如何利用公式C (α-β)来推导cos(α+β)=?③分析观察C (α+β)的结构有何特征?④在公式C (α-β)、C (α+β)的基础上能否推导sin(α+β)=?sin(α-β)=?⑤公式S (α-β)、S (α+β)的结构特征如何?⑥对比分析公式C (α-β)、C (α+β)、S (α-β)、S (α+β),能否推导出tan(α-β)=?tan (α+β)=?⑦分析观察公式T (α-β)、T (α+β)的结构特征如何?⑧思考如何灵活运用公式解题?活动:对问题①,学生默写完后,教师打出课件,然后引导学生观察两角差的余弦公式,点拨学生思考公式中的α,β既然可以是任意角,是怎样任意的?你会有些什么样的奇妙想法呢?鼓励学生大胆猜想,引导学生比较cos(α-β)与cos(α+β)中角的内在联系,学生有的会发现α-β中的角β可以变为角-β,所以α-(-β)=α+β〔也有的会根据加减运算关系直接把和角α+β化成差角α-(-β)的形式〕.这时教师适时引导学生转移到公式C (α-β)上来,这样就很自然地得到cos(α+β)=cos [α-(-β)]=cos αcos(-β)+sin αsin(-β)=cos αcos β-sin αsin β.所以有如下公式:(α+β)对问题②,教师引导学生细心观察公式C (α+β)的结构特征,可知“两角和的余弦,等于这两角的余弦积减去这两角的正弦积”,同时让学生对比公式C (α-β)进行记忆,并填空:cos75°=cos(_________)==__________=___________.对问题③,上面学生推得了两角和与差的余弦公式,教师引导学生观察思考,怎样才能得到两角和与差的正弦公式呢?我们利用什么公式来实现正、余弦的互化呢?学生可能有的想到利用诱导公式⑸⑹来化余弦为正弦(也有的想到利用同角的平方和关系式sin 2α+cos 2α=1来互化,此法让学生课下进行),因此有sin(α+β)=cos [2π-(α+β)]=cos [(2π-α)-β]=cos(2π-α)cos β+sin(2π-α)sin β =sin αcos β+cos αsin β.在上述公式中,β用-β代之,则sin(α-β)=sin [α+(-β)]=sin αcos(-β)+cos αsin(-β)=sin αcos β-cos αsin β. (α+β)(α-β).同时进一步体会本节公式的探究过程及公式变化特点,体验三角公式的这种简洁美、对称美.为强化记忆,教师可让学生填空,如sin(θ+φ)=___________,sin 75sin 72cos 75cos 72ππππ+=__________. 对问题⑥,教师引导学生思考,在我们推出了公式C (α-β)、C (α+β)、S (α+β)、S (α-β)后,自然想到两角和与差的正切公式,怎么样来推导出tan(α-β)=?,tan(α+β)=?呢?学生很容易想到利用同角三角函数关系式,化弦为切得到.在学生探究推导时很可能想不到讨论,这时教师不要直接提醒,让学生自己悟出来.当cos(α+β)≠0时,tan(α+β)=.sin sin cos cos sin cos cos sin )cos()sin(βαβαβαβββ-+=++a a 如果cos αcos β≠0,即cos α≠0且cos β≠0时,分子、分母同除以cos αcos β得tan(α+β)=)tan(tan 1tan tan βαβα--+,据角α、β的任意性,在上面的式子中,β用-β代之,则有tan(α-β)=.tan tan 1tan tan )tan(tan 1)tan(tan βαβαβαβα+-=---+ 由此推得两角和、差的正切公式,简记为T (α-β)、T (α+β).对问题⑥,让学生自己联想思考,两角和与差的正切公式中α、β、α±β的取值是任意的吗?学生回顾自己的公式探究过程可知,α、β、α±β都不能等于2π+k π(k ∈Z ),并引导学生分析公式结构特征,加深公式记忆.对问题⑦⑧,教师与学生一起归类总结,我们把前面六个公式分类比较可得C (α+β)、S (α+β)、T (α+β)叫和角公式;S (α-β)、C (α-β)、T (α-β)叫差角公式.并由学生归纳总结以上六个公式的推导过程,从而得出以下逻辑联系图.可让学生自己画出这六个框图.通过逻辑联系图,深刻理解它们之间的内在联系,借以理解并灵活运用这些公式.同时教师应提醒学生注意:不仅要掌握这些公式的正用,还要注意它们的逆用及变形用.如两角和与差的正切公式的变形式tan α+tan β=tan(α+β)(1-tan αtan β),tan α-tan β=tan(α-β)(1+tan αtan β),在化简求值中就经常应用到,使解题过程大大简化,也体现了数学的简洁美.对于两角和与差的正切公式,当tan α,tan β或tan (α±β)的值不存在时,不能使用T (α±β)处理某些有关问题,但可改用诱导公式或其他方法,例如:化简tan(2π-β),因为tan 2π的值不存在,所以改用诱导公式tan(2π-β)=βββπβπsin cos )2cos()2sin(=--来处理等.(三)应用示例思路1例1 已知sin α=53-,α是第四象限角,求sin(4π-α),cos(4π+α),tan(4π-α)的值. 活动:教师引导学生分析题目中角的关系,在面对问题时要注意认真分析条件,明确要求.再思考应该联系什么公式,使用公式时要有什么准备,准备工作怎么进行等.例如本题中,要先求出cos α,tan α的值,才能利用公式得解,本题是直接应用公式解题,目的是为了让学生初步熟悉公式的应用,教师可以完全让学生自己独立完成.解:由sin α=53-,α是第四象限角,得cos α=54)53(1sin 122=--=-a . ∴tan α=a a cos sin =43-. 于是有sin(4π-α)=sin 4πcos α-cos 4πsin α=,1027)53(225422=-⨯-⨯ cos(4π+α)=cos 4πcos α-sin 4πsin α=,1027)53(225422=-⨯-⨯ tan(α-4π)=4tan tan 14tan tan ππa a +-=a a tan 11tan +-=7)43(1143-=-+--. 点评:本例是运用和差角公式的基础题,安排这个例题的目的是为了训练学生思维的有序性,逐步培养他们良好的思维习惯.变式训练1.不查表求cos75°,tan105°的值.解:cos75°=cos(45°+30°)=cos45°cos30°-sin45°sin30° =42621222322-=⨯-⨯, tan105°=tan(60°+45°)= 311345tan 60tan 145tan 60tan -+=-+ =-(2+3). 2.设α∈(0,2π),若sin α=53,则2sin(α+4π)等于( ) A.57 B.51 C.27 D.4 答案:A例 2 已知sin α=32,α∈(2π,π),cos β=43-,β∈(π,23π).求sin(α-β),cos(α+β),tan(α+β).活动:教师可先让学生自己探究解决,对探究困难的学生教师给以适当的点拨,指导学生认真分析题目中已知条件和所求值的内在联系.根据公式S (α-β)、C (α+β)、T (α+β)应先求出cosα、sin β、tan α、tan β的值,然后利用公式求值,但要注意解题中三角函数值的符号.解:由sin α=32,α∈(2π,π),得 cos α=a 2sin 1--=-2)32(1--=35-,∴tan α=552-. 又由cos β=31-,β∈(π,23π). sin β=β2cos 1--=47)43(12-=---, ∴tan β=37.∴sin(α-β)=sin αcos β-cos αsin β =32×(43-)-(12356)47()35(--=-⨯-. ∴cos(α+β)=cos αcos β-sin αsin β=(35-)×(43-)-32×(47-) =.127253+∴tan(α+β)=35215755637)552(137552tan tan 1tan tan ++-=⨯--+-=-+βαβα=17727532+-. 点评:本题仍是直接利用公式计算求值的基础题,其目的还是让学生熟练掌握公式的应用,训练学生的运算能力.变式训练引导学生看章头图,利用本节所学公式解答课本章头题,加强学生的应用意识.解:设电视发射塔高CD=x 米,∠CAB=α,则sin α=6730, 在Rt △ABD 中,tan(45°+α)=3030+x tan α. 于是x=30tan )45tan(30-+αα , 又∵sin α=6730,α∈(0,2π),∴cos α≈6760,tan α≈21. tan(45°+α)=211211tan 1tan 1-+≈-+αα=3, ∴x=21330⨯-30=150(米). 答:这座电视发射塔的高度约为150米.例3 在△ABC 中,sinA=53(0°<A<45°),cosB=135(45°<B<90°),求sinC 与cosC 的值. 活动:本题是解三角形问题,在必修5中还作专门的探究,这里用到的仅是与三角函数诱导公式与和差公式有关的问题,难度不大,但应是学生必须熟练掌握的.同时也能加强学生的应用意识,提高学生分析问题和解决问题的能力.教师可让学生自己阅读、探究、讨论解决,对有困难的学生教师引导学生分析题意和找清三角形各角之间的内在联系,从而找出解决问题的路子.教师要提醒学生注意角的范围这一暗含条件.解:∵在△ABC 中,A+B+C=180°,∴C=180°-(A+B).又∵sinA=53且0°<A<45°,∴cosA=54. 又∵cosB=135且45°<B<90°,∴sinB=1312. ∴sinC=sin [180°-(A+B)]=sin(A+B)=sinAcosB+cosAsinB =53×135+54×1312=6563, cosC=cos [180°-(A+B)]=-cos(A+B)=sinAsinB-cosAcosB=53×1312-54×135=6516. 点评:本题是利用两角和差公式,来解决三角形问题的典型例子,培养了学生的应用意识,也使学生更加认识了公式的作用,解决三角形问题时,要注意三角形内角和等于180°这一暗含条件.变式训练在△ABC 中,已知sin(A-B)cosB+cos(A-B)sinB ≥1,则△ABC 是( )A.锐角三角形B.钝角三角形C.直角三角形D.等腰非直角三角形答案:C思路2例1 若sin(43π+α)=135,cos(4π-β)=53,且0<α<4π<β<43π,求cos(α+β)的值. 活动:本题是一个典型的变角问题,也是一道经典例题,对训练学生的运算能力以及逻辑思维能力很有价值.尽管学生思考时有点难度,但教师仍可放手让学生探究讨论,教师不可直接给出解答.对于探究不出的学生,教师可恰当点拨引导,指导学生解决问题的关键是寻找所求角与已知角的内在联系,引导学生理清所求的角与已知角的关系,观察选择应该选用哪个公式进行求解,同时也要特别提醒学生注意:在求有关角的三角函数值时,要特别注意确定准角的范围,准确判断好三角函数符号,这是解决这类问题的关键.学生完全理清思路后,教师应指导学生的规范书写,并熟练掌握它.对于程度比较好的学生可让其扩展本题,或变化条件,或变换所求的结论等.如教师可变换α,β角的范围,进行一题多变训练,提高学生灵活应用公式的能力,因此教师要充分利用好这个例题的训练价值.解:∵0<α<4π<β<43π,∴43π<43π+α<π,-2π<4π-β<0, 又已知sin(43π+α)=135,cos(4π-β)=53, ∴cos(43π+α)=1312-,sin(4π-β)=54-. ∴cos(α+β)=sin [2π+(α+β)]=sin [(43π+α)-(4π-β)] =sin(43π+α)cos(4π-β)-cos(43π+α)sin(4π-β) =135×53-(1312-)×(54-)=6533-. 本题是典型的变角问题,即把所求角利用已知角来表示,实际上就是化归思想.这需要巧妙地引导,充分让学生自己动手进行角的变换,培养学生灵活运用公式的能力.变式训练已知α,β∈(43π,π),sin(α+β)=53-,sin(β-4π)=1312,求cos(α+4π)的值. 解:∵α,β∈(43π,π),sin(α+β)=53-,sin(β-4π)=1312, ∴23π<α+β<2π,2π<β-4π<43π.∴cos(α+β)=54,cos(β-4π)=135-. ∴cos(α+4π)=cos [(α+β)-(β-4π)] =cos(α+β)cos(β-4π)+sin(α+β)sin(β-4π) =54×(135-)+(53-)×1312=6556-.例2 化简.sin sin )sin(sin sin )sin(sin sin )sin(aa a a θθθβθβββ-+-+- 活动:本题是直接利用公式把两角的和、差化为两单角的三角函数的形式,教师可以先让学生自己独立地探究,然后进行讲评.解:原式=aa a a a a sin sin sin cos cos sin sin sin sin cos cos sin sin sin sin cos cos sin θθθθβθβθββββ-+-+- =a a a a a a a a sin sin sin sin sin cos cos sin sin sin sin sin sin cos sin cos sin sin sin sin sin sin sin cos sin cos sin βθβθβθθβθβθβθβθβαθβ-+-+- =asin sin sin 0βθ =0.点评:本题是一个很好的运用公式进行化简的例子,通过学生独立解答,培养学生熟练运用公式的运算能力.变式训练 化简)cos(sin sin 2cos sin 2)sin(βαβαβαβα++-+ 解:原式=βαβαβαβαβαβαsin sin cos cos sin sin 2cos sin 2sin cos cos sin -+- =).tan()cos()sin(cos cos sin sin cos sin sin cos αβαβαββαβαβαβα-=--=+-(四)作业已知0<β<4π,4π<α<43π,cos(4π-α)=53,sin(43π+β)=135,求sin(α+β)的值. 解:∵4π<α<43π,∴2π-<4π-α<0.∴sin(4π-α)=2)53(1--=54-.又∵0<β<4π,∴43π<43π+β<π,cos(43π+β)=2)135(1--=1312-.∴sin(α+β)=-cos(2π+α+β)=-cos [(43π+β)-(4π-α)]=-cos(43π+β)cos(4π-α)-sin(43π+β)sin(4π-α)=-(1312-)×53135-×(54-)=6556.(五)课堂小结1.先由学生回顾本节课都学到了哪些数学知识和数学方法,有哪些收获与提高,在公式推导中你悟出了什么样的数学思想?对于这六个公式应如何对比记忆?其中正切公式的应用有什么条件限制?怎样用公式进行简单三角函数式的化简、求值与恒等式证明.2.教师画龙点睛:我们本节课要理解并掌握两角和与差的正弦、余弦、正切公式及其推导,明白从已知推得未知,理解数学中重要的数学思想——转化思想,并要正确熟练地运用公式解题.在解题时要注意分析三角函数名称、角的关系,一个题目能给出多种解法,从中比较最佳解决问题的途径,以达到优化解题过程,规范解题步骤,领悟变换思路,强化数学思想方法之目的.3.1.2两角和与差的正弦、余弦、正切公式(2)教案教学分析1.两角和与差的正弦、余弦、正切公式是在研究了两角差的余弦公式的基础上,进一步研究具有“两角和差”关系的正弦、余弦、正切公式的.在这些公式的推导中,教科书都把对照、比较有关的三角函数式,认清其区别,寻找其联系和联系的途径作为思维的起点,如比较cos(α-β)与cos(α+β),它们都是角的余弦只是角形式不同,但不同角的形式从运算或换元的角度看都有内在联系,即α+β=α-(-β)的关系,从而由公式C (α-β)推得公式C (α+β),又如比较sin(α-β)与cos(α-β),它们包含的角相同但函数名称不同,这就要求进行函数名的互化,利用诱导公式(5)(6)即可推得公式S (α-β)、S (α+β)等.2.通过对“两角和与差的正弦、余弦、正切公式”的推导,揭示了两角和、差的三角函数与这两角的三角函数的运算规律,还使学生加深了数学公式的推导、证明方法的理解.因此本节内容也是培养学生运算能力和逻辑思维能力的重要内容,对培养学生的探索精神和创新能力,发现问题和解决问题的能力都有着十分重要的意义.3.本节的几个公式是相互联系的,其推导过程也充分说明了它们之间的内在联系,让学生深刻领会它们的这种联系,从而加深对公式的理解和记忆.本节几个例子主要目的是为了训练学生思维的有序性,逐步培养他们良好的思维习惯,教学中应当有意识地对学生的思维习惯进行引导,例如在面对问题时,要注意先认真分析条件,明确要求,再思考应该联系什么公式,使用公式时要具备什么条件等.另外,还要重视思维过程的表述,不能只看最后结果而不顾过程表述的正确性、简捷性等,这些都是培养学生三角恒等变换能力所不能忽视的. 二、三维目标1.知识与技能:在学习两角差的余弦公式的基础上,通过让学生探索、发现并推导两角和与差的正弦、余弦、正切公式,了解它们之间的内在联系,并通过强化题目的训练,加深对公式的理解,培养学生的运算能力及逻辑推理能力,从而提高解决问题的能力. 2.过程与方法:通过两角和与差的正弦、余弦、正切公式的运用,会进行简单的求值、化简、恒等证明,使学生深刻体会联系变化的观点,自觉地利用联系变化的观点来分析问题,提高学生分析问题解决问题的能力.3.情感态度与价值观:通过本节学习,使学生掌握寻找数学规律的方法,提高学生的观察分析能力,培养学生的应用意识,提高学生的数学素质. 三、重点难点教学重点:两角和与差的正弦、余弦、正切公式及其推导. 教学难点:灵活运用所学公式进行求值、化简、证明. 四、课时安排 2课时五、教学设想 (一)导入新课思路 1.(复习导入)让学生回忆上节课所学的六个公式,并回忆公式的来龙去脉,然后让一个学生把公式默写在黑板上或打出幻灯.教师引导学生回顾比较各公式的结构特征,说出它们的区别和联系,以及公式的正用、逆用及变形用,以利于对公式的深刻理解.这节课我们将进一步探究两角和与差的正弦、余弦、正切公式的灵活应用.思路2.(问题导入)教师可打出幻灯,出示一组练习题让学生先根据上节课所学的公式进行解答.1.化简下列各式(1)cos (α+β)cos β+sin (α+β)sin β;(2)cos sin 1tan cos sin cos sin sin 22---+--x x xx x x x ; (3).tan tan cos sin )sin()sin(2222αββαβαβα+-+ 2.证明下列各式(1);tan tan 1tan tan )cos()sin(βαβαβαβα++=-+(2)tan (α+β)tan (α-β)(1-tan 2tan 2β)=tan 2α-tan 2β; (3).sin sin )cos(2sin )2sin(αββααβα=+-+答案:1.(1)cos α;(2)0;(3)1.2.证明略.教师根据学生的解答情况进行一一点拨,并对上节课所学的六个公式进行回顾复习,由此展开新课.(二)推进新课、新知探究、提出问题①请同学们回忆这一段时间我们一起所学的和、差角公式.②请同学们回顾两角和与差公式的区别与联系,可从推导体系中思考.活动:待学生稍做回顾后,教师打出幻灯,出示和与差角公式,让学生进一步在直观上发现它们内在的区别与联系,理解公式的推导充分发挥了向量的工具作用,更要体会由特殊到一般的数学思想方法.教师引导学生观察,当α、β中有一个角为90°时,公式就变成诱导公式,所以前面所学的诱导公式其实是两角和与差公式的特例.在应用公式时,还要注意角的相对性,如α=(α+β)-β,)2()2(2βαβαβα---=+等.让学生在整个的数学体系中学会数学知识,学会数学方法,更重要的是学会发现问题的方法,以及善于发现规律及其内在联系的良好习惯,提高数学素养.sin (α±β)=sin αcos β±cos αsin β〔S(α±β)〕; cos (α±β)=cos αcos βsin αsin β〔C (α±β)〕;tan (α±β)=βαβαtan tan 1tan tan ±〔T (α±β)〕.讨论结果:略.(三)应用示例思路1例1 利用和差角公式计算下列各式的值.(1)sin72°cos42°-cos72°sin42°; (2)cos20°cos70°-sin20°sin70°;(3)15tan 115tan 1-+活动:本例实际上是公式的逆用,主要用来熟悉公式,可由学生自己完成.对部分学生,教师点拨学生细心观察题中式子的形式有何特点,再对比公式右边,马上发现(1)同公式S (α-β)的右边,(2)同公式C (α+β)右边形式一致,学生自然想到公式的逆用,从而化成特殊角的三角函数,并求得结果.再看(3)式与T (α+β)右边形式相近,但需要进行一定的变形.又因为tan45°=1,原式化为15tan 45tan 115tan 45tan -+,再逆用公式T (α+β)即可解得.解:(1)由公式S (α-β)得 原式=sin(72°-42°)=sin30°=21. (2)由公式C (α+β)得原式=cos(20°+70°)=cos90°=0. (3)由公式T (α+β)得原式=15tan 45tan 115tan 45tan -+=tan(45°+15°)=tan60°=3. 点评:本例体现了对公式的全面理解,要求学生能够从正、反两个角度使用公式.与正用相比,反用表现的是一种逆向思维,它不仅要求有一定的反向思维意识,对思维的灵活性要求也高,而且对公式要有更全面深刻的理解.变式训练 1.化简求值:(1)cos44°sin14°-sin44°cos14°; (2)sin14°cos16°+sin76°cos74°;(3)sin(54°-x)cos(36°+x)+cos(54°-x)sin(36°+x).解:(1)原式=sin(14°-44°)=sin(-30°)=-sin30°=21-. (2)原式=sin14°cos16°+cos14°sin16°=sin(14°+16°)=sin30°=21. (3)原式=sin [(54°-x)+(36°+x)]=sin90°=1.2.计算.75tan 175tan 1+- 解:原式=75tan 45tan 175tan 45tan +-=tan(45°-75°)=tan(-30°)=-tan30°=33-.例2 已知函数f(x)=sin(x+θ)+cos (x-θ)的定义域为R ,设θ∈[0,2π],若f(x)为偶函数,求θ的值.活动:本例是一道各地常用的、基础性较强的综合性统考题,其难度较小,只需利用偶函数的定义,加上本节学到的两角和与差的三角公式展开即可,但不容易得到满分.教师可先让学生自己探究,独立完成,然后教师进行点评.解:∵f(x)为偶函数,∴f(-x)=f(x),即sin(-x+θ)+cos(-x-θ)=sin(x+θ)+cos(x-θ), 即-sinxcos θ+cosxsin θ+cosxcos θ-sinxsin θ =sinxcos θ+cosxsin θ+cosxcos θ+sinxsin θ. ∴sinxcos θ+sinxsin θ=0.∴sinx(sin θ+cos θ)=0对任意x 都成立.∴2sin(θ+4π)=0,即sin(θ+4π)=0. ∴θ+4π=k π(k ∈Z ).∴θ=k π-4π(k ∈Z ).又θ∈[0,2π),∴θ=43π或θ=47π.点评:本例学生可能会根据偶函数的定义利用特殊值来求解.教师应提醒学生注意,如果将本例变为选择或填空,可利用特殊值快速解题,作为解答题利用特殊值是不严密的,以此训练学生逻辑思维能力.变式训练 已知:2π<β<α<43π,cos(α-β)=1312,sin(α+β)=54-,求cos2β的值.解:∵2π<β<α<43π,∴0<α-β<4π,π<α+β<23π.又∵cos(α-β)=1312,sin(α+β)= 54-,∴sin(α-β)=135,cos(α+β)=53-.∴cos2β=cos [(α+β)-(α-β)]=cos(α+β)cos(α-β)+sin(α+β)sin(α-β) =53-×1312+(54-)×135=6556-.例3 求证:cos α+3sin α=2sin(6π+α). 活动:本题虽小但其意义很大,从形式上就可看出来,左边是两个函数,而右边是一个函数,教师引导学生给予足够的重视.对于此题的证明,学生首先想到的证法就是把等式右边利用公式S (α+β)展开,化简整理即可得到左边此为证法,这是很自然的,教师要给予鼓励.同时教师可以有目的的引导学生把等式左边转化为公式S (α+β)的右边的形式,然后逆用公式化简即可求得等式右边的式子,这种证明方法不仅仅是方法的变化,更重要的是把两个三角函数化为一个三角函数.证明:方法一:右边=2(sin6πcos α+cos 6πsin α)=2(21cos α+23sin α)=cos α+3sin α=左边.方法二:左边=2(21cos α+23sin α)=2(sin 6πcos α+cos 6πsin α)=2sin(6π+α)=右边. 点评:本题给出了两种证法,方法一是正用公式的典例,而方法二则是逆用公式证明的,此法也给了我们一种重要的转化方法,要求学生熟练掌握其精神实质.本例的方法二将左边的系数1与3分别变为了21与23,即辅助角6π的正、余弦.关于形如asinx+bcosx (a ,b 不同时为零)的式子,引入辅助角变形为Asin(x+φ)的形式,其基本想法是“从右向左”用和角的正弦公式,把它化成Asin(x+φ)的形式.一般情况下,如果a=AC os φ,b=Asin φ,那么asinx+bcosx=A(sinxcos φ+cosxsin φ)=Asin(x+φ).由sin 2φ+cos 2φ=1,可得 A 2=a 2+b 2,A=±22b a +,不妨取A=22b a +,于是得到cos φ=22ba a +,sin φ=22b a b +,从而得到tan φ=ba ,因此asinx+bcosx=22b a +sin(x+φ),通过引入辅助。
人教版高一数学必修4 第三章 《三角恒等变换》单元教学设计

三角恒等变换 单元教学设计一、本单元内容在《课程标准》与《考试大纲》中的目标表述1、本单元教学内容的范围3.1两角和与差的正弦、余弦和正切公式 3.1.1 两角差的余弦公式3.1.2 两角和与差的正弦、余弦、正切公式 3.1.3二倍角的正弦、余弦、正切公式 3.2 简单的三角恒等变换2、本单元教学内容在模块内容体系中的地位和作用变换是数学的重要工具,也是数学学习的主要对象之一.代数变换是学生熟悉的,与代数变换一样,三角变换也是只变其形不变其质的,它可以揭示那些外形不同但实质相同的三角函数式之间的内在联系.在本册第一章,学生接触了同角三角函数式的变换.在本章,学生将运用向量方法推导两角差的余弦公式,由此出发推导其它三角函数恒等变换公式,并运用这些公式进行简单的三角恒等变换.通过本章学习,要进一步提高学生的推理能力和运算能力.三角恒等变换在数学及应用科学中应用广泛,同时有利于发展学生的推理能力和计算能力.本章将通过三角恒等变换揭示一些问题的数学本质.3、本单元教学内容总体教学目标(1)和差角公式与二倍角公式经历用向量的数量积推导出两角差的余弦公式的过程,掌握用向量证明数学问题的方法,进一步体会向量法的作用.能从两角差的余弦公式导出两角和的余弦公式,以及两角和与差的正弦、正切公式,了解公式间的内在联系.能应用公式解决比较简单的有关应用问题.经历运用正弦、余弦、正切的和角公式,推导出它们对应的倍角公式及公式2C的两种变形,再运用二倍角的变形公式推导出半角的正弦、余弦和正切公式的过程,掌握倍角公式和半角公式,能正确运用公式进行简单的三角函数式的化简、求值、恒等式的证明.了解公式之间的内在联系,培养学生的逻辑推理能力.(2)简单的三角变换运用三角变换公式进行简单的三角变换,通过公式的综合运用,掌握三角变换的特点,预测变换的目标,设计变换的过程.4、本单元教学内容重点和难点分析(1)两角和与差的正弦、余弦、和正切公式重点:两角和与差的余弦公式求值和证明;难点:两角和的余弦公式的推导.(2)简单的三角变换重点:运用三角变换公式进行简单的三角恒等变换;难点:公式的综合运用,根据三角变换的特点,设计变换的过程.5.人教A版教材特点用向量证明差角公式,引导学生用向量研究三角问题;建立和角公式与旋转变换之间的联系;引导学生独立的由和角公式推导出倍角公式与和差化积、积化和差;和角公式在三角恒等变换及三角形计算中的应用.提供了“练习题”,“习题A、习题B”,“复习参考题A ”,“复习参考题B”,等多种形式的练习方式,为教学提供了丰富的可选择的空间.三、与本单元教学内容相适应的教学方式和教学方法概述1、选取与内容密切相关的,典型的,丰富的和学生熟悉的素材,用生动活泼的语言,创设能够体现数学的概念和结论,数学的思想和方法,以及数学应用的学习情境,使学生产生对数学的亲切感,引发学生“看个究竟”的冲动,以达到培养其兴趣的目的.通过“观察”,“思考”,“探究”等栏目,引发学生的思考和探索活动,切实改进学生的学习方式.在教学中强调类比,推广,特殊化,化归等数学思想方法,尽可能养成其逻辑思维的习惯.本单元公式较多,有些是要求学生记忆的,有些是不要求学生记忆的,但要求会推导、会运用;建议在教学中,注重公式内在的联系,尽量引导学生利用已有知识推导公式;在推导中记忆公式,运用公式,解决实际问题;四、设计意图与特色本章的内容分为两节:“两角和与差的正弦、余弦和正切公式”,“简单的三角恒等变换”,在学习本章之前我们学习了向量的相关知识,因此设计的意图是选择两角差的余弦公式作为基础,运用向量的知识来予以证明,降低了难度,使学生容易接受;本章是以两角差的余弦公式作为基础来推导其它的公式;本章在内容的安排上有明暗两条线,明线是建立公式,学会变换,暗线是发展推理和运算的能力,因此在本章全部内容的安排上,特别注意恰时恰点的提出问题,引导学生用对比、联系、化归的观点去分析、处理问题,强化运用数学思想方法指导设计变换思路的意识;本章在内容的安排上贯彻“删减繁琐的计算、人为技巧化的难题和过分强调细枝末叶的内容”的理念,严格控制了三角恒等变换及其应用的繁、难程度,尤其注意不以半角公式、积化和差、和差化积公式作为变换的依据,而只把这些公式的推导作为变换的基本练习.五、本单元教学内容及课时安排建议本章教学时间约8课时,具体分配如下:3.1两角和与差的正弦、余弦、和正切公式约3课时3.2简单的恒等变换约3课时复习约2课时六、课时教学设计课题§3.1 两角和与差的正弦、余弦和正切公式一、课标要求:本节的中心内容是建立相关的十一个公式,通过探索证明和初步应用,体会和认识公式的特征及作用.二、设计意图与特色本节内容都是用例题来展现的.通过例题的解答,引导学生对变换对象目标进行对比、分析,促使学生形成对解题过程中如何选择公式,如何根据问题的条件进行公式变形,以及变换过程中体现的换元、逆向使用公式等数学思想方法的认识,从而加深理解变换思想,提高学生的推理能力.三、学习重点与难点1.重点:引导学生通过独立探索和讨论交流,会导出两角和差的三角函数的十一个公式,并了解它们的内在联系,为运用这些公式进行简单的恒等变换打好基础;2.难点:两角差的余弦公式的探索与证明.课题 3.1.1 两角差的余弦公式(第一课时)一、学习目标(1)掌握借助单位圆,运用三角函数定义和向量夹角的余弦公式推导出两角差的余弦公式;(2)通过简单运用,使学生初步理解公式的结构及功能,为建立其它和(差)公式打好基础;(3)通过教学活动,使学生经历发现、猜想、论证的数学化的过程,并体验到数学学习的严谨、求实的科学态度,逐步培养学生探索问题的精神.二、学习重、难点1.重点:通过探索得到两角差的余弦公式;2.难点:探索过程的组织和适当引导,这里不仅有学习积极性的问题,还有探索过程必用的基础知识是否已经具备的问题,运用已学知识和方法的能力问题,等等.三、学习过程1、学习引导探究(一):两角差的余弦公式思考1:设α,β为两个任意角, 你能判断cos(α-β)=cosα-cosβ恒成立吗?思考2:我们设想cos(α-β)的值与α,β的三角函数值有一定关系,观察下表中的数据,你有什么发现?思考3:一般地,你猜想cos(α-β)等于什么?思考4:如图,设α,β为锐角,且α>β,角α的终边与单位圆的交点为P 1, ∠P 1OP =β,那么cos(α-β)表示哪条线段长?思考5:上图中,如何用线段分别表示sin β和cos β?思考6:cos αcos β=OAcos α,它表示哪条线段长? sin αsin β=PAsin α,它表示哪条线段长?思考7:利用OM =OB +BM =OB +CP 可得什么结论?思考8:上述推理能说明对任意角α,β,都有cos(α-β)=cos αcos β+sin αsin β成立吗?思考9:根据cos αcos β+sin αsin β的结构特征,你能联想到一个相关计算原理吗?思考10:如图,设角α,β的终边与单位圆的交点分别为A 、B ,则向量OA 、OB 的坐标分别是什么?其数量积是什么?思考11:向量OA 与OB 的夹角θ与α、β有什么关系?根据量积定义,OA ⋅OB 等于什么?由此可得什么结论?思考12:公式cos(α-β)=cos αcos β+sin αsin β称为差角的余弦公式,记作()C αβ-,该公式有什么特点?如何记忆? 探究(二):两角差的余弦公式的变通思考1:若已知α+β和β的三角函数值,如何求cos α的值?思考2:利用α-(α-β)=β可得cos β等于什么?思考3:若cos α+cos β=a ,sin α+sin β=b ,则cos(α-β)等于什么?思考4:若cos α-cos β=a ,sin α-sin β=b ,则cos(α-β)等于什么?2、随堂练习⑴、________15cos =⑵、)cos(),23,(,43cos ),,2(,32sin βαππββππαα-∈-=∈=求已知 ⑶、15sin cos 173πθθθ=-已知,是第二象限角,求()的值3、知识拓展例11cos sin 7αβααββ=+=已知,为锐角,,(),求cos 例2 已知1cos()cos sin()sin,3且⎪⎭⎫⎝⎛∈ππα2,23 , 求)4cos(πα-的值. 四、反思小结1.在差角的余弦公式的形成过程中,蕴涵着丰富的数学思想、方法和技巧,如数形结合,化归转换、归纳、猜想、构造、换元、向量等,我们要深刻理解和领会.2.已知一个角的正弦(或余弦)值,求该角的余弦(或正弦)值时, 要注意该角所在的象限,从而确定该角的三角函数值符号.3.在差角的余弦公式中,α,β既可以是单角,也可以是复角,运用时要注意角的变换,如,2β=(α+β)-(α-β) 等. 同时,公式的应用具有灵活性,解题时要注意正向、逆向和变式形式的选择.五、自我测评1cos79cos34sin 79sin34 +=、() A 12B 1 CD 222、4,(,),cos()( )524ππααπα=-∈-=已知cos 则B -C -D 10101010AA cos sin cos sin2012AB 3、在平面直角坐标系中,已知两点(80,80),B(20,),则的值是( )A14sin sin 1cos ,cos()2αβαβαβ-=-=--=、若则 5cos cos cos 0,sin sin sin 0,cos()αβγαβγαβ++=++=-=、若则1116cos cos cos 714αβααββ=+=-、已知,都是锐角,,(),求的值。
第三章三角恒等变换教案

高中数学必修4 第3章 三角恒等变换 3.1.1 两角差的余弦公式一、教学目标掌握用向量方法建立两角差的余弦公式.通过简单使用,使学生初步理解公式的结构及其功能,为建立其它和(差)公式打好基础. 二、教学重、难点1. 教学重点:通过探索得到两角差的余弦公式;2. 教学难点:探索过程的组织和适当引导,这里不但有学习积极性的问题,还有探索过程必用的基础知识是否已经具备的问题,使用已学知识和方法的水平问题,等等. 三、教学设想: (一)导入:问题1: 我们在初中时就知道 2cos 452=,3cos302=,由此我们能否得到()cos15cos 4530?=-=大家能够猜测,是不是等于cos 45cos30-呢?根据我们在第一章所学的知识可知我们的猜测是错误的!下面我们就一起探讨两角差的余弦公式()cos ?αβ-= (二)探讨过程:在第一章三角函数的学习当中我们知道,在设角α的终边与单位圆的交点为1P ,cos α等于角α与单位圆交点的横坐标,也能够用角α的余弦线来表示。
思考?.1角函数线来探求公式怎样联系单位圆上的三(1) 怎样构造角β和角αβ-?(注意:要与它们的正弦线、余弦线联系起来.)?)2(的余弦线和余弦线的正弦线怎样作出角βαβα-,、、思考2:怎样联系向量的数量积探求公式?(1)结合图形,明确应该选择哪几个向量,它们是怎样表示的?(2)怎样利用向量的数量积的概念的计算公式得到探索结果? 两角差的余弦公式:βαβαβαsin sin cos cos )cos(⋅+⋅=-(三)例题讲解例1、利用和、差角余弦公式求cos 75、cos15的值. 解:分析:把75、15构造成两个特殊角的和、差.()231cos75cos 4530cos 45cos30sin 45sin 30222=+=-=⨯=()231cos15cos 4530cos 45cos30sin 45sin 302222=-=+=⨯=点评:把一个具体角构造成两个角的和、差形式,有很多种构造方法,例如:()cos15cos 6045=-,要学会灵活使用.例2、已知4sin 5α=,5,,cos ,213παπββ⎛⎫∈=- ⎪⎝⎭是第三象限角,求()cos αβ-的值.解:因为,2παπ⎛⎫∈ ⎪⎝⎭,4sin 5α=由此得3cos 5α===-又因为5cos ,13ββ=-是第三象限角,所以12sin 13β===-所以3541233cos()cos cos sin sin 51351365αβαβαβ⎛⎫⎛⎫⎛⎫-=+=-⨯-+⨯-=- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭点评:注意角α、β的象限,也就是符号问题.思考:此题中没有),2ππα⎝⎛∈,呢? (四)练习:不查表计算以下各式的值:︒︒+︒︒20sin 80sin 20cos 80cos 1)(︒+︒15sin 2315cos 212)(解: ︒︒+︒︒20sin 80sin 20cos 80cos 1)( 2160cos )2080cos(=︒=︒-︒= (五)小结:两角差的余弦公式,首先要理解公式结构的特征,理解公式的推导过程,熟知由此衍变的两角和的余弦公式.在解题过程中注意角α、β的象限,也就是符号问题,学会灵活使用.(1)牢记公式.S S C C C ⋅+⋅=-)(βα(2)在“给值求值”题型中灵活处理已、未知关系. (六)作业3.1.2两角和与差的正弦、余弦、正切公式一、教材分析本节的主要内容是两角和与差的正弦、余弦和正切公式,为了引起学生学习本章的兴趣,理解以两角差的余弦公式为基础,推导两角和、差正弦和正切公式的方法,体会三角恒等变换特点的过程,理解推导过程,掌握其应用从而激发学生对本章内容的学习兴趣和求知欲。
人教版高中必修4(B版)第三章三角恒等变换教学设计

人教版高中必修4(B版)第三章三角恒等变换教学设计一、教学目标1.理解三角恒等变换的概念和性质。
2.掌握正弦、余弦、正切的恒等变换公式。
3.能够使用三角函数的恒等变换公式求解三角函数的值。
二、教学重点难点1.三角恒等变换概念和性质的理解。
2.正弦、余弦、正切的恒等变换公式的记忆和应用。
三、教学内容及方法1. 教学内容1.三角恒等变换的概念和性质。
2.正弦、余弦、正切的恒等变换公式。
2. 教学方法1.给出例题,并通过例题引出概念和性质。
2.讲解正弦、余弦、正切的恒等变换公式,并进行示例演练。
3.练习题的讲解和答疑。
四、教学过程设计1. 导入环节1.介绍本节课的主题和目标。
2.提问学生对三角恒等变换的了解和认识,引出三角恒等变换的概念和性质。
2. 讲解环节1.以例题的形式引出正弦、余弦、正切的恒等变换公式,讲解公式的推导过程和应用方法。
2.通过多组例题演示如何使用恒等变换公式求解三角函数的值。
3. 练习环节1.发放练习题,让学生进行练习并自行检验答案。
2.推广题目,让学生进行自主探究,并对想法进行讨论和答疑。
五、教学评估1.通过课后作业检查和测试等方式进行评估,考察学生对三角恒等变换的掌握情况。
2.针对评估结果进行适当调整和讲解,弥补学生掌握不足和漏洞。
六、教学资源1.PowerPoint演示文稿。
2.练习题和解答。
3.可视化三角恒等变换的工具软件,如GeoGebra或Desmos。
七、反思总结三角恒等变换是高中数学中比较基础而又重要的概念之一。
因此,在教学过程中,既要重视学生的掌握程度,也要注意教学内容和方式的生动和丰富。
此次教学中,我结合多组例题,并使用工具软件进行可视化演示,使学生可以更加深入地理解三角恒等变换的概念和性质,同时也更好地掌握了正弦、余弦、正切的恒等变换公式。
最后课后的总结和评估,也能帮助学生更深入地理解和记忆知识点。
人教A版高中数学必修4第三章 三角恒等变换3.2 简单的三角恒等变换教案(1)

3.2《简单的三角恒等变换》教学设计【教学目标】1会用已学公式进行三角函数式的化简、求值和证明,引导学生推导半角公式,积化和差、和差化积公式(公式不要求记忆),2使学生进一步提高运用转化、换元、方程等数学思想解决问题的能力. 【导入新课】 习引入:复习倍角公式2S α、2C α、2Tα先让学生默写三个倍角公式,注意等号两边角的关系,特别注意2C α.既然能用单角表示倍角,那么能否用倍角表示单角呢? 新授课阶段半角公式的推导及理解 : 例1、 试以cos α表示222sin,cos ,tan 222ααα.解析:我们可以通过二倍角2cos 2cos 12αα=-和2cos 12sin 2αα=-来做此题.(二倍角公式中以α代2α,2α代α) 解:因为2cos 12sin2αα=-,可以得到21cos sin22αα-=;因为2cos 2cos 12αα=-,可以得到21cos cos 22αα+=. 两式相除可以得到222sin 1cos 2tan 21cos cos 2ααααα-==+.点评:⑴以上结果还可以表示为:1cos sin 221cos cos22αααα-=±+=±1cos tan 21cos ααα-=±+并称之为半角公式(不要求记忆),符号由2α角的象限决定.⑵降倍升幂公式和降幂升倍公式被广泛用于三角函数式的化简、求值、证明. ⑶代数式变换往往着眼于式子结构形式的变换,三角恒等变换常常首先寻找式子所包含的各个角之间的联系,并以此为依据选择可以联系他们的适当公式,这是三角式恒等变换的重要特点.例2 求证:(1)()()1sin cos sin sin 2αβαβαβ=++-⎡⎤⎣⎦; (2)sin sin 2sin cos22θϕθϕθϕ+-+=. 解析:回忆并写出两角和与两角差的正余弦公式,观察公式与所证式子的联系. 证明:(1)因为()sin αβ+和()sin αβ-是我们所学习过的知识,因此我们从等式右边着手.()sin sin cos cos sin αβαβαβ+=+;()sin sin cos cos sin αβαβαβ-=-.两式相加得()()2sin cos sin sin αβαβαβ=++-; 即()()1sin cos sin sin 2αβαβαβ=++-⎡⎤⎣⎦; (2)由(1)得()()sin sin 2sin cos αβαβαβ++-=①;设,αβθαβϕ+=-=, 那么,22θϕθϕαβ+-==.把,αβ的值代入①式中得sin sin 2sincos22θϕθϕθϕ+-+=.点评:在例2证明中用到了换元思想,(1)式是积化和差的形式,(2)式是和差化积的形式,在后面的练习当中还有六个关于积化和差、和差化积的公式.例3 求函数sin 3cos y x x =+的周期,最大值和最小值. 解析:利用三角恒等变换,先把函数式化简,再求相应的值. 解: 13sin 3cos 2sin cos 2sin 223y x x x x x π⎛⎫⎛⎫=+=+=+ ⎪ ⎪ ⎪⎝⎭⎝⎭, 所以,所求的周期22T ππω==,最大值为2,最小值为2-.点评:例3是三角恒等变换在数学中应用的举例,它使三角函数中对函数()sin y A x ωϕ=+的性质研究得到延伸,体现了三角变换在化简三角函数式中的作用.课堂小结用和(差)角公式、倍角公式进行简单的恒等变换.我们要对三角恒等变换过程中体现的换元、逆向使用公式等数学思想方法加深认识,学会灵活运用.作业课本p143 习题3.2 A 组1、(1)(5) 3 、5 拓展提升1.已知cos (α+β)cos (α-β)=31,则cos 2α-sin 2β的值为( )A .-32B .-31C .31D .32 2.在△ABC 中,若sin A sin B =cos 22C,则△ABC 是( )A .等边三角形B .等腰三角形C .不等边三角形D .直角三角形3.sin α+sin β=33(cos β-cos α),且α∈(0,π),β∈(0,π),则α-β等于( )A .-3π2 B .-3π C .3πD .3π2 4.已知cos (α+β)cos (α-β)=31,则cos 2α-sin 2β的值为( )A .-32B .-31C .31D .32 5.在△ABC 中,若sin A sin B =cos 22C,则△ABC 是( )A .等边三角形B .等腰三角形C .不等边三角形D .直角三角形6.sin α+sin β=33(cos β-cos α),且α∈(0,π),β∈(0,π),则α-β等于( )A .-3π2 B .-3πC .3πD .3π2 7.已知sin (α+β)sin (β-α)=m ,则cos 2α-cos 2β等于( ) A .-m B .m C .-4m D .4m二、填空题8.sin20°cos70°+sin10°sin50°=_________.9.已知α-β=3π2,且cos α+cos β=31,则cos (α+β)等于_________. 三、解答题10.已知f (x )=-21+2sin 225sinxx,x ∈(0,π). (1)将f (x )表示成cos x 的多项式; (2)求f (x )的最小值.12.已知△ABC 的三个内角A 、B 、C 满足:A +C =2B ,B C A cos 2cos 1cos 1-=+,求cos 2CA -的值.13. 已知sin A +sin3A +sin5A =a ,cos A +cos3A +cos5A =b , 求证:(2cos2A +1)2=a 2+b 2.14. 求证:cos 2x +cos 2(x +α)-2cos x cos αcos (x +α)=sin 2α.15. 求函数y =cos3x ·cos x 的最值.参考答案一、选择题:1.C 2. B 3. D 4.C 5. B 6. D 7. B 二、填空题:8.41 9.-97三、解答题10.解:(1)f (x )=2cos 23cos 22sin 2sin 23cos 22sin 22sin 25sinx x x xx x x x ==-=cos2x +cos x =2cos 2x +cos x-1.(2)∵f (x )=2(cos x +41)2-89,且-1≤cos x ≤1, ∴当cos x =-41时,f (x )取得最小值-89. 11 分析:本小题考查三角函数的基础知识,利用三角公式进行恒等变形和运算的能力. 解:由题设条件知B =60°,A +C =120°, ∵-︒60cos 2=-22,∴CA cos 1cos 1+=-22. 将上式化简为cos A +cos C =-22cos A cos C , 利用和差化积及积化和差公式,上式可化为 2cos2C A +cos 2CA -=-2[cos (A +C )+cos (A -C )], 将cos2C A +=cos60°=21,cos (A +C )=cos120°=-21代入上式得cos 2CA -=22-2cos (A -C ),将cos (A -C )=2cos 2(2C A -)-1代入上式并整理得42cos 2(2C A -)+2cos 2C A --32=0,即[2cos2C A --2][22cos 2CA -+3]=0. ∵22cos 2C A -+3≠0,∴2cos 2CA --2=0. ∴cos 2C A -=22.12.证明:由已知得 ⎩⎨⎧=+=+,,b A A A a A A A 3cos 2cos 3cos 23sin 2cos 3sin 2 ∴⎩⎨⎧=+=+.)12cos 2(3cos )12cos 2(3sin b A A a A A ,两式平方相加得(2cos2A +1)2=a 2+b 2. 13.证明:左边=21(1+cos2x )+21[1+cos (2x +2α)]-2cos x cos αcos (x +α) =1+21[cos2x +cos (2x +2α)]-2cos x cos αcos (x +α) =1+cos (2x +α)cos α-cos α[cos (2x +α)+cos α] =1+cos (2x +α)cos α-cos αcos (2x +α)-cos 2α =1-cos 2α=sin 2α =右边,∴原不等式成立. 14.解:y =cos3x ·cos x =21(cos4x +cos2x ) =21(2cos 22x -1+cos2x ) =cos 22x +21cos2x -21 =(cos2x +41)2-169. ∵cos2x ∈[-1,1], ∴当cos2x =-41时,y 取得最小值-169; 当cos2x =1时,y 取得最大值1.。
高中数学 第三章《三角恒等变换》教学设计 新人教A版必修4

课题:书法---写字基本知识课型:新授课教学目标:1、初步掌握书写的姿势,了解钢笔书写的特点。
2、了解我国书法发展的历史。
3、掌握基本笔画的书写特点。
重点:基本笔画的书写。
难点:运笔的技法。
教学过程:一、了解书法的发展史及字体的分类:1、介绍我国书法的发展的历史。
2、介绍基本书体:颜、柳、赵、欧体,分类出示范本,边欣赏边讲解。
二、讲解书写的基本知识和要求:1、书写姿势:做到“三个一”:一拳、一尺、一寸(师及时指正)2、了解钢笔的性能:笔头富有弹性;选择出水顺畅的钢笔;及时地清洗钢笔;选择易溶解的钢笔墨水,一般要固定使用,不能参合使用。
换用墨水时,要清洗干净;不能将钢笔摔到地上,以免笔头折断。
三、基本笔画书写1、基本笔画包括:横、撇、竖、捺、点等。
2、教师边书写边讲解。
3、学生练习,教师指导。
(姿势正确)4、运笔的技法:起笔按,后稍提笔,在运笔的过程中要求做到平稳、流畅,末尾处回锋收笔或轻轻提笔,一个笔画的书写要求一气呵成。
在运笔中靠指力的轻重达到笔画粗细变化的效果,以求字的美观、大气。
5、学生练习,教师指导。
(发现问题及时指正)四、作业:完成一张基本笔画的练习。
板书设计:写字基本知识、一拳、一尺、一寸我的思考:通过导入让学生了解我国悠久的历史文化,激发学生学习兴趣。
这是书写的起步,让学生了解书写工具及保养的基本常识。
基本笔画书写是整个字书写的基础,必须认真书写。
课后反思:学生书写的姿势还有待进一步提高,要加强训练,基本笔画也要加强训练。
课题:书写练习1课型:新授课教学目标:1、教会学生正确书写“杏花春雨江南”6个字。
2、使学生理解“杏花春雨江南”的意思,并用钢笔写出符合要求的的字。
重点:正确书写6个字。
难点:注意字的结构和笔画的书写。
教学过程:一、小结课堂内容,评价上次作业。
二、讲解新课:1、检查学生书写姿势和执笔动作(要求做到“三个一”)。
2、书写方法是:写一个字看一眼黑板。
(老师读,学生读,加深理解。
必修4第三章三角恒等变换单元教学设计

弦 公 式 求 求值
用,,并进一步
cos1050 及
熟悉公式的特
cos15 的值
征,为以后灵活
应用作铺垫。
归纳小 从知识、方 公式推导中向量的应用
使学生对本节
结
法两个方面 公式的结构特征
知识有一个清
对本节课的 在三角变换时, 本公式应用中, 首先应考虑根据题 晰完整地认识,
内容进行归 目的条件与结论来进行角的变换
然后相
只 剩 下 cos xcos y sin x sin y 问 题 得
通过这个 练习,培养 学生良好 的发现问 题解决问 题的能力.
解.思维过程可以逆向, (考虑由 cos( x y)
入手,寻找 cos x cos y,sin xsin y 想到平
方.)
归纳小 结
从知识, 方法两个方面来对本节课的内 容进行归纳总结.
(四)教学过程
教学 环节
教学内容
师生互 动
设计意图
复
习 复习公式
cos
引
cos
入
先让学生默写两角和与差的余弦公式, 然后
指出这两个公式是讨论复角
与单角
cos cos cos cos
sin sin sin sin
, 的余弦函数间的关系,且此关系对任
意角 , 均成立,并且要注意
cos
cos cos
是错误
情感目标: 培养学生探索和创新的意识, 构建良好的数学思维品质. (二)教学重点,难点
本节课的重点是使学生掌握两角和与差的余弦公式. 难点是两角差的余弦公式的推导与证 明.
(三) 学法与教学用具
1. 学法:启发式教学
2. 教学用具:多媒体
(四)教学过程
高中数学 第三章《三角恒等变换》教学设计 新人教A版必修4
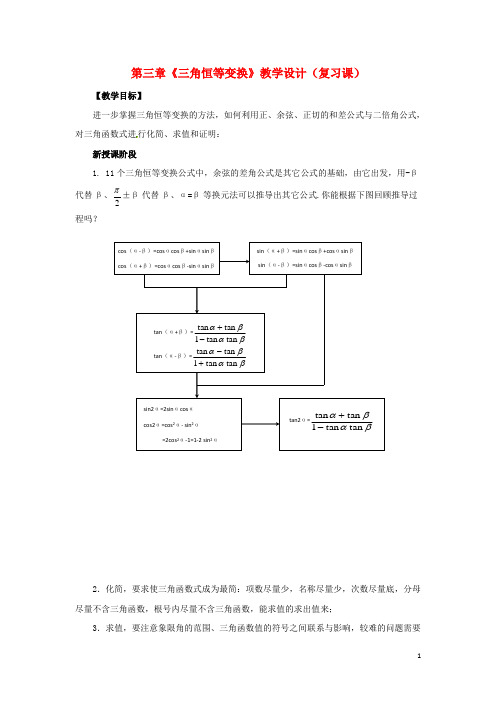
第三章《三角恒等变换》教学设计(复习课)【教学目标】进一步掌握三角恒等变换的方法,如何利用正、余弦、正切的和差公式与二倍角公式,对三角函数式进行化简、求值和证明:新授课阶段1. 11个三角恒等变换公式中,余弦的差角公式是其它公式的基础,由它出发,用-β代替β、2π±β代替β、α=β等换元法可以推导出其它公式.你能根据下图回顾推导过程吗?2.化简,要求使三角函数式成为最简:项数尽量少,名称尽量少,次数尽量底,分母尽量不含三角函数,根号内尽量不含三角函数,能求值的求出值来;3.求值,要注意象限角的范围、三角函数值的符号之间联系与影响,较难的问题需要cos (α-β)=cos αcos β+sin αsin β cos (α+β)=cos αcos β-sin αsin βsin (α+β)=sin αcos β+cos αsin β sin (α-β)=sin αcos β-cos αsin βtan (α+β)=βαβαtan tan 1tan tan -+ tan (α-β)=βαβαtan tan 1tan tan +- sin2α=2sin αcos α cos2α=cos 2α- sin 2α=2cos 2α-1=1-2 sin 2αtan2α=βαβαtan tan 1tan tan -+根据上三角函数值进一步缩小角的范围.4.证明是利用恒等变换公式将等式的左边变同于右边,或右边变同于,或都将左右进行变换使其左右相等.5. 三角恒等变换过程与方法,实际上是对三角函数式中的角、名、形的变换,即(1)找差异:角、名、形的差别;(2)建立联系:角的和差关系、倍半关系等,名、形之间可以用哪个公式联系起来;(3)变公式:在实际变换过程中,往往需要将公式加以变形后运用或逆用公式,如升、降幂公式, cosα= cosβcos (α-β)- sinβsin (α-β),1= sin 2α+cos 2α,0030tan 130tan 1-+=000030tan 45tan 130tan 45tan -+=tan (450+300)等.例1 知),2(,61)4sin()4sin(ππ∈α=α-πα+π,求sin4α的值. 解:∵61)4sin()4sin(=α-πα+π ∴31)4cos()4sin(2=α+πα+π∴31)]4(2sin[=α+π ∴cos2α =31又∵),2(ππ∈α ∴2α∈ (π, 2π)∴sin2α = 322)31(12cos 122-=--=α-- ∴sin4α = 2sin2αcos2α = 92431)322(2-=⨯-⨯ 例2 已知θ是三角形中的一个最小的内角,且12sin 2cos 2sin 2cos 2222+=θ-θ-θ+θa a a ,求a 的取值范围. 解:原式变形:1)2sin 2(cos )2sin 2(cos 2222+=θ-θ-θ-θa a即1cos )1(+=θ-a a ,显然1≠a (若1=a ,则 0 = 2)∴11cos -+=θa a 又∵30π≤θ<,∴1cos 21<θ≤ 即:11121<-+≤a a 解之得:3-≤a例3 求证:)6(sin )3cos(cos sin 22α-π-α+πα+α的值是与α无关的定值.证:)3cos(cos )]23cos(1[21)2cos 1(21α+πα+α-π--α-=原式)sin 3sin cos 3(cos cos ]2cos )23[cos(21απ-απα+α-α-π=211(cos cos 2sin sin 2cos 2)cos sin 2332ππαααααα=+-+-1111cos 22cos 2(1cos 2)2442444ααααα=+-++-= ∴)6(sin )3cos(cos sin 22α-π-α+πα+α的值与α无关 例4 已知331cos 2sin 2cos(), , 45221tan πππααααα-++=≤<-求的值.解:由3cos()45πα+=得3cos 225αα-=解方程组2235sin cos 1αααα=⎨⎪+=⎩得sin 10cos αα⎧=-⎪⎪⎨⎪=⎪⎩或sin 10cos αα⎧=⎪⎪⎨⎪=⎪⎩sin 310cos 0 22cos αππααα⎧=-⎪⎪≤<∴≤∴⎨⎪=⎪⎩Q 21cos 2sin 22sin 2sin cos 1tan 1tan ααααααα-++∴=--22(2(281010101775⨯+⨯==--例5 求值:020210sin 21)140cos 1140sin 3(⋅-.解:原式=0020*******sin 21140cos 140sin 140sin 140cos 3⋅- 16160sin 200sin 1680cos 80sin 200sin 810sin 2180sin 41200sin 80sin 410sin 21)40cos 40sin ()140sin 140cos 3)(140sin 140cos 3(00000020002000000=-=-=⋅⋅-=⋅-+-=例6.已知函数1)4()cos x f x xπ-=.(Ⅰ)求()f x 的定义域;(Ⅱ)设α的第四象限的角,且tan α43=-,求()f α的值. 解:(Ⅰ)由 cos 0x ≠得()2x k k Z ππ≠+∈,故()f x 在定义域为},,2x x k k Z ππ⎧≠+∈⎨⎩(Ⅱ)因为4tan 3α=-,且α是第四象限的角, 所以43sin ,cos ,55αα=-= 故12sin(2)4()cos f πααα--= 2212(sin 2cos 2)22cos ααα--=1sin 2cos 2cos ααα-+=22cos 2sin cos cos αααα-= 2(cos sin )αα=-145=. 例7 已知sin (4π-x )=135,0<x <4π,求)(x x +4πcos 2cos 的值.分析:角之间的关系:(4π-x )+(4π+x )=2π及2π-2x =2(4π-x ),利用余角间的三角函数的关系便可求之.解:∵(4π-x )+(4π+x )=2π,∴cos(4π+x )=sin (4π-x ). 又cos2x =sin (2π-2x )=sin2(4π-x )=2sin (4π-x )cos (4π-x ), ∴)(x x +4πcos 2cos =2cos (4π-x )=2×1312=1324.例8 求证:(sin cos 1)(sin cos 1)tan sin 22x x x x xx +--+=解:原式=22(sin 12sin 1)(sin 12sin 1)22sin 2x xx x x+---++ =22(2sin cos 2sin )(2sin cos 2sin )2222224sin cos cos 22x x x x x x x xx-+=(cos sin )(cos sin )sin 22222cos cos 2x x x x x x x-+⋅ =x x x x x cos 2cos 2sin 2sin 2cos 22⋅-)(=x x x x cos 2cos 2sincos ⋅⋅=tan 2x .例9 已知223sin 2sin 1αβ+=,3sin2-2sin2=0αβ,, αβ且都是锐角,求+2αβ 的值.解:由223sin 2sin 1αβ+=得3sin 2α=1-2sin 2β=cos2β.由3sin2-2sin2=0αβ得sin2β=23sin2α.∴cos(α+2β)=cos αcos2β-sin αsin2β=3cos αsin 2α-sin α·23sin2α=0.∵α、β∈(0,2π),∴α+2β∈(0,2π3). ∴α+2β=2π. 课堂小结三角恒等式的证明方法有:从等式一边推导变形到另一边,一般是化繁为简. 等式两边同时变形成同一个式子.将式子变形后再证明. 作业 见同步练习 拓展提升1.若34x ππ<<,则1cos 1cos 22x x+-+等于 (A 2cos()42x π- (B )2cos()42xπ-- (C )2sin()42x π- (D )2sin()42xπ--2.函数y=21sin2x+sin 2x,x R ∈的值域是( )(A)[-21,23] (B) [2122,2122++-] (C) [-23,21] (D)[2122,2122---]3.已知x ∈(-2π,0),cos x =54,则tan2x 等于 ( )A.247B.-247 C.724D.-724 4.已知t an2θ=32,则θθθθsin cos 1sin cos 1+++-的值为( ) A . 32B .-32 C .23 D .-235..sin 2cos 0αα+=,则sin 2cos2αα+= . 6.已知sin 2m θ=,若0,4πθ⎛⎫∈ ⎪⎝⎭,则sin cos ______θθ-=. 若,42ππθ⎛⎫∈ ⎪⎝⎭ , 则sin cos ______θθ-=. 7.若111cos sin θθ-=,则sin 2θ的值为_______.8.已知锐角三角形ABC 中,.51)sin(,53)sin(=-=+B A B A 求tan tan AB的值.9. ()41,cos ,tan , cos .53αβααββ=-=-已知、为锐角求的值10.设函数()cos 223cos ()f x x x x x R =+∈的最大值为M ,最小正周期为T . (1) 求M ,T ;(2) 若有10个互不相等的正数i x 满足()i f x =M ,且10i x π≤(i=1,2,…10), 求12x x +…10x +的值.参考答案 1.C2.B 提示:用二倍角公式及两角和与差的正弦或余弦公式3.D 4.A 提示:222sin 2sin cos1cos sin 222tan 1cos sin 22cos 2sin cos 222θθθθθθθθθθθ+-+==+++ 5..75- 提示:由已知得tan 2α=-,22sin 2cos 22sin cos cos sin αααααα+=+- 2222222sin cos cos sin 2tan 1tan 7sin cos tan 15ααααααααα+-+-===-++ 6.1,1m m --- 提示:2(sin cos )12sin cos θθθθ-=-=1sin 21m θ-=-当0,sin cos 4πθθθ⎛⎫∈< ⎪⎝⎭时,当,sin cos 42ππθθθ⎛⎫∈> ⎪⎝⎭时, 7.222-+ 提示:去分母后两边平方可得 8 解:,51)sin(,53)sin(=-=+B A B A Θ .2tan tan 51sin cos ,52cos sin .51sin cos cos sin ,53sin cos cos sin =⇔⎪⎪⎩⎪⎪⎨⎧==⇔⎪⎪⎩⎪⎪⎨⎧=-=+∴B A B A B A B A B A B A B A 9 解:43,cos , sin .55ααα=∴=Q 是锐角.,22 π<β-α<π-∴βα为锐角、又Θ ()可求出,31tan -=-βαΘ()(),1010sin ,10103cos -=-=-βαβα()cos cos βααβ∴=--⎡⎤⎣⎦()()cos cos sin sin ααβααβ=-+-4310310510510⎛⎫=⋅+- ⎪ ⎪⎝⎭910.50= 10 解:(1)()cos 2322sin(2)6f x x x x π=+=+Q 2,M T π∴== (2)()i f x M =由知:2sin(2)26i x π+=,22,62i x k k Z πππ+=+∈故即 ,6i x k k Z ππ=+∈,又i x 是互不相等的正数且10i x π≤(i=1,2,…10),故,6i x k ππ=+k =0,1,…9.所以12x x +…10x +1403π=。
高中数学 第3章 三角恒等变换教学设计 苏教版必修4(2021年整理)

高中数学第3章三角恒等变换教学设计苏教版必修4编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(高中数学第3章三角恒等变换教学设计苏教版必修4)的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为高中数学第3章三角恒等变换教学设计苏教版必修4的全部内容。
高中数学第3章三角恒等变换教学设计苏教版必修4错误!知识网络教学分析三角函数及其三角恒等变换不仅有着广泛的实际应用,而且是进一步学习中学后继内容和高等数学的基础,因而成为高考中对基础知识、基本技能和基本思想方法考查的重要内容之一.切实掌握三角函数的基本变换思想是复习掌握好本章的关键.三角函数的恒等变形,不仅在三角函数的化简、求值问题中应用,而且在研究第一章三角函数的图象与性质时、在后续内容解三角形中也应用广泛.解决三角函数的恒等变形问题,其关键在掌握基本变换思想,运用三角恒等变形的主要途径--变角,变函数,变结构,注意公式的灵活应用.在本章的学习中,化归的数学思想和方法被多次运用,有了化归思想,就可以理解三角恒等式推导和变形的思路.在本节课的教学中,可以先组织学生自己回顾在本章教学中所学到的知识,自己绘制本章内容的结构框架图,梳理本章的知识体系,构建学生的知识结构.三角公式是三角变换的基本依据,在三角恒等变换的复习中,可以引导学生利用向量的数量积推导出两角差的余弦公式,并由此公式推导出两角和与差的正弦、余弦、正切公式,二倍角的正弦、余弦、正切公式,引导学生推导积化和差、和差化积、半角公式及万能公式.通过对这些公式的探求,使学生学会预测变换的目标、选择变换的公式、设计变换的途径,帮助学生进一步提高推理能力和运算能力.学完本章后,前一章平面向量更有了用武之地,它是沟通代数、几何与三角函数的一种重要工具,三角函数又具有较强的渗透力,切实提高三角函数的综合能力是复习好本章的保证.因此,我们可以通过整合,将三角函数,平面向量结成一个知识板块来复习,并进行三角与向量相融合的综合训练,这样更有利于学生对平面向量、三角函数及三角恒等变换的深刻理解及运用.三维目标1.通过复习全章知识方法,掌握两角和与差的正弦、余弦、正切公式,掌握二倍角的正弦、余弦、正切公式.并能正确地运用上述公式化简三角函数式、求某些角的三角函数值、证明较简单的三角恒等式以及解决一些简单的实际问题.2.掌握简单的三角恒等变换的基本思想方法,并结合向量解决一些基本的综合问题.3.通过三角恒等变换体会数学的逻辑性的特征,进一步理解数学的化归思想、方程思想和代换意识,认识事物之间是相互依存、互相联系的.学会用联系和发展的观点认识事物,培养学生学会思考问题的方法,培养他们勇于探索创新的精神,磨练学生的意志.重点难点教学重点:和角公式、差角公式、倍角公式及其灵活应用.教学难点:和角公式、差角公式、倍角公式在三角恒等变换中的综合运用.课时安排2课时错误!第1课时导入新课思路1.(直接导入)在第一章三角函数的基础上,我们又一起探究学习了第3章三角恒等变换的有关知识,并掌握了一定的分析问题与解决问题的方法,提高了我们的思维能力与运算能力.现在我们一起对本章进行小结与复习,进一步巩固本章所学的知识,请同学们画出本章的知识框图,由此进入复习.思路2。
高中数学第三章三角恒等变换3.3三角函数的积化和差与和差化积教案新人教B版必修4

(一)课前准备(预计用时:5分钟)
学生预习:
-发放预习材料,引导学生提前了解三角函数积化和差与和差化积的学习内容,标记出有疑问或不懂的地方。
-设计预习问题,如“积化和差与和差化积公式在生活中的应用”,激发学生思考,为课堂学习三角函数的内容做好准备。
教师备课:
-深入研究教材,明确教学目标和教学重难点。
-准备一些典型例题的解析图解,通过图解的方式让学生更清晰地看到解题步骤和思路。
-设计一些互动式电子白板练习,让学生可以在课堂上即时操作,增强互动性和参与感。
3.实验器材:
-虽然本节课不涉及物理实验,但如果条件允许,可以准备一些简单的实验器材,如直角三角形模型、角度测量仪等,用于直观展示三角函数中的角度关系。
- $\sin 30^\circ \cos 45^\circ - \cos 30^\circ \sin 45^\circ = \sin(30^\circ - 45^\circ)$
2.艺术性和趣味性:
回顾旧知:
-简要回顾上节课学习的三角恒等变换内容,帮助学生建立知识之间的联系。
-提出问题,检查学生对旧知的掌握情况,为学习新课打下基础。
(三)新课呈现(预计用时:25分钟)
知识讲解:
-清晰、准确地讲解积化和差与和差化积的知识点,结合实例帮助学生理解。
-突出重点,强调难点,通过对比、归纳等方法帮助学生加深记忆。
学生学习效果
1.知识与技能:
-学生能够理解并掌握三角函数积化和差与和差化积的基本概念和公式。
-学生能够运用积化和差与和差化积的公式进行三角函数的表达式转换和简化计算。
-学生通过课堂练习和课后作业,提高了对三角函数运算的熟练性和准确性。
-学生能够将实际问题中的角度关系转化为数学表达式,解决实际问题。
人教A版高一年级必修4第三章第二节 简单的三角恒等变换教学设计

3.2 简单的三角恒等变换一、课标要求:本节主要包括利用已有的十一个公式进行简单的恒等变换,以及三角恒等变换在数学中的应用.二、编写意图与特色本节内容都是用例题来展现的.通过例题的解答,引导学生对变换对象目标进行对比、分析,促使学生形成对解题过程中如何选择公式,如何根据问题的条件进行公式变形,以及变换过程中体现的换元、逆向使用公式等数学思想方法的认识,从而加深理解变换思想,提高学生的推理能力.三、教学目标通过例题的解答,引导学生对变换对象目标进行对比、分析,促使学生形成对解题过程中如何选择公式,如何根据问题的条件进行公式变形,以及变换过程中体现的换元、逆向使用公式等数学思想方法的认识,从而加深理解变换思想,提高学生的推理能力.四、教学重点与难点教学重点:引导学生以已有的十一个公式为依据,以推导积化和差、和差化积、半角公式的推导作为基本训练,学习三角变换的内容、思路和方法,在与代数变换相比较中,体会三角变换的特点,提高推理、运算能力.教学难点:认识三角变换的特点,并能运用数学思想方法指导变换过程的设计,不断提高从整体上把握变换过程的能力.五、学法与教学用具学法:讲授式教学六、教学过程:学习和(差)公式,倍角公式以后,我们就有了进行变换的性工具,从而使三角变换的内容、思路和方法更加丰富,这为我们的推理、运算能力提供了新的平台.下面我们以习题课的形式讲解本节内容.例1、试以cosα表示222 sin,cos,tan222ααα.解:我们可以通过二倍角2cos2cos12αα=-和2cos12sin2αα=-来做此题.因为2cos12sin2αα=-,可以得到21cossin22αα-=;因为2cos2cos12αα=-,可以得到21coscos22αα+=.又因为222sin1cos2tan21coscos2ααααα-==+.思考:代数式变换与三角变换有什么不同?代数式变换往往着眼于式子结构形式的变换.对于三角变换,由于不同的三角函数式不仅会有结构形式方面的差异,而且还会有所包含的角,以及这些角的三角函数种类方面的差异,因此三角恒等变换常常首先寻找式子所包含的各个角之间的联系,这是三角式恒等变换的重要特点.例2、求证: (1)、()()1sin cos sin sin 2αβαβαβ=++-⎡⎤⎣⎦; (2)、sin sin 2sin cos 22θϕθϕθϕ+-+=.证明:(1)因为()sin αβ+和()sin αβ-是我们所学习过的知识,因此我们从等式右边着手.()sin sin cos cos sin αβαβαβ+=+;()sin sin cos cos sin αβαβαβ-=-. 两式相加得()()2sin cos sin sin αβαβαβ=++-; 即()()1sin cos sin sin 2αβαβαβ=++-⎡⎤⎣⎦;(2)由(1)得()()sin sin 2sin cos αβαβαβ++-=①;设,αβθαβϕ+=-=, 那么,22θϕθϕαβ+-==.把,αβ的值代入①式中得sin sin 2sin cos 22θϕθϕθϕ+-+=.思考:在例2证明中用到哪些数学思想?例2 证明中用到换元思想,(1)式是积化和差的形式,(2)式是和差化积的形式,在后面的练习当中还有六个关于积化和差、和差化积的公式.例3、求函数sin y x x =的周期,最大值和最小值.解:s i n 3c o s y x x =这种形式我们在前面见过,1sin 2sin 2sin 223y x x x x x π⎛⎫⎛⎫=+=+=+ ⎪ ⎪ ⎪⎝⎭⎝⎭, 所以,所求的周期22T ππω==,最大值为2,最小值为2-.点评:例3是三角恒等变换在数学中应用的举例,它使三角函数中对函数()sin y A x ωϕ=+的性质研究得到延伸,体现了三角变换在化简三角函数式中的作用.七、课堂小结此节虽只安排一到两个课时的时间,但也是非常重要的内容,我们要对变换过程中体现的换元、逆向使用公式等数学思想方法加深认识,学会灵活运用.八、作业布置习题3.2 A 组 1题(1)(2)(3)(4)九、课后反思。
【精品】高中数学第三章三角恒等变换3.3几个三角恒等式教案苏教版必修4

3.3 几个三角恒等式整体设计教学分析本节主要内容为利用已有的公式进行推导发现.本节的编写意图与特色是教师引导学生发现创造,从而加深理解变换思想,提高学生的推理能力.三角恒等变换所涉及的问题各种各样,内容十分丰富,我们希望能总结出一些有规律性的数学思想、方法和技巧,提高对三角变换的理性认识.科学发现是从问题开始的,没有问题就不可能有深入细致的观察.为了让学生经历一个完整的探索发现过程,教科书从三角函数运算的角度提出了研究课题.这是从数学知识体系的内部发展需要提出问题的方法.用这种方法提出问题可以更好地揭示知识间的内在联系,体会推理论证和逻辑思维在数学发现活动中的作用.从运算的角度提出问题,还可以帮助学生认识到三角变换也是一种运算,丰富对运算的认识,从而把对三角变换的研究纳入整体的数学体系之中.类比对数运算,由两角和与差的正弦公式易推出积化和差公式.在推导出了公式sin α+sin β=2sin α+β2cos α-β2以后,可以让学生推导其余的和差化积及积化和差公式.本节后面的练习中之所以用证明的形式给出这个问题,只是为了让学生有一个正确完整的结论.和差化积、积化和差、万能代换以及半角公式都不要求记忆和运用,要注意不应该加大三角变换的难度,不要在三角变换中“深挖洞”.高考在该部分内容上的难度一降再降几乎不涉及了.三维目标1.通过类比推导出积化和差与和差化积公式及万能公式.体会化归、换元、方程、逆向使用公式等数学思想,提高学生的推理能力.体会三角恒等变换在数学中的应用.2.通过和差化积公式和积化和差公式的推导,让学生经历数学探索和发现过程,激发学生数学发现的欲望和信心.重点难点教学重点:推导积化和差、和差化积公式.教学难点:认识三角变换的特点,并能运用数学思想方法指导变换过程的设计,不断提高从整体上把握变换过程的能力.课时安排 1课时教学过程导入新课思路1.(复习导入)在前面的几节课中我们学习了两角和与差的三角函数的计算公式,并运用这些公式解决了一些三角函数的化简、求值以及三角恒等式的证明问题,在我们运用三角函数知识解决一些问题的时候,我们也会遇到形如sin α+sin β,sin α-sin β,cos α+cos β,cos α-cos β的形式,那么,我们能否运用角α、β的有关三角函数值表示它们呢?这就是我们本节课所要研究的问题.思路2.(类比导入)我们知道log a m +log a n =log a (mn),那么sin α+sin β等于什么呢? 推进新课新知探究和差化积公式的推导、万能公式的应用.在引入对数概念以后,我们还研究了它的运算,并得到了一些重要的结论,如log a m +log a n =log a (mn).同样,在定义了三角函数以后,我们也应该考虑它的运算,如 sin α+sin β=? 观察和角公式sin(α+β)=sin αcos β+cos αsin β, sin(α-β)=sin αcos β-cos αsin β, 容易得到sin(α+β)+sin(α-β)=2sin αcos β.① 由此,有sin αcos β=12[sin(α+β)+sin(α-β)].①的左边已经是两个正弦的和,因此,只要进行简单的变形,就可以回答sin α+sin β=?这个问题了.令α+β=θ,α-β=φ,代入①得 sin θ+sin φ=2sin θ+φ2cos θ-φ2,从而有sin α+sin β=2sin α+β2cos α-β2.②为了更好地发挥本例的训练功能,把两个三角式结构形式上的不同点作为思考的出发点,引导学生思考,哪些公式包含sin αcos β呢?想到sin(α+β)=sin αcos β+cos αsin β.从方程角度看这个等式,sin αcos β,cos αsin β分别看成两个未知数.二元方程要求得确定解,必须有两个方程,这就促使学生考虑还有没有其他包含sin αcos β的公式,列出sin(α-β)=sin αcos β-cos αsin β后,解相应地以sin αcos β,cos αsin β为未知数的二元一次方程组,就容易得到所需要的结果.得到以和的形式表示的积的形式后,解决它的反问题,即用积的形式表示和的形式,在思路和方法上都与前者没有什么区别.只需做个变换,令α+β=θ,α-β=φ,则α=θ+φ2,β=θ-φ2,代入①式即得②式.证明:(1)因为sin(α+β)=sin αcos β+cos αsin β,sin(α-β)=sin αcos β-cos αsin β,将以上两式的左右两边分别相加,得 sin(α+β)+sin(α-β)=2sin αcos β, 即sin αcos β=12[sin(α+β)+sin(α-β)].(2)由(1)可得sin(α+β)+sin(α-β)=2sin αcos β.① 设α+β=θ,α-β=φ,那么α=θ+φ2,β=θ-φ2.把α、β的值代入①,即得sin θ+sin φ=2sin θ+φ2cos θ-φ2.类似的还能得到sin α-sin β=2cos α+β2sin α-β2,cos α+cos β=2cos α+β2cos α-β2,cos α-cos β=-2sin α+β2sin α-β2.以上四个公式我们称其为和差化积公式.教师给学生适时引导,指出这两个方程所用到的数学思想,可以总结出在本例的证明过程中,用到了换元的思想,如把α+β看作θ,α-β看作φ,从而把包含α,β的三角函数式变换成θ,φ的三角函数式.另外,把sin αcos β看作x ,cos αsin β看作y ,把等式看作x ,y 的方程,通过解方程求得x ,这就是方程思想的体现.利用前面所学的三角函数公式还能推出很多有用的恒等式,我们先来探究一个具体问题.设tan α2=t.(1)求证:sin α=2t 1+t 2,cos α=1-t 21+t 2,tan α=2t1-t 2;①(2)当t =2时,利用以上结果求3cos 2α2-2sin α+sin 2α2的值. (1)证明:由二倍角公式,得sin α=2sin α2cos α2=2sin α2cos α2cos 2α2+sin 2α2=2tanα21+tan2α2=2t1+t 2,tan α=2tanα21-tan2α2=2t1-t 2.再由同角三角函数间的关系,得 cos α=sin αtan α=2t 1+t 22t 1-t 2=1-t21+t2.(2)解:3cos2α2-2sin α+sin 2α2=2cos 2α2+1-2sin α=2+cos α-2sin α =2+1-t 21+t 2-4t1+t 2=3+t 2-4t 1+t =-15. 公式①称为万能代换公式,利用万能代换公式,可以用tan α2的有理式统一表示α角的任何三角函数值.图1中的直角三角形可以帮助你更好地理解万能代换公式.图1应用示例思路1例1已知sinx -cosx =12,求sin 3x -cos 3x 的值.活动:教师引导学生利用立方差公式进行对公式变换化简,然后再求解.由于(a -b)3=a 3-3a 2b +3ab 2-b 3=a 3-b 3-3ab(a -b),∴a 3-b 3=(a -b)3+3ab(a -b).解完此题后,教师引导学生深挖本例的思想方法,由于sinxcosx 与sinx±cosx 之间的转化,提升学生的运算、化简能力及整体代换思想.本题也可直接应用上述公式求解,即sin 3x -cos 3x =(sinx -cosx)3+3sinxcosx(sinx -cosx)=1116.此方法往往适用于sin 3x±cos 3x 的化简问题.解:由sinx -cosx =12,得(sinx -cosx)2=14,即1-2sinxcosx =14,∴sinxcosx=38.∴sin 3x -cos 3x =(sinx -cosx)(sin 2x +sinxcosx +cos 2x) =12(1+38)=1116. 点评:本题考查的是公式的变形、化简、求值,注意公式的灵活运用和化简的方法.例2已知cos A cos 2B +sin A sin 2B =1,求证:cos B cos 2A +sin Bsin 2A=1.活动:此题可从多个角度进行探究,由于所给的条件等式与所要证明的等式形式一致,只是将A 、B 的位置互换了,因此应从所给的条件等式入手,而条件等式中含有A 、B 角的正、余弦,可利用平方关系来减少函数的种类.从结构上看,已知条件是a 2+b 2=1的形式,可利用三角代换.证法一:∵cos 4A cos 2B +sin 4A sin 2B =1,∴cos 4Asin 2B +sin 4Acos 2B =sin 2Bcos 2B.∴cos 4A(1-cos 2B)+sin 4Acos 2B =(1-cos 2B)cos 2B , 即cos 4A -cos 2B(cos 4A -sin 4A)=cos 2B -cos 4B. ∴cos 4A -2cos 2Acos 2B +cos 4B =0.∴(cos 2A -cos 2B)2=0.∴cos 2A =cos 2B.∴sin 2A =sin 2B. ∴cos 4B cos 2A +sin 4B sin 2A =cos 2B +sin 2B =1. 证法二:令cos 2A cosB =cos α,sin 2AsinB =sin α,则cos 2A =cosBcos α,sin 2A =sinBsin α.两式相加得1=cosBcos α+sinBsin α,即cos(B -α)=1.∴B-α=2k π(k∈Z ),即B =2k π+α(k∈Z ).∴cos α=cosB ,sin α=sinB. ∴cos 2A =cosBcos α=cos 2B ,sin 2A =sinBsin α=sin 2B. ∴cos 4B cos 2A +sin 4B sin 2A =cos 4B cos 2B +sin 4B sin 2B=cos 2B +sin 2B =1. 点评:要善于从不同的角度来观察问题,本例从角与函数的种类两方面观察,利用平方关系进行了合理消元.思路2例题 证明1+sinx cosx =tan(π4+x2).活动:教师引导学生思考,对于三角恒等式的证明,可从三个角度进行推导:①左边→右边;②右边→左边;③左边→中间条件←右边.教师可以鼓励学生试着多角度的化简推导.注意式子左边包含的角为x ,三角函数的种类为正弦,余弦,右边是半角x2,三角函数的种类为正切.证法一:从右边入手,切化弦,得 tan(π4+x 2)=π4+x 2π4+x 2=sin π4cos x 2+cos π4sin x 2cos π4cos x 2-sin π4sin x 2=cos x 2+sinx 2cos x 2-sinx 2,由左右两边的角之间的关系,想到分子分母同乘以cos x 2+sin x2,得x 2+sin x 22x 2+sin x 2x 2-sin x 2=1+sinxcosx. 证法二:从左边入手,分子分母运用二倍角公式的变形,降倍升幂,得 1+sinxcosx=x 2+sin x 22x 2+sin x 2x 2-sin x 2=cos x 2+sin x 2cos x 2-sin x 2.由两边三角函数的种类差异,想到弦化切,即分子分母同除以cos x2,得1+tan x 21-tan x 2=tan π4+tanx 21-tan π4tanx 2=tan(π4+x 2). 点评:本题考查的是半角公式的灵活运用,以及恒等式的证明所要注意的步骤与方法.变式训练求证:1+sin4θ-cos4θ2tan θ=1+sin4θ+cos4θ1-tan 2θ. 分析:运用比例的基本性质,可以发现原式等价于1+sin4θ-cos4θ1+sin4θ+cos4θ=2tan θ1-tan 2θ,此式右边就是tan2θ. 证明:原等式等价于1+sin4θ-cos4θ1+sin4θ+cos4θ=tan2θ.而上式左边=sin4θ+-cos4θsin4θ++cos4θ=2sin2θcos2θ+2sin 22θ2sin2θcos2θ+2cos 22θ=2sin2θθ+sin2θ2cos2θ2θ+cos2θ=tan2θ=右边.∴上式成立,即原等式得证.知能训练1.若sin α=513,α在第二象限,则tan α2的值为( )A .5B .-5 C.15 D .-152.设5π<θ<6π,cos θ2=a ,则sin θ4等于( )A.1+a2B.1-a2 C .-1+a2D .-1-a23.已知sin θ=-35,3π<θ<7π2,则tan θ2=__________.答案:1.A 2.D 3.-3课堂小结1.先让学生自己回顾本节学习的数学知识:和、差、倍角的正弦、余弦公式的应用,半角公式、代数式变换与三角变换的区别与联系.积化和差与和差化积公式及其推导,三角恒等式与条件等式的证明.2.教师画龙点睛:本节学习的数学方法:公式的使用,换元法,方程思想,等价转化,三角恒等变形的基本手段.作业课本复习题9、10.设计感想1.本节主要学习了怎样推导半角公式,积化和差,和差化积公式,在解题过程中,应注意对三角式的结构进行分析,根据结构特点选择合适公式,进行公式变形.还要思考一题多解、一题多变,并体会其中的一些数学思想,如换元、方程思想,“1”的代换,逆用公式等.2.在近几年的高考中,对三角变换的考查仍以基本公式的应用为主,突出对求值的考查.特别是对平方关系及和角公式的考查应引起重视,其中遇到对符号的判断是经常出问题的地方,同时要注意结合诱导公式的应用.备课资料一、1.一道给值求角类问题错解点击.解决给值求角这类问题时,要注意根据问题给出的三角函数值及角的范围,选择适当的三角函数,确定所求角的恰当范围,利用函数值在此范围内的单调性求出所求角.解答此类问题一定要重视角的范围对三角函数值的制约关系,常见的错误为不根据已知条件确定角的范围而盲目求值,造成增解.例题:若sin α=55,sin β=1010,α、β均为锐角,求α+β的值. 错解:∵α为锐角, ∴cos α=1-sin 2α=255.又β为锐角,∴cos β=1-sin 2β=31010.∴sin(α+β)=sin αcos β+cos αsin β=22. ∵α,β均为锐角, ∴0°<α+β<180°. ∴α+β=45°或135°.点评:上述解法欠严密,仅由sin(α+β)=22,0°<α+β<180°而得到α+β=45°或135°是正确的.但题设中sin α=55<12,sin β=1010<12,使得0°<α+β<60°,故上述结论是错误的.事实上,由0°<α+β<180°,应选择求cos(α+β)=22(∵余弦函数在此范围内是单调的),易求得cos(α+β)=22,则α+β=45°,因此,解决给值求角这类问题一般分三步:第一步是确定角所在的范围;第二步是求角的某一个三角函数值(要尽量使所选择的三角函数在所确定的范围内单调);第三步是得到结论,求得所求角的值.2.如何进行三角恒等变式的证明. 三角恒等式证明的基本方法:师:如何利用同角三角函数的基本关系式对三角恒等式进行证明呢? (1)可从一边开始,证得它等于另一边,一般是由繁到简. (2)可用左右归一法,即证明左右两边都等于同一个式子. (3)可采用切割化弦,将其转化为所熟知的正、余弦.(4)可用分析法,即假定结论成立,经推理论证,找到一个显然成立的式子(或已知条件). (5)可用拼凑法,即针对题设与结论间的差异,有针对性地变形,以消除其差异,简言之,即化异求同.(6)可采用比较法,即“左边右边=1”或“左边-右边=0”.证明三角恒等式的实质是消除等式两边的差异,就是有目的地进行化简,因此,在证明时要注意将上述方法综合起来考虑,要灵活运用公式,消除差异,其思维模式可归纳为三点:(1)发现差异:观察角、函数、运算结构的差异; (2)寻求联系:运用相关公式,找出转化差异的联系; (3)合理转化:选择恰当的公式,实现差异的转化. 二、备用习题1.已知tanx =-3,则sin2x =________,cos2x =________. 2.已知tan α=2,则cos2α等于( ) A .-13 B .±13C .-35D .±353.下列各式化成和差的形式分别是: (1)sin(π3+2x)cos(π3-2x);(2)cos α+β2sin α-β2.4.设α、β≠k π+π2(k∈Z ),且cos2α+sin 2β=0.求证:tan 2α=2tan 2β+1.5.已知△ABC 的三个内角A 、B 、C 满足A +C =2B ,且1cosA +1cosC =-2cosB ,试求cosA -C2的值.6.不查表求值: tan6°tan42°tan66°tan78°. 参考答案: 1.-35 -45 2.C3.(1)34+12sin4x ;(2)12(sin α-sin β). 4.证明:∵cos2α+sin 2β=0,∴1-tan 2α1+tan 2α+sin 2βsin 2β+cos 2β=0,即1-tan 2α1+tan 2α+tan 2β1+tan 2β=0. 化简得tan 2α=2tan 2β+1.5.解:由题设条件,知B =60°,A +C =120°, 设A -C2=α,则A =60°+α,C =60°-α. 代入1cosA +1cosC =-2cosB ,可得1+α+1-α=-22,即2cos α-3sin α+2cos α+3sin α=-22,可化为4cos 2α+2cos α-3=0, 解得cos α=22或-324(舍去). ∴co s A -C 2=22.6.解:原式=tan54°tan6°tan66°tan42°tan78°tan54°=-+tan54°=tan18°tan42°tan78°tan54°=-+tan54°=tan54°tan54°=1.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
必修4第三章三角恒等变换单元教学设计案例 3.1.1两角和与差的余弦(一)教学目标知识目标:掌握用向量方法建立两角差的余弦公式,通过简单运用,使学生初步理解公式的结构及其功能,为建立其它和(差)公式打好基础.能力目标:进一步理解向量法解决问题的方法,培养学生运用数学工具在实践中探索知识,进而获取知识的能力.情感目标:培养学生探索和创新的意识,构建良好的数学思维品质.(二)教学重点,难点本节课的重点是使学生掌握两角和与差的余弦公式.难点是两角差的余弦公式的推导与证明.、(三)学法与教学用具1. 学法:启发式教学2. 教学用具:多媒体(四)教学过程思考并讨论:(投影) 1) 问题解决的思路与方法 2)体现了α与β的任意性吗3)探究 cos()的公式—由学生回答上述问题,教师点评:结论如下1)主要利用了向量这个工具,体会其作用与便利之处.。
回归到余弦的定义,数形结合,利用单位圆简化了计算。
2)α与β有任意性,有Z k k OQ OP ∈+±=-,2,πβα 说一该公式具有一般性。
3)把公式C α-β中的β换成-β,则有板书:cos [α-(-β)]=cos α·cos (-β)+sin α·sin(-β)=cos α·cos β-sin α·sin β,/cos15的值从知识、方案例3.1(2)(一)教学目标1.知识目标:掌握公式结构特点,会用公式求值.2.#3.能力目标:培养学生的观察,分析,类比,联想能力,间接推理能力,自学能力.4.情感能力:发展学生正向,逆向思维能力,构建良好的数学思维品质.(二)教学重点,难点重点是公式的结构特点,会用公式求值.难点是公式的逆向和变形运用.(三)教学方法教师按照课本的知识结构先设计若干问题,课前印发给学生,引导他们阅读课本,课堂上在教师三导(引导,指导,辅导)下,以学生为主体,对所设问题进行读,议,练,讲,其间教师通过提问,参与讨论,巡视学生练习及板演,观察学生情绪等渠道,及时搜集反馈信息,及时作出评价,再发指令,使教学过程处于动态平衡中.(四)教学过程`)απ,.数值.(2)(3)再求三角函数值的正负.(4)代入时,从左至右依次代入.(5)注意cos2,2ππαβ得αβπ+,再进一步参11cos()14αβ+=-.确定sin()αβ+的值.思考题:1.已知cos()=31求 (sin +sin )2+(cos +cos )2的值。
2.sin sin =21,cos cos =21, (0, 2π),(0, 2π), ^求cos()的值§3.1.2 两角和与差的正弦一、教学目标1、知识与技能目标:能从两角差的余弦公式导出两角和、差正弦公式,了解它们的内在联系。
-2、过程与方法目标:引导学生推导和角公式,使学生认识整个公式体系的推理和形成的过程。
从这一过程中,使学生领会其中体现出来的数学基本思想、蕴含的创新思想,掌握研究数学的基本方法,从而提高数学素质。
3、情感、态度与价值观目标:通过公式的推导,了解它们的内在联系和知识的发展过程,体会一般与特殊的关系与转化,培养利用联系、变化的辩证唯物主义观点去分析问题的能力。
体会学科间的联系。
二、教学重点、难点1. 教学重点:两角和、差正弦公式的应用和旋转变换公式。
2. 教学难点:利用两角和的正弦公式变sin cos a b αα+为一个角的三角函数的形式。
三、教学方法研讨式教学,讲授式教学 四、教学过程:#(一)复习式导入:大家首先回顾一下两角和与差的余弦公式:()cos cos cos sin sin αβαβαβ+=-;()cos cos cos sin sin αβαβαβ-=+.这是两角和与差的余弦公式,下面大家思考一下两角和与差的正弦公式是怎样的呢 提示:在第一章我们用诱导公式五(或六)可以实现正弦、余弦的互化,这对我们解决今天的问题有帮助吗让学生动手完成两角和与差正弦公式.()()sin cos cos cos cos sin sin 2222ππππαβαβαβαβαβ⎡⎤⎡⎤⎛⎫⎛⎫⎛⎫+=-+=-+=-+- ⎪ ⎪ ⎪⎢⎥⎢⎥⎣⎦⎝⎭⎝⎭⎝⎭⎣⎦sin cos cos sin αβαβ=+.()()()()sin sin sin cos cos sin sin cos cos sin αβαβαβαβαβαβ-=+-=-+-=-⎡⎤⎣⎦让学生观察认识两角和与差正弦公式的特征()sin αβ+=sin cos cos sin αβαβ+ ①里加外加,里减外减&()sin sin cos cos sin αβαβαβ-=- ②,,,αβαβ顺序不变简单应用:(视学生情况,2可酌情删减)1、求00sin 75,sin15)2、(口答)课本138页练习A 1——4题 (二)例题讲解 例题安排:例1与例2是三角与向量的综合问题,其过程是一次旋转变换。
例1是例2的一个特例,在编排上体现了由特殊到一般的认识规律,例2求证的结论是一组旋转变换公式。
由此,在安排上,例1作为重点讲解,而例2则留给学生自己课下解决。
培养学生举一反三,由特殊到一般的学习能力。
例3与例4也是由特殊到一般的关系。
先讲例3降低了难度,为例4打好了基础,这样例4便也可由同学仿照例3研讨得出。
》例5 体现了数学学科与物理学科的联系,增强了学生的学习兴趣,可留作思考作业课下完成。
例1、已知向量(3,4)OP =,逆时针旋转045到'OP 的位置。
求点'(',')P x y =的坐标 解题分析:问题1、P 点坐标知道吗问题2、OP 旋转到'OP ,什么变了,什么没变问题3、通过前面的学习,你能利用三角函数的知识解决这个问题吗 解:设xOP α∠= 由(3,4)OP =可知(3,4)P所以235OP ==,而'5OP OP ==又因为34cos ,sin 55αα==同理()()00''cos 45,sin 4555x y αα=+=+所以()()000'5cos 455cos cos 45sin sin 453242552522x ααα=+=-⎛⎫=- ⎪ ⎪⎝⎭=-同理()()000'5sin 455sin cos 45cos sin 454232552522y ααα=+=+⎛⎫=+ ⎪ ⎪⎝⎭=所以'()22P -例2(学生课下仿照例1研讨完成)已知点(,)P x y ,与原点的距离保持不变,逆时针旋转θ角到点()'','P x y 。
求证:'cos sin 'sin cos x x y y x y θθθθ=-⎧⎨=+⎩[证明:设xOP α∠=,OP r =则cos ,sin x y rr αα==同理 ()()''cos ,sin x y rrαθαθ=+=+ 从而()()'cos cos cos sin sin cos sin x r r x y αθαθαθθθ=+=-=- ()()'sin sin cos cos sin sin cos y r r x y αθαθαθθθ=+=+=+即 'cos sin 'sin cos x x y y x y θθθθ=-⎧⎨=+⎩例3x x -解题分析:此题与我们所学的两角和与差正弦、余弦不相象,但我们能否发现规律呢【x x-))()1cos cos sin30cos cos30sin 22sin 302x x x x x x x ⎫⎪⎪⎝⎭==-=-思考:是怎么得到的发现=我们是构造一个角使它的正、余弦分别等于12和例4、(教师引导学生仿照例3研讨完成)求函数sin cos y a x b x =+的最大值、最小值和周期,其中,a b 是不同时为零的实数。
解:由例3 知 sin cos y a xb x =+可写为y x x ⎫=⎪⎭,'其中cosθθ==则,原式)()cos sin sin cos x x x θθθ=+=+所以函数sincos y a x b x =+2π注:此题结论可作为公式记住,可方便解题。
例5、(学生课下完成)已知三个电流瞬时值的函数式分别是()()00123,2sin 45,4sin 45I t I t I t ωωω==-=+,求它们合成后的电流瞬时值的函数式,并指出这个函数的振幅和初相。
解: 123II I I =++…()()()())()0000002sin 454sin 452sin cos 45cos sin 454sin cos 45cos sin 45sin cos cos sin t t t t t t t t t t t t t t t ωωωωωωωωωωωωωθωθωθ=+-++=+-++=⎫=⎪⎭=+=+其中01arctan 142'4θ=≈所以()0142'I t ω=+0142' (三)小结:本节我们学习了两角和与差正弦公式及其应用,我们要熟记公式,在解题过程中要善于发现规律,学会灵活运用.(四)作业:课本141页 习题3 —1 A 第2——4题3.1.3两角和与差的正切)一、教学目标:1、知识与技能:⑴掌握公式及其推导过程,理解公式成立的条件;会用公式求值。
⑵培养学生的观察、分析、类比、联想能力;间接推理能力;自学能力。
2、过程与方法:由学生熟知的两角和与差的正弦、余弦公式,引导学生推导出两角和与差的正切公式,通过教师的提问,学生观察,分析,讨论及练习。
及时搜集反馈信息,动态调整教学过程,引导学生攻克难点,掌握重点。
3、情感态度、价值观:发展学生的正向、逆向思维和发散思维能力,构建良好的数学思维品质。
二、教学重点:公式的结构特点及其推导方法、成立条件,运用公式求值。
教学难点:公式的逆向和变形应用。
-三、教学过程:1、复习引入复习:两角和与差的正、余弦公式S+,S, C+ ,C()sin +sin cos +cos sin αβαβαβ= ()sin sin cos cos sin αβαβαβ-=- ()cos cos cos sin sin αβαβαβ+=- ()cos cos cos sin sin αβαβαβ-=+提出问题:复角αβ±与单角α,β的正弦、余弦函数存在以上关系,那么能否用tan tan αβ和来表示()tan αβ±呢、2、两角和与差正切公式的推导及理解 T +,T⑴tan(+)公式的推导(让学生回答) ∵cos (+)0tan(+)=βαβαβαβαβαβαsin sin cos cos sin cos cos sin )cos()sin(-+=++ 当cos cos 0时分子分母同时除以cos cos得:()tan tan tan 1tan tan αβαβαβ++=-以代得:()()()()tan tan tan tan tan tan 1tan tan 1tan tan αβαβαβαβαβαβ+---=+-==⎡⎤⎣⎦--+|⑵思考讨论:①公式是如何推导出来的有什么限制条件 ②公式有何特点如何记忆 ③公式有何用处有何变形⑶注意:1、必须在定义域范围内使用上述公式。
