第二章 随机变量及其分布
合集下载
概率论课件第二章
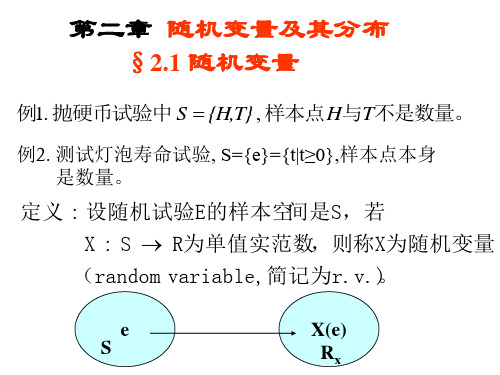
第二章 随机变量及其分布 §2.1 随机变量
例1. 抛硬币试验中S {H,T}, 样本点H与T不是数量。
例2. 测试灯泡寿命试验, S={e}={t|t≥0},样本点本身 是数量。
定义 : 设随机试验E的样本空间是S,若 X : S R为单值实范数,则称X为随机变量 (random variable, 简记为r.v.) 。
2. 特例: (1,) 是参数为的指数分布. (=1) 3. 伽玛函数的性质: (i) (+1)= ();
1 (iii)( ) . 2
(ii) 对于正整数n, (n+1)=n!;
§5. 随机变量的函数的分布
一、 X为离散型r.v. 例1.设X具有以下的分布律,求Y=(X-1)2分布律: X -1 0 1 2 pk 0.2 0.3 0.1 0.4
(二) 贝努利试验
(二项分布)
定 义 : 设 试 验E只 有 两 个 可 能 结 果 A与 A , 且 P( A ) p ( 0 p 1), 将 试 验E独 立 重 复 地 进 行 n次 , 这 样 的 试 验 称 为 贝 努 利 试 验.
设X是n重贝努利试验中事件A发生的次数, 则X 是一个随机变量, 于是
§4. 连续型随机变量及其概率密度
F(x) , 存在非负函 1.定义 : 对于r.v.X的分布函数 数f(x) , 使对于任意的实数 x, 有
则称X为连续型r.v.f(x)称为X概率密度函数, 简称概率密度. 连续型r.v.的分布函数是连续函数.
F(x ) f(t)dt
x
2.概率密度 f(x)的性质:
25
标准正态分布的上分位点:
设X ~ N(0,1), 若z 满足条件
例1. 抛硬币试验中S {H,T}, 样本点H与T不是数量。
例2. 测试灯泡寿命试验, S={e}={t|t≥0},样本点本身 是数量。
定义 : 设随机试验E的样本空间是S,若 X : S R为单值实范数,则称X为随机变量 (random variable, 简记为r.v.) 。
2. 特例: (1,) 是参数为的指数分布. (=1) 3. 伽玛函数的性质: (i) (+1)= ();
1 (iii)( ) . 2
(ii) 对于正整数n, (n+1)=n!;
§5. 随机变量的函数的分布
一、 X为离散型r.v. 例1.设X具有以下的分布律,求Y=(X-1)2分布律: X -1 0 1 2 pk 0.2 0.3 0.1 0.4
(二) 贝努利试验
(二项分布)
定 义 : 设 试 验E只 有 两 个 可 能 结 果 A与 A , 且 P( A ) p ( 0 p 1), 将 试 验E独 立 重 复 地 进 行 n次 , 这 样 的 试 验 称 为 贝 努 利 试 验.
设X是n重贝努利试验中事件A发生的次数, 则X 是一个随机变量, 于是
§4. 连续型随机变量及其概率密度
F(x) , 存在非负函 1.定义 : 对于r.v.X的分布函数 数f(x) , 使对于任意的实数 x, 有
则称X为连续型r.v.f(x)称为X概率密度函数, 简称概率密度. 连续型r.v.的分布函数是连续函数.
F(x ) f(t)dt
x
2.概率密度 f(x)的性质:
25
标准正态分布的上分位点:
设X ~ N(0,1), 若z 满足条件
概率论与数理统计第二章 随机变量及其分布

15
例4: 甲、乙两名棋手约定进行10盘比赛,以赢的盘数 较多者为胜. 假设每盘棋甲赢的概率都为0.6,乙赢的概 率为0.4,且各盘比赛相互独立,问甲、乙获胜的概率 各为多少? 解 每一盘棋可看作0-1试验. 设X为10盘棋赛中甲赢的 盘数,则 X ~ b(10, 0.6) . 按约定,甲只要赢6盘或6盘 以上即可获胜. 所以
定义:若随机变量X所有可能的取值为x1,x2,…,xi,…,且 X 取这些值的概率为 P(X=xi)= pi , i=1, 2, ... (*)
则称(*)式为离散型随机变量X 的分布律。 分布律的基本性质: (1) 表格形式表示: pi 0, i=1,2,... (2)
i
pi 1
X pk
x1 p1
这里n=500值较大,直接计算比较麻烦. 利用泊松定理作近似计算: n =500, np = 500/365=1.3699>0 ,用 =1.3699 的泊松分布作近似 计算:
(1.3669) 5 1.3669 P{ X 5} e 0.01 5!
23
例2: 某人进行射击,其命中率为0.02,独立射击400次,试求击 中的次数大于等于2的概率。 解 将每次射击看成是一次贝努里试验,X表示在400次射击中 击的次数,则X~B(400, 0.02)其分布律为
k 0,1
14
(2) 二项分布 设在一次伯努利试验中有两个可能的结果,且有 P(A)=p 。则在 n 重伯努利试验中事件 A发生的次数 X是一个 离散型随机变量,其分布为
P ( X k ) C nk p k q n k
k =0, 1, 2 ,, n
称X 服从参数为n,p的二项分布,记为 X~b(n, p) 对于n次重复一个0-1试验. 随机变量X表示: n次试验中, A发生的次数. 如: 掷一枚硬币100次, 正面出现的次数X服从二项分布. b(100, 1/2) 事件 X~
第二章随机变量及其分布函数

28
例2.2.9 设在时间t分钟内通过某交叉路口的汽车 数服从参数与t成正比的泊松分布. 已知在一分钟内 没有汽车通过的概率为0.2,求在2分钟内多于一辆 车通过的概率.
S={红色、白色} ?
将 S 数量化
非数量 可采用下列方法
X ()
红色 白色
S
1 0R
3
即有 X (红色)=1 , X (白色)=0.
1, 红色, X () 0, 白色.
这样便将非数量的 S={红色,白色} 数量化了.
4
实例2 抛掷骰子,观察出现的点数.
则有
S={1,2,3,4,5,6} 样本点本身就是数量 X () 恒等变换
20
泊松分布是一个非常常用的分布律,它常与 单位时间、单位面积等上的计数过程相联系. 例如一小时内来到某百货公司中顾客数、单位 时间内某电话交换机接到的呼唤次数和布匹 上单位面积的疵点数等随机现象都可以用泊
松分布来描述. 附表 2 给出了不同 值对应的
泊松分布函数的值.
21
泊松分布的取值规律
记 P(k; ) k e ,则
P
1 2
X
5
2
P(X
1 X
2)
P(X 1) P(X 2) 5
9
12
例 2.2.2 一只口袋中有 m 只白球, n m 只黑球.连 续无放回地从这口袋中取球,直到取出黑球为止.设 此时取出了 X 只白球,求 X 的分布律.
解 X 的可能取值为 0,1,2,, m ,且事件{X i}意 味着总共取了 i+1 次球,其中最后一次取的是黑球而 前面 i 次取得都是白球.
或 X ~ Bn, p.
二项分布的背景是伯努利试验:如果每次试验中事 件A发生的概率均为p,则在n重伯努利试验中A发生 的次数服从参数为n,p的二项分布。
第二章随机变量及其概率分布(概率论)

当 x ≥ 1 时,F ( x) = P( X ≤ x) =P( X = 0) + P( X = 1) =1 ⎧0 x < 0
所以 F ( x) = ⎪⎨0.3 0 ≤ x < 1. ⎪⎩1 1 ≤ x
⎧0 x < 0 分布函数为 F ( x) = ⎪⎨0.3 0 ≤ x < 1
⎪⎩1 1 ≤ x
分布函数图形如下
F(x) 1 0.3
x 01
3
例 设X的概率分布律如下,求X的分布函数. X012 P 0.4 0.35 0.25
解
⎧0
x<0
F
(
x)
=
⎪⎪ ⎨
⎪
0.4 0.75
0≤ x<1 1≤ x<2
⎪⎩ 1
x≥2
由此可见
(1)离散型随机变量的分布函数是分段函数,分 段区间是由X的取值点划分成的左闭右开区间; (2)函数值从0到1逐段递增,图形上表现为阶梯 形跳跃递增; (3)函数值跳跃高度是X取值区间中新增加点的 对应概率值.
z 泊松在数学方面贡献很多。最突出的是1837 年在提出泊松分布。
z 除泊松分布外,还有许多数学名词是以他的 名字命名的,如泊松积分、泊松求和公式、 泊松方程、泊松定理。
当一个随机事件,以固定的平均瞬时速率 λ随机独立地出现时,那么这个事件在单 位时间(面积或体积)内出现的次数或个数 就近似地服从泊松分布。
解: 依题意, X可取值 0, 1, 2, 3.
设 Ai ={第i个路口遇红灯}, i=1,2,3
路口3
路口2
P(X=0)= P(A1)=1/2,
路口1
X=该汽车首次停下时通过的路口的个数. 设 Ai={第i个路口遇红灯}, i=1,2,3
概率统计 第二章 随机变量及其分布

引入适当的随机变量描述下列事件: 例1:引入适当的随机变量描述下列事件: 个球随机地放入三个格子中, ①将3个球随机地放入三个格子中,事件 A={有 个空格} B={有 个空格} A={有1个空格},B={有2个空格}, C={全有球 全有球} C={全有球}。 进行5次试验, D={试验成功一次 试验成功一次} ②进行5次试验,事件 D={试验成功一次}, F={试验至少成功一次 试验至少成功一次} G={至多成功 至多成功3 F={试验至少成功一次},G={至多成功3次}
例2
xi ∈( a ,b )
∑
P( X = xi )
设随机变量X的分布律为 设随机变量X
0 1 2 3 4 5 6 0.1 0.15 0.2 0.3 0.12 0.1 0.03
试求: 试求:
P( X ≤ 4), P (2 ≤ X ≤ 5), P ( X ≠ 3)
0.72 0.7
F ( x) = P{ X ≤ x} =
k : xk ≤ x
∑p
k
离散型随机变量的分布函数是阶梯函数, 离散型随机变量的分布函数是阶梯函数 分布函数的跳跃点对应离散型随机变量的 可能取值点,跳跃高度对应随机变量取对应 可能取值点 跳跃高度对应随机变量取对应 值的概率;反之 反之,如果某随机变量的分布函数 值的概率 反之 如果某随机变量的分布函数 是阶梯函数,则该随机变量必为离散型 则该随机变量必为离散型. 是阶梯函数 则该随机变量必为离散型
X
x
易知,对任意实数a, 易知,对任意实数 b (a<b), P {a<X≤b}=P{X≤b}-P{X≤a}= F(b)-F(a) ≤ = ≤ - ≤ = -
P( X > a) = 1 − F (a)
第二章 随机变量及其分布

来表示。
2. 二项分布的推导过程与说明
3. 举例( 例2,例3,例4 )
C. 泊松分布
1. 定义:如果随机变量X的概率密度如下:
P(X k)
λ k k!
e
λ
,
k =0,1,2,… ( >0) ,
(2.4)
则称X服从参数为 的泊松分布,记作:
X ~ ()
2. 说明
3. 举例
返回目录
§3 随机变量的分布函数
P{X=4}=0.218 P{X=5}=0.175 P{X=6}=0.109 P{X=7}=0.055
P{X=k} < 0.001 , 当 k ≥ 11时
P{ X=8 }=0.022 P{ X=9 }=0.007 P{X=10}=0.02
例3:
某人进行射击,设每次射击的命中率为0.02,独立射 击400次,试求至少击中两次的概率。
解:以p表示每组信号灯禁止汽车通过的概率,
X所有可能取值为0,1,2,3,4。得X的分布律 为:P{X= k}= (1-p)k p , k=0,1,2,3, P{X= 4}= (1-p)4。用表格表示如下:
X
01
2
34
pk
p (1-p) p (1-p)2 p (1-p)3 p (1-p)4
代入p=1/2可得结果,可验证此结果满足分布 律两性质。
• 而有的实验结果与数值无直接关系,我们可 以把它映射为数值来表示,如:硬币抛掷中出 现正面用“0”来表示,出现反面用“1”来表示。
例1:在一袋中装有编号分别为1,2,3的3只球,
在袋中任取一只球,放回,再取一只球,记录它 们的编号。考察两只球的编号之和。则实验的样 本空间S={e}={(i,j)} i,j=1,2,3。 i,j分别为第一,第 二次取到球的号码。 以X表示两球号码之 和,得到样本空间 的每一个样本点e, X都有一值与之对 应,如图2-1。
2. 二项分布的推导过程与说明
3. 举例( 例2,例3,例4 )
C. 泊松分布
1. 定义:如果随机变量X的概率密度如下:
P(X k)
λ k k!
e
λ
,
k =0,1,2,… ( >0) ,
(2.4)
则称X服从参数为 的泊松分布,记作:
X ~ ()
2. 说明
3. 举例
返回目录
§3 随机变量的分布函数
P{X=4}=0.218 P{X=5}=0.175 P{X=6}=0.109 P{X=7}=0.055
P{X=k} < 0.001 , 当 k ≥ 11时
P{ X=8 }=0.022 P{ X=9 }=0.007 P{X=10}=0.02
例3:
某人进行射击,设每次射击的命中率为0.02,独立射 击400次,试求至少击中两次的概率。
解:以p表示每组信号灯禁止汽车通过的概率,
X所有可能取值为0,1,2,3,4。得X的分布律 为:P{X= k}= (1-p)k p , k=0,1,2,3, P{X= 4}= (1-p)4。用表格表示如下:
X
01
2
34
pk
p (1-p) p (1-p)2 p (1-p)3 p (1-p)4
代入p=1/2可得结果,可验证此结果满足分布 律两性质。
• 而有的实验结果与数值无直接关系,我们可 以把它映射为数值来表示,如:硬币抛掷中出 现正面用“0”来表示,出现反面用“1”来表示。
例1:在一袋中装有编号分别为1,2,3的3只球,
在袋中任取一只球,放回,再取一只球,记录它 们的编号。考察两只球的编号之和。则实验的样 本空间S={e}={(i,j)} i,j=1,2,3。 i,j分别为第一,第 二次取到球的号码。 以X表示两球号码之 和,得到样本空间 的每一个样本点e, X都有一值与之对 应,如图2-1。
概率论第二章

2.分布函数单调不减 分布函数单调不减 3.分布函数为右连续函数 分布函数为右连续函数
分布函数与密度函数的关系
x
F ( x) = ∫
−∞
f (t )dt
密度函数性质
1. f ( x) ≥ 0 2. f ( x)dx = 1 ∫
−∞ +∞
3. P ( x ∈ (a, b)) = ∫ f ( x)dx
,−∞ < x < +∞
• 其中 µ , σ (σ > 0 ) 为常数 则称 服从参数为 为常数,则称 则称X服从参数为 2 的正态 µ ,σ 分布(或高斯分布 记为X~ N ( µ , σ 2 ) 或高斯分布),记为 分布 或高斯分布 记为 • 正态分布密度函数的图形关于直线 x = 对称,即对 对称 即对 任意常数 a, f ( µ − a ) = f ( µ + a ) • x = µ 时, f (x ) 取到最大值 取到最大值.
(1) P (Y ≥ 2 ) = 1 − 0 .9876 5 − 5 × 0 .9876 4 × 0 .0124 = 0 .0015
(2) P (Y ≥ 2 Y ≥ 1) = P ((Y ≥ 2) ∩ (Y ≥ 1)) P(Y ≥ 2) 0.0015 = = = 0.0248 5 P (Y ≥ 1) P(Y ≥ 1) 1 − 0.9876
, = 0, , k 1 L5 ,
例2 射击进行到目标被击中或4发子 弹被用完为止.如果每次射击的命中 率都是0.4,求总射击次数X的分布律.
解 X=k所对应的事件为前k-1次射击均 未击中,第k次射击击中,故X的分布律 为:
X
P
1
2
2
3
3
4
4
分布函数与密度函数的关系
x
F ( x) = ∫
−∞
f (t )dt
密度函数性质
1. f ( x) ≥ 0 2. f ( x)dx = 1 ∫
−∞ +∞
3. P ( x ∈ (a, b)) = ∫ f ( x)dx
,−∞ < x < +∞
• 其中 µ , σ (σ > 0 ) 为常数 则称 服从参数为 为常数,则称 则称X服从参数为 2 的正态 µ ,σ 分布(或高斯分布 记为X~ N ( µ , σ 2 ) 或高斯分布),记为 分布 或高斯分布 记为 • 正态分布密度函数的图形关于直线 x = 对称,即对 对称 即对 任意常数 a, f ( µ − a ) = f ( µ + a ) • x = µ 时, f (x ) 取到最大值 取到最大值.
(1) P (Y ≥ 2 ) = 1 − 0 .9876 5 − 5 × 0 .9876 4 × 0 .0124 = 0 .0015
(2) P (Y ≥ 2 Y ≥ 1) = P ((Y ≥ 2) ∩ (Y ≥ 1)) P(Y ≥ 2) 0.0015 = = = 0.0248 5 P (Y ≥ 1) P(Y ≥ 1) 1 − 0.9876
, = 0, , k 1 L5 ,
例2 射击进行到目标被击中或4发子 弹被用完为止.如果每次射击的命中 率都是0.4,求总射击次数X的分布律.
解 X=k所对应的事件为前k-1次射击均 未击中,第k次射击击中,故X的分布律 为:
X
P
1
2
2
3
3
4
4
第二章随机变量及其分布

若随机变量X的概率分布为
Pn (k ) P( X k)C p (1 p)
k n k
nk
, k 0,1,, n
其中0<p<1,称X服从参数为n和p的二项分布, 记作 X~B(n,p)
例5:一随机数字序列要有多长才能使0至少出 现一次的概率不小于0.9?
泊松分布
若随机变量X的概率分布为
和 2 都是常数, 任意, >0, 其中 2 则称X服从参数为 和 的正态分布. 2 记作 X ~ N ( , )
正态分布 N ( , )的图形特点
2
正态分布的密度曲线是一条关于 对 称的钟形曲线. 特点是“两头小,中间大,左右对称”.
设X~ N ( , ) ,
, x
t2 2
( x )
1 ( x) 2
x
e dt
正态分布与标准正态分布的关系 标准正态分布的重要性在于,任何一个 一般的正态分布都可以通过线性变换转化为 标准正态分布.
F ( x) (
x
)
正态分布的概率计算
( x ) 1 ( x )
5.P( X x) 0
P ( a X b) P ( a X b) P ( a X b) P ( a X b)
例1 :已知连续型随机变量X有概率密度
k x 1 0 x 2 f ( x) 其它 0 求系数k及分布函数F(x),并计算P(0.5<X<3).
2
2
( x)dx
的 2 值,并称之为 关于的双侧分位点。 X
2.3
离散型随机变量函数的分布
例1 已知X的分布列为 X Pk -2 -1 0 1 2 3
第2章 随机变量及其分布

, 解 死亡人数 X ~ B(10000 0.005)
40 (1) P{ X 40} C10000 0.005400.9959960 .
k C10000 0.005k 0.99510000 k . (2) P{ X 70} k 0 70
计算相当复杂,下面介绍一个实用的近似公式。
2
2、在有些试验中,试验结果看来与数值无关,但我 们可以引进一个变量来表示它的各种结果.也就是说, 把试验结果数值化. 例1 抛一枚硬币,观察正反面的出现情况. 显然,该试验有两个可能的结果: H , T
我们引入记号:
1, X X (e ) 0,
eH , e T
于是我们就可以用 { X 1}表示出现的是正面, 而用 { X 0} 表示出现的是反面。 X就是一个随机变量。
路口1
路口2
路口3
1 P{ X 0} P( A1 ) . 2
10
路口1
路口2
路口3
1 P{ X 1} P ( A1 A2 ) . 4
路口1
路口2
路口3
1 P{ X 2} P ( A1 A2 A3 ) . 8
11
路口1
路口2
路口3
1 P{ X 3} P ( A1 A2 A3 ) . 8
24
定义
若随机变量X的概率分布为
k! 则称X服从参数为 的泊松分布,记为 X ~ ( ) .
验证规范性:
P{ X k }
k
e , k 0,1,2, , ( 0)
k!
k 0
k
e ,
k! e
k 0
概率论与数理统计第二章

1 ,max= 2
4. 渐近线 以X轴为渐进线
5. 曲线的变化规律
设X~ N ( , ) ,
2
X的分布函数是
1 F ( x) 2
x
(t ) 2 22Fra bibliotekedt , x
标准正态分布
0, 1 的正态分布称为标准正态分布.
若随机变量X的概率分布为: P(X=1)=p,0<p<1 P(X=0)=1-p=q 则称X服从参数为p的两点分布.
二项分布
例4 设射手每一次击中目标的概率为p,现连续 射击n次,求恰好击中次数X 的概率分布.
若随机变量X的概率分布为
Pn (k ) P( X k)C p (1 p)
k n k
3. F(x+0)=F(x)
例1:设随机变量X的分布函数为
a be x , x 0 F ( x) x0 0 ,
求常数a, b及概率 P( X 2)
2.2
离散型随机变量的概率分布
定义1 :设xk(k=1,2, …)是离散型随机变量X 所取的一切可能值,pk是X取 xk值的概率,称
0
1 8
1
a
2
2a
Pk
(1)求常数a ; (2) P( X 1), P(2 X 0), P( X 2)
例2 在五件产品中有两件次品,从中任取出两 件。用随机变量X表示其中的次品数,求X的分 布律和分布函数.
X
P
0
0.3
1
0.6
2
0.1
1.0 0.9
0 0.3 F ( x) 0.9 1.0
均匀分布
概率论 第二章 随机变量与概率分布

(2)P{0 X 2}, P{0 X 2}.
解 (1)X的分布函数为
0,
x 1
F
(
x)
1313,
1 2
5 6
,
1 x 1 1 x 2
1
1
1
1,
2 x
3 2 6
解 (2)P{0 X 2} F (2) F (0) 1 1 2 ,
33 P{0 X 2} P{0 X 2} P{X 2} 21 1.
a-b ab
2
0 1
x
2
解得:a=1/2 b=1/
X的密度为: f(x) = F(x) =
1 (1+ x2 )
(-<x<)
P{X2>1}=1-P{-1X 1}
=1-{F(1)-F(-1)}=1/ 2
例6. 设随机变量X的密度函数为:
ke-3x x>0
事件:{取到2白、1黑}={X=2}={Y=1}
4. 随机变量的分类 通常分为两类:
所有取值可以逐 个一一列举
离散型随机变量
随 机 变 量
全部可能取值不仅
如“取到次品的个数”,无穷多,而且还不能
一一列举,而是充满
“收到的呼叫数”等. 满一个或几个区间.
连续型随机变量 非离散型随机变量
非离散型非连续型
§4. 连续型随机变量的概率密度 1. 定义:对于随机变量X的分布函数F(x), 如果存在非负函数f(x),使对于任意实数x有:
F( x) x f (t)dt
则称X为连续型随机变量;称f(x)为X的概率 密度函数。简称概率密度。
概率密度的性质:
(1). f(x)0;
(2).
f
(
x)dx
解 (1)X的分布函数为
0,
x 1
F
(
x)
1313,
1 2
5 6
,
1 x 1 1 x 2
1
1
1
1,
2 x
3 2 6
解 (2)P{0 X 2} F (2) F (0) 1 1 2 ,
33 P{0 X 2} P{0 X 2} P{X 2} 21 1.
a-b ab
2
0 1
x
2
解得:a=1/2 b=1/
X的密度为: f(x) = F(x) =
1 (1+ x2 )
(-<x<)
P{X2>1}=1-P{-1X 1}
=1-{F(1)-F(-1)}=1/ 2
例6. 设随机变量X的密度函数为:
ke-3x x>0
事件:{取到2白、1黑}={X=2}={Y=1}
4. 随机变量的分类 通常分为两类:
所有取值可以逐 个一一列举
离散型随机变量
随 机 变 量
全部可能取值不仅
如“取到次品的个数”,无穷多,而且还不能
一一列举,而是充满
“收到的呼叫数”等. 满一个或几个区间.
连续型随机变量 非离散型随机变量
非离散型非连续型
§4. 连续型随机变量的概率密度 1. 定义:对于随机变量X的分布函数F(x), 如果存在非负函数f(x),使对于任意实数x有:
F( x) x f (t)dt
则称X为连续型随机变量;称f(x)为X的概率 密度函数。简称概率密度。
概率密度的性质:
(1). f(x)0;
(2).
f
(
x)dx
重点!!第二章随机变量及其分布

例如:◆ 掷一颗骰子面上出现的点数;
◆ 昆虫的产卵数; ◆五月份北京的最高温度; ◆ 每天进入上海站的旅客数;
(2)在有些试验中,试验结果看来与数值无 关,但我们可以引进一个变量来表示它的各 种结果.也就是说,把试验结果数值化。
例如:裁判员在运动场上不叫运动员的名 字而叫号码,名字与号码之间建立了一种
0 X ~ 1 2 1 1 4 2 1 8 3 1 8
即
例2.7 一骰子掷两次,用X表示所得点数之和,求X取可能
值的概率。
解 X的所有可能取值为2,3,4,…,12,其分布律为
二、常用的离散型随机变量及其分布
(1) (0—1)分布
如果随机变量X的分布律为
P X = k = p 1 - p , k = 0,1, 0 < p < 1 .
它是一个随机变量。
事件{收到不少于1次呼叫} {没有收到呼叫} {X= 0}
{ X 1}
三、 随机变量的分类
离散型随机变量 随机变量 非离散型随机变量 混合型随机变量 我们将研究两类随机变量: (1)离散型随机变量 (2)连续型随机变量 连续型随机变量
例2.1 对一均匀硬币抛一次,观察正反面情况。 =>样本空间 {H , T }, 定义随机变量
注:若将本例中的“有放回”改为”无放回”, 那么各次试 验条件就不同了, 不在是伯努利试验, 只能用古典概型求解。
1 C95 C52 P( X 2) 3 0.00618 C100
定理2.3泊松(Poisson) 设>0,n是正整数,若npn=,则对任
一固定的非负整数k,有
n k k lim C n pn (1 pn ) n k
第二章随机变量及其分布 随机事件

f ( x)
. x
数学 分析
R
称这种定义在样本空间上的实值函数 X=X()为随机变量. 2. 定义(P38 定义1) 设随机试验 E 的样本空间为 , 若对每一个样 本点 ,有唯一实数 X()与之对应, 则称实值函数 X()为 随机变量, 简记为 X . 随机变量通常用大写字母 X, Y, Z 或希腊字母 ,η 等表示
pk
p1 p2
…
pk
…
P(X=xk ) 特征性质: 1.P ( X xk ) = P( )= 1 注2 分布列的性质: 0 pk 1; pk 注3 随机变量的分布列不等同于其分布函数,
累积概率函数
k 1 k 1
统称为分布
例2
分布函数
可互相确定 ? ! ?
分布列
点概率函数
例如,从某一学校随机选一学生,测量他的 身高. 我们可以把可能的身高看作随机变量 X , 然后我们可以提出关于X 的各种问题. 如 P(X >1.7 )=? P(X ≤1.5 )= ? P(1.5<X<1.7) =? 一旦我们实际选定了一个学生并量了其身高 之后,我们就得到 X 的一个具体的值,记作 x . 这时要么 x≥1.7, 要么 x <1.7, 再求 P(x ≥1.7)就没有意义了. 随机变量 X 所取的值一般采用小写字母 x, y, z 等表示
. ..
.
. ] x
!
1 e x, x 0; 例2(P38 例1) 验证函数 F ( x ) 其它, 0,
分段函数
可以作为某个随机变量的分布函数. 解 (1) 由函数表达式显然有 非负有界性 0 F(x) 1,
2
.
0
浙大第二章随机变量及其分布

即分布函数是密度函数的可变上限的 定积分.
由上式可得,在 f (x)的连续点,
dF(x) f(x) dx
常见的连续型随机变量 正态分布、均匀分布、指数分布
(I)正态分布
正态分布是应用最广泛的一种连 续型分布.
正态分布在十九世纪前叶由 高 斯(Gauss)加以推广,所以通常 称为高斯分布.
德莫佛
泊松分布的定义及图形特点
p (k;) :P {Xk} e k, k 0 ,1 ,2 , ,
k! 其中 >0 是常数,则称 X 服从参数为 的
λ
泊松分布,记作X~P( ).
λ
λ
由泊松定理,n重贝努里试 验中稀有事件出现的次数近 似地服从泊松分布.
我们把在每次试验中出现概 率很小的事件称作稀有事件. 如地震、火山爆发、特大洪 水、意外事故等等
德莫佛(De Moivre)最早发现了 二项分布的一个近似公式,这一 公式被认为是正态分布的首次露 面.
(1) 正态分布的定义
若r.v. X 的概率密度为 f(x) 1 e , (x2 2)2 x
2
其中 和 都是常数, 任意, >0, 则称X服从参数为 和 的正态分布.
记作 X~N(,2) (Norm
2 当x→ ∞时,f(x) → 0,
这说明曲线 f(x)向左右伸展时,越来越贴 近x轴。即f (x)以x轴为渐近线。
f(x) 1 e , (x2 2)2 x
2
用求导的方法可以证明,
为f (x)的两个拐点的横坐 标。
x=μ σ
这是高等数学的内容,如果 忘记了,课下再复习一下。
X ~ U[a, b]
用X表示n重贝努里试验中事件A(成功) 出现的次数,则
X~B(n,p)
由上式可得,在 f (x)的连续点,
dF(x) f(x) dx
常见的连续型随机变量 正态分布、均匀分布、指数分布
(I)正态分布
正态分布是应用最广泛的一种连 续型分布.
正态分布在十九世纪前叶由 高 斯(Gauss)加以推广,所以通常 称为高斯分布.
德莫佛
泊松分布的定义及图形特点
p (k;) :P {Xk} e k, k 0 ,1 ,2 , ,
k! 其中 >0 是常数,则称 X 服从参数为 的
λ
泊松分布,记作X~P( ).
λ
λ
由泊松定理,n重贝努里试 验中稀有事件出现的次数近 似地服从泊松分布.
我们把在每次试验中出现概 率很小的事件称作稀有事件. 如地震、火山爆发、特大洪 水、意外事故等等
德莫佛(De Moivre)最早发现了 二项分布的一个近似公式,这一 公式被认为是正态分布的首次露 面.
(1) 正态分布的定义
若r.v. X 的概率密度为 f(x) 1 e , (x2 2)2 x
2
其中 和 都是常数, 任意, >0, 则称X服从参数为 和 的正态分布.
记作 X~N(,2) (Norm
2 当x→ ∞时,f(x) → 0,
这说明曲线 f(x)向左右伸展时,越来越贴 近x轴。即f (x)以x轴为渐近线。
f(x) 1 e , (x2 2)2 x
2
用求导的方法可以证明,
为f (x)的两个拐点的横坐 标。
x=μ σ
这是高等数学的内容,如果 忘记了,课下再复习一下。
X ~ U[a, b]
用X表示n重贝努里试验中事件A(成功) 出现的次数,则
X~B(n,p)
第二章 随机变量及其分布

2013-7-8
宁波工程学院 理学院
第二章 随机变量及其分布
第24页
课堂练习
设 X ~ p(x),且 p(x) = p(x),F(x)是 X 的分布函数, 则对任意实数 a>0,有( ② ) a 1 a ① F(a) =1 p( x )dx ② F(a)= p( x )dx 0 0 2 ③ F(a) = F(a) ④ F(a) = 2F(a) 1
3 x
0,
, x 0, x 0.
2013-7-8
宁波工程学院 理学院
第二章 随机变量及其分布
第20页
离散型
1. 分布列: pn = P(X=xn) ( 唯一 ) 2. F(x) =
xi x
连续型
1. 密度函数 X ~ p(x) ( 不唯一 )? 2. F ( x) p(t )dt
P{X 0}, P{0 X 1}, P{X 2}, P{X 2}
2013-7-8
宁波工程学院 理学院
第二章 随机变量及其分布
第10页
2.1.3 离散随机变量的分布列
设离散随机变量 X 的可能取值为: x1,x2,……,xn,…… 称 pi=P(X=xi), i =1, 2, …… 为 X 的分布列.
2013-7-8
宁波工程学院 理学院
第二章 随机变量及其分布
第6页
两类随机变量
若随机变量 X 可能取值的个数为有限个或 可列个,则称 X 为离散随机变量. 若随机变量 X 的可能取值充满某个区间 [a, b],则称 X 为连续随机变量. 前例中的 X, Y, Z ,O为离散随机变量; 而电视机寿命T 为连续随机变量.
2013-7-8
宁波工程学院 理学院
第二章 随机变量及其分布
第24页
课堂练习
设 X ~ p(x),且 p(x) = p(x),F(x)是 X 的分布函数, 则对任意实数 a>0,有( ② ) a 1 a ① F(a) =1 p( x )dx ② F(a)= p( x )dx 0 0 2 ③ F(a) = F(a) ④ F(a) = 2F(a) 1
3 x
0,
, x 0, x 0.
2013-7-8
宁波工程学院 理学院
第二章 随机变量及其分布
第20页
离散型
1. 分布列: pn = P(X=xn) ( 唯一 ) 2. F(x) =
xi x
连续型
1. 密度函数 X ~ p(x) ( 不唯一 )? 2. F ( x) p(t )dt
P{X 0}, P{0 X 1}, P{X 2}, P{X 2}
2013-7-8
宁波工程学院 理学院
第二章 随机变量及其分布
第10页
2.1.3 离散随机变量的分布列
设离散随机变量 X 的可能取值为: x1,x2,……,xn,…… 称 pi=P(X=xi), i =1, 2, …… 为 X 的分布列.
2013-7-8
宁波工程学院 理学院
第二章 随机变量及其分布
第6页
两类随机变量
若随机变量 X 可能取值的个数为有限个或 可列个,则称 X 为离散随机变量. 若随机变量 X 的可能取值充满某个区间 [a, b],则称 X 为连续随机变量. 前例中的 X, Y, Z ,O为离散随机变量; 而电视机寿命T 为连续随机变量.
2013-7-8
2.1随机变量及其分布(1,2)课件

(4) F ( x ) 至多有可数多个间断点, 且在其间断点处,
是右连续的, 即对任何实数 a 有 lim F x F (a )
x a
任一随机变量 的分布函数 都满足以上性质, 反之, 任一满足以上性质的函数, 都可作为某一 随机变量的分布函数.
X 服从离散均匀分布.
三、分布函数 离散型随机变量的特点是: 其取值范围是有限集
或可列集. 其概率分布可用列表法表示: X x1 , x2 , x3 , ..., xn , ... p p1 , p2 , p3 , ..., pn , ...
但有些随机变量是非离散的,它的取值可能是 某一
区间内的一切值.
x x
lim F x 1
(4) F ( x ) 至多有可数多个间断点, 且在其间断点处,
是右连续的, 即对任何实数 a 有 lim F x F (a ) 证(1)0 F ( x ) P{ X x } 1 (2) a b 时, X a
1 P{ X 2 } P{ X 4 } P{ X 6 } ... P{ X 2n } ...
p 2 p 4 p 6 ... p 2 n ... 1 p2 1 2 2 2 1 p p 2p 1 p 2
p2
若离散型 r , v . X 的概率分布为
X p x1 p1
A x2 xk
p2
pk
则对于集合 xn n 1,2,3,... 的任一子集 A, 事件
“ X 在 A 中取值” 即“X A ” 的概率为
P{ X A } pk
xk A
只有两种对立结果: 对于贝努利试验, “A发生” 与“A不发生” 设事件A发生的概率为 p ( 0 p 1 ) 则事件 A 发生的概率为 q 1 p 令X表示 一次贝努利试验中, A发生的次数, 即
是右连续的, 即对任何实数 a 有 lim F x F (a )
x a
任一随机变量 的分布函数 都满足以上性质, 反之, 任一满足以上性质的函数, 都可作为某一 随机变量的分布函数.
X 服从离散均匀分布.
三、分布函数 离散型随机变量的特点是: 其取值范围是有限集
或可列集. 其概率分布可用列表法表示: X x1 , x2 , x3 , ..., xn , ... p p1 , p2 , p3 , ..., pn , ...
但有些随机变量是非离散的,它的取值可能是 某一
区间内的一切值.
x x
lim F x 1
(4) F ( x ) 至多有可数多个间断点, 且在其间断点处,
是右连续的, 即对任何实数 a 有 lim F x F (a ) 证(1)0 F ( x ) P{ X x } 1 (2) a b 时, X a
1 P{ X 2 } P{ X 4 } P{ X 6 } ... P{ X 2n } ...
p 2 p 4 p 6 ... p 2 n ... 1 p2 1 2 2 2 1 p p 2p 1 p 2
p2
若离散型 r , v . X 的概率分布为
X p x1 p1
A x2 xk
p2
pk
则对于集合 xn n 1,2,3,... 的任一子集 A, 事件
“ X 在 A 中取值” 即“X A ” 的概率为
P{ X A } pk
xk A
只有两种对立结果: 对于贝努利试验, “A发生” 与“A不发生” 设事件A发生的概率为 p ( 0 p 1 ) 则事件 A 发生的概率为 q 1 p 令X表示 一次贝努利试验中, A发生的次数, 即
概率论第二章

将 p = 0.5 代入,得
1 0 X ~ 0 .5 0.25 2 0.125 3 0 .0625 0 .0625 4
下面,重点介绍三种离散型随机变量的概率分 布。 (一)0-1分布 分布 若X 的分布律为 k 1− k P { X = k } = p (1 − p ) , k = 0 ,1 或者 0 1 X p pk 1− p 则称随机变量 X 服从参数为 的0-1分布 参数为p的 分布. 参数为 如果试验的结果只有两个:成功与失败,并且成 功的概率为p,则成功的次数 X 服从参数为p的0-1 分布。
P{ X ≥ 2} = 1 − P{ X = 0} − P{ X = 1}
P{ X ≥ 2} = 1 − P{ X = 0} − P{ X = 1}
= 1 − (0.99) − 20(0.01)(0.99) = 0.0169 设A为“四个人中至少有一个人来不及维修”这 一事件,则有
20 19
P( A) ≥ P{ X ≥ 2} = 0.0169
P{ X ≥ 2} = 1 − P{ X = 0} − P{ X = 1}
= 1 − (0.98)
400
− 400(0.02)(0.98)
399
直接计算上式比较麻烦,为此需要一个近似计算 公式。我们先引入一个重要的分布。
(三) 泊松分布 三 泊松分布(Poisson Distribution) 如果随机变量 X 的分布律为:
例6 社会上定期发行某种奖券,中奖率为p.某人 每次购买一张奖券,如果没有中奖则下次继续购买1 张,直至中奖为止.求该人购买次数的分布律. 解 设该人购买的次数为X ,则X的可能取值为
1, 2 , L .
{X = 1} 表示第一次购买就中奖,其概率为p.
概率论第二章

三。几种常用的离散型分布 (一)二项分布
B ( n, p )
在贝努里试验中,如果每次试验事件 发生的概率为 发生的概率为P, 在贝努里试验中,如果每次试验事件A发生的概率为 ,即
P ( A) = p,0 < p < 1, q = 1 − p
并设随机变量X表示在 次试验中事件 发生的次数 并设随机变量 表示在n次试验中事件 发生的次数, 表示在 次试验中事件A发生的次数 则称X服从二项分布,记作 则称 服从二项分布,记作X~ B ( n, 服从二项分布 其分布列为: p ) ,其分布列为: k k n−k 。 ) P{ X = k} = Cn p (1 − p) , k = 0,1,..., n (2。3) 特别, 特别,当n=1时,X~ B (1, 时
G ( p)
在贝努里试验中,如果每次试验事件 发生的概率为 发生的概率为P, 在贝努里试验中,如果每次试验事件A发生的概率为 ,即
P ( A) = p,0 < p < 1, q = 1 − p
并设随机变量X表示事件 首次发生的试验次数 则称X 并设随机变量 表示事件A首次发生的试验次数,则称 表示事件 首次发生的试验次数, 服从几何分布, 其分布列为: 服从几何分布, 几何分布 记作 X ~ G ( p ) ,其分布列为:
0 3 3 解:P ( X = 0) = C2 C3 / C5 = 1 / 10,
1 3 P( X = 1) = C2C32 / C5 = 6 / 10, 2 1 3 P( X = 2) = C2 C3 / C5 = 3 / 10,
通式为: 通式为:
2
k 3 3 P( X = k ) = C2 C3 − k / C5 , k = 0,1,2
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(3) k 0 = [(n + 1) p ] = [7.7] = 7 故最可能命中 7 炮. 8.设有 80 台同类型设备, 各台工作与否是相互独立的,发生故障的概率都是 0.01, 且一台设备的故障能由一个人处理. 考虑两种配备维修工人的方法, 其一是由 4 人维护, 每人负责 20 台; 其二是由 3 人共同维护 80 台. 试比较这两种方法在设备发生故障时不 能及时维修的概率的大小. 解 按第一种方法以 X 表示第一人负责的 20 台中同一时刻发生故障的台数,则
P{0 ≤ X ≤ 2} = P{U{ X = k}} = ∑ b( k ;800,0.0005)
k =0 k =0
2
2
4 42 ≈ ∑ P(k ,4) = e (1 + + ) ≈ 0.2381 1! 2! k =0
2 −4
习 题 2-3 1、判别下列函数是否为某随机变量的分布函数?
⎧0, x < −2, ⎪ (1) F ( x) = ⎨1 / 2, − 2 ≤ x < 0, ⎪1, x ≥ 0; ⎩ ⎧0, x < 0, ⎪ (2) F ( x) = ⎨sin x, 0 ≤ x < π , ⎪1, x ≥ π ; ⎩ ⎧0, x < 0, ⎪ (3) F ( x) = ⎨ x + 1 / 2, 0 ≤ x < 1 / 2, ⎪1, x ≥ 1 / 2. ⎩
14
6. 设随机变量 X 的概率分布为: P{ X = K } = (1) P{
k , k = 1,2,3,4,5 .试求: 15
1 5 (2) P{1 ≤ X ≤ 3} ; (3) P{ X > 3}. < X < }; 2 2 1 5 1 2 1 解 (1) P{ < X < } = P{ X = 1} + P{ X = 2} = + = ; 2 2 15 15 5 1 2 3 2 (2) P{1 ≤ X ≤ 3} = P{ X = 1} + P{ X = 2} + P{ X = 3} = + + = 15 15 15 5 4 5 3 (3) P{ X > 3} = P{ X = 4} + P{ X = 5} = + = . 15 15 5
2、 掷一枚均匀的硬币三次, 观察前后三次出现的正面次数之和 “大于 2” , “等于 2” , “小于 2”的情况,定义一个随机变量,并写出该随机变量取每一个特定值的概率. 解 分别用 w1 , w2 , w3 表示试验的三个结果“大于 2” , “等于 2” , “小于 2”则
Ω = {w1 , w2 , w3 } 定义随机变量 X 如下:
∴ P{ X ≥ 3} = 1 − P{ X < 3} = 1 − P{ X = 0} − P{ X = 1} − P{ X = 2}
= 1 − e −0.7 (
0.7 0 0.71 0.7 2 + + ) ≈ 0.0341. 0! 1! 2!
10.纺织厂女工照顾 800 个纺锭,每一纺锭在某一段时间 τ 内断头的概率为 0.005. 求在 τ 这段时间内断头次数不大于 2 的概率. 解:以 X 表示纺锭断头次数则 n = 800, p = 0.005, np = 4 ,应用泊松定理,所求概率 为
ω
X
HHH 3
HHT 2
HTH 2
THH 2
HTT 1
THT 1
TTH 1
TTT 0
则 X 是随机变量,易见, 使 X 取值为 2({ X = 2}) 的样本点构成的子集为 A = {HHT , HTH , THH }, 故 P{ X = 2} = P( A) = 3 / 8, 类似地,有
P{ X ≤ 1} = P{HTT , THT , TTH , TTT } = 4 / 8.
P{ X = 4} =
2×3 +1 7 2× 4 +1 1 2 × 5 + 1 11 = , P{ X = 5} = = , P{ X = 6} = = 36 36 36 4 பைடு நூலகம்6 36
故 X 的概率分布为
X pi
1 1 26
2 3 1 5 12 36
4 5 6 7 1 11 36 4 36
2.一汽车沿一街道行驶, 需要通过三个均设有红绿信号灯的路口, 每个信号灯为红 或绿与其它信号灯为红或绿相互独立, 且红绿两种信号灯显示的时间相等. 以 X 表示 该汽车首次遇到红灯前已通过的路口的个数, 求 X 的概率分布. 解 由题意知, X 的所有可能取值为 0,1,2,3 则
P{ X = 0} =
1 1 1 1 , P{ X = 1} = × = , 2 2 2 4 1 1 1 1 1 1 1 1 P{ X = 2} = × × = , P{ X = 3} = × × = 2 2 2 8 2 2 2 8 X pi 0 1 2 1 2 1 1 4 8 3 1 8
故 X 的概率分布为
解 满足分布函数的三条性质 (1) 单调非减; (2) F (−∞) = lim F ( x) = 0, F (+∞) = lim F ( x) = 1;
x→−∞ x→+∞
(3) 右连续性. 所以(1) (3)是分布函数.(2)不是 2、设随机变量 X 的分布函数为
F ( x) = A + B arctan x (−∞ < x < +∞).
∞
第二种方法中发生故障而不能及时维修的概率小,且维修工人减少一人. 9.某一城市每天发生火灾的次数 X 服从参数 λ = 0.7 的泊松分布, 求该城市一天内 发生 3 次或 3 次以上火灾的概率.
15
解 Q X ~ P (0.7) ∴ P{ X = k} =
0.7 k −0.7 e , (k = 0,1,L) k!
X ~ b( 20,0.01) , 以 Ai 表 示 事 件 第 i 人 负 责 的 台 中 发 生 故 障 不 能 及 时 维 修 ,
( i = 1,2,3,4 ) ,则 80 台中发生故障而不能及时维修的概率为:
P( A1 U A2 U A3 U A4 ) ≥ P ( A1 ) = P{ X ≥ 2}
求: (1) X 的的分布函数; (2) P{X ≤ 1 / 2}, P{3 / 2 < X ≤ 5 / 2}, P{2 ≤ X ≤ 3}. 解 (1) F ( x) = P{ X ≤ x} 当 x < −1 时, { X ≤ x} = ∅, 故 F ( x) = 0 当 − 1 ≤ x < 2 时, F ( x ) = P{ X ≤ x} = P{ X = −1} = 当 2 ≤ x < 4 时, F ( x ) = P{ X = −1} + P{ X = 2} =
试求: (1)系数 A与B ; (2) P{ X ≤ 0} ; (3) P{−1 < X ≤ 1}.
16
解 (1) 因为 F ( +∞ ) = A + B ⋅ 所以 A =
π
= 1 , F ( −∞ ) = A + B ⋅ ( − ) = 0 , 2 2
π
1 1 ,B = 2 π 1 1 + arctan x (−∞ < x < +∞ ). 2 π
习 题 2-2
1 同时掷两枚骰子观察它们出现的点数,求两枚骰子出现的最大点数的概率分布. 解 设 X 表示骰子出现的最大点数,则 X 的所有可能取值为 1,2,3,4,5,6
13
P{ X = 1} =
1 2 ×1 + 1 1 2× 2 +1 5 = , P{ X = 3} = , P{ X = 2} = = 36 36 12 36 36
7.若每次射击中靶的概率为 0.7,射击 10 炮求: (1)命中 3 炮的概率; (2)至少命 中 3 炮的概率; (3)最可能命中几炮. 解 设 X 表示射击 10 炮中中靶的次数,则 X ~ b(10,0.7) 故
3 (1) P{ X = 3} = C10 0.7 3 0.37 = 0.009; 0 1 2 (2) P{ X ≥ 3} = 1 − (C10 0.7 0 0.310 + C10 0.710.39 + C10 0.7 2 0.38 ) = 0.998;
3.已知随机变量 X 的概率分布为:
X pi
1
θ
2
2 3 3 且 P{ X ≥ 2} = 求θ . 2 2θ (1 − θ ) (1 − θ ) 4
3 4
解 由 P{ X ≥ 2} = P{ X = 2} + P{ X = 3} = 2θ (1 − θ ) + (1 − θ ) 2 = 1 − θ 2 = 求得 θ = ± 故取 θ =
1 4
1 1 3 + = 4 2 4
当 x ≥ 4 时, F ( x ) = P{ X = −1} + P{ X = 2} + P{ X = 4} = 1
x < −1 ⎧ 0, ⎪1 / 4, − 1 ≤ x < 2 ⎪ 故 F ( x) = ⎨ ⎪3 / 4, 2 ≤ x < 4 ⎪ x≥2 ⎩ 1, 1 1 (2) P{X ≤ 1 / 2} = F ( ) − F ( −∞) = 4 2 5 3 3 1 1 P{3 / 2 < X ≤ 5 / 2} = F ( ) − F ( ) = − = 2 2 4 4 2 3 1 1 P{2 ≤ X ≤ 3} = − = 4 4 2 x<0 ⎧ 0, ⎪ x / 2, 0 ≤ x <1 ⎪ 4、 设 X 的分布函数为 F ( x) = ⎨ . ⎪ x − 1 / 2, 1 ≤ x < 1.5 ⎪ x ≥ 1.5 ⎩ 1,
