九年级切线长定理练习题
数学九年级上册-切线长定理及三角形的内切圆七大题型人教版原卷版

专题24.7 切线长定理及三角形的内切圆【七大题型】【人教版】【题型1 利用切线长定理求周长】 (1)【题型2 三角形内切圆中求角度】 (2)【题型3 三角形内切圆中求面积】 (4)【题型4 三角形内切圆中求线段长度】 (5)【题型5 三角形内切圆中求半径】 (5)【题型6 三角形内切圆中求最值】 (6)【题型7 外接圆和内切圆的综合运用】 (7)【题型1 利用切线长定理求周长】【例1】(2022秋•宜兴市校级期中)如图,△ABC 是一张三角形的纸片,⊙O 是它的内切圆,点D 是其中的一个切点,已知AD =10cm ,小明准备用剪刀沿着与⊙O 相切的任意一条直线MN 剪下一块三角形(△AMN ),则剪下的△AMN 的周长为 .【变式1-1】(2022秋•莒南县期末)如图,PA 、PB 切⊙O 于A 、B 两点,CD 切⊙O 于点E ,分别交PA、PB于点C、D.若PA、PB的长是关于x的一元二次方程x2﹣mx+m﹣1=0的两个根,求△PCD 的周长.【变式1-2】(2022•雨花区校级三模)如图,△ABC中,∠C=90°,BC=5,⊙O与△ABC的三边相切于点D、E、F,若⊙O的半径为2,则△ABC的周长为( )A.14B.20C.24D.30【变式1-3】(2022秋•崇川区月考)如图,P是⊙O外一点,PA、PB分别和⊙O相切于点A、B,C是劣AB弧上任意一点,过C作⊙O切线DE,交PA、PB于点D、E,已知PA的长为5cm,∠DOE=65°,点M、N分别在PA、PB的延长线上,MN与⊙O相切于点F,已知DN、EM的长是方程x2﹣10x+k=0的两根.(1)求∠P的度数;(2)求△PDE的周长;(3)求四边形DEMN的周长.【题型2 三角形内切圆中求角度】【例2】(2022•温州模拟)如图,在Rt△ABC中,∠A=90°,⊙O是它的内切圆,与AB,BC,CA分别切于点D,E,F,若∠ACB=40°,则∠DOE= .【变式2-1】(2022秋•昌平区期末)如图,⊙O是△ABC的内切圆,切点分别为D,E,F,已知∠A=40°,连接OB,OC,DE,EF,则∠BOC= °,∠DEF= °.【变式2-2】(2022•万年县校级模拟)如图,△ABC中,内切圆I与AB,BC,CA分别切于F,D,E,连接BI,CI,再连接FD,ED,(1)若∠A=40°,求∠BIC与∠FDE的度数.(2)若∠BIC=α;∠FDE=β,试猜想α,β的关系,并证明你的结论.【变式2-3】(2022秋•邗江区期中)如图,在△ABC中,AB=AC,AD⊥BC于点D,点M是△ABC内一点,连接BM交AD于点N,已知∠AMB=108°,若点M是△CAN的内心,则∠BAC的度数为( )A.36°B.48°C.60°D.72°【题型3 三角形内切圆中求面积】【例3】(2022秋•黄冈期中)如图,边长为1的正方形ABCD的边AB是⊙O的直径,CF是⊙O的切线,E为切点,F点在AD上,BE是⊙O的弦,求△CDF的面积.【变式3-1】(2022•武汉模拟)如图,AB是⊙O的直径,C是⊙O上一点,E是△ABC的内心,2OE⊥EB.若AE=2,则△ABE的面积为( )222A.B.2C.D.1【变式3-2】(2022春•海曙区校级期中)如图,花边带上正三角形的内切圆半径为1cm.如果这条花边带有100个圆和100个正三角形,则这条花边的面积为( )33A.150πB.150C.300D.200【变式3-3】(2022•齐齐哈尔一模)如图,正方形ABCD边长为4cm,以正方形的一边BC为直径在正方形ABCD内作半圆,过A作半圆的切线,与半圆相切于F点,与DC相交于E点,则△ADE的面积( )cm2A.12B.24C.8D.6【题型4 三角形内切圆中求线段长度】【例4】(2022秋•乌兰察布期末)如图,⊙O分别切△ABC的三条边AB、BC、CA于点D、E、F、若AB=5,AC=6,BC=7,求AD、BE、CF的长.【变式4-1】(2022秋•崇川区月考)如图,已知△ABC的内切圆O与三边分别切于D、E、F,∠A=60°,CB=6cm,△ABC的周长为16cm,则DF的长等于( )A.2cm B.3cm C.4cm D.6cm【变式4-2】(2022秋•龙凤区期末)如图,在Rt△ABC中,∠C=90°,AC=3,BC=4,⊙O是△ABC 的内切圆,点D是斜边AB的中点,则OD的长度是 .【变式4-3】(2022•永定区模拟)如图,已知在矩形ABCD中,AB=12,BC=16,⊙O1和⊙O2分别是△ABC和△ADC的内切圆,点E、F为切点,则EF的长是 cm.【题型5 三角形内切圆中求半径】【例5】(2022•定安县二模)如图,在矩形ABCD中,AD<AB,AD=9,AB=12,则△ACD内切圆的半径是( )A .1B .2C .3D .4【变式5-1】(2022秋•张店区期末)如图,在Rt △ABC 中,∠C =90°,BC =3,AB =5,⊙O 是Rt △ABC 的内切圆,则⊙O 的半径为( )A .1B .C .2D .323【变式5-2】(2022秋•虎丘区校级期中)若四边形ABCD 有内切圆(与四边形四边均相切),四边形面积为S ,各边长分别为a ,b ,c ,d ,则该圆的直径为( )A .B .C .D .a +b +c +dS Sa +c c−d S(a +b)2S a +b +c +d【变式5-3】(2022秋•南丹县期末)如图,△ABC 的内切圆⊙O 分别与AB ,AC ,BC 相切于点D ,E ,F .若∠C =90°,AC =6,BC =8,则⊙O 的半径等于 .【题型6 三角形内切圆中求最值】【例6】(2022春•长兴县月考)如图,矩形ABCD ,AD =6,AB =8,点P 为BC 边上的中点,点Q 是△ACD 的内切圆圆O 上的一个动点,点M 是CQ 的中点,则PM 的最大值是 .【变式6-1】(2022秋•扬州月考)如图是一块△ABC余料,已知AB=20cm,BC=7cm,AC=15cm,现将余料裁剪成一个圆形材料,则该圆的最大面积是 .【变式6-2】(2022•温州自主招生)设等边△ABC的内切圆半径为2,圆心为I.若点P满足PI=1,则△ABC与△APC的面积之比的最大值为 .【变式6-3】(2022秋•滨湖区期末)已知点C是⊙O上一动点,弦AB=6,∠ACB=120゜.(1)如图1,若CD平分∠ACB,求证:AC+BC=CD;(2)如图2,△ABC内切圆半径为r.①用含r的代数式表示AC+BC;②求r的最大值.【题型7 外接圆和内切圆的综合运用】【例7】(2022秋•滨湖区期末)设两直角边分别为3、4的直角三角形的外接圆和内切圆的半径长分别为R和r,则R﹣r= .【变式7-1】(2022•鞍山模拟)如图,⊙O内切于Rt△ABC,切点分别为D、E、F,∠C=90°.已知∠AOC=120°,则∠OAC= °,∠B= °.已知AC=4cm,BC=3cm,则△ABC 的外接圆的半径为 cm,内切圆的半径为 cm.【变式7-2】(2022•游仙区模拟)如图,在△ABC中,∠BAC=60°,其周长为20,⊙I是△ABC的内切3圆,其半径为,则△BIC的外接圆直径为 .【变式7-3】(2022秋•鄞州区校级月考)如图,在Rt△ABC中,AC=8,BC=6,∠C=90°.⊙I分别切AC,BC,AB于点D,E,F,求Rt△ABC的内心I与外心O之间的距离.。
3.7 切线长定理(练习)(解析版)

第三章 圆第七节 切线长定理精选练习一、单选题1.(2021·北京九年级专题练习)如图,PA ,PB 为⊙O 的两条切线,点A ,B 是切点,OP 交⊙O 于点C ,交弦AB 于点D .下列结论中错误的是( )A .PA =PBB .AD =BDC .OP ⊥ABD .∠PAB =∠APB【答案】D【分析】利用切线长定理、等腰三角形的性质即可得出答案.【详解】解:由切线长定理可得:∠APO =∠BPO ,PA =PB ,从而AB ⊥OP ,AD =BD .因此A .B .C 都正确.无法得出∠PAB =∠APB ,可知:D 是错误的.综上可知:只有D 是错误的.故选:D .【点睛】本题考查了切线长定理、等腰三角形的性质,关键是利用切线长定理、等腰三角形的性质解答.2.(2021·全国九年级课时练习)如图,AB 是⊙O 的直径,点P 在BA 的延长线上,PA =AO ,PD 与⊙O 相切于点D ,BC ⊥AB 交PD 的延长线于点C ,若⊙O 的半径为1,则BC的长是( )A .1.5B .2CD 【答案】D【分析】连接OD ,根据切线的性质求出∠ODP =90°,根据勾股定理求出PD ,证明BC 是⊙O 的切线,根据切线长定理得出C D =BC ,再根据勾股定理求出BC 即可.【详解】连接OD ,如图所示∵PC 切⊙O 于D ∴∠ODP =90°∵⊙O 的半径为1,PA =AO ,AB 是⊙O 的直径 ∴PO =1+1=2,PB =1+1+1=3,OD =1∴由勾股定理得:PD ==∵BC ⊥AB ,AB 过O ∴BC 切⊙O 于B ∵PC 切⊙O 于D ∴CD =BC设CD =CB =x 在Rt △PBC 中,由勾股定理得:PC 2=PB 2+BC 2即222)3x x +=+ 解得:x 即BC故选:D【点睛】本题考查了切线的性质和判定,及切线长定理,切线的性质定理为:圆的切线垂直于过切点的半径,切线长定理为:从圆外一点可以引圆的两条切线,它们的切线长相等,这一点和圆心的连线平分两条切线的夹角.同时考查了利用勾股定理解直角三角形.3.(2021·湖北武汉市·九年级一模)如图,经过A 、C 两点的⊙O 与△ABC 的边BC 相切,与边AB 交于点D ,若∠AD C =105°,BC =CD =3,则AD 的值为( )A .B .CD 【答案】A【分析】连接OC 、OD ,作OE AB ^于点E .易求出75CBD CDB Ð=Ð=°,30BCD Ð=°.再由切线的性质,即可求出60OCD Ð=°,即三角形OCD 为等边三角形.得出结论60ODC Ð=°,3OC OD CD ===.从而即可求出45ADO Ð=°,即三角形OED 为等腰直角三角形,由此即可求出DE 的长,最后根据垂径定理即可求出AD 的长.【详解】如图,连接OC 、OD ,作OE AB ^于点E .∵BC CD =,∴CBD CDB Ð=Ð,∵105ADC Ð=°,∴75CBD CDB Ð=Ð=°,∴18027530BCD Ð=°-´°=°.由题意可知OC BC ^,即90OCB Ð=°,∴903060OCD OCB BCD Ð=Ð-Ð=°-°=°,∵OD =OC ,∴三角形OCD 为等边三角形.∴60ODC Ð=°,3OC OD CD ===.∴1056045ADO ADC ODC Ð=Ð-Ð=°-°=°,∴三角形OED 为等腰直角三角形,∴3DE ===∴22AD DE ===故选:A .本题考查切线的性质,等腰三角形的性质,三角形外角的性质,等腰直角三角形与等边三角形的判定和性质以及垂径定理,综合性强.正确的连接辅助线是解答本题的关键.4.如图,直线AB,BC,CD分别与⊙O相切于E,F,G,且AB//CD,若OB=3cm,OC=4cm,则四边形EBCG的周长等于( )A.5cm B.10cm C.745cm D.625cm【答案】C【分析】连接OF,利用切线性质和切线长定理可证明BE=BF,CG=CF,∠OBE=∠OBF,∠OCG=∠OCF,OF⊥BC,再根据平行线的性质证得∠BOC=90°,进而由勾股定理求得BC长,根据三角形的面积公式求得OF,进而可求得四边形的周长.【详解】解:连接OF,∵直线AB,BC,CD分别与⊙O相切于E,F,G,∴BE=BF,CG=CF,∠OBE=∠OBF,∠OCG=∠OCF,OF⊥BC,∵AB∥CD,∴∠ABC+∠DCB=180°,∴∠OBF+∠OCF=90°,即∠BOC=90°,∴在Rt△BOC中,OB=3cm,OC=4cm,由勾股定理得:BC==,由1122OB OC BC OF××=××得:OF=341255´=cm,∴OE=OG=OF= 125cm,∴四边形EBCG的周长为BE+BC+CG+EG=2OE+2BC=2×125+2×5=745cm,【点睛】本题考查切线的性质、切线长定理、平行线的性质、勾股定理、三角形的面积公式,熟练掌握切线长定理的运用,证得∠BOC =90°和利用等面积法求出OF 是解答的关键.5.(2021·山西吕梁市·九年级月考)如图,四边形ABCD 内接于⊙O ,AB =BC .AT 是⊙O 的切线,∠BAT =55°,则∠D 等于( )A .110°B .115°C .120°D .125°【答案】A【分析】连接AC ,OA ,OB ,先结合切线的性质以及圆的性质求得ACB BAT Ð=Ð,再结合等腰三角形的性质以及圆的内接四边形的性质求得2D ACB Ð=Ð即可.【详解】如图所示,连接AC ,OA ,OB ,则()11802AOB OBA OAB =°-ÐÐÐ=,∵2AOB ACB Ð=Ð,∴90ACB OAB =°-ÐÐ,∴90ACB OAB Ð=°-Ð,∵AT 是⊙O 的切线,∴90BAT OAB Ð=°-Ð,∴55ACB BAT Ð=Ð=°,∵AB BC =,∴1802ABC ACB Ð=°-Ð,根据圆的内接四边形可得:180D ABC Ð=°-Ð,∴2110D ACB Ð=Ð=°,故选:A .【点睛】本题考查圆的综合问题,理解圆的切线的性质以及内接四边形的性质是解题关键.6.(2021·浙江九年级专题练习)如图,⊙O 的弦AB =8,M 是弦AB 上的动点,若OM 的最小值是3,则⊙O 的半径是( )A .4B .5C .6D .7【答案】B【分析】过O 点作OH ⊥AB 于H ,连接OA ,如图,根据垂径定理得到AH =BH =4,利用垂线段最短得到OH =3,然后利用勾股定理计算出OA 即可.【详解】解:过O 点作OH ⊥AB 于H ,连接OA ,如图,∵OH ⊥AB ,∴AH =BH =12AB =12×8=4,∵OM 的最小值是3,∴OH =3,在Rt △OAH 中,OA =5,即⊙O 的半径是5.故选:B .【点睛】本题考查了垂径定理:直于弦的直径平分这条弦,并且平分弦所对的两条弧.也考查了勾股定理.7.(2020·聊城市茌平区实验中学九年级月考)如图,P 为O 外一点,PA 、PB 分别切O 于点A 、B ,CD 切O 于点E 且分别交PA 、PB 于点C ,D ,若PA =4,则△PCD 的周长为( )A .5B .7C .8D .10【答案】C【分析】根据切线长定理求解即可【详解】解:∵PA 、PB 分别切O 于点A 、B ,CD 切O 于点E ,PA=4,∴PA=PB=4,AC=CE ,BD=DE ,∴△PCD 的周长为PC+CE+DE+PD=PC+AC+BD+PD=PA+PB=4+4=8,故选:C .【点睛】本题考查切线长定理,熟练掌握切线长定理及其应用是解答的关键.8.(2021·北京九年级专题练习)如图,ABC D 的内切圆O e 与A B ,BC ,CA 分别相切于点D ,E ,F ,且2AD =,ABC D 的周长为14,则BC 的长为( )A .3B .4C .5D .6【答案】C 【分析】根据切线长定理得到AF =AD =2,BD =BE ,CE =CF ,由△ABC 的周长为14,可求BC 的长.【详解】解:O Qe 与A B ,BC ,CA 分别相切于点D ,E ,F2AF AD \==,BD BE =,CE CF =,ABC D Q 的周长为14,14AD AF BE BD CE CF \+++++=2()10BE CE \+=5BC \=故选:C .【点睛】本题考查了三角形的内切圆与内心,切线长定理,熟练掌握切线长定理是解题的关键.二、填空题9.如图,PA 、PB 、CD 是⊙O 的切线,A 、B 、E 是切点,CD 分别交PA 、PB 于C 、D 两点,若∠COD =70°,则∠AP B =_______.【答案】40°【分析】先利用切线长定理,得出∠BDO =∠CDO ,∠ACO =∠DCO ,再利用三角形内角和求出∠CDO +∠DCO 后得到∠BDC+∠A CD 的值,最后利用三角形外角的性质得到关于∠P 的方程,解方程即可得出答案.【详解】解:∵PA 、PB 、CD 是⊙O 的切线,∴∠BDO =∠CDO ,∠ACO =∠DCO ,∵∠COD =70°,∴∠CDO +∠DCO =180°-70°=110°,∴∠BDC +∠ACD =2(∠CDO +∠DCO )=2 ×110°=220°,∵∠BDC =∠DCP +∠P ,∠ACD =∠CDP +∠P ,∴∠DCP +∠P +∠CDP +∠P =220°,即180°+∠P =220°,∴∠P =40°,即∠APB =40°,故答案为:40°.【点睛】本题综合考查了圆的切线长定理、三角形的内角和定理、三角形外角的性质等,解决本题的关键是要牢记各定理与性质的内容,能灵活运用它们进行不同的角之间的转化,考查了学生推理分析的能力.10.(2021·浙江九年级其他模拟)如图,已知AD 是BAC Ð的平分线,以线段AB 为直径作圆,交BAC Ð和角平分线于C ,D 两点.过D 向AC 作垂线DE 垂足为点E .若24DE CE ==,则直径AB =_______.【答案】10【分析】连接CD 、OD 、OC 、BD ,运用勾股定理求得CD 的长,再证明DE 是圆O 的切线,运用全等三角形的判定与性质以及余角的性质得出∠CDE =∠BAD ,易得BD =CD ,然后再根据正切函数求得AD ,最后根据勾股定理解答即可.【详解】解:如图:连接CD 、OD 、OC 、BD∵AE ⊥DE , 24DE CE ==∴CD =∵OA =OD∴∠OAD =∠ODA∴∠BOD =∠OAD +∠ODA = 2∠OAD∵∠ODA =∠OAD∴∠EAD =∠ODA∴OD //AE∴OD ⊥DE ,即DE 是圆O 的切线∴∠CDE +∠ODC =90°∵AB是直径∴∠BAD+∠B=90°在△BOD和△DOC中OC=OB,DO=DO,BD=CD ∴△BOD≌△DOC∴∠ODC=∠OBD∴∠CDE=∠BAD∵∠BAD=∠DAC∴∠COD=∠BOD∴BD=CD=∵tan∠BAD=BDAD= tan∠CDE=12CEDE=,∴AD=∴AB10=.故填10.【点睛】本题主要考查了三角形的性质、圆的切线的判定与性质、勾股定理、三角函数等知识点,灵活应用相关知识成为解答本题的关键.11.(2020·湖北孝感市·九年级月考)如图,PA、PB是⊙O的切线,A、B为切点,点C、D在⊙O上.若∠P=108°,则∠B+∠D=_____.【答案】216°【分析】连接AB,根据切线得出PA=PB,求出∠PBA=∠PAB=36°,根据圆内接四边形的对角互补得出∠D+∠CBA=180°,再求出答案即可.【详解】解:连接AB,∵PA、PB是⊙O的切线,A、B为切点,∴PA=PB,∴∠PAB=∠PBA,∵∠APB=108°,∴∠PBA=∠PAB=12×(180°﹣∠APB)=36°,∵A、D、C、B四点共圆,∴∠D+∠CBA=180°,∴∠PBC+∠D=∠PBA+∠CBA+∠D=36°+180°=216°,故答案为:216°.【点睛】本题考查了切线长定理,圆周角定理,等腰三角形的性质,三角形内角和定理,圆内接四边形等知识点,能综合运用知识点进行推理和计算是解此题的关键.12.(2021·河北石家庄市·石家庄外国语学校九年级月考)已知△ABC中,⊙I为△ABC的内切圆,切点为H,若B C=6,AC=8,AB=10,则点A到圆上的最近距离等于_____.-【答案】2【分析】连接IA,IA与⊙I半径的差即为点A到圆上的最近距离,只需求出IA和⊙I半径即可得答案.【详解】解:连接IA,设AC、BC分别切⊙I于E、D,连接IE、ID,如图:∵BC=6,AC=8,AB=10,∴BC2+AC2=AB2∴∠C=90°∵⊙I为△ABC的内切圆,∴∠IEC=∠IDC=90°,IE=ID,∴四边形IDCE是正方形,设它的边长是x,则IE=EC=CD=ID=IH=x,∴AE=8﹣x,BD=6﹣x,由切线长定理可得:AH=8﹣x,BH=6﹣x,而AH+BH=10,∴8﹣x+6﹣x=10,解得x=2,∴AH=6,IH=2,∴IA,∴点A到圆上的最近距离为﹣2,故答案为:﹣2.【点睛】本题考查勾股定理、切线长定理、三角形的内切圆等知识,是重要考点,难度较易,掌握相关知识是解题关键.三、解答题13.(2021·浙江温州市·九年级一模)如图,点C ,D 在以AB 为直径的半圆O 上, AD BC=,切线DE 交AC 的延长线于点E ,连接OC .(1)求证:∠ACO =∠ECD .(2)若∠CDE =45°,DE =4,求直径AB 的长.【答案】(1)证明见详解;(2)【分析】(1)由 AD BC=,可得∠A =∠B ,内接四边形可得出∠ECD=∠B ,进而得出∠ACO =∠ECD ;(2))连接OD ,由切线的性质可得出∠ODE =90°,进而得出∠CDO =∠DCO=45°,再根据已知条件计算出∠E=∠ECD ,得到CD=DE =4,再利用勾股定理求出半径,进而得出答案;【详解】(1)证明:∵ AD BC=,∴∠A =∠B ;∵ABDC 是内接四边形∴∠ECD=∠B∴∠ECD=∠A∵AO =CO ;∴∠ACO =∠A∴∠ACO =∠ECD(2)连接OD∵DE 是圆的切线∴∠ODE =90°,∵∠CDE =45°,OC=OD∴∠CDO =∠DCO =45°,∴∠COD =90°,∵ AD BC=,∴ AC DC=,∴∠AOC =∠DOB=45°,∴AO =OC ,∴∠ACO =∠A=1804567.52°-°=° ;∵∠DCO =45°,∴∠ECD =180°-45°-67.5°=67.5°,∵∠E=180°-∠CDE -∠ECD =180°-45°-67.5°=67.5°,∴∠E=∠ECD∴CD=DE =4,∵∠COD =90°,∴222CD OC OD =+∴2216OC OD +=,即28OC =∴OC= 故⊙O 的半径为∴直径AB 的长,【点睛】本题属于圆综合题,考查了圆周角定理,内接四边形,切线性质定理,等腰三角形的判定与性质,勾股定理等知识,熟练掌握性质及定理是解决本题的关键.14.(2021·江苏无锡市·九年级期中)如图,AB 为⊙O 的直径,PD 切⊙O 于点C ,与BA 的延长线交于点D ,DE ⊥P O 交PO 延长线于点E ,连接PB ,∠EDB =∠EPB .(1)求证:PB 是⊙O 的切线.(2)若PB =3,tan ∠PDB =34,求⊙O 的半径.【答案】(1)见解析;(2)32【分析】(1)根据三角形的内角和定理可证E PBO Ð=Ð,然后根据垂直定义可得90E Ð=°,从而得出半径CB PB ^,根据切线的判定定理即可证出结论;(2)连接OC ,根据题意求出45BD PD ==,,再结合切线长定理得到3PC =,2CD =,从而设O e 的半径是r ,利用勾股定理求解即可.【详解】(1),EDB EPB DOE POB Ð=ÐÐ=ÐQ ,E PBO \Ð=Ð,DE PO ^Q ,90E \Ð=°,90PBO \Ð=°,\半径CB PB ^,PB \是O e 的切线.(2)如图,连接OC ,33tan 904PB PDB PBD =Ð=Ð=°Q ,,tan 45BD PB PDB PD \=Ð===g ,.PB Q 和PC 是O e 的切线,3PC PB \==,2CD PD PC \=-=,设O e 的半径是r ,则4OD DB OB r =-=-,PD Q 切O e 于点C ,OC PD \^,222CD OC OD \+=,()22224r r \+=-,32r \=.【点睛】本题考查圆的综合问题,理解切线的判定与性质定理以及正切函数的定义是解题关键.15.(2021·天津九年级学业考试)已知AB 为O e 的直径,点C ,D 为O e 上的两点,AD 的延长线于BC 的延长线交于点P ,连接CD ,30CAB Ð=°.(Ⅰ)如图①,若 2=CBCD ,4AB =,求AD 的长;(Ⅱ)如图②,过点C 作O e 的切线交AP 于点M ,若6CD AD ==,求CM 的长.【答案】(1)AD =;(2)CM = .【分析】(1)根据弧、圆周角之间的关系可求得∠BAD =45°,连接BD ,可得△ABD 为等腰直角三角形,求解即可;(2)根据弦、圆心角之间关系、等边对等角以及三角形外角的性质可求得∠PDM =60°,OC //AP ,再根据切线的性质定理易得△CDM 为直角三角形,解直角三角形即可.【详解】解:(1)∵ 2=CBCD ,30CAB Ð=°,∴1152CAD CAB Ð=Ð=°,∴∠BAD =45°,连接BD ,∵AB 为直径,∴∠BDA =90°,∴cos45AD AB =×°=(2)连接OD 、OC ,∵30CAB Ð=°,∴∠COB =60°,∠AOC =120°,∵6CD AD ==,∴∠AOD =∠COD =60°,∴∠ACD =∠CAD =30°,∠BAP =∠CAD +∠CAB =60°=∠COB ,∴OC //AP ,∠CDP =∠ACD +∠CAD =60°,∵CM 为O e 的切线,∴∠OCM =90°,∴∠AMC =180°-∠OCM =90°,在Rt △CDM 中,sin 60CM CD =×°=.【点睛】本题考查切线的性质定理,等腰三角形等边对等角,弧、圆心角、圆周角、弦之间的关系,解直角三角形.正确作出辅助线是解题关键.。
人教版九年级数学上册切线长定理测试题

第3课时切线长定理一、选择题1.下列说法中,不正确的是 ( ) A.三角形的内心是三角形三条内角平分线的交点B.锐角三角形、直角三角形、钝角三角形的内心都在三角形内部C.垂直于半径的直线是圆的切线D.三角形的内心到三角形的三边的距离相等2.给出下列说法:①任意一个三角形一定有一个外接圆,并且只有一个外接圆;②任意一个圆一定有一个内接三角形,并且只有一个内接三角形;③任意一个三角形一定有一个内切圆,并且只有一个内切圆;④任意一个圆一定有一个外切三角形,并且只有一个外切三角形.其中正确的有 ( )A.1个 B.2个 C.3个 D.4个3.一个直角三角形的斜边长为8,内切圆半径为1,则这个三角形的周长等于 ( ) A.21 B.20 C.19 D.184.如图,PA、PB分别切⊙O于点A、B,AC是⊙O的直径,连结AB、BC、OP,则与∠PAB相等的角(不包括∠PAB本身)有 ( )A.1个 B.2个C.3个 D.4个4题图5题图6题图5.如图,已知△ABC的内切圆⊙O与各边相切于点D、E、F,则点O是△DEF的 ( )A.三条中线的交点 B.三条高的交点C.三条角平分线的交点 D.三条边的垂直平分线的交点6.一个直角三角形的斜边长为8,内切圆半径为1,则这个三角形的周长等于 ( )A.21 B.20 C.19 D.18二、填空题6.如图,⊙I是△ABC的内切圆,切点分别为点D、E、F,若∠DEF=52o,则∠A的度为________.6题图 7题图 8题图7.如图,一圆内切于四边形ABCD,且AB=16,CD=10,则四边形ABCD的周长为________.PBAO8.如图,已知⊙O 是△ABC 的内切圆,∠BAC=50o,则∠BOC 为____________度. 三、解答题9. 如图,AE 、AD 、BC 分别切⊙O 于点E 、D 、F ,若AD=20,求△ABC 的周长.10. 如图,PA 、PB 是⊙O 的两条切线,切点分别为点A 、B ,若直径AC= 12,∠P=60o,求弦AB 的长.11. 如图,PA 、PB 是⊙O 的切线,A 、B 为切点,∠OAB =30°.(1)求∠APB 的度数;(2)当OA =3时,求AP 的长.12.已知:如图,⊙O 内切于△ABC ,∠BOC =105°,∠ACB =90°,AB =20cm .求BC 、AC 的长.13.已知:如图,△ABC三边BC=a,CA=b,AB=c,它的内切圆O的半径长为r.求△ABC的面积S.14.如图,在△ABC中,已知∠ABC=90o,在AB上取一点E,以BE为直径的⊙O恰与AC相切于点D,若AE=2 cm,AD=4 cm.(1)求⊙O的直径BE的长;(2)计算△ABC的面积.15.已知:如图,⊙O是Rt△ABC的内切圆,∠C=90°.(1)若AC=12cm,BC=9cm,求⊙O的半径r;(2)若AC=b,BC=a,AB=c,求⊙O的半径r.四、体验中考16.(2011年安徽)△ABC 中,AB =AC ,∠A 为锐角,CD 为AB 边上的高,I 为△ACD 的内切圆圆心,则∠AIB 的度数是( ) A .120° B .125° C .135° D .150°17.(2011年绵阳)一个钢管放在V 形架内,右图是其截面图,O 为钢管的圆心.如果钢管的半径为25 cm ,∠MPN = 60︒,则OP =( )A .50 cmB .253cmC .3350cm D .503cm 18. (2011年甘肃定西)如图,在△ABC 中,5cm AB AC ==,cos B 35=.如果⊙O 的半径为10cm ,且经过点B 、C ,那么线段AO = cm .17题图 18题图 19题图19. (2011年湖南怀化)如图,PA 、PB 分别切⊙O 于点A 、B ,点E 是⊙O 上一点,且60=∠AEB ,则=∠P __ ___度.参考答案◆随堂检测1. C2. B (提示:②④错误)3. 760(提示:连接ID,IF ∵∠DEF=520∴∠DIF=1040∵D、F是切点∴DI⊥AB,IF⊥AC∴∠ADI=∠AFI=900∴∠A=1800-1040=760)4. 52 (提示:AB+CD=AD+BC)5. 1150 (提示:∵∠A=500∴∠ABC+∠ACB=1300∵OB,OC分别平分∠ABC,∠ACB ∴∠OBC+∠OCB=650∴∠BOC=1800-650=1150)◆课下作业 ●拓展提高1. D (提示:AD=AF,BD=BE,CE=CF ∴周长=821218⨯+⨯=)2. C3. D4. 解:∵AD,AE 切于⊙O 于D,E ∴AD=AE=20 ∵AD,BF 切于⊙O 于D,F ∴BD=BF 同理:CF=CE ∴C △ABC =AB+BC+AC=AB+BF+FC+AC=AB+BD+EC+AC=AD+AE=405. 解:连接BC ∵PA,PB 切⊙O 于A,B ∴PA=PB ∵∠P=600 ∴△ABC 是正三角形 ∵∠PAB=600∵PA 是⊙O 切线 ∴CA ⊥AP ∴∠CAP=900 ∴∠CAB=300 ∵直径AC ∴∠ABC=900 ∴cos300=ABAC∴AB=6. 解:(1)∵在△ABO 中,OA =OB ,∠OAB =30°∴∠AOB =180°-2×30°=120°∵PA 、PB 是⊙O 的切线∴OA ⊥PA ,OB ⊥PB .即∠OAP =∠OBP =90° ∴在四边形OAPB 中,∠APB =360°-120°-90°-90°=60°.(2)如图①,连结OP∵PA 、PB 是⊙O 的切线∴PO 平分∠APB ,即∠APO =12∠APB =30° 又∵在Rt △OAP 中,OA =3, ∠APO =30°∴AP =tan 30OA°=7. 解:(1)连接OD ∴OD ⊥AC ∴△ODA 是Rt △设半径为r ∴AO=r+2 ∴(r+2)2—r 2=16 解之得:r=3 ∴BE=6(2) ∵∠ABC=900 ∴OB ⊥BC ∴BC 是⊙O 的切线 ∵CD 切⊙O 于D ∴CB=CD 令CB=x∴AC=x+4,BC=4,AB=x ,AB=8 ∵2228(4)x x +=+ ∴6x = ∴S △ABC =186242⨯⨯= ●体验中考 1. C2. A (提示:∠MPN=600可得∠OPM=300 可得OP=2OM=50)3.3(提示:连接OB ,易得:∠ABC=∠AOB ∴cos ∠AOB=cos ∠35=OBOA AO=)4. ∠P=600专项训练二概率初步一、选择题1.(徐州中考)下列事件中的不可能事件是( )A.通常加热到100℃时,水沸腾 B.抛掷2枚正方体骰子,都是6点朝上C.经过有交通信号灯的路口,遇到红灯 D.任意画一个三角形,其内角和是360°2.小张抛一枚质地均匀的硬币,出现正面朝上的可能性是( )A.25% B.50% C.75% D.85%3.(2016·贵阳中考)2016年5月,为保证“中国大数据产业峰会及中国电子商务创新发展峰会”在贵阳顺利召开,组委会决定从“神州专车”中抽调200辆车作为服务用车,其中帕萨特60辆、狮跑40辆、君越80辆、迈腾20辆,现随机从这200辆车中抽取1辆作为开幕式用车,则抽中帕萨特的概率是( )A.110B.15C.310D.254.(金华中考)小明和小华参加社会实践活动,随机选择“打扫社区卫生”和“参加社会调查”其中一项,那么两人同时选择“参加社会调查”的概率为( )A.14B.13C.12D.345.在一个不透明的袋中装着3个红球和1个黄球,它们只有颜色上的区别,随机从袋中摸出2个小球,两球恰好是一个黄球和一个红球的概率为( )A.12B.13C.14D.166.现有两枚质地均匀的正方体骰子,每枚骰子的六个面上都分别标有数字1、2、3、4、5、6.同时投掷这两枚骰子,以朝上一面所标的数字为掷得的结果,那么所得结果之和为9的概率是( )A.13B.16C.19D.1127.分别转动图中两个转盘一次,当转盘停止转动时,两个指针分别落在某个数所表示的区域,则两个数的和是2的倍数或3的倍数的概率等于( )A.316B.38C.58D.1316第7题图第8题图8.(2016·呼和浩特中考)如图,△ABC是一块绿化带,将阴影部分修建为花圃,已知AB=15,AC=9,BC=12,阴影部分是△ABC的内切圆,一只自由飞翔的小鸟将随机落在这块绿化带上,则小鸟落在花圃上的概率为( )A.16B.π6C.π8D.π5二、填空题9.已知四个点的坐标分别是(-1,1),(2,2),⎝ ⎛⎭⎪⎫23,32,⎝ ⎛⎭⎪⎫-5,-15,从中随机选取一个点,在反比例函数y =1x 图象上的概率是________.10.(黄石中考)如图所示,一只蚂蚁从A 点出发到D ,E ,F 处寻觅食物.假定蚂蚁在每个岔路口都可能随机选择一条向左下或右下的路径(比如A 岔路口可以向左下到达B 处,也可以向右下到达C 处,其中A ,B ,C 都是岔路口).那么,蚂蚁从A 出发到达E 处的概率是________.11.(贵阳中考)现有50张大小、质地及背面图案均相同的《西游记》任务卡片,正面朝下放置在桌面上,从中随机抽取一张并记下卡片正面所绘人物的名字后原样放回,洗匀后再抽.通过多次试验后,发现抽到绘有孙悟空这个人物卡片的频率约为0.3.估计这些卡片中绘有孙悟空这个人物的卡片张数约为________.12.(荆门中考)荆楚学校为了了解九年级学生“一分钟内跳绳次数”的情况,随机选取了3名女生和2名男生,则从这5名学生中,选取2名同时跳绳,恰好选中一男一女的概率是________.13.(重庆中考)点P 的坐标是(a ,b ),从-2,-1,0,1,2这五个数中任取一个数作为a 的值,再从余下的四个数中任取一个数作为b 的值,则点P (a ,b )在平面直角坐标系中第二象限内的概率是________.14.★从-1,1,2这三个数字中,随机抽取一个数记为a ,那么,使关于x 的一次函数y =2x +a 的图象与x 轴、y 轴围成的三角形的面积为14,且使关于x 的不等式组⎩⎨⎧x +2≤a ,1-x ≤2a有解的概率为________.三、解答题15.(南昌中考)在一个不透明的袋子中装有仅颜色不同的10个小球,其中红球4个,黑球6个.(1)先从袋子中取出m (m >1)个红球,再从袋子中随机摸出1个球,将“摸出黑球”记为事件A ,请完成下列表格:(2)先从袋子中取出m 个红球,再放入m 个一样的黑球并摇匀,随机摸出1个黑球的概率等于45,求m 的值.16.(菏泽中考)锐锐参加我市电视台组织的“牡丹杯”智力竞答节目,答对最后两道单选题就顺利通关,第一道单选题有3个选项,第二道单选题有4个选项,这两道题锐锐都不会,不过锐锐还有两个“求助”可以用(使用“求助”一次可以让主持人去掉其中一题的一个错误选项).(1)如果锐锐两次“求助”都在第一道题中使用,那么锐锐通关的概率是________; (2)如果锐锐两次“求助”都在第二道题中使用,那么锐锐通关的概率是________; (3)如果锐锐将每道题各用一次“求助”,请用树状图或者列表来分析他顺利通关的概率.17.(丹东中考)甲、乙两人进行摸牌游戏.现有三张形状大小完全相同的牌,正面分别标有数字2,3,5.将三张牌背面朝上,洗匀后放在桌子上.(1)甲从中随机抽取一张牌,记录数字后放回洗匀,乙再随机抽取一张.请用列表法或画树状图的方法,求两人抽取相同数字的概率;(2)若两人抽取的数字之和为2的倍数,则甲获胜;若抽取的数字之和为5的倍数,则乙获胜.这个游戏公平吗?请用概率的知识加以解释.18.一只不透明的袋子中装有4个质地、大小均相同的小球,这些小球分别标有数字3,3,5,x,甲、乙两人每次同时从袋中各随机摸出1个球,并计算摸出的这2个球上数字之和,记录后将小球放回袋中搅匀,进行重复实验.实验数据如下表:(1)如果实验继续进行下去,根据上表数据,出现“和为8”的频率稳定在它的概率附近,估计出现“和为8”的概率是________;(2)如果摸出的这两个小球上数字之和为9的概率是13,那么x的值可以取4吗?请用列表法或画树状图法说明理由;如果x的值不可以取4,请写出一个符合要求的x的值.参考答案与解析1.D 2.B 3.C 4.A 5.A 6.C 7.C8.B 解析:∵AB =15,BC =12,AC =9,∴AB 2=BC 2+AC 2,∴△ABC 为直角三角形,∴△ABC 的内切圆半径为12+9-152=3,∴S △ABC =12AC ·BC =12×12×9=54,S 圆=9π,∴小鸟落在花圃上的概率为9π54=π6.9.12 10.12 11.15 12.35 13.15 14.13 15.解:(1)4 2或3 (2)根据题意得6+m 10=45,解得m =2,所以m 的值为2. 16.解:(1)14 解析:第一道肯定能对,第二道对的概率为14,所以锐锐通关的概率为14;(2)16 解析:锐锐两次“求助”都在第二道题中使用,则第一道题对的概率为13,第二道题对的概率为12,所以锐锐能通关的概率为12×13=16;(3)锐锐将每道题各用一次“求助”,分别用A ,B 表示剩下的第一道单选题的2个选项,a ,b ,c 表示剩下的第二道单选题的3个选项,树状图如图所示.共有6种等可能的结果,锐锐顺利通关的只有1种情况,∴锐锐顺利通关的概率为16.17.解:(1)所有可能出现的结果如下表,从表格可以看出,总共有9种结果,每种结果出现的可能性相同,其中两人抽取相同数字的结果有3种,所以两人抽取相同数字的概率为13;(2)不公平.从表格可以看出,两人抽取数字之和为2的倍数有5种,两人抽取数字之和为5的倍数有3种,所以甲获胜的概率为59,乙获胜的概率为13.∵59>13,∴甲获胜的概率大,游戏不公平.2 3 52 2 23 2 5 2 3 2 3 3 3 5 3 52 53 5 5 518.解:(1)0.33(2)图略,当x 为4时,数字和为9的概率为212=16≠13,所以x 不能取4;当x =6时,摸出的两个小球上数字之和为9的概率是13.。
九年级数学 切线长定理 专题练习(含解析)

∴梯形对边和为:8+8=16, 则这个等腰梯形的上底与下底长的和为 16. 故选:D. 分析:直接利用圆外切四边形对边和相等,进而求出即可. 6.如图,⊙O 是△ABC 的内切圆,点 D、E 分别为边 AB、AC 上的点,且 DE 为⊙O 的切 线,若△ABC 的周长为 25,BC 的长是 9,则△ADE 的周长是( ) A.7 B.8 C.9 D.16
答案:C
解析:解答: ∵AB、AC 是⊙O 的两条切线,B、C 是切点, ∴∠B=∠C=90°,∠BOC=180°-∠A=110°. 故选 C. 分析:利用切线的性质可得,∠B=∠C=90°,再用四边形的内角和为 360 度可解. 10.如图,PA、PB 是⊙O 的两条切线,切点是 A、B.如果 OP=4,PA= 2 3 ,那么∠AOB 等于( ) A.90° B.100° C.110° D.120°
答案:B 解析:解答:∵PA、PB 都是⊙O 的切线, ∴PA=PB, 又∵∠P=60°, ∴△PAB 是等边三角形,即 AB=PA=8, 故选 B. 分析: 根据切线长定理知 PA=PB,而∠P=60°,所以△PAB 是等边三角形,由此求得弦 AB 的长. 8.如图,PA、PB 分别是⊙O 的切线,A、B 为切点,AC 是⊙O 的直径,已知∠BAC=35°, ∠P 的度数为( ) A.35° B.45° C.60° D.70°
答案:D 解析:解答: 根据切线的性质定理得∠PAC=90°, ∴∠PAB=90°-∠BAC=90°-35°=55°. 根据切线长定理得 PA=PB, 所以∠PBA=∠PAB=55°, 所以∠P=70°. 故选 D. 分析: 根据切线长定理得等腰△PAB,运用内角和定理求解. 9.如 图 , AB、 AC 是 ⊙O 的 两 条 切 线 , B、 C 是 切 点 , 若 ∠A=70°, 则 ∠BOC 的 度 数 为 ( ) A.130° B.120° C.110° D.100°
部编数学九年级上册专题24.7切线长定理及三角形的内切圆【七大题型】(人教版)(解析版)含答案

专题24.7 切线长定理及三角形的内切圆【七大题型】【人教版】【题型1 利用切线长定理求周长】 (1)【题型2 三角形内切圆中求角度】 (5)【题型3 三角形内切圆中求面积】 (9)【题型4 三角形内切圆中求线段长度】 (13)【题型5 三角形内切圆中求半径】 (17)【题型6 三角形内切圆中求最值】 (20)【题型7 外接圆和内切圆的综合运用】 (25)【题型1 利用切线长定理求周长】【例1】(2022秋•宜兴市校级期中)如图,△ABC 是一张三角形的纸片,⊙O 是它的内切圆,点D 是其中的一个切点,已知AD =10cm ,小明准备用剪刀沿着与⊙O 相切的任意一条直线MN 剪下一块三角形(△AMN ),则剪下的△AMN 的周长为 20cm .【分析】利用切线长定理得出DM =MF ,FN =EN ,AD =AE ,进而得出答案.A B C I【解答】解:∵△ABC是一张三角形的纸片,⊙O是它的内切圆,点D是其中的一个切点,AD=10cm,∴设E、F分别是⊙O的切点,故DM=MF,FN=EN,AD=AE,∴AM+AN+MN=AD+AE=10+10=20(cm).故答案是:20cm.【变式1-1】(2022秋•莒南县期末)如图,PA、PB切⊙O于A、B两点,CD切⊙O于点E,分别交PA、PB于点C、D.若PA、PB的长是关于x的一元二次方程x2﹣mx+m﹣1=0的两个根,求△PCD的周长.【分析】由PA、PB切⊙O于A、B两点,CD切⊙O于点E,根据切线长定理,可得PA=PB,又由PA、PB的长是关于x的一元二次方程x2﹣mx+m﹣1=0的两个根,根据根与系数的关系,可求得PA与PB的长,又由CD切⊙O于点E,即可得△PCD的周长等于PA+PB.【解答】解:∵PA、PB的长是关于x的一元二次方程x2﹣mx+m﹣1=0的两个根,∴PA+PB=m,PA•PB=m﹣1,∵PA、PB切⊙O于A、B两点,∴PA=PB=m2,即m2•m2=m﹣1,即m2﹣4m+4=0,解得:m=2,∴PA=PB=1,∵PA、PB切⊙O于A、B两点,CD切⊙O于点E,∴AD=ED,BC=EC,∴△PCD的周长为:PD+CD+PC=PD+DE+EC+PC=PD+AD+BC+PC=PA+PB=2.【变式1-2】(2022•雨花区校级三模)如图,△ABC中,∠C=90°,BC=5,⊙O与△ABC的三边相切于点D、E、F,若⊙O的半径为2,则△ABC的周长为( )A.14B.20C.24D.30【分析】设AD=x,由切线长定理得AE=x,根据题意可得四边形OECF为正方形,则CE=CF=2,BD=BF=3,在直角三角形ABC中,利用勾股定理求出x,然后求其周长.【解答】解:连接OE、OF,设AD=x,由切线长定理得AE=x,∵⊙O与Rt△ABC的三边分别点D、E、F,∴OE⊥AC,OF⊥BC,∴四边形OECF为正方形,∵⊙O的半径为2,BC=5,∴CE=CF=2,BD=BF=3,∴在Rt△ABC中,∵AC2+BC2=AB2,即(x+2)2+52=(x+3)2,解得x=10,∴△ABC的周长为12+5+13=30.故选:D.【变式1-3】(2022秋•崇川区月考)如图,P是⊙O外一点,PA、PB分别和⊙O相切于点A、B,C是劣弧AB上任意一点,过C作⊙O切线DE,交PA、PB于点D、E,已知PA的长为5cm,∠DOE=65°,点M、N分别在PA、PB的延长线上,MN与⊙O相切于点F,已知DN、EM的长是方程x2﹣10x+k=0的两根.(1)求∠P的度数;(2)求△PDE的周长;(3)求四边形DEMN的周长.【分析】(1)只要证明∠AOB=130°,∠PAO=∠PBO=90°,再利用四边形内角和定理即可解决问题;(2)利用切线长定理即可解决问题;(3)因为DN、EM的长是方程x2﹣10x+k=0的两根.可得DN+EM=10,再利用切线长定理即可解决问题;【解答】解:(1)连接OA、OB、OC.∴PA、PB、DE是⊙O的切线,∴PA⊥OA,OB⊥PB,∠DOA=∠DOC,∠EOB=∠EOC,∵∠DOE=65°,∴∠AOB=130°,∠PAO=∠PBO=90°,∴∠P=360°﹣90°﹣90°﹣130°=50°.(2)∵PA、PB、DE是⊙O的切线,∴DA=DC,EC=EB,PA=PB=5,∴△PDE的周长=PD+DE+PE=PD+DA+PE+EB=PA+PB=10.(3)∵DN、EM的长是方程x2﹣10x+k=0的两根.∴DN+EM=10,∴PN,PM,MN是⊙O的切线,∴AN=NF,MF=MB,DA=DC,EC=EB,∴四边形EMND的周长=EM+MN+DN+DE=EM+BM+NA+DA+EB+DN=2(DN+EM)=20.【题型2 三角形内切圆中求角度】【例2】(2022•温州模拟)如图,在Rt△ABC中,∠A=90°,⊙O是它的内切圆,与AB,BC,CA分别切于点D,E,F,若∠ACB=40°,则∠DOE= 130° .【分析】利用直角三角形性质求出∠ABC=50°,再利用切线性质求出∠BDO=∠BEO=90°,再利用四边形内角和为360°,即可求得答案.【解答】解:在Rt△ABC中,∵∠A=90°,∠ACB=40°,∴∠ABC=90°﹣∠ACB=90°﹣40°=50°,∵⊙O是Rt△ABC的内切圆,与AB,BC,CA分别切于点D,E,F,∴AB、BC是⊙O的切线,∴∠BDO=∠BEO=90°,∴∠DOE=360°﹣∠BDO﹣∠BEO﹣∠ABC=130°,故答案为:130°.【变式2-1】(2022秋•昌平区期末)如图,⊙O是△ABC的内切圆,切点分别为D,E,F,已知∠A=40°,连接OB,OC,DE,EF,则∠BOC= 110 °,∠DEF= 70 °.【分析】连接OD和OF,根据内切圆的性质可得OB,OC平分∠ABC,∠ACB,再根据三角形内角和定理即可求出角BOC的度数;根据切线的性质可得∠DOF的度数,进而根据圆周角定理可得∠DEF的度数.【解答】解:如图,连接OD和OF,∵⊙O是△ABC的内切圆,切点分别为D,E,F,∠A=40°,∴OB,OC平分∠ABC,∠ACB,∴∠BOC=180°﹣∠OBC﹣∠OCB(∠ABC+∠ACB)=180°−12×140°=180°−12=110°,∵OD⊥AB,OF⊥AC,∴∠ADO=∠AFO=90°,∴∠DOF=360°﹣90°﹣90°﹣40°=140°,∠DOF=70°.∴∠DEF=12故答案为:110,70.【变式2-2】(2022•万年县校级模拟)如图,△ABC中,内切圆I与AB,BC,CA分别切于F,D,E,连接BI,CI,再连接FD,ED,(1)若∠A=40°,求∠BIC与∠FDE的度数.(2)若∠BIC=α;∠FDE=β,试猜想α,β的关系,并证明你的结论.(∠ABC+∠ACB),求出∠ABC+∠ACB 【分析】(1)根据圆I是△ABC的内切圆求出∠IBC+∠ICB=12的度数,求出∠IBC+∠ICB即可;连接IF、IE,求出∠FIE,即可求出∠FDE;(2)由(1)得出∠BIC=180°﹣(∠IBC+∠ICB),∠FDE=180°﹣2∠A,根据三角形的内角和定理求出∠BIC =90°+12∠A ,代入即可求出答案.【解答】解:(1)∵圆I 是△ABC 的内切圆,∴∠IBC =12∠ABC ,∠ICB =12∠ACB ,∴∠IBC +∠ICB =12(∠ABC +∠ACB ),∵∠ABC +∠ACB =180°﹣∠A =140°,∴∠IBC +∠ICB =70°,∴∠BIC =180°﹣(∠IBC +∠ICB )=110°,如图,连接IF 、IE ,∵圆I 是△ABC 的内切圆,∴∠IFA =∠IEA =90°,∵∠A =40°,∴∠FIE =360°﹣∠IFA ﹣∠IEA ﹣∠A =140°,∴∠EDF =12∠EIF =70°,答:∠BIC =110°,∠FDE =70°;(2)解:α=180°﹣β,证明:由圆周角定理得:∠FIE =2∠FDE ,由(1)知:2∠FDE =180°﹣∠A ,即∠A =180°﹣2∠FDE ,∴∠A =180°﹣∠EIF ,由(1)知:2∠FDE =180°﹣∠A ,∴∠A =180°﹣2∠FDE =180°﹣2β,∠BIC =180°﹣(∠IBC +∠ICB )=180°−12(∠ABC +∠ACB )=180°−1(180°﹣∠A)2∠A,=90°+12(180°﹣2β),∴∠BIC=α=90°+12即α=180°﹣β.【变式2-3】(2022秋•邗江区期中)如图,在△ABC中,AB=AC,AD⊥BC于点D,点M是△ABC内一点,连接BM交AD于点N,已知∠AMB=108°,若点M是△CAN的内心,则∠BAC的度数为( )A.36°B.48°C.60°D.72°【分析】过点M作ME⊥AD于点E,根据已知条件可得△ABC是等腰三角形,AD是BC边的中垂线,证明ME∥BC,可得∠NME=∠NBD,由点M是△CAN的内心,可得点M在∠NAC和∠ANC的角平分线上,设∠NAM=x,∠NBD=y,所以∠BAC=4x,∠NBD=∠NCD=∠NME=y,∠ENM=∠CNM=2y,然后利用∠AMB=108°,列出方程组y−x=18°2y+x=72°,求解即可得结论.【解答】解:如图,过点M作ME⊥AD于点E,∵AB=AC,AD⊥BC,∴△ABC是等腰三角形,AD是BC边的中垂线,∴NB=NC,∠BAD=∠CAD,∴∠NBD=∠NCD,∵ME⊥AD,AD⊥BC,∴ME∥BC,∴∠NME=∠NBD,∵点M是△CAN的内心,∴点M在∠NAC和∠ANC的角平分线上,∴∠NAM=∠CAM,∠ANM=∠CNM,设∠NAM=x,∠NBD=y,∴∠BAC=4x,∠NBD=∠NCD=∠NME=y,∴∠ENM=∠CNM=∠NBC+∠NCB=2y,∵∠AMB=108°,∴∠AME=∠AMB﹣∠EMN=108°﹣y,在△AEM中,∠EAM+∠AME=90°,∴x+108°﹣y=90°,∴y﹣x=18°,在△ANM中,∠NAM+∠ANM=180°﹣108°,∴x+2y=72°,y−x=18°2y+x=72°,解得x=12°y=30°,∴∠BAC=4x=48°.故选:B.【题型3 三角形内切圆中求面积】【例3】(2022秋•黄冈期中)如图,边长为1的正方形ABCD的边AB是⊙O的直径,CF是⊙O的切线,E 为切点,F点在AD上,BE是⊙O的弦,求△CDF的面积.【分析】设AF=x,由切线长定理可得EF=AF=x,则FD=1﹣x,CF=CE+EF=CB+EF=1+x,利用勾股定理建立方程求出x的值,再根据三角形的面积公式即可求出问题的答案.【解答】解:设AF=x,∵四边形ABCD是正方形,∴∠DAB=90°,∴DA⊥AB,∴AD是圆的切线,∵CF是⊙O的切线,E为切点,∴EF=AF=x,∴FD=1﹣x,∵CB⊥AB,∴CB为⊙O的切线,∴CB=CE,∴CF=CE+EF=CB+EF=1+x.∴在Rt△CDF中由勾股定理得到:CF2=CD2+DF2,即(1+x)2=1+(1﹣x)2,解得x=14,∴DF=1﹣x=34,∴S△CDF =12×1×34=38.【变式3-1】(2022•武汉模拟)如图,AB是⊙O的直径,C是⊙O上一点,E是△ABC的内心,OE⊥EB.若AE=ABE的面积为( )A .B .2CD .1【分析】延长BE 交⊙O 于点F ,连接AF ,OF ,根据AB 是⊙O 的直径,可得∠AFB =∠C =90°,证明△FEA 是等腰直角三角形,可得AF =EF =2,根据垂径定理可得EF =BE =2,进而可得△ABE 的面积.【解答】解:如图,延长BE 交⊙O 于点F ,连接AF ,OF ,∵AB 是⊙O 的直径,∴∠AFB =∠C =90°,∴∠CAB +∠CBA =90°,∵E 是△ABC 的内心,∴∠EAB =12∠CAB ,∠EBA =12∠CBA ,∴∠EAB +∠EBA =12(∠CAB +∠CBA )=45°,∴∠FEA =45°,∴△FEA 是等腰直角三角形,∴AE ==,∵AE =∴AF =EF =2,∵OE ⊥EB ,∴EF =BE =2,∴△ABE 的面积为:12BE •AF =12×2×2=2.故选:B .【变式3-2】(2022春•海曙区校级期中)如图,花边带上正三角形的内切圆半径为1cm .如果这条花边带有100个圆和100个正三角形,则这条花边的面积为( )A .150πB .C .D .200【分析】画出图形,连接AD ,OB ,则AD 过O ,求出∠OBD =30°,求出OB ,根据勾股定理求出BD ,同法求出CD ,求出BC 的长后求得一个三角形的面积即可求得花边的面积.【解答】解:从中选择一个等边三角形和其内接圆如图,⊙O 是△ABC 的内切圆,⊙O 切AB 于F ,切AC 于E ,切BC 于D ,连接AD ,OB ,则AD 过O (因为等边三角形的内切圆的圆心再角平分线上,也在底边的垂直平分线上),∵△ABC 是等边三角形,∴∠ABC =60°,∵⊙O 是△ABC 的内切圆,∴∠OBC =12∠ABC =30°,∵⊙O 切BC 于D ,∴∠ODB =90°,∵OD =1,∴OB =2,由勾股定理得:BD ==∴BC =∴S △ABC =12BC •AD =12××3=∴这条花边的面积=100S △ABC =故选:C .【变式3-3】(2022•齐齐哈尔一模)如图,正方形ABCD 边长为4cm ,以正方形的一边BC 为直径在正方形ABCD 内作半圆,过A 作半圆的切线,与半圆相切于F 点,与DC 相交于E 点,则△ADE 的面积( )cm2A.12B.24C.8D.6【分析】由于AE与圆O切于点F,根据切线长定理有AF=AB=4cm,EF=EC;设EF=EC=xcm.则DE=(4﹣x)cm,AE=(4+x)cm,然后在三角形BCE中由勾股定理可以列出关于x的方程,解方程即可求出,然后就可以求出△ADE的面积.【解答】解:∵AE与圆O切于点F,显然根据切线长定理有AF=AB=4cm,EF=EC,设EF=EC=xcm,则DE=(4﹣x)cm,AE=(4+x)cm,在三角形ADE中由勾股定理得:(4﹣x)2+42=(4+x)2,∴x=1cm,∴CE=1cm,∴DE=4﹣1=3cm,=AD•DE÷2=3×4÷2=6cm2.∴S△ADE故选:D.【题型4 三角形内切圆中求线段长度】【例4】(2022秋•乌兰察布期末)如图,⊙O分别切△ABC的三条边AB、BC、CA于点D、E、F、若AB =5,AC=6,BC=7,求AD、BE、CF的长.【分析】由切线长定理,可知:AF =AD ,CF =CE ,BE =BD ,用未知数设AD 的长,然后表示出BD 、CF 的长,即可表示出BE 、CE 的长,根据BE +CE =7,可求出AD 的长进而求出BE 、CF 的长.【解答】解:假设AD =x ,∵⊙O 分别切△ABC 的三条边AB 、BC 、CA 于点D 、E 、F ;∴根据切线长定理得出AD =AF ,BD =BE ,EC =FC ,∴AF =x ,∵AB =5,AC =6,BC =7,∴BE =BD =AB ﹣AD =5﹣x ,FC =EC =AC ﹣AF =6﹣x ,∴BC =BE +EC =5﹣x +6﹣x =7,解得:x =2,∴AD =2,BE =BD =5﹣2=3,CF =AC ﹣AF =6﹣2=4.【变式4-1】(2022秋•崇川区月考)如图,已知△ABC 的内切圆O 与三边分别切于D 、E 、F ,∠A =60°,CB =6cm ,△ABC 的周长为16cm ,则DF 的长等于( )A .2cmB .3cmC .4cmD .6cm【分析】利用三角形内切圆的性质以及切线长定理得出BD =BE ,CE =CF ,AD =AF ,进而得出△ADF 是等边三角形,即可得出答案.【解答】解:∵△ABC 的内切圆O 与三边分别切于D 、E 、F ,CB =6cm ,△ABC 的周长为16cm ,∴BD =BE ,CE =CF ,AD =AF ,∵BE +EC =BD +FC =6,∴AD =AF =12(AB +AC +BC ﹣BC ﹣BD ﹣CF )=12(16﹣6﹣6)=2,∵∠A =60°,∴△ADF 是等边三角形,∴DF =2.故选:A .【变式4-2】(2022秋•龙凤区期末)如图,在Rt △ABC 中,∠C =90°,AC =3,BC =4,⊙O 是△ABC的内切圆,点D是斜边AB的中点,则OD的长度是 .【分析】如图连接OE、OF、OQ,设⊙O的半径是r,由勾股定理求出AB=5,根据△ABC的内切圆,得到OE⊥AC,OF⊥BC,OE=OF,推出四边形CFOE是正方形,得到CE=CF=OF=OE,根据3﹣r+4﹣r=5求出r、AQ、OQ的长求出AD、DQ的长【解答】解:如图连接OE、OF、OQ,设⊙O的半径是r,由勾股定理得:AB=5,∵⊙O是三角形ABC的内切圆,∴OE⊥AC,OF⊥BC,OE=OF,AE=AQ,BF=BQ,∵∠C=90°,∴∠C=∠CFO=∠CEO=90°,∴四边形CFOE是正方形,∴CE=CF=OF=OE,∴3﹣r+4﹣r=5,r=1,AQ=AE=3﹣1=2,OQ=1,∵D是AB的中点,,∴AD=52,∴DQ=AD﹣AQ=12∴OD2=OQ2+DQ2,∴OD=【变式4-3】(2022•永定区模拟)如图,已知在矩形ABCD中,AB=12,BC=16,⊙O1和⊙O2分别是△ABC和△ADC的内切圆,点E、F为切点,则EF的长是 4 cm.【分析】根据矩形的性质得到AC=20,△ABC≌△CDA,则⊙O1和⊙O2的半径相等.如图,过O1作AB、BC的垂线分别交AB、BC于N、P,过O2作BC,CD、AD的垂线分别交BC,CD、AD于Q,G、H,由∠B=90°,推出四边形O1NBP是正方形,设圆的半径为r,根据切线长定理12﹣r+16﹣r=20,解得r=4,过O1作O1M⊥FO2于M,则O1M=PQ=8,QM=BN=4,同法可得DG=4,根据EF=AC﹣AE﹣CF计算即可.【解答】解:∵矩形ABCD中,AB=12,BC=16,∴AC=20,△ABC≌△CDA,则⊙O1和⊙O2的半径相等.如图,过O1作AB、BC的垂线分别交AB、BC于N、P,过O2作BC,CD、AD的垂线分别交BC,CD、AD于Q,G、H,∵∠B=90°,∴四边形O1NBP是正方形,设圆的半径为r,根据切线长定理12﹣r+16﹣r=20,解得r=4,∴BP=BN=4,同法可得DG=4,∴AN=AE=CG=CF=8,∴EF=AC﹣AE﹣CF=20﹣16=4故答案为:4.【题型5 三角形内切圆中求半径】【例5】(2022•定安县二模)如图,在矩形ABCD中,AD<AB,AD=9,AB=12,则△ACD内切圆的半径是( )A.1B.2C.3D.4【分析】根据矩形性质和勾股定理可得AC=15,设△ACD内切圆的圆心为O,△ACD内切圆的半径为r,连接OE,OF,OG,得四边形DFOG是正方形,然后根据切线长定理即可解决问题.【解答】解:在矩形ABCD中,∠B=90°,AD=BC=9,AB=12,根据勾股定理,得AC==15,设△ACD内切圆的圆心为O,△ACD内切圆的半径为r,如图,连接OE,OF,OG,得四边形DFOG是正方形,∴DF=DG=r,∴AG=AE=AD﹣DG=9﹣r,CF=CE=CD﹣DF=AB﹣DF=12﹣r,∵AE+CE=AC,∴9﹣r+12﹣r=15,解得r=3.∴△ACD内切圆的半径是3.故选:C.【变式5-1】(2022秋•张店区期末)如图,在Rt△ABC中,∠C=90°,BC=3,AB=5,⊙O是Rt△ABC 的内切圆,则⊙O的半径为( )A .1BC .2D .【分析】根据三角形内切圆与内心的性质和三角形面积公式解答即可.【解答】解:∵∠C =90°,BC =3,AB =5,∴AC ==4,如图,分别连接OA 、OB 、OC 、OD 、OE 、OF ,∵⊙O 是△ABC 内切圆,D 、E 、F 为切点,∴OD ⊥BC ,OE ⊥AC ,OF ⊥AB 于D 、E 、F ,OD =OE =OF ,∴S △ABC =S △BOC +S △AOC +S △AOB =12BC •DO +12AC •OE +12AB •FO =12(BC +AC +AB )•OD ,∵∠C =90°,∴12×AC •BC =12(BC +AC +AB )•OD ,∴OD =3×4345=1.故选:A .【变式5-2】(2022秋•虎丘区校级期中)若四边形ABCD 有内切圆(与四边形四边均相切),四边形面积为S ,各边长分别为a ,b ,c ,d ,则该圆的直径为( )A .a b c d SB .S a cC .c−d S(a b)D .2S a b c d【分析】连接OA 、OB 、OC 、OD .由S 四边形ABCD =S △OAB +S △OBC +S △OCD +S △AOD ,由S 四边形ABCD =12AB •r +12BC •r +12CD •r +12AD •r =12(a +b +c +d )•r =S ,即可推出r =2S a b c d .【解答】解:如图,连接OA 、OB 、OC 、OD .∵S 四边形ABCD =S △OAB +S △OBC +S △OCD +S △AOD又∵S △OAB =12AB •r ,S △OBC =12BC •r ,S △OCD =12CD •r ,S △AOD =12AD •r ,∴S 四边形ABCD =12AB •r +12BC •r +12CD •r +12AD •r =12(a +b +c +d )•r =S ,∴r =2S a b c d .故选:D .【变式5-3】(2022秋•南丹县期末)如图,△ABC 的内切圆⊙O 分别与AB ,AC ,BC 相切于点D ,E ,F .若∠C =90°,AC =6,BC =8,则⊙O 的半径等于 2 .【分析】连结OD ,OE ,OF ,设⊙O 半径为r ,根据勾股定理可得AB =10,证明四边形OECF 是正方形,可得CF =CE =OF =r ,然后根据切线长定理可得AE =AE =AC ﹣CE =6﹣r ,BF =BD =BC ﹣CF =8﹣r ,进而可以解决问题.【解答】解:如图,连结OD ,OE ,OF ,设⊙O 半径为r ,∵∠C =90°,AC =6,BC =8,∴AB ==10,∵△ABC 的内切圆⊙O 与AB ,BC ,AC 分别相切于点D ,F ,E ,∴AC ⊥OE ,AB ⊥OD ,BC ⊥OE ,且OF =OD =OE =r ,∴四边形OECF 是正方形,∴CF =CE =OF =r ,∴AE =AE =AC ﹣CE =6﹣r ,BF =BD =BC ﹣CF =8﹣r ,∵AD +BD =AB =10,∴6﹣r +8﹣r =10,∴r =2.∴⊙O 的半径等于2.故答案为:2.【题型6 三角形内切圆中求最值】【例6】(2022春•长兴县月考)如图,矩形ABCD ,AD =6,AB =8,点P 为BC 边上的中点,点Q 是△ACD 的内切圆圆O 上的一个动点,点M 是CQ 的中点,则PM +1 .【分析】由矩形性质和勾股定理可得AC =10,设△ADC 内切圆半径为r ,由面积法可得r =2,连接BQ ,易证PM 为△BCQ 的中位线,得出PM =12BQ ,当BQ 经过圆心O 时,BQ 最长,则此时PM 最大,作OE ⊥AD 与点E ,OF ⊥AB 与点F ,则BF =AB ﹣AF =8﹣2=6,OF =AE =AD ﹣DE =6﹣2=4,由勾股定理可得BO =BQ =BO +OQ =2,从而可得PM 的结果.【解答】解:∵四边形ABCD 为矩形,∴∠D =90°,CD =AB =8,∴AC ==10,设△ADC 的内切圆半径为r ,则有12r(AC +AD +DC)=12×6×8,即12r(10+6+8)=24,解得:r =2.连接BQ ,∵P为BC中点,M为CQ中点,∴PM为△BQC的中位线,BQ,∴PM=12当BQ经过圆心O时,BQ最长,则此时PM最大,作OE⊥AD与点E,OF⊥AB与点F,则BF=AB﹣AF=8﹣2=6,OF=AE=AD﹣DE=6﹣2=4,∴BO=∴BQ=BO+OQ=+2,BQ=1.∴PM=12+1.【变式6-1】(2022秋•扬州月考)如图是一块△ABC余料,已知AB=20cm,BC=7cm,AC=15cm,现将余料裁剪成一个圆形材料,则该圆的最大面积是 4πcm2. .r 【分析】当该圆为三角形内切圆时面积最大,设内切圆半径为r,则该三角形面积可表示为:12•BC•AD,利用勾股定理可得AD,易得三角形(AB+AC+BC)=21r,利用三角形的面积公式可表示为12ABC的面积,可得r,求得圆的面积.【解答】解:如图1所示,S △ABC =12•r •(AB +BC +AC )=12r ×42=21r ,过点A 作AD ⊥BC 交BC 的延长线于点D ,如图2,设CD =x ,由勾股定理得:在Rt △ABD 中,AD 2=AB 2﹣BD 2=400﹣(7+x )2,在Rt △ACD 中,AD 2=AC 2﹣x 2=225﹣x 2,∴400﹣(7+x )2=225﹣x 2,解得:x =9,∴AD =12,∴S △ABC =12BC ×AD =12×7×12=42,∴21r =42,∴r =2,该圆的最大面积为:S =πr 2=π•22=4π(cm 2),故答案为:4πcm 2.【变式6-2】(2022•温州自主招生)设等边△ABC 的内切圆半径为2,圆心为I .若点P 满足PI =1,则△ABC 与△APC 的面积之比的最大值为 6 .【分析】P 满足PI =1,则P 在以I 为圆心,以1位半径的圆上,当P 是⊙O 和BE 的交点时,△ACP 的面积最小,即△ABC 与△APC 的面积之比最大.此时PE =2﹣1=1,则△ABC 与△APC 的面积的比值是BE 与PE 的比值,据此即可求解.【解答】解:点P 满足PI =1,则P 在以I 为圆心,以1位半径的圆上.作BE ⊥AC ,则BE 一定过点I ,连接AI .∵在直角△AIE 中,∠IAE =12∠BAC =12×60°=30°,IE =2,∴AI =2IE =4,∴BE =IE +BI =IE +AI =2+4=6.当P是⊙I和BE的交点时,△ACP的面积最小,即△ABC与△APC的面积之比最大.此时PE=2﹣1=1,则△ABC与△APC的面积的比值是BEPE =61=6.故答案是:6.【变式6-3】(2022秋•滨湖区期末)已知点C是⊙O上一动点,弦AB=6,∠ACB=120゜.(1)如图1,若CD平分∠ACB,求证:AC+BC=CD;(2)如图2,△ABC内切圆半径为r.①用含r的代数式表示AC+BC;②求r的最大值.【分析】(1)在CD上截取CE=BC,由∠ACD=∠BCD=60°得到△BCE为等边三角形,根据圆周角定理得∠ABD=∠ACD=60°,则BE=BC=CE,∠1+∠ABE=60°,∠ABE+∠2=60°,所以∠1=∠2,于是可根据“AAS”判断△ACB≌△DEB,得到AC=DE,由此得到CD=CE+DE=BC+AC;(2)①作弦CD平分∠ACB,设△ABC的内心为P点,作PQ⊥AB于Q,PH⊥BC于H,PF⊥AC于F,根据内心的性质得PF=PQ=PH=r,由∠ACD=∠BCD=60°得到∠CPF=∠CPH=30°,根据含30度的直角三角形三边的关系得到CF,CH==,然后根据切线长定理得到AF=AQ=AC﹣CF=AC,BH=BQ=BC﹣CH=BC,而AB=AQ+BQ,所以AC+BC=6,整理得AC+BC=6+;②由于AC+BC=CD得到CD=6,所以当CD为直径时,r最大;当CD为直径,根据垂径定理的推论得CD⊥AB,AM=BM=12AB=3,AC=BC,可计算出CD=AC=2CD=+=6+,可解得r=6﹣【解答】(1)证明:在CD上截取CE=BC,如图1,∵CD平分∠ACB,∠ACB=120゜,∴∠ACD=∠BCD=60°,∴△BCE为等边三角形,∠ABD=∠ACD=60°,∴BE=BC=CE,∠1+∠ABE=60°,∠ABE+∠2=60°,∴∠1=∠2,在△ACB和△DEB中∠A=∠D∠1=∠2,BC=BE∴△ACB≌△DEB,∴AC=DE,∴CD=CE+DE=BC+AC;(2)解:①作弦CD平分∠ACB,设△ABC的内心为P点,作PQ⊥AB于Q,PH⊥BC于H,PF⊥AC 于F,如图,则PF=PQ=PH=r,∵CD平分∠ACB,∠ACB=120゜,∴∠ACD=∠BCD=60°,∴∠CPF=∠CPH=30°,∴CF=,CH==,∴AF=AQ=AC﹣CF=AC,BH=BQ=BC﹣CH=BC,而AB=AQ+BQ,∴AC+BC=6,∴AC+BC=6+;②∵AC+BC=CD,∴CD=6+,∴当CD为直径时,r最大,如图3,当CD为直径,∴CD⊥AB,垂足为M,AB=3,AC=BC,∴AM=BM=12∵∠ACD=60°,∴∠CAM=30°,∴CD∴AC=2CD=∴+6,∴r=6﹣即r的最大值为6﹣【题型7 外接圆和内切圆的综合运用】【例7】(2022秋•滨湖区期末)设两直角边分别为3、4的直角三角形的外接圆和内切圆的半径长分别为R 和r,则R﹣r= 1.5 .【分析】利用三角形的外心与内心的性质即可进行计算.【解答】解:因为直角三角形的外接圆半径等于斜边长的一半,所以R==2.5;如图,若Rt △ABC 的边AC =3,BC =4,根据勾股定理,得AB =5,其内切圆⊙O 分别切AB 、BC 、AC 于D 、E 、F .设OE =OF =OD =r ,∴S △ABC =S △AOB +S △BOC +S △AOC ,即12AC •BC =12AB •OD +12BC •OE +12AC •OF ,12×3×4=12×5×r +12×4×r +12×3×r ,6=12r (5+4+3),6=6r ,∴r =1,则R ﹣r =2.5﹣1=1.5.故答案为:1.5.【变式7-1】(2022•鞍山模拟)如图,⊙O 内切于Rt △ABC ,切点分别为D 、E 、F ,∠C =90°.已知∠AOC =120°,则∠OAC = 15 °,∠B = 60 °.已知AC =4cm ,BC =3cm ,则△ABC 的外接圆的半径为 52 cm ,内切圆的半径为 1 cm .【分析】由三角形内心的性质得到OC 平分∠ACB ,求得∠ACO =12∠ACB =45°,根据三角形的内角和得到结论;根据勾股定理得到AB ==5,于是得到结论.【解答】解:∵⊙O 内切于Rt △ABC ,∠C =90°,∴OC 平分∠ACB ,∴∠ACO =12∠ACB =45°,∵∠AOC =120°,∴∠OAC =180°﹣45°﹣120°=15°,∵AO 平分∠BAC ,∴∠BAC =2∠OAC =30°,∴∠B =90°﹣30°=60°;∵AC =4cm ,BC =3cm ,∠C =90°,∴AB ==5,∴△ABC 的外接圆的半径为52;设内切圆的半径为r ,∴r =34−52=1,故答案为:15,60,52,1.【变式7-2】(2022•游仙区模拟)如图,在△ABC 中,∠BAC =60°,其周长为20,⊙I 是△ABC 的内切BIC 的外接圆直径为 .【分析】设△BIC 的外接圆圆心为O ,连接OB ,OC ,作CD ⊥AB 于点D ,在圆O 上取点F ,连接FB ,FC ,作OE ⊥BC 于点E ,设AB =c ,BC =a ,AC =b ,根据三角形内心定义可得S △ABC =12lr =12×20×=12AB •CD ,可得bc =40,根据勾股定理可得BC =a =7,再根据I 是△ABC 内心,可得IB 平分∠ABC ,IC 平分∠ACB ,根据圆内接四边形性质和圆周角定理可得∠BOC =120°,再根据垂径定理和勾股定理即可求出OB 的长.【解答】解:如图,设△BIC 的外接圆圆心为O ,连接OB ,OC ,作CD ⊥AB 于点D ,在圆O 上取点F ,连接FB ,FC ,作OE ⊥BC 于点E ,设AB =c ,BC =a ,AC =b ,∵∠BAC =60°,∴AD =12b ,CD ,∴BD =AB ﹣AD =c −12b ,∵△ABC 周长为l =20,△ABC 的内切圆半径为r∴S △ABC =12lr =12×20×12AB •CD ,∴=•c ,∴bc =40,在Rt △BDC 中,根据勾股定理,得BC 2=BD 2+CD 2,即a 2=(c −12b )2+)2,整理得:a 2=c 2+b 2﹣bc ,∵a +b +c =20,∴a 2=c 2+b 2﹣bc =(b +c )2﹣3bc =(20﹣a )2﹣3×40,解得a =7,∴BC =a =7,∵I 是△ABC 内心,∴IB 平分∠ABC ,IC 平分∠ACB ,∵∠BAC=60°,∴∠ABC+∠ACB=120°,∴∠IBC+∠ICB=60°,∴∠BIC=120°,∴∠BFC=180°﹣120°=60°,∴∠BOC=120°,∵OE⊥BC,,∠BOE=60°,∴BE=CE=72÷∴OB=72【变式7-3】(2022秋•鄞州区校级月考)如图,在Rt△ABC中,AC=8,BC=6,∠C=90°.⊙I分别切AC,BC,AB于点D,E,F,求Rt△ABC的内心I与外心O之间的距离.【分析】连接ID、IE、IF,如图,由AC=8,BC=6,∠C=90°,根据圆周角定理的推论和勾股定理AB=5,连接OI,设⊙I的得到AB为△ABC的外接圆的直径,AB=10,则外心O为AB的中点,BO=12半径为r,根据切线的性质和切线长定理得ID⊥AC,IE⊥BC,IF⊥AB,AD=AF,BE=BF,易得四边形IDCE为正方形,则DC=CE=r,所以AD=AC﹣DC=8﹣r,BE=BC﹣CE=6﹣r,即AF=8﹣r,BF=6﹣r,利用AF+BF=AB得8﹣r+6﹣r=10,解得r=2,所以BF=4,则OF=OB﹣BF=1,在Rt△IOF中,根据勾股定理得IO【解答】解:连接ID、IE、IF,如图,∵AC=8,BC=6,∠C=90°,∴AB为△ABC的外接圆的直径,AB=10,∴外心O为AB的中点,AB=5,∴BO=12连接OI,如图,设⊙I的半径为r,∵⊙I分别切AC,BC,AB于点D,E,F,∴ID⊥AC,IE⊥BC,IF⊥AB,AD=AF,BE=BF,而∠C=90°,∴四边形IDCE为正方形,∴DC=CE=r,∴AD=AC﹣DC=8﹣r,BE=BC﹣CE=6﹣r,∴AF=8﹣r,BF=6﹣r,而AF+BF=AB,∴8﹣r+6﹣r=10,解得r=2,∴BF=6﹣r=4,∴OF=OB﹣BF=5﹣4=1,在Rt△IOF中,IF=2,OF=1,∴IO=即Rt△ABC的内心I与外心O。
2021年九年级数学中考复习专题之圆:切线长定理综合运用(一)
2021年九年级数学中考复习专题之圆:切线长定理综合运用(一)一.选择题1.如图所示,P是⊙O外一点,PA,PB分别和⊙O切于A,B两点,C是上任意一点,过C作⊙O的切线分别交PA,PB于D,E.若△PDE的周长为12,则PA的长为()A.12 B.6 C.8 D.42.如图,△MBC中,∠B=90°,∠C=60°,MB=,点A在MB上,以AB为直径作⊙O与MC相切于点D,则CD的长为()A.B.C.2 D.33.如图中,CA,CD分别切圆O1于A,D两点,CB、CE分别切圆O2于B,E两点.若∠1=60°,∠2=65°,判断AB、CD、CE的长度,下列关系何者正确()A.AB>CE>CD B.AB=CE>CD C.AB>CD>CE D.AB=CD=CE4.如图,AB、AC是⊙O的切线,B、C为切点,∠A=50°,点P是圆上异于B、C,且在上的动点,则∠BPC的度数是()A.65°B.115°C.115°或65°D.130°或65°5.如图,半圆O的直径在梯形ABCD的底边AB上,且与其余三边BC、CD、DA相切,若BC=2,DA=3,则AB的长()A.等于4 B.等于5 C.等于6 D.不能确定6.如图,已知PA,PB分别切⊙O于点A、B,∠P=60°,PA=8,那么弦AB的长是()A.4 B.8 C.4D.87.如图所示,PA,PB是⊙O的切线,且∠APB=40°,下列说法不正确的是()A.PA=PB B.∠APO=20°C.∠OBP=70°D.∠AOP=70°8.如图,⊙O是△ABC的内切圆,点D、E分别为边AC、BC上的点,且DE为⊙O的切线,若△ABC的周长为25,BC的长是9,则△ADE的周长是()A.7 B.8 C.9 D.169.如图,半圆O的直径在梯形ABCD的底边AB上,且与其余三边BC,CD,DA相切,若AB=10,BC=4,则AD的长()A.4 B.5 C.6 D.710.已知:如图,以定线段AB为直径作半圆O,P为半圆上任意一点(异于A、B),过点P作半圆O的切线分别交过A、B两点的切线于D、C,连接OC、BP,过点O作OM∥CD分别交BC与BP于点M、N.下列结论:①S四边形ABCD=AB•CD;②AD=AB;③AD=ON;④AB为过O、C、D三点的圆的切线.其中正确的个数有()A.1个B.2个C.3个D.4个二.填空题11.如图,⊙O是四边形ABCD的内切圆,连接OA、OB、OC、OD.若∠AOB=108°,则∠COD的度数是.12.一个菱形的周长是20cm,两对角线之比是4:3,则该菱形的内切圆的半径是cm.13.如图,P是⊙O的直径AB的延长线上一点,PC、PD切⊙O于点C、D.若PA=6,⊙O的半径为2,则∠CPD=.14.如图,已知:PA、PB、EF分别切⊙O于A、B、D,若PA=10cm,那么△PEF周长是cm.若∠P=35°,那么∠AOB=,∠EOF=.15.如图,P是⊙O外的一点,PA、PB分别与⊙O相切于点A、B,C是上的任意一点,过点C的切线分别交PA、PB于点D、E,若△PDE的周长是10,则PA=.三.解答题16.已知:如图,PA、PB是⊙O的切线,切点分别是A、B,Q为AB上一点,过Q点作⊙O的切线,交PA、PB于E、F点,已知PA=12cm,求△PEF的周长.17.如图,AC是⊙O的直径,∠ACB=60°,连接AB,分别过A、B作圆O的切线,两切线交于点P,若已知⊙O的半径为1,求△PAB的周长.18.如图,点B在⊙O外,以B点为圆心,OB长为半径画弧与⊙O相交于两点C,D,与直线OB相交A点.当AC=5时,求AD的长.19.如图所示,在梯形ABCD中,AD∥BC,AB⊥BC,以AB为直径的⊙O与DC相切于E.已知AB=8,边BC比AD大6.(1)求边AD、BC的长;(2)在直径AB上是否存在一动点P,使以A、D、P为顶点的三角形与△BCP相似?若存在,求出AP的长;若不存在,请说明理由.20.如图,P是⊙O外的一点,PA、PB分别与⊙O相切于点A、B,C是上的任意一点,过点C的切线分别交PA、PB于点D、E.(1)若PA=4,求△PED的周长;(2)若∠P=40°,求∠AFB的度数.参考答案一.选择题1.解:∵PA,PB分别和⊙O切于A,B两点,∴PA=PB,∵DE是⊙O的切线,∴DA=DC,EB=EC,∵△PDE的周长为12,即PD+DE+PE=PD+DC+EC+PE=PD+AD+EB+PE=PA+PB=2PA=12,∴PA=6.故选:B.2.解:在直角△BCM中,tan60°==,得到BC==2,∵AB为圆O的直径,且AB⊥BC,∴BC为圆O的切线,又CD也为圆O的切线,∴CD=BC=2.故选:C.3.解:∵∠1=60°,∠2=65°,∴∠ABC=180°﹣∠1﹣∠2=180°﹣60°﹣65°=55°,∴∠2>∠1>∠ABC,∴AB>BC>AC,∵CA,CD分别切圆O1于A,D两点,CB、CE分别切圆O2于B,E两点,∴AC=CD,BC=CE,∴AB>CE>CD.故选:A.4.解:如图,连接OB、OC,∵AB、AC是⊙O的切线,∴∠OBA=∠OCA=90°,∵∠A=50°,∴∠BOC=130°,∵∠BOC=2∠P,∴∠BPC=65°;故选:C.5.解:如图,连接OC,OD,设⊙O的半径为r,∵BC、CD、DA与半⊙O相切,∴AD边上的高和AO边上的高都为r,∴AO=AD,同理BO=BC,∴AB=AO+BO=AD+BC=2+3=5.故选:B.6.解:∵PA,PB分别切⊙O于点A、B,∴PA=PB,又∠P=60°,∴△APB是等边三角形,∴AB=PA=8.故选:B.7.解:∵PA,PB是⊙O的切线,且∠APB=40°,∴PA=PB,∠APO=∠BPO,∠A=∠B=90°,∴∠OBP=∠OAP,∴C是错误的.故选:C.8.解:∵AB、AC、BC、DE都和⊙O相切,∴BI=BG,CI=CH,DG=DF,EF=EH.∴BG+CH=BI+CI=BC=9,∴C△ADE=AD+AE+DE=AD+AE+DF+EF=AD+DG+EH+AE=AG+AH=C△ABC﹣(BG+EH+BC)=25﹣2×9=7.故选:A.9.解:连接OC,OD,设⊙O的半径为r,∵BC、CD、DA与半⊙O相切,∴AD和AO的高为r,∴AO=AD,同理BO=BC,∴AB=AO+BO=AD+BC,又知AB=10,BC=4,故知AD=6,故选:C.10.解:连接OD、AP,∵DA、DP、BC分别是圆的切线,切点分别是A、P、B,∴DA=DP,CP=CB,∠A=90°=∠B=∠DPO,∴AD+BC=DP+CP=CD,∴S四边形ABCD=(AD+BC)•AB=AB•CD,∴①正确;∵AD=DP<OD,∵四边形ODPN是平行四边形,得到OD=NP<BP<AB,则AD<AB,∴②错误;∵AB是圆的直径,∴∠APB=90°,∵DP=AD,AO=OP,∴D、O在AP的垂直平分线上,∴OD⊥AP,∵∠DPO=∠APB=90°,∴∠OPB=∠DPA=∠DOP,∵OM∥CD,∴∠POM=∠DPO=90°,在△DPO和△NOP中∠PON=∠DPO,OP=OP,∠DOP=∠OPN,∴△DPO≌△NOP,∴ON=DP=AD,∴③正确;∵AP⊥OD,OA=OP,∴∠AOD=∠POD,同理∠BOC=∠POC,∴∠DOC=×180°=90°,∴△CDO的外接圆的直径是CD,∵∠A=∠B=90°,取CD的中点Q,连接OQ,∵OA=OB,∴AD∥OQ∥BC,∴∠AOQ=90°,∴④正确.故选:C.二.填空题(共5小题)11.解:如图所示:连接圆心与各切点,在Rt△DEO和Rt△DFO中,∴Rt△DEO≌Rt△DFO(HL),∴∠1=∠2,同理可得:Rt△AFO≌Rt△AMO,Rt△BMO≌Rt△BNO,Rt△CEO≌Rt△CNO,∴∠3=∠4,∠5=∠7,∠6=∠8,∴∠5+∠6=∠7+∠8=108°,∴2∠2+2∠3=360°﹣2×108°,∴∠2+∠3=∠DOC=72°.故答案为:72°.12.解:如图所示:菱形ABCD,对角线AC,BD,可得菱形内切圆的圆心即为对角线交点,设AB与圆相切于点E,可得OE⊥AB,∵一个菱形的周长是20cm,两对角线之比是4:3,∴AB=5cm,设BO=4x,则AO=3x,故(4x)2+(3x)2=25,解得:x=1,则AO=3,BO=4,故EO•AB=AO•BO,解得:EO=.故答案为:.13.解:∵PA=6,⊙O的半径为2,∴PB=PA﹣AB=6﹣4=2,∴OP=4,∵PC、PD切⊙O于点C、D.∴∠OPC=∠OPD,∴CO⊥PC,∴sin∠OPC==,∴∠OPC=30°,∴∠CPD=60°,故答案为:60°.14.解:∵PA、PB、EF分别切⊙O于A、B、D.∴AE=ED,DF=FR∴△PEF周长是PE+PF+EF=PE+EA+PF+FR=PA+PR=2PA=20cm;∵PA、PB、EF分别切⊙O于A、B∴∠PAO=∠PRO=90°∴∠AOB=360°=90°﹣90°﹣35°=145°;∴∠EOF=∠AOB=72.5°故答案是:20,145°,72.5°.15.解:∵DA,DC都是圆O的切线,∴DC=DA,同理EC=EB,PA=PB,∴△PDE的周长=PD+PE+DE=PD+DC+PE+BE=PA+PB=2PA=10,∴PA=5;故答案为5.三.解答题(共5小题)16.解:∵PA、PB是⊙O的切线,切点分别是A、B,∴PA=PB=12,∵过Q点作⊙O的切线,交PA、PB于E、F点,∴EB=EQ,FQ=FA,∴△PEF的周长是:PE+EF+PF=PE+EQ+FQ+PF,=PE+EB+PF+FA=PB+PA=12+12=24,答:△PEF的周长是24.17.解:∵PA,PB是圆O的切线.∴PA=PB,∠PAB=60°∴△PAB是等边三角形.在直角△ABC中,AB=AC•sin60°=2×=∴△PAB的周长为PA+PB+AB=3.18.解:连接OC、OD.∵OA是⊙B的直径,∴∠OCA=∠ODA=90°,∴AC、AD都是⊙O的切线.∴AD=AC=5.19.解:(1)方法1:过D作DF⊥BC于F,在Rt△DFC中,DF=AB=8,FC=BC﹣AD=6,∴DC2=62+82=100,即DC=10.(1分)设AD=x,则DE=AD=x,EC=BC=x+6,∴x+(x+6)=10.∴x=2.∴AD=2,BC=2+6=8.(4分)方法2:连OD、OE、OC,由切线长定理可知∠DOC=90°,AD=DE,CB=CE,设AD=x,则BC=x+6,由射影定理可得:OE2=DE•EC.(2分)即:x(x+6)=16,解得x1=2,x2=﹣8,(舍去)∴AD=2,BC=2+6=8.(4分)(2)存在符合条件的P点.设AP=y,则BP=8﹣y,△ADP与△BCP相似,有两种情况:①△ADP∽△BCP时,∴y=;(6分)②△ADP∽△BPC时,∴y=4.(7分)故存在符合条件的点P,此时AP=或4.(8分)20.解:(1)∵DA,DC都是圆O的切线,∴DC=DA,同理EC=EB,∵P是⊙O外的一点,PA、PB分别与⊙O相切于点A、B∴PA=PB,∴三角形PDE的周长=PD+PE+DE=PD+DC+PE+BE=PA+PB=2PA=8,即三角形PDE的周长是8;(2)连接AB,∵PA=PB,∴∠PAB=∠PBA,∵∠P=40°,∴∠PAB=∠PBA=(180﹣40)=70°,∵BF⊥PB,BF为圆直径∴∠ABF=∠PBF=90°﹣70°=20°∴∠AFB=90°﹣20°=70°.答:(1)若PA=4,△PED的周长为8;(2)若∠P=40°,∠AFB的度数为70°.。
浙教版九年级数学下册2.2:切线长定理 同步练习题(含解析)
浙教版九年级下册2.2 切线长定理同步练习一.选择题(共16小题)1.如图,P A、PB、分别切⊙O于A、B两点,∠P=40°,则∠C的度数为()A.40°B.140°C.70°D.80°2.如图,P A,PB分别是⊙O的切线,A,B分别为切点,点E是⊙O上一点,且∠AEB=60°,则∠P为()A.120°B.60°C.30°D.45°3.如图,⊙O内切于四边形ABCD,AB=10,BC=7,CD=8,则AD的长度为()A.8B.9C.10D.114.如图,P A、PB分别切⊙O于A、B,P A=10cm,C是劣弧AB上的点(不与点A、B重合),过点C的切线分别交P A、PB于点E、F.则△PEF的周长为()A.10cm B.15cm C.20cm D.25cm5.如图,AD、AE、CB均为⊙O的切线,D、E、F分别为切点,AD=8,则△ABC的周长为()A.8B.10C.12D.166.如图,⊙O是四边形ABCD的内切圆,切点依次是E、F、G、H,下列结论一定正确的有()个①AF=BG②CG=CH③AB+CD=AD+BC④BG<CG.A.1B.2C.3D.47.如图,AB、AC是⊙O的切线,B、C为切点,∠A=50°,点P是圆上异于B、C,且在上的动点,则∠BPC的度数是()A.65°B.115°C.115°或65°D.130°或65°8.如图,已知P A,PB分别切⊙O于点A、B,∠P=60°,P A=8,那么弦AB的长是()A.4B.8C.4D.89.如图所示,P A,PB是⊙O的切线,且∠APB=40°,下列说法不正确的是()A.P A=PB B.∠APO=20°C.∠OBP=70°D.∠AOP=70°10.如图,AE、AD和BC分别切⊙O于点E、D、F,如果AD=20,则△ABC的周长为()A.20B.30C.40D.5011.如图,从圆O外一点P引圆O的两条切线P A,PB,切点分别为A,B.如果∠APB=60°,P A=8,那么弦AB的长是()A.4B.8C.D.12.如图,圆O的圆心在梯形ABCD的底边AB上,并与其它三边均相切,若AB=10,AD =6,则CB长()A.4B.5C.6D.无法确定13.如图,一圆内切四边形ABCD,且AB=16,CD=10,则四边形的周长为()A.50B.52C.54D.5614.如图,若△ABC的三边长分别为AB=9,BC=5,CA=6,△ABC的内切圆⊙O切AB、BC、AC于D、E、F,则AF的长为()A.5B.10C.7.5D.415.已知⊙O的半径是4,P是⊙O外的一点,且PO=8,从点P引⊙O的两条切线,切点分别是A,B,则AB=()A.4B.C.D.16.如图,P A、PB分别切⊙O于A、B两点,如果∠P=60°,P A=2,那么AB的长为()A.1B.2C.3D.4二.填空题(共4小题)17.如图,四边形ABCD是⊙O的外切四边形,且AB=10,CD=15,则四边形ABCD的周长为.18.如图,菱形ABCD,∠B=60°,AB=4,⊙O内切于菱形ABCD,则⊙O的半径为.19.如图,P A,PB是⊙O的切线,A,B为切点,∠OAB=38°,则∠P=°.20.如图,四边形ABCD外切于圆,AB=16,CD=10,则四边形的周长是.三.解答题(共7小题)21.如图,P A、PB是⊙O的切线,A、B为切点,AC是⊙O的直径,∠BAC=20°,求∠P 的度数.22.如图,P A、PB是⊙O的切线,CD切⊙O于点E,△PCD的周长为12,∠APB=60°.求:(1)P A的长;(2)∠COD的度数.23.如图,P A、PB是⊙O的切线,切点分别是A、B,直线EF也是⊙O的切线,切点为Q,交P A、PB于点E、F,已知P A=12cm,∠P=40°①求△PEF的周长;②求∠EOF的度数.24.如图,P A、PB、DE切⊙O于点A、B、C、D在P A上,E在PB上,(1)若P A=10,求△PDE的周长.(2)若∠P=50°,求∠O度数.25.如图,P A,PB是⊙O的切线,A、B为切点,AC是⊙O的直径,∠P=60°.(1)求∠BAC的度数;(2)当OA=2时,求AB的长.26.已知:如图,P A、PB是⊙O的切线,切点分别是A、B,Q为AB上一点,过Q点作⊙O 的切线,交P A、PB于E、F点,已知P A=12cm,求△PEF的周长.27.如图,已知AB为⊙O的直径,P A,PC是⊙O的切线,A,C为切点,∠BAC=30°.(Ⅰ)求∠P的大小;(Ⅱ)若AB=2,求P A的长(结果保留根号).参考答案一.选择题(共16小题)1.如图,P A、PB、分别切⊙O于A、B两点,∠P=40°,则∠C的度数为()A.40°B.140°C.70°D.80°【分析】连接OA,OB根据切线的性质定理,切线垂直于过切点的半径,即可求得∠OAP,∠OBP的度数,根据四边形的内角和定理即可求的∠AOB的度数,然后根据圆周角定理即可求解.【解答】解:∵P A是圆的切线.∴∠OAP=90°,同理∠OBP=90°,根据四边形内角和定理可得:∠AOB=360°﹣∠OAP﹣∠OBP﹣∠P=360°﹣90°﹣90°﹣40°=140°,∴∠ACB=∠AOB=70°.故选:C.2.如图,P A,PB分别是⊙O的切线,A,B分别为切点,点E是⊙O上一点,且∠AEB=60°,则∠P为()A.120°B.60°C.30°D.45°【分析】连接OA,BO,由圆周角定理知可知∠AOB=2∠E=120°,P A、PB分别切⊙O 于点A、B,利用切线的性质可知∠OAP=∠OBP=90°,根据四边形内角和可求得∠P =180°﹣∠AOB=60°.【解答】解:连接OA,BO;∵∠AOB=2∠E=120°,∴∠OAP=∠OBP=90°,∴∠P=180°﹣∠AOB=60°.故选:B.3.如图,⊙O内切于四边形ABCD,AB=10,BC=7,CD=8,则AD的长度为()A.8B.9C.10D.11【分析】根据圆外切四边形的性质对边和相等进而得出AD的长.【解答】解:∵⊙O内切于四边形ABCD,∴AD+BC=AB+CD,∵AB=10,BC=7,CD=8,∴AD+7=10+8,解得:AD=11.故选:D.4.如图,P A、PB分别切⊙O于A、B,P A=10cm,C是劣弧AB上的点(不与点A、B重合),过点C的切线分别交P A、PB于点E、F.则△PEF的周长为()A.10cm B.15cm C.20cm D.25cm【分析】根据切线长定理由P A、PB分别切⊙O于A、B得到PB=P A=10cm,由于过点C的切线分别交P A、PB于点E、F,再根据切线长定理得到EA=EC,FC=FB,然后三角形周长的定义得到△PEF的周长=PE+EF+PF=PE+EC+FC+PF,用等线段代换后得到三角形PEF的周长等于P A+PB.【解答】解:∵P A、PB分别切⊙O于A、B,∴PB=P A=10cm,∵EA与EC为⊙的切线,∴EA=EC,同理得到FC=FB,∴△PEF的周长=PE+EF+PF=PE+EC+FC+PF=PE+EA+FB+PF=P A+PB=10+10=20(cm).故选:C.5.如图,AD、AE、CB均为⊙O的切线,D、E、F分别为切点,AD=8,则△ABC的周长为()A.8B.10C.12D.16【分析】由AD、AE、CB均为⊙O的切线,D、E、F分别为切点,根据切线长定理,可得CE=CF,BD=BF,AE=AD=8,继而可求得△ABC的周长为AE+AD的和.【解答】解:∵AD、AE、CB均为⊙O的切线,D、E、F分别为切点,∴CE=CF,BD=BF,AE=AD=8,∴△ABC的周长为:AC+BC+AB=AC+CF+BF+AB=AC+CE+BD+AB=AE+AD=16.故选:D.6.如图,⊙O是四边形ABCD的内切圆,切点依次是E、F、G、H,下列结论一定正确的有()个①AF=BG②CG=CH③AB+CD=AD+BC④BG<CG.A.1B.2C.3D.4【分析】根据切线长定理(从圆外一点引圆的两条切线,它们的切线长相等,圆心和这一点的连线,平分两条切线的夹角)对以下选项进行分析.【解答】解:如图,连接OE、OF、OH、OG.①∵⊙O是四边形ABCD的内切圆,切点依次是E、F、G、H,∴BF=BG、AF=AE,只有当点F是边AB的中点时,AF=BF=BG,否则,等式AF=BG不成立;故本选项不一定正确;②根据题意,知,CG、CH都是⊙O的切线,∴CG=CH.故本选项正确;③根据题意,知AF=AE,DH=DE,BF=BG,CG=CH,则AF+BF+CH+DH=AE+BG+CG+DE,即AB+CD=AD+BC.故本选项正确;④当点G是边BC的中点时,BG=CG.故本选项错误;综上所述,正确的说法有2个;故选:B.7.如图,AB、AC是⊙O的切线,B、C为切点,∠A=50°,点P是圆上异于B、C,且在上的动点,则∠BPC的度数是()A.65°B.115°C.115°或65°D.130°或65°【分析】连接OB、OC,根据四边形的内角和定理,求得∠BOC=130°,再由圆周角定理求得∠P的度数即可.【解答】解:如图,连接OB、OC,∵AB、AC是⊙O的切线,∴∠OBA=∠OCA=90°,∵∠A=50°,∴∠BOC=130°,∵∠BOC=2∠P,∴∠BPC=65°;故选:AC.8.如图,已知P A,PB分别切⊙O于点A、B,∠P=60°,P A=8,那么弦AB的长是()A.4B.8C.4D.8【分析】根据切线长定理和等边三角形的判定方法,发现等边三角形即可求解.【解答】解:∵P A,PB分别切⊙O于点A、B,∴P A=PB,又∠P=60°,∴△APB是等边三角形,∴AB=P A=8.故选:B.9.如图所示,P A,PB是⊙O的切线,且∠APB=40°,下列说法不正确的是()A.P A=PB B.∠APO=20°C.∠OBP=70°D.∠AOP=70°【分析】根据切线长定理得A,B是正确的;再根据切线的性质定理以及直角三角形的两个锐角互余得D是正确的;根据切线的性质定理得C错误.【解答】解:∵P A,PB是⊙O的切线,且∠APB=40°,∴P A=PB,∠APO=∠BPO,∠A=∠B=90°,∴∠OBP=∠OAP,∴C是错误的.故选:C.10.如图,AE、AD和BC分别切⊙O于点E、D、F,如果AD=20,则△ABC的周长为()A.20B.30C.40D.50【分析】根据切线长定理:从圆外一点引圆的两条切线,它们的切线长相等,将△ABC 的周长转化为切线长求解.【解答】解:据切线长定理有AD=AE,BE=BF,CD=CF;则△ABC的周长=AB+BC+AC=AB+BF+CF+AC=AB+BE+AC+CD=AD+AE=2AD=40.故选:C.11.如图,从圆O外一点P引圆O的两条切线P A,PB,切点分别为A,B.如果∠APB=60°,P A=8,那么弦AB的长是()A.4B.8C.D.【分析】根据切线长定理知P A=PB,而∠P=60°,所以△P AB是等边三角形,由此求得弦AB的长.【解答】解:∵P A、PB都是⊙O的切线,∴P A=PB,又∵∠P=60°,∴△P AB是等边三角形,即AB=P A=8,故选:B.12.如图,圆O的圆心在梯形ABCD的底边AB上,并与其它三边均相切,若AB=10,AD =6,则CB长()A.4B.5C.6D.无法确定【分析】方法1、设圆O的半径是R,圆O与AD、DC、CB相切于点E、F、H,连接OE、OD、OF、OC、OH,则圆的半径R,可以看作△BOC,△COD,△AOD的高,根据S梯形ABCD=S△BOC+S△COD+S△DOA,以及梯形的面积公式即可求解.方法2、利用切线的性质得出∠ADO=∠ODC,进而得出∠ADO=∠AOD,即可得出OA =6,即:OB=4,同理:BC=OB即可得出结论.【解答】解:方法1、设圆O的半径是R,圆O与AD、DC、CB相切于点E、F、H,连接OE、OD、OF、OC、OH.设CD=y,CB=x.设S梯形ABCD=S则S=(CD+AB)R=(y+10)R﹣﹣﹣﹣(1)S=S△BOC+S△COD+S△DOA=xR+yR+×6R﹣﹣﹣﹣(2)联立(1)(2)得x=4;方法2、连接OD.OC∵AD,CD是⊙O的切线,∴∠ADO=∠ODC,∵CD∥AB,∴∠ODC=∠AOD,∴∠ADO=∠AOD∴AD=OA∵AD=6,∴OA=6,∵AB=10,∴OB=4,同理可得OB=BC=4,故选:A.13.如图,一圆内切四边形ABCD,且AB=16,CD=10,则四边形的周长为()A.50B.52C.54D.56【分析】根据切线长定理,可以证明圆外切四边形的性质:圆外切四边形的两组对边和相等,从而可求得四边形的周长.【解答】解:由题意可得圆外切四边形的两组对边和相等,所以四边形的周长=2(16+10)=52.故选:B.14.如图,若△ABC的三边长分别为AB=9,BC=5,CA=6,△ABC的内切圆⊙O切AB、BC、AC于D、E、F,则AF的长为()A.5B.10C.7.5D.4【分析】由切线长定理,可知:AF=AD,CF=CE,BE=BD,用未知数设AF的长,然后表示出BD、CF的长,即可表示出BE、CE的长,根据BE+CE=5,可求出AF的长.【解答】解:设AF=x,根据切线长定理得AD=x,BD=BE=9﹣x,CE=CF=CA﹣AF =6﹣x,则有9﹣x+6﹣x=5,解得x=5,即AF的长为5.故选:A.15.已知⊙O的半径是4,P是⊙O外的一点,且PO=8,从点P引⊙O的两条切线,切点分别是A,B,则AB=()A.4B.C.D.【分析】在Rt△POA中,用勾股定理,可求得P A的长,进而可根据∠APO的正弦值求出AC的长,即可求出AB的长.【解答】解:如图所示,P A、PB切⊙O于A、B,因为OA=4,PO=8,则AP==4,∠APO=30°,∵∠APB=2∠APO=60°故△P AB是等边三角形,AB=AP=4故选:C.16.如图,P A、PB分别切⊙O于A、B两点,如果∠P=60°,P A=2,那么AB的长为()A.1B.2C.3D.4【分析】由切线长定理知P A=PB,根据已知条件即可判定△P AB是等边三角形,由此可求得AB的长.【解答】解:∵P A、PB分别切⊙O于A、B,∴P A=PB;∵∠P=60°,∴△P AB是等边三角形;∴AB=P A=2,故选B.二.填空题(共4小题)17.如图,四边形ABCD是⊙O的外切四边形,且AB=10,CD=15,则四边形ABCD的周长为50.【分析】根据切线长定理得到AE=AH,BE=BF,CF=CG,DH=DG,得到AD+BC=AB+CD=25,根据四边形的周长公式计算,得到答案.【解答】解:∵四边形ABCD是⊙O的外切四边形,∴AE=AH,BE=BF,CF=CG,DH=DG,∴AD+BC=AB+CD=25,∴四边形ABCD的周长=AD+BC+AB+CD=25+25=50,故答案为:50.18.如图,菱形ABCD,∠B=60°,AB=4,⊙O内切于菱形ABCD,则⊙O的半径为.【分析】作辅助线,构建直角△AOB,分别计算OA、OB的长,根据面积法可得OE的长.【解答】解:设AB和BC上的切点分别为E、F,连接OA、OE、OB、OF,则OE⊥AB,OF⊥BC,∵⊙O内切于菱形ABCD,∴OE=OF,∴OB平分∠ABC,∵∠ABC=60°,∴∠ABO=30°,同理得∠BAO=60°,∴∠AOB=90°,∴AO=AB=2,OB=2,∴S△AOB=AB•OE=AO•OB,4OE=2×,OE=,故答案为:.19.如图,P A,PB是⊙O的切线,A,B为切点,∠OAB=38°,则∠P=76°.【分析】由切线的性质得出P A=PB,P A⊥OA,得出∠P AB=∠PBA,∠OAP=90°,由已知得出∠PBA=∠P AB=90°﹣∠OAB=52°,再由三角形内角和定理即可得出结果.【解答】解:∵P A,PB是⊙O的切线,∴P A=PB,P A⊥OA,∴∠P AB=∠PBA,∠OAP=90°,∴∠PBA=∠P AB=90°﹣∠OAB=90°﹣38°=52°,∴∠P=180°﹣52°﹣52°=76°;故答案为:76.20.如图,四边形ABCD外切于圆,AB=16,CD=10,则四边形的周长是52.【分析】利用圆外切四边形的性质定理可以得出,四边形的周长是对边和的2倍,即可得.【解答】解:由题意可得圆外切四边形的两组对边和相等,所以四边形的周长=2(16+10)=52.故答案为:52.三.解答题(共7小题)21.如图,P A、PB是⊙O的切线,A、B为切点,AC是⊙O的直径,∠BAC=20°,求∠P 的度数.【分析】根据切线长定理得等腰△P AB,运用三角形内角和定理求解即可.【解答】解:根据切线的性质得:∠P AC=90°,所以∠P AB=90°﹣∠BAC=90°﹣20°=70°,根据切线长定理得P A=PB,所以∠P AB=∠PBA=70°,所以∠P=180°﹣70°×2=40°.22.如图,P A、PB是⊙O的切线,CD切⊙O于点E,△PCD的周长为12,∠APB=60°.求:(1)P A的长;(2)∠COD的度数.【分析】(1)可通过切线长定理将相等的线段进行转换,得出三角形PDE的周长等于P A+PB的结论,即可求出P A的长;(2)根据三角形的内角和求出∠ADC和∠BEC的度数和,然后根据切线长定理,得出∠EDO和∠DEO的度数和,再根据三角形的内角和求出∠DOE的度数.【解答】解:(1)∵CA,CE都是圆O的切线,∴CA=CE,同理DE=DB,P A=PB,∴三角形PDE的周长=PD+CD+PC=PD+PC+CA+BD=P A+PB=2P A=12,即P A的长为6;(2)∵∠P=60°,∴∠PCE+∠PDE=120°,∴∠ACD+∠CDB=360°﹣120°=240°,∵CA,CE是圆O的切线,∴∠OCE=∠OCA=∠ACD;同理:∠ODE=∠CDB,∴∠OCE+∠ODE=(∠ACD+∠CDB)=120°,∴∠COD=180﹣120°=60°.23.如图,P A、PB是⊙O的切线,切点分别是A、B,直线EF也是⊙O的切线,切点为Q,交P A、PB于点E、F,已知P A=12cm,∠P=40°①求△PEF的周长;②求∠EOF的度数.【分析】①根据切线长定理得出P A=PB,EB=EQ,FQ=F A,由PE+EF+PF=PE+EQ+FQ+PF即可求出答案.②连接OE,OF,求出∠OEF+∠OFE的度数,即可得出∠EOF的度数.【解答】解:①∵P A、PB是⊙O的切线,∴P A=PB,又∵直线EF是⊙O的切线,∴EB=EQ,FQ=F A,∴△PEF的周长=PE+PF+EF=PE+PF+EB+F A=P A+PB=2P A=24cm;②连接OE,OF,则OE平分∠BEF,OF平分∠AFE,则∠OEF+∠OFE=(∠P+∠PFE)+∠(P+∠PEF)=(180°+40°)=110°,∴∠EOF=180°﹣110°=70°.24.如图,P A、PB、DE切⊙O于点A、B、C、D在P A上,E在PB上,(1)若P A=10,求△PDE的周长.(2)若∠P=50°,求∠O度数.【分析】(1)于P A、PB、DE都是⊙O的切线,可根据切线长定理将切线P A、PB的长转化为△PDE的周长;(2)连接OA、OC、0B,利用切线长定理即可得到∠O=∠AOB,根据四边形的内角和可得∠AOB+∠P=180°,进而求出∠O的度数.【解答】解:(1)∵P A、PB、DE分别切⊙O于A、B、C,∴P A=PB,DA=DC,EC=EB;∴C△PDE=PD+DE+PE=PD+DA+EB+PE=P A+PB=10+10=20;∴△PDE的周长为20;(2)连接OA、OC、0B,∵OA⊥P A,OB⊥PB,OC⊥DE,∴∠DAO=∠EBO=90°,∴∠P+∠AOB=180°,∴∠AOB=180°﹣50°=130°∵∠AOD=∠DOC,∠COE=∠BOE,∴∠DOE=∠AOB=×130°=65°.25.如图,P A,PB是⊙O的切线,A、B为切点,AC是⊙O的直径,∠P=60°.(1)求∠BAC的度数;(2)当OA=2时,求AB的长.【分析】(1)根据切线长定理推出AP=BP,根据等腰三角形性质和三角形的内角和定理求出∠P AB=60°,求出∠P AO=90°即可;(2)根据直角三角形性质求出OP,根据勾股定理求出AP,根据等边三角形的判定和性质求出即可.【解答】解:(1)∵P A,PB是⊙O的切线,∴AP=BP,∵∠P=60°,∴∠P AB=60°,∵AC是⊙O的直径,∴∠P AC=90°,∴∠BAC=90°﹣60°=30°.(2)连接OP,则在Rt△AOP中,OA=2,∠APO=30°,∴OP=4,由勾股定理得:,∵AP=BP,∠APB=60°,∴△APB是等边三角形,∴.26.已知:如图,P A、PB是⊙O的切线,切点分别是A、B,Q为AB上一点,过Q点作⊙O 的切线,交P A、PB于E、F点,已知P A=12cm,求△PEF的周长.【分析】根据切线长定理得出P A=PB,EB=EQ,FQ=F A,代入PE+EF+PF=PE+EQ+FQ+PF即可求出答案.【解答】解:∵P A、PB是⊙O的切线,切点分别是A、B,∴P A=PB=12,∵过Q点作⊙O的切线,交P A、PB于E、F点,∴EB=EQ,FQ=F A,∴△PEF的周长是:PE+EF+PF=PE+EQ+FQ+PF,=PE+EB+PF+F A=PB+P A=12+12=24,答:△PEF的周长是24.27.如图,已知AB为⊙O的直径,P A,PC是⊙O的切线,A,C为切点,∠BAC=30°.(Ⅰ)求∠P的大小;(Ⅱ)若AB=2,求P A的长(结果保留根号).【分析】(Ⅰ)根据切线的性质及切线长定理可证明△P AC为等边三角形,则∠P的大小可求;(Ⅱ)由(Ⅰ)知P A=PC,在Rt△ACB中,利用30°的特殊角度可求得AC的长.【解答】解:(Ⅰ)∵P A是⊙O的切线,AB为⊙O的直径,∴P A⊥AB,∴∠BAP=90°;∵∠BAC=30°,∴∠CAP=90°﹣∠BAC=60°.又∵P A、PC切⊙O于点A、C,∴P A=PC,∴△P AC为等边三角形,∴∠P=60°.(Ⅱ)如图,连接BC,则∠ACB=90°.在Rt△ACB中,AB=2,∠BAC=30°,∵cos∠BAC=,∴AC=AB•cos∠BAC=2cos30°=.∵△P AC为等边三角形,∴P A=AC,∴P A=.。
2.5.5切线长定理同步练习2023学年苏科版九年级数学上册

切线长定理同步练习一、选择题(共10小题,每小题4分,共40分)1. 如图,P 为⊙O 外一点,PA ,PB 是⊙O 的切线,切点分别为A ,B ,若PA =5,则PB 的长是( )A .2B .3C .4D .52. 如图,PA 、PB 为圆O 的切线,切点分别为A 、B ,PO 交AB 于点C ,PO 的延长线交圆O 于点D ,下列结论不一定成立的是( )A .PA =PB B .∠BPD =∠APDC .AB ⊥PD D .AB 平分PD3. 如图,PA 切⊙O 于点A ,PB 切⊙O 于点B ,OP 交⊙O 于点C ,下列结论中,错误的是( )A .∠1=∠2B .PA =PBC .AB ⊥OPD .∠PAB =2∠14.如图,PA ,PB 为⊙O 的切线,A ,B 分别为切点,∠APB =60°,点P 到圆心O 的距离OP =2,则⊙O 的半径为( )A .12B .1C .32D .2 5.如图,AB 是⊙O 的直径,点C 为⊙O 外一点,CA ,CD 是⊙O 的切线,A ,D 为切点,连接BD ,AD.若∠ACD =30°,则∠DBA 的大小是( )A .15°B .30°C .60°D .75°6. 一把直尺、含60°角的直角三角尺和光盘如图摆放,AB =3,则光盘的直径是( )A .3B .3 3C .6D .6 37. 如图,PA 、PB 分别与⊙O 相切于A 、B 两点,点C 为⊙O 上一点,连接AC 、BC ,若∠P =50°,则∠ACB 的度数为( )A .60°B .75°C .70°D .65°8. 如图,从⊙O 外一点P 引圆的两条切线PA 、PB ,切点分别为A 、B ,点C 是劣弧AB 上一点,过点C 的切线分别交PA 、PB 于点M ,N ,若⊙O 的半径为2,∠P =60°,则△PMN 的周长为( )A .4B .6C .4 3D .6 39. 如图,在矩形ABCD 中,AB =4,AD =5,AD 、AB 、BC 分别与⊙O 相切于E 、F 、G 三点,过点D 作⊙O 的切线交BC 于点M ,切点为N ,则DM 的长为( )A.133B.92C.4313 D .2 5 10. 如图,AB 为半圆O 的直径,AD ,BC 分别切半圆O 于A ,B 两点,CD 切半圆O 于点E ,AD 与CD 交于点D ,BC 与CD 交于点C ,连接OD 、OC ,下列结论:①AD +BC =CD ;②OD =OC ;③S 梯形ABCD =12CD·OA ;④∠DOC =90°.其中正确的有( )A .①④B .①②③C .②③④D .③④二.填空题(共6小题,每小题4分,共24分)11.如图,PA ,PB 切⊙O 于点A ,B ,已知∠APB =60°,⊙O 的半径为2,则切线PA 的长为_______.12. 如图,AB ,AC ,BD 是⊙O 的切线,P ,C ,D 为切点,如果AB =5,AC =3,则BD 的长为_______.13. 如图,PA ,PB 是⊙O 的切线,切点分别为A ,B ,点C 在AB ︵上,过点C 的切线分别交PA ,PB 于点E ,F.若△PEF 的周长为6,则线段PA 的长为________.14. 如图,在四边形ABCD 中,AB =16,CD =10,AB ,BC ,CD ,AD 与⊙O 分别相切于点E ,F ,G ,H ,则四边形ABCD 的周长为______.15. 如图,PA ,PB 分别切⊙O 于点A ,B ,点C 在⊙O 上,且∠ACB =50°,则∠P =______.16. 如图,在△ABC 中,∠C =90°,AC =3,BC =4,则△ABC 的内切圆半径r =________.三.解答题(共6小题, 56分)17.(6分) 如图,四边形ABCD的各边与⊙O分别相切于点E,F,G,H,说明AB+CD 与BC+AD的大小关系.18.(8分) 如图,PA,PB是⊙O的切线,A,B为切点,CD切⊙O于点E,连接OC,OD,△PCD的周长为12,∠P=60°.求PA的长.19.(8分) 如图,PA,PB是⊙O的两条切线,A,B是切点,若∠APB=60°,PO=2,求⊙O的半径的长.20.(10分) 如图,已知AB为⊙O的直径,PA,PC是⊙O的切线,A,C为切点,∠BAC =30°.求∠P的大小.21.(12分) 已知:AB是⊙O的直径,AB=2,弦DE=1,直线AD与BE相交于点C,弦DE在⊙O上运动且保持长度不变,过点D的切线交BC于点F.若DE∥AB,求证:CF=EF;22.(12分) 如图,直线AB,BC,CD分别与⊙O相切于点E,F,G,且AB∥CD,OB=6 cm,OC=8 cm.求:(1)∠BOC的度数;(2)BE+CG的长;(3)⊙O的半径.参考答案1-5DDDBD 6-10DDCAA11.2 312.213.314.5215.80°16. 117. 解:由切线长定理,得AE =AH ,BE =BF ,CF =CG ,DG =DH ,∴AB +CD =AE +BE +CG +DG =AH +BF +CF +DH =AH +DH +BF +CF =BC +AD ,即AB +CD =BC +AD.18. 解:∵CA ,CE 都是⊙O 的切线,∴CA =CE ,同理DE =DB ,PA =PB ,∴△PDC 的周长=PD +CD +PC =PD +PC +CA +BD =PA +PB =2PA =12,即PA 的长为619. ∵PA ,PB 是⊙O 的两条切线,∴∠APO =∠BPO =12∠APB ,∠PAO =90°.∵∠APB =60°,∴∠APO =30°.∵PO =2,∴AO =1.20. 解:∵PA 是⊙O 的切线,AB 为⊙O 的直径,∴PA ⊥AB ,∴∠BAP =90°.∵∠BAC =30°,∴∠CAP =90°-∠BAC =60°.又∵PA ,PC 切⊙O 于点A ,C ,∴PA =PC ,∴△PAC 为等边三角形,∴∠P =60°21. 证明:连接OD ,OE.∵AB =2,∴OA =OD =OE =OB =1.∵DE =1,∴OD =OE =DE.∴△ODE 是等边三角形.∴∠ODE =∠OED =60°.∵DE ∥AB ,∴∠AOD =∠ODE =60°,∠BOE =∠OED =60°.∴△AOD 和△BOE 都是等边三角形.∴∠OAD =∠OBE =60°. ∵DE ∥AB ,∴∠CDE =∠OAD =60°,∠CED =∠OBE =60°.∴△CDE 是等边三角形.∵DF 是⊙O 的切线,∴DF ⊥OD.∴∠ODF =90°.∴∠EDF =90°-∠CED =90°-60°=30°.∴∠DFE =180°-∠EDF -∠CED =180°-30°-60°=90°.∴DF ⊥CE.∴CF =EF.22. 解:(1)连接OF ,根据切线长定理,得BE =BF ,CF =CG ,∠OBF =∠OBE ,∠OCF =∠OCG.∵AB ∥CD ,∴∠ABC +∠BCD =180°,∴∠OBF +∠OCF =90°,∴∠BOC =90°(2)由(1)知,∠BOC =90°.∵OB =6 cm ,OC =8 cm ,∴由勾股定理,得BC =OB 2+OC 2 =10 cm ,∴BE +CG =BC =10 cm(3)∵OF ⊥BC ,∴OF =OB·OC BC =4.8 cm。
切线长定理和三角形内切圆(两大类题型)—2023-2024学年九年级数学下册(浙教版)(解析版)

切线长定理和三角形内切圆(两大类题型)【题型1利用切线长定理的性质求线段长度或周长】【题型2 三角形的内切圆与内心】【题型1利用切线长定理的性质求线段长度或周长】1.如图,AB、AC、BD是⊙O的切线,切点分别是P、C、D.若AB=10,AC =6,则BD的长是()A.3B.4C.5D.6【答案】B【解答】解:∵AC、AP为⊙O的切线,∴AC=AP=6,∵BP、BD为⊙O的切线,∴BP=BD,∴BD=PB=AB﹣AP=10﹣6=4.故选:B.2.如图,P为⊙O外一点,P A、PB分别切⊙O于点A、B,CD切⊙O于点E,分别交P A、PB于点C、D,若P A=8,则△PCD的周长为()A.8B.12C.16D.20【答案】C【解答】解:∵P A、PB分别切⊙O于点A、B,CD切⊙O于点E,∴P A=PB=8,AC=EC,BD=ED,∴PC+CD+PD=PC+CE+DE+PD=P A+AC+PD+BD=P A+PB=8+8=16,即△PCD的周长为16.故选:C.3.以正方形ABCD的AB边为直径作半圆O,过点C作直线切半圆于点F,交AB边于点E,若△CDE的周长为12,则直角梯形ABCE周长为()A.12B.13C.14D.15【答案】C【解答】解:设AE的长为x,正方形ABCD的边长为a,∵CE与半圆O相切于点F,∴AE=EF,BC=CF,∵EF+FC+CD+ED=12,∴AE+ED+CD+BC=12,∵AD=CD=BC=AB,∴正方形ABCD的边长为4;在Rt△CDE中,ED2+CD2=CE2,即(4﹣x)2+42=(4+x)2,解得:x=1,∵AE+EF+FC+BC+AB=14,∴直角梯形ABCE周长为14.故选:C.4.如图,⊙O是△ABC的内切圆,点D、E分别为边AB、AC上的点,且DE 为⊙O的切线,若△ABC的周长为25,BC的长是9,则△ADE的周长是()A.7B.8C.9D.16【答案】A【解答】解:∵AB、AC、BC、DE都和⊙O相切,∴BI=BG,CI=CH,DG=DF,EF=EH.∴BG+CH=BI+CI=BC=9,∴C△ADE =AD+AE+DE=AD+AE+DF+EF=AD+DG+EH+AE=AG+AH=C△ABC﹣(BG+EH+BC)=25﹣2×9=7.故选:A.5.如图所示,P是⊙O外一点,P A,PB分别和⊙O切于A,B两点,C是上任意一点,过C作⊙O的切线分别交P A,PB于D,E.若△PDE的周长为12,则P A的长为()A.12B.6C.8D.4【答案】B【解答】解:∵P A,PB分别和⊙O切于A,B两点,∴P A=PB,∵DE是⊙O的切线,∴DA=DC,EB=EC,∵△PDE的周长为12,即PD+DE+PE=PD+DC+EC+PE=PD+AD+EB+PE=P A+PB=2P A=12,∴P A=6.故选:B.6.如图,⊙O为△ABC的内切圆,AC=10,AB=8,BC=9,点D,E分别为BC,AC上的点,且DE为⊙O的切线,则△CDE的周长为()A.9B.7C.11D.8【答案】C【解答】解:设AB,AC,BC,DE和圆的切点分别是P,N,M,Q,CM=x,根据切线长定理,得CN=CM=x,BM=BP=9﹣,AN=AP=10﹣x.则有9﹣x+10﹣x=8,解得:x=5.5.所以△CDE的周长=CD+CE+QE+DQ=2x=11.故选:C.7.如图,⊙O内切于正方形ABCD,点O为圆心,作∠MON=90°,其两边分别交BC,CD于点M,N,交⊙O于点E,F,若CM+CN=6,则弧EF的长为()A.3πB.2.25πC.2πD.1.5π【答案】D【解答】解:设⊙O与正方形ABCD的边CD相切于点G,与BC相切于点H,如解图,连接OG,OH,则四边形OHCG是正方形,∵∠GON+∠NOH=90°∠HOM+∠NOH=90°,∴∠GON=∠HOM,又∵∠OGN=∠OHM=90°,OG=OH,∴△OGN≌△OHM(ASA),∴GN=HM,∴⊙O的半径=,∴.故选:D.8.如图,在等腰三角形ABC中,O为底边BC的中点,以O为圆心作半圆与AB,AC相切,切点分别为D,E.过半圆上一点F作半圆的切线,分别交AB,AC于M,N.那么的值等于()A.B.C.D.1【答案】B【解答】解:连OM,ON,如图,∵MD,MF与⊙O相切,∴∠1=∠2,同理得∠3=∠4,而∠1+∠2+∠3+∠4+∠B+∠C=360°,AB=AC∴∠2+∠3+∠B=180°;而∠1+∠MOB+∠B=180°,∴∠3=∠MOB,即有∠4=∠MOB,∴△OMB∽△NOC,∴=,∴BM•CN=BC2,∴=.故选:B.9.如图,⊙O内切于正方形ABCD,O为圆心,作∠MON=90°,其两边分别交BC,CD于点N,M,若CM+CN=10,则⊙O的面积为.【答案】25π【解答】解:设⊙O与正方形ABCD的边CD切于E,与BC切于F,连接OE,OF,则四边形OECF是正方形,∴CF=CE=OE=OF,∠OEM=∠OFN=∠EOF=90°,∵∠MON=90°,∴∠EOM=∠FON,∴△OEM≌△OFN(ASA),∴EM=NF,∴CM+CN=CE+CF=10,∴OE=5,∴⊙O的面积为25π,故答案为:25π.10.如图,四边形ABCD是O的外切四边形,且AB=8,CD=12,则四边形ABCD的周长为.【答案】40.【解答】解:∵四边形ABCD是⊙O的外切四边形,∴AD+BC=AB+CD=20,∴四边形ABCD的周长=AD+BC+AB+CD=40,故答案为:40.11.如图,一圆内切于四边形ABCD,且AB=16cm,CD=10cm,则四边形的周长为.【答案】52cm.【解答】解:设四边形ABCD的内切圆圆心为O,⊙O与AB、BC、CD、AD 分别相切于点E、F、G、H,∵AH=AE,BF=BE,DH=DG,CF=CG,AB=16cm,CD=10cm,∴AD+BC=AH+BF+DH+CF=AE+BE+DG+CG=AB+CD=16+10=26(cm),∴AB+CD+AD+BC=26+26=52(cm),∴四边形ABCD的周长为52cm,故答案为:52cm.12.如图,⊙O与△ABC的边AB、AC、BC分别相切于点D、E、F,如果AB =4,AC=5,AD=1,那么BC的长为.【答案】见试题解答内容【解答】解:∵AB、AC、BC都是⊙O的切线,∴AD=AE,BD=BF,CE=CF,∵AB=4,AC=5,AD=1,∴AE=1,BD=3,CE=CF=4,∴BC=BF+CF=3+4=7.13.如图所示,P是⊙O外一点,P A,PB分别和⊙O切于A,B两点,C是上任意一点,过C作⊙O的切线分别交P A,PB于D,E.(1)若△PDE的周长为10,则P A的长为;(2)连接CA、CB,若∠P=50°,则∠BCA的度数为度.【答案】见试题解答内容【解答】解:(1)∵P A、PB、DE分别切⊙O于A、B、C,∴P A=PB,DA=DC,EC=EB;=PD+DE+PE=PD+DA+EB+PE=P A+PB=10;∴C△PDE∴P A=PB=5;(2)连接OA、OB、AC、BC,在⊙O上取一点F,连接AF、BF,∵P A、PB分别切⊙O于A、B;∴∠P AO=∠PRO=90°∴∠AOB=360°﹣90°﹣90°﹣50°=130°;∴∠AFB=∠AOB=65°,∵∠AFB+∠BCA=180°∴∠BCA=180°﹣65°=115°;故答案为:5,115°.14.如图,分别过⊙O上A、B、C三点作⊙O切线,切线两两交于P、M、N,P A=9,则△PMN的周长为.【答案】18.【解答】解:∵P A、PB、MN分别与⊙O切于A、B、C,∴P A=PB,MA=MC,NB=NC,∴△PMN的周长=PM+MN+PN=PM+MC+CN+PN=PM+MA+NB+PN=P A+PB=9+9=18,故答案为:18.15.如图,以正方形ABCD的AB边为直径作半圆O,过点C作直线切半圆于点F,交AD边于点E,若△CDE的周长为12,则直角梯形ABCE周长为.【答案】见试题解答内容【解答】解:设AE的长为x,正方形ABCD的边长为a,∵CE与半圆O相切于点F,∴AE=EF,BC=CF,∵EF+FC+CD+ED=12,∴AE+ED+CD+BC=12,∵AD=CD=BC=AB,∴正方形ABCD的边长为4;在Rt△CDE中,ED2+CD2=CE2,即(4﹣x)2+42=(4+x)2,解得:x=1,∴AE+EF+FC+BC+AB=14,∴直角梯形ABCE周长为14.故答案为:14.【题型2 三角形的内切圆与内心】16.如图,在△ABC中,内切圆O与BC,CA,AB分别切于D,E,F若∠A=50°,则∠EDF=()A.55°B.65°C.75°D.85°【答案】B【解答】解:如图所示,连接OE,OF,∵内切圆O与CA,AB分别切于E,F,∴∠AFO=∠AEO=90°,∵∠A=50°,∴∠EOF=360°﹣∠A﹣∠AFO﹣∠AEO=130°,∵点D在圆O上,∴,故选:B.17.如图,点Ⅰ为△ABC的内心,若∠A为50°,则∠BIC的度数为()A.105°B.100°C.115°D.130°【答案】C【解答】解:∵点I为三角形的内心,∴∠CBI=∠ABC,∠BCI=∠ACB,∴∠CBI+∠BCI=(∠ABC+∠ACB),∵∠A=50°,∴∠ABC+∠ACB=180°﹣∠A=130°,∴∠CBI+∠BCI=(∠ABC+∠ACB)=65°,∴∠BIC=180°﹣(∠CBI+∠BCI)=115°.故选:C.18.如图,在一张Rt△ABC纸片中,∠ACB=90°,BC=5,AC=12,⊙O是它的内切圆.小明用剪刀沿着⊙O的切线DE剪下一块三角形ADE,则△ADE 的周长为()A.19B.17C.22D.20【答案】D【解答】解:如图,设△ABC的内切圆切三边于点F,H,G,连接OF,OH,OG,∴四边形OHCG是正方形,由切线长定理可知:AF=AG,∵DE是⊙O的切线,∴MD=MF,EM=EG,∵∠ACB=90°,BC=5,AC=12,∴AB==13,∵⊙O是△ABC的内切圆,∴内切圆的半径=(AC+BC﹣AB)=2,∴CG=2,∴AG=AC﹣CG=12﹣2=10,∴△ADE的周长=AD+DE+AE=AD+DF+EG+AE=AF+AG=2AG=20.故选:D.19.如图,在△ABC中,AB=8,AC=6,O为△ABC的内心,若△ABO的面积为20,则△ACO的面积为()A.20B.15C.18D.12【答案】B【解答】解:∵O为△ABC的内心,∴点O到AB,AC的距离相等,∴△AOB、△AOC面积的比=AB:AC=8:6=4:3.∵△ABO的面积为20,∴△ACO的面积为15.故选:B.20.如图,△ABC的内切圆⊙O与AB,BC,AC分别相切于点D,E,F,∠B =90°,AB=6,BC=8,则△ABC的内切圆半径r为()A.4B.3C.2D.1【答案】C【解答】解:连接OD、OE、OF,OA、OB、OC,∵∠B=90°,AB=6,BC=8,∴AC===10,∵⊙O与AB,BC,AC分别相切于点D,E,F,∴OD⊥AB,OE⊥BC,OF⊥AC,OD=OE=OF=r,,∵AB•OD+BC•OE+AC•OD=AB•BC=S△ABC∴×6r+×8r+×10r=×6×8,解得r=2,故选:C.21.如图,在Rt△ABC中,∠C=90°,AC=8,BC=6,⊙O是△ABC的内切圆,则阴影部分面积是()A.2B.πC.4﹣πD.π﹣2【答案】C【解答】解:Rt △ABC 中,AC =8,BC =6,∴AB ==10,∴S △ABC =AC •BC =24,C △ABC =AC +BC +AB =24,∴内切圆半径r ==2,∴S 圆=πr 2=π,设⊙O 与AC 切于点D ,与BC 切于点E ,连接OD 、OE ,则四边形ODCE 为正方形,∴S 阴影=S 正方形ODCE ﹣S 扇形DOE =2×2﹣×2×2π=4﹣π.故选:C .22.如图,已知Rt △ABC 中,∠ACB =90°,⊙O 为△ABC 的内切圆,若,且△ABC 的面积为24,则△ABC 的周长为( )A .48B .C .24D .【答案】C 【解答】解:过O 点作OD ⊥AB 于D 点,OE ⊥AC 于E 点,OF ⊥BC 于F 点,连接OA 、OB ,如图,∵⊙O 为△ABC 的内切圆,∴OD =OE =OF ,OC 平分∠ACB ,∴∠OCE=∠OCF=∠ACB=45°,∴OE=OC=×2=2,∴OD=OF=2,∵S△AOB +S△AOC+S△BOC=S△ABC,∴×2×AB+×2×AC+×2×BC=24,即AB+AC+BC=24,∴△ABC的周长为24.故选:C.23.如图,△ABC中,∠A=80°,点O是△ABC的内心,则∠BOC的度数为()A.100°B.160°C.80°D.130°【答案】D【解答】解:∵∠A=80°,∴∠ABC+∠ACB=180°﹣∠A=100°,∵点O是△ABC的内心,∴∠OBC+∠OCB=(∠ABC+∠ACB)=50°,∴∠BOC=180°﹣50°=130°.故选:D.24.如图,⊙O为Rt△ABC的内切圆,切点分别为M,N,Q,已知∠ABC=90°,CM=2,AM=3,则⊙O的半径为()A.B.C.1D.2【答案】C【解答】解:连接OM、ON、OQ,根据切线长定理可得,AN=AM=3、CQ=CM=2,∠ONB=∠OQB=90°,又∵ON=OQ=r,∠ABC=90°,∴四边形ONBQ为正方形,即QB=BN=r,在Rt△ABC中,AB2+BC2=AC2,∵CM=2,AM=3,∴AB=3+r,BC=2+r,AC=2+3=5∴(3+r)2+(2+r)2=52,解得r1=1,r2=﹣6(舍去),∴⊙O的半径为1,故选:C.25.如图,△ABC的内切圆⊙I与BC,CA,AB分别相切于点D,E,F,若⊙I 的半径为r,∠A=α,则(BF+CE﹣BC)的值和∠FDE的大小分别为()A.2r,90°﹣αB.0,90°﹣αC.2r,D.0,【答案】D【解答】解:如图,连接IF,IE.∵△ABC的内切圆⊙I与BC,CA,AB分别相切于点D,E,F,∴BF=BD,CD=CE,IF⊥AB,IE⊥AC,∴BF+CE﹣BC=BD+CD﹣BC=BC﹣BC=0,∠AFI=∠AEI=90°,∴∠EIF=180°﹣α,∴∠EDF=∠EIF=90°﹣α.故选:D.26.如图,在△ABC中,∠A=80°,⊙O是△ABC的内切圆,连接OB、OC,交⊙O于点D、E,已知OD=3,则图中阴影部分的面积是()A.4πB.C.3πD.【答案】B【解答】解:如图,⊙O分别与BC、AB相切于M、N,连接OM,ON,∴OM⊥BC,ON⊥AB,∵OM=ON,∴OB平分∠ABC,同理OC平分∠ACB,∴∠OBC=∠ABC,∠OCB=∠ACB,∴∠OBC+∠OCB=(∠ABC+∠ACB)=(180°﹣∠A)=×(180°﹣80°)=50°,∴∠BOC =180°﹣50°=130°,∵OD =3,∴扇形ODE 的面积==.故选:B .27.如图,在Rt △ABC 中,∠C =90°,AC =4,BC =3,⊙O 为Rt △ABC 的内切圆,则图中阴影部分的面积为(结果保留π)( )A .B .6﹣C .5﹣D .3+【答案】C【解答】解:Rt △ABC 中,AC =4,BC =3,∴AB ==5,∴S △ABC =AC •BC =6,C △ABC =AC +BC +AB =12,∴内切圆半径r ==1,∴S 圆=πr 2=π,设⊙O 与AC 切于点D ,与BC 切于点E ,连接OD 、OE ,则四边形ODCE 为正方形,∴S 阴影=S △ABC ﹣S 圆﹣S 正方形=6﹣π﹣1=5﹣π.故选:C .28.如图,⊙O 是△ABC 的内切圆,若△ABC 的周长为18,面积为9,则⊙O 的半径是( )A .1B .C .1.5D .2【答案】A 【解答】解:如图,设⊙O 与△ABC 的各边分别相切于点E 、F 、G ,连接OE ,OF ,OG ,OA ,OB ,OC ,设⊙O 的半径为r ,则OE ⊥AB ,OF ⊥AC ,OG ⊥BC ,OE =OF =OG =r ,∵S △ABC =S △ABO +S △ACO +S △BOC ,=AB •r +AC •r +BC •r ,=(AB +AC +BC )•r ,又△ABC 的周长为18,面积为9,∴9=×18•r ,∴r =1,故选:A .29.如图,在△ABC 中,∠C =90°,AC =4,BC =3.⊙O 是△ABC 的内切圆,分别与AC 、BC 、AB 相切于点D 、E 、F ,则圆心O 到顶点A 的距离是( )A.B.3C.D.【答案】C【解答】解:如图,连结OD,OE,OF,设⊙O半径为r,∵∠C=90°,AC=4,BC=3,∴AB==5,∵⊙O是△ABC AC、BC、AB相切于点D、E、F,,∴AC⊥OD,AB⊥OF,BC⊥OE,且OF=OD=OE=r,∴四边形OECF是正方形,∴CE=CD=OD=r,∴AD=AF=AC﹣CD=4﹣r,BF=BE=BC﹣CE=3﹣r,∵AF+BF=AB=5,∴3﹣r+4﹣r=5,∴r=1.∴OD=CD=1,∴AD=3.∴AO==,故选:C.30.如图,等腰△ABC的内切圆⊙O与AB,BC,CA分别相切于点D,E、F,且AB=AC=13,BC=10,则DE的长是()A.B.C.D.【答案】D【解答】解:连接OA、OE、OB,OB交DE于H,如图,∵等腰△ABC的内切圆⊙O与AB,BC,CA分别相切于点D,E,F,∴OA平分∠BAC,OE⊥BC,OD⊥AB,BE=BD,∵AB=AC,∴AO⊥BC,∴点A、O、E共线,即AE⊥BC,∴BE=CE=5,在Rt△ABE中,AE==12,∵BD=BE=5,∴AD=8,设⊙O的半径为r,则OD=OE=r,AO=12﹣r,在Rt△AOD中,r2+82=(12﹣r)2,解得r=,在Rt△BOE中,OB=5=,∵BE=BD,OE=OD,∴OB垂直平分DE,∴DH=EH,OB⊥DE,∵HE•OB=OE•BE,∴HE===,∴DE=2EH=.故选:D.31.如图,⊙I是Rt△ABC的内切圆,∠ACB=90°,过点I作MN∥AB分别交CA,CB于N,M,若BM=3,AN=4,则⊙I的半径是()A.B.C.D.【答案】D【解答】解:设切点分别为E,F,G,连接IE,IF,IG,过点M作MP⊥AB 于P,过点N作NQ⊥AB于Q,∵⊙I是Rt△ABC的内切圆,∴IE⊥BC,IF⊥AC,IG⊥AB,IE=IF=IG,∵NQ⊥AB,∴∠AQN=∠IFN=90°,∵MN∥AB,∴∠A=∠INF,∵MP⊥AB,NQ⊥AB,IG⊥AB,MN∥AB,∴NQ=IG=MP,∴NQ=IF,∴△AQN≌△NFI(AAS),∴IN=AN=4,同理可得IM=BM=3,∵IE⊥BC,∴∠MEI=90°,∵∠ACB=90°∴∠MEI=∠ACB∴IE∥AC,∴∠MIE=∠INF,∴△MEI∽△IFN,∴,设ME=3x,IF=4x,则IE=IF=4x,在Rt△MEI中,由勾股定理,得(3x)2+(4x)2=32,解得:(负根已经舍去),∴,故选:D.32.如图,把Rt△OAB置于平面直角坐标系中,点A的坐标为(0,4),点B 的坐标为(3,0),点P是Rt△OAB内切圆的圆心.将Rt△OAB沿y轴的正方向作无滑动滚动.使它的三边依次与x轴重合.第一次滚动后,圆心为P1,第二次滚动后圆心为P2…依此规律,第2019次滚动后,Rt△OAB内切圆的圆心P2019的坐标是()A.(673,1)B.(674,1)C.(8076,1)D.(8077,1)【答案】D【解答】解:∵点A的坐标为(0,4),点B的坐标为(3,0),∴OA=4,OB=3,∴AB==5,∴Rt△OAB内切圆的半径=(3+4﹣5)=1,∴P的坐标为(1,1),∵将Rt△OAB沿x轴的正方向作无滑动滚动,使它的三边依次与x轴重合,第一次滚动后圆心为P1,第二次滚动后圆心为P2,…,∴P3(3+5+4+1,1),即(13,1),每滚动3次一个循环,∵2019÷3=673,∴第2019次滚动后,Rt△OAB内切圆的圆心P2019的横坐标是673×(3+5+4)+1,即P2019的横坐标是8077,∴P2019的坐标是(8077,1);故选D.33.如图,△ABC是一张周长为18cm的三角形纸片,BC=5cm,⊙O是它的内切圆,小明准备用剪刀在⊙O的右侧沿着与⊙O相切的任意一条直线MN剪下△AMN,则剪下的三角形的周长为()A.13cmB.8cmC.6.5cmD.随直线MN的变化而变化【答案】B【解答】解:由切线长定理得,BD=BG,CP=CG,MH=MD,NH=NP,∴BD+CP=BG+CG=5,∴AD+AP=18﹣10=8,∴△AMN的周长=AM+MN+AN=AM+MD+AN+NP=AD+AP=8,故选:B.34.如图,在Rt△ABC中,∠ACB=90°,⊙O是△ABC的内切圆,三个切点分别为D,E,F,若BF=3,AF=10,则△ABC的面积是30.【答案】30.【解答】解:∵⊙O是△ABC的内切圆,切点分别为D,E,F,∴OE⊥AC,OD⊥BC,CD=CE,BD=BF=3,AF=AE=10,∴AB=AF+BF=13,∵∠C=90°,OD=OE,∴四边形OECD是正方形,设EC=CD=x,在Rt△ABC中,BC2+AC2=AB2,故(x+3)2+(x+10)2=132,解得:x1=2,x2=﹣15(舍去),∴BC=5,AC=12,=×5×12=30,∴S△ABC故答案为:30.。
冀教版九年级数学下册同步练习题-切线长定理
29.4 切线长定理知识点一切线长定理1. 如图,PA、PB分别切⊙O于点A、B,AC是⊙O的直径,连结AB、BC、OP,则与∠PAB相等的角(不包括∠PAB本身)有( ) A.1个B.2个C.3个D.4个第1题图第2题图2.如图,PA、PB切⊙O于点A、B,PA=8,CD切⊙O于点E,交PA、PB于C、D两点,则△PCD的周长是()A.8 B.18 C.16 D.143.如图,PA,PB分别是⊙O的切线,A,B分别为切点,点E是⊙O上一点,且∠AEB=60°,则∠P为()A.120°B.60°C.30°D.45°第3题图第4题图4.如图,一圆内切于四边形ABCD,且AB=16,CD=10,则四边形ABCD的周长为________.5.如图,AB、AC、BD是⊙O的切线,P、C、D为切点,如果AB=5,AC=3,则BD的长为__________.第5题图第6题图6.PA、PB切⊙O于A、B两点,CD切⊙O于点E,交PA、PB于C、D,若⊙O的半径为r,△PCD的周长等于3r,则tan∠APB的值是______________.P BAO7. 如图,AE 、AD 、BC 分别切⊙O 于点E 、D 、F ,若AD=20,求△ABC 的周长.8. 如图,PA 、PB 是⊙O 的两条切线,切点分别为点A 、B ,若直径AC= 12,∠P=60o ,求弦AB 的长.9.. 如图,PA 、PB 是⊙O 的切线,A 、B 为切点,∠OAB =30°.(1)求∠APB 的度数;(2)当OA =3时,求AP 的长.知识点二 三角形的内切圆1.下列说法中,不正确的是 ( )A .三角形的内心是三角形三条内角平分线的交点B.锐角三角形、直角三角形、钝角三角形的内心都在三角形内部C.垂直于半径的直线是圆的切线D.三角形的内心到三角形的三边的距离相等2.给出下列说法:①任意一个三角形一定有一个外接圆,并且只有一个外接圆;②任意一个圆一定有一个内接三角形,并且只有一个内接三角形;③任意一个三角形一定有一个内切圆,并且只有一个内切圆;④任意一个圆一定有一个外切三角形,并且只有一个外切三角形.其中正确的有( ) A.1个B.2个C.3个D.4个3.一个直角三角形的斜边长为8,内切圆半径为1,则这个三角形的周长等于( ) A.21 B.20 C.19 D.184.一个直角三角形的斜边长为8,内切圆半径为1,则这个三角形的周长等于( )A.21 B.20 C.19 D.185.△ABC中,AB=AC,∠A为锐角,CD为AB边上的高,I为△ACD的内切圆圆心,则∠AIB的度数是()A.120°B.125°C.135°D.150°6.如图,⊙I是△ABC的内切圆,切点分别为点D、E、F,若∠DEF=52o,则∠A=________.7.已知:如图,⊙O内切于△ABC,∠BOC=105°,∠ACB=90°,AB=20cm.求BC、AC 的长.8.已知:如图,△ABC三边BC=a,CA=b,AB=c,它的内切圆O的半径长为r.求△ABC的面积S.9.已知:如图,⊙O是Rt△ABC的内切圆,∠C=90°.(1)若AC=12cm,BC=9cm,求⊙O的半径r;(2)若AC=b,BC=a,AB=c,求⊙O的半径r.。
北师大版九年级数学下册 3.7 切线长定理(含答案)
北师大版九年级数学下3.7 切线长定理(含答案)一、选择题1.如图1,P为⊙O外一点,PA,PB分别切⊙O于A,B两点,若PA=3,则PB等于()图1A.2 B.3 C.4 D.52.如图2,从⊙O外一点P引⊙O的两条切线PA,PB,切点分别为A,B.如果∠APB=60°,PA=8,那么弦AB的长是()图2A.4 B.8 C.4 3 D.8 33.如图3,若△ABC的三边长分别为AB=9,BC=5,CA=6,△ABC的内切圆⊙O与AB,BC,CA分别切于点D,E,F,则AF的长为()图3A.5 B.10 C.7.5 D.44.如图4,PA切⊙O于点A,PB切⊙O于点B,OP交⊙O于点C,下列结论中,错误的是( )图4A.∠1=∠2 B.PA=PB C.AB⊥OP D.PA2=PC·PO5.2019·深圳模拟如图5,AB是⊙O的直径,C为⊙O外一点,CA,CD是⊙O的切线,A,D为切点,连接BD,AD.若∠ACD=48°,则∠DBA的度数是()图5A.32°B.48°C.60°D.66°6.如图6,已知PA,PB分别切⊙O于点A,B,C是劣弧AB上一动点,过点C作⊙O的切线交PA于点M,交PB于点N.已知∠P=56°,则∠MON的度数是()图6A.56°B.60°C.62°D.不可求7.把直尺、三角尺和圆形螺母按图7所示放置在桌面上,∠CAB=60°,D为切点,若量得AD=6 cm,则圆形螺母的外直径是()图7A.12 cm B.24 cmC.6 3 cm D.12 3 cm二、填空题8.如图8,四边形ABCD是⊙O的外切四边形,且AB=10,CD=12,则四边形ABCD的周长为________.图89.如图9所示,在Rt△ABC中,∠C=90°,AC的长为8,BC的长为15,则△ABC的内切圆⊙O的直径是________.图910.如图10,P是⊙O的直径AB的延长线上一点,PC,PD分别切⊙O于点C,D.若PA=6,⊙O的半径为2,则∠CPD=________°.图1011.如图11所示,已知PA,PB,EF分别切⊙O于点A,B,D,若PA=15 cm,则△PEF的周长是________cm;若∠P=50°,则∠EOF=________°.图1112.如图12所示,⊙O与△ABC中AB,AC边的延长线及BC边相切,且∠ACB=90°,∠A,∠ABC,∠ACB所对的边长依次为3,4,5,则⊙O的半径是________.图12三、解答题13.一个夹角为120°的墙角处放置了一个圆柱形的容器,俯视图如图13,在俯视图中⊙O与两边的墙分别切于B,C两点(圆柱形容器的直径不易直接测量).(1)写出图中相等的线段;(2)请你设计一种可以通过计算求出⊙O的直径的测量方法(写出主要解题过程).图1314.如图14,△ABC外切于⊙O,切点分别为D,E,F,∠A=60°,BC=7,⊙O的半径为 3.求:(1)BF+CE的长;(2)△ABC的周长.图1415.如图15,边长为1的正方形ABCD的边AB是⊙O的直径,CF是⊙O的切线,E为切点,点F在AD 上,BE是⊙O的弦,求△CDF的面积.图15附加题如图16,以Rt△ABC的直角边AB为直径作⊙O,与斜边AC交于点D,过点D作⊙O的切线交BC边于点E,连接OE.(1)求证:EB=EC=ED.(2)在线段DC上是否存在点F,使得BC2=4DF·DC?若存在,找出点F,并予以证明;若不存在,请说明理由.图16参考答案1.[答案] B2.[答案] B3.[解析] A设AF=x,根据切线长定理得AD=x,BD=BE=9-x,CE=CF=CA-AF=6-x,则有9-x+6-x=5,解得x=5,即AF的长为5.4.[解析] D如图,连接OA,OB.∵P A切⊙O于点A,PB切⊙O于点B,∴P A=PB,∴△ABP是等腰三角形.易证∠1=∠2,∴AB⊥OP.故A,B,C均正确.设OP 交AB 于点D ,易证△P AD ∽△POA , ∴P A ∶PO =PD ∶P A ,∴P A 2=PD ·PO . 故D 错误.5.[解析] D ∵CA ,CD 是⊙O 的切线, ∴CA =CD , ∴∠CAD =∠CDA . ∵∠ACD =48°, ∴∠CAD =∠CDA =66°. ∵CA ⊥AB ,AB 是⊙O 的直径,∴∠DBA +∠DAB =90°,∠CAD +∠DAB =90°, ∴∠DBA =∠CAD =66°. 6.[答案] C7.[解析] D 设圆形螺母的圆心为O ,与AB 切于点E ,连接OD ,OE ,OA ,如图所示.∵AD ,AB 为圆O 的切线,∴AO 为∠DAB 的平分线,OD ⊥AC . 又∵∠CAB =60°,∴∠OAE =∠OAD =12∠DAB =60°.在Rt △AOD 中,∠OAD =60°,AD =6 cm , ∴tan ∠OAD =tan60°=3,即OD6=3, ∴OD =6 3 cm ,∴圆形螺母的外直径为12 3 cm. 8.[答案] 44[解析] ∵四边形ABCD 是⊙O 的外切四边形,∴AD +BC =AB +CD =22,∴四边形ABCD 的周长=AD +BC +AB +CD =44.。
切线长定理-三角形的内切圆(基础篇)-2022-2023学年九年级数学下册基础知识专项讲练(浙教版)

专题2.8 切线长定理三角形的内切圆(基础篇)(专项练习)一、单选题1.用尺规作图作三角形的内切圆,用到了哪个基本作图()A.作一条线段等于已知线段B.作一个角等于已知角C.作一个角的平分线D.作一条线段的垂直平分线2.一个等腰直角三角形的内切圆与外接圆的半径之比为()A2B2C21D213.已知三角形的周长为12,面积为6,则该三角形内切圆的半径为()A.4B.3C.2D.14.如图,PA、PB是O的切线,AC是O的直径,62P∠=,则BOC∠的度数为()A.60B.62C.31D.705.如图,从⊙O外一点P引圆的两条切线P A,PB,切点分别是A,B,若⊙APB=60°,P A=5,则弦AB的长是()A.52B532C.5D.36.如图,P A和PB是⊙O的两条切线,A,B为切点,点D在AB上,点E,F分别在线段P A和PB上,且AD=BF,BD=AE.若⊙P=α,则⊙EDF的度数为()A .90°﹣αB .32αC .2αD .90°﹣12α7.如图,已知PA 、PB 是O 的两条切线,A 、B 为切点,连接OP 交AB 于C ,交O 于D ,连接OA 、OB ,则图中等腰三角形、直角三角形的个数分别为( )A .1,2B .2,2C .2,6D .1,68.若Rt ABC 的外接圆半径为R ,内切圆半径为r ,则其内切圆的面积与Rt ABC 的面积比为( )A .22rr Rπ+ B .2rR rπ+ C .42rR rπ+ D .4rR rπ+9.已知⊙ABC 中,⊙ACB =90°,CD 、CE 分别是⊙ABC 中线和高线,则( )A .D 点是⊙ABC 的内心B .D 点是⊙ABC 的外心 C .E 点是⊙ABC 的内心D .E 点是⊙ABC 的外心10.如图,点E 是⊙ABC 的内心,AE 的延长线和⊙ABC 的外接圆相交于点D ,连接BD ,CE ,若⊙CBD =32°,则⊙BEC 的大小为( )A .64°B .120°C .122°D .128°二、填空题11.如图,已知点O 是ABC ∆的内心,若120BOC ∠=,则A ∠=__________.12.如图,Rt ⊙ABC 中,⊙C =90°,若AC =4,BC =3,则⊙ABC 的内切圆半径r =_____.13.如图,P 是⊙O 外一点,P A 、PB 分别和⊙O 切于A 、B ,C 是弧AB 上任意一点,过C 作⊙O 的切线分别交P A 、PB 于D 、E ,若△PDE 的周长为20cm ,则P A 长为__________.14.如图,AB 是⊙O 的直径,弦BC=2cm ,⊙ABC=60°.若动点P 以2cm/s 的速度从B 点出发沿着B→A 的方向运动,点Q 以1cm/s 的速度从A 点出发沿着A→C 的方向运动,当点P 到达点A 时,点Q 也随之停止运动.设运动时间为t (s ),当⊙APQ 是直角三角形时,t 的值为_________.15.如图所示,AB 、AC 为⊙O 的切线,B 和C 是切点,延长OB 到D ,使BD =OB ,连接AD .∠DAC =78°,那么∠AOD 等于_____度.16.如图,AB AC 、是O 的切线,B C 、为切点,连接BC .若50A ∠=︒,则ABC ∠=__________.17.在菱形ABCD 中,对角线AC 与BD 相交于点O ,AC =8、BD =6,则菱形ABCD 的内切圆半径为 ________.18.如图,四边形ABCD 为O 的内接四边形,I 是BCD △的内心,点O 与点I 关于直线BD 对称,则A ∠的度数是__________.三、解答题19.如图,ABC 中,50,75ABC ACB ∠=︒∠=︒,点O 是ABC 的内心.求BOC ∠的度数.20.如图,Rt ABC 中,90ABC ∠=︒,O 为BC 上一点,以O 为圆心,OB 长为半径的圆恰好与AC 相切于点D ,交BC 于点E ,连接DO ,并延长交于O 点F .(1)求证:BAO F ∠=∠;(2)若3AD =,2CD =,求O 的半径及EF 的长.21.如图,线段AB 经过O 的圆心O ,交圆O 于点A ,C ,1BC =,AD 为O 的弦,连接BD ,30BAD ABD ∠=∠=︒,连接DO 并延长交O 于点E ,连接BE 交O 于点M .(1)求证:直线BD 是O 的切线; (2)求线段BM 的长.22.如图,点E 是ABC 的内心,AE 的延长线和ABC 的外接圆O 相交于点D ,过D 作直线DG ∥B C .(1)若80ACB ∠=︒,则ADB =∠______;AEB ∠= ______. (2)求证:DE CD =;(3)求证:DG 是O 的切线C .23.如图,在ABC 中,AB AC =,以AB 为直径的O 交BC 于点P ,交CA 的延长线于点D ,连接BD .(1)求作O的切线PQ,PQ交AC于点Q;(要求:尺规作图,不写作法,保留作图迹).(2)在(1)的条件下,求证:QC DQ24.如图,四边形ABCD是⊙O的内接四边形,AB = 6,BC = 8,⊙ABC = 90°,弧AD = 弧DC.(1)求边CD的长;(2)已知⊙ABE与⊙ABD关于直线AB对称.⊙尺规作图:作⊙ABE;(保留作图痕迹,不写作法)⊙连接DE,求线段DE的长.参考答案1.C【分析】根据三角形内心的定义解答.解:三角形的内切圆的圆心叫三角形的内心,是三角形三个角平分线的交点,⊙用尺规作图作三角形的内切圆,用到了作角的平分线的作法,故选:C.【点拨】此题考查了三角形内心的定义,正确理解定义是解题的关键.2.D【分析】设等腰直角三角形的直角边是12条直角边的和与斜边的差的一半,22-其外接圆半径是斜边的一半,22222-21.解:设等腰直角三角形的直角边是12;⊙22-外接圆半径是22,⊙2222-21.故选:D.【点拨】本题考查三角形的内切圆与外接圆的知识,解题的关键是熟记直角三角形外接圆的半径和内切圆的半径公式:直角三角形的内切圆半径等于两条直角边的和与斜边的差的一半;直角三角形外接圆的半径是斜边的一半.3.D【分析】设内切圆的半径为r,根据公式:12rC S三角形三角形,列出方程即可求出该三角形内切圆的半径.解:设内切圆的半径为r11262r解得:r=1故选D.【点拨】此题考查的是根据三角形的周长和面积,求内切圆的半径,掌握公式:1 2rC S三角形三角形是解决此题的关键.4.B【分析】(1)根据切线长定理推出AP=BP,根据等腰三角形性质和三角形的内角和定理求出⊙PAB=59°,求出⊙BAC⊙BOC即可.解:PA,PB是⊙O的切线,∴AP=BP,⊙P=62°,∴⊙PAB=o o180-622=59°,AC是⊙O的直径,∴⊙PAC=90°,∴⊙BAC=90°-59°=31°,∴∠BOC=2⊙BAC=62°,故选B.【点拨】本题考查了等腰三角形的性质,切线长定理,切线的性质,圆周角定理等知识点的应用,题型较好,综合性比较强,通过做此题培养了学生分析问题和解决问题的能力.5.C【分析】先利用切线长定理得到P A=PB,再利用⊙APB=60°可判断⊙APB为等边三角形,然后根据等边三角形的性质求解.解:⊙P A,PB为⊙O的切线,⊙P A=PB,⊙⊙APB=60°,⊙⊙APB为等边三角形,⊙AB=P A=5.故选:C.【点拨】本题考查了切线长定理以及等边三角形的判定与性质.此题比较简单,注意掌握数形结合思想的应用.6.D 【分析】根据切线性质,证得DAE △⊙FBD ,通过等量代换得出EDF DAE ∠=∠,再根据等腰三角形的性质,由⊙P =α,求得DAE ∠即可.解: ⊙P A 和PB 是⊙O 的两条切线,A ,B 为切点,⊙P A =PB ,⊙PAB PBA ∠=∠,即DAE DBF ∠=∠ 在DAE △与FBD 中, ⊙AD BF DAE DBF AE BD =⎧⎪∠=∠⎨⎪=⎩⊙DAE △⊙FBD (SAS ), ⊙DEA FDB ∠=∠, 在DAE △中,180DAE AED EDA ∠+∠+∠=︒,⊙DEA FDB ∠=∠,⊙180DAE FDB EDA ∠+∠+∠=︒, ⊙180EDF FDB EDA ∠+∠+∠=︒, ⊙EDF DAE ∠=∠, ⊙⊙P =α,P A =PB , ⊙PAB PBA ∠=∠⊙在PAB △中,1902BAP α∠=︒-,即1902DAE α∠=︒-,⊙EDF DAE ∠=∠, ⊙1902EDF α∠=︒-故选:D .【点拨】本题考查了切线的性质,全等三角形的性质以及等腰三角形的性质,通过全等证明,等量代换求得EDF DAE ∠=∠是解题关键.7.C 【分析】根据切线长定理及半径相等得,⊙APB 为等腰三角形,⊙AOB 为等腰三角形,共两个;根据切线长定理和等腰三角形三线合一的性质,直角三角形有:⊙AOC ,⊙AOP ,⊙APC ,⊙OBC ,⊙OBP ,⊙CBP ,共6个.解:因为OA 、OB 为圆O 的半径,所以OA =OB ,所以⊙AOB 为等腰三角形,根据切线长定理,PA =PB ,故⊙APB 为等腰三角形,共两个,根据切线长定理,PA =PB ,⊙APC =⊙BPC ,PC =PC ,所以⊙PAC⊙⊙PBC ,故AB⊙PE ,根据切线的性质定理⊙OAP =⊙OBP =90°,所以直角三角形有:⊙AOC ,⊙AOP ,⊙APC ,⊙OBC ,⊙OBP ,⊙CBP ,共6个.故选C .【点拨】此题综合考查了切线的性质和切线长定理及等腰三角形的判定,有利于培养同学们良好的思维品质.8.B【分析】画好符合题意的图形,由切线长定理可得:,,,CE CF r AE AG m BF BG n ======结合勾股定理可得:22,mn Rr r =+再求解直角三角形的面积()()21==22ACB S m r n r Rr r +++,从而可得直角三角形的内切圆的面积与直角三角形的面积之比.解:如图,由题意得:902ACB AB R ∠=︒=,,111O E O F O G r ===,由切线长定理可得:,,,CE CF r AE AG BF BG ====设,,AE AG m BF BG n ====()()()222m r n r m n ∴+++=+,2,m n R += ()2mn m n r r ∴=++,22,mn Rr r ∴=+而()()()211=+22ACB S m r n r mn mr nr r ++=++ ()221=222Rr r Rr r +++ 2=2Rr r +122.22O ABC Sr r S Rr r R r ππ∴==++故选B .【点拨】本题考查的是三角形的内切圆与三角形的外接圆,切线长定理,勾股定理的应用,掌握以上知识是解题的关键.9.B【分析】根据直角三角形斜边上的中线等于斜边的一半,可得D 是⊙ABC 的外心,据此即可求解.解:在△ABC 中,⊙ACB =90°,⊙CD 是△ABC 中线,⊙D 点是△ABC 的外心.故选:B .【点拨】本题考查了三角形的外心,直角三角形斜边上的中线等于斜边的一半,掌握以上知识是解题的关键.10.C【分析】根据圆周角定理可求⊙CAD=32°,再根据三角形内心的定义可求⊙BAC ,再根据三角形内角和定理和三角形内心的定义可求⊙EBC+⊙ECB ,再根据三角形内角和定理可求⊙BEC 的度数.解:在⊙O 中,⊙⊙CBD=32°,⊙⊙CAD=32°,⊙点E 是⊙ABC 的内心,⊙⊙BAC=64°,⊙⊙EBC+⊙ECB=(180°-64°)÷2=58°,⊙⊙BEC=180°-58°=122°.故选:C.【点拨】本题考查了三角形的内心,圆周角定理,三角形内角和定理,关键是得到⊙EBC+⊙ECB的度数.11.60【分析】先利用120BOC∠=,可求出⊙OBC+⊙OCB,再利用三角形的内心即为三个内角角平分线的交点,可求出⊙ABC+⊙ACB,然后就可求出⊙A.解:⊙120BOC∠=⊙⊙OBC+⊙OCB=180°-⊙BOC=60°∆的内心又⊙点O是ABC⊙BO、CO分别平分⊙ABC和⊙ACB⊙⊙ABC+⊙ACB=2(⊙OBC+⊙OCB)=120°⊙⊙A=180°-(⊙ABC+⊙ACB)=60°故答案为60【点拨】此题考查的是三角形内心的定义和三角形内角和定理.12.1解:如图,设⊙ABC的内切圆与各边相切于D,E,F,连接OD,OE,OF,则OE⊙BC,OF⊙AB,OD⊙AC,设半径为r,CD=r,⊙⊙C=90°,AC=4,BC=3,⊙AB=5,⊙BE=BF=3﹣r,AF=AD=4﹣r,⊙4﹣r+3﹣r=5,⊙r=1,⊙⊙ABC的内切圆的半径为1,故答案为1.13.10cm【分析】根据切线长定理,可将△PDE的周长转化为两条切线长的和,已知了△PDE的周长,即可求出切线的长.解:根据切线长定理得:AD=CD,CE=BE,P A=PB,则△PDE的周长=PD PE DE PD PE DC EC PA PB++=+++=+=2P A=20,∴P A=10.故答案为:10.cm【点拨】本题考查的是切线长定理,三角形的周长的计算,掌握切线长定理是解题的关键14.或3-解:因为AB是⊙O的直径,所以⊙ACB=90°,又因为BC=2,⊙ABC=60°;所以AB=2BC=4cm;因为运动时间为t(s),所以AQ=t,BP=2t,所以AP=4-2t,⊙当⊙AQP=90°时,因为⊙A=30°,AP=4-2t,所以PQ=2-t,AQ=3PQ,所以t=3(2-t),所以t=3-;⊙当⊙APQ=90°时,PQ=12AQ,AP=3PQ,所以4-2t=32t,解得t=,综上所述,当t的值为或3-时,⊙APQ是直角三角形.【点拨】1.圆的性质;2.直角三角形的判定与性质.15.64【分析】由已知条件推导出⊙CAO=⊙OAB=⊙BAD,⊙ABD=90°,由此根据⊙DAC=78°,能求出⊙AOD的大小.解:⊙AB、AC为⊙O的切线,B和C是切点,BD=OB,AB∴垂直平分OD,⊙CAO=⊙OABAO AD∴=∴⊙OAB=⊙BAD,⊙⊙CAO=⊙OAB=⊙BAD,⊙ABD=90°,⊙⊙DAC=78°,⊙⊙BAO=13⊙DAC=26°,⊙∠AOD=90°-26°=64°.故答案为:64.【点拨】本题考查角的大小的求法,解题时要认真审题,注意切线性质的灵活运用是解题的关键.16.65°【分析】根据切线长定理即可得出AB=AC,然后根据等边对等角和三角形的内角和定理即可求出结论.解:⊙AB AC、是O的切线,⊙AB=AC⊙⊙ABC=⊙ACB=12(180°-⊙A)=65°故答案为:65°.【点拨】此题考查的是切线长定理和等腰三角形的性质,掌握切线长定理和等边对等角是解决此题的关键.17.125##2.4【分析】根据菱形的性质,可得AC⊙BD,11,22AO AC DO BD==,再由勾股定理可得5AD=,然后设菱形ABCD的内切圆半径为r,根据三角形的面积,即可求解.解:在菱形ABCD中,AC⊙BD,11,22AO AC DO BD==,⊙AC=8、BD=6,⊙AO=4,DO=3,⊙225 AD AO DO+,设菱形ABCD 的内切圆半径为r ,⊙12AOD SAD r =⨯ , ⊙12AODS AO DO =⨯, ⊙1153422r ⨯=⨯⨯ ,解得:125r = , 即菱形ABCD 的内切圆半径为125. 故答案为:125【点拨】本题主要考查了菱形的性质,内切圆,熟练掌握菱形的性质是解题的关键. 18.72︒【分析】连接OB 、OD 、BI 、DI ,利用轴对称的性质证得四边形OBID 是菱形,得到⊙BOD =⊙BID ,⊙OBD =⊙BDO =⊙IBD =⊙IDB ,根据圆周角定理得到⊙BOD =2⊙A ,由圆内接四边形性质得到180A C ∠+∠=︒,求出⊙BID =180°-12A ∠,由此得到2⊙A =180°-12A ∠,求出⊙A =72︒. 解:连接OB 、OD 、BI 、DI ,⊙点O 与点I 关于直线BD 对称,⊙OB =BI ,OD =DI ,⊙OB =OD ,⊙OB =BI =OD =DI ,⊙四边形OBID 是菱形,⊙⊙BOD =⊙BID ,⊙OBD =⊙BDO =⊙IBD =⊙IDB ,⊙⊙BOD =2⊙A ,⊙BID =180°-(⊙IBD +⊙IDB ),⊙⊙IBD +⊙IDB =()11802C ︒-∠,180A C ∠+∠=︒, ⊙ ⊙IBD +⊙IDB =12A ∠,⊙⊙BID =180°-12A ∠, ⊙2⊙A =180°-12A ∠, 解得⊙A =72︒,故答案为:72︒.【点拨】此题考查了圆内接四边形对角互补的性质,三角形内心定义,菱形的判定及性质,三角形内角和定理,轴对称的性质,熟记各知识点是解题的关键.19.117.5°【分析】由点O 是ABC ∆的内心,50ABC ∠=︒,75ACB ∠=︒,根据三角形的内心是三角形三条角平分线的交点,即可求得OBC ∠与OCB ∠的度数,又由三角形内角和定理,即可求得BOC ∠的度数.解:点O 是ABC 的内心,50ABC ∠=︒,75ACB ∠=︒,11502522OBC ABC ∴∠=∠=⨯︒=︒,117537.522OCB ACB ∠=∠=⨯︒=︒, 1801802537.5117.5BOC OBC OCB ∴∠=︒-∠-∠=︒-︒-︒=︒.【点拨】此题考查了三角形内心的性质.此题难度不大,解题的关键是掌握三角形的内心是三角形三条角平分线的交点.20.(1)见分析(2)O 的半径为1.5,65EF =【分析】(1)连接DE ,根据切线长定理可得⊙BAO =⊙DAO ,⊙PDC =90°,从而得到⊙BAO =12⊙BAD ,从而得到⊙BAO =12()1902C COD ︒-∠=∠=⊙F ,即可求证; (2)根据切线长定理可得AB =AD =3,再由勾股定理可得BC =4,设O 的半径为x ,则OD =x ,OC =4-x ,在Rt COD 中,由勾股定理可得O 的半径为1.5,由(1)可得1tan tan 2F BAO =∠=,在Rt DEF △中,由勾股定理,即可求解. (1)证明:如图,连接DE ,⊙90ABC ∠=︒,⊙AB 与O 相切,⊙AD 与O 相切,⊙⊙BAO =⊙DAO ,⊙PDC =90°,⊙⊙BAO =12⊙BAD ,⊙⊙BAD =90°-⊙C ,⊙C =90°-⊙COD , ⊙⊙BAO =12()1902C COD ︒-∠=∠=⊙F ; (2)解:⊙AB 与O 相切,AD 与O 相切,⊙AB =AD =3,⊙CD =2,⊙AC =5,⊙BC =4,设O 的半径为x ,则OD =x ,OC =4-x ,在Rt COD 中,由勾股定理得:222OD CD OC +=,⊙()222x 24x +=-,解得:x =1.5,⊙O 的半径为1.5,即OB =1.5,⊙DF 为直径,DF =3,⊙⊙DEF =90°,⊙BAO F ∠=∠,⊙ 1.51tan tan 32OB F BAO AB =∠===, ⊙EF =2DE ,在Rt DEF △中,由勾股定理得:222DF DE EF =+,⊙222132EF EF ⎛⎫=+ ⎪⎝⎭,解得:65EF =65EF =(舍去).【点拨】本题主要考查了切线长定理,圆周角定理,勾股定理,熟练掌握切线长定理,圆周角定理是解题的关键.21.(1)见分析37 【分析】(1)根据圆周角定理可得260BOD BAD ∠=∠=︒,从而得到90ODB ∠=︒ ,即可求证; (2)连接DM ,Rt ⊙BOD 中,根据直角三角形的性质可得 BO =2OD ,从而得到1OD OC ==,3BD =DE O 为的直径,可得2DE =,90DME ∠=︒,从而得到7BE =,再由1122BDE S BD DE BE DM =⋅=⋅△,可得221DM =解.(1)证明:⊙⊙BOD =2⊙BAD ,⊙260BOD BAD ∠=∠=︒,又⊙30ABD ∠=︒,⊙90ODB ∠=︒ ,即OD BD ⊥,又⊙OD 为O 的半径,⊙直线BD 是O 的切线;(2)解:如图,连接DM ,Rt ⊙BOD 中,30DBO ∠=︒,⊙2BO OD OC BC ==+,又1BC =,OD OC =,⊙1OD OC ==,⊙3BD =⊙DE O 为的直径,⊙2DE =,90DME ∠=︒,在Rt ⊙BDE 中,227BE DE BD +⊙1122BDE S BD DE BE DM =⋅=⋅△, ⊙221BD DE DM BE ⋅= 在Rt ⊙BDM 中,2237BM BD DM =- 【点拨】本题主要考查了切线的判定,圆周角定理,直角三角形的性质,勾股定理等知识,熟练掌握切线的判定,圆周角定理,直角三角形的性质,勾股定理是解题的关键.22.(1)80°,130°;(2)见分析过程;(3)见分析过程.【分析】(1)由圆周角定理可得∠ACB =∠ADB =70°,由三角形的内心的性质可得∠AEB =125°;(2)由三角形的内心的性质可得AE 平分∠BAC ,BE 平分∠ABC ,可得∠BAE =∠CAE ,∠ABE =∠CBE ,由外角的性质可得∠BED =∠DBE ,可证DE =CD ;(3)由垂径定理可得OD ⊥BC ,由平行线的性质可得OD ⊥DG ,可得结论.(1)解:如图,连接BD ,OD ,∵AB AB =,∴∠ACB =∠ADB =80°,∴∠ABC +∠BAC =100°,∵点E 是△ABC 的内心,∴AE 平分∠BAC ,BE 平分∠ABC ,∴∠BAE =∠CAE ,∠ABE =∠CBE ,∴∠BAE +∠ABE =50°,∴∠AEB =130°,故答案为:80°,130°;(2)证明:∵∠BAE =∠CAE ,∴BD =CD ,∴BD =CD ,∵∠BAE =∠CAE =∠CBD ,∠ABE =∠CBE ,∴∠BED =∠BAE +∠ABE =∠CBD +∠CBE =∠DBE ,∴BD =DE ,∴DE =CD ;(3)证明:∵BD =CD ,∴OD ⊥BC ,∵DG ∥BC ,∴OD ⊥DG ,又∵OD 是半径,∴DG 是⊙O 的切线.【点拨】本题考查了三角形的内心,圆的有关性质,切线的判定和性质,灵活运用这些性质解决问题是解题的关键.23.(1)见详解;(2)见详解.【分析】(1)作射线OP ,以点P 为圆心,任意长为半径画弧交射线于M ,N ,以点M ,N 为圆心,大于12MN 为半径画弧,两弧交于点E ,作直线PE ,交AC 于点Q ,则直线PQ 即为所求;(2)如图,连接AP ,则BP =PC ,根据中位线的性质证得OP AC ∥,由切线的性质,平行线的性质证PQ AC ⊥,根据直径所对的圆周角是直角,得90D ∠=︒,证得PQ BD ∥问题得证.(1)解:如图所示,直线PQ 即为所求;(2)证明:如图,连接AP ,AB AC =,BP PC ∴=,OA OB =,OP AC ∴∥,OP 是O 的切线,OP PQ ∴⊥,PQ AC ∴⊥,AB 是O 的直径,90D ∴∠=︒ ,BD AC ⊥,BD DC ∴∥,1CQ PC DQ BP∴==, DQ CQ ∴=.【点拨】本题考查了圆的综合题、圆的半径相等、切线的判定和性质、直径所对的圆周角是直角、三角形中位线的判定和性质、平行线的判定和性质、等腰三角形的性质等知识,作辅助线是解决本题的关键.24.(1)52图见分析⊙14【分析】(1)先求出直径AC,再得到⊙ADC是等腰直角三角形,利用勾股定理即可求解;(2)⊙以B点为圆心,BD为半径,和以A点为圆心,AD为半径画弧,交点为E点,再顺次连接即可;⊙过A点作AH⊙BD,先求出BD的长,再证明⊙BDE是等腰直角三角形,故可求出DE 的长.解:(1)⊙AB = 6,BC = 8,⊙ABC = 90°,⊙AC22+=,AC是⊙O的直径6810⊙⊙ADC=90°⊙弧AD = 弧DC⊙AD=CD⊙⊙ADC是等腰直角三角形⊙AD2+CD2=AC2解得CD=52(2)⊙如图,⊙ABE为所求;⊙过A点作AH⊙BD,⊙弧AD = 弧DC⊙ABC=45°⊙⊙ABD=⊙CBD=12⊙⊙ABH是等腰直角三角形⊙AB2=BH2+AH2,AH=BH⊙AH=BH2⊙AD=CD2⊙在Rt⊙ADH中,DH2242-=AD AH⊙BD=BH+DH=2⊙⊙ABE与⊙ABD关于直线AB对称⊙⊙EBD=2⊙ABD=90°,BE=BD=2⊙⊙BDE是等腰直角三角形⊙DE2214+.BE BD【点拨】此题主要考查圆内的线段长度求解、尺规作图,解题的关键是熟知圆周角的性质、等腰直角三角形的判定与性质及对称性的应用.。
九年级数学切线长定理及弦切角练习题

切线长〔一〕填空1.:如图7-143,直线BC切⊙O于B点,AB=AC,AD=BD,那么∠A=____.∠2.:如图7-144,直线DC与⊙O相切于点C,AB为⊙O直径,AD⊥DC 于D,∠DAC=28°侧∠CAB=____.3.:直线AB与圆O切于B点,割线ACD与⊙O交于C和D4.:如图7-145,PA切⊙O于点A,割线PBC交⊙O于B和C两点,P=15°,∠ABC=47°,那么∠C=____.5.:如图7-146,三角形ABC的∠C=90°,内切圆O与△ABC的三边分别切于D,E,F 三点,∠DFE=56°,那么∠B=____.6.:如图7-147,△ABC内接于⊙O,DC切⊙O于C点,∠1=∠2,那么ABC为____三角形.7.:如图7-148,圆O为△ABC外接圆,AB为直径,DC切⊙O于C点,A=36°,那么∠ACD=.〔二〕选择8.:△ABC内接于⊙O,∠ABC=25°,∠ACB=75°,过A点作⊙O的切线交BC的延伸线于P,那么∠APB等于[ ]A.°;B.55°;C.50°;D.40°.9.:如图7-149,PA,PB切⊙O于A,B两点,AC为直径,那么图中与∠PAB相等的角的个数为[]A.1个;B.2个;C.4个;D.5个.10.如图7-150,四边形ABCD为圆内接四边形,AB是直径,MN切⊙O于C点,∠BCM=38°,那么∠ABC的度数是[]A.38°;B.52°;C.68°;D.42°.11.如图7-151,PA切⊙O于点A,PCB交⊙O于C,B两点,且PCB过点O,AE⊥BP交⊙O于E,那么图中与∠CAP相等的角的个数是[]A.1个;B.2个;C.3个;D.4个.〔三〕计算12.:如图7-152,PT与⊙O切于C,AB为直径,∠BAC=60°,AD为⊙O 一弦.求∠ADC与∠PCA的度数.13.:如图7-153,PA切⊙O于A,PO交⊙O于B,C,PD均分∠APC.求∠ADP的度数.14.:如图7-154,⊙O的半径OA⊥OB,过A点的直线交OB于P,交⊙O于Q,过Q引⊙O的切线交OB延伸线于C,且PQ=QC.求∠A的度数.15.:如图7-155,⊙O内接四边形ABCD,MN切⊙O于C,∠BCM=38°,AB为⊙O直径.求∠ADC的度数.16.:如图7-156,PA,PC切⊙O于A,C两点,B点17.:如图7-157,AC为⊙O的弦,PA切⊙O于点A,PC过O点与⊙O交于B,∠C=33°.求∠P的度数.18.:如图7-158,四边形ABCD内接于⊙O,EF切⊙O19.BA是⊙O的弦,TA切⊙O于点A,∠BAT=100°,点M在圆周上但与A,B不重合,求∠AMB 的度数.20.:如图7-159,PA切圆于A,BC为圆直径,∠BAD=∠P,PA=15cm,PB=5cm.求BD的长.21.:如图7-160,AC是⊙O直径,PA⊥AC于A,PB切⊙O于B,BEAC于E.假定AE=6cm,EC=2cm,求BD的长.22.:如图7-161所示,P为⊙O外一点,PA切⊙O于A,从PA中点M引⊙O割线MNB,∠PNA=138°.求∠PBA的度数.23.:如图7-162,DC切⊙O于C,DA交⊙O于P和B两点,AC交⊙O于Q,PQ为⊙O直径交BC于E,∠BAC=17°,∠D=45°.求∠PQC与∠PEC的度数.24.:如图7-163,QA切⊙O于点A,QB交⊙O于B25.:如图7-164,QA切⊙O于A,QB交⊙O于B和C26.:在图7-165中,PA切⊙O于A,AD均分∠BAC,PE均分∠APB,AD=4cm,PA=6cm.求EP的长.27.;如图7-166,PA为△ABC外接圆的切线,A为切点,DE∥AC,PE=PD.AB=7cm,AD=2cm.求DE的长.28.:如图7-167,BC是⊙O的直径,DA切⊙O于A,DA=DE.求∠BAE的度数.29.:如图7-168,AB为⊙O直径,CD切⊙O于CAE∠CD于E,交BC于F,AF=BF.求∠A的度数.30.:如图7-169,PA,PB分别切⊙O于A,B,PCD为割线交⊙O于C,D.假定AC=3cm,AD=5cm,BC=2cm,求DB的长.31.:如图7-170,ABCD的极点A,D,C在圆O上,AB的延伸线与⊙O 交于M,CB的延伸线与⊙O交于点N,PD切⊙O于D,∠ADP=35°,∠ADC=108°.求∠M的度数.32.:如图7-171,PQ为⊙O直径,DC切⊙O于C,DP交⊙O于B,交CQ延伸线于A,∠D=45°,∠PEC=39°.求∠A的度数.33.:如图7-172,△ABC内接于⊙O,EA切⊙O于A,过B作BD∥AE交AC延伸线于D.假定AC=4cm,CD=3cm,求AB的长.34.:如图7-173,△ABC内接于圆,FB切圆于B,CF⊥BF于F交圆于E,∠1=∠2.求∠1的度数.35.:如图7-174,PC为⊙O直径,MN切⊙O于A,PB⊥MN于B.假定PC=5cm,PA=2cm.求PB的长.36.:如图7-175,AD为⊙O直径,CBE,CD分别切⊙37.:如图7-176,圆内接四边形ABCD的AB边经过圆心,AD,BC的延伸线订交于E,过C点的切线CF⊥AE于F.求证:〔1〕△ABE为等腰三角形;〔2〕假定BC=1cm,AB=3cm,求EF的长.38.:如图7-177,AB,AC切⊙O于B,C,OA交⊙O于F,E,交BC于D.〔1〕求证:E为△ABC心里;〔2〕假定∠BAC=60°,AB=a,求OB与OD的长.〔四〕证明39.:在△ABC中,∠C=90°,以C为圆心作圆切AB边于F点,AD,BC 分别与⊙C切于D,E两点.求证:AD∥BE.40.:PA,PB与⊙O分别切于A,B两点,延伸OB到C,41.:⊙O与∠A的两边分别相切于D,E.在线段AD,AE〔或在它们的延伸线〕上各取一点B,C,使DB=EC.求证:OA⊥BC.⊥EC于H,AO交BC于D.求证:BC·AH=AD·CE.*43.:如图7-178,MN切⊙O于A,弦BC交OA于E,过C点引BC的垂线交MN于D.求:AB∥DE.44.:如图7-179,OA是⊙O半径,B是OA延伸线上一点,BC切⊙O于C,CD⊥OA于D.求证:CA均分∠BCD.45.:如图7-180,BC是⊙O直径,EF切⊙O于A点,AD⊥BC于D.求证:AB均分∠DAE,AC均分∠DAF.46.:如图7-181,在△ABC中,AB=AC,∠C=2∠A,以AB为弦的圆O与BC切干点B,与AC 交于D点.求证:AD=DB=BC.47.:如图7-182,过△ADG的极点A作直线与DG的延伸线订交于C,过G作△ADG的外接圆的切线二均分线段AC于E.求证:AG2=DG·CG.48.:如图7-183,PA,PB分别切⊙O于A,B两点,PCD为割线.求证:AC·BD=BC·AD.BC=BA,连结AC交圆于点E.求证:四边形ABDE是平行四边形.50.:如图7-185,∠1=∠2,⊙O过A,D两点且交AB,AC于E,F,BC切⊙O于D.求证:EF∥BC.51.:如图7-186,AB是半圆直径,EC切半圆于点C,BE⊥CE交AC于F.求证:AB=BF.52.:如图7-187,AB为半圆直径,PA⊥AB,PC切半圆于C点,CD⊥AB于D交PB于M.求证:CM=MD.〔五〕作图53.求作以线段AB为弦,所含圆周角为锐角∠α〔见图7-188〕的弧〔不写作法,写出、求作,答出所求〕.54.求作一个以α为一边,所对角为∠α,此边上高为h的三角形.55.求作一个以a为一边,m为此边上中线,所对角为∠α的三角形〔不写作法,答出所求〕.切线长定理及弦切角练习题(答案)〔一〕填空1.36° 2.28° 3.50°4.32°5.22° 6.等腰7.54°〔二〕选择8.C 9.D 10.B 11.C〔三〕计算12.30°,30°.13.45°.提示:连结AB交PD于E.只要证明∠ADE=∠AED,证明时利用三角形外角定理及弦切角定理.∠14.30°.提示:因为PQ=QC,所以∠QCP=∠QPC.连结OQ,那么知∠POQ与QCP互余.又∠OAQ=∠OQA与∠QPC互余,所以∠POQ=∠OAQ=∠OQA.而它们的和为90°〔因为∠AOC=90°〕.所以∠OAQ=30°16.°.提示:解法一连结AC,那么∠PAC=∠PCA.又∠P=45°,所以PAC=∠°.进而∠B=∠°.解法二连结OA,OC,那么∠AOC=180°-∠P=135°,所以17.24°.提示:连结OA,那么∠POA=66°.18.60°.提示:连结BD,那么∠ADB=40°,∠DBC=20°.设∠ABD=∠BDC〔因为AB//CD〕=x°,那么因∠B+∠D=180°,所以2x°+60°=180°,x°=60°,进而∠ADE=∠ABD=60°.19.100°或80°.提示:M可在弦AB对的两弧的每一个上.进而22.42°.提示:∠ABM=∠NAM.于是明显△ABM∽△NAM,NMP,所以△PMB∽△NMP,进而∠PBM=∠NPM.再由∠ABM=∠NAM,就有∠PBA=∠PBM+∠NAM=∠NPM+∠NAM=180°-∠PNA=42°.23.28°,39°.提示:连结PC.24.41°.提示:求出∠QAC和∠ACB的度数.25.100°.以DB=9.因为2DP=2×9,由此得DP2=9.又DP>0,所以DP=3,进而,DE=23=6〔cm〕.28.45°.提示:连结AC.因为DA=DE,所以∠ABE+∠BAE=∠AED=∠EAD=CAD+∠CAE,但∠ABE=∠CAD,所以∠BAE=∠CAE.因为∠BAE+∠CAE=90°,所以∠BAE=45°.29.60°.提示:解法一连结AC,那么AC⊥BC.又AF⊥CE,所以∠ACE=∠F.又DC切⊙O于C,所以∠ACE=∠B.所以∠F=∠B.因为AF=BF,所以∠BAF=∠B=∠F.所以∠BAF=60°.31.37°.提示:连结AC,那么∠M=∠ACN=∠CAD.32.17°.提示:连结PC,那么∠QPC+∠PBC=90°.45°=∠D=〔∠BPQ+∠QPC〕∠DCP=〔∠BPQ+∠QPC〕-∠PBC=[∠BPQ+〔90°-∠PBC〕]-∠PBC.所以2∠PBC-∠BPQ=45°.〔1〕又∠PBC+∠BPQ=39°,〔2〕进而∠PBC=28°,∠BPQ=11°.于是∠A=∠PBC-∠BPQ=17°.34.30°.提示:连结BE,由∠1=∠2,可推出∠EBF=∠ECB=∠EBC,而这三个角的和为90°,所以每个角为30°.36.60°.提示:连结OB,那么OB⊥CE,进而∠C=∠BOE=60°.37.〔1〕提示:连结OC,那么∠E=∠OCB=∠OBC=∠CDE,所以△ABE为等腰三角形.38.〔1〕提示:连结BE.只要证明∠ABE=∠DBE.〔四〕证明39.提示:AC,BC各均分∠A,∠B.想法证出∠A+∠B=180°.40.提示:连结OP,想法证出∠BPC=∠BPO.42.提示:在△BCE和△DAH中,∠BCE=∠DAH〔它们都与∠DCH互补〕.又A,D,C,H共圆,所以∠CEB=∠ACB=∠AHD,进而△BCE∽△DAH.这就得所要证明的比率式.43.提示:连结AC.先证明A,E,C,D四点共圆.由此得∠ADE=〔∠ACE=〕MAB,所以AB//DE.44.提示:证法一延伸AO交⊙O于点E,连结EC,那么∠BCA=∠E,且∠ACD=E.所以∠BCA=∠ACD.∠证法二连结OA,那么∠BCA与∠OCA互余;又∠ACD与∠OAC互余,而∠OCA=OAC,所以∠BCA=∠ACD.46.提示:由得∠A=36°,∠B=∠C=72°,∠DBC=∠A=36°,所以∠ABD=36°,进而AD=BD.又∠C=∠CDB=72°,所以BD=BC.47.提示:过A作CD的平行线交BC于H,那么AH=CG.而后证AG2=DG·AH=DG·CG.49.提示:因为BC=BA,所以∠A=〔∠C=〕∠D;又∠CED=∠DBF〔BF是AB的延伸线〕,所以它们的补角∠DEA=∠ABD.进而四边形ABDE是平行四边形.50.提示:连结DE,那么∠BDE=∠1=∠2=∠FED.所以EF//BC.51.提示:连结BC,那么∠ACB=90°=∠FCB.因为CE⊥BE,所以∠F=∠ECB.因为EC切半圆于C,所以∠ECB=∠A,所以∠A=∠F,所以AB=BF.52.提示:连结AC,BC并延伸BC交AP延伸线于点N.第一所以CM=MD.。
鲁教版九年级下册数学第五章 圆 切线长定理

5.7切线长定理
第五章圆
提示:点击 进入习题
1C 2C 3D 4C
5A
答案显示
6C 7C
8 5 3 cm
提示:点击 进入习题
9C 10 见习题 11 见习题 12 见习题
13 见习题 14 见习题 15 见习题 16 见习题 17 见习题
答案显示
1.下列说法正确的是( C ) A.过任意一点总可以作圆的两条切线 B.圆的切线长就是圆的切线的长度 C.过圆外一点所画的圆的两条切线的切线长相等 D.过圆外一点所画的圆的切线的切线长一定大于圆的 半径
根据勾股定理得 PA=2 3.∵MA,MC 为⊙O 的两条切线,
∴MA=MC.又 NB,NC 为⊙O 的两条切线,∴NC=NB. ∴△PMN 的周长=PM+PN+MN=PM+PN+MC+NC
=PM+PN+MA+NB=PA+PB=2PA=4 3.
【答案】C
7.【2020·永州】如图,已知PA,PB是⊙O的两条切线, A,B为切点,线段OP交⊙O于点M.给出下列四种说法:
A.DC=DT B.AD= 2DT
C.BD=BO D.2OC=5AC
【点拨】如图,连接OD. ∵OT是半径,OT⊥AB,∴DT是⊙O的切线. ∵DC是⊙O的切线,∴DC=DT,故选项A正确. ∵OA=OB,∠AOB=90°,∴∠A=∠B=45°.
∵DC 是切线,∴CD⊥OC.∴∠ACD=90°. ∴∠A=∠ADC=45°.∴AC=CD=DT.
解:△OBC 是直角三角形. 理由:∵AB,BC,CD 分别与⊙O 相切于点 E,F,G, ∴∠OEB=∠OFB=∠OFC=∠OGC=90°,BE=BF, CF=CG.∵OE=OF=OG,△ OBE≌△OBF,
人教版-数学-九年级上册-新版数学九上 切线长定理 配套练习

第5题切线长定理配套练习 姓名一、选择题:1.如图l ,已知PA ,PB 是⊙O 的切线,A 、B 为切点,AC 是 ⊙O 的直径,∠P=40°,则∠BAC 度数是( )A .70°B .40°C .50°D .20°2.已知圆的半径为6,圆心到圆外一点的距离为10,则该点到圆的切线长为( )A .7B . 8C .9D .103.下列命题中,是真命题的是( ) A .三角形的内心是三角形三条高的交点B .三角形的内心是三角形三条边垂直平分线的交点C .三角形的内心到三角形三边的距离相等D .三角形的内心是三角形各个顶点的距离相等4.如图,△ABC 的内切圆⊙O 与BC 、CA 、AB 分别 相切于点D 、E 、F ,且AB=3cm ,BC=4cm ,CA=5cm , 求AF 、BD 、CE 的长分别为( )A 、1,3,4B 、1,2,3C 、2,3,二、填空题:5.如图,PA 、PB 切⊙O 于A 、B ,∠P=60°,OP=4,则⊙O 的半径=_________.6.如图,已知圆外切等腰梯形ABCD 的中位线EF=15cm ,那么等腰梯形ABCD 的周长=___________.7.如图,PA 切⊙O 于A ,PB 切⊙O 于B ,∠APB=90°,OP=4,则⊙O 的半径=_________.8.如图,△ABC 中,∠ABC=50°,∠ACB=80°,点O 是 △ABC 的内心,则∠BOC 的度数为 。
A第1题APO .B第6题第7题FEDBC三、解答题:9.如图,⊙O是△ABC的内切圆,与AB、BC、CA分别切于点D、E、F,∠DOE=120°,∠EOF=150°,求△ABC的三个内角的度数.的度数.11.△ABC的内切圆⊙O与AC、AB、BC分别相切于点D、E、F,且AB=5厘米,BC=9厘米,AC=6厘米,求AE、BF和CD的长.12.如图,△ABC中,∠C =90º ,它的内切圆O分别与边AB、BC、CA相切于点D、E、F,且BD=12,AD=8,求⊙O的半径r.。
2024-2025学年初中数学九年级上册(人教版)同步练习第06讲切线长定理与弦切角定理(原卷版)
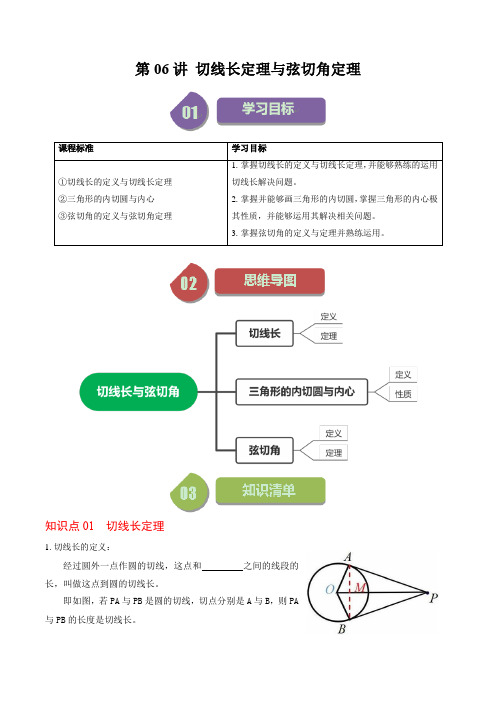
第06讲切线长定理与弦切角定理课程标准学习目标①切线长的定义与切线长定理②三角形的内切圆与内心③弦切角的定义与弦切角定理1.掌握切线长的定义与切线长定理,并能够熟练的运用切线长解决问题。
2.掌握并能够画三角形的内切圆,掌握三角形的内心极其性质,并能够运用其解决相关问题。
3.掌握弦切角的定义与定理并熟练运用。
知识点01 切线长定理1.切线长的定义:经过圆外一点作圆的切线,这点和之间的线段的长,叫做这点到圆的切线长。
即如图,若PA与PB是圆的切线,切点分别是A与B,则PA 与PB的长度是切线长。
2.切线长定理:从圆外一点作圆的切线,可以作条,它们的长度。
圆心和这一点的连线两条切线的夹角。
即P A PB,∠APO∠BPO。
推广:有切线长定理的结论可得:①△APO△BPO⇒∠AOP∠B OP⇒AM⌒AM⌒⇒AB OP。
题型考点:①切线长定理的应用。
【即学即练1】1.如图,⊙O与△ABC的边AB、AC、BC分别相切于点D、E、F,如果AB=4,AC=5,AD=1,那么BC的长为.【即学即练2】2.如图,△ABC中,∠A=60°,BC=6,它的周长为16.若⊙O与BC,AC,AB三边分别切于E,F,D 点,则DF的长为()A.2B.3C.4D.6【即学即练3】3.如图,P为⊙O外一点,P A、PB分别切⊙O于A、B,CD切⊙O于点E,分别交P A、PB于点C、D,若P A=5,则△PCD的周长为()A.5B.7C.8D.104.如图所示,P是⊙O外一点,P A,PB分别和⊙O切于A,B两点,C是上任意一点,过C作⊙O的切线分别交P A,PB于D,E.若△PDE的周长为12,则P A的长为()A.12B.6C.8D.4知识点02 三角形的内切圆与内心1.内切圆的定义:如图:与三角形各边都的圆叫三角形的。
三角形叫做圆的。
2.内心:三角形的的圆心叫做三角形的内心,三角形的内心就是三角形三个内角的交点。
所以圆心到三角形三边的距离相等。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
九年级切线长定理练习
题
This model paper was revised by LINDA on December 15, 2012.
九年级切线长定理练习题
一、选择题
1.下列说法中,不正确的是 ( ) A.三角形的内心是三角形三条内角平分线的交点
B.锐角三角形、直角三角形、钝角三角形的内心都在三角形内部
C.垂直于半径的直线是圆的切线
D.三角形的内心到三角形的三边的距离相等
2.给出下列说法:
①任意一个三角形一定有一个外接圆,并且只有一个外接圆;
②任意一个圆一定有一个内接三角形,并且只有一个内接三角形;
③任意一个三角形一定有一个内切圆,并且只有一个内切圆;
④任意一个圆一定有一个外切三角形,并且只有一个外切三角形.
其中正确的有 ( )
A.1个 B.2个 C.3个 D.4个3.一个直角三角形的斜边长为8,内切圆半径为1,则这个三角形的周长等于
( )
A.21 B.20 C.19 D.18
4. 如图,PA、PB分别切⊙O于点A、B,AC是⊙O的直径,连结AB、BC、OP,
则与∠PAB相等的角(不包括∠PAB本身)有 ( ) A.1个 B.2个C.3个 D.4个4题图5题图 6题图5.如图,已知△ABC的内切圆⊙O与各边相切于点D、E、F,则点O是△DEF的 ( )
A.三条中线的交点 B.三条高的交点
C.三条角平分线的交点 D.三条边的垂直平分线的交点
6.一个直角三角形的斜边长为8,内切圆半径为1,则这个三角形的周长等于
( )
A.21 B.20 C.19 D.18
二、填空题
P
B
A
O
6.如图,⊙I 是△ABC 的内切圆,切点分别为点D 、E 、F ,若∠DEF=52o , 则∠A 的度为________.
6题图 7题图 8题图
7.如图,一圆内切于四边形ABCD ,且AB=16,CD=10,则四边形ABCD 的周长为________.
8.如图,已知⊙O 是△ABC 的内切圆,∠BAC=50o ,则∠BOC 为____________度.
三、解答题
9. 如图,AE 、AD 、BC 分别切⊙O 于点E 、D 、F ,若AD=20,求△ABC 的周长.
10. 如图,PA 、PB 是⊙O 的两条切线,切点分别为点
A 、
B ,若
直径AC= 12,∠P=60o
,求弦AB 的长.
11. 如图,PA 、PB 是⊙O 的切线,A 、B 为切点,∠OAB =
30°.
(1)求∠APB 的度数;
(2)当OA =3时,求AP 的长.
12.已知:如图,⊙O 内切于△ABC ,∠BOC =105°,∠ACB =90°,AB =20cm .求BC 、AC 的
长.
13.已知:如图,△ABC 三边BC =a ,CA =b ,AB =c ,
它的内
切圆O 的半径长为r .求△ABC 的面积S .
14. 如图,在△ABC 中,已知∠ABC=90o ,在AB 上取一点E ,以BE 为直径的⊙O 恰与AC 相切于点D ,若AE=2 cm ,
AD=4 cm .
(1)求⊙O 的直径BE 的长;
(2)计算△ABC 的面积.
15.已知:如图,⊙O 是Rt △ABC 的内切圆,∠C =90°.
(1)若AC =12cm ,BC =9cm ,求⊙O 的半径r ;
(2)若AC =b ,BC =a ,AB =c ,求⊙O 的半径r .
四、体验中考
16.(2011年安徽)△ABC 中,AB =AC ,∠A 为锐角,CD 为AB 边上的高,I 为△ACD 的内切圆圆心,则∠AIB 的度数是( )
A .120°
B .125°
C .135°
D .150°
17.(2011年绵阳)一个钢管放在V 形架内,右图是其截面图,O 为钢管的圆心.如果钢
管的半径为25 cm ,∠MPN = 60,则OP =( )
A .50 cm
B .253cm
C .
3
3
50cm D .503cm 18. (2011年甘肃定西)如图,在△ABC 中,5cm AB AC ==,cos B 3
5
=.如果⊙O 的半径
,且经过点B 、C ,那么线段AO = cm .
17题图 18题图 19题图
19. (2011年湖南怀化)如图,PA 、PB 分别切⊙O 于点A 、B ,点E 是⊙O 上一点,且 60=∠AEB ,则=∠P __ ___度.。
