多边形的内角和练习题
多边形的内角和与外角和练习题

解
设一个外角为x°,则内角为(x+36)° 因为多边形的内角与相邻的外角互补;
所以 x+x+36=180
解得
x=72
360÷72=5
答 这个多边形的五边形.
10.∠A+∠B+∠C+∠D+∠E+∠F+∠G=540°.
A
G
B
E
D
O
F C
11. 如图在 ABC中,D是ACB 与 ABC的角平分 线的交点,BD的延长线交AC于E,且 EDC 50, 则 A的度数为多少?
12.如图,在六边形ABCDEF中,AF // CD, AB// DE, 且 A 120,∠B 80 ,则 ∠C 的度数是多少,D 的度 数是多少?
13.如图,在ABC中,BD是ABC的角平分线,DE//BC, 交AB于E,∠A= 45 , ∠BDC= 60 ,求ΔBDE各内
角的度数.
A
E
DBCຫໍສະໝຸດ 14.如图,已知DC是△ABC中∠ACB的外角平分线, 说明为什么∠BAC>∠B.
(第 13 题)
360°
C
7.当一个多边形的边数增加时,其外角和 ( )
A 8.某.增学加生在计算B四.减个少多边形C的.内不角变和时,得D到.不下能列确四定
个答案,其中错误的是( C )
A.180° D.1080°
B.540°
C.1900°
9. 一个正多边形的一个内角比相邻外角大36°,求这 个正多边形的边数.
多边形内角和与外 角和的练习题
复习
n边形内角和公式、外角和公式?
1. n边形的内角和等于(n-2)·180. 2. n边形的外角和都等于360°.
1、一个多边形的每个外角都是 30,这个多边形 2、的正边十数二是边_形__的1_2。每个内角的度数是_1_5_.0
多边形的内角和 小学数学 课后练习
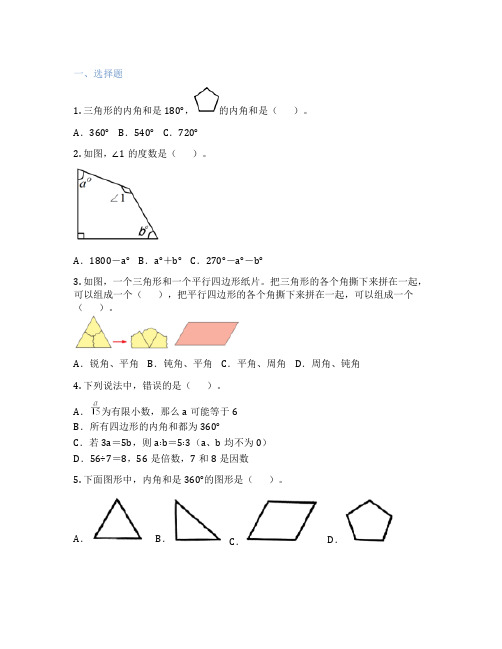
一、选择题1. 三角形的内角和是180°,的内角和是()。
A.360°B.540°C.720°2. 如图,∠1的度数是()。
A.1800-a°B.a°+b°C.270°-a°-b°3. 如图,一个三角形和一个平行四边形纸片。
把三角形的各个角撕下来拼在一起,可以组成一个(),把平行四边形的各个角撕下来拼在一起,可以组成一个()。
A.锐角、平角B.钝角、平角C.平角、周角D.周角、钝角4. 下列说法中,错误的是()。
A.为有限小数,那么a可能等于6B.所有四边形的内角和都为360°C.若3a=5b,则a∶b=5∶3(a、b均不为0)D.56÷7=8,56是倍数,7和8是因数5. 下面图形中,内角和是360°的图形是()。
A.B.C.D.二、填空题6. 如图所示,四边形的内角和是( )。
7. 探究多边形的内角和与它的边数的关系,一个八边形的内角和是______°。
多边形……边数3 4 5 6 ……内角和180°360°540°720°……8. 在一个直角三角形中,有一个锐角是30°,另一个锐角是( )。
在一个等腰三角形中,有一条边,长是5厘米,另一条边,长是2厘米,围成这个等腰三角形至少需要( )厘米长的绳子。
(接头处忽略不计)9. 三角形内角和是( )°,下面梯形的内角和是( )°。
10. 图形探索:根据情境完成填空。
情境描述:一天,六(1)班的牛牛同学在作业本上画了一个任意的四边形,接着他又分别以四边形的四个顶点为圆心画了4个半径是3cm的扇形,再给这4个扇形涂上阴影,如图,画完后,他好奇地发现一个数学问题:阴影部分的面积是多少呢?经过他深入探索,他突然兴奋地嚷道:“太简单了!用四年级学过的多边形的内角和知识不就解决了吗。
八年级数学多边形及其内角和(含解析答案)

多边形和内角和练习题温故而知新:1.多边形多边形的内角和:n边形内角和等于_(n-2)·180°__多边形的外角和:任意多边形外角和等于__360°_多边形的对角线:凸n边形共有_1(3)2n n-_条对角线。
2.平面镶嵌定义:用一些不重叠摆放的多边形把平面的一部分完全覆盖,通常把这类问题叫做用多边形覆盖平面(或平面镶嵌)问题.说明:正三角形、正方形和正六边形可以镶嵌平面图案,正五边形不能镶嵌平面图案.多边形的对角线例 1 今年暑假,佳一学校安排全校师生的假期社会实践活动,将每班分成三个组,每组派1名教师作为指导教师,为了加强同学间的联系,学校要求该班每两人之间(包括指导教师)每周至少通一次电话,现知该校七(1)班共有50名学生,那么该班师生之间每周至少要通几次电话?为了解决这一问题,小明把该班师生人数n与每周至少通话次数s之间的关系用下列模型表示,如图。
解析:师生53人看作是53边形的53个顶点,n边形的对角线条数公式为:1(3)2n n-。
答案:解:将七(1)班师生53人看作是53边形的53个顶点,由多边形对角线条数公式1(3)2n n-得1⨯⨯-=53(533)13252所以1325+53=1378次。
答:该班每周师生之间至少要通1378次电话小结:(1)建立数学模型是解决实际问题的基本方法;(2)n边形的对角线的条数公式是1(3)n n-2多边形的内角和与外角和例2 已知一个多边形的外角和等于内角和的1/3,求这个多边形的边数。
解析:多边形的外角和为360°,根据多边形的内角和及外角和列方程.答案:解:设这个多边形的边数为n,根据题意,得1n-⨯=(2)1803603解得 n=8答:这个多边形的边数是8.小结:利用方程求解是解决此类问题的一般方法。
例3 如图,小陈从O点出发,前进5米后向右转20°,再前进5米后又向右转20°,……这样一直走下去,他第一次回到出发点O时一共走了()A.60米B.100米C.90米D.120米解析:根据多边形的外角和求出这个多边形的边数。
多边形的内角和练习题

多边形的内角和,外角和1.多边形2.正多边形3.对角线:从多边形的一个顶点可以引条对角线,把多边形分成个三角形4.多边形的内角和:5.多边形的外角和:1、多边形的每个外角等于与它相邻的内角,则它是几边形?每个外角是多少度?2、多边形的内角和等于它的外角和的3倍,它是几边形?3、一个多边形的内角和是它的外角和的2倍还多180,求多边形的边数4、内角和等于外角和5倍的多边形是几边形?5、多边形的内角和与外角和的比为7:2,求边数6、多边形的每个内角都相等,且每个内角比相邻的外角大60度,则它是几边形?7、是否存在一个多边形,它的每个外角等于相邻内角的1/5?8.一个多边形的内角和是外角和的一半,则它是1.已知三角形ABC的三个内角满足关系∠B+∠C=3∠A,则此三角形().A.一定有一个内角为45°B.一定有一个内角为60°C.一定是直角三角形D.一定是钝角三角形2.如果一个三角形的三个外角之比为2:3:4,则与之对应的三个内角度数之比为().A.4:3:2 B.3:2:4C.5:3:1 D.3:1:53.如图7-6,下列说法中错误的是().A.∠1不是三角形ABC的外角B.∠B<∠1+∠2C.∠ACD是三角形ABC的外角D.∠ACD>∠A+∠B图7-64.下列判断中正确的是().A.四边形的外角和大于内角和B.若多边形边数从3增加到n(n为大于3的自然数),它们外角和的度数不变C.一个多边形的内角中,锐角的个数可以任意多D.一个多边形的内角和为1880°5.一个五边形有三个角是直角,另两个角都等于n,则n的值为().A.108°B.125°C.135°D.150°6.多边形每一个内角都等于150°,则从此多边形一个顶点发出的对角线有( ).A .7条B .8条C .9条D .10条7.现有长度分别为2cm 、4cm 、6cm 、8cm 的木棒,从中任取三根,能组成三角形的个数为( ).A . 1B . 2C . 3D . 48.(n+1)边形的内角和比n 边形的内角和大( )A 、180°B 、360°C 、n ·180°D 、n ·360°9.如图7-9,三角形ABC 中,D 为BC 上的一点,且S △ABD =S △ADC ,则AD 为( ).A .高B .角平分线C .中线D .不能确定10.如图7-10,已知∠1=∠2,则AH 必为三角形ABC 的( ).A .角平分线B .中线C .一角的平分线D .角平分线所在射线11.已知,如图7-1,∠ACD =130°,∠A =∠B ,那么∠A 的度数是 .12.如图7-2,根据图形填空:(1)AD 是△ABC 中∠BAC 的角平分线,则∠ =∠ =图7-1 图7-2 图7-3图7-9 图7-10 图7-11∠.(2)AE是△ABC中线,则==.(3)AF是△ABC的高,则∠=∠=90°.13.如图7-3所示,图中有个三角形,个直角三角形.14.一个多边形的每个外角都为30°,则这个多边形的边数为;一个多边形的每个内角都为135°,则这个多边形的边数为.。
多边形内角和练习题

多边形内角和练习题一、选择题1. 一个多边形的内角和为540°,它是几边形?A. 四边形B. 五边形C. 六边形D.七边形2. 一个六边形的内角和是多少度?A. 360°B. 720°C. 900°D. 1080°3. 下列哪个多边形的内角和等于其外角和?A. 三角形B. 四边形C. 五边形D. 六边形4. 一个多边形的内角和是1440°,它是几边形?A. 八边形B. 九边形C. 十边形D. 十一边形二、填空题1. 一个______边形的内角和是______°。
2. 若一个多边形的内角和为1800°,则它是______边形。
3. 一个凸多边形的内角和是360°,那么这个多边形是______。
4. 已知一个多边形的内角和为n×180°360°,那么这个多边形是______边形。
三、解答题1. 计算一个十边形的内角和。
2. 已知一个多边形的内角和是840°,求这个多边形的边数。
3. 一个多边形的内角和是1200°,求它的外角和。
4. 若一个多边形的内角和是1350°,求它的每个内角的平均度数。
5. 一个多边形的内角和是1440°,求它的每个外角的平均度数。
6. 已知一个多边形的内角和是1800°,求它的外角和。
7. 一个多边形的内角和是360°,判断这个多边形是什么形状。
四、应用题1. 在一个正多边形的每个内角都是135°,求这个正多边形的边数。
2. 一个正多边形的每个外角都是30°,求这个正多边形的内角和。
3. 一个正多边形的内角和是1080°,求这个正多边形的边长。
4. 在一个正多边形中,每个内角比每个外角大60°,求这个正多边形的边数。
5. 一个正多边形的内角和是它的外角和的两倍,求这个正多边形的边数。
多边形的内角和计算练习题

多边形的内角和计算练习题一、选择题1、一个多边形的内角和是 720°,则这个多边形是()A 四边形B 五边形C 六边形D 七边形2、如果一个多边形的内角和是外角和的 3 倍,那么这个多边形的边数是()A 8B 9C 10D 113、下列角度中,不能成为多边形内角和的是()A 600°B 720°C 900°D 1080°4、一个多边形的内角和比它的外角和的 2 倍还大 180°,这个多边形的边数为()A 7B 8C 9D 105、若一个多边形的每一个外角都等于 40°,则这个多边形的边数是()A 7B 8C 9D 10二、填空题1、一个多边形的内角和是 1800°,则它是_____边形。
2、若一个多边形的每一个内角都等于 150°,则这个多边形是_____边形。
3、一个多边形的每一个外角都是36°,则这个多边形是_____边形。
4、若一个多边形的内角和与外角和的总和为 1800°,则这个多边形是_____边形。
5、一个多边形的边数增加 1,则内角和增加_____度。
三、解答题1、已知一个多边形的内角和与外角和的差为 1080°,求这个多边形的边数。
2、若一个多边形的内角和是外角和的5 倍,求这个多边形的边数。
3、一个多边形的每一个内角都比相邻的外角大 36°,求这个多边形的边数。
4、一个多边形除一个内角外,其余内角之和是 2570°,求这个内角的度数以及多边形的边数。
5、小明在计算一个多边形的内角和时,少算了一个内角的度数,结果得出内角和为 600°,你能帮他算出这个多边形的内角和以及少算的那个内角的度数吗?6、如图,在四边形 ABCD 中,∠A = 140°,∠D = 80°。
(1)∠B +∠C =?(2)若四边形 ABCD 的内角和为 360°,求∠B 和∠C 的度数分别是多少?7、一个多边形截去一个角后,形成的新多边形的内角和为2520°,求原多边形的边数。
多边形及其内角和练习题(含答案)

多边形及其内角和练习题(含答案)1.如果四边形ABCD中∠A+∠C+∠D=280°,那么∠B的角度是多少?选项:A.80° B.90° C.170° D.20°2.如果一个多边形的内角和为1080°,那么这个多边形有多少条边?选项:A.9 B.8 C.7 D.63.内角和等于外角和的两倍的多边形是什么形状?选项:A.五边形B.六边形C.七边形D.八边形4.六边形的内角和是多少度?5.正十边形的每个内角的度数是多少?每个外角的度数是多少?6.图中有多少种不同的四边形?7.四边形的四个内角可以都是锐角吗?可以都是钝角吗?可以都是直角吗?为什么?8.求下列图形中x的值:9.在四边形ABCD中,已知∠A=∠C=90°,BE平分∠ABC,DF平分∠ADC。
BE与DF有什么位置关系?为什么?10.有10个城市进行篮球比赛,每个城市派出3个代表队参加比赛,规定同一城市间的代表队不进行比赛,其他代表队都要比赛一场。
按照这个规定,所有代表队需要打多少场比赛?11.在一个五边形的每个顶点处以1为半径画圆,求圆与五边形重合的面积。
12.(1) 已知一个多边形的内角和为540°,那么这个多边形是什么形状?选项:A.三角形 B.四边形 C.五边形 D.六边形 (2) 五边形的内角和是多少度?13.一个多边形的每个顶点处取一个外角,这些外角中最多有几个钝角?选项:A.1个 B.2个 C.3个 D.4个14.(1) 四边形有几条对角线?五边形有几条对角线?六边形有几条对角线?猜想并探索:n边形有几条对角线?(2) 一个n边形的边数增加1,对角线增加多少条?15.如果一个多边形的边数增加1,那么这个多边形的内角和会增加多少度?如果将n边形的边数增加1倍,那么它的内角和会增加多少度?16.壁虎想捕捉一只害虫,它在油罐下底边A处,害虫在油罐上边缘B处。
(完整版)《正多边形的内角和》专项练习题

(完整版)《正多边形的内角和》专项练习题题目一已知一个正五边形的每个内角为120度,请计算这个正五边形的内角和。
解答一正多边形的内角和公式为:内角和 = (n - 2) × 180度其中,n表示正多边形的边数。
根据题目已知条件,正五边形的边数为5,代入公式可知:内角和 = (5 - 2) × 180度 = 3 × 180度 = 540度所以,这个正五边形的内角和为540度。
题目二已知一个正六边形的某个内角为100度,请计算这个正六边形的每个内角和正六边形的内角和。
解答二正多边形的每个内角的计算公式为:每个内角 = 内角和 / 正多边形的边数正多边形的内角和公式为:内角和 = (n - 2) × 180度根据题目已知条件,正六边形的某个内角为100度,代入公式可求得每个内角和正六边形的内角和:每个内角 = 100度 / 6 = 16.67度内角和 = (6 - 2) × 180度 = 4 × 180度 = 720度所以,这个正六边形的每个内角为16.67度,内角和为720度。
题目三已知一个正七边形的每个内角为140度,请计算这个正七边形的边数。
解答三正多边形的内角和公式为:内角和 = (n - 2) × 180度根据题目已知条件,正七边形的每个内角为140度,代入公式可求得边数:140度 = (n - 2) × 180度解方程可得:n - 2 = 140度 / 180度n - 2 = 14/18n - 2 = 7/9n ≈ 2 + 7/9n ≈ 2.78所以,这个正七边形的边数约为2.78,即大约为3个边。
注意:由于正多边形的边数必须为整数,所以这个结果不符合实际情况,可能存在题目或计算错误。
以上是关于正多边形内角和的专项练题的完整解答。
参考资料:。
多边形的内角和与外角和练习题

多边形的内角和与外角和一、填空题1。
若一凸多边形的内角和等于它的外角和,则它的边数是______。
2。
五边形的内角和等于______度。
3。
十边形的对角线有_____条。
4.正十五边形的每一个内角等于_______度。
5.内角和是1620°的多边形的边数是________.6。
用正n边形拼地板,则n的值可能是_______。
二、选择题7.一个多边形的内角和是720°,则这个多边形是( )A。
四边形 B.五边形 C。
六边形 D.七边形8。
一个多边形的内角和比它的外角和的3倍少180°,这个多边形的边数是( )A。
5 B.6 C.7 D.89。
若正n边形的一个外角为60°,则n的值是( )A。
4 B。
5 C。
6 D。
810。
下列角度中,不能成为多边形内角和的是()A.600°B.720°C.900° D。
1080°11。
若一个多边形的内角和与外角和之和是1800°,则此多边形是()A.八边形 B。
十边形 C。
十二边形 D.十四边形12。
用下列两种正多边形能拼地板的是( )A.正三角形和正八边形B.正方形和正八边形 C。
正六边形和正八边形 D。
正十边形和正八边形三、解答题13。
一个多边形的每一个外角都等于45°,求这个多边形的内角和。
14.已知一个多边形的内角和是1440°,求这个多边形的对角线的条数。
15.一个多边形,除一个内角外,其余各内角之和等于1000°,求这个内角及多边形的边数。
16、已知一个多边形的内角和是外角和的6倍,求这个多边形的边数17、一个正多边形的一个内角的度数比相邻外角的6倍还多12°,求这个正多边形的内角和.18.一个多边形中,每个内角都相等,并且每个外角等于它的相邻内角的23,求这个多边形的边数及内角和。
19。
若两个多边形的边数之比是1:2,内角和度数之比为1:3,求这两个多边形的边数。
多边形的内角和与外角和综合练习题

多边形的内角和与外角和综合练习题多边形是几何学中的基础概念,拥有不同边数的多边形呈现出各种形状。
在研究多边形的性质时,我们常常关注多边形的内角和与外角和。
本文将通过综合练习题来巩固和加深对多边形内、外角和的理解。
练习题1:已知凸多边形的一个内角为75°,其余内角的度数依次递增,最大的内角是其中的第几个内角?解析:凸多边形的每个内角的度数总和等于(边数 - 2) × 180°。
由于题目没有给出具体的边数,我们无法计算出每个内角的具体度数,但可以根据给定信息确定出最大的内角所在的位置。
由于内角度数递增且凸多边形的每个内角都小于180°,最大的内角一定是最后一个内角。
练习题2:已知凸多边形的内角和为1080°,该多边形的边数是多少?解析:根据凸多边形的每个内角的度数总和等于(边数 - 2) × 180°,我们可以得到方程 (边数 - 2) × 180° = 1080°。
则边数 - 2 = 6,边数 = 8。
所以该多边形的边数为8。
练习题3:已知一个内角和为1620°的凸多边形,求它的边数。
解析:同样地,根据凸多边形的每个内角的度数总和等于(边数 - 2) × 180°,我们可以得到方程 (边数 - 2) × 180° = 1620°。
则边数 - 2 = 9,边数 = 11。
所以该多边形的边数为11。
练习题4:一个凸多边形的一个内角的度数是其他内角度数的3倍,且所有内角度数的和为1080°,求这个多边形的边数。
解析:我们设这个内角的度数为3x,则其他内角的度数分别为x。
根据凸多边形的每个内角的度数总和等于(边数 - 2) × 180°,我们可以得到方程 3x + x(边数 - 1) = 1080°。
化简得到 x(边数 + 2) = 1080°。
多边形及其内角和练习题含答案

9-2多边形的内角和及外角和练习一一.填空题1.若一凸多边形的内角和等于它的外角和,则它的边数是______ •2.五边形的内角和等于______ •3.十边形的对角线有_________ 条.4・正十五边形的每一个内角等于_______ . 5.内角和是1620°的多边形的边数是_・6.用正n边形拼地板,则n的值可能是______ ・二、选择题7.一个多边形的内角和是720°,则这个多边形是()A.四边形B.五边形C.六边形D.七边形8•—个多边形的内角和比它的外角和的3倍少180。
,这个多边形的边数是() A.5 B.6 C.7 9.若正n 边形的一个外() A.4 B.5 C.6 10.下列角度中,不能成为多边形内角和的是(A. 600°B. 720°C. 900°D.8角为60 °,则n 的值是D.8)D. 1080°11.若一个多边形的内角和及外角和之和是1800。
,则此多边形是()A.八边形B.十边形C・十二边形 D.十四边形12.用下列两种正多边形能拼地板的是()A.正三角形和正八边形B.正方形和正八边形C.正六边形和正八边形D.正十边形和正八边形三、解答题13.一个多边形的每一个外角都等于45。
,求这个多边形的内角和.14.己知一个多边形的内角和是1440。
,求这个多边形的对角线的条数.15•—个多边形,除一个内角外,其余各内角之和等于1000°,求这个内角及多边形的边数・11・3多边形及其内角和16•—个多边形中,每个内角都相等,并且每个外角等于它的相邻内角的2/3,求这个多边形的边数及内角和.17.如图,一个六边形的木个内角都是120° , AB二1, BC=CD=3, DE=2,求该六边形的周长.19.若两个多边形的边数之比是1:2,内角和度数之比为1:3,求这两个多边形的边数.20.如果多边形恰有四个内角是钝角,那么多边形的边数共有几种可能?其中最多是几边形?最少是几边形?21.下列地板是由正方形、正六边形、正十二边形拼成的,试说明由这三种正多边形能拼地板的理由・22•已知四边形ABCD 中,ZA:ZB=7:5, ZA-ZC=ZB, ZC=ZD-40° , 求各内角的度数.23.一个多边形除了一个内角等于a,其余角的和等于2750°,求这个多边形的边数及a •21.下列地板是由正方形、正六边形、正十二边形拼成的,试说明由这三种正多边形能拼地板的理由.22•已知四边形ABCD中,ZA: ZB=7:5, ZA-ZC=ZB, ZC=ZD-40°求各内角的度数.23. 一个多边形除了一个内角等于a ,其余角的和等于2750°,求这个多边形的边数及a.24.一个广场地面的一部分如图所示,地面的中央是一块正六边形的地砖,周围用正三角形和正方形的大理石地砖拼成,从里往外共12层(不包括中央的正六边形地砖),每一层的外界都围成一个多边形•若中央正六边形地砖的边长是0. 5米,则第12层的外边界所围成的多边形的周长是多少1.四边形ABCD中,如果ZA+ZC+ZD=280° ,则ZB的度数是()A. 80°B. 90°C. 170°D. 20°2.一个多边形的内角和等于1080° ,这个多边形的边数是()A. 9B. 8C. 7D. 63.内角和等于外角和2倍的多边形是()A.五边形B.六边形C.七边形D.八边形4.六边形的内角和等于 _______ .5.正十边形的每一个内角的度数等于_______ ,每一个外角的度数等于 ________ .6.如图,你能数出多少个不同的四边形?7.四边形的四个内角可以都是锐角吗?可以都是钝角吗?可以都是宜角吗?&求下列图形中x的值:综合创新作业9.(综合题)已知:如图,在四边形ABCD中,ZA=ZC=90° , BE平分ZABC, DF平分Z ADC. BE及DF有怎样的位置关系?为什么?多边形及其内角和练习题(含答案)10.(应用题)有10个城市进行篮球比赛,每个城市均派3个代表队参加比赛,规定同一城市间代表队不进行比赛,其他代表队都要比赛一场,问按此规定,所有代表队要打多少场比赛?11.(创新题)如图,以五边形的每个顶点为圆心,以1为半径画圆,求圆及五边形重合的面积.12.(1)(2005年,南通)己知一个多边形的内角和为540。
多边形的内角和

08
探究4
n边形内角和公式的应用
B
A
C
D
G
F
E
n边形内角和=(n-2) ·180°
例1:已知四边形ABCD,∠A+∠C=180°,求∠B+∠D=?
A
B
C
D
点评:四边形的一组对角互补,另一组对角也互补。
解:四边形的内角和为:
(4-2) ×180 =360 °
∴ ∠B+∠D= 360 °- (A+∠C)=180°
分成三角形的个数
计算规律
三角形
四边形
五边形
六边形
七边形
n边形
…
…
…
…
…
…
3
4
5
6
7
n
0
n-3
1
2
3
4
1
2
3
4
5
n-2
(n-2) ·180°
5 ×180°
4 ×180°
3 ×180°
2 ×180°
1 ×180°
总结:n边形内角和公式
B
A
C
D
G
F
E
n边形内角和=(n-2) ·180°
01
把一个五边形分成几个三角形,还有其他的分法吗?
02
A
03
B
04
C
05
D
06
E
07
F
08
180° × 4 – 180° = 540°
探究2
01
E
02
A
03
B
04
C
05
D
06
O
多边形的内角和 小学数学 练习题

一、选择题1. 小英画了一个多边形,这个多边形的内角和不可能是()。
A.B.C.2. 如图,一个等腰直角三角形的纸片沿虚线剪去涂色的部分。
剩下图形的内角和是()。
A.135°B.180°C.270°D.360°3. 下列说法错误的是()。
A.四边形的内角和是360°B.2022年2月有29天C.真分数的倒数一定大于14. 下列说法中正确的是()。
①199×99+199=(99+1)×199。
②在一道乘法算式中,其中一个乘数乘20,另一个乘数也乘20,积不变。
③梯形的内角和与平行四边形的内角和相等。
④一个三角形中最小的内角是50°,那么这是一个锐角三角形。
A.①②B.①③C.②④D.①④5. 根据三角形的内角和,我们可以推出梯形的内角和是()。
A.180°B.360°C.540°二、填空题6. 一个九边形的内角和是( )°。
一个n边形的内角和是( )°。
7. 探究找规律题,观察下面的图形并填表。
……图形三角形四边形五边形六边形……n边形边数 3 4 5 6 …n分成三角形的个数 1 2 3 4 …( )内角和180°180°×2 180°×3 180°×4 ……( )8. 用一张正方形纸折一折,填一填。
内角和________°,________形内角和________°,________形内角和________°。
9. 下图∠1=69°,∠2=( )°。
10. 下面的每个小正方形的边长是1分米。
(1)上图( )轴对称图形。
(填“是”或“不是”)(2)图①向( )平移( )格可以与图②重合。
(3)图①的面积是( )平方分米。
(4)图①的内角和是( )度。
初二多边形及其内角和的练习题

初二多边形及其内角和的练习题多边形是初中数学中的重要概念,它是指由三条或者更多条线段组成的图形。
而多边形的内角和是指该多边形内所有角的度数之和。
在初二数学学习中,学生需要掌握多边形及其内角和的相关概念和计算方法。
下面就是一些关于初二多边形及其内角和的练习题,供同学们参考和练习。
练习题一:1.一个四边形的两个内角分别为90°和75°,其余两个内角的度数之和是多少?2.一个五边形的两个内角分别为120°和130°,其余三个内角的度数之和是多少?3.一个七边形的一个内角为135°,其余六个内角的度数之和是多少?练习题二:1.一个六边形的每个内角的度数分别是110°、120°、135°、100°、90°,求其内角和。
2.一个八边形的每个内角的度数都相等,求每个内角度数以及内角和。
3.一个五边形的内角和与一个四边形的内角和之比是2:3,求该五边形的最大内角的度数。
练习题三:1.一个六边形的内角和是新课标中一次函数中函数关系图形翻转180°的内角和,求这个内角和。
2.一个n边形的内角和是(n-2)×180°,n是一个整数且大于3,当n=15时,这个多边形的内角和是多少?3.一个六边形的两个顶角的度数之差为30°,这两个顶角的度数分别是多少?练习题四:1.一个五边形的一个内角与一个六边形的一个内角是对顶角,这两个内角的度数之比是2:3,求这个五边形内所有角的度数之和。
2.一个五边形内角和与一个六边形内角和之比是1:4,这个五边形的最小内角为60°,求这个五边形内所有角的度数之和。
3.一个六边形的内角和是一个七边形的一半,这个六边形的最大内角为120°,求这个六边形的所有内角的度数之和。
以上是关于初二多边形及其内角和的一些练习题。
通过做题可以帮助同学们巩固对多边形及其内角和的理解,并提高解决相关问题的能力。
多边形及其内角和(精选精练)(专项练习)(教师版) 2024-2025学年八年级数学上册基础知识专项

专题11.8多边形及其内角和(精选精练)(专项练习)一、单选题(本大题共10小题,每小题3分,共30分)1.(23-24六年级下·山东烟台·期中)过多边形一个顶点的所有对角线将这个多边形分成3个三角形,这个多边形是()A .五边形B .六边形C .七边形D .八边形2.(23-24八年级下·安徽阜阳·阶段练习)一个正多边形的内角和为1080︒.则这个正多边形的边数为()A .9B .8C .7D .63.(2024·福建福州·模拟预测)如图1是颐和园小长廊五角加膛窗,其轮廓是一个正五边形,如图2是它的示意图,它的一个外角α的度数为()A .70︒B .72︒C .60︒D .108︒4.(2020·辽宁葫芦岛·三模)如图,多边形ABCDEFG 中,108E F G ∠=∠=∠=︒,72C D ∠=∠=︒,则A B ∠∠+的值为()A .108︒B .72︒C .54︒D .36︒5.(2024·内蒙古赤峰·三模)如果一个正多边形的一个外角是45︒,则这个正多边形是正()边形A .六B .八C .十D .十二6.(2024·湖北荆门·模拟预测)小聪利用所学的数学知识,给同桌出了这样一道题:假如从点A 出发,沿直线走9米后向左转θ,接着沿直线前进9米后,再向左转θ,…,如此下去,当他第一次回到点A 时,发现自己一共走了72米,则θ的度数为()A.60︒B.75︒C.30︒D.45︒7.(2024·云南玉溪·三模)若一个正多边形的每一个外角都是36︒,则该正多边形的内角和的度数是().A.1440︒B.360︒C.1800︒D.2160︒∠=︒,则1∠的度数为8.(2024·河北石家庄·三模)如图,五边形ABCDE是正五边形,AF DG∥,若226()A.86︒B.64︒C.62︒D.52︒9.(23-24九年级下·河北邯郸·期中)综合实践课上,嘉嘉用八个大小相等的含45°角的直角三角板拼成了一个环状图案,如图1,若淇淇尝试用含60°角的直角三角板拼成类似的环状图案,如图2,除了图上3个还需要含60°角的直角三角板的数量为()A.3个B.6个C.9个D.12个10.(2024·河北沧州·二模)用“筝形”和“镖形”两种不同的瓷砖铺设成如图所示的地面,则“筝形”瓷砖中的∠的度数为()内角BCDA.120︒B.135︒C.144︒D.150︒二、填空题(本大题共8小题,每小题4分,共32分)11.(2024八年级下·全国·专题练习)一个八边形的内角和是.12.(23-24六年级下·山东济南·期中)若从n边形的一个顶点最多能引出2条对角线,则n是.13.(2024·湖北咸宁·一模)一个多边形的内角和为540︒,这个多边形的边数是.14.(2024·陕西宝鸡·模拟预测)一个正多边形的内角比外角大90︒,则这个多边形的内角和为.15.(23-24八年级上·辽宁营口·期中)如果把一个多边形剪去一个内角,剩余部分的内角和为1440︒,那么原多边形有条边.16.(19-20七年级下·江苏扬州·期末)如图,∠A+∠B+∠C+∠D+∠E+∠F+∠G=.17.(2024·陕西西安·模拟预测)一个正多边形的外角和与内角和的比为1:3,则这个多边形是正边形.18.(2024·云南昆明·二模)如图,一个正n边形被树叶遮掩了一部分,若直线a,b所夹锐角为36︒,则n的值是.三、解答题(本大题共6小题,共58分)19.(8分)(21-22八年级下·广西桂林·期中)列式计算:求图中x的值.20.(8分)(23-24八年级上·江西南昌·期末)如果多边形的每个内角都比与它相邻的外角的4倍多30︒.(1)这个多边形的内角和是多少度?(2)求这个多边形的对角线的总条数.21.(10分)(23-24八年级上·新疆昌吉·期中)如图,在五边形ABCDE 中,100120AE CD A B �靶=,,∥(1)若110D ∠=︒,请求E ∠的度数;(2)试求出C ∠及五边形外角和的度数.22.(10分)(23-24七年级下·湖南衡阳·阶段练习)如图,阅读佳佳与明明的对话,解决下列问题:(1)多边形内角和为什么不可能为2020︒?(2)明明求的是几边形的内角和?(3)错当成内角的那个外角为多少度?23.(10分)(2024·浙江杭州·一模)问题情境:在探索多边形的内角与外角关系的活动中,同学们经历了观察、猜想、实验、计算、推理、验证等过程,提出了问题,请解答.(1)若四边形的一个内角的度数是α.①求和它相邻的外角的度数(用含α的代数式表示);②求其他三个内角的和(用含α的代数式表示).n>,除了一个内角,其余内角的和为920︒,求n的值.(2)若一个n边形(3)深入探究:n>的一个外角与和它不相邻的(n)1-个内角的和之间满足的等量关系,说明理由.(3)探索n边形(3)24.(12分)(1)已知图①中的三角形ABC,分别作AB,BC,CA的延长线BD,CE,AF,测量∠CBD,∠ACE,∠BAF的度数,并计算∠CBD+∠ACE+∠BAF.由此你有什么发现?请利用所学知识解释说明;(2)类似地,已知图②中的四边形PQRS,分别作PQ,QR,RS,SP的延长线QG,RH,SM,PN,测量∠RQG,∠SRH,∠PSM,∠QPN的度数,并计算∠RQG+∠SRH+∠PSM+∠QPN.由此你又有什么发现?(3)综合(1)(2)的发现,你还能进一步得到什么猜想?参考答案:1.A【分析】本题考查了多边形的对角线数量问题,根据n 边形从一个顶点出发可引出()3n -条对角线,可组成()2n -个三角形,依此可求出n 的值,得到答案.【详解】解:设这个多边形是n 边形,由题意得:23n -=,解得:5n =,即这个多边形是五边形,故选:A .2.B【分析】本题多边形内角和公式,解题关键是理解并熟记多边形内角和公式.根据多边形内角和定理:可得方程()18021080x ︒⨯-=︒,再解方程即可.【详解】解:设多边形边数有x 条,由题意得:()18021080x ︒⨯-=︒解得:8x =故选B3.B【分析】本题主要考查多边形的内角和外角,熟练掌握正多边形的外角和为360︒是解题的关键.根据多边形的外角和为360︒即可作答.【详解】解:360572÷=︒.故选:B .4.B【分析】连接CD ,设AD 与BC 交于点O ,根据多边形的内角和公式即可求出∠E +∠F +∠G +∠EDC +∠GCD ,根据各角的关系即可求出∠ODC +∠OCD ,然后根据对顶角的相等和三角形的内角和定义即可求出结论.【详解】解:连接CD ,设AD 与BC 交于点O∵∠E +∠F +∠G +∠EDC +∠GCD=180°×(5-2)=540°,108E F G ∠=∠=∠=︒,72∠=∠=︒GCB EDA ,∴108°+108°+108°+72°+∠ODC +72°+∠OCD=540°∴∠ODC +∠OCD=72°∵∠AOB=∠COD∴∠A +∠B=180°-∠AOB=180°-∠COD=∠ODC +∠OCD=72°故选B .【点拨】此题考查的是多边形的内角和公式和对顶角的性质,掌握多边形的内角和公式和对顶角相等是解决此题的关键.5.B【分析】本题考查了正多边形的外角性质,根据正多边形的外角都相等以及外角和为360︒,列式36045︒÷︒进行计算,即可作答.【详解】解:∵一个正多边形的一个外角是45︒,∴360458︒÷︒=,∴这个正多边形是正八边形,故选:B .6.D【分析】本题考查了多边形的内角与外角,解决本题的关键是明确第一次回到出发点A 时,所经过的路线正好构成一个正多边形.第一次回到出发点A 时,所经过的路线正好构成一个正多边形,用8972=÷,求得边数,再根据多边形的外角和为360︒,即可求解.【详解】解:∵第一次回到出发点A 时,所经过的路线正好构成一个正多边形,∴正多边形的边数为:8972=÷,根据多边形的外角和为360︒,∴则他每次转动θ的角度为:360845︒÷=︒,故选:D .7.A【分析】本题主要考查了多边形的内角和与外角和,掌握内角和公式是解题的关键.根据任何多边形的外角和都是360︒,可以求出多边形的边数,再根据多边形的内角和公式,就得到多边形的内角和.【详解】解:根据题意得:该多边形的边数为:3601036︒=︒,∴该正多边形的内角和为:()1021801440-⨯︒=︒.故选:A .8.C【分析】此题考查了多边形的内角和外角及平行线的性质,熟记多边形内角和公式及平行线的性质是解题的关键.连接AD ,根据多边形的内角和及平行线的性质求解即可.【详解】如图,连接AD ,∵五边形ABCDE 是正五边形,()521801085E BAE -⨯︒∴∠=∠==︒,EA ED =,()34180108236∴∠=∠=︒-︒÷=︒,5108472∴∠=︒-∠=︒,226∠=︒ ,2598,DAF ∴∠=∠+∠=︒,AF DG 98,ADG ∴∠=︒1362.ADG ∴∠=∠-∠=︒故选:C .9.C【分析】本题主要考查了正多边形的外角和.多边形由拼图方法可知:环状图案的外围是正多边形,根据正多边形外角和等于360︒即可求出正多边形的边数.【详解】解:依题意可知:用含60°角的直角三角板按图示拼成类似的环状图案是正多边形,正多边形的外角180(9060)30=︒-︒+︒=︒,故正多边形的边数为3603012︒÷︒=(条)∴除了图上3个还需要含60°角的直角三角板的数量为1239-=(个)故选C .10.C【分析】本题主要考查了多边形内角和定理,根据5个“筝形”组成一个正十边形,结合多边形内角和定理求解即可【详解】解;由图可知,5个“筝形”组成一个正十边形,∴()180********BCD ︒⨯-∠==︒,故选:C11.1080︒/1080度【分析】本题考查了多边形内角和定理,直接套用多边形的内角和()2180n -⋅︒进行计算可求八边形的内角和,【详解】解:内角和:()8218061801080-⨯︒=⨯︒=︒.故答案为:1080︒12.5【分析】本题考查了多边形的对角线,牢记n 边形从一个顶点出发可引出(3)n -条对角线是解题的关键.据此求解即可.【详解】解:∵从n 边形的一个顶点最多能引出2条对角线,∴32n -=,∴5n =.故答案为:5.13.5【分析】本题考查多边形的内角和公式,n 边形的内角和公式为()2180n -⨯︒,由此列方程即可得到答案.【详解】解:设这个多边形的边数为n ,则()2180540n -⨯︒=︒,解得5n =,故答案为:5.14.1080︒/1080度【分析】本题考查了多边形外角和与内角和,掌握其计算公式是解题的关键.多边形的内角和公式为:()2180n -⨯︒(其中n 为多边形的边数),多边形的外角和是360︒.因为多边形的外角和是360︒,且正多边形的每个内角都相等,每个外角也都相等,设这个正多边形的一个外角为x ,则内角为90x +︒,根据内角与外角的和为180︒可列出方程.【详解】设外角是x ,则内角是180x ︒-,则18090x x ︒--=︒,解得45x =︒.则多边形的边数是:360458︒÷︒=.∴内角和是:()821801080-⨯︒=︒.故答案为:1080︒.15.11或10或9【分析】本题考查了多边形的内角和度数,熟记相关结论是解题关键.【详解】解:以五边形为例,如图所示:剪去一个内角后,多边形的边数可能加1,可能不变,也可能减1设新多边形的边数为n ,则()21801440n -⨯︒=︒,解得:10n =∴原多边形可能有11或10或9条边.故答案为:11或10或9.16.540°【分析】连接ED ,由三角形内角和可得∠A+∠B=∠BED+∠ADE ,再由五边形的内角和定理得出结论.【详解】连接ED ,∵∠A+∠B=180°-∠AOB ,∠BED+∠ADE=180°-∠DOE ,∠AOB=∠DOE ,∴∠A+∠B=∠BED+∠ADE ,∵∠CDE+∠DEF+∠C+∠F+∠G=(5-2)×180°=540°,即∠CDO+∠ADE+BED+∠BEF+∠C+∠F+∠G=540°,∴∠A+∠B+∠C+∠CDO+∠BEF+∠F+∠G=540°.故答案为:540°.【点拨】本题考查了三角形的内角和公式,以及多边形的内角和公式,熟记多边形的内角和公式为(n -2)×180°是解答本题的关键.17.八【分析】本题主要考查了多边形的内角和,熟练掌握多边形的内角和公式,是解决问题的关键设这个正多边形的边数为n ,根据正多边形的外角和与内角和的比为1:3,利用多边形内角和公式与外角和列方程解答并检验,即得【详解】设这是个正n 边形,∵这个正多边形的外角和与内角和的比为1:3,∴()360121803n =-⨯,解得,8n =,经体验8n =是所列方程的解,且符合题意,∴这是个正八边形,故答案为:八18.5【分析】本题主要考查了多边形的内角和外角,解题关键是熟练掌握正多边形的定义及性质和外角和.先根据题意画出图形,再根据已知条件求出2∠和3∠的度数,然后根据正多边形的性质和外角和,求出正多边形的边数即可.【详解】解:如图所示:由题意得:136∠=︒,123180∠+∠+∠=︒ ,2318036144∴∠+∠=︒-︒=︒,正多边形每个外角都相等,23144272∴∠=∠=︒÷=︒,正多边形的外角和为360︒,∴它的边数为:360725÷=,n ∴的值为5,故答案为:5.19.100【分析】本题考查了四边形的内角和定理,根据题意,列式109060360x x +++︒+︒=︒计算即可.【详解】根据题意,列式109060360x x +++︒+︒=︒,解得100x =,故图中x 的值为100.20.(1)1800︒(2)54【分析】本题主要考查多边形内角与外角的知识点,此题要结合多边形的内角和公式寻求等量关系,构建方程求解即可.另外还要注意从n 边形一个顶点可以引3n -()条对角线.(2)求出多边形的边数,利用多边形内角和公式即可得到答案;(3)根据n 边形有()32n n -条对角线,即可解答.【详解】(1)解:设这个正多边形的一个外角为x ︒,依题意有430180x x ++=,解得30x =,3603012︒÷︒=∴这个正多边形是十二边形.∴这个正多边形的内角和为(122)1801800-⨯︒=︒(2)解:对角线的总条数为4(1231)252-=⨯(条).21.(1)70E ∠=︒(2)140C ∠=︒,五边形外角和的度数是360︒【分析】本题主要考查多边形内角和、外角和及平行线的性质,熟练掌握多边形内角和及平行线的性质是解题的关键.(1)根据平行线的性质可进行求解;(2)根据多边形内角和、外角和及平行线的性质可进行求解.【详解】(1)解:∵AE CD ∥,∴180D E ∠+∠=︒,∴180********E D ∠∠=︒-=︒-︒=︒;(2)解:五边形ABCDE 中,()52180540A B C D E ∠+∠+∠+∠+∠=-⨯︒=︒,∵180D E ∠+∠=︒,100A ∠=︒,120B ∠=︒,∴()540C D E A B∠∠∠∠∠=︒-+--140=︒;五边形外角和的度数是360︒.22.(1)见解析(2)十三边形或十四边形(3)110︒或20︒【分析】本题主要考查了多边形内角和定理,多边形内角和外角的关系以及二元一次方程组的应用.(1)根据多边形内角和定理公式计算判断即可.(2)设应加的内角为x ,多加的外角为y ,依题意可列方程为()21802020n y x -=-+ ,结合角的属性建立不等式求整数解即可.(3)分别计算十三边形的内角和以及十四边形的内角和,分别列出关于x ,y 的二元一次方程组求解即可.【详解】(1)设多边形的边数为n ,由题意得()18022020n -= ,解得2139n =,∵n 为正整数,∴多边形的内角和不可能为2020︒.(2)设应加的内角为x ,多加的外角为y ,依题意可列方程为()21802020n y x -=-+ ,∵180180x y -<-< ,∴()202018018022020180n -<-<+ ,解得22121499n <<,又∵n 为正整数,∴n 13=或14n =.故明明求的是十三边形或十四边形的内角和.(3)十三边形的内角和为()1801321980⨯-= ,∴2020198040y x -=-= ,又180x y += ,∴70x = ,110y = .十四边形的内角和为()1801422160⨯-= ,∴21602020140x y -=-= ,又180x y += ,∴160x = ,20y = .所以错当成内角的那个外角为110︒或20︒.23.(1)①180α︒-,②360α︒-(2)8n =;(3)(3)180n βα-=-⨯︒,理由见解析【分析】(1)①根据一个内角与它相邻的外角的和是180︒进行计算即可;②四边形的内角和是360︒进行计算即可;(2)根据多边形的内角和的计算方法进行计算即可;(3)表示出和它不相邻的(n )1-个内角的和即可.【详解】解:(1)①四边形的一个内角的度数是α,则与它相邻的外角的度数180α︒-;②由于四边形的内角和是360︒其中一个内角为α,则其它三个内角的和为360α︒-;(2)由题意得,(2)180920n α-⨯︒-=︒,3n > 的正整数,0180α︒<<︒,8n ∴=,即这个多边形为八边形;(3)设n 边形(3)n >的一个外角为α,它不相邻的(n )1-个内角的和为β,则有180(2)180n αβ︒-+=-⨯︒,即(3)180n βα-=-⨯︒.24.(1)见解析,∠CBD +∠ACE +∠BAF =360°,三角形中的外角和为360°,见解析;(2)∠RQG +∠SRH +∠PSM +∠QPN =360°,见解析;(3)多边形的外角和和都是360°,见解析【分析】(1)经测量得出∠CBD =138°,∠ACE =117°,∠BAF =105°,∠CBD +∠ACE +∠BAF =360°,则据此得出结论三角形中的外角和为360°,根据平角是180°和多边形内角和证明即可;(2)分别测量出几个角并求出这几个角的和,得出结论:在四边形的外角和是360°;根据(1)中证明方法证明即可;(3)猜想:多边形的外角和和都是360°.根据(1),(2)方法证明即可;【详解】解:(1)经测量知∠CBD =138°,∠ACE =117°,∠BAF =105°,∴∠CBD +∠ACE +∠BAF =360°,发现:三角形中的外角和为360°,理由:∵∠CBD+∠ABC=180°,∠ACE+∠ACB=180°,∠BAC+∠BAF=180°,∴∠CBD+∠ACE+∠BAF+∠ABC+∠ACB+∠BAC=540°,又∵∠ABC+∠ACB+∠BAC=180°,∴∠CBD+∠ACE+∠BAF=360°;(2)∠RQG=125°,∠SRH=113°,∠PSM=48°,∠QPN=74°,所以∠RQG+∠SRH+∠PSM+∠QPN=360°;发现:在四边形的外角和是360°;∵∠RQG+∠PQR=180°,∠SRH+∠QRS=180°,∠PSM+∠RSP=180°,∠QPN+∠QPS=180°,∵∠RQG+∠PQR+∠SRH+∠QRS+∠PSM+∠RSP+∠QPN+∠QPS=720°,∵∠PQR+∠QRS+∠RSP+∠QPS=360°,∴∠RQG+∠SRH+∠PSM+∠QPN=360°.(3)猜想:多边形的外角和都是360°.设多边形为n边形,则n边形的每一个内角与它相邻的外角的和为180°,∴n边形的外角和=180°n﹣(n﹣2)×180°=180°n﹣180°n+360°=360°.【点拨】此题考查多边形外角和的知识,利用平角是180°结合多边形内角和证明即可.。
八年级数学同步练习-多边形及其内角和

11.3多边形及其内角和1、若一个凸多边形的内角和为720°,则这个多边形的边数为().A. 4B. 5C. 6D. 72、若多边形的边数由3增加到n(n为大于3的整数),则其外角和的度数().A. 增加B. 减少C. 不变D. 不能确定3、如果一个多边形的内角和等于它的外角和的2倍,则这个多边形是().A. 三角形B. 四边形C. 五边形D. 六边形4、正十边形的每一个内角的度数为().A. 120°B. 135°C. 140°D. 144°5、一个多边形的每一个外角都是45°,则这个多边形的边数为().A. 6B. 7C. 8D. 96、如图,小明从A点出发,沿直线前进12米后向左转36°,再沿直线前12米,又向左转36°⋯照这样走下去,他第一次回到出发地A点时,一共走了米.7、若一个正多边形的内角和为720°,则这个正多边形的每一个内角是().A. 60°B. 90°C. 108°D. 120°8、如果过一个多边形的一个顶点的对角线有6条,则该多边形是().A. 九边形B. 八边形C. 七边形D. 六边形9、从n边形的一个顶点作对角线,把这个n边形分成三角形的个数是().A. n个B. (n−1)个C. (n−2)个D. (n−3)个10、下面的平面图形中,不能镶嵌平面的图形是().A. 正三角形B. 正六边形C. 正四边形D. 正五边形11、如图,将一个长方形剪去一个角,则剩下的多边形为().A. 五边形B. 四边形或五边形C. 三角形或五边形D. 三角形或四边形或五边形12、一个多边形截去一个角后,形成另一个多边形的内角和为720°,那么原多边形的边数为().A. 5B. 5或6C. 5或7D. 5或6或713、如图,∠1是五边形ABCDE的一个外角,若∠1=65°,则∠A+∠B+∠C+∠D=°.14、如图,∠1,∠2,∠3,∠4是五边形ABCDE的外角,且∠1=∠2=∠3=∠4=70°,则∠AED的度数是.15、若正多边形的内角和是1080°,则该正多边形的边数是.16、一个多边形的每一个外角都等于40°,则它的边数为.17、如果一个多边形的内角和是外角和的3倍,则这个多边形的边数是().A. 8B. 9C. 10D. 1118、某多边形的内角和加上其外角和等于1080°,则此多边形的边数是().A. 4B. 5C. 6D. 719、一个正多边形的外角与它相邻的内角之比为1:4,那么这个多边形的边数为().A. 8B. 9C. 10D. 1220、如图所示,小华从A点出发,沿直线前进10米后左转24°,再沿直线前进10米,又向左转24°,⋅⋅⋅,照这样走下去,他第一次回到出发地A点时,一共走的路程是().A. 140米B. 150米C. 160米D. 240米21、经过多边形一个顶点的所有对角线把多边形分成10个三角形,多边形的边数是().A. 8条B. 9条C. 12条D. 11条22、如果一个多边形的每个外角是40°,那么从这个多边形的一个顶点出发,可以引出条对角线.23、如果限于用一种正多边形镶嵌,下列正多边形不能镶嵌成一个平面图形的是().A. 正三角形B. 正方形C. 正五边形D. 正六边形24、如果一个正方形被截掉一个角后,得到一个多边形,那么这个多边形的内角和是.25、一个多边形截去一个角后,形成另一个多边形的内角和为2520°,则原多边形的边数是().A. 17B. 16C. 15D. 16或15或1726、如图,在五边形ABCDE中,∠A+∠B+∠E=300°,DP、CP分别平分∠EDC、∠BCD,则∠P=().A. 50°B. 55°C. 60°D. 65°27、如图是由射线AB,BC,CD,DE,EA组成的平面图形,则∠1+∠2+∠3+∠4+∠5=°.28、如图,∠A+∠B+∠C+∠D+∠E+∠F=°.1 、【答案】 C;【解析】设这个多边形的边数为n,则(n−2)×180°=720°,解得n=6,故这个多边形为六边形.故选C.2 、【答案】 C;【解析】因为多边形外角和固定为360°,所以外角和的度数是不变的.故选:C.3 、【答案】 D;【解析】设多边形为n边形,由题意,得(n−2)⋅180=360×2,解得n=6.故选D.4 、【答案】 D;【解析】方法一 : ∵一个十边形的每个外角都相等,∴十边形的一个外角为360÷10=36°.∴每个内角的度数为180°−36°=144°;故选:D.方法二 : 由多边形的内角和公式可知,正十边形的内角和为180°×(10−2)=1440°.所以每个内角的度数为1440°÷10=144°.故选D.5 、【答案】 C;【解析】由多边形外角和为360°,=8,则边数:360°45°所以多边形为8边形.故选C.6 、【答案】120;【解析】由题意得:360°÷36°=10,则他第一次回到出发地A点时,一共走了12×10=120(米).7 、【答案】 D;【解析】(n−2)×180°=720°,∴n−2=4,∴n=6.则这个正多边形的每一个内角为720°÷6=120°.故选:D.8 、【答案】 A;【解析】∵过一个多边形的一个顶点的对角线有6条,∴多边形的边数为6+3=9,∴这个多边形是九边形.9 、【答案】 C;【解析】从n边形的一个顶点作对角线,把这个n边形分成(n−2)个三角形.10 、【答案】 D;【解析】 A选项 : 正三角形的一个内角度数为180°−360°÷3=60°,是360°的约数,能镶嵌平面,不符合题意,故A错误;B选项: 正六边形的一个内角度数为180°−360°÷6=120°,是360°的约数,能镶嵌平面,不符合题意,故B错误;C选项 : 正四边形的一个内角度数为180°−360°÷4=90°,是360°的约数,能镶嵌平面,不符合题意,故C错误;D选项 : 正五边形的一个内角度数为180°−360°÷5=108°,不是360°的约数,不能镶嵌平面,符合题意,故D正确;11 、【答案】 D;【解析】沿对角线剪则剩下三角形.剪痕过一个顶点,并与一面相交得四边形.剪痕与相邻的两边相交,得五边形.12 、【答案】 D;【解析】如图:剪切的三种情况:①不经过顶点剪,则比原来边数多1,②只过一个顶点剪,则和原来边数相等,③按照顶点连线剪,则比原来的边数少1,设内角和为720°的多边形的边数是n,则(n−2)⋅180°=720°,解得:n=6,则原多边形的边数为5或6或7,故选:D.13 、【答案】425;【解析】∠A+∠B+∠C+∠D+∠AED=180°×(5−2)=540°,∵∠1+∠AED=180°,∠1=65°,∴∠AED=180°−65°=115°,∴∠A+∠B+∠C+∠D=540°−∠AED=540°−115°=425°.14 、【答案】100°;【解析】如图:∵五边形ABCDE的外角和是360°,∴∠5=360°−70°×4=80°,∴∠AED=180°−80°=100°.15 、【答案】8;【解析】根据n边形的内角和公式,得:(n−2)⋅180=1080,解得n=8.∴这个多边形的边数是8.故答案为:8.16 、【答案】9;【解析】解法一:360°÷40°=9.多边形外角和是360°,边数=外角数=内角数.解法二:∵外角都是40°,∴内角都是140°,设它为n边形则度数总和为140n°,又∵n边形的度数和是(n−2)×180°,所以140n=(n−2)×180,解得n=9.17 、【答案】 A;【解析】设该多边形边数为n,则内角和为180°(n−2),外角和为360°,∴180°⋅(n−2)=3×360°,解得n=8,故选A.18 、【答案】 C;【解析】多边形外角和为360°,则此多边形内角和为720°,+2=6.∴边数为=720°180°19 、【答案】 C;【解析】由外角与它相邻的内角是邻补角可得:x+4x=180°,一个外角度数x=36°,∴正多边形的边数为360°÷36°=10.20 、【答案】 B;【解析】∵多边形的外角和为360°,而每一个外角为24°,∴多边形的边数为360°÷24°=15,∴小华一共走了:15×10=150米.故选:B.21 、【答案】 C;【解析】从n边形的一个顶点出发可引出(n−3)条对角线,可组成(n−2)个三角形,即可得n−2=10,解得n=12.故选C.22 、【答案】6;【解析】多边形的边数:360°÷40°=9,从一个顶点出发可以引对角线的条数:9−3=6(条).23 、【答案】 C;【解析】 A选项 : 正三角形每个内角是60°,能整除360°,能镶嵌.B选项 : 正方形每个内角是180°−360°÷4=90°,能整除360°,能镶嵌.C选项 : 正五边形每个内角为180°−360°÷5=108°,不能整除360°,不能镶嵌.D选项 : 正六边形每个内角为180°−360°÷6=120°,能整除360°,能镶嵌.24 、【答案】540°或360°或180°;【解析】n边形的内角和是(n−2)⋅180°,所得新的多边形的边数增加1,则新的多边形的内角和是(4+1−2)×180°=540°,所得新的多边形的边数不变,则新的多边形的内角和是(4−2)×180°=360°,所得新的多边形的边数减少1,则新的多边形的内角和是(4−1−2)×180°=180°,因而所成的新多边形的内角和是540°或360°或180°.25 、【答案】 D;【解析】一个多边形截去一个角后,多边形的边数可能增加了一条,也可能不变或者减少了一条,根据(n−2)×180°=2520°,解得n=16.∴多边形的边数为15,16或17.故选D.26 、【答案】 C;【解析】方法一 : ∵在五边形ABCDE中,∠A+∠B+∠E=300°,∴∠EDC+∠BCD=240°,又∵DP、CP分别平分∠EDC、∠BCD,∴∠PDC+∠PCD=120°,∴△CDP中,∠P=180°−(∠PDC+∠PCD)=180°−120°=60°.方法二 : 五边形的内角和为(5−2)×180°=540°∵∠A+∠B+∠E=300°,∴∠EDC+∠BCD=240°.∵DP、CP分别平分∠EDC,∠BCD,∴∠PDC=12∠EDC,∠PCD=12∠BCD,∴∠PDC+∠PCD=12(∠EDC+∠BCD)=12×240°=120°∴∠P=60°.故选C.27 、【答案】360;【解析】∠1+∠2+∠3+∠4+∠5=(180°−∠BAE)+(180°−∠ABC)+(180°−∠BCD)+(180°−∠CDE)+(180°−∠DEA)=180°×5−(∠BAE+∠ABC+∠BCD+∠CDE+∠DEA)=900°−(5−2)×180°=900°−540°=360°.故答案为:360°.28 、【答案】360;【解析】如下图所示∵∠AHG=∠A+∠B,∠DNG=∠C+∠D,∠EGN=∠E+∠F,∴∠AHG+∠DNG+∠EGN=∠A+∠B+∠C+∠D+∠E+∠F,又∵∠AHG、∠DNG、∠EGN是△GHN的三个不同的外角,∴∠AHG+∠DNG+∠EGN=360°,∴∠A+∠B+∠C+∠D+∠E+∠F=360°.故答案为:360.。
小学数学多边形的内角和的练习题

小学数学多边形的内角和的练习题多边形是我们数学中经常涉及到的一个概念,它有着丰富的性质和特点。
其中一个重要的性质就是多边形的内角和,在解决多边形相关问题时,计算内角和是必不可少的。
本文将为小学生提供一些多边形的内角和的练习题,通过这些练习题的解答,巩固对多边形内角和的理解和计算能力。
练习一:计算三角形的内角和三角形是最简单的多边形,它由三条边组成,每个角都是尖角,即小于 90 度。
请计算以下三角形的内角和:1. 一个直角三角形,其中一个角是90度,另外两个角是多少度?解答:直角三角形的两个角是直角(90度)和锐角,因此另外两个角的度数加起来等于 90 度,即两个角分别是 90 度 - X 度和 X 度,其中 X 度是一个锐角。
2. 一个等腰三角形,其中两个角相等,每个角是多少度?解答:等腰三角形的两个角是相等的,因此每个角的度数相同。
设每个角的度数为 X 度,则另外一个角也是 X 度。
根据三角形内角和的性质,我们可以得到等式:X 度 + X 度 + X 度 = 180 度,解方程得到:3X 度 = 180 度,X 度 = 60 度。
所以每个角是60度。
练习二:计算四边形的内角和四边形是有四条边、四个顶点以及四个内角的多边形。
请计算以下四边形的内角和:1. 一个长方形,其中一个角是直角(90度),其他三个角分别是多少度?解答:长方形的对角线相交于90度,即对角线将长方形划分成两个相等的直角三角形。
因此,任意一个角的度数等于直角三角形的一个角度,即90度。
所以,其他三个角的度数也都是90度。
2. 一个平行四边形,其中两组对边平行,每个角是多少度?解答:平行四边形的对边是平行的,因此它可以划分成两组相等的对边分别是相对的。
根据平行四边形的性质,我们可以得知每个角的度数相等。
设每个角的度数为 X 度,则另外一个角也是 X 度。
根据四边形内角和的性质,我们可以得到等式:X 度 + X 度 + X 度 + X 度 = 360 度,解方程得到:4X 度 = 360 度,X 度 = 90 度。
2023-2024学年人教版数学八年级上册 11.3多边形及其内角和同步练习(含答案)

2023-2024学年人教版数学八年级上册11.3多边形及其内角和同步练习(含答案)2023-2024学年人教版数学八年级上册11.3 多边形及其内角和同步练习一、单选题1.五边形的内角和为()A.720° B.540° C.360° D.180°2.下列角度中,不能成为多边形内角和的是()A.600° B.720° C.900° D.1080°3.一个多边形的内角和是外角和的2倍,这个多边形是()A.四边形B.五边形C.六边形D.八边形4.若从一个正多边形的一个顶点出发,最多可以引5条对角线,则它的一个内角为()A.B.C.D.5.如果一个四边形的面积正好等于它的两条对角线乘积的一半,那么这个四边形一定是()A.菱形B.矩形C.正方形D.对角线互相垂直的四边形6.在一个凸n边形的纸板上切下一个三角形后,剩下一个内角和为1080°的多边形,则n的值为()A.7 B.8C.9 D.以上都有可能7.一个多边形纸片剪去一个内角后,得到一个内角和为2340°的新多边形,则原多边形的边数为()A.14或15或16 B.15或16或17 C.15或16 D.16或178.下列说法中,正确的个数有()①若一个多边形的外角和等于360°,则这个多边形的边数为4;②三角形的高相交于三角形的内部;③三角形的一个外角大于任意一个内角;④一个多边形的边数每增加一条,这个多边形的内角和就增加;⑤对角线共有5条的多边形是五边形.A.1个B.2个C.3个D.4个二、填空题9.若一个正多边形的一个外角等于18°,则这个正多边形的边数是.10.一个多边形的内角和与外角和的比是4:1,则它的边数是.11.如图,点O是正五边形ABCDE的中心,连接BD、OD,则∠BDO =°.12.平面上,将边长相等的正三角形、正方形、正五边形、正六边形的一边重合并叠在一起,如图,则∠3+∠1﹣∠2=.13.如图所示,∠1+∠2+∠3+∠4+∠5+∠6=度.三、解答题14.一个多边形,它的内角和比外角和的4倍多180°,求这个多边形的边数及内角和度数.15.如图,是四边形的一个外角,且.那么与互补吗?为什么?16.如图,CD∠AF,∠CDE=∠BAF,AB∠BC,∠C=120°,∠E=80°,试求∠F的度数.17.如图,四边形ABCD中,BA丄DA,CD丄BC,BE、DF分别是∠ABC、∠ADC的平分线.(1)∠1与∠2有什么数量关系,为什么?(2)BE与DF有什么位置关系?请说明理由.18.如图,将六边形纸片ABCDEF沿虚线剪去一个角(∠BCD)后,得到∠1+∠2+∠3+∠4+∠5=460°.(1)求六边形ABCDEF的内角和;(2)求∠BGD的度数.19.如图,五边形中,.(1)求的度数;(2)直接写出五边形的外角和.参考答案1.B 2.A 3.C 4.D 5.D 6.D 7.A 8.B 9.2010.1011.1812.24°13.360 °14.解:根据题意,得(n﹣2)180=1620,解得:n=11.则这个多边形的边数是11,内角和度数是1620度.15.解:与互补,理由如下:∠ ,∠ABC+=180∠∠ABC+∠D=180 ,∠四边形内角和等于360 ,∠ + =360°-(∠ABC+∠D)=180°∠ 与互补.解:如图,连结AD在四边形ABCD中,∠BAD+∠ADC+∠B+∠C=360°.∠AB∠BC,∠∠B=90°.又∠∠C=120°,∠∠BAD+∠ADC=150°.∠CD∠AF,∠∠CDA=∠DAF.又∠∠CDE =∠BAF,∠∠EDA=∠BAD.在四边形ADEF∠DAF+∠EDA+∠F+∠E=360°,∠∠F+∠E=360°(∠ADC+∠BAD)=210°.又∠∠E=80°,∠∠F=130°17.(1)解:∠1+∠2=90°;理由如下:∠BE,DF分别是∠ABC,∠ADC的平分线,∠∠ABC=2∠1,∠ADC=2∠2,∠BA丄DA,CD丄BC,∠∠A=∠C=90°,∠∠ABC+∠ADC=180°,∠2(∠1+∠2)=180°,∠∠1+∠2=90°;(2)解:BE∠DF;理由如下:在∠FCD中,∠∠C=90°,∠∠DFC+∠2=90°,∠∠1+∠2=90°,∠∠1=∠DFC,∠BE∠DF.18.(1)解:六边形ABCDEF的内角和为:180°×(6-2)=720°;(2)解:∠∠1+∠2+∠3+∠4+∠5=460°,∠∠GBC+∠C+∠CDG=720°-460°=260°,∠∠G=360°-(∠GBC+∠C+∠CDG)=100°.19.(1)解:∠AE∠CD,∠∠D+∠E=180°,∠五边形ABCDE中,∠A=100°,∠B=120°,∠.(2)解:根据多边形的外角和定理:五边形的外角和是:°。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
七年级数学多边形的内角和练习题
一、基础知识:
1.四边形ABCD中,如果∠A+∠C+∠D=280°,则∠B的度数是()
A.80° B.90° C.170° D.20°
2.一个多边形的内角和等于1080°,这个多边形的边数是()
A.9 B.8 C.7 D.6
3.内角和等于外角和2倍的多边形是()
A.五边形 B.六边形 C.七边形 D.八边形
4.六边形的内角和等于_______度.
5.正十边形(每条边相等,每个内角相等的十边形)的每一个内角的度数等于______,每一个外角的度数等于_______.
6.如图,你能数出多少个不同的四边形?
7.四边形的四个内角可以都是锐角吗?可以都是钝角吗?可以都是直角吗?•为什么?
8.求下列图形中x的值:二、知识运用:
9.(综合题)已知:如图,在四边形ABCD中,∠A=∠C=90°,BE平分∠ABC,•DF平分∠ADC。
BE与DF有怎样的位置关系?为什么?
10.(应用题)有10个城市进行篮球比赛,每个城市均派3个代表队参加比赛,规定同一城市间代表队不进行比赛,其他代表队都要比赛一场,问按此规定,•所有代表队要打多少场比赛?(想一下与我们什么几何模型类似)
11.(创新题)如图,以五边形的每个顶点为圆心,以1为半径画圆,求圆与五边形重合的面积.
12.(1)(2005年,南通)已知一个多边形的内角和为540°,则这个多边形为()
A.三角形 B.四边形 C.五边形 D.六边形
(2)(2005年,福建泉州)五边形的内角和等于_______度.
13.(易错题)一个多边形的每一个顶点处取一个外角,这些外角中最多有钝角(• )
A.1个 B.2个 C.3个 D.4个
三、能力拓展:
14.(探究题)
(1)四边形有几条对角线?
五边形有几条对角线?
六边形有几条对角线?
……
猜想并探索:
n边形有几条对角线?
(2)一个n边形的边数增加1,对角线增加多少条?
15.(开放题)如果一个多边形的边数增加1,•那么这个多边形的内角和增加多少度?若将n边形的边数增加1倍,则它的内角和增加多少度?16.壁虎在一座油罐的下底边沿A处.它发现在自己的正上方──油罐上边缘的B•处有一只害虫.壁虎决定捕捉这只害虫.为了不引起害虫的注意,它故意不走直线,而是绕着油罐,沿着一条螺旋路线,从背后对害虫进行突然袭击如图7-3-5.结果,•壁虎的偷袭得到成功,获得了一顿美餐.
请问:壁虎沿着螺旋线爬行是最短的路程吗(线段AB除外)?。
