清华大学理论力学惯量矩阵分析解析
理论力学 12 动量矩定理

轴转动(zhuàn dòng)。已知均质杆 OA 长为 l ,质 C1 量为 m 1,均质圆盘 C 2 的半径为 r ,质量为 m 2,
试求复摆对 O 轴的动量矩。
A
C2 r
解: J O 的计算(jìsuàn):
JO
1 12
m1
l
2
m1
l 2
2
1 2 m2
r2
m2
l
r
2
图 12-9
由几何关系知: r R h z
h 薄圆片对 y 轴转动惯量 d J y 为:
1 r2 dm 4
精品资料
dJ y
1 4
r 2dm
z 2dm
1 4
r2
z2
r 2dz
1
4
R4 h4
h
z 4
R2 h2
h
z 2
z2
dz
整个(zhěnggè)圆锥体对于 y 轴的转动惯量为:
J y
h 0
1 4
底圆直径的转动惯量。已知圆锥体质量为 M ,
z
底圆半径为 R ,高为 h ,如图12-6所示。 r
h z dz
解:把圆锥体分成许多(xǔduō)厚度为 d z 的薄圆片,该薄圆片的质量为
d m r2d z
为圆锥体的密度,r为薄圆片的半径。
O
y
R
x
图 12-6
圆锥体的质量为
M 1R2h
3
薄圆片对自身直径的转动惯量为
精品资料
12.1 转动惯量、平行(píngxíng) 轴定1理2.1.1 转动惯量
质点系的运动,不仅(bùjǐn)与作用在质点系上的力有关, 还与质点系各质点的质量其及分布情况有关。质心是描述质 点系质量分布的一个特征量,转动惯量(Moment of inertia)则 是描述质点系质量分布的另一个特征量。
清华大学理论力学lecture08_131809805

定:FAy 与 FCy !
A
C
FAy FAx
A
FCy
FCx
C
B
D
yl
x z
FD D
B 超静定结构!
E
刚体模型无法求解超静定结构的所有约束力,需要采用变形体模型。
由两个或两个以上刚体组成的系统,称为刚体系统。刚体系统 平衡问题的特点是:仅仅考察系统整体平衡,无法求得全部未知力。
例:如图所示的结构由AC、CD、DE和BE四部分组成,载荷及尺 寸如图。求A、B、C处的约束力。
S6 2qa
B
NB
将处于平衡状态的变形体更换为刚体则平衡状态不变 F1
F3
。这个结论称为硬化原理。换句话说变形体平衡时其
所受力系满足主矢为零、对任一点的主矩为零。
例:已知四连杆机构ABCD 受
力P、Q 作用。试分析机构平
衡时P、Q 的关系。
D
A
450 900
Q
B
300 600
P
C
F2 F4 y
x z
FD D
FAx=-2FD 解毕! C
例题:图示结构,已 知 : FP、l、r 求: 固定端 A和铰E 二处约束力。
解:解除约束,画整体和杆BEC
的受力分析图,如图所示。
l
讨论:如何求 FDE 及 M A ?
B
1.5l
C
E
ll
l
B
Cr
E
D
y
x
z
FC
A
杆DE为二
D 力构件!
2FC
A FAx
MA
FAy
FBy FBx
解: 解除约束,画受力分析 图。DA和BC为二力构件。
【精品】理论力学11动量矩定理分析解析幻灯片

0 Fox m2l amgFOy
FOymgm2lam 4g
§11-4 刚体对轴的转动惯量
一.定义: Jz miri2
z
i
对于质量连续分布的刚体,上式可写成积分
形式
Jz r2 dm
由定义可知,转动惯量不仅与 质量有关,而且与质量的分布有关;
ri
vi
mi
在国际单位制中,转动惯量的单位
是: kg·m2。同一刚体对不同轴的转
Jz mz2
回转半径的几何意义是:假想地将物体的质量集 中到一点处,并保持物体对轴的转动惯量不变,则该 点到轴的距离就等于回转半径的长度。
3、平行轴定理
定理:刚体对于任一轴的转动惯量,等于刚体 对于通过质心、并与该轴平行的轴的转动惯量,加 上刚体的质量与两轴间距离平方的乘积,
zC
z1
m
C
Jz1 JzC md2
dLO dt
MO(Fi(e))
若 Mz(F(e))0,则 Lz 常量。
dLz dt
Mz (Fi (e) )
例 高炉运送矿石的卷扬机如图。已知鼓轮的半径为R,质量 为m1,绕O轴转动。小车和矿石的总质量为m2。作用在鼓轮上
的力偶矩为M,鼓轮对转轴的转动惯量为J,轨道倾角为a。
设绳质量和各处摩擦不计,求小车的加速度a。
O u
A
mg
mg
解:以系统为研究对象,受力如图。
由于SMO(F (e))=0,且系统初始静止,所以LO=0。
设重物A上升的速度为v,则人的绝对速度va的大小为
va uv
v
LOmarvmv0 r
FOy
O
FOx
u
A mg mg
L Om (uv)rm v0r
第八章 通信系统的矩阵几何解析法

(moments)
2001-4-25
牛志升@清华大学
19
M/E2/1排队系统的求解
?嵌入马尔可夫过程
?确定马尔可夫性成立的嵌入点(顾客退去时刻) ?针对嵌入点建立马尔可夫平衡方程式 ?导入状态变量(退去时刻队列长度)的概率母函
数 ?求出队列长度的z变换及其特征量(moment) ?求出等待时间的LST及其特征量(moment)
1,2
A1 B2 B1 1
λ
A0
2,2
A1 A2 2
λ
3,2
A1 A0 A2 3
λ
A0 A2
23
0
2001-4-25
牛志升@清华大学
PH/M/s排队系统的矩阵几何解(1)
2001-4-25
牛志升@清华大学
24
PH/M/s排队系统的矩阵几何解(2)
2001-4-25
牛志升@清华大学
25
PH/M/s排队系统的矩阵几何解(3)
2,2
μ2 μ1 μ2
?
λ 状态转移率(Q)矩阵
μ2
λ
3,2
λ
2001-4-25
牛志升@清华大学
18
M/E2/1排队系统的求解
?多维马尔可夫过程
?多维线性方程式组(pQ=0 & pe=1) ?导入概率母函数使之转化为一维线性方程式 ?求解出状态变量(队列长度)的概率母函数 ?通过微分得出状态变量(队列长度)的矩
2001-4-25
牛志升@清华大学
11
矩阵几何法的基本定理(3)
2001-4-25
牛志升@清华大学
12
M/PH/1排队系统的矩阵几何解(1)
2001-4-25
清华大学版理论力学课后习题答案大全-----第5章点的复合运动分析
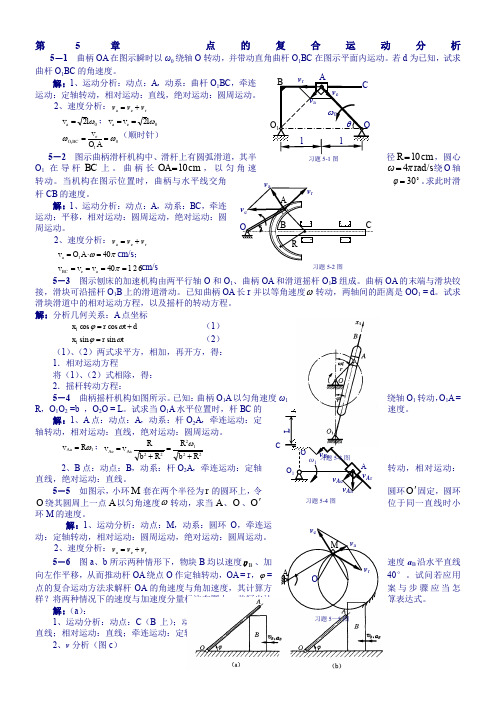
第5章 点的复合运动分析5-1 曲柄OA 在图示瞬时以ω0绕轴O 转动,并带动直角曲杆O 1BC 在图示平面内运动。
若d 为已知,试求曲杆O 1BC 的角速度。
解:1、运动分析:动点:A ,动系:曲杆O 1BC ,牵连运动:定轴转动,相对运动:直线,绝对运动:圆周运动。
2、速度分析:r e a v v v += 0a 2ωl v =;0e a 2ωl v v == 01e 1ωω==AO v BC O (顺时针)5-2 图示曲柄滑杆机构中、滑杆上有圆弧滑道,其半径cm 10=R ,圆心O 1在导杆BC 上。
曲柄长cm 10=OA ,以匀角速rad/s 4πω=绕O 轴30=φ。
求此时滑转动。
当机构在图示位置时,曲柄与水平线交角杆CB 的速度。
解:1、运动分析:动点:A ,动系:BC ,牵连运动:平移,相对运动:圆周运动,绝对运动:圆周运动。
2、速度分析:r e a v v v += πω401a =⋅=A O v cm/s ; 12640a e ====πv v v BC cm/s5-3 图示刨床的加速机构由两平行轴O 和O 1、曲柄OA 和滑道摇杆O 1B 组成。
曲柄OA 的末端与滑块铰接,滑块可沿摇杆O 1B 上的滑道滑动。
已知曲柄OA 长r 并以等角速度ω转动,两轴间的距离是OO 1 = d 。
试求滑块滑道中的相对运动方程,以及摇杆的转动方程。
解:分析几何关系:A 点坐标 d t r x +=ωϕcos cos 1 (1) t r x ωϕsin sin 1= (2) (1)、(2)两式求平方,相加,再开方,得: 1.相对运动方程 将(1)、(2)式相除,得: 2.摇杆转动方程:5-4 曲柄摇杆机构如图所示。
已知:曲柄O 1A 以匀角速度ω1绕轴O 1转动,O 1A = R ,O 1O 2 =b ,O 2O = L 。
试求当O 1A 水平位置时,杆BC 的速度。
解:1、A 点:动点:A ,动系:杆O 2A ,牵连运动:定轴转动,相对运动:直线,绝对运动:圆周运动。
清华大学版理论力学课后习题答案大全第10章动能定理及其应用习题解

CA(a)ωO(a)第10章动能定理及其应用10-1计算图示各系统的动能:1.质量为m ,半径为r 的均质圆盘在其自身平面内作平面运动。
在图示位置时,若已知圆盘上A、B 两点的速度方向如图示,B 点的速度为v B ,θ =45º(图a )。
2.图示质量为m 1的均质杆OA ,一端铰接在质量为m 2的均质圆盘中心,另一端放在水平面上,圆盘在地面上作纯滚动,圆心速度为v (图b )。
3.质量为m 的均质细圆环半径为R ,其上固结一个质量也为m 的质点A 。
细圆环在水平面上作纯滚动,图示瞬时角速度为ω(图c )。
解:1.2222221632(2121)2(212121B B B C C C mv r v mr v m J mv T =⋅+=+=ω2.222122222214321(21212121vm v m r v r m v m v m T +=⋅++=3.22222222)2(212121ωωωωmR R m mR mR T =++=10-2图示滑块A 重力为1W ,可在滑道内滑动,与滑块A 用铰链连接的是重力为2W 、长为l 的匀质杆AB 。
现已知道滑块沿滑道的速度为1v ,杆AB 的角速度为1ω。
当杆与铅垂线的夹角为ϕ时,试求系统的动能。
解:图(a )BA T T T +=)2121(21222211ωC C J v g W v g W ++=21221121212211122]cos 22)2[(22ωϕω⋅⋅+⋅++++=l g W l l v l v l g W v g W ]cos 31)[(2111221222121ϕωωv l W l W v W W g +++=10-3重力为P F 、半径为r 的齿轮II 与半径为r R 3=的固定内齿轮I 相啮合。
齿轮II 通过匀质的曲柄OC 带动而运动。
曲柄的重力为Q F ,角速度为ω,齿轮可视为匀质圆盘。
试求行星齿轮机构的动能。
理论力学(哈工大版)第十二章动量矩定理(全面版)资料

理论力学(哈工大版)第十二章动量矩定理(全面版)资料第八章 动量矩定理8-1 质点系的动量矩(待强化) 一.动量矩的概念质点对点O 的动量矩:v m r v m m O ⨯=)( 质点对轴 z 的动量矩:)()(xy O z v m m v m m = 对着轴看:顺时针为负 逆时针为正质点对点O 的动量矩与对轴z 的动量矩之间的关系:[])( )(v m m v m m z z O = kg·m2/s 。
二.质点系的动量矩 质系对点O 动量矩:i i i i i OO v m r v m mL ⨯==∑∑)(质系对轴z 动量矩:[]z Oii zz L v m m L)(==∑三.质点系的动量矩的计算c c c mv r L L ⨯+=0质点系对任意定点O 的动量矩,等于质点系对质心的动量矩,与将质点系的动量集中于质心对于O 点动量矩的矢量和。
质点系对质心的绝对运动动量矩,等于质点系对随质心平动的参考系的相对运动动量矩。
结论:在计算质点系对于质心的动量矩时,用质点相对于惯性参考系的绝对速度vi ,或用质点相对于固结在质心上的平动参考系的相对速度vi `,所得结果是一样的。
四、刚体的动量矩 1.平动刚体C C C O O v m r v m m L ⨯==)( )(C z z v m m L =2.定轴转动刚体ωZ z J L =3.平面运动刚体C C C C C O m m L v O C L v r L +⨯=+⨯= ω⋅+=C C z z J v m m L )(平面运动刚体对垂直于质量对称平面的固定轴的动量矩,等于刚体随同质心作平动时质心的动量对该轴的动量矩与绕质心轴作转动时的动量矩之和。
8-2 动量矩定理(待强化) 一.质点的动量矩定理)()]([ , )(F m v m F r v r O O m dtdm dt d =⨯=⨯ 质点对任一固定点的动量矩对时间的导数,等于作用在质点上的力对同一点之矩。
清华大学大学物理转动定律转动惯量
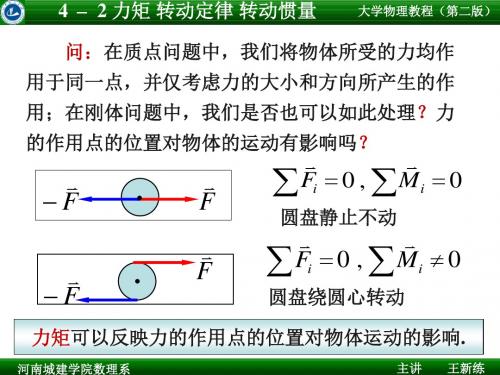
4 – 2 力矩 转动定律 转动惯量
大学物理教程(第二版)
飞轮的质量为什么 大都分布于外轮缘?
河南城建学院数理系 主讲
竿 子 长 些 还 是 短 些 较 安 全 ?
王新练
4 – 2 力矩 转动定律 转动惯量
大学物理教程(第二版)
例1 如图, 有一半径为 R 质量为 的匀质圆 m 盘, 可绕通过盘心 O 垂直盘面的水平轴转动. 转轴与圆 盘之间的摩擦略去不计. 圆盘上绕有轻而细的绳索, 绳 的一端固定在圆盘上, 另一端系质量为 m 的物体. 试求 物体下落时的加速度、绳中的张力和圆盘的角加速度.
例2 有一半径为R质量为 m 匀质圆盘, 以角速度ω 0绕 通过圆心垂直圆盘平面的轴转动.若有一个与圆盘大小相 同的粗糙平面(俗称刹车片)挤压此转动圆盘,故而有正压 力N 均匀地作用在盘面上, 从而使其转速逐渐变慢.设正 压力N 和刹车片与圆盘间的摩擦系数均已被实验测出.试 问经过多长时间圆盘才停止转动? 解: 在圆盘上取面积微元, 面积元所受对转轴的摩擦力矩 大小
圆盘静止不动
Fi 0 , Mi 0
圆盘绕圆心转动
力矩可以反映力的作用点的位置对物体运动的影响.
主讲 王新练
4 – 2 力矩 转动定律 转动惯量
大学物理教程(第二版)
一
力矩
刚体绕 O z 轴旋转 , 力
且在转动平面内, r 为由点O 到力的作用点 P 的径 矢. M F 对转轴 Z 的力矩 z F M r F M r * M Fr sin Fd O P
4 – 2 力矩 转动定律 转动惯量 转动定律
大学物理教程(第二版)
M J
J mi ri
2
理论力学简答题

答:在非惯性系中a =a—65x r f简答题答案1、说明科里奥利加速度产生的原因。
答:(1)质点具有相对速度B时,致使质点在活动参考系中的位置发生变化,从而改变了速度的大小;(2)质点跟随活动参考系转动时,相对速度方向的变化2、试推导出质点在非惯性系中的动力学方程,并说明方程中各项的含义。
动力学方程为ma'=ma—m(6x r'一m6x(6x r')—2m6x v fma表示外力;m6x r'是由非惯性系的加速转动引起的,与非惯性系的角加速度有关;m6x(6x r')成为惯性离心力;2m6x v'科里奥利惯性力。
3.试举两例说明由于地球自转而产生的力学效应,并简述其原因.答:①如物体的重力随地理纬度的增大而增大,这是地球自转产生惯性离心力的影响。
②自由落体的偏东。
地球上物体的运动方程为:X的正方向向南,y的正方向向东,Z的正方向竖直向上。
自由落体的运动方向mx=F+2m6y sin九x<my=F—2m6(x sin九+z cos九)mz=F—mg+2m6y cos九z向着z轴的负方向,'小于零,从运动方程知,物体向东方向受到附加的科里奥利力的作用,即自由落体的偏东。
4.为什么落体会偏东答:地球上物体的运动方程为:d d t-dr')r x m iii"dT 丿—艺r'x F(e)+r xCiii—1艺m rd d tM ‘—dL 1dtmx —F +2m W ysin 九x<my —F —2m 3(x sin 九+z cos 九)mz —F —mg +2m W ycos 九zX 的正方向向南,y 的正方向向东,Z 的正方向竖直向上。
自由落体的运动方向向着Z 轴的负方向,z小于零,从运动方程知,物体向东方向受到附加的科里奥利力的作用,即自由落体的偏东。
5、应用非惯性系动力学方程导出质点组对质心的角动量定理.答:在非惯性系中d 2r '--二m L —F (e)+F (i)+(—m r )id t 2iiiC工r 'x F(e)iii —1艺mr '—0iii—16、分别说明质点组动量守恒定律、动量矩守恒定律、机械能守恒定律成立条件。
理论力学B知识点总结

理论力学B知识点总结一、刚体运动1. 刚体的定义刚体是指无穿透形变、受力形变的物体。
在刚体运动中,刚体上任意两点的距离在运动过程中保持不变。
2. 刚体的运动刚体的运动包括平移运动和转动运动。
在平移运动中,刚体上所有点都沿着相同的方向移动;在转动运动中,刚体围绕着某一固定轴线做转动运动。
3. 刚体的运动描述描述刚体运动需要了解刚体的位移、速度和加速度。
刚体的位移是指刚体上任一点在运动中的位置变化;速度是位移对时间的变化率;而加速度则是速度对时间的变化率。
4. 刚体的自由度刚体在运动中的自由度取决于其平移和转动的自由度。
一个刚体的自由度等于其平移自由度和转动自由度之和。
5. 刚体的转动惯量刚体的转动惯量是指刚体绕轴线转动时对于外力的惯性作用。
转动惯量的大小取决于刚体的形状和质量分布。
二、惯性参考系1. 惯性参考系的定义惯性参考系是指在其中做任意匀速直线运动的参考系。
在惯性参考系中,牛顿力学定律成立。
2. 非惯性参考系非惯性参考系是指其中做非匀速直线运动或者转动运动的参考系。
在非惯性参考系中,牛顿力学定律不成立,会出现虚拟力的存在。
3. 惯性力在非惯性参考系中,需要引入惯性力来修正牛顿力学定律。
惯性力的大小和方向取决于非惯性参考系的加速度。
4. 某些相对静止的参考系也可以看作是惯性参考系。
例如地球上的局部平面参考系和地心参考系。
三、欧拉定理1. 惯性张量惯性张量是描述刚体转动惯量的张量。
它可以表示刚体对于不同轴线转动惯量的大小和方向。
2. 惯性张量的对角化对角化惯性张量可以将刚体转动问题简化为主轴转动问题。
3. 刚体的转动运动刚体的转动运动可以分解为绕着主轴的简谐振动。
这对于描述刚体的稳定平衡以及刚体的自由振动具有重要意义。
四、运动方程1. 刚体的运动方程刚体的运动方程包括平动方程和转动方程。
平动方程描述刚体的质心运动,转动方程描述刚体围绕质心的转动运动。
2. 惯量矩阵惯量矩阵是描述刚体转动惯量的矩阵。
《理论力学》一

《理论力学》一一.填空题1. 限制质点运动的物体(如曲线、曲面等 )称为( 约束 )。
2.惯性力( 约束 )对应的反作用力,( 称作 )牛顿第三定律。
3. 如果力只是位置的函数,并且它的旋度等于零,即满足0F F F z y x)(zy x =∂∂∂∂∂∂=⨯∇k j ir F 则这种力叫做( 惯性力 )。
4.真实力与参考系的选取( 无关 ),而惯性力却与参与系的选取(相关)。
5.质点系的动能等于质心的动能与各质点相对(速度矢量和)的动能之和。
6. 限制质点运动的物体(如曲线、曲面等 )称为(约束 )。
7.同一质点系中各质点之间的相互作用力称为(约束反力 )二.选择题1. e a r r θθθθ)2(&&&&+=称为质点的( C )。
a. 法向加速度 b. 切向加速度c. 横向加速度d. 径向加速度2.][)(r F m en '⨯⨯-=ωω称为Aa.平动惯性力b.离心惯性力c.科氏惯性力3. ττdtdv a =称为质点的( C )。
a. 法向加速度 b. 横向加速度c. 切向加速度d. 径加速度4. 质点系中所有内力对任一力矩的矢量和Aa. 等于零b. 不等于零c. 不一定等于零 5. e a r rr r )(2θ&&&-=称为质点的( A )。
a.径向加速度b.横向加速度c.切向加速度d.法向加速度6.质点系内力所作的功Aa. 等于零b. 不等于零c. 不一定等于零 7. n a v n ρ2=称为质点的( B )。
a. 横向加速度 b. 法向加速度c. 径向加速度d. 切向加速度8.如果作用在质点上的力都是保守力,或虽是非保守力作用但非保守力不作功或所作功之和等于零。
则质点系机械能Aa. 守恒b. 不守恒c. 不一定守恒 9.)2(v F r m c ⨯-=ω称为Aa.科氏惯性力b.离心惯性力c.平动惯性力三.简答题1.在曲线坐标系中,单位矢量和基矢有无区别若有,区别何在答:有区别,主要是角度变化。
清华大学版理论力学课后习题答案大全第9章动量矩定理及其应用

习题9-2图习题20-3图OxF Oy F gm gDdα习题20-3解图第9章动量矩定理及其应用9-1计算下列情形下系统的动量矩。
1.圆盘以ω的角速度绕O 轴转动,质量为m 的小球M 可沿圆盘的径向凹槽运动,图示瞬时小球以相对于圆盘的速度v r 运动到OM =s 处(图a );求小球对O 点的动量矩。
2.图示质量为m 的偏心轮在水平面上作平面运动。
轮心为A ,质心为C ,且AC =e ;轮子半径为R ,对轮心A 的转动惯量为J A ;C 、A 、B 三点在同一铅垂线上(图b )。
(1)当轮子只滚不滑时,若v A 已知,求轮子的动量和对B 点的动量矩;(2)当轮子又滚又滑时,若v A 、ω已知,求轮子的动量和对B 点的动量矩。
解:1、2s m L O ω=(逆)2、(1)1()(Remv e v m mv p A A C +=+==ω(逆)Rv me J R e R mv J e R mv L AA A C CB )()()(22-++=++=ω(2))(e v m mv p A C ω+==ωωωω)()()())(()(2meR J v e R m me J e R e v m J e R mv L A A A A C C B +++=-+++=++=9-2图示系统中,已知鼓轮以ω的角速度绕O 轴转动,其大、小半径分别为R 、r ,对O 轴的转动惯量为J O ;物块A 、B 的质量分别为m A 和m B ;试求系统对O 轴的动量矩。
解:ω)(22r m R m J L B A O O ++=9-3图示匀质细杆OA 和EC 的质量分别为50kg 和100kg ,并在点A 焊成一体。
若此结构在图示位置由静止状态释放,计算刚释放时,杆的角加速度及铰链O 处的约束力。
不计铰链摩擦。
解:令m =m OA =50kg ,则m EC =2m 质心D 位置:(设l =1m)m6565===l OD d 刚体作定轴转动,初瞬时ω=0lmg lmg J O ⋅+⋅=22α222232)2(212131ml ml l m ml J O =+⋅⋅+=即mglml 2532=α2rad/s 17.865==g lαgl a D 362565t =⋅=α由质心运动定理:OyD F mg a m -=⋅33t4491211362533==-=mg g mmg F Oy N (↑)0=ω,0n=Da ,0=Ox F 习题9-1图(a )(b )习题9-5解图习题9-5图9-4卷扬机机构如图所示。
第1章 张量分析(清华大学张量分析,你值得拥有)

g1 1
gi xi g2 ix1 sin x2 jx1 cos x2
g2 r
曲线坐标系:斜角直线坐标系的延伸
※三维球坐标系
(x, y, z) (x1, x2, x3)
(r, , ) (x1, x2 , x3 )
x3
r
gr g
g
x2
r x1i x2 j x3k xigi x1
新、老坐标之间的变换和逆变换: xi = xi xi'
gidxi gi' dx i'
dxi
=
xi xi'
dx i '
dx i
i'
i'
→
gi
i i'
dx
i'
g i
'
dx
i'
再由:
gidxi
g i
'
dx
i
'
→
gi'
i i'
gi
dxi'
=
xi' xi
dxi
i i
'
dx
i
→
gidxi
gi'
i i
'
dx
定义式(实体形式,几何表达):
u v u v cos
v cos
12-2 惯量矩阵

T
三 维 刚 体 动 力 学 基 础
Aij = ii ⋅ i ′j
z′
z
ri
O
mi
y′
ri′ = A ri T ′ = ∑ mi (ri′2 E − rr ′ ′ JO i i )
T = ∑ mi (ri 2 E − AT rr i i A) T = AT ∑ mi (ri 2 E − rr i i )A
确定惯性主轴的解析方法—特征值问题
第12章 矢量L 与ω一般不共线: L = J ω O O O
三 维 刚 体 动 力 学 基 础
如果ω 沿某一惯性主轴z: ω = ωz k LO =Jzω — LO与ω共线 LO = λω LO = JO ω JO ω = λ ω — 惯性矩阵的特征值问题 J x − λ − J xy − J xz ω x − J yx J y − λ − J yz ω y = 0 ω − − − J J J λ zx zy z z JO是实对称阵,必存在三个实特征值(即 为主转动惯量),相应的特征向量就是三个 惯性主轴。
思考题 - 用几何法确定中心惯性主轴
第12章
x
z
三 维 刚 体 动 力 学 基 础
y z
y
x
1 mL2 12 JC = 0 0
0 1 mL2 12 0
0 0 0
2 2 mR 5 JC = 0 0
0 2 mR 2 5 0
0 0 2 mR 2 5
ri di e
y
T = eT ∑ mi [ ri 2 E − rr i i ]e
x0
x
J e = eT JO e
理论力学答案完整版(清华大学出版社)3

之差称为静不定次数。这类问题需要补充与静不定次数相同数量的变形协调方程才能求解。 未知约束力分量的数目小于独立平衡方程的数目,这类平衡问题是不存在的。 解题要领:
(2)AD 梁上,固定铰链 A 处有 2 个约束力,辊轴铰链 B、C 和 D 各有 1 个约束力, 共有 5 个约束力,这 5 个约束力组成平面一般力系,可以列出 3 个独立的平衡方程。所以, AD 梁是 2 次静不定。
(3)曲梁 AB 两端都是固定端约束,各有 3 个共 6 个约束力组成平面一般力系,而独 立的平衡方程只有 3 个。所以是 3 次静不定。
2 要区分物体维持平衡时的摩擦力与能够产生的最大静摩擦力,两者不可混淆。 3 有摩擦时的平衡问题往往还伴随物体的翻倒问题,要全面考虑,择其合理解。 4 自锁问题通常利用摩擦角概念和二力平衡条件或三力平衡汇交定理解题,具有几何直观、 概念清楚和便于理解的特点。关键是要确定临界平衡时的摩擦角。 5 滚动摩擦问题的考虑类似于滑动摩擦问题。
FA = 63.22 kN . ∑ Fy = 0, FA + FC sin 60o + FB − F1 sin 60o − F2 − q × 3 = 0 ,
FB = 88.74 kN .
题 3-3(a)图
(b)解:以 AB 以梁为研究对象,画受力图,列平衡方程
∑ Fx = 0 , FD cos 45o − FB cos 45o − F2 cos30o = 0 , ∑ mC = 0, FD sin 45o × 4 + FB sin 45o × 8 − M − F1 × 2
理论力学答案完整版(清华大学出版社)6

v A = OA ⋅ ω = 1.2 m/s , AB 杆作平面运动,在图示瞬时,由 v A , v B 知, AB
杆作瞬时平移,有
vB = v A = 1.2 m/s . BE 作平移, vE = vB . 有 v D , v E 找得 ED 杆速度瞬
心为 D 点.在图示位置上可得
题 6-6 图
OE = AB − OA − EB = OD , o 由此可知 ∠ODE = ∠OED = 30 , ED 杆角速度为
( xC , y C ,ϑ ) 确定,所以 AB 杆的平面运动方程为: xC = r cos ω 0 t , y C = r sin ω 0 t , θ = ϕ = ω0t .
题 6-1 图
6-2 杆 AB 的 A 端沿水平线以等速 v 运动,在运动时杆恒与一半圆周相切,半圆周半径为 R,如图所示。如杆与水平线的夹角为 θ ,试以角 θ 表示杆的角速度。 解: 解法一:杆 AB 作平面运动。选取 A 为基点, 由速度基点法 vC = v A + vCA , 作图示几何关系,图中 v A = v ,解得
r1 = r2 = 300 3 mm, O1 A = 750 mm ,AB = 1500 mm ; 又平衡杆的角速度 ω O1 = 6 rad/s。 知:
曲柄 OB 和齿轮 1 的角速度。 求当 θ = 60 和 β = 90 时,
o o
解:由图所示可知:点 C 是 AB 杆和轮 II 的速度瞬心, 故
2
2
ωDE =
vE 10 = 3 = 5.77 rad/s , CE 3 3.6 = 2.08 m/s , 3
D 点的速度为
vD = CD ⋅ ωDE =
曲柄 OD 的角速度为
清华大学版理论力学课后习题答案大全_____第6章刚体平面运动分析汇总

清华⼤学版理论⼒学课后习题答案⼤全_____第6章刚体平⾯运动分析汇总6章刚体的平⾯运动分析6-1 图⽰半径为r 的齿轮由曲柄OA 带动,沿半径为R 的固定齿轮滚动。
曲柄OA 以等⾓加速度α绕轴O 转动,当运动开始时,⾓速度0ω= 0,转⾓0?= 0。
试求动齿轮以圆⼼A 为基点的平⾯运动⽅程。
解:?c o s )(r R x A += (1) ?sin )(r R y A +=(2)α为常数,当t = 0时,0ω=0?= 0 221t α?=(3)起始位置,P 与P 0重合,即起始位置AP ⽔平,记θ=∠OAP ,则AP 从起始⽔平位置⾄图⽰AP 位置转过θ??+=A因动齿轮纯滚,故有?=CP CP 0,即θ?r R = ?θr R =, ??rr R A += (4)将(3)代⼊(1)、(2)、(4)得动齿轮以A 为基点的平⾯运动⽅程为:+=+=+=222212sin )(2cos )(t r r R t r R y t r R x A A A α?αα6-2 杆AB 斜靠于⾼为h 的台阶⾓C 处,⼀端A 以匀速v 0沿⽔平向右运动,如图所⽰。
试以杆与铅垂线的夹⾓θ表⽰杆的⾓速度。
解:杆AB 作平⾯运动,点C 的速度v C 沿杆AB 如图所⽰。
作速度v C 和v 0的垂线交于点P ,点P 即为杆AB 的速度瞬⼼。
则⾓速度杆AB 为hv AC v AP v ABθθω2000cos cos ===轮A 和垫滚B 与地⾯之间以及垫滚B 与拖车之间⽆滑动。
解:R v R v A A ==ωR vR v B B 22==ωB A ωω2=6-4 直径为360mm 的滚⼦在⽔平⾯上作纯滚动,杆BC ⼀端与滚⼦铰接,另⼀端与滑块C 铰接。
设杆BC 在⽔平位置时,滚⼦的⾓速度ω=12 rad/s ,θ=30?,?=60?,BC =270mm 。
试求该瞬时杆BC 的⾓速度和点C 的速度。
习题6-1图习题6-2图习题6-2解图习题6-3解图习题6-3图v A = vv B = v ωAωB习题6-6图习题6-6解图解:杆BC 的瞬⼼在点P ,滚⼦O 的瞬⼼在点D BDv B ?=ωBPBD BP v B BC ?==ωω =30sin 27030cos 36012 rad/s 8=PC v BC C ?=ωm/s 87.130cos 27.08=??=6-5 在下列机构中,那些构件做平⾯运动,画出它们图⽰位置的速度瞬⼼。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
x
y
A
y0
Je eT JOe
Je J xl2 J ym2 Jzn2 2J xylm 2J yzmn 2J zxnl
转轴:研究不同坐标系中惯性矩阵的关系
第12章
三 维 刚 体 动 力 学 基 础
旧系Oxyz —A 新系O'x'y'z' i = iA Aij ii ij
ri AT ri
JO mi (ri2E ririT ) mi (ri2E AT ririT A) AT mi (ri2E ririT ) A
z
z
O
x x
mi
ri y
y
JO AT JO A
若保持坐标原点不变,改变坐标轴相对于物 体的方位,则惯性矩阵的元素将随之变化。
主轴坐标系
在惯性矩阵中, 若 Jxy = Jyx = 0; Jzx = Jxz = 0; Jzy = Jyz = 0 则Oxyz称为主轴坐标系,三轴称为惯性主 轴, Jx , J y , Jz 称为主转动惯量。惯性矩阵为
Jx 0 0 J 0 Jy 0
0 0 Jz
若点O与质心C重合,则轴Cx、Cy、Cz称为 中心惯性主轴,相应的转动惯量Jx、Jy、Jz 称为中心主转动惯量。
0
1 4
mR
2
0
0
1 2
0 mR2
z
c
y
a
b
J
C
1 12
m(b2 0 0
c2
)0
1 12
m(a
2
0
c
2
0
)0 112m(a2
b2
)
第12章
三 维 刚 体 动 力 学 基 础
思考题 - 用几何法确定中心惯性主轴
x
y
z
JC
1 12
mL2 0 0
移心:研究对两点的转动惯量的关系
第12章
三 维 刚 体 动 力 学 基 础
ri ρi s ri i s
JO mi (ri2 E ri riT ) mi[(i s)T (i s)E (i s)(i s)T ]
mi[(i2 iT s sT i s2 )E (i iT i sT siT ssT )]
mi yi zi 0
如果均质刚体有对称轴, 则此轴是轴上各点的惯性 主轴
x mi
xi
z i
0
mi yi zi 0
z1 z2 对称面 o1 o2 P
z 对称轴
y
思考题 - 用几何法确定中心惯性主轴
第12章
三 维x 刚 体 动 力 学x 基 础
z
y JC
1 4
mR2 0
0
0
1 12
mL2
0
0 00
z
x
y
JC
2 5
mR2 0
0
0
2 5
mR2
0
0
2 5
0 mR
2
第12章
三 维 刚 体 动 力 学 基 础
确定惯性主轴的解析方法—特征值问题
矢量LO与一般不共线: LO = JO 如果沿某一惯性主轴z: = z k
LO=Jz — LO与共线
第2节
惯量矩阵
2020年2月29日
第12章
三 维 刚 体 动 力 学 基 础
对过O点任意轴e的转动惯量
e l m nT
Je midi2
z0
mi
mi[ri2 (e ri )(ri e)] z ri di
mi[eT ri2Ee eT ririTe]
e
O
eT mi[ri2E ririT ]e x0
LO = Jx x i + Jy y j + Jz z k
求任意点惯量矩阵的一般方法是:先求出中 心主轴坐标系中的惯量矩阵,再用移心和转 轴变换求解。
第12章
三 维 刚 体 动 力 学 基 础
确定惯性主轴的几何方法
如果均质刚体有对称平面,
则平面上某点的惯性主轴 之一必与平面垂直
mi xi zi 0
惯性主轴。
第12章
三 维 刚 体 动 力 学 基 础
返回
JO JC m(s2E ssT )
Jo J c J m (Jm 为质心C对O的惯量矩阵)
J z J z md 2
(转动惯量的移轴公式)
J xy J xy msxsy
Z
z mi
在若干平行轴中,刚体对通
过质心之轴的转动惯量最小
O
X
ri s
ρi
y
xC
Y
第12章
三 维 刚 体 动 力 学 基 础
LO =
LO = JO
JO = — 惯性矩阵的特征值问题
J x J xy J xz x
y
0
J zx J zy J z z
JO是实对称阵,必存在三个实特征值(即 为主转动惯量),相应的特征向量就是三个
