光在各向同性介质及其界面所发生的现象
光通过各向同性介质及其界面所发生的现象课件

当光从折射率较小的介质射入折射 率较大的介质时,若入射角大于临 界角,光会发生全反射现象。
光的散射与吸收
光的散射
吸收光谱
光在各向同性介质中传播时,由于微 小颗粒或分子的存在,使得光线方向 发生改变,形成散射现象。
不同物质对光的吸收具有选择性,通 过分析物质对不同波长光的吸收情况 ,可以得到该物质的吸收光谱。
当光遇到障碍物或通过小孔时,光波 会绕过障碍物或小孔边缘,产生衍射 现象,形成明暗相间的衍射条纹。
THANKS
[ 感谢观看 ]
光的速度
光在各向同性介质中的传 播速度与介质折射率有关 ,折射率越大,光速越小 。
光的偏振
在各向同性介质中,自然 光经过反射、折射后仍为 自然光,不发生偏振现象 。
光的折射与反射
折射定律
当光从一种介质进入另一种介质 时,入射角与折射角遵循斯涅尔
定律。
反射定律
光在各向同性介质的界面上发生反 射时,反射光线与入射光线、法线 在同一平面上,且反射角等于入射 角。
全反射
当光从一个折射率较小的介质射入折 射率较大的介质时,如果入射角大于 临界角,光将被完全反射回原介质, 不进入折射率较大的介质。
临界角
当光射到界面时,入射角等于临界角 的光线会发生全反射。
光的干涉与衍射现象
光的干涉
当两束或多束相干光波相遇时,它们 会相互叠加,形成明暗相间的干涉条 纹。
光的衍射
光的全反射
01
当光从一个折射率较小的介质射 入折射率较大的介质时,如果入 射角大于临界角,光将会被完全 反射回原介质,不进入新介质。
02
全反射现象在光学、光纤通信等 领域有广泛应用,如光纤通信就 是利用光的全反射原理传递信息 的。
光传播的基本定律

光传播的基本定律
光传播的基本定律包括以下几个方面:
1. 光的直线传播定律:光在各向同性介质中沿直线传播。
当光线遇到边界时,可能会发生折射、反射和漫射等现象。
2. 折射定律(斯涅尔定律):当光从一个介质传播到另一个介质时,入射角、折射角和两个介质的折射率之间有一定的关系,由斯涅尔定律描述。
该定律可以用来解释光在透明介质中的传播现象。
3. 反射定律(兰伯特定律):光在边界面上发生反射时,入射角、反射角和两个介质之间的界面法线之间有一定的关系,由兰伯特定律描述。
该定律可以用来解释光在镜面上的反射现象。
4. 色散定律:不同波长的光在介质中传播时会发生不同的折射现象,即光的色散。
色散定律描述了光的折射角和波长之间的关系。
5. 光的干涉与衍射定律:当光通过狭缝、缝隙或物体表面时,会发生干涉和衍射现象。
干涉定律和衍射定律描述了这些现象中光的相干性和波的绕射效应。
这些定律是光学领域中描述光传播的基本规律,在理论研究和光学应用中有重要的指导作用。
光从晶体到各向同性介质界面的反射和透射

第2 9卷第 1 期辽 宁 石 油 化 工 大 学 学 报Vo l . 2 9 No . 12009 年 3 月J O U RNAL O F L IAON IN G U N IV ER SI T Y O F P E T ROL EU M & C H EM I CAL T E C H NOL O GY Mar . 2009文章编号 :1672 - 6952 (2009) 01 - 0091 - 06光从晶体到各向同性介质界面的反射和透射裴芳芳 , 陈西园(辽宁石油化工大学理学院 ,辽宁抚顺 113001)摘 要 : 为了分析光在晶体界面的能量损失 ,给出了一种求解反射率和透射率的方法 。
分析了光从单轴晶体 入射到各向同性介质表面时的折射和反射 ,根据在界面处电磁场的边界条件和位相匹配条件 ,得到了在晶体界面的 菲涅耳公式 。
在晶体光轴取向任意的条件下 ,给出了反射的 o 光 、e 光以及折射光的偏振状态和振幅以及表明各光束间能量关系的折射率和反射率的理论表达式 ,为晶体器件特性的研究提供了有力的理论工具 。
数值模拟表明 ,所 得结果满足能量守恒 ;射入各向同性介质中光的电场 (或磁场) 与原入射光的电场 ( 或磁场) 不再平行 ; 光轴的取向和 入射角的大小对折射光的偏振方向和能量有重大影响 。
关键词 : 单轴晶体 ; 边界条件 ; 透射率 ; 反射率 中图分类号 : TN012 ; O436文献标识码 : ARef l ectio n a nd Ref ractio n at Int e r f a ce of Cr y s t al :Fro m Cr y s t al to Iso t ropic Me d i u mP EI Fa n g - f a n g , C H EN Xi - yua n( S c h ool o f S cie n ce , L i aoni n g U n i ve r s i t y o f Pet role u m & Che m i c a l Tec h n ol o g y ,Fus h u n L i a oni n g 113001 , P. R. Chi n a )R e cei ve d 5 J u n e 2008 ; re v i se d 10 Oct o be r 2008 ; acce p t e d 20 Oct o be r 2008Abstract :In o r der to analyze t h e ener g y lo s s of a beam at cr y st al surf a ce s , a met h o d wa s p r opo s ed to calculat e t h eco r r e s po n di n g ref l ectivit y and t r a n smi s sivit y . Acco r d ing to t h e elect r o m agnet ic b o u n da r y co n dit io n s and t h e p h a s e matchingco nditio n s , ref lectio n a nd ref ractio n of a beam i ncident f ro m a cr yst al upo n an i so t ropic medium were st udied , and t h e Fre s nelfo r mula s at t he int erf ace bet ween t he cr y st al and t he i so t r opic medium were deduced. A s t he o rient atio n of op tical a x i s i sa r bit ra r y , t he pola rizatio n st at es a nd t he amp lit udes of t he o ray a nd e ray a nd t he ref ract ed ray were given , a nd t h e t h eo r eticalexp ressio n s of t he ref lectivit y and t h e t ra n smi ssivit y rep re senting ener gy relatio n s bet ween t h e ray s were o bt ained , w h ichp ro v ide a t h eo ret ical ba si s fo r develop ing and app lying cr yst al device s. N umerical simulatio n s sho w t hat t he re s u lt s a r eacco r dant wit h co n servatio n of ener gy ; elect rical f ield o r magnet ic f ield of t he ray ref ract ed to t he i so t rop ic med ium d oes n o t p a rallel to t he elect ric f ield o r t he magnet ic f ield of o riginal incident ray ; t he directio n of op t ical axi s a nd t he magnit u d e ofincident a n gle have a great eff e ct o n t h e ener g y a n d t h e po la r izatio n directio n of t h e ref racted ray. K ey words : U n iaxial cr y st al ; Bo u nda r y co n ditio n ; Tra n smi s sivit y ; Ref l ectivit yC o r r espo n ding a ut h o r . Tel . : + 86 - 413 - 6863324 ; f a x : + 86 - 413 - 6860766 ; e - mail :p e iff 222 @to m . co m随着激光技术的发展 ,光学偏振元件的大量使用 ,需要研究光在晶体表面反射和折射问题的情况越来越多[ 1 - 5 ]。
光在两种介质界面上传播特性分析

第一章引言1.1课题的目的和意义光入射到不同介质的表面时会发生反射与折射,反射与折射时振动相位的变化;入射光与折射光的振幅与光强的关系;倏逝波和全反射时的能量流动情况;以及界面反射与折射对光的偏振态的影响;还有光在正负折射率介质上的传播情况。
该课题的要求是分别对以上几个方面的问题进行探讨,并得出结论。
1.2目前的状况及前景首先从问题的本身来说,光在两种介质界面上传播机理,是光学里非常普遍的现象。
随着光学的反展,使得它由古典几何光学问题,发展成为现代光学问题。
由以往的以几何光学理论进行研究,发展到现在的以电磁波的理论去研究。
因研究方法的改变,研究的层次也在改变,由以往的简单的光路问题,延展到振幅与光强问题、振动相位问题、偏振态问题以及在新材料上的应用(出现了负折射率的材料)。
受传统教材的限制,这些问题常常没有得到全面的研究。
1.3课题研究的内容为了更好的学习和研究两种介质表面上光的传播特性。
总的来说,本文分别在五个大的部分进行深入的探讨:第一部分:利用费马原理从光程的角度来阐述光的传播规律,使得其更简明更具有普遍意义。
费马原理指出光线从A点到B点,是沿着光程为极值的路径传播的。
第二部分:利用菲涅耳公式对反射、折射时的振动相位变化关系进行了探讨,从菲涅耳公式出发,分两种情况进行了讨论。
第一种情况:光由光疏介质入射到光密介质时光振动矢量的相位变化;第二种情况:光由光密介质入射到光疏介质时光振动矢量的相位关系。
第三部分:对入射光与折射光的振幅、光强进行了分析。
利用菲涅耳公式和电磁场能量、能流理论,分析光在两种同性介质分界面上的入射、反射和折射时的现象,并得出了两个结论:(1)在一定条件下,折射光的振幅可大于入射光的振幅;(2)在一定条件下,折射光的光强可以大于入射光的光强。
第四部分:探讨全反射时出现的倏逝波,并应用Maxwell的电磁理论,对光的全反射现象进行了推导,并得到与全反射密切相关的倏逝波,并对倏逝波进行了详细的讨论。
一、 菲涅耳公式(Fresnel formula)
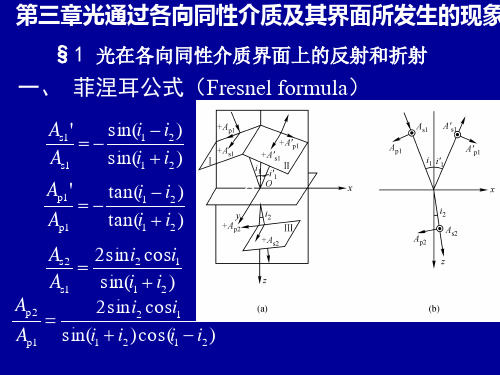
1
4
紫光的散射强度大约是红光的10倍。
4. 偏振性
O z
y p B’
y D A’ B
AP z
x
D’ 实验 自然光入射到散射物质中,观察到:
正侧方(z)线偏振 斜方向(C)部分偏振 对着x方向(x)自然光
解释 用电偶极子次级辐射可解释 实验现象
分解成 +
被微粒散射时,各方向上的振幅可看成以上 两个分振动的合成。 退偏振 线偏振光照射某些气体或液体,从侧向 观察时,散射光变成部分偏振的,称为退偏 振。其机理是介质分子本身是各向异性的。
2.正交棱镜法
研究色散,目的是寻找 n f ( )的函数形式。 正交棱镜装置
三棱镜P1→AH(光谱) P1 P2→A’H’(光谱) n f ( ) ——弯曲光谱的形状。
3.正常色散与反常色散(Normal dispersion and abnormal dispersion)
正常色散曲线的信息
dut余虹一菲涅耳公式fresnelformula第三章光通过各向同性介质及其界面所发生的现象1光在各向同性介质界面上的反射和折射布儒斯特角线偏振光四用反射和折射法获得偏振光布儒斯特定律玻璃片堆要提高反射线偏振光的强度可利用玻璃片堆的多次反射
第三章光通过各向同性介质及其界面所发生的现象 §1 光在各向同性介质界面上的反射和折射 一、 菲涅耳公式(Fresnel formula)
dI Idx dI a Idx I dI d I I 0 a dx a 为吸收系数 I I 0 e a d ,
0
d
a AC ,式中A是一个与浓度无关 稀溶液:
的常量,C为溶液的浓度。
§ 3 光的色散(Dispersion of Light) 1.色散的特点
河北工业大学 2020 年硕士研究生招生考试611光学

河北工业大学2020年硕士研究生招生考试自命题科目考试大纲科目代码:611科目名称:光学适用专业:物理学一、考试要求本《光学》考试大纲适用于河北工业大学理学院物理学学科研究生招生专业课考试。
主要考察对于光学的基本概念、方法及运用所学知识分析问题和解决问题的能力。
本科目考试的重点是要求考生掌握光学的基本概念、基本理论和基本计算,能够应用光学的基础知识,分析和计算光学问题。
二、考试形式试卷题型主要包括计算题、分析论述题等。
考试时间为3小时,总分为150分。
三、考试内容(一)几何光学几何光学的基本定律和费马原理,成像的基本概念;光在平面上的反射和折射,棱镜;傍轴条件下的单球面折射成像,薄透镜的成像公式和放大率;共轴球面系统;共轴球面系统傍轴成像的矩阵方法;光学系统中的光阑,像差。
(二)光波场的描述简谐波的数学描述,波动方程和叠加原理;傅里叶分析,光的偏振态。
(三)光通过各向同性介质及其界面所发生的现象光在各向同性介质界面的反射和折射;菲涅尔公式,布儒斯特定律;光的吸收,光的色散和散射。
(四)光的干涉波的叠加和干涉,相干光波的条件和获得方法;杨氏实验,两束平行光的干涉;薄膜干涉,等倾干涉和等厚干涉;迈克尔逊干涉仪;光学薄膜;光拍。
(五)光的衍射光的衍射现象,惠更斯---菲涅尔原理;衍射现象分类;夫琅禾费正弦光栅衍射,夫琅禾费单缝、矩形孔和圆孔衍射;夫琅禾费多缝衍射,菲涅尔圆孔和圆屏衍射。
(六)光在各向异性介质中的传播双折射和双反射;产生线偏振光的元件,用波片改变光的偏振态;偏振态的检测,偏振光的干涉;旋光现象及其应用。
四、参考书目游璞,于国萍.光学.北京:高等教育出版社,2003.五、特别提示考生需要携带无编程无存储无记忆功能的计算器。
光通过各向同性介质及其界面所发生的现象

光的折射
总结词
当光从一种介质进入另一种介质时,由于速度的改变,光会改变其传播方向,产生折射现象。
详细描述
光的折射是指光从一个介质进入另一个介质时,由于速度的改变而发生方向改变的现象。折射角的大 小与入射角的大小、介质的折射率等因素有关。当光线从折射率较小的介质进入折射率较大的介质时 ,折射角小于入射角;反之,折射角大于入射角。
光的折射与反射
折射定律
当光从一种介质进入另一种介质时,会发生折射现象,折射 角与入射角、介质折射率有关。
反射定律
光在界面上发生反射时,反射角等于入射角,与界面法线垂 直。
光的散射与吸收
光的散射
光在介质中传播时,由于微小颗粒或分子的散射作用,使得光向各个方向散射。
光的吸收
光在介质中传播时,部分光能被介质吸收转化为其他形式的能量,导致光强减 弱。
详细描述
热辐射是由于物质的原子或分子的振 动和转动状态发生变化而产生的电磁 波。热辐射的强度和波长与物质的温 度有关,是热传递的一种方式。
光化学反应
总结词
光化学反应是指光子与物质相互作用时,激 发物质分子并导致化学反应发生的现象。
详细描述
光化学反应需要特定波长的光子激发,使物 质分子吸收光能后发生化学键断裂或形成, 从而生成新的物质。光化学反应在光合作用、 染料敏化太阳能电池等领域有重要应用。
自由空间光通信
利用激光在空气中传输信 息,适用于短距离、高速 率的通信。
水下光通信
利用光在水中传输信息, 适用于水下探测和通信。
光学传感
光电传感器
利用光电效应将光信号转换为电信号,用于检测 物体是否存在或移动。
光纤传感器
利用光纤中光的传输特性变化检测物理量,如温 度、压力、位移等。
第三章光在各向同性介质及其界面所发生的现象

E′s n1 cosi1 −n2 cosi2 sin( i1 −i2 ) 1 = rs = =− E s n1 cosi1 + n2 cosi2 sin( i1 +i2 ) 1 2n1 cosi1 2cosi1 sin i2 tp = = = E p n2 cosi1 + n1 cosi2 sin( i1 +i2 ) cos(i1 −i2 ) 1 E2s 2n1 cosi1 2cosi1 sin i2 ts = = = E s n1 cosi1 + n2 cosi2 sin( i1 +i2 ) 1
n2 透 光 2 = I2σ cos i2 = 射 W 2
′ ′2 W E1 1 反 率 = 射 R = = r2 2 W E1 1 W n2 cos i 2 E2 2 透 率 = 射 T = W n1 cos i1 E12 1
例 E = Aexp[−i(ωt −ϕ)] :1 E2 = Aexp[−i(ωt −ϕ −π)] = −Aexp[−i(ωt −ϕ)] E2 Aexp[−i(ωt −ϕ −π)] = = −1 E Aexp[−i(ωt −ϕ)] 1
振幅比中出现负号——表示它们之间有 振幅比中出现负号——表示它们之间有 的位相差。 π 的位相差。
反射光E 反射光 1’ Er = E1 exp −i(ω1t − k1 ⋅ r )] ′ ′ ′ [ 折射光E2 Et = E2 exp −i(ω2t − k2 ⋅ r )] 折射光 [ 已知 E 、 1、 1 ω k。 1 求: E′、 1、 1、 2、 2、 2。 ω′ k′ E ω k 1 可知
Es 1
n cos i1 + n2 cos i2 1
例2.光波掠入射
i1 ≈ 90º ; rp= rs= -1;
光波在各向同性介质界面的反射和折射 ppt课件

ppt课件
17
(2)大角度入射(掠射)的反射特性
由图1-24(a),有
n1<n2,光疏到光密。θ 1≈900的掠射情况。
rs 0, rp 0
在入射点处,反射光矢量Er与入射光矢量Ei方向近似相 反,将产生半波损失。 n1>n2,光密到光疏。掠射θ 1≈900>θ c。全反射。 在入射点处,反射光产生半波损失的条件:
ki sin i kr sin r , ki sin i kt sin t n1 sin i n1 sin r , n1 sin i n2 sin t
反射定律
T 1-21
折射定律
描述光在介质面上的传播方向
ppt课件 3
1.2.2 菲涅耳公式
描述入射光、反射光和折射光 之间的振幅、相位关系。 1.s分量和p分量 垂直入射面的振动分量- -s分量 T 1-23 平行入射面的振动分量- -p分量 规定分量和分量的正方向如图所示 2.反射系数和透射系数 定义:s分量、p分量的反射系数、透射系数分别为
① n1<n2,光疏到光密。先考察θ 1=00的正入射情况。 由图1-24(a),有
rs 0, rp 0
考虑P30 T1-23,有关光场振动正方向的规定,则有
可见:在入射点处,合成的反射光矢量Er相对入射光场Ei反 向,相位发生π突变,或半波损失。 对于θ 1非零、小角度入射时,都将近似产生π相位突变,或 半波损失。
入射光中s分量和p分量的透射率(不相同)为
n2 cos 2 2 sin 21 sin 2 2 Ts ts n1 cos1 sin 2 (1 2 )
n2 cos 2 2 sin 21 sin 2 2 Tp tp 2 n1 cos1 sin (1 2 ) cos2 (1 2 )
Fresnel(菲涅尔)公式

n 3
2、菲涅尔菱形棱镜 Fresnel Prism
n=1.5
i i1
1
i =48.50 or 54.50
1
δ=δ -δ =450 ps
1/4 波片:线偏振入射光转化为椭圆偏振光。
13
全内反射情况下的透射场
P 1
P' 1
S 1
n 1
k 1
i
1
i'
1
S' 1
k' 1
n 2
k
x
i
2
2
P 2
z
S 2
i1
i1
−1
−
ωt
⎞⎤ ⎟⎟⎠⎥⎦⎥
=
exp
⎛ ⎜⎜⎝
∓k2
z
n12 n22
sin2
i1
⎞ − 1 ⎟⎟⎠
⋅ exp
⎡⎣i
( k2 x
sin
i2
−
ωt
)⎤⎦
因此,透射场具有如下形式:
⎛
( ) E 2
S P
(r, t )
=
( ) A 2
S P
exp
⎡⎣i
(k2
⋅r
−ωt )⎤⎦
=
( ) A 2
S P
exp ⎜⎜⎝
=
n2 2
ε0 μ0
A2 2 cos i2
R = W1′ = W1
A1′ 2 A1 2
=
r2
T = W2 = n2 cos i2 A2 2 = n2 cos i2 t 2 W1 n1 cos i1 A1 2 n1 cos i1
R+T =1
σ cosi 1
σ cosi 1
第五章光在各向同性介质界面上的反射和折射 光学课件

r
1.0
内反射垂直入射时无相位变化
i1 00
反射光与入 射光同相位
0.2 0.2
1.0
rs
rp iB i c
公式
90 0 i1
E s1
E P1 E 1 E s1
E P 1 E 1
p
s
0
iB i c 90 0
i1
光在各向同性的介质界面反射时, 一般会引起偏振态的变化:
若知入射光的偏振态和入射角, 可以由其反射特征辨别 反射光的偏振态, 方法可以分为两步:
得 p 分量 振幅反射比:
rp
Ep1 Ep1
tg(i1i2), tg(i1i2)
振幅透射比:
tp
Ep2 Ep1
2sini2cois1. sini1(i2)
返回
(b) 讨论S分量
对于 s 分量, 同理有
H pc 1 io 1 H sp c 1 io 1 H spc 2 io 2 , s
Es1Es1Es2 .
若圆偏振光的光矢量随时间变化是右旋的,
则这种圆偏振光叫做右旋圆偏振光,反之,叫做
左旋圆偏振光. 若光矢量在时间上是右旋的,
则在空间上一定是左旋, 即“空左时右”.
y
y
x
z
0
x
ห้องสมุดไป่ตู้
在垂直于光传播方向的平面 内,右旋圆偏振光的电矢量
随时间变化顺时针旋转
右旋圆偏振光在 三维空间中电矢量左旋
(3) 椭圆偏振光
在垂直于光传播方向的固定平面内, 光矢量的 方向和大小都在随时间改变, 光矢量的端点描出一 个椭圆, 这样的 偏振光 叫做椭圆偏振光.
y
以上三种偏振光称为完 全偏振光, 可以由两个互相 垂直的,有相位关系的, 同 频率的线偏振光合成. 反之, 一完全偏振光也可以分解为 两个任意方向, 相互垂直, 有相位关系的同频率的线偏 振光.
光的直线传播原理

光的直线传播原理光的直线传播原理可以从两个方面来解释,分别是几何光学和波动光学。
首先,从几何光学的角度来看,光的直线传播原理是基于光在均匀介质中的传播规律。
根据直线传播原理,光在同质、各向同性的均匀介质中沿直线传播。
这意味着光在传播过程中不会发生偏折,也不会发生弯曲。
这个原理可以通过光的射线模型来解释,即将光传播的方向看作一条射线,这条射线沿直线传播直到遇到界面或其他介质。
这个原理主要是由光的物理性质决定的。
光是由电磁波组成的,其传播的速度在真空中是一个常数,即光速。
当光进入均匀介质中时,由于介质密度的变化引起光速的改变,但是光的传播方向不会发生改变,仍然沿着直线传播。
这是因为光的传播速度的改变只会导致光的频率和波长的改变,而不会影响光的传播方向。
另外,还有一个与几何光学相关的概念是光的反射和折射。
当光在介质的表面遇到边界时,根据光的反射和折射定律,光会发生反射和折射现象。
反射是指光与界面发生碰撞后沿原射线方向返回的现象,折射是指光经过界面后改变传播方向的现象。
这些现象都可以用几何光学中的射线来解释和理解。
然而,光的直线传播原理并不完全适用于一些特殊情况,比如在不同介质的交界面上会发生光的偏折现象。
这可以通过其他光的特性,比如波动性来解释。
从波动光学的角度来看,光的传播可以视为一种波的传播。
根据波动光学的原理,光是一种横波,它沿着传播方向传播,同时也沿垂直于传播方向的方向进行振动。
这个振动可以用波长、频率和振幅来描述。
当光从一种介质传播到另一种介质时,由于介质密度的变化,光的传播速度会发生改变,这将引起光波的折射现象。
根据折射定律,光从一种介质射向另一种介质时,入射角和折射角之间有一个确定的关系,这是由光在介质中传播速度的改变引起的。
这个现象在波动光学中称为光的折射。
此外,光的直线传播原理也与光的传播距离有关。
在传播距离很短的情况下,比如光在一个均匀介质中传播,由于物理尺寸的影响可以忽略不计,光的传播可以近似为直线传播。
光在不同介质中的传播特性

光在不同介质中的传播特性光是一种电磁波,它在不同介质中的传播特性是我们研究光学的重要内容。
不同介质对光的传播速度、折射和反射等产生不同的影响。
本文将从这些方面来讨论光在不同介质中的传播特性。
一、光在空气中的传播特性在空气中,光的传播速度非常快,约为每秒30万公里。
这是因为空气是一种低密度的介质,其中没有太多分子和原子来干扰光的传播。
所以在日常生活中,我们看到的光照明可以瞬间到达我们的眼睛,使我们能够清晰地看到周围的物体。
当光从一种介质射向另一种介质时,会发生折射现象。
在光从空气射入水中时,会发生折射现象。
这是因为光在不同介质中的传播速度不同。
当光从空气射入水中时,由于水的密度较大,光的传播速度变慢。
根据折射定律,光线在折射时会发生弯曲,即发生折射。
二、光在水中的传播特性光在水中的传播速度比在空气中要慢,约为每秒22万公里。
这是由于水的分子较空气的分子密集,导致光需要与更多的分子发生相互作用,从而减慢传播速度。
在水中,光线也可以发生折射和反射的现象。
折射是当光从一种介质射向另一种介质时,由于传播速度的不同而改变方向的现象。
在光从水射入空气时,由于水中的传播速度较慢,光线会朝着垂直于水面的方向弯曲,即向上倾斜。
这是因为光在射入空气时恢复了较快的传播速度。
反射是当光遇到界面时,一部分光线被反弹回原来的介质中的现象。
在光从水射入空气时,一部分光线会被反射回水中。
根据反射定律,入射角等于反射角。
入射角是光线与法线(垂直于界面的线)的夹角,反射角是光线与法线的夹角。
三、光在玻璃中的传播特性光在玻璃中的传播速度比在空气和水中都要慢,约为每秒20万公里。
这是因为玻璃是一种高密度的介质,其中的分子更加紧密,抵抗光的传播速度。
在玻璃中,光线也会发生折射和反射的现象。
折射定律适用于光从空气或水射入玻璃中。
光线在从空气或水射入玻璃中时,会向法线方向弯曲。
这是因为光的传播速度在玻璃中更加缓慢。
反射现象也适用于光从空气或水射入玻璃中。
第1章光在各向同性介质中的传输特性

第 1 章 光在各向同性介质中的传输特性 图 1-2 平面波图示
第 1 章 光在各向同性介质中的传输特性
2)
(1) 单色平面光波的三角函数表示 (1-20)式是波动方程在平 面光波情况下的一般解形式,根据具体条件的不同,可以采取 不同的具体函数表示。 最简单、 最普遍采用的是三角函数形 式,即
f=Acos(ωt-kz)+Bsin(ωt+kz)
令
p z vt
可以证明
q z vt
p
1 2
z
1 v
t
q
1 2
z
1 v
t
因而,上面的方程变为 2 f 0 pq
第 1 章 光在各向同性介质中的传输特性
求解该方程,f可表示为
f f1( p) f2(q) f1(z vt) f2(z vt) (1-20)
对于式中的f1(z-vt), (z-vt)为常数的点都处于相同的振动状态。 如图1-2(a)所示,t=0时的波形为Ⅰ,t=t1时的波形Ⅱ相对于波形 Ⅰ平移了vt1, ……。由此见,f1(z-vt)表示的是沿z方向、以速度v 传播的波。类似地,分析可知f2(z+vt)表示的是沿-z方向、以速度 v传播的波。将某一时刻振动相位相同的点连结起来,所组成的 曲面叫波阵面。由于此时的波阵面是垂直于传播方向z的平面(图 1-2(b)),所以f1和f2是平面光波,(1-20)式是平面光波情况下波动 方程的一般解。在一般情况下,沿任一方向k、以速度v传播的平 面波,如图1 - 2(c)所示。
第 1 章 光在各向同性介质中的传输特性
第 1 章 光在各向同性介质中的传输特性
1.1 光波的特性 1.2 光波在各向同性介质界面上的反射和折射 1.3 光波在金属表面上的反射和折射
高中物理 光的干涉(3)

n2 cos i2 A22 n1 cos i1 A12
n2 cos i2 n1 cos i1
t2
按照能量守恒: W1 W1'W2
RT 1
可以证明:
Rs Ts 1
Rp Tp 1
设光从空气垂直射向折射率为1.5的玻璃的表面:
n1 1, n2 1.5
R
r2
1 2
c 0n1 A12
cos i1
从界面上带走的能量:
I2
W1'
I1'cos i1
1 2
c 0n1 A1'2
cos i1
W2
I2
cos i2
1 2
c 0n2 A22
cos i2
反射率R:
R W1' W1
I1' I1
A1'2 A12
r2
透射率T:
T
W2 W1
I2 cos i2 I1 cos i1
2n1 cos i1
n2 cos i1 n1 cos i2
在反射和折射过程中,p、s两个分量的振动是相互
独立的。
半波损失的解释
几种特殊的反射情况:
• n1< n2,在接近正入射或掠入射下,反射
光的合成振动相对于入射光的合成振动发生 了的相位突变,或称半波突变。
相位差对应于半个波长的光程差,也 称半波损失。
1.5 光在各向同性介质界面上的反射和折射
菲涅耳公式
1823年法国的菲涅耳把光当 作弹性波,导出了反射光和透射 光的相对振幅,进一步说明了反 射定律和折射定律。
物理光学-在各向同性介质界面上反、折射(1.2.1-2)
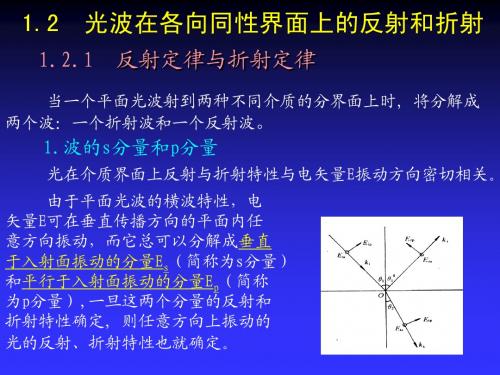
2.菲涅耳公式
消去Ers分量
⇒ ts =
[Eis − ( Ets − Eis )]n1 cosθ1 = Ets n2 cosθ 2
Ets 2 n1 cos θ1 2 n1 cos θ1 = = Eis n1 cos θ1 + n2 cos θ 2 n1 cos θ1 + ( n1 sin θ1 sin θ 2 ) cos θ 2 2 sin θ 2 cos θ 1 sin( θ 1 + θ 2 )
消去Etp分量
2E ip n1 cosθ1 = E tp (n 2 cosθ1 + n1 cosθ 2 )
⇒ tp = E
tp
E ip
=
2 n 1 cos θ 1 n 2 cos θ 1 + n 1 cos θ 2
=
2 cosθ1 sinθ 2 sin(θ1 + θ 2 ) cos(θ1 − θ 2 )
H is + H rs = H ts
n1 ( E ip + E rp ) = E tp n2
1 1 E ip + E µ 1V1 µ 1V1
rp
=
1 E µ 1V 2
tp
n1 (Eip + Erp ) cosθ2 n2
Erp (n 2 cosθ1 + n1 cosθ2 ) = Eip (n 2 cosθ1 − n1 cosθ2 )
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
h
20
若r、t 为正值,表明反
射、透射分量相对入射
光在分界面处没有的位
相跃变,若r、t 为负值,
则有的位相变化。
看图时: 1)看随着i1变化,
r、t 的大小变化;
2)看随着i1变化,
r、t 的正负变化。
h
21
外反射情况下( n1 < n2 )的位相跃变
1 )透射时
tp
E 2p E 1p
0,
ts
h
17
(3)位相跃变(相移)
为什么图中r 的值 会有正、有负?负值 表示什么?
1)r, t 为正值表示 其分量方向与约定 的正方向相同。若 为负值,则分量方 向与约定方向相反
h
18
2)r,t 是瞬时值比,也可看作是复振幅比。 对复振幅比,比值中即包含振幅比的大 小,也包含相位的变化。
rs E1S / E1S
E1s E1s
sin(i1 sin(i1
i2) i2)
tp
E2 p E1p
2cosi1 sini2 sin(i1 i2)cos(i1 i2)
ts
E2s E1s
2cosi1 sini2 sin(i1 i2) h
13
1.2 反射(透射)振幅比 位相跃变(相移)
已知 r 、t 及 由 i1、n1、n2 决定。
h
24
s
2 tan
1
n2 n1
( n1 n2
)2
sin
2
i1
1
cos i1
p
2 tan
1
n1 n2
(
n1 n2
)2
sin
2
i1
1
cos i1
h
25
当 i1=48.5°(54.5 °)时 P分量比S分量位相超前 /4
菲涅耳菱形菱镜
h
26
例.1 比较 i1 0 时外反射和内反射时
反射光的振动方向与 入射光的振动方向的关系
第三章 光通过各向同性介质 及其界面所发生的现象
§1 光在各向同性介质界面上的反射和折射 各向同性介质: 折射率或波速沿各个方向相同。
1.1 菲涅耳反射折射公式
h
1
问题 光通过各向同性介质时会发生反射、 折射等各种物理现象。反射、折射定律 只解决了入射、反射、折射光传播方向 间的关系,未涉及到三者间的振幅、位 相、偏振态间的关系。
※ 反射光波在界面处发生了的位相跃变
h
31
例3.薄膜上下表面的反射
1)i1 < iB n1 < n2 < n3
2)i1 < iB n1 < n2
光在上下两表面反 射均是光疏光密
第一界面外反射, 第二界面内反射。
(1)(2) 两 光 束 间 无 附 加位相差,振动同相
(1)(2)两光束间有附 加位相差,振动反相
pk k
n1 < n2
p k p k
n1 >n2
h
27
光波正入射 i1=0, i2=0 ( i1 0, i2 0 )
若 n1 < n2
rp= - rs=n2-n1 / n2+n1
rs< 0 有的位相跃变 rp > 0 没有的位相跃变
p
k
k
对观察者来说
反射光P、S分量都与入射光P、S分量方向相反
h
34
1.3 反射率和透射率 目的:讨论入射光,反射光,折射光间的能流关系 (1)定义:
反射率:R=反射光能流/入射光能流=W’1/W1
透射率:T=折射光能流/入射光能流=W2/ W1
能流:单位时间通过某横截面积的能量(W)
平均能流密度:单位时间,单位面积,垂直能 流方向所通过的能量(I)。
可见:W=I×光束横截面积
上述R、T的表达式适用于
1)内、外反射 2)任意入射角 3)任意偏振态
h
37
(3)反射率曲线(R~i1曲线)
① 由图可见
1)RS随i1 而单调上升
2)i1< iB时, i1RP , i1> iB时,i1 RP 。
3) R 随i1 而单调上升。 i1 ≈0º R=Rmin i1 ≈90º, R=1
(
入射光E1
E1S E1P
反射光E1’
E’1S E’1P
p,
s,
k组成右
手螺旋正交系
折射光E2
E2S E2P
表示在界面入射点附近,S正方向向外
h
7
定义
反射振幅比:rs
E1s E1s
,
rp
E1 p E1 p
;
透射振幅比:ts
E2s E1s
,
tp
E2 p E1 p
;
h
8
菲涅耳公式
rp
E1p E1 p
菲涅耳公式可以解决上述问题。
h
2
问题:单色平行光入射到无限大平面的交界面 上 (不考虑散射)讨论反射、折射光的状态
入射光E1
反射光E1’
折射光E2
E 1 、 1 、 k 1 、 E 2 、 2 、 k 2 。
h
3
入射光
E i E 1 e x i (1 t p k 1 r ) []
记此时的 i1=iB , 称为布儒斯特角
rp=0
说明,不论入射光的偏 振态如何,反射光只是 振动面垂直入射面的S 光,反射光中没有P光
i2
tp= ts =2n1 / n2+n1
ts
E 2s E 1s
2 n 1 cos i1 n 1 cos i1 n 2 cos
i2
h
12
例2.光波掠入射
i1 90º ;
rp= rs= -1; tp= ts=0 E1p
tan(i1 i2) tan(i1 i2)
;
rs
E 2s 0 E 1s
在入射点处
E 2 p,
E 2 s 与 E 1 p , E 1 s 同相 ,
无位相跃变。
h
22
2 )反射时 rs 0 有 的位相跃变。 当 i 1 i B 时, r p 0 没有 的位相跃变。 当 i 1 i B 时, r p 0 有 的位相跃变。
h
23
内反射情况下( n1 > n2 )的位相跃变
※可见:i1< 30 º时R可近似认为是为常数
h
39
③
K1
i1=iB时
K2,
RP = 0
i1 i2 2
反 射 光 中 只S有 分 量 , 是 完 全 偏 振 光 。 透 射 光 中 P光 占 优 势 是 部 分 偏。振 光
例:n1=1.0, n2=1.5 n1=1.5, n2=1.0
RS=15% , RP = 0
i2 i2
i1= 0, i2= 0
( i1 0, i2 0 )
rs
E 1s n 1 cos E 1 s n 1 cos
i1 n 2 cos i1 n 2 cos
i2 i2
rp= -rs =n2-n1 / n2+n1
tp
E 2p E 1p
2 n 1 cos i1 n 2 cos i1 n 1 cos
2n1 cos i1 n2 cos i1 n1 cos i2
2 cos i1 sin i2 sin(i1 i2 ) cos(i1 i2 )
ts
E2s E1s
2n1 cos i1 n1 cos i1 n2 cos i2
2 cos i1 sin i2 sin(i1 i2 )
可见:①r, t 及 由i1,n1,n2决定。②在反射和折
h
29
一般在 i1〈 iB时:
光从光疏介质光密介质,反射光 相对入射光在界面处有的位相跃变。
光从光密介质光疏介质,反射光 相对入射光在界面处无的位相跃变。
h
30
例2.掠入射(n1 < n2 )
i1 900, rp= rs= -1
k
i1 900 时, 可近似认为反射光与入射光在同一直
线上,两分量的方向均相反。
W1
n1 cosih1 E12
36
反射率 RW1 E12 r2 W1 E12
透射率 T W2 W1
n2 cosi2 n1cosi1
E22 E12
n2 cosi2 n1cosi1
t2
可见:能流分配关系R、T仅与i1、i2、n1、n2有关
按能量守恒定律 对非吸收介质有
W1 =W1’+ W2 R+T=1
n1=1.0, n2=1.5 n1=1.5, n2=1.0
iB=56 º19’ iB=33º41’
可见:光线反转入射时,两边iB角互余。
h
40
1. 4 布儒斯特定律
i1= iB
当 i1+i2= /2 时
i1+i2=/2 i2 rp=0 rs=n12-n2 2/ n22+n1 2 tp= n1 / n2 ts=2n1 / n22+n12
E~1S eit / E~1S eit
E~1S / E~1S
h
19
例: E1 A exp[ i( t )] E 2 A exp[ i( t )] A exp[ i( t )]
E 2 A exp[ i( t )] 1 E1 A exp[ i( t )]
振幅比中出现负号——表示它们之间有 的位相差。
与另一列波的相干叠加问题,一般讨论相邻
两束光波的位相差问题。
h
33
(4)斯托克斯公式
a ra
n1 i1
n2
i2 ta
tt’a rra ra
