平面几何习题大全
五年级下册数学《平面几何》练习题大全

五年级下册数学《平面几何》练习题大全
一、选择题
1. 以下哪个选项是平行四边形的一个性质?
A. 两组对边分别相等
B. 四条边都相等
C. 对角线互相平分
D. 有一个角是直角
2. 如果一个四边形的对边平行且相等,那么它一定是?
A. 矩形
B. 菱形
C. 平行四边形
D. 梯形
3. 在三角形中,若一个角的度数是90度,那么这个三角形是?
A. 锐角三角形
B. 直角三角形
C. 钝角三角形
D. 等边三角形
二、填空题
1. 矩形是一种特殊的平行四边形,它的特点是_____。
2. 在三角形中,如果一个角的度数大于90度,那么这个角被
称为_____角。
3. 若一个四边形的对边相等且平行,则这个四边形是_____。
三、解答题
1. 画出一个任意三角形,并标出它的三个内角。
2. 已知一个平行四边形的对边相等,证明它是矩形。
3. 若已知三角形ABC中,AB=AC,求证∠BAC=60度。
四、应用题
1. 小明的书桌是一个矩形,已知矩形的长是80cm,宽是40cm,求书桌的面积。
2. 小红有一个平行四边形的框架,已知对边相等,其中一个角是直角,求这个平行四边形的面积。
3. 如图,三角形ABC中,AB=AC,D是BC的中点,求证AD是∠BAC的角平分线。
请注意,以上题目只是示例,并不是完整的练习题大全。
您可以根据需要继续添加或修改题目。
史上最全之初中平面几何经典题集锦

初中平面几何经典(史上最全)如图 ,在凸四边形 ABCD 中∠ABC =120° , ∠BCD =90°. 则 AD =______已知如图:正方形 ABCD ,BE =BD ,CE 平行于 BD ,BE 交 CD 于 F ,求证:DE =DF0ABC AB=AC,A=20,AB D AD BC BDC∠∠在等腰三角形中,在上取一点,使=,求ABCD00 ABC ABC=46D BC DC=AB DAB=21CAD ∆∠∠∠在中,,是边上一点,,,求ABC ,AB=AC,D BC ,E AD ,BDE CED BAC BD CD ∆∠∠∠在中为边上一点为上一点且满足=2=,求证:=200ABC ,BAC 60,ATB BTC CTA 120M BC TA+TB+TC=2AM∆∠=∠=∠=∠=在中点为的中点,求证:002,ABC ,D AC ,CBD ABD 60BDC 30,AB BC BD ,:DB DC ∆∠-∠=∠===如图中是边上的一个点求证ABC,O ,O AB AC X Y OX OY ≤三角形为重心过作任一条直线、于、,求证:2在直角梯形ABCD 中, ∠ABC =∠BAD =90°, AB =16.对角线AC 与BD 交于点E ,过E 作EF ⊥AB 于点F , O 为边AB 的中点, 且FE+EO =8.求AD +BC的值.已知四边形ABCD 中,AB=DC,E、F 分别为AD 与BC 的中点,连接EF 与BA 的延长线相交于N,与CD 的延长线相交于M,求证:∠BNF=∠CMF0ABC ,CB>CA,BAC 80,D AB CB-CA=BD,I ABC ,IDA _____∆∠=∆∠=在中为上一点,满足为的内心则1,G ABC ,D CB ,BD=BC 2AE DG AC E,?AC ∆=如图为的重心点在延长线上且过的直线交于点则,H O ABC BAC ABC 2,AH ?∆∠∆=如图、分别为的垂心、外心,=45若的外接圆半径为则ABC =90AD BAC BD DC=21∆∠∠∠0已知在中,C,是 的平分线交BC于D,::,则B=?,AB ,C AB D ACDE DB CA BE如图是半圆的直径点平分弧,点平分弧、交于点E,则=?0ABC ,CB>CA,ABC 35CB=CA+AI,I ABC ,BAC _____∆∠=∆∠=在中,满足为的内心则AB PC OP BP=2AP=6CP=⊥在圆内的点P在弦上,点C在圆上,若,,则?0RT ABC ABC=90D BC E CE AD AE=EF,AC=7,FC=3,cos ACB=?∆∠∠在中,,为线段的中点,在线段AB上与交于点F,则ABC BC=12AC=5AI BE D E F DE IF AB G AG=∆如图,直角中,,,角A和角B的平分线交于点I,、与边交于点、,为线段的中点,交于点,ABC A BC BC CA AB AB CC =AC BB ∆'''''’’中,G为重心,分别为、、的中点,如果A、C、G、B共圆,求证:00ABCDE AB=BC CD=DE BD=2ABC=150CDE=30ABCDE ∠∠如图,五边形满足,,,,,则五边形的面积为_00493ABC AB=AC BC=cos 25E BEC+ACB=180AED=120DE=ABC D ∆∠=∠∠∠如图,在中,,,为BC中点,点为三角形内部一点,,_ABCD O ABC AMN ABCD ∆∆如图,在平行四边形中,为对角线的交点,MN分别是BO、CD的中点,若,求证:为正方形OPQR ABC AOR BOP CRQ OPQR ∆∆∆∆如图,正方形内接于,已知、、的面积分别为1,3,1那么正方形的边长是__E F AB AD BFDE AE+EC=AF+FC AB+BC=AD+DC如图,、分别为线段、上的点,与交于点C,若,求证:已知:如图,O 是半圆的圆心,C 、E 是圆上的两点,CD ⊥AB ,EF ⊥AB ,EG ⊥CO .求证:CD =GF .已知:△ABC 中,H 为垂心,O 为外心,且OM ⊥BC 于M .(1)求证:AH =2OM ;(2)若∠BAC =600,求证:AH =AO .AFGCEBO D ·ADHEMCBO如图,分别以△ABC 的AC 和BC 为一边,在△ABC 的外侧作正方形ACDE 和正方形CBFG ,点P 是EF 的中点. 求证:点P 到边AB 的距离等于AB 的一半.如图,四边形ABCD 为正方形,DE ∥AC ,且CE =CA ,直线EC 交DA 延长线于F .求证:AE =AF .设P 是正方形ABCD 一边BC 上的任一点,PF ⊥AP ,CF 平分∠DCE .求证:PA =PF .PCGFBQADEE DA CBFFEP C BA设P 是平行四边形ABCD 内部的一点,且∠PBA =∠PDA .求证:∠PAB =∠PCB .平行四边形ABCD 中,设E 、F 分别是BC 、AB 上的一点,AE 与CF 相交于P ,且AE =CF .求证:∠DPA =∠DPC .设P 是边长为1的正△ABC 内任一点,L =PA +PB +PC ,求证:3 ≤L <2.PADCBFPDECBAAPC BABC AB=AC AC D BC=BD+AD A ∆∠∠如图:是一个等腰三角形,其中,若B的角平分线交于,求的度数00AB=CD=1ABC=90CBD=30AC∠∠如图:已知,,,求PA=PB APB 2ACB AC PB D P =4PD=3AD DC ∠∠如图:若,=,与交于点,且B,,则=?ABC DEC AD BE 18S =2cosC=?∆∆如图,,是锐角三角形的两条高,若S=,,则。
新平面几何100题1-60

1、设I是△ABC的内心,D是边BC上的一点,E是BC延长线上一点,且满足BDDC =BEEC.设H是D到直线IE的垂足,证明:∠AHE=∠IDE.B2、设O、H分别是△ABC的外心和垂心,点A关于直线OH的对称点是P,点P和点A不在直线BC的同侧,E、F分别在AB和AC上,满足BE=PC,CF=PB,直线AP、OH相交于点K,证明:EK⊥FK.B CP3、设正△ABC的外接圆和内切圆分别是Γ、ω,P为ω上一动点,P1、P2、P3分别为P在BC、CA、AB上的射影,圆ω1、ω2、ω3分别与BC、CA、AB切于P1、P2、P3且与Γ内切(它们的圆心与A、B、C分别在BC、CA、AB的异侧).证明:圆ω1、ω2、ω3两两外公切线的长度之和是一个定值.A4、设正△ABC内接于⊙O,E、F分别是AC,BC上一点,使得AE=2CE,BF=2CF. P为⊙O上的一点,PD⊥EF于D,交AB于K,作PS⊥BC于S,连接SK并交AO于T.证明:DS=DT.T5、设E、F分别位于△ABC的AC,AB边上,BE、CF交于D,△AEF的外接圆交△ABC的外接圆于点A、P,△AEF的外接圆在A处的切线交△ABC于A、Q两点,设N、M分别为AQ、BC的中点.证明:∠APD=∠MNQ.Q6、已知△ABC的外心为O,A′、B′、C′分别是边BC、CA、AB上的点,且满足A、B′、C′、O共圆,C、A′、B′、O共圆.以B′为圆心,B′C为半径的圆和以C′为圆心,BC′为半径的圆的根轴为l a.类似定义l b、l c.证明:直线l a、l b、l c交出的三角形垂心与△ABC的垂心重合.7、设凸四边形ABCD顶点不共圆,记点A在直线BC、BD、CD上的射影分别为P、Q、R,其中P、Q分别在BC、BD内,R在CD的延长线上.记点D在直线AC、BC、AB上的射影分别为X、Y、Z,其中X、Y分别在线段AC、BC内,Z在BA的延长线上,设△ABD的垂心为H,证明:BH的中点在△PQR外接圆和△XYZ外接圆的根轴上.8、在圆内接四边形ABCD中,AB>BC,AD>DC,I、J分别为△ABC、△ADC的内心.以AC为直径的圆与线段IB交于点X、与JD的延长线交于点Y.证明:若B、I、J、D四点共圆,则点X、Y关于直线AC对称.9、设△ABC的外接圆和内切圆的圆心分别为O、I,点M和点Q分别在边AB和AC上,点N和点P分别在边BC上(N在线段BP上),且满足五边形AMNPQ的五条边长相等.记点S为直线MN和QP的交点,l为∠MSQ的角平分线.证明:l和OI平行.S11、凸四边形ABCD中,P、Q、R、S分别是线段AB、BC、CD、DA上的点.若相交的线段PR、QS把四边形ABCD分为4个四个对角线互相垂直的凸四边形.证明:P、Q、R、S四点共圆.B12、不等腰三角形ABC的外接圆为Ω,内心为I,射线AI与BC交于D,与Ω交于除A以外的另一点M,以DM为直径的圆与Ω交于除M以外的另一点K,直线MK与BC交于点S,设N为IS的中点,L1、L2为△KID的外接圆与△MAN的外接圆的交点.证明:IL1或IL2的中点在Ω上.S113、在非等腰△ABC中,D、E、F分别为BC、CA、AB的中点.过D作△ABC的内切圆的切线(不同于直线BC),交直线EF于点X.类似定义Y和Z.证明:X、Y、Z三点共线.ZBD14、圆外切四边形ABCD的内切圆⊙I分别切DC、DA于E、F,K为BD上一点,KA、KC分别交⊙I于M、N,MF与NE交于L.证明:L在直线BD上.L15、四边形ABCD内接于⊙O,∠A、∠C的角平分线相交于点I,∠B、∠D的角平分线相交于点J,直线IJ不经过点O,且与边AB、CD的延长线分别交于点P、R,与边BC、DA分别交于点Q、S.线段PR、QS的中点分别为M、N.证明:OM⊥ON.R16、在圆内接四边形ABCD中,M、N分别是线段BC、AD的中点,对角线AC、BD交于点E. P是边BC上的点,满足PBPC =(BDAC)2.设E在PN上的投影是H,证明:△BEC的外接圆与△MPH的外接圆相切.17、圆内接四边形ABCD的对角线相交于P,存在一个圆Γ与AB、BC、AD、DC的延长线切于点X、Y、Z、T.过A、B的圆Ω与圆Γ外切于S.证明:SP⊥ST.18、对于平面上的凸四边形ABCD,设直线l交直线AB于X,交直线CD于X′,交直线BC于Y,交直线DA于Y′,交直线AC于Z,交直线BD于Z′.已知以上六点在l上按照X、Y、Z、X′、Y′、Z′的顺序排列.证明:以XX′、YY′、ZZ′为直径的三个圆共点.19、设O是三角形ABC的外心,D是AB上一点,作与⊙O内切,与线段CD、BD相切的⊙I;作与⊙O内切,与线段CD、AD相切的⊙J.证明:若A、B、I、J四点共圆,则D是三角形ABC中的∠ACB内旁切圆在AB上的切点.20、设⊙O 1与⊙O 2交于P 、Q 两点,过P 作两条割线AB 、CD ,过Q 作两条平行割线A′B′、C′D′,取△PAC 、△PBD 、△QB′D′、△QA′C′的九点圆圆心F 1、F 2、F 3、F 4.证明:四边形F 1F 2F 3F 4是矩形.D'A'C21、设⊙O是四边形ABCD的内切圆. AC、BD交于P,I、J分别是△ABC、△ADC的内心,OP,IJ交于K,T是K在BD上的射影.证明:I、J、P、T四点共圆.B22、设O、I B、I C分别是锐角三角形ABC的外接圆圆心,∠B内的旁切圆圆心和∠C内的旁切圆圆心.在AC边上取点E和Y,使得∠ABY=∠CBY,BE⊥AC,在AB边上取点F和Z,使得∠ACZ=∠BCZ,CF⊥AB,直线I B F和I C E交于点P.证明:PO⊥YZ.I B I C23、四边形ABCD内接于⊙O,AC、BD交于点P,直线AB、CD交于点Q. K是P在QO上的射影,KP、BC交于X,M是BC的中点,P′是P关于BC的对称点,K′是K关于M的对称点. P′K′分别交BC于Y,交KP于Z.证明:△XYZ的外接圆与△QBC的外接圆相切.D24、对边不平行的凸四边形ABCD中,BA延长线与CD延长线交于点E,AD延长线与BC延长线交于点F,K是△CDF的外接圆与△ADE的外接圆的交点(K≠D).设∠BAD、∠ABC、∠BCD、∠ADC的外角平分线分别为l A、l B、l C、l D,l A和l B、l B和l C、l C和l D、l D和l A分别交于点G、H、I、J.△CDF的外接圆中,弧DF(不含C)的中点为Q,直线EH与△AED的外接圆交于另一点M.设GJ中垂线与IH中垂线(不重合)交于点P.证明:P、M、Q、K四点共圆.25、设D是△ABC外接圆⊙O上任意一点,过D作⊙O的切线l.证明:l关于△ABC三边对称的直线围成的三角形的外接圆与⊙O相切.26、设O为△ABC内一点,O在BC、CA、AB上的射影分别为U、V、W.X、Y、Z分别在BC、CA、AB上,X′、Y′、Z′分别是X关于U、Y关于V,Z关于W的对称点,点X、Y、Z关于△ABC的密克点为S,点X′、Y′、Z′关于△ABC的密克点为T.证明:OS=OT.B CX'U27、点D、E、F分别在△ABC的边AB、BC、CA上,满足AD+AF=BC、BD+BE=AC、CE+CF=AB. △ADF、△BDE、△CEF的外接圆与△ABC外接圆的另一个交点分别为A1、B1、C1,P是D、E、F关于△ABC的密克点,证明:P为△A1B1C1的垂心.128、设AA′、BB′、CC′是锐角△ABC的外接圆的三条直径,P为△ABC内任意一点,点P在BC、CA、AB上的射影分别是D、E、F,X、Y、Z分别是A′关于D、B′关于E,C′关于F的对称点.证明:△XYZ∽△ABC.29、设H是锐角△ABC的外接圆的垂心,P是外接圆弧BC上一点,连接PH交弧AC于M,弧AB上一点K满足直线KM平行于点P关于△ABC的西姆松线,设Q为外接圆上一点满足30、设△ABC的内切圆⊙I分别切BC、CA、AB于点D、E、F,延长EI交DF于G,BE、CF交⊙I于另外的点X、Y.设J为△AEF外接圆的另一个交点,△XJI外接圆与⊙I的另一个交点为S,T在⊙I上满足TS⊥AI,连接YT、XS交于P,直线DP与⊙I的另一个交点为Q.证明:KQ是⊙I的直径.C31、在△ABC中,内切圆⊙I分别切BC、CA、AB于点D、E、F,M、N分别是AB、AC的中点,EF、MN交于S,DS与⊙I的另一个交点为J.证明:J在△ABC的九点圆上.B C32、过△ABC内心I任作一直线l,内切圆分别切BC、CA、AB于点X、Y、Z,边BC、CA、AB的中点分别为D、E、F,直线l分别交△BIC外接圆、△CIA外接圆、△AIB外接圆于另一点D′、E′、F′,过点X、Y、Z分别作平行于DD′、EE′、FF′的直线l1、l2、l3.证明:直线l1、l2、l3交于一点.33、已知△ABC的外接圆为⊙O,A′为点A在⊙O上的对径点.作等边△BCD,使得A、D位的于BC的异侧,过点A′作A′D的垂线,分别与AC、AB交于E、F两点.以EF为底,作底角为π6等腰△ETF,并使得A、T位于BC的异侧.证明:AT经过△ABC的九点圆圆心.ED34、设△ABC的内切圆⊙I与边BC、CA、AB分别切于点D、E、F,记⊙I B、⊙I C分别为△ABC的顶点B、C所对的旁切圆,P、Q分别为I B E,I C F的中点,若DE、DF与I B I C交于点K、J,EJ 与FK交于点M,PE与△PAC的外接圆交于另一点X,QF与△QAB的外接圆交于另一点Y.证明:BY、CX、AM三线共点.35、已知凸四边形ABCD内两动点P、Q满足∠APB=∠AQB=∠CPD=∠CQD.证明:动直线PQ要么均经过一个定点,要么相互平行.36、在凸四边形ABCD中,∠ABC=∠ADC<π,∠ABC、∠ADC的平分线交于点P,并分2别与AC交于点E、F,M为AC的中点,BM、DM与△BDP的外接圆分别交于另一点X、Y,EX与PY交于点Q.证明:AC⊥PQ.B37、凸六边形A1A2A3A4A5A6满足A1A2=A3A4=A5A6,A2A3=A4A5=A6A1,点X、Y在38、已知凸四边形ABCD内接于⊙O,⊙I切AC、BD及⊙O,E为弧BC的中点,AE与BD相交于点M,DE与AC相交于点N.证明:△EMN外接圆与⊙I相切.39、锐角△ABC 中BC >AC >AB ,I 、O 、H 分别为其内心、外心、垂心,D 、E 分别在BC 、AC 上使AE =BD ,CD +CE =AB .记K 为BE 与AD 交点,证明:KH =2IO .ABC40、在锐角△ABC中,AB>AC,设Γ为其外接圆,H为垂心,F为由顶点A处所引高的垂足,M为边BC的中点.Q、K为圆Γ上的点,使得∠HQA=∠HKQ=π.若点A、B、C、K、Q互2不相同,且按此顺序排列在Γ上,证明:△KQH的外接圆与△FKM的外接圆相切.41、设△ABC内接于⊙O,过A作⊙O的切线交BC于T,G为△ABC的重心,直线TG分别交AB、AC于E、F,AG交⊙O于K,证明:AK平分∠EKF.K42、在凸四边形ABCD中,AB≠BC,ω1和ω2分别是△ABC和△ADC的内切圆.已知存在一个圆ω与射线BA相切(切点不在线段BA上),与射线BC相切(切点不在线段BC上),且与直线AD和直线CD都相切.证明:圆ω1和ω2的两条外公切线的交点在圆ω上.43、P为△ABC内一点,L、M、N分别为边BC、CA、AB的中点,且PL∶PM∶PN=BC∶CA∶AB.延长AP、BP、CP分别交△ABC的外接圆于点D、E、F.证明:△APF、△APE、△BPF、△BPD、△CPD、△CPE的外接圆圆心六点共圆.B44、给定△ABC,求线段BC上满足下列条件的所有点P:如果X、Y是直线PA与△PAB、△PAC外接圆的两条外公切线的交点,则(PAXY )2+PB∙PCAB∙AC=1.45、在凸四边形ABCD中,∠ABC=∠CDA=π2,H是A在BD上的射影,边AB上的S和边AD上的T使H在△SCT内部,∠CHS−∠CSB=π2,∠THC−∠DTC=π2,证明:直线BD和△TSH的外接圆相切.CD46、在△ABC中,⊙O、⊙I分别为其外接圆与内切圆,⊙I与BC切于点D,M为ID中点,A0与A 关于点O对称,直线A0M交⊙O于异于点A0的一点X,证明:△ADX的外接圆与直线BC相切.47、已知P 是凸四边形ABCD 的边AB 上的一点,ω是△CPD 的内切圆,I 为其圆心,若ω分别与△APD 以及△CPB 的内切圆切于点K 和L ,AC 与BD 交于点E ,AK 、BL 交于点F .证明:E 、I 、F 共线.BAD48、在锐角△ABC中,ω、Ω、R分别表示其内切圆、外接圆及外接圆的半径.圆ωA与Ω内切于点A且与ω外切;圆ΩA与Ω内切于点A且与ω内切.设P A和Q A分别是ωA和ΩA的圆心.同样定义P B和Q B、P C和Q C.证明:8P A Q A∙P B Q B∙P C Q C≤R349、已知△ABC的垂心为H,外心为O,设A、B、C关于BC、CA、AB的对称点分别为D、E、F.证明:D、E、F共线当且仅当OH=2R,其中R为△ABC外接圆半径.FCO50、设∠XAY是一个固定的角,B、C分别是射线AX、AY上的动点,∠XAY内有一动点P满足PA、PB、PC的长度都保持不变.求△ABC面积的最小值.。
高三数学平面几何练习题及答案

高三数学平面几何练习题及答案一、选择题1. 已知直线l与x轴的交点为A(2, 0),与y轴的交点为B(0, -3)。
则直线l的斜率是:A. 3B. -3C. 1/3D. -1/3答案: B. -32. 已知平面上两点P(2, 4)、Q(5, 7),则向量PQ的坐标表示为:A. (3, 3)B. (2, 3)C. (5, 7)D. (7, 11)答案: A. (3, 3)3. 已知点A(-3, 4)、B(1, -2),则直线AB的斜率为:A. 2B. -2C. 3/2D. -3/2答案: D. -3/24. 在直角坐标系中,点P(3, 4)关于y轴的对称点为:A. (3, -4)B. (-3, 4)C. (4, 3)D. (-4, 3)答案: B. (-3, 4)5. 直线y = 2x + 3与直线y = -x + 1的交点坐标为:A. (1, 2)B. (2, 1)C. (-1, 2)D. (2, -1)答案: C. (-1, 2)二、填空题1. 已知向量AB = (-3, 2),向量BC = (-1, 4),则向量AC = ______。
答案: (-4, 6)2. 已知点A(2, 3)、B(5, 7),则直线AB的斜率为______。
答案: 4/33. 已知线段的中点坐标为M(3, -2),其中一端点为N(5, 1),则另一端点坐标为______。
答案: (1, -5)4. 平面上一点P(x, y),与坐标轴的距离之和为7,且x > 0,y > 0。
则点P可能的坐标是______。
答案: (4, 3)5. 直线y = 3x + 2与y轴交点的坐标为(0, b),则b = ______。
答案: 2三、解答题1. 已知四边形ABCD,其中AB为水平线段,CD为垂直线段。
已知AB的中点坐标为M(2, 3),CD的中点坐标为N(5, 4)。
求四边形ABCD的中心点坐标。
解答:四边形的中心点坐标为两个中点的坐标的平均值。
平面几何100题及答案(前80题)
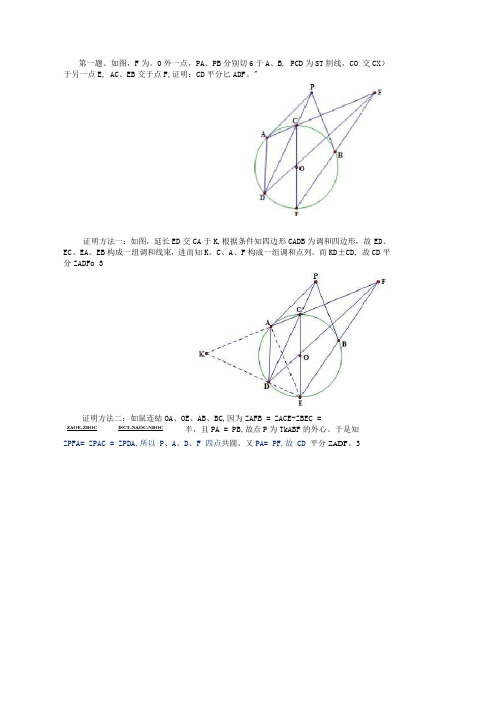
第一题、如图,F为。
0外一点,PA、PB分别切6于A、B, PCD为ST割线,CO 交CX)于另一点E, AC、EB交于点F,证明:CD平分匕ADF。
"证明方法一:如图,延长ED交CA于K,根据条件知四边形CADB为调和四边形,故ED、EC、EA、EB构成一组调和线束,进而知K、C、A、F构成一组调和点列。
而KD±CD, 故CD平分ZADFo 3证明方法二:如鼠连結OA、OE、AB、BC,因为ZAFB = ZACE-ZBEC =ZAOE-ZBOC ISCT-NAOC-NBOC 半,且PA = PB,故点P为TkABF的外心。
于是知ZPFA= ZPAC = ZPDA,所以P、A、D、F 四点共圆。
又PA= PF,故CD 平分Z A DF。
3第二题、如图,AB为©0直径,C、D为O。
上两点,且在AB同侧,。
在C、D两处的切城交于点E, BC、AD交于点F, EF交AB于证明:E、C、页、D四点共圆。
“证明:如图,延长白C、BD交于点K,则BC1AK, AD丄BK,从而知F^)AKAB的垂心。
又在圆内接六边形CCADDB中使用帕斯卡定理,知K、E、F三点共线,从而KM丄卽于価。
于是知匕CMF = ZCAF= ZCDE,所以E、C、页、D四点共圆。
K第三题、如图,AB为。
直径,C、D为伽上两点'且在AB同侧,O0在C. D两处的切线交于点E, BC、AD交于点F, EB交0。
于点G,证明;ZCEF = 2/AGF。
“证明:如图,根据条件知匕CF D =典牌=(脸-®;(i对-命)=Z CAB + / DBA = ZECF + ZEDF;且EC = ED;故点E 为△CED 外心。
于是知/EFC = ZECF = ZCAB = ZCGE,敌E、C、F、G四点共圆。
所以“ZCGF = ZCEF = 2(90° - ZECF)= 2(90° - ZCAB)= 2ZABC 二2ZAGC " 0lWZAGF = —=—,即得ZCEF = 2ZAGFo,2 2第四題、如图,AB为直径,P为AB延长线上一点,PC切于C,点C关于朋的对称点为点D, CE1AD于E, F为CE中点,AF交于K,求证:AP为ZXPCK外扬圆的切线。
平面几何练习题

平面几何练习题题一:求三角形边长和周长已知一个三角形的两边长分别为a和b,夹角为C°,求第三边c的长度和三角形的周长P。
解:根据余弦定理可知,余弦公式为:c² = a² + b² - 2ab·cos(C)。
根据上述公式,可以计算得到c的长度。
根据三角形的定义可知,三角形的周长P等于三边之和,即P = a + b + c。
题二:求三角形的面积已知一个三角形的底边长为b,高为h,求三角形的面积S。
解:根据三角形的面积公式可知,S = 0.5 * b * h。
题三:判断点是否在三角形内部已知一个三角形的三个顶点坐标分别为A(x₁,y₁),B(x₂,y₂),C(x₃,y₃),以及一个待判断的点D(x,y),判断点D是否在三角形ABC的内部。
解:利用行列式的性质可以判断点D是否在三角形ABC内部。
设点D的坐标为(x,y),则点D在三角形ABC内部的条件为:|(x₁ - x) (y₁ - y) 1||(x₂ - x) (y₂ - y) 1| > 0|(x₃ - x) (y₃ - y) 1|如果等式左侧的行列式结果大于0,则点D在三角形ABC内部;如果等式左侧的行列式结果小于0,则点D在三角形ABC的外部;如果等式左侧的行列式结果等于0,则点D在三角形ABC所在的边界上。
题四:求矩形的面积和周长已知一个矩形的长为L,宽为W,求矩形的面积S和周长P。
解:矩形的面积公式为S = L * W,周长公式为P = 2 * (L + W)。
题五:求圆的面积和周长已知一个圆的半径为r,求圆的面积S和周长C(circumference)。
解:圆的面积公式为S = π * r²,其中π取近似值3.14159;圆的周长公式为C = 2 * π * r。
题六:判断点是否在圆内部已知一个圆的圆心坐标为O(x₀,y₀),半径为r,以及一个待判断的点P(x,y),判断点P是否在圆O内部或者在圆的边界上。
平面几何习题及答案

平面几何习题及答案
平面几何是数学中的重要部分,通过题的练可以加深对基本概念和定理的理解。
本文提供一些常见的平面几何题及其答案,供研究和练使用。
1. 题1
已知三角形ABC的三边长度分别为a、b和c,求三角形的面积S。
解答:
首先,可以使用海伦公式计算半周长p:
p = (a + b + c) / 2
然后,使用海伦公式计算三角形的面积S:
S = sqrt(p * (p - a) * (p - b) * (p - c))
其中,sqrt表示平方根。
2. 题2
已知三角形ABC的底边AB是一条固定的线段,顶角C的位置可以变化,求三角形的最大面积。
解答:
根据三角形面积公式S = 1/2 * base * height,当底边AB固定时,三角形的最大面积出现在高度最大的位置。
在这种情况下,高度等于底边长度的一半。
因此,三角形的最大面积为:S = 1/2 * AB * (AB/2) = AB^2 / 4
3. 题3
已知平行四边形ABCD的两条对角线交于点O,求平行四边形的面积S。
解答:
由于对角线互相平分,所以可以将平行四边形分为两个相等的三角形。
假设对角线AB和CD的交点为O,那么平行四边形的面积等于两个三角形的面积之和。
设对角线AB和CD的长度分别为d1和d2,那么平行四边形的面积为:
S = 2 * (1/2 * d1 * d2) = d1 * d2
通过以上题的练,可以提高对平面几何的理解和应用能力。
希望本文对研究者有所帮助。
参考资料
- 平面几何概念和定理的教材或课堂讲义。
初中数学-平面几何练习题

初中数学-平面几何练习题
以下是一些初中数学平面几何的练题,供同学们进行练和巩固知识。
1.### 题目:计算三角形面积
已知三角形ABC的底边AC的长度为12cm,高BD的长度为8cm。
请计算三角形ABC的面积。
2.### 题目:判断平行线
已知直线AB // 直线CD,直线EF // 直线CD。
请判断直线AB 是否和直线EF平行。
3.### 题目:求直角三角形斜边长度
已知直角三角形ABC中,直角边AB的长度为8cm,直角边AC的长度为6cm。
请计算斜边BC的长度。
4.### 题目:计算矩形周长和面积
已知矩形ABCD的长为10cm,宽为6cm。
请计算矩形ABCD
的周长和面积。
5.### 题目:判断正方形
已知四边形ABCD是一个正方形,且边长为3cm。
请判断四边形EFGH是否为正方形。
6.### 题目:计算梯形面积
已知梯形ABCD的底边AB长度为8cm,顶边CD长度为6cm,高EF长度为4cm。
请计算梯形ABCD的面积。
以上是初中数学平面几何的一些练习题,希望能帮助同学们巩
固知识,提高解题能力。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
平面几何习题大全下面的平面几何习题均是我两年来收集的,属竞赛围。
共分为五种类型,1,几何计算;2,几何证明;3,共点线与共线点;4,几何不等式;5,经典几何。
几何计算-1命题设点D是Rt△ABC斜边AB上的一点,DE⊥BC于点E,DF⊥AC于点F。
若AF=15,BE=10,则四边形DECF的面积是多少?解:设DF=CE=x,DE=CF=y. ∵Rt△BED∽Rt△DFA, ∴BE/DE=DF/AF<==> 10/y=x/15 <==> xy=150.所以,矩形DECF的面积150.几何证明-1命题在圆接四边形ABCD中,O为圆心,己知∠AOB+∠COD=180.求证:由O向四边形ABCD 所作的垂线段之和等于四边形ABCD的周长的一半。
证明(一) 连OA,OB,OC,OD,过圆心O点分别作AB,BC,CD,DA的垂线,垂足依次为P,Q,R,S。
易证ΔAPO≌ΔORD,所以 DR=OP,AP=OR,故 OP+OR=DR+AP=(CD+AB)/2。
同理可得:OQ+OS=(DA+BC)/2。
因此有 OP+OQ+OR+OS=(AB+BC+CD+DA)/2。
证明(二) 连OA,OB,OC,OD,因为∠AOB+∠COD=180°,OA=OD,所以易证RtΔAPO≌RtΔORD,故得 DR=OP,AP=OR,即 OP+OR=DR+AP=(CD+AB)/2。
同理可得:OQ+OS=(DA+BC)/2。
因此有 OP+OQ+OR+OS=(AB+BC+CD+DA)/2。
几何不等式-1命题设P是正△ABC任意一点,△DEF是P点关于正△ABC的接三角形[AP,BP,CP延长分别交BC,CA,AB于D,E,F],记面积为S1;△KNM是P点关于正△ABC的垂足三角形[过P点分别作BC,CA,AB垂线交于K,N,M],记面积为S2。
求证:S2≥S1 。
证明设P点关于正△ABC的重心坐标为P(x,y,z),a为正△ABC的边长,则正△ABC的面积为S=(a^2√3)/4。
由三角形重心坐标定义易求得:AD=za/(y+z),CD=ya/(y+z),CE=xa/(z+x),AE=za/(z+x),AF=ya/(x+y),BF=xa/(x+y).故得:△AEF的面积X=AE*AF*sin60°/2=Syz/(z+x)(x+y);△BFD的面积Y=BF*BD*sin60°/2=Szx/(x+y)(y+z);△CDE的面积Z=CD*CE*sin60°/2=Sxy/(y+z)(z+x).从而有 S1=S-X-Y-Z=2xyzS/(y+z)(z+x)(x+y)。
因为P点是△KNM的费马点,从而易求得:PK=(xa√3)/[2(x+y+z)],PN=(ya√3)/[2(x+y+z)],PM=(za√3)/[2(x+y+z)].故得:S2=(PN*PM+PM*PK+PK*PN)*sin120/2=3S(yz+zx+xy)/[4(x+y+z)^2]。
所以待证不等式S2≥S1等价于:(3/4)*(yz+zx+xy)/(x+y+z)^2≥2xyz/(y+z)(z+x)(x+y);<====> 3(y+z)(z+x)(x+y)(yz+zx+xy)≥8xyz(x+y+z)^2;上式展开等价于3x^3(y^2+z^2)+3y^3(z^2+x^2)+3z^3(x^2+y^2)-2xyz(x^2+y^2+z^2)-4xyz(yz+zx+xy)≥0; 上式化简等价于x^2(x+2y+2z)(y-z)^2+y^2(y+2z+2x)(z-x)^2+z^2(z+2x+2y)(x-y)^2≥0.因为P点在正△ABC,故x>0,y>0,z>0,所以上式显然成立。
命题得证。
几何不等式-2命题设P是三角形ABC一点,直线AP,BP,CP与三边的交点分别为D,E,F。
则三角形DEF叫做点P的塞瓦三角形。
试证点P的塞瓦三角形DEF的面积不超过三角形ABC面积的四分之一。
证明设三角形ABC的面积为S, 塞瓦三角形DEF的面积为S1, 三角形AEF的面积为Sa, 三角形BFD的面积为Sb, 三角形CDE的面积为Sc。
令BD=xBC,CE=yCA,AF=zAB,则CD=(1-x)BC,AE=(1-y)CA,BF=(1-z)AB。
那么Sa=(AE*AF*sinA)/2=z*(1-y)*S,Sb=(BD*BF*sinB)/2=x*(1-z)*S,Sc=(CD*CE*sinC)/2=y*(1-x)*S。
所以有S1=S-Sa-Sb-Sc=S*[1-z*(1-y)-x*(1-z)-y*(1-x)]=S*[1-(x+y+z)+yz+zx+xy] ,据此命题[S≥4S1]转化为证明4*[1-(x+y+z)+yz+zx+xy]≤1根据塞瓦定理得:xyz=(1-x)*(1-y)*(1-z)上述恒等式展开等价于1+yz+zx+xy=2xyz+x+y+z将其代入得:8xyz≤1.由算术--几何平均不等式得:2√[x(1-x)]≤1,2√[y(1-y)]≤1,2√[z(1-z)]≤1,上述三式相乘得:8√[xyz(1-x)*(1-y)*(1-z)]≤1 , <==> 8xyz≤1 .几何不等式-3命题设P是三角形ABC一点,点P在三边BC,CA,AB上的射影分别为D,E,F。
则三角形DEF叫做点P的垂足三角形。
试证点P的垂足三角形DEF的面积不超过三角形ABC面积的四分之一。
证明设P点垂足ΔDEF面积为F,ΔABC面积为Δ,令PD=r1,PE=r2,PC=r3,BC=a,CA=b,AB=c,R表示三角形ABC的外接圆半径。
则有F=[r2*r3*sinA+r3*r1*sinB+r1*r2*sinC]/2=[a*r2*r3+b*r3*r1+c*r1*r2]/(4R)。
故命题转化为求证a*r2*r3+b*r3*r1+c*r1*r2≤RΔ (1)据恒等式:abc=4RΔ,则上式为a*r2*r3+b*r3*r1+c*r1*r2≤abc/4 (2)设P点的ΔABC重心坐标为P(x,y,z),对(2)式作置换等价于R^2*(x+y+z)^2≥yza^2+zxb^2+xyc^2 (3)(3)展开化简为(R*x)^2+(R*y)^2+(R*z)^2+(2*R^2-a^2)*yz+(2*R^2-b^2)*zx+(2*R^2-c^2)*xy≥0上式配方整理得:[R*x+(2*R^2-c^2)*y/(2R)+(2*R^2-b^2)*z/(2R)]^2+[c*y*cosC-b*z*cosB]^2≥0,显然成立。
易验证当x:y:z=a*cosA:b*cosB:c*cosC,即外心时取等号。
几何不等式-4命题试比较给定一三角形的最大接矩形的面积与最大接正方形的面积大小。
证明设给定三角形ABC的边长分别为a,b,c,相对应的高线分别为ha,hb,hc,给定三角形ABC的面积为S。
不妨设a>b>c,则ha<hb<hc,运用化归法易证明:给定三角形ABC的最大接矩形与最大接正方形的一边与三角形一边重合,另外两端在另外两边上。
下面在a>b>c条件下,求出最大接矩形与最大接正方形的面积。
(1)对于给定三角形的最大接矩形的面积可如下求:设矩形长为x[与BC边重合],宽为y,矩形的面积为S1。
运用相似比可得:(ha-y)/x=ha/a <==> x=a*(ha-y)/ha,所以S1=y*a*(ha-y)/ha=-[1/(a*ha)]*[a^2*y^2-2*a*S*y]=-[1/(2*S)]*(a*y-S)^2+S^/2≤S/2。
当y=S/a=ha/2,x=a/2时,S1的最大值为S/2。
所以给定三角形的最大接矩形的面积为S/2,它共有三种形状,即(长,宽)=(a/2,ha/2);(长,宽)=(b/2,hb/2);(长,宽)=(c/2,hc/2)。
注意这里长与宽相对而言。
(2)对于给定三角形的最大接正方形的面积可如下求:设正方形边长为x,正方形的面积为S2。
运用相似比可得:(ha-x)/x=ha/a <==> x=2*S/(a+ha),因为a>b>c,易证得:a+ha>b+hb>c+hc,所以给定三角形的最大接正方形的面积:S2=[2*S/(c+hc)]^2。
(3)下面确定给定三角形ABC的最大接矩形的面积与最大接正方形的面积大小。
[2*S/(c+hc)]^2≤S/2<==> 8*S≤(c+hc)^2因为c^2+(hc)^2≥2*c*hc=4*S,所以8*S≤(c+hc)^2显然成立。
当c=hc时等号成立。
几何不等式-5命题在等腰直角三角形中,∠BAC=90°,E,F在BC边上[E点靠近B点,F点靠近C 点]。
求证:(1) 如果∠EAF≤45°,则BE^2+CF^2≥EF^2;(2) 如果∠EAF≥45°,则BE^2+CF^2≤EF^2.证明设AE为y,AF为z,AB=AC=a。
在△ABE,△ACF中[∠ABE=45°,∠ACF=45°],根据余弦定理得:BE^2=y^2-a^2+a*BE*√2;y^2=a^2+BE^2-a*BE*√2;z^2=a^2+CF^2-a*CF*√2; CF^2=z^2-a^2+a*CF*√2.两式相加得:BE^2+CF^2=y^2+z^2-2a^2+a√2(BE+CF)=y^2+z^2-2a^2+a√2(a√2-EF)=y^2+z^2-a√2EF。
注意到:△AEF面积的两种表示式yzsin(∠EAF)/2=aEF/(2√2) a√2EF=2yzsin∠EAF所以有 BE^2+CF^2=y^2+z^2-2yzsin∠EAF而在△AEF中,根据余弦定理得:EF^2=y^2+z^2-2yzcos∠EAF对比上述两式,当∠EAF=45°时,有BE^2+CF^2=EF^2。
(1) 如果∠EAF≤45°,则tan∠EAF≤1,即BE^2+CF^2≥EF^2;(2) 如果∠EAF≥45°,则tan∠EAF≥1,即BE^2+CF^2≤EF^2.附证如图,等腰直角三角形ABC,E,F在BC上,不妨设F在E右侧将△AFC旋转90度到△ADB∠ABC=∠ACB=∠ABD=45==>∠DBE=90 BD=CF==>BE^2+CF^2=BE^2+BD^2=DE^2DE^2=AD^2+AE^2-2AD*AE*cos∠DAEEF^2=AF^2+AE^2-2AF*AE*cos∠EAFAD=AFDE^2-EF^2=2AF*AE(cos∠EAF-cos∠DAE)∠DAE=∠DAB+∠BAE=∠CAF+∠BAE=90-∠EAF(1)∠EAF≤45°,则90°>∠DAE≥∠EAF>0°,DE^2-EF^2=2AF*AE(cos∠EAF-cos∠DAE)≥0DE^2≥EF^2BE^2+CF^2≥EF^2(2)∠EAF≥45°,则0°<∠DAE≤∠EAF<90°,DE^2-EF^2=2AF*AE(cos∠EAF-cos∠DAE)≤0DE^2≤EF^2BE^2+CF^2≤EF^2几何不等式-6命题非钝角三角形的三条中线组成的三角形,它的外接圆半径大于原三角形外接圆半径的5/6。
