等边三角形性质与判定公开课PPT课件
合集下载
等边三角形的性质和判定市公开课一等奖省优质课获奖课件

知识点1:等边三角形性质 1.等边三角形两条高线相交所成钝角度数是( ) B A.105° B.120° C.135° D.150° 2.如图是一个等边三角形纸片,剪去一个角后得到一个四边形,则图 中∠α+∠β度数是( ) C A.180° B.220° C.240° D.300°
第2页
3.(·泉州)如图,在正三角形ABC中,AD⊥BC于点D,则∠BAD= ____3°0.
第14页
方法技能:
1.等边三角形性质: (1)三个内角都相等,每一个角都等于60°; (2)等边三角形是轴对称图形,它有3条对称轴,分别为三边垂直 平分线; (3)等边三角形是特殊等腰三角形,它含有等腰三角形一切性 质. 2.等边三角形判定: (1)三边都相等三角形是等边三角形; (2)三个角都相等三角形是等边三角形; (3)有一个角是60°等腰三角形是等边三角形. 易错提醒:
(1)证实:∵CE=CD,∴∠E=∠CDE,∴∠ACB= 2∠E.又∵AD=DE,∴∠E=∠DAC.∵AD是△ABC 角平分线,∴∠BAC=2∠DAC=2∠E,∴∠ACB= ∠BAC,∴BA=BC,又∵AB=AC,∴AB=BC= AC,∴△ABC是等边三角形 (2)解:当AD为△ABC中线或高时,结论依然成立
第4页
知识点2:等边三角形判定
6.以下三角形:①有两个角等于60°;②有一个角等于60°等腰三角形;
③三个外角(每个顶点处各取一个外角)都相等三角形;④一腰上中线也
是这条腰上高等腰三角形.其中是等边三角形有( )
D
A.①②③ B.①②④
C.①③ D.①②③④
7.如图,△ABC是等边三角形,D,E,F为各边中点,则图中等边三角
4.如图,已知P,Q是△ABCBC边上两点,BP=PQ=QC=AP=AQ, 则∠BAC度数为_______°. 120
第2页
3.(·泉州)如图,在正三角形ABC中,AD⊥BC于点D,则∠BAD= ____3°0.
第14页
方法技能:
1.等边三角形性质: (1)三个内角都相等,每一个角都等于60°; (2)等边三角形是轴对称图形,它有3条对称轴,分别为三边垂直 平分线; (3)等边三角形是特殊等腰三角形,它含有等腰三角形一切性 质. 2.等边三角形判定: (1)三边都相等三角形是等边三角形; (2)三个角都相等三角形是等边三角形; (3)有一个角是60°等腰三角形是等边三角形. 易错提醒:
(1)证实:∵CE=CD,∴∠E=∠CDE,∴∠ACB= 2∠E.又∵AD=DE,∴∠E=∠DAC.∵AD是△ABC 角平分线,∴∠BAC=2∠DAC=2∠E,∴∠ACB= ∠BAC,∴BA=BC,又∵AB=AC,∴AB=BC= AC,∴△ABC是等边三角形 (2)解:当AD为△ABC中线或高时,结论依然成立
第4页
知识点2:等边三角形判定
6.以下三角形:①有两个角等于60°;②有一个角等于60°等腰三角形;
③三个外角(每个顶点处各取一个外角)都相等三角形;④一腰上中线也
是这条腰上高等腰三角形.其中是等边三角形有( )
D
A.①②③ B.①②④
C.①③ D.①②③④
7.如图,△ABC是等边三角形,D,E,F为各边中点,则图中等边三角
4.如图,已知P,Q是△ABCBC边上两点,BP=PQ=QC=AP=AQ, 则∠BAC度数为_______°. 120
等边三角形性质与判定ppt课件

5、 △ABC是等腰三角形,周长为15cm且 ∠A=60°,则BC=_____5__
.
如图,已知,△ABC是等边三角形,BD
是中线,BD=6,延长BC到E。使CE=CD,
求DE长。
A
D
B
C
E
.
等边三角形判定探索 (判定方法):
1.三个内角都相等的三角形是等边三角形.
∵∠A=∠B=∠C=60 ° ∴AB=AC=BC (等角对等边)
提示:在△ABC中
60°
AB=AC
B
C
∴∠B=∠C =60°
∵∠A+∠B+ ∠ C=180°
∴∠A=60° ∵ ∠A= ∠ C ∴BC=AB
像△ABC这样三边相 等的三角形,我们把
∴AB=BC=AC
它叫做等边三角形也
叫正三角形
.
A
B )60° 60(° C
⑴ 等边三角形的三边都相等
⑵ 等边三角形的三个内角都相等,并且 每一个角都等于60°.
等腰三角形是轴对称图形
等腰三角形的两腰相等AB=AC
两底角相等∠B=∠C(等边对等角)
B
C
D
等腰三角形顶角的平分线、底边上的中线和底边上
的高线互相重合(三线合一)
3.等腰三角形的判定方法
如果一个三角形有两个角相等,那么这两个角所 对的边也相等。(简写成“等角对等边”)
.
A
如右图所示,在△ABC中,AB=AC, ∠ B=60 °,你能得到什么结论。
∵ AD=AE
D
∴∠ADE=∠AED
∴△ADE是等边三角形
B
A E C
.Leabharlann 如图,D、E、F分别是等边三 角形ABC三边上三点,且 AD=BE=CF。 试问:△DEF是什么三角形?
.
如图,已知,△ABC是等边三角形,BD
是中线,BD=6,延长BC到E。使CE=CD,
求DE长。
A
D
B
C
E
.
等边三角形判定探索 (判定方法):
1.三个内角都相等的三角形是等边三角形.
∵∠A=∠B=∠C=60 ° ∴AB=AC=BC (等角对等边)
提示:在△ABC中
60°
AB=AC
B
C
∴∠B=∠C =60°
∵∠A+∠B+ ∠ C=180°
∴∠A=60° ∵ ∠A= ∠ C ∴BC=AB
像△ABC这样三边相 等的三角形,我们把
∴AB=BC=AC
它叫做等边三角形也
叫正三角形
.
A
B )60° 60(° C
⑴ 等边三角形的三边都相等
⑵ 等边三角形的三个内角都相等,并且 每一个角都等于60°.
等腰三角形是轴对称图形
等腰三角形的两腰相等AB=AC
两底角相等∠B=∠C(等边对等角)
B
C
D
等腰三角形顶角的平分线、底边上的中线和底边上
的高线互相重合(三线合一)
3.等腰三角形的判定方法
如果一个三角形有两个角相等,那么这两个角所 对的边也相等。(简写成“等角对等边”)
.
A
如右图所示,在△ABC中,AB=AC, ∠ B=60 °,你能得到什么结论。
∵ AD=AE
D
∴∠ADE=∠AED
∴△ADE是等边三角形
B
A E C
.Leabharlann 如图,D、E、F分别是等边三 角形ABC三边上三点,且 AD=BE=CF。 试问:△DEF是什么三角形?
中考数学冲刺复习——等边三角形的性质与判定(共34张PPT)

2019/5/21
25
4.如图1,△ABC和△ADE都是等边三角形. (1)求证:BD=CE; (2)如图2,若BD的中点为P,CE的中点为Q,请判断△APQ的形状,并说明理由.
2019/5/21
26
5. (1)如图(a)所示,△ABC和△CDE都是等边三角形,且B、C、D三点共线,联结AD、BE相交于点P, 求证:BE=AD.
2019/5/21
27
E
E
E
C A
C A
C A
P
P
P
B
D
B
D
B
D
F
2019/5/21
F
F
28
E
C A
P
B
D
F
2019/5/21
29
04
等边三角形 的综合练习
1.已知如图等腰△ABC,AB=AC,∠BAC=120°,AD⊥BC于点D,点P是BA延长线上一点,点O是线段AD上一点, OP=OC,下面的结论:①∠APO+∠DCO=30°;②△OPC是等边三角形;③AC=AO+AP;④S△ABC=S四边形 AOCP.其中正确的是( ) A.①②③B.①②④C.①③④D.①②③④
(2)如图(b)所示,在△BCD中,∠BCD<120°,分别以BC、CD和BD为边在△BCD外部作等边三角 形ABC、等边三角形CDE和等边三角形BDF,联结AD、BE和CF交于点P,下列结论中正确的是 (只填序号即可) ①AD=BE=CF;②∠BEC=∠ADC;③∠DPE=∠EPC=∠CPA=60°;
4
2019/5/21
5
2019/5/21
6
2019/5/21
7
等边三角形的性质和判定PPT教学课件

1.5
5140 9766
1.5
6130
1164 7
2.2
7070
1343 3
2.2
8010
1521 9
28
2.2
8950
1700 5
30
2.2
9890
1879 1
➢ 上图采用周边传动刮泥机结构 主要由中心支座、桁架、传动装置、刮板等部分组成,
该机为全桥(或半桥)周边传动刮泥,传动是由电机经行 星摆线针轮减速机直接或通过链条驱动滚轮,以中心支座 为圆心在池壁顶做圆周运行。 ------结构简单,耗电省,运行可靠,目前已广泛推广
3.在△ABC中,∠A=∠B=∠C,你能得到AB=BC=CA 吗?为什么? 你从中能得到什么结论? 三个角都相等的三角形是等边三角形. 4.在△ABC中,AB=AC,∠A=60°.(1)求证:△ABC是 等边三角形; (2)如果把∠A=60°改为∠B=60°或∠C=60°,那么结论 还成立吗? (3)由上你可以得到什么结论? 有一个角是60°的等腰三角形是等边三角形.
将污泥与3-4倍污泥量的水混合而进行沉降分离 (仅适用于消化污泥)
目的:降低污泥中的碱度和粘度,以节省混凝 剂的用量,提高浓缩效果,缩短浓缩时间。
过程:泥水混合—淘洗—沉淀
三、加热加压调理
可使部分有机物分解,亲水性有机胶体物质水解,颗粒 结构改变,从而改善污泥的浓缩与脱水性能
(一)高温加压调理 流程 图5-6
第五章 污泥的浓缩与脱水
第一节 概述 一、污泥的种类
按来源分: 生活污水污泥、工业废水污泥、给水污泥
按污泥从水中的分离过程分: 沉淀污泥(初沉池污泥、混凝沉淀污泥、化学沉
淀污泥)及生物污泥(包括腐殖污泥、剩余活性污泥 )
等边三角形的性质及判定ppt课件
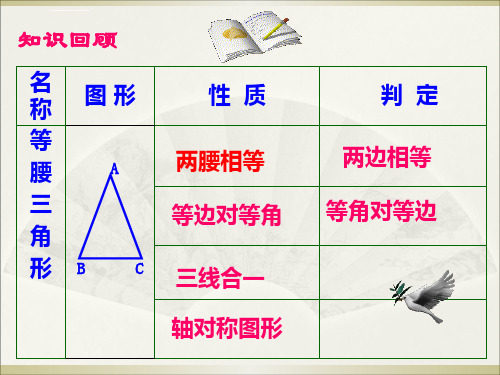
名 称 等 边 三 角 形B
图形
A C
性质 三条边都相等 三个角都相等,且都为60° 三线合一
轴对称图形,有三条对称轴
认 识 到 了 贫 困户贫 困的根 本原因 ,才能 开始对 症下药 ,然后 药到病 除。近 年来国 家对扶 贫工作 高度重 视,已 经展开 了“精 准扶贫 ”项目
等边三角形的判定:
B
A
N
认 识 到 了 贫 困户贫 困的根 本原因 ,才能 开始对 症下药 ,然后 药到病 除。近 年来国 家对扶 贫工作 高度重 视,已 经展开 了“精 准扶贫 ”项目
2、在Rt△ABC 中, 如果∠BCA= 90° , ∠A= 30 °,CD 是高,
(1)BD=1,则BC、AB各等于多少;
(2)求证:BD=1/2BC=1/4AB
解(1)由已知可求得
C
∠BCD= 30 °
于是在Rt△ADC 与Rt△BDC 中用本定理得BC=2,AB=4
A
DB
(2)在Rt△ADC 与Rt△BDC运用本定理
BD=1/2BC
BC=1/2AB
∴ BD=1/2BC=1/4AB
认 识 到 了 贫 困户贫 困的根 本原因 ,才能 开始对 症下药 ,然后 药到病 除。近 年来国 家对扶 贫工作 高度重 视,已 经展开 了“精 准扶贫 ”项目
认 识 到 了 贫 困户贫 困的根 本原因 ,才能 开始对 症下药 ,然后 药到病 除。近 年来国 家对扶 贫工作 高度重 视,已 经展开 了“精 准扶贫 ”项目
知识回顾
名 称
图形
性质
等
腰
A
两腰相等
三
等边对等角
角
形B
C 三线合一
轴对称图形
等边三角形的性质和判定 (优质课)获奖课件

3.在△ABC中,∠A=∠B=∠C,你能得到AB=BC=CA 吗?为什么? 你从中能得到什么结论? 三个角都相等的三角形是等边三角形. 4.在△ABC中,AB=AC,∠A=60°.(1)求证:△ABC是 等边三角形; (2)如果把∠A=60°改为∠B=60°或∠C=60°,那么结论 还成立吗? (3)由上你可以得到什么结论? 有一个角是60°的等腰三角形是等边三角形.源自 语文小魔方站作品 盗版必究
谢谢您下载使用!
更多精彩内容,微信扫描二维码获取 扫描二维码获取更多资源
附赠 中高考状元学习方法
前言
高考状元是一个特殊的群体,在许多 人的眼中,他们就如浩瀚宇宙里璀璨夺目 的星星那样遥不可及。但实际上他们和我 们每一个同学都一样平凡而普通,但他们 有是不平凡不普通的,他们的不平凡之处 就是在学习方面有一些独到的个性,又有 着一些共性,而这些对在校的同学尤其是 将参加高考的同学都有一定的借鉴意义。
11.2 与三角形有关的角
11.2.2 三角形的外角
1.了解三角形的外角. 2.知道三角形的外角等于与它不相邻的两个内角的 和. 3.学会运用简单的说理来计算三角形相关的角.
重点 三角形外角的性质. 难点 运用三角形外角性质进行有关计算时能准确地推 理.
一、复习引入 什么是三角形的内角?它是由什么组成的? 三角形内角和定理的内容是什么? 教师提出问题,学生举手回答问题. 二、探究新知 1.探究三角形外角的概念. 教师布置学生自学教材第14页最后一段话的内容,然后完 成以下问题: (1)举例说明什么是三角形的外角.(上黑板画图说明) (2)如图,∠ADB,∠BPC,∠BDC,∠DPC分别是哪个三 角形的外角?
四、练习与小结 练习:教材练习. 教师布置练习,学生举手回答. 小结:谈谈你对三角形外角的认识. 教师引导学生谈谈对三角形外角的认识.主要从定义和 性质两个方面入手. 五、布置作业 习题11.2第5,6,8题,选做题:第11题.
《等边三角形》PPT优质课件

∴∠DBE= 1 ∠ABC=30°.
2
∵DE=DB,∴∠E=∠DBE=30°.
B
D CE
∵∠ACB=∠CDE+∠E,∴∠CDE=∠ACB-∠E=30°.
探索新知
知识点1 等边三角形的性质 【变式】如图,等边三角形ABC的边长为3,点D是AC的中点,点E在BC 的延长线上,若DE=DB,求CE的长.
知识点1 等边三角形的性质
A
BC边上的中线,高和所对角的平分线“三线合一”.
AB边上的中线,高和所对角的平分线“三线合一”.
B
C AC边上的中线,高和所对角的平分线“三线合一”.
等边三角形每条边上的中线、高和所对角的平分线相互重 合,即“三线合一”.
探索新知
知识点1 等边三角形的性质
思考3 把等腰三角形的对称性用于等边三角形,能得到什么结 论?
知识点1 等边三角形的性质
图形 性边 质角
三线 合一
等腰三角形
两条边相等 两个底角相等
底边上的中线、高和顶角 的平分线互相重合
对称 性
1条对称轴
等边三角形
三条边都相等 三个角都相等, 且都是60º 每一边上的中线、高和这一边 所对的角的平分线互相重合
3条对称轴
探索新知
知识点1 等边三角形的性质 例1 如图,△ABC是等边三角形,BD平分∠ABC,延长BC到点E,使 得CE=CD.求证:BD=DE.
有一个角是60°的等腰 三角形是等边三角形.
探索新知
知识点2 等边三角形的判定
例2 如图,△ABC是等边三角形,DE∥BC,分别交AB,AC于点D,E.
求证:△ADE是等边三角形.
证明:∵△ABC是等边三角形,∴∠A=∠B=∠C.
等边三角形的性质和判定PPT课件(华师大版)(1)

解:∵△ABC是等边三角形, ∴∠A=∠B=∠C=60°.
∵DE⊥AC,EF⊥BC,DF⊥AB,
∴∠AED=∠EFC=∠FDB=90°, ∴∠ADE=90°-∠A=90°-60°=30°, ∴∠EDF=180°-30°-90°=60°. 同理可得∠DEF=∠EFD=60°. 即△DEF各个内角的度数都是60°.
例5 AB=AC,∠BAC=120°,AD⊥AB,AE⊥AC. (1)∠C=________,∠B=________; (2)求证:△ADE是等边三角形.
导引:(1)由AB=AC,∠BAC=120°, 可求出∠B,∠C 的度数为30°. (2)三个角都是60°的三角形是等 边三角形.
解:(1)30°;30°. (2)∵AD⊥AB,AE⊥AC(已知), ∴∠BAD=∠EAC=90°(垂直的定义). ∴∠B=∠C=30°(已知), ∴∠ADB=∠AEC=60°(直角三角形的两个锐角 互余). ∴∠ADB=∠AEC=∠EAD=60°. ∴△ADE是等边三角形(三个角都相等的三角形是 等边三角形).
要点精析:(1)它是特殊的等腰三角形,具备等腰三 角 形的所有性质;(2)它是特殊的等腰三角形,任意两边都 可作为腰,任意一个角都可以作为顶角.
(来源于教材)
2.等边三角形的性质:(1)等边三角形的三条边 都相等;(2)等边三角形的三个内角都相等,并且每一 个角都等于60°.(3)等边三角形是轴对称图形,它有 三条对称轴,分别为三边的垂直平分线;(4)各边上的 高、中线、对应的角平分线重合,且长度相等.
例1 如图13.3-5, △ABC是等边三角形,D,E,
F分别是三边AB,AC,BC上的点,且
DE⊥AC,EF⊥BC,DF⊥AB,计算△DEF
各个内角的度数.
等边三角形-PPT课件

图形,有三条对称轴.
B
C
请同学们认真快速的完成: 讲学稿中练一练(1)
1、已知等边△ABC中,AB=3cm则△ABC 的周长为___9_c_m___
2、用一个5倍的放大镜照等边三角形 △ABC,则∠A=__6_0_°___
3、△ABC是等边三角形,则∠A的外角= ____1__2_0° 4、等边三角形两条高相交所成的钝角 的度数是_1_2__0_°__
?
细心观察,探索等边三角形性质
结合等腰三角形的性质,你能填出等边三角形对应 的结论吗?
图形
等腰 三角形
等边 三角形
边
两边相等 (定义)
三边相等 (定义)
角
轴对称图形
两底角相等 (等边对等角)
是(三线合一) 一条对称轴
相等
是(三线合一)
每个角都等于60° 三条对称轴
细心观察,探索等边三角形性质
对“等边三角形的三个内角都相等,并且每一个角 都等于60°”这一结论进行证明.
∵ DE∥BC,
∴ ∠B =∠ADE,∠C =∠AED. D
E
∴ ∠A=∠ADE =∠AED.
∴ △ADE 是等边三角形.
B
C
动脑思考,变式训练
变式: △ABC 是等边三角形,若点D、E 在边AB、 AC 的延长线上,且 DE∥BC,结论还成立吗?
证明:∵ △ABC 是等边三角形,
∴ ∠A =∠ABC =∠ACB =60°. A
思考1 一个三角形的满足什么条件是等边三角形?到的这两个命题进行证明.
一般三角形
等边三角形
等腰三角形
满足什么条件的三角 形是等腰三角形?
方法一:从边看
有两边相等的三角形是 等腰三角形(定义)
等边三角形性质与判定公开课 ppt课件

2020/12/15
12
• 1.三边都相等的三角形叫做_等__边_三角形. • 2.等边三角形的每个内角都等于_6_0__度. • 3.等边三角形有__3__条对称轴.
4.已知△ABC中,∠A=∠B=60°,AB=3cm 则△ABC的周长是_9_c_m_____
5. △ABC是等腰三角形,周长为15cm且 ∠A=60°,则BC=___5_c_m__
(2) 等边三角形的判定:
1.三边相等的三角形是等边三角形. 2.三个内角都等于60 °的三角形是等边三角形. 3.有一个内角等于60 °的等腰三角形是等边三角形.
2020/12/15
17
4
等边三角形的定义
三条边都相等的三角形叫做等边三角形 (也叫正三角形)。
A
等边三角形是特殊的 等腰三角形
B
C
2020/12/15
5
图形
等腰三角形
等边三角形
边 :两条边相等
性
三条边都相等
角 :两个底角相等
三个角都相等,且都是60º
质 重要 底边上的中线、高和 每一边上的中线、高和这一边 线段:顶角的平分线互相重合 所对的角的平分线互相重合
B
D
2020/12/15
A
C
E
15
拓展练习
如图,等边三角形ABC中,
A
AD是BC上的高,
∠ BDE=∠CDF=60 °,
图中有哪些与BD相等的线段? E
F
2020/12/15
B DC
16
(1).等边三角形的性质. 1.等边三角形的内角都相等,且都等于60 ° 2.等边三角形是轴对称图形,有三条对称轴. 3.等边三角形各边上中线,高和所对角的平 分线都重合(三线合一).
《13.3.2.1等边三角形的性质与判定》PPT课件

D
E
B
C
是 12 cm.
5.如图,在△ABC中,∠ACB=90°,∠CAB=30°, 以AB为边在△ABC外作等边△ABD,E是AB的中点, 连接CE并延长交AD于F.求证:△AEF≌△BEC.
证明:∵△ABD是等边三角形, ∴∠DAB=60°, ∵∠CAB=30°,∠ACB=90°, ∴∠EBC=90°-30°=60°, ∴∠FAE=∠EBC. ∵E为AB的中点, ∴AE=BE. 又∵ ∠AEF=∠BEC, ∴△AEF≌△BEC(ASA).
图①
图②
解:(1)AN=BM. 理由:∵△ACM与△CBN都是等边三角形, ∴AC=MC,CN=CB,∠ACM=∠BCN=60°. ∴∠ACN=∠MCB. ∴△ACN≌△MCB(SAS). ∴AN=BM.
图①
(2)△CEF是等边三角形. 证明:∵∠ACE=∠FCM=60°, ∴∠ECF=60°. ∵△ACN≌△MCB, ∴∠CAE=∠CMB. ∵AC=MC, ∴△ACE≌△MCF(ASA), ∴CE=CF. ∴△CEF是等边三角形.
方法总结:等边三角形是特殊的三角形,它的三个 内角都是60°,这个性质常应用在求三角形角度的 问题上,一般需结合“等边对等角”、三角形的内角 和与外角的性质.
变式训练: 如图,△ABC是等边三角形,BD平分∠ABC,延长
BC到E,使得CE=CD.求证:BD=DE.
证明:∵△ABC是等边三角形,BD是角平分线, ∴∠ABC=∠ACB=60°,∠DBC=30°. 又∵CE=CD, ∴∠CDE=∠CED. 又∵∠BCD=∠CDE+∠CED, ∴∠CDE=∠CED=30°. ∴∠DBC=∠DEC. ∴DB=DE(等角对等边).
例2 △ABC为正三角形,点M是BC边上任 意一点,点N是CA边上任意一点,且BM= CN,BN与AM相交于Q点,(1)∠BQM等于 多少度?(2)若四边形QMCN的面积为2,
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
对称性:轴对称图形(1条) 轴对称图形(3条)
.
4
等边三角形的性质
1 .三条边相等。
2.等边三角形的内角都相等,且等于60°
3.等边三角形各边上中线,高和所对角的 平分线都重合(三线合一)
4.等边三角形是轴对称图形,有三条对称轴。
.
5
如图,已知,△ABC是等边三角 形,BD是中线,BD=6,延长 BC到E。使CE=CD,求DE长。 A
较AD与BE的大小,能得到什么结论?
说明理由.
B
D
A
.
C
E
13
拓展练习
如图,等边三角形ABC中,
A
AD是BC上的高,
∠ BDE=∠CDF=60 °,
图中有哪些与BD相等的线段? E
F
B
.
DC
14
(1).等边三角形的性质. 1.等边三角形的内角都相等,且都等于60 ° 2.等边三角形是轴对称图形,有三条对称轴. 3.等边三角形各边上中线,高和所对角的平 分线都重合(三线合一).
D
B
C
E
.
6
满足什么条件的三角 形是等腰三角形?
方法一:从边看
有两边相等的三角形是 等腰三角形(定义)
? 满足什么条件的三角
形是等边三角形
方法一:
三边都相等的三角形是 等边三角形(定义)
方法二:从角看
有两个角相等的三角 形是等腰三角形。
方法二:
三个角都相等的三角形 是等边三角形。
.
7
小明认为还有第三种方法“两条边相等且 有一个角是60°的三角形也是等边三角形”, 你同意吗?
交AB、AC于D , E。 求证:△ADE是等边三角形
A
D
E
B
C
若将DE ∥ BC改为AD=AE呢?
若将DE ∥ BC改为∠ADE=600呢?
.
10
• 1.三边都相等的三角形叫做_等__边_三角形. • 2.等边三角形的每个内角都等于_6_0__度. • 3.等边三角形有__3__条对称轴.
4.已知△ABC中,∠A=∠B=60°,AB=3cm 则△ABC的周长是__9_c形。
∵AB=BC=AC ∴△ABC是等边三角形
三个角都相等的三角形是等边三角形。 ∵ ∠A= ∠ B= ∠ C
∴△ABC是等边三角形
有一个角是60°的等腰三角形是等边三角形。 ∵ ∠A=600 , AB=BC
∴△ABC是等边. 三角形
9
例1. 如图,△ABC是等边三角形, DE ∥ BC,
(2) 等边三角形的判定:
1.三边相等的三角形是等边三角形. 2.三个内角都等于60 °的三角形是等边三角形. 3.有一个内角等于60 °的等腰三角形是等边三角形.
.
15
5. △ABC是等腰三角形,周长为15cm且 ∠A=60°,则BC=_____5_c_m
.
11
如图,D、E、F分别是等边三 角形ABC三边上三点,且 AD=BE=CF。 试问:△DEF是什么三角形?
A D
F
B E
C
.
12
能力提升
如图, △ABC和△CDE都是等边三角形,
且点A、C、E在一直线上, 试比
龙门中学理科组
.
1
.
2
等边三角形的定义
三条边都相等的三角形叫做等边三角形 (也叫正三角形)。
A
等边三角形是特殊的 等腰三角形
B
C
.
3
图形
等腰三角形
等边三角形
边 :两条边相等
性
角 :两个底角相等
三条边都相等 三个角都相等,且都是60º
质 重要 底边上的中线、高和 每一边上的中线、高和这一边 线段:顶角的平分线互相重合 所对的角的平分线互相重合
