北大《自动控制原理》讲义 第三讲
自动控制原理(程鹏)第三章课件

目录
• 控制系统概述 • 控制系统稳定性分析 • 控制系统误差分析 • 控制系统性能分析 • 控制系统校正与优化
01
CATALOGUE
控制系统概述
控制系统的定义与分类
总结词
控制系统的定义与分类
详细描述
控制系统是指在一定环境条件下,在设定值与被控变量之间构成的闭环反馈回 路。根据不同的分类标准,控制系统可以分为多种类型,如线性与非线性、时 不变与时变、离散与连续等。
优化系统结构
通过优化系统结构,改善系统性能 ,减小误差。
04
04
CATALOGUE
控制系统性能分析
时域性能指标
峰值时间
指系统输出达到峰值所需要的时间。
调节时间
指系统输出从设定值变化到稳态值的95%所需的时间。
超调量
指系统输出超过设定值达到的最大偏差量。
稳态误差
指系统输出达到稳态值后与设定值的偏差量。
串联校正
在系统前向通道中加入补偿环节,改 善系统动态特性。
并联校正
在系统反馈回路中加入补偿环节,改 善系统静态特性。
复合校正
结合串联和并联校正,全面提升系统 性能。
控制系统优化方法
线性二次型最优控制
通过最小化某一二次型代价函数,实现控制 系统性能优化。
极点配置
通过调整系统极点位置,优化系统动态特性 。
频域分析法
通过分析系统的频率响应或波德图来判断系统 的稳定性。
根轨迹法
通过绘制系统的根轨迹图来判断系统的稳定性。
控制系统稳定性的意义
01
系统稳定性是控制系统正常工作 的前提条件,只有稳定的控制系 统才能实现有效的控制。
自动控制原理(3)

= (1/T)*e
- t /T
# 3—4 二阶系统分析
由二阶微分方程描述的系统——二阶 系统。
一、数学模型 二阶系统传递函数的通式为: s + 2ζwns+wn 1 (s)=――――――― (Ts) 2 +2ζTs +1
2 wn
(s)=――――――― 2 2
T=1/wn
# 3—4二阶系统分析
自动控制原理
第三章
第三章 控制系统的时域分析
研究系统的动态特性,实质就是研究系统在 输入信号作用下,输出量是怎样按输入量的作用 而变化,也即系统对输入如何发生响应。
3—1 控制系统分析的方法
一、控制系统的典型输入
控制系统的输入信号具有随机的性质,往往不能用分析的 方法准确地表示出来。但对同一个系统,各种不同的输入所引起 的过渡过程所表征的系统特性在本质上是一致的,故在比较两个 系统的特性时,采用相同的输入是方便的。 单位脉冲函数:
三、一阶系统的单位斜坡响应
1、响应特性
R(s)=1/s2 C (s)=[1/s2 (Ts+1)]
取C(s)的拉氏反变换,得:
# 3—3 一阶系统分析 --1 2 g(t) = L [1/s (Ts+1)] --1 2 = L [1/s -T/s+ T/(s+1/T)]
- t /T
g(t) =( t – T)+T*e (t > 0) = Css + Ctt 式中Css=(t-T)为响应的稳态分量, - t /T Ctt=T*e 为响应的瞬态分量,当时间 t 时,Ctt衰减到0。
响应的初始速度为: -t/T de(t)/dt|t=0 =1 – e |t=0 = 0
自动控制原理讲义1-3章
第一章自动控制原理的基本概念主要内容:自动控制的基本知识开环控制与闭环控制自动控制系统的分类及组成自动控制理论的发展§1.1 引言控制观念生产和科学实践中,要求设备或装置或生产过程按照人们所期望的规律运行或工作。
同时,干扰使实际工作状态偏离所期望的状态。
例如:卫星运行轨道,导弹飞行轨道,加热炉出口温度,电机转速等控制控制:为了满足预期要求所进行的操作或调整的过程。
控制任务可由人工控制和自动控制来完成。
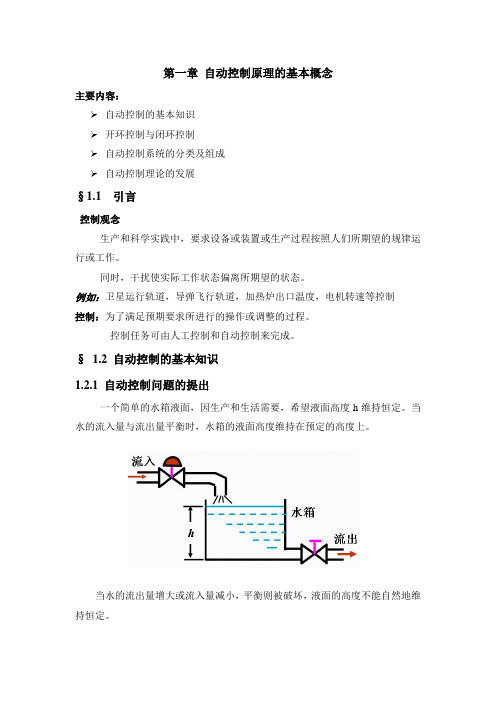
§ 1.2 自动控制的基本知识1.2.1 自动控制问题的提出一个简单的水箱液面,因生产和生活需要,希望液面高度h维持恒定。
当水的流入量与流出量平衡时,水箱的液面高度维持在预定的高度上。
当水的流出量增大或流入量减小,平衡则被破坏,液面的高度不能自然地维持恒定。
所谓控制就是强制性地改变某些物理量(如上例中的进水量),而使另外某些特定的物理量(如液面高度h)维持在某种特定的标准上。
人工控制的例子。
这种人为地强制性地改变进水量,而使液面高度维持恒定的过程,即是人工控制过程。
1.2.2 自动控制的定义及基本职能元件1. 自动控制的定义自动控制就是在没有人直接参与的情况下,利用控制器使被控对象(或过程)的某些物理量(或状态)自动地按预先给定的规律去运行。
当出水与进水的平衡被破坏时,水箱水位下降(或上升),出现偏差。
这偏差由浮子检测出来,自动控制器在偏差的作用下,控制阀门开大(或关小),对偏差进行修正,从而保持液面高度不变。
2. 自动控制的基本职能元件自动控制的实现,实际上是由自动控制装置来代替人的基本功能,从而实现自动控制的。
画出以上人工控制与动控制的功能方框图进行对照。
比较两图可以看出,自动控制实现人工控制的功能,存在必不可少的三种代替人的职能的基本元件:测量元件与变送器(代替眼睛)自动控制器(代替大脑)执行元件(代替肌肉、手)这些基本元件与被控对象相连接,一起构成一个自动控制系统。
下图是典型控制系统方框图。
自动控制原理第三章

P75 二阶系统的 结构图
20
2019/4/2
《自动控制原理》第三章
1、无阻尼情况 ( 0)
s 1 ct (t ) L [ 2 ] cos nt t 0 2 s n
等幅振 荡
特征方程有一对共轭虚根 s1,2 jn 2、欠阻尼情况 (0 1)
2019/4/2
《自动控制原理》第三章
7
三.劳斯稳定判据的应用
1、判断系统的稳定性 例: a3 s 3 a2 s 2 a1s a0 0 解:
判断稳定性。
s
3
a3 a2 a1a2 a3 a0 a2 a0
a1 a0 0
0 0
s2 s1 s
0
三阶系统稳定的充要条件是: ai
2019/4/2
瞬态ct (t ) e
ct (t )
t
T
, 稳态css (t ) 1(t )
css (t )
dc(t ) 1 e t /T dt t 0 T
c(t )
t 0
1 T
+
=
2019/4/2
《自动控制原理》第三章
18
二.一阶系统的动态性能指标
c(t )
t 3T
(1 e
t /T
)
t 3T
1 e
3T /T
0.95
T0 T 1 K0
ts 3T
ts 是一阶系统的动态性能指标。
增大系统的开环放大系数K0 会使T 减小,使ts 减小。
2019/4/2
《自动控制原理》第三章
19
第四节
二阶系统的动态性能指标
二阶标准型 或称典型二阶系 统传递函数
[工学]自动控制原理第3章
![[工学]自动控制原理第3章](https://img.taocdn.com/s3/m/d9a77406bf23482fb4daa58da0116c175f0e1e8a.png)
三、劳斯判据 系统特征方程的标准形式: ■ 系统稳定的必要条件: 特征方程所有系数均为正,则系统可能稳定,可 ■ 用劳斯判据判稳。 ■ 系统稳定的充分条件: 特征方程所有系数组成劳斯表,其第一列元素必须
为正。 ■ 列劳斯表:
26
例 四阶系统特征方程式: 试判别系统的稳定性,并说明特征根中具有正部根 的个数。 列劳斯表:
(1)用
代入特征方程;
(2)将z看作新坐标, 用劳斯判据再次判稳。
30
3.6 稳态误差分析及计算
一、误差及稳态误差概念定义
1.误差: (2种定义) 输入端定义 输出端定义 两者之间的关系
31
32
2.稳态误差: 稳定系统误差的终值。 3.稳态误差的计算公式: 终值定理 二、稳态误差计算 1.在给定输入信号作用下的分析: 令
28
四、劳斯判据的其它应用 1.分析系统参数对稳定性的影响 例 系统如图所示,求使系统稳定的K值的 范围。解 : 系统闭环特征方程为 列劳斯表
系统稳定必须满足 所以
29
2.确定系统的相对稳定性
稳定裕量: 系统离稳定的边界有多少余量。也就是实部最大的特 征根与虚轴的距离。
若要求系统有 的稳定裕量, 则
18
例 有一位置随动系统,结构图如下图所示,其中K=4 。 求该系统的自然振荡角频率和阻尼比; 求该系统的超调量和调节时间; 若要阻尼比等于0.707,应怎样改变系统 放大倍数K ?
解(1)系统的闭环传递函数为
写成标准形式
可知
19
(2)超调量和调节时间
(3)要求
时,
四、提高二阶系统动态性能的方法 1.比例——微分(PD)串联校 正
将其代入超调量公式得
, 叫 峰值时间。
自动控制原理(任彦硕)第三章PPT

传递函数模型
01
传递函数是描述线性时不变系 统动态特性的重要数学模型, 其形式为G(s) = (s^2 + 2s + 5)/(s^2 + 3s + 2)。
02
传递函数反映了系统对输入信 号的响应能力,包括幅频特性 和相频特性两个方面。
控制系统的工程实现案例
案例一
温度控制系统:通过模拟电路实现温 度控制系统的模拟,实现对温度的精 确控制。
案例二
飞行器控制系统:利用数字计算机实 现对飞行器的姿态、高度和速度等参 数的控制,提高飞行器的稳定性和安 全性。
感谢您的观看
THANKS
数字实现是指利用数字计算机来实现 控制系统的方法。
数字计算机具有精度高、稳定性好、 易于编程和实现等优点,因此在控制 系统的工程实现中得到了广泛应用。
数字实现的步骤
数字实现通常包括离散化、编程、仿 真和实际运行等步骤。离散化是将连 续的时间变量离散化,以便于数字计 算机处理;编程则是将离散化的系统 模型转化为计算机程序;仿真是在计 算机上模拟系统的动态行为,以便于 调试和优化;实际运行则是将优化后 的控制系统在实际环境中运行。
03
通过传递函数可以方便地分析 系统的稳定性、极点和零点等 重要特性,进而进行系统分析 和设计。
动态结构图
动态结构图是描述控制系统 动态特性的图形化表示方法 ,通过结构图可以直观地了 解系统各部分之间的相互关
系和信号传递过程。
动态结构图包括方框图、信 号流图和梅森图等形式,其 中方框图是最常用的一种形
自动控制原理(任彦硕第三 章
目录
• 控制系统概述 • 控制系统的数学模型 • 控制系统的性能分析 • 控制系统的校正与设计 • 控制系统的工程实现
l自动控制原理 第三讲 拉氏变换

Lecture3-Laplace TransformsK.J.ÅströmReview of control system analysis1.The Basic Feedback Loopplace T ransforms3.Analysis of Feedback Loops4.Qualitative Understanding of Signals and Systems5.SummaryTheme:Streamline manipulation of equations and block diagrams.Construction of a Block DiagramThe block diagram gives an overview.T o draw a block diagram:•Understand how the system works.•Identify the major components and the relevant signals.•Key questions:Where is the essential dynamics?What are appropriate abstractions?•Describe the dynamics of the blocks in terms of standard models.dt n+a1dn−1ydt n−1+...+b n u is characterized by two polynomialsA(s)=s n+a1s n−1+a2s n−2+...+a n−1s+a nB(s)=b1s n−1+b2s n−2+...+b n−1s+b n•The roots of A(s)are called poles of the system.•The roots of B(s)are called zeros of the system.•The transfer function of the system is G(s)=B(s)Linear Time Invariant Systems(LTI)d n ydt n−1+...+a n y=b1dn−1uInterpretation of the Impulse Responsey(t)=nk=1C k−1(t)eαk t+t(t−τ)u(τ)dτLet the system be initially at rest,i.e.C k=0and let the inputbe an impulse at time0.The output is theny(t)= (t)If the input is a unit step the output(the step response)isy(t)=t(t−τ)dτ=t(τ)dτExperimental determination of step and impulse responses.Recall Cruise ControlProcess modeldvdt2+(0.02+k)dedtThe mathematical tool of Laplace transforms is ideally suitedfor these type of calculations.An essential part of the languageof control.place TransformsConsider a function f defined on 0≤t <∞and a real number σ>0.Assume that f grows slower than e σt for large t .The Laplace transform F =L f of f is defined asL f =F (s )= ∞e −stf (t )dtExample 1:f (t )=1,F (s )=∞e −st dt =−1sExample 2:f (t )=e −at ,F (s )=∞e −(s +a )t dt =−1s +adt=∞e −stf (t )dt =e −st f (t )∞0+s∞e −stf (t )dt =−f (0)+s L fs)dv =f (0)Final value theoremlim s →0sF (s )=lim s →0∞0se −st f (t )dt =lims →0∞e −vf (vPropertiesLinearity:L (a f +b )=a L f +b L Differentiation:L dfs L fTime shift:L f (t −T )=e −sTL fTime stretch:L f (at )=1a ),a >0.Convolution:L t0f (t −τ) (τ)d τ=F (s )G (s )Final value Theorem †:lim s →0sF (s )=lim t →∞f (t )Initial value Theorem †:lim s →∞sF (s )=lim t →0f (t )•†:V alid only if limits exist!A (s )=B (s )s −α1+C 2s −αnC k =lim s →αk(s −αk )F (s )=B (αk )The time function corresponding to the transform isf (t )=C 1e α1t +C 2e α2t +...+C n e αn tParameters αk give shape and numbers C k give magnitudes.Notice that αk may be complex numbers.With multiple roots the constants C k are instead polynomials.Manipulating LTI Systems The differentiation property L dfCruise ControlProcess model:dvsE(s)Pure algebra gives relation between Laplace transforms of slopeΘreference V r and E by eliminating V and Us(s+0.02)+ks+k iE(s)=10sΘ(s)+s(s+0.02)V r(s)2+2ω0s+ω20Θ(s)=10θ0ω0te−ω0tω0te−ω0tThe largest error e max=10θ0e−1occurs for t=1/ωparegraph belowθ0=0.04ζ=1,ω0=0.05(dotted),ω0=0.1Discussion•What do we mean by a solution to a problem?•A historical perspectiveClosed form expressions,tables,curves •The role of computers•The necessity of insight and understanding•The need to check results•What properties can wefind easily using“back of an envelope”calculation.•A perspective on use of Laplace transforms in control engineering•A more general(biased personal)perspective.T echnology changes fast but engineering education changes slowly.U(s)=L yCar Model in Cruise Control Process modeldvU(s)=1U(s)=−10Transfer Function of PID ControllerThe error e is the input and the control signal u is the outputu=ke+k ite(τ))dτ+k ddeE(s)=k+k iTransfer Function of CarA simple model of a car on a horizontal road tells how its position y depends on the throttle.Let the mass be m and assume that the propelling force is proportional to the throttle wefindmd2yU(s)=kTransfer Function of Time DelayConsider a system where the output y is the input u delayed Ttime units.The input output relation isy(t)=u(t−T)and the transfer function isG(s)=Y(s)Transfer Function of Standard Model Consider the systemd n ydt n−1+...+a n y=b1dn−1us n+a1s n−1+a2s n−2+...+a n−1s+a nSolutionIntroduce Laplace transforms and transfer functions.We haveE =R − N +P (D +CE )Solving for E givesE =11+PCN −P5.Qualitative Understanding of Signals andSystemsTime responses can in principle be computed.T ables of Laplace transforms is a help but the work is quite tedious.Time responses are easy to compute using different types of software.•It is a good rule to always make order of magnitude calculations to make sure that results are reasonable whenever you use software.•Much insight can be obtained form very simple calcula-tions (series expansions and factorization).•Some results will be presented.•It will be discussed more in future lecturesA (s )=B (s )s −α1+C 2s −αnC k =lim s →αk(s −αk )F (s )=B (αk )Parameters αk (roots of A (s ))are easy to compute.The signal y (t )has the formy (t )=C 1e α1t +C 2e α2t +...+C n e αn tParameters αk give shape and C k give magnitudes.A (s )=s +5Example...For small s the Laplace transform is Y(s) 2.5/s,which implies that for large t the time function is y(t) 2.5.For larges we have Y(s) 1/s2.This means that for small t the time function isC(s)=s+5Insight from Transfer Functions•Derive transfer function G(s)=B(s)Insight from Transfer Functions•Make a series expansion of G(s)for small s(low fre-quency behavior,large t)G(s)=c−1s+c−2s k+...If c0=0like a static gain.If c−1=0and c−1=0like an integrator.If c−1=c−2=...=c−k+1=0and c k=0like k integrators.ExamplesE XAMPLE 1—PID CONTROLLERThe PID controller has the transfer functionG (s )=k +k is+k +k d sThis is already in series expansion form.For slow signals(small s )it behaves like an integrator and for fast signals (large s )it behaves like a differentiator.E XAMPLE 2—PID CONTROLLER WITHD ERIVATIVEF ILTERG (s )=k 1+11+s T d /NBehaves like a static gain k (1+N )for fast signals (large s ).。
自动控制原理第六章第三讲超前网络及其串联校正

根据截止频率
的要求,计算超前网络参数a和T;
求出T;
即可得超前网络的传递函数:
则已校正系统的传递函数为:
绘出校正后的对数幅频特性:
验证已校系统的相角裕度 ,若不满足 要求,应重选 ,一般使其增大。
步骤:
确定开环增益K(根据稳态误差的要求);
(
s
E
)
(
1
s
G
)
(
s
G
)
(
2
s
G
)
(
s
C
)
(
s
G
r
+
系统输出:
系统误差:
当:
时,
对输入的 误差全补偿条件
说明: 以上结论仅在理想条件下成立:
无论是输出响应完全复现输入或是完全不受扰动影响, 都是在传递函数零、极点对消能够完全实现的基础上得到的。
由于控制器和对象都是惯性的装置, 故G1(s)和G2(s)的分母多项式的s阶数比分子多项式的s阶数高。 据补偿式可见, 要求选择前馈装置的传递函数是它们的倒数, 即Gr(s)或Gn(s)的分子多项式的s阶数应高于其分母多项式的s阶数, 这就要求前馈装置是一个理想的(甚至是高阶的)微分环节。
滞后-超前网络贡献的幅值衰减的最大值
由相角裕度要求,估算网络滞后部分的交接频率 , 得:
01
结束
02
绘制已校正系统Bode图,校验性能指标
03
反馈校正
开环传函为:
工作原理 设图中局部反馈回路为G2c(s), 其频率特性为 :
反馈校正、复合校正基本原理
整个反馈回路的 传递函数等效为:
理想的微分环节实际不存在, 所以完全实现传递函数的零、极点对消在实际上也是做不到的。
北大《自动控制原理》讲义 第三讲
P.83 图3-13 给出了欠阻尼二阶系统阻尼比与超调量之间 的关系。 (5)调节时间 ts 的计算
为了简化调节时间的计算,一般用包络线来代替实 际响应估算调节时间。
在 0.8 ,误差带 0.05 5% 时,可用以下近似 估算公式:
ts
] 3.单位理想脉冲
δ(t)=
∞ t=0
0
且 (t)dt 1 0
0 t ≠0
L[δ(t)]=1
4正弦asinωt
L[a sin t] a s2 2
三 典型时间响应
1. 单位阶跃响应 Φ(s)*R(s)=Φ(s)*1/s h(t)=L-1 [Φ(s)*1/s]
2. 单位斜坡响应 Ct(s)= Φ(s)*R(s)= Φ(s)*1/s² Ct (t)=L-1 [Φ(s)*1/s2]
] L1[ C1 C2 1]
(s s1 )(s s2 )s
s s1 s s2 s
1 C1e s1t C2e s2t
C1=ωn2/( s1 -s2)s1; C1=ωn2/( s2 -s1)s2
-பைடு நூலகம்
图3.7二阶系统动态结构
二阶系统的响应特点和特征根的性质
ξ>1称过阻尼,由上知,s1 ,s2为两个不等的负实根 。
2 n
dc(t) dt
n2c(t)
n2r(t)
2
C(s)
R(s)
(s)
(s2
n
2 ns
n2
1. 单位阶段响应h(t)的一般式
2
C(s) (s) • R(s)
n
•1
s2 2 ns n2 s
则单位阶跃响应一般式
h(t)
自动控制原理课件第3次课 拉氏变换

不满足以上条件的方程,就成为非线性方程。
哈尔滨工程大学自动化学院
20
自动控制原理
第一章 自动控制的一般概念
常见非线性情况
饱和非线性 死区非线性
间隙非线性
继电器非线性
哈尔滨工程大学自动化学院
21
自动控制原理
第一章 自动控制的一般概念
单摆(非线性)
是未知函数 的非线性函数,
所以是非线性模型。
哈尔滨工程大学自动化学院
25
自动控制原理
第一章 自动控制的一般概念
多变量函数泰勒级数法
y f ( x1 , x2 )
增量方程
静态方程
哈尔滨工程大学自动化学院
26
自动控制原理
第一章 自动控制的一般概念
单变量函数泰勒级数法
函数y=f(x)在其平衡点(x0, y0)附近的泰勒级数展开式为:
略去含有高于一次的增量∆x=x-x0的项,则: 注:非线性系统的线性化 模型,称为增量方程。 注:y = f (x0)称为系统的 静态方程
机械旋转系统
哈尔滨工程大学自动化学院
12
自动控制原理
相似物理系统
第一章 自动控制的一般概念
哈尔滨工程大学自动化学院
13
自动控制原理
第一章 自动控制的一般概念
Part 2-1-3 提取数学模型的步骤 划分环节,确定输入量和输出量 逐个列写各元件的微分方程
消去中间变量
写成标准形式
实例 二级RC无源网络
自动控制原理
第一章 自动控制的一般概念
第二章 控制系统的数学模型
本章主要内容:
2-I 控制系统的数学模型
2-2 非线性数学模型的线性化
自动控制原理 第七章 第三讲 离散系统的动态性能分析

4 不同典型输入作用下, D(z)的确定 不同典型输入作用下, 的确定
a. 单位阶跃 (m=1, A(z)=1)
−1
R(z) =
1 1 − z −1
z −1 [1 − Φ ( z )] = (1 − z ) D ( z ) = (1 − z −1 )G ( z ) 1 误差的Z变换 变换: 误差的 变换: E ( z ) = [1 − Φ ( z )] =1 −1 (1 − z )
输输输输
1.4 1.2 1 0.8 0.6 0.4 0.2 0 0 2 4 6 10 12 时时(sec) 8 14 16 18
den=[1 [
-0.104 0.368] ]
dstep(num, den)
MATLAB绘制的阶跃响应曲线
二、闭环极点与动态响应的关系 (1)闭环实数极点分布与相应的动态响应形式 )
z=
w=
z +1 z −1
w +1 w −1
代入特征方程中,应用 代入特征方程中,应用Routh判据判稳 判据判稳
离散系统的稳态误差计算
1. 终值定理法
R(s) + E(s) T E *(s) C(s)
G(s)
-
系统的误差
E (z) =
1 R( z) 1 + G( z )
设闭环系统稳定, 根据终值定理 终值定理可以求出在输入信号作用下采样 设闭环系统稳定 根据终值定理可以求出在输入信号作用下采样 系统的稳态误差终值 系统的稳态误差终值: 稳态误差终值
t →∞ z →1 z →1
(*)
b.
当典型输入信号分别为单位阶跃 、 单位斜坡和 单位加速度信号时 当典型输入信号分别为 单位阶跃、 单位斜坡 和 单位加速度信号 时 , 单位阶跃 变换分别如下所示 其Z变换分别如下所示 变换分别如下所示: 1 Tz − 1 T 2 z − 1 (1 + z − 1 ) R(z) = , R(z) = , R(z) = 1 − z −1 (1 − z − 1 ) 2 2 (1 − z − 1 ) 3
自动控制原理第三章ppt课件

2
0
1.8 0.4
0.1
1.6 0.5
0.2
1.4 0.6
0.3
1.2 0.7
1 0.8
0.8
0.6 0.4 0.2
0 0
0.9 1.0 1.5
246
阻尼比越小,超调量越大,上升时间越短。
2
nt
8 10 12
阻尼比取0.40.8时,超调 量适宜,调节
时间短
可以看出:随着 的增加,c(t)将从无衰减的周期运动变为有
K K
H O
0.9 10
三、一阶系统的单位脉冲响应
输入 r(t)=δ(t)或R(s)=1 一阶系统的单位脉冲响应
c(t) 1 e t/T
T
ts 3T
ts 3T
动
态
性
能
对于脉冲扰动信号,具有. 自动调节能指力
26
四. 一阶系统的斜坡响应
输出与输 入之间的 位置误差 随时间而 增大,最 后趋于常 值T
阻尼系统,系统发散,系统不稳定。
2 当时 0,特征方程有一对共轭的虚根,称为零(无)阻尼系
统,系统的阶跃响应为持续的等幅振荡。
3. 当时 0 1 ,特征方程有一对实部为负的共轭复根,
称为欠阻尼系统,系统的阶跃响应为衰减的振荡过程。
4 当 1 时,特征方程有一对相等的实根,称为临界
阻尼系统,系统的阶跃响应为非振荡过程。
1 s
n2 s2 n2
1 s
时间响应
s 1
s2 n2 s
c(t)1cosnt
4. 临界阻尼运动 =1
1
C(s)
Gc
(s)
R(s)
(s
n2 n
自动控制原理自学课件 第三章 控制系统的时域分析—3高阶系统时域分析

n
工程上: b
P
n
5
7
s1
j
s3 5 n s2
n
由上图可见,当阻尼比 不变时,随着实数极点向虚 轴方向移动,系统的超调量不断下降,而峰值时间、 上升时间则不断加长。在b《1时,及闭环实数极点的 数值小于或等于闭环复数极点的实部数值时,三阶系 统将呈现过阻尼特性。 8
首先讨论典型三阶系统的瞬态响应,然后进行更具一般形式 的高阶系统的瞬态响应分析。从下面的讨论中,可以看到:
高阶系统的瞬态响应是由若干个一阶系统和二阶系 统的瞬态响应线性叠加而成。
1
1.三阶系统的单位阶跃响应
典型三阶系统的闭环传函可表示成: 2 Pn C (s) (s) , 0 1, P 0 2 2 R ( s ) ( s P )( s 2 n s n )
2
a3 0 a3 exp Pt 0
新增极点引发的自由运动模态项对过渡过程的影响是: 使最大超调减小,使调节时间增加
3
1.闭环极点对过渡过程的影响
s1, 2 n jn 1 2 s3 P
ct 1 a1 exp n t cos d t a2 exp n t sin d t a3 exp Pt
1
14
结论: 高阶系统的响应,是由一阶系统和二阶系统的
时间响应函数项叠加而成。只有所有闭环极点都具有负 实部,即所有极点均位于左半S平面,系统才是稳定的。 闭环极点负实部的绝对值越大,其对应的响应分量衰减 得越迅速,反之衰减得越慢。闭环极点决定系统响应类 型(发散、收敛),闭环零、极点共同决定系统响应形 状。
a3 1 Bs D C s 2 2 s s P s 2 n s n
最新自动控制原理第三章-3.1ppt课件

可得系统调节时间
3T 0.05
ts
4T
0.02
1 1/T斜 率
0.632
h(t)1et/T
0
T
t
显然,峰值时间tp和超调量σp%都不存在,所以一
阶系统的单位阶跃响应的主要性能指标就是其调
节时间ts,它表征了系统过渡过程的快慢。一阶
系统的时间常数T越小,调节时间ts 越短,响应
曲线越快接近稳态值。
自动控制原理第三章-3.1
主要内容
1. 什么是时域分析法 2. 时域分析法的条件 3. 一阶系统的时域分析
一. 什么是时域分析法
分析控制系统的方法 1.建立系统的数学模型 2.采用相应的分析方法
• 时域分析法
• 根轨迹方法 经典控制理论 • 频域分析法
时域分析法定义
根据系统的微分方程,以拉普拉斯变换作为数学工具, 直接解出控制系统的时间响应,然后根据响应的表达式 以及时间响应曲线来分析系统的控制性能,并找出系统 结构,参数与这些性能之间的关系的方法。
2.典型时间响应
动态过程——动态性能 (又叫瞬态过程或过渡过程) 稳态过程——稳态性能
➢ 动态性能指标 定义:描述稳定的系统在单位阶跃函数作用下,动 态过 程随时间t变化的指标,称为动态性能指标。
•延迟时间 •上升时间 •峰值时间 •调节时间 •超调量
典型单位阶跃响应
h(t)
1.0
td 0.5
误差带5%或2%
1. 可以用时间常数去度量 系统输出量的数值
t T时 , c(t ) 1 e 1 0.632 63 .2%
t 2T时 , c(t ) 1 e 2 0.865 86 .5%
t 3T时 , c(t ) 1 e 3 0.95 95 %
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
T dc(t) c(t) r(t) dt
Φ(s)=C(s)/R(s)=1 / (Ts+1)
一. 单位阶跃响应
c(s) (s) • R(s) 1 • 1 Ts 1 s
h(t) L1[
1
• 1] L1[1
1
1t
] 1e T
Ts 1 s
s s 1
T
图3.4一阶系统单位阶跃响应曲线
二.典型外作用
1 单位阶跃1(t)
1(t )
1 t>=0 0 t<0
L[1(t)] 1 s
图3.1 典型外作用
2.单位斜度t*1(t)
t t>=0
t*1(t)=
0 t<0
L[t •1(t )]
1 s2
] 3.单位理想脉冲
δ(t)=
∞ t=0
0
且 (t)dt 1 0
0 t ≠0
L[δ(t)]=1
图3.5 系统结构图
例3.2 试 证一阶响应曲线的次割距相等,且等于T。
证:
1 - h(t A ) tB - tA
dh(t ) dt
t t A
图3.6一阶系统响应的次割距
1 tA
1 (1 e T )
1
1 tA
eT
tB tA
T
tB- tA=T
3t 2
0.4 ~ 0.8 % 25.4% ~1.5%
P.83 图3-13 给出了欠阻尼二阶系统阻尼比与超调量之间 的关系。 (5)调节时间 ts 的计算
为了简化调节时间的计算,一般用包络线来代替实 际响应估算调节时间。
在 0.8 ,误差带 0.05 5% 时,可用以下近似 估算公式:
ts
2 n
dc(t) dt
n2c(t)
n2r(t)
2
C(s)
R(s)
(s)
(s2
n
2 ns
n2
1. 单位阶段响应h(t)的一般式
2
C(s) (s) • R(s)
n
•1
s2 2 ns n2 s
则单位阶跃响应一般式
h(t)
L1[C(s)]
L1[
(s 2
n 2n s
n2
•
1] s
L1[
n2
sin( n
1 2tr ) 1
1 2
sin(n 1 2 tr ) 0
tr
d
n
1 2
(3)峰值时间 t p 的计算
dh(t ) dt ttp
n e nt p sin d t p 0 1 2
sin d t p 0
d t p 0, , 2 , d t p ,
tp
d
过阻尼系统响应缓慢,对于一般要求时间响应快的 系统过阻尼响应是不希望的。 但在有些应用场合则需要过阻尼响应特性: 例如(1)大惯性的温度控制系统、压力控制系统等。
(2)指示仪表、记录仪表系统,既要无超调、时间 响应尽可能快。 另外,有些高阶系统可用过阻尼二阶系统近似。
过阻尼
1
h(t) 1 e t / T1 e t / T2 T2 / T1 1 T1 / T2 1
n2
K T
10K
, 10K 25 ,
K 2.5
s
1 T1
s
1 T2
s2
1 T1
1 T2
s
1 T1T2
,
n2
1 T1T2
1
T1
T2
1 5
0.2
ts 4.75T1 4.750.2 0.95 (s)
td
1 0.6 0.2 2 n
1.8 5
0.36 (s)
tr
11.5 n
2
3.5 5
本章重点
通过本章学习,应 重点掌握典型输入信号 的定义与特征、控制系 统暂态和稳态性能指标 的定义及计算方法、一 阶及二阶系统暂态响应 的分析方法、控制系统 稳定性的基本概念及稳 定判据的应用、控制系 统的稳态误差概念和误 差系数的求取等内容。
3.1 典型响应和性能指标
一.典型初状态
•
••
c(0 ) c(0) c(0 ) 0
(t 0)
2 css (t) t n
ctt (t) 1 ent sin( d t 2 ) n 1 2
2 e(t) r(t) c(t)
n n
1 ent sin( d t 2 ) 1 2
ess
(t)
r(t)
c
ss
(t)
t
css
(t)
2 n
de(t)
dt 0 t p d
e(t p )
3.5
n
也可以用以下公式估算:ts
4
ts
n
3
2% (0 0.9)
5%
1
n
1
n
4
ln
3 ln
1 1 2
1 1 2
n
2% 5%
二阶系统单位阶跃响应的性能指标归纳如下:
1 0.6 0.2 2
td
n
或
tr d
n 1 2
1 0.7 td n
tp
K
R(s) s2 (1 K )s K
K
K
C(s)
s(s 1)
1 s
(2) n K 1 K
2K
(3) p % e / 1 2 100%,
ln(1 / p )
0.456
2 (ln 1 ) 2
p
(4) n
3.53 (rad / s)
t p 1 2
(5) K n 2 12.46
一般取c(∞)的±5%,有时取±2%)并且以后不 再超过此值所需的最小时间。
4、稳态误差еss 对单位负反馈系统,当时间t趋于无穷大时,系
统的单位阶跃响应的实际值(即稳态值)与期望值( 即输入量1(t))之差,定义为稳态误差,即
еss =1-с(∞)
3-2 一阶系统分析 1. 数学模型
图3.3一阶系统典型结构
n
1 2
(4)超调量 % 的计算
h(t p ) 1 entp sin( n 1 2 t p ) 1 e / 1 2 sin( )
1 2
1 2
sin( ) 1 2 h(t p ) 1 e / 1 2
根据超调量的定义,并考虑到 h() 1
% e / 1 2 100%
n2
es1t
n2
es2t 1
(s1 s2 )s1
(s2 s1)s2
1
0.5
e ( 2 1)nt
0.5
e( 2 1)nt
2 2 1 1
2 2 1 1
ts
1
n
(6.45
1.7)
5%误差带 ξ>=0.7
图3.8过阻尼二阶系统h(t)曲线
四 临界阻尼二阶系统的单位阶跃响应
s1,2= -ωn
(t 0)
动态性能指标:延迟时间、上升时间、调节时间
因为求上述指标,要解一个超越方程,只能用数值 方法求解。利用曲线逆合法给出近似公式
(1)延迟时间 td 计算
1
1 0.6 0.2 2
td
n
(2)上升时间 tr 计算 p.86 图3-16
1
11.5 2 tr n
(3)调节时间 ts 计算
p.86 图3-17 ts ~ T1 T1 T2
s2
2
ns
n2
s
1 T1
s
1 T2
,
1 (T1 / T2 ) 2 T1 / T2
1 T1 / T2 1
ts 4.75T1
例:角度随动系统如图所示,设 K 为开环增益,
T=0.1 (s)为伺服电动机的时间常数。
若要求:单位阶跃响应无超调,而且 ts 1(s) ,求K 的取值、系统的延迟时间和上升时间
解:
1. (s)
C(s)
100/ s
10
1
10
R(s) 1 100 0.1 0.1s 1 0.1s 1
s
ts=3T=3*0.1=0.3秒
2. (s) 100 / s 1/ K H
1
100 s
KH
0.01 s 1 KH
-
T=0.01/ KH ts=3T=0.03/ KH 0.1=0.03/ KH KH=0.3
4正弦asinωt
L[a sin t] a s2 2
三 典型时间响应
1. 单位阶跃响应 Φ(s)*R(s)=Φ(s)*1/s h(t)=L-1 [Φ(s)*1/s]
2. 单位斜坡响应 Ct(s)= Φ(s)*R(s)= Φ(s)*1/s² Ct (t)=L-1 [Φ(s)*1/s2]
3. 单位脉冲响应 K(s)= Φ(s)*R(s) =Φ(s)*1=Φ(s) K(t)=L-1[Φ(s)]
四.阶跃响应的性能指标
图3.2 单位阶跃响应曲线及性能指标
1、峰值时间tp 指输出响应超过稳态值而达到第一个峰值所
需时间。 2、超调量σ% 指暂态过程中输出响应的最大值超过稳态值
的百分数。
% h(t p P h() •100 %
h()
3、调节时间ts 指当c(t)和c(∞)之间误差达到规定允许值(
解:因为考虑系统尽 r (s) 量快的无超调响应,
则可选阻尼比为临界
阻尼 1
ts 4.75T1
K
c (s)
s(Ts 1)
(s) K K /T Ts 2 s K s 2 1 s K TT
D(s) s2 1 s K 0 TT
T 0.1,
2
n
1 T
10 ,
