人教版八年上第十二章轴对称测试题(附答案)

合集下载

人教版八年级上第十二章轴对称测试题

第十二章轴对称单元测试题一、选择题(每小题5分，其25分)1．下列四个图案中，轴对称图形的个数是( )2．下列命题中，不正确的是( )(A)关于直线对称的两个三角形一定全等. (B)两个圆形纸片随意平放在水平桌面上构成轴对称图形.(C)若两图形关于直线对称，则对称轴是对应点所连线段的垂直平分线.(D)等腰三角形一边上的高、中线及这边对角平分线重台.3．下列四个图案中．具有一个共有性质则下面四个数字中，满足上述性质的一个是( ) (A)6 (B)7 (C)8 (D)94.等腰三角形的一个内角是50。

，则另外两个角的度数分别是( )(A) 65°，65°. (B) 50°,80°． (C) 65°，65°或50°，80°. (D) 50°,50°. 5.如果等腰三角形两边长是6cm 和3cm ,那么它的周长是( )(A) 9cm (B) 12cm (C) 1215cm cm 或 (D) 15cm .二、填空题(每小题5分，共20分)6．等腰三角形是对称图形，它至少有条对称轴.7．小明上午在理发店理发时，从镜子内看到背后墙上普通时钟的时针与分针的位置如图所示，此时时间是 .8．已知△ABC 是轴对称图形．且三条高的交点恰好是C 点，则△ABC 的形状是 .9．已知点A(一2，4)，B(2，4)，C(1．2)，D(1-2)，E(一3，1)，F(3，1)是平面坐标系内的6个点，选择其中三个点连成一个三角形，剩下三个点连成另一个三角形，若这两个三角形关于y 轴对称，就称为一组对称三角形，那么，坐标系中可找出组对称三角形． 10．如图，△ABC 中，AB=AC ．∠A=36°，AB 的中垂线DE 交AC 于D ，交AB 于E.下述结论(1)BD 平分∠ABC ；(2)AD=BD=BC ；(3)△BDC 的周长等于AB+BC ；(4)D 是AC 中点，其中正确的命题序号是 .三、画一画11.(6分)以“○○，△△，＿＿＿”(即两个圆,两个三角形,三条线段)为条件,画出一个有实际意义的对称图形.四、解答题12．(10分)在△ABC 中,∠C=90°，DE 垂直平分斜边AB ，分别交AB 、BC 于D 、E 。

数学八年级上册《轴对称》单元检测(含答案)

[点睛]本题考查了轴对称和轴对称图形的性质,难度适中．
9.如图,在中, , , 平分 , ,则图中共有等腰三角形（）
A. 个B. 个C. 个D. 个
[答案]D
[解析]
[分析]
根据等腰三角形性质和三角形内角和定理求出∠A C B＝∠B＝（180°−∠A）＝72°,求出∠A C D＝∠B C D＝ ∠A C B＝36°,求出∠C D B＝∠A＋∠A C D＝72°,根据平行线的性质得出∠ED B＝∠A＝36°,∠DEB＝∠A C B＝72°,∠C DE＝∠A C D＝36°,推出∠A＝∠A C D＝∠B C D＝∠C DE＝36°,∠B＝∠A C D＝∠DEB＝∠C D B＝72°即可．
A. B. C. D.
3.一个角是等腰三角形是（）
A.等腰直角三角形B.等边三角形C.直角三角形D.上述都正确
4.如图,在一个规格为（即个小正方形）的球台上,有两个小球 , ．若击打小球 ,经过球台边的反弹后,恰好击中小球 ,那么小球击出时,应瞄准球台边上的点（）
A. B. C. D.
5.如图,桌面上有M、N两球,若要将M球射向桌面的任意一边,使一次反弹后击中N球,则4个点中,可以瞄准的是( )
[详解]解：∵A B＝A C,
∴∠A B C＝∠C,
∵B D＝B A,
∴∠A＝∠B D A,
∴∠A＞∠C,
∴2∠A＜180°且3∠A＞180°,
∴60°＜∠A＜90°,即60＜x＜90．
故选C．
[点睛]此题考查了等腰三角形的性质,三角形内角和为180°和三角形外角的性质,关键是得到2∠A＜180°且3∠A＞180°．
[答案]D
[解析]
[分析]
此题根据△A B C中∠A为锐角与钝角分为两种情况解答．

人教版八年级数学上册《轴对称》测试卷(含答案)

人教版八年级数学上册《轴对称》测试卷（含答案）一、选择题(每小题3分,共30分)1.点A(m,3)与B(4,n)关于x轴对称,则m,n的值分别为( )A.4,3B.-4,-3C.-4,3D.4，-32.下列交通标志中,是轴对称图形的是( )3.下列轴对称图形中,对称轴最多的是( )A.线段B.等边三角形C.五角星D.圆4.下列三角形中,不是轴对称图形的是( )A.等腰直角三角形B.有一个角是30°的直角三角形C.两内角分别是30°，120°的三角形D.两内角分别是30°,75°的三角形5.如图,ABCD 是矩形纸片，翻折∠B、∠D,使AD、BC 边与对角线AC重叠，且顶点B、D恰好落在同一点0上,折痕分别是CE、AF,则AE等于( )EBA.√3B.2C.1.5D.√26.到三角形三个顶点距离相等的点是( )A.三条中线的交点B.三条高的交点C.三条角平分线的交点D.三边垂直平分线的交点7.如图,在等腰梯形ABCD中,AD //BC,AB=CD,AC=BD,AC平分∠BCD,若∠ABC=72°,则图中等腰三角形共有( )A.8个B.6个C.4个D.2个8.如图,在△ABC 中,AB<AC,BC边的垂直平分线交BC于D,交AC 于E,连BE,AB=6cm，△ABE 的周长为14cm,则AC的长为( )A.4cmB.6cmC.8cmD.10cm9.如图,已知AB=AC=BD,则∠1与∠2的关系是( )A.∠1=2∠2B.2∠1+∠2=180°C.∠1+3∠2=180°D.3∠1-∠2=180°10.如图,在△ABC中,∠BAC=90,AB=AC,BD平分∠ABC交AC于D,AE⊥BD,交BC于E，下列说法:①AB=BE;②∠CAE=1∠C;③AD=CE;④CD=CE.其中正确的是( )2A.①②③B.②③④C.①②④D.①②③④二、填空题(每小题3分,共18分)11.已知点A(m-1,3)与点B(2,n+1)关于x轴对称,则m=_________,n=__________.12.等腰三角形的一个角是80°,则它顶角的度数是_______________度.13.在△ABC 中.①若AB=BC=CA,则△ABC为等边三角形;②若∠A=∠B=∠C,则△ABC 为等边三角形;③有两个角都是60°的三角形是等边三角形;④一个角为60°的等腰三角形是等边三角形.上述结论中正确的有__个.14.如图,在△ABC 中,∠A=90°,∠ABC=60°,∠ABC,∠ACB的平分线交于点O,OE // AB交BC于E,OF //AC交BC于F,若AB=1,则△OEF 的周长为_____________.15.如图,AD是等边△ABC底边上的中线,AC的垂直平分线交AC 于点E,交AD于点F ,若AD=9,则DF长为____.16.已知Rt△ABC 中,∠C=90°,∠A=30°.在直线BC或AC上取一点P,使得△PAB是等腰三角形，则符合条件的P点有________个.三、解答题(72分)17.(8分)如图,△ABC 中,点D是BC边的中点,DE⊥AB于E,DF⊥AC于F,BE=CF.求证:∠BAD=∠CAD.18.(8分)如图,在△ABC中,D,E分别是AC,AB边上的点,BD,CE相交于点0,给出下列条件:①∠EBO=∠DCO;②∠BEO=∠CDO;③BE=CD;④OB=OC.(1)上述四个条件中,哪两个条件可判定△ABC是等腰三角形?(用序号写出所有的情形);(2)选择(1)中的一种情形,证明△ABC是等腰三角形.19.(8分)在平面直角坐标系中,△ABC的三个顶点坐标分别为A(-3,0),B(-3,-4),C(-1,-4).(1)求△ABC的面积;(2)在图中作出△ABC关于x轴对称的图形△DEF,并写出D,E,F 的坐标.20.(8分)如图,在△ABC中,∠ACB=2∠B,∠BAC的平分线AD交BC于D,过C作CN⊥AD交AD于H,交AB于N.(1) 求证:△ANC为等腰三角形;(2)试判断BN与CD的数量关系,并说明理由.21.(8分)已知如图,在△ABC中,AB=BC=2,∠ABC=120°,BC//x轴,点B的坐标是(一3,1).(1)写出顶点C的坐标;(2)作出△ABC 关于y轴对称的△A'B'C';(3)求以点A,B,B',A'为顶点的四边形的周长.22.(10 分)在△ABC 中,AB=CB.(1)若AC=AB,如图1,CM⊥AB 于点M,MN⊥AC 于点N,NP ⊥BC 于点P.若CP=2,则BP=_______;(2)若∠BAC=45°,如图2,CD平分∠ACB交AB于点D,过边AC上一点E作EF //CD,交AB于点F,AG是△AEF的高,探究高AG与边EF的数量关系;(3)若∠ABC=90°,点E是射线BC上的一个动点,作AF⊥AE且AF=AE,连CF交直线AB于点G.若BCCE =53，则AGBG=__________.23.(10分)图1,在△ABC中,AB=AC,∠BAC=30°，点D 是△ABC内一点,DB=DC,∠DCB=30°，点E是BD延长线上一点,AE=AB.(1)直接写出∠ADE 的度数___________;(2)求证:DE=AD+DC;(3)作BP 平分∠ABE,EF⊥BP,垂足为F(如图2),若EF=3,求BP 的长.24.(12分)如图1,A 是OB 的垂直平分线上的一点,P为y轴上一点，且∠OPB=∠OAB.(1)若∠AOB=60°,PB=4,求点P的坐标;(2)在(1)的条件下,求证:PA+PO=PB;(3)如图2,若点A是OB 的垂直平分线上的一点,已知A(2,5),∠OPB=∠OAB,求PO+PB 的值.参考答案：。

人教版八年级上册数学《轴对称》单元测试题附答案

A. 3B. 4C. 8D. 9
7.已知点P（5，-2）与点Q关于y轴对称，则Q点的坐标为（）
A. （-5，2）B. （－5，－2）C. （5，2）D. （5，－2）
8.如图，在锐角△ABC中，AB＝4 ，∠BAC＝45°，∠BAC的平分线交BC于点D，M、N分别是AD和AB上的动点，则BM＋MN的最小值是（）
23.已知，如图，是的平分线，，点在上，，，垂足分别是、 .试说明： .
24.如图，△ABC中，AC=BC，点D在BC上，作∠ADF=∠B，DF交外角∠ACE的平分线CF于点F．
（1）求证：CF∥AB；
（2）若∠CAD=20°，两个村庄A、B，要在河边建一自来水厂向A村与B村供水．
(4)小明站在五个学生的身后，这五个学生正向前方某人用手势示意一个五位数，从小明站的地方看(如图③所示)，这个五位数是23456.请你判断出他们示意的真实五位数是多少?
27.如图，已知△ABC中，AB＝AC＝12厘米，BC＝9厘米，AD＝BD＝6厘米．
(1)如果点P在线段BC上以3厘米秒速度由B点向C点运动，同时点Q在线段CA上由C点向A点运动．
10.把26个英文字母按规律分成5组，现在还有5个字母D、M、Q、X、Z，请你按原规律补上，其顺序依次为（）
①F，R，P，J，L，G，（）②H，I，O，（）③N，S，（）
④B，C，K，E，（）⑤V，A，T，Y，W，U，（）
A.Q X Z M DB.D M Q Z X
C.Z X M D QD.Q X Z D M
人教版数学八年级上学期
《轴对称》单元测试
(时间：120分钟满分：150分)
一、单选题（共10题；共28分）
1.下列交通标志是轴对称图形的是（）

人教版八年级上册第12章轴对称复习测试及答案4份WORD

图130，请你求出其余两角30和120”；王华同学说：75和75”．还有一些同学也提出了不同的看法．）假如你也在课堂中，你的意见如何？为什么？75和75或30和120．30+α+α=180，75．75和75．++β=，3030180120．30和120．“分类讨论”，“考虑问题要全面”等能体现分类讨论思想的给.为顶点将平角五等份，并沿五等份的折线折叠，再等于（）.如图，一平面镜与水平面成45°角固定在水平桌面上，一小球以桌面向平面镜匀速滚去，则小球在平面镜里所成的像（的速度，做竖直向上运动 B. 以1m/s的速度，做竖直向下运动的速度，做竖直向上运动 D. 以2m/s的速度，做竖直向下运动如图，在Rt△ABC中，∠C=90°，直线BD交AC于上；然后再沿虚线上的半圆，再展开，则展开后二、填空题（每小题3分，共24分）1．已知△ABC是轴对称图形，且三条高的交点恰好是C点，则△的形状是___________.2. 如图6，DE是AB的垂直平分线，D是垂足，DE交BC于AC=18cm，则△AEC的周长为_______cm.3. 已知点A，B，C，D的坐标分别为A（-2，1），B（1，2），C（-2，-1），D（1，-2），则线段AB与CD关于______.4.在如图7的4×4正方形网格中，∠1+∠2+∠3+∠4+∠5+∠的顶点A，B，C，D按顺时针方向排列，若在平面直角坐标系内，、D两点对应的坐标，0），且A、C两点关于x中，∠B=∠C，FD⊥BC，________.__________.成轴对称且也以格点为顶点的三角A AB CC．3 D．4 6，则此等腰三角形的周长为（）=90°，AB的垂直平分线交．的对称轴，如果AD∥BC（用直尺、圆规作图，保留作图痕迹，不写作法，不要求证明）2008年北京2004年雅典1988年汉城1980年莫斯科ＡＢＣＤ．如图1，在平面直角坐标系中，下列各中是点E关于x轴的对称点的是（加拿大澳大利亚瑞士乌拉圭A．加拿大、乌拉圭B．加拿大、瑞士、澳大利亚，请你找出格纸中所有与。

新人教版八年级数学上册第十二章轴对称测试题及答案ABC卷

课标人教版八年级（上）数学检测试卷轴对称 A 卷（考试时间为60分钟，满分100分）姓名：______________一、填空题（每小题3分，共30分） 1．长方形的对称轴有___________条． 2．等腰直角三角形的底角为_____________．3．等边三角形的边长为a ，则它的周长为_____________． 4．（-2，1）点关于x 轴对称的点坐标为__________．5．如图，∠A =36°，∠DBC =36°，∠C =72°，则图中等腰三角形有_______个． 6．如图，△ABC 中，DE 是AC 的垂直平分线，AE =3cm ，△ABD 的周长为13cm ，则△ABC 的周长为____________．7．△ABC 中，AB 边上的中线CD 将△ABC 分成两个等腰三角形，则∠ACB =_______度． 8．等腰三角形的顶角为x 度，则一腰上的高线与底边的夹角是___________度．9．在“线段，角，半圆，长方形，梯形，三角形，等边三角形”这七个图形中，是轴对称的图形有_______个．10．如图，四边形ABCD 沿直线l 对折后互相重合，如果AD ∥BC ，有下列结论:①AB ∥CD ；②AB =CD ；③AB ⊥BC ；④AO =OC 其中正确的结论是_______________．（把你认为正确的结论的序号都填上）二、选择题（每小题3分，共30分）11．下列平面图形中，不是轴对称图形的是（）12．下列英文字母属于轴对称图形的是（）（A ）（B ）（C ）（D ）ABC D第5题第6题ABDCE第10题ABCDl O（A ） N （B ） S （C ） H （D ） K13．下列图形中对称轴最多的是（）（A ）圆（B ）正方形（C ）等腰三角形（D ）线段14．如图，△ABC 中，AB =AC ，D 是BC 中点，下列结论中不正确的是（）（A ）∠B =∠C （B ）AD ⊥BC （C ）AD 平分∠BAC （D ）AB =2BD15．△ABC 中，AB =AC ．外角∠CAD =100°，则∠B 的度数（）（A ）80° （B ）50° （C ）40° （D ）30°16．等腰三角形的一个角是80°，则它的底角是（）（A ）50° （B ） 80° （C ） 50°或80° （D ） 20°或80°17．如果一个三角形两边的垂直平分线的交点在第三边上，那么这个三角形是（）（A ）锐角三角形．（B ）直角三角形．（C ）钝角三角形．（D ）不能确定．18．如图，是屋架设计图的一部分，点D 是斜梁AB 的中点，立柱BC 、DE 垂直于横梁AC ，AB =8m ，∠A =30°，则DE 等于（）（A ）1m （B ） 2m （C ）3m （D ） 4m19．以下叙述中不正确的是（）A 、等边三角形的每条高线都是角平分线和中线B 、有一内角为 60的等腰三角形是等边三角形C 、等腰三角形一定是锐角三角形D 、在一个三角形中，如果两条边不相等，那么它们所对的角也不相等；反之，如果两个角不相等，那么它们所对的边也不相等。

人教版八年级上册数学《轴对称》单元测试卷(含答案)

人教版八年级上册数学《轴对称》单元测试卷姓名：__________班级：__________考号：__________一、选择题（本大题共10小题，每小题3分，共30分。

在每小题给出的四个选项中，只有一个选项是符合题目要求的）1.下列“QQ 表情”中属于轴对称图形的是（）2.如图，AC AD =，BC BD =，则有（）A ．AB 垂直平分CD B ．CD 垂直平分ABC ．AB 与CD 互相垂直平分D ．CD 平分ACB ∠3.下列图形中对称轴最多的是（）A ．圆B ．正方形C ．等腰三角形D ．线段4.如图，ΔABC 与ΔA 'B 'C '关于直线l 对称，则∠B 的度数为（）A ．．．30．．°B ．．．50．．°C ．．．90．．°D ．．．100．．．° 5.如图，等腰ABC △中，底边BC a =，36A ∠=︒，ABC ∠的平分线交AC 于D ，BCD ∠的平分线交BD 于E ，则图中等腰三角形共有（）个．A ．3B ．4C ．5D ．6BD CA6.如图所示，将一张正方形纸片对折两次，然后在上面打3个洞，则纸片展开后是7.如图，在ABC ∆中，AB AC =，ABC ∠，ACB ∠的平分线相交于点F ，过F 作DE BC ∥ ，交AB 于点D ，交AC 于E ．图中是等腰三角形有（）个．A ．3B ．4C ．5D ．68.已知等腰三角形的周长为24cm ，一腰长是底边长的2倍，则腰长是( )A ．4.8cmB ．9.6cmC ．2.4cmD ．1.2cm9.若等腰三角形中有一个角等于50︒，则这个等腰三角形的顶角的度数为( )A ．50︒B ．80︒C ．65︒或50︒D ．50︒或80︒ 10.如图1所示为三角形纸片ABC ，AB 上有一点P ．已知将A ，B ，C 往内折至P 时，出现折线 SR 、TQ 、QR ，其中Q 、R 、S、T 四点会分别在BC 、AC 、AP 、BP 上，如图2所示．若ABC △、四边形PTQR 的面积分别为16、5，则PRS △的面积为（）EDCB AF E C B AD二、填空题（本大题共5小题，每小题3分，共15分）11.已知ABC ∆中，AB AC =．36A ∠=︒，则C ∠= ．12.等腰三角形一个角为70°,它的另外两个角为 .13.如图，在ABC ∆中，120BAC ∠=︒，AD BC ⊥于D ，且AB BD DC +=，那么C ∠的度数是_______14.如图，ABC △中，AD 平分BAC ∠，AB BD AC +=，则:B C ∠∠= ．15.如图，将ABC ∆绕着C 点按顺时针方向旋转20︒，B 点落在'B 点位置，A 点落在'A 点位置，若''AC AB ⊥，则________BAC ∠=D CB AAB CB'A'CB A三、解答题（本大题共7小题，共55分）16.在正方形ABCD 所在平面上找一点P ，使APB ∆是等腰直角三角形，这样的点P 你能发现几个?请作出这些点．17.求作线段AB 的垂直平分线18.如图，在ABC ∆中，AB AC =，D 是ABC ∆外的一点，且60ABD ∠=，60ACD ∠=．求证：BD DC AB +=．19.如图，P 是ABC ∆的外角EAC ∠的平分线AD 上的点（不与A 重合）求证：PB PC AB AC +>+DCB A BDC B AEDPCB A20.尺规作图：把右图补成以虚线l为对称轴的轴对称图形，你会得到一只美丽蝴蝶的图案（不用写作法、保留作图痕迹）．21.已知BD是等腰ABC∆三个内角的度数．∆一腰上的高，且50ABD∠=︒，求ABC22.已知：如图，ABC=，且P点到ABC ∠及两点M、N。

人教版八年级上册数学《轴对称》单元测试题(附答案)

14.如图，在△ABC中，∠ABC＝∠ACB，点P为△ABC内一点，且∠PBC＝∠PCA，∠BPC＝110°，则∠A＝_____．
15.如图，若∠A＝15°，AB＝BC＝CD＝DE＝EF，则∠DEF等于_____．
三、解答题
16.如图，在平面直角坐标系中，A（1，2），B（3，1），C（﹣2，﹣1）．
∴∠CBD=∠A+∠ACB=36°，
∵BC=CD，
∴∠CDB=∠CBD=36°，
∴∠DCE=∠A+∠CDA=18°+36°=54°，
∵CD=DE，
∴∠CED=∠DCE=54°，
∴∠EDF=∠A+∠AED=18°+54°=72°，
∵DE=EF，
∴∠EFD=ห้องสมุดไป่ตู้EDF=72°，
∴∠GEF=∠A+∠AFE=18°+72°=90°．
证明：（1）FC=AD；
（2）AB=BC+AD。
24.如图，在中，是的中点，过点的直线交于点，交的平行线于点，交于点，连接、．
(1)求证：；
(2)请你判断与的大小关系，并说明理由．
参考答案
一、选择题
1.下列图形中，不是轴对称图形的是（）
A. B. C. D.
【答案】A
A.10B.16C.8D.4
10.如图，在△ABC中，AB=AC=11，∠BAC=120°，AD是△ABC的中线，AE是∠BAD的角平分线，DF∥AB交AE的延长线于点E，则DF的长为（）
A. 4.5B. 5C. 5.5D. 6
11.如图，等边△ABC 边长为4，AD是边BC上的中线，F是边AD上的动点，E是边AC上一点，若AE=2，则EF+CF取得最小值时，∠ECF的度数为（）

人教版数学八年级上册《轴对称》单元检测题附答案

14.如图，树AB垂直于地面，为测树高，小明在C处测得∠ACB＝15°，他沿CB方向走了20米，到达D处，测得∠ADB＝30°，则计算出树的高度是__________米．
15.如图，在△ABC中，AC＝8，BC＝5，AB的垂直平分线DE交AB于点D，交边AC于点E，则△BCE的周长为______已知点P(3，－1)关于y轴对称点Q的坐标是(a＋b，1－b)，则ab的值为______.
【答案】－10
【解析】
试题解析：∵点P(3,−1)关于y轴的对称点Q的坐标是(a+b,1−b)，
∴a+b=−3，1−b=−1，
解得：b=2，a=−5，
故答案为
14.如图，树AB垂直于地面，为测树高，小明在C处测得∠ACB＝15°，他沿CB方向走了20米，到达D处，测得∠ADB＝30°，则计算出树的高度是__________米．
点睛：本题考查的是等腰三角形的性质及三角形外角的性质，根据题意得出∠B1C2A1，∠B2A3A2及∠B3A4A3的度数，找出规律是解答此题的关键．
6.下列图标中是轴对称图形的是（）
A. B. C. D.
【答案】D
【解析】
【详解】解:A、不是轴对称图形，故本选项错误；
B、不是轴对称图形，故本选项错误；
人教版数学八年级上学期
《轴对称》单元测试
考试时间：90分钟满分：100分
一、选择题(每小题3分，共30分)
1.已知等腰三角形的顶角为50°，则这个等腰三角形的底角为（）．
A. 50°B. 65°C. 80°D. 50°或65
2.如图，若是等边三角形，，是的平分线，延长到，使，则
A 7B.8C.9D.10
∵一边长为6，
∴它的周长为18.

数学八年级上册《轴对称》单元测试题(带答案)

∴∠A=40°．
∵A B=A C，
∴
故选A．
[点睛]此题考查等腰三角形的性质及三角形的内角与外角等知识点的掌握情况．根据已知求得∠A=40°是正确解答本题的关键．
二、填空题
11.请写出两个具有轴对称性的汉字.
[答案]甲、由、中、田、日等(答案不唯一).
[解析]
[分析]
根据轴对称图形的概念，即可写出:甲，日，田等字．
6.已知M(0，2)关于x轴对称的点为N，线段MN的中点坐标是()
A.(0，﹣2)B.(0，0)C.(﹣2，0)D.(0，4)
[答案]B
[解析]
根据轴对称的性质，知线段MN的中点就是原点，即线段MN的中点坐标是(0，0)．
故选B
7.在△A B C中,A B=A C,D为B C的中点,则下列结论:①∠B=∠C;②A D⊥B C;③∠B A C=2∠B A D;④A B,A C边上的中线的长相等.其中正确的结论有( )
故答案选:A．
[点睛]本题考查了用坐标表示轴对称的知识点，熟练掌握点关于x轴、y轴对称的点的坐标特点是解题的关键．
3.已知线段A B和点C,D,且C A=C B,D A=D B,那么直线C D是线段A B的( )
A. 垂线B. 平行线
C. 垂直平分线D. 过中点的直线
[答案]C
[解析]
[分析]
由已知C A=C B根据线段垂直平分线的性质的逆定理可得点C在A B的垂直平分线上，同理得点D的位置
[答案]D
[解析]
[分析]
此题中没有明确指出等边三角形的边长是等腰三角形的底边还是腰长，所以我们应该分两种情况进行分析．先求出等边三角形的边长，再分两种情况进行分析求解．
[详解]解:∵等边三角形周长为45Cm，

数学八年级上人教新课标第12章轴对称习题精选2汇总

第12章《轴对称》（测试时间90分钟，测试总分100分）一、选择题（每题3分，共30分）2. 点M（1，2）关于x轴对称的点的坐标为（）A：（－1，－2） B：（－1，2） C：（1，－2） D：（2，－ 1）3．下列图形中对称轴最多的是( )A：等腰三角形 B：正方形 C：圆 D：线段4．已知直角三角形中30°角所对的直角边为2㎝，则斜边的长为（）A：2 ㎝ B：4 ㎝ C：6 ㎝ D：8㎝5．下列说法正确的是( )A：等腰三角形的高、中线、角平分线互相重合 B：顶角相等的两个等腰三角形全等C：等腰三角形的两个底角相等 D：等腰三角形一边不可以是另一边的二倍6．若等腰三角形的周长为26cm，一边为11cm，则腰长为（）A：11cm B：7.5cm C：11cm或7.5cm D：以上都不对7．如图：DE是∆ABC中AC边的垂直平分线，若BC=8厘米，AB=10厘米，则∆EBC的周长为（）厘米A：16 B：18 C：26 D：288．如图：∠EAF=15°，AB=BC=CD=DE=EF，则∠DEF等于（）A：90° B： 75° C：70° D： 60°9．若等腰三角形腰上的高是腰长的一半,则这个等腰三角形的底角是（）A：75°或15° B：75° C：15° D：75°和30°10．如图所示，是四边形ABCD的对称轴，AD∥BC，现给出下列结论：①AB∥CD；②AB=BC；③AB⊥BC；④AO=OC 其中正确的结论有（）A：1个 B：2个 C：3个 D：4个二、填空题（每题3分，共18分）11．等腰三角形的一边长是6，另一边长是3，则周长为________________；CEBDAlOCB DACA FECBA12．等腰三角形的一内角等于50°，则其它两个内角各为；13．如图：在Rt △ABC 中，∠C=90°，∠A=30°，AB ＋BC=12㎝，则AB= ㎝； 14．如图：点P 为∠AOB 内一点，分别作出P 点关于OA 、OB 的对称点P 1，P 2，连接P 1P 2交OA 于M ，交OB 于N ，P 1P 2=15，则△PMN 的周长为； 15.等腰三角形一腰上的高与另一腰上的夹角为30°，则顶角的度数为；16.如图：是屋架设计图的一部分,点D 是斜梁AB 的中点,立柱BC 、DE 垂直于横梁AC,AB=8m,∠A=30°,则DE 等于；三、解答题（17题6分,18题～19题每题7分,20题～23题8分，共52分）17.（6分）如图：某地有两所大学和两条相交叉的公路，（点M ，N 表示大学，AO ，BO 表示公路）.现计划修建一座物资仓库，希望仓库到两所大学的距离相等，到两条公路的距离也相等。

人教版八年第十二章轴对称练习题

1. 写出下列各点关于已知直线的对称点：（1）（3,2）关于直线x=1的对称点为，关于直线y=-1的对称点为 .（2）（5，-3）关于直线x=6的对称点为，关于直线y=-4的对称点为 .2.如图，已知点M 、N 和∠AOB,求作一点P ，使点P 到点M,N的距离相等，且到角两边的距离相等.3.已知A(-1,2)和B(-3，-2),试在y 轴上确定一点P ，使其到A 、B 的距离和最小，求P 点的坐标.4.如图，已知AD 是∠BAC 的角平分线，AD 的垂直平分线交AB 于点E ，交BC 的延长线于点F.（1）你知道与∠FAC 相等的角是哪一个？为什么？（2）小明认为直线DE 与AC 不可能相交，你同意他的说法吗，为什么？5.如图，△ABC 中，AB ＞AC,BC 的垂直平分线DF 交△ABC 的外角平分线AD 于D,DE ⊥AB 于点E ，求证：BE-AC=AE.6.如图，在Rt △ABC 中，∠C=90°，DE 是AB 的垂直平分线，交BC 于点E,连接AE, ∠CAE: ∠BAE=1:2，求∠B 的度数.1.如图，在直角坐标系中，点A 的坐标为（1，0），以OA 为边在第四象限内作等边△AOB ，点C 为x 轴上一动点.（O C ＞1），连接BC ，以BC 为边在第四象限内作等边△CBD ，直线DA 交y 轴于点E.（1）试问△OBC 与△ABD 全等吗？并证明你的结论.（2）随着点C 位置的变化，点E 的位置是否会发生变化，请你说明理由._ O _ B 2题图_ E _ F _ D _ C _ B _ A 4题图 _E _F _D _ C _ B _ A 5题图 _E _ D _ C _ B _ A 6题图_ y _ x _ O _ E _ D _C _B _ A2.已知，如图在△ABC 中，AB=AC ，D 为AC 上任意一点，延长BA 到E 使AE=AD ，连接DE.求证：D E ⊥BC.3.如图，在△ABC 中，∠ACB=100°，AC=AE ，BC=BD ，求∠DCE 的度数.4.如图，在△ABC 中，AB=AC ，AD 和BE 是高，它们交于点H ，且AE=BE.求证：AH=2BD_ E _ D _ C _ B _ A _ E _ D _ C _ B _ A_ H _ E _ D _ C _ B _ A1.如图，OP 是∠AOB 的平分线，OM 是∠AOP 的平分线，PN ⊥OA 于N ，交OM 于M ，则MN 与MP 的大小关系是怎样？2.如图，△ABC 中，D 、E 分别是边AC 、AB 上的点，BD 与CE 相交于点O ，给出下列四个条件：①∠EBO=∠DCO ；②∠BEO=∠COD ；③BE=CD ；④OB=OC.把其中两个条件作为题设，可能推出△ABC 是等腰三角形的有多少种？3.如图，在△ABC 中，AB 、AC 的垂直平分线分别交BC 于点E 、F ，若∠BAC=115°，求∠EAF 的度数.4.如图，在△ABC 中，AB=AC ，在AB 边上取一点D ，在AC 的延长线上取一点E ，使BD=CE ，连接DE 交BC 于点G.求证：DG=GE_ N _ P _ M _ O _ B _ A _ E _ D _ C _B _ A _ F _ E _C _B _ A G _ E _ D _C _ B _ A5.如图A （9，0）、B （0，6）、C （0，－2），连接AB ，经过点C 的直线L 与AB 交于点E ，与X 轴交于点D （3，0），且EB=EC ，求△EAD 的面积.6.如图：△ABC 中AB=AC ，D 是BC 上一点，∠BAD=30°，E 是AC 上一点，且AD=AE ，求∠EDC 的度数.7.如图，AD 是△ABC 的边BC 上的高，由下列条件中的某一个就能推出△ABC 是等腰三角形的是（把所有正确答案的序号填写在横线上）.①∠BAD=∠ACD ；②∠BAD=∠CAD ；③AB+BD=AC+CD ；④AB －BD=AC －CD8.如图，△ABC 是等边三角形，CE 是∠ACD 的平分线，且CE=BD ，判断△ADE 的形状._ x _ y _ E _ D _ C _ O _ B _A _ E _ D _ C _B _A _ D _ C _B _ A _E _ A1.在△ABC 中，∠A=100°，∠ABC=40°，BD 是∠ABC 的平分线，延长BD 至E ，使DE=AD 。

轴对称测试题及答案

DCBA第14题第15题第16题O新人教版八年级数学上册第十二章轴对称测试题及答案一、选择题（本大题共12小题，每小题2分，共24分）1.下列几何图形中，是轴对称图形且对称轴的条数大于1的有（）⑴长方形；⑵正方形；⑶圆；⑷三角形；⑸线段；⑹射线；⑺直线.A. 3个B. 4个C. 5个D. 6个2.下列说法正确的是（）A.任何一个图形都有对称轴B.两个全等三角形一定关于某直线对称C.若△ABC与△DEF成轴对称，则△ABC≌△DEFD.点A，点B在直线L两旁，且AB与直线L交于点O，若AO＝BO，则点A与点B关于直线L对称3.如图所示是一只停泊在平静水面的小船，它的“倒影”应是图中的（）4.在平面直角坐标系中，有点A（2，－1），点A关于y轴的对称点是（）A.（－2，－1）B.（－2，1）C.（2，1）D.（1，－2）5.已知点A的坐标为（1，4），则点A关于x轴对称的点的纵坐标为（）A. 1B. －1C. 4D. －46.等腰三角形是轴对称图形，它的对称轴是（）A.过顶点的直线B.底边上的高C.底边的中线D.顶角平分线所在的直线.7.已知点A（－2，1）与点B关于直线x＝1成轴对称，则点B的坐标为（）A.（4，1）B.（4，－1）C.（－4，1）D.（－4，－1）8.已知点P（1，a）与Q（b，2）关于x轴成轴对称，又有点Q（b，2）与点M（m，n）关于y轴成轴对称，则m－n的值为（）A. 3B.－3C. 1D. －19.等腰三角形的一个内角是50°，则另外两个角的度数分别为（）A.65°，65°B.50°，80°C.65°，65°或50°，80°D.50°，50°10.等腰三角形一腰上的高与另一腰的夹角为60°，则这个等腰三角形的顶角为（）A. 30°B. 150°C. 30°或150°D.12°11.等腰三角形底边长为6cm，一腰上的中线把它的周长分成两部分的差为2cm，则腰长为（）A. 4cmB. 8cmC. 4cm或8cmD. 以上都不对12.已知∠AOB＝30°，点P在∠AOB的内部，点P1和点P关于OA对称，点P2和点P关于OB对称，则P1、O、P2三点构成的三角形是（）A.直角三角形B.钝角三角形C.等腰直角三角形D.等边三角形二、填空题：（本大题共8小题，每小题3分，共24分）13.等边三角形是轴对称图形，它有条对称轴.14.如图，如果△A1B1C1与△ABC关于y轴对称，那么点A的对应点A1的坐标为21题⑴L21题⑵BEDCBA15.如图是某时刻在镜子中看到准确时钟的情况，则实际时间是.16.已知∠AOB＝30°，点P在OA上，且OP＝2，点P关于直线OB的对称点是Q，则PQ＝.17.等腰三角形顶角为30°，腰长是4cm，则三角形的面积为.18.点P（1，2）关于直线y＝1对称的点的坐标是；关于直线x＝1对称的的坐标是.19.三角形三内角度数之比为1∶2∶3，最大边长是8cm，则最小边的长是.20.在△ABC和△ADC中，下列3个论断：①AB＝AD；②∠BAC＝∠DAC；③BC＝DC.将两个论断作为条件，另一个论断作为结论构成一个命题，写出一个真命题：.三、解答题：（本大题共52分）21.（每小题5分，共10分）作图题：（不写作法，保留作图痕迹）⑴如图，已知线段AB和直线L，作出与线段AB关于直线L对称的图形.⑵已知∠AOB和C、D两点，求作一点P，使PC＝PD，且P到∠AOB两边的距离相等.22.（5分）如图所示，在平面直角坐标系中，A（－1，5），B（－1，0），C（－4，3）.⑴求出△ABC的面积.⑵在图形中作出△ABC关于y轴的对称图形△A1B1C1.⑶写出点A1，B1，C1的坐标.23.（5分）如图所示，梯形ABCD关于y轴对称，点A的坐标为（－3，3），点B的坐标为（－2，0）.⑴写出点C和点D的坐标；⑵求出梯形ABCD的面积.24.（5分）如图，△ABC中，DE是AC的垂直平分线，AE＝3cm，△ABD的周长为13cm.求△ABC的周长.P DC B A P ED C B ANM F E CB A 25.（6分）如图，D 是等边三角形ABC 内一点，DB ＝DA ，BP ＝AB ，∠DPB ＝∠DBC.求证：∠BPD ＝30°.26.（8分）如图，△ABC 为任意三角形，以边AB 、AC 为边分别向外作等边三角形ABD 和等边三角形ACE ，连接CD 、BE 并且相交于点P. 求证：⑴CD ＝BE. ⑵∠BPC ＝120°27.（6分）下面有三个结论：⑴ 等腰三角形两底角的平分线的交点到底边两端的距离相等.⑵ 等腰三角形两腰上中线的交点到底边两端的距离相等.⑶ 等腰三角形两腰上的高的交点到底边两端的距离相等.请你任选一个结论进行证明.28.（7分）如图，在△ABC 中，AB ＝AC ，∠A ＝120°，BC ＝6，AB 的垂直平分线交BC 于M ，交AB 于E ，AC 的垂直平分线交BC 于N ，交AC 于F ，求证：BM ＝MN ＝NC.参考答案和提示：一、选择题：1.C ；2.C ；3.B ；4.A ；5.D ；6.D ；7.A ；8.B ；9.C ；10.C ；11.C ；12.D ；二、填空题：13. 3；14.（－1，3）；15. 4点40分；16. 2；17. 4cm 2；18.（1，0），（1，2）； 19.4cm ；20.等腰三角形的顶角平分线和底边上的中线重合.三、解答题：21.略；22.⑴＝×5×3＝7.5（平方单位）；⑵略；⑶A 1（1，5），B 1（1，0）；C 1（4，3）.ED CB A23.⑴C（2，0），D（3，3）.⑵＝（4＋6）×3＝15（平方单位）.24.∵DE是线段AC的垂直平分线∴AD＝CD∵△ABD的周长为13cm∴AB＋BC＝13cm∵AE＝3cm∴AC＝2AE＝6cm. ∴△ABC的周长为：AB＋BC＋AC＝19cm.25.连接CD，并延度CD交AB于E，证CE垂直平分AB，可得∠DCB＝30°再证△BDC≌△BDP即可.26.略；27.略28.连接MA、NA，证明：MA＝NA＝MN.。

八年级(初二)上册数学第十二章轴对称测试题(附答案)

第十二章轴对称一、填空题(每小题2分，共20分)1、等腰三角形是对称图形，它至少有条对称轴.2、等腰三角形的顶角与底角的度数之比为4：1，则它的各内角度数为 _______________ .3、已知△ABC 是轴对称图形．且三条高的交点恰好是C 点，则△ABC 的形状是 ___________.4、直线y=kx+4与坐标轴围成的三角形是等腰三角形，则k=5、已知点P(一3，2)，点P 关于X 轴的对称点坐标为 ____6、Rt △ABC 中，∠ACB=90°，CD 是高，∠A=30°，BD=5cm ，则AB=7、观察上图中的图片，请说出图中小亮衣服上的数字是：8、如果等腰三角形一腰上的高与腰的夹角为30°，则该三角形的顶角的度数为 9、已知点A(一2，4)，B(2，4)，C(1，2)，D(-1，2)，E(一3，1)，F(3，1)是平面坐标系内的6个点，选择其中三个点连成一个三角形，剩下三个点连成另一个三角形，若这两个三角形关于y 轴对称，就称为一组对称三角形，那么，坐标系中可找出 ____________组对称三角形．10、小强拿了一张正方形的纸如图（1），沿虚线对折一次得图（2），再对折一次得图（3），然后用剪刀沿图（3）中的虚线（虚线与底边平行）剪去一个角，再打开后的形状应是二、选择题(每小题3分，共18分)第6B ADC12、下列命题中，不正确的是( )(A)关于直线对称的两个三角形一定全等.(B)两个大小一样的圆形纸片随意平放在水平桌面上构成轴对称图形. (C)若两图形关于直线对称，则对称轴是对应点所连线段的垂直平分线. (D)等腰三角形一边上的高、中线及这边对角平分线重台.13、将长方形ABCD 沿折痕EF 折叠，使CD 落在GH 的位置，若∠BGH=55°，则∠HEF=（） (A)55° (B) 65°(C)72.5 (D)75° 12、等腰三角形的一个内角是50。

人教八年级数学上第12章《轴对称图形》单元检试题含解析

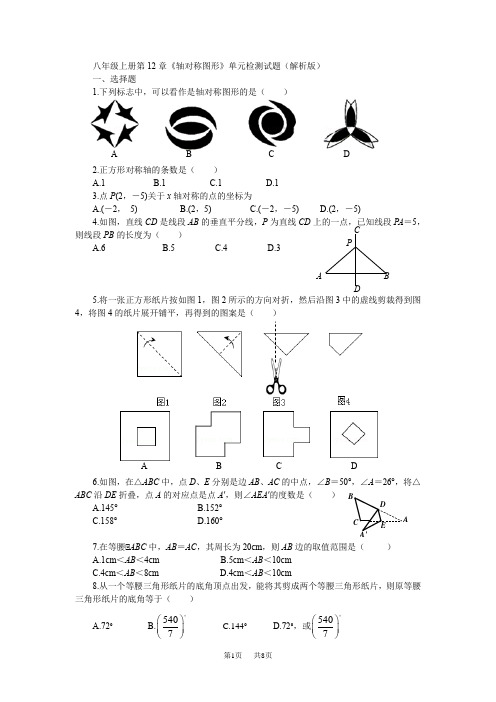
八年级上册第12章《轴对称图形》单元检测试题（解析版）一、选择题1.下列标志中，可以看作是轴对称图形的是（）2.正方形对称轴的条数是（）A.1B.1C.1D.13.点P (2，－5)关于x 轴对称的点的坐标为A.(－2， 5)B.(2，5)C.(－2，－5)D.(2，－5)4.如图，直线CD 是线段AB 的垂直平分线，P 为直线CD 上的一点，已知线段P A ＝5，则线段PB 的长度为（） A.6 B.5 C.4 D.35.将一张正方形纸片按如图1，图2所示的方向对折，然后沿图3中的虚线剪裁得到图4，将图4的纸片展开铺平，再得到的图案是（）6.如图，在△ABC 中，点D 、E 分别是边AB 、AC 的中点，∠B ＝50°，∠A ＝26°，将△ABC 沿DE 折叠，点A 的对应点是点A ′，则∠AEA ′的度数是（） A.145° B.152°C.158°D.160°7.在等腰△ABC 中，AB ＝AC ，其周长为20cm ，则AB 边的取值范围是（）A.1cm ＜AB ＜4cmB.5cm ＜AB ＜10cmC.4cm ＜AB ＜8cmD.4cm ＜AB ＜10cm8.从一个等腰三角形纸片的底角顶点出发，能将其剪成两个等腰三角形纸片，则原等腰三角形纸片的底角等于（）A.72°B.5407⎛⎫ ⎪⎝⎭ C.144° D.72°，或5407⎛⎫ ⎪⎝⎭DCBA P D CB A A BCD D EC9.如图，点P 是∠AOB 外的一点，点M ，N 分别是∠AOB 两边上的点，点P 关于OA 的对称点Q 恰好落在线段MN 上，点P 关于OB 的对称点R 落在MN 的延长线上.若PM ＝2.5cm ，PN ＝3cm ，MN ＝4cm ，则线段QR 的长为（）cm A.4.5 B.5.5 C.6.5 D.710.如图所示，已知△ABC 和△ADE 均是等边三角形，点B 、C 、E 在同一条直线上，AE 与BD 交于点O ，AE 与CD 交于点G ，AG 与BD 交于点F ，连结OC 、FG ，则下列结论：①AE ＝BD ；②AG ＝BF ；③FG ∥BE ；④∠BOC ＝∠EOC ，其中正确的结论个数（）A.1个B.2个C.3个D.4个二、填空题11.如图，在Rt △ABC 中，∠ABC ＝90°，AC ＝10cm ，点D 为AC 的中点，则BD ＝＿＿＿cm.12.如图，∠A ＝30°，∠C ′＝60°，△ABC 与△A ′B ′C ′关于直线l 对称，则∠B ＝＿＿＿.13.已知OC 是∠AOB 的平分线，点P 在OC 上，PD ⊥OA ，PE ⊥OB ，垂足分别为点D 、E ，PD ＝10，则PE 的长度为＿＿＿.14.如图，在Rt △ABC 中，∠C ＝90°，D 为AB 的中点，DE ⊥AC 于点E ，∠A ＝30°，AB ＝8，则DE 的长度是＿＿＿.15.如图，在等腰三角形纸片ABC 中，AB ＝AC ，∠A ＝50°，折叠该纸片，使点A 落在点B 处，折痕为DE ，则∠CBE ＝＿＿＿.B ′ A ′ BC A C ′l C B AD MR PO B A NQG FO D C B A E D C BA ED A E16.如图，在△ABC 中，按以下步骤作图：①分别以点B 、C 为圆心，以大于12BC 的长为半径作弧，两弧相交于M 、N 两点；②作直线MN 交AB 于点D ，连接CD .若CD ＝AC ，∠B ＝25°，则∠ACB 的度数为＿＿＿.17.在一次夏令营活动中，小明同学从营地A 出发，要到A 地的北偏东60°方向的C 处，他先沿正东方向走了200m 到达B 地，再沿北偏东30°方向走，恰能到达目的地C （如图），那么，由此可知，B 、C 两地相距＿＿＿m.18.如图，在第1个△A 1BC 中，∠B ＝30°，A 1B ＝CB ；在边A 1B 上任取一点D ，延长CA 1到A 2，使A 1A 2＝A 1D ，得到第2个△A 1A 2D ；在边A 2D 上任取一点E ，延长A 1A 2到A 3，使A 2A 3＝A 2E ，得到第3个△A 2A 3E ，…按此做法继续下去，则第n 个三角形中以A n 为顶点的内角度数是＿＿＿.三、解答题 19.在平面直角坐标系中，已知点A (－3，1)，B (－1，0)，C (－2，－1)，请在图中画出△ABC ，并画出与△ABC 关于y 轴对称的图形.20.如图，△ABC 与△DEF 关于直线l 对称，请用无刻度的直尺，在下面两个图中分别作出直线l .21.如图，在等边△ABC 中，AB ＝2，点P 是AB 边上任意一点（点P 可以与点A 重合），过点P 作PE ⊥BC ，垂足为E ，过点E 作EF ⊥AC ，垂足为F ，过点F 作FQ ⊥AB ，垂足为Q ，求当BP 的长等于多少时，点P 与点Q 重合？22.如图，在△ABC 中，点D 在AB 上，且CD ＝CB ，点E 为BD 的中点，点F 为AC 的F C E B D A F C E B A (D ) B A C 30° 北 60° L N M P C B AE FQA 1 A 2A 3 A 4 CB D E F … B AC O y x 3 1 -3 -1 A中点，连结EF 交CD 于点M ，连接AM .（1）求证：EF ＝12AC . （2）若∠BAC ＝45°，求线段AM 、DM 、BC 之间的数量关系.23.如图，O 为△ABC 内部一点，OB ＝312，P 、R 为O 分别以直线AB 、直线BC 为对称轴的对称点.（1）请指出当∠ABC 在什么角度时，会使得PR 的长度等于7？并完整说明PR 的长度为何在此时会等于7的理由.（2）承（1）小题，请判断当∠ABC 不是你指出的角度时，PR 的长度是小于7还是会大于7？并完整说明你判断的理由.24.如图，在△ABC 中，点D ，E 分别在边AC ，AB 上，BD 与CE 交于点O ，给出下列三个条件：①∠EBO ＝∠DCO ；②BE ＝CD ；③OB ＝OC .（1）上述三个条件中，由哪两个条件可以判定△ABC 是等腰三角形？（用序号写出所有成立的情形）（2）请选择（1）中的一种情形，写出证明过程.25.如图，在等边三角形ABC 中，点D ，E 分别在边BC ，AC 上，且DE ∥AB ，过点E 作EF ⊥DE ，交BC 的延长线于点F .（1）求∠F 的度数.（2）若CD ＝2，求DF 的长.26.如图，已知△BAD 和△BCE 均为等腰直角三角形，∠BAD ＝∠BCE ＝90°，点M 为DE 的中点.过点E 与AD 平行的直线交射线AM 于点N .（1）当A ，B ，C 三点在同一直线上时（如图1），求证：M 为AN 的中点.（2）将如图1中△BCE 绕点B 旋转，当A ，B ，E 三点在同一直线上时（如图2），求证：△CAN 为等腰直角三角形.（3）将如图1中△BCE 绕点旋转到图3的位置时，（2）中的结论是否仍然成立？若成立，试证明之；若不成立，请说明理由.AB CD E O E D C B A F NC A O P R B27.如图，△ABC 中，AB ＝AC ，△A ＝36°，称满足此条件的三角形为黄金等腰三角形．请完成以下操作：（画图不要求使用圆规，以下问题所指的等腰三角形个数均不包括△ABC ）（1）在图1中画1条线段，使图中有2个等腰三角形，并直接写出这2个等腰三角形的顶角度数分别是＿＿＿度和＿＿＿度.（2）在图2中画2条线段，使图中有4个等腰三角形.（3）继续按以上操作发现：在△ABC 中画n 条线段，则图中有＿＿＿个等腰三角形，其中有＿＿＿个黄金等腰三角形.28.（1）操作发现：如图①，D 是等边△ABC 边BA 上一动点（点D 与点B 不重合），连结DC ，以DC 为边在BC 上方作等边△DCF ，连结AF .你能发现线段AF 与BD 之间的数量关系吗？并证明你发现的结论.（2）类比猜想：如图②，当动点D 运动至等边△ABC 边BA 的延长线上时，其它作法与（1）相同.猜想AF 与BD 在（1）中的结论是否仍然成立？（3）深入探究：Ⅰ.如图③，当动点D 在等边△ABC 边BA 上运动时（点D 与点B 不重合），连接DC ，以DC 为边在其上方、下方分别作等边△DCF 和等边△DCF ′，连接AF 、BF ′，探究AF 、BF ′与AB 有何等量关系？并证明你探究的结论.Ⅱ.如图④，当动点D 运动至等边△ABC 边BA 的延长线上运动时，其它作法与图③相同.Ⅰ中的结论是否成立？若不成立，是否有新的结论？并证明你得出的结论.参考答案：F DC B A 图① FD C B A 图② F D C B A 图③ F ′ F AC F ′D 图④B DC B A E M N 图2D C B AE M N图3 图1 C B A E F 图2 C B A E 图3C B A一、1.D.点拨：A 、不是轴对称图形，不符合题意；B 、不是轴对称图形，不符合题意；C 、不是轴对称图形，不符合题意；D 、是轴对称图形，符合题意.故应选D .2.D.3.B.点拨：把点P (2，－5)的纵坐标－5改成它的相反数5，即可得到点P 关于x 轴对称点的坐标.4.B.点拨：由根据线段垂直平分线性质可以直接判断线段P A 与线段PB 的长度相等.5.B.点拨：按照图中的顺序向右上翻折，向左上角翻折，剪去左上角，展开得到图形B .故应选B .6.B.点拨：∵D 、E 分别是边AB 、AC 的中点，∴DE ∥BC ，∴∠ADE ＝∠B ＝50°，∵∠A ＝26°，∴∠ADE ＝180°－50°－26°＝104°；再由折叠可知：∠AED ＝∠A ′ED ＝104°，∴∠AEA ′＝360°－104°－104°＝152°.7.B.点拨：∵在等腰△ABC 中，AB ＝AC ，其周长为20cm ，∴设AB ＝AC ＝x ，则BC ＝20－2x cm ，∴2x ＞20－2x ，且20－2x ＞0，解得5cm ＜x ＜10cm.故应选B .8.D .点拨：如图，等腰三角形ABC 中，因为AB ＝AC ，所以∠ABC ＝∠C ，设顶角为α、底角为β，则根据三角形三内角和为180°，得α+2β＝180.此时，由于过B 点画直线交AC 于D ，则△ADB 与△BDC 都是等腰三角形，若AD ＝DB ＝BC ，则β＝2α，α+2β＝180°，解得α＝36°，β＝72°；若AD ＝DB ，BC ＝DC ，则β＝3α，α+2β＝180°，解得α＝7180，β＝7540 .所以原等腰三角形纸片的底角等于72°，或5407⎛⎫ ⎪⎝⎭.故应选D .9.A.点拨：∵点P 关于OA 的对称点Q 恰好落在线段MN 上，点P 关于OB 的对称点R 落在MN 的延长线上，∴PM ＝MQ ，PN ＝NR .∵PM ＝2.5cm ，PN ＝3cm ，MN ＝4cm ，∴RN =3cm ，MQ ＝2.5cm ，NQ ＝MN －MQ ＝4－2.5＝1.5（cm ），则线段QR 的长为：RN +NQ ＝3+1.5＝4.5（cm ）.故应选A .10.D.点拨：因为BC ＝AC ，∠BCD ＝∠ACE ＝120°，CD ＝CE ，所以△BCD ≌△ACE ，从而得①AE ＝BD 是正确的；又因为△BCD ≌△ACE ，所以∠FBC ＝∠GAC ，根据BC ＝AC ，∠BCF ＝∠ACG ＝60°，得△BCF ≌△ACG ，所以②AG ＝BF 是正确的；由△BCF ≌△ACG ，得CF ＝CG ，而∠FCG ＝60°，所以∠CGF ＝∠CFG ＝∠FCG ＝60°，所以③FG ∥BE 是正确的；如图，过C 作CM ⊥BD 于M ，CN ⊥AE 于N ，易得△BCM ≌△CAN ，所以CM ＝CN ，所以④∠BOC ＝∠EOC 是正确的.故应选D .二、11.5. 12.90°.点拨：因为△ABC 与△A ′B ′C ′关于直线l 对称，∠C ′＝60°，所以∠C ′＝∠C ＝60°，在△ABC 中，因为∠A ＝30°，所以∠B ＝180°－30°－60°＝90°.13.10.点拨：由角平分线的性质及题中已知条件可得PD ＝PE ，又因为PD ＝10，所以PE ＝10.14.2.点拨：∵D 为AB 的中点，AB ＝8，∴AD ＝4，∵ DE ⊥AC 于点E ，∴∠DEA ＝90°，∵∠A ＝30°，∴DE ＝12AD ＝2； G F O D C B AE M N DC B A15.15°.点拨：∵折叠该纸片，使点A 落在点B 处，折痕为DE ，∴EA ＝EB ，∴∠EBA ＝∠A .又∵AB ＝AC ，∠A ＝50°，∴∠B ＝65°，∠EBA ＝50°，∴∠CBE ＝15°.16.105°.点拨：由①的作图可知CD ＝BD ，∴∠DCB ＝∠B ＝25°，∴∠ADC ＝50°.又∵CD ＝AC ，∴∠A ＝∠ADC ＝50°，∴∠ACD ＝80°，∴∠ACB ＝80°+25°＝105°.17.200.点拨：由条件，得∠ABC ＝90°+30°＝120°，∠BAC ＝90°－60°＝30°，所以∠ACB ＝180°－∠ABC －∠BAC ＝180°－120°－30°＝30°，所以∠ACB ＝∠BAC ，所以BC ＝AB ＝200，即B 、C 两地相距200m. 18.(12)n －1·75°.点拨：∵A 1B ＝CB ，∠B ＝30°，∴∠C ＝∠BA 1C ＝12(180°－∠B )＝75°，又∵A 1A 2＝A 1D ，∴∠A 1A 2D ＝∠A 1DA 2＝12∠DA 1C ＝12×75°（三角形外角等于不相邻两内角之和）＝2112-×75°＝2112-⎛⎫ ⎪⎝⎭×75°；同样，∵A 2A 3＝A 2E ，∴∠A 2A 3E ＝∠A 2EA 3＝12∠DA 2A 1＝12×12×75°＝14×75°＝3112-×75°＝3112-⎛⎫ ⎪⎝⎭×75°；同理，∠A 3A 4F ＝∠A 3F A 4＝12∠EA 3A 2＝4112-⎛⎫ ⎪⎝⎭×75°；…第n 个三角形中以A n 为顶点的内角度数是112n -⎛⎫ ⎪⎝⎭×75°.三、19.如图，△ABC 就是所求的三角形，A ，B ，C 三点关于y 轴的对称点分别为A ′(3，1)，B ′(1，0)，C ′(2，－1)，△A ′B ′C ′就是△ABC 关于y 轴对称的图形.20.如图1和2所示中的直线l 就是分别所求作的对称轴.21.设BP ＝x ，在Rt △PBE 中，∠BPE ＝30°，所以BE ＝12x ，则EC ＝2－12x ，在Rt △EFC 中，∠FEC ＝30°，所以FC ＝12EC ＝1－14x ，所以AF ＝2－FC ＝2－(1－14x )＝1+14x ，同理，AQ ＝12AF ＝12+18x ，当点P 与点Q 重合时，有BP +AQ ＝2，即x +(12+18x )＝2，解得x ＝43，故当BP ＝43时，点P 与点Q 重合. 22.（1）证明：∵CD ＝CB ，E 为BD 的中点，∴CE ⊥BD ，∴∠AEC ＝90°.又∵F 为AC 的中点，∴EF ＝12AC .（2）∵∠BAC ＝45°，∠AEC ＝90°，∴∠ACE ＝∠BAC ＝45°，∴AE ＝图2 F C E B D A l 图1 F C E B A (D ) l B A C O y x 3 1 -3 -1 A ′ B ′ C ′CE.又∵F为AC的中点，∴EF⊥AC，∴EF为AC的垂直平分线，∴AM＝CM，∴AM+DM ＝CM+DM＝CD.又∵CD＝CB，∴AM+DM＝BC.23.（1）∠ABC＝90°时，PR＝7.证明：连接PB、RB，∵P、R为O分别以直线AB、直线BC为对称轴的对称点，∴PB＝OB＝312，RB＝OB＝312，∵∠ABC＝90°，∴∠ABP+∠CBR＝∠ABO+∠CBO＝∠ABC＝90°，∴点P、B、R三点共线，∴PR＝2×312＝7.（2）PR的长度是小于7.理由：∠ABC≠90°，则点P、B、R三点不在同一直线上，∴PB+BR＞PR，∵PB+BR＝2OB＝2×312＝7，∴PR＜7.24.（1）①②、①③.（2）选①②证明如下：在△BOE和△COD中，∵∠EBO＝∠DCO，∠EOB＝∠DOC，BE＝CD，∴△BOE≌△COD（AAS），∴BO＝CO，∠OBC＝∠OCB，∴∠EOB+∠OBC＝∠DOC+∠OCB，即∠ABC＝∠ACB，∴AB＝AC，即△ABC是等腰三角形.25.（1）∵三角形ABC为等边三角形，∴∠B＝60°，∵DE∥AB，∴∠EDC＝∠B＝60°，∵EF⊥DE，∴∠DEF＝90°，∴∠F＝90°－∠EDC＝30°.（2）∵∠ACB＝60°，∠EDC＝60°，∴△EDC是等边三角形，∴ED＝DC＝2，∵∠DEF＝90°，∠F＝30°，∴DF＝2DE＝4.26.（1）∵点M为DE的中点，∴DM＝ME．∵AD∥EN，∴∠ADM＝∠NEM，又∵∠DMA ＝∠EMN，∴△DMA≌△EMN，∴AM＝MN，即M为AN的中点.（2）由（1）中△DMA≌△EMN 可知DA＝EN，又∵DA＝AB，∴AB＝NE，∵∠ABC＝∠NEC＝135°，BC＝CE，∴△ABC≌△NEC，∴AC＝CN，∠ACB＝∠NCE，∵∠BCE＝∠BCN+∠NCE＝90°，∴∠BCN+∠ACB＝90°，∴∠CAN＝90°，∴△CAN为等腰直角三角形.（3）由（2）可知AB ＝NE，BC＝CE.又∵∠ABC＝360°－45°－45°－∠DBE＝270°－∠DBE＝270°－(180°－∠BDE－∠BED)＝90°+∠BDE+∠BED＝90°+∠ADM－45°+∠BED＝45+∠MEN+∠BED＝∠CEN，∴△ABC≌△NEC，再同（2）可证△CAN为等腰直角三角形，∴（2）中的结论是否仍然成立.27.（1）如图1所示.∵AB＝AC，∠A＝36°，∴当AE＝BE，则∠A＝∠ABE＝36°，则∠AEB＝108°，则∠EBC＝36°，∴这2个等腰三角形的顶角度数分别是108度和36度.（2）画法不惟一.如，如图2所示.四个等腰三角形分别是：△ABE，△BCE，△BEF，△CEF.（3）如图3所示.当1条直线可得到2个等腰三角形；当2条直线可得到4个等腰三角形；当3条直线可得到6个等腰三角形；…∴在△ABC中画n条线段，则图中有2n个等腰三角形，其中有n个黄金等腰三角形.28.（1）AF＝BD.证明：因为△ABC和△DCF均是等边三角形，所以∠ACB＝∠DCF，所以∠ACB－∠ACD＝∠DCF－∠ACD，即∠BCD＝∠ACF.在△BDC和△AFC中，BC＝AC，∠BCD＝∠ACF，DC＝FC，所以△BDC≌△AFC，所以AF＝BD.（2）仍然成立.证法同（1）.（3）Ⅰ：AF+BF′＝AB.证明：由（1）可证AF＝BD，同理可证△ADC≌△BF′C，所以BF′＝AD，所以AF+BF′＝AB.Ⅱ.在Ⅰ中的结论不成立，新结论是：AF－BF′＝AB.证明：同（1）可证△BDC≌△AFC，所以AF＝BD，同理可证△ADC≌△BF′C，所以BF′＝AD，因为BD－AD＝AB，所以AF－BF′＝AB.。

人教版八年级数学上册轴对称解答题综合测试卷(word含答案)

人教版八年级数学上册轴对称解答题综合测试卷（word 含答案）一、八年级数学轴对称解答题压轴题（难）1．如图，在△ABC 中，AB=BC=AC=20 cm ．动点P ，Q 分别从A ，B 两点同时出发，沿三角形的边匀速运动．已知点P ，点Q 的速度都是2 cm/s ，当点P 第一次到达B 点时，P ，Q 两点同时停止运动．设点P 的运动时间为t （s ）．（1）∠A=______度；（2）当0＜t ＜10，且△APQ 为直角三角形时，求t 的值；（3）当△APQ 为等边三角形时，直接写出t 的值．【答案】（1）60；（2）103或203；（3）5或20 【解析】【分析】(1)根据等边三角形的性质即可解答；（2）需分∠APQ=90°和∠AQP=90°两种情况进行解答；（3）需分以下两种情况进行解答：①由∠A=60°，则当AQ=AP 时，△APQ 为等边三角形；②当P 于B 重合，Q 与C 重合时，△APQ 为等边三角形.【详解】解：（1）60°．（2）∵∠A=60°，当∠APQ=90°时，∠AQP=90°－60°=30°．∴QA=2PA ．即2022 2.t t -=⨯解得 10.3t = 当∠AQP=90°时，∠APQ=90°－60°=30°．∴PA=2QA ．即2(202)2.t t -=解得 20.3t = ∴当0＜t ＜10，且△APQ 为直角三角形时，t 的值为102033或．（3）①由题意得：AP=2t ，AQ=20-2t∴当AQ=AP时，△APQ为等边三角形∴2t=20-2t，解得t=5②当P于B重合，Q与C重合，则所用时间为：4÷2=20综上，当△APQ为等边三角形时，t=5或20．【点睛】本题考查了等边三角形和直角三角形的判定以及动点问题，解答的关键在于正确的分类讨论以及对所学知识的灵活应用.2．如图1，△ABC 中，AB＝AC，∠BAC＝90º，D、E 分别在 BC、AC 边上，连接 AD、BE 相交于点 F，且∠CAD＝12∠ABE．(1)求证：BF＝AC；(2)如图2，连接 CF，若 EF＝EC，求∠CFD 的度数；(3)如图3，在⑵的条件下，若 AE＝3，求 BF 的长.【答案】（1）答案见详解；（2）45°，（3）4.【解析】【分析】（1）设∠CAD=x，则∠ABE=2x，∠BAF=90°-x，∠AFB=180°-2x-(90°-x)= 90°-x，进而得到∠BAF =∠AFB，即可得到结论；(2)由∠AEB=90°-2x，进而得到∠EFC=（90°-2x）÷2=45°-x，由BF＝AB，可得：∠EFD=∠BFA=90°-x，根据∠CFD=∠EFD-∠EFC，即可求解；(3)设EF＝EC=x，则AC=AE+EC=3+x，可得BE=BF+EF=3+x+x=3+2x，根据勾股定理列出方程，即可求解.【详解】（1）设∠CAD=x，∵∠CAD＝12∠ABE，∠BAC＝90º，∴∠ABE=2x，∠BAF=90°-x，∵∠ABE+∠BAF+∠AFB=180°，∴∠AFB=180°-2x-(90°-x)= 90°-x，∴∠BAF =∠AFB，∴BF＝AB；∵AB＝AC，（2）由（1）可知：∠CAD=x ，∠ABE=2x ，∠BAC ＝90º，∴∠AEB=90°-2x ，∵EF ＝EC ，∴∠EFC=∠ECF ，∵∠EFC+∠ECF=∠AEB=90°-2x ，∴∠EFC=（90°-2x ）÷2=45°-x ，∵BF ＝AB ,∴∠BFA=∠BAF=(180°-∠ABE)÷2=(180°-2x)÷2=90°-x ，∴∠EFD=∠BFA=90°-x ，∴∠CFD=∠EFD-∠EFC=(90°-x ）-(45°-x)=45°；（3）由（2）可知：EF ＝EC ，∴设EF ＝EC =x ，则AC=AE+EC=3+x ，∴AB=BF=AC=3+x ，∴BE=BF+EF=3+x+x=3+2x ，∵∠BAC ＝90º，∴222AB AE BE +=，∴222(3)3(32)x x ++=+，解得：11x =，23x =-（不合题意，舍去）∴BF=3+x=3+1=4.【点睛】本题主要考查等腰三角形的性质定理和勾股定理，用代数式表示角度和边长，把几何问题转化为代数和方程问题，是解题的关键.3．如图，在等腰直角ABC △中，AB AC =，90BAC ∠=︒，点D 是ABC △ 内一点，连接 AD ，AE AD ⊥ 且 AE AD =，连接 BD 、CE 交于点 F .（1）如图 1，求BFC ∠的度数；（2）如图 2，连接ED 交 BC 于点 G ，连接 AG ，若 AG 平分BAD ∠，求证：2EAC EDF ∠=∠；（3）如图 3，在（2）的条件下，BF 交 AG 、AC 分别于点M 、N ，DH AM ⊥，连接 HN ，若ADN ∆的面积与DHN 的面积差为 6，6DF =，求四边形 AMFE 的面积.【答案】（1）∠BFC =90°；（2）见解析；（3）20AMFE S =四边形.【解析】【分析】（1）根据SAS 证明ABD ACE ≌，所以ABD ACF ∠=∠，所以90BFC BAC ∠=∠=︒.（2）根据题意先求出180ABG ADG ∠+∠=︒，在AB 上截取AK AD =，连接KG ，由AKG ADG ≌，180BKG AKG ∠+∠=︒，可证得BKG KBG ∠=∠，GB GK DG ==，所以DBG BDG EDF α∠=∠=∠=，因为2CAE BAD α∠=∠=，所以2CAE EDF ∠=∠．（3）根据题意和（2）中结论先证明AD AN AE ==，过 A 作BF 、CE 垂线，垂足分别为R 、T ，连接AF ，证明ANR AET ≌，所以AR AT =，然后根据等腰三角形的性质可得出DM FN =，过点H 作HP FM ⊥，垂足为P ，所以HP PM DP ==，设DP x =，DR y =，所以ADN DHN S S ∆∆-= 1122DN AR DN HP ⋅⋅-⋅ ()6y x y =+=，226DF x y =+=，求出x ，y ，不难得到AEF ANF ADM S S S ∆∆∆===4，然后可得20AMFE S =四边形.【详解】（1）因为ABC 是等腰直角三角形，所以AB AC =，90BAC DAE ∠=︒=∠，所以BAD CAE ∠=∠，因为AD AE =，所以ABD ACE ≌，所以ABD ACF ∠=∠，所以90BFC BAC ∠=∠=︒.（2）因为AD AE =，90DAE ∠=︒，所以45AED ACG ∠=︒=∠，所以CAE CGE ∠=∠，由（1）知：BAD CAE ∠=∠，所以BAD CGD ∠=∠，设2BAD CGD α∠==∠，所以1802BGD α∠=︒-，所以180BAD BGD ∠+∠=︒，所以180ABG ADG ∠+∠=︒，因为AG 平分BAD ∠，所以BAG DAG α∠=∠=，在AB 上截取AK AD =，连接KG ，因为AG AG =，所以AKG ADG ≌，所以AKG ADG ∠=∠，DG KG =，因为180BKG AKG ∠+∠=︒，所以BKG KBG ∠=∠，所以GB GK DG ==，所以DBG BDG EDF α∠=∠=∠=，因为2CAE BAD α∠=∠=，所以2CAE EDF ∠=∠．（3）由（2）知：BAG DBG α∠=∠=，因为90BAC ∠=︒，45ABC ∠=︒，所以45ABN α∠=︒-，因为2BAD α∠=，所以45ADN α∠=︒+，因为902DAN α∠=︒-，所以45AND ADN α∠=︒+=∠，所以AD AN =，因为AD AE =，所以AE AN =，过 A 作BF 、CE 垂线，垂足分别为R 、T ，连接AF ，因为45ACE ABD α∠=∠=︒-，2CAE α∠=，所以45AET ANR α∠=︒+=∠，因为AE AN =，所以ANR AET ≌，所以AR AT =，所以FA 平分BFT ∠，所以45AFN AFE ∠=∠=︒，因为45AMN ∠=︒，所以AFM AMF ∠=∠，所以AF AM =，所以FR MR =，因为DR RN =，所以DM FN =，过点H 作HP FM ⊥，垂足为P ，因为45AMN ∠=︒，90DHM ∠=︒，所以45MHP DHP HDP ∠=∠=∠=︒，所以HP PM DP ==，设DP x =，所以2DM FN x ==，设DR y =，所以2DN y =，所以2MR x y =+，因为45MAR ∠=︒，所以2AR MR x y ==+，所以ADN DHN S S ∆∆-= 1122DN AR DN HP ⋅⋅-⋅ ()6y x y =+=，因为226DF x y =+=，所以3x y +=，所以2y =，1x =，因为AF AF =，ANF AEF ∠=∠，所以AEF ANF ≌，所以FN EF =，因为AR AT =，所以AEF ANF ADM S S S ∆∆∆==，因为142ADM S DM AR ∆=⋅⋅=，所以20ADM ADN ANF AEF AMFE S S S S S ∆∆∆∆=+++=四边形.【点睛】本题是三角形综合题，考查了等腰三角形的性质、三角形内角和定理、全等三角形的判定和性质等知识点，解题的难点在于学会添加常用辅助线，构造三角形全等解决问题，属于中考压轴题.4．（1）如图①，D是等边△ABC的边BA上一动点（点D与点B不重合），连接DC，以DC为边，在BC上方作等边△DCF，连接AF，你能发现AF与BD之间的数量关系吗？并证明你发现的结论；（2）如图②，当动点D运动至等边△ABC边BA的延长线时，其他作法与（1）相同，猜想AF与BD在（1）中的结论是否仍然成立？若成立，请证明；（3）Ⅰ.如图③，当动点D在等边△ABC边BA上运动时（点D与B不重合），连接DC，以DC为边在BC上方和下方分别作等边△DCF和等边△DCF′，连接AF，BF′，探究AF，BF′与AB有何数量关系？并证明你的探究的结论；Ⅱ．如图④，当动点D在等边△ABC的边BA的延长线上运动时，其他作法与图③相同，Ⅰ中的结论是否成立？若不成立，是否有新的结论？并证明你得出的结论．【答案】（1）AF=BD，理由见解析；（2）AF与BD在（1）中的结论成立，理由见解析；（3）Ⅰ. AF+BF′=AB，理由见解析，Ⅱ．Ⅰ中的结论不成立，新的结论是AF=AB+BF′，理由见解析．【解析】【分析】（1）由等边三角形的性质得BC=AC，∠BCA=60°，DC=CF，∠DCF=60°，从而得∠BCD=∠ACF，根据SAS证明△BCD≌△ACF，进而即可得到结论；（2）根据SAS证明△BCD≌△ACF，进而即可得到结论；（3）Ⅰ．易证△BCD≌△ACF（SAS），△BCF′≌△ACD（SAS），进而即可得到结论；Ⅱ．证明△BCF′≌△ACD，结合AF=BD，即可得到结论．【详解】（1）结论：AF=BD，理由如下：如图1中，∵△ABC是等边三角形，∴BC=AC，∠BCA=60°，同理知，DC=CF，∠DCF=60°，∴∠BCA-∠DCA=∠DCF-∠DCA，即：∠BCD=∠ACF，在△BCD和△ACF中，∵BC AC BCD ACF DC FC =∠=∠=⎧⎪⎨⎪⎩，∴△BCD ≌△ACF （SAS ），∴BD =AF ；（2）AF 与BD 在（1）中的结论成立，理由如下：如图2中，∵△ABC 是等边三角形，∴BC =AC ，∠BCA =60°，同理知，DC =CF ，∠DCF =60°，∴∠BCA +∠DCA =∠DCF +∠DCA ，即∠BCD =∠ACF ，在△BCD 和△ACF 中，∵BC AC BCD ACF DC FC =∠=∠=⎧⎪⎨⎪⎩，∴△BCD ≌△ACF （SAS ），∴BD =AF ；（3）Ⅰ．AF +BF ′=AB ，理由如下：由（1）知，△BCD ≌△ACF （SAS ），则BD =AF ；同理：△BCF ′≌△ACD （SAS ），则BF ′=AD ，∴AF +BF ′=BD +AD =AB ；Ⅱ．Ⅰ中的结论不成立，新的结论是AF =AB +BF ′，理由如下：同理可得：BCF ACD ∠=∠′，F C DC =′，在△BCF ′和△ACD 中，BC AC BCF ACD F C DC =∠⎧⎪=∠=⎪⎨⎩′′， ∴△BCF ′≌△ACD （SAS ），∴BF ′=AD ，又由（2）知，AF =BD ，∴AF =BD =AB +AD =AB +BF ′，即AF =AB +BF ′．【点睛】本题主要考查等边三角形的性质定理，三角形全等的判定和性质定理，熟练掌握三角形全等的判定和性质定理，是解题的关键．5．如图1，在ABC 中，90BAC ∠=︒，点D 为AC 边上一点，连接BD ，点E 为BD 上一点，连接CE ，CED ABD ∠=∠，过点A 作AG CE ⊥，垂足为G ，交ED 于点F ．(1)求证：2FAD ABD ∠=∠；(2)如图2，若AC CE =，点D 为AC 的中点，求证：AB AC =；(3)在(2)的条件下，如图3，若3EF =，求线段DF 的长．【答案】（1）详见解析；（2）详见解析；（3）6【解析】【分析】（1）根据直角三角形的性质可得90ADB ABD ∠=︒-∠，90EFG CED ∠=︒-∠，然后根据三角形的内角和和已知条件即可推出结论；（2）根据直角三角形的性质和已知条件可得AFD ADF ∠=∠，进而可得AF AD =，BFA CDE ∠=∠，然后即可根据AAS 证明ABF ∆≌CED ∆，可得AB CE =，进一步即可证得结论；（3）连接AE ，过点A 作AH AE ⊥交BD 延长线于点H ，连接CH ，如图4．先根据已知条件、三角形的内角和定理和三角形的外角性质推出45AED ∠=︒，进而可得AE AH =，然后即可根据SAS 证明△ABE ≌△ACH ，进一步即可推出90CHD ∠=︒，过点A 作AK ED ⊥于K ，易证△AKD ≌△CHD ，可得DK DH =，然后即可根据等腰三角形的性质推得DF =2EF ，问题即得解决．【详解】（1）证明：如图1，90BAC ∠=︒，90ADB ABD ∴∠=︒-∠，AG CE ⊥，90FGE ∴∠=︒，90EFG AFD CED ∴∠=∠=︒-∠，180FAD AFD ADF CED ABD ∴∠=︒-∠-∠=∠+∠，CED ABD ∠=∠，2FAD ABD ∴∠=∠；（2）证明：如图2，90AFD CED ∠=︒-∠，90ADB ABD ∠=︒-∠，CED ABD ∠=∠，AFD ADF ∴∠=∠，AF AD ∴=，BFA CDE ∠=∠，∵点D 为AC 的中点，∴AD=CD ，AF CD ∴=，ABF ∴∆≌CED ∆（AAS ），AB CE ∴=，CE AC =，AB AC ∴=；（3）解：连接AE ，过点A 作AH AE ⊥交BD 延长线于点H ，连接CH ，如图4． 90BAC ∠=︒，BAE CAH ∴∠=∠，设ABD CED α∠=∠=，则2,902FAD ACG αα∠=∠=︒-，CA CE =，45AEC EAC α∴∠=∠=︒+，45AED ∴∠=︒，45AHE ∴∠=︒，AE AH ∴=，AB AC =，∴△ABE ≌△ACH （SAS ），135AEB AHC ∴∠=∠=︒，90CHD ∴∠=︒，过点A 作AK ED ⊥于K ，90AKD CHD ∴∠=∠=︒，AD CD =，ADK CDH ∠=∠，∴△AKD ≌△CHD （AAS ），DK DH ∴=，∵,,AK DF AF AD AE AH ⊥==，,FK DK EK HK ∴==，3DH EF ∴==，6DF ∴=．【点睛】本题考查了直角三角形的性质、三角形的内角和定理、三角形的外角性质、等腰直角三角形的判定和性质、全等三角形的判定和性质以及等腰三角形的性质等知识，考查的知识点多、综合性强、难度较大，正确添加辅助线、构造等腰直角三角形和全等三角形的模型、灵活应用上述知识是解题的关键．6．如图，在等边ABC ∆中，线段AM 为BC 边上的中线．动点D 在直线AM 上时，以CD 为一边在CD 的下方作等边CDE ∆，连结BE ．（1）求CAM ∠的度数；（2）若点D 在线段AM 上时，求证：ADC BEC ∆≅∆；（3）当动点D 在直线AM 上时，设直线BE 与直线AM 的交点为O ，试判断AOB ∠是否为定值？并说明理由．【答案】（1）30°；（2）证明见解析；（3）AOB ∠是定值，60AOB ∠=︒.【解析】【分析】（1）根据等边三角形的性质可以直接得出结论；（2）根据等边三角形的性质就可以得出AC AC =，DC EC =，，60ACB DCE ∠=∠=︒，由等式的性质就可以BCE ACD ∠=∠，根据SAS 就可以得出ADC BEC ∆≅∆；（3）分情况讨论：当点D 在线段AM 上时，如图1，由（2）可知ACD BCE ≅∆∆，就可以求出结论；当点D 在线段AM 的延长线上时，如图2，可以得出ACD BCE ≅∆∆而有30CBE CAD ∠=∠=︒而得出结论；当点D 在线段MA 的延长线上时，如图3，通过得出ACD BCE ≅∆∆同样可以得出结论．【详解】（1）ABC ∆是等边三角形，60BAC ∴∠=︒．线段AM 为BC 边上的中线，12CAM BAC ∴∠=∠， 30CAM ∴∠=︒．（2）ABC ∆与DEC ∆都是等边三角形，AC BC ∴=，CD CE =，60ACB DCE ∠=∠=︒，ACD DCB DCB BCE ∴∠+∠=∠+∠，ACD BCE ∠∠∴=．在ADC ∆和BEC ∆中AC BC ACD BCE CD CE =⎧⎪∠=∠⎨⎪=⎩，()ACD BCE SAS ∴∆≅∆；（3）AOB ∠是定值，60AOB ∠=︒，理由如下：①当点D 在线段AM 上时，如图1，由（2）可知ACD BCE ≅∆∆，则30CBE CAD ∠=∠=︒，又60ABC ∠=︒，603090CBE ABC ∴∠+∠=︒+︒=︒，ABC ∆是等边三角形，线段AM 为BC 边上的中线AM ∴平分BAC ∠，即11603022BAM BAC ∠=∠=⨯︒=︒ 903060BOA ∴∠=︒-︒=︒．②当点D 在线段AM 的延长线上时，如图2，ABC ∆与DEC ∆都是等边三角形，AC BC ∴=，CD CE =，60ACB DCE ∠=∠=︒，ACB DCB DCB DCE ∴∠+∠=∠+∠，ACD BCE ∠∠∴=，在ACD ∆和BCE ∆中AC BC ACD BCE CD CE =⎧⎪∠=∠⎨⎪=⎩，()ACD BCE SAS ∴∆≅∆，30CBE CAD ∴∠=∠=︒，同理可得：30BAM ∠=︒，903060BOA ∴∠=︒-︒=︒．③当点D 在线段MA 的延长线上时，ABC ∆与DEC ∆都是等边三角形，AC BC ∴=，CD CE =，60ACB DCE ∠=∠=︒，60ACD ACE BCE ACE ∴∠+∠=∠+∠=︒，ACD BCE ∠∠∴=，在ACD ∆和BCE ∆中AC BC ACD BCE CD CE =⎧⎪∠=∠⎨⎪=⎩，()ACD BCE SAS ∴∆≅∆，CBE CAD ∴∠=∠，同理可得：30CAM ∠=︒150CBE CAD ∴∠=∠=︒30CBO ∴∠=︒，∵30BAM ∠=︒，903060BOA ∴∠=︒-︒=︒．综上，当动点D 在直线AM 上时，AOB ∠是定值，60AOB ∠=︒．【点睛】此题考查等边三角形的性质，全等三角形的判定及性质，等边三角形三线合一的性质，解题中注意分类讨论的思想解题.7．在等边△ABC 中，点D 在BC 边上，点E 在AC 的延长线上，DE =DA (如图1)．(1)求证：∠BAD =∠EDC ；(2)若点E 关于直线BC 的对称点为M (如图2)，连接DM ，AM ．求证：DA =AM ．【答案】(1)见解析；(2)见解析【解析】【分析】（1）根据等边三角形的性质，得出∠BAC =∠ACB =60°，然后根据三角形的内角和和外角性质，进行计算即可.（2）根据轴对称的性质，可得DM=DA ，然后结合（1）可得∠MDC =∠BAD ，然后根据三角形的内角和，求出∠ADM=60°即可.【详解】解：(1)如图1，∵△ABC是等边三角形，∴∠BAC=∠ACB=60°，∴∠BAD=60°﹣∠DAE，∠EDC=60°﹣∠E，又∵DE=DA，∴∠E=∠DAE，∴∠BAD=∠EDC．(2)由轴对称可得，DM=DE，∠EDC=∠MDC，∵DE=DA，∴DM=DA，由(1)可得，∠BAD=∠EDC，∴∠MDC=∠BAD，∵△ABD中，∠BAD+∠ADB=180°﹣∠B=120°，∴∠MDC+∠ADB=120°，∴∠ADM=60°，∴△ADM是等边三角形，∴AD=AM．【点睛】本题主要考察了轴对称和等边三角形的性质，解题的关键是熟练掌握这些性质.8．如图，在平面直角坐标系中，A（﹣3，0），点 B是 y轴正半轴上一动点，点C、D在 x 正半轴上．（1）如图，若∠BAO＝60°，∠BCO＝40°，BD、CE 是△ABC的两条角平分线，且BD、CE交于点F，直接写出CF的长_____．（2）如图，△ABD是等边三角形，以线段BC为边在第一象限内作等边△BCQ，连接 QD并延长，交 y轴于点 P，当点 C运动到什么位置时，满足 PD＝23DC？请求出点C的坐标；（3）如图，以AB为边在AB的下方作等边△ABP，点B在 y轴上运动时，求OP的最小值．【答案】（1）6；（2）C的坐标为（12，0）；（3）3 2 .【解析】【分析】（1）作∠DCH ＝10°，CH 交 BD 的延长线于 H ，分别证明△OBD ≌△HCD 和△AOB ≌△FHC ，根据全等三角形的对应边相等解答；（2）证明△CBA ≌△QBD ，根据全等三角形的性质得到∠BDQ ＝∠BAC ＝60°，求出 CD ，得到答案；（3）以 OA 为对称轴作等边△ADE ，连接 EP ，并延长 EP 交 x 轴于点 F ．证明点 P 在直线 EF 上运动，根据垂线段最短解答．【详解】解：（1）作∠DCH ＝10°，CH 交 BD 的延长线于 H ，∵∠BAO ＝60°，∴∠ABO ＝30°，∴AB ＝2OA ＝6，∵∠BAO ＝60°，∠BCO ＝40°，∴∠ABC ＝180°﹣60°﹣40°＝80°，∵BD 是△ABC 的角平分线，∴∠ABD ＝∠CBD ＝40°，∴∠CBD ＝∠DCB ，∠OBD ＝40°﹣30°＝10°，∴DB ＝DC ，在△OBD 和△HCD 中，==OBD HCD DB DC ODC HDC ∠∠⎧⎪=⎨⎪∠∠⎩∴△OBD ≌△HCD （ASA ），∴OB ＝HC ，在△AOB 和△FHC 中，==ABO FCH OB HC AOB FHC ∠∠⎧⎪=⎨⎪∠∠⎩∴△AOB ≌△FHC （ASA ），∴CF=AB=6，故答案为6；（2）∵△ABD 和△BCQ 是等边三角形，∴∠ABD ＝∠CBQ ＝60°，∴∠ABC ＝∠DBQ ，在△CBA 和△QBD 中，BA BD ABC DBQ BC BQ =⎧⎪∠=∠⎨⎪=⎩∴△CBA ≌△QBD （SAS ），∴∠BDQ ＝∠BAC ＝60°，∴∠PDO ＝60°，∴PD ＝2DO ＝6，∵PD ＝23DC ， ∴DC ＝9，即 OC ＝OD+CD ＝12，∴点 C 的坐标为（12，0）；（3）如图3，以 OA 为对称轴作等边△ADE ，连接 EP ，并延长 EP 交 x 轴于点F ．由（2）得，△AEP ≌△ADB ，∴∠AEP ＝∠ADB ＝120°，∴∠OEF ＝60°，∴OF ＝OA ＝3，∴点P 在直线 EF 上运动，当 OP ⊥EF 时，OP 最小，∴OP ＝12OF ＝32则OP 的最小值为32．【点睛】本题考查的是等边三角形的性质，全等三角形的判定和性质，垂线段最短，掌握全等三角形的判定定理和性质定理是解题的关键．9．如图1，在△ABC中，∠ACB=90°，AC=12BC，点D为BC的中点，AB =DE，BE∥AC．（1）求证：△ABC≌△DEB；（2）连结AD、AE、CE，如图2．①求证：CE是∠ACB的角平分线；②请判断△ABE是什么特殊形状的三角形，并说明理由．【答案】（1）详见解析；（2）①详见解析；②△ABE是等腰三角形，理由详见解析.【解析】【分析】（1）由AC//BE，∠ACB=90°可得∠DBE=90°，由AC=12BC，D是BC中点可得AC=BD，利用HL即可证明△ABC≌△DEB；（2）①由（1）得BE=BC，由等腰直角三角形的性质可得∠BCE=45°，进而可得∠ACE=45°，即可得答案；②根据SAS可证明△ACE≌△DCE，可得AE=DE，由AB=DE可得AE=AB即可证明△ABE是等腰三角形.【详解】（1）∵∠ACB=90°，BE∥AC∴∠CBE=90°∴△ABC和△DEB都是直角三角形∵AC=12BC，点D为BC的中点∴AC=BD又∵AB=DE∴△ABC≌△DEB（H.L.）（2）①由（1）得：△ABC≌△DEB ∴BC=EB又∵∠CBE=90°∴∠BCE=45°∴∠ACE=90°-45°=45°∴∠BCE=∠ACE∴CE是∠ACB的角平分线②△ABE是等腰三角形，理由如下：在△ACE和△DCE中AC DCACE BCECE CE=⎧⎪∠=∠⎨⎪=⎩∴△ACE≌△DCE（SAS）.∴AE=DE又∵AB=DE∴AE=AB∴△ABE是等腰三角形【点睛】本题考查全等三角形的判定与性质及等腰三角形的判断与性质，熟练掌握判定定理是解题关键.10．如图1，△ABD，△ACE都是等边三角形，（1）求证：△ABE≌△ADC；（2）若∠ACD=15°，求∠AEB的度数；（3）如图2，当△ABD与△ACE的位置发生变化，使C、E、D三点在一条直线上，求证：AC∥BE．【答案】(1)见解析(2) ∠AEB=15°(3) 见解析【解析】试题分析：（1）由等边三角形的性质可得AB=AD，AE=AC，∠DAB=∠EAC=60°，即可得∠DAC=∠BAE，利用SAS即可判定△ABE≌△ADC；（2）根据全等三角形的性质即可求解；（3）由（1）的方法可证得△ABE≌△ADC，根据全等三角形的性质和等边三角形的性质可得∠AEB=∠ACD =60°，即可得∠AEB=∠EAC，从而得AC∥BE．试题解析：（1）证明：∵△ABD，△ACE都是等边三角形∴AB=AD，AE=AC，∠DAB=∠EAC=60°，∴∠DAC=∠BAE，在△ABE和△ADC中，∴，∴△ABE≌△ADC；（2）由（1）知△ABE≌△ADC，∴∠AEB=∠ACD，∵∠ACD=15°，∴∠AEB=15°；（3）同上可证：△ABE≌△ADC，∴∠AEB=∠ACD，又∵∠ACD=60°，∴∠AEB=60°，∵∠EAC=60°，∴∠AEB=∠EAC，∴AC∥BE．点睛：本题主要考查了等边三角形的性质、全等三角形的判定及性质，证得△ABE≌△ADC 是解决本题的关键.。

人教版-八年级上册-第十二章轴对称(全章)

人教版第12章轴对称考点一：关于“轴对称图形”与“轴对称”的认识【知识要点】轴对称图形：如果_____个图形沿某条直线折叠后，直线两旁的部分能够________，那么这个图形叫轴对称图形，这条直线叫做____________。

轴对称：对于____个图形，如果沿着一条直线对折后，它们能完全重合，那么称这两个图形成________，这条直线就是对称轴。

两个图形中的对应点叫做__________ 【例题解析】1、在26个大写英文字母中，是轴对称图形的有。

2、在三角形、等腰三角形、梯形、直角梯形、等腰梯形、平行四边形中，是轴对称图形的有。

其中的对称轴最多，有条。

3、下列几何图形中，○1线段○2角○3直角三角形○4半圆，其中一定是轴对称图形的有（）A ．1个B ．2个C ．3个D ．4个 4、．图9-19中，轴对称图形的个数是（）A ．4个B ．3个C ．2个D ．1个5、正三角形有条对称轴，正四边形有条对称轴，正n 边形有___条对称轴。

考点二：垂直平分线的性质定理及判定定理【知识要点】（一）性质定理：线段的垂直平分线上的点到线段两端点的距离相等。

几何语言：。

ABOPPB PAABPOABO=∴⊥的中点，且为线段点【例题分析】1．（2012•黄冈）如图，在△ABC中，AB=AC，∠A=36°，AB的垂直平分线交AC 于点E，垂足为点D，连接BE，则∠EBC的度数为_________ ．2．如图所示，∠BAC=105°，若MP和NQ分别垂直平分AB和AC．求∠PAQ的度数．3．（2012•常州）如图，在四边形ABCD中，AD∥BC，对角线AC的中点为O，过点O作AC的垂线分别与AD、BC相交于点E、F，连接AF．求证：AE=AF．4．（2010•娄底）如图，在四边形ABCD中，AD∥BC，E为CD的中点，连接AE、BE，BE⊥AE，延长AE交BC的延长线于点F．求证：（1）FC=AD；（2）AB=BC+AD．（二）判定定理：【知识要点】到线段两端点距离相等的点在这条线段的垂直平分线上几何语言：的垂直平分线上在线段点AB P PBPA ∴=引申——垂直平分线的判定要满足的条件： 1、直线过线段的中点 2、直线垂直于已知线段【例题分析】1．如图，△ABC 中，AB=AC ，PB=PC ，连AP 并延长交BC 于D ，求证：AD 垂直平分BC2．如图，AD 是△ABC 的角平分线，DE 、DF 分别是△ABD 和△ACD 的高，求证：AD 垂直平分EF ．。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

八年级上第十二章轴对称测试题2011-8-30
一.选择题（每小题5分）
1.下列四个图案中，轴对称图形的个数是（）
A 3
B 2
C 1
D 0
2.下列命题中，不正确的是（）
A.关于直线对称的两个三角形一定全等（）
B.两个圆形纸片随意平放在水平桌面上构成轴对称图形
C.若两图形关于直线对称，则对称轴是对称点所连线段的垂直平分线
D.等腰三角形一边上的高、中线及这边对角平分线重合
3.下列四个图案中，具有一个共有性质．则下面四个数字中，满足上述性质的一
个是（）A.6 B.7 C.8 D.9
4．等腰三角形的一个内角是50°，则另外两个角的度数分别是（）
A.65°,65°
B.50°，80°
C.65°,65°或50°,80°
D.50°,50°
5．如果等腰三角形两边长是6㎝和3㎝，那么它的周长是（）
A. 9 ㎝
B. 12 ㎝
C. 12 ㎝或15 ㎝
D. 15 ㎝
二.填空题（每小题5分，共25分）
6.等腰三角形是对称图形，它至少有条对称轴.
7.小明上午在理发店理发时，从镜子内看到背后墙上普通时钟的时针与分针的位
置如图所示，此时时间是.
8.已知△ABC
是轴对称图形，且三条高的交点恰好是C点，则△ABC的形状
是.
9.已知点A（-2，4），B(2,4)，C(-1,2),D(1,2),E(-3,1),F(3,1)是平面坐标系内的6
个点，选择其中三个点连成一个三角形，剩下三个点连成另一个三角形.若这
两个三角形关于y轴对称，就称为一组对称三角形，那么坐标系中可找出
组对称三角形.
10.如图，△ABC中，AB=AC, ∠A=36 °，AB的中垂线DE交AC于D,交AB于
E,下述结论：（1）BD平分∠ABC;(2)AD=BD=BC;(3) △BDC的周长等于
AB+BC;(4)D是AC中点.其中正确的命题序号是.
三、画一画
11.（8分）“以○○，△△，－－－”（即两个圆，两个三角形，三条线段）为条件
画出一个有实际意义的对称图形.
（第10题）
（第1题）
（第3题）
（第7题）
_ E
_ D
_ C
_ B
_ A
八年数学试卷第1页（共4页）八年数学试卷第2页（共4页）
八年级数学试卷第3页（共4页）八年级数学试卷第4页（共4页）
四、解答题 12.（13分）在△ABC 中，∠C=90 °，DE 垂直平分斜边AB,分别交AB,BC 于D,E.若∠CAE=∠B+30 °，求∠AEB.
13.(13分)在△ABC 中，AB=AC, ∠A=120 °，BC=6 ㎝，AB 的垂直平分
线交BC 于M ，交AB 于E, AC 的垂直平分线交BC 于N ，交AC 于F,求证：BM=MN=NC.
五、应用题
14.（16分）某班举行文艺晚会，桌子摆成两直条（如图中的AO,BO ），AO 桌面上摆满了橘子，BO 桌面上摆满了糖果，坐在C 处的学生小明先那橘子再拿糖果，然后回到座位，请你帮助他设计一条行走路线，使其所走的总路程最短？（尺规作图，并写出作法）
答案：1.C ；2.D ；3.C ；4.C ；5.D ；6.轴，1；7.10时45分；8.等腰三角形；9.4；10.（1）
（2），（3）.11.题略；12.140度；13.提示：连接MA ，NB ，证明：MA=NB=MN ； 14.分两种情况讨论：若∠AOB 小于90°，行走路线为C E F C ，若∠AOB
行于90°，从C 点沿直线走到O 处，再直线返回C 处.
_
E _ D _
C _
B _ A （第12题）
__ O _ A （第14题）。