高三数学教学质量检测试题(doc 13页)
辽宁省八校2024-2025学年高三上学期12月联合教学质量检测数学试题+答案

2024-2025学年度上学期高三12月联合教学质量检测高三数学试卷满分150分,考试用时120分钟注意事项:1.答题前,先将自己的姓名、准考证号填写在试卷和答题卡上,并将准考证号条形码贴在答题卡上的指定位置.2.选择题的作答:每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑.写在试卷、草稿纸和答题卡上的非答题区域均无效.3.非选择题的作答:用黑色签字笔直接答在答题卡上对应的答题区域内.写在试卷、草稿纸和答题卡上的非答题区域均无效.4.考试结束后,请将本试卷和答题卡一并上交.一、单项选择题(本大题共8小题,每小题5分,共40分.在每小题所给的四个选项中,只有一项是符合题目要求的)1.设i 为虚数单位,若z =2-ii 3,则z =()A.2+iB.2-iC.1+2iD.1-2i2.已知cos α1+sin α=-3,则cos αsin α-1的值为()A.33B.-33C.3D.-33.意大利数学家斐波那契的《算经》中记载了一个有趣的数列:1,1,2,3,5,8,13,21,34,55,89,144,⋯⋯这就是著名的斐波那契数列,该数列的前2024项中有( )个奇数A.1012B.1348C.1350D.13524.在△ABC 中,H 为BC 的中点,M 为AH 的中点,若AM =λAB +μAC ,则λ+μ等于()A.23B.12C.16D.135.已知a =log 35,b =log 23,c =e ln 43,则()A.a <b <cB.c <b <aC.b <c <aD.c <a <b6.某人有两把雨伞用于上下班,如果一天上班时他也在家而且天下雨,只要有雨伞可取,他将拿一把去办公室,如果一天下班时他也在办公室而且天下雨,只要有雨伞可取,他将拿一把回家.;如果天不下雨,那么他不带雨伞.假设每天上班和下班时下雨的概率均为13,不下雨的概率均为23,且与过去情况相互独立.现在两把雨伞均在家里,那么连续上班两天,他至少有一天淋雨的概率为()A.1681B.2081C.827D.28817.已知直线l :4x +3y +5=0与圆C :(x -4)2+(y -3)2=4,点P ,Q 在直线l 上,过点P 作圆C 的切线,切点分别为A ,B ,当P A 取最小值时,则QA +QB 的最小值为()A.31B.231C.82D.2338.在平行四边形ABCD 中,DA =DB ,E 是平行四边形ABCD 内(包括边界)一点,DE ⋅DA DA =DE ⋅DBDB,若CE =xCB +yCD ,则x +y 的取值范围为()A.1,2B.1,32C.12,32D.0,1二、多项选择题(本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求,全部选对得6分,部分选对的得部分分,有选错的得0分)9.对任意A ,B ⊆R ,记A ⊕B =x x ∈A ∪B ,x ∉A ∩B ,并称A ⊕B 为集合A ,B 的对称差.例如:若A =1,2,3 ,B =2,3,4 ,则A ⊕B =1,4 .下列命题中,为真命题的是()A.若A ,B ⊆R 且A ⊕B =B ,则A =∅B.若A ,B ⊆R 且A ⊕B =∅,则A =BC.若A ,B ⊆R 且A ⊕B ⊆A ,则A ⊆BD.存在A ,B ⊆R ,使得A ⊕B ≠∁R A ⊕∁R B10.在菱形ABCD 中,AB =2,∠BAD =60°,E 为AB 的中点,将△ADE 沿直线DE 翻折至△A 1DE 的位置,使得二面角A 1-DE -C 为直二面角,若P 为线段A 1C 的中点,则()A.BP ⎳平面A 1DEB.DP ⊥ECC.异面直线PB ,A 1D 所成的角为π3D.A 1B 与平面PBD 所成角的余弦值为42711.随机事件A ,B 满足P A =12,P B =23,P A B =34,则下列说法正确的是()A.P AB =P A P BB.P A B =38C.P A +B =34D.P AB A +B P AB =P 2A P 2B三、填空题(本大题共3小题,每小题5分,共15分)12.已知数列a n 的通项公式为a n =tn 2-78t +174 n +172,n ≤2t n,n >2,若数列a n 是单调递增数列,则实数t 的取值范围是.13.已知函数f (x )=2sin ωx +π4(ω>0)在区间0,1 上的值域为m ,n ,且n -m =3,则ω的值为.14.欧拉(1707-1783),他是数学史上最多产的数学家之一,他发现并证明了欧拉公式e iθ=cos θ+i sin θ,从而建立了三角函数和指数函数的关系,若将其中的θ取作π就得到了欧拉恒等式e i π+1=0,它是令人着迷的一个公式,它将数学里最重要的几个量联系起来,两个超越数--自然对数的底数e ,圆周率π,两个单位--虚数单位i 和自然数单位1,以及被称为人类伟大发现之一的0,数学家评价它是“上帝创造的公式”,请你根据欧拉公式:e iθ=cos θ+i sin θ,将复数ei π3+e i π表示成a +bi (a ,b ∈R ,i 为虚数单位)的形式;若z n =1,则z =z k (k =0,1,2,⋯,n -1),这里z k =cos 2k πn +i sin 2k πn(k =0,1,2,⋯,n -1),称z k 为1的一个n 次单位根,简称单位根.类比立方差公式,我们可以获得x 5-1=(x -1)x 4+x 3+x 2+x 1+1 ,复数z =e2πi5,则z -2 z 2-2 z 3-2 z 4-2 的值是.四、解答题(本大题共5小题,共77分.解答应写出必要的文字说明、证明过程或演算步骤)15.已知数列a n 的前n 项和S n =na n -3n (n -1),n ∈N *,且a 3=17.(1)求a 1;(2)求数列a n 的前n 项和S n ;(3)设数列b n 的前n 项和T n ,且满足b n =n S n ,求证:T n <233n +2.16.在△ABC 中,角A ,B ,C 所对的边分别为a ,b ,c ,且cos C c =-cos Aa +2b.(1)求角C 的大小;(2)若AC =BC =2,如图,D ,E 是AB 上的动点,且∠DCE 始终等于30°,记∠CED =α.当α为何值时,△CDE 的面积取到最小值,并求出最小值.17.如图,在以A ,B ,C ,D ,E ,F 为顶点的五面体中,四边形ABCD 与四边形CDEF 均为等腰梯形,AB ∥CD ,CD ∥EF ,AB =DE =EF =CF =2,CD =4,AD =BC =10,AE =23,M 对CD 的中点.(1)证明:平面ABCD ⊥平面CDEF ;(2)求平面AEM 与平面BEM 所成角的正弦值;(3)设点N 是△ADM 内一动点,ND ⋅NM=0,当线段AN 的长最小时,求直线EN 与直线BF 所成角的余弦值.18.已知A ,B 分别是双曲线C :x 2a 2-y 2b2=1(a >0,b >0)的左、右顶点,点P 22,n 是双曲线C 上的一点,直线P A ,PB 的斜率分别为k 1,k 2,且k 1k 2=|AB |=4.(1)求双曲线C 的方程;(2)已知过点(4,0)的直线l :x =my +4,交C 的左,右两支于D ,E 两点(异于A ,B ).(i )求m 的取值范围;(ii )设直线AD 与直线BE 交于点Q ,求证:点Q 在定直线上.19.已知函数f x =x 2e x ,g x =ln x .(1)求函数y =f (x )的单调区间;(2)若曲线y =e x +m 与y =g x +1 存在两条公切线,求整数m 的最小值;(3)已知a ∈-1e ,0 ,函数h x =x -1 g x -1 -ax有3个零点为:x 1,x 2,x 3,且x 1<x 2<x 3,证明:x 1+x 2+x 3>2e.参考答案1.D【分析】结合复数的四则运算,以及共轭复数的定义,即可求解.【详解】z =2-i i 3=2-i-i =1+2i ,故z=1-2i .故选:D .2.A【分析】由cos α1+sin α⋅cos αsin α-1=-1即可求解.【详解】因为cos α1+sin α⋅cos αsin α-1=cos 2αsin 2α-1=1-sin 2αsin 2α-1=-1,且cos α1+sin α=-3,所以cos αsin α-1=33.故选:A 3.C【分析】对数列中的数进行归纳,发现规律,结合题意得到答案.【详解】对数列中的数归纳发现,每3个数中前2个都是奇数,后一个是偶数,又2022=3×674,故该数列前2024项有2×674+2=1350个奇数.故选:C 4.B【分析】由向量的线性运算结合图形特征,求出λ,μ的值即可.【详解】在△ABC 中,H 为BC 的中点,M 为AH 的中点,则AM =12AH =12×12AB +AC ,所以λ=μ=14,λ+μ=12.故选:B 5.D【分析】利用对数函数的单调性以及基本不等式比较大小.【详解】由已知得c =eln 43=43,比较a =log 35和c =43的大小,其中c =43=log 3343,因为53=125>3433=81,所以53>343,又因为y =log 3x 在0,+∞ 单调递增,所以a =log 35>c =log 3343,即a >c ;比较b =log 23和c =log 2243的大小,其中33=81>2433=16,即3>243,因为y =log 2x 在0,+∞ 上单调递增,所以b =log 23>c =log 2243,即b >c ;比较a =log 35,b =log 23的大小,因为a =log 35<log 327=log 3332=32,b =log 23>log 222=log 2232=32,所以a <b ,即c <a <b ,故选:D .6.D【分析】计算对立事件的概率,从下雨次数入手,分类讨论计算两天都不淋雨的概率,即可得至少有一天淋雨的概率.【详解】解:“至少有一天淋雨”的对立事件为“两天都不淋雨”,连续上两天班,上班、下班的次数共有4次.(1)4次均不下雨,概率为:234=1681;(2)有1次下雨但不淋雨,则第一天或第二天上班时下雨,概率为:2×13×233=1681;(3)有2次下雨但不淋雨,共3种情况:①同一天上下班均下雨;②两天上班时下雨,下班时不下雨;③第一天上班时下雨,下班时不下雨,第二天上班时不下雨,下班时下雨;概率为:2×132×232+13×23×13×23+13×23×23×13=1681;(4)有3次下雨但不被淋雨,则第一天或第二天下班时不下雨,概率为:2×133×23=481;(5)4次均下雨,概率为:134=181;两天都不淋雨的概率为:1681+1681+1681+481+181=5381,所以至少有一天淋雨的概率为:1-5381=2881.故选:D .7.C【分析】由切线长公式知当PC ⊥l 时,P A 最小,结合点到直线距离公式求得P A 的最小值,然后作A 关于直线l 的对称点A ,可知当点Q 为A B 与直线l 的交点时,QA +QB 最小,由对称知,此时P 与Q 重合,从而易得最小值.【详解】由C :(x -4)2+(y -3)2=4可知圆心为4,3 ,半径r =2,由题意P A =PC2-AC 2=PC2-4,所以当PC ⊥l 时,P A 取最小值,由点到直线的距离公式可得PC min =4×4+3×3+516+9=6,此时P A =PB =36-4=42,过A 作直线l 的对称点A ,连接QA ,A B ,A B 与直线l 的交点即为所求的点Q ,由于P A 与PB 关于直线PC 对称,PC ⊥l ,P A 与P A 关于直线l 对称,因此P A 与A B 就是同一条直线,即点P 即为所求的点Q ,所以QA +QB 的最小值为2PB =82.故选:C8.B【分析】先根据题意,得到点E 的轨迹,然后利用向量计算即可.【详解】因为DE ⋅DA DA =DE ⋅DBDB得DE cos ∠EDA =DEcos ∠EDB ,即cos ∠EDA =cos ∠EDB所以点E 在∠BDA 的角平分线上,设AB 的中点为M因为DA =DB ,所以点E 在线段DM 上,不妨设DE =λDM,λ∈0,1 ,所以CE =CD +λDM易知DM =DA +AM =CB -12CD所以CE =CD +λCB -12CD =1-λ2CD+λCB因为CE =xCB +yCD所以x +y =1-λ2+λ=1+λ2因为λ∈0,1所以x +y =1+λ2∈1,32故选:B【点睛】关键点点睛:DE ⋅DA DA =DE ⋅DBDB表示了DA ,DB 两个向量的角平分线.9.AB【分析】根据集合的新定义,结合选项以及交并补的性质逐一判断即可.【详解】解:对于A ,因为A ⊕B =B ,所以B =x x ∈A ∪B ,x ∉A ∩B ,所以A ⊆B ,且B 中的元素不能出现在A ∩B 中,因此A =∅,即A 正确;对于B ,因为A ⊕B =∅,所以∅=x x ∈A ∪B ,x ∉A ∩B ,即A ∪B 与A ∩B 是相同的,所以A =B ,即B 正确;对于C ,因为A ⊕B ⊆A ,所以x x ∈A ∪B ,x ∉A ∩B ⊆A ,所以B ⊆A ,即C 错误;对于D ,由于∁R A ⊕∁R B =x |x ∈∁R A ∪∁R B ,x ∉∁R A ∩∁R B=x x ∈∁R A ∩B ,x ∉∁R A ∪B =x |x ∈A ∪B ,x ∉A ∩B ,而A ⊕B =x x ∈A ∪B ,x ∉A ∩B ,故A ⊕B =∁R A ⊕∁R B ,即D 错误.故选:AB .10.AC【分析】建立空间直角坐标系,用向量法证明线面关系即可判断A ,B 选项;用向量法分别表示向量PB ,A 1D ,A 1B ,以及求出平面PBD 的法向量,代入异面直线所成的角的向量公式可判断C 选项,代入直线与平面所成角的余弦公式即可判定D 选项.【详解】如图,建立空间直角坐标系,则A 1(0,0,1),B (1,0,0),C (2,3,0),D (0,3,0),P 1,32,12.对于A ,因为BP =0,32,12,平面A 1DE 的一个法向量为m =(1,0,0),所以BP ⋅m=0,所以BP ⎳平面A 1DE ,故A 正确.对于B ,因为DP =1,-32,12,EC =(2,3,0),所以DP ⋅EC =12≠0,所以DP ,EC 不垂直,故B 错误.对于C ,因为PB =0,-32,-12 ,A 1D =(0,3,-1),所以cos PB ,A 1D =PB ⋅A 1DPB A 1D =12,所以异面直线PB ,A 1D 所成的角为π3,故C 正确.对于D ,设平面PBD 的法向量为n=(x ,y ,z ),因为BP =0,32,12,BD =(-1,3,0),所以n ⋅BP =32y +12z =0,n⋅BD =-x +3y =0,令x =3,得n =3,1,-3 .设A 1B 与平面PBD 所成的角为θ,因为A 1B=(1,0,-1),所以sin θ=cos A 1B ,n =A 1B ⋅nA 1B n =237×2=427,cos θ=1-sin 2θ=1-4272=77,故D 错误.故选:AC .11.CD【分析】根据题意由相互独立事件的概率性质分析可判断A ,B ;由概率加法公式可分析C ;计算P AB A +B ,验证P AB A +B P AB =P 2A P 2B 是否正确即可判断D .【详解】由已知P A =12,P B =13,因为P A B =P A B P B=34,所以P A B =P A B P B =34×13=14,所以P AB =P B -P A B =13-14=112,所以P AB ≠P A P B ,故A 错误;因为P A B =P A -P A B =12-14=14,故B 错误;P A +B =P A +P B -P AB =12+13-112=34,故C 正确;P AB A +B =P AB P A +B=11234=19,又P A B =14,P A =12,P B =13,所以P AB A +B P AB =P 2A P 2B ,故D 正确.故选:CD .【点睛】方法点睛:解决本题的关键是概率的性质和应用,以及条件概率的计算.12.2,+∞【分析】根据是递增数列以及解析式,可得a 的范围,又a 3>a 2>a 1,代入求解,即可求得答案.【详解】因为数列a n 是递增数列,当n >2时,a n =t n ,可得t >1,当n ≤2时,a 1<a 2,即t -78t +174 +172<4t -278t +174 +172,解得t >2,又a 3>a 2,所以t 3>4t -278t +174 +172,解得t >32或-32<t <0.综上,实数t 的取值范围是2,+∞ .故答案为:2,+∞ .13.11π12【分析】利用整体代入法,结合正弦函数的图像求解即可.【详解】x ∈0,1 ,故ωx +π4∈π4,ω+π4,因为f (x )=2sin ωx +π4在区间0,1 上的值域为m ,n ,且n -m =3,故必有n =2,m =-1,,如图所示,则ω+π4=7π6,故ω=11π12.故答案为:11π1214.-12+32i 31【分析】根据欧拉公式直接可得求出第一空;根据单位根的概念,代入化简即可求出第二空.【详解】e i π3=cosπ3+i sin π3=12+32,e i π=cosπ+i sinπ=-1,所以e i π3+e i π=-12+32i ,由题意可得z 5=1,所以z 5-1=(z -1)z 4+z 3+z 2+z 1+1 =0,又因为z ≠1,所以z 4+z 3+z 2+z 1+1=0,则z -2 z 2-2 z 3-2 z 4-2=z -2 z 4-2 z 2-2 z 3-2 =z 5+4-2z -2z 4 z 5+4-2z 2-2z 3 =5-2z -2z 4 5-2z 2-2z 3=25-10z 2-10z 3-10z +4z 3+4z 4-10z 4+4z 6+4z 7=25-10z 2-10z 3-10z +4z 3+4z 4-10z 4+4z +4z 2=25-6z 4+z 3+z 2+z 1 =31-6z 4+z 3+z 2+z 1+1 =31.故答案为:-12+32i ;31.【点睛】关键点点睛:本题的关键在于对欧拉公式的使用和复数四则运算法则的熟练运用.15.(1)a 1=5(2)S n =3n 2+2n(3)证明见解析【分析】(1)令n =2,n =3解方程即可求解,(2)利用S n ,a n 的关系,作差可得等差数列,即可求解,(3)利用放缩法可得b n <23n +2+3n -1=23(3n +2-3n -1),即可利用累加法求解.【详解】(1)在S n =na n -3n (n -1),n ∈N *中,a 3=17,令n =2,n =3可得a 1+a 2=2a 2-6a 1+a 2+a 3=3a 3-18 ⇒a 2-a 1=6a 1+a 2=16 ,∴a 1=5.(2)S n =na n -3n (n -1),①当n ≥2时,S n -1=(n -1)a n -1-3(n -1)(n -2),②①-②可得a n =na n -(n -1)a n -1-6(n -1)⇒(n -1)a n =(n -1)a n -1+6(n -1)(n ≥2),∴a n =a n -1+6,∴a n 是公差为6的等差数列,∴a n =a 1+6(n -1)=6n -1,∴S n =na n -3n (n -1)=n (6n -1)-3n (n -1)=3n 2+2n .(3)证明:由(2)可得b n =n 3n 2+2n=13n +2,∴b n =13n +2=223n +2<23n +2+3n -1=23(3n +2-3n -1),∴T n =b 1+b 2+⋅⋅⋅+b n <23[(5-2)+(8-5)+⋅⋅⋅+(3n +2-3n -1)]=23(3n +2-2)<233n +2.16.(1)C =120°(2)α=75°,最小值为2-3【分析】(1)根据正弦定理将分式化简,结合两角和的正弦公式可求得结果;(2)在△ACE 中,根据正弦定理表示出CE ,在△BCD 中,根据正弦定理表示出CD ,根据三角形面积公式得到△CDE 的面积,即可求出结果.【详解】(1)在△ABC 中,由正弦定理可得cos C sin C =-cos Asin A +2sin B,所以sin A cos C +2sin B cos C =-cos A sin C ,所以sin A +C =-2sin B cos C ,即得sin B =-2sin B cos C ,因为0°<B <180°,所以sin B >0,所以cos C =-12,因为0°<C <180°,所以C =120°;(2)因为AC =BC =2,由(1)知C =120°,所以A =B =30°,在△ACE 中,由正弦定理可得AC sin α=CE sin30°,所以CE =1sin α,在△BCD 中,由正弦定理可得BC sin 150°-α =CD sin30°,所以CD =1sin 150°-α,所以S △CDE =12⋅CD ⋅CE ⋅sin30°=14sin αsin 150°-α =12sin 2α-60° +3,因为0<α<150°,所以0<2α-60°<240°,当sin 2α-60° =1时,S △CDE 取得最小值2-3,此时2α-60°=90°,即α=75°,所以当α=75°时,△CDE 的面积取到最小值,最小值为2-3.17.(1)证明见解析(2)4313(3)32.【分析】(1)取DM 的中点O ,证明AO ⊥OE ,AO ⊥DM ,EO ⊥DM ,然后得线面垂直,再得面面垂直;(2)以O 为坐标原点,分别以OE ,OC ,OA 为x ,y ,z 轴建立如图所示的空间直角坐标系,用空间向量法求二面角;(3)由向量的数量积为0,确定N 的轨迹,再由最小值确定其位置,得其坐标,然后由空间向量法求线面角.【详解】(1)取DM 的中点O ,连结OA ,OE ,由已知得,△EMD 是边长为2的等边三角形,△ADM 是以AD =AM =10为腰的等腰三角形,则OE ⊥DM ,OA ⊥DM ,OA =3,OE =3,故AO 2+OE 2=AE 2,故OA ⊥OE ,OE ∩DM =O ,OE ⊂平面CDEF ,DM ⊂平面CDEF ,所以OA ⊥平面CDEF ,又OA ⊂平面ABCD ,所以平面ABCD ⊥平面CDEF ;(2)以O 为坐标原点,分别以OE ,OC ,OA 为x ,y ,z 轴建立如图所示的空间直角坐标系,则A 0,0,3 ,E 3,0,0 ,M 0,1,0 ,B 0,2,3 ,BE =(3,-2,-3),AE =3,0,-3 ,EM =-3,1,0 ,MB=0,1,3 ,设平面AEM 的法向量为n=x ,y ,z ,则n ⋅AE =0n ⋅EM =0,即3x -3z =0-3x +y =0 ,取z =1,则n=3,3,1 ,设平面BEM 的一个法向量为m=a ,b ,c ,由m ⋅EM=-3a +b =0m ⋅BE =3a -2b +3c =0,取a =3,得m =3,3,-1 ,所以cos m ,n =m ⋅n m ⋅n=1113,因为m ,n ∈0,πsin <m ,n >=4313,故平面AEM 与平面BEM 所成角的正弦值为4313.(3)点N 是△ADM 内一动点且ND ⋅NM=0,则点N 在以DM 为直径的圆上,当线段AN 的长最小时,点N 在AO 与圆的交点处,此时N 0,0,1 ,EN =-3,0,1 ,BF=3,0,-3 ,设直线EN 与直线BF 所成角为θ,所以cos θ=cos EN ,BF =EN ⋅BFEN BF=32,所以直线EN 与直线BF 所成角得余弦值为32.18.(1)x 24-y 216=1(2)(i )m <-12或m >12;(ii )证明见解析【分析】(1)根据k 1k 2=|AB |=4求出a =2,n 2=16,从而得到(22)24-16b2=1,求出b 2=16,得到双曲线方程;(2)(i )由题意知直线l 的方程为x =my +4,D x 1,y 1 ,E x 2,y 2 ,联立双曲线方程,结合根的判别式和y 1y 2>0得到不等式,求出m 的取值范围;(ii )在(i )的基础上,得到两根之和,两根之积,得到y 1y 2=-3y 1+y 22m,表达出直线AD 和直线BE 的方程,联立得到x =2my 1y 2+2y 1+6y 23y 2-y 1,将y 1y 2=-3y 1+y 2 2m代入,化简得到x =1,得到答案.【详解】(1)由题意可知A (-a ,0),B (a ,0),因为|AB |=2a =4,所以a =2.因为P (22,n ),k 1k 2=n 22+2⋅n 22-2=n 2(22)2-4=n 24=4,得n 2=16,又因为P(22,n)在双曲线上,则(22)24-16b2=1,所以b2=16.所以双曲线C的方程为x2 4-y216=1.(2)(i)由题意知直线l的方程为x=my+4,D x1,y1,E x2,y2.联立x24-y216=1x=my+4,化简得4m2-1y2+32my+48=0,因为直线l与双曲线左右两支相交,所以y1y2>0,即m满足:4m2-1≠032m2-1924m2-1>0y1y2=484m2-1>0,所以m<-12或m>12.(ii)y1+y2=-32m4m2-1,y1y2=484m2-1,则y1y2=-3y1+y22m,直线AD的方程为y=y1x1-2(x-2),直线BE的方程为y=y2x2-2(x-2).联立直线AD与BE的方程,得y1x1+2(x+2)=y2x2-2(x-2),所以y2my2+2-y1my1+6x=2y1my1+6+2y2my2+2,所以6y2-2y1x=4my1y2+4y1+12y2,所以x=2my1y2+2y1+6y23y2-y1=-3y1-3y2+2y1+6y23y2-y1=3y2-y13y2-y1=1,所以点Q的横坐标始终为1,故点Q在定直线x=1上【点睛】圆锥曲线中,针对非对称韦达,一般思路为设出直线方程,与圆锥曲线联立,得到两根之和,两根之积,并两者相除,得到两者的关系,再代入后续的计算中,达到化简的目的.19.(1)单调递增区间是-∞,-2 和0,+∞ ,单调递减区间是-2,0 (2)-1(3)证明见解析【分析】(1)先求导,然后根据导函数的正负判断f x 的单调性,由此可确定出单调区间;(2)根据条件写出切线方程,通过联立思想求解出m 关于切点坐标的表示,由此构造函数分析单调性和最小值,即可确定出整数m 的最小值;(3)将问题转化为方程x -1 g x -1 =ax有三个根x 1,x 2,x 3,借助图象分析出x 1,x 2,x 3的范围,然后通过转化将待证明的问题变为证明x 2-1 ln x 2-1 -2e +1-x 2 ln 2e +1-x 2 >0,再通过构造函数分析单调性和最值完成证明.【详解】(1)f x =2xe x +x 2e x =x x +2 e x ,令f x =0,解得x =0或x =-2,当x ∈-∞,-2 时,f x >0,f x 单调递增,当x ∈-2,0 时,f x <0,f x 单调递减,当x ∈0,+∞ 时,f x >0,f x 单调递增,所以f x 的单调递增区间是-∞,-2 和0,+∞ ,单调递减区间是-2,0 .(2)设切线分别与y =ex +m和y =ln x +1 交于A x 4,e x 4+m ,B x 5,ln x 5+1 ,y =ex +m的导数为y =ex +m,y =ln x +1 的导数为y =1x +1,所以A 处切线方程为y =e x 4+m x -x 4 +e x 4+m ,B 处切线方程为y =1x 5+1x -x 5 +ln x 5+1 ,由公切线可知,e x 4+m =1x 5+1⇔x 4+m =-ln x 5+1 ex 4+m-x 4ex 4+m=ln x 5+1 -x 5x 5+1 ,所以1x 5+1--ln x 5+1 -m x 5+1=ln x 5+1 -x 5x 5+1,化简可得m =x 5ln x 5+1 -x 5-1,因为公切线有两条,所以m =x 5ln x 5+1 -x 5-1x 5>-1 有两个根;设t x =x ln x +1 -x -1x >-1 ,所以t x =ln x +1 +xx +1-1=ln x +1 -1x +1,因为y =ln x +1 ,y =-1x +1均在-1,+∞ 上单调递增,所以t x =ln x +1 -1x +1在-1,+∞ 上单调递增,且t 0 =-10,t 1 =ln2-12 ln e -12=0,所以存在唯一x 0∈0,1 使得t x 0=0,当x ∈-1,x 0 时,t x <0,t x 单调递减,当x ∈x 0,+∞ 时,t x >0,t x 单调递增,所以t x min =t x 0 =x 0ln x 0+1 -x 0-1且ln x 0+1 -1x 0+1=0,所以t x min =t x 0 =x 0x 0+1-x 0-1=-x 0+1+1x 0+1+1,由对勾函数性质可知y =x 0+1+1x 0+1在x 0∈0,1 时单调递增,所以x 0+1+1x 0+1∈2,52 ,所以t x min =t x 0 ∈-32,-1 ,且x →-1时,t x →+∞,x →+∞时,t x →+∞,所以若m =t x 有两个根,则m >t x 0 ,故整数m 的最小值为-1.(3)h x =x -1 g x -1 -ax的定义域为-∞,-1 ∪1,+∞ ,由题意可知,x 1,x 2,x 3是方程x -1 g x -1 =ax的三个根;当x ∈-∞,-1 时,令p x =x -1 ln -x -1 ,所以p x =ln -x -1 +x -1x +1,令r x =ln -x -1 +x -1x +1,所以rx =1x +1+x +1-x -1 x +12=1x +1+2x +1 2=x +3x +1 2,当x ∈-∞,-3 时,r x <0,r x 单调递减,当x ∈-3,-1 时,r x >0,r x单调递增,所以r x min =r -3 =ln2+2>0,所以p x min =p -3 =ln2+2>0,所以p x 在-∞,-1 上单调递增,且p -2 =0;当x ∈1,+∞ 时,令q x =x -1 ln x -1 ,所以q x =ln x -1 +1,由q x =0解得x =1+1e ,当x ∈1,1+1e 时,q x <0,q x 单调递减,当x ∈1+1e,+∞ 时,q x >0,q x 单调递增,且q 1+1e =1e ln 1e =-1e<0,q 2 =0,作出y =x -1 ln x -1 ,y =ax 的简图如下图所示,由图象可知,-2<x 1<-1,1<x 2<1+1e<x 3<2,要证x 1+x 2+x 3>2e ,只需证x 2+x 3>2e +2,即证x 3>2e+2-x 2,因为1<x 2<1+1e ,所以1+1e <2e +2-x 2<2e+1<2,又因为q x =x -1 ln x -1 在1+1e ,2上单调递增,所以只需证q x 3 >q2e +2-x 2 ,且q x 3 =q x 2 ,所以只需证q x 2 >q 2e +2-x 2 ,即证x 2-1 ln x 2-1 -2e +1-x 2 ln 2e +1-x 2 >0(*);设s x =x -1 ln x -1 -2e +1-x ln 2e +1-x x ∈1,1+1e ,所以s x =ln x -1 +x -1x -1--1 ln 2e +1-x -2e +1-x ⋅12e+1-x⋅-1 ,所以s x =ln x -1 +ln 2e +1-x +2=ln x -1 2e+1-x +2,因为y =x -1 2e +1-x =-x 2+2+2e x -2e +1 ,对称轴x =1+1e且开口向下,所以y =x -1 2e +1-x 在1,1+1e 上单调递增,所以s x <ln 1+1e -1 +ln 2e +1-1-1e +2=0,所以s x 在1,1+1e上单调递减,所以s x >s 1+1e=1e ln 1e -1e ln 1e =0,所以s x >0对x ∈1,1+1e恒成立,所以(*)成立,即x 1+x 2+x 3>2e成立.【点睛】方法点睛:利用导数证明或判定不等式问题:(1)通常要构造新函数,利用导数研究函数的单调性与极值(最值),从而得出不等关系;(2)利用可分离变量,构造新函数,直接把问题转化为函数的最值问题,从而判定不等关系;(3)适当放缩构造法:根据已知条件适当放缩或利用常见放缩结论,从而判定不等关系;(4)构造“形似”函数,变形再构造,对原不等式同解变形,根据相似结构构造辅助函数.答案第1页,共2页。
安徽省合肥市第一中学2025届高三上学期教学质量检测(11月月考)数学试题(含答案)

安徽省合肥市第一中学2025届高三上学期教学质量检测(11月月考)数学试题一、单选题:本题共8小题,每小题5分,共40分。
在每小题给出的选项中,只有一项是符合题目要求的。
1.已知集合A={x|y=log3(x2−1)},集合B={y|y=3−x},则A∩B=( )A. (0,1)B. (1,2)C. (1,+∞)D. (2,+∞)2.若sinθ(sinθ+cosθ)=25,则tanθ=( )A. 2或−13B. −2或13C. 2D. −23.已知函数f(x)=a−e x1+ae x⋅cos x,则“a=1”是“函数f(x)的是奇函数”的( )A. 充分不必要条件B. 必要不充分条件C. 充要条件D. 既不充分也不必要条件4.函数f(x)={ax2+e x,x≥0x3−ax2+a,x<0在R上单调,则a的取值范围是( )A. (0,1)B. (0,1]C. [0,1)D. [0,1]5.在▵ABC中,内角A,B,C的对边分别为a,b,c,已知▵ABC的外接圆半径为1,且a2+c2−b2=2ac,1+2sin A 1−2cos A =sin2C1+cos2C,则▵ABC的面积是( )A. 22B. 32C. 1D. 26.已知一个正整数N=a×1010(1≤a<10),且N的15次方根仍是一个整数,则这个数15次方根为().(参考数据:lg2≈0.3,lg3≈0.48,lg5≈0.7)A. 3B. 4C. 5D. 67.已知函数f(x)=x ln x,g(x)=e x−x2+a,若∃x1,x2∈[1,2],使得f(x1)=g(x2),则实数a的取值范围是( )A. (4−e2,ln4+1−e)B. [4−e2,ln4+1−e]C. (ln4+4−e2,1−e)D. [ln4+4−e2,1−e]8.已知正数x,y满足9x2−1+9y2−1=9xy,则4x2+y2的最小值为( )A. 1B. 2C. 3D. 4二、多选题:本题共3小题,共18分。
安徽省合肥市2021届高三第三次教学质量检测数学理试题 Word版含答案

合肥市2021年高三第三次教学质量检测数学试题(理科)本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,满分150分,考试时间120分钟,祝各位考生考试顺当! 第Ⅰ卷(选择题 共50分)一、选择题:本大题共10小题,每小题5分,共50分,在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知()(1)2a i bi i +-=(其中,a b 均为实数,i 为虚数单位),则||a bi +等于 A.2 B.2 C.1 D.1或22.命题“对于任意x R ∈,都有0x e >”的否定是A.对于任意x R ∈,都有0x e ≤B.不存在x R ∈,使得0x e ≤C.存在0x R ∈,使得00x e >D.存在0x R ∈,都有00x e ≤ 3.若函数|2|2y x =--的定义域为集合{|22}A x R x =∈-≤≤,值域为集合B ,则 A.A B = B.A B ⊂ C.B A ⊂ D.A B =∅ 4.在等差数列{}n a 中,已知1823(4)a a =-,则该数列的前11项和11S 等于 A.33 B.44 C.55 D.66 5.执行如图所示的程序框图,若将推断框内“100S >”改为关于n 的不等式“0n n ≥”且要求输出的结果不变,则正整数0n的取值A.是4B.是5C.是6D.不唯一 6.在极坐标系中,已知点(4,1),(3,1)2A B π+,则线段AB 的长度是 A.1 B.214π+ C.7 D.5 7.某三棱锥的三视图如图所示,则该三棱锥的各个面中,最大的面积是 A.62 B.1C.22 D.648.某校方案组织高一班级四个班开展研学旅行活动,初选了,,,A B C D 四条不同的研学线路,每个班级只能在这四条线路中选择其中的一条,且同一线路最多只能有两个班级选择,则不同的选择方案有A.240种B.204种C.188种D.96种 9.在ABC ∆中,角,,A B C 的对边分别是,,a b c ,若2sin sin a b c B A +=,则A ∠的大小是A.2πB.3πC.4πD.6π10.定义在R 上的函数()f x 满足:()1f x >且()'()1,(0)5f x f x f +>=,其中'()f x 是()f x 的导函数,则不等式ln[()1]ln 4f x x +>-的解集为A.(0,)+∞B.(,0)(3,)-∞+∞C.(,0)(0,)-∞+∞D.(,0)-∞ 第Ⅱ卷(非选择题 共100分)二、填空题:本大题共5小题,每小题5分,共25分,把答案填在答题卡的相应位置上. 11.某校为了了解教科研工作开展状况与老师年龄之间的关系,将该校不小于35岁的80名老师按年龄分组,分组区间为[35,40),[40,45),[45,50),[50,55),[55,60),由此得到频率分布直方图如图,则这80名老师中年龄小于45岁的老师有人12.设 6260126(32)(21)(21)(21)x a a x a x a x -=+-+-++-,则1350246a a a a a a a ++=+++ 13.在平面直角坐标系中,不等式组02y x x y ≤≤⎧⎨+≤⎩表示的平面区域为1Ω,直线:(1)0(0)l kx y k k ---=<将区域1Ω分为左右两部分,记直线l 的右边区域为2Ω,在区域1Ω内随机投掷一点,其落在区域2Ω内的概率13P =,则实数k 的取值为14.设点F 是抛物线22y x =的焦点,过抛物线上一点P ,沿x 轴正方向作射线//PQ x 轴,若FPQ ∠的平分线PR 所在直线的斜率为2-,则点P 的坐标为 15.已知向量,OA OB 满足1||||1,2OA OB OA OB ==⋅=,动点C 满足OC xOA yOB =+,给出以下命题: ①若1x y +=,则点C 的轨迹是直线; ②若||||1x y +=,则点C 的轨迹是矩形; ③若1xy =,则点C 的轨迹是抛物线; ④若1x y =,则点C 的轨迹是直线;⑤若221x y xy ++=,则点C 的轨迹是圆. 以上命题正确的是 (写出你认为正确的全部命题的序号)三、解答题:本大题共6小题,共75分,解答应写出文字说明,证明过程或演算步骤.16(本小题满分12分) 已知函数5()sin()cos()(0)412f x x x ππωωω=+++>的最小正周期为4π. (Ⅰ)求ω的值 (Ⅱ)设12,[,]22x x ππ∈-,求12|()()|f x f x -的最大值.17(本小题满分12分) 已知数列{}n a 满足*()2n n n S a n N =∈,(其中n S 是数列{}n a 的前n 项和,且22a =. (Ⅰ)求数列{}n a 的通项公式;(Ⅱ)设2((n n n n a b a n ⎧⎪=⎨⎪⎩为奇数为偶数)),求数列{}n b 的前2n 项和2n T .18(本小题满分12分) 已知椭圆22221(0)x y a b a b +=>>,过其右焦点F 且垂直于x 轴的弦MN 的长度为b .(Ⅰ)求该椭圆的离心率;(Ⅱ)已知点A 的坐标为(0,)b ,椭圆上存在点,P Q ,使得圆224x y +=内切于APQ ∆,求该椭圆的方程.19(本小题满分13分)如图,在多面体ABCDEF 中,四边形ABCD 是边长为1的正方形,BF ⊥平面,//.ABCD DE BF (Ⅰ)求证:AC EF ⊥;(Ⅱ)若2,1,BF DE ==在EF 上取点G ,使//BG 平面ACE ,求直线AG 与平面ACE 所成角θ的正弦值.20(本小题满分13分) 某校高三班级争辩性学习小组共6人,方案同时参观科普展,该科普展共有甲,乙,丙三个展厅,6人各自随机地确定参观挨次,在每个展厅参观一小时后去其他展厅,全部展厅参观结束后集合返回,设大事A 为:在参观的第一小时时间内,甲,乙,丙三个展厅恰好分别有该小组的2个人;大事B 为:在参观的其次个小时时间内,该小组在甲展厅人数恰好为2人. (Ⅰ)求()P A 及(|)P B A ; (Ⅱ)设在参观的第三个小时时间内,该小组在甲展厅的人数为ξ,则在大事A 发生的前提下,求ξ的概率分布列及数学期望. 21(本小题满分13分) 已知函数()ln 2 3.f x x x =-+ (Ⅰ)求函数()f x 的单调区间; (Ⅱ)设函数2()1t g x x x =-+,若()()g x f x >对0x >恒成立,求整数t 的最小值.。
2022届江苏省南通市高三上学期9月第一次教学质量监测数学试题(word版含答案)

3.某亲子栏目中,节目组给6位小朋友布置一项搜寻空投食物的任务.已知:①食物投掷点有远、近两处;②由于小朋友甲年纪尚小,所以要么不参与该项任务,要么参与搜寻近处投掷点的食物,但不参与时另需1位小朋友在大本营陪同;③所有参与搜寻任务的小朋友被均匀分成两组,一组去远处,一组去近处.那么不同的搜寻方案有()
一、单项选择题:本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的,请把答案填涂在答题卡相应位置上.
1.已知集合 ,则 ()
A. B. 或
C. D. 或
【答案】B
2.已知复数 ,则 在复平面内对应的点所在的象限为()
A.第一象限B.第二象限C.第三象限D.第四象限
C.若 D.若 ,则 与平行
【答案】BD
11.若二项式 展开式中二项式系数之和为 ,展开式的各项系数之和为 ,各项系数的绝对值之和为 ,则下列结论正确的是()
A.
B.存在 ,使得
C. 的最小值为2
D.
【答案】AB
12.“阿基米德多面体”也称为半正多面体(semi-regularsolid),是由边数不全相同的正多边形为面围成的多面体,它体现了数学的对称美.如图所示,将正方体沿交于一顶点的三条棱的中点截去一个三棱锥,共可截去八个三棱锥,得到八个面为正三角形、六个面为正方形的一种半正多面体.已知 ,则关于如图半正多面体的下列说法中,正确的有()
A.该半正多面体的体积为
B.该半正多面体过 三点的截面面积为
C.该半正多面体外接球的表面积为
D.该半正多面体的顶点数 、面数 、棱数 满足关系式
【答案】ACD
三、填空题:本题共4小题,每小题5分,共20分
13.已知 ,则实数 的取值分别为______.
安徽省六安市2024届高三上学期期末教学质量检测数学试题含答案

六安市2024年高三教学质量检测数学试题(答案在最后)注意事项:1.答卷前,考生务必将自己的姓名和座位号填写在答题卡上.2、回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑.如需改动,用橡皮擦干净后,再选涂其他答案标号.回答非选择题时,将答案写在答题卡上.写在本试卷上无效.3.考试结束后,将本试卷和答题卡一并交回.一、单选题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合{}2log 1,A x x x =≤∈Z,{}220B x xx =+-<,则A B = ()A.{}0,1 B.{}2,1-- C.{}1,0- D.{}1-【答案】D 【解析】【分析】解出对数不等式和一元二次不等式,再根据交集含义即可.【详解】2log ||1x ≤,即22log ||log 2x ≤,则22x -≤≤且0x ≠,则{}2,1,1,2A =--,{}21B x x =-<<,所以{}1A B ⋂=-.故选:D .2.已知复数z 的共轭复数在复平面内对应的点为()2,2-,则复数1z的虚部为()A.1-B.i- C.14-D.1i 4-【答案】C 【解析】【分析】得到22i z =+,利用复数除法法则得到111i 44z =-,求出虚部.【详解】由已知得22i z =+,()()122i 1i 11i 22i 22i 444z --===-+-,则复数1z 的虚部为14-.故选:C3.已知向量a =,向量(1,b =- ,则a 与b 的夹角大小为()A.30︒B.60︒C.120︒D.150︒【答案】D 【解析】【分析】根据给定条件,利用向量夹角的坐标表示求解即得.【详解】向量a =,(1,b =-,则cos ,222a b 〈〉==-⨯ ,而0,180a b ︒≤〈〉≤︒ ,所以a,b的夹角为150︒.故选:D4.等差数列{}n a 的公差不为0,其前n 项和为n S ,若()83124m S a a a =++,则m =()A.11B.12C.13D.14【答案】C 【解析】【分析】由等差数列的前n 项和公式与通项公式转化为基本量计算即可.【详解】设等差数列{}n a 的公差为d ,所以81828S a d =+,则有()11118282214a d a d a m d a +=+++-+⎡⎤⎣⎦,即()141d m d =+,又0d ≠,所以114m +=,所以13m =.故选:C.5.函数()e 4,1ln ,1x x x f x x x ⎧+-<=⎨≥⎩,若()()()21105f a f a f +≤--,则实数a 的取值范围是()A.{}1- B.(],1-∞-C.[)1,-+∞ D.11,e⎡⎫--⎪⎢⎣⎭【答案】A 【解析】【分析】原不等式变形为()()25110f a f a ⎡⎤+≤-⎣⎦,再利用分段函数的单调性即可得到不等式,解出即可.【详解】当1x <时,()e 4xf x x =+-,因为e ,4x y y x ==-在(),1∞-上单调递增,此时()f x 单调递增,当1x ≥时,易知()ln f x x =单调递增,且当1x =时,1e 14e 30ln1+-=-<=,则()f x 在R 上单调递增,因为211a +≥,则()()()()()222215ln 1ln5ln5151f a f a a f a ⎡⎤++=++=+=+⎣⎦,所以由()()()21105f a f a f +≤--得()()25110f a f a ⎡⎤+≤-⎣⎦,所以()25110a a +≤-,解得1a =-.故选:A .6.已知ππcos 2cos 63αα⎛⎫⎛⎫-=+⎪ ⎪⎝⎭⎝⎭,则2πsin 23α⎛⎫+= ⎪⎝⎭()A.35 B.45C.45-D.35-【答案】B 【解析】【分析】根据诱导公式结合二倍角公式,利用齐次式计算可得.【详解】因为πππ632αα⎛⎫⎛⎫-++=⎪ ⎪⎝⎭⎝⎭,所以ππcos sin 63αα⎛⎫⎛⎫-=+ ⎪ ⎪⎝⎭⎝⎭,则ππsin 2cos 33αα⎛⎫⎛⎫+=+ ⎪ ⎪⎝⎭⎝⎭,即πtan 23α⎛⎫+= ⎪⎝⎭,所以222πππ2sin cos 2tan 2πππ4333sin 22sin cos πππ3335sin cos tan 1333ααααααααα⎛⎫⎛⎫⎛⎫+++ ⎪ ⎪ ⎪⎛⎫⎛⎫⎛⎫⎝⎭⎝⎭⎝⎭+=++=== ⎪ ⎪ ⎪⎛⎫⎛⎫⎛⎫⎝⎭⎝⎭⎝⎭+++++ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭.故选:B.7.圆()222:0O x y r r +=>上一点1,22A r r ⎛⎫⎪⎝⎭关于x 轴的对称点为B ,点E ,F 为圆O 上的两点,且满足EAB FAB ∠=∠,则直线EF 的斜率为()A.B.3C.3D.13【答案】B 【解析】【分析】根据圆的性质以及斜率乘积与直线垂直的关系即可.【详解】由EAB FAB ∠=∠知BOE BOF ∠=∠,所以OB EF ⊥,而212OB OArk k r =-=-=,∴3EF k =.故选:B.8.某种生命体M 在生长一天后会分裂成2个生命体M 和1个生命体N ,1个生命体N 生长一天后可以分裂成2个生命体N 和1个生命体M ,每个新生命体都可以持续生长并发生分裂.假设从某个生命体M 的生长开始计算,记n a 表示第n 天生命体M 的个数,n b 表示第n 天生命体N 的个数,则11a =,10b =,则下列结论中正确的是()A.413a = B.数列{}nnb a 为递增数列C.5163ni b==∑ D.若{}n n a b λ+为等比数列,则1λ=【答案】B 【解析】【分析】根据给定条件,求出递推公式,进而求出数列{},{}n n a b 的通项公式,再逐项分析判断即得.【详解】依题意,12n n n a a b +=+,12n n n b b a +=+,则113()n n n n a b a b +++=+,而111a b +=,因此数列{}n n a b +是首项为1,公比为3的等比数列,13n n n a b -+=,又11n n n n a b a b ++=--,因此111n n a a b b -=-=,于是1312n n a -+=,1312n n b --=,对于A ,3431142a +==,A 错误;对于B ,11131213131n n n n n b a ----==-++,显然数列12{}31n -+是递减数列,因此{}n n b a 为递增数列,B 正确;对于C ,51014134058ni b==++++=∑,C 错误;对于D ,1122331,2,54a b a b a b λλλλλ==+=++++,由{}n n a b λ+为等比数列,得2(2)54λλ+=+,解得1λ=或1λ=-,当1λ=时,13n n n b a λ-+=,显然数列{}n n a b λ+是等比数列,当1λ=-时,1n n a b λ+=,显然数列{}n n a b λ+是等比数列,因此当数列{}n n a b λ+是等比数列时,1λ=或1λ=-,D 错误.故选:B【点睛】思路点睛:涉及求数列单调性问题,可以借助作差或作商的方法判断单调性作答,也可以借助函数单调性进行判断.二、选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分.9.下列函数中,既是偶函数,又在区间()0,∞+上单调递增的是()A.ln y x =B.ln y x= C.2y x -= D.e e x xy -=+【答案】AD 【解析】【分析】A 选项,根据函数奇偶性得到()ln f x x =为偶函数,且在()0,∞+单调递增,A 正确;B 不满足奇偶性,C 不满足单调性;D 选项,满足为偶函数,且求导得到函数在()0,x ∈+∞上单调递增,得到答案.【详解】A 选项,()ln f x x =定义域为()(),00,x ∈-∞⋃+∞,且()()ln ln f x x x f x -=-==,故()ln f x x =为偶函数,且()0,x ∈+∞时,ln y x =单调递增,故A 正确;B 选项,ln y x =的定义域为()0,∞+,故不是偶函数,故B 项错误;C 选项,()0,x ∈+∞时,2y x -=单调递减,故C 项错误;D 选项,()e exxg x -=+的定义域为R ,且()()e e x xg x g x --=+=,故()e exxg x -=+是偶函数,且()0,x ∈+∞时,()e e0xxg x -'=->,函数单调递增,故D 项正确.故选:AD10.地震释放的能量E 与地震震级M 之间的关系式为lg 4.8 1.5E M =+,2022年9月18日我国台湾地区发生的6.9级地震释放的能量为1E ,2023年1月28日伊朗西北发生的5.9级地震释放的能量为2E ,2023年2月6日土耳其卡赫拉曼马拉什省发生的7.7级地震释放的能量为3E ,下列说法正确的是()A.1E 约为2E 的10倍B.3E 超过2E 的100倍C.3E 超过1E 的10倍D.3E 低于1E 的10倍【答案】BC 【解析】【分析】根据题意,结合对数运算公式,即可判断.【详解】A.()12lg lg 1.5 6.9 5.9E E -=⨯-,所以 1.51210E E =,故A 错误;B.()32lg lg 1.57.7 5.9E E -=⨯-, 2.73210100E E =>,故B 正确;C.()31lg lg 1.57.7 6.9E E -=⨯-, 1.2311010E E =>,故C 项正确,D 项错误.故选:BC11.已知函数()f x 的导函数为()f x ',对任意的正数x ,都满足()()()22f x xf x f x x <<-',则下列结论正确的是()A.()1122f f ⎛⎫< ⎪⎝⎭B.()()1122f f <C.()11422f f ⎛⎫<- ⎪⎝⎭D.()()11214f f <+【答案】BC 【解析】【分析】设()()()0f x g x x x=>,利用导数求出()g x 的单调性,据此即可判断A 和B 选项,设()()()220f x x h x x x-=>,根据导数求出()h x 的单调性,据此即可求解C 和D 选项.【详解】设()()()0f x g x x x=>,则()()()20xf x f x g x x'-='>,所以()g x 在()0,∞+上单调递增,由()112g g ⎛⎫>⎪⎝⎭得()1122f f ⎛⎫> ⎪⎝⎭,故A 项错误;由()()12g g <得()()1122f f <,故B 项正确;设()()()220f x x h x x x-=>,则()()()()()()()()243222220f x x f x x x xf x f x x h x x x ---⋅--=''=<',所以()h x 在()0,∞+上单调递减,由()112h h ⎛⎫<⎪⎝⎭得()11422f f ⎛⎫<- ⎪⎝⎭,故C 项正确:由()()12h h >得()()11214f f >+,故D 项错误.故选:BC.12.在棱长为1的正方体1111ABCD A B C D -中,P 为棱上一点,满足1PA PC d +=(d 为定值),记P 点的个数为n ,则下列说法正确的是()A.当d =2n =B.1d <<+时,6n =C.当d =时,15n =D.n 的最大值为18【答案】AD 【解析】【分析】由点P 的位置进行分类讨论判断求解即可.【详解】当点P 位于A 或1C 处时,d当P 在AB 棱上由A 到B 移动时,d 1,当P 在AD ,1AA ,1C C ,11C B ,11C D 等棱上移动时,d 1+当P 在1BB 棱上由B 到1B 移动时,d 由11+;当P 在BC ,DC ,1D D ,11A B ,11A D 等棱上移动时,d 也是由1+再由增大到1+.故选:AD.三、填空题:本题共4小题,每小题5分,共20分.13.抛物线24y x =的焦点F 与x 轴上一点A 的连线的中点P 恰在抛物线上,则线段AF 的长为______.【答案】316##0.1875【解析】【分析】根据题意求线段AF 的中点坐标,结合抛物线的定义分析求解.【详解】因为24y x =,即214x y =,可知抛物线的焦点10,16F ⎛⎫⎪⎝⎭,准线为116y =-,设(),0A a ,则线段AF的中点为1,232a ⎛⎫⎪⎝⎭,则113321632PF =+=,所以3216AF PF ==.故答案为:316.14.如图,在四边形ABCD 中,AD AB ⊥,120ADC ∠=︒,AB =,1AD =,2CD =,求四边形ABCD 绕直线AD 旋转一周所成几何体的表面积为______.【答案】(12π+【解析】【分析】作出辅助线,求出各边长度,求出以AB 为半径的圆的面积,以CD 为母线和CE 为半径的圆锥的侧面积,以BC 为母线的圆台的面积,相加后得到答案.【详解】作CE AD ⊥,CFAB ⊥,E ,F 为垂足,因为120ADC ∠=︒,所以60EDC ∠=︒,因为2CD =,所以1DE =,CE =,故==AF CE ,又AB =1AD =,故2CF AE AD DE ==+=,BF AB AF =-=,由勾股定理得CB ==,四边形ABCD 绕直线AD 旋转一周所成几何体的表面积分为三部分,以AB 为半径的圆的面积(2π12π=,以CD 为母线和CE 为半径的圆锥的侧面积πrl =,以BC 为母线的圆台的侧面积+=所以该几何体的表面积为(12π+.故答案为:(12π+15.已知函数()()()22cos0f x x ωω=>的最小正周期为π,将函数()y f x =的图象上的所有点向右平移π6个单位长度,再将所得的图象上各点的横坐标缩短为原来的12,纵坐标不变,得到()y g x =的图象,则()y g x =在ππ,124⎡⎤⎢⎥⎣⎦上的值域为______.【答案】1,22⎡⎤⎢⎥⎣⎦【解析】【分析】化简()f x 的解析式,根据()f x 的最小正周期求得ω,根据三角函数图象变换的知识求得()g x ,进而求得()g x 在ππ,124⎡⎤⎢⎣⎦上的值域.【详解】()cos21f x x ω=+,2ππ2ω=,22ω=,()cos21f x x =+,将函数()y f x =的图象上的所有点向右平移π6个单位长度,得到ππcos 21cos 2163y x x ⎡⎤⎛⎫⎛⎫=-+=-+ ⎪ ⎢⎥⎝⎭⎝⎭⎣⎦,再将所得的图象上各点的横坐标缩短为原来的12,得到()πcos 413g x x ⎛⎫=-+ ⎪⎝⎭,因为ππ,124x ⎡⎤∈⎢⎥⎣⎦,所以π2π40,33x ⎡⎤-∈⎢⎥⎣⎦,所以π1cos 4,132x ⎛⎫⎡⎤-∈- ⎪⎢⎥⎝⎭⎣⎦,所以()y g x =在ππ,124⎡⎤⎢⎣⎦上的值域为1,22⎡⎤⎢⎥⎣⎦.故答案为:1,22⎡⎤⎢⎥⎣⎦16.已知2F 是双曲线2222:1(0,0)x y C a b a b-=>>的右焦点,圆222:O x y a +=与双曲线C 的渐近线在第一象限交于点A ,点B 在双曲线C 上,222BF F A =-,则双曲线C 的渐近线方程为______.【答案】2y x =±【解析】【分析】求出点A 的坐标及2AF 长,由222BF F A =-可得点A 为2BF 的中点,再结合双曲线定义求解即得.【详解】由222BF F A =-,得点A 为2BF 的中点,记1F 为C 的左焦点,连接1BF ,令半焦距为c ,则122BF OA a ==,由222b y x ax y a ⎧=⎪⎨⎪+=⎩,解得2a x cab y c ⎧=⎪⎪⎨⎪=⎪⎩,即2(,)a ab A c c ,而2(,0)F c ,因此2222()()a ab AF c b c c=-+=,由双曲线定义得222b a a -=,即2b a =,所以双曲线C 的渐近线方程为2y x =±.故答案为:2y x=±四、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.17.已知数列{}n a 的前n 项和为n S ,()()140n n S a λλλ-=->.(1)求证:数列{}n a 为等比数列;(2)当2λ=时,设1221log log n n n a n a n b a a ++++=+,求数列{}n b 的前n 项和n T .【答案】(1)证明见解析(2)261939n n nT n +=+【解析】【分析】(1)根据11,1,2n n n S n a S S n -=⎧=⎨-≥⎩作差得到1n n a a λ+=,即可得证;(2)由(1)可得12n n a +=,则321122323n n n b n n n n ++=+=+-++++,再利用裂项相消法计算可得.【小问1详解】证明:因为()()140n n S a λλλ-=->,当1n =时,()1114S a λλ-=-,解得14a =,由()14n n S a λλ-=-得()1114n n S a λλ++-=-,两式作差得()()()111144n n n n S S a a λλλλ++---=---,即()111n n n a a a λλλ++-=-,则1n n a a λ+=,又0λ>,所以数列{}n a 是首项为4,公比为λ的等比数列.【小问2详解】当2λ=时,由(1)得11422n n n a -+=⨯=,又223121322232log log log log 2322n n n n n n n a n a n n n b a a n n ++++++++++=+=+=+++,所以322131112232323n n n n n b n n n n n n +++++-=+=+=+-++++++,所以1111112344523n T n n n ⎛⎫⎛⎫⎛⎫=+-+-+⋅⋅⋅+-⎪ ⎪ ⎪++⎝⎭⎝⎭⎝⎭1111112344523n n n ⎛⎫=+-+-+⋅⋅⋅+- ⎪++⎝⎭21161923339n n n n n +⎛⎫=+-=⎪++⎝⎭.18.在ABC 中,内角A ,B ,C 所对应的边分别为a ,b ,c .(1)若12b a =,6sin sin B A -=,求角A 的值;(2)若π3A =,且b 是a 和3c 的等差中项,求cos B 的值.【答案】(1)π3A =或2π3(2)1cos 7B =-【解析】【分析】(1)根据题意利用正弦定理边化角即可得结果;(2)由等差中项可得23a b c =-,结合余弦定理解得83b c =,73a c =,代入余弦定理即可得结果.【小问1详解】因为12b a =,由正弦定理sin sin b a B A=得1sin sin 2B A =,又因为6sin sin B A -=sin 2A =,且()0,πA ∈,所以π3A =或2π3.【小问2详解】显然0,0,0a b c >>>,由b 是a 和3c 的等差中项得23b a c =+,即230a b c =->,可得32b c >,因为π3A =,由余弦定理2222cos a b c bc A =+-可得()22223b c b c bc -=+-,化简得2231180b bc c -+=,即()()380b c b c --=,解得83b c =或b c =(舍去),由23a b c =-,可得73a c =,由余弦定理222cos 2a c b B ac +-=,得22278133cos 7723c c c B c c ⎛⎫⎛⎫+- ⎪ ⎪⎝⎭⎝⎭==-⎛⎫⨯ ⎪⎝⎭.19.已知函数()()36R f x x ax a =+-∈.(1)若函数()f x 的图象在2x =处的切线与x 轴平行,求函数()f x 的图象在3x =-处的切线方程;(2)讨论函数()f x 的单调性.【答案】19.15480x y -+=20.答案见解析【解析】【分析】(1)先求导函数再求斜率最后写出切线方程;(2)分类讨论列表根据导函数求单调性.【小问1详解】()23f x x a ='+.由题意()2120f a ='+=,解得12a =-,所以()3126f x x x =--,()33f -=,()315f '-=()f x 在3x =-处的切线方程为15480x y -+=【小问2详解】()23f x x a ='+.①当0a ≥时,()0f x '≥,()f x 在R 上单调递增.②当0a <时,由()0f x '=得x =,()f x 在R 上的变化情况如下表:由上表可得()f x 在,∞⎛- ⎝上单调递增,在⎛ ⎝上单调递减,在∞⎫+⎪⎪⎭上单调递增.综上,当0a ≥时,增区间为(),∞∞-+,无减区间;当0a <时,增区间为,∞⎛- ⎝和∞⎫+⎪⎪⎭,减区间为⎛ ⎝.20.如图,在三棱锥A BCD -中,CE BD ⊥,垂足为点E ,AH ⊥平面BCD ,垂足H 在CE 上,点F 在AC 上,且CEF CAH ∠=∠.(1)证明:AC ⊥平面BDF ;(2)若22BE DE ==,22CH EH ==,三棱锥A BCD -的体积为BF 与平面ABD 所成角的正弦值.【答案】(1)证明见解析(2)5.【解析】【分析】(1)利用线面垂直得到线线垂直,由CEF CAH ∠=∠,可得出AC EF ⊥,利用线面垂直的判定定理可以证得AC ⊥平面BDF ;(2)通过三棱锥A BCD -的体积,可以求出AH ,进一步求AC ,由两个三角形AHC ,EFC 相似,得出F 为AC 的中点,然后建立空间直角坐标系,求平面ABD 的法向量,进而可以求得直线与平面所成角的正弦值.【小问1详解】由AH ⊥平面BCD ,BD ⊂平面BCD ,得AH BD ⊥,又CE BD ⊥,而AH ⊂平面ACE ,CE ⊂平面ACE ,AH CE H = ,所以BD ⊥平面ACE ,又AC ⊂平面ACE ,所以BD AC ⊥.再由AH ⊥平面BCD ,EC ⊂平面BCD ,得AH EC ⊥,得90AHC ∠=︒,又CEF CAH ∠=∠,ACH ECF ∠=∠,得90EFC AHC ︒∠=∠=,即AC EF ⊥.又EF ⊂平面BDF ,BD ⊂平面BDF ,EF BD E = ,所以AC ⊥平面BDF .【小问2详解】由条件知11133322A BCD BCD V S AH BD CE AH AH -=⋅=⨯⨯⨯⨯==所以AH =,在Rt AHC 中,2228412AC AH CH =+=+=,所以AC =由(1)知Rt Rt AHC EFC ~△△,所以FC ECHC AC =,即2FC =,得FC =,可知F 为AC 的中点,过点H 作HG BD ∥交BC 于点G由(1)易得HG ,HC ,HA 两两垂直,以{HG 、HC 、}HA正交基底,建立空间直角坐标系H xyz -,如图所示由题意可知,(0,0,A ,()2,1,0B -,()0,1,0E -,()0,2,0C,(F .则(0,1,EA = ,()2,0,0EB =,(2,BF =- ,设平面ABD 的一个法向量为(),,n x y z =,则020EA n y EB n x ⎧⋅=+=⎪⎨⋅==⎪⎩,令1z =-,则y =,所以平面ABD的一个法向量()0,1n =-,设直线BF 与平面ABD 所成角θ,则sin =cos<,5n BF n BF n BFθ⋅>===⋅.故直线BF 与平面ABD所成角的正弦值为5.21.平面内一动点P 到直线:4l y =的距离,是它到定点()0,1F 的距离的2倍.(1)求动点P 的轨迹Γ的方程;(2)经过点F 的直线(不与y 轴重合)与轨迹Γ相交于M ,N 两点,过点M 作y 轴平行线交直线l 于点T ,求证:直线NT 过定点.【答案】(1)22143y x +=(2)证明见解析【解析】【分析】(1)由题意得4y -=,化简即可得解;(2)设直线MN 的方程以及,,M N T 的坐标,联立若椭圆方程,由韦达定理得()121232kx x x x =+,表示出NT 的方程,令0x =,证明此时y 为定值即可得证.【小问1详解】由题意,设动点P 的坐标为(),x y,则4y -=,平方整理得22143y x +=,所以点P 的轨迹Γ方程为22143y x+=.【小问2详解】由题意,设直线MN 的方程为1y kx =+,()11,M x y ,()22,N x y ,则()1,4T x .将1y kx =+代入22143y x +=得()2234690k x kx ++-=,所以122634k x x k -+=+,122934x x k -=+,显然0∆>,所以()121232kx x x x =+.因为直线NT 的方程为()212144y y x x x x --=--,令0x =,则()21221221122121214144x x kx x x y x x kx x y x x x x x x -+---===---()()21122121213545222x x x x x x x x x x --+-===--,因此,直线NT 过定点50,2⎛⎫ ⎪⎝⎭.【点睛】关键点点睛:本题第二问的关键是采用设线法,设直线MN 的方程为1y kx =+,再将其椭圆方程联立得到韦达定理式,再化积为和得到()121232kx x x x =+,再得到直线NT 的方程,令0x =计算即可.22.已知函数()()()22ln 211R 2m f x x x m x m =+-++∈.(1)求函数()f x 的极值;(2)设函数()f x 有两个极值点12,x x ,求证:()()122f x f x f m ⎛⎫+< ⎪⎝⎭.【答案】(1)答案见解析(2)证明见解析【解析】【分析】(1)求定义域,求导,对导函数因式分解,分0m ≤,12m =,12m >,102m <<,得到函数的单调性,进而得到函数的极值情况;(2)由(1)得110,,22m ∞⎛⎫⎛⎫∈⋃+ ⎪ ⎪⎝⎭⎝⎭,并得到()()12212ln 222f x f x m m m +=---,2222ln 44f m m ⎛⎫=-+ ⎪ ⎪⎝⎭,作差法得到()()21222f x f x f m ⎛⎫⎫+-=-- ⎪⎪ ⎪⎭⎝⎭,结合m 的范围得到结论.【小问1详解】()()22ln 2112m f x x x m x =+-++的定义域为()0,∞+,()()()()()()2212212210mx m x x mx f x mx m x x x x-++--'=+-+==>①若0m ≤,则()20f '=,()0,2x ∈时()0f x '>,()2,x ∞∈+时()0f x '<,故()f x 在()0,2x ∈上单调递增,在()2,x ∞∈+上单调递减,所以函数的极大值为()22ln221f m =--,无极小值,②若12m =,则()()2202x f x x'-=≥,()f x 在()0,∞+上单调递增,无极值.③若12m >,由()()()210x mx f x x--'==得2x =或1x m =,10,x m ⎛⎫∈ ⎪⎝⎭时()0f x '>,1,2x m ⎛⎫∈ ⎪⎝⎭时()0f x '<,()2,x ∞∈+时()0f x '>,故()f x 在10,m ⎛⎫ ⎪⎝⎭,()2,∞+上单调递增,在1,2m ⎛⎫⎪⎝⎭上单调递减,所以极大值为112ln 12f m m m ⎛⎫=---⎪⎝⎭,极小值为()22ln221f m =--.④若102m <<,由()()()210x mx f x x--'==得2x =或1x m =,()0,2x ∈时()0f x '>,12,x m ⎛⎫∈ ⎪⎝⎭时()0f x '<,1,x m ∞⎛⎫∈+ ⎪⎝⎭时()0f x '>,故()f x 在()0,2,1,m ∞⎛⎫+⎪⎝⎭上单调递增,在12,m ⎛⎫⎪⎝⎭上单调递减,所以极大值为()22ln221f m =--,极小值为112ln 12f m m m ⎛⎫=---⎪⎝⎭.综上,当0m ≤时,极大值为()22ln221f m =--,无极小值;当102m <<时,极大值为()22ln221f m =--,极小值为112ln 12f m m m ⎛⎫=--- ⎪⎝⎭;当12m =时,()f x 无极值;当12m >时,极大值为112ln 12f m m m ⎛⎫=--- ⎪⎝⎭,极小值为()22ln221f m =--.【小问2详解】由(1)知函数()f x 有两个极值点时,110,,22m ∞⎛⎫⎛⎫∈⋃+ ⎪ ⎪⎝⎭⎝⎭.()()()121122ln2212ln 12f x f x f f m m m m ⎛⎫+=+=----- ⎪⎝⎭212ln222m m m=---,()222224ln 222122ln 44f m m m m m ⎛⎫=+-++=-++ ⎪ ⎪⎝⎭,所以()()122122462f x f x f m m m ⎛⎫+-=--++- ⎪⎪⎝⎭22442⎫=-+-=-⎪⎭,因为110,,22m ∞⎛⎫⎛⎫∈⋃+ ⎪ ⎪⎝⎭⎝⎭2≠,所以()()212220f x f x f m ⎛⎫⎫+-=-+< ⎪⎪ ⎪⎭⎝⎭,即()()1222f x f x f m ⎛⎫+<- ⎪ ⎪⎝⎭.【点睛】方法点睛:在导数解答题中,单调性问题是绕不开的一个问题,因为单调性是解决后续问题的关键,利用导函数求解函数单调性步骤,先求定义域,再求导,导函数能因式分解的要进行因式分解,根据导函数的正负号,确定函数的单调区间,若不能直接求出,可能需要多次求导.。
辽宁省2024-2025学年高三上学期10月联考数学教学质量检测试卷(含解析)

注意事项:1. 答题前,先将自己的姓名、准考证号填写在试卷和答题卡上,并将准考证号条形码贴在答题卡上的指定位置.2. 选择题的作答:每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑.写在试卷、草稿纸和答题卡上的非答题区域均无效.3. 非选择题的作答:用黑色签字笔直接答在答题卡上对应的答题区域内.写在试卷、草稿纸和答题卡上的非答题区域均无效.4. 考试结束后,请将本试卷和答题卡一并上交.一、单项选择题(本大题共8小题,每小题5分,共40分.在每小题所给的四个选项中,只辽宁省2024-2025学年高三上学期10月联考数学教学质量检测试卷有一项是符合题目要求的)1. 已知集合{}21A x x =-<,{}3B x a x a =<<+,若{}15A B x x ⋃=<<,则a =()A. 0B. 1C. 2D. 3【答案】C 【解析】【分析】先求出集合A ,再根据并集得出参数的值.【详解】因为()1,3A =,()1,5A B ⋃=,又因为(),3B a a =+,所以35,a +=即a =2.故选:C.2. 如图,在ABC V 中,点D 是BC 边的中点,3AD GD = ,则用向量AB ,AC表示BG 为( )A. 2133BG AB AC=-+u u u u r uu r u u u r B. 1233BG AB AC=-+u u u r u uu r u u u r C. 2133BG AB AC=-u u u r u u u r u u u r D. 2133BG AB AC=+u u u r u u u r u u ur【答案】A 【解析】【分析】利用向量的线性运算求解即可.【详解】3AD GD =,故23AG AD = ,则()2212133233B C G BA BA BA AG AD AB A AB AC =+=+=+⨯+=-+.故选:A3. 在等比数列{}n a 中,记其前n 项和为n S ,已知3212a a a =-+,则84S S 的值为( )A. 2 B. 17 C. 2或8D. 2或17【答案】D 【解析】【分析】根据等比数列通项公式求得1q =或2q =-,再利用等比数的求和公式求解即可.【详解】解:由等比数列的通项公式可得21112a q a q a =-+,整理得220q q +-=,解得1q =或2q =-.当q =1时,1841824S a S a ==;当2q =-时,()()814844184111117111a q S q q q S q a q q ---====-+--.所以84S S 的值为2或17.故选:D .4. 每年10月1日国庆节,根据气象统计资料,这一天吹南风的概率为25%,下雨的概率为20%,吹南风或下雨的概率为35%,则既吹南风又下雨的概率为( )A. 5% B. 10%C. 15%D. 45%【答案】B 【解析】【分析】根据概率公式直接得出结论.【详解】由题知,既吹南风又下雨的概率为25%20%35%10%+-=.故选:B5. 若直线:3l y kx k =+-与曲线:C y =恰有两个交点,则实数k 的取值范围是( )A. 4,+3∞⎛⎫⎪⎝⎭B. 43,32⎛⎤⎥⎝⎦C. 40,3⎛⎫ ⎪⎝⎭D. 43,32⎡⎫⎪⎢⎣⎭【答案】B 【解析】【分析】先得到直线过定点()1,3P ,作出直线l 与曲线C ,由图求出直线l 过点()1,0A -时的斜率和直线l 与曲线C 相切时的斜率即可树形结合得解.【详解】由()313y kx k k x =+-=-+可知直线l 过定点()1,3P ,曲线:C y =两边平方得()2210x y y +=≥,所以曲线C 是以()0,0为圆心,半径为1且位于直线x 轴上方的半圆,当直线l 过点()1,0A -时,直线l 与曲线C 有两个不同的交点,此时3032k k k =-+-⇒=,当直线l 与曲线C 相切时,直线和圆有一个交点,圆心()0,0到直线l的距离1d ,两边平方解得43k =,所以结合图形可知直线l 与曲线C 恰有两个交点,则4332k <≤.故选:B.6. 已知()ππsin 0,32f x x ωϕωϕ⎛⎫⎛⎫=++>< ⎪⎪⎝⎭⎝⎭为偶函数,()()sin g x x ωϕ=+,则下列结论不正确的A. π6ϕ=B. 若()g x 的最小正周期为3π,则23ω=C. 若()g x 在区间()0,π上有且仅有3个最值点,则ω的取值范围为710,33⎛⎫⎪⎝⎭D. 若π4g ⎛⎫= ⎪⎝⎭,则ω的最小值为2【答案】D 【解析】【分析】先根据()f x 是偶函数求ϕ判断A 选项;根据最小正周期公式计算可以判断B 选项;据有且仅有3个最值点求范围判断C 选项;据函数值求参数范围结合给定范围求最值可以判断D 选项.【详解】()ππsin 0,32f x x ωϕωϕ⎛⎫⎛⎫=++>< ⎪⎪⎝⎭⎝⎭为偶函数,则πππππ,Z,,,3226k k ϕϕϕ+=+∈<∴=∣∣A 选项正确;若()g x 的最小正周期为3π,由()sin()g x x ωϕ=+则2π23π,3T ωω==∴=,B 选项正确;πππ(0,π),(,π)666x x ωω∈+∈+ 若()g x 在区间()0,π上有且仅有3个最值点,则5ππ7π710π,26233ωω<+≤<≤,C 选项正确;若π()sin(6g x x ω=+ πππsin +446g ω⎛⎫⎛⎫== ⎪ ⎪⎝⎭⎝⎭,则πππ+2π463k ω=+或ππ2π+2π463k ω=+,Z k ∈,则 283k ω=+或28,Z k k ω=+∈,又因为0ω>,则ω的最小值为23,D 选项错误.故选:D.7. 已知()612a x x x ⎛⎫-- ⎪⎝⎭的展开式中,常数项为1280-,则a =( )A. ―2B. 2C. D. 1【解析】【分析】根据已知条件,结合二项式定理并分类讨论,即可求解.【详解】由题意,62a x x ⎛⎫- ⎪⎝⎭的通项公式为()()6662166C 2C 2rr r r r rr r a T x a x x ---+-⎛⎫=⋅=- ⎪⎝⎭,令620r -=,则3r =,令621r -=-,则72r =不符合题意,所以()612a x x x ⎛⎫-- ⎪⎝⎭的常数项为()3336C 21280a --=-,解得2a =-.故选:A .8. 已知函数22()log f x x mx x =-+,若不等式()0f x >的解集中恰有两个不同的正整数解,则实数m的取值范围是( )A. 23log 33,89+⎡⎫⎪⎢⎣⎭B. 23log 33,94+⎛⎫⎪⎝⎭C. 23log 33,94+⎡⎫⎪⎢⎣⎭ D. 23log 33,89+⎛⎫⎪⎝⎭【答案】C 【解析】【分析】不等式()0f x >可化为2log 1xmx x-<,利用导数分析函数()2log x g x x =的单调性,作函数()1h x mx =-,()2log xg x x=的图象,由条件结合图象列不等式求m 的取值范围.【详解】函数22()log f x x mx x =-+的定义域为(0,+∞),不等式()0f x >化为:2log 1xmx x-<.令()1h x mx =-,()2log x g x x=,()2222221log e log log e log x xx x g x x x --='=,故函数()g x 在()0,e 上单调递增,在()e,∞+上单调递减.当1x >时,()0g x >,当1x =时,()0g x =,当01x <<时,()0g x <,当x →+∞时,()0g x →,当0x >,且0x →时,()g x ∞→-,画出()g x 及()h x 的大致图象如下,因为不等式()0f x >的解集中恰有两个不同的正整数解,故正整数解为1,2.故()()()()2233h g h g ⎧<⎪⎨≥⎪⎩,即22log 2212log 3313m m ⎧-<⎪⎪⎨⎪-≥⎪⎩,解得23log 3943m +≤<.故选:C.二、多项选择题(本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求,全部选对得6分,部分选对的得部分分,有选错的得0分)9. 已知复数232023i i i i 1iz ++++=+ ,则下列结论正确的是( )A. 1i 2z -=-B. 1i 2z -=C. 1i 2z +=-D. z =【答案】ACD 【解析】【分析】利用234i+i +i +i 0=对分子化简,然后利用复数的除法化简,可求共轭复数、复数的模依次判断即可得出结果.【详解】因为i,411,42i ,i,431,4nn k n k k n k n k=+⎧⎪-=+⎪=∈⎨-=+⎪⎪=⎩Z ,所以234i+i +i +i 0=,所以()()()()2342323202323505i+i +i +i i i i 1i i i i i i i i 111i 1i 1i 1i 1i 1i 1i 22z +++--++++++-======-++++++- ,所以A 正确,B 错误,111i i=222z +=---,C 准确,所以z ==D 正确.故选:ACD10. “费马点”是由十七世纪法国数学家费马提出并征解的一个问题. 该问题是:“在一个三角形内求作一点,使其与此三角形的三个顶点的距离之和最小”.意大利数学家托里拆利给出了解答,当 ABC V 的三个内角均小于120°时,使得120AOB BOC COA ︒∠=∠=∠=的点O 即为费马点;当 ABC V 有一个内角大于或等于120°时,最大内角的顶点为费马点.下列说法正确的是( )A. 正三角形的的费马点是正三角形的中心B. 若P 为ABC V 的费马点, 且 0PA PB PC ++=u u r u u r u u u r r,则ABC V 一定为正三角形C. 若ABC V 三边长分别为2D. ABC V 的内角A ,B ,C 所对的边分别为a ,b , c , π22A ,bc ∠==,若点P 为ABC V 的费马点,则PA PB PB PC PC PA ⋅+⋅+⋅=.【答案】ABC 【解析】【分析】对A ,根据正三角形中心的性质结合费马点定义易判断;对B ,取AB 的中点D ,由0PA PB PC ++=可得点P 是ABC V 的重心,再结合条件可得点P 是ABC V 的中心,得证;对C ,利用三角形旋转,结合费马点定义,构造正三角形转化线段长求解;对D ,由向量数量积定义,结合费马点定义和三角形等面积法列式求解.【详解】对于A ,如图O 是正三角形ABC 的中心,根据正三角形的性质易得o 120AOB AOC BOC ∠=∠=∠=,所以点O 是正三角形ABC 的费马点,故A 正确;对于B ,如图,取AB 的中点D ,则2PA PB PD += ,因为0PA PB PC ++=,所以2PC PD =-u u u r u u u r,所以,,C P D 三点共线,且点P 是ABC V 的重心,又点P 是ABC V 费马点,则o 120APB APC BPC ∠=∠=∠=,则o 60APD BPD ∠=∠=,又AD BD =,易得PA PB =,同理可得PC PB =,所以PA PB PC ==所以点P 是ABC V 的外心,所以点P 是ABC V 的中心,即ABC V 是正三角形.故B 正确;对于C ,如图,在Rt ABC △中,1AB =,BC =,2AC =,o 30ACB ∠=,点O 是Rt ABC △的费马点,将COA 绕点C 顺时针旋转o 60,得到CED △,易证COE ,ACD 是正三角形,则OC OE =,OA DE =,CD AC =,且点,,,B O E D 共线,所以o90BCD ∠=,所以BD ===又OA OB OC DE OE OB DB ++=++==,的.故C 正确;对于D ,由费马点定义可得o 120APB APC BPC ∠=∠=∠=,设PA x =,PB y =,PC z =,,,0x y z >,由ABC PAB PAB PAB S S S S =++V V V V,可得111122222xy xz yz ++=⨯,整理得xy yz xz ++=,所以111222PA PB PB PC PC PA xy yz xz ⎛⎫⎛⎫⎛⎫⋅+⋅+⋅=⋅-+⋅-+⋅- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭ ()1122xy yz xz =-++=-=,故D 错误.故选:ABC.【点睛】关键点点睛:解答本题首先要理解费马点的含义,解答D 选项的关键在于利用三角形等面积法求出xy yz xz ++=.11. 在四面体ABCD 中,棱AB 的长为4,AB BD ⊥,CD BD ⊥,2BD CD ==,若该四面体的体积为)A. 异面直线AB 与CD 所成角的大小为π3B. AC的长可以为C. 点D 到平面ABCD. 当二面角A BC D --是钝角时,其正切值为【答案】ACD【解析】【分析】根据等体积法可结合三角形的面积公式可得sin CDE ∠=A ,根据余弦定理即可求解B ,根据等体积法即可求解C ,根据二面角的几何法,结合同角关系即可求解D.【详解】在平面ABD 内过D 作DE AB ∥,且ED AB =,由于AB BD ⊥,故四边形ABDE 为矩形,CD BD ⊥,DE BD ⊥,BD DE C = ,CD ⊂平面CDE ,DE ⊂平面CDE ,故BD ⊥平面CDE ,故11233C ABD C EDA B CDE CDE CDE V V V S BD S ---===⋅=⨯=,11sin 24sin 4sin 22CDE S CD DE CDE CDE CDE=⋅⋅∠=⨯⨯∠=∠故1124sin 233C ABD CDE V S CDE -=⨯=⨯∠⨯=,因此sin CDE ∠=由于()0,CDE π∠∈,所以3CDE π∠=或23π,由于CDE ∠为异面直线AB 与CD 所成角或其补角,故异面直线AB 与CD 所成角的大小为3π,A 正确,当23CDE π∠=时,CE ===,由于BD ⊥平面CDE ,AE BD ,∴AE ⊥平面CDE ,CE ⊂平面CDE ,故AE CE ⊥,此时AC ==当3CDE π∠=时,CE ===,由于BD ⊥平面CDE ,AE BD ,∴AE ⊥平面CDE ,CE ⊂平面CDE ,故AE CE ⊥,此时4AC ==,故B 错误,由于BC ==,4AB =,当AC =cos BAC ∠==sin BAC ∠=,11sin 422ABC S AB AC BAC =⋅⋅∠=⨯⨯= ,当4AC =时,161683cos 2444BAC +-∠==⨯⨯,故sin BAC ∠=,1sin 2ABC S AB AC BAC =⋅∠= ,故点D 到平面ABC的距离为d ===,C 正确,当4AC =时,4AB AC ==,2CD BD ==,取BC 中点为O ,连接OA ,OD ,则AOD ∠即为二面角A BC D --的平面角,12OD BC ===,AO ==所以22cos 0AOD ∠===<,故AOD ∠为钝角,符合题意,此时sin tan cos AODAOD AOD∠∠==∠,当4AC =,由于2DBCS =,点A 到平面BDC距离为d ===,设A 在平面BDC 的投影为H ,则AH =,故HD==HC ==,因此点O 为以D ,C为圆心,以半径为,显然交点位于BC ,同D 的一侧,故此时二面角A BC D --为锐角,不符合要求,故D 正确,故选:ACD三、填空题(本大题共3小题,每小题5分,共15分)12. 已知,a b +∈R ,41a b +=,则aba b+的最大值是________.【答案】19【解析】的【分析】先求出11a b+的最小值,再将aba b +化为111a b+,即可求得答案.【详解】因为,a b +∈R ,41a b +=,故()111144559b a a b a b a b a b ⎛⎫+=++=++≥+= ⎪⎝⎭,当且仅当4b a a b=,结合41a b +=,即11,63==a b 时等号成立,所以11119ab a b a b =≤++,即ab a b +的最大值是19,故答案为:1913. 刻画空间的弯曲性是几何研究的重要内容,在数学上用曲率刻画空间弯曲性.规定:多面体的顶点的曲率等于2π与多面体在该点的面角之和的差(多面体的面的内角叫做多面体的面角,角度用弧度制),多面体面上非顶点的曲率均为零,多面体的总曲率等于该多面体各顶点的曲率之和.例如:正四面体(四个面都是等边三角形围成的几何体)在每个顶点有3个面角,每个面角是π3,所以正四面体在每个顶点的曲率为π2π3π3-⨯=,故其总曲率为4π.我们把平面四边形ABCD 外的点P 连接顶点A 、B 、C 、D 构成的几何体称为四棱锥,根据曲率的定义,四棱锥的总曲率为______.【答案】4π【解析】【分析】根据曲率的定义求解即可.【详解】由定义可得多面体的总曲率2π=⨯顶点数各面内角和,因为四棱锥有5个顶点,5个面,分别为4个三角形和1个四边形,所以任意四棱锥的总曲率为()2π5π42π14π⨯-⨯+⨯=.故答案为:4π.14. 过双曲线22221(0,0)y x a b a b-=>>的上焦点1F ,作其中一条渐近线的垂线,垂足为H ,直线1F H 与双曲线的上、下两支分别交于,M N ,若3NH HM =,则双曲线的离心率e =__________.【解析】【分析】设双曲线右焦点为2F ,HM t =,3NH t =,由题意结合双曲线定义可依次求出1F H 、1OF 、1F M 、1F N 、2F N 和2F M ,接着分别在1Rt F OH 、12F MF △和12F NF △中结合余弦定理求出1cos OF M ∠,进而建立等量关系式求出t ,从而求得2b a =,进而由离心率公式即可得解.【详解】设双曲线右焦点为2F ,由题()10,F c ,双曲线的一条渐近线方程为ay x b=-即0ax by +=,过该渐近线作垂线,则由题1F H b =,1OF c =,设HM t =,则由题3NH t =,1F M b t =-,13F N b t =+,所以232F N b t a =+-,22F M b t a =-+,所以在1Rt F OH 中,111cos F H bOF M OF c∠==①,在12F MF △中,()()()()()22222211221112||||22cos 222F M F F F M b t c b t a OF M b t c F M F F +--+--+∠==-⋅②,在12F NF △中,()()()()()22222211221112||||3232cos 2322F N F F F N b t c b t a OF M b t c F N F F +-++-+-∠==+⋅③,由①②得()()()()()2222222b t c b t a bb tc c-+--+=-,化简解得ab t a b =+,由①③得()()()()()2223232232b t c b t a b b t c c++-+-=+,化简解得()3ab t b a =-,所以()23ab abb a a b b a =⇒=+-,故双曲线的离心率c e a====.【点睛】思路点睛:依据题意设双曲线右焦点为2F ,HM t =,则结合双曲线定义可得1Rt F OH 、12F MF △和12F NF △的边长均是已知的,接着结合余弦定理均可求出三个三角形的公共角1OF M ∠的余弦值1cos OF M ∠,从而可建立等量关系式依次求出t 和2b a =,进而由离心率公式得解.四、解答题(本大题共5小题,共77分.解答应写出必要的文字说明、证明过程或演算步骤)15. 设n S 为数列{}n a 的前n 项和,满足()*1N n n S a n =-∈.(1)求数列{}n a 的通项公式;(2)记22212n n T S S S =+++ ,求n T .【答案】(1)1()2n n a = (2)1235111((3232n nn n T --=+-⋅【解析】【分析】(1)应用1n n n S S a --=,再结合等比数列定义及通项公式计算即可;(2)先化简得出21111()()24n n n S --+=,再应用分组求和及等比数列前n 项和公式计算.小问1详解】因为数列{a n }的前n 项和,满足1n n S a =-,当2n ≥时,可得111n n S a --=-,两式相减得1n n n a a a -=-,即12n n a a -=,所以112n n a a -=,令1n =,可得1111S a a =-=,解得112a =,所以数列{a n }构成首项为12,公比为12的等比数列,所以{a n }的通项公式为1111()(222n nn a -=⋅=.【小问2详解】由(1)知1(2nn a =,可得11(2nn S =-,所以222111111()]12()()1((22224[1n n n n n n S -=-⋅=+=-+-,【则222121111()[1()]244(111)111124n n n n T S S S -⋅-=+++=+++-+-- 1235111()()3232n n n --=+-⋅.16. 如图,正四棱台ABCD EFGH -中,24,EG AC MN ==上为上下底面中心的连线,且MN 与侧面.(1)求点A 到平面MHG 的距离;(2)求二面角E HM G --的余弦值.【答案】(1(2)23-【解析】【分析】(1)由题意建立空间直角坐标系,求得平面法向量,利用点面距向量公式,可得答案;(2)求得两个平面的法向量,利用面面角的向量公式,可得答案.【小问1详解】由题意,易知,,MN MA MB 两两垂直,分别以,,MA MB MN 为,,x y z 轴建立直角坐标系,如下图:则()()()()1,0,0,0,0,0,0,2,1,2,0,1A M H G --,取()()0,2,1,2,0,1MH MG =-=-,设平面MHG 的法向量(),,n x y z = ,则2020n MH y z n MG x z ⎧⋅=-+=⎪⎨⋅=-+=⎪⎩,令2z =,则1,1x y ==,所以平面MHG 的一个法向量()1,1,2n =,取()1,0,0MA = ,点A 到平面MHG的距离MA n d n ⋅===.【小问2详解】由(1)可知()()()()2,0,1,0,2,1,0,0,0,2,0,1E H M G --,取()()()()2,2,0,2,0,1,2,2,0,2,0,1HE ME HG MG ===-=-,设平面EHM 的法向量()1111,,m x y z = ,则11111122020m HE x y m ME x z ⎧⋅=+=⎪⎨⋅=+=⎪⎩ ,令11x =-,则221,2y z ==,所以平面EHM 的一个法向量()11,1,2m =-,设平面HMG 的法向量()2222,,m x y z = ,则22222222020m HG x y m MG x z ⎧⋅=-+=⎪⎨⋅=-+=⎪⎩ ,令21x =,则111,2y z ==,所以平面EHG 的一个法向量()21,1,2m =,设二面角E HM G --的大小为θ,则12121142cos 1143m m m m θ⋅-++=-=-=-++⋅ .17. 某汽车公司最新研发了一款新能源汽车,并在出厂前对100辆汽车进行了单次最大续航里程(理论上是指新能源汽车所装载的燃料或电池所能够提供给车行驶的最远里程)的测试.现对测试数据进行整理,得到如下的频率分布直方图:(1)估计这100辆汽车的单次最大续航里程的平均值x (同一组中的数据用该组区间的中点值代表);(2)由频率分布直方图计算得样本标准差s 的近似值为49.75.根据大量的汽车测试数据,可以认为这款汽车的单次最大续航里程X 近似地服从正态分布()2,N μσ,其中μ近似为样本平均数x ,σ近似为样本标准差S.(ⅰ)利用该正态分布,求()250.25399.5P X <<;(ⅱ)假设某企业从该汽车公司购买了20辆该款新能源汽车,记Z 表示这20辆新能源汽车中单次最大续航里程位于区间(250.25,399.5)的车辆数,求E (Z );参考数据:若随机变量ξ服从正态分布()2,N μσ,则()0.6827P μσξμσ-<<+=,()()220.9545,330.99731P P μσξμσμσξμσ-<<+=-<<+=.(3)某汽车销售公司为推广此款新能源汽车,现面向意向客户推出“玩游戏,送大奖”活动,客户可根据抛掷硬币的结果,操控微型遥控车在x 轴上从原点O 出发向右运动,已知硬币出现正、反面的概率都12,客户每掷一次硬币,遥控车向右移动一次,若掷出正面,则遥控车向移动一个单位,若掷出反面,则遥控车向右移动两个单位,直到遥控车移到点(59,0)(胜利大本营)或点(60,0)(失败大本营)时,游戏结束,若遥控车最终停在“胜利大本营”,则可获得购车优惠券.设遥控车移到点(),0n 的概率为()160n P n ≤≤,试证明数列{}1n n P P --是等比数列()259n ≤≤,求出数列{}()160n P n ≤≤的通项公式,并比较59P 和60P 的大小.【答案】(1)300 (2)(ⅰ)0.8186;(ⅱ)16.372(3)证明见解析,158211,159362111,60362n n n P n -⎧⎛⎫-⋅-≤≤⎪ ⎪⎪⎝⎭=⎨⎛⎫⎪+⋅= ⎪⎪⎝⎭⎩,5960P P >【解析】【分析】(1)根据平均数的求法求得正确答案.(2)(ⅰ)根据正态分布的对称性求得正确答案.(ⅱ)根据二项分布的知识求得正确答案.(3)根据已知条件构造等比数列,然后利用累加法求得n P ,利用差比较法比较59P 和60P 的大小.【小问1详解】2050.12550.23050.453550.24050.05300x ≈⨯+⨯+⨯+⨯+⨯=.【小问2详解】(ⅰ)0.95450.6827(250.25399.5)0.68270.81862P X -<<=+=.(ⅱ))∵Z 服从二项分布()20,0.8186B ,∴()200.818616.372E Z =⨯=.【小问3详解】当359n ≤≤时,()12112111,222n n n n n n n P P P P P P P -----=+-=--,1221111131,,222244P P P P ==⨯+=-=.∴{}1(259)n n P P n --≤≤是以14为首项,12-为公比的等比数列,2111(259)42n n n P P n --⎛⎫-=⋅-≤≤ ⎪⎝⎭.22132111111,,,(259)44242n n n P P P P P P n --⎛⎫⎛⎫-=-=⋅-⋯-=⋅-≤≤ ⎪⎪⎝⎭⎝⎭.累加得:115816058111422111111,(259),1362236212n n n n P P P n P P --⎛⎫⎛⎫-- ⎪ ⎪ ⎪⎝⎭⎛⎫⎛⎫⎝⎭-==-⋅-≤≤==+⋅ ⎪ ⎪⎝⎭⎝⎭+.∴158211,159362111,60362n n n P n -⎧⎛⎫-⋅-≤≤⎪ ⎪⎪⎝⎭=⎨⎛⎫⎪+⋅= ⎪⎪⎝⎭⎩∵58585960111111033232P P ⎛⎫⎛⎫⎛⎫-=-⨯=-> ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭,∴5960P P >.注:比较59P 和60P 的另一个过程:58596059592112111,13623622P P P P ⎛⎫=-⋅>-==-<< ⎪⎝⎭.18. 已知函数()1e xx f x +=.(1)求函数()f x 的极值;(2)若不等式()e ln 1xf x a x +≥恒成立,求实数a 的取值范围;(3)已知直线l 是曲线()y f x =在点()(),t f t 处的切线,求证:当1t >时,直线l 与曲线()y f x =相交于点()(),s f s ,其中s t <.【答案】(1)极大值为1,没有极小值 (2)[]e,0- (3)证明见解析【解析】【分析】(1)求导,利用导数判断()f x 的单调性和极值;(2)根据题意可得ln 0x a x +≥恒成立,构建()ln ,0g x x a x x =+>,分类讨论a 的符号,利用导数求最值,结合恒成立问题分析求解;(3)根据导数的几何意义可得当1t >时,方程2110e e ex t tx tx t t ++++-=有小于t 的解,构建()211e e ex t tx tx t t h x +++=+-,其中x t <,1t >,利用导数研究函数零点分析证明.小问1详解】由题意可知:()f x 的定义域为R ,且()ex xf x '-=,令()0f x '=时,0x =,则x ,f ′(x ),()f x 的关系为x(),0∞-0(0,+∞)f ′(x )+0-()f x 单调递增极大值单调递减所以,当0x =时,()f x 取到极大值为1,没有极小值.【小问2详解】若()e ln 1xf x a x +≥,即ln 0x a x +≥恒成立,设()ln ,0g x x a x x =+>,则()1a x a g x x x'+=+=,①当0a =时,则()0g x x =>恒成立,符合题意;②当0a >时,则()0g x '≥,可知()g x 在(0,+∞)上单调递增,因为11e e 10a a g --⎛⎫=-< ⎪⎝⎭,所以ln 0x a x +≥不恒成立;③当0a <时,x ,()g x ',()g x 的关系为x()0,a -a-(),a ∞-+()g x '-+【()g x 单调递减极小值单调递增可知()g x 的最小值为()()min ln g x a a a =-+-,则()ln 0a a a -+-≥,因为0a <,则()1ln 0a --≥,解得e 0a ≤-<;综上所述:实数a 的取值范围是[]e,0-.【小问3详解】因为()1e x x f x +=,()e x x f x '-=,则()1e t tf t +=,e t t k -=即切点坐标为1,e t t t +⎛⎫⎪⎝⎭,切线l 斜率为e tt k -=,可得l 的方程为()1e e t t t t y x t +--=-,即21e et tt t t y x -++=+,联立方程21e e 1e t txt t t y x x y ⎧-++=+⎪⎪⎨+⎪=⎪⎩,可得2110e e e x t tx tx t t ++++-=,由题可知:当1t >时,方程2110e e ex t tx tx t t ++++-=有小于t 的解,设()211e e ex t tx tx t t h x +++=+-,其中x t <,1t >且()0h t =,则()e e x t x t h x '-=+,设()()F x h x =',则()1e xx F x '-=,因为1t >,x ,()F x ',F (x )的关系为x(),1∞-1()1,t ()F x '-+F (x )单调递减1e et t -+,单调递增可知F (x )的最小值()()()min 10F x F F t =<=,且()1e 0e ttF -=+>,可知()01,1x ∃∈-,使()00F x =,当()0,x x ∞∈-时,()0F x >,即h ′(x )>0;当()0,x x t ∈时,()0F x <,即h ′(x )<0;可知h (x )在()0,x ∞-内单调递增;在()0,x t 内单调递减,可知h (x )的最大值()()()0max 0h x h x h t '=>=,且()()2110e t t h -+-=<,可知h (x )存在小于t 的零点,所以当1t >时,直线l 与曲线y =f (x )相交于点()(),s f s ,其中s t <,得证.【点睛】方法点睛:两招破解不等式的恒成立问题(1)分离参数法第一步:将原不等式分离参数,转化为不含参数的函数的最值问题;第二步:利用导数求该函数的最值;第三步:根据要求得所求范围.(2)函数思想法第一步:将不等式转化为含待求参数的函数的最值问题;第二步:利用导数求该函数的极值;第三步:构建不等式求解.19. 蝴蝶定理因其美妙的构图,像是一只翩翩起舞的蝴蝶,一代代数学名家蜂拥而证,正所谓花若芬芳蜂蝶自来.如图,已知圆M 的方程为222()x y b r +-=,直线x my =与圆M 交于()11,C x y ,()22,D x y ,直线x ny =与圆M 交于()33,E x y ,()44,F x y .原点O 在圆M 内.设CF 交x 轴于点P ,ED 交x 轴于点Q .(1)当0b =,r =,12m =-,2n =时,分别求线段OP 和OQ 的长度;(2)①求证:34121234y y y y y y y y ++=.②猜想|OP |和|OQ |的大小关系,并证明.【答案】(1)53OP OQ == (2)①证明见解析;②猜测OP OQ =,证明见解析.【解析】【分析】(1)联立直线与圆的方程,可求,,,C D E F 各点的坐标,利用直线的两点式方程,可得直线CF 和ED 的方程,并求它们与x 轴的交点坐标,可得问题答案.(2)①联立直线与圆的方程,求出两根之和与两根之积,找到相等代换量,从而证明成立.②分别求出点P 和点Q 的横坐标表达式,结合①中的结论,从而证明成立.【小问1详解】当0b =,r =,12m =-,2n =时,圆M :225x y +=,直线CD :12x y =-,由22512x y x y ⎧+=⎪⎨=-⎪⎩⇒12x y =⎧⎨=-⎩或12x y =-⎧⎨=⎩,故()1,2C -,()1,2D -;直线EF :2x y =,由2252x y x y⎧+=⎨=⎩⇒21x y =⎧⎨=⎩或21x y =-⎧⎨=-⎩,故()2,1E ,()2,1F --.所以直线CF :122112y x ++=+-+,令0y =得53x =-,即5,03P ⎛⎫- ⎪⎝⎭;直线ED :122112y x --=---,令0y =得53x =,即5,03Q ⎛⎫ ⎪⎝⎭.所以:53OP OQ ==.【小问2详解】①由题意:22b r <.由()222x y b r x my ⎧+-=⎪⎨=⎪⎩⇒()()222my y b r +-=⇒()2222120m y by b r +-+-=,则1y ,2y 是该方程的两个解,由韦达定理得:12222122211b y y m b r y y m ⎧+=⎪⎪+⎨-⎪⋅=⎪+⎩,所以1222122y y b y y b r +=⋅-.同理可得:3422342y y b y y b r +=⋅-,所以34121234y y y y y y y y ++=⋅⋅.②猜测OP OQ =,证明如下:设点(),0P p ,(),0Q q .因为,,C P F 三点共线,所以:414100y y x p x p --=--⇒411414x y x y p y y -=-,又因为点C 在直线x my =上,所以11x my =;点F 在直线x ny =上,所以44x ny =.所以()1441141414y y n m ny y my y p y y y y --==--;同理因为,,E Q D 三点共线,可得:()2323y y n m q y y -=-.由①可知:34121234y y y y y y y y ++=⋅⋅⇒12341111y y y y +=+⇒14321111y y y y -=-⇒23411423y y y y y y y y --=⋅⋅⇒231414230y y y y y y y y ⋅⋅+=--, 所以()()14231423y y n m y y n m p q y y y y --+=+--()23141423y y y y n m y y y y ⎛⎫=-+ ⎪--⎝⎭0=.即p q =-,所以OP OQ =成立.【点睛】关键点点睛:本题的关键是联立直线与圆的方程,结合一元二次方程根与系数的关系,进行化简处理,设计多个字母的运算,整个运算过程一定要小心、仔细.。
陕西省汉中市2023届高三上学期教学质量第一次检测理科数学试题(含答案解析)
()
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件
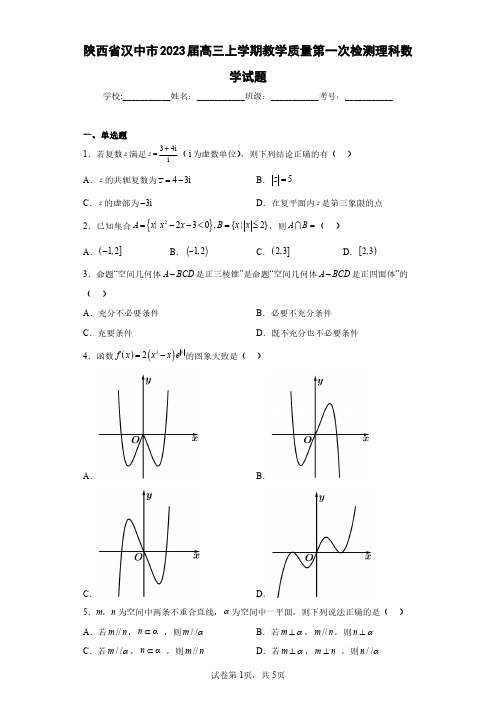
4.函数 f x 2 x3 x e x 的图象大致是( )
A.
B.
C.
D.
5.m,n 为空间中两条不重合直线, 为空间中一平面,则下列说法正确的是( )
A.若 m // n , n ,则 m / /
B.若 m , m // n ,则 n
7.A 【分析】先将原函数用诱导公式变形为正弦函数表示,再根据“左加右减”的原则判断即可.
【详解】
y
cos
2x
3
cos
2x
5 6
2
sin
2x
5 6
sin
2
x
5 12
故可由
y
sin2x 的图象向左平移
5 12
个单位长度得到.
故选:A.
8.C
【分析】分别安排各场馆的志愿者,利用组合计数和乘法计数原理求解.
三、解答题
17.已知 a,b, c 分别为 ABC 内角 A, B,C 的对边,且 2b a cosC c cosA
(1)求角 C ; (2)若 c2 2ab,ABC 的面积为 3 ,求 a b 的值. 18.如图,多面体 ABCDEF 中,四边形 ABCD 为菱形, ABB FA 2ED 2 .
A.
1 3
B. 2 5
C.
1 2
D. 3 5
11.若双曲线
x2 a2
y2 b2
1(a
0, b
0)
的实轴的两个端点与抛物线
x2
8by
的焦点是一个直
角三角形的顶点,则该双曲线的离心率为( )
2024届重庆市普通高中高三第三次教学质量检测试题考试数学试题

2024届重庆市普通高中高三第三次教学质量检测试题考试数学试题注意事项:1. 答题前,考生先将自己的姓名、准考证号填写清楚,将条形码准确粘贴在考生信息条形码粘贴区。
2.选择题必须使用2B 铅笔填涂;非选择题必须使用0.5毫米黑色字迹的签字笔书写,字体工整、笔迹清楚。
3.请按照题号顺序在各题目的答题区域内作答,超出答题区域书写的答案无效;在草稿纸、试题卷上答题无效。
4.保持卡面清洁,不要折叠,不要弄破、弄皱,不准使用涂改液、修正带、刮纸刀。
一、选择题:本题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.定义在R 上函数()f x 满足()()f x f x -=,且对任意的不相等的实数[)12,0,x x ∈+∞有()()12120f x f x x x -<-成立,若关于x 的不等式()()()2ln 3232ln 3f mx x f f mx x --≥--++在[]1,3x ∈上恒成立,则实数m 的取值范围是( ) A .1ln6,126e ⎡⎤+⎢⎥⎣⎦B .1ln3,126e ⎡⎤+⎢⎥⎣⎦C .1ln3,23e ⎡⎤+⎢⎥⎣⎦D .1ln6,23e ⎡⎤+⎢⎥⎣⎦2.执行如下的程序框图,则输出的S 是( )A .36B .45C .36-D .45- 3.用数学归纳法证明,则当时,左端应在的基础上加上( )A .B .C .D .4.在关于x 的不等式2210ax x ++>中,“1a >”是“2210ax x ++>恒成立”的( ) A .充分不必要条件 B .必要不充分条件 C .充要条件D .既不充分也不必要条件5.已知复数z 满足()11z i i +=-(i 为虚数单位),则z 的虚部为( )A .i -B .iC .1D .1-6.己知函数()()1,0,ln ,0,kx x f x x x ->⎧=⎨--<⎩若函数()f x 的图象上关于原点对称的点有2对,则实数k 的取值范围是( )A .(),0-∞B .()0,1C .()0,∞+D .10,2⎛⎫ ⎪⎝⎭7.用一个平面去截正方体,则截面不可能是( ) A .正三角形B .正方形C .正五边形D .正六边形8.已知集合2{|1}A x x =<,{|ln 1}B x x =<,则 A .{|0e}A B x x =<< B .{|e}A B x x =< C .{|0e}A B x x =<<D .{|1e}AB x x =-<<9.已知集合{}1,0,1,2A =-,{}|lg(1)B x y x ==-,则A B =( )A .{2}B .{1,0}-C .{}1-D .{1,0,1}-10.已知i 为虚数单位,实数,x y 满足(2)x i i y i +=-,则||x yi -= ( ) A .1B .2C .3D .511.如图,点E 是正方体ABCD -A 1B 1C 1D 1的棱DD 1的中点,点F ,M 分别在线段AC ,BD 1(不包含端点)上运动,则( )A .在点F 的运动过程中,存在EF //BC 1B .在点M 的运动过程中,不存在B 1M ⊥AEC .四面体EMAC 的体积为定值D .四面体FA 1C 1B 的体积不为定值 12.51(1)x x-+展开项中的常数项为 A .1B .11C .-19D .51二、填空题:本题共4小题,每小题5分,共20分。
数学丨浙江省湖州、衢州、丽水2025届高三11月三地市高三教学质量检测试卷数学试卷及答案

湖州、衢州、丽水2024年11月三地市高三教学质量检测试卷数学1.本试题卷共4页,满分150分,考试时间120分钟.2.考生答题前,务必将自己的姓名、准考证号用黑色字迹的签字笔或钢笔填写在答题纸上.3.选择题的答案须用2B 铅笔将答题纸上对应题目的答案标号涂黑,如要改动,须将原填涂处用橡皮擦净.4.非选择题的答案须用黑色字迹的签字笔或钢笔写在答题纸上相应区域内,作图时可先使用2B 铅笔,确定后须用黑色字迹的签字笔或钢笔描黑,答案写在本试题卷上无效.一、单项选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合{}6,5,4,3,2,1=A ,{}A x xB ∈=2,则=B A A.{}1 B.{}2,1 C.{}4,2,1 D.{}6,5,4,3,2,12.已知复数=-1i z (其中i 是虚数单位),则+=2z z A.2B.13.双曲线的另一种定义:动点(,)M x y 与定点(,0)F c 的距离和它与定直线2:al x c=的距离的比是常数ca(0a c <<),则点M 的轨迹是一个双曲线.动点M 与定点F 的距离和它与定直线:3l x =M 的轨迹方程为A.2212y x -= B.2212y x -= C.2212x y -= D.2212x y -=4.为研究光照时长x (小时)和种子发芽数量y (颗)之间的关系,某课题研究小组采集了9组数据,绘制散点图如图所示,并对,x y 进行线性回归分析.若在此图中加上点P 后,再次对,x y 进行线性回归分析,则下列说法正确的是A.,x y 不具有线性相关性B.决定系数2R 变大C.相关系数r 变小D.残差平方和变小5.已知ABC ∆的外接圆圆心为O ,且2AB AC AO += ,||||OA AB = ,则向量BA在向量BC 上的投影向量为A.14BCB.C.14BC-D. 6.古代农耕常用水车作为灌溉引水的工具,是人类的一项古老的发明,也是人类改造自然的成果之一.如图是一个半径为r 的水车,以水车的中心为原点,过水车的中心且平行于水平面的直线为x 轴,建立平面直角坐标系,一个水斗从点2)A -出发,沿圆周按逆时针方向匀速旋转,且旋转一周用时60秒.经过t 秒后,水斗旋转到P 点,设P 点的坐标为(,)x y ,其纵坐标满足sin()(0y r t t ωϕ=+ ,0ω>,||)2πϕ<,当45t =秒时,||PA =A.B.C. D.47.已知长方体1111ABCD A B C D -,E 是棱11C D 的中点,平面1AB E 将长方体分割成两部分,则体积较小部分与体积较大部分的体积之比为A .715B .12C .724D .7178.已知函数()x x x f 2cos 3cos -=,(0,)x π∈,若()f x 有两个零点()1212,x x x x <,则A .{}21,5x x ∈πB .123x x =C .121cos cos 2x x +=D .41cos cos 21-=x x 第6题图二、多项选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.9.已知0a >,0b >,则下列说法正确的是A.若1=+b a ,则2log log 22-≤+b a B.若1=+b a ,则1<+b a C.若1a b -=,则1212a b-≥ D.若1=-b a ,则221a b +>10.现有一个抽奖活动,主持人将奖品放在编号为1、2、3的箱子中,甲从中选择了1号箱子,但暂时未打开箱子,主持人此时打开了另一个箱子(主持人知道奖品在哪个箱子,他只打开甲选择之外的一个空箱子).记i A (1,2,3i =)表示第i 号箱子有奖品,j B (2,3j =)表示主持人打开第j 号箱子.则下列说法正确的是A.321()2P B A =B.131()3P A B =C.若再给甲一次选择的机会,则甲换号后中奖概率增大D.若再给甲一次选择的机会,则甲换号后中奖概率不变11.如图,在直三棱柱111ABC A B C -中,12AC BC CC ===,AC BC ⊥,Q 是线段AB 的中点,P 是线段1BC 上的动点(含端点),则下列命题正确的是A.三棱锥1P A QC -的体积为定值B.在直三棱柱111ABC A B C -内部能够放入一个表面积为4π的球C.直线PQ 与AC 所成角的正切值的最小值是22D .1A P PQ +第11题图三、填空题:本题共3小题,每小题5分,共15分.12.在()12nx -(*n ∈N )的展开式中,x 的系数为10-,则n =▲.13.已知椭圆()2222:10x y C a b a b +=>>,过左焦点F 作直线l 与圆222:4c M x y +=相切于点E ,与椭圆C 在第一象限的交点为P ,且3PE EF =,则椭圆离心率为▲.14.若()()3(2)222f x x x =-+-+,已知数列{}n a 中,首项1120a =,32123n n a a aa a n=++++L ,*n ∈N ,则()791ii f a ==∑▲.四、解答题:本题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.15.(本小题满分13分)如图,在三棱锥P ABC -中,底面ABC 是边长为2的等边三角形,⊥PC 平面ABC ,点E 是PB 的中点,点F 在线段CE 上且:2:1CF EF =,G 为三角形ABC 的重心.(1)求证:GF ∥平面P AB ;(2)当PC 的长为何值时,二面角E AC B --的大小为60︒.16.(本小题满分15分)在ABC ∆中,角A ,B ,C 对应的的三边分别是a ,b ,c,且2bB c-=.(1)求角C 的值;(2)若1=c ,B A tan 3tan 2=,求ABC ∆的面积.17.(本小题满分15分)第15题图已知数列{}n a 的首项是1,其前n 项和是n S ,且121++=+n a a n n ,*n ∈N .(1)求32,a a 的值及数列{}n a 的通项公式;(2)若存在实数λ,使得关于n 的不等式25n S n λ+≤,*n ∈N 有解,求实数λ取到最大值时n 的值.18.(本小题满分17分)已知函数()21ln1x f x ax x -=+-(R a ∈).(1)当1=a 时,求曲线()x f y =在点()()2,2f 处的切线方程;(2)若103a <≤,3,22x ⎡⎤∈⎢⎥⎣⎦,证明:()2f x <;(3)若1x >,恒有()32ln 22f x ≥+,求实数a 的取值范围.19.(本小题满分17分)直线族是指具有某种共同性质的直线的全体,例如()R ∈+=k kx y 1表示过点()1,0的直线族(不包括直线y 轴),直线族的包络曲线定义为:直线族中的每一条直线都是该曲线上某点处的切线,且该曲线上的每一点处的切线都是该直线族中的某条直线.(1)圆()22:34M x y +-=是直线族1(,)mx ny m n +=∈R 的包络曲线,求,m n 满足的关系式;(2)若点()00,N x y 不在直线族Ω:()2y tx t t =-∈R 的任意一条直线上,求0y 的取值范围及直线族Ω的包络曲线E 的方程;(3)在(1)(2)的条件下,过曲线E 上动点P 向圆M 做两条切线PA ,PB ,交曲线E 于点A ,B ,求PAB ∆面积S 的最小值.湖州、衢州、丽水2024年11月三地市高三教学质量检测试卷数学参考答案一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.题号12345678答案BCBCAADD二、选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.题号91011答案ACDBCACD三、填空题:本题共3小题,每小题5分,共15分.12.513.14.158四、解答题:本题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.15.(本小题满分13分)如图,在三棱锥P ABC -中,底面ABC 是边长为2的等边三角形,⊥PC 平面ABC ,点E 是PB 的中点,点F 在线段CE 上且:2:1CF EF =,G 为三角形ABC 的重心.(1)求证:GF ∥平面P AB ;(2)当PC 的长为何值时,二面角E AC B --的大小为60︒.解:(1)如图1,连接CG 并延长,交AB 与点H ,由于,G F 分别为,ABC PBC ∆∆重心,所以2CF CGFE GH==,故//GF EH ,……………………3分EH ⊂面PAB ,FG ⊄面PAB ,所以//FG 面PAB .……………………6分(2)解法一:如图2,取线段BC 的中点D ,连接ED ,过点D 作DK AC ⊥,垂足为K ,连接EK .因为//,ED PC PC ABC ⊥平面,所以ED ABC ⊥平面,所以EKD ∠为二面角B AC E --的平面角,所以60EKD ∠= ……………………………………………………10分因为2DK =,所以32ED =,于是有3PC =.……………………13分解法二:如图3,以AC 的中点O 为坐标原点建立空间直角坐标系Ozxy ,设PC h =,则()0,1,0A -,)B,()0,1,0C,1,22h E ⎫⎪⎪⎝⎭.……………………8分设平面EAC 的一个法向量为()1,,n x y z =则1100n AC n AE ⎧⋅=⎪⎨⋅=⎪⎩,得3022220hz x y y ++=⎪⎨⎪=⎩取(,0,n h =,………………………………………………………………11分易得平面ABC 的一个法向量()20,0,1n =因为二面角E AC B --的大小为060,所以1212121cos ,2n n n n n n ⋅==,解得:3h =.………………………………………………………………13分图1图2图316.(本小题满分15分)在ABC∆中,角A,B,C对应的的三边分别是a,b,c,B=.(1)求角C的值;(2)若1=c,BA tan3tan2=,求ABC∆的面积.解:(1B=sin cosA B C B-=,…………2分sin cosB C B C B-=(+),cos sinB C B=,.………………………………………………………………5分故2cos2C=,又0Cπ<<,所以4Cπ=.……………………………………………7分(2)若1=c ,tan 12tan 3tan 3tan )341tan A A B A Aπ-==-+=-⨯-(,22tan 5tan 30A A --=解得tan 3A =,1tan 2A =-(舍去),……………………10分则tan 2B =,所以sin A =,sin B =,由sin sin a cA C=,得a =,……13分故113sin 1225S ac B ==⨯⨯,ABC ∆的面积为53.……………………15分17.(本小题满分15分)已知数列{}n a 的首项是1,其前n 项和是n S ,且121++=+n a a n n ,*n ∈N .(1)求32,a a 的值及数列{}n a 的通项公式;(2)若存在实数λ,使得关于n 的不等式25n S n λ+≤,*n ∈N 有解,求实数λ取到最大值时n 的值.解:(1)由题可得当1n =时,21214a a =++=当2n =时,322219a a =+⨯+=.……………………2分当2n ≥时,121-=--n a a n n ,所以112211n n n n n a a a a a a a a ---=-+-++-+ 2212331n n n =-+-++= ,……5分当1n =时,11a =也满足2n a n =,综上所述,数列{}n a 的通项公式为2n a n =.…………………………………7分(未检验1n =时的情形,扣1分)(2)由题可得25n n S λ≤-,设25n n b n S =-,若要使得关于n 的不等式25n S n λ+≤(*n ∈N )有解,则()max n b ≤λ,当2n ≥时,2125250n n n b b a n --=-=-≥,则5n ≤,…………………………………12分故当4n =或5n =时,n b 的最大值为70,所以实数λ取到最大值70时,此时n 的值为4或5.………………………………………………………………………15分(λ最大值未给出不扣分)18.(本小题满分17分)已知函数()21ln 1x f x ax x -=+-(R a ∈).(1)当1=a 时,求曲线()x f y =在点()()2,2f 处的切线方程;(2)若103a <≤,3,22x ⎡⎤∈⎢⎥⎣⎦,证明:()2f x <;(3)若1x >,恒有()32ln 22f x ≥+,求实数a 的取值范围.解:(1)()()()11211f x x x -'=+--(1x >或12x <),…………………………3分则()223f '=,又()2ln 32f =+,所以所求的切线方程为()()2ln 3223y x -+=-,即22ln 333y x =++.…………………5分(定义域未给出,扣1分)(2)()()()1211f x a x x -'=+--……………………7分因为322x ≤≤,所以()()1112113x x --≤≤---,而310≤<a ,所以()0f x '≤,故()f x 在区间3,22⎡⎤⎢⎥⎣⎦上单调递减,………………………………9分所以()3312ln 22ln 22222f x f ⎛⎫≤=+≤+< ⎪⎝⎭成立.………………………………10分(3)当32x =时,3332ln 22ln 2222f a ⎛⎫=+≥+ ⎪⎝⎭,所以1a ≥.………………………12分下证:当1a ≥,1x >时()32ln 22f x ≥+恒成立.令()21ln 1x g a xa x -=+-,1a ≥所以()()211ln1x g a g x x -≥=+-,………………………………………………………14分所以()21ln 1x f x x x -≥+-,令()21ln 1x x x x ϕ-≥+-,则()()()()()()2311211211x x x x x x x ϕ--'=+=----,当31,2x ⎛⎫∈ ⎪⎝⎭时,()0x ϕ'<,()x ϕ单调递减,当3,2x ⎛⎫∈+∞ ⎪⎝⎭时,()0x ϕ'>,()x ϕ单调递增,所以()332ln 222x ϕϕ⎛⎫≥=+ ⎪⎝⎭,所以a 的取值范围为[)1,+∞.……………………………………………………17分19.(本小题满分17分)直线族是指具有某种共同性质的直线的全体,例如()R ∈+=k kx y 1表示过点()1,0的直线族(不包括直线y 轴),直线族的包络曲线定义为:直线族中的每一条直线都是该曲线上某点处的切线,且该曲线上的每一点处的切线都是该直线族中的某条直线.(1)圆()22:34M x y +-=是直线族1(,)mx ny m n +=∈R 的包络曲线,求,m n 满足的关系式;(2)若点()00,N x y 不在直线族Ω:()2y tx t t =-∈R 的任意一条直线上,求0y 的取值范围及直线族Ω的包络曲线E 的方程;(3)在(1)(2)的条件下,过曲线E 上动点P 向圆M 做两条切线PA ,PB ,交曲线E 于点A ,B .求PAB ∆面积S 的最小值.解:(1)由题可得,直线族1(,)mx ny m n +=∈R 为圆M 的切线,………………2分故满足,2d =,所以,m n 满足2254610n m n --+=.……………4分(2)将点()00,N x y 代入()2R y tx t t =-∈,可得关于t 的方程2000t x t y -+=,因为点()00,N x y 不在直线族()2R y tx t t =-∈上,故方程2000t x t y -+=无实数解,所以20040x y ∆=-<,那么2004x y >,故00y >因为区域2004x y >的边界为抛物线24x y =,…………………………………7分下证:24x y =是()2R y tx t t =-∈的包络曲线.证明:联立直线()2R y tx t t =-∈与24x y =,可得22440x tx t -+=,所以0∆=,故直线族Ω:()2R y tx t t =-∈为抛物线24x y =的切线.因此直线族Ω的包络曲线E 的方程为24x y =.…………………………………10分(3)设()11,A x y ,()22,B x y ,()22,P u u 则2111224PA y u x u k x u -+==-,故()11:2420PA x u x y ux +--=由直线PA 与M 相切,所以2d =,整理得()22111250u y ux u -++-=,1)同理可得,()22221250u y ux u -++-=,2)由1)2)可得直线()22:1250AB u y ux u -++-=.………………………………12分直线AB 与2:4C x y =联立得()22212504u y ux u x y ⎧-++-=⎪⎨=⎪⎩,(显然12≠u )可得22228204011ux u x u u -++=--,由韦达定理可得21212228204,11u u x x x x u u -+=-⋅=--.因此(()222411u AB u+=-,………………………………………………14分由于点()22,P u u 到直线AB 的距离422251u u d u ++=+,所以PAB ∆面积为()()4222225251PAB S u u u ∆=++-,令21u m -=,则()824PAB S f m m m ∆⎛==++ ⎝,由()()01f m m '==≥-,解得4m =,所以()f m 在()0,4上单调递减,在()4,+∞上单调递增,那么()()min 4PAB S f ∆==25u =时取到),所以PAB ∆面积S的最小值是17分。
浙江省杭州市2024届高三下学期4月教学质量检测数学试题含答案

2023学年第二学期杭州市高三年级教学质量检测数学试题卷(答案在最后)考生须知:1.本试卷分试题卷和答题卷两部分.满分150分,考试时间120分钟.2.请用黑色字迹的钢笔或签字笔在答题卡指定的区域(黑色边框)内作答,超出答题区域的作答无效!3.考试结束,只需上交答题卡.一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.函数()sin f x x=的最小正周期是A.4πB.2πC.πD.2π【答案】C 【解析】【详解】sin x 的图象是将sin x 的图象在x 轴下方的部分对称翻折上来所得,所以周期是sin x 周期的一半,即周期为π.2.已知m ,n 表示两条不同直线,α表示平面,下列说法正确的是A.若//,//,m n αα则//m n B.若m α⊥,n α⊂,则m n ⊥C.若m α⊥,m n ⊥,则//n α D.若//m α,m n ⊥,则n α⊥【答案】B 【解析】【详解】试题分析:线面垂直,则有该直线和平面内所有的直线都垂直,故B 正确.考点:空间点线面位置关系.3.已知,a b 是两个单位向量,若向量a 在向量b 上的投影向量为12b,则向量a 与向量a b - 的夹角为()A.30°B.60°C.90°D.120°【答案】B【解析】【分析】由条件结合投影向量的定义可求,a b,再根据向量夹角余弦公式求结论.【详解】因为向量a 在向量b 上的投影向量为12b ,,a b是两个单位向量,所以1cos ,2a a b b b ⋅= ,所以1cos ,2a b = ,又[],0,πa b ∈ ,所以π,3a b = ,所以()21111122a ab a a b ⋅-=-⋅=-⨯⨯=,又11a a b =-=== ,,所以()1cos ,2a ab a a b a a b ⋅--==⋅- ,又[],0,πa a b -∈ ,所以向量a 与向量a b - 的夹角为π3,即60 .故选:B.4.设甲:“函数()2sin f x x ω=在ππ,34⎡⎤-⎢⎣⎦单调递增”,乙:“02ω<≤”,则甲是乙的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件【答案】A 【解析】【分析】根据函数单调性求出ω的范围,即可判断答案.【详解】若“函数()2sin f x x ω=在ππ,34⎡⎤-⎢⎥⎣⎦单调递增”,则0ω>,由ππ22x ω-≤≤得ππ22x ωω-≤≤,则ππ23ππ24ωω⎧-≤-⎪⎪⎨⎪≥⎪⎩,解得302ω<≤,所以,甲是乙的充分不必要条件.故选:A5.设数列{}{},n n a b 满足11111,2,2nn n n n a b a b n a b ++==+=+=.设n S 为数列{}n n a b +的前n 项的和,则7S =()A.110B.120C.288D.306【答案】A 【解析】【分析】利用分组求和法,结合已知,可得答案.【详解】711223344556677S a b a b a b a b a b a b a b =+++++++++++++()()()()()()11232345456767a b a b b a a b b a a b b a =+++++++++++++246112222422622448161264110=++⨯++⨯++⨯+=++++++=.故选:A.6.将5名志愿者分配到三个社区协助开展活动,每个志愿者至少去一个社区,每个社区至少1名,则不同的分配方法数是()A.300B.240C.150D.50【答案】C 【解析】【分析】先分组,人员构成可能为1、1、3或1、2、2,再将3组全排列即可得.【详解】先将5名志愿者分成3组,若这三组的人员构成为1、1、3,则共有35C 种分组方案,若这三组的人员构成为1、2、2,则共有225322C C A 种分组方案,再将这3组志愿者随机分配到三个社区,共有33A 种分配方案,故共有2233535322C C 103C +A 106150A 2⎛⎫⨯⎛⎫⋅=+⨯= ⎪ ⎪⎝⎭⎝⎭种分配方法.故选:C.7.设集合{1,1}M =-,{|0N x x =>且1}x ≠,函数()xxf x a a λ-=+(0a >且1a ≠),则()A.(),,M a f x λ∀∈∃∈N 为增函数B.(),,M a f x λ∃∈∀∈N 为减函数C.(),,M a f x λ∀∈∃∈N 为奇函数D.(),,M a f x λ∃∈∀∈N 为偶函数【答案】D 【解析】【分析】结合指数函数的单调性与奇偶性检验各选项即可.【详解】当1λ=时,()x xf x a a -=+,1a >时,()f x 在(,0)-∞上不是增函数,故A 不正确;当1λ=-时,()xxf x a a-=-,1a >时,()f x 在(0,)+∞上为增函数,B 不正确;当1λ=时,()x xf x a a -=+,()()x x f x a a f x --=+=,()f x 为偶函数,故C 不正确;当1λ=时,()x xf x a a -=+,()()x x f x a a f x --=+=,()f x 为偶函数,故D 正确;故选:D.8.在ABC 中,已知sin cos sin ,cos sin cos A A n C n C B B ==.若πtan 34A ⎛⎫+=- ⎪⎝⎭,则n =()A.无解B.2C.3D.4【答案】A 【解析】【分析】由πtan 34A ⎛⎫+=- ⎪⎝⎭可得tan 2A =,进而得到tan tan tan 2A B C =⋅=,借助三角形内角和与两角和的正切公式可得tan tan 2B C +=,设tan B t =,有2220t t -+=,可得该方程无解,故不存在这样的n .【详解】由π1tan tan 341tan AA A+⎛⎫+==- ⎪-⎝⎭,即tan 2A =,则cos 0A ≠,由sin cos sin ,cos sin cos A An C n C B B ==,知cos 0C ≠,则tan tan tan AC B=,则tan tan tan 2A B C =⋅=,又()()tan tan tan tan πtan tan tan 1tan tan B CA B C B C B C B C+=--=-+=-=+-⋅,故tan tan 2B C +=,设tan B t =,则tan 2C t =-,有()22t t -=,即2220t t -+=,4840∆=-=-<,即该方程无解,故不存在这样三角形,即n 无解.故选:A.二、选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求.全部选对得6分,部分选对的得部分分,有选错的得0分.9.已知关于x 的方程210(22)x tx t ++=-<<的两根为1z 和2z ,则()A.12z z =B.121z z ⋅=C.12=z zD.1122z z z z ⎛⎫= ⎪⎝⎭【答案】ABC 【解析】【分析】求出方程的两根,即可判断A ,利用韦达定理判断B ,计算出两根的模,即可判断C ,利用复数代数形式的除法运算及B 项的结论化简12z z ,即可判断D.【详解】关于x 的方程210(22)x tx t ++=-<<,则240t ∆=-<,4i 2t x -±∴=,不妨设1422t z =-+,24i 22t z =--,12z z ∴=,故A 正确;由韦达定理可得121z z =,故B正确;121z z ==,故C 正确;121z z = ,∴2222111212222z z t t z z z z ⎛⎫-===-+=- ⎪ ⎪⎝⎭,则21222z t z ⎛⎫-=+ ⎪⎝⎭,当0t ≠时,12R z z ∉,此时1122z z z z ⎛⎫≠ ⎪⎝⎭,故D 错误.故选:ABC .10.已知函数()f x 对任意实数x 均满足()()2211f x f x +-=,则()A.()()f x f x -=B.1f=C.()113f -=D.函数()f x在区间上不单调【答案】ACD 【解析】【分析】令x 等价于x -,则()()2211f x f x -+-=,可推导出()()f x f x -=,进而可判断A ,利用赋值法可判断B ,C ;先算出满足21x x =-的x 值,由此可得1123f f ⎛⎫+==⎪⎪⎝⎭,即可判断D .【详解】对于A ,令x 等价于x -,则()()2211f x f x -+-=,所以()()()2112f x f x f x ---==,故A 正确;对于B ,令1x =,则()()2101f f +=,令0x =,则()()2011f f +=,解得:()()1013f f ==,令x =,()211ff +=,则13f =,故B 错误;对于C ,由A 知,()()f x f x -=,所以()()1113f f -==,故C 正确;对于D ,令21x x =-,所以210x x --=,解得:12x ±=,令12x =,则112122ff ⎛⎫⎛+++= ⎪ ⎪ ⎝⎭⎝⎭,所以15123f ⎛⎫+= ⎪ ⎪⎝⎭,因为152+∈,15123f f⎛⎫==⎪ ⎪⎝⎭,所以函数()f x 在区间上不单调,故D 正确.故选:ACD .11.过点()2,0P 的直线与抛物线C :24y x =交于,A B 两点.抛物线C 在点A 处的切线与直线2x =-交于点N ,作NM AP ⊥交AB 于点M ,则()A.直线NB 与抛物线C 有2个公共点B.直线MN 恒过定点C.点M 的轨迹方程是()()22110x y x -+=≠D.3MNAB的最小值为【答案】BCD 【解析】【分析】设出直线AB 的方程为2x ty =+,代入24y x =,然后写出切线方程,结合韦达定理可判断AB ;根据B 可得M 的轨迹方程,从而判断C ;利用弦长公式及点到直线的距离公式表示出3MN AB,然后利用导数的知识求出最值进而判断D.【详解】设直线AB 的方程为2x ty =+,221212,,,44y y A y B y ⎛⎫⎛⎫⎪ ⎪⎝⎭⎝⎭联立224x ty y x=+⎧⎨=⎩,消去x 得2480y ty --=,则12124,8y y t y y +==-,对于A :抛物线C 在点A 处的切线为21124y y y x ⎛⎫=+ ⎪⎝⎭,当2x =-时得12112144282222y y y y y yty -=-=+=-=,即()2,2N t -,所以直线NB 的方程为1221222242424y y y y y y x y --⎛⎫-=- ⎪⎝⎭--,整理得1144y y x y =--,联立112444y y x y y x ⎧=--⎪⎨⎪=⎩,消去x 的122116604y y y y ++=,解得18y y =-,即直线NB 与抛物线C 相切,A 错误;对于B :直线MN 的方程为()122x y t t +=--,整理得y x t=-,此时直线MN 恒过定点()0,0,B 正确;对于C :又选项B 可得点M 在以线段OP 为直径的圆上,点O 除外,故点M 的轨迹方程是()()22110x y x -+=≠,C 正确;对于D:222t MN +==,AB ===则()()3253222222221t t MN AB t ⎛⎫++==+,,m m =≥则()352221MN m ABm =-,设()()5222,1m f m m m=≥-则()()()()()()()2426242244221018121511m m m m m m mf m m m -----'==--,当>m 时,()0f m '>,()f mm <<时,()0f m '<,()f m 单调递减,所以()()2min 25255851f m f ===-,D 错误.故选:BC.【点睛】方法点睛:直线与抛物线联立问题第一步:设直线方程:有的题设条件已知点,而斜率未知;有的题设条件已知斜率,点不定,都可由点斜式设出直线方程.第二步:联立方程:把所设直线方程与抛物线方程联立,消去一个元,得到一个一元二次方程.第三步:求解判别式Δ:计算一元二次方程根的判别式Δ>0.第四步:写出根之间的关系,由根与系数的关系可写出.第五步:根据题设条件求解问题中的结论.三、填空题:本题共3小题,每小题5分,共15分.12.写出与圆221x y +=相切且方向向量为(的一条直线的方程______.【答案】2y =+或2y =-(写出一个即可)【解析】【分析】由条件可设直线方程为y b =+,结合条件列方程求b 即可得结论.【详解】因为切线的方向向量为(,故可设切线方程为y b =+,因为直线y b =+与圆221x y +=相切,又圆221x y +=的圆心坐标为()0,0,半径为1,圆心()0,0到直线y b =+2b =,所以12b =,所以2b =或2b =-,所以与圆221x y +=相切且方向向量为(的直线为2y =+或2y =-,故答案为:2y =+或2y =-(写出一个即可).13.函数()2f x=______.【答案】【解析】【分析】借助换元法令t =,可得()()325f x h t t t t==-+-,借助导数求取函数()h t 的单调性后,即可得解.【详解】令0t =>,则21x t =-,故()()()2223321125f tt t x t t t-++==-+---,令()()3250h t t t t t=-+->,则()()(242222231235235t t t t t t th t t t '++--++=-++==-,当(t ∈时,()0h t '>,当)t ∈+∞时,()0h t '<,则()h t在(上单调递增,在)+∞时单调递减,故()35h t h≤=-+⨯即函数()2f x =.故答案为:.14.机场为旅客提供的圆锥形纸杯如图所示,该纸杯母线长为12cm ,开口直径为8cm .旅客使用纸杯喝水时,当水面与纸杯内壁所形成的椭圆经过母线中点时,椭圆的离心率等于______.【答案】17【解析】【分析】依题意,利用等腰三角形ABC 求得cos α,再由余弦定理求出椭圆长轴长,作出圆锥的轴截面交椭圆于点,P Q ,建立坐标系,利用三角形重心性质和相似三角形求出点P 坐标,代入椭圆方程即可求得半短轴长,利用离心率定义计算即得.【详解】如图,设BCD α∠=,因12,8AB AC BC ===,故41cos 123α==,又6CD =,由余弦定理,22212cos 3664268683BD CD BC CD BC α=+-⋅=+-⨯⨯⨯=,即BD =,设椭圆中心为O ,作圆锥的轴截面AMN ,与底面直径BC 交于E ,与椭圆交于,P Q ,连AE 交BD 于G ,以点O 为原点,DB 为x 轴,建立直角坐标系.则23AG AE =,又由APQ AMN 得216,33PQ MN ==133DG DB ==,从而33OG =-=则得8(,)33P -,不妨设椭圆方程为22221x y a b+=,把a =和点P坐标代入方程,解得b =,则3c ==,故.17c e a ===故答案为:31717.四、解答题:本大题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.15.已知等差数列{}n a 的前n 项和为n S ,且()*4224,21n n S S a a n ==+∈N .(1)求数列{}n a 的通项公式;(2)数列{}n b 满足13b =,令21n n n n a b a b ++⋅=⋅,求证:192nk k b =<∑.【答案】(1)()21n a n n *=-∈N (2)证明见解析【解析】【分析】(1)设等差数列{}n a 的首项为1a ,公差为d ,由题意可得()()11114684212211a d a da n d a n d +=+⎧⎨+-=+-+⎩,解方程求出1,a d ,即可求出数列{}n a 的通项公式;(2)由(1)可得12123n n b n b n +-=+,由累乘法可求出{}n b 的通项公式,再由裂项相消法求解即可.【小问1详解】设等差数列{}n a 的首项为1a ,公差为d .由4224,21n n S S a a ==+,得()()11114684212211a d a da n d a n d +=+⎧⎨+-=+-+⎩,解得:1a 1,d 2==,所以()()12121n a n n n *=+-=-∈N .【小问2详解】由(1)知,()()12123n n n b n b +-=+,即12123n n b n b n +-=+,12321n n b n b n --=+,122521n n b n b n ---=-,……,322151,75b b b b ==,利用累乘法可得:1211212325313212175n n n n n b b b n n b b b b b n n -----=⋅⋅⋅⋅⋅⋅⋅=⋅⋅⋅⋅⋅⋅⋅+-,12311nkn nk bb b b b b -==+++++∑ ()()9911212122121n n n n ⎛⎫==- ⎪-+-+⎝⎭9111111112335572121n n ⎡⎤⎛⎫=-+-+-++- ⎪⎢⎥-+⎝⎭⎣⎦ 911221n ⎛⎫=- ⎪+⎝⎭所以191912212nk k b n =⎛⎫=-< ⎪+⎝⎭∑.16.已知函数()()()21ln 22f x a x x a =+-∈R .(1)讨论函数()f x 的单调性;(2)若函数()f x 有两个极值点,(ⅰ)求实数a 的取值范围;(ⅱ)证明:函数()f x 有且只有一个零点.【答案】(1)答案见解析;(2)(ⅰ)10a -<<;(ⅱ)证明见解析【解析】【分析】(1)求出函数的导函数,再分1a ≤-、10a -<<、0a ≥三种情况,分别求出函数的单调区间;(2)(ⅰ)由(1)直接解得;(ⅱ)结合函数的最值与零点存在性定理证明即可.【小问1详解】函数()()()21ln 22f x a x x a =+-∈R 的定义域为()2,-+∞,且()()21122x a a f x x x x -+++='=-++,当1a ≤-时,()0f x '≤恒成立,所以()f x 在()2,-+∞单调递减;当10a -<<时,令()0f x '=,即()2110x a -+++=,解得11x =,21x =,因为10a -<<,所以011a <+<,则211-<<-,所以当()2,1x ∈-时()0f x '<,当()1x ∈时()0f x ¢>,当)1,x ∈+∞时()0f x '<,所以()f x 在()2,1--上单调递减,在()1上单调递增,在)1,-+∞上单调递减;当0a ≥时,此时12≤-,所以()1x ∈-时()0f x ¢>,当)1,x ∈+∞时()0f x '<,所以()f x 在()1--上单调递增,在)1,-+∞上单调递减.综上可得:当1a ≤-时()f x 在()2,-+∞单调递减;当10a -<<时()f x 在()2,1-上单调递减,在()1-上单调递增,在)1,-+∞上单调递减;当0a ≥时()f x 在()1--上单调递增,在)1,-+∞上单调递减.【小问2详解】(ⅰ)由(1)可知10a -<<.(ⅱ)由(1)()f x 在()2,1-上单调递减,在()1-上单调递增,在)1,-+∞上单调递减,所以()f x 在1x =-处取得极大值,在1x =-处取得极小值,又10a -<<,所以011a <+<,则112<<,又())))211ln1102f x fa =-=+-<极大值,又())110f f<<,所以()f x 在()1,+∞上没有零点,又10a -<<,则44a<-,则440e e a -<<,442e 2e 2a --<-<-,则240e 24a ⎛⎫<-< ⎪⎝⎭,所以2441e 24e 202a af ⎛⎫⎛⎫-=--> ⎪ ⎪⎝⎭⎝⎭,所以()f x 在()2,1--上存在一个零点,综上可得函数()f x 有且只有一个零点.17.如图,在多面体ABCDPQ 中,底面ABCD 是平行四边形,60,244,DAB BC PQ AB M ∠=︒===为BC 的中点,,,PQ BC PD DC QB MD ⊥⊥∥.(1)证明:90ABQ ∠=︒;(2)若多面体ABCDPQ 的体积为152,求平面PCD 与平面QAB 夹角的余弦值.【答案】(1)证明见解析;(2)10.【解析】【分析】(1)根据余弦定理求解DM =,即可求证DM DC ⊥,进而根据线线垂直可证明线面垂直,即可得线线垂直,(2)根据体积公式,结合棱柱与棱锥的体积关系,结合等体积法可得PM h ==坐标系,求解法向量求解.【小问1详解】在DCM △中,由余弦定理可得DM =,所以222DM DC CM +=,所以90MDC ∠=︒,所以DMDC ⊥.又因为DC PD ⊥,,,DM PD D DM DP ⋂=⊂平面PDM ,所以DC ⊥平面PDM ,PM ⊂平面PDM .所以DC PM ⊥.由于//,2PQ BM PQ BM ==,所以四边形PQBM 为平行四边形,所以PM QB ∥.又AB DC ,所以AB BQ ⊥,所以90ABQ ∠=︒.【小问2详解】因为QB MD ⊥,所以PM MD ⊥,又PM CD ⊥,,,DC MD D DC MD ⋂=⊂平面ABCD ,所以PM ⊥平面ABCD .取AD 中点E ,连接PE ,设PM h =.设多面体ABCDPQ 的体积为V ,则33P CDEM A PEM P CDEM P AEM P CDEM ABQ PEM V V V V V V V ------=+=+=+三棱柱四棱锥四棱锥四棱锥112π152212551sin 333323AEM AEM AEM AEM CDEM S h S h S h S h S h h =⨯+⨯=⨯+⨯=⨯=⨯⨯⨯⨯=△△△△四边形.解得PM h ==建立如图所示的空间直角坐标系,则()())2,0,,1,0A B C-,)(((),,,0,0,0DP Q M .则平面QAB 的一个法向量()1,0,0n =.所以()0,1,0,CD PD ==-,设平面PCD 的一个法向量(),,m x y z =,则0,0,m CD n PD ⎧⋅=⎪⎨⋅=⎪⎩即0,0,y =⎧⎪-=取()3,0,1m = .所以cos 10m n m n θ⋅==⋅ .所以平面PAD 与平面PMD夹角的余弦值为10.18.已知,A B 是椭圆22:14xE y +=的左,右顶点,点()(),00M m m >与椭圆上的点的距离的最小值为1.(1)求点M 的坐标.(2)过点M 作直线l 交椭圆E 于,C D 两点(与,A B 不重合),连接AC ,BD 交于点G .(ⅰ)证明:点G 在定直线上;(ⅱ)是否存在点G 使得CG DG ⊥,若存在,求出直线l 的斜率;若不存在,请说明理由.【答案】(1)()3,0;(2)(ⅰ)证明见解析;(ⅱ)存在,4525±【解析】【分析】(1)设()00,P x y,利用两点距离距离得PM =,然后根据330,22m m ≤分类讨论求解即可;(2)(ⅰ)设直线()()1122:3,,,,l x ty C x y D x y =+,与椭圆方程联立方程,结合韦达定理得121265y y ty y +=-,写出直线AC ,BD 的方程,进而求解即可;(ⅱ)由题意点G 在以AB为直径的圆上,代入圆的方程求得4,33G ⎛⎫± ⎪ ⎪⎝⎭,写出直线AC 的方程,与椭圆联立,求得点C 的坐标,进而可得答案.【小问1详解】设()00,P x y 是椭圆上一点,则220044x y +=,因为()022PM x ==-≤≤,①若min30,12m PM <≤==,解得0m =(舍去),②若min3,12m PM >==,解得1m =(舍去)或3m =,所以M 点的坐标位()3,0.【小问2详解】(ⅰ)设直线()()1122:3,,,,l x ty C x y D x y =+,由22314x ty x y =+⎧⎪⎨+=⎪⎩,得()224650t y ty +++=,所以12122265,44t y y y y t t +=-=++,所以121265y y ty y +=-,①由216800t ∆=->,得t>或t <,易知直线AC 的方程为()1122y y x x =++,②直线BD 的方程为()2222y y x x =+-,③联立②③,消去y ,得()()()()121212221211212552221x y ty y ty y y x x x y ty y ty y y ++++===--++,④联立①④,消去12ty y ,则()()12212155265526y y y x x y y y-+++==---++,解得43x =,即点G 在直线43x =上;(ⅱ)由图可知,CG DG ⊥,即AG BG ⊥,所以点G 在以AB 为直径的圆上,设4,3G n ⎛⎫ ⎪⎝⎭,则22443n ⎛⎫+= ⎪⎝⎭,所以253n =±,即425,33G ⎛⎫± ⎪ ⎪⎝⎭.故直线AC 的方程为()25y x =±+,直线AC 的方程与椭圆方程联立,得291640x x +-=,解得2A x =-,所以412929C x =-⋅-=,所以9C y =±,故25l MC k k ==±.19.在概率统计中,常常用频率估计概率.已知袋中有若干个红球和白球,有放回地随机摸球n 次,红球出现m 次.假设每次摸出红球的概率为p ,根据频率估计概率的思想,则每次摸出红球的概率p 的估计值为p m n=.(1)若袋中这两种颜色球的个数之比为1:3,不知道哪种颜色的球多.有放回地随机摸取3个球,设摸出的球为红球的次数为Y ,则()3,Y B p ~.注:()p P Y k =表示当每次摸出红球的概率为p 时,摸出红球次数为k 的概率)(ⅰ)完成下表;k0123()14P Y k =2764164()34P Y k =9642764(ⅱ)在统计理论中,把使得..()p P Y k =的取值达到最大时的........p ,作为p 的估计值,记为 p ,请写出 p 的值.(2)把(1)中“使得()p P Y k =的取值达到最大时的p 作为p 的估计值 p ”的思想称为最大似然原理.基于最大似然原理的最大似然参数估计方法称为最大似然估计.具体步骤:先对参数θ构建对数似然函数()l θ,再对其关于参数θ求导,得到似然方程()0l θ'=,最后求解参数θ的估计值.已知(),Y B n p ~的参数p 的对数似然函数为()11()ln 1ln(1)nnii i i l p Xp X p ===+--∑∑,其中0,1,i i X i ⎧=⎨⎩第次摸出白球第次摸出红球.求参数p 的估计值,并且说明频率估计概率的合理性.【答案】(1)(ⅰ)表格见解析;(ⅱ)1,0,143,2,3ˆ4y p y ⎧=⎪⎪=⎨⎪=⎪⎩;(2)11ni i X n =∑,答案见解析【解析】【分析】(1)(ⅰ)分14p =与34p =计算即可得;(ⅱ)结合题意与所得表格即可得解;(2)求取函数()11()ln 1ln(1)nnii i i l p Xp X p ===+--∑∑的导数,借助导数得到函数的最大值点,即可得解.【小问1详解】因为袋中这两种颜色球的个数之比为1:3,且()3,Y B p ~,所以p 的值为14或34;(ⅰ)当14p =时,()()211134271C 164P Y p p ==-=,()()2213492C 164P Y p p ==-=,当34p =时,()()30033410C 164P Y p p ==-=,()()22334272C 164P Y p p ==-=,表格如下k0123()14P Y k =27642764964164()34P Y k =16496427642764(ⅱ)由上表可知()()33C 1kk kp P Y k p p -==-.当0y =或1时,参数14p =的概率最大;当2y =或3时,参数34p =的概率最大.所以1,0,143,2,3ˆ4y p y ⎧=⎪⎪=⎨⎪=⎪⎩;【小问2详解】由()11()ln 1ln(1)nnii i i l p Xp X p ===+--∑∑,则()()111111n ni i i i l p X X p p =='=---∑∑,令()1111101n n i i i i X X p p ==--=-∑∑,即()11111111nniii i nnniiii i i X n X pnpXXX=====---===-∑∑∑∑∑,故11n i i p X n ==∑,即当110,n i i X n p =⎛⎫∈ ⎪⎝⎭∑时,()0l p '>,当11,1n i i p X n =⎛⎫∈ ⎪⎝⎭∑时,()0l p '<,故()l p 在110,n i i X n =⎛⎫ ⎪⎝⎭∑上单调递增,在11,1n i i X n =⎛⎫⎪⎝⎭∑上单调递减,即当11n i i p X n ==∑时,()l p 取最大值,故11ˆni i pX n ==∑,因此,用最大似然估计的参数 p 与频率估计概率的 p 是一致的,故用频率估计概率是合理的.【点睛】关键点点睛:本题关键点在于借助导数求取函数()l p 取最大值时的p ,得到11ˆni i pX n ==∑.。
2022-2023学年浙江省杭州市高三年级上学期教学质量检测数学试题卷+答案解析(附后)

2022-2023学年浙江省杭州市高三年级上学期教学质量检测数学试题卷1. 设集合,,则( )A. B.C. D.2.若复数其中i为虚数单位,则( )A. B.2 C. D. 43. 已知,则( )A. B. C. D.4. 已知二次函数的图象如图所示,若将函数的图象向右平移2个单位长度得到函数的图象,则不等式的解集是( )A. B. C. D.5. 已知非零向量,的夹角的余弦值为,且,则( )A. 1B.C.D. 26. 冬末春初,人们容易感冒发热.某公司规定:若任意连续7天,每天不超过5人体温高于,则称没有发生群体性发热.根据下列连续7天体温高于人数的统计量,能判定该公司没有发生群体性发热的为( )①中位数为3,众数为②均值小于1,中位数为③均值为3,众数为④均值为2,标准差为A. ①③B. ③④C. ②③D. ②④7. 设抛物线的焦点为F,直线l过点F与抛物线C交于A,B两点,以AB为直径的圆与y轴交于D,E两点,且,则直线l的方程为( )A. B.C. D.8. 若过点可以作曲线的两条切线,则( )A. B.C. D.9. 已知函数则( )A. 的图象是轴对称图形,不是中心对称图形B. 在上单调递增,在上单调递减C.的最大值为,最小值为0D.的最大值为,最小值为10. 甲箱中有5个红球,2个白球和3个黑球,乙箱中有4个红球,3个白球和3个黑球.先从甲箱中随机取出一球放入乙箱,分别以,和表示由甲箱取出的球是红球,白球和黑球的事件;再从乙箱中随机取出一球,以B表示由乙箱取出的球是红球的事件,则下列结论正确的是A. 事件B与事件相互独立B.C. D.11. 若函数在区间上单调递增,则( )A. 存在,使得函数为奇函数B. 函数的最大值为C. 的取值范围为D. 存在4个不同的,使得函数的图象关于直线对称12. 已知函数,设为实数,且,则( )A. 函数的图象关于点对称B. 不等式的解集为C. 若,则D. 若,则13.的展开式中的系数为__________.14. 将函数的图象向右平移个单位长度,则平移后的图象中与y轴最近的对称轴方程是________.15. 已知双曲线,若过点能作该双曲线的两条切线,则该双曲线离心率e 的取值范围为____.16. 已知不等式,对恒成立,则a的取值范围是__________.17. 已知等比数列的前n项和为,数列是公比为2的等比数列.求数列的通项公式;求数列的前n项和18. 设的内角A,B,C的对边分别为a,b,若,求当为锐角三角形,时,求的周长的取值范围.19. 已知函数满足求函数的解析式;若关于x的方程恰有四个不同的实数根,求实数k的取值范围.20. 第24届冬季奥运会于2022年2月4日在北京开幕,本次冬季奥运会共设7个大项,15个分项,109个小项.为调查学生对冬季奥运会项目的了解情况,某大学进行了一次抽样调查,若被调查的男女生人数均为,统计得到以下列联表,经过计算可得男生女生合计了解6n不了解5n合计10n10n求n的值,并判断有多大的把握认为该校学生对冬季奥运会项目的了解情况与性别有关;①为弄清学生不了解冬季奥运会项目的原因,采用分层抽样的方法从抽取的不了解冬季奥运会项目的学生中随机抽取9人,再从这9人中抽取3人进行面对面交流,求“至少抽到一名女生”的概率;②将频率视为概率,用样本估计总体,从该校全体学生中随机抽取10人,记其中对冬季奥运会项目了解的人数为X,求X的数学期望.附表:附:,21. 已知椭圆的离心率为,上顶点为M,下顶点为N,,设点在直线上,过点T的直线TM,TN分别交椭圆C于点E和点求椭圆C的标准方程;求证:直线EF恒过定点,并求出该定点;若的面积为的面积的k倍,则当t为何值时,k取得最大值?22. 已知函数若1是的极值点,求a的值.求的单调区间.若有两个实数解,,直接写出a的取值范围;为正实数,若对于符合题意的任意,,当时都有,求的取值范围.答案和解析1.【答案】D【解析】【分析】本题考查集合并集的求解,简单对数不等式的求解,属于基础题.先分别化简集合A,B,然后根据并集的定义求得【解答】解:,,则可得2.【答案】C【解析】【分析】本题主要考查复数的除法运算,考查复数模的计算,属于基础题.利用复数的四则运算,可知,再由复数的模,即可求解.【解答】解:,则3.【答案】A【解析】【分析】本题考查三角求值问题,属于基础题.根据二倍角的正切公式求得,进而将齐次式弦化切代值求解即可.【解答】解:,,4.【答案】B【解析】【分析】本题考查二次函数解析式的求解,图象的平移变换,考查不等式的求解,为基础题.根据定义求得平移后的解析式,结合图像与特殊点求解不等式即可.【解答】解:设,结合图象可知,可得,且,所以,将的图象向右平移2个单位长度得到函数的图象,如图,由,又在上递增,且,,所以由图像可得不等式的解集为故选:5.【答案】A【解析】【分析】本题主要考查垂直关系与向量数量积的关系,考查向量数量积的运算,属于基础题.由,可得,由,的夹角的余弦值为,可得,化简即可得到所求值.【解答】解:因为,则,可得,由题可知,的夹角的余弦值为,则,原式整理得,因为,为非零向量,将等式两边同时除以,得,解得舍或6.【答案】D【解析】【分析】本题考查平均数、中位数、众数的实际应用,属于中档题.根据已知逐项推测是否有某天超过5人体温高于即可判定.【解答】解:将7天体温高于人数由小到大依次记为、、、、、、对于①,满足中位数为3,众数为2的7个数可以为:2、2、2、3、3、4、6,与题意矛盾,①不能判定;对于②,假设,即该公司发生了群体性发热,因中位数为1,则,平均数为,矛盾,故假设不成立,即该公司没有发生群体性发热,②可以判定;对于③,满足众数为4,均值为3的7个数可以为:0、1、2、4、4、4、6,与题意矛盾,③不能判定;对于④,假设,即该公司发生群体性发热,若均值为2,则方差为,即,与标准差为矛盾,故假设不成立,即该公司没有发生群体性发热,④可以判定.7.【答案】C【解析】【分析】本题考查直线与抛物线的位置关系,考查抛物线中焦点弦的性质,属于中档题.分直线l斜率不存在时,与直线l斜率存在时,进行求解.【解答】解:由题意,抛物线的焦点为,当直线l斜率不存在时,,可求得,和题意矛盾,舍去;当直线l斜率存在时,设直线,,,联立,得,,,,,即,圆的半径,圆心为AB中点,其横坐标,,结合几何关系可得:则有,求解得则该直线方程为8.【答案】B【解析】【分析】本题考查导数的几何意义,属于中档题.设切点坐标为,根据点在切线方程上,将问题转化为关于的一元二次方程有两个正根,由此求解.【解答】解:设切点为,,,切点处切线的斜率,则切线方程为:,又切线过点,则,整理得,则关于的一元二次方程有两个正根,由根与系数的关系可得,,所以且,根据根的判别式可得,化简可得9.【答案】ABD【解析】【分析】本题考查利用导数研究函数的单调性与最值,函数的对称性,属于中档题.根据函数图象的对称性可判断选项利用导数研究函数单调性,进而判断选项B;根据函数单调性确定函数最值,进而判断选项C,【解答】解:对于A,由于,故有对称轴,因此的图象是轴对称图形,不是中心对称图形;故A正确;对于B,函数的定义域为,,令则,故在区间上单调递增,在上单调递减;故B正确;对于C、D,由B选项可得,,又,故故C错误,D正确.10.【答案】BD【解析】【分析】本题考查条件概率,全概率公式,属于中档题.事件B与事件,,都不是相互独立事件,求,由全概率公式求,可求事件B的概率;再根据条件概率判断【解答】解:事件B与事件,,都不相互独立,故A不正确,,故B正确;,故C不正确,,故D正确.故选11.【答案】BCD【解析】【分析】本题考查函数的图象和性质,属于中档题.利用函数的图象和性质逐个判断即可.【解答】解:对于A,函数,函数最大值,最小值分别为,故不存在使得函数为奇函数,故A错误;对于B,,,函数的最大值为,当取得,故B正确;对于C,由于在区间上单调递增,故,解得,故C正确;对于D,令,,解得,,由知的取值为,,,,故D正确,12.【答案】ABD【解析】【分析】本题考查指数型复合函数图象的应用,考查函数图象的对称性,利用单调性解不等式,属于较难题.对由可判断;对根据函数单调递增可求解;对CD,根据的性质画出函数图象,表示出直线AD的方程,根据B,C均在直线AD上方建立不等关系可得.【解答】解:对,函数的图象关于点对称,故A正确;对在R上单调递增,且,则化为,则,解得,故不等式的解集为,故B正确:对C,,则可得,且关于点对称,在R上单调递增,可得函数图象如下:B,C均在直线AD上方,其中直线AD的方程为,则可得,,所以,,,即,故C错误,D正确.13.【答案】40【解析】【分析】本题考查二项式定理,求解指定项的系数,属于基础题.根据二项式展开式公式求解即可.【解答】解:结合二项展开式有:,故系数为14.【答案】【解析】【分析】本题考查三角函数的平移变换,对称轴方程,属于中档题.利用三角函数图象的平移可得新函数,求的所有对称轴,,从而可判断平移后的图象中与y轴最近的对称轴的方程.【解答】解:因为函数的图象向右平移个单位长度可得,则的对称轴为,,即,,当时,,当时,,所以平移后的图象中与y轴最近的对称轴的方程是,故答案为:15.【答案】【解析】【分析】本题考查求双曲线的离心率,属于中档题.根据过点能作该双曲线的两条切线判断该点在双曲线外部,得到a的范围,从而求出离心率的范围.【解答】解:过能作两条切线说明该点在双曲线外部,故,故,,又点不在该双曲线渐近线上,故,即,综上,16.【答案】【解析】【分析】本题考查利用导数求解不等式恒成立问题,需要构造函数,属于难度.运用同构原不等式可变为,,再讨论a和1的大小关系,构造函数,运用导数即可求解.【解答】解:,即,令,即对恒成立,当时,即:在恒成立,显然不恒成立,舍去;当时:在时,显然恒成立,在时,即,令,,则在上恒单调递增,且,则有,则对任意的恒成立,设,,可知在上递增,在上单调递减,可得,即得,综上17.【答案】解:由题意,知①所以②①-②,得,因为为等比数列,所以,又因为,所以,所以因为,①②①-②,得,所以【解析】本题主要考查等比数列通项公式的求解,考查错位相减法求和,属于基础题.根据前n项和与通项的关系构造两个等式进行作差求解;由错位相差法求解.18.【答案】解:由题意,知,即,因为,所以根据正弦定理,得,所以,,所以,因为,且锐角三角形,所以,所以,所以则,即周长的取值范围是【解析】本题考查正余弦定理解三角形,两角和与差的三角函数公式,辅助角公式,正弦函数的性质,属于中档题.利用余弦定理可计算出,从而可得B的值;根据正弦定理,得所以,,从而得到,再根据A的范围,求出的范围即可.19.【答案】解:由题意,得,,所以,解得:显然,所以,只需要函数与的图象有四个不同交点,当时,函数在上单调递增,在上单调递减,所以当时,当时,函数在上单调递减,在上单调递增,所以,则,又当时,由此,可作出与的草图,如图所示.根据图象,知或,解得或,即实数k的取值范围为【解析】本题考查函数解析式的求解,已知函数零点个数求参,为中档题.将代入方程,与原方程联立即可求解;方程化简为,讨论函数的单调性与零点,属性结合即可得k的范围.20.【答案】解:据题意列出2x2列联表如下所示:男生女生合计了解6n5n11n不了解4n5n9n合计10n10n20n由,得,,所以,因为,所以有的把握认为该校学生对冬季奥运会项目的了解情况与性别有关.①由列联表知不了解冬奥会的学生中,男生:女生,故抽取的9人中,男生为4人,女生为5人,则抽取的3人中,记“至少抽到一名女生”为事件A,所以②样本中了解冬奥会的频率为,将频率视为概率,用样本估计总体,即从全校学生中任取一人,恰好了解冬奥会的概率为由题意得,对冬季奥运会项目的了解的人数X服从二项分布,且X∽,所以X的数学期望【解析】本题考查独立性检验,考查二项分布求均值问题,属于中档题.根据题意填写列联表,利用公式,求得,结合附表即可求解;①由列联表,结合对立事件的概率公式,即可求解;②将频率视为概率,用样本估计总体,对冬季奥运会项目的了解的人数X服从二项分布,且X∽,即可求解.21.【答案】解:由题知,,故,由题意知直线TM的方程为,直线TN的方程为由,得同理,所以直线EF的方程为:,即所以,直线EF过定点因为,所以当且仅当,即时,等号成立.所以当时,k取得最大值【解析】本题考查椭圆的标准方程、直线与椭圆的位置关系的应用,属于较难题.由可得,进而结合离心率求解a,即可得椭圆方程;设出直线TM、TN方程,与分别椭圆方程联立,求得E、F坐标,进而求得直线EF方程,即可得定点的坐标;用t表示出与的面积,进而表示出k,利用基本不等式求最值即可得最大值.22.【答案】解:因为,因为1是的极值点,所以,解得所以,易知时,时,,即在上单调递增,在上单调递减,所以1是的极大值点,满足题设.综上,由知,①当时,,所以在上单调递增;②当时,令,解得令,解得所以在上单调递增,在上单调递减,综上:当时,在上单调递增;当时,在上单调递增,在上单调递减.由题意,知在上有两个解.设,则当时,,即在上单调递增,至多有一个零点,不符合题意;当时,易知在上单调递增,在上单调递减,即的极大值为令,即,解得当时,因为,所以在有唯一零点;当时,令,则,再令,则,故在上单调递增,所以,即,故在上单调递增,所以,因为,所以,即,即,即,故,所以,故,又在上单调递减,所以在有唯一零点;综上:当时,在上两个零点,即有两个解,时,,即由得,,,故,又,所以,即,即,故,令,则,令,则,所以在上单调递增,即,当,即时,,故,下证令,则,所以在上单调递增,故,综上,,故恒成立;当,即时,,故,即不恒成立,即不恒成立,不满足题意;综上:,即【解析】本题考查利用导数研究函数极值,零点,及恒成立问题,为难题.由极值点的意义求解;求导,对a分类讨论求解;设,则,对a分类讨论求解;由得,,故,则,故,令,则,构造函数利用导数求解.。
陕西省西北农林科技大学附属中学2024届高三第四次教学质量检测试题考试数学试题

陕西省西北农林科技大学附属中学2024届高三第四次教学质量检测试题考试数学试题注意事项1.考试结束后,请将本试卷和答题卡一并交回.2.答题前,请务必将自己的姓名、准考证号用0.5毫米黑色墨水的签字笔填写在试卷及答题卡的规定位置. 3.请认真核对监考员在答题卡上所粘贴的条形码上的姓名、准考证号与本人是否相符.4.作答选择题,必须用2B 铅笔将答题卡上对应选项的方框涂满、涂黑;如需改动,请用橡皮擦干净后,再选涂其他答案.作答非选择题,必须用05毫米黑色墨水的签字笔在答题卡上的指定位置作答,在其他位置作答一律无效. 5.如需作图,须用2B 铅笔绘、写清楚,线条、符号等须加黑、加粗.一、选择题:本题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.我国古代有着辉煌的数学研究成果,其中的《周髀算经》、《九章算术》、《海岛算经》、《孙子算经》、《缉古算经》,有丰富多彩的内容,是了解我国古代数学的重要文献.这5部专著中有3部产生于汉、魏、晋、南北朝时期.某中学拟从这5部专著中选择2部作为“数学文化”校本课程学习内容,则所选2部专著中至少有一部是汉、魏、晋、南北朝时期专著的概率为( ) A .35B .710C .45D .9102.已知双曲线C :()222210,0x y a b a b -=>>的焦距为2c ,焦点到双曲线C ,则双曲线的渐近线方程为()A .y =B .y =C .y x =±D .2y x =±3.在ABC ∆中,“cos cos A B <”是“sin sin A B >”的( ) A .充分而不必要条件 B .必要而不充分条件 C .充分必要条件D .既不充分也不必要条件4.相传黄帝时代,在制定乐律时,用“三分损益”的方法得到不同的竹管,吹出不同的音调.如图的程序是与“三分损益”结合的计算过程,若输入的x 的值为1,输出的x 的值为( )A .6481B .3227C .89D .16275.已知空间两不同直线m 、n ,两不同平面α,β,下列命题正确的是( ) A .若m α且n α,则m n B .若m β⊥且m n ⊥,则n βC .若m α⊥且m β,则αβ⊥D .若m 不垂直于α,且n ⊂α,则m 不垂直于n6.已知实数集R ,集合{|13}A x x =<<,集合|2B x y x ⎧==⎨-⎩,则()R A C B ⋂=( ) A .{|12}x x <≤ B .{|13}x x << C .{|23}x x ≤<D .{|12}x x <<7.已知函数31,0()(),0x x f x g x x ⎧+>=⎨<⎩是奇函数,则((1))g f -的值为( )A .-10B .-9C .-7D .18.已知ABC ∆中,角A 、B 所对的边分别是a ,b ,则“a b >”是“A B >”的( ) A .充分不必要条件 B .必要不充分条件 C .既不充分也不必要条件D .充分必要条件9.已知数列{}n a 的通项公式为22n a n =+,将这个数列中的项摆放成如图所示的数阵.记n b 为数阵从左至右的n 列,从上到下的n 行共2n 个数的和,则数列n n b ⎧⎫⎨⎬⎩⎭的前2020项和为( )A .10112020B .20192020C .20202021D .1010202110.在正方体1111ABCD A B C D -中,球1O 同时与以A 为公共顶点的三个面相切,球2O 同时与以1C 为公共顶点的三个面相切,且两球相切于点F .若以F 为焦点,1AB 为准线的抛物线经过12O O ,,设球12O O ,的半径分别为12r r ,,则12r r =( ) A .512- B .32- C .212-D .23-11.已知角a 的终边经过点()()4,30P m m m -≠,则2sin cos a a +的值是( ) A .1或1-B .25或25- C .1或25-D .1-或2512.集合{}2|4,M y y x x ==-∈Z 的真子集的个数为( )A .7B .8C .31D .32二、填空题:本题共4小题,每小题5分,共20分。
安徽省合肥市第一中学2025届高三上学期第二次教学检测数学试卷(含解析)

合肥一中2024~2025学年度高三第二次教学质量检测数学试题(考试时间:120分钟 满分:150分)注意事项:1.答题前,务必在答题卡和答题卷规定的地方填写自己的姓名、准考证号和座位号后两位.2.答题时,每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑.如需改动,用橡皮擦干净后,再选涂其他答案标号.3.答题时,必须使用0.5毫米的黑色墨水签字笔在答题卷上书写,要求字体工整、笔迹清晰.作图题可先用铅笔在答题卷规定的位置绘出,确认后再用0.5毫米的黑色墨水签字笔描清楚.必须在题号所指示的答题区域作答,超出答题区域书写的答案无效,在试题卷、草稿纸上答题无效.4.考试结束,务必将答题卡和答题卷一并上交.一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一个选项是正确的.请把正确的选项填涂在答题卡相应的位置上.1.已知集合,,则图中阴影部分所表示的集合是( )A .B .C .D .2.命题“,使”的否定是( )A .,使B .不存在,使C .,使D .,使3.函数的部分图象大致为( )A .B.{}2,1,0,1,2M =--(){}22log 1N y y x ==+{}2,1--{}2,1,0--{}0,1,2{}1,0-x ∃∈R 210x x +-≠x ∃∈R 210x x +-=x ∈R 210x x +-≠x ∀∉R 210x x +-=x ∀∈R 210x x +-=()3sin 1x x f x x =+C .D .4.“曲线恒在直线的下方”的一个充分不必要条件是( )A .B .C .D .5.当阳光射入海水后,海水中的光照强度随着深度增加而减弱,可用表示其总衰减规律,其中是消光系数,(单位:米)是海水深度,(单位:坎德拉)和(单位:坎德拉)分别表示在深度处和海面的光强.已知某海域6米深处的光强是海面光强的,则该海域消光系数的值约为( )(参考数据:,)A .0.2B .0.18C .0.15D .0.146.在中,内角,,的对边分别为,,,已知,,则外接圆的面积为( )A .B .C .D .7.已知函数的图象关于直线对称,且在上没有最小值,则的值为( )A .B .4C .D .8.已知是内一点,且,点在内(不含边界),若,则的取值范围是( )A .B .C .D .二、选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求.全部选对得6分,部分选对的得部分分,选对但不全的得部分分,有选错的得0分.9.已知平面向量,,且,则( )ln y x =y x b =+1b >-1e b -<<-10b -<<0b <0e KD D I I -=K D D I 0I D 40%K ln 20.7≈ln 5 1.6≈ABC △A B C a bc a =()(()sin sin sin sin A B b c B C -+=+ABC △π3π4π5π()()πsin 04f x x ωω⎛⎫=+> ⎪⎝⎭π6x =()f x π0,4⎛⎫ ⎪⎝⎭ω3292152O ABC △0OA OB OC ++= M OBC △AM xAB y AC =+ 2x y +1,12⎛⎫ ⎪⎝⎭2,13⎛⎫ ⎪⎝⎭()1,251,2⎛⎫ ⎪⎝⎭()2,a m = ()1,1b =- 22a b a b +=-A .B .C .D .10.已知,若对任意的,不等式恒成立,则( )A .B .C .的最小值为32D .的最小值为11.已知函数的定义域为,函数为偶函数,函数为奇函数,则下列说法正确的是( )A .函数的一个对称中心为B .C .函数为周期函数,且一个周期为4D .三、填空题:本题共3小题,每小题5分,共15分.12.已知,则______.13.已知函数,方程有四个不同根,,,,且满足,则的最大值为______.14.定义表示实数,中的较大者,若,,是正实数,则的最小值是______.四、解答题:本题共5小题,第15题满分13分,第16题、第17题满分15分,第18题、第19题满分17分,共77分.解答应写出文字说明、证明过程或演算步骤.15.(13分)的内角,,的对边分别为,,,已知.(1)若,,求的面积;2m =π,3a b = a b ⊥ a =1b >()1,x ∈+∞32440ax x abx b +--≤0a <216a b =216a b +24a ab a b +++8-()f x R ()()()11F x f x x =+-+()()231G x f x =+-()f x ()2,1()01f =-()f x ()()()()()012345f f f f f ++++=π4tan 43α⎛⎫+=- ⎪⎝⎭cos 2α=()22log ,012,04x x f x x x x ⎧>⎪=⎨++≤⎪⎩()f x a =1x 2x 3x 4x 1234x x x x <<<()2312432x x x x x +-{}max ,x y x y a b c 123max ,max ,max ,a b c b c a ⎧⎫⎧⎫⎧⎫++⎨⎬⎨⎬⎨⎬⎩⎭⎩⎭⎩⎭ABC △A B C a b c ()2222cos 02a b c c b A b+--+=4a =8b c +=ABC △(2)若角为钝角,求的取值范围.16.(15分)已知函数.(Ⅰ)当时,关于的方程在区间内有两个不相等的实数根,求实数的取值范围;(Ⅱ)求函数在区间上的最小值.17.(15分)摩天轮是一种大型转轮状的机械建筑设施,游客坐在摩天轮的座舱里慢慢地往上转,可以从高处俯瞰四周景色.如图,某摩天轮最高点距离地面高度为120m ,转盘直径为110m ,设置有48个座舱,开启后按逆时针方向匀速旋转,游客在座舱转到距离地面最近的位置进舱,转一周大约需要30min .(1)游客甲坐上摩天轮的座舱,开始转动后距离地面的高度为,求在转动一周的过程中,关于的函数解析式;(2)若甲、乙两人分别坐在两个相邻的座舱里,在运行一周的过程中,求两人距离地面的高度差(单位:m )关于的函数解析式,并求高度差的最大值(精确到0.1m ).参考公式:.参考数据:,.18.(17分)已知函数.(1)当时,,求实数的取值范围;(2)若,求证:;(3)若,,为正实数,且,求证:.19.(17分)已知实数集,定义:(与可以相同).记为集合C c b()()()ln 1f x x x a x a R =+-∈0a =x ()f x m =1,32⎡⎤⎢⎥⎣⎦m ()f x 1,e e⎡⎤⎢⎥⎣⎦min t m H H t h t sin sin 2sincos 22θϕθϕθϕ+-+=πsin 0.207915≈πsin 0.065448≈()sin f x x =0x ≥()f x ax ≤a π02αβ<<<()()()cos f f βαβαα-<-*n ∈N 00a =12,,,n a a a 121n a a a +++= 1π12n i =≤<{}12,,,n X x x x = {},i j i j X X x x x x X ⊗=∈i x j x X中的元素个数.(1)若,请直接给出和;(2)若均为正数,且,求的最小值;(3)若,求证:.合肥一中2024~2025学年度高三第二次教学质量检测数学参考试卷1.A【详解】,所以阴影部分.故选:A .2.D【详解】命题“,使”的否定是,使.故选:D .3.A【详解】易知函数的定义域为,故可排除C ,D ;又,,所以可排除B ,故选:A .4.C【详解】由曲线恒在直线下方,可得,恒成立,即所以“曲线恒在直线的下方”的充要条件是,故选:C .5.C 【详解】依题意得,,化成对数式,,解得,.故选:C .6.C【详解】因为,且,所以,由正弦定理,可得,即,X {}1,2,3,6X =X X ⊗X X ⊗12,,,n x x x 300X X ⊗=X 11X =17X X ⊗≥{}0N y y =≥(){}2,1M N =--R ðx ∃∈R 210x x +-≠x ∀∈R 210x x +-=()3sin 1x x f x x =+{}1x x ≠-π14->-3ππsin π4404ππ1144f ⎛⎫-- ⎪⎛⎫⎝⎭-==> ⎪⎝⎭⎛⎫-+-+ ⎪ ⎪⎝⎭⎝⎭ln y x =y x b =+ln x x b <+ln b x x >-1b >-ln y x =y x b =+1b >-6040%e K D I I -==26ln ln 2ln 50.95K -==-≈-0.15K ≈a =()(()sin sin sin sin A B b c B C -+=+()()()sin sin sin sin A B a b c B C -+=+()()()a b a b c b c -+=+222a b c bc =++所以,又因,所以,所以外接圆的半径为..故选:C .7.A【详解】由的图象关于直线对称可得,,解得或,,由于在上没有最小值,所以,所以,故选:A .8.C【详解】因为内一点,,所以为的重心,又在内(不含边界),且当与重合时,最小,此时所以,即,当与重合时,最大,此时,所以,,即,因为在内且不含边界,所以取开区间,即,故选:C .二.多选题9.ACD【详解】由,,可得,,2221cos 22b c a A bc +-==-()0,πA ∈2π3A =ABC △22sin a A ==2π24πS =⋅=()()πsin 04f x x ωω⎛⎫=+> ⎪⎝⎭π6x =ππππ642k ω+=±+k ∈Z 362k ω=+962k ω=-+k ∈Z ()f x π0,4⎛⎫ ⎪⎝⎭π5π0544ωω≤⇒<≤32ω=ABC △0OA OB OC ++= O ABC △M OBC △M O 2x y +()21113233AM AB AC AB AC AB AC λμ⎡⎤=+=⨯+=+⎢⎥⎣⎦ 13x y ==21x y +=M C 2x y +AM AC = 0x =1y =22x y +=M OBC △()21,2x y +∈()2,a m = ()1,1b =- ()24,2a b m +=- ()20,2a b m -=+由,可得,解得,故A 正确;由,可得,故D 正确;又,则,,故B 错误,C 正确.故选:ACD .10.ABD【详解】因为,即恒成立,又因为,,所以当,当时,,因为对任意的,不等式恒成立,所以当时,,当时,,所以对于函数,必有,单调递减,且零点为,所以,所以,所以A 正确,B 正确;对于C ,因为,所以所以,当且仅当,即时取等号,与条件不符,所以C 错误;对于D ,,令,当且仅当时,等号成立.则原式,22a b a b +=- ()()221622m m +-=+2m =()2,2a = a == cos ,0a b a b a b ⋅=== π,2a b = a b ⊥ 32440ax x abx b +--≤()()240ax x b +-≤1b >1x >1x <<20x b -<x >20x b ->()1,x ∈+∞32440ax x abx b +--≤0x <<40ax +≥x >40ax +≤4y ax =+0a <x =40+=216a b =40=a =216161632a b b b +=+≥=1616b b=1b =216164a ab a b b b b b ⎛⎛⎫+++=-=+- ⎪ ⎝⎭⎝216448b b ⎛⎫=+-=-- ⎪⎝⎭m =4m ≥4b =()2484m m m =--≥由二次函数的性质可得的最小值为,此时,,所以D 正确,故选:ABD .11.ABD【详解】对于A ,因为为奇函数,所以,即,所以,所以,所以函数的图象关于点对称,所以A 正确,对于B ,在中,令,得,得,因为函数为偶函数,所以,所以,所以,令,则,所以,得,所以B 正确,对于C ,因为函数的图象关于点对称,,所以,所以,所以4不是的周期,所以C 错误,对于D ,在中令,则,令,则,因为,所以,因为,所以,所以D 正确,故选:ABD .三.填空题(共1小题)12..【详解】因为,所以,可得,则.故答案为:.()2484y m m m =--≥8-4b =2a =-()()231G x f x =+-()()G x G x -=-()()231231f x f x ⎡⎤--=-+-⎣⎦()()23232f x f x -++=()()222f x f x -++=()f x ()2,1()()222f x f x -++=0x =()222f =()21f =()()()11F x f x x =+-+()()F x F x -=()()()()1111f x x f x x ---=+-+()()112f x f x x +--=1x =()()202f f -=()102f -=()01f =-()f x ()2,1()01f =-()43f =()()04f f ≠()f x ()()222f x f x -++=1x =()()132f f +=2x =()()042f f +=()01f =-()43f =()21f =()()()()()012345f f f f f ++++=2425-π4tan 43α⎛⎫+=- ⎪⎝⎭tan 141tan 3αα+=--tan 7α=22222222cos sin 1tan 1724cos 2cos sin 1tan 1725ααααααα---====-+++2425-13..【详解】作出函数图像可得,从而得,且,从而得,原式,令,,,令,则,,在单调递增,,最大值为.14.【详解】按和分类:记,当时,当且仅当,,时,等号成立;当时,,12981222x x +=-2324log log x x -=341x x =(]23log 1,2x -∈(]312,4x ∈∴()23122322331122x x x x x x +=-=+ 232312y x x =+(]312,4x ∈ (]2314,16x ∴∈231t x =()2f t t t=+(]4,16t ∈()f t )+∞()9129,28f t ⎛⎤∴∈ ⎥⎝⎦∴12983c a ≤3c a ≥123max ,max ,max ,M a b c b c a ⎧⎫⎧⎫⎧⎫=++⎨⎬⎨⎬⎨⎬⎩⎭⎩⎭⎩⎭3c a ≤23235333a a M a a c a a a ≥++≥++=+≥=a =b =c =3c a ≥2325M a c c c c c c c ≥++≥++=+≥=当且仅当,,时,等号成立.综上所述,的最小值是四.解答题15.(13分)【详解】(1)由和正弦定理得,,因,则有,因,,则,又,故.由余弦定理,,代入得,,因,则有,即得,故的面积(2)由正弦定理,可得,因,代入化简得:.因为钝角,故由可得,则,即,故的取值范围是.16.(15分)【详解】(Ⅰ)当时,,,由,,故可列表:a =b =c =M ()2cos cos 0c b A a C -+=()sin 2sin cos sin cos 0C B A A C -+=()()sin cos sin cos sin sin πsin C A A C A C B B +=+=-=()sin 12cos 0B A -=0πB <<sin 0B >1cos 2A =0πA <<π3A =2222cos a b c bc A =+-2216b c bc +-=8b c +=()2316b c bc +-=16bc =ABC △11sin 1622S bc A ==⨯=sin sin b c B C =sin sin c C b B =2π3C B =-2πsin sin 13sin sin 2B cC b B B ⎛⎫- ⎪⎝⎭====C π022ππ32B B ⎧<<⎪⎪⎨⎪->⎪⎩π06B <<0tan B <<32>2c b >c b ()2,+∞0a =()ln f x x x x =-()ln 11ln f x x x =+-='∴()0132f x x ⎧>⎪⎨≤≤⎪⎩'ln 013132x x x >⎧⎪⇔⇔<≤⎨≤≤⎪⎩()0111232f x x x ⎧'<⎪⇔≤<⎨≤≤⎪⎩13,关于的方程在区间内有两个不相等的实数根时;(Ⅱ),由得.①当,即时,,在上为增函数,;②当,即时,在上,为减函数,在上,为增函数,;③当,即时,,在上为减函数,.综上所述,.17.【详解】如图,设座舱距离地面最近的位置为点,以轴心为原点,与地面平行的直线为轴建立直角坐标系.x121,12⎛⎫ ⎪⎝⎭()1,3y '-+y11ln222--]1-Z3ln33-11ln 203ln 3322--<<- ∴x ()f x m =1,32⎡⎤⎢⎥⎣⎦111ln 222m -<≤--()()ln 0f x x a x =+>'()0f x '=ax e -=1aee -<1a >()0f x '>()f x 1,e e ⎡⎤⎢⎥⎣⎦()min 12a f x f e e -⎛⎫== ⎪⎝⎭1a e e e -≤≤11a -≤≤1,a e e -⎡⎤⎢⎥⎣⎦()0f x '<()f x ,a e e -⎡⎤⎣⎦()0f x '>()f x ()()mina af x f e e --==-aee ->1a <-()0f x '<()f x 1,e e ⎡⎤⎢⎥⎣⎦()()min e f x f ea ==()min2,1,11,1a a a e f x e a ea a --⎧>⎪⎪=--≤≤⎨⎪<-⎪⎩P O x(1)设时,游客甲位于点,以为终边的角为;根据摩天轮转一周大约需要30min ,可知座舱转动的角速度约,由题意可得,.(2)如图,甲、乙两人的位置分别用点,表示,则.经过后甲距离地面的高度为,点相对于点始终落后,此时乙距离地面的高度为.则甲、乙距离地面的高度差,利用,可得,.当(或),即(或22.8)时,的最大值为.所以,甲、乙两人距离地面的高度差的最大值约为7.2m .18.(17分)【详解】(1)首先,,故,设,则,,由,可知当时,,在区间上单调递增,故,满足;当时,由在区间上单调递增,且,,故存在,使得,且时,,单调递减,此时,,与题设矛盾.综上所述,实数的取值范围.0min t =()0,55P -OP π2-πrad min 15ππ55sin 65152H t ⎛⎫=-+⎪⎝⎭030t ≤≤A B 2ππ4824AOB ∠==min t 1ππ55sin 65152H t ⎛⎫=-+⎪⎝⎭B A πrad 242π13π55sin 651524H t ⎛⎫=-+ ⎪⎝⎭12πππ13πππ13ππ55sin sin 55sin sin 15215241522415h H H t t t t ⎛⎫⎛⎫⎛⎫⎛⎫=-=---=-+- ⎪ ⎪ ⎪⎪⎝⎭⎝⎭⎝⎭⎝⎭sin sin 2sincos22θϕθϕθϕ+-+=πππ110sinsin 481548h t ⎛⎫=- ⎪⎝⎭030t ≤≤πππ15482t -=3π27.8t ≈h π110sin 7.248≈ππ122f a ⎛⎫=≤⎪⎝⎭2πa ≥()sin g x ax x =-0x ∀≥()0g x ≥()cos g x a x =-'1a ≥()0g x '≥()g x []0,+∞()()00g x g ≥=21πa ≤<()g x 'π0,2⎛⎫ ⎪⎝⎭()010g a =-<'π02g a ⎛⎫=> ⎪⎝⎭'0π0,2x ⎛⎫∈ ⎪⎝⎭()00g x '=()00,x x ∈()0g x '<()g x ()()00g x g <=a [)1,+∞(2)由,可知,即故只要证设,,则,在区间上单调递增,即,,故原不等式成立.(3)一方面,由于,故可令,其中,,结合第(2)问的结论,,另一方面,()()()()()cos cos cos f f f f βαβααββαααα-<-⇔-<-π02αβ<<<cos cos βαββ>()()cos cos f f ββαβββ-<-()()cos cos f f βββααα-<-()()cos g x f x x x =-π0,2x ⎛⎫∈ ⎪⎝⎭()()cos cos sin sin 0g x x x x x x x =--=>'()g x π0,2⎛⎫⎪⎝⎭()()g g αβ<()()cos cos f f βββααα-<-01121201n a a a a a a a =<<+<<+++= 012π02n θθθθ=<<<<= 12sin i i a a a θ=+++ 1,2,,i n =1ni =1ni ==111sin sin cos ni i i i θθθ-=--=∑()()1110111cos πcos 2nni i i i i n i i i θθθθθθθθ---==--<=-=-=∑∑1ni =()()1011112nii i i i n a a a a a a a =-+≥++++++++∑1011121nii i i i na a a a a a a =-+=++++++++∑,综上可得,.19.(17分)【详解】(1),;(2)一方面,积有个,另一方面,积有个,故,当中所有元素互素时,等号成立.要使得时,最小,可令中所有元素互素,此时,,解得:,故的最小值为24;(3)考虑集合中所有元素变为原来的相反数时,集合不改变,不妨设中正数个数不少于负数个数.①当中元素均为非负数时,设,于是,,此时,集合中至少有,,,…,,,,…,这18个元素,即;②当中元素至少有一个为负数时,设是中全体元素,且,于是,.由是中的个元素,且非正数;又是中的7个元素,且为正数,故中元素不少于17个,即;另外,当时,满足,11ni i a ===∑1π12i n=≤<{}1,2,3,4,6,9,12,18,36X X ⊗=9X X ⊗=i i x x ⋅n ()i j i j x x x x ⋅≠()21C 2nn n -=()()1122n n n n X X n -+⊗≤+=X 300X X ⊗=X X ()13002n n +=24n =X X X X ⊗X X 12110x x x ≤<<< 1223242113111011x x x x x x x x x x x x <<<<<<< X X ⊗12x x 23x x 24x x 211x x 311x x 411x x 1011x x 18X X ⊗≥X 11120l l k z z z y y y -<<<<<<< …X ()11k l k l +=≥6k ≥1112123k k k l k z y z y z y z y z y z y >>>>>>> X X ⊗110k l +-=23242526364656y y y y y y y y y y y y y y <<<<<<X X ⊗X X ⊗17X X ⊗≥{}2340,1,2,2,2,2X =±±±±±{}23456780,1,2,2,2,2,2,2,2,2X X ⊗=-±±±±±±±-17X X ⊗=故.17X X ⊗≥。
山东省临沂市2024-2025学年高三上学期期中教学质量检测数学试题

山东省临沂市2024-2025学年高三上学期期中教学质量检测数学试题一、单选题1.已知集合{}26A x x x =-<,{}3,2,1,1,2,3B =---,则A B = ()A .{}2,1,1,2,3--B .{}2,1,1,2--C .{}1,1,2,3-D .{}1,1,2-2.已知非零实数a ,b 满足a b >,则()A .11a b<B .22a b >C .33a b >D .22ac bc >3.在平行四边形ABCD 中,点E 为线段CD 的中点,记AB m = ,AD n = ,则AE =()A .12m n- B .12m n- C .12m n+ D .12m n+ 4.已知函数()341x f x x =--,则不等式()0f x >的解集是()A .()0,2B .()(),02,-∞+∞ C .()1,0-D .()(),10,-∞-⋃+∞5.已知()1sin 3αβ-=,tan 2tan αβ=,则()sin αβ+=()A .3B .3C .3D .16.“3a <”是“不等式220x ax -+≥在()0,∞+上恒成立”的()A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件7.已知函数sin 1y x ω=+(0ω>)与函数1221x xy +=+的图象在区间(2π,2π)-内交点的坐标分别为1122(,)(,),,(,)n n x y x y x y ,则1()ni i i x y =+∑的值可能是()A .2B .4C .5D .88.已知数列{}n a 的前n 项和为n S ,11a =,21a =,122n n n a a a --=+,(3n ≥),则9S =()A .341B .340C .61D .60二、多选题9.已知z 为复数,且210z z ++=,则()A .31z =B .1z z +=C .1z z -=D .1z z ⋅=10.已知()332f x x x =-+,则()A .()f x 有三个零点B .()()10104f f -+=C .当()2,x ∞∈-+时,()0f x ≥D .曲线=存在两条过点()2,0-的切线11.定义“01数列”{}n a 如下:①{}0,1i a ∈,1,2,,i n = ;②{}n a 共有+m k 项(*,m k ∈N ,m k ≥),其中m 项为0,k 项为1,且对任意的j m k +≤,*j ∈N ,12,,,j a a a 中0的个数不少于1的个数.记“01数列”的个数为(),f m k ,则()A .()3,25f =B .()()()4,44,13,2f f f =+C .()(),,1f m m f m m =-D .当m k >时,()()(),,11,f m k f m k f m k =-+-三、填空题12.已知n S 为数列{}n a 的前n 项和,若2n S n =,则2024a 的值为.13.已知函数()f x 的定义域为D ,写出一个同时具有下列性质①②③的函数:.对任意12,x x D ∈,12x x ≠,①若12x x <,12()()f x f x <;②1212()()()f x x f x f x =;③1212()()()22x x f x f x f ++>.14.已知关于x 的方程()sin 1cos 220a x b x b ++++=有解,则22a b +的最小值为.四、解答题15.已知函数()()sin f x A x =+ωϕ(0ω>,π2ϕ<)图象的一个最高点的坐标为π,23⎛⎫⎪⎝⎭,与之相邻的一个对称中心的坐标为7π,012⎛⎫⎪⎝⎭.(1)求()f x 的解析式;(2)若()()121f x f x ==,求12x x -的最小值,16.已知等比数列{}n a 满足1212a a -=,2314a a -=.(1)求数列{}n a 的通项公式;(2)记数列{}n a 的前n 项和为n S ,前n 项积为n T ,求证:2n n S T +≤.17.在ABC V 中,已知内角A ,B ,C 所对的边分别为a ,b ,csin cos A a C =,sin(2)A C B -=.(1)求sin B ;(2)若4b =,求ABC V 的面积.18.已知函数()1ln e x f x x -=+.(1)求()f x 的导函数()f x '的极值;(2)不等式()1f x kx ≥-对任意[)1,x ∞∈+恒成立,求k 的取值范围;(3)对任意k ∈R ,直线y kx b =+与曲线()y f x =有且仅有一个公共点,求b 的取值范围.19.已知集合{}1,2,3,,A m = ,其中*m ∈N ,3m ≥.对于集合A 的n (*n ∈N ,3n ≥)元子集B ,若B 中不存在三个元素构成等差数列,则称集合B 为集合A 的“缺等差子集”(1)当5m =时,写出集合A 包含元素1和2的“缺等差子集”;(2)当14m =时,求集合A 的“缺等差子集”元素个数的最大值;(3)当()1312km =+,且2k ≥时,是否存在满足2k n =的集合A 的“缺等差子集”,请说明理由.。
2023-2024学年安徽省合肥市第一中学高三上学期第二次教学质量检测数学试题+答案解析

2023-2024学年安徽省合肥市第一中学高三上学期第二次教学质量检测数学试题一、单选题:本题共8小题,每小题5分,共40分。
在每小题给出的选项中,只有一项是符合题目要求的。
1.已知复数z满足为虚数单位,则()A.3B.C.5D.2.已知集合R,,若,则实数a的取值范围为A.RB.C.D.3.已知角的终边过点,则()A. B. C. D.4.在正项等比数列中,若,,则()A.1B.2C.3D.5.陀螺又称陀罗,是中国民间最早的娱乐健身玩具之一,在山西夏县新石器时代的遗址中就发现了石制的陀螺.如图所示的陀螺近似看作由一个圆锥与一个圆柱的组合体,其中圆柱的底面半径为2,圆锥与圆柱的高均为2,若该陀螺是由一个球形材料削去多余部分制成,则该球形材料的体积的最小值为()A. B. C. D.6.2023年杭州亚运会期间,甲、乙、丙3名运动员与5名志愿者站成一排拍照留念,若甲与乙相邻、丙不排在两端,则不同的排法种数有()A.1120B.7200C.8640D.144007.已知椭圆C:的离心率为,左、右焦点分别为,,P是C上一动点,若点P到焦点的最大距离为,则的取值范围为()A. B. C. D.8.已知数列的前n项和为,且,若,则()A. B. C. D.二、多选题:本题共4小题,共20分。
在每小题给出的选项中,有多项符合题目要求。
全部选对的得5分,部分选对的得2分,有选错的得0分。
9.已知数列的前n项和为,,,若N,是常数,则()A.数列是等比数列B.数列是等比数列C. D.10.已知函数是偶函数,其图象的两个相邻对称轴间的距离为,将函数的图象向右平移个单位长度得到函数的图象,则()A. B.在上单调递增C.函数的图象关于点对称D.函数的图象在处取得极大值11.在直角坐标系xOy中,抛物线C:的准线方程为,过C的焦点F作直线PQ交C于,两点,则()A. B.C.可能是直角三角形D.以FP为直径的圆与y轴相切12.在四面体ABCD中,,点D关于直线AC的对称点为,则() A.B.的最大值为C.若BD与平面ABC夹角的正切值为,则D.四面体ABCD体积的最大值为1三、填空题:本题共4小题,每小题5分,共20分。
河南省信阳市2023-2024学年高三第一次教学质量检测数学试题(含答案解析)

河南省信阳市2023-2024学年高三第一次教学质量检测数学
试题
学校:___________姓名:___________班级:___________考号:___________
一、单选题
二、多选题
..
..
.四个实数1-,2,x ,y 按照一定顺序可以构成等比数列,则xy 的可能取值有(
.1
8-
B .2-16
-D ..已知0a >,0b >,且a +,则不正确的是(
)
.14
ab ≥
B .2a 216a b
+≥D ..函数()f x 及其导函数f ',且()f x 是奇函数,设()4f x x -+,则以下结论正确的有(
.函数()2g x -的图象关于直线.若()g x 的导函数为g ,则()00g '=.()h x 的图象存在对称中心
.设数列{}a 为等差数列,44=,则()()h a h a ++三、填空题
四、解答题
参考答案:
又根据对称性可知()1f x 与12y =
形成的封闭图形的面积为又()()2124f x f x =-,[]4,8x ∈,所以2f 即212a a =,
故以此类推,有12n n a a +=,*n ∈N ,
所以数列{}n a 是以2为首项,2为公比的等比数列,
所以(
)1232122
12
n
n a a a a ⨯-+++⋅⋅⋅⋅⋅⋅+=
=-由8122510511+-=<,91221022511+-=>。
河南省部分示范性高中2024-2025学年高三上学期11月质量检测数学试题(含解析)

11绝密★启用前2025届高三第一学期11月质量检测数学全卷满分150分,考试时间120分钟.注意事项:1.答题前,先将自己的姓名、准考证号填写在试卷和答题卡上,并将条形码粘贴在答题卡上的指定位置.2.请按题号顺序在答题卡上各题目的答题区域内作答,写在试卷、草稿纸和答题卡上的非答题区域均无效.3.选择题用2B 铅笔在答题卡上把所选答案的标号涂黑;非选择题用黑色签字笔在答题卡上作答;字体工整,笔迹清楚.4.考试结束后,请将试卷和答题卡一并上交.一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合,,则()A. B. C. D.2.若,则( )A. B. C. D.3.要得到函数的图象,只需要把函数的图象( )A.向右平移个单位长度 B.向左平移个单位长度C.向右平移个单位长度 D.向左平移个单位长度4.已知直线:,:,设甲:;乙:,则()A.甲是乙的充分条件但不是必要条件B.甲是乙的必要条件但不是充分条件C.甲是乙的充要条件D.甲既不是乙的充分条件也不是乙的必要条件(){}lg 1A x y x =∈=-Z {}220B x x x =--≤A B ⋂={}1,0,1-{}1,0-[)1,1-()1,2-1i zz+=z =11i 22-+11i 22--11i 22-11i 22+()π2cos 23g x x ⎛⎫=-⎪⎝⎭()π2sin 26f x x ⎛⎫=- ⎪⎝⎭π3π3π6π61l ()1210a x y -++=2l ()120ax a y +-+=12l l ⊥2a =115.设为非零向量,若,则( )A.B. C. D.6.设为等比数列的前n 项和,若,,则( )A.1B.2C.3D.57.若关于的不等式在上恒成立,则的取值范围是( )A.B.C.D.8.已知函数的定义域为,且,,设,则( )A.B. C. D.二、多选题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.9.记数列的前项和为,且,则()A.B.数列是公差为1的等差数列C.数列的前项和为D.数列的前项和为10.已知函数,,是的两个零点,且,则( )A.B.为的极小值点C.的极大值为4,a b ,22b a a b b a ⎛⎫⎛⎫+⊥+⊥ ⎪ ⎪⎝⎭⎝⎭cos ,a b <>=1313-1212-n S {}n a 11a =-284a a =84S S =x ()1ln ex ax ax x +≥+()0,+∞a 10,e⎛⎤ ⎥⎝⎦(]0,e 1,e⎡⎫+∞⎪⎢⎣⎭[)e,+∞()f x R ()()()()22f x y f x y f x f y ++-=+()11f =()()*n a f n n =∈N 20211k ka ==-∑10211940589840531760{}n a n n S ()2*n S n n n =+∈N36a =n n S a ⎧⎫⎨⎬⎩⎭1n S ⎧⎫⎨⎬⎩⎭n 1nn +(){}1nn a -20232024-()32f x x ax bx c =+++0x =3x =()f x ()30f '=4a b c ++=3x =()f x ()f xD.满足的解集是11.已知函数的定义域为,对于任意非零实数,均有,且,则下列结论正确的为( )A. B.为奇函数C.D.三、填空题:本题共3小题,每小题5分,共15分.12.若是第二象限角,且,则___________.13.在平面直角坐标系中,,若点P 满足,则面积的最大值为___________.14.在中,,,两点分别在边AB ,AC 上,若,则的最大值为___________.四、解答题:本题共5小题,共77分.解答应写出必要的文字说明、证明过程及演算步骤.15.(本小题满分13分)已知函数为奇函数.(1)求a 的值;(2)求满足的x 的取值范围.16.(本小题满分15分)已知函数的最小正周期为,且的最大值为2.(1)求和的值;(2)若函数在区间内有且仅有两个零点,,求的取值范围及的值.17.(本小题满分15分)在中,内角的对边分别为,记的面积为S.(1)求的值;()()1f x f >{}4x x >()f x R ,x y ()f x x >()()()11f x y f x f y x y+=+()00f =()f x ()()221xxf f ->()()20242024f x f x ≥α3tan 4α=-πcos 4α⎛⎫+= ⎪⎝⎭xOy ()1,0A 2222PO PA +=POA ABC π3A =2AB =,D E DE DB =AD ()2log 12a f x x ⎛⎫=- ⎪-⎝⎭()()2log 2f x x <+-()()πcos cos 03f x x x a ωωω⎛⎫=++> ⎪⎝⎭π()f x ωa ()()g x f x m =-ππ,33⎡⎤-⎢⎥⎣⎦1x 2x m ()12f x x +ABC ,,A B C ,,a b c ABC 2AC S ⋅=A(2)已知D 为AC 的中点,,求的周长.18.(本小题满分17分)已知数列的前项和为,数列满足,,.(1)求的通项公式;(2)设,求使得成立的n 的最小整数.(表示不超过的最大整数)19.(本小题满分17分)已知曲线的图象上存在两点,记直线的方程为,若恰为曲线的一条切线,且直线与曲线相切于两点,,,则称函数为“切线上界”函数.(1)试判断函数是否为“切线上界”函数.若是,求出一组点;否则,请说明理由;(2)已知为“切线上界”函数,求实数的取值范围;(3)证明:当时,为“切线上界”函数.2025届高三第一学期11月质量检测•数学参考答案、提示及评分细则S =BD =ABC {}n a n n S {}n b 21n n b a =+()12112n n n S nb n b b b -=+-+++ 111a b =={}n a nn nnS c a =[][][]122024n c c c +++≥ []x x ()y f x =,A B AB ()y g x =AB ()y f x =()y g x =()y f x =,A B x ∀∈R ()()f x g x ≤()f x ()22sin sin 2F x x x =+,A B ()()2ln 1,0,,0,x x G x x a x ⎧+>=⎨--<⎩a 0ω>()sin H x x x ω=+题号12345678答案B A D BDCBC题号91011答案ACDBCDACD一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.【答案】B【解析】由,解得,且,由,解得,所以,故选B.2.【答案】A【解析】因为,所以,所以,故选A.3.【答案】D【解析】,所以只需把的图象向左平移个单位长度,故选D.4.【答案】B【解析】当时,直线,此时,当时,,解得,所以甲是乙的必要条件但不是充分条件,故选B.5.【答案】D【解析】设.由,可得,即.同理,由可得,所以.故选D.6.【答案】C【解析】由,则,因为,所以,所以,故选C.10x ->1x <x ∈Z ()()22210x x x x --=-+…12x -……{}1,0A B ⋂=-111i z z z +=+=()()1i 1i 1i 1i 1i 12z ++===--+-1i 2z -+=()ππππ2cos 22sin 22sin 23326g x x x x ⎛⎫⎛⎫⎛⎫=-=-+=+ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭()π2sin 26f x x ⎛⎫=- ⎪⎝⎭π61a =12:210,:20l y l x +=+=12l l ⊥1a ≠1121a aa -⨯=--2a =,ab θ<>=2b a b ⎛⎫+⊥ ⎪⎝⎭ 202b a b ⋅+= 2||cos 2b a b θ⋅=-2a b a ⎛⎫+⊥ ⎪⎝⎭ 2||cos 2a ab θ⋅⋅=- 1,cos ,2a b a b =<>=- 284a a =52a =±4510a q a =>452,2a q =-=848441131S q q S q-==+=-7.【答案】B【解析】易知在上恒成立,即,设,易知单调递增,因为,所以,即,令,则,当时,单调递减,当时,单调递增,所以的最小值为,所以的取值范围是(,故选B.8.【答案】C【解析】令,则,所以,令,则,所以,令,则,所以,即,设,则,所以,即,所以,,故选C.二、多选题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.9.【答案】ACD (全部选对得6分,选对1个得2分,选对2个得4分,有选错的得0分)【解析】,A 选项正确;()10,ln e x a a x ax x >++…()0,∞+1ln ln 1e ln e ln a xx a x x-+-+…()e xf x x =+()f x ()1ln lnf a x f x ⎛⎫- ⎪⎝⎭…1ln lna x x-…ln ln a x x -…()ln g x x x =-()111x g x x x-=-='()0,1x ∈()()0,g x g x '<()1,x ∞∈+()()0,g x g x '>()g x ()11g =ln 1,a a …0,e]0x y ==()()()()002020f f f f +=+()00f =1x y ==()()()()202121f f f f +=+()24f =1,y x n ==()()()()()1122122f n f n f n f f n ++-=+=+()()()()112f n f n f n f n +-=--+112n n n n a a a a +--=-+1n n n b a a +=-11212,3n n b b b a a --==-=()32121n b n n =+-=+121n n a a n +-=+213521n a a n n =++++-= 2020202222111111111111111111211213243518201921k k k k a k k k ===⎛⎫⎛⎫==-=⨯-+-+-++-+- ⎪ ⎪---+⎝⎭⎝⎭∑∑∑ 11115891222021840⎛⎫=+--= ⎪⎝⎭3326a S S =-=当时,,且,所以,则数列是公差为的等差数列,B 选项错误;,前项和为,C 选项正确;,D 选项正确,故选ACD.10.【答案】BCD (全部选对得6分,选对1个得2分,选对2个得4分,有选错的得0分)【解析】是的两个零点,与轴相切,且.所以,所以,A 选项错误;为的极小值点,B 选项正确;,所以为的极大值点,.C 选项正确;因为,D 选项正确;故选BCD.11.【答案】ACD (全部选对得6分,选对1个得2分,选对2个得4分,有选错的得0分)【解析】令,则,则,故选项A 正确;由已知,有,①当时,;②当时,.又,则当时,.若为奇函数,则函数为偶函数,与①②矛盾,故选项B 错误;由选项B 可知,故选项C 正确;当时,由选项A 知显然;当时,令,且,由选项B 易知,函数在定义域内单调递增,2n …12n n n a S S n -=-=12a =12,2n n n S n a n a +==n n S a ⎧⎫⎨⎬⎩⎭12()111111n S n n n n ==-++n 1n n +20231(1)2(12342023)2024nnn a=-=-+-+--=-∑ 0,3x x ==()f x ()f x x ()30f '=()()2(3),114f x x x f a b c =-=+++=3a b c ++=()()()()2(3)23331,3f x x x x x x x =-+-=--='()f x ()()()()2(3)23333f x x x x x x '=-+-=--1x =()f x ()14f =()()414f f ==y x =-()()()0110f f x f x x x=-=-()00f =x ∀∈R ()f x x >0x >()1f x x>0x <()1f x x<()()()()()()11f x y f x y f x f y f x f y x y x y x y ++=+⇔=⋅+()22420,x f f x x x ⎛⎫ ⎪⎝⎭=>∴0x <()01f x x<<()f x ()f x x()()()()()22222212222x xxxx x x xx xf f f f f -----+==>⋅+0x =()00,f =∴()()20242024f x f x …0x ≠21,x y x x x +==21x x >()()()()2121121211f x f x f x x f x x x x x x -=⋅>-∴()f x x()(),00,∞∞-⋃+当时,,则;当时,,则,故选项D 正确;故选ACD.三、填空题:本题共3小题,每小题5分,共15分.12.【答案及评分细则】【解析】依题意,,所以13.【答案及评分细则】【解析】设,依题意,,整理可得,,所以点在圆心为,半径为的圆上,所以面积的最大值为.14.【答案及评分细则】【解析】设,则,在中,由正弦定理:,可得:,所以时,四、解答题:本题共5小题,共77分.解答应写出必要的文字说明、证明过程及演算步骤.15.【答案】(1)4(2)【解析及评分细则】(1)依题意,,整理得,,∴0x >()()20242024f x f x xx>()()20242024f x f x …0x <()()20242024f x f x xx<()()20242024f x f x …34sin ,cos 55αα==-)πcos cos sin 4ααα⎛⎫+=-= ⎪⎝⎭13(),P x y ()22222(1)2x y x y ++-+=221439x y ⎛⎫-+= ⎪⎝⎭P 1,03⎛⎫⎪⎝⎭23POA 1211233⨯⨯=8-,AD x ADE ∠θ==2DE DB x ==-ADE sin sin AD DEAED A∠=πsin 3xθ=⎛⎫+ ⎪⎝⎭2πsin 3x -228x ==-=-π6θ=max 8AD =-()0,1()()22log 1log 1022a a f x f x x x ⎛⎫⎛⎫+-=-+-=⎪ ⎪-+⎝⎭⎝⎭()()2222(2)log 04a x f x f x x ⎡⎤--+-==⎢⎥-⎣⎦或(舍),;(2)由(1)可知,,,,即,整理得,,解得,满足的的取值范围是.16.【答案】(1)(2)【解析及评分细则】(1),所以,设的最小正周期为,则,所以,的最大值为,所以;(2)由(1)可知,,在区间内有且仅有两个零点,2(2)4,4a a ∴-=∴=0a =4a ∴=()()222222log ,log 2log 2x x f x x x x ++⎛⎫=+-=⎪-⎝⎭()20,20,0,220,xx x x x +⎧>⎪-⎪>∴∈⎨⎪+>⎪⎩()()2log 2f x x ∴<+-2222x xx x++<-()()22210x x x x +-=+-<21x -<<∴()()2log 2f x x <+-x ()0,151,4a ω==()12772,44m f x x <+=…()π1cos cos cos cos 32f x x x a x x x a ωωωωω⎛⎫⎛⎫=++=+ ⎪ ⎪ ⎪⎝⎭⎝⎭()11cos2cos cos 24x f x x x x a a ωωωω⎛⎫+=+= ⎪ ⎪⎝⎭πcos 21324x aω⎛⎫+ ⎪⎝⎭=++()f x T 2ππ2T ω==1ω=()f x 11224a ++=54a =()πcos 23322x f x ⎛⎫+ ⎪⎝⎭=+()()g x f x m =-ππ,33⎡⎤-⎢⎥⎣⎦12,x x即为方程的两个根,令,易知在上单调递增,在上单调递减,根据三角函数图象,,解得.,解得,.17.【答案】(1)(2)【解析及评分细则】(1),又,由,解得,得;(2),设,则,在中,由余弦定理可得,,在中,由余弦定理可得,,两式相加可得,,由(1)可得,,12,x x πcos 2233x m ⎛⎫+=- ⎪⎝⎭ππππ2,,,,π3333t x x t ⎡⎤⎡⎤=+∈-∴∈-⎢⎥⎢⎥⎣⎦⎣⎦cos y t =π,03⎡⎤-⎢⎥⎣⎦[]0,π12312m ∴-< (724)m <…12ππ22033x x ∴+++=12π3x x +=-()122ππcos π37333224f x x f ⎛⎫-+ ⎪⎛⎫⎝⎭∴+=-=+= ⎪⎝⎭π35+2cos S AC A =⋅= 1sin 2S bc A =sin cos bc A A =tan A =()0,πA ∈ π3A =1sin 62bc A bc ==∴= ADB ∠θ=πCDB ∠θ=-ADB 222222b b c θ⎛⎫=+-⨯ ⎪⎝⎭CDB ()2222π22b b a θ⎛⎫=+-⨯- ⎪⎝⎭222227422b bc a b +=+=()()22222,23230c b a bc c bc b c b c b +-=∴--=-+=或(舍),,,的周长为18.【答案】(1)(2)46【解析及评分细则】(1)因为,则,两式相减可得,即,又因为,则,整理可得,则,两式相减可得,则,且,可知数列是首项为2,公比为2的等比数列,则,所以;(2),易知,当时,,所以,32bc ∴=c b =-2222222337,224b b b a b c bc b a ⎛⎫∴=+-=+-=∴=⎪⎝⎭236,6,2,3,2b bc b c a =∴=∴=== ABC ∴ 5+21nn a =-()121n n nb n b b S +-++= ()121112n n n n b nb b b S +++++++= 1211n n n b b b b a ++++++= 121122222n n n b b b b a ++++++= 21n n b a =+()()()()121111112n n n a a a a a ++++++++++= 1112n n S n a ++++=2n n S n a +=11122n n n a a a +++=-()1121n n a a ++=+112a +={}1n a +11222n n n a -+=⨯=21n n a =-()22221n n n n n n n a n nS n c n a a -===--[][][][][][]123454916252111,222,234,246,259371531c c c c c ⎡⎤⎡⎤⎡⎤⎡⎤=⨯-==⨯-==⨯-==⨯-==⨯-=⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎣⎦6n …()()()()30123111211122(11)C C C C CC 21266n nn n n n n n nnn n n n n n n n ----++=+=+++++++++=…()232261161112211066nn n n n n n n -++++----=>…所以,所以当时,,所以,解得,所以使得成立的的最小整数为46.19.【答案】(1)详见解析(2)(3)详见解析【解析及评分细则】(1)令,解得,为的极大值点,且的一条切线.为“切线上界”函数,可取,满足题意;(2)设,则,当时,单调递减,当时,单调递减,,整理可得,点处的切线方程为:,同理点处的切线方程为:,整理可得,,依题意,两点处的切线方程重合,,[]222121n n n c n n ⎡⎤=-=-⎢⎥-⎣⎦6n …[][][]2121246251261213n c c c n n +++=++++⨯-+⨯-++-=- 232024n -…46n …[][][]122024n c c c +++ …n 1,4∞⎛⎫- ⎪⎝⎭()2π2sin sin21cos2sin21214F x x x x x x ⎛⎫=+=-+=+-⎪⎝⎭…()π1214F x x ⎛⎫=-= ⎪⎝⎭3ππ,8x k k =+∈Z ()3ππ8x k k ∴=+∈Z ()F x 1y =()y F x =()F x ∴3π11π,1,,188A B ⎛⎛+ ⎝⎝()()()()121122,,,,x x A x G x B x G x >()()12G x G x =''0x >()()1,1G x G x x =+''0x <()()2,G x x G x -'='120x x ∴>>A ()1111ln 111x xy x x x =++-++B ()22222y x a x x x ++=--2222y x x x a =-+-,A B ()212112112,1ln 1,1x x x x x a x ⎧=-⎪+⎪∴⎨⎪+-=-⎪+⎩()()121111ln 11141a x x x ∴=--++++设,则,单调递减,,设点处的切线为:,令,,当时时,,设点处的切线为:,,综上的取值范围为;(3)易知,,设,两点处的切线方程分别为:,,,,不妨取,()()()211ln 1104(1)1x x x x x ϕ=--++>++()232311122102(1)(1)12(1)x x x x x x x ϕ'++=-+-=-<++++()x ϕ∴()110,,44a a ϕ∞⎛⎫∴<=∈- ⎪⎝⎭A ()()1111ln 111x xE x x x x =++-++()()()()1111ln 111x xP x E x G x x x x =-=++-++()()ln 10x x -+>()11111P x x x =-++'()10,x x ∈()()10,,P x x x ∞<∈+'()0P x '>()()()()()10,0,P x P x P x G x E x ∴=∴∴………B ()2222Y x x x x a =-+-()()()()()()()2222222222220,0,Y x G x x x x a x a x x xx x x Y x G x G x Y x -=-+-++=+-=-∴-………a 1,4∞⎛⎫- ⎪⎝⎭()1cos H x x ωω=+'()()111222,sin ,,sin A x x x B x x x ωω++,A B ()11111cos sin cos y x x x x x ωωωωω=++-()22221cos sin cos y x x x x x ωωωωω=++-121112221cos 1cos sin cos sin cos x x x x x x x x ωωωωωωωωωω+=+⎧∴⎨-=-⎩()1221121cos cos ,cos sin sin x x x x x x x ωωωωωω∴=-=-212π,k x x k ω=+∈Z,解得,令,则,直线的方程为,,当时,为“切线上界”函数.1212πcos sin sin 0k x x x ωωω∴=-=()1ππ2k x k ω+=∈Z 12π5π,22x x ωω==11sin 1,cos 0x x ωω==∴AB 1y x =+()sin 1H x x x x ω=++ …∴0ω>()sin H x x x ω=+。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高三数学教学质量检测试题(doc 13页)试卷类型:A 2009年佛山市普通高中高三教学质量检测(二)数学 (文科)2009.4本试卷共4页,21小题,满分150分.考试用时120分钟.注意事项:1.答卷前,考生要务必填写答题卷上的有关项目.2.选择题每小题选出答案后,用铅笔把答案代号涂在答题卡对应的格内.3.非选择题必须用黑色字迹的钢笔或签字实数a 等于A .12-B .2-C .12 D .2 5.已知α、β是不同的平面,m 、n 是不同的直线,则下列命题不.正确的是 A .若m m ,α⊥∥,,β⊂n n 则βα⊥m ∥,,n =βαα 则m ∥nC .若m ∥n ,α⊥m ,则α⊥n m m ,α⊥,β⊥则α∥β.6.已知函数2,[1,1](),[1,1]x f x x x ∈-⎧=⎨∉-⎩,若[()]2f f x =,则x 的取值范围是 A .∅ B .[1,1]- C .(,1)(1,)-∞-+∞ D .{2}[1,1]- 7.如图,是函数tan()42y x ππ=-的部()OB OA OB -=A .4B .2 D .4-8. 若双曲线22221(0,0)x y a b ab-=>>近线的距离等于焦距的14,是A 5B .62C .2D .33B A yx 1 O 第7题图9. 已知函数2xy =的定义域为[],m n (,m n 为整数),值域为[]1,2.则满足条件的整数数对(,)m n 共有 A .1个 B .2个 C .3个 D .4个10. 家电下乡政策是应对金融危机、积极扩大内需的重要举措.我市某家电制造集团为尽快实现家电下乡提出四种运输方案,据预测,这四种方案均能在规定时间T 内完成预期的运输任务Q 0,各种方案的运输总量Q 与时间t 的函数关系如下图所示.在这四种方案中,运输效率(单.位时间的运.....输.量.)逐步提高的是二、填空题:本大共5小题,考生作答4小题,每Q OQ tAQ OQtCQOQtDOQ 0Q tB小题5分,满分20分) (一)必做题(11~13题)11. 命题“若0c >,则函数2()f x x x c =+-有两个零点.”的逆.否命题...是 . 12. 已知{}na 是公比为实数q 的等比数列,若4576,,a a a a +成等差数列,则q 等于 .13.在直角坐标系中,若不等式组0,,(1)1y y x y k x ≥⎧⎪≤⎨⎪≤--⎩表示一个三角形区域,则实数k 的取值范围是 .(二)选做题(14~15题,考生只能从中选做一题)14. (几何证明选讲)如图,过圆外点P 作⊙O 的割线PAB 与切线PE ,E 为切点,连结AE 、BE ,APE ∠的平分线分别与AE 、BE 相交于点C 、D ,若30AEB ∠=︒,则PCE ∠= .15. (坐标系与参数方程)在极坐标系中,和极轴垂直且相交的直线l 与圆4ρ=相交于A 、B 两点,若||4AB =,则直线l 的极坐标方程为 .· PE B A C DO 第14题图AE D CB A 1 B 1C 1 第17题图三、解答题:本大题共6小题,满分80分,解答须写出文字说明、证明过程或演算步骤. 16.(本题满分12分)在ABC ∆中,,,a b c 分别为内角,,A B C 所对的边,且满足sin 32A A =.(Ⅰ)求A 的大小;(Ⅱ)现给出三个条件:①2a =; ②45B =︒;③3c b =试从中选出两个可以确定ABC ∆的条件,写出你的选择并以此为依据求ABC ∆的面积.(只需写出一个选定方案即可,选多种方案以第一种方案记分)17.(本题满分12分)如图,侧棱垂直底面的三棱柱111ABC A B C -的底面ABC 位于平行四边形ACDE 中,2AE =,4AC =,60E ∠=︒,点B 为DE 中点,连结1A E .(Ⅰ)求证:平面1A BC ⊥平面11A ABB .(Ⅱ)设四棱锥1A AEBC -与四棱锥111A B BCC - 的体积分别为1V 、2V ,求12:V V 的值.第18题图 甲 乙 1 2 3 418.(本题满分14分)佛山市在每年的春节后,市政府都会发动公务员参与到植树活动中去林管部门在植树前,为保证树苗的质量,都会在植树前对树苗进行检测.现从甲乙两种树苗中各抽测了10株树苗的高度,量出的高度如下(单位:厘米) 甲:37,21,31,20,29,19,32,23,25,33乙:10,30,47,27,46,14,26,10,44,46(Ⅰ)根据抽测结果,完成答题卷中的茎叶图,并根据 你填写的茎叶图,对甲、乙两种树苗的高度作比较,写出两个统计结论;(Ⅱ)设抽测的10株甲种树苗高度平均值为x ,将这10株树苗的高度依次输入按程序框图进行的运算,问输出的S 大小为多少?并说明S 的统计学意义。
开0S = 2()iS S x x =+- 1i =输入ix 1i i =+否10?i ≥ 是输出S结束10SS =19.(本题满分14分)桑基鱼塘是广东省珠江三角洲一种独具地方特色的农业生产形式,某研究单位打算开发一个桑基鱼塘项目,该项目准备购置一块占地1800平方米的矩形地块,中间挖成三个矩形池塘养鱼,挖出的泥土堆在池塘四 周形成基围(阴影部分所示)种植桑树,鱼塘周围 的基围宽均为2米,如图所示,池塘所占面积为S平方米,:1:2a b .(Ⅰ) 试用,x y 表示S ;(Ⅱ) 若要使S 最大,则,x y 的值各为多少?a 米b 米x 米y 米 第19题图y xO A B C第20题图 20.(本题满分14分)如图,已知曲线21:1C y x=-与x 轴相交于A 、B两点,与y 轴相交于点C ,圆2C 经过A 、B 、C 三点.(Ⅰ)求圆2C 的方程;(Ⅱ)过点(0,)(1)P m m <-的直线1l 与圆2C 相切,试探讨1l 与1C 的位置关系;(Ⅲ)当4m =-时,过点P 作直线2l 与2C 相交于M N、两点,,MQ QN MP PNλλ==-,(0λ≠且1λ≠±).证明:点Q 恒在一条定直线上.21.(本题满分14分)已知函数211()()1(1)tf x t x x x =--++,其中t 为常数,且0t >.(Ⅰ)求函数()tf x 在(0,)+∞上的最大值; (Ⅱ)数列{}n a 中,123a =,112n n n n a a a a ++=-,求{}na 的通项公式;(Ⅲ)证明:对任意的0x >,12()nnaf x ≥,12n =,,.2009年佛山市普通高中高三教学质量检测(二)数学试题(文科)参考答案和评分标准一、选择题(每题5分,共50分) 题号 1 2 3 4 5 6 7 8 9 10答案C A B C BD A D C B二、填空题(每题5分,共20分)11.若函数2()f x x x c =+-没有两个零点,则0c ≤.(或“若函数2()f x xx c=+-至多有一个零点,则0c ≤.”)12.1213.(,1)-∞- 14.75︒ 15. cos 23ρθ=三、解答题:本大题共6小题,满分80分,解答须写出文字说明、证明过程或演算步骤. 16.(本题满分12分)解: 解:(Ⅰ)依题意得2sin()23A π+=,即sin()13A π+= ………………………………………………3分∵0A π<<, ∴4333A πππ<+<, ∴32A ππ+=, ∴6A π= ………………………5分 (Ⅱ)方案一:选择①② …………………………………………………………………………………6分由正弦定理sin sin a bA B=,得sin 22sin ab B A==……………………………………………8分26,sin sin()sin cos cos sin 4A B C C A B A B A B π++=∴=+=+=…………………10分1126sin 2223122S ab C +∴==⨯⨯=. ………………………………………………12分方案二:选择①③…………………………………………………………………………………………6分由余弦定理2222cos b c bc A a +-=,有222334b b b +-=,则2b =,23c =,…………………10分所以111sin 2233222S bc A ==⨯⨯=…………………………………………………………12分A EDBA 1B 1 说明:若选择②③,由3c b=得,6sin 31C B ==>不成立,这样的三角形不存在.17.(本题满分12分)解: 解:(Ⅰ)方法一、在平行四边形ACDE 中,∵2AE =,4AC =,60E ∠=︒,点B 为DE 中点. ∴60ABE ∠=︒,30CBD ∠=︒,从而90ABC ∠=︒,即AB BC ⊥…1分又1AA ⊥面ABC ,BC ⊂面ABC∴1AA BC ⊥,而1AA AB A =, ∴BC ⊥平面11A ABB ………………………………………………4分∵BC ⊂平面1A BC∴平面1A BC ⊥平面11A ABB …………………………………………………5分方法二、∵2AE =,4AC =,60E ∠=︒,点B 为DE 中点. ∴2AB =,3BC =,22216AB BC AC +==,∴AB BC ⊥……………………………………1分又1AA ⊥面ABC,BC ⊂面ABC,∴1AA BC⊥,而1AA AB A=,∴BC ⊥平面11A ABB ………4分∵BC ⊂平面1A BC∴平面1A BC ⊥平面11A ABB …………………………………………………5分(Ⅱ)方法一、设平行四边形ACDE 的面积为S,1AA h =, ……………………………………………6分则四棱锥1A AEBC-的体积1131344V Sh Sh=⋅=, ………………………………………………………8分四棱锥111A B BCC -的体积分别为2211323V Sh Sh=⋅= …………………………………………………10分∴1211:():()3:443V VSh Sh ==. ………………………………………………………………………12分 方法二、设1AA h =,则四棱锥1A AEBC -的体积11112433332AEBC V S AA h h+=⋅=⋅=,………8分∵111A B B B ⊥,1111A B B C ⊥,1111B BB C B =, ∴11A B ⊥面11BCC B甲 乙 1 2 3 4 0 6 0 4 4 7 6 0 679 0 7 1 3 3 2 5 1 9 ∴四棱锥111A B BCC -的体积分别为112111142323333BCC B V S A B h h=⋅⋅=⨯⨯ ……………………10分 ∴124:(3):(3)3:43V Vh h ==. ……………………………………………………………………12分18.(本题满分14分) 解:(Ⅰ)茎叶图如右. ………………………………………3分 统计结论:①甲种树苗的平均高度小于乙种树苗的平均高度;②甲种树苗比乙种树苗长得更整齐;③甲种树苗的中位数为27,乙种树苗的中位数为28.5;④甲种树苗的高度基本上是对称的,而且大多数集中在均值附近,乙种树苗的高度分布较为分散. ………………………………………………7分(给分说明:写出的结论中,1个正确得2分.)(Ⅱ)27,35.x S ==……………………………………………………………………………………11分S表示10株甲树苗高度的方差,是描述树苗高度离散程度的量.S值越小,表示长得越整齐,S 值越大,表示长得越参差不齐. ……………………………………14分 19.(本题满分14分)解:(Ⅰ)由题可得:1800,2xy b a ==,则636y a b a =++=+…………………………………………2分6(4)(6)(316)(316)3y S x a x b x a x -=-+-⨯=-=-16183263x y =--………………………6分(Ⅱ)方法一:161618326183261832480135233S x y x y =--≤-⨯=-=…………………11分当且仅当1663x y =,即40,45x y ==时,S 取得最大值1352. ……………………………………14分方法二:161800960018006321832(6)3S x x x x=--⨯+=-+960018322618324801352x x≤-⨯=-=……………………………………………11分当且仅当96006x x =,即40x =时取等号,S 取得最大值.此时180045y x==. …………………14分 方法三:设9600()1832(6)S f x x x==-+(0)x > …………………………………………………8分2296006(40)(40)()6x x f x x x -+'=-=………………………………………………………………9分令()0f x '=得40x =当040x <<时,()0f x '>,当40x >时,()0f x '<. ∴当40x =时,S 取得最大值.此时45y =. …………………………………………………………14分 20.(本题满分14分)解:(Ⅰ) 由题可得(1,0)A -、(10)B ,、(0,1)C -,则OA OB OC== ………………………………1分因此圆2C 为以原点为圆心,1为半径的圆 且圆2C 的方程为221x y +=.……………………………………………………………………………3分(Ⅱ)依题意,直线1l 斜率存在,可设其直线方程为y kx m =+, ……………………………………4分因为直线1l 与圆2C 相切,211m k =+,即221k m =-, (6)分联立1l 与1C 的方程21y kx m y x =+⎧⎨=-⎩,可得210x kx m ---=,…………………………………………7分因此224443km m m ∆=++=++当0∆<,即13m -<<-时,直线1l 与1C 没有公共点;……………………………………………8分当0∆=,即3m =-时,直线1l 与1C 有且只有一个公共点;…………………………………………9分当0∆>,即3m <-时,直线1l 与1C 有两个公共点. ………………………………………………10分(Ⅲ)设点1122(,),(,),(,)Q x y M x y N x y ,由MQ QN λ=得,()()121212121()()1x x x x x x x y y y y y yy λλλλλλ+=+⎧-=-⎧⎪⇒⎨⎨-=-+=+⎩⎪⎩……①……② 同理由MP PN λ=-可得()()()12121014x x y y λλλλ-=-⨯⎧⎪⎨-=-⨯-⎪⎩……③……④⨯+⨯①③②④得()2222222121241x x y y y λλλ-+-=-- ………………………………………12分又222211221,1xy x y +=+=,1λ≠±.所以41y -=,即14y =-, ∴点Q 恒在一条定直线14y =-上. ……………………………………………………………………14分21.(本题满分14分)解:(Ⅰ)由()211()1(1)tf x t x x x =--++,得则()()2243(1)2(1)21()(1)(1)(1)t x t x x t x f x x x x -+--⋅+-'=--=+++………………………………………2分0x >,∴当x t <时,()0tf x '>;当x t >时,()0tf x '<,∴当x t =时,()tf x 取得最大值1()1t f t t=+.………………………………………………………4分(Ⅱ)由题意知1111122n n a a +=⋅+,即11111(1)2n na a +-=-……………………………………………6分∴数列1{1}na -是以11112a-=为首项,12为公比的等比数列,∴11111()22n na --=⋅, 即n a =221nn+ ……………………………………………………………8分(Ⅲ)令12nt =>,则212111()()1(1)2nnf x x x x =--++…………………………………………10分由(Ⅰ)可知, 1122112()()122112nnn n n n n f x f a ≤===++. ……………………………………13分∴对任意的0x >,不等式12()(12)nnaf x n ≥=,,成立.…………………………………………14分。
