抛物线基础练习题(基础有梯度)

合集下载

初三抛物线的基础练习题

初三抛物线的基础练习题一、填空题1. 一个抛物线的方程为y=2y^2+3y−4，其中横坐标为3时，纵坐标为_______。

2. 已知一个抛物线的顶点坐标为(2,-5)，则该抛物线的方程为_______。

3. 抛物线y=−y^2+2y+3的对称轴方程为y=_______。

4. 已知抛物线y=−y^2+yy+3的对称轴方程为y=2，则抛物线的顶点坐标为_______。

5. 抛物线的焦点是(0,3)，其对称轴方程为y=4，则该抛物线的方程为_______。

二、选择题1. 下列哪个二次函数的图像是一个抛物线？A. y=2y^2+3y+4B. y=2y+5C. y=y^3−4y^2+3y−2D. y=3√y2. 已知一个抛物线的焦点为(5,3)，则该抛物线的对称轴方程为：A. y=5B. y=3C. y=−5D. y=−33. 已知一个抛物线的方程为y=−y^2+4y−3，求其顶点坐标。

A. (2,-1)B. (3,2)C. (-2,1)D. (-3,-2)4. 若一个抛物线的焦点为(-2,-6)，则该抛物线的方程为：A. y=−2y^2−6y−2B. y=−2y^2+6y−2C. y=2y^2−6y+2D. y=2y^2−6y−25. 一个抛物线的焦点为(1,4)，顶点坐标为(2,9)，则该抛物线的方程为：A. y=2y^2−12y+15B. y=−2y^2+12y−15C. y=−2y^2+12y+15D. y=2y^2−12y−15三、解答题1. 求抛物线y=y^2+2y−3的焦点、对称轴方程和顶点坐标。

2. 若y=yy^2+yy+y的抛物线的焦点为(4,1)，顶点坐标为(2,3)，则该抛物线的方程为什么？求出y、y和y的值。

3. 求抛物线y=−y^2+4的焦点、对称轴方程和顶点坐标。

4. 已知一个抛物线的焦点为(3,2)，过点(1,4)，求该抛物线的方程。

5. 抛物线的焦点为(0,5)，顶点坐标为(1,6)，求该抛物线的方程和对称轴方程。

抛物线基础练习题(基础有梯度)

抛物线基础练习题一. 选择题1．抛物线212y x =的准线方程是A.3x =B. 3x =-C. 3y =D. 3y =- 2．若直线10ax y -+=经过抛物线24y x =的焦点，则实数a = A.1 B.2 C. 1- D. 2- 3．抛物线22y x =-和22y x =-的焦点坐标分别是A.1,08⎛⎫- ⎪⎝⎭ 和10,2⎛⎫- ⎪⎝⎭B. 10,8⎛⎫- ⎪⎝⎭ 和1,02⎛⎫- ⎪⎝⎭ C. 1,02⎛⎫- ⎪⎝⎭和10,8⎛⎫- ⎪⎝⎭ D. 10,2⎛⎫- ⎪⎝⎭和1,08⎛⎫- ⎪⎝⎭4．若抛物线22y px =的焦点与椭圆22162x y +=的右焦点重合，则p 的值为A ．2-B ．2C ．4-D ．45．若双曲线2221613x y p-=的左焦点在抛物线22y px =的准线上，则p 的值为A ．2B ．3C ．4D ．6．设椭圆22221(00)x y m n m n+=>>，的右焦点与抛物线28y x =的焦点相同，离心率为12，则此椭圆的方程为A ．2211216x y +=B ．2211612x y +=C ．2214864x y += D ．2216448x y += 7．若点P 是抛物线22y x =上的一个动点，则点P 到点（0，2）的距离与P 到该抛物线准线的距离之和的最小值为A B ．3 C D ．928．已知直线1:4360l x y -+=和2:1l x =-，抛物线24y x =上一动点P 到1l 和2l 的距离之和的最小值是 A ．115B ．3C ．2D ．37169．已知点P 在24y x =上，那么点P 到点(21)Q -，的距离与点P 到抛物线焦点距离之和取得最小值时，点P 的坐标为1⎛⎫1⎛⎫10．已知22y px =的焦点为F ，点111222()()P x y P x y ，，，，333()P x y ，在抛物线上，且2132x x x =+，则Ａ.123FP FP FP +=Ｂ.222123FP FP FP +=Ｃ.2132FP FP FP =+ Ｄ.2213FPFP FP =⋅ 11．连结抛物线24x y =的焦点F 与点(1,0)M 所得线段与抛物线交于点A ，设点O 为坐标原点，则三角形OAM 的面积为A ．1-B ．32- C ．1D ．32+12．已知直线(2)(0)y k x k =+>与抛物线2:8C y x =相交于A 、B 两点，F 为C 的焦点，若2FA FB =，则k =A ．13B ．C ．23D ．13．过点(1,0)-作抛物线21y x x =++的切线，则其中一条切线方程是A ．220x y ++=B ．330x y -+=C ．10x y ++=D ．10x y -+=14．设P 为曲线2:23C y x x =++上一点，且曲线C 在点P 处切线倾斜角的范围是[0,]4π，则点P 横坐标的取值范围是A ．1[1,]2--B ．[1,0]-C ．[0,1]D ．1[,1]215．抛物线2y x =-上的点到直线4380x y +-=距离的最小值为 A ．43B ．75 C ．85D ．316．设抛物线24x y =的焦点为F ，A 、B 、C 为该抛物线上三点，若0FA FB FC ++=，则FA +FB +FC =A ．9B ．6C ．4D ．317．设O 是坐标原点,F 是22(0)y px p =>的焦点,A 是抛物线上的点,FA 与x 轴正向的夹角为60,则OA =A ．214pB ．2C ．6p D ．1336p 18．已知抛物线的准线方程为20x y +-=，焦点是(5,5)F ，则抛物线的顶点坐标是.(3,5)A B ．(5,3)C ．(2,2)D ．(3,3)二. 填空题19．若抛物线顶点是坐标原点,焦点坐标是()2,0F -,则抛物线方程是 20．若抛物线顶点是坐标原点,准线方程是()0y m m =≠,则抛物线方程是 21．若点P 到直线1x =-的距离比它到点(20)，的距离小1，则点P 的轨迹方程为22．已知动圆过定点,02p ⎛⎫⎪⎝⎭，且与直线2p x =-相切，其中0p >.则动圆圆心C 的轨迹的方程是23．与圆0422=-+x y x 外切且与y 轴相切的动圆的圆心的轨迹方程是 24．抛物线2y ax =的准线方程是2y =,则a =25．在抛物线22y px =上,横坐标为4的点到焦点的距离为5,则p =26．已知抛物线21y ax =-的焦点是坐标原点，则以抛物线与两坐标轴的三个交点为顶点的三角形面积为27．已知F 是抛物线24C y x =：的焦点，A B ，是C 上的两个点，线段AB 的中点为(22)M ，，则ABF =△S ．28．已知圆C 的圆心与抛物线24y x =的焦点关于直线y x =对称，直线4320x y --=与圆C 相交于A B ，两点，若6AB =，则圆C 的方程为三. 解答题29. 在ABC ∆中，角C B A ,,所对边分别为c b a ,,，已知,2,32==c a bc B A 2cot tan 1=⋅+，求ABC ∆的面积S.30．为拉动经济增长，某市决定新建一批重点工程，分为基础设施工程、民生工程和产业建设工程三类。

高中数学抛物线练习(有答案)

1抛物线的定义：平面内与一个定点F 和一条定直线l 的距离相等的点的轨迹叫做抛物线，定点F 叫做抛物线的焦点，定直线l 叫做抛物线的准线． 2抛物线的图形和性质：①顶点是焦点向准线所作垂线段中点。

②焦准距：FK p =③通径：过焦点垂直于轴的弦长为2p 。

④顶点平分焦点到准线的垂线段：2p OF OK ==。

⑤焦半径为半径的圆：以P 为圆心、FP 为半径的圆必与准线相切。

所有这样的圆过定点F 、准线是公切线。

⑥焦半径为直径的圆：以焦半径 FP 为直径的圆必与过顶点垂直于轴的直线相切。

所有这样的圆过定点F 、过顶点垂直于轴的直线是公切线。

⑦焦点弦为直径的圆：以焦点弦PQ 为直径的圆必与准线相切。

所有这样的圆的公切线是准线。

3抛物线标准方程的四种形式：，，px y px y 2222-==。

，py x py x 2222-== 4抛物线px y 22=的图像和性质：①焦点坐标是：⎪⎭⎫⎝⎛02，p ，②准线方程是：2p x -=。

③焦半径公式：若点),(00y x P 是抛物线px y 22=上一点，则该点到抛物线的焦点的距离（称为焦半径）是：02p PF x =+， ④焦点弦长公式：过焦点弦长121222p pPQ x x x x p =+++=++ ⑤抛物线px y 22=上的动点可设为P ),2(2y py 或2(2,2)P pt pt 或P px y y x 2),(2=其中一般情况归纳：抛物线的定义：例1：点M 与点F (－4，0)的距离比它到直线l ：x －6=0的距离4.2，求点M 的轨迹方程．分析：点M 到点F 的距离与到直线x =4的距离恰好相等，符合抛物线定义．例2：斜率为1的直线l 经过抛物线y 2=4x 的焦点，与抛物线相交于点A 、B ，求线段A 、B 的长．分析：这是灵活运用抛物线定义的题目．基本思路是：把求弦长AB 转化为求A 、B 两点到准线距离的和．解：如图8－3－1，y 2=4x 的焦点为F (1，0)，则l 的方程为y =x －1．由⎩⎨⎧+==142x y x y 消去y 得x 2－6x +1=0．设A (x 1，y 1)，B (x 2，y 2) 则x 1+x 2=6．又A 、B 两点到准线的距离为A '，B '，则()()()8262112121=+=++=+++='+'x x x x B B A A点评：抛物线的定义本身也是抛物线最本质的性质，在解题中起到至关重要的作用。

抛物线基础题(含答案)

抛物线（A)一.选择题：1．准线为x ＝2的抛物线的标准方程是A ．24y x =- Ｂ．28y x =- C.24y x = D.28y x = (答：B) 2．焦点是（-5，０)的抛物线的标准方程是A.25y x =B.210y x =-C.220y x =-D.220x y =- (答:C)3．抛物线F 是焦点,则p 表示A. Ｆ到准线的距离B.F 到准线距离的14 B. C. F 到准线距离的18D. F 到ｙ轴距离的 (答:B) 4．动点M （ｘ，ｙ)到点Ｆ(4，0)的距离比它到直线x+5＝0的距离小１，则点M 的轨迹方程是Ａ.40x += B.40x -= C.28y x = Ｄ.216y x = （答:D ） 5．若抛物线2(1)y a x =+的准线方程是x=－3，那么抛物线的焦点坐标是Ａ.（3,0) B.(２,０) Ｃ.1，0) Ｄ.（-1,0）（答:C)6． 24x y =点于直线0x y -=对称的抛物线的焦点坐标为 A 10,16⎛⎫ ⎪⎝⎭ B 10,16⎛⎫- ⎪⎝⎭ C 1,016⎛⎫ ⎪⎝⎭Ｄ1,016⎛⎫- ⎪⎝⎭ （答:A) 7．动点P 到直线40x +=的距离减去它到()2,0M 的距离之差等于2,则点Ｐ的轨迹是A 直线B 椭圆Ｃ双曲线Ｄ抛物线（答:D)8．抛物线的顶点在原点,焦点在y 轴上,抛物线上一点(),3P m -到焦点的距离为5，则抛物线的准线方程是A 4y = Ｂ4y =- C 2y = D 2y =- （答：C ）9．抛物线()20y ax a =<的焦点坐标和准线方程分别为 A 11,044x a a ⎛⎫= ⎪⎝⎭B 11,044x a a ⎛⎫-=- ⎪⎝⎭C 110,44y a a ⎛⎫=- ⎪⎝⎭D 110,44y a a⎛⎫-=- ⎪⎝⎭ (答:Ｃ) 10. 在28y x =上有一点Ｐ，它到焦点的距离是20，则P 点的坐标是A ()8,12 Ｂ()18,12- C ()18,12或()18,12- D ()12,18或()12,18-（答:Ｃ）11．物线210y x =的焦点到准线的距离是 A.10 B.5 C.20 D.52 (答:B) 12．抛物线28x y =-的焦点坐标是Ａ.()4,0- B ．()0,4- Ｃ.()2,0- Ｄ.()0,2- (答：Ｄ)二.填空题：1． 2(0)y ax a =≠的焦点坐标是答：(,0)4a2． 24y x =的焦点坐标是准线方程是 (答：（0,116),116y =- 3．顶点在原点,焦点为(0,－2）的抛物线的方程为 (答：28x y =-）4．抛物线22(0)y px p =>上一点Ｍ到焦点的距离是()2p a a >，则点M 到准线的距离是点Ｍ的横坐标是 (答：,2p a a -） 5．一条隧道的顶部是抛物拱形，拱高１.1米,跨度是2．2米,则拱形的抛物线方程是（答：21.1x y =-)6．抛物线22(0)y px p =>点()23-，到其焦点的距离是5,则p ＝_______(答：4） 7．抛物线()()12,1812,18-24x y =上一点A 的纵坐标为4,则点Ａ与抛物线的焦点为___＿＿__（答：5)三．解答题:1．根据下列条件写出抛物线的标准方程（1）焦点是F(３,0) (答：212y x =）（2）准线方程是14x =- (答:2y x =）（3）焦点到准线距离是２ (答：2x y =±24y x =±)2．求顶点在原点，对称轴为坐标轴,过点(2，-8)的抛物线方程,并指出焦点和准线。

(完整版)抛物线进阶练习题

(完整版)抛物线进阶练习题本文档提供了一系列的进阶级抛物线练题，旨在帮助您巩固抛物线的相关知识和技巧。

以下是题目详解：题目一：抛物线的焦点和准线已知抛物线的顶点坐标为$(h,k)$，准线与$x$轴的交点为$(p,0)$，根据已知条件回答以下问题：1. 要求导出抛物线焦点的坐标。

2. 计算准线的方程。

题目二：求解抛物线与直线的交点已知一条直线的方程$y=ax+b$和抛物线的方程$y=cx^2+dx+e$，根据已知条件回答以下问题：1. 求出抛物线与直线的交点坐标。

2. 根据交点坐标，判断抛物线与直线是否相交。

题目三：抛物线的平移和缩放已知标准抛物线的方程$y=x^2$，根据已知条件回答以下问题：1. 若将抛物线平移至点$(a,b)$，求出平移后抛物线的方程。

2. 若将抛物线沿着$x$轴缩放$k$倍，求出缩放后抛物线的方程。

题目四：抛物线的最值已知抛物线的方程$y=ax^2+bx+c$，根据已知条件回答以下问题：1. 求抛物线的顶点坐标。

2. 根据顶点坐标，判断抛物线的开口方向和最值。

题目五：抛物线的面积和弧长已知抛物线的方程$y=ax^2+bx+c$，根据已知条件回答以下问题：1. 计算抛物线在区间$[x_1,x_2]$上的面积。

2. 计算抛物线在区间$[x_1,x_2]$上的弧长。

题目六：实际应用根据实际问题回答以下问题：1. 小球从离地面为$h$的地方以初速度$v$沿着与地面垂直方向抛出，求解小球的抛物线轨迹方程。

2. 根据抛物线轨迹方程，计算小球在某个时刻$t$的高度。

以上是关于抛物线进阶练题的完整题目。

希望这些练题能够帮助您巩固和拓展抛物线的知识与技巧。

祝您练愉快，取得好成绩！> 注意：本文档所给题目仅为举例，实际练习中可根据需要进行调整和扩展。

抛物线基础训练题经典含答案

抛物线基础训练题1.动点P 到点A (0，2)的距离比到直线l :y =-4的距离小2，则动点P 的轨迹方程为 D A. x y 42= B. x y 82= C.y x 42= D.y x 82=2.已知直线l 与抛物线x y 82=交于A 、B 两点，且l 经过抛物线的焦点F ，A 点的坐标为(8，8)，则线段AB 的中点到准线的距离是 A A.425 B.225 C.825D.253.已知抛物线的焦点在直线y x 2--4=0上，则此抛物线的标准方程是C A.x y 162= B.y x 82-= C. x y 162=或y x 82-= D. x y 162=或y x 82=4.直线y =kx -2与抛物线x y 82=交于A 、B 两点，且AB 的中点横坐标为2，则k 的值是 BA.-1B.2C.-1或2D.以上都不是5.动圆M 经过点A (3，0)且与直线l :x =-3相切，则动圆圆心M 的轨迹方程是 A A. x y 122= B. xy 62= C. xy 32= D.x y 242=6.θ是任意实数，则方程ｘ２＋ｙ２ｓｉｎθ＝４的曲线不可能是（C ）Ａ.椭圆 .双曲线 .抛物线 .圆7.双曲线ky x 224+＝１的离心率ｅ∈（１，２），则k 的取值范围是（B ） .(－∞，０) Ｂ.（－12，０）Ｃ.（－３，０）Ｄ.（－60，－12）8.以12422y x -=1的焦点为顶点，顶点为焦点的椭圆方程为（D ） A.1121622=+y x B.1161222=+y x C. 141622=+y x D.116422=+y x9.抛物线y =x ２上到直线２x -y =4距离最近的点的坐标是（ B ）.(45,23) .(1，1) .( 49,23) .(2，4)10.1122222222=-=-ay b x b y a x 与（ａ＞ｂ＞０）的渐近线（D ）.重合Ｂ.不重合，但关于x 轴对应对称 .不重合，但关于y 轴对应对称Ｄ.不重合，但关于直线y =x 对应对称 11．抛物线22x y =的焦点坐标是（ C ）A ．)0,1(B ．)0,41(C ．)81,0(D ． )41,0(12 已知抛物线的顶点在原点，焦点在y 轴上，其上的点)3,(-m P 到焦点的距离为5，则抛物线方程为（ D ） A ．y x 82= B ．y x 42= C ．y x 42-= D ．y x 82-=13．抛物线x y 122=截直线12+=x y 所得弦长等于（ A ）A ．15 B ．152C ．215 D ．1514．顶点在原点，坐标轴为对称轴的抛物线过点(－2,3)，则它的方程是（ B ） A ．y x 292-=或x y 342=B ．x y 292-=或y x 342= C ．y x 342=D ．x y 292-=15．抛物线x y =2上到其准线和顶点距离相等的点的坐标为 )42,81(±______________．16．已知圆07622=--+x y x ，与抛物线)0(22>=p px y 的准线相切，则=p _2__________．17抛物线22y x =的准线方程为（ B ） A ．14y =-B ．18y =-C ．1y =D ．12y =18抛物线24x y =上的一点M 到焦点的距离为1，则点M 的纵坐标是（ B ）A ．1617B ．1615C ．87D ．019抛物线28x y =-的准线方程是（ B ）A ． 321=x B ． 2=y C ． 321=y D ． 2-=y20抛物线2x y =在点M （21，41）处的切线的倾斜角是（ B ）A ．30°B ．45°C ．60°D ．90°21若抛物线22y px =的焦点与椭圆22162x y +=的右焦点重合，则p 的值为（ D ）。

(完整版)高二抛物线基础测试题

高二抛物线基础测试题一、选择题：1．顶点在原点，焦点是F (0,5)的抛物线方程是( )A ．y 2＝20xB ．x 2＝20yC ．y 2＝120xD ．x 2＝120y2．抛物线y ＝－x 2的焦点坐标为( )A.⎝ ⎛⎭⎪⎫0，14B.⎝⎛⎭⎪⎫0，－14 C.⎝ ⎛⎭⎪⎫14，0 D.⎝ ⎛⎭⎪⎫－14，03．抛物线y ＝ax 2的准线方程是y ＝2，则实数a 的值为( )A.18 B ．－18 C ．8 D ．－84．(2010年高考陕西卷)已知抛物线y 2＝2px (p >0)的准线与圆x 2＋y 2－6x －7＝0相切，则p 的值为( )A.12 B ．1 C ．2 D ．45．(2010年高考湖南卷)设抛物线y 2＝8x 上一点P 到y 轴的距离是4，则点P 到该抛物线焦点的距离是( )A ．4B ．6C ．8D ．126．若点P 到定点F (4,0)的距离比它到直线x ＋5＝0的距离小1，则点P 的轨迹方程是( )A ．y 2＝－16xB ．y 2＝－32xC ．y 2＝16xD ．y 2＝16x 或y ＝0(x <0)7．以x 轴为对称轴的抛物线的通径(过焦点且与x 轴垂直的弦)长为8，若抛物线的顶点在坐标原点，则其方程为( )A ．y 2＝8xB ．y 2＝－8xC ．y 2＝8x 或y 2＝－8xD ．x 2＝8y 或x 2＝－8y8．已知抛物线y 2＝2px (p >0)的焦点F ，点P 1(x 1，y 1)、P 2(x 2，y 2)、P 3(x 3，y 3)在抛物线上，且2x 2＝x 1＋x 3，则有( )A ．|FP 1|＋|FP 2|＝|FP 3|B ．|FP 1|2＋|FP 2|2＝|FP 3|2C ．|FP 1|＋|FP 3|＝2|FP 2|D ．|FP 1|·|FP 3|＝|FP 2|29．抛物线y 2＝12x 截直线y ＝2x ＋1所得弦长等于( )A.15 B ．215C.152D ．15.10．以抛物线y 2＝2px (p >0)的焦半径|PF |为直径的圆与y 轴的位置关系为( )A ．相交B ．相离C ．相切D ．不确定11．过抛物线的焦点且垂直于其对称轴的弦是AB ，抛物线的准线交x 轴于点M ，则∠AMB 是( )A ．锐角B ．直角C．钝角D．锐角或钝角12．(2010年高考山东卷)已知抛物线y2＝2px(p>0)，过其焦点且斜率为1的直线交抛物线于A、B两点，若线段AB的中点的纵坐标为2，则该抛物线的准线方程为( )A．x＝1 B．x＝－1C．x＝2 D．x＝－2二．填空题13．已知直线x－y－1＝0与抛物线y＝ax2相切，则a＝________.14．抛物线y2＝4x上的点P到焦点F的距离是5，则P点的坐标是________．15．抛物线y2＝4x与直线2x＋y－4＝0交于两点A与B，F是抛物线的焦点，则|FA|＋|FB|＝________. 16．边长为1的等边三角形AOB，O为原点，AB⊥x轴，则以O为顶点，且过A、B的抛物线方程是________．三、解答题(解答应写出文字说明，证明过程或演算步骤.)17．若抛物线y2＝－2px(p>0)上有一点M，其横坐标为－9.它到焦点的距离为10，求抛物线方程和M点的坐标．18．抛物线的焦点F在x轴上，直线y＝－3与抛物线相交于点A，|AF|＝5，求抛物线的标准方程．19．已知抛物线y2＝－x与直线l：y＝k(x＋1)相交于A，B两点．(1)求证：OA⊥OB；(2)当△OAB的面积等于10时，求k的值．高二抛物线基础测试题参考答案一.选择题：题号 1 2 3 4 5 6 7 8 9 10 11 12 答案 BBBCBCCCACBB1．解析：选B.由p2＝5得p ＝10，且焦点在y 轴正半轴上，故x 2＝20y .2．解析：选B.x 2＝－y ，∴2p ＝1，p ＝12，∴焦点坐标为⎝ ⎛⎭⎪⎫0，－14.3．解析：选B.由y ＝ax 2，得x 2＝1a y ，14a ＝－2，a ＝－18.4．解析：选C.由抛物线的标准方程得准线方程为x ＝－p2.由x 2＋y 2－6x －7＝0得(x －3)2＋y 2＝16.∵准线与圆相切，∴3＋p2＝4，∴p ＝2.5解析：选B.如图所示，抛物线的焦点为F (2,0)，准线方程为x ＝－2，由抛物线的定义知：|PF |＝|PE |＝4＋2＝6.6．解析：选C.∵点F (4,0)在直线x ＋5＝0的右侧，且P 点到点F (4,0)的距离比它到直线x ＋5＝0的距离小1，∴点P 到F (4,0)的距离与它到直线x ＋4＝0的距离相等．故点P 的轨迹为抛物线，且顶点在原点，开口向右，p ＝8，故P 点的轨迹方程为y 2＝16x . 7．解析：选C.通径2p ＝8且焦点在x 轴上，故选C. 8．解析：选C.由抛物线定义知|FP 1|＝x 1＋p2，|FP 2|＝x 2＋p 2，|FP 3|＝x 3＋p2，∴|FP 1|＋|FP 3|＝2|FP 2|，故选C.9．解析：选A.令直线与抛物线交于点A (x 1，y 1)，B (x 2，y 2)由⎩⎪⎨⎪⎧y ＝2x ＋1y 2＝12x 得4x 2－8x ＋1＝0，∴x 1＋x 2＝2，x 1x 2＝14，∴|AB |＝1＋22x 1－x 22＝5[x 1＋x 22－4x 1x 2]＝15.10．解析：选C.|PF |＝x P ＋p 2，∴|PF |2＝x P 2＋p4，即为PF 的中点到y 轴的距离．故该圆与y 轴相切．11．解析：选B.由题意可得|AB |＝2p .又焦点到准线距离|FM |＝p ，F 为AB 中点，∴|FM |＝12|AB |，∴△AMB 为直角三角形且∠AMB ＝90°.12．解析：选B.∵y 2＝2px (p >0)的焦点坐标为⎝ ⎛⎭⎪⎫p2，0，∴过焦点且斜率为1的直线方程为y ＝x －p 2，即x ＝y ＋p2，将其代入y 2＝2px 得y 2＝2py ＋p 2，即y 2－2py－p 2＝0.设A (x 1，y 1)，B (x 2，y 2)，则y 1＋y 2＝2p ，∴y 1＋y 22＝p ＝2，∴抛物线的方程为y 2＝4x ，其准线方程为x ＝－1. 二．填空题13解析：由⎩⎪⎨⎪⎧x －y －1＝0y ＝ax2，得ax 2－x ＋1＝0，由Δ＝1－4a ＝0，得a ＝14. 答案：1414．解析：设P (x 0，y 0)，则|PF |＝x 0＋1＝5，∴x 0＝4， ∴y 20＝16，∴y 0＝±4. 答案：(4，±4) 15．解析：设A (x 1，y 1)，B (x 2，y 2)，则|FA |＋|FB |＝x 1＋x 2＋2.又⎩⎪⎨⎪⎧y 2＝4x 2x ＋y －4＝0⇒x 2－5x ＋4＝0， ∴x 1＋x 2＝5，x 1＋x 2＋2＝7. 答案：7 16．解析：焦点在x 轴正半轴上时，设方程为y 2＝2px (p >0)代入点(32，12)得p ＝312，焦点在x 轴负半轴上时，设方程为y 2＝－2px (p >0)，∴p ＝－312.综上，所求方程为y 2＝±36x . 答案：y 2＝±36x 三、解答题17．若抛物线y 2＝－2px (p >0)上有一点M ，其横坐标为－9.它到焦点的距离为10，求抛物线方程和M 点的坐标．解：由抛物线定义知焦点为F (－p 2，0)，准线为x ＝p2，由题意设M 到准线的距离为|MN |，则|MN |＝|MF |＝10，即p2－(－9)＝10， ∴p ＝2.故抛物线方程为y 2＝－4x ，将M (－9，y )代入y 2＝－4x ，解得y ＝±6， ∴M (－9,6)或M (－9，－6)．18．抛物线的焦点F 在x 轴上，直线y ＝－3与抛物线相交于点A ，|AF |＝5，求抛物线的标准方程．解：设所求抛物线的标准方程为： y 2＝ax (a ≠0)，A (m ，－3)．则由抛物线的定义得5＝|AF |＝|m ＋a4|，又(－3)2＝am .所以，a ＝±2或a ＝±18.故所求抛物线的方程为y 2＝±2x 或y 2＝±18x .19．已知抛物线y 2＝－x 与直线l ：y ＝k (x ＋1)相交于A ，B 两点．(1)求证：OA ⊥OB ；(2)当△OAB 的面积等于10时，求k 的值．解：(1)证明：联立⎩⎪⎨⎪⎧y 2＝－xy ＝k x ＋1，消去x ，得ky 2＋y －k ＝0.设A (x 1，y 1)，B (x 2，y 2)，则y 1＋y 2＝－1k，y 1·y 2＝－1.因为y 21＝－x 1，y 22＝－x 2，所以(y 1·y 2)2＝x 1·x 2，所以x 1·x 2＝1，所以x 1x 2＋y 1y 2＝0，即OA →·OB →＝0，所以OA ⊥OB .(2)设直线l 与x 轴的交点为N ，则N 的坐标为(－1,0)，所以S △AOB ＝12|ON |·|y 1－y 2|＝12×|ON |×y 1＋y 22－4y 1·y 2 ＝12×1× 1k 2＋4＝10，解得k 2＝136，所以k ＝±16.。

2022年高考数学一轮复习专题专题41抛物线基础巩固检测题解析版.docx

专题41抛物线基础巩固检测题(解析版)一、单选题1.过抛物线十=4》的焦点F 的直线交抛物线于AB 两点，若F 是线段AB 的中点,则 |AB |=()A. 1B. 2C. 3D. 4【答案】D 【分析】依据题意可知线段AB 为抛物线的通径可得结果. 【详解】由题可知：线段为抛物线的通径所以|AB| = 4 故选：D2. F 为抛物线y2=2px(p>0)上一点，点尸到抛物线准线和对称轴的距离分别为10和6,则P=()【答案】D 【分析】由抛物线：/=2px(p>0)可得准线/的方程为：x = --|,设点P(x,y),再由点尸到抛物线准线和对称轴的距离分别为10和6,可得x + ^ = 10, y = ±6,再与抛物线方 2 程y2=2px(p 〉0),联立解方程组，即可求解.【详解】解：由题意可得：抛物线V=2px(p>0)的准线/的方程为：x =-宣设点P(x, y),又因点P 到抛物线准线和对称轴的距离分别为10和6, 即。

的值分别为18或2.故选：D. 【点睛】B. 4C. 4 或9D. 2或18所以有，》+农102y = ±6 ,解得＜y 2 =2 pxx = l 、或＜ [p = 18|x = 9[P = 2‘A. 2本题考查了抛物线的标准方程及其性质，考查理解辨析能力及运算求解能力，属于基础题.3.已知抛物线方程为必=4>,则该抛物线的焦点坐标为( )A. (0,-1)B. ^-―C.D. (0,1)【答案】D【分析】根据抛物线方程求出。

=2，即可得抛物线的焦点坐标.【详解】由抛物线方程x2=4y可知2p = 4,所以p = 2,又抛物线的焦点在V轴正半轴上，所以该抛物线的焦点坐标为(0,1).故选：D4.已知抛物线C:x2=2py(p〉0)的焦点在直线x+y-1 = 0上，又经过抛物线C的焦点且倾斜角为60。

的直线交抛物线C于A、8两点，则|仙|=( )A. 12B. 14C. 16D. 18【答案】C【分析】直线x+y-l =。

(完整版)抛物线基础练习题

完整版)抛物线基础练习题抛物线基础练习题1.抛物线方程及性质1.1 抛物线的标准方程为 $y = ax^2 + bx + c$，其中 $a$、$b$、$c$ 是实数常数。

a 的值决定了抛物线的开口方向。

当 $a。

0$ 时，抛物线开口向上。

当 $a < 0$ 时，抛物线开口向下。

1.2 抛物线的对称轴是垂直于 x-轴的直线，可以通过以下公式求得：x = -\frac{b}{2a}$$2.抛物线图像绘制2.1 绘制抛物线图像的步骤：确定抛物线的方程。

找出对称轴的 x 坐标。

绘制对称轴，并确定对称轴上的一点。

根据对称轴上的点，绘制抛物线的图像。

2.2 使用上述步骤绘制以下抛物线的图像：2.2.1 $y = x^2$，开口向上的抛物线。

首先，我们可以得知对称轴的 x 坐标为 $x = 0$。

确定对称轴上的一点 P(0,0)，然后根据 P 点的坐标起始绘制抛物线图像。

绘制结果如下图所示：抛物线图像](image.png)3.练习题请计算并回答下列问题：1.当抛物线方程为 $y = -2x^2 + 3x + 1$ 时，求其对称轴的 x 坐标。

2.给定抛物线方程 $y = 4x^2 + 2x + 1$，求其开口方向。

4.答案解析解答上述练习题：1.根据公式 $x = -\frac{b}{2a}$，代入 $a=-2$ 和 $b=3$，我们可以计算得到对称轴的 x 坐标为 $x = -\frac{3}{2}$。

2.根据抛物线方程 $y = 4x^2 + 2x + 1$，我们可以得知 $a = 4.0$，所以抛物线的开口方向是向上。

希望以上内容能够帮助你理解抛物线的基本概念和绘制方法。

如果还有其他问题，请随时提问。

抛物线练习题(含答案)

抛物线练习题一、选择题1．在直角坐标平面内，到点(1,1)和直线x ＋2y ＝3距离相等的点的轨迹是( )A ．直线B ．抛物线C ．圆D ．双曲线 2．抛物线y 2＝x 上一点P 到焦点的距离是2，则P 点坐标为( )A.⎝ ⎛⎭⎪⎫32，±62B.⎝ ⎛⎭⎪⎫74，±72C.⎝ ⎛⎭⎪⎫94，±32 D.⎝ ⎛⎭⎪⎫52，±102 3．抛物线y ＝ax 2的准线方程是y ＝2，则a 的值为( )A.18 B ．－18C ．8D ．－8 4．设抛物线y 2＝8x 上一点P 到y 轴的距离是4，则点P 到该抛物线焦点的距离是( )A ．4B ．6C ．8D ．12 5．设过抛物线的焦点F 的弦为AB ，则以AB 为直径的圆与抛物线的准线的位置关系是( )A ．相交B ．相切C ．相离D ．以上答案都有可能6．过点F (0,3)且和直线y ＋3＝0相切的动圆圆心的轨迹方程为( )A ．y 2＝12xB ．y 2＝－12xC ．x 2＝12yD ．x 2＝－12y 7．抛物线y 2＝8x 上一点P 到x 轴距离为12，则点P 到抛物线焦点F 的距离为( )A ．20B ．8C ．22D ．24 8．抛物线的顶点在坐标原点，焦点是椭圆4x 2＋y 2＝1的一个焦点，则此抛物线的焦点到准线的距离为( )A ．2 3 B. 3 C.12 3 D.143 9．设抛物线的顶点在原点，其焦点F 在y 轴上，又抛物线上的点(k ，－2)与F 点的距离为4，则k 的值是( )A ．4B ．4或－4C ．－2D ．2或－210．抛物线y ＝1mx 2(m <0)的焦点坐标是( ) A.⎝ ⎛⎭⎪⎫0，m 4 B.⎝ ⎛⎭⎪⎫0，－m 4 C.⎝ ⎛⎭⎪⎫0，14m D.⎝⎛⎭⎪⎫0，－14m 11．抛物线的顶点在原点，对称轴是x 轴，抛物线上的点(－5,25)到焦点的距离是6，则抛物线的方程为( )A ．y 2＝－2xB ．y 2＝－4xC ．y 2＝2xD ．y 2＝－4x 或y 2＝－36x12．已知抛物线y 2＝2px (p >0)的准线与圆(x －3)2＋y 2＝16相切，则p 的值为( )A.12B ．1C ．2D ．4二、填空题13．过抛物线焦点F 的直线与抛物线相交于A 、B 两点，若A 、B 在抛物线准线上的射影是A 1、B 1，则∠A 1FB 1= 。

抛物线基础题(含答案)

抛物线1．在平面内，“点P 到某定点的距离等于到某定直线的距离”是“点P 的轨迹为抛物线”的( )A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件答案 B2．若动点P 到定点F (－4,0)的距离与到直线x ＝4的距离相等，则P 点的轨迹是( )A ．抛物线B ．线段C ．直线D ．射线答案 A3. 已知动点P 到定点(0,2)的距离和它到直线l ：y ＝－2的距离相等，则点P 的轨迹方程为________。

答案 x 2＝8y 4. 已知动点M 的坐标满足方程5x 2＋y 2＝|3x ＋4y －12|，则动点M 的轨迹是( )A ．椭圆B ．双曲线C ．抛物线D ．圆答案 C5. 对抛物线y ＝4x 2，下列描述正确的是( )A ．开口向上，焦点为(0,1)B ．开口向上，焦点为⎝ ⎛⎭⎪⎫0，116C ．开口向右，焦点为(1,0)D ．开口向右，焦点为⎝ ⎛⎭⎪⎫0，116答案 B6．抛物线y ＝ax 2(a ≠0)的准线方程是y ＝2，则a 的值为( )A.18B ．－18 C ．8 D ．－8解析因为y ＝ax 2(a ≠0)，化为标准方程为x 2＝1a y ，其准线方程为y ＝2，所以2＝1－4a，所以a ＝－18。

故选B 。

答案 B7. 抛物线y ＝－116x 2的焦点坐标为( )A.⎝ ⎛⎭⎪⎫－164，0 B ．(－4,0) C.⎝ ⎛⎭⎪⎫0，－164 D ．(0，－4) 解析抛物线方程化为x 2＝－16y 。

其焦点坐标为(0，－4)。

答案 D8. 抛物线方程为7x ＋4y 2＝0，则焦点坐标为________。

解析抛物线方程化为y 2＝－74x ，所以抛物线开口向左，2p ＝74，p 2＝716，故焦点坐标为⎝ ⎛⎭⎪⎫－716，0。

答案 ⎝ ⎛⎭⎪⎫－716，09．顶点在坐标原点，对称轴为坐标轴，又过点(－2,3)的抛物线方程是( )A ．y 2＝94xB ．x 2＝43yC ．y 2＝－94x 或x 2＝－43yD ．y 2＝－92x 或x 2＝43y 答案 D10．已知抛物线y ＝mx 2(m >0)的焦点与椭圆4y 29＋x22＝1的一个焦点重合，则m ＝________。

抛物线基础练习题(基础有梯度)

抛物线基础练习题(基础有梯度)一.选择题1.抛物线y^2=12x的准线方程是y=3.2.直线ax-y+1=0经过抛物线y^2=4x的焦点，实数a=2.3.抛物线y=-2x^2和y^2=-2x的焦点坐标分别是(-1,0)和(0,-1)。

4.若抛物线y=2px的焦点与椭圆x^2/16+y^2/9=1的右焦点重合，则p的值为4.5.双曲线x^2/16-y^2/4=1的左焦点在抛物线y^2=2px的准线上，则p的值为3.6.设椭圆x^2/16+y^2/4=1(m>0,n>0)的右焦点与抛物线y^2=8x的焦点相同，离心率为1/2，则此椭圆的方程为x^2/12+y^2/16=1.7.若点P是抛物线y^2=2x上的一个动点，则点P到点(0,2)的距离与P到该抛物线准线的距离之和的最小值为5/2.8.已知直线.9.已知点P在抛物线y^2=4x上，点P到点Q(2,-1)的距离与点P到抛物线焦点距离之和取得最小值时，点P的坐标为(1,2)。

10.已知y^2=2px的焦点为F，点P1(x1,y1)，P2(x2,y2)，P3(x3,y3)在抛物线上，且2x2=x1+x3，则FP1+FP2=FP3.11.连结抛物线x^2=4y的焦点F与点M(1,0)所得线段与抛物线交于点A，设点O为坐标原点，则三角形OAM的面积为2/3.一.解答题1.将直线方程化为一般式：2x-3y+6=0，代入抛物线方程得y^2=-8x-2kx-16k，根据对称性，过抛物线焦点的直线方程为x=-2，代入抛物线方程得y^2=16-16k，由题意得点A坐标为(-2,4)，点B坐标为(-2,-4)，则点F坐标为(-2,0)，代入抛物线方程得焦距2p=4，解得p=2，代入y^2=16-16k得k=3/4，因此k的值为C.（注意题干中的格式错误）2.过点(-1,0)的切线斜率为f’(-1)=2(-1)+1=-1，切线方程为y=-x-1，联立y=x^2+x+1得x^2+2x+2=0，无实根，因此不存在过点(-1,0)的切线，选项都不正确。

抛物线基础练习题(基础有梯度)

抛物线基础练习题一.选择题1．抛物线212yx的准线方程是A.3x B. 3xC.3y D.3y 2．若直线10axy 经过抛物线24y x 的焦点，则实数aA.1B.2C. 1D. 23．抛物线22yx和22yx 的焦点坐标分别是A.1,08和10,2B. 10,8和1,02C.1,02和10,8D. 10,2和1,084．若抛物线22ypx 的焦点与椭圆22162xy的右焦点重合，则p 的值为A ．2B ．2C ．4D ．45．若双曲线2221613xy p的左焦点在抛物线22ypx 的准线上，则p 的值为A ．2B ．3C ．4D ．426．设椭圆22221(00)xy mnmn，的右焦点与抛物线28yx 的焦点相同，离心率为12，则此椭圆的方程为A ．2211216xyB ．2211612xyC ．2214864xyD ．2216448xy7．若点P 是抛物线22y x 上的一个动点，则点P 到点（0，2）的距离与P 到该抛物线准线的距离之和的最小值为A ．172B ．3C ．5D ．928．已知直线1:4360l x y 和2:1l x，抛物线24yx 上一动点P 到1l 和2l 的距离之和的最小值是A ．115B ．3C ．2D ．37169．已知点P 在24y x 上，那么点P 到点(21)Q ，的距离与点P 到抛物线焦点距离之和取得最小值时，点P 的坐标为A ．114，B ．114，C ．(12)，D ．(12)，。

(完整版)抛物线练习题(含答案)

抛物线练习题一、选择题1．在直角坐标平面内，到点(1,1)和直线x ＋2y ＝3距离相等的点的轨迹是( )A ．直线B ．抛物线C ．圆D ．双曲线2．抛物线y 2＝x 上一点P 到焦点的距离是2，则P 点坐标为( )A.⎝⎛⎭⎫32，±62B.⎝⎛⎭⎫74，±72C.⎝⎛⎭⎫94，±32D.⎝⎛⎭⎫52，±102 3．抛物线y ＝ax 2的准线方程是y ＝2，则a 的值为( )A.18 B ．－18C ．8D ．－8 4．设抛物线y 2＝8x 上一点P 到y 轴的距离是4，则点P 到该抛物线焦点的距离是( )A ．4B ．6C ．8D ．125．设过抛物线的焦点F 的弦为AB ，则以AB 为直径的圆与抛物线的准线的位置关系是( )A ．相交B ．相切C ．相离D ．以上答案都有可能6．过点F (0,3)且和直线y ＋3＝0相切的动圆圆心的轨迹方程为( )A ．y 2＝12xB ．y 2＝－12xC ．x 2＝12yD ．x 2＝－12y7．抛物线y 2＝8x 上一点P 到x 轴距离为12，则点P 到抛物线焦点F 的距离为( )A ．20B ．8C ．22D ．248．抛物线的顶点在坐标原点，焦点是椭圆4x 2＋y 2＝1的一个焦点，则此抛物线的焦点到准线的距离为( )A ．2 3 B. 3 C.12 3 D.143 9．设抛物线的顶点在原点，其焦点F 在y 轴上，又抛物线上的点(k ，－2)与F 点的距离为4，则k 的值是( )A ．4B ．4或－4C ．－2D ．2或－210．抛物线y ＝1mx 2(m <0)的焦点坐标是( ) A.⎝⎛⎭⎫0，m 4 B.⎝⎛⎭⎫0，－m 4 C.⎝⎛⎭⎫0，14m D.⎝⎛⎭⎫0，－14m 11．抛物线的顶点在原点，对称轴是x 轴，抛物线上的点(－5,25)到焦点的距离是6，则抛物线的方程为( )A ．y 2＝－2xB ．y 2＝－4xC ．y 2＝2xD ．y 2＝－4x 或y 2＝－36x12．已知抛物线y 2＝2px (p >0)的准线与圆(x －3)2＋y 2＝16相切，则p 的值为( )A.12 B ．1 C ．2 D ．4二、填空题13．过抛物线焦点F的直线与抛物线相交于A、B两点，若A、B在抛物线准线上的射影是A1、B1，则∠A1FB1= 。

高考数学复习---抛物线基础知识巩固练习题(含答案)

9．已知过抛物线 y2＝2px(p＞0)的焦点，斜率为 2 2的直线交抛物线于 A(x1， y1)，B(x2，y2)(x1＜x2)两点，且|AB|＝9.
(1)求该抛物线的方程； (2)O 为坐标原点，C 为抛物线上一点，若O→C＝O→A＋λO→B，求 λ 的值．
[解] (1)由题意得直线 AB 的方程为 y＝2 2·x－p2，与 y2＝2px 联立，消去 y 有 4x2－5px＋p2＝0，所以 x1＋x2＝54p.
x2＝4y [△FPM 为等边三角形，则|PM|＝|PF|，由抛物线的定义得 PM 垂直
于抛物线的准线，设 Pm，m2p2，则点 Mm，－p2，因为焦点 F0，p2，△FPM 是
等边三角形，
m2p2＋p2＝4，所以
p2＋p22＋m2＝4，
m2＝12，
解得
因此抛物线方程为 x2＝4y.]
p＝2，
三、解答题
2.
则直线 AB 的方程为 y＝2 2(x－1)，与抛物线方程联立整理得 2x2－5x＋2＝0，xA＋xB＝52，所以 xB＝12，所以|BF|＝12＋1＝32.]
8．已知抛物线 x2＝2py(p＞0)的焦点为 F，点 P 为抛物线上的动点，点 M 为其准线上的动点，若△FPM 为边长是 4 的等边三角形，则此抛物线的方程为 ________．
A．1
B．2
C．3
D．4
A [∵x2＝2y，∴y＝x22，∴y′＝x，
∵抛物线 C 在点 B 处的切线斜率为 1，∴B1，12，
∵抛物线 x2＝2y 的焦点 F 的坐标为0，12，
∴直线 l 的方程为 y＝12，∴|AF|＝|BF|＝1.]
3．(2019·桂林模拟)设经过抛物线C的焦点的直线l与抛物

抛物线练习题带答案,知识点总结(基础版)

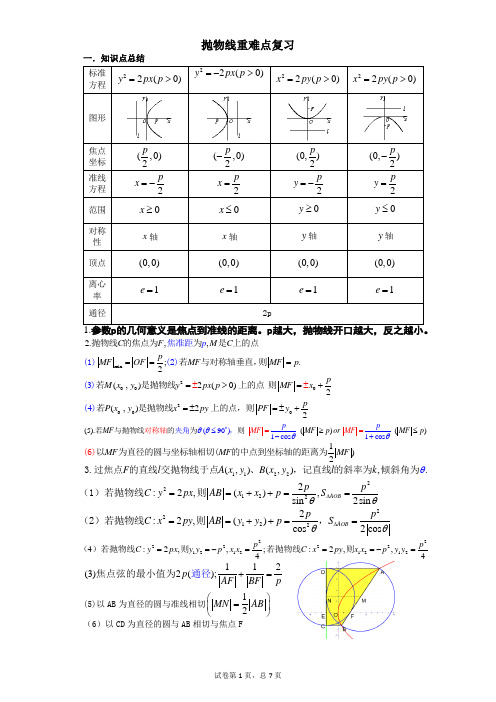
抛物线重难点复习一．知识点总结2.,,C F p M C 焦抛物线的焦点为为是准距上的点min ;.2pMF OF MF MF p ===(1)(2)若与对称轴垂直，则2000(,)2(0)23p M x y y px p MF x =>=±+±若是抛物线上的点则() 2000(,)224p P x y x py PF y =±=±+若是抛物线上的(点，则) (5).()(90)1cos s ()1co p MF MF pp or MF p MF MF θθθθ≥≤-+==≤ 若与抛物线的为则夹角，对称轴1)2MF MF MF 以为直径的圆与坐标轴相切(的中点到坐标轴的距离为(6)1122(,)(,),.F l A x y B x y l k θ3.过焦点的直线交抛物线于点、，记直线的斜率为倾斜角为221222:2,(),sin 2sin AOB p p C y px AB x x p S θθ∆==++==（1）若抛物线则221222:2,()cos 2cos AOB p p C x py AB y y p S θθ∆==++==（2）若抛物线则， 222222121212124:2,,;:2,,44p p C y px y y p x x C x py x x p y y ==-===-=（）若抛物线则若抛物线则112(3)2();p AF BF p+=通焦点弦的最径小值为 (5)以AB 为直径的圆与准线相切12MN AB ⎛⎫=⎪⎝⎭（6）以CD 为直径的圆与AB 相切与焦点F1．已知抛物线22(0)y px p =>上横坐标为 3 的点到其焦点的距离为 4，则p =________. 【答案】2【解析】抛物线y 2=2px （p ＞0， ∵抛物线y 2=2px （p ＞04，∴p=2.故答案为2.2．已知F 是抛物线y 2=2x 的焦点，A ,B 是该抛物线上的两点，|AF |+|BF |=11，则线段AB 的中点到y 轴的距离为（） A. 3 B. 4 C. 5 D. 7 【答案】C 【解析】∵F 是抛物线y 2=2x 的焦点∴F (12,0) ,准线方程x =−12，设A (x 1,y 1),B (x 2,y 2)∴|AF |+|BF |=x 1+1+x 2+1=11x 1+x 2=10,∴线段AB 的中点横坐标为5∴线段AB 5，所以B 选项是正确的.3．已知抛物线C ：的焦点为F ，()00A x y ，是C 上一点，则0x =（）A. 2B. 2±C. 4D. 4± 【答案】D【解析】28x y =，如图，由抛物线的几何意义，可知0022AF Al y y ===+，所以02y =，所以04x =±，故选D 。

实际问题与二次函数—抛物线型(基础)(含答案)

实际问题与二次函数—抛物线型（基础）一、单选题(共8道，每道10分)1.赵州桥的桥拱可以用抛物线的一部分表示，函数关系为，当水面宽度AB为20m 时，水面与桥拱顶的高度DO等于( )A.2mB.4mC.10mD.16m答案：B解题思路：根据题意点B的横坐标为10，把代入中，得．∴A(-10，-4)，B(10，-4)即水面与桥拱顶的高度DO等于4m．试题难度：三颗星知识点：略2.如图所示，中堂中学教学楼前喷水池喷出的抛物线水柱，水柱喷出的竖直高度y（m）与水平距离x（m）满足，则水柱的最大高度是( )A.2mB.4mC.6mD.答案：C解题思路：∵抛物线水柱的解析式为，∴水柱的最大高度是6m．试题难度：三颗星知识点：略3.如图，若被击打的小球飞行高度h（单位：m）与飞行时间t（单位：s）之间具有的关系为，则小球从飞出到落地所用的时间为( )s．A.1B.2C.4D.8答案：C解题思路：根据题意，令h=0得，，∴解得，，即小球从飞出到落地所用的时间为4s试题难度：三颗星知识点：略4.汽车刹车后行驶的距离s（单位：米）关于行驶的时间t（单位：秒）的函数解析式为（b为常数）．已知t=时，s=6，则汽车刹车后行驶的最大距离为( ) A.米 B.8米C.米D.10米答案：C解题思路：根据题意，t=时，s=6代入得，，解得，b=15∴函数解析式为，∴当时，s取得最大值，此时即汽车刹车后行驶的最大距离为米试题难度：三颗星知识点：略5.如图，隧道的截面是抛物线，可以表示为，该隧道内设双行道，限高为3m，那么每条行道宽是( )A.不大于4mB.恰好4mC.不小于4mD.大于4m，小于8m答案：A解题思路：由题意，把代入中得，．由于该隧道内设双行道，所以每条行道宽应不大于4m．试题难度：三颗星知识点：略6.有一座抛物线型拱桥，正常水位时桥下水面宽度为20米，拱顶距离水面4米，建立如图所示的平面直角坐标系，若正常水位时，桥下水深6米．为保证过往船只顺利航行，桥下水面宽度不得小于18米，则当水深超过( )米时，就会影响过往船只的顺利航行．A.2.76米B.6.76米C.6米D.7米答案：B解题思路：1．解题要点①理解题意，建立数学模型将题目中的数据转化为图中对应的线段长，确定关键点坐标，求出抛物线解析式．观察图形，抛物线的顶点为(0，0)，由题意，抛物线过点(10，-4)，故可求出抛物线的解析式．②明确目标及判断标准，利用二次函数图象性质求解要求影响过往船只顺利航行的水深，可先分析临界状态，即分析当水面宽度为18米时的水深．由二次函数的对称性，可转化为分析当x=9时的水深．首先可得对应的y值，结合拱顶到水底的总距离为6+4=10，可求出保证过往船只顺利航行的临界水深．③求解验证，回归实际2．解题过程设该抛物线的解析式为，由题意得，抛物线过点(10，-4)，代入解析式得，∴，∴该抛物线的解析式为．令x=9，可得y=-3.24，此时水深为6+4-3.24=6.76米，即桥下水深6.76米时正好可以保证过往船只顺利航行，所以当水深超过6.76米时就会影响过往船只的顺利航行．试题难度：三颗星知识点：略7.你知道吗？平时我们在跳大绳时，绳甩到最高处的形状可近似地看作抛物线．如图所示，正在甩绳的甲、乙两名学生拿绳的手间距为4m，距地面均为1m，学生丙、丁分别站在距甲拿绳的手水平距离1m，2.5m处，绳子在甩到最高处时刚好通过他们的头顶．已知学生丙的身高是1.5m，则学生丁的身高为（建立的平面直角坐标系如图所示）( )A.1.5mB.1.625mC.1.66mD.1.67m答案：B解题思路：设抛物线的解析式为，由题意，抛物线过点(-1，1)，(3，1)，(0，1.5)，∴解得，，∴．当时，，即学生丁的身高是1.625m．试题难度：三颗星知识点：略8.某公园草坪的防护栏由100段形状相同的抛物线型构件组成．如图，为了牢固起见，每段护栏需要间距0.4m加设一根不锈钢的支柱，若防护栏的最高点距底部0.5m，则这条防护栏需要不锈钢支柱的总长度至少为( )A.1.6mB.80mC.160mD.0.8m答案：C解题思路：建立如图所示的坐标系：设抛物线的解析式为，由题意得B(0，0.5)，C(1，0)，∴，∴，∴抛物线的解析式为．当时；当时．∴（米），∴这条防护栏需要不锈钢支柱的总长度至少为1.6×100=160（米）．试题难度：三颗星知识点：略。

抛物线基础练习题(基础有梯度)精编版

抛物线基础练习题一. 选择题1．抛物线212y x =的准线方程是A.3x =B. 3x =-C. 3y =D. 3y =- 2．若直线10ax y -+=经过抛物线24y x =的焦点，则实数a = A.1 B.2 C. 1- D. 2- 3．抛物线22y x =-和22y x =-的焦点坐标分别是A.1,08⎛⎫- ⎪⎝⎭ 和10,2⎛⎫- ⎪⎝⎭B. 10,8⎛⎫- ⎪⎝⎭ 和1,02⎛⎫- ⎪⎝⎭ C. 1,02⎛⎫- ⎪⎝⎭和10,8⎛⎫- ⎪⎝⎭ D. 10,2⎛⎫- ⎪⎝⎭和1,08⎛⎫- ⎪⎝⎭4．若抛物线22y px =的焦点与椭圆22162x y +=的右焦点重合，则p 的值为 A ．2- B ．2 C ．4- D ．45．若双曲线2221613x y p-=的左焦点在抛物线22y px =的准线上，则p 的值为A ．2B ．3C ．4D ．6．设椭圆22221(00)x y m n m n +=>>，的右焦点与抛物线28y x =的焦点相同，离心率为12，则此椭圆的方程为A ．2211216x y +=B ．2211612x y += C ．2214864x y += D ．2216448x y += 7．若点P 是抛物线22y x =上的一个动点，则点P 到点（0，2）的距离与P 到该抛物线准线的距离之和的最小值为A B ．3 C D ．928．已知直线1:4360l x y -+=和2:1l x =-，抛物线24y x =上一动点P 到1l 和2l 的距离之和的最小值是 A ．115B ．3C ．2D ．37169．已知点P 在24y x =上，那么点P 到点(21)Q -，的距离与点P 到抛物线焦点距离之和取得最小值时，点P 的坐标为A ．114⎛⎫- ⎪⎝⎭，B ．114⎛⎫⎪⎝⎭， C ．(12)， D ．(12)-，10．已知22y px =的焦点为F ，点111222()()P x y P x y ，，，，333()P x y ，在抛物线上，且2132x x x =+，则Ａ.123FP FP FP +=Ｂ.222123FP FP FP +=Ｃ.2132FP FP FP =+ Ｄ.2213FPFP FP =⋅ 11．连结抛物线24x y =的焦点F 与点(1,0)M 所得线段与抛物线交于点A ，设点O 为坐标原点，则三角形OAM 的面积为A ．1-B ．32- C ．1D ．3212．已知直线(2)(0)y k x k =+>与抛物线2:8C y x =相交于A 、B 两点，F 为C 的焦点，若2FA FB =，则k =A ．13B ．3C ．23D ．313．过点(1,0)-作抛物线21y x x =++的切线，则其中一条切线方程是A ．220x y ++=B ．330x y -+=C ．10x y ++=D ．10x y -+=14．设P 为曲线2:23C y x x =++上一点，且曲线C 在点P 处切线倾斜角的范围是[0,]4π，则点P 横坐标的取值范围是A ．1[1,]2--B ．[1,0]-C ．[0,1]D ．1[,1]215．抛物线2y x =-上的点到直线4380x y +-=距离的最小值为 A ．43B ．75 C ．85D ．316．设抛物线24x y =的焦点为F ，A 、B 、C 为该抛物线上三点，若0FA FB FC ++=，则FA +FB +FC =A ．9B ．6C ．4D ．317．设O 是坐标原点,F 是22(0)y px p =>的焦点,A 是抛物线上的点,FA 与x 轴正向的夹角为60,则OA =A ．214pB ．2C pD ．1336p18．已知抛物线的准线方程为20x y +-=，焦点是(5,5)F ，则抛物线的顶点坐标是.(3,5)A B ．(5,3)C ．(2,2)D ．(3,3)二. 填空题19．若抛物线顶点是坐标原点,焦点坐标是()2,0F -,则抛物线方程是 20．若抛物线顶点是坐标原点,准线方程是()0y m m =≠,则抛物线方程是 21．若点P 到直线1x =-的距离比它到点(20)，的距离小1，则点P 的轨迹方程为22．已知动圆过定点,02p ⎛⎫⎪⎝⎭，且与直线2p x =-相切，其中0p >.则动圆圆心C 的轨迹的方程是23．与圆0422=-+x y x 外切且与y 轴相切的动圆的圆心的轨迹方程是 24．抛物线2y ax =的准线方程是2y =,则a =25．在抛物线22y px =上,横坐标为4的点到焦点的距离为5,则p =26．已知抛物线21y ax =-的焦点是坐标原点，则以抛物线与两坐标轴的三个交点为顶点的三角形面积为27．已知F 是抛物线24C y x =：的焦点，A B ，是C 上的两个点，线段AB 的中点为(22)M ，，则ABF =△S ．28．已知圆C 的圆心与抛物线24y x =的焦点关于直线y x =对称，直线4320x y --=与圆C 相交于A B ，两点，若6AB =，则圆C 的方程为三. 解答题29. 在ABC ∆中，角C B A ,,所对边分别为c b a ,,，已知,2,32==c a bc B A 2cot tan 1=⋅+，求ABC ∆的面积S.30．为拉动经济增长，某市决定新建一批重点工程，分为基础设施工程、民生工程和产业建设工程三类。