土木工程制图-点线面投影篇6教学提纲
点线面投影教案

者用于画多面正投影图。
◆直线段和平面形的投影特性
一、直线段的投影特性
线段的投影,由线段上一系列点的投影决定。
由于两平面的P与H的交线ab必定为直线,所以直线的投影一般
仍是直线。线段上其它点的投影,也必定位于由此两端点所决定的线段投影上。
线段对于一个投影面的相对位置有:平行、倾斜、垂直三种情况,其投影特性如下:
画图时,对于投影面平行线,应先画它所平行的投影面上的那个投影(反映实长的斜线)
3、投影面垂直线
垂直一个投影面的直线,称为投影面垂直线。垂直于H面的称为铅垂
线,垂直于V面的称为正垂线,垂直于W面的称为侧垂线。
P、78表3—2列举了几种投影面垂直线的投影图例及其投影特征。
三、两直线的相对位置
两直线的相对位置有平行、相交、交叉三种情况。前两种统称为共面直线,交叉位置的两直线则称为异面直线。
由前向后投射在正面(V)上所得的视图叫主视图,由上向下投射在水平面(H)面上所得的视图叫俯视图,由左向右投射在侧面(W)上所得的视图叫左视图。把这三个视图按正确的投影关系配置的视图,常称为三面视图或三视图。
3、投影面的展开
为了把三面视图画在同一张图纸上,必须把三个互相垂直相交的投影
面展开摊平成一个平面。其方法如下图所示,正面(V)保持不动,水平面(H)绕X轴向下旋转900与正面(V)成一平面,侧面(W)绕Z轴向右旋转900,也与正面(V)成一平面,展开后三个投影面就在同一图纸平面上。
点的投影规律:
点的相邻两个投影的连线,必定垂直投影轴。
点的投影到投影轴的各段投影连线长度,分别等于点到三个投影面的距离,而且两两相等。
点是最基本的几何元素,以上两点投影规律不但为画和读点的投影图所依据,也为今后各种图示、读图以及图解问题所应用。
土木工程制图第三章点-直线和平面的投影PPT课件

(3)投影面垂直线的投影特点为:在它所垂直的投 影面上的投影积聚为一点,另外两个投影垂直 于相应的投影轴,如图3.15所示。
可编辑课件PPT
24
投影面垂直线
土木工程制图
ax
a●
解法二: 用圆规直接量 取aaz=aax
a● ax
a●
az
a
●
可编辑课件PPT
7
例2:已知点的两面投影,求第三 投影,如下图所示。
土木工程制图
(a) 已知
(b) 作图
分析:因为根据点的任意可编两辑面课件投PPT影可以求出第三投影。 8
四、特殊位置的点
土木工程制图
注意:A点的侧面投影a"应在OYW轴上,C点的水平投影
(b) 正平线
21
(c) 侧平线
投影面平行线投影特性
土木工程制图
水平线
a b Z a
Xa β γ b YH
实长
实长
b b α
YW X
b
正平线
a Z a
γ
b
侧平线
a
Z a
β
b
α
YW X a
a
b
YH
YH
与H面的夹角:α
实长
b
YW
与V面的夹角:β
投影特性
与W面的夹角:γ
1)在其平行的那个投影面上的投影反映实长, 并反映直线与另两投影面的真实倾角。
O b
a AB实长
△Z
△Z
A0 a′
OX
B0
a
YH
土木工程制图-点线面投影篇1教学提纲

二,点在两投影面体系中的投影
V
1 两投影面体系(two view system)
的建立
X
ⅡⅠ Ⅲ
O
◆正面投影面(vertical projection plane) Ⅳ H
(简称正面或V面)
◆水平投影面(horizontal projection
plane) (简称水平面或H面)
两投影面体系
◆投影轴(projection axis)
V a
●
X ax
Z
az
A
●
O
● a W
a● H
ay Y
① aa⊥OX轴 aa⊥OZ轴 ② aax= aaz =Aa(A到V面的距离)
aay= aaz =Aa(A到W面的距离) aax= aay =Aa(A到H面的距离)
例1:已知点的两个投影,求第三投影。
解法一:
a●
Z az ● a
解法二:
a●
Z az ●a
a ● b ●
Z a
●
b
●
o
Y
a●
B点在A点
之右、之前、 之下
●
b
Y
例4:已知点A(12,8,10),点B在点A的下方
5mm、左0 mm、前0 mm,试完成点B的投影。
分析:点 B 在点 A 的正下方 5 mm,
即点 B(12,8,5)。
Z
a'
az a”
5 b'
X
ax
b”
aOYW
YW
a ≡b
aYH
如何根据点的二面投影求第三面投影
三.两点间的相对位置 四.重影点及可见性
作业
T3-1,2,3,4
画法几何与土木建筑制图 第6章 投影变换

b d c
b d c
b1
a1(d1)
c1
4、 投影面垂直面变换为投影面平行面
换H面
正垂面
“水平面”(实形)
换V面
b
铅垂面
“正平面”(实形)
V V1
a1
X1
b1
c1
A a
b
a
B
V X
a
H
c
C
X
a
b(c)
H
c
b(c) c1
b1
a1
实形
5、 一般位置线变换为投影面垂直线:二次换面
b a
a2 (b2) H2
(2)轨迹圆在旋转轴所平行面上的投影,为平行于投影轴的直线。
三、 换面法的投影规律
1. 换面法的投影规律(1)以点的一次变换为例-替换V面
替换投影面
V a
新投影面
V a 替换投影
A
a1 V1
X ax
新投影
旧轴
X ax
新投影
a1
a
ax1
X1 H
a
ax1
保留投影面
H
保留投影
新轴
X1
新投影到不变投影连线垂直于新投影轴:a1a ⊥ X1
新投影到新投影轴的距离等于旧投影到旧投影轴的距
V1称为新投影面;V称为被更换的投影面;H称为被保留的 投影面。 X1称为新投影轴;X称为被更换的投影轴。
二、 新投影面的选择原则
V1
a1
X1
b1
c1
A a
V
b
B
a
c
C
b(c) H
V1∥ABC
V1┴H
新投影面的选择必须符合以下两个基本条件: (1) 新投影面必须和空间几何元素处于有利解题的位置(平行或垂直) (2) 新投影面必须垂直于于原投影体系中的一个被保留的投影面。
第三讲点线面的投影

第三讲点、线、面的投影(6学时)主要内容: 1.点的投影;(2学时)2.直线的投影;(3学时)(1)直线对投影面的相对位置及投影特性;(2)直角三角形法求一般位置线的实长及对投影面倾角;(3)直线上的点/点分割线段成定比;(4)两直线的相对位置,直角投影定理。
3.平面的投影;(1学时)(1)平面的表示法与投影特性(2)平面上的点和线教学目的: 1.掌握点线面在三面投影体系中的正投影规律;2.掌握点直面在第一角投影中各种位置的投影特性和作图方法;3.掌握直线对投影面的倾角、线段实长和平面图形实形的求法。
学时分配: 6学时(理论学时)教学方式:多媒体教学与普通教学结合。
第一节点的投影(2学时)一.点的二面投影1.二面投影体系的建立及点的二面投影点是形体最基本的元素。
在几何学中无大小、薄厚、宽窄,只占有位置。
空间点用大写字母表示,投影点用小写字母表示。
如图3-1所示,设立一个投影面P,则A1、 A2、 A3点在投影面P上的正投影是唯一的。
但反过来,若知道了点的一个投影,却不能确定点的空间位置(缺少一个坐标)。
因此要确定一个点的空间位置,只有一个投影是不够的。
如图3-2所示,设立两个互相垂直的投影面正立投影面V (也称正面或V 面)、水平投影面H (也称水平面或H 面),从而构成二投影面体系。
V 面和H 面的交线OX 称为投影轴。
A 点的在V 面上的投影称为A 点的正面投影或A 点的正投影、A 点的V 投影,用a’表示。
A 点的在H 面上的投影称为A 点的水平投影或A 点的H 投影,用a 表示。
我们需要把这种空间关系在一种图纸上(一个平面上)表达出来。
保持V 面不动,H 面绕OX 轴向下旋转90º直至与V 面重合,从而得到点的二面投影图。
为简便起见,投影图中投影面的边框不必画出,如图3-3所示。
在点的二面投影体系中,X 、Y 、Z 三个坐标均能体现,故点的二面投影就唯一确立了点在空间的相对位置(相对二面投影体系)。
土木工程制图平面立体的投影及线面投影分析精品PPT课件

(1)水平投影∥OYH ;(2)正面投影∥OZ;(3)侧面投影反映线 段实长和对H、V的倾角。
第3章 平面立体的投影及线面投影分析
16
§3.2 立体上直线的投影分析
投影面平行线的投影特性归纳为: 平行于哪个投影面的直线,在它所平行的那个投影面上的 投影反映线段的实长和对另两投影面的倾角,另外的两投影则 平行于相应的投影轴。
不可能三投影都出现平行。
第3章 平面立体的投影及线面投影分析
35
§3.2 立体上直线的投影分析
四、两直线间的相对几何关系
3. 交错 交错直线同面投影的交点,是二交错直线上一对重影点的投影。
第3章 平面立体的投影及线面投影分析
36
§3.2 立体上直线的投影分析
四、两直线间的相对几何关系
3. 交错 交错直线同面投影的交点,是二交错直线上一对重影点的投影。 重影点投影的可见性由它们与投影面的距离判定。
来 无意,也不可能设计出来能为大家“统一”使用的电子讲稿。
由 于各校的专业实际、学时、学生水平、教学条件以及教师的教 学风格的不同,必然对演示文稿会有不同的要求,期望有不同 的风格。本套演示文稿仅仅是提供一种借鉴,做了一些基本的 准备,使用者在使用前一定要根据自己的实际情况对其做个性 化处理:删除本页的声明,调整内容结构,改进编排顺序,简 化、削减文稿中的文字份量,加强图形、图片、视频、动画的 表现效果,充实你的精彩表演方法,把它改造成符合你自己需 要的、能更好展示教学水平的、表演技艺出众的实用化作品, 以提高课堂教学效果。第祝3你章 圆平面满立成体功的投!影及线面投影分析
单击开始自动演播 的辅助投影面V1
ab∥cd , a'b'∥c'd' , a"b"∥c"d"
土木工程制图-点线面投影篇7教学提纲

a'
5' m'
3(' 4')
1'
k'
2'
c'
n'
X
b' m c O 作 图
a
( 2)5
4k
13
PH n
b
① 过mn作铅垂面 ② 求铅垂面与ABC交线 ③求交线与MN交点K ④判别可见性
利用重影点
根据重影点Ⅲ、Ⅳ可判别出正面投影的可见性;
根据重影点Ⅱ、Ⅴ可判别出水平投影的可见性。
可见性判断
a'
5' m
2)自点S作SD △ABC。
3)过点S任作一直线SE,与SD构成一平面即为所求。
例:过点S作一平面垂直于平面△ABC。
a'
c'
空间及投影分析
平面ABC是一般位置
b' s'
b
平面,过点s'作正平
线垂直于平面内一般
位置直线AC的 投影
a'c',再过点s作水平
c
线垂直于ac,则两相
交直线所示平面即为
a
s
e
O
3
f
k
m
d
b
2
c
4
作图: • 利用辅助面法求DE与△ABC的交点K • 利用辅助面法求DF与△ABC的交点M • 连接KM,即△ABC与△DEF的交线
(1)线面交点法
b'
e'
2'
PV
a'(1') 5' k' d'
X
a1
m' 6' 4' 3' 7'
土木工程制图第4章 点、线、面的投影

a′ ′ b′ ′ d′ ′ c′ ′ c b d
x
a
对于一般位置直 线,只要有两个同面 投影互相平行, 投影互相平行,空间 两直线就平行。 两直线就平行。
结论: 结论:AB//CD
例2:判断图中两条直线是否平行。 :判断图中两条直线是否平行。
②
c′ ′ a′ ′ d′ ′ c b d a b′ ′ b″ ″ c″ ″ a″ ″ d″ ″
γ
B a″ b″ a′ X
α
α γ
A
a
b
a
b YH
投影特性: 1. ab || OX ; a″ b″|| OZ 2. a′ b′=AB 3. 反映α、γ角的真实大小
(3)侧平线—只平行于侧面投影面的直线
a′ a′ A b′ a″ b′ X O a b″ B b b YH Z a″
β α
b″
β α
a
●
d′ ′
两直线相交吗? 为什么? 两直线相交吗? 为什么? 同名投影可能相交, ★ 同名投影可能相交, 交点” 但 “交点”不符合空间 一个点的投影规律。 一个点的投影规律。 ★ “交点”是两直线上 交点” 交点 重影点的投影, 的一 对重影点的投影, 用其可帮助判断两直线 的空间位置。 的空间位置。
b″ Y
投影特性:1. a b、 a′b′、a″ b″均小于实长 2. a b、a′b′、a″ b″均倾斜于投影轴 3.不反映 α 、 β 、γ 实角
一般位置直线的投影特点: 一般位置直线的投影特点:
三个投影都倾斜于投影轴; 三个投影都倾斜于投影轴; 倾斜于投影轴 各投影均不反映实长。 各投影均不反映实长。 不反映实长
a a b
b YH
投影特性: 1. a″b″ 积聚 成一点 2. ab ⊥ OYH ; a′b′⊥ OZ 3. ab = a′b′ =AB
土木工程制图第6章立体的投影

6.5 平面与立体相截——
图6-21 求圆柱体被单一平截面切后所得切割体的投影
6.5 平面与立体相截——
6.5.3 多个平截面下的切割体
求基本体被多个平截面切后的投影的作图步骤如下: (1)求每个平截面下的截交线。
(2)画出多个平截面间的交线,交线的两端点在体表
6.5 平面与立体相截——
图6-16 求直线与三棱锥贯穿点的投影
6.5 平面与立体相截——
6.5.1 切割体概述
切割体是基本体经过切割后形成的体。切割的面称 为截面,可以是平截面或曲截面。基本体经过切割后在 其表面产生的交线称为截交线。截交线具有共有性,既 在体的表面上,又在截面上。截交线还具有封闭性。图 6-18所示为平截面和圆柱形截面下的截交线。本节仅介 绍截面为平截面的情况。
(3)判断可见性。将可见段画成实线,不可见段画成虚线。
6.3 基本体表面的线
图6-11 求圆柱表面线的投影
6.4 直线与立体相交——贯穿点
6.4.1 直线与直柱体相交
【例6-5】
如图6-14(a)所示,求直线AB 【解】分析:因为直线经过两个侧面,所以与三棱柱有两个交点。由 于柱的侧面投影具有积聚性,两交点在积聚投影面上的投影在三边形 上,因此可以直接得到贯穿点的水平投影,而且该两点也在直线上, 故可直接投到直线的正面投影上。作图步骤如图6-14(b) (1)确定贯穿点的水平投影1、2。在积聚投影面上的求出各点投影。 (2)在直线上求出贯穿点的正面投影1′、2′ (3) a′1′、b′2′画成实线。
②重影性。三角形的每个线框都是 锥体侧面的可见表面投影和不可见 表面投影的重合。底面多边形是底 面和所有侧面投影的重合。此时, 在与底面平行的投影面上,侧面都 是可见的,底面是不可见的。
画法几何与土木工程制图 第2章 点、线、面的投影
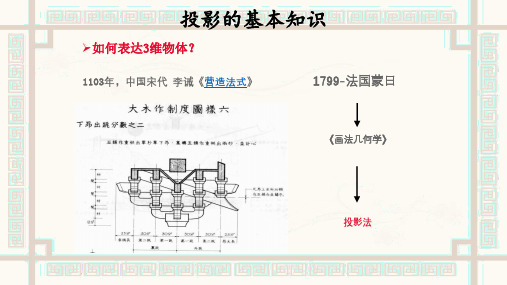
平面的投影
二、平面的分类
正垂面(⊥V面)
αγ γ α
平面的投影
二、平面的分类
铅垂面(⊥H面)
β
γ
β γ
平面的投影
二、平面的分类
侧垂面(⊥W面)
β α
β α
投影面垂直面的投影特性
平面的投影
在其垂直的投影面上的投影积聚为一线段,且反映与另两 投影面的倾角的真实大小
在其余两个投影面上的投影都是其类似形。
二、平面的分类
正平面(//V面)
平面的投影
′
′
′
′
″″
″″
′
′
′
′
″″ ″″
二、平面的分类
水平面(//H面)
平面的投影
′′
′′ ″″
″″
′′
′′
″″ ″ ″
平面的投影
二、平面的分类
侧平面(//W面)
′ ′ ′′
″
″
″
″
′ ′ ′′
″ ″
″″
平面的投影
投影面平行面的投影特性
H-水平投影 a V-正面投影 a ' W-侧面投影 a''
投影面展开过程
点的投影
3.点的投影规律
点的正面投影和水平投影的连线垂直于OX轴。
a' a⊥OX
点的正面投影和侧面投影的连线垂直于OZ轴。
a' a" ⊥OZ
点的水平投影到OX轴的距离等于点的侧面投影到OZ轴的距离。
aax =a" az
点的投影
′
′
′
′ ′
′
一、平面的表示法
2.迹线表示法
平面的投影
土木工程制图-第二章点、直线、平面的投影

平行直线的投影
例题
33
1.平行二直线的投影
34
[例题7] 给出平行四边形ABDC的两条边AB、AC的H、V投影,试完成ABDC的投影。 d d'
三、两交叉直线
交叉直线的投影
交叉二直线重影点投影的可见性判断
例题
36
1.交叉二直线的投影
凡不满足平行和相交条件的直线为交叉二直线。
一、 点的投影
a
a (b)
(1) 点的正投影是点,在过该点垂直于投影面的投射线的垂足处; (2) 如果两点位于某一投影面的同一投射线上,则此两点在该投影面上的投影必定重合。
3
点在三投影面体系中的投影
点的三面投影 点的三面投影规律 三面投影的投影关系 点的坐标 例题
1.点的三面投影
O
a'
a
a"
e"(f")
c'(d')
15
2.2 直线的投影
3
例题
2
1
直线的投影
直线的投影特性
16
一、直线的投影
a
c
b
(a)
(b)
B
a(c)(b)
(c)
c
a
b
17
一般位置直线
01
投影面的平行线 投影面的垂直线 例题
01
直线的投影特性
01
1、一般位置直线的投影特性
b
b'
a"
b"
a
a'
A
B
YW
19
2、投影面平行线的投影特性
1
2
d
d'
武汉理工大学土木工程制图第六、七章建筑形体的投影(二)

H投影为一
d
圆,另两投
影为三角形a。
s
b′ d″
c″
a″ b″ S
b
D
B
c
A
CV
(4)表面上取点: 素线法
已知a′, 求a、a″
s′
纬圆法 s″
素线法 a′
a″
S
1′
宽
s
a 1
宽
A
Ⅰ
纬圆法:
已知b′, 求b、b″
1′ b′
宽
1s
b
b″
S
宽
B
例:已知A、B的一个投影,求另两投影。
作图如下:
A为特殊点
例1:补全圆球被切后的H、W投影。
6` 中点 4`5` a`b`
2`3`7`8`
1`
78=1`6` 3 8 5 b
1
6
2
a
74
85```b```3``6``
a`` 作图:截交线为椭圆
4`` 7`` 2``
1、求特殊点: ⅠⅡⅢⅣⅤⅥ
1``
2、求椭圆长轴
上的ⅦⅧ
3、求一般点:
A、B
4、将各点连
成光滑的曲线
已知:
a′、b″, 求另两
投影。
AO
b
Y
a
已知: a′,求另外两投影。 a′
作辅助正平圆
Y
a″
Y
a
二、平面与曲面立体相交:
1、圆柱被切:下列三种情况
圆柱上的截交线
截平面 的位置
倾斜于圆柱轴线
垂直于圆柱轴线
截交线 的形状
椭圆
圆
立
体
图
平行于圆柱轴线 两条直素线
土木工程制图复习提纲

土木工程制图复习提纲1、点的投影重点掌握点的投影规律作图及其应用。
应用——涉及立体的截交线和相贯线上取点作图方法2、直线的投影•重点掌握特殊位置直线(投影面的平行线和投影面的垂直线)的投影特性及其运用;•了解一般位置直线的真长与倾角作图方法(直角三角形法)及其运用;•了解直线上点的从属性与定比性及其运用;•重点掌握两直线平行、相交、交叉的投影特性及其运用;•重点掌握一边平行于投影面的直角投影规律及其运用.3、平面的投影•重点掌握特殊位置平面的投影特性;•重点掌握平面上取点、取线的方法;•了解平面倾角与平面上最大倾斜线的关系及其应用;4、线面相对位置•重点掌握特殊位置元素间的平行、相交、垂直相交的作图方法。
(而对一般位置元素间平行、相交、垂直问题可结合投影变换方法予以解决)5、投影变换•掌握直线、平面变换的基本作图方法;•重点掌握投影变换的运用。
6、曲线、曲面和立体的投影•重点掌握基本几何形体投影图的阅读与画法;•重点掌握基本几何形体表面上点、线段的投影作图方法及其点、线段的可见性. 7、平面与立体相交•重点掌握平面立体、回转体的截交线投影作图。
掌握截交线的空间分析与投影分析;空间分析过程就是要分析截交线的形状,平面立体的截交线形状为平面多边形,曲面立体截交线形状通常情况下为平面曲线,特殊情况下可以含有直线段。
投影分析过程就是要明确截交线的哪个投影已知,而所要求解的是截交线的哪个投影。
掌握截交线的投影作图方法;对平面立体截交线而言,若截交线方向不明确,可用线面交点法求解作图,若截交线与立体上的某棱线或底面平行则可用面面交线法求解作图。
对曲面立体截交线而言,若截交线投影为非圆曲线时,可利用曲面立体表面取点方法,作出足够多的公有点后光滑连线获得;若截交线投影为圆、圆弧或直线段,可利用尺规作图求解。
掌握截交线投影作图的基本步骤⑴空间分析;⑵投影分析;⑶投影作图;⑷整理立体图线8、两立体相交对两平面立体的相贯线,其分析方法和投影作图与多个截平面截切平面立体类型相同,相贯线为空间多边形;对平面立体与曲面立体相贯线,其分析方法和投影作图与多个截平面截切曲面立体类型相同,相贯线为多条平面曲线组成的空间曲线;对两曲面立体相贯线,其相贯线为空间曲线,首先应作出相贯线上足够多的公有点(特殊点和一般点),然后光滑连线。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
⒈ 投影面垂直面 V 在它垂直的投影面上
的投影积聚成直线。该直 X 线与投影轴的夹角反映空 间平面与另外两投影面夹 角的大小。
Z
βγ
oW
H
Y
另外两个投影面上的投影有类似性。
一、各种位置面的投影特性
⒉ 投影面平行面
V
在它所平行的投影面上 的投影反映实形。
A
W
另两个投影面上的投影
分别积聚成与相应的投影轴
H
平行的直线。
一、各种位置面的投影特性
Z
⒊ 一般位置平面 V
三个投影都类似。
X
O
W
H Y
与投影轴平行
a b
c
a b
与投影轴 a 倾斜
c a
水平面
b c c
b
铅垂面
二、属于平面的点和线
1、面上作线的方法:
面上作线先找点
解法一
m a
m a
b n c
b nc
根据定理二
解法二
d
a'
c'
交即直s线d/,/a则b、两平
e'
面平s行e/。/ac
b
d
s´d´//a´b´,
s´e´//a´c´,
a
s
相交直线SD和SE
所确定的平面即
c
为所求。
e
例2:判别平面△ABC与四边形DEFG是否平行。
e'
d' X
d
e
f'
m'
b'
n'
g' a'
g a
n
m f
b
分析:在任一平 c' 面线面作dd内 , 内图′′mn′′作 若 也/:///两 在 能aa′′bc相 另 作′′ 交 一 出直 平 与
之再对作应出平其行水的平两 O相投交影直d线m和,d则n。两 c 平由面于平d行m/。/ab、
dn//ac 所以△ABC与四 边形DEFG平行。
例3:判断下列平面与平面 P 是否平行。
PV
QV
PH
QH
(a)
(b)
(c)
(d)
P∥aபைடு நூலகம்c
§ 3-2 相交问题
直线与平面相交 平面与平面相交
u直线与平面相交
bk a
n
平面ABC是一铅垂
面,其水平投影积聚成
一条直线,该直线与mn
的交点即为K点的水平
c
投影。
用线
作图
上取
c ① 求交点
点法
n ② 判别可见性 直观法
由水平投影可知,KN段 在平面前,故正面投影上
kn为可见。
⑵ 直线为特殊位置
空间及投影分析
交点是 分界点
a
a
b m
直线MN为铅垂线,其水平
k●
投影积聚成一个点,故交点K
例3:过点M作一直线与 平面平行。
c'
b'
m'
●
若平面为特殊位置平
a'
n'
面,则直线应与该平
面的积聚投影平行。
a
c
m
●
n
b
n
n
有无数解
直线与平面平行判定:
若一直线平行于平面内任一 直线,则该直线与平面平行。
若平面为特殊位置平面,则直 线应与该平面的积聚投影平行。
例1:判断直线与平面是否平行?
b'
k'
d'
a'
c'
e'
kb d
a
e
ck 不平行de, 故直线与平面
不平行。
c
例2:判断直线与平面是否平行?
m' e' e
m
d' n' f'
平行
s'
d
f s
n
不平行
a' b'(d') c' k'
d a
k
c
b
例3:判断直线与平面是否平行?
(a)
(b)
(c)
(d)
△∥b、c、d
二、平面与平面平行
b
① 若一平面上的两相 交直线对应平行于另 一平面上的两相交直 线,则这两平面相互 平行。
§3-1 平行问题
′′
′
′
′
′
一、 直线与平面平行
几何条件
若一直线平行于某平面的一条 直线,则此直线平行于该平面。
例1:过点M作直线MN平行于平面ABC。
b
d
n
c m
a
●
b
d
n
a
m●
c
有多少解?
有无数解
例2:过M点作直线MN 平行于V 面和平面ABC。
b
正平线
d
a
c m
n
●
c
a
d
m●
n
b
唯一解
H
行,且平行于平面的同面迹线
Y
作属于平面的投影面平行线时,应先作 平行于投影轴的那个投影,再按补作属 于平面的直线所缺投影作出其它投影。
王雷
§3-1 平行问题
线、面相对位置包括平行、相交(垂直)。
平行问题
包 括
直线与平面平行 平面与平面平行
一、 直线与平面平行
几何条件
若一直线平行于某平面的一条 直线,则此直线平行于该平面。
b′
n′
●
e′
h′ ●m′
c′
f′
b
n ●
d(e)
a ● h(f) m c
a
b
n ●
d(e)
m● h(f) c
同面的异侧,异面的同侧, 可见性相反。
(2)两平面互交
b
f
m ●
d
a
k ●
n
●
e
c
f
b
一、投影积聚性法
当直线或平面垂直投影面时,利用其 投影积聚性来求解的方法。
• 积聚性投影的出现,相当于共有元素的一 个投影已知,就使问题的性质转化为面上 找点或线上找点的问题。
• 可见性一般能直接看出,不必另行作图判断。
1. 线、面相交
⑴ 平面为特殊位置
空间及投影分析
交点是
b
分界点
k ●
a
m
m
●
c 的水平投影也积聚在该点上。
●
n 1(2)
作图
用面上
b m(nk)● 2
●
1
① 求交点
取点法
c ② 判别可见性 利用重影点
点Ⅰ位于平面上,在前;
点Ⅱ位于MN上,在后。
故k2为不可见。
⒉ 两平面相交
⑴ 一个平面为特殊位置 空间及投影分析
d′ a′
h′
平面DEFH是一铅垂
交线是 面,它的水平投影有积
b
c a
b d
a
c
根据定理三
二、属于平面的点和线
2、面上取点的方法:
首先面上取线、 然后线上找点
①
bd
●k
c
a
b
d
a
●k
c
②
a a
b
k●
c
k● b c
在面内作辅助线求解 利用平面的积聚性求解
三、属于平面的投影面平行线
V
在任意平面上都存在着无数 条水平线、正平线、侧平线
X
Z
o
W
平行于同一投影面的直线彼此平
交点是直线与平面的共有点。
●
●
要讨论的问题:
Ø 求交点。 Ø 判别可见性,即判别两者之间的相互遮挡关系。
§ 3-2 相交问题
u平面与平面相交
直线与平面相交 平面与平面相交
d'
h′
交线为直线,是两平面的 共有线。
要讨论的问题:
b′
n● ′
e′
● m′
c′
f′
Ø 求交线。(共有点)
Ø 判别可见性,即判别两者之间的相互遮挡关系。
② 若两投影面垂直面 相互平行,则它们具 有积聚性的那组投影 必相互平行。
c d a
c
a
d
b
b d
a c
e
d
b
ac
e
e f
f e f
h h f
例1: 已知平面△ABC与面外一点S,试过点S 作一平面与平面△ABC平行。
d' 分作析图::过点作两
b'
相过交点直S作线直对线应平
s'
行SD于//平AB面,S内E/两/B相C.
m′
●
分界线 聚性,其与ac、bc的交 点m 、n 即为两个共有
b′
n′
●
点的水平投影,故mn即
c′
为交线MN的水平投影。
e′
f′
作图 ① 求交线
a
② 判别可见性
直观法
bn ● d(e)
h(f)
●
m
同面的异侧,异面的同侧
可见性相反
c
交线是可见与否分界线
d′
h′
a′
● m′
b′
n′
●
e′
c′
f′
d′
