最新线段和差的最值问题
线段和差的最值问题教学课件讲议

A
A
B
B
m
P
m P'
A
m B
A B'
m
P'
P
B
过B作关于直线m的对称点B’,连接AB’交点直线m于P,此 时PB=PB’,PA-PB最大值为AB’
应用:1、抛物线 ya2xbxc交x轴于A,B两点,交
y轴于点C, 已知抛物线的对称轴为是x 1 ,B (3 ,0 )C ,(0 , 3 )
(1)求抛物线的解析式; (2)在抛物线的对称轴上是否存在一点P,使点P 到B,C两点的距离之差最大?若存在,求出它 们之差的最大值,并求出点P的坐标,若不存在
请说明理由。
y
A
O
C
Bx
2、如图所示,直线 y 3x2 与x轴交于点C,与y轴交于点B,
点A为 y 轴正半轴上的一点,⊙A经过点B和点O,直线BC交⊙A
线段和差的最值问题
1.常见的几何最值问题有:线段最值问 题, 线段和差最值问题,周长最值问题、 面积 最值问题等;
2.几何最值问题的基本原理。 ①两点之间线段最短 ②垂线段最短 ③三角形两边之差小于第三边 ④利用函数关系求最值
一、两条线段和的最小值
已知:直线m外两点A,B,在直线m上求 一点P,使PA+PB最小;
(1)点A、B在直线m两侧:
(2)点A、B在直线同侧:
A
A
m B
m P
A
B
A
B m
B m
P
A'
例1:在△ABC中,AC=BC=2,
∠ACB=90O,D是BC边的中点,E是AB
上的一动点,则EC+ED的最小值
初中几何中线段和差的最大值与最小值典型分析(最全)

初中几何中线段和差的最大值与最小值典型分析(最全)-CAL-FENGHAI-(2020YEAR-YICAI)_JINGBIAN初中几何中线段和(差)的最值问题一、两条线段和的最小值。
基本图形解析:(对称轴为:动点所在的直线上)一)、已知两个定点:1、在一条直线m 上,求一点P ,使PA+PB 最小; (1)点A 、B 在直线m 两侧:(2)点A 、B 在直线同侧:A 、A ’ 是关于直线m 的对称点。
2、在直线m 、n 上分别找两点P 、Q ,使PA+PQ+QB 最小。
(1)两个点都在直线外侧:(2)一个点在内侧,一个点在外侧: (3)两个点都在内侧:mm A Bm B mA Bmnmnnmn(4)、台球两次碰壁模型变式一:已知点A 、B 位于直线m,n 的内侧,在直线n 、m 分别上求点D 、E 点,使得围成的四边形ADEB 周长最短.填空:最短周长=________________变式二:已知点A 位于直线m,n 的内侧, 在直线m 、n 分别上求点P 、Q 点PA+PQ+QA 周长最短.二)、一个动点,一个定点: (一)动点在直线上运动:n点B 在直线n 上运动,在直线m 上找一点P ,使PA+PB 最小(在图中画出点P 和点B ) 1、两点在直线两侧:2、两点在直线同侧:(二)动点在圆上运动点B 在⊙O 上运动,在直线m 上找一点P ,使PA+PB 最小(在图中画出点P 和点B )1、点与圆在直线两侧:2、点与圆在直线同侧:m nmnmnmmm三)、已知A 、B 是两个定点,P 、Q 是直线m 上的两个动点,P 在Q 的左侧,且PQ 间长度恒定,在直线m 上要求P 、Q 两点,使得PA+PQ+QB 的值最小。
(原理用平移知识解)(1)点A 、B 在直线m 两侧:过A 点作AC ∥m,且AC 长等于PQ 长,连接BC,交直线m 于Q,Q 向左平移PQ 长,即为P 点,此时P 、Q 即为所求的点。
线段和差的最值问题解题策略课件

高阶练习题
总结词
挑战综合应用
详细描述
高阶练习题难度较高,需要综合运用线段和 差最值问题的多种解题策略,挑战解题者的 思维深度和广度,培养综合应用能力。
06 问题拓展与思考
相关问题链接
线段和差与面积关系
探讨线段和差与面积的最值问题,如何通过线段和差来求解面积 的最值。
线段和差与其他几何量关系
研究线段和差与周长、体积等其他几何量的最值问题之间的联系。
生产制造中的应用
探讨线段和差最值问题在生产制造、工艺设计和 优化中的实际应用,如何提高生产效率和降低成 本。
THANKS
02 解题策略
代数法
通过代数运算,将问题转化为函数最值问题,利用求导或不 等式性质求解。
代数法是解决线段和差最值问题的基本方法之一。首先,将 问题中的线段长度表示为变量,然后通过代数运算,将问题 转化为一个函数最值问题。接下来,利用求导或不等式性质 ,找到函数的最值点,从而得到线段和差的最值。
几何法
详细描述
解决这类问题需要理解线段的性质和 几何定理,如勾股定理、三角形的三 边关系等。通过这些定理可以推导出 线段和差的最值条件,从而找到解决 问题的关键点。
三角形中的线段和差问题
总结词
三角形中的线段和差问题涉及到三角 形的边长和角度,需要结合三角形的 性质进行求解。
详细描述
解决这类问题需要掌握三角形的边角 关系,如正弦定理、余弦定理等。通 过这些定理可以推导出线段和差与角 度之间的关系,从而找到最值条件。
将参数方程转换为普通方程,便 于计算和比较线段长度。
05 练习题与解析
基础练习题
总结词
掌握基础概念
详细描述
基础练习题主要涉及线段和差最值问题的基本概念和简单应用,适合初学者通过练习理解和掌握基本 解题方法。
线段和差最值问题解题技巧

线段和差最值问题解题技巧
1. 嘿,你知道吗?平移线段有时就像变魔术一样神奇!比如在这个问题里,把这两条线段平移到一起,你看,是不是一下子就找到答案啦!
2. 哇塞,利用对称性质来解决线段和差最值问题,那可真是绝了呀!就像给问题找到了一把万能钥匙。
比如这个图形,通过对称,一下子就柳暗花明了呢!
3. 哎呀呀,有时候转换思维超重要的啦!别死磕一种方法呀,就像走不通的路咱就换一条呗。
像这个例子,转换一下思考角度,答案不就出来啦!
4. 嘿,当遇到难题不要慌,想想三角形三边关系呀!这就好比给你指了一条明路。
比如看到这样的条件,马上想起三边关系,难题迎刃而解咯!
5. 哇哦,构造辅助线简直就是秘密武器呀!就如同给问题搭了一座桥。
像这个情况,构造出合适的辅助线,一下子就突破难关啦!
6. 哈哈,把复杂问题简单化,不就轻松多了吗?就像把一大团乱麻理清楚。
看这个例子,简单化之后,答案显而易见呀!
7. 哟呵,关注特殊点和特殊位置呀,这可是关键呢!如同发现了宝藏的线索。
像这个情况,抓住特殊点,难题瞬间攻克啦!
8. 嘿呀,寻找等量关系也很重要呀,就像在迷宫里找到了正确的路线。
看看这个例子,一旦找到等量关系,答案就水到渠成啦!
9. 最后我想说,掌握了这些解题技巧,遇到线段和差最值问题根本不用怕呀!它们就是我们的得力助手,能让我们在数学的海洋里畅游无阻呀!。
2020年中考备考专题复习课件:线段的和(差)最值问题(共18张PPT)

线段和(差)的最值问题
一、已知两个定点,一条直线,求 直线上一点,到两定点之和最小。
方法:作其中一点关于直 线的对称点 ,连接另一 点与对称点 ,与直线的 A 交点就是所要求的点。
基本图形 : FA+FB=F+FB`=AB` 此时,和最小
A
Bm
Bm F
B`
根据:两点间线段最短
5
BD
的最小值为4
5
B
C
5
E D
C
典型题解析
4.如图,△ABC为等边三角形,AB=2,若P为△ABC内一动点,
且满足∠PAB =∠ACP,则线段PB长度的最小值为___________.
C
解析:由∠PAB =∠ACP,且 ∠PAB+∠PAC=600,可得∠P=1200, 所以P应该是在AC所对的弧上运 动。由A、P、C三点确定辅助圆, 当B、P、O三点在一条直线上时, PB长度最小,根据两点间线段最 短。
解析:此题 A、C是两定点,点P在OB上为动点, 故可作C关于OB的对称点C`,连接AC`交OB于点P.
∵OA⊥OB, ∴∠AOB=900. ∵∠AOC=600, ∴∠BOC=300. ∴∠AOC`=300 ∴∠AOC=∠C`OC=600, ∠AOC`=1200 ∴OC⊥AC` ∴∠OAC`=300,AH=HC`.
y A
解析 :由PA-PB≤AB,故取等号时,差 最大,也就是当点P与点H重合时,差最 大。
∵A(-2,3) , B(3,1),
∴AB= 52 + 22 = 29 即:PA-PB长度最大为 29
y A
B
x
O
P
H
PO
B
线段差的最大值与线段和的最小值问题
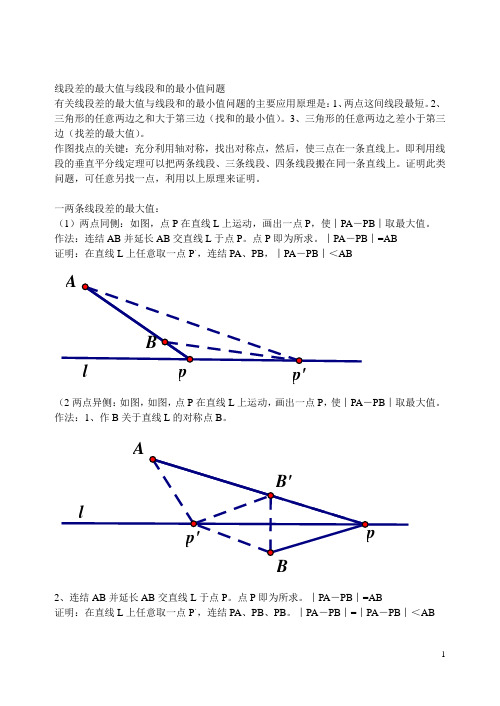
线段差的最大值与线段和的最小值问题有关线段差的最大值与线段和的最小值问题的主要应用原理是:1、两点这间线段最短。
2、三角形的任意两边之和大于第三边(找和的最小值)。
3、三角形的任意两边之差小于第三边(找差的最大值)。
作图找点的关键:充分利用轴对称,找出对称点,然后,使三点在一条直线上。
即利用线段的垂直平分线定理可以把两条线段、三条线段、四条线段搬在同一条直线上。
证明此类问题,可任意另找一点,利用以上原理来证明。
一两条线段差的最大值:(1)两点同侧:如图,点P在直线L上运动,画出一点P,使︱PA-PB︱取最大值。
作法:连结AB并延长AB交直线L于点P。
点P即为所求。
︱PA-PB︱=AB证明:在直线L上任意取一点P。
,连结PA、PB,︱PA-PB︱<ABp'(2两点异侧:如图,如图,点P在直线L上运动,画出一点P,使︱PA-PB︱取最大值。
作法:1、作B关于直线L的对称点B。
B2、连结AB并延长AB交直线L于点P。
点P即为所求。
︱PA-PB︱=AB证明:在直线L上任意取一点P。
,连结PA、PB、PB。
︱PA-PB︱=︱PA-PB︱<AB(三角形任意两边之差小于第三边)二、两条线段和的最小值问题:(1))两点同侧:如图,点P在直线L上运动,画出一点P使P A+PB取最小值。
(三角形的任意两边之和大于第三边(找和的最小值),P A+PB=AB(2)两点异侧:如图,点P在直线L上运动,画出一点P使P A+PB取最小值。
(两点之间线段最短)三、中考考点:08年林金钟老师的最后一题:如图,在矩形ABCO中,B(3,2),E(3,1),F(1,2)在X轴与Y轴上是否分别存在点M、N,使得四边形EFNM的周长最小?若存在,请求出周长的最小值,若不存在,请说明理由。
提示:EF长不变。
即求F N+NM+MF的最小值。
利用E关于X轴的对称点E,F的对称点F,把这三条线段搬到同一条直线上。
一、以正方形为载体,求线段和的最小值例1. 如图1,四边形ABCD 是正方形,边长是4,E 是BC 上一点,且CE =1,P 是对角线BD 上任一点,则PE +PC 的最小值是_____________。
线段和差极值题型
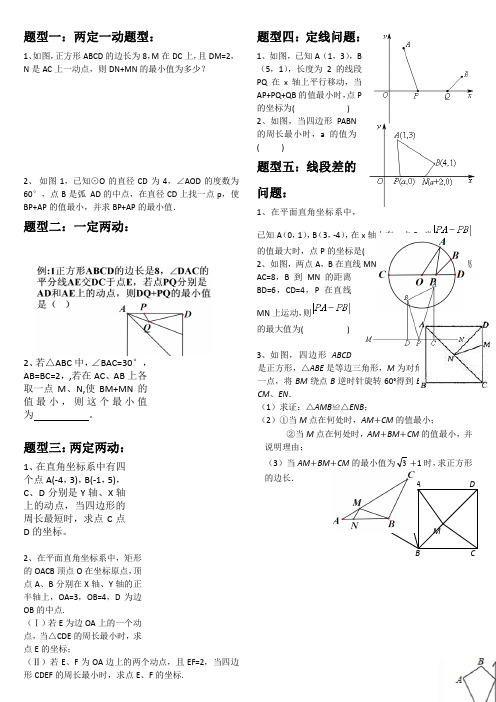
DCM A NE题型一:两定一动题型:1、如图,正方形ABCD 的边长为8,M 在DC 上,且DM=2,N 是AC 上一动点,则DN+MN 的最小值为多少?2、 如图1,已知⊙O 的直径CD 为4,∠AOD 的度数为60°,点B 是弧 AD 的中点,在直径CD 上找一点p ,使BP+AP 的值最小,并求BP+AP 的最小值.题型二:一定两动:2、若△ABC 中,∠BAC=30°,AB=BC=2,,若在AC 、AB 上各取一点M 、N,使BM+MN 的值最小,则这个最小值为。
题型三:两定两动:1、在直角坐标系中有四个点A(-4,3),B(-1,5),C 、D 分别是Y 轴、X 轴上的动点,当四边形的周长最短时,求点C 点D 的坐标。
2、在平面直角坐标系中,矩形的OACB 顶点O 在坐标原点,顶点A 、B 分别在X 轴、Y 轴的正半轴上,OA=3,OB=4,D 为边OB 的中点. (Ⅰ)若E 为边OA 上的一个动点,当△CDE 的周长最小时,求点E 的坐标;(Ⅱ)若E 、F 为OA 边上的两个动点,且EF=2,当四边形CDEF 的周长最小时,求点E 、F 的坐标.题型四:定线问题:1、如图,已知A (1,3),B (5,1),长度为2的线段PQ 在x 轴上平行移动,当AP+PQ+QB 的值最小时,点P 的坐标为( )2、如图,当四边形PABN 的周长最小时,a 的值为( )题型五:线段差的问题:1、在平面直角坐标系中,已知A (0,1),B (3,-4),在x 轴上有一点P ,当的值最大时,点P 的坐标是( )2、如图,两点A ,B 在直线MN 的同侧,A 到MN 的距离AC=8,B 到MN 的距离BD=6,CD=4,P 在直线MN 上运动,则的最大值为( )3、如图,四边形ABCD是正方形,△ABE 是等边三角形,M 为对角线BD 上任意一点,将BM 绕点B 逆时针旋转60°得到BN ,连接AM 、CM 、EN .(1)求证:△AMB ≌△ENB ;(2)①当M 点在何处时,AM +CM 的值最小;②当M 点在何处时,AM +BM +CM 的值最小,并说明理由;(3)当AM +BM +CM 的最小值为3+1时,求正方形的边长.。
中考复习之线段和差最值之费马点问题-附练习题含参考答案
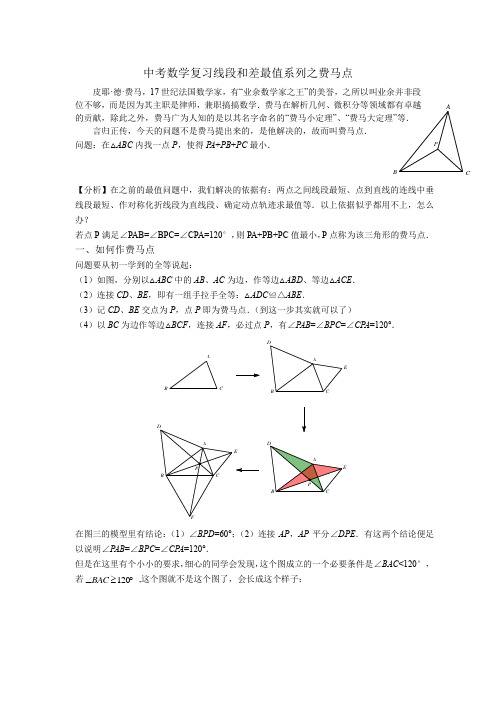
ABCP中考数学复习线段和差最值系列之费马点皮耶·德·费马,17世纪法国数学家,有“业余数学家之王”的美誉,之所以叫业余并非段位不够,而是因为其主职是律师,兼职搞搞数学.费马在解析几何、微积分等领域都有卓越的贡献,除此之外,费马广为人知的是以其名字命名的“费马小定理”、“费马大定理”等.言归正传,今天的问题不是费马提出来的,是他解决的,故而叫费马点. 问题:在△ABC 内找一点P ,使得P A +PB +PC 最小.【分析】在之前的最值问题中,我们解决的依据有:两点之间线段最短、点到直线的连线中垂线段最短、作对称化折线段为直线段、确定动点轨迹求最值等.以上依据似乎都用不上,怎么办?若点P 满足∠PAB=∠BPC=∠CPA=120°,则PA+PB+PC 值最小,P 点称为该三角形的费马点.一、如何作费马点问题要从初一学到的全等说起:(1)如图,分别以△ABC 中的AB 、AC 为边,作等边△ABD 、等边△ACE . (2)连接CD 、BE ,即有一组手拉手全等:△ADC ≌△ABE .(3)记CD 、BE 交点为P ,点P 即为费马点.(到这一步其实就可以了)(4)以BC 为边作等边△BCF ,连接AF ,必过点P ,有∠P AB =∠BPC =∠CP A =120°.在图三的模型里有结论:(1)∠BPD =60°;(2)连接AP ,AP 平分∠DPE .有这两个结论便足以说明∠P AB =∠BPC =∠CP A =120°.但是在这里有个小小的要求,细心的同学会发现,这个图成立的一个必要条件是∠BAC <120°,若120BAC ∠≥︒ ,这个图就不是这个图了,会长成这个样子:EB ACAB CDE此时CD 与BE 交点P 点还是我们的费马点吗?显然这时候就不是了,显然P 点到A 、B 、C 距离之和大于A 点到A 、B 、C 距离之和.所以,是的,你想得没错,此时三角形的费马点就是A 点!当然这种情况不会考的,就不多说了.二、为什么是这个点为什么P 点满足∠P AB =∠BPC =∠CP A =120°,P A +PB +PC 值就会最小呢?归根结底,还是要重组这里3条线段:P A 、PB 、PC 的位置,而重组的方法是构造旋转!在上图3中,如下有△ADC ≌△ABE ,可得:CD =BE .类似的手拉手,在图4中有3组,可得:AF =BE =CD .巧的,它们仨的长度居然一样长!更巧的是,其长度便是我们要求的P A +PB +PC 的最小值,这一点是可以猜想得到的,毕竟最小值这个结果,应该也是个特别的值! 接下来才是真正的证明:考虑到∠APB =120°,∴∠APE =60°,则可以AP 为边,在PE 边取点Q 使得PQ =AP ,则△APQ 是等边三角形.△APQ 、△ACE 均为等边三角形,且共顶点A ,故△APC ≌△AQE ,PC =QE . 以上两步分别转化P A =PQ ,PC =QE ,故P A +PB +PC =PB +PQ +QE =BE .没有对比就没有差别,我们换个P 点位置,如下右图,同样可以构造等边△APQ ,同样有△APC ≌△AQE ,转化P A =PQ ,PC =QE ,显然,P A +PB +PC =PB +PQ +QE >BE .还剩下第3个问题!如果说费马点以前还算是课外的拓展内容,那现在,已经有人把它搬上了中考舞台!【中考再现】问题背景:如图1,将△ABC 绕点A 逆时针旋转60°得到△ADE ,DE 与BC 交于点P ,可推出结论:P A +PC =PE .问题解决:如图2,在△MNG 中,MN =6,∠M =75°,MG=O 是△MNG 内一点,则点O 到△MNG 三个顶点的距离和的最小值是______.【分析】本题的问题背景实际上是提示了解题思路,构造60°的旋转,当然如果已经了解了费马点问题,直接来解决就好了!如图,以MG 为边作等边△MGH ,连接NH ,则NH 的值即为所求的点O 到△MNG 三个顶点的距离和的最小值.(此处不再证明)过点H 作HQ ⊥NM 交NM 延长线于Q 点,根据∠NMG =75°,∠GMH =60°,可得∠HMQ =45°,∴△MHQ 是等腰直角三角形, ∴MQ =HQ =4,∴NH== 练习题1.如图,在△ABC 中,△ACB=90°,AB=AC=1,P 是△ABC 内一点,求P A +PB +PC 的最小值.2. 如图,已知矩形ABCD ,AB =4,BC =6,点M 为矩形内一点,点E 为BC 边上任意一点,则MA +MD +ME 的最小值为______.NG图2图1ABCD EPHGN M464Q HGN MABCDME3.如图,矩形ABCD中,AB=10,BC=15,现在要找两点E、F,则EA+EB+EF+FC+FD的最小值为__________4.如图,等腰Rt∆ABC中,AB=4,P为∆ABC内部一点,则PA+PB+PC的最小值为_______5.如图,∆ABC中,AB=4,,∠ABC=75°,P为∆ABC内的一个动点,连接PA、PB、PC,则PA+PB+PC的最小值为________6.如图,P为正方形ABCD对角线BD上一动点,若AB=2,则PA+PB+PC的最小值为______7.在Rt∆ABC中,∠ACB=90°,AC=1,,点O为Rt∆ABC内一点,连接AO、BO、CO,且∠AOC=∠COB=∠BOA=120°,则OA+OB+OC=_______8.如图,在四边形ABCD中,∠B=60°,AB=BC=3,AD=4,∠BAD=90°,点P是四边形内部一点,则PA+PB+PD的最小值是______9.如图,点P是矩形ABCD对角线BD上的一个动点,已知AB=2,,则PA+PB+PC 的最小值为_______10.如图,菱形ABCD的对角线AC上有一动点P,BC=6,∠ABC=150°,则PA+PB+PD的最小值为__________11.已知,在∆ABC中,∠ACB=30°点P是ABC内一动点,则PA+PB+PC的最小值为__________12.如图,设点P到等边三角形ABC两顶点A、B的距离分别为2则PC的最大值为______13.如图,设点P到正方形ABCD两顶点A、D的距离为2PC的最大值为________14.如图,设点P到正方形ABCD两顶点A、D的距离为2则PO的最大值为_________.15.如图,在Rt∆ABC中,∠BAC=90⁰,AB=AC,点D是BC边上一动点,连接AD,把AD 绕点A逆时针旋转90⁰,得到AE,连接CE、DE,点F是DE的中点,连接CF问题:在点D运动的过程中,在线段AD上存在一点P,使PA+PB+PC的值最小,当PA+PB+PC 取最小值时,AP的长为m,用含有m的式子表示CE的长.参考答案1.7.8.7 9.3 10. 12.2+13.2+1 15.32m +。
数学线段和(差)的最值问题
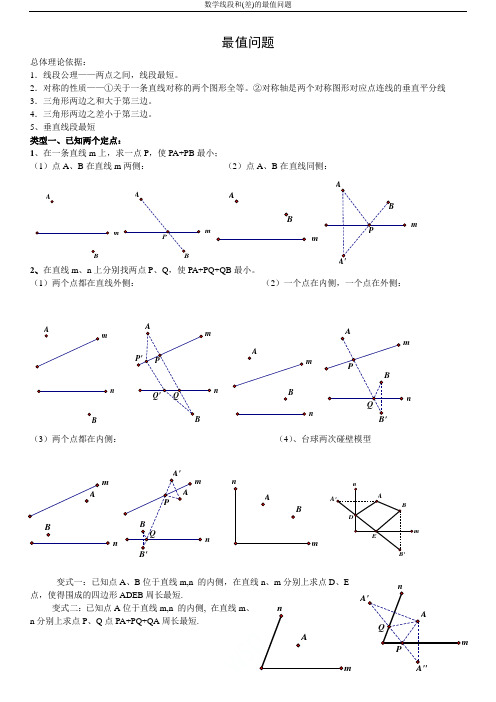
最值问题总体理论依据:1.线段公理——两点之间,线段最短。
2.对称的性质——①关于一条直线对称的两个图形全等。
②对称轴是两个对称图形对应点连线的垂直平分线3.三角形两边之和大于第三边。
4.三角形两边之差小于第三边。
5、垂直线段最短类型一、已知两个定点:1、在一条直线m上,求一点P,使PA+PB最小;(1)点A、B在直线m两侧:(2)点A、B在直线同侧:2、在直线m、n上分别找两点P、Q,使PA+PQ+QB最小。
(1)两个点都在直线外侧:(2)一个点在内侧,一个点在外侧:(3)两个点都在内侧:(4)、台球两次碰壁模型变式一:已知点A、B位于直线m,n 的内侧,在直线n、m分别上求点D、E点,使得围成的四边形ADEB周长最短.变式二:已知点A位于直线m,n 的内侧,n分别上求点P、Q点PA+PQ+QA周长最短.mmABmABnmnnmnnnmBmO xyB DA C P 例题1、一次函数y kx b =+的图象与x 、y 轴分别交于点A (2,0),B (0,4).(1)求该函数的解析式;(2)O 为坐标原点,设OA 、AB 的中点分别为C 、D ,P 为OB 上一动点, 求PC +PD 的最小值,并求取得最小值时P 点坐标.例2、如图,矩形OABC 顶点O 位于原点,OA,OC 分别在x 轴、y 轴上.B 点坐标为(3,2),E 为AB 中点,F 为BC 边的三等分点.在x 轴、y 轴上是否分别存在点M 、N ,使得四边形MNFE 的周长最小?如果存在,求出周长的最小值;如果不存在,请说明理由.类型二、一个动点,一个定点: (一)动点在直线上运动:点B 在直线n 上运动,在直线m 上找一点P ,使PA+PB 最小(在图中画出点P 和点B ) 1、两点在直线两侧: 2、两点在直线同侧:(二)动点在圆上运动点B 在⊙O 上运动,在直线m 上找一点P ,使PA+PB 最小(在图中画出点P 和点B ) 1、点与圆在直线两侧: 2、点与圆在直线同侧:m nAPmn ABmnAP mnABmOP'PmO BB' mOAP mO A B例题3、如图,在锐角△ABC中,AB=24,∠BAC=45°,∠BAC的平分线交BC于点D,M、N分别是AD和AB上的动点,则BM+MN的最小值是.例题4、如图,E,F是正方形ABCD的边AD上两个动点,满足AE=DF.连接CF交BD于点G,连接BE交AG于点H.若正方形的边长为2,则线段DH长度的最小值是.类型三、已知A、B是两个定点,P、Q是直线m上的两个动点,P在Q的左侧,且PQ间长度恒定,在直线m上要求P、Q两点,使得PA+PQ+QB的值最小。
最新二次函数中的最值问题整理(中考数学必考知识点)

二次函数中的最值问题归纳(中考数学必考知识点)一.线段和差最值1、如图,在平面直角坐标系中,抛物线y=ax2+bx﹣4与x轴交于点A(﹣2,0),B(4,0),与y轴交于点C,点D为BC的中点.(1)求该抛物线的函数表达式;(2)点G是该抛物线对称轴上的动点,若GA+GC有最小值,求此时点G的坐标;第二问解题思路:(1)根据点G是该抛物线对称轴上的动点可得当点G在直线BC与抛物线对称轴的交点上时,GA+GC最小,先求出点C的坐标.(2)再设直线BC的解析式为y=kx﹣4(k≠0),根据待定系数求得直线BC 的解析式为y=x﹣4,然后求出抛物线的对称轴为直线x=1,联立两解析式求解即可.2、如图,在平面直角坐标系中,直线y=4x+4与x轴交于A点,与y轴交于C点,抛物线)经过A,C两点,与x轴相交于另一点B,连接BC.点P是线段BC上方抛物线上的一个动点,过点P作PQ⊥BC交线段BC于点Q.(1)求抛物线的解析式;(2)点D为抛物线对称轴上的一个动点,求|DC﹣DB|的最大值;第二问解题思路:(1)作点C关于抛物线的对称轴的对称点N(2,4).(2)连接BN交抛物线的对称轴于点D,则点D为所求点,进而求解.二.线段最值3、如图,抛物线y=﹣x2+bx+c与x轴交于A、B两点(点A在点B的左侧),点A的坐标为(﹣1,0),与y轴交于点C(0,3),作直线BC.动点P在x轴上运动,过点P作PM⊥x轴,交抛物线于点M,交直线BC于点N,设点P的横坐标为m.(1)求抛物线的解析式和直线BC的解析式;(2)当点P在线段OB上运动时,求线段MN的最大值;第二问解题思路:(1)用m可分别表示出N、M的坐标,则可表示出MN的长.(2)再利用二次函数的最值可求得MN的最大值.变式训练:如图,已知抛物线经过点A(﹣6,0),B(2,0),与y轴交于点C.(1)求抛物线的解析式;(2)若点P为该抛物线上一动点.当点P在直线AC下方时,过点P作PE∥x轴,交直线AC于点E,作PF∥y轴.交直线AC于点F,求EF的最大值;4、如图,在平面直角坐标系中,直线y=4x+4与x轴交于A点,与y轴交于C点,抛物线)经过A,C两点,与x轴相交于另一点B,连接BC.点P是线段BC上方抛物线上的一个动点,过点P作PQ⊥BC交线段BC于点Q.(1)求抛物线的解析式;(2)求PQ的最大值,并写出此时点P的坐标;第二问解题思路:由PQ=HP sin∠PHQ=PH知,当PH最大时,PG最大,进而求解变式训练:如图,二次函数y=ax2+bx+2的图象与x轴相交于点A(﹣1,0)、B(4,0),与y轴相交于点C.(1)求该函数的表达式;(2)点P为该函数在第一象限内的图象上一点,过点P作PQ⊥BC,垂足为点Q,连接PC.线段PQ的最大值;变式训练:如图,抛物线y=x2﹣(a+1)x+a与x轴交于A、B两点(点A位于点B的左侧),与y轴交于点C.对称轴为直线x=﹣1.(1)a=;(2)点P为直线AC下方抛物线上的一动点,过P作PE⊥AC于点E,过P作PF⊥x轴于点F,交直线AC于点G,求PE+PG的最大值;5、如图,抛物线y=ax2+bx+3交x轴于点A(3,0)和点B(﹣1,0),交y轴于点C.(1)求抛物线的表达式;(2)D是直线AC上方抛物线上一动点,连接OD交AC于点N,求的最大值,并求出此时D的坐标.第二问解题思路:过点D作DH∥y轴,交AC于点H,由(1)设D(m,﹣m2+2m+3),直线AC的解析式为y=kx+n,然后可求出直线AC的解析式,则有H(m,﹣m+3),进而可得DH=﹣m2+3m,最后根据△OCN∽△DHN可进行求解.变式训练:如图,在平面直角坐标系中,直线y=x+2与x轴交于点A,与y轴交于点C,抛物线y=﹣x2+bx+c经过A、C两点,与x轴的另一交点为点B.(1)求抛物线的函数表达式;(2)点D为直线AC上方抛物线上一动点;连接BC、CD,设直线BD交线段AC于点E,△CDE的面积为S1,△BCE的面积为S2,求的最大值;三.周长和面积6、如图,抛物线过点O(0,0),E(10,0),矩形ABCD的边AB在线段OE上(点B在点A的左侧),点C,D在抛物线上.设B(t,0),当t=2时,BC=4.(1)求抛物线的函数表达式;(2)当t为何值时,矩形ABCD的周长有最大值?最大值是多少?第二问解题思路:由抛物线的对称性得AE=OB=t,据此知AB=10﹣2t,再由x=t时BC=t2﹣t,根据矩形的周长公式列出函数解析式,配方成顶点式即可得变式训练:如图1,抛物线y=ax2+bx+c与x轴相交于点B,C(点B在点C左侧),与y轴相交于点A(0,4),已知点C坐标为(4,0),△ABC面积为6.(1)求抛物线的解析式;(2)点M是直线AC下方抛物线上一点,过点P作直线AC的垂线,垂足为点H,过点P作PQ∥y轴交AC于点Q,求△PHQ周长的最大值及此时点P的坐标;7、如图,抛物线y=ax2+x+c经过坐标轴上A、B、C三点,直线y=﹣x+4过点B和点C.(1)求抛物线的解析式;(2)E是直线BC上方抛物线上一动点,连接BE、CE,求△BCE面积的最大值及此时点E的坐标;第二问解题思路:过E点作EG∥y轴交BC于点G,设E(t,﹣t2+t+4),则G(t,﹣t+4),可得S=﹣(t﹣2)2+4,当t=2时,△BCE的面积有最大值4,此时E △BCE(2,4)变式训练:二次函数y=ax2+bx+4(a≠0)的图象经过点A(﹣4,0),B(1,0),与y轴交于点C,点P为第二象限内抛物线上一点.(1)求二次函数的表达式;(2)如图,连接P A,PC,AC,求S的最大值;△P AC变式训练:已知抛物线y=﹣x2+bx+c与x轴交于A(﹣1,0),B(3,0)两点.(1)直接写出抛物线的函数解析式;(2)点N是第一象限内抛物线上的一动点,连接NA分别交BC、y轴于D、E两点,若△NBD、△CDE的面积分别为S1、S2,求S1﹣S2的最大值;四.AP+kBP型8、如图,已知二次函数y=ax2+bx+c的图象与x轴相交于A(﹣1,0),B(3,0)两点,与y轴相交于点C(0,﹣3),P是第四象限内这个二次函数的图象上一个动点,设点P的横坐标为m,过点P作PH⊥x轴于点H,与BC交于点M.(1)求这个二次函数的表达式;(3)求PM+2BH的最大值;第二问解题思路:设P点坐标为(m,m2﹣2m﹣3),则M点坐标为(m,m﹣3),H点坐标为(m,0),将PM+2BH转化为二次函数求最值即可变式训练:抛物线y=﹣x2+bx+c与x轴交于A、B(3,0)两点,与y轴交于点C,点和点P都在抛物线上.(1)求出抛物线表达式;(2)如图,若点P在直线AD的上方,过点P作PH⊥AD,垂足为H,①当点P是抛物线顶点时,求PH的长,②求AH+PH的最大值;变式训练:如图,已知抛物线y=x2+bx+c与x轴相交于A(﹣1,0),B(m,0)两点,与y轴相交于点C(0,﹣3),抛物线的顶点为D.(1)求抛物线的解析式;(2)若P是直线BC下方抛物线上任意一点,过点P作PH⊥x轴于点H,与BC交于点M.①求线段PM长度的最大值.②在①的条件下,若F为y轴上一动点,求PH+HF+CF的最小值.。
初中几何中线段和与差最值问题

初中几何中线段和(差)的最值问题一、两条线段和的最小值。
基本图形解析: 一)、已知两个定点:1、在一条直线m 上,求一点P ,使PA+PB 最小; (1)点A 、B 在直线m 两侧:(2)点A 、B 在直线同侧:2、在直线m 、n 上分别找两点P 、Q ,使PA+PQ+QB 最小。
(1)两个点都在直线外侧:m m BmABmm(2)一个点在内侧,一个点在外侧:(3)两个点都在内侧:nmnnnmB(4)、台球两次碰壁模型变式一:已知点A 、B 位于直线m,n 的内侧,在直线n 、m 分别上求点D 、E 点,使得围成的四边形ADEB 周长最短.变式二:已知点A 位于直线m,n 的内侧, 在直线m 、n 分别上求点P 、Q 点PA+PQ+QA 周长最短.二)、一个动点,一个定点: (一)动点在直线上运动:点B 在直线n 上运动,在直线m 上找一点P ,使PA+PB 最小(在图中画出点P 和点B )1、两点在直线两侧:2、两点在直线同侧:(二)动点在圆上运动点B 在⊙O 上运动,在直线m 上找一点P ,使PA+PB 最小(在图中画出点P 和点B ) 1、点与圆在直线两侧:m nmnmnmmm2、点与圆在直线同侧:三)、已知A 、B 是两个定点,P 、Q 是直线m 上的两个动点,P 在Q 的左侧,且PQ 间长度恒定,在直线m 上要求P 、Q 两点,使得PA+PQ+QB 的值最小。
(原理用平移知识解) (1)点A 、B 在直线m 两侧:作法:过A 点作AC ∥m,且AC 长等于PQ 长,连接BC,交直线m 于Q,Q 向左平移PQ 长,即为P 点,此时P 、Q 即为所求的点。
(2)点A 、B 在直线m 同侧:mmQ基础题1.如图1,∠AOB=45°,P是∠AOB内一点,PO=10,Q、R分别是OA、OB上的动点,求△PQR周长的最小值为.mABEQPmABQ2、如图2,在锐角三角形ABC中,AB=4,∠BAC=45°,∠BAC的平分线交BC于点D,M,N分别是AD和AB上的动点,则BM+MN 的最小值为.3、如图3,在锐角三角形ABC中,AB=52,∠BAC=45,BAC的平分线交BC于D,M、N分别是AD和AB上的动点,则BM+MN的最小值是。
线段差最值问题典型题

线段差最值问题典型题哎,今天咱们聊聊线段差最值的问题,听起来是不是有点高深?别担心,咱们轻松点,像喝茶聊天一样,慢慢说。
线段差最值,其实就是在某个范围内,怎么把线段的差距给最大化或者最小化,想想就挺有意思,是吧?想象一下,你和小伙伴在一块玩,比赛看谁的跳远最远,结果你跳了三米,他跳了两米。
简单粗暴,一看就知道你赢了,差了整整一米!这就像数学里的线段差,简单直接。
不过,如果咱们把这比赛放到一个更复杂的场景,那就得费点脑筋了。
比方说,今天你们去参加一个趣味运动会,有个项目是“跳远赛”,这可不是随便跳跳就行的。
得测量一下你和小伙伴的成绩,看看谁的跳得最远,谁的差距最大。
好吧,回到数学上。
假设有一条线段,长度不一,咱们要计算这些线段之间的差距。
这时候就得用到线段的最值问题。
简简单单说,就是求一堆线段中,最长的和最短的差几何。
这个就像咱们生活中,有的人一掷千金,有的人却拮据得像干粮都不够的样子,真的是天上一个地上一个,差距大得吓人。
不过,想要搞清楚这个线段的差值,得先理清思路。
比如,你有三条线段,分别是2米、5米和7米。
看看,最大值是7米,最小值是2米。
哎呀,算算,7减2,不就是5米吗?这就是咱们想要的结果,简单吧!说白了,这个问题就像是一道汤,越简单的材料,越能煮出美味的味道。
再举个例子,假设你现在有一把尺子,想要测量一条特别长的线段,结果发现你手里的尺子短得可怜,根本量不清楚。
这个时候,你是不是就得想办法把线段拆分开?这就涉及到把线段分成更小的部分,然后逐个测量,最后再合起来。
这样一来,你就能得到更准确的差值。
这种拆分的过程,仿佛在告诉我们,生活中遇到复杂的问题,不妨分开来看,简单又有效!说到这里,大家可能会想,“这不就是个简单的数学题吗?”但背后蕴含的哲理可深了。
就像人生,咱们常常在面对各种挑战,有时候事情复杂得让人头大,但如果咱们能把它分解成小块,一步一步来,最终就能迎刃而解。
真的是一分耕耘,一分收获啊。
线段和差的最值问题PPT课件

第一步 寻找、构造几何模型
要求△PBC的周长最小? 只要PB+PC最小就好了!
经典模型:牛喝水!
7
第二步 计算——勾股定理
把PB+PC转化为PA+PC !
当P运动到H时,PA+PC最 AC 22 32 183
小
练习:已知二次函数图像的顶点坐 标为C(3,-2),且在x轴上截得的线 段AB的长为4,在y轴上有一点P, 使△APC的周长最小,求P点坐标。
边) 1、已知直线m外两点A,B,在直线m上求一点P,使PA与PB的差最 大 (1)点A、B在直线m同侧: (2)点A、B在直线m异侧:
A
A
B
B
m
P
m P'
A
m B
A B'
m
P'
P
B
过B作关于直线m的对称点B’,连接AB’交点直线m于P, 此时PB=PB’,PA-PB最大值为AB’
17
应用:1、抛物线 y ax2 bx c 交x轴于A,B两点,交
中考专题复习
——求线段和差的最值
1
1.常见的几何最值问题有:线段最值问 题, 线段和差最值问题,周长最值问题、 面积 最值问题等;
2.几何最值问题的基本原理。 ①两点之间线段最短 ②垂线段最短 ③三角形两边之差小于第三边 ④利用函数关系求最值
2
一、两条线段和的最小值
已知:直线m外两点A,B,在直线m上 求一点P,使PA+PB最小;
此时A′C=MC-MA′
26
举一反三 典例2 (2016·江苏淮安)如图,在Rt△ABC 中,∠C=90°,AC=6,BC=8,点F在边AC上,并且CF=2,点E 为边BC上的动点,将△CEF沿直线EF翻折,点C落在点P处, 则点P到边AB距离的最小值是 1.2 .
几何图形中线段和差最值问题

点的个数动一动-C组变式:由两个点到多个点,增加层次性-如图,正方形ABCD中,AB=2,-1若M是AB边上的中点, 是对角-线AC上任意一点,求PM+PB2的最-M2-小值-2若M1、M2是AB边上的三等分点-,P1、P2依次是对角 AC上任意两点-求P1M1+P1B2+P2M1+P2M22的-最小值
八会归纳-线段和的最值问题-利用对称性构-如何去解?-造三点一线-化归:-引申、条件变换、移植转-换、增加解题层次性 -课本例题或常见题-考题
点的个数动一动-C组变式:由两个点到多个点,增加层次性-如图,正方形ABCD中,AB=2,-1若M是AB边上的中点, 是对角-线AC上任意一点,求PM+PB2的最-小值-2若M1、M2是AB边上的三等分点,-P1、P2依次是对角线AC 任意两点,求-P1M1+P1B2+P2M1+P2M22的最小值-3若M、M2Mg是AB边上的10等分-点,P1、P2 g依次是对角线AC上任意-点,直接写出P1M1+P1B2+P2M1+P2M22-++P,Mg+PgMg2的最小值
A组-已知抛物线-y0x2--5-x+2-22-若一个动点M自P0,1-出发,先到达对称轴上某点(设为点F,最后运动 点-A。确定使点M运动的总路径最短的点F的位置,并求出这-个最短路程的长。-0,2A-A'5,2-0,1PT-d-X -1
B组-变一变-若一个动点M自P出发,先到达x轴上的某点(设为点E,,再-到达抛物线的对称轴上某并求出这个最短-路程的长-0,2A-0,1P1-X--1
A-Mi'-D-P,M1+P,B2+P2M1+P2M2-MD2-M1'M22-C
抛物线与线段和差最值问题(含答案)

抛物线与线段和差最值问题(含答案)线段和差最值问题是数学中常见的优化问题,需要运用一些基本的数学知识和技巧来解决。
下面分别给出四道相关的例题。
一、如图,抛物线$y=\frac{1}{2}x+bx-2$与$x$轴交于$A$、$B$两点,与$y$轴交于点$C$,且$A(-1,\frac{1}{2})$。
1)求抛物线的解析式以及顶点$D$的坐标;2)判断$\triangle ABC$的形状,证明你的结论;3)点$M(m,0)$是$x$轴上的一个动点,当$MC+MD$的值最小时,求$m$的值。
二、如图,在平面直角坐标系中,抛物线$y=ax^2+bx+c$经过$A(-2,-4)$、$B(2,0)$、$O(0,0)$三点。
1)求抛物线$y=ax^2+bx+c$的解析式;2)若点$M$是该抛物线对称轴上的一点,求$AM+OM$的最小值。
三、如图,已知直线$y=\frac{1}{12}x+1$与$y$轴交于点$A$,与$x$轴交于点$D$,抛物线$y=x+bx+c$与直线交于$A$、$E$两点,与$x$轴交于$B$、$C$两点,且$B$点坐标为$(1,0)$。
1)求该抛物线的解析式;2)在抛物线的对称轴上找一点$M$,使$|AM-MC|$的值最大,求出点$M$的坐标。
四、已知抛物线$y=\frac{1}{2}x+bx$经过点$A(4,\frac{5}{2})$,设点$C(1,-3)$,请在抛物线的对称轴上确定一点$D$,使得$AD-CD$的值最大,则$D$点的坐标为。
解题思路:1、对于第一题,先求出抛物线的解析式,再通过求导得到顶点的坐标,最后利用勾股定理求出最小值点的坐标。
2、对于第二题,先利用三点求解得到抛物线的解析式,再通过对称性求出对称轴,最后利用距离公式求解最小值。
3、对于第三题,先求解抛物线的解析式,再通过求导得到对称轴和顶点的坐标,最后利用距离公式求解最大值点的坐标。
4、对于第四题,先求解抛物线的解析式,再通过对称性求出对称轴和顶点的坐标,最后利用距离公式求解最大值点的坐标。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
小结
经典模型:台球两次碰壁问题 经验储存:没有经验,难有思路
例6:在平面直角坐标系中,Rt△AOB 的顶点坐标分别是A(-2,0),O(0,0), B(0,4),把△AOB绕O点按顺时针旋 转90度,得到△COD,(1)求C、D 的坐标,(2)求经过A、B、D三点的 抛物线。(3)在(2)中的抛物线的 对称轴上取两点E、F(E在F点的上 方),且EF=1,当四边形ACEF的周 长最小时,求E、F的坐标。
CB 323232
小结
E? F!
3.如图,∠AOB=45,角内有一动点 P ,PO=10,在AO,BO上有两动点Q, R,求△PQR周长的最小值。
D
B
R P
O
Q
A
E
4.如图,四边形ABCD是正方形,△ABE是等边
三角形,M为对角线BD(不含B点)上任意一
点,将BM绕点B逆时针旋转60°得到BN,连接
2、对于动点Q(1,n), 求PQ+QB的最小值 .
第一步 寻找、构造几何模型 要求PQ+QB的最小值?
经典模型:牛喝水!
第二步 计算——勾股定理
把PQ+QB转化为PQ+QA ! 当Q运动到E时,PQ+QA最小
AP 3232 3 2
第二步 计算——勾股定理
把PQ+QB转化为PQ+QA ! 当Q运动到E时,PQ+QA最小
1、已知在对抛物线的对称轴上存 在一点P,使得△PBC的周长最小, 请求出点P的坐标 .
第一步 寻找、构造几何模型 要求△PBC的周长最小? 只要PB+PC最小就好了!
经典模型:牛喝水!
第二步 计算——勾股定理
把PB+PC转化为PA+PC !
当P运动到H时,PA+PC最小 AC 2232 13
B
CE D/
F
AO
D
例5、例6中的最小值问题所涉及到的路 径,虽然都是由三条动线段连接而成, 且路径都是“定点→动点→动点→定 点”,但是例5中的量动点间的线段长度 不确定,而例6的两动点间的线段长度为 定值,正是由于这点的不同,使得它们 的解题方法有很大差异,例5是根据两点 之间线段最短找到动点的位置,例6是通 过构造平行四边形先找到所求的其中一 个动点的位置,另一个位置也随之确定。
例3:已知二次函数图像的顶点坐标 为C(3,-2),且在x轴上截得的线段 AB的长为4,在y轴上有一点P,使 △APC的周长最小,求P点坐标。
A/ O PA B C
Байду номын сангаас
例4:抛物线y=ax2+bx+c经过点A(4,3),B(2,0),当x=3和x=-3时, 这条抛物线上对应点的纵坐标相等, 经过点C(0,-2)的直线a与x轴平 行。(1)求直线AB和抛物线,(2) 设直线AB上点D的横坐标为-1,P(m, n)是抛物线上的一动点,当△POD 的周长最小时,求P点坐标。
EN、AM、CM.
⑴ 求证:△AMB≌△ENB;
⑵ ①当M点在何处时,AM+CM的值最小;
②当M点在何处时,AM+BM+CM的值最小,
并说明理由;
A
D
N
E
M
B
C
结束语
谢谢大家聆听!!!
32
A D
P OB
C
A D
OB P
C
例3,例4中最小值问题,所涉及到的
路径虽然都是有两条动线段连接而成, 且路径都是“定点→动点→定点”, 但是动点运动的路线不同,例3是直线, 例4是曲线,因此它们的解法有很大不 同,例3是根据两点之间线段最短找到 动点的位置,例4是根据垂线段最短找 到所求的两个动点的位置。
例5:在x轴、y轴上是否分别存在点M、 N,使得四边形MNFE的周长最小?如
果存在,求出周长的最小值;如果不 存在,请说明理由.
第一步 寻找、构造几何模型
要求四边形MNFE F/
F
的周长最小?
N
E
M
E/
把三条线段转移 到同一条直线上 就好了!
第二步 计算——勾股定理
E'F' 3242 5
EF 1222 5
线段和差的最值问题
两条线段和的最小值 两条线段差的最大值
两点之间,线段最短
三角形两边之差小于第三边
当P运动到E时,PA+PB 最小
当Q运动到F时,QD-QC 最大
当P运动到E时,PA+PB最小 当Q运动到F时,QD-QC最大
第一步,寻找、构造几何模型 第二步,计算
例1:在△ABC中,AC=BC=2,
∠ACB=90O,D是BC边的中点,E是AB
上的一动点,则EC+ED的最小值
为
。
A
p
E
C
D
B
例2:△ABC中,AC=3,BC=4, AB=5,试在AB上找一点P,在BC上 取一点M,使CP+PM的值最小,并 求出这个最小值。 C/
A
P
BM
C
例1、例2中的最小值问题,所涉及到的 路径,虽然都是由两条线段连接而成, 但是路径中的动点与定点的个数不同, 例1 中的路径为“定点→动点→定点”, 是两个定点一个动点,而例2中的路径 是“定点→动点→动点”,是一个定点 两个动点,所以两个题的解法有较大差 异,例1是根据两点之间线段最短求动 点的位置,例2是根据垂线段最短找两 个动点的位置。
