自由曲线自由曲面的设计共63页
合集下载
《自由曲线与曲面》PPT课件

7.6 B样条曲线
• Gordon和Riesenfeld于1974年用B样条基函数代替了Bernstein基函数,构造了B样条 曲线。
• 比Bezier曲线更贴近控制多边形,曲线更光滑(很容易产生C2连续性),曲线的次数 可根据需要指定
• 增加了对曲线的局部修改功能,B样条曲线是分段组成的,所以控制多边形的顶点对曲 线的控制灵活而直观。
2.一阶导数
• 将式(7-12)求导,有
n
p' (t) Pi Cni [i t i1 (1 t)ni (n i) t i (1 t)ni1 ] i0 在闭区间〔0,1〕内,将t=0和t=1 代入上式,得到
p' (0) n (P1 P0 ) p' (1) n (Pn Pn1)
可以证明,二次Bezier曲线是一段抛物线。
3.三次Bezier曲线
• 当n=3时,Bezier曲线的控制多边形有四个控制点P0、P1、P2和P3,Bezier曲线 是三次多项式。
3
p(t) Pi Bi,3 (t) (1 t)3 P0 3t(1 t)2 P1 3t 2 (1- t) P2 t3 P3 i0 (t3 3t 2 - 3t 1)P0 (3t 3 6t 2 3t)P1 (3t3 3t 2 ) P2 t3P3
• 通常单一的曲线段或曲面片难以表达复杂的形状,必须将一些曲线段连接成组合曲线, 或将一些曲面片连接成组合曲面,才能描述复杂的形状。
• 为了保证在连接点处平滑过渡,需要满足连续性条件。连续性条件有两种:参数连续 性和几何连续性。
•
参数连续性
• 零阶参数连续性,记作C0,指相 邻两个曲线段在交点处具有相同的 坐标。
菅光宾
数字媒体系
• 7.1 基本概念 • 7.4 Bezier曲线 • 7.5 Bezier曲面 • 7.6 B样条曲线 • 7.7 B样条曲面
自由曲线与曲面

主要内容
11.1 解析曲面 11.2 Bezier曲面 11.3 B样条曲面 11.4 NURBS曲面 11.5 曲面的其它表达 11.6 曲面求交算法
11.1 解析曲面(代数曲面)
代数曲面在造型系统中常见,但远远不能满足复 杂曲面造型的要求
适合构造简单曲面,不能构造自由曲面 不同类型曲面拼接连续性难以保证 不同曲面求交公式不一,程序实现量大 工程设计交互性差
通常样条曲面的求交算法采用离散逼近、迭代求精 与跟踪的方法,求交精度不高,计算量大,速度慢,对 共点、共线、共面难以处理,从而影响布尔运算的效率 和稳定性。
基本的求交算法:
由于计算机内浮点数有误差,求交计算必须引进容差。假定
容差为e,则点被看成是半径为e的球,线被看成是半径为e的圆管, 面被看成是厚度为2e的薄板。
c)然后固定指标i,以第一步求出的n+1条截面曲线的控制顶 点阵列中的第i排即: di,j, j 0,1,, n 为“数据点”,以上一 步求出的跨界切矢曲线的第i个顶点为”端点切矢”,在节点矢 量V上应用曲线反算,分别求出m+3条插值曲线即控制曲线的 B样条控制顶点di.j ,i 0,1,,m 2; j 0,1,,n 2 ,即为所求双
superquadric
superquadric曲面在商用 CAD系统应用相对较少,但 在动画软件中常用
superquadric toroids
(
x
)2/E2
(
y
)2/E2
E2/E1 a
(
z
)2/E1
1
rx
ry
rz
superquadric ellipsoids
(
x
)2/E2
(
y
E2/E1 )2/E2
11.1 解析曲面 11.2 Bezier曲面 11.3 B样条曲面 11.4 NURBS曲面 11.5 曲面的其它表达 11.6 曲面求交算法
11.1 解析曲面(代数曲面)
代数曲面在造型系统中常见,但远远不能满足复 杂曲面造型的要求
适合构造简单曲面,不能构造自由曲面 不同类型曲面拼接连续性难以保证 不同曲面求交公式不一,程序实现量大 工程设计交互性差
通常样条曲面的求交算法采用离散逼近、迭代求精 与跟踪的方法,求交精度不高,计算量大,速度慢,对 共点、共线、共面难以处理,从而影响布尔运算的效率 和稳定性。
基本的求交算法:
由于计算机内浮点数有误差,求交计算必须引进容差。假定
容差为e,则点被看成是半径为e的球,线被看成是半径为e的圆管, 面被看成是厚度为2e的薄板。
c)然后固定指标i,以第一步求出的n+1条截面曲线的控制顶 点阵列中的第i排即: di,j, j 0,1,, n 为“数据点”,以上一 步求出的跨界切矢曲线的第i个顶点为”端点切矢”,在节点矢 量V上应用曲线反算,分别求出m+3条插值曲线即控制曲线的 B样条控制顶点di.j ,i 0,1,,m 2; j 0,1,,n 2 ,即为所求双
superquadric
superquadric曲面在商用 CAD系统应用相对较少,但 在动画软件中常用
superquadric toroids
(
x
)2/E2
(
y
)2/E2
E2/E1 a
(
z
)2/E1
1
rx
ry
rz
superquadric ellipsoids
(
x
)2/E2
(
y
E2/E1 )2/E2
第四章 自由曲线

13
4.1.3 插值、拟合和光顺 插值、
• 拟合
– 以求各点偏差平方和的极小值的方法,求得 以求各点偏差平方和的极小值的方法 求得F(x)中的系数 中的系数. 求得 中的系数
ϕ(a j ) = ∑dk [∑a j xkj − yk ]2
k =1 j =0
n
m
– 求极值 求极值:
∂ϕ =2 ∂ai
∑ ∑
y
yy = f ຫໍສະໝຸດ x)y = f (x)y = ϕ(x)
y = ϕ(x)
y1
y2
x2
x
y1
y2
y3 x3
x
12
o
x1
(a)
o
x1
x2
(b)
4.1.3 插值、拟合和光顺 插值、
• 拟合
– 当插值点太多 构造插值函数使其通过所有的点是相当困 当插值点太多,构造插值函数使其通过所有的点是相当困 难的. 难的 – 选择一个次数较低的函数 在某种意义上逼近这些点 拟合 选择一个次数较低的函数,在某种意义上逼近这些点 在某种意义上逼近这些点.拟合 方法很多,最常用的有最小二乘法 最常用的有最小二乘法. 方法很多 最常用的有最小二乘法 – 最小二乘法 一组点 最小二乘法:一组点 一组点(xi,yi),i=1,2…n要求构造一个 要求构造一个m(m<n要求构造一个 m 1)次多项式函数 次多项式函数 j
dk [
k =1 j =0
n
m
i a j xkj − yk ]xk = 0
– 有m+1个方程 可以解出 个方程,可以解出 个未知数a0,a1,…am,代入定 个方程 可以解出m+1个未知数 个未知数 代入定 义即可求得多项式函数F(x). 义即可求得多项式函数 14
FSS自由曲面设计

在3D空间做曲线: 1- 定义主平面 2- 创建
创建的类型:
Through points: 通过每一个点; Control points: 所做的点是控制点 Near points: 线的类型不同
• 如果任选点,曲线将位于定义平面上 • 如果选已经存在的点,那么将产生空间曲线 • 如果需要的不是上述情况 ,激活Disable geometry
似于Loft
步骤: 1- 选 profile 2- 选 Spine 3- 选 Guide
注意:
-所有元素必须是互 相接触的
江达公司
• Translation: profile 沿 spine 轮廓转换 • On contour: profile 位于轮廓三面体 (T, N, B) • Fixed direction: 定义方向
效果图 测量数据
FSS创建曲面
FSK
FSS创建曲面
GSD详细设计
DSE
QSR
真实渲染
FSS创建曲面
GSD详细设计
验证、 修改
GSD详细设计
使用其它 模块完成
江达公司
23
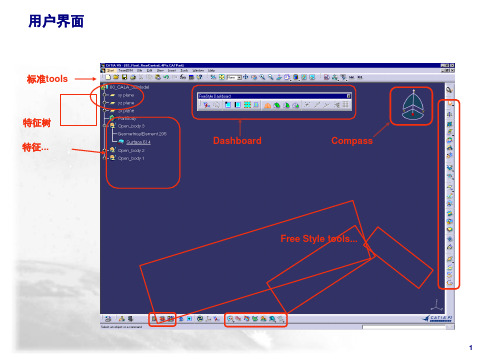
CATIA 介绍
FreeStyle Sketch Tracer
江达公司
24
调入一个图片
江达公司
25
确定图的位置、比例
江达公司
26
显示曲面特性。
10
Blend
Blend 曲线
Blend :做出一条新曲线 连接两条曲线,并定义连接方式 1- 选一条曲线 2- 第二条 3- 定义连接类型
接触点: 显示接触点 (dashboard). 并可以调整接触点
连续值: 显示 (dashboard)并调整
自由曲线与曲面-123页精选文档

2.参数样条表示 在计算机图形学应用中使用几种不同的样条描述。
每种描述是一个带有某特定边界条件多项式的特殊 类型。
02.12.2019
5
例如空间一条曲线用三次参数方程可以表示如下:
x(u)﹦axu 3﹢bxu 2﹢cxu﹢dx y(u)﹦ayu 3﹢byu 2﹢cyu﹢dy z(u)﹦azu 3﹢bzu 2﹢czu﹢dz u[0,1] 或
二阶几何连续性,记为G2连续,指两个曲线段在相交 处其一阶和二阶导数均成比例。G2连续下,两个曲线段在 交点处的曲率相等。
02.12.2019
4
7.1.4 参数样条曲线 1.样条曲线
在计算机图形学中,术语样条曲线指由多项式曲 线段连接而成的曲线,在每段的边界处满足特定连 续条件。而样条曲面可用两组正交样条曲线来描述。 样条用来设计曲线和曲面形状,典型的CAD应用包 括汽车、飞机和航天飞机表面设计以及船壳设计。
Hermite样条插值(以法国数学家Charles Hermite
命名)使用型值点和型值点处的一阶导数建立边界条
件。设Pk和Pk+1为第K个和第K+1个型值点,Hermite样 条插值边界条件规定为:
P(0) ﹦Pk P(1) ﹦Pk+1 P’(0)﹦Dk P’(1)﹦Dk+1 其中,Dk和Dk+1分别为Pk和Pk+1处的一阶导数。 将参数方程写成矩阵形式为:
﹢(-3xk﹢3xk+1-2xk'-xk+1')u2+xk'u﹢xk y(u)﹦(2yk-2yk+1+yk'﹢yk+1')u3
﹢(-3yk﹢3yk+1-2yk'-yk+1')u2+yk'u﹢yk z(u)﹦(2zk-2zk+1+zk'﹢zk+1')u3
每种描述是一个带有某特定边界条件多项式的特殊 类型。
02.12.2019
5
例如空间一条曲线用三次参数方程可以表示如下:
x(u)﹦axu 3﹢bxu 2﹢cxu﹢dx y(u)﹦ayu 3﹢byu 2﹢cyu﹢dy z(u)﹦azu 3﹢bzu 2﹢czu﹢dz u[0,1] 或
二阶几何连续性,记为G2连续,指两个曲线段在相交 处其一阶和二阶导数均成比例。G2连续下,两个曲线段在 交点处的曲率相等。
02.12.2019
4
7.1.4 参数样条曲线 1.样条曲线
在计算机图形学中,术语样条曲线指由多项式曲 线段连接而成的曲线,在每段的边界处满足特定连 续条件。而样条曲面可用两组正交样条曲线来描述。 样条用来设计曲线和曲面形状,典型的CAD应用包 括汽车、飞机和航天飞机表面设计以及船壳设计。
Hermite样条插值(以法国数学家Charles Hermite
命名)使用型值点和型值点处的一阶导数建立边界条
件。设Pk和Pk+1为第K个和第K+1个型值点,Hermite样 条插值边界条件规定为:
P(0) ﹦Pk P(1) ﹦Pk+1 P’(0)﹦Dk P’(1)﹦Dk+1 其中,Dk和Dk+1分别为Pk和Pk+1处的一阶导数。 将参数方程写成矩阵形式为:
﹢(-3xk﹢3xk+1-2xk'-xk+1')u2+xk'u﹢xk y(u)﹦(2yk-2yk+1+yk'﹢yk+1')u3
﹢(-3yk﹢3yk+1-2yk'-yk+1')u2+yk'u﹢yk z(u)﹦(2zk-2zk+1+zk'﹢zk+1')u3
FSS-自由曲面设计PPT课件
3D curve
创建关联的 3D 曲线,这意味着在创建或编辑时可以添加或删除点(控制点或穿越点)。 A:创建关联的 3D 曲线的三种方式: 1.通过点 (Through points):结果曲线为一条通过每个选定点的多弧曲线 2.控制点 (Control points):所单击的点为结果曲线的控制点 3.近似点 (Near points):结果曲线为一条具有固定度数并平滑通过选定点的单弧 B: more frame
将曲线投影到曲面上 选线 + ctrl + 选面
19
Creating Blend Curves
创建混合/桥接曲线 1.选线 2.上下文选项
20
Styling corner
在其它两个平面曲线之间的给定半径连接曲线
21
Matching Curves
曲线匹配 需要两个元素 1.曲线(匹配时变形,与第二个元素匹配) 2.曲线/曲线上的点/3D点/端点 选点就近匹配原则
• 重新回到 xyz 模式--------------------------------------------------------------
• 坐标与实体链接转换-----------------------------------------------------------
• 如果与实体链接, 创建一个坐标平面 -------------------------------------------
15
Creating a Styling Sweep
四种扫描方式: 1.简单扫描(轮廓、脊线) 2.扫描扑捉(轮廓、脊线、引导线)
轮廓线沿引导线不发生变形 3.扫描拟合(轮廓、脊线、引导线)
轮廓线沿引导线发生变形 4.近轮廓扫描(轮廓、脊线、引导线、
(计算机图形学)自由曲线曲面

参数连续性,用C 表示 C0连续(0阶参数连续) —— 指曲线相连,前一段曲线的终点
阶数
t=1与后一段曲线的起点t=0相同,即 相邻两段曲线结合点处有相同坐标。
C1连续(一阶参数连续) ——代表两个相邻曲线段的方程在相交
点处有相同的一阶导数(切线)。 (一阶导数反映了曲线对参数 t 的变 化速度)
B2,3(t)ຫໍສະໝຸດ Ot4个基函数
7.2.2 Bernstein基函数及曲线的性质
Bi ,n (t ) n! i i t i (1 t ) ni C n t (1 t ) ni i!(n i)!
t∈〔0,1〕(i=0,1,2……n) ,t∈〔0,1〕
1.非负性: Bi,n (t ) 0
void CTestView::DrawBezier()//绘制Bezier曲线 { CDC *pDC=GetDC(); CPen NewPen,*pOldPen; NewPen.CreatePen(PS_SOLID,1,RGB(0,0,255));//曲线颜色 pOldPen=pDC->SelectObject(&NewPen); pDC->MoveTo(P[0]); for(double t=0.0;t<=1.0;t+=0.01) { double x=0,y=0; for(int i=0;i<=n;i++) { x+=P[i].x*C(n,i)*pow(t,i)*pow(1-t,n-i); y+=P[i].y*C(n,i)*pow(t,i)*pow(1-t,n-i); } pDC->LineTo(Round(x),Round(y)); } pDC->SelectObject(pOldPen); NewPen.DeleteObject(); ReleaseDC(pDC); }
计算机图形学第4章 自由曲线与曲面2

(1) P3 Q0 (2) 0 P3 P2 (Q1 Q0 )
三点共线,且Q1,P2在连接点的异侧
二阶几何连续条件?
自学
21
4.6 Bezier曲线
反求控制顶点
给定n+1个型值点,要求构造一条Bezier曲线通过这些点
Q0 P0 ... 0 n 1 n 1 n (i / n) ... PnCn (i / n) n Qi P0Cn (1 i / n) P 1C n (1 i / n) ... Qn Pn
17
4.6 Bezier曲线
二次Bezier曲线
n=2,抛物线 P(0)=P0,P(1)=P2; P'(0)=2(P1- P0), P'(1)=2(P2- P1) P(1/2)=[P1+ (P0+ P2)/2]/2
P1
P(0.5)
P(0)
P0
M
P2
P(1)
说明二次Bezier曲线在 t=1/2 处的点经过P0P2 上 的中线P1M的中点。
优于Bezier曲线之处:
26
4.7 B样条曲线
三次B样条曲线对三次Bezier曲线进行改进, 它克服了Bezier曲线的不足,同时保留了 Bezier曲线的直观性和凸包性,是一种工程设 计中更常用的拟合曲线。
三次B样条曲线的构造:
由前面可知,三次参数曲线可以表示成: P(t)=F0,3(t)P0 + F1,3(t)P1 + F2,3(t)P2 + F3,3 (t)P3 F0,3(t) ,F1,3(t) ,F2,3(t) ,F3,3 (t)是待定参数 P2 P1 P(t) 由P0,P1,P2,P3确定 Q(s) 由P1,P2,P3,P4确定 P3 P4
自由曲线曲面造型技术PPT课件

•
•
•
•
•
•
•
•
•
•
•
O
x
第42页/共62页
已知 mn个节点
其中
互不相同,不妨设
构造一个二元函数
通过全部已知节点,即
再用
计算插值,即
第43页/共62页
第二种(散乱节点):
y
•
••
• •
•
• •
•
•
•
•
•
•
•
0
x
第44页/共62页
已知n个节点
其中
互不相同,
构造一个二元函数
通过全部已知节点,即
再用
第7页/共62页
1.1.1 曲面变形
(• 传D统e的fNoURrBmS模a型t仅i允o许n调整o控r制S顶h点a或p权因e子B来l局e部n改d变i曲n面g形)状。
• 计算机动画业和实体造型业需要与曲面表示方法无关的变形方法或性状调配方法。
第8页/共62页
1.1.2 曲面重建(Reconstuction)
是集几何造型与数控编程于一体的集成化软 件,具有统一的数据结构,数据管理和用户界面. 系统采用NURBS(Non Uniform Rational BSpline)方法为造型核心,统一表示二次曲线曲 面和自由曲线曲面.从根本上解决了不规则的 任意边界的曲面造型问题,解决了复杂零件的 四,五坐标加工编程问题,适用于各种刀具端铣 和侧铣,大大提高了系统的数控编程能力.可以 大面积切除毛坯余量,提高加工效率.系统具有
y
+
++
+
i +
+
(xi,yi)
自由曲线-自由曲面设计

若令 d k x
n
a
j 0
m
k 0
i k
Si ,
d
k 0
n
i yk xk Ti;则可得方程组: k
j
S i j Ti
这里有m+1个方程,可以解出m+1个系数未知数 a0,a1,…am,代入定义即可求出多项式F(x)逼近已知 的n个型值点;
一组实验数据: x 0 10 20 30 40
多项式拟合最小二乘法
设已知型值点为(xi,yi)(i=1,2,…n),现构造一个 m(m<n-1)次多项式函数y=F(x)逼近这些型值点; 逼近的好坏可用各点偏差的加权平方和来衡量:
(a0 , a1 ,..., am ) d k [ F ( xk ) yk ]2
k 0 n
F ( x) a j x j 使得偏 令F(x)为一个m次多项式,
j 0
m
差平方和 达到极小;
最小二乘法解决逼近问题
根据求极值问题的方法可知,使 (a j ) 达到极小的 a j (j=0,1…,m)必须满足下列方程组:
n m i 2 d k a j xkj y k xk 0 ai k 0 j 0
i 0,1,..... m
1972年,德布尔(de Boor)给出了B样条的标准计算 方法;
1974年,通用汽车公司的戈登(Gordon)和里森费尔 德(Riesenfeld)在B样条理论的基础上,提出了B样 条曲线、曲面;
1975年,美国的佛斯普里尔(Versprill)提出了有理B 样条方法; 80年代后期,美国的皮格尔(Piegl)和蒂勒(Tiller)将 有理B样条发展成非均匀有理B样条(NURBS)方法;
自由曲线和曲面 图形学 孔令德 计算机图形学基础教程 大学课件98页PPT文档

Hermite曲线段定义:给定曲线段的两个端点P i 和 P i+1和两端点处的一阶导数Ri和Ri+1构造而成。
下面用已知条件求出Hermite曲线段的参数方程
11
通常用三次参数方程描述空间一条自由曲 线:
x(t) y(t)
axt3 ayt3
bxt2 byt2
cxt cyt
dx dy
,t∈[0,1]
z(t) azt3 bzt2 czt dz
其中,t为参数,且0<=t<=1时,t=0对应曲线段的起点,t =1时,对应曲线段的终点。
以直线为例:已知直线的起点坐标P1(x1,y1) 和终点坐标P2(x2,y2),直线的显式方程:
yy1yx22 xy11(xx1)
9
直线的隐函数方程表示为:
f(x)yy1y x2 2 x y1 1(xx1)0
直线的参数方程表示为:
yxyx11
(x2 (y2
d
t∈〔0,1〕;
13
7.1.3 拟合和逼近
• 型值点 指通过测量或计算得到的曲线或曲面上少量描述曲线或 曲面几何形状的数据点。
• 控制点
指用来控制或调整曲线(面)形状的特殊点(不一定在曲线上)
• 插值点 求给定型值点之间曲线(面)上的点 要求建立的曲线与曲面数学模型,严格通过已知的每一
自由曲线曲面——
无法用标准方程描述的曲线曲 面,通常由一系列实测数据点 确定。如汽车的外形曲线曲面、 等高线等。
3
图7-1 汽车的曲面
4
7.1 基本概念
7.1.1 样条曲线曲面 7.1.2 曲线曲面的表示形式 7.1.3 拟合和逼近 7.1.4 连续性条件
下面用已知条件求出Hermite曲线段的参数方程
11
通常用三次参数方程描述空间一条自由曲 线:
x(t) y(t)
axt3 ayt3
bxt2 byt2
cxt cyt
dx dy
,t∈[0,1]
z(t) azt3 bzt2 czt dz
其中,t为参数,且0<=t<=1时,t=0对应曲线段的起点,t =1时,对应曲线段的终点。
以直线为例:已知直线的起点坐标P1(x1,y1) 和终点坐标P2(x2,y2),直线的显式方程:
yy1yx22 xy11(xx1)
9
直线的隐函数方程表示为:
f(x)yy1y x2 2 x y1 1(xx1)0
直线的参数方程表示为:
yxyx11
(x2 (y2
d
t∈〔0,1〕;
13
7.1.3 拟合和逼近
• 型值点 指通过测量或计算得到的曲线或曲面上少量描述曲线或 曲面几何形状的数据点。
• 控制点
指用来控制或调整曲线(面)形状的特殊点(不一定在曲线上)
• 插值点 求给定型值点之间曲线(面)上的点 要求建立的曲线与曲面数学模型,严格通过已知的每一
自由曲线曲面——
无法用标准方程描述的曲线曲 面,通常由一系列实测数据点 确定。如汽车的外形曲线曲面、 等高线等。
3
图7-1 汽车的曲面
4
7.1 基本概念
7.1.1 样条曲线曲面 7.1.2 曲线曲面的表示形式 7.1.3 拟合和逼近 7.1.4 连续性条件
