2020年中考数学函数专题(附答案)
2020年中考数学复习专题练:《二次函数实际应用 》(含答案)

2020年中考数学复习专题练:《二次函数实际应用》1.金松科技生态农业养殖有限公司种植和销售一种绿色羊肚菌,已知该羊肚菌的成本是12元/千克,规定销售价格不低于成本,又不高于成本的两倍.经过市场调查发现,某天该羊肚菌的销售量y(千克)与销售价格x(元/千克)的函数关系如下图所示:(1)求y与x之间的函数解析式;(2)求这一天销售羊肚菌获得的利润W的最大值;(3)若该公司按每销售一千克提取1元用于捐资助学,且保证每天的销售利润不低于3600元,问该羊肚菌销售价格该如何确定.2.某超市以20元/千克的进货价购进了一批绿色食品,如果以30元/千克销售这些绿色食品,那么每天可售出400千克.由销售经验可知,每天的销售量y(千克)与销售单价x (元)(x≥30)存在如图所示的一次函数关系.(1)试求出y与x的函数关系式;(2)设该超市销售该绿色食品每天获得利润w元,当销售单价为何值时,每天可获得最大利润?最大利润是多少?3.为倡导节能环保,降低能源消耗,提倡环保型新能源开发,造福社会.某公司研发生产一种新型智能环保节能灯,成本为每件40元.市场调查发现,该智能环保节能灯每件售价y(元)与每天的销售量为x(件)的关系如图,为推广新产品,公司要求每天的销售量不少于1000件,每件利润不低于5元.(1)求每件销售单价y(元)与每天的销售量为x(件)的函数关系式并直接写出自变量x的取值范围;(2)设该公司日销售利润为P元,求每天的最大销售利润是多少元?(3)在试销售过程中,受国家政策扶持,毎销售一件该智能环保节能灯国家给予公司补贴m(m≤40)元.在获得国家每件m元补贴后,公司的日销售利润随日销售量的增大而增大,则m的取值范围是(直接写出结果).4.网络销售是一种重要的销售方式.某乡镇农贸公司新开设了一家网店,销售当地农产品.其中一种当地特产在网上试销售,其成本为每千克2元.公司在试销售期间,调查发现,每天销售量y(kg)与销售单价x(元)满足如图所示的函数关系(其中2<x≤10).(1)若5<x≤10,求y与x之间的函数关系式;(2)销售单价x为多少元时,每天的销售利润最大?最大利润是多少元?5.现代城市绿化带在不断扩大,绿化用水的节约是一个非常重要的问题.如图1、图2所示,某喷灌设备由一根高度为0.64m的水管和一个旋转喷头组成,水管竖直安装在绿化带地面上,旋转喷头安装在水管顶部(水管顶部和旋转喷头口之间的长度、水管在喷灌区域上的占地面积均忽略不计),旋转喷头可以向周围喷出多种抛物线形水柱,从而在绿化带上喷灌出一块圆形区域.现测得喷的最远的水柱在距离水管的水平距离3m处达到最高,高度为1m.(1)求喷灌出的圆形区域的半径;(2)在边长为16m的正方形绿化带上固定安装三个该设备,喷灌区域可以完全覆盖该绿化带吗?如果可以,请说明理由;如果不可以,假设水管可以上下调整高度,求水管高度为多少时,喷灌区域恰好可以完全覆盖该绿化带.(以上需要画出示意图,并有必要的计算、推理过程)6.某商家在购进一款产品时,由于运输成本及产品成本的提高,该产品第x天的成本y(元/件)与x(天)之间的关系如图所示,并连续60天均以80元/件的价格出售,第x天该产品的销售量z(件)与x(天)满足关系式z=x+15.(1)第25天,该商家的成本是元,获得的利润是元;(2)设第x天该商家出售该产品的利润为w元.①求w与x之间的函数关系式;②求出第几天的利润最大,最大利润是多少?7.某品牌服装公司经过市场调査,得到某种运动服的月销量y(件)是售价x(元/件)的一次函数,其售价、月销售量、月销售利润w(元)的三组对应值如下表:注:月销售利润=月销售量×(售价一进价)售价x(元/件)130 150 180月销售量y(件)210 150 60月销售利润w(元)10500 10500 6000(1)求y关于x的函数解析式(不要求写出自变量的取值范围);(2)当售价是多少时,月销售利润最大?最大利润是多少元?(3)为响应号召,该公司决定每售出1件服装,就捐赠a元(a>0),商家规定该服装售价不得超过200元,月销售量仍满足上关系,若此时月销售最大利润仍可达9600元,求a的值.8.“武汉加油!中国加油!”疫情牵动万人心,每个人都在为抗击疫情而努力.某厂改造了10条口罩生产线,每条生产线每天可生产口罩500个.如果每增加一条生产线,每条生产线就会比原来少生产20个口罩.设增加x条生产线后,每条生产线每天可生产口罩y 个.(1)直接写出y与x之间的函数关系式;(2)若每天共生产口罩6000个,在投入人力物力尽可能少的情况下,应该增加几条生产线?(3)设该厂每天可以生产的口罩w个,请求出w与x的函数关系式,并求出增加多少条生产线时,每天生产的口罩数量最多,最多为多少个?9.九年级孟老师数学小组经过市场调查,得到某种运动服的月销量y(件)是售价x(元/件)的一次函数,其售价、月销售量、月销售利润w(元)的三组对应值如下表:售价x(元/件)130 150 180月销售量y(件)210 150 60月销售利润w(元)10500 10500 6000注:月销售利润=月销售量×(售价﹣进价)(1)①求y关于x的函数解析式(不要求写出自变量的取值范围);②运动服的进价是元/件;当售价是元/件时,月销利润最大,最大利润是元.(2)由于某种原因,该商品进价降低了m元/件(m>0),商家规定该运动服售价不得低于150元/件,该商店在今后的售价中,月销售量与售价仍满足(1)中的函数关系式,若月销售量最大利润是12000元,求m的值.10.小明经过市场调查,整理出他妈妈商店里一种商品在第x(1≤x≤30)天的销售量的相关信息如下表:时间第x(天)1≤x≤20 20≤x≤30售价(元/件)x+30 50每天销量(件)160﹣4x已知该商品的进价为每件20元,设销售该商品的每天利润为y元.(1)求出y与x的函数关系式;(2)问销售该商品第几天时,当天销售利润最大,最大利润是多少?(3)该商品在销售过程中,共有多少天每天销售利润不低于2400元?请直接写出结果.11.我市某乡镇在“精准扶贫”活动中销售农产品,经分析发现月销售量y(万件与月份x (月)的关系为:每件产品的利润z(元)与月份x(月)的关系如表:x 1 2 3 4 5 6 7 8 9 10 11 12 z19 18 17 16 15 14 13 12 10 10 10 10 (1)请你根据表格直接写出每件产品利润z(元)与月份x(月)的函数关系式;(2)若月利润w(万元)=当月销售量y(万件)x当月每件产品的利润z(元),求月利润w(万元)与月份x(月)的关系式;(3)当x为何值时,月利润w有最大值,最大值为多少?12.某商品的进价为每件50元,售价为每件60元,每个月可卖出200件.若每件商品的售价上涨1元,则每个月少卖10件(每件售价不能高于72元),设每件商品的售价上涨x 元(x为正整数),每个月的销售量为y件.(1)求y与x的函数关系式并直接写出自变量x的取值范围;(2)设每月的销售利润为w元,每件商品的售价定为多少元时,每个月可获得最大利润?最大月利润是多少元?13.某超市销售一种高档蔬菜“莼菜”,其进价为16元/kg.经市场调查发现:该商品的日销售量y(kg)是售价x(元/kg)的一次函数,其售价、日销售量对应值如表:售价x(元/kg)20 30 40日销售量y(kg)80 60 40(1)求y关于x的函数解析式(不要求写出自变量的取值范围);(2)x为多少时,当天的销售利润w(元)最大?最大利润为多少?(3)由于产量日渐减少,该商品进价提高了a元/kg(a>0),物价部门规定该商品售价不得超过36元/kg,该商店在今后的销售中,日销售量与售价仍然满足(1)中的函数关系.若日销售最大利润是864元,求a的值.14.为满足市场需求,新生活超市在端午节前夕购进价格为3元/个的粽子,根据市场预测,该品牌粽子每个售价4元时,每天能出售500个,并且售价每上涨0.1元,其销售量将减少10个,为了维护消费者利益,物价部门规定,该品牌粽子的售价不能超过进价的200%.(1)请你利用所学知识帮助超市给该品牌粽子定价,使超市每天的销售利润为800元.(2)定价为多少时每天的利润最大?最大利润是多少?15.甲船从A处起以15km/h的速度向正北方向航行,这时乙船从A的正东方向20km的B 处起以20km/h的速度向西航行,多长时间后,两船的距离最小?最小距离是多少?16.某商场经营一种海产品,进价是每千克20元,根据市场调查发现,每日的销售量y(千克)与售价x(元/千克)是一次函数关系,如图所示:(1)求y与x的函数关系式(不求自变量取值范围);(2)某日该商场出售这种海产品获得了21000元的利润,该海产品的售价是多少?(3)若某日该商场这种海产品的销售量不少于650千克,该商场销售这种海产品获得的最大利润是多少?17.某网店专售一款电动牙刷,其成本为20元/支,销售中发现,该商品每天的销售量y(支)与销售单价x(元/支)之间存在如图所示的关系.(1)请求出y与x的函数关系式;(2)该款电动牙刷销售单价定为多少元时,每天销售利润最大?最大利润是多少元?(3)近期武汉爆发了“新型冠状病毒”疫情,该网店店主决定从每天获得的利润中抽出200元捐赠给武汉,为了保证捐款后每天剩余利润不低于550元,如何确定该款电动牙刷的售单价?18.某网店专售一品牌牙膏,其成本为22元/支,销售中发现,该商品每天的销售量y(支)与销售单价x(元/支)之间存在如图所示的关系.(1)请求出y与x之间的函数关系式;(2)该品牌牙膏销售单价定为多少元时,每天销售利润最大?最大利润是多少元?(3)在武汉爆发“新型冠状病毒”疫情期间,该网店店主决定从每天获得的利润中抽出100元捐赠给武汉,为了保证捐款后每天剩余的利润不低于350元,在抗“新型冠状病毒”疫情期间,市场监督管理局加大了对线上、线下商品销售的执法力度,对商品售价超过成本价的20%的商家进行处罚,请你给该网店店主提供一个合理化的销售单价范围.19.某工艺品厂生产一款工艺品,已知这款工艺品的生产成本为60元/件.经市场调研发现,这款工艺品每天的销售量y(件)与售价x(元/件)之间存在着如表所示的一次函数关系:售价x/(元/件)…70 90 …销售量y/件…3000 1000 …(1)求销售量y(件)与售价x(元/件)之间的函数关系式.(2)求每天的销售利润w(元)与售价x(元/件)之间的函数关系式.(3)如何定价才能使该工艺品厂每天获得的销售利润为40000元?20.如图,用一段长为30m的篱笆围成一个一边靠墙的矩形菜园,墙长为18m.设矩形菜园的边AB的长为xm,面积为Sm2.(I)写出S关于x的函数解析式,并求出x的取值范围;(Ⅱ)当该矩形菜园的面积为72m2时,求边AB的长;(Ⅲ)当边AB的长为多少时,该矩形菜园的面积最大?最大面积是多少?参考答案1.解:(1)①当12≤x≤20时,设y=kx+b.代(12,2000),(20,400),得解得∴y=﹣200x+4400②当20<x≤24时,y=400.综上,y=(2)①当12≤x≤20时,W=(x﹣12)y=(x﹣12)(﹣200x+4400)=﹣200(x﹣17)2+5000当x=17时,W的最大值为5000;②当20<x≤24时,W=(x﹣12)y=400x﹣4800.当x=24时,W的最大值为4800.∴最大利润为5000元.(3)①当12≤x≤20时,W=(x﹣12﹣1)y=(x﹣13)(﹣2000x+4400)=﹣200(x﹣17.5)2+4050令﹣200(x﹣17.5)2+4050=3600x 1=16,x2=19∴定价为16≤x≤19②当20<x≤24时,W=400(x﹣13)=400x﹣5200≥3600 ∴22≤x≤24.综上,销售价格确定为16≤x≤19或22≤x≤24.2.解:(1)设y与x的函数关系式为y=kx+b,,得,即y与x的函数关系式是y=﹣20x+1000(30≤x≤50);(2)w=(x﹣20)y=(x﹣20)(﹣20x+1000)=﹣20x2+1400x﹣20000=﹣20(x﹣35)2+4500,故当x=35时,w取得最大值,此时w=4500,答:当销售单价为35元/千克时,每天可获得最大利润4500元.3.解:(1)设每件销售单价y(元)与每天的销售量为x(件)的函数关系式为y=kx+b,把(1500,55)与(2000,50)代入y=kx+b得,,解得:,∴每件销售单价y(元)与每天的销售量为x(件)的函数关系式为y=﹣x+70,当y≥45时,﹣x+70≥45,解得:x≤2500,∴自变量x的取值范围1000≤x≤2500;(2)根据题意得,P=(y﹣40)x=(﹣x+70﹣40)x=﹣x2+30x=﹣(x ﹣1500)2+22500,∵﹣<0,P有最大值,当x<1500时,P随x的增大而增大,∴当x=1500时,P的最大值为22500元,答:每天的最大销售利润是22500元;(3)由题意得,P=(﹣x+70﹣40+m)x=﹣x2+(30+m)x,∵对称轴为x=50(30+m),∵1000≤x≤2500,∴x 的取值范围在对称轴的左侧时P 随x 的增大而增大,50(30+m )≥2500,解得:m ≥20,∴m 的取值范围是:20≤m ≤40.故答案为:20≤m ≤40.4.解:(1)设y =kx +b ,把(5,600),(10,400)代入y =kx +b , 得解得 ∴y =﹣40x +800.(2)设每天的销售利润为w 元当2<x ≤5时,w =600(x ﹣2)=600x ﹣1200当x =5时,w max =600×5﹣1200=1800(元);当5<x ≤10时,w =(﹣40x +800)(x ﹣2)=﹣40(x ﹣11)2+3240当x =10时,w max =﹣40×1+3240=3200综上所述,当x =10时,每天的销售利润最大,最大是3200元.5.解:(1)根据题意,以水管在地面安装处为坐标原点,以该处和喷的最远的水柱落地处所在直线为x 轴,建立平面直角坐标系,则喷的最远的水柱所在的抛物线顶点为(3,1),过(0,0.64).可设该抛物线对应的函数表达式是y =a (x ﹣3) 2+1,代入(0,0.64),解得,a =﹣. 所以y =﹣ (x ﹣3) 2+1.令y =0,解得x 1=﹣2(舍),x 2=8.4 分所以,喷灌出的圆形区域的半径为8 m .(2)在边长为16 m 的正方形绿化带上按如图的位置固定安装三个该设备,如图1,喷灌出的圆形区域的半径的最小值是=,8<,这样安装不能完全覆盖;如图2,设CD=x,则BC=16﹣x,DE=8,AB=16,由勾股定理得:82+x2=(16﹣x)2+162解得:x=14∴2r==∴喷灌出的圆形区域的半径的最小值是,8<,这样安装也不能完全覆盖;<,如果喷灌区域可以完全覆盖该绿化带.则一个设备喷灌出的圆形区域的半径的最小值应为m.设水管向上调整a m,则调整后喷的最远的水柱所在的抛物线函数表达式是y=﹣(x﹣3) 2+1+a.代入(,0),解得,a=.0.64+=答:水管高度为时,喷灌区域恰好可以完全覆盖该绿化带.6.解:(1)由图象可知,此时的产量为z=25+15=40(件),设直线BC的关系为y=kx+b,∴,∴,∴y=x+10,故第25天,该商家的成本是:25+10=35(元)则第25天的利润为:(80﹣35)×40=1800(元);故答案为:35,1800;(2)①当0≤x≤20时,w=(80﹣30)(x+15)=50x+750,当20<x≤60时,w=[80﹣(x+10)](x+15)=﹣x2+55x+1050 ∴w=.②当0≤x≤20时w=(80﹣30)(x+15)=50x+750,=1750元;当x=20时,w最大当20<x≤60时,w=﹣x2+55x+1050∵﹣1<0,抛物线开口向下,对称轴为x=∴当x=27或x=28时,w=﹣272+55×27+1050=1806(元)∵1806>1750∴第27天或28天的利润最大,最大为1806元.7.解:(1)设y关于x的函数解析式为:y=kx+b(k≠0)由题意得:,解得:∴y关于x的函数解析式为y=﹣3x+600;(2)运动服的进价是:130﹣10500÷210=80(元)月销售利润w=(x﹣80)(﹣3x+600)=﹣3x2+840x﹣48000=﹣3(x﹣140)2+10800∴当售价是140元时,月销售利润最大,最大利润为10800元;(3)由题意得:w=(x﹣80﹣a)(﹣3x+600)=﹣3x2+(840+3a)x﹣48000﹣600a∴当x=140+a时,w有最大值.∵a>0,且a≤140﹣80∴140<140+a≤170<200∵商家规定该服装售价不得超过200元,此时月销售最大利润仍可达9600元,∴当x=140+a时,有,解得,a=120﹣80,或a=120+80(舍去),故a=120﹣80.8.解:(1)由题意可知该函数关系为一次函数,其解析式为:y=500﹣20x;∴y与x之间的函数关系式为y=500﹣20x(0≤x≤25,且x为整数);(2)由题意得:(10+x)(500﹣20x)=6000,整理得:x2﹣15x+50=0,解得:x1=5,x2=10,∵尽可能投入少,∴x2=10舍去.答:应该增加5条生产线.(3)w=(10+x)(500﹣20x)=﹣202+300x+5000=﹣20(x﹣7.5)2+6125,∵a=﹣20<0,开口向下,∴当x=7.5时,w最大,又∵x为整数,∴当x=7或8时,w最大,最大值为6120.答:当增加7或8条生产线时,每天生产的口罩数量最多,为6120个.9.解:(1)设y关于x的函数解析式为:y=kx+b(k≠0)由题意得:解得:∴y关于x的函数解析式为y=﹣3x+600;(2)运动服的进价是:130﹣10500÷210=80(元)月销售利润w=(x﹣80)(﹣3x+600)=﹣3x2+840x﹣48000=﹣3(x﹣140)2+10800∴当售价是140元时,月销售利润最大,最大利润为10800元.故答案为:80;140;10800;(3)由题意得:w=[x﹣(80﹣m)](﹣3x+600)=﹣3x2+(840﹣3m)x﹣48000+600m对称轴为x=140﹣∵m>0∴140﹣<140<150∵商家规定该运动服售价不得低于150元/件∴由二次函数的性质,可知当x=150时,月销售量最大利润是12000元∴﹣3×1502+(840﹣3m)×150﹣48000+600m=12000解得:m=10∴m的值为10.10.(1)当1≤x<20时,y=(160﹣4x)(x+30﹣20)=﹣4x2+120x+1600;当20≤x≤30时,y=(50﹣20)(160﹣4x)=﹣120x+4800;综上:y=(2)当1≤x<20时,y=﹣4x2+120x+1600=﹣4(x﹣15)2+2500∵a=﹣4<0∴当x=15时,y有最大值,最大值为2500元;当20≤x≤30时,y=﹣120x+4800;∵k=﹣120<0∴y随x的增大而减小∴当x=20时,y有最大值,最大值为2400元,综上可知,当x=15时,当天的销售利润最大,最大利润为2500元.(3)当1≤x<20时,令y=﹣4(x﹣15)2+2500=2400,解得:x1=10,x2=20(舍)∵a=﹣4<0∴当1≤x<20时,有10天每天销售利润不低于2400元;当20≤x≤30时,令y=﹣120x+4800=2400解得:x=20由(2)可知,2400为此时间段的最大值.综上,共有11天每天销售利润不低于2400元.11.解:(1)观察表中数据可得,当1≤x≤8时,z=﹣x+20;当9≤x≤12时,z=10.∴z与x的关系式为:z=;(2)当1≤x≤6时,w=(﹣x+20)(x+8)=﹣x2+12x+160;当7≤x≤8时,w=(﹣x+20)(﹣x+20)=x2﹣40x+400;当9≤x≤12时,w=10(﹣x+20)=﹣10x+200;∴w与x的关系式为:(3)当1≤x≤6时,w=﹣x2+12x+160=﹣(x﹣6)2+196,∴x=6时,w有最大值为196;当7≤x≤8时,w=x2﹣40x+400=(x﹣20)2,w随x增大而减小,∴x=7时,w有最大值为169;当9≤x≤12时,w=﹣10x+200,w随x增大而减小,∴x=9时,w有最大值为110;∵110<169<196,∴x=6时,w有最大值为196.12.解:(1)由题意得:y=200﹣10x∵每件售价不能高于72元∴1≤x≤12,且x为正整数;(2)由题意得:w=(60+x﹣50)(200﹣10x)=(10+x)(200﹣10x)=﹣10x2+100x+2000=﹣10(x﹣5)2+2250∴当x=5时,60+x=65时,即销售单价为65元时,每个月可获得最大利润,最大月利润是2250元.13.解:(1)①依题意设y=kx+b,则有解得:∴y关于x的函数解析式为y=﹣2x+120;(2)根据题意得,w=(﹣2x+120)×(x﹣16)=﹣2x2+152x﹣1920=﹣2(x﹣38)2+968,∴当售价是38元/件时,日销售利润最大,最大利润是968元;(3)根据题意得,w=(﹣2x+120)×(x﹣16﹣a)=﹣2x2+(152+2a)x﹣1920﹣120a∵a>0,对称轴为直线x=﹣=38+>36,又∵﹣2<0,售价不得超过36元/kg,∴当x≤36时,w随x的增大而增大,∴当x=36时,w有最大值864元,∴﹣2×362+(152+2a )×36﹣1920﹣120a =864,∴解得:a =2,∴a 的值为2.14.解:(1)设每个粽子的定价为x 元时,每天的利润为800元, 根据题意得,, 解得x 1=7,x 2=5,∵售价不能超过进价的200%,∴x ≤3×200%,即x ≤6,∴x =5,∴定价为5元时,每天的利润为800元.(2)设每个粽子的定价为m 元,则每天的利润为w ,则有: w =(m ﹣3)(500﹣10×)=(m ﹣3)(500﹣100m +400)=﹣100(m ﹣3)(m ﹣9)=﹣100(m 2﹣12m +27)=﹣100[(m ﹣6)2﹣9]=﹣100(m ﹣6)2+900∵二次项系数为﹣100<0,m ≤6,∴当定价为6元时,每天的利润最大,最大的利润是900元.15.解:根据题意画出示意图如下:设x 小时后,两船相距ykm ,根据题意,得:y2=(15x)2+(20﹣20x)2=225x2+400﹣800x+400x2=(25x﹣16)2+144∴当x=时,y2有最小值144,则y的最小值为12,答:小时后,两船的距离最小,最小距离是12km.16.解:(1)设y与x之间的函数关系式为y=kx+b,将(25,950),(40,800)代入可得:解得,∴y与x之间的函数关系式为y=﹣10x+1200.(2)根据题目信息可得:(﹣10x+1200)(x﹣20)=21000,整理可得:x2﹣140x+4500=0,解得x=50或x=90.∴该海产品的售价是50元/kg或90元/kg.(3)设所获利润为W,则根据题目信息可得:W=(﹣10x+1200)(x﹣20)=﹣10(x﹣70)2+25000.∵﹣10x+1200≥650,∴x≤55.∴当x=55时,W有最大值.W的最大值为:﹣10(55﹣70)2+25000=22750(元).∴该商场销售这种海产品获得的最大利润是22750元.17.解:(1)设y与x的函数关系式为y=kx+b,将(30,100),(35,50)代入y=kx+b,得,解得,∴y与x的函数关系式为y=﹣10x+400;(2)设该款电动牙刷每天的销售利润为w 元,由题意得 w =(x ﹣20)•y=(x ﹣20)(﹣10x +400)=﹣10x 2+600x ﹣8000=﹣10(x ﹣30)2+1000,∵﹣10<0,∴当x =30时,w 有最大值,w 最大值为1000.答:该款电动牙刷销售单价定为30元时,每天销售利润最大,最大销售利润为1000 元;(3)设捐款后每天剩余利润为 z 元,由题意可得 z =﹣10x 2+600x ﹣8000﹣200=﹣10x 2+600x ﹣8200,令z =550,即﹣10x 2+600x ﹣8200=550,﹣10(x 2﹣60x +900)=﹣250,x 2﹣60x +900=25,解得x 1=25,x 2=35,画出每天剩余利润z 关于销售单价x 的函数关系图象如解图,由图象可得:当该款电动牙刷的销售单价每支不低于25元,且不高于35元时,可保证捐款后每天剩余利润不低于550 元.18.解:(1)根据题意设y =kx +b (k ≠0),将(30,100)、(35,50)代入得, 解得,∴y与x之间的关系式为y=﹣10x+400;(2)设每天的利润为W元,则W=(x﹣22)y=(x﹣22)(﹣10x+400)=﹣10x2+620x﹣8800=﹣10(x﹣31)2+810,∴销售单价定为31元时,每天最大利润为810元.(3)﹣10x2+620x﹣8800﹣100=350,解得x=25或x=37,结合图象和二次函数的特点得出25≤x≤37,又x≤22×(1+20%),综上可得25≤x≤26.4,∴按要求网店店主的销售单价范围为大于或等于25元且小于或等于26.4元.19.解:(1)设销售量y(件)与售价x(元/件)之间的函数关系式为y=kx+b,,得,即销售量y(件)与售价x(元/件)之间的函数关系式是y=﹣100x+10000;(2)由题意可得,w=(x﹣60)y=(x﹣60)(﹣100x+10000)=﹣100x2+16000x+600000,即每天的销售利润w(元)与售价x(元/件)之间的函数关系式是w=﹣100x2+16000x+600000;(3)当w=40000时,40000=﹣100x2+16000x+600000,解得,x1=x2=80,答:当定价为80元时,才能使该工艺品厂每天获得的销售利润为40000元.20.解:(Ⅰ)∵AB=CD=xm,∴BC=(30﹣2x)m,由题意得S=x(30﹣2x)=﹣2x2+30x(6≤x<15);(Ⅱ)令s=72得:﹣2x2+30x=72,解得:x=3或x=12,当x=3时,30﹣2x=24>18,∴x取12,答:AB的长为12米.(Ⅲ)∵S=﹣2x2+30x=﹣2(x﹣7.5)2+112.5,=112.5,∴当x=7.5时,S有最大值,S最大。
2020年重庆中考复习数学函数图象专题训练一(含答案)

(2)①∵b=8,∴y=|﹣x2+8x﹣7|﹣4,当 x=﹣ 时,y= ;当 x=4 时,y=5;
∴m= ,n=5;②如图所示:
(3)函数关于 x=4 对称;
第 17 页(共 34 页)
(4)当 ,|﹣x2+8x﹣7|=m+4 有四个根,
解(1)当 x=0 时,y=﹣2+2+3=3,即 m=3, 当 x=3 时,y=﹣0.5+1+3=3.5,即 n=3.5 (2)图象如图所示:
(3)图象关于直线 x=2 对称
第 16 页(共 34 页)
(4)∵﹣ (x﹣2)2+|x﹣2|+3=k 有 3 个不相等的实数根,即函数 y=﹣ (x﹣2)2+|x﹣2|+3 图象与
y=k 图象有三个交点,由图象得,k=3. 2、(2019 秋•北碚区校级月考)已知关于 x 函数 y=|﹣x2+bx﹣7|﹣4,点(4,5)在函数上,且 b 为整数,
根据我们已有的研究函数的经验,请对该函数及其图象进行如下探究,并完成以下问题:
(1)求 b= 8 ; (2)函数图象探究:
①下表是 y 与 x 的几组对应值,请直接写出 m 与 n 的值:m=
;
(2)在给出的平面直角坐标系中,画出这个函数的图象并写出这个函数的一条性质
;
(3)进一步探究函数图象并解决问题:
①直线 y=k 与函数 y=a|x2+bx|+c 有三个交点,则 k= ;
②已知函数 y=x﹣3 的图象如图所示,结合你所画的函数图象,写出不等式 a|x2+bx|+c≤x﹣3 的解
集:
图1
(3)请结合所画函数图象,写出函数图象的一条性质; (4)解决问题:若函数y1 与y2 2a 2 至少有2 个交点,求a 的取值范围.
2020年初三数学下册中考专题复习 二次函数面积最值问题(含答案)

2020年初三数学下册中考专题复习二次函数面积最值问题1.如图,关于x的二次函数y=x2+bx+c的图象与x轴交于点A(1,0)和点B,与y轴交于点C(0,3),抛物线的对称轴与x轴交于点D.(1)求二次函数的表达式;(2)在y轴上是否存在一点P,使△PBC为等腰三角形?若存在.请求出点P的坐标;(3)有一个点M从点A出发,以每秒1个单位的速度在AB上向点B运动,另一个点N 从点D与点M同时出发,以每秒2个单位的速度在抛物线的对称轴上运动,当点M到达点B时,点M、N同时停止运动,问点M、N运动到何处时,△MNB面积最大,试求出最大面积.2.如图,在平面直角坐标系中,平行四边形ABOC如图放置,将此平行四边形绕点O顺时针旋转90°得到平行四边形A′B′OC′.抛物线y=﹣x2+2x+3经过点A、C、A′三点.(1)求A、A′、C三点的坐标;(2)求平行四边形ABOC和平行四边形A′B′OC′重叠部分△C′OD的面积;(3)点M是第一象限内抛物线上的一动点,问点M在何处时,△AMA′的面积最大?最大面积是多少?并写出此时M的坐标.3.如图,直线AB和抛物线的交点是A(0,﹣3),B(5,9),已知抛物线的顶点D的横坐标是2.(1)求抛物线的解析式及顶点坐标;(2)在x轴上是否存在一点C,与A,B组成等腰三角形?若存在,求出点C的坐标,若不在,请说明理由;(3)在直线AB的下方抛物线上找一点P,连接PA,PB使得△PAB的面积最大,并求出这个最大值.4.如图,抛物线C1:y=x2﹣2x与抛物线C2:y=ax2+bx开口大小相同、方向相反,它们相交于O,C两点,且分别与x轴的正半轴交于点B,点A,OA=2OB.(1)求抛物线C2的解析式;(2)在抛物线C2的对称轴上是否存在点P,使PA+PC的值最小?若存在,求出点P的坐标,若不存在,说明理由;(3)M是直线OC上方抛物线C2上的一个动点,连接MO,MC,M运动到什么位置时,△MOC面积最大?并求出最大面积.5.如图,在平面直角坐标系中,二次函数的图象交坐标轴于A(﹣1,0),B(4,0),C(0,﹣4)三点,点P是直线BC下方抛物线上一动点.(1)求这个二次函数的解析式;(2)是否存在点P,使△POC是以OC为底边的等腰三角形?若存在,求出P点坐标;若不存在,请说明理由;(3)动点P运动到什么位置时,△PBC面积最大,求出此时P点坐标和△PBC的最大面积.6.如图,二次函数y=﹣x2+3x+m的图象与x轴的一个交点为B(4,0),另一个交点为A,且与y轴相交于C点(1)求m的值及C点坐标;(2)在直线BC上方的抛物线上是否存在一点M,使得它与B,C两点构成的三角形面积最大,若存在,求出此时M点坐标;若不存在,请简要说明理由(3)P为抛物线上一点,它关于直线BC的对称点为Q①当四边形PBQC为菱形时,求点P的坐标;②点P的横坐标为t(0<t<4),当t为何值时,四边形PBQC的面积最大,请说明理由.7.如图,抛物线y=ax2+bx+与直线AB交于点A(﹣1,0),B(4,),点D是抛物线A、B两点间部分上的一个动点(不与点A、B重合),直线CD与y轴平行,交直线AB于点C,连接AD,BD.(1)求抛物线的表达式;(2)设点D的横坐标为m,△ADB的面积为S,求S关于m的函数关系式,并求出当S 取最大值时的点C的坐标.8.如图A(0,3),B(3,0),C(1,0)分别是抛物线:y=ax2+bx+c(a≠0)上的三点,点P为抛物线上一动点.(1)求此抛物线的解析式.(2)当△PAB是以AB为一直角边的直角三角形时,求此时点P的坐标.(3)若点P在抛物线上A、B两点之间移动时,是否存在一个位置,使△PAB的面积最大?若存在,请求此时点P的坐标.若不存在,请说明理由.9.如图,抛物线y=ax2+bx+c经过A(0,3)、B(﹣1,0)、D(2,3),抛物线与x轴的另一交点为E.点P为直线AE上方抛物线上一动点,设点P的横坐标为t.(1)求抛物线的表达式;(2)当t为何值时,△PAE的面积最大?并求出最大面积;(3)是否存在点P使△PAE为直角三角形?若存在,求出t的值;若不存在,说明理由.10.如图,抛物线y=ax2+bx+c与x轴交于A(﹣1,0)B(3,0)两点,与y轴交于点C (0,﹣3)(1)求出该抛物线的函数关系式及对称轴(2)点P是抛物线上的一个动点,设点P的横坐标为t(0<t<3).当△PCB的面积的最大值时,求点P的坐标(3)在(1)的条件下,点P在抛物线上,点Q在抛物线的对称轴上,若以BC为边,以点B、C、P、Q为顶点的四边形是平行四边形时,求P点的坐标.11.如图,抛物线y=﹣x2+bx+c与x轴交于点A(﹣1,0)和点B,与y轴交于C(0,3),直线y=+m经过点C,与抛物线的另一交点为点D,点P是直线CD上方抛物线上的一个动点,过点P作PF⊥x轴于点F,交直线CD于点E,设点P的横坐标为m.(1)求抛物线解析式并求出点D的坐标;(2)连接PD,△CDP的面积是否存在最大值?若存在,请求出面积的最大值;若不存在,请说明理由;(3)当△CPE是等腰三角形时,请直接写出m的值.12.如图1,在平面直角坐标系中,直线y=x﹣与抛物线y=﹣x2+bx+c交于A、B两点,点A在x轴上,点B的横坐标为﹣8.点P是直线AB上方的抛物线上的一动点(不与点A、B重合),过点P作x轴的垂线,垂足为E,交直线AB于点C,作PD⊥AB于点D,交x轴于点F.(1)求该抛物线的解析式;(2)求sin∠ACE的值;(3)连接PA、PB(如图2所示),设△PAB的面积为S,点P的横坐标为x,求S关于x的函数关系式,并求出S的最大值.13.如图,⊙M的圆心M(﹣1,2),⊙M经过坐标原点O,与y轴交于点A.经过点A的一条直线l解析式为:y=﹣x+4与x轴交于点B,以M为顶点的抛物线经过x轴上点D(2,0)和点C(﹣4,0).(1)求抛物线的解析式;(2)求证:直线l是⊙M的切线;(3)点P为抛物线上一动点,且PE与直线l垂直,垂足为E;PF∥y轴,交直线l于点F,是否存在这样的点P,使△PEF的面积最小.若存在,请求出此时点P的坐标及△PEF面积的最小值;若不存在,请说明理由.14.如图,已知抛物线y=ax2﹣x+c与x轴相交于A、B两点,并与直线y=x﹣2交于B、C两点,其中点C是直线y=x﹣2与y轴的交点,连接AC.(1)求抛物线的解析式;(2)证明:△ABC为直角三角形;(3)△ABC内部能否截出面积最大的矩形DEFG?(顶点D、E、F、G在△ABC各边上)若能,求出最大面积;若不能,请说明理由.15.如图,在平面直角坐标系中,矩形OCDE的三个顶点分别是C(3,0),D(3,4),E (0,4).点A在DE上,以A为顶点的抛物线过点C,且对称轴x=1交x轴于点B.连接EC,AC.点P,Q为动点,设运动时间为t秒.(1)填空:点A坐标为;抛物线的解析式为.(2)在图①中,若点P在线段OC上从点O向点C以1个单位/秒的速度运动,同时,点Q在线段CE上从点C向点E以2个单位/秒的速度运动,当一个点到达终点时,另一个点随之停止运动.当t为何值时,△PCQ为直角三角形?(3)在图②中,若点P在对称轴上从点A开始向点B以1个单位/秒的速度运动,过点P做PF⊥AB,交AC于点F,过点F作FG⊥AD于点G,交抛物线于点Q,连接AQ,CQ.当t为何值时,△ACQ的面积最大?最大值是多少?16.如图,抛物线y=ax2+bx+c(a≠0)与x轴交于点A和点B(1,0),与y轴交于点C(0,3),其对称轴l为x=﹣1,P为抛物线上的一个动点.(1)求抛物线的解析式并写出其顶点坐标;(2)当点P的纵坐标为2时,求点P的横坐标;(3)当点P在运动过程中,求四边形PABC面积最大时的值及此时点P的坐标.17.如图,在平面直角坐标系中,顶点为(4,﹣1)的抛物线交y轴于A点,交x轴于B,C两点(点B在点C的左侧),已知A点坐标为(0,3).(1)求此抛物线的解析式;(2)过点B作线段AB的垂线交抛物线于点D,如果以点C为圆心的圆与直线BD相切,请判断抛物线的对称轴l与⊙C有怎样的位置关系,并给出证明;(3)已知点P是抛物线上的一个动点,且位于A,C两点之间,问:当点P运动到什么位置时,△PAC的面积最大?并求出此时P点的坐标和△PAC的最大面积.18.如图,已知抛物线y=﹣+bx+4与x轴相交于A、B两点,与y轴相交于点C,若已知B点的坐标为B(8,0).(1)求抛物线的解析式及其对称轴方程.(2)连接AC、BC,试判断△AOC与△COB是否相似?并说明理由.(3)在抛物线上BC之间是否存在一点D,使得△DBC的面积最大?若存在请求出点D 的坐标和△DBC的面积;若不存在,请说明理由.19.如图1,抛物线y=﹣x2+bx+c(a≠0)与x轴交于A(﹣4,0)、B(1,0)两点,与y轴交于C点,对称轴x=﹣,点N(n,0)是线段AB上的一个动点(N与A、B两点不重合),请回答下列问题:(1)求出抛物线的解析式,并写出C点的坐标;(2)试求出当n为何值时,△ANC恰能构成是等腰三角形.(3)如图2,过N作NF∥BC,与AC相交于D点,连结CN,请问在N点的运动过程中,△CDN的面积是否存在最大值;若存在,试求出该最大面积,若不存在,请说明理由.20.抛物线y=ax2+bx+c与x轴交于点A(1,0)和点B(5,0),与y轴交于点C(0,3).该抛物线与直线相交于C,D两点,点P是抛物线上的动点且位于x轴下方,直线PM∥y轴,分别与x轴和直线CD交于点M,N.(1)求该抛物线所对应的函数解析式;(2)连结PC,PD,如图1,在点P运动过程中,△PCD的面积是否存在最大值?若存在,求出这个最大值;若不存在,说明理由;(3)连结PB,过点C作CQ⊥PM,垂足为点Q,如图2,是否存在点P,使得△CNQ 与△PBM相似?若存在,求出满足条件的点P的坐标;若不存在,说明理由.详细答案一.解答题(共20小题)1.【解答】解:(1)把A(1,0)和C(0,3)代入y=x2+bx+c,解得:b=﹣4,c=3,∴二次函数的表达式为:y=x2﹣4x+3;(2)令y=0,则x2﹣4x+3=0,解得:x=1或x=3,∴B(3,0),∴BC=3,点P在y轴上,当△PBC为等腰三角形时分三种情况进行讨论:如图1,①当CP=CB时,PC=3,∴OP=OC+PC=3+3或OP=PC﹣OC=3﹣3∴P1(0,3+3),P2(0,3﹣3);②当BP=BC时,OP=OB=3,∴P3(0,﹣3);③当PB=PC时,∵OC=OB=3∴此时P与O重合,∴P4(0,0);综上所述,点P的坐标为:(0,3+3)或(0,3﹣3)或(0,﹣3)或(0,0);(3)如图2,设A运动时间为t,由AB=2,得BM=2﹣t,则DN=2t,∴S△MNB=×(2﹣t)×2t=﹣t2+2t=﹣(t﹣1)2+1,即当M(2,0)、N(2,2)或(2,﹣2)时△MNB面积最大,最大面积是1.2.【解答】解:(1)当y=0时,﹣x2+2x+3=0,解得x1=3,x2=﹣1,则C(﹣1,0),A ′(3,0);当x=0时,y=3,则A(0,3);(2)∵四边形ABOC为平行四边形,∴AB∥OC,AB=OC,而C(﹣1,0),A(0,3),∴B(1,3)=×3×1=,∴OB==,S△AOB又∵平行四边形ABOC旋转90°得平行四边形A′B′OC′,∴∠ACO=∠OC′D,OC′=OC=1,又∵∠ACO=∠ABO,∴∠ABO=∠OC′D.又∵∠C′OD=∠AOB,∴△C′OD∽△BOA,∴=()2=()2=,=×=;∴S△C′OD(3)设M点的坐标为(m,﹣m2+2m+3),0<m<3,作MN∥y轴交直线AA′于N,易得直线AA′的解析式为y=﹣x+3,则N(m,﹣m+3),∵MN=﹣m2+2m+3﹣(﹣m+3)=﹣m2+3m,∴S△AMA′=S△ANM+S△MNA′=MN•3=(﹣m2+3m)=﹣m2+m=﹣(m﹣)2+,∴当m=时,S△AMA'的值最大,最大值为,此时M点坐标为().3.【解答】解:(1)抛物线的顶点D的横坐标是2,则x=﹣=2…①,抛物线过是A(0,﹣3),则:函数的表达式为:y=ax2+bx﹣3,把B点坐标代入上式得:9=25a+5b﹣3…②,联立①、②解得:a=,b=﹣,c=﹣3,∴抛物线的解析式为:y=x2﹣x﹣3,当x=2时,y=﹣,即顶点D的坐标为(2,﹣);(2)A(0,﹣3),B(5,9),则AB=13,①当AB=AC时,设点C坐标(m,0),则:(m)2+(﹣3)2=132,解得:m=±4,即点C坐标为:(4,0)或(﹣4,0);②当AB=BC时,设点C坐标(m,0),则:(5﹣m)2+92=132,解得:m=5,即:点C坐标为(5,0)或(5﹣2,0),③当AC=BC时,设点C坐标(m,0),则:点C为AB的垂直平分线于x轴的交点,则点C坐标为(,0),故:存在,点C的坐标为:(4,0)或(﹣4,0)或(5,0)或(5﹣2,0)或(,0);(3)过点P作y轴的平行线交AB于点H,设:AB所在的直线过点A(0,﹣3),则设直线AB的表达式为y=kx﹣3,把点B坐标代入上式,9=5k﹣3,则k=,故函数的表达式为:y=x﹣3,设:点P坐标为(m,m2﹣m﹣3),则点H坐标为(m,m﹣3),S△P AB=•PH•x B=(﹣m2+12m),取得最大值为:,当m=2.5时,S△P AB答:△PAB的面积最大值为.4.【解答】解:(1)令:y=x2﹣2x=0,则x=0或2,即点B(2,0),∵C1、C2:y=ax2+bx开口大小相同、方向相反,则a=﹣1,则点A(4,0),将点A的坐标代入C2的表达式得:0=﹣16+4b,解得:b=4,故抛物线C2的解析式为:y=﹣x2+4x;(2)联立C1、C2表达式并解得:x=0或3,故点C(3,3),作点C关于C2对称轴的对称点C′(1,3),连接AC′交函数C2的对称轴与点P,此时PA+PC的值最小为:线段AC′的长度=3,此时点P(2,2);(3)直线OC的表达式为:y=x,过点M作y轴的平行线交OC于点H,设点M(x,﹣x2+4x),则点H(x,x),=MH×x C=(﹣x2+4x﹣x)=﹣x2+x,则S△MOC∵﹣<0,故x=,最大值为.故当点M(,)时,S△MOC5.【解答】解:(1)设抛物线解析式为y=ax2+bx+c,把A、B、C三点坐标代入可得,解得,∴抛物线解析式为y=x2﹣3x﹣4;(2)作OC的垂直平分线DP,交OC于点D,交BC下方抛物线于点P,如图1,∴PO=PC,此时P点即为满足条件的点,∵C(0,﹣4),∴D(0,﹣2),∴P点纵坐标为﹣2,代入抛物线解析式可得x2﹣3x﹣4=﹣2,解得x=(小于0,舍去)或x=,∴存在满足条件的P点,其坐标为(,﹣2);(3)∵点P在抛物线上,∴可设P(t,t2﹣3t﹣4),过P作PE⊥x轴于点E,交直线BC于点F,如图2,∵B(4,0),C(0,﹣4),∴直线BC解析式为y=x﹣4,∴F(t,t﹣4),∴PF=(t﹣4)﹣(t2﹣3t﹣4)=﹣t2+4t,=S△PFC+S△PFB=PF•OE+PF•BE=PF•(OE+BE)=PF•OB=(﹣t2+4t)∴S△PBC×4=﹣2(t﹣2)2+8,最大值为8,此时t2﹣3t﹣4=﹣6,∴当t=2时,S△PBC∴当P点坐标为(2,﹣6)时,△PBC的最大面积为8.6.【解答】解:(1)将B(4,0)代入y=﹣x2+3x+m,解得,m=4,∴二次函数解析式为y=﹣x2+3x+4,令x=0,得y=4,∴C(0,4),(2)存在,理由:∵B(4,0),C(0,4),∴直线BC解析式为y=﹣x+4,当直线BC向上平移b单位后和抛物线只有一个公共点时,△MBC面积最大,∴,∴x2﹣4x+b=0,∴△=16﹣4b=0,∴b=4,∴,∴M(2,6),(3)①如图,∵点P在抛物线上,∴设P(m,﹣m2+3m+4),当四边形PBQC是菱形时,点P在线段BC的垂直平分线上,∵B(4,0),C(0,4)∴线段BC的垂直平分线的解析式为y=x,∴m=﹣m2+3m+4,∴m=1±,∴P(1+,1+)或P(1﹣,1﹣),②如图,设点P(t,﹣t2+3t+4),过点P作y轴的平行线l,过点C作l的垂线,∵点D在直线BC上,∴D(t,﹣t+4),∵PD=﹣t2+3t+4﹣(﹣t+4)=﹣t2+4t,BE+CF=4,=2S△PCB=2(S△PCD+S△PBD)=2(PD×CF+PD×BE)=4PD=﹣4t2+16t,∴S四边形PBQC∵0<t<4,=16∴当t=2时,S四边形PBQC最大7.【解答】解:(1)∵由题意得解得:,∴y=﹣x2+2x+.(2)设直线AB为:y=kx+b.则,解得直线AB的解析式为y=+.如图所示:记CD与x轴的交点坐标为E.过点B作BF⊥DC,垂足为F.设D(m,﹣m2+2m+)则C(m,m+).∵CD=(﹣m2+2m+)﹣(m+)=m2+m+2,∴S=AE•DC+CD•BF=CD(AE+BF)=DC=m2+m+5.∴S=m2+m+5.∵﹣<0,∴当m=时,S有最大值.∴当m=时,m+=×+=.∴点C(,).8.【解答】解:(1)将A(0,3),B(3,0),C(1,0)代入y=ax2+bx+c,得:,解得:,∴抛物线的解析式为y=x2﹣4x+3.(2)设点P的坐标为(m,m2﹣4m+3).∵点A的坐标为(0,3),点B的坐标为(3,0),∴AP2=(m﹣0)2+(m2﹣4m+3﹣3)2=m4﹣8m3+17m2,BP2=(m﹣3)2+(m2﹣4m+3)2=m4﹣8m3+23m2﹣30m+18,AB2=(3﹣0)2+(0﹣3)2=18.分两种情况考虑:①当∠BAP=90°时,AB2+AP2=BP2,即18+m4﹣8m3+17m2=m4﹣8m3+23m2﹣30m+18,整理,得:m2﹣5m=0,解得:m1=0(舍去),m2=5,∴点P的坐标为(5,8);②当∠ABP=90°时,AB2+BP2=AP2,即18+m4﹣8m3+23m2﹣30m+18=m4﹣8m3+17m2,整理,得:m2﹣5m+6=0,解得:m3=2,m3=3(舍去),∴点P的坐标为(2,﹣1).综上所述:当△PAB是以AB为一直角边的直角三角形时,点P的坐标为(5,8)或(2,﹣1).(3)存在,如图过点P作PD∥y轴交直线AB于点D.设直线AB的解析式为y=kx+d(k≠0),将A(0,3),B(3,0)代入y=kx+d,得:,解得:,∴直线AB的解析式为y=﹣x+3.设点P的坐标为(n,n2﹣4n+3)(0<n<3),则点D的坐标为(n,﹣n+3),∴PD=(﹣n+3)﹣(n2﹣4n+3)=﹣n2+3n,=OB•PD=﹣n2+n=﹣(n﹣)2+.∴S△P AB∵﹣<0,取得最大值,此时最大值为,∴当n=时,S△P AB∴当△PAB的面积取最大值时,点P的坐标为(,﹣).9.【解答】解:(1)由题意得:,解得:,∴抛物线解析式为y=﹣x2+2x+3;(2)∵A(0,3),D(2,3),∴抛物线对称轴为x=1,∴E(3,0),设直线AE的解析式为y=kx+3,∴3k+3=0,解得,k=﹣1,∴直线AE的解析式为y=﹣x+3,如图1,作PM∥y轴,交直线AE于点M,设P(t,﹣t2+2t+3),M(t,﹣t+3),∴PM=﹣t2+2t+3+t﹣3=﹣t2+3t,∴==,∴t=时,△PAE的面积最大,最大值是.(3)由图可知∠PEA≠90°,∴只能有∠PAE=90°或∠APE=90°,①当∠PAE=90°时,如图2,作PG⊥y轴,∵OA=OE,∴∠OAE=∠OEA=45°,∴∠PAG=∠APG=45°,∴PG=AG,∴t=﹣t2+2t+3﹣3,即﹣t2+t=0,解得t=1或t=0(舍去),②当∠APE=90°时,如图3,作PK⊥x轴,AQ⊥PK,则PK=﹣t2+2t+3,AQ=t,KE=3﹣t,PQ=﹣t2+2t+3﹣3=﹣t2+2t,∵∠APQ+∠KPE=∠APQ+∠PAQ=90°,∴∠PAQ=∠KPE,且∠PKE=∠PQA,∴△PKE∽△AQP,∴,∴,即t2﹣t﹣1=0,解得:t=或t=<0(舍去),综上可知存在满足条件的点P,t的值为1或.10.【解答】解:(1)设抛物线解析式为y=a(x+1)(x﹣3),∵抛物线与y轴交于点C(0,﹣3),∴﹣3=a(0+1)(0﹣3),∴a=1∴设抛物线解析式为y=(x+1)(x﹣3)=x2﹣2x﹣3,对称轴为直线x=1;(2)设P(t,t2﹣2t﹣3),S△PCB=S△POC+S△POB﹣S△BOC=×3t+×3×|t2﹣2t﹣3|﹣=∵a=<0,∴函数有最大值,当t=时,面积最大,∴P()(3)设Q(1,n)),①当PQ、PC为平行四边形的对角线时,P(4,n+3),∴42﹣2×4﹣3=n+3,n=2,∴P(4,5);②当CQ、BP为平行四边形的对角线时,P(﹣2,n﹣3),∴(﹣2)2﹣2×(﹣2)﹣3=n﹣3,n=8,∴P(﹣2,5);综上所述,以BC为边,以点B、C、P、Q为顶点的四边形是平行四边形时,P点的坐标(4,5),(﹣2,5).11.【解答】解:(1)把A(﹣1,0),C(0,3)分别代入y=﹣x2+bx+c得,解得,∴抛物线的解析式为y=﹣x2+2x+3;把C(0,3)代入y=﹣x+m,解得m=3,∴直线CD的解析式为y=﹣x+3,解方程组,解得或,∴D点坐标为(,);(2)存在.设P(m,﹣m2+2m+3),则E(m,﹣m+3),∴PE=﹣m2+2m+3﹣(﹣m+3)=﹣m2+m,=••(﹣m2+m)=﹣m2+m=﹣(m﹣)2+,∴S△PCD当m=时,△CDP的面积存在最大值,最大值为;(3)当PC=PE时,m2+(﹣m2+2m+3﹣3)2=(﹣m2+m)2,解得m=0(舍去)或m=;当CP=CE时,m2+(﹣m2+2m+3﹣3)2=m2+(﹣m+3﹣3)2,解得m=0(舍去)或m=(舍去)或m=;当EC=EP时,m2+(﹣m+3﹣3)2=(﹣m2+m)2,解得m=(舍去)或m =,综上所述,m的值为或或.12.【解答】解:(1)当x=﹣8时,y=x﹣=﹣,则B(﹣8,﹣),当y=0时,x﹣=0,解得x=2,则A(2,0),把B(﹣8,﹣),A(2,0)代入y=﹣x2+bx+c得,解得,∴抛物线的解析式y=﹣x2﹣x+;(2)当x=0时,y=x﹣=﹣,则G(0,﹣),在Rt△AOG中,∵OG=,OA=2,∴AG==,∴sin∠AGO===,∵PC⊥x轴,∴PC∥OG,∴∠ACE=∠AGO,∴sin∠ACE=;(3)设P(x,﹣x2﹣x+),则C(x,x﹣),∴PC=﹣x2﹣x+﹣(x﹣)=﹣x2﹣x+4,∴S=•(2+8)•(﹣x2﹣x+4)=﹣x2﹣x+20=﹣(x+3)2+,当x=﹣3时,S的最大值为.13.【解答】解:(1)设抛物线的解析式为y=a(x﹣2)(x+4),将点M的坐标代入得:﹣9a=2,解得:a=﹣.∴抛物线的解析式为y=﹣x2﹣x+.(2)连接AM,过点M作MG⊥AD,垂足为G.把x=0代入y=﹣x+4得:y=4,∴A(0,4).将y=0代入得:0=﹣x+4,解得x=8,∴B(8,0).∴OA=4,OB=8.∵M(﹣1,2),A(0,4),∴MG=1,AG=2.∴tan∠MAG=tan∠ABO=.∴∠MAG=∠ABO.∵∠OAB+∠ABO=90°,∴∠MAG+∠OAB=90°,即∠MAB=90°.∴l是⊙M的切线.(3)∵∠PFE+∠FPE=90°,∠FBD+∠PFE=90°,∴∠FPE=∠FBD.∴tan∠FPE=.∴PF:PE:EF=:2:1.∴△PEF的面积=PE•EF=×PF•PF=PF2.∴当PF最小时,△PEF的面积最小.设点P的坐标为(x,﹣x2﹣x+),则F(x,﹣x+4).∴PF=(﹣x+4)﹣(﹣x2﹣x+)=﹣x+4+x2+x﹣=x2﹣x+=(x﹣)2+.∴当x=时,PF有最小值,PF的最小值为.∴P(,).∴△PEF的面积的最小值为=×()2=.14.【解答】(1)解:∵直线y=x﹣2交x轴、y轴于B、C两点,∴B(4,0),C(0,﹣2),∵y=ax2﹣x+c过B、C两点,∴,解得,∴y=x2﹣x﹣2.(2)证明:如图1,连接AC,∵y=x2﹣x﹣2与x负半轴交于A点,∴A(﹣1,0),在Rt△AOC中,∵AO=1,OC=2,∴AC=,在Rt△BOC中,∵BO=4,OC=2,∴BC=2,∵AB=AO+BO=1+4=5,∴AB2=AC2+BC2,∴△ABC为直角三角形.(3)解:△ABC内部可截出面积最大的矩形DEFG,面积为,理由如下:①一点为C,AB、AC、BC边上各有一点,如图2,此时△AGF∽△ACB∽△FEB.设GC=x,AG=﹣x,∵,∴,∴GF=2﹣2x,∴S=GC•GF=x•(2)=﹣2x2+2x=﹣2[(x﹣)2﹣]=﹣2(x﹣)2+,即当x=时,S最大,为.②AB边上有两点,AC、BC边上各有一点,如图3,此时△CDE∽△CAB∽△GAD,设GD=x,∵,∴,∴AD=x,∴CD=CA﹣AD=﹣x,∵,∴,∴DE=5﹣x,∴S=GD•DE=x•(5﹣x)=﹣x2+5x=﹣[(x﹣1)2﹣1]=﹣(x﹣1)2+,即x=1时,S最大,为.综上所述,△ABC内部可截出面积最大的矩形DEFG,面积为.15.【解答】解:(1)∵抛物线的对称轴为x=1,矩形OCDE的三个顶点分别是C(3,0),D(3,4),E(0,4),点A在DE上,∴点A坐标为(1,4),设抛物线的解析式为y=a(x﹣1)2+4,把C(3,0)代入抛物线的解析式,可得a(3﹣1)2+4=0,解得a=﹣1.故抛物线的解析式为y=﹣(x﹣1)2+4,即y=﹣x2+2x+3;(2)依题意有:OC=3,OE=4,∴CE===5,当∠QPC=90°时,∵cos∠QCP==,∴=,解得t=;当∠PQC=90°时,∵cos∠QCP==,∴=,解得t=.∴当t=或t=时,△PCQ为直角三角形;(3)∵A(1,4),C(3,0),设直线AC的解析式为y=kx+b,则,解得.故直线AC的解析式为y=﹣2x+6.∵P(1,4﹣t),将y=4﹣t代入y=﹣2x+6中,得x=1+,∴Q点的横坐标为1+,将x=1+代入y=﹣(x﹣1)2+4中,得y=4﹣.∴Q点的纵坐标为4﹣,∴QF=(4﹣)﹣(4﹣t)=t﹣,=S△AFQ+S△CFQ∴S△ACQ=FQ•AG+FQ•DG=FQ(AG+DG)=FQ•AD=×2(t﹣)=﹣+t=﹣(t2+4﹣4t﹣4)=﹣(t﹣2)2+1,∴当t=2时,△ACQ的面积最大,最大值是1.16.【解答】解:(1)∵抛物线y=ax2+bx+c(a≠0)与x轴交于点A和点B(1,0),与y 轴交于点C(0,3),其对称轴l为x=﹣1,∴A(﹣3,0),∴解得:,∴二次函数的解析式为y=﹣x2﹣2x+3=﹣(x+1)2+4,∴顶点坐标为(﹣1,4).(2)设点P(x,2)即y=﹣x2﹣2x+3=2,解得x1=﹣1或x2=﹣﹣1,∴点P(﹣1,2)或(﹣﹣1,2).(3)设点P(x,y),则y=﹣x2﹣2x+3,=S△OBC+S△OAP+S△OPC,∵S四边形BCP A∴=,∵﹣<0,∴当x=﹣时,四边形PABC的面积有最大值,所以点P(﹣,).17.【解答】解:(1)设抛物线为y=a(x﹣4)2﹣1,∵抛物线经过点A(0,3),∴3=a(0﹣4)2﹣1,;∴抛物线为;(2)相交.证明:连接CE,则CE⊥BD,当时,x1=2,x2=6.A(0,3),B(2,0),C(6,0),对称轴x=4,∴OB=2,AB==,BC=4,∵AB⊥BD,∴∠OAB+∠OBA=90°,∠OBA+∠EBC=90°,∴△AOB∽△BEC,∴=,即=,解得CE=,∵>2,故抛物线的对称轴l与⊙C相交.(3)如图,过点P作平行于y轴的直线交AC于点Q;可求出AC的解析式为;设P点的坐标为(m,),则Q点的坐标为(m,);∴PQ=﹣m+3﹣(m2﹣2m+3)=﹣m2+m.=S△P AQ+S△PCQ=×(﹣m2+m)×6∵S△P AC=﹣(m﹣3)2+;∴当m=3时,△PAC的面积最大为;此时,P点的坐标为(3,).18.【解答】解:(1)∵B点的坐标为B(8,0),∴﹣16+8b+4=0,解得b=,∴抛物线的解析式为y═﹣+x+4,对称轴方程为x=﹣=3;(2)∵由(1)知,抛物线的对称轴方程为x=3,B(8,0)∴A(﹣2,0),C(0,4),∴OA=2,OC=4,OB=8,∴tan∠ACO=tan∠CBO=,∴∠ACO=∠CBO.∵∠AOC=∠COB=90°,∴△AOC∽△COB.(3)设BC解析式为y=kx+b,把(8,0),(0,4)分别代入解析式得,,解得,解得y=﹣x+4,作DH⊥x轴,交BC于H.设D(t,﹣t2+t+4),H(t,﹣t+4),S△BCD=DH•OB=×(﹣t2+t+4+t﹣4)×8=﹣t2+8t=﹣(t2﹣8t+42﹣16)=﹣(t﹣4)2+16,当t=4时,△DBC的最大面积为16,此时D点坐标为(4,6).19.【解答】解:(1)∵抛物线y=﹣x2+bx+c(a≠0)与x轴交于A(﹣4,0)、B(1,0)两点,不妨设抛物线的解析式为y=﹣(x+4)(x﹣1),即y=﹣x2﹣x+2.∴C(0,2).(2)分两种情形:①当AN=AC时,如图1中,∵AC==2,∴n﹣(﹣4)=2,∴n=2﹣4.②当NA=NC时,如图2中,在Rt△NOC中,OC=2,∵NC=NA=n﹣(﹣4)=n+4,ON=n,∴n2+22=(n+)2,解得n=﹣.综上所述,当n=2﹣4或﹣时,△ANC是等腰三角形.(3)如图3中,由题意可知:直线BC的解析式为y=﹣2x+2,直线AC的解析式为y=x+2,设N(n,0),易知N在线段OB上时,△CDN的面积较小,不妨设n<0,∵ND∥BC,设ND的解析式为y=﹣2x+b,代入(n,0)可得b=2n,∴ND的解析式为y=﹣2x+2n,由,可得点D的纵坐标:y D=(8+2n),=S△AOC﹣S△ADN﹣S△CON∴S△CDN=[2×4﹣2|n|﹣(8+2n)(n+4)=﹣(n+)2+,∵﹣<0,∴当n=﹣时,△DCN的面积最大,最大值为.20.【解答】解:(1)∵抛物线y=ax2+bx+c经过点A(1,0)、点B(5,0)和点C(0,3),因为与y轴相较于点C,所以c=3.∴,解得,∴该抛物线对应的函数解析式为y=x2﹣x+3;(2)∵点P是抛物线上的动点且位于x轴下方,∴可设P(t,t2﹣t+3)(1<t<5),∵直线PM∥y轴,分别与x轴和直线CD交于点M、N,∴M(t,0),N(t,t+3),∴PN=t+3﹣(t2﹣t+3)=﹣(t﹣)2+直线CD与抛物线解析式可得,解得或,∴C(0,3),D(7,),分别过C、D作直线PN的垂线,垂足分别为E、F,如图1,则CE=t,DF=7﹣t,=S△PCN+S△PDN=PN•CE+PN•DF=PN=[﹣(t﹣)2+]=﹣(t ∴S△PCD﹣)2+,∴当t=时,△PCD的面积有最大值,最大值为;(3)存在.∵∠CQN=∠PMB=90°,∴当△CNQ与△PBM相似时,有或两种情况,∵CQ⊥PM,垂足为Q,∴Q(t,3),且C(0,3),N(t,t+3),∴CQ=t,NQ=t+3﹣3=t,∴,∵P(t,t2﹣t+3),M(t,0),B(5,0),∴BM=5﹣t,PM=0﹣(t2﹣t+3)=﹣t2+t﹣3,当时,则PM=BM,即﹣t2+t﹣3=(5﹣t),解得t=2或t=5(舍去),此时P(2,﹣);当时,则BM=PM,即5﹣t=(﹣t2+t﹣3),解得t=或t=5(舍去),此时P(,﹣);综上可知存在满足条件的点P,其坐标为(2,﹣)或(,﹣).。
2020年中考数学《一次函数》专题复习(带答案)

2020年中考数学《一次函数》专题复习(名师精选全国真题,值得下载练习)一.选择题1.(2019•辽阳)若ab<0且a>b,则函数y=ax+b的图象可能是()A.B.C.D.2.(2019•大庆)正比例函数y=kx(k≠0)的函数值y随着x增大而减小,则一次函数y =x+k的图象大致是()A.B.C.D.3.(2019•娄底)如图,直线y=x+b和y=kx+2与x轴分别交于点A(﹣2,0),点B(3,0),则解集为()A.x<﹣2 B.x>3 C.x<﹣2或x>3 D.﹣2<x<3 4.(2019•雅安)如图,在平面直角坐标系中,直线l1:y=x+1与直线l2:y=x 交于点A1,过A1作x轴的垂线,垂足为B1,过B1作l2的平行线交l1于A2,过A2作x轴的垂线,垂足为B2,过B2作l2的平行线交l1于A3,过A3作x轴的垂线,垂足为B3…按此规律,则点A n的纵坐标为()A.()n B.()n+1 C.()n﹣1+D.5.(2019•鄂尔多斯)在“加油向未来”电视节目中,王清和李北进行无人驾驶汽车运送货物表演,王清操控的快车和李北操控的慢车分别从A,B两地同时出发,相向而行.快车到达B地后,停留3秒卸货,然后原路返回A地,慢车到达A地即停运休息,如图表示的是两车之间的距离y(米)与行驶时间x(秒)的函数图象,根据图象信息,计算a、b的值分别为()A.39,26 B.39,26.4 C.38,26 D.38,26.4 6.(2019•遵义)如图所示,直线l1:y=x+6与直线l2:y=﹣x﹣2交于点P(﹣2,3),不等式x+6>﹣x﹣2的解集是()A.x>﹣2 B.x≥﹣2 C.x<﹣2 D.x≤﹣2 7.(2019•锦州)如图,一次函数y=2x+1的图象与坐标轴分别交于A,B两点,O为坐标原点,则△AOB的面积为()A.B.C.2 D.48.在平面直角坐标系中,函数y=kx+b的图象如图所示,则下列判断正确的是()A.k>0 B.b<0 C.k•b>0 D.k•b<09.(2019•鞍山)如图,若一次函数y=﹣2x+b的图象与两坐标轴分别交于A,B两点,点A的坐标为(0,3),则不等式﹣2x+b>0的解集为()A.x>B.x<C.x>3 D.x<3 10.(2019•辽阳)一条公路旁依次有A,B,C三个村庄,甲乙两人骑自行车分别从A 村、B村同时出发前往C村,甲乙之间的距离s(km)与骑行时间t(h)之间的函数关系如图所示,下列结论:①A,B两村相距10km;②出发1.25h后两人相遇;③甲每小时比乙多骑行8km;④相遇后,乙又骑行了15min或65min时两人相距2km.其中正确的个数是()A.1个B.2个C.3个D.4个11.(2019•桂林)如图,四边形ABCD的顶点坐标分别为A(﹣4,0),B(﹣2,﹣1),C(3,0),D(0,3),当过点B的直线l将四边形ABCD分成面积相等的两部分时,直线l所表示的函数表达式为()A.y=x+B.y=x+C.y=x+1 D.y=x+ 12.(2019•包头)如图,在平面直角坐标系中,已知A(﹣3,﹣2),B(0,﹣2),C(﹣3,0),M是线段AB上的一个动点,连接CM,过点M作MN⊥MC交y轴于点N,若点M、N在直线y=kx+b上,则b的最大值是()A.﹣B.﹣C.﹣1 D.0 13.(2019•广元)如图,过点A0(0,1)作y轴的垂线交直线l:y=x于点A1,过点A1作直线l的垂线,交y轴于点A2,过点A2作y轴的垂线交直线l于点A3,…,这样依次下去,得到△A0A1A2,△A2A3A4,△A4A5A6,…,其面积分别记为S1,S2,S3,…,则S100为()A.()100B.(3)100C.3×4199D.3×2395 14.(2019•聊城)某快递公司每天上午9:00﹣10:00为集中揽件和派件时段,甲仓库用来揽收快件,乙仓库用来派发快件,该时段内甲、乙两仓库的快件数量y(件)与时间x(分)之间的函数图象如图所示,那么当两仓库快递件数相同时,此刻的时间为()A.9:15 B.9:20 C.9:25 D.9:30 15.(2019•鄂州)如图,在平面直角坐标系中,点A1、A2、A3…A n在x轴上,B1、B2、B3…B n在直线y=x上,若A1(1,0),且△A1B1A2、△A2B2A3…△A n B n A n+1都是等边三角形,从左到右的小三角形(阴影部分)的面积分别记为S1、S2、S3…S n.则S n可表示为()A.22n B.22n﹣1C.22n﹣2D.22n﹣3二.填空题16.(2019•济南)某市为提倡居民节约用水,自今年1月1日起调整居民用水价格.图中l1、l2分别表示去年、今年水费y(元)与用水量x(m3)之间的关系.小雨家去年用水量为150m3,若今年用水量与去年相同,水费将比去年多元.17.如图,在平面直角坐标系中,点A,C分别在x轴、y轴上,四边形ABCO是边长为4的正方形,点D为AB的中点,点P为OB上的一个动点,连接DP,AP,当点P满足DP+AP的值最小时,直线AP的解析式为.18.(2019•阜新)甲、乙两人分别从A,B两地相向而行,匀速行进甲先出发且先到达B地,他们之间的距离s(km)与甲出发的时间t(h)的关系如图所示,则乙由B地到A地用了h.19.(2019•鄂尔多斯)如图,有一条折线A1B1A2B2A3B3A4B4…,它是由过A1(0,0),B1(4,4),A2(8,0)组成的折线依次平移8,16,24,…个单位得到的,直线y =kx+2与此折线有2n(n≥1且为整数)个交点,则k的值为.20.(2019•大连)甲、乙两人沿同一条直路走步,如果两人分别从这条直路上的A,B 两处同时出发,都以不变的速度相向而行,图1是甲离开A处后行走的路程y(单位:m)与行走时间x(单位:min)的函数图象,图2是甲、乙两人之间的距离y(单位:m)与甲行走时间x(单位:min)的函数图象,则a﹣b=.21.(2019•娄底)已知点P(x0,y0)到直线y=kx+b的距离可表示为d=,例如:点(0,1)到直线y=2x+6的距离d==.据此进一步可得两条平行线y=x和y=x﹣4之间的距离为.22.(2019•本溪)如图,点B1在直线l:y=x上,点B1的横坐标为2,过B1作B1A1⊥l,交x轴于点A1,以A1B1为边,向右作正方形A1B1B2C1,延长B2C1交x轴于点A2;以A2B2为边,向右作正方形A2B2B3C2,延长B3C2交x轴于点A3;以A3B3为边,向右作正方形A3B3B4C3,延长B4C3交x轴于点A4;…;按照这个规律进行下去,点∁n的横坐标为(结果用含正整数n的代数式表示)23.(2019•贵阳)在平面直角坐标系内,一次函数y=k1x+b1与y=k2x+b2的图象如图所示,则关于x,y的方程组的解是.24.(2019•东营)如图,在平面直角坐标系中,函数y=x和y=﹣x的图象分别为直线l1,l2,过l1上的点A1(1,)作x轴的垂线交l2于点A2,过点A2作y 轴的垂线交l1于点A3,过点A3作x轴的垂线交l2于点A4,…依次进行下去,则点A2019的横坐标为.25.(2019•天门)如图,在平面直角坐标系中,四边形OA1B1C1,A1A2B2C2,A2A3B3C3,…都是菱形,点A1,A2,A3,…都在x轴上,点C1,C2,C3,…都在直线y=x+上,且∠C1OA1=∠C2A1A2=∠C3A2A3=…=60°,OA1=1,则点C6的坐标是.26.(2019•徐州)函数y=x+1的图象与x轴、y轴分别交于A、B两点,点C在x轴上.若△ABC为等腰三角形,则满足条件的点C共有个.三.解答题27.(2019•恩施州)某县有A、B两个大型蔬菜基地,共有蔬菜700吨.若将A基地的蔬菜全部运往甲市所需费用与B基地的蔬菜全部运往甲市所需费用相同.从A、B两基地运往甲、乙两市的运费单价如下表:甲市(元/吨)乙市(元/吨)A基地20 25B基地15 24(1)求A、B两个蔬菜基地各有蔬菜多少吨?(2)现甲市需要蔬菜260吨,乙市需要蔬菜440吨.设从A基地运送m吨蔬菜到甲市,请问怎样调运可使总运费最少?28.(2019•沈阳)在平面直角坐标系中,直线y=kx+4(k≠0)交x轴于点A(8,0),交y轴于点B.(1)k的值是;(2)点C是直线AB上的一个动点,点D和点E分别在x轴和y轴上.①如图,点E为线段OB的中点,且四边形OCED是平行四边形时,求▱OCED的周长;②当CE平行于x轴,CD平行于y轴时,连接DE,若△CDE的面积为,请直接写出点C的坐标.29.(2019•大连)如图,在平面直角坐标系xOy中,直线y=﹣x+3与x轴,y轴分别相交于点A,B,点C在射线BO上,点D在射线BA上,且BD=OC,以CO,CD为邻边作▱COED.设点C的坐标为(0,m),▱COED在x轴下方部分的面积为S.求:(1)线段AB的长;(2)S关于m的函数解析式,并直接写出自变量m的取值范围.30.(2019•徐州)如图①,将南北向的中山路与东西向的北京路看成两条直线,十字路口记作点A.甲从中山路上点B出发,骑车向北匀速直行;与此同时,乙从点A出发,沿北京路步行向东匀速直行.设出发xmin时,甲、乙两人与点A的距离分别为y1m、y2m.已知y1、y2与x之间的函数关系如图②所示.(1)求甲、乙两人的速度;(2)当x取何值时,甲、乙两人之间的距离最短?31.(2019•宁夏)在综合与实践活动中,活动小组对学校400米的跑道进行规划设计,跑道由两段直道和两端是半圆弧的跑道组成.其中400米跑道最内圈为400米,两端半圆弧的半径为36米.(π取3.14).(1)求400米跑道中一段直道的长度;(2)在活动中发现跑道周长(单位:米)随跑道宽度(距最内圈的距离,单位:米)的变化而变化.请完成下表:跑道宽度/米0 1 2 3 4 5 …跑道周长/米400 …若设x表示跑道宽度(单位:米),y表示该跑道周长(单位:米),试写出y与x的函数关系式:(3)将446米的跑道周长作为400米跑道场地的最外沿,那么它与最内圈(跑道周长400米)形成的区域最多能铺设道宽为1.2米的跑道多少条?32.(2019•哈尔滨)如图,在平面直角坐标系中,点O为坐标原点,直线y=x+4与x 轴交于点A,与y轴交于点B,直线BC与x轴交于点C,且点C与点A关于y轴对称;(1)求直线BC的解析式;(2)点P为线段AB上一点,点Q为线段BC上一点,BQ=AP,连接PQ,设点P 的横坐标为t,△PBQ的面积为S(S≠0),求S与t之间的函数关系式(不要求写出自变量t的取值范围);(3)在(2)的条件下,点E在线段OA上,点R在线段BC的延长线上,且点R的纵坐标为﹣,连接PE、BE、AQ,AQ与BE交于点F,∠APE=∠CBE,连接PF,PF的延长线与y轴的负半轴交于点M,连接QM、MR,若tan∠QMR=,求直线PM的解析式.参考答案一.选择题1.解:∵ab<0,且a>b,∴a>0,b<0,∴函数y=ax+b的图象经过第一、三、四象限.故选:A.2.解:∵正比例函数y=kx(k≠0)的函数值y随x的增大而减小,∴k<0,∵一次函数y=x+k的一次项系数大于0,常数项小于0,∴一次函数y=x+k的图象经过第一、三象限,且与y轴的负半轴相交.故选:A.3.解:∵直线y=x+b和y=kx+2与x轴分别交于点A(﹣2,0),点B(3,0),∴解集为﹣2<x<3,故选:D.4.解:联立直线l1与直线l2的表达式并解得:x=,y=,故A1(,);则点B1(,0),则直线B1A2的表达式为:y=x+b,将点B1坐标代入上式并解得:直线B1A2的表达式为:y3=x﹣,将表达式y3与直线l1的表达式联立并解得:x=,y=,即点A2的纵坐标为;同理可得A3的纵坐标为,…按此规律,则点A n的纵坐标为()n,故选:A.5.解:速度和为:24÷(30﹣18)=2米/秒,由题意得:,解得:b=26.4,因此慢车速度为:=0.8米/秒,快车速度为:2﹣0.8=1.2米/秒,快车返回追至两车距离为24米的时间:(26.4﹣24)÷(1.2﹣0.8)=6秒,因此a=33+6=39秒.故选:B.6.解:当x>﹣2时,x+6>﹣x﹣2,所以不等式x+6>﹣x﹣2的解集是x>﹣2.故选:A.7.解:一次函数y=2x+1中,当x=0时,y=1;当y=0时,x=﹣0.5;∴A(﹣0.5,0),B(0,1)∴OA=0.5,OB=1∴△AOB的面积=0.5×1÷2=故选:A.8.解:∵一次函数y=kx+b的图象经过一、二、四象限,∴k<0,b>0.∴kb<0,故选:D.9.解:∵一次函数y=﹣2x+b的图象交y轴于点A(0,3),∴b=3,令y=﹣2x+3中y=0,则﹣2x+3=0,解得:x=,∴点B(,0).观察函数图象,发现:当x<时,一次函数图象在x轴上方,∴不等式﹣2x+b>0的解集为x<.故选:B.10.解:由图象可知A村、B村相离10km,故①正确,当1.25h时,甲、乙相距为0km,故在此时相遇,故②正确,当0≤t≤1.25时,易得一次函数的解析式为s=﹣8t+10,故甲的速度比乙的速度快8km/h.故③正确当1.25≤t≤2时,函数图象经过点(1.25,0)(2,6)设一次函数的解析式为s=kt+b 代入得,解得∴s=8t+10当s=2时.得2=8t﹣10,解得t=1.5h由1.5﹣1.25=0.25h=15min同理当2≤t≤2.5时,设函数解析式为s=kt+b将点(2,6)(2.5,0)代入得,解得∴s=﹣12t+30当s=2时,得2=﹣12t+30,解得t=由﹣1.25=h=65min故相遇后,乙又骑行了15min或65min时两人相距2km,④正确.故选:D.11.解:由A(﹣4,0),B(﹣2,﹣1),C(3,0),D(0,3),∴AC=7,DO=3,∴四边形ABCD分成面积=AC×(|y B|+3)==14,可求CD的直线解析式为y=﹣x+3,设过B的直线l为y=kx+b,将点B代入解析式得y=kx+2k﹣1,∴直线CD与该直线的交点为(,),直线y=kx+2k﹣1与x轴的交点为(,0),∴7=×(3﹣)×(+1),∴k=或k=0,∴k=,∴直线解析式为y=x+;故选:D.12.解:连接AC,则四边形ABOC是矩形,∴∠A=∠ABO=90°,又∵MN⊥MC,∴∠CMN=90°,∴∠AMC=∠MNB,∴△AMC∽△NBM,∴,设BN=y,AM=x.则MB=3﹣x,ON=2﹣y,∴,即:y=x2+x∴当x=﹣=﹣时,y最大=×()2+=,∵直线y=kx+b与y轴交于N(0,b)当BN最大,此时ON最小,点N(0,b)越往上,b的值最大,∴ON=OB﹣BN=2﹣=,此时,N(0,)b的最大值为.故选:A.13.解:∵点A0的坐标是(0,1),∴OA0=1,∵点A1在直线y=x上,∴OA1=2,A0A1=,∴OA2=4,∴OA3=8,∴OA4=16,得出OA n=2n,∴A n A n+1=2n•,∴OA198=2198,A198A199=2198•,∵S1=(4﹣1)•=,∵A2A1∥A200A199,∴△A0A1A2∽△A198A199A200,∴=()2,∴S=2396•=3×2395故选:D.14.解:设甲仓库的快件数量y(件)与时间x(分)之间的函数关系式为:y1=k1x+40,根据题意得60k1+40=400,解得k1=6,∴y1=6x+40;设乙仓库的快件数量y(件)与时间x(分)之间的函数关系式为:y2=k2x+240,根据题意得60k2+240=0,解得k2=﹣4,∴y2=﹣4x+240,联立,解得,∴此刻的时间为9:20.故选:B.15.解:∵△A1B1A2、△A2B2A3…△A n B n A n+1都是等边三角形,∴A1B1∥A2B2∥A3B3∥…∥A n B n,B1A2∥B2A3∥B3A4∥…∥B n A n+1,△A1B1A2、△A2B2A3…△A n B n A n+1都是等边三角形,∵直线y=x与x轴的成角∠B1OA1=30°,∠OA1B1=120°,∴∠OB1A1=30°,∴OA1=A1B1,∵A1(1,0),∴A1B1=1,同理∠OB2A2=30°,…,∠OB n A n=30°,∴B2A2=OA2=2,B3A3=4,…,B n A n=2n﹣1,易得∠OB1A2=90°,…,∠OB n A n+1=90°,∴B1B2=,B2B3=2,…,B n B n+1=2n﹣1,∴S1=×1×=,S2=×2×2=2,…,S n=×2n﹣1×2n﹣1=;故选:D.二.填空题(共11小题)16.解:设当x>120时,l2对应的函数解析式为y=kx+b,,得,即当x>120时,l2对应的函数解析式为y=6x﹣240,当x=150时,y=6×150﹣240=660,由图象可知,去年的水价是480÷160=3(元/m3),故小雨家去年用水量为150m3,需要缴费:150×3=450(元),660﹣450=210(元),即小雨家去年用水量为150m3,若今年用水量与去年相同,水费将比去年多210元,故答案为:210.17.解:∵四边形ABCO是正方形,∴点A,C关于直线OB对称,连接CD交OB于P,连接P A,PD,则此时,PD+AP的值最小,∵OC=OA=AB=4,∴C(0,4),A(4,0),∵D为AB的中点,∴AD=AB=2,∴D(4,2),设直线CD的解析式为:y=kx+b,∴,∴,∴直线CD的解析式为:y=﹣x+4,∵直线OB的解析式为y=x,∴,解得:x=y=,∴P(,),设直线AP的解析式为:y=mx+n,∴,解得:,∴直线AP的解析式为y=﹣2x+8,故答案为:y=﹣2x+8.18.解:由图可得,甲的速度为:36÷6=6(km/h),则乙的速度为:=3.6(km/h),则乙由B地到A地用时:36÷3.6=10(h),故答案为:10.19.解:∵A1(0,0),A2(8,0),A3(16,0),A4(24,0),…,∴A n(8n﹣8,0).∵直线y=kx+2与此折线恰有2n(n≥1且为整数)个交点,∴点A n+1(8n,0)在直线y=kx+2上,∴0=8nk+2,解得:k=﹣.故答案为:﹣.20.解:从图1,可见甲的速度为=60,从图2可以看出,当x=时,二人相遇,即:(60+V乙)×=120,解得:乙的速度V乙=80,∵乙的速度快,从图2看出乙用了b分钟走完全程,甲用了a分钟走完全程,a﹣b==,故答案为.21.解:当x=0时,y=x=0,即点(0,0)在直线y=x上,因为点(0,0)到直线y=x﹣4的距离为:d===2,因为直线y=x和y=x﹣4平行,所以这两条平行线之间的距离为2.故答案为2.22.解:过点B1、C1、C2、C3、C4分别作B1D⊥x轴,C1D1⊥x轴,C2D2⊥x轴,C3D3⊥x轴,C4D4⊥x轴,……垂足分别为D、D1、D2、D3、D4……∵点B1在直线l:y=x上,点B1的横坐标为2,∴点B1的纵坐标为1,即:OD=2,B1D=1,图中所有的直角三角形都相似,两条直角边的比都是1:2,∴点C1的横坐标为:2++()0,点C2的横坐标为:2++()0+()0×+()1=+()0×+()1点C3的横坐标为:2++()0+()0×+()1+()1×+()2=+()0×+()1×++()2点C4的横坐标为:=+()0×+()1×+()2×+()3……点∁n的横坐标为:=+()0×+()1×+()2×+()3×+()4×……+()n﹣1=+[()0+()1×+()2+()3+()4……]+()n﹣1==故答案为:23.解:∵一次函数y=k1x+b1与y=k2x+b2的图象的交点坐标为(2,1),∴关于x,y的方程组的解是.故答案为.24.解:由题意可得,A1(1,),A2(1,﹣),A3(﹣3,﹣),A4(﹣3,3),A5(9,3),A6(9,﹣9),…,可得A2n+1的横坐标为(﹣3)n∵2019=2×1009+1,∴点A2019的横坐标为:(﹣3)1009=﹣31009,故答案为:﹣31009.25.解:∵OA1=1,∴OC1=1,∴∠C1OA1=∠C2A1A2=∠C3A2A3=…=60°,∴C1的纵坐标为:sin60°•OC1=,横坐标为cos60°•OC1=,∴C1(,),∵四边形OA1B1C1,A1A2B2C2,A2A3B3C3,…都是菱形,∴A1C2=2,A2C3=4,A3C4=8,…,∴C2的纵坐标为:sin60°•A1C2=,代入y=x+求得横坐标为2,∴C2(2,),C3的纵坐标为:sin60°•A2C3=2,代入y=x+求得横坐标为5,∴C3(5,2),∴C4(11,4),C5(23,8),∴C6(47,16);故答案为(47,16).26.解以点A为圆心,AB为半径作圆,与x轴交点即为C;以点B为圆心,AB为半径作圆,与x轴交点即为C;作AB的中垂线与x轴的交点即为C;故答案为4;三.解答题(共6小题)27.解:(1)设A、B两基地的蔬菜总量分别为x吨、y吨.于是有:,解得:,答:A、B两基地的蔬菜总量分别为300吨和400吨;(2)由题可知:,∴0≤m<260,∵w=20m+25(300﹣m)+15(260﹣m)+24[400﹣(260﹣m)]=4m+14760,∵4>0,∴w随m的增大而增大,∴w最小=14760答:当A基地运300吨到乙市,B基地运260吨到甲市,B基地运140吨到乙市时,总运费最少为14760元.28.解:(1)将A(8,0)代入y=kx+4,得:0=8k+4,解得:k=﹣.故答案为:﹣.(2)①由(1)可知直线AB的解析式为y=﹣x+4.当x=0时,y=﹣x+4=4,∴点B的坐标为(0,4),∴OB=4.∵点E为OB的中点,∴BE=OE=OB=2.∵点A的坐标为(8,0),∴OA=8.∵四边形OCED是平行四边形,∴CE∥DA,∴==1,∴BC=AC,∴CE是△ABO的中位线,∴CE=OA=4.∵四边形OCED是平行四边形,∴OD=CE=4,OC=DE.在Rt△DOE中,∠DOE=90°,OD=4,OE=2,∴DE==2,∴C平行四边形OCED=2(OD+DE)=2(4+2)=8+4.②设点C的坐标为(x,﹣x+4),则CE=|x|,CD=|﹣x+4|,∴S△CDE=CD•CE=|﹣x2+2x|=,∴x2﹣8x+33=0或x2﹣8x﹣33=0.方程x2﹣8x+33=0无解;解方程x2﹣8x﹣33=0,得:x1=﹣3,x2=11,∴点C的坐标为(﹣3,)或(11,﹣).29.解:(1)当x=0时,y=3,当y=0时,x=4,∴直线y=﹣x+3与x轴点交A(4,0),与y轴交点B(0,3)∴OA=4,OB=3,∴AB=,因此:线段AB的长为5.(2)当CD∥OA时,如图,∵BD=OC,OC=m,∴BD=m,由△BCD∽△BOA得:,即:,解得:m=;①当<m≤3时,如图1所示:过点D作DF⊥OB,垂足为F,此时在x轴下方的三角形与△CDF全等,∵△BDF∽△BAO,∴,∴DF=,同理:BF=m,∴CF=2m﹣3,∴S△CDF==(2m﹣3)×=m2﹣2m,即:S=m2﹣2m,(<m≤3)②当0<m≤时,如图2所示:DE=m≤,此时点E在△AOB的内部,S=0 (0<m≤);③当﹣3<m≤0时,如图3所示:同理可得:点D(﹣m,m+3)设直线CD关系式为y=kx+b,把C(0,m)、D(﹣m,m+3)代入得:,解得:k=﹣,b=m,直线CD关系式为y=﹣x+m,当y=0时,0=﹣x+m,解得x=m2F(,0)∴S△COF=OC•OF=(﹣m)×=﹣m3,即:S=﹣m3,(﹣3<m≤0)④当m<﹣3时,如图4所示:同理可得:点D(﹣m,m+3)此时,DF=﹣m﹣3,OC=﹣m,OF=﹣,∴S梯形OCDF=(﹣m﹣3﹣m)×(﹣)=即:S=(m<﹣3)综上所述:S与m的函数关系式为:S=.30.解:(1)设甲、乙两人的速度分别为am/min,bm/min,则:y1=y2=bx由图②知:x=3.75或7.5时,y1=y2,∴,解得:∴y1=1200﹣240x,令y1=0,则x=5∴y1=y2=80x答:甲的速度为240m/min,乙的速度为80m/min.(2)设甲、乙之间距离为d,则d2=(1200﹣240x)2+(80x)2=64000(x﹣)2+144000,∴当x=时,d2的最小值为144000,即d的最小值为120;答:当x=时,甲、乙两人之间的距离最短.31.解:(1)400米跑道中一段直道的长度=(400﹣2×36×3.14)÷2=86.96 米,答:400米跑道中一段直道的长度约为86.96米.(2)当跑道宽度为1米时,此时弯道的半径为36+1=37米,周长为86.96×2+2×3.14×37=406.28米,当跑道宽度为2米时,此时弯道的半径为36+2=38米,周长为86.96×2+2×3.14×38=412.56米,当跑道宽度为3米时,此时弯道的半径为36+3=39米,周长为86.96×2+2×3.14×39=418.84米,当跑道宽度为4米时,此时弯道的半径为36+4=40米,周长为86.96×2+2×3.14×40=425.12米,当跑道宽度为5米时,此时弯道的半径为36+1=41米,周长为86.96×2+2×3.14×41=431.4米,表格填写如下:y与x的函数关系式为:y=2πx+400=6.28x+400;(3)当y=446时,即6.28x+400=446,解得:x≈7.32 m7.32÷1.2≈6 条∴最多能铺设道宽为1.2米的跑道6条.32.解:(1)∵y=x+4,∴A(﹣3,0)B(0,4),∵点C与点A关于y轴对称,∴C(3,0),设直线BC的解析式为y=kx+b,将B(0,4),C(3,0)代入,,解得k=﹣,b=4,∴直线BC的解析式y=﹣;(2)如图1,过点A作AD⊥BC于点点D,过点P作PN⊥BC于N,PG⊥OB于点G.∵OA=OC=3,OB=4,∴AC=6,AB=BC=5,∴sin∠ACD=,即,∴AD=,∵点P为直线y=x+4上,∴设P(t,t+4),∴PG=﹣t,cos∠BPG=cos∠BAO,即,∴,∵sin∠ABC=,∴PN==,∵AP=BQ,∴BQ=5+,∴S=,即S=;(3)如图,延长BE至T使ET=EP,连接AT、PT、AM、PT交OA于点S.∵∠APE=∠EBC,∠BAC=∠BCA,∴180°﹣∠APE﹣∠BAC=180°﹣∠EBC﹣∠ACB,∴∠PEA=∠BEC=∠AET,∴PT⊥AE,PS=ST,∴AP=AT,∠TAE=∠P AE=∠ACB,AT∥BC,∴∠TAF=∠FQB,∵∠AFT=∠BFQ,AT=AP=BQ,∴△ATF≌△QBF,∴AF=QF,TF=BF,∵∠PSA=∠BOA=90°,∴PT∥BM,∴∠TBM=∠PTB,∵∠BFM=∠PFT,∴△MBF≌△PTF,∴MF=PF,BM=PT,∴四边形AMQP为平行四边形,∴AP∥MQ,MQ=AP=BQ,∴∠MQR=∠ABC,过点R作RH⊥MQ于点H,∵sin∠ABC=sin∠MQR=,设QR=25a,HR=24a,则QH=7a,∵tan∠QMR=,∴MH=23a,BQ=MQ=23a+7a=30a,BR=BQ+QR=55a,过点R作RK⊥x轴于点K.∵点R的纵坐标为﹣,∴RK=,∵sin∠BCO=,∴CR=,BR=,∴,a=,∴BQ=30a=3,∴5+=3,t=,∴P(),∴,∵BM=PT=2PS=,BO=4,∴OM=,∴M(0,),设直线PM的解析式为y=mx+n,∴,解得,∴直线PM的解析式为y=.。
2020年中考数学专题复习 一次函数及其应用(解析版)

2020中考数学专题复习一次函数及其应用(含答案)一、选择题(本大题共6道小题)1. 若点P在一次函数y=-x+4的图象上,则点P一定不在()A.第一象限B.第二象限C.第三象限D.第四象限2. 对于正比例函数y=-2x,当自变量x的值增加1时,函数y的值增加()A.-2B.2C.-D.3. 正比例函数y=kx(k≠0)的函数值y随着x的增大而减小,则一次函数y=x+k的图象大致是 ()4. 若一次函数y=kx+b(k,b为常数,且k≠0)的图象过点A(0,-1),B(1,1),则不等式kx+b>1的解集为()A.x<0B.x>0C.x<1D.x>15. 在同一平面直角坐标系中,直线y=4x+1与直线y=-x+b的交点不可能在()A.第一象限B.第二象限C.第三象限D.第四象限6. 一次函数y=kx-1的图象经过点P,且y的值随x值的增大而增大,则点P的坐标为()A.(-5,3)B.(1,-3)C.(2,2)D.(5,-1)二、填空题(本大题共6道小题)7. 直线y=2x-1与x轴的交点坐标为.8. 已知点A(x1,y1)、B(x2,y2)在直线y=kx+b上,且直线经过第一、二、四象限,当x1<x2时,y1与y2的大小关系为.9. 星期天,小明上午8:00从家里出发,骑车到图书馆去借书,再骑车回到家,他离家的距离y(千米)与时间t(分)的关系如图所示,则上午8:45小明离家的距离是千米.10. 如图所示,一次函数y=ax+b的图象与x轴相交于点(2,0),与y轴相交于点(0,4),结合图象可知,关于x的方程ax+b=0的解是x=.11. 如图,直线y=kx+b(k<0)经过点A(3,1),当kx+b<x时,x的取值范围为.12. 在平面直角坐标系中,点P(x0,y0)到直线Ax+By+C=0的距离公式为:d=,则点P(3,-3)到直线y=-x+的距离为.三、解答题(本大题共4道小题)13. 小王骑车从甲地到乙地,小李骑车从乙地到甲地,小王的速度小于小李的速度,两人同时出发,沿同一条公路匀速前进.图中的折线表示两人之间的距离y(km)与小王的行驶时间x(h)之间的函数关系.请你根据图象进行探究:(1)小王和小李的速度分别是多少?(2)求线段BC所表示的y与x之间的函数解析式,并写出自变量x的取值范围.14. 为了节能减排,我市某校准备购买某种品牌的节能灯,已知3只A型节能灯和5只B型节能灯共需50元,2只A型节能灯和3只B型节能灯共需31元.(1)求1只A型节能灯和1只B型节能灯的售价各是多少元?(2)学校准备购买这两种型号的节能灯共200只,要求A型节能灯的数量不超过B型节能灯的数量的3倍,请设计出最省钱的购买方案,并说明理由.15. 如图,在平面直角坐标系xOy中,过点A(-2,0)的直线交y轴正半轴于点B,将直线AB绕着点O顺时针旋转90°后,分别与x轴、y轴交于点D,C.(1)若OB=4,求直线AB的函数关系式;(2)连接BD,若△ABD的面积是5,求点B的运动路径长.16. 现代互联网技术的广泛应用,催生了快递行业的高速发展,小明计划给朋友快递一部分物品,经了解有甲、乙两家快递公司比较合适.甲公司表示:快递物品不超过1千克的,按每千克22元收费;超过1千克,超过的部分按每千克15元收费.乙公司表示:按每千克16元收费,另加包装费3元,设小明快递物品为x 千克.(1)根据题意,填写下表:快递物品质量0.5 1 3 4 …(千克)甲公司收费22 …(元)乙公司收费11 51 67 …(元)(2)设甲快递公司收费y1元,乙快递公司收费y2元,分别写出y1,y2关于x的函数关系式.(3)当x>3时,小明应选择哪家快递公司更省钱?请说明理由.2020中考数学一次函数及其应用-答案一、选择题(本大题共6道小题)1. 【答案】C[解析]∵-1<0,4>0,∴一次函数y=-x+4的图象经过第一、二、四象限,即不经过第三象限.∵点P在一次函数y=-x+4的图象上,∴点P一定不在第三象限.故选C.2. 【答案】A3. 【答案】A[解析]因为正比例函数y=kx(k≠0)的函数值y随着x的增大而减小,所以k<0,所以一次函数y=x+k的函数值y随着x增大而增大,图象与y轴交于负半轴,故选A.4. 【答案】D[解析]如图所示:不等式kx+b>1的解集为x>1.故选D.5. 【答案】D[解析]因为直线y=4x+1只经过第一、二、三象限,所以其与直线y=-x+b的交点不可能在第四象限.故选D.6. 【答案】C[解析]∵一次函数y=kx-1的图象经过点P,且y的值随x值的增大而增大,∴k>0.由y=kx-1得k=.分别将选项中坐标代入该式,只有当(2,2)时k==>0.二、填空题(本大题共6道小题)7. 【答案】,08. 【答案】y1>y2[解析]∵一次函数图象经过第二、四象限,∴k<0,y随x的增大而减小,∴当x1<x2时,y1>y2.9. 【答案】1.510. 【答案】2[解析]考查一元一次方程与一次函数的关系,即关于x的方程ax+b=0的解就是一次函数y=ax+b的图象与x轴交点(2,0)的横坐标2.11. 【答案】x>3[解析]当x=3时,x=×3=1,∴点A在一次函数y=x的图象上,且一次函数y=x的图象经过第一、三象限,∴当x>3时,一次函数y=x的图象在y=kx+b的图象上方,即kx+b<x.12. 【答案】[解析]∵y=-x+,∴2x+3y-5=0,∴点P(3,-3)到直线y=-x+的距离为:=.故答案为.三、解答题(本大题共4道小题)13. 【答案】解:(1)从线段AB得:两人从相距30 km的两地同时出发,1 h后相遇,则v小王+v小李=30 km/h,小王从甲地到乙地行驶了3 h,∴v小王=30÷3=10(km/h),∴v小李=20 km/h.(2)C点的意义是小李骑车从乙地到甲地用了30÷20=1.5(h),此时小王和小李的距离是1.5×10=15(km),∴C点坐标是(1.5,15).设直线BC的解析式为y=kx+b,将B(1,0),C(1.5,15)分别代入解析式,得解得:∴线段BC的解析式为y=30x-30(1≤x≤1.5).14. 【答案】解:(1)设1只A型节能灯的售价是x元,1只B型节能灯的售价是y元,根据题意,得解得答:1只A型节能灯的售价是5元,1只B型节能灯的售价是7元.(2)设购买A型节能灯a只,则购买B型节能灯(200-a)只,总费用为w元,w=5a+7(200-a)=-2a+1400,∵a≤3(200-a),∴a≤150,∵-2<0,w随a的增大而减小,∴当a=150时,w取得最小值,此时w=1100,200-a=50.答:最省钱的购买方案是:购买A型节能灯150只,B型节能灯50只.15. 【答案】解:(1)因为OB=4,且点B在y轴正半轴上,所以点B的坐标为(0,4).设直线AB的函数关系式为y=kx+b,将点A(-2,0),B(0,4)的坐标分别代入,得解得所以直线AB的函数关系式为y=2x+4.(2)设OB=m,因为△ABD的面积是5,所以AD·OB=5.所以(m+2)m=5,即m2+2m-10=0.解得m=-1+或-1-(舍去).因为∠BOD=90°,所以点B的运动路径长为×2π×(-1+)=π.16. 【答案】解:(1)11526719[解析]当x=0.5时,y甲=22×0.5=11.当x=3时,y甲=22+15×2=52;当x=4时,y甲=22+15×3=67;当x=1时,y乙=16×1+3=19.故答案为:11;52;67;19.(2)当0<x≤1时,y1=22x;当x>1时,y1=22+15(x-1)=15x+7.∴y1=y2=16x+3(x>0).(3)当x>3时,当y1>y2时,有15x+7>16x+3,解得x<4;当y2=y2时,有15x+7=16x+3,解得x=4;当y1<y2时,有15x+7<16x+3,解得x>4.∴当3<x<4时,小明选择乙公司省钱;当x=4时,两家公司费用一样;当x>4时,小明选择甲公司省钱.。
2020年中考数学专题复习:函数模型的应用(含答案)

2020年中考数学专题复习:函数模型的应用1.超市以每千克40元的价格购进夏威夷果,计划以每千克60元的价格销售,为了让顾客得到更大的实惠,现决定降价销售,已知这种夏威夷果销售量y(千克)与每千克降价x(元)(0<x <20)之间满足一次函数关系,其图象如图所示:(1)求y与x之间的函数关系式;(2)超市要想获利2090元,则这种夏威夷果每千克应降价多少元?2.如图①,某商场在一楼到二楼之间设有上、下行自动扶梯和步行楼梯.甲、乙两人从二楼同时下行,甲乘自动扶梯,乙走步行楼梯,甲离一楼地面的高度h(单位:m)与下行时间x(单位:s)之间具有函数关系h=-310x+6,乙离一楼地面的高度y(单位:m)与下行时间x(单位:s)的函数关系如图②所示.(1)求y关于x的函数解析式;(2)请通过计算说明甲、乙两人谁先到达一楼地面.3.某智能品牌店,在销售某型号运动手环时,以高出进价的50%标价.已知按标价九折销售该型号运动手环8个与将标价直降100元销售7个获利相同.(1)求该型号运动手环的进价和标价分别是多少元?(2)若该型号运动手环的进价不变,按(1)中的标价出售,该店平均每月可售出38个;若每个运动手环每降价20元,每月可多售出2辆,求该型号运动手环降价多少元时,每月获利最大?最大利润是多少?4.一水果店以进价为每千克16元购进万荣苹果,销售中发现,销售单价定为20元时,日销售量为50千克;当销售单价每上涨1元,日销售量就减少5千克,设销售单价为x(元),每天的销售量为y(千克),每天获利为w(元).(1)求y与x之间的函数关系式;(2)求w与x之间的函数关系式;该苹果售价定为每千克多少元时,每天的销售利润最大?最大利润是多少元?(3)如果商家规定这种苹果每天的销售量不低于40千克,求商家每天销售利润的最大值是多少元?5.挂灯笼成为我国的一种传统文化. 小明在春节前购进甲、乙两种红灯笼,用3120元购进甲灯笼与用4200元购进乙灯笼的数量相同,已知乙灯笼每对进价比甲灯笼每对进价多9元.(1)求甲、乙两种灯笼每对的进价;(2)经市场调查发现,乙灯笼每对售价50元时,每天可售出98对,售价每提高1元,则每天少售出2对;物价部门规定其销售单价不高于每对65元,设乙灯笼每对涨价x元,小明一天通过乙灯笼获得利润y元.①求出y与x之间的函数解析式;②乙种灯笼的销售单价为多少元时,一天获得利润最大?最大利润是多少元?6.甲、乙两个批发店销售同一种苹果.在甲批发店,不论一次购买数量是多少,价格均为6元/kg.在乙批发店,一次购买数量不超过50 kg时,价格为7元/kg;一次购买数量超过50 kg时,其中有50 kg的价格仍为7元/kg,超出50 kg部分的价格为5元/kg.设小王在同一个批发店一次购买苹果的数量为x kg(x>0).(Ⅰ)根据题意填表:(Ⅱ)设在甲批发店花费y1元,在乙批发店花费y2元,分别求y1,y2关于x的函数解析式;(Ⅲ)根据题意填空:①若小王在甲批发店和在乙批发店一次购买苹果的数量相同,且花费相同,则他在同一个批发店一次购买苹果的数量为________kg;②若小王在同一个批发店一次购买苹果的数量为120 kg,则他在甲、乙两个批发店中的________批发店购买花费少;③若小王在同一个批发店一次购买苹果花费了360元,则他在甲、乙两个批发店中的________批发店购买数量多.7.某工厂计划生产甲乙两种产品共2500吨,每生产1吨甲产品可获得利润0.3万元,每生产1吨乙产品可获得利润0.4万元,设该工厂生产了甲产品x(吨),生产甲、乙两种产品获得的总利润为y(万元).(1)求y与x之间的函数表达式;(2)若每生产1吨甲产品需要A原料0.25吨,每生产1吨乙产品需要A原料0.5吨,受市场影响,该厂能获得的A原料至多为1000吨,其它原料充足.求出该工厂生产甲、乙两种产品各为多少吨时,能获得最大利润.8. 某商场销售一批足球文化衫,已知该文化衫的进价为每件40元,当售价为每件60元时,每个月可销售出100件,根据市场行情,现决定涨价销售,调查表明,每件商品的售价每上涨1元,每月少销售出2件,设每件商品的售价为x 元.每个月的销售为y 件.(1)求y 与x 之间的函数关系式;(2)当每件商品的售价定为多少元时,每个月的利润恰好为2250元;(3)当每件商品的售价定为多少元时,每个月获得利润最大?最大月利润为多少?9. 某公司计划在某地区销售一款5G 产品,根据市场分析,该产品的销售价格将随销售周期的变化而变化,设该产品在第x (x 为正整数)个销售周期每台的销售价格为y 元,y 与x 之间满足如图所示的一次函数关系.(1)求y 与x 之间的关系式;(2)设该产品在第x 个销售周期的销售数量为p (万台),p 与x 的关系可以用p =12x +12来描述.根据以上信息,试问:哪个销售周期的销售收入最大?此时该产品每台的销售价格是多少元?10. 某商店销售一种商品,经市场调查发现,该商品的周销售量y (件)是售价x (元/件)的一次函数,其售价,周销售量,周销售利润w (元)的三组对应值如下表:售价x (元/件) 50 60 80 周销售量y (件) 100 80 40 周销售利润w (元)100016001600(1)①求y 关于x 的函数解析式(不要求写出自变量的取值范围);②该商品进价是________元/件;当售价是____元/件时,周销售利润最大,最大利润是______元;(2)由于某种原因,该商品进价提高了m元/件(m>0),物价部门规定该商品售价不得超过65元/件,该商店在今后的销售中,周销售量与售价仍然满足(1)中的函数关系.若周销售最大利润是1400元,求m的值.参考答案1. 解:(1)设一次函数解析式为y =kx +b , ∵当x =2,y =120;当x =4,y =140;∴⎩⎪⎨⎪⎧2k +b =120,4k +b =140, 解得⎩⎪⎨⎪⎧k =10,b =100.∴y 与x 之间的函数关系式为y =10x +100;(4分) (2)由题意得(60-40-x )(10x +100)=2090, 整理得x 2-10x +9=0, 解得x 1=1,x 2=9. ∵让顾客得到更大的实惠, ∴x =9,答:超市要想获利2090元,则这种夏威夷果每千克应降价9元.(7分)2. 解:(1)设y 关于x 的函数解析式为y =kx +b ,把点(0,6)(15,3)代入y =kx +b 得⎩⎪⎨⎪⎧6=b ,3=15k +b ,解得⎩⎪⎨⎪⎧k =-15,b =6,∴y 关于x 的函数解析式为y =-15x +6;(2)甲:当h=0时,得x=20.乙:当y=0时,得x=30.∵20<30,∴甲先到达一楼地面.3.解:(1)设该型号运动手环的进价为x元,根据题意得[(1+50%)x×0.9-x]×8=[(1+50%)x-100-x]×7,∴x=1000,∴(1+50%)x=1500元,∴该型号运动手环的进价为1000元,标价为1500元;(4分) (2)设该型号运动手环降价y元,利润为w元.根据题意得w=(38+y20×2)(1500-1000-y)=(38+0.1y)(500-y)=-0.1(y-60)2+19360,当y=60时,w有最大值19360.∴降价60元,每月获利最大,最大利润为19360元.(8分)4.解:(1)根据题意得y=50-5(x-20)=-5x+150;(2分)(2)根据题意得w=(x-16)(-5x+150)=-5x2+230x-2400,(4分)∴w与x的函数关系式为:w=-5x2+230x-2400=-5(x-23)2+245.∵-5 <0,∴当x=23时,w有最大值,最大值为245.(5分)答:w与x之间的函数关系式为w=-5x2+230x-2400.该苹果售价定为每千克23元时,每天销售利润最大,最大利润是245元;(6分)(3)根据题意得-5x+150≥40,解得x≤22.∵w=-5(x-23)2+245.∵-5<0,w≤23时,w随x增大而增大,∴当x=22时w有最大值,其最大值为-5×(22-23)2+245=240(元).答:商家每天销售利润的最大值是240元.(10分)5.解:(1)设甲种灯笼进价为x元/对,则乙种灯笼的进价为(x+9)元/对,由题意得3120 x=4200 x+9,解得x=26,经检验,x=26是原方程的解,且符合题意,∴x+9=26+9=35,答:甲种灯笼单价为26元/对,乙种灯笼的单价为35元/对;(4分) (2)①y=(50+x-35)(98-2x)=-2x2+68x+1470,答:y与x之间的函数解析式为:y=-2x2+68x+1470;(7分)②∵a=-2<0,∴函数y有最大值,该二次函数的对称轴为:x=-b2a=17,物价部门规定其销售单价不高于每对65元,∴x+50≤65,∴x≤15,∵x<17时,y随x的增大而增大,∴当x =15时,y 最大=2040. ∴15+50=65.答:乙种灯笼的销售单价为每对65元时,一天获得利润最大,最大利润是2040元.(10分) 6. 解:(Ⅰ)180,900,210,850;【解法提示】甲批发店花费:当x =30时,花费为30×6=180;当x =150时,花费为150×6=900.乙批发店花费:当x =30时,花费为30×7=210;当x =150时,花费为50×7+(150-50)×5=850.(Ⅱ)y 1=6x (x >0), 当0<x ≤50时,y 2=7x ;当x >50时,y 2=7×50+5(x -50),即y 2=5x +100;即y 2=⎩⎪⎨⎪⎧7x (0<x ≤50),5x +100(x >50).(Ⅲ)①100;②乙;③甲.【解法提示】①当0<x ≤50时,甲批发店和乙批发店花费不可能相同,则x >50时,令y 1=y 2,则6x =5x +100,解得x =100;②当x =120时,y 1=6×120=720,y 2=5×120+100=700,∵720>700,∴在乙批发店购买花费少;③对甲批发店而言:令y 1=360,则6x =360,解得x =60.对乙批发店而言:当x =50时,花费为350<360,则令5x +100=360,解得x =52,∵60>52,∴小王花费360元时,在甲批发店购买数量多.7. 解:(1)y =x ·0.3+(2500-x )·0.4=-0.1x +1000; (2)由题意得x ·0.25+(2500-x )·0.5≤1000,解得x ≥1000. 又∵x ≤2500,∴1000≤x ≤2500. 由(1)可知,-0.1<0,∴y 的值随着x 的增加而减小,∴当x =1000时,y 取最大值,此时生产乙种产品2500-1000=1500(吨) 答:工厂生产甲产品1000吨,乙产品1500吨时,能获得最大利润. 8. 解:(1)根据题意得y = 100-2(x -60)=-2x +220(60≤x ≤110); (2)由题意可得:(-2x +220)(x -40)=2250. x 2-150x +5525=0, 解得x 1=65,x 2=85.答:当每件商品的售价定为65元或85元时,利润恰好是2250元; (3)设利润为W 元,∴W =(x -40)(-2x +220)=-2x 2+300x -8800=-2(x -75)2+2450. ∵a =-2<0, ∴抛物线开口向下. ∵60≤x ≤110,∴当x =75时,W 有最大值,W 最大=2450(元).答:当售价定为75元时,获得最大利润,最大利润是2450元. 9. 解:(1)设y 关于x 的函数关系式为y =kx +b (k ≠0),由图象可知,将点(1,7000),(5,5000)代入得⎩⎪⎨⎪⎧k +b =7000,5k +b =5000,解得⎩⎪⎨⎪⎧k =-500,b =7500,∴y 关于x 的函数关系式为y =-500x +7500;(2)设销售收入为W ,根据题意得W =yp =(-500x +7500)·(12x +12), 整理得W =-250(x -7)2+16000,∵-250<0,∴W 在x =7时取得最大值,最大值为16000元,此时该产品每台的销售价格为-500×7+7500=4000元.答:第7个销售周期的销售收入最大,此时该产品每台的销售价格为4000元.10. 解:(1)①y =-2x +200;②40,70,1800;(2)由题意可知w =(-2x +200)×(x -40-m )=-2x 2+(280+2m )x -8000-200m ,对称轴为直线x =140+m 2, ∵m >0,∴对称轴x =140+m 2>70, ∵抛物线开口向下,在对称轴左侧,y 随x 的增大而增大,∴当x =65时,y max =1400,代入表达式解得m =5.。
2020年中考数学专题培优:二次函数图像和性质(含答案)
2020年中考数学专题培优 二次函数图像和性质(含答案)一、单选题(共有10道小题)1.抛物线247y x x =--的顶点坐标是( )A .(2,-11)B .(-2,7)C .(2,11)D .(2,-3)2.把抛物线23y x =先向上平移2个单位,再向右平移3个单位,所得抛物线的解析式是( )A.()2332y x =+- B.()2322y x =++ C.()2332y x =--D.()2332y x =-+3.若抛物线22y x x c =-+与y 轴的交点坐标为(0,-3),则下列说法不正确的是( ) A.抛物线的开口向上 B.抛物线的对称轴是直线x =1C.当x =1时,y 的最大值为-4D.抛物线与x 轴的交点坐标为(-1,0),(3,0)。
4.如图,二次函数()2,0y ax bx c a =++≠的图象与x 轴交于A 、B 两点,与y 轴交于C 点,且对称轴为1x =,点B 坐标为(-1,0).则下面的四个结论中正确的个数是()①20a b +=;②420a b c +<-;③0ac >;④当0y <时,1x <-或2x >. A .1 B .2 C .3 D .45.将抛物线216212=-+yx x 向左平移2个单位后,得到新抛物线的解析式为( ) A .21(8)52=-+y x B .21(4)52=-+y x C .21(8)32=-+y x D .21(4)32=-+y x6.已知二次函数()²,0y ax bx c c =++≠的图象如图所示,下列说法错误..的是 ( )A.图像关于直线1x =对称B.函数()²,0y ax bx c c =++≠的最小值是-4C.-1和3是方程()²0,0ax bx c c ++=≠ 的两个根D.当1x <时,y 随x 的增大而增大7.对于二次函数22y x x =-+,有下列四个结论,其中正确的结论的个数为()CA B -1x=1xy O -11-4xyO①它的对称轴是直线1x =;②设221112222,2y x x y x x =-+=-+,则21x x >时,有21y y >;③它的图象与x 轴的两个交点是(0,0)和(2,0) ④当02x << 时,0y > A.1B.2C.3D.48.已知二次函数c bx ax y ++=2的y 与x 的部分对应值如下表:x …… -1 0 1 3 …… y …… -3 1 3 1 ……则下列判断中正确的是( )A.抛物线开口向上B.抛物线与y 轴交于负半轴C.图象对称轴为直线x=1D.方程02=++c bx ax 有一个根在3与4之间9.如图,一段抛物线24(22)=-+-yx x ≤≤为1C ,与x 轴交于0A ,1A 两点,顶点为1D ;将1C 绕点1A 旋转180°得到2C ,顶点为2D ;1C 与2C 组成一个新的图象,垂直于y 轴的直线l 与新图象交于点111()P x y ,,222()Px y ,,与线段12D D 交于点333()P x y ,,设123x x x ,,均为正数,123=++t x x x ,则t 的取值范围是( )A .68t <≤B .68t ≤≤C .1012t <≤D .1012t ≤≤10.在同一平面直角坐标系中,函数y mx m =+,和函数222,)0y mx x m m =-++≠(是常数,且的图象可能是( )二、填空题(共有7道小题) 11.抛物线开口方向对称轴顶点坐标yxC 2C 1A 0D 2D 1A 1OAx y O B xyO C x yODxyO()232y x =--()2132y x =+12.抛物线()2241y x =--的开口 ,顶点坐标是 ,对称轴是 ; 当x = 时,y 有最 值为 ;在对称轴左侧,即当x 时,y 随x 的增大而 , 在对称轴右侧,即当x 时,y 随x 的增大而 .13.在平面直角坐标系中,若将抛物线()132++-=x y 先向左平移2个单位长度,再向下平移3个单位长度,则经过这两次平移后所得抛物线的顶点坐标是 .14.二次函数422-+=x x y 的图象的开口方向是 ,对称轴是 ,顶点坐标是15.抛物线3422+-=x x y 绕坐标原点旋转180°所得的抛物线的表达式是 .16.若抛物线c x x y +-=42的顶点在直线1+=x y 上,求c 的值______ 17.已知点P (m ,n )在抛物线a x ax y --=2上,当m ≥﹣1时,总有n ≤1成立,则a 的取值范围是 .三、解答题(共有6道小题)18.抛物线()233y x =- 与x 轴交点为A ,与y 轴交点为B ,求A ,B 两点坐标及△AOB 的面积19.已知,在同一平面直角坐标系中,反比例函数xy 5=与二次函数c x x y ++-=22的图象交于点A (-1,m ). (1)求m ,c 的值;(2)求二次函数图象的对称轴和顶点坐标.20.已知抛物线32++=bx ax y 的对称轴是直线x=1.(1)求证:2a+b=0;(2)若关于x 的方程082=-+bx ax 的一个根为4,求方程的另一个根.21.当k 分别取-1,1,2时,函数()2145y k x x k =--+-都有最大值吗?请写出你的判断,并说明理由;若有最大值,请求出最大值。
2020年九年级中考数学专题专练--几何函数压轴题专练(含答案)
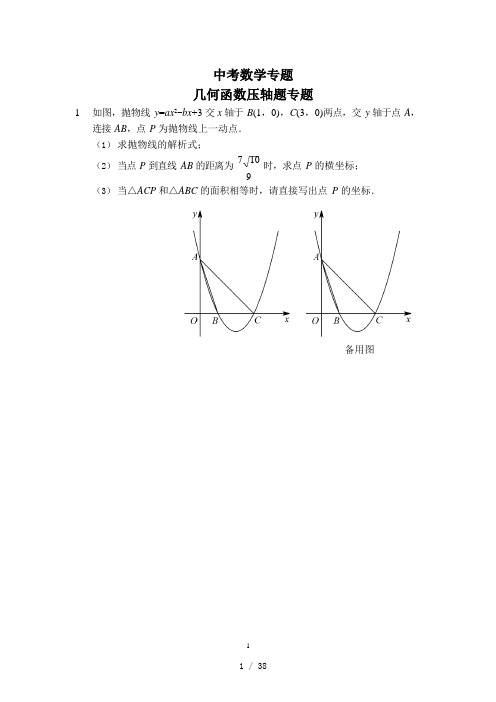
中考数学专题几何函数压轴题专题1.如图,抛物线y=ax2-bx+3 交x 轴于B(1,0),C(3,0)两点,交y 轴于点A,连接AB,点P 为抛物线上一动点.(1)求抛物线的解析式;(2)当点P 到直线AB 的距离为7 10时,求点P 的横坐标;9(3)当△ACP 和△ABC 的面积相等时,请直接写出点P 的坐标.备用图2.如图1,在平面直角坐标系中,直线y=x+4 与抛物线y =-1x2 +bx +c (b,c 2是常数)交于A,B 两点,点A 在x 轴上,点B 在y 轴上.设抛物线与x 轴的另一个交点为点C.(1)求该抛物线的解析式.(2)点P 是抛物线上一动点(不与点A,B 重合).①如图2,若点P 在直线AB 上方,连接OP 交AB 于点D,求PD的最大值;OD②如图3,若点P 在x 轴上方,连接PC,以PC 为一边作正方形CPEF.随着点P 的运动,正方形的大小、位置也随之改变,当顶点E 或F 恰好落在y 轴上时,直接写出对应的点P 的坐标.23. 如图,抛物线y=ax2+bx+4(a≠0)交x 轴于点A(4,0),B(-2,0),交y 轴于点C.(1)求抛物线的解析式.(2)点Q 是x 轴上位于点A,B 之间的一个动点,点E 为线段BC 上一个动点,若始终保持∠EQB=∠CAB,连接CQ,设△CQE 的面积为S,点Q 的横坐标为m,求出S 关于m 的函数关系式,并求出当S 取最大值时点Q 的坐标.(3)点P 为抛物线上位于AC 上方的一个动点,过点P 作PF⊥y 轴,交直线AC 于点F,点D 的坐标为(2,0),若O,D,F 三点中,当其中一点恰好位于另外两点的垂直平分线上时,我们把这个点叫做另外两点的“和谐点”,请判断这三点是否有“和谐点”的存在,若存在,请直接写出此时点P 的坐标;若不存在,请说明理由.4.如图,抛物线y =-3x2 +bx +c 与x 轴交于A,B 两点,与y 轴交于点C,直4线y =3x + 3 经过点A,C.4(1)求抛物线的解析式.(2)P 是抛物线上一动点,过P 作PM∥y 轴交直线AC 于点M,设点P 的横坐标为t.①若以点C,O,M,P 为顶点的四边形是平行四边形,求t 的值.②当射线MP,MC,MO 中一条射线平分另外两条射线的夹角时,直接写出t 的值.5.如图1,抛物线y=ax2+bx+2 与x 轴交于A,B 两点,与y 轴交于点C,AB=4,矩形OBDC 的边CD=1,延长DC 交抛物线于点E.(1)求抛物线的解析式.(2)如图2,点P 是直线EO 上方抛物线上的一个动点,过点P 作y 轴的平行线交直线EO 于点G,作PH⊥EO,垂足为H.设PH 的长为a,点P 的横坐标为m,求a 关于m 的函数关系式(不必写出m 的取值范围),并求出a 的最大值.(3)如果点N 是抛物线对称轴上的一点,抛物线上是否存在点M,使得以M,A,C,N 为顶点的四边形是平行四边形?若存在,直接写出所有满足条件的点M 的坐标;若不存在,请说明理由.6.如图,在平面直角坐标系中,△ABC 是直角三角形,∠ACB=90°,AC=BC,OA=1,OC=4,抛物线y=x2+bx+c 经过A,B 两点,抛物线的顶点为D.(1)求b,c 的值.(2)点E 是直角三角形ABC 斜边AB 上一动点(点A,B 除外),过点E 作x 轴的垂线交抛物线于点F,当线段EF 的长度最大时,求点E 的坐标.(3)在(2)的条件下:①求以点E,B,F,D 为顶点的四边形的面积;② 在抛物线上是否存在一点P,使△EFP 是以EF 为直角边的直角三角形?若存在,直接写出所有点P 的坐标;若不存在,说明理由.7.如图,抛物线y=ax2+bx+3(a≠0)的对称轴为直线x=-1,抛物线交x 轴于A,C 两点,与直线y=x-1 交于A,B 两点,直线AB 与抛物线的对称轴交于点E.(1)求抛物线的解析式;(2)点P 在直线AB 上方的抛物线上运动,若△ABP 的面积最大,求此时点P 的坐标;(3)在平面直角坐标系中,以点B,E,C,D 为顶点的四边形是平行四边形,请直接写出符合条件点D 的坐标.8.如图,已知抛物线y =ax2 +3x + 4 的对称轴是直线x=3,且与x 轴相交于A,2B 两点(B 点在A 点右侧),与y 轴交于C 点.(1)求抛物线的解析式和A,B 两点的坐标.(2)若点P 是抛物线上B,C 两点之间的一个动点(不与B,C 重合),则是否存在一点P,使△PBC 的面积最大?若存在,请求出△PBC 的最大面积;若不存在,试说明理由.(3)若M 是抛物线上任意一点,过点M 作y 轴的平行线,交直线BC 于点N,当MN=3 时,求点N 的坐标.9.如图,抛物线y=1x2 +bx +c 经过点A( 2 3(1)求该抛物线的解析式;,0)和点B(0,-2).(2)若△OAB 以每秒2 个单位长度的速度沿射线BA 方向运动,设运动时间为t,点O,A,B 的对应点分别为D,E,C,直线DE 交抛物线于点M.①当点M 为DE 的中点时,求t 的值;②连接AD,当△ACD 为等腰三角形时,请直接写出点M 的坐标.备用图310.如图,抛物线y=ax2+bx-2 的对称轴是直线x=1,与x 轴交于A,B 两点,与y 轴交于点C,点A 的坐标为(-2,0),点P 为抛物线上的一个动点,过点P 作PD⊥x 轴于点D,交直线BC 于点E.(1)求抛物线解析式.(2)若点P 在第一象限内,当OD=4PE 时,求四边形POBE 的面积.(3)在(2)的条件下,若点M 为直线BC 上一点,点N 为平面直角坐标系内一点,是否存在这样的点M 和点N,使得以点B,D,M,N 为顶点的四边形是菱形?若存在,直接写出点N 的坐标;若不存在,请说明理由.11.如图,在平面直角坐标系中,∠ACB=90°,OC=2OB,tan∠ABC=2,点B 的坐标为(1,0),抛物线y=-x2+bx+c 经过A,B 两点.(1)求抛物线的解析式.(2)点P 是直线AB 上方抛物线上的一点,过点P 作PD 垂直x 轴于点D,交线段AB 于点E,使PE 1DE .2①求点P 的坐标和△PAB 的面积.②在直线PD 上是否存在点M,使△ABM 为直角三角形?若存在,直接写出符合条件的所有点M 的坐标;若不存在,请说明理由.12.如图,抛物线y=ax2+bx+2 与直线y=-x 交第二象限于点E,与x 轴交于A(-3,0),B 两点,与y 轴交于点C,EC∥x 轴.(1)求抛物线的解析式;(2)点P 是直线y=-x 上方抛物线上的一个动点,过点P 作x 轴的垂线交直线于点G,作PH⊥EO,垂足为H.设PH 的长为l,点P 的横坐标为m,求l 与m 的函数关系式(不必写出m 的取值范围),并求出l 的最大值;(3)如果点N 是抛物线对称轴上的一个动点,抛物线上存在一动点M,若以M,A,C,N 为顶点的四边形是平行四边形,请直接写出所有满足条件的点M 的坐标.13. 如图所示,已知抛物线y=ax2+bx+c(a≠0)经过点A(-2,0),B(4,0),C(0,-8),与直线y=x-4 交于B,D 两点.(1)求抛物线的解析式及点D 的坐标;(2)点P 为直线BD 下方抛物线上的一个动点,求△BDP 面积的最大值及此时点P 的坐标;(3)点Q 是线段BD 上异于B,D 的动点,过点Q 作QF⊥x 轴于点F,交抛物线于点G,当△QDG 为直角三角形时,直接写出点Q 的坐标.1314.如图,抛物线y=ax2+bx+c 交x 轴于点A(1,0)和点B(3,0),交y 轴于点C,抛物线上一点D 的坐标为(4,3).(1)求该抛物线所对应的函数解析式;(2)如图1,点P 是直线BC 下方抛物线上的一个动点,PE∥x 轴,PF∥y 轴,求线段EF 的最大值;(3)如图2,点M 是线段CD 上的一个动点,过点M 作x 轴的垂线,交抛物线于点N,当△CBN 是直角三角形时,请直接写出所有满足条件的点M 的坐标.15.如图,已知抛物线y=ax2+4x+c 与x 轴交于点M,与y 轴交于点N,抛物线的对称轴与x 轴交于点P,OM=1,ON=5.(1)求抛物线的解析式.(2)点A 是y 轴正半轴上一动点,点B 是抛物线对称轴上的任意一点,连接AB,AM,BM,且AB⊥AM.①AO 为何值时,△ABM∽△OMN,请说明理由;②若Rt△ABM 中有一边的长等于MP 时,请直接写出点 A 的坐标.16.如图,已知A(-2,0),B(4,0),抛物线y=ax2+bx-1 过A,B 两点,并与过点A 的直线y =-1x -1 交于点C.2(1)求抛物线解析式及对称轴.(2)在抛物线的对称轴上是否存在一点P,使四边形ACPO 的周长最小?若存在,求出点P 的坐标;若不存在,请说明理由.(3)点M 为y 轴右侧抛物线上一点,过点M 作直线AC 的垂线,垂足为N.问:是否存在这样的点N,使以点M,N,C 为顶点的三角形与△AOC 相似?若存在,求出点N 的坐标;若不存在,请说明理由.17.如图,直线l:y =1x +m 与x 轴交于点A(4,0),与y 轴交于点B,抛物线2y=ax2+bx+c(a≠0)经过A,B 两点,且与x 轴交于另一点C(-1,0).(1)求直线及抛物线的解析式;(2)点P 是抛物线上一动点,当点P 在直线l 下方的抛物线上运动时,过点P 作PM∥x 轴交l 于点M,过点P 作PN∥y 轴交l 于点N,求PM+PN 的最大值;(3)在(2)的条件下,当PM+PN 的值最大时,将△PMN 绕点N 旋转,当点M 落在x 轴上时,直接写出此时点P 的坐标.18.如图,已知抛物线y=ax2+x+c 与y 轴交于点C(0,3),与x 轴交于点A 和点B(3,0),点P 是抛物线上的一个动点.(1)求这条抛物线的表达式;(2)若点P 是点B 与点C 之间的抛物线上的一个动点,过点P 向x 轴作垂线,交BC 于点D,求线段PD 长度的最大值;(3)当点P 移动到抛物线的什么位置时,使得∠PCB=75°,请求出此时点P 的坐标.19.在平面直角坐标系内,直线y =1x + 2 分别与x 轴、y 轴交于点A,C.抛物2线y =-1x2 +bx +c 经过点A 与点C,且与x 轴的另一个交点为点B.点D2在该抛物线上,且位于直线AC 的上方.(1)求上述抛物线的表达式;(2)若连接AD,CD,试求出点D 到直线AC 的最大距离以及此时△ADC 的面积;(3)过点D 作DF⊥AC,垂足为点F,连接CD.若△CFD 与△AOC 相似,求点D 的坐标.20.如图,抛物线y=ax2+bx-3 过A(1,0),B(-3,0),直线AD 交抛物线于点D,点D 的横坐标为-2,点P(m,n)是线段AD 上的动点.(1)求直线AD 及抛物线的解析式.(2)过点P 的直线垂直于x 轴,交抛物线于点Q,求线段PQ 的长度l 与m 的关系式,m 为何值时,PQ 最长?(3)在平面内是否存在整点R(横、纵坐标都为整数),使得P,Q,D,R 为顶点的四边形是平行四边形?若存在,直接写出点R 的坐标;若不存在,说明理由.21.如图,抛物线y=-x2+bx+c 交x 轴于A,B 两点,交y 轴于点C,直线y=x-5经过点B,C.(1)求抛物线的解析式;(2)点P 是直线BC 上方抛物线上的一动点,求△BCP 面积S 的最大值;(3)在抛物线上找一点M,连接AM,使得∠MAB=∠ABC,请直接写出点M 的坐标.21参考答案:2、3、4、5、6、7、8、9、10、11、12、13、14、15、16、17、18、19、20、21、。
2020年中考数学压轴题专题复习:一次函数与反比例函数-答案

2020年中考数学压轴题专题复习:一次函数与反比例函数一、选择题(本大题共6道小题)1. 如图,A 、B 两点在反比例函数y =k 1x 的图象上,C 、D 两点在反比例函数y =k 2x的图象上,AC ⊥x 轴于点E ,BD ⊥x 轴于点F ,AC =2,BD =3,EF =103,则k 2-k 1=( )A. 4B.143 C. 163D. 62. 已知一次函数y =kx +b -x 的图象与x 轴的正半轴相交,且函数值y 随自变量x 的增大而增大,则k ,b 的取值情况为( )A. k >1,b <0B. k >1,b >0C. k >0,b >0D. k >0,b <03. 下列函数中,满足y 的值随x 的值增大而增大的是( )A. y =-2xB. y =3x -1C. y =1xD. y =x 24. 设函数y =kx (k ≠0,x >0)的图象如图所示,若z =1y,则z 关于x 的函数图象可能为( )5. 二次函数y =ax 2+bx +c (a ,b ,c 为常数且a ≠0)的图象如图所示,则一次函数y =ax+b 与反比例函数y =cx的图象可能是( )6. 若式子k-1+(k-1)0有意义,则一次函数y=(1-k)x+k-1的图象可能是()二、填空题(本大题共5道小题)7. 已知反比例函数y =k x的图象在每一个象限内y 随x 的增大而增大,请写一个符合条件的反比例函数解析式____________.8. 如图所示,已知点C (1,0),直线y =-x +7与两坐标轴分别交于A ,B 两点,D ,E分别是AB ,OA 上的动点,则△CDE 周长的最小值是________.9. 将函数y =2x +b (b 为常数)的图象位于x 轴下方的部分沿x 轴翻折至其上方后,所得的折线是函数y =|2x +b |(b 为常数)的图象,若该图象在直线y =2下方的点的横坐标x 满足0<x <3,则b 的取值范围为____________.10. 如图,一次函数y =kx +b 的图象分别与反比例函数y =a x的图象在第一象限交于点A (4,3),与y 轴的负半轴交于点B ,且OA =OB .(1)求函数y =kx +b 和y =ax的表达式;(2)已知点C (0,5),试在该一次函数图象上确定一点M ,使得MB =MC .求此时点M 的坐标.11. 如图,已知点A ,C 在反比例函数y =a x的图象上,点B ,D 在反比例函数y =b x的图象上,a >b >0,AB ∥CD ∥x 轴,AB ,CD 在x 轴的两侧,AB =34,CD =32,AB 与CD 间的距离为6,则a -b 的值是________.三、解答题(本大题共4道小题)12. 如图,在平面直角坐标系xOy 中,直线y =-x +3与x 轴交于点C ,与直线AD 交于点A (43,53),点D 的坐标为(0,1). (1)求直线AD 的解析式;(2)直线AD 与x 轴交于点B ,若点E 是直线AD 上一动点(不与点B 重合),当△BOD 与△BCE相似时,求点E的坐标.13. 九年级(3)班数学兴趣小组经过市场调查整理出某种商品在第x天(1≤x≤90,且x为整数)的售价与销售量的相关信息如下,已知商品的进价为30元/件,设该商品的售价为y(单位:元/件),每天的销售量为p(单位:件),每天的销售利润为w(单位:元).(1)求出w与x的函数关系式;(2)问销售该商品第几天时,当天的销售利润最大?并求出最大利润;(3)该商品在销售过程中,共有多少天每天的销售利润不低于5600元?请直接写出结果.14. 如图,已知抛物线y=x2-(m+3)x+9的顶点C在x轴正半轴上,一次函数y=x+3与抛物线交于A、B两点,与x、y轴分别交于D、E两点.(1)求m的值;(2)求A、B两点的坐标;(3)点P(a,b)(-3<a<1)是抛物线上一点,当△P AB的面积是△ABC面积的2倍时,求a、b的值.15. 如图,二次函数y=ax2+bx的图象经过点A(2,4)与B(6,0).(1)求a,b的值;(2)点C是该二次函数图象上A、B两点之间的一动点,横坐标为x(2<x<6).写出四边形OACB的面积S关于点C的横坐标x的函数表达式,并求S的最大值.答案一、选择题(本大题共6道小题)1. 【答案】A 【解析】设E (x 1,0),F (x 2,0),则A (x 1,k 1x 1),D (x 2,k 2x 2),B (x 2,k 1x 2),C (x 1,k 2x 1),∴AC =k 1-k 2x 1=2,BD =k 2-k 1x 2=3,∴k 1-k 2=2x 1,k 2-k 1=3x 2,∴2x 1+3x 2=0,又∵EF =x 2-x 1=103,∴x 2=43,∴k 2-k 1=3x 2=3×43=4.2. 【答案】A 【解析】原解析式可变形为y =(k -1)x +b ,∵函数值y 随自变量x 的增大而增大,∴k -1>0,∴k >1,∵图象与x 轴正半轴相交,∴b <0,∴满足题意的k 、b 情况为k >1,b <0.3. 【答案】B 【解析】一次函数y =-2x 中,y 随x 增大而减小;一次函数y =3x -1中,y 随x 的增大而增大;反比例函数y =1x 中,在每一个分支上,y 随x 的增大而减小;二次函数y =x 2中,当x >0时,y 随x 增大而增大,当x <0时,y 随x 的增大而减小,故答案为B .4. 【答案】D 【解析】函数y =k x(k ≠0,x >0)的图象在第一象限,则k >0,x >0.由已知得z =1y =1k x=xk,所以z 关于x 的函数图象是一条射线,且在第一象限,故选D.5. 【答案】C 【解析】抛物线开口向上,所以a >0,对称轴在y 轴右侧,所以a 、b异号,所以b <0,抛物线与y 轴交于负半轴,所以c <0,所以直线y =ax +b 过第一、三、四象限,反比例函数y =cx位于第二、四象限,故答案为C.6. 【答案】C 【解析】式子k -1+(k -1)0有意义,则k >1,所以1-k <0,k -1>0,所以一次函数y =(1-k )x +k -1的图象经过第一、二、四象限.二、填空题(本大题共5道小题)7. 【答案】y =-2x(答案不唯一) 【解析】∵反比例函数的图象在每一个象限内y 随x的增大而增大,∴k <0,∴k 可取-2(答案不唯一).8. 【答案】10 【解析】作点C 关于y 轴的对称点C 1(-1,0),点C 关于直线AB 的对称点C 2,连接C 1C 2交OA 于点E ,交AB 于点D ,则此时△CDE 的周长最小,且最小值等于C 1C 2的长.∵OA =OB =7,∴CB =6,∠ABC =45°.∵AB 垂直平分CC 2,∴∠CBC 2=90°,∴C 2的坐标为(7,6).在Rt △C 1BC 2中,C 1C 2=C 1B 2+C 2B 2=82+62=10.即△CDE 周长的最小值是10.9. 【答案】-4<b<-2 【解析】先求出直线y =2与y =|2x +b|的交点的横坐标,再由已知条件列出关于b 的不等式组,便可求出结果.由⎩⎪⎨⎪⎧y =2y =|2x +b|,得⎩⎪⎨⎪⎧y =2y =2x +b或⎩⎪⎨⎪⎧y =2y =-2x -b ,解得x =2-b 2或x =-2+b2,∵0<x<3,∴⎩⎨⎧2-b2<3-b +22>0,解得-4<b<-2.10. 【答案】(1)【思路分析】由点A 的坐标和OA =OB 可得点B 的坐标,用待定系数法即可求出一次函数的解析式;将点A 的坐标代入反比例函数解析式中即可求出反比例函数的解析式.解:∵点A(4,3),∴OA =42+32=5,∴OB =OA =5, ∴B(0,-5),将点A(4, 3),点B(0, -5)代入函数y =kx +b 得,⎩⎪⎨⎪⎧4k +b =3b =-5,解得⎩⎪⎨⎪⎧k =2b =-5,(2分) ∴一次函数的解析式为y =2x -5, 将点A(4, 3)代入y =ax 得,3=a 4, ∴a =12,∴反比例函数的解析式为y =12x, ∴所求函数表达式分别为y =2x -5和y =12x.(4分) (2)【思路分析】由题意可知,使MB =MC 的点在线段BC 的垂直平分线上,故求出线段BC 的垂直平分线和一次函数的交点即可.解:如解图,∵点B 的坐标为(0, -5),点C 的坐标为(0, 5),∴x 轴是线段BC 的垂直平分线, ∵MB =MC ,∴点M 在x 轴上,又∵点M 在一次函数图象上,∴点M 为一次函数的图象与x 轴的交点,如解图所示, 令2x -5=0,解得x =52,(6分)∴此时点M 的坐标为(52, 0).(8分)11. 【答案】3 【解析】设点A 的纵坐标为y 1,点C 的纵坐标为y 2,∵AB ∥CD ∥x轴,∴点B 的纵坐标为y 1,点D 的纵坐标为y 2,∵点A 在函数y =ax 的图象上,点B 在函数y =b x 的图象上,且AB =34,∴a y 1-b y 1=34,∴y 1=4(a -b )3,同理y 2=2(b -a )3,又∵AB与CD 间的距离为6,∴y 1- y 2=4(a -b )3-2(b -a )3=6,解得a -b =3.三、解答题(本大题共4道小题)12. 【答案】解:(1)设直线AD 的解析式为y =kx +b(k≠0), 将D(0,1)、A(43,53)代入解析式得⎩⎪⎨⎪⎧b =143k +b =53, 解得⎩⎪⎨⎪⎧b =1k =12,∴直线AD 的解析式为y =12x +1.(3分) (2)直线AD 的解析式为y =12x +1,令y =0,得x =-2, ∴B(-2,0),即OB =2.∵直线AC 的解析式为y =-x +3,令y =0,得x =3,∴C(3,0),即BC =5,设E(x ,12x +1), ①当E 1C ⊥BC 时,∠BOD =∠BCE 1=90°,∠DBO =∠E 1BC ,∴△BOD ∽△BCE 1,此时点C 和点E 1的横坐标相同,将x =3代入y =12x +1, 解得:y =52, ∴E 1(3,52).(6分) ②当CE 2⊥AD 时,∠BOD =∠BE 2C =90°,∠DBO =∠CBE 2,∴△BOD ∽△BE 2C ,如解图,过点E 2作E 2F ⊥x 轴于点F ,则∠E 2FC =∠BFE 2=90°.∵∠E 2BF +∠BE 2F =90°,∠CE 2F +∠BE 2F =90°,∴∠E 2BF =∠CE 2F ,∴△E 2BF ∽△CE 2F ,则E 2F BF =CF E 2F, 即E 2F 2=CF·BF ,(12x +1)2=(3-x)(x +2),解得:x 1=2,x 2=-2(舍去),∴E 2(2,2);(9分)③当∠EBC =90°时,此情况不存在.综上所述,点E 的坐标为E 1(3,52)或E 2(2,2).(10分)13. 【答案】解:(1)当0≤x≤50时,设商品的售价y 与时间x 的函数关系式为y =kx +b(k 、b 为常数且k≠0),∵y =kx +b 经过点(0,40),(50,90),∴⎩⎪⎨⎪⎧b =4050k +b =90, 解得⎩⎪⎨⎪⎧k =1b =40, ∴y =x +40,∴y 与x 的函数关系式为:y =⎩⎨⎧x +40 (0≤x≤50,且x 为整数)90 (50<x≤90,且x 为整数),(2分) 由数据可知每天的销售量p 与时间x 成一次函数关系.设每天的销售量p 与时间x 的函数关系式为p =mx +n(m ,n 为常数,且m≠0), ∵p =mx +n 过点(60,80),(30,140),∴⎩⎪⎨⎪⎧60m +n =8030m +n =140,解得⎩⎪⎨⎪⎧m =-2n =200, ∴p =-2x +200(0≤x≤90,且x 为整数),(3分)当0≤x≤50时,w =(y -30)·p=(x +40-30)(-2x +200),=-2x 2+180x +2000,当50<x≤90时,w =(90-30)×(-2x +200)=-120x +12000,综上所述,每天的销售利润w 与时间x 的函数关系式是:w =⎩⎨⎧-2x 2+180x +2000 (0≤x≤50,且x 为整数)-120x +12000 (50<x≤90,且x 为整数).(5分) (2)当0≤x≤50时,w =-2x 2+180x +2000=-2(x -45)2+6050,∵a =-2<0且0≤x≤50,∴x =45时,w 最大=6050(元),(6分)当50<x≤90时,w =-120x +12000,∵k =-120<0,∴w 随x 增大而减小.∴x =50时,w 最大=6000(元),∵6050>6000,∴x =45时,w 最大=6050(元),即销售第45天时,当天获得的销售利润最大,最大利润是6050元.(8分)(3)24天.(10分)【解法提示】①当0≤x ≤50,若w 不低于5600元,则w =-2x 2+180x +2000≥5600,解得30≤x ≤60,∴30≤x ≤50;②当50<x ≤90时,若w 不低于5600元,则w =-120x +12000≥5600,解得x ≤1603, ∴50<x ≤1603, 综合①②可得30≤x ≤1603, ∴从第30天到第53天共有24天利润不低于5600元.14. 【答案】解:(1)∵抛物线y =x 2-(m +3)x +9的顶点在x 轴的正半轴上,∴方程x 2-(m +3)x +9=0有两个相等的实数根,∴b 2-4ac =[-(m +3)]2-4×9=0,解得m =3或m =-9,又∵抛物线对称轴大于0,即m +3>0,∴m =3.(3分)(2)由(1)可知抛物线解析式为y =x 2-6x +9,联立一次函数y =x +3,可得⎩⎪⎨⎪⎧y =x 2-6x +9y =x +3, 解得⎩⎪⎨⎪⎧x =1y =4或⎩⎪⎨⎪⎧x =6y =9, ∴A(1,4),B(6,9).(6分)(3)如解图,分别过A 、B 、P 三点作x 轴的垂线,垂足分别为R 、S 、T ,∵A(1,4),B(6,9),C(3,0),P(a ,b),∴AR =4,BS =9,RC =3-1=2,CS =6-3=3,RS =6-1=5,PT =b ,RT =1-a ,ST =6-a ,∴S △ABC =S 梯形ABSR -S △ARC -S △BCS =12×(4+9)×5-12×2×4-12×3×9=15, S △PAB =S 梯形PBST -S 梯形ARTP -S 梯形ARSB =12(9+b)(6-a)-12(b +4)(1-a)-12×(4+9)×5=12(5b -5a -15).(8分)又∵S △PAB =2S △ABC ,∴12(5b -5a -15)=30,即b -a =15, ∴b =15+a ,∵P 点在抛物线上,∴b =a 2-6a +9,∴15+a =a 2-6a +9,解得a =7±732, ∵-3<a<1,∴a =7-732, ∴b =15+7-732=37-732.(10分)15. 【答案】解:(1)∵二次函数y =ax 2+bx 的图象经过点A(2,4)与B(6,0).∴⎩⎪⎨⎪⎧4a +2b =436a +6b =0, 解得⎩⎪⎨⎪⎧a =-12b =3.(4分) (2)如解图①,过点A 作x 轴的垂线,垂足为点D(2,0),连接CD ,过点C 作CE ⊥AD ,CF ⊥x 轴,垂足分别为点E ,点F ,则S △OAD =12OD·AD =12×2×4=4, S △ACD =12AD·CE =12×4×(x -2)=2x -4, S △BCD =12BD·CF =12×4×(-12x 2+3x)=-x 2+6x , 则S =S △OAD +S △ACD +S △BCD =4+(2x -4)+(-x 2+6x)=-x 2+8x.∴S 关于x 的函数表达式为S =-x 2+8x(2<x<6).(10分)∵S =-(x -4)2+16,∴当x =4时,四边形OACB 的面积S 取最大值,最大值为16.(12分)图①【一题多解】解法一:由(1)知y =-12x 2+3x ,如解图②,连接AB ,则 S =S △AOB +S △ABC ,其中S △AOB =12×6×4=12, 设直线AB 解析式为y 1=k 1x +b 1,将点A(2,4),B(6,0)代入,易得,y 1=-x +6,过C 作直线l ⊥x 轴交AB 于点D ,∴C(x ,-12x 2+3x),D(x ,-x +6), ∴S △ABC =S △ADC +S △BDC =12·CD·(x -2)+12·CD·(6-x)=12·CD·4=2CD , 其中CD =-12x 2+3x -(-x +6)=-12x 2+4x -6, ∴S △ABC =2CD =-x 2+8x -12,∴S =S △ABC +S △AOB =-x 2+8x -12+12=-x 2+8x =-(x -4)2+16(2<x<6), 即S 关于x 的函数表达式为S =-x 2+8x(2<x<6),∴当x =4时,四边形OACB 的面积S 取最大值,最大值为16.图②解法二:∵点C 在抛物线y =-12x 2+3x 上, ∴点C(x ,-12x 2+3x), 如解图③,过点A 作AD ⊥x 轴,垂足为点D ,过点C 作CE ⊥x 轴,垂足为点E ,则 点D 的坐标为(2,0),点E 的坐标为(x ,0),∴S =S △OAD +S 梯形ADEC +S △CEB =12×2×4+12(4-12x 2+3x)(x -2)+12(6-x)(-12x 2+3x)=-x 2+8x ,∵S =-x 2+8x =-(x -4)2+16(2<x<6),∴当x =4时,四边形OACB 的面积S 取最大值,最大值为16.图③。
2020年中考数学第一轮复习专题 第19课 一次函数(含答案)

第19课一次函数本节内容考纲要求考查一次函数图象、性质及应用,体会一次函数与方程(组)、不等式之间的联系,一次函数的实际应用。
广东省近5年试题规律:主要考查一次函数的表达式、图象及性质,有时以选择、填空题出现,但多以一次函数的应用、一次函数与反比例函数的综合题出现,可作压轴题。
知识清单知识点一一次函数与正比例函数的概念课前小测1.(正比例函数的性质)关于正比例函数y=﹣3x,下列结论正确的是()A.图象不经过原点B.y随x的增大而增大时,y=1C.图象经过第二、四象限D.当x=132.(一次函数的性质)一次函数y=﹣2x﹣1的图象不经过下列各象限中的()A.第一象限B.第二象限C.第三象限D.第四象限3.(一次函数的性质)若正比例函数y=3x的图象经过A(﹣2,y1),B(﹣1,y2)两点,则y1与y2的大小关系为()A.y1<y2B.y1>y2C.y1≤y2D.y1≥y24.(一次函数与方程的关系)若直线y=kx+b的图象经过点(1,3),则方程kx+b=3的解是()A.1 B.2 C.3 D.45.(求一次函数解析式)已知一次函数y=﹣x+b的图象过点(8,2),那么此一次函数的解析式为.经典回顾考点一一次函数图象与性质【例1】函数y=x﹣2的图象不经过()A.第一象限B.第二象限C.第三象限D.第四象限【点拔】本题考查了一次函数的性质,对于一次函数y=kx+b,k>0,函数经过第一、三象限,k<0,函数经过第二、四象限.考点二一次函数与方程、不等式【例2】(2019•黔东南州)如图所示,一次函数y=ax+b(a、b为常数,且a>0)的图象经过点A(4,1),则不等式ax+b<1的解集为.【点拔】本题考查了一次函数与不等式的关系及数形结合思想的应用.解决此类问题关键是仔细观察图形,注意几个关键点(交点、原点等),做到数形结合.考点三一次函数的解析式【例3】(2019•广东模拟)如图,一次函数y=kx+b的图象经过A、B两点,与x 轴交于点C.(1)写出点A、B、C的坐标;(2)求此一次函数的解析式;(3)求△AOC的面积.【点拔】考查一次函数图象上点的坐标特征、待定系数法求函数的关系式、以及将点的坐标转化为三角形的底和高,进而求三角形的面积.考点四一次函数的应用【例4】(2019•新疆)某水果店以每千克8元的价格购进苹果若干千克,销售了部分苹果后,余下的苹果每千克降价4元销售,全部售完.销售金额y(元)与销售量x(千克)之间的关系如图,请根据图象提供的信息完成下列问题:(1)降价前苹果的销售单价是元/千克;(2)求降价后销售金额y(元)与销售量x(千克)之间的函数解析式,并写出自变量的取值范围;(3)该水果店这次销售苹果盈利了多少元?【点拔】本题考查一次函数的应用,解答本题明确题意,利用一次函数的性质和数形结合的思想解答.对应训练1.(2018•常德)若一次函数y=(k﹣2)x+1的函数值y随x的增大而增大,则()A.k<2 B.k>2 C.k>0 D.k<0 2.(2019•鞍山)如图,若一次函数y=﹣2x+b的图象与两坐标轴分别交于A,B 两点,点A的坐标为(0,3),则不等式﹣2x+b>0的解集为()A.x>B.x<C.x>3 D.x<3 3.(2018•邵阳)如图所示,一次函数y=ax+b的图象与x轴相交于点(2,0),与y轴相交于点(0,4),结合图象可知,关于x的方程ax+b=0的解是.4.(2016•宜昌)如图,直线y=3x+3与两坐标轴分别交于A、B两点.(1)求∠ABO的度数;(2)过A的直线l交x轴正半轴于C,AB=AC,求直线l的函数解析式.5.(2019•深圳)有A、B两个发电厂,每焚烧一吨垃圾,A发电厂比B发电厂多发40度电,A焚烧20吨垃圾比B焚烧30吨垃圾少1800度电.(1)求焚烧1吨垃圾,A和B各发电多少度?(2)A、B两个发电厂共焚烧90吨的垃圾,A焚烧的垃圾不多于B焚烧的垃圾两倍,求A厂和B厂总发电量的最大值.中考冲刺夯实基础1.(2019•广安)一次函数y=2x﹣3的图象经过的象限是()A.一、二、三B.二、三、四C.一、三、四D.一、二、四2.(2019•梧州)直线y=3x+1向下平移2个单位,所得直线的解析式是()A.y=3x+3 B.y=3x﹣2 C.y=3x+2 D.y=3x﹣1 3.(2019•大庆)正比例函数y=kx(k≠0)的函数值y随着x增大而减小,则一次函数y=x+k的图象大致是()A.B.C.D.4.(2019•铁岭)在平面直角坐标系中,函数y=kx+b的图象如图所示,则下列判断正确的是()A.k>0 B.b<0 C.k•b>0 D.k•b<0 5.(2019•锦州)如图,一次函数y=2x+1的图象与坐标轴分别交于A,B两点,O为坐标原点,则△AOB的面积为()A.B.C.2 D.4 6.(2019•本溪)函数y=5x的图象经过的象限是.7.(2019•成都)已知一次函数y=(k﹣3)x+1的图象经过第一、二、四象限,则k的取值范围是.8.(2019•杭州)某函数满足当自变量x=1时,函数值y=0,当自变量x=0时,函数值y=1,写出一个满足条件的函数表达式.能力提升9.(2019•辽阳)若ab<0且a>b,则函数y=ax+b的图象可能是()A.B.C.D.10.(2019•枣庄)如图,一直线与两坐标轴的正半轴分别交于A,B两点,P是线段AB上任意一点(不包括端点),过点P分别作两坐标轴的垂线与两坐标轴围成的矩形的周长为8,则该直线的函数表达式是()A.y=﹣x+4 B.y=x+4 C.y=x+8 D.y=﹣x+8 11.(2019•鄂尔多斯)如图,有一条折线A1B1A2B2A3B3A4B4…,它是由过A1(0,0),B1(4,4),A2(8,0)组成的折线依次平移8,16,24,…个单位得到的,直线y=kx+2与此折线有2n(n≥1且为整数)个交点,则k的值为.12.(2019•本溪)如图,点B1在直线l:y=12x上,点B1的横坐标为2,过B1作B1A1⊥l,交x轴于点A1,以A1B1为边,向右作正方形A1B1B2C1,延长B2C1交x轴于点A2;以A2B2为边,向右作正方形A2B2B3C2,延长B3C2交x轴于点A3;以A3B3为边,向右作正方形A3B3B4C3,延长B4C3交x轴于点A4;…;按照这个规律进行下去,点∁n的横坐标为(结果用含正整数n的代数式表示)13.(2019•丹东)如图,在平面直角坐标系中,点A,C分别在x轴、y轴上,四边形ABCO是边长为4的正方形,点D为AB的中点,点P为OB上的一个动点,连接DP,AP,当点P满足DP+AP的值最小时,直线AP的解析式为.14.(2019•天门)某农贸公司销售一批玉米种子,若一次购买不超过5千克,则种子价格为20元/千克,若一次购买超过5千克,则超过5千克部分的种子价格打8折.设一次购买量为x千克,付款金额为y元.(1)求y关于x的函数解析式;(2)某农户一次购买玉米种子30千克,需付款多少元?第19课 一次函数课前小测1.C . 2.A . 3.A . 4.A . 5.y =﹣x +10.经典回顾考点一 一次函数图象与性质 【例1】B .考点二 一次函数与方程、不等式 【例2】x <4. 考点三 一次函数的解析式【例3】解:(1)A (2,4)、B (0,2)、C (﹣2,0); (2)将B (0,2)、C (﹣2,0)代入y =kx +b 得:202k b b -+=⎧⎨=⎩解得:k =1,b =2,∴一次函数的解析式为:y =x +2;(3)S △AOC =12×2×4=4,答:△AOC 的面积为4. 考点四 一次函数的应用 【例4】解:(1)16;(2)(760﹣640)÷(16﹣4)=10,设降价后y (元)与x (千克)之间的函数解析式是y =kx +b ,得:4064050760k b k b +=⎧⎨+=⎩,得12160k b =⎧⎨=⎩, ∴y =12x +160(40<x ≤50); (3)760﹣8×50=360(元)答:该水果店这次销售苹果盈利了360元. 对应训练 1.B . 2.B . 3.x =2.4.解:(1)对于直线y令x =0,则y 令y =0,则x =﹣1,故点A 的坐标为(0,点B 的坐标为(﹣1,0),则AO BO =1, 在Rt △ABO 中, ∵tan ∠ABO =AOBO∴∠ABO =60°; (2)在△ABC 中, ∵AB =AC ,AO ⊥BC , ∴AO 为BC 的中垂线, 即BO =CO ,则C 点的坐标为(1,0),设直线l 的解析式为:y =kx +b ,则0b k b ⎧=⎪⎨+=⎪⎩,解得:k b ⎧=⎪⎨=⎪⎩ 即函数解析式为:y5.解:(1)设焚烧1吨垃圾,A 发电厂发电a 度,B 发电厂发电b 度,得:4030201800a b a b -=⎧⎨-=⎩,解得300260a b =⎧⎨=⎩, 答:焚烧1吨垃圾,A 发电厂发电300度,B 发电厂发电260度;(2)设A 发电厂焚烧x 吨垃圾,则B 发电厂焚烧(90﹣x )吨垃圾,总发电量为y 度,则y =300x +260(90﹣x )=40x +23400,∵x ≤2(90﹣x ),∴x ≤60,∵y 随x 的增大而增大,∴当x =60时,y 有最大值为:40×60+23400=25800(元).答:A 厂和B 厂总发电量的最大是25800度.中考冲刺夯实基础1.C .2.D .3.A .4.D .5.A .6.一、三7.k <3;8.y =﹣x +1.能力提升9.A.10.A.11.﹣14n.12.1 732nn-⨯.13.y=﹣2x+8.14.解:(1)根据题意,得①当0≤x≤5时,y=20x;②当x>5,y=20×0.8(x﹣5)+20×5=16x+20;(2)把x=30代入y=16x+20,∴y=16×30+20=500;∴一次购买玉米种子30千克,需付款500元;。
2020年中考数学压轴题专题复习:二次函数-答案

∴y=x+40,
∴y与x的函数关系式为:
y= ,(2分)
由数据可知每天的销售量p与时间x成一次函数关系.
设每天的销售量p与时间x的函数关系式为p=mx+n(m,n为常数,且m≠0),
∵p=mx+n过点(60,80),(30,140),
∴ ,解得 ,
∴p=-2x+200(0≤x≤90,且x为整数),(3分)
11.【答案】(1+ ,2)或(1- ,2)【解析】抛物线y=-x2+2x+3与y轴交于点C,则点C坐标是(0,3),∵点D(0,1),点P在抛物线上,且△PCD是以CD为底的等腰三角形,∴易得点P的纵坐标是2,当y=2时,∴-x2+2x+3=2,则x2-2x-1=0,解得方程的两根是x= =1± ,∴点P的坐标是(1+ ,2)或(1- ,2).
14.【答案】
解:(1)把B(-2,6),C(2,2)代入抛物线的解析式得:
,(1分)
解得 ,(2分)
∴抛物线的解析式为y= x2-x+2.(3分)
(2)抛物线解析式化为顶点式:y= (x-1)2+ ,则抛物线顶点D(1, ),(4分)
如解图①所示,过点B、D、C分别向x轴作垂线,垂足分别为点M、N、H,则有:
6.【答案】C【解析】抛物线开口向上,所以a>0,对称轴在y轴右侧,所以a、b异号,所以b<0,抛物线与y轴交于负半轴,所以c<0,所以直线y=ax+b过第一、三、四象限,反比例函数y= 位于第二、四象限,故答案为C.
二、填空题(本大题共5道小题)
7.【答案】(1,4)【解析】∵A(0,3)、B(2,3),两点纵坐标相同,∴A、B两点关于直线x=1对称,∴抛物线的对称轴是直线x=1,即- =1,解得b=2,∵当x=0时,y=3,∴c=3,∴抛物线的解析式为y=-x2+2x+3,当x=1时,y=-x2+2x+3=-12+2×1+3=4,∴抛物线的顶点坐标是(1,4).
2020年中考数学 三轮专题 二次函数查漏补缺 (含答案)

2020中考数学 三轮专题 二次函数查漏补缺 (含答案)命题点1 二次函数的性质1.抛物线y =2(x -3)2+1的顶点坐标是( ) A. B. C. D.2.二次函数2+bx +c (a ≠0)图象上部分点的坐标(x ,y )对应值列表如下:则该函数图象的对称轴是( ) A. 直线x =-3 B. 直线x =-2 C. 直线x =-1 D. 直线x =03.二次函数y =x 2-2x +4化为y =a (x -h )2+k 的形式,下列正确的是( ) A. y =(x -1)2+2 B. y =(x -1)2+3 C. y =(x -2)2+2 D. y =(x -2)2+44.抛物线y =12x 2,y =x 2,y =-x 2的共同性质是:①都是开口向上;②都以点(0,0)为顶点;③都以y 轴为对称轴;④都关于x 轴对称.其中正确的个数有( )A. 1个B. 2个C. 3个D. 4个5.已知函数y =-x 2-2x ,当________时,函数值y 随x 的增大而增大.命题点2 二次函数图象的平移6.如果将抛物线y =x 2+2向下平移1个单位,那么所得新抛物线的表达式是( ) A. y =(x -1)2+2 B. y =(x +1)2+2 C. y =x 2+1 D. y =x 2+37.要将抛物线y =x 2+2x +3平移后得到抛物线y =x 2,下列平移方法正确的是( ) A. 向左平移1个单位,再向上平移2个单位 B. 向左平移1个单位,再向下平移2个单位 C. 向右平移1个单位,再向上平移2个单位 D. 向右平移1个单位,再向下平移2个单位8.若抛物线y =x 2-2x +3不动,将平面直角坐标系........xOy 先沿水平方向向右平移1个单位,再沿铅直方向向上平移3个单位,则原抛物线图象的解析式应变为( )A. y =(x -2)2+3B. y =(x -2)2+5C. y =x 2-1D. y =x 2+49.在平面直角坐标系中,把一条抛物线先向上平移3个单位长度,然后绕原点旋转180°得到抛物线y =x 2+5x +6,则原抛物线的解析式是( )A. y =-(x -52)2-114B. y =-(x +52)2-114C. y =-(x -52)2-14D. y =-(x +52)2+14命题点3 二次函数图象与系数的关系10.某同学在用描点法画二次函数y =ax 2+bx +c 图象时,列出了下面的表格:由于粗心,A. -11 B. -2 C. 1 D. -511.以x 为自变量的二次函数y =x 2-2(b -2)x +b 2-1的图象不经过第三象限,则实数b 的取值范围是( )A. b ≥54B. b ≥1或b ≤-1C. b ≥2D. 1≤b ≤212.已知直线y =bx -c 与抛物线y =ax 2+bx +c 在同一直角坐标系中的图象可能是( )13.抛物线y=x2+bx+c(其中b,c是常数)过点A(2,6),且抛物线的对称轴与线段y=0(1≤x≤3)有交点,则c的值不可能是()A. 4B. 6C. 8D. 1014.二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:①b<0;②c>0;③a+c<b;④b2-4ac>0,其中正确的个数是()A. 1B. 2C. 3D. 4第14题图第15题图15.如图,抛物线y=ax2+bx+c(a>0)的对称轴是过点(1,0)且平行于y轴的直线,若点P(4,0)在该抛物线上,则4a-2b+c的值为________.命题点4二次函数图象与方程、不等式16.若二次函数y=ax2-2ax+c的图象经过点(-1,0),则方程ax2-2ax+c=0的解为()A. x1=-3,x2=-1B. x1=1,x2=3C. x1=-1,x2=3D. x1=-3,x2=117.若二次函数y=2x2-4x-1的图象与x轴交于A(x1,0)、B(x2,0)两点,则1x1+1x2的值为________.第18题图18.如图,直线y=x+m和抛物线y=x2+bx+c都经过点A(1,0)和B(3,2),不等式x2+bx+c>x+m的解集为____________.命题点5 二次函数的实际应用19.竖直上抛的小球离地高度是它运动时间的二次函数.小军相隔1秒依次竖直向上抛出两个小球.假设两个小球离手时离地高度相同,在各自抛出后1.1秒时到达相同的最大离地高度.第一个小球抛出后t 秒时在空中与第二个小球的离地高度相同,则t =________.20.某电商销售一款夏季时装,进价40元/件,售价110元/件,每天销售20件,每销售一件需缴纳电商平台推广费用a 元(a >0).未来30天,这款时装将开展“每天降价1元”的夏令促销活动,即从第1天起每天的单价均比前一天降1元.通过市场调研发现,该时装单价每降1元,每天销量增加4件.在这30天内,要使每天缴纳电商平台推广费用后的利润随天数t (t · 为正整数....)的增大而增大,a 的取值范围应为________. 21.如图,需在一面墙上绘制几个相同的抛物线型图案,按照图中的直角坐标系,最左边的抛物线可以用y =ax 2+bx (a ≠0)表示.已知抛物线上B ,C 两点到地面的距离均为34 m ,到墙边OA 的距离分别为12 m ,32m.(1)求该抛物线的函数关系式,并求图案最高点到地面的距离;(2)若该墙的长度为10 m ,则最多可以连续绘制几个这样的抛物线型图案?第21题图22.某果园有100棵橙子树,平均每棵树结600个橙子,现准备多种一些橙子树以提高果园产量,但是如果多种树,那么树之间的距离和每一棵树所接受的阳光就会减少.根据经验估计,每多种一棵树,平均每棵果树就会少结5个橙子,假设果园多种x棵橙子树.(1)直接写出平均每棵树结的橙子数y(个)与x之间的关系式;(2)果园多种多少棵橙子树时,可以使橙子的总产量最大?最大为多少个?23.一茶叶专卖店经销某种品牌的茶叶,该茶叶的成本价是80元/kg,销售单价不低于120元/kg,且不高于180元/kg.经销一段时间后得到如下数据:设y与x(1)直接写出y与x的函数关系式,并指出自变量x的取值范围;(2)当销售单价为多少时,销售利润最大?最大利润是多少?命题点6二次函数综合题24.如图,已知抛物线y=-x2+mx+3与x轴交于点A,B两点,与y轴交于点C,点B 的坐标为(3,0).(1)求m的值及抛物线的顶点坐标;(2)点P是抛物线对称轴l上的一个动点,当P A+PC的值最小时,求点P的坐标.第24题图25.正方形OABC的边长为4,对角线相交于点P,抛物线L经过O、P、A三点,点E 是正方形内的抛物线上的动点.(1)建立适当的平面直角坐标系,①直接写出O,P,A三点坐标;②求抛物线L的解析式;(2)求△OAE与△OCE面积之和的最大值.第25题图26.已知二次函数y =ax 2-2ax +c (a >0)的图象与x 轴的负半轴和正半轴分别交于A 、B 两点,与y 轴交于点C ,它的顶点为P ,直线CP 与过点B 且垂直于x 轴的直线交于点D ,且CP ∶PD =2∶3.(1)求A 、B 两点的坐标;(2)若tan ∠PDB =54,求这个二次函数的关系式.第26题图参考答案1. A 【解析】∵抛物线y =a (x -h )2+k 的顶点坐标是(h ,k ),∴y =2(x -3)2+1的顶点坐标是(3,1).2. B 【解析】由表格的数据可以看出,x =-3和x =-1时y 的值相同,都是-3,所以可以判断出,点(-3,-3)和点(-1,-3)关于二次函数图象的对称轴对称,利用公式x =x 1+x 22,可求出对称轴为直线x =x 1+x 22=-3-12=-42=-2. 3. B 【解析】将二次函数的一般式经过配方转化成顶点式,可以加上一次项系数的一半的平方来凑完全平方式.y =x 2-2x +4=x 2-2x +1+3=(x -1)2+3.4. B 【解析】抛物线y =12x 2,y =x 2,y =-x 2的共同性质是:5. x ≤-1 【解析】∵函数y =-x 2-2x ,其图象的对称轴为x =-b2a =-1,且a =-1<0,∴在对称轴的左边y 随x 的增大而增大,∴x ≤-1.6. C 【解析】根据图象平移变换口诀“左加右减,上加下减”进行解答.把抛物线y =x 2+2向下平移1个单位得y =x 2+2-1=x 2+1.7. D 【解析】y =x 2+2x +3=(x +1)2+2,该抛物线的顶点坐标是(-1,2),抛物线y =x 2的顶点坐标是(0,0),则平移的方法可以是:将抛物线y =x 2+2x +3向右移1个单位,再向下平移2个单位得抛物线y =x 2.8. C 【解析】由抛物线y =x 2-2x +3得y =(x -1)2+2.保持抛物线不动,将平面直角坐标系先沿水平方向向右平移1个单位,其实质相当于抛物线向左平移1个单位,再将平面直角坐标系向上平移3个单位,则相当于抛物线向下平移3个单位,根据抛物线平移规律:左加右减,上加下减,可得新的抛物线解析式为y =(x -1+1)2+2-3=x 2-1.9. A 【解析】∵抛物线的解析式为:y =x 2+5x +6,∴绕原点旋转180°变为y =-x 2+5x -6,即y =-(x -52)2+14,∴再向下平移3个单位长度得到的抛物线解析式为y =-(x -52)2+14-3=-(x -52)2-114. 10. D 【解析】由函数图象关于对称轴对称,得点(-1,-2),(0,1),(1,-2)在函数图象上,把点(-1,-2),(0,1),(1,-2)代入函数解析式,得⎩⎪⎨⎪⎧a -b +c =-2c =1a +b +c =-2,解得⎩⎪⎨⎪⎧a =-3b =0c =1,∴函数解析式为y =-3x 2+1,x =2时y =-11.11. A 【解析】∵二次函数图象不经过第三象限,∴分两种情况讨论:(1)当对称轴在x ≥0范围内,即b -2≥0时,需满足在x =0时,函数值大于等于0,即y =b 2-1≥0,解得b ≥2;(2)当对称轴在x <0范围内,即b -2<0时,需满足函数图象顶点的纵坐标大于等于0,即4(b 2-1)-[-2(b -2)]24=4b -5≥0,解得54≤b <2;综上所述,b 的取值范围为b ≥54. 12. C 【解析】在A 中,抛物线的对称轴在y 轴右边,∴-b2a>0,∵a >0,∴b <0;而从一次函数图象知b >0,∴选项A 错误;在B 中,抛物线对称轴-b2a >0,∵a <0,∴b>0;而从一次函数图象知b <0,∴选项B 错误;在C 中,抛物线的对称轴在y 轴左边,∴-b2a <0,∵a >0,∴b >0;抛物线与y 轴负半轴相交,∴c <0;而从一次函数图象知b >0,-c >0,∴c <0,∴选项C 正确;在D 中,抛物线与y 轴的正半轴相交,c >0,由一次函数图象知-c >0,即c <0,∴选项D 错误.13. A 【解析】 由题知,对称轴与线段y =0(1≤x ≤3)有交点,则有1≤-b2≤3,可得到:-6≤b ≤-2,由抛物线经过点A (2,6),代入可得4+2b +c =6,∴b =2-c 2,∴-6≤2-c2≤-2, 解得6≤c ≤14,∴c 的值不可能是4.14. C 【解析】∵图象开口向下,∴a <0,∵对称轴在y 轴右侧,∴a ,b 异号,∴b >0,故①错误;∵图象与y 轴交于x 轴上方,∴c >0,故②正确;当x =-1时,a -b +c <0,则a +c <b ,故③正确;图象与x 轴有两个交点,则b 2-4ac >0,故④正确.15. 0 【解析】设抛物线与x 轴的另一个交点是Q ,∵抛物线的对称轴是过点(1,0)的直线,与x 轴的一个交点是P(4,0),∴与x 轴的另一个交点Q(-2,0),把(-2,0)代入解析式得:0=4a -2b +c ,∴4a -2b +c =0.16. C 【解析】∵图象过点(-1,0),∴将点(-1,0)代入方程得a +2a +c =0,即3a +c =0.当x =3时,将(3,0)代入方程也得到3a +c =0成立,当x =-3时,将(-3,0)代入方程也得到15a +c =0(与3a +c =0不相符),∴方程的两个根为x 1=-1,x 2=3.17. -4 【解析】由题意可知,x 1,x 2为方程2x 2-4x -1=0的两根,所以x 1+x 2=2,x 1x 2=-12,则1x 1+1x 2=x 1+x 2x 1x 2=2-12=-4.18. x<1或x>3 【解析】∵直线y =x +m 和抛物线y =x 2+bx +c 都经过点A(1,0)和B(3,2),∴根据图象可知,不等式x 2+bx +c >x +m 的解集为x <1或x >3.19. 1.6 秒 【解析】本题主要考查了二次函数的对称性问题.由题意可知,各自抛出后1.1秒时到达相同最大离地高度,即到达二次函数图象的顶点处,故此二次函数图象的对称轴为t =1.1;由于两次抛小球的时间间隔为1秒,所以当第一个小球和第二个小球到达相同高度时,则这两个小球必分居对称轴左右两侧,由于高度相同,则在该时间节点上,两小球对应时间到对称轴距离相同. 故该距离为0.5秒, 所以此时第一个小球抛出后t =1.1+0.5=1.6秒时与第二个小球的离地高度相同.20. 0<a ≤5 【解析】设未来30天每天获得的利润为y ,y =(110-40-t)(20+4t)-(20+4t)a 化简,得y =-4t 2+(260-4a)t +1400-20a ,每天缴纳电商平台推广费用后的利润随天数t(t 为整数)的增大而增大,则-(260-4a )2×(-4)≥30,解得a ≤5,又∵a >0,∴a 的取值范围是0<a ≤5.21. 解:(1)由题意知,抛物线y =ax 2+bx(a ≠0)经过点B(12,34),C(32,34),则⎩⎨⎧14a +12b =3494a +32b =34,解得⎩⎪⎨⎪⎧a =-1b =2,∴抛物线的解析式是y =-x 2+2x.(3分) 根据对称性知,抛物线的对称轴是x =-b2a =1,当x =1时,y =1, ∴顶点坐标是(1,1).答:图案最高点到地面的距离是1 m .(5分) (2)∵抛物线的对称轴是x =1,∴一个图案与地面两交点间的距离是2 m ,10÷2=5. 答:最多可以连续绘制5个这样的抛物线型图案.(8分)22. 解:(1)平均每棵树结的橙子个数y(个)与x 之间的关系为:y =600-5x(0≤x ≤120).(3分)(2)设果园多种x 棵橙子树时,可使橙子的总产量为w ,(4分) 则w =(600-5x)(100+x) =-5x 2+100x +60000 =-5(x -10)2+60500.(7分)答:果园多种10棵橙子树时,可使橙子的总产量最大,最大为60500个.(8分) 23. 解:(1)y =-12x +160,120≤x ≤180.(3分)(2)设销售利润为W 元,则W =y(x -80)=(-12x +160)(x -80),(4分)即W =-12x 2+200x -12800=-12(x -200)2+7200.(5分)∵-12<0,∴当x <200时,W 随x 的增大而增大, 又120≤x ≤180,∴当x =180时,W 取最大值, 此时,W =-12(180-200)2+7200=7000.答:当销售单价为180元时,销售利润最大,最大利润是7000元.(8分) 24. 解:(1)把B(3,0)代入抛物线解析式,得0=-32+3m +3, 解得m =2,(2分)∴y =-x 2+2x +3,∵y =-x 2+2x +3=-(x -1)2+4,∴顶点坐标为(1,4).(4分)第24题解图(2)如解图,连接BC 交抛物线对称轴l 于点P ,连接AP ,此时PA +PC 的值最小.(6分) 由抛物线y =-x 2+2x +3得点C 的坐标为(0,3), 设直线 BC 的解析式为y =kx +b(k ≠0), 把点B(3,0),C(0,3)的坐标代入,得⎩⎪⎨⎪⎧0=3k +b 3=b , ∴⎩⎪⎨⎪⎧k =-1b =3, ∴直线BC 的解析式为y =-x +3.(8分) 当x =1时,y =-1+3=2.∴当PA +PC 的值最小时,点P 的坐标为(1,2).(10分)25.【思路分析】①建立坐标系时应使正方形内抛物线上点的坐标是正数,以点O 为坐标原点建立平面直角坐标系,即可表示出O 、P 、A 三点的坐标;②用待定系数法即可求得抛物线的解析式.解:如解图,以OA 所在的直线为横轴,水平向右为正方向,以OC 所在直线为纵轴,垂直向上为正方向,建立平面直角坐标系.第25题解图①O(0,0),P(2,2),A(4,0);(3分)②设抛物线L 的解析式为y =ax 2+bx +c ,将点O ,P ,A 的坐标分别代入y =ax 2+bx +c ,得 ⎩⎪⎨⎪⎧c =04a +2b +c =216a +4b +c =0, 解得⎩⎪⎨⎪⎧a =-12b =2c =0,∴抛物线L 的解析式为y =-12x 2+2x.(6分)(2)【思路分析】用点E 的横坐标表示△OAE 与△OCE 的面积之和,根据二次函数的性质即可确定最大值.解:设点E 的横坐标为m.∵点E 在正方形内的抛物线上,∴点E 的纵坐标为-12m 2+2m,∴S △OAE +S △OCE =12×4×(-12m 2+2m)+12×4×m =-m 2+6m =-(m -3)2+9.(10分)∴当m =3时,△OAE 与△OCE 的面积之和的值最大,最大值是9.(12分) 26. 解:(1)y =ax 2-2ax +c第26题解图=a(x 2-2x)+c =a(x -1)2+c -a ∴P 点坐标为(1,c -a).(2分)如解图,过点C 作CE ⊥PQ ,垂足为E ,延长CE 交BD 于点F ,则CF ⊥BD. ∵P(1,c -a), ∴CE =OQ =1. ∵PQ ∥BD ,∴△CEP ∽△CFD , ∴CP CD =CE CF. 又∵CP ∶PD =2∶3, ∴CE CF =CP CD =22+3=25, ∴CF =2.5,(4分)∴OB =CF =2.5,∴BQ =OB -OQ =1.5, ∴AQ =BQ =1.5,∴OA =AQ -OQ =1.5-1=0.5, ∴A(-0.5,0),B(2.5,0).(5分) (2)∵tan ∠PDB =54,∴CF DF =54, ∴DF =45CF =45×2.5=2,(6分)∵△CFD ∽△CEP ,∴PE DF =CE CF, ∴PE =DF·CE CF =2×12.5=0.8.∵P(1,c -a),C(0,c),∴PE =PQ -OC =c -(c -a)=a , ∴a =0.8,(8分)∴y =0.8x 2-1.6x +c.把A(-0.5,0)代入得:0.8×(-0.5)2-1.6×(-0.5)+c =0, 解得c =-1.(9分)∴这个二次函数的关系式为:y =0.8x 2-1.6x -1.(10分)。
2020年中考数学压轴专题:函数的图象与性质专题(含答案)

2020中考数学 压轴专题 函数的图象与性质专题(含答案)1. 如图,在平面直角坐标系中,一次函数y =mx +5(m ≠0)的图象与反比例函数y =足为点M .(1)求一次函数和反比例函数的表达式;(2)求△OAM 的面积S ;(3)在y 轴上求一点P ,使PA +PB 的值最小并求出此时点P 的坐标.第1题图将B (4,1)代入y =mx +5得:1=4m +5,△m =-1,△y =-x +5;(3)如解图,作点A 关于y 轴的对称点N ,则N (-1,4).连接BN 交y 轴于点P ,点P 即为所求.设直线BN的关系式为y=kx+b,第1题解图第2题图△A(4,0),令x=0,则y=3,△等腰Rt△ABC中,△BAC=90°,(2)△如解图,连接PO,△P(a,1),△△S△ABP=S△ABC,第2题解图3.如图△,在直角坐标系中,点A的坐标为(0,12),经过原点的直线l1与经过点A的直线l2相交于点B(m,n).(1)若m=9,n=3,求直线l1和l2的解析式;(2)将△BAO绕点B顺时针旋转180°得△BFE,如图△,连接AE,OF.△证明:四边形OFEA是平行四边形;△若四边形OFEA是正方形,求m和n的值.第3题解图4.如图,在△ABC中,点A(4,0),点B在x轴上,点C在第四象限且横坐标为2,直线l1:y=-3x+3经过点B,C;直线l2经过点C,与x轴交于点P(点P在点B 右侧),设点P的横坐标为m.(2)若P是AB的中点,求m的值;(3)当S△PBC=3时,求直线l2的解析式.第4题图解:(1)(1,0),(2,-3);【解法提示】△y=-3x+3经过点B,C,点B在x轴上,点C横坐标为2,△B(1,0),C(2,-3).(2)△P 是AB 中点,(3)△S△PBC =3,△PB =2,△P (3,0),设直线l 2的解析式为y =kx +b ,则有3=02=3k b k b ++-⎧⎨⎩, 解得=3=9k b -⎧⎨⎩,△直线l 2的解析式为y =3x -9.5. 如图,在平面直角坐标系中,点A 的坐标为(4,0),点B 的坐标为(0,4),点M 是线段AB 上任意一点(A ,B 两点除外).(1)求直线AB 的解析式;(2)过点M 分别作MC △OA 于点C ,MD △OB 于点D ,当点M 在AB 上运动时,你认为四边形OCMD 的周长是否发生变化?并说明理由;(3)当点M 把线段AB 分成的两部分的比为1:3时,请求出点M 的坐标.第5题图解:(1)设直线AB 的解析式为y=kx +b ,由题意可得4=0=4k bb+⎧⎨⎩,解得=1=4kb-⎧⎨⎩,△AB的解析式为y=-x+4;(2)不发生变化.理由:设M点的坐标为(x,-x+4),则MD=|x|=x,MC=|-x+4|=-x+4,△四边形OCMD的周长=2(MD+MC)=2[x+(-x+4)]=8,△四边形OCMD的周长不发生变化;(3)△DM△x轴,则点M的横坐标为1,此时纵坐标=-x+4=-1+4=3,△M(1,3);则点M的横坐标为3,此时纵坐标=-x+4=-3+4=1,△M(3,1),综上可知,点M的坐标为(1,3)或(3,1).6.如图,已知一次函数y=2x-4的图象与x轴、y轴分别相交于点A、B,点P在该函数的图象上,P到x轴、y轴的距离分别为d1、d2.(1)当P为线段AB的中点时,求d1+d2的值;(2)直接写出d1+d2的范围,并求当d1+d2=3时点P的坐标;(3)若在线段AB上存在无数个P点,使d1+ad2=4(a为常数),求a的值.解:(1)对于一次函数y=2x-4,令x=0,得到y=-4;令y=0,得到x=2,△A(2,0),B(0,-4),△P为AB的中点,△P(1,-2),△d1+d2=3;(2)d1+d2≥2;设P(m,2m-4),△d1+d2=|m|+|2m-4|,当0≤m≤2时,d1+d2=m+4-2m=4-m=3,解得m=1,此时P1(1,-2);当m>2时,d1+d2=m+2m-4=3,当m<0时,不存在,(3)设P(m,2m-4),△d1=|2m-4|,d2=|m|,△P在线段AB上,△0≤m≤2,△d1=4-2m,d2=m,△d1+ad2=4,△4-2m+am=4,即(a-2)m=0,△有无数个点,△a=2.7.M,N,高为3的等边三角形ABC,边BC在x轴上,将此三角形沿着x轴的正方向平移,在平移过程中,得到△A1B1C1,当点B1与原点重合时,解答下列问题:(1)求出点A1的坐标,并判断点A1是否在直线l上;(2)求出边A1C1所在直线的解析式;(3)在坐标平面内找一点P,使得以P、A1、C1、M为顶点的四边形是平行四边形,求出P点的坐标.第7题图解:(1)如解图,作A1H△x轴于H.在Rt△A1OH中,△A1H=3,△A1OH=60°,由解图可知,当以P、A1、C1、M为顶点的四边形是平行四边形时,P1 (3第7题解图8.如图,在平面直角坐标系xoy中,平行四边形ABCO的顶点A,B的坐标分别是A(3,0),B(0,2).(1)求点C的坐标及直线AB的解析式;(2)动点P在直线23y x=上运动.△当PB=PC时,求出P点的坐标;△将直线23y x=怎样平移,能将平行四边形ABCO的面积平分?并求出此时它与直线AB交点Q的坐标;(3)在x轴上是否存在两点M、N(M在N左侧),使MN=1,且CM+MN+BN的值最小?若存在,求出M、N两点的坐标,并求出这个最小值;若不存在,请说明理由.第8题图解:(1)△四边形ABCO是平行四边形,△CB△OA,CB=OA=3,△点C的坐标为(-3,2),设直线AB的解析式为y=kx+b,代入A(3,0),B(0,2)得032k bb=+⎧⎨=⎩,解得232kb⎧=-⎪⎨⎪=⎩,△223y x=-+;(2)△当PB=PC时,P点在BC的垂直平分线上,即直线x=-32上,又△点P在直线23y x=上,△23()132y=⨯-=-,△P点的坐标为(-32,-1);△若将平行四边形ABCO的面积平分,则直线必过平行四边形ABCO对角线的交点,即过点(0,1),△将直线23y x=向上平移1个单位即可,此时直线的解析式为213y x=+,联立方程组223213y xy x⎧=-+⎪⎪⎨⎪=+⎪⎩,解得3432xy⎧=⎪⎪⎨⎪=⎪⎩,△它与直线AB 的交点Q 的坐标为(34,32); (3)存在.如解图,将点 C 向右平移1个单位长度得C ',作C '关于x 轴的对称点C '',连接C ''B ,交 x 轴于点 N ,将 N 点向左平移1个单位得M ,M 、N 即为所求作的点. 由题意可知,点C '(-2,2),△以点C '关于x 轴的对称点C ''(-2,-2),设直线C ''B 的解析式为y kx b =+,代入C ''(-2,-2),B (0,2)得222k bb -=-+⎧⎨=⎩,解得22k b =⎧⎨=⎩ , △22yx =+,△点 N 的坐标为(-1,0),点 M 的坐标为(-2,0), △CM +MN +BN 的最小值即为C ''B +MN1+=1+.第8题解图9. 如图,在平面直角坐标系中,O 为坐标原点,直角三角形OBD 的直角顶点D 在(1)求图象经过点B 的反比例函数的解析式;(2)点E 是(1)中反比例函数图象上一点,连接BE 、DE ,若BE =DE ,求四边形OBED 的面积.第9题图△BD =2OD ,△OD =2,BD =4,△B (2,4),(2)如解图,作EF △BD 于点F ,由BD △x 轴, △△EFD =△ODF ,△EF △x 轴, △BE =DE ,EF △BD 于点F ,△x =4,△E (4,2),EF =2,第9题解图10.于点B,平行于x轴的直线y=n(0<n<6)交反比例函数的图象于点M,交AB于点N,连接BM.(1)求m的值和反比例函数的表达式;(2)直线y=n沿y轴方向平移,当n为何值时,△BMN的面积最大?第10题图解:(1)△直线y=2x+6经过点A(1,m),△m=2×1+6=8,△A(1,8),△k=8,△n=3时,△BMN的面积最大.11.点,且A点的橫坐标为1.(1)求一次函数的函数表达式;(2)当y1>y2时,求x的取值范围;(3)已知反比例函数在第一象限的图象上有一点C橫坐标为3,求△ABC的面积.第11题图将点A(1,6)代入y1=x+m,得:1+m=6,解得m=5,则一次函数解析式为y1=x+5;则点A (1,6)、点B (-6,-1),由图象可知y 1>y 2时-6<x <0或x >1;则点C (3,2),如解图,连接AC ,BC ,则AD =2、CD =4、BE =9、CE =3,第11题解图12. B (m ,n )(m >1),过点B 作y 轴的垂线,垂足为点C . (1)求该反比例函数解析式;(2)当△ABC 面积为2时,求点B 的坐标;(3)P 为线段AB 上一动点(P 不与A 、B 重合),在(2)的情况下,直线y =ax -1与线段AB 交于点P ,直接写出a 的取值范围.第12题图△k=1×2=2,△mn=2,(3)将A(1,2)代入y=ax-1中,2=a-1,解得a=3;△直线y=ax-1与线段AB交于点P,P为线段AB上一动点(P不与点A、B重合),第13题图解:(1)根据题意得点B的横坐标为0,点A的纵坐标为0,△B(0,6),A(-8,0),△OA=8,OB=6,△CB平分△ABO,CD△AB,CO△BO,△CD=CO,△BC=BC,△Rt△BCD△Rt△BCO,△BD=BO=6,△AD=AB-BD=4,△△ADC=△AOB=90°,△CAD=△BAO,△△ACD△△ABO,△AC=5,△OC=OA-AC=3,△C(-3,0),△△EDB=△AOB=90°,BD=BO,△EBD=△ABO,△△EBD△△ABO,△BE=AB=10,△OE=BE-OB=4,△E(0,-4),设直线CE的解析式为y=kx-4,△-3k-4=0,解得(2)存在.第13题解图。
2020届中考数学冲刺复习专题:反比例函数(含答案)

2020届中考数学冲刺复习专题:反比例函数1.如图,已知反比例函数y 1=的图象与一次函数y 2=k 2x +b 的图象在第一象限交于A (1,3),B (3,m )两点,一次函数的图象与x 轴交于点C . (1)求反比例函数和一次函数的表达式; (2)当x 为何值时,y 2>0?(3)已知点P (0,a )(a >0),过点P 作x 轴的平行线,在第一象限内交一次函数y 2=k 2x +b 的图象于点M ,交反比例函数y 1=的图象于点N .结合函数图象直接写出当PM >PN 时a 的取值范围.2.如图,过原点的直线y 1=mx (m ≠0)与反比例函数y 2=(k <0)的图象交于A 、B 两点,点A 在第二象限,且点A 的横坐标为﹣1,点D 在x 轴负半轴上,连接AD 交反比例函数图象于另一点E ,AC 为∠BAD 的平分线,过点B 作AC 的垂线,垂足为C ,连接CE ,若AD =2DE ,△AEC 的面积为.(1)根据图象回答:当x 取何值时,y 1<y 2; (2)求△AOD 的面积;(3)若点P 的坐标为(m ,k ),在y 轴的轴上是否存在一点M ,使得△OMP 是直角三角形,若存在,请直接写出点M 的坐标;若不存在,请说明理由.3.定义:若实数x ,y ,x ',y '满足x =kx '+2,y =ky '+2(k 为常数,k ≠0),则在平面直角坐标系xOy中,称点(x,y)为点(x',y')的“k值关联点”.例如,点(3,0)是点(1,﹣2)的“1值关联点”.(1)在A(2,3),B(1,3)两点中,点是P(1,﹣1)的“k值关联点”;(2)若点C(8,5)是双曲线y=(t≠0)上点D的“3值关联点”,求t的值和点D的坐标;(3)设两个不相等的非零实数m,n满足点E(m2+mn,2n2)是点F(m,n)的“k值关联点”,求点F到原点O的距离的最小值.4.如图,直线y=ax+2与x轴、y轴分别相交于A,B两点,与双曲线y=(x>0)相交于点P,PC⊥x轴于点C,且PC=4,点A的坐标为(﹣4,0).(1)求双曲线的解析式;(2)若点Q为双曲线上点P右侧的一点,过点Q作QH⊥x轴于点H,当以点Q,C,H为顶点的三角形与△AOB相似时,求点Q的坐标.5.如图(1),正方形ABCD顶点A、B在函数y=(k>0)的图象上,点C、D分别在x轴、y轴的正半轴上,当k的值改变时,正方形ABCD的大小也随之改变.(1)若点A的横坐标为5,求点D的纵坐标;(2)如图(2),当k=8时,分别求出正方形A′B′C′D′的顶点A′、B′两点的坐标;(3)当变化的正方形ABCD与(2)中的正方形A′B′C′D′有重叠部分时,求k的取值范围.6.如图,四边形ABCD是平行四边形,点A(1,0),B(4,1),C(4,4).反比例函数y=(x>0)的图象经过点D,点P是一次函数y=kx+4﹣4k(k≠0)的图象与该反比例函数图象的一个公共点.(1)求反比例函数的解析式;(2)通过计算,说明一次函数y=kx+4﹣4k(k≠0)的图象一定过点C;(3)对于一次函数y=kx+4﹣4k(k≠0),当随x的增大而增大时,确定点P横坐标的取值范围(不必写过程).7.如图①,M,N为矩形ABCD一组邻边AD,CD上两点,若==m,则称M,N为邻边AD,CD上的一对共轭点,m为这两点的共轭系数.如图②,在平面直角坐标系中,反比例函数y=(x>0)的图象与矩形OABC的一组邻边分别交于点M,N.(1)求证:M,N为BC,BA上的一对共轭点;=8.求M,N的共轭系数;(2)若M(1,4),S四边形ONBM(3)若B(8,6),把△BMN沿MN翻折得△B′MN,当B′在ON上时,求M,N的共轭系数.8.如图,点A,B分别在x轴,y轴上,过A,B作AB垂线,交反比例函数y=(k>0,x >0)的图象于D,C,四边形ABCD为矩形,CF⊥y轴于F,DE⊥x轴于E,CF=a,BF=b,OA=x,OB=y.(1)求证:AE=a.(2)请写出两个不同的关于a,b,x,y的关系式.(3)求证:∠OAB=45°.9.正方形ABCD的顶点A(1,1),点C(3,3),反比例函数y=(x>0).(1)如图1,双曲线经过点D时求反比例函数y=(x>0)的关系式;(2)如图2,正方形ABCD向下平移得到正方形A′B′C′D′,边A'B'在x轴上,反比例函数y=(x>0)的图象分别交正方形A′B′C′D′的边C'D′、边B′C′于点F、E,①求△A'EF的面积;②如图3,x轴上一点P,是否存在△PEF是等腰三角形,若存在直接写出点P坐标,若不存在明理由.10.如图,在平面直角坐标系中,一次函数y=kx+b(k≠0)与反比例函数y=(m≠0)的图象相交于A(2,4),B(n,﹣2)两点.(1)求一次函数和反比例函数的表达式;(2)点C是第一象限内反比例函数图象上的一点,且点C在A的右侧,过点C作CD平行于y轴交直线AB于点D,若以C为圆心,CD长为半径的⊙C恰好与y轴相切,求点C 的坐标.11.如图,如图,一次函数y=﹣x+b与反比例函数的图象交于点A(m,1)和B(1,﹣3).(1)填空:一次函数的解析式为,反比例函数的解析式为;(2)点P是x轴正半轴上一点,连接AP,BP.当△ABP是直角三角形时,求出点P的坐标.12.在平面直角坐标系中,我们定义:横坐标与纵坐标均为整数的点为整点.如图,已知双曲线y=(x>0)经过点A(2,2),记双曲线与两坐标轴之间的部分为G(不含双曲线与坐标轴).(1)求k的值;(2)求G内整点的个数;(3)设点B(m,n)(m>3)在直线y=2x﹣4上,过点B分别作平行于x轴y轴的直线,交双曲线y=(x>0)于点C、D,记线段BC、BD、双曲线所围成的区域为W,若W内部(不包括边界)不超过8个整点,求m的取值范围.13.如图,一次函数y=kx+b与反比例函数y=的图象在第一象限交于点A(4,3),与y轴的负半轴交于点B,且OA=OB.(1)求一次函数y=kx+b和y=的表达式;(2)在x轴上是否存在一点C,使得△ABC是以AB为腰的等腰三角形,若存在,求出点C的坐标;若不存在,请说明理由.(3)反比例函数y=(1≤x≤4)的图象记为曲线C1,将C1向右平移3个单位长度,得曲线C2,则C1平移至C2处所扫过的面积是(直接写出答案).14.如图,已知直线y=2x+2与x轴交于点A,与y轴交于点C,矩形ACBE的顶点B在第一象限的反比例函数y=图象上,过点B作BF⊥OC,垂足为F,设OF=t.(1)求∠ACO的正切值;(2)求点B的坐标(用含t的式子表示);(3)已知直线y=2x+2与反比例函数y=图象都经过第一象限的点D,联结DE,如果DE⊥x轴,求m的值.15.如图1,平面直角坐标系xOy中,A(﹣4,3),反比例函数y=(k<0)的图象分别交矩形ABOC的两边AC,BC于E,F(E,F不与A重合),沿着EF将矩形ABOC折叠使A,D 重合.(1)①如图2,当点D 恰好在矩形ABOC 的对角线BC 上时,求CE 的长; ②若折叠后点D 落在矩形ABOC 内(不包括边界),求线段CE 长度的取值范围. (2)若折叠后,△ABD 是等腰三角形,请直接写出此时点D 的坐标.16.如图是反比例函数的图象,点A (a ,b ),C (c ,d )分别在图象的两支上,以AC为对角线作矩形ABCD 且AB ∥x 轴.(1)当线段AC 过原点时,分别写出a 与c ,b 与d 的一个等量关系式; (2)当A 、C 两点在直线y =x +2上时,求矩形ABCD 的周长; (3)当AB =BC 时,探究a 与c 的数量关系.17.如图,一次函数y 1=k 1x +4与反比例函数y 2=的图象交于点A (2,m )和B (﹣6,﹣2),与y 轴交于点C .(1)k 1= ,k 2= ; (2)根据函数图象知,①当y 1>y 2时,x 的取值范围是 ; ②当x 为 时,y 2>﹣2x .(3)过点A 作AD ⊥x 轴于点D ,点P 是反比例函数在第一象限的图象上一点,设直线OP 与线段AD 交于点E ,当S 四边形ODAC :S △ODE =4:1时,求点P 的坐标.(4)点M 是y 轴上的一个动点,当△MBC 为直角三角形时,直接写出点M 的坐标.18.如图1,在平面直角坐标系中,放置有一个Rt △ABC ,顶点A 与原点O 重合,边AC 与x 轴重合,∠ACB =90°,AC =BC =4,反比例函数y =的图象分别与AB 和BC 交于点D 、E ,且此时点D 恰为AB 的中点.(1)求反比例函数的表达式及点E 的坐标;(2)连接DE ,在x 轴上存在一点P ,可使得△DEP 成为以DE 为腰的等腰三角形,试求出所有符合条件的点P 的坐标;(3)如图2,保持反比例函数图象不变,将△ABC 沿x 轴向左平移,使得点E 成为BC 的中点,求此时点D 的坐标.19.如图,反比例函数y =(x >0)过点A (3,4),直线AC 与x 轴交于点C (6,0),交y 轴于点E ,过点C 作x 轴的垂线BC 交反比例函数图象于点B .(1)求k的值与B点的坐标;(2)将直线EC向右平移,当点E正好落在反比例函数图象上的点E'时,直线交x轴于点F.请判断点B是否在直线EF上并说明理由;(3)在平面内有点M,使得以A、B、F、M四点为顶点的四边形为平行四边形,请直接写出符合条件的所有M点的坐标.20.已知直线y=2x+b与反比例函数y=的(k>0)图象交于点A,过点A作AB⊥x轴于点B,点D为线段AC的中点,BD交y轴于点E,(1)若k=8,且点A的横坐标为1,求b的值;(2)已知△BEC的面积为4,则k的值为多少?(3)若将直线旋转,k=8,点E为△ABC的重心且OE=2,求直线AC的解析式.参考答案1.解:(1)∵反比例函数的图象过点A(1,3),∴,∴k1=3,∴反比例函数表达式为:;∵点B(3,m)在函数的图象上,∴,∴B(3,1).∵一次函数y2=k2x+b的图象过点A(1,3),B(3,1),∴,解得,∴一次函数的表达式为:y2=﹣x+4;∴反比例函数和一次函数的表达式分别为,y2=﹣x+4.(2)∵当y2=0时,﹣x+4=0,x=4,∴C(4,0),由图象可知,当x<4时,y2>0.(3)如图,由图象可得,当1<a<3时,PM>PN.2.解:(1)∵直线y1=mx(m≠0)与反比例函数y2=(k<0)的图象交于A、B两点,且点A的横坐标为﹣1,∴点A,点B关于原点对称,∴点B的横坐标为1,∴当x取﹣1<x<0或x>1时,y1<y2;(2)连接OC,OE,由图象知,点A,点B关于原点对称,∴OA=OB,∵AC⊥CB,∴∠ACB=90°,∴OC=AB=AO,∴∠OAC=∠OCA,∵AC为∠BAD的平分线,∴∠OAC=∠DAC,∴∠OCA=∠DAC,∴AD∥OC,∴S△AEO =S△ACE=,∵AD=2DE,∴AE=DE,∴S△AOD =2S△AOE=3;(3)作EF⊥x轴于F,作AH⊥x轴于H,则EF∥AH,∵AD=2DE,∴DE=EA,∵EF∥AH,∴==1,∴DF=FH,∴EF是△DHA的中位线,∴EF=AH,∵S△OEF =S△OAH=﹣,∴OF•EF=OH•HA,∴OH=OF,∴OH=HF,∴DF=FH=HO=DO,∴S△OAH =S△ADO=3=1,∴﹣=1,∴k=﹣2,∴y=﹣,∵点A在y=﹣的图象上,∴把x=﹣1代入得,y=2,∴A(﹣1,2),∵点A在直线y=mx上,∴m=﹣2,∴P(﹣2,﹣2),在y轴上找到一点M,使得△OMP是直角三角形,当∠OMP=90°时,PM⊥y轴,则OM=2,∴点M的坐标为(0.﹣2);当∠OPM=90°时,过P作PG⊥y轴于G,则△OPM是等腰直角三角形,∴OM=2PG=4,∴点M的坐标为(0.﹣4);综上所述,点M的坐标为(0.﹣2)或(0,﹣4).3.解:(1)若点A(2,3)是P(1,﹣1)的“k值关联点”,∴k=≠,不合题意,若点B(1,3)是P(1,﹣1)的“k值关联点”,∴k===﹣1,符合题意,故答案为:B;(2)设点D坐标为(x,y),∵点C(8,5)是点D的“3值关联点”,∴∴∴点D坐标为(2,1),∵点D是双曲线y=(t≠0)上点,∴t=2×1=2;(3)∵点E(m2+mn,2n2)是点F(m,n)的“k值关联点”,∴,∴m2n+mn2﹣2n=2n2m﹣2m,∴(m﹣n)(mn+2)=0,∵m≠n,∴mn=﹣2,∴m=,∵(m﹣n)2≥0,∴m2+n2﹣2mn≥0,∴m2+n2≥2mn,∴m2+n2=+n2≥2×n×=4,∴点F到原点O的距离==,∴点F到原点O的距离的最小值为2.4.解:(1)把A(﹣4,0)代入y=ax+2,得,﹣4a +2=0,解得a =, 故直线AB 的解析式为y =x +2, 把y =4代入y =x +2,得,x +2=4, 解得x =4, ∴点P (4,4).把P (4,4)代入y =,得k =16, 故双曲线的解析式为y =;(2)把x =0代入y =x +2,得y =2, ∴点B 的坐标为(0,2), ∴OB =2, ∵A (﹣4,0), ∴OA =4, 设Q (m ,),则CH =m ﹣4,QH =,由题意可知∠AOB =∠QHC =90°, 当△AOB ∼△QHC 时,,即,解得:m 1=2+2,m 2=2﹣2(不合题意,舍去), ∴点Q 的坐标为(2+2,4﹣4),当△BOA ∼△QHC 时,,即,解得m 1=8,m 2=﹣4(不合题意,舍去), ∴点Q 的坐标为(8,2). 综上可知,点Q 的坐标为(2+2,4﹣4)或(8,2).5.解:(1)如图,过点A 作AE ⊥y 轴于点E ,则∠AED =90°.∵四边形ABCD为正方形,∴AD=DC,∠ADC=90°,∴∠ODC+∠EDA=90°.∵∠ODC+∠OCD=90°,∴∠EDA=∠OCD,在△AED和△DOC中,∴△AED≌△DOC(AAS),∴OD=EA=5,∴点D的纵坐标为5;(2)作A′M⊥y轴于M,B′N⊥x轴于点N,设OD′=a,OC′=b,同理可得△B′C′N≌△C′D′O≌△A′D′E,∴C′N=OD′=A′M=a,B′N=C′O=D′M=b,∴A′(a,a+b),B′(a+b,b),∵点A′、B′在反比例函数y=的图象上,∴a(a+b)=8,b(a+b)=8,∴解得a=b=2或a=b=﹣2(舍去),∴A′、B′两点的坐标分别为(2,4),(4,2);(3)设直线A′B′的解析式为y=mx+n,把A′(2,4),B′(4,2)代入得,解得,∴直线A′B′解析式为y=﹣x+6,同样可求得直线C′D′解析式为y=﹣x+2,由(2)可知△OCD是等腰直角三角形,设点A的坐标为(m,2m),点D坐标为(0,m),当A点在直线C′D′上时,则2m=﹣m+2,解得m=,此时点A的坐标为(,),∴k=×=;当点D在直线A′B′上时,有m=6,此时点A的坐标为(6,12),∴k=6×12=72;综上可知:当变化的正方形ABCD与(2)中的正方形A′B′C′D′有重叠部分时,k的取值范围为≤x≤72.6.解:(1)∵四边形ABCD是平行四边形,∴AD=BC,∵B(4,1),C(4,4),∴BC⊥x轴,AD=BC=3,而A点坐标为(1,0),∴点D的坐标为(1,3).∵反比例函数y=(x>0)的函数图象经过点D(1,3),∴3=,∴m=3,∴反比例函数的解析式为y=;(2)当x=4时,y=kx+4﹣4k=4k+4﹣4k=4,∴一次函数y=kx+4﹣4k(k≠0)的图象一定过点C;(3)设点P的横坐标为a,∵一次函数y=kx+4﹣4k(k≠0)过C点,并且y随x的增大而增大时,∴k>0,P点的纵坐标要小于4,横坐标大于4,当纵坐标小于4时,∵y=,∴<3,解得:a>1,则a的范围为a>1或a<4.7.解:(1)∵点M,N是反比例函数y=图象上的点,∴BC•AN=CM•AB,∴,∴,∴M,N为BC,BA上的一对共轭点;(2)如图,连接OM,ON,∵M(1,4),∴k=1×4=4,OC=4,∴反比例函数解析式为:y =, ∴S △CMO =S △OAN =2,∴S 矩形ABCO =S △CMO +S △OAN +S 四边形ONBM =12, ∵CO =4, ∴BC =3, ∴BM =BC ﹣CM =2, ∴m =;(3)如图,延长BC 至D ,使得MD =BM ,过点D 作DF ⊥x 轴于F ,交NO 的延长线于点E ,∵点B (8,6)∴AB =CO =6,BC =AO =8, ∵AN •AO =CM •CO , ∴,∴AN =CM , ∴=,设BN =3x ,BM =4x ,则DM =4x , ∵把△BMN 沿MN 翻折得△B ′MN , ∴BM =B 'M ,∠B =∠MB 'N =90°,在Rt △DME 和Rt △B 'ME 中,DM =B 'M =BM ,EM =EM , ∴Rt △DME ≌Rt △B 'ME (HL ), ∴∠DME =∠EMB ', ∴∠EMN =90°,∴∠DME +∠BMN =90°,且∠BMN +∠BNM =90°, ∴∠DME =∠MNB ,且∠B =∠D =90°,∴△DME∽△BNM,∴∴DE=x,∵∠EOF=∠AON,∠NAO=∠EFO=90°,∴△EFO∽△NAO,∴,∴∴x=0(舍去),x=,∴BN=,AN=6﹣BN=,∴m==.8.(1)证明:∵四边形ABCD为矩形,CF⊥y轴于F,DE⊥x轴于E,∴∠BFC=∠ABC=∠BAD=∠AED=90°,BC=AD,∴∠CBF+∠ABO=∠ABO+∠OAB=90°,∴∠CBF=∠OAB,∵∠BAO+∠DAE=∠DAE+∠ADE=90°,∴∠BAO=∠ADE,∴∠CBF=∠ADE,∴△BCF≌△DAE(AAS),∴AE=CF=a;(2)解:由(1)知,BF=DE=b,∵OA=x,OB=y,∴C(a,b+y),D(a+x,b),∵点D,C在反比例函数y=(k>0,x>0)的图象上,∴a(b+y)=b(a+x)=k,即ay=bx①;∵∠BFC=∠AOB=90°,∠CBF=∠BAO,∴△CBF∽△BAO,∴,∴=②;(3)解:由(2)中的①÷②得,x2=y2,∵x>0,y>0,∴x=y,∴OA=OB,∴△AOB是等腰直角三角形,∴∠OAB=45°.9.解:(1)∵点A(1,1),点C(3,3),∴点D(1,3),将点D的坐标代入反比例函数表达式得:k=3,故反比例函数表达式为:y=;(2)平移后点A′、B′、C′、D′的坐标分别为:(1,0)、(3,0),(3,2)、(1,2),则平移后点E纵坐标为3,则点E(3,1),同理点F(,2),△A'EF的面积=S正方形A′B′C′D′﹣S△A′B′E﹣S△A′D′F﹣S△EFC′=2×2×2×﹣2×1﹣××1=;(3)点E、F的坐标分别为:(3,1)、(,2),设点P(m,0),则EF2=(3﹣)2+(2﹣1)2=,EP2=(m﹣3)2+1,PF2=(m﹣)2+4,当EF=EP时,即=(m﹣3)2+1,解得:m=或;当EF=PF时,同理可得:m=;当EP=PF时,同理可得:m=,故点P的坐标为(,0)或(,0)或(,0)或(,0)或(,0).10.解:(1)∵A(2,4),B(n,﹣2)在反比例函数y=(m≠0)的图象上,∴m=2×4=8,﹣2=,∴n=﹣4,∴反比例函数的解析式为:y=;∵一次函数y=kx+b过A(2,4),B(n,﹣2),∴,∴,∴一次函数解析式为:y=x+2;(2)设点C(a,),则点D(a,a+2),∴CD=a+2﹣,∵以C为圆心,CD长为半径的⊙C恰好与y轴相切,∴a=a+2﹣∴a=4,∴点C(4,2).11.解:(1)∵点A(m,1)和B(1,﹣3)在反比例函数的图象上,∴k=1×(﹣3)=﹣3,k=m×1,∴m=﹣3,∴点A(﹣3,1),∴反比例函数解析式为:y=;∵一次函数y=﹣x+b过点B(1,﹣3),∴﹣3=﹣1+b,∴b=﹣2,∴一次函数解析式为:y=﹣x﹣2;故答案为:y=﹣x﹣2,;(2)如图1,当∠ABP=90°时,过点P作CD⊥x轴,过点A作AC⊥DC于C,过点B作BD⊥CD于D,设点P的坐标为(x,0),∴AC=x+3,CP=1,PD=3,BD=x﹣1,∵∠APB=90°,∴∠APC+∠BPD=90°,又∵∠APC+∠CAP=90°,∴∠CAP=∠BPD,又∵∠C=∠BDP=90°,∴△ACP∽△PBD,∴,∴,∴x1=﹣1,x2=﹣1﹣(舍去),∴点P(﹣1+,0);当∠ABP=90°时,∵直线y=﹣x﹣2与x轴交于点C,与y轴交于点D,∴点C(﹣2,0),点D(0,﹣2),∴OC=2,OD=2,CD=2,BC=3,∵tan∠OCD=,∴,∴CP=6,∵点C(﹣2,0),∴点P(4,0),综上所述:点P的坐标为(,0)或(4,0).12.解:(1)∵双曲线y=经过点A(2,2),∴2=解得,k=4;(2)对于双曲线y=,当x=1时,y=4,∴在直线x=1上,当0<y<4时,有整点(1,1),(1,2),(1,3)当x=2时,y=2,∴在直线x=2上,当0<y<2时,有整点(2,1);当x=3时,,∴在直线x=3上,当0<y<时,有整点(3,1);当x=4时,y=1,∴在直线x=4上,当0<y<1时,没有整点.∴G内整点的个数为5个;(3)当m=4时,点B(4,4),点C(1,4),点D(4,1),此时在区域W内(不包含边界)有(2,3)、(3,2)、(3,3)共3个整点,线段BD 上有4个整点,线段BC上有4个整点,∵点(4,4)重合,点(4,1)、(1,4)在边界上,∴当m>4时,区域W内至少有3+4+4﹣3=8个整点.当m=4.5时,点B(4.5,5),点C(,5),线段BC上有4个整点,此时区域W内整点个数为8个.当m>4.5时,区域W内部整点个数增加.∴若W内部(不包括边界)不超过8个整点,3<m≤4.5.13.解:(1)∵点A(4,3)在反比例函数y=的图象上,∴a=4×3=12,∴反比例函数的解析式为y=,由勾股定理得,OA==5,∴OB=OA=5,∴点B的坐标为(0,﹣5),把A(4,3)、B(0,﹣5),∴,解得,,∴一次函数为y=2x﹣5;(2)存在,设点C的坐标为(m,0),由勾股定理得,AB==4,AC=,BC=,当AB=AC=4时,=4,解得,m1=﹣﹣4,m2=﹣+4,∴点C的坐标为(﹣﹣4,0)或(﹣+4,0),当BC=AB=4时,=4,解得,m=,∴点C的坐标为(﹣,0)或(,0),综上所述,△ABC是以AB为腰的等腰三角形时,点C的坐标为(﹣﹣4,0)或(﹣+4,0)或(﹣,0)或(,0);(3)当x=1时,y=12,当x=4时,y=3,如图2,将C1向右平移3个单位长度,得曲线C2,则C1平移至C2处所扫过的面积=平行四边形EFNM的面积=3×(12﹣3)=27,故答案为:27.14.解:(1)∵直线y=2x+2与x轴交于点A,与y轴交于点C,∴点A(﹣1,0),点C(0,2)∴OA=1,OC=2,∴tan∠ACO==;(2)∵四边形ACBE是矩形,∴∠ACB=90°,∴∠ACO+∠BCF=90°,且∠BCF+∠CBF=90°,∴∠ACO=∠CBF,∵OF=t,∴CF=2﹣t,∵tan∠CBF=tan∠ACO=,∴BF=4﹣2t,∴点B(4﹣2t,t);(3)如图,连接DE,交x轴于H点,∵DE⊥x轴,∴∠AHE=90°,∴∠HAE+∠AEH=90°,且∠CAO+∠HAE=90°,∠CAO+∠ACO=90°,∠ACO+∠BCF=90°,∴∠AEH=∠BCF,且∠CFB=∠AHE,AE=BC,∴△BCF≌△AEH(AAS)∴AH=BF=4﹣2t,CF=HE,∵点A(﹣1,0),∴点H(3﹣2t,0),∴当x=3﹣2t时,y=2(3﹣2t)+2=8﹣4t,∴点D坐标为(3﹣2t,8﹣4t),∵点D,点B都在反比例函数y=上,∴(3﹣2t)(8﹣4t)=t(4﹣2t)∴t1=2(不合题意舍去),t2=;∴点B(,)∴m=×=.15.解:(1)①如图2中,连接AD交EF于H.∵四边形ABOC是矩形,A(﹣4,3),∴∠A=90°,OB=AC=4,AB=OC=3,∵E,F在y=时,∴可以假设E(,3),F(﹣4,),∴AE=4+,AF=3+,∴AE:AF=4:3,∵AC:BC=4:3,∴=,∵∠EAF=∠CAB,∴△EAF∽△CAB,∴∠AEF=∠ACB,∴EF∥BC,∵A,D关于EF对称,点D落在BC上,∴EF垂直平分线段AD,∴AH=DH,∵EF∥BC,∴=,∴AE=EC=2.②如图3中,当点D落在OB上时,连接AD交EF于H.∵∠EAF=∠ABD=90°,∠AEF=∠BAD,∴△AEF∽△BAD,∴=,则==,∴BD=AB÷=,设AF=x,则FB=3﹣x,FD=AF=x在Rt△BDF中,∵FB2+BD2=DF2,∴(3﹣x)2+()2=x2,解得x=,∴AF=,∴AE=AF=,∴EC=4﹣AE=4﹣=,∴<CE<4时,折叠后点D落在矩形ABOC内(不包括边界),线段CE长度的取值范围为:<CE<4.(2)∵△ABD是等腰三角形,F与B不重合,∴AB≠BD.①如图4中,当AD=BD时,∠BAD=∠ABD,由(1)可知∠BAD=∠AEF,∴∠ABD=∠AEF.作DM∥OB交AB于M,交OC于N.则DM⊥AB,MN=AC=4,∴∠BMD=∠EAF=90°,BM=AB=,∴△AEF∽△ABD,∴=,则==,∴MD=BM÷=,∴DN=MN﹣MD=4﹣=,∴D(﹣,).②如图5中,当AD=AB时,作DM∥OB交AB于M,交OC于N.则DM⊥AB,MN=AC=4,∴∠AMD=∠EAF=90°,由(1)可得∠BAD=∠AEF,∴△AEF∽△MAD,∴=,则==,设AM=4a,则MD=3a,在Rt△MAD中,∵AM2+DM2=AD2,∴(4a )2+(3a )2=32, ∴a =, ∴AM =,MD =,∴BM =AB =AM =3﹣=,DN =MN ﹣MD =4﹣=,∴D (﹣,).综上所述,满足条件的点D 的坐标为(﹣,)或(﹣,).16.解:(1)当线段AC 过原点时,点A 、C 中点为:(0,0), 故(a +c )=0,(b +d )=0, 即:a +c =0,b +d =0;(2)由题意得:,解之得,.∴A (1,3),C (﹣3,﹣1).∴AB =1﹣(﹣3)=4,BC =3﹣(﹣1)=4,4×4=16. 答:矩形ABCD 的周长为16.(3)∵点A (a ,b )、C (c ,d )均在的图象上,∴,.∵AB =BC , ∴. ∴ac =﹣3.答:a 与c 的数量关系是ac =﹣3.17.解:(1)将点B (﹣6,﹣2)代入y 1=k 1x +4, ﹣2=﹣6k 1+4,解得:k 1=1; 将点B (﹣6,﹣2)代入y 2=①,﹣2=,解得:k 2=12.故答案为:1;12.(2)①观察函数图象可知:当﹣6<x <0或x >2时,一次函数图象在反比例函数图象上方,∴当y 1>y 2时,x 的取值范围是﹣6<x <0或x >2. 故答案为:﹣6<x <0或x >2.②过点O 作直线l :y =﹣2x ,如图1所示.观察图形可知:x >0时,反比例函数图象在直线l 上方, 故答案为:x >0.(3)依照题意,画出图形,如图2所示.当x =2时,m =x +4=6, ∴点A 的坐标为(2,6); 当x =0时,y 1=x +4=4, ∴点C 的坐标为(0,4).∵S 四边形ODAC =(OC +AD )•OD =×(4+6)×2=10,S 四边形ODAC :S △ODE =4:1, ∴S △ODE =OD •DE =×2DE =10×, ∴DE =2.5,即点E 的坐标为(2,2.5). 设直线OP 的解析式为y =kx , 将点E (2,2.5)代入y =kx ,得 2.5=2k ,解得:k =, ∴直线OP 的解析式为y =x ②.联立①②并解得:,,∵点P 在第一象限, ∴点P 的坐标为(,).(4)依照题意画出图形,如图3所示.当∠CMB =90°时,BM ∥x 轴, ∴点M 的坐标为(0,﹣2); 当∠CBM =90°时,∵直线AC 的解析式为y =x +4, ∴∠BCM =45°,∴△BCM 为等腰直角三角形,∴CM=﹣2x B=12,∴点M的坐标为(0,﹣8).综上所述:当△MBC为直角三角形时,点M的坐标为(0,﹣2)或(0,﹣8).18.解:(1)∵∠ACB=90°,AC=BC=4,∴点B、C的坐标分别为:(4,4)、(4,0),∵D为AB的中点,故点D(2,2),将点D的坐标代入反比例函数表达式得:2=,解得:k=4,故反比例函数表达式为:y=①,设点E(4,m),将点E的坐标代入上式并解得:m=1,故点E(4,1);(2)设点P(m,0),而点D、E的坐标分别为:(2,2)、(4,1),DE2=(4﹣2)2+(2﹣1)2=5,PD2=(m﹣2)2+4;PE2=(m﹣4)2+1,当DE=PD时,则5=(m﹣2)2+4,解得:m=1或3;当DE=PE时,同理可得:m=2或6(舍去6);故点P的坐标为:(1,0)或(2,0)或(3,0);(3)设三角形ABC向左平移了m个单位,则点C、B的坐标分别为:(4﹣m,0)、(4﹣m,4),∵点E为BC的中点,∴点E(4﹣m,2),将点E的坐标代入反比例函数表达式得:2=,解得:m=2,故点C、B的坐标分别为:(2,0)、(2,4),点A(﹣2,0),设直线AB的表达式为:y=sx+t,则,解得:,故直线AB的表达式为:y=x+2②,联立①②并解得:或(舍去);故点D的坐标为:(﹣1,+1).19.解:(1)把点A(3,4)代入y=(x>0),得k=xy=3×4=12,故该反比例函数解析式为:y=.∵点C(6,0),BC⊥x轴,∴把x=6代入反比例函数y=,得:y==2,∴B(6,2).综上所述,k的值是12,B点的坐标是(6,2);(2)设直线A、C的表达式为:y=kx+b,则,解得:,故直线AC的表达式为:y=﹣x+8,令x=0,则y=8,故点E(0,8),设直线EC向右平移m个单位,则平移后直线的表达式为:y=﹣(x﹣m)+8,则点E′(m,8),∵点E′在反比例函数上,∴将点E′坐标代入反比例函数表达式得:8m=12,解得:m=,则平移后直线的表达式为:y=﹣(x﹣)+8=﹣x+10,令y=0,则x=,故点F(,0);当x=6时,y=﹣x+10=2,故点B在直线EF上;(3)设点M的坐标为(s,t),而点A、B、F的坐标分别为:(3,4)、(6,2)、(,0);①当AB是边时,点A向右平移3个单位向下平移2个单位得到B,同样点M(N)向右平移3个单位向下平移2个单位得到N(M),故或,解得:或,故点M的坐标为:(,﹣2)或(,2);②当AB是对角线时,由中点公式得:,解得:,故点M的坐标为(,6);综上,点M的坐标为:(,﹣2)或(,2)或(,6).20.解:(1)由题意,A(1,8),把A(1,8)代入y=2x+b得到b=6.(2)设A(m,),则B(m,0),把A(m,)代入y=2x+b得到b=﹣2m,∴直线AC的解析式为y=2x+﹣2m,令y=0,得到x=m﹣,∴C(m﹣,0),∵AD=DC,∴D(m﹣,),设直线BD的解析式为y=k′x+b′,则有,解得,∴直线BD的解析式为y=﹣2x+2m,∴E(0,2m),∴OE=2m,BC=OC+OB==4,∵S△ECB∴•BC•EO=4,∴××2m=4,∴k=8.(3)连接AE,延长AE交BC于J.由(2)可知,E(0,2m),∵OE=2,∴2m=2,∴m=1,∴C((1﹣,0),B(1,0),A(1,k),∴直线AE的解析式为:y=(k﹣2)x+2,令y=0,得到x=,∴J(,0),∵E是△ABC的重心,∴CJ=JB,∴=(1+1﹣),解得k=6或0(舍弃),∴直线AC的解析式为y=2x+4.。
2020中考数学 专题练习:一次函数的应用(含答案)

(2)如果狮山公园铺设广场砖的面积为1600m2 ,那么公园应选择哪个工程队施工更合算?
y元
48000 28000
0 500 1000 图 12
x m2
6.绿谷商场“家电下乡 ”指定 型号冰箱、彩电的进价和售价如下表所示:
类别
冰箱
彩电
进价(元/台)
2 320
1 900
售价(元/台)
2 420
S(km) 8
6·
4· B
2·
·0
A
2 t(h)
3.在一次运输任务中,一辆汽车将一批货物从甲地运往乙地,到达乙地卸货后返回.设汽 车从甲地出发 x(h) 时,汽车与甲地的距离为 y(km),y 与 x 的函数关系如图所示. 根据图像信息,解答下列问题: (1)这辆汽车的往、返速度是否相同?请说明理由; (2)求返程中 y 与 x 之间的函数表达式; (3)求这辆汽车从甲地出发 4h 时与甲地的距离.
②哪种进货方案商场获得利润最大(利润=售价 进价),最大利润是多少?
7.星期天 8:00~8:30,燃气公司给平安加气站的储气罐注入天然气.之后,
y(立方米)
一位工作人员以每车 20 立方米的加气量,依次给在加气站排队等候的若干 10 000 8 000
辆车加气.储气罐中的储气量 y (立方米)与时间 x (小时)的函数关系
如图所示. (1)8:00~8:30,燃气公司向储气罐注入了多少立方米的天然气?
2 000 0 0.5 10.5 x(小时)
(2)当 x ≥ 0.5 时,求储气罐中的储气量 y (立方米)与时间 x (小时)
的函数解析式; (3)请你判断,正在排队等候的第 18 辆车能否在当天 10:30 之前加完气?请说明理由.
2020年中考数学复习专题练:《一次函数综合 》(含答案)

2020年中考数学复习专题练:《一次函数综合》1.如图,直线与x轴交于A点,与y轴交于B点,动点P从A点出发,沿AO方向向点O匀速运动,同时动点Q从B点出发,沿BA方向向点A匀速运动,P,Q两点的运动速度都是每秒1个单位,当一个点停止运动,另一个点也随之停止运动,连接PQ,设运动时间为t(s).(1)求A,B两点的坐标;(2)当t为何值时△AQP的面积为;(3)当t为何值时,以点A,P,Q为顶点的三角形与△ABO相似,并直接写出此时点Q 的坐标.2.已知直线y=2x+b与x轴交于点A,与y轴交于点B,将线段BO绕着点B逆时针旋转90°得到线段BC,过点C作CD⊥x轴于点D,四边形OBCD的面积为36.(1)求直线AB的解析式;(2)点P为线段OD上一点,连接CP,点H为CP上一点,连接BH,且BH=BC,过点H 作CP的垂线交CD、OB于E、F,连接AE、AC,设点P的横坐标为t,△ACE的面积为S,求S与t的函数解析式;(3)在(2)的条件下,连接OH,过点F作FK⊥OH交x轴于点K,若PD=PK,求点P 的坐标.3.如图,已知直线y=kx+2与x轴、y轴分别相交于点A、点B,∠BAO=30°,若将△AOB沿直钱CD折叠,使点A与点B重合,折痕CD与x轴交于点C,与AB交于点D.(1)求k的值;(2)求点C的坐标;(3)求直线CD的表达式.4.如图1,在平面直角坐标系中,OB=10,F是y轴正半轴上一点.(1)若OF=2,求直线BF的解析式;(2)设OF=t,△OBF的面积为s,求s与t的函数关系(直接写出自变量t的取值范围);(3)如图3,在(2)的条件下,过点B作BA⊥x轴,点C在x轴上,OF=OC,连接AC,CD⊥直线BF于点D,∠ACB=2∠CBD,AC=13,OF=OC,AC.BD交于点E,求此时t的值.5.如图,在平面直角坐标系中,点A 的坐标为(0,1),点B 的坐标为(﹣3,﹣1),将线段AB 向右平移m (m >0)个单位,点A 、B 的对应点分别为点A ′,B ′.(1)画出线段AB ,当m =4时,点B ′的坐标是 ;(2)如果点B ′又在直线x =上,求此时A ′、B ′两点的坐标;(3)在第(2)题的条件下,在第一象限中是否存在这样的点P ,使得△A ′B ′P 是以A ′B ′为腰的等腰直角三角形?如果存在,直接写出点P 的坐标;如果不存在,试说明理由.6.如图,在平面直角坐标系xOy 中,直线l 1:y =x +2与x 轴交于点A ,直线l 2:y =3x ﹣6与x 轴交于点D ,与l 1相交于点C .(1)求点D 的坐标;(2)在y 轴上一点E ,若S △ACE =S △ACD ,求点E 的坐标;(3)直线l 1上一点P (1,3),平面内一点F ,若以A 、P 、F 为顶点的三角形与△APD 全等,求点F 的坐标.7.如图,在平面直角坐标系中,长方形OABC的顶点O为坐标原点,顶点A,C分别在x轴正半轴和y轴正半轴上,顶点B的坐标为(12,8),直线y=kx+8﹣6k(k<0)交边AB 于点P,交边BC于点Q.(1)当k=﹣1时,求点P,Q的坐标;(2)若直线PQ∥AC,BH是Rt△BPQ斜边PQ上的高,求BH的长;(3)若PQ平分∠OPB,求k的值.8.如图,直线y=﹣x+4与x轴交于A点,与y轴交于B点,动点P从A点出发,以每秒2个单位的速度沿AO方向向点O匀速运动,点E是点B以Q为对称中心的对称点,同时动点Q从B点出发,以每秒1个单位的速度沿BA方向向点A匀速运动,当一个点停止运动,另一个点也随之停止运动,连结PQ,设P,Q两点运动时间为t秒(0<t≤1.5).(1)直接写出A,B两点的坐标.(2)当t为何值时,PQ∥OB?(3)四边形PQBO面积能否是△ABO面积的;若能,求出此时t的值;若不能,请说明理由;(4)当t为何值时,△APQ为直角三角形?(直接写出结果)9.定义:在平面直角坐标系中,对于任意两点A(a,b),B(c,d),若点T(x,y)满足x=,y=,那么称点T是点A和B的融合点.例如:M(﹣1,8),N(4,﹣2),则点T(1,2)是点M和N的融合点.如图,已知点D(3,0),点E是直线y =x+2上任意一点,点T(x,y)是点D和E的融合点.(1)若点E的纵坐标是6,则点T的坐标为;(2)求点T(x,y)的纵坐标y与横坐标x的函数关系式:(3)若直线ET交x轴于点H,当△DTH为直角三角形时,求点E的坐标.10.已知:在平面直角坐标系中,点O为坐标原点,直线y=kx+8(k<0)分别交x轴,y 轴于点C,B,点A在第一象限,连接AB,AC,四边形ABOC是正方形.(1)如图1,求直线BC的解析式;(2)如图2,点D,E分别在AB,OC上,点E关于y轴的对称点为点F,点G在EF上,且EG=2FG,连接DE,DG,设点G的横坐标为t,△DEG的面积为S,求S与t之间的函数关系式,并直接写出自变量t的取值范围;(3)如图3,在(2)的条件下,连接BE,BF,CD,点M在BF上,且FM=EG,点N在BE上,连接MN交DG于点H,∠BNM=∠BEF,且MH=NH,若CD=5BD,求S的值.11.如图,在平面直角坐标系xOy中,直线l:y=kx+b与x轴交于点A(﹣6,0),与y1轴交于点B(0,4),与直线l:y=x相交于点C.2(1)求直线l的函数表达式;1(2)求△COB的面积;(3)在x轴上是否存在一点P,使△POC是等腰三角形.若不存在,请说明理由;若存在,请直接写出点P的坐标.12.如图,直线y=x+4与x轴.y轴分别交于A.B两点直线BC与x轴交于点C(4,0).(1)求直线BC的解析式;(2)D(2,m)为线段BC上的点,作点D关于直线上x=﹣4的对称点E.CE交直线:x =﹣4于F,求线段CF的长;(3)y轴上是否存在一点M.使得以A、B、M为顶点的三角形为等腰三角形?若存在,请直接写出点M的坐标;若不存在,请说明理由.13.将矩形AOCB如图放置在平面直角坐标系中,E为边OC上的一个动点,过点E作ED⊥AE 交BC边于点D,且OA,OC的长是方程x2﹣20x+96=0的两个实数根,且OC>OA.(1)设OE=x,CD=y,求y与x的函数关系(不求x的取值范围).(2)当D为BC的中点时,求直线AE的解析式;(3)在(2)的条件下,平面内是否存在点F,使得以A,D,B,F为顶点的四边形为平行四边形?若存在,请直接写出点F的坐标;若不存在,请说明理由.14.如图,直线y=ax+b交x轴于点A,交y轴于点B,且a,b满足a=+4,直线y=kx﹣4k过定点C,点D为直线y=kx﹣4k上一点,∠DAB=45°.(1)a=,b=,C坐标为;(2)如图1,k=﹣1时,求点D的坐标;(3)如图2,在(2)的条件下,点M是直线y=kx﹣4k上一点,连接AM,将AM绕A顺时针旋转90°得AQ,OQ最小值为.15.在平面直角坐标系中,直线AB与x轴交于点A,与y轴交于点B,与直线OC:y=x交1于点C.=﹣x+10时,如图1.(1)当直线AB解析式为y2①求点C的坐标;②根据图象求出当x满足什么条件时﹣x+10<x.(2)如图2,作∠AOC的平分线ON,若AB⊥ON,垂足为E,△OAC的面积为9,且OA=6.P,Q分别为线段OA、OE上的动点,连接AQ与PQ,试探索AQ+PQ是否存在最小值?若存在,求出这个最小值:若不存在,说明理由.16.如图1,在第四象限的矩形ABCD,点A与坐标原点O重合,且AB=4,AD=3.点Q从B 点出发以每秒1个单位长度的速度沿B→C→D运动,当点Q到达点D时,点Q停止运动,设点Q运动的时间为t秒.(1)请直接写出图1中,点C的坐标,并求出直线OC的表达式;(2)求△ACQ的面积S关于t的函数关系式,并写出t的取值范围;(3)如图2,当点Q开始运动时,点P从C点出发以每秒2个单位长度的速度运动向点A运动,当点P到达A点时点Q和点P同时停止运动,当△QCP与△ABC相似时,求出相应的t值.17.如图,在平面直角坐标系中,直线y=x+4与x轴交于点A,与y轴交于点B.(1)求点A,B的坐标;(2)点P从B点出发,沿射线BO方向运动,速度为每秒一个单位,当t为何值时,△ABP为直角三角形?(直接写出答案)(3)点E(5,0)过点E作直线l⊥x轴,点C在直线l上,点D在x轴上,以A、B、C、D四个点组成的四边形是平行四边形,请直接写出点D坐标.18.在平面直角坐标系中,一次函数y=﹣x+3图象与x轴交于点A,与y轴交于点B.(1)请直接写出点A坐标,点B坐标;(2)点C是直线AB上一个动点,当△AOC的面积是△BOC的面积的2倍时,求点C的坐标;(3)点D为直线AB上的一个动点,在平面内找另一个点E,且以O、B、D、E为顶点的四边形是菱形,请直接写出满足条件的菱形的周长.19.如图,在平面直角坐标系中,OA=OB,△OAB的面积是2.(1)求线段OB的中点C的坐标.(2)连结AC,过点O作OE⊥AC于E,交AB于点D.①直接写出点E的坐标.②连结CD,求证:∠ECO=∠DCB;(3)点P为x轴上一动点,点Q为平面内一点,以点A、C、P、Q为顶点作菱形,直接写出点Q的坐标.20.如图,正方形AOBC的边长为2,点O为坐标原点,边OB,OA分别在x轴,y轴上,点D是BC的中点,点P是线段AC上的一个点,如果将OA沿直线OP对折,使点A的对应点A′恰好落在PD所在直线上.(1)若点P是端点,即当点P在A点时,A′点的位置关系是,OP所在的直线是,当点P在C点时,A′点的位置关系是,OP所在的直线表达式是.(2)若点P不是端点,用你所学的数学知识求出OP所在直线的表达式.(3)在(2)的情况下,x轴上是否存在点Q,使△DPQ的周长为最小值?若存在,请求出点Q的坐标;若不存在,请说明理由.参考答案1.解:(1)令y=0,则﹣x+6=0,解得:x=8,令x=0时,y=6,∴点A(8,0),点B(0,6);(2)由(1)得:OA=8,OB=6,在Rt△AOB中,AB===10,∵当一个点停止运动,另一个点也随之停止运动,∴0<t≤8,∵点P的速度是每秒1个单位,点Q的速度是每秒1个单位,∴AP=t,AQ=AB﹣BQ=10﹣t,∴点Q到AP的距离为AQ•sin∠OAB=(10﹣t)×=(10﹣t),∴△AQP的面积S=×t×(10﹣t)=,解得t=5+(不合题意舍去)或t=5﹣,∴当t为(5﹣)秒时△AQP的面积为;(3)若∠APQ=90°,则△APQ∽△AOB,此时=,即:=,解得:t=,若∠AQP=90°,则△APQ∽△ABO,此时=,即:=,解得t=,∵0<t≤8,∴t的值为或,①当t=时,OP=8﹣=,PQ=AP•tan∠OAB=×=,∴点Q的坐标为:(,);②当t=时,AQ=,过点Q作QM⊥x轴于M,如图所示:∴AM=AQ•cos∠OAB=×=,则OM=8﹣=,QM=AQ•sin∠OAB=×=,∴点Q的坐标为:(,);综上所述,当t为秒或秒时,以点A,P,Q为顶点的三角形与△ABO相似,此时点Q的坐标分别为(,)、(,).2.解:(1)∵将线段BO绕着点B逆时针旋转90°得到线段BC,∴OB=BC,∠OBC=90°,∵CD⊥x轴于点D,∴∠CDO=90°,∵∠BOD=90°,∴四边形OBCD为正方形,∵四边形OBCD的面积为36.∴OB=6,∴B(0,6),∵直线y=2x+b与y轴交于点B,∴b=6,∴直线AB的解析式为y=2x+6;(2)∵直线y=2x+6与x轴交于点A,∴A(﹣3,0),如图1,过点B作BL⊥CP,垂足为L,交CD于点M,∵BH=BC,∴CL=HL,∵BL⊥CP,EF⊥CP,∴BM∥EF,∴CM=ME,∵∠CBM+∠BMC=∠BMC+∠MCL=90°∴∠CBM=∠PCD,∵∠BCM=∠PDC,BC=CD,∴△BCM≌△CDP(ASA),∴CM=PD,∴PD=CM=ME=6﹣t,∴CE=2CM=2(6﹣t),∵AD=OA+OD=9,∴S===﹣9t+54(0≤t≤6);(3)设PD=a,如图2,∵BF∥CD,BM∥EF,∴四边形BFEM是平行四边形,∴BF=EM=PD=a,∴OF=OP,连接FP,设FK与OH交于A',∴∠OFP=45°,∵∠FOP+∠FHP=180°,∴F、O、P、H四点共圆,∴∠OFP=∠OHP=45°,∴∠OHF=45°,∵FK⊥OH,∴∠FA'H=90°,∴∠EFK=45°,如图3,过点E作ER⊥EF交射线FK于点R,∴△EFR为等腰直角三角形,∴EF=ER,过点F作FG⊥CD于点G,过点R作x轴的平行线交y轴于点Q,交CD的延长线于点N,连接KE、∴∠RNE=∠FGE=90°,∠FEG=∠ERN,∴△EFG≌△REN(AAS),∴EN=FG,EG=RN=PD=a,∵CG=BF=a,GE=a,设ED=b,∴DN=CE=2a=OQ,OF=a+b,∵PD=PK=a,OD=CD=2a+b,∴OK=b,∵OK∥QR,∴,即,∴b(3a+b)=(a+b)2,∴a=b,∴3a=6,∴a=2,∴P(4,0).3.解:(1)令x=0,则y=2,即:OB=2,由勾股定理得:OA=6,则k=﹣;(2)设:BC=AC=a,则OC=6﹣a,在△BOC中,(2)2+(6﹣a)2=a2,解得:a=4,则点C(2,0);(3)点D时AB的中点,则点D(3,),将点C、D的坐标代入一次函数:y=kx+b得:,解得:,故直线CD的表达式为:y=x﹣2.4.解:(1)∵OB=10,OF=2,∴B(﹣10,0),F(0,2),设直线BF的解析式为y=kx+b,∵直线y=kx+b经过点B(﹣10,0),F(0,2),∴,解得:,∴直线BF的解析式为y=x+2;(2)△OBF的面积为S==5t(t>0);(3)如图,延长AB至点R,使BR=AB,连接CR,延长CD交y轴于点T,过点T,作TM ∥x轴交BA的延长线于点M,过点T作TK⊥CR交RC的延长线于点K,连接RT,∵AB⊥BC,AB=BR,∴BC垂直平分AR,∴AC=CR=13,∴∠ACB=∠RCB,设∠CBD=α,则∠ACB=2α,∵BD⊥CD,∴∠BDC=90°,∴∠BCD=90°﹣α,∵∠ACB=∠RCB=2α,∴∠ACK=180°﹣4α,∴∠KCT=∠BCK﹣∠BCD=∠BCA+∠ACK﹣∠BCD=90°﹣α,∴∠KCT=∠BCD,∵TK⊥KR,OT⊥OC,∴OT=TK,∵TC=TC,∴Rt△OTC≌Rt△KTC(HL),∴OC=CK=TK=t,∵OF=OC,∠BOF=∠TOC,∠FBO=∠OTC,∴△BOF≌△TOC(AAS),∴OB=OT=10,∴TK=10,∵∠ABO+∠BOT=90°+90°=180°.∴MB∥OT,∵MT∥OB,∴四边形OBMT为平行四边形,∵OB=OT,∠BOT=90°.∴四边形OBMT为正方形,∴MB=MT=OT=10,∴MT=TK,∵RT=RT,∴Rt△RMT≌Rt△RTK(HL),∴RK=RM=CR+CK=13+t,∴BR=RM﹣MB=3+t,∵BC=OB+OC=10+t,在Rt△BRC中,BR2+BC2=RC2,∴(3+t)2+(10+t)2=132,解得:t=2(t=﹣15舍去).∴t的值为2.5.解:(1)∵点A的坐标为(0,1),点B的坐标为(﹣3,﹣1),将线段AB向右平移m(m>0)个单位,∴A'(m,1),B'(m﹣3,﹣1),当m=4时,A'(4,1),B'(1,﹣1),故答案(1,﹣1);(2)由(1)知,B'(m﹣3,﹣1),∵点B′又在直线x=上,∴m﹣3=,∴m=6,由(1)知,A'(m,1),B'(m﹣3,﹣1),∴A'(6,1),B'(3,﹣1);(3)存在,理由:如图,由(2)知,A'(6,1),B'(3,﹣1),过点B'作GH∥x轴,过点P作PG⊥GH于G,过点A'作A'H⊥GH于H,∴H(6,﹣1),∴A'H=2,B'H=3,∵△PA'B'是等腰直角三角形,∴A'B'=PB',∠A'B'P=90°,∴∠PB'G+∠A'B'H=90°,∵∠PB'G+∠B'PG=90°,∴∠B'PG=∠A'B'H,∴△PB'G≌△A'B'H(AAS),∴B'G=A'H=2,PG=B'H=3,∴P(1,2),同理:P'(4,4),即:点P的坐标为(1,2)或(4,4).:y=3x﹣6与x轴交于点D,6.解:(1)∵直线l2∴令y=0,则3x﹣6=0,∴x =2,∴D (2,0);(2)如图1,∵直线l 1:y =x +2与x 轴交于点A , ∴令y =0.∴x +2=0,∴x =﹣2,∴A (﹣2,0),由(1)知,D (2,0), ∴AD =4,联立直线l 1,l 2的解析式得,, 解得,, ∴C (4,6),∴S △ACD =AD •|y C |=×4×6=12, ∵S △ACE =S △ACD ,∴S △ACE =12,直线l 1与y 轴的交点记作点B , ∴B (0,2),设点E (0,m ),∴BE =|m ﹣2|,∴S △ACE =BE •|x C ﹣x A |=|m ﹣2|×|4+2|=4|m ﹣2|=12, ∴m =﹣2或m =6,∴点E (0,﹣2)或(0,6);(3)如图2,①当点F 在直线l 1上方时,∵以A 、P 、F 为顶点的三角形与△APD 全等,∴Ⅰ、当△APF'≌△APD时,连接DF',BD,由(2)知,B(0,2),由(1)知,A(﹣2,0),D(2,0),∴OB=OA=OD,∴∠ABO=∠DBO=45°,∴∠ABD=90°,∴DB⊥l,1∵△APF'≌△APD,∴PF'=PD,AF'=AD,∴直线l是线段DF'的垂直平分线,1对称,∴点D,F'关于直线l1∴DF'⊥l,1∴DF'过点B,且点B是DF'的中点,∴F'(﹣2,4),Ⅱ、当△PAF≌△APD时,∴PF=AD,∠APF=∠PAD,∴PF∥AD,∵点D(2,0),A(﹣2,6),∴点D向左平移4个单位,∴点P向左平移4个单位得,F(1﹣4,6),∴F(﹣3,3),②当点F在直线l下方时,1∵△PAF''≌△APD,由①Ⅱ知,△PAF≌△APD,∴△PAF≌△PAF'',∴AF=AF'',PF=PF'',∴点F与点F'关于直线l对称,1,∴FF''⊥l1∵DF'⊥l,1∴FF'∥DF',而点F'(﹣2,4)先向左平移一个单位,再向下平移一个单位,∴D(2,0),向左平移1个单位,再向下平移一个单位得F''(2﹣1,0﹣1),∴F''(1,﹣1),即:点F的坐标为(﹣3,3)或(﹣2,4)或(1,﹣1).7.解:(1)当k=﹣1时,该直线表达式为y=﹣x+14,∵四边形OABC是长方形,点P,Q分别在边AB,BC上,点B(12,8),∴点P的横坐标为12,点Q的纵坐标为8,当x=12时,y=﹣1×12+14=2,当y=8时,﹣x+14=8,解得x=6,∴点P,Q的坐标分别是P(12,2),Q(6,8);(2)如图1,过点B作BH⊥PQ于H,∵长方形OABC的顶点B的坐标是(12,8),∴点A的坐标为(12,0),点C的坐标为(0,8).设直线AC表达式为y=ax+b,则解得,,∴直线AC的解析式为y=﹣x+8,∵PQ∥AC,∴k=﹣.∴直线PQ表达式为y=﹣x+12,∵当x=12时,y=4;当y=8时,8=﹣x+12,∴x=6,∴BP=4,BQ=6.在Rt△BPQ中,根据勾股定理得,PQ==2,∵S=BQ•BP=PQ•BH,△PBQ∴×4×6=××BH,∴BH=;(3)∵当x=12时,y=6k+8;当y=8时,x=6.∴点P的坐标为(12,6k+8),点Q的坐标为(6,8).∴AP=6k+8,AO=12,BQ=CQ=6,AB=OC=8.∴BP=8﹣(6k+8)=﹣6k,过点Q作QM⊥OP于点M,连接OQ,如图2,∵PQ平分∠OPB,∴∠QPB=∠QPM,又∵∠PMQ=∠B=90°,PQ=PQ,∴△BPQ≌△MPQ(AAS),∴QM=QB=6,MP=BP=﹣6k,在Rt△OCQ中,根据勾股定理得,OQ=10,在Rt△OQM中,根据勾股定理得OM=8,∴OP=OM+MP=8﹣6k,∵在Rt△OAP中,OA2+AP2=OP2,即122+(6k+8)2=(8﹣6k)2.解得,k=﹣.8.解:(1)令y=0,则﹣x+4=0,解得x=4,x=0时,y=4,∴OA=6,OB=8,∴点A(4,0),B(0,4);(2)在Rt△AOB中,由勾股定理得,AB===4,∵点P的速度是每秒2个单位,点Q的速度是每秒1个单位,∴AP=2t,AQ=AB﹣BQ=4﹣t,若PQ ∥OB ,则∠APQ =∠AOB =90°,则 ∴,解得t =;(3)如图,作QH ⊥OA 于H ,∴QH ∥OB ,∴△QAH ∽△BAO , ∴,即,∴QH =4﹣t ,当四边形PQBO 面积是△ABO 面积的时,S △APQ =S △AOB , ∴•2t •(4﹣t )=×, 整理得t 2﹣4t +4=0,解得t =(2﹣)或t =(2+)(舍去)∴t 的值为=(2﹣)四边形PQBO 面积是△ABO 面积的.(4)若∠APQ =90°,由(2)可知t =;若∠AQP =90°,则cos ∠OAB =, ∴=,解得t =8﹣4,∵0<t ≤1.5,∴t 的值为,∴当t 为时,△APQ 为直角三角形.9.解:(1)∵点E 是直线y =x +2上一点,点E 的纵坐标是6,∴x+2=6,解得,x=4,∴点E的坐标是(4,6),∵点T(x,y)是点D和E的融合点,∴x==,y==2,∴点T的坐标为(,2),故答案为:(,2);(2)设点E的坐标为(a,a+2),∵点T(x,y)是点D和E的融合点,∴x=,y=,解得,a=3x﹣3,a=3y﹣2,∴3x﹣3=3y﹣2,整理得,y=x﹣;(3)设点E的坐标为(a,a+2),则点T的坐标为(,),当∠THD=90°时,点E与点T的横坐标相同,∴=a,解得,a=,此时点E的坐标为(,),当∠TDH=90°时,点T与点D的横坐标相同,∴=3,解得,a=6,此时点E的坐标为(6,8),当∠DTH=90°时,该情况不存在,综上所述,当△DTH为直角三角形时,点E的坐标为(,)或(6,8).10.解:(1)当x=0时,y=kx+8=8所以B(0,8),OB=8∵四边形ABOC是正方形∴OB=OC=8∴C(8,0)得8k+8=0∴k=﹣1∴y=﹣x+8(2)∵点E关于y轴的对称点为点F∴OE=OF=EF∵EG=2FGEG=EF∴OE=3OG=﹣3t∴EG=﹣4t∴S=(﹣8≤t<0)(3)作ML∥EF,交BE于点L,作EQ⊥LG,则∠BEF=∠BLM 显然BM=BL,MF=LE∴LE=GE∴∠3=∠BEF而已知∠2=∠BEF∴∠2=∠3,MN∥EQ∴∠2=∠BLM∵∠1+∠2=∠BLM∴∠1=∠2∵GL⊥MN∴GL过MN的中点∴G,L,D在一条直线上∵CD=5BD∴(5BD)2﹣(8﹣BD)2=82得BD=2∴82+(﹣3t)2=(2﹣4t)2得t=﹣2∴S=3211.解:(1)将点A(﹣6,0),B(0,4)代入y=kx+b中,得,∴,的函数表达式为y=x+4;∴直线l1(2)由(1)知,直线l的函数表达式为y=x+4①,1:y=x,∵直线l2联立①②解得,,∴C(6,8),∵B(0,4),∴OB=4,=OB•|x C|=×4×6=12;∴S△COB(3)设P(m,0),∵O(0,0),C(6,8),∴OP=|m|.OC=10,CP=,∵△POC是等腰三角形,①当OP=OC时,∴|m|=10,∴m=±10,∴P(﹣10,0)或(10,0),②当OP=CP时,∴|m|=,∴m=,∴P(,0),③当OC=CP时,∴10=,∴m=0(舍)或m=12,∴P(12,0),即:满足条件的点P的坐标为(﹣10,0)或(10,0)或(12,0)或(,0).12.解:(1)∵直线y=x+4与x轴、y轴分别交于A、B两点,∴A(﹣4,0),B(0,4),设直线BC的解析式为:y=kx+4,∴4k+4=0,∴k=﹣,∴直线BC的解析式为:y=﹣x+4;(2)如图1,∵D(2,m)为线段BC上的点,∴m=﹣2+4=2,∴D(2,2),∵点D关于直线上x=﹣4的对称点E,∴E(﹣10,2),∴直线CE的解析式为y=﹣x+,当x=﹣4时,y=,∴F(﹣4,),∴AF =,AC =8, ∴CF ==2;(3)存在,如图2,∵AO =4,OB =4,∴AB =8,∠ABO =30°,∠BAO =60°,当BA =BM =8时,以A 、B 、M 为顶点的三角形为等腰三角形, ∴OM =8+4或OM =8﹣4, ∴M 1(0,8+4),M 3=(0.4﹣8); 当AB =MM =8时,以A 、B 、M 为顶点的三角形为等腰三角形, ∴OM =OB =4,∴M 4(0,﹣4),当MA =MB 时,以A 、B 、M 为顶点的三角形为等腰三角形, ∴∠MAB =∠MBA =30°,∴∠MAO =30°,∴OM =, ∴M 2(0,),综上所述,点M 的坐标为M 1(0,8+4),M 2(0,),M 3=(0.4﹣8),M 4(0,﹣4).13.解:(1)x2﹣20x+96=0 (x﹣8)(x﹣12)=0x 1=8,x2=12,∵OC>OA,∴OA=8,OC=12,∵ED⊥AE,∴∠AEO+∠DEC=90°,又∵∠AEO+∠OAE=90°,∴∠OAE=∠CED,又∠AOE=∠ECD=90°,∴△AOE∽△ECD,∴=,即=,∴y=﹣x2+x;(2)当D为BC的中点时,y=4,∴﹣x2+x=4,解得,x1=4,x2=8,设直线AE的解析式为:y=kx+b,当x=4时,点E的坐标为(4,0),解得,,∴直线AE的解析式为:y=﹣2x+8;当x=8时,点E的坐标为(8,0),解得,,∴直线AE的解析式为:y=﹣x+8,∴当D为BC的中点时,直线AE的解析式为y=﹣2x+8或y=﹣x+8;(3)当点F在线段OA上时,FA=BD=4,∴OF=4,即点F的坐标为(0,4),当点F在线段OA的延长线上时,FA=BD=4,∴OF=12,即点F的坐标为(0,12),当点F在线段BC右侧、AB∥DF时,DF=AB=12,∴点F的坐标为(24,4),综上所述,以A,D,B,F为顶点的四边形为平行四边形时,点F的坐标为(0,4)或(0,12)或(24,4).14.解:(1)∵4﹣b≥0,b﹣4≥0,∴b=4,则a=4,对于直线y=kx﹣4k,当y=0时,x=4,∴点C的坐标为(4,0),故答案为:4;4;(4,0);(2)当D在线段BC上时,作BE⊥BA交AD的延长线于点E,作EF⊥y轴于F,则∠BEF+∠EBO=90°,∠ABO+∠EBO=90°,∴∠BEF=∠ABO,∵∠DAB=45°,∴BA=BE,在△AOB和△BFE中,,∴△AOB≌△BFE(AAS),∴BF=OA,EF=OB=4,对于直线y=4x+4,当y=0时,x=﹣1,∴OA=1,∴E(4,3)设直线AE解析式为y=mx+n,,解得,,则直线AE解析式为y=x+,,解得,,∴D(,);当D在CB延长线上时,同理可得D(,);(3)设M(m,﹣m+4),由(2)可得,△ANM≌△QHA,∴MN=AH=﹣m+4,AN=QH=m+1,∴Q(﹣m+3,﹣m﹣1)则OQ2=(﹣m+3)2+(﹣m﹣1)2=2(m﹣1)2+8,当m=1时,OQ最小为,故答案为:2.15.解:(1)①由題意,,解得:,所以C(4,4).②观察图象可知x>4时,直线AB位于直线OC的下方,即x>4时,﹣x+10<x.(2)由题意,在OC上截取OM=OP,连结MQ,∵ON平分∠AOC,∴∠AOQ=∠COQ,又OQ=OQ.∴△POQ≌△MOQ(SAS),∴PQ=MQ,∴AQ+PQ=AQ+MQ,当A、Q、M在同一直銭上,且AM⊥OC吋,AQ+MQ最小,即AQ+PQ存在最小値;∴AB⊥ON,∴∠AEO=∠CEO,∴△AEO≌△CEO(ASA),∴OC=OA=6,∵△OAC的面积为9,∴OC•AM=9,∴AM=3,∴AQ+PQ存在最小值,最小值为3.16.解:(1)∵在第四象限的矩形ABCD,点A与坐标原点O重合,且AB=4,AD=3,∴点C的坐标为(4,﹣3),设直线OC的函数解析式为y=kx,﹣3=4k,得k=﹣,即直线OC的表达式为y=﹣x;(2)当0≤t<3时,S==﹣2t+6,当3<t≤7时,S==,由上可得,S=;(3)∵AB=4,BC=3,∠ABC=90°,∴AC=5,当△ABC∽△QPC时,则,∵AC=5,QC=3﹣t,CB=3,CP=2t,∴,解得,t=;当△ABC∽△PQC时,,∵AC=5,PC=2t,BC=3,QC=3﹣t,∴,解得,t =;由上可得,当△QCP 与△ABC 相似时,t 值是或. 17.解:(1)∵直线y =x +4,∴当y =0时,x =﹣3,当x =0时,y =4,∴点A 的坐标为(﹣3,0),点B 的坐标为:(0,4);(2)当t 为4或时,△ABP 为直角三角形,理由:当∠BPA =90°时,此时点P 与点O 重合,此时t =OB =4,当∠BAP =90°时,△BAO ∽△BPA ,则,∵点A 的坐标为(﹣3,0),点B 的坐标为:(0,4),∴OA =3,OB =4,∵∠BOA =90°,∴AB =5, ∴,解得,BP =,由上可得,当t 为4或时,△ABP 为直角三角形; (3)点D 坐标是(2,0)或(8,0),理由:当四边形ABC 1D 1是平行四边形时,∵点A 的坐标为(﹣3,0),点B 的坐标为:(0,4),点E 的坐标为(5,0), ∴BC 1=5,∵四边形ABC 1D 1是平行四边形,∴BC 1=AD 1,∴AD 1=5,∵点A 的坐标为(﹣3,0),∴点D 1的坐标为(2,0);当四边形ABD 2C 2是平行四边形时,则ED 2=OA ,∵点A 的坐标为(﹣3,0),点E 的坐标为(5,0),∴OA=3,∴OD=8,2的坐标为(8,0);∴D2由上可得,点D坐标是(2,0)或(8,0).18.解:(1)在y=﹣x+3中,令x=0,则y=3;令y=0,则x=3;∴A(3,0),B(0,3);故答案为:(3,0);(0,3).(2)∵A(3,0),B(0,3),∴OA=3,OB=3,=OA×OB=×3×3=,∴S△AOB设C(m,n),①当点C在线段AB上时,如图1,∵△AOC的面积是△BOC的面积的2倍,∴S△AOC=,∴∴m=2或m=﹣2(舍去),∵点C在直线y=﹣x+3上,∴﹣2+3=n,∴n=1,∴C(2,1).②当点C在线段AB的延长线上时,如图2,∵△AOC的面积是△BOC的面积的2倍,∴S△BOC =S△AOB,∴×OB×|m|=,∴m=﹣3或m=3(舍去),∴C(﹣3,6).综合以上可得点C的坐标为(2,1)或(﹣3,6).(3)如图3,以OB为边的菱形OBDE中,∵OB=3,∴周长为3×4=12,如图4,以OB边的菱形OBDE中,同理周长为12.如图5,以OB为对角线的菱形ODBE中,∵OB=OA=3,∴∠OBA=45°,∴∠DBE=90°,∴四边形ODBE为正方形,∴BD=3×.∴四边形ODBE的周长为4×.综上可得以O、B、D、E为顶点的菱形的周长为12或6.故答案为:12或6.19.解:(1)∵OA=OB,△OAB的面积是2.∴OA•OB=2,∴OA=OB=2,线段OB的中点C的坐标为:(﹣1,0),答:线段OB的中点C的坐标为:(﹣1,0).(2)①过点E作EF⊥OB,∵∠AOC=90°,OA=2,OC=1,∴AC=,∵OE⊥AC,由面积法得:OE===,∵∠EOF+∠AOE=∠EAO+∠AOE=90°,∴∠EOF=∠EAO,∴tan∠EOF=tan∠EAO=,设EF=x,则OF=2x,∴由勾股定理得:,解得:x=,2x=,∴点E坐标为:(﹣,).②证明:过点B作OB的垂线,交OE于点G,由(2)①可知,∠EOF=∠EAO,∴在△AOC和△OBG中,∴△AOC≌△OBG(ASA),∴∠ECO=∠BGD,BG=OC,∵C为线段OB的中点,∴BG=BC,∵OA =OB ,∠AOC =∠OBG =90°,∴∠GBD =∠CBD =45°,∴在△BGD 和△BCD 中,∴△BGD ≌△BCD (SAS )∴∠DCB =∠BGD ,又∠ECO =∠BGD ,∴∠ECO =∠DCB .(3)由菱形对角线互相垂直的性质,易知,P 1(1,0),Q 1(0,﹣2)符合题意; ∵AC =,∴分别以点C 和点A 为圆心,以为半径作圆,与x 轴可得两个交点P 2(﹣,0),P 3(,0)从而得Q 2(﹣,2),Q 3(,2), 由tan ∠ACO =2,可知,当以AC 为菱形的对角线时,AC 被另一条对角线垂直平分,,从而另一条对角线P 4Q 4的一半为,从而P 4C =,∴P 4(,0),Q 4(﹣,2)综上,点Q 的坐标为:(0,﹣2)、(﹣,2)、(,2),(﹣,2).20.解:(1)由轴对称的性质可得,若点P 是端点,即当点P 在A 点时,A ′点的位置关系是点A ,OP 所在的直线是y 轴;当点P 在C 点时,∵∠AOC =∠BOC =45°,∴A′点的位置关系是点B,OP所在的直线表达式是y=x.故答案为:A,y轴;B,y=x.(2)连接OD,∵正方形AOBC的边长为2,点D是BC的中点,∴==.由折叠的性质可知,OA′=OA=2,∠OA′D=90°.∴A′D=1.设点P(x,2),PA′=x,PC=2﹣x,CD=1.∴(x+1)2=(2﹣x)2+12.解得x=.所以P(,2),∴OP所在直线的表达式是y=3x.(3)存在.若△DPQ的周长为最小,即是要PQ+DQ为最小.∵点D关于x轴的对称点是D′(2,﹣1),∴设直线PD'的解析式为y=kx+b,,解得,∴直线PD′的函数表达式为y=﹣x+.当y=0时,x=.∴点Q(,0).。
2020年中考数学 考前大专题复习:函数(解析版)

2020中考数学考前大专题复习:函数(含答案)一、选择题(本大题共6道小题)1. 二次函数y=x2-ax+b的图象如图所示,对称轴为直线x=2,下列结论不正确的是()A.a=4B.当b=-4时,顶点的坐标为(2,-8)C.当x=-1时,b>-5D.当x>3时,y随x的增大而增大2. 正比例函数y=kx(k≠0)的函数值y随着x的增大而减小,则一次函数y=x+k的图象大致是 ()3. 如图所示,在平面直角坐标系中,半径均为1个单位长度的半圆O1,O2,O3,…,组成一条平滑的曲线,点P从原点O出发沿这条曲线向右运动,速度为每秒π2个单位长度,则第2019秒时,点P的坐标是()A.(2018,0)B.(2019,1)C.(2019,-1)D.(2020,0)4. 如图,☉O的半径为2,双曲线的解析式分别为y=1x和y=-1x,则阴影部分的面积为()A.4πB.3πC.2πD.π5. 如图,在Rt△ABO中,∠OBA=90°,A(4,4),点C在边AB上,且ACCB=13,点D为OB的中点,点P为边OA上的动点,当点P在OA上移动时,使四边形PDBC 周长最小的点P的坐标为()A.(2,2)B.52,52C.83,83D.(3,3)6. 如图,函数y={1x(x>0),-1x(x<0)的图象所在坐标系的原点是()A.点MB.点NC.点PD.点Q二、填空题(本大题共6道小题)7. 元朝朱世杰的《算学启蒙》一书记载:“今有良马日行二百四十里,驽马日行一百五十里,驽马先行一十二日,问良马几何日追及之”,如图K11-3是两匹马行走路程s关于行走时间t的函数图象,则两图象交点P的坐标是.图K11-38. 如图,已知直线y=kx+b过A(-1,2),B(-2,0)两点,则0≤kx+b≤-2x的解集为.9. 已知抛物线y=ax2+bx+c(a≠0)的对称轴是直线x=1,其部分图象如图所示,下列说法中:①b>0;②a-b+c<0;③b+2c>0;④当-1<x<0时,y>0,正确的是(填写序号).10. 如图,矩形OABC的顶点A,C分别在y轴、x轴的正半轴上,D为AB的中点,反比例函数y=kx(k>0)的图象经过点D,且与BC交于点E,连接OD,OE,DE,若△ODE的面积为3,则k的值为.11. 如图,平行于x轴的直线与函数y=k1x(k1>0,x>0),y=k2x(k2>0,x>0)的图象分别相交于A,B两点,点A在点B的右侧,C为x轴上的一个动点.若△ABC的面积为4,则k1-k2的值为.12. 如图,抛物线y=-14x2+12x+2与x轴相交于A,B两点,与y轴相交于点C,点D在抛物线上,且CD∥AB.AD与y轴相交于点E,过点E的直线PQ平行于x 轴,与拋物线相交于P,Q两点,则线段PQ的长为.三、解答题(本大题共5道小题)13. 已知二次函数y=2x2+bx+1的图象过点(2,3).(1)求该二次函数的表达式;(2)若点P(m,m2+1)也在该二次函数的图象上,求点P的坐标.14. 某商店销售一种商品,经市场调查发现,该商品的周销售量y(件)是售价x(元/件)的一次函数,其售价、周销售量、周销售利润w(元)的三组对应值如下表: 售价x(元/件) 50 60 80周销售量y(件) 100 80 40周销售利润w(元)1000 1600 1600注:周销售利润=周销售量×(售价-进价)(1)①求y关于x的函数解析式(不要求写出自变量的取值范围);②该商品进价是元/件;当售价是元/件时,周销售利润最大,最大利润是元;(2)由于某种原因,该商品进价提高了m元/件(m>0),物价部门规定该商品售价不得超过65元/件,该商店在今后的销售中,周销售量与售价仍然满足(1)中的函数关系.若周销售最大利润是1400元,求m的值.15. 如图①,在平面直角坐标系xOy中,已知抛物线y=ax2-2ax-8a与x轴相交于A,B两点(点A在点B的左侧),与y轴交于点C(0,-4).(1)点A的坐标为,点B的坐标为,线段AC的长为,抛物线的解析式为.(2)点P是线段BC下方抛物线上的一个动点.如果在x轴上存在点Q,使得以点B,C,P,Q为顶点的四边形是平行四边形,求点Q的坐标.①16. 如图,已知抛物线y=ax2+bx+4(a≠0)的对称轴为直线x=3,抛物线与x轴相交于A,B两点,与y轴相交于点C,已知B点的坐标为(8,0).(1)求抛物线的解析式;(2)点M为线段BC上方抛物线上的一点,点N为线段BC上的一点,若MN∥y 轴,求MN的最大值;(3)在抛物线的对称轴上是否存在点Q,使△ACQ为等腰三角形?若存在,求出符合条件的Q点坐标;若不存在,请说明理由.17. 如图,在直角坐标系中,抛物线经过点A(0,4)、B(1,0)、C(5,0),其对称轴与x轴相交于点M.(1)求抛物线的解析式和对称轴;(2)在抛物线的对称轴上是否存在一点P,使△P AB的周长最小?若存在,请求出点P的坐标;若不存在,请说明理由;(3)连接AC,在直线AC下方的抛物线上,是否存在一点N,使△NAC的面积最大?若存在,请求出点N的坐标;若不存在,请说明理由.2020中考数学考前大专题复习:函数-答案一、选择题(本大题共6道小题)1. 【答案】C[解析]选项A,由对称轴为直线x=2可得--a2=2,∴a=4,正确;选项B,∵a=4,b=-4,∴代入解析式可得,y=x2-4x-4,当x=2时,y=-8,∴顶点的坐标为(2,-8),正确;选项C,由图象可知,x=-1时,y<0,即1+4+b<0,∴b<-5,∴错误;选项D,由图象可以看出当x>3时,在对称轴的右侧,y随x的增大而增大,正确,故选C.2. 【答案】A[解析]因为正比例函数y=kx(k≠0)的函数值y随着x的增大而减小,所以k<0,所以一次函数y=x+k的函数值y随着x增大而增大,图象与y轴交于负半轴,故选A.3. 【答案】C[解析]点P运动一个半圆用时为2π2÷π2=2(秒).∵2019=1009×2+1,∴2019秒时,P在第1010个半圆的中点处,∴此时点P坐标为(2019,-1).故选C.4. 【答案】C[解析]根据反比例函数y=1x,y=-1x及圆的中心对称性和轴对称性知,将二、四象限的阴影部分旋转到一、三象限对应部分,显然所有阴影部分的面积之和等于一、三象限内两个扇形的面积之和,也就相当于一个半径为2的半圆的面积.∴S阴影=12π×22=2π.故选C.5. 【答案】C[解析]由题可知:A(4,4),D(2,0),C(4,3),点D关于AO的对称点D'坐标为(0,2),设l D'C:y=kx+b,将D'(0,2),C(4,3)代入,可得y=14x+2,解方程组{y=14x+2,y=x,得{x=83,y=83.∴P83,83.故选C.6. 【答案】A[解析]∵函数y=1x(x>0)与y=-1x(x<0)的图象关于y轴对称,∴直线MP是y轴所在直线,∵两支曲线分别位于一、二象限,∴直线MN是x轴所在直线,∴坐标原点为M.二、填空题(本大题共6道小题)7. 【答案】(32,4800)[解析]根据题意,得{s=240(t-12),s=150t,解得{t=32,s=4800.故答案为(32,4800).8. 【答案】-2≤x≤-1[解析]如图,直线OA的解析式为y=-2x,当-2≤x≤-1时,0≤kx+b≤-2x.9. 【答案】①③④[解析]根据图象可得:a<0,c>0,对称轴:直线x=-b2a=1,∴b=-2a.∵a<0,∴b>0,故①正确;把x=-1代入y=ax 2+bx +c ,得y=a -b +c.由抛物线的对称轴是直线x=1,且过点(3,0),可得当x=-1时,y=0,∴a -b +c=0,故②错误;当x=1时,y=a +b +c>0.∵b=-2a ,∴-b2+b +c>0,即b +2c>0,故③正确; 由图象可以直接看出④正确.故答案为:①③④.10. 【答案】4[解析]过点D 作DH ⊥x 轴于H 点,交OE 于M ,∵反比例函数y=kx (k>0)的图象经过点D ,E ,∴S △ODH =S △ODA =S △OEC =k2,∴S △ODH -S △OMH =S △OEC -S △OMH ,即S △OMD =S 四边形EMHC , ∴S △ODE =S 梯形DHCE =3,设D (m ,n ),∵D 为AB 的中点,∴B (2m ,n ).∵反比例函数y=kx (k>0)的图象经过点D ,E ,∴E 2m ,n2,∴S 梯形DHCE =12n 2+nm=3, ∴k=mn=4.11. 【答案】8[解析]过点B 作BE ⊥x 轴,垂足为点E ,过点A 作AF ⊥x 轴,垂足为点F ,直线AB 交y 轴于点D ,因为△ABC 与△ABE 同底等高, 所以S △ABE =S △ABC =4, 因为四边形ABEF 为矩形, 所以S 矩形ABEF =2S △ABE =8, 因为k 1=S 矩形OF AD ,k 2=S 矩形OEBD , 所以k 1-k 2=S 矩形OF AD -S 矩形OEBD =S 矩形ABEF =8.12. 【答案】2√5 [解析]当y=0时,-14x 2+12x +2=0,解得x 1=-2,x 2=4,∴点A 的坐标为(-2,0).当x=0时,y=-14x 2+12x +2=2,∴点C 的坐标为(0,2). 当y=2时,-14x 2+12x +2=2,解得x 1=0,x 2=2, ∴点D 的坐标为(2,2).设直线AD 的解析式为y=kx +b (k ≠0), 将A (-2,0),D (2,2)代入y=kx +b ,得{-2k +b =0,2k +b =2,解得{k =12,b =1,∴直线AD 的解析式为y=12x +1.当x=0时,y=12x +1=1,∴点E 的坐标为(0,1). 当y=1时,-14x 2+12x +2=1,解得x 1=1-√5,x 2=1+√5, ∴点P 的坐标为(1-√5,1),点Q 的坐标为(1+√5,1), ∴PQ=1+√5-(1-√5)=2√5.三、解答题(本大题共5道小题)13. 【答案】解:(1)∵二次函数y=2x 2+bx +1的图象过点(2,3), ∴3=8+2b +1,∴b=-3,∴该二次函数的表达式为y=2x 2-3x +1. (2)∵点P (m ,m 2+1)在该二次函数的图象上, ∴m 2+1=2m 2-3m +1,解得m 1=0,m 2=3, ∴点P 的坐标为(0,1)或(3,10).14. 【答案】解:(1)①设y 与x 的函数关系式为y=kx +b ,依题意,有{50k +b =100,60k +b =80,解得{k =-2,b =200,∴y 与x 的函数关系式是y=-2x +200..②设进价为t 元/件,由题意,1000=100×(50-t ),解得t=40,∴进价为40元/件; 周销售利润w=(x -40)y=(x -40)(-2x +200)=-2(x -70)2+1800,故当售价是70元/件时,周销售利润最大,最大利润是1800元.故答案为40,70,1800.(2)依题意有,w=(-2x +200)(x -40-m )=-2x 2+(2m +280)x -8000-200m=-2x -m+14022+12m 2-60m +1800.∵m>0,∴对称轴x=m+1402>70,∵-2<0,∴抛物线开口向下, ∵x ≤65,∴w 随x 的增大而增大,∴当x=65时,w 有最大值(-2×65+200)(65-40-m ), ∴(-2×65+200)(65-40-m )=1400, ∴m=5.15. 【答案】[解析](1)令y=0求得点A ,B 坐标,再由点C 坐标求得抛物线的解析式及线段AC 的长;(2)过点C 作x 轴的平行线交抛物线于点P ,通过分类讨论确定点Q 坐标. 解:(1)点A 的坐标为(-2,0),点B 的坐标为(4,0); 线段AC 的长为2√5, 抛物线的解析式为:y=12x 2-x -4. (2)过点C 作x 轴的平行线交抛物线于点P .∵点C (0,-4),∴-4=12x 2-x -4,解得x 1=2,x 2=0,∴P (2,-4).∴PC=2,若四边形BCPQ 为平行四边形,则 BQ=CP=2,∴OQ=OB +BQ=6,∴Q (6,0).若四边形BPCQ 为平行四边形,则BQ=CP=2, ∴OQ=OB -BQ=2,∴Q (2,0).故以点B ,C ,P ,Q 为顶点的四边形是平行四边形时,Q 点的坐标为(6,0),(2,0).16. 【答案】(1)根据题意得,ab 2 =3,即b =-6a ,则抛物线的解析式为y =ax 2-6ax +4,将B (8,0)代入得,0=64a -48a +4,解得a =-14,b =32,∴抛物线的解析式为y =-14x 2+32x +4;(2)设直线BC 的解析式为y =kx +d ,由抛物线解析式可知:当x =0时,y =4,即点C (0,4),将B (8,0),C (0,4)代入得:804k d d +=⎧⎨=⎩,解得⎩⎪⎨⎪⎧k =-12d =4,∴直线BC 的解析式为y =-12x +4,设点M 的横坐标为x (0<x <8),则点M 的纵坐标为-14x 2+32x +4,点N 的纵坐标为-12x +4,∵点M 在抛物线上,点N 在线段BC 上,MN ∥y 轴,∴MN =-14x 2+32x +4-(-12x +4)=-14x 2+32x +4+12x -4=-14x 2+2x=-14(x -4)2+4,∴当x =4时,MN 的值最大,最大值为4;(3)存在.理由如下:令-14x 2+32x +4=0,解得x 1=-2,x 2=8,∴A (-2,0),又∵C (0,4),由勾股定理得,AC =22+42=25,如解图,过点C 作CD ⊥对称轴于点D ,连接AC .解图∵抛物线对称轴为直线x =3,则CD =3,D (3,4).①当AC =CQ 时,DQ =CQ 2-CD 2=(25)2-32=11,当点Q 在点D 的上方时,点Q 到x 轴的距离为4+11,此时,点Q 1(3,4+11),当点Q 在点D 的下方时,点Q 到x 轴的距离为4-11,此时点Q 2(3,4-11);②当AQ =CQ 时,点Q 为对称轴与x 轴的交点,AQ =5,CQ =32+42=5, 此时,点Q 3(3,0);③当AC =AQ 时,∵AC =25,点A 到对称轴的距离为5,25<5,∴不可能在对称轴上存在Q 点使AC =AQ ,综上所述,当点Q 的坐标为(3,4+11)或(3,4-11)或(3,0)时,△ACQ 为等腰三角形.17. 【答案】(1)设抛物线的解析式为y =a (x -1)(x -5)(a ≠0),把点A (0,4)代入上式,解得a =45,∴y =45(x -1)(x -5)=45x 2-245x +4=45(x -3)2-165,∴抛物线的对称轴是直线x =3;(2)存在,P 点坐标为(3,85).理由如下:如解图①,连接AC 交对称轴于点P ,连接BP ,BA ,解图①∵点B 与点C 关于对称轴对称,∴PB =PC ,∴C △P AB =AB +AP +PB =AB +AP +PC =AB +AC ,∴此时△P AB 的周长最小,设直线AC 的解析式为y =kx +b (k ≠0),把A (0,4),C (5,0)代入y =kx +b 中,得⎩⎨⎧=+=054b k b ,解得,454⎪⎩⎪⎨⎧=-=b k ∴直线AC 的解析式为y =-45x +4,∵点P 的横坐标为3,∴y =-45×3+4=85,∴P 点坐标为(3,85);(3)在直线AC 下方的抛物线上存在点N ,使△NAC 面积最大.如解图②,设N 点的横坐标为t ,此时点N (t ,45t 2-245t +4)(0<t <5). 过点N 作y 轴的平行线,分别交x 轴、AC 于点F 、G ,过点A 作AD ⊥NG ,垂足为点D .解图②由(2)可知直线AC 的解析式为y =-45x +4,把x =t 代入y =-45x +4得y =-45t +4,则G (t ,-45t +4).此时NG =-45t +4-(45t 2-245t +4)=-45t 2+4t ,∵AD +CF =OC =5,∴S △NAC =S △ANG +S △CNG=12NG ·AD +12NG ·CF=12NG ·OC=12×(-45t 2+4t )×5=-2t 2+10t=-2(t -52)2+252,∴当t =52时,△NAC 的面积最大,最大值为252,由t =52,得y =45t 2-245t +4=-3,∴N 点坐标为(52,-3).。
2020年中考数学一次函数专题复习(含答案)

2020年中考数学一次函数专题复习【名师精选全国真题,值得下载练习】第Ⅰ卷(选择题)一.选择题1.已知一次函数的图象过点(0,3),且与两坐标轴在第一象限所围成的三角形面积为3,则这个一次函数的表达式为()A.y=1.5x+3 B.y=1.5x﹣3 C.y=﹣1.5x+3 D.y=﹣1.5x﹣3 2.如图,直线y=kx+b与直线y=3x﹣2相交于点(,﹣),则不等式3x﹣2<kx+b 的解为()A.x>B.x<C.x>﹣D.x<﹣3.如图,一次函数y=x+6的图象与x轴,y轴分别交于点A,B,过点B的直线l平分△ABO的面积,则直线l相应的函数表达式为()A.y=x+6 B.y=x+6 C.y=x+6 D.y=x+6 4.已知点(1,y1),(﹣1,y2),(﹣2,y3)都在直线y=﹣x+b上,则y1,y2,y3的值的大小关系是()A.y1>y2>y3B.y1<y2<y3C.y3>y1>y2D.y3>y1>y2 5.已知一次函数y=(m+1)x+m2﹣1的图象经过原点,则m的值为()A.1 B.﹣1 C.±1 D.06.在一次800米的长跑比赛中,甲、乙两人所跑的路程s(米)与各自所用时间t(秒)之间的函数图象分别为线段OA和折线OBCD,则下列说法不正确的是()A.甲的速度保持不变B.乙的平均速度比甲的平均速度大C.在起跑后第180秒时,两人不相遇D.在起跑后第50秒时,乙在甲的前面7.若点P在一次函数y=﹣4x+2的图象上,则点P一定不在()A.第一象限B.第二象限C.第三象限D.第四象限8.关于函数y=﹣2x﹣1,下列结论正确的是()A.图象必经过(﹣2,1)B.若两点A(x1,y1),B(x2,y2)在该函数图象上,且x1<x2,y1<y2C.函数的图象向下平移1个单位长度得y=﹣2x﹣2的图象D.当x>0.5时,y>09.在某次物理实验课上,小明同学测得在弹簧的弹性限度内弹簧的长度y与物体质量x 的关系如下表,则y与x的关系式是()x/g0 20 40 60 ……y/cm10 11 12 13 ……A.y=x B.y=0.1x+10 C.y=0.05x+10 D.y=0.2x+10 10.如图,直线y=kx+b交x轴于点A(﹣2,0),直线y=mx+n交x轴于点B(5,0),这两条直线相交于点C(1,p),则不等式组的解集为()A.x<5 B.x<﹣2 C.﹣2<x<5 D.﹣2<x<1 11.如图,直线y=﹣x+4与x轴,y轴分别交于A,B两点,把△AOB绕点A顺时针旋转90°后得到△AO′B',则点B'的坐标是()A.(7,3)B.(4,5)C.(7,4)D.(3,4)12.如图,已知平面直角坐标系中,A点在x轴上,C点在y轴上,OC=6,OA=OB =10,且BC∥OA,PQ∥AB交AC于D点,且∠ODQ=90°,则D点的坐标为()A.B.C.D.第Ⅱ卷(非选择题)二.填空题13.已知一次函数y=kx+b的图象经过点A(0,﹣3)和B(1,﹣1),则此函数的表达式为.14.已知函数y=(k﹣1)x﹣1,若y随x的增大而减小,则k的取值范围为.15.一次函数y1=kx+b与y2=x+a的图象如图,则下列结论:则正确的序号有.①k<0;②a>0;③关于x的方程kx﹣x=a﹣b的解是x=3;④当x>3时,y1<y2中.16.如图,OA和BA分别表示甲、乙两名学生运动的一次函数的图象,图中s和t分别表示路程和时间,根据图象判定快者比慢者每秒多跑米.17.如图,10个边长为1的正方形摆放在平面直角坐标系中,经过A(1,0)点的一条直线l将这10个正方形分成面积相等的两部分,则该直线的解析式为.18.十一黄金周,小明和小亮乘甲车从沙坪坝出发,以一定的速度匀速前往铁山坪体验“飞越丛林”.出发15分钟后,小明发现忘带身份证和钱包,便下车换乘乙车匀速回家去取(小明换车、取身份证和钱包的时间忽略不计),小亮仍乘甲车并以原速继续前行,小明回家取了身份证和钱包后,为节约时间,又立即乘乙车以原来速度的倍匀速按原路赶往铁山坪,由于国庆期间车流量较大,在小明乘乙车以加速后的速度匀速赶往铁山坪期间,甲车恰好因故在途中持续堵塞了5分钟,结果乙车先到达目的地.甲、乙两车之间的距离y(千米)与乙车行驶时间x(小时)之间的部分图象如图所示,则乙车出发小时到达目的地.三.解答题19.如图,一次函数的图象l1分别与x,y轴交于A,B两点,正比例函数的图象l2与l1交于点C(m,4).(1)求m的值及l2的解析式;(2)若点D在x轴上,使得S△DOC=2S△BOC的值,请求出D点的坐标;(3)一次函数y=kx+1的图象为l3,且l1,l2,l3不能围成三角形,则k的值为.20.甲、乙两车从A城出发匀速行驶至B城,在整个行驶过程中,甲、乙两车离开A 城的距离y(千米)与行驶时间x(小时)之间的函数关系如图所示,已知甲对应的函数关系式为y=60x,根据图象提供的信息,解决下列问题:(1)求乙离开A城的距离y与x的关系式;(2)求乙出发后几小时追上甲车?21.某企业生产并销售某种产品,整理出该商品在第x(1≤x≤90,x为整数)天的售价y 与x函数关系如图所示,已知该商品的进价为每件30元,第x天的销售量为(200﹣2x)件.(1)试求出售价y与x之间的函数关系式;(2)请求出该商品在销售过程中的最大利润;22.在平面直角坐标系中,直线y=x+2与x轴,y轴分别交于点A,B,点D的坐标为(0,3),点E是线段AB上的一点,以DE为腰在第二象限内作等腰直角△DEF,∠EDF=90°.(1)请直接写出点A,B的坐标:A(,),B(,);(2)设点F的坐标为(a,b),连接FB并延长交x轴于点G,求点G的坐标.23.【模型建立】如图1,等腰直角三角形ABC中,∠ACB=90°,CB=CA,直线ED经过点C,过A作AD⊥ED于点D,过B作BE⊥ED于点E.求证:△BEC≌△CDA;【模型应用】①已知直线l1:y=x+4与x轴交于点A,与y轴交于点B,将直线l1绕着点A逆时针旋转45°至直线l2,如图2,求直线l2的函数表达式;②如图3,在平面直角坐标系中,点B(8,6),作BA⊥y轴于点A,作BC⊥x轴于点C,P是线段BC上的一个动点,点Q是直线y=2x﹣6上的动点且在第一象限内.问点A、P、Q能否构成以点Q为直角顶点的等腰直角三角形,若能,请直接写出此时点Q的坐标,若不能,请说明理由.参考答案一.选择题1.解:设这个一次函数的表达式为y=kx+b(k≠0),与x轴的交点是(a,0).∵一次函数y=kx+b(k≠0)图象过点(0,3),∴b=3.∵这个一次函数与两坐标轴所围成的三角形面积为3,∴×3×|a|=3,解得:a=2或﹣2.∵一次函数的图象与两坐标轴在第一象限围成的三角形,∴a=﹣2把(﹣2,0)代入y=kx+3,得k=1.5,则函数的解析式是y=1.5x+3.故选:A.2.解:不等式3x﹣2<kx+b的解集为x<.故选:B.3.解:∵一次函数y=x+6的图象与x轴,y轴分别交于点A,B,∴令y=0,则求得x=﹣8,令x=0,求得y=6,∴A(﹣8,0),B(0,6),∵过点B的直线l平分△ABO的面积,∴AC=OC,∴C(﹣4,0),设直线l的解析式为y=kx+6,把C(﹣4,0)代入得﹣4k+6=0,解得k=,∴直线l的解析式为y=x+6,故选:D.4.解:∵直线y=﹣x+b,k=﹣1<0,∴y随x的增大而减小,又∵﹣2<﹣1<1,∴y1<y2<y3.故选:B.5.解:∵一次函数y=(m+1)x+m2﹣1的图象经过原点,∴,解得m=1.故选:A.6.解:由图象可知,甲的速度保持不变,故选项A正确;甲的速度为:800÷180=4米/秒,乙的平均速度为:800÷220=3米/秒,∵4>3,∴乙的平均速度比甲的平均速度小,故选项B错误;在起跑后第180秒时,甲到达终点,乙离终点还有一段距离,他们不相遇,故选项C 正确;在起跑后第50秒时,乙在甲的前面,故选项D正确;故选:B.7.解:∵﹣4<0,2>0,∴一次函数y=﹣4x+2的图象经过第一、二、四象限,即不经过第三象限.∵点P在一次函数y=﹣4x+2的图象上,∴点P一定不在第三象限.故选:C.8.解:A、把x=﹣2代入函数y=﹣2x﹣1得,(﹣2)×(﹣2)﹣1=3≠1,故点(﹣2,1)不在此函数图象上,故本选项错误;B、∵函数y=﹣2x+1中.k=﹣2<0,∴y随x的增大而减小,若两点A(x1,y1),B(x2,y2)在该函数图象上,且x1<x2,y1>y2,故本选项错误;C、根据平移的规律,函数y=﹣2x﹣的图象向下平移1个单位长度得y=﹣2x﹣1﹣1,即y=﹣2x﹣2,故本选项正确;D、把x=0.5代入函数y=﹣2x﹣1=﹣2,故本选项错误.故选:C.9.解:在弹簧的弹性限度内弹簧的长度y与物体质量x的关系为一次函数关系,设y与x的关系式为y=kx+b,把,代入,可得,解得,∴y与x的关系式为y=0.05x+10,故选:C.10.解:y=kx+b<0,则x<﹣2,y=mx+n>0,则x<5,不等式组的解集即为:x<﹣2,故选:B.11.解:当x=0时,y=4,所以B点坐标为(0,4),所以OB=4,当y=0时,x=3,所以A点坐标为(3,0),所以OA=3.根据旋转的性质可知:O′A=OA=3,O′B′=OB=4,且O′A⊥x轴,O′B′∥x轴,∴B′点到x轴距离为3,到y轴距离为4+3=7,因为B′点在第一象限,所以点B′的坐标为(7,3).故选:A.12.解:如图,作BH⊥OA于H.作DK⊥OA于K.∵BC∥OA,BH∥OC,∴四边形OCBH是平行四边形,∵∠AOC=90°,∴四边形OCBH是矩形,∴OC=BH=6,∵OA=OB=10,∴OH===8,∴AH=OA﹣BH=2,∵C(0,6),A(10,0),∴直线AC的解析式为y=﹣x+6,∵∠ODQ=90°,∴∠DOQ+∠OQD=90°,∵AB∥PQ,∴∠BAH=∠OQD,∵∠BAH+∠ABH=90°,∴∠DOK=∠ABH,∵∠OKD=∠AHB=90°,∴△OKD∽△BHA,∴=,∴==,设DK=m,则OK=3m,∴D(3m,m),代入y=﹣x+6,可得m=,∴D(,),故选:A.二.填空题(共6小题)13.解:由题意可得方程组,解得,则此函数的解析式为:y=2x﹣3,故答案为y=2x﹣3.14.解:∵一次函数y=(k﹣1)x﹣1,当k﹣1<0时,即k<1时,一次函数图象经过第二、四象限,y随x的增大而减小,所以k的取值范围为k<1.故答案为k<1.15.解:∵直线y1=kx+b经过第一、三象限,∴k<0,所以①正确;∵直线y2=x+a与y轴的交点在x轴下方,∴a<0,所以②错误;∵一次函数y1=kx+b与y2=x+a的图象的交点的横坐标为3,∴关于x的方程kx+b=x+a的解是x=3,所以③正确;当x>3时,y1<y2,所以④正确.故答案为①③④.16.解:如图所示:快者的速度为:64÷8=8(m/s),慢者的速度为:(64﹣12)÷8=6.5(m/s),8﹣6.5=1.5(米),所以快者比慢者每秒多跑1.5米.故答案为:1.517.解:将由图中1补到2的位置,∵10个正方形的面积之和是10,∴梯形ABCD的面积只要等于5即可,∴设BC=4﹣x,则[(4﹣x)+3]×3÷2=5,解得,x=,∴点B的坐标为(,3),设过点A和点B的直线的解析式为y=kx+b,,解得,,即过点A和点B的直线的解析式为y=,故答案为:y=.18.解:设甲车的速度为a千米/小时,乙车回家时的速度是b千米/小时,a=b,,设a=8m,b=9m(m>0),由图象得乙车行驶小时两边相距千米,﹣=,m=5,∴a=40,b=45,设t小时两车相距3千米,=+3+(t﹣)×40,t=,故答案为:.三.解答题(共5小题)19.解:(1)把C(m,4)代入一次函数y=﹣x+5,可得4=﹣m+5,解得m=2,∴C(2,4),设l2的解析式为y=ax,则4=2a,解得a=2,∴l2的解析式为y=2x;(2)过C作CD⊥AO于D,CE⊥BO于E,则CD=4,CE=2,在y=﹣x+5中,令x=0,则y=5;令y=0,则x=10,∴A(10,0),B(0,5),∴AO=10,BO=5,∵S△DOC=2S△BOC,∴OD×4=2×,∴OD=5,∴D点的坐标为(5,0)或(﹣5,0);(3)一次函数y=kx+1的图象为l3,且11,l2,l3不能围成三角形,∴当l3经过点C(2,4)时,k=;当l2,l3平行时,k=2;当11,l3平行时,k=﹣;故k的值为或2或﹣,故答案为或2或﹣.20.解:(1)设乙对应的函数关系式为y=kx+b将点(4,300),(1,0)代入y=kx+b得:解得:,∴乙对应的函数关系式y=100x﹣100;(2)易得甲车对应的函数解析式为y=60x,联立,解得:,2.5﹣1=1.5(小时),∴乙车出发后1.5小时追上甲车.21.解:(1)当0≤x≤50时,设y与x的解析式为:y=kx+40,则50k+40=90,解得k=1,∴当0≤x≤50时,y与x的解析式为:y=x+40,∴售价y与x之间的函数关系式为:y=;(2)y=x+40,∵k=1>0,y随x的增大而增大,∴x=50时,该商品在销售过程中的利润最大,最大值为:(90﹣30)×(200﹣2×50)=6000(元).答:第50天时,该商品在销售过程中的利润最大,最大利润为6000元.22.解:(1)∵直线y=x+2与x轴,y轴分别交于点A,B,∴点A(﹣2,0),点B(0,2)故答案为:(﹣2,0),(0,2)(2)如图,过点F作FM⊥y轴,过点E作EN⊥y轴,∴∠FMD=∠EDF=90°∴∠FDM+∠DFM=90°,∠FDM+∠EDN=90°,∴∠DFM=∠EDN,且FD=DE,∠FMD=∠END=90°,∴△DFM≌△EDN(AAS)∴EN=DM,FM=BN,∵点F的坐标为(a,b),∴FM=DN=﹣a,DM=b﹣3,∴点E坐标(﹣b+3,3+a),∵点E是线段AB上的一点,∴3+a=﹣b+3+2∴a+b=2,∴点F(a,2﹣a)设直线BF的解析式为y=kx+2,∴2﹣a=ka+2∴k=﹣1,∴直线BF的解析式为y=﹣x+2,∴点G(2,0)23.解:(1)证明:∵△ABC为等腰直角三角形∴CB=CA又∵AD⊥CD,BE⊥EC∴∠D=∠E=90°∠ACD+∠BCE=180°﹣90°=90°又∵∠EBC+∠BCE=90°∴∠ACD=∠EBC在△ACD与△CBE中,∠D=∠E,∠ACD=∠EBC,CA=BC,∴△ACD≌△CBE(AAS);(2)过点B作BC⊥AB交l2于C,过C作CD⊥y轴于D,∵∠BAC=45°∴△ABC为等腰Rt△由(1)可知:△CBD≌△BAO∴BD=AO,CD=OB∵,y=0,x=﹣3∴A(﹣3,0),x=0,y=4∴B(0,4)∴BD=AO=3,CD=OB=4∴OD=4+3=7.∴C(﹣4,7),直线l2表达式中的k为:﹣7,点C(﹣4,7),则l2的解析式:y=﹣7x﹣21;(3)如下图,设点Q(m,2m﹣6),当∠AQP=90°时,由(1)知,△AMQ≌△QNP(AAS),∴AM=QN,即|8﹣m|=6﹣(2m﹣6),解得:m=4或,故:Q(4,2),.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2020年中考数学函数专题(附答案)一、单选题(共12题;共24分)1.在函数中,自变量的取值范围是( )A. B. C. D.2.已知抛物线y=﹣x2+2x﹣3,下列判断正确的是()A. 开口方向向上,y有最小值是﹣2B. 抛物线与x轴有两个交点C. 顶点坐标是(﹣1,﹣2)D. 当x<1时,y随x增大而增大3.长方形的周长为24 cm,其中一边长为x cm(其中0<x<12),面积为y cm2,则该长方形中y与x的关系式可以写为( )A. y=x2B. y=(12-x)2C. y=(12-x)·xD. y=2(12-x)4.已知将二次函数y=x2+bx+c的图象向右平移2个单位再向下平移3个单位,所得图象的解析式为y=x2﹣4x ﹣5,则b,c的值为()A. b=0,c=6B. b=0,c=﹣5C. b=0,c=﹣6D. b=0.c=55.下列四个函数中,自变量的取值范围为≥1的是()A. B. C. D.6.已知二次函数y=a(x﹣2)2+c,当x=x1时,函数值为y1;当x=x2时,函数值为y2,若|x1﹣2|>|x2﹣2|,则下列表达式正确的是()A. y1+y2>0B. y1﹣y2>0C. a(y1﹣y2)>0D. a(y1+y2)>07.从地面竖立向上抛出一个小球,小球的高度h(单位:m)与小球运动时间t(单位:s)之间的关系式为h=30t-5t2,那么小球从抛出至回落到地面所需要的时间是().A. 6sB. 4sC. 3sD. 2s8.已知一元二次方程:①x2+2x+3=0,②x2-2x-3=0.下列说法正确的是( )A. ①②有实数解B. ①无实数解,②有实数解C. ①有实数解,②无实数解D. ①②都无实数解9.如图,在边长4的正方形ABCD中,E是边BC的中点,将△CDE沿直线DE折叠后,点C落在点F处,冉将其打开、展平,得折痕DE。
连接CF、BF、EF,延长BF交AD于点G。
则下列结论:①BG= DE;②CF⊥BG;③sin∠DFG= ;④S△DFG= .其中正确的有()A. 1个B. 2个C. 3个D. 4个10.在下列点中,与点A(-2,-4)的连线平行于y轴的是()A. (2,-4)B. (4,-2)C. (-2,4)D. (-4,2)11.我们把1,1,2,3,5,8,13,21,…,这组数称为斐波那契数列,为了进一步研究,依次以这列数为半径作90°圆弧,,,…,得到斐波那契螺旋线,然后顺次连结P1P2,P2P3,P3P4,…,得到螺旋折线(如图),已知点P1(0,1),P2(-1,0),P3(0,-1),则该折线上的点P9的坐标为()A. (-6,24)B. (-6,25)C. (-5,24)D. (-5,25)12.如图(1),四边形ABCD中,AB∥CD,∠ADC=90°,P从A点出发,以每秒1个单位长度的速度,按A→B→C→D的顺序在边上匀速运动,设P点的运动时间为t秒,△PAD的面积为S,S关于t的函数图象如图(2)所示,当P运动到BC中点时,△APD的面积为()A. 4B. 5C. 6D. 7二、填空题(共8题;共16分)13.抛物线y=(x﹣1)2+3的顶点坐标为________.14.如图,10个边长为1的正方形如图摆放在平面直角坐标系中,经过原点的一条直线l将这10个正方形分成面积相等的两部分,则该直线l的解析式为________.15.两个反比例函数y=,y=在第一象限内的图象如图所示.点P1,P2,P3、…、P2007在反比例函数y=上,它们的横坐标分别为x1、x2、x3、…、x2007,纵坐标分别是1,3,5…共2007个连续奇数,过P1,P2,P3、…、P2007分别作y轴的平行线,与y=的图象交点依次为Q1(x1′,y1′)、Q1(x2′,y2′)、…、Q2(x2007′,y2007′),则|P2007Q2007|=________.16.如图,矩形OABC的顶点A,C分别在x轴,y轴上,顶点B在第一象限,AB=1.将线段OA绕点O按逆时针方向旋转60°得到线段OP,连接AP,反比例函数(k≠0)的图象经过P,B两点,则k的值为________.17.如图,在平面直角坐标系中,点A(4 ,0)是x轴上一点,以OA为对角线作菱形OBAC,使得∠BOC.=60°,现将抛物线y=x2沿直线OC平移到y=a(x﹣m)2+h,那么h关于m的关系式是________,当抛物线与菱形的AB边有公共点时,则m的取值范围是________.18.如图,AB是半圆O的直径,点C为⊙O上一点,AE和过点C的切线互相垂直,垂足为E,AE交⊙O于点D,直线EC交AB的延长线于点P,连接AC,BC,,AD=3.给出下列结论:①AC平分∠BAD;②△ABC∽△ACE;③AB=3PB;④S△ABC=5,其中正确的是________(写出所有正确结论的序号).19.如图,矩形ABCD中,AD=2,AB=5,P为CD边上的动点,当△ADP与△BCP相似时,DP=________.20.如图所示,在一张长为4cm、宽为3cm的矩形纸片上,现要剪下一个腰长2cm的等腰三角形(要求:等腰三角形的一个顶点与矩形的一个顶点重合,另两个顶点在矩形的边上),则剪下的等腰三角形面积为 ________三、综合题(共5题;共60分)21.已知:如图M2-10,抛物线y=ax2+x+c与x轴交于点A(-1,0),B(3,0).(1)试确定该抛物线的函数表达式;(2)已知点C是该抛物线的顶点,求△OBC的面积;(3)若点P是线段BC上的一动点,求OP的最小值.22.如图,在水平地面点A处有一网球发射器向空中发射网球,网球飞行路线是一条抛物线,在地面上落点为B.有人在直线AB上点C(靠点B一侧)竖直向上摆放无盖的圆柱形桶,试图让网球落入桶内.已知AB=4米,AC=3米,网球飞行最大高度OM=5米,圆柱形桶的直径CD为0.5米,高为0.3米(网球的体积和圆柱形桶的厚度忽略不计).(1)如图,建立直角坐标系,求此抛物线的解析式;(2)如果竖直摆放7个圆柱形桶时,网球能不能落入桶内?(3)当竖直摆放圆柱形桶至多多少个时,网球可以落入桶内?23.如图,一次函数y=kx+b与反比例函数y= 的图象交于点A(1,6),B(3,n)两点.(1)求反比例函数和一次函数的表达式;(2)点M是一次函数y=kx+b图象位于第一象限内的一点,过点M作MN⊥x轴,垂足为点N,过点B作BD⊥y轴,垂足为点D,若△MON的面积小于△BOD的面积,直接写出点M的横坐标x的取值范围.24.如图,抛物线y=﹣x2+ x+2与x轴交于点A,B,与y轴交于点C.(1)试求A,B,C的坐标;(2)将△ABC绕AB中点M旋转180°,得到△BAD.①求点D的坐标;②判断四边形ADBC的形状,并说明理由;(3)在该抛物线对称轴上是否存在点P,使△BMP与△BAD相似?若存在,请直接写出所有满足条件的P 点的坐标;若不存在,请说明理由.25.如图,在平面直角坐标系中,平行四边形ABOC如图放置,将此平行四边形绕点O顺时针旋转90°得到平行四边形A′B′OC′.抛物线y=﹣x2+2x+3经过点A、C、A′三点.(1)求A、A′、C三点的坐标;(2)求平行四边形ABOC和平行四边形A′B′OC′重叠部分△C′OD的面积;(3)点M是第一象限内抛物线上的一动点,问点M在何处时,△AMA′的面积最大?最大面积是多少?并写出此时M的坐标.答案一、单选题1. C2. D3. C4.C5. A6. C7. A8.B9. C 10. C 11. B 12. B二、填空题13. 顶点坐标是(1,3). 14. y= 15. 16.17. h=﹣m;≤m≤ 18. ①②③④ 19.1或4或2.5 20.2或三、综合题21. (1)解:抛物线y=ax2+x+c与x轴交于点A(-1,0),B(3,0),∴解得,∴抛物线的解析式为y= x2+x+(2)解:y= x2+x+ =- (x-1)2+2,∴抛物线的顶点C的坐标为(1,2).∴S△OBC= ×3×2=3(3)解:当OP是BC边上的高时,OP的值最小.∵B(3,0),C(1,2),∴BC= =2 .∵S△OBC= BC·OP=3,∴OP= ,即OP的最小值是22. (1)解:M(0,5),B(2,0),C(1,0),D(,0),设抛物线的解析式为y=ax2+k,∵抛物线过点M和点B,则k=5,.即抛物线解析式为;(2)解:当x=1时,y= ;当x= 时,y= .即P(1,),Q(,)当竖直摆放7个圆柱形桶时,桶高= ×7=2.1.∵2.1<且2.1<,∴网球不能落入桶内;(3)解:设竖直摆放圆柱形桶m个时网球可以落入桶内,由题意,得,≤0.3m≤ ,解得:≤m≤ ;∵m为整数,∴m的值为8,9,10,11,12.∴当竖直摆放圆柱形桶至多12个时,网球可以落入桶内.23.(1)解:将点A(1,6)代入反比例函数中,得:6=,所以m=6,所以反比例函数的解析式为,∵点B(3,n)在反比例函数上,∴n=2,即点B的坐标为(3,2).将点A(1,6)、点B(3,2)代入y=kx+b中,得解得,故一次函数的解析式为y=-2x+8(2)解:依照题意作出图形,如图所示:设M点的坐标为(x,-2x+8),则N点的坐标为(x,0).∵点B为(3,2),∴点D为(0,2).∴OD=2,BD=3,ON=x,MN=8-2x.∵△MON的面积小于△BOD的面积,∴ON•MN< OD•BD,即x(8-2x)<2×3,解得:x<1或x>3,∵点M在第一象限内,则x>0,x<4,∴.24. (1)解:当y=0时,0=﹣x2+ x+2,解得:x1=﹣1,x2=4,则A(﹣1,0),B(4,0),当x=0时,y=2,故C(0,2)(2)解:①过点D作DE⊥x轴于点E,∵将△ABC绕AB中点M旋转180°,得到△BAD,∴DE=2,AO=BE=1,OM=ME=1.5,∴D(3,﹣2);②∵将△ABC绕AB中点M旋转180°,得到△BAD,∴AC=BD,AD=BC,∴四边形ADBC是平行四边形,∵AC= ,BC= ,AB=5,∴AC2+BC2=AB2,∴△ACB是直角三角形,∴∠ACB=90°,∴四边形ADBC是矩形(3)解:由题意可得:BD= ,AD=2 ,则,当△BMP∽△ADB时,,可得:BM=2.5,则PM=1.25,故P(1.5,1.25),当△BMP1∽△ABD时,P1(1.5,﹣1.25),当△BMP2∽△BDA时,可得:P2(1.5,5),当△BMP3∽△BDA时,可得:P3(1.5,﹣5),综上所述:点P的坐标为:(1.5,1.25),(1.5,﹣1.25),(1.5,5),(1.5,﹣5).25. (1)解:当y=0时,﹣x2+2x+3=0,解得x1=3,x2=﹣1,则C(﹣1,0),A′(3,0),当x=0时,y=3,则A(0,3)(2)解:∵四边形ABOC为平行四边形,∴AB OC,AB=OC,而C(﹣1,0),A(0,3),∴B(1,3),∴OB==,S△AOB=×3×1=,又∵平行四边形ABOC旋转90°得平行四边形A′B′OC′,∴∠ACO=∠OC′D,OC′=OC=1,又∵∠ACO=∠ABO,∴∠ABO=∠OC′D.又∵∠C′OD=∠AOB,∴△C′OD∽△BOA,∴=( )2=()2=,∴S△C′OD=× =(3)解:设M点的坐标为(m,﹣m2+2m+3),0<m<3,作MN y轴交直线AA′于N,易得直线AA′的解析式为y=﹣x+3,则N(m,﹣m+3),∵MN=﹣m2+2m+3﹣(﹣m+3)=﹣m2+3m,∴S△AMA′=S△ANM+S△MNA′=MN•3=(﹣m2+3m)=﹣m2+ m=﹣(m﹣)2+ ,∴当m=时,S△AMA'的值最大,最大值为,此时M点坐标为(,).。
